Page 1

3B SCIENTIFIC
Bedienungsanleitung
01/10 ALF
®
PHYSICS
Kräftetisch U52004
1 Fuß
2 Klemmen mit Umlenkrollen
3 Mittelstab
4 Halterung
für Schnüre
5 Arbeitsplatte
6 Gewichtaufhänger mit Schlitz-
gewichten
1. Beschreibung
Der Kräftetisch dient zum Nachweis, dass die Kraft
eine vektorielle Größe ist sowie zur quantitativen
Untersuchung der Zusammensetzung und Zerlegung von Kräften.
Der Kräftetisch besteht aus einer kreisförmigen
Arbeitsplatte auf stabilem Fuß mit doppelter Skalierung der Winkeleinteilung. Über drei Umlenkrollen mit Befestigungsklammern werden Gewichte an
Schnüren mit Haken aufgehängt. Die drei Schlitzgewichtsätze aus Messing bestehen aus je 2x 5 g, 2x
10 g, 2x 20 g und 2x 50 g Gewichten sowie einem
50 g Gewichtaufhänger.
2. Technische Daten
Abmessungen: ca. 300 mm x 390 mm Ø
Skala: 0 bis 360° mit 1° Teilung
Masse: ca. 3 kg
3. Prinzip
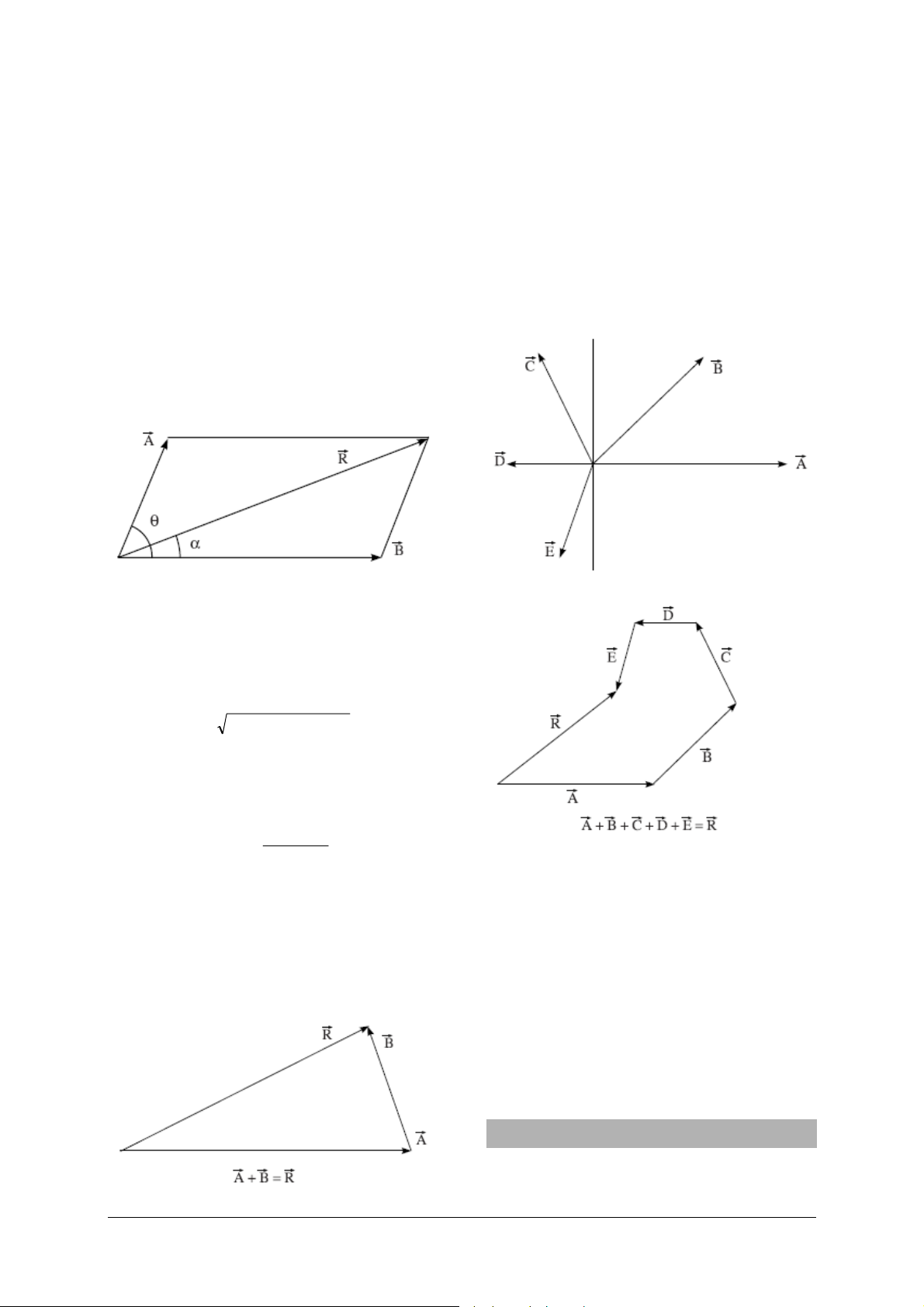
Kräfte sind vektorielle Größen. Deshalb kann die
resultierende Ersatzkraft zweier auf einen Punkt
wirkender Kräfte nicht allein aus ihren Größen
bestimmt werden sondern es muss auch ihre Richtung Berücksichtigung finden. Die Resultierende
1
Page 2
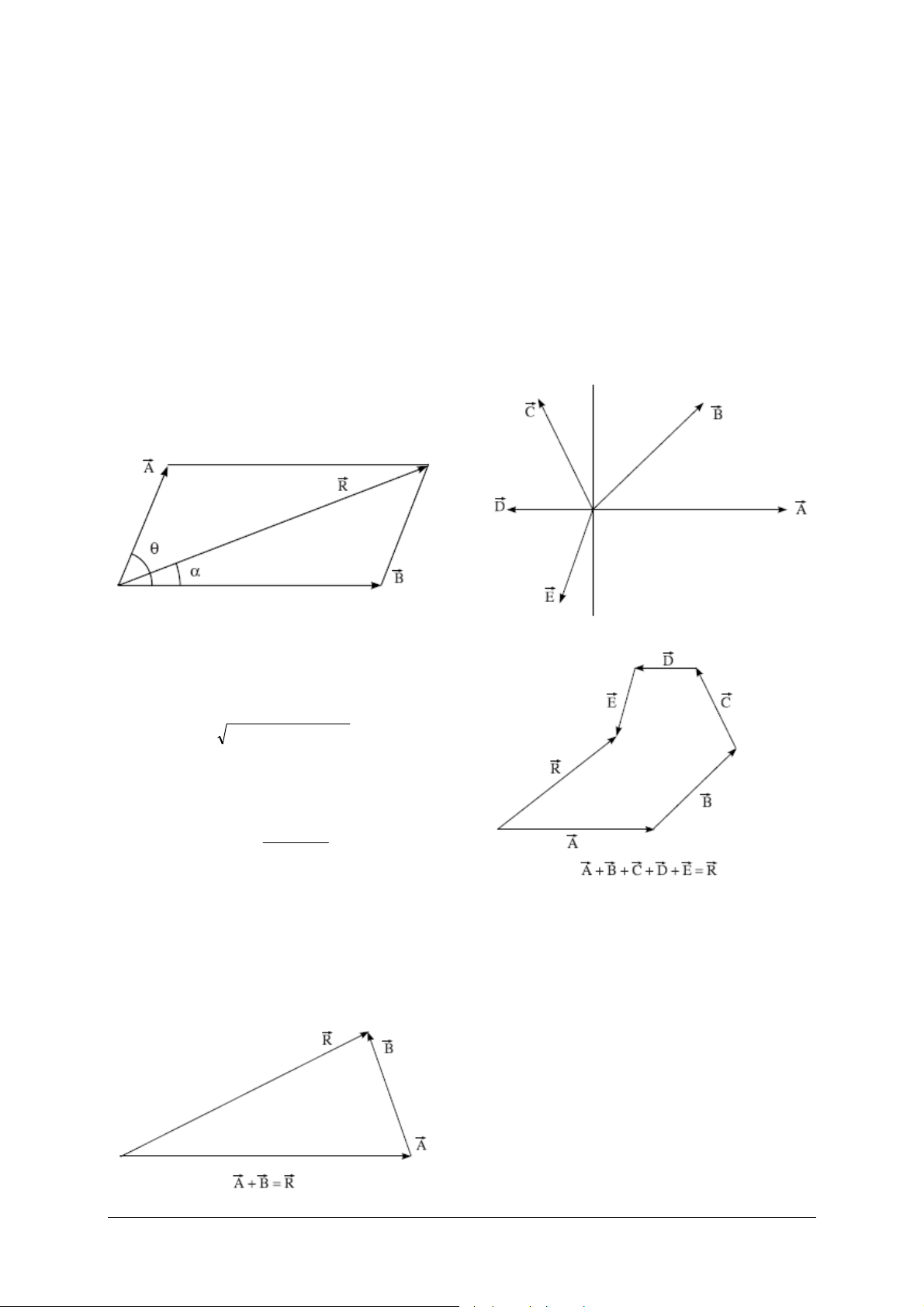
zweier oder mehrerer in einer Ebene auf einen
A
r
A
Punkt wirkender Kräfte ist eine einzelne Kraft in
der gleichen Ebene, die die gleiche Wirkung hervorruft, wie die Kombination der individuellen
Kräfte. Hat eine Kraft also die gleiche Größe wie die
Resultierende, wirkt aber entgegengesetzt in der
Richtung, so befindet sich der Körper im Gleichgewichtszustand. Die Resultierende kann analytisch
oder mit graphischen Methoden mittels verschiedener Gesetze (Kräfteparallelogramm, Kräftedreieck, Kräftepolygon) bestimmt werden.
Nach dem Gesetz des Kräfteparallelogramms werden zwei Kräfte, die gleichzeitig auf einen Körper
wirken, in ihrer Größe und in ihrer Richtung durch
zwei aneinander liegenden Seiten eines Parallelogramms repräsentiert. Die Resultierende ergibt sich
sowohl in Größe als auch in Richtung aus der Diagonalen, die ihren Ausgang im gleichen Punkt hat.
Daraus ergibt sich, dass sich ein Körper im Gleichgewicht befindet, wenn drei Kräfte auf ihn wirken,
die durch die Seiten eines Dreiecks repräsentiert
werden.
Wirken mehr als zwei Kräfte gleichzeitig auf einen
Körper, findet das Gesetz des Kräftepolygons seine
Anwendung. Danach werden mehrere Kräfte mit
gemeinsamem Angriffspunkt in ihrer Größe und in
ihrer Richtung durch ein offenes Polygon repräsentiert, bei denen die Seiten den gleichen Richtungssinn haben. Die resultierende Ersatzkraft ergibt
sich aus der Seite, die das Polygon schließt im entgegengesetzten Richtungssinn wie die anderen
Seiten.
Dieser Satz lässt sich mathematisch folgendermaßen ausdrücken. Wenn zwischen zwei Kräften
r
und
B
, die auf einen Körper wirken, der Winkel θ
liegt, ergibt sich die Resultierende
22
Ist α der Winkel zwischen der Resultierenden und
der Kraft
r
, so ist
tan
=α
r
R
aus:
θ++= cosABBAR 2
θ
sinB
θ+
cosBA
Nach dem Gesetz des Kräftedreiecks werden zwei
Kräfte, die gleichzeitig auf einen Körper wirken, in
ihrer Größe und in ihrer Richtung durch zwei Seiten eines Dreiecks repräsentiert, die den gleichen
Richtungssinn haben. Die Resultierende ergibt sich
sowohl in Größe als auch in Richtung aus der dritten Seite im entgegengesetzten Richtungssinn wie
die ersten beiden Seiten.
Daher befindet sich ein Körper, auf den mehrere
Kräfte wirken, im Gleichgewicht, wenn sich die
Kräfte als geschlossenes Polygon darstellen lassen.
Die Vektorsumme der individuellen Kräfte ist
gleich Null und deshalb ist die Resultierende auch
Null.
Eine nähere Betrachtung dieses Sachverhalts zeigt,
dass das Gesetz des Kräftepolygons nur eine einfache Erweiterung des Gesetzes des Kräftedreiecks ist.
Der Kräftetisch ist ein geeignetes Instrument zur
Demonstration der Vektoraddition und des Gleichgewichts von Kräften sowie zur Bestätigung der
graphischen und analytischen Methoden. Der
Gleichgewichtszustand zwischen zwei oder drei
Kräften lässt sich demonstrieren und sowohl die
Größe als auch die Richtung jeder Kraft einfach
bestimmen.
2
Page 3

4. Bedienung
4.1 Aufbau des Geräts
• Fuß auf ebene Fläche stellen.
• Mittelstab senkrecht im Fuß festschrauben.
• Arbeitsplatte mit Kraft auf den Mittelstab auf-
drücken.
• Unterlegscheibe auf die Mittelbohrung aufle-
gen und Halterung für Schnüre einschrauben.
• Umlenkrollen mit Klemmen an den 0°, 120°
und 240° Markierungen der Arbeitsplatte anbringen.
• Ring über die Halterung im Mittelpunkt der
Arbeitsplatte legen.
• Schnüre über die Umlenkrollen legen, Ge-
wichtaufhänger anhängen und gleiche Schlitzgewichte auflegen.
• Ring sollte sich im Gleichgewicht befinden.
4.2 Versuchsbeispiel: Vektor Addition
• Kräftetisch wie oben beschrieben aufbauen.
• Eine 20 g und eine 50 g Masse auf je einen
Gewichtsanhänger bei 0° und 120° auflegen.
• Durch Auflegen von Massen auf den dritten
Gewichtsanhänger und Wahl eines geeignetes
Winkels Gleichgewicht herstellen. Zur Überprüfung Ring anheben und fallen lassen. Fällt der
Ring zurück ins Zentrum, ist ein Gleichgewichtszustand erreicht. Falls nicht, müssen
weitere Justierungen vorgenommen werden.
• Größe und Richtung der Kraft berechnen, die
nötig ist ein Gleichgewicht zu erreichen. Vergleich der theoretischen Größe mit dem experimentell gewonnenen Wert.
• Die verschiedenen Kräfte in Richtung und
Größe maßstabgerecht zeichnen; Bestätigung
des Gesetzes des Kräftedreiecks.
• Versuch mit verschiedenen Massen und Win-
keln wiederholen.
3B Scientific GmbH • Rudorffweg 8 • 21031 Hamburg • Deutschland • www.3bscientific.com
Technische Änderungen vorbehalten
© Copyright 2010 3B Scientific GmbH
Page 4

Page 5

3B SCIENTIFIC
Instruction sheet
01/10 ALF
®
PHYSICS
Force Table U52004
1 Base
2 Clamps with pulleys
3 Centre rod
4 Mount for cords
5 Work disc
6 Weight holder with slotted
weights
1. Description
The force table serves to prove that force is a vector
quantity. It is also used for quantitative investigation of how forces combine and resolve.
The force table consists of a circular work disc on a
stable base with a dual angle scale. Weights are
attached to three pulleys with securing clamps. The
three sets of brass weights consist of 2x 5 g, 2x 10 g,
2x 20 g and 2x 50 g weights and weight holders
weighing 50 g.
2. Technical data
Dimensions: 300 mm x 390 mm dia. approx.
Scale: 0 to 360° with 1° resolution
Weight: 3 kg approx.
3. Principle
Forces are vector quantities. This means that the
resultant of two forces working at a single point is
not simply the sum of the forces but is dependent
1
Page 6
on the direction in which the forces act. The resul-
A
r
r
A
r
tant of two forces acting at the same point in a
single plane is defined as that force which, acting
alone in the same plane, would have the same
effect as the combination of the two forces. A force
of equal magnitude to the resultant but acting in
the opposite direction therefore maintains the
body in equilibrium. The resultant can be obtained
by analysis or by graphical means using various
laws (parallelogram of forces, triangle of forces,
polygon of forces).
A parallelogram of forces represents two forces
acting simultaneously on a body as two adjacent
sides of a parallelogram. The magnitude and direction of their resultant is then given by the diagonal
originating from the same point.
From this it can be determined that a body is in
equilibrium if three forces are acting upon it,
which can be represented by the three sides of a
triangle.
If more than two forces act on a body at once, the
law of the polygon of forces is used. This represents
several forces acting at the same point as following
sides of a polygon where one side remains open. As
for the triangle, following the side that closes the
polygon in the opposite direction gives the resultant force.
This theorem can be expressed mathematically as
follows: When two forces
and Br acting on a
body with an angle θ between them, the resultant
R
is given by:
22
θ++= cosABBAR 2
If α is the angle between the resultant and force
then:
θ
sinB
tan
=α
θ+
cosBA
With the law of the triangle of forces, two forces
acting simultaneously on a body are represented in
terms of magnitude and direction by two following
sides of a triangle. The magnitude and direction of
the resultant is then given by following the third
side of the triangle in the opposite direction.
Therefore a body is in equilibrium when several
forces act upon it that can be represented as a
closed polygon. The vector sum of the individual
forces is equal to zero and so is the resultant force.
On closer observation, this law can be seen to be a
simple extension of the law of the triangle of
forces. The force table is suitable for demonstrating
vector addition and equilibrium of forces and for
confirming the graphic and analytical methods.
The equilibrium between two or three forces can
be demonstrated and the magnitude and direction
of each force easily determined.
4. Operation
4.1 Equipment Setup
• Place the base on an even surface.
• Screw the centre rod vertically into the base.
2
Page 7

• Press the work disc with force onto the centre
rod.
• Place the washer onto the central bore and
screw in the mount for cords.
• Attach the pulleys with clamps at the positions
on the work disc marked 0°, 120° and 240°.
• Place the ring above the mount in the centre of
the work disc.
• Run the cords over the pulleys, suspend the
weight holders and attach the slotted weights.
• The ring should be in a state of equilibrium.
4.2 Sample experiment: Vector Addition
• Set up the force table as above.
• Add a 20 g mass to one weight holder and a
50 g mass to another at 0° and 120°.
• By adding weights to a third weight holder and
selecting a suitable angle it is possible to establish equilibrium. To check the equilibrium, lift
the ring and let it drop. If it falls back to the
centre, equilibrium has been attained. If not,
then further adjustments are necessary.
• Calculate the magnitude and direction of the
forces required to attain equilibrium. Compare
the values obtained in the experiment to those
determined by the theory.
• Draw the forces to scale showing their magni-
tude and direction to confirm the law of the
triangle of forces.
• Repeat the experiment with different masses
and angles.
3B Scientific GmbH • Rudorffweg 8 • 21031 Hamburg • Germany • www.3bscientific.com
Subject to technical amendments
© Copyright 2010 3B Scientific GmbH
Page 8

Page 9

3B SCIENTIFIC
Instructions d'utilisation
01/10 ALF
®
PHYSICS
Table de forces U52004
1 Pied
2 Fixations avec galets de renvoi
3 Barre du milieu
4 Support pour cordes
5 Plaque de travail
6 Suspensions avec poids à fente
1. Description
La table de forces permet de démontrer que la
force est une grandeur vectorielle et d’effectuer
une étude quantitative sur la composition et la
décomposition de forces.
La table de forces est constitué d’une plaque de
travail circulaire montée sur un pied stable avec
une double graduation angulaire. Des poids sont
accrochés à des cordes par des crochets sur trois
galets de renvoi à fixations. Les trois jeux de poids
à fente, laiton, comprennent chacun 2x 5 g, 2x 10
g, 2x 20 g et 2x 50 g poids ainsi qu’une suspension
de poids de 50 g.
2. Caractéristiques techniques
Dimensions : env. 300 mm, x Ø 390 mm
Graduation : 0° à 360°, en pas de 1°
Masse : env. 3 kg
3. Principe
Les forces sont des grandeurs vectorielles. Aussi la
force résultante de deux forces agissant sur un
point ne peutelle pas être déterminée uniquement
à partir de ses grandeurs, il faut également tenir
compte de sa direction. La résultante de deux ou
1
Page 10

de plusieurs forces agissant sur un point d’un plan
A
r
A
r
est une force unique du même plan qui a le même
effet que la combinaison des forces individuelles. Si
une force présente donc la même grandeur que la
résultante, mais qu’elle agit dans la direction opposée, le corps est en équilibre. La résultante peut
être déterminée de manière analytique ou par des
méthodes graphiques à l’aide de différentes règles
(parallélogramme, triangle, polygone de forces).
D’après la règle du parallélogramme de forces,
deux forces agissant en même temps sur un corps
sont représentées dans leur grandeur et dans leur
direction par deux côtés opposés d’un parallélogramme. Tant la grandeur que la direction de la
résultante sont déterminées par la diagonale dont
le point de départ se situe sur le même point.
trios forces, représentées par les côtés d’un triangle, agissent sur lui.
Si plus de deux forces agissent en même temps sur
un corps, on appliquera la règle du polygone de
forces. D’après cette règle, la grandeur et la direction de plusieurs forces ayant le même point
d’attaque sont représentées par un polygone ouvert, dont les côtés ont le même sens. La résultante
est déterminée par le côté qui ferme le polygone
dans le sens opposé aux autres côtés.
Cet énoncé peut être exprimé mathématiquement
de la manière suivante. Si l’écart entre deux forces
r
et Br agissant sur un corps représente l’angle θ,
R
la résultante
est déterminée par
22
θ++= cosABBAR 2
Si α est l’angle entre la résultante et la force
:
θ
sinB
tan
=α
θ+
cosBA
D’après la règle du triangle de forces, deux forces
agissant en même temps sur un corps sont
représentées dans leur grandeur et dans leur direction par deux côtés de même sens d’un triangle.
Tant la grandeur que la direction de la résultante
sont déterminées par le troisième côté opposé aux
deux premiers.
Il en résulte qu’un corps est en équilibre lorsque
Aussi un corps, sur lequel agissent plusieurs forces,
estil en équilibre lorsque les forces peuvent être
représentées par un polygone fermé. La somme
vectorielle des forces individuelles est égale à zéro
et, par conséquent, la résultante est également
nulle.
En observant cette situation de plus près, on constate que la règle du polygone de forces ne
représente qu’une simple extension de la règle du
triangle de forces.
La table de forces est un instrument qui permet de
démontrer l’addition vectorielle et l’équilibre de
forces ainsi que de confirmer les methods graphiques et analytiques. Il est possible de démontrer
l’équilibre entre deux ou trois forces et de déterminer tant la grandeur que la direction de chaque
force.
2
Page 11

4. Manipulation
4.1 Montage de l’appareil
• Placer le pied sur une surface plane.
• Visser la barre du milieu dans le pied.
• Positionner avec force la plaque de travail sur
la barre du milieu.
• Placer le plateau inférieur sur la perforation
centrale et visser le support pour cordes.
• Disposer les galets de renvoi avec des fixations
aux repères 0°, 120° et 240° de la plaque de
travail.
• Placer l’anneau au-dessus du support au centre
de la plaque de travail.
• Placer les cordes sur les galets de renvoi, accro-
cher les poids à fentes sur les suspensions et
utiliser des poids à fente identiques.
• L’anneau doit être en équilibre.
4.2 Exemple d’expérience : Addition vectorielle
• Monter la table comme décrit ci-dessus.
• Placer une masse de 20 g et une de 50 g à 0° et
120° sur chacune des suspensions de poids.
• Etablir un équilibre en accrochant des masses
à la troisième suspension et en choisissant un
angle approprié. Aux fins de contrôle, soulever
l’anneau, puis le laisser retomber. Si l’anneau
revient au centre, l’équilibre est obtenu. Si ce
n’est pas le cas, procéder à des ajustages supplémentaires.
• Calculer la grandeur et la direction de la force
nécessaires pour obtenir un équilibre. Comparer la grandeur théorique avec la valeur obtenue par l’expérience.
• Dessiner à l’échelle la direction et la grandeur
des différentes forces ; confirmation de la règle
du triangle de forces.
• Répéter l’expérience avec différentes masses et
différents angles.
3B Scientific GmbH • Rudorffweg 8 • 21031 Hamburg • Allemagne • www.3bscientific.com
Sous réserve de modifications techniques
© Copyright 2010 3B Scientific GmbH
Page 12

Page 13

3B SCIENTIFIC
Istruzioni per l'uso
01/10 ALF
®
PHYSICS
Tavolo delle forze U52004
1 Piede
2 Morsetti con pulegge
3 Asta centrale
4 Supporto per corde
5 Piano di lavoro
6 Supporti per pesi con pesi a
fessura
1. Descrizione
La tavolo delle forze serve per dimostrare che la
forza è una grandezza vettoriale e per l’analisi
quantitativa della composizione e della scomposizione delle forze.
La tavolo delle forze è costituito da un piano di
lavoro circolare su piede stabile con doppia scala
della graduazione angolare. I pesi vengono appesi
a corde dotate di ganci su tre pulegge con fermi di
fissaggio. I tre set di pesi a fessura, in ottone, sono
costituiti ciascuno da pesi di 2x 5 g, 2x 10 g, 2x 20 g
2x 50 g , e da un supporto per pesi da 50 g.
2. Dati tecnici
Dimensioni: ca. 300 mm x 390 mm Ø
Scala: da 0 a 360° con divisione da 1°
Peso: ca. 3 kg
3. Principio
Le forze sono grandezze vettoriali. Quindi la forza
risultante di due forze che agiscono su un unico
punto non può essere determinata solo in base alle
loro intensità, ma necessariamente anche in base
alla loro direzione. La risultante di due o più forze
1
Page 14

che agiscono in un piano su un punto è un’unica
A
r
r
A
r
forza sullo stesso piano, che causa lo stesso effetto
dato dalla combinazione delle singole forze. Quindi
se una forza ha la stessa intensità della risultante,
ma agisce in direzione contraria, il corpo si trova in
stato di equilibrio. La risultante può essere determinata in modo analitico o con metodi grafici
mediante diverse leggi (parallelogramma delle
forze, triangolo delle forze, poligono delle forze).
Secondo la legge del parallelogramma delle forze,
le intensità e le direzioni di due forze che agiscono
contemporaneamente su un corpo vengono rappresentate da due lati adiacenti di un parallelogramma. L’intensità e la direzione della risultante
sono rappresentate dalla diagonale che si origina
dallo stesso punto.
Si evince che un corpo si trova in equilibrio se su di
esso agiscono tre forze rappresentate dai lati di un
triangolo.
Se su un corpo agiscono più di due forze conte
poraneamente, si applica la legge del poligono
delle forze. Le intensità e le direzioni di più forze
con punto di applicazione comune vengono rappresentate da un poligono aperto i cui lati hanno
lo stesso verso. La forza risultante è costituita dal
lato che chiude il poligono nel verso contrario
rispetto agli altri lati.
È possibile esprimere questo teorema in modo
matematico come segue. Se due forze
e Br che
agiscono su un corpo comprendono l’angolo θ, la
R
risultante
si ottiene da:
22
θ++= cosABBAR 2
Se α è l’angolo compreso fra la risultante e la forza
, si ha
θ
sinB
tan
=α
θ+
cosBA
Secondo la legge del triangolo delle forze,
l’intensità e la direzione di due forze che agiscono
contemporaneamente su un corpo vengono rappresentate da due lati di un triangolo che hanno lo
stesso verso. L’intensità e la direzione della risultante sono rappresentate dal terzo lato nel verso
contrario rispetto ai due lati precedenti.
Quindi un corpo su cui agiscono più forze si trova
in equilibrio se le forze possono essere rappresentate da un poligono chiuso. La somma vettoriale
delle single forze è uguale a zero e quindi anche la
risultante è uguale a zero.
Una riflessione più approfondita su questa affermazione mostra che la legge del poligono delle
forze non è altro che un’estensione della legge del
triangolo delle forze.
La tavolo delle forze è uno strumento idoneo per
dare una dimostrazione della somma vettoriale e
dell’equilibrio delle forze e anche per confermare i
metodi grafici e analitici. È possible dimostrare lo
stato di equilibrio fra due o tre forze e determinare
in modo semplice l’intensità e la direzione di ogni
forza.
2
Page 15

4. Utilizzo
4.1 Assemblaggio dell’apparecchio
• Posizionare il piede su una superficie piana.
• Fissare in verticale l’asta centrale nel piede.
• Infilare il piano di lavoro sull’asta centrale.
• Mettere la rondella sul foro centrale e avvitarci
il supporto per corde.
• Applicare le pulegge con morsetti in corrispon-
denza delle marcature a 0°, 120° e 240° presenti sul piano di lavoro.
• Collocare l’anello sul sostegno al centro del
piano di lavoro.
• Posizionare le corde sopra le pulegge; agganci-
are il supporto per pesi e collocare gli stessi pesi a fessura.
• L’anello dovrebbe essere in equilibrio.
4.2 Esempio di esperimento: addizione di vettori
• Assemblare la tavola delle forze come descritto
in precedenza.
• Collocare un peso da 20 g e un peso da 50 g su
un supporto per pesi a 0° e 120°.
• Sul terzo supporto per pesi collocare i pesi
necessary e scegliere un angolo adatto per
ristabilire l’equilibrio. Eseguire la verifica sollevando l’anello e lasciandolo ricadere. Se
l’anello ricade in centro, si ha una situazione di
equilibrio. In caso contrario, è necessario procedere ad ulteriori aggiustamenti.
• Calcolare l’intensità e la direzione della forza
necessaria per raggiungere l’equilibrio, confrontare i dati teorici con i valori ottenuti
sperimentalmente.
• Disegnare in scala l’intensità e la direzione
delle diverse forze; conferma della legge del
triangolo delle forze.
• Ripetere l’esperimento con diversi pesi e an-
goli.
3B Scientific GmbH • Rudorffweg 8 • 21031 Amburgo • Germania • www.3bscientific.com
Con riserva di modifiche tecniche
© Copyright 2010 3B Scientific GmbH
Page 16

Page 17

3B SCIENTIFIC
Instrucciones de uso
01/10 ALF
®
PHYSICS
Mesa de fuerzas U52004
1 Base
2 Sujetadores co poleas
3 Varilla central
4 Soporte para cordones
5 Placa de trabajo
6 Colgador de pesas con pesas
ranuradas
1. Descripción
La mesa de fuerzas se utiliza para demostrar que la
fuerza es una dimension vectorial, así como para el
estudio cuantitativo de la unión y descomposición
de fuerzas.
La mesa de fuerzas se compone de una placa de
trabajo circular, apoyada sobre una base estable,
con doble escala de división angular. Sobre las tres
poleas de inversión, con soportes de sujeción, se
colgarán pesas de cordones con ganchos. Los tres
juegos de pesas ranuradas, de latón, están compuestos, cada uno, de 2 pesas de 5 g, 2 de 10 g, 2
de 20 g y 2 de 50 g, así como de un colgador de
pesas de 50 g.
2. Datos técnicos
Dimensiones: aprox. 300 mm x 390 mm Ø
Escala: de 0 a 360°, con divisiones de 1°
Peso: aprox. 3 kg
3. Principio
Las fuerzas son magnitudes vectoriales. Es por ello
que una fuerza resultante de dos fuerzas, que actúan sobre un punto, no puede medirse sólo a
partir de su dimensión, sino que también hay que
tener en cuenta su dirección. La fuerza resultante
de dos o más fuerzas que actúan sobre un mismo
1
Page 18

punto, a un mismo nivel, es otra fuerza única en el
A
r
r
A
mismo nivel, que tiene el mismo efecto que la
combinación de las fuerzas individuales. Por lo
tanto, si una fuerza tiene la misma magnitud que
la resultante, pero actúa en sentido contrario, el
cuerpo se encontrará en estado de equilibrio. Las
fuerzas resultantes pueden determinarse con
métodos analíticos o gráficos a través de diversas
reglas (paralelograma de fuerzas, triángulo de
fuerzas o polígono de fuerzas).
Según la regla del paralelograma de fuerzas, las
dimensiones y sentidos de dos fuerzas, que actúan
al mismo tiempo sobre un cuerpo, se representan
por medio de los dos lados contiguos de un paralelograma. La fuerza resultante se obtiene, en su
dimensión y en su sentido, de la diagonal que
parte del mismo punto.
equilibrio cuando sobre él actúan tres fuerzas representadas por los lados de un triángulo.
Si más de dos fuerzas actúan a la vez sobre un
cuerpo, podremos entonces aplicar la regla del
polígono de fuerzas. Según esta regla, se representarían las dimensiones y direcciones de varias fuerzas, que actúan sobre un mismo punto, mediante
un polígono abierto en el que todos los lados tuvieran la misma dirección. La fuerza resultante se
obtiene del lado que cierra el polígono y que tiene
una dirección contraria a todos los demás lados del
mismo.
Esta regla puede expresarse matemáticamente de
acuerdo con lo siguiente: Si entre dos fuerzas
r
B
, que actúan sobre un mismo cuerpo, se encuen-
tra el ángulo θ, se obtiene la fuerza resultante
22
α es el ángulo entre la fuerza resultante y la fuerza
r
θ++= cosABBAR 2
y
R
:
, de modo que:
θ
sinB
=α
tan
θ+
cosBA
Según la regla del triángulo de fuerzas, para dos
fuerzas que actúan al mismo tiempo sobre un
cuerpo, su magnitud y dirección se representarían
con los dos lados de un triángulo, que tienen la
misma dirección. La fuerza resultante se obtiene,
tanto en su magnitude como en su dirección, del
tercer lado del triángulo que tiene sentido contrario a los dos primeros lados.
De ello se deduce que un cuerpo se encuentra en
Según este esquema, un cuerpo sobre el que actúan diversas fuerzas se encuentra en equilibrio
cuando estas fuerzas se pueden representar por
medio de un polígono cerrado. La suma de los
vectores de las fuerzas individuales es igual a cero,
y por tanto la fuerza resultante es también cero.
Un estudio más detenido de este fenómeno muestra que la regla del polígono de fuerzas es simplemente una ampliación de la regla del triángulo de
fuerzas.
La mesa de fuerzas es un instrumento indicado
para la demostración de la suma vectorial y del
equilibrio de fuerzas, así como para la determinación de los métodos gráficos y analíticos. Con él
puede mostrarse el equilibrio entre dos o tres fuerzas, e incluso pueden determinarse con facilidad
las magnitudes y sentido de cada fuerza.
2
Page 19

4. Manejo
4.1 Montaje del aparato
• Coloque la base sobre una superficie plana.
• Atornille la varilla central sobre la base, en
sentido vertical.
• Aplice la placa de trabajo con presión sobre la
varilla central.
• Arandela Poner la arandela sobre el taladro
central y atornillar el soporte para los cordones.
• Ajuste las poleas de inversión, con los sujeta-
dores, en las marcas de 0°, 120° y 240° de la
placa de trabajo.
• Coloque el anillo, sobre el soporte, en el centro
de la placa de trabajo.
• Coloque los cordones sobre las poleas de inver-
sión, cuelgue los soportes de pesas y emplace
sobre ellos pesas ranuradas de igual peso.
• El anillo debe encontrarse en equilibrio.
4.2 Ejemplo de experimento: Suma vectorial
• Monte la mesa de fuerzas como se indicó ante-
riormente.
• Cuelgue de cada colgador una pesa de 20 g y
otra de 50 g, en las marcas de 0° y 120°.
• Consiga el equilibrio colocando pesas en el
tercer colgador, seleccionando para este fin un
ángulo adecuado. Como comprobación eleve el
anillo y déjelo caer. Si el anillo vuelve a su posición, en el centro, habrá alcanzado el equilibrio. Si no es así, deberá realizar más ajustes
hasta conseguir este resultado.
• Calcule la magnitud y sentido de la fuerza
necesarios para alcanzar el equilibrio, compare
la magnitude teórica con el valor obtenido experimentalmente.
• Dibuje a escala las diferentes fuerzas, tanto en
sentido como en magnitud. Comprobación de
la regla del triángulo de fuerzas.
• Repita el experimento con diferentes pesos y
ángulos.
3B Scientific GmbH • Rudorffweg 8 • 21031 Hamburgo ▪ Alemania • www.3bscientific.com
Se reservan las modificaciones técnicas
© Copyright 2010 3B Scientific GmbH
Page 20

Page 21

3B SCIENTIFIC
Manual de instruções
01/10 ALF
®
PHYSICS
Mesa de forças U52004
1 Pé
2 Pinças com polias de desvio
3 Barra central
4 Suporte para corda
5 Placa de trabalho
6 Suspensório para pesos com
pesos de entalhe
1. Descrição
A mesa de forças serve para a comprovação que a
força é uma magnitude vetorial assim como para a
análise quantitativa da composição e
decomposição de forças.
A mesa de forças consiste numa placa de trabalho
circular sobre um pé estável com escala dupla da
divisão angular. Por sobre as três polias de desvio
com pinças de fixação são pendurados pesos com
ganchos em cordas. Os três conjuntos de pesos de
entalhe de latão consistem em pesos de 2x 5 g, 2x
10 g, 2x 20 g e 2x 50 g cada um, assim como um
suspensório de pesos de 50 g.
2. Dados técnicos
Dimensões: aprox. 300 mm x 390 mm Ø
Escala: 0 até 360° com divisão de 1°
Massa: aprox. 3 kg
3. Princípio
Forças são magnitudes vetoriais. Por isso, a força
compensatória resultante de duas forças agindo
num mesmo ponto, não pode ser determinada só
pelas suas magnitudes, mas também devem ser
levadas em consideração as suas direções. A
1
Page 22

resultante de duas ou mais forças agindo num
A
r
r
A
r
mesmo plano é uma força única no mesmo plano,
a qual produz o mesmo efeito que a combinação
das forças individuais.
Portanto, se uma força tem a mesma magnitude
que a resultante, mais age contrária em direção, o
corpo encontra-se então em situação de equilíbrio.
A resultante pode ser determinada de modo
analítico ou com métodos gráficos por meio de
diferentes leis (paralelogramo de forças, triângulo
de forças, polígono de forças).
Segundo a lei do paralelogramo de forças, duas
forces que agem simultaneamente sobre um corpo
são representadas na sua magnitude e direção por
dois lados adjacentes de um paralelogramo. A
resultante se produz tanto em magnitude como em
direção a partir das diagonais que têm a sua saída
no mesmo ponto.
Disto resulta que um corpo se encontra em
equilíbrio quando três forças agem sobre ele, que
são representadas pelos três lados de um
triângulo.
Se mais de duas forças agem simultaneamente
sobre um corpo, então, a lei do polígono de forças
encontra a sua aplicação. Segundo esta lei, várias
forças com ponto de ataque comum na sua
magnitude e direção são representadas por um
polígono aberto, cujos lados possuem o mesmo
sentido de direção. A força compensatória
resultante decorre do lado que fecha o polígono
em direção contrária dos outros lados.
Este teorema pode ser expresso matematicamente
da seguinte forma. Quando entre duas forças
r
B
que agem sobre um corpo, existe o ângulo θ, a
R
resultante
decorre de:
22
θ++= cosABBAR 2
Se α é o ângulo entre a resultante e a força
e
,
então será
θ
sinB
=α
tan
θ+
cosBA
Segundo a lei do triângulo de forças, duas forças
que agem simultaneamente sobre um corpo são
representadas na sua magnitude e direção por dois
lados de um triângulo que têm o mesmo sentido
de direção. A resultante decorre, tanto em
magnitude como na sua direção, do terceiro lado
em sentido de direção contrária a ambos os lados
anteriores.
Por isso, um corpo sobre o qual agem várias forças,
encontra-se em equilíbrio, quando as forças podem
ser representadas em forma de um polígono
fechado. A soma dos vetores das forças individuais
é igual a zero, e por isso, a resultante também é
zero.
Uma observação mais detalhada destes fatos
mostra que a lei do polígono de forças é só uma
extensão simples da lei do triângulo de forças.
A mesa de forças é um instrumento adequado para
a demonstração da adição de vetores e do
equilíbrio de forças, assim como para a
comprovação dos métodos gráficos e analíticos. O
estado de equilíbrio entre duas ou três forças pode
ser demonstrado, e tanto a magnitude como a
direção de cada força pode ser determinada com
facilidade.
2
Page 23

4. Utilização
4.1 Montagem do aparelho
• Colocar o pé sobre uma superfície plana.
• Aparafusar a barra central verticalmente no pé.
• Pressionar a placa de trabalho com força sobre
a barra central.
• Colocar a arruela sobre a furação central e
aparafusar o suporte para as cordas.
• Montar as polias de desvio com pinças nas
marcas de 0°, 120° e 240° da placa de
trabalho.
• Colocar o anel sobre o suporte no ponto
central da placa de trabalho.
• Colocar as cordas sobre as polias de desvio,
pendurar os suspensórios para pesos e colocar
pesos de entalhe iguais.
• O anel deveria encontrar-se em equilíbrio.
4.2 Exemplo de Experiência: adição de vetores
• Montar a mesa de força como descrito acima.
• Colocar uma massa de 20 g e outra de 50 g
num suspensório de pesos em 0° e 120°.
• Estabelecer o equilíbrio colocando massas e
escolhendo um ângulo adequado no terceiro
suspensório. Para a verificação, levantar o anel
e deixá-lo cair. Se o anel cair de volta no
centro, foi atingido o estado de equilíbrio. Em
caso contrário, mais ajustes devem ser feitos.
• Calcular a magnitude e a direção da força
necessária para atingir o equilíbrio.
Comparação da magnitude teórica com o valor
obtido experimentalmente.
• Desenhar conforme a escala as diferentes
forças em direção e magnitude; comprovação
da lei do triângulo de forças.
• Repetir a experiência com massas e ângulos
diferentes.
3B Scientific GmbH • Rudorffweg 8 • 21031 Hamburgo • Alemanha • www.3bscientific.com
Sob reserva de alterações técnicas
© Copyright 2010 3B Scientific GmbH
Page 24

 Loading...
Loading...