Texas Instruments TI-Nspire CAS Reference Guide [it]

CAS

Guida di riferimento

La presente Guida è relativa alla versione 1.4 del software TI-Nspire. Per ottenere la versione più aggiornata della documentazione, visitare il sito education.ti.com/guides.

Informazioni importanti

Salvo per quanto dichiarato espressamente nella licenza che accompagna un programma, Texas Instruments non rilascia alcuna garanzia, esplicita o implicita, incluse fra le altre le garanzie implicite di commerciabilità e di idoneità ad uno scopo particolare, per quanto riguarda programmi o materiali cartacei e rende disponibili tali materiali esclusivamente su base "tal quale." In nessun caso Texas Instruments è responsabile verso chicchessia di danni speciali, collaterali, incidentali o consequenziali in relazione con o derivanti dall'acquisto o dall’uso di questi materiali, e la sola ed esclusiva responsabilità di Texas Instruments, indipendentemente dalla forma dell'azione, non supera l'importo indicato nella licenza per il programma. Inoltre Texas Instruments non è responsabile di rivendicazioni di alcun genere contro l'uso di questi materiali da parte di chiunque.

Licenza

Leggere per intero la licenza installata in C:\Program Files\TI

Education\TI-Nspire CAS

Macintosh®, Windows®, Excel®, Vernier EasyLink®, EasyTemp®, Go!®Link, Go!®Motion, e Go!®Temp sono marchi dei rispettivi proprietari.

Sommario

Informazioni importanti Modelli di espressione

Modello di frazione ..................................... 1

Modello di esponente ................................. 1

Modello di radice quadrata ........................ 1

Modello di radice ennesima ........................1

Modello di funzione esponenziale e ..........2

Modello di log ..............................................2

Modello di funzione piecewise a 2 tratti ...2 Modello di funzione piecewise a N tratti ...2

Modello di sistema di 2 equazioni ..............3

Modello di sistema di N equazioni ............. 3

Modello di valore assoluto ..........................3

Modello di gg°pp’ss.ss’’ ............................... 3

Modello di matrice (2 x 2) ...........................3

Modello di matrice (1 x 2) ...........................3

Modello di matrice (2 x 1) ...........................4

Modello di matrice (m x n) ..........................4

Modello di sommatoria (G) .......................... 4

Modello di prodotto (Π) ..............................4

Modello di derivata prima .......................... 4

Modello di derivata ennesima .................... 5

Modello di integrale definito ..................... 5

modello di integrale indefinito .................. 5

Modello di limite ......................................... 5

Elenco alfabetico A

abs() (Valore assoluto) ................................. 6

amortTbl() .................................................... 6

and ................................................................6

angle() (Angolo) ........................................... 7

ANOVA (Analisi della varianza) .................. 7

ANOVA2way (Analisi della varianza a due

dimensioni) ................................................... 8

Ans (Ultimo risultato) ................................ 10

approx() Approssima .................................10

approxRational() ........................................ 10

arcLen() (Lunghezza arco) .........................10

augment() (Affianca/concatena) ...............11

avgRC() (Tasso di variazione media) ......... 11

bal() .............................................................12

4Base2 ......................................................... 12

4Base10 ....................................................... 13

4Base16 ....................................................... 13

binomCdf() (Funzione della probabilità cumulativa per la distribuzione binomiale) . 13

binomPdf() ................................................. 13

ceiling() (Arrotondato per eccesso) ...........14

cFactor() (Fattore complesso) ....................14

char() (Stringa di caratteri) ........................ 14

charPoly() (Polinomio caratteristico) .........15

2way ........................................................ 15

Cdf() ........................................................ 15

GOF ......................................................... 15

Pdf() ........................................................ 16

ClearAZ (Cancella AZ) ................................ 16

ClrErr .......................................................... 16

colAugment() (Affianca colonna) ............. 17

colDim() (Dimensione colonna) ................ 17

colNorm() (Norma colonna) ...................... 17

comDenom() (Denominatore comune) .... 17

conj() (Coniugato) ...................................... 18

constructMat() (Costruisci matrice) ........... 18

CopyVar (Copia variabile) ......................... 18

corrMat() (Matrice di correlazione) ..........19

4cos (Coseno) .............................................. 19

cos() (Coseno) ............................................. 20

cosê() (Arcocoseno) ................................... 21

cosh() (Coseno iperbolico) ......................... 21

coshê() (Arcocoseno iperbolico) ............... 21

cot() (Cotangente) ..................................... 22

cotê() (Arcocotangente iperbolica) .......... 22

coth() (Cotangente iperbolica) ................. 22

cothê() Arcocotangente iperbolica .......... 23

count() ........................................................ 23

countif() ..................................................... 23

crossP() (Prodotto vettoriale) .................... 24

csc() (Cosecante) ......................................... 24

cscê() (Cosecante inversa) .......................... 24

csech (Cosecante iperbolica) ..................... 24

cschê() (Cosecante iperbolica inversa) ...... 25

cSolve() (Risolvi in campo complesso) ....... 25

CubicReg (Regressione cubica) ................. 27

cumSum() (Somma cumulativa) ................ 27

Cycle (Ripeti) .............................................. 28

4Cylind (Forma cilindrica) .......................... 28

cZeros() (Zeri complessi) ............................ 28

dbd() ........................................................... 30

4DD (Visualizza angolo decimale) ............. 30

4Decimal (Decimale) .................................. 30

Define (Definisci) ....................................... 31

Define LibPriv (Definisci libreria privata) . 31 Define LibPub (Definisci libreria pubblica) .. 32

DelVar ........................................................ 32

deSolve() Soluzione di equazioni

differenziali ............................................... 32

det() (Determinante) ................................. 34

diag() (Diagonale) ...................................... 34

dim() (Dimensione) .................................... 34

Disp ............................................................. 35

4DMS (Gradi/primi/secondi) ....................... 35

dominantTerm() (Termine dominante) .... 36

dotP() (Prodotto scalare) ........................... 36

e^() (Funzione esponenziale) .................... 37

eff() ............................................................. 37

eigVc() (Autovettore) ................................ 37

iii

eigVl() (Autovalore) ...................................38

Else ..............................................................38

ElseIf ............................................................38

EndFor .........................................................38

EndFunc ......................................................38

EndIf ............................................................38

EndLoop ......................................................38

EndPrgm .....................................................38

EndTry .........................................................38

EndWhile ....................................................39

exact() (Esatto) ...........................................39

Exit (Esci) .....................................................39

4exp (Espressione) .......................................39

exp() (e alla potenza) .................................39

exp4list() ......................................................40

expand() (Espandi) .....................................40

expr() (Da stringa a espressione) ...............41

ExpReg (Regressione esponenziale) ..........41

factor() (Fattorizza) ....................................42

FCdf() (Probabilità di distribuzione F) ......43

Fill (Riempi) .................................................43

FiveNumSummary ......................................44

floor() (Arrotondato per difetto) ..............44

fMax() (Massimo funzione) .......................44

fMin() (Minimo funzione) ..........................45

For ...............................................................45

format() (Formato) .....................................46

fPart() Funzione parte frazionaria ............46

FPdf() (Probabilità di distribuzione F) ......46

freqTable4list() ............................................46

FTest_2Samp (Verifica F su due campioni) ... 47

frequency() .................................................47

Func .............................................................48

gcd() (Massimo comun divisore) ................48

geomCdf() (Probabilità geometrica

cumulata) ....................................................48

geomPdf() (Probabilità per la distribuzione

geometrica discreta) ..................................49

getDenom() (Ottieni/restituisci

denominatore) ...........................................49

getLangInfo() (Ottieni informazioni sulla

lingua) .........................................................49

getMode() ...................................................49

getNum() (Ottieni/restituisci numeratore) 50 getVarInfo() (Ottieni informazioni variabile) 51

Goto (Vai a) ................................................51

4Grad (Gradianti o Gradi centesimali) .......52

identity() (Identità) ....................................52

If ..................................................................52

ifFn() ............................................................53

imag() (Parte immaginaria) .......................53

impDif() (Derivata implicita) ......................54

Indirection (Conversione indiretta) ...........54

inString() (All’interno della stringa) ..........54

int() (Funzione parte intera) ......................54

intDiv() Divisione intera ............................ 54

integrate .................................................... 54

() ......................................................... 55

invc invF() (Distribuzione F cumulativa inversa) .. 55 invNorm() (Distribuzione normale

cumulativa inversa) .................................... 55

invt() (Funzione della probabilità t di

Student) ...................................................... 55

iPart() (Parte intera) ................................... 55

irr() .............................................................. 55

isPrime() (Numero primo) .......................... 56

Lbl (Etichetta) ............................................. 56

lcm() (Minimo comune multiplo) .............. 56

left() (Sinistra) ............................................ 57

libShortcut() (Collegamento a libreria) ....57

limit() o lim() (Limite) ................................ 57

LinRegBx (Regressione lineare) ................. 58

LinRegMx (Regressione lineare) ............... 59

LinRegtIntervals (Regressione lineare) ..... 59

LinRegtTest (t Test regressione lineare) ... 61

@list() (Differenza in una lista) .................. 61

list4mat() (Da lista a matrice) ..................... 62

4ln (Conversione in logaritmo naturale) ... 62

ln() (Logaritmo naturale) .......................... 62

LnReg (Regressione logaritmica) .............. 63

Local (Variabile locale) .............................. 64

log() (Logaritmo) ....................................... 64

4logbase ...................................................... 65

Logistic (Regressione logistica) ................. 65

LogisticD (Rgressione logistica) ................. 66

Loop ............................................................ 67

LU (Scomposizione inferiore - superiore) . 67

mat4list() (Da matrice a lista) ..................... 68

max() (Massimo) ......................................... 68

mean() Media ............................................. 68

median() (Mediana) ................................... 68

MedMed (Linea mediana-mediana) ......... 69

mid() (In mezzo alla stringa) ..................... 69

min() (Minimo) ........................................... 70

mirr() ........................................................... 70

mod() (Modulo) ......................................... 71

mRow() (Operazione con righe di matrice) .. 71 mRowAdd() (Moltiplicazione e somma di

righe di matrice) ........................................ 71

MultReg (Regressione lineare multipla) ... 71 MultRegIntervals (Intervalli di confidenza della previsione di regressione multipla) . 72 MultRegTests (Verifica sulla regressione

lineare multipla) ........................................ 72

nCr() (Combinazioni) ................................. 73

nDeriv() (Derivata numerica) .................... 74

newList() (Nuova lista) ............................... 74

newMat() (Nuova matrice) ........................ 74

nfMax() (Massimo di una funzione calcolato

numericamente) ........................................ 74

nfMin() (Minimo di una funzione calcolato

numericamente) ......................................... 75

nInt() (Integrale numerico) ........................ 75

nom() ..........................................................75

norm() (Norma di Froebius) .......................76

normalLine() (Retta normale) ...................76

normCdf() (Probabilità di distribuzione

normale) ..................................................... 76

normPdf() (Densità di probabilità) ............ 76

not ..............................................................76

nPr() (Disposizioni semplici) ......................77

npv() ............................................................78

nSolve() (Soluzione numerica) ...................78

OneVar (Statistiche a una variabile) .........79

or .................................................................80

ord() Codice numerico di carattere ...........80

P4Rx() (Coordinata x rettangolare) ...........80

P4Ry() (Coordinata y rettangolare) ...........81

PassErr .........................................................81

piecewise() (Funzione definita a tratti) ....81

poissCdf() (Probabilità cumulata per la

distribuzione discreta di Poisson) .............81

poissPdf() (Probabilità per la distribuzione

discreta di Poisson) .................................... 82

4Polar (Visualizza come vettore polare) ...82

polyCoeffs() ................................................ 83

polyDegree() .............................................. 83

polyEval() (Calcola polinomio) .................. 83

polyGcd() .................................................... 84

polyQuotient() ........................................... 84

polyRemainder() ........................................ 84

PowerReg (Regressione su potenza) .........85

Prgm ...........................................................86

Product (PI) (Prodotto) .............................. 86

product() (Prodotto) .................................. 86

propFrac() (Frazione propria) ....................86

QR (Scomposizione QR) ............................. 87

QuadReg (Regressione quadratica) ..........88

QuartReg (Regressione quartica) .............. 89

R4Pq() (Coordinata polare) ........................ 90

R4Pr() Coordinata polare ........................... 90

4Rad in angolo radiante ............................ 90

rand() (Numero casuale) ............................90

randBin() (Numero casuale da distribuzione

binomiale) .................................................. 91

randInt() (Intero casuale) ...........................91

randMat() (Matrice casuale) ......................91

randNorm() (Normale casuale) .................. 91

randPoly() (Polinomio casuale) .................91

randSamp() (Campione casuale) ...............91

RandSeed (Seme numero casuale) ............92

real() (Reale) ...............................................92

4Rect (Visualizza come vettore rettangolare) 92

ref() (Forma a scalini per righe) ................ 93

remain() (Resto) ......................................... 93

Return (Restituisci) ..................................... 93

right() (Destra) ........................................... 93

root() .......................................................... 94

rotate() (Ruota) .......................................... 94

round() (Arrotondamento) ....................... 95

rowAdd() (Somma di righe di matrice) .... 95

rowDim() (Dimensione righe matrice) ...... 95

rowNorm() (Norma righe matrice) ........... 95

rowSwap() (Inverti righe matrice) ............ 96

rref() (Forma a scalini ridotta per righe) ..96

sec() (Secante) ............................................ 96

sec/() (Secante inversa) ............................. 97

sech() (Secante iperbolica) ........................ 97

sechê() (Secante iperbolica inversa) ......... 97

seq() (Sequenza) ........................................ 97

series() (Serie) ............................................. 98

setMode() ................................................... 99

shift() (Sposta) .......................................... 100

sign() (Segno) ........................................... 101

simult() Sistema di equazioni simultanee ....

101

4sin (Seno) ................................................ 102

sin() (Seno) ............................................... 102

sinê() (Arcoseno) ...................................... 103

sinh() (Seno iperbolico) ........................... 103

sinhê() (Arcoseno iperbolico) .................. 103

SinReg (Regressione sinusoidale) ............ 104

solve() (Risolvi) ......................................... 105

SortA (Ordinamento ascendente) ........... 107

SortD (Ordinamento discendente) ......... 107

4Sphere (Visualizza come vettore sferico) ....

108

sqrt() (Radice quadrata) .......................... 108

stat.results (Risultati dell’analisi statistica) ... 109 stDevPop() (Deviazione standard della

popolazione) ............................................ 110

stDevSamp() (Deviazione standard del

campione) ................................................ 110

stat.values (Valori dei risultati) ............... 110

Stop .......................................................... 111

Store (Memorizza) ................................... 111

string() (Da espressione a stringa) ..........111

subMat() (Sottomatrice) .......................... 111

Sum (Sigma) ............................................. 111

sum() (Somma) ......................................... 112

sumIf() ...................................................... 112

system() (Sistema) .................................... 112

T (Trasposizione) ...................................... 113

tan() (Tangente) ...................................... 113

tanê() (Arcotangente) ............................. 114

tangentLine() (Retta tangente) .............. 114

tanh() (Tangente iperbolica) ................... 114

tanhê() (Arcotangente iperbolica) ......... 115

taylor() ...................................................... 115

tCdf() (Probabilità di distribuzione t di

Student) ................................................... 115

tCollect() (Riduzione trigonometrica) .... 116

tExpand() (Espansione trigonometrica) ..116

Then ..........................................................116

tInterval (Intervallo di confidenza t) .......116

tInterval_2Samp (Intervallo di confidenza t

su due campioni) ......................................117

tmpCnv() (Converti temperatura) ...........118

@tmpCnv() (Converti un intervallo di

temperature) ............................................118

tPdf() (Densità di probabilità t di Student) .. 118

trace() (Traccia) .........................................119

Try (Tentativo) ..........................................119

tTest (Verifica t) ........................................120

tTest_2Samp (Verifica t su due campioni) ....

120

tvmFV() .....................................................121

tvmI() .........................................................121

tvmN() .......................................................121

tvmPmt() ...................................................121

tvmPV() .....................................................121

TwoVar (Risultati a due variabili) ............122

unitV() (Vettore unità) .............................123

varPop() (Varianza della popolazione) ...124

varSamp() (Varianza campione) ..............124

when() (Quando) ......................................124

While .........................................................125

“With” ......................................................125

xor .............................................................125

zeros() (Zeri) .............................................126

zInterval (Intervallo di confidenza Z) ......127

zInterval_1Prop (Intervallo di confidenza z

per una proporzione) ..............................128

zInterval_2Prop (Intervallo di confidenza z

per due proporzioni) ...............................128

zInterval_2Samp (Intervallo di confidenza z

su due campioni) ......................................128

zTest (Verifica z) .......................................129

zTest_1Prop (Verifica z per una proporzione) 129 zTest_2Prop (Verifica z per due proporzioni) 130 zTest_2Samp (Verifica su due campioni) 130

Simboli

+ (addizione) ............................................ 132

N(sottrazione) ........................................... 132

·(moltiplicazione) ................................... 133

à (divisione) .............................................. 134

^ (elevamento a potenza) .......................134

(quadrato) ............................................ 135

.+ (punto addizione) ................................ 135

.. (punto sottrazione). ............................. 135

·(punto moltiplicazione). ...................... 136

. / (punto divisione) .................................. 136

.^ (punto elevato a potenza) .................. 136

ë(negazione) ............................................ 137

% (percentuale) ....................................... 137

= (uguale) ................................................. 138

ƒ (diverso) ................................................ 138

< (minore di) ............................................ 139

{ (minore di o uguale a) .......................... 139

> (maggiore di) ........................................ 139

| (maggiore di o uguale a) ...................... 139

! (fattoriale) ............................................. 140

& (aggiunge) ............................................ 140

d() (derivata) ............................................ 140

‰() (integrale) ............................................ 140

‡() (radice quadrata) ............................... 141

Π() (prodotto) .......................................... 142

G() (somma) .............................................. 142

GInt() ......................................................... 143

GPrn() ........................................................ 144

# (conversione indiretta) ......................... 144

í (notazione scientifica) .......................... 144

G (gradianti) ............................................. 145

ô(radianti) ................................................ 145

¡ (gradi) .................................................... 145

¡, ’, ’’ (gradi/primi/secondi) ...................... 146

 (angolo) ................................................ 146

’ (primo) .................................................... 146

_ (trattino basso) ...................................... 147

4 (converti) ................................................ 147

10^() .......................................................... 147

^ê (reciproco) ........................................... 148

| (“with”) .................................................. 148

& (memorizza) ......................................... 149

:= (assegna) .............................................. 149

0b, 0h ........................................................ 150

Codici di errore e messaggi Informazioni sul servizio di

manutenzione e riparazione del prodotto TI e sulla garanzia

Guida di riferimento di TI-Nspire™

La presente Guida elenca i modelli, le funzioni, i comandi e gli operatori disponibili per il calcolo di espressioni matematiche.

CAS

Modelli di espressione

I modelli di espressione rappresentano un metodo veloce per introdurre espressioni matematiche in notazione matematica standard. Un modello, quando inserito, viene visualizzato nella riga di introduzione come tanti quadratini al posto degli elementi che si possono inserire. Un cursore indica quale elemento si può inserire.

Utilizzare i tasti freccia o premere

un valore o un’espressione per esso. Premere

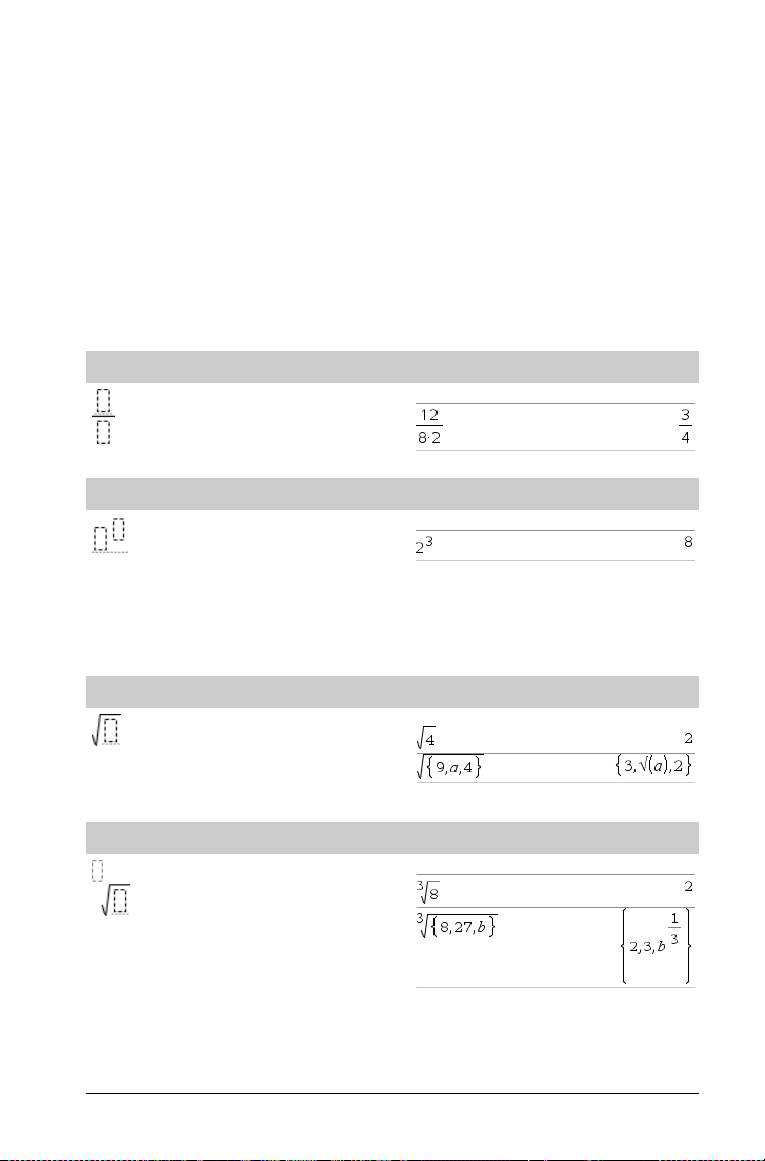
Modello di frazione

Nota: vedere anche / (divisione) a pagina 134.

e per spostare il cursore su ciascun elemento e digitare

· o /· per calcolare l’espressione.

Tasti /p

Esempio:

Modello di esponente

Nota: digitare il primo valore, premere l, quindi digitare

l’esponente. Per riportare il cursore sulla linea di base, premere la freccia a destra (¢).

Nota: vedere anche ^ (potenza) a pagina 134.

Modello di radice quadrata

Nota: vedere anche

Modello di radice ennesima

Nota: vedere anche root() a pagina 94.

‡

() (radice quadrata) a pagina 141.

Tasto l

Esempio:

Tasti /q

Esempio:

Tasti /l

Esempio:

Guida di riferimento di TI-Nspire™ CAS 1

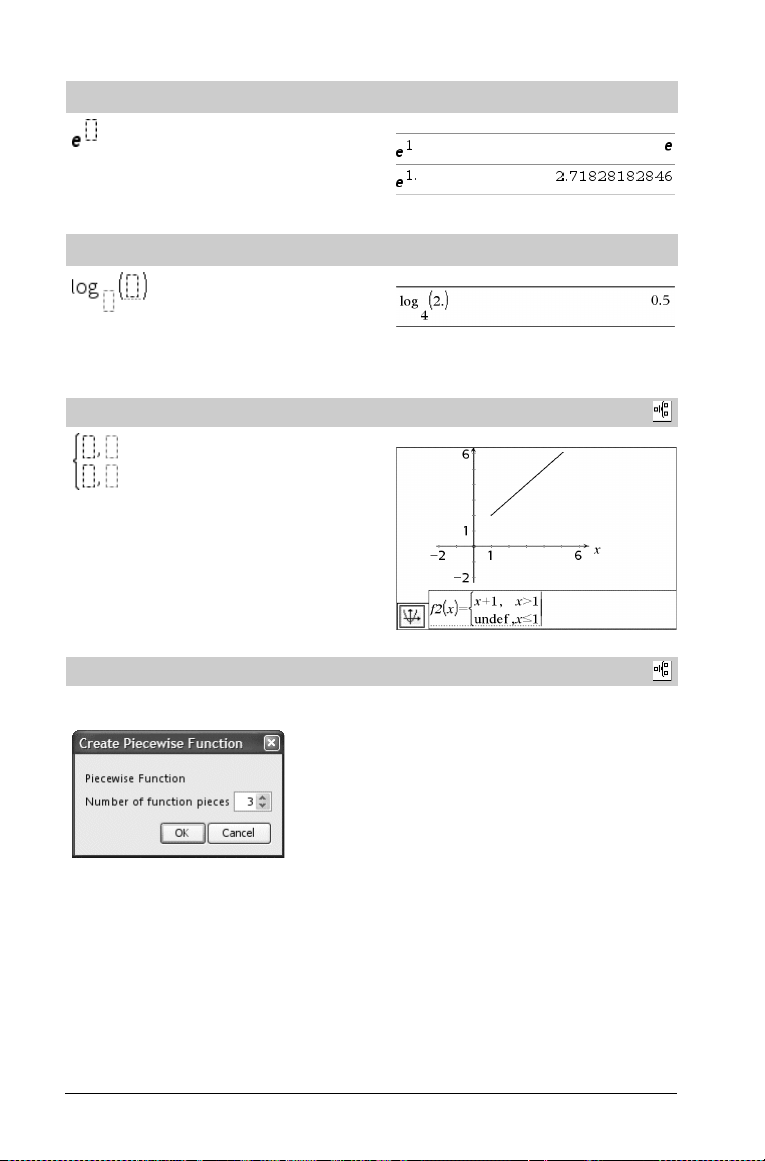
Modello di funzione esponenziale e

Esponenziale naturale e elevato a potenza

Nota: vedere anche e^() a pagina 37.

Tasti u

Esempio:

Modello di log

Calcola il logaritmo nella base specificata. Per la base 10 predefinita, omettere la base.

Nota: vedere anche log() a pagina 64.

Modello di funzione piecewise a 2 tratti

Consente di creare espressioni e condizioni per funzioni definite a due-tratti. Per aggiungere un tratto, fare clic sul modello e ripeterlo.

Nota: vedere anche piecewise() a pagina 81.

Modello di funzione piecewise a N tratti

Consente di creare espressioni e condizioni per una funzione definita a N-tratti. Richiede l’introduzione di N.

Tasto /

Esempio:

Catalogo >

Esempio:

Catalogo >

Esempio: vedere l’esempio del Modello di funzione piecewise a 2 tratti.

Nota: vedere anche piecewise() a pagina 81.

2 Guida di riferimento di TI-Nspire™ CAS

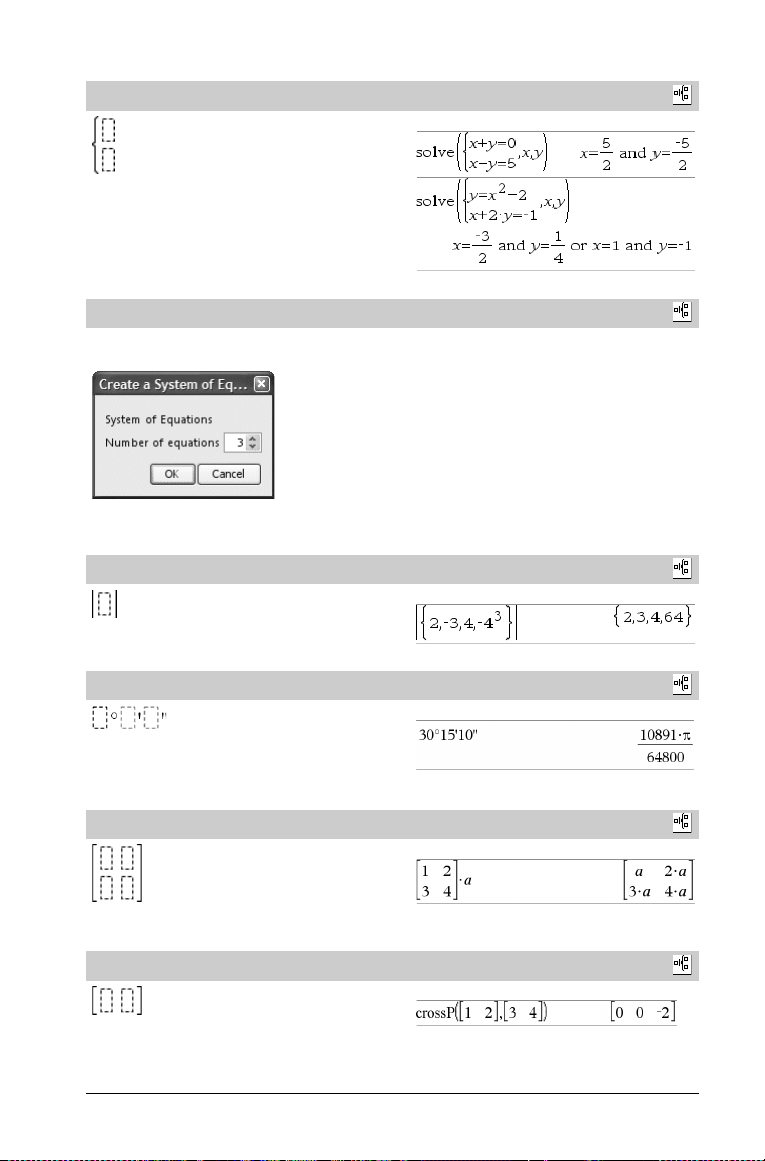
Modello di sistema di 2 equazioni

Crea un sistema di due equazioni. Per aggiungere una riga a un sistema esistente, fare clic sul modello e ripeterlo.

Nota: vedere anche system() a pagina 112.

Catalogo >

Esempio:

Modello di sistema di N equazioni

Consente di creare un sistema di N equazioni. Richiede l’introduzione di N.

Nota: vedere anche system() a pagina 112.

Modello di valore assoluto

Nota: vedere anche abs() a pagina 6.

Modello di gg°pp’ss.ss’’

Consente di inserire angoli nel formato gg°pp’ss.ss’’, dove gg è il numero di gradi decimali, pp è il numero di primi e ss.ss è il numero di secondi.

Modello di matrice (2 x 2)

Catalogo >

Esempio: vedere l’esempio del Modello di sistema di equazioni (2 equazioni).

Catalogo >

Esempio:

Catalogo >

Esempio:

Catalogo >

Esempio:

Crea una matrice 2 x 2.

Modello di matrice (1 x 2)

Esempio:

Catalogo >

Guida di riferimento di TI-Nspire™ CAS 3

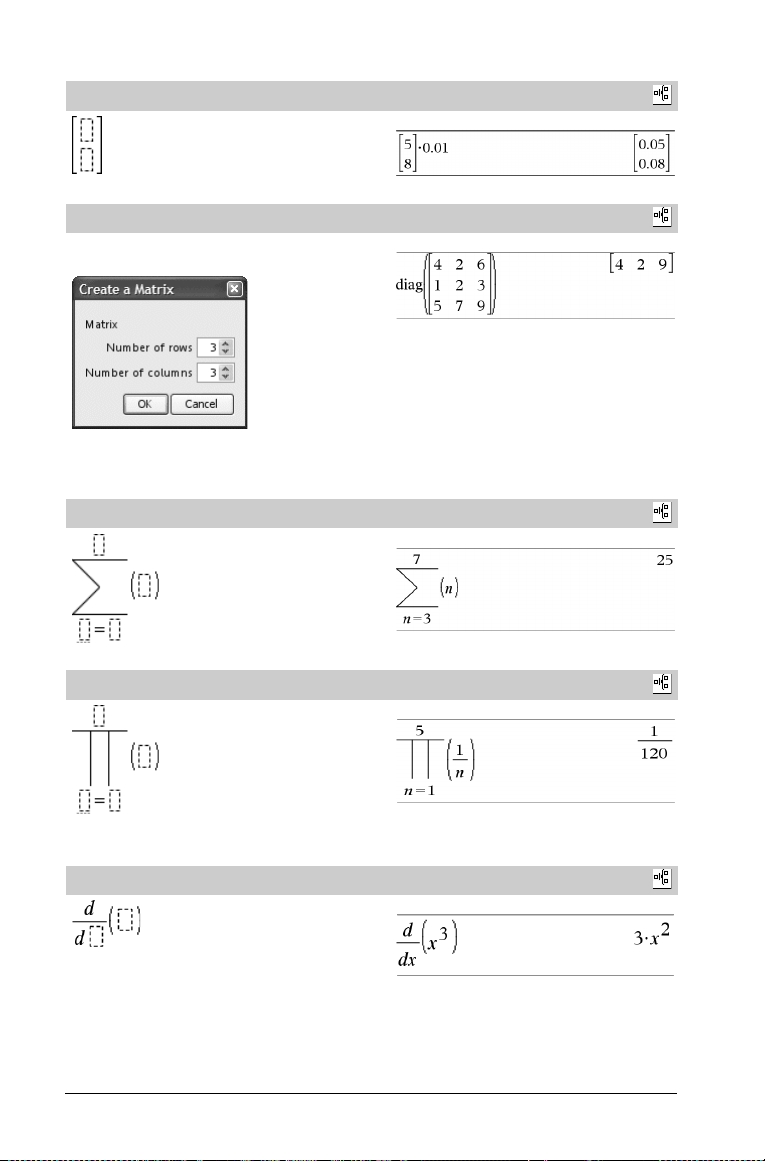
Modello di matrice (2 x 1)

Catalogo >

Esempio:

Modello di matrice (m x n)

Il modello appare dopo la richiesta di specificare il numero di righe e colonne.

Nota: se si crea una matrice con un numero elevato di righe e colonne, è possibile che la visualizzazione richieda un po’ di tempo.

Modello di sommatoria (G)

Modello di prodotto (Π)

Catalogo >

Esempio:

Catalogo >

Esempio:

Catalogo >

Esempio:

Nota: vedere anche Π() (prodotto) a pagina 142.

Modello di derivata prima

Nota: vedere anche

d() (derivata)

Esempio:

a pagina 140.

Catalogo >

4 Guida di riferimento di TI-Nspire™ CAS

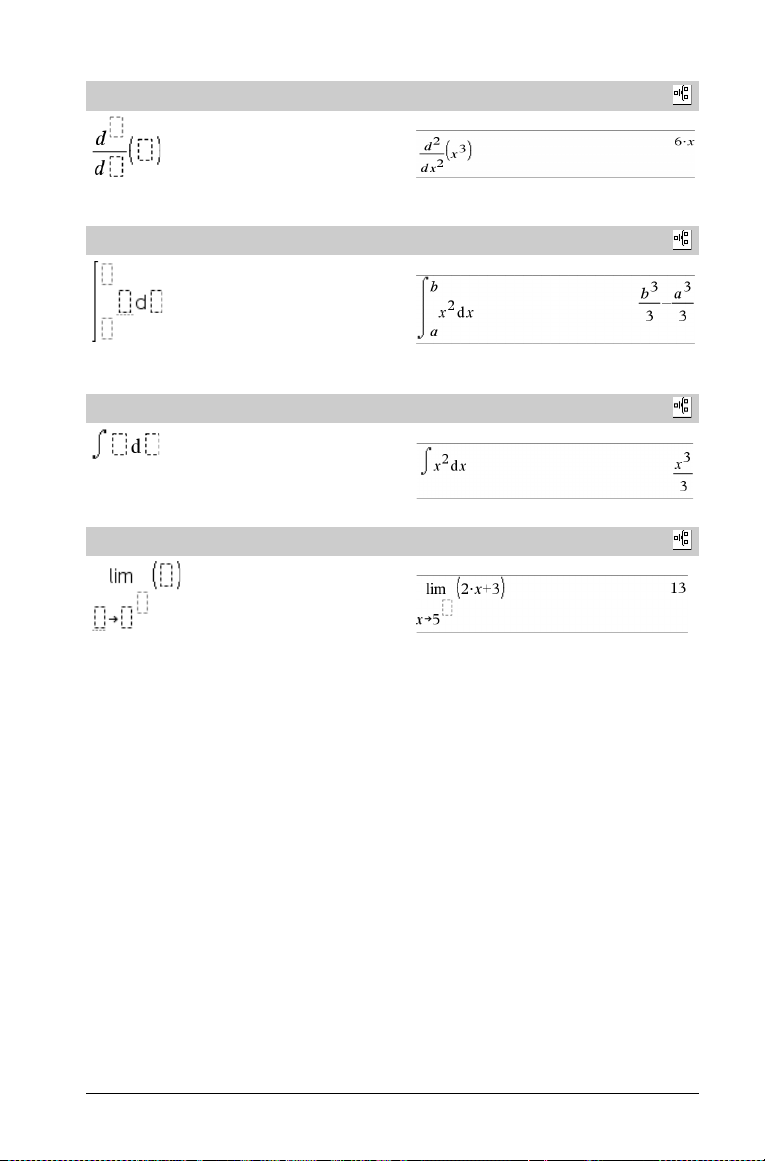
Modello di derivata ennesima

Catalogo >

Esempio:

Nota: vedere anche

d() (derivata)

a pagina 140.

Modello di integrale definito

Nota: vedere anche ‰() integrate() a pagina 140.

modello di integrale indefinito

Nota: vedere anche ‰() integrate() a pagina 140.

Modello di limite

Utilizzare N o (N) per il limite da sinistra. Utilizzare + per il limite da destra.

Nota: vedere anche limit() a pagina 57.

Catalogo >

Esempio:

Catalogo >

Esempio:

Catalogo >

Esempio:

Guida di riferimento di TI-Nspire™ CAS 5

Elenco alfabetico

Gli elementi i cui nomi sono composti da caratteri non alfabetici (come ad esempio +, !, >) sono elencati alla fine della presente sezione, a partire da pagina 132. Se non diversamente specificato, tutti gli esempi della presente sezione sono stati eseguiti in modalità reset predefinita e tutte le variabili sono intese come non definite.

abs() (Valore assoluto)

abs(Espr1) ⇒ espressione abs(

Lista1) ⇒ lista

abs(Matrice1) ⇒ matrice

Restituisce il valore assoluto dell’argomento.

Nota: vedere anche Modello di valore assoluto a pagina 3.

Se l’argomento è un numero complesso, restituisce il modulo del numero.

Nota: tutte le variabili non definite vengono considerate come

variabili reali.

amortTbl()

amortTbl(NPmt,N,I,PV, [Pmt], [FV], [PpY], [CpY], [PmtAt],

[

valoreArrotondato]) ⇒ matrice

Funzione di ammortamento che restituisce una matrice come una tabella di ammortamento per un set di argomenti TVM.

NPmt è il numero di rate da includere nella tabella. La tabella inizia con la prima rata.

N, I, PV, Pmt, FV, PpY, CpY e PmtAt sono descritti nella tabella degli argomenti TVM a pagina 122.

• Se si omette Pmt, viene utilizzata l’impostazione predefinita Pmt=tvmPmt(N,I,PV,FV,PpY,CpY,PmtAt).

• Se si omette FV, viene utilizzata l’impostazione predefinita FV=0.

• Le impostazioni predefinite di PpY, CpY e PmtAt sono le stesse delle funzioni TVM.

valoreArrotondato specifica il numero di cifre decimali di arrotondamento. Impostazione predefinita=2.

Le colonne nella matrice risultante appaiono nel seguente ordine: numero di rate, interesse pagato, capitale versato e saldo.

Il saldo visualizzato nella riga n è il saldo dopo la rata n. È possibile utilizzare la matrice di output come input per le altre

funzioni di ammortamento GInt() e GPrn() a pagina 143, e bal() a pagina 12.

Catalogo

and

Espressione booleana1 and Espressione booleana2

⇒ Espressione booleana

Lista booleana1 and Lista booleana2

⇒ Lista booleana

Matrice booleana1 and Matrice booleana2

⇒ Matrice booleana

Restituisce vero o falso o una forma semplificata dell’espressione immessa originariamente.

Catalogo

6 Guida di riferimento di TI-Nspire™ CAS

and

Intero1 and Intero2 ⇒ intero

Confronta due interi reali bit per bit utilizzando un’operazione Internamente, entrambi gli interi vengono convertiti in numeri binari a 64 bit con segno. Quando vengono confrontati bit corrispondenti, il risultato sarà 1 se entrambi sono uguali a 1; in caso contrario il risultato sarà 0. Il valore restituito rappresenta il risultato dei bit e viene visualizzato nella modalità base che è stata impostata.

È possibile inserire gli interi in qualsiasi base numerica. Se si tratta di un numero binario o esadecimale, utilizzare rispettivamente il prefisso 0b o 0h. Senza prefisso, gli interi vengono considerati decimali (base 10).

Se viene indicato un intero decimale troppo grande per una forma binaria con segno a 64 bit, verrà utilizzata un’operazione a modulo simmetrico per portare il valore nell’intervallo appropriato.

and.

Catalogo

In modalità base Esadecimale:

Importante: è zero, non la lettera O.

In modalità base Bin:

In modalità base Dec:

Nota: un numero binario può contenere fino a 64 cifre (oltre al

prefisso 0b). Un numero esadecimale può contenere fino ad 16 cifre.

angle() (Angolo)

angle(Espr1) ⇒ espressione

Restituisce l’angolo dell’argomento, interpretando l’argomento come numero complesso.

Nota: tutte le variabili non definite vengono considerate come

variabili reali.

angle(Lista1) ⇒ lista angle(Matrice1) ⇒ matrice

Restituisce una lista o una matrice di angoli degli elementi contenuti in Lista1 o Matrice1, interpretando ciascun elemento come un numero complesso che rappresenta un punto di coordinate rettangolari bidimensionali.

ANOVA (Analisi della varianza)

ANOVA Lista1,Lista2[,Lista3,...,Lista20][,Flag]

Esegue l’analisi della varianza a una dimensione per confrontare le medie di un numero di popolazioni compreso tra due e venti. Il riepilogo dei risultati è memorizzato nella variabile stat.results. (Vedere pagina 109).

Flag=0 per Dati, Flag=1 per Statistiche

Catalogo

In modalità angolo in gradi:

In modalità angolo in gradianti (gradi centesimali):

In modalità angolo in radianti:

Catalogo

Variabile di output

Descrizione

stat.F Valore della statistica F

stat.PVal Livello minimo di significatività in corrispondenza del quale l’ipotesi nulla può essere rifiutata

Guida di riferimento di TI-Nspire™ CAS 7

Variabile di output

stat.df Grado di liberà dei gruppi

stat.SS Somma dei quadrati dei gruppi

stat.MS Quadrati medi dei gruppi

stat.dfError Gradi di libertà degli errori

stat.SSError Somma dei quadrati degli errori

stat.MSError Quadrato medio degli errori

stat.sp Deviazione standard aggregata

stat.xbarlist Media dell’input delle liste

stat.CLowerList Intervalli di confidenza al 95% per la media di ogni lista di input

stat.CUpperList Intervalli di confidenza al 95% per la media di ogni lista di input

Descrizione

ANOVA2way (Analisi della varianza a due dimensioni)

ANOVA2way Lista1,Lista2[,Lista3,…,Lista20][,RigaLiv]

Esegue l’analisi a due dimensioni della varianza per confrontare le medie di un numero di popolazioni compreso tra due e venti. Il riepilogo dei risultati è memorizzato nella variabile stat.results. (Vedere pagina 109).

RigaLiv=0 per Blocco

RigaLiv=2,3,...,Lun-1, per Due fattori, dove Lun=lunghezza(Lista1)=lunghezza(Lista2) = … = lunghezza(Lista10) e Lun / RigaLiv ∈ {2,3,…}

Output: design blocco

Variabile di output

stat.F Statistica F del fattore colonna

stat.PVal Livello minimo di significatività in corrispondenza del quale l’ipotesi nulla può essere rifiutata

stat.df Gradi di libertà del fattore colonna

stat.SS Somma dei quadrati del fattore colonna

stat.MS Quadrati medi del fattore colonna

stat.FBlock Statistica F per fattore

stat.PValBlock Probabilità minima in cui l’ipotesi nulla può essere rifiutata

stat.dfBlock Gradi di libertà per fattore

stat.SSBlock Somma dei quadrati per fattore

stat.MSBlock Quadrati medi per fattore

stat.dfError Gradi di libertà degli errori

stat.SSError Somma dei quadrati degli errori

stat.MSError Quadrati medi degli errori

Descrizione

Catalogo

8 Guida di riferimento di TI-Nspire™ CAS

Variabile di output

stat.s Deviazione standard dell’errore

Output FATTORE COLONNA

Descrizione

Variabile di output

stat.Fcol Statistica F del fattore colonna

stat.PValCol Valore di probabilità del fattore colonna

stat.dfCol Gradi di libertà del fattore colonna

stat.SSCol Somma dei quadrati del fattore colonna

stat.MSCol Quadrati medi del fattore colonna

Output FATTORE RIGA

Variabile di output

stat.Frow Statistica F del fattore riga

stat.PValRow Valore di probabilità del fattore riga

stat.dfRow Gradi di libertà del fattore riga

stat.SSRow Somma dei quadrati del fattore riga

stat.MSRow Quadrati medi del fattore riga

Output di INTERAZIONE

Variabile di output

stat.FInteract F dell’interazione

stat.PValInteract Valore di probabilità dell’interazione

stat.dfInteract Gradi di liberà dell’interazione

stat.SSInteract Somma dei quadrati dell’interazione

stat.MSInteract Quadrati medi dell’interazione

Descrizione

Output di ERRORE

Variabile di output

stat.dfError Gradi di libertà degli errori

stat.SSError Somma dei quadrati degli errori

stat.MSError Quadrati medi degli errori

Descrizione

Guida di riferimento di TI-Nspire™ CAS 9

Variabile di output

s Deviazione standard dell’errore

Descrizione

Ans (Ultimo risultato)

Ans ⇒ valore

Restituisce il risultato dell’ultima espressione calcolata.

approx() Approssima

approx(Espr1) ⇒ espressione

Restituisce il calcolo dell’argomento come espressione contenente valori decimali, ove possibile, indipendentemente dalla modalità corrente Auto o Approssimato .

Equivale a inserire l’argomento e a premere

approx(Lista1) ⇒ lista approx(Matrice1) ⇒ matrice

Restituisce una lista o una matrice nella quale ciascun elemento è stato calcolato con valori decimali, ove possibile.

approxRational()

approxRational(Espr[, tol]) ⇒ espression approxRational(Lista[, tol]) ⇒ lista approxRational(Matrice[, tol]) ⇒ matrice

Restituisce l’argomento come frazione utilizzando una tolleranza tol. Se tol è omesso, viene utilizzata una tolleranza di 5.E-14.

·.

Tasti

Catalogo

arcLen() (Lunghezza arco)

arcLen(Espr1,Var ,Inizio,Fine) ⇒ espressione

Restituisce la lunghezza dell’arco di Espr1 da Inizio a Fine in funzione della variabile Va r .

La lunghezza dell’arco viene calcolata come un integrale, basandosi sulla definizione di una funzione.

arcLen(Lista1,Var ,Inizio,Fine) ⇒ lista

Restituisce una lista delle lunghezze dell’arco di ciascun elemento di Lista1 da Inizio a Fine in funzione di Var .

Catalogo

10 Guida di riferimento di TI-Nspire™ CAS

augment() (Affianca/concatena)

augment(Lista1, Lista2) ⇒ lista

Restituisce una nuova lista in cui Lista2 viene aggiunta (accostata) alla fine di Lista1.

augment(Matrice1, Matrice2) ⇒ matrice

Restituisce una nuova matrice in cui Matrice2 viene aggiunta alla fine di Matrice1. Se si usa il carattere "," le matrici devono avere uguale numero di righe; Matrice2 viene aggiunta a Matrice1 come nuove colonne. Non modifica Matrice1 o Matrice2.

Catalogo

avgRC() (Tasso di variazione media)

avgRC(Espr1, Var [=Valore] [, H]) ⇒ espressione avgRC(Espr1, Var [=Valore] [, Lista1]) ⇒ lista avgRC(Lista1, Va r [=Valore] [, H]) ⇒ lista avgRC(Matrice1, Var [=Valore] [, H]) ⇒ matrice

Restituisce il rapporto incrementale (tasso di variazione media). Espr1 può essere un nome di funzione definito dall’utente

(vedere Func). Quando è specificato, valore ha la priorità su qualsiasi precedente

assegnazione di variabile o qualsiasi sostituzione corrente “tale quale” della variabile.

H è il valore di incremento. Se H è omesso, viene impostato per default su 0.001.

Si noti che la funzione simile nDeriv() utilizza la formula del rapporto incrementale bilaterale.

Catalogo

Guida di riferimento di TI-Nspire™ CAS 11

bal()

bal(NPmt,N,I,PV,[Pmt], [FV], [PpY], [CpY], [PmtAt],

[

valoreArrotondato]) ⇒ valore

bal(NPmt,tabellaAmmortamento) ⇒ valore

Funzione di ammortamento che calcola il saldo del piano di rientro dopo una rata specificata.

N, I, PV, Pmt, FV, PpY, CpY e PmtAt sono descritti nella tabella degli argomenti TVM a pagina 122.

NPmt specifica il numero della rata a partire dalla quale deve essere calcolato il saldo.

N, I, PV, Pmt, FV, PpY, CpY e PmtAt sono descritti nella tabella degli argomenti TVM a pagina 122.

• Se si omette Pmt, viene utilizzata l’impostazione predefinita Pmt=tvmPmt(N,I,PV,FV,PpY,CpY,PmtAt).

• Se si omette FV, viene utilizzata l’impostazione predefinita FV=0.

• Le impostazioni predefinite di PpY, CpY e PmtAt sono le stesse delle funzioni TVM.

valoreArrotondato specifica il numero di cifre decimali di arrotondamento. Impostazione predefinita=2.

bal(NPmt,tabellaAmmortamento) calcola il saldo dopo la rata

numero NPmt sulla base della tabella di ammortamento tabellaAmmortamento. L’argomento tabellaAmmortamento deve essere una matrice avente la forma descritta in amortTbl() a pagina

Nota: vedere anche GInt() e GPrn() a pagina 143.

Base2

Intero1 4Base2 ⇒ intero

Converte Intero1 in un numero binario. I numeri binari o esadecimali hanno sempre, rispettivamente, il prefisso 0b o 0h.

0b numeroBinario 0h numeroEsadecimale

Zero, non la lettera O, seguito da b o h. Un numero binario può contenere fino a 64 cifre. Un numero

esadecimale può contenere fino ad 16 cifre. Senza prefisso, Intero1 viene considerato decimale (base 10). Il

risultato viene visualizzato in modalità binaria, indipendentemente dalla modalità Base impostata.

Se viene indicato un intero decimale troppo grande per una forma binaria con segno a 64 bit, verrà utilizzata un’operazione a modulo simmetrico per portare il valore nell’intervallo appropriato.

Catalogo

12 Guida di riferimento di TI-Nspire™ CAS

Base10

4Base10 ⇒ intero

Intero1

Converte Intero1 in numero decimale (base 10). Le voci binarie o esadecimali devono sempre avere, rispettivamente, il prefisso 0b o 0h.

0b numeroBinario 0h numeroEsadecimale

Zero, non la lettera O, seguito da b o h. Un numero binario può contenere fino a 64 cifre. Un numero

esadecimale può contenere fino ad 8 cifre. Senza prefisso, Intero1 viene considerato decimale (base10). Il

risultato viene visualizzato in modalità decimale, indipendentemente dalla modalità Base impostata.

Base16

Intero1 4Base16 ⇒ intero

Converte Intero1 in un numero esadecimale. I numeri binari o esadecimali hanno sempre, rispettivamente, il prefisso 0b o 0h.

0b numeroBinario 0h numeroEsadecimale

Zero, non la lettera O, seguito da b o h. Un numero binario può contenere fino a 64 cifre. Un numero

esadecimale può contenere fino ad 16 cifre. Senza prefisso, Intero1 viene considerato decimale (base 10). Il

risultato viene visualizzato in modalità esadecimale, indipendentemente dalla modalità Base impostata.

Se viene indicato un intero decimale troppo grande per una forma binaria con segno a 64 bit, verrà utilizzata un’operazione a modulo simmetrico per portare il valore nell’intervallo appropriato.

Catalogo

binomCdf() (Funzione della probabilità cumulativa per la distribuzione binomiale)

binomCdf(n,p,valoreInferiore,valoreSuperiore) ⇒ numero se

valoreInferiore e valoreSuperiore sono numeri, lista se valoreInferiore e valoreSuperiore sono liste

binomCdf(

è un numero,

Calcola la probabilità cumulativa per la distribuzione binomiale discreta con il numero di prove n e le probabilità di successo p per ciascuna prova.

Per P(X  valoreSuperiore), impostare valoreInferiore=0

binomPdf()

binomPdf(n,p) ⇒ numero binomPdf(n,p,Va lX ) ⇒ numero se Va l X è un numero, lista se

Val X è una lista

Calcola una probabilità in corrispondenza di valX per la distribuzione binomiale discreta con il numero n di prove e la probabilità p di successo per ogni prova.

n,p,valoreSuperiore) ⇒ numero se valoreSuperiore

lista se valoreSuperiore è una lista

Catalogo

Guida di riferimento di TI-Nspire™ CAS 13

ceiling() (Arrotondato per eccesso)

ceiling(Espr1) ⇒ intero

Restituisce il più vicino numero intero ‚ all’argomento.

L’argomento può essere un numero reale o complesso.

Nota: vedere anche floor().

ceiling(Lista1) ⇒ lista ceiling(Matrice1) ⇒ matrice

Restituisce una lista o matrice del valore arrotondato per eccesso di ciascun elemento.

cFactor() (Fattore complesso)

cFactor(Espr1[,Var ]) ⇒ espressione cFactor(Lista1[,Va r]) ⇒ lista cFactor(Matrice1[,Var ]) ⇒ matrice

cFactor(Espr1) restituisce la scomposizione in fattori di Espr1

rispetto a tutte le variabili con un denominatore comune. Espr1 viene scomposto, per quanto possibile, in fattori razionali

lineari, anche se ciò introduce nuovi numeri non reali. Questa procedura è utile qualora si desideri ottenere una scomposizione in fattori relativamente a più di una variabile.

cFactor(Espr1,Var ) restituisce Espr1 scomposto in fattori

relativamente alla variabile Va r . Espr1 viene scomposto, per quanto possibile, in fattori li neari in Var ,

pur con costanti non reali, anche se vengono introdotte costanti irrazionali o sottoespressioni che sono irrazionali in altre variabili.

I fattori ed i rispettivi termini vengono ordinati con Var come variabile principale. Le potenze simili di Va r sono ridotte in ciascun fattore. Includere Va r se si desidera che la scomposizione in fattori tenga conto solo di tale variabile e che le espressioni irrazionali siano incluse in qualsiasi altra variabile per aumentare la scomposizione in fattori relativamente a Va r . Si può verificare una scomposizione in fattori incidentale relativamente ad altre variabili.

Nell’impostazione Auto della modalità Auto/Approssimato, l’inclusione di Va r permette inoltre l’approssimazione con coefficienti a virgola mobile nel caso in cui i coefficienti irrazionali non possano essere esplicitamente espressi in termini concisi con le funzioni incorporate. Anche qualora vi sia una sola variabile, se si include Va r la scomposizione in fattori può risultare più completa.

Nota: vedere anche factor().

Catalogo

Per vedere l’intero risultato, premere £, quindi utilizzare ¡ e

¢ per spostare il cursore

char() (Stringa di caratteri)

char(Intero) ⇒ carattere

Restituisce un carattere stringa corrispondente al numero Intero del set di caratteri del palmare. L’intervallo valido per intero Intero è compreso tra 0 e 65535.

Catalogo

14 Guida di riferimento di TI-Nspire™ CAS

charPoly() (Polinomio caratteristico)

charPoly(matriceQuadrata,Var) ⇒ espressione polinomiale charPoly(matriceQuadrata,Espr) ⇒ espressione polinomiale charPoly(matriceQuadrata1,Matrice2) ⇒ espressione

polinomiale

Restituisce il polinomio caratteristico di matriceQuadrata. Il polinomio caratteristico di n×n matrice A, indicato da pA(l), è il polinomio definito da

pA(l) = det(l• I NA)

dove I indica la matrice identica n×n. matriceQuadrata1 e matriceQuadrata2 devono avere le stesse

dimensioni.

2way

2way MatriceOss

chi22way MatriceOss

Esegue una verifica c2 per l’associazione di numeri nella tabella a due variabili nella matrice osservata MatriceOss. Il riepilogo dei risultati è memorizzato nella variabile stat.results. (Vedere pagina 109).

Catalog

Catalogo

Variabile di output

Descrizione

stat.c2 Statistica Chi quadrato: somma (osservati - attesi)2/attesi

stat.PVal Livello minimo di significatività in corrispondenza del quale l’ipotesi nulla può essere rifiutata

stat.df Gradi di libertà per le statistiche chi quadrato

stat.ExpMat Matrice della tabella di numeri elementari attesi, assumendo l’ipotesi nulla

stat.CompMat Matrice di contributi statistici chi quadrato elementari

Cdf()

Cdf(valoreInferiore,valoreSuperiore,gl) ⇒ numero se

valoreInferiore e valoreSuperiore sono numeri, lista se valoreInferiore e valoreSuperiore sono liste

chi2Cdf(

valoreInferiore,valoreSuperiore,gl) ⇒ numero se valoreInferiore e valoreSuperiore sono numeri, list se valoreInferiore e valoreSuperiore sono liste

Calcola la probabilità della distribuzione c2 tra il valoreInferiore e il valoreSuperiore per i gradi di libertà gl specificati.

Catalogo

Per P(X  valoreSuperiore), impostare valoreInferiore= 0.

GOF

GOF listaOss,listaAtt,gl

chi2GOF listaOss,listaAtt,gl

Esegue una verifica per confermare che i dati del campione appartengono a una popolazione conforme a una data distribuzione. listaOss è una lista di conteggi e deve contenere numeri interi. Il riepilogo dei risultati è memorizzato nella variabile stat.results. (Vedere pagina 109).

Catalogo

Guida di riferimento di TI-Nspire™ CAS 15

Variabile di output

Descrizione

stat.c2 Statistica Chi quadrato: sum((osservati - attesi)2/attesi

stat.PVal Livello minimo di significatività in corrispondenza del quale l’ipotesi nulla può essere rifiutata

stat.df Gradi di libertà per le statistiche chi quadrato

stat.CompList Contributi statistici chi quadrato elementari

Pdf()

Pdf(Val X ,gl) ⇒ numero se Va lX è un numero, lista se Va l X

è una lista

chi2Pdf(

Val X ,gl) ⇒ numero se Va lX è un numero, lista se

Val X è una lista

Catalogo

Calcola la funzione della densità di probabilità (pdf) per la distribuzione c2 a un dato valore Va l X per i gradi di libertà

gl specificati.

ClearAZ (Cancella AZ)

ClearAZ

Cancella tutte le variabili con il nome di un solo carattere nello spazio attività corrente.

ClrErr

Cancella lo stato di errore e imposta la variabile di sistema errCode su zero.

L’istruzione Else del blocco Try...Else...EndTry dovrebbe utilizzare

ClrErr o PassErr. Se l’errore deve essere elaborato o ignorato,

utilizzare ClrErr. Se non si sa quale azione applicare all’errore, utilizzare PassErr per inviarlo al successivo blocco di gestione degli errori. Se non ci sono ulteriori blocchi di gestione degli errori

Try...Else...EndTry in attesa di applicazione, la finestra di dialogo

dell’errore viene visualizzata come normale.

Nota: vedere anche PassErr a pagina 81 e Try a pagina 119. Nota per l’introduzione dell’esempio: nell’applicazione

Calcolatrice sul palmare, è possibile introdurre definizioni composte da più righe premendo @ invece di · alla fine di ciascuna

riga. Sulla tastiera del computer, mantenere premuto Alt e premere

Invio.

Catalogo

Per un esempio di ClrErr, vedere l’esempio 2 del comando Try a pagina 119.

16 Guida di riferimento di TI-Nspire™ CAS

colAugment() (Affianca colonna)

colAugment(Matrice1, Matrice2) ⇒ matrice

Restituisce una nuova matrice in cui Matrice2 viene aggiunta alla fine di Matrice1. Le matrici devono avere uguale numero di colonne; Matrice2 viene aggiunta a Matrice1 come nuove colonne. Non modifica Matrice1 o Matrice2.

Catalogo

colDim() (Dimensione colonna)

colDim(Matrice) ⇒ espressione

Restituisce il numero delle colonne contenute in Matrice.

Nota: vedere anche rowDim().

colNorm() (Norma colonna)

colNorm(Matrice) ⇒ espressione

Restituisce il massimo delle somme dei valori assoluti degli elementi nelle colonne di Matrice.

Nota: non sono ammessi elementi non definiti di una matrice.

Vedere anche rowNorm().

comDenom() (Denominatore comune)

comDenom(Espr1[,Va r]) ⇒ espressione comDenom(Lista1[,Var ]) ⇒ lista comDenom(Matrice1[,Var ]) ⇒ matrice

comDenom(Espr1) restituisce una frazione ridotta con

numeratore e denominatore completamente espansi.

comDenom(Espr1,Va r) restituisce una frazione ridotta con

numeratore e denominatore espansi rispetto a Va r . I termini ed i rispettivi fattori sono ordinati considerando Va r la variabile principale. Le potenze simili di Va r sono ridotte. Si può verificare una scomposizione in fattori incidentale dei coefficienti ridotti. Questo procedimento, rispetto all’omissione di Va r , permette di risparmiare tempo, memoria e spazio sullo schermo, rendendo inoltre l’espressione più comprensibile. Le successive operazioni eseguite sul risultato sono più veloci e non rischiano di esaurire la memoria.

Catalogo

Se Va r non compare in Espr1, comDenom(Espr1,Var) restituisce una frazione ridotta con numeratore e denominato re non espansi. Tali risultati permettono di solito di risparmiare ulteriore tempo, memoria e spazio sullo schermo. Le successive operazioni eseguite sul risultato sono più veloci e non rischiano di esaurire la memoria, grazie a tali risultati, parzialmente scomposti in fattori.

Guida di riferimento di TI-Nspire™ CAS 17

comDenom() (Denominatore comune)

Anche qualora non vi sia nessun denominatore, la funzione comden è spesso un modo veloce per ottenere una scomposizione in fattori parziale, se

factor() è troppo lento oppure se si rischia di esaurire la

memoria.

Suggerimento: inserire questa definizione della funzione comden() e utilizzarla regolarmente come alternativa a comDenom() e factor().

Catalogo

conj() (Coniugato)

conj(Espr1) ⇒ espressione conj(Lista1) ⇒ lista conj(Matrice1) ⇒ matrice

Restituisce il complesso coniugato dell’argomento.

Nota: tutte le variabili non definite vengono considerate come

variabili reali.

constructMat() (Costruisci matrice)

constructMat(Espr,Var 1 ,Va r2 ,numRighe,numColonne)

⇒ matrice

Restituisce una matrice sulla base degli argomenti. Espr è un’espressione nelle variabili Va r 1 e Va r2 . Gli elementi nella

matrice risultante sono formati calcolando Espr per ciascun valore incrementato di Va r 1 e Va r 2 .

Var 1 è incrementato automaticamente da 1 a numRighe. All’interno di ciascuna riga, Va r2 è incrementato da 1 a numColonne.

CopyVar (Copia variabile)

CopyVar Var 1 , Va r 2 CopyVar Var 1 ., Va r2 .

CopyVar Var 1 , Var 2 copia il valore della variabile Va r 1 nella

variabile Var 2 , creando Va r2 se necessario. La variabile Va r 1 deve contenere un valore.

Se Var 1 è il nome di una funzione esistente d efinita dall’utente, copia la definizione di quella funzione nella funzione Va r 2. La funzione

Var 1 deve essere definita. Var 1 deve soddisfare i requisiti validi per i nomi di variabile oppure

deve essere un’espressione indiretta che viene semplificata in un nome di variabile che soddisfa i suddetti requisiti.

Catalogo

Catalog

18 Guida di riferimento di TI-Nspire™ CAS

CopyVar (Copia variabile)

CopyVar Var 1 ., Va r2 . copia tutti i membri del gruppo di variabili

. nel gruppo Va r2 ., creando Va r 2 . se necessario.

Var 1 Var 1 . deve essere il nome di un gruppo di variabili esistente , come ad

esempio i risultati statistici stat.nn o le variabili create utilizzando la funzione

LibShortcut(). Se Var 2 . esiste già, questo comando

sostituisce tutti i membri che sono comuni a entrambi i gruppi e aggiunge i membri che non esistono ancora. Se esiste una variabile semplice (non un gruppo) denominata Va r 2, si produce un errore.

Catalog

corrMat() (Matrice di correlazione)

corrMat(Lista1,Lista2[,…[,Lista20]])

Calcola la matrice di correlazione per la matrice affiancata [Lista1 Lista2 . . . Lista20].

cos (Coseno)

Espr

cos

Rappresenta Espr rispetto al coseno. È un operatore di conversione della visualizzazione. Può essere utilizzato solo alla fine della riga di introduzione.

cos riduce tutte le potenze di

sin(...) modulo 1Ncos(...)^2 in modo che qualsiasi potenza rimanente di cos(...) abbia esponenti compresi nell’intervallo (0, 2). Pertanto, il risultato non conterrà sin(...) se e solo se sin(...) si presenta nell’espressione data solamente con esponenti pari.

Nota: questo operatore di conversione non è supportato nelle

modalità di misurazione degli angoli in Gradi o Gradianti (gradi centesimali). Prima di utilizzarlo, accertarsi che la modalità angolare sia impostata su Radianti e che Espr non contenga riferimenti espliciti ad angoli in gradi o gradianti.

Catalogo

Catalog

Guida di riferimento di TI-Nspire™ CAS 19

cos() (Coseno)

cos(Espr1) ⇒ espressione cos(Lista1) ⇒ lista

cos(Espr1) restituisce sotto forma di espressione il coseno

dell’argomento.

cos(Lista1) restituisce una lista dei coseni di tutti gli elementi di

Lista1.

Nota: conformemente alla modalità di misurazione degli angoli

impostata, l’argomento viene interpretato come angolo in gradi, gradianti o radianti. È possibile utilizzareó,G oôper escludere

provvisoriamente la modalità d’angolo selezionata.

Tasto n

In modalità angolo in gradi:

In modalità angolo in gradianti (gradi centesimali):

In modalità angolo in radianti:

cos(matriceQuadrata1) ⇒ matriceQuadrata

Restituisce il coseno della matrice di matriceQuadrata1. Ciò non equivale a calcolare il coseno di ogni elemento.

Quando una funzione scalare f(A) opera su matriceQuadarata1 (A), il risultato viene calcolato dall’algoritmo:

Calcola gli autovalori (Ii) e gli autovettori (Vi) di A.

matriceQuadrata1 deve essere diagonalizzabile. Inoltre, non può avere variabili simboliche alle quali non sia stato assegnato un valo re.

Forma le matrici:

Quindi A = X B Xêe f(A) = X f(B) Xê. Ad esempio, cos(A) = X cos(B) Xê dove:

cos (B) =

Tutti i calcoli vengono eseguiti in virgola mobile.

In modalità angolo in radianti:

20 Guida di riferimento di TI-Nspire™ CAS

cosê() (Arcocoseno)

cosê(Espr1) ⇒ espressione cosê(Lista1) ⇒ lista

Tasti /n

In modalità angolo in gradi:

cosê(Espr1) restituisce sotto forma di espressione l’angolo il cui

coseno è Espr1.

cosê(Lista1) restituisce la lista dell’inversa dei coseni di ciascun

elemento di Lista1.

Nota: conformemente alla modalità di misurazione degli angoli

impostata, il risultato è in gradi, gradianti o radianti.

cosê(matriceQuadrata1) ⇒ matriceQuadrata

Restituisce il coseno inverso della matrice di matriceQuadrata1. Ciò non equivale a calcolare il coseno inverso di ogni elemento. Per informazioni sul metodo di calcolo, vedere cos().

matriceQuadrata1 deve essere diagonalizzabile. Il risultato contiene sempre numeri a virgola mobile.

cosh() (Coseno iperbolico)

cosh(Espr1) ⇒ espressione cosh(Lista1) ⇒ lista

cosh(Espr1) restituisce sotto forma di espressione il coseno

iperbolico dell’argomento.

cosh(Lista1) restituisce una lista dei coseni iperbolici di ciascun

elemento di Lista1.

cosh(matriceQuadrata1) ⇒ matriceQuadrata

Restituisce il coseno iperbolico della matrice di matriceQuadrata1. Ciò non equivale a calcolare il coseno iperbolico di ogni elemento. Per informazioni sul metodo di calcolo, vedere cos().

matriceQuadrata1 deve essere diagonalizzabile. Il risultato contiene sempre numeri a virgola mobile.

In modalità angolo in gradianti (gradi centesimali):

In modalità angolo in radianti:

In modalità angolo in radianti e i n modalità formato rettangolare complesso:

Per vedere l’intero risultato, premere £, quindi utilizzare ¡ e

¢ per spostare il cursore

Catalogo

In modalità angolo in radianti:

coshê() (Arcocoseno iperbolico)

coshê(Espr1) ⇒ espressione coshê(Lista1) ⇒ lista

cosh

(Espr1) restituisce sotto forma di espressione l’inversa del

coseno iperbolico dell’argomento.

cosh

(Lista1) restituisce una lista dell’inversa dei coseni iperbolici

di ciascun elemento di Lista1.

Catalogo

Guida di riferimento di TI-Nspire™ CAS 21

coshê() (Arcocoseno iperbolico)

coshê(matriceQuadrata1) ⇒ matriceQuadrata

Restituisce l’inversa del coseno iperbolico della matrice di matriceQuadrata1. Ciò non equivale a calcolare l’inversa del coseno iperbolico di ogni elemento. Per informazioni sul metodo di calcolo, vedere cos().

matriceQuadrata1 deve essere diagonalizzabile. Il risultato contiene sempre numeri a virgola mobile.

Catalogo

In modalità angolo in radianti e in modalità formato rettangolare complesso:

Per vedere l’intero risultato, premere £, quindi utilizzare ¡ e

¢ per spostare il cursore

cot() (Cotangente)

cot(Espr1) ⇒ espressione cot(Lista1) ⇒ lista

Restituisce la cotangente dell’espressione1 oppure restituisce una lista delle cotangenti di tutti gli elementi di lista1.

Nota: conformemente alla modalità di misurazione degli angoli

impostata, l’argomento viene interpretato come angolo in gradi, gradianti o radianti. È possibile utilizzare ó,G oôper escludere

provvisoriamente la modalità d’angolo selezionata.

cotê() (Arcocotangente iperbolica)

cotê(Espr1) ⇒ espressione cotê(Lista1) ⇒ lista

Restituisce l’angolo la cui cotangente è Espr1 oppure restituisce una lista contenente l’inversa delle cotangenti di ciascun elemento di Lista1.

Nota: conformemente alla modalità di misurazione degli angoli

impostata, il risultato è in gradi, gradianti o radianti.

coth() (Cotangente iperbolica)

coth(Espr1) ⇒ espressione coth(Lista1) ⇒ lista

Restituisce la cotangente iperbolica di Espr1 o restituisce una lista delle cotangenti iperboliche di tutti gli elementi di Lista1.

Catalogo

In modalità angolo in gradi:

In modalità angolo in gradianti (gradi centesimali):

In modalità angolo in radianti:

Catalogo

In modalità angolo in gradi:

In modalità angolo in gradianti (gradi centesimali):

In modalità angolo in radianti:

Catalogo

22 Guida di riferimento di TI-Nspire™ CAS

cothê() Arcocotangente iperbolica

cothê(Espr1) ⇒ espressione cothê(Lista1) ⇒ lista

Restituisce la cotangente iperbolica inversa di Espr1 oppure restituisce una lista contenente l’inversa delle cotangenti iperboliche di ciascun elemento di Lista1.

Catalogo

count()

count(Valore1oLista1 [,Valore2oLista2 [,...]]) ⇒ valore

Restituisce il totale accumulato di tutti gli elementi negli argomenti che danno come risultato valori numerici.

Gli argomenti possono essere un’espressione, un valore, una lista o una matrice. È possibile mischiare tipi di dati e utilizzare argomenti di varie dimensioni.

Per una lista, una matrice o un intervallo di celle, viene calcolato ciascun elemento per determinare se dovrebbe essere incluso nel conteggio.

In Foglio elettronico, è possibile utilizzare un intervallo di celle al posto di qualsiasi argomento.

countif()

countif(Lista,Criteri) ⇒ valore

Restituisce il totale accumulato di tutti gli elementi di Lista che soddisfano i Criteri specificati.

Criteri può essere:

• Un valore, un’espressione o una stringa. Ad esempio, 3 conta

solo quegli elementi di Lista che sono semplificati nel numero 3.

• Un’espressione booleana contenente il simbolo ? come

segnaposto di ciascun elemento. Ad esempio, ?<5 conta solo quegli elementi di Lista che sono minori di 5.

In Foglio elettronico, è possibile utilizzare un intervallo di celle al posto di Lista.

Nota: vedere anche sumIf() a pagina 112 e frequency() a

pagina 47.

Catalogo

Nell’ultimo esempio, sono contati solo 1/2 e 3+4*i. I restanti argomenti, presupponendo che x sia indefinito, non danno come risultato valori numerici.

Catalogo

Conta il numero di elementi uguali a 3.

Conta il numero di elementi uguali a “def”.

Conta il numero di elementi uguali a x; questo esempio presuppone che la variabile x sia indefinita.

Conta 1 e 3.

Conta 3, 5 e 7.

Conta 1, 3, 7 e 9.

Guida di riferimento di TI-Nspire™ CAS 23

crossP() (Prodotto vettoriale)

crossP(Lista1, Lista2) ⇒ lista

Restituisce sotto forma di lista il prodotto vettoriale di Lista1 e Lista2.

Lista1 e Lista2 devono essere uguali, 2 o 3.

crossP(Vettore1, Vet t or e 2 ) ⇒ vettore

Restituisce un vettore riga o colonna (a seconda degli argomenti) corrispondente al prodotto vettoriale di Ve t t or e 1 per Vettore2.

Vettore1 e Vettore2 devono essere entrambi vettori riga o vettori colonna. Le dimensioni di entrambi devono essere uguali, 2 o 3.

Catalogo

csc() (Cosecante)

csc(Espr1) ⇒ espressione csc(Lista1) ⇒ lista

Restituisce la cosecante di Espr1 oppure restituisce una lista contenente le cosecanti di tutti gli elementi in Lista1.

cscê() (Cosecante inversa)

cscê(Espr1) ⇒ espressione cscê(Lista1) ⇒ lista

Restituisce l’angolo la cui cosecante è Espr1 oppure restituisce una lista contenente l’inversa delle cosecanti di ciascun elemento di Lista1.

Nota: conformemente alla modalità di misurazione degli angoli

impostata, il risultato è in gradi, gradianti o radianti.

csech (Cosecante iperbolica)

csch(Espr1) ⇒ espressione csch(Lista1) ⇒ lista

Restituisce la cosecante iperbolica di Espr1 oppure restituisce una lista di cosecanti iperboliche di tutti gli elementi di Lista1.

Catalogo

In modalità angolo in gradi:

In modalità angolo in gradianti (gradi centesimali):

In modalità angolo in radianti:

Catalogo

In modalità angolo in gradi:

In modalità angolo in gradianti (gradi centesimali):

In modalità angolo in radianti:

Catalogo

24 Guida di riferimento di TI-Nspire™ CAS

cschê() (Cosecante iperbolica inversa)

cschê(Espr1) ⇒ espressione cschê(Lista1) ⇒ lista

Restituisce la cosecante iperbolica inversa di Espr1 oppure restituisce una lista contenente le cosecanti iperboliche inverse di ciascun elemento di Lista1.

Catalogo

cSolve() (Risolvi in campo complesso)

cSolve(Equazione, Va r ) ⇒ espressione booleana cSolve(Equazione, Var=Campione) ⇒ espressione booleana cSolve(Disequazione, Va r ) ⇒ espressione booleana

Restituisce possibili soluzioni complesse di un’equazione o di una disequazione rispetto a Va r. Il fine è quello di produrre tutte le possibili soluzioni reali e non reali. Anche se Equazione è reale,

cSolve() ammette risultati non reali nel modo reale.

Sebbene tutte le variabili non definite che non terminano con un trattino basso (_) siano elaborate come se fossero reali, cSolve() può risolvere equazioni polinomiali a soluzioni complesse.

cSolve() imposta temporaneamente il dominio complesso durante

la soluzione, sebbene il dominio corrente sia reale. Nel dominio complesso, le potenze frazionarie con denominatori dispari utilizzano l’ambito principale invece di quello reale. Pertanto le soluzioni ottenute con solve() per le equazioni contenenti tali potenze frazionarie non sono necessariamente un sottoinsieme di quelle ottenute con cSolve().

cSolve() inizia con metodi simbolici esatti. Con l’eccezione della

modalità Esatto, cSolve() utilizza eventualmente anche la scomposizione in fattori complessa approssimata iterativa di polinomi.

Nota: vedere anche cZeros(), solve() e zeros(). Nota: se Equazione è di tipo non polinomiale con funzioni quali

abs(), angle(), conj(), real() o imag(), è necessario inserire un

trattino basso (premere /_) dopo Va r . Per impostazione predefinita, una variabile viene considerata come valore reale.

Se si utilizza var_, la variabile verrà considerata come un numero complesso.

È necessario utilizzare var_ anche per qualsiasi altra variabile in Equazione che potrebbe avere valori non reali. In caso contrario, si potrebbero ottenere dei risultati inaspettati.

Catalogo

In modalità Mostra cifre impostata su Fissa 2:

Per vedere l’intero risultato, premere £, quindi utilizzare ¡ e

¢ per spostare il cursore

z viene considerato come reale:

z_ viene considerato come complesso:

Guida di riferimento di TI-Nspire™ CAS 25

cSolve() (Risolvi in campo complesso)

cSolve(Eqn1 and Eqn2 [and …],

VarOCampione1, VarOCampione2 [, …])

⇒ espressione booleana

cSolve(SistemaDiEquazioni, VarOCampione1,

VarOCampione2 [, …]) ⇒ espressione booleana

Restituisce possibili soluzioni complesse ai sistemi di equazioni algebriche, dove ogni varOCampione specifica una variabile in base alla quale risolvere l’equazione.

In alternativa è possibile specificare un valore campione iniziale per la variabile. Ogni varOCampione deve avere la forma:

variabile

– oppure – variabile = numero reale o non reale

Ad esempio, x è valido come pure x=3+i. Se tutte le equazioni sono polinomiali e NON si indica alcun valore

campione iniziale, lessicale di Gröbner/Buchberger per tentare di determinare tutte le soluzioni complesse.

Le soluzioni complesse comprendono soluzioni reali e non reali, come nell’esempio a destra.

I sistemi di equazioni polinomiali possono avere variabili aggiuntive senza valori, ma rappresentano valori numerici dati che potrebbero essere sostituiti successivamente.

cSolve() utilizza il metodo di eliminazione

Catalogo

Nota: gli esempi che seguono usano il trattino basso (premere

/_) in modo che le variabili vengano considerate

come complesse.

Per vedere l’intero risultato, premere £, quindi utilizzare ¡ e

¢ per spostare il cursore

Per vedere l’intero risultato, premere £, quindi utilizzare ¡ e

¢ per spostare il cursore

È inoltre possibile includere variabili risolutorie che non compaiono nelle equazioni. Queste soluzioni mostrano come le famiglie di soluzioni possano contenere costanti arbitrarie della forma ck, dove k è un suffisso intero compreso tra 1 e 255.

Per i sistemi polinomiali, i tempi di calcolo o l’insufficienza di memoria possono dipendere in gran parte dall’ordine in cui sono elencate le variabili risolutorie. Se la scelta iniziale esaurisce la memoria (o la pazienza), provare a ridisporre le variabili all’interno delle equazioni e/o della lista varOCampione.

Se non viene indicato alcun valore campione e se anche una sola equazione è non polinomiale per una qualsiasi variabile, ma tutte le equazioni sono lineari per tutte le variabili risolutorie cSolve() utilizza l’eliminazione gaussiana per tentare di determinare tutte le soluzioni.

Se un sistema non è né polinomiale per tutte le sue variabili né lineare per le variabili risolutorie, cSolve() determina al più una soluzione utilizzando un metodo di approssimazione iterativa. A tale scopo, il numero di variabili risolutorie deve essere uguale al numero di equazioni e tutte le altre variabili delle equazioni devono poter esser e semplificate in numeri.

26 Guida di riferimento di TI-Nspire™ CAS

Per vedere l’intero risultato, premere £, quindi utilizzare ¡ e

¢ per spostare il cursore

cSolve() (Risolvi in campo complesso)

Spesso si rende necessario utilizzare un valore campione non reale per determinare una soluzione non reale. Per ottenere una convergenza, può essere necessario che il valore campione debba essere abbastanza prossimo alla soluzione.

Catalogo

Per vedere l’intero risultato, premere £, quindi utilizzare ¡ e

¢ per spostare il cursore

CubicReg (Regressione cubica)

CubicReg X, Y[, [Freq] [, Categoria, Includi]]

Calcola la regressione polinomiale cubica y = a·x3+b· x2+c·x+d sulle liste X e Y con frequenza Freq. Il riepilogo

dei risultati è memorizzato nella variabile stat.results. (Vedere pagina 109).

Tutte le liste devono avere le stesse dimensioni, ad eccezione di

Includi. X e Y sono liste di variabili indipendenti e dipendenti. Freq è una lista opzionale di valori di frequenza. Ciascun elemento di

Freq specifica la frequenza di occorrenza di ogni dato corrispondente

di X e Y. Il valore predefinito è 1. Tutti gli elementi devono essere numeri interi | 0.

Categoria è una lista di codici numerici di categoria dei dati corrispondenti di X e Y.

Includi è una lista di uno o più codici di categoria. Solo quei dati il cui codice di categoria è inserito in questa lista vengono inclusi nel calcolo.

Variabile di output

stat.RegEqn

stat.a, stat.b, stat.c, stat.d

stat.R

stat.Resid Residui della regressione

stat.XReg Lista di punti dati della Lista X modificata attualmente usata nella regressione secondo le restrizioni di

stat.YReg Lista di punti dati della Lista Y modificata attualmente usata nella regressione secondo le restrizioni di

stat.FreqReg Lista di frequenze corrispondenti a stat.XReg e stat.YReg

Descrizione

Equazione di regressione: a·x3+b·x2+c·x+d

Coefficienti di regressione

Coefficiente di determinazione

Freq, Lista Categoria e Includi Categorie

Catalogo

cumSum() (Somma cumulativa)

cumSum(Lista1) ⇒ lista

Restituisce una lista delle somme cumulative degli eleme nti in Lista1, incominciando dall’elemento 1.

Catalogo

Guida di riferimento di TI-Nspire™ CAS 27

cumSum() (Somma cumulativa)

cumSum(Matrice1) ⇒ matrice

Restituisce una matrice delle somme cumulative degli elementi di Matrice1. Ciascun elemento è la somma cumulativa della colonna, dall’alto al basso.

Catalogo

Cycle (Ripeti)

Ripeti

Trasferisce il controllo della funzione alla iterazione immediatamente successiva del ciclo corrente (For, While o Loop).

Cycle non è ammesso al di fuori delle tre strutture di ciclo (For, While o Loop).

Nota per l’introduzione dell’esempio: nell’applicazione

Calcolatrice sul palmare, è possibile introdurre definizioni composte da più righe premendo @ invece di · alla fine di ciascuna

riga. Sulla tastiera del computer, mantenere premuto Alt e premere

Invio.

Cylind (Forma cilindrica)

Vettore 4Cylind

Visualizza il vettore riga o colonna nella forma cilindrica [r,q, z].

Vettore deve avere esattamente tre elementi. Può essere una riga o una colonna.

cZeros() (Zeri complessi)

cZeros(Espr, Va r ) ⇒ lista

Restituisce una lista di possibili valori reali e non reali per Va r per i quali Espr=0. cZeros() calcola

exp4list(cSolve(Espr=0,Var ),Va r ). Per il resto, cZeros() è simile

a zeros().

Nota: vedere anche cSolve(), solve() e zeros().

Nota: se Espr è di tipo non polinomiale con funzioni quali abs(), angle(), conj(), real(), or imag(), è necessario inserire un

trattino basso (premere /_) dopo Va r . Per impostazione predefinita, una variabile viene considerata come valore reale. Se si

utilizza var_, la variabile verrà considerata come un numero complesso.

È necessario utilizzare var_ anche per qualsiasi altra variabi le in Espr che potrebbe avere valori non reali. In caso contrario, si potrebbero ottenere dei risultati inaspettati.

Catalogo

Funzione che elenca le somme degli interi da 1 a 100 saltando

50.

Catalogo

In modalità Mostra cifre impostata su Fissa 3:

Per vedere l’intero risultato, premere £, quindi utilizzare ¡ e

¢ per spostare il cursore

z viene considerato come reale:

z_ viene considerato come complesso:

28 Guida di riferimento di TI-Nspire™ CAS

cZeros() (Zeri complessi)

cZeros({Espr1, Espr2 [, … ] }, {

VarOCampione1,VarOCampione2 [, … ] }) ⇒ matrice

Restituisce le possibili posizioni in cui le espressioni sono simultaneamente zero. Ogni VarOCampione specifica un’incognita il cui valore si desidera calcolare.

In alternativa è possibile specificare un valore campione iniziale per la variabile. Ogni varOCampione deve avere la forma:

variabile

– oppure –

variabile = numero reale o non reale

Ad esempio, x è valido come pure x=3+i. Se tutte le equazioni sono polinomiali e NON si indica alcun valore

campione iniziale, cZeros() utilizza il metodo di eliminazione lessicale di Gröbner/Buchberger per tentare di determinare tutti gli zeri complessi.

Gli zeri complessi comprendono zeri reali e non reali, come nell’esempio a destra.

Ciascuna riga della matrice risultante rappresenta uno zero alternativo, con i componenti ordinati come nella lista VarOCampione. Per estrarre una riga, indicizzare la matrice per [riga].

Le espressioni polinomiali simultanee possono avere variabili aggiuntive senza valori, ma rappresentano valori numerici dati che potrebbero essere sostituiti successivamente.

Catalogo

Nota: gli esempi che seguono usano il trattino basso (premere

/_) in modo che le variabili vengano considerate

come complesse.

Estrarre la riga 2:

È inoltre possibile includere variabili incognite che non compaiono nelle espressioni. Questi zeri mostrano come le famiglie di zeri possano contenere costanti arbitrarie della forma ck, dove k è un suffisso intero compreso tra 1 e 255.

Per i sistemi polinomiali, i tempi di calcolo o l’insufficienza di memoria possono dipendere in gran parte dall’ordine in cui sono elencate le incognite. Se la scelta iniziale esaurisce la memoria (o la pazienza), provare a ridisporre le variabili all’interno delle espressioni e/o della lista VarOCampione.

Se non viene indicato alcun valore campione e se anche una sola espressione è non polinomiale per una qualsiasi variabile ma tutte le espressioni sono lineari per tutte le incognite, cZeros() utilizza l’eliminazione gaussiana per tentare di determinare tutti gli zeri.

Guida di riferimento di TI-Nspire™ CAS 29

cZeros() (Zeri complessi)

Se un sistema non è né polinomiale per tutte le sue variabili né lineare per le incognite, cZeros() determina al più uno zero utilizzando un metodo di approssimazione iterativa. A tale scopo, il numero di incognite deve essere uguale al numero di espressioni e tutte le altre variabili delle espressioni devono poter essere semplificate in numeri.

Spesso si rende necessario utilizzare un valore campione non reale per determinare uno zero non reale. Per ottenere una convergenza, può essere necessario che il valore campione debba essere abbastanza prossimo allo zero.

Catalogo

dbd()

dbd(data1,data2) ⇒ valore

Restituisce il numero di giorni tra la data1 e la data2 usando il metodo di conteggio dei giorni effettivi.

data1 e data2 possono essere numeri o liste di numeri all’interno di un intervallo di date del calendario normale. Se sia data1 che data2 sono liste, esse devono contenere lo stesso numero di elementi.

data1 e data2 devono essere comprese tra gli anni 1950 e 2049. È possibile inserire le date in uno dei due formati, che differiscono

esclusivamente per la posizione del punto decimale. MM.GGAA (formata usato generalmente negli Stati Uniti)

GGMM.AA (formato usato generalmente in Europa)

DD (Visualizza angolo decimale)

Val o r e1 4DD ⇒ valore Lista1 4DD ⇒ lista Matrice1 4DD ⇒ matrice

Restituisce l’equivalente decimale dell’argomento espresso in gradi. L’argomento è un numero, una lista o una matrice interpretata in gradianti, radianti o gradi dall’impostazione della modalità Angolo.

4Decimal (Decimale)

4Decimal

Espr1

4Decimal

Lista1 Matrice1

Visualizza l’argomento nella forma decimale. Questo operatore può essere utilizzato solo alla fine della riga di introduzione.

Decimal

⇒ espressione ⇒ espressione

⇒ espressione

Catalogo

In modalità angolo in gradi:

In modalità angolo in gradianti (gradi centesimali):

In modalità angolo in radianti:

Catalogo

30 Guida di riferimento di TI-Nspire™ CAS

Define (Definisci)

Define Var = Espressione Define Funzione(Param1, Param2, ...) = Espressione

Definisce la variabile Va r o la funzione Funzione definita dall’utente. Parametri, quali Param1, sono segnaposto per il passaggio di

argomenti alla funzione. Quando si chiama una funzione definita dall’utente, occorre fornire argomenti (ad esempio, valori o variabili) corrispondenti ai parametri. Una volta chiamata, la funzione calcola

Espressione utilizzando gli argomenti forniti. Var e Funzione non possono essere il nome di una variabile di

sistema né una funzione o un comando predefiniti.

Nota: questa forma di Define equivale all’esecuzione

dell’espressione: espressione & Funzione(Param1,Param2).

Define Funzione(Param1, Param2, ...) = Func

Blocco

EndFunc

Programma(Param1, Param2, ...) = Prgm

Define

Blocco

EndPrgm

In questa forma, il programma o la funzione definita dall’utente può eseguire un blocco di istruzioni multiple.

Blocco può essere una singola istruzione o una serie di istruzioni su righe separate. Inoltre Blocco può includere espressioni e istruzioni (quali If, Then, Else e For).

Nota per l’introduzione dell’esempio: nell’applicazione

Calcolatrice sul palmare, è possibile introdurre definizioni composte da più righe premendo @ invece di · alla fine di ciascuna

riga. Sulla tastiera del computer, mantenere premuto Alt e premere

Invio. Nota: vedere anche Define LibPriv a pagina 31 e Define

LibPub

a pagina 32.

Catalogo

Define LibPriv (Definisci libreria privata)

Define LibPriv Var = Espressione Define LibPriv Funzione(Param1, Param2, ...) = Espressione

Define LibPriv Funzione(Param1, Param2, ...) = Func

Blocco

EndFunc Define LibPriv

Blocco

EndPrgm

Funziona come Define, eccetto che definisce una variabile, una funzione o un programma libreria privata. Funzioni e programmi privati non sono elencati nel Catalogo.

Nota: vedere anche Define a pagina 31 e Define LibPub a

pagina 32.

Programma(Param1, Param2, ...) = Prgm

Catalogo

Guida di riferimento di TI-Nspire™ CAS 31

Define LibPub (Definisci libreria pubblica)

Define LibPub Var = Espressione Define LibPub Funzione(Param1, Param2, ...) = Espressione

Define LibPub Funzione(Param1, Param2, ...) = Func

Blocco

EndFunc Define LibPub

Blocco

EndPrgm

Funziona come Define, eccetto che definisce una variabile, una funzione o un programma libreria pubblica. Funzioni e programmi pubblici vengono elencati nel Catalogo dopo che la libreria è stata salvata e aggiornata.

Nota: vedere anche Define a pagina 31 e Define LibPriv a

pagina 31.

Programma(Param1, Param2, ...) = Prgm

Catalogo

DelVar

DelVar Var 1 [, Va r 2] [, Va r 3 ] ... DelVar

Var .

Elimina dalla memoria la variabile o il gruppo di variabili specificato.

DelVar Var . elimina tutti i membri del gruppo di variabili Va r.

(come ad esempio i risultati statistici stat.nn o le variabili create utilizzando la funzione LibShortcut()). Il punto (.) in questa forma del comando DelVar ne limiti l’applicabilità all’eliminazione di un

gruppo di variabili; non può essere applicato alla variabile semplice Var .

deSolve() Soluzione di equazioni differenziali

deSolve(ODE1°O2°Ordine, Var , varDipendente)

⇒ soluzione generale

Restituisce un’equazione che specifica in modo esplicito o implicito una soluzione generale per l’equazione differenziale ordinaria (ODE) di 1° o 2° ordine. Nell’ODE:

• Usare il simbolo di primo (premere ') per indicare la derivata

prima della variabile dipendente rispetto alla variabile indipendente.

• Usare due simboli di primo per indicare la derivata seconda corrispondente.

Il simbolo di primo viene utilizzato solo per le derivate all’interno di deSolve(). Negli altri casi utilizzare d().

La soluzione generale di un’equazione di primo ordine contiene una costante arbitraria della forma ck, dove k è un suffisso intero compreso tra 1 e 255. La soluzione di un’equazione di secondo ordine contiene due costanti di questo tipo.

Catalog

Catalogo

32 Guida di riferimento di TI-Nspire™ CAS

deSolve() Soluzione di equazioni differenziali

Applicare solve() ad una soluzione implicita per tentare di convertirla in una o più soluzioni esplicite equivalenti.

Quando si confrontano i risultati ottenuti con le soluzioni date dal libro di testo o dal manuale, tenere presente che metodi diversi introducono constanti arbitrarie in punti diversi dei calcoli, il che può dare soluzioni generali diverse.

deSolve(ODE1°Ordine and condizioneIniziale, Var ,

varDipendente)

⇒ soluzione particolare

Restituisce una soluzione particolare che soddisfa ODE1°Ordine e condizioneIniziale. Di solito ciò risulta più semplice che non

determinare una soluzione generale, sostituire i valori iniziali, calcolare la soluzione in base ad una costante arbitraria e quindi sostituire il valore nella soluzione generale.

condizioneIniziale è un’equazione della forma: varDipendente (valoreInizialeDipendente) =

valoreInizialeDipendente valoreInizialeIndipendente e valorInizialeDipendente possono

essere variabili come x0 e y0 che non contengono alcun valore. Una differenziazione implicita può servire a verificare le soluzioni implicite.

deSolve(ODE2°Ordine and condIniziale1 and condIniziale2,

Var , varDipendente) ⇒ soluzione particolare

Restituisce una soluzione particolare che soddisfa ODE2°ordine e che ha un valore specifico della variabile dipendente e la derivata prima nello stesso punto.

Per condIniziale1, utilizzare la forma:

varDipendente (valoreInizialeDipendente) = valoreInizialeDipendente

Per condIniziale2, utilizzare la forma: depVar (valoreInizialeIndipendente) = valore1°DerivataIniziale

Catalogo

deSolve(ODE2°Ordine and condLimite1 and

condLimite2, Var , varDipendente) ⇒ soluzione particolare

Restituisce una soluzione particolare che soddisfa ODE2°Ordine e che ha valori specificati in due punti diversi.

Guida di riferimento di TI-Nspire™ CAS 33

det() (Determinante)

det(matriceQuadrata[, Tolleranza]) ⇒ espressione

Restituisce il determinante di matriceQuadrata. In alternativa, un elemento qualsiasi della matrice viene considerato

zero se il suo valore assoluto è minore di Tolleranza. Tale tolleranza viene utilizzata solo se la matrice contiene elementi a vir gola mobile e non contiene variabili simboliche alle quali non sia stato assegnato un valore. In caso contrario, Tolleranza viene ignorato.

• Se si usa

Approssimato

virgola mobile.

•Se Tolleranza viene omesso o non è utilizzato, la tolleranza predefinita viene calcolata come:

5EM14 ·max(dim(matriceQuadrata))·

rowNorm(matriceQuadrata)

oppure se si imposta la modalità Auto o

su Approssimato, i calcoli verranno eseguiti in

Catalogo

diag() (Diagonale)

diag(Lista) ⇒ matrice diag(matriceRiga) ⇒ matrice diag(matriceColonna) ⇒ matrice

Restituisce una matrice avente i valori dell’argomento lista o matrice nella diagonale principale.

diag(matriceQuadrata) ⇒ matriceRiga

Restituisce una matrice riga contenente gli elementi della diagonale principale di matriceQuadrata.

matriceQuadrata deve essere quadrata.

dim() (Dimensione)

dim(Lista) ⇒ intero

Restituisce le dimensioni di Lista.

dim(Matrice) ⇒ lista

Restituisce le dimensioni di Matrice nella forma di una lista a due elementi {righe, colonne}.

dim(Stringa) ⇒ intero

Restituisce il numero di caratteri contenuti nella stringa Stringa.

Catalogo

34 Guida di riferimento di TI-Nspire™ CAS

Disp

Disp [esprOrString1] [, esprOrString2] ...

Visualizza gli argomenti nella cronologia di Calculator. Gli argomenti possono essere visualizzati in successione, separati da sottili spazi.

Questo comando è utile soprattutto in programmi e funzioni per assicurare la visualizzazione dei calcoli intermedi.

Nota per l’introduzione dell’esempio: nell’applicazione

Calcolatrice sul palmare, è possibile introdurre definizioni composte da più righe premendo @ invece di · alla fine di ciascuna

riga. Sulla tastiera del computer, mantenere premuto Alt e premere

Invio.

DMS (Gradi/primi/secondi)

Espr 4DMS Lista 4DMS Matrice 4DMS

Interpreta l’argomento come un angolo e visualizza il numero DMS equivalente (GGGGGG¡PP’SS.ss’’). Per ulteriori informazioni sul formato DMS (gradi, primi, secondi) vedere ¡, ’, ’’ a pagina 146.

Nota: 4quando DMS viene utilizzato in modalità angolo in radianti,

converte i radianti in gradi. Se i dati inseriti sono seguiti dal simbolo dei gradi ¡, non verrà eseguita alcuna conversione. 4DMS può essere utilizzato solo alla fine di una riga di introduzione.

In modalità angolo in gradi:

Catalogo

Guida di riferimento di TI-Nspire™ CAS 35

dominantTerm() (Termine dominante)

dominantTerm(Espr1, Var [, Punto]) ⇒ espressione dominantTerm(Espr1, Var [, Punto]) | Va r >Punto

⇒ espressione

dominantTerm(Espr1, Var [, Punto]) | Va r <Punto

⇒ espressione

Restituisce il termine dominante di una rappresentazione di serie di potenze di Espr1 sviluppate intorno a Punto. Il termine dominante è quello la cui grandezza cresce più rapidamente in prossimità di Va r = Punto. La potenza risultante di (Var N Punto) può avere esponente negativo e/o frazionario. Il coefficiente di questa potenza può includere logaritmi di (Va r N Punto) e altre funzioni di Va r che sono

dominate da tutte le potenze di (Va r N Punto) aventi lo stesso segno esponenziale.

Il valore predefinito di Punto è 0. Punto può essere ˆ o Nˆ, in questi casi il termine dominante sarà quello avente l’esponente più grande di Va r anziché l’esponente più piccolo di Va r.

dominantTerm(…) restituisce “dominantTerm(…)” se non è

in grado di determinare una tale rappresentazione, come ad esempio per singolarità essenziali quali sin(1/z) in z=0, e

N1/z

corrispondenza di z=0 o ez in z = ˆ o Nˆ.

Se la serie o una delle suoe derivate presenta una discontinuità in corrispondenza del Punto, il risultato potrebbe contenere sottoespressioni della forma sign(…) o abs(…) per una variabile di

sviluppo reale o della forma (-1) sviluppo complessa, che termina con "_". Se si pensa di utilizzare il termine dominante solo per i valori da una sola parte di Punto, aggiungere a dominantTerm(...) quello appropriato tra "| Var > Punto", "| Var < Punto", "| "Va r ‚ Punto" o "Va r  Punto" per ottenere un risultato più semplice.

dominantTerm() si distribuisce su liste e matrici indicate come

primo argomento.

dominantTerm() è utile per conoscere l’espressione più semplice

possibile che sia asintotica rispetto a un’altra espressione come Var " Punto. dominantTerm() è utile inoltre quando non è ovvio quale sarà il grado del primo termine diverso da zero di una serie e non si desidera procedere per ipotesi iterative, sia interattivamente che per mezzo di un loop di programma.

Nota: vedere anche series() a pagina 98.

floor(…angle(…)…)

per una variabile di

Catalogo

dotP() (Prodotto scalare)

dotP(Lista1, Lista2) ⇒ espressione

Catalogo

Restituisce il prodotto scalare di due liste.

dotP(Ve t to r e 1, Vettore2) ⇒ espressione

Restituisce il prodotto scalare di due vettori. Entrambi devono essere vettori riga o colonna.

36 Guida di riferimento di TI-Nspire™ CAS

e^() (Funzione esponenziale)

e^(Espr1) ⇒ espressione

Restituisce e elevato alla potenza di Espr1.

Nota: vedere anche e modello di funzione esponenziale a

pagina 2.

Nota: premere u per visualizzare

carattere E dalla tastiera.

Un numero complesso può essere inserito nella forma polare re Usare questa forma solo nella modalità di misurazione degli angoli in radianti; nella modalità in gradi o gradianti causa un errore del dominio.

e^(Lista1) ⇒ lista

Restituisce e elevato alla potenza di ciascun elemento di Lista1.

e^(matriceQuadrata1) ⇒ matriceQuadrata

Restituisce l’esponenziale della matrice di matriceQuadrata1. Ciò non equivale a calcolare e elevato alla potenza di ciascun elemento. Per informazioni sul metodo di calcolo, vedere cos().

matriceQuadrata1 deve essere diagonalizzabile. Il risultato contiene sempre numeri a virgola mobile.

eff()

eff(tassoNominale,CpY) ⇒ valore

Funzione finanziaria che converte il tasso di interesse nominale tassoNominale in un tasso effettivo annuo, essendo CpY il numero di periodi di capitalizzazione per anno.

tassoNominale deve essere un numero reale e CpY deve essere un numero reale > 0.

Nota: vedere anche nom() a pagina 75.

^( è diverso da accedere al

Tasto u

Catalogo

eigVc() (Autovettore)

eigVc(matriceQuadrata) ⇒ matrice

Restituisce una matrice contenente gli autovettori per una matriceQuadrata reale o complessa, in cui ogni colonna del risultato corrisponde ad un autovalore. Tenere presente che un autovettore non è univoco; esso infatti può essere scalato per qualsiasi fattore costante. Gli autovettori vengono normalizzati, cioè se V = [x1, x2,

…, xn], allora:

+ … + x

= 1

matriceQuadrata viene dapprima equilibrata con similitudini fino a quando le norme di riga e colonna sono il più vicino possibili allo stesso valore. matriceQuadrata viene quindi ridotta nella forma superiore di Hessenberg mentre gli autovettori vengono calcolati con una scomposizione in fattori di Schur.

In modalità formato rettangolare complesso:

Per vedere l’intero risultato, premere £, quindi utilizzare ¡ e

¢ per spostare il cursore

Catalogo

Guida di riferimento di TI-Nspire™ CAS 37

eigVl() (Autovalore)

eigVl(matriceQuadrata) ⇒ lista

Restituisce la lista degli autovalori di una matriceQuadrata reale o complessa.

matriceQuadrata viene dapprima equilibrata con similitudini fino a quando le norme di riga e colonna sono il più vicino possibili allo stesso valore. matriceQuadrata viene quindi ridotta nella forma superiore di Hessenberg mentre gli autovalo ri vengono calcolati dalla matrice superiore di Hessenberg.

In modalità formato rettangolare complesso:

Per vedere l’intero risultato, premere £, quindi utilizzare ¡ e

Catalogo

¢ per spostare il cursore

Else Vedere If a pagina 52.

ElseIf

If Espressione booleana1 Then

Blocco1

ElseIf Espressione booleana2 Then

Block2

BloccoN

EndIf

Nota per l’introduzione dell’esempio: nell’applicazione

Calcolatrice sul palmare, è possibile introdurre definizioni composte da più righe premendo @ invece di · alla fine di ciascuna

riga. Sulla tastiera del computer, mantenere premuto Alt e premere

Invio.

EndFor Vedere For a pagina 45.

EndFunc Vedere Func a pagina 48.

EndIf Vedere If a pagina 52.

EndLoop Vedere Loop a pagina 67.

EndPrgm Vedere Prgm a pagina 86.

Catalogo

EndTry Vedere Try a pagina 119.

38 Guida di riferimento di TI-Nspire™ CAS

EndWhile Vedere While a pagina 125.

exact() (Esatto)

exact(Espr1 [, Tolleranza]) ⇒ espressione exact(Lista1 [, Tolleranza]) ⇒ lista exact(Matrice1 [, Tolleranza]) ⇒ matrice

Utilizza l’aritmetica della modalità Esatto per restituire, se possibile, l’equivalente razionale dell’argomento.

Tolleranza specifica la tolleranza per la conversione; l’impostazione predefinita è 0 (zero).

Exit (Esci)

Esci

Permette di uscire dal blocco corrente For, While o Loop.

Exit non è ammesso al di fuori delle tre strutture iterative (For, While o Loop).

Nota per l’introduzione dell’esempio: nell’applicazione

Calcolatrice sul palmare, è possibile introdurre definizioni composte da più righe premendo @ invece di · alla fine di ciascuna

riga. Sulla tastiera del computer, mantenere premuto Alt e premere

Invio.

Descrizione della funzione:

Catalogo

exp (Espressione)

Espr

exp

Rappresenta Espr rispetto all’esponente naturale e. È un operatore di conversione della visualizzazione. Può essere utilizzato solo alla fine della riga di introduzione.

exp() (e alla potenza)

exp(Espr1) ⇒ espressione

Catalog

Tasto u

Restituisce e elevato alla potenza di Espr1. Restituisce e elevato alla potenza di Va l or e 1 .

Nota: vedere anche e modello di funzione esponenziale a pagina 2.

Guida di riferimento di TI-Nspire™ CAS 39

exp() (e alla potenza)

exp(Lista1) ⇒ lista

Restituisce e elevato alla potenza di ciascun elemento di Lista1.

exp(matriceQuadrata1) ⇒ matriceQuadrata

Restituisce l’esponenziale della matrice di matriceQuadrata1. Ciò non equivale a calcolare e elevato alla potenza di ciascun elemento. Per informazioni sul metodo di calcolo, vedere

matriceQuadrata1 deve essere diagonalizzabile. Il risultato contiene sempre numeri a virgola mobile.

cos().

Tasto u

exp4list()

exp4list(Espr,Va r ) ⇒ lista

Ricerca in Espr le equazioni separate dalla parola “or” e restituisce una lista contenente la parte destra delle equazioni nella forma Var = E s pr . In questo modo viene semplificato il compito di estrarre alcuni valori delle soluzioni inclusi nei risultati delle funzioni solve(),

cSolve()

, fMin() e fMax().

Nota: exp4list() non è necessario con le funzioni zeros e cZeros() in quanto queste restituiscono direttamente una lista

contenente i valori delle soluzioni.

expand() (Espandi)

expand(Espr1 [, Va r ]) ⇒ espressione expand(Lista1 [,Va r ]) ⇒ lista expand(Matrice1 [,Var ]) ⇒ matrice

expand(Espr1) restituisce l’espansione di Espr1 relativamente a

tutte le sue variabili. Si tratta di un’espansione polinomiale per i polinomi e di una parziale espansione di frazioni per le espressioni razionali.

La funzione expand() permette di trasformare Espr1 in una somma e/o differenza di termini semplici. Al contrario, factor() permette di trasformare Espr1 in un prodotto e/o in un quoziente di fattore semplici.

expand(Espr1,Var ) restituisce l’espa nsione di Espr1 relativamente

a Va r. Le potenze simili di Va r sono ridotte. I termini ed i rispettivi fattori sono ordinati considerando Va r la variabile principale. Si può verificare accidentalmente la scomposizione in fattori o l’espansione dei coefficienti ridotti. Questo procedimento, rispetto all’omissione di Var , permette di risparmiare tempo, memoria e spazio sullo schermo, rendendo inoltre l’espressione più comprensibile.

Catalogo

Anche in presenza di una sola variabile, Va r permette di rendere più completa la scomposizione in fattori del denominatore utilizzata per la parziale espansione di frazioni.

Suggerimento: per le espressioni razionali, propFrac() costituisce un’alternativa più veloce ma meno completa di expand().

Nota: vedere anche comDenom() per l’espansione di un

numeratore di una frazione con denominatore espanso.

40 Guida di riferimento di TI-Nspire™ CAS

expand() (Espandi)

expand(Espr1,[Va r]) distribuisce inoltre logaritmi e potenze

frazionarie indipendentemente da Va r . Per una maggiore distribuzione dei logaritmi e delle potenze frazionarie, possono essere richieste condizioni per garantire che alcuni fattori siano non negativi.

expand(Espr1,[Va r]) distribuisce inoltre valori assoluti, sign() e

gli esponenziali, indipendentemente da Va r .

Nota: vedere anche tExpand() per l’espansione di funzioni

trigonometriche con angoli somma e multipli di angoli.

Catalogo

expr() (Da stringa a espressione)

expr(Stringa) ⇒ espressione

Restituisce la stringa di caratteri contenuta in Stringa come espressione e la esegue subito.

ExpReg (Regressione esponenziale)

ExpReg X, Y [, [Freq] [, Categoria, Includi]]

Calcola la regressione esponenziale y = a·(b)xsulle liste X e Y con frequenza Freq. Il riepilogo dei risultati è memorizzato nella variabile stat.results. (Vedere pagina 109).

Tutte le liste devono avere le stesse dimensioni, ad eccezione di

Includi. X e Y sono liste di variabili indipendenti e dipendenti. Freq è una lista opzionale di valori di frequenza. Ciascun elemento di

Freq specifica la frequenza di occorrenza di ogni dato corrispondente

di X e Y. Il valore predefinito è 1. Tutti gli elementi devono essere numeri interi | 0.

Categoria è una lista di codici numerici di categoria dei dati corrispondenti di X e Y.

Includi è una lista di uno o più codici di categoria. Solo quei dati il cui codice di categoria è inserito in questa lista vengono inclusi nel calcolo.

Catalogo

Variabile di output

stat.RegEqn

Descrizione

Equazione di regressione: a·(b)

stat.a, stat.b Coefficienti di regressione

stat.r

Coefficiente di determinazione lineare di dati trasformati

Guida di riferimento di TI-Nspire™ CAS 41

Variabile di output

stat.r Coefficiente di correlazione per dati trasformati (x, ln(y))

stat.Resid Residui associati al modello esponenziale

stat.ResidTrans Residui associati all’adattamento lineare dei dati trasformati

stat.XReg Lista di punti dati della Lista X modificata attualmente usata nella regressione secondo le restrizioni di

stat.YReg Lista di punti dati della Lista Y modificata attualmente usata nella regressione secondo le restrizioni di

stat.FreqReg Lista di frequenze corrispondenti a stat.XReg e stat.YReg

Descrizione

Freq, Lista Categoria e Includi Categorie

factor() (Fattorizza)

factor(Espr1[, Va r ]) ⇒ espressione factor(Lista1[,Va r ]) ⇒ lista factor(Matrice1[,Var ]) ⇒ matrice

factor(Espr1) restituisce la scomposizione in fattori di Espr1 per tutte le sue variabili con denominatore comune.

Espr1 viene scomposto in fattori razionali lineari (per quanto

possibile) senza introdurre nuove sottoespressioni non reali. Questa procedura è utile qualora si desideri ottenere una scomposizione in fattori relativamente a più di una variabile.

factor(Espr,Va r) restituisce la scomposizione in fattori di Espr1 relativamente alla variabile Va r .

Espr1 viene scomposto (per quanto possibile) in fattori reali che sono

lineari in Va r, anche se introduce costanti irrazionali o sottoespressioni irrazionali in altre variabili.

Nota: vedere anche comDenom() per ottenere una veloce

scomposizione in fattori parziale quando factor() non è sufficientemente veloce o la memoria è esaurita.

Nota: vedere anche cFactor() per una scomposizione completa dei

coefficienti complessi nel tentativo di ottenere fattori lineari.

Catalogo

42 Guida di riferimento di TI-Nspire™ CAS

factor() (Fattorizza)

factor(numeroRazionale) restituisce il numero razionale

scomposto in fattori primi. Per i numeri composti, il tempo di elaborazione cresce in modo esponenziale secondo il numero di cifre del secondo fattore più grande. Ad esempio, la scomposizione in fattori di un intero di 30 cifre può richiedere più di un giorno, mentre la scomposizione di un numero di 100 cifre può richiedere più di un secolo.

Nota: per arrestare (interrompere) un calcolo, premere w.

Se si desidera soltanto determinare se un numero è primo, utilizzare

isPrime(). Ciò risulta molto più veloce, in particolare se

numeroRazionale non è primo e se il secondo fattore più grande ha più di cinque cifre.

Catalogo

FCdf() (Probabilità di distribuzione F)

FCdf(estremoInf,estremoSup,glNumer,glDenom) ⇒ numero se

estremoInf e estremoSup sono numeri, lista se estremoInf e estremoSup sono liste

FCdf(

estremoInf,estremoSup,glNumer,glDenom) ⇒ numero se estremoInf e estremoSup sono numeri, lista se estremoInf e estremoSup sono liste

Calcola la probabilità della distribuzione F tra estremoInf e estremoSup per il glNumer (gl, gradi di libertà) e glDenom

specificati.

Per P(X  valoreSuperiore), impostare valoreInferiore= 0.

Fill (Riempi)

Fill Espr, varMatrice ⇒ matrice

Sostituisce ciascun elemento della variabile varMatrice con Espr. varMatrice deve esistere già.

Fill Espr, varLista ⇒ lista

Sostituisce ciascun elemento della variabile varLista con Espr. varLista deve esistere già.

Catalogo

Guida di riferimento di TI-Nspire™ CAS 43

FiveNumSummary

FiveNumSummary X[,[Freq][,Categoria,Includi]]

Fornisce una versione abbreviata delle statistiche a 1 variabile nella lista X. Il riepilogo dei risultati è memorizzato nella variabile

stat.results. (Vedere pagina 109). X rappresenta una lista contenente i dati. Freq è una lista opzionale di valori di frequenza. Ciascun elemento di

Freq specifica la frequenza di occorrenza di ogni dato corrispondente

di X. Il valore predefinito è 1. Tutti gli elementi devono essere numeri interi | 0.

Categoria è una lista di codici numerici di categoria dei dati corrispondenti di X.

Includi è una lista di uno o più codici di categoria. Solo quei dati il cui codice di categoria è inserito in questa lista vengono inclusi nel calcolo.

Catalog

Variabile di output

Descrizione

stat.MinX Minimo dei valori x

stat.Q1X 1° quartile di x

stat.MedianX Mediana di x

stat.Q3X 3° quartile di x

stat.MaxX Massimo dei valori x

floor() (Arrotondato per difetto)

floor(Espr1) ⇒ intero

Restituisce il numero intero più grande che è { all’argomento. Questa funzione è identica a int().

L’argomento può essere un numero reale o complesso.

floor(Lista1) ⇒ lista floor(Matrice1) ⇒ matrice

Restituisce una lista o matrice del valore arrotondato per difetto di ciascun elemento.

Nota: vedere anche ceiling() e int().

fMax() (Massimo funzione)

fMax(Espr, Var) ⇒ Espressione booleana fMax(Espr, Var ,estremoInferiore) fMax(

Espr, Va r,estremoInferiore,estremoSuperiore)

fMax(

Espr, Va r) | estremoInferiore<Va r<estremoSuperiore

Restituisce un’espressione booleana che specifica i possibili valori di Var che massimizzano Espr o che individuano il suo estremo superiore.

Catalogo

44 Guida di riferimento di TI-Nspire™ CAS

fMax() (Massimo funzione)

È possibile utilizzare l’operatore "|" per restringere l’intervallo della soluzione e/o specificare altri vincoli.

Quando la modalità Auto o Approssimato è impostata su Approssimato, fMax() ricerca ripetutamente un massimo locale approssimato. Questo procedimento è generalmente più veloce, soprattutto se si utilizza l’operatore "|" per limitare la ricerca ad un intervallo relativamente piccolo che contiene esattamente un massimo locale.

Nota: vedere anche fMin() e max().

Catalogo

fMin() (Minimo funzione)

fMin(Espr, Var) ⇒ Espressione booleana fMin(Espr, Var ,estremoInferiore) fMin(

Espr, Va r,estremoInferiore,estremoSuperiore)

fMin(

Espr, Va r) | estremoInferiore<Var <estremoSuperiore

Restituisce un’espressione booleana che specifica i possibili valori di Var che minimizzano Espr o che individuano il suo estremo inferiore.

È possibile utilizzare l’operatore "|" per restringere l’intervallo della soluzione e/o specificare altri vincoli.

Quando la modalità Auto o Approssimato è impostata su Approssimato, fMin() ricerca ripetutamente un minimo locale approssimato. Questo procedimento è generalmente più veloce, soprattutto se si utilizza l’operatore “|” per limitare la ricerca ad un intervallo relativamente piccolo che contiene esattamente un minimo locale.

Nota: vedere anche fMax() e min().

For

For Var , Basso, Alto [, Incr]

Blocco

EndFor

Esegue iterativamente le istruzioni di Blocco per ciascun valore di Var , da Basso a Alto, secondo incrementi pari a Incr.

Var non deve essere una variabile di sistema. Incr può essere un valore positivo o negativo. Il valore predefinito è

1. Blocco può essere una singola istruzione o una serie di istruzioni

separate dal carattere ":".

Nota per l’introduzione dell’esempio: nell’applicazione

Calcolatrice sul palmare, è possibile introdurre definizioni composte da più righe premendo @ invece di · alla fine di ciascuna

riga. Sulla tastiera del computer, mantenere premuto Alt e premere

Invio.

Catalogo

Guida di riferimento di TI-Nspire™ CAS 45

format() (Formato)

format(Espr[, stringaFormato]) ⇒ stringa

Restituisce Espr come stringa di caratteri basata sul modello di formato.

Espr deve poter essere semplificata in un numero. stringaFormato è una stringa e deve essere espressa nella forma:

“F[n]”, “S[n]”, “E[n]”, “G[n][c]”, dove le porzioni racchiuse tra parentesi [ ] sono facoltative.

F[n]: formato fisso. n rappresenta il numero di cifre da visualizzare dopo la virgola decimale.

S[n]: formato scientifico. n rappresenta il numero di cifre da visualizzare dopo la virgola decimale.

E[n]: formato tecnico. n rappresenta il numero di cifre dopo la prima cifra significativa. L’esponente è modificato secondo multipli di tre e la virgola decimale viene spostata verso destra di zero, una o due cifre.

G[n][c]: analogo al formato fisso, separa inoltre le cifre a sinistra del separatore decimale in gruppi di tre. c specifica il carattere separatore dei gruppi; il valore predefinito è la virgola. Se c è un punto, il separatore decimale viene visualizzato come virgola.

[Rc]: tutti gli indicatori precedenti possono essere seguiti dal suffisso di radice Rc, dove c è un singolo carattere che specifica che cosa sostituire al punto della radice.

Catalogo

fPart() Funzione parte frazionaria

fPart(Espr1) ⇒ espressione fPart(Lista1) ⇒ lista fPart(Matrice1) ⇒ matrice

Restituisce la parte frazionaria dell’argomento. Per una lista o una matrice, restituisce le parti frazionarie degli

elementi. L’argomento può essere un numero reale o complesso.

FPdf() (Probabilità di distribuzione F)

FPdf(valX,glNumer,glDenom) ⇒ numero se Val X è un

lista se Val X è una lista

numero,

FPdf(

valX,glNumer,glDenom) ⇒ numero se Val X è un

lista se Val X è una lista

numero,

Calcola la probabilità di distribuzione F in valX per il glNumer (gradi di libertà) e glDenom specificati.

freqTable4list()

freqTable4list(Lista1,Lista ListaInteriFreq) ⇒ lista

Restituisce una lista contenente gli elementi di Lista1 espansi secondo le frequenze in ListaInteriFreq. Questa funzione può essere utilizzata per costruire una tabella di frequenze per l’applicazione Dati e statistiche.

Lista1 può essere qualsiasi lista valida. ListaInteriFreq deve avere la stessa dimensione di Lista1 e deve

contenere solo elementi interi non negativi. Ciascun elemento specifica il numero di volte che l’elemento corrispondente di Lista1 verrà ripetuto nella lista dei risultati. Un valore zero esclude l’elemento corrispondente di Lista1.

Catalogo

Catalog

46 Guida di riferimento di TI-Nspire™ CAS

frequency()

frequency(Lista1,listaContenitori) ⇒ lista

Restituisce una lista contenente i conteggi degli elementi di Lista1. I conteggi sono basati su intervalli (contenitori) definiti nell’argomento listaContenitori.

Se listaContenitori è {b(1), b(2), …, b(n)}, gli intervalli specificati

?{b(1), b(1)<?{b(2),…,b(n-1)<?{b(n), b(n)>?}. La lista

sono { risultante è un elemento più lungo di listaContenitori.

Ciascun elemento del risultato corrisponde al numero di elementi di Lista1 che rientrano nell’intervallo di quel contenitore. Espresso nei termini della funzione countIf(), il risultato è { countIf(list, ?{b(1)),

countIf(list, b(1)<?{b(2)), …, countIf(list, b(n-1)<?{b(n)), countIf(list, b(n)>?)}.

Gli elementi di Lista1 che non possono essere “inseriti in un contenitore” vengono ignorati.

In Foglio elettronico, è possibile utilizzare un intervallo di celle al posto di entrambi gli argomenti.

Nota: vedere anche countIf() a pagina 23.

Catalogo

Spiegazione del risultato:

2 elementi di Datalist sono {2.5 4 elementi di Datalist sono> 2.5 e {4.5 3 elementi di Datalist sono >4.5

L’elemento "hello" è una stringa e non può essere collocata in alcun contenitore definito.

FTest_2Samp (Verifica F su due campioni)

Catalogo

FTest_2Samp Lista1,Lista2[,Freq1[,Freq2[,Ipotesi]]]

FTest_2Samp

(Input lista dati)

Lista1,Lista2[,Freq1[,Freq2[,Ipotesi]]]

FTest_2Samp sx1,n1,sx2,n2[,Ipotesi]

FTest_2Samp

(Input statistiche riepilogo)

Consente di eseguire una verifica F su due campioni. Il riepilogo dei risultati è memorizzato nella variabile stat.results. (Vedere pagina

109).

Per Ha: s1 > s2, impostare Ipotesi>0 Per Ha: s1 ƒ s2 (default), impostare Ipotesi =0 Per Ha: s1 < s2, impostare Ipotesi<0

Variabile di output

stat.F

stat.PVal Livello minimo di significatività in corrispondenza del quale l’ipotesi nulla può essere rifiutata

stat.dfNumer Gradi di libertà del numeratore = n1-1

stat.dfDenom Gradi di libertà del denominatore = n2-1

stat.sx1, stat.sx2 Deviazioni standard dei campioni delle sequenze di dati di Lista 1 e Lista 2

stat.x1_bar stat.x2_bar

stat.n1, stat.n2 Dimensione dei campioni

sx1,n1,sx2,n2[,Ipotesi]

Descrizione

Statistica ó calcolata per la sequenza di dati

Medie dei campioni delle sequenze di dati di Lista 1 e Lista 2

Guida di riferimento di TI-Nspire™ CAS 47

Func

Blocco

EndFunc

Modello per la creazione di una funzione definita dall’utente. Blocco può essere una singola istruzione, una serie di istruzioni

separate dal carattere “:” o una serie di istruzioni su righe separate. La funzione può utilizzare l’istruzione risultato.

Nota per l’introduzione dell’esempio: nell’applicazione

Calcolatrice sul palmare, è possibile introdurre definizioni composte da più righe premendo @ invece di · alla fine di ciascuna

riga. Sulla tastiera del computer, mantenere premuto Alt e premere

Invio.

Return per restituire un dato

Catalogo

Definizione di una funzione Piecewise (definita a tratti):

Risultato della rappresentazione grafica g(x)

gcd() (Massimo comun divisore)

gcd(Numero1, Numero2) ⇒ espressione

Restituisce il massimo comune divisore (gcd) dei due argomenti. Il

gcd di due frazioni è il massimo comune divisore dei rispettivi

numeratori diviso per il minimo comune multiplo (lcm) dei loro denominatori.

In modalità Auto o Approssimato, il gcd di numeri decimali in vir gola mobile è 1.0.

gcd(Lista1, Lista2) ⇒ lista

Restituisce i massimi comuni divisori degli elementi corrispondenti in Lista1 e Lista2.

gcd(Matrice1, Matrice2) ⇒ matrice

Restituisce i massimi comuni divisori degli elementi corrispondenti in Matrice1 e Matrice2.

geomCdf() (Probabilità geometrica cumulata)

geomCdf(p,valoreInferiore,valoreSuperiore) ⇒ numero se

valoreInferiore e valoreSuperiore sono numeri, lista se valoreInferiore e valoreSuperiore sono liste

geomCdf(

p,valoreSuperiore) ⇒ numero se valoreSuperiore è

lista se valoreSuperiore è una lista

un numero,

Calcola una probabilità geometrica cumulata da valoreInferiore a valoreSuperiore con la probabilità di esiti favorevoli p specificata.

Per P(X  valoreSuperiore), impostare valoreSuperiore = 1.

Catalogo

48 Guida di riferimento di TI-Nspire™ CAS

geomPdf() (Probabilità per la distribuzione geometrica discreta)

geomPdf(p,valX) ⇒ numero se Val X è un numero, lista se

Val X è una lista

Calcola una probabilità in corrispondenza di Va l X, il numero della prova in cui si è verificato il primo caso favorevole, per la distribuzione geometrica discreta con la probabilità di esiti favorevoli p specificata.

Catalogo

getDenom() (Ottieni/restituisci denominatore)

getDenom(Espr1) ⇒ espressione

Trasforma l’argomento in un’espressione con denominatore comune ridotto e successivamente restituisce il denominatore.

getLangInfo() (Ottieni informazioni sulla lingua)

getLangInfo() ⇒ stringa

Restituisce una stringa che corrisponde all’abbreviazione della lingua attiva corrente. Può essere utilizzato, ad esempio, in un programma o in una funzione per determinare la lingua corrente.

Inglese = "en" Danese = "da" Tedesco = "de" Finlandese = "fi" Francese = "fr" Italiano = "it" Olandese = "nl" Olandese - Belgio = "nl_BE" Norvegese = "no" Portoghese = "pt" Spagnolo = "es" Svedese = "sv"

getMode()

getMode(interoNomeModo) ⇒ valore getMode(0) ⇒ lista

getMode(interoNomeModo) restituisce un valore che rappresenta

l’impostazione corrente del modo interoNomeModo.

getMode(0) restituisce una lista contenente coppie di numeri.

Ciascuna coppia è costituita da un numero intero per il modo e da un numero intero per l’impostazione.

Per un elenco dei modi e delle relative impostazioni, vedere la tabella seguente.

Se si salvano le impostazioni con getMode(0) & var, è possibile utilizzare setMode(var) in una funzione o in un programma per ripristinare temporaneamente le impostazioni solo all’interno dell’esecuzione della funzione o del programma. Vedere setMode() a pagina 99.

Catalogo

Catalog

Catalogo

Guida di riferimento di TI-Nspire™ CAS 49

Nome modo

Mostra cifre (Display digits)

Angolo (Angle)

Formato esponenziale (Exponential Format)

Reale o Complesso (Real or Complex)

Auto o Approssimato (Auto or Approx.)

Formato vettoriale (Vector Format)

Base

Sistema unità di misura (Unit system)

Intero modo Interi impostazioni

=Mobile, 2=Mobile1, 3=Mobile2, 4=Mobile3, 5=Mobile4, 6=Mobile5, 7=Mobile6,

8=Mobile7, 9=Mobile8, 10=Mobile9, 11=Mobile10, 12=Mobile11, 13=Mobile12, 14=Fissa0, 15=Fissa1, 16=Fissa2, 17=Fissa3, 18=Fissa4, 19=Fissa5, 20=Fissa6, 21=Fissa7, 22=Fissa8, 23=Fissa9, 24=Fissa10, 25=Fissa11, 26=Fissa12

=Radianti, 2=Gradi, 3=Gradianti

=Normale, 2=Scientifico, 3=Tecnico

=Reale, 2=Rettangolare, 3=Polare

=Auto, 2=Approssimato, 3=Esatto

=Rettangolare, 2=Cilindrico, 3=Sferico

=Decimale, 2=Esadecimale, 3=Binario

=SI, 2=Eng/US

getNum() (Ottieni/restituisci numeratore)

getNum(Espr1) ⇒ espressione

Trasforma l’argomento in un’espressione con denominatore comune ridotto e successivamente restituisce il numeratore.

Catalogo

50 Guida di riferimento di TI-Nspire™ CAS

getVarInfo() (Ottieni informazioni variabile)

getVarInfo() ⇒ matrice o stringa getVarInfo(StringaNomeLibreria) ⇒ matrice o stringa

getVarInfo() restituisce una matrice di informazioni (nome

variabile, tipo e accessibilità libreria) per tutte le va riabili e gli oggetti libreria definiti nell’attività corrente.

Se non ci sono variabili definite, "NONE".

getVarInfo(StringaNomeLibreria) restituisce una matrice di

informazioni per tutti gli oggetti libreria definiti nella libreria StringaNomeLibreria. StringaNomeLibreria deve essere una stringa (testo racchiuso tra virgolette) o una variabile stringa.

getVarInfo() restituisce la stringa

Se la libreria StringaNomeLibreria non esiste, si produce un errore.

Notare l’esempio sulla sinistra, in cui il risultato di getVarInfo() è assegnato alla variabile vs. Se si tenta di visualizzare la riga 2 o la riga 3 di vs viene restituito un errore “Invalid list or matrix (Lista o matrice non valida)” perché almeno uno degli elementi di queste righe (ad esempio, variabile b) viene ricalcolato in una matrice.

Questo errore potrebbe ripresentarsi quando si utilizza Ans per ricalcolare un risultato di getVarInfo().

Questo errore viene generato perché la versio ne corrente del software non supporta una struttura di matrice generalizzata quando un elemento di una matrice può essere o una matrice o una lista.

Catalog

Goto (Vai a)

Goto nomeEtichetta

Catalogo

Trasferisce il controllo all’etichetta nomeEtichetta. nomeEtichetta deve essere definito nella stessa funzione mediante

un’istruzione Lbl.

Nota per l’introduzione dell’esempio: nell’applicazione

Calcolatrice sul palmare, è possibile introdurre definizioni composte da più righe premendo @ invece di · alla fine di ciascuna

riga. Sulla tastiera del computer, mantenere premuto Alt e premere

Invio.

Guida di riferimento di TI-Nspire™ CAS 51

Grad (Gradianti o Gradi centesimali)

4 Grad ⇒ espressione

Espr1

Converte Espr1 in una misura di angolo in gradianti.

In modalità angolo in gradi:

In modalità angolo in radianti:

Catalogo

identity() (Identità)

identity(Intero) ⇒ matrice

Restituisce la matrice identità con la dimensione di Intero. Intero deve essere un numero intero positivo.

If Espressione booleana Istruzione If Espressione booleana Then

Blocco

EndIf

Se il valore di Espressione booleana è vero, viene eseguita la singola istruzione Istruzione o il blocco di istruzioni Blocco prima di procedere con l’esecuzione.

Se il valore di Espressione booleana è falso, la funzione continua senza eseguire l’istruzione o il blocco di istruzioni.

Blocco può essere una singola espressione o una serie di espressioni separate dal carattere ":".

Nota per l’introduzione dell’esempio: nell’applicazione

Calcolatrice sul palmare, è possibile introdurre definizioni composte da più righe premendo @ invece di · alla fine di ciascuna

riga. Sulla tastiera del computer, mantenere premuto Alt e premere

Invio. If Espressione booleana Then

Blocco1

Else

Blocco2

EndIf

Se il valore di Espressione booleana è vero, viene eseguito Blocco1 e successivamente viene saltato Blocco2.

Se il valore di Espressione booleana è falso, viene saltato Blocco1, ma viene eseguito Blocco2.

Blocco1 e Blocco2 possono essere una singola istruzione.

Catalogo

52 Guida di riferimento di TI-Nspire™ CAS

If Espressione booleana1 Then

Blocco1

ElseIf

Espressione booleana2 Then

Blocco2

Espressione booleanaN Then

BloccoN

EndIf

Permette il passaggio a un’altra funzione. Se il valore di Espressione

booleana1 è vero, viene eseguito Blocco1. Se il valore di Espressione booleana1 è falso, viene calcolata Espressione boolenana2, ecc.

Catalogo

ifFn()

ifFn(EsprBooleana,Valore_s e_vero [,Valore_se_falso [,

Valore_se_sconosciuto]]) ⇒ espressione, lista o matrice

Calcola l’espressione booleana EsprBooleana (o ciascun elemento di EsprBooleana) e produce un risultato sulla base delle seguenti

regole:

• EsprBooleana può verificare un singolo valore, una lista o una

matrice.

• Se un elemento di EsprBooleana dà come risultato una

condizione vera, viene restituito l’elemento corrispondente di Valore_se_vero.

• Se un elemento di EsprBooleana dà come risultato una

condizione falsa, viene restituito l’elemento corrispondente di Valore_se_falso. Se Valore_se_falso è omesso, viene restituito undef.

• Se un elemento di EsprBooleana non dà come risultato una

condizione vera né una condizione falsa, viene restituito l’elemento corrispondente di Valore_se_sconosciuto. Se Valore_se_sconosciuto è omesso, viene restituito undef.

• Se il secondo, terzo o quarto argomento della funzione ifFn() è

una singola espressione, la verifica booleana viene applicata a tutte le posizioni in EsprBooleana.

Nota: se l’istruzione EsprBooleana semplificata implica una lista o

una matrice, tutti gli altri argomenti della lista o della matrice devono avere uguali dimensioni e il risultato avrà uguali dimensioni.

imag() (Parte immaginaria)

imag(Espr1) ⇒ espressione

Restituisce la parte immaginaria dell’argomento.

Nota: tutte le variabili non definite vengono considerate come

variabili reali. vedere anche real() a pagina 92

Catalogo

Il valore di verifica di 1 è minore di 2.5, così l’elemento Valore_se_vero corrispondente di 5 viene copiato nella lista del risultato.

Il valore di verifica di 2 è minore di 2.5, così l’elemento Valore_se_vero corrispondente di 6 viene copiato nella lista del risultato.

Il valore di verifica di 3 è minore di 2.5, così l’elemento Valore_se_falso corrispondente di 10 viene copiato nella lista del risultato.

Valore_se_vero è un singolo valore e corrisponde a qualsiasi posizione selezionata.

Valore_se_falso non è specificato. Viene utilizzato Undef.

Un elemento selezionato da Valo re_se_v ero. Un elemento selezionato da Valore_se_sconosciuto.

Catalogo

Guida di riferimento di TI-Nspire™ CAS 53

imag() (Parte immaginaria)

imag(Lista1) ⇒ lista

Restituisce una lista delle parti immaginarie degli elementi.

imag(Matrice1) ⇒ matrice

Restituisce una matrice delle parti immaginarie degli elementi.

Catalogo

impDif() (Derivata implicita)

impDif(Equazione, Var , varDipendente[,Ord])

⇒ espressione

dove l’impostazione predefinita dell’ordine Ord è 1. Calcola la derivata implicita di equazioni in cui una variabile è definita

implicitamente rispetto a un’altra.

Indirection (Conversione indiretta) Vedere

inString() (All’interno della stringa)

inString(stringaRicerca, sottoStringa[, Inizio]) ⇒ intero

Restituisce la posizione del carattere nella stringa stringaRicerca dal quale inizia per la prima vola la stringa sottoStringa.

Inizio, se incluso, specifica la posizione del carattere all’interno di stringaRicerca in cui comincia la stringa. L’impostazione predefinita

è 1 (il primo carattere di stringaRicerca). Se stringaRicerca non contiene sottoStringa o Inizio è > della

lunghezza di stringaRicerca, viene restituito zero.

int() (Funzione parte intera)

int(Espr) ⇒ intero int(Lista1) ⇒ lista int(Matrice1) ⇒ matrice

Restituisce il più grande dei numeri interi che è minore o uguale all’argomento. Questa funzione è identica a floor().

L’argomento può essere un numero reale o complesso. Con una lista o con una matrice, restituisce il numero intero maggiore

di ciascuno degli elementi.

Catalogo

a pagina 144.

#()

Catalogo

intDiv() Divisione intera

intDiv(Numero1, Numero2) ⇒ intero intDiv(Lista1, Lista2) ⇒ lista intDiv(Matrice1, Matrice2) ⇒ matrice

Catalogo

Restituisce la parte intera di (Numero1 ÷ Numero2). Con liste e matrici, restituisce la parte intera di

(argomento 1 ÷ argomento 2) per ciascuna coppia di elementi.

integrate

Vedere

, a pagina 140.

‰()

54 Guida di riferimento di TI-Nspire™ CAS

invc2()

invc2(Area,gl)

Area,gl)

invChi2(

Calcola la funzione della probabilità c2 (chi quadrato) cumulativa inversa specificata dal grado di libertà, gl, per una data Area sotto la curva.

Catalogo

invF() (Distribuzione F cumulativa inversa)

invF(Area,glNumer,glDenom)

Area,glNumer,glDenom)

invF(

Calcola la funzione della distribuzione F cumulativa inversa specificata da glNumer e glDenom per una data Area sotto la curva.

invNorm() (Distribuzione normale cumulativa inversa)

invNorm(area[,m[,s]])

Calcola la funzione della distribuzione normale cumulativa inversa per una data Area sotto la curva della distribuzione normale specificata da m e s.

invt() (Funzione della probabilità t di Student)

invt(Area,gl)

Calcola la funzione della probabilità t di Student inversa, specificata dal grado di libertà, gl per una data Area sotto la curva.

iPart() (Parte intera)

iPart(Numero) ⇒ intero iPart(Lista1) ⇒ lista iPart(Matrice1) ⇒ matrice

Restituisce la parte intera dell’argomento. Per una lista o per una matrice, restituisce la parte intera di ciascun

argomento. L’argomento può essere un numero reale o complesso.

irr()

irr(CF0,CFLista [,CFFreq]) ⇒ valore

Funzione finanziaria che calcola l’indice di rendimento interno di un investimento (Internal Rate of Return).

CF0 è il cash flow iniziale al tempo 0; deve essere un numero reale. CFLista è una lista di importi di cash flow dopo il cash flow iniziale

CF0. CFFreq è una lista opzionale in cui ciascun elemento specifica la

frequenza di occorrenza di un importo di cash flow raggruppato (consecutivo), che è l’elemento corrispondente di CFLista. L’impostazione predefinita è 1; è possibile inserire valori che siano numeri interi positivi < 10000.

Nota: vedere anche mirr() a pagina 70.

Catalogo

Guida di riferimento di TI-Nspire™ CAS 55

isPrime() (Numero primo)

isPrime(Numero) ⇒ espressione costante booleana

Restituisce vero o falso per indicare se numero è un numero intero

‚ 2 divisibile solo per se stesso e per 1.

Se Numero ha più di 306 cifre e non ha fattori {1021,

isPrime(Numero) visualizza un messaggio di errore.

Se si desidera soltanto determinare se un Numero è primo, utilizzare

isPrime() invece di factor(). Ciò risulta molto più veloce, in

particolare se Numero non è primo e il secondo fattore più grande ha più di cinque cifre.

Nota per l’introduzione dell’esempio: nell’applicazione

Calcolatrice sul palmare, è possibile introdurre definizioni composte da più righe premendo @ invece di · alla fine di ciascuna

riga. Sulla tastiera del computer, mantenere premuto Alt e premere

Invio.

Catalogo

Funzione per trovare il numero primo successivo dopo il numero specificato:

Lbl (Etichetta)

Lbl nomeEtichetta

Definisce un’etichetta chiamata nomeEtichetta in una funzione. È possibile utilizzare un’istruzione Goto nomeEtichetta per trasferire

il controllo del programma all’istruzione immediatamente successiva all’etichetta.

nomeEtichetta deve soddisfare gli stessi requisiti validi per i nomi delle variabili.

Nota per l’introduzione dell’esempio: nell’applicazione

Calcolatrice sul palmare, è possibile introdurre definizioni composte da più righe premendo @ invece di · alla fine di ciascuna

riga. Sulla tastiera del computer, mantenere premuto Alt e premere

Invio.

lcm() (Minimo comune multiplo)

lcm(Numero1, Numero2) ⇒ espressione lcm(List1, Lista2) ⇒ lista lcm(Matrice1, Matrice2) ⇒ matrice

Restituisce il minimo comune multiplo (lcm) di due argomenti. Il lcm di due frazioni è il minimo comune multiplo dei loro numeratori diviso per il massimo comune divisore (gcd) dei loro denominatori. Il lcm dei numeri frazionari a virgola mobile è il loro prodotto.

Per due liste o matrici, restituisce i minimi comuni multipli dei corrispondenti elementi.

Catalogo

56 Guida di riferimento di TI-Nspire™ CAS

left() (Sinistra)

left(stringaOrigine[, Num]) ⇒ stringa

Restituisce i caratteri Num più a sinistra contenuti nella stringa di caratteri stringaOrigine.

Se si omette Num, restituisce l’intera stringaOrigine.

left(Lista1[, Num]) ⇒ lista

Restituisce gli elementi Num più a sinistra contenuti in Lista1. Se si omette Num, restituisce l’intera Lista1.

left(Confronto) ⇒ espressione

Restituisce il primo membro di un’equazione o di una disequazione.

Catalogo

libShortcut() (Collegamento a libreria)

libShortcut(stringaNomeLibr, stringaNomeCollegamento [, LibPrivFlag]) ⇒ lista di variabili

Crea una gruppo di variabili nell’attività corrente che contiene i riferimenti a tutti gli oggetti nel documento libreria specificato stringaNomeLibr. Aggiunge inoltre i membri del gruppo al menu Variables (Variabili). È quindi possibile fare riferimento a ciascun oggetto utilizzando la relativa stringaNomeCollegamento.

Impostare LibPrivFlag=0 per escludere oggetti libreria privata (default) Impostare LibPrivFlag=1 per includere oggetti libreria privata

Per copiare un gruppo di variabili, vedere CopyVar a pagina 18. Per eliminare un gruppo di variabili, vedere DelVar a pagina 32.

limit() o lim() (Limite)

limit(Espr1, Va r, Punto [,Direzione]) ⇒ espressione limit(Lista1, Va r, Punto [, Direzione]) ⇒ lista limit(Matrice1, Var , Punto [, Direzione]) ⇒ matrice

Restituisce il limite richiesto.

Nota: vedere anche Modello di limite a pagina 5.

Direzione: negativa=da sinistra, positiva=da destra, altrimenti=entrambe. (se il valore è omesso, Direzione viene impostata per default su entrambe).

Catalogo

Questo esempio presuppone un documento libreria memorizzato e aggiornato, denominato linalg2, che contiene oggetti definiti come clearmat, gauss1 e gauss2.

Catalogo

I limiti tendenti a + ˆ e a - ˆ sono sempre convertiti in limiti unilaterali dalla parte finita.

A seconda dei casi, limit() restituisce il limite cercato oppure undef quando non può determinare un limite univoco. Ciò non significa necessariamente che non esista un limite univoco. undef significa che il risultato è un numero non conosciuto di grandezza finita o infinita, oppure è l’intero insieme di tali numeri.

Guida di riferimento di TI-Nspire™ CAS 57

limit() o lim() (Limite)

limit() utilizza metodi quali la regola de L’Hopital, per cui vi sono

limiti univoci che non possono essere determinati da questa funzione. Se Espr1 contiene variabili indefinite diverse da Va r , può risultare necessario ridurle per ottenere un risultato più conciso.

I limiti sono molto sensibili agli errori di arrotondamento. Pertanto, si consiglia di evitare nel calcolo dei limiti, per quanto possibile, l’impostazione Approssimato della modalità Auto o

Approssimato

possibile che i numeri, che dovrebbero essere zero o avere una grandezza infinita, si comportino in modo diverso e che i limiti, che dovrebbero avere una grandezza finita diversa da zero, non l’abbiano.

e i numeri approssimati. In caso contrario, è

Catalogo

LinRegBx (Regressione lineare)

LinRegBx X,Y[,Freq[,Categoria,Includi]]

Calcola la regressione lineare y = a+b·x sulle liste X e Y con frequenza Freq. Il riepilogo dei risultati è memorizzato nella variabile stat.results. (Vedere pagina 109).

Tutte le liste devono avere le stesse dimensioni, ad eccezione di Includi.

Catalogo

X e Y sono liste di variabili indipendenti e dipendenti. Freq è una lista opzionale di valori di frequenza. Ciascun elemento di

Freq specifica la frequenza di occorrenza di ogni dato corrispondente

di X e Y. Il valore predefinito è 1. Tutti gli elementi devono essere numeri interi | 0.

Categoria è una lista di codici numerici di categoria dei dati corrispondenti di X e Y.

Includi è una lista di uno o più codici di categoria. Solo quei dati il cui codice di categoria è inserito in questa lista vengono inclusi nel calcolo.

Variabile di output

stat.RegEqn

Descrizione

Equazione di regressione: a+b·x

stat.a, stat.b Coefficienti di regressione

stat.r

coefficiente di determinazione

stat.r Coefficiente di correlazione

stat.Resid Residui della regressione

stat.XReg Lista di punti dati della Lista X modificata attualmente usata nella regressione secondo le restrizioni di

stat.YReg Lista di punti dati della Lista Y modificata attualmente usata nella regressione secondo le restrizioni di

Freq, Lista Categoria e Includi Categorie

stat.FreqReg Lista di frequenze corrispondenti a stat.XReg e stat.YReg

58 Guida di riferimento di TI-Nspire™ CAS

LinRegMx (Regressione lineare)

LinRegMx X,Y[,Freq[,Categoria,Includi]]

Calcola la regressione lineare y = m·x+b sulle liste X e Y con frequenza Freq. Il riepilogo dei risultati è memorizzato nella variabile stat.results. (Vedere pagina 109).

Tutte le liste devono avere le stesse dimensioni, ad eccezione di

Includi. X e Y sono liste di variabili indipendenti e dipendenti. Freq è una lista opzionale di valori di frequenza. Ciascun elemento di

Freq specifica la frequenza di occorrenza di ogni dato corrispondente

di X e Y. Il valore predefinito è 1. Tutti gli elementi devono essere numeri interi | 0.

Categoria è una lista di codici numerici di categoria dei dati corrispondenti di X e Y.

Includi è una lista di uno o più codici di categoria. Solo quei dati il cui codice di categoria è inserito in questa lista vengono inclusi nel calcolo.

Catalogo

Variabile di output

stat.RegEqn

Descrizione

Equazione di regressione: m·x+b

stat.m, stat.b Coefficienti di regressione

stat.r

coefficiente di determinazione

stat.r Coefficiente di correlazione

stat.Resid Residui della regressione

stat.XReg Lista di punti dati della Lista X modificata attualmente usata nella regressione secondo le restrizioni di

stat.YReg Lista di punti dati della Lista Y modificata attualmente usata nella regressione secondo le restrizioni di

Freq, Lista Categoria e Includi Categorie

stat.FreqReg Lista di frequenze corrispondenti a stat.XReg e stat.YReg

LinRegtIntervals (Regressione lineare)

LinRegtIntervals X,Y[,Freq[,0[,livelloConfidenza]]]

Per pendenza Calcola un intervallo di confidenza di livello C per la pendenza.

LinRegtIntervals X,Y[,Freq[,1,Val X [,livelloConfidenza]]]

Per risposta. Calcola un valore y previsto, un intervallo di previsione del livello C per una singola osservazione e un interva llo di confidenza del livello C per la risposta media.

Il riepilogo dei risultati è memorizzato nella variabile stat.results. (Vedere pagina 109).

Catalogo

Tutte le liste devono avere la stessa dimensione.

X e Y sono liste di variabili indipendenti e dipendenti. Freq è una lista opzionale di valori di frequenza. Ciascun elemento di

Freq specifica la frequenza di occorrenza di ogni dato corrispondente

di X e Y. Il valore predefinito è 1. Tutti gli elementi devono essere numeri interi | 0.

Guida di riferimento di TI-Nspire™ CAS 59

Variabile di output

stat.RegEqn

stat.a, stat.b Coefficienti di regressione

stat.df Gradi di libertà

stat.r

stat.r Coefficiente di correlazione

stat.Resid Residui della regressione

Solo tipo per pendenza

Descrizione

Equazione di regressione: a+b·x

Coefficiente di determinazione

Variabile di output

[stat.CLower, stat.CUpper]

stat.ME Margine di errore dell’intervallo di confidenza

stat.SESlope Errore standard della pendenza

stat.s Errore standard sulla linea

Solo tipo per risposta

Variabile di output

[stat.CLower, stat.CUpper]

stat.ME Margine di errore dell’intervallo di confidenza

stat.SE Errore standard della risposta media

[stat.LowerPred , stat.UpperPred]

stat.MEPred Margine di errore dell’intervallo di previsione

stat.SEPred Errore standard per la previsione

stat.y

Descrizione

Intervallo di confidenza per la pendenza

Descrizione

Intervallo di confidenza per la risposta media

Intervallo di previsione per una singola osservazione

a + b·ValX

60 Guida di riferimento di TI-Nspire™ CAS

LinRegtTest (t Test regressione lineare)

LinRegtTest X,Y[,Freq[,Ipotesi]]

Calcola una regressione lineare sulle liste X e Y e un t test sul valore della pendenza b e il coefficiente di correlazione r per l’equazione y=a+bx. Viene verificata l’ipotesi nulla H0:b=0 (in modo

equivalente, r=0) in relazione a una di tre ipotesi alternative.

Tutte le liste devono avere la stessa dimensione.

X e Y sono liste di variabili indipendenti e dipendenti. Freq è una lista opzionale di valori di frequenza. Ciascun elemento di

Freq specifica la frequenza di occorrenza di ogni dato corrispondente

di X e Y. Il valore predefinito è 1. Tutti gli elementi devono essere numeri interi | 0.

Ipotesi è un valore opzionale che specifica una di tre ipotesi alternative rispetto alla quale verrà testata l’ipotesi nulla (H0:b=r=0).

Per Ha: bƒ0 e rƒ0 (default), impostare Ipotesi=0 Per Ha: b<0 e r<0, impostare Ipotesi<0 Per Ha: b>0 e r>0, impostare Ipotesi>0

Il riepilogo dei risultati è memorizzato nella variabile stat.results. (Vedere pagina 109).

Catalogo

Variabile di output

stat.RegEqn

stat.t Statistica T per il test di significatività

stat.PVal Livello minimo di significatività in corrispondenza del quale l’ipotesi nulla può essere rifiutata

stat.df Gradi di libertà

stat.a, stat.b Coefficienti di regressione

stat.s Errore standard sulla linea

stat.SESlope Errore standard della pendenza

stat.r

stat.r Coefficiente di correlazione

stat.Resid Residui della regressione

list() (Differenza in una lista)

Descrizione

Equazione di regressione: a + b·x

Coefficiente di determinazione

Catalogo

@list(Lista1) ⇒ lista

Restituisce una lista contenente le differenze tra elementi consecutivi in Lista1. Ogni elemento di Lista1 viene sottratto dal successivo elemento di Lista1. La lista risultante è sempre composta da un elemento in meno della Lista1 originale.

Guida di riferimento di TI-Nspire™ CAS 61

list4mat() (Da lista a matrice)

list4mat(Lista [, elementiPerRiga]) ⇒ matrice

Restituisce una matrice completata riga per riga con gli elementi di

Lista. elementiPerRiga, se incluso, specifica il numero di elementi per riga.

L’impostazione predefinita corrisponde al numero di elementi di Lista (una riga).

Se Lista non completa la matrice risultante, viene aggiunta una serie di zeri.

ln (Conversione in logaritmo naturale)

Espr 4ln ⇒ espressione

Causa la conversione dell’input Espr in un’espressione contenente solo logaritmi naturali (ln).

Catalogo

ln() (Logaritmo naturale)

ln(Espr1) ⇒ espressione ln(Lista1) ⇒ lista

Restituisce il logaritmo naturale dell’argomento. In una lista, restituisce i logaritmi naturali degli elementi.

ln(matriceQuadrata1) ⇒ matriceQuadrata

Restituisce il logaritmo naturale della matrice matriceQuadrata1. Ciò non equivale a calcolare il logaritmo naturale di ogni elemento. Per informazioni sul metodo di calcolo, vedere cos().

matriceQuadrata1 deve essere diagonalizzabile. Il risultato contiene sempre numeri a virgola mobile.

Tasti /u

Se la modalità del formato complesso è Reale:

Se la modalità del formato complesso è Rettangolare:

In modalità angolo in radianti e in modalità formato rettangolare complesso:

Per vedere l’intero risultato, premere £, quindi utilizzare ¡ e

¢ per spostare il cursore

62 Guida di riferimento di TI-Nspire™ CAS

LnReg (Regressione logaritmica)

LnReg X, Y[, [Freq] [, Categoria, Includi]]

Calcola la regressione logaritmica y = a+b·ln(x) sulle liste X e Y con frequenza Freq. Il riepilogo dei risultati è memorizzato nella variabile stat.results. (Vedere pagina 109).

Tutte le liste devono avere le stesse dimensioni, ad eccezione di

Includi. X e Y sono liste di variabili indipendenti e dipendenti. Freq è una lista opzionale di valori di frequenza. Ciascun elemento di

Freq specifica la frequenza di occorrenza di ogni dato corrispondente

di X e Y. Il valore predefinito è 1. Tutti gli elementi devono essere numeri interi | 0.

Categoria è una lista di codici numerici di categoria dei dati corrispondenti di X e Y.

Includi è una lista di uno o più codici di categoria. Solo quei dati il cui codice di categoria è inserito in questa lista vengono inclusi nel calcolo.

Catalogo

Variabile di output

stat.RegEqn

stat.a, stat.b Coefficienti di regressione

stat.r

stat.r Coefficiente di correlazione per dati trasformati (ln(x), y)

stat.Resid Residui associati al modello logaritmico

stat.ResidTrans Residui associati all’adattamento lineare dei dati trasformati

stat.XReg Lista di punti dati della Lista X modificata attualmente usata nella regressione secondo le restrizioni di

stat.YReg Lista di punti dati della Lista Y modificata attualmente usata nella regressione secondo le restrizioni di

stat.FreqReg Lista di frequenze corrispondenti a stat.XReg e stat.YReg

Descrizione

Equazione di regressione: a+b·ln(x)

Coefficiente di determinazione lineare di dati trasformati

Freq, Lista Categoria e Includi Categorie

Guida di riferimento di TI-Nspire™ CAS 63

Local (Variabile locale)

Local Var 1 [, Va r 2] [, Va r 3 ] ...

Definisce le var specificate come variabili locali. Tali variabili esistono solamente durante il calcolo di una funzione e vengono cancellate al termine dell’esecuzione di tale funzione.

Nota: le variabili locali permettono di risparmiare memoria in quanto

esistono solo temporaneamente. Inoltre, esse non influiscono sui valori delle variabili globali esistenti. Le variabili locali devono essere utilizzate per i cicli For e per salvare in maniera provvi soria i valori in una funzione su diverse righe, poiché le modifiche sulle variabili globali non sono ammesse in una funzione.

Nota per l’introduzione dell’esempio: nell’applicazione

Calcolatrice sul palmare, è possibile introdurre definizioni composte da più righe premendo @ invece di · alla fine di ciascuna

riga. Sulla tastiera del computer, mantenere premuto Alt e premere

Invio.

Catalogo

log() (Logaritmo)

log(Espr1[,Espr2]) ⇒ espressione log(Lista1[,Espr2]) ⇒ lista

Restituisce il logaritmo in base-Espr2 dell’argomento.

Nota: vedere anche Modello di logaritmo a pagina 2.

In una lista, restituisce il logaritmo in base-Espr2 degli elementi. Se Espr2 viene omesso, come base viene utilizzato 10.

log(matriceQuadrata1[,Espr2]) ⇒ matriceQuadrata

Restituisce il logaritmo in base-Espr2 della matrice di matriceQuadrata1. Ciò non equivale a calcolare il logaritmo in base- Espr2 di ogni elemento. Per informazioni sul metodo di calcolo,

vedere cos(). matriceQuadrata1 deve essere diagonalizzabile. Il risultato contiene

sempre numeri a virgola mobile. Se l’argomento base viene omesso, come base viene utilizzato 10.

Tasti /

Se la modalità del formato complesso è Reale:

Se la modalità del formato complesso è Rettangolare:

In modalità angolo in radianti e in modalità formato rettangolare complesso:

Per vedere l’intero risultato, premere £, quindi utilizzare ¡ e

¢ per spostare il cursore

64 Guida di riferimento di TI-Nspire™ CAS

logbase

4logbase(Espr1) ⇒ espressione

Espr

Causa la semplificazione dell’input Espr in un’espressione che utilizza la base Espr1.

Catalogo

Logistic (Regressione logistica)

Logistic X, Y[, [Freq] [, Categoria, Includi]]

Calcola la regressione logistica y = (c/(1+a·e con frequenza Freq. Il riepilogo dei risultati è memorizzato nella variabile stat.results. (Vedere pagina 109).

Tutte le liste devono avere le stesse dimensioni, ad eccezione di Includi.

-bx

)) sulle liste X e Y

Catalogo

X e Y sono liste di variabili indipendenti e dipendenti. Freq è una lista opzionale di valori di frequenza. Ciascun elemento di

Freq specifica la frequenza di occorrenza di ogni dato corrispondente

di X e Y. Il valore predefinito è 1. Tutti gli elementi devono essere numeri interi | 0.

Categoria è una lista di codici numerici di categoria dei dati corrispondenti di X e Y.

Includi è una lista di uno o più codici di categoria. Solo quei dati il cui codice di categoria è inserito in questa lista vengono inclusi nel calcolo.

Variabile di output

stat.RegEqn

Descrizione

Equazione di regressione: c/(1+a·e

-bx

)

stat.a, stat.b, stat.c Coefficienti di regressione

stat.Resid Residui della regressione

stat.XReg Lista di punti dati della Lista X modificata attualmente usata nella regressione secondo le restrizioni di

stat.YReg Lista di punti dati della Lista Y modificata attualmente usata nella regressione secondo le restrizioni di

Freq, Lista Categoria e Includi Categorie

stat.FreqReg Lista di frequenze corrispondenti a stat.XReg e stat.YReg

Guida di riferimento di TI-Nspire™ CAS 65

LogisticD (Rgressione logistica)

LogisticD X, Y [, [Iterazioni], [Freq] [, Categoria, Includi]]

Calcola la regressione logistica y = (c/(1+a·e con frequenza Freq, utilizzando un numero specificato di Iterazioni. Il riepilogo dei risultati è memorizzato nella variabile stat.results. (Vedere pagina 109).

Tutte le liste devono avere le stesse dimensioni, ad eccezione di

Includi. X e Y sono liste di variabili indipendenti e dipendenti. Iterazioni è un valore opzionale che specifica quante volte al

massimo verrà tentata una soluzione. Se omesso, viene utilizzato 64. Di solito valori più alti danno una maggiore accuratezza ma richiedono tempi di esecuzione più lunghi, e viceversa.

Freq è una lista opzionale di valori di frequenza. Ciascun elemento di Freq specifica la frequenza di occorrenza di ogni dato corrispondente

di X e Y. Il valore predefinito è 1. Tutti gli elementi devono essere numeri interi

Categoria è una lista di codici numerici di categoria dei dati corrispondenti di X e Y.

Includi è una lista di uno o più codici di categoria. Solo quei dati il cui codice di categoria è inserito in questa lista vengono inclusi nel calcolo.

| 0.

-bx

)+d) sulle liste X e Y

Catalogo

Variabile di output

stat.RegEqn

stat.a, stat.b, stat.c, stat.d

stat.Resid Residui della regressione

stat.XReg Lista di punti dati della Lista X modificata attualmente usata nella regressione secondo le restrizioni di

stat.YReg Lista di punti dati della Lista Y modificata attualmente usata nella regressione secondo le restrizioni di

stat.FreqReg Lista di frequenze corrispondenti a stat.XReg e stat.YReg

Descrizione

Equazione di regressione: c/(1+a·e

Coefficienti di regressione

Freq, Lista Categoria e Includi Categorie

-bx

)+d)

66 Guida di riferimento di TI-Nspire™ CAS

Loop

Blocco

EndLoop

Esegue ciclicamente le istruzioni di Blocco. Si noti che un ciclo viene eseguito infinite volte, se non si trovano istruzioni all’interno di Blocco.

Blocco è una sequenza di istruzioni separate dal carattere.

Nota per l’introduzione dell’esempio: nell’applicazione

Calcolatrice sul palmare, è possibile introdurre definizioni composte da più righe premendo

riga. Sulla tastiera del computer, mantenere premuto Alt e premere

Invio.

@ invece di · alla fine di ciascuna

Goto o Exit

Catalogo

LU (Scomposizione inferiore - superiore)

LU Matrice, nomeMatriceL, nomeMatriceU,

nomeMatriceP[, Tol ]

Calcola la scomposizione LU (lower-upper, inferiore-superiore) di una matrice reale o complessa. La matrice triangolare inferiore è memorizzata in nomeMatriceL, quella superiore in nomeMatriceU, la matrice di permutazione (che descrive gli scambi di riga eseguiti durante i calcoli) in nomeMatriceP.

nomeMatriceL · nomeMatriceU = nomeMatriceP · matrice

In alternativa, un elemento qualsiasi della matrice viene considerato zero se il suo valore assoluto è minore di To l. Tale tolleranza viene utilizzata solo se la matrice contiene elementi a virgola mobile e non contiene variabili simboliche alle quali non sia stato assegnato un valore. In caso contrario, To l viene ignorato.

•Se si usa

•Se Tol viene omesso o non è utilizzato, la tolleranza predefinita

L’algoritmo di scomposizione in fattori LU usa il pivoting parziale per lo scambio di righe.

· oppure se si imposta la modalità Auto

o Approssimato

in virgola mobile.

viene calcolata come: 5EM14 ·max(dim(Matrice)) ·rowNorm(Matrice)

su Approssimato, i calcoli verranno eseguiti

Catalogo

Guida di riferimento di TI-Nspire™ CAS 67

mat4list() (Da matrice a lista)

mat4list(Matrice) ⇒ lista

Restituisce una lista completata con gli elementi di Matrice. Gli elementi sono copiati da Matrice riga per riga.

max() (Massimo)

max(Espr1, Espr2) ⇒ espressione max(Lista1, Lista2) ⇒ lista max(Matrice1, Matrice2) ⇒ matrice

Restituisce il massimo di due argomenti; se questi sono due liste o matrici, restituisce una lista o matrice contenente il valore massimo di ciascuna coppia di elementi corrispondenti.

max(Lista) ⇒ espressione

Restituisce l’elemento massimo di lista.

max(Matrice1) ⇒ matrice

Restituisce un vettore riga contenente l’elemento massimo di ciascuna colonna di Matrice1.

Nota: vedere anche fMax() e min().

mean() Media

mean(Lista[, listaFreq]) ⇒ espressione

Restituisce la media degli elementi di Lista. Ogni elemento di listaFreq conta il numero di occorrenze consecutive

dell’elemento corrispondente di Lista.

mean(Matrice1[, matriceFreq])

⇒ matrice

Restituisce un vettore riga contenente le medie di tutte le colonne di

Matrice1.

Ogni elemento di matriceFreq conta il numero di occorrenze consecutive dell’elemento corrispondente di Matrice1.

In modalità formato vettore rettangolare:

Catalogo

median() (Mediana)

median(Lista) ⇒ espressione

Restituisce la mediana degli elementi di Lista.

Catalogo

68 Guida di riferimento di TI-Nspire™ CAS

median() (Mediana)

median(Matrice1) ⇒ matrice

Restituisce un vettore riga contenente le mediane degli elementi delle colonne di Matrice1.

Nota: tutti gli elementi nella lista o nella matrice devono essere

semplificati in numeri.

Catalogo

MedMed (Linea mediana-mediana)

MedMed X,Y [, Freq] [, Categoria, Includi]]

Calcola la linea mediana-mediana y = (m·x+b) sulle liste X e Y con frequenza Freq. Il riepilogo dei risultati è memorizzato nella variabile stat.results. (Vedere pagina 109).

Tutte le liste devono avere le stesse dimensioni, ad eccezione di

Includi. X e Y sono liste di variabili indipendenti e dipendenti. Freq è una lista opzionale di valori di frequenza. Ciascun elemento di

Freq specifica la frequenza di occorrenza di ogni dato corrispondente

di X e Y. Il valore predefinito è 1. Tutti gli elementi devono essere numeri interi | 0.

Categoria è una lista di codici numerici di categoria dei dati corrispondenti di X e Y.

Includi è una lista di uno o più codici di categoria. Solo quei dati il cui codice di categoria è inserito in questa lista vengono inclusi nel calcolo.

Variabile di output

stat.RegEqn

stat.m, stat.b Coefficienti del modello

stat.Resid Residui della linea mediana-mediana

stat.XReg Lista di punti dati della Lista X modificata attualmente usata nella regressione secondo le restrizioni di

stat.YReg Lista di punti dati della Lista Y modificata attualmente usata nella regressione secondo le restrizioni di

stat.FreqReg Lista di frequenze corrispondenti a stat.XReg e stat.YReg

Descrizione

Equazione linea mediana-mediana: m·x+b

Freq, Lista Categoria e Includi Categorie

Catalogo

mid() (In mezzo alla stringa)

mid(stringaOrigine, Inizio[, Cont]) ⇒ stringa

Restituisce Cont caratteri dalla stringa di caratteri stringaOrigine, incominciando dal numero di carattere di Inizio.

Se Cont viene omesso o se è maggiore della dimensione di stringaOrigine, restituisce tutti i caratteri di stringaOrigine, incominciando dal numero di carattere di Inizio.

Cont deve essere ‚ 0. Se Cont = 0, viene restituita una stringa vuota.

Catalogo

Guida di riferimento di TI-Nspire™ CAS 69

mid() (In mezzo alla stringa)

mid(listaOrigine, Inizio [, Cont]) ⇒ lista

Restituisce Cont elementi da listaOrigine, iniziando dal numero di elemento di Inizio.

Se Cont viene omesso o è maggiore della dimensione di listaOrigine, restituisce tutti gli elementi di listaOrigine, incominciando dal numero di elemento di Inizio.

Cont deve essere

mid(listaStringaOrigine, Inizio[, Cont]) ⇒ lista

Restituisce Cont stringhe della lista delle stringhe listaStringheOrigine, incominciano dal numero di elemento di Inizio.

‚ 0. Se Cont = 0, restituisce una lista vuota.

min() (Minimo)

min(Espr1, Espr2) ⇒ espressione min(Lista1, Lista2) ⇒ lista min(Matrice1, Matrice2) ⇒ matrice

Restituisce il minimo di due argomenti. Se gli argomenti sono due liste o matrici, viene restituita una lista o una matrice contenente il valore minimo di ciascuna coppia di elementi corrispondenti.

min(Lista) ⇒ espressione

Restituisce l’elemento minimo di Lista.

min(Matrice1) ⇒ matrice

Restituisce un vettore di riga contenente l’elemento minimo di ciascuna colonna di Matrice1.

Nota: vedere anche fMin() e max().

Catalogo

mirr()

mirr(tassoFinanziamento,tassoReinvestimento,CF0,CFLista [,CFFreq])

Funzione finanziaria che restituisce l’indice interno di rendimento modificato di un investimento.

tassoFinanziamento è il tasso di interesse che si paga sugli importi di cash flow.

tassoReinvestimento è il tasso di interesse in corrispondenza del quale i cash flow vengono reinvestiti.

Catalogo

CF0 è il cash flow iniziale al tempo 0; deve essere un numero reale. CFLista è una lista di importi di cash flow dopo il cash flow iniziale

CF0. CFFreq è una lista opzionale in cui ciascun elemento specifica la

Nota: vedere anche irr() a pagina 55.

70 Guida di riferimento di TI-Nspire™ CAS

mod() (Modulo)

mod(Espr1, Espr2) ⇒ espressione mod(Lista1, Lista2) ⇒ lista mod(Matrice1, Matrice2) ⇒ matrice

Restituisce il primo argomento modulo secondo argomento, come definito dalle identità:

mod(x,0) = x mod(x,y) = x

Quando il secondo argomento è diverso da zero, il risultato è periodico in tale argomento. Il risultato può essere zero oppure ha lo stesso segno del secondo argomento.

Se gli argomenti sono due liste o due matrici, viene restituita una lista o una matrice contenente il modulo di ciascuna coppia di elementi corrispondenti.

Nota: vedere anche remain() a pagina 93

-ìy floor(x/y)

Catalogo

mRow() (Operazione con righe di matrice)

mRow(Espr, Matrice1, Indice) ⇒ matrice

Restituisce una copia di Matrice1 dove ciascun elemento della riga Indice di Matrice1 viene moltiplicato per Espr.

mRowAdd() (Moltiplicazione e somma di righe di matrice)

mRowAdd(Espr, Matrice1, Indice1, Indice2) ⇒ matrice

Restituisce una copia di Matrice1 dove ciascun elemento della riga Indice2 di Matrice1 viene sostituito con:

Espr × riga Indice1 + riga Indice2

MultReg (Regressione lineare multipla)

MultReg Y, X1[,X2[,X3,…[,X10]]]

Calcola la regressione lineare multipla della lista Y sulle liste X1, X2,

…, X10. Il riepilogo dei risultati è memorizzato nella variabile

stat.results. (Vedere pagina 109).

Tutte le liste devono avere la stessa dimensione.

Variabile di output

stat.RegEqn

Descrizione

Equazione di regressione: b0+b1·x1+b2·x2+ ...

stat.b0, stat.b1, ... Coefficienti di regressione

stat.R

Coefficiente di determinazione multipla

stat.yList yList = b0+b1·x1+ ...

stat.Resid Residui della regressione

Catalogo

Guida di riferimento di TI-Nspire™ CAS 71

MultRegIntervals (Intervalli di confidenza della previsione di regressione multipla)

MultRegIntervals Y,

X1[,X2[,X3,…[,X10]]],listaValX[,livelloConfidenza]

Calcola un valore y previsto, un intervallo di previsione del livello C per una singola osservazione e un intervallo di confidenza del livello C per la risposta media.

Il riepilogo dei risultati è memorizzato nella variabile stat.results. (Vedere pagina 109).

Tutte le liste devono avere la stessa dimensione.

Catalogo

Variabile di output

stat.RegEqn

Descrizione

Equazione di regressione: b0+b1·x1+b2·x2+ ...

stat.y Una stima del punto: y = b0 + b1 · xl + ... per listaValX

stat.dfError Gradi di libertà degli errori

stat.CLower, stat.CUpper Intervallo di confidenza per una risposta media

stat.ME Margine di errore dell’intervallo di confidenza

stat.SE Errore standard della risposta media

stat.LowerPred, stat.UpperrPred

Intervallo di previsione per una singola osservazione

stat.MEPred Margine di errore dell’intervallo di previsione

stat.SEPred Errore standard per la previsione

stat.bList Lista dei coefficienti di regressione, {b0,b1,b2,...}

stat.Resid Residui della regressione

MultRegTests (Verifica sulla regressione lineare multipla)

MultRegTests Y, X1[,X2[,X3,…[,X10]]]

Il test di regressione lineare multipla calcola una regressione lineare multipla sui dati assegnati e fornisce la statistica F test globale e le statistiche t test per i coefficienti.

Il riepilogo dei risultati è memorizzato nella variabile stat.results. (Vedere pagina 109).

Output

Catalogo

Variabile di output

stat.RegEqn

Descrizione

Equazione di regressione: b0+b1·x1+b2·x2+ ...

stat.F Statistica della verifica F globale

stat.PVal Valore P associato alla statistica F globale

stat.R

stat.AdjR

Coefficiente di determinazione multipla

Coefficiente modificato di determinazione multipla

72 Guida di riferimento di TI-Nspire™ CAS

Variabile di output

stat.s Deviazione standard dell’errore

stat.DW Statistica d Durbin-Watson; utilizzata per determinare se la correlazione automatica di primo ordine è

stat.dfReg Gradi di liberà della regressione

stat.SSReg Somma dei quadrati della regressione

stat.MSReg Quadrato medio della regressione

stat.dfError Gradi di libertà degli errori

stat.SSError Somma dei quadrati degli errori

stat.MSError Quadrato medio degli errori

stat.bList {b0,b1,...} Lista dei coefficienti

stat.tList Lista di statistiche t, una per ogni coefficiente di bList

stat.PList Lista di valori P per ogni statistica t

stat.SEList Lista di errori standard per coefficienti di bList

stat.yList listay = b0+b1·x1+...

stat.Resid Residui della regressione

stat.sResid Residui standardizzati; valore ottenuto dividendo un residuo per la sua deviazione standard

stat.CookDist Distanza di Cook; misura dell’influenza di un’osservazione basata sui valori residui e di leverage

stat.Leverage Misura della distanza dei valori della variabile indipendente dai rispettivi valori medi

Descrizione

presente nel modello

nCr() (Combinazioni)

nCr(Espr1, Espr2) ⇒ espressione

Date le espressioni intere Espr1 e Espr2 conEspr1 ‚ Espr2 ‚ 0,

nCr() è il numero di combinazioni degli elementi di Espr1 presi nel

numero di Espr2 per volta (questa procedura è nota anche come coefficiente binomiale). Entrambi gli argomenti possono essere numeri interi o espressioni simboliche.

nCr(Espr1, 0) ⇒ 1

Espr1, interoNeg) ⇒ 0

nCr(

Espr1, interoPos) ⇒ Espr1·(Espr1N1)...

nCr(

(Espr1NinteroPos+1)/ interoPos!

Espr1, nonIntero) ⇒ espressione!/

nCr(

((Espr1NnonIntero)!·nonIntero!)

Lista1, Lista2) ⇒ lista

nCr(

Restituisce una lista di combinazioni sulla base delle coppie di elementi corrispondenti nelle due liste. Le liste degli argomenti devono avere dimensioni uguali.

Catalogo

Guida di riferimento di TI-Nspire™ CAS 73

nCr() (Combinazioni)

nCr(Matrice1, Matrice2) ⇒ matrice

Restituisce una matrice di combinazioni, sulla base delle coppie di elementi corrispondenti nelle due matrici. Le matrici degli argomenti devono avere le stesse dimensioni.

Catalogo

nDeriv() (Derivata numerica)

nDeriv(Espr1, Va r [=Valore] [, H]) ⇒ espressione nDeriv(Espr1, Va r [, H] | Var = Va l or e ) ⇒ espressione nDeriv(Espr1, Va r [=Valore], Lista) ⇒ list nDeriv(Lista1, Va r [=Valore] [, H]) ⇒ lista nDeriv(Matrice1, Va r [=Valore] [, H]) ⇒ matrice

Restituisce la derivata numerica sotto forma di espressione, utilizzando la formula del rapporto incrementale bilaterale.

Quando è specificato, valore ha la priorità su qualsiasi precedente assegnazione di variabile o qualsiasi sostituzione corrente “tale che” della variabile.

H è il valore di incremento. Se H è omesso, viene impostato per default su 0.001.

Se si utilizza Lista1 o Matrice1, l’operazione viene mappata sui valori della lista o sugli elementi della matrice.

Nota: vedere anche avgRC() e d().

newList() (Nuova lista)

newList(numElementi) ⇒ lista

Restituisce una lista le cui dimensioni sono numElementi. Ciascun elemento è zero.

newMat() (Nuova matrice)

newMat(numRighe, numColonne) ⇒ matrice

Restituisce una matrice di zeri le cui dimensioni sono date da numRighe per numColonne.

nfMax() (Massimo di una funzione calcolato numericamente)

nfMax(Espr, Var ) ⇒ valore nfMax(Espr, Var , estremoInf) ⇒ valore

nfMax(Espr, Var , estremoInf, estremoSup) ⇒ valore nfMax(Espr, Var) | estremoInf<Var <estremoSup ⇒ valore

Restituisce un possibile valore calcolato numericamente della variabile Var che produce il massimo locale di Espr.

Se si specificano estremoInf e estremoSup, la funzione cerca il massimo locale tra questi valori.

Nota: vedere anche fMax() e d().

Catalogo

74 Guida di riferimento di TI-Nspire™ CAS

nfMin() (Minimo di una funzione calcolato numericamente)

nfMin(Espr, Var ) ⇒ valore nfMin(

Espr, Va r, estremoInf) ⇒ valore Espr, Va r, estremoInf, estremoSup) ⇒ valore

nfMin( nfMin(

Espr, Var) | estremoInf<Var <estremoSup ⇒ valore

Restituisce un possibile valore calcolato numericamente della variabile Var che produce il minimo locale di Espr.

Se si specificano estremoInf e estremoSup, la funzione cerca il minimo locale tra questi valori.

Nota: vedere anche fMin() and d().

Catalogo

nInt() (Integrale numerico)

nInt(Espr1, Var, Inferiore, Superiore) ⇒ espressione

Se la funzione da integrare Espr1 non contiene nessun’altra variabile oltre a Var e se Inferiore e Superiore sono costanti, ˆ positivo o ˆ negativo, allora nInt() restituisce un’approssimazione di

‰(Espr1,Var , Inferiore, Superiore). Tale approssimazione è una

media pesata di alcuni valori esemplificativi della funzione da integrare nell’intervallo Inferiore<Va r <Superiore.

L’obiettivo sono sei cifre significative. L’algoritmo adattivo termina quando sembra che l’obiettivo sia stato raggiunto, oppure quando sembra che ulteriori esempi non potrebbero portare alcun miglioramento significativo.

Viene visualizzato un avvertimento ("Accuratezza dubbia") quando sembra che l’obiettivo non sia stato raggiunto.

È possibile nidificare nInt() per un’integrazione numerica multipla. I limiti di integrazione possono dipendere da variabili di integrazione esterne ad essi.

Nota: vedere anche ‰() a pagina 140.

nom()

nom(tassoEffettivo,CpY) ⇒ valore

Funzione finanziaria che converte il tasso di interesse effettivo annuo tassoEffettivo in un tasso nominale, essendo CpY il numero di periodi di capitalizzazione per anno.

tassoEffettivo deve essere un numero reale e CpY deve essere un numero reale > 0.

Nota: vedere anche eff() a pagina 37.

Catalogo

Guida di riferimento di TI-Nspire™ CAS 75

norm() (Norma di Froebius)

norm(Matrice) ⇒ espressione norm(Vettore) ⇒ espressione

Restituisce la norma di Frobenius.

Catalogo

normalLine() (Retta normale)

normalLine (Espr1,Va r ,Punto) ⇒ espressione normalLine(Espr1,Va r =Punto) ⇒ espressione

Restituisce la retta normale alla curva rappresentata da Espr1 nel punto specificato in Va r=Punto.

Accertarsi che la variabile indipendente non sia definita. Per esempio, se f1(x):=5 e x:=3, allora normalLine(f1(x),x,2) restituisce "false".

normCdf() (Probabilità di distribuzione normale)

normCdf(valoreInferiore,valoreSuperiore[,m[,s]]) ⇒ numero

valoreInferiore e valoreSuperiore sono numeri, lista se

valoreInferiore e valoreSuperiore sono liste Calcola la probabilità di distribuzione normale tra valoreInferiore e

valoreSuperiore per m (default=0) e s (default=1) specificati. Per P(X  valoreSuperiore), impostare valoreInferiore = .ˆ.

normPdf() (Densità di probabilità)

normPdf(Val X [,m[,s]]) ⇒ numero se Va l X è un numero, lista

Val X è una lista

Calcola la funzione della densità di probabilità per la distribuzione normale in un valore valX specificato per m s specificati.

not

not EsprBooleana1 ⇒ espressione booleana

Restituisce vero o falso o una forma semplificata dell’argomento.

Catalogo

76 Guida di riferimento di TI-Nspire™ CAS

not

not Intero1 ⇒ intero

Restituisce il complemento a uno di un intero reale. Internamente, Intero1 viene convertito in numero binario a 64 bit con segno. Il valore di ciascun bit viene scambiato (0 diventa 1 e viceversa) per il complemento a uno. I risultati vengono visualizzati nella modalità Base che è stata impostata.

È possibile inserire l’intero in qualsiasi base numerica. Se si tratta di un numero binario o esadecimale, utilizzare rispettivamente il prefisso 0b o 0h. Senza prefisso, l’intero viene considerato decimale (base 10).

Se viene indicato un intero decimale troppo grande per una forma binaria con segno a 64 bit, verrà utilizzata un’operazione a modulo simmetrico per portare il valore nell’intervallo appropriato.

In modalità base Esadecimale:

Importante: è zero, non la lettera O.

In modalità base Bin:

Catalogo

nPr() (Disposizioni semplici)

nPr(Espr1, Espr2) ⇒ espressione

Per Espr1 ed Espr2 intere, dove Espr1 ‚ Espr2 ‚ 0, nPr() corrisponde al numero di disposizioni semplici degli elementi di Espr1 prese nel numero di Espr2 alla volta. Entrambi gli argomenti possono essere numeri interi o espressioni simboliche.

nPr(Espr, 0) ⇒ 1

Espr, interoNeg) ⇒ 1/((Espr+1)·(Espr+2)...

nPr(

(

espressioneNinteroNeg))

Espr, interoPos)

nPr(

⇒ Espr·(EsprN1)... (EsprNinteroPos+1)

Espr, nonIntero) ⇒ Espr! / (EsprNnonIntero)!

nPr(

Lista1, Lista2) ⇒ lista

Restituisce una lista delle disposizioni semplici sulla base delle coppie di elementi corrispondenti nelle due liste. Le liste degli argomenti devono avere dimensioni uguali.

nPr(Matrice1, Matrice2) ⇒ matrice

Restituisce una matrice di disposizioni semplici sulla base delle coppie di elementi corrispondenti nelle due matrici. Le matrici degli argomenti devono avere le stesse dimensioni.

Per vedere l’intero risultato, premere

£, quindi utilizzare ¡ e

¢ per spostare il cursore

Nota: un numero binario può contenere fino a 64 cifre (oltre al

prefisso 0b). Un numero esadecimale può contenere fino ad 16 cifre.

Catalogo

Guida di riferimento di TI-Nspire™ CAS 77

npv()

npv(tassoInteresse,CFO,CFLista[,CFFreq])

Funzione finanziaria che calcola il valore presente netto (Net Present Value), la somma dei valori presenti per i cash flow in entrata (somme ricevute) e in uscita (somme pagate). Un risultato positivo per npv indica un investimento proficuo.

tassoInteresse è il tasso a cui scontare i cash flow (il costo del denaro) di un dato periodo.

CF0 è il cash flow iniziale al tempo 0; deve essere un numero reale. CFLista è una lista di importi di cash flow dopo il cash flow iniziale

CF0. CFFreq è una lista in cui ciascun elemento specifica la frequenza di

occorrenza di un importo di cash flow raggruppato (consecutivo), che è l’elemento corrispondente di CFLista. L’impostazione pr edefinita è 1; è possibile inserire valori che siano numeri interi positivi < 10000.

Catalogo

nSolve() (Soluzione numerica)

nSolve(Equazione,Var [=Campione]) ⇒ numero o

stringa_errore

nSolve(Equazione,Var [=Campione],estremoInf)

⇒ numero o stringa_errore

nSolve(Equazione,Var [=Campione],estremoInf,estremoSup)

⇒ numero o stringa_errore

nSolve(Equazione,Var [=Campione]) |

estremoInf<Var <estremoSup

⇒ numero o stringa_errore

Ricerca iterativamente una soluzione numerica reale approssimata dell’Equazione per la sua variabile. Specificare la variabile come:

variabile

– o – variabile = numero reale

Ad esempio, x è valido come pure x=3.

nSolve() risulta spesso più veloce di solve() o di zeros(),

soprattutto se viene utilizzato l’operatore "|" pe r limitare la ricerca in un intervallo piccolo che contenga esattamente una soluzione semplice.

nSolve() cerca di determinare un punto in cui il resto sia zero

oppure due punti relativamente vicini, nei quali il resto abbia segni opposti e la grandezza del resto non sia eccessiva. Se non è possibile ottenere ciò utilizzando un numero limitato di punti campione, viene restituita la stringa "Nessuna soluzione trovata".”

Nota: vedere anche cSolve(), cZeros(), solve() e zeros().

Catalogo

Nota: se vi sono soluzioni multiple, è possibile usare un valore

campione per trovare una soluzione particolare.

78 Guida di riferimento di TI-Nspire™ CAS

OneVar (Statistiche a una variabile)

OneVar [1,]X[,[Freq][,Categoria,Includi]] OneVar [

n,]X1,X2[X3[,…[,X20]]]

Calcola le statistiche ad una variabile fino a 20 liste. Il riepilogo dei risultati è memorizzato nella variabile stat.results. (Vedere pagina

109). Tutte le liste devono avere le stesse dimensioni, ad eccezione di

Includi. Gli argomenti di X sono liste di dati. Freq è una lista opzionale di valori di frequenza. Ciascun elemento di

Freq specifica la frequenza di occorrenza di ogni dato corrispondente

di X. Il valore predefinito è 1. Tutti gli elementi devono essere numeri interi | 0.

Categoria è una lista di codici numerici di categoria dei dati corrispondenti di X.

Includi è una lista di uno o più codici di categoria. Solo quei dati il cui codice di categoria è inserito in questa lista vengono inclusi nel calcolo.

Variabile di output

stat.v

Statistiche.Gx

stat.Gx

stat.sx Deviazione standard del campione di X

stat.ssssx Deviazione standard della popolazione di X

stat.n Numero dei punti di dati

stat.MinX Minimo dei valori x

stat.Q1X 1° quartile di x

stat.MedianX Mediana di x

stat.Q3X 3° quartile di x

stat.MaxX Massimo dei valori x

stat.SSX Somma dei quadrati delle deviazioni dalla media di x

Descrizione

Media dei valori X

Somma dei valori X

Catalogo

Guida di riferimento di TI-Nspire™ CAS 79

EsprBooleana1 or EsprBooleana2

⇒ espressione booleana

Restituisce vero o falso o una forma semplificata dell’espressione immessa originariamente.

Restituisce vero se la semplificazione di una o di entrambe le espressioni risulta vera. Restituisce falso solo se il calcolo di entrambe le espressioni risulta falso.

Nota: vedere xor. Nota per l’introduzione dell’esempio: nell’applicazione

Calcolatrice sul palmare, è possibile introdurre definizioni composte da più righe premendo @ invece di · alla fine di ciascuna

riga. Sulla tastiera del computer, mantenere premuto Alt e premere

Invio.

Intero1 or Intero2 ⇒ intero

Confronta due interi reali bit per bit tramite un’operazione or. Internamente, entrambi gli interi vengono convertiti in numeri binari a 64 bit con segno. Quando vengono confrontati bit corrispondenti, il risultato sarà 1 se uno dei due bit è uguale a 1; se entrambi i bit sono uguali a 0, il risultato sarà 0. Il valore restituit o rappresenta il risultato dei bit e viene visualizzato nella modalità base che è stata impostata.

Se viene indicato un intero decimale troppo grande per una forma binaria con segno a 64 bit, verrà utilizzata un’operazione a modulo simmetrico per portare il valore nell’intervallo appropriato.

Nota: vedere xor.

Catalogo

In modalità base Esadecimale:

Importante: è zero, non la lettera O.

In modalità base Bin:

Nota: un numero binario può contenere fino a 64 cifre (oltre al

prefisso 0b). Un numero esadecimale può contenere fino ad 16 cifre.

ord() Codice numerico di carattere

ord(Stringa) ⇒ intero ord(Lista1) ⇒ lista

Restituisce il codice numerico del primo carattere nella stringa di caratteri Stringa, oppure una lista dei primi caratteri di ciascun elemento della lista.

Catalogo

P4Rx() (Coordinata x rettangolare)

P4Rx(rEspr, qEspr) ⇒ espressione

P4Rx(rLista, qLista) ⇒ lista P4Rx(rMatrice, qMatrice) ⇒ matrice

Restituisce la coordinata x equivalente della coppia (r, q).

Nota: l’argomento q viene interpretato come angolo in gradi,

gradianti o radianti, conformemente alla modalità di misurazione degli angoli impostata. Se l’argomento è un’espressione, si può

utilizzare il simbolo ó,G o ô per escludere tale impostazione provvisoriamente.

In modalità angolo in radianti:

80 Guida di riferimento di TI-Nspire™ CAS

Catalogo

P4Ry() (Coordinata y rettangolare)

P4Ry(rEspr, qEspr) ⇒ espressione P4Ry(rLista, qLista) ⇒ lista P4Ry(rMatrice, qMatrice) ⇒ matrice

Restituisce la coordinata y equivalente della coppia (r, q).

Nota: l’argomento q viene interpretato come angolo in gradi,

gradianti o radianti, conformemente alla modalità di misurazione degli angoli impostata. Se l’argomento è un’espressione, si può

utilizzare il simbolo provvisoriamente.

ó,

o ô per escludere tale impostazione

In modalità angolo in radianti:

Catalogo

PassErr

Passa un errore al livello successivo. Se la variabile di sistema errCode è zero, PassErr non esegue

alcuna azione. L’istruzione Else del blocco Try...Else...EndTry dovrebbe utilizzare

ClrErr o PassErr. Se l’errore deve essere elaborato o ignorato,

Try...Else...EndTry in attesa di applicazione, la finestra di dialogo

dell’errore viene visualizzata come normale.

Nota: vedere anche ClrErr a pagina 16e Try a pagina 119. Nota per l’introduzione dell’esempio: nell’applicazione

Calcolatrice sul palmare, è possibile introdurre definizioni composte da più righe premendo @ invece di · alla fine di ciascuna

riga. Sulla tastiera del computer, mantenere premuto Alt e premere

Invio.

piecewise() (Funzione definita a tratti)

piecewise(Espr1 [, Condizione1 [, Espr2 [, Condizione2 [, … ]]]])

Restituisce definizioni di una funzione piecewise (definita a tratti) sotto forma di elenco. È inoltre possibile creare definizioni piecewise utilizzando un modello.

Nota: vedere anche Modello di funzione piecewise a

pagina 2.

poissCdf() (Probabilità cumulata per la distribuzione discreta di Poisson)

poissCdf(l,valoreInferiore,valoreSuperiore) ⇒ numero se

valoreInferiore e valoreSuperiore sono numeri, lista se valoreInferiore e valoreSuperiore sono liste

poissCdf(

l,valoreSuperiore) (per

P(0

XvaloreSuperiore) ⇒ numero se valoreSuperiore è un

numero, lista se

Calcola una probabilità cumulata per la distribuzione discreta di Poisson con la media l specificata.

valoreSuperiore è una lista

Per P(X  valoreSuperiore), impostare valoreInferiore=0

Catalogo

Per un esempio di PassErr, vedere l’esempio 2 del comando

Try a pagina 119.

Catalogo

Guida di riferimento di TI-Nspire™ CAS 81

poissPdf() (Probabilità per la distribuzione discreta di Poisson)

poissPdf(l,Val X ) ⇒ numero se Va l X è un numero, lista se

Val X è una lista

Calcola una probabilità per la distribuzione discreta di Poisson con la media l specificata.

Polar (Visualizza come vettore polare)

4Polare

Vettore

Visualizza vettore in forma polare [r q]. Il vettore deve essere bidimensionale e può essere sia una riga che una colonna.

Nota: 4Polar è un’istruzione in formato di visualizzazione, n on una

funzione di conversione. Tale istruzione può essere impiegata solo alla fine di una riga di introduzione e non aggiorna ans.

Nota: vedere anche 4Rect a pagina 92.

valoreComplesso 4Polar

Visualizza vettoreComplesso in forma polare.

• In modalità angolo in gradi, restituisce (rq).

• In modalità angolo in radianti, restituisce reiq.

valoreComplesso può avere una forma complessa qualsiasi. Tuttavia

una voce re

q causa un errore nella modalità di misurazione degli

angoli in gradi.

Nota: è necessario usare le parentesi per un inserimento polare

(rq).

Catalogo

In modalità angolo in radianti:

In modalità angolo in gradianti (gradi centesimali):

In modalità angolo in gradi:

82 Guida di riferimento di TI-Nspire™ CAS

polyCoeffs()

polyCoeffs(Poli [,Var ]) ⇒ lista

Restituisce una lista di coefficienti di polinomio Poli in funzione della variabile Var .

Poli deve essere un’espressione polinomiale in Va r . Si consiglia di non omettere Va r a meno che Poli non sia un’espressione in una variabile singola.

Catalogo

Espande il polinomio e seleziona x per la Va r omessa.

polyDegree()

polyDegree(Poli [,Var ]) ⇒ valore

Restituisce il grado dell’espressione polinomiale Poli in funzione della variabile Va r. Se si omette Va r, la funzione polyDegree() seleziona un’impostazione predefinita dalle variabili contenute nel polinomio Poli.

Poli deve essere un’espressione polinomiale in Va r . Si consiglia di non omettere Va r a meno che Poli non sia un’espressione in una sola variabile.

polyEval() (Calcola polinomio)

polyEval(Lista1, Espr1) ⇒ espressione polyEval(Lista1, Lista2) ⇒ espressione

Interpreta il primo argomento come coefficiente di un polinomio di grado decrescente e restituisce il polinomio calcolato per il valore del secondo argomento.

Catalogo

Polinomi costanti

Il grado può essere estratto, ma non i coefficienti. Questo perché è possibile estrarre il grado senza espandere il polinomio.

Catalogo

Guida di riferimento di TI-Nspire™ CAS 83

polyGcd()

polyGcd(Espr1,Espr2) ⇒ espressione

Restituisce il massimo comune divisore (gcd) dei due argomenti. Espr1 e Espr2 devono essere espressioni polinomiali. Non sono ammessi come argomenti liste, matrici e booleani.

Catalogo

polyQuotient()

polyQuotient(Poli1,Poli2 [,Var ]) ⇒ espressione

Restituisce il quoziente del polinomio Poli1 diviso per il polinomio Poli2 in funzione della variabile specificata Va r .

Poli1 e Poli2 devono essere espressioni polinomiali in Va r . Si

consiglia di non omettere Va r a meno che Poli1 e Poli2 non siano espressioni nella stessa variabile singola.

polyRemainder()

polyRemainder(Poli1,Poli2 [,Var ]) ⇒ espressione

Restituisce il resto del polinomio Poli1 diviso per il polinomio Poli2 in funzione della variabile specificata Va r .

Poli1 e Poli2 devono essere espressioni polinomiali in Va r . Si consiglia di omettere Va r a meno che Poli1 e Poli2 non siano espressioni nella stessa variabile singola.

Catalogo

84 Guida di riferimento di TI-Nspire™ CAS

PowerReg (Regressione su potenza)

PowerReg X,Y [, Freq] [, Categoria, Includi]]

Calcola la regressione su potenza y = (a·(x)b) sulle liste X e Y con frequenza Freq. Il riepilogo dei risultati è memorizzato nella variabile stat.results. (Vedere pagina 109).

Tutte le liste devono avere le stesse dimensioni, ad eccezione di

Includi. X e Y sono liste di variabili indipendenti e dipendenti. Freq è una lista opzionale di valori di frequenza. Ciascun elemento di

Freq specifica la frequenza di occorrenza di ogni dato corrispondente

di X e Y. Il valore predefinito è 1. Tutti gli elementi devono essere numeri interi | 0.

Categoria è una lista di codici numerici di categoria dei dati corrispondenti di X e Y.

Includi è una lista di uno o più codici di categoria. Solo quei dati il cui codice di categoria è inserito in questa lista vengono inclusi nel calcolo.

Catalogo

Variabile di output

stat.RegEqn

Descrizione

Equazione di regressione: a·(x)

stat.a, stat.b Coefficienti di regressione

stat.r

Coefficiente di determinazione lineare di dati trasformati

stat.r Coefficiente di correlazione per dati trasformati (ln(x), ln(y))

stat.Resid Residui associati al modello di potenza

stat.ResidTrans Residui associati all’adattamento lineare dei dati trasformati

stat.XReg Lista di punti dati della Lista X modificata attualmente usata nella regressione secondo le restrizioni di

stat.YReg Lista di punti dati della Lista Y modificata attualmente usata nella regressione secondo le restrizioni di

Freq, Lista Categoria e Includi Categorie

stat.FreqReg Lista di frequenze corrispondenti a stat.XReg e stat.YReg

Guida di riferimento di TI-Nspire™ CAS 85

Prgm

Blocco

EndPrgm

Modello per la creazione di un programma definito dall’utente. Deve essere utilizzato con il comando

Define LibPriv.

Blocco può essere una singola istruzione, una serie di istruzioni separate dal carattere “:” o una serie di istruzioni su righe separate.

Nota per l’introduzione dell’esempio: nell’applicazione

Calcolatrice sul palmare, è possibile introdurre definizioni composte

Define, Define LibPub o

Calcolare il massimo comune divisore e visualizzare i risultati intermedi.

Catalogo

da più righe premendo @ invece di · alla fine di ciascuna riga. Sulla tastiera del computer, mantenere premuto Alt e premere

Invio.

Product (PI) (Prodotto) Vedere P() a pagina 142.

product() (Prodotto)

product(Lista[, Inizio[, Fine]]) ⇒ espressione

Restituisce il prodotto degli elementi contenuti in Lista. Inizio e Fine sono opzionali e specificano un intervallo di elementi.

product(Matrice1[, Inizio[, Fine]]) ⇒ matrice

Restituisce un vettore di riga contenente i prodotti degli elementi nelle colonne di Matrice1. Inizio e Fine sono opzionali e specificano un intervallo di elementi.

propFrac() (Frazione propria)

propFrac(Espr1[, Va r ]) ⇒ espressione

propFrac(numero_razionale) restituisce numero_razionale sotto

forma di somma di un numero intero e di una frazione, aventi lo stesso segno e denominatore di grandezza maggiore del numeratore.

Catalogo

86 Guida di riferimento di TI-Nspire™ CAS

propFrac() (Frazione propria)

propFrac(espressione_razionale,Var ) restituisce la somma delle

frazioni proprie ed un polinomio rispetto a Va r . Il grado di Va r nel denominatore supera il grado di Va r nel numeratore di ciascuna frazione propria. Le potenze simili di Va r sono ridotte. I termini ed i rispettivi fattori sono ordinati considerando Va r la variabile principale.

Se Va r è omesso, viene eseguita l’espansione della frazione propria rispetto alla variabile più significativa. I coefficienti della parte polinomiale vengono trasformati in propri rispetto alla prima va riabile più significativa, e così di seguito.

Nelle espressioni razionali, propFrac() costituisce un’alternativa più veloce ma meno completa di expand().

Catalogo

QR (Scomposizione QR)

QR Matrice, MatriceQ, MatriceR[, Tol ]

Calcola la scomposizione QR di Householder di una matrice reale o complessa. Le matrici Q ed R che si ottengono vengono memorizzate nei Matrice specificati. La matrice Q è unitaria. La matrice R è triangolare superiore.

•Se si usa

•Se Tol viene omesso o non è utilizzato, la tolleranza predefinita

La scomposizione QR viene calcolata in modo numerico tramite trasformazioni di Householder; la soluzione simbolica tramite GramSchmidt. Le colonne in nomeMatriceQ sono i vettori della base ortonormale con estensione pari allo spazio definito da matrice.

· oppure se si imposta la modalità Auto

o Approssimato

in virgola mobile.

viene calcolata come: 5Eë14 ·max(dim(Matrice)) ·rowNorm(Matrice)

su Approssimato, i calcoli verranno eseguiti

Catalogo

Il numero a virgola mobile (9.) in m1 fa sì che i risultati vengano calcolati nella forma a virgola mobile.

Guida di riferimento di TI-Nspire™ CAS 87

QuadReg (Regressione quadratica)

QuadReg X,Y [, Freq] [, Categoria, Includi]]

Calcola la regressione polinomiale quadratica y =

·x

+b·x+c sulle liste X e Y con frequenza Freq. Il riepilogo dei

risultati è memorizzato nella variabile stat.results. (Vedere pagina

109). Tutte le liste devono avere le stesse dimensioni, ad eccezione di

Includi. X e Y sono liste di variabili indipendenti e dipendenti. Freq è una lista opzionale di valori di frequenza. Ciascun elemento di

Freq specifica la frequenza di occorrenza di ogni dato corrispondente

di X e Y. Il valore predefinito è 1. Tutti gli elementi devono essere numeri interi

Categoria è una lista di codici numerici di categoria dei dati corrispondenti di X e Y.

Includi è una lista di uno o più codici di categoria. Solo quei dati il cui codice di categoria è inserito in questa lista vengono inclusi nel calcolo.

| 0.

Catalogo

Variabile di output

stat.RegEqn

stat.a, stat.b, stat.c Coefficienti di regressione

stat.R

stat.Resid Residui della regressione

stat.XReg Lista di punti dati della Lista X modificata attualmente usata nella regressione secondo le restrizioni di

stat.YReg Lista di punti dati della Lista Y modificata attualmente usata nella regressione secondo le restrizioni di

stat.FreqReg Lista di frequenze corrispondenti a stat.XReg e stat.YReg

Descrizione

Equazione di regressione: a·x2+b·x+c

coefficiente di determinazione

Freq, Lista Categoria e Includi Categorie

88 Guida di riferimento di TI-Nspire™ CAS

QuartReg (Regressione quartica)

QuartReg X,Y [, Freq] [, Categoria, Includi]]

Calcola la regressione polinomiale quartica

y = a

·x

+b·x3+c· x2+d·x+e sulle liste X e Y con frequenza Freq.

Il riepilogo dei risultati è memorizzato nella variabile stat.results. (Vedere pagina 109).

Tutte le liste devono avere le stesse dimensioni, ad eccezione di

Includi. X e Y sono liste di variabili indipendenti e dipendenti. Freq è una lista opzionale di valori di frequenza. Ciascun elemento di

Freq specifica la frequenza di occorrenza di ogni dato corrispondente

di X e Y. Il valore predefinito è 1. Tutti gli elementi devono essere numeri interi

Categoria è una lista di codici numerici di categoria dei dati corrispondenti di X e Y.

Includi è una lista di uno o più codici di categoria. Solo quei dati il cui codice di categoria è inserito in questa lista vengono inclusi nel calcolo.

| 0.

Catalogo

Variabile di output

stat.RegEqn

stat.a, stat.b, stat.c, stat.d, stat.e

stat.R

stat.Resid Residui della regressione

stat.XReg Lista di punti dati della Lista X modificata attualmente usata nella regressione secondo le restrizioni di

stat.YReg Lista di punti dati della Lista Y modificata attualmente usata nella regressione secondo le restrizioni di

stat.FreqReg Lista di frequenze corrispondenti a stat.XReg e stat.YReg

Descrizione

Equazione di regressione: a·x4+b·x3+c· x2+d·x+e

Coefficienti di regressione

coefficiente di determinazione

Freq, Lista Categoria e Includi Categorie

Guida di riferimento di TI-Nspire™ CAS 89

R4Pq() (Coordinata polare)

R4Pq (xEspr, yEspr) ⇒ espressione R4Pq (xLista, yLista) ⇒ lista R4Pq (xMatrice, yMatrice) ⇒ matrice

Restituisce la coordinata q equivalente alla coppia di argomenti (x,y).

Nota: conformemente alla modalità di misurazione degli angoli

impostata, il risultato è in gradi, gradianti o radianti.

R4Pr() Coordinata polare

R4Pr (xEspr, yEspr) ⇒ espressione R4Pr (xLista, yLista) ⇒ lista R4Pr (xMatrice, yMatrice) ⇒ matrice

Restituisce la coordinata r equivalente alla coppia di argomenti (x,y).

Catalogo

In modalità angolo in gradi:

In modalità angolo in gradianti (gradi centesimali):

In modalità angolo in radianti:

Catalogo

In modalità angolo in radianti:

Rad in angolo radiante

Espr14Rad ⇒ espressione

Converte l’argomento in una misura d’angolo in radianti.

rand() (Numero casuale)

rand() ⇒ espressione rand(numTentativi) ⇒ lista

rand() restituisce un numero casuale compreso tra 0 e 1. rand(numTentativi) restituisce una lista contenente numTentativi

valori casuali compresi tra 0 e 1.

In modalità angolo in gradi:

In modalità angolo in gradianti (gradi centesimali):

Imposta il seme dei numeri casuali.

Catalogo

90 Guida di riferimento di TI-Nspire™ CAS

randBin() (Numero casuale da distribuzione binomiale)

randBin(n, p) ⇒ espressione randBin(n, p, numTentativi) ⇒ lista

randBin(n, p) restituisce un numero reale casuale da una

distribuzione binomiale specificata.

randBin(n, p, numTentativi) restituisce una lista contenente

numTentativi numeri reali casuali da una distribuzione binomiale specificata.

Catalogo

randInt() (Intero casuale)

randInt(EstremoInf,EstremoSup) ⇒ espressione randInt(EstremoInf,EstremoSup,numTentativi) ⇒ lista

randInt(EstremoInf,EstremoSup) restituisce un intero casuale

all’interno dell’intervallo specificato dagli numeri interi EstremoInf e EstremoSup.

randInt(EstremoInf,EstremoSup,numTentativi) restituisce un

elenco contenente NumTentativi interi casuali all’interno dell’intervallo specificato.

randMat() (Matrice casuale)

randMat(numRighe, numColonne) ⇒ matrice

Restituisce una matrice di numeri interi compresi tra -9 e 9 della dimensione specificata.

Entrambi gli argomenti devono potere essere semplificati in numeri interi.

randNorm() (Normale casuale)

randNorm(m, s [,numProve]) ⇒ espressione

Restituisce un numero decimale dalla distribuzione normale specifica. Può essere qualsiasi numero reale, anche se con maggiore probabilità

sarà compreso nell’intervallo [mN3·s, m+3·s].

randPoly() (Polinomio casuale)

randPoly(Va r , Ordine) ⇒ espressione

Restituisce un polinomio in Va r dell’Ordine specificato. I coefficienti sono numeri interi casuali compresi nell’intervallo tr a ë9 e 9. Il primo coefficiente non può essere zero.

Ordine deve essere tra 0 e 99.

Catalogo

Nota: i valori di questa matrice cambiano ogni volta che si

preme ·.

Catalogo

randSamp() (Campione casuale)

randSamp(Lista,NumTentativi[,noSostituzione]) ⇒ lista

Restituisce una lista contenente un campione casuale di NumTentativi da Lista con l’opzione di sostituire (noSostituzione=0) o meno (noSostituzione=1) il campione. L’impostazione predefinita prevede la sostituzione del campione.

Catalogo

Guida di riferimento di TI-Nspire™ CAS 91

RandSeed (Seme numero casuale)

RandSeed Numero

Se Numero = 0, imposta i semi ai valori predefiniti per il generatore di numeri casuali. Se Numero semi, memorizzati nelle variabili di sistema seed1 e seed2.

ƒ 0, viene utilizzato per generare due

Catalogo

real() (Reale)

real(Espr1) ⇒ espressione

Restituisce la parte reale dell’argomento.

Nota: tutte le variabili non definite vengono considerate come

variabili reali. vedere anche imag() a pagina 53.

real(Lista1) ⇒ lista

Restituisce le parti reali di tutti gli elementi.

real(Matrice1) ⇒ matrice

Restituisce le parti reali di tutti gli elementi.

Rect (Visualizza come vettore rettangolare)

Vettore 4Rect

Visualizza Vettore nella forma rettangolare [x, y, z]. Le dimensioni del vettore devono essere 2 o 3 e il vettore può essere una riga o una colonna.

Nota: 4Rect è un’istruzione del formato di visualizzazione, non una

funzione di conversione. Tale istruzione può essere impiegata solo alla fine di una riga di introduzione e non aggiorna ans.

Nota: vedere anche 4Polar a pagina 82.

valoreComplesso 4Rect

Visualizza valoreComplesso nella forma rettangolare a+bi. valoreComplesso può avere una forma complessa qualsiasi. Tuttavia

un inserimento nella forma re misurazione degli angoli in gradi.

Nota: è necessario usare le parentesi per un inserimento polare

(rq).

causa un errore nella modalità di

Catalogo

In modalità angolo in radianti:

In modalità angolo in gradianti (gradi centesimali):

In modalità angolo in gradi:

Nota: per inserire  dalla tastiera, selezionarlo nell’elenco dei

simboli del Catalogo.

92 Guida di riferimento di TI-Nspire™ CAS

ref() (Forma a scalini per righe)

ref(Matrice1[, To l ]) ⇒ matrice

Restituisce la forma a scalini per righe di Matrice1. In alternativa, un elemento qualsiasi della matrice viene considerato

zero se il suo valore assoluto è minore di To l. Tale tolleranza viene utilizzata solo se la matrice contiene elementi a virgola mobile e non contiene variabili simboliche alle quali non sia stato assegnato un valore. In caso contrario, To l viene ignorato.

•Se si usa

•Se Tol viene omesso o non è utilizzato, la tolleranza predefinita

Nota: vedere anche rref() a pagina 96.

o Approssimato

in virgola mobile.

viene calcolata come: 5Eë14 ·max(dim(Matrice1)) ·rowNorm(Matrice1)

· oppure se si imposta la modalità Auto

su Approssimato, i calcoli verranno eseguiti

Catalogo

remain() (Resto)

remain(Espr1, Espr2) ⇒ espressione remain(Lista1, Lista2) ⇒ lista remain(Matrice1, Matrice2) ⇒ matrice

Restituisce il resto del primo argomento rispetto al secondo argomento, come definito dalle identità:

remain(x,0)  x remain(x,y)  xNy·iPart(x/y)

Si noti che, di conseguenza remain(Nx,y)  Nremain(x,y). Il risultato può essere zero oppure può avere lo stesso segno del primo argomento.

Nota: vedere anche mod() a pagina 71.

Return (Restituisci)

Return [Espr]

Restituisce Espr quale risultato della funzione. Questo comando viene utilizzato all’interno di un blocco Func...EndFunc.

Nota: utilizzare Return senza alcun argomento all’interno di un

blocco Prgm...EndPrgm per uscire da un programma.

Nota per l’introduzione dell’esempio: nell’applicazione

Calcolatrice sul palmare, è possibile introdurre definizioni composte da più righe premendo @ invece di · alla fine di ciascuna

riga. Sulla tastiera del computer, mantenere premuto Alt e premere

Invio.

right() (Destra)

right(Lista1[, Num]) ⇒ lista

Restituisce i Num elementi più a destra contenuti in Lista1. Se si omette Num, restituisce l’intera Lista1.

Catalogo

Guida di riferimento di TI-Nspire™ CAS 93

right() (Destra)

right(stringaOrigine[, Num]) ⇒ stringa

Restituisce i caratteri Num più a destra contenuti nella stringa di caratteri stringaOrigine.

Se si omette Num, restituisce l’intera stringaOrigine.

right(Confronto) ⇒ espressione

Restituisce il secondo membro di un’equazione o di una disequazione.

Catalogo

root()

root(Espr) ⇒ radice root(Espr1, Espr2) ⇒ radice

root(Espr) restituisce la radice quadrata di Espr. root(Espr1, Espr2) restituisce la radice Espr2-esima di Espr1.

Espr1 può essere una costante reale o complessa a virgola mobile, una costante razionale intera o complessa o un’espressione simbolica generale.

Nota: vedere anche Modello di radice ennesima a pagina 1.

rotate() (Ruota)

rotate(Intero1[,numRotazioni]) ⇒ intero

Ruota i bit di un numero intero binario. È possibile inserire Intero1 in qualsiasi base numerica; esso viene convertito automaticamente in forma binaria a 64 bit con segno. Se Intero1 è troppo grande per questa forma, un’operazione a modulo simmetrico lo porta all’interno dell’intervallo.

Se numRotazioni è positivo, la rotazione avviene verso sinistra. Se numRotazioni è negativo, la rotazione avviene verso destra. L’impostazione predefinita è ë1 (ruota a destra di un bit).

Ad esempio, in una rotazione a destra:

Ogni bit ruota verso destra. 0b00000000000001111010110000110101 L’ultimo bit a destra diventa l’ultimo a sinistra. Dà: 0b10000000000000111101011000011010 I risultati vengono visualizzati nella modalità Base che è stata

impostata.

rotate(Lista1[,numRotazioni]) ⇒ lista

Restituisce una copia di Lista1 ruotata a destra o a sinistra di numRotazioni elementi. Non modifica Lista1.

Se numRotazioni è positivo, la rotazione avviene verso sinistra. Se numRotazioni è negativo, la rotazione avviene verso destra.

L’impostazione predefinita è ë1 (ruota a destra di un bit).

Catalogo

In modalità base Bin:

Per vedere l’intero risultato, premere £, quindi utilizzare ¡ e

¢ per spostare il cursore

In modalità base Esadecimale:

Importante: per inserire un numero binario o esadecimale, utilizzare sempre il prefisso 0b o 0h (è uno zero, non la lettera O).

In modalità base Dec:

94 Guida di riferimento di TI-Nspire™ CAS

Texas Instruments TI-Nspire CAS Reference Guide [it]

Specifications and Main Features

Frequently Asked Questions

User Manual

Informazioni importanti

Sommario

Modelli di espressione

Guida di riferimento di TI-Nspire™ CAS 1

Elenco alfabetico