
CAS
Guía de Referencia
Este manual de instrucciones es válido para el software TI-Nspire versión
1.4. Para obtener la versión más reciente de la documentación, vaya a
education.ti.com/guides.

Información importante
A menos que la licencia que acompaña a este programa recoja
expresamente lo contrario, Texas Instruments no otorga ningún tipo de
garantía, ya sea implícita o explícita, con carácter enunciativo mas no
limitativo, a ninguna garantía implícita de comerciabilidad o idoneidad
para ningún propósito determinado, en relación con ningún programa o
material impreso, y pone a disposición esos materiales únicamente tal y
como están. Texas Instruments queda eximida de toda responsabilidad
por daños especiales, colaterales, accidentales o derivados en relación
con o a causa de la adquisición o el uso de estos materiales. La
responsabilidad única de Texas Instruments independientemente de la
acción legal adoptada, no podrá exceder la cantidad señalada en la
licencia del programa. Además, Texas Instruments quedará exenta de
toda responsabilidad frente a cualquier reclamación,
independientemente de la clase que sea, en referencia al uso de estos
materiales por un tercero.
Licencia
Sírvase ver la licencia completa instalada en C:\Program Files\TI
Education\TI-Nspire CAS.
© 2008 Texas Instruments Incorporated
Macintosh®, Windows®, Excel®, Vernier EasyLink®, EasyTemp®,
Go!®Link, Go!®Motion, y Go!®Temp son marcas comerciales de sus
propietarios respectivos.
ii

Índice
Información importante
Plantillas de expresión
Plantilla de fracción .....................................1
Plantilla de exponente ................................1
Plantilla de raíz cuadrada ............................1
Plantilla de raíz enésima ............................. 1
Plantilla de base e ........................................2
Plantilla de logaritmo ..................................2
Plantilla de función definida a trozos
(2 partes) ...................................................... 2
Plantilla de función definida a trozos
(N partes) ......................................................2
Plantilla de sistema de 2 ecuaciones ...........3
Plantilla de sistema de N ecuaciones ..........3
Plantilla de valor absoluto .......................... 3
Plantilla de gg°mm’ss.ss’’ .............................3
Plantilla de matriz (2 x 2) ............................3
Plantilla de matriz (1 x 2) ............................4
Plantilla de matriz (2 x 1) ............................4
Plantilla de matriz (m x n) ........................... 4
Plantilla de suma (G) .................................... 4
Plantilla de producto (Π) ............................. 4
Plantilla de primera derivada ......................5
Plantilla de derivada enésima .....................5
Plantilla de integral definida ......................5
Plantilla de integral indefinida ...................5
Plantilla de límite .........................................5
Listado alfabético
A
abs() ..............................................................6
amortTbl() .................................................... 6
and ................................................................6
angle() ..........................................................7
ANOVA .........................................................7
ANOVA de 2 variables .................................8
Ans ..............................................................10
approx() ......................................................10
approxRational() ........................................ 10
arcLen() .......................................................10
augment() ...................................................10
avgRC() ....................................................... 11
B
bal() .............................................................11
4Base2 .........................................................12
4Base10 .......................................................12
4Base16 .......................................................12
binomCdf() ................................................. 13
binomPdf() ................................................. 13
C
ceiling() .......................................................13
cFactor() ......................................................13
char() ...........................................................14
charPoly() ....................................................14
2
de 2 elementos ...................................... 14
c
2
Cdf() ........................................................ 15
c
2
GOF ......................................................... 15
c
2
Pdf() ........................................................ 16
c
ClearAZ ....................................................... 16
ClrErr .......................................................... 16
colAugment() ............................................. 16
colDim() ...................................................... 16
colNorm() ................................................... 17
comDenom() .............................................. 17
conj() .......................................................... 17
constructMat() ........................................... 18
CopyVar ...................................................... 18
corrMat() .................................................... 18
4cos ............................................................. 19
cos() ............................................................ 19
cosê() .......................................................... 20
cosh() .......................................................... 21
coshê() ........................................................ 21
cot() ............................................................ 21
cotê() .......................................................... 22
coth() .......................................................... 22
cothê() ........................................................ 22
count() ........................................................ 22
countif() ..................................................... 23
crossP() ....................................................... 23
csc() ............................................................. 23
cscê() ........................................................... 24
csch() ........................................................... 24
cschê() ......................................................... 24
cSolve() ....................................................... 24
CubicReg .................................................... 26
cumSum() ................................................... 27
Cycle ........................................................... 27
4Cylind ........................................................ 27
cZeros() ....................................................... 28
D
dbd() ........................................................... 29
4DD ............................................................. 30
4Decimal ..................................................... 30
Define (Definir) .......................................... 30
Define LibPriv ............................................ 31
Define LibPub ............................................ 32
DelVar ........................................................ 32
deSolve() .................................................... 32
det() ............................................................ 34
diag() .......................................................... 34
dim() ........................................................... 34
Disp ............................................................. 35
4GMS ........................................................... 35
dominantTerm() ........................................ 36
dotP() .......................................................... 36
E
e^() ............................................................. 37
eff() ............................................................. 37
eigVc() ........................................................ 37
eigVl() ......................................................... 38
Else ............................................................. 38
ElseIf ........................................................... 38
iii

EndFor .........................................................38
EndFunc ......................................................38
EndIf ............................................................38
EndLoop ......................................................38
EndPrgm .....................................................38
EndTry .........................................................38
EndWhile ....................................................39
exact() .........................................................39
Exit ..............................................................39
4exp .............................................................39
exp() ............................................................39
exp4lista() ....................................................40
expand() ......................................................40
expr() ...........................................................41
ExpReg ........................................................41
F
factor() ........................................................42
FCdf() ..........................................................43
Fill ................................................................43
FiveNumSummary ......................................43
floor() ..........................................................44
fMax() .........................................................44
fMin() ..........................................................45
For ...............................................................45
format() ......................................................46
fPart() ..........................................................46
FPdf() ..........................................................46
freqTable4lista() ..........................................46
frequency() .................................................47
FTest_2Samp ..............................................47
Func .............................................................48
G
gcd() ............................................................48
geomCdf() ...................................................48
geomPdf() ...................................................49
getDenom() ................................................49
getLangInfo() .............................................49
getMode() ...................................................49
getNum() ....................................................50
getVarInfo() ................................................51
Goto ............................................................51
4Grad ...........................................................52
I
identity() .....................................................52
If ..................................................................52
ifFn() ............................................................53
imag() ..........................................................53
impDif() .......................................................54
Indirection ..................................................54
inString() .....................................................54
int() .............................................................54
intDiv() ........................................................54
integrate .....................................................54
2
() .........................................................55
invc
invF() ...........................................................55
invNorm() ....................................................55
invt() ............................................................55
iPart() ..........................................................55
irr() ..............................................................55
isPrime() ......................................................56
L
Lbl ............................................................... 56
lcm() ............................................................ 56
left() ............................................................ 57
libShortcut() ............................................... 57
limit() o lim() .............................................. 57
LinRegBx ..................................................... 58
LinRegMx ................................................... 59
LinRegtIntervals ......................................... 60
LinRegTTest (Test t de regresión lineal) ...61
@List() .......................................................... 62
list4mat() ..................................................... 62
4ln ................................................................ 62
ln() .............................................................. 62
LnReg .......................................................... 63
Local ........................................................... 64
log() ............................................................ 64
4logbase ...................................................... 65
Logistic ....................................................... 65
LogisticD ..................................................... 66
Loop ............................................................ 67
LU ................................................................ 67
M
mat4list() ..................................................... 68
max() ........................................................... 68
mean() ........................................................ 68
median() ..................................................... 68
MedMed ..................................................... 69
mid() ........................................................... 69
min() ........................................................... 70
mirr() ........................................................... 70
mod() .......................................................... 71
mRow() ....................................................... 71
mRowAdd() ................................................ 71
MultReg ...................................................... 71
MultRegIntervals ....................................... 72
MultRegTests ............................................. 72
N
nCr() ............................................................ 73
nDeriv() ....................................................... 74
newList() ..................................................... 74
newMat() .................................................... 74
nfMax() ....................................................... 74
nfMin() ....................................................... 75
nInt() ........................................................... 75
nom() .......................................................... 75
norm() ......................................................... 76
normalLine() ............................................... 76
normCdf() ................................................... 76
normPdf() ................................................... 76
not .............................................................. 76
nPr() ............................................................ 77
npv() ........................................................... 78
nSolve() ....................................................... 78
O
OneVar ....................................................... 79
or ................................................................ 80
ord() ............................................................ 80
iv

P
P4Rx() ...........................................................80
P4Ry() ...........................................................81
PassErr .........................................................81
piecewise() ..................................................81
poissCdf() .................................................... 81
poissPdf() ....................................................82
4Polar ..........................................................82
polyCoeffs() ................................................ 82
polyDegree() .............................................. 83
polyEval() .................................................... 83
polyGcd() ....................................................83
polyQuotient() ........................................... 84
polyRemainder() ........................................ 84
PowerReg ...................................................85
Prgm ...........................................................86
Product (PI) ................................................. 86
product() ..................................................... 86
propFrac() ................................................... 86
Q
QR ...............................................................87
QuadReg .....................................................88
QuartReg ....................................................89
R
R4Pq() ..........................................................90
R4Pr() ...........................................................90
4Rad ............................................................. 90
rand() .......................................................... 90
randBin() ..................................................... 91
randInt() ..................................................... 91
randMat() ................................................... 91
randNorm() ................................................. 91
randPoly() ................................................... 91
randSamp() ................................................. 91
RandSeed .................................................... 92
real() ...........................................................92
4Rect ............................................................92
ref() .............................................................93
remain() ......................................................93
Return ......................................................... 93
right() ..........................................................93
root() ...........................................................94
rotate() .......................................................94
round() ........................................................95
rowAdd() ....................................................95
rowDim() ....................................................95
rowNorm() .................................................. 95
rowSwap() .................................................. 96
rref() ............................................................96
S
sec() .............................................................96
sec/() ...........................................................97
sech() ...........................................................97
sechê() ......................................................... 97
seq() ............................................................97
series() .........................................................98
setMode() ................................................... 99
shift() ........................................................100
sign() .........................................................101
simult() ..................................................... 101
4sin ............................................................ 102
sin() ........................................................... 102
sinê() ......................................................... 103
sinh() ......................................................... 103
sinhê() ....................................................... 103
SinReg ...................................................... 104
solve() ....................................................... 105
SortA ........................................................ 107
SortD ........................................................ 107
4Sphere ..................................................... 108
sqrt() ......................................................... 108
stat.results ................................................ 109
stat.values ................................................ 110
stDevPop() ................................................ 110
stDevSamp() ............................................. 110
Stop .......................................................... 111
Store ......................................................... 111
string() ...................................................... 111
subMat() ................................................... 111
Sum (Sigma) ............................................. 111
sum() ......................................................... 112
sumIf() ...................................................... 112
system() .................................................... 112
T
T (transponer) .......................................... 113
tan() .......................................................... 113
tanê() ........................................................ 114
tangentLine() ........................................... 114
tanh() ........................................................ 114
tanhê() ...................................................... 115
taylor() ...................................................... 115
tCdf() ........................................................ 115
tCollect() ................................................... 116
tExpand() .................................................. 116
Then ......................................................... 116
tInterval .................................................... 116
tInterval_2Samp ....................................... 117
tmpCnv() .................................................. 117
@tmpCnv() ................................................ 118
tPdf() ........................................................ 118
trace() ....................................................... 118
Try ............................................................. 119
tTest .......................................................... 119
tTest_2Samp ............................................. 120
tvmFV() ..................................................... 120
tvmI() ........................................................ 121
tvmN() ...................................................... 121
tvmPmt() .................................................. 121
tvmPV() ..................................................... 121
TwoVar ..................................................... 122
U
unitV() ...................................................... 123
V
varPop() .................................................... 123
varSamp() ................................................. 124
W
when() ...................................................... 124
While ........................................................ 125
v

“With” ......................................................125
X
xor .............................................................125
Z
zeros() .......................................................126
zInterval ....................................................127
zInterval_1Prop ........................................128
zInterval_2Prop ........................................128
zInterval_2Samp .......................................128
zTest ..........................................................129
zTest_1Prop ..............................................129
zTest_2Prop ..............................................130
zTest_2Samp .............................................130
Símbolos
+ (suma) ....................................................132
N(resta) ......................................................132
·(multiplicación) ......................................133
à (división) ................................................133
^ (potencia) ..............................................134
2
(cuadrado) ............................................135
x
.+ (punto suma) ........................................135
.. (punto resta) .........................................135
·(punto multiplic.) ..................................135
.
. / (punto división) ....................................136
.^ (punto de potencia) .............................136
ë(negación) ...............................................136
% (porcentaje) .........................................136
= (igual) .....................................................137
ƒ (no igual) ...............................................137
< (menor que) ...........................................138
{ (menor o igual que) ..............................138
> (mayor que) ...........................................138
| (mayor o igual que) .............................. 138
! (factorial) ............................................... 139
& (añadir) ................................................. 139
d() (derivada) ........................................... 139
‰() (integral) .............................................. 139
‡() (raíz cuadrada) ................................... 140
Π() (producto) .......................................... 141
G() (suma) ................................................. 141
GInt() ......................................................... 142
GPrn() ........................................................ 143
# (dirección) ............................................. 143
í (notación científica) .............................. 143
g (grado centesimal) ................................ 144
ô(radián) ................................................... 144
¡ (grado) ................................................... 144
¡, ', '' (grados/minutos/segundos) ........... 145
(ángulo) ................................................ 145
' (primo) .................................................... 145
_ (subrayado) ........................................... 146
4 (convertir) .............................................. 146
10^() .......................................................... 146
^ê (inverso de un valor) ........................... 147
| (“with”) .................................................. 147
& (almacenar) ..........................................148
:= (asignar) ............................................... 148
© (comentario) ......................................... 148
0b, 0h ........................................................ 149
Códigos y mensajes de error
Información sobre productos,
servicios y garantías de TI
vi
Guía de referencia de TI-Nspire™
En esta guía se describen las plantillas, funciones, órdenes y operadores que podrá utilizar para
calcular expresiones matemáticas.
CAS
Plantillas de expresión
Las plantillas de expresión son un medio fácil de introducir expresiones matemáticas en
notación estándar. Cada plantilla que se inserta aparece en la línea de entrada y presenta
bloques pequeños para indicar los elementos que se pueden introducir. Los elementos se
indican por medio de un cursor.
Utilice las teclas de flecha o pulse
y escriba un valor o una expresión. Pulse
Plantilla de fracción
Nota: Consulte también / (división), en la página 133.
e para desplazar el cursor a cada posición del elemento,
· o /· para calcular la expresión.
/
Teclas
Ejemplo:
p
Plantilla de exponente
Nota: Escriba el primer valor, pulse l, y escriba el exponente.
Para desplazar el cursor hasta la línea de base, pulse la tecla de flecha
(¢).
Nota: Consulte también ^ (potencia), en la página 134.
Plantilla de raíz cuadrada
Nota: Consulte también
página 140.
Plantilla de raíz enésima
Nota: Consulte también root(), en la página 94.
‡
() (raíz cuadrada), en la
Ejemplo:
Ejemplo:
Ejemplo:
Teclas
Teclas
Tecla l
/
q
/
l
Guía de referencia de TI-Nspire™ CAS 1
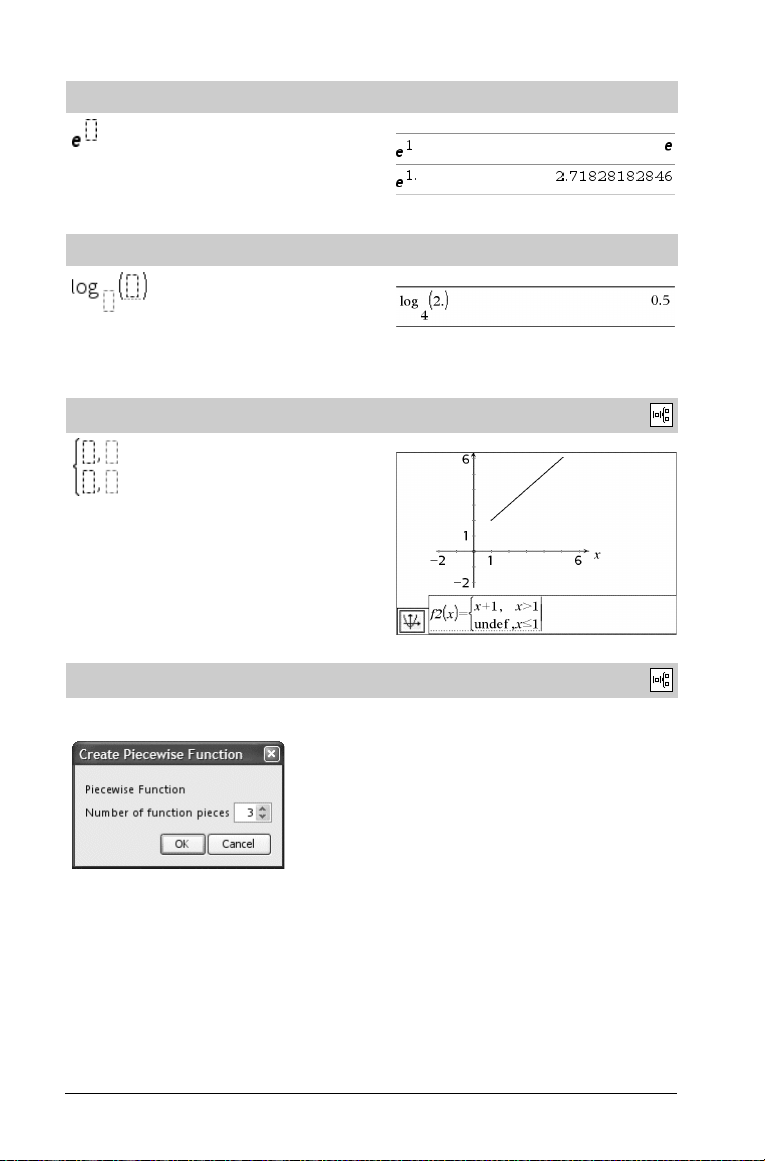
Plantilla de base e
Base el número e y exponente cualquiera
Nota: Consulte también e^(), en la página 37.
Teclas u
Ejemplo:
Plantilla de logaritmo
Calcula el logaritmo de la base que se indique. En el caso de la base
por defecto, 10, no hay que indicar la base.
Nota: Consulte también log(), en la página 64.
Plantilla de función definida a trozos (2 partes)
Permite crear expresiones y condiciones para una función definida a
trozos -con dos partes. Para añadir un trozo, haga clic en la plantilla y
repita los pasos.
Nota: Consulte también piecewise(), en la página 81.
Plantilla de función definida a trozos (N partes)
Permite crear expresiones y condiciones para una función definida a
trozos con N-partes. Solicita la introducción del número de partes, N.
Tecla /s
Ejemplo:
Catálogo >
Ejemplo:
Catálogo >
Ejemplo:
Consulte el ejemplo de la plantilla definida a trozos (2 partes).
Nota: Consulte también piecewise(), en la página 81.
2 Guía de referencia de TI-Nspire™ CAS
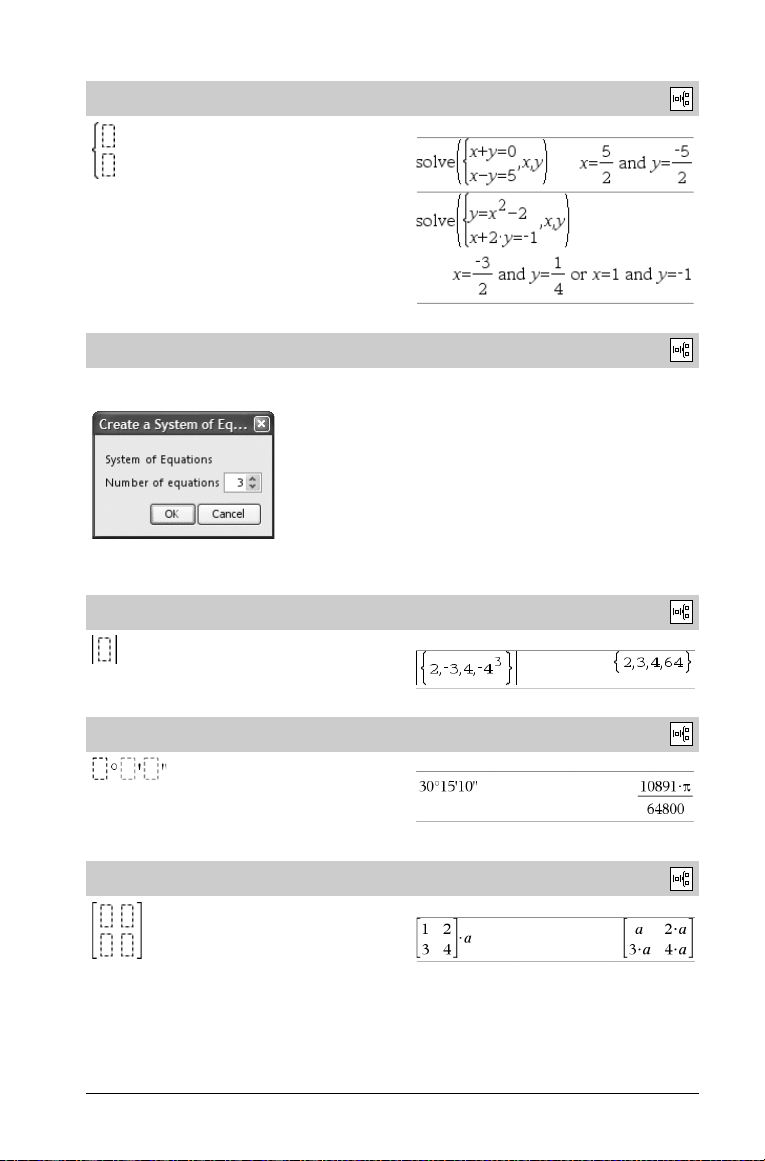
Plantilla de sistema de 2 ecuaciones
Crea un sistema de dos ecuaciones. Para añadir una fila a un sistema
existente, haga clic en la plantilla y repita los pasos anteriores.
Nota: Consulte también system(), en la página 112.
Catálogo >
Ejemplo:
Plantilla de sistema de N ecuaciones
Permite crear un sistema de N ecuaciones. Solicita la introducción del
número de ecuaciones, N.
Nota: Consulte también system(), en la página 112.
Plantilla de valor absoluto
Nota: Consulte también abs(), en la página 6.
Plantilla de gg°mm’ss.ss’’
Permite introducir ángulos en formato gg°mm’ss.ss’’, donde gg es
el número de grados sexagesimales, mm corresponde al número de
minutos y ss.ss al de segundos.
Plantilla de matriz (2 x 2)
Catálogo >
Ejemplo:
Consulte el ejemplo de Plantilla de sistema de ecuaciones (2
ecuaciones).
Catálogo >
Ejemplo:
Catálogo >
Ejemplo:
Catálogo >
Ejemplo:
Crea una matriz de 2 por 2.
Guía de referencia de TI-Nspire™ CAS 3
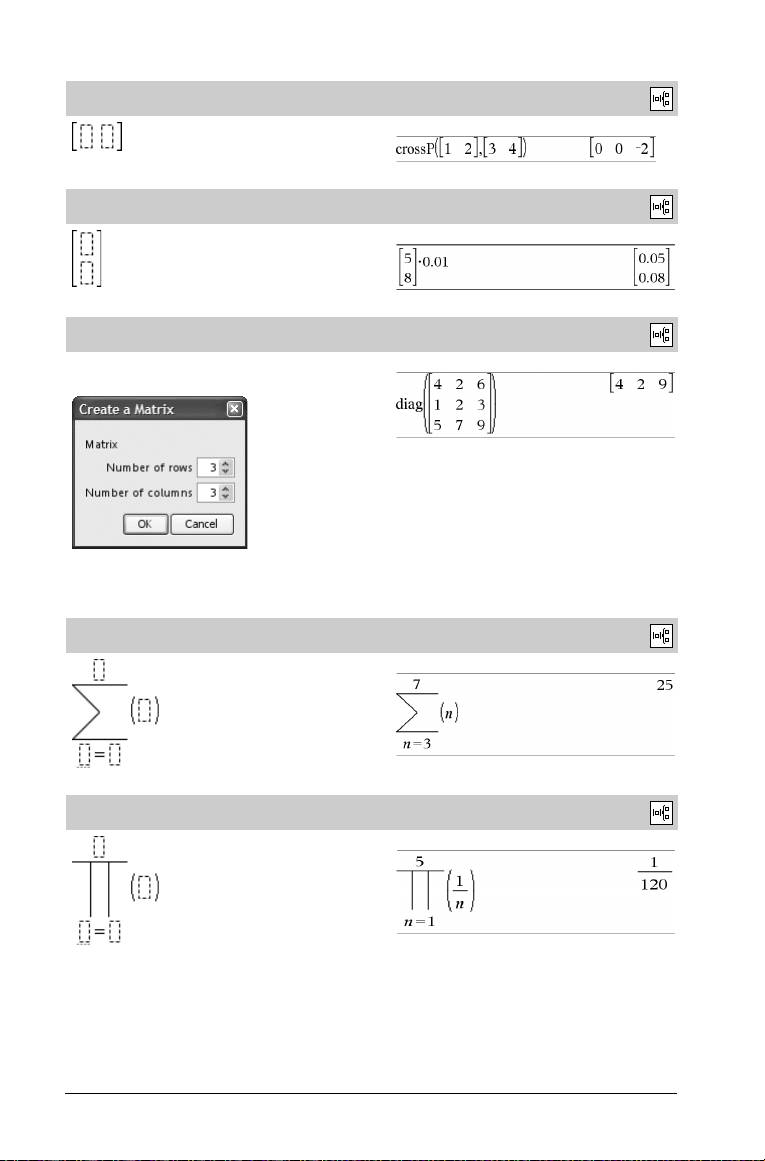
Plantilla de matriz (1 x 2)
.
Catálogo >
Ejemplo:
Plantilla de matriz (2 x 1)
Plantilla de matriz (m x n)
La plantilla aparece tras la solicitud para especificar el número de filas
y columnas.
Nota: Si la matriz que ha creado tiene gran cantidad de filas y
columnas puede tardar unos minutos en aparecer.
Plantilla de suma (G)
Catálogo >
Ejemplo:
Catálogo >
Ejemplo:
Catálogo >
Ejemplo:
Plantilla de producto (Π)
Ejemplo:
Nota: Consulte también Π() (producto), en la página 141.
Catálogo >
4 Guía de referencia de TI-Nspire™ CAS
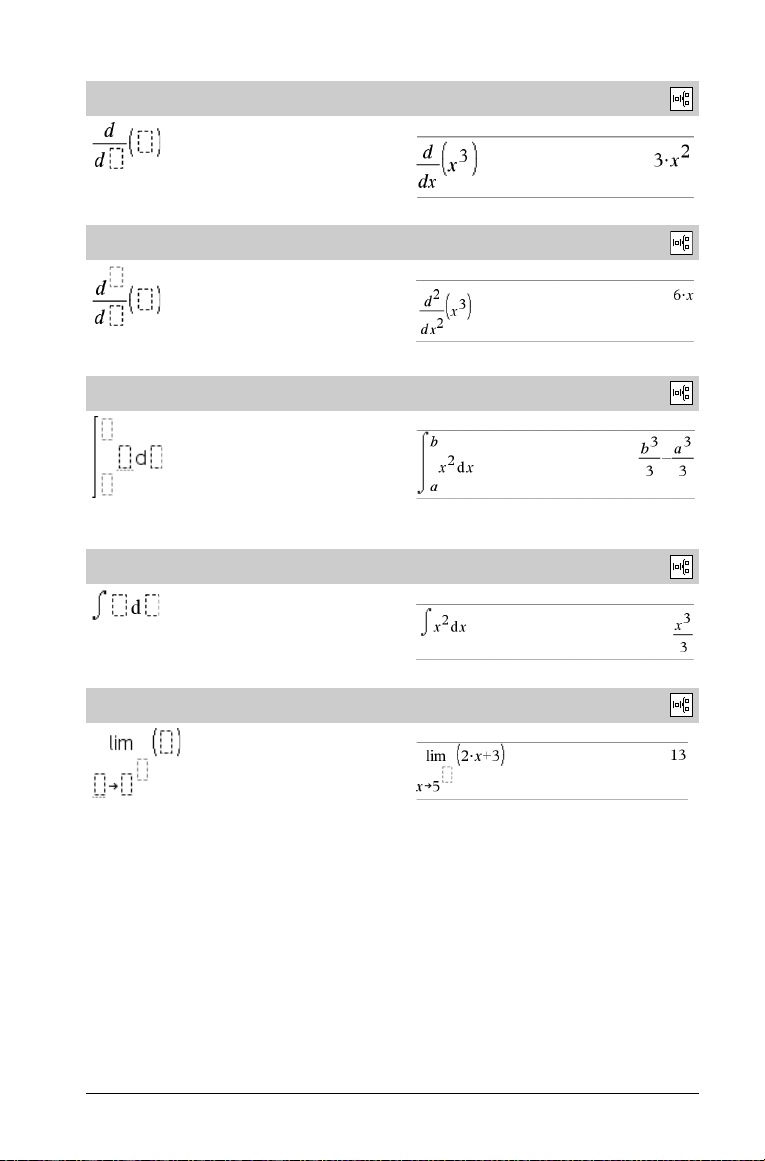
Plantilla de primera derivada
Catálogo >
Ejemplo:
Nota: Consulte también
d() (derivada)
, en la página 139.
Plantilla de derivada enésima
Nota: Consulte también
d() (derivada)
, en la página 139.
Plantilla de integral definida
Nota: Consulte también ‰() integrate(), en la página 139.
Plantilla de integral indefinida
Nota: Consulte también ‰() integrate(), en la página 139.
Plantilla de límite
Catálogo >
Ejemplo:
Catálogo >
Ejemplo:
Catálogo >
Ejemplo:
Catálogo >
Ejemplo:
Utilice N o (N) para el límite izquierdo. Utilice + para el límite
derecho.
Nota: Consulte también limit(), en la página 57.
Guía de referencia de TI-Nspire™ CAS 5

Listado alfabético
Los elementos con nombres no alfabéticos (por ejemplo, +, ! y >) se incluyen al final de esta
sección, en una lista que comienza en la página 132. A menos que se especifique lo contrario,
todos los ejemplos de esta sección se han realizado en el modo de restablecimiento
predeterminado y suponiendo que todas las variables están sin definir.
A
abs()
abs(Expr1) ⇒ expresión
abs(
Lista1) ⇒ lista
abs(Matriz1) ⇒ matriz
Calcula el valor absoluto de un argumento.
Nota: Consulte también Plantilla de valor absoluto, en la
página 3.
Si el argumento es un número complejo, el r esultado es el módulo del
número.
Nota: Se considera que todas las variables no definidas son variables
reales.
amortTbl()
amortTbl(NPmt,N,I,PV, [Pmt], [FV], [PpY], [CpY], [PmtAt],
redondValor]) ⇒ matriz
[
Función de amortización que genera una matriz como una tabla de
amortización para un conjunto de argumentos de TVM (valor
temporal del dinero).
NPmt es el número de pagos que se han de incluir en la tabla. La
tabla se inicia con el primer pago.
N, I, PV, Pmt, FV, PpY, CpY y PmtAt se describen en la tabla de
argumentos para TVM, en la página 121.
• Si se omite el valor de Pmt, se aplica de forma predeterminada
Pmt=tvmPmt(N,I,PV,FV,PpY,CpY,PmtAt).
• Si se omite el valor de FV, se aplica de forma predeterminada
FV=0.
• Los valores predeterminados para PpY, CpY y PmtAt son los
mismos que los de las funciones de TVM.
redondValor especifica el número de decimales de redondeo. Valor
predeterminado = 2.
Las columnas de la matriz de resultados siguen este orden: Número
de pago, interés pagado, principal amortizado y principal que resta
por pagar.
El principal que resta por pagar n corresponde al principal que resta
por pagar tras el pago n.
La matriz de salida se puede utilizar como entrada de las otras
funciones de amortización, GInt() y GPrn(), en la página 142, y
bal(), en la página 11.
Catálogo
Catálogo
>
>
and
ExprBooleana1 and ExprBooleana2 ⇒ Expresión booleana
ListaBooleana1 and ListaBooleana2 ⇒ Lista booleana
MatrizBooleana1 and MatrizBooleana2 ⇒ Matriz booleana
Muestra el resultado verdadero o falso o una forma simplificada de la
entrada original.
Catálogo
>
6 Guía de referencia de TI-Nspire™ CAS

and
Entero1 and Entero2 ⇒ entero
Compara bit a bit dos números enteros reales mediante una
and. Internamente, ambos enteros se convierten en
operación
números binarios con signo de 64 bits. Cuando se comparan los bits
correspondientes, el resultado es 1 si ambos bits son 1; en caso
contrario, el resultado será 0. El valor obtenido representa el
resultado de los bits, y aparece conforme al modo base especificado.
Los números enteros se pueden introducir en cualquier base. Para una
entrada binaria o hexadecimal es necesario utilizar el prefijo 0b o 0h,
respectivamente. Si no se indica un prefijo, los enteros se consideran
decimales (base 10).
Si el entero decimal que se introduce es demasiado largo para un
formato binario con signo de 64 bits, se utiliza una operación de
módulo simétrico para llevar el valor al rango apropiado.
Catálogo
>
En modo base Hex:
Importante: Cero, no la letra O.
En modo base Bin:
En modo base Dec:
Nota: Una entrada binaria puede tener hasta 64 dígitos (sin
contar el prefijo 0b). Una entrada hexadecimal puede tener
hasta 16 dígitos.
angle()
angle(Expr1) ⇒ expresión
Devuelve el ángulo del argumento, interpretando el argumento como
un número complejo.
Nota: Se considera que todas las variables no definidas son variables
reales.
angle(Lista1) ⇒ lista
angle(Matriz1) ⇒ matriz
Devuelve una lista o matriz de ángulos de los elementos en Lista1 o
Matriz1, interpretando cada elemento como un número complejo
que representa las coordenadas de un punto del plano.
ANOVA
ANOVA Lista1,Lista2[,Lista3,...,Lista20][,Etiqueta]
Realiza un análisis de varianza de un factor para comparar la media
de 2 a 20 poblaciones. El resumen de los resultados se guarda en la
variable stat.results. (Consulte la página 109.)
Etiqueta = 0 para Datos, Etiqueta = 1 para Estadística
Catálogo
En el modo de ángulo en grados:
En el modo de ángulo en grados centesimales:
En el modo de ángulo en radianes:
Catálogo
>
>
Vari able de
salida
Descripción
stat.F Valor de la estadística F
stat.PVal Nivel de significancia mínimo al que se puede rechazar la hipótesis nula
stat.df Grados de libertad de los grupos
Guía de referencia de TI-Nspire™ CAS 7
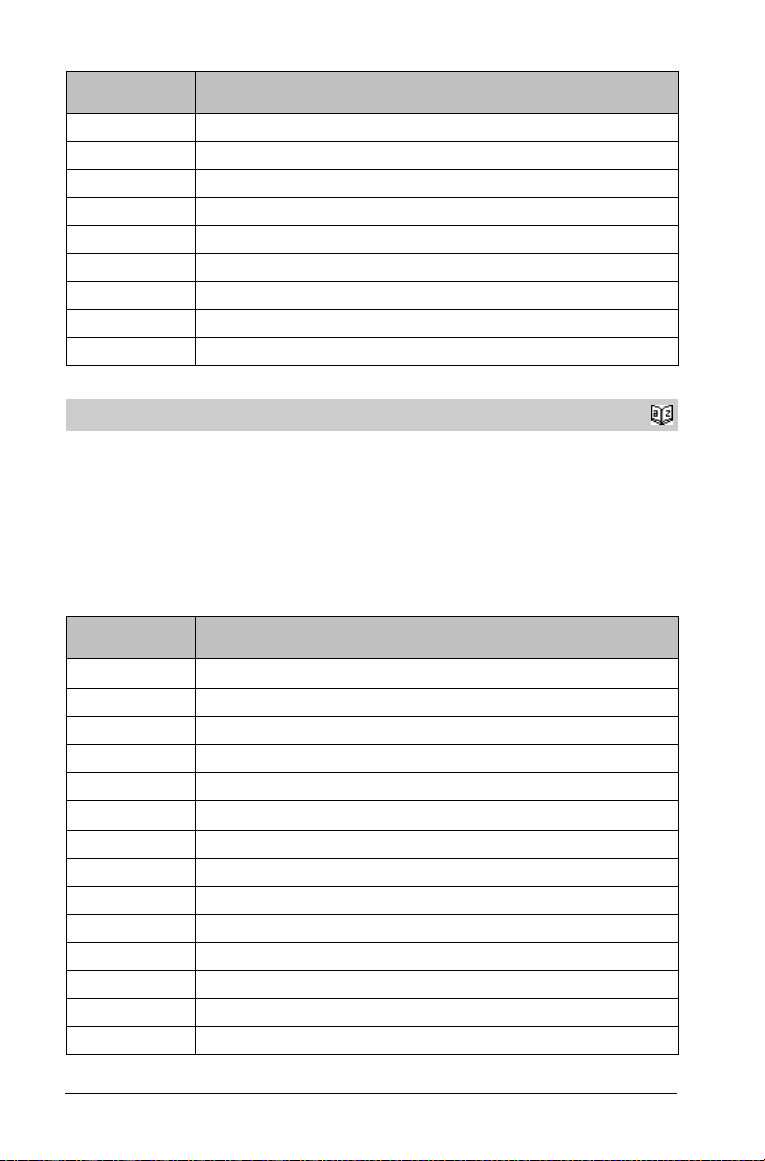
Vari able de
salida
stat.SS Suma de los cuadrados de los grupos
stat.MS Media de los cuadrados de los grupos
stat.dfError Grados de libertad de los errores
stat.SSError Suma de los cuadrados de los errores
stat.MSError Media de los cuadrados de los errores
stat.sp Desviación estándar sondeada
stat.xbarlist Media de las entradas de las listas
stat.CLowerList 95% de los intervalos de confianza para la media de cada lista de entrada
stat.CUpperList 95% de los intervalos de confianza para la media de cada lista de entrada
Descripción
ANOVA de 2 variables
ANOVA2way Lista1,Lista2[,Lista3,…,Lista20][,nivelFila]
Realiza un análisis de varianza de dos factores comparando las
medias de 2 a 20 poblaciones. El resumen de los resultados se guarda
en la variable stat.results. (Consulte la página 109.)
nivelFila = 0 para Bloque
nivelFila=2,3,...,Len-1, para Dos Factor, donde
Len=lenght(Lista1)=length(Lista2) = … = length(Lista10) y
Len / nivelFila ∈ {2,3,…}
Salidas: Estudio conjunto
Vari able de
salida
stat.F Estadístico F de la variable columna
stat.PVal Nivel de significancia mínimo al que se puede rechazar la hipótesis nula
stat.df Grados de libertad de la variable columna
stat.SS Suma de los cuadrados de la variable columna
stat.MS Media de los cuadrados de la variable columna
stat.FBlock Estadístico F de la variable
stat.PValBlock Probabilidad mínima a la que se puede rechazar la hipótesis nula
stat.dfBlock Grados de libertad de la variable
stat.SSBlock Suma de los cuadrados de la variable
stat.MSBlock Media de los cuadrados de la variable
stat.dfError Grados de libertad de los errores
stat.SSError Suma de los cuadrados de los errores
stat.MSError Media de los cuadrados de los errores
stat.s Desviación estándar del error
Descripción
Catálogo
>
8 Guía de referencia de TI-Nspire™ CAS

Salidas para la variable COLUMNA
Vari able de
salida
stat.
Fcol Estadístico F de la variable columna
stat.PValCol Valor de probabilidad de la variable columna
stat.dfCol Grados de libertad de la variable columna
stat.SSCol Suma de los cuadrados de la variable columna
stat.MSCol Media de los cuadrados de la variable columna
Salidas para la variable FILA
Vari able de
salida
stat.FRow Estadístico F de la variable fila
stat.PValRow Valor de probabilidad de la variable fila
stat.dfRow Grados de libertad de la variable fila
stat.SSRow Suma de los cuadrados de la variable fila
stat.MSRow Media de los cuadrados de la variable fila
Salidas para INTERACCIÓN
Vari able de
salida
stat.FInteract Estadístico F de la interacción
stat.PValInteract Probabilidad de la interacción
stat.dfInteract Grados de libertad de la interacción
stat.SSInteract Suma de los cuadrados de la interacción
stat.MSInteract Media de los cuadrados de la interacción
Descripción
Descripción
Descripción
Salida para ERROR
Vari able de
salida
stat.dfError Grados de libertad de los errores
stat.SSError Suma de los cuadrados de los errores
stat.MSError Media de los cuadrados de los errores
s Desviación estándar del error
Descripción
Guía de referencia de TI-Nspire™ CAS 9

Ans
Ans ⇒ valor
Devuelve el resultado de la expresión calculada en último lugar.
Teclas
/v
approx()
approx(Expr1) ⇒ expresión
Devuelve el cálculo del argumento como una expresión que contiene
cifras decimales, siempre que sea posible, sin tener en cuenta el modo
actual, Auto or Approximate (Auto o Aproximado) .
Equivale a introducir el argumento y pulsar
approx(Lista1) ⇒ lista
approx(Matriz1) ⇒ matriz
Devuelve una lista o una matriz en donde cada elemento se ha
calculado hasta un valor decimal, siempre que sea posible.
approxRational()
approxRational(Expr[, tol]) ⇒ expresión
approxRational(Lista[, tol]) ⇒ lista
approxRational(Matriz[, tol]) ⇒ matriz
Muestra el argumento como una fracción que utiliza la toler ancia tol.
Si se omite el valor de tol, se utiliza una tolerancia de 5.E-14.
arcLen()
arcLen(Expr1,Var ,Inic,Fin) ⇒ expresión
Devuelve la longitud de arco de Expr1 desde Inicio a Fin con
respecto a la variable Va r.
La longitud de arco se calcula mediante una integral.
/
·.
Catálogo
Catálogo
Catálogo
>
>
>
arcLen(Lista1,Var ,Inic,Fin) ⇒ lista
Devuelve una lista de las longitudes de arco de cada elemento de
Lista1 desde Inicio a Fin con respecto aVar .
augment()
augment(Lista1, Lista2) ⇒ lista
Devuelve una nueva lista que es Lista2 añadida al final de Lista1.
Catálogo
>
10 Guía de referencia de TI-Nspire™ CAS
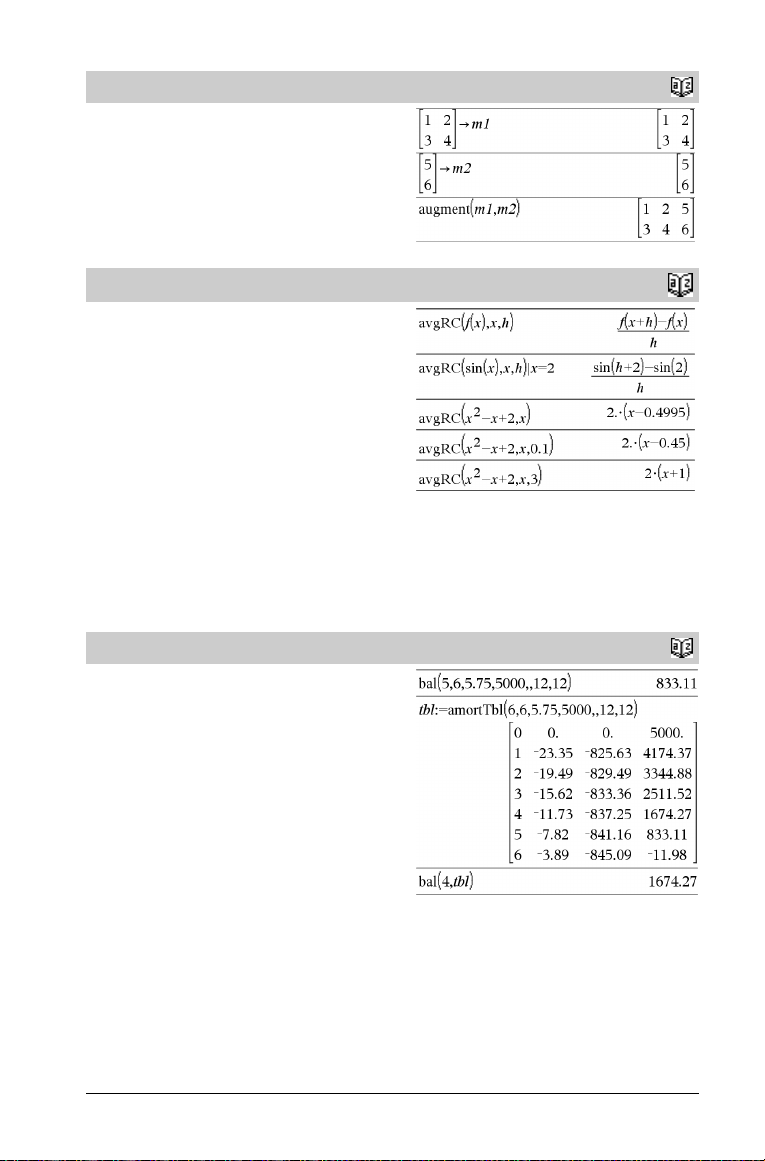
augment()
augment(Matriz1, Matriz2) ⇒ matriz
Devuelve una nueva matriz que es Matriz2 añadida a Matriz1.
Cuando se utiliza el carácter “,”, las matrices deben tener el mismo
número de filas, y Matriz2 se añade a Matriz1 como si fueran
nuevas columnas. No se altera el contenido de Matriz1 ni Matriz2.
Catálogo
>
avgRC()
avgRC(Expr1, Va r [=Valor] [, H]) ⇒ expresión
avgRC(Expr1, Va r [=Valor] [, Lista1]) ⇒ lista
avgRC(Lista1, Va r [=Valor] [, H]) ⇒ lista
avgRC(Matriz1, Var [=Valor] [, H]) ⇒ matriz
Devuelve el cociente incremental positivo (tasa media de cambio).
Expr1 se puede utilizar como un nombre de función definido por el
usuario (consulte Func).
Cuando se especifica, valor sobrescribe cualquier otra asignación de
variable anterior o cualquier sustitución “tal como” actual de la
variable.
H es el valor de paso. Si se omite, H adopta el valor predeterminado
0,001.
Observe que la función similar nDeriv() utiliza el cociente de
diferencia central.
B
bal()
bal(NPmt,N,I,PV ,[Pmt], [FV], [PpY], [CpY], [PmtAt],
redondValor]) ⇒ valor
[
bal(NPmt,amortTable) ⇒ valor
Función de amortización que calcula el principal que resta por pagar
tras un pago especificado.
N, I, PV, Pmt, FV, PpY, CpY y PmtAt se describen en la tabla de
argumentos para TVM, en la página 121.
NPmt especifica el número de pagos tras el cual se desean calcular
los datos.
N, I, PV, Pmt, FV, PpY, CpY y PmtAt se describen en la tabla de
argumentos para TVM, en la página 121.
• Si se omite el valor de Pmt, se aplica de forma predeterminada
Pmt=tvmPmt(N,I,PV,FV,PpY,CpY,PmtAt).
• Si se omite el valor de FV, se aplica de forma predeterminada
FV=0.
• Los valores predeterminados para PpY, CpY y PmtAt son los
mismos que los de las funciones de TVM.
redondValor especifica el número de decimales de redondeo. Valor
predeterminado = 2.
bal(NPmt,amortTable) calcula el principal que resta por pagar tras
el número de pago NPmt, según una tabla de amortización
amortTable. El argumento amortTable debe ser una matriz en la
forma descrita en la sección amortTbl(), en la página 6.
Nota: Consulte también GInt() y GPrn(), en la página 142.
Catálogo
Catálogo
>
>
Guía de referencia de TI-Nspire™ CAS 11

Base2
4
4Base2 ⇒ entero
Entero1
Convierte Entero1 en un número binario. Los números binarios o
hexadecimales llevan siempre un prefijo 0b o 0h, respectivamente.
0b NúmeroBinario
0h NúmeroHexadecimal
Cero, no la letra O, seguido de b o h.
Un número binario puede tener hasta 64 dígitos. Un número
hexadecimal puede tener hasta 16 dígitos.
Si no se indica un prefijo, Entero1 se considera decimal (base 10).
El resultado aparece en formato binario, sea cual sea el modo de la
base.
Si el entero decimal que se introduce es demasiado largo para un
formato binario con signo de 64 bits, se utiliza una operación de
módulo simétrico para llevar el valor al rango apropiado.
Base10
4
Entero1 4Base10 ⇒ entero
Convierte Entero1 en un número decimal (base 10). Una entrada
binaria o hexadecimal debe llevar siempre el prefijo 0b o 0h,
respectivamente.
0b NúmeroBinario
0h NúmeroHexadecimal
Cero, no la letra O, seguido de b o h.
Un número binario puede tener hasta 64 dígitos. Un número
hexadecimal puede tener hasta 16 dígitos.
Si no se indica un prefijo, Entero1 se considera decimal. El resultado
aparece en formato decimal, sea cual sea el modo de la base.
Base16
4
Entero1 4Base16 ⇒ entero
Convierte Entero1 en un número hexadecimal. Los números binarios
o hexadecimales llevan siempre un prefijo 0b o 0h, respectivamente.
0b NúmeroBinario
0h NúmeroHexadecimal
Cero, no la letra O, seguido de b o h.
Un número binario puede tener hasta 64 dígitos. Un número
hexadecimal puede tener hasta 16 dígitos.
Si no se indica un prefijo, Entero1 se considera decimal (base 10).
El resultado aparece en formato hexadecimal, sea cual sea el modo
de la base.
Si el entero decimal que se introduce es demasiado largo para un
formato binario con signo de 64 bits, se utiliza una operación de
módulo simétrico para llevar el valor al rango apropiado.
Catálogo
Catálogo
Catálogo
>
>
>
12 Guía de referencia de TI-Nspire™ CAS

binomCdf()
binomCdf(n,p,Extremoinferior,Extremosuperior) ⇒ número si
Extremoinferior y Extremosuperior son números, lista si
Extremoinferior y Extremosuperior son listas
binomCdf(n,p,Extremosuperior) ⇒ número si
Extremosuperior es un número, lista si Extremosuperior es una
lista
Calcula una probabilidad acumulada para la distribución binomial
discreta para un número de pruebas n y probabilidad de éxito p en
cada prueba.
Para P(X Extremosuperior), defina Extremoinferior=0
Catálogo
>
binomPdf()
binomPdf(n,p) ⇒ número
binomPdf(n,p,XVal) ⇒ número si XVal es un número, lista si
XVal es una lista
Calcula una probabilidad para la distribución binomial discreta para
un número de pruebas n y probabilidad de éxito p en cada prueba.
C
ceiling()
ceiling(Expr1) ⇒ entero
Devuelve el menor entero que sea ‚ el argumento.
El argumento puede ser un número real o complejo.
Nota: Consulte también floor().
ceiling(Lista1) ⇒ lista
ceiling(Matriz1) ⇒ matriz
Devuelve una lista o una matriz con los correspondientes menores
enteros.
cFactor()
cFactor(Expr1[,Var ]) ⇒ expresión
cFactor(Lista1[,Va r]) ⇒ lista
cFactor(Matriz1[,Var ]) ⇒ matriz
cFactor(Expr1) devuelve Expr1 factorizado con respecto a todas
sus variables, sobre un denominador común.
Expr1 se factoriza tanto como sea posible hacia factores racionales
lineales incluso aunque dé lugar a números no reales. Esta alternativa
resulta apropiada si desea que la factorización se realice co n respecto
a más de una variable.
Catálogo
Catálogo
Catálogo
>
>
>
Guía de referencia de TI-Nspire™ CAS 13

cFactor()
cFactor(Expr1,Var ) devuelve Expr1 factorizado con respecto a la
variable Var .
Expr1 se factoriza tanto como sea posible hacia factores que son
lineales en Va r, aunque sean constantes no reales, incluso aunque
genere constantes irracionales o subexpresiones que sean irr acionales
en otras variables.
Los factores y sus términos se ordenan con Va r como variable
principal. En cada factor se recogen potencias de Va r similares.
Incluya Va r si la factorización es necesaria sólo con respecto a la
variable y no tiene inconveniente en aceptar expresiones irracionales
en cualquier otra variable para incrementar la factorización con
respecto a Var . Puede haber alguna factorización incidental con
respecto a otras variables.
Para el ajuste Auto del modo Auto or Approximate, la inclusión
de Var permite también una aproximación con coeficientes de coma
flotante cuando no sea posible expresar los coeficientes explícita y
concisamente en términos de las funciones integradas. Incluso
cuando sólo hay una variable, la inclusión de Va r puede generar una
factorización más completa.
Nota: Consulte también factor().
Catálogo
>
Para ver todos los resultados, pulse £ y utilice ¡ y ¢ para
mover el cursor.
char()
char(Entero) ⇒ carácter
Devuelve una cadena de caracteres que contiene el carácter dado
por el número Entero del juego de caracteres de la unidad portátil.
El rango válido para Entero es 0–65535.
charPoly()
charPoly(Matrizcuadrada,Var) ⇒ expresión polinómica
charPoly(Matrizcuadrada,Expr) ⇒ expresión polinómica
charPoly(Matrizcuadrada1,Matriz2) ⇒ expresión polinómica
Devuelve el polinomio característico de Matrizcuadrada. El
polinomio característico de la matriz cuadrada A de dimensión nxn,
indicado por medio de pA(l), es el polinomio definido por
pA(l) = det(l• I NA)
donde I indica la matriz de identidad n×n.
Matrizcuadrada1 y Matrizcuadrada2 deben tener las mismas
dimensiones.
2
c
de 2 elementos
2
c
2way ObsMatriz
chi22way ObsMatriz
Calcula un test de c2 para determinar si hay asociación con la tabla
de recuentos de dos elementos incluida en la matriz observada
ObsMatriz. El resumen de los resultados se guarda en la variable
stat.results. (Consulte la página 109.)
Catálogo
Catálogo
Catálogo
>
>
>
14 Guía de referencia de TI-Nspire™ CAS

Vari able de
salida
Descripción
stat.c2 Estadística de chi cuadrado: suma (observada - esperada)2/esperada
stat.PVal Nivel de significancia mínimo al que se puede rechazar la hipótesis nula
stat.df Grados de libertad para la estadística de chi cuadrado
stat.ExpMat Matriz de tabla de recuentos de elementos esperada, suponiendo una hipótesis nula
stat.CompMat Matriz de contribuciones para estadística de chi cuadrado de los elementos
2
c
Cdf()
2
c
Cdf(Extremoinferior,Extremosuperior,gl) ⇒ número si
Extremoinferior y Extremosuperior son números, lista si
Extremoinferior y Extremosuperior son listas
chi2Cdf(
Extremoinferior,Extremosuperior,gl) ⇒ número si
Extremoinferior y Extremosuperior son números, lista si
Extremoinferior y Extremosuperior son listas
Calcula la probabilidad de distribución de c2 entre el
Extremoinferior y el Extremosuperior para los grados de libertad gl
especificados.
Para P(X Extremosuperior), defina Extremoinferior=0.
2
c
GOF
2
c
GOF obsLista,expLista,gl
chi2GOF obsLista,expLista,gl
Lleva a cabo un test para confirmar que los datos de la muestra son
de una población que cumple una distribución especificada. obsList
es una lista de recuentos y debe contener números enteros.
El resumen de los resultados se guarda en la variable stat.results.
(Consulte la página 109).
Catálogo
Catálogo
>
>
Vari able de
salida
Descripción
stat.c2 Estadística de chi cuadrado: suma (observada - esperada)2/esperada
stat.PVal Nivel de significancia mínimo al que se puede rechazar la hipótesis nula
stat.df Grados de libertad para la estadística de chi cuadrado
stat.CompList Contribuciones para estadística de chi cuadrado de los elementos
Guía de referencia de TI-Nspire™ CAS 15

2
c
Pdf()
2
c
Pdf(XVal,gl) ⇒ número si XVal es un número, lista si XVal
es una lista
chi2Pdf(
XVal,gl) ⇒ número si XVal es un número, lista si
XVal es una lista
Calcula la función de densidad de probabilidad (pdf) para la
distribución de c2 para un valor XVal especificado para los grados de
libertad gl especificados.
Catálogo
>
ClearAZ
ClearAZ
Borra todas las variables cuyo nombre esté compuesto por un único
carácter del espacio del problema actual.
ClrErr
ClrErr
Borra el estado de error y define la variable del sistema errCode en
cero.
La cláusula Else del bloque Try...Else...EndTry debería utilizar
ClrErr o PassErr. Si va a procesar o ignorar el error, utilice ClrErr.
Si desconoce el tratamiento que se va a dar al error, utilice PassErr
para enviarlo al siguiente gestor de errores. Si no hay más gestores de
errores de tipo Try...Else...EndTry, el cuadro de diálogo de errores
aparecerá en su forma normal.
Nota: Consulte también PassErr, en la página 81, y Try , en la
página 119.
Nota para introducir el ejemplo: En la aplicación Calculadora
de la unidad portátil, puede introducir definiciones formadas por
varias líneas si pulsa @ en lugar de · al final de cada línea.
En el teclado del ordenador, mantenga pulsada la tecla Alt y pulse
Enter (Intro).
colAugment()
colAugment(Matriz1, Matriz2) ⇒ matriz
Devuelve una nueva matriz que es Matriz2 añadida a Matriz1.
Las dos matrices han de tener el mismo número de columnas, y
Matriz2 se añade a Matriz1 como si fueran nuevas filas. No se altera
el contenido de Matriz1 ni Matriz2.
Catálogo
>
Catálogo
>
Para ver un ejemplo de ClrErr, consulte el ejemplo 2 de la
orden Try, en la página 119.
Catálogo
>
colDim()
colDim(Matriz) ⇒ expresión
Catálogo
>
Devuelve el número de columnas de Matriz.
Nota: Consulte también rowDim().
16 Guía de referencia de TI-Nspire™ CAS

colNorm()
colNorm(Matriz) ⇒ expresión
Devuelve el máximo de las sumas de los valores absolutos de los
elementos de las columnas de MatriZ.
Nota: No se admiten elementos de matriz sin definir. Consulte
rowNorm().
también
Catálogo
>
comDenom()
comDenom(Expr1[,Va r]) ⇒ expresión
comDenom(Lista1[,Var ]) ⇒ lista
comDenom(Matriz1[,Var ]) ⇒ matriz
comDenom(Expr1) devuelve una fracción con un numerador
totalmente desarrollado sobre un denominador también totalmente
desarrollado.
comDenom(Expr1,Va r) devuelve una fracción reducida con un
numerador y un denominador desarrollados con respecto a Va r . Los
términos y sus factores se ordenan con Va r como variable principal.
Se agrupan potencias similares de Va r . Puede haber alguna
factorización incidental de los coeficientes agrupados. Comparada
con la omisión de Va r, supone ahorro de tiempo, memoria y espacio
de pantalla, al tiempo que hace que la expresión sea más
comprensible. También hace que el resultados de las operaciones
siguientes se genere más rápidamente con menos riesgo de agotar la
memoria.
Si Va r no ocurre en Expr1, comDenom(Expr1,Var ) devuelve una
fracción reducida de un numerador no desarrollado sobre un
denominador no desarrollado. Estos resultados suelen ahorrar
tiempo, memoria y espacio en pantalla. Tales resultados con
factorización parcial hacen que los resultados de las operaciones
siguientes se generen más rápido y con menos gasto de memoria.
Incluso si no hay denominador, la función comden suele ser un
medio rápido de conseguir una factorización parcial si factor() es
demasiado lento o consume mucha memoria.
Sugerencia: Introduzca esta definición de función comden() y
pruébela cada cierto tiempo como método alternativo de
comDenom() y factor().
Catálogo
>
conj()
conj(Expr1) ⇒ expresión
conj(Lista1) ⇒ lista
conj(Matriz1) ⇒ matriz
Catálogo
>
Muestra el complejo conjugado del argumento.
Nota: Se considera que todas las variables no definidas son variables
reales.
Guía de referencia de TI-Nspire™ CAS 17

constructMat()
constructMat(Expr,Var 1 ,Var 2 ,númeroFilas,númeroColumnas)
⇒ matriz
Devuelve una matriz basada en los argumentos.
Expr es una expresión en las variables Va r 1 y Var 2 . Los elementos de
la matriz resultante se forman calculando Expr para cada valor
incrementado de Va r1 y Va r 2 .
Var 1 se incrementa automáticamente desde
En cada fila, Va r2 se incrementa desde 1 hasta númeroColumnas.
1 hasta númeroFilas.
Catálogo
>
CopyVar
CopyVar Var 1 , Va r 2
CopyVar Var 1 ., Va r2 .
CopyVar Var 1 , Var 2 copia el valor de la variable Va r 1 hasta la
variable Var 2 , creando Va r2 si es necesario. La variable Va r 1 debe
tener un valor.
Si Va r1 es el nombre de una función definida por el usuario, copia su
definición en la función Va r2 . La función Va r 1 debe estar definida.
Var 1 debe cumplir los requisitos de nomenclatura aplicables a las
variables o ser una expresión que pueda convertirse en un nombre de
variable que cumpla dichos requisitos.
CopyVar Var 1 ., Va r 2. copia todos los miembros del grupo de
variables Var 1 . en el grupo Va r 2. creando Va r 2 . si es necesario.
Var 1 . debe ser el nombre de un grupo de var iables existente, como el
resultado estadístico stat.nn, o bien variables creadas con la función
LibShortcut(). Si Var 2 . ya existe, la orden sustituye todos los
miembros que son comunes a ambos grupos y añade los que no
existen. Si ya existe una variable sencilla (no un grupo) con el nombre
Var 2 , devuelve un error.
corrMat()
corrMat(Lista1,Lista2[,…[,Lista20]])
Calcula la matriz de correlación de la matriz aumentada [Lista1,
Lista2, ..., Lista20].
Catálogo
Catálogo
>
>
18 Guía de referencia de TI-Nspire™ CAS
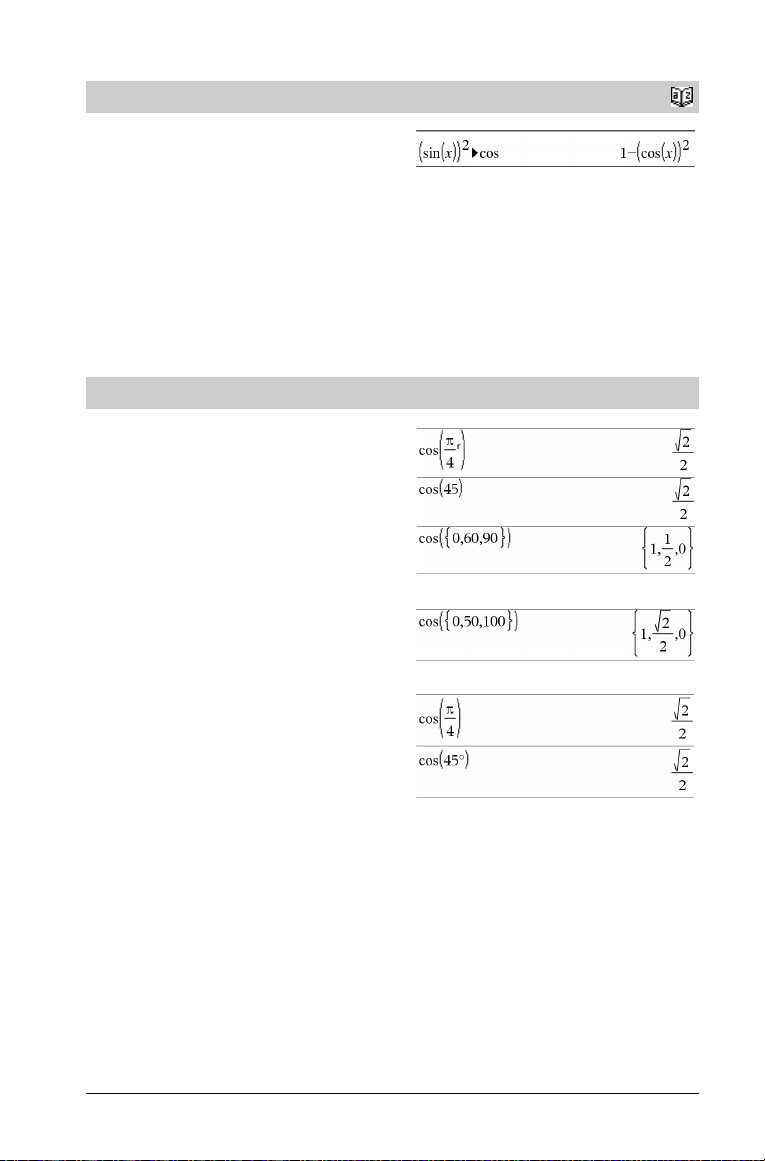
4
cos
4cos
Expr
Representa Expr en función de coseno. Es un operador de conversión
de presentación, y se puede utilizar únicamente al final de la línea de
entrada.
4
cos reduce todas las potencias de
sin(...) módulo 1Ncos(...)^2
para que las restantes potencias de cos(...) tengan exponentes en el
rango (0, 2). Por lo tanto, en el resultado no aparecerá en función de
sin(...) si y sólo si sin(...) se aparece en la expresión dada sólo en
potencias pares.
Nota: Este operador de conversión no es válido para los modos de
ángulo en grados o grados centesimales. Antes de utilizarlo,
asegúrese de que el modo ángulo está definido en radianes y que
Expr no contiene referencias explícitas a ángulos en grados o grados
centesimales.
Catálogo
>
cos()
cos(Expr1) ⇒ expresión
cos(Lista1) ⇒ lista
cos(Expr1) devuelve el coseno del argumento en forma de
expresión.
cos(Lista1) devuelve una lista de los cosenos de todos los elementos
de Lista1.
Nota: El argumento se interpreta como un ángulo en gra dos, grados
centesimales o radianes, según el modo de ángulo actual. Puede
utilizar ó,G o ôpara sobrescribir el modo de ángulo temporalmente.
Tecla n
En el modo de ángulo en grados:
En el modo de ángulo en grados centesimales:
En el modo de ángulo en radianes:
Guía de referencia de TI-Nspire™ CAS 19

cos()
cos(Matrizcuadrada1) ⇒ Matrizcuadrada
Devuelve el coseno de la matriz Matrizcuadrada1. El resultado no es
igual que calcular el coseno de cada elemento.
Cuando la función escalar f(A) actúa sobre Matrizcuadrada1 (A), el
resultado se calcula mediante el algoritmo:
Calcula los valores propios (li) y los vectores propios (Vi) de A.
Matrizcuadrada1 debe ser diagonizable. Además, no puede tener
variables simbólicas que no tengan un valor asignado.
Escriba las matrices:
A continuación, A = X B Xêy f(A) = X f(B) Xê. Por ejemplo, cos(A) =
X cos(B) Xê donde:
cos(B) =
Todos los cálculos se realizan utlizando la coma aritmética flotante.
Tecla n
En el modo de ángulo en radianes:
cosê()
cosê(Expr1) ⇒ expresión
cosê(Lista1) ⇒ lista
cosê(Expr1) devuelve el ángulo cuyo coseno es Expr1 en forma de
expresión.
cosê(Lista1) devuelve una lista de los cosenos inversos de cada
elemento de Lista1.
Nota: El resultado se muestra como un ángulo en grados, grados
centesimales o radianes, según el modo de ángulo actual.
cosê(Matrizcuadrada1) ⇒ Matrizcuadrada
Devuelve el coseno inverso de la matriz Matrizcuadrada1. El
resultado no es igual que calcular el coseno inverso de cada
elemento. Para obtener más información sobre el método de cálculo,
consulte cos().
Matrizcuadrada1 debe ser diagonizable. El resultado contiene
siempre números con coma flotante.
En el modo de ángulo en grados:
En el modo de ángulo en grados centesimales:
En el modo de ángulo en radianes:
En el modo de ángulo en radianes y formato complejo
rectangular:
Para ver todos los resultados, pulse £ y utilice ¡ y ¢ para
mover el cursor.
Teclas
/
n
20 Guía de referencia de TI-Nspire™ CAS

cosh()
cosh(Expr1) ⇒ expresión
cosh(Lista1) ⇒ lista
cosh(Expr1) devuelve el coseno hiperbólico del argumento en
forma de expresión.
cosh(Lista1) devuelve una lista de cosenos hiperbólicos de cada
elemento de Lista1.
cosh(Matrizcuadrada1) ⇒ Matrizcuadrada
Devuelve el coseno hiperbólico de la matriz Matrizcuadrada1. El
resultado no es igual que calcular el coseno hiperbólico de cada
elemento. Para obtener más información sobre el método de cálculo,
cos().
consulte
Matrizcuadrada1 debe ser diagonizable. El resultado contiene
siempre números con coma flotante.
En el modo de ángulo en radianes:
Catálogo
>
coshê()
coshê(Expr1) ⇒ expresión
coshê(Lista1) ⇒ lista
ê
cosh
(Expr1) devuelve el coseno hiperbólico inverso del argumento
en forma de expresión.
ê
cosh
(Lista1) devuelve una lista de cosenos hiperbólicos inversos
de cada elemento de Lista1.
coshê(Matrizcuadrada1) ⇒ Matrizcuadrada
Devuelve el coseno hiperbólico inverso de la matriz
Matrizcuadrada1. El resultado no es igual que calcular el coseno
hiperbólico inverso de cada elemento. Para obtener más información
sobre el método de cálculo, consulte cos().
Matrizcuadrada1 debe ser diagonizable. El resultado contiene
siempre números con coma flotante.
cot()
cot(Expr1) ⇒ expresión
cot(Lista1) ⇒ lista
Devuelve la cotangente de Expr1 o una lista de las cotangentes de
todos los elementos de Lista1.
Nota: El argumento se interpreta como un ángulo en gra dos, grados
centesimales o radianes, según el modo de ángulo actual. Puede
utilizar ó,G oôpara sobrescribir el modo de ángulo temporalmente.
Catálogo
>
En el modo de ángulo en radianes y formato complejo
rectangular:
Para ver todos los resultados, pulse £ y utilice ¡ y ¢ para
mover el cursor.
Catálogo
>
En el modo de ángulo en grados:
En el modo de ángulo en grados centesimales:
En el modo de ángulo en radianes:
Guía de referencia de TI-Nspire™ CAS 21

cotê()
cotê(Expr1) ⇒ expresión
cotê(Lista1) ⇒ lista
Devuelve el ángulo cuya cotangente es Expr1 o una lista de las
cotangentes inversas de cada elemento de Lista1.
Nota: El resultado se muestra como un ángulo en grados, radianes o
grados centesimales, según el modo de ángulo actual.
Catálogo
En el modo de ángulo en grados:
En el modo de ángulo en grados centesimales:
En el modo de ángulo en radianes:
>
coth()
coth(Expr1) ⇒ expresión
coth(Lista1) ⇒ lista
Devuelve la cotangente hiperbólica de Expr1 o una lista de las
cotangentes hiperbólicas de todos los elementos de Lista1.
cothê()
cothê(Expr1) ⇒ expresión
cothê(Lista1) ⇒ lista
Devuelve la cotangente hiperbólica inversa de Expr1 o una lista de
las cotangentes hiperbólicas inversas de todos los elementos de
Lista1.
count()
count(Valor1 o Lista1 [,Valor2 o Lista2 [,...]]) ⇒ valor
Devuelve el recuento acumulado de todos los elementos de los
argumentos que sirven para calcular valores numéricos.
Cada argumento puede ser una expresión, valor, lista o matriz. Es
posible mezclar tipos de datos y utilizar argumentos con distintas
dimensiones.
En listas, matrices o rangos de celdas, se calcula cada elemento para
determinar si debe incluirse en el recuento.
En la aplicación Listas y Hojas de cálculo, puede utilizarse un rango de
celdas en lugar de cualquier argumento.
Catálogo
>
Catálogo
>
Catálogo
>
En el último ejemplo, sólo se han contado los valores 1/2 y
3+4*i. Los restantes argumentos, suponiendo que x esté sin
definir, no se utilizan para calcular valores numéricos.
22 Guía de referencia de TI-Nspire™ CAS

countif()
countif(Lista,Criterios) ⇒ valor
Devuelve el recuento acumulado de todos los elementos de Lista que
cumplen los Criterios especificados.
Los criterios pueden ser:
• Un valor, una expresión o una cadena. Por ejemplo, 3 cuenta sólo
los elementos de Lista que se simplifican al valor 3.
• Una expresión booleana que contenga el símbolo ? como lugar
donde introducir cada elemento. Por ejemplo, ?<5 cuenta sólo
los elementos de Lista que son menores de 5.
En la aplicación Listas y Hojas de cálculo, puede utilizarse un rango de
celdas en lugar de Lista.
Nota: Consulte también sumIf(), en la página 112, y
frequency(), en la página 47.
Catálogo
>
Cuenta el número de elementos que son iguales a 3.
Cuenta el número de elementos que son iguales a “def”.
Cuenta el número de elementos que son iguales a x; en este
ejemplo se supone que la variable x está sin definir.
Cuenta 1 y 3.
Cuenta 3, 5 y 7.
Cuenta 1, 3, 7 y 9.
crossP()
crossP(Lista1, Lista2) ⇒ lista
Devuelve el producto vectorial de Lista1 y Lista2 en forma de lista.
Lista1 y Lista2 deben tener la misma dimensión, que deberá ser 2 o
3.
crossP(Vector1, Vector2) ⇒ vector
Devuelve un vector fila o columna (depende del argument o) que es el
producto vectorial de Vector1 y Vector2.
Tanto Vector1 como Vector2 deben ser vectores fila, o vectores
columna. Los dos vectores deben tener la misma dimensión, que
deberá ser 2 o 3.
csc()
csc(Expr1) ⇒ expresión
csc(Lista1) ⇒ lista
Devuelve la cosecante de Expr1 o una lista de las cosecantes de
todos los elementos de Lista1.
Catálogo
Catálogo
En el modo de ángulo en grados:
En el modo de ángulo en grados centesimales:
En el modo de ángulo en radianes:
>
>
Guía de referencia de TI-Nspire™ CAS 23
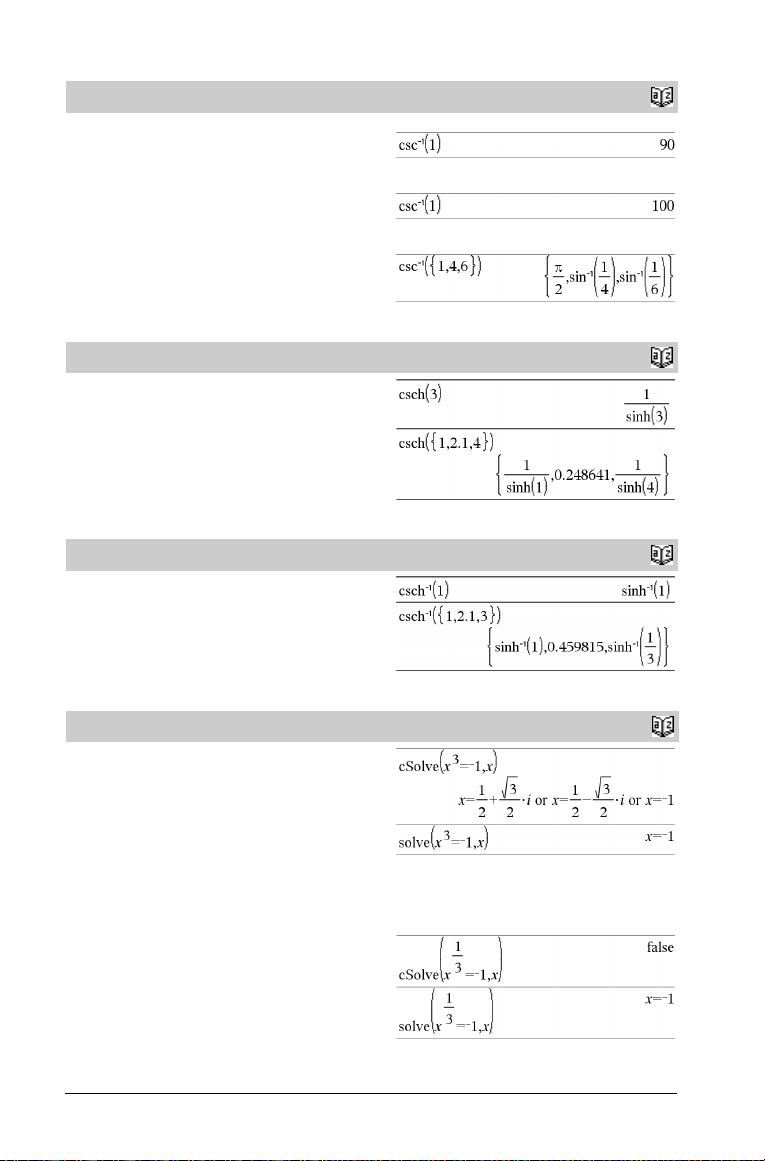
cscê()
cscê(Expr1) ⇒ expresión
cscê(Lista1) ⇒ lista
Devuelve el ángulo cuya cosecante es Expr1 o una lista de las
cosecantes inversas de todos los elementos de Lista1.
Nota: El resultado se muestra como un ángulo en grados, grados
centesimales o radianes, según el modo de ángulo actual.
Catálogo
En el modo de ángulo en grados:
En el modo de ángulo en grados centesimales:
En el modo de ángulo en radianes:
>
csch()
csch(Expr1) ⇒ expresión
csch(Lista1) ⇒ lista
Devuelve la cosecante hiperbólica de Expr1 o una lista de las
cosecantes hiperbólicas de todos los elementos de Lista1.
cschê()
cschê(Expr1) ⇒ expresión
cschê(Lista1) ⇒ lista
Devuelve la cosecante hiperbólica inversa de Expr1 o una lista de las
cosecantes hiperbólicas inversas de todos los elementos de Lista1.
cSolve()
cSolve(Ecuación, Va r ) ⇒ Expresión boolena
cSolve(Equación, Var=Conjetura) ⇒ Expresión booleana
cSolve(Desigualdad, Va r ) ⇒ Expresión booleana
Devuelve las posibles soluciones complejas de una ecuación o
desigualdad para Va r. El objetivo es presentar todas las posibles
soluciones, tanto reales como no reales. Incluso si Ecuación es real,
cSolve() permite resultados no reales en formato complejo.
Aunque todas las variables no definidas no terminen con un carácter
de subrayado (_) se procesan como si fueran reales, cSolve() puede
resolver ecuaciones polinómicas mediante soluciones complejas.
Durante la solución, cSolve() define temporalmente el dominio
como complejo incluso aunque el dominio actual sea real. En el
dominio complejo, las potencias de fracción que tengan
denominadores impares utilizan la rama principal en lugar de la real.
Por lo tanto, las soluciones de solve() en ecuaciones que requieran
tales potencias de fracción no constituyen necesariamente un
subconjunto derivado de cSolve().
Catálogo
Catálogo
Catálogo
>
>
>
24 Guía de referencia de TI-Nspire™ CAS

cSolve()
cSolve() se inicia con métodos simbólicos exactos. cSolve() utiliza
también factoriales polinómicos complejos aproximados i terativos, en
caso necesario.
Nota: Consulte también cZeros(), solve() y zeros().
Nota: Si Ecuación no es un polinomio con funciones como abs(),
angle(), conj(), real() o imag(), deberá insertarse un carácter de
subrayado (pulse /_) al final de Va r. De forma
predeterminada, las variables se tratan como valores reales.
Si utiliza var_, la variable será tratada como un número complejo.
También deberá utilizar var_ para cualquier otra variable de
Ecuación que pueda tener valores no reales. De lo contrario puede
obtener resultados imprevistos.
cSolve(Ecuación1 and Ecuación2 [and …],
VarOConjetura1, VarOConjetura2 [, … ])
⇒ Expresión booleana
cSolve(SistemaDeEcuaciones, VarOConjetura1,
VarOConjetura2 [, …]) ⇒ Expresión booleana
Devuelve las posibles soluciones complejas para las ecuaciones
algebraicas simultáneas, donde cada varOConjetura especifica una
variable para la que se desea resolver.
Opcionalmente se puede especificar un valor inicial para una vari able.
Cada varOConjetura debe tener la forma:
variable
– o –
variable = número real o no real.
Por ejemplo, x es válido y también x=3+i.
Si todas las ecuaciones son polinómicas y NO se ha especificado
ningún valor inicial, cSolve() utiliza el método de eliminación léxica
de Gröbner/Buchberger para tratar de determinar todas las
soluciones complejas.
Las soluciones complejas pueden incluir tanto números reales como
no reales, tal y como se indica en el ejemplo de la derecha.
Catálogo
>
En modo Mostrar dígitos como Fijo 2:
Para ver todos los resultados, pulse £ y utilice ¡ y ¢ para
mover el cursor.
z tratado como real:
z_ tratado como complejo:
Nota: Los ejemplos siguientes utiliza n un carácter de subrayado
(pulse /_) para que las variables se puedan
considerar como números complejos.
Para ver todos los resultados, pulse £ y utilice ¡ y ¢ para
mover el cursor.
Las ecuaciones polinómicas simultáneas pueden tener variables extr a
que carezcan de valores pero que representen valores numéricos
dados que puedan ser sustituidos más adelante.
Para ver todos los resultados, pulse £ y utilice ¡ y ¢ para
mover el cursor.
Guía de referencia de TI-Nspire™ CAS 25

cSolve()
También puede incluir variables de solución que no aparezcan en las
ecuaciones. Dichas soluciones muestran cómo las familias de
soluciones pueden contener constantes arbitrarias de la forma ck,
donde k sea un sufijo entero de 1 a 255.
Para sistemas polinómicos, el tiempo de cálculo o el agotamiento de
la memoria pueden depender del orden con el que aparecen las
variables de solución. Si la opción de memoria, o su paciencia, se
agota, pruebe a reorganizar las variables de las ecuaciones, la lista de
varOConjetura o ambos elementos.
Si no incluye ningún valor inicial y alguna de las ecuaciones es no
polinómica en cualquier variable pero todas las ecuaciones son
lineales en todas las variables de solución, cSolve() utiliza un
método de eliminación gaussiana para tratar de determinar todas las
soluciones.
Si el sistema no es polinómico en todas sus variables ni lineal en
todas sus variables de solución, cSolve() determina una solución
como máximo utilizando un método de iteración aproximada. Para
ello, el número de las variables de la solución debe ser igual al
número de ecuaciones, y todas las demás variables de las ecuaciones
deben simplificarse en números.
A veces puede ser necesario utilizar un valor inicial no real para
determinar una solución no real. Por convergencia, es probable que el
valor inicial esté bastante próximo a la solución.
Catálogo
>
Para ver todos los resultados, pulse £ y utilice ¡ y ¢ para
mover el cursor.
Para ver todos los resultados, pulse £ y utilice ¡ y ¢ para
mover el cursor.
CubicReg
CubicReg X, Y[, [Frec] [, Categoría, Incluir]]
Calcula la regresión polinómica cúbica y = a·x3+b· x2+c·x+d de
las listas X e Y con la frecuencia Frec. El resumen de los resultados se
guarda en la variable stat.results. (Consulte la página 109).
Todas las listas, salvo Incluir, deben tener la misma dimensión.
X e Y son listas que contienen, respectivamente, la variable
independiente y la variable dependiente.
Frec es una lista opcional de valores de frecuencia. Cada elemento
de Frec especifica la frecuencia de ocurrencia de cada punto de datos
en X e Y. El valor predeterminado es 1. Todos los elementos deben
ser enteros | 0.
Categoría es una lista de códigos numéricos de categoría para los
datos de X e Y.
Incluir es una lista de uno o varios códigos de categoría. En el cálculo
sólo se incluyen los elementos de datos cuyo código de categoría se
encuentre en la lista.
Vari able de
salida
stat.RegEqn
stat.a, stat.b, stat.c,
stat.d
2
stat.R
Descripción
Ecuación de regresión: a·x3+b·x2+c·x+d
Coeficientes de regresión
Coeficiente de determinación
Catálogo
>
26 Guía de referencia de TI-Nspire™ CAS

Vari able de
salida
Descripción
stat.Resid Residuos de la regresión
stat.XReg Lista de puntos de datos en la Lista X modificada utilizada realmente en la regresión basada en
stat.YReg Lista de puntos de datos en la Lista Y modificada utilizada realmente en la regresión basada en las
restricciones de Frec, Lista Categoría e Incluir Categoría
restricciones de Frec, Lista Categoría e Incluir Categoría
stat.FreqReg Lista de frecuencias correspondiente a stat.XReg y stat.YReg
cumSum()
cumSum(Lista1) ⇒ lista
Devuelve una lista de las sumas acumuladas de los elementos de
Lista1, a partir del elemento 1.
cumSum(Matriz1) ⇒ matriz
Devuelve una matriz de las sumas acumuladas de los elementos de
Matriz1. Cada elemento es la suma acumulada de los elementos de
la columna desde arriba hacia abajo.
Cycle
Cycle
Transfiere el control de forma inmediata a la siguiente iteración del
bucle actual (For, While o Loop).
Cycle no está admitido fuera de las tres estructuras de bucle (For,
While o Loop).
Nota para introducir el ejemplo: En la aplicación Calculadora
de la unidad portátil, puede introducir definiciones formadas por
varias líneas si pulsa @ en lugar de · al final de cada línea.
En el teclado del ordenador, mantenga pulsada la tecla Alt y pulse
Enter (Intro).
Catálogo
>
Catálogo
>
Listado de función que suma los enteros de 1 a 100 omitiendo
50.
Cylind
4
Catálogo
>
Vec t o r 4Cylind
Muestra el vector de la fila o la columna en formato cilíndrico [r,q,
z].
Vec t o r debe tener tres elementos exactamente. Puede ser una fila o
una columna.
Guía de referencia de TI-Nspire™ CAS 27

cZeros()
cZeros(Expr, Va r ) ⇒ lista
Devuelve una lista de posibles valores, tanto reales como no reales,
para Va r que hacen Expr=0. cZeros() lo consigue calculando
exp4lista(cSolve(Expr=0,Var ),Va r ). De lo contrario, cZeros() es
similar a zeros().
Nota: Consulte también cSolve(), solve() y zeros().
Nota: Si Expr no es un polinomio con funciones como abs(),
angle(), conj(), real() o imag(), deberá insertarse un carácter de
subrayado (pulse /_) al final de Va r. De forma
predeterminada, las variables se tratan como valores reales. Si utiliza
var_ , la variable será tratada como un número complejo.
También deberá utilizar var_ para cualquier otra variable de Expr
que pueda tener valores no reales. De lo contrario puede obtener
resultados imprevistos.
cZeros({Expr1, Expr2 [, … ] },
VarOConjetura1,VarOConjetura2 [, … ] }) ⇒ matriz
{
Devuelve las posibles posiciones donde las expresiones son cero
simultáneamente. Cada VarOConjetura especifica una incógnita
cuyo valor se desea determinar.
Opcionalmente se puede especificar un valor inicial para una vari able.
Cada varOConjetura debe tener la forma:
variable
– o –
variable = número real o no real
Por ejemplo, x es válido y también x=3+i.
Si todas las expresiones son polinomios y NO se ha especificado
ningún valor inicial, cZeros() utiliza el método de eliminación léxica
de Gröbner/Buchberger para tratar de determinar todos los ceros
complejos.
Los ceros complejos pueden incluir tanto números reales como no
reales, tal y como se indica en el ejemplo de la derecha.
Cada fila de la matriz resultante representa un cero alternativo, con
los componentes ordenados igual que en la lista de VarOConjetura.
Para extraer una fila, indexe la matriz por [fila].
Catálogo
>
En modo Mostrar dígitos como Fijo 3:
Para ver todos los resultados, pulse
mover el cursor.
z tratado como real:
z_ tratado como complejo:
Nota: Los ejemplos siguientes utilizan un carácter de
subrayado _ (pulse /_) para que las variables se
puedan considerar como números complejos.
£ y utilice ¡ y ¢ para
Extraer fila 2:
Los polinomios simultáneos pueden tener variables extra que
carezcan de valores pero que representen valores numéricos dados
que puedan ser sustituidos más adelante.
28 Guía de referencia de TI-Nspire™ CAS

cZeros()
También puede incluir variables incógnitas que no aparezcan en las
expresiones. Dichos ceros muestran cómo las familias de soluciones
pueden contener constantes arbitrarias de la forma ck, donde k sea
un sufijo entero de 1 a 255.
Para sistemas de polinomios, el tiempo de cálculo o el agotamiento
de la memoria pueden depender del orden con que el aparecen las
incógnitas. Si la opción de memoria inicial, o su paciencia, se agota,
pruebe a reorganizar las variables de las expresiones, la lista de
VarOConjetura o ambos elementos.
Si no incluye ningún valor inicial y alguna de las expresiones no es
polinómica en cualquier variable pero todas las expresiones son
lineales en todas las incógnitas, cZeros() utiliza un método de
eliminación gaussiana para tratar de determinar todos los ceros.
Si el sistema no es polinómico en todas sus variables ni lineal en sus
incógnitas, cZeros() determina una solución como máximo
utilizando un método de iteración aproximada. Para ello, el número
de las variables de la solución debe ser igual al número de
expresiones, y todas las demás variables de las expresiones deben
simplificarse en números.
A veces puede ser necesario utilizar un valor inicial no real para
determinar un cero no real. Por convergencia, es probable que un
valor inicial esté bastante próximo a cero.
D
Catálogo
>
dbd()
dbd(fecha1,fecha2) ⇒ valor
Devuelve el número de días entre fecha1 y fecha2 utilizando el
método de recuento de días reales.
fecha1 y fecha2 pueden ser números o listas de números
comprendidos en el rango de fechas del calendario estándar. Si tanto
fecha1 como fecha2 son listas, deben tener la misma longitud.
fecha1 y fecha2 deben estar comprendidas en los años 1950 y 2049.
Puede introducir las fechas en cualquiera de los dos formatos.
El separador decimal permite diferenciar los formatos de fecha.
MM.DDAA (es el formato de uso más frecuente en EE. UU.)
DDMM.AA (es el formato de uso más frecuente en Europa)
Catálogo
>
Guía de referencia de TI-Nspire™ CAS 29

DD
4
4DD ⇒ valor
Expr1
Lista1 4DD ⇒ list
Matriz1
4DD ⇒ matriz
Devuelve el equivalente decimal del argumento expresado en grados.
El argumento es un número, lista o matriz que se interpreta en
grados, radianes o grados centesimales según el modo de ángulo
actual.
Catálogo
En el modo de ángulo en grados:
En el modo de ángulo en grados centesimales:
En el modo de ángulo en radianes:
>
4Decimal
4Decimal
Expresión1
4Decimal
Lista1
4
Decimal
Matriz1
Muestra el argumento en formato decimal. El operador sólo se puede
utilizar al final de la línea de entrada.
Define (Definir)
Define Var = Expresión
Define Function(Param1, Param2, ...) = Expresión
Define la variable Va r o la función definida por el usuario Function.
Los parámetros, como Param1, son lugares donde insertar los
argumentos que pasan a la función. Al designar una función definida
por el usuario es necesario facilitar los argumentos (por ejemplo,
valores o variables) correspondientes a los parámetros. Cuando se
activa, la función calcula el valor de Expresión con los argumentos
facilitados.
Var y Function no pueden ser el nombre de una variable del sistema
ni de una orden o función integrada.
Nota: Esta forma de la orden Define equivale a ejecutar la
expresión: expresión & Function(Param1,Param2).
⇒ expresión
⇒ expresión
⇒ expresión
Catálogo
Catálogo
>
>
30 Guía de referencia de TI-Nspire™ CAS

Define (Definir)
Define Function(Param1, Param2, ...) = Func
Bloque
EndFunc
Program(Param1, Param2, ...) = Prgm
Define
Bloque
EndPrgm
De esta forma, la función o programa definidos por el usuario pueden
ejecutar un bloque de varias sentencias.
Bloque puede ser una sentencia sencilla o una serie de sentencias
escritas en varias líneas. Bloque puede incluir también expresiones e
instrucciones (como If, Then, Else y For).
Nota para introducir el ejemplo: En la aplicación Calculadora
de la unidad portátil, puede introducir definiciones formadas por
varias líneas si pulsa @ en lugar de · al final de cada línea.
En el teclado del ordenador, mantenga pulsada la tecla Alt y pulse
Enter (Intro).
Nota: Consulte también Define LibPriv, en la página 31 y
Define LibPub, en la página 32.
Catálogo
>
Define LibPriv
Define LibPriv Var = Expresión
Define LibPriv Function(Param1, Param2, ...) = Expresión
Define LibPriv Function(Param1, Param2, ...) = Func
Bloque
EndFunc
Define LibPriv
Bloque
EndPrgm
Funciona igual que Define, salvo en que define una variable de
biblioteca, función o programa privados. Las funciones y los
programas privados no aparecen en el Catálogo.
Nota: Consulte también Define, en la página 30 y Define
LibPub
Program(Param1, Param2, ...) = Prgm
, en la página 32.
Catálogo
>
Guía de referencia de TI-Nspire™ CAS 31

Define LibPub
Define LibPub Var = Expresión
Define LibPub Function(Param1, Param2, ...) = Expresión
Define LibPub Function(Param1, Param2, ...) = Func
Bloque
EndFunc
Define LibPub
Bloque
EndPrgm
Funciona igual que Define, salvo en que define una variable de
biblioteca, función o programa públicos. Las funciones y los
programas públicos aparecen en el Catálogo una vez que la biblioteca
ha sido guardada y actualizada.
Nota: Consulte también Define, en la página 30 y Define
LibPriv
Program(Param1, Param2, ...) = Prgm
, en la página 31.
Catálogo
>
DelVar
DelVar Var 1 [, Va r 2] [, Va r 3 ] ...
DelVar
Var .
Borra la variable o el grupo de variables especificado de la memoria.
DelVar Var . borra todos los miembros del grupo de variables Va r.
(por ejemplo, el estadístico stat.nn resultados o variables creadas
utilizando la función LibShortcut()). El punto (.) en este formato
de orden de DelVar impide borrar un grupo de variables; no tiene
efecto sobre la variable sencilla Va r .
deSolve()
deSolve(ODE1erO2ºOrden, Var , depVar)
⇒ una solución general
Devuelve una ecuación que implícita o explícitamente especifica una
solución general para la ecuación deferencial ordinaria (ODE) de
primer o segundo grado. En la ODE:
• Utilice el símbolo principal (pulse ') para indicar la primera
derivada de la variable dependiente con respecto a la variable
independiente.
• Utilice los dos símbolos principales para indicar la segunda
derivada correspondiente.
El símbolo principal se utiliza sólo para las derivadas incluidas en
deSolve(). En los demás casos, utilice d().
La solución general de una ecuación de primer grado contiene una
constante arbitraria de la forma ck, donde k es un sufijo entero de 1 a
255. La solución de la ecuación de segundo grado contiene dos
constantes de ese tipo.
Catálogo
Catálogo
>
>
32 Guía de referencia de TI-Nspire™ CAS

deSolve()
Aplique solve() a una solución implícita si desea tratar de
convertirla en una o varias soluciones equivalentes explícitas.
Al comparar los resultados con las soluciones del libro o el manual,
tenga en cuenta que métodos distintos introducen constantes
arbitrarias en diferentes puntos del cálculo, lo que puede generar
diversas soluciones generales.
deSolve(ODE1erOrden and Condinicial, Var , Vardependiente)
⇒ una solución particular
Devuelve una solución particular que satisface la ODE de primer
orden y la Condición inicial. Es un método que suele resultar más
fácil que determinar una solución general, sustituir los valores
iniciales, hallar la constante arbitraria y, finalmente, sustituir el valor
en la solución general.
Condición inicial es una ecuación de la forma:
depVar (ValorIndependienteInicial) = ValorDependienteInicial
El ValorIndependienteInicial y el ValorDependienteInicial pueden
ser variables como x0 e y0 que tengan valores no almacenados. La
diferenciación implícita puede facilitar la comprobación de las
soluciones implícitas.
deSolve(ODE2ºOrden and Condinicial1 and Condinicial2,
Var , Vardependiente) ⇒ una solución particular
Devuelve una solución concreta que satisface la ODE2ºOrden y tiene
un valor especificado de la variable dependiente y de su primera
derivada en un punto.
Para Condinicial1, utilice la forma:
depVar (ValorIndependienteInicial) = ValorDependienteInicial
Para Condinicial2, utilice la forma:
depVar (ValorIndependienteInicial) = Valor1ªDerivadaInicial
Catálogo
>
deSolve(ODE2ºOrden and Condextremo1 and
Condextremo2, Var , Vardependiente) ⇒ una solución
particular
Devuelve una solución particular que satisface la ODE de segundo
orden y tiene el valor especificado en dos puntos diferentes.
Guía de referencia de TI-Nspire™ CAS 33

det()
det(Matrizcuadrada[, Tolerancia]) ⇒ expresión
Devuelve la determinante de Matrizcuadrada.
Opcionalmente, cualquier elemento de la matriz se trata com o cero si
su valor absoluto es menor que Tolerancia. Esta tolerancia se utiliza
sólo si la matriz tiene entradas de coma flotante y no contiene
ninguna variable simbólica que no tenga asignado un valor. De lo
contrario, se ignorará el valor de Tolerancia.
/
• Si utiliza
Approximate (Auto o Aproximado)
cálculos se efectuarán utilizando la coma flotante aritmética.
•Si el valor de Tolerancia se omite o no se utiliza, la tolerancia
predeterminada se calcula como:
5EM14 ·max(dim(Matrizcuadrada))·
rowNorm(Matrizcuadrada)
·
o define el modo Auto or
en Aproximado, los
Catálogo
>
diag()
diag(Lista) ⇒ matriz
diag(Matrizfila) ⇒ matriz
diag(Matrizcolumna) ⇒ matriz
Devuelve una matriz con los valores de la lista de argumentos o de la
diagonal principal de la matriz.
diag(Matrizcuadrada) ⇒ Matrizfila
Devuelve una matriz fila con los elementos de la diagonal principal de
Matrizcuadrada.
Matrizcuadrada debe ser cuadrada.
dim()
dim(Lista) ⇒ entero
Devuelve la dimensión de Lista.
dim(Matriz) ⇒ lista
Devuelve las dimensiones de la matriz como una lista de dos
elementos {filas, columnas}.
dim(Cadena) ⇒ entero
Devuelve el número de caracteres contenido en la cadena de
caracteres Cadena.
Catálogo
Catálogo
>
>
34 Guía de referencia de TI-Nspire™ CAS

Disp
Disp [exprOCadena1] [, exprOCadena2] ...
Muestra los argumentos del historial de Calculadora. Los argumentos
aparecen uno tras otro separados por pequeños espacios.
Resulta especialmente útil en programas y funciones ya que permite
garantizar la presentación de cálculos intermedios.
Nota para introducir el ejemplo: En la aplicación Calculadora
de la unidad portátil, puede introducir definiciones formadas por
varias líneas si pulsa @ en lugar de · al final de cada línea.
En el teclado del ordenador, mantenga pulsada la tecla Alt y pulse
Enter (Intro).
GMS
4
Expr 4GMS
List 4GMS
Matriz 4GMS
Interpreta el argumento como un ángulo y muestra el número GMS
equivalente (GGGGGG¡MM'SS.ss''). Consulte ¡, ', '', en la página
145 para ver información sobre el formato GMS(grados, minutos,
segundos).
Nota: 4GMS se convertirá de radianes a grados cuando se utilice en
modo radianes. Si la entrada va seguida de un símbolo de grados, ¡,
no se producirá conversión alguna. Sólo se puede utilizar 4GMS al
final de una línea de entrada.
En el modo de ángulo en grados:
Catálogo
Catálogo
>
>
Guía de referencia de TI-Nspire™ CAS 35

dominantTerm()
dominantTerm(Expr1, Va r [, Punto]) ⇒ expresión
dominantTerm(Expr1, Va r [, Punto]) | Va r >Punto
⇒ expresión
dominantTerm(Expr1, Va r [, Punto]) | Va r <Punto
⇒ expresión
Devuelve el término dominante de una representación de series de
potencias de Expr1 ampliadas a partir de Punto. El término
dominante es aquel cuya magnitud crece más rápidamente a media
que se aproxima a Va r = Punto. La potencia resultante de (Va r N
Punto) puede tener un exponente negativo y/o fraccionario. El
coeficiente de esta potencia puede incluir logaritmos de (Va r N
Punto) y otras funciones de Va r que estén dominadas por todas las
potencias de (Va r N Punto) con el mismo signo de exponente.
Punto valor predeterminado 0. Punto puede ser ˆ o Nˆ, en cuyo
caso el término dominante será el que tenga el exponente mayor de
Var , no el de menor exponente de Va r.
dominantTerm(…) devuelve “dominantTerm(…)” si no
puede obtener una representación concreta como, por ejemplo,
singularidades esenciales como sin(1/z) en z=0, e
z = ˆ o Nˆ.
Si la serie o una de sus derivadas tiene un salto de discontinuidad en
Punto, el resultado puede contener subexpresiones en la forma
sign(…) o abs(…) para una variable de desarrollo real, o (-
floor(…angle(…)…)
1)
una que termine con "_". Si piensa utilizar el término dominan te sólo
para los valores de un lado de Punto, añada a dominantTerm(...)
el valor apropiado de "| Va r > Punto", "| Va r < Punto", "| "Va r ‚
para una variable de desarrollo complejo, como
N1/z
en z=0, o ez en
Punto" o "Var Punto" para obtener un resultado más simple.
dominantTerm() se distribuye sobre los primeros argumentos,
listas y matrices.
dominantTerm() resulta útil cuando desea conocer la expresión
más simple posible que es asintótica a otra expresión como
Var " Punto. dominantTerm() también resulta útil cuando no es
evidente el grado del primer término distinto de cero de una serie, y
no desea realizar aproximaciones iterativas, ya sea de forma
interactiva o mediante un bucle de programa.
Nota: Consulte también series(), en la página 98.
Catálogo
>
dotP()
dotP(Lista1, Lista2) ⇒ expresión
Catálogo
>
Devuelve el producto escalar de dos listas.
dotP(Vector1, Vector2) ⇒ expresión
Devuelve el producto escalar de dos vectores.
Los dos vectores deben ser fila o columna.
36 Guía de referencia de TI-Nspire™ CAS

E
e^()
e^(Expr1) ⇒ expresión
Devuelve el valor de e elevado al exponente Expr1.
Nota: Consulte también Plantilla de base e, en la página 2.
Nota: Pulsar u para mostrar
e
^( no es lo mismo que pulsar el
carácter E del teclado.
i
Puede introducir un número complejo en la forma polar re
obstante, deberá utilizar esta forma sólo en el modo de ángulo en
radianes: genera un error de dominio en e l modo de ángulo en grados
o grados centesimales.
e^(Lista1) ⇒ lista
q
. No
Devuelve el valor de e elevado a cada elemento de Lista1.
e^(Matrizcuadrada1) ⇒ Matrizcuadrada
Devuelve la matriz exponencial de Matrizcuadrada1. El resultado no
es igual que calcular e elevado a cada elemento. Para obtener más
información sobre el método de cálculo, consulte cos().
Matrizcuadrada1 debe ser diagonizable. El resultado contiene
siempre números con coma flotante.
eff()
eff(Tasanominal,CpY) ⇒ valor
Función financiera que convierte la tasa de interés nominal
Tasanominal en una tasa anual efectiva, siendo CpY el número de
periodos compuestos por año.
Tasanominal debe ser un número real; CpY debe ser un número real
> 0.
Nota: Consulte también nom(), en la página 75.
Tecla u
Catálogo
>
eigVc()
eigVc(Matrizcuadrada) ⇒ matriz
Devuelve una matriz que contiene los vectores propios para una
Matrizcuadrada real o compleja, donde cada columna del resultado
corresponde a un valor propio. Tenga en cuenta que los vectores
propios no son únicos; pueden venir multiplicados por cualquier
factor constante. Los vectores propios están normalizados, de tal
modo que si V = [x1, x2, … , xn], entonces:
2
2
+ … + x
2
= 1
n
x
+x
1
2
Matrizcuadrada se transforma en primer lugar hasta que las normas
de la fila y la columna se aproximen al mismo valor tanto como sea
posible. A continuación se reduce Matrizcuadrada hasta la forma
superior de Hessenberg y los vectores propios se calculan por medio
de una factorización de Schur.
En el formato complejo rectangular:
Para ver todos los resultados, pulse £ y utilice ¡ y ¢ para
mover el cursor.
Catálogo
>
Guía de referencia de TI-Nspire™ CAS 37

eigVl()
eigVl(Matrizcuadrada) ⇒ lista
Devuelve una lista de valores propios de una Matrizcuadrada real o
compleja.
Matrizcuadrada se transforma en primer lugar hasta que las normas
de la fila y la columna se aproximen al mismo valor tanto como sea
posible. A continuación se reduce Matrizcuadrada hasta la forma
superior de Hessenberg y los valores propios se calculan a par tir de la
matriz superior de Hessenberg.
Else Consulte If, en la página 52.
En el modo de formato complejo rectangular:
Para ver todos los resultados, pulse £ y utilice ¡ y ¢ para
mover el cursor.
Catálogo
>
ElseIf
If ExprBooleana1 Then
Bloque1
ElseIf ExprBooleana2 Then
Bloque2
©
ElseIf ExprBooleanaN Then
BloqueN
EndIf
©
Nota para introducir el ejemplo: En la aplicación Calculadora
de la unidad portátil, puede introducir definiciones formadas por
varias líneas si pulsa @ en lugar de · al final de cada línea.
En el teclado del ordenador, mantenga pulsada la tecla Alt y pulse
Enter (Intro).
EndFor Consulte For, en la página 45.
EndFunc Consulte Func, en la página 48.
EndIf Consulte If, en la página 52.
EndLoop Consulte Loop, en la página 67.
EndPrgm Consulte Prgm, en la página 86.
Catálogo
>
EndTry Consulte Try, en la página
119
38 Guía de referencia de TI-Nspire™ CAS
.

EndWhile Consulte While, en la página 125.
exact()
exact(Expr1 [, Tolerancia]) ⇒ expresión
exact(Lista1 [, Tolerancia]) ⇒ lista
exact(Matriz1 [, Tolerancia]) ⇒ matriz
Utiliza el modo aritmético Exact para devolver, siempre que sea
posible, el número racional equivalente de un argumento.
Tolerancia especifica la tolerancia de la conversión; el valor
predeterminado es 0 (cero).
Exit
Exit
Sale del bloque For, While o Loop actual.
Exit no está admitido fuera de las tres estructuras de bucle (For,
While o Loop).
Nota para introducir el ejemplo: En la aplicación Calculadora
de la unidad portátil, puede introducir definiciones formadas por
varias líneas si pulsa @ en lugar de · al final de cada línea.
En el teclado del ordenador, mantenga pulsada la tecla Alt y pulse
Enter (Intro).
Listado de funciones:
Catálogo
Catálogo
>
>
4
exp
4
Expr
exp
Representa Expr en función de potencias de base e. Es un operador
de conversión de presentación, y se puede utilizar únicamente al final
de la línea de entrada.
exp()
exp(Expr1) ⇒ expresión
Catálogo
Tecla u
>
Devuelve el valor de e elevado al exponente Expr1.
Nota: Consulte también Plantilla de base e, en la página 2.
i
Puede introducir un número complejo en la forma polar re
obstante, deberá utilizar esta forma sólo en el modo de ángulo en
radianes: genera un error de dominio en e l modo de ángulo en grados
o grados centesimales.
q
. No
Guía de referencia de TI-Nspire™ CAS 39

exp()
exp(Lista1) ⇒ lista
Devuelve el valor de e elevado a cada elemento de Lista1.
exp(Matrizcuadrada1) ⇒ Matrizcuadrada
Devuelve la matriz exponencial de Matrizcuadrada1. El resultado no
es igual que calcular e elevado a cada elemento. Para obtener más
información sobre el método de cálculo, consulte
Matrizcuadrada1 debe ser diagonizable. El resultado contiene
siempre números con coma flotante.
cos().
Tecla u
exp4lista()
exp4list(Expr,Va r ) ⇒ lista
Examina Expr para ecuaciones separadas por la palabra “or”, y
devuelve una lista que contiene los extremos derechos de las
ecuaciones en la forma Va r= E x p r. Es una forma fácil de extraer
algunos valores solución incluidos en los resultados de las funciones
solve(), cSolve(), fMin() y fMax().
Nota: exp4list() no aparece necesariamente con las funciones
zeros y cZeros() ya que éstas devuelven directamente una lista de
valores solución.
expand()
expand(Expr1 [, Va r ]) ⇒ expresión
expand(Lista1 [,Va r ]) ⇒ lista
expand(Matriz1 [,Var ]) ⇒ matriz
expand(Expr1) devuelve Expr1 desarrollada con respecto a todas
sus variables. El desarrollo es una expresión polinómica para los
polinomios y de fracción parcial para las expresiones racionales.
El objetivo de expand() es convertir Expr1 en una suma o una
diferencia de términos sencillos o en ambas. Por el contrario, el
objetivo de factor() es convertir Expr1 en un producto o un
cociente de factores sencillos o en ambos.
expand(Expr1,Va r) devuelve Expr1 desarrollado con respecto a
Var . Se agrupan potencias similares de Va r. Los términos y sus
factores se ordenan con Va r como variable principal. Puede haber
alguna factorización o desarrollo incidental de los coeficientes
agrupados. Comparada con la omisión de Va r , supone ahorro de
tiempo, memoria y espacio de pantalla, al tiempo que hace que la
expresión sea más comprensible.
Catálogo
Catálogo
>
>
Incluso cuando sólo hay una variable, el uso de Va r puede hacer que
la factorizacion del denominador utilizado para un desarrollo de
fracción parcial sea más completa.
Sugerencia: Para expresiones racionales, propFrac() es más rápido
pero ofrece una alternativa más reducida que expand().
Nota: Consulte también comDenom() para ver más información
de un numerador desarrollado sobre un denominador también
desarrollado.
40 Guía de referencia de TI-Nspire™ CAS

expand()
expand(Expr1,[Va r]) desarr olla también logaritmos y potencias de
fracción al margen del valor de Va r . El desarrollo de logaritmos y
potencias puede requerir el uso de algunas restricciones en las
desigualdades para garantizar que algunos factores sean no
negativos.
expand(Expr1, [Va r]) desarrolla también valores absolutos,
sign() y exponenciales, sin tener en cuenta Va r.
Nota: Consulte también tExpand() para ver información sobre
suma de ángulos y desarrollo de varios ángulos.
Catálogo
>
expr()
expr(Cadena) ⇒ expresión
Devuelve la cadena de caracteres contenida en Cadena como una
expresión y la ejecuta de inmediato.
ExpReg
ExpReg X, Y [, [Frec] [, Categoría, Incluir]]
Calcula la regresión exponencial y = a·(b)xen las listas X e Y con la
frecuencia Frec. El resumen de los resultados se guarda en la variable
stat.results. (Consulte la página 109).
Todas las listas, salvo Incluir, deben tener la misma dimensión.
X e Y son listas que contienen, respectivamente, la variable
independiente y la variable dependiente.
Frec es una lista opcional de valores de frecuencia. Cada elemento
de Frec especifica la frecuencia de ocurrencia de cada punto de datos
en X e Y. El valor predeterminado es 1. Todos los elementos deben
ser enteros | 0.
Categoría es una lista de códigos numéricos de categoría para los
datos de X e Y.
Incluir es una lista de uno o varios códigos de categoría. En el cálculo
sólo se incluyen los elementos de datos cuyo código de categoría se
encuentre en la lista.
Catálogo
Catálogo
>
>
Vari able de
salida
stat.RegEqn
Descripción
Ecuación de regresión: a·(b)
x
stat.a, stat.b Coeficientes de regresión
stat.r
2
Coeficiente de determinación lineal para los datos transformados
Guía de referencia de TI-Nspire™ CAS 41

Vari able de
salida
stat.r Coeficiente de correlación para los datos transformados (x, ln(y))
stat.Resid Residuos asociados con el modelo exponencial
stat.ResidTrans Residuos asociados con el ajuste lineal de los datos transformados
stat.XReg Lista de puntos de datos en la Lista X modificada utilizada realmente en la regresión basada en
stat.YReg Lista de puntos de datos en la Lista Y modificada utilizada realmente en la regresión basada en las
stat.FreqReg Lista de frecuencias correspondiente a stat.XReg y stat.YReg
Descripción
restricciones de Frec, Lista Categoría e Incluir Categoría
restricciones de Frec, Lista Categoría e Incluir Categoría
F
factor()
factor(Expr1[, Va r ]) ⇒ expresión
factor(Lista1[,Va r ]) ⇒ lista
factor(Matriz1[,Var ]) ⇒ matriz
factor(Expr1) devuelve Expr1 factorizado con respecto a todas sus
variables sobre un denominador común.
Expr1 se factoriza tanto como sea posible en factores lineales sin
introducir nuevas subexpresiones no reales. Esta alternativa resulta
apropiada si la factorización se realiza con respecto a más de una
variable.
factor(Expr1,Var ) devuelve Expr1 factorizado con respecto a la
variable Var .
Expr1 se factoriza tanto como sea posible en factores reales que
sean lineales en Va r, incluso si introduce constantes irracionales o
subexpresiones que sean irracionales en otras variables.
Los factores y sus términos se ordenan con Va r como variable
principal. En cada factor se agrupan potencias de Va r similares.
Incluya Va r si la factorización es necesaria sólo con respecto a la
variable y no tiene inconveniente en aceptar expresiones irracionales
en cualquier otra variable para incrementar la factorización con
respecto a Var . Puede haber alguna factorización incidental con
respecto a otras variables.
Para el ajuste Auto del modo Auto or Approximate, la inclusión
de Var permite también una aproximación con coeficientes de coma
flotante cuando no sea posible expresar explícita y concisamente los
coeficiente en términos de funciones integradas. Incluso cuando sólo
haya una variable, la inclusión de Va r puede generar una
factorización más completa.
Nota: Consulte también comDenom() como método rápido de
alcanzar una factorización parcial cuando factor() no es lo bastante
rápido o si se agota la memoria.
Nota: Consulte también cFactor() para factorizar al máximo los
coeficientes complejos en busca de factores lineales.
Catálogo
>
42 Guía de referencia de TI-Nspire™ CAS

factor()
factor(Númeroracional) devuelve el número racional factorizado
en primos. Para los números compuestos, el tiempo de cálculo crece
exponencialmente con el número de dígitos del segundo factor más
grande. Por ejemplo, factorizar un número entero de 30 dígitos puede
tardar más de un día; factorizar uno de 100 dígitos podría tardar más
de un siglo.
Nota: Para detener (interrumpir) un cálculo, pulse w.
Si sólo desea determinar si el número es primo, utilice
una opción mucho más rápida, especialmente si Númeroracional no
es primo y el segundo factor más grande tiene más de cinco dígitos.
isPrime(). Es
Catálogo
>
FCdf()
FCdf(Extremoinferior,Extremosuperior,dfNumer,dfDenom) ⇒
número si Extremoinferior y Extremosuperior son números, lista
si
Extremoinferior y Extremosuperior son listas
FCdf(
Extremoinferior,Extremosuperior,dfNumer,dfDenom) ⇒
número si Extremoinferior y Extremosuperior son números, lista
si
Extremoinferior y Extremosuperior son listas
Calcula la probabilidad de la distribución F entre el Extremoinferior
y el Extremosuperior para los dfNumer (grados de libertad) y
dfDenom especificados.
Para P(X Extremosuperior), defina Extremoinferior=0.
Fill
Fill Expr, matrizVar ⇒ matriz
Sustituye cada elemento de la variable matrizVar con Expr.
matrizVar debe ser un valor ya existente.
Fill Expr, listaVar ⇒ lista
Sustituye cada elemento de la variable listaVar con Expr.
listaVar debe ser un valor ya existente.
FiveNumSummary
FiveNumSummary X[,[Frec][,Categoría,Incluir]]
Ofrece una versión abreviada de la estadística de una variable en la
lista X. El resumen de los resultados se guarda en la variable
stat.results. (Consulte la página 109).
X representa una lista que contiene los datos.
Frec es una lista opcional de valores de frecuencia. Cada elemento
de Frec especifica la ocurrencia de cada valor X correspondiente.
El valor predeterminado es 1. Todos los elementos deben ser enteros
| 0.
Categoría es una lista de códigos numéricos de categoría para los
valores X correspondientes.
Incluir es una lista de uno o varios códigos de categoría. En el cálculo
sólo se incluyen los elementos de datos cuyo código de categoría se
encuentre en la lista.
Catálogo
Catálogo
Catálogo
>
>
>
Guía de referencia de TI-Nspire™ CAS 43

Vari able de
salida
Descripción
stat.MinX Mínimo de valores de x
stat.Q1X Primer cuartil de x
stat.MedianX Mediana de x
stat.Q3X Tercer cuartil de x
stat.MaxX Máximo de valores de x
floor()
floor(Expr1) ⇒ entero
Devuelve el mayor entero que es { el argumento. Esta función es
idéntica a int().
El argumento puede ser un número real o complejo.
floor(Lista1) ⇒ lista
floor(Matriz1) ⇒ matriz
Devuelve una lista o una matriz con las correspondientes partes
enteras de los elementos.
Nota: Consulte también ceiling() e int().
fMax()
fMax(Expr, Var) ⇒ Expresión booleana
fMax(Expr, Va r,Extremoinferior)
fMax(
Expr, Va r,Extremoinferior,Extremosuperior)
fMax(
Expr, Va r) | Extremoinferior<Va r <Extremosuperior
Devuelve una expresión booleana expecificando los valores
candidatos para Va r que maximizan Expr o localizan su extremo
superior mínimo.
Puede utilizar el operador “|” para restringir el intervalo de
soluciones, especificar otros límites o ambos.
Para el ajuste Approximate (Aproximado) del modo Auto or
Approximate (Auto o Aproximado)
iterativamente un máximo local aproximado. Suele ser más ráp ido, en
especial si se utiliza el operador “|” para restringir la búsqueda a un
intervalo relativamente pequeño que contenga exactamente un
máximo local.
Nota: Consulte también fMin() y max().
, fMax() busca
Catálogo
Catálogo
>
>
44 Guía de referencia de TI-Nspire™ CAS

fMin()
fMin(Expr, Var) ⇒ Expresión booleana
fMin(Expr, Var ,Extremoinferior)
fMin(
Expr, Va r,Extremoinferior,Extremosuperior)
fMin(
Expr, Va r) | Extremoinferior<Va r <Extremosuperior
Devuelve una expresión booleana expecificando los valores
candidatos para Va r que minimizan Expr o localizan su extremo
inferior máximo.
Puede utilizar el operador “|” para restringir el intervalo de
soluciones, especificar otros límites o ambos.
Para el ajuste Approximate (Aproximado) del modo Auto or
Approximate (Auto o Aproximado)
iterativamente un mínimo local aproximado. Suele ser más rápido, en
especial si se utiliza el operador “|” para restringir la búsqueda a un
intervalo relativamente pequeño que contenga exactamente un
mínimo local.
Nota: Consulte también fMax() y min().
, fMin() busca
Catálogo
>
For
For Var , Inferior, Superior [, Paso]
Bloque
EndFor
Ejecuta la sentencia de Bloque iterativamente por cada valor de Va r ,
de Inferior a Superior, en incrementos de Paso.
Var no debe ser una variable del sistema.
Paso puede ser un valor positivo o negativo. El v alor predeterminado
es 1.
Bloque puede ser una sentencia sencilla o una serie de sentencias
separadas por el carácter “:”.
Nota para introducir el ejemplo: En la aplicación Calculadora
de la unidad portátil, puede introducir definiciones formadas por
varias líneas si pulsa @ en lugar de · al final de cada línea.
En el teclado del ordenador, mantenga pulsada la tecla Alt y pulse
Enter (Intro).
Catálogo
>
Guía de referencia de TI-Nspire™ CAS 45

format()
format(Expr[, formatoCadena]) ⇒ cadena
Devuelve Expr como una cadena de caracteres basada en la plantilla
de formato.
Expr debe simplificarse a un número.
formatoCadena es una cadena y debe estar en la forma: “F[n]”,
“S[n]”, “E[n]”, “G[n][c]”, donde [ ] indica partes opcionales.
F[n]: Formato fijo. n es el número de dígitos que aparece después del
decimal.
S[n]: Formato científico. n es el número de dígitos que aparece
después del decimal.
E[n]: Formato de ingeniería. n es el número de dígitos que aparece
después del primer dígito significante. El exponente se ajusta a un
múltiplo de tres, y el decimal se mueve hacia la derecha en cero, uno
o dos dígitos.
G[n][c]: Igual que el formato fijo pero, además, separa en grupos de
tres los dígitos situados a la izquierda del radical. c especifica el
carácter separador de grupo; el valor pred eterminado es coma. Si c es
un punto, el radical aparecerá como una coma.
[Rc]: Todos los especificadores anteriores pueden llevar el sufijo
indicador de rádix RC, donde c es un único carácter que especifica el
que se va a utilizar como separador.
Catálogo
>
fPart()
fPart(Expr1) ⇒ expresión
fPart(Lista1) ⇒ lista
fPart(Matriz1) ⇒ matriz
Devuelve la parte decimal de un argumento.
Para una lista o una matriz, devuelve la parte decimal de los
elementos.
El argumento puede ser un número real o complejo.
FPdf()
FPdf(XVal,glNúmero,glDenom) ⇒ número si XVal es un
lista si XVal es una lista
número,
Calcula la probabilidad de la distribución F en XVal con los grados
de libertad especificados para glNum y glDenom.
freqTable4lista()
freqTable4list(Lista1,ListaEnterosFrecuencia) ⇒ lista
Devuelve una lista que contiene los elementos de Lista1 ampliados
según las frecuencias de ListaEnterosFrecuencia. Esta función se
puede utilizar para construir una tabla de frecuencias para la
aplicación Datos y Estadística.
Lista1 puede ser cualquier lista válida.
ListaEnterosFrecuencia debe tener la misma dimensión que Lista1
y contener elementos enteros no negativos solamente. Cada
elemento especifica el número de veces que el correspondiente
elemento de Lista1 se va a repetir en la lista resultante. Un valor de
cero excluye el correspondiente elemento de Lista1.
Catálogo
Catálogo
Catálogo
>
>
>
46 Guía de referencia de TI-Nspire™ CAS

frequency()
frequency(Lista1,Listabin) ⇒ lista
Devuelve una lista con el recuento de los elementos contenidos en
Lista1. El recuento se basa en los rangos definidos en Listabin.
Si Listabin es {b(1), b(2), …, b(n)}, los rangos especificados son
{
?{b(1), b(1)<?{b(2),…,b(n-1)<?{b(n), b(n)>?}. La lista resultante
es un elemento más extenso que Listabin.
Cada elemento del resultado se corresponde con el número de
elementos de Lista1 comprendidos en el rango. Expresado en
términos de la función
?{b(1)), countIf(list, b(1)<?{b(2)), …, countIf(list, b(n-1)<?{b(n)),
countIf(list, b(n)>?)}.
Los elementos de Lista1 que no se pueden “incluir en un rango” son
desestimados.
En la aplicación Listas y Hojas de cálculo, puede utilizar un rango de
celdas en lugar de ambos argumentos.
Nota: Consulte también countIf(), en la página 23.
countIf(), el resultado es { countIf(list,
Catálogo
>
Explicación del resultado:
2 elementos de Datalist que son {2.5
4 elementos de Datalist que son >2.5 y {4.5
3 elementos de Datalist que son >4.5
El elemento "hello" es una cadena y no se puede incluir en
ninguno de los rangos definidos.
FTest_2Samp
FTest_2Samp Lista1,Lista2[,Frec1[,Frec2[,Hipótesis]]]
FTest_2Samp
(Entrada de lista de datos)
Lista1,Lista2[,Frec1[,Frec2[,Hipótesis]]]
FTest_2Samp sx1,n1,sx2,n2[,Hipótesis]
FTest_2Samp
(Entrada de resumen estadístico)
Realiza un test F de dos muestras. El resumen de los resultados se
guarda en la variable stat.results. (Consulte la página 109.)
Para Ha: s1 > s2, defina Hipótesis>0
Para Ha: s1 ƒ s2 (predeterminado), defina Hipótesis =0
Para Ha: s1 < s2, defina Hipótesis<0
Vari able de
salida
stat.F
stat.PVal Nivel de significancia mínimo al que se puede rechazar la hipótesis nula
stat.dfNumer Grados de libertad del numerador = n1-1
stat.dfDenom Grados de libertad del denominador = n2-1
stat.sx1, stat.sx2 Desviaciones estándar de la muestra de las sucesiones de datos en Lista 1 y Lista 2
stat.x1_bar
stat.x2_bar
stat.n1, stat.n2 Tamaño de las muestras
sx1,n1,sx2,n2[,Hipótesis]
Descripción
Estadística ó calculada para la sucesión de datos
Medias de la muestra de las sucesiones de datos en Lista 1 y Lista 2
Catálogo
>
Guía de referencia de TI-Nspire™ CAS 47

Func
Func
Bloque
EndFunc
Plantilla para crear una función definida por el usuario.
Bloque puede ser una sentencia sencilla, una serie de sentencias
separadas por el carácter “:”, o una serie de sentencias escritas en
varias líneas. La función puede utilizar la instrucción
devolver un resultado concreto.
Nota para introducir el ejemplo: En la aplicación Calculadora
de la unidad portátil, puede introducir definiciones formadas por
varias líneas si pulsa @ en lugar de · al final de cada línea.
En el teclado del ordenador, mantenga pulsada la tecla Alt y pulse
Enter (Intro).
Return para
G
Definir una función a trozos:
Resultado de representar gráficamente g(x)
Catálogo
>
gcd()
gcd(Val or 1, Valor2) ⇒ expresión
Devuelve el máximo común divisor de los dos argumentos. El gcd de
dos fracciones es el gcd de sus numeradores dividido por el lcm de
sus denominadores.
En modo Auto o Aproximado, el gcd de números con decimal
flotante es 1.0.
gcd(Lista1, Lista2) ⇒ lista
Devuelve el máximo común divisor correspondiente a cada elemento
de Lista1 y Lista2.
gcd(Matriz1, Matriz2) ⇒ matriz
Devuelve el máximo común divisor correspondiente a cada elemento
de Matriz1 y Matriz2.
geomCdf()
geomCdf(p, Extremoinferior,Extremosuperior) ⇒ número si
Extremoinferior y Extremosuperior son números, lista si
Extremoinferior y Extremosuperior son listas
geomCdf(
p,Extremosuperior) ⇒ número si Extremosuperior
es un número,
Calcula la probabilidad geométrica acumulada de Extremoinferior a
Extremosuperior con la probabilidad de éxito p especificada.
Para P(X Extremosuperior), defina Extremoinferior = 1.
lista si Extremosuperior es una lista
Catálogo
Catálogo
>
>
48 Guía de referencia de TI-Nspire™ CAS

geomPdf()
geomPdf(p,XVal) ⇒ número si XVal es un número, lista si
XVal es una lista
Calcula la probabilidad de que se verifique XVal, número del intento
en el que se va a producir el primer acierto, para la distribución
geométrica discreta con la probabilidad de aciertos p especificada.
Catálogo
>
getDenom( )
getDenom(Expr1) ⇒ expresión
Transforma el argumento en una expresión con un común
denominador reducido y, a continuación, devuelve su denominador.
getLangInfo( )
getLangInfo() ⇒ cadena
Devuelve una cadena que se corresponde con el nombre corto del
idioma activo en cada momento. Por ejemplo, puede utilizar el
nombre en un programa o una función para determinar el idioma
actual.
Inglés = "en"
Danés = "da"
Alemán = "de"
Finlandés = "fi"
Francés = "fr"
Italiano = "it"
Neerlandés = "nl"
Flamenco = "nl_BE"
Noruego = "no"
Portugués = "pt"
Español = "es"
Sueco = "sv"
getMode()
getMode(Mod oNombre Entero ) ⇒ valor
getMode(0) ⇒ lista
getMode(Mod oNombre Entero ) devuelve un valor que representa
la configuración actual del modo ModoNombreEntero.
getMode(0) devuelve una lista que contiene pares de números.
Cada par consta de un entero de modo y un entero de configuración.
Para ver una lista de los modos y sus configuraciones, consulte la
tabla siguiente.
Si guarda los valores de configuración con getMode(0) & var,
puede utilizar setMode(var) en una función o un programa para
restaurar temporalmente la configuración sólo durante la ejecución
de la función o el programa. Consulte setMode(), en la página 99.
Catálogo
Catálogo
Catálogo
>
>
>
Guía de referencia de TI-Nspire™ CAS 49

Nombre del
modo
Display Digits
(Mostrar dígitos)
Angle (Ángulo)
Exponential Format
(Formato
exponencial)
Real or Complex
(Real o complejo)
Auto or Approximate
(Auto o aproximado)
Vector Format
(Formato vectorial)
Base
Unit System (Sistema
de unidades)
Modo
del
entero
1
2
3
4
5
6
7
8
Configuración de enteros
1
=Flotante, 2=Flotante1, 3=Flotante2, 4=Flotante3, 5=Flotante4, 6=Flotante5,
7=Flotante6, 8=Flotante7, 9=Flotante8, 10=Flotante9, 11=Flotante10, 12=Flotante11,
13=Flotante12, 14=Fijo0, 15=Fijo1, 16=Fijo2, 17=Fijo3, 18=Fijo4, 19=Fijo5, 20=Fijo6,
21=Fijo7, 22=Fijo8, 23=Fijo9, 24=Fijo10, 25=Fijo11, 26=Fijo12
1
=Radianes, 2=Grados, 3=Grados centesimales
1
=Normal, 2=Científico, 3=Ingeniería
1
=Real, 2=Rectangular, 3=Polar
1
=Auto, 2=Aproximado, 3=Exacto
1
=Rectangular, 2=Cilíndrico, 3=Esférico
1
=Decimal, 2=Hex, 3=Binario
1
=SI, 2=Inglés/EE UU
getNum()
getNum(Expr1) ⇒ expresión
Transforma el argumento en una expresión con un común
denominador reducido y, a continuación, devuelve su numerador.
Catálogo
>
50 Guía de referencia de TI-Nspire™ CAS

getVarInfo()
getVarInfo() ⇒ matriz o cadena
getVarInfo(CadenaNombreBiblioteca) ⇒ matriz o cadena
getVarInfo() devuelve una matriz de información (nombre de
variable, tipo y accesibilidad a la biblioteca) de todas las variables y
objetos de biblioteca definidos en el problema actual.
Si no hay ninguna variable definida,
cadena "NONE".
getVarInfo(CadenaNombreBiblioteca) devuelve una matriz de
información para todos los objetos de biblioteca definidos en
CadenaNombreBiblioteca. CadenaNombreBiblioteca debe ser una
cadena (texto entre comillas) o una variable de cadena.
Si la biblioteca CadenaNombreBibliotea no existe, devuelve un
error.
Observe el ejemplo de la izquierda en donde el resultado de
getVarInfo() se ha asignado a la variable vs. El intento de mostrar
la fila 2 o la fila 3 de vs devuelve un error “Lista o matriz no válidas”
ya que, al menos uno de los elementos de las filas (por ejemplo,
variable b) se recalcula en una matriz.
Este error se produce también cuando se utiliza Ans para recalcular
un resultado getVarInfo().
El sistema muestra el error anterior porque la versión actual del
software no admite una estructura de matriz generalizada donde un
elemento de una matriz puede ser tanto una matriz como una lista.
getVarInfo() devuelve la
Catálogo
>
Goto
Goto Nombreetiqueta
Catálogo
>
Transfiere el control a la etiqueta Nombreetiqueta.
Nombreetiqueta debe estar definido en la misma función por medio
de una instrucción Lbl.
Nota para introducir el ejemplo: En la aplicación Calculadora
de la unidad portátil, puede introducir definiciones formadas por
varias líneas si pulsa @ en lugar de · al final de cada línea.
En el teclado del ordenador, mantenga pulsada la tecla Alt y pulse
Enter (Intro).
Guía de referencia de TI-Nspire™ CAS 51

Grad
4
4 Grad ⇒ expresión
Expr1
Convierte Expr1 a grados centesimales
I
En el modo de ángulo en grados:
En el modo de ángulo en radianes:
Catálogo
>
identity()
identity(Entero) ⇒ matriz
Devuelve la matriz identidad de dimensión Entero.
Entero debe ser un número entero positivo.
If
If Declarac ExprBooleana
If ExprBooleana Then
Bloque
EndIf
If ExprBooleana evalúa la condición como verdadera, ejecuta la
sentencia sencilla Declarac o el bloque de sentencias Bloque antes
de continuar con la ejecución.
If BooleanExpr evalúa la condición como falsa, continúa el proceso
sin ejecutar la sentencia o el bloque de sentencias.
Bloque puede ser una sentencia sencilla o una serie de sentencias
separadas por el carácter “:”.
Nota para introducir el ejemplo: En la aplicación Calculadora
de la unidad portátil, puede introducir definiciones formadas por
varias líneas si pulsa @ en lugar de · al final de cada línea.
En el teclado del ordenador, mantenga pulsada la tecla Alt y pulse
Enter (Intro).
If ExprBooleana Then
Bloque1
Else
Bloque2
EndIf
If ExprBooleana evalúa la condición como verdadera, ejecuta
Bloque1 e ignora Bloque2.
If ExprBooleana evalúa la condición como falsa, ignora Bloque1
pero ejecuta Bloque2.
Bloque1 y Bloque2 pueden ser una sentencia sencilla.
Catálogo
Catálogo
>
>
52 Guía de referencia de TI-Nspire™ CAS

If
If ExprBooleana1 Then
Bloque1
ElseIf
ExprBooleana2 Then
Bloque2
©
ElseIf
ExprBooleanaN Then
BloqueN
EndIf
Permite la ramificación. If ExprBooleana1 evalúa la condición como
verdadera, ejecuta Bloque1. If ExprBooleana1 evalúa la condición
como falsa, evalúa ExprBooleana2, etc.
Catálogo
>
ifFn()
ifFn(ExprBooleana,Valor_Si_verd [,Valor_Si_falso
[,
Valor_Si_desconocido]]) ⇒ expresión, lista o matriz
Evalúa la expresión booleana ExprBooleana (o cada elemento de
ExprBooleana ) y genera un resultado conforme a las reglas
siguientes:
• ExprBooleana puede verificar un valor, lista o matriz únicos.
• Si un elemento de ExprBooleana verifica la condición, devuelve
el elemento correspondiente de Valor_Si_verd.
• Si un elemento de ExprBooleana no verifica la condición,
devuelve el elemento correspondiente de Valor_Si_falso. Si se
omite Valor_Si_falso, devuelve un valor sin definir.
• Si un elemento de ExprBooleana resultara no ser verdadero ni
falso, se devolverá el elemento correspondiente
Valor_Si_desconocido. Si se omite Valor_Si_desconocido,
devuelve un valor sin definir.
• Si el argumento segundo, tercero o cuarto de la función ifFn()
es una expresión sencilla, la prueba booleana se aplica a cada
posición de ExprBooleana.
Nota: Si la sentencia ExprBooleana simplificada afecta a una lista o
una matriz, todos los demás argumentos de listas o matrices deberán
tener las mismas dimensiones, y el resultado tendrá también la
misma dimensión.
imag()
imag(Expr1) ⇒ expresión
Devuelve la parte imaginaria de un argumento.
Nota: Se considera que todas las variables no definidas son variables
reales. Consulte también real(), en la página 92.
Catálogo
>
Al ser 1 menor que 2.5 su valor correspondiente en
Valor_Si_verd, el 5, se copia.
Al ser 2 menor que 2.5 su valor correspondiente en
Valor_Si_verd, el 6, se copia.
Al ser 3 mayor que 2.5 su valor correspondiente en
Valor_Si_falso, el 10, se copia.
Valor_Si_verd es un valor sencillo y corresponde a cualquier
posición seleccionada.
Valor_Si_falso está sin especificar. Se utilizar Undef (sin
definir).
Un elemento seleccionado de Valor_Si_verd. Un elemento
seleccionado de Valor_Si_desconocido.
Catálogo
>
Guía de referencia de TI-Nspire™ CAS 53

imag()
imag(Lista1) ⇒ lista
Devuelve una lista de las partes imaginarias de los elementos.
imag(Matriz1) ⇒ matriz
Devuelve una matriz de las partes imaginarias de los elementos.
Catálogo
>
impDif()
impDif(Ecuación, Var , Vardependiente[,Ord])
⇒ expresión
donde el valor predeterminado de Orden es 1.
Calcula la derivada implícita de las ecuaciones en las que una variable
se define implícitamente en términos de la otra.
Indirection Consulte
inString()
inString(Cadenabsq, subCadena[, Inic]) ⇒ entero
Devuelve la posición del carácter en la cadena Cadenabsq donde
comienza la primera ocurrencia de la cadena subCadena.
Inic, si va incluido, especifica la posición del carácter de Cadenabsq
donde se inicia la búsqueda. Valor predeterminado = 1 (el primer
carácter de Cadenabsq).
Si Cadenabsq no contiene subCadena o Inic es > la longitud de
Cadenabsq, devuelve cero.
int()
int(Expr) ⇒ entero
int(Lista1) ⇒ lista
int(Matriz1) ⇒ matriz
Devuelve el mayor entero menor o igual que el argumento.
Esta función es idéntica a floor().
El argumento puede ser un número real o complejo.
Para una lista o una matriz, devuelve la correspondiente parte entera
de cada elemento.
Catálogo
, en la página 143.
#()
Catálogo
Catálogo
>
>
>
intDiv()
intDiv(Número1, Número2) ⇒ entero
intDiv(Lista1, Lista2) ⇒ lista
intDiv(Matriz1, Matriz2) ⇒ matriz
Catálogo
>
Devuelve la parte entera con su signo de (Número1 ÷ Número2).
Para las listas y las matrices, devuelve la parte entera con su signo de
(argumento 1 ÷ argumento 2) para cada par de elementos.
integrate
Consulte
, en la página 139.
‰()
54 Guía de referencia de TI-Nspire™ CAS

invc2()
invc2(Área,gl)
Área,gl)
invChi2(
Calcula la probabilidad acumulada inversa c2 (chi cuadrado)
especificada por el grado de libertad, gl de un Área dada bajo la
curva.
Catálogo
>
invF()
invF(Área,glNumer,glDenom)
Área,glNumer,glDenom)
invF(
Calcula la función de distribución acumulada normal inversa F
especificada por el glNumer y el glDenom de un Área dada bajo la
curva.
invNorm()
invNorm(Área[,m[,s]])
Calcula la función de distribución acumulada normal inversa de un
Área dada bajo la curva de distribución normal especificada por m y
s.
invt()
invt(Área,gl)
Calcula la función de probabilidad acumulada inversa de t de Student
especificada por el grado de libertad, gl, de un Área dada bajo la
curva.
iPart()
iPart(Número) ⇒ entero
iPart(Lista1) ⇒ lista
iPart(Matriz1) ⇒ matriz
Devuelve la parte entera de un argumento.
Para las listas y las matrices, devuelve la parte entera de cada
elemento.
El argumento puede ser un número real o complejo.
irr()
irr(CF0,CFLista [,CFFrec]) ⇒ valor
Función financiera que calcula la tasa interna de retorno de una
inversión.
CF0 es el flujo de caja inicial en el tiempo 0; debe ser un número real.
CFLista es una lista de cantidades de flujo de caja tras el flujo de
caja inicial CF0.
CFFrec es una lista opcional en la que cada elemento especifica la
frecuencia de ocurrencia de una cantidad de flujo de caja agrupada
(consecutiva), que es el elemento correspondiente de CFLista. El
valor predeterminado es 1; si introduce valores, deberán ser números
enteros positivos < 10.000.
Nota: Consulte también mirr(), en la página 70.
Catálogo
Catálogo
Catálogo
Catálogo
Catálogo
>
>
>
>
>
Guía de referencia de TI-Nspire™ CAS 55

isPrime()
isPrime(Número) ⇒ Expresión booleana constante
Devuelve verdadero (true) o falso (false) para indicar si número es un
número entero
Si Número supera los 306 dígitos y no tiene factores {1021,
isPrime(Número) muestra un mensaje de error.
Si sólo desea determinar si Número es primo, utilice
lugar de
si Número no es primo y tiene un segundo factor más grande que
supera los cinco dígitos.
Nota para introducir el ejemplo: En la aplicación Calculadora
de la unidad portátil, puede introducir definiciones formadas por
varias líneas si pulsa @ en lugar de · al final de cada línea.
En el teclado del ordenador, mantenga pulsada la tecla Alt y pulse
Enter (Intro).
‚ 2 divisible sólo por sí mismo y por 1.
factor(). Es una opción mucho más rápida, especialmente
isPrime() en
L
Catálogo
Función para hallar el siguiente primo tras un número
especificado:
>
Lbl
Lbl Nombreetiqueta
Define una etiqueta con el nombre Nombreetiqueta dentro de una
función.
Puede utilizar la instrucción Goto Nombreetiqueta para transferir el
control a la instrucción situada inmediatamente después de la
etiqueta.
Nombreetiqueta debe cumplir los mismos requisitos de nombre que
las variables:
Nota para introducir el ejemplo: En la aplicación Calculadora
de la unidad portátil, puede introducir definiciones formadas por
varias líneas si pulsa @ en lugar de · al final de cada línea.
En el teclado del ordenador, mantenga pulsada la tecla Alt y pulse
Enter (Intro).
lcm()
lcm(Número1, Número2) ⇒ expresión
lcm(Lista1, Lista2) ⇒ lista
lcm(Matriz1, Matriz2) ⇒ matriz
Devuelve el mínimo común múltiplo de los dos argumentos. El lcm
de dos fracciones es el lcm de sus numeradores dividido por el gcd
de sus denominadores. El lcm de números con decimal flotante es su
producto.
Para dos listas o dos matrices, devuelve el mínimo común múltiplo de
los elementos correspondientes.
Catálogo
Catálogo
>
>
56 Guía de referencia de TI-Nspire™ CAS

left()
left(Cadenaorigen[, Número]) ⇒ cadena
Devuelve el Número de caracteres situados a la izquierda y
contenidos en la cadena de caracteres Cadenaorigen.
Si se omite Número, devuelve todos los de Cadenaorigen.
left(Lista1[, Número]) ⇒ lista
Devuelve el Número de caracteres situados a la izquierda y
contenidos en Lista1*.
Si se omite Número, devuelve todos los de Lista1.
left(Comparación) ⇒ expresión
Devuelve el miembro de la zquierda de una ecuación o una
desigualdad.
Catálogo
>
libShortcut()
libShortcut(CadenaNombreBiblioteca,
CadenaNombreAccesoDirecto
[, EtiquetaBibliotecaPriv]) ⇒ lista de variables
Crea un grupo de variables en el problema actual que contiene
referencias a todos los objetos del documento de biblioteca
CadenaNombreBiblioteca especificado. También añade los
miembros del grupo al menú Variables. Luego podrá hacer referencia
a cada objeto utilizando su CadenaNombreAccesoDirecto.
Defina EtiquetaBibliotecaPriv=0 para excluir objetos de biblioteca
privada (valor predeterminado)
Defina EtiquetaBiblioteca=1 para incluir objetos de biblioteca
privada.
Para copiar un grupo de variables, consulte CopyVar, en la
página 18.
Para borrar un grupo de variables, consulte DelVar, en la página 32.
limit() o lim()
limit(Expr1, Va r, Punto [,Dirección]) ⇒ expresión
limit(Lista1, Va r, Punto [, Dirección]) ⇒ lista
limit(Matriz1, Var , Punto [, Dirección]) ⇒ matriz
Devuelve el límite solicitado.
Nota: Consulte también Plantilla de límite, en la página 5.
Dirección: negativa = por la izquierda, positiva = por la derecha, en
caso contrario = ambas. (Si se omite, el valor predeterminado para
Dirección es ambas.)
Catálogo
>
En este ejemplo se supone la existencia de un documento de
biblioteca llamado linalg2 almacenado y actualizado
correctamente y que contiene objetos definidos com o clearmat,
gauss1 y gauss2.
Catálogo
>
Los límites hacia ˆ positivo y hacia ˆ negativo se convierten siempre
en el límite lateral del lado correspondiente.
Guía de referencia de TI-Nspire™ CAS 57

limit() o lim()
Dependiendo de las circunstancias, limit() se devuelve a sí mismo o
"sin definir" cuando no es posible determinar un límite único. Esto no
significa necesariamente que no exista un límite único. Sin definir
significa que el resultado es tanto un número desconocido, con una
magnitud finita o infinita, como el conjunto completo de esos mismos
números.
limit() utiliza métodos como la regla de L'Hôpital para obtener el
límite en el caso de indeterminación. Si Expr1 contiene otras
variables sin definir que no sean Va r , puede que deba restringirlas
para obtener resultados más concisos.
Los límites pueden ser muy sensibles a errores de redondeo. En la
medida de lo posible, evite el uso del ajuste Aproximado del modo
Auto or Approximate (Auto o Aproximado) y aproxime los
números cuando calcule los límites. De lo contrario, es probable que
los límites que deban tener una magnitud cero o infinito no presenten
estos resultados, y los límites que deban tener una magnitud no cero
o finita tampoco los cumplan.
Catálogo
>
LinRegBx
LinRegBx X,Y[,[Frec][,Categoría,Incluir]]
Calcula la regresión lineal y = a+b·x de las listas X e Y con una
frecuencia Frec. El resumen de los resultados se guarda en la variable
stat.results. (Consulte la página 109).
Catálogo
Todas las listas, salvo Incluir, han de tener la misma dimensión.
X e Y son listas que contienen, respectivamente, la variable
independiente y la variable dependiente.
Frec es una lista opcional de valores de frecuencia. Cada elemento
de Frec especifica la frecuencia de ocurrencia de cada punto de datos
en X e Y. El valor predeterminado es 1. Todos los elementos deben
ser enteros | 0.
Categoría es una lista de códigos numéricos de categoría para los
datos de X e Y.
Incluir es una lista de uno o varios códigos de categoría. En el cálculo
sólo se incluyen los elementos de datos cuyo código de categoría se
encuentre en la lista.
Vari able de
salida
stat.RegEqn
Descripción
Ecuación de regresión: a+b·x
stat.a, stat.b Coeficientes de regresión
stat.r
2
Coeficiente de determinación
stat.r Coeficiente de correlación
stat.Resid Residuos de la regresión
stat.XReg Lista de puntos de datos en la Lista X modificada utilizada realmente en la regresión basada en
stat.YReg Lista de puntos de datos en la Lista Y modificada utilizada realmente en la regresión basada en las
restricciones de Frec, Lista Categoría e Incluir Categorías
restricciones de Frec, Lista Categoría e Incluir Categorías
stat.FreqReg Lista de frecuencias correspondiente a stat.FreqReg y stat.YReg
>
58 Guía de referencia de TI-Nspire™ CAS

LinRegMx
LinRegMx X,Y[,[Frec][,Categoría,Incluir]]
Calcula la regresión lineal y = m·x+b para las listas X e Y con una
frecuencia Frec. El resumen de los resultados se guarda en la variable
stat.results. (Consulte la página 109).
Todas las listas, salvo Incluir, han de tener la misma dimensión.
X e Y son listas que contienen, respectivamente, la variable
independiente y la variable dependiente.
Frec es una lista opcional de valores de frecuencia. Cada elemento
de Frec especifica la frecuencia de ocurrencia de cada punto de datos
en X e Y. El valor predeterminado es 1. Todos los elementos deben
ser enteros | 0.
Categoría es una lista de códigos numéricos de categoría para los
datos de X e Y.
Incluir es una lista de uno o varios códigos de categoría. En el cálculo
sólo se incluyen los elementos de datos cuyo código de categoría se
encuentre en la lista.
Catálogo
>
Vari able de
salida
stat.RegEqn
stat.m, stat.b Coeficientes de regresión
2
stat.r
stat.r Coeficiente de correlación
stat.Resid Residuos de la regresión
stat.XReg Lista de puntos de datos en la Lista X modificada utilizada realmente en la regresión basada en
stat.YReg Lista de puntos de datos en la Lista Y modificada utilizada realmente en la regresión basada en las
stat.FreqReg Lista de frecuencias correspondiente a stat.XReg y stat.YReg
Descripción
Ecuación de regresión: m·x+b
Coeficiente de determinación
restricciones de Frec, Lista Categoría e Incluir Categorías
restricciones de Frec, Lista Categoría e Incluir Categorías
Guía de referencia de TI-Nspire™ CAS 59

LinRegtIntervals
LinRegtIntervals X,Y[,Frec[,0[,NivelC]]]
Para la pendiente. Calcula el intervalo de confianza de nivel C para la
pendiente.
LinRegtIntervals X,Y[,Frec[,1,Xval[,NivelC]]]
Para la respuesta. Calcula el valor de Y previsto, un intervalo de
predicción de nivel C para una única observación y un intervalo de
confianza de nivel C para la respuesta media.
El resumen de los resultados se guarda en la variable stat.results.
(Consulte la página 109).
Todas las listas deben tener las mismas dimensiones.
X e Y son listas que contienen, respectivamente, la variable
independiente y la variable dependiente.
Frec es una lista opcional de valores de frecuencia. Cada elemento
de Frec especifica la frecuencia de ocurrencia de cada punto de datos
en X e Y. El valor predeterminado es 1. Todos los elementos deben
ser enteros | 0.
Catálogo
>
Vari able de
salida
stat.RegEqn
stat.a, stat.b Coeficientes de regresión
stat.df Grados de libertad
2
stat.r
stat.r Coeficiente de correlación
stat.Resid Residuos de la regresión
Sólo para tipo de pendiente
Vari able de
salida
[stat.CLower,
stat.CUpper]
stat.ME Margen de error del intervalo de confianza
stat.SESlope Error estándar de la pendiente
stat.s Error estándar para la recta
Sólo para el tipo de respuesta
Vari able de
salida
[stat.CLower,
stat.CUpper]
stat.ME Margen de error del intervalo de confianza
Descripción
Ecuación de regresión: a+b·x
Coeficiente de determinación
Descripción
Intervalo de confianza para la pendiente.
Descripción
Intervalo de confianza para la respuesta media
60 Guía de referencia de TI-Nspire™ CAS

Vari able de
salida
stat.SE Error estándar de la respuesta media
[stat.LowerPred ,
stat.UpperPred]
stat.MEPred Margen de error del intervalo de predicción
stat.SEPred Error estándar para la predicción
stat.y
Descripción
Intervalo de predicción para una única observación
a + b·XVal
LinRegTTest (Test t de regresión lineal)
LinRegtTest X,Y[,Frec[,Hipótesis]]
Calcula una regresión lineal en las listas X e Y junto con un test t para
el valor de la pendiente b y el coeficiente de correlación r para la
ecuación y=a+bx. Prueba la hipótesis nula H0:b=0 (equivalencia,
r=0) frente a una de las tres alternativas siguientes.
Todas las listas deben tener la misma dimensión.
X e Y son listas que contienen, respectivamente, la variable
independiente y la variable dependiente.
Frec es una lista opcional de valores de frecuencia. Cada elemento
de Frec especifica la frecuencia de ocurrencia de cada punto de datos
en X e Y. El valor predeterminado es 1. Todos los elementos deben
ser enteros | 0.
Hipótesis es un valor opcional que especifica una de las tres hipótesis
alternativas frente a las que se va a probar la hipótesis nula
(H0:b=r=0).
Para Ha: bƒ0 y rƒ0 (predeterminado), defina Hipótesis=0
Para Ha: b<0 y r<0, defina Hipótesis<0
Para Ha: b>0 y r>0, defina Hipótesis>0
El resumen de los resultados se guarda en la variable stat.results.
(Consulte la página 109).
Vari able de
salida
stat.RegEqn
stat.t t Test estadístico para significancia
stat.PVal Nivel de significancia mínimo al que se puede rechazar la hipótesis nula
stat.df Grados de libertad
stat.a, stat.b Coeficientes de regresión
stat.s Error estándar para la recta
stat.SESlope Error estándar de la pendiente
2
stat.r
stat.r Coeficiente de correlación
stat.Resid Residuos de la regresión
Descripción
Ecuación de regresión: a + b·x
Coeficiente de determinación
Catálogo
>
Guía de referencia de TI-Nspire™ CAS 61

List()
@
@List(Lista1) ⇒ lista
Devuelve una lista que contiene las diferencias entre elementos
consecutivos de Lista1. Cada elemento de Lista1 se resta del
siguiente elemento de Lista1. La lista resultante tiene siempre un
elemento menos que la Lista1 original.
Catálogo
>
list4mat()
list4mat(Lista [, elementosPorFila]) ⇒ matriz
Devuelve una matriz rellena fila a fila con los elementos de Lista.
elementosPorFila, si se incluye, especifica el número de elementos
por fila. El valor predeterminado es el número de elementos de Lista
(una fila).
Si Lista no rellena la matriz resultante se añaden ceros.
ln
4
Expr 4ln ⇒ expresión
Hace que Expr se convierta en una expresión que contiene sólo
logaritmos naturales (ln).
ln()
ln(Expr1) ⇒ expresión
ln(Lista1) ⇒ lista
Devuelve el logaritmo natural del argumento.
Para una lista, devuelve los logaritmos naturales de los elementos.
ln(Matrizcuadrada1) ⇒ Matrizcuadrada
Devuelve el logaritmo natural de la matriz Matrizcuadrada1. El
resultado no es igual que calcular el logaritmo natural de cada
elemento. Para obtener más información sobre el método de cálculo,
consulte cos().
Matrizcuadrada1 debe ser diagonizable. El resultado contiene
siempre números con coma flotante.
Catálogo
Catálogo
/
Teclas
Si el modo de formato complejo es Real:
Si el modo de formato complejo es Rectangular:
En el modo de ángulo en radianes y formato complejo
rectangular:
>
>
u
Para ver todos los resultados, pulse £ y utilice ¡ y ¢ para
mover el cursor.
62 Guía de referencia de TI-Nspire™ CAS

LnReg
LnReg X, Y[, [Frec] [, Categoría, Incluir]]
Calcula la regresión logarítmica y = a+b·ln(x) de las listas X e Y con
una frecuencia Frec. El resumen de los resultados se guarda en la
variable stat.results. (Consulte la página 109).
Todas las listas, salvo Incluir, deben tener la misma dimensión.
X e Y son listas que contienen, respectivamente, la variable
independiente y la variable dependiente.
Frec es una lista opcional de valores de frecuencia. Cada elemento
de Frec especifica la frecuencia de ocurrencia de cada punto de datos
en X e Y. El valor predeterminado es 1. Todos los elementos deben
ser enteros | 0.
Categoría es una lista de códigos numéricos de categoría para los
datos de X e Y.
Incluir es una lista de uno o varios códigos de categoría. En el cálculo
sólo se incluyen los elementos de datos cuyo código de categoría se
encuentre en la lista.
Catálogo
>
Vari able de
salida
stat.RegEqn
stat.a, stat.b Coeficientes de regresión
2
stat.r
stat.r Coeficiente de correlación para los datos transformados (ln(x), y)
stat.Resid Residuos asociados al modelo logarítmico
stat.ResidTrans Residuos asociados con el ajuste lineal de los datos transformados
stat.XReg Lista de puntos de datos en la Lista X modificada utilizada realmente en la regresión basada en
stat.YReg Lista de puntos de datos en la Lista Y modificada utilizada realmente en la regresión basada en las
stat.FreqReg Lista de frecuencias correspondiente a stat.XReg y stat.YReg
Descripción
Ecuación de regresión: a+b·ln(x)
Coeficiente de determinación lineal para los datos transformados
restricciones de Frec, Lista Categoría e Incluir Categorías
restricciones de Frec, Lista Categoría e Incluir Categorías
Guía de referencia de TI-Nspire™ CAS 63

Local
Local Var 1 [, Va r 2] [, Va r 3 ] ...
Declara las vars especificadas como variables locales. Las variables
sólo están presentes durante el cálculo de la función y se borran
cuando finaliza la ejecución de la misma.
Nota: Las variables locales permiten ahorrar memoria puest o que su
existencia es sólo temporal. Además, no interfieren con l os valores de
ninguna variable global existente. Las variables locales deben
utilizarse para bucles For y para guardar temporalmente los valores
de una función de varias líneas, ya que no está permitido modificar
variables globales de una función.
Nota para introducir el ejemplo: En la aplicación Calculadora
de la unidad portátil, puede introducir definiciones formadas por
varias líneas si pulsa @ en lugar de · al final de cada línea.
En el teclado del ordenador, mantenga pulsada la tecla Alt y pulse
Enter (Intro).
Catálogo
>
log()
log(Expr1[,Expr2]) ⇒ expresión
log(Lista1[,Expr2]) ⇒ lista
Devuelve el logaritmo base -Expr2 del primer argumento.
Nota: Consulte también Plantilla de registro, en la página 2.
Para una lista, devuelve el logaritmo base -Expr2 de los elementos.
Si se omite el segundo argumento, la base utilizada será 10.
log(Matrizcuadrada1[,Expr]) ⇒ Matrizcuadrada
Devuelve el logaritmo base Expr de la matriz Matrizcuadrada1. El
resultado no es igual que calcular el logaritmo base -Expr de cada
elemento. Para obtener más información sobre el método de cálculo,
consulte cos().
Matrizcuadrada1 debe ser diagonizable. El resultado contiene
siempre números con coma flotante.
Si se omite el argumento base, la utilizada será 10.
/s
Teclas
Si el modo de formato complejo es Real:
Si el modo de formato complejo es Rectangular:
En el modo de ángulo en radianes y formato complejo
rectangular:
Para ver todos los resultados, pulse £ y utilice ¡ y ¢ para
mover el cursor.
64 Guía de referencia de TI-Nspire™ CAS

logbase
4
4logbase(Expr1) ⇒ expresión
Expr
Simplifica la Expresión de entrada a una expresión que utiliza base
Expr1.
Catálogo
>
Logistic
Logistic X, Y[, [Frec] [, Categoría, Incluir]]
Calcula la regresión logística y = (c/(1+a·e
con una frecuencia Frec. El resumen de los resultados se guarda en la
variable stat.results. (Consulte la página 109).
-bx
)) de las listas X e Y
Catálogo
Todas las listas, salvo Incluir, deben tener la misma dimensión.
X e Y son listas que contienen, respectivamente, la variable
independiente y la variable dependiente.
Frec es una lista opcional de valores de frecuencia. Cada elemento
de Frec especifica la frecuencia de ocurrencia de cada punto de datos
en X e Y. El valor predeterminado es 1. Todos los elementos deben
ser enteros | 0.
Categoría es una lista de códigos numéricos de categoría para los
datos de X e Y.
Incluir es una lista de uno o varios códigos de categoría. En el cálculo
sólo se incluyen los elementos de datos cuyo código de categoría se
encuentre en la lista.
Vari able de
salida
stat.RegEqn
Descripción
Ecuación de regresión: c/(1+a·e
-bx
)
stat.a, stat.b, stat.c Coeficientes de regresión
stat.Resid Residuos de la regresión
stat.XReg Lista de puntos de datos en la Lista X modificada utilizada realmente en la regresión basada en
stat.YReg Lista de puntos de datos en la Lista Y modificada utilizada realmente en la regresión basada en las
restricciones de Frec, Lista Categoría e Incluir Categorías
restricciones de Frec, Lista Categoría e Incluir Categorías
stat.FreqReg Lista de frecuencias correspondiente a stat.XReg y stat.YReg
>
Guía de referencia de TI-Nspire™ CAS 65

LogisticD
LogisticD X, Y [ , [Iteraciones] , [Frec] [, Categoría, Incluir] ]
Calcula la regresión logística y = (c/(1+a·e
con una frecuencia Frec, utilizando un número de Iteraciones
especificado. El resumen de los resultados se guarda en la variable
stat.results. (Consulte la página 109).
Todas las listas, salvo Incluir, deben tener la misma dimensión.
X e Y son listas que contienen, respectivamente, la variable
independiente y la variable dependiente.
Iteraciones es un valor opcional que especifica el número máximo de
veces que se debe intentar la solución. Si se omite, se utiliza 64. Por
lo general, los valores más grandes ofrecen más precisión aunque
requieren más tiempo de ejecución, y viceversa.
Frec es una lista opcional de valores de frecuencia. Cada elemento
de Frec especifica la frecuencia de ocurrencia de cada punto de datos
en X e Y. El valor predeterminado es 1. Todos los elementos deben
| 0.
ser enteros
Categoría es una lista de códigos numéricos de categoría para los
datos de X e Y.
Incluir es una lista de uno o varios códigos de categoría. En el cálculo
sólo se incluyen los elementos de datos cuyo código de categoría se
encuentre en la lista.
-bx
)+d) de las listas X e Y
Catálogo
>
Vari able de
salida
stat.RegEqn
stat.a, stat.b, stat.c,
stat.d
stat.Resid Residuos de la regresión
stat.XReg Lista de puntos de datos en la Lista X modificada utilizada realmente en la regresión basada en
stat.YReg Lista de puntos de datos en la Lista Y modificada utilizada realmente en la regresión basada en
stat.FreqReg Lista de frecuencias correspondiente a stat.XReg y stat.YReg
Descripción
Ecuación de regresión: c/(1+a·e
Coeficientes de regresión
restricciones de Frec, Lista Categoría e Incluir Categorías
restricciones de Frec, Lista Categoría e Incluir Categorías
-bx
)+d)
66 Guía de referencia de TI-Nspire™ CAS

Loop
Loop
Bloque
EndLoop
Ejecuta repetidamente las sentencias de Bloque. El bucle se repetirá
indefinidamente a menos que haya incluido una instrucción
Exit para que se ejecute en el Bloque.
Bloque es una serie de sentencias separadas por el carácter “:”.
Nota para introducir el ejemplo: En la aplicación Calculadora
de la unidad portátil, puede introducir definiciones formadas por
varias líneas si pulsa
En el teclado del ordenador, mantenga pulsada la tecla Alt y pulse
Enter (Intro).
@ en lugar de · al final de cada línea.
Goto o
Catálogo
>
LU
LU Matriz, NombreMatInf, NombreMatSup, NombreMatP[, Tol]
Calcula la descomposición LU (inferior-superior) Doolittle de una
matriz real o compleja. La matriz triangular inferior se guarda en
NombreMatInf, la matriz triangular superior en NombreMatSup y la
matriz de permutación (que describe las filas intercambiadas durante
el cálculo) en NombreMatP.
NombreMatInf · NombreMatSup = NombreMatP · matriz
Opcionalmente, cualquier elemento de matriz se trata como cero si su
valor absoluto es menor que el de To l . Esta tolerancia se utiliza sólo si
la matriz tiene entradas de coma flotante y no contiene ninguna
variable simbólica que no tenga asignado un valor. De lo contrario se
ignorará el valor de To l.
• Si utiliza
•Si el valor de To l se omite o no se utiliza, la tolerancia
El algoritmo de factorización LU se vale de un sistema de giro parcial
para el intercambio de las filas.
/
Approximate (Auto o Aproximado)
cálculos se efectuarán utilizando la coma flotante aritmética.
predeterminada se calculará como:
5EM14 ·max(dim(Matriz)) ·rowNorm(Matriz)
· o define el modo Auto or
en Aproximado, los
Catálogo
>
Guía de referencia de TI-Nspire™ CAS 67

M
mat4list()
mat4list(Matriz) ⇒ lista
Devuelve una matriz construida a partir de los elementos de Matriz.
Los elementos proceden de Matriz y se han copiado fila a fila.
max()
max(Expr1, Expr2) ⇒ expresión
max(Lista1, Lista2) ⇒ lista
max(Matriz1, Matriz2) ⇒ matriz
Devuelve el máximo de los dos argumentos. Si los argumentos son
dos listas o dos matrices, devuelve una lista o una matriz que
contiene el valor máximo de cada par de elementos correspondientes.
max(Lista) ⇒ expresión
Devuelve el elemento máximo de lista.
max(Matriz1) ⇒ matriz
Devuelve un vector fila que contiene el elemento máximo de cada
columna de Matriz1.
Nota: Consulte también fMax() y min().
mean()
mean(Lista[, Listafrecuencia]) ⇒ expresión
Devuelve la media de los elementos de Lista.
Cada elemento de Listafrecuencia cuenta el número de ocurrencias
consecutivas del elemento correspondiente en Lista.
mean(Matriz1[, Matrizfrecuencia]) ⇒ matriz
Devuelve un vector fila de las medias de todas las columnas de
Matriz1.
Cada elemento de Matrizfrecuencia cuenta el número de
ocurrencias consecutivas del elemento correspondiente en Matriz1.
En el formato de vector rectangualr:
Catálogo
Catálogo
Catálogo
>
>
>
median()
median(Lista) ⇒ expresión
Devuelve la mediana de los elementos de Lista.
Catálogo
>
68 Guía de referencia de TI-Nspire™ CAS

median()
median(Matriz1) ⇒ matriz
Devuelve un vector de fila que contiene las medianas de las col umnas
de Matriz1.
Nota: Es necesario simplificar a números todas las entradas de la
lista o la matriz.
Catálogo
>
MedMed
MedMed X,Y [, Frec] [, Categoría, Incluir]]
Calcula la recta mediana-mediana y = (m·x+b) de las listas X e Y
con una frecuencia Frec. El resumen de los resultados se guarda en la
variable stat.results. (Consulte la página 109).
Todas las listas, salvo Incluir, deben tener la misma dimensión.
X e Y son listas que contienen, respectivamente, la variable
independiente y la variable dependiente.
Frec es una lista opcional de valores de frecuencia. Cada elemento
de Frec especifica la frecuencia de ocurrencia de cada punto de datos
en X e Y. El valor predeterminado es 1. Todos los elementos deben
ser enteros | 0.
Categoría es una lista de códigos numéricos de categoría para los
datos de X e Y.
Incluir es una lista de uno o varios códigos de categoría. En el cálculo
sólo se incluyen los elementos de datos cuyo código de categoría se
encuentre en la lista.
Vari able de
salida
stat.RegEqn
stat.m, stat.b Coeficientes de modelo
stat.Resid Residuos de la recta mediana-mediana
stat.XReg Lista de puntos de datos en la Lista X modificada utilizada realmente en la regresión basada en
stat.YReg Lista de puntos de datos en la Lista Y modificada utilizada realmente en la regresión basada en las
stat.FreqReg Lista de frecuencias correspondiente a stat.XReg y stat.YReg
Descripción
Ecuación de la recta mediana-mediana: m·x+b
restricciones de Frec, Lista Categoría e Incluir Categorías
restricciones de Frec, Lista Categoría e Incluir Categorías
Catálogo
>
mid()
mid(Cadenaorigen, Inicio[, Cont]) ⇒ cadena
Devuelve los caracteres Cont incluidos en la cadena Cadenaorigen,
a partir del número de carácter de Inicio.
Si Cont se omite o es mayor que la dimensión de Cadenaorigen,
devuelve todos los caracteres de Cadenaorigen, a partir del número
de carácter de Inicio.
Cont debe ser ‚ 0. Si Cont = 0, devuelve una cadena vacía.
Catálogo
>
Guía de referencia de TI-Nspire™ CAS 69

mid()
mid(Listaorigen, Inicio [, Cont]) ⇒ lista
Devuelve Cont de los elementos incluidos en Listaorigen, a partir del
número de elemento de Inicio.
Si Cont se omite o es mayor que la dimensión de Listaorigen,
devuelve todos los elementos de Lista origen, a partir del número de
elemento de Inicio.
Cont debe ser
mid(ListaCadenaorigen, Inicio[, Cont]) ⇒ lista
Devuelve Cont de las cadenas incluidas en la lista de cadenas
ListaCadenaorigen, a partir del número de elemento de Inicio.
‚ 0. Si Cont = 0, devuelve una lista vacía.
min()
min(Expr1, Expr2) ⇒ expresión
min(Lista1, Lista2) ⇒ lista
min(Matriz1, Matriz2) ⇒ matriz
Devuelve el mínimo de los dos argumentos. Si los argumentos son
dos listas o dos matrices, devuelve una lista o una matriz que
contiene el valor mínimo de cada par de elementos correspondientes.
min(Lista) ⇒ expresión
Devuelve el elemento mínimo de Lista.
min(Matriz1) ⇒ matriz
Devuelve un vector fila que contiene el elemento mínimo de cada
columna de Matriz1.
Nota: Consulte también fMin() y max().
Catálogo
Catálogo
>
>
mirr()
mirr(TasaFinan,TasaReinver,CF0,CFLista[,CFFrec])
Función financiera que calcula la tasa interna mo dificada o de retorno
de una inversión.
TasaFinan es la tasa de interés que se paga sobre las cantidades del
flujo de caja.
TasaReinver es la tasa de interés a la que se reinvierten los flujos de
caja.
Catálogo
>
CF0 es el flujo de caja inicial en el tiempo 0; debe ser un número real.
CFLista es una lista de cantidades de flujo de caja tras el flujo de
caja inicial CF0.
CFFrec es una lista opcional en la que cada elemento especifica la
frecuencia de ocurrencia de una cantidad de flujo de caja agrupada
(consecutiva), que es el elemento correspondiente de CFLista. El
valor predeterminado es 1; si introduce valores, deberán ser números
enteros positivos < 10.000.
Nota: Consulte también irr(), en la página55.
70 Guía de referencia de TI-Nspire™ CAS

mod()
mod(Expr1, Expr2) ⇒ expresión
mod(Lista1, Lista2) ⇒ lista
mod(Matriz1, Matriz2) ⇒ matriz
Devuelve el primer argumento módulo del segundo argumento según
estas definiciones:
mod(x,0) = x
mod(x,y) = x
Cuando el segundo argumento es distinto de cero, el resultado es
periódico en dicho argumento. El resultado puede ser cero o tener el
mismo signo que el segundo argumento.
Si los argumentos son dos listas o dos matrices, devuelve una lista o
una matriz que contiene el módulo de cada par de elementos
correspondientes.
Nota: Consulte también remain(), en la página 93
-ìy floor(x/y)
Catálogo
>
mRow()
mRow(Expr, Matriz1, Índice) ⇒ matriz
Devuelve una copia de Matriz1 con cada elemento de la fila Índice
de Matriz1 multiplicado por el valor de Expr.
mRowAdd()
mRowAdd(Expr, Matriz1, Índice1, Índice2) ⇒ matriz
Devuelve una copia de Matriz1 con cada elemento de la fila Índice2
de Matriz1 sustituido por:
Expr · fila Índice1 + fila Índice2
MultReg
MultReg Y, X1[,X2[,X3,…[,X10]]]
Calcula la regresión lineal múltiple de la lista Y en las listas X1, X2,
…, X10. El resumen de los resultados se guarda en la variable
stat.results. (Consulte la página 109).
Todas las listas deben tener la misma dimensión.
Vari able de
salida
stat.RegEqn
Descripción
Ecuación de regresión: b0+b1·x1+b2·x2+ ...
stat.b0, stat.b1, ... Coeficientes de regresión
stat.R
2
Coeficiente de determinación múltiple
stat.yLista yLista = b0+b1·x1+ ...
stat.Resid Residuos de la regresión
Catálogo
Catálogo
Catálogo
>
>
>
Guía de referencia de TI-Nspire™ CAS 71

MultRegIntervals
MultRegIntervals Y, X1[,X2[,X3,…[,X10]]],XValLista[,NivelC]
Calcula el valor de y que se prevé, un intervalo de predicción de nivel
C para una única observación y un intervalo de confianza de nivel C
para la respuesta media.
El resumen de los resultados se guarda en la variable stat.results.
(Consulte la página 109).
Todas las listas deben tener la misma dimensión.
Catálogo
>
Vari able de
salida
stat.RegEqn
Descripción
Ecuación de regresión: b0+b1·x1+b2·x2+ ...
stat.y Punto estimado: y = b0 + b1 · xl + ... para XValLista
stat.dfError Grados de libertad de los errores
stat.CLower, stat.CUpper Intervalo de confianza para una respuesta media
stat.ME Margen de error del intervalo de confianza
stat.SE Error estándar de la respuesta media
stat.LowerPred,
stat.UpperrPred
Intervalo de predicción para una única observación
stat.MEPred Margen de error del intervalo de predicción
stat.SEPred Error estándar para la predicción
stat.bList Lista de coeficientes de regresión, {b0,b1,b2,...}
stat.Resid Residuos de la regresión
MultRegTests
MultRegTests Y, X1[,X2[,X3,…[,X10]]]
Test de regresión lineal múltiple, calcula un a regresión lineal múltiple
de los datos dados y proporciona el test estadístico F general y el test
estadístico t para los coeficientes.
El resumen de los resultados se guarda en la variable stat.results.
(Consulte la página 109).
Salidas
Catálogo
>
Vari able de
salida
stat.RegEqn
Descripción
Ecuación de regresión: b0+b1·x1+b2·x2+ ...
stat.F Test estadístico F general
stat.PVal Valor P asociado con el test estadístico F general
stat.R
stat.AdjR
2
2
Coeficiente de determinación múltiple
Coeficiente de determinación múltiple ajustado
72 Guía de referencia de TI-Nspire™ CAS

Vari able de
salida
stat.s Desviación estándar del error
stat.DW Estadística de Durbin-Watson; utilizada para determinar si en el modelo está presente la correlación
stat.dfReg Grados de libertad de la regresión
stat.SSReg Suma de cuadrados de la regresión
stat.MSReg Media de cuadrados de la regresión
stat.dfError Grados de libertad de los errores
stat.SSError Suma de los cuadrados de los errores
stat.MSError Media de los cuadrados de los errores
stat.bList {b0,b1,...} Lista de coeficientes
stat.tList Lista de los estadísticos t, uno por cada coeficiente de la ListaB
stat.PList Lista de valores P para cada estadístico t
stat.SEList Lista de errores estándar para los coeficientes de la ListaB
stat.yLista yLista = b0+b1·x1+...
stat.Resid Residuos de la regresión
stat.sResid Residuos estandarizados; obtenidos al dividir un residuo por su desviación estándar
stat.CookDist Distancia de Cook; medida de la influencia de una observación basada en el valor residual y medio
stat.Leverage Medida de la distancia entre los valores de la variable independiente y los valores medios
Descripción
automática de primer orden
N
nCr()
nCr(Expr1, Expr2) ⇒ expresión
Para Expr1 y Expr2 enteros con Expr1 ‚ Expr2 ‚ 0, nCr() es el
número de combinaciones de elementos de Expr1 tomando Expr2
cada vez. (También se conoce como coeficiente binomial). Ambos
argumentos pueden ser expresiones enteras o simbólicas.
nCr(Expr, 0) ⇒ 1
Expr, EnteroNeg) ⇒ 0
nCr(
Expr, EnteroPos) ⇒ Expr·(ExprN1)...
nCr(
(ExprNEnteroPos+1)/ EnteroPos!
Expr, NoEntero) ⇒ expresión!/
nCr(
((ExprNNoEntero)!·NoEntero!)
Lista1, Lista2) ⇒ lista
nCr(
Devuelve una lista de combinaciones basada en los pares de
elementos correspondientes de las dos listas. Los argumentos deben
tener el mismo tamaño que la lista.
Catálogo
>
Guía de referencia de TI-Nspire™ CAS 73

nCr()
nCr(Matriz1, Matriz2) ⇒ matriz
Devuelve una matriz de combinaciones basada en los pares de
elementos correspondientes de las dos matrices. Los argumentos
deben tener el mismo tamaño que la matriz.
Catálogo
>
nDeriv()
nDeriv(Expr1, Va r [=Valor] [, H]) ⇒ expresión
nDeriv(Expr1, Va r [, H] | Var = Va lo r ) ⇒ expresión
nDeriv(Expr1, Va r [=Valor], Lista) ⇒ lista
nDeriv(Lista1, Va r [=Valor] [, H]) ⇒ lista
nDeriv(Matriz1, Va r [=Valor] [, H]) ⇒ matriz
Devuelve la derivada numérica como una expresión. Utili za la fórmula
de cociente de diferencia central.
Cuando se especifica, valor sobrescribe cualquier otra asignación de
variable anterior o cualquier sustitución “tal como” actual de la
variable.
H es el valor de paso. Si se omite, H adopta el valor predeterminado
0,001.
Cuando se utiliza Lista1 o Matriz1, la operación se aplica a los
valores de la lista o los elementos de la matriz.
Nota: Consulte también avgRC() y d().
newList()
newList(númElementos) ⇒ lista
Devuelve una lista con la dimensión númElementos. Cada elemento
es cero.
newMat()
newMat(númeroFilas, númeroColumnas) ⇒ matriz
Devuelve la matriz de ceros de dimensión númeroFilas por
númeroColumnas.
nfMax()
nfMax(Expr, Va r) ⇒ valor
nfMax(Expr, Va r, Extremoinferior) ⇒ valor
nfMax(Expr, Va r, Extremoinferior, Extremosuperior) ⇒ valor
nfMax(Expr, Var) |
Extremoinferior<Var <Extremosuperior ⇒ valor
Devuelve el posible valor numérico de la variable Va r donde se
produce el máximo local de Expr.
Si se facilitan los valores de Extremoinferior y Extremosuperior, la
función busca el máximo local entre dichos valores.
Nota: Consulte también fMax() y d().
Catálogo
Catálogo
Catálogo
Catálogo
>
>
>
>
74 Guía de referencia de TI-Nspire™ CAS

nfMin()
nfMin(Expr, Va r) ⇒ valor
nfMin(Expr, Va r, Extremoinferior) ⇒ valor
nfMin(Expr, Va r, Extremoinferior, Extremosuperior) ⇒ valor
nfMin(Expr, Var) |
Extremoinferior<Var <Extremosuperior ⇒ valor
Devuelve el posible valor numérico de la variable Va r donde se
produce el mínimo local de Expr.
Si se facilitan los valores de Extremoinferior y Extremosuperior, la
función busca el mínimo local entre dichos valores.
Nota: Consulte también fMin() y d().
Catálogo
>
nInt()
nInt(Expr1, Var, Inferior, Superior) ⇒ expresión
Si el integrando Expr1 no contiene otra variable que Va r , y si los
valores Inferior y Superior son constantes, ˆ positivo o ˆ negativo,
entonces nInt() devuelve una aproximación de ‰(Expr1, Va r ,
Inferior, Superior). Esta aproximación es una media ponderada de
algunos valores de ejemplo del integrando en el intervalo
Inferior<Va r<Superior.
El objetivo es conseguir seis dígitos significativos. El algoritmo de
búsqueda termina cuando parece que se ha logrado el objetivo, o
cuando parece que ningún otro ejemplo adicional ofrecerá una
mejoría satisfactoria.
La pantalla muestra una advertencia (“Exactitud dudosa”) cuan do no
parece que vaya a alcanzarse el objetivo.
Anide la función nInt() para realizar varias integraciones numéricas.
Los límites de la integración pueden depender de las variables de
integración que quedan fuera de las mismas.
Nota: Consulte también ‰(), en la página 139.
nom()
nom(TasaEfectiva,CpY) ⇒ valor
Función financiera que convierte la tasa de interés anual efectiva
TasaEfectiva en una tasa nominal, siendo CpY el número de
periodos compuestos por año.
TasaEfectiva debe ser un número real; CpY debe ser un número real
> 0.
Nota: Consulte también eff(), en la página 37.
Catálogo
Catálogo
>
>
Guía de referencia de TI-Nspire™ CAS 75

norm()
norm(Matriz) ⇒ expresión
norm(Ve c to r ) ⇒ expresión
Devuelve la norma de Frobenius.
Catálogo
>
normalLine()
normalLine (Expr1,Va r ,Punto) ⇒ expresión
normalLine(Expr1,Va r =Punto) ⇒ expresión
Devuelve la recta normal a la curva representada por Expr1 en el
punto especificado en Va r=Punto.
Asegúrese de que la variable independiente no esté definida.
Por ejemplo, Si f1(x):=5 y x:=3, entonces normalLine(f1(x),x,2)
devuelve "falso".
normCdf()
normCdf(Extremoinferior,Extremosuperior[,m[,s]]) ⇒ númer
o si Extremoinferior y Extremosuperior son números, lista si
Extremoinferior y Extremosuperior son listas
Calcula la probabilidad de distribución normal entre Extremoinferior
y Extremosuperior para los valores de m (predeterminado=0) y s
(predeterminado=1) especificados.
Para P(X Extremosuperior), defina Extremoinferior = .ˆ.
normPdf()
normPdf(XVal[,m[,s]]) ⇒ número si XVal es un número, lista
XVal es una lista
si
Calcula la función de densidad de probabilidad para la distribución
normal para un valor XVal especificado para unos valores m y s
especificados.
not
not ExprBooleana ⇒ Expresión booleana
Indica si el argumento es verdadero (true), falso (false) o muestra una
forma simplificada del mismo.
Catálogo
Catálogo
Catálogo
Catálogo
>
>
>
>
76 Guía de referencia de TI-Nspire™ CAS

not
not Entero1 ⇒ entero
Devuelve el complemento a uno para un número entero real.
Internamente, Entero1 se convierte en un número binario con signo
de 64 bits. El valor de cada bit se invierte (0 se convierte en 1, y
viceversa) por el complemento de uno. Los resultados se muestran
conforme al modo de la base.
Los números enteros se pueden introducir en cualquier base. Para una
entrada binaria o hexadecimal es necesario utilizar el prefijo 0b o 0h,
respectivamente. Si no se indica un prefijo, el entero se considera
como decimal (base 10).
Si el entero decimal que se introduce es demasiado largo para un
formato binario con signo de 64 bits, se utiliza una operación de
módulo simétrico para llevar el valor al rango apropiado.
En modo base Hex:
Importante: Cero, no la letra O.
En modo base Bin:
Catálogo
>
nPr()
nPr(Expr1, Expr2) ⇒ expresión
Para Expr1 y Expr2 enteros con Expr1 ‚ Expr2 ‚ 0, nPr() es el
número de variaciones de elementos de Expr1 tomando Expr2 cada
vez. Ambos argumentos pueden ser números enteros o expresiones
simbólicas.
nPr(Expr, 0) ⇒ 1
Expr, EnteroNeg) ⇒ 1/((Expr+1)·(Expr+2)...
nPr(
(
expresiónNEnteroNeg))
nPr(
Expr, EnteroPos) ⇒ Expr·(ExprN1)...
ExprNEnteroPos+1)
(
Expr, NoEntero) ⇒ Expr! / (ExprNNoEntero)!
nPr(
nPr(
Lista1, Lista2) ⇒ lista
Devuelve una lista de variaciones basada en los pares de elementos
correspondientes de las dos listas. Los argumentos deben tener el
mismo tamaño que la lista.
nPr(Matriz1, Matriz2) ⇒ matriz
Devuelve una lista de variaciones basada en los pares de elementos
correspondientes de las dos matrices. Los argumentos deben tener el
mismo tamaño que la matriz.
Para ver todos los resultados, pulse
mover el cursor.
Nota: Una entrada binaria puede tener hasta 64 dígitos (sin
contar el prefijo 0b). Una entrada hexadecimal puede tener
hasta 16 dígitos.
£ y utilice ¡ y ¢ para
Catálogo
>
Guía de referencia de TI-Nspire™ CAS 77

npv()
npv(Tas a In t er és ,CFO,CFList[,CFFrec])
Función financiera que calcula el valor presente neto; la suma de los
valores presentes para las entradas y salidas de flujos de caja. Un
resultado de npv positivo indica una inversión rentable.
TasaInterés es la tasa de descuento que se aplica a los flujos de caja
(coste del dinero) en un periodo de tiempo.
CF0 es el flujo de caja inicial en el tiempo 0; debe ser un número real.
CFLista es una lista de cantidades de flujo de caja tras el flujo inicial
CF0.
CFFrec es una lista opcional en la que cada elemento especifica la
frecuencia de ocurrencia de una cantidad de flujo de caja agrupada
(consecutiva), que es el elemento correspondiente de CFLista. El
valor predeterminado es 1; si introduce valores, deberán ser números
enteros positivos < 10.000.
Catálogo
>
nSolve()
nSolve(Ecuación,Var [=Conjetura]) ⇒ número o error_cadena
nSolve(Ecuación,Var [=Conjetura],Extremoinferior)
⇒ número o error_cadena
nSolve(Ecuación,Var [=Conjetura],Extremoinferior,Extremosup
erior) ⇒ número o error_cadena
nSolve(Ecuación,Var [=Conjetura]) |
Extremoinferior<Var <Extremosuperior
⇒ número o error_cadena
Busca repetidamente una solución numérica real aproximada de
Ecuación para su única variable. Especifique la variable como:
variable
– o –
variable = número real
Por ejemplo, x es válido y también lo es x=3.
nSolve() suele ser más rápido que solve() o zeros(), en especial
si se utiliza el operador “|” para restringir la búsqueda a un intervalo
relativamente pequeño que contenga exactamente una solución
sencilla.
nSolve() intenta determinar un punto donde el residuo es cero, o
dos puntos relativamente cercanos donde el residuo tenga signos
opuestos y su diferencia no sea excesiva. Si no consigue alcanzar un
número modesto de puntos de ejemplo, devuelve la cadena “no
solution found (no se ha encontrado una solución”).
Nota: Consulte también cSolve(), cZeros(), solve() y zeros().
Catálogo
>
Nota: Si hay varias soluciones, puede utilizar una conjetura que
le ayude a hallar una solución concreta.
78 Guía de referencia de TI-Nspire™ CAS

O
OneVar
OneVar [1,]X[,[Frec][,Categoría,Incluir]]
OneVar [
n,]X1,X2[X3[,…[,X20]]]
Calcula una estadística de una variable para un máximo de 20 listas.
El resumen de los resultados se guarda en la variable stat.results.
(Consulte la página 109.)
Todas las listas, salvo Incluir, han de tener la misma dimensión.
Los argumentos de X son listas de datos.
Frec es una lista opcional de valores de frecuencia. Cada elemento
de Frec especifica la ocurrencia de cada valor X correspondiente. El
valor predeterminado es 1. Todos los elementos deben ser enteros |
0.
Categoría es una lista de códigos numéricos de categoría para los
valores X correspondientes.
Incluir es una lista de uno o varios códigos de categoría. En el cálculo
sólo se incluyen los elementos de datos cuyo código de categoría se
encuentre en la lista.
Vari able de
salida
stat.v
stat.Gx
2
stat.Gx
stat.sx Desviación estándar de la muestra x
stat.ssssx Desviación estándar de población x
stat.n Número de puntos de datos
stat.MinX Mínimo de valores de x
stat.Q1X Primer cuartil de x
stat.MedianX Mediana de x
stat.Q3X Tercer cuartil de x
stat.MaxX Máximo de valores de x
stat.SSX Suma de cuadrados de desviaciones con respecto a la media de x
Descripción
Media de los valores de x
Suma de los valores de x
Suma de los valores de x
2
Catálogo
>
Guía de referencia de TI-Nspire™ CAS 79

or
ExprBooleana1 or ExprBooleana2
⇒ Expresión booleana
Indica si la entrada original es verdadera (true), falsa (false) o muest ra
una forma simplificada de la misma.
Devuelve "verdadero" si una cualquiera o las dos expresiones se
evalúan como verdadero. Devuelve "falso" sólo si las dos expresiones
se evalúan como falso.
Nota: Consulte xor.
Nota para introducir el ejemplo: En la aplicación Calculadora
de la unidad portátil, puede introducir definiciones formadas por
varias líneas si pulsa @ en lugar de · al final de cada línea.
En el teclado del ordenador, mantenga pulsada la tecla Alt y pulse
Enter (Intro).
Entero1 or Entero2 ⇒ entero
Compara bit a bit dos números enteros reales mediante una
operación or. Internamente, ambos enteros se convierten en números
binarios con signo de 64 bits. Cuando se comparan los bits
correspondientes, el resultado es 1 si cualquiera de ellos es 1; el
resultado será 0 sólo si los dos bits son 0. El valor obtenido representa
el resultado de los bits, y aparece conforme al modo base
especificado.
Los números enteros se pueden introducir en cualquier base. Para una
entrada binaria o hexadecimal es necesario utilizar el prefijo 0b o 0h,
respectivamente. Si no se indica un prefijo, los enteros se consideran
decimales (base 10).
Si el entero decimal que se introduce es demasiado largo para un
formato binario con signo de 64 bits, se utiliza una operación de
módulo simétrico para llevar el valor al rango apropiado.
Nota: Consulte xor.
Catálogo
>
En modo base Hex:
Importante: Cero, no la letra O.
En modo base Bin:
Nota: Una entrada binaria puede tener hasta 64 dígitos (sin
contar el prefijo 0b). Una entrada hexadecimal puede tener
hasta 16 dígitos.
ord()
ord(Cadena) ⇒ entero
ord(Lista1) ⇒ lista
Devuelve el código numérico del primer carácter de la cadena de
caracteres Cadena, o una lista de los primeros caracteres de cada
elemento de la lista.
Catálogo
>
P
P4Rx()
P4Rx(rExpr, qExpr) ⇒ expresión
P4Rx(rLista, qLista) ⇒ lista
P4Rx(rMatriz, qMatriz) ⇒ matriz
Devuelve la coordenada X equivalente del par
(r, q).
Nota: El argumento q se interpreta como un ángulo en grados,
radianes o grados centesimales, según el modo de ángulo actual. Si el
argumento es una expresión, puede utilizar ó,G o ôpara sobrescribir
el modo de ángulo temporalmente.
En el modo de ángulo en radianes:
80 Guía de referencia de TI-Nspire™ CAS
Catálogo
>

P4Ry()
P4Ry(rExpr, qExpr) ⇒ expresión
P4Ry(rLista, qLista) ⇒ lista
P4Ry(rMatriz, qMatriz) ⇒ matriz
Devuelve la coordenada Y equivalente del par (r, q).
Nota: El argumento q se interpreta como un ángulo en grados,
radianes o grados centesimales, según el modo de ángulo actual. Si el
argumento es una expresión, puede utilizar
el modo de ángulo temporalmente.
G
ó,
o ôpara sobrescribir
En el modo de ángulo en radianes:
Catálogo
>
PassErr
PassErr
Pasa un error al siguiente nivel.
Si la variable del sistema errCode es cero, PassErr no realiza acción
alguna.
La cláusula Else del bloque Try...Else...EndTry debería utilizar
ClrErr o PassErr. Si va a procesar o ignorar el error, utilice ClrErr.
Si desconoce el tratamiento que se va a dar al error, utilice PassErr
para enviarlo al siguiente gestor de errores. Si no hay más gestores de
errores de tipo Try...Else...EndTry, el cuadro de diálogo de errores
aparecerá en su forma normal.
Nota: Consulte también ClrErr, en la página 16, y Try, en la página
119.
Nota para introducir el ejemplo: En la aplicación Calculadora
de la unidad portátil, puede introducir definiciones formadas por
varias líneas si pulsa @ en lugar de · al final de cada línea.
En el teclado del ordenador, mantenga pulsada la tecla Alt y pulse
Enter (Intro).
piecewise()
piecewise(Expr1 [, Cond1 [, Expr2 [, Cond2 [, … ]]]])
Devuelve definiciones para una función definida a trozos en forma de
lista. También puede crear definiciones de funciones definidas a
trozos con una plantilla.
Nota: Consulte también Plantilla para funciones definidas a
trozos
, en la página 2.
poissCdf()
poissCdf(l,Extremoinferior,Extremosuperior) ⇒ número si
Extremoinferior y Extremosuperior son números, lista si
Extremoinferior y Extremosuperior son listas
poissCdf(
l,Extremosuperior) (para
P(0
XExtremosuperior) ⇒ número si Extremosuperior es un
número, lista si
Calcula la probabilidad acumulada para la distribución de Poisson
discreta con la media especificada l.
Extremosuperior es una lista
Para P(X Extremosuperior), defina Extremoinferior=0
Catálogo
>
Para ver un ejemplo de PassErr, consulte el Ejemplo 2 de la
orden Try, en la página 119.
Catálogo
>
Catálogo
>
Guía de referencia de TI-Nspire™ CAS 81

poissPdf()
poissPdf(l,XVal) ⇒ número si XVal es un número, lista si
XVal es una lista
Calcula la probabilidad para la distribución de Poisson discreta con la
media especificada l.
Polar
4
4Polar
Vec t o r
Muestra el vector en formato polar [r q]. El vector debe ser
bidimensional y ser fila o columna.
Nota: 4Polar es una orden para un formato de presentación, no
una función de conversión. Se puede utilizar sólo al final de una línea
de entrada y no actualiza el valor de ans.
Nota: Consulte también 4Rect, en la página 92.
complexValue 4Polar
Muestra complexVector en formato polar.
• El modo de ángulo en grados devuelve (rq).
• El modo de ángulo en radianes devuelve re
complexValue puede tener cualquier formato complejo. Sin embargo,
una entrada re
Nota: Debe utilizar paréntesis para una entrada polar (rq).
i
q
generará un error si el modo de ángulo es grados.
i
q
.
Catálogo
Catálogo
En el modo de ángulo en radianes:
En el modo de ángulo en grados centesimales:
En el modo de ángulo en grados:
>
>
polyCoeffs()
polyCoeffs(Poli [,Var ]) ⇒ lista
Devuelve la lista de los coeficientes de un polinomio Poli con
respecto a la variable Va r.
Poli debe ser una expresión polinómica en Va r . Se recomienda no
omitir Va r a menos que Poli sea una expresión en una variable
sencilla.
Catálogo
>
Desarrolle el polinomio y seleccione x para la Var omitida.
82 Guía de referencia de TI-Nspire™ CAS

polyDegree()
polyDegree(Poli [,Var ]) ⇒ valor
Devuelve el grado de la expresión polinómica Poli con respecto a la
variable Var . Si omite Va r , la función polyDegree() seleccionará
un valor predeterminado de entre las variables contenidas en el
polinomio Poli.
Poli debe ser una expresión polinómica en Va r . Se recomienda no
omitir Va r a menos que Poli sea una expresión en una variable
sencilla.
Catálogo
>
Constantes polinómicas
Es posible extraer el grado aunque no se puedan extraer los
coeficientes. El motivo es que el grado se puede extraer sin
desarrollar el polinomio.
polyEval()
polyEval(Lista1, Expr1) ⇒ expresión
polyEval(Lista1, Lista2) ⇒ expresión
Interpreta el primer argumento como los coeficientes de un polinomio
de grado descendente y devuelve el valor numérico del polinomio
calculado para el segundo argumento.
polyGcd()
polyGcd(Expr1,Expr2) ⇒ expresión
Devuelve el máximo común divisor de los dos argumentos.
Expr1 y Expr2 deben ser expresiones polinómicas.
No se admiten listas, matrices ni argumentos booleanos.
Catálogo
Catálogo
>
>
Guía de referencia de TI-Nspire™ CAS 83

polyQuotient()
polyQuotient(Poli1,Poli2 [,Var ]) ⇒ expresión
Devuelve el cociente del polinomio Poli1 dividido por el polinomio
Poli2 con respecto a la variable especificada Va r .
Poli1 y Poli2 deben ser expresiones polinómicas en Va r . Se
recomienda no omitir Va r a menos que Poli1 y Poli2 sean
expresiones de la misma variable sencilla.
Catálogo
>
polyRemainder()
polyRemainder(Poli1,Poli2 [,Var ]) ⇒ expresión
Devuelve el resto del polinomio Poli1 dividido por el polinom io Poli2
con respecto a la variable especificada Va r .
Poli1 y Poli2 deben ser expresiones polinómicas en Va r . Se
recomienda no omitir Va r a menos que Poli1 y Poli2 sean
expresiones de la misma variable sencilla.
Catálogo
>
84 Guía de referencia de TI-Nspire™ CAS

PowerReg
PowerReg X,Y [, Frec] [, Categoría, Incluir]]
Calcula la regresión potencial y = (a·(x)b) de las listas X e Y con
una frecuencia Frec. El resumen de los resultados se guarda en la
variable stat.results. (Consulte la página 109).
Todas las listas, salvo Incluir, deben tener la misma dimensión.
X e Y son listas que contienen, respectivamente, la variable
independiente y la variable dependiente.
Frec es una lista opcional de valores de frecuencia. Cada elemento
de Frec especifica la frecuencia de ocurrencia de cada punto de datos
en X e Y. El valor predeterminado es 1. Todos los elementos deben
ser enteros | 0.
Categoría es una lista de códigos numéricos de categoría para los
datos de X e Y.
Incluir es una lista de uno o varios códigos de categoría. En el cálculo
sólo se incluyen los elementos de datos cuyo código de categoría se
encuentre en la lista.
Catálogo
>
Vari able de
salida
stat.RegEqn
Descripción
Ecuación de regresión: a·(x)
b
stat.a, stat.b Coeficientes de regresión
stat.r
2
Coeficiente de determinación lineal para los datos transformados
stat.r Coeficiente de correlación para los datos transformados (ln(x), ln(y))
stat.Resid Residuos asociados con el modelo potencial
stat.ResidTrans Residuos asociados con el ajuste lineal de los datos transformados
stat.XReg Lista de puntos de datos en la Lista X modificada utilizada realmente en la regresión basada en
stat.YReg Lista de puntos de datos en la Lista Y modificada utilizada realmente en la regresión basada en las
restricciones de Frec, Lista Categoría e Incluir Categorías
restricciones de Frec, Lista Categoría e Incluir Categorías
stat.FreqReg Lista de frecuencias correspondiente a stat.XReg y stat.YReg
Guía de referencia de TI-Nspire™ CAS 85

Prgm
Prgm
Bloque
EndPrgm
Plantilla para crear una programa definido por el usuario. Debe
utilizarse junto con la orden
LibPriv
.
Bloque puede ser una sentencia sencilla, una serie de sentencias
separadas por el carácter “:”, o una serie de sentencias escritas en
varias líneas.
Nota para introducir el ejemplo: En la aplicación Calculadora
de la unidad portátil, puede introducir definiciones formadas por
Define, Define LibPub o Define
varias líneas si pulsa @ en lugar de · al final de cada línea.
En el teclado del ordenador, mantenga pulsada la tecla Alt y pulse
Enter (Intro).
Catálogo
Calcular el valor de GCD y mostrar resultados intermedios.
>
Product (PI)
product()
product(Lista[, Inicio[, Fin]]) ⇒ expresión
Devuelve el producto de los elementos contenidos en Lista. Inicio y
Fin son opcionales. Permiten especificar un rango de elementos.
product(Matriz1[, Inicio[, Final]]) ⇒ matriz
Devuelve un vector fila que contiene los productos de los elementos
de las columnas de Matriz1. Inicio y Fin son opcionales. Permiten
especificar un rango de elementos.
propFrac()
propFrac(Expr1[, Va r ]) ⇒ expresión
propFrac(número_racional) devuelve número_racional como la
suma de un entero y una fracción que tienen el mismo signo y un
denominador mayor que el numerador.
Consulte Π(), en la página 141.
Catálogo
>
Catálogo
>
86 Guía de referencia de TI-Nspire™ CAS

propFrac()
propFrac(expresión_racional,Var ) devuelve la suma de las
fracciones propias y un polinomio con respecto a Va r . El grado de Va r
del denominador supera el grado de Va r del numerador en cada
fracción propia. Se agrupan potencias similares de Va r . Los términos
y sus factores se ordenan con Va r como variable principal.
Si se omite Va r, se efectúa un desarrollo en fracciones propias con
respecto a la variable más relevante. Los coeficientes de la parte
polinómica se corrigen con respecto a su primera variable más
importante y, así, sucesivamente.
Para expresiones racionales, propFrac() es más rápido pero ofrece
una alternativa más reducida que expand().
Puede utilizar la función propFrac() para representar fracciones
mixtas y demostrar sumas y restas de fracciones mixtas.
Q
Catálogo
>
QR
QR Matriz, qMatriz, rMatriz[,To l]
Calcula la factorización QR de Householder de una matriz real o
compleja. Las matrices resultantes Q y R se almacenan con los
Matrices especificados. La matriz Q es unitaria. La matriz R es una
matriz triangular superior.
Opcionalmente, cualquier elemento de la matriz se trata com o cero si
su valor absoluto es menor que el de To l. Esta tolerancia se utiliza
sólo si la matriz tiene entradas de coma flotante y no contiene
ninguna variable simbólica que no tenga asignado un valor. De lo
contrario se ignorará el valor de To l.
• Si utiliza
•Si el valor de To l se omite o no se utiliza, la tolerancia
/
Approximate (Auto o Aproximado)
· o define el modo Auto or
cálculos se efectuarán utilizando la coma flotante aritmética.
predeterminada se calculará como:
5Eë14 ·max(dim(Matriz)) ·rowNorm(Matriz)
en Aproximado, los
Catálogo
>
El número de coma flotante (9.) en m1 hace que los resultados
se calculen en formato de coma flotante.
Guía de referencia de TI-Nspire™ CAS 87

QR
La factorización QR se calcula numéricamente mediante el uso de
transformaciones de Householder. La solución simbólica se calcula
mediante un proceso de Gram-Schmidt. Las columnas de
NombreMatq son los vectores de base ortonormal que definen el
espacio dado por matriz.
Catálogo
>
QuadReg
QuadReg X,Y [, Frec] [, Categoría, Incluir]]
Calcula la regresión polinómica cuadrática y = a ·x2+b·x+c de las
listas X e Y con una frecuencia Frec. El resumen de los resultados se
guarda en la variable stat.results. (Consulte la página 109).
Todas las listas, salvo Incluir, deben tener la misma dimensión.
X e Y son listas que contienen, respectivamente, la variable
independiente y la variable dependiente.
Frec es una lista opcional de valores de frecuencia. Cada elemento
de Frec especifica la frecuencia de ocurrencia de cada punto de datos
en X e Y. El valor predeterminado es 1. Todos los elementos deben
ser enteros | 0.
Categoría es una lista de códigos numéricos de categoría para los
datos de X e Y.
Incluir es una lista de uno o varios códigos de categoría. En el cálculo
sólo se incluyen los elementos de datos cuyo código de categoría se
encuentre en la lista.
Vari able de
salida
stat.RegEqn
stat.a, stat.b, stat.c Coeficientes de regresión
2
stat.R
stat.Resid Residuos de la regresión
stat.XReg Lista de puntos de datos en la Lista X modificada utilizada realmente en la regresión basada en
stat.YReg Lista de puntos de datos en la Lista Y modificada utilizada realmente en la regresión basada en las
stat.FreqReg Lista de frecuencias correspondiente a stat.XReg y stat.YReg
Descripción
Ecuación de regresión: a·x2+b·x+c
Coeficiente de determinación
restricciones de Frec, Lista Categoría e Incluir Categorías
restricciones de Frec, Lista Categoría e Incluir Categorías
Catálogo
>
88 Guía de referencia de TI-Nspire™ CAS

QuartReg
QuartReg X,Y [, Frec] [, Categoría, Incluir]]
Calcula la regresión polinómica cuártica
4
y = a
·x
+b·x3+c· x2+d·x+e de las listas X e Y para una
frecuencia Frec. El resumen de los resultados se guarda en la variable
stat.results. (Consulte la página 109).
Todas las listas, salvo Incluir, han de tener la misma dimensión.
X e Y son listas que contienen, respectivamente, la variable
independiente y la variable dependiente.
Frec es una lista opcional de valores de frecuencia. Cada elemento
de Frec especifica la frecuencia de ocurrencia de cada punto de datos
en X e Y. El valor predeterminado es 1. Todos los elementos deben
| 0.
ser enteros
Categoría es una lista de códigos numéricos de categoría para los
datos de X e Y.
Incluir es una lista de uno o varios códigos de categoría. En el cálculo
sólo se incluyen los elementos de datos cuyo código de categoría se
encuentre en la lista.
Catálogo
>
Vari able de
salida
stat.RegEqn
stat.a, stat.b, stat.c,
stat.d, stat.e
2
stat.R
stat.Resid Residuos de la regresión
stat.XReg Lista de puntos de datos en la Lista X modificada utilizada realmente en la regresión basada en
stat.YReg Lista de puntos de datos en la Lista Y modificada utilizada realmente en la regresión basada en las
stat.FreqReg Lista de frecuencias correspondiente a stat.XReg y stat.YReg
Descripción
Ecuación de regresión: a·x4+b·x3+c· x2+d·x+e
Coeficientes de regresión
Coeficiente de determinación
restricciones de Frec, Lista Categoría e Incluir Categorías
restricciones de Frec, Lista Categoría e Incluir Categorías
Guía de referencia de TI-Nspire™ CAS 89

R
R4Pq()
R4Pq (Exprx, Expry) ⇒ expresión
R4Pq (Listax, Listay) ⇒ lista
R4Pq (Matrizx, Matrizy) ⇒ matriz
Devuelve la coordenada q equivalente del par de argumentos
(x,y).
Nota: El resultado se muestra como un ángulo en grados, grados
centesimales o radianes, según el modo de ángulo actual.
R4Pr()
R4Pr (Exprx, Expry) ⇒ expresión
R4Pr (Listax, Listay) ⇒ lista
R4Pr (Matrizx, Matrizy) ⇒ matriz
Devuelve la coordenada r equivalente del par de argumentos (x,y).
Catálogo
En el modo de ángulo en grados:
En el modo de ángulo en grados centesimales:
En el modo de ángulo en radianes:
Catálogo
En el modo de ángulo en radianes:
>
>
4
Rad
Expr14Rad ⇒ expresión
Convierte el argumento a radianes.
rand()
rand() ⇒ expresión
rand(númeroPruebas) ⇒ lista
rand() devuelve un valor aleatorio entre 0 y 1.
rand(númeroPruebas) devuelve una lista que contiene
númeroPruebas valores aleatorios entre 0 y 1.
En el modo de ángulo en grados:
En el modo de ángulo en grados centesimales:
Define el número raíz aleatorio.
Catálogo
Catálogo
>
>
90 Guía de referencia de TI-Nspire™ CAS

randBin()
randBin(n, p) ⇒ expresión
randBin(n, p, númeroPruebas) ⇒ lista
randBin(n, p) devuelve un número real aleatorio de una
distribución binomial especificada.
randBin(n, p, númeroPruebas) devuelve una lista que contiene
númeroPruebas números reales aleatorios de una distribución
binomial especificada.
Catálogo
>
randInt()
randInt(Extremoinferior,Extremosuperior) ⇒ expresión
randInt(Extremoinferior,Extremosuperior,númeroPruebas) ⇒
lista
randInt(Extremoinferior,Extremosuperior) devuelve un entero
aleatorio comprendido en el rango especificado por los límites
enteros Extemoinferior y Extremosuperior.
randInt(Extremoinferior,Extremosuperior,númeroPruebas)
devuelve una lista que contiene númeroPruebas enteros aleatorios
comprendidos en el rango especificado.
randMat()
randMat(númeroFilas, númeroColumnas) ⇒ matriz
Devuelve una matriz de números enteros entre -9 y 9 de la dimensión
especificada.
Ambos argumentos deben simplificarse a números enteros.
randNorm()
randNorm(m, s [,númeroPruebas]) ⇒ expresión
Devuelve un número decimal a partir de la distribución normal
especificada. Puede ser cualquier número real, pero estará
concentrado principalmente en el intervalo [mN3·s, m+3·s].
randPoly()
randPoly(Va r , Orden) ⇒ expresión
Devuelve un polinomio en Va r del Orden especificado. Los
coeficientes son número enteros aleatorios comprendidos en el rango
de ë9 a 9. El coeficiente inicial nunca es cero.
Orden debe ser 0–99.
Catálogo
>
Catálogo
>
Nota: Los valores de la matriz cambiarán cada vez que se pulse
·.
Catálogo
>
Catálogo
>
randSamp()
randSamp(Lista,númeroPruebas[,noResp]) ⇒ lista
Devuelve una lista que contiene una muestra aleatoria de
númeroPruebas pruebas procedentes de una Lista con una opción
para muestra con reemplazamiento (noResp=0), o muestra sin
reemplazamiento (noResp=1). El valor predeterminado es sustituir el
ejemplo.
Catálogo
>
Guía de referencia de TI-Nspire™ CAS 91

RandSeed
RandSeed Número
Si Número = 0, define el valor raíz en los ajustes predeterminados de
fábrica para el generador de números aleatorios. Si Número
utiliza para generar dos números raíz, que se almacenan en las
variables del sistema como seed1 y seed2.
ƒ 0, se
Catálogo
>
real()
real(Expr1) ⇒ expresión
Devuelve la parte real del argumento.
Nota: Se considera que todas las variables no definidas son variables
reales. Consulte también imag(), en la página 53.
real(Lista1) ⇒ lista
Devuelve la parte real de todos los elementos.
real(Matriz1) ⇒ matriz
Devuelve la parte real de todos los elementos.
Rect
4
Vec t o r 4Rect
Muestra el Ve ct o r en formato rectangular [x, y, z]. El vector debe ser
bidimensional o tridimensional y ser fila o columna.
Nota: 4Rect es una orden para un formato de presentación, no una
función de conversión. Se puede utilizar sólo al final de una línea de
entrada y no actualiza el valor de ans.
Nota: Consulte también 4Polar, en la página 82.
complexValue 4Rect
Muestra complexValue en formato rectangular a+bi. complexValue
puede tener cualquier formato complejo. Sin embargo, una entrada
i
q
re
generará un error si el modo de ángulo es grados.
Nota: Debe utilizar paréntesis para una entrada polar (rq).
En el modo de ángulo en radianes:
Catálogo
Catálogo
>
>
En el modo de ángulo en grados centesimales:
En el modo de ángulo en grados:
Nota: Para introducir , selecciónelo en la lista de símbolos
del catálogo.
92 Guía de referencia de TI-Nspire™ CAS

ref()
ref(Matriz1[, To l]) ⇒ matriz
Devuelve una forma de fila escalonada de Matriz1.
Opcionalmente, cualquier elemento de matriz se trata como cero si su
valor absoluto es menor que To l. Esta tolerancia se utiliza sólo si la
matriz tiene entradas de coma flotante y no contiene ninguna
variable simbólica que no tenga asignado un valor. De lo contrario se
ignorará el valor de To l.
• Si utiliza
•Si el valor de To l se omite o no se utiliza, la tolerancia
Nota: Consulte también rref(), en la página 96.
/
Approximate (Auto o Aproximado)
cálculos se efectuarán utilizando la coma flotante aritmética.
predeterminada se calculará como:
5Eë14 ·max(dim(Matriz1)) ·rowNorm(Matriz1)
· o define el modo Auto or
en Aproximado, los
Catálogo
>
remain()
remain(Expr1, Expr2) ⇒ expresión
remain(Lista1, Lista2) ⇒ lista
remain(Matriz1, Matriz2) ⇒ matriz
Devuelve el resto del primer argumento con respecto al segundo
argumento, según se define en las identidades:
remain(x,0) x
remain(x,y) xNy·iPart(x/y)
Como consecuencia, observe que remain(Nx,y) Nremain(x,y).
El resultado puede ser cero o tener el mismo signo que el primer
argumento.
Nota: Consulte también mod(), en la página 71.
Return
Return [Expr]
Devuelve Expr como resultado de la función. Se utiliza en un bloque
Func...EndFunc.
Nota: Utilice Return sin argumento en un bloque
Prgm...EndPrgm para salir de un programa.
Nota para introducir el ejemplo: En la aplicación Calculadora
de la unidad portátil, puede introducir definiciones formadas por
varias líneas si pulsa @ en lugar de · al final de cada línea.
En el teclado del ordenador, mantenga pulsada la tecla Alt y pulse
Enter (Intro).
right()
right(Lista1[, Número]) ⇒ lista
Devuelve Número elementos situados a la derecha y contenidos en
Lista1.
Si se omite Número, devuelve todos los de Lista1.
Catálogo
Catálogo
Catálogo
>
>
>
Guía de referencia de TI-Nspire™ CAS 93

right()
right(Cadenaorigen[, Número]) ⇒ cadena
Devuelve Número caracteres situados a la derecha en la cadena de
caracteres Cadenaorigen.
Si se omite Número, devuelve todos los de Cadenaorigen.
right(Comparación) ⇒ expresión
Devuelve el miembro de la derecha de una ecuación o una
desigualdad.
Catálogo
>
root()
root(Expr) ⇒ root
root(Expr1, Expr2) ⇒ raíz
root(Expr) devuelve la raíz cuadrada de Expr.
root(Expr1, Expr2) devuelve la raíz Expr2 de Expr1. Expr1 puede
ser una constante de coma flotante real o compleja, una constante
racional entera o compleja o una expresión simbólica general.
Nota: Consulte también Plantilla de raíz enésima, en la
página 1.
rotate()
rotate(Entero1[,númeroDeRotaciones]) ⇒ entero
Rota los bits de un entero binario. Entero1 se puede introducir en
cualquier base numérica; se convierte automáticamente a un formato
binario con signo de 64 bits. Si el módulo de Entero1 es demasiado
largo para este formato, se utiliza una operación de módulo simétrico
para llevar el valor al rango apropiado.
Si númeroDeRotaciones es positivo, la rotación es hacia la izquierda.
Si númeroDeRotaciones es negativo, la rotación es hacia la derech a.
El valor predeterminado es ë1 (rotar un bit hacia la derecha).
Por ejemplo, en una rotación hacia la derecha:
Cada bit se rota hacia la derecha.
0b00000000000001111010110000110101
El bit situado en el extremo derecho se rota hacia la izquierda.
generando:
0b10000000000000111101011000011010
El resultado se muestra en conformidad con el modo de base.
rotate(Lista1[,númeroDeRotaciones]) ⇒ lista
Devuelve una copia de Lista1 rotada hacia la derecha o la izquierda
tantos elementos como indica númeroDeRotaciones. No altera el
contenido de Lista1.
Si númeroDeRotaciones es positivo, la rotación es hacia la izquierda.
Si númeroDeRotaciones es negativo, la rotación es hacia la derech a.
El valor predeterminado es ë1 (rotar un elemento hacia la derecha).
Catálogo
>
Catálogo
>
En modo base Bin:
Para ver todos los resultados, pulse £ y utilice ¡ y ¢ para
mover el cursor.
En modo base Hex:
Importante: Para introducir un número binario o hexadecimal,
utilice siempre el prefijo 0b o 0h (cero, no la letra O).
En modo base Dec:
94 Guía de referencia de TI-Nspire™ CAS
 Loading...
Loading...