Texas Instruments TI-Nspire CAS Reference Guide [sv]

CAS

Referenshandbok

Denna handbok avser TI-Nspire programvara version 1.4. För att erhålla den senaste versionen av dokumentationen, besök education.ti.com/guides.

Viktigt information

Med undantag för vad som uttryckligen anges i den licens som medföljer ett program lämnar Texas Instruments inga garantier, vare sig uttryckliga eller underförstådda, inklusive garantier avseende säljbarhet eller lämplighet för visst ändamål beträffande något program- eller bokmaterial, och tillhandahåller sådant material "i befintligt skick". Under inga omständigheter skall Texas Instruments hållas ansvarigt för några speciella, indirekta eller tillfälliga skador eller följdskador i samband med inköpet eller användningen av materialet, och Texas Instruments:s enda och uteslutande skadeståndsskyldighet, oberoende av anspråkets form, skall inte överstiga det belopp som anges i licensen för programmet. Inte heller skall Texas Instruments hållas ansvarigt för anspråk av något som helst slag beträffande användningen av materialet av annan part.

Licens

Se den fullständiga licensen som installerats i C:\Program Files\TI Education\TI-Nspire CAS.

Macintosh®, Windows®, Excel®, Vernier EasyLink®, EasyTemp®, Go!®Link, Go!®Motion, och Go!®Temp är varumärken som tillhör sina respektive ägare.

Innehåll

Viktigt information Mallar för uttryck

Mall för Bråk ................................................1

Mall för Exponent ........................................1

Mall för Kvadratrot ......................................1

Mall för N:te rot ........................................... 1

e exponent mall ........................................... 2

Mall för Log ..................................................2

Stegvis mall (2 steg) ..................................... 2

Stegvis mall (N steg) .................................... 2

Mall för System med 2 ekvationer .............. 3

Mall för System med N ekvationer .............3

Mall för Absolutbelopp ...............................3

Mall för dd°mm’ss.ss’’ ..................................3

Matrismall (2 x 2) .........................................3

Matrismall (1 x 2) .........................................4

Matrismall (2 x 1) .........................................4

Matrismall (m x n) ........................................ 4

Mall för Summa (G) ...................................... 4

Mall för Produkt (Π) ....................................4

Mall för Första derivata ...............................5

Mall för N:te derivata ..................................5

Mall för Bestämd integral ........................... 5

Mall för obestämd integral .........................5

Mall för Gränsvärde ..................................... 5

Alfabetisk lista A

abs() ..............................................................6

amortTbl() .................................................... 6

and (och) ......................................................6

angle() ..........................................................7

ANOVA ......................................................... 7

ANOVA2way ................................................ 8

Ans (svar) ....................................................10

approx() ......................................................10

approxRational() ........................................ 10

arcLen() .......................................................10

augment() ................................................... 10

avgRC() ....................................................... 11

bal() .............................................................11

4Base2 ......................................................... 12

4Base10 ....................................................... 12

4Base16 ....................................................... 12

binomCdf() ................................................. 12

binomPdf() ................................................. 13

ceiling() .......................................................13

cFactor() ......................................................13

char() ...........................................................14

charPoly() ....................................................14

2way ........................................................14

Cdf() .........................................................14

GOF ......................................................... 15

Pdf() ........................................................ 15

ClearAZ ....................................................... 15

ClrErr .......................................................... 15

colAugment() ............................................. 16

colDim() ...................................................... 16

colNorm() ................................................... 16

comDenom() .............................................. 16

conj() .......................................................... 17

constructMat() ........................................... 17

CopyVar ...................................................... 17

corrMat() .................................................... 18

4cos ............................................................. 18

cos() ............................................................ 19

cosê() .......................................................... 20

cosh() .......................................................... 20

coshê() ........................................................ 20

cot() ............................................................ 21

cotê() .......................................................... 21

coth() .......................................................... 21

cothê() ........................................................ 22

count() ........................................................ 22

countif() ..................................................... 22

crossP() ....................................................... 23

csc() ............................................................. 23

cscê() ........................................................... 23

csch() ........................................................... 23

cschê() ......................................................... 24

cSolve() ....................................................... 24

CubicReg .................................................... 26

cumSum() ................................................... 26

Cycle ........................................................... 27

4Cylind ........................................................ 27

cZeros() ....................................................... 27

dbd() ........................................................... 29

4DD ............................................................. 29

4Decimal ..................................................... 29

Define (Definiera) ...................................... 30

Define LibPriv ............................................ 30

Define LibPub ............................................ 31

DelVar ........................................................ 31

deSolve() .................................................... 31

det() ............................................................ 33

diag() .......................................................... 33

dim() ........................................................... 33

Disp ............................................................. 34

4DMS ........................................................... 34

dominantTerm() ........................................ 35

dotP() .......................................................... 35

e^() ............................................................. 36

eff() ............................................................. 36

eigVc() ........................................................ 36

eigVl() ......................................................... 37

Else ............................................................. 37

ElseIf ........................................................... 37

EndFor ........................................................ 37

EndFunc ...................................................... 37

iii

EndIf ............................................................37

EndLoop ......................................................37

EndPrgm .....................................................37

EndTry .........................................................37

EndWhile ....................................................38

exact() .........................................................38

Exit ..............................................................38

4exp .............................................................38

exp() ............................................................38

exp4list() ......................................................39

expand() ......................................................39

expr() ...........................................................40

ExpReg ........................................................40

factor() ........................................................41

FCdf() ..........................................................42

Fill ................................................................42

FiveNumSummary ......................................42

floor() ..........................................................43

fMax() .........................................................43

fMin() ..........................................................43

For ...............................................................44

format() ......................................................44

fPart() ..........................................................44

FPdf() ..........................................................44

freqTable4list() ............................................45

frequency() .................................................45

FTest_2Samp ..............................................45

Func .............................................................46

gcd() ............................................................46

geomCdf() ...................................................46

geomPdf() ...................................................47

getDenom() ................................................47

getLangInfo() .............................................47

getMode() ...................................................47

getNum() ....................................................48

getVarInfo() ................................................49

Goto ............................................................49

4Grad ...........................................................50

identity() .....................................................50

If ..................................................................50

ifFn() ............................................................51

imag() ..........................................................51

impDif() .......................................................52

Indirection ..................................................52

inString() .....................................................52

int() .............................................................52

intDiv() ........................................................52

integrate .....................................................52

() .........................................................53

invc

invF() ...........................................................53

invNorm() ....................................................53

invt() ............................................................53

iPart() ..........................................................53

irr() ..............................................................53

isPrime() ......................................................54

Lbl ............................................................... 54

lcm() ............................................................ 54

left() ............................................................ 55

libShortcut() ............................................... 55

limit() eller lim() ......................................... 55

LinRegBx ..................................................... 56

LinRegMx ................................................... 57

LinRegtIntervals ......................................... 57

LinRegtTest ................................................ 59

@List() .......................................................... 59

list4mat() ..................................................... 60

4ln ................................................................ 60

ln() .............................................................. 60

LnReg .......................................................... 60

Local ........................................................... 61

log() ............................................................ 62

4logbase ...................................................... 62

Logistic ....................................................... 63

LogisticD ..................................................... 63

Loop ............................................................ 64

LU ................................................................ 65

mat4list() ..................................................... 65

max() ........................................................... 66

mean() ........................................................ 66

median() ..................................................... 66

MedMed ..................................................... 67

mid() ........................................................... 67

min() ........................................................... 68

mirr() ........................................................... 68

mod() .......................................................... 68

mRow() ....................................................... 69

mRowAdd() ................................................ 69

MultReg ...................................................... 69

MultRegIntervals ....................................... 69

MultRegTests ............................................. 70

nCr() ............................................................ 71

nDeriv() ....................................................... 71

newList() ..................................................... 72

newMat() .................................................... 72

nfMax() ....................................................... 72

nfMin() ....................................................... 72

nInt() ...........................................................72

nom() .......................................................... 73

norm() ......................................................... 73

normalLine() ............................................... 73

normCdf() ................................................... 73

normPdf() ................................................... 74

not .............................................................. 74

nPr() ............................................................ 74

npv() ........................................................... 75

nSolve() ....................................................... 75

OneVar ....................................................... 76

or (eller) ..................................................... 77

ord() ............................................................ 77

P4Rx() .......................................................... 77

P4Ry() ...........................................................78

PassErr .........................................................78

piecewise() ..................................................78

poissCdf() .................................................... 78

poissPdf() ....................................................78

4Polar ..........................................................79

polyCoeffs() ................................................ 79

polyDegree() .............................................. 80

polyEval() .................................................... 80

polyGcd() .................................................... 80

polyQuotient() ........................................... 81

polyRemainder() ........................................ 81

PowerReg ...................................................81

Prgm ...........................................................82

Product (PI) .................................................82

product() ..................................................... 83

propFrac() ................................................... 83

QR ...............................................................84

QuadReg .....................................................84

QuartReg ....................................................85

R4Pq() ..........................................................86

R4Pr() ...........................................................86

4Rad ............................................................. 86

rand() .......................................................... 86

randBin() ..................................................... 87

randInt() ..................................................... 87

randMat() ................................................... 87

randNorm() ................................................. 87

randPoly() ................................................... 87

randSamp() ................................................. 87

RandSeed .................................................... 88

real() ...........................................................88

4Rect ............................................................88

ref() .............................................................89

remain() ......................................................89

Return ......................................................... 89

right() ..........................................................89

root() ...........................................................90

rotate() .......................................................90

round() ........................................................ 91

rowAdd() .................................................... 91

rowDim() .................................................... 91

rowNorm() .................................................. 91

rowSwap() .................................................. 91

rref() ............................................................92

sec() .............................................................92

sec/() ...........................................................92

sech() ...........................................................93

sechê() ......................................................... 93

seq() ............................................................93

series() .........................................................94

setMode() ................................................... 95

shift() ..........................................................96

sign() ...........................................................97

simult() ........................................................97

4sin ..............................................................98

sin() .............................................................98

sinê() ........................................................... 99

sinh() ........................................................... 99

sinhê() ......................................................... 99

SinReg ...................................................... 100

solve() ....................................................... 101

SortA ........................................................ 103

SortD ........................................................ 103

4Sphere ..................................................... 104

sqrt() ......................................................... 104

stat.values ................................................ 105

stat.results ................................................ 105

stDevPop() ................................................ 106

stDevSamp() ............................................. 106

Stop .......................................................... 107

Store ......................................................... 107

string() ...................................................... 107

subMat() ................................................... 107

Sum (Sigma) ............................................. 107

sum() ......................................................... 107

sumIf() ...................................................... 108

system() .................................................... 108

T(transponera) ......................................... 109

tan() .......................................................... 109

tanê() ........................................................ 110

tangentLine() ........................................... 110

tanh() ........................................................ 110

tanhê() ...................................................... 111

taylor() ...................................................... 111

tCdf() ........................................................ 111

tCollect() ................................................... 112

tExpand() .................................................. 112

Then ......................................................... 112

tInterval .................................................... 112

tInterval_2Samp ....................................... 113

tmpCnv() .................................................. 113

@tmpCnv() ................................................ 114

tPdf() ........................................................ 114

trace() ....................................................... 114

Try ............................................................. 115

tTest .......................................................... 115

tTest_2Samp ............................................. 116

tvmFV() ..................................................... 116

tvmI() ........................................................ 117

tvmN() ...................................................... 117

tvmPmt() .................................................. 117

tvmPV() ..................................................... 117

TwoVar ..................................................... 118

unitV() ...................................................... 119

varPop() .................................................... 119

varSamp() ................................................. 119

when() ...................................................... 120

While ........................................................ 120

“With” ...................................................... 120

xor .............................................................121

zeros() .......................................................121

zInterval ....................................................123

zInterval_1Prop ........................................123

zInterval_2Prop ........................................123

zInterval_2Samp .......................................124

zTest ..........................................................124

zTest_1Prop ..............................................125

zTest_2Prop ..............................................125

zTest_2Samp .............................................126

Symboler

+ (addera) .................................................127

N(subtrahera) ............................................127

·(multiplicera) .........................................128

à (dividera) ...............................................128

^ (potens) ..................................................129

(kvadrat) ...............................................130

.+ (punkt addera) .....................................130

.. (punkt subtrahera) ................................130

·(punkt multiplicera) .............................130

. / (punkt dividera) ...................................131

.^ (punkt potens) ......................................131

ë(negation) ...............................................131

% (procent) ..............................................131

= (lika med) ...............................................132

ƒ (inte lika med) .......................................132

< (mindre än) ............................................132

{ (mindre än eller lika med) ....................133

> (större än) ..............................................133

| (större än eller lika med) ......................133

! (fakultet) ................................................133

& (lägg till) ............................................... 133

d() (derivata) ............................................ 134

‰() (integrera) ............................................134

‡() (kvadratrot) ........................................ 135

Π() (produkt) ............................................ 135

G() (summa) .............................................. 136

GInt() ......................................................... 137

GPrn() ........................................................ 137

# (indirection) .......................................... 138

í (grundpotensform) ............................... 138

g (nygrad) ................................................. 138

ô(radian) ................................................... 138

¡ (grader) .................................................. 139

¡, ', '' (grad/minut/sekund) ...................... 139

 (vinkel) .................................................. 139

' (prim) ...................................................... 140

_ (understrykning) ................................... 140

4 (konvertera) ........................................... 140

10^() .......................................................... 141

^ê (inverterat värde) ................................ 141

| (“with”) .................................................. 141

& (lagra) ................................................... 142

:= (tilldela) ................................................ 142

0b, 0h ........................................................ 143

Felkoder och meddelanden Service och garanti för TI-

produkter

TI-Nspire™

Denna handbok beskriver de mallar, funktioner, kommandon och operatorer som är tillgängliga för utvärdering av matematiska uttryck.

CAS Referenshandbok

Mallar för uttryck

Mallar för uttryck erbjuder ett enkelt sätt att mata skriva in uttryck med matematiska standardtecken. När du matar in en mall visas den på inmatningsraden med små block i positioner där du kan skriva in element. En markör visar vilket element du kan skriva in.

Använd piltangenterna eller tryck på

ett värde eller uttryck för det aktuella elementet. Tryck på utvärdera uttrycket.

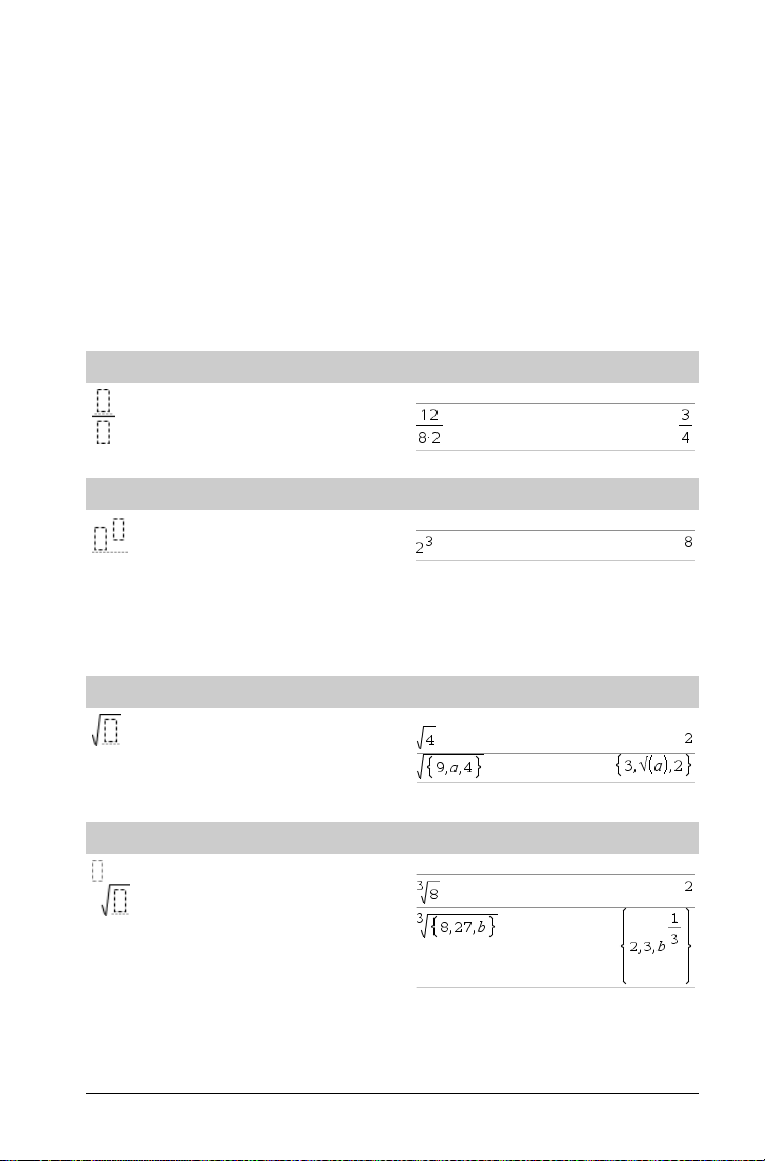
Mall för Bråk

Obs: Se även / (dela) på sidan 128.

e för att flytta till varje elements position, och skriv

· eller /· för att

/p tangenter

Exempel:

Mall för Exponent

Obs: Skriv in det första värdet, tryck på l och skriv sedan in

exponenten. För att återföra markören till basraden, tryck på högerpilen (¢).

Obs: Se även ^ (potens) på sidan 129.

Mall för Kvadratrot

Obs: Se även

Mall för N:te rot

‡

() (kvadratrot) på sidan 135.

Obs: Se även root() på sidan 90.

l tangent

Exempel:

/q tangenter

Exempel:

/l tangenter

Exempel:

TI-Nspire™ CAS Referenshandbok 1

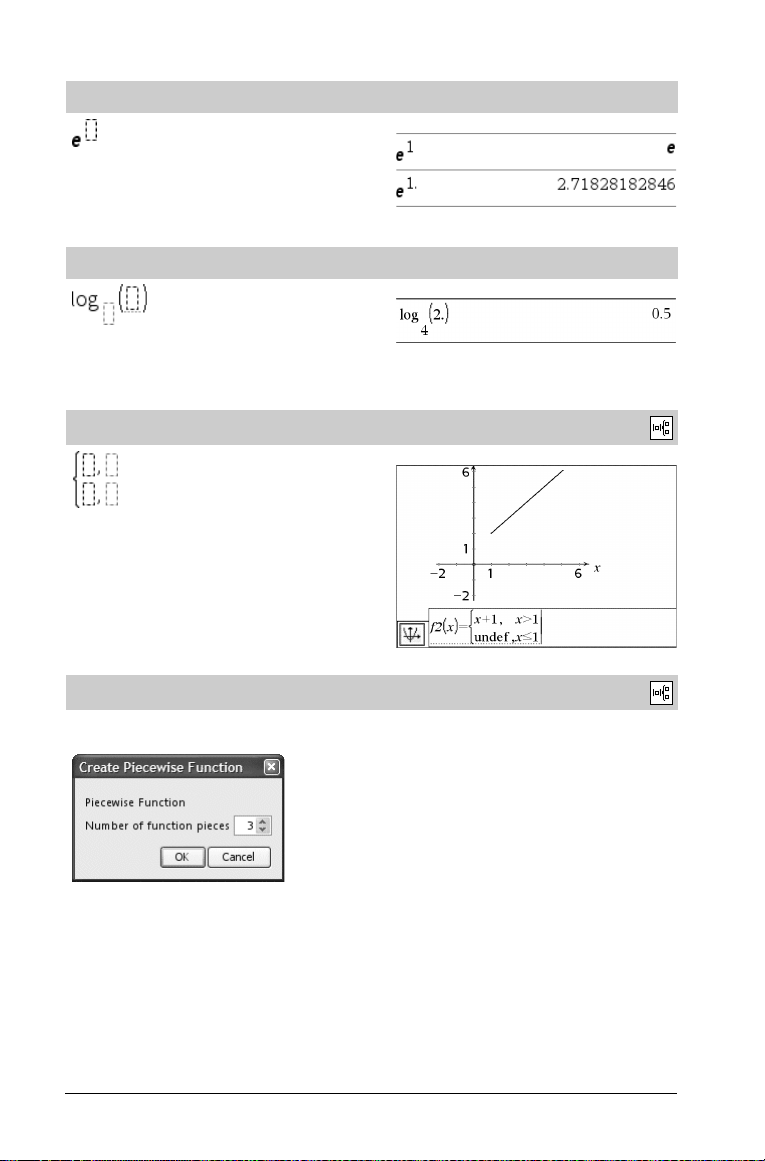
e exponent mall

Basen för den naturliga logaritmen e upphöjd till

Obs: Se även e^() på sidan 36.

u tangenter

Exempel:

Mall för Log

Beräknar logaritmen till en specificerad bas. För en förinställning av bas 10, utelämna basen.

Obs: Se även log() på sidan 62.

Stegvis mall (2 steg)

Låter dig skapa uttryck och villkor för en stegvis funktion med två steg.- För att lägga till ett steg, klicka i mallen och upprepa mallen.

Obs: Se även stegvis() på sidan 78.

Stegvis mall (N steg)

Låter dig skapa uttryck och villkor för en stegvis funktion med N steg.Promptar för N.

Exempel:

Exempel: Se exemplet på Stegvis mall (2 steg).

/s tangent

Katalog >

Obs: Se även stegvis() på sidan 78.

2 TI-Nspire™ CAS Referenshandbok

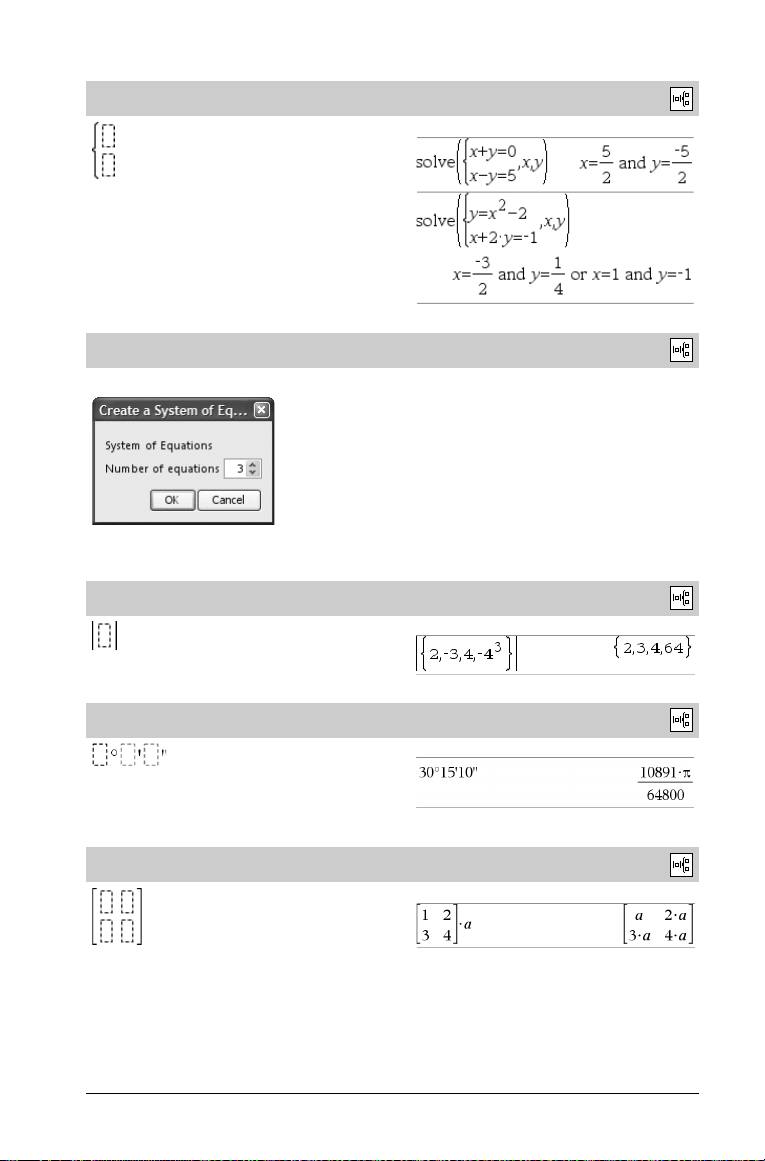
Mall för System med 2 ekvationer

Skapar ett system med två ekvationer. För att lägga till en rad i ett befintligt system, klicka i mallen och upprepa mallen.

Obs: Se även system() på sidan 108.

Katalog >

Exempel:

Mall för System med N ekvationer

Låter dig skapa ett system med N ekvationer. Promptar för N.

Obs: Se även system() på sidan 108.

Mall för Absolutbelopp

Obs: Se även abs() på sidan 6.

Mall för dd°mm’ss.ss’’

Låter dig skriva in vinklar i formatet dd°mm’ss.ss’’, där dd är antalet decimala grader, mm är antalet minuter och ss.ss är antalet sekunder.

Matrismall (2 x 2)

Katalog >

Exempel: Se exemplet på mall för Ekvationssystem (2 ekvationer).

Katalog >

Exempel:

Katalog >

Exempel:

Katalog >

Exempel:

Skapar en 2 x 2-matris.

TI-Nspire™ CAS Referenshandbok 3

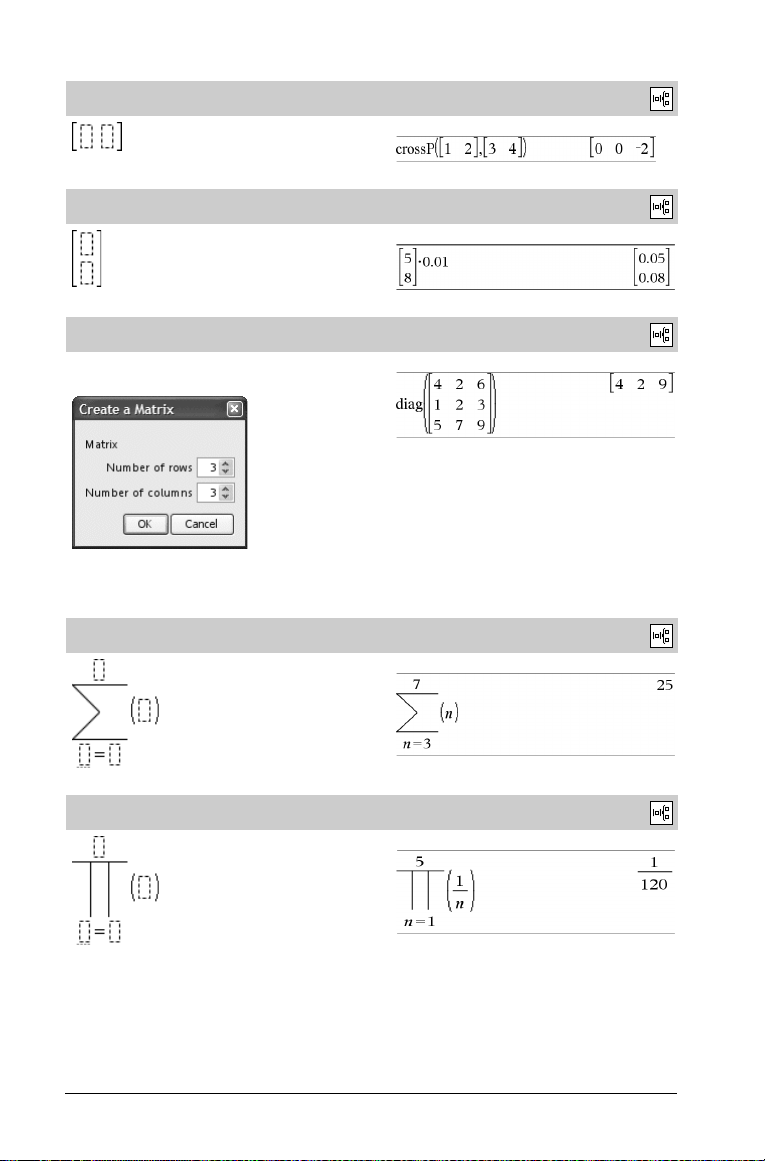
Matrismall (1 x 2)

Katalog >

Exempel:

Matrismall (2 x 1)

Matrismall (m x n)

Mallen visas när du har uppmanats att specificera antalet rader och kolumner.

Obs: Om du skapar en matris med många rader och kolumner kan det ta några sekunder innan den visas.

Mall för Summa (G)

Katalog >

Exempel:

Katalog >

Exempel:

Katalog >

Exempel:

Mall för Produkt (Π)

Exempel:

Obs: Se även Π() (produkt) på sidan 135.

Katalog >

4 TI-Nspire™ CAS Referenshandbok

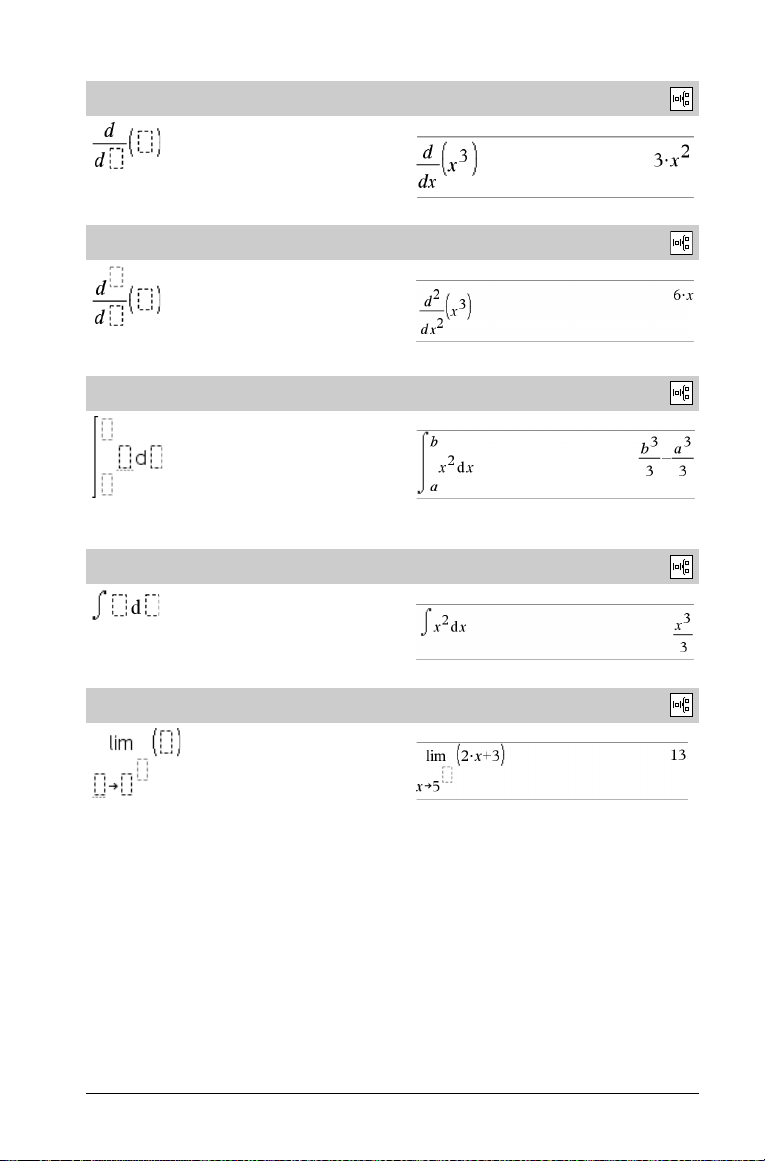
Mall för Första derivata

Katalog >

Exempel:

Obs: Se även

d() (derivata)

på sidan 134.

Mall för N:te derivata

Obs: Se även

d() (derivata)

på sidan 134.

Mall för Bestämd integral

Obs: Se även ‰() integrera() på sidan 134.

Mall för obestämd integral

Obs: Se även ‰() integrera() på sidan 134.

Mall för Gränsvärde

Katalog >

Exempel:

Katalog >

Exempel:

Katalog >

Exempel:

Katalog >

Exempel:

Använd N eller (N) för det vänstra gränsvärdet. Använd + för det högra gränsvärdet.

Obs: Se även gränsvärde() på sidan 55.

TI-Nspire™ CAS Referenshandbok 5

Alfabetisk lista

Poster som inte är alfabetiska (t.ex. +, ! och >) listas i slutet av detta avsnitt och börjar på sidan

127. Om inget annat anges har alla exempel i detta avsnitt utförts i det förinställda återställningsläget och alla variabler betraktas som odefinierade.

abs()

abs(Expr1) ⇒ uttryck abs(

List1) ⇒ lista

abs(Matrix1) ⇒ matris

Ger argumentets absolutbelopp.

Obs: Se även Mall för Absolutbelopp på sidan 3.

Om argumentet är ett komplext tal erhålls talets modul.

Obs: Alla odefinierade variabler behandlas som reella variabler.

amortTbl()

amortTbl(NPmt,N,I,PV, [Pmt], [FV], [PpY], [CpY], [PmtAt],

roundValue]) ⇒ matris

[

Amorteringsfunktion som ger en matris i form av en amorteringstabell för en uppsättning av TVM-argument.

NPmt är antalet inbetalningar som skall inkluderas i tabellen. Tabellen börjar med den första inbetalningen.

N, I, PV, Pmt, FV, PpY, CpY och PmtAt beskrivs i tabellen över TVM-argument, se sidan 117.

• Om du utelämnar Pmt används förinställningen Pmt=tvmPmt(N,I,PV,FV,PpY,CpY,PmtAt).

• Om du utelämnar FV används förinställningen FV=0.

• Förinställningarna av PpY, CpY och PmtAt är desamma som för TVM-funktionerna.

roundValue anger antalet decimaler för avrundning. Förinställning: 2. Kolumnerna i resultatmatrisen har följande ordning:

Inbetalningsnummer, räntebelopp, kapitalbelopp och balans. Balansen som visas på rad n är balansen efter inbetalning n. Du kan använda resultatmatrisen som indata för de andra

amorteringsfunktionerna GInt() och GPrn(), se sidan 137, och

bal(), se sidan 11.

Katalog

and (och)

BooleanExpr1 and BooleanExpr2 ⇒ Booleskt uttryck BooleanList1 and BooleanList2 ⇒ Boolesk lista BooleanMatrix1 and BooleanMatrix2 ⇒ Boolesk matris

Ger resultatet sant eller falskt eller en förenklad form av den ursprungliga inmatningen.

Katalog

6 TI-Nspire™ CAS Referenshandbok

and (och)

Integer1 and Integer2 ⇒ heltal

Jämför två reella heltal bit för bit med en omvandlas båda heltalen till 64-bitars binära tal. När motsvarande bitar jämförs blir resultatet 1 om båda bitarna är 1, annars blir resultatet 0. Det erhållna värdet representerar bitresultatet och visas enligt Bas-läget.

Du kan skriva in heltalen i valfri talbas. För en binär eller hexadecimal inmatning måste du använda prefixet 0b respektive 0h. Utan prefix behandlas heltalen som decimala (bas 10).

Om du skriver in ett decimalt heltal som är alltför stort för att anges i 64-bitars binär form används en symmetrisk moduloberäkning för att få ned värdet till lämplig nivå.

och-operation. Internt

Katalog

I hexadecimalt basläge:

Viktigt: Noll, inte bokstaven O.

I binärt basläge:

I decimalt basläge:

Obs: En binär inmatning kan ha upp till 64 siffror (exklusive

prefixet 0b). En hexadecimal inmatning kan ha upp till 16 siffror.

angle()

angle(Expr1) ⇒ uttryck

Ger argumentets vinkel med argumentet tolkat som ett komplext tal.

Obs: Alla odefinierade variabler behandlas som reella variabler.

vinkel(List1) ⇒ lista vinkel(Matrix1) ⇒ matris

Ger en lista eller matris över vinklarna hos elementen i List1 eller Matrix1, där varje element tolkas som ett komplext tal som

representerar en tvådimensionell rektangulär koordinatpunkt.

ANOVA

ANOVA List1,List2[,List3,...,List20][,Flag]

Utför en 1-vägs variansanalys för att jämföra medelvärdena hos 2 till 20 populationer. En sammanfattning av resultaten visas i variabeln

stat.results. (Se sidan 105.) Flag=0 för Data, Flag=1 för Statistik

I vinkelläget Grader:

I vinkelläget Nygrader:

I vinkelläget Radianer:

Katalog

Resultatvariabel Beskrivning

stat.F Värdet på F-statistiken

stat.PVal Lägsta signifikansnivå vid vilken nollhypotesen kan förkastas

stat.df Frihetsgrader hos grupperna

stat.SS Kvadratsumma hos grupperna

TI-Nspire™ CAS Referenshandbok 7

Resultatvariabel Beskrivning

stat.MS Kvadratmedelvärde hos grupperna

stat.dfError Frihetsgrader hos felen

stat.SSError Kvadratsumma hos felen

stat.MSError Kvadratmedelvärde hos felen

stat.sp Sammanslagen (pooled) standardavvikelse

stat.xbarlist Medelvärdet på listornas indata

stat.CLowerList 95 % konfidensintervall för medelvärdet hos varje indatalista

stat.CUpperList 95 % konfidensintervall för medelvärdet hos varje indatalista

ANOVA2way

ANOVA 2-vägsList1,List2[,List3,…,List20][,LevRow]

Beräknar en 2-vägs variansanalys för att jämföra medelvärdena hos 2 till 20 populationer. En sammanfattning av resultaten visas i variabeln stat.results. (Se sidan 105.)

LevRow=0 för Block

LevRow=2,3,...,Len-1, for Two Factor, where Len=length(List1)=length(List2) = … = length(List10) and Len / LevRow ∈ {2,3,…}

Utdata: Block Design

Resultatvariabel Beskrivning

stat.FF statistik för kolumnfaktorn

stat.PVal Lägsta signifikansnivå vid vilken nollhypotesen kan förkastas

stat.df Frihetsgrader hos kolumnfaktorn

stat.SS Kvadratsumma hos kolumnfaktorn

stat.MS Kvadratmedelvärde hos kolumnfaktorn

Statistik.FBlock F statistik för faktor

stat.PValBlock Lägsta sannolikhet vid vilken nollhypotesen kan förkastas

stat.dfBlock Frihetsgrader hos faktor

stat.SSBlock Kvadratsumma hos faktor

stat.MSBlock Kvadratmedelvärde hos faktor

stat.dfError Frihetsgrader hos felen

stat.SSError Kvadratsumma hos felen

stat.MSError Kvadratmedelvärde hos felen

stat.s Standardavvikelse hos felet

Katalog

8 TI-Nspire™ CAS Referenshandbok

Utdata för KOLUMNFAKTOR

Resultatvariabel Beskrivning

stat.Fcol F statistik för kolumnfaktorn

stat.PValCol Sannolikhetsvärde på kolumnfaktorn

stat.dfCol Frihetsgrader hos kolumnfaktorn

stat.SSCol Kvadratsumma hos kolumnfaktorn

stat.MSCol Kvadratmedelvärde hos kolumnfaktorn

Utdata för RADFAKTOR

Resultatvariabel Beskrivning

stat.FRow F statistik för radfaktorn

stat.PValRow Sannolikhetsvärde på radfaktorn

stat.dfRow Frihetsgrader hos radfaktorn

stat.SSRow Kvadratsumma hos radfaktorn

stat.MSRow Kvadratmedelvärde hos radfaktorn

Utdata för INTERAKTION

Resultatvariabel Beskrivning

stat.FInteract F statistik för interaktionen

stat.PValInteract Sannolikhetsvärde på interaktionen

stat.dfInteract Frihetsgrader hos interaktionen

stat.SSInteract Kvadratsumma hos interaktionen

stat.MSInteract Kvadratmedelvärde hos interaktionen

Utdata för FEL

Resultatvariabel Beskrivning

stat.dfError Frihetsgrader hos felen

stat.SSError Kvadratsumma hos felen

stat.MSError Kvadratmedelvärde hos felen

s Standardavvikelse hos felet

TI-Nspire™ CAS Referenshandbok 9

Ans (svar)

Ans ⇒ värde

Ger resultatet på det senast beräknade uttrycket.

tangenter

approx()

approx(Expr1) ⇒ uttryck

Visar resultatet av beräkningen av argumentet som ett uttryck med decimala värden, när så är möjligt, oavsett den aktuella inställn ingen av Auto eller Ungefärlig .

Detta motsvarar att skriva in argumentet och trycka på

·.

approx(List1) ⇒ lista approx(Matrix1) ⇒ matris

Ger en lista eller matris där varje element har beräknats till ett decimalt värde, när så är möjligt.

approxRational()

approxRational(Expr[, tol]) ⇒ uttryck approxRational(List[, tol]) ⇒ lisa approxRational(Matrix[, tol]) ⇒ matris

Ger argumentet som ett bråk med hjälp av toler ansen hos tol. Om tol utelämnas används en tolerans på 5.E-14.

arcLen()

arcLen(Expr1,Var ,St art,End) ⇒ uttryck

Ger båglängden hos Expr1 från Start till End med hänsyn till variabeln Var .

Båglängden beräknas som en integral baserat på ett definierat funktionsläge.

Katalog

arcLen(List1,Var ,Start,End) ⇒ lista

Ger en lista på båglängden hos varje element i List1 från Start till End med hänsyn till Va r.

augment()

augment(List1, List2) ⇒ lista

Ger en ny lista med List2 inlagd i slutet på List1.

Katalog

10 TI-Nspire™ CAS Referenshandbok

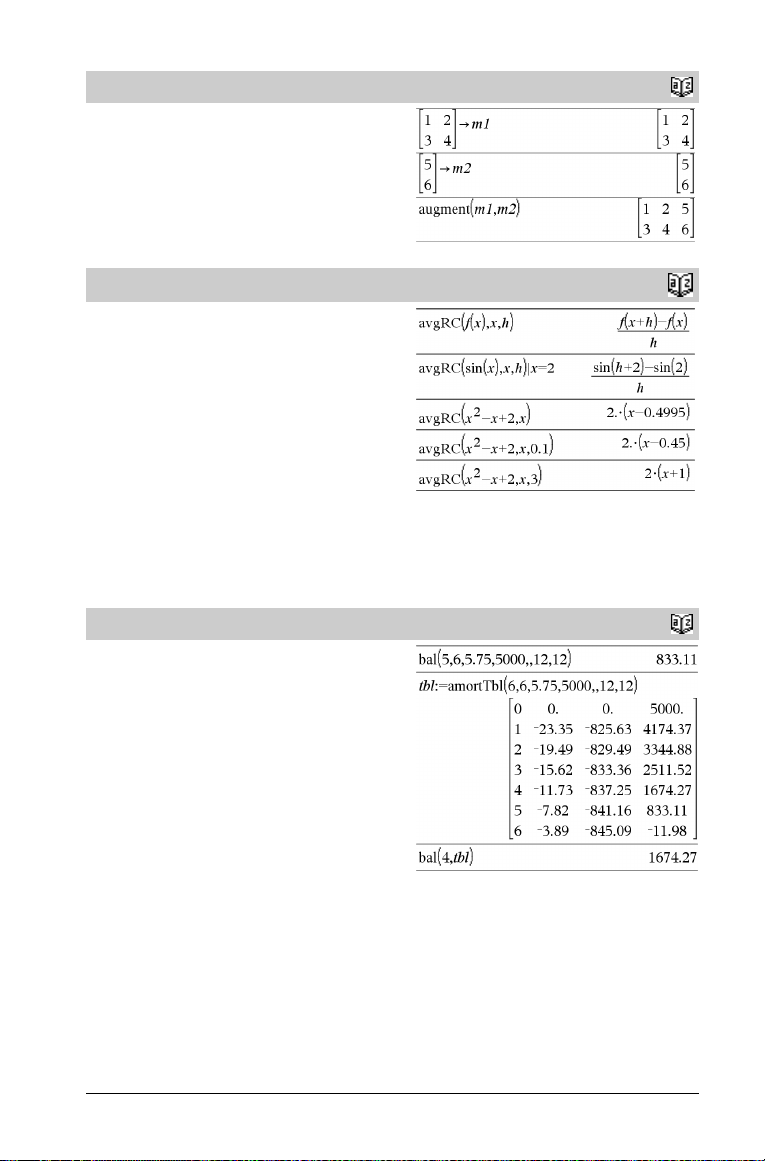
augment()

augment(Matrix1, Matrix2) ⇒ matris

Ger en ny matris med Matrix2 fogad till Matrix1. När kommatecknet (,) används måste matriserna ha samma raddimensioner och Matrix2 fogas till Matrix1 som nya kolumner. Ändrar inte Matrix1 eller Matrix2.

Katalog

avgRC()

avgRC(Expr1, Va r [=värde] [, H]) ⇒ uttryck avgRC(Expr1, Va r [=värde] [, List1]) ⇒ lista avgRC(List1, Va r [=värde] [, H]) ⇒ lista avgRC(Matrix1, Var [=värde] [, H]) ⇒ matris

Ger differenskvoten i positiv riktning. Expr1 kan vara ett användardefinierat funktionsnamn (se Func). När värde specificeras övertar det eventuella tidigare

variabeltilldelningar eller aktuella ersättningar av typ “så att” för variabeln.

H är stegvärdet. Om H uelämnas används förinställningen 0.001. Observera att den liknande funktionen nDeriv() använder den

symmetriska differenskvoten.

bal()

bal(NPmt,N,I,PV,[Pmt], [FV], [PpY], [CpY], [PmtAt],

roundValue]) ⇒ värde

[

bal(NPmt,amortTable) ⇒ värde

Amorteringsfunktion som beräknar planerad balans efter en specificerad inbetalning.

N, I, PV, Pmt, FV, PpY, CpY och PmtAt beskrivs i tabellen över TVM-argument, se sidan 117.

NPmt anger numret på den inbetalning efter vilken du vill att data skall beräknas.

N, I, PV, Pmt, FV, PpY, CpY och PmtAt beskrivs i tabellen över TVM-argument, se sidan 117.

• Om du utelämnar Pmt används förinställningen Pmt=tvmPmt(N,I,PV,FV,PpY,CpY,PmtAt).

• Om du utelämnar FV används förinställningen FV=0.

• Förinställningarna av PpY, CpY och PmtAt är desamma som för TVM-funktionerna.

roundValue anger antalet decimaler för avrundning. Förinställning: 2.

bal(NPmt,amortTable) beräknar lånebalansen efter inbetalning

nummer NPmt, baserat på amorteringstabell amortTable. Argumentet amortTable måste vara en matris i den form som beskrivs under amortTbl() på sidan 6.

Obs: Se även GInt() och GPrn() på sidan137.

Katalog

TI-Nspire™ CAS Referenshandbok 11

Base2

4Base2 ⇒ heltal

Integer1

Omvandlar Integer1 till ett binärt tal. Binära och hexadecimala tal har alltid prefixet 0b respektive 0h.

0b binaryNumber 0h hexadecimalNumber

Noll, inte bokstaven O, följt av b eller h. Ett binärt tal kan ha upp till 64 siffror. Ett h exadecimalt tal kan ha upp

till 16 siffror. Utan prefix behandlas Integer1 som ett decimalt tal (bas 10).

Resultatet visas i binär form, oavsett Bas-läget. Om du skriver in ett decimalt heltal som är alltför stort för att anges i

64-bitars binär form används en symmetrisk moduloberäkning för att få ned värdet till lämplig nivå.

Base10

Integer1 4Base10 ⇒ heltal

Omvandlar Integer1 till ett decimalt tal (bas 10). En binär eller hexadecimal inmatning måste alltid ha prefixet 0b respektive 0h.

0b binaryNumber 0h hexadecimalNumber

Noll, inte bokstaven O, följt av b eller h. Ett binärt tal kan ha upp till 64 siffror. Ett h exadecimalt tal kan ha upp

till 16 siffror. Utan prefix behandlas Integer1 som ett decimalt tal. Resultatet visas

i decimal form, oavsett Bas-läget.

Base16

Integer1 4Base16 ⇒ heltal

Konverterar Integer1 till ett hexadecimalt tal. Binära och hexadecimala tal har alltid prefixet 0b respektive 0h.

0b binaryNumber 0h hexadecimalNumber

Noll, inte bokstaven O, följt av b eller h. Ett binärt tal kan ha upp till 64 siffror. Ett h exadecimalt tal kan ha upp

till 16 siffror. Utan prefix behandlas Integer1 som ett decimalt tal (bas 10).

Resultatet visas i hexadecimal form, oavsett Bas-läget. Om du skriver in ett decimalt heltal som är alltför stort för att anges i

64-bitars binär form används en symmetrisk moduloberäkning för att få ned värdet till lämplig nivå.

Katalog

binomCdf()

binomCdf(n,p,lowBound,upBound) ⇒ tal om lowBound och

upBound är tal, lista om lowBound och upBound är listor

binomCdf(

Beräknar en kumulativ sannolikhet för den diskreta binomialfördelningen med n antal försök och sannolikheten p för att lyckas vid varje försök.

För P(X  upBound), sätt lowBound=0

n,p,upBound) ⇒ tal om upBound är ett tal, lista

upBound är en lista

Katalog

12 TI-Nspire™ CAS Referenshandbok

binomPdf()

binomPdf(n,p) ⇒ tal binomPdf(n,p,XVal) ⇒ tal om XVal är ett tal, lista om XVal

är en lista

Beräknar en sannolikhet för den diskreta binomialfördelni ngen med n antal försök och sannolikheten p för att lyckas vid varje försök.

Katalog

ceiling()

ceiling(Expr1) ⇒ heltal

Ger det närmaste heltal som är ‚ argumentet.

Argumentet kan vara ett reellt eller ett komplext tal.

Obs: Se även floor().

ceiling(List1) ⇒ lista ceiling(Matrix1) ⇒ matris

Ger en lista eller matris över taket för varje element.

cFactor()

cFactor(Expr1[,Var ]) ⇒ uttryck cFactor(List1[,Va r]) ⇒ lista cFactor(Matrix1[,Var ]) ⇒ matris

cFactor(Expr1) ger en faktorisering av Expr1 baserad på uttryckets

alla variabler med en gemensam nämnare. Expr1 faktoriseras så långt det går till linjära, rationella faktorer även

om detta inför nya icke-reella tal. Detta alternativ är lämpligt om du vill ha en faktorisering baserad på mer än en variabel.

cFactor(Expr1,Var ) ger en faktorisering av Expr1 baserad på

variabeln Var . Expr1 faktoriseras så långt det går till faktorer som är linjära i Va r ,

med kanske icke-reella konstanter, även om detta inför irrationella konstanter eller deluttryck som är irrationella i andra variabler.

Faktorerna och deras termer sorteras med Va r som huvudvariabel. Liknande potenser av Va r samlas in i varje faktor. Inkludera Va r om faktorisering baserad på endast denna variabel behövs och du är villig att acceptera irrationella uttryck i andra variabler för att öka faktoriseringen baserad på Va r . Viss tillfällig faktorisering kan ske vad gäller andra variabler.

Med inställningen Auto i läge Auto eller Ungefärlig medger inkludering av Va r också en uppskattning med koefficienter med flytande decimalkomma när irrationella koefficienter inte explicit kan uttryckas kortfattat med termerna i de inbyggda funktionerna. Även med endast en variabel kan inkludering av Va r ge en mer fullständig faktorisering.

Obs: Se även faktor().

Katalog

För att se hela resultatet, tryck på £ och använd sedan ¡ och

¢ för att flytta markören.

TI-Nspire™ CAS Referenshandbok 13

char()

char(Integer) ⇒ tecken

Ger en teckensträng som innehåller tecknet med numret Integer från handenhetens teckenuppsättning. Det giltiga området för Integer är 0–65535.

Katalog

charPoly()

charPoly(squareMatrix,Var) ⇒ polynom charPoly(squareMatrix,Expr) ⇒ polynom charPoly(squareMatrix1,Matrix2) ⇒ polynom

Ger det karakteristiska polynomet för squareMatrix. Det karakteristiska polynomet för n×n matris A, betecknat pA(l), är polynomet definierat av

pA(l) = det(l• I NA)

där I betecknar enhetsmatrisen n×n. squareMatrix1 och squareMatrix2 måste ha samma dimensioner.

2way

2way ObsMatrix

chi22way ObsMatrix

Beräknar ett c2-test för association på 2-vägstabellen öv er antal i den observerade matrisen ObsMatrix. En sammanfattning av resultaten visas i variabeln stat.results. (Se sidan 105.)

Resultatvariabel Beskrivning

stat.c2 Chi-kvadratstatistik: summa (observerad - förväntad)2/förväntad

stat.PVal Lägsta signifikansnivå vid vilken nollhypotesen kan förkastas

stat.df Frihetsgrader hos chi-kvadratstatistiken

stat.ExpMat Matris över förväntad elementräknetabell, baserad på nollhypotesen

stat.CompMat Matris över elementbidrag till chi-kvadratstatistiken

Katalog

Cdf()

Cdf(lowBound,upBound,df) ⇒ tal om lowBound och

upBound är tal, lista om lowBound och upBound är listor

chi2Cdf(

lowBound,upBound,df) ⇒ tal om lowBound och

upBound är tal, lista om lowBound och upBound är listor

Beräknar sannolikheten för c2-fördelning mellan lowBound och upBound för den specificerade frihetsgraden df.

Katalog

För P(X  upBound), sätt lowBound = 0.

14 TI-Nspire™ CAS Referenshandbok

GOF

GOF obsList,expList,df

chi2GOF obsList,expList,df

Utför ett test för att bekräfta att urvalsdata är från en population som följer en specificerad fördelning. obsList är en lista med data och måste innehålla heltal. En sammanfattning av resultaten visas i variabeln stat.results. (Se sidan 105.)

Resultatvariabel Beskrivning

stat.c2 Chi-kvadratstatistik: summa (observerad - förväntad)2/förväntad

stat.PVal Lägsta signifikansnivå vid vilken nollhypotesen kan förkastas

stat.df Frihetsgrader hos chi-kvadratstatistiken

stat.CompList Elementbidrag till chi-kvadratstatistiken

Pdf()

Pdf(XVal,df) ⇒ tal om XVal är ett tal, lista om XVal är en

lista

chi2Pdf(

XVal,df) ⇒ tal om XVal är ett tal, lista om XVal är en

lista

Beräknar värde hos täthetsfunktionen (pdf) för c2-fördelningen vid ett specificerat XVal-värde för den specificerade frihetsgraden df.

Katalog

ClearAZ

Rensar alla variabler som har ett enda tecken i det aktuella problemet.

ClrErr

Rensar felstatusen och ställer in systemvariabeln errCode på noll. Villkoret Else i blocket Try...Else...EndTry bör använda ClrErr

eller PassErr. Om felet skall processas eller ignoreras, använd

ClrErr. Om det är okänt hur felet skall hanteras, an vänd PassErr för

att skicka felet vidare till nästa felhanterare. Om det inte finns någon ytterligare felhanterare för Try...Else...EndTry visas feldialogrutan som normal.

Obs: Se även PassErr på sidan 78 och Try på sidan 115. Anmärkning om inmatningen av exemplet: I

handenhetens applikation Calculator kan du skriva in flerradiga

För ett exempel på ClrErr, se exempel 2 under kommandot Try på sidan 115.

Katalog

definitioner genom att trycka på @ i stället för · i slutet av varje rad. På datorns tangentbord, håll ned Alt och tryck på Enter.

TI-Nspire™ CAS Referenshandbok 15

colAugment()

colAugment(Matrix1, Matrix2) ⇒ matris

Ger en ny matris med Matrix2 fogad till Matrix1. Matriserna måste ha samma kolumndimensioner och Matrix2 fogas till Matrix1 som nya rader. Ändrar inte Matrix1 eller Matrix2.

Katalog

colDim()

colDim(Matrix) ⇒ uttryck

Ger antalet kolumner i Matrix.

Obs: Se även rowDim().

colNorm()

colNorm(Matrix) ⇒ uttryck

Ger maximum av summorna av absolutbeloppen på elementen i kolumnerna i Matrix.

Obs: Odefinierade matriselement är ej tillåtna. Se även rowNorm().

comDenom()

comDenom(Expr1[,Va r]) ⇒ uttryck comDenom(List1[,Var ]) ⇒ lista comDenom(Matrix1[,Var ]) ⇒ matris

comDenom(Expr1) ger en reducerad kvot mellan en fullt

expanderad täljare och en fullt expanderad nämnare.

comDenom(Expr1,Va r) ger en reducerad kvot mellan täljare och

nämnare som expanderats enligt Va r . Termerna och deras faktorer sorteras med Var som huvudvariabel. Liknande potenser av Va r samlas in. Viss tillfällig faktorisering kan ske av de insamlade koefficienterna. Jämfört med att utesluta Va r sparar detta ofta tid, minne och skärmutrymme, vilket gör uttrycket mer begripligt. Det gör också att påföljande operationer på resultatet går snabbare och med mindre risk att minnet tar slut.

Katalog

Om Va r inte förekommer i Expr1 ger comDenom(Expr1,Va r ) en reducerad kvot mellan en oexpanderad täljare och en oexpanderad nämnare. Sådana resultat sparar i regel ännu mer tid, minne och skärmutrymme. Sådana delvis faktoriserade resultat gör också att påföljande operationer på resultatet går mycket snabbare och med mycket mindre risk att minnet tar slut.

16 TI-Nspire™ CAS Referenshandbok

comDenom()

Även om det inte finns någon nämnare är funktionen comden ofta ett snabbt sätt att erhålla en delvis faktorisering om factor() är för långsam eller om den utarmar minnet.

Tips: Mata in denna comden() funktionsdefinition och prova den

rutinmässigt som ett alternativ till

comDenom() och factor().

Katalog

conj()

conj(Expr1) ⇒ uttryck conj(List1) ⇒ lista conj(Matrix1) ⇒ matris

Ger argumentets komplexkonjugat.

Obs: Alla odefinierade variabler behandlas som reella variabler.

constructMat()

constructMat(Expr,Var 1 ,Var 2 ,numRows,numCols)

⇒ matris

Ger en matris baserad på argumenten. Expr är ett uttryck i variablerna Va r 1 och Va r2 . Element i den

resulterande matrisen skapas genom att utvärdera Expr för varje ökat värde på Va r1 och Va r 2 .

Var 1 ökas automatiskt från 1 till och med numRows. Inom varje rad ökas Va r2 från 1 till och med numCols.

CopyVar

CopyVar Var 1 , Va r 2 CopyVar Var 1 ., Var 2 .

CopyVar Var 1 , Va r2 kopierar värdet på variabel Var 1 till variabel

Var 2 , och skapar Va r 2 vid behov. Variabeln Va r1 måste ha ett värde. Om Va r1 är namnet på en befintlig användardefinierad funktion

kopieras definitionen på denna funktion till funktionen Va r 2 . Funktionen Va r1 måste vara definierad.

Var 1 måste uppfylla kraven för namngivning av variabler eller måste vara ett indirection-uttryck som förenklas till ett variabelnamn som uppfyller kraven.

Katalog

TI-Nspire™ CAS Referenshandbok 17

CopyVar

CopyVar Var 1 ., Var 2 . kopierar alla led i variabelgruppen Va r 1 . till

gruppen Var 2 Var 1 . måste vara namnet på en befintlig variabelgrupp, t.ex. den

statistiska stat.nn-resultaten, eller variabler skapade med funktionen

LibShortcut(). Om Var 2 . redan finns ersätter detta kommando alla

led som är gemensamma för båda grupperna och lägger till de led som inte redan finns. Om en enkel variabel (icke-grupp) med namnet Var 2 finns inträffar ett fel.

. och skapar Va r2 . vid behov.

Katalog

corrMat()

corrMat(List1,List2[,…[,List20]])

Beräknar korrelationsmatrisen för den sammanfogade matrisen [List1, List2, ..., List20].

cos

Expr

cos

Representerar Expr i termer av cosinus. Detta är en omvandlingsoperator för visning. Den kan endast användas i sl utet av inmatningsraden.

cos reducerar alla potenser av

sin(...) modulo 1Ncos(...)^2 så att eventuella återstående potenser av cos(...) har exponenter i området (0, 2). Resultatet kommer sålunda att vara fritt från sin(...) om, och endast om, sin(...) finns i det givna uttrycket vid jämna potenser.

Obs: Denna omvandlingsoperator stöds inte i vinkellägena Grader

och Nygrader. Innan du använder den, kontrollera att vinkelläget är inställt på Radianer och att Expr inte innehåller explicita referenser till vinklar i grader eller nygrader.

Katalog

18 TI-Nspire™ CAS Referenshandbok

cos()

cos(Expr1) ⇒ uttryck cos(List1) ⇒ lista

cos(Expr1) ger argumentets cosinus som ett uttryck. cos(List1) ger en lista på cosinus för alla element i List1. Obs: Argumentet tolkas som en vinkel i grader, nygrader eller

radianer enligt det inställda vinkelläget. Du kan använda ó,G eller

ôför att tillfälligt överstyra vinkelläget.

n tangent

I vinkelläget Grader:

I vinkelläget Nygrader:

I vinkelläget Radianer:

cos(squareMatrix1) ⇒ kvadratMatris

Ger matrisen med cosinus för squareMatrix1. Detta är inte detsamma som att beräkna cosinus för varje element.

När en skalär funktion f(A) används på squareMatrix1 (A) beräknas resultatet med algoritmen:

Beräkna egenvärdena (li) och egenvektorerna (Vi) för A.

squareMatrix1 måste vara möjlig att diagonalisera. Den får inte heller ha symboliska variabler som inte har tilldelats ett värde.

Forma matriserna:

Då är A = X B Xêoch f(A) = X f(B) Xê. Exempelvis cos(A) = X cos(B) Xê där:

cos(B) =

Alla beräkningar utförs med flyttalsaritmetik.

I vinkelläget Radianer:

TI-Nspire™ CAS Referenshandbok 19

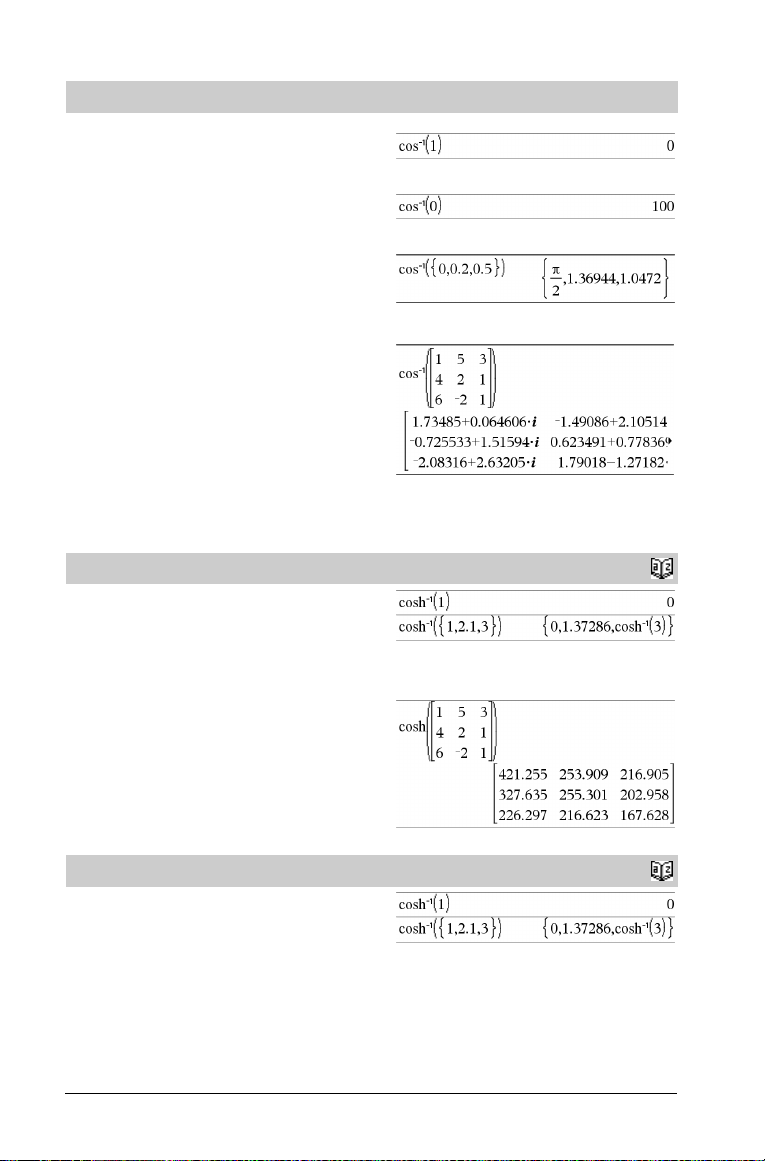
cosê()

cosê(Expr1) ⇒ uttryck cosê(List1) ⇒ lista

/n tangenter

I vinkelläget Grader:

cosê(Expr1) ger den vinkel vars cosinus är Expr1 som ett uttryck.

cosê(List1) ger en lista på invers cosinus för varje element i List1.

Obs: Resultatet erhålls som en vinkel i grader, nygrader eller radianer

beroende på det aktuella vinkelläget.

cosê(squareMatrix1) ⇒ squareMatrix

Ger matrisen med invers cosinus för squareMatrix1. Detta är inte detsamma som att beräkna invers cosinus för varje element. Se cos() för information om beräkningsmetoden.

squareMatrix1 måste vara möjlig att diagonalisera. Resultatet visas alltid i flyttalsform.

cosh()

cosh(Expr1) ⇒ uttryck cosh(List1) ⇒ lista

cosh(Expr1) ger argumentets hyperboliska cosinus som ett uttryck. cosh(List1) ger en lista på hyperbolisk cosinus för varje element i

List1.

cosh(squareMatrix1) ⇒ kvadratMatris

Ger matrisen med hyperbolisk cosinus för squareMatrix1. Detta är inte detsamma som att beräkna hyperbolisk cosinus för varje element. Se cos() för information om beräkningsmetoden.

squareMatrix1 måste vara möjlig att diagonalisera. Resultatet visas alltid i flyttalsform.

I vinkelläget Nygrader:

I vinkelläget Radianer:

I vinkelläget Radianer och i Rektangulärt komplext format:

För att se hela resultatet, tryck på £ och använd sedan ¡ och

¢ för att flytta markören.

Katalog

I vinkelläget Radianer:

coshê()

coshê(Expr1) ⇒ uttryck coshê(List1) ⇒ lista

cosh

(Expr1) ger argumentets inversa hyperboliska cosinus som ett

uttryck.

cosh

(List1) ger en lista på invers hyperbolisk cosinus för varje

element i List1.

Katalog

20 TI-Nspire™ CAS Referenshandbok

coshê()

coshê(squareMatrix1) ⇒ kvadratMatris

Ger matrisen med invers hyperbolisk cosinus för squareMatrix1. Detta är inte detsamma som att beräkna invers hyperbolisk cosinus för varje element. Se

squareMatrix1 måste vara möjlig att diagonalisera. Resultatet visas alltid i flyttalsform.

cos() för information om beräkningsmetoden.

Katalog

I vinkelläget Radianer och i Rektangulärt komplext format:

cot()

cot(Expr1) ⇒ uttryck cot(List1) ⇒ lista

Ger cotangens för Expr1 eller en lista på cotangens för alla element i List1.

Obs: Argumentet tolkas som en vinkel i grader, nygrader eller

radianer enligt det inställda vinkelläget. Du kan använda ó,G ellerôför att tillfälligt överstyra vinkelläget.

cotê()

cotê(Expr1) ⇒ uttryck cotê(List1) ⇒ lista

Ger den vinkel vars cotangens är Expr1 eller en lista på invers cotangens för varje element i List1.

Obs: Resultatet erhålls som en vinkel i grader, nygrader eller radianer

beroende på det aktuella vinkelläget.

För att se hela resultatet, tryck på

¢ för att flytta markören.

I vinkelläget Grader:

I vinkelläget Nygrader:

I vinkelläget Radianer:

I vinkelläget Grader:

I vinkelläget Nygrader:

I vinkelläget Radianer:

£ och använd sedan ¡ och

Katalog

coth()

coth(Expr1) ⇒ uttryck coth(List1) ⇒ lista

Ger hyperbolisk cotangens för Expr1 eller en lista på hyperbolisk cotangens för alla element i List1.

Katalog

TI-Nspire™ CAS Referenshandbok 21

cothê()

cothê(Expr1) ⇒ uttryck cothê(List1) ⇒ lista

Ger den inversa hyperboliska cotangensen för Expr1 eller en lista på invers hyperbolisk cotangens för alla element i List1.

Katalog

count()

count(Val u e 1 or L i s t1 [,Value2orList2 [,...]]) ⇒ värde

Ger det totala ackumulerade antalet element i argumenten som utvärderas till numeriska värden.

Varje argument kan vara ett uttryck, ett värde, en lista eller en matris. Du kan blanda datatyper och använda argument med olika dimensioner.

För en lista, en matris, eller ett område av celler, utvärderas varje element för att bestämma om det skall inkluderas i räkningen.

I applikationen Listor och kalkylblad kan du använda ett område av celler i stället för ett argument.

countif()

countif(List,Criteria) ⇒ värde

Ger det totala ackumulerade antalet element i List som uppfyller specificerade Criteria.

Criteria kan vara:

• Ett värde, ett uttryck eller en sträng. Som exempel räknar 3

endast de element i List som förenklas till värdet 3.

• Ett booleskt uttryck som innehåller symbolen ? fungerar som

platshållare för varje element. Som exempel räknar ?<5 endast de element i List som är lägre än 5.

I applikationen Listor och kalkylblad kan du använda ett område av celler i stället för List.

Obs: Se även sumIf() på sidan 108 och frequency() på sidan 45.

Katalog

I det sista exemplet räknas endast 1/2 och 3+4*i. De återstående argumenten, förutsatt att x är odefinierad, utvärderas inte till numeriska värden.

Katalog

Räknar antalet element som är lika med 3.

Räknar antalet element som är lika med “def.”

Räknar antalet element som är lika med x. I detta exempel förutsätts att variabeln x är odefinierad.

Räknar 1 och 3.

Räknar 3, 5 och 7.

Räknar 1, 3, 7 och 9.

22 TI-Nspire™ CAS Referenshandbok

crossP()

crossP(List1, List2) ⇒ lista

Ger vektorprodukten av List1 och List2 som en lista. List1 och List2 måste ha samma dimension och dimensionen måste

vara antingen 2 eller 3.

crossP(Vector1, Vector2) ⇒ vektor

Ger en rad- eller kolumnvektor (beroende på argumenten) som är vektorprodukten av Vector1 och Vector2.

Både Vector1 och Vector2 måste vara radvektorer eller båda måste vara kolumnvektorer. Båda vektorerna måste ha samma dimension och dimensionen måste vara antingen 2 eller 3.

Katalog

csc()

csc(Expr1) ⇒ uttryck csc(List1) ⇒ lista

Ger cosekanten för Expr1 eller en lista på cosekanten för alla element i List1.

cscê()

cscê(Expr1) ⇒ uttryck cscê(List1) ⇒ lista

Ger den vinkel vars cosekant är Expr1 eller en lista på den inversa cosekanten för varje element i List1.

Obs: Resultatet erhålls som en vinkel i grader, nygrader eller radianer

beroende på det aktuella vinkelläget.

csch()

csch(Expr1) ⇒ uttryck csch(List1) ⇒ lista

Ger den hyperboliska cosekanten för Expr1 eller en lista på den hyperboliska cosekanten för alla element i List1.

I vinkelläget Grader:

I vinkelläget Nygrader:

I vinkelläget Radianer:

I vinkelläget Grader:

I vinkelläget Nygrader:

I vinkelläget Radianer:

Katalog

TI-Nspire™ CAS Referenshandbok 23

cschê()

cschê(Expr1) ⇒ uttryck cschê(List1) ⇒ lista

Ger den inversa hyperboliska cosekanten för Expr1 eller en lista på den inversa hyperboliska cosekanten för alla element i List1.

Katalog

cSolve()

cSolve(Equation, Va r ) ⇒ Booleskt uttryck cSolve(Equation, Va r =G u e s s) ⇒ Booleskt uttryck cSolve(Inequality, Va r ) ⇒ Booleskt uttryck

Ger möjliga komplexa lösningar på en ekvation eller olikhet för Va r. Målet är att producera "kandidater" för alla reella och icke-reella lösningar. Även om Equation är reell medger cSolve() icke-reella resultat i Real Complex Format.

Även om alla odefinierade variabler som inte slutar med ett understrykningstecken (_) behandlas som om de vore reella kan

cSolve() lösa polynomekvationer för komplexa lösningar. cSolve() ställer temporärt in området på komplext under lösningen

även om det aktuella området är reellt. I det komplexa området använder rationella potenser med udda nämnare principaldelen framför den reella delen. Följaktligen är lösningar från solve() på ekvationer som innehåller sådana rationella potenser inte nödvändigtvis deluppsättningar av lösningarna från cSolve().

cSolve() börjar med exakta symboliska metoder. cSolve()

använder om nödvändigt också iterativ ungefärlig komplex polynomfaktoruppdelning.

Obs: Se även cZeros(), solve() och zeros(). Obs: Om Equation är ett icke-polynom med funktioner såsom

abs(), angle(), conj(), real() eller imag() bör du placera ett

understrykningstecken (tryck på /_) i slutet på Va r . Som förinställning behandlas en variabel som ett reellt värde.

Om du använder var_ behandlas variabeln som komplex. Du bör också använda var_ för övriga variabler i Equation som kan

ha icke-reella värden. Annars kan du få oväntade resultat.

Katalog

I läge Display Digits (Visa siffror) för Fix 2:

För att se hela resultatet, tryck på £ och använd sedan ¡ och

¢ för att flytta markören.

z behandlas som reellt:

z_ behandlas som komplext:

24 TI-Nspire™ CAS Referenshandbok

cSolve()

cSolve(Eqn1 and Eqn2 [and …],

VarOrGuess1, VarOrGuess2 [, … ]) ⇒ Booleskt uttryck

cSolve(SystemOfEqns, VarOrGuess1,

VarOrGuess2 [, …]) ⇒ Booleskt uttryck

Ger möjliga komplexa lösningar på ekvationssystem där varje VarOrGuess specificerar en variabel som du vill lösa.

Du kan som alternativ specificera en initial gissning för en variabel. Varje VarOrGuess måste ha formen:

variable

– eller – variable = reellt eller icke-reellt tal

Som exempel är x giltigt och likaså x=3+i. Om alla ekvationer är polynom och om du INTE specificerar några

initiala gissningar använder cSolve() eliminationsmetoden Gröbner/ Buchberger för att försöka bestämma alla komplexa lösningar.

Komplexa lösningar kan innehålla både reella och icke-reella lösningar, som i exemplet till höger.

Ekvationssystem som innehåller polynom kan ha extra variabler som saknar värden, men representerar givna numeriska värden som kan ersättas senare.

Du kan också inkludera lösningsvariabler som inte visas i ekvationerna. Dessa lösningar visar hur familjer av lösningar kan innehålla godtyckliga konstanter med formen ck där k är ett heltalssuffix från 1 till och med 255.

För polynomsystem kan beräkningstiden och användningen av minne i hög grad bero på i vilken ordning du listar lösningsvariabler. Om ditt första val utarmar minnet, eller tar på ditt tålamod, kan du försöka med att arrangera om variablerna i ekvationerna och/eller i listan VarOrGuess.

Om du inte inkluderar några gissningar och om någon ekvation är ett icke-polynom i någon variabel, men alla ekvationer är linjära i alla lösningsvariabler, använder cSolve() Gauss eliminationsmetod för att försöka bestämma alla lösningar.

Katalog

Obs: I följande exempel används ett understrykningstecken

(tryck på /_) så att variablerna behandlas som komple xa.

För att se hela resultatet, tryck på £ och använd sedan ¡ och

¢ för att flytta markören.

För att se hela resultatet, tryck på £ och använd sedan ¡ och

¢ för att flytta markören.

För att se hela resultatet, tryck på £ och använd sedan ¡ och

¢ för att flytta markören.

Om ett system är varken polynomt i alla dess variabler eller linjärt i dess lösningsvariabler bestämmer cSolve() högst en lösning med en ungefärlig iterativ metod. För att göra detta måste antalet lösningsvariabler vara lika med antalet ekvationer och alla övriga variabler i ekvationerna måste förenklas till tal.

TI-Nspire™ CAS Referenshandbok 25

cSolve()

En icke-reell gissning är ofta nödvändig för att bestämma en icke-reell lösning. För konvergens kan en gissning behöva vara ganska nära en lösning.

Katalog

För att se hela resultatet, tryck på £ och använd sedan ¡ och

¢ för att flytta markören.

CubicReg

CubicReg X, Y[, [Freq] [, Category, Include]]

Utför en tredjegrads regressionsanalys y = a·x3+b· x2+c·x+d på listorna X och Y med frekvensen Freq. En sammanfattning av resultaten visas i variabeln stat.results. (Se sidan 105.)

Alla listor utom Include måste ha samma dimensioner.

X och Y är listor på oberoende och beroende variabler. Freq är en frivillig lista på frekvensvärden. Varje element i Freq

specificerar frekvensen för varje motsvarande X- och Y-datapunkt. Det förinställda värdet är 1. Alla element måste vara heltal | 0.

Category är en lista på numeriska kategorikoder för motsvarande Xoch Y-data.

Include är en lista på en eller flera av kategorikoderna. Endast de dataobjekt vars kategorikod är med på listan tas med i beräkningen.

Resultatvariabel Beskrivning

stat.RegEqn

stat.a, stat.b, stat.c, stat.d

stat.R

stat.Resid Residualer från regressionsanalysen

stat.XReg Lista på datapunkter i den modifierade X List som används i regressionen baserat på begränsningar i

stat.YReg Lista på datapunkter i den modifierade Y List som används i regressionen baserat på begränsningar i

stat.FreqReg Lista på frekvenser som motsvarar stat.XReg och stat.YReg

Regressionsekvation: a·x3+b·x2+c·x+d

Regressionskoefficienter

Determinationskoefficient

Freq, Category List och Include Categories

Katalog

cumSum()

cumSum(List1) ⇒ lista

Ger en lista på de kumulativa summorna av elementen i List1 och börjar med element 1.

Katalog

26 TI-Nspire™ CAS Referenshandbok

cumSum()

cumSum(Matrix1) ⇒ matris

Ger en matris över de kumulativa summorna av elementen i Matrix1. Varje element är den kumulativa summan av kolumnen uppifrån och ned.

Katalog

Cycle

Överför omedelbart kontroll till nästa iteration i den aktuella slingan (For, While eller Loop).

Cycle tillåts inte utanför de tre slingstrukturerna (For, While eller Loop).

Anmärkning om inmatningen av exemplet: I

handenhetens applikation Calculator kan du skriva in flerradiga definitioner genom att trycka på @ i stället för · i slutet av

varje rad. På datorns tangentbord, håll ned Alt och tryck på Enter.

Cylind

Vec t o r 4Cylind

Visar rad- eller kolumnvektorn i cylindrisk form [r,q, z].

Vec t o r måste ha exakt tre element. Den kan vara antingen en rad eller en kolumn.

cZeros()

cZeros(Expr, Va r ) ⇒ lista

Ger en lista på möjliga reella och icke-reella värden på Va r som gör Expr=0. cZeros() gör detta genom att beräkna

exp4list(cSolve(Expr=0,Var ),Va r ). Annars är cZeros() lika zeros().

Obs: Se även cSolve(), solve() och zeros().

Obs: Om Expr är ett icke-polynom med funktioner såsom abs(), angle(), conj(), real() eller imag() bör du placera ett

understrykningstecken (tryck på /_) i slutet på Va r . Som förinställning behandlas en variabel som ett reellt värde. Om du

använder var_ behandlas variabeln som komplex. Du bör också använda var_ för övriga variabler i Expr som kan ha

icke-reella värden. Annars kan du få oväntade resultat.

cZeros({Expr1, Expr2 [, … ] },

{

VarOrGuess1,VarOrGuess2 [, … ] }) ⇒ matris

Ger möjliga positioner där uttrycken är noll samtidigt. Varje VarOrGuess specificerar en okänd vars värde du söker.

Katalog

Funktion som listar heltal från 1 till 100 utom 50.

Katalog

I läge Display Digits (Visa siffror) för Fix 3:

För att se hela resultatet, tryck på £ och använd sedan ¡ och

¢ för att flytta markören.

z behandlas som reellt:

z_ behandlas som komplext:

TI-Nspire™ CAS Referenshandbok 27

cZeros()

Du kan som alternativ specificera en initial gissning för en variabel. Varje VarOrGuess måste ha formen:

variable

– eller –

variable = reellt eller icke-reellt tal

Som exempel är x giltigt och likaså x=3+i. Om alla ekvationer är polynom och om du INTE specificerar några

initiala gissningar använder cZeros() eliminationsmetoden Gröbner/ Buchberger för att försöka bestämma alla komplexa nollställen.

Komplexa nollställen kan innehålla både reella och icke-reella nollställen, som i exemplet till höger.

Varje rad i den resulterande matrisen representerar ett alternativt nollställe, med komponenterna ordnade på samma sätt som i listan VarOrGuess. För att extrahera en rad, indexera matrisen med [row].

System av polynom kan ha extra variabler som saknar värden, men representerar givna numeriska värden som kan ersättas senare.

Katalog

Obs: I följande exempel används ett understrykningstecken _

/_) så att variablerna behandlas som

(tryck på komple xa.

Extrahera rad 2:

Du kan också inkludera okända variabler som inte visas i uttrycken. Dessa nollställen visar hur familjer av nollställen kan innehålla godtyckliga konstanter med formen ck, där k är ett he ltalssuffix från 1 till och med 255.

För polynomsystem kan beräkningstiden och användningen av minne i hög grad bero på i vilken ordning du listar okända. Om ditt första val utarmar minnet, eller tar på ditt tålamod, kan du försöka med att arrangera om variablerna i uttrycken och/eller i listan VarOrGuess.

Om du inte inkluderar några gissningar och om något uttryck är ett icke-polynom i någon variabel, men alla uttryck är linjära i alla okända, använder cZeros() Gauss eliminationsmetod för att försöka bestämma alla nollställen.

Om ett system är varken polynomt i alla dess variabler eller linjärt i dess okända bestämmer cZeros() högst ett nollställe med en ungefärlig iterativ metod. För att göra detta måste antalet okända vara lika med antalet uttryck och alla övriga variabler i uttrycken måste förenklas till tal.

28 TI-Nspire™ CAS Referenshandbok

cZeros()

En icke-reell gissning är ofta nödvändig för att bestämma ett ickereellt nollställe. För konvergens kan en gissning behöva vara ganska nära ett nollställe.

Katalog

dbd()

dbd(date1,date2) ⇒ värde

Ger antalet dagar mellan date1 och date2 med dagräkningsmetoden. date1 och date2 kan vara tal eller listor på tal inom den normala

kalendern. Om både date1 och date2 är listor måste de vara lika långa.

date1 och date2 måste vara mellan 1950 och 2049. Du kan mata in datumen i ett av två format. Decimalplaceringen

skiljer sig mellan de två datumformaten. MM.DDYY (format som ofta används i USA)

DDMM.YY (format som ofta används i Europa)

Expr1 4DD ⇒ värde List1 4DD ⇒ lista Matrix1 4DD ⇒ matris

Ger den decimala ekvivalenten till argumentet uttryckt i grader. Argumentet är ett tal, en lista eller en matris som tolkas av vinkelläget i nygrader, radianer eller grader.

4Decimal

Expression1 List1 Matrix1

Visar argumentet i decimal form. Operatorn kan endast användas i slutet av inmatningsraden.

4Decimal

Decimal

⇒ uttryck

I vinkelläget Grader:

I vinkelläget Nygrader:

I vinkelläget Radianer:

Katalog

TI-Nspire™ CAS Referenshandbok 29

Define (Definiera)

Define Var = Uttryck Define Function(Param1, Param2, ...) = Uttryck

Definierar variabeln Va r eller den användardefinierade funktionen Function.

Parametrar såsom Param1 utgör platshållare för att överföra argument till funktionen. När du anropar en användardefinierad funktion måste du ha argument (t.ex. värden eller variabler) som överensstämmer med parametrarna. När funktionen anropas beräknar den Expression med de givna argumenten.

Var och Function får inte vara namnet på en systemvariabel eller inbyggd funktion eller ett kommando.

Obs: Denna form av Define är ekvivalent med att exekvera

uttrycket: expression & Function(Param1,Param2).

Define Function(Param1, Param2, ...) = Func

Block

EndFunc

Program(Param1, Param2, ...) = Prgm

Define

Block

EndPrgm

I denna form kan den användardefinierade funktionen eller programmet exekvera ett block av flera påståenden.

Block kan vara antingen ett enstaka påstående eller en serie av påståenden på separata rader. Block kan även inkludera uttryck och instruktioner (t.ex. If, Then, Else och For).

Anmärkning om inmatningen av exemplet:

I handenhetens applikation Calculator kan du skriva in flerradiga definitioner genom att trycka på @ i stället för · i slutet av

varje rad. På datorns tangentbord, håll ned Alt och tryck på Enter.

Obs: Se även Define LibPriv på sidan 30 och Define LibPub på

sidan 31.

Katalog

Define LibPriv

Define LibPriv Var = Uttryck Define LibPriv Function(Param1, Param2, ...) = Uttryck

Define LibPriv Function(Param1, Param2, ...) = Func

Block

EndFunc Define LibPriv

Block

EndPrgm

Fungerar på samma sätt som Define förutom att en privat biblioteksvariabel, funktion eller program definieras. Privata funktioner och program visas inte i Katalogen.

Obs: Se även Define på sidan 30 och Define LibPub på

sidan 31.

Program(Param1, Param2, ...) = Prgm

Katalog

30 TI-Nspire™ CAS Referenshandbok

Define LibPub

Define LibPub Var = Uttryck Define LibPub Function(Param1, Param2, ...) = Uttryck

Define LibPub Function(Param1, Param2, ...) = Func

Block

EndFunc Define LibPub

Block

EndPrgm

Fungerar på samma sätt som Define förutom att en allmän biblioteksvariabel, funktion eller program definieras. Allmänna funktioner och program visas i Katalogen när biblioteket har sparats och uppdaterats.

Obs: Se även Define på sidan 30 och Define LibPriv på

sidan 30.

Program(Param1, Param2, ...) = Prgm

Katalog

DelVar

DelVar Var 1 [, Va r 2] [, Va r 3 ] ... DelVar

Var .

Tar bort den specificerade variabeln eller variabelgruppen från minnet.

DelVar Var . tar bort alla led i variabelgruppen Var . variabelgrupp

(t.ex. den statistiska stat.nn-resultaten eller variabler skapade med funktionen LibShortcut()). Punkten (.) i denna form av DelVarkommandot begränsar kommandot till borttagning av en

variabelgrupp: den enkla variabeln Va r påverkas inte.

deSolve()

deSolve(1stOr2ndOrderODE, Var , depVar)

⇒ en allmän lösning

Ger en ekvation som explicit eller implicit specificerar en generell lösning på den ordinära differentialekvationen (ODE) av 1:a eller 2:a ordningen. I ODE:

• Använd en primsymbol (tryck på ') för att beteckna

förstaderivatan av den beroende variabeln med avseende på den oberoende variabeln.

• Använd två primsymboler för att beteckna motsvarande andraderivata.

Primsymbolen används endast för derivata inom deSolve(). Använd d() i övriga fall.

Den generella lösningen på en ekvation av 1:a ordningen innehåller en godtycklig konstant med formen ck, där k är ett heltalssuffix från 1 till och med 255. Lösningen på en ekvation av 2:a ordningen innehåller två sådana konstanter.

Katalog

TI-Nspire™ CAS Referenshandbok 31

deSolve()

Använd solve() på en implicit lösning om du vill försöka konvertera den till en eller flera ekvivalenta explicita lösningar.

När du jämför dina resultat med lösningar i läroböcker eller egna lösningar för hand, tänk på att olika metoder inför godtyckliga konstanter på olika ställen i beräkningen, vilket kan ge olika generella lösningar.

deSolve(1stOrderODE and initCond, Var , depVar)

⇒ en partikulärlösning

Ger en partikulärlösning som uppfyller 1stOrderODE och initCond. Detta är vanligen enklare än att bestämma en allmä n lösning, ersätta initiala värden, lösa den godtyckliga konstanten och sedan ersätta värdet i den allmänna lösningen.

initCond är en ekvation med formen: depVar (initialIndependentValue) = initialDependentValue initialIndependentValue och initialDependentValue kan vara

variabler såsom x0 och y0 som saknar lagrade värden. Implicit derivering kan underlätta verifieringen av implicita lösningar.

deSolve(2ndOrderODE and initCond1 and initCond2,

Var , depVar) ⇒ en partikulärlösning

Ger en partikulärlösning som uppfyller 2nd Order ODE och har ett specificerat värde på den beroende variabeln och dess förstaderivata i en punkt.

För initCond1, använd formen: depVar (initialIndependentValue) = initialDependentValue För initCond2, använd formen: depVar (initialIndependentValue) = initial1stDerivativeValue

Katalog

deSolve(2ndOrderODE and bndCond1 and

bndCond2, Var , depVar) ⇒ en partikulärlösning

Ger en partikulärlösning som uppfyller 2ndOrderODE och har specificerade värden i två punkter.

32 TI-Nspire™ CAS Referenshandbok

det()

det(squareMatrix[, Tolerance]) ⇒ uttryck

Ger determinanten för squareMatrix. Alternativt behandlas varje matriselement som noll om dess

absolutvärde är mindre än Tolerance. Denna tolerans används endast om matrisen har inmatning i flyttalsform och inte innehåller några symboliska variabler som inte har tilldelats ett värde. Annars ignoreras Tolerance.

• Om du använder

Approximate

flyttalsaritmetik.

• Om Tolerance utelämnas eller inte används beräknas standardtoleransen som:

5EM14 ·max(dim(squareMatrix))·

rowNorm(squareMatrix)

eller ställer in Auto or

på Approximate utförs beräkningarna med

Katalog

diag()

diag(List) ⇒ matris diag(rowMatrix) ⇒ matris diag(columnMatrix) ⇒ matris

Ger en matris med värdena i argumentlistan eller matrisen i dess huvuddiagonal.

diag(squareMatrix) ⇒ radMatris

Ger en radmatris som innehåller elementen från huvuddiagonalen hos squareMatrix.

squareMatrix måste vara kvadratisk.

dim()

dim(List) ⇒ heltal

Ger dimensionen på List.

dim(Matrix) ⇒ lista

Ger dimensionerna på en matris som en list a med två element {rader, kolumner}.

dim(Strin g) ⇒ heltal

Ger antalet tecken i teckensträngen Stri ng.

Katalog

TI-Nspire™ CAS Referenshandbok 33

Disp

Disp [exprOrString1] [, exprOrString2] ...

Visar argumenten i Calculator-historiken. Argumenten visas i ordningsföljd med utslutning som separatorer.

Huvudsakligen användbart i program och funktioner för att säkerställa visningen av mellanliggande beräkningar.

Anmärkning om inmatningen av exemplet: I

handenhetens applikation Calculator kan du skriva in flerradiga definitioner genom att trycka på @ i stället för · i slutet av

varje rad. På datorns tangentbord, håll ned Alt och tryck på Enter.

DMS

Expr 4DMS List 4DMS Matrix 4DMS

Tolkar argumentet som en vinkel och visar motsvarande DMS-värde (DDDDDD¡MM'SS.ss''). Se ¡, ', '' på sidan 139 för DMS-format (grad,

minuter, sekunder).

Obs: 4DMS konverterar från radianer till grader vid användning i

läget radianer. Om inmatningen följs av en gradsymbol ¡ sker ingen konvertering. Du kan bara använda 4DMS i slutet av en inmatningsrad.

I vinkelläget Grader:

Katalog

34 TI-Nspire™ CAS Referenshandbok

dominantTerm()

dominantTerm(Expr1, Va r [, Point]) ⇒ uttryck dominantTerm(Expr1, Va r [, Point]) | Va r >Point

⇒ uttryck

dominantTerm(Expr1, Va r [, Point]) | Va r <Point

⇒ uttryck

Ger den dominanta termen i en potensserierepresentation av Expr1 expanderat kring Point. Den dominanta termen är den term som snabbast ökar i storlek nära Va r = Point. Den resulterande potensen av (Var N Point) kan ha en negativ och/eller exponent i bråkform.

Koefficienten för denna potens kan inkludera logaritmer av (Va r N Point) och andra funktioner av Va r som domineras av alla potenser av (Var N Point) som har samma exponenttecken.

Point förinställs till 0. Point kan vara ˆ eller Nˆ, varvid den dominanta termen kommer att vara den term som har den största exponenten av Va r snarare än den minsta exponenten av Va r .

dominantTerm(…) ger “dominantTerm(…)” om den inte kan

bestämma en sådan representation, t.ex. för essentiel la singulariteter såsom sin(1/z) vid z=0, e

Om serien eller någon av dess derivator har en språngdiskontinuitet vid Point innehåller resultatet troligen deluttryck i formen sign(…) eller abs(…) för en reell expansionsvariabel, eller (-

floor(…angle(…)…)

med "_". Om du tänker använda den dominanta termen endast för värden på ena sidan av Point, bifoga då till dominantTerm(...) den lämpliga av "| Va r > Point", "| Va r < Point", "| "Va r ‚ Point" eller "Va r  Point" för att erhålla ett enklare resultat.

dominantTerm() fördelas över 1:a-argumentlistor och matriser. dominantTerm() kan användas när du vill veta det enklaste

uttrycket som är asymptotiskt med ett annat uttryck såsom Var " Point. dominantTerm() kan också användas när det inte är uppenbart vilken grad den första icke-nolltermen i en serie kommer att ha, och du inte vill gissa varken iterativt eller interaktivt eller använda en programslinga.

Obs: Se även series() på sidan 94.

N1/z

vid z=0, eller ez vid z = ˆ eller Nˆ.

för en komplex expansionsvariabel, vilken slutar

Katalog

dotP()

dotP(List1, List2) ⇒ uttryck

Katalog

Ger “prick”-produkten av två listor.

dotP(Vector1, Vector2) ⇒ uttryck

Ger “prick”-produkten av två vektorer. Båda måste vara radvektorer eller båda måste vara kolumnvektorer.

TI-Nspire™ CAS Referenshandbok 35

e^()

e^(Expr1) ⇒ uttryck

Ger e upphöjt till potensen Expr1.

Obs: Se även e exponentmall på sidan 2. Obs: Att trycka på u för att visa

tecknet E på tangentbordet.

Du kan skriva in ett komplext tal i den polära formen re dock denna form endast i vinkelläget Radianer: den orsakar ett områdesfel i vinkelläget Grader eller Nygrader.

e^(List1) ⇒ lista

Ger e upphöjt till potensen för varje element i List1.

e^(squareMatrix1) ⇒ kvadratMatris

Ger matrisen med exponenten för squareMatrix1. Detta är inte detsamma som att beräkna e upphöjt till potensen för varje element. Se cos() för information om beräkningsmetoden.

squareMatrix1 måste vara möjlig att diagonalisera. Resultatet visas alltid i flyttalsform.

eff()

eff(nominalRate,CpY) ⇒ värde

Finansiell funktion som konverterar den nominella räntan nominalRate till en årlig effektiv ränta, given av CpY som antalet ränteperioder per år.

nominalRate måste vara ett reellt tal och CpY måste vara ett reellt tal > 0.

Obs: Se även nom() på sidan 73.

eigVc()

eigVc(squareMatrix) ⇒ matris

Ger en matris som innehåller egenvektorerna för en reell eller komplex squareMatrix där varje kolumn i resultatet motsvarar ett egenvärde. Observera att en egenvektor inte är unik: den kan vara skalad med vilken konstant faktor som helst. Egenvektorerna är normaliserade, vilket innebär att om V = [x1, x2, …, xn], så är:

+ … + x

= 1

squareMatrix balanseras först med liknande transformationer tills rad- och kolumnnormerna har så nära samma värde som möjligt. squareMatrix reduceras sedan till övre Hessenberg-form och egenvektorerna beräknas med en Schur-faktorisering.

^( skiljer sig från att trycka på

. Använd

u-tangent

Katalog

I Rektangulärt komplext format:

För att se hela resultatet, tryck på £ och använd sedan ¡ och

¢ för att flytta markören.

36 TI-Nspire™ CAS Referenshandbok

eigVl()

eigVl(squareMatrix) ⇒ lista

Ger en lista på egenvärdena för en reell eller komplex squareMatrix. squareMatrix balanseras först med likhetstransformationer tills rad-

och kolumnnormerna har så nära samma värde som möjligt. squareMatrix reduceras sedan till övre Hessenberg-form och egenvektorerna beräknas från den övre Hessenberg-matrisen.

I läget Rektangulärt komplext format:

För att se hela resultatet, tryck på £ och använd sedan ¡ och

Katalog

¢ för att flytta markören.

Else Se If på sidan50.

ElseIf

If BooleanExpr1 Then

Block1

ElseIf BooleanExpr2 Then

Block2

BlockN

EndIf

Anmärkning om inmatningen av exemplet: I

handenhetens applikation Calculator kan du skriva in flerradiga definitioner genom att trycka på @ i stället för · i slutet av

varje rad. På datorns tangentbord, håll ned Alt och tryck på Enter.

EndFor Se For på sidan44.

EndFunc Se Func på sidan 46.

EndIf Se If på sidan50.

EndLoop Se Loop på sidan 64.

EndPrgm Se Prgm på sidan 82.

Katalog

EndTry Se Try på sidan 115.

TI-Nspire™ CAS Referenshandbok 37

EndWhile Se While på sidan 120.

exact()

exact(Expr1 [, Tolerance]) ⇒ uttryck exact(List1 [, Tolerance]) ⇒ lista exact(Matrix1 [, Tolerance]) ⇒ matris

Använder det aritmetiska läget Exact för att, när så är möjligt, ge argumentet som ett rationellt tal.

Tolerance specificerar konverteringens tolerans: förinställningen är 0 (noll).

Exit

Avslutar det aktuella blocket For, While eller Loop.

Exit tillåts inte utanför de tre slingstrukturerna (For, While eller Loop).

Anmärkning om inmatningen av exemplet: I

handenhetens applikation Calculator kan du skriva in flerradiga definitioner genom att trycka på @ i stället för · i slutet av

varje rad. På datorns tangentbord, håll ned Alt och tryck på Enter.

Funktionslista:

Katalog

exp

Expr

exp

Representerar Expr i termer av basen för den naturliga logaritmen e. Detta är en omvandlingsoperator för visning. Den kan endast användas i slutet av inmatningsraden.

exp()

exp(Expr1) ⇒ uttryck

Ger e upphöjt till potensen Expr1.

Obs: Se även e exponentmall på sidan 2.

Du kan skriva in ett komplext tal i den polära formen re dock denna form endast i vinkelläget Radianer: den orsakar ett områdesfel i vinkelläget Grader eller Nygrader.

. Använd

Katalog

u-tangent

38 TI-Nspire™ CAS Referenshandbok

exp()

exp(List1) ⇒ lista

Ger e upphöjt till potensen för varje element i List1.

exp(squareMatrix1) ⇒ kvadratMatris

Ger matrisen med exponenten för squareMatrix1. Detta är inte detsamma som att beräkna e upphöjt till potensen för varje element. Se

cos() för information om beräkningsmetoden.

squareMatrix1 måste vara möjlig att diagonalisera. Resultatet visas alltid i flyttalsform.

u-tangent

exp4list()

exp4list(Expr,Va r ) ⇒ lista

Undersöker Expr för ekvationer som är separerade med ordet “eller,” och ger en lista med de högra sidorna av ekvationerna med formen Var = E x pr . Detta ger dig en enkel metod att extrahera vissa lösningsvärden i resultaten från funktionerna solve(), cSolve(),

fMin() och fMax().

Obs: exp4list() behövs inte med funktionerna zeros och cZeros() eftersom de direkt ger en lista på lösningsvärden.

expand()

expand(Expr1 [, Va r ]) ⇒ uttryck expand(List1 [,Va r ]) ⇒ lista expand(Matrix1 [,Var ]) ⇒ matris

expand(Expr1) ger Expr1 utvecklat med avseende på alla dess

variabler. Utvecklingen är en polynomutveckling för polynom och partiell bråkutveckling för rationella uttryck.

Målsättningen med expand() är att transformera Expr1 till en summa av och/eller skillnad mellan enkla termer. Som kontrast är målsättningen med factor() att transformera Expr1 till en produkt av och/eller kvot mellan enkla faktorer.

expand(Expr1,Va r) ger Expr1 utvecklat med avseende på Va r.

Liknande potenser av Va r samlas in. Termerna och deras faktorer sorteras med Var som huvudvariabel. Viss tillfällig faktorisering eller utveckling kan ske av de insamlade koefficienterna. Jämfört med att utesluta Va r sparar detta ofta tid, minne och skärmutrymme, vilket gör uttrycket mer begripligt.

Katalog

Även med endast en variabel kan användning av Va r göra den faktorisering av nämnare som används för partialbråks utveckling mer fullständig.

Tips: För rationella uttryck är propFrac() ett snabbare, men mindre extremt alternativ till expand().

Obs: Se även comDenom() för en expanderad täljare över en

expanderad nämnare.

TI-Nspire™ CAS Referenshandbok 39

expand()

expand(Expr1,[Va r]) fördelar också logaritmer och rationella

potenser oberoende av Va r . För ökad fördelning av logaritmer och rationella potenser kan olikhetsbegränsningar vara nödvändiga för att säkerställa att vissa faktorer är naturliga tal.

expand(Expr1, [Va r]) fördelar också absolutvärden, sign() och

exponentialer oberoende av Va r .

Obs: Se även tExpand() för utveckling av trigonometriska utryck.

Katalog

expr()

expr(Stri ng) ⇒ uttryck

Ger teckensträngen i Str ing som ett uttryck och exekverar det omedelbart.

ExpReg

ExpReg X, Y [, [Freq] [, Category, Include]]

Beräknar den exponentiella regressionen y = a·(b)xpå listorna X och Y med frekvensen Freq. En sammanfattning av resultaten visas i variabeln stat.results. (Se sidan 105.)

Alla listor utom Include måste ha samma dimensioner.

X och Y är listor på oberoende och beroende variabler. Freq är en frivillig lista på frekvensvärden. Varje element i Freq

specificerar frekvensen för varje motsvarande X- och Y-datapunkt. Det förinställda värdet är 1. Alla element måste vara heltal | 0.

Category är en lista på numeriska kategorikoder för motsvarande Xoch Y-data.

Include är en lista på en eller flera av kategorikoderna. Endast de dataobjekt vars kategorikod är med på listan tas med i beräkningen.

Resultatvariabel Beskrivning

stat.RegEqn

Regressionsekvation: a·(b)

stat.a, stat.b Regressionskoefficienter

stat.r

Koefficient för linjär bestämning av transformerade data

stat.r Korrelationskoefficient för transformerade data (x, ln(y))

stat.Resid Residualer associerade med den exponentiella modellen

Katalog

40 TI-Nspire™ CAS Referenshandbok

Resultatvariabel Beskrivning

stat.ResidTrans Residualer associerade med linjär anpassning av transformerade data

stat.XReg Lista på datapunkter i den modifierade X List som används i regressionen baserat på begränsningar i

stat.YReg Lista på datapunkter i den modifierade Y List som används i regressionen baserat på begränsningar i

stat.FreqReg Lista på frekvenser som motsvarar stat.XReg och stat.YReg

Freq, Category List och Include Categories

factor()

factor(Expr1[, Va r ]) ⇒ uttryck factor(List1[,Va r ]) ⇒ lista factor(Matrix1[,Var ]) ⇒ matris

factor(Expr1) ger en faktorisering av Expr1 baserad på uttryckets

alla variabler med en gemensam nämnare.

Expr1 faktoriseras så långt det går till linjära, rationella fak torer utan

att införa nya icke-reella deluttryck. Detta alternativ är lämpligt om du vill ha en faktorisering baserad på mer än en variabel.

factor(Expr1,Var ) ger en faktorisering av Expr1 baserad på variabeln Var .

Expr1 faktoriseras så långt det går till reella faktorer som är linjära i Var , även om detta inför irrationella konstanter eller deluttryck som

är irrationella i andra variabler. Faktorerna och deras termer sorteras med Va r som huvudvariabel.

Liknande potenser av Va r samlas in i varje faktor. Inkludera Va r om faktorisering baserad på endast denna variabel behövs och du är villig att acceptera irrationella uttryck i andra variabler för att öka faktoriseringen baserad på Va r . Viss tillfällig faktorisering kan ske vad gäller andra variabler.

Med inställningen Auto i läge Auto or Approximate medger inkludering av Va r en uppskattning med koefficienter i flyttalsform när irrationella koefficienter inte explicit kan uttryckas kortfattat med termerna i de inbyggda funktionerna. Även med endast en variabel kan inkludering av Va r ge en mer fullständig faktorisering.

Obs: Se även comDenom() för ett snabbt sätt att erhålla partiell

faktorisering när factor() inte är snabb nog eller om den utarmar minnet.

Obs: Se även cFactor() för faktorisering hela vägen till komplexa

koefficienter i sökningen efter linjära faktorer.

factor(rationalNumber) ger det rationella talet faktoriserat i

primtal. För sammansatta tal ökar beräkningstiden exponentiel lt med antalet siffror i den näst största faktorn. Som exempel kan faktorisering av ett 30-siffrigt heltal ta mer än en dag och faktorisering av ett 100-siffrigt tal kan ta mer än 100 år.

Obs: För att stoppa (avbryta) en beräkning, tryck på w.

Om du endast vill bestämma om ett tal är ett primtal, använd

isPrime() i stället. Detta går mycket fortare, särskilt om

rationalNumber inte är ett primtal och om den näst största faktorn har mer än fem siffror.

Katalog

TI-Nspire™ CAS Referenshandbok 41

FCdf()

FCdf(lowBound,upBound,dfNumer,dfDenom) ⇒ number om

lowBound och upBound är tal, lista om lowBound och upBound

är listor

FCdf(

lowBound,upBound,dfNumer,dfDenom) ⇒ tal om

lowBound och upBound är tal, lista om lowBound och upBound

är listor

Beräknar sannolikheten för F-fördelning mellan lowBound och upBound för specificerad dfNumer (frihetsgrader) och dfDenom.

För P(X  upBound), sätt lowBound = 0.

Katalog

Fill

Fill Expr, matrixVar ⇒ matris

Ersätter varje element i variabeln matrixVar med Expr. matrixVar måste redan existera.

Fill Expr, listVar ⇒ lista

Ersätter varje element i variabeln listVar med Expr. listVar måste redan existera.

FiveNumSummary

FiveNumSummary X[,[Freq][,Category,Include]]

Ger en förkortad version av envariabelstatistiken för listan X. En sammanfattning av resultaten visas i variabeln stat.results. (Se sidan 105.)

X representerar en lista på aktuella data. Freq är en frivillig lista på frekvensvärden. Varje element i Freq

specificerar frekvensen för varje motsvarande X-värde. Det förinställda värdet är 1. Alla element måste vara heltal | 0.

Category är en lista på numeriska kategorikoder för motsvarande Xvärden.

Include är en lista på en eller flera av kategorikoderna. Endast de dataobjekt vars kategorikod är med på listan tas med i beräkningen.

Resultatvariabel Beskrivning

stat.MinX Minsta x-värde

stat.Q1X Undre kvartil för x

stat.MedianX Median för x

stat.Q3X Övre kvartil för x

stat.MaxX Största x-värde

Katalog

42 TI-Nspire™ CAS Referenshandbok

floor()

floor(Expr1) ⇒ heltal

Ger det största heltal som är { argumentet. Denna funktion är identisk med int().

Argumentet kan vara ett reellt eller ett komplext tal.

floor(List1) ⇒ lista floor(Matrix1) ⇒ matris

Ger en lista eller matris med golvvärden för varje element.

Obs: Se även ceiling() och int().

Katalog

fMax()

fMax(Expr, Var) ⇒ Booleskt uttryck fMax(Expr, Va r,lowBound) fMax(

Expr, Va r,lowBound,upBound)

fMax(

Expr, Va r) | lowBound<Va r <upBound

Ger ett booleskt uttryck som specificerar möjliga värden på Va r som maximerar Expr eller lokaliserar dess lägsta övre gräns.

Du kan använda operatorn “|” för att begränsa lösningsintervallet och/eller specificera andra begränsningar.

Med inställningen Approximate i läge Auto or Approximate söker fMax() iterativt efter ett ungefärligt lokalt maximum. Detta går ofta fortare, särskilt om du använder operatorn “|” för att begränsa sökningen till ett relativt litet intervall som innehåller exakt ett lokalt maximum.

Obs: Se även fMin() och max().

fMin()

fMin(Expr, Var) ⇒ Booleskt uttryck fMin(Expr, Var ,lowBound) fMin(

Expr, Va r,lowBound,upBound)

fMin(

Expr, Va r) | lowBound<Va r <upBound

Ger ett booleskt uttryck som specificerar möjliga värden på Va r som minimerar Expr eller lokaliserar dess största nedre gräns.

Du kan använda operatorn “|” för att begränsa lösningsintervallet och/eller specificera andra begränsningar.

Med inställningen Approximate i läge Auto or Approximate söker fMin() iterativt efter ett ungefärligt lokalt minimum. D etta går ofta fortare, särskilt om du använder operatorn “|” för att begränsa sökningen till ett relativt litet intervall som innehåller exakt ett lokalt minimum.

Obs: Se även fMax() och min().

Katalog

TI-Nspire™ CAS Referenshandbok 43

For

For Var , Low, High [, St ep]

Block

EndFor

Exekverar iterativt påståendena i Block för varje värde på Va r , från Low till High, i steg enligt Step.

Var får inte vara en systemvariabel. Step kan vara positivt eller negativt. Det förinställda värdet är 1. Block kan vara antingen ett enstaka påstående eller en serie av

påståenden separerade med tecknet “:”.

Anmärkning om inmatningen av exemplet: I

handenhetens applikation Calculator kan du skriva in flerradiga definitioner genom att trycka på @ i stället för · i slutet av

varje rad. På datorns tangentbord, håll ned Alt och tryck på Enter.

Katalog

format()

format(Expr[, formatString]) ⇒ sträng

Ger Expr som en teckensträng baserad på formatmallen. Expr måste förenklas till ett tal. formatString är en sträng och måste ha formen: “F[n]”, “S[n]”,

“E[n]”, “G[n][c]”, där [ ] indikerar frivilliga delar. F[n]: Fast format. n är antalet siffror som skall visas efter

decimalpunkten. S[n]: Scientific format (Grundpotensform). n är antalet siffror som

skall visas efter decimalpunkten. E[n]: Engineering format. n är antalet siffror efter den första

signifikanta siffran. Exponenten justeras till en multipel av tre och decimalpunkten flyttas åt höger med noll, en eller två siffror.

G[n][c]: Samma som fast format, men separerar också siffor till vänster om basen i grupper om tre. c specificerar det gruppseparerande tecknet och är förinställt på kommatecken. Om c är en punkt visas basen som ett kommatecken.

[Rc]: Samtliga ovanstående specifikationssymboler kan förses med suffix med Rc-basflaggan, där c är ett enstaka tecken som specificerar vad som skall ersättas för baspunkten.

fPart()

fPart(Expr1) ⇒ uttryck fPart(List1) ⇒ lista fPart(Matrix1) ⇒ matris

Ger argumentets bråkdel. Ger, för en lista eller matris, elementens bråkdelar. Argumentet kan vara ett reellt eller ett komplext tal.

FPdf()

FPdf(XVal,dfNumer,dfDenom) ⇒ tal om XVal är ett tal, lista

XVal är en lista

Beräknar sannolikheten för F-fördelning vid XVal för specificerad dfNumer (frihetsgrader) och dfDenom.

Katalog

44 TI-Nspire™ CAS Referenshandbok

freqTable4list()

freqTable4list(List1,freqIntegerList) ⇒ lista

Ger en lista som innehåller elementen från List1 expanderad enligt frekvenserna i freqIntegerList. Denna funktion kan användas för att skapa en frekvenstabell för applikationen Data & Statistik.

List1 kan vara vilken giltig lista som helst. freqIntegerList måste ha samma dimensioner som List1 och får

endast innehålla icke-negativa heltalselement. Varje element specificerar antalet gånger motsvarande List1-element kommer att upprepas i resultatlistan. Ett värde på noll utesluter motsvarande List1-element.

Katalog

frequency()

frequency(List1,binsList) ⇒ lista

Ger en lista med antalet element i List1. Talen baseras på områden (bins = staplar) som du definierar i binsList.

Om binsList är {b(1), b(2), …, b(n)} är de specificerade områdena {?{b(1), b(1)<?{b(2),…,b(n-1)<?{b(n), b(n)>?}. Den resulterande listan är ett element längre än binsList.

Varje element i resultatet motsvarar antalet element från List1 som är i området för denna stapel. Uttryckt enligt funktionen countIf() är resultatet { countIf(list, ?{b(1)), countIf(list, b(1)<?{b(2)), …, countIf(list, b(n-1)<?{b(n)), countIf(list, b(n)>?)}.

Element i List1 som inte kan “placeras i en stapel” ignoreras. I applikationen Listor och kalkylblad kan du använda ett område av

celler i stället för båda argumenten.

Obs: Se även countIf() på sidan 22.

FTest_2Samp

FTest_2Samp List1,List2[,Freq1[,Freq2[,Hypoth]]]

FTest_2Samp

(Indatalista)

List1,List2[,Freq1[,Freq2[,Hypoth]]]

FTest_2Samp sx1,n1,sx2,n2[,Hypoth]

FTest_2Samp

(Summary stats indata)

Utför ett 2-sampel F test. En sammanfattning av resultaten visas i variabeln stat.results. (Se sidan 105.)

eller Ha: s1 > s2, sätt Hypoth>0 För Ha: s1 ƒ s2 (förinställning), sätt Hypoth =0 För Ha: s1 < s2, sätt Hypoth<0

sx1,n1,sx2,n2[,Hypoth]

Katalog

Förklaring av resultat:

2 element från Datalist är {2.5 4 element från Datalist är >2.5 och {4.5 3 element från Datalist är >4.5

Elementet "hello" är en sträng och kan inte placeras i någon av de definierade staplarna.

Katalog

Resultatvariabel Beskrivning

stat.F

stat.PVal Lägsta signifikansnivå vid vilken nollhypotesen kan förkastas

stat.dfNumer täljare, frihetsgrader = n1-1

stat.dfDenom nämnare, frihetsgrader = n2-1

stat.sx1, stat.sx2 Standardavvikelser hos urvalet i datasekvenserna i List 1 och List 2

Beräknad ó-statistik för datasekvensen

TI-Nspire™ CAS Referenshandbok 45

Resultatvariabel Beskrivning

stat.x1_bar stat.x2_bar

stat.n1, stat.n2 Storlek på urvalen

Medelvärden hos urvalet i datasekvenserna i List 1 och List 2

Func

Block

EndFunc

Mall för att skapa en användardefinierad funktion. Block kan vara ett enstaka påstående, en serie av påståenden

separerade med tecknet “:” eller en serie av påståenden på separata rader. Funktionen kan använda instruktionen Return för att ge ett specifikt resultat.

Anmärkning om inmatningen av exemplet: I

handenhetens applikation Calculator kan du skriva in flerradiga definitioner genom att trycka på @ i stället för · i slutet av

varje rad. På datorns tangentbord, håll ned Alt och tryck på Enter.

gcd()

gcd(Val ue 1, Value2 ) ⇒ uttryck

Ger den största gemensamma delaren för de två argumenten.

gcd för två bråk är gcd för deras täljare dividerat med lcm för deras

nämnare. I läge Auto eller Approximate (Ungefärlig) är gcd 1.0 för bråktal i

flyttalsform.

gcd(List1, List2) ⇒ lista

Ger största gemensamma delare för motsvarande element i List1 och List2.

gcd(Matrix1, Matrix2) ⇒ matris

Ger största gemensamma delare för motsvarande element i Matrix1 och Matrix2.

Definiera en stegvis funktion:

Resultat från plottning av g(x)

Katalog

geomCdf()

geomCdf(p,lowBound,upBound) ⇒ tal om lowBound och

upBound är tal, lista om lowBound och upBound är listor

geomCdf(

p,upBound) ⇒ tal om upBound är ett tal, lista om

upBound är en lista Beräknar en kumulativ geometrisk sannolikhet från lowBound till

upBound med den specificerade sannolikheten p för att lyckas.

För P(X  upBound), sätt lowBound = 1.

Katalog

46 TI-Nspire™ CAS Referenshandbok

geomPdf()

geomPdf(p,XVal) ⇒ tal om XVal är ett tal, lista om XVal är

en lista

Beräknar en sannolikhet vid XVal, vid vilket försök i försöksomgången som man lyckas första gången, för den diskreta geometriska fördelningen med den specificerade sannolikheten p för att lyckas.

Katalog

getDenom( )

getDenom(Expr1) ⇒ uttryck

Transformerar argumentet till ett uttryck med reducerad gemensam nämnare och ger sedan dess nämnare.

getLangInfo( )

getLangInfo() ⇒ sträng

Ger en sträng som motsvarar det korta namnet på det aktuella aktiva språket. Du kan exempelvis använda den i ett program eller i en funktion för att bestämma det aktuella språket.

Engelska = "en" Danska = "da" Tyska = "de" Finska = "fi" Franska = "fr" Italienska = "it" Holländska = "nl" Belgisk holländska = "nl_BE" Norska = "no" Portugisiska = "pt" Spanska = "es" Svenska = "sv"

getMode()

getMode(ModeNameInteger) ⇒ värde getMode(0) ⇒ lista

getMode(ModeNameInteger) ger ett värde som representerar den

aktuella lägesinställningen för ModeNameInteger.

getMode(0) ger en lista på talpar. Varje par består av ett

lägesheltal och ett inställningsheltal. Se nedan för en lista på lägen och deras inställningar.

Om du sparar inställningarna med getMode(0) & var kan du använda setMode(var) i en funktion eller ett program för att temporärt återställa inställningarna endast inom exekveringen av funktionen eller programmet. Se setMode() på sidan 95.

Katalog

TI-Nspire™ CAS Referenshandbok 47

Lägets namn

Display Digits (Antal siffror)

Angle (Vinkel)

Exponential Format (Exponentiellt format)

Real or Complex (Reellt eller Komplext)

Auto or Approx. (Auto eller Ungefärlig)

Vector Format (Vektorformat)

Base (Bas)

Unit System (Enhetssystem)

Lägesheltal Heltal för inställningar

=Float, 2=Float1, 3=Float2, 4=Float3, 5=Float4, 6=Float5, 7=Float6, 8=Float7,

9=Float8, 10=Float9, 11=Float10, 12=Float11, 13=Float12, 14=Fix0, 15=Fix1, 16=Fix2, 17=Fix3, 18=Fix4, 19=Fix5, 20=Fix6, 21=Fix7, 22=Fix8, 23=Fix9, 24=Fix10, 25=Fix11, 26=Fix12

=Radian, 2=Degree, 3=Gradian

=Normal, 2=Scientific, 3=Engineering

=Real, 2=Rectangular, 3=Polar

=Auto, 2=Approximate, 3=Exact

=Rectangular, 2=Cylindrical, 3=Spherical

=Decimal, 2=Hex, 3=Binary

=SI, 2=Eng/US

getNum()

getNum(Expr1) ⇒ uttryck

Transformerar argumentet till ett uttryck med reducerad gemensam nämnare och ger sedan dess täljare.

Katalog

48 TI-Nspire™ CAS Referenshandbok

getVarInfo()

getVarInfo() ⇒ matris eller sträng getVarInfo(LibNameString) ⇒ matris eller sträng

getVarInfo() ger en matris med information (variabelnamn, typ

och åtkomlighet till bibliotek) för alla variabler och biblioteksobjekt som är definierade i det aktuella problemet.

Om inga variabler är definierade ger "NONE".

getVarInfo(LibNameString) ger en matris med information för

alla biblioteksobjekt som är definierade i bibliotek et LibNameString. LibNameString måste vara en sträng (text omsluten med

citationstecken) eller en strängvariabel.

getVarInfo() strängen

Om biblioteket LibNameString inte finns uppstår ett fel.

Se exemplet till vänster där resultatet av getVarInfo() tilldelas variabeln vs. Ett försök att visa rad 2 eller rad 3 av vs ger ett “Ogiltig lista eller matris”-fel eftersom minst ett av elementen i dessa rader (t.ex. variabel b) omvärderas till en matris.

Detta fel kan också inträffa när Ans används för att utvärdera ett

getVarInfo()-resultat på nytt.

Systemet ger ovanstående fel eftersom den aktuella versionen av programvaran inte stöder en generaliserad matrisstruktur där ett element i en matris kan vara antingen en matris eller en lista.

Katalog

Goto

Goto labelName

Katalog

Överför kontroll till etiketten labelName. labelName måste definieras i samma funktion med en Lbl-

instruktion.

Anmärkning om inmatningen av exemplet: I

handenhetens applikation Calculator kan du skriva in flerradiga definitioner genom att trycka på @ i stället för · i slutet av

varje rad. På datorns tangentbord, håll ned Alt och tryck på Enter.

TI-Nspire™ CAS Referenshandbok 49

Grad

4 Grad ⇒ uttryck

Expr1

Konverterar Expr1 till en vinkelmätning i nygrader.

I vinkelläget Grader:

I vinkelläget Radianer:

Katalog

identity()

identity(Integer) ⇒ matris

Ger enhetsmatrisen med ett mått på Integer (Heltal). Integer måste vara positivt heltal.

If BooleanExpr Statement If BooleanExpr Then

Block

EndIf

If BooleanExpr utvärderar till sant och exekverar sedan det enstaka påståendet Statement eller blocket av påståenden Block innan exekveringen fortsätter.

If BooleanExpr utvärderar till falskt och fortsätter exekveringen utan att exekvera påståendet eller blocket av påståenden.

Block kan vara antingen ett enstaka påstående eller en serie av påståenden separerade med tecknet “:”.

Anmärkning om inmatningen av exemplet: I

handenhetens applikation Calculator kan du skriva in flerradiga definitioner genom att trycka på @ i stället för · i slutet av

varje rad. På datorns tangentbord, håll ned Alt och tryck på Enter.

If BooleanExpr Then

Block1

Else

Block2

EndIf

If BooleanExpr utvärderar till sant, exekverar Block1 och hoppar sedan över Block2.

If BooleanExpr utvärderar till falskt, hoppar över Block1 och exekverar Block2.

Block1 och Block2 kan vara enstaka påståenden.

Katalog

50 TI-Nspire™ CAS Referenshandbok

If BooleanExpr1 Then

Block1

ElseIf

BooleanExpr2 Then

Block2

BooleanExprN Then

BlockN

EndIf

Medger förgrening. If BooleanExpr1 utvärderar till sant och exekverar Block1. If BooleanExpr1 utvärderar till falskt, utvärderar BooleanExpr2, etc.

Katalog

ifFn()

ifFn(BooleanExpr,Val u e _ If _ t r ue [,Value_If_false [,

Value_If_unknown]]) ⇒ uttryck, lista eller matris

Utvärderar det booleska uttrycket BooleanExpr (eller varje element från BooleanExpr) och producerar ett resultat baserat på följande regler:

• BooleanExpr kan testa ett enstaka värde, en lista eller en matris.

• Om ett element i BooleanExpr utvärderas som sant erhålls motsvarande element från Value_If_true.

• Om ett element i BooleanExpr utvärderas som falskt erhålls motsvarande element från Value_If_false. Om du utelämnar Value_If_false erhålls undef.

• Om ett element i BooleanExpr är varken sant eller falskt erhålls motsvarande element från Value_If_unknown. Om du utelämnar Value_If_unknown erhålls undef.

• Om det andra, tredje eller fjärde argumentet i funktionen ifFn() är ett enstaka uttryck tillämpas det booleska testet på varje position i BooleanExpr.

Obs: Om det förenklade påståendet BooleanExpr inbegriper en lista

eller matris måste alla övriga list- eller matrisargument ha samma dimensioner, och resultatet får då samma dimensioner.

imag()

imag(Expr1) ⇒ uttryck

Ger argumentets imaginärdel.

Obs: Alla odefinierade variabler behandlas som reella variabler. Se

även real() på sidan 88

Katalog

Testvärdet på 1 är mindre än 2.5, varför dess motsvarande Value_If_True element 5 kopieras till resultatlistan.

Testvärdet på 2 är mindre än 2.5, varför dess motsvarande Value_If_True element 6 kopieras till resultatlistan.

Testvärdet på 3 är inte mindre än 2.5, varför dess motsvarande

Value_If_False element 10 kopieras till resultatlistan.

Value_If_true är ett enstaka värde och motsvarar varje vald

position.

Value_If_false är ej specificerat. Undef används.

Ett valt element från Value_If_true. Ett valt element från Value_If_unknown.

Katalog

imag(List1) ⇒ lista

Ger en lista på elementens imaginärdelar.

TI-Nspire™ CAS Referenshandbok 51

imag()

imag(Matrix1) ⇒ matris

Ger en matris på elementens imaginärdelar.

Katalog

impDif()

impDif(Equation, Var , dependVar[,Ord])

⇒ uttryck

där ordern Ord förinställs på 1. Beräknar den implicita derivatan för ekvationer i vilka en variabel är

implicit definierad med termer från en annan.

Indirection Se

inString()

inString(srcString, subString[, Start]) ⇒ heltal

Ger teckenpositionen i strängen srcString där den första förekomsten av strängen subString börjar.

Start, om inkluderad, specificerar teckenpositionen inom srcString där sökningen börjar. Förinställning = 1 (det första tecknet i srcString).

Återgår till noll om srcString inte innehåller subString eller om Start är > längden på srcString.

int()

int(Expr) ⇒ heltal int(List1) ⇒ lista int(Matrix1) ⇒ matris

Ger det största heltalet som är mindre än eller lika med argumentet. Denna funktion är identisk med floor().

Argumentet kan vara ett reellt eller ett komplext tal. Ger, för en lista eller matris, det största heltalet för varje element.

Katalog

på sidan 138.

#()

Katalog

intDiv()

intDiv(Number1, Number2) ⇒ heltal intDiv(List1, List2) ⇒ lista intDiv(Matrix1, Matrix2) ⇒ matris

Katalog

Ger heltalsdelen av (Number1 ÷ Number2). Ger, för listor och matriser, heltalsdelen av

(argument 1 ÷ argument 2) för varje elementpar.

integrate

på sidan 134.

‰()

52 TI-Nspire™ CAS Referenshandbok

invc2()

invc2(Area,df)

Area,df)

invChi2(

Beräknar den inversa kumulativa sannolikhetsfunktionen c2 (chikvadrat) specificerad av frihetsgraden df för en given Area under kurvan.

Katalog

invF()

invF(Area,dfNumer,dfDenom)

Area,dfNumer,dfDenom)

invF(

Beräknar den inversa kumulativa fördelningsfunktionen F specificerad av dfNumer och dfDenom för en given Area under kurvan.

invNorm()

invNorm(Area[,m[,s]])

Beräknar den inversa kumulativa normalfördelningsfunktionen för en given Area under normalfördelningskurvan specificerad av m och s.

invt()

invt(Area,df)

Beräknar den inversa kumulativa sannolikhetsfunktionen student-t specifierad av Degree of Freedom (Frihetsgrad), df, för en given Area under kurvan.

iPart()

iPart(Number) ⇒ heltal iPart(List1) ⇒ lista iPart(Matrix1) ⇒ matris

Ger argumentets heltalsdel. Ger, för listor och matriser, heltalsdelen för varje element. Argumentet kan vara ett reellt eller ett komplext tal.

irr()

irr(CF0,CFList [,CFFreq]) ⇒ value

Finansiell funktion som beräknar internräntan på en investering. CF0 är det initiala kassaflödet vid tidpunkt 0 och måste vara e tt reellt

tal. CFList är en lista på kassaflödesbelopp efter det initiala kassaflödet

CF0. CFFreq är en frivillig lista i vilken varje element specificerar

frekvensen för ett grupperat (konsekutivt) kassaflödesbelopp, vilket är det motsvarande elementet i CFList. Förinställningen är 1. Om du vill mata in värden måste de vara positiva heltal < 10.000.

Obs: Se även mirr() på sidan 68.

Katalog

TI-Nspire™ CAS Referenshandbok 53

isPrime()

isPrime(Number) ⇒ Booleskt konstantuttryck

Ger sant eller falskt för att indikera om number är ett heltal ‚ 2 som är jämnt delbart endast med sig självt och 1.

Om Number överskrider cirka 306 siffror och saknar faktorer visar isPrime(Number) ett felmeddelande.

Om du endast vill bestämma om Number är ett primtal, använd

isPrime() i stället för factor(). Detta går mycket fortare, särskilt

om Number inte är ett primtal och dess näst största faktor har mer än cirka fem siffror.

Anmärkning om inmatningen av exemplet: I

handenhetens applikation Calculator kan du skriva in flerradiga definitioner genom att trycka på @ i stället för · i slutet av

varje rad. På datorns tangentbord, håll ned Alt och tryck på Enter.

{1021

Katalog

Funktion för att hitta nästa primtal efter ett specificerat tal:

Lbl

Lbl labelName

Definierar en etikett med namnet labelName inom en funktion. Du kan använda en Goto labelName-instruktion för att överföra

kontroll till instruktionen direkt efter etiketten. labelName måste uppfylla samma krav på namngivning som ett

variabelnamn.

Anmärkning om inmatningen av exemplet: I

handenhetens applikation Calculator kan du skriva in flerradiga definitioner genom att trycka på @ i stället för · i slutet av

varje rad. På datorns tangentbord, håll ned Alt och tryck på Enter.

lcm()

lcm(Number1, Number2) ⇒ uttryck lcm(List1, List2) ⇒ lista lcm(Matrix1, Matrix2) ⇒ matris

Ger den minsta gemensamma multipeln för de två argumenten. lcm för två bråk är lcm för deras täljare dividerat med gcd för deras nämnare. lcm för tal i flyttalsform är deras produkt.

Ger, för två listor eller matriser, den minsta gemensamma multipeln för de motsvarande elementen.

Katalog

54 TI-Nspire™ CAS Referenshandbok

left()

left(sourceString[, Num]) ⇒ sträng

Ger Num-tecknen längst till vänster i teckensträngen sourceString. Om du utelämnar Num erhålls alla i sourceString.

left(List1[, Num]) ⇒ lista

Ger Num-elementen längst till vänster i List1. Om du utelämnar Num erhålls alla i List1.

left(Comparison) ⇒ uttryck

Ger den vänstra sidan av en ekvation eller olikhet.

Katalog

libShortcut()

libShortcut(LibNameString, ShortcutNameString [, LibPrivFlag]) ⇒ lista på variabler

Skapar en variabelgrupp i det aktuella problemet som innehåller referenser till alla objekt i det specificerade biblioteksdokumentet libNameString. Lägger också till gruppmedlemmarna på menyn Variables. Du kan sedan referera till varje objekt med hjälp av dess ShortcutNameString.

Ställ LibPrivFlag=0 för att utesluta privata biblioteksobjekt (förinställning) Ställ LibPrivFlag=1 för att inkludera privata biblioteksobjekt

För att kopiera en variabelgrupp, se CopyVar på sidan 17. För att ta bort en variabelgrupp, se DelVar på sidan 31.

limit() eller lim()

limit(Expr1, Va r, Point [,Direction]) ⇒ uttryck limit(List1, Va r, Point [, Direction]) ⇒ lista limit(Matrix1, Var , Point [, Direction]) ⇒ matris

Ger det begärda gränsvärdet.

Obs: Se även Limit template på sidan 5.

Direction (Riktning): negativ=från vänster, positiv=från höger, annars=båda. (Om Direction utelämnas förinställs den till båda.)

Katalog

Detta exempel förutsätter ett korrekt lagrat och uppdaterat biblioteksdokument med namnet linalg2 och som innehåller objekt definierade som clearmat, gauss1 och gauss2.

Katalog

Gränsvärden vid positiv ˆ och vid negativ ˆ konverteras alltid till ensidiga gränsvärden från den ändliga sidan.

Beroende på omständigheterna ger limit() sig självt eller undef när den inte kan bestämma ett unikt gränsvärde. Detta innebär nödvändigtvis inte att ett unikt gränsvärde inte existerar. "undef" innebär att resultatet antingen är ett okänt tal med ändlig eller oändlig storlek, eller hela uppsättningen av sådana tal.

TI-Nspire™ CAS Referenshandbok 55

limit() eller lim()

limit() använder metoder såsom L’Hopital’s regel, så det finns unika

gränsvärden som den inte kan bestämma. Om Expr1 innehåller odefinierade variabler utöver Va r kan du behöva begränsa dem för att erhålla ett mer kortfattat resultat.

Gränsvärden kan vara mycket känsliga för avrundningsfel. Undvik om möjligt inställningen Approximate (Ungefärlig) i läge Auto or

Approximate

Annars har gränsvärden som skulle vara noll eller ha oändlig storlek sannolikt inte dessa egenskaper, och gränsvärden som skulle ha ändlig icke nollstorlek kanske inte har detta.

och ungefärliga tal när du beräknar gränsvärden.

Katalog

LinRegBx

LinRegBx X,Y[,[Freq][,Category,Include]]

Utför den linjära regressionsanalysen y = a+b·x på listorna X och Y med frekvensen Freq. En sammanfattning av resultaten visas i variabeln stat.results. (Se sidan 105.)

Katalog

Alla listor utom Include måste ha samma dimensioner. X och Y är listor på oberoende och beroende variabler. Freq är en frivillig lista på frekvensvärden. Varje element i Freq

specificerar frekvensen för varje motsvarande X- och Y-datapunkt. Det förinställda värdet är 1. Alla element måste vara heltal | 0.

Category är en lista på numeriska kategorikoder för motsvarande Xoch Y-data.

Include är en lista på en eller flera av kategorikoderna. Endast de dataobjekt vars kategorikod är med på listan tas med i beräkningen.

Resultatvariabel Beskrivning

stat.RegEqn

Regressionsekvation: a+b·x

stat.a, stat.b Regressionskoefficienter

stat.r

Determinationskoefficient

stat.r Korrelationskoefficient

stat.Resid Residualer från regressionen

stat.XReg Lista på datapunkter i den modifierade X List som används i regressionen baserat på begränsningar i

stat.YReg Lista på datapunkter i den modifierade Y List som används i regressionen baserat på begränsningar i

Freq, Category List och Include Categories

stat.FreqReg Lista på frekvenser som motsvarar stat.FreqReg och stat.YReg

56 TI-Nspire™ CAS Referenshandbok

LinRegMx

LinRegMx X,Y[,[Freq][,Category,Include]]

Beräknar den linjära regressionen y = m·x+b på listorna X och Y med frekvensen Freq. En sammanfattning av resultaten visas i variabeln stat.results. (Se sidan 105.)

Katalog

Alla listor utom Include måste ha samma dimensioner. X och Y är listor på oberoende och beroende variabler. Freq är en frivillig lista på frekvensvärden. Varje element i Freq

specificerar frekvensen för varje motsvarande X- och Y-datapunkt. Det förinställda värdet är 1. Alla element måste vara heltal | 0.

Category är en lista på numeriska kategorikoder för motsvarande Xoch Y-data.

Include är en lista på en eller flera av kategorikoderna. Endast de dataobjekt vars kategorikod är med på listan tas med i beräkningen.

Resultatvariabel Beskrivning

stat.RegEqn

Regressionsekvation: m·x+b

stat.m, stat.b Regressionskoefficienter

stat.r

Determinationskoefficient

stat.r Korrelationskoefficient

stat.Resid Residualer från regressionen

stat.XReg Lista på datapunkter i den modifierade X List som används i regressionen baserat på begränsningar i

stat.YReg Lista på datapunkter i den modifierade Y List som används i regressionen baserat på begränsningar i

Freq, Category List och Include Categories

stat.FreqReg Lista på frekvenser som motsvarar stat.XReg och stat.YReg

LinRegtIntervals

LinRegtIntervals X,Y[,Freq[,0[,CLev]]]

För Slope (Lutning). Beräknar ett nivå-C-konfidensintervall för lutningen.

LinRegtIntervals X,Y[,Freq[,1,Xval[,CLev]]]

För Response (Svar). Beräknar ett prognostiserat y-värde, ett nivå-Cprediktionsintervall för en enstaka observation och ett nivå-Ckonfidensintervall för medelvärdet på svaret.

En sammanfattning av resultaten visas i variabeln stat.results. (Se sidan 105.)

Katalog

Alla listor måste ha samma dimensioner.

X och Y är listor på oberoende och beroende variabler. Freq är en frivillig lista på frekvensvärden. Varje element i Freq

specificerar frekvensen för varje motsvarande X- och Y-datapunkt. Det förinställda värdet är 1. Alla element måste vara heltal | 0.

TI-Nspire™ CAS Referenshandbok 57

Resultatvariabel Beskrivning

stat.RegEqn

stat.a, stat.b Regressionskoefficienter

stat.df Frihetsgrader

stat.r

stat.r Korrelationskoefficient

stat.Resid Residualer från regressionen

Endast för typen Slope

Resultatvariabel Beskrivning

[stat.CLower, stat.CUpper]

stat.ME Konfidensintervall - felmarginal

stat.SESlope Standardfel hos lutning

stat.s Standardfel hos linjen

Endast för typen Response

Resultatvariabel Beskrivning

[stat.CLower, stat.CUpper]

stat.ME Konfidensintervall - felmarginal

stat.SE Standardfel hos medelsvar

[stat.LowerPred , stat.UpperPred]

stat.MEPred Prognostiseringsintervall - felmarginal

stat.SEPred Standardfel för prognostisering

stat.y

Regressionsekvation: a+b·x

Determinationskoefficient

Konfidensintervall för lutningen

Konfidensintervall för medelvärdet på svaret

Prediktionsintervall för en enstaka observation

a + b·XVal

58 TI-Nspire™ CAS Referenshandbok

LinRegtTest

LinRegtTest X,Y[,Freq[,Hypoth]]

Utför en linjär regressionsanalys på listorna X och Y och ett t-test på lutningens värde b samt korrelationskoefficienten r för ekvationen y=a+bx. Det testar nollhypotesen H0:b=0 (equivalently, r=0) mot en av tre alternativa hypoteser.

Alla listor måste ha samma dimensioner.

X och Y är listor på oberoende och beroende variabler. Freq är en frivillig lista på frekvensvärden. Varje element i Freq

specificerar frekvensen för varje motsvarande X- och Y-datapunkt. Det förinställda värdet är 1. Alla element måste vara heltal | 0.

Hypoth är ett valfritt värde som specificerar en av tre alternativa hypoteser mot vilka nollhypotesen (H0:b=r=0) kommer att testas.

För Ha: bƒ0 och rƒ0 (förinställning), ställ Hypoth=0 För Ha: b<0 och r<0, ställ Hypoth<0 För Ha: b>0 och r>0, ställ Hypoth>0

En sammanfattning av resultaten visas i variabeln stat.results. (Se sidan 105.)

Resultatvariabel Beskrivning

stat.RegEqn

stat.t t-Statistik för signifikanstest

stat.PVal Lägsta signifikansnivå vid vilken nollhypotesen kan förkastas

stat.df Frihetsgrader

stat.a, stat.b Regressionskoefficienter

stat.s Standardfel hos linjen

stat.SESlope Standardfel hos lutning

stat.r

stat.r Korrelationskoefficient

stat.Resid Residualer från regressionen

Regressionsekvation: a + b·x

Determinationskoefficient

Katalog

List()

Katalog

@List(List1) ⇒ lista

Ger en lista på skillnaderna mellan konsekut iva element i List1. Varje element i List1 subtraheras från nästa element i List1. Den resulterande listan är alltid ett element kortare än den ursprungliga List1.

TI-Nspire™ CAS Referenshandbok 59

list4mat()

list4mat(List [, elementsPerRow]) ⇒ matris

Ger en matris fylld rad efter rad med elementen från List. elementsPerRow, om inkluderad, specificerar antalet element per

rad. Förinställningen är antalet element i List (en rad). Om List inte fyller den resulterande listan läggs nollor till.

Expr 4ln ⇒ uttryck

Medför att inmatningen Expr konverteras till ett uttryck som endast innehåller naturliga logaritmer (ln).

Katalog

ln()

ln(Expr1) ⇒ uttryck ln(List1) ⇒ lista

Ger argumentets naturliga logaritm. Ger, för en lista, elementens naturliga logaritmer.

ln(squareMatrix1) ⇒ kvadratMatris

Ger matrisen med naturlig logaritm för squareMatrix1. Detta är inte detsamma som att beräkna den naturliga logaritmen för varje element. För information om beräkningsmetoden, se cos().

squareMatrix1 måste vara möjlig att diagonalisera. Resultatet visas alltid i flyttalsform.

LnReg

LnReg X, Y[, [Freq] [, Category, Include]]

Utför en en logaritmisk regressionsanalys y = a+b·ln(x) på listorna X och Y med frekvensen Freq. En sammanfattning av resultaten visas i variabeln stat.results. (Se sidan 105.)

Alla listor utom Include måste ha samma dimensioner.

X och Y är listor på oberoende och beroende variabler. Freq är en frivillig lista på frekvensvärden. Varje element i Freq

specificerar frekvensen för varje motsvarande X- och Y-datapunkt. The default value is 1. All elements must be integers | 0.

Category är en lista på numeriska kategorikoder för motsvarande Xoch Y-data.

Include är en lista på en eller flera av kategorikoderna. Endast de dataobjekt vars kategorikod är med på listan tas med i beräkningen.

Om det komplexa formatläget är Real:

Om det komplexa formatläget är Rectangular:

I vinkelläget Radianer och i Rektangulärt komplext format:

För att se hela resultatet, tryck på £ och använd sedan ¡ och

tangenter

¢ för att flytta markören.

Katalog

60 TI-Nspire™ CAS Referenshandbok

Resultatvariabel Beskrivning

stat.RegEqn

Regressionsekvation: a+b·ln(x)

stat.a, stat.b Regressionskoefficienter

stat.r

Koefficient för linjär bestämning av transformerade data

stat.r Korrelationskoefficient för transformerade data (ln(x), y)

stat.Resid Residualer associerade med den logaritmiska modellen

stat.ResidTrans Residualer associerade med linjär anpassning av transformerade data

stat.XReg Lista på datapunkter i den modifierade X List som används i regressionen baserat på begränsningar i

stat.YReg Lista på datapunkter i den modifierade Y List som används i regressionen baserat på begränsningar i

Freq, Category List och Include Categories

stat.FreqReg Lista på frekvenser som motsvarar stat.XReg och stat.YReg

Local

Local Var 1 [, Va r 2] [, Va r 3 ] ...

Betecknar specificerade vars som lokala variabler. Dessa variabler existerar endast under utvärderingen av ett uttryck och tas bort när exekveringen av uttrycket är klar.

Obs: Lokala variabler sparar minne eftersom de endast existerar

tillfälligt. De stör heller inga befintliga globala variabe lvärden. Lokala variabler måste användas för For-slingor och för att temporärt spara värden i en flerradig funktion eftersom modifieringar av globala värden inte är tillåtna i en funktion.

Anmärkning om inmatningen av exemplet:

I handenhetens applikation Calculator kan du skriva in flerradiga definitioner genom att trycka på @ i stället för · i slutet av

varje rad. På datorns tangentbord, håll ned Alt och tryck på Enter.

Katalog

TI-Nspire™ CAS Referenshandbok 61

log()

log(Expr1[,Expr2]) ⇒ uttryck log(List1[,Expr2]) ⇒ lista

Ger bas-Expr2-logaritmen för det första argumentet.

Obs: Se även Log template på sidan 2.

Ger, för en lista, bas-Expr2-logaritmen för elementen. Om det andra argumentet utelämnas används 10 som bas.

Om det komplexa formatläget är Real:

Om det komplexa formatläget är Rectangular:

tangenter

log(squareMatrix1[,Expr]) ⇒ kvadratMatris

Ger matrisen med bas-Expr-logaritm för squareMatrix1. Detta är inte detsamma som att beräkna bas-Expr-logaritmen för varje element. Se cos() för information om beräkningsmetoden.

squareMatrix1 måste vara möjlig att diagonalisera. Resultatet visas alltid i flyttalsform.

Om basargumentet utelämnas används 10 som bas.

logbase

Expr 4logbase(Expr1) ⇒ uttryck

Medför att inmatningen Expression förenklas till ett uttryck med basen Expr1.

I vinkelläget Radianer och i Rektangulärt komplext format:

För att se hela resultatet, tryck på £ och använd sedan ¡ och

¢ för att flytta markören.

Katalog

62 TI-Nspire™ CAS Referenshandbok

Logistic

Logistic X, Y[, [Freq] [, Category, Include]]

Utför den logistiska regressionsanalysen y = (c/(1+a·e listorna X och Y med frekvensen Freq. En sammanfattning av resultaten visas i variabeln stat.results. (Se sidan 105.)

-bx

)) på

Katalog

Alla listor utom Include måste ha samma dimensioner. X och Y är listor på oberoende och beroende variabler. Freq är en frivillig lista på frekvensvärden. Varje element i Freq

specificerar frekvensen för varje motsvarande X- och Y-datapunkt. Det förinställda värdet är 1. Alla element måste vara heltal | 0.

Category är en lista på numeriska kategorikoder för motsvarande Xoch Y-data.

Include är en lista på en eller flera av kategorikoderna. Endast de dataobjekt vars kategorikod är med på listan tas med i beräkningen.

Resultatvariabel Beskrivning

stat.RegEqn

Regressionsekvation: c/(1+a·e

-bx

)

stat.a, stat.b, stat.c Regressionskoefficienter

stat.Resid Residualer från regressionen

stat.XReg Lista på datapunkter i den modifierade X List som används i regressionen baserat på begränsningar i

stat.YReg Lista på datapunkter i den modifierade Y List som används i regressionen baserat på begränsningar i

Freq, Category List och Include Categories

stat.FreqReg Lista på frekvenser som motsvarar stat.XReg och stat.YReg

LogisticD

LogisticD X, Y [, [Iterations], [Freq] [, Category, Include] ]

Utför den logistiska regressionsanalysen y = (c/(1+a·e listorna X och Y med frekvensen Freq, med ett specificerat antal

Iterationer. En sammanfattning av resultaten visas i variabeln stat.results. (Se sidan 105.)

-bx

)+d) på

Katalog

Alla listor utom Include måste ha samma dimensioner. X och Y är listor på oberoende och beroende variabler. Iterations är ett valfritt värde som specificerar det maximala antalet

gånger en lösning kommer att provas. Om denna utelämnas används

64. Normalt ger större värden bättre noggrannhet, men längre

exekveringstider, och vice versa. Freq är en frivillig lista på frekvensvärden. Varje element i Freq

specificerar frekvensen för varje motsvarande X- och Y-datapunkt. Det förinställda värdet är 1. Alla element måste vara heltal | 0.

Category är en lista på numeriska kategorikoder för motsvarande Xoch Y-data.

Include är en lista på en eller flera av kategorikoderna. Endast de dataobjekt vars kategorikod är med på listan tas med i beräkningen.

TI-Nspire™ CAS Referenshandbok 63

Resultatvariabel Beskrivning

stat.RegEqn

stat.a, stat.b, stat.c, stat.d

Regressionsekvation: c/(1+a·e

Regressionskoefficienter

-bx

)+d)

stat.Resid Residualer från regressionen

stat.XReg Lista på datapunkter i den modifierade X List som används i regressionen baserat på begränsningar i

stat.YReg Lista på datapunkter i den modifierade Y List som används i regressionen baserat på begränsningar i

Freq, Category List och Include Categories

stat.FreqReg Lista på frekvenser som motsvarar stat.XReg och stat.YReg

Loop

Block

EndLoop

Exekverar påståendena i Block upprepade gånger. Observera att slingan upprepas i all oändlighet såvida inte en Goto- eller Exitinstruktion exekveras inom Block.

Block är en serie av påståenden separerade med tecknet “:”.

Anmärkning om inmatningen av exemplet:

I handenhetens applikation Calculator kan du skriva in flerradiga definitioner genom att trycka på @ i stället för · i slutet av

varje rad. På datorns tangentbord, håll ned Alt och tryck på Enter.

Katalog

64 TI-Nspire™ CAS Referenshandbok

LU Matrix, lMatName, uMatName, pMatName[, Tol ]

Beräknar uppdelningen Doolittle LU (undre-övre) av en reell eller komplex matris. Den undertriangulära matrisen lagras i lMatName, den övre triangulära matrisen lagras i uMatName och permutationsmatrisen (som beskriver radväxlingarna som har gjorts under beräkningen) lagras i pMatName.

lMatName · uMatName = pMatName · matris

Alternativt behandlas varje matriselement som noll om dess absolutvärde är mindre än To l. Denna tolerans används endast om matrisen har inmatning med tal i flyttalsform och inte innehåller några symboliska variabler som inte har tilldelats ett värde. Annars ignoreras To l.

• Om du använder

Approximate

flyttalsaritmetik.

• Om Tol utelämnas eller inte används beräknas standardtoleransen som:

5EM14 ·max(dim(Matrix)) ·rowNorm(Matrix)

Faktoriseringsalgoritmen LU använder partiell pivotering med radutbyten.

· eller ställer in Auto or

på Approximate utförs beräkningarna med

Katalog

mat4list()

mat4list(Matrix) ⇒ lista

Ger en lista med elementen i Matrix. Elementen kopieras från Matrix rad för rad.

TI-Nspire™ CAS Referenshandbok 65

Katalog

max()

max(Expr1, Expr2) ⇒ uttryck max(List1, List2) ⇒ lista max(Matrix1, Matrix2) ⇒ matris

Ger de två argumentens maximum. Ger, om argumenten är två listor eller matriser, en lista eller matris som innehåller maximumvärdet för varje par av motsvarande element.

max(List) ⇒ uttryck

Ger maximumelementet i list.

max(Matrix1) ⇒ matris

Ger en radvektor som innehåller maximumelemen tet för varje kolumn i Matrix1.

Obs: Se även fMax() och min().

Katalog

mean()

mean(List[, freqList]) ⇒ uttryck

Ger medelvärdet för elementen i List. Varje freqList-element räknar antalet förekomster av motsvarande

element i List.

mean(Matrix1[, freqMatrix]) ⇒ matris

Ger en radvektor med medelvärdena för alla kolumner i Matrix1.

Varje freqMatrix-element räknar antalet förekomster av motsvarande element i Matrix1.

median()

median(List) ⇒ uttryck

Ger medianen för elementen i List.

median(Matrix1) ⇒ matris

Ger en radvektor som innehåller medianerna för kolumnerna i Matrix1.

Obs: Alla inmatningar i listan eller matrisen måste förenklas till tal.

I vektorformatet Rectangular:

Katalog

66 TI-Nspire™ CAS Referenshandbok

MedMed

MedMed X,Y [, Freq] [, Category, Include]]

Beräknar median-median-linjen y = (m·x+b) på listorna X och Y med frekvensen Freq. En sammanfattning av resultaten visas i variabeln stat.results. (Se sidan 105.)

Alla listor utom Include måste ha samma dimensioner.

X och Y är listor på oberoende och beroende variabler. Freq är en frivillig lista på frekvensvärden. Varje element i Freq

specificerar frekvensen för varje motsvarande X- och Y-datapunkt. Det förinställda värdet är 1. Alla element måste vara heltal | 0.

Category är en lista på numeriska kategorikoder för motsvarande Xoch Y-data.

Include är en lista på en eller flera av kategorikoderna. Endast de dataobjekt vars kategorikod är med på listan tas med i beräkningen.

Resultatvariabel Beskrivning

stat.RegEqn

stat.m, stat.b Modellkoefficienter

stat.Resid Residualer från median-median-linjen

stat.XReg Lista på datapunkter i den modifierade X List som används i regressionen baserat på begränsningar i

stat.YReg Lista på datapunkter i den modifierade Y List som används i regressionen baserat på begränsningar i

stat.FreqReg Lista på frekvenser som motsvarar stat.XReg och stat.YReg

Ekvation för median-median-linje m·x+b

Freq, Category List och Include Categories

Katalog

mid()

mid(sourceString, Start[, Count]) ⇒ sträng

Ger Count-tecknen från teckensträngen sourceString och börjar med teckennumret Start.

Ger, om Count utelämnas eller är större än dimensionen på sourceString, alla tecken från sourceString med start från teckennumret Start.

Count måste vara ‚ 0. Om Count = 0 erhålls en tom sträng.

mid(sourceList, Start [, Count]) ⇒ lista

Ger Count-elementen från sourceList och börjar med elementnumret Start.

Ger, om Count utelämnas eller är större än dimensionen på sourceList, alla element från sourceList med start från elementnumret Start.

Count måste vara ‚ 0. Om Count = 0 erhålls en tom lista.

mid(sourceStringList, Start[, Count]) ⇒ lista

Ger Count-strängarna från stränglistan sourceStringList och börjar med elementnumret Start.

Katalog

TI-Nspire™ CAS Referenshandbok 67

min()

min(Expr1, Expr2) ⇒ uttryck min(List1, List2) ⇒ lista min(Matrix1, Matrix2) ⇒ matris

Ger de två argumentens minimum. Ger, om argumenten är två listor eller matriser, en lista eller matris som innehåller minimumvärdet för varje par av motsvarande element.

min(List) ⇒ uttryck

Ger minimumelementet för List.

min(Matrix1) ⇒ matris

Ger en radvektor som innehåller minimumelement et för varje kolumn i Matrix1.

Obs: Se även fMin() och max().

Katalog

mirr()

mirr(financeRate,reinvestRate,CF0,CFList[,CFFreq])

Finansiell funktion som beräknar den modifierade internräntan på en investering.

financeRate är den räntesats som du betalar på kassaflödesbeloppen.

rein vestRa te är den räntesats vid vilken kassaflödena återinvesteras. CF0 är det initiala kassaflödet vid tidpunkt 0 och måste vara ett r eellt

tal. CFList är en lista på kassaflödesbelopp efter det initiala kassaflödet

CF0. CFFreq är en frivillig lista i vilken varje element specificerar

Obs: Se även irr() på sidan 53.

mod()

mod(Expr1, Expr2) ⇒ uttryck mod(List1, List2) ⇒ lista mod(Matrix1, Matrix2) ⇒ matris

Ger det första argumentet modulo det andra argumentet definierat av identiteterna:

mod(x,0) = x mod(x,y) = x -ìy floor(x/y)

När det andra argumentet är skilt från noll är resultatet periodiskt i det argumentet. Resultatet är antingen noll eller har samma tecken som det andra argumentet.

Ger, om argumenten är två listor eller matriser, en lista eller matris som innehåller modulen för varje par av motsvarande element.

Obs: Se även remain() på sidan 89

Katalog

68 TI-Nspire™ CAS Referenshandbok

mRow()

mRow(Expr, Matrix1, Index) ⇒ matris

Ger en kopia av Matrix1 med varje element i rad Index i Matrix1 multiplicerat med Expr.

Katalog

mRowAdd()

mRowAdd(Expr, Matrix1, Index1, Index2) ⇒ matris

Ger en kopia av Matrix1 med varje element i rad Index2 i Matrix1 ersatt med:

Expr · rad Index1 + rad Index2

MultReg

MultReg Y, X1[,X2[,X3,…[,X10]]]

Beräknar den multipla linjära regressionen i lista Y på listorna X1, X2,

…, X10. En sammanfattning av resultaten visas i variabeln

stat.results. (Se sidan 105.)

Alla listor måste ha samma dimensioner.

Resultatvariabel Beskrivning

stat.RegEqn

Regressionsekvation: b0+b1·x1+b2·x2+ ...

stat.b0, stat.b1, ... Regressionskoefficienter

stat.R

Koefficient för multipel bestämning

stat.yList yList = b0+b1·x1+ ...

stat.Resid Residualer från regressionsanalysen

MultRegIntervals

MultRegIntervals Y, X1[,X2[,X3,…[,X10]]],XValList[,CLevel]

Beräknar ett prognostiserat y-värde, ett nivå-C-prediktionsintervall för en enstaka observation och ett nivå-C-konfidensintervall för medelvärdet på svaret.

En sammanfattning av resultaten visas i variabeln stat.results. (Se sidan 105.)

Alla listor måste ha samma dimensioner.

Katalog

Resultatvariabel Beskrivning

stat.RegEqn

Regressionsekvation: b0+b1·x1+b2·x2+ ...

stat.y En punktuppskattning: y = b0 + b1 · xl + ... för XValList

stat.dfError Fel hos frihetsgrader

TI-Nspire™ CAS Referenshandbok 69

Resultatvariabel Beskrivning

stat.CLower, stat.CUpper Konfidensintervall för ett medelvärde på svaret

stat.ME Konfidensintervall - felmarginal

stat.SE Standardfel hos medelvärdet på svaret

stat.LowerPred, stat.UpperrPred

Prediktionsintervall för en enstaka observation

stat.MEPred Prediktionsintervall - felmarginal

stat.SEPred Standardfel för prognostisering

stat.bList Lista på regressionskoefficienter, {b0,b1,b3,...}

stat.Resid Residualer från regressionen

MultRegTests

MultRegTests Y, X1[,X2[,X3,…[,X10]]]

Ett multipelt linjärt regressionstest utför en multipel linjär regressionsanalys på givna data och ger den globala F-teststatistiken och t-teststatistiken för koefficienterna.

En sammanfattning av resultaten visas i variabeln stat.results. (Se sidan 105.)

Katalog

Utdata

Resultatvariabel Beskrivning

stat.RegEqn

Regressionsekvation: b0+b1·x1+b2·x2+ ...

stat.F Global F-teststatistik

stat.PVal P-värde associerat med global F-statistik

stat.R

stat.AdjR

Koefficient för multipel bestämning

Justerad koefficient för multipel bestämning

stat.s Standardavvikelse hos felet

stat.DW Durbin-Watson-statistik: används för att bestämma om modellen innehåller autokorrelation av första

ordningen

stat.dfReg Frihetsgrader hos regressionen

stat.SSReg Regressionens kvadratsumma

stat.MSReg Regression medelkvadrat

stat.dfError Fel hos frihetsgrader

stat.SSError Felens kvadratsumma

stat.MSError Felens medelkvadrat

stat.bList {b0,b1,...} Lista på koefficienter

stat.tList Lista på t-statistik för varje koefficient i bList

stat.PList Lista på P-värden för varje t-statistik

stat.SEList Lista på standardfel för koefficienter i bList

70 TI-Nspire™ CAS Referenshandbok

Resultatvariabel Beskrivning

stat.yList yList = b0+b1·x1+...

stat.Resid Residualer från regressionen

stat.sResid Standardiserade residualer: erhållna genom att dividera en residual med dess standardavvikelse

stat.CookDist Cooks avstånd: mått på den influens som en observation har, baserat på residual och stigning

stat.Leverage Mått på hur långt värdena i den oberoende variabeln är från sina medelvärden

nCr()

nCr(Expr1, Expr2) ⇒ uttryck

För heltal Expr1 och Expr2 med Expr1 ‚ Expr2 ‚ 0 är nCr() antalet kombinationer av Expr1 saker tagna Expr2 åt gången . (Detta kallas också en binomial koefficient.) Båda argumenten kan vara heltal eller symboliska uttryck.

nCr(Expr, 0) ⇒ 1

Expr, negInteger) ⇒ 0

nCr(

Expr, posInteger) ⇒ Expr·(ExprN1)...

nCr(

(ExprNposInteger+1)/ posInteger!

Expr, nonInteger) ⇒ expression!/

nCr(

((ExprNnonInteger)!·nonInteger!)

List1, List2) ⇒ lista

nCr(

Ger en lista på kombinationer baserat på motsvarande elementpar i de två listorna. Argumenten måste ha samma liststorlek.

nCr(Matrix1, Matrix2) ⇒ matris

Ger en matris över kombinationer baserat på motsvarande elementpar i de två matriserna. Argumenten måste ha samma matrisstorlek.

nDeriv()

nDeriv(Expr1, Va r [=Value] [, H]) ⇒ uttryck nDeriv(Expr1, Va r [, H] | Var = Va lu e ) ⇒ uttryck nDeriv(Expr1, Va r [=Value], List) ⇒ lista nDeriv(List1, Va r [=Value] [, H]) ⇒ lista nDeriv(Matrix1, Va r [=Value] [, H]) ⇒ matris

Ger den numeriska derivatan som ett uttryck. Använder formeln för symmetrisk differenskvot.

När Va lu e specificeras överstyr värdet eventuella tidigare variabeltilldelningar eller aktuella ersättningar av typ “så att” för variabeln.

H är stegvärdet. Om H uelämnas används förinställningen 0.001. När du använder List1 eller Matrix1 avbildas operationen över

värdena i listan eller över matriselementen.

Obs: Se även avgRC() och d().

Katalog

TI-Nspire™ CAS Referenshandbok 71

newList()

newList(numElements) ⇒ lista

Ger en lista med dimensionen på numElements. Varje element är noll.

Katalog

newMat()

newMat(numRows, numColumns) ⇒ matris

Ger en matris med nollor med dimensionen numRows gånger numColumns.

nfMax()

nfMax(Expr, Va r) ⇒ värde nfMax(Expr, Va r, lowBound) ⇒ värde nfMax(Expr, Va r, lowBound, upBound) ⇒ värde nfMax(Expr, Var) | lowBound<Va r<upBound ⇒ värde

Ger ett möjligt numeriskt värde på variabeln Va r där lok alt maximum för Expr inträffar.

Om du inför lowBound och upBound söker funktionen efter lokalt maximum mellan dessa värden.

Obs: Se även fMax() och d().

nfMin()

nfMin(Expr, Va r) ⇒ värde nfMin(Expr, Va r, lowBound) ⇒ värde nfMin(Expr, Va r, lowBound, upBound) ⇒ värde nfMin(Expr, Var) | lowBound<Var <upBound ⇒ värde

Ger ett möjligt numeriskt värde på variabeln Va r där lokalt minimum för Expr inträffar.

Om du inför lowBound och upBound söker funktionen efter lokalt minimum mellan dessa värden.

Obs: Se även fMin() och d().

nInt()

nInt(Expr1, Var, Lower, Upper) ⇒ uttryck

Om integranden Expr1 inte innehåller någon variabel utöver Va r , och om Lower och Upper är konstanter, positiv ˆ eller negativ ˆ, ger

nInt() en uppskattning av ‰(Expr1, Va r, Lower, Upper). Denna

uppskattning är ett vägt genomsnitt av vissa sampelvärden hos integranden i intervallet Lower<Va r <Upper.

Målsättningen är sex signifikanta siffror. Den adaptiva algoritmen bestämmer när det verkar sannolikt att målet har uppnåtts, eller när det verkar osannolikt att ytterligare sampling ger en nämnvärd förbättring.

En varning (“Questionable accuracy”) visas när det verkar som om målet inte har uppnåtts.

Katalog

Man kan kapsla in nInt() för att utföra multipel numerisk integrering. Integrationsgränser kan bero på integrationsvariabler utanför gränserna.

72 TI-Nspire™ CAS Referenshandbok

nInt()

Obs: Se även ‰() på sidan 134.

Katalog

nom()

nom(effectiveRate,CpY) ⇒ värde

Finansiell funktion som konverterar den årliga effektiva räntan effectiveRate till en nominell ränta, given av CpY som antalet sammansatta ränteperioder per år.

effectiveRate måste vara ett reellt tal och CpY måste vara ett reellt tal > 0.

Obs: Se även eff() på sidan 36.

norm()

norm(Matrix) ⇒ uttryck norm(Ve c to r ) ⇒ uttryck

Ger Frobenius norm.

normalLine()

normalLi ne (Expr1,Va r,Point) ⇒ uttryck normalLine(Expr1,Va r =Point) ⇒ uttryck

Ger normalen för kurvan representerad av Expr1 vid punkten som specificeras i Var =Point.

Kontrollera att den oberoende variabeln inte är definierad. Om exempelvis f1(x):=5 och x:=3 ger normalLine(f1(x),x,2) "falskt".

Katalog

normCdf()

normCdf(lowBound,upBound[,m[,s]]) ⇒ tal om lowBound

upBound är tal, lista om lowBound och upBound är listor

och

Beräknar sannolikheten vid en normalfördelning mellan lowBound och upBound för specificerad m (förinställning=0) och s (förinställning=1).

Katalog

För P(X  upBound), sätt lowBound = .ˆ.

TI-Nspire™ CAS Referenshandbok 73

normPdf()

normPdf(XVal[, m[,s]]) ⇒ tal om XVal är ett tal, lista om

XVal är en lista

Beräknar värde hos täthetsfunktionen för normalfördelning vid ett specificerat XVal-värde för specificerad m och s.

Katalog

not

not BooleanExpr ⇒ Booleskt uttryck

Ger en sann, falsk eller förenklad form av argumentet.

not Integer1 ⇒ heltal

Ger ettkomplementet till ett reellt heltal. Internt omvandlas Integer1 till ett 64-bitars binärt tal. Värdet på varje bit växlas (0 blir 1 och vice versa) för ettans komplement. Resultaten visas enligt det inställda basläget.

Du kan skriva in heltalet i valfri talbas. För en binär eller hexadecimal inmatning måste du använda prefixet 0b respektive 0h. Utan prefix behandlas heltalet som ett decimalt tal (bas 10).

Om du skriver in ett decimalt heltal som är alltför stort för att anges i 64-bitars binär form används en symmetrisk moduloperation för att få ned värdet till lämplig nivå.

nPr()

nPr(Expr1, Expr2) ⇒ uttryck

För heltal Expr1 och Expr2 med Expr1 ‚ Expr2 ‚ 0 är nPr() antalet permutationer av Expr1 saker tagna Expr2 åt gången. Båda argumenten kan vara heltal eller symboliska uttryck.

nPr(Expr, 0) ⇒ 1 nPr(

Expr, negInteger) ⇒ 1/((Expr+1)·(Expr+2)...

expressionNnegInteger))

(

nPr(

Expr, posInteger) ⇒ Expr·(ExprN1)...

ExprNposInteger+1)

(

Expr, nonInteger) ⇒ Expr! / (ExprNnonInteger)!

nPr(

Katalog

I hexadecimalt basläge:

Viktigt: Noll, inte bokstaven O.

I binärt basläge:

För att se hela resultatet, tryck på £ och använd sedan ¡ och

¢ för att flytta markören.

Obs: En binär inmatning kan ha upp till 64 siffror (exklusive

prefixet 0b). En hexadecimal inmatning kan ha upp till 16 siffror.

Katalog

nPr(

List1, List2) ⇒ lista

Ger en lista på permutationer baserat på motsvarande elementpar i de två listorna. Argumenten måste ha samma liststorlek.

nPr(Matrix1, Matrix2) ⇒ matris

Ger en matris över permutationer baserat på motsvarande elementpar i de två matriserna. Argumenten måste ha samma matrisstorlek.

74 TI-Nspire™ CAS Referenshandbok

npv()

npv(InterestRate,CFO,CFList[,CFFreq])

Finansiell funktion som beräknar nettovärdet, dvs. summan av aktuella värden för kassainflöden och kassautflöden. Ett positivt resultat för npv indikerar en vinstgivande investering.

InterestRate är räntan med vilken kassaflödena (kapitalanskaffningskostnaderna) diskonteras under en period.

CF0 är det initiala kassaflödet vid tidpunkt 0 och måste vara e tt reellt tal.

CFList är en lista på kassaflödesbelopp efter det initiala kassaflödet CF0.

CFFreq är en lista i vilken varje element specificerar frekvensen för

ett grupperat (konsekutivt) kassaflödesbelopp, vilket är det motsvarande elementet i CFList. Förinställningen är 1. Om du vill mata in värden måste de vara positiva heltal < 10.000.

Katalog

nSolve()

nSolve(Equation,Var [=Guess]) ⇒ tal eller fel_sträng nSolve(Equation,Var [=Guess],lowBound)

⇒ tal eller fel_sträng

nSolve(Equation,Var [=Guess],lowBound,upBound) ⇒ tal

eller fel_sträng

nSolve(Equation,Var [=Guess]) | lowBound<Va r <upBound

⇒ tal eller fel_sträng

Söker iterativt efter en ungefärlig reell numerisk lösning på Equation för dess variabel. Specificera variabeln som:

variabel

– eller – variabel = reellt tal

Som exempel är x giltigt och likaså x=3.

nSolve() är ofta mycket snabbare än solve() eller zeros(), särskilt

om operatorn “|” används för att begränsa sökningen till ett litet intervall som innehåller exakt en enkel lösning.

nSolve() försöker att bestämma antingen en punkt där residualen är

noll eller två relativt närliggande punk ter där residualen har motsatta tecken och inte är överdrivet stor. Om detta inte kan uppnås med ett måttligt antal samplingspunkter erhålls strängen “no solution found”.

Obs: Se även cSolve(), cZeros(), solve() och zeros().

Katalog

Obs: Om det finns flera lösningar kan du använda en gissning

för att lättare hitta en viss lösning.

TI-Nspire™ CAS Referenshandbok 75

OneVar

OneVar [1,]X[,[Freq][,Category,Include]] OneVar [

n,]X1,X2[X3[,…[,X20]]]

Beräknar 1-variabelstatistik på upp till 20 listor. En sammanfattning av resultaten visas i variabeln stat.results. (Se sidan 105.)

Alla listor utom Include måste ha samma dimensioner.

X-argumenten är datalistor. Freq är en frivillig lista på frekvensvärden. Varje element i Freq

specificerar frekvensen för varje motsvarande X-värde. Det förinställda värdet är 1. Alla element måste vara heltal | 0.

Category är en lista på numeriska kategorikoder för motsvarande Xvärden.

Include är en lista på en eller flera av kategorikoderna. Endast de dataobjekt vars kategorikod är med på listan tas med i beräkningen.

Resultatvariabel Beskrivning

stat.v

stat.Gx

stat.sx Standardavvikelse för x (sampling)

stat.ssssx Standardavvikelse för x (population)

stat.n Antal datapunkter

stat.MinX Minsta x-värde

stat.Q1X Undre kvartil för x

stat.MedianX Median för x

stat.Q3X Övre kvartil för x

stat.MaxX Största x-värde

stat.SSX Kvadratsumma av avvikelser från medelvärdet på x

Medelvärde av x-värden

Summa av x-värden

Summa av x2-värden

Katalog

76 TI-Nspire™ CAS Referenshandbok

or (eller)

BooleanExpr1 or BooleanExpr2

⇒ Booleskt uttryck

Ger resultatet sant eller falskt eller en förenklad form av den ursprungliga inmatningen.

Ger sant om ettdera eller båda uttrycken förenklas till sant. Ger resultatet falskt om båda uttrycken utvärderas som falska.

Obs: Se xor. Anmärkning om inmatningen av exemplet:

I handenhetens applikation Calculator kan du skriva in flerradiga definitioner genom att trycka på @ i stället för · i slutet av

varje rad. På datorns tangentbord, håll ned Alt och tryck på Enter.

Katalog

Integer1 or Integer2 ⇒ heltal

Jämför två reella heltal bit för bit med en or-operation. Internt omvandlas båda heltalen till 64-bitars binära tal. När motsvarande bitar jämförs blir resultatet 1 om båda bitarna är 1. Resultatet blir 0 endast om båda bitarna är 0. Det erhållna värdet representerar bitresultaten och visas enligt det inställda basläget.

Du kan skriva in heltalen i valfri talbas. För en binär eller hexadecimal inmatning måste du använda prefixet 0b respektive 0h. Utan prefix behandlas heltalen som decimala (bas 10).

Om du skriver in ett decimalt heltal som är alltför stort för att anges i 64-bitars binär form används en symmetrisk modulooperation för att få ned värdet till lämplig nivå.

Obs: Se xor.

ord()

ord(Str ing) ⇒ integer ord(List1) ⇒ lista

Ger den numeriska koden för det första tecknet i teckensträngen Strin g eller en lista på de första tecknen i varje listelement.

P4Rx()

P4Rx(rExpr, qExpr) ⇒ uttryck P4Rx(rList, qList) ⇒ lista P4Rx(rMatrix, qMatrix) ⇒ matris

Ger den ekvivalenta x-koordinaten för paret (r, q).

Obs: Argumentet q tolkas som en vinkel i antingen grader, nygrader

eller i radianer beroende på det aktuella vinkelläget. Om argumentet är ett uttryck kan du använda ó,G eller ôför att tillfälligt överstyra

vinkelläget.

I hexadecimalt basläge:

Viktigt: Noll, inte bokstaven O.

I binärt basläge:

Obs: En binär inmatning kan ha upp till 64 siffror (exklusive

prefixet 0b). En hexadecimal inmatning kan ha upp till 16 siffror.

Katalog

I vinkelläget Radianer:

TI-Nspire™ CAS Referenshandbok 77

P4Ry()

P4Ry(rExpr, qExpr) ⇒ uttryck P4Ry(rList, qList) ⇒ lista P4Ry(rMatrix, qMatrix) ⇒ matris

Ger den ekvivalenta y-koordinaten för paret (r, q).

Obs: Argumentet q tolkas som en vinkel i antingen grader, radianer

eller nygrader beroende på det aktuella vinkelläget. Om argumentet är ett uttryck kan du använda

vinkelläget.

ó,

eller ôför att tillfälligt överstyra

I vinkelläget Radianer:

Katalog

PassErr

Flyttar ett fel till nästa nivå. Om systemvariabeln errCode är noll utför PassErr ingenting. Villkoret Else i blocket Try...Else...EndTry bör använda ClrErr

eller PassErr. Om felet skall processas eller ignoreras, använd

ClrErr. Om det är okänt hur felet skall hanteras, använd PassErr för

att skicka felet vidare till nästa felhanterare. Om det inte finns någon ytterligare felhanterare för Try...Else...EndTry visas feldialogrutan som normal.

Obs: Se även ClrErr på sidan 15 och Try på sidan 115. Anmärkning om inmatningen av exemplet:

I handenhetens applikation Calculator kan du skriva in flerradiga definitioner genom att trycka på @ i stället för · i slutet av

varje rad. På datorns tangentbord, håll ned Alt och tryck på Enter.

piecewise()

piecewise(Expr1 [, Condition1 [, Expr2 [, Condition2 [, … ]]]])

Ger definitioner för en stegvis funktion i form av en lista. Du kan också skapa stegvisa definitioner med hjälp av en mall.

Obs: Se även Piecewise template på sidan 2.

poissCdf()

poissCdf(l,lowBound,upBound) ⇒ tal om lowBound och

upBound är tal, lista om lowBound och upBound är listor

poissCdf(

l,upBound) (för P(0XupBound) ⇒ tal om

upBound är ett tal, lista om upBound är en lista

Beräknar en kumulativ sannolikhet för den diskreta Poissonfördelningen med det specificerade medelvärdet l.

För P(X  upBound), sätt lowBound=0

Katalog

För ett exempel på PassErr, se exempel 2 under kommandot

Try på sidan 115.

Katalog

poissPdf()

poissPdf(l,XVal) ⇒ tal om XVal är ett tal, lista om XVal är

en lista

Beräknar en sannolikhet för den diskreta Poisson-fördelni ngen med det specificerade medelvärdet l.

Katalog

78 TI-Nspire™ CAS Referenshandbok

Polar

4Polar

Vec t o r

Visar vector i polär form [r q]. Vektorn måste ha dimensionen 2 och kan vara en rad eller en kolumn.

Obs: 4Polar är en visa format-instruktion, inte en

konverteringsfunktion. Du kan endast använda den i slutet av en inmatningsrad, och den uppdaterar inte ans.

Obs: Se även 4Rect på sidan 88.

complexValue 4Polar

Visar complexVector i polär form.

• Vinkelläget Grader ger (rq).

• Vinkelläget Radianer ger re

complexValue kan ha valfri komplex form. En inmatning av re orsakar dock ett fel i vinkelläget Grader.

Obs: Du måste använda parenteserna för en (rq) polär inmatning.

I vinkelläget Radianer:

I vinkelläget Nygrader:

I vinkelläget Grader:

Katalog

polyCoeffs()

polyCoeffs(Poly [,Var ]) ⇒ lista

Ger en lista på koefficienterna för polynomet Poly med avseende på variabeln Var .

Poly måste vara ett polynomuttryck i Va r . Vi rekommenderar att du inte utelämnar Va r såvida inte Poly är ett uttryck i bara en variabel.

Katalog

Expanderar polynomet och väljer x för den utelämnade Va r.

TI-Nspire™ CAS Referenshandbok 79

polyDegree()

polyDegree(Poly [,Var ]) ⇒ värde

Ger graden för polynomuttrycket Poly med avseende på variabeln Var . Om du utelämnar Va r väljer funktionen polyDegree() en förinställning från variablerna i polynomet Poly.

Poly måste vara ett polynomuttryck i Va r . Vi rekommenderar att

du inte utelämnar Va r såvida inte Poly är ett uttryck i en singulär variabel.

Katalog

Konstanta polynom

Graden kan extraheras även om koefficienterna inte kan extrahera den. Detta beror på att graden kan extraheras utan att utveckla polynomet.

polyEval()

polyEval(List1, Expr1) ⇒ uttryck polyEval(List1, List2) ⇒ uttryck

Tolkar det första argumentet som koefficienten för ett polynom med fallande ordning och ger polynomet utvärderat för det andra argumentets värde.

polyGcd()

polyGcd(Expr1,Expr2) ⇒ uttryck

Ger den största gemensamma delaren för de två argumenten. Expr1 och Expr2 måste vara polynomuttryck. Listargument, matrisargument och booleska argument är ej tillåtna.

Katalog

80 TI-Nspire™ CAS Referenshandbok

polyQuotient()

polyQuotient(Poly1,Poly2 [,Var ]) ⇒ uttryck

Ger kvoten på polynomet Poly1 dividerat med polynomet Poly2 med avseende på den specificerade variabeln Va r .

Poly1 och Poly2 måste vara polynomuttryck i Va r . Vi rekommenderar att du inte utelämnar Va r såvida inte Poly1 och Poly2 är uttryck i samma variabel.

Katalog

polyRemainder()

polyRemainder(Poly1,Poly2 [,Var ]) ⇒ uttryck

Ger resten på polynomet Poly1 dividerat med polynomet Poly2 med avseende på den specificerade variabeln Va r .

Poly1 och Poly2 måste vara polynomuttryck i Va r . Vi rekommenderar att du inte utelämnar Va r såvida inte Poly1 och Poly2 är uttryck i samma variabel.

PowerReg

PowerReg X,Y [, Freq] [, Category, Include]]

Utför potensregressionsanalys y = (a·(x)b) på listorna X och Y med frekvensen Freq. En sammanfattning av resultaten visas i variabeln stat.results. (Se sidan 105.)

Alla listor utom Include måste ha samma dimensioner.

X och Y är listor på oberoende och beroende variabler. Freq är en frivillig lista på frekvensvärden. Varje element i Freq

specificerar frekvensen för varje motsvarande X- och Y-datapunkt. Det förinställda värdet är 1. Alla element måste vara heltal | 0.

Category är en lista på numeriska kategorikoder för motsvarande Xoch Y-data.

Include är en lista på en eller flera av kategorikoderna. Endast de dataobjekt vars kategorikod är med på listan tas med i beräkningen.

Katalog

TI-Nspire™ CAS Referenshandbok 81

Resultatvariabel Beskrivning

stat.RegEqn

Regressionsekvation: a·(x)

stat.a, stat.b Regressionskoefficienter

stat.r

Koefficient för linjär bestämning av transformerade data

stat.r Korrelationskoefficient för transformerade data (ln(x), ln(y))

stat.Resid Residualer associerade med potensmodellen

stat.ResidTrans Residualer associerade med linjär anpassning av transformerade data

stat.XReg Lista på datapunkter i den modifierade X List som används i regressionen baserat på begränsningar i

stat.YReg Lista på datapunkter i den modifierade Y List som används i regressionen baserat på begränsningar i

Freq, Category List och Include Categories

stat.FreqReg Lista på frekvenser som motsvarar stat.XReg och stat.YReg

Prgm

Block

EndPrgm

Mall för att skapa ett användardefinierat program. Måste användas med kommandot Define, Define LibPub eller Define LibPriv.

Block kan vara ett enstaka påstående, en serie av påståenden separerade med tecknet “:” eller en serie av påståenden på separata rader.

Anmärkning om inmatningen av exemplet:

I handenhetens applikation Calculator kan du skriva in flerradiga definitioner genom att trycka på @ i stället för · i slutet av

varje rad. På datorns tangentbord, håll ned Alt och tryck på Enter.

Product (PI)

Beräkna GCD och visa mellanliggande resultat.

Se Π() på sidan 135.

Katalog

82 TI-Nspire™ CAS Referenshandbok

product()

product(List[, Start[, end]]) ⇒ uttryck

Ger produkten av elementen i List. Start och end är valfria. De specificerar ett område med element.

product(Matrix1[, Start[, end]]) ⇒ matris

Ger en radvektor som innehåller produkterna av elementen i kolumnerna i Matrix1. Start och end är valfria. De specificerar ett område med rader.

Katalog

propFrac()

propFrac(Expr1[, Va r ]) ⇒ uttryck

propFrac(rational_number) ger rational_number som summan

av ett heltal och ett bråk med samma tecken och med större nämnare än täljare.

propFrac(rational_expression,Var ) ger summan av egentliga bråk

och ett polynom med avseende på Va r. Graden hos Va r i nämnaren överskrider graden hos Va r i täljaren i varje egentligt bråk. Liknande potenser av Var samlas in. Termerna och deras faktorer sorteras med Var som huvudvariabel.

Om Va r utelämnas utförs en utveckling av ett egentligt bråk med avseende på den mest betydande variabeln. Koefficienterna för polynomdelen görs sedan egentliga, först med avseende på deras mest betydande variabel och så vidare.

För rationella uttryck är propFrac() ett snabbare, men mindre extremt alternativ till expand().

Du kan använda funktionen propFrac() för att representera blandade bråk och demonstrera addition och subtraktion av blandade bråk.

Katalog

TI-Nspire™ CAS Referenshandbok 83

QR Matrix, qMatName, rMatName[, Tol ]

Beräknar faktoriseringen Householder QR av en reell eller komplex matris. De resulterande Q- och R-matriserna lagras i specificerad MatNames. Q-matrisen är unitär. R-matrisen är övertriangulär.

Alternativt behandlas varje matriselement som noll om dess absolutvärde är mindre än To l. Denna tolerans används endast om matrisen har inmatning i flyttalsform och inte innehåller några symboliska variabler som inte har tilldelats ett värde. Annars ignoreras To l.

• Om du använder

Approximate

flyttalsaritmetik.

• Om Tol utelämnas eller inte används beräknas standardtoleransen som:

5Eë14 ·max(dim(Matrix)) ·rowNorm(Matrix)

QR-faktoriseringen beräknas numeriskt med Householdertransformationer. Den symboliska lösningen beräknas med GramSchmidt. Kolumnerna i qMatName är de ortonormerade basvektorerna som täcker utrymmet som definieras av matrix.

· eller ställer in Auto or

på Approximate utförs beräkningarna med

Katalog

Siffran för flytande komma (9.) i m1 medför att resultat beräknas med flyttalsaritmetik.

QuadReg

QuadReg X,Y [, Freq] [, Category, Include]]

Utför den kvadratiska regressionsanalysen y = a·x2+b·x+c på listorna X och Y med frekvensen Freq. En sammanfattning av resultaten visas i variabeln stat.results. (Se sidan 105.)

Alla listor utom Include måste ha samma dimensioner.

X och Y är listor på oberoende och beroende variabler. Freq är en frivillig lista på frekvensvärden. Varje element i Freq

specificerar frekvensen för varje motsvarande X- och Y-datapunkt. Det förinställda värdet är 1. Alla element måste vara heltal | 0.

Category är en lista på numeriska kategorikoder för motsvarande Xoch Y-data.

Include är en lista på en eller flera av kategorikoderna. Endast de dataobjekt vars kategorikod är med på listan tas med i beräkningen.

Katalog

84 TI-Nspire™ CAS Referenshandbok

Resultatvariabel Beskrivning

stat.RegEqn

Regressionsekvation: a·x2+b·x+c

stat.a, stat.b, stat.c Regressionskoefficienter

stat.R

Determinationskoefficient

stat.Resid Residualer från regressionen

stat.XReg Lista på datapunkter i den modifierade X List som används i regressionen baserat på begränsningar i

stat.YReg Lista på datapunkter i den modifierade Y List som används i regressionen baserat på begränsningar i

Freq, Category List och Include Categories

stat.FreqReg Lista på frekvenser som motsvarar stat.XReg och stat.YReg

QuartReg

QuartReg X,Y [, Freq] [, Category, Include]]

Katalog

Utför en fjärdegrads regressionsanalys y = a·x4+b·x3+c· x2+d·x+e på listorna X och Y med frekvensen

Freq. En sammanfattning av resultaten visas i variabeln stat.results. (Se sidan 105.)

Alla listor utom Include måste ha samma dimensioner.

X och Y är listor på oberoende och beroende variabler. Freq är en frivillig lista på frekvensvärden. Varje element i Freq

specificerar frekvensen för varje motsvarande X- och Y-datapunkt. Det förinställda värdet är 1. Alla element måste vara heltal | 0.

Category är en lista på numeriska kategorikoder för motsvarande Xoch Y-data.

Include är en lista på en eller flera av kategorikoderna. Endast de dataobjekt vars kategorikod är med på listan tas med i beräkningen.

Resultatvariabel Beskrivning

stat.RegEqn

stat.a, stat.b, stat.c, stat.d, stat.e

stat.R

Regressionsekvation: a·x4+b·x3+c· x2+d·x+e

Regressionskoefficienter

Determinationskoefficient

stat.Resid Residualer från regressionen

stat.XReg Lista på datapunkter i den modifierade X List som används i regressionen baserat på begränsningar i

stat.YReg Lista på datapunkter i den modifierade Y List som används i regressionen baserat på begränsningar i

Freq, Category List och Include Categories

stat.FreqReg Lista på frekvenser som motsvarar stat.XReg och stat.YReg

TI-Nspire™ CAS Referenshandbok 85

R4Pq()

R4Pq (xExpr, yExpr) ⇒ uttryck R4Pq (xList, yList) ⇒ lista R4Pq (xMatrix, yMatrix) ⇒ matris

Ger den ekvivalenta q-koordinaten för argumentparen (x,y).

Obs: Resultatet erhålls som en vinkel i grader, nygrader eller radianer

beroende på det aktuella vinkelläget.

R4Pr()

R4Pr (xExpr, yExpr) ⇒ uttryck R4Pr (xList, yList) ⇒ lista R4Pr (xMatrix, yMatrix) ⇒ matris

Ger den ekvivalenta r-koordinaten för argumentparen (x,y).

I vinkelläget Grader:

I vinkelläget Nygrader:

I vinkelläget Radianer:

Katalog

Rad

Expr14Rad ⇒ uttryck

Konvertar argumentet till en vinkel i radianer.

rand()

rand() ⇒ uttryck rand(#Trials) ⇒ lista

rand() ger ett slumpvärde mellan 0 och 1. rand(#Trials) ger en lista med #Trials slumpvärden mellan 0 och 1.

I vinkelläget Grader:

I vinkelläget Nygrader:

Bestämmer slumptalsfröet.

Katalog

86 TI-Nspire™ CAS Referenshandbok

randBin()

randBin(n, p) ⇒ uttryck randBin(n, p, #Trials) ⇒ lista

randBin(n, p) ger ett reellt slumptal från en specificerad

binomialfördelning.

randBin(n, p, #Trials) ger en lista med #Trials reella slumptal från

en specificerad binomialfördelning.

Katalog

randInt()

randInt(lowBound,upBound) ⇒ uttryck randInt(lowBound,upBound,#Trials) ⇒ lista

randInt(lowBound,upBound) ger ett slumptal med heltalsvärde

inom det område som specificeras av heltalsgränserna lowBound och upBound.

randInt(lowBound,upBound,#Trials) ger en lista med #Trials

slumptal med heltalsvärden inom det specificerade området.

randMat()

randMat(numRows, numColumns) ⇒ matris

Ger en matris med heltal mellan -9 och 9 med specificerad dimension. Båda argumenten måste förenklas till heltal.

randNorm()

randNorm(m, s [,numTrials]) ⇒ uttryck

Ger ett decimalt tal från den specificerade normalfördelningen. Det kan vara ett reellt tal, men det blir kraftigt koncentrerat i intervallet

[mN3·s, m+3·s].

randPoly()

randPoly(Va r , Order) ⇒ uttryck

Ger ett polynom i Va r med specificerad Order. Koefficienterna är slumpheltal i området ë9 t.o.m. 9. Den första koefficienten är inte noll.

Order måste vara 0–99.

Catalog

Katalog

Obs: Värdena i denna matris ändras varje gång du trycker på

·.

Katalog

randSamp()

randSamp(List,numTrials[,noRepl]) ⇒ lista

Ger en lista på ett slumpmässigt urval av numTrials försök från List med ett alternativ för urvalsutbyte (noRepl=0) eller inget urvalsutbyte (noRepl=1). Förinställningen är med urvalsutbyte.

Katalog

TI-Nspire™ CAS Referenshandbok 87

RandSeed

RandSeed Number

Om Number = 0 ställs fröna in på fabriksinställningarna för slumptalsgeneratorn. Om Number två frön, vilka lagras i systemvariablerna seed1 och seed2.

ƒ 0 används det för att generera

Katalog

real()

real(Expr1) ⇒ uttryck

Ger argumentets reella del.

Obs: Alla odefinierade variabler behandlas som reella variabler. Se

även imag() på sidan 51.

real(List1) ⇒ lista

Ger de reella delarna av alla element.

real(Matrix1) ⇒ matris

Ger de reella delarna av alla element.

Rect

Vec t o r 4Rect

Visar Vec t o r i rektangulär form [x, y, z]. Vektorn måste ha dimensionen 2 eller 3 och kan vara en rad eller en kolumn.

Obs: 4Rect är en visa format-instruktion, inte en

konverteringsfunktion. Du kan endast använda den i slutet av en inmatningsrad, och den uppdaterar inte ans.

Obs: Se även 4Polar på sidan 79.

complexValue 4Rect

Visar complexValue i rektangulär form a+bi. complexValue kan ha valfri komplex form. En inmatning av re

vinkelläget Grader.

Obs: Du måste använda parenteserna för en (rq) polär inmatning.

orsakar dock ett fel i

I vinkelläget Radianer:

Katalog

I vinkelläget Nygrader:

I vinkelläget Grader:

Obs: För att skriva in tecknet , välj det från symbollistan i

Catalog.

88 TI-Nspire™ CAS Referenshandbok

ref()

ref(Matrix1[, To l]) ⇒ matris

Ger radtrappstegsformen av Matrix1. Alternativt behandlas varje matriselement som noll om dess

absolutvärde är mindre än To l. Denna tolerans används endast om matrisen har inmatning i flyttalsform och inte innehåller några symboliska variabler som inte har tilldelats ett värde. Annars ignoreras To l.

• Om du använder

Approximate

flyttalsaritmetik.

• Om Tol utelämnas eller inte används beräknas standardtoleransen som:

5Eë14 ·max(dim(Matrix1)) ·rowNorm(Matrix1)

Obs: Se även rref() på sidan 92.

· eller ställer in Auto or

på Approximate utförs beräkningarna med

Katalog

remain()

remain(Expr1, Expr2) ⇒ uttryck remain(List1, List2) ⇒ lista remain(Matrix1, Matrix2) ⇒ matris

Ger resten på det första argumentet med avseende på det andra argumentet definierat av identiteterna:

remain(x,0)  x remain(x,y)  xNy·iPart(x/y)

Som en följd av detta, obeservera att remain(Nx,y) 

Nremain(x,y ). Resultatet är antingen noll eller har samma tecken

som det första argumentet.

Obs: Se även mod() på sidan 68.

Return

Return [Expr]

Ger Expr som resultatet av funktionen. Använd inom ett

Func...EndFunc-block. Obs: Använd Return utan ett argument inom ett

Prgm...EndPrgm-block för att gå ur ett program. Anmärkning om inmatningen av exemplet:

I handenhetens applikation Calculator kan du skriva in flerradiga definitioner genom att trycka på @ i stället för · i slutet av

varje rad. På datorns tangentbord, håll ned Alt och tryck på Enter.

right()

right(List1[, Num]) ⇒ lista

Ger Num-elementen längst till höger i List1. Om du utelämnar Num erhålls alla i List1.

Katalog

TI-Nspire™ CAS Referenshandbok 89

right()

right(sourceString[, Num]) ⇒ sträng

Ger Num-tecknen längst till höger i teckensträngen sourceString. Om du utelämnar Num erhålls alla i sourceString.

right(Comparison) ⇒ uttryck

Ger den högra sidan av en ekvation eller olikhet.

Katalog

root()

root(Expr) ⇒ rot root(Expr1, Expr2) ⇒ rot

root(Expr) ger kvadratroten ur Expr. root(Expr1, Expr2) ger Expr2-roten ur Expr1. Expr1 kan vara en

reell eller komplex konstant i flyttalsform, ett heltal eller komplex rationell konstant eller ett allmänt symboliskt uttryck.

Obs: Se även Nth root template på sidan 1.

rotate()

rotate(Integer1[,#ofRotations]) ⇒ heltal

Roterar bitarna i ett binärt heltal. Du kan skriva in Integer1 i valfri talbas. Det konverteras automatiskt till 64-bitars binär form. Om storleken på Integer1 är alltför stor för denna form för en symmetrisk modulooperation talet inom området.

Om #ofRotations är positiv sker rotationen åt vänster. Om #ofRotations är negativ sker rotationen åt höger. Förinställningen är

ë1 (rotera en bit åt höger).

Vid exempelvis höger rotation:

Varje bit roteras åt höger. 0b00000000000001111010110000110101 Biten längst till höger roteras till positionen längst till vänster. ger: 0b10000000000000111101011000011010 Resultatet visas enligt det inställda basläget.

rotate(List1[,#ofRotations]) ⇒ lista

Ger en kopia av List1 roterad åt höger eller vänster av #ofRotations- elementen. Ändrar inte List1.

Om #ofRotations är positiv sker rotationen åt vänster. Om #ofRotations är negativ sker rotationen åt höger. Förinställningen är

ë1 (rotera ett element åt höger).

rotate(String1[,#ofRotations]) ⇒ sträng

Ger en kopia av String1 roterad åt höger eller vänster av #ofRotations-tecknen. Ändrar inte String1.

Om #ofRotations är positiv sker rotationen åt vänster. Om #ofRotations är negativ sker rotationen åt höger. Förinställningen är

ë1 (rotera ett tecken åt höger).

Katalog

I binärt basläge:

För att se hela resultatet, tryck på £ och använd sedan ¡ och

¢ för att flytta markören.

I hexadecimalt basläge:

Viktigt: När du skriver in ett binärt eller hexadecimalt tal, använd alltid prefixet 0b eller 0h (noll, inte bokstaven O).

I decimalt basläge:

90 TI-Nspire™ CAS Referenshandbok

round()

round(Expr1[, digits]) ⇒ uttryck

Ger argumentet avrundat till det specificerade antalet siffror efter decimalpunkten.

digits måste vara ett heltal i området 0–12. Om digits inte inkluderas erhålls argumentet avrundat till 12 signifikanta siffror.

Obs: Läget Display digits (Visa siffror) kan påverka hur detta visas.

round(List1[, digits]) ⇒ lista

Ger en lista på elementen avrundade till det specificerade antalet siffror.

round(Matrix1[, digits]) ⇒ matris

Ger en matris över elementen avrundade till det specificerade antalet siffror.

Katalog

rowAdd()

rowAdd(Matrix1, rIndex1, rIndex2) ⇒ matris

Ger en kopia av Matrix1 med rad rIndex2 ersatt av summan av raderna rIndex1 och rIndex2.

rowDim()

rowDim(Matrix) ⇒ uttryck

Ger antalet rader i Matrix.

Obs: Se även colDim() på sidan 16.

rowNorm()

rowNorm(Matrix) ⇒ uttryck

Ger maximum av summorna av absolutbeloppen på elementen i raderna i Matrix.

Obs: Alla matriselement måste förenklas till tal. Se även colNorm()

på sidan 16.

rowSwap()

rowSwap(Matrix1, rIndex1, rIndex2) ⇒ matris

Ger Matrix1 med raderna rIndex1 och rIndex2 växlade.

Katalog

TI-Nspire™ CAS Referenshandbok 91

rref()

rref(Matrix1[, To l]) ⇒ matris

Ger den reducerade radtrappstegsformen av Matrix1.

• Om du använder

Approximate

flyttalsaritmetik.

• Om Tol utelämnas eller inte används beräknas standardtoleransen som:

5Eë14 ·max(dim(Matrix1)) ·rowNorm(Matrix1)

Obs: Se även ref() på sidan 89.

· eller ställer in Auto or

på Approximate utförs beräkningarna med

Katalog

sec()

sec(Expr1) ⇒ uttryck sec(List1) ⇒ lista

Ger sekansfunktionen för Expr1 eller en lista på sekansfunktionerna för alla element i List1.

Obs: Argumentet tolkas som en vinkel i grader, nygrader eller

radianer enligt det inställda vinkelläget. Du kan använda ó,G ellerôför att tillfälligt överstyra vinkelläget.

sec/()

sec/(Expr1) ⇒ uttryck sec/(List1) ⇒ lista

Ger den vinkel vars sekansfunktion är Expr1 eller en lista på de inversa sekansfunktionerna för alla element i List1.

Obs: Resultatet erhålls som en vinkel i grader, nygrader eller radianer

beroende på det aktuella vinkelläget.

I vinkelläget Grader:

I vinkelläget Nygrader:

I vinkelläget Radianer:

Katalog

92 TI-Nspire™ CAS Referenshandbok

sech()

sech(Expr1) ⇒ uttryck sech(List1) ⇒ lista

Ger den hyperboliska sekansfunktionen för Expr1 eller en lista på de hyperboliska sekansfunktionerna för elementen i List1.

Katalog

sechê()

sechê(Expr1) ⇒ uttryck sechê (List1) ⇒ lista

Ger den inversa hyperboliska sekansfunktionen för Expr1 eller en lista på den inversa hyperboliska sekansfunktionen för alla element i List1.

seq()

seq(Expr, Va r, Low, High[, St ep]) ⇒ lista

Stegvis ökning av Va r från Low till High med det steg som anges av Step, utvärderar Expr och ger resultatet som en lista. Det

ursprungliga innehållet i Va r är fortfarande kvar när seq() har utförts.

Var får inte vara en systemvariabel. Det förinställda värdet på Ste p är 1.

Katalog

I vinkelläget Radianer och i Rektangulärt komplext läge:

Katalog

Tryck på Ctrl+Enter /· för att urvärdera:

TI-Nspire™ CAS Referenshandbok 93

series()

series(Expr1, Var , Order [, Point]) ⇒ uttryck series(Expr1, Var , Order [, Point]) | Va r >Point ⇒ uttryck series(Expr1, Var , Order [, Point]) | Va r <Point ⇒ uttryck

Ger en generaliserad trunkerad potensserierepresentation av Expr1 utvecklat kring Point genom Order-graden Order kan vara ett rationellt tal vilket som helst. De resulterande potenserna av (Va r N Point) kan inkludera negativa och/eller exponenter i bråkform. Koefficienterna för dessa potenser kan inkludera logaritmer av (Va r N Point) och andra funktioner av Va r som domineras av alla potenser av (Va r N Point) som har samma exponenttecken.

Point förinställs till 0. Point kan vara ˆ eller Nˆ, varvid utvecklingen sker genom Order-graden i 1/(Va r N Point).

series(...) ger “series(...)” om den inte kan bestämma en sådan

representation, t.ex. för väsentliga singulariteter såsom sin(1/z) vid

N1/z

z=0, e

vid z=0, eller ez vid z = ˆ eller Nˆ.

Om serien eller någon av dess derivator har en språngdiskontinuitet vid Point innehåller resultatet troligen deluttryck i formen sign(…) eller abs(…) för en reell expansionsvariabel, eller

floor(…angle(…)…)

(-1) med "_". Om du tänker använda serien endast för värden på ena sidan av Point, lägg då till den lämpliga av "| Va r > Point", "| Va r < Point", "| "Var ‚ Point" eller "Va r  Point" för att erhålla ett enklare resultat.

series() kan ge symboliska approximationer av obestämda och

bestämda integraler, för vilka symboliska lösningar annars inte kan erhållas.

series() fördelas över 1:a-argumentlistor och matriser. series() är en generaliserad version av taylor().

Som det sista exemplet till höger illustrerar kan visningsrutinerna nedåt i resultatet som produceras av series(...) arrangera om termer så att den dominanta termen inte är längst till vänster.

Obs: Se även dominantTerm() på sidan 35.

för en komplex expansionsvariabel, vilken slutar

Catalog

94 TI-Nspire™ CAS Referenshandbok

Texas Instruments TI-Nspire CAS Reference Guide [sv]

Specifications and Main Features

Frequently Asked Questions

User Manual

Viktigt information

Innehåll

Mallar för uttryck

TI-Nspire™ CAS Referenshandbok 1

Alfabetisk lista