Texas instruments TI-NSPIRE CAS REFERENCE Manual

CAS

Guide de référence

Informations importantes

Sauf spécification contraire prévue dans la Licence fournie avec le programme, Texas Instruments n’accorde aucune garantie expresse ou implicite, ce qui inclut sans pour autant s’y limiter les garanties implicites quant à la qualité marchande et au caractère approprié à des fins particulières, liés aux programmes ou aux documents et fournit seulement ces matériels en l’état. En aucun cas, Texas Instruments n’assumera aucune responsabilité envers quiconque en cas de dommages spéciaux, collatéraux, accessoires ou consécutifs, liés ou survenant du fait de l’acquisition ou de l’utilisation de ces matériels. La seule et unique responsabilité incombant à Texas Instruments, indépendamment de la forme d’action, ne doit pas excéder la somme établie dans la licence du programme. En outre, Texas Instruments ne sera pas responsable des plaintes de quelque nature que soit, à l’encontre de l’utilisation de ces matériels, déposées par une quelconque tierce partie.

Licence

Veuillez consulter la licence complète, copiée dans C:\Program Files\TI

Education\TI-Nspire CAS

Microsoft®, Windows®, Excel®, Vernier EasyTemp®, Vernier Go!®Temp et Vernier Go!®Motion sont des marques commerciales de leur propriétaire respectif.

Contents

Modèles d'expression

Modèle Fraction ...........................................1

Modèle Exposant .........................................1

Modèle Racine carrée .................................. 1

Modèle Racine n-ième .................................1

Modèle e Exposant ...................................... 2

Modèle Logarithme ..................................... 2

Modèle Fonction définie par morceaux (2

morceaux) .....................................................2

Modèle Fonction définie par morceaux (n

morceaux) .....................................................2

Modèle Système de 2 équations .................3

Modèle Système de n équations .................3

Modèle Valeur absolue ............................... 3

Modèle dd°mm’ss.ss’’ ...................................3

Modèle Matrice (2 x 2) ................................ 3

Modèle Matrice (1 x 2) ................................ 3

Modèle Matrice (2 x 1) ................................ 4

Modèle Matrice (m x n) ............................... 4

Modèle Somme (G) ....................................... 4

Modèle Produit (Π) ...................................... 4

Modèle Dérivée première ........................... 4

Modèle Dérivée n-ième ............................... 5

Modèle Intégrale définie ............................ 5

Modèle Intégrale indéfinie .........................5

Modèle Limite .............................................. 5

Liste alphabétique A

abs() ..............................................................6

amortTbl() ....................................................6

and ................................................................6

angle() ..........................................................7

ANOVA .........................................................7

ANOVA2way ................................................ 8

ans ...............................................................10

approx() ......................................................10

approxRational() ........................................ 10

arcLen() .......................................................10

augment() ...................................................11

avgRC() ....................................................... 11

bal() .............................................................12

4Base2 .........................................................12

4Base10 .......................................................13

4Base16 .......................................................13

binomCdf() ................................................. 13

binomPdf() ................................................. 13

ceiling() .......................................................14

cFactor() ......................................................14

char() ...........................................................14

2way ........................................................15

Cdf() .........................................................15

GOF ......................................................... 15

Pdf() .........................................................16

clearAZ ....................................................... 16

ClrErr .......................................................... 16

colAugment() ............................................. 16

colDim() ...................................................... 16

colNorm() ................................................... 17

comDenom() .............................................. 17

conj() .......................................................... 17

CopyVar ...................................................... 18

corrMat() .................................................... 18

cos() ............................................................ 18

cosê() .......................................................... 19

cosh() .......................................................... 20

coshê() ........................................................ 20

cot() ............................................................ 20

cotê() .......................................................... 21

coth() .......................................................... 21

cothê() ........................................................ 21

count() ........................................................ 21

countif() ..................................................... 22

crossP() ....................................................... 22

csc() ............................................................. 22

cscê() ........................................................... 23

csch() ........................................................... 23

cschê() ......................................................... 23

cSolve() ....................................................... 23

CubicReg .................................................... 25

cumSum() ................................................... 26

Cycle ........................................................... 26

4Cylind ........................................................ 26

cZeros() ....................................................... 27

dbd() ........................................................... 28

4DD ............................................................. 29

4Decimal ..................................................... 29

Define ......................................................... 29

Define LibPriv ............................................ 30

Define LibPub ............................................ 31

DelVar ........................................................ 31

deSolve() .................................................... 31

det() ............................................................ 32

diag() .......................................................... 33

dim() ........................................................... 33

Disp ............................................................. 33

4DMS ........................................................... 34

dominantTerm() ........................................ 34

dotP() .......................................................... 34

e^() ............................................................. 35

eff() ............................................................. 35

eigVc() ........................................................ 36

eigVl() ......................................................... 36

Else ............................................................. 36

ElseIf ........................................................... 36

EndFor ........................................................ 36

EndFunc ...................................................... 37

EndIf ........................................................... 37

EndLoop ..................................................... 37

EndPrgm ..................................................... 37

iii

EndTry .........................................................37

EndWhile ....................................................37

exact() .........................................................37

Exit ..............................................................37

exp() ............................................................38

exp4list() ......................................................38

expand() ......................................................38

expr() ...........................................................39

ExpReg ........................................................40

factor() ........................................................40

Fill ................................................................41

floor() ..........................................................42

fMax() .........................................................42

fMin() ..........................................................42

For ...............................................................43

format() ......................................................43

fPart() ..........................................................43

FPdf() ..........................................................44

frequency() .................................................44

FTest_2Samp ..............................................44

Func .............................................................45

gcd() ............................................................45

geomCdf() ...................................................45

geomPdf() ...................................................46

getDenom() ................................................46

getMode() ...................................................46

getNum() ....................................................47

getVarInfo() ................................................47

Goto ............................................................47

4Grad ...........................................................48

identity() .....................................................48

If ..................................................................48

ifFn() ............................................................49

imag() ..........................................................49

impDif() .......................................................50

Indirection ..................................................50

inString() .....................................................50

int() .............................................................50

intDiv() ........................................................50

integrate .....................................................50

() .........................................................51

invc

invF() ...........................................................51

invNorm() ....................................................51

invt() ............................................................51

iPart() ..........................................................51

irr() ..............................................................51

isPrime() ......................................................52

Lbl ...............................................................52

lcm() ............................................................52

left() ............................................................53

limit() ou lim() ............................................53

LinRegBx .....................................................53

LinRegMx ....................................................54

LinRegtIntervals .........................................55

LinRegtTest .................................................56

@list() ........................................................... 56

list4mat() ..................................................... 56

4ln ................................................................ 57

ln() .............................................................. 57

LnReg .......................................................... 57

Local ........................................................... 58

log() ............................................................ 58

4logbase ...................................................... 59

Logistic ....................................................... 59

LogisticD ..................................................... 60

Loop ............................................................ 60

LU ................................................................ 61

mat4list() ..................................................... 61

max() ........................................................... 62

mean() ........................................................ 62

median() ..................................................... 62

MedMed ..................................................... 63

mid() ........................................................... 63

min() ........................................................... 64

mirr() ........................................................... 64

mod() .......................................................... 64

mRow() ....................................................... 65

mRowAdd() ................................................ 65

MultReg ...................................................... 65

MultRegIntervals ....................................... 65

MultRegTests ............................................. 66

nCr() ............................................................ 67

nDeriv() ....................................................... 68

newList() ..................................................... 68

newMat() .................................................... 68

nfMax() ....................................................... 68

nfMin() ....................................................... 68

nInt() ........................................................... 69

nom() .......................................................... 69

norm() ......................................................... 69

normCdf() ................................................... 69

normPdf() ................................................... 70

not .............................................................. 70

nPr() ............................................................ 70

npv() ........................................................... 71

nSolve() ....................................................... 71

OneVar ....................................................... 72

or ................................................................ 72

ord() ............................................................ 73

P4Rx() .......................................................... 73

P4Ry() .......................................................... 73

PassErr ........................................................ 74

piecewise() .................................................74

poissCdf() .................................................... 74

poissPdf() .................................................... 74

4Polar .......................................................... 74

polyCoeffs() ................................................ 75

polyDegree() .............................................. 76

polyEval() .................................................... 76

polyGcd() .................................................... 76

polyQuotient() ........................................... 77

polyRemainder() ........................................ 77

PowerReg ...................................................77

Prgm ...........................................................78

Product (PI) ................................................. 78

product() ..................................................... 79

propFrac() ................................................... 79

QR ...............................................................80

QuadReg .....................................................80

QuartReg ....................................................81

R4Pq() ..........................................................82

R4Pr() ...........................................................82

4Rad .............................................................82

rand() ..........................................................82

randBin() ..................................................... 83

randInt() ..................................................... 83

randMat() ................................................... 83

randNorm() ................................................. 83

randPoly() ................................................... 83

randSamp() ................................................. 83

RandSeed .................................................... 84

real() ...........................................................84

4Rect ............................................................84

ref() .............................................................85

remain() ......................................................85

Return .........................................................85

right() ..........................................................85

root() ...........................................................86

rotate() .......................................................86

round() ........................................................87

rowAdd() ....................................................87

rowDim() ....................................................87

rowNorm() ..................................................87

rowSwap() ..................................................88

rref() ............................................................88

sec() .............................................................88

sec/() ...........................................................89

sech() ...........................................................89

sechê() ......................................................... 89

seq() ............................................................89

series() .........................................................90

setMode() ................................................... 91

shift() ..........................................................92

sign() ...........................................................93

simult() ........................................................93

sin() .............................................................94

sinê() ...........................................................94

sinh() ...........................................................95

sinhê() .........................................................95

SinReg .........................................................96

solve() .........................................................96

SortA ...........................................................98

SortD ...........................................................99

4Sphere ....................................................... 99

sqrt() ...........................................................99

stat.results ................................................ 100

stat.values .................................................100

stDevPop() ................................................ 101

stDevSamp() ............................................. 101

Stop .......................................................... 102

Store ......................................................... 102

string() ...................................................... 102

subMat() ................................................... 102

Sum (Sigma) ............................................. 102

sum() ......................................................... 102

sumIf() ...................................................... 103

system() .................................................... 103

T (transposée) .......................................... 104

tan() .......................................................... 104

tanê() ........................................................ 105

tanh() ........................................................ 105

tanhê() ...................................................... 105

taylor() ...................................................... 106

tCdf() ........................................................ 106

tCollect() ................................................... 107

tExpand() .................................................. 107

Then ......................................................... 107

TInterval ................................................... 107

TInterval_2Samp ...................................... 108

tmpCnv() .................................................. 108

@tmpCnv() ................................................ 109

tPdf() ........................................................ 109

Try ............................................................. 109

tTest .......................................................... 110

tTest_2Samp ............................................. 111

tvmFV() ..................................................... 111

tvmI() ........................................................ 111

tvmN() ...................................................... 112

tvmPmt() .................................................. 112

tvmPV() ..................................................... 112

TwoVar ..................................................... 113

unitV() ...................................................... 114

varPop() .................................................... 114

varSamp() ................................................. 114

when() ...................................................... 115

While ........................................................ 115

With .......................................................... 116

xor ............................................................ 116

zeros() ....................................................... 116

zInterval ................................................... 118

zInterval_1Prop ........................................ 118

zInterval_2Prop ........................................ 119

zInterval_2Samp ...................................... 119

zTest ......................................................... 120

zTest_1Prop .............................................. 120

zTest_2Prop .............................................. 121

zTest_2Samp ............................................ 121

Symboles

+ (somme) .................................................122

N(soustraction) ..........................................122

·(multiplication) ......................................123

à (division) ................................................124

^ (puissance) .............................................124

(carré) ...................................................125

.+ (addition élément par élément) ..........125

.. (soustraction élément par élément) ....125

·(multiplication élément par élément) .126

. / (division élément par élément) ...........126

.^ (puissance élément par élément) ........126

ë(opposé) ..................................................127

% (pourcentage) ......................................127

= (égal à) ...................................................128

ƒ (différent de) .........................................128

< (inférieur à) ...........................................129

{ (inférieur ou égal à) ..............................129

> (supérieur à) ..........................................129

| (supérieur ou égal à) .............................129

! (factorielle) .............................................130

& (ajouter) ................................................130

d() (dérivée) ..............................................130

‰() (intégrale) ............................................130

‡() (racine carrée) .....................................131

Π() (produit) .............................................132

G() (somme) .............................................. 132

GInt() ......................................................... 133

GPrn() ........................................................ 134

# (indirection) .......................................... 134

í (notation scientifique) .......................... 134

g (grades) ................................................. 135

ô(radians) ................................................. 135

¡ (degré) ................................................... 135

¡, ', '' (degré/minute/seconde) ................. 135

 (angle) .................................................. 136

' (guillemets) ............................................ 136

_ (soulignement) ...................................... 136

4 (conversion) ........................................... 137

10^() .......................................................... 137

^ê (inverse) ............................................... 137

| (“sachant que”) ...................................... 138

& (stocker) ................................................139

:= (assigner) .............................................. 139

0b, 0h ........................................................ 140

Codes et messages d'erreur Informations sur les services et la

garantie TI

Guide de référence TI-Nspire™

Ce guide fournit la liste des modèles, fonctions, commandes et opérateurs disponibles pour le calcul d'expressions mathématiques.

CAS

Modèles d'expression

Les modèles d'expression facilitent la saisie d'expressions mathématiques en notation standard. Lorsque vous utilisez un modèle, celui-ci s'affiche sur la ligne de saisie, les petits carrés correspondants aux éléments que vous pouvez saisir. Un curseur identifie l'élément que vous pouvez saisir.

Utilisez les touches fléchées ou appuyez sur

puis tapez la valeur ou l'expression correspondant à chaque élément. Appuyez sur

e pour déplacer le curseur sur chaque élément,

· ou

/· pour calculer l'expression.

Modèle Fraction

Exemple :

Remarque : Voir aussi / (division), page 124.

Touches /p

Modèle Exposant

Remarque : Tapez la première valeur, appuyez sur l, puis

entrez l'exposant. Pour ramener le curseur sur la ligne de base, appuyez sur la flèche droite (¢).

Remarque : Voir aussi ^ (puissance), page 124.

Modèle Racine carrée

Remarque : Voir aussi

Modèle Racine n-ième

Remarque : Voir aussi root(), page 86.

‡

() (racine carrée), page 131.

Touche l

Exemple :

Touches /q

Exemple :

Touches /l

Exemple :

Guide de référence TI-Nspire™ CAS 1

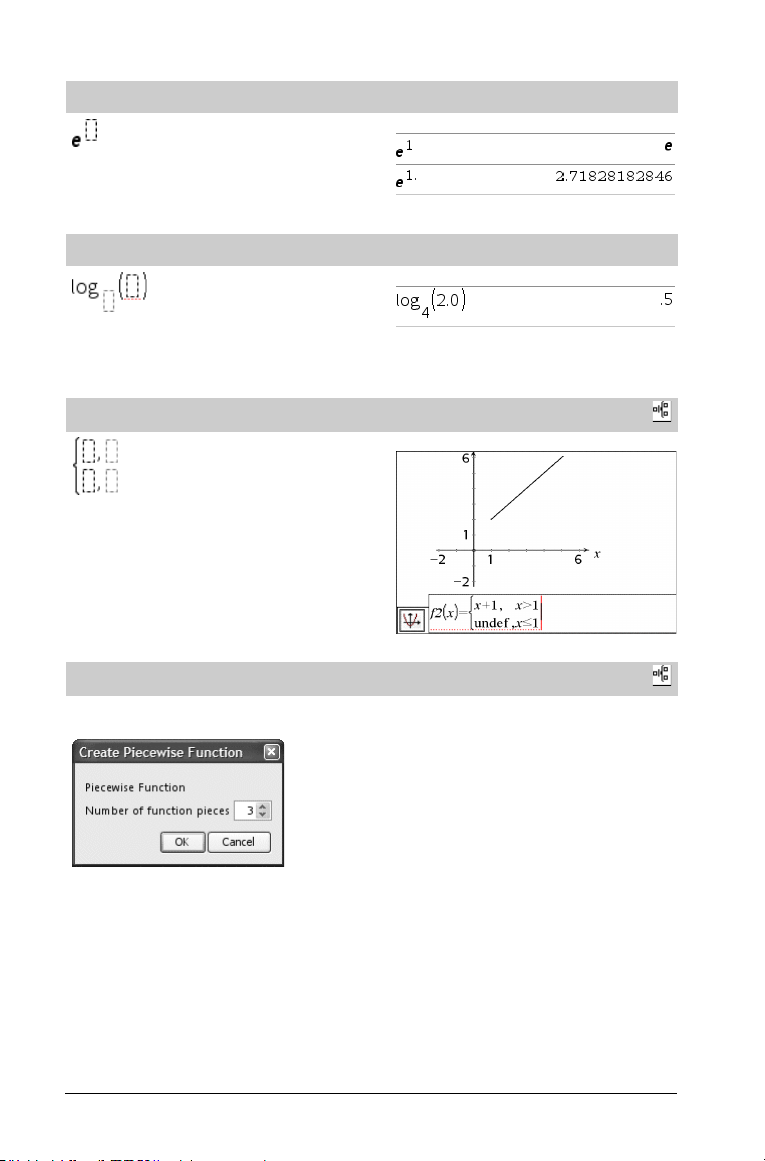
Modèle e Exposant

La base du logarithme népérien e élevée à une puissance

Remarque : Voir aussi e^(), page 35.

Touches u

Exemple :

Modèle Logarithme

Calcule le logarithme selon la base spécifiée. Par défaut la base est 10, dans ce cas ne spécifiez pas de base.

Remarque : Voir aussi log(), page 58.

Modèle Fonction définie par morceaux (2 morceaux)

Permet de créer des expressions et des conditions pour une fonction définie par deux morceaux.- Pour ajouter un morceau supplémentaire, cliquez dans le modèle et appliquez-le de nouveau.

Remarque : Voir aussi piecewise(), page 74.

Modèle Fonction définie par morceaux (n morceaux)

Permet de créer des expressions et des conditions pour une fonction définie par n- morceaux. Le système vous invite à définir n.

Touches /s

Exemple :

Catalogue >

Exemple :

Catalogue >

Exemple : Voir l'exemple donné pour le modèle Fonction définie par morceaux (2 morceaux).

Remarque : Voir aussi piecewise(), page 74.

2 Guide de référence TI-Nspire™ CAS

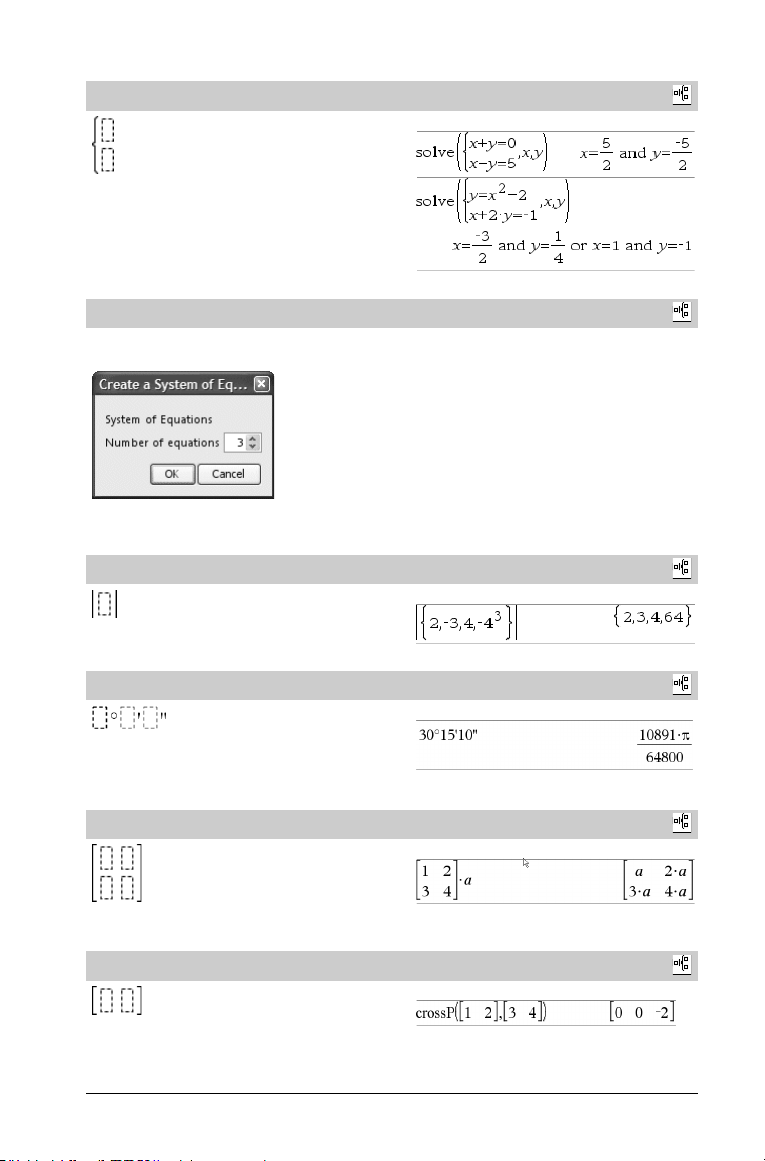
Modèle Système de 2 équations

Crée un système de deux équations. Pour ajouter une nouv elle ligne à un système existant, cliquez dans le modèle et appliquez-le de nouveau.

Remarque : Voir aussi system(), page 103.

Catalogue >

Exemple :

Modèle Système de n équations

Permet de créer un système de n équations. Le système vous invite à définir n.

Remarque : Voir aussi system(), page 103.

Modèle Valeur absolue

Remarque : Voir aussi abs(), page 6.

Modèle dd°mm’ss.ss’’

Permet d'entrer des angles en utilisant le format dd°mm’ss.ss’’, où

dd correspond au nombre de degrés décimaux, mm au nombre de

minutes et ss.ss au nombre de secondes.

Modèle Matrice (2 x 2)

Catalogue >

Exemple : Voir l'exemple donné pour le modèle Système de 2 équations.

Catalogue >

Exemple :

Catalogue >

Exemple :

Catalogue >

Exemple :

Crée une matrice de type 2 x 2.

Modèle Matrice (1 x 2)

Exemple :

Catalogue >

Guide de référence TI-Nspire™ CAS 3

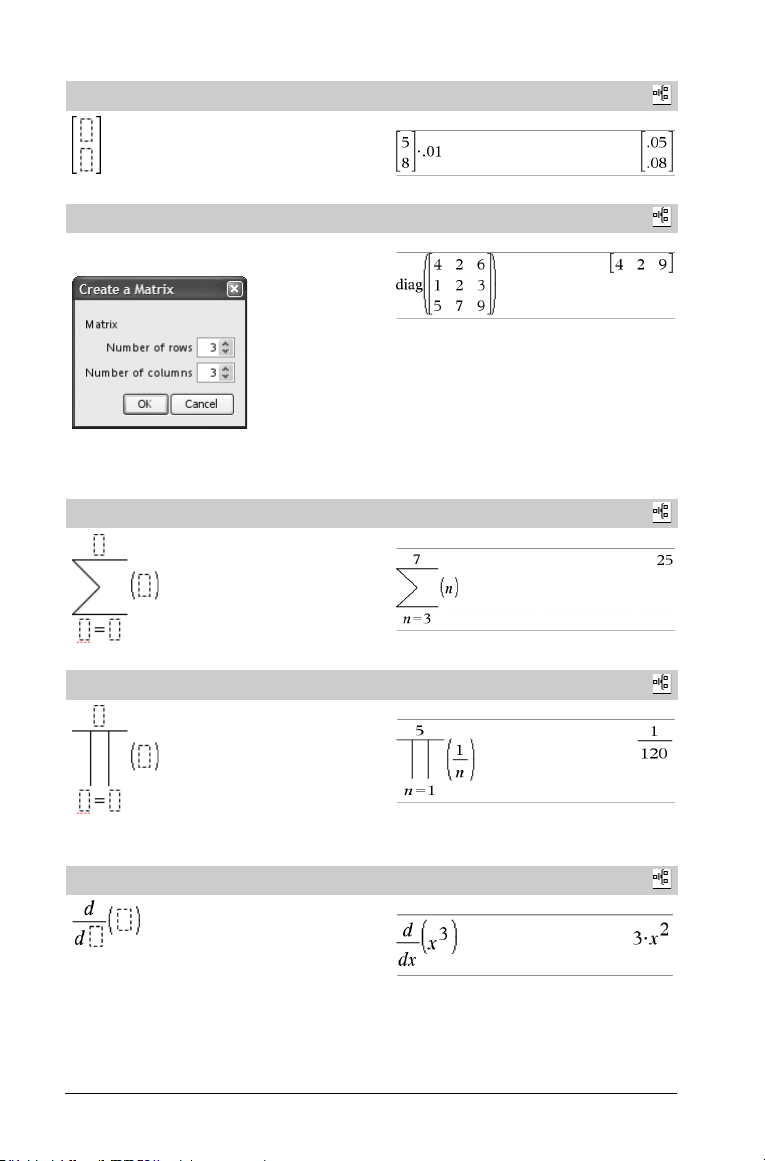
Modèle Matrice (2 x 1)

Catalogue >

Exemple :

Modèle Matrice (m x n)

Le modèle s'affiche après que vous ayez saisi le nombre de lignes et de colonnes.

Remarque : si vous créez une matrice dotée de nombreuses lignes et colonnes, son affichage peut prendre quelques minutes.

Modèle Somme (G)

Modèle Produit (Π)

Catalogue >

Exemple :

Catalogue >

Exemple :

Catalogue >

Exemple :

Remarque : Voir aussi Π() (produit), page 132.

Modèle Dérivée première

Remarque : Voir aussi

d() (dérivée)

Exemple :

, page 130.

Catalogue >

4 Guide de référence TI-Nspire™ CAS

Modèle Dérivée n-ième

Catalogue >

Exemple :

Remarque : Voir aussi

d() (dérivée)

, page 130.

Modèle Intégrale définie

Remarque : Voir aussi ‰() integrate(), page 130.

Modèle Intégrale indéfinie

Remarque : Voir aussi ‰() integrate(), page 130.

Modèle Limite

Utilisez N ou (N) pour définir la limite à gauche et la touche + pour la limite à droite.

Remarque : Voir aussi limit(), page 53.

Catalogue >

Exemple :

Catalogue >

Exemple :

Catalogue >

Exemple :

Guide de référence TI-Nspire™ CAS 5

Liste alphabétique

Les éléments dont le nom n'est pas alphabétique (comme +, !, et >) apparaissent à la fin de cette section, à partir de la page 122. Sauf indication contraire, tous les exemples fournis dans cette section ont été réalisés en mode de réinitialisation par défaut et toutes les variables sont considérées comme indéfinies.

abs()

abs(Expr1) ⇒ expression abs(

Liste1) ⇒ liste

abs(Matrice1) ⇒ matrice

Donne la valeur absolue de l'argument.

Remarque : Voir aussi Modèle Valeur absolue, page 3.

Si l'argument est un nombre complexe, donne le module de ce nombre.

Remarque : toutes les variables non affectées sont considérées

comme réelles.

amortTbl()

amortTbl(NPmt,N,I,PV, [Pmt], [FV], [PpY], [CpY], [PmtAt],

[

valArrondi]) ⇒ matrice

Fonction d'amortissement affichant une matrice représentant un tableau d'amortissement pour un ensemble d'arguments TVM.

NPmt est le nombre de versements à inclure au tableau. Le tableau commence avec le premier versement.

N, I, PV, Pmt, FV, PpY, CpY et PmtAt sont décrits dans le tableau des arguments TVM, page 112.

• Si vous omettez Pmt, il prend par défaut la valeur Pmt=tvmPmt(N,I,PV,FV,PpY,CpY,PmtAt).

• Si vous omettez FV, il prend par défaut la valeur FV=0.

• Les valeurs par défaut pour PpY, CpY et PmtAt sont les mêmes que pour les fonctions TVM.

valArrondi spécifie le nombre de décimales pour arrondissement. Valeur par défaut=2.

Les colonnes dans la matrice résultante apparaissent dans l'ordre suivant : Numéro de versement, montant versé pour les intérêts, montant versé pour le capital et solde.

Le solde affiché à la ligne n correspond au solde après le versement n. Vous pouvez utiliser la matrice de sortie pour insérer les valeurs des

autres fonctions d'amortissement GInt() et GPrn(), page 133 et

bal(), page 12.

Catalogue

and

Expr booléenne1 and Expr booléenne2

⇒ Expression booléenne

Liste booléenne1 et Liste booléenne2 ⇒ Liste booléenne Matrice booléenne1 et Matrice booléenne2 ⇒ Matrice booléenne

Donne true (vrai) ou false (faux) ou une forme simplifiée de l'entrée initiale.

Catalogue

6 Guide de référence TI-Nspire™ CAS

and

Entier1 et Entier2 ⇒ entier

Compare les représentations binaires de deux entiers réels en appliquant un convertis en nombres binaires 64 bits signés. Lorsque les bits comparés correspondent, le résultat est 1 si dans les de ux cas il s'agit d'un bit 1 ; dans les autres cas, le résultat est 0. La valeur donnée représente le résultat des bits et elle est affichée selon le mode Base utilisé.

Les entiers de tout type de base sont admis. Pour une entrée binaire ou hexadécimale, vous devez utiliser respectivement le préfixe 0b ou 0h. Tout entier sans préfixe est considéré comme un nombre en écriture décimale (base 10).

Si vous entrez un nombre dont le codage binaire signé dépasse 64 bits, il est ramené à l'aide d'une congruence dans la plage appropriée.

and bit à bit. En interne, les deux entiers sont

Catalogue

En mode base Hex :

Important : utilisez le chiffre zéro et pas la lettre O.

En mode base Bin :

En mode base Dec :

Remarque : une entrée binaire peut comporter jusqu'à 64

chiffres (sans compter le préfixe 0b) ; une entrée hexadécimale jusqu'à 16 chiffres.

angle()

angle(Expr1) ⇒ expression

Donne l'argument de l'expression passée en paramètre, celle-ci étant interprétée comme un nombre complexe.

Remarque : toutes les variables non affectées sont considérées

comme réelles.

angle(Liste1) ⇒ liste angle(Matrice1) ⇒ matrice

Donne la liste ou la matrice des arguments des éléments de Liste1 ou Matrice1, où chaque élément est interprété comme un nombre

complexe représentant un point de coordonnée rectangulaire à deux dimensions.

ANOVA

ANOVA Liste1,Liste2[,Liste3,...,Liste20][,Indicateur]

Effectue une analyse unidirectionnelle de variance pour comparer les moyennes de deux à vingt populations. Un récapitulatif du résultat est stocké dans la variable stat.results. (Voir page 100.)

Indicateur=0 pour Données, Indicateur=1 pour Stats

En mode Angle en degrés :

En mode Angle en grades :

En mode Angle en radians :

Catalogue

Variable de sortie Description

stat.F Valeur de F statistique

stat.PVal Plus petite probabilité permettant de rejeter l'hypothèse nulle

stat.df Degré de liberté des groupes

Guide de référence TI-Nspire™ CAS 7

Variable de sortie Description

stat.SS Somme des carrés des groupes

stat.MS Moyenne des carrés des groupes

stat.dfError Degré de liberté des erreurs

stat.SSError Somme des carrés des erreurs

stat.MSError Moyenne des carrés des erreurs

stat.sp Écart-type du groupe

stat.xbarlist Moyenne des entrées des listes

stat.CLowerList Limites inférieures des intervalles de confiance de 95 % pour la moyenne de chaque liste d'entrée

stat.CUpperList Limites supérieures des intervalles de confiance de 95 % pour la moyenne de chaque liste d'entrée

ANOVA2way

ANOVA2way Liste1,Liste2[,…[,Liste10]][,NivLign]

Effectue une analyse de variance à deux facteurs pour comparer les moyennes de deux à vingt populations. Un récapitulatif du résultat est stocké dans la variable stat.results. (Voir page 100.)

NivLign=0 pour Bloc

NivLign=2,3,...,Len-1, pour 2 facteurs, où Long=length(Liste1)=length(Liste2) = … = length(Liste10) et Long / NivLign ∈ {2,3,…}

Sorties : Bloc

Variable de sortie Description

stat.FF statistique du facteur de colonne

stat.PVal Plus petite probabilité permettant de rejeter l'hypothèse nulle

stat.df Degré de liberté du facteur de colonne

stat.SS Somme des carrés du facteur de colonne

stat.MS Moyenne des carrés du facteur de colonne

stat.FBlock F statistique du facteur

stat.PValBlock Plus petite probabilité permettant de rejeter l'hypothèse nulle

stat.dfBlock Degré de liberté du facteur

stat.SSBlock Somme des carrés du facteur

stat.MSBlock Moyenne des carrés du facteur

stat.dfError Degré de liberté des erreurs

stat.SSError Somme des carrés des erreurs

stat.MSError Moyenne des carrés des erreurs

stat.s Écart-type de l'erreur

Catalogue

8 Guide de référence TI-Nspire™ CAS

Sorties FACTEUR DE COLONNE

Variable de sortie Description

stat.Fcol F statistique du facteur de colonne

stat.PValCol Valeur de probabilité du facteur de colonne

stat.dfCol Degré de liberté du facteur de colonne

stat.SSCol Somme des carrés du facteur de colonne

stat.MSCol Moyenne des carrés du facteur de colonne

Sorties FACTEUR DE LIGNE

Variable de sortie Description

stat.Frow F statistique du facteur de ligne

stat.PValRow Valeur de probabilité du facteur de ligne

stat.dfRow Degré de liberté du facteur de ligne

stat.SSRow Somme des carrés du facteur de ligne

stat.MSRow Moyenne des carrés du facteur de ligne

Sorties INTERACTION

Variable de sortie Description

stat.FInteract F statistique de l'interaction

stat.PValInteract Valeur de probabilité de l'interaction

stat.dfInteract Degré de liberté de l'interaction

stat.SSInteract Somme des carrés de l'interaction

stat.MSInteract Moyenne des carrés de l'interaction

Sorties ERREUR

Variable de sortie Description

stat.dfError Degré de liberté des erreurs

stat.SSError Somme des carrés des erreurs

stat.MSError Moyenne des carrés des erreurs

s Écart-type de l'erreur

Guide de référence TI-Nspire™ CAS 9

ans

ans ⇒ valeur

Donne le résultat de la dernière expression calculée.

Touches

approx()

approx(Expr1) ⇒ expression

Donne une approximation décimale de l'argument sous forme d'expression, dans la mesure du possible, indépendamment du mode

Auto ou Approché utilisé.

Ceci est équivalent à la saisie de l'argument suivie d'une pression sur

·.

approx(Liste1) ⇒ liste approx(Matrice1) ⇒ matrice

Donne une liste ou une matrice d'éléments pour lesquels une approximation décimale a été calculée, dans la mesure du possible.

approxRational()

approxRational(Expr1[, tol]) ⇒ expression approxRational(Liste1[, tol]) ⇒ liste approxRational(Matrice1[, tol]) ⇒ matrice

Donne l'argument sous forme de fraction en utilisant une tolérance tol. Si tol est omis, la tolérance 5.E-14 est utilisée.

arcLen()

arcLen(Expr1,Var ,Début,Fin) ⇒ expression

Donne la longueur de l'arc de la courbe définie par Expr1 entre les points d'abscisses Début et Fin en fonction de la variable Va r .

La longueur d'arc est calculée sous forme d'intégrale e n supposant la définition du mode fonction.

Catalogue

arcLen(Liste1,Var ,Début,Fin) ⇒ liste

Donne la liste des longueurs d'arc de chaque élément de Liste1 entre les points d'abscisses Début et Fin en fonction de la variable Va r .

10 Guide de référence TI-Nspire™ CAS

augment()

augment(Liste1, Liste2) ⇒ liste

Donne une nouvelle liste obtenue en plaçant les éléments de Liste2 à la suite de ceux de Liste1.

augment(Matrice1, Matrice2) ⇒ matrice

Donne une nouvelle matrice obtenue en ajoutant les lignes/colonnes de la Matrice2 à celles de la Matrice1. Les matrices doivent avoir le même nombre de lignes et Matrice2 est ajoutée à Matrice1 via la création de nouvelles colonnes. Matrice1 et Matrice2 ne sont pas modifiées.

Catalogue

avgRC()

avgRC(Expr1, Va r [=valeur] [, H]) ⇒ expression

Donne le taux d'accroissement moyen (quotient à différence antérieure) de l'expression.

Expr1 peut être un nom de fonction défini par l'utilisateur (voir

Func).

Si valeur est spécifiée, celle-ci prévaut sur toute affectation de variable ou substitution précédente de type “sachant que” pour la variable.

H correspond à la valeur de l'incrément. Si H n'est pas précisé, il est fixé par défaut à 0.001.

Notez que la fonction comparable nDeriv() utilise le quotient à différence symétrique.

Catalogue

Guide de référence TI-Nspire™ CAS 11

bal()

bal(NPmt,N,I,PV ,[Pmt], [FV], [PpY], [CpY], [PmtAt],

[

valArrondi]) ⇒ valeur

bal(NPmt,tblAmortissement) ⇒ valeur

Fonction d'amortissement destinée à calculer le solde après versement d'un montant spécifique.

N, I, PV, Pmt, FV, PpY, CpY et PmtAt sont décrits dans le tableau des arguments TVM, page 112.

NPmt indique le numéro de versement après lequel vous souhaitez que les données soient calculées.

N, I, PV, Pmt, FV, PpY, CpY et PmtAt sont décrits dans le tableau des arguments TVM, page 112.

• Si vous omettez Pmt, il prend par défaut la valeur Pmt=tvmPmt(N,I,PV,FV,PpY,CpY,PmtAt).

• Si vous omettez FV, il prend par défaut la valeur FV=0.

• Les valeurs par défaut pour PpY, CpY et PmtAt sont les mêmes que pour les fonctions TVM.

valArrondi spécifie le nombre de décimales pour arrondissement. Valeur par défaut=2.

bal(NPmt,tblAmortissement) calcule le solde après le numéro de

paiement NPmt, sur la base du tableau d'amortissement tblAmortissement. L'argument tblAmortissement doit être une matrice au format décrit à tblAmortissement(), page 6.

Remarque : voir également GInt() et GPrn(), page 133.

Base2

Entier1 4Base2 ⇒ entier

Convertit Entier1 en nombre binaire. Les nombres binaires et les nombres hexadécimaux présentent toujours respectivement un préfixe, 0b ou 0h.

0b nombreBinaire 0h nombreHexadécimal

Zéro et pas la lettre O, suivi de b ou h. Une entrée binaire peut comporter jusqu'à 64 chiffres (sans compter

le préfixe 0b) ; une entrée hexadécimale jusqu'à 16 chiffres. Si Entier1 est entré sans préfixe, il est considéré comme un nombre

en écriture décimale (base 10). Le résultat est affiché sous forme binaire, indépendamment du mode Base utilisé.

Si vous entrez un nombre dont le codage binaire signé dépasse 64 bits, il est ramené à l'aide d'une congruence dans la plage appropriée.

Catalogue

12 Guide de référence TI-Nspire™ CAS

Base10

4Base10 ⇒ entier

Entier1

Convertit Entier1 en un nombre décimal (base 10). Toute entrée binaire ou hexadécimale doit avoir respectivement un préfixe 0b ou 0h.

0b nombreBinaire 0h nombreHexadécimal

Zéro et pas la lettre O, suivi de b ou h. Une entrée binaire peut comporter jusqu'à 64 chiffres (sans compter

le préfixe 0b) ; une entrée hexadécimale jusqu'à 8 chiffres. Sans préfixe, Entier1 est considéré comme décimal. Le résultat est

affiché en base décimale, quel que soit le mode Base en cours d'utilisation.

Base16

Entier1 4Base16 ⇒ entier

Convertit Entier1 en nombre hexadécimal. Les nombres binaires et les nombres hexadécimaux présentent toujours respectivement un préfixe, 0b ou 0h.

0b nombreBinaire 0h nombreHexadécimal

Zéro et pas la lettre O, suivi de b ou h. Une entrée binaire peut comporter jusqu'à 64 chiffres (sans compter

le préfixe 0b) ; une entrée hexadécimale jusqu'à 16 chiffres. Si Entier1 est entré sans préfixe, il est considéré comme un nombre

en écriture décimale (base 10). Le résultat est affiché sous forme hexadécimal, indépendamment du mode Base utilisé.

Si vous entrez un nombre dont le codage binaire signé dépasse 64 bits, il est ramené à l'aide d'une congruence dans la plage appropriée.

Catalogue

binomCdf()

binomCdf(n,p) ⇒ nombre binomCdf(n,p,LimitInf) ⇒ nombre si LimitInf est un nombre,

liste si LimitInf est une liste

binomCdf(

LimitSup sont des nombres, liste si LimitInf et LimitSup sont

des listes

Calcule la fonction de répartition d'une loi binomiale discrèt e avec un nombre n d'essais et une probabilité p de réussite pour chaque essai. Si ValX est omis, donne la liste des probabilités de la loi binomiale de paramètres n et p.

binomPdf()

binomPdf(n,p) ⇒ nombre binomPdf(n,p,Va lX ) ⇒ nombre si Va l X est un nombre, liste si

Val X est une liste

Calcule la probabilité de Va lX pour la loi binomiale discrète avec un nombre n d'essais et la probabilité p de réussite pour chaque essai.

n,p,LimitInf,LimitSup) ⇒ nombre si LimitInf et

Catalogue

Guide de référence TI-Nspire™ CAS 13

ceiling()

ceiling(Expr1) ⇒ entier

Donne le plus petit entier ‚ à l'argument.

L'argument peut être un nombre réel ou un nombre complexe.

Remarque : Voir aussi floor().

ceiling(Liste1) ⇒ liste ceiling(Matrice1) ⇒ matrice

Donne la liste ou la matrice de plus petites valeurs supérieures ou égales à chaque élément.

cFactor()

cFactor(Expr1[,Var ]) ⇒ expression cFactor(Liste1[,Va r]) ⇒ liste cFactor(Matrice1[,Var ]) ⇒ matrice

cFactor(Expr1) factorise Expr1 dans C en fonction de toutes ses

variables et sur un dénominateur commun. La factorisation de Expr1 décompose l'expression en autant de

facteurs rationnels linéaires que possible même si cela introduit de nouveaux nombres non réels. Cette alternative peut s'avérer utile pour factoriser l'expression en fonction de plusieurs variables.

cFactor(Expr1,Var ) factorise Expr1 dans C en fonction de la

variable Var . La factorisation de Expr1 décompose l'expression en autant de

facteurs possible qui sont linéaires dans Va r, avec peut-être des constantes non réelles, même si cela introduit des constantes irrationnelles ou des sous-expressions qui sont irrationnelles dans d'autres variables.

Les facteurs et leurs termes sont triés, Var étant la variable principale. Les mêmes puissances de Va r sont regroupées dans chaque facteur. Incluez Va r si la factorisation ne doit s'effectuer que par rapport à cette variable et si vous acceptez les expressions irrationnelles dans les autres variables pour augmenter la factorisation par rapport à Va r . Une factorisation incidente peut se produire par rapport aux autres variables.

Avec le réglage Auto du mode Auto ou Approché

(Approximate)

approximation avec des coefficients en virgule flottante dans le cadre de laquelle les coefficients irrationnels ne peuvent pas être exprimés explicitement suivant les termes des fonctions intégrées. Même en présence d'une seule variable, l'utilisation de Va r peut contribuer à une factorisation plus complète.

Remarque : voir aussi factor().

l'utilisation de Va r permet également une

Catalogue

Pour afficher le résultat entier, appuyez sur £, puis utilisez les touches ¡ et ¢ pour déplacer le curseur.

char()

char(Entier) ⇒ caractère

Donne le caractère dont le code dans le jeu de caractères de l'unité nomade est Entier. La plage valide pour Entier est comprise entre 0 et 65535.

Catalogue

14 Guide de référence TI-Nspire™ CAS

2way

2way MatriceObservée

chi22way MatriceObservée

Effectue un test matrice observée MatriceObservée. Un récapitulatif du résultat est stocké dans la variable stat.results. (Voir page 100.)

d'association sur le tableau 2*2 de valeurs dans la

Variable de sortie Description

stat.c2 Stats Khi2 : sum(observée - attendue)2/attendue

stat.PVal Plus petite probabilité permettant de rejeter l'hypothèse nulle

stat.df

Degré de liberté des statistiques khi

stat.ExpMat Matrice du tableau de valeurs élémentaires attendues, acceptant l'hypothèse nulle

stat.CompMat

Cdf()

Cdf(LimitInf,LimitSup,df) ⇒ nombre si LimitInf et LimitSup

sont des nombres,

chi2Cdf(

LimitInf,LimitSup,df) ⇒ nombre si LimitInf et

LimitSup sont des nombres, liste si LimitInf et LimitSup sont

des listes

Calcule la fonction de répartition de la loi c2 à df degrés de liberté entre LimitInf et LimitSup.

GOF

GOF ListeObservée,ListeAttendue,df

chi2GOF ListeObservée,ListeAttendue,df

Effectue un test pour s'assurer que les données des échantillons sont issues d'une population conforme à la loi spécifiée. Un récapitulatif du résultat est stocké dans la variable stat.results. (Voir page 100.)

Matrice des contributions statistiques khi2 élémentaires

liste si LimitInf et LimitSup sont des listes

Catalogue

Variable de sortie Description

stat.c2 Stats Khi2 : sum(observée - attendue)2/attendue

stat.PVal Plus petite probabilité permettant de rejeter l'hypothèse nulle

stat.df

stat.CompList

Degré de liberté des statistiques khi

Contributions statistiques khi2 élémentaires

Guide de référence TI-Nspire™ CAS 15

Pdf()

Pdf(Val X ,df) ⇒ nombre si Va lX est un nombre, liste si Va l X

est une liste

chi2Pdf(

Val X ,df) ⇒ nombre si Va lX est un nombre, liste si

Val X est une liste

Calcule la densité de probabilité (pdf) de la loi c2 à df degrés de liberté en une valeur Va l X spécifiée.

Catalogue

clearAZ

Supprime toutes les variables à une lettre de l'activité courante.

ClrErr

Efface le statut d'erreur et règle la variable système errCode sur zéro. L'instruction Else du bloc Try...Else...EndTry doit utiliser EffErr

ou PassErr. Si vous comptez rectifier ou ignorer l'erreur, sélectionnez EffErr. Si vous ne savez pas comment traiter l'erreur, sélectionnez PassErr pour la transférer au traitement d'erreurs suivant. S'il n'y a plus d'autre traitement d'erreurs

Try...Else...EndTry

normalement.

Remarque : voir également PassErr, page 74 et Try, page 109. Remarque pour la saisie des données de l'exemple :

dans l'application Calculs de l'unité nomade, vous pouvez entrer des définitions sur plusieurs lignes en appuyant sur @ à la place de

, la boîte de dialogue Erreur s'affiche

· à chaque fin de ligne. Sur le clavier de l'ordinateur, maintenez

enfoncée la touche Alt tout en appuyant sur Entrée (Enter).

colAugment()

colAugment(Matrice1, Matrice2) ⇒ matrice

Donne une nouvelle matrice obtenue en ajoutant les lignes/colonnes de la Matrice2 à celles de la Matrice1. Les matrices doivent avoir le même nombre de colonnes et Matrice2 est ajou tée à Matrice1 via la création de nouvelles lignes. Matrice1 et Matrice2 ne sont pas modifiées.

Catalogue

Pour obtenir un exemple de ClrErr, reportez-vous à l'exemple 2 de la commande Try , page 110.

Catalogue

colDim()

colDim(Matrice) ⇒ expression

Donne le nombre de colonnes de la matrice Matrice.

Remarque : voir aussi rowDim().

Catalogue

16 Guide de référence TI-Nspire™ CAS

colNorm()

colNorm(Matrice) ⇒ expression

Donne le maximum des sommes des valeurs absolues des éléments situés dans chaque colonne de la matrice Matrice.

Remarque : les éléments non définis de matrice ne sont pas

autorisés. Voir aussi

rowNorm().

Catalogue

comDenom()

comDenom(Expr1[,Va r]) ⇒ expression comDenom(Liste1[,Var ]) ⇒ liste comDenom(Matrice1[,Var ]) ⇒ matrice

comDenom(Expr1) donne le rapport réduit d'un numérateur

entièrement développé sur un dénominateur entièrement développement.

comDenom(Expr1,Va r) donne le rapport réduit d'un numérateur

et d'un dénominateur développé par rapport à Va r . Les termes et leurs facteurs sont triés, Va r étant la variable principale. Les mêmes puissances de Va r sont regroupées. Une factorisation incidente des coefficients regroupés peut se produire. L'utilisation de Va r permet de gagner du temps, de la mémoire et de l'espace sur l'écran tout en facilitant la lecture de l'expression. Les opérations suivantes basées sur le résultat obtenu sont également plus rapides et moins consommatrices de mémoire.

Si Var n'intervient pas dans Expr1, comDenom(Expr1,Va r ) donne le rapport réduit d'un numérateur non développé sur un dénominateur non développé. Ce type de résultat offre généralement un gain de temps, de mémoire et d'espace sur l'écran. La factorisation partielle du résultat contribue également à accélérer les opérations suivantes basées sur le résultat et à utiliser moins de mémoire.

Même en l'absence de tout dénominateur, la fonction comden permet d'obtenir rapidement une factorisation partielle si la fonction

factor() est trop lente ou si elle utilise trop de mémoire. Conseil : entrez cette définition de la fonction comden() et

utilisez-la régulièrement comme solution alternative à

comDenom() et à factor().

Catalogue

conj()

conj(Expr1) ⇒ expression conj(Liste1) ⇒ liste conj(Matrice1) ⇒ matrice

Catalogue

Donne le conjugué de l'argument.

Remarque : toutes les variables non affectées sont considérées

comme réelles.

Guide de référence TI-Nspire™ CAS 17

CopyVar

CopyVar Var 1 , Va r 2

Si Va r1 correspond au nom d'une variable existante, copie la valeur de cette variable dans variable Var 2. La variable Va r 1 doit avoir une valeur.

Si Va r1 correspond au nom d'une fonction existante définie par l'utilisateur, copie la définition de cette fonction dans la fonction

Var 2 . La fonction Va r 1 doit être définie. Var 1 doit être conforme aux règles de dénomination des variables ou

correspondre à une expression d'indirection correspondant à un nom de variable conforme à ces règles.

Catalogue

corrMat()

corrMat(Liste1,Liste2[,…[,Liste20]])

Calcule la matrice de corrélation de la matrice augmentée [Liste1 Liste2 ... List20].

cos()

cos(Expr1) ⇒ expression cos(Liste1) ⇒ liste

cos(Expr1) calcule le cosinus de l'argument et l'affiche sous forme

d'expression.

cos(Liste1) donne la liste des cosinus des éléments de Liste1. Remarque : l'argument est interprété comme la mesure d'un angle

en degrés, en grades ou en radians, suivant le mode angulaire en cours d'utilisation. Vous pouvez utiliser ó,G ou ô pour préciser

l'unité employée temporairement pour le calcul.

En mode Angle en degrés :

En mode Angle en grades :

En mode Angle en radians :

Catalogue

Touche n

18 Guide de référence TI-Nspire™ CAS

cos()

cos(matriceCarrée1) ⇒ matriceCarrée

Calcule le cosinus de la matrice matriceCarrée1. Ce calcul est différent du calcul du cosinus de chaque élément.

Si une fonction scalaire f(A) opère sur matriceCarrée1 (A), le résultat est calculé par l'algorithme suivant :

Calcul des valeurs propres (li) et des vecteurs propres (Vi) de A.

matriceCarrée1 doit être diagonalisable et ne peut pas présenter de variables symboliques sans valeur affectée.

Formation des matrices :

Alors A = X B Xêet f(A) = X f(B) Xê. Par exemple, cos(A) = X cos(B) Xê où :

cos (B) =

Tous les calculs sont exécutés en virgule flottante.

Touche n

En mode Angle en radians :

cosê()

cosê(Expr1) ⇒ expression cosê(Liste1) ⇒ liste

cosê(Expr1) donne l'arc cosinus de Expr1 et l'affiche sous forme

d'expression.

cosê(Liste1) donne la liste des arcs cosinus de chaque élément de

Liste1.

Remarque : donne le résultat en degrés, en grades ou en radians,

suivant le mode angulaire utilisé.

cosê(matriceCarrée1) ⇒ matriceCarrée

Donne l'arc cosinus de matriceCarrée1. Ce calcul est différent du calcul de l'arc cosinus de chaque élément. Pour plus d'informations sur la méthode de calcul, reportez-vous à cos().

matriceCarrée1 doit être diagonalisable. Le résultat contient toujours des chiffres en virgule flottante.

En mode Angle en degrés :

En mode Angle en grades :

En mode Angle en radians :

En mode Angle en radians et en mode Format complexe Rectangulaire :

Touches /n

Pour afficher le résultat entier, appuyez sur £, puis utilisez les touches ¡ et ¢ pour déplacer le curseur.

Guide de référence TI-Nspire™ CAS 19

cosh()

cosh(Expr1) ⇒ expression cosh(Liste1) ⇒ liste

cosh(Expr1) donne le cosinus hyperbolique de l'argument et

l'affiche sous forme d'expression.

cosh(Liste1) donne la liste des cosinus hyperboliques de chaque

élément de Liste1.

cosh(matriceCarrée1) ⇒ matriceCarrée

Donne le cosinus hyperbolique de la matrice matriceCarrée1. Ce calcul est différent du calcul du cosinus hyperbolique de chaque élément. Pour plus d'informations sur la méthode de calcul, reportez-

cos().

vous à matriceCarrée1 doit être diagonalisable. Le résultat contient

toujours des chiffres en virgule flottante.

En mode Angle en radians :

Catalogue

coshê()

coshê(Expr1) ⇒ expression coshê(List1) ⇒ liste

cosh

(Expr1) donne l'argument cosinus hyperbolique de

l'argument et l'affiche sous forme d'expression.

cosh

(Liste1) donne la liste des arguments cosinus hyperboliques

de chaque élément de Liste1.

coshê(matriceCarrée1) ⇒ matriceCarrée

Donne l'argument cosinus hyperbolique de la matrice matriceCarrée1. Ce calcul est différent du calcul de l'argument cosinus hyperbolique de chaque élément. Pour plus d'informations sur la méthode de calcul, reportez-vous à cos().

matriceCarrée1 doit être diagonalisable. Le résultat contient toujours des chiffres en virgule flottante.

cot()

cot(Expr1) ⇒ expression cot(Liste1) ⇒ liste

Affiche la cotangente de Expr1 ou retourne la liste des cotangentes des éléments de Liste1.

Remarque : l'argument est interprété comme la mesure d'un angle

en degrés, en grades ou en radians, suivant le mode angulaire en cours d'utilisation. Vous pouvez utiliser ó,G ou ô pour préciser

l'unité employée temporairement pour le calcul.

Catalogue

En mode Angle en radians et en mode Format complexe Rectangulaire :

Pour afficher le résultat entier, appuyez sur £, puis utilisez les touches ¡ et ¢ pour déplacer le curseur.

Catalogue

En mode Angle en degrés :

En mode Angle en grades :

En mode Angle en radians :

20 Guide de référence TI-Nspire™ CAS

cotê()

cotê(Expr1) ⇒ expression cotê(Liste1) ⇒ liste

Donne l'arc cotangente de Expr1 ou affiche une liste comportant les arcs cotangentes de chaque élément de Liste1.

Remarque : donne le résultat en degrés, en grades ou en radians,

suivant le mode angulaire utilisé.

En mode Angle en degrés :

En mode Angle en grades :

En mode Angle en radians :

Catalogue

coth()

coth(Expr1) ⇒ expression coth(Liste1) ⇒ liste

Affiche la cotangente hyperbolique de Expr1 ou donne la liste des cotangentes hyperboliques des éléments de Liste1.

cothê()

cothê(Expr1) ⇒ expression cothê(Liste1) ⇒ liste

Affiche l'argument cotangente hyperbolique de Expr1 ou donne la liste comportant les arguments cotangentes hyperboliques des éléments de Liste1.

count()

count(Valeur1ouListe1 [,Valeur2ouListe2[,...]]) ⇒ valeur

Affiche le nombre total des éléments dans les arguments qui s'évaluent à des valeurs numériques.

Un argument peut être une expression, une valeur, une liste ou une matrice. Vous pouvez mélanger les types de données et utiliser des arguments de dimensions différentes.

Pour une liste, une matrice ou une plage de cellules, chaque élément est évalué afin de déterminer s'il doit être inclus dans le comptage.

Dans l'application Tableur & listes, vous pouvez utiliser une plage de cellules à la place de n'importe quel argument.

Catalogue

Dans le dernier exemple, seuls 1/2 et 3+4*i sont comptabilisés. Les autres arguments, dans la mesure où x est indéfini, ne correspondent pas à des valeurs numériques.

Guide de référence TI-Nspire™ CAS 21

countif()

countif(Liste,Critère) ⇒ valeur

Affiche le nombre total d'éléments dans Liste qui répondent au critère spécifié.

Le critère peut être :

• Une valeur, une expression ou une chaîne. Par exemple, 3 compte uniquement les éléments dans Liste qui ont pour valeur

• Une expression booléenne contenant le symbole ? comme paramètre substituable à tout élément. Par exemple, ?<5 ne compte que les éléments dans Liste qui sont inférieurs à 5.

Dans l'application Tableur & listes, vous pouvez utiliser une plage de cellules à la place de Liste.

Remarque : voir également sumIf(), page 103 et frequency(),

page 44.

Catalogue

Compte le nombre d'éléments égaux à 3.

Compte le nombre d'éléments égaux à “def.”

Compte le nombre d'éléments égaux à x; cet exemple part du principe que la variable x est indéfinie.

Compte 1 et 3.

Compte 3, 5 et 7.

Compte 1, 3, 7 et 9.

crossP()

crossP(Liste1, Liste2) ⇒ liste

Donne le produit vectoriel de Liste1 et de Liste2 et l'affiche sous forme de liste.

Liste1 et Liste2 doivent être de même dimension et cette dimension doit être égale à 2 ou 3.

crossP(Vecteur1, Vecteur2) ⇒ vecteur

Donne le vecteur ligne ou le vecteur colonne (en fonction des arguments) obtenu en calculant le produit vectoriel de Vecteur1 et Vec t e u r2 .

Ces deux vecteurs, Vecteur1 et Vecteur2, doivent être de même type (ligne ou colonne) et de même dimension, cette dimension devant être égale à 2 ou 3.

csc()

csc(Expr1) ⇒ expression csc(Liste1) ⇒ liste

Affiche la cosécante de Expr1 ou donne une liste comportant les cosécantes de tous les éléments de Liste1.

En mode Angle en degrés :

En mode Angle en grades :

En mode Angle en radians :

Catalogue

22 Guide de référence TI-Nspire™ CAS

cscê()

cscê(Expr1) ⇒ expression cscê(Liste1) ⇒ liste

Affiche l'angle dont la cosécante correspond à Expr1 ou donne la liste des arcs cosécante de chaque élément de Liste1.

Remarque : donne le résultat en degrés, en grades ou en radians,

suivant le mode angulaire utilisé.

En mode Angle en degrés :

En mode Angle en grades :

En mode Angle en radians :

Catalogue

csch()

csch(Expr1) ⇒ expression csch(Liste1) ⇒ liste

Affiche la cosécante hyperbolique de Expr1 ou donne la liste des cosécantes hyperboliques de tous les éléments de Liste1.

cschê()

cschê(Expr1) ⇒ expression cschê(Liste1) ⇒ liste

Affiche l'argument cosécante hyperbolique de Expr1 ou donne la liste des arguments cosécantes hyperboliques de tous les éléments de Liste1.

cSolve()

cSolve(Équation, Va r ) ⇒ Expression booléenne cSolve(Inéquation, Va r ) ⇒ Expression booléenne

Résout dans C une équation ou une inéquation pour Va r . L'objectif est de trouver toutes les solutions réelles et non réelles possibles. Même si Équation est à coefficients réels, cSolve() autorise les résultats non réels en mode Format complexe : Réel.

Bien que toutes les variables non affectées dont le nom ne se termine pas par (_) soient considérées comme réelles, cSolve() permet de résoudre des systèmes d'équations polynomiales en utilisant des solutions complexes.

cSolve() définit temporairement le domaine sur complexe pendant

la résolution, même si le domaine courant est réel. Dans le domaine complexe, les puissances fractionnaires possédant un dénominateur impair utilisent la branche principale plutôt que la branche réelle. Par conséquent, les solutions de solve() pour les équations impliquant de telles puissances fractionnaires n'appartiennent pas nécessairement à un sous-ensemble de celles de cSolve().

Catalogue

Guide de référence TI-Nspire™ CAS 23

cSolve()

cSolve() commence la résolution en utilisant les méthodes

symboliques exactes. Excepté en mode Exact, cSolve() utilise aussi une factorisation itérative approchée des polynômes complexes, si nécessaire.

Remarque : voir aussi cZeros(), solve() et zeros(). Remarque : si Équation n'est pas polynomiale avec les fonctions

comme

abs(), angle(), conj(), real() ou imag(), ajoutez un

caractère de soulignement (en appuyant sur Var . Par défaut, les variables sont considérées comme réelles.

Si vous utilisez var_ , la variable est considérée comme complexe. Vous pouvez également utiliser var_ pour toutes les autres variables

de Équation pouvant avoir des valeurs non réelles. Sinon, vous risquez d'obtenir des solutions inattendues.

cSolve(Équation1 and Équation2 [and … ],

VarOuInit1, Var O u In i t 2 [, … ]}) ⇒ Expression booléenne

{

Donne les solutions complexes possibles d'un système d'équations algébriques, où chaque VarOuInit définit une variable dont vous cherchez la valeur.

Vous pouvez également spécifier une condition initiale pour les variables. Chaque VarOuInit doit utiliser le format suivant :

variable

– ou – variable = nombre réel ou non réel

Par exemple, x est autorisé, de même que x=3+i. Si toutes les équations sont polynomiales et si vous NE spécifiez PAS

de condition initiale, cSolve() utilise la méthode d'élimination lexicale Gröbner/Buchberger pour tenter de trouver toutes les solutions complexes.

Les solutions complexes peuvent combiner des solutions réelles et des solutions non réelles, comme illustré dans l'exemple ci-contre.

/_) à la fin de

Catalogue

En mode Afficher chiffres, Fixe 2 :

Pour afficher le résultat entier, appuyez sur £, puis utilisez les touches ¡ et ¢ pour déplacer le curseur.

z est considéré comme réel :

z_ est considéré comme complexe :

Remarque : les exemples suivants utilisent un caractère de

soulignement (obtenu en appuyant sur /_) pour que toutes les variables soient considérées comme complexes.

Pour afficher le résultat entier, appuyez sur £, puis utilisez les touches ¡ et ¢ pour déplacer le curseur.

Les systèmes d'équations polynomiales peuvent comporter des variables supplémentaires auxquelles aucune valeur n'est affectée, mais qui représentent des valeurs numériques données pouvant s'y substituer par la suite.

Pour afficher le résultat entier, appuyez sur £, puis utilisez les touches ¡ et ¢ pour déplacer le curseur.

24 Guide de référence TI-Nspire™ CAS

cSolve()

Vous pouvez également utiliser des variables qui n'apparaissent pas dans les équations. Ces solutions montrent comment des solutions peuvent dépendre de paramètres arbitraires de type ck, où k est un suffixe entier compris entre 1 et 255.

Pour les systèmes d'équations polynomiales, le temps de calcul et l'utilisation de la mémoire peuvent considérablement varier en fonction de l'ordre dans lequel les variables inconnues sont spécifiées. Si votre choix initial ne vous satisfait pas pour ces raisons, vous pouvez modifier l'ordre des variables dans les équations et/ou la liste des variables VarOuInit.

Si vous choisissez de ne pas spécifier de condition et s'il l'une des équations n'est pas polynomiale en l'une des variables, mais que toutes les équations sont linéaires par rapport à toutes les variables de solution inconnues, cSolve() utilise l'élimination gaussienne pour tenter de trouver toutes les solutions.

Si un système d'équations n'est pas polynomial par rapport à toutes ses variables ni linéaire par rapport aux inconnues, cSolve() cherche au moins une solution en utilisant la méthode itérative approchée. Pour cela, le nombre d'inconnues doit être égal au nombre d'équations et toutes les autres variables contenues dans les équations doivent pouvoir être évaluées à des nombres.

Une condition non réelle est souvent nécessaire pour la détermination d'une solution non réelle. Pour assurer une convergence correcte, la valeur utilisée doit être relativement proche de la solution.

Catalogue

Pour afficher le résultat entier, appuyez sur £, puis utilisez les touches ¡ et ¢ pour déplacer le curseur.

CubicReg

CubicReg X, Y[, [Fréq] [, Catégorie, Inclure]]

Effectue un ajustement polynomial de degré 3 et met à jour toutes les variables statistiques. Un récapitulatif du résultat est stocké dans la variable stat.results. (Voir page 100.)

Toutes les listes doivent comporter le même nombre de lignes, à l'exception de Inclure.

X représente la liste des valeurs de x. Y représente la liste des valeurs de y. Fréq représente la liste des fréquences. Catégorie représente les numéros de catégories. Inclure représente la liste des catégories à utiliser.

Variable de sortie Description

stat.RegEqn

stat.a, stat.b, stat.c, stat.d

stat.R

stat.Resid

stat.XReg Liste des points de données de la liste Liste X modifiée, actuellement utilisée dans l'ajustement basé sur

Équation d'ajustement : a·x3+b·x2+c·x+d

Coefficients d'ajustement

Coefficient de détermination

Valeurs résiduelles de l'ajustement des courbes = y - (a·x3+b·x2+c·x+d)

les restrictions de Fréq, Liste de catégories et Inclure les catégories

Catalogue

Guide de référence TI-Nspire™ CAS 25

Variable de sortie Description

stat.YReg Liste des points de données de la liste Liste Y modifiée, actuellement utilisée dans l'ajustement basé sur

stat.FreqReg Liste des fréquences correspondant à stat.XReg et stat.YReg

les restrictions de Fréq, Liste de catégories et Inclure les catégories

cumSum()

cumSum(Liste1) ⇒ liste

Donne la liste des sommes cumulées des éléments de Liste1, en commençant par le premier élément (élément 1).

cumSum(Matrice1) ⇒ matrice

Donne la matrice des sommes cumulées des éléments de Matrice1. Chaque élément correspond à la somme cumulée de tous les éléments situés au-dessus, dans la colonne correspondante.

Cycle

Procède au passage immédiat à l'itération suivante de la boucle courante (For, While ou Loop).

La fonction Cycle ne peut pas s'utiliser indépendamment de l'une

des trois structures de boucle (For, While ou Loop).

Remarque pour la saisie des données de l'exemple :

dans l'application Calculs de l'unité nomade, vous pouvez entrer des définitions sur plusieurs lignes en appuyant sur @ à la place de

· à chaque fin de ligne. Sur le clavier de l'ordinateur, maintenez

enfoncée la touche Alt tout en appuyant sur Entrée (Enter).

Catalogue

Liste de fonctions qui additionne les entiers compris entre 1 et 100, en sautant 50.

Cylind

Vec t e u r 4Cylind

Affiche le vecteur ligne ou colonne en coordonnées cylindriques [r,q, z].

Vec t e u r doit être un vecteur à trois éléments. Il peut s'agir d'un vecteur ligne ou colonne.

Catalogue

26 Guide de référence TI-Nspire™ CAS

cZeros()

cZeros(Expr, Va r ) ⇒ liste

Donne la liste des valeurs réelles et non réelles possibles de Va r qui annulent Expr. Pour y parvenir, cZeros() calcule

exp4list(cSolve(Expr=0,Var ),Va r ). Pour le reste, cZeros() est

comparable à zeros().

Remarque : voir aussi cSolve(), solve() et zeros().

Remarque : si Expr n'est pas polynomiale par rapport aux

fonctions comme abs(), angle(), conj(), real() ou imag(), vous pouvez utiliser un caractère de soulignement (obtenu e n appuyant sur

/_) à la fin du nom de Var . Par défaut, les variables sont

considérées comme réelles. Si vous utilisez var_, la variable est considérée comme complexe.

Vous pouvez également utiliser var_ pour les autres variables de Expr pouvant avoir des valeurs non réelles. Sinon, vous risquez d'obtenir des solutions inattendues.

cZeros({Expr1, Expr2 [, … ] },

VarOuInit1,Va r O uI n i t 2 [, … ] }) ⇒ matrice

{

Donne les valeurs possibles auxquelles les expressions s'annulent simultanément. Chaque VarOuInit définit une inconnue dont vous recherchez la valeur.

Vous pouvez également spécifier une condition initiale pour les variables. Chaque VarOuInit doit utiliser le format suivant :

variable

– ou –

variable = nombre réel ou non réel

Par exemple, x est autorisé, de même que x=3+i. Si toutes les expressions sont polynomiales et si vous NE spécifiez

PAS de condition initiale, cZeros() utilise la méthode d'élimination lexicale Gröbner/Buchberger pour tenter de trouver tous les zéros complexes.

Les zéros complexes peuvent combiner des zéros réels et des zéros non réels, comme illustré dans l'exemple ci-contre.

Chaque ligne de la matrice résultante représente un n_uplet, l'ordre des composants étant identique à celui de la liste VarOuInit. Pour extraire une ligne, indexez la matrice par [ligne].

Catalogue

En mode Afficher chiffres, Fixe 3 :

Pour afficher le résultat entier, appuyez sur touches ¡ et ¢ pour déplacer le curseur.

z est considéré comme réel :

z_ est considéré comme complexe :

Remarque : les exemples suivants utilisent un _ (obtenu en

appuyant sur /_) pour que toutes les variables soient considérées comme complexes.

£, puis utilisez les

Extraction ligne 2 :

Guide de référence TI-Nspire™ CAS 27

cZeros()

Vous pouvez également utiliser des inconnues qui n'apparaissent pas dans les expressions. Ces exemples montrent comment des ensembles de zéros peuvent dépendre de constantes arbitraires de type ck, où k est un suffixe entier compris entre 1 et 255.

Pour les systèmes d'équations polynomiales, le temps de calcul et l'utilisation de la mémoire peuvent considérablement varier en fonction de l'ordre dans lequel les inconnues sont spécifiées. Si votre choix initial ne vous satisfait pas pour ces raisons, vous pouvez modifier l'ordre des variables dans les expressions et/ou la liste VarOuInit.

Si vous choisissez de ne pas spécifier de condition et s'il l'une des expressions n'est pas polynomiale en l'une des variables, mais que toutes les expressions sont linéaires par rapport à toutes les inconnues, cZeros() utilise l'élimination gaussienne pour tenter de trouver tous les zéros.

Si un système d'équations n'est pas polynomial en toutes ses variables ni linéaire par rapport à ses inconnues, cZeros() cherche au moins un zéro en utilisant une méthode itérative approchée. Pour cela, le nombre d'inconnues doit être égal au nombre d'expressions et toutes les autres variables contenues dans les expressions doivent pouvoir être évaluées à des nombres.

Une condition non réelle est souvent nécessaire pour la détermination d'un zéro non réel. Pour assurer une convergence correcte, la valeur utilisée doit être relativement proche d'un zéro.

Catalogue

dbd()

dbd(date1,date2) ⇒ valeur

Calcule le nombre de jours entre date1 et date2 à l'aide de la méthode de calcul des jours.

date1 et date2 peuvent être des chiffres ou des listes de chiffres compris dans une plage de dates d'un calendrier normal. Si date1 et date2 sont toutes deux des listes, elles doivent être de la même longueur.

date1 et date2 doivent être comprises entre 1950 et 2049. Vous pouvez saisir les dates à l'un des deux formats. L'emplacement

de la décimale permet de distinguer les deux formats. MM.JJAA (format communément utilisé aux Etats-Unis)

JJMM.AA (format communément utilisé en Europe)

Catalogue

28 Guide de référence TI-Nspire™ CAS

4DD ⇒ valeur

Val e u r Liste1 4DD ⇒ liste Matrice1

4DD ⇒ matrice

Donne l'équivalent décimal de l'argument exprimé en degrés. L'argument est un nombre, une liste ou une matrice interprété suiva nt le mode Angle utilisé (grades, radians ou degrés).

En mode Angle en degrés :

En mode Angle en grades :

En mode Angle en radians :

Catalogue

4Decimal

Expr1

4Decimal

Liste1 Matrice1

Affiche l'argument sous forme décimale. Cet opérateur ne peut être utilisé qu'à la fin d'une ligne.

Define

Define Var = Expression Define Fonction(Param1, Param2, ...) = Expression

Définit la variable Va r ou la fonction définie par l'utilisateur Fonction.

Les paramètres, tels que Param1, sont des paramètres substituables utilisés pour transmettre les arguments à la fonction. Lors de l'appel d'une fonction définie par l'utilisateur, des arguments (par exemple, les valeurs ou variables) qui correspondent aux paramètres doivent être fournis. La fonction évalue ensuite Expression en utilisant les arguments fournis.

Var et Fonction ne peuvent pas être le nom d'une variable système ni celui d'une fonction ou d'une commande prédéfinie.

Remarque : cette utilisation de Define est équivalente à celle de

l'instruction : expression & Fonction(Param1,Param2).

Decimal

⇒ expression ⇒ expression

⇒ expression

Catalogue

Guide de référence TI-Nspire™ CAS 29

Define

Define Fonction(Param1, Param2, ...) = Func

Bloc

EndFunc

Programme(Param1, Param2, ...) = Prgm

Define

Bloc

EndPrgm

Dans ce cas, la fonction définie par l'utilisateur ou le programme permet d'exécuter plusieurs instructions (bloc).

Bloc peut correspondre à une instruction unique ou à une série d'instructions réparties sur plusieurs lignes. Bloc peut également contenir des expressions et des instructions (comme If, Then, Else et For).

Remarque pour la saisie des données de l'exemple :

dans l'application Calculs de l'unité nomade, vous pouvez entrer des définitions sur plusieurs lignes en appuyant sur @ à la place de

· à chaque fin de ligne. Sur le clavier de l'ordinateur, maintenez

enfoncée la touche Alt tout en appuyant sur Entrée (Enter).

Remarque : voir aussi Define LibPriv, page 30 et Define LibPub

, page 31.

Catalogue

Define LibPriv

Define LibPriv Var = Expression Define LibPriv Fonction(Param1, Param2, ...) = Expression

Define LibPriv Fonction(Param1, Param2, ...) = Func

Bloc

EndFunc Define LibPriv

Bloc

EndPrgm

S'utilise comme Define, mais permet de définir des objets (variables, fonctions, programmes) dans la bibliothèque privée. Les fonctions et programmes privés ne s'affichent pas dans le Catalogue.

Remarque : voir aussi Define, page 29 et Define LibPub, page

31.

Programme(Param1, Param2, ...) = Prgm

Catalogue

30 Guide de référence TI-Nspire™ CAS

Define LibPub

Define LibPub Var = Expression Define LibPub Fonction(Param1, Param2, ...) = Expression

Define LibPub Fonction(Param1, Param2, ...) = Func

Bloc

EndFunc Define LibPub

Bloc

EndPrgm

S'utilise comme Define, mais permet de définir des objets (variables, fonctions, programmes) dans la bibliothèque publique. Les fonctions et programmes publics s'affichent dans le Catalogue après l'enregistrement et le rafraîchissement de la bibliothèque.

Remarque : voir aussi Define, page 29 et Define LibPriv, page

30.

Programme(Param1, Param2, ...) = Prgm

Catalogue

DelVar

DelVar Var 1 [, Va r 2] [, Va r 3 ] ...

Supprime de la mémoire les variables spécifiées.

deSolve()

deSolve(ode1OrdreOu2Ordre, varIndépendante,

varDépendante) ⇒ une solution générale

Donne une équation qui définit explicitement ou implicitement la solution générale de l'équation différentielle du 1er ou du 2ème ordre. Dans l'équation différentielle :

• Utilisez uniquement le symbole « prime » (obtenu en appuyant

sur ') pour indiquer la dérivée première de la fonction (variable dépendante) par rapport à la variable (variable

indépendante).

• Utilisez deux symboles « prime » pour indiquer la dérivée seconde correspondante.

Le symbole « prime » s'utilise pour les dérivées uniquement dans deSolve(). Dans tous les autres cas, utilisez d().

La solution générale d'une équation du 1er ordre comporte une constante arbitraire de type ck, où k est un suffixe entier compris entre 1 et 255. La solution générale d'une équation de 2ème ordre contient deux constantes de ce type.

Appliquez solve() à une solution implicite si vous voulez tenter de la convertir en une ou plusieurs solutions explicites équivalente déterminées explicitement.

Si vous comparez vos résultats avec ceux de vos manuels de cours ou ceux obtenus manuellement, sachez que certaines méthodes introduisent des constantes arbitraires en plusieurs e ndroits du calcul, ce qui peut induire des solutions générales différentes.

Catalogue

Guide de référence TI-Nspire™ CAS 31

deSolve()

deSolve(ode1Ordre and ConditionInitiale, varIndépendante,

varDépendante) ⇒ une solution particulière

Donne une solution particulière qui satisfait à la fois ode1Ordre et ConditionInitiale. Ceci est généralement plus simple que de

déterminer une solution générale car on substitue le s valeurs initiales, calcule la constante arbitraire, puis substitue cette valeur dans la solution générale.

ConditionInitiale est une équation de type : varDépendante (valeurIndépendanteInitiale) =

ValeurDépendanteInitiale varIndépendanteInitiale et varDépendanteInitiale peuvent être

des variables comme x0 et y0 non affectées. La différentiation implicite peut aider à vérifier les solutions implicites.

deSolve(ode2Ordre and ConditionInitiale1 and

ConditionInitiale2, varIndépendante, varDépendante)

⇒ une solution particulière

Donne une solution particulière qui satisfait ode2Ordre et qui a une valeur spécifique de la variable dépendante et sa dérivée première en un point.

Pour ConditionInitiale1, utilisez :

varDépendante (valeurIndépendanteInitiale) = ValeurDépendanteInitiale

Pour ConditionInitiale2, utilisez : varDépendante (ValeurIndépendanteinitiale) =

ValeurInitialeDérivée1

deSolve(ode2Ordre and ConditionBorne1 and

ConditionBorne2, varIndépendante, varDépendante)

⇒ une solution particulière

Donne une solution particulière qui satisfait ode2Ordre et qui a des valeurs spécifiques en deux points différents.

Catalogue

det()

det(matriceCarrée[, Tol ]) ⇒ expression

Donne le déterminant de matriceCarrée. L'argument facultatif Tol permet de considérer comme nul tout

élément de la matrice dont la valeur absolue est inférieure à Tol . Cet argument n'est utilisé que si la matrice contient des nombres en virgule flottante et ne contient pas de variables symbolique sans valeur affectée. Dans le cas contraire, To l est ignoré.

• Si vous utilisez

Approché (Approximate)

calculs sont exécutés en virgule flottante.

•Si Tol est omis ou inutilisé, la tolérance par défaut est calculée comme suit :

5EM14 ·max(dim(matriceCarrée))·

rowNorm(matriceCarrée)

· ou définissez le mode Auto ou

sur Approché (Approximate), les

Catalogue

32 Guide de référence TI-Nspire™ CAS

diag()

diag(Liste) ⇒ matrice diag(matriceLigne) ⇒ matrice diag(matriceColonne) ⇒ matrice

Donne une matrice diagonale, ayant sur sa diagonale principale les éléments de la liste passée en argument.

diag(matriceCarrée) ⇒ matriceLigne

Donne une matrice ligne contenant les éléments de la diagonale principale de matriceCarrée.

matriceCarrée doit être une matrice carrée.

Catalogue

dim()

dim(Liste) ⇒ entier

Donne le nombre d'éléments de Liste.

dim(Matrice) ⇒ liste

Donne les dimensions de la matrice sous la forme d'une liste à deux éléments {lignes, colonnes}.

dim(Chaîne) ⇒ entier

Donne le nombre de caractères contenus dans Chaîne.

Disp

Disp [exprOuChaîne1] [, exprOuChaîne2] ...

Affiche les arguments dans l'historique de Calculator. Les arguments apparaissent les uns après les autres, séparés par des espaces fines.

Très utile dans les programmes et fonctions pour l'affichage de calculs intermédiaires.

Remarque pour la saisie des données de l'exemple :

dans l'application Calculs de l'unité nomade, vous pouvez entrer des définitions sur plusieurs lignes en appuyant sur @ à la place de

· à chaque fin de ligne. Sur le clavier de l'ordinateur, maintenez

enfoncée la touche Alt tout en appuyant sur Entrée (Enter).

Catalogue

Guide de référence TI-Nspire™ CAS 33

DMS

4DMS

Expr Liste 4DMS Matrice 4DMS

Interprète l'argument comme un angle et affiche le nombre DMS équivalent (DDDDDD¡MM'SS.ss''). Voir ¡, ', '' page 135 pour le

détail du format DMS (degrés, minutes, secondes).

Remarque : 4DMS convertit les radians en degrés lorsque

l'instruction est utilisée en mode radians. Si l'entrée est suivie du symbole des degrés pouvez utiliser 4DMS qu'à la fin d'une ligne.

¡, aucune conversion n'est effectuée. Vous ne

En mode Angle en degrés :

Catalogue

dominantTerm()

dominantTerm(Expr1, Va r [, Point]) ⇒ expression dominantTerm(Expr1, Va r [, Point]) | Va r >Point

⇒ expression

dominantTerm(Expr1, Va r [, Point]) | Va r <Point

⇒ expression

Donne le terme dominant du développement en série généralisé de Expr1 au Point. Le terme dominant est celui dont le module croît le plus rapidement en Va r = Point. La puissance de (Var N Point) peut avoir un exposant négatif et/ou fractionnaire. Le coefficient de cette puissance peut inclure des logarithmes de (Va r N Point) et d'autres

fonctions de Va r dominés par toutes les puissances de (Va r N Point) ayant le même signe d'exposant.

La valeur par défaut de Point est 0. Point peut être ˆ ou Nˆ, auxquels cas le terme dominant est celui qui a l'exposant de Va r le plus grand au lieu de celui qui l'exposant de Va r le plus petit.

dominantTerm(…) donne “dominantTerm(…)” s'il ne

parvient pas à déterminer la représentation, comme pour les singularités essentielles de type sin(1/z) en z=0, e

en z = ˆ ou Nˆ.

Si la série ou une de ses dérivées présente une disconti nuité en Point, le résultat peut contenir des sous-expressions de type sign(…) ou

abs(…) pour une variable réelle ou (-1) variable complexe, qui se termine par "_". Si vous voulez utiliser le terme dominant uniquement pour des valeurs supérieures ou inférieures à Point, vous devez ajouter à dominantTerm(...) l'élément approprié "| Var > Point", "| Var < Point", "| "Va r ‚

N1/z

floor(…angle(…)…)

en z=0 ou ez

pour une

Point" ou "Va r  Point" pour obtenir un résultat simplifié.

dominantTerm() est appliqué à chaque élément d'une liste ou

d'une matrice passée en 1er argument.

dominantTerm() est utile pour connaître l'expression la plus

simple correspondant à l'expression asymptotique d'un équivalent d'une expression quand Va r " Point. dominantTerm() peut également être utilisé lorsqu'il n'est pas évident de déterminer le degré du premier terme non nul d'une série et que vous ne souhaitez pas tester les hypothèses de manière interactive ou via une boucle.

Remarque : voir aussi series(), page 90.

Catalogue

dotP()

dotP(Liste1, Liste2) ⇒ expression

Catalogue

Donne le produit scalaire de deux listes.

34 Guide de référence TI-Nspire™ CAS

dotP()

dotP(Vecteur1, Vec t e ur 2 ) ⇒ expression

Donne le produit scalaire de deux vecteurs. Les deux vecteurs doivent être de même type (ligne ou colonne).

Catalogue

e^()

e^(Expr1) ⇒ expression

Donne e élevé à la puissance de Expr1.

Remarque : voir aussi Modèle e Exposant, page 2. Remarque : une pression sur u pour afficher

différente d'une pression sur le caractère E du clavier.

Vous pouvez entrer un nombre complexe sous la forme polaire re N'utilisez toutefois cette forme qu'en mode Angle en radians ; elle provoque une erreur de domaine en mode Angle en degrés ou en grades.

e^(Liste1) ⇒ liste

Donne une liste constituée des exponentielles des éléments de Liste1.

e^(matriceCarrée1) ⇒ matriceCarrée

Donne l'exponentielle de matriceCarrée1. Le résultat est différent de la matrice obtenue en prenant l'exponentielle de chaque élément. Pour plus d'informations sur la méthode de calcul, reportez-vous à

cos().

matriceCarrée1 doit être diagonalisable. Le résultat contient toujours des chiffres en virgule flottante.

eff()

eff(tauxNominal,CpY) ⇒ valeur

Fonction financière permettant de convertir un taux d'i ntérêt nominal tauxNominal en un taux annuel effectif, CpY étant le nombre de périodes de calcul par an.

tauxNominal doit être un nombre réel et CpY doit être un nombre réel > 0.

Remarque : voir également nom(), page 69.

^( est

Touche u

Catalogue

Guide de référence TI-Nspire™ CAS 35

eigVc()

eigVc(matriceCarrée) ⇒ matrice

Donne une matrice contenant les vecteurs propres d'une matriceCarrée réelle ou complexe, chaque colonne du résultat correspond à une valeur propre. Notez qu'il n'y a pas unicité des vecteurs propres. Ils peuvent être multipliés par n'importe quel facteur constant. Les vecteurs propres sont normés, ce qui signifie que si V = [x1, x2, … , xn], alors :

+ … + x

= 1

matriceCarrée est d'abord transformée en une matrice semblable dont la norme par rapport aux lignes soit le plus proche de celle par rapport aux colonnes. La matriceCarrée est ensuite réduite à la forme de Hessenberg supérieure et les vecteurs propres calculés via une factorisation de Schur.

Catalogue

En mode Format complexe Rectangulaire :

Pour afficher le résultat entier, appuyez sur £, puis utilisez les touches ¡ et ¢ pour déplacer le curseur.

eigVl()

eigVl(matriceCarrée) ⇒ liste

Donne la liste des valeurs propres d'une matriceCarrée réelle ou complexe.

matriceCarrée est d'abord transformée en une matrice semblable dont la norme par rapport aux lignes soit le plus proche de celle par rapport aux colonnes. La matriceCarrée est ensuite réduite à la forme de Hessenberg supérieure et les valeurs propres calculées à partir de la matrice de Hessenberg supérieure.

Else Voir If, page 48.

ElseIf

If Expr booléenne1 Then

Bloc1

ElseIf Expr booléenne2 Then

Bloc2

BlocN

EndIf

Remarque pour la saisie des données de l'exemple :

dans l'application Calculs de l'unité nomade, vous pouvez entrer des définitions sur plusieurs lignes en appuyant sur @ à la place de

En mode Format complexe Rectangulaire :

Pour afficher le résultat entier, appuyez sur £, puis utilisez les touches ¡ et ¢ pour déplacer le curseur.

Catalogue

· à chaque fin de ligne. Sur le clavier de l'ordinateur, maintenez

enfoncée la touche Alt tout en appuyant sur Entrée (Enter).

EndFor Voir For, page 43.

36 Guide de référence TI-Nspire™ CAS

EndFunc Voir Func, page 45.

EndIf Voir If, page 48.

EndLoop Voir Loop, page 60.

EndPrgm Voir Prgm, page 78.

EndTry Voir Try, page 109.

EndWhile Voir While, page 115.

exact()

exact(Expr1 [, To l]) ⇒ expression exact(Liste1 [, To l ]) ⇒ liste exact(Matrice1 [, To l ]) ⇒ matrice

Utilise le mode Exact quel que soit le mode Exact/Approché en cours d'utilisation pour donner, si possible, la valeur formelle de l'argument.

Tol fixe la tolérance admise pour cette approximati on. Par défaut, cet argument ; est égal à 0 (zéro).

Exit

Permet de sortir de la boucle For, While ou Loop courante.

Exit ne peut pas s'utiliser indépendamment de l'une des trois

structures de boucle (For, While ou Loop).

Remarque pour la saisie des données de l'exemple :

dans l'application Calculs de l'unité nomade, vous pouvez entrer des définitions sur plusieurs lignes en appuyant sur @ à la place de

· à chaque fin de ligne. Sur le clavier de l'ordinateur, maintenez

enfoncée la touche Alt tout en appuyant sur Entrée (Enter).

Liste des fonctions :

Catalogue

Guide de référence TI-Nspire™ CAS 37

exp()

exp(Expr1) ⇒ expression

Donne l'exponentielle de Expr1.

Remarque : voir aussi Modèle e Exposant, page 2.

exp(Liste1) ⇒ liste

i q

Donne une liste constituée des exponentielles des éléments Liste1.

exp(matriceCarrée1) ⇒ matriceCarrée

cos().

matriceCarrée1 doit être diagonalisable. Le résultat contient toujours des chiffres en virgule flottante.

Touche u

exp4list()

exp4list(Expr,Va r ) ⇒ liste

Recherche dans Expr les équations séparées par le mot « or » et retourne une liste des membres de droite des équations du type Var = E x pr . Cela permet en particulier de récupérer facilement sous forme de liste les résultats fournis par les fonctions solve(),

cSolve()

, fMin() et fMax().

Remarque : exp4list() n'est pas nécessaire avec les fonctions zeros et cZeros() étant donné que celles-ci donnent directement

une liste de solutions.

expand()

expand(Expr1 [, Va r ]) ⇒ expression expand(Liste1 [,Va r ]) ⇒ liste expand(Matrice1 [,Var ]) ⇒ matrice

expand(Expr1) développe Expr1 en fonction de toutes ses

variables. C'est un développement polynomial pour les expressions polynomiales et une décomposition en éléments simples pour les expressions rationnelles.

L'objectif de expand() est de transformer Expr1 en une somme et/ ou une différence de termes simples. Par opposition, l'objectif de

factor() est de transformer Expr1 en un produit et/ou un quotient

de facteurs simples.

Catalogue

38 Guide de référence TI-Nspire™ CAS

expand()

expand(Expr1,Va r) développe Expr1 en fonction de Va r. Les

mêmes puissances de Va r sont regroupées. Les termes et leurs facteurs sont triés, Var étant la variable principale. Une factorisation ou un développement incident des coefficients regroupés peut se produire. L'utilisation de Va r permet de gagner du temps, de la mémoire et de l'espace sur l'écran tout en facilitant la lecture de l'expression.

Même en présence d'une seule variable, l'utilisation de Va r peut contribuer à une factorisation du dénominateur, utilisée pour une décomposition en éléments simples, plus complète.

Conseil : pour les expressions rationnelles, propFrac() est une alternative plus rapide mais moins extrême à expand().

Remarque : voir aussi comDenom() pour un numérateur

développé sur un dénominateur développé.

expand(Expr1,[Va r]) « distribue » également des logarithmes et

des puissances fractionnaires indépendamment de Va r . Pour un plus grand développement des logarithmes et des puissances fractionnaires, l'utilisation de contraintes peut s'avérer nécessaire pour s'assurer que certains facteurs ne sont pas négatifs.

expand(Expr1, [Va r]) « distribue » également des valeurs

absolues, sign(), et des exponentielles, indépendamment de Va r .

Remarque : voir aussi tExpand() pour le développement

contenant des sommes et des multiples d'angles.

Catalogue

expr()

expr(Chaîne) ⇒ expression

Convertit la chaîne de caractères contenue dans Chaîne en une expression. L'expression obtenue est immédiatement évaluée.

Catalogue

Guide de référence TI-Nspire™ CAS 39

ExpReg

ExpReg X, Y [, [Fréq] [, Catégorie, Inclure]]

Calcule un ajustement exponentiel. Un récapitulatif du résultat est stocké dans la variable stat.results. (Voir page 100.)

Tous les arguments doivent être de mêmes dimensions, à l'exception de Inclure.

Variable de sortie Description

stat.RegEqn

stat.a, stat.b

stat.r

stat.r Coefficient de corrélation linéaire

stat.Resid

stat.ResidTrans Valeurs résiduelles associées à l'ajustement linéaire des données transformées

stat.XReg Liste des points de données de la liste Liste X modifiée, actuellement utilisée dans l'ajustement basé sur

stat.YReg Liste des points de données de la liste Liste Y modifiée, actuellement utilisée dans l'ajustement basé sur

stat.FreqReg Liste des fréquences correspondant à stat.XReg et stat.YReg

Équation d'ajustement : a·(b)

Coefficients d'ajustement : y = a·(b)x.

Coefficient de détermination

Valeurs résiduelles de l'ajustement des courbes = y - a·(b)x.

les restrictions de Fréq, Liste de catégories et Inclure les catégories

Catalogue

factor()

factor(Expr1[, Va r ]) ⇒ expression factor(Liste1[,Va r ]) ⇒ liste factor(Matrice1[,Var ]) ⇒ matrice

factor(Expr1) factorise Expr1 en fonction de l'ensemble des

variables associées sur un dénominateur commun.

La factorisation Expr1 décompose l'expression en autant de

facteurs rationnels linéaires que possible sans introduire de nouvelles sous-expressions non réelles. Cette alternative peut s'avérer utile pour factoriser l'expression en fonction de plusieurs variables.

40 Guide de référence TI-Nspire™ CAS

Catalogue

factor()

factor(Expr1,Var ) factorise Expr1 en fonction de la variable Va r.

La factorisation de Expr1 décompose l'expression en autant de

facteurs réels possible linéaires par rapport à Va r, même si cela introduit des constantes irrationnelles ou des sous-expressions qui sont irrationnelles dans d'autres variables.

Les facteurs et leurs termes sont triés, Var étant la variable principale. Les mêmes puissances de Va r sont regroupées dans chaque facteur. Utilisez Va r si la factorisation ne doit s'effectuer que par rapport à cette variable et si vous acceptez les expressions irrationnelles dans les autres variables pour augmenter la factorisation par rapport à Va r . Une factorisation incidente peut se produire par rapport aux autres variables.

Avec le réglage Auto du mode Auto ou Approché

(Approximate)

approximation des coefficients en virgule flottante dans le cas où les coefficients irrationnels ne peuvent pas être exprimés explicitement en termes de fonctions usuelles. Même en présence d'une seule variable, l'utilisation de Va r peut contribuer à une factorisation plus complète.

Remarque : voir aussi comDenom() pour obtenir rapidement

une factorisation partielle si la fonction factor() est trop lente ou si elle utilise trop de mémoire.

Remarque : voir aussi cFactor() pour une factorisation à

coefficients complexes visant à chercher des facteurs linéaires.

factor(nombreRationnel) factorise le nombre rationnel en facteurs

premiers. Pour les nombres composites, le temps de calcul augmente de façon exponentielle avec le nombre de chiffres du deuxième facteur le plus grand. Par exemple, la factorisation d'un entier composé de 30 chiffres peut prendre plus d'une journée et celle d'un nombre à 100 chiffres, plus d'un siècle.

Remarque : pour arrêter un calcul, appuyez sur w.

Si vous souhaitez uniquement déterminer si un nombre est un nombre premier, utilisez isPrime(). Cette méthode est plus rapide, en particulier si nombreRationnel n'est pas un nombre premier et si le deuxième facteur le plus grand comporte plus de cinq chiffres.

, l'utilisation de Va r permet également une

Catalogue

Fill

Fill Expr, VarMatrice ⇒ matrice

Catalogue

Remplace chaque élément de la variable VarMatrice par Expr. VarMatrice doit avoir été définie.

Fill Expr, VarListe ⇒ liste

Remplace chaque élément de la variable VarListe par Expr. Var L i s te doit avoir été définie.

Guide de référence TI-Nspire™ CAS 41

floor()

floor(Expr1) ⇒ entier

Donne le plus grand entier { à l'argument (partie entière). Cette fonction est comparable à int().

L'argument peut être un nombre réel ou un nombre complexe.

floor(Liste1) ⇒ liste floor(Matrice1) ⇒ matrice

Donne la liste ou la matrice de la partie entière de chaque élément.

Remarque : voi aussi ceiling() et int().

Catalogue

fMax()

fMax(Expr, Var) ⇒ Expression booléenne fMax(Expr, Va r,LimitInf) fMax(

Expr, Va r,LimitInf,LimitSup)

fMax(

Expr, Va r) | LimitInf<Va r <LimitSup

Donne une expression booléenne spécifiant les valeurs possibles de Var pour laque lle Expr est à son maximum ou détermine au moins sa limite supérieure.

Vous pouvez utiliser l'opérateur « | » pour préciser l'intervalle de recherche et/ou spécifier d'autres contraintes.

Avec le réglage Approché (Approximate) du mode Auto ou

Approché (Approximate)

façon itérative un maximum local approché. C'est souvent plus rapide, surtout si vous utilisez l'opérateur « | » pour limiter la recherche à un intervalle relativement réduit qui contient exactement un maximum local.

Remarque : voir aussi fMin() et max().

, fMax() permet de rechercher de

fMin()

fMin(Expr, Var) ⇒ Expression booléenne fMin(Expr, Var ,LimitInf) fMin(

Expr, Va r,LimitInf,LimitSup)

fMin(

Expr, Va r) | LimitInf<Va r <LimitSup

Donne une expression booléenne spécifiant les valeurs possibles de Var pour laquelle Expr est à son minimum ou détermine au moins sa limite inférieure.

Vous pouvez utiliser l'opérateur « | » pour préciser l'intervalle de recherche et/ou spécifier d'autres contraintes.

Avec le réglage Approché (Approximate) du mode Auto ou

Approché (Approximate)

façon itérative un minimum local approché. C'est souvent plus ra pide, surtout si vous utilisez l'opérateur « | » pour limiter la recherche à un intervalle relativement réduit qui contient exactement un minimum local.

Remarque : voir aussi fMax() et min().

, fMin() permet de rechercher de

Catalogue

42 Guide de référence TI-Nspire™ CAS

For

For Var , Début, Fin [, Incrément]

Bloc

EndFor

Exécute de façon itérative les instructions de Bloc pour chaque valeur de Var , à partir de Début jusqu'à Fin, par incréments équivalents à

Incrément. Var ne doit pas être une variable système. Incrément peut être une valeur positive ou négative. La valeur par

défaut est 1. Bloc peut correspondre à une ou plusieurs instructions, séparées par

un « : ».

Remarque pour la saisie des données de l'exemple :

dans l'application Calculs de l'unité nomade, vous pouvez entrer des définitions sur plusieurs lignes en appuyant sur @ à la place de

· à chaque fin de ligne. Sur le clavier de l'ordinateur, maintenez

enfoncée la touche Alt tout en appuyant sur Entrée (Enter).

Catalogue

format()

format(Expr[, chaîneFormat]) ⇒ chaîne

Donne Expr sous la forme d'une chaîne de caractères correspondant au modèle de format spécifié.

Expr doit avoir une valeur numérique. chaîneFormat doit être une chaîne du type : « F[n] », « S[n] », « E[n]

», « G[n][c] », où [ ] identifie les parties facultatives. F[n] : format Fixe. n correspond au nombre de chiffres à afficher après

le séparateur décimal. S[n] : format Scientifique. n correspond au nombre de chiffres à

afficher après le séparateur décimal. E[n] : format Ingénieur. n correspond au nombre de chiffres après le

premier chiffre significatif. L'exposant est ramené à un multiple de trois et le séparateur décimal est décalé vers la droite de zéro, un ou deux chiffres.

G[n][c] : identique au format Fixe, mais sépare également les chiffres à gauche de la base par groupes de trois. c spécifie le caractère séparateur des groupes et a pour valeur par défaut la virgule. Si c est un point, la base s'affiche sous forme de virgule.

[Rc] : tous les formats ci-dessus peuvent se voir ajouter en suffixe l'indicateur de base Rc, où c correspond à un caractère unique spécifiant le caractère à substituer au point de la base.

fPart()

fPart(Expr1) ⇒ expression fPart(Liste1) ⇒ liste fPart(Matrice1) ⇒ matrice

Donne la partie fractionnaire de l'argument. Dans le cas d'une liste ou d'une matrice, donne les parties

fractionnaires des éléments. L'argument peut être un nombre réel ou un nombre complexe.

Catalogue

Guide de référence TI-Nspire™ CAS 43

FPdf()

FPdf(Val X ,dfNumer,dfDenom) ⇒ nombre si Va lX est un

liste si Val X est une liste

nombre,

FPdf(

Val X ,dfNumer,dfDenom) ⇒ nombre si Va l X est un

liste si Val X est une liste

nombre,

Calcule la densité de la loi F (Fisher) de degrés de liberté dfNumer et dfDenom en Val X .

Catalogue

frequency()

frequency(Liste1,ListeBinaires) ⇒ liste

Affiche une liste contenant le nombre total d'éléments dans Liste1. Les comptages sont effectués à partir de plages (binaires) définies par l'utilisateur dans listeBinaires.

Si listeBinaires est {b(1), b(2), …, b(n)}, les plages spécifiées sont {?{b(1), b(1)<?{b(2),…,b(n-1)<?{b(n), b(n)>?}. Le résultat comporte un élément de plus que listeBinaires.

Chaque élément du résultat correspond au nombre d'éléments dans Liste1 présents dans la plage. Exprimé en termes de fonction

countIf(), le résultat est { countIf(liste, ?{b(1)), countIf(liste,

b(1)<?{b(2)), …, countIf(liste, b(n-1)<?{b(n)), countIf(liste, b(n)>?)}.

Les éléments de Liste1 qui ne sont pas “placés dans une plage” ne sont pas pris en compte.

Dans l'application Tableur & listes, vous pouvez utiliser une plage de cellules à la place des deux arguments.

Remarque : voir également countIf(), page 22.

FTest_2Samp

FTest_2Samp Liste1,Liste2[,Fréq1[,Fréq2[,Hypoth]]]

FTest_2Samp

(Entrée de liste de données)

Liste1,Liste2[,Fréq1[,Fréq2[,Hypoth]]]

FTest_2Samp sx1,n1,sx2,n2[,Hypoth]

FTest_2Samp

(Récapitulatif des statistiques fournies en entrée) Effectue un test F sur deux échantillons. Un récapitulatif du résultat

est stocké dans la variable stat.results. (Voir page 100.)

Hypoth > 0 correspond à Ha : s1 > s2 Hypoth = 0 correspond à Ha : s1 ƒ s2 (par défaut) Hypoth < 0 correspond à Ha : s1 < s2

sx1,n1,sx2,n2[,Hypoth]

Catalogue

Explication du résultat :

2 éléments de Datalist sont {2,5 4 éléments de Datalist sont >2,5 et {4,5 3 éléments de Datalist sont >4,5

L'élément « hello » est une chaîne et ne peut être placé dans aucune des plages définies.

Catalogue

Variable de sortie Description

stat.F

stat.PVal Plus petite probabilité permettant de rejeter l'hypothèse nulle

stat.dfNumer Numérateur degrés de liberté = n1-1

stat.dfDenom Dénominateur degrés de liberté = n2-1.

stat.sx1, stat.sx2 Écarts types de population d'échantillon des séquences de données dans Liste 1 et Liste 2.

Statistique ó estimée pour la séquence de données

44 Guide de référence TI-Nspire™ CAS

Variable de sortie Description

stat.x1_bar stat.x2_bar

stat.n1, stat.n2 Taille des échantillons

Moyenne de population d'échantillon des séquences de données dans Liste 1 et Liste 2.

Func

Bloc

EndFunc

Modèle de création d'une fonction définie par l'utilisateur. Bloc peut correspondre à une instruction unique ou à une série

d'instructions séparées par le caractère “:” ou à une série d'instructions réparties sur plusieurs lignes. La fonction peut utiliser l'instruction Return pour donner un résultat spécifique.

Remarque pour la saisie des données de l'exemple :

dans l'application Calculs de l'unité nomade, vous pouvez entrer des définitions sur plusieurs lignes en appuyant sur @ à la place de

· à chaque fin de ligne. Sur le clavier de l'ordinateur, maintenez

enfoncée la touche Alt tout en appuyant sur Entrée (Enter).

gcd()

gcd(Nombre1, Nombre2) ⇒ expression

Donne le plus grand commun diviseur des deux arguments. Le gcd de deux fractions correspond au gcd de leur numérateur divisé par le

lcm de leur dénominateur.

En mode Auto ou Approché, le gcd de nombre fractionnaires en virgule flottante est égal à 1.

gcd(Liste1, Liste2) ⇒ liste

Donne la liste des plus grands communs diviseurs des éléments correspondants de Liste1 et Liste2.

gcd(Matrice1, Matrice2) ⇒ matrice

Donne la matrice des plus grands communs diviseurs des éléments correspondants de Matrice1 et Matrice2.

Catalogue

Définition d'une fonction par morceaux :

Résultat de la représentation graphique de g(x)

Catalogue

geomCdf()

geomCdf(p, LimitInf, LimitSup) ⇒ nombre si LimitInf et

LimitSup sont des nombres, liste si LimitInf et LimitSup sont

des listes

Calcule la fonction de répartition de la loi géométrique entre LimitInf et LimitSup en fonction de la probabilité de réussite p spécifiée.

Pour p  LimitSup, définissez LimitInf = 1.

Catalogue

Guide de référence TI-Nspire™ CAS 45

geomPdf()

geomPdf(p,Val X ) ⇒ nombre si Va lX est un nombre, liste si

Val X est une liste

Calcule la probabilité que le premier succès intervienne au rang Val X , pour la loi géométrique discrète en fonction de la probabilité de réussite p spécifiée.

Catalogue

getDenom( )

getDenom(Expr1) ⇒ expression

Transforme l'argument en une expression dotée d'un dénominateur commun réduit, puis en donne le numérateur.

getMode()

getMode(EntierNomMode) ⇒ valeur getMode(0) ⇒ liste

getMode(EntierNomMode) affiche une valeur représentant le

réglage actuel du mode EntierNomMode.

getMode(0) affiche une liste contenant des paires de chiffres.

Chaque paire consiste en un entier correspondant au mode et un entier correspondant au réglage.

Pour obtenir une liste des modes et de leurs réglages, reportez-vous au tableau ci-dessous.

Si vous enregistrez les réglages avec getMode(0) & var, vous pouvez utiliser setMode(var) dans une fonction ou un programme pour restaurer temporairement les réglages au sein de l'exécution de la fonction ou du programme uniquement. Voir également

setMode(), page 91.

Nom du mode

Afficher chiffres

Angle

Format Exponentiel

Réel ou Complexe

Auto ou Approché

Format Vecteur

Base

Système d'unités

Entier du mode

Entiers de réglage

=Flottant, 2=Flottant 1, 3=Flottant 2, 4=Flottant 3, 5=Flottant 4, 6=Flottant 5,

7=Flottant 6, 8=Flottant 7, 9=Flottant 8, 10=Flottant 9, 11=Flottant 10, 12=Flottant 11, 13=Flottant 12, 14=Fixe 0, 15=Fixe 1, 16=Fixe 2, 17=Fixe 3, 18=Fixe 4, 19=Fixe 5, 20=Fixe 6, 21=Fixe 7, 22=Fixe 8, 23=Fixe 9, 24=Fixe 10, 25=Fixe 11, 26=Fixe 12

=Radian, 2=Degré, 3=Grade

=Normal, 2=Scientifique, 3=Ingénieur

=Réel, 2=Rectangulaire, 3=Polaire

=Auto, 2=Approché, 3=Exact

=Rectangulaire, 2=Cylindrique, 3=Sphérique

=Décimale, 2=Hexadécimale, 3=Binaire

=SI, 2=Ang/US

Catalogue

46 Guide de référence TI-Nspire™ CAS

getNum()

getNum(Expr1) ⇒ expression

Transforme l'argument en une expression dotée d'un dénominateur commun réduit, puis en donne le dénominateur.

Catalogue

getVarInfo()

getVarInfo() ⇒ matrice ou chaîne getVarInfo(ChaîneNomBibliothèque) ⇒ matrice ou chaîne

getVarInfo() donne une matrice d'informations (nom de variable,

type et bibliothèque accessible) pour toutes les variables et objets de bibliothèques définis dans l'activité courante.

Si aucune variable n'est définie, getVarInfo() donne la chaîne "NONE" (AUCUNE).

getVarInfo(ChaîneNomBibliothèque) donne une matrice

d'informations pour tous les objets de bibliothèque définis dans la bibliothèque NomBibliothèque. ChaîneNomBibliothèque doit être une chaîne (texte entre guillemets) ou une variable.

Si la bibliothèque NomBibliothèque n'existe pas, une erreur est générée.

Goto

Goto nomÉtiquette

Transfère le contrôle du programme à l'étiquette nomÉtiquette. nomÉtiquette doit être défini dans la même fonction à l'aide de

l'instruction Lbl.

Remarque pour la saisie des données de l'exemple :

dans l'application Calculs de l'unité nomade, vous pouvez entrer des définitions sur plusieurs lignes en appuyant sur @ à la place de

· à chaque fin de ligne. Sur le clavier de l'ordinateur, maintenez

enfoncée la touche Alt tout en appuyant sur Entrée (Enter).

Catalogue

Guide de référence TI-Nspire™ CAS 47

Grad

4 Grad ⇒ expression

Expr1

Convertit Expr1 en une mesure d'angle en grades.

En mode Angle en degrés :

En mode Angle en radians :

Catalogue

identity()

identity(Entier) ⇒ matrice

Donne la matrice identité (matrice unité) de dimension Entier. Entier doit être un entier positif.

If Expr booléenne Instruction If Expr booléenne Then

Bloc

EndIf

Si Expr booléenne passe le test de condition, exécute l'instruction Instruction ou le bloc d'instructions Bloc avant de poursuivre

l'exécution de la fonction. Si Expr booléenne ne passe pas le test de condition, poursuit

l'exécution en ignorant l'instruction ou le bloc d'instructions. Bloc peut correspondre à une ou plusieurs instructions, séparées par

un « : ».

Remarque pour la saisie des données de l'exemple :

dans l'application Calculs de l'unité nomade, vous pouvez entrer des définitions sur plusieurs lignes en appuyant sur @ à la place de

· à chaque fin de ligne. Sur le clavier de l'ordinateur, maintenez

enfoncée la touche Alt tout en appuyant sur Entrée (Enter).

If Expr booléenne Then

Bloc1

Else

Bloc2

EndIf

Si Expr booléenne passe le test de condition, exécute Bloc1 et ignore Bloc2.

Si Expr booléenne ne passe pas le texte de condition, ignore Bloc1, mais exécute Bloc2.

Bloc1 et Bloc2 peuvent correspondre à une seule instruction.

Catalogue

48 Guide de référence TI-Nspire™ CAS

If Expr booléenne1 Then

Bloc1

ElseIf

Expr booléenne2 Then

Bloc2

Expr booléenneN Then

BlocN

EndIf

Permet de traiter les conditions multiples. Si Expr booléenne1 passe le test de condition, exécute Bloc1. Si Expr booléenne1 ne passe pas le test de condition, calcule Expr booléenne2, etc.

Catalogue

ifFn()

ifFn(exprBooléenne,Valeur_si_Vrai [,Valeur_si_Faux [,

Valeur_si_Inconnu]]) ⇒ expression, liste ou matrice

Evalue l'expression booléenne exprBooléenne(ou chacun des éléments de exprBooléenne) et produit un résultat reposant sur les règles suivantes :

• exprBooléenne peut tester une valeur unique, une liste ou une matrice.

• Si un élément de exprBooléenne est vrai, l'élément correspondant de Valeur_si_Vrai s'affiche.

• Si un élément de exprBooléenne est faux, l'élément correspondant de Valeur_si_Faux s'affiche. Si vous omettez Valeur_si_Faux, undef s'affiche.

• Si un élément de exprBooléenne n'est ni vrai ni faux, l'élément correspondant de Valeur_si_Inconnu s'affiche. Si vous omettez Valeur_si_Inconnu, undef s'affiche.

• Si le deuxième, troisième ou quatrième argument de la fonction

ifFn() est une expression unique, le test booléen est appliqué à

toutes les positions dans exprBooléenne.

Remarque : si l'instruction simplifiée exprBooléenne implique une

liste ou une matrice, tous les autres arguments de type liste ou matrice doivent avoir la ou les même(s) dimension(s) et le résultat aura la ou les même(s) dimension(s).

imag()

imag(Expr1) ⇒ expression

Donne la partie imaginaire de l'argument.

Remarque : toutes les variables non affectées sont considérées

comme réelles. Voir aussi real(), page 84

Catalogue

La valeur d'essai 1 est inférieure à 2,5, ainsi l'élément correspondant dans Valeur_si_Vrai (5) est copié dans la liste de résultats.

La valeur d'essai 2 est inférieure à 2,5, ainsi l'élément correspondant dans Valeur_si_Vrai(6) est copié dans la liste de résultats.

La valeur d'essai 3 n'est pas inférieure à 2,5, ainsi l'élément correspondant dans Valeur_si_Faux (10) est copié dans la liste de résultats.

Valeur_si_Vrai est une valeur unique et correspond à n'importe quelle position sélectionnée.

Valeur_si_Faux n'est pas spécifié. Undef est utilisé.

Un élément sélectionné à partir de Valeur_si_Vrai. Un élément sélectionné à partir de Valeur_si_Inconnu.

Catalogue

Guide de référence TI-Nspire™ CAS 49

imag()

imag(Liste1) ⇒ liste

Donne la liste des parties imaginaires des éléments.

imag(Matrice1) ⇒ matrice

Donne la matrice des parties imaginaires des éléments.

Catalogue

impDif()

impDif(Équation, varIndépendante, varDépendante[,Ordre ])

⇒ expression

Catalogue

où la valeur par défaut de l'argument Ordre est 1. Calcule la dérivée implicite d'une équation dans la quelle une variable

est définie implicitement par rapport à une autre.

Indirection Voir

inString()

inString(chaîneSrce, sousChaîne[, Début]) ⇒ entier

Donne le rang du caractère de la chaîne chaîneSrce où commence la première occurrence de sousChaîne.

Début, s'il est utilisé, indique le point de départ de la recherche dans chaîneSrce. Par défaut, la recherche commence à partir du premier

caractère de chaîneSrce. Si chaîneSrce ne contient pas sousChaîne ou si Début est > à la

longueur de ChaîneSrce, on obtient zéro.

int()

int(Expr) ⇒ entier int(Liste1) ⇒ liste int(Matrice1) ⇒ matrice

Donne le plus grand entier inférieur ou égal à l'argument. Cette fonction est identique à floor() (partie entière).

Catalogue

L'argument peut être un nombre réel ou un nombre complexe. Dans le cas d'une liste ou d'une matrice, donne la partie entière de

chaque élément.

, page 134.

#()

intDiv()

intDiv(Nombre1, Nombre2) ⇒ entier intDiv(Liste1, Liste2) ⇒ liste intDiv(Matrice1, Matrice2) ⇒ matrice

Donne le quotient dans la division euclidienne de (Nombre1 ÷ Nombre2).

Dans le cas d'une liste ou d'une matrice, donne le quotient de (argument 1 ÷ argument 2) pour chaque paire d'éléments.

integrate

Catalogue

Voir

, page 130.

‰()

50 Guide de référence TI-Nspire™ CAS

invc2()

invc2(Zone,df)

Zone,df)

invchi2(

Calcule l'inverse de la fonction de répartition de la loi c2 (Khi2) de degré de liberté df en un point donné (Zone).

Catalogue

invF()

invF(Zone,dfNumer,dfDenom)

Zone,dfNumer,dfDenom)

invF(

Calcule l'inverse de la fonction de répartition de la loi F (Fisher) de paramètres spécifiée par dfNumer et dfDenom en un point donné (Zone).

invNorm()

invNorm(Zone[,m,s])

Calcule l'inverse de la fonction de répartition de la loi normale de paramètres mu et sigma (m et s) en un point donné (zone).

invt()

invt(Zone,df)

Calcule l'inverse de la fonction de répartition de la loi student-t de degré de liberté df en un point donné (Zone).

iPart()

iPart(Nombre) ⇒ entier iPart(Liste1) ⇒ liste iPart(Matrice1) ⇒ matrice

Donne l'argument moins sa partie fractionnaire. Dans le cas d'une liste ou d'une matrice, applique la fonction à

chaque élément. L'argument peut être un nombre réel ou un nombre complexe.

irr()

irr(MT0,ListeMT [,FréqMT]) ⇒ valeur

Fonction financière permettant de calculer le taux interne de rentabilité d'un investissement.

MT0 correspond au mouvement de trésorerie initial à l'heure 0 ; il doit s'agir d'un nombre réel.

Liste MT est une liste des montants de mouvements de trésorerie après le mouvement de trésorerie initial MT0.

FréqMT est une liste facultative dans laquelle chaque élément indique la fréquence d'occurrence d'un montant de mouvement de trésorerie groupé (consécutif), correspondant à l'élément de ListeMT. La valeur par défaut est 1 ; si vous saisissez des valeurs, elles doivent être des entiers positifs < 10 000.

Remarque : voir également mirr(), page 64.

Catalogue

Guide de référence TI-Nspire™ CAS 51

isPrime()

isPrime(Nombre) ⇒ Expression booléenne constante

Donne true ou false selon que nombre est ou n'est pas un entier naturel premier

Si Nombre dépasse 306 chiffres environ et n'a pas de diviseur inférieur à

Si vous souhaitez uniquement déterminer si Nombre est un nombre premier, utilisez rapide, en particulier si Nombre n'est pas un nombre premier et si le deuxième facteur le plus grand comporte plus de cinq chiffres.

Remarque pour la saisie des données de l'exemple :

dans l'application Calculs de l'unité nomade, vous pouvez entrer des définitions sur plusieurs lignes en appuyant sur @ à la place de

‚ 2, divisible uniquement par lui-même et 1.

{1021, isPrime(Nombre) affiche un message d'erreur.

isPrime() et non factor(). Cette méthode est plus

· à chaque fin de ligne. Sur le clavier de l'ordinateur, maintenez

enfoncée la touche Alt tout en appuyant sur Entrée (Enter).

Catalogue

Fonction permettant de trouver le nombre premier suivant un nombre spécifié :

Lbl

Lbl nomÉtiquette

Définit une étiquette en lui attribuant le nom nomÉtiquette dans une fonction.

Vous pouvez utiliser l'instruction Goto nomÉtiquette pour transférer le contrôle du programme à l'instruction suivant immédiatement l'étiquette.

nomÉtiquette doit être conforme aux mêmes règles de dénomination que celles applicables aux noms de variables.

Remarque pour la saisie des données de l'exemple :

dans l'application Calculs de l'unité nomade, vous pouvez entrer des définitions sur plusieurs lignes en appuyant sur @ à la place de

· à chaque fin de ligne. Sur le clavier de l'ordinateur, maintenez

enfoncée la touche Alt tout en appuyant sur Entrée (Enter).

lcm()

lcm(Nombre1, Nombre2) ⇒ expression lcm(Liste1, Liste2) ⇒ liste lcm(Matrice1, Matrice2) ⇒ matrice

Donne le plus petit commun multiple des deux arguments. Le lcm de deux fractions correspond au lcm de leur numérateur divisé par le

gcd de leur dénominateur. Le lcm de nombres fractionnaires en

virgule flottante correspond à leur produit. Pour deux listes ou matrices, donne les plus p etits communs multiples

des éléments correspondants.

Catalogue

52 Guide de référence TI-Nspire™ CAS

left()

left(chaîneSrce[, Nomb]) ⇒ chaîne

Donne la chaîne formée par les Nomb premiers caractères de la chaîne chaîneSrce.

Si Nomb est absent, on obtient chaîneSrce.

left(Liste1[, Nomb]) ⇒ liste

Donne la liste formée par les Nomb premiers éléments de Liste1. Si Nomb est absent, on obtient Liste1.

left(Comparaison) ⇒ expression

Donne le membre de gauche d'une équation ou d'une inéquation.

Catalogue

limit() ou lim()

limit(Expr1, Va r, Point [,Direction]) ⇒ expression limit(Liste1, Var , Point [, Direction]) ⇒ liste limit(Matrice1, Var , Point [, Direction]) ⇒ matrice

Donne la limite recherchée.

Remarque : voir aussi Modèle Limite, page 5.

Direction : négative=limite à gauche, positive=limite à droite, sinon=gauche et droite. (Si Direction est absent, la valeur par défaut est gauche et droite.)

Les limites en +ˆ et en -ˆ sont toujours converties en limites unilatérales.

Dans certains cas, limit() retourne lui-mêm e ou undef (non défini) si aucune limite ne peut être déterminée. Cela ne signifie pas pour autant qu'aucune limite n'existe. undef signifie que le ré sultat est soit un nombre inconnu fini ou infini soit l'ensemble complet de ces nombres.

limit() utilisant des méthodes comme la règle de L’Hôpital, il existe

des limites uniques que cette fonction ne permet pas de déterminer. Si Expr1 contient des variables non définies autres que Va r , il peut s'avérer nécessaire de les contraindre pour obtenir un résultat plus précis.

Les limites peuvent être affectées par les erreurs d'arrondi. Dans la mesure du possible, n'utilisez pas le réglage Approché (Approximate) du mode Auto ou Approché (Approximate) ni des nombres approchés lors du calcul de limites. Sinon, les limites normalement nulles ou infinies risquent de ne pas l'être.

Catalogue

LinRegBx

LinRegBx X,Y[,Fréq[,Catégorie,Inclure]]

Effectue une régression linéaire de type y=a+bx sur X et Y en utilisant la fréquence Fréq. Un récapitulatif du résultat est stocké dans la variable stat.results. (Voir page 100.)

Catalogue

Guide de référence TI-Nspire™ CAS 53

Variable de sortie Description

stat.RegEqn

stat.a, stat.b Coefficients d'ajustement

stat.r

stat.r Coefficient de corrélation linéaire

stat.Resid

stat.XReg Liste des points de données de la liste Liste X modifiée, actuellement utilisée dans l'ajustement basé sur

stat.YReg Liste des points de données de la liste Liste Y modifiée, actuellement utilisée dans l'ajustement basé sur

stat.FreqReg Liste des fréquences correspondant à stat.FreqReg et stat.YReg

Équation d'ajustement : a+b

Coefficient de détermination

Valeurs résiduelles de l'ajustement des courbes : y - (a+b·x)

les restrictions de Fréq, Liste de catégories et Inclure les catégories

·x

LinRegMx

LinRegMx X,Y[,Fréq[,Catégorie,Inclure]]

Effectue une régression linéaire de type y=mx+b sur X et Y en utilisant la fréquence Fréq. Un récapitulatif du résultat est stocké dans la variable stat.results. (Voir page 100.)

Variable de sortie Description

stat.RegEqn

stat.m, stat.b

stat.r

stat.r Coefficient de corrélation linéaire

stat.Resid

stat.XReg Liste des points de données de la liste Liste X modifiée, actuellement utilisée dans l'ajustement basé sur

stat.YReg Liste des points de données de la liste Liste Y modifiée, actuellement utilisée dans l'ajustement basé sur

stat.FreqReg Liste des fréquences correspondant à stat.XReg et stat.YReg

Équation d'ajustement : m·x+b

Coefficients d'ajustement : y = m·x+b

Coefficient de détermination

Valeurs résiduelles de l'ajustement des courbes : y - (m·x+b)

les restrictions de Fréq, Liste de catégories et Inclure les catégories

Catalogue

54 Guide de référence TI-Nspire™ CAS

LinRegtIntervals

LinRegtIntervals X,Y[,Fréq[,0[,CLevel]]]

Pour pente

LinRegtIntervals X,Y[,Fréq[,1,Val X [,CLevel]]]

Pour prévision Calcule l'intervalle t de régression linéaire pour un ajustement de la

courbe des paires de points de données, où y(k) = a + b types d'intervalle sont disponible : Slope et Predict. Un récapitulatif du résultat est stocké dans la variable stat.results. (Voir page 100.)

Variable de sortie Description

stat.RegEqn

stat.a,b Estimations des paramètres de décalage et de pente pour l'ajustement de courbe

stat.df Degrés de liberté

stat.r

stat.r Coefficient de corrélation linéaire

stat.Resid

Pour les intervalles de type Slope uniquement

Variable de sortie Description

[stat.CLower, stat.CUpper]

stat.ME Marge d'erreur de l'intervalle de confiance b de la pente

stat.SESlope

stat.s

Équation d'ajustement : a+b·x

Coefficient de détermination

Valeurs résiduelles de l'ajustement des courbes : y - (a+b·x)

Intervalle de confiance sur la pente contenant le CLevel de dist.

SE Slope = s/sqrt(sum(x-xbar)2)

Écart-type de l'erreur d'ajustement pour y - (a + b·x)

·x(k). Deux

Catalogue

Pour les intervalles de type Predict uniquement

Variable de sortie Description

[stat.CLower, stat.CUpper]

stat.ME Marge d'erreur de l'intervalle de confiance

stat.SE Erreur type de l'intervalle de confiance

[stat.LowerPred , stat.UpperPred]

stat.MEPred Marge d'erreur de l'intervalle prévu

stat.SEPred Erreur type de l'intervalle prévu

stat.y

Intervalle de confiance sur la prévision contenant le CLevel de dist.

Intervalle prévu sur la prévision contenant le CLevel de dist.

a + b·ValX

Guide de référence TI-Nspire™ CAS 55

LinRegtTest

LinRegtTest X,Y[,Fréq[,Hypoth]]]

Calcule l'ajustement de la courbe de régression linéaire des paires de points de données, où y(k) = a + b·x(k), et teste les hypothèses nulles H0: b = 0 par rapport à l'une des alternatives suivantes :

Hypoth > 0 correspond à Ha : s1 > s2 Hypoth = 0 correspond à Ha : Hypoth < 0 correspond à Ha :

Un récapitulatif du résultat est stocké dans la variable stat.results. (Voir page 100.)

Variable de sortie Description

stat.RegEqn

stat.a, stat.b Estimations des paramètres de décalage et de pente pour l'ajustement de courbe

stat.df Degrés de liberté

stat.s

stat.t T-Statistique pour la signification de la pente

stat.PVal Probabilité que l'hypothèse alternative est fausse

stat.r Coefficient de corrélation de régression linéaire

stat.r

stat.SESlope

stat.Resid Valeurs résiduelles de l'ajustement linéaire

s1 ƒ s2 (par défaut) s1 < s2

Équation d'ajustement : a + b·x

Écart-type de l'erreur d'ajustement pour y - (a + b·x)

Coefficient de détermination

SE Slope = s/sqrt(sum(x-x_bar)2)

Catalogue

list()

Catalogue

@list(Liste1) ⇒ liste

Donne la liste des différences entre les éléments consécutifs de Liste1. Chaque élément de Liste1 est soustrait de l'élément suivant

de Liste1. Le résultat comporte toujours un élément de moins que la liste Liste1 initiale.

list4mat()

list4mat(Liste [, élémentsParLigne]) ⇒ matrice

Donne une matrice construite ligne par ligne à partir des éléments de Liste.

Si élémentsParLigne est spécifié, donne le nombre d'éléments par ligne. La valeur par défaut correspond au nombre d'éléments de Liste (une ligne).

Si Liste ne comporte pas assez d'éléments pour la matrice, on complète par zéros.

Catalogue

56 Guide de référence TI-Nspire™ CAS

4ln ⇒ expression

Expr

Convertit Expr en une expression contenant uniquement des logarithmes népériens (ln).

Catalogue

ln()

ln(Expr1) ⇒ expression ln(Liste1) ⇒ liste

Donne le logarithme népérien de l'argument. Dans le cas d'une liste, donne les logarithmes népériens de tous les

éléments de celle-ci.

ln(matriceCarrée1) ⇒ matriceCarrée

Donne le logarithme népérien de la matrice matriceCarrée1. Ce calcul est différent du calcul du logarithme népérien de chaque élément. Pour plus d'informations sur la méthode de calcul, reportezvous à cos().

matriceCarrée1 doit être diagonalisable. Le résultat contient toujours des chiffres en virgule flottante.

LnReg

LnReg X, Y[, [Fréq] [, Catégorie, Inclure]]

Calcule la régression logarithmique. Un récapitulatif du résultat est stocké dans la variable stat.results. (Voir page 100.)

Tous les arguments doivent être de mêmes dimensions, à l'exception de Inclure.

Touches /u

En mode Format complexe Réel :

En mode Format complexe Rectangulaire :

En mode Angle en radians et en mode Format complexe Rectangulaire :

Pour afficher le résultat entier, appuyez sur £, puis utilisez les touches ¡ et ¢ pour déplacer le curseur.s

Catalogue

Variable de sortie Description

stat.RegEqn

stat.a, stat.b

stat.r

Équation d'ajustement : a+b·ln(x)

Coefficients d'ajustement : y = a+b·ln(x)

Coefficient de détermination

stat.r Coefficient de corrélation linéaire

Guide de référence TI-Nspire™ CAS 57

Variable de sortie Description

stat.Resid

stat.ResidTrans Valeurs résiduelles associées à l'ajustement linéaire des données transformées

stat.XReg Liste des points de données de la liste Liste X modifiée, actuellement utilisée dans l'ajustement basé sur

stat.YReg Liste des points de données de la liste Liste Y modifiée, actuellement utilisée dans l'ajustement basé sur

stat.FreqReg Liste des fréquences correspondant à stat.XReg et stat.YReg

Valeurs résiduelles de l'ajustement des courbes = yN(a+b·ln(x)).

les restrictions de Fréq, Liste de catégories et Inclure les catégories

Local

Local Var 1 [, Va r 2] [, Va r 3 ] ...

Déclare les variables vars spécifiées comme variables locales. Ces variables existent seulement lors du calcul d'une fonction et sont supprimées une fois l'exécution de la fonction terminée.

Remarque : les variables locales contribuent à libérer de la

mémoire dans la mesure où leur existence est temporaire. De même, elle n'interfère en rien avec les valeurs des variables globales existantes. Les variables locales s'utilisent dans les boucles For et pour enregistrer temporairement des valeurs dans les fonctions de plusieurs lignes dans la mesure où les modifications sur les variables globales ne sont pas autorisées dans une fonction.

Remarque pour la saisie des données de l'exemple :

dans l'application Calculs de l'unité nomade, vous pouvez entrer des définitions sur plusieurs lignes en appuyant sur @ à la place de

· à chaque fin de ligne. Sur le clavier de l'ordinateur, maintenez

enfoncée la touche Alt tout en appuyant sur Entrée (Enter).

log()

log(Expr1[,Expr2]) ⇒ expression log(Liste1[,Expr2]) ⇒ liste

Donne le logarithme de base Expr2 de l'argument.

Remarque : voir aussi Modèle Logarithme, page 2.

Dans le cas d'une liste, donne le logarithme de base Expr2 des éléments.

Si Expr2 est omis, la valeur de base 10 par défaut est utilisée.

En mode Format complexe Réel :

Catalogue

Touches /

En mode Format complexe Rectangulaire :

58 Guide de référence TI-Nspire™ CAS

log()

log(matriceCarrée1[,Expr]) ⇒ matriceCarrée

Donne le logarithme de base Expr de matriceCarrée1. Ce calcul est différent du calcul du logarithme de base Expr de chaque élément. Pour plus d'informations sur la méthode de calcul, reportez-vous à

cos().

matriceCarrée1 doit être diagonalisable. Le résultat contient toujours des chiffres en virgule flottante.

Si l'argument de base est omis, la valeur de base 10 par défaut est utilisée.

logbase

Expr1 4logbase(Expr2) ⇒ expression

Provoque la simplification de l'expression entrée en une expression utilisant uniquement des logarithmes de base Expr2.

Touches /

En mode Angle en radians et en mode Format complexe Rectangulaire :

Pour afficher le résultat entier, appuyez sur £, puis utilisez les touches ¡ et ¢ pour déplacer le curseur.

Catalogue

Logistic

Logistic X, Y[, [Fréq] [, Catégorie, Inclure]]

Effectue une régression logistique sur X et Y en utilisant la fréquence Fréq. Un récapitulatif du résultat est stocké dans la variable stat.results. (Voir page 100.)

Variable de sortie Description

stat.RegEqn

stat.a, stat.b, stat.c Coefficients d'ajustement

stat.Resid

stat.XReg Liste des points de données de la liste Liste X modifiée, actuellement utilisée dans l'ajustement basé sur

stat.YReg Liste des points de données de la liste Liste Y modifiée, actuellement utilisée dans l'ajustement basé sur

stat.FreqReg Liste des fréquences correspondant à stat.XReg et stat.YReg

Équation d'ajustement : c/(1+a·e

Valeurs résiduelles de l'ajustement des courbes = y - (c/(1+a·e

les restrictions de Fréq, Liste de catégories et Inclure les catégories

-bx

)

-bx

)).

Catalogue

Guide de référence TI-Nspire™ CAS 59

LogisticD

LogisticD X, Y [ , [Itérations] , [Fréq] [, Catégorie, Inclure] ]

Calcule la régression logistique. Un récapitulatif du résultat est stocké dans la variable stat.results. (Voir page 100.)

Tous les arguments doivent être de mêmes dimensions, à l'exception de Inclure.

Itérations spécifie le nombre maximum d'itérations utilisées lors de

ce calcul. Si Itérations est omis, la valeur par défaut 64 est utilisée. On obtient généralement une meilleure précision en choisissant une valeur élevée, mais cela augmente également le temps de calcul, et vice versa.

Variable de sortie Description

stat.RegEqn

stat.a, stat.b, stat.c, stat.d

stat.Resid

stat.XReg Liste des points de données de la liste Liste X modifiée, actuellement utilisée dans l'ajustement basé sur

stat.YReg Liste des points de données de la liste Liste Y modifiée, actuellement utilisée dans l'ajustement basé sur

stat.FreqReg Liste des fréquences correspondant à stat.XReg et stat.YReg

Équation d'ajustement : a/(1+b·e

Coefficients d'ajustement

Valeurs résiduelles de l'ajustement des courbes = y - (a/(1+b·e

les restrictions de Fréq, Liste de catégories et Inclure les catégories

-c·x

)+d)

-c·x

)+d)

Catalogue

Loop

Bloc

EndLoop

Exécute de façon itérative les instructions de Bloc. Notez que la boucle se répète indéfiniment, jusqu'à l'exécution d'une instruction

Goto ou Exit à l'intérieur du Bloc.

Bloc correspond à une série d'instructions, séparées par un « : ».

Remarque pour la saisie des données de l'exemple :

dans l'application Calculs de l'unité nomade, vous pouvez entrer des définitions sur plusieurs lignes en appuyant sur @ à la place de

Catalogue

· à chaque fin de ligne. Sur le clavier de l'ordinateur, maintenez

enfoncée la touche Alt tout en appuyant sur Entrée (Enter).

60 Guide de référence TI-Nspire™ CAS

LU Matrice, NomMatl, NomMatu, NomMatp[, Tol ]

Calcule la décomposition LU (lower-upper) de Doolittle d'une matrice réelle ou complexe. La matrice triangulaire inféri eure est stockée dans NomMatl, la matrice triangulaire supérieure dans NomMatu et la matrice de permutation (qui décrit les échanges de lignes exécutés pendant le calcul) dans NomMatp.

NomMatl · NomMatu = NomMatp · matrice

L'argument facultatif Tol permet de considérer comme nul tout élément de la matrice dont la valeur absolue est inférieure à Tol . Cet argument n'est utilisé que si la matrice contient des nombres en virgule flottante et ne contient pas de variables symbolique sans valeur affectée. Dans le cas contraire, To l est ignoré.

• Si vous utilisez

Approché (Approximate)

calculs sont exécutés en virgule flottante.

•Si Tol est omis ou inutilisé, la tolérance par défaut est calculée comme suit :

5EM14 ·max(dim(Matrice)) ·rowNorm(Matrice)

L'algorithme de factorisation LU utilise la méthode du Pivot partiel avec échanges de lignes.

· ou définissez le mode Auto ou

sur Approché (Approximate), les

Catalogue

mat4list()

mat4list(Matrice) ⇒ liste

Donne la liste obtenue en copiant les éléments de Matrice ligne par ligne.

Guide de référence TI-Nspire™ CAS 61

Catalogue

max()

max(Expr1, Expr2) ⇒ expression max(Liste1, Liste2) ⇒ liste max(Matrice1, Matrice2) ⇒ matrice

Donne le maximum des deux arguments. Si les arguments sont deux listes ou matrices, donne la liste ou la matrice formée de la valeur maximale de chaque paire d'éléments correspondante.

max(Liste) ⇒ expression

Donne l'élément maximal de liste.

max(Matrice1) ⇒ matrice

Donne un vecteur ligne contenant l'élément maximal de chaque colonne de la matrice Matrice1.

Remarque : voir aussi fMax() et min().

Catalogue

mean()

mean(Liste[, listeFréq]) ⇒ expression

Donne la moyenne des éléments de Liste. Chaque élément de la liste listeFréq totalise le nombre d'occurrence s

de l'élément correspondant de Liste.

mean(Matrice1[, matriceFréq]) ⇒ matrice

Donne un vecteur ligne des moyennes de toutes les colonnes de

Matrice1.

Chaque élément de matriceFréq totalise le nombre d'occurrences de l'élément correspondant de Matrice1.

median()

median(Liste) ⇒ expression

Donne la médiane des éléments de Liste.

median(Matrice1) ⇒ matrice

Donne un vecteur ligne contenant les médianes des colonnes de Matrice1.

Remarque : tous les éléments de la liste ou de la matrice doivent

correspondre à des valeurs numériques.

En mode Format Vecteur Rectangulaire :

Catalogue

62 Guide de référence TI-Nspire™ CAS

MedMed

MedMed X,Y [, Fréq] [, Catégorie, Inclure]]

Calcule la régression linéaire médiane-médiane (MedMed). Un récapitulatif du résultat est stocké dans la variable stat.results. (Voir page 100.)

Tous les arguments doivent être de mêmes dimensions, à l'exception de Inclure.

Variable de sortie Description

stat.RegEqn

stat.a, stat.b

stat.Resid

stat.XReg Liste des points de données de la liste Liste X modifiée, actuellement utilisée dans l'ajustement basé sur

stat.YReg Liste des points de données de la liste Liste Y modifiée, actuellement utilisée dans l'ajustement basé sur

stat.FreqReg Liste des fréquences correspondant à stat.XReg et stat.YReg

Équation d'ajustement : m·x+b

Coefficients d'ajustement : y = m·x+b

Valeurs résiduelles de l'ajustement des courbes = y - (m·x+b).

les restrictions de Fréq, Liste de catégories et Inclure les catégories

Catalogue

mid()

mid(chaîneSrce, Début[, Nbre]) ⇒ chaîne

Donne la portion de chaîne de Nbre de caractères extraite de la chaîne chaîneSrce, en commençant au numéro de caractère Début.

Si Nbre est omis ou s'il dépasse le nombre de caractères de la chaîne chaîneSrce, on obtient tous les caractères de chaîneSrce, compris entre le numéro de caractère Début et le dernier caractère.

Nbre doit être ‚ 0. Si Nbre = 0, on obtient une chaîne vide.

mid(listeSource, Début [, Nbre]) ⇒ liste

Donne la liste de Nbre d'éléments extraits de listeSource, en commençant à l'élément numéro Début.

Si Nbre est omis ou s'il dépasse le nombre d'éléments de la liste listeSource, on obtient tous les éléments de listeSource, compris entre l'élément numéro Début et le dernier élément.

Nbre doit être ‚ 0. Si Nbre = 0, on obtient une liste vide.

mid(listeChaînesSource, Début[, Nbre]) ⇒ liste

Donne la liste de Nbre de chaînes extraites de la liste listeChaînesSource, en commençant par l'élément numéro Début.

Catalogue

Guide de référence TI-Nspire™ CAS 63

min()

min(Expr1, Expr2) ⇒ expression min(Liste1, Liste2) ⇒ liste min(Matrice1, Matrice2) ⇒ matrice

Donne le minimum des deux arguments. Si les arguments sont deux listes ou matrices, donne la liste ou la matrice formée de la valeur minimale de chaque paire d'éléments correspondante.

min(Liste) ⇒ expression

Donne l'élément minimal de Liste.

min(Matrice1) ⇒ matrice

Donne un vecteur ligne contenant l'élément minimal de chaque colonne de la matrice Matrice1.

Remarque : voir aussi fMin() et max().

Catalogue

mirr()

mirr(tauxFinancement,tauxRéinvestissement,MT0,ListeMT [,FréqMT]) ⇒ expression

Fonction financière permettant d'obtenir le taux interne de rentabilité modifié d'un investissement.

tauxFinancement correspond au taux d'intérêt que vous payez sur les montants de mouvements de trésorerie.

tauxRéinvestissement est le taux d'intérêt auquel les mouvements de trésorerie sont réinvestis.

MT0 correspond au mouvement de trésorerie initial à l'heure 0 ; il doit s'agir d'un nombre réel.

Liste MT est une liste des montants de mouvements de trésorerie après le mouvement de trésorerie initial MT0.

Remarque : voir également irr(), page 51.

mod()

mod(Exp1, Expr2) ⇒ expression mod(Liste1, List2) ⇒ liste mod(Matrice1, Matrice2) ⇒ matrice

Donne le premier argument modulo le deuxième argument, défini par les identités suivantes :

mod(x,0) = x mod(x,y) = x -Ïy floor(x/y)

Lorsque le deuxième argument correspond à une valeur non nulle, le résultat est de période dans cet argument. Le résultat est soit zéro soit une valeur de même signe que le deuxième argument.

Si les arguments sont deux listes ou deux matrices, on obtient une liste ou une matrice contenant la congruence de chaque paire d'éléments correspondante.

Remarque : voir aussi remain(), page 85

Catalogue

64 Guide de référence TI-Nspire™ CAS

mRow()

mRow(Expr, Matrice1, Index) ⇒ matrice

Donne une copie de Matrice1 obtenue en multipliant chaque élément de la ligne Index de Matrice1 par Expr.

Catalogue

mRowAdd()

mRowAdd(Expr, Matrice1, Index1, Index2) ⇒ matrice

Donne une copie de Matrice1 obtenue en remplaçant chaque élément de la ligne Index2 de Matrice1 par :

Expr × ligne Index1 + ligne Index2

MultReg

MultReg Y, X1, X2, …, X10

Calcule la régression linéaire multiple de la liste Y sur les listes X1, X2, …, X10. Un récapitulatif du résultat est stocké dans la variable stat.results. (Voir page 100.)

Variable de sortie Description

stat.RegEqn

Équation d'ajustement : b0 + b1·x1 + b2·x2 + ...

stat.b0, stat.b1, ... Coefficients de l'équation de régression

stat.R

Coefficient de détermination multiple

stat.ylist ylist = b0+b1·x1+ ...

stat.Resid

y - liste y

MultRegIntervals

MultRegIntervals Y,X1,X2[,…[,X10]],listeValX[,CLevel]

Calcule un intervalle de confiance pour la valeur que prendra y en y et en y en utilisant la régression multiple. Un récapitulatif du résultat

est stocké dans la variable stat.results. (Voir page 100.)

Catalogue

Variable de sortie Description

stat.RegEqn

Équation d'ajustement : b0 + b1·x1 + b2·x2 + ...

stat.y Prévision d'un point : y = b0 + b1 · xl + ... pour listeValX

stat.dfError Degré de liberté des erreurs

stat.CLower, stat.CUpper

Intervalle de confiance pour une moyenne y

Guide de référence TI-Nspire™ CAS 65

Variable de sortie Description

stat.ME Marge d'erreur de l'intervalle de confiance

stat.se Erreur type de l'intervalle de confiance

stat.LowerPred, stat.UpperrPred

Intervalle de prévision de y

stat.MEPred Marge d'erreur de l'intervalle que vous pouvez prédire

stat.SEPred Erreur type d'un intervalle que vous pouvez prédire

stat.bList Liste de coefficients de régression, {b0,b1,...}

stat.xvalist

stat.Resid

Valeurs X d'entrée servant à calculer y

Valeurs résiduelles de l'ajustement des courbes y = b0 + b1 · x1 + b2 · x2 + ...

MultRegTests

MultRegTests Y,X1,X2[,X3[,...[,X10]]]

Le test t de régression linéaire multiple calcule une régression li néaire sur les données et effectue un test F statistique de linéarité. Un récapitulatif du résultat est stocké dans la variable stat.results. (Voir page 100.)

Catalogue

Sorties

Variable de sortie Description

stat.RegEqn

Équation d'ajustement : b0 + b1·x1 + b2·x2 +...

stat.F Statistique du test F global

stat.PVal Plus petite probabilité permettant de rejeter l'hypothèse nulle

stat.R

stat.AdjR

Coefficient de détermination multiple

Coefficient ajusté de détermination multiple

stat.s Écart-type de l'erreur

stat.DW Statistique de Durbin-Watson ; sert à déterminer si la corrélation automatique de premier ordre est

présente dans le modèle.

stat.dfReg Degrés de liberté de la régression

stat.SSReg Somme des carrés de la régression

stat.MSReg Moyenne des carrés de la régression

stat.dfError Degrés de liberté des erreurs

stat.SSError Somme des carrés des erreurs

stat.MSError Moyenne des carrés des erreurs

stat.bList

stat.tList

{b0,b1,...} Liste des coefficients de l'équation de régression ? = b0+b1·x1+...

Liste des statistiques t pour chaque coefficient dans y(liste B)

stat.PList Liste des valeurs de probabilité pour chaque statistique t

66 Guide de référence TI-Nspire™ CAS

Variable de sortie Description

stat.ylist ylist = b0+b1·x1+ . .

stat.SEList Liste des pentes SE de chaque coefficient dans B

stat.Resid

stat.sResid Valeurs résiduelles normalisées ; valeur obtenue en divisant une valeur résiduelle par son écart-type.

stat.CookDist Distance de Cook ; Mesure de l'influence d'une observation basée sur la valeur résiduelle et le levier

stat.Leverage Mesure de la distance séparant les valeurs de la variable indépendante de leurs valeurs moyennes

y - liste y

nCr()

nCr(Expr1, Expr2) ⇒ expression

Pour les expressions Expr1 et Expr2 avec Expr1 ‚ Expr2 ‚ 0,

nCr() donne le nombre de combinaisons de Expr1 éléments pris

parmi Expr2 éléments. (Appelé aussi « coefficient binomial ».) Les deux arguments peuvent être des entiers ou des expressions symboliques.

nCr(Expr, 0) ⇒ 1

Expr, entierNég) ⇒ 0

nCr(

Expr, entierPos) ⇒ Expr·(ExprN1)...

nCr( (ExprNentierPos+1)/ entierPos!

Expr, nonEntier) ⇒ expression!/

nCr( ((ExprNnonEntier)!·nonEntier!)

Liste1, Liste2) ⇒ liste

nCr(

Donne une liste de combinaisons basées sur les paires d'éléments correspondantes dans les deux listes. Les arguments doivent être des listes comportant le même nombre d'éléments.

nCr(Matrice1, Matrice2) ⇒ matrice

Donne une matrice de combinaisons basées sur les paires d'éléments correspondantes dans les deux matrices. Les arguments doivent être des matrices comportant le même nombre d'éléments.

Catalogue

Guide de référence TI-Nspire™ CAS 67

nDeriv()

nDeriv(Expr1, Va r [=Valeur] [, H]) ⇒ expression nDeriv(Expr1, Va r [, H] | Var = Va le u r ) ⇒ expression

nDeriv(Expr1, Va r [=Valeur], Liste) ⇒ liste nDeriv(Liste1, Va r [=Valeur] [, H]) ⇒ liste nDeriv(Matrice1, Va r [=Valeur] [, H]) ⇒ matrice

Donne la dérivée numérique sous forme d'expression. Utilise la formule de quotient à différence symétrique.

Si valeur est spécifiée, celle-ci prévaut sur toute affectation de variable ou substitution précédente de type “sachant que” pour la variable.

H correspond à la valeur de l'incrément. Si H n'est pas précisé, il est fixé par défaut à 0.001.

Si vous utilisez Liste1 ou Matrice1, l'opération s'étend aux valeurs de la liste ou aux éléments de la matrice.

Remarque : voir aussi avgRC() et d().

Catalogue

newList()

newList(nbreÉléments) ⇒ liste

Donne une liste de dimension nbreÉléments. Tous les éléments sont nuls.

newMat()

newMat(nbreLignes, nbreColonnes) ⇒ matrice

Donne une matrice nulle de dimensions nbreLignes, nbreColonnes.

nfMax()

nfMax(Expr, Va r) ⇒ valeur nfMax(Expr, Va r, LimitInf) ⇒ valeur nfMax(Expr, Va r, LimitInf, LimitSup) ⇒ valeur nfMax(Expr, Var) | LimitInf<Va r <LimitSup ⇒ valeur

Donne la valeur numérique possible de la variable Va r au point où le maximum local de Expr survient.

Si LimitInf et LimitSup sont spécifiés, la fonction recherche le maximum local entre ces valeurs.

Remarque : voir aussi fMax() et d().

nfMin()

nfMin(Expr, Va r) ⇒ valeur nfMin(

Expr, Va r, LimitInf) ⇒ valeur Expr, Va r, LimitInf, LimitSup) ⇒ valeur

nfMin( nfMin(

Expr, Var) | LimitInf<Var <LimitSup ⇒ valeur

Donne la valeur numérique possible de la variable Va r au point où le minimum local de Expr survient.

Si LimitInf et LimitSup sont spécifiés, la fonction recherche le minimum local entre ces valeurs.

Remarque : voir aussi fMin() et d().

Catalogue

68 Guide de référence TI-Nspire™ CAS

nInt()

nInt(Expr1, Var, Borne1, Borne2) ⇒ expression

Si l'intégrande Expr1 ne contient pas d'autre variable que Va r et si Borne1 et Borne2 sont des constantes, en +

nInt() donne le calcul approché de ‰(Expr1, Var , Borne1, Borne2).

Cette approximation correspond à une moyenne pondérée de certaines valeurs d'échantillon de l'intégrande dans l'intervalle

<Va r<Borne2.

Borne1

L'objectif est d'atteindre une précision de six chiffres significatifs. L'algorithme s'adaptant, met un terme au calcul lorsqu'il semble avoir atteint cet objectif ou lorsqu'il paraît improbable que des échantillons supplémentaires produiront une amélioration notable.

Le message « Précision incertaine » s'affiche lorsque cet objectif ne semble pas atteint.

Il est possible de calculer une intégrale multiple en imbriquant plusieurs appels nInt(). Les bornes d'intégration peuvent dépendre des variables d'intégration les plus extérieures.

Remarque : voir aussi ‰(), page 130.

ˆ ou en -ˆ, alors

Catalogue

nom()

nom(tauxEffectif,CpY) ⇒ valeur

Fonction financière permettant de convertir le taux d'intérêt effectif tauxEffectif à un taux annuel nominal, CpY étant le nombre de périodes de calcul par an.

tauxEffectif doit être un nombre réel et CpY doit être un nombre réel > 0.

Remarque : voir également eff(), page 35.

norm()

norm(Matrice) ⇒ expression

Donne la norme de Frobenius.

normCdf()

normCdf(LimitInf,LimitSup[,m,s]) ⇒ nombre si LimitInf et

LimitSup sont des nombres, liste si LimitInf et LimitSup sont

des listes

Calcule la fonction de répartition de la loi normale d'une variable de paramètres m et s spécifiés entre les bornes lowerBound et upperBound.

Pour p(X  LimitSup), définissez LimitInf = .ˆ.

Catalogue

Guide de référence TI-Nspire™ CAS 69

normPdf()

normPdf(Val X [,m,s]) ⇒ nombre si Va lX est un nombre, liste

Val X est une liste

Calcule la densité de probabilité de la loi normale à la valeur Va l X spécifiée pour les paramètres m et s.

Catalogue

not

not Expr booléenne1 ⇒ Expression booléenne

Donne true (vrai) ou false (faux) ou une forme simplifiée de l'argument.

not Entier1 ⇒ entier

Donne le complément à 1 d'un entier. En interne, Entier1 est converti en nombre binaire 64 bits signé. La valeur de chaque bit est inversée (0 devient 1, et vice versa) pour le complément à 1. Le résultat est affiché en fonction du mode Base utilisé.

Si vous entrez un nombre dont le codage binaire signé dépasse 64 bits, il est ramené à l'aide d'une congruence dans la plage appropriée.

nPr()

nPr(Expr1, Expr2) ⇒ expression

Pour les expressions Expr1 et Expr2 avec Expr1 ‚ Expr2 ‚ 0,

nPr() donne le nombre de permutations de Expr1 éléments pris

parmi Expr2 éléments. Les deux arguments peuvent être des entiers ou des expressions symboliques.

nPr(Expr, 0) ⇒ 1

Expr, entierNég) ⇒ 1/((Expr+1)·(Expr+2)...

nPr( (

expressionNentierNég))

Expr, entierPos)

nPr(

⇒ Expr·(ExprN1)... (ExprNentierPos+1)

nPr(

Expr, nonEntier)

⇒ Expr! / (ExprNnonEntier)!

Catalogue

En mode base Hex :

Important : utilisez le chiffre zéro et pas la

lettre O.

En mode base Bin :

Pour afficher le résultat entier, appuyez sur £, puis utilisez les touches ¡ et ¢ pour déplacer le curseur.

Remarque : une entrée binaire peut comporter jusqu'à 64

chiffres (sans compter le préfixe 0b) ; une entrée hexadécimale jusqu'à 16 chiffres.

Catalogue

nPr(

Liste1, Liste2) ⇒ liste

Donne une liste de permutations basées sur les paires d'éléments correspondantes dans les deux listes. Les arguments doivent être des listes comportant le même nombre d'éléments.

70 Guide de référence TI-Nspire™ CAS

nPr()

nPr(Matrice1, Matrice2) ⇒ matrice

Donne une matrice de permutations basées sur les paires d'éléments correspondantes dans les deux matrices. Les arguments doivent être des matrices comportant le même nombre d'éléments.

Catalogue

npv()

npv(tauxIntérêt,MTO,ListeMT[,FréqMT])

Fonction financière permettant de calculer la va leur actuelle nette ; la somme des valeurs actuelles des mouvements d'entrée et de sortie de fonds. Un résultat positif pour NPV indique un investissement rentable.

tauxIntérêt est le taux à appliquer pour l'escompte des mouvements de trésorerie (taux de l'argent) sur une période donnée.

MT0 correspond au mouvement de trésorerie initial à l'heure 0 ; il doit s'agir d'un nombre réel.

Liste MT est une liste des montants de mouvements de trésorerie après le mouvement de trésorerie initial MT0.

FréqMT est une liste dans laquelle chaque élément indique la fréquence d'occurrence d'un montant de mouvement de trésorerie groupé (consécutif), correspondant à l'élément de ListeMT. La valeur par défaut est 1 ; si vous saisissez des valeurs, elles doivent être des entiers positifs < 10 000.

nSolve()

nSolve(Équation,Var [=Condition]) ⇒ chaîne_nombre ou

erreur

nSolve(Équation,Var [=Condition],LimitInf)

⇒ chaîne_nombre ou erreur

nSolve(Équation,Var [=Condition],LimitInf,LimitSup)

⇒ chaîne_nombre ou erreur

nSolve(Équation,Var [=Condition]) | LimitInf<Va r <LimitSup

⇒ chaîne_nombre ou erreur

Recherche de façon itérative une solution numérique réelle approchée pour Équation en fonction de sa variable. Spécifiez la variable comme suit :

variable

– ou – variable = nombre réel

Par exemple, x est autorisé, de même que x=3.

nSolve() est souvent plus rapide que solve() ou zeros(),

notamment si l'opérateur « | » est utilisé pour limiter la recherche à un intervalle réduit qui contient exactement une seule solution.

nSolve() tente de déterminer un point où la valeur résiduelle est

zéro ou deux points relativement rapprochés où la valeur résiduelle a un signe négatif et où son ordre de grandeur n'est pas excessif. S'il n'y parvient pas en utilisant un nombre réduit de points d'échantillon, la chaîne « Aucune solution n'a été trouvée » s'affiche.

Remarque : voir aussi cSolve(), cZeros(), solve(), et zeros().

Catalogue

Remarque : si plusieurs solutions sont possibles, vous pouvez

utiliser une condition pour mieux déterminer une solution particulière.

Guide de référence TI-Nspire™ CAS 71

OneVar

OneVar [1,]X[,[Fréq][,Catégorie,Inclure]] OneVar [

n,]X1,X2[X3[,…[,X20]]]

Effectue le calcul de statistiques à une variable sur un maximum de 20 listes. Un récapitulatif du résultat est stocké dans la variable stat.results. (Voir page 100.)

Tous les arguments doivent être de mêmes dimensions, à l'exception de Inclure.

X représente la liste des valeurs de x. Fréq représente la liste des fréquences. Catégorie représente les numéros de catégories. Inclure représente la liste des catégories à utiliser.

Variable de sortie Description

stat.v

stat.Gx

stat.sx Écart-type de l'échantillon de x

stat.ssssx Écart-type de la population de x

stat.n Nombre de points de données

stat.MinX Minimum des valeurs de x

stat.Q1X 1er quartile de x

stat.MedianX Médiane de x

stat.Q3X 3ème quartile de x

stat.MaxX Maximum des valeurs de x

stat.SSX Somme des carrés des écarts par rapport à la moyenne de x

Moyenne des valeurs x

Somme des valeurs x

Somme des valeurs x2.

Catalogue

Expr booléenne1 or Expr booléenne2

⇒ Expression booléenne

Donne true (vrai) ou false (faux) ou une forme simplifiée de l'entrée initiale.

Donne true si la simplification de l'une des deux ou des deux expressions est vraie. Donne false uniquement si la simplification des deux expressions est fausse.

Remarque : voir xor. Remarque pour la saisie des données de l'exemple :

dans l'application Calculs de l'unité nomade, vous pouvez entrer des définitions sur plusieurs lignes en appuyant sur @ à la place de

Catalogue

· à chaque fin de ligne. Sur le clavier de l'ordinateur, maintenez

enfoncée la touche Alt tout en appuyant sur Entrée (Enter).

72 Guide de référence TI-Nspire™ CAS

Entier1 or Entier2 ⇒ entier

Compare les représentations binaires de deux entiers réels en appliquant un or bit par bit. En interne, les deux entiers sont convertis en nombres binaires 64 bits signés. Lorsque les bits comparés correspondent, le résultat est 1 si dans les deux cas il s'agit d'un bit 1 ; le résultat est 0 si, dans les deux cas, il s'agit d'un bit 0. La valeur donnée représente le résultat des bits et elle est affichée selon le mode Base utilisé.

Si vous entrez un nombre dont le codage binaire signé dépasse 64 bits, il est ramené à l'aide d'une congruence dans la plage appropriée.

Remarque : voir xor.

Catalogue

En mode base Hex :

Important : utilisez le chiffre zéro et pas la lettre O.

En mode base Bin :

Remarque : une entrée binaire peut comporter jusqu'à 64

chiffres (sans compter le préfixe 0b) ; une entrée hexadécimale jusqu'à 16 chiffres.

ord()

ord(Chaîne) ⇒ entier ord(Liste1) ⇒ liste

Donne le code numérique du premier caractère de la chaîne de caractères Chaîne ou une liste des premiers caractères de tous les éléments de la liste.

P4Rx()

P4Rx(ExprR, qExpr) ⇒ expression

P4Rx(ListeR, qListe) ⇒ liste P4Rx(MatriceR, qMatrice) ⇒ matrice

Donne la valeur de l'abcisse du point de coordonnées polaires (r, q).

Remarque : l'argument q est interprété comme une mesure en

degrés, en grades ou en radians, suivant le mode Angle utilisé. Si l'argument est une expression, vous pouvez utiliser ó,G ou ôpour

ignorer temporairement le mode Angle sélectionné.

P4Ry()

P4Ry(ExprR, qExpr) ⇒ expression P4Ry(ListeR, qListe) ⇒ liste P4Ry(MatriceR, qMatrice) ⇒ matrice

Donne la valeur de l'ordonnée du point de coordonnées polaires (r, q).

Remarque : l'argument q est interprété comme une mesure en

degrés, en grades ou en radians, suivant le mode Angle utilisé. Si l'argument est une expression, vous pouvez utiliser ó,G ou ôpour

ignorer temporairement le mode Angle sélectionné.

En mode Angle en radians :

Catalogue

Guide de référence TI-Nspire™ CAS 73

PassErr

Passe une erreur au niveau suivant. Si la variable système errCode est zéro, L'instruction Else du bloc Try...Else...EndTry doit utiliser EffErr

ou PassErr. Si vous comptez rectifier ou ignorer l'erreur, sélectionnez

EffErr. Si vous ne savez pas comment traiter l'erreur, PassErr pour la transférer au niveau suivant. S'il n'y a

sélectionnez plus d'autre programme de traitement des erreurs

Try...Else...EndTry, la boîte de dialogue Erreur s'affiche

normalement.

Remarque : voir également ClrErr, page 16 et Try, page 109. Remarque pour la saisie des données de l'exemple :

dans l'application Calculs de l'unité nomade, vous pouvez entrer des définitions sur plusieurs lignes en appuyant sur @ à la place de

PassErr ne fait rien.

· à chaque fin de ligne. Sur le clavier de l'ordinateur, maintenez

enfoncée la touche Alt tout en appuyant sur Entrée (Enter).

Pour obtenir un exemple de 2 de la commande

Try, page 110.

Catalogue

PassErr, reportez-vous à l'exemple

piecewise()

piecewise(Expr1 [, Condition1 [, Expr2 [, Condition2 [, … ]]]])

Permet de créer des fonctions définies par morceaux sous forme de liste. Il est également possible de créer des fonctions définies par morceaux en utilisant un modèle.

Remarque : voir aussi Modèle Fonction définie par morceaux

, page 2.

poissCdf()

poissCdf(l,LimitInf[,LimitSup]) ⇒ nombre si LimitInf et

LimitSup sont des nombres, liste si LimitInf et LimitSup sont

des listes

Calcule la fonction de répartition d'une loi de Poisson discrète de moyene l spécifiée entre les bornes lowerBound et upperBound.

Pour P(X  LimitSup), définissez LimitInf=0

poissPdf()

poissPdf(l,Val X ) ⇒ nombre si Va lX est un nombre, liste si

Val X est une liste

Calcule la probabilité de ValX pour la loi de Poisson de moyenne l spécifiée.

Polar

Vec t e u r 4Polar

Affiche vecteur sous forme polaire [r q]. Le vecteur doit être un vecteur ligne ou colonne et de dimension 2.

Remarque : 4Polar est uniquement une instruction d'affichage et

non une fonction de conversion. On ne peut l'utili ser qu'à la fin d'une ligne et elle ne modifie pas le contenu du registre ans.

Remarque : voir aussi 4Rect, page 84.

Catalogue

74 Guide de référence TI-Nspire™ CAS

Polar

valeurComplexe 4Polar

Affiche valeurComplexe sous forme polaire.

• Le mode Angle en degrés affiche (rq).

• Le mode Angle en radians affiche reiq.

valeurComplexe peut prendre n'importe quelle forme complexe. Toutefois, une entrée re degrés.

Remarque : vous devez utiliser les parenthèses pour les entrées

polaires (rq).

q génère une erreur en mode Angle en

En mode Angle en radians :

En mode Angle en grades :

En mode Angle en degrés :

Catalogue

polyCoeffs()

polyCoeffs(Poly [,Var ]) ⇒ liste

Affiche une liste des coefficients du polynôme Poly pour la variable Var .

Poly doit être une expression polynomiale de Va r Nous conseillons

de ne pas omettre Va r à moins que Poly ne soit une expression dans une variable unique.

Catalogue

Etend le polynôme et sélectionne x pour la variable omise Var .

Guide de référence TI-Nspire™ CAS 75

polyDegree()

polyDegree(Poly [,Var ]) ⇒ valeur

Affiche le degré de l'expression polynomiale Poly pour la variable Var . Si vous omettez Va r , la fonction polyDegree() sélectionne

une variable par défaut parmi les variables contenues dans le polynôme Poly.

Poly doit être une expression polynomiale de Va r Nous conseillons de ne pas omettre Va r à moins que Poly ne soit une expression dans une variable unique.

Catalogue

Polynômes constants

Il est possible d'extraire le degré, même si cela n'es t pas possible pour les coefficients. Cela s'explique par le fait qu'un degré peut être extrait sans développer le polynôme.

polyEval()

polyEval(Liste1, Expr1) ⇒ expression polyEval(Liste1, Liste2) ⇒ expression

Interprète le premier argument comme les coefficients d'un polynôme ordonné suivant les puissances décroissantes et calcule la valeur de ce polynôme au point indiqué par le deuxième argument.

polyGcd()

polyGcd(Expr1,Expr2) ⇒ expression

Donne le plus grand commun diviseur des deux arguments. Expr1 et Expr2 doivent être des expressions polynomiales. Les listes, matrices et arguments booléens ne sont pas autorisés.

Catalogue

76 Guide de référence TI-Nspire™ CAS

polyQuotient()

polyQuotient(Poly1,Poly2 [,Var ]) ⇒ expression

Affiche le quotient de polynôme Poly1 divisé par le polynôme Poly2 par rapport à la variable spécifiée Var .

Poly1 et Poly2 doivent être des expressions polynomiales de Va r . Nous conseillons de ne pas omettre Va r à moins que Poly1 et Poly2 ne soient des expressions dans une même variable unique.

Catalogue

polyRemainder()

polyRemainder(Poly1,Poly2 [,Var ]) ⇒ expression

Affiche le reste du polynôme Poly1 divisé par le polynôme Poly2 par rapport à la variable spécifiée Var .

Poly1 et Poly2 doivent être des expressions polynomiales de Va r . Nous conseillons de ne pas omettre Va r à moins que Poly1 et Poly2 ne soient des expressions dans une même variable unique.

PowerReg

PowerReg X,Y [, Fréq] [, Catégorie, Inclure]]

Calcule l'ajustement par une fonction de puissance. Un récapitulatif du résultat est stocké dans la variable stat.results. (Voir page 100.)

Tous les arguments doivent être de mêmes dimensions, à l'exception de Inclure.

Catalogue

Guide de référence TI-Nspire™ CAS 77

Variable de sortie Description

stat.RegEqn

stat.a, stat.b

stat.r

stat.r Coefficient de corrélation linéaire

stat.Resid

stat.ResidTrans Valeurs résiduelles associées à l'ajustement linéaire des données transformées

stat.XReg Liste des points de données de la liste Liste X modifiée, actuellement utilisée dans l'ajustement basé sur

stat.YReg Liste des points de données de la liste Liste Y modifiée, actuellement utilisée dans l'ajustement basé sur

stat.FreqReg Liste des fréquences correspondant à stat.XReg et stat.YReg

Équation d'ajustement : a·(x)

Coefficients d'ajustement : y = a·(x)

Coefficient de détermination

Valeurs résiduelles de l'ajustement des courbes = y - a·(x)b.

les restrictions de Fréq, Liste de catégories et Inclure les catégories

Prgm

Bloc

EndPrgm

Modèle de création d'un programme défini par l'utilisateur. À utiliser avec la commande Define, Define LibPub, ou Define LibPriv.

Bloc peut correspondre à une instruction unique ou à une série d'instructions séparées par le caractère “:” ou à une série d'instructions réparties sur plusieurs lignes.

Remarque pour la saisie des données de l'exemple : dans

l'application Calculs de l'unité nomade, vous pouvez entrer des définitions sur plusieurs lignes en appuyant sur @ à la place de

· à chaque fin de ligne. Sur le clavier de l'ordinateur, maintenez

enfoncée la touche Alt tout en appuyant sur Entrée (Enter).

Product (PI)

Catalogue

Calcule le plus grand commun diviseur et affiche les résultats intermédiaires.

Voir Π(), page 132.

78 Guide de référence TI-Nspire™ CAS

product()

product(Liste[, Début[, Fin]]) ⇒ expression

Donne le produit des éléments de Liste. Début et Fin sont facultatifs. Ils permettent de spécifier une plage d'éléments.

product(Matrice1[, Début[, Fin]]) ⇒ matrice

Donne un vecteur ligne contenant les produits des éléments ligne par ligne de Matrice1. Début et Fin sont facultatifs. Ils permettent de spécifier une plage de colonnes.

Catalogue

propFrac()

propFrac(Expr1[, Va r ]) ⇒ expression

propFrac(nombre_rationnel) décompose nombre_rationnel sous

la forme de la somme d'un entier et d'une fraction de même signe et dont le dénominateur est supérieur au numérateur (fraction propre).

propFrac(expression_rationnelle,Var ) donne la somme des

fractions propres et d'un polynôme par rapport à Va r . Le degré de Var dans le dénominateur est supérieur au degré de Va r dans le numérateur pour chaque fraction propre. Les mêmes puissances de Var sont regroupées. Les termes et leurs facteurs sont triés, Va r étant la variable principale.

Si Var est omis, le développement des fractions propres s'effectue par rapport à la variable la plus importante. Les coefficients de la partie polynomiale sont ensuite ramenés à leur forme propre par rapport à leur variable la plus importante, et ainsi de suite.

Pour les expressions rationnelles, propFrac() est une alternative plus rapide mais moins extrême à expand().

Catalogue

Guide de référence TI-Nspire™ CAS 79

QR Matrice, NomMatq, NomMatr[, Tol ]

Calcule la factorisation QR Householder d'une matrice réelle ou complexe. Les matrices Q et R obtenues sont stockées dans les NomsMat spécifiés. La matrice Q est unitaire. La matrice R est triangulaire supérieure.

• Si vous utilisez

Approché (Approximate)

calculs sont exécutés en virgule flottante.

•Si Tol est omis ou inutilisé, la tolérance par défaut est calculée comme suit :

5Eë14 ·max(dim(Matrice)) ·rowNorm(Matrice)

La factorisation QR sous forme numérique est calculée en utilisant la transformation de Householder. La factorisation symbolique est calculée en utilisant la méthode de Gram-Schmidt. Les colonnes de NomMatq sont les vecteurs de base orthonormaux de l'espace vectoriel engendré par les vecteurs colonnes de matrice.

· ou définissez le mode Auto ou

sur Approché (Approximate), les

Catalogue

Le nombre en virgule flottante (9.) dans m1 fait que les résultats seront tous calculés en virgule flottante.

QuadReg

QuadReg X,Y [, Fréq] [, Catégorie, Inclure]]

Calcule l'ajustement par un polynôme de degré 2. Un récapitulatif du résultat est stocké dans la variable stat.results. (Voir page 100.)

Tous les arguments doivent être de mêmes dimensions, à l'exception de Inclure.

Variable de sortie Description

stat.RegEqn

Équation d'ajustement : a·x2+b·x+c

Catalogue

80 Guide de référence TI-Nspire™ CAS

stat.a, stat.b, stat.c Coefficients d'ajustement

stat.R

stat.Resid

stat.XReg Liste des points de données de la liste Liste X modifiée, actuellement utilisée dans l'ajustement basé sur

stat.YReg Liste des points de données de la liste Liste Y modifiée, actuellement utilisée dans l'ajustement basé sur

Coefficient de détermination

Valeurs résiduelles de l'ajustement des courbes = y - (a·x2+b·x+c).

les restrictions de Fréq, Liste de catégories et Inclure les catégories

stat.FreqReg Liste des fréquences correspondant à stat.XReg et stat.YReg

QuartReg

QuartReg X,Y [, Fréq] [, Catégorie, Inclure]]

Calcule l'ajustement par un polynôme de degré 4. Un récapitulatif du résultat est stocké dans la variable stat.results. (Voir page 100.)

Tous les arguments doivent être de mêmes dimensions, à l'exception de Inclure.

Catalogue

Variable de sortie Description

stat.RegEqn

stat.a, stat.b, stat.c, stat.d, stat.e

stat.R

stat.Resid

stat.XReg Liste des points de données de la liste Liste X modifiée, actuellement utilisée dans l'ajustement basé sur

stat.YReg Liste des points de données de la liste Liste Y modifiée, actuellement utilisée dans l'ajustement basé sur

Équation d'ajustement : a·x4+b·x3+c· x2+d·x+e

Coefficients d'ajustement

Coefficient de détermination

Valeurs résiduelles de l'ajustement des courbes = y - (a·x4+b·x3+c· x2+d·x+e).

les restrictions de Fréq, Liste de catégories et Inclure les catégories

stat.FreqReg Liste des fréquences correspondant à stat.XReg et stat.YReg

Guide de référence TI-Nspire™ CAS 81

R4Pq()

R4Pq (ExprX, ExprY) ⇒ expression R4Pq (ListeX, ListeY) ⇒ liste R4Pq (MatriceX, MatriceY) ⇒ matrice

Donne la coordonnée q d'un point de coordonnées rectangulaires (x,y).

Remarque : donne le résultat en degrés, en grades ou en radians,

suivant le mode angulaire utilisé.

R4Pr()

R4Pr (ExprX, ExprY) ⇒ expression R4Pr (ListeX, ListeY) ⇒ liste R4Pr (MatriceX, MatriceY) ⇒ matrice

Donne la coordonnée r d'un point de coordonnées rectangulaires (x,y).

En mode Angle en degrés :

En mode Angle en grades :

En mode Angle en radians :

Catalogue

Rad

Expr14Rad ⇒ expression

Convertit l'argument en mesure d'angle en radians.

rand()

rand() ⇒ expression rand(nmbreEssais) ⇒ liste

rand() donne un nombre aléatoire compris entre 0 et 1. rand(nbreEssais) donne une liste de nombres aléatoires compris

entre 0 et 1 pour le nombre d'essais nbreEssais.

En mode Angle en degrés :

En mode Angle en grades :

Réinitialise le générateur de nombres aléatoires.

Catalogue

82 Guide de référence TI-Nspire™ CAS

randBin()

randBin(n, p) ⇒ expression randBin(n, p, nbreEssais) ⇒ liste

randBin(n, p) donne un nombre aléatoire tiré d'une distribution

binomiale spécifiée.

randBin(n, p, nbreEssais) donne une liste de nombres aléatoires

tirés d'une distribution binomiale spécifiée pour un nombre d'essais nbreEssais.

Catalogue

randInt()

randInt(LimiteInf,LimiteSup) ⇒ expression randInt(LimiteInf,LimiteSup,nbreEssais) ⇒ liste

randInt(LimiteInf,LimiteSup) donne un entier aléatoire pris entre

les limites entières LimiteInf et LimiteSup.

randInt(LimiteInf,LimiteSup,nbreEssais) donne une liste d'entiers

aléatoires pris entre les limites spécifiées pour un nombre d'essais nbreEssais.

randMat()

randMat(nbreLignes, nbreColonnes) ⇒ matrice

Donne une matrice aléatoire d'entiers compris entre -9 et 9 de la dimension spécifiée.

Les deux arguments doivent pouvoir être simplifiés en entiers.

randNorm()

randNorm(m, s [,nbreEssais]) ⇒ expression

Donne un nombre décimal aléatoire issu de la loi normale spécifiée. Il peut s'agir de tout nombre réel, mais le résultat obtenu sera

essentiellement compris dans l'intervalle [mN3·s, m+3·s].

randPoly()

randPoly(Va r , Ordre) ⇒ expression

Donne un polynôme aléatoire de la variable Va r de degré Ordre spécifié. Les coefficients sont des entiers aléatoires compris entre ë9 et 9. Le premier coefficient sera non nul.

Ordre doit être un entier compris entre 0 et 99.

Catalogue

Remarque : Les valeurs de cette matrice changent chaque

fois que l'on appuie sur ·.

Catalogue

randSamp()

randSamp(Liste,nbreEssais[,sansRem]) ⇒ liste

Donne une liste contenant un échantillon aléatoire de nbreEssais éléments choisis dans Liste avec option de remise (sansRem=0) ou sans option de remise (sansRem=1). L'option par défaut est avec remise.

Catalogue

Guide de référence TI-Nspire™ CAS 83

RandSeed

RandSeed Nombre

Si Nombre = 0, réinitialise le générateur de nombres aléatoires. Si

ƒ 0, sert à générer deux nombres initiaux qui sont stockés

Nombre

dans les variables système seed1 et seed2.

Catalogue

real()

real(Expr1) ⇒ expression

Donne la partie réelle de l'argument.

Remarque : toutes les variables non affectées sont considérées

comme réelles. Voir aussi imag(), page 49.

real(Liste1) ⇒ liste

Donne la liste des parties réelles de tous les éléments.

real(Matrice1) ⇒ matrice

Donne la matrice des parties réelles de tous les éléments.

Rect

Vec t e u r 4Rect

Affiche Vecteur en coordonnées rectangulaires [x, y, z]. Le vecteur doit être un vecteur ligne ou colonne de dimension 2 ou 3.

Remarque : 4Rect est uniquement une instruction d'affichage et

non une fonction de conversion. On ne peut l'utili ser qu'à la fin d'une ligne et elle ne modifie pas le contenu du registre ans.

Remarque : Voir aussi 4Polar, page 74.

valeurComplexe 4Rect

Affiche valeurComplexe sous forme rectangulaire (a+bi). valeurComplexe peut prendre n'importe quelle forme rectangulaire.

Toutefois, une entrée re degrés.

Remarque : vous devez utiliser les parenthèses pour les entrées

polaires (rq).

génère une erreur en mode Angle en

En mode Angle en radians :

En mode Angle en grades :

Catalogue

En mode Angle en degrés :

Remarque : pour taper  à partir du clavier, sélectionnez-le

dans la liste des symboles du Catalogue.

84 Guide de référence TI-Nspire™ CAS

ref()

ref(Matrice1[, To l ]) ⇒ matrice

Donne une réduite de Gauss de la matrice Matrice1. L'argument facultatif Tol permet de considérer comme nul tout

• Si vous utilisez

Approché (Approximate)

calculs sont exécutés en virgule flottante.

•Si Tol est omis ou inutilisé, la tolérance par défaut est calculée comme suit :

5Eë14 ·max(dim(Matrice1)) ·rowNorm(Matrice1)

Remarque : voir aussi rref(), page 88.

· ou définissez le mode Auto ou

sur Approché (Approximate), les

Catalogue

remain()

remain(Expr1, Expr2) ⇒ expression remain(Liste1, Liste2) ⇒ liste remain(Matrice1, Matrice2) ⇒ matrice

Donne le reste de la division euclidienne du premier argument par le deuxième argument, défini par les identités suivantes :

remain(x,0)  x remain(x,y)  xNy·iPart(x/y)

Vous remarquerez que remain(Nx,y)  Nremain(x,y). Le résultat peut soit être égal à zéro , soit être du même signe que le premier argument.

Remarque : voir aussi mod(), page 64.

Return

Return [Expr]

Donne Expr comme résultat de la fonction. S'utilise dans les blocs

Func...EndFunc. Remarque : Vous pouvez utiliser Return sans argument dans un

bloc Prgm...EndPrgm pour quitter un programme.

Remarque pour la saisie des données de l'exemple :

dans l'application Calculs de l'unité nomade, vous pouvez entrer des définitions sur plusieurs lignes en appuyant sur @ à la place de

· à chaque fin de ligne. Sur le clavier de l'ordinateur, maintenez

enfoncée la touche Alt tout en appuyant sur Entrée (Enter).

right()

right(Liste1[, Nomb]) ⇒ liste

Donne les Nomb éléments les plus à droite de la liste Liste1. Si Nomb est absent, on obtient Liste1.

Catalogue

Guide de référence TI-Nspire™ CAS 85

right()

right(chaîneSrce[, Nomb]) ⇒ chaîne

Donne la chaîne formée par les Nomb caractères les plus à droite de la chaîne de caractères chaîneSrce.

Si Nomb est absent, on obtient chaîneSrce.

right(Comparaison) ⇒ expression

Donne le membre de droite d'une équation ou d'une inéquation.

Catalogue

root()

root(Expr) ⇒ root root(Expr1, Expr2) ⇒ root

root(Expr) affiche la racine carrée de Expr. root(Expr1, Expr2) affiche la racine Expr2 de Expr1. Expr1 peut

être un nombre réel ou une constant complexe en virgule flottant e, un entier ou une constante rationnelle complexe, ou une expression symbolique générale.

Remarque : voir aussi Modèle Racine n-ième, page 1.

rotate()

rotate(Entier1[,nbreRotations]) ⇒ entier

Permute les bits de la représentation binaire d'un entier. Entier1 peut être un entier de n'importe quelle base ; il est automatiquement converti sous forme binaire (64 bits) signée. Si Entier1 est trop important pour être codé sur 64 bits, il est ramené à l'aide d'une congruence dans la plage appropriée.

Si nbreRotations est positif, la permutation circulaire s'effectue vers la gauche. Si nbreRotations est négatif, la permutation circulaire s'effectue vers la droite. La valeur par défaut est ë1 (permutation circulation de un bit vers la droite).

Par exemple, dans une permutation circulaire vers la droite :

Tous les bits permutent vers la droite. 0b00000000000001111010110000110101 Le bit le plus à droite passe à la position la plus à gauche. donne : 0b10000000000000111101011000011010 Le résultat est affiché selon le mode Base utilisé.

rotate(Liste1[,nbreRotations]) ⇒ liste

Donne une copie de Liste1 dont les éléments ont été permutés circulairement vers la gauche ou vers la droite de nbreRotations éléments. Ne modifie en rien Liste1.

Catalogue

En mode base Bin :

Pour afficher le résultat entier, appuyez sur £, puis utilisez les touches ¡ et ¢ pour déplacer le curseur.

En mode base Hex :

Important : pour une entrée binaire ou hexadécimale, vous devez utiliser respectivement le préfixe 0b ou 0h (zéro, pas la lettre O).

En mode base Dec :

86 Guide de référence TI-Nspire™ CAS

rotate()

rotate(Chaîne1[,nbreRotations]) ⇒ chaîne

Donne une copie de Chaîne1 dont les caractères ont été permutés circulairement vers la gauche ou vers la droite de nbreRotations caractères. Ne modifie en rien Chaîne1.

Catalogue

round()

round(Expr1[, n]) ⇒ expression

Arrondit l'argument au nombre de chiffres n spécifié après la virgule. n doit être un entier compris entre 0 et 12. Si n est omis, arrondit

l'argument à 12 chiffres significatifs.

Remarque : le mode d'affichage des chiffres peut affecter le

résultat affiché.

round(Liste1[, n]) ⇒ liste

Donne la liste des éléments arrondis au nombre de chiffres n spécifié.

round(Matrice1[, n]) ⇒ matrice

Donne la matrice des éléments arrondis au nombre de chiffres n spécifié.

rowAdd()

rowAdd(Matrice1, IndexL1, IndexL2) ⇒ matrice

Donne une copie de Matrice1 obtenue en remplaçant dans la matrice la ligne IndexL2 par la somme des lignes IndexL1 et IndexL2.

rowDim()

rowDim(Matrice) ⇒ expression

Donne le nombre de lignes de Matrice.

Remarque : voir aussi colDim(), page 16.

Catalogue

rowNorm()

rowNorm(Matrice) ⇒ expression

Donne le maximum des sommes des valeurs absolues des éléments de chaque ligne de Matrice.

Remarque : la matrice utilisée ne doit contenir que des éléments

numériques. Voir aussi colNorm(), page 17.

Catalogue

Guide de référence TI-Nspire™ CAS 87

rowSwap()

rowSwap(Matrice1, IndexL1, IndexL2) ⇒ matrice

Donne la matrice Matrice1 obtenue en échangeant les lignes IndexL1 et IndexL2.

Catalogue

rref()

rref(Matrice1[, Tol ]) ⇒ matrice

Donne la réduite de Gauss-Jordan de Matrice1.

• Si vous utilisez

Approché (Approximate)

calculs sont exécutés en virgule flottante.

•Si Tol est omis ou inutilisé, la tolérance par défaut est calculée comme suit :

5Eë14 ·max(dim(Matrice1)) ·rowNorm(Matrice1)

Remarque : Voir aussi ref(), page 85.

· ou définissez le mode Auto ou

sur Approché (Approximate), les

sec()

sec(Expr1) ⇒ expression sec(Liste1) ⇒ liste

Affiche la sécante de Expr1 ou retourne la liste des sécantes des éléments de Liste1.

Remarque : l'argument est interprété comme la mesure d'un angle

en degrés, en grades ou en radians, suivant le mode angulaire en cours d'utilisation. Vous pouvez utiliser ó,G ou ô pour préciser

l'unité employée temporairement pour le calcul.

En mode Angle en degrés :

Catalogue

88 Guide de référence TI-Nspire™ CAS

sec/()

sec/(Expr1) ⇒ expression sec/(Liste1) ⇒ liste

Affiche l'angle dont la sécante correspond à Expr1 ou retourne la liste des arcs sécantes des éléments de Liste1.

Remarque : donne le résultat en degrés, en grades ou en radians,

suivant le mode angulaire utilisé.

En mode Angle en degrés :

En mode Angle en grades :

En mode Angle en radians :

Catalogue

sech()

sech(Expr1) ⇒ expression sech(Liste1) ⇒ liste

Affiche la sécante hyperbolique de Expr1 ou retourne la liste des sécantes hyperboliques des éléments de liste1.

sechê()

sechê(Expr1) ⇒ expression sechê (Liste1) ⇒ liste

Donne l'argument sécante hyperbolique de Expr1 ou retourne la liste des arguments sécantes hyperboliques des éléments de Liste1.

seq()

seq(Expr, Va r, Début, Fin[, Incrément]) ⇒ liste

Incrémente la valeur de Va r comprise entre Début et Fin en fonction de l'incrément Incrément spécifié, calcule Expr et affiche le résultat sous forme de liste. Le contenu initial de Va r est conservé après l'application de seq().

Var ne doit pas être une variable système. La valeur par défaut de Incrément est 1.

Catalogue

En mode Angle en radians et en mode Format complexe Rectangulaire :

Catalogue

Appuyez sur Ctrl + Entrée /· pour calculer :

Guide de référence TI-Nspire™ CAS 89

series()

series(Expr1, Var , Ordre [, Point]) ⇒ expression series(Expr1, Var , Ordre [, Point]) | Var >Point ⇒ expression series(Expr1, Var , Ordre [, Point]) | Var <Point ⇒ expression

Donne un développement en série généralisé, tronqué, de Expr1 en Point jusqu'au degré Ordre. Ordre peut être un nombre rationnel

quelconque. Les puissances de (Va r N Point) peuvent avoir des exposants négatifs et/ou fractionnaires. Les coefficients de ces puissances peuvent inclure les logarithmes de (Va r N Point) et d'autres fonctions de Va r dominés par toutes les puissances de (Va r

N Point) ayant le même signe d'exposant.

La valeur par défaut de Point est 0. Point peut être ˆ ou Nˆ,

auxquels cas le développement s'effectue jusqu'au degré Ordre en 1/ (Va r N Point).

series(...) donne “series(...)” s'il ne parvient pas à déterminer la

représentation, comme pour les singularités essentielles sin(1/z) en

N1/z

z=0, e

en z=0 ou ez en z = ˆ ou Nˆ.

Si la série ou une de ses dérivées présente une disconti nuité en Point, le résultat peut contenir des sous-expressions de type sign(…) ou

abs(…) pour une variable réelle ou (-1) variable complexe, qui se termine par "_". Si vous voulez utiliser la série uniquement pour des valeurs supérieures ou inférieures à Point, vous devez ajouter l'élément approprié "| Va r > Point", "| Var < Point", "| "Va r ‚ Point" ou "Va r  Point" pour obtenir un résultat simplifié.

series() peut donner des approximations symboliques pour des

intégrales indéfinies et définies pour lesquelles autrement, il n'e st pas possible d'obtenir des solutions symboliques.

series() est appliqué à chaque élément d'une liste ou d'une matrice

passée en 1er argument.

series() est une version généralisée de taylor().

Comme illustré dans l'exemple ci-contre, le développement des routines de calcul du résultat donnée par series(...) peut réorganiser l'ordre des termes de sorte que le terme dominant ne soit pas le terme le plus à gauche.

Remarque : voir aussi dominantTerm(), page 34.

floor(…angle(…)…)

pour une

Catalogue

90 Guide de référence TI-Nspire™ CAS

setMode()

setMode(EntierNomMode, EntierRéglage) ⇒ entier setMode(liste) ⇒ liste des entiers

Accessible uniquement dans une fonction ou un programme.

setMode(EntierNomMode, EntierRéglage) règle

provisoirement le mode EntierNomMode sur le nouveau réglage EntierRéglage et affiche un entier correspondant au réglage

d'origine de ce mode. Le changement est limité à la durée d'exécution du programme/de la fonction.

EntierNomMode indique le mode que vous souhaitez régler. Il doit s'agir d'un des entiers du mode du tableau ci-dessous.

EntierRéglage indique le nouveau réglage pour ce mode. Il doit s'agir de l'un des entiers de réglage indiqués ci-dessous pour le mode spécifique que vous configurez.

setMode(liste) permet de modifier plusieurs réglages. liste

contient les paires d'entiers de mode et d'entiers de réglage.

setMode(liste) affiche une liste dont les paires d'entiers

représentent les modes et réglages d'origine. Si vous avez enregistré tous les réglages du mode avec

getMode(0) & var, setMode(var) permet de restaurer ces

réglages jusqu'à fermeture du programme ou de la fonction. Voir

getMode(), page 46. Remarque : Les réglages de mode actuels sont transférés dans

les sous-programmes appelés. Si un sous-programme change un quelconque réglage du mode, le changement sera perdu dès le retour au programme appelant.

Remarque pour la saisie des données de l'exemple :

dans l'application Calculs de l'unité nomade, vous pouvez entrer des définitions sur plusieurs lignes en appuyant sur @ à la

place de · à chaque fin de ligne. Sur le clavier de l'ordinateur, maintenez enfoncée la touche Alt tout en appuyant

sur Entrée (Enter).

Catalogue

Affiche la valeur approchée de p à l'aide du réglage par défaut de Afficher chiffres, puis affiche p avec le réglage Fixe 2. Vérifiez que la valeur par défaut est bien restaurée après l'exécution du programme.

Nom du mode

Afficher chiffres

Angle

Format Exponentiel

Réel ou Complexe

Auto ou Approché

Format Vecteur

Base

Système d'unités

Entier du mode

Entiers de réglage

=Flottant, 2=Flottant 1, 3=Flottant 2, 4=Flottant 3, 5=Flottant 4, 6=Flottant 5,

=Radian, 2=Degré, 3=Grade

=Normal, 2=Scientifique, 3=Ingénieur

=Réel, 2=Rectangulaire, 3=Polaire

=Auto, 2=Approché, 3=Exact

=Rectangulaire, 2=Cylindrique, 3=Sphérique

=Décimale, 2=Hexadécimale, 3=Binaire

=SI, 2=Ang/US

Guide de référence TI-Nspire™ CAS 91

shift()

shift(Entier1[,nbreDécal]) ⇒ entier

Décale les bits de la représentation binaire d'un entier. Entier1 peut être un entier de n'importe quelle base ; il est automatiquement converti sous forme binaire (64 bits) signée. Si Entier1 est trop important pour être codé sur 64 bits, il est ramené à l'aide d'une congruence dans la plage appropriée.

Si nbreDécal est positif, le décalage s'effectue vers la gauche. Si nbreDécal est négatif, le décalage s'effectue vers la droite. La valeur par défaut est ë1 (décalage d'un bit vers la droite).

Dans un décalage vers la droite, le de rnier bit est éliminé et 0 ou 1 est inséré à gauche selon le premier bit. Dans un décalage vers la gauche, le premier bit est éliminé et 0 est inséré comme dernier bit.

Par exemple, dans un décalage vers la droite : Tous les bits sont décalés vers la droite. 0b0000000000000111101011000011010 Insère 0 si le premier bit est un 0

ou 1 si ce bit est un 1. donne : 0b00000000000000111101011000011010 Le résultat est affiché selon le mode Base utilisé. Les zéros de tête ne

sont pas affichés.

shift(Liste1 [,nbreDécal]) ⇒ liste

Donne une copie de Liste1 dont les éléments ont été décalés vers la gauche ou vers la droite de nbreDécal éléments. Ne modifie en rien Liste1.

Si nbreDécal est positif, le décalage s'effectue vers la gauche. Si nbreDécal est négatif, le décalage s'effectue vers la droite. La valeur par défaut est ë1 (décalage d'un élément vers la droite).

Les éléments introduits au début ou à la fin de liste par l'opération de décalage sont remplacés par undef (non défini).

shift(Chaîne1 [,nbreDécal]) ⇒ chaîne

Donne une copie de Chaîne1 dont les caractères ont été décalés vers la gauche ou vers la droite de nbreDécal caractères. Ne modifie en rien Chaîne1.

Si nbreDécal est positif, le décalage s'effectue vers la gauche. Si nbreDécal est négatif, le décalage s'effectue vers la droite. La valeur par défaut est ë1 (décalage d'un caractère vers la droite).

Les caractères introduits au début ou à la fin de Chaîne par l'opération de décalage sont remplacés par un espace.

Catalogue

En mode base Bin :

En mode base Hex :

Important : pour une entrée binaire ou hexadécimale, vous

devez utiliser respectivement le préfixe 0b ou 0h (zéro, pas la lettre O).

En mode base Dec :

92 Guide de référence TI-Nspire™ CAS

sign()

sign(Expr1) ⇒ expression sign(Liste1) ⇒ liste sign(Matrice1) ⇒ matrice

Pour une Expr1 réelle ou complexe, donne Expr1/ Expr1ƒ 0.

abs(Expr1) si

Donne 1 si l'expression Expression1 est positive. Donne ë1 si l'expression Expr1 est négative.

sign(0) donne „1 en mode Format complexe Réel ; sinon, donne lui-

même.

sign(0) représente le cercle d'unité dans le domaine complexe.

Dans le cas d'une liste ou d'une matrice, donne les signes de tous les éléments.

En mode Format complexe Réel :

Catalogue

simult()

simult(matriceCoeff, vecteurConst[, tol]) ⇒ matrice

Donne un vecteur colonne contenant les solutions d'un système d'équations.

matriceCoeff doit être une matrice carrée qui contient les coefficients des équations.

vecteurConst doit avoir le même nombre de lignes (même dimension) que matriceCoeff et contenir le second membre.

• Si vous réglez le mode Auto ou Approché (Approximate) sur Approché (Approximate), les calculs sont exécutés en virgule flottante.

•Si Tol est omis ou inutilisé, la tolérance par défaut est calculée comme suit :

5Eë14 ·max(dim(matriceCoeff)) ·rowNorm(matriceCoeff)

simult(matriceCoeff, matriceConst[, tol]) ⇒ matrice

Permet de résoudre plusieurs systèmes d'équations, ayant les mêmes coefficients mais des seconds membres différents.

Chaque colonne de matriceConst représente le second membre d'un système d'équations. Chaque colonne de la matrice obtenue contient la solution du système correspondant.

Catalogue

Résolution de x et y : x + 2y = 1 3x + 4y = ë1

La solution est x=ë3 et y=2.

Résolution : ax + by = 1 cx + dy = 2

Résolution :

x + 2y = 1

3x + 4y = ë1

x + 2y = 2

3x + 4y = ë3

Pour le premier système, x=ë3 et y=2. Pour le deuxième système, x=ë7 et y=9/2.

Guide de référence TI-Nspire™ CAS 93

sin()

sin(Expr1) ⇒ expression sin(Liste1) ⇒ liste

sin(Expr1) donne le sinus de l'argument sous forme d'expression. sin(Liste1) donne la liste des sinus des éléments de Liste1. Remarque : l'argument est interprété comme mesure d'angle en

degrés, en grades ou en radians, suivant le mode angulaire sélectionné. Vous pouvez utiliser ó,G ou ô pour ignorer

temporairement le mode angulaire sélectionné.

En mode Angle en degrés :

En mode Angle en grades :

En mode Angle en radians :

Touche

sin(matriceCarrée1) ⇒ matriceCarrée

Donne le sinus de la matrice matriceCarrée1. Ce calcul est différent du calcul du sinus de chaque élément. Pour plus d'informations sur la méthode de calcul, reportez-vous à cos().

matriceCarrée1 doit être diagonalisable. Le résultat contient toujours des chiffres en virgule flottante.

sinê()

sinê(Expr1) ⇒ expression sinê(Liste1) ⇒ liste

sinê(Expr1) donne l'arc sinus de Expr1 sous forme d'expression.

sinê(List1) donne la liste des arcs sinus des éléments de Liste1.

Remarque : donne le résultat en degrés, en grades ou en radians,

suivant le mode angulaire utilisé.

En mode Angle en radians :

En mode Angle en degrés :

En mode Angle en grades :

En mode Angle en radians :

Touches

94 Guide de référence TI-Nspire™ CAS

Texas instruments TI-NSPIRE CAS REFERENCE Manual

Specifications and Main Features

Frequently Asked Questions

User Manual