Texas instruments DERIVE 5 Introduction

Download

™

Introduction to

by Bernhard Kutzler & Vlasta Kokol-Voljc

TI EXPLORATIONS™SOFTWARE

Bernhard KUTZLER

Vlasta KOKOL-VOLJC

Introduction to

The following Derive™ 5 documentation is being provided as a courtesy of the authors, Bernhard Kutzler / Vlasta Kokol and the publisher Texas Instruments. We invite you to use the following abbreviated document during your personal evaluation of Derive™ 5. Use of the document for any other purpose is strictly prohibited.

A book for learning how to use D

ERIVE

Kutzler, Bernhard & Kokol-Voljc, Vlasta

Introduction to D

ERIVE

2000



2000 Kutzler & Kokol-Voljc OEG, Austria

1. Edition, 1. Printing: March 2000

Typesetting: Bernhard Kutzler, Leonding, Austria

Cover art: Texas Instruments Incorporated, Dallas, Texas, USA

The author and publisher make no warranty of any kind, expressed or implied, with regard to the

documentation contained in this book. The author and publisher shall not be liable in any event for

incidental or consequental damages in connection with, or arising out of, the furnishing, performance

or use of this text.

No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any

form, or by any means, electronic, mechanical, photocopying, recording or otherwise, without prior

permission, in writing, from the publisher.

ERIVE

is a trademark of Texas Instruments Incorporated

INDOWS

, W

INDOWS

95, W

INDOWS

NT, and WIN32S are registered trademarks of Microsoft Corp.

Introduction ............................................................................................................................................. 1

Chapter 1: First Steps ............................................................................................................................. 3

Chapter 2: Documenting Polynomial Zero Finding ........................................................................... 23

Chapter 3: The Whole and Its Parts – Subexpressions ..................................................................... 43

Chapter 4: Equations and Inequalities ................................................................................................ 63

Chapter 5: Approximate Versus Exact Computations ...................................................................... 83

Chapter 6: Sequences and Families of Curves ................................................................................... 95

Chapter 7: Investigations in Space .................................................................................................... 117

Chapter 8: What Is ‘Simple’? .............................................................................................................. 135

Chapter 9: Vectors, Matrices, and Sets ............................................................................................. 153

Chapter 10: Parametric Plots ............................................................................................................. 171

Chapter 11: Towards a Module for Analytical Geometry ............................................................... 185

Chapter 12: Some Calculus ................................................................................................................ 203

Chapter 13: More on Plotting ............................................................................................................. 221

ERIVE

Chapter 14: What Else Can D

ERIVE

Learn More about D

Appendix A: D

Appendix B: Factory Default D

Index ..................................................................................................................................................... 269

ERIVE

................................................................................................................... 261

Startup Options ................................................................................................ 263

Do? ............................................................................................ 243

ERIVE

................................................................................................ 265

iii

Preface

The desire to make D

Many thanks to Albert Rich and Theresa Shelby, the principal authors of D

continuous support during the writing of this book.

Many thanks to Patricia Littlefield and David Stoutemyer who polished the language of this

book.

Bernhard Kutzler & Vlasta Kokol-Voljc, February 2000

ERIVE

5 easily and quickly accessible led to this book.

ERIVE

5, for their

Introduction

ERIVE

is a mathematical computer program. It processes algebraic variables, expressions,

equations, functions, vectors, and matrices like a scientific calculator processes floating point

numbers. D

calculus, and plot graphs in 2 and 3 dimensions. The main strength of D

algebra and powerful graphics. It is an excellent tool for doing and applying mathematics, for

documenting mathematical work, and for teaching and learning mathematics.

For a teacher and student, D

mathematics. By providing numeric, algebraic, and graphic capabilities together with seamless

integration of these, D

mathematics. You will find that many topics can be treated more efficiently and effectively than

by using traditional methods. Many problems that require extensive and laborious training at

school can be solved with a single keystroke using D

performing long mathematical calculations. While D

mechanical/algorithmic parts of solving a problem, students can concentrate on the

mathematical meaning of concepts. Instead of teaching and learning boring technical skills,

teachers and students can concentrate on the exciting and useful techniques of problem solving.

It has proven to be highly supportive for the cognitive development of advanced mathematical

concepts.

For an engineer, D

operations and functions and for visualizing problems and their solutions in various ways. If you

use D

knowledgeable mathematical assistant that is easy to use.

ERIVE

can perform numeric and symbolic computations, algebra, trigonometry,

ERIVE

are symbolic

ERIVE

is the ideal tool for supporting the teaching and the learning of

ERIVE

enables new approaches in teaching, learning, and understanding

ERIVE

: It eliminates the drudgery of

ERIVE

takes the burden of doing the

ERIVE

is the ideal tool for fast and effective access to numerous mathematical

ERIVE

for your everyday mathematical work, you will find it a tireless, powerful, and

This book is for learning how to use D

ERIVE

5 by private study. Install D

ERIVE

5 on your

computer. Starting with the first chapter, you will learn step by step how to use the program.

Follow all instructions and examples. The text leads you through several mathematical topics

that are used for learning how to solve mathematical problems with D

ERIVE

examples also provide ideas for using D

during teaching; some of them are explained in

ERIVE

. Many of the

more detail in “Educator’s footnotes.” Paragraphs starting with the symbol  give instructions

about what you should do on your computer. Hundreds of screen dumps ensure that you will not

get lost on this journey.

2 Introduction

By solving typical mathematical high school level problems, you will learn to handle D

ERIVE

5 as

much as necessary for everyday use and for teaching or learning mathematics. You will learn

how to use the major commands, keys, and functions. At the end of each chapter you will find a

summary of the features learned in that chapter. The Quick Reference Guide at the end of the

book is a summary of commands, keys, functions, and utility files, which is organized by tasks.

The index at the end is useful if you need to locate a particular portion of the text.

All you need to run D

INDOWS

NT.

ERIVE

5 is a PC compatible computer with W

It is assumed that you know how to use computers and the W

screen shots in this book were produced from D

ERIVE

on W

INDOWS

95 or 98, some of the screens may appear slightly different.

ERIVE

running on W

This book introduces all features and functions that are required for routine use of D

There is more functionality than can be described here. This book is

ERIVE

. A complete reference to all features is included with the software as online help. Some

INDOWS

95, W

INDOWS

operating system. The

INDOWS

not

a reference manual for

INDOWS

98, or

NT. If you are running

ERIVE

of the chapters give examples of how to use the online help.

ERIVE

We plan to write additional texts on D

http://series.bk-teachware.com

for new texts and local dealer information.

5. Please regularly look at the web site

Have fun reading and discovering.

Chapter 1: First Steps

ERIVE

makes it easy to perform mathematical operations: Enter an expression, apply a

command, and a new expression is obtained. All expressions can be used for new

computations—just like on a piece of paper. This chapter teaches the basic techniques of using

ERIVE

5. Note: For simplicity, we will abbreviate D

This text assumes that you use a factory default D

match those in this book. If you just installed D

version of D

ERIVE

that was used by someone else, we recommend that you turn it into a factory

default version now. Appendix B gives instructions on how to do this.

ERIVE

Start D

by double clicking on the D

desktop, you probably will find D

ERIVE

on the



The following screen appears after a few seconds:

ERIVE

. Only then will your screen images fully

ERIVE

, it is a factory default version. If you use a

icon. If there is no D

Start

menu or via

5 as D

ERIVE

throughout this text.

ERIVE

icon on your computer’s

Start>Programs

ERIVE

The D

•

screen comprises (from top to bottom):

the Titlebar

the Menu Bar

the Command Toolbar

a (currently empty) Algebra Window, also called the View

the Status Bar

the Expression Entry Toolbar, also called the entry line

the Greek Symbol Toolbar and the Math Symbol Toolbar

4 Chapter 1: First Steps

Work with D

After starting D

ERIVE

by entering expressions and applying commands, thus creating a worksheet.

ERIVE

, the system is ready to accept user input via the Expression Entry Toolbar,

as is indicated by the blinking cursor in the toolbar’s entry field. Input mode can be implemented

with the Command Toolbar’s tenth button from the left, labeled



Learn more about the button

The message

Author Expression

Enter new expression in active work sheet



Prepare for entering an expression: Move the mouse pointer onto

by moving the mouse pointer onto it.

below the cursor is the button’s title. The Status Bar message

is the button’s function description.

, then click (i.e. press

and release) the left mouse button.



Enter the fraction:

2/3



End the input with the ‘Enter’-key

ERIVE

displays this expression as a fraction with a horizontal line, a numerator, and a

(¢)

denominator, i.e. in “2-dimensional” output format, as opposed to the “1-dimensional” or “linear”

input format used for entering the number. The expression’s unique label number, #1, is shown

ERIVE

to the left of the expression. D

focus

) is still in the entry line. Also observe that a copy of the input is still in the entry field and is

is again ready to accept the next input, i.e. input control (the

entirely highlighted. This has the same meaning as in text editors and word processors. You can

remove the highlighting with the right arrow key, then edit the string of symbols, or you can

replace the marked string by typing new symbols.

Kutzler & Kokol-Voljc: Introduction to D

(¢)

Replace the last input by



Enter

1/2+1&3

ERIVE

with an intentional typographical error:

When a syntax error is detected, the cursor is moved to the location of the error and the cause of

the error is displayed in the Status Bar’s first pane. In the above example D

ERIVE

discovered an

unexpected special character. In some cases (for example, when entering an opening

parenthesis instead of the division symbol) there are several errors possible, and D

ERIVE

can only

guess.



Update the input to the backspace key Conclude with

(¢)

1/2+1/3

(æ_)

: Use the

) to delete the incorrect character, then type the division operator.

(Del)

key (or the right arrow key

(Æ)

followed by

The expression and its label, #2, are displayed. The new expression is highlighted in reverse

video. Expression #1 is no longer highlighted.

If you mistyped the input and want to delete the highlighted expression for a retry, use

move the focus into the algebra window, use the ‘Delete’ key

expression, then use the

Author Expression

button to move the focus back into the entry line.

(Del)

to delete the highlighted

(Esc)

An alternative technique for replacing an expression will be explained in Chapter 2.



Simplify expression #2 using the Command Toolbar’s

Simplify

button .

The result becomes the next expression with the label #3. By default, simplified expressions are

displayed centered. This makes it easy to distinguish between entry and result. As with many

ERIVE

other behaviors of D

Even after using the

expression,

. To enter the square root symbol, use the respective button on the Math

, this can be customized if desired.

Simplify

button, the focus still is in the entry line. Enter the next

Symbol Toolbar:



Enter

as: 24

(¢)

6 Chapter 1: First Steps



Simplify using

This is different from what an “ordinary” calculator would produce. A mathematician once

“How do you recognize a mathematician?”

asked:

mathematician considers expression #5 a beautiful result.”

and suggested the following answer:

Most students strive to replace

such an expression by the corresponding floating point approximation. D

ERIVE

can do this as

“A

well: Highlight expression #4 so that you can apply a different command to it.



Highlight expression #4 by moving the mouse pointer anywhere in the row occupied by the expression, then clicking the left mouse button.

Selecting an expression with the mouse button is one technique of highlighting it. An alternative

technique is first to move the focus into the algebra window (if necessary) using the

then using the cursor keys

(½)

(¼)

to move the highlighting one expression up or down.

(Esc)

key,



Approximate using the Command Toolbar’s

Approximate

button .

While an expression is highlighted, the Status Bar’s second pane shows the automatically

generated expression annotation. The third pane shows the computing time in case the expres-

sion was obtained as a result of a computation. For expression #6 this is:

The automatically generated annotation explains how the expression was obtained.

Approx(#4)

means that the expression was obtained by applying the

command) to expression #4. The computation time displayed in the third pane,

Approximate

0.000s

button (or

indicates that the calculation took less than 0.001 seconds (the time may be different on your

computer).



Highlight expression #4, . . .



. . . then expression #5.,

The annotation of expression #4,

expression #5,

Simp(#4)

User

, means that it was entered by the user; the annotation of

, indicates that the expression was obtained by applying the

Simplify

button (or command) to expression #4. The first pane is always available for messages

associated with a menu item, button, or command status.

ERIVE

worksheets also can include text and other objects. The easiest way of entering text is via

the Command Toolbar’s

Insert Text

button . New expressions are added at the end of the

Kutzler & Kokol-Voljc: Introduction to D

ERIVE

worksheet. Other objects (including text objects) are added after the highlighted object. To

insert a text object above the square root of 24, first highlight the object that is now above it.



Highlight expression #3.



Display a function description of the

Insert Text

button by moving the mouse pointer

onto it.



Insert a text object by clicking on the

Insert Text

button .

Highlighting of a text object is indicated by a frame around it. The blinking cursor inside

indicates text editing mode.



Enter the text:

We compute the square root of 24:

A text object allows simple text editing similar to what you can do in standard text editors. Later

you will learn how to change the font size, alignment, color, etc.

As a next example compute

. Due to the previous activity, the focus now is in the algebra

1234

window. Before you can enter another expression, move the focus into the entry line.



1234^56

Enter

by using the

of digits followed by

Author Expression

(¢)

. The exponentiation operator ^ can be found on both the

button , then typing the respective string

keyboard and the Math Symbol Toolbar. (It is the sixth symbol from the left in the first row.)



Simplify using

This is a very big number. For those who want to know the number of digits, there are two

methods to find out: First, you can count them. Second, you can approximate the number.

8 Chapter 1: First Steps



Approximate using

The answer is displayed in scientific notation. Since the count of whole digits is one more than

the power of 10, the number has 173+1 = 174 digits.

In the next exercise, you will learn a different technique of entering expressions by using the

buttons preceding the entry field.



Type into the entry line

x/3+x/4

this time

without concluding with

(¢)

Note the five buttons left of the entry field. The usual technique of moving the mouse pointer

onto a button reveals the first one,

, as the

has the same effect as concluding the input with the



Enter the above expression with

Simplify

Unlike ordinary calculators, D

button .

ERIVE

can perform nonnumeric (symbolic, algebraic) computations

Author Expression

(¢)

button. Selecting this button

key. Try it:

, then simplify as usual using the Command Toolbar’s

such as simplifying expression #10 into expression #11.

For the next example use the Expression Entry Toolbar’s second button,



To simplify

2xx

immediately, type

x+2x

then select the entry line’s

Simplify

button .

This button simplified the entered expression immediately without the usual display of the

unsimplified expression. Note the result’s annotation:

For the next example use the Expression Entry Toolbar’s third button,



Enter and simplify

Simplify

button .

sinxy x

by typing

xy+sinx

Simp(User)

then using the entry line’s

Author and

Kutzler & Kokol-Voljc: Introduction to D

ERIVE

This button produced two expressions, #13 and #14 and has the same effect as entering the

unsimplified expression with

(¢)

, then simplifying it with . It is, therefore, a convenient

shortcut for the frequently used “enter and simplify.” This example also shows how convenient

fast input is in D

ERIVE

. You can enter expressions just as you would write them on paper. For ‘

times y ‘ simply enter xy. No multiplication operator is needed between x and y. For ‘Sine of x ‘

simply enter sinx. No parentheses are needed around x.

The Expression Entry Toolbar has buttons for entering, simplifying, entering & simplifying,

approximating, and entering & approximating expressions.

The simplified expression #14 differs from the unsimplified expression #13 only in the order in

which its terms are displayed. While unsimplified expressions are displayed as they were entered

(except for the 2-dimensional pretty print format), simplified expressions are displayed in a

standardized format using a certain term ordering.

Back to how simple it is to enter expressions. A consequence of the convenient fast input, such

xy+sinx

for

⋅+

sin( )xy x

, is that variable names can consist of only one character (for

example x and y). This suffices most of the time, but if you need to use multicharacter variable

names, D

ERIVE

allows this, too (for example

time

or x12). Using multicharacter variable names

will be explained in Chapter 14.

Clearly, you cannot omit all parentheses. For example, you will need to parenthesize the

denominator to enter a rational expression such as

. If the parentheses are omitted in this

example, the resulting expression has a different meaning.



Enter:

2/x+1

Oops—the expression on the screen looks different from the intended expression! D

ERIVE

applies operations in the conventional order, for example multiplication and division before

addition and subtraction. As you can see from the above example, the 2-dimensional screen

display of an input provides you with valuable feedback about the soundness of your input.

Educator’s footnote:

the students to input expressions given to them on the chalkboard or a piece of paper. Because D features 2-dimensional output of expressions, the students get an immediate feedback. If the expression on the screen looks different from the one on the chalkboard or paper, then the input was wrong, and they must try again. When the teacher lets students input expressions of increasing complexity, they learn how to “linearize” expressions by trying and experimenting (trial and error), and learn to understand the structure of expressions. In this way, they improve their competence in recognizing structures, which is one of the basic mathematical skills important in many areas.

A very simple educational exercise with D

ERIVE

, therefore, consists of asking

ERIVE

10 Chapter 1: First Steps

When correcting the most recent input, you can take advantage of the fact that a copy of the

most recent input and the focus are still in the entry line.



To edit the expression use the right arrow key input to

Now it looks correct. Since you don’t need expression #15 any more, delete it.



Prepare for deletion: Highlight expression #15 either with the mouse or with the keyboard’s arrow keys after moving the focus into the algebra window using

2/(x+1)

by adding the parentheses, then enter the expression with

(Æ)

to remove the highlighting. Change the

(¢)

(Esc)



Delete expression #15: Use the

The expression that was expression #15 disappeared. The expression that was expression #16

has become expression #15. By default, automatic renumbering adjusts expression numbers so

that they begin with #1 and have no gaps.

Errors such as omitting a whole pair of parentheses may change the meaning of an expression,

as was the case in the previous example. If only one parenthesis is omitted, the input becomes a

meaningless character string, and D

syntax error message:



ERIVE

parenthesis can be spotted while a missing opening parenthesis obviously cannot, the first

alternative is used for the error message. Depending on how the expression should look, you

have to either delete the closing parenthesis or insert an opening parenthesis somewhere before

it. For the above example there are six possible repairs:

input

4x-1/x-5)

Enter

attempts to position the cursor in front of the expected error. Since a superfluous closing

4x-1/x-5 4x-1/x-(5) 4x-1/(x-5) 4x-(1/x-5) 4(x-1/x-5) (4x-1/x-5)

after moving the focus into the entry line with

Delete Object

ERIVE

will issue a warning in the form of an appropriate

button or press the

(Del)

key.

output

To choose the third variant insert an opening parenthesis between the division operator and the

variable x.

−−

45x

−−

45x

−



45x

−−

 



−−

45x





45x

−−

Kutzler & Kokol-Voljc: Introduction to D



Edit the input string to

4x-1/(x-5)

511

ERIVE

then press

(¢)

When working with D

When focus is in the entry line,

Author Expression

the

ERIVE

, focus can be either in the entry line or in the algebra window (View).

(Esc)

will move focus into the View. When focus is in the View,

button or its hot key equivalent,

(F2)

, moves it into the entry line.

Another method to move focus is using the mouse. Focus is where one last moved the mouse

pointer to and then pressed the left mouse button.



Ensure that focus is in the entry line by moving the mouse pointer into the entry line’s entry field, then clicking with the left mouse button.

The disadvantage of this method is that it removes highlighting if there was any, so now you

cannot simply replace the old input with a new one by starting to type the new input string. You

could use the backspace key several times to delete the old string, but a more elegant way is to

use the tab key.



Highlight the contents of the entry line with the tab key

x^2

Enter and simplify

button or to use the entry line’s

obtained from the Math Symbol Toolbar (



Type

√

x^2

√

. It is up to you to either use the ‘Enter’ key followed by the

then press

Enter and Simplify

(Ctrl)+(¢)

) or entered as

. This is the same as

button. The square root symbol √ can be

(ÿ)

(Ctrl)-(Q)

, i.e. this is a simple way to

Simplify

perform an “enter and simplify” operation without using the mouse.

As an alternative, introduce a pair of parentheses around



Enter and simplify:

Educator’s footnote:

students how many different expressions they can generate by inserting 1, 2 (or more) pairs of parentheses into a valid string of characters. This is another excellent exercise to help students gain an understanding of the structure of expressions.

(x^2)

√

This is another example for an elementary educational use of D

x^2

ERIVE

. Ask

12 Chapter 1: First Steps

The last two examples are remarkable for two reasons. First, they demonstrate the importance

of using parentheses to differentiate between

). Second, expression #20 shows how carefully D

()

The third power of

−

is entered as follows:

(meaning

ERIVE

) and

()

simplifies expressions.

(meaning



This did not change anything. Now you have an opportunity to apply one of those commands for

which there is no equivalent Command Toolbar button.



(α-1)^3

Enter

Try to expand expression #21, first by simplifying with

Prepare for opening the

Simplify

Open the

. (Insert Alpha with the Greek Symbol Toolbar button

command.

Simplify

menu by clicking the left mouse button.

menu by moving the mouse pointer above the Menu Bar’s

This menu offers several commands. The

expression.



Select this command by moving the mouse pointer above the word

Expand

command is appropriate for expanding an

Expand

. . .

Kutzler & Kokol-Voljc: Introduction to D



. . . then invoke the command by clicking on it with the left mouse button.

513

ERIVE

opens the

Expand Expression

dialog box. You will obtain similar dialog boxes with all

commands that require specification of parameters. The above dialog box requires the

specification of the expansion variable and the amount of expansion. Often it is enough to accept

the default specifications and immediately exit the dialog box with the ‘Enter’ key or by clicking

xpand_)

the default button, which here is

displayed.) Use the

(_Cancel_)

(_E

button or the

you want an unsimplified application of the



Perform the expansion with the suggested parameters by using

(¢)

because this is the default button or click on

A keyboard alternative for selecting the

following standard W

the underscore under the letter S in

underscore, but now without the

INDOWS

technique:

Simplify

(Alt)

. (The default button is the one prominently

(Esc)

EXPAND

Expansion

(Alt)+(S)

), then press

key to cancel the command. Use

function.

(_E

xpand_)

(_E

xpand_)

command from the

opens the

(E)

Simplify

menu (use

(again the letter with the

(_OK_)

(either press

menu is the

(S)

because of

, which is used only to open menus.) This technique

works for all menu commands.

For all buttons from the Command Toolbar there exist corresponding menu commands. Use

commands for the next example. Enter, simplify, then approximate



To enter the above expression, select the

sin(¹/4)

(¢)

. (Obtain π from either the Greek or the Math Symbol Toolbar. A button

Author>Expression

sin 4

command, then type

()

for this frequently used character is in both of these toolbars.)



Simplify expression #24 with the

Simplify>Basic

command.

14 Chapter 1: First Steps

This is another “beautiful” result. Before computing an approximation, add an appropriate

comment to the worksheet in form of a text object.



Insert a text object with the

Insert>Text Object

command, then type:

The following is an approximation of sin(pi/4)



(Try to) conclude the input with

(¢)

The ‘Enter’ key, used from within text editing mode, added an extra line to the text object. This

is not what was intended.



Delete the extra line using the backspace key

Note that while D

ERIVE

is in text editing mode, you have no access to certain buttons and menu

(æ_)

commands as you can see in the Command Toolbar. The inaccessible buttons and menu

commands appear dimmed. For example, the

Approximate

button is not available in text editing

mode now, because a text object is highlighted.

You need to highlight an expression before you can approximate it.



Highlight expression #24, then approximate it with

Simplify>Approximate

Other than the Command Toolbar’s

Approximate

button, the

Simplify>Approximate

command

invokes a dialog box in which you are asked to specify the number of digits of precision. The

currently displayed default value of 10 digits is also used by the

Simplify>Approximate

command allows you to temporarily change the default value for the next

Approximate

button. The

computation. Change the number to 35, then use the default dialog exit.

(_A

 35

pproximate_)

Kutzler & Kokol-Voljc: Introduction to D

ERIVE

In D

you can specify virtually any precision, meaning number of significant digits used for

515

ERIVE

arithmetic. The practical limitations are given by the available memory and your patience. Note

that computing time increases with increasing precision.

Update your text to indicate the chosen precision.



Bring the text object into editing mode by clicking into it. Position the cursor immediately after the word:



Change the text appropriately by using the backspace key adding:

35-digit

(æ_)

Reducing the text’s font size requires the Formatting Toolbar to be on.



Open the



Turn the Formatting Toolbar on by selecting the

View Toolbars

submenu with the

Window>View Toolbars

Formatting Toolbar

to delete the letter n, then

command.

For editing D

ERIVE

text, use the same techniques as in standard word processing programs. This

toolbar indicates that the font size is 12 points. Before you can reduce the font size to 10 points,

you need to highlight the respective portion of text.



Highlight the entire sentence. Either use the technique of dragging the mouse pointer (hold the left mouse button down) from one end of the text to the other, or put the cursor at the text’s end (or beginning), then repeatedly use the left (or right) arrow key together with the shift key, or place the cursor anywhere in the text, then triple-click.

16 Chapter 1: First Steps



Prepare for changing the font size: Open the

clicking on



Select the number 10.

Alternatively, you could make the

Font Size

field’s dropdown selection menu by

field active, then overwrite 12 with 10.

Now, announce the next example with an appropriate text.



Prepare for entering text using the

Insert Text

button .

Oops—this is the wrong position. The new text should appear at the end of the document. Since

Insert Text

the

button (as well as the

Insert>Text Object

command) adds the text object after the

highlighted object, you need to highlight expression #26 first.



Select expression #26.

Although the frame around the unintentionally inserted, empty text object disappeared, it is still

there. It can be deleted like any other object only after it is highlighted.



Highlight the text object by clicking into it.



Try to delete it, using the

(Del)

key.

This has no effect. Remember: Clicking inside a text object starts text editing mode. To select a

text object for deletion, copying, or moving, click (precisely) onto the frame or into the narrow

space left (or right) of the text object, or press



Select the text object for deletion using

(Esc)

from within text editing.

Kutzler & Kokol-Voljc: Introduction to D

517

ERIVE

The text object is selected now as is indicated by the frame around it. Make sure there is no

cursor inside it. If there is, press



Delete the empty text object using the

(Esc)

again.

(Del)

key.



Insert a new text object after the highlighted expression #26 (using the text “

Next we

.”

Note that this text again has font size 12 as you can see in the Formatting Toolbar’s

), then start entering

Font Size

field. Earlier you only changed the format of existing text. Changing the default format of all new

text objects is done via a command from the



To change the default setting of future text objects, select the

Text Objects

command.

Options>Display

menu.

Options>Display>Font of New

18 Chapter 1: First Steps



Change the font size to 10 points by scrolling within the

Size

selection menu appropriately,

then selecting the number 10, or by overwriting 12 with 10 via the keyboard.



Close the dialog with

(_OK_)

When continuing to write into the text object you started (you may need to click into the text

object to put it into text editing mode), it still is in 12 point size, because the setting you just

changed effects



Delete the text object for a retry with the new default text font size. Select it by clicking into it then using



Enter a new text object with the following contents:

new

text objects only.

(Esc)

. Delete with

(Del)

The text has font size 10 points now. You will not need the Formatting Toolbar any more in this

session, so switch it off to provide more space for other purposes. Switching a toolbar off

requires the same procedure as switching it on.



Turn the Formatting Toolbar off using

Window>View Toolbars>Formatting Toolbar

Experiment with the commands from the

changing the “look” of a D

ERIVE

worksheet.

Options>Display

submenu to become familiar with

Kutzler & Kokol-Voljc: Introduction to D

519

ERIVE



Select the

Options>Display

menu’s first choice (i.e.

Alignment of New Objects

This invokes a dialog box that allows you to control the alignment of all the objects that can be

ERIVE

in a D

worksheet.

obtained by adding an operator to an expression without simplifying.

Unsimplified Expressions

are expressions entered by you or expressions

Simplified Expressions

expressions obtained from simplifying or approximating an expression. It is helpful to display

user input left justified and the answers centered, as it is done by the default setting.



To keep the settings as they are, exit the dialog with

Try the next command in the



Try the menu’s second choice, change the text size by clicking on the

Options>Display

Options>Display>Font of All Expressions

Large

(_Cancel_)

submenu.

radio button.

or the

(Esc)

key.

(left picture), then

are

20 Chapter 1: First Steps



Carry out the change by leaving the dialog box with

(_OK_)

This font is useful for demonstration purposes, especially when using an overhead projector with

a display palette. For personal work the small font may be preferable. Therefore, switch back to

it and try a different color instead.



To undo the change of expression size, select again, then change the text size back to small by clicking on the picture.) Prepare for changing the font color by opening the

Options>Display>Font of All Expressions

Small

radio button (left

Color

selection menu.



Select a color of your choice by clicking on it, then close the dialog with

(_OK_)

Earlier you entered π via the Greek or Math Symbol Toolbar. There are several methods for

entering special constants such as π, the base of the natural logarithm e, or the imaginary unit i.



To enter a sum of three π‘s, first move the focus into the entry line using

from one of the two symbol toolbars, the second one by typing pi, and the third one as

(Ctrl)+(P)

. (The pluses in between are all entered via the keyboard.)

(F2)

. Enter the first

These are the three methods of entering the number π. While some look different in the entry

line, they all look and mean the same once they are entered:



Conclude the input of the sum of three π‘s with

(¢)

Kutzler & Kokol-Voljc: Introduction to D

521

ERIVE

There are also three methods for entering the base of the natural logarithm e. Use all three of

them to enter a sum of three e’s, then add the ordinary letter e to see the difference between a

variable with this name and the famous constant. There is also another method of simplifying an

expression.



Enter the first e from the Math Symbol Toolbar using the third one as

(Ctrl)+(E)

. Then type:

+e=

(Note the use of the postfix equals operator.)

, the second one by typing #e, and



End the input of the sum of three e’s and the variable e with

(¢)

The postfix equals operator causes an automatic simplification and the generation of an equation

whose left hand side is the unsimplified expression and whose right hand side is the simplified

expression. This method displays both the unsimplified and simplified expression on the same

line, saving lines on the screen.

Similarly there are three methods for entering the imaginary unit. You can obtain I from the

Math Symbol Toolbar, type #i, or enter it via the key combination

(Ctrl)+(I)

Conclude this chapter as follows.



Enter the text “

ERIVE

Exit D



. The

ERIVE

Exit D

To exit without saving the worksheet, select

This is the end of the first chapter.

Exit

command can be found in the

using the

File>Exit

command.

(_N

File

o_)

”

menu.

22 Chapter 1: First Steps

Summary

Algebra Window

(Del)

File>Exit Simplify>Expand Options>Display Window>View Toolbars>Formatting Toolbar

(½), (¼)

(Esc)

click left mouse button into row occupied by the expression ......................... highlight expression

click left mouse button into text object .................................................. edit contents of text object

click onto text object frame or left or right of it, or press

............................................................................................. delete highlighted expression

Insert>Text Object

Author>Expression

implify>Basic

implify>Approximate

.................................................................................................................................. exit D

................................................................................. expand highlighted expression

............................................................................................... change display settings

........................................................................ move highlighting one expression up, down

............................................................................................................................. cancel command

.....................................................................highlight text object (without text editing)

(F5)

......................................................................... simplify highlighted expression

............................. insert text object after the highlighted object

(F2)

............................. enter expression, move focus into entry line

................................................... approximate highlighted expression

.................................... toggle the formatting toolbar

(Esc)

from within text editing ...............

ERIVE

Expression Entry Toolbar

(¢)

................................................................................................................ enter simplified expression

...................................................................................... enter expression and simplified expression

(Esc)

(ÿ)

, etc................................................................................................................................... Greek letters

(postfix equals operator) ................................................................................ enforce simplification

...................................................................................................................... enter expression

............................................................................................ move focus into the algebra window

...................................................................................................... highlight contents of entry field

(Ctrl)+(P)

(Ctrl)+(E)

(Ctrl)+(I)

(Ctrl)+(Q)

or pi ...........................................................................................................................

or #e .............................................................................. base of natural logarithm

or #i ................................................................................................. imaginary unit

sqrt

..................................................................................... square root symbol

Chapter 2: Documenting Polynomial Zero Finding

The emphasis in this chapter is on creating a simple mathematical document about the finding of

the zeros of a polynomial. At the same time you will learn the corresponding basic techniques of

ERIVE

using D



Start D

ERIVE

Your first session with D

information about the status of D

performed with the

this file. The

default settings or start D

changes from the first chapter. This book is written so that each chapter starts with a factory

default D



Start with a factory default D

Start the new document with an appropriate headline.



Insert a text object containing the text “

You will look for the zeros of the polynomial

Derive Startup

ERIVE

. We recommend that you do the same.

ERIVE

left a trace in the form of an initialization file. This file stores

ERIVE

before you last shut it down. For example, the change

Options>Display>Font of New Text Objects

dialog gives you the choice to either start D

ERIVE

with the settings from the initialization file, i.e. with some of the

ERIVE

by exiting the dialog with

Finding the zeros of a polynomial

432

xxxx

=+ − −−

()ypx

24 442

command is among the data in

ERIVE

with the factory

(_Y

es_)

.”

3571

24 Chapter 2: Documenting Polynomial Zero Finding



Enter the above polynomial by preparing for expression input with

, then typing:

y=x^4/2+3x^3/4-5x^2-7x/4-1/2

(Intentionally leave out the /4 in the middle term.)

From here on, the key

(¢)

or the button

(_OK_)

will be displayed only in ambiguous situations.

It will not be used any more for simple inputs such as the above. It is important for some of the

features you are going to study and use in this chapter that you work with the above polynomial.

Therefore, make sure it was entered properly.

As you know, it was not! The /4 in the middle term is missing. This is easily repaired by applying

Edit>Derive Object

the



Edit the highlighted expression by selecting the

command to the highlighted expression.

Edit>Derive Object

command.

This brings a copy of the expression into the entry line with the cursor positioned at its left end,

so the system is ready for editing.



Insert /4 after

(¢)

The

key performed a

5x^2

, then end the input with

replacement

of the old expression with the new one. There is no need

to delete the old expression when using the

(¢)

Edit>Derive Object

command.

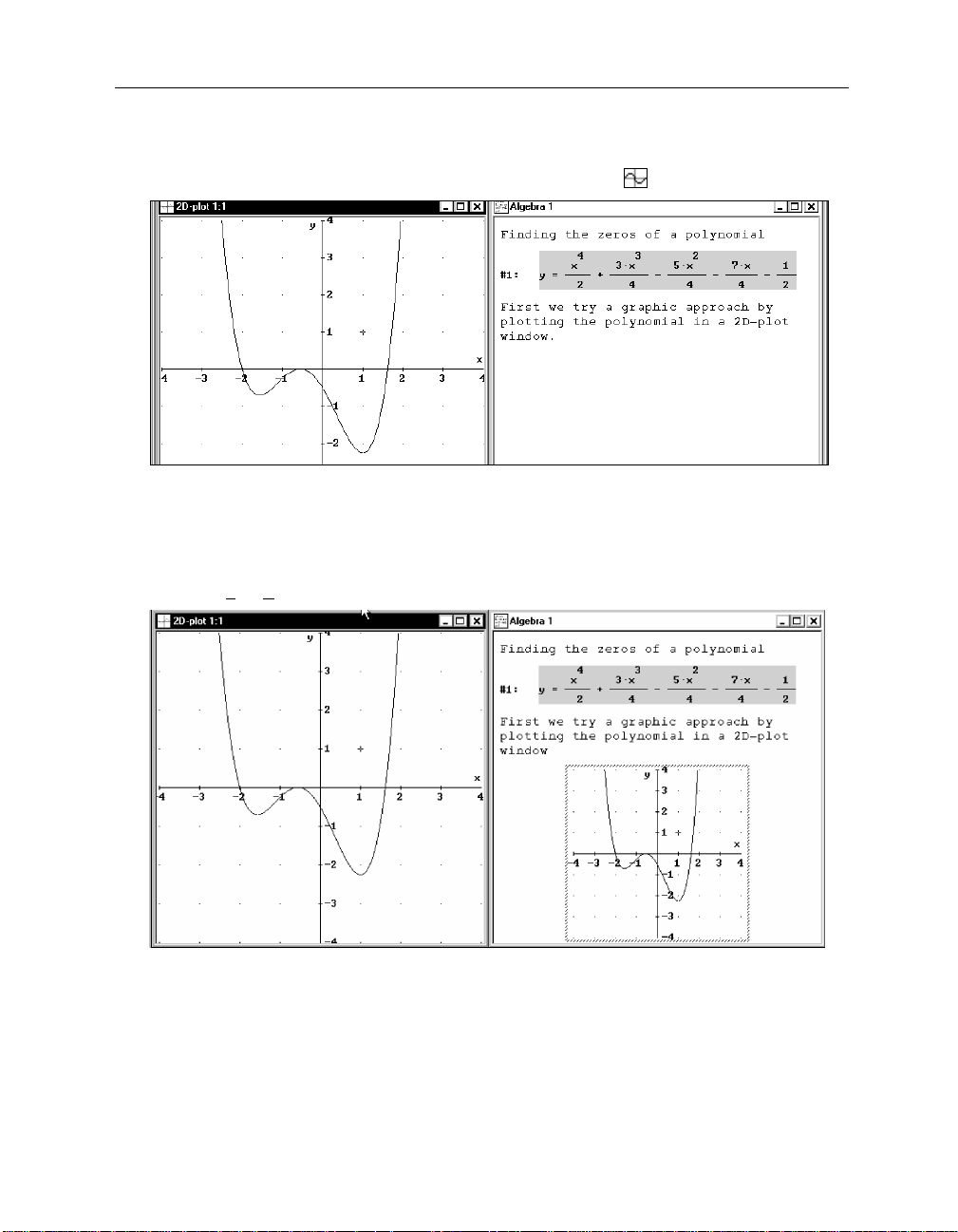
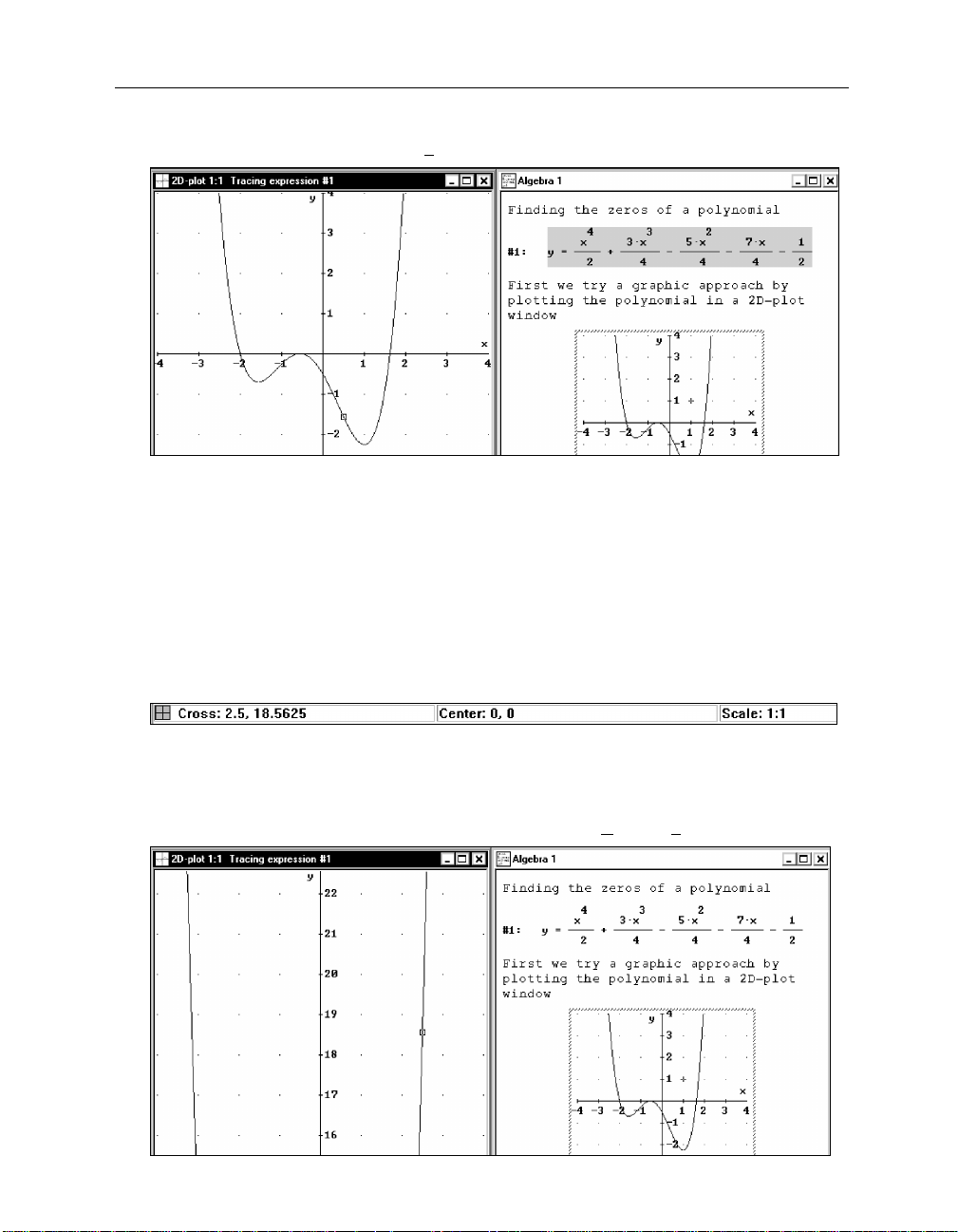
Consider looking at a house from several different positions. From each position you will see

details that you can’t see from other positions. Based on this idea, mathematicians use a variety

of different representations for mathematical objects. The fourth degree polynomial that you

entered is displayed as an

algebraic

representation. Next you will produce a

graphical

representation, because this representation is particularly useful for obtaining information about

the zeros. In other words, you will plot

its graph.

Since the major goal in this session is to properly document the mathematical work, . . .



. . . insert the text

“First we try a graphic approach by plotting the polynomial in a 2D-plot

window.”

“Plot” is a technical term. As such, it includes different aspects of drawing and graphical representation. It does not stand for mathematical accuracy, and in this book it will be used with three different meanings: for the activity of producing a graphical representation, for a graphical representation as an object, and for the corresponding D

ERIVE

command.

Kutzler & Kokol-Voljc: Introduction to D

525

ERIVE



Prepare for plotting a 2D graph: Open a 2D-plot window by clicking on the

button

or selecting the

ERIVE

created a plot window, so that you now have two windows to work with: an algebra

window and a 2D-plot window. Use the usual W

Window>New 2D plot Window

INDOWS

techniques to flip between windows or

command.

change their sizes and positions.



Put the two windows side by side using the

Window>Tile Vertically

command.

2D-plot Window

Each window is labeled with the window type in its upper left corner (

2D-plot

and

Algebra

). The

active window’s Title Bar is dark; the inactive window’s Title Bar is dimmed. Since the plot

window is active, the Menu Bar, the Command Toolbar, and the Status Bar are all different from

26 Chapter 2: Documenting Polynomial Zero Finding

that of the algebra window. In particular, the Status Bar displays the following graphics

information:

Cross

•

gives the coordinates of a movable cross,

Center

gives the coordinates of the picture center,

Scale

gives the scale factors of both axes,

The crossed square icon preceding the word

Cross

indicates Cartesian coordinates.



Draw the graph using the

Oops—the

Plot Expression

The reason is that the

Plot Expression

button .

button is dimmed inaccessible.

button (as well as its equivalent, the

Insert>Plot

command) plots the point set given by the algebra window’s highlighted expression, but

currently the second text object is highlighted and a text object can’t be plotted.



Highlight the polynomial by clicking on it (this makes the algebra window the active window), then make the 2D-plot window active again by clicking its Title Bar.

There are several techniques to make a different window active:

•

From the algebra window use the Command Toolbar’s

the 2D-plot window use the Command Toolbar’s

•

Click on the window you want to make active. This method, however, must be used with

2D-plot window

Algebra window

button and from

button .

care: Clicking on an algebra window with the left mouse button is likely to alter the

highlighting, clicking on a 2D-plot window with the left mouse button is likely to move the

graphics cross, this might have unexpected effects. Therefore, it is better to click with the

right mouse button to change windows, or to click, with any mouse button, into the window’s

Title Bar.

•

From the algebra window use the

window use the

•

From the algebra window use the

(Alt)+(W)

the

Window>x Algebra

(x)

and

keys as abbreviations of the above.

Window>y 2D-plot

command and from the graphics

command. (The numbers x and y may vary.)

(Alt)+(W)

and

(y)

keys and from the graphics window use

Kutzler & Kokol-Voljc: Introduction to D

527

ERIVE

Now the



Plot Expression

button is available, and you are ready to plot the polynomial.

Draw the polynomial’s graph using the

Plot Expression

button .

Now we have both an algebraic and a graphical representation of the polynomial available.

However, the graphical representation is

outside

the algebra window’s worksheet in its own

independent plot window.



Copy the current plot window into the algebra window’s worksheet by using the 2D-plot window’s

File>Embed

command.

This “freezes” the current status of the plot window into the worksheet. The plot window is

interactive; the embedded plot image is not. The embedded plot image can be brought back into

an interactive plot window at any time with a double mouse click.

The graphical representation is useful for exploring the polynomial’s zeros. However, from the

current picture it is not clear whether the polynomial has two, three, or four distinct zeros. An

answer can be found by inspecting the graph with the moveable graphics cross. Its coordinates

are displayed in the status line, which now shows the cross at the initial position (1,1):

28 Chapter 2: Documenting Polynomial Zero Finding

The color of the cross can be changed using the

Options>Display>Cross

command.

When the plot window is active, the cross can be repositioned by either moving the mouse

pointer and clicking the left mouse button or by using the arrow keys



Move the mouse pointer to (1,-1), or near it, then click with the left mouse button to move

(Æ), (æ), (½)

, and

(¼)

the cross to this position (left picture). Use the arrow keys to move the cross to (0.5,0.5). Try

(Ctrl)+(Æ), (Ctrl)+(æ), (Ctrl)+(½)

(Ctrl)+(¼)

, and

to move the cross in bigger

steps.

(Home)

The

key moves the cross to the plot window center.

The trace mode is very useful for inspecting curves. This mode can be switched on and off with

Trace Plots

the

(F3)

. As is customary in W

button , the

Options>Trace Plots

INDOWS

programs, a button with the same effect as a command is

command, or the corresponding hot key

displayed in the respective menu left of the command, while the hot key is displayed right of the

command. Check this out for the



Open the

Options

menu.

Options>Trace Plots

command:

Kutzler & Kokol-Voljc: Introduction to D

529

ERIVE



Turn trace mode on by selecting the

Trace Plots

command.

When trace mode is switched on, the cross changes its shape into a square and jumps vertically

to the curve, with its horizontal coordinate unchanged. The expression number of the traced

curve is displayed in the plot window’s Title Bar (here:

mode is switched on, the square can be moved only along the curve. This can be done using

and

(æ)

, or using

(Ctrl)+(Æ)

(Ctrl)+(æ)

and

Tracing Expression #1

). When trace

(Æ)

for “big steps.” It can also be done by moving

the mouse pointer and clicking with the left mouse button to the new position. If there are

several graphs displayed, use



Become familiar with moving the square. Use the arrow keys and the mouse to move the

(½)

and

(¼)

to select another graph.

square. Finally, click the left mouse button at the point (2.5,0).

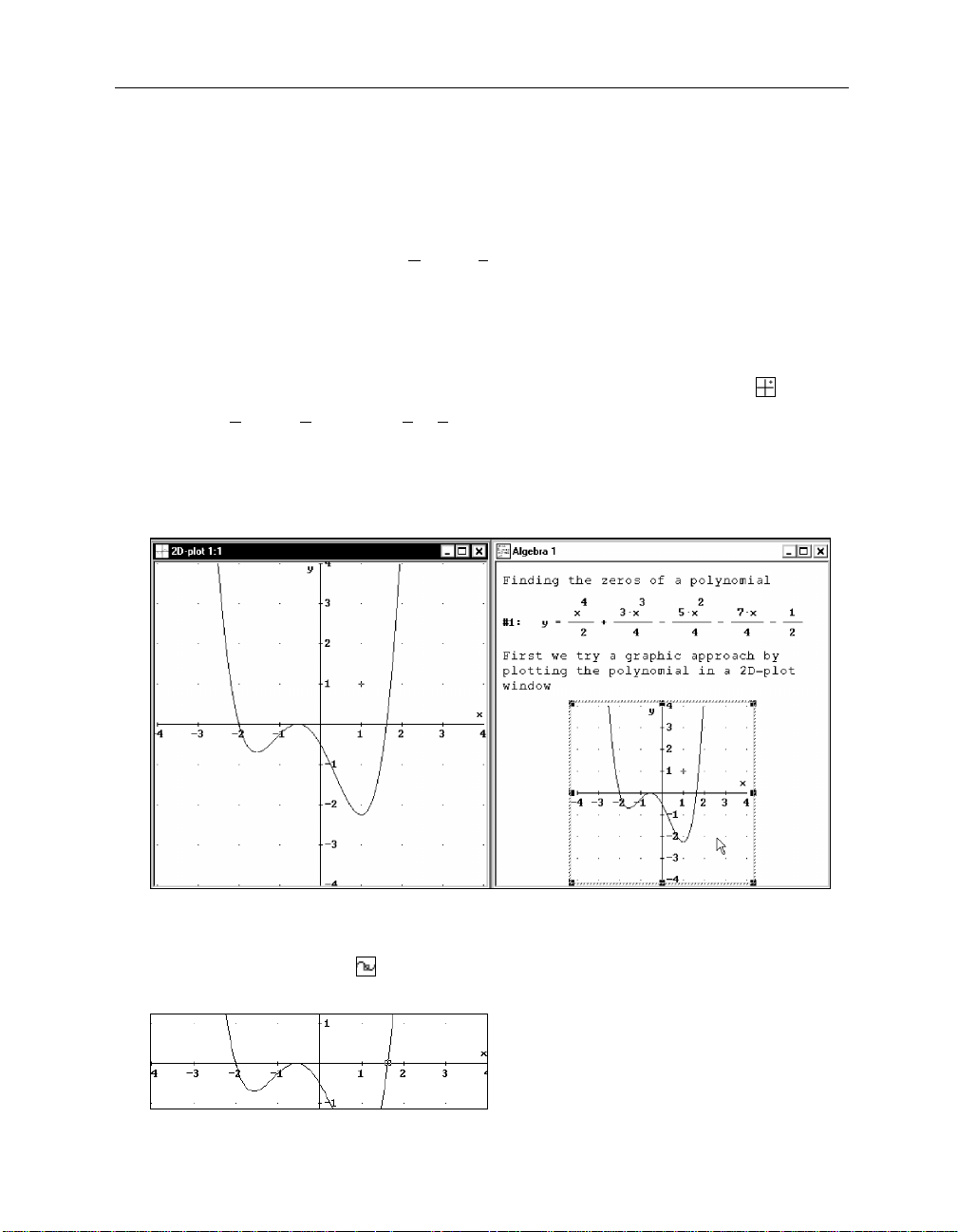
What happened to the square? It disappeared. Looking at the status line indicates the reason. The

square’s vertical coordinate is 18.5625, so it is far from the current plot area. You can ask D

ERIVE

to move the plot area where the cross or square is.



Move the plot area where the cross is by flipping the switch

Options>Follow Cross

30 Chapter 2: Documenting Polynomial Zero Finding

The plot window “follows” the square. This means that the plot ranges for the horizontal and the

vertical axes are changed automatically to ensure that the cross is visible. Since this mode can

destroy a chosen plot range, follow mode should be used carefully and is therefore switched off

by default.



Turn follow mode off by selecting

Options>Follow Cross

again.

There are several ways to restore a previous range:

•

While follow mode is on, you can click the left mouse button at a horizontal position where

the corresponding vertical curve coordinate is within the original plot range. This requires

some knowledge and reasoning about the curve.

•

Independent of the follow mode status you may use the

•

Select the

Set>Plot Range

Set>Plot Region

or the

Center on origin

command, use the

button .

(_Reset_)

button,

then leave the dialog.

•

If available, double click on an embedded version of the original graph. This last option is

particularly convenient.



Restore the original graph by double clicking on the embedded graph.

Trace mode was lost because the embedded graph was produced before trace mode was turned

on. Switch trace mode on again to start looking for the polynomial’s zeros.



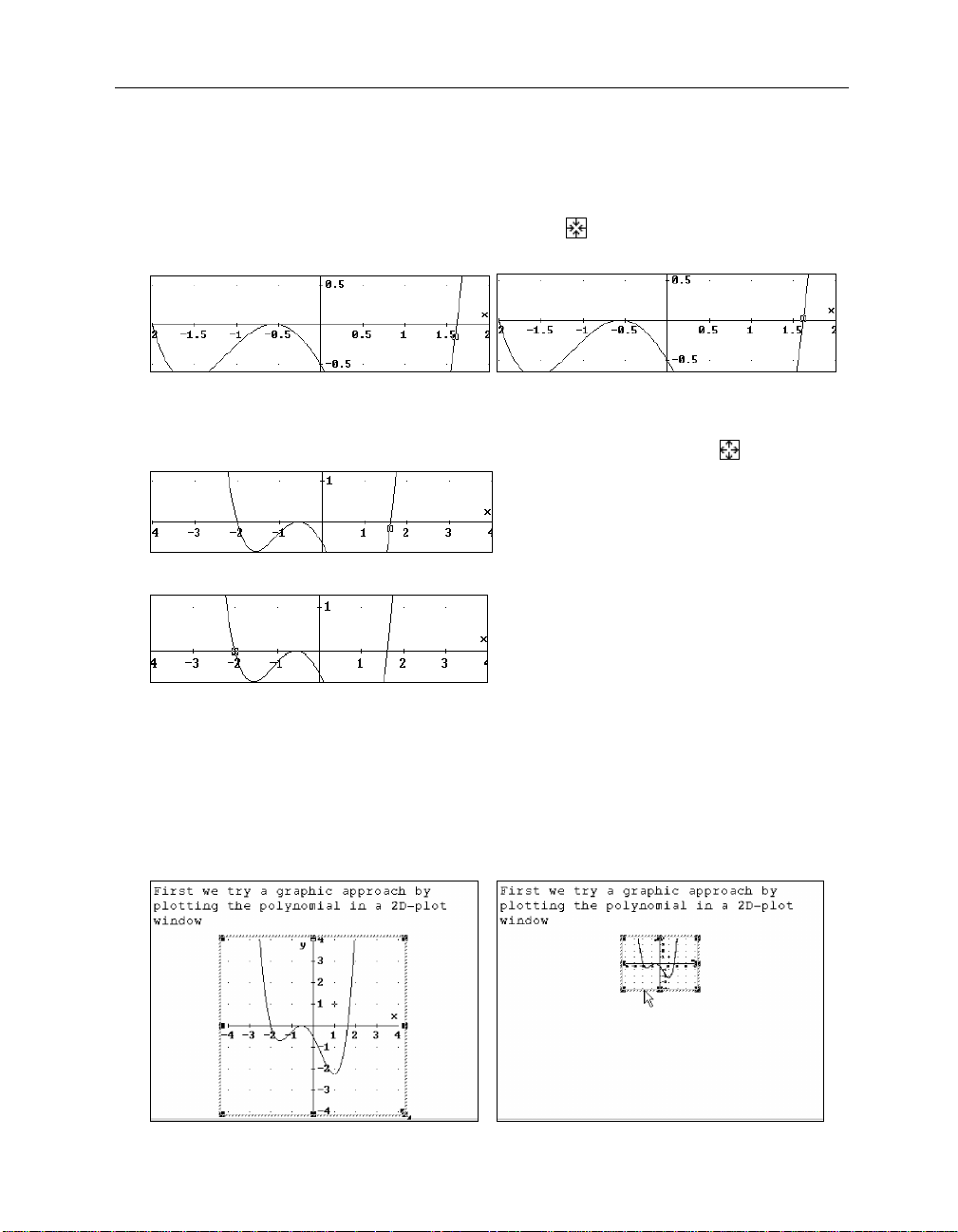
Switch trace mode on with

, then move the square to the rightmost zero, as near as you

can get to the horizontal axis.

ERIVE

displays the square coordinates as

different.) Using the left arrow key

Cross: 1.62, 0.01688368

(æ)

once moves the square to

. (Your numbers might be

Cross: 1.6, -0.1512

. You have

Kutzler & Kokol-Voljc: Introduction to D

531

ERIVE

not found a position at which the y-coordinate is zero, but you can say that the polynomial zero

must be between 1.6 and 1.62, probably being closer to 1.62. An obvious approach for getting

closer is magnification.



Zoom in using the Command Toolbar’s

Zoom in

button (left picture), then move the

square closer to the rightmost zero.

Now you get

Cross: 1.62, 0.01688368

Cross: 1.61, -0.06817304

and

(or whatever numbers you

obtain) hence the polynomial zero is between 1.61 and 1.62.



Restore the original scale factors by zooming out with the



Find an approximation for the leftmost zero by moving the square to it.

Zoom out

button .

The leftmost zero seems to be at exactly x=-2.

Document what you found so far by inserting appropriate text objects.



Switch to the algebra window. Resize the embedded plot: Select the image by clicking on it. The image is surrounded by 8 black squares, which can be used to resize it. Move the mouse pointer to the lower right corner until a double-headed arrow appears. Press and hold the left mouse button. With the left mouse button held down, drag the pointer towards the image center. When a suitable size is reached, release the mouse button.

32 Chapter 2: Documenting Polynomial Zero Finding

When you don’t like the change of the aspect ratio such is in the above pictures, you can easily

restore it. You will learn how to do this in Chapter 4.

Insert a text object documenting the method and result of your findings.



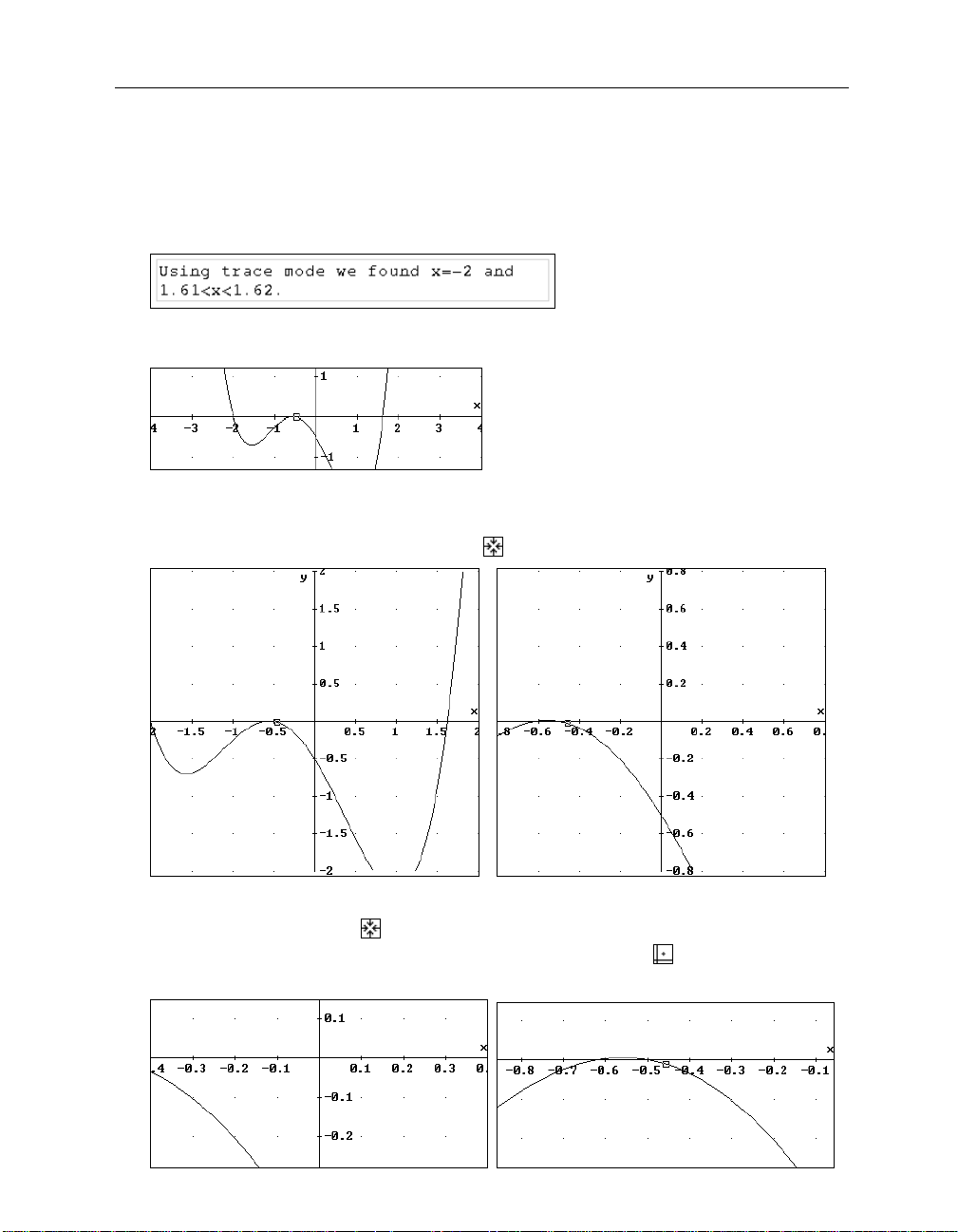
Insert a new text object and enter the following text (use the numbers you found):



Search for more zeros: Make the plot window active, then move the square to the uncertain middle section.

You will find that there is one zero between -0.62 and -0.6. Another zero seems to be at exactly

x=-0.5. To obtain a picture with intersections of the graph, magnify again.



Zoom in, this time using the

Zoom in

button twice.

It becomes obvious that there are two zeros. Continue to magnify the graph.



Zooming in once more with

switched off (left picture). The very useful

lets the square leave the plot window because follow mode is

Center on cross

button shifts the plot range

so that the square/cross is in the center of the new plot image.

Kutzler & Kokol-Voljc: Introduction to D

533

ERIVE

Move the square to get a better approximation of the left zero.



Move the square near the left zero and note the cross coordinates in the Status Bar.

Now the change of sign happens between x=-0.62 and x=-0.618. Produce a graph with steeper

intersections to get a more accurate answer.



Zoom in vertically only, using the

Zoom vertical in

button .

A highly recommended tool is the

Set range with box

button , which allows to choose a crop

rectangle graphically.



Prepare for choosing a crop rectangle by using the

Set range with box

button .

The mouse cursor turns into a crosshair.



Choose a crop rectangle: Click and hold the left mouse button at the top left corner of the desired area. Drag the mouse down and to the right until the box encloses the desired area.



Release the mouse button.

Set 2D-Plot Range

The

dialog box is displayed, reflecting the numerical equivalents of the

choices you just made with the mouse. This dialog box could be obtained in the first place using

Set>Plot Range

the

command. But a graphical choice of the plot range is often more convenient.

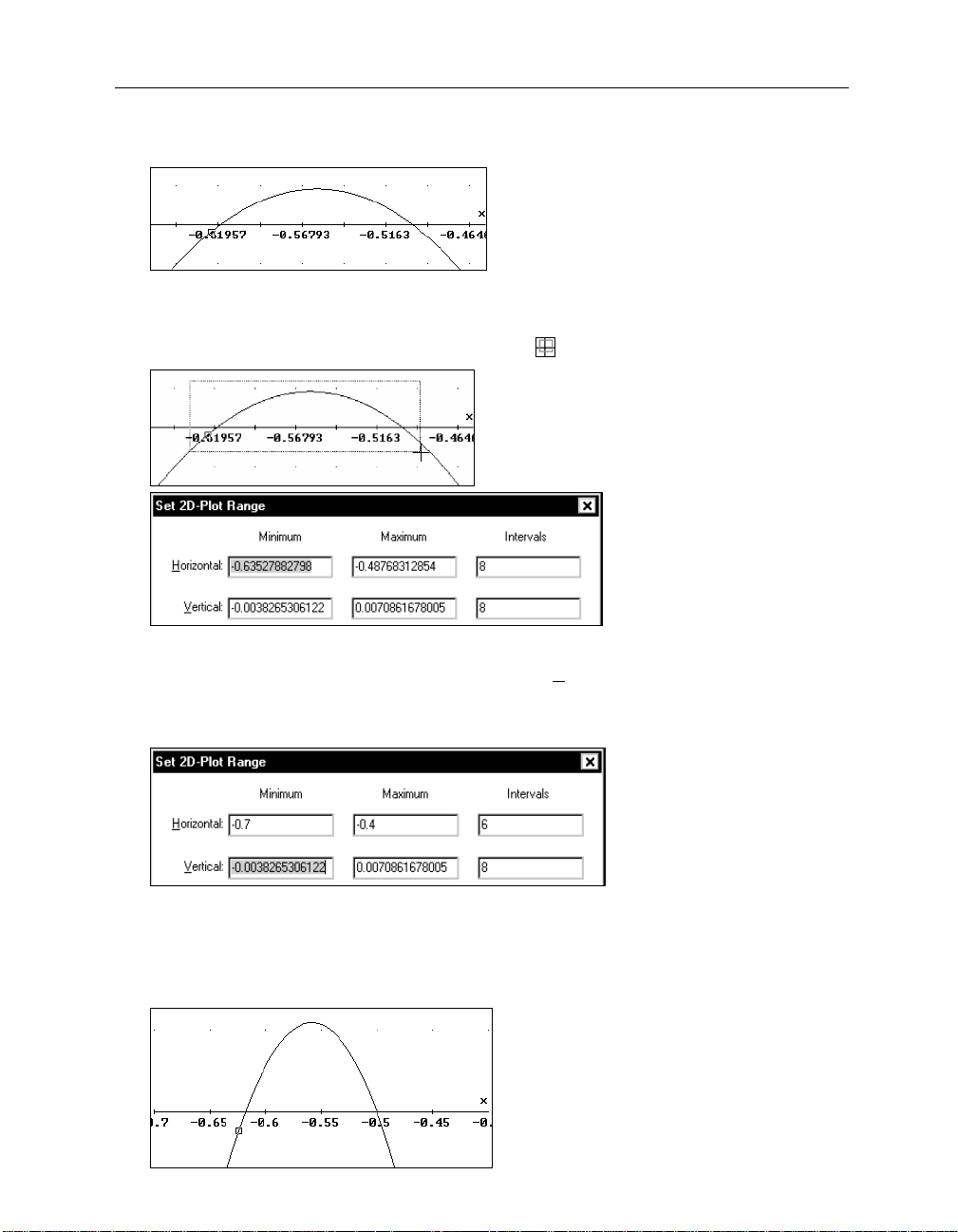
34 Chapter 2: Documenting Polynomial Zero Finding



See what happens if you confirm with

(_OK_)

Notice the complicated numbers below the tick marks (your numbers are likely to be different)

and in the Status Bar scale factors. This is caused by the graphical box selection.



Zoom in again using the

Set range with box

button .

It is helpful to edit the suggested numerical values to the nearest simple values. Start by

overwriting the highlighted value of the input field for the

(ÿ)

key

 -0.7

to make the next input field active. Enter the following values.

(ÿ)

-0.4

(ÿ)

Horizontal Minimum

. Then use the tab

Make the values for the

Maximum

the

fields. For example, 6 intervals for a horizontal range of length 0.3 (= difference of

Intervals

fields fit to the difference of the values for the

-0.7 and -0.4) ensures nice numbers below the tick marks.

 -0.01

(ÿ)

0.01

(ÿ)

(_OK_)

Minimum

and

Kutzler & Kokol-Voljc: Introduction to D



Use the trace mode square to find approximations of the two zeros.

535

ERIVE

The left zero lies between -0.6181818 and -0.6174242; and the other zero probably is at -0.5. All

the above work now should be documented in the algebra window’s worksheet by embedding

the graph and adding an appropriate text object.



From the 2D-plot window select the

File>Embed

command, then switch to the algebra

window and resize the embedded plot appropriately.



Insert a new text object documenting the method and result of your findings:

Close the plot window, then open the algebra window to full size.



Close the plot window by clicking the left mouse button on the

button that is located in

the window’s upper right corner. Open the algebra window to full size by clicking on the

button, which is located left of the algebra window’s button.

Next compute the zeros by solving the corresponding polynomial equation. Before doing so,

enter an appropriate textual description of your approach.

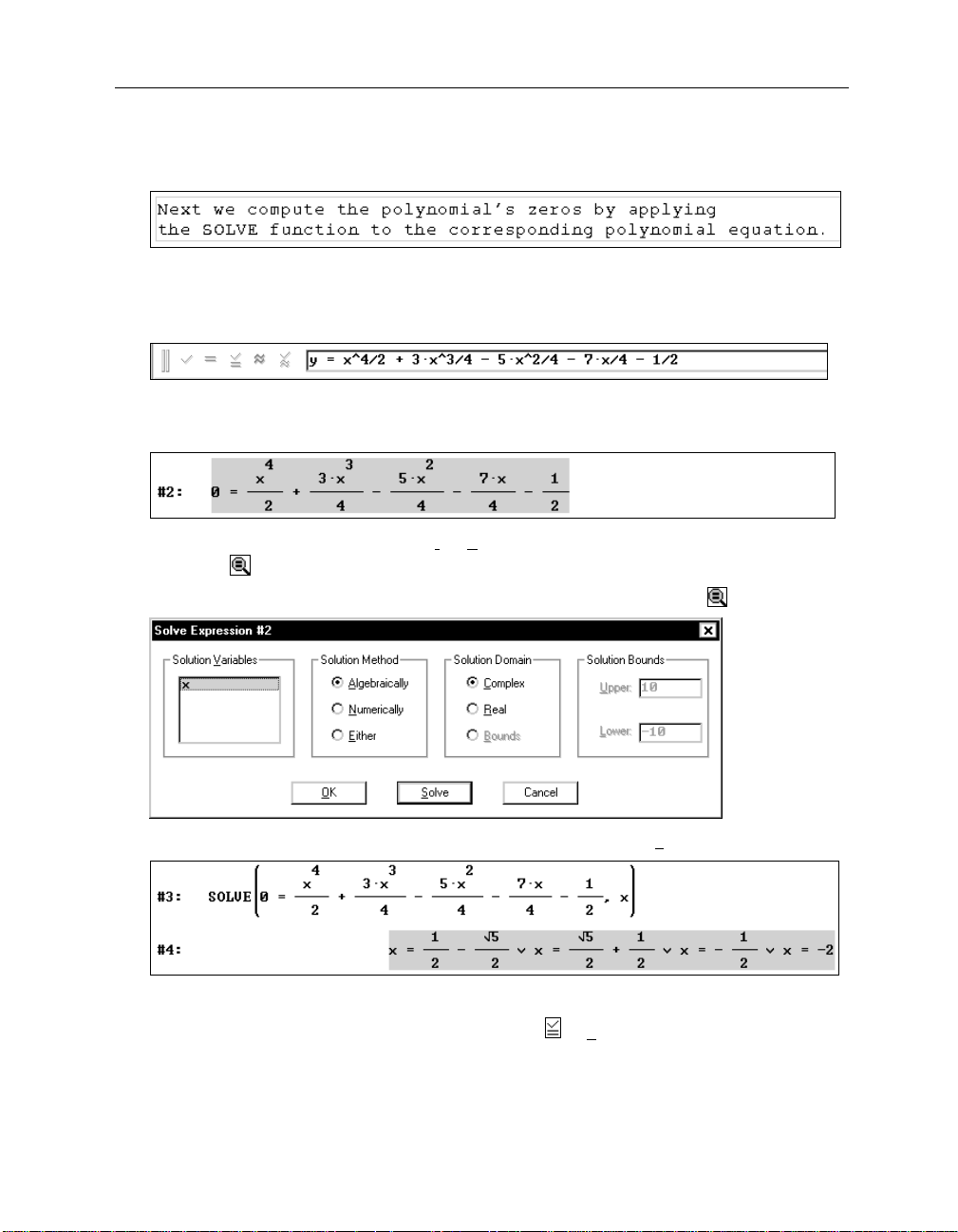
36 Chapter 2: Documenting Polynomial Zero Finding



Enter the text: “

to the corresponding polynomial equation.

Next we compute the polynomial’s zeros by applying the SOLVE function

”

Generate the corresponding polynomial equation.



Highlight the polynomial #1, move focus into the entry line with

(F2)

(which is the hot key

for authoring expressions), then auto-paste a copy of the polynomial using the hot key

(F2)

may become your most frequently used hot key.



Replace y with 0 then conclude the input with

For solving this equation either use the

Solve>Expression

(¢)

command or the corresponding

toolbar button .



Prepare for solving the equation by applying the

Solve Expression

button .

(F3)

(_S



Solve the equation. Accept all suggested parameters by selecting

olve_)

Here ∨ is the mathematical symbol for the logical operator OR.

(_S

Similar to the Entry Toolbar’s

Enter and Simplify

button ,

unsimplified expression (which is the formal application of the

olve_)

generated both an

SOLVE

function to the equation)

and a simplified expression (which is the solution of the equation.) The exit

generated the unsimplified expression only.

(_OK_)

would have

Kutzler & Kokol-Voljc: Introduction to D

537

ERIVE



Enter the text “

Expression #4 gives the four exact zeros of the polynomial.

”

In order to compare these results with what you found graphically, approximate expression #4.

Before doing so, again add a textual description of your approach.



Enter the text “

graphically.



Approximate expression #4 by first highlighting it, and then applying the

We approximate #4 so that we can compare it with what we found

”

Approximate

button .

To turn this worksheet into a good piece of mathematical documentation, do some more editing,

then print and save it. First, add a signature documenting author(s) and date.



Switch the Formatting Toolbar on using

Window>View Toolbars>Formatting Toolbar

All fields and buttons are dimmed as long as there is no text object in editing mode.



Add a text object at the end of the worksheet using

. Choose a special format for the

signature: In the Formatting Toolbar change the font size to 8 points and click on the

Right Justify

button .



This document was created by . . . on . . ..”

Enter “

Next change the topmost text object into an attention-catching title line.



Highlight the first text object’s contents using the usual text processing techniques.

Choose a format that is suitable for a title line, for example . . .



. . . change to 14 point font size, bold (



Switch the Formatting Toolbar off using

), centered ( ), then add a blank line.

Window>View Toolbars>Formatting Toolbar

38 Chapter 2: Documenting Polynomial Zero Finding

Before sending a document to the printer, it is a good idea to do a print preview.



Look at the print preview using the

File>Print Preview

command.

Print preview offers various options including a button for zooming in.



Zoom in with

(_Zoom_I

n_)

The magnifying glass shaped cursor in the upper right quarter of the page indicates that an

alternative to using the

(_Zoom_In_)

button is to click with the left mouse button.

Kutzler & Kokol-Voljc: Introduction to D

539

ERIVE

Make the expressions slightly larger. Change the expression font size via the

Options>Printing

submenu.



Prepare for changing the expression font size: Close the print preview window with

(_C

lose_)

, then select the command

Here you can select the expression font size, choose between

the printing of



Change the font size to 11 points, then close the dialog with Apply again the

Annotation

File>Print Preview

Computation Time

s and

Options>Printing>Expression Layout

Regular

and

Bold

s. (By default neither is printed).

(_OK_)

command, this time zooming in twice.

font, and control

The worksheet is now ready to be printed.

40 Chapter 2: Documenting Polynomial Zero Finding

(_P



Prepare for printing the document using print preview’s

rint_)

button.

Make sure that the printer is properly connected, switched on, and set. In the

you can change the printer or the printing properties, change the print range from

Printing

All

dialog box

to either a

range of pages or the highlighted expressions, or change the number of copies from the default 1

to the number you want.



Send the document to the printer with

(_OK_)

Kutzler & Kokol-Voljc: Introduction to D

541

ERIVE

Saving the worksheet preserves your work for later use or modification.



Save the worksheet by selecting the

File>Save As

command.

ERIVE

suggests storing the file in the subdirectory

Math

. You may choose a different directory

by selecting one from the selection menu that is offered for the



Accept the suggestion and enter the file name

(_S

Close the dialog with

ave_)

Notice the Title Bar. Previously there was

Algebra 1 chapter02.dfw

worksheet. Now there is

chapter02.dfw

. The suffix

[

.dfw

is the default that is chosen when you do not specify a suffix as

[

chapter02

Algebra 1

]

as the indication of an unnamed algebra

]

, indicating an algebra worksheet with name

part of the filename.



Exit from D

ERIVE

Save in

in the

field.

File name

input field.

42 Chapter 2: Documenting Polynomial Zero Finding

Summary

Algebra Window

Solve>Expression

............................................................................................ open 2D-plot window or switch to one

........................................................................................................... right justify highlighted object

.................................................................................................................... center highlighted object

File>Save As File>Print Preview Edit>Derive Object Options>Display>Cross Options>Printing>Expression Layout Window>New 2D plot Window

double-click left mouse button on embedded plot ................. open embedded plot in plot window

.......................................................................................... save worksheet using a name

............................................................................................................ print preview

(Ctrl)+(ª)+(E)

double-click left or right of expr. ...................... edit highlighted expression

.......................................................... change appearance of graphics cross

................................................................. open new 2D-plot window

............................................................. solve equation

...................................................... format expression layout

2D-plot Window

Insert>Plot

Options>Trace Plots

................................................................................................................. center plot region on cross

................................................................................................................ center plot region on origin

(F9)

(F10)

(F7)

.................................................................................................. graphically choose a crop rectangle

File>Embed Set>Plot Range Options>Follow Cross

(Æ), (¼),(æ), (½)

(Ctrl)+(Æ), (Ctrl)+(¼), (Ctrl)+(æ), (Ctrl)+(½)

(Home)

............................................................................................. move cross to plot window center

...................................................................................... plot highlighted expression

(F3)

......................................................................................................................................zoom in

................................................................................................................................. zoom out

.................................................................................................................... zoom in vertically

....................................................................... copy plot window into algebra worksheet

................................................................................................... set plot range borders

........................................................................................... toggle follow mode

................................................. move cross one pixel (one dot) on the screen

......................................................................... toggle trace mode

......................... move cross several pixels

All Windows

Window>Tile Vertically

................. arrange windows as right-left split (active window on the left)

Index

............................................................. 124

.............................................................. 35

5x – 6 = 2x + 15 ......................................... 63

=−

zx y

cos( )zxy

=⋅

∨

........................................................... 67, 75

∧

................................................................. 75

° ................................................................ 147

:∈ ...................................................... 137, 138

:= .......................................... 66, 96, 138, 167

∞

............................................................... 138

↓

............................................................... 161

(¢) (¼) (½) (ª)+(¼) (ª)+(½) (ª)+(Æ) (ª)+(æ) (Æ) (æ) (Alt)+(PrtSc) (Ctrl)+(¢) (Ctrl)+(¼) (Ctrl)+(½) (Ctrl)+(ª)+(¼) (Ctrl)+(ª)+(½) (Ctrl)+(ª)+(M) (Ctrl)+(Æ) (Ctrl)+(æ) (Ctrl)+(C) (Ctrl)+(E) (Ctrl)+(P) (Ctrl)+(Q) (Ctrl)+(V) (Ctrl)+(X) (Del)

............................................. 117

................................. 125, 132

..................................................... 4, 106

.................................. 6, 28, 29, 118, 209

.......................................... 45, 121

.......................................... 46, 121

......................................... 5, 28, 29, 118

...................................... 201

.............................. 11, 64, 106

............................................ 28

................................... 53

................................... 201

...................................... 28, 29

...................................... 54, 201

.............................................. 20

.............................................. 11

.............................................. 54

...................................... 54, 201

........................................................... 5

(Esc)

........................................ 5, 13, 16, 243

(F2)

.................................................... 11, 126

(F3)

........................................ 28, 36, 49, 122

(F4)

...................................................... 49, 64

(F9)

.......................................................... 128

(Home)

........................................................ 28

(PgDn)

...................................................... 119

(PgUp)

...................................................... 119

(PrtSc) (ÿ)

(Insert expression) .dfw 2:1 2D-plot Window 3D-plot window

.................................................... 201

...................................................... 11, 34

............................. 49, 64

............................................................. 41

............................................................... 56

button ..................... 25

button ..................... 117

abort computation .................................... 90

absolute value function .... 74, 139, 154, 198

accuracy ..................................................... 86

activate window ........................................ 26

aggressive simplification ....................... 151

algebra window ..................................... 3, 25

Algebra Window

algebraic equation .................................. 232

algebraic representation .......................... 24

Algebraically

algebra-state variable ................... 66, 68, 84

algorithmic limitations ............................. 87

aliasing ..................................................... 133

Alpha .......................................................... 12

alternative to

analytic geometry ................................... 185

AND

.............................................................. 75

ANGLE

........................................................ 155

angle between two vectors .................... 154

Angular unit

annotation ................................................ 105

button .................... 26

radio button ....................... 91

Edit>Derive Object

............................................ 148

........... 78

270 Index

annotation of expression .......................... 6

annotation’s position ............................. 106

apostrophe ................................................ 51

Apply parameters to rest of plot list

... 175

applying differentiation ......................... 207

Approximate

button ............................ 6

approximate computations ................... 230

approximate mode ................................... 83

approximate step by step ........................ 88

approximation tools ................................. 83

arbitrary number of digits ....................... 83

area .......................................................... 212

aspect ratio ....................................... 31, 115

assignment expression ...................... 66, 96

assignment operator .............................. 138

Asterisk

................................................... 247

audit trail ................................................... 66

Author and Simplify Author Expression Author Expression Author Matrix Author Vector Author>Expression Author>Matrix Author>Vector Auto Plot Color

button ................. 8

button .................. 4

button .................. 8

button ....................... 162

button ...................... 153

................................. 13

........................................ 162

........................................ 153

scheme ........................ 125

automatic color cycling mode .............. 156

automatic renumbering ..................... 10, 52

auto-paste .................................................. 36

autoscale mode ...................................... 118

avoid display ............................................. 72

avoid generation of duplicates ............. 197

axes .......................................................... 129

axes labels ............................................... 103

axes titles ................................................ 107

back accent operator ` ........................... 164

background color ................................... 130

backspace ........................................... 14, 15

base of natural logarithm e ..................... 21

Basic File Binary Bold

books about D

................................................ 201

...................................................... 252

button ......................................... 37

ERIVE

............................... 261

Boolean combination ............................... 77

border lines/curves ............................. 76, 77

Bottom Maximum Bottom Minimum

................................... 125

.................................... 125

box ............................................................ 129

brackets ............................................. 72, 137

branch ...................................................... 230

Branch

..................................................... 232

bring embedded plots alive ..................... 56

Buchberger ................................................ 73

built-in functions ..................................... 187

C File

........................................................ 201

Calculus>Differentiate Calculus>Integrate Calculus>Limit Calculus>Table Calculus>Vector

................................ 104, 203

cancellation ....................................... 90, 145

cannot integrate ...................................... 214

case insensitive mode .............................. 65

Case Sensitivity

catastrophic cancellation ......................... 90

cautious .................................................... 230

Center

......................................................... 26

center coordinates .................................. 101

Center Justify Center on cross Center on origin

button ......................... 37

change of sign ........................................... 33

change windows ....................................... 26

Character

mode ................................ 66, 246

character string ....................................... 188

circle ................................................... 68, 199

CIRCUMCIRCLE

........................................... 199

circumscribed circle ............................... 196

clipart ....................................................... 243

clipboard .................................... 54, 191, 201

button ....................................... 68

close window ............................................ 35

coefficient ................................................ 111

COL

............................................................ 166

Collect

...................................................... 144

colon-epsilon ........................................... 138

........................... 205

................................. 211

....................................... 110

..................................... 109

................................ 66, 246

button ...................... 32

button ..................... 32

Kutzler & Kokol-Voljc: Introduction to D

5 271

ERIVE

colon-equals ........................................ 66, 96

color ........................................................... 98

Color by

.................................................. 125

Command Toolbar ..................................... 3

commands ................................................. 12

common denominator ............................. 60

complex branch ...................................... 230

Complex

factorization ............................. 60

complex plotting mode .......................... 231

complex-valued function ....................... 229

Compressed

........................................... 247

computer clock ...................................... 254

computing time .......................................... 6

Confucius ................................................ 244

conjecture ............................................... 229

conjunction ............................................... 77

connect points ................................ 155, 194

constants, famous .................................. 135

constant-x grid curves ........................... 121

constant-y grid curves ........................... 121

constrained optimization ........................ 77

contiguous objects ................................... 53

convenience ............................................ 203

convenient fast input ................................. 9

conversion constant ............................... 148

coordinate geometry .............................. 185

Copy

button ........................................ 54

correct input ............................................. 10

count number of digits .............................. 8

crop rectangle ........................................... 33

Cross

......................................................... 26

cross product .................................. 154, 158

crosshair .................................................... 33

cube ................................................. 118, 128

cubic root ........................................ 229, 232

curve’s shape .......................................... 174

Custom Cut

.................................................... 124

button ............................................ 54

cylindrical coordinates .......................... 182

danger of approximate arithmetic ......... 90

data matrix .............................................. 159

decide ........................................................ 87

decimal fractions ...................................... 83

decimal numbers .................................... 249

Declare>Function Definition Declare>Input Settings Declare>Output Settings Declare>Simplification Set Declare>Variable Domain

................ 193

.................... 66, 245

......... 47, 246, 249

..... 84, 144, 232

............. 136, 229

default ................................................ 68, 141

default text font size ................................. 17

definite integral ....................................... 211

DEG

............................................................ 147

degrees ............................................. 148, 155

Delete

....................................................... 122

delete all plots ........................................... 98

delete expression ...................................... 60

Delete Object

button .............. 10, 60, 98

delete text object ...................................... 16

delete variable declaration expr. .......... 141

demo files ................................................ 261

derivative ................................................. 206

Derive Startup

dialog ............................... 23

determinant of matrix ............................ 164

DfW

file .................................................... 189

dialog box .................................................. 13

DIB File

.................................................... 201

die ............................................................. 253

DIF

............................................................. 215

DIF_APPS.MTH

....................................... 207

difference of sets .................................... 168

differential equation ............................... 216

differentiation ......................................... 205

Digits

field ......................................... 84, 249

digits of precision ..................................... 15

DIM

..................................................... 253, 259

dimmed buttons ........................................ 14

disguised subexpression .......................... 51

disjunction ................................... 75, 77, 236

display large expressions ........................ 20

display of axes ......................................... 108

document mathematical work ................ 24

documentation ........................................ 146

domain declaration ................................. 138

dot operator ..................................... 154, 163

Double Click Feature ............................... 45

double click on embedded plot ............... 30

drag line ..................................................... 51

272 Index

drag text field ......................................... 107

DSOLVE1_GEN

........................................... 216

.................................................................. 21

edges of triangle ..................................... 194

Edit

........................................................... 122

ERIVE

edit D

Edit>Copy Edit>Copy Plot Window Edit>Cut Edit>Delete Edit>Delete All Annotations Edit>Delete All Plots Edit>Derive Object Edit>Mark and Copy Edit>Paste Edit>Plot Edit>Select All Edit>Undelete

Educator’s footnote Educator’s footnote

effect of using integer parameters ....... 174

Einstein ................................................... 135

elapsed time .............................................. 90

ELEMENT

ellipses ..................................................... 160

embed plot window ................................. 27

end of the document .............................. 191

Ending Value

enter and simplify ................................ 9, 11

Enter key

equation with infinitely many sol. .......... 65

equation with no solution ....................... 65

equivalence transformations .................. 63

equivalent .................................................. 87

exact precision mode .............................. 83

exchange two windows ......................... 228

exit D

expand ............................................... 12, 145

expansion variables ................................. 47

explicit form ............................................. 70

explicit solution ...................................... 217

exponentiation operator ........................... 7

Expression display

text ........................................ 15

......................................... 54, 201

........................ 201

............................................ 54, 201

............................................... 60

................ 197

....................... 98, 173

............................ 24, 78

.............................. 201

................................................ 54

......................................... 121, 123

.......................................... 78

........................................... 60

.. 9, 11, 46, 64, 65, 93

........... 138, 143, 146

............................................. 72, 161

.......................................... 109

(¢)

........................................... 4

ERIVE

................................................ 21

................................ 247

Expression Entry Toolbar ......................... 3

expression font size .................................. 39

extent of expression ................................. 44

extract element from list ......................... 72

factor polynomial ...................................... 59

factorial .................................................... 256

factory default ............... 1, 23, 245, 264, 265

factory default box ................................. 117

factory default plot range ...................... 102

factory default precision mode ............... 86

FALSE

........................................................... 65

family member .......................................... 95

family of curves ............................... 174, 217

family of lines .................................... 97, 112

family of points ............................... 100, 102

family of tangents ................................... 210

family of triangles ................................... 224

famous constants .................................... 135

File>Embed File>Exit File>Export File>Load>Data File File>Load>Demo File File>Load>Utility File File>New File>Open File>Page Setup File>Print File>Print Preview File>Save As File>Update File>Write

filter ............................................................ 92

Find Derivative Find Integral Find Limit

finite sequence .......................................... 96

FIT

.............................................................. 159

fixpoint method ...................................... 257

flattened circle .......................................... 68

floatable toolbars .................................... 244

floating point arithmetic ................ 139, 231

focus ....................................................... 4, 11

............................................... 27

..................................................... 21

.............................................. 201

............................... 256

............................. 261

..................... 188, 193

.................................................... 54

.......................................... 55, 191

..................................... 201

................................................. 201

............................ 38, 201

............................. 41, 189, 201

............................... 71, 108, 115

................................................ 201

button ...................... 205

button ........................... 211

button ...................... 104, 203

Kutzler & Kokol-Voljc: Introduction to D

5 273

ERIVE

follow mode .............................................. 30

font ........................................................... 105

font color ................................................... 20

Font Size

................................................... 16

Formatting Toolbar ....... 15, 37, 85, 113, 243

Fortran File

............................................. 201

four-function calculator ........................ 136

function as ordered pairs ...................... 169

function definition ................................... 96

function invocations .............................. 187

function plots ............................................ 70

functional programming ........................ 259

fundamental theorem of algebra .......... 232

Gaussian elimination method ................. 73

generic coefficient ................................. 112

Gradient

.................................................. 124

graphical representation ......................... 24

graphics cross ................................... 27, 121

graphics square ........................................ 29

Greek letters ........................................... 145

Greek Symbol Toolbar .................. 3, 12, 51

grid ..................................................... 70, 122

grid intervals ........................................... 101

grid point ........................................... 98, 114

grid size ........................................... 123, 131

Groebner-bases method .......................... 73

Help>Contents Help>Index

heritage .................................................... 110

Hexadecimal

highlight contents of entry line ............... 11

highlight entire expression ..................... 45

highlight expression with mouse ............. 6

highlight multiple objects ........................ 52

highlight text ............................................. 15

highlight text object ................................. 16

highlighting subexpression ..................... 43

holes ........................................................ 139

horizontal drag line .................................. 51

horizontal length .................................... 101

horizontal line ................................... 97, 105

....................................... 261

...................................... 165, 206

........................................... 252

horizontal scroll bar ................................. 86

HOWOFTEN

................................................. 254

hyperbola ................................................... 70

................................................................... 21

....................................................... 200, 256

imaginary component ..................... 139, 231

imaginary unit ........................................... 21

implicit plot ................................. 70, 93, 235

implicit solution ...................................... 217

import numerical data ............................ 256

inaccessible buttons ................................. 14

inactive window ........................................ 25

increment button ...................................... 84

incrementally rotated figures ................ 223

indefinite integration .............................. 211

index variable ............................................ 96

inequalities ................................................ 73

inequality in two variables ....................... 75

INF

..................................................... 104, 138

infinity ...................................... 104, 138, 204

influence of parameter ........................... 177

initialization file ................................ 23, 264

inner product ........................................... 154

Input Mode Insert Annotation

insert expression .............................. 49, 191

Insert Text Insert>Annotation Insert>OLE Object Insert>Plot Insert>Text Object

inside the sphere ..................................... 240

inspect a graph .......................................... 27

INT

..................................................... 211, 216

integers .................................................... 142

integration ....................................... 205, 211

integration constant ............................... 211

interactive plot .......................................... 27

interchange window positions .............. 157

Internet Mailing List ............................... 261

interrupt ................................................... 259

INTERSECT

intersection of sets ................................. 168

........................................ 66, 245

button ................. 105

button ................................. 6

.......................... 105, 195

.................................. 244

......................... 26, 126, 180, 238

.................................... 14

................................................. 189

274 Index

inverse function .............................. 226, 233

isolated points ................................ 194, 228

ITERATE

ITERATES

..................................................... 257

................................................... 257

jagged ...................................................... 131

JPEG File

................................................ 201

label number ............................................... 4

labeled box .............................................. 117

labels ............................................ 4, 195, 224

least squares fit ....................................... 159

length of vector ...................................... 154

LIM

.................................................... 203, 215

limit .................................................. 104, 203

limitations ........................... 83, 87, 107, 234

LINE_ORTH

................................................ 187

list .............................................................. 72

ln(0) ......................................................... 149

logarithmic expressions ........................ 148

logical statement .................................... 151

magnify .............................................. 31, 119

Magnify plot Math

Math Symbol Toolbar ............................ 3, 5

mathematical document .......................... 23

mathematical identities ......................... 233

matrix ............................... 100, 110, 161, 256

matrix extraction ................................... 167

matrix inverse ......................................... 164

matrix multiplication ............................. 163

Matrix Operations

maximum color ...................................... 124

memory requested ................................. 263

menu .......................................................... 12

Menu Bar ..................................................... 3

MIDPOINT

million ........................................................ 86

minimal restriction ................................. 137

minimum color ....................................... 124

Mode

button .......... 119, 131, 240

file .................................................. 188

.................................. 166

................................................... 187

field ................................................. 84

models ........................................................ 63

move cross ................................................. 28

move highlighting ........................................ 6

move objects ............................................. 51

move the annotation ............................... 196

multi-character variable names ................. 9

multi-line display .................................... 201

multiple angles ........................................ 144

Multiplication Operator

......................... 248

named constants ..................................... 109

naming convention ................................. 187

New

button ........................................... 54

Newsletter ............................................... 261

noncontiguous objects ............................. 53

nonnegative ............................................. 136

nonreal valued function ......................... 228

nonsquare matrices ................................ 165

notation .................................................... 249

NSOLVE

......................................................... 91

Number of Panels Numerically

.......................... 123, 126

radio button ......................... 91

observation point .................................... 122

odd multiples ........................................... 142

ODE1.MTH

OLE Objects ............................................ 243

one-digit odd integers ............................. 169

one-letter variables ................................. 245

one-row matrices .................................... 190

online help ............................................... 206

Open

open menu ................................................. 13

open window to full size .......................... 35

optimization ............................................... 77

Options>Approximate BeforePlotting Options>Autoscale New Plots Options>Change Plot Color Options>Display Options>Display>Alignment of New O Options>Display>Axes Options>Display>Cross Options>Display>Font of All Express

............................................... 216

button ...................................... 191

103

..... 118, 128

........... 99, 173

..................................... 128

. 17

.................. 108, 141

.......................... 28

.. 19

Kutzler & Kokol-Voljc: Introduction to D

5 275

ERIVE

Options>Display>Font of New Text Options>Display>Grids Options>Display>Plot Color Options>Display>Points Options>Follow Cross Options>Hide Labels Options>Plot Real and Imaginary P Options>Printing>Expression Layout Options>Printing>Header and Footer Options>Renumber Expression Options>Simplify Before Plotting Options>Startup Options>Trace Plots

......................................................... 67, 75

........................ 115

........ 99, 155, 194

............................ 29

............................ 224

............................ 259, 265

....................... 28, 122

...... 17

.................. 99

... 229

. 39

224

............ 52

....... 102

ordered pairs .......................................... 169

orient the plot ......................................... 117

oscillations ....................... 127, 133, 234, 235

outermost function ................................ 145

outermost operator ............................ 43, 45

parametric form ..................................... 172

Parametric Plot Parameters

parenthesis .............................................. 137

part of a circle ........................................ 172

Pascal File Paste

.............................................. 201

button ....................................... 54

pathnames ............................................... 263

pattern ............................................. 216, 223

percentage of memory used .................... 90

Percentage of physical memory

PERP_BISECTOR

......................................... 187

perpendicular ......................................... 158

perpendicular bisector .......................... 185

perpendicular vector form .................... 185

persistent parentheses ....................... 43, 47

phase angle ............................................. 232

photograph .............................................. 243

physical screen length ............................. 69

pi .................................................... 13, 20, 83

pixels ......................................................... 69

plot ....................................................... 24, 74

plot a vector .............................................. 97

Plot

button ................................. 117, 126

Plot Color

tab ......................................... 124

................. 174

......... 263

Plot Expression Plot Parameters Plot Properties

button ..................... 26

tab ............................... 123

dialog ............................ 123

plot unsimplified expressions ............... 102

LOTINT

..................................................... 212

point ........................................................... 98

point of intersection ............................... 189

polar .................................................. 235, 236

polynomial ......................................... 56, 111

postfix equals .............................. 21, 82, 135

POWER_SET

................................................ 169

powers of trig functions ......................... 145

precision mode ........................................ 248

Precision

section ...................................... 84

prime numbers ........................................ 160

Principal

................................................... 232

print ............................................................ 40

print annotations ...................................... 39

print bold ................................................... 39

print computation times .......................... 39

print preview ............................................. 38

print regular ............................................... 39

procedural programming ................ 256, 259

program ............................................ 188, 256

programming languages ......................... 201

progress bar/dialog box ........................... 90

Prompt to use factory default

...... 259, 263

prove .................................................. 87, 151

pseudo-random number generator ....... 252

quadrant ........................................... 139, 150

quartic equation ........................................ 91

quintic equation ........................................ 90

radian mode ............................................. 147

Radical

radix bases ....................................... 246, 251

Rainbow

RANDOM

random numbers ..................................... 252

Rational Real

real branch ............................................... 230

factorization ................................ 59

........................................... 124, 127

..................................................... 252

factorization ............................... 59

.......................................................... 137

276 Index

real numbers ........................................... 142

Real

radio button ..................................... 92

rectangular part of the screen .............. 201

recursive functions ................................ 256

remove highlighting ................................. 10

rendering program ................................. 139

replace a subexpression .......................... 50

replace expression’s variables ................ 49

replace old expression with new one .... 24

reposition annotation ............................ 107

representations ......................................... 24

reset plot window .................................. 231

resize embedded plot ......................... 31, 70

restore original view .............................. 120

restore plot range ..................................... 30

restore scale factors ................................ 31

Right Justify

button ........................... 37

root functions ......................................... 232

Rotate down Rotate left Rotate plots Rotate right Rotate up

rotate,

ROTATE_FIG

button .......................... 118

button ............................. 118

button .......................... 119

button ........................... 118

button ............................... 118

ROTATE

................................. 118, 222

.............................................. 222

rotation around x or y axis ................... 179

rotation control ...................................... 131

rotation matrix ....................................... 221

round-off errors ........................ 88, 139, 231

ROW

........................................................... 166

scaffolding method .................................. 65

scalar product ......................................... 154

Scale

.......................................................... 26

Scheme

scientific notation .................................. 249

screen images ......................................... 201

scroll bar ............................................. 85, 86

segment ................................................... 155

SELECT

select embedded plot ............................... 31

select variable ........................................... 48

selected plot ............................................ 122

semi-colons ..................................... 162, 190

................................................... 124

.............................................. 160, 253

Sensitive Set 2D Aspect Ratio Set Eye Position Set range with box Set>Aspect Ratio Set>Coordinate System Set>Eye Position Set>Plot Range Set>Plot Region

radio button ............................. 66

dialog ..................... 69

button ................... 120

button ................. 33

....... 69, 80, 172, 198, 240

........ 182, 236, 237

.................................... 120

..................... 30, 33, 99, 130

....................... 30, 101, 130

sets ............................................................ 168

shaded area ................................................ 75

shallowest operator .................................. 44

shift the function ..................................... 175

show the equation ................................... 199

shrink ....................................................... 119

Shrink plot

button ............................. 119

simplification ........................................... 233

Simplification Settings

dialog ................ 83

simplification tools ................................... 83

Simplified Expressions

........................... 19

simplify a subexpression ......................... 47

Simplify Simplify>Approximate Simplify>Basic Simplify>Expand Simplify>Factor Simplify>Subexpression Substitution Simplify>Variable Substitution

button .............................. 5, 135

....................... 14, 83

.................................. 13, 135

...................................... 12

.................................. 59, 91

.. 51

.............. 49

Simpson’s rule ......................................... 215

simulate .................................................... 253

singularities ............................................. 150

size of points ............................................. 99

slow down ............................................... 123

smallest subexpression ............................ 45

Solution Domain Solution Method Solution Variables

SOLUTIONS

SOLVE

................................................. 190

..................................... 36, 91, 151, 190

field .............................. 92

field ..................... 67, 73

solve equation numerically ...................... 91

solve equation step by step ...................... 63

Solve Expression

button ............. 36, 63

solve polynomial equation ....................... 35

solve system of equations ........................ 71

Solve>Expression

.................................... 36

Kutzler & Kokol-Voljc: Introduction to D

5 277

ERIVE

Solve>System

.......................... 71, 159, 190

sphere ...................................................... 236

spherical plot .......................................... 236

spiral staircase ........................................ 177

square brackets ................................ 72, 137

square root ............................................ 5, 11

Start

menu .................................................. 3

Starting Value

........................................ 109

Status Bar .................................................... 3

steeper intersections ............................... 33

step size ............................................. 96, 109

stepwise approximation .......................... 88

stepwise computations ............................ 47

stepwise simplification .......................... 146

stop rotation ........................................... 120

stop tracing ............................................. 122

structure of expressions .......................... 43

SUB

............................................................ 161

subexpressions ......................................... 43

subscript .................................................... 96

substitution ............................................... 49

subtract 2x ................................................ 63

suffix .......................................................... 41

summation theorem ............................... 144

surfaces in three dimensions ................ 117

syntactical replace operation ................. 51

syntax error ................................................ 5

system of equations ................................. 71

system of inequalities .............................. 78

TABLE

........................................................ 109

tabs ............................................................ 55

tangent ..................................................... 206

tangent plane .......................................... 124

TARGA File

template .................................................. 207

term ordering .............................................. 9

term structure ........................................... 44

text editing mode ........................... 7, 14, 15

text object ................................................... 7

THROWS

TIFF File

tile windows .............................................. 25

Titlebar .................................... 8, 29, 41, 189

............................................. 201

..................................................... 253

.................................................. 201

too many windows ................................... 68

toolbars .................................................... 244

Top Maximum Top Minimum

......................................... 125

.......................................... 125

touch ........................................................ 240

trace curve ............................................... 121

trace mode ......................................... 28, 120

trace mode does not work ....................... 70

Trace Plots

button .............. 28, 120, 122

Tracing Toolbar ...................................... 121

Transformation Direction

...................... 144

transformation rule ................................ 136

translation ................................................ 175

transpose of matrix ................................ 164

triangle,

Trig Powers

TRIANGLE

.................... 193, 195, 221

..................................... 144, 145

trigonometric collect mode ................... 145

trigonometric identities ......................... 142

Trigonometry

.......................................... 144

trigonometry expansion mode .............. 145

Trivial

factorization .................................. 60

TRUE

............................................................ 65

turn axes off ............................................ 141

two-sided limit ........................................ 203

undo command ......................................... 60

undo variable declaration ...................... 141

union of sets ............................................ 168

unique ....................................................... 234

unnamed worksheet ................................. 41

unselect expression ................................ 191

unselect plot............................................. 123

unselect variable ....................................... 48

unsimplified expressions ................. 19, 102

unwrap ....................................................... 86

update plot object ..................................... 70

User Group .............................................. 261

user-defined color scheme .................... 122

user-defined functions ........................... 187

utility files ................................ 207, 259, 263

variable domains ..................................... 136

variable names ............................................ 9

278 Index

variable ordering ................................ 47, 67

Variable Substitution

VECT2D

...................................................... 156

VECT3D

...................................................... 157

VECTOR

Vector dimension

........................................ 95, 160, 210

button .... 49, 136

.................................. 153

vertical length ......................................... 101

vertical scroll bar ..................................... 85

View ....................................................... 3, 11

visualize ..................................... 93, 117, 155

window type ............................................. 25

Window>Display Tabs

............................ 55

Window>New 2D plot Window Window>New 3D-plot Window Window>Tile Vertically Window>View Toolbars Window>View Toolbars>Formatting T

............... 25

..... 132, 179

............................ 25

.......................... 15

. 37

word mode ......................................... 66, 246

worksheet .................................................... 4

Wrap

button ........................................ 86

Zoom in Zoom out Zoom vertical in Zoom vertical out

button ............................ 31, 127

button ................. 31, 133, 213

button ...................... 31

button ............ 31, 213

Texas Instruments U.S.A. 7800 Banner Drive Dallas, Texas 75251

ti-cares@ti.com

Texas instruments DERIVE 5 Introduction

Specifications and Main Features

Frequently Asked Questions

User Manual

Table of Contents

Preface

Introduction

Chapter 1: First Steps

Summary

Chapter 2: Documenting Polynomial Zero Finding

Summary

Index