Motorola DSP56000 User Manual

Download

DSP56000

24-BIT

DIGITAL SIGNAL PROCESSOR

FAMILY MANUAL

Motorola, Inc. Semiconductor Products Sector DSP Division 6501 William Cannon Drive, West Austin, Texas 78735-8598

Order this document by DSP56KFAMUM/AD

Motorola reserves the right to make changes without further notice to any products herein to improve reliability, function or design. Motorola does not assume any liability arising out of the application or use of any product or circuit described herein; neither does it convey any license under its patent rights nor the rights of others. Motorola products are not authorized for use as components in life support devices or systems intended for surgical implant into the body or intended to support or sustain life. Buyer agrees to notify Motorola of any such intended end use whereupon Motorola shall determine availability and suitability of its product or products for the use intended. Motorola and M are registered trademarks of Motorola, Inc. Motorola, Inc. is an Equal Employment Opportunity /Afﬁrmative Action Employer.

OnCE is a trade mark of Motorola, Inc.  Motorola Inc., 1994



“1 ≤ N ≤

”.

Order this document by

MOTOROLA

SEMICONDUCTOR

DSP56KFAMUM/AD

TECHNICAL DATA

DSP56K Family

Addendum to

24-bit Digital Signal Processor Family Manual

This document, containing changes, additional features, further explanations, and clarifications, is a supplement to the original document:

DSP56KFAMUM/AD Family Manual DSP56K Family

24-bit Digital Signal Processors

Change the following:

Page 11-4, Section 11.2.1 - Delete “4. NeXT Page A-83, third line - Replace Page A-104, Under the “Operation:” heading - Replace “ Page A-104, Second sentence after “Description:” heading - Replace “

of D.

” with “

One is added to the LSB of D; i.e. bit 0 of A0 or B0.

“1;leN;le24”

under Mach”.

with

24”

D -1 ⇒ D

” with “

”

D+1 ⇒ D

One is added from the LSB

”.

Page A-130, First symbolic description under the “Operation:” heading - Replace “ “

If S[n]=1

Page A-218, Timing description - Replace “ Timing:

6 + ea + ap oscillator clock cycles

Page A-219, Timing description - Replace “ Timing:

6 + ea + ap oscillator clock cycles

Page A-225, Timing description - Replace “ Timing:

2+mvp oscillator clock cycles

Page A-261, Timing description - Replace “ Timing:

oscillator clock cycles

Page A-261, Memory description - Replace “Memory:

program words

Page B-11, An inch below the middle of the page - Replace the “ Page B-16, 7

”.

instruction from bottom - Replace “

2+mvp oscillator clock cycles

4+mvp oscillator clock cycles

4 oscillator clock cycles

1 program words

cir

” instruction with “

lsl A,n0

” with “

lsl B A,n0

” with “ Timing:

” with “Memory:

If S[n]=0

” with “ Timing:

clr

” with

2+mvp

1+ mv

”.

MOTOROLA INC., 1995

MOTOROLA

SEMICONDUCTOR

TECHNICAL DATA



MOTOROLA INC., 1995

OnCE

is a trade mark of Motorola, Inc.

Motorola reserves the right to make changes without further notice to any products herein. Motorola makes no warranty, representation or guarantee regarding the suitability of its products for any particular purpose, nor does Motorola assume any liability arising out of the application or use of any product or circuit, and specifically disclaims any and all liability, including without limitation consequential or incidental damages. “Typical” parameters can and do vary in different applications. All operating parameters, including “Typical”, must be validated for each customer application by customer's technical experts. Motorola does not convey any license under its patent rights nor the rights of others. Motorola products are not designed, intended, or authorized for use as components in systems intended for surgical implant into the body, or other applications intended to support or sustain life, or for any other application in which the failure of the Motorola product could create a situation where personal injury or death may occur. Should Buyer purchase or use Motorola products for any such unintended or unauthorized application, Buyer shall indemnify and hold Motorola and its officers, employees, subsidiaries, affiliates, and distributors harmless against all claims, costs, damages, and expenses, and reasonable attorney fees arising out of, directly or indirectly, any claim of personal injury or death associated with such unintended or unauthorized use, even if such claim alleges that Motorola was negligent regarding the design or manufacture of the part.

Motorola and

b are registered trademarks of Motorola, Inc.

Literature Distribution Centers: USA: Motorola Literature Distribution; P.O. Box 20912; Phoenix, Arizona 85036. EUROPE: Motorola Ltd.; European Literature Center; 88 Tanners Drive, Blakelands, Milton

Keynes, MK14 5BP, Great Britain.

TABLE OF CONTENTS

Paragraph Page

Number Title Number

SECTION 1

DSP56K FAMILY INTRODUCTION

1.1 INTRODUCTION . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .1-3

1.2 ORIGIN OF DIGITAL SIGNAL PROCESSING . . . . . . . . . . . . . . . . . . . . . . . .1-3

1.3 SUMMARY OF DSP56K FAMILY FEATURES . . . . . . . . . . . . . . . . . . . . . . . .1-9

1.4 MANUAL ORGANIZATION . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .1-11

SECTION 2

DSP56K CENTRAL ARCHITECTURE

OVERVIEW

2.1 DSP56K CENTRAL ARCHITECTURE OVERVIEW . . . . . . . . . . . . . . . . . . . .2-3

2.2 DATA BUSES . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .2-3

2.3 ADDRESS BUSES . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .2-4

2.4 DATA ALU . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .2-5

2.5 ADDRESS GENERATION UNIT . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .2-5

2.6 PROGRAM CONTROL UNIT . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .2-5

2.7 MEMORY EXPANSION PORT (PORT A) . . . . . . . . . . . . . . . . . . . . . . . . . . .2-6

2.8 ON-CHIP EMULATOR (OnCE) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .2-6

2.9 PHASE-LOCKED LOOP (PLL) BASED CLOCKING . . . . . . . . . . . . . . . . . . .2-6

SECTION 3

DATA ARITHMETIC LOGIC UNIT

3.1 DATA ARITHMETIC LOGIC UNIT . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .3-3

3.2 OVERVIEW AND DATA ALU ARCHITECTURE . . . . . . . . . . . . . . . . . . . . . .3-3

3.3 DATA REPRESENTATION AND ROUNDING . . . . . . . . . . . . . . . . . . . . . . .3-10

3.4 DOUBLE PRECISION MULTIPLY MODE . . . . . . . . . . . . . . . . . . . . . . . . . .3-16

MOTOROLA

TABLE OF CONTENTS

iii

Table of Contents (Continued)

Paragraph Page

Number Title Number

3.5 DATA ALU PROGRAMMING MODEL . . . . . . . . . . . . . . . . . . . . . . . . . . . . .3-19

3.6 DATA ALU SUMMARY . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .3-19

SECTION 4

ADDRESS GENERATION UNIT

4.1 ADDRESS GENERATION UNIT AND ADDRESSING MODES . . . . . . . . . . .4-3

4.2 AGU ARCHITECTURE . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .4-3

4.3 PROGRAMMING MODEL . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .4-6

4.4 ADDRESSING . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .4-8

SECTION 5

PROGRAM CONTROL UNIT

5.1 PROGRAM CONTROL UNIT . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .5-3

5.2 OVERVIEW . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .5-3

5.3 PROGRAM CONTROL UNIT (PCU) ARCHITECTURE . . . . . . . . . . . . . . . . .5-5

5.4 PROGRAMMING MODEL . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .5-8

SECTION 6

INSTRUCTION SET INTRODUCTION

6.1 INSTRUCTION SET INTRODUCTION . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .6-3

6.2 SYNTAX . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .6-3

6.3 INSTRUCTION FORMATS . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .6-3

6.4 INSTRUCTION GROUPS . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .6-20

SECTION 7

PROCESSING STATES

7.1 PROCESSING STATES . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .7-3

7.2 NORMAL PROCESSING STATE . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .7-3

7.3 EXCEPTION PROCESSING STATE (INTERRUPT PROCESSING) . . . . . .7-10

TABLE OF CONTENTS MOTOROLA

Table of Contents (Continued)

Paragraph Page

Number Title Number

7.4 RESET PROCESSING STATE . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .7-33

7.5 WAIT PROCESSING STATE . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .7-36

7.6 STOP PROCESSING STATE . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .7-37

SECTION 8

PORT A

8.1 PORT A OVERVIEW . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .8-3

8.2 PORT A INTERFACE . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .8-3

SECTION 9

PLL CLOCK OSCILLATOR

9.1 PLL CLOCK OSCILLATOR INTRODUCTION . . . . . . . . . . . . . . . . . . . . . . . .9-3

9.2 PLL COMPONENTS . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .9-3

9.3 PLL PINS . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .9-9

9.4 PLL OPERATION CONSIDERATIONS . . . . . . . . . . . . . . . . . . . . . . . . . . . .9-11

SECTION 10

ON-CHIP EMULATION (OnCE)

10.1 ON-CHIP EMULATION INTRODUCTION . . . . . . . . . . . . . . . . . . . . . . . . . .10-3

10.2 ON-CHIP EMULATION (OnCE) PINS . . . . . . . . . . . . . . . . . . . . . . . . . . . . .10-3

10.3 OnCE CONTROLLER AND SERIAL INTERFACE . . . . . . . . . . . . . . . . . . . .10-6

10.4 OnCE MEMORY BREAKPOINT LOGIC . . . . . . . . . . . . . . . . . . . . . . . . . . .10-11

10.5 OnCE TRACE LOGIC . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .10-13

10.6 METHODS OF ENTERING THE DEBUG MODE . . . . . . . . . . . . . . . . . . . .10-14

10.7 PIPELINE INFORMATION AND GLOBAL DATA BUS REGISTER . . . . . .10-16

10.8 PROGRAM ADDRESS BUS HISTORY BUFFER . . . . . . . . . . . . . . . . . . .10-18

10.9 SERIAL PROTOCOL DESCRIPTION . . . . . . . . . . . . . . . . . . . . . . . . . . . . .10-19

10.10 DSP56K TARGET SITE DEBUG SYSTEM REQUIREMENTS . . . . . . . . .10-19

10.11 USING THE OnCE . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .10-20

MOTOROLA

TABLE OF CONTENTS

Table of Contents (Continued)

Paragraph Page

Number Title Number

SECTION 11

ADDITIONAL SUPPORT

11.1 USER SUPPORT . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .11-3

11.2 MOTOROLA DSP PRODUCT SUPPORT . . . . . . . . . . . . . . . . . . . . . . . . . .11-4

11.3 DSP56KADSx APPLICATION DEVELOPMENT SYSTEM . . . . . . . . . . . . .11-6

11.4 Dr. BuB ELECTRONIC BULLETIN BOARD . . . . . . . . . . . . . . . . . . . . . . . . .11-7

11.5 MOTOROLA DSP NEWS . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .11-16

11.6 MOTOROLA FIELD APPLICATION ENGINEERS . . . . . . . . . . . . . . . . . . .11-16

11.7 DESIGN HOTLINE– 1-800-521-6274 . . . . . . . . . . . . . . . . . . . . . . . . . . . . .11-16

11.8 DSP HELP LINE – (512) 891-3230 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .11-16

11.9 MARKETING INFORMATION– (512) 891-2030 . . . . . . . . . . . . . . . . . . . . .11-16

11.10 THIRD-PARTY SUPPORT INFORMATION – (512) 891-3098 . . . . . . . . . .11-16

11.11 UNIVERSITY SUPPORT – (512) 891-3098 . . . . . . . . . . . . . . . . . . . . . . . .11-16

11.12 TRAINING COURSES – (602) 897-3665 or (800) 521-6274 . . . . . . . . . . .11-17

11.13 REFERENCE BOOKS AND MANUALS . . . . . . . . . . . . . . . . . . . . . . . . . . .11-17

APPENDIX A

INSTRUCTION SET DETAILS

A.1 APPENDIX A INTRODUCTION . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A-3

A.2 INSTRUCTION GUIDE . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A-3

A.3 NOTATION . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A-4

A.4 ADDRESSING MODES . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A-10

A.5 CONDITION CODE COMPUTATION . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A-15

A.6 PARALLEL MOVE DESCRIPTIONS . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A-20

A.7 INSTRUCTION DESCRIPTIONS . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A-21

A.8 INSTRUCTION TIMING . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A-294

A.9 INSTRUCTION SEQUENCE RESTRICTIONS . . . . . . . . . . . . . . . . . . . . . A-305

A.10 INSTRUCTION ENCODING . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A-311

APPENDIX B

BENCHMARK PROGRAMS

B.1 INTRODUCTION . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B-3

B.2 BENCHMARK PROGRAMS . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B-3

TABLE OF CONTENTS MOTOROLA

LIST of FIGURES

Figure Page

Number Title Number

1-1 Analog Signal Processing . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1-4

1-2 Digital Signal Processing . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1-5

1-3 DSP Hardware Origins . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 1-9

2-1 DSP56K Block Diagram . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2-4

3-1 DSP56K Block Diagram . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3-4

3-2 Data ALU . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3-5

3-3 MAC Unit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3-7

3-4 DATA ALU Accumulator Registers . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3-8

3-5 Saturation Arithmetic . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3-10

3-6 Integer-to-Fractional Data Conversion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3-11

3-7 Bit Weighting and Alignment of Operands . . . . . . . . . . . . . . . . . . . . . . . . . . 3-12

3-8 Integer/Fractional Number Comparison . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3-13

3-9 Integer/Fractional Multiplication Comparison . . . . . . . . . . . . . . . . . . . . . . . . 3-14

3-10 Convergent Rounding . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3-15

3-11 Full Double Precision Multiply Algorithm . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3-16

3-12 Single X Double Multiply Algorithm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3-17

3-13 Single X Double Multiply-Accumulate Algorithm . . . . . . . . . . . . . . . . . . . . . . 3-18

3-14 DSP56K Programming Model . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3-19

4-1 DSP56K Block Diagram . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4-4

4-2 AGU Block Diagram . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4-5

4-3 AGU Programming Model . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4-7

4-4 Address Register Indirect — No Update . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4-10

4-5 Address Register Indirect — Postincrement . . . . . . . . . . . . . . . . . . . . . . . . . 4-11

4-6 Address Register Indirect — Postdecrement . . . . . . . . . . . . . . . . . . . . . . . . 4-12

4-7 Address Register Indirect — Postincrement by Offset Nn . . . . . . . . . . . . . . 4-13

4-8 Address Register Indirect — Postdecrement by Offset Nn . . . . . . . . . . . . . . 4-14

4-9 Address Register Indirect — Indexed by Offset Nn . . . . . . . . . . . . . . . . . . . 4-15

4-10 Address Register Indirect — Predecrement . . . . . . . . . . . . . . . . . . . . . . . . . 4-16

4-11 Circular Buffer . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4-19

4-12 Linear Addressing with a Modulo Modifier . . . . . . . . . . . . . . . . . . . . . . . . . . 4-20

4-13 Modulo Modifier Example . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4-21

MOTOROLA

Revision 2.1 DSP56004 DESIGN SPECIFICATION vii

LIST of FIGURES

vii

List of Figures (Continued)

Figure Page

Number Title Number

4-14 Bit-Reverse Address Calculation Example . . . . . . . . . . . . . . . . . . . . . . . . . . 4-24

4-15 Address Modifier Summary . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4-26

5-1 Program Address Generator . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5-3

5-2 DSP56K Block Diagram . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5-4

5-3 Three-Stage Pipeline . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5-7

5-4 Program Control Unit Programming Model . . . . . . . . . . . . . . . . . . . . . . . . . . 5-8

5-5 Status Register Format . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5-9

5-6 OMR Format . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5-14

5-7 Stack Pointer Register Format . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5-15

5-8 SP Register Values . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5-15

5-9 DSP56K Central Processing Module Programming Model . . . . . . . . . . . . . . 5-18

6-1 DSP56K Central Processing Module Programming Model . . . . . . . . . . . . . . 6-4

6-2 General Format of an Instruction Operation Word . . . . . . . . . . . . . . . . . . . . 6-5

6-3 Operand Sizes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6-6

6-4 Reading and Writing the ALU Extension Registers . . . . . . . . . . . . . . . . . . . . 6-7

6-5 Reading and Writing the Address ALU Registers . . . . . . . . . . . . . . . . . . . . . 6-7

6-6 Reading and Writing Control Registers . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6-8

6-7 Special Addressing – Immediate Data . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6-15

6-8 Special Addressing – Absolute Addressing . . . . . . . . . . . . . . . . . . . . . . . . . 6-16

6-9 Special Addressing – Immediate Short Data . . . . . . . . . . . . . . . . . . . . . . . . 6-17

6-10 Special Addressing – Short Jump Address . . . . . . . . . . . . . . . . . . . . . . . . . . 6-18

6-11 Special Addressing – Absolute Short Address . . . . . . . . . . . . . . . . . . . . . . . 6-19

6-12 Special Addressing – I/O Short Address . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6-20

6-13 Hardware DO Loop . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6-25

6-14 Nested DO Loops . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6-26

6-15 Classifications of Parallel Data Moves . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6-27

6-16 Parallel Move Examples . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6-28

7-1 Fast and Long Interrupt Examples . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7-13

7-2 Interrupt Priority Register (Addr X:$FFFF) . . . . . . . . . . . . . . . . . . . . . . . . . . 7-14

7-3 Interrupting an SWI . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7-18

7-4 Illegal Instruction Interrupt Serviced by a Fast Interrupt . . . . . . . . . . . . . . . . 7-19

7-5 Illegal Instruction Interrupt Serviced by a Long Interrupt . . . . . . . . . . . . . . . . 7-20

7-6 Repeated Illegal Instruction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7-21

7-7 Trace Exception . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7-23

7-8 Fast Interrupt Service Routine . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7-27

7-9 Two Consecutive Fast Interrupts . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7-28

7-10 Long Interrupt Service Routine . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7-30

7-11 JSR First Instruction of a Fast Interrupt . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7-31

7-12 JSR Second Instruction of a Fast Interrupt . . . . . . . . . . . . . . . . . . . . . . . . . . 7-32

viii

LIST of FIGURES MOTOROLA

List of Figures (Continued)

Figure Page

Number Title Number

7-13 Interrupting an REP Instruction . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7-34

7-14 Interrupting Sequential REP Instructions . . . . . . . . . . . . . . . . . . . . . . . . . . . 7-35

7-15 Wait Instruction Timing . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7-36

7-16 Simultaneous Wait Instruction and Interrupt . . . . . . . . . . . . . . . . . . . . . . . . . 7-37

7-17 STOP Instruction Sequence . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7-38

7-18 STOP Instruction Sequence Followed by IRQA . . . . . . . . . . . . . . . . . . . . . . 7-39

7-19 STOP Instruction Sequence Recovering with RESET . . . . . . . . . . . . . . . . . 7-42

8-1 Port A Signals . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8-4

9-1 PLL Block Diagram . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9-3

9-2 DSP56K Block Diagram . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9-4

9-3 PLL Control Register (PCTL) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9-6

10-1 OnCE Block Diagram . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10-3

10-2 DSP56K Block Diagram . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10-4

10-3 OnCE Controller and Serial Interface . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10-6

10-4 OnCE Command Register . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10-7

10-5 OnCE Status and Control Register (OSCR) . . . . . . . . . . . . . . . . . . . . . . . . . 10-9

10-6 OnCE Memory Breakpoint Logic . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10-12

10-7 OnCE Trace Logic Block Diagram . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10-14

10-8 OnCE Pipeline Information and GDB Registers . . . . . . . . . . . . . . . . . . . . . . 10-16

10-9 OnCE PAB FIFO . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10-17

B-1 20-Tap FIR Filter Example . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B-5

B-2 Radix 2, In-Place, Decimation-In-Time FFT. . . . . . . . . . . . . . . . . . . . . . . . . . B-7

B-3 8-Pole 4-Multiply Cascaded Canonic IIR Filter . . . . . . . . . . . . . . . . . . . . . . . B-9

B-4 LMS FIR Adaptive Filter . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . B-11

B-5 Real Input FFT Based on Glenn Bergland Algorithm. . . . . . . . . . . . . . . . . . . B-12

MOTOROLA

LIST of FIGURES

LIST of TABLES

Table Page

Number Title Number

1-1 Benchmark Summary in Instruction Cycles. . . . . . . . . . . . . . . . . . . . . . . . . 1-6

3-1 Limited Data Values. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3-11

4-1 Address Register Indirect Summary . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4-8

4-2 Address Modifier Summary . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4-17

4-3 Bit-Reverse Addressing Sequence Example. . . . . . . . . . . . . . . . . . . . . . . . 4-23

6-1 Addressing Modes Summary . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6-21

7-1 Instruction Pipelining . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7-3

7-2 Status Register Interrupt Mask Bits . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7-14

7-3 Interrupt Priority Level Bits . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7-15

7-4 External Interrupt . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7-15

7-5 Central Processor Interrupt Priorities Within an IPL . . . . . . . . . . . . . . . . . . 7-15

7-6 Interrupt Sources . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7-16

9-1 Multiplication Factor Bits MF0-MF11 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9-6

9-2 Division Factor Bits DF0-DF3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9-7

9-3 PSTP and PEN Relationship . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9-8

9-4 Clock Output Disable Bits COD0-COD1 . . . . . . . . . . . . . . . . . . . . . . . . . . . 9-9

10-1 Chip Status Information . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10-5

10-2 OnCE Register Addressing . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10-7

10-3 Memory Breakpoint Control Table . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10-10

A-1 Instruction Description Notation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A-5

A-2 DSP56K Addressing Modes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A-11

A-3 DSP56K Addressing Mode Encoding . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A-12

A-4 Addressing Mode Modifier Summary . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A-14

A-5 Condition Code Computations for Instructions (No Parallel Move) . . . . . . . A-19

A-6 Instruction Timing Summary . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A-301

A-7 Parallel Data Move Timing . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A-302

A-8 MOVEC Timing Summary . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A-302

A-9 MOVEP Timing Summary . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A-302

LIST of TABLES MOTOROLA

List of Tables (Continued)

Table Page

Number Title Number

A-10 Bit Manipulation Timing Summary . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A-303

A-11 Jump Instruction Timing Summary. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A-303

A-12 RTI/RTS Timing Summary . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A-304

A-13 Addressing Mode Timing Summary . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A-304

A-14 Memory Access Timing Summary. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A-305

A-15 Single-Bit Register Encodings . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A-312

A-16 Single-Bit Special Register Encodings . . . . . . . . . . . . . . . . . . . . . . . . . . . . A-312

A-17 Double-Bit Register Encodings . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A-312

A-18 Triple-Bit Register Encodings. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A-313

A-19 (a)Four-Bit Register Encodings for 12 Registers in Data ALU . . . . . . . . . . . A-313

A-19 (b)Four-Bit Register Encodings for 16 Condition Codes . . . . . . . . . . . . . . . . A-313

A-20 Five-Bit Register Encodings for 28 Registers in

Data ALU and Address ALU . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A-314

A-21 Six-Bit Register Encodings for 43 Registers On-Chip . . . . . . . . . . . . . . . . . A-314

A-22 Write Control Encoding . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A-314

A-23 Memory Space Bit Encoding . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A-314

A-24 Program Controller Register Encoding . . . . . . . . . . . . . . . . . . . . . . . . . . . . A-315

A-25 Condition Code and Address Encoding . . . . . . . . . . . . . . . . . . . . . . . . . . . A-315

A-26 Effective Addressing Mode Encoding . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A-316

A-27 Operation Code K0-2 Decode . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A-331

A-28 Operation Code QQQ Decode . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A-332

A-29 Nonmultiply Instruction Encoding . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A-333

A-30 Special Case #1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A-334

A-31 Special Case #2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . A-334

B-1 27-MHz Benchmark Results for the DSP56001R27 . . . . . . . . . . . . . . . . . . B-4

MOTOROLA

LIST of TABLES

List of Tables (Continued)

Table Page

Number Title Number

xii

LIST of TABLES MOTOROLA

SECTION 1

DSP56K FAMILY INTRODUCTION

MOTOROLA DSP56K FAMILY INTRODUCTION 1 - 1

SECTION CONTENTS

SECTION 1.1 INTRODUCTION ........................................................................3

SECTION 1.2 ORIGIN OF DIGITAL SIGNAL PROCESSING ..........................3

SECTION 1.2 SUMMARY OF DSP56K FAMILY FEATURES ..........................9

SECTION 1.3 MANUAL ORGANIZATION ........................................................11

1 - 2 DSP56K FAMILY INTRODUCTION

MOTOROLA

INTRODUCTION

1.1 INTRODUCTION

The DSP56K Family is Motorola’s series of 24-bit general purpose Digital Signal Processors (DSPs

). The family architecture features a central processing module that is

common to the various family members, such as the DSP56002 and the DSP56004.

Note: The DSP56000 and the DSP56001 are not based on the central processing module

architecture and should not be used with this manual. They will continue to be described in the DSP56000/DSP56001 User’s Manual (DSP56000UM/AD Rev. 2).

This manual describes the DSP56K Family’s central processor and instruction set. It is intended to be used with a family member’s User’s Manual, such as the DSP56002 User’s Manual .

The User’s Manual presents the device’s specifics, including pin descriptions, operating modes, and peripherals. Packaging and timing information can be found in the device’s Technical Data Sheet.

This chapter introduces general DSP theory and discusses the features and benefits of the Motorola DSP56K family of 24-bit processors. It also presents a brief description of each of the sections of the manual.

1.2 ORIGIN OF DIGITAL SIGNAL PROCESSING

DSP is the arithmetic processing of real-time signals sampled at regular intervals and digitized. Examples of DSP processing include the following:

• Filtering of signals

• Convolution, which is the mixing of two signals

• Correlation, which is a comparison of two signals

• Rectification, amplification, and/or transformation of a signal All of these functions have traditionally been performed using analog circuits. Only recent-

ly has semiconductor technology provided the processing power necessary to digitally perform these and other functions using DSPs.

Figure 1-1 shows a description of analog signal processing. The circuit in the illustration filters a signal from a sensor using an operational amplifier, and controls an actuator with the result. Since the ideal filter is impossible to design, the engineer must design the filter for acceptable response, considering variations in temperature, component aging, power supply variation, and component accuracy. The resulting circuit typically has low noise immunity, requires adjustments, and is difficult to modify.

*This manual uses the acronym DSP for Digital Signal Processing or Digital Signal Processor, de-

pending on the context.

MOTOROLA DSP56K FAMILY INTRODUCTION 1 - 3

x(t) INPUT FROM

SENSOR

ORIGIN OF DIGITAL SIGNAL PROCESSING

ANALOG FILTER

x(t)

y(t)

OUTPUT

ACTUATOR

y(t)

GAIN

FREQUENCY

yt()

---------

xt()

FREQUENCY CHARACTERISTICS

IDEAL

FILTER

------

–=

----------------------------- +

1 jwR

fCf

Figure 1-1 Analog Signal Processing

The equivalent circuit using a DSP is shown in Figure 1-2. This application requires an analog-to-digital (A/D) converter and digital-to-analog (D/A) converter in addition to the DSP. Even with these additional parts, the component count can be lower using a DSP due to the high integration available with current components.

Processing in this circuit begins by band-limiting the input with an anti-alias filter, eliminating out-of-band signals that can be aliased back into the pass band due to the sampling process. The signal is then sampled, digitized with an A/D converter, and sent to the DSP.

The filter implemented by the DSP is strictly a matter of software. The DSP can directly implement any filter that can also be implemented using analog techniques. Also, adaptive filters can be easily implemented using DSP, whereas these filters are extremely difficult to implement using analog techniques.

The DSP output is processed by a D/A converter and is low-pass filtered to remove the effects of digitizing. In summary, the advantages of using the DSP include the following:

1- 4 DSP56K FAMILY INTRODUCTION

MOTOROLA

ORIGIN OF DIGITAL SIGNAL PROCESSING

• Fewer components

• Stable, deterministic performance

• Wide range of applications

• High noise immunity and

•

Self-test can be built in

•

No filter adjustments

•

Filters with much closer tolerances

•

Adaptive filters easily implemented

power-supply rejection

LOW-PASS

ANTIALIASING

FILTER

ANALOG IN ANALOG OUT

SAMPLER AND

ANALOG-TO-DIGITAL

CONVERTER

A/D D/A

x(n) y(n) y(t)x(t)

IDEAL

FILTER

GAIN

DSP OPERATION

FIR FILTER

ck() nk–()×

∑

k0=

FINITE IMPULSE

RESPONSE

DIGITAL-TO-ANALOG

CONVERTER

RECONSTRUCTION

LOW-PASS

FILTER

FREQUENCY

ANALOG

FILTER

DIGITAL

FILTER

GAIN

FREQUENCY

GAIN

FREQUENCY

Figure 1-2 Digital Signal Processing

MOTOROLA DSP56K FAMILY INTRODUCTION 1 - 5

ORIGIN OF DIGITAL SIGNAL PROCESSING

The DSP56K family is not designed for a particular application but is designed to execute commonly used DSP benchmarks in a minimum time for a single-multiplier architecture. For example, a cascaded, 2nd-order, four-coefficient infinite impulse response (IIR) biquad section has four multiplies for each section. For that algorithm, the theoretical minimum number of operations for a single-multiplier architecture is four per section. Table 1-1 shows a list of benchmarks with the number of instruction cycles a DSP56K chip uses compared to the number of multiplies the algorithm requires.

Table 1-1 Benchmark Summary in Instruction Cycles

Number of

Benchmark Number of Cycles

Algorithm Multiplies

Real Multiply 3 1 N Real Multiplies 2N N Real Update 4 1 N Real Updates 2N N N Term Real Convolution (FIR) N N N Term Real * Complex Convolution 2N N Complex Multiply 6 4 N Complex Multiplies 4N N Complex Update 7 4 N Complex Updates 4N 4N N Term Complex Convolution (FIR) 4N 4N

- Order Power Series 2N 2N

N 2nd - Order Real Biquad Filter 7 4 N Cascaded 2 N Radix Two FFT Butterﬂies 6N 4N

- Order Biquads 4N 4N

These benchmarks and others are used independently or in combination to implement functions whose characteristics are controlled by the coefficients of the benchmarks being executed. Useful functions using these and other benchmarks include the following:

1- 6 DSP56K FAMILY INTRODUCTION

MOTOROLA

ORIGIN OF DIGITAL SIGNAL PROCESSING

Digital Filtering

Finite Impulse Response (FIR) Infinite Impulse Response (IIR) Matched Filters (Correlators) Hilbert Transforms Windowing Adaptive Filters/Equalizers

Signal Processing

Compression (e.g., Linear Predictive

Coding of Speech Signals) Expansion Averaging Energy Calculations Homomorphic Processing Mu-law/A-law to/from Linear Data

Conversion

Data Processing

Encryption/Scrambling Encoding (e.g., Trellis Coding) Decoding (e.g., Viterbi Decoding)

Numeric Processing

Scaler, Vector, and Matrix Arithmetic Transcendental Function Computation

(e.g., Sin(X), Exp(X)) Other Nonlinear Functions Pseudo-Random-Number Generation

Modulation

Amplitude Frequency Phase

Spectral Analysis

Fast Fourier Transform (FFT) Discrete Fourier Transform (DFT) Sine/Cosine Transforms Moving Average (MA) Modeling Autoregressive (AR) Modeling ARMA Modeling

Useful applications are based on combining these and other functions. DSP applications affect almost every area in electronics because any application for analog electronic circuitry can be duplicated using DSP. The advantages in doing so are becoming more compelling as DSPs become faster and more cost effective.Some typical applications for DSPs are presented in the following list:

Telecommunication

Tone Generation Dual-Tone Multifrequency (DTMF) Subscriber Line Interface Full-Duplex Speakerphone Teleconferencing Voice Mail Adaptive Differential Pulse Code Modulation (ADPCM) Transcoder Medium-Rate Vocoders Noise Cancelation Repeaters Integrated Services Digital Network

(ISDN) Transceivers

Secure Telephones

Data Communication

High-Speed Modems Multiple Bit-Rate Modems High-Speed Facsimile

Radio Communication

Secure Communications Point-to-Point Communications Broadcast Communications Cellular Mobile Telephone

Computer

Array Processors Work Stations Personal Computers Graphics Accelerators

MOTOROLA DSP56K FAMILY INTRODUCTION 1 - 7

ORIGIN OF DIGITAL SIGNAL PROCESSING

Image Processing

Pattern Recognition Optical Character Recognition Image Restoration Image Compression Image Enhancement Robot Vision

Graphics

3-D Rendering Computer-Aided Engineering (CAE) Desktop Publishing Animation

Instrumentation

Spectral Analysis Waveform Generation Transient Analysis Data Acquisition

Speech Processing

Speech Synthesizer Speech Recognizer Voice Mail Vocoder Speaker Authentication Speaker Verification

Audio Signal Processing

Digital AM/FM Radio Digital Hi-Fi Preamplifier Noise Cancelation Music Synthesis Music Processing Acoustic Equalizer

High-Speed Control

Laser-Printer Servo Hard-Disk Servo Robotics Motor Controller Position and Rate Controller

Vibration Analysis

Electric Motors Jet Engines Turbines

Medical Electronics

Cat Scanners Sonographs X-Ray Analysis Electrocardiogram Electroencephalogram Nuclear Magnetic Resonance Analysis

Digital Video

Digital Television High-Resolution Monitors

Radar and Sonar Processing

Navigation Oceanography Automatic Vehicle Location Search and Tracking

Seismic Processing

Oil Exploration Geological Exploration

As shown in Figure 1-3, the keys to DSP are as follows:

• The Multiply/Accumulate (MAC) operation

• Fetching operands for the MAC

• Program control to provide versatile operation

• Input/Output to move data in and out of the DSP MAC is the basic operation used in DSP. The DSP56K family of processors has a dual

Harvard architecture optimized for MAC operations. Figure 1-3 shows how the DSP56K

1- 8 DSP56K FAMILY INTRODUCTION

MOTOROLA

SUMMARY OF DSP56K FAMILY FEATURES

architecture matches the shape of the MAC operation. The two operands, C() and X(), are directed to a multiply operation, and the result is summed. This process is built into the chip by using two separate memories (X and Y) to feed a single-cycle MAC. The entire process must occur under program control to direct the correct operands to the multiplier and save the accumulator as needed. Since the two memories and the MAC are independent, the DSP can perform two moves, a multiply and an accumulate, in a single operation. As a result, many of the benchmarks shown in Table 1-1 can be executed at or near the theoretical maximum speed for a single-multiplier architecture.

1.3 SUMMARY OF DSP56K FAMILY FEATURES

The high throughput of the DSP56K family of processors makes them well suited for communication, high-speed control, numeric processing and computer and audio applications. The main features that contribute to this high throughput include:

• Speed — Speeds high enough to easily address applications traditionally served by low-end floating point DSPs.

FIR FILTER

ck() nk–()×

A/D D/A

x(n) y(n) y(t)x(t)

∑

k0=

∑

MEMORY

PROGRAM

∑

MAC

Figure 1-3 DSP Hardware Origins

MOTOROLA DSP56K FAMILY INTRODUCTION 1 - 9

SUMMARY OF DSP56K FAMILY FEATURES

• Precision — The data paths are 24 bits wide, providing 144 dB of dynamic range; intermediate results held in the 56-bit accumulators can range over 336 dB.

• Parallelism — Each on-chip execution unit (AGU, program control unit, data ALU), memory, and peripheral operates independently and in parallel with the other units through a sophisticated bus system. The data ALU, AGU, and program control unit operate in parallel so that an instruction prefetch, a 24-bit x 24-bit multiplication, a 56bit addition, two data moves, and two address-pointer updates using one of three types of arithmetic (linear, modulo, or reverse-carry) can be executed in a single instruction cycle. This parallelism allows a four-coefficient IIR filter section to be executed in only four cycles, the theoretical minimum for single-multiplier architecture. At the same time, the two serial controllers can send and receive full-duplex data, and the host port can send/receive simplex data.

• Flexibility — While many other DSPs need external communications circuitry to interface with peripheral circuits (such as A/D converters, D/A converters, or host processors), the DSP56K family provides on-chip serial and parallel interfaces which can support various configurations of memory and peripheral modules

• Sophisticated Debugging — Motorola’s on-chip emulation technology (OnCE) allows simple, inexpensive, and speed independent access to the internal registers for debugging. OnCE tells application programmers exactly what the status is within the registers, memory locations, buses, and even the last five instructions that were executed.

• Phase-locked Loop (PLL) Based Clocking — PLL allows the chip to use almost any available external system clock for full-speed operation while also supplying an output clock synchronized to a synthesized internal core clock. It improves the synchronous timing of the processors’ external memory port, eliminating the timing skew common on other processors.

• Invisible Pipeline — The three-stage instruction pipeline is essentially invisible to the programmer, allowing straightforward program development in either assembly language or a high-level language such as a full Kernighan and Ritchie C.

• Instruction Set — The instruction mnemonics are MCU-like, making the transition from programming microprocessors to programming the chip as easy as possible. The orthogonal syntax controls the parallel execution units. The hardware DO loop instruction and the repeat (REP) instruction make writing straight-line code obsolete.

1- 10 DSP56K FAMILY INTRODUCTION

MOTOROLA

MANUAL ORGANIZATION

DSP56001 Compatibility — All members of the DSP56K family are downward

compatible with the DSP56001, and also have added flexibility, speed, and functionality.

• Low Power — As a CMOS part, the DSP56000/DSP56001 is inherently very low power and the STOP and WAIT instructions further reduce power requirements.

1.4 MANUAL ORGANIZATION

This manual describes the central processing module of the DSP56K family in detail and provides practical information to help the user:

• Understand the operation of the DSP56K family

• Design parallel communication links

• Design serial communication links

• Code DSP algorithms

• Code communication routines

• Code data manipulation algorithms

• Locate additional support

•

The following list describes the contents of each section and each appendix: Section 2 – DSP56K Central Architecture Overview

The DSP56K central architecture consists of the data arithmetic logic unit (ALU), address generation unit (AGU), program control unit, On-Chip Emulation (OnCE) circuitry, the phase locked loop (PLL) based clock oscillator, and an external memory port (Port A). This section describes each subsystem and the buses interconnecting the major components in the DSP56K central processing module.

Section 3 – Data Arithmetic Logic Unit

This section describes in detail the data ALU and its programming model.

Section 4 – Address Generation Unit

This section specifically describes the AGU, its programming model, address indirect modes, and address modifiers.

Section 5 – Program Control Unit

This section describes in detail the program control unit and its programming model.

Section 6 – Instruction Set Introduction

This section presents a brief description of the syntax, instruction formats, operand/memory references, data organization, addressing modes, and instruction set. A detailed description of each instruction is given in APPENDIX A - INSTRUCTION SET DETAILS.

MOTOROLA DSP56K FAMILY INTRODUCTION 1 - 11

MANUAL ORGANIZATION

Section 7 – Processing States

This section describes the five processing states (normal, exception, reset, wait, and stop).

Section 8 – Port A

This section describes the external memory port, its control register, and control signals.

Section 9 – PLL Clock Oscillator

This section describes the PLL and its functions

Section 10 – On-Chip Emulator (OnCE)

This section describes the OnCE circuitry and its functions.

Section 11 – Additional Support

This section presents a brief description of current support products and services and information on where to obtain them.

Appendix A – Instruction Set Details

A detailed description of each DSP56K family instruction, its use, and its affect on the processor are presented.

Appendix B – Benchmarks

DSP5K family benchmark results are listed in this appendix.

1- 12 DSP56K FAMILY INTRODUCTION MOTOROLA

SECTION 2

DSP56K CENTRAL ARCHITECTURE

OVERVIEW

MOTOROLA DSP56K CENTRAL ARCHITECTURE OVERVIEW 2 - 1

SECTION CONTENTS

SECTION 2.1 DSP56K CENTRAL ARCHITECTURE OVERVIEW ..................3

SECTION 2.2 DATA BUSES .............................................................................3

SECTION 2.3 ADDRESS BUSES .....................................................................4

SECTION 2.4 DATA ALU ..................................................................................5

SECTION 2.5 ADDRESS GENERATION UNIT ................................................5

SECTION 2.6 PROGRAM CONTROL UNIT .....................................................5

SECTION 2.7 MEMORY EXPANSION PORT (PORT A) ..................................6

SECTION 2.8 ON-CHIP EMULATOR (OnCE) ..................................................6

SECTION 2.9 PHASE-LOCKED LOOP (PLL) BASED CLOCKING ..................6

2 - 2 DSP56K CENTRAL ARCHITECTURE OVERVIEW

MOTOROLA

DSP56K CENTRAL ARCHITECTURE OVERVIEW

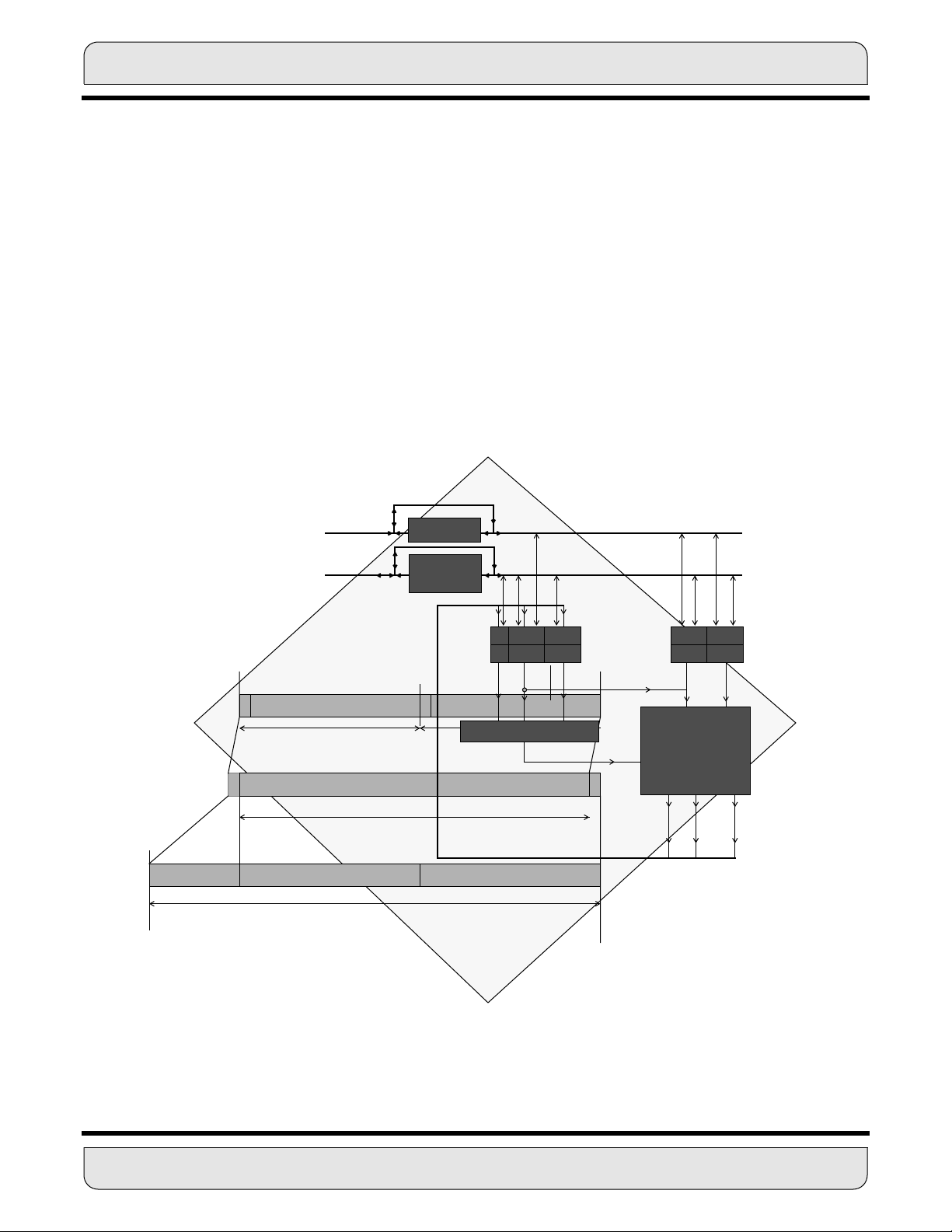
2.1 DSP56K CENTRAL ARCHITECTURE OVERVIEW

The DSP56K family of processors is built on a standard central processing module. In the expansion area around the central processing module, the chip can support various configurations of memory and peripheral modules which may change from family member to family member. This section introduces the architecture and the major components of the central processing module.

The central components are:

• Data Buses

• Address Buses

• Data Arithmetic Logic Unit (data ALU)

• Address Generation Unit (AGU)

• Program Control Unit (PCU)

• Memory Expansion (Port A)

• On-Chip Emulator (OnCE™) circuitry

• Phase-locked Loop (PLL) based clock circuitry

Figure 2-1 shows a block diagram of a typical DSP56K family processor, including the central processing module and a nonspecific expansion area for memory and peripherals. The following paragraphs give brief descriptions of each of the central components. Each of the components is explained in detail in subsequent chapters.

2.2 DATA BUSES

The DSP56K central processing module is organized around the registers of three independent execution units: the PCU, the AGU, and the data ALU. Data movement between the execution units occurs over four bidirectional 24-bit buses: the X data bus (XDB), the Y data bus (YDB), the program data bus (PDB), and the global data bus (GDB). (Certain instructions treat the X and Y data buses as one 48-bit data bus by concatenating them.) Data transfers between the data ALU and the X data memory or Y data memory occur over XDB and YDB, respectively. XDB and YDB are kept local on the chip to maximize speed and minimize power dissipation. All other data transfers, such as I/O transfers with peripherals, occur over the GDB. Instruction word prefetches occur in parallel over the PDB.

The bus structure supports general register-to-register, register-to-memory, and memoryto-register data movement. It can transfer up to two 24-bit words and one 56-bit word in the same instruction cycle. Transfers between buses occur in the internal bus switch.

MOTOROLA DSP56K CENTRAL ARCHITECTURE OVERVIEW 2 - 3

PERIPHERAL

PINS

24-Bit 56K

Module

PERIPHERAL

MODULES

ADDRESS

GENERATION

UNIT

ADDRESS BUSES

PROGRAM

RAM/ROM

EXPANSION

X MEMORY

RAM/ROM

EXPANSION

YAB XAB PAB

Y MEMORY

RAM/ROM

EXPANSION

AREA

EXTERNAL ADDRESS

BUS

SWITCH

ADDRESS

INTERNAL

DATA

BUS

SWITCH

PLL

CLOCK

GENERATOR

PROGRAM

INTERRUPT

CONTROLLER

PROGRAM

DECODE

CONTROLLER

Program Control Unit

MODC/NMI MODB/IRQB MODA/IRQA

RESET

PROGRAM

ADDRESS

GENERA TOR

YDB XDB PDB GDB

DATA ALU

24X24+56→56-BIT MAC

TWO 56-BIT ACCUMULATORS

BUS

CONTROL

EXTERNAL DATA BUS

SWITCH

OnCE™

16 BITS 24 BITS

PORT A

CONTROL

DATA

Figure 2-1 DSP56K Block Diagram

2.3 ADDRESS BUSES

Addresses are specified for internal X data memory and Y data memory on two unidirectional 16-bit buses — X address bus (XAB) and Y address bus (YAB). Program memory addresses are specified on the bidirectional program address bus (PAB). External mem-

2- 4 DSP56K CENTRAL ARCHITECTURE OVERVIEW

MOTOROLA

DATA ALU

ory spaces are addressed over a single 16-bit unidirectional address bus driven by a three-input multiplexer that can select the XAB, the YAB, or the PAB. Only one external memory access can be made in an instruction cycle. There is no speed penalty if only one external memory space is accessed in an instruction cycle. However, if two or three external memory spaces are accessed in a single instruction, there will be a one or two instruction cycle execution delay, respectively.

A bus arbitrator controls external access.

2.3.1 Internal Bus Switch

Transfers between buses occur in the internal bus switch. The internal bus switch, which is similar to a switch matrix, can connect any two internal buses without adding any pipeline delays. This flexibility simplifies programming.

2.3.2 Bit Manipulation Unit

The bit manipulation unit is physically located in the internal bus switch block because the internal data bus switch can access each memory space. The bit manipulation unit performs bit manipulation operations on memory locations, address registers, control registers, and data registers over the XDB, YDB, and GDB.

2.4 DATA ALU

The data ALU performs all of the arithmetic and logical operations on data operands. It consists of four 24-bit input registers, two 48-bit accumulator registers, two 8-bit accumulator extension registers, an accumulator shifter, two data bus shifter/limiter circuits, and a parallel, single-cycle, nonpipelined Multiply-Accumulator (MAC) unit.

2.5 ADDRESS GENERATION UNIT

The AGU performs all of the address storage and address calculations necessary to indirectly address data operands in memory. It operates in parallel with other chip resources to minimize address generation overhead. The AGU has two identical address arithmetic units that can generate two 16-bit addresses every instruction cycle. Each of the arithmetic units can perform three types of arithmetic: linear, modulo, and reverse-carry.

2.6 PROGRAM CONTROL UNIT

The program control unit performs instruction prefetch, instruction decoding, hardware DO loop control, and interrupt (or exception) processing. It consists of three components: the program address generator, the program decode controller, and the program interrupt controller. It contains a 15-level by 32-bit system stack memory and the following six di-

MOTOROLA DSP56K CENTRAL ARCHITECTURE OVERVIEW 2 - 5

MEMORY EXPANSION PORT (PORT A)

rectly addressable registers: the program counter (PC), loop address (LA), loop counter (LC), status register (SR), operating mode register (OMR), and stack pointer (SP). The 16-bit PC can address 65,536 locations in program memory space.

There are four mode and interrupt control pins that provide input to the program interrupt controller. The Mode Select A/External Interrupt Request A(MODA/IRQA lect B/External Interrupt Request B (MODB/IRQB and receive interrupt requests from external sources.

) pins select the chip operating mode

) and Mode Se-

The Mode Select C/Non-Maskable Interrupt (MODC/NMI mode options and non-maskable interrupt input.

The RESET pin resets the chip. When it is asserted, it initializes the chip and places it in the reset state. When it is deasserted, the chip assumes the operating mode indicated by the MODA, MODB, and MODC pins.

2.7 MEMORY EXPANSION PORT (PORT A)

Port A synchronously interfaces with a wide variety of memory and peripheral devices over a common 24-bit data bus. These devices include high-speed static RAMs, slower memory devices, and other DSPs and MPUs in master/slave configurations. This variety is possible because the expansion bus timing is programmable and can be tailored to match the speed requirements of the different memory spaces. Not all DSP56K family members feature a memory expansion port. See the individual device’s User’s Manual to determine if a particular chip includes this feature.

2.8 ON-CHIP EMULATOR (OnCE)

DSP56K on-chip emulation (OnCE) circuitry allows the user to interact with the DSP56K and its peripherals non-intrusively to examine registers, memory, or on-chip peripherals. It provides simple, inexpensive, and speed independent access to the internal registers for sophisticated debugging and economical system development.

) pin provides further operating

Dedicated OnCE pins allow the user to insert the DSP into its target system and retain debug control without sacrificing other user accessible on-chip resources. The design eliminates the costly cabling and the access to processor pins required by traditional emulator systems.

2.9 PHASE-LOCKED LOOP (PLL) BASED CLOCKING

The PLL allows the DSP to use almost any available external system clock for full-speed operation, while also supplying an output clock synchronized to a synthesized internal clock. The PLL performs frequency multiplication, skew elimination, and low-power division.

2- 6 DSP56K CENTRAL ARCHITECTURE OVERVIEW

MOTOROLA

SECTION 3

DATA ARITHMETIC LOGIC UNIT

MOTOROLA DATA ARITHMETIC LOGIC UNIT 3 - 1

SECTION CONTENTS

SECTION 3.1 DATA ARITHMETIC LOGIC UNIT .............................................3

SECTION 3.2 OVERVIEW AND DATA ALU ARCHITECTURE .......................3

3.2.1 Data ALU Input Registers (X1, X0, Y1, Y0) ........................................5

3.2.2 MAC and Logic Unit ............................................................................6

3.2.3 Data ALU A and B Accumulators ........................................................7

3.2.4 Accumulator Shifter ............................................................................ 9

3.2.5 Data Shifter/Limiter ............................................................................. 9

3.2.5.1 Limiting (Saturation Arithmetic) .................................................. 9

3.2.5.2 Scaling ........................................................................................ 10

SECTION 3.3 DATA REPRESENTATION AND ROUNDING ..........................10

SECTION 3.4 DOUBLE PRECISION MULTIPLY MODE .................................16

SECTION 3.5 DATA ALU PROGRAMMING MODEL .......................................19

SECTION 3.6 DATA ALU SUMMARY ..............................................................19

3 - 2 DATA ARITHMETIC LOGIC UNIT

MOTOROLA

DATA ARITHMETIC LOGIC UNIT

3.1 DATA ARITHMETIC LOGIC UNIT

This section describes the operation of the Data ALU registers and hardware. It discusses data representation, rounding, and saturation arithmetic used within the Data ALU, and concludes with a discussion of the programming model.

3.2 OVERVIEW AND DATA ALU ARCHITECTURE

As described in Section 2, The DSP56K family central processing module is composed of three execution units that operate in parallel. They are the Data ALU, address generation unit (AGU), and the program control unit (PCU) (see Figure 3-1). These three units are register oriented rather than bus oriented and interface over the system buses with memory and memory-mapped I/O devices.

The Data ALU (see Figure 3-2) is the first of these execution units to be presented. It balances speed with the capability to process signals that have a wide dynamic range and performs all arithmetic and logical operations on data operands.

The Data ALU registers may be read or written over the XDB and the YDB as 24- or 48bit operands. The source operands for the Data ALU, which may be 24, 48, or 56 bits, always originate from Data ALU registers. The results of all Data ALU operations are stored in an accumulator.

The 24-bit data words provide 144 dB of dynamic range. This range is sufficient for most real-world applications since the majority of data converters are 16 bits or less – and certainly not greater than 24 bits. The 56-bit accumulator inside the Data ALU provides 336 dB of internal dynamic range so that no loss of precision will occur due to intermediate processing. Special circuitry handles data overflows and roundoff errors.

The Data ALU can perform any of the following operations in a single instruction cycle: multiplication, multiply-accumulate with positive or negative accumulation, convergent rounding, multiply-accumulate with positive or negative accumulation and convergent rounding, addition, subtraction, a divide iteration, a normalization iteration, shifting, and logical operations.

The components of the Data ALU are:

• Four 24-bit input registers

• A parallel, single-cycle, nonpipelined multiply-accumulator/logic unit (MAC)

• Two 48-bit accumulator registers

• Two 8-bit accumulator extension registers

• An accumulator shifter

• Two data bus shifter/limiter circuits

MOTOROLA DATA ARITHMETIC LOGIC UNIT 3 - 3

PERIPHERAL

PINS

24 Bit 56K

Module

OVERVIEW AND DATA ALU ARCHITECTURE

PERIPHERAL

MODULES

ADDRESS

GENERATION

UNIT

PROGRAM

RAM/ROM

EXPANSION

YAB XAB PAB

X MEMORY

RAM/ROM

EXPANSION

Y MEMORY

RAM/ROM

EXPANSION

AREA

EXTERNAL ADDRESS

BUS

SWITCH

ADDRESS

INTERNAL

DATA

BUS

SWITCH

PLL

CLOCK

GENERATOR

PROGRAM

INTERRUPT

CONTROLLER

PROGRAM

DECODE

CONTROLLER

Program Control Unit

MODC/NMI MODB/IRQB MODA/IRQA

RESET

PROGRAM

ADDRESS

GENERA TOR

YDB XDB PDB GDB

DATA ALU

24X24+56→56-BIT MAC

TWO 56-BIT ACCUMULATORS

BUS

CONTROL

EXTERNAL DATA BUS

SWITCH

OnCE™

16 BITS 24 BITS

PORT A

CONTROL

DATA

Figure 3-1 DSP56K Block Diagram

The following paragraphs describe each of these components and provide a description of data representation, rounding, and saturation arithmetic.

3 - 4 DATA ARITHMETIC LOGIC UNIT

MOTOROLA

OVERVIEW AND DATA ALU ARCHITECTURE

3.2.1 Data ALU Input Registers (X1, X0, Y1, Y0)

X1, X0, Y1, and Y0 are four 24-bit, general-purpose data registers. They can be treated as four independent, 24-bit registers or as two 48-bit registers called X and Y, developed by concatenating X1:X0 and Y1:Y0, respectively. X1 is the most significant word in X and Y1 is the most significant word in Y. The registers serve as input buffer registers between the XDB or YDB and the MAC unit. They act as Data ALU source operands and allow new operands to be loaded for the next instruction while the current instruction uses the

X DATA BUS Y DATA BUS

2424

X0 X1 Y0 Y1

SHIFTER

24 24

MULTIPLIER

ACCUMULATOR,

ROUNDING,

AND LOGIC UNIT

A (56) B (56)

5656

SHIFTER/LIMITER

Figure 3-2 Data ALU

MOTOROLA DATA ARITHMETIC LOGIC UNIT 3 - 5

OVERVIEW AND DATA ALU ARCHITECTURE

register contents. The registers may also be read back out to the appropriate data bus to implement memory-delay operations and save/restore operations for interrupt service routines.

3.2.2 MAC and Logic Unit

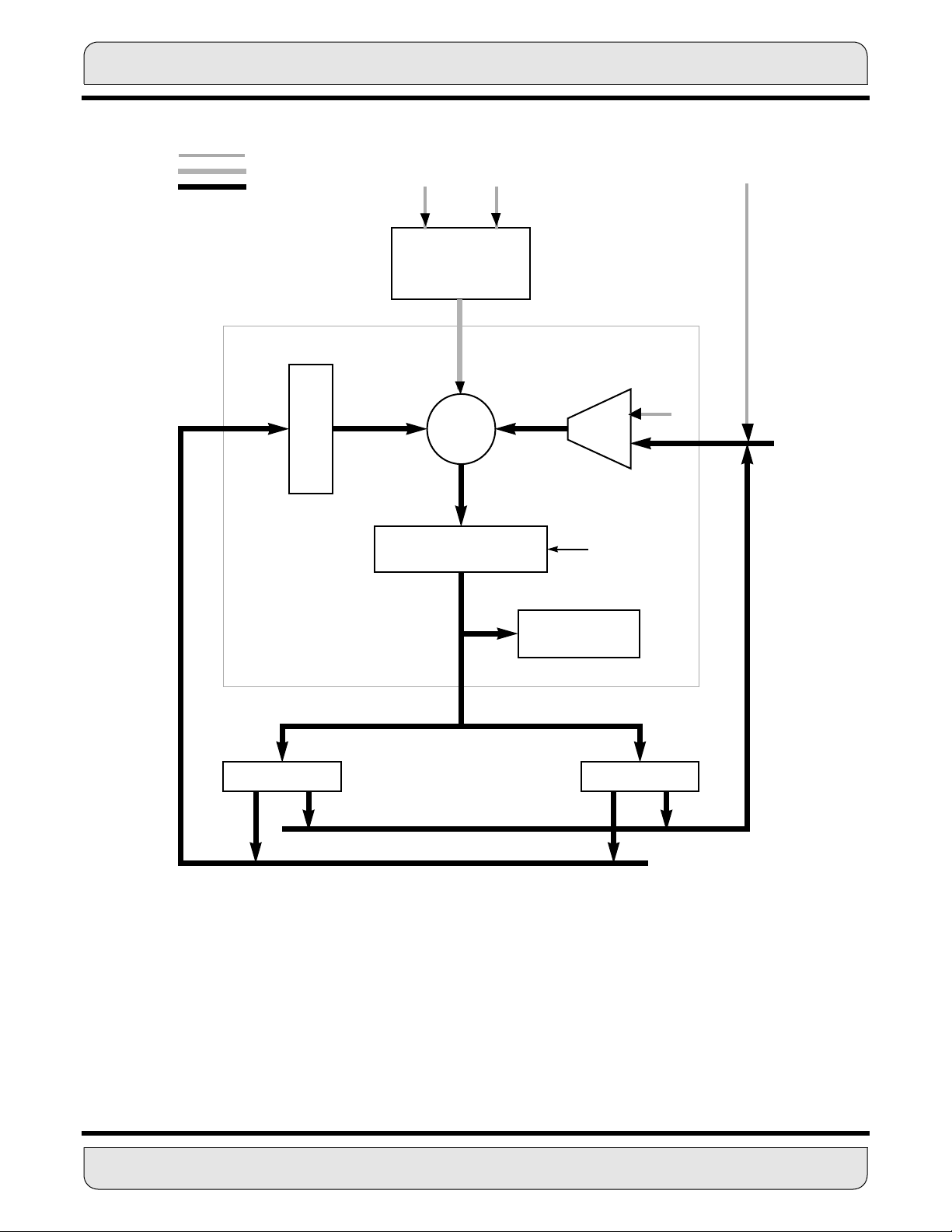
The MAC and logic unit shown in Figure 3-3 conduct the main arithmetic processing and perform all calculations on data operands in the DSP.

For arithmetic instructions, the unit accepts up to three input operands and outputs one 56-bit result in the following form: extension:most significant product:least significant product (EXT:MSP:LSP). The operation of the MAC unit occurs independently and in parallel with XDB and YDB activity, and its registers facilitate buffering for Data ALU inputs and outputs. Latches on the MAC unit input permit writing an input register which is the source for a Data ALU operation in the same instruction.

The arithmetic unit contains a multiplier and two accumulators. The input to the multiplier can only come from the X or Y registers (X1, X0, Y1, Y0). The multiplier executes 24-bit x 24-bit, parallel, twos-complement fractional multiplies. The 48-bit product is right justified and added to the 56-bit contents of either the A or B accumulator. The 56-bit sum is stored back in the same accumulator (see Figure 3-3). An 8-bit adder, which acts as an extension accumulator for the MAC array, accommodates overflow of up to 256 and allows the two 56-bit accumulators to be added to and subtracted from each other. The extension adder output is the EXT portion of the MAC unit output. This multiply/accumulate operation is not pipelined, but is a single-cycle operation. If the instruction specifies a multiply without accumulation (MPY), the MAC clears the accumulator and then adds the contents to the product.

In summary, the results of all arithmetic instructions are valid (sign-extended and zerofilled) 56-bit operands in the form of EXT:MSP:LSP (A2:A1:A0 or B2:B1:B0). When a 56bit result is to be stored as a 24-bit operand, the LSP can be simply truncated, or it can be rounded (using convergent rounding) into the MSP.

Convergent rounding (round-to-nearest) is performed when the instruction (for example, the signed multiply-accumulate and round (MACR) instruction) specifies adding the multiplier’s product to the contents of the accumulator. The scaling mode bits in the status register specify which bit in the accumulator shall be rounded.

The logic unit performs the logical operations AND, OR, EOR, and NOT on Data ALU registers. It is 24 bits wide and operates on data in the MSP portion of the accumulator. The LSP and EXT portions of the accumulator are not affected.

3 - 6 DATA ARITHMETIC LOGIC UNIT

MOTOROLA

OVERVIEW AND DATA ALU ARCHITECTURE

24 BITS 48 BITS 56 BITS

X0,X1,

Y0, OR Y1

24-BITx24-BIT

FRACTIONAL

MULTIPLIER

S H

I F T E R

CONVERGENT - ROUNDING

FORCING FUNCTION

X0,X1,

Y0, OR Y1

–

56 - BIT

ARITHMETIC AND

LOGIC UNIT

SCALING

MODE BITS

X0,X1,

Y0, OR Y1

CONDITION

CODE GENERATOR

ACCUMULATOR A ACCUMULATOR B

Figure 3-3 MAC Unit

3.2.3 Data ALU A and B Accumulators

The Data ALU features two general-purpose, 56-bit accumulators, A and B. Each consists of three concatenated registers (A2:A1:A0 and B2:B1:B0, respectively). The 8-bit sign extension (EXT) is stored in A2 or B2 and is used when more than 48-bit accuracy is needed; the 24-bit most significant product (MSP) is stored in A1 or B1; the 24-bit least

MOTOROLA DATA ARITHMETIC LOGIC UNIT 3 - 7

OVERVIEW AND DATA ALU ARCHITECTURE

DATA ALU ACCUMULATOR REGISTERS

Accumulator A

A2 A1 A0

7023 023 0

Accumulator B

55 055 0

7023 023 0

B1 B0

EXT MSP LSP

*Read as sign extension bits, written as don’t care.

EXT MSP LSP

Figure 3-4 DATA ALU Accumulator Registers

significant product (LSP) is stored in A0 or B0 as shown in Figure 3-4. Overflow occurs when a source operand requires more bits for accurate representation

than are available in the destination. The 8-bit extension registers offer protection against overflow. In the DSP56K chip family, the extreme values that a word operand can assume are - 1 and + 0.9999998. If the sum of two numbers is less than - 1 or greater than + 0.9999998, the result (which cannot be represented in a 24 bit word operand) has underflowed or overflowed. The 8-bit extension registers can accurately represent the result of 255 overflows or 255 underflows. Whenever the accumulator extension registers are in use, the V bit in the status register is set.

Automatic sign extension occurs when the 56-bit accumulator is written with a smaller operand of 48 or 24 bits. A 24-bit operand is written to the MSP (A1 or B1) portion of the accumulator, the LSP (A0 or B0) portion is zero filled, and the EXT (A2 or B2) portion is sign extended from MSP. A 48-bit operand is written into the MSP:LSP portion (A1:A0 or B1:B0) of the accumulator, and the EXT portion is sign extended from MSP. No sign extension occurs if an individual 24-bit register is written (A1, A0, B1, or B0).When either A or B is read, it may be optionally scaled one bit left or one bit right for block floatingpoint arithmetic. Sign extension can also occur when writing A or B from the XDB and/or YDB or with the results of certain Data ALU operations (such as the transfer conditionally (Tcc) or transfer Data ALU register (TFR) instructions).

Overflow protection occurs when the contents of A or B are transferred over the XDB and YDB by substituting a limiting constant for the data. Limiting does not affect the content of A or B – only the value transferred over the XDB or YDB is limited. This overflow protection occurs after the contents of the accumulator has been shifted according to the scaling mode. Shifting and limiting occur only when the entire 56-bit A or B accumulator is specified as the source for a parallel data move over the XDB or YDB. When individual registers A0, A1, A2, B0, B1, or B2 are specified as the source for a parallel data move,

3 - 8 DATA ARITHMETIC LOGIC UNIT

MOTOROLA

OVERVIEW AND DATA ALU ARCHITECTURE

shifting and limiting are not performed.

3.2.4 Accumulator Shifter

The accumulator shifter (see Figure 3-3) is an asynchronous parallel shifter with a 56-bit input and a 56-bit output that is implemented immediately before the MAC accumulator input. The source accumulator shifting operations are as follows:

• No Shift (Unmodified)

• 1-Bit Left Shift (Arithmetic or Logical) ASL, LSL, ROL

• 1-Bit Right Shift (Arithmetic or Logical) ASR, LSR, ROR

• Force to zero

3.2.5 Data Shifter/Limiter

The data shifter/limiter circuits (see Figure 3-3) provide special post-processing on data read from the Data ALU A and B accumulators out to the XDB or YDB. There are two independent shifter/limiter circuits (one for XDB and one for the YDB); each consists of a shifter followed by a limiting circuit.

3.2.5.1 Limiting (Saturation Arithmetic)

The A and B accumulators serve as buffer registers between the MAC unit and the XDB and/or YDB. They act both as Data ALU source and destination operands.Test logic exists in each accumulator register to support the operation of the data shifter/limiter circuits. This test logic detects overflows out of the data shifter so that the limiter can substitute one of several constants to minimize errors due to the overflow. This process is called saturation arithmetic

The Data ALU A and B accumulators have eight extension bits. Limiting occurs when the extension bits are in use and either A or B is the source being read over XDB or YDB. If the contents of the selected source accumulator can be represented without overflow in the destination operand size (i.e., accumulator extension register not in use), the data limiter is disabled, and the operand is not modified. If contents of the selected source accumulator cannot be represented without overflow in the destination operand size, the data limiter will substitute a limited data value with maximum magnitude (saturated) and with the same sign as the source accumulator contents: $7FFFFF for 24-bit or $7FFFFF FFFFFF for 48-bit positive numbers, $800000 for 24-bit or $800000 000000 for 48-bit negative numbers. This process is called saturation arithmetic. The value in the accumulator register is not shifted and can be reused within the Data ALU. When limiting does occur, a flag is set and latched in the status register.Two limiters allow two-word operands to be limited independently in the same instruction cycle. The two data limiters can also be com-

MOTOROLA DATA ARITHMETIC LOGIC UNIT 3 - 9

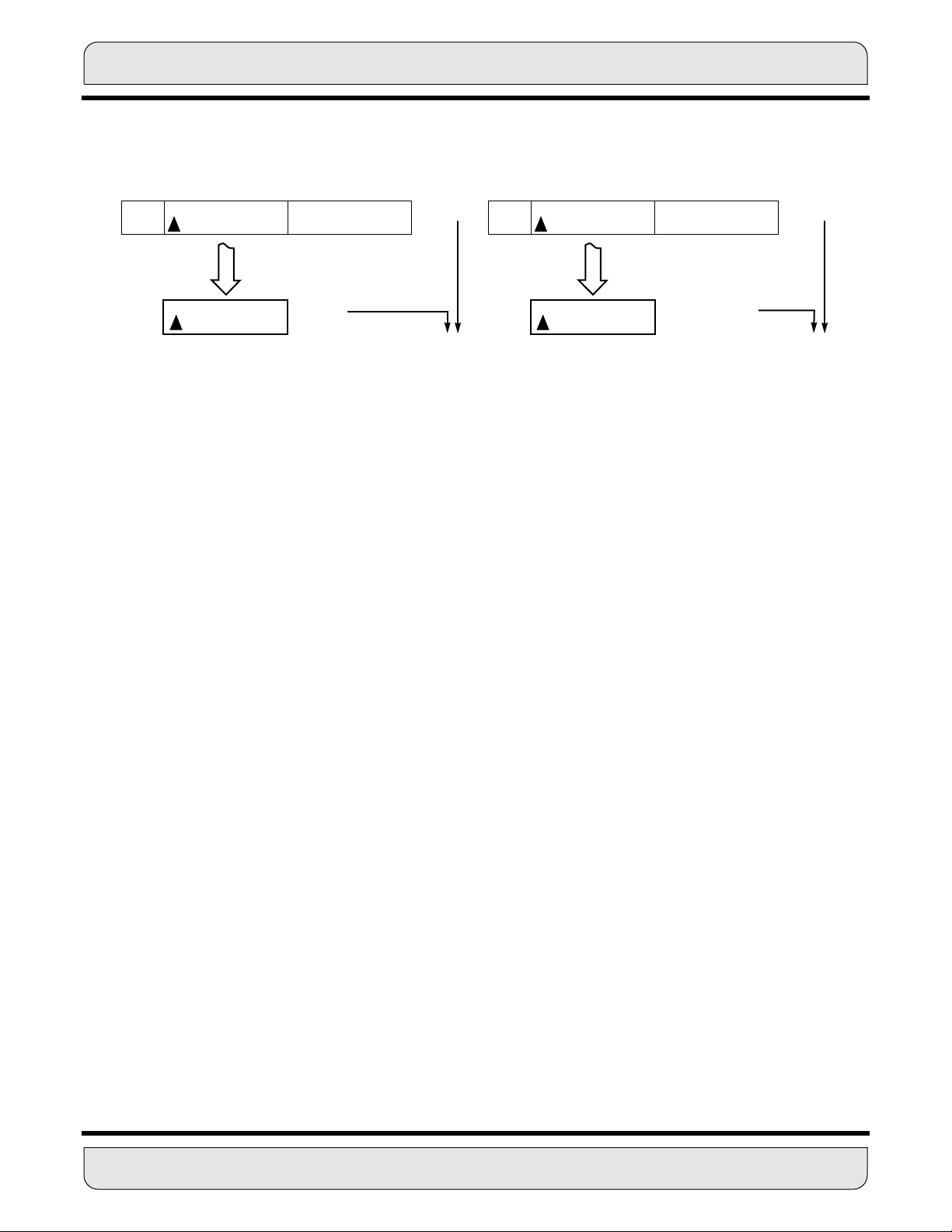
DATA REPRESENTATION AND ROUNDING

WITHOUT LIMITING* WITH LIMITING*

55 0

0 . . . 0 1 0 0 . . . . . . . . . . . 0 0 0 0 . . . . . . . . . . . . 0 0

7 0 23 0 23 0

MOVE A1, X0

1 0 0 . . . . . . . . . . . 0 0 0 1 1 . . . . . . . . . . . 1 1

23 0 23 0

* Limiting automatically occurs when the 56 - bit operands A or B (not A2, A1, A0, B2, B1, or B0) are read. The contents

of A or B are NOT changed.

X0 = -1.0 X0 = +0.9999999

A = +1.0

|ERROR| = 2.0

55 0

0. . . 0 1 0 0 . . . . . . . . . . . 0 0 0 0 . . . . . . . . . . . . 0 0

7 0 23 0 23 0

MOVE A, X0

|ERROR| = .0000001

A = +1.0

Figure 3-5 Saturation Arithmetic

bined to form one 48-bit data limiter for long-word operands. For example, if the source operand were 01.100 (+ 1.5 decimal) and the destination reg-

ister were only four bits, the destination register would contain 1.100 (- 1.5 decimal) after the transfer, assuming signed fractional arithmetic. This is clearly in error as overflow has occurred. To minimize the error due to overflow, it is preferable to write the maximum (“limited”) value the destination can assume. In the example, the limited value would be

0.111 (+ 0.875 decimal), which is clearly closer to + 1.5 than - 1.5 and therefore introduces less error.

Figure 3-5 shows the effects of saturation arithmetic on a move from register A1 to register X0. The instruction “MOVE A1,X0” causes a move without limiting, and the instruction “MOVE A,X0” causes a move of the same 24 bits with limiting. The error without limiting is 2.0; whereas, it is 0.0000001 with limiting. Table 3-1 shows a more complete set of limiting situations.

3.2.5.2 Scaling

The data shifters can shift data one bit to the left or one bit to the right, or pass the data unshifted. Each data shifter has a 24-bit output with overflow indication and is controlled by the scaling mode bits in the status register. These shifters permit dynamic scaling of fixed-point data without modifying the program code. For example, this permits block floating-point algorithms such as fast Fourier transforms to be implemented in a regular fashion.

3.3 DATA REPRESENTATION AND ROUNDING

The DSP56K uses a fractional data representation for all Data ALU operations. Figure 3-

3 - 10 DATA ARITHMETIC LOGIC UNIT

MOTOROLA

DATA REPRESENTATION AND ROUNDING

Table 3-1 Limited Data Values

Destination

Memory Reference

X and Y

L (X:Y)

Source

Operand

X:A X:B

Y:A Y:B

X:A Y:A X:A Y:B X:B Y:A X:B Y:B L:AB L:BA

L:A L:B

Accumulator

Sign

Limited Value (Hexadecimal) Type of

XDB YDB

7FFFFF

800000

— —

7FFFFF

800000

7FFFFF

800000

7FFFFF

800000

7FFFFF

800000

7FFFFF

800000

7FFFFF

800000

7FFFFF

800000

7FFFFF

800000

FFFFFF

000000

— —

Access

One 24 bit

Two 24 bit

One 48 bit

7 shows the bit weighting of words, long words, and accumulator operands for this representation. The decimal points are all aligned and are left justified.

Data must be converted to a fractional number by scaling before being used by the DSP or the user will have to be very careful in how the DSP manipulates the data. Moving $3F to a 24-bit Data ALU register does not result in the contents being $00003F as might be expected. Assuming numbers are fractional, the DSP left justifies rather than right justifies. As a result, storing $3F in a 24-bit register results in the contents being $3F0000. The simplest example of scaling is to convert all integer numbers to fractional numbers by shifting the decimal 24 places to the left (see Figure 3-6). Thus, the data has not changed; only the position of the decimal has moved.

S3F.

S.3F

S = SIGN BIT

3F = HEXADECIMAL DATA TO BE CONVERTED

Figure 3-6 Integer-to-Fractional Data Conversion

For words and long words, the most negative number that can be represented is -1 whose internal representation is $800000 and $800000000000, respectively. The most positive word is $7FFFFF or 1 - 2

-23

and the most positive long word is $7FFFFFFFFFFF

MOTOROLA DATA ARITHMETIC LOGIC UNIT 3 - 11

DATA REPRESENTATION AND ROUNDING

or 1 - 2

-47

. These limitations apply to all data stored in memory and to data stored in the Data ALU input buffer registers. The extension registers associated with the accumulators allow word growth so that the most positive number that can be used is approximately 256 and the most negative number is approximately -256. When the accumulator extension registers are in use, the data contained in the accumulators cannot be stored exactly in memory or other registers. In these cases, the data must be limited to the most positive or most negative number consistent with the size of the destination and the sign of the accumulator (the most significant bit (MSB) of the extension register).

To maintain alignment of the binary point when a word operand is written to accumulator A or B, the operand is written to the most significant accumulator register (A1 or B1), and its MSB is automatically sign extended through the accumulator extension register. The least significant accumulator register is automatically cleared. When a long-word operand is written to an accumulator, the least significant word of the operand is written to the least significant accumulator register A0 or B0 and the most significant word is written to

DATA ALU

–2

–23

WORD OPERAND

X1, X0 Y1, Y0 A1, A0 B1, B0

LONG - WORD OPERAND

X1:X0 = X Y1:Y0 = Y A1:A0 = A10 B1:B0 = B10

ACCUMULATOR A OR B

Figure 3-7 Bit Weighting and Alignment of Operands

–2

–24

–2

A2, B2 A1, B1 A0, B0

SIGN EXTENSION OPERAND ZERO

–24

–47

3 - 12 DATA ARITHMETIC LOGIC UNIT

MOTOROLA

DATA REPRESENTATION AND ROUNDING

A1 or B1(see Figure 3-8).

TWOS COMPLEMENT INTEGER

N BITS

(N–1)

–2

•

TO [+2

(N–1)

–1]

TWOS COMPLEMENT FRACTIONAL

FRACTIONAL = INTEGER EXCEPT FOR X AND

•

N BITS

–1 TO [+1–2

–(N–1)

]

Figure 3-8 Integer/Fractional Number Comparison

A comparison between integer and fractional number representation is shown in Figure

. The number representation for integers is between ± 2

3-8

(N-1)

; whereas, the fractional representation is limited to numbers between ± 1. To convert from an integer to a fractional number, the integer must be multiplied by a scaling factor so the result will always be between ± 1. The representation of integer and fractional numbers is the same if the numbers are added or subtracted but is different if the numbers are multiplied or divided. An example of two numbers multiplied together is given in Figure 3-9. The key difference is that the extra bit in the integer multiplication is used as a duplicate sign bit and as the least significant bit (LSB) in the fractional multiplication. The advantages of fractional data representation are as follows:

• The MSP (left half) has the same format as the input data.

• The LSP (right half) can be rounded into the MSP without shifting or updating the

exponent.

• A significant bit is not lost through sign extension.

• Conversion to floating-point representation is easier because the industry-standard

floating-point formats use fractional mantissas.

• Coefficients for most digital filters are derived as fractions by the high-level language

programs used in digital-filter design packages, which implies that the results can be used without the extensive data conversions that other formats require.

Should integer arithmetic be required in an application, shifting a one or zero, depending on the sign, into the MSB converts a fraction to an integer.

The Data ALU MAC performs rounding of the accumulator register to single precision if requested in the instruction (the A1 or B1 register is rounded according to the contents of the A0 or B0 register). The rounding method is called round-to-nearest (even) number, or convergent rounding. The usual rounding method rounds up any value above one-half

MOTOROLA DATA ARITHMETIC LOGIC UNIT 3 - 13

DATA REPRESENTATION AND ROUNDING

SIGNED MULTIPLICATION N x N - 2N – 1 BITS

INTEGER FRACTIONAL

S S

SIGNED MULTIPLIER

S MSP LSP •

2N — 1 PRODUCT

SIGN EXTENSION

2N BITS

S S

SIGNED MULTIPLIER

S• MSP LSP

2N — 1 PRODUCT

2N BITS

ZERO FILL

Figure 3-9 Integer/Fractional Multiplication Comparison

and rounds down any value below one-half. The question arises as to which way onehalf should be rounded. If it is always rounded one way, the results will eventually be biased in that direction. Convergent rounding solves the problem by rounding down if the number is odd (LSB=0) and rounding up if the number is even (LSB=1). Figure 3-10 shows the four cases for rounding a number in the A1 (or B1) register. If scaling is set in the status register, the resulting number will be rounded as it is put on the data bus. However, the contents of the register are not scaled.

3 - 14 DATA ARITHMETIC LOGIC UNIT

MOTOROLA

DATA REPRESENTATION AND ROUNDING

CASE I: IF A0 < $800000 (1/2), THEN ROUND DOWN (ADD NOTHING)

BEFORE ROUNDING

A2 A1 A0

XX . .XX XXX . . .XXX0100 011XXX . . . . XXX

55 48 47 24 23 0

CASE II: IF A0 > $800000 (1/2), THEN ROUND UP (ADD 1 TO A1) BEFORE ROUNDING

A2 A1 A0

XX . .XX XXX . . .XXX0100 1110XX . . . . XXX

55 48 47 24 23 0

CASE III: IF A0 = $800000 (1/2), AND THE LSB OF A1 = 0,THEN ROUND DOWN (ADD NOTHING)

BEFORE ROUNDING

A2 A1 A0

XX . .XX XXX . . . XXX0100 10000 . . . . . . 000

55 48 47 24 23 0

AFTER ROUNDING

A2 A1 A0*

XX . . XX XXX . . . XXX0100 000 . . . . . . . . 000

55 48 47 24 23 0

AFTER ROUNDING

A2 A1 A0*

XX . .XX XXX . . . XXX0101 000 . . . . . . . . 000

55 48 47 24 23 0

AFTER ROUNDING

A2 A1 A0*

XX . .XX XXX . . . XXX0100 000 . . . . . . . . 000

55 48 47 24 23 0

CASE IV: IF A0 = $800000 (1/2), AND THE LSB = 1, THEN ROUND UP (ADD 1 TO A1)

BEFORE ROUNDING

A2 A1 A0

XX . .XX XXX . . .XXX0101 10000 . . . . . . 000

55 48 47 24 23 0

*A0 is always clear; performed during RND, MPYR, MACR

AFTER ROUNDING

A2 A1 A0*

XX . .XX XXX . . .XXX0110 000 . . . . . . . . 000

55 48 47 24 23 0

Figure 3-10 Convergent Rounding

MOTOROLA DATA ARITHMETIC LOGIC UNIT 3 - 15

DOUBLE PRECISION MULTIPLY MODE

3.4 DOUBLE PRECISION MULTIPLY MODE

The Data ALU double precision multiply operation multiplies two 48-bit operands with a 96-bit result. The processor enters the dedicated Double Precision Multiply Mode when the user sets bit 14 (DM) of the Status Register (bit 6 of the MR register). The mode is disabled by clearing the DM bit. For information on the DM bit, see Section 5.4.2.13 Double Precision Multiply Mode (Bit 14).

CAUTION:

While in the Double Precision Multiply Mode, only the double precision m ultiply algorithms shown in Figure 3-11, Figure 3-12, and Figure 3-13 may be executed by the Data ALU; any other Data ALU operation will give indeterminate results.

Figure 3-11 shows the full double precision multiply algorithm. To allow for pipeline delay, the ANDI instruction should not be immediately followed by a Data ALU instruction. For example, the ORI instruction sets the DM mode bit, but, due to the instruction execution pipeline, the Data ALU enters the Double Precision Multiply mode only after

Y:X:

MSP2

LSP2

DP2 DP0

MSP1

LSP1

DP3 DP1

DP3_DP2_DP1_DP0 = MSP1_LSP1 x MSP2_LSP2

ori #$40,mr ;enter mode move x:(r1)+,x0 y:(r5)+,y0 ;load operands mpy y0,x0,a x:(r1)+,x1 y:(r5)+,y1 ;LSP*LSP➞a mac x1,y0,a a0,y:(r0) ;shifted(a)+

; MSP*LSP➞a

mac x0,y1,a ;a+LSP*MSP➞a

mac y1,x1,a a0,x:(r0)+ ;shifted(a)+

; MSP*MSP➞a move a,l:(r0)+ andi #$bf,mr ;exit mode non-Data ALU operation ;pipeline delay

Figure 3-11 Full Double Precision Multiply Algorithm

3 - 16 DATA ARITHMETIC LOGIC UNIT

MOTOROLA

DOUBLE PRECISION MULTIPLY MODE

one instruction cycle. The ANDI instruction clears the DM mode bit, but, due to the instruction execution pipeline, the Data ALU leaves the mode after one instruction cycle.

The double precision multiply algorithm uses the Y0 register at all stages. If the use of the Data ALU is required in an interrupt service routine, Y0 should be saved together with other Data ALU registers to be used, and should be restored before leaving the interrupt routine.

If just single precision times double precision multiply is desired, two of the multiply operations may be deleted and replaced by suitable initialization and clearing of the accumulator and Y0. Figure 3-12 shows the single precision times double precision algorithm.

Y:X:

SPMSP1

LSP1

DP2DP3

DP1

DP3_DP2_DP1 = MSP1_LSP1 x SP

clr a #0,y0 ;clear a and y0 ori #$40,mr ;enter DP mode move x:(r1)+,x0 y:(r5)+,y1 ;load LSP1 and SP mac x0,y1,a x:(r1)+,x1 ;LSP1*SP➞a,

;load MSP1

mac y1,x1,a a0,x:(r0)+ ;shifted(a)+

; SP*MSP1➞a,

;save DP1 move a,l:(r0)+ ;save DP3_DP2 andi #$bf,mr ;exit DP mode non-Data ALU operation ;pipeline delay

Figure 3-12 Single × Double Multiply Algorithm

Figure 3-13 shows a single precision times double precision multiply-accumulate algorithm. First, the least significant parts of the double precision values are multiplied by the single precision values and accumulated in the “Double Precision Multiply” mode. Then the DM bit is cleared and the least significant part of the result is saved to memory. The most significant parts of the double precision values are then multiplied by the single pre-

MOTOROLA DATA ARITHMETIC LOGIC UNIT 3 - 17

DOUBLE PRECISION MULTIPLY MODE

cision values and accumulated using regular MAC instructions. Note that the maximum number of single times double MAC operations in this algorithm are limited to 255 since overflow may occur (the A2 register is just eight bits long). If a longer sequence is required, it should be split into sub-sequences each with no more than 255 MAC operations.

Y:X:

SPiMSPi

DP3_DP2_DP1 =

move #N-1,m5 clr a #0,y0 ;clear a and y0 ori #$40,mr ;enter DP mode move x:(r1)+,x0 y:(r5)+,y1 ;load LSPi and SPi rep #N ;0<N<256 mac x0,y1,a x:(r1)+,x0 y:(r5)+,y1 ;LSPi*SPi➞a andi #$bf,mr ;exit DP mode move a0,x:(r0)+ ;save DP1 move a1,y0 move a2,a move y0,a0 ;a2:a1➞a1:a0 rep #N mac x0,y1,a x:(r1)+,x0 y:(r5)+,y1 ;load MSPi and SPi move a,l:(r0)+ ;save DP3_DP2

LSPi

DP3 DP1

DP2

∑ MSPi_LSPi x SPi

Figure 3-13 Single × Double Multiply-Accumulate Algorithm

3 - 18 DATA ARITHMETIC LOGIC UNIT MOTOROLA

DATA ALU PROGRAMMING MODEL

3.5 DATA ALU PROGRAMMING MODEL

The Data ALU features 24-bit input/output data registers that can be concatenated to accommodate 48-bit data and two 56-bit accumulators, which are segmented into three 24bit pieces that can be transferred over the buses. Figure 3-14 illustrates how the registers in the programming model are grouped.

DATA ALU

INPUT REGISTERS

X Y

47 0

23 0 23 0

A2 A1 A0

23 8 7 0 23 0 23 0

*Read as sign extension bits, written as don’t care.

DATA ALU

ACCUMULATOR REGISTERS

55 055 0

23 8 7 0 23 0 23 0

47 0

Y1 Y0

23 0 23 0

B1 B0

Figure 3-14 DSP56K Programming Model

3.6 DATA ALU SUMMARY

The Data ALU performs arithmetic operations involving multiply and accumulate operations. It executes all instructions in one machine cycle and is not pipelined. The two 24-bit numbers being multiplied can come from the X registers (X0 or X1) or Y registers (Y0 or Y1). After multiplication, they are added (or subtracted) with one of the 56-bit accumulators and can be convergently rounded to 24 bits. The convergent-rounding forcing function detects the $800000 condition in the LSP and makes the correction as necessary. The final result is then stored in one of the accumulators as a valid 56-bit number. The condition code bits are set based on the rounded output of the logic unit.

MOTOROLA DATA ARITHMETIC LOGIC UNIT 3 - 19

DATA ALU SUMMARY

3 - 20 DATA ARITHMETIC LOGIC UNIT MOTOROLA

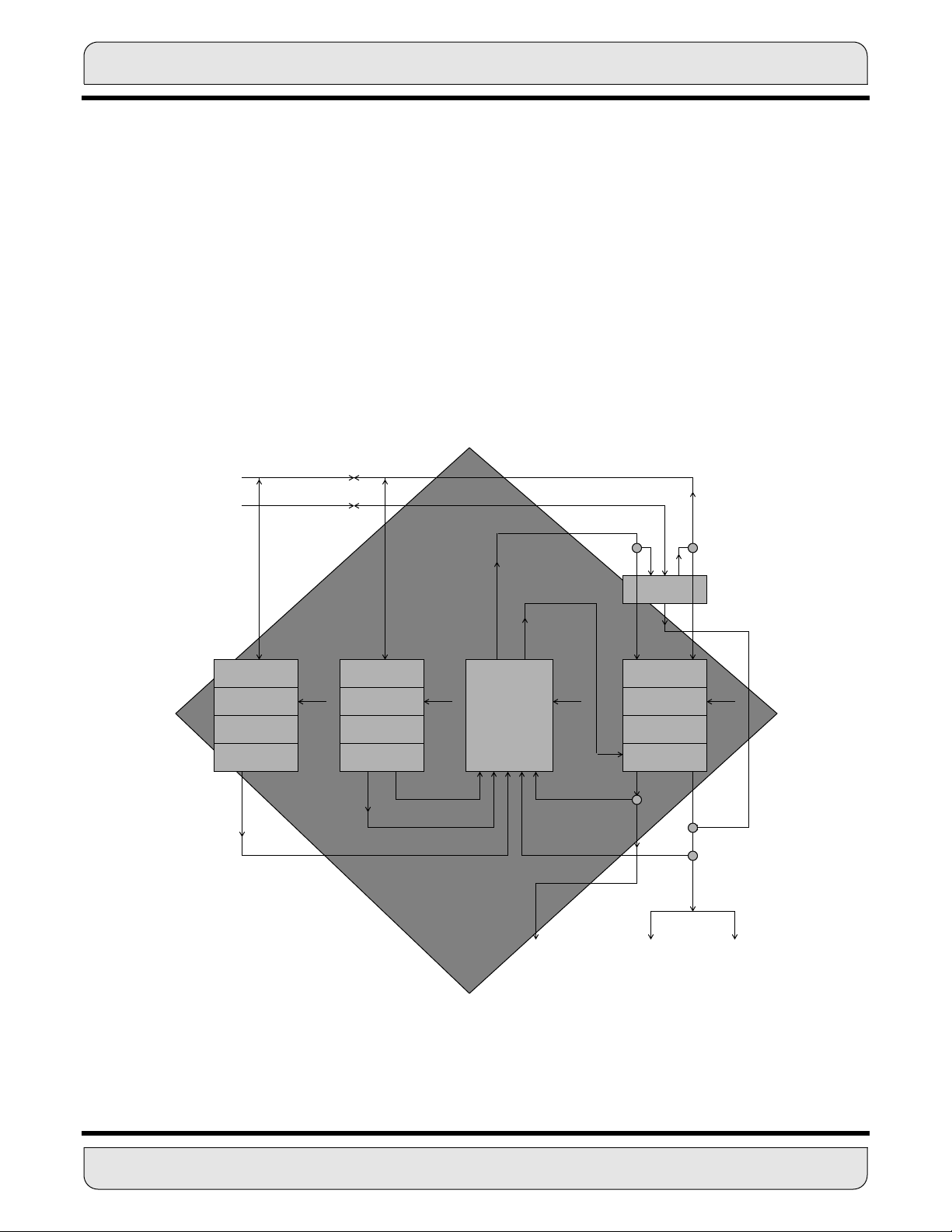
SECTION 4

ADDRESS GENERATION UNIT

MOTOROLA ADDRESS GENERATION UNIT 4 - 1

SECTION CONTENTS

SECTION 4.1 ADDRESS GENERATION UNIT AND ADDRESSING MODES ....3

SECTION 4.2 AGU ARCHITECTURE ..................................................................3

4.2.1 Address Register Files (Rn) ................................................................3

4.2.2 Offset Register Files (Nn) ....................................................................4

4.2.3 Modifier Register Files (Mn) ................................................................5

4.2.4 Address ALU .......................................................................................5

4.2.5 Address Output Multiplexers ...............................................................6

SECTION 4.3 PROGRAMMING MODEL .............................................................6

4.3.1 Address Register Files (R0 - R3 and R4 - R7) ....................................7

4.3.2 Offset Register Files (N0 - N3 and N4 - N7) .......................................7

4.3.3 Modifier Register Files (M0 - M3 and M4 - M7) ...................................8

SECTION 4.4 ADDRESSING ...............................................................................8

4.4.1 Address Register Indirect Modes ........................................................9

4.4.1.1 No Update ...................................................................................9

4.4.1.2 Postincrement By 1 .....................................................................9

4.4.1.3 Postdecrement By 1 ...................................................................9

4.4.1.4 Postincrement By Offset Nn .......................................................10

4.4.1.5 Postdecrement By Offset Nn ......................................................11

4.4.1.6 Indexed By Offset Nn ..................................................................12

4.4.1.7 Predecrement By 1 .....................................................................13

4.4.2 Address Modifier Arithmetic Types .....................................................14

4.4.2.1 Linear Modifier (Mn=$FFFF) .......................................................16

4.4.2.2 Modulo Modifier ..........................................................................18

4.4.2.3 Reverse-Carry Modifier (Mn=$0000) ..........................................22

4.4.2.4 Address-Modifier-Type Encoding Summary ...............................25

4 - 2 ADDRESS GENERATION UNIT

MOTOROLA

ADDRESS GENERATION UNIT AND ADDRESSING MODES

4.1 ADDRESS GENERATION UNIT AND ADDRESSING MODES

This section contains three major subsections. The first subsection describes the hardware architecture of the address generation unit (AGU), the second subsection describes the programming model, and the third subsection describes the addressing modes, explaining how the Rn, Nn, and Mn registers work together to form a memory address.

4.2 AGU ARCHITECTURE

The AGU is shown in the DSP56K block diagram in Figure 4-1. It uses integer arithmetic to perform the effective address calculations necessary to address data operands in memory, and contains the registers used to generate the addresses. It implements linear, modulo, and reverse-carry arithmetic, and operates in parallel with other chip resources to minimize address-generation overhead.

The AGU is divided into two identical halves, each of which has an address arithmetic logic unit (ALU) and four sets of three registers (see Figure 4-2). They are the address registers (R0 - R3 and R4 - R7), offset registers (N0 - N3 and N4 - N7), and the modifier registers (M0 - M3 and M4 - M7). The eight Rn, Nn, and Mn registers are treated as register triplets — e.g., only N2 and M2 can be used to update R2. The eight triplets are R0:N0:M0, R1:N1:M1, R2:N2:M2, R3:N3:M3, R4:N4:M4, R5:N5:M5, R6:N6:M6, and R7:N7:M7.

The two arithmetic units can generate two 16-bit addresses every instruction cycle — one for any two of the XAB, YAB, or PAB. The AGU can directly address 65,536 locations on the XAB, 65,536 locations on the YAB, and 65,536 locations on the PAB. The two independent address ALUs work with the two data memories to feed the data ALU two operands in a single cycle. Each operand may be addressed by an Rn, Nn, and Mn triplet.

4.2.1 Address Register Files (Rn)

Each of the two address register files (see Figure 4-2) consists of four 16-bit registers. The two files contain address registers R0 - R3 and R4 - R7, which usually contain addresses used as pointers to memory. Each register may be read or written by the global data bus (GDB). When read by the GDB, 16-bit registers are written into the two least significant bytes of the GBD, and the most significant byte is set to zero. When written from the GBD, only the two least significant bytes are written, and the most significant byte is truncated. Each address register can be used as input to its associated address ALU for a register update calculation. Each register can also be written by the output of its respective address ALU. One Rn register from the low address ALU and one Rn register from the high address ALU can be accessed in a single instruction.

MOTOROLA ADDRESS GENERATION UNIT 4 - 3

PERIPHERAL

PINS

PERIPHERAL

MODULES

24-Bit 56K

Module

ADDRESS

GENERATION

UNIT

AGU ARCHITECTURE

PROGRAM

RAM/ROM

EXP ANSION

X MEMORY

RAM/ROM

EXPANSION

YAB XAB PAB

Y MEMORY

RAM/ROM

EXPANSION

AREA

EXTERNAL ADDRESS

BUS

SWITCH

ADDRESS

INTERNAL

DATA

BUS

SWITCH

PLL

CLOCK

GENERAT OR

PROGRAM

INTERRUPT

CONTROLLER

PROGRAM

DECODE

CONTROLLER

Program Control Unit

MODC/NMI MODB/IRQB MODA/IRQA

RESET

PROGRAM

ADDRESS

GENERA TOR

YDB XDB PDB GDB

DATA ALU

24X24+56→56-BIT MAC

TWO 56-BIT ACCUMULATORS

BUS

CONTROL

EXTERNAL

DATA BUS

SWITCH

OnCE™

16 BITS 24 BITS

PORT A

CONTROL

DATA

Figure 4-1 DSP56K Block Diagram

4.2.2 Offset Register Files (Nn)

Each of two offset register files shown in Figure 4-2 consists of four 16-bit registers. The two files contain offset registers N0 - N3 and N4 - N7, which contain either data or offset values used to update address pointers. Each offset register can be read or written by the

4 - 4 ADDRESS GENERATION UNIT

MOTOROLA

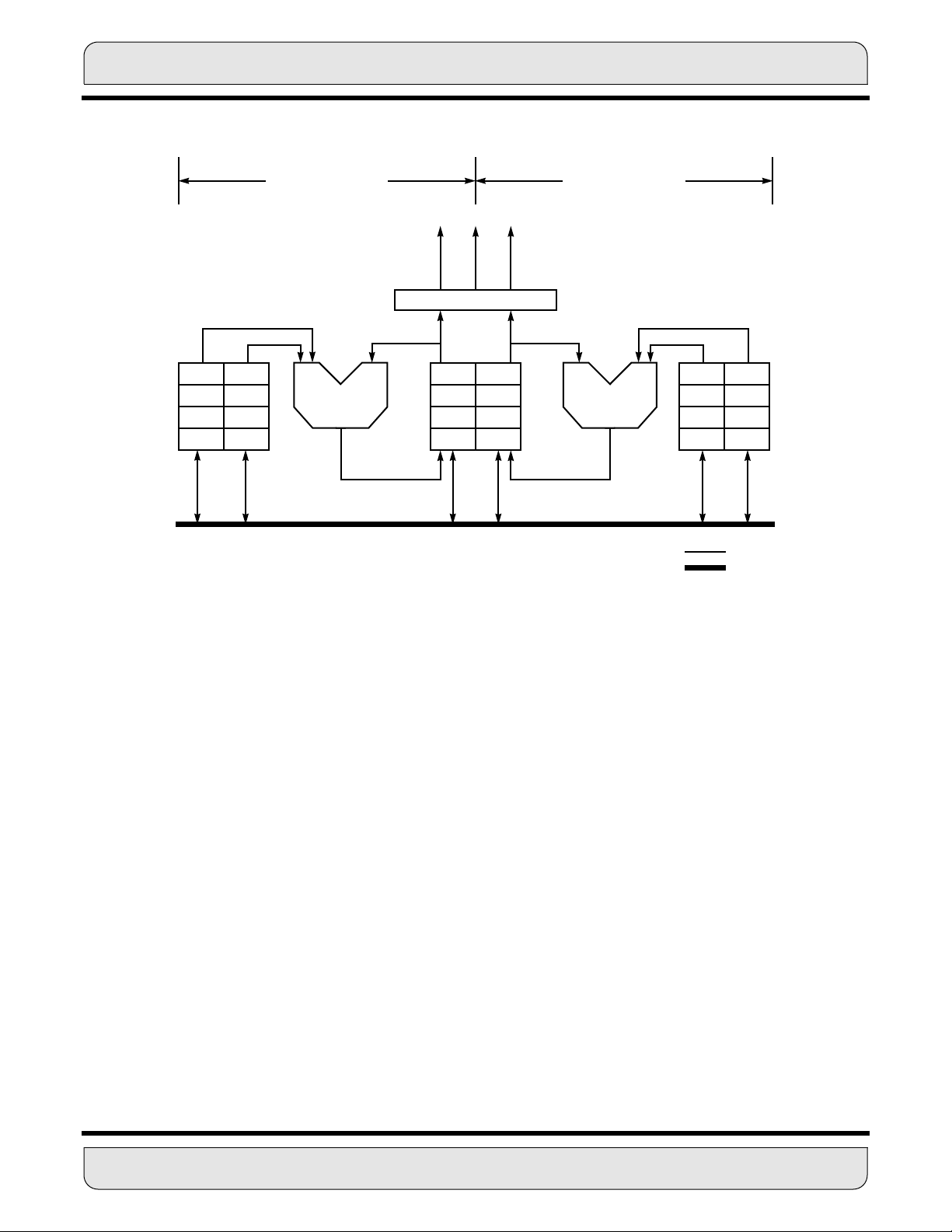
AGU ARCHITECTURE

LOW ADDRESS ALU HIGH ADDRESS ALU

XAB YAB PAB

TRIPLE MULTIPLEXER

N0 N1

M1 M2

N2 N3 M3

ADDRESS

ALU

GLOBAL DATA BUS

R0 R1

R5 R6

R2 R3 R7

ADDRESS

ALU

M4 M5

N5 N6

M6 M7 N7

16 bits 24 bits

Figure 4-2 AGU Block Diagram

GDB. When read by the GDB, the contents of a register are placed in the two least significant bytes, and the most significant byte on the GDB is zero extended. When a register is written, only the least significant 16 bits of the GDB are used; the upper portion is truncated.

4.2.3 Modifier Register Files (Mn)

Each of the two modifier register files shown in Figure 4-2 consists of four 16-bit registers. The two files contain modifier registers M0 - M3 and M4 - M7, which specify the type of arithmetic used during address register update calculations or contain data. Each modifier register can be read or written by the GDB. When read by the GDB, the contents of a register are placed in the two least significant bytes, and the most significant byte on the GDB is zero extended. When a register is written, only the least significant 16 bits of the GDB are used; the upper portion is truncated. Each modifier register is preset to $FFFF during a processor reset.

4.2.4 Address ALU

The two address ALUs are identical (see Figure 4-2) in that each contains a 16-bit full adder (called an offset adder), which can add 1) plus one, 2) minus one, 3) the contents of the respective offset register N, or 4) the twos complement of N to the contents of the

MOTOROLA ADDRESS GENERATION UNIT 4 - 5

selected address register. A second full adder (called a modulo adder) adds the summed result of the first full adder to a modulo value, M or minus M, where M-1 is stored in the respective modifier register. A third full adder (called a reverse-carry adder) can add 1) plus one, 2) minus one, 3) the offset N (stored in the respective offset register), or 4) minus N to the selected address register with the carry propagating in the reverse direction — i.e., from the most significant bit (MSB) to the least significant bit (LSB). The offset adder and the reverse-carry adder are in parallel and share common inputs. The only difference between them is that the carry propagates in opposite directions. Test logic determines which of the three summed results of the full adders is output.

Each address ALU can update one address register, Rn, from its respective address register file during one instruction cycle and can perform linear, reverse-carry, and modulo arithmetic. The contents of the selected modifier register specify the type of arithmetic to be used in an address register update calculation. The modifier value is decoded in the address ALU.

PROGRAMMING MODEL

The output of the offset adder gives the result of linear arithmetic (e.g., Rn and is selected as the modulo arithmetic unit output for linear arithmetic addressing modifiers. The reverse-carry adder performs the required operation for reverse-carry arithmetic and its result is selected as the address ALU output for reverse-carry addressing modifiers. Reverse-carry arithmetic is useful for 2 addressing. For modulo arithmetic, the modulo arithmetic unit will perform the function (Rn Nn. If the modulo operation requires wraparound for modulo arithmetic, the summed output of the modulo adder gives the correct updated address register value; if wraparound is not necessary, the output of the offset adder gives the correct result.

4.2.5 Address Output Multiplexers

The address output multiplexers (see Figure 4-2) select the source for the XAB, YAB, and PAB. These multiplexers allow the XAB, YAB, or PAB outputs to originate from R0 - R3 or R4 - R7.

4.3 PROGRAMMING MODEL

The programmer’s view of the AGU is eight sets of three registers (see Figure 4-3). These registers can act as temporary data registers and indirect memory pointers. Automatic updating is available when using address register indirect addressing. The Mn registers can be programmed for linear addressing, modulo addressing, and bit-reverse addressing.

N) modulo M, where N can be one, minus one, or the contents of the offset register

-point fast Fourier transform (FFT)

1; Rn

4 - 6 ADDRESS GENERATION UNIT

MOTOROLA

PROGRAMMING MODEL

23 16 15 0

* * * * * * * *

ADDRESS REGISTERS

* Written as don’t care; read as zero

R7 R6 R5 R4 R3 R2 R1 R0

23 16 15 0

* * * * * * * *

OFFSET REGISTERS

N7 N6

N5 N4 N3 N2 N1 N0

23 16 15 0

* * * * * * * *

MODIFIER REGISTERS

M7 M6 M5 M4 M3 M2 M1 M0

UPPER FILE

LOWER FILE

Figure 4-3 AGU Programming Model

4.3.1 Address Register Files (R0 - R3 and R4 - R7)

The eight 16-bit address registers, R0 - R7, can contain addresses or general-purpose data. The 16-bit address in a selected address register is used in the calculation of the effective address of an operand. When supporting parallel X and Y data memory moves, the address registers must be thought of as two separate files, R0 - R3 and R4 - R7. The contents of an Rn may point directly to data or may be offset. In addition, Rn can be preupdated or post-updated according to the addressing mode selected. If an Rn is updated, modifier registers, Mn, are always used to specify the type of update arithmetic. Offset registers, Nn, are used for the update-by-offset addressing modes. The address register modification is performed by one of the two modulo arithmetic units. Most addressing modes modify the selected address register in a read-modify-write fashion; the address register is read, its contents are modified by the associated modulo arithmetic unit, and the register is written with the appropriate output of the modulo arithmetic unit. The form of address register modification performed by the modulo arithmetic unit is controlled by the contents of the offset and modifier registers discussed in the following paragraphs. Address registers are not affected by a processor reset.

4.3.2 Offset Register Files (N0

N3 and N4

N7)

The eight 16-bit offset registers, N0 - N7, can contain offset values used to increment/decrement address registers in address register update calculations or can be used for 16-bit general-purpose storage. For example, the contents of an offset register can be used to step through a table at some rate (e.g., five locations per step for waveform generation), or the contents can specify the offset into a table or the base of the table for indexed addressing. Each address register, Rn, has its own offset register, Nn, associated with it.

MOTOROLA ADDRESS GENERATION UNIT 4 - 7

ADDRESSING

Table 4-1 Address Register Indirect Summary

Address Register Indirect

No Update No XXXX X (Rn) Postincrement by 1 Yes XXXX X (Rn)+ Postdecrement by 1 Yes XXXX X (Rn)– Postincrement by Offset Nn Yes XXXX X (Rn)+Nn

NOTE:

S = System Stack Reference C = Program Control Unit Register Reference D = Data ALU Register Reference A = Address ALU Register Reference P = Program Memory Reference X = X Memory Reference Y = Y Memory Reference L = L Memory Reference

XY = XY Memory Reference

Uses Mn

Modiﬁer

SCDAPXYLXY

Operand Reference

Assembler

Syntax

Offset registers are not affected by a processor reset.

4.3.3 Modifier Register Files (M0

M3 and M4 - M7)

The eight 16-bit modifier registers, M0 - M7, define the type of address arithmetic to be performed for addressing mode calculations, or they can be used for general-purpose storage. The address ALU supports linear, modulo, and reverse-carry arithmetic types for all address register indirect addressing modes. For modulo arithmetic, the contents of Mn also specify the modulus. Each address register, Rn, has its own modifier register, Mn, associated with it. Each modifier register is set to $FFFF on processor reset, which specifies linear arithmetic as the default type for address register update calculations.

4.4 ADDRESSING

The DSP56K provides three different addressing modes: register direct, address register indirect, and special. Since the register direct and special addressing modes do not necessarily use the AGU registers, they are described in SECTION 6 - INSTRUCTION SET INTRODUCTION. The address register indirect addressing modes use the registers in

4 - 8 ADDRESS GENERATION UNIT

MOTOROLA

ADDRESSING

the AGU and are described in the following paragraphs.

4.4.1 Address Register Indirect Modes

When an address register is used to point to a memory location, the addressing mode is called “address register indirect” (see Table 4-1). The term indirect is used because the register contents are not the operand itself, but rather the address of the operand. These addressing modes specify that an operand is in memory and specify the effective address of that operand.

A portion of the data bus movement field in the instruction specifies the memory space to be referenced. The contents of specific AGU registers that determine the effective address are modified by arithmetic operations performed in the AGU. The type of address arithmetic used is specified by the address modifier register, Mn. The offset register, Nn, is only used when the update specifies an offset.

Not all possible combinations are available, such as + (Rn). The 24-bit instruction word size is not large enough to allow a completely orthogonal instruction set for all instructions used by the DSP.

An example and description of each mode is given in the following paragraphs. SECTION 6 - INSTRUCTION SET INTRODUCTION and APPENDIX A - INSTRUCTION SET DETAILS give a complete description of the instruction syntax used in these examples. In particular, XY: memory references refer to instructions in which an operand in X memory and an operand in Y memory are referenced in the same instruction.

4.4.1.1 No Update

The address of the operand is in the address register, Rn (see Table 4-1). The contents of the Rn register are unchanged by executing the instruction. Figure 4-4 shows a MOVE instruction using address register indirect addressing with no update. This mode can be used for making XY: memory references. This mode does not use Nn or Mn registers.

4.4.1.2 Postincrement By 1

The address of the operand is in the address register, Rn (see Table 4-1 and Figure 4-5). After the operand address is used, it is incremented by 1 and stored in the same address register. This mode can be used for making XY: memory references and for modifying the contents of Rn without an associated data move.

4.4.1.3 Postdecrement By 1

The address of the operand is in the address register, Rn (see Table 4-1 and Figure 4-6). After the operand address is used, it is decremented by 1 and stored in the same address register. This mode can be used for making XY: memory references and for

MOTOROLA ADDRESS GENERATION UNIT 4 - 9

EXAMPLE: MOVE A1,X: (R0)

ADDRESSING

BEFORE EXECUTION

A2 A1 A0

55 48 47 24 23 0

0123456789ABCD 7 0 23 0 23 0

X MEMORY

23 0

XXXXXX

$1000 $1000

15 0

$1000

15 0

XXXX

15 0

$FFFF

AFTER EXECUTION

A2 A1 A0

55 48 47 24 23 0

0 123456789ABCD 7 0 23 0 23 0

X MEMORY

23 0

$234567

15 0

$1000

15 0

XXXX

15 0

$FFFF

Assembler Syntax: (Rn) Memory Spaces: P:, X:, Y:, XY:, L: Additional Instruction Execution Time (Clocks): 0 Additional Effective Address Words: 0

Figure 4-4 Address Register Indirect — No Update

modifying the contents of Rn without an associated data move.

4.4.1.4 Postincrement By Offset Nn

The address of the operand is in the address register, Rn (see Table 4-1 and Figure 4-7). After the operand address is used, it is incremented by the contents of the Nn register and stored in the same address register. The contents of the Nn register are unchanged. This mode can be used for making XY: memory references and for modifying the contents of

4 - 10 ADDRESS GENERATION UNIT

MOTOROLA

EXAMPLE: MOVE B0,Y: (R1)+

BEFORE EXECUTION AFTER EXECUTION

ADDRESSING

B2 B1 B0

55 48 47 24 23 0

AF654321FEDCBA

7 0 23 0 23 0

Y MEMORY

23 0

$2501 $2500

XXXXXX XXXXXX

15 0

$2500

15 0

XXXX

15 0

$FFFF

B2 B1 B0

55 48 47 24 23 0

AF654321FEDCBA

7 0 23 0 23 0

Y MEMORY

23 0

$2501 $2500

XXXXXXX

$FEDCBA

15 0

$2501

15 0

XXXX

15 0

$FFFF

Assembler Syntax: (Rn)+ Memory Spaces: P:, X:, Y:, XY:, L: Additional Instruction Execution Time (Clocks): 0 Additional Effective Address Words: 0

Figure 4-5 Address Register Indirect — Postincrement

Rn without an associated data move.

4.4.1.5 Postdecrement By Offset Nn

The address of the operand is in the address register, Rn (see Table 4-1 and Figure 4-8). After the operand address is used, it is decremented by the contents of the Nn register and stored in the same address register. The contents of the Nn register are unchanged. This mode cannot be used for making XY: memory references, but it can be used to mod-

MOTOROLA ADDRESS GENERATION UNIT 4 - 11

EXAMPLE: MOVE Y0,Y: (R3)-

ADDRESSING

BEFORE EXECUTION

Y1 Y0

47 24 23 0

1231 23 4564 56

23 0 23 0

Y MEMORY

23 0

$4735 $4734

XXXXXX XXXXXX

15 0

$4735

15 0

XXXX

15 0

$FFFF

AFTER EXECUTION

47 24 23 0

23 0 23 0

Y1 Y0

12 31 23 4 564 56

Y MEMORY

23 0

$4735

$4734

456456 XXXXXX

15 0

$4734

15 0

XXXX

15 0

$FFFF

Assembler Syntax: (Rn)– Memory Spaces: P:, X:, Y:, XY:, L: Additional Instruction Execution Time (Clocks): 0 Additional Effective Address Words: 0

Figure 4-6 Address Register Indirect — Postdecrement

ify the contents of Rn without an associated data move.

4.4.1.6 Indexed By Offset Nn

The address of the operand is the sum of the contents of the address register, Rn, and the contents of the address offset register, Nn (see Table 4-1 and Figure 4-9). The contents of the Rn and Nn registers are unchanged. This addressing mode, which requires

4 - 12 ADDRESS GENERATION UNIT

MOTOROLA

EXAMPLE: MOVE X1,X: (R2)+N2

ADDRESSING

BEFORE EXECUTION

47 24 23 0

23 0 23 0

X1 X0

A5 B4C6 000001

X MEMORY

23 0

$3204

$3200

XXXXXX

15 0

$3200

15 0

$0004 $0004

15 0

$FFFF

AFTER EXECUTION

X1 X0

47 24 23 0

A5B4C6 000001

23 0 23 0

X MEMORY

23 0

$3204

$3200

XXXXXX

$A5B4 C6

15 0

$3204

15 0

$FFFF

Assembler Syntax: (Rn)+Nn Memory Spaces: P:, X:, Y:, XY:, L: Additional Instruction Execution Time (Clocks): 0 Additional Effective Address Words: 0

Figure 4-7 Address Register Indirect — Postincrement by Offset Nn

an extra instruction cycle, cannot be used for making XY: memory references.

4.4.1.7 Predecrement By 1

The address of the operand is the contents of the address register, Rn, decremented by 1 before the operand address is used (see Table 4-1 and Figure 4-10). The contents of Rn are decremented and stored in the same address register. This addressing mode requires an extra instruction cycle. This mode cannot be used for making XY: memory references, nor can it be used for modifying the contents of Rn without an associated data

MOTOROLA ADDRESS GENERATION UNIT 4 - 13

EXAMPLE: MOVE X:(R4)–N4,A0

ADDRESSING

BEFORE EXECUTION

A2 A1 A0

55 48 47 24 23 0

0 F74105A 3FA6B0 7 0 23 0 23 0

X MEMORY

23 0

$7706

$7703

$505050

XXXXXX

15 0

$7706

15 0

$0003

15 0

$FFFF

AFTER EXECUTION

A2 A1 A0

55 48 47 24 23 0

0F74105A505050 7 0 23 0 23 0

X MEMORY

23 0

$7706

$7703

$505050

XXXXXX

15 0

$7703

15 0

$0003

15 0

$FFFF

Assembler Syntax: (Rn)–Nn Memory Spaces: P:, X:, Y:, L: Additional Instruction Execution Time (Clocks): 0 Additional Effective Address Words: 0

Figure 4-8 Address Register Indirect — Postdecrement by Offset Nn

move.

4.4.2 Address Modifier Arithmetic Types

The address ALU supports linear, modulo, and reverse-carry arithmetic for all address register indirect modes. These arithmetic types easily allow the creation of data structures in memory for FIFOs (queues), delay lines, circular buffers, stacks, and bit-reversed FFT buffers.

4 - 14 ADDRESS GENERATION UNIT

MOTOROLA

EXAMPLE: MOVE Y1,X: (R6+N6)

ADDRESSING

BEFORE EXECUTION

Y1 Y0

47 24 23 0

62100 9BA4C22

23 0 23 0

X MEMORY

23 0

$6004

$6000

XXXXXX

15 0

$6000

15 0

$0004 $0004

15 0

$FFFF

AFTER EXECUTION

Y1 Y0

47 24 23 0

62100 9B A4 C22

23 0 23 0

X MEMORY

23 0

$6004

$6000

$621009

XXXXXX

15 0

$6000

15 0

$FFFF

Assembler Syntax: (Rn+Nn) Memory Spaces: P:, X:, Y:, L: Additional Instruction Execution Time (Clocks): 2 Additional Effective Address Words: 0

Figure 4-9 Address Register Indirect — Indexed by Offset Nn

The contents of the address modifier register, Mn, defines the type of arithmetic to be performed for addressing mode calculations. For modulo arithmetic, the contents of Mn also specifies the modulus, or the size of the memory buffer whose addresses will be referenced. See Table 4-2 for a summary of the address modifiers implemented on the

MOTOROLA ADDRESS GENERATION UNIT 4 - 15

EXAMPLE: MOVE X: –(R5),B1

ADDRESSING

BEFORE EXECUTION

B2 B1 B0

55 48 47 24 23 0

3BB62D04A554C0 7 0 23 0 23 0

X MEMORY

23 0

$3007 $3006

$ABCDEF $123456

15 0

$3007

15 0

XXXX

15 0

$FFFF

AFTER EXECUTION

B2 B1 B0

55 48 47 24 23 0

3B12345 6A554C 0 7 0 23 0 23 0

X MEMORY

23 0

$3007 $3006

$ABCDEF $123456

15 0

$3006

15 0

XXXX

15 0

$FFFF

Assembler Syntax: –Rn Memory Spaces: P:, X:, Y:, L: Additional Instruction Execution Time (Clocks): 2 Additional Effective Address Words: 0

Figure 4-10 Address Register Indirect — Predecrement

DSP56K. The MMMM column indicates the hex value which should be stored in the Mn register.

4.4.2.1 Linear Modifier (Mn=$FFFF)

When the value in the modifier register is $FFFF, address modification is performed using normal 16-bit linear arithmetic (see Table 4-2). A 16-bit offset, Nn, and + 1 or –1 can be used in the address calculations. The range of values can be considered as signed (Nn from –32,768 to + 32,767) or unsigned (Nn from 0 to + 65,535) since there is no arithmetic

4 - 16 ADDRESS GENERATION UNIT

MOTOROLA

ADDRESSING

difference between these two data representations. Addresses are normally considered unsigned, and data is normally considered signed.

4.4.2.2 Modulo Modifier

When the value in the modifier register falls into one of two ranges (Mn=$0001 to $7FFF or Mn= $8001 to $BFFF with the reserved gaps noted in the table), address modification is performed using modulo arithmetic (see Table 4-2).

Modulo arithmetic normally causes the address register value to remain within an address range of size M, whose lower boundary is determined by Rn. The upper boundary is determined by the modulus, or M. The modulus value, in turn, is determined by Mn, the value in the modifier register (see Figure 4-11).

There are certain cases where modulo arithmetic addressing conditions may cause the address register to jump linearly to the same relative address in a different buffer. Other cases firmly restrict the address register to the same buffer, causing the address register to wrap around within the buffer. The range in which the value contained in the modifier register falls determines how the processor will handle modulo addressing.

4.4.2.2.1 Mn=$0001 to $7FFF

In this range, the modulus (M) equals the value in the modifier register (Mn) plus 1. The memory buffer’s lower boundary (base address) value, determined by Rn, must have zeros in the k LSBs, where 2

≥

M, and therefore must be a multiple of 2

. The upper

boundary is the lower boundary plus the modulo size minus one (base address plus M–

1). Since M

) is created where these circular buffers can be located. If M<2k, there will be a space

between sequential circular buffers of (2

2k, once M is chosen, a sequential series of memory blocks (each of length

≤

)–M.

For example, to create a circular buffer of 21 stages, M is 21, and the lower address boundary must have its five LSBs equal to zero (2

≥ 21, thus k ≥ 5). The Mn register is

loaded with the value 20. The lower boundary may be chosen as 0, 32, 64, 96, 128, 160, etc. The upper boundary of the buffer is then the lower boundary plus 21. There will be an unused space of 11 memory locations between the upper address and next usable lower address. The address pointer is not required to start at the lower address boundary or to end on the upper address boundary; it can initially point anywhere within the defined modulo address range. Neither the lower nor the upper boundary of the modulo region is stored; only the size of the modulo region is stored in Mn. The boundaries are determined by the contents of Rn. Assuming the (Rn)+ indirect addressing mode, if the address register pointer increments past the upper boundary of the buffer (base address plus M–1), it will wrap around through the base address (lower boundary). Alternatively, assuming the (Rn)- indirect addressing mode, if the address decrements past the lower boundary

MOTOROLA ADDRESS GENERATION UNIT 4 - 17

ADDRESSING

Table 4-2 Address Modifier Summary

MMMM Addressing Mode Arithmetic

0000 Reverse Carry (Bit Reverse) 0001 Modulo 2 0002 Modulo 3

7FFE Modulo 32767

7FFF Modulo 32768 8000 Reserved 8001 Multiple Wrap-Around Modulo 2 8002 Reserved 8003 Multiple Wrap-Around Modulo 4

: Reserved

8007 Multiple Wrap-Around Modulo 8

: Reserved

800F Multiple Wrap-Around Modulo 2

: Reserved

801F Multiple Wrap-Around Modulo 2

: Reserved

803F Multiple Wrap-Around Modulo 2

: Reserved

807F Multiple Wrap-Around Modulo 2

: Reserved

80FF Multiple Wrap-Around Modulo 2

: Reserved

81FF

: Reserved

83FF

: Reserved

87FF Multiple Wrap-Around Modulo 2

: Reserved

8FFF

: Reserved

9FFF Multiple Wrap-Around Modulo 2

: Reserved

BFFF Multiple Wrap-Around Modulo 2

: Reserved

Multiple Wrap-Around Modulo 2

4 - 18 ADDRESS GENERATION UNIT MOTOROLA

ADDRESSING

UPPER BOUNDARY

ADDRESS POINTER

CIRCULAR

BUFFER

M = MODULUS

LOWER BOUNDARY

Figure 4-11 Circular Buffer

(base address), it will wrap around through the base address plus M–1 (upper boundary). If an offset (Nn) is used in the address calculations, the 16-bit absolute value, |Nn|, must

be less than or equal to M for proper modulo addressing in this range. If Nn>M, the result is data dependent and unpredictable, except for the special case where Nn=P x 2

, a multiple of the block size where P is a positive integer. For this special case, when using the (Rn)+ Nn addressing mode, the pointer, Rn, will jump linearly to the same relative address in a new buffer, which is P blocks forward in memory (see Figure 4-12).

Similarly, for (Rn)–Nn, the pointer will jump P blocks backward in memory. This technique is useful in sequentially processing multiple tables or N-dimensional arrays. The range of values for Nn is –32,768 to + 32,767. The modulo arithmetic unit will automatically wrap around the address pointer by the required amount. This type of address modification is useful for creating circular buffers for FIFOs (queues), delay lines, and sample buffers up to 32,768 words long as well as for decimation, interpolation, and waveform generation. The special case of (Rn)

± Nn mod M with Nn=P x 2

is useful for performing the same algorithm on multiple blocks of data in memory — e.g., parallel infinite impulse response (IIR) filtering.

An example of address register indirect modulo addressing is shown in Figure 4-13. Starting at location 64, a circular buffer of 21 stages is created. The addresses generated are offset by 15 locations. The lower boundary = L x (2

) where 2k ≥ 21; therefore, k=5 and

the lower address boundary must be a multiple of 32. The lower boundary may be chosen

MOTOROLA ADDRESS GENERATION UNIT 4 - 19

ADDRESSING

(Rn) ± Nn MOD M WHERE Nn = 2

(i.e., P = 1)

Figure 4-12 Linear Addressing with a Modulo Modifier

as 0, 32, 64, 96, 128, 160, etc. For this example, L is arbitrarily chosen to be 2, making the lower boundary 64. The upper boundary of the buffer is then 84 (the lower boundary plus 20 (M–1)). The Mn register is loaded with the value 20 (M–1). The offset register is arbitrarily chosen to be 15 (Nn

≤M). The address pointer is not required to start at the lower

address boundary and can begin anywhere within the defined modulo address range — i.e., within the lower boundary + (2

) address region. The address pointer, Rn, is arbitrarily chosen to be 75 in this example. When R2 is post-incremented by the offset by the MOVE instruction, instead of pointing to 90 (as it would in the linear mode) it wraps around to 69. If the address register pointer increments past the upper boundary of the buffer (base address plus M–1), it will wrap around to the base address. If the address decrements past the lower boundary (base address), it will wrap around to the base address plus M–1.

If Rn is outside the valid modulo buffer range and an operation occurs that causes Rn to be updated, the contents of Rn will be updated according to modulo arithmetic rules. For example, a MOVE B0,X:(R0)+ N0 instruction (where R0=6, M0=5, and N0=0) would apparently leave R0 unchanged since N0=0. However, since R0 is above the upper boundary, the AGU calculates R0+ N0–M0–1 for the new contents of R0 and sets R0=0.

4 - 20 ADDRESS GENERATION UNIT MOTOROLA

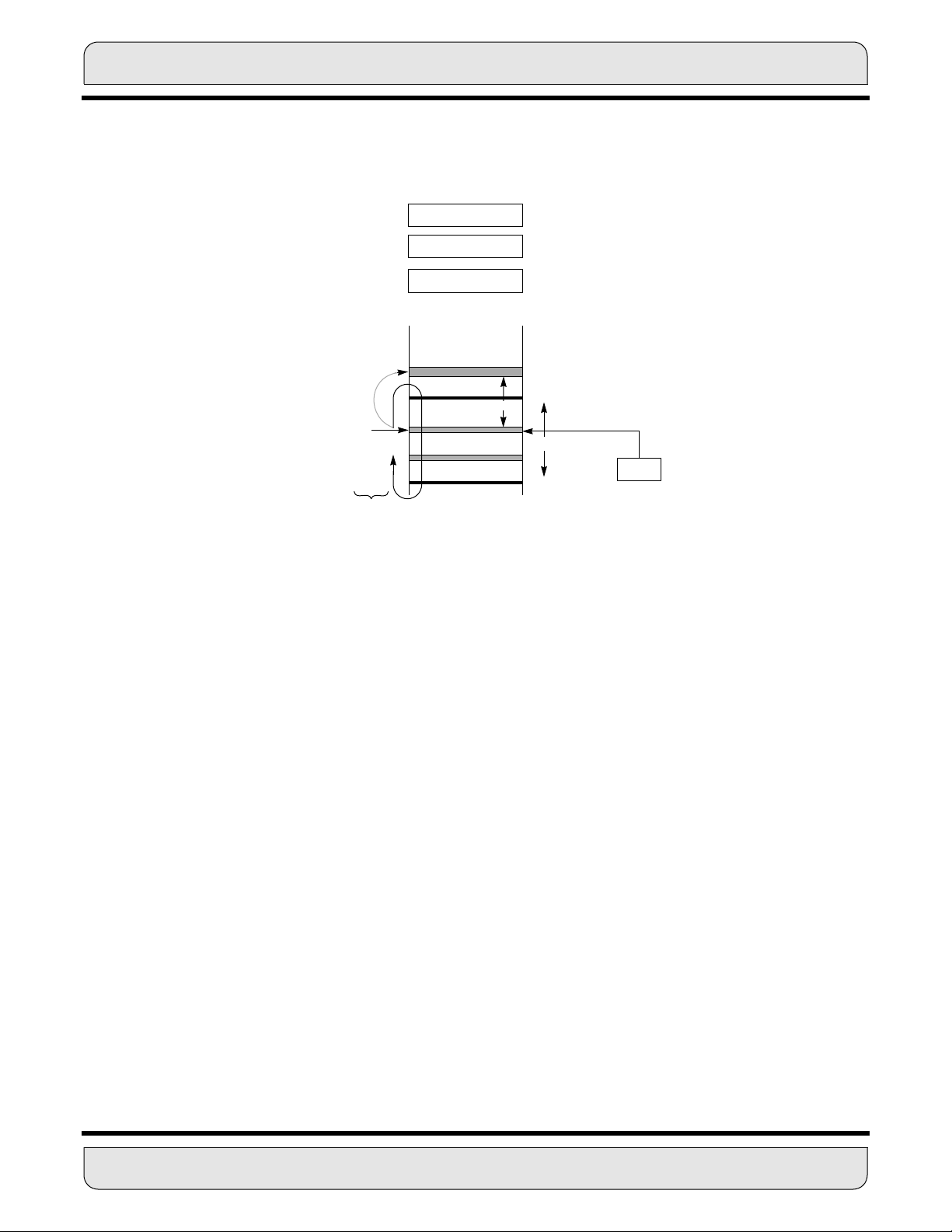
ADDRESSING

EXAMPLE: MOVE X0,X:(R2)+N

LET:

00.....0010100

MODULUS=21

0..010 00000 k=5

00.....0001111

00.....1001011

(90)

(75)

(69)

OFFSET=15

POINTER=75

(84)

XD BUS

(64)

Figure 4-13 Modulo Modifier Example

The MOVE instruction in Figure 4-13 takes the contents of the X0 register and moves it to a location in the X memory pointed to by (R2), and then (R2) is updated modulo 21. The new value of R2 is not 90 (75+ 15), which would be the case if linear arithmetic had been used, but rather is 69 since modulo arithmetic was used.

4.4.2.2.2 Mn=$8001 to $BFFF

In this range, the modulo (M) equals (Mn+1)-$8000, where Mn is the value in the modifier register (see Table 4-2). This range firmly restricts the address register to the same buffer, causing the address register to wrap around within the buffer. This multiple wraparound addressing feature reduces argument overhead and is useful for decimation, interpolation, and waveform generation.

The address modification is performed modulo M, where M may be any power of 2 in the range from 2

to 214. Modulo M arithmetic causes the address register value to remain within an address range of size M defined by a lower and upper address boundary. The value M-1 is stored in the modifier register Mn least significant 14 bits while the two most significant bits are set to ‘10’. The lower boundary (base address) value must have zeroes in the k LSBs, where 2

= M, and therefore must be a multiple of 2k. The upper boundary

is the lower boundary plus the modulo size minus one (base address plus M-1).

MOTOROLA ADDRESS GENERATION UNIT 4 - 21

ADDRESSING

For example, to create a circular buffer of 32 stages, M is chosen as 32 and the lower address boundary must have its 5 least significant bits equal to zero (2

= 32, thus k = 5). The Mn register is loaded with the value $801F. The lower boundary may be chosen as 0, 32, 64, 96, 128, 160, etc. The upper boundary of the buffer is then the lower boundary plus 31.

The address pointer is not required to start at the lower address boundary and may begin anywhere within the defined modulo address range (between the lower and upper boundaries). If the address register pointer increments past the upper boundary of the buffer (base address plus M-1) it will wrap around to the base address. If the address decrements past the lower boundary (base address) it will wrap around to the base address plus M-1. If an offset Nn is used in the address calculations, it is not required to be less than or equal to M for proper modulo addressing since multiple wrap around is supported for (Rn)+Nn, (Rn)-Nn and (Rn+Nn) address updates (multiple wrap-around cannot occur with (Rn)+, (Rn)- and -(Rn) addressing modes).

The multiple wrap-around address modifier is useful for decimation, interpolation and waveform generation since the multiple wrap-around capability may be used for argument reduction.

4.4.2.3 Reverse-Carry Modifier (Mn=$0000)

Reverse carry is selected by setting the modifier register to zero (see Table 4-2). The address modification is performed in hardware by propagating the carry in the reverse direction — i.e., from the MSB to the LSB. Reverse carry is equivalent to bit reversing the contents of Rn (i.e., redefining the MSB as the LSB, the next MSB as bit 1, etc.) and the offset value, Nn, adding normally, and then bit reversing the result. If the + Nn addressing mode is used with this address modifier and Nn contains the value 2

(k–1)

(a power of two), this addressing modifier is equivalent to bit reversing the k LSBs of Rn, incrementing Rn by 1, and bit reversing the k LSBs of Rn again. This address modification is useful for addressing the twiddle factors in 2k-point FFT addressing and to unscramble 2 data. The range of values for Nn is 0 to + 32K (i.e., Nn=2

), which allows bit-reverse ad-

-point FFT

dressing for FFTs up to 65,536 points. To make bit-reverse addressing work correctly for a 2

point FFT, the following proce-

dures must be used:

1. Set Mn=0; this selects reverse-carry arithmetic.

2. Set Nn=2

(k–1)

4 - 22 ADDRESS GENERATION UNIT MOTOROLA

ADDRESSING

3. Set Rn between the lower boundary and upper boundary in the buffer memory. The lower boundary is L x (2

), where L is an arbitrary whole number. This boundary gives a 16-bit binary number “xx . . . xx00 . . . 00”, where xx . . . xx=L and 00 . . . 00 equals k zeros. The upper boundary is L x (2

)+ ((2k)–1). This boundary gives a 16-bit binary number “xx . . . xx11 . . . 11”, where xx . . . xx=L and 11 . . . 11 equals k ones.

4. Use the (Rn)+ Nn addressing mode.

As an example, consider a 1024-point FFT with real data stored in the X memory and imaginary data stored in the Y memory. Since 1,024=2 is zero to select bit-reverse addressing. Offset register (Nn) contains the value 512 (2

), and the pointer register (Rn) contains 3,072 (L x (2k)=3 x (210)), which is the lower

, k=10. The modifier register (Mn)

(k–

boundary of the memory buffer that holds the results of the FFT. The upper boundary is 4,095 (lower boundary + (2

)–1=3,072+ 1,023).

Postincrementing by + N generates the address sequence (0, 512, 256, 768, 128, 640,...), which is added to the lower boundary. This sequence (0, 512, etc.) is the scrambled FFT data order for sequential frequency points from 0 to 2

π. Table 4-3 shows the successive

contents of Rn when using (Rn)+ Nn updates.

Table 4-3 Bit-Reverse Addressing

Sequence Example

Rn Contents

3072 0 3584 512 3328 256 3840 768 3200 128 3712 640

Offset From

Lower Boundary

The reverse-carry modifier only works when the base address of the FFT data buffer is a multiple of 2

, such as 1,024, 2,048, 3,072, etc. The use of addressing modes other than

postincrement by + Nn is possible but may not provide a useful result.

MOTOROLA ADDRESS GENERATION UNIT 4 - 23

ADDRESSING

The term bit reverse with respect to reverse-carry arithmetic is descriptive. The lower boundary that must be used for the bit-reverse address scheme to work is L x (2

). In the previous example shown in Table 4-3, L=3 and k=10. The first address used is the lower boundary (3072); the calculation of the next address is shown in Figure 4-14. The k LSBs of the current contents of Rn (3,072) are swapped:

EACH UPDATE, (Rn)+Nn, IS EQUIVALENT TO:

L k BITS

1. BIT REVERSING: Rn=000011 0000000000=3072

0000000000

2. INCREMENT Rn BY 1: Rn=000011 0000000000 +1

000011 0000000001

3. BIT REVERSING AGAIN: Rn=000011 0000000001

1000000000

000011 1000000000=3584

Figure 4-14 Bit-Reverse Address Calculation Example

• Bits 0 and 9 are swapped.

• Bits 1 and 8 are swapped.

• Bits 2 and 7 are swapped.

• Bits 3 and 6 are swapped.

• Bits 4 and 5 are swapped. The result is incremented (3,073), and then the k LSBs are swapped again:

• Bits 0 and 9 are swapped.

• Bits 1 and 8 are swapped.

• Bits 2 and 7 are swapped.

• Bits 3 and 6 are swapped.

• Bits 4 and 5 are swapped. The result is Rn equals 3,584.

4 - 24 ADDRESS GENERATION UNIT MOTOROLA

ADDRESSING

4.4.2.4 Address-Modifier-Type Encoding Summary

There are three address modifier types:

• Linear Addressing

• Reverse-Carry Addressing

• Modulo Addressing Bit-reverse addressing is useful for 2

-point FFT addressing. Modulo addressing is useful for creating circular buffers for FIFOs (queues), delay lines, and sample buffers up to 32,768 words long. The linear addressing is useful for general-purpose addressing. There is a reserved set of modifier values (from 32,768 to 65,534) that should not be used.

Figure 4-15 gives examples of the three addressing modifiers using 8-bit registers for simplification (all AGU registers are 16 bit). The addressing mode used in the example, postincrement by offset Nn, adds the contents of the offset register to the contents of the address register after the address register is accessed. The results of the three examples are as follows:

• The linear address modifier addresses every fifth location since the offset register

contains $5.

• Using the bit-reverse address modifier causes the postincrement by offset Nn

addressing mode to use the address register, bit reverse the four LSBs, increment by 1, and bit reverse the four LSBs again.

• The modulo address modifier has a lower boundary at a predetermined location, and

the modulo number plus the lower boundary establishes the upper boundary. This boundary creates a circular buffer so that, if the address register is pointing within the boundaries, addressing past a boundary causes a circular wraparound to the other boundary.

MOTOROLA ADDRESS GENERATION UNIT 4 - 25

ADDRESSING

LINEAR ADDRESS MODIFIER

M0 = 255 = 11111111 FOR LINEAR ADDRESSING WITH R0 ORIGINAL REGISTERS: N0 = 5, R0 = 75 = 0100 1011 POSTINCREMENT BY OFFSET N0: R0 = 80 = 0101 0000 POSTINCREMENT BY OFFSET N0: R0 = 85 = 0101 0101 POSTINCREMENT BY OFFSET N0: R0 = 90 = 0101 1010

MODULO ADDRESS MODIFIER

M0 = 19 = 0001 0011 FOR MODULO 20 ADDRESSING WITH R0 ORIGINAL REGISTERS: N0 = 5, R0 = 75 = 0100 1011 POSTINCREMENT BY OFFSET N0: R0 = 80 = 0101 0000 POSTINCREMENT BY OFFSET N0: R0 = 65 = 0100 0001 POSTINCREMENT BY OFFSET N0: R0 = 70 = 0100 0110

UPPER

BOUNDARY

LOWER

BOUNDARY

83 80

65 64

REVERSE-CARRY ADDRESS MODIFIER

M0 = 0= 0000 0000 FOR REVERSE-CARRY ADDRESSING WITH R0 ORIGINAL REGISTERS: N0 = 8, R0 = 64 = 0100 0000 POSTINCREMENT BY OFFSET N0: R0 = 72 = 0100 1000 POSTINCREMENT BY OFFSET N0: R0 = 68 = 0100 0100 POSTINCREMENT BY OFFSET N0: R0 = 76 = 0100 1100

Figure 4-15 Address Modifier Summary

4 - 26 ADDRESS GENERATION UNIT MOTOROLA

SECTION 5

PROGRAM CONTROL UNIT

MOTOROLA PROGRAM CONTROL UNIT 5 - 1

SECTION CONTENTS

SECTION 5.1 PROGRAM CONTROL UNIT .................................................... 3

SECTION 5.2 OVERVIEW ................................................................................ 3

SECTION 5.3 PROGRAM CONTROL UNIT (PCU) ARCHITECTURE ............ 5

5.3.1 Program Decode Controller ................................................................ 5

5.3.2 Program Address Generator (PAG) ................................................... 5

5.3.3 Program Interrupt Controller ............................................................... 6

5.3.4 Instruction Pipeline Format ................................................................. 6

SECTION 5.4 PROGRAMMING MODEL ......................................................... 8

5.4.1 Program Counter ................................................................................ 8

5.4.2 Status Register ................................................................................... 9

5.4.2.1 Carry (Bit 0) .................................................................................10

5.4.2.2 Overflow (Bit 1) ...........................................................................10

5.4.2.3 Zero (Bit 2) ..................................................................................10

5.4.2.4 Negative (Bit 3) ...........................................................................10

5.4.2.5 Unnormalized (Bit 4) ...................................................................10

5.4.2.6 Extension (Bit 5) ..........................................................................11

5.4.2.7 Limit (Bit 6) ..................................................................................11

5.4.2.8 Scaling Bit (Bit 7) .........................................................................11

5.4.2.9 Interrupt Masks (Bits 8 and 9) .....................................................12

5.4.2.10 Scaling Mode (Bits 10 and 11) ..................................................12

5.4.2.11 Reserved Status (Bit 12) ...........................................................13

5.4.2.12 Trace Mode (Bit 13) ..................................................................13

5.4.2.13 Double Precision Multiply Mode (Bit 14) ...................................13

5.4.2.14 Loop Flag (Bit 15) ......................................................................13

5.4.3 Operating Mode Register ................................................................... 14

5.4.4 System Stack ...................................................................................... 14

5.4.5 Stack Pointer Register ........................................................................15

5.4.5.1 Stack Pointer (Bits 0–3) ..............................................................16

5.4.5.2 Stack Error Flag (Bit 4) ................................................................16

5.4.5.3 Underflow Flag (Bit 5) .................................................................16

5.4.5.4 Reserved Stack Pointer Registration (Bits 6–23) ........................17

5.4.6 Loop Address Register ....................................................................... 17

5.4.7 Loop Counter Register ....................................................................... 17

5.4.8 Programming Model Summary ........................................................... 17

5 - 2 PROGRAM CONTROL UNIT

MOTOROLA

PROGRAM CONTROL UNIT

5.1 PROGRAM CONTROL UNIT

This section describes the hardware of the program control unit (PCU) and concludes with a description of the programming model. The instruction pipeline description is also included since understanding the pipeline is particularly important in understanding the DSP56K family of processors.

5.2 OVERVIEW

The program control unit is one of the three execution units in the central processing module (see Figure 5-2). It performs program address generation (instruction prefetch), instruction decoding, hardware DO loop control, and exception (interrupt) processing. The programmer sees the program control unit as six registers and a hardware system stack (SS) as shown in Figure 5-1. In addition to the standard program flow-control resources, such as a program counter (PC), complete status register (SR), and SS, the program control unit features registers (loop address (LA) and loop counter (LC)) dedicated to supporting the hardware DO loop instruction.

The SS is a 15-level by 32-bit separate internal memory which stores the PC and SR for subroutine calls, long interrupts, and program looping. The SS also stores the LC and LA registers. Each location in the SS is addressable as a 16-bit register, system stack high (SSH) and system stack low (SSL). The stack pointer (SP) points to the SS locations.

PAB PDB

16 24

CLOCK

OMR

PC LA LC SP

24 24

GLOBAL DATA BUS

32 x 15

STACK

INTERRUPTS

CONTROL

Figure 5-1 Program Address Generator

MOTOROLA PROGRAM CONTROL UNIT 5 - 3

PERIPHERAL

PINS

PERIPHERAL

24-Bit

56K Mod-

MODULES

ADDRESS

GENERATION

UNIT

OVERVIEW

PROGRAM

RAM/ROM

EXPANSION

YAB XAB PAB

X MEMORY

RAM/ROM

EXPANSION

Y MEMORY

RAM/ROM

EXPANSION

AREA

EXTERNAL ADDRESS

BUS

SWITCH

ADDRESS

INTERNAL

DATA

BUS

SWITCH

PLL

CLOCK

GENERATOR

PROGRAM

INTERRUPT

CONTROLLER

PROGRAM

DECODE

CONTROLLER

Program Control Unit

MODC/NMI MODB/IRQB MODA/IRQA

RESET

PROGRAM

ADDRESS

GENERA TOR

YDB XDB PDB GDB

DATA ALU

24X24+56→56-BIT MAC

TWO 56-BIT ACCUMULATORS

BUS

CONTROL

EXTERNAL

DATA BUS

SWITCH

OnCE™

16 BITS 24 BITS

PORT A

CONTROL

DATA

Figure 5-2 DSP56K Block Diagram

All of the PCU registers are read/write to facilitate system debugging. Although none of the registers are 24 bits, they are read or written over 24-bit buses. When they are read, the least significant bits (LSBs) are significant, and the most significant bits (MSBs) are zeroed as appropriate. When they are written, only the appropriate LSBs are significant, and the MSBs are written as don’t care.

5 - 4 PROGRAM CONTROL UNIT

MOTOROLA

PROGRAM CONTROL UNIT (PCU) ARCHITECTURE

The program control unit implements a three-stage (prefetch, decode, execute) pipeline and controls the five processing states of the DSP: normal, exception, reset, wait, and stop.

5.3 PROGRAM CONTROL UNIT (PCU) ARCHITECTURE

The PCU consists of three hardware blocks: the program decode controller (PDC), the program address generator (PAG), and the program interrupt controller (PIC).

5.3.1 Program Decode Controller

The PDC contains the program logic array decoders, the register address bus generator, the loop state machine, the repeat state machine, the condition code generator, the interrupt state machine, the instruction latch, and the backup instruction latch. The PDC decodes the 24-bit instruction loaded into the instruction latch and generates all signals necessary for pipeline control. The backup instruction latch stores a duplicate of the prefetched instruction to optimize execution of the repeat (REP) and jump (JMP) instructions.

5.3.2 Program Address Generator (PAG)

The PAG contains the PC, the SP, the SS, the operating mode register (OMR), the SR, the LC register, and the LA register (see Figure 5-1).

The PAG provides hardware dedicated to support loops, which are frequent constructs in DSP algorithms. A DO instruction loads the LC register with the number of times the loop should be executed, loads the LA register with the address of the last instruction word in the loop (fetched during one loop pass), and asserts the loop flag in the SR. The DO instruction also supports nested loops by stacking the contents of the LA, LC, and SR prior to the execution of the instruction. Under control of the PAG, the address of the first instruction in the loop is also stacked so the loop can be repeated with no overhead. While the loop flag in the SR is asserted, the loop state machine (in the PDC) will compare the PC contents to the contents of the LA to determine if the last instruction word in the loop was fetched. If the last word was fetched, the LC contents are tested for one. If LC is not equal to one, then it is decremented, and the SS is read to update the PC with the address of the first instruction in the loop, effectively executing an automatic branch. If the LC is equal to one, then the LC, LA, and the loop flag in the SR are restored with the stack contents, while instruction fetches continue at the incremented PC value (LA + 1). More information about the LA and LC appears in Section 5.3.4 Instruction Pipeline Format.

The repeat (REP) instruction loads the LC with the number of times the next instruction is to be repeated. The instruction to be repeated is only fetched once, so throughput is increased by reducing external bus contention. However, REP instructions are not

MOTOROLA PROGRAM CONTROL UNIT 5 - 5

PROGRAM CONTROL UNIT (PCU) ARCHITECTURE

interruptible since they are fetched only once. A single-instruction DO loop can be used in place of a REP instruction if interrupts must be allowed.

5.3.3 Program Interrupt Controller

The PIC receives all interrupt requests, arbitrates among them, and generates the interrupt vector address.

Interrupts have a flexible priority structure with levels that can range from zero to three. Levels 0 (lowest level), 1, and 2 are maskable. Level 3 is the highest interrupt priority level (IPL) and is not maskable. Two interrupt mask bits in the SR reflect the current IPL and indicate the level needed for an interrupt source to interrupt the processor. Interrupts cause the DSP to enter the exception processing state which is discussed fully in SECTION 7 – PROCESSING STATES.

The four external interrupt sources include three external interrupt request inputs (IRQA IRQB

, and NMI) and the RESET pin. IRQA and IRQB can be either level sensitive or negative edge triggered. The nonmaskable interrupt (NMI interrupt. MODA/IRQA deasserted. The sampled values are stored in the operating mode register (OMR) bits MA, MB, and MC, respectively (see Section 5.4.3 for information on the OMR). Only the fourth external interrupt, RESET

The PIC also arbitrates between the different I/O peripherals. The currently selected peripheral supplies the correct vector address to the PIC.

5.3.4 Instruction Pipeline Format

The program control unit uses a three-level pipelined architecture in which concurrent instruction fetch, decode, and execution occur. This pipelined operation remains essentially hidden from the user and makes programming straightforward. The pipeline is illustrated in Figure 5-3, which shows the operations of each of the execution units and all initial conditions necessary to follow the execution of the instruction sequence shown in the figure. The pipeline is described in more detail in Section 7.2.1 Instruction Pipeline.

The first instruction, I1, should be interpreted as follows: multiply the contents of X0 by the contents of Y0, add the product to the contents already in accumulator A, round the result to the “nearest even,” store the result back in accumulator A, move the contents in X data memory (pointed to by R0) into X0 and postincrement R0, and move the contents in Y data memory (pointed to by R4) into Y1 and postincrement R4. The second instruction, I2, should be interpreted as follows: clear accumulator A, move the contents in X0 into the location in X data memory pointed to by R0 and postincrement R0. Before the clear oper-

, MODB/IRQB, and MODC/NMI pins are sampled when RESET is

, and Illegal Instruction have higher priority than NMI.

) is edge sensitive and is a level 3

5 - 6 PROGRAM CONTROL UNIT

MOTOROLA

PROGRAM CONTROL UNIT (PCU) ARCHITECTURE

EXAMPLE PROGRAM SEGMENT

Instruction 1 MACR X0,Y1,A X:(R0)+,X0 Y:(R4)+,Y1 Instruction 2 CLR A X0,X:(R0)+ A,Y:(R4)Instruction 3 MAC X0,Y1,A X:(R0)+,X0 Y:(R4)+,Y1

SERIAL EXECUTION OF INSTRUCTIONS

SEQUENCE OF OPERATIONS

Instruction/Data Fetch

Instruction Decode

Instruction Execution

PARALLEL PROCESSING OF INSTRUCTIONS

INSTRUCTION FETCH

INSTRUCTION DECODE

INSTRUCTION EXECUTION

PARALLEL

OPERATIONS

ADDRESS

UPDATE

(AGU)

INITIAL

CONDITIONS

R0=$0005 R4=$0008

Instruction Cycle 1

INSTRUCTION

FETCH

LOGIC

Instruction Cycle 1 Instruction Cycle 2

Instruction Cycle 2

INSTRUCTION

FETCH

EXECUTION OF EXAMPLE PROGRAM

I1 I2

LOGIC

INSTRUCTION

DECODE

LOGIC

Instruction Cycle 3 Instruction Cycle 5Instruction Cycle

INSTRUCTION

FETCH

LOGIC

INSTRUCTION

DECODE

LOGIC

INSTRUCTION

EXECUTION

LOGIC

Instruction Cycle 3

I3 I2 I1

R0=5+1 R4=8+1

INSTRUCTION

EXECUTION

INSTRUCTION FETCH LOGIC

DECODE

LOGIC

Instruction Cycle 4 Instruction Cycle 5

I4 I3 I2

R0=6+1 R4=9–1

FETCH

LOGIC

INSTRUCTION

DECODE

LOGIC

INSTRUCTION

EXECUTION

LOGIC

I5 I4 I3

R0=7+1 R4=8+1

INSTRUCTION

EXECUTION

(DATA ALU)

X MEMORY

AT ADDRESS

$0005 $0006 $0007

Y MEMORY

AT ADDRESS

$0008 $0009

A: A2=$00 A1=$000066 A0=$000000

X0=$400000 Y1=$000077

DATA

$000005 $000006 $000007

DATA

$000008 $000009

A: A2=$00 A1=$0000A2 A0=$000000

X0=$000005 Y1=$000008

$000005 $000006 $000007

$000008 $000009

A: A2=$00 A1=$000000 A0=$000000

X0=$000005 Y1=$000008

$000005 $000005 $000007

$000008 $0000A2

A: A2=$00 A1=$000000 A0=$000050

X0=$000007 Y1=$000008

$000005 $000005 $000007

$000008 $0000A2

Figure 5-3 Three-Stage Pipeline

MOTOROLA PROGRAM CONTROL UNIT 5 - 7

PROGRAMMING MODEL

PROGRAM CONTROL UNIT

23 1615 0

LOOP ADDRESS

23 1615 0

PROGRAM

COUNTER (PC)

31 SSH 1615 SSL 0

23 1615 0

LOOP COUNTER (LC)

23 1615 8 7 0

MR CCR

STATUS

SYSTEM STACK

Figure 5-4 Program Control Unit Programming Model

23 8 7 6 5 4 3 2 1 0

OPERATING MODE REGISTER (OMR)

23 6 5 0

STACK POINTER (SP)

MADE MB

* READ AS ZERO, SHOULD BE WRITTEN

WITH ZERO FOR FUTURE COMPATIBILITY

ation, move the contents in accumulator A into the location in Y data memory pointed to by R4 and postdecrement R4. The third instruction, I3, is the same as I1, except the rounding operation is not performed.

5.4 PROGRAMMING MODEL

The program control unit features LA and LC registers which support the DO loop instruction and the standard program flow-control resources, such as a PC, complete SR, and SS. With the exception of the PC, all registers are read/write to facilitate system debugging. Figure 5-4 shows the program control unit programming model with the six registers and SS. The following paragraphs give a detailed description of each register.

5.4.1 Program Counter

This 16-bit register contains the address of the next location to be fetched from program memory space. The PC can point to instructions, data operands, or addresses of operands. References to this register are always inherent and are implied by most instructions.

5 - 8 PROGRAM CONTROL UNIT

MOTOROLA

PROGRAMMING MODEL

MR CCR

15 14 13 12 11 10 9 8 76 543210

LF DM T S1 S0 I1 I0 S L E U N Z V C

CARRY OVERFLOW

ZERO NEGATIVE UNNORMALIZED

EXTENSION LIMIT SCALING INTERRUPT MASK

SCALING MODE RESERVED TRACE MODE

DOUBLE PRECISION

MULTIPLY MODE

LOOP FLAG

All bits are cleared after hardware reset except bits 8 and 9 which are set to ones. Bits 12 and 16 to 23 are reserved, read as zero and should be written with zero for future compatibility

Figure 5-5 Status Register Format

This special-purpose address register is stacked when program looping is initialized, when a JSR is performed, or when interrupts occur (except for no-overhead fast interrupts).

5.4.2 Status Register

The 16-bit SR consists of a mode register (MR) in the high-order eight bits and a condition code register (CCR) in the low-order eight bits, as shown in Figure 5-5. The SR is stacked when program looping is initialized, when a JSR is performed, or when interrupts occur, (except for no-overhead fast interrupts).

The MR is a special purpose control register which defines the current system state of the processor. The MR bits are affected by processor reset, exception processing, the DO, end current DO loop (ENDDO), return from interrupt (RTI), and SWI instructions and by instructions that directly reference the MR register, such as OR immediate to control register (ORI) and AND immediate to control register (ANDI). During processor reset, the interrupt mask bits of the MR will be set. The scaling mode bits, loop flag, and trace bit will be cleared.

MOTOROLA PROGRAM CONTROL UNIT 5 - 9

PROGRAMMING MODEL

The CCR is a special purpose control register that defines the current user state of the processor. The CCR bits are affected by data arithmetic logic unit (ALU) operations, parallel move operations, and by instructions that directly reference the CCR (ORI and ANDI). The CCR bits are not affected by parallel move operations unless data limiting occurs when reading the A or B accumulators. During processor reset, all CCR bits are cleared.

5.4.2.1 Carry (Bit 0)

The carry (C) bit is set if a carry is generated out of the MSB of the result in an addition. This bit is also set if a borrow is generated in a subtraction. The carry or borrow is generated from bit 55 of the result. The carry bit is also affected by bit manipulation, rotate, and shift instructions. Otherwise, this bit is cleared.

5.4.2.2 Overflow (Bit 1)

The overflow (V) bit is set if an arithmetic overflow occurs in the 56-bit result. This bit indicates that the result cannot be represented in the accumulator register; thus, the register has overflowed. Otherwise, this bit is cleared.

5.4.2.3 Zero (Bit 2)

The zero (Z) bit is set if the result equals zero; otherwise, this bit is cleared.

5.4.2.4 Negative (Bit 3)

The negative (N) bit is set if the MSB (bit 55) of the result is set; otherwise, this bit is cleared.

5.4.2.5 Unnormalized (Bit 4)

The unnormalized (U) bit is set if the two MSBs of the most significant product (MSP) portion of the result are identical. Otherwise, this bit is cleared. The MSP portion of the A or B accumulators, which is defined by the scaling mode and the U bit, is computed as follows:

S1 S0 Scaling Mode U Bit Computation

0 0 No Scaling U = (Bit 47 ⊕ Bit 46) 0 1 Scale Down U = (Bit 48 ⊕ Bit 47) 1 0 Scale Up U = (Bit 46 ⊕ Bit 45)

5 - 10 PROGRAM CONTROL UNIT

MOTOROLA

PROGRAMMING MODEL

5.4.2.6 Extension (Bit 5)

The extension (E) bit is cleared if all the bits of the integer portion of the 56-bit result are all ones or all zeros; otherwise, this bit is set. The integer portion, defined by the scaling mode and the E bit, is computed as follows:

S1 S0 Scaling Mode Integer Portion

0 0 No Scaling Bits 55,54........48,47

0 1 Scale Down Bits 55,54........49,48

1 0 Scale Up Bits 55,54........47,46

If the E bit is cleared, then the low-order fraction portion contains all the significant bits; the high-order integer portion is just sign extension. In this case, the accumulator extension register can be ignored. If the E bit is set, it indicates that the accumulator extension register is in use.

5.4.2.7 Limit (Bit 6)

The limit (L) bit is set if the overflow bit is set. The L bit is also set if the data shifter/limiter circuits perform a limiting operation; otherwise, it is not affected. The L bit is cleared only by a processor reset or by an instruction that specifically clears it, which allows the L bit to be used as a latching overflow bit (i.e., a “sticky” bit). L is affected by data movement operations that read the A or B accumulator registers.

5.4.2.8 Scaling Bit (Bit 7)

The scaling bit (S) is used to detect data growth, which is required in Block Floating Point FFT operation. Typically, the bit is tested after each pass of a radix 2 FFT and, if it is set, the scaling mode should be activated in the next pass. The Block Floating Point FFT algorithm is described in the Motorola application note APR4/D, “Implementation of Fast Fourier Transforms on Motorola’s DSP56000/DSP56001 and DSP96002 Digital Signal Processors.” This bit is computed according to the following logical equations when the result of accumulator A or B is moved to XDB or YDB. It is a “sticky” bit, cleared only by an instruction that specifically clears it.

MOTOROLA PROGRAM CONTROL UNIT 5 - 11

PROGRAMMING MODEL

If S1=0 and S0=0 (no scaling) then S = (A46 XOR A45) OR (B46 XOR B45)

If S1=0 and S0=1 (scale down) then S = (A47 XOR A46) OR (B47 XOR B46)

If S1=1 and S0=0 (scale up) then S = (A45 XOR A44) OR (B45 XOR B44)

If S1=1 and S0=1 (reserved) then the S flag is undefined.

where Ai and Bi means bit i in accumulator A or B.

5.4.2.9 Interrupt Masks (Bits 8 and 9)

The interrupt mask bits, I1 and I0, reflect the current IPL of the processor and indicate the IPL needed for an interrupt source to interrupt the processor. The current IPL of the processor can be changed under software control. The interrupt mask bits are set during hardware reset but not during software reset.

I1 I0 Exceptions Permitted Exceptions Masked

0 0 IPL 0,1,2,3 None 0 1 IPL 1,2,3 IPL 0 1 0 IPL 2,3 IPL 0,1 1 1 IPL 3 IPL 0,1,2

5.4.2.10 Scaling Mode (Bits 10 and 11)

The scaling mode bits, S1 and S0, specify the scaling to be performed in the data ALU shifter/limiter, and also specify the rounding position in the data ALU multiply-accumula-

5 - 12 PROGRAM CONTROL UNIT

MOTOROLA

PROGRAMMING MODEL

tor (MAC). The scaling modes are shown in the following table:

S1 S0

0 0 23 No Scaling 0 1 24 Scale Down (1-Bit Arithmetic Right Shift) 1 0 22 Scale Up (1-Bit Arithmetic Left Shift) 1 1 — Reserved for Future Expansion

Rounding

Bit

Scaling Mode

The scaling mode affects data read from the A or B accumulator registers out to the XDB and YDB. Different scaling modes can occur with the same program code to allow dynamic scaling. Dynamic scaling facilitates block floating-point arithmetic. The scaling mode also affects the MAC rounding position to maintain proper rounding when different portions of the accumulator registers are read out to the XDB and YDB. The scaling mode bits, which are cleared at the start of a long interrupt service routine, are also cleared during a processor reset.

5.4.2.11 Reserved Status (Bit 12)

This bits is reserved for future expansion and will read as zero during DSP read operations.

5.4.2.12 Trace Mode (Bit 13)

The trace mode (T) bit specifies the tracing function of the DSP56000/56001 only . (With other members of the DSP56K family, use the OnCE trace mode described in Section

10.5.) For the DSP56000/56001, if the T bit is set at the beginning of any instruction execution, a trace exception will be generated after the instruction execution is completed. If the T bit is cleared, tracing is disabled and instruction execution proceeds normally. If a long interrupt is executed during a trace exception, the SR with the trace bit set will be stacked, and the trace bit in the SR is cleared (see SECTION 7 – PROCESSING STATES for a complete description of a long interrupt operation). The T bit is also cleared during processor reset.

5.4.2.13 Double Precision Multiply Mode (Bit 14)

The processor is in double precision multiply mode when this bit is set. (See Section 3.4 for detailed information on the double precision multiply mode.) When the DM bit is set, the operations performed by the MPY and MAC instructions change so that a double precision 48-bit by 48-bit double precision multiplication can be performed in six instruc-

MOTOROLA PROGRAM CONTROL UNIT 5 - 13

PROGRAMMING MODEL

23 8 76543210

SD MC YD DE MB MA

OPERATING MODE A, B DATA ROM ENABLE INTERNAL Y MEMORY DISABLE OPERATING MODE C RESERVED STOP DELAY RESERVED RESERVED

Figure 5-6 OMR Format

tions. The DSP56K software simulator accurately shows how the MPY, MAC, and other Data ALU instructions operate while the processor is in the double precision multiply mode.

5.4.2.14 Loop Flag (Bit 15)

The loop flag (LF) bit is set when a program loop is in progress. It detects the end of a program loop. The LF is the only SR bit that is restored when a program loop is terminated. Stacking and restoring the LF when initiating and exiting a program loop, respectively, allow the nesting of program loops. At the start of a long interrupt service routine, the SR (including the LF) is pushed on the SS and the SR LF is cleared. When returning from the long interrupt with an RTI instruction, the SS is pulled and the LF is restored. During a processor reset, the LF is cleared.

5.4.3 Operating Mode Register

The OMR is a 24-bit register (only six bits are defined) that sets the current operating mode of the processor. Each chip in the DSP56K family of processors has its own set of operating modes which determine the memory maps for program and data memories, and the startup procedure that occurs when the chip leaves the reset state. The OMR bits are only affected by processor reset and by the ANDI, ORI, and MOVEC instructions, which directly reference the OMR.

The OMR format with all of its defined bits is shown in Figure 5-6. For product-specific OMR bit definitions, see the individual chip’s user manual for details on its respective operating modes.

5.4.4 System Stack

The SS is a separate 15X32-bit internal memory divided into two banks, the SSH and the

5 - 14 PROGRAM CONTROL UNIT

MOTOROLA

PROGRAMMING MODEL

SSL, each 16 bits wide. The SSH stores the PC contents, and the SSL stores the SR contents for subroutine calls, long interrupts, and program looping. The SS will also store the LA and LC registers. The SS is in stack memory space; its address is always inherent and implied by the current instruction.

The contents of the PC and SR are pushed on the top location of the SS when a subroutine call or long interrupt occurs. When a return from subroutine (RTS) occurs, the contents of the top location in the SS are pulled and put in the PC; the SR is not affected. When an RTI occurs, the contents of the top location in the SS are pulled to both the PC and SR.

The SS is also used to implement no-overhead nested hardware DO loops. When the DO instruction is executed, the LA:LC are pushed on the SS, then the PC:SR are pushed on the SS. Since each SS location can be addressed as separate 16-bit registers (SSH and SSL), software stacks can be created for unlimited nesting.

The SS can accommodate up to 15 long interrupts, seven DO loops, 15 JSRs, or combinations thereof. When the SS limit is exceeded, a nonmaskable stack error interrupt occurs, and the PC is pushed to SS location zero, which is not implemented in hardware. The PC will be lost, and there will be no SP from the stack interrupt routine to the program that was executing when the error occurred.

54 3210

UF SE P3 P2 P1 P0

STACK POINTER STACK ERROR FLAG UNDERFLOW FLAG

Figure 5-7 Stack Pointer Register Format

5.4.5 Stack Pointer Register

The 6-bit SP register indicates the location of the top of the SS and the status of the SS (underflow, empty, full, and overflow). The SP register is referenced implicitly by some instructions (DO, REP, JSR, RTI, etc.) or directly by the MOVEC instruction. The SP register format is shown in Figure 5-7. The SP register works as a 6-bit counter that addresses (selects) a 15-location stack with its four LSBs. The possible SP values are shown in Figure 5-8 and described in the following paragraphs.

5.4.5.1 Stack Pointer (Bits 0–3)

The SP points to the last location used on the SS. Immediately after hardware reset,

MOTOROLA PROGRAM CONTROL UNIT 5 - 15

PROGRAMMING MODEL

these bits are cleared (SP=0), indicating that the SS is empty. Data is pushed onto the SS by incrementing the SP, then writing data to the location to

which the SP points. An item is pulled off the stack by copying it from that location and then by decrementing the SP.

5.4.5.2 Stack Error Flag (Bit 4)

The stack error flag indicates that a stack error has occurred, and the transition of the stack error flag from zero to one causes a priority level-3 stack error exception.

When the stack is completely full, the SP reads 001111, and any operation that pushes data onto the stack will cause a stack error exception to occur. The SR will read 010000 (or 010001 if an implied double push occurs).

Any implied pull operation with SP equal to zero will cause a stack error exception, and the SP will read 111111 (or 111110 if an implied double pull occurs).

The stack error flag is a “sticky bit” which, once set, remains set until cleared by the user. There is a sequence of instructions that can cause a stack overflow and, without the sticky bit, would not be detected because the stack pointer is decremented before the stack error interrupt is taken. The sticky bit keeps the stack error bit set until the user clears it by writing a zero to SP bit 4. It also latches the overflow/underflow bit so that it cannot be changed by stack pointer increments or decrements as long as the stack error is set. The overflow/underflow bit remains latched until the first move to SP is executed.

Note: When SP is zero (stack empty), instructions that read the stack without SP post-

decrement and instructions that write to the stack without SP preincrement do not cause a stack error exception (i.e., 1) DO SSL,xxxx 2) REP SSL 3) MOVEC or move peripheral

UF SE P3 P2 P1 P0

1 1 1 1 1 0 STACK UNDERFLOW CONDITION AFTER DOUBLE PULL 1 1 1 1 1 1 STACK UNDERFLOW CONDITION 0 0 0 0 0 0 STACK EMPTY (RESET); PULL CAUSES UNDERFLOW 0 0 0 0 0 1 STACK LOCATION 1

0 0 1 1 1 0 STACK LOCATION 14 0 0 1 1 1 1 STACK LOCATION 15; PUSH CAUSES OVERFLOW 0 1 0 0 0 0 STACK OVERFLOW CONDITION 0 1 0 0 0 1 STACK OVERFLOW CONDITION AFTER DOUBLE PUSH

Figure 5-8 SP Register Values

5 - 16 PROGRAM CONTROL UNIT

MOTOROLA

PROGRAMMING MODEL

data (MOVEP) when SSL is specified as a source or destination).

5.4.5.3 Underflow Flag (Bit 5)

The underflow flag is set when a stack underflow occurs. The underflow flag is a “sticky bit” when the stack error flag is set. That is, when the stack error flag is set, the underflow flag will not change state. The combination of “underflow=1” and “stack error=0” is an illegal combination and will not occur unless it is forced by the user. If this condition is forced by the user, the hardware will correct itself based on the result of the next stack operation.

5.4.5.4 Reserved Stack Pointer Registration (Bits 6–23)

SP register bits 6 through 23 are reserved for future expansion and will read as zero during read operations.

5.4.6 Loop Address Register

The LA is a read/write register which is stacked into the SSH by a DO instruction and is unstacked by end-of-loop processing or by an ENDDO instruction. The contents of the LA register indicate the location of the last instruction word in a program loop. When that last instruction is fetched, the processor checks the contents of the LC register (see the following section). If the contents are not one, the processor decrements the LC and takes the next instruction from the top of the SS. If the LC is one, the PC is incremented, the loop flag is restored (pulled from the SS), the SS is purged, the LA and LC registers are pulled from the SS and restored, and instruction execution continues normally.

5.4.7 Loop Counter Register

The LC register is a special 16-bit counter which specifies the number of times a hardware program loop shall be repeated. This register is stacked into the SSL by a DO instruction and unstacked by end-of-loop processing or by execution of an ENDDO instruction. When the end of a hardware program loop is reached, the contents of the LC register are tested for one. If the LC is one, the program loop is terminated, and the LC register is loaded with the previous LC contents stored on the SS. If LC is not one, it is decremented and the program loop is repeated. The LC can be read under program control, which allows the number of times a loop will be executed to be monitored/changed dynamically. The LC is also used in the REP instruction

5.4.8 Programming Model Summary

The complete programming model for the DSP56K central processing module is shown in Figure 5-9. Programming models for the peripherals are shown in the appropriate user manuals.

MOTOROLA PROGRAM CONTROL UNIT 5 - 17

PROGRAMMING MODEL

DATA ARITHMETIC LOGIC UNIT

47 X 0

23 0 23 0

23 1615 0

* * * * * * * *

23 8 7 0#23 0

R7 R6 R5 R4 R3 R2 R1 R0

POINTER

REGISTERS

ACCUMULATOR REGISTERS

55 A 0

55 B 0

ADDRESS GENERATION UNIT

23 1615 0

* * * * * * * *

OFFSET

REGISTERS

INPUT REGISTERS

47 Y 0

23 0 23 0

N7 N6 N5 N4 N3 N2 N1 N0

23 0

23 1615 0

* * * * * * * *

M7 M6 M5 M4 M3 M2 M1 M0

MODIFIER

REGISTERS

UPPER FILE

LOWER FILE

PROGRAM CONTROL UNIT

23 1615 0

LOOP ADDRESS

23 1615 0

PROGRAM

COUNTER (PC)

31 SSH 16 15 SSL 0

23 1615 0

LOOP COUNTER (LC)

23 1615 8 7 0

MR CCR

STATUS

23 8 7 6 5 4 3 2 1 0

OPERATING MODE REGISTER (OMR)

23 6 5 0

STACK POINTER (SP)

* READ AS ZERO, SHOULD BE WRITTEN

WITH ZERO FOR FUTURE COMPATIBILITY

# READ AS SIGN EXTENSION BITS,

WRITTEN AS DON’T CARE

SYSTEM STACK

Figure 5-9 DSP56K Central Processing Module Programming Model

MADE MB

5 - 18 PROGRAM CONTROL UNIT MOTOROLA

SECTION 6

INSTRUCTION SET INTRODUCTION

Fetch F1 F2 F3 F3e F4 F5 F6 . . . Decode D1 D2 D3 D3e D4 D5 . . . Execute E1 E2 E3 E3e E4 . . . Instruction Cycle: 1 2 3 4 5 6 7 . . .

MOTOROLA INSTRUCTION SET INTRODUCTION 6 - 1

SECTION CONTENTS

SECTION 6.1 INSTRUCTION SET INTRODUCTION ......................................3

SECTION 6.2 SYNTAX .....................................................................................3

SECTION 6.3 INSTRUCTION FORMATS ........................................................3

6.3.1 Operand Sizes ....................................................................................5

6.3.2 Data Organization in Registers ...........................................................6

6.3.2.1 Data ALU Registers ...................................................................... 6

6.3.2.2 AGU Registers .............................................................................. 7

6.3.2.3 Program Control Registers ........................................................... 8

6.3.3 Data Organization in Memory ............................................................. 9

6.3.4 Operand References ..........................................................................11

6.3.4.1 Program References ..................................................................... 11

6.3.4.2 Stack References ......................................................................... 11

6.3.4.3 Register References ..................................................................... 11

6.3.4.4 Memory References ..................................................................... 11

6.3.4.4.1 X Memory References ............................................................11

6.3.4.4.2 Y Memory References ............................................................12

6.3.4.4.3 L Memory References .............................................................12

6.3.4.4.4 YX Memory References ..........................................................12

6.3.5 Addressing Modes ..............................................................................12

6.3.5.1 Register Direct Modes .................................................................. 13

6.3.5.1.1 Data or Control Register Direct ...............................................13

6.3.5.1.2 Address Register Direct ..........................................................13

6.3.5.2 Address Register Indirect Modes .................................................. 13

6.3.5.3 Special Addressing Modes ........................................................... 14

6.3.5.3.1 Immediate Data .......................................................................14

6.3.5.3.2 Absolute Address ....................................................................14

6.3.5.3.3 Immediate Short ......................................................................14

6.3.5.3.4 Short Jump Address ...............................................................14

6.3.5.3.5 Absolute Short ........................................................................14

6.3.5.3.6 I/O Short ..................................................................................16

6.3.5.3.7 Implicit Reference ...................................................................16

6.3.5.4 Addressing Modes Summary ........................................................ 20

SECTION 6.4 INSTRUCTION GROUPS ..........................................................20

6.4.1 Arithmetic Instructions ........................................................................ 22

6.4.2 Logical Instructions .............................................................................23

6.4.3 Bit Manipulation Instructions ...............................................................24

6.4.4 Loop Instructions ................................................................................24

6.4.5 Move Instructions ................................................................................26

6.4.6 Program Control Instructions .............................................................. 27

6 - 2 INSTRUCTION SET INTRODUCTION

MOTOROLA

INSTRUCTION SET INTRODUCTION

6.1 INSTRUCTION SET INTRODUCTION

The programming model shown in Figure 6-1 suggests that the DSP56K central processing module architecture can be viewed as three functional units which operate in parallel: data arithmetic logic unit (data ALU), address generation unit (AGU), and program control unit (PCU). The instruction set keeps each of these units busy throughout each instruction cycle, achieving maximal speed and maintaining minimal program size.

This section introduces the DSP56K instruction set and instruction format. The complete range of instruction capabilities combined with the flexible addressing modes used in this processor provide a very powerful assembly language for implementing digital signal processing (DSP) algorithms. The instruction set has been designed to allow efficient coding for DSP high-level language compilers such as the C compiler. Execution time is minimized by the hardware looping capabilities, use of an instruction pipeline, and parallel moves.

6.2 SYNTAX

The instruction syntax is organized into four columns: opcode, operands, and two parallelmove fields. The assembly-language source code for a typical one-word instruction is shown in the following illustration. Because of the multiple bus structure and the parallelism of the DSP, up to three data transfers can be specified in the instruction word – one on the X data bus (XDB), one on the Y data bus (YDB), and one within the data ALU. These transfers are explicitly specified. A fourth data transfer is implied and occurs in the program control unit (instruction word prefetch, program looping control, etc.). Each data transfer involves a source and a destination.

Opcode Operands XDB YDB

MAC X0,Y0,A X:(R0)+,X0 Y:(R4)+,Y0 The opcode column indicates the data ALU, AGU, or program control unit operation to be

performed and must always be included in the source code. The operands column specifies the operands to be used by the opcode. The XDB and YDB columns specify optional data transfers over the XDB and/or YDB and the associated addressing modes. The address space qualifiers (X:, Y:, and L:) indicate which address space is being referenced. Parallel moves are allowed in 30 of the 62 instructions. Additional information is presented in APPENDIX A - INSTRUCTION SET DETAILS.

6.3 INSTRUCTION FORMATS

The DSP56K instructions consist of one or two 24-bit words – an operation word and an optional effective address extension word. The general format of the operation word is

MOTOROLA INSTRUCTION SET INTRODUCTION 6 - 3

Motorola DSP56000 User Manual

Specifications and Main Features

Frequently Asked Questions

User Manual