HP F2231AA User Manual

Download

12c financial calculator

user's guide

Edition 4 HP Part Number 0012C-90001

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 1 of 209 Printed Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

Notice

THIS MANUAL AND ANY EXAMPLES CONTAINED HEREIN ARE PROVIDED “AS IS” AND ARE SUBJECT TO CHANGE WITHOUT NOTICE. HEWLETT-PACKARD COMPANY MAKES NO WARRANTY OF ANY KIND WITH REGARD TO THIS MANUAL, INCLUDING, BUT NOT LIMITED TO, THE IMPLIED WARRANTIES OF MERCHANTABILITY, NON-INFRINGEMENT AND FITNESS FOR A PARTICULAR PURPOSE.

HEWLETT-PACKARD CO. SHALL NOT BE LIABLE FOR ANY ERRORS OR FOR INCIDENTAL OR CONSEQUENTIAL DAMAGES IN CONNECTION WITH THE FURNISHING, PERFORMANCE, OR USE OF THIS MANUAL OR THE EXAMPLES CONTAINED HEREIN.

Copyright 1981, 2004 Hewlett-Packard Development Company, L.P. Reproduction, adaptation, or translation of this manual is prohibited without prior written permission of Hewlett-Packard Company, except as allowed under the copyright laws.

Hewlett-Packard Company 4995 Murphy Canyon Rd, Suite 301 San Diego, CA 92123

Printing History

Edition 4 August 2004

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 2 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

Introduction

About This Handbook

This hp 12c user's guide is intended to help you get the most out of your investment in your hp 12c Programmable Financial Calculator. Although the excitement of acquiring this powerful financial tool may prompt you to set this handbook aside and immediately begin “pressing buttons,” in the long run you’ll profit by reading through this handbook and working through the examples it contains.

Following this introduction is a brief section called Making Financial Calculations Easy—which shows you that your hp 12c does just that! The remainder of this handbook is organized basically into three parts:

z Part I (sections 1 through 7) describes how to use the various financial,

mathematics, statistics, and other functions (except for programming) provided in the calculator:

z Section 1 is about Getting Started. It tells you how to use the keyboard,

how to do simple arithmetic calculations and chain calculations, and how to use the storage registers (“memories”).

z Section 2 tells you how to use the percentage and calendar functions. z Section 3 tells you how to use the simple interest, compound interest, and

amortization functions.

z Section 4 tells you how to do discounted cash flow analysis, bond, and

depreciation calculations.

z Section 5 tells you about miscellaneous operating features such as

Continuous Memory, the display, and special function keys.

z Sections 6 and 7 tell you how to use the statistics, mathematics, and

number-alteration functions.

z Part II (sections 8 through 11) describe how to use the powerful

programming capabilities of the hp 12c.

z Part III (sections 12 through 16) give you step-by-step solutions to specialized

problems in real estate, lending, savings, investment analysis, and bonds. Some of these solutions can be done manually, while others involve running a program. Since the programmed solutions are both self-contained and step-by-step, you can easily employ them even if you don’t care to learn how to create your own programs. But if you do start to create your own programs, look over the programs used in the solutions: they contain examples of good programming techniques and practices.

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 3 of 209 Printed Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

4 Introduction

z The various appendices describe additional details of calculator operation as

well as warranty and service information.

z The Function Key Index and Programming Key Index at the back of the

handbook can be used as a handy page reference to the comprehensive information inside the manual

Financial Calculations in the United Kingdom

The calculations for most financial problems in the United Kingdom are identical to the calculations for those problems in the United States — which are described in this handbook. Certain problems, however, require different calculation methods in the United Kingdom than in the United States. Refer to Appendix F for more information.

For More Solutions to Financial Problems

In addition to the specialized solutions found in Sections 12 through 16 of this handbook, many more are available in the optional hp 12c Solutions Handbook. Included are solutions to problems in lending, forecasting, pricing, statistics, savings, investment analysis, personal finance, securities, Canadian mortgages, learning curves in manufacturing, and queuing theory. A Solutions Handbook is available online (www.hp.com/calculators

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 4 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

Contents

Introduction.................................................................... 3

About This Handbook.....................................................................3

Financial Calculations in the United Kingdom.....................................4

For More Solutions to Financial Problems...........................................4

Part I. Problem Solving ......................................... 15

Section 1: Getting Started............................................. 16

Power On and Off........................................................................16

Low-Power Indication..............................................................16

The Keyboard ..............................................................................16

Keying in Numbers ................................................................17

Digit Separators ....................................................................17

Negative Numbers ................................................................17

Keying in Large Numbers .......................................................18

The CLEAR Keys ....................................................................18

Simple Arithmetic Calculations .......................................................19

Chain Calculations.......................................................................20

Storage Registers..........................................................................23

Storing and Recalling Numbers...............................................23

Clearing Storage Registers......................................................24

Storage Register Arithmetic .....................................................24

Section 2: Percentage and Calendar Functions................ 26

Percentage Functions.....................................................................26

Percentages ..........................................................................26

Net Amount..........................................................................27

Percent Difference..................................................................27

Percent of Total......................................................................28

Calendar Functions.......................................................................29

Date Format..........................................................................29

Future or Past Dates................................................................30

Number of Days Between Dates..............................................31

Section 3: Basic Financial Functions ............................... 32

The Financial Registers..................................................................32

Storing Numbers Into the Financial Registers .............................32

Displaying Numbers in the Financial Registers...........................32

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 5 of 209 Printed Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

6 Contents

Clearing the Financial Registers.............................................. 33

Simple Interest Calculations........................................................... 33

Financial Calculations and the Cash Flow Diagram.......................... 34

The Cash Flow Sign Convention.............................................. 36

The Payment Mode ............................................................... 37

Generalized Cash Flow Diagrams........................................... 37

Compound Interest Calculations..................................................... 39

Specifying the Number of Compounding Periods and the Periodic

Interest Rate ......................................................................... 39

Calculating the Number of Payments or Compounding Periods ... 39

Calculating the Periodic and Annual Interest Rates..................... 43

Calculating the Present Value ................................................. 44

Calculating the Payment Amount............................................. 46

Calculating the Future Value................................................... 48

Odd-Period Calculations ........................................................ 50

Amortization ............................................................................... 54

Section 4: Additional Financial Functions ....................... 57

Discounted Cash Flow Analysis: NPV and IRR................................. 57

Calculating Net Present Value (NPV) ....................................... 58

Calculating Internal Rate of Return (IRR) ................................... 63

Reviewing Cash Flow Entries................................................... 64

Changing Cash Flow Entries................................................... 65

Bond Calculations ....................................................................... 66

Bond Price ............................................................................67

Bond Yield............................................................................67

Depreciation Calculations ............................................................. 68

Section 5: Additional Operating Features ....................... 70

Continuous Memory..................................................................... 70

The Display................................................................................. 71

Status Indicators ................................................................... 71

Number Display Formats ....................................................... 71

Scientific Notation Display Format........................................... 72

Special Displays ................................................................... 73

The key ..............................................................................74

The Key..............................................................................74

Arithmetic Calculations With Constants.................................... 75

Recovering From Errors in Digit Entry....................................... 75

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 6 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

Contents 7

Section 6: Statistics Functions........................................ 76

Accumulating Statistics..................................................................76

Correcting Accumulated Statistics ...................................................77

Mean .........................................................................................77

Standard Deviation.......................................................................79

Linear Estimation ..........................................................................80

Weighted Mean...........................................................................81

Section 7: Mathematics and Number-Alteration Functions 83

One-Number Functions .................................................................83

The Power Function.......................................................................85

Part II. Programming............................................. 87

Section 8: Programming Basics ..................................... 88

Why Use Programs?.....................................................................88

Creating a Program......................................................................88

Running a Program.......................................................................89

Program Memory .........................................................................90

Identifying Instructions in Program Lines....................................91

Displaying Program Lines........................................................92

The 00 Instruction and Program Line 00 ............................93

Expanding Program Memory ..................................................94

Setting the Calculator to a Particular Program Line .....................95

Executing a Program One Line at a Time.........................................96

Interrupting Program Execution.......................................................97

Pausing During Program Execution...........................................97

Stopping Program Execution .................................................101

Section 9: Branching and Looping ............................... 103

Simple Branching.......................................................................103

Looping ....................................................................................104

Conditional Branching ................................................................107

Section 10: Program Editing ......................................... 113

Changing the Instruction in a Program Line....................................113

Adding Instructions at the End of a Program ..................................114

Adding Instructions Within a Program...........................................115

Adding Instructions by Replacement.......................................115

Adding Instructions by Branching...........................................116

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 7 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

8 Contents

Section 11: Multiple Programs ...................................... 120

Storing Another Program ............................................................ 120

Running Another Program........................................................... 122

Part III. Solutions .................................................. 123

Section 12: Real Estate and Lending .............................. 124

Annual Percentage Rate Calculations With Fees............................. 124

Price of a Mortgage Traded at a Discount or Premium.................... 126

Yield of a Mortgage Traded at a Discount or Premium ................... 128

The Rent or Buy Decision ............................................................ 130

Deferred Annuities ..................................................................... 134

Section 13: Investment Analysis .................................... 136

Partial-Year Depreciation............................................................. 136

Straight-Line Depreciation..................................................... 136

Declining-Balance Depreciation ............................................ 139

Sum-of-the-Years-Digits Depreciation ...................................... 141

Full- and Partial-Year Depreciation with Crossover .......................... 144

Excess Depreciation................................................................... 148

Modified Internal Rate of Return................................................... 148

Section 14: Leasing...................................................... 151

Advance Payments..................................................................... 151

Solving For Payment ............................................................ 151

Solving for Yield ................................................................. 154

Advance Payments With Residual ................................................ 156

Solving for Payment............................................................. 156

Solving For Yield................................................................. 158

Section 15: Savings...................................................... 160

Nominal Rate Converted to Effective Rate ..................................... 160

Effective Rate Converted to Nominal Rate ..................................... 161

Nominal Rate Converted to Continuous Effective Rate..................... 162

Section 16: Bonds ........................................................ 163

30/360 Day Basis Bonds........................................................... 163

Annual Coupon Bonds ............................................................... 166

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 8 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

Contents 9

Appendixes................................................................ 169

Appendix A: The Automatic Memory Stack ................... 170

Getting Numbers Into the Stack: The Key..............................171

Termination of Digit Entry .....................................................172

Stack Lift.............................................................................172

Rearranging Numbers in the Stack ...............................................172

The key .....................................................................172

The Key.......................................................................172

One-Number Functions and the Stack...........................................173

Two-Number Functions and the Stack............................................173

Mathematics Functions .........................................................173

Percentage Functions............................................................ 174

Calendar and Financial Functions.................................................175

The LAST X Register and the Key .........................................176

Chain Calculations.....................................................................176

Arithmetic Calculations with Constants ..........................................177

Appendix B: More About L...................................... 179

Appendix C: Error Conditions ...................................... 181

Error 0: Mathematics..................................................................181

Error 1: Storage Register Overflow ...............................................182

Error 2: Statistics ........................................................................182

Error 3: IRR................................................................................182

Error 4: Memory ........................................................................182

Error 5: Compound Interest..........................................................183

Error 6: Storage Registers............................................................183

Error 7: IRR................................................................................184

Error 8: Calendar.......................................................................184

Error 9: Service..........................................................................184

Pr Error .....................................................................................184

Appendix D: Formulas Used ........................................ 185

Percentage ................................................................................185

Interest......................................................................................185

Simple Interest.....................................................................185

Compound Interest...............................................................186

Amortization..............................................................................186

Discounted Cash Flow Analysis....................................................187

Net Present Value ................................................................187

Internal Rate of Return ..........................................................187

Calendar ..................................................................................187

Actual Day Basis .................................................................187

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 9 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

10 Contents

30/360 Day Basis.............................................................. 187

Bonds ...................................................................................... 188

Depreciation ............................................................................. 189

Straight-Line Depreciation..................................................... 189

Sum-of-the-Years-Digits Depreciation ...................................... 189

Declining-Balance Depreciation ............................................ 190

Modified Internal Rate of Return................................................... 190

Advance Payments..................................................................... 190

Interest Rate Conversions ............................................................ 191

Finite Compounding............................................................ 191

Continuous Compounding.................................................... 191

Statistics ................................................................................... 191

Mean................................................................................ 191

Weighted Mean ................................................................. 191

Linear Estimation................................................................. 191

Standard Deviation ............................................................. 192

Factorial ............................................................................ 192

The Rent or Buy Decision ............................................................ 192

Appendix E: Battery, Warranty, and Service Information 193

Battery ..................................................................................... 193

Low-Power Indication.................................................................. 193

Installing a New Battery ...................................................... 193

Verifying Proper Operation (Self-Tests) .......................................... 194

Warranty.................................................................................. 196

Service..................................................................................... 197

Regulatory Information ............................................................... 199

Temperature Specifications.......................................................... 199

Noise Declaration ..................................................................... 199

Disposal of Waste Equipment by Users in Private Household in the

European Union ........................................................................ 200

Appendix F: United Kingdom Calculations .................... 201

Mortgages................................................................................ 201

Annual Percentage Rate (APR) Calculations ................................... 202

Bond Calculations ..................................................................... 202

Function Key Index...................................................... 203

Programming Key Index .............................................. 206

Subject Index.............................................................. 208

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 10 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

Making Financial

Calculations Easy

Before you begin to read through this handbook, let’s take a look at how easy financial calculations can be with your hp 12c. While working through the examples below, don’t be concerned about learning how to use the calculator; we’ll cover that thoroughly beginning with Section 1.

Example 1:

college education 14 years from today. You expect that the cost will be about $6,000 a year ($500 a month) for 4 years. Assume she will withdraw $500 at the beginning of each month from a savings account. How much would you have to deposit into the account when she enters college if the account pays 6% annual interest compounded monthly?

This is an example of a compound interest calculation. All such problems involve at least three of the following quantities:

z n: the number of compounding periods. z i: the interest rate per compounding period. z PV: the present value of a compounded amount. z PMT: the periodic payment amount. z FV: the future value of a compounded amount.

In this particular example:

z n is 4 years × 12 periods per year = 48 periods. z i is 6% per year ÷ 12 periods per year = 0.5% per period. z PV is the quantity to be calculated — the present value when the financial

z PMT is $500. z FV is zero, since by the time your daughter graduates she (hopefully!) will

To begin, turn the calculator on by pressing the ; key. Then, press the keys shown in the

Suppose you want to ensure that you can finance your daughter’s

transaction begins.

not need any more money.

Keystrokes

column below.

If you are not familiar with the use of an hp calculator keyboard, refer to the description on

pages 16 and 17.

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 11 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

12 Making Financial Calculations Easy

Note: A battery symbol (¼) shown in the lower-left corner of the display

when the calculator is on signifies that the available battery power is nearly exhausted. To install new batteries, refer to Appendix E.

The calendar functions and nearly all of the financial functions take some time to produce an answer. (This is typically just a few seconds, but the ¼, !, L, and S functions could require a half-minute or more.) During these calculations, the word running flashes in the display to let you know that the calculator is running.

Keystrokes Display

fCLEARHf2

4gA

6gC

500P

g× $

0.00

48.00

0.50

500.00

-21,396.61

Clears previous data inside the calculator and sets display to show two decimal places.

Calculates and stores the number of compounding periods.

Calculates and stores the periodic interest rate.

Stores periodic payment amount.

Sets payment mode to Begin.

Amount required to be deposited.

Example 2:

by the time your daughter enters college 14 years from now. Let’s say that she has a paid-up $5,000 insurance policy that pays 5.35% annually, compounded semiannually. How much would it be worth by the time she enters college?

In this example, we need to calculate FV, the future value.

Keystrokes Display

fCLEARG

14\2µn

5.35\2z¼

5000Þ$

We now need to determine how to accumulate the required deposit

-21,396.61

28.00

2.68

-5,000.00

10,470.85

Clears previous financial data inside the calculator.

Calculates and stores the number of compounding periods.

Calculates and stores the periodic interest rate.

Stores the present value of the policy.

Value of policy in 14 years.

Don’t be concerned now about the minus sign in the display. That and other details will be

explained in Section 3.

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 12 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

Making Financial Calculations Easy 13

Example 3:

provide about half the required amount. An additional amount must be set aside to provide the balance (21,396.61 – 10,470.85 = 10,925.76). Suppose you make monthly payments, beginning at the end of next month, into an account that pays 6% annually, compounded monthly. What payment amount would be required in order to accumulate $10,925.75 in the 14 years remaining?

Keystrokes Display

fCLEARG

14gA

6gC

10925.76M

gÂ

Example 4:

with 6% annual interest compounded monthly, but you can afford to make $45.00 monthly payments. What is the minimum interest rate that will enable you to accumulate the required amount?

In this problem, we do not need to clear the previous financial data inside the calculator, since most of it is unchanged from the preceding example.

Keystrokes Display

45ÞP

12§

The preceding example showed that the insurance policy will

10,470.85

168.00

0.50

10.925.76

–41.65

Suppose you cannot find a bank that currently offers an account

–45.00

0.42

5.01

Clears previous financial data inside the calculator.

Calculates and stores the number of compounding periods.

Calculates and stores the periodic interest rate.

Stores the future value required.

Sets payment mode to End.

Monthly payment required.

Stores payment amount.

Periodic interest rate.

Annual interest rate.

This is only a small sampling of the many financial calculations that can now be done easily with your hp 12c. To begin learning about this powerful financial tool, just turn the page.

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 13 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

Part I

Problem Solving

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 15 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

Section 1

Getting Started

Power On and Off

To begin using your hp 12c, press the ; key*. Pressing ; again turns the calculator off. If not manually turned off, the calculator will turn off automatically 8

to 17 minutes after it was last used.

Low-Power Indication

A battery symbol (¼) shown in the upper-left corner of the display when the calculator is on signifies that the available battery power is nearly exhausted. To replace the batteries, refer to Appendix E.

The Keyboard

Many keys on the hp 12c perform two or even three functions. The primary function of a key is indicated by the characters printed in white on the upper face of the key. The alternate function(s) of a key are indicated by the characters printed in gold above the key and the characters printed in blue on the lower face of the key. These alternate functions are specified by pressing the appropriate prefix key before the function key:

z To specify the alternate function printed in

above a key, press the gold prefix key (f), then press the function key.

z To specify the primary function printed on the uppe

face of a key, press the key alone.

z To specify the alternate function printed in blue on the

lower face of a key, press the blue prefix key (g), then press the function key.

Note that the ; key is lower than the other keys to help prevent its being pressed

inadvertently.

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 16 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

old

Section 1: Getting Started 17

Throughout this handbook, references to the operation of an alternate function appear as only the function name in a box (for example, “The L function …”). References to the selection of an alternate function appear preceded by the appropriate prefix key (for example, “Pressing functions shown on the keyboard in gold under the bracket labeled “CLEAR” appear throughout this handbook preceded by the word “CLEAR” (for example, “The CLEARH function …” or “Pressing fCLEARH …”).

If you press the f or g prefix key mistakenly, you can cancel it by pressing

CLEARX. This can also be pressed to cancel the ?, :, and i keys. (These keys are “prefix” keys in the sense that other keys must be pressed after them in order to execute the corresponding function.) Since the X key is also used to display the mantissa (all 10 digits) of a displayed number, the mantissa of the number in the display will appear for a moment after the X key is released.

Pressing the f or g prefix key turns on the corresponding status indicator — f or g — in the display. Each indicator turns off when you press a function key (executing an alternate function of that key), another prefix key, or fCLEARX.

…”). References to the

Keying in Numbers

To key a number into the calculator, press the digit keys in sequence, just as if you were writing the number on paper. A decimal point must be keyed in (using the decimal point key) if it is part of the number unless it appears to the right of the last digit.

Digit Separators

As a number is keyed in, each group of three digits to the left of the decimal point is automatically separated in the display. When the calculator is first turned on after coming from the factory — or after Continuous Memory is reset — the decimal point in displayed numbers is a dot, and the separator between each group of three digits is a comma. If you wish, you can set the calculator to display a comma for the decimal point and a dot for the three-digit separator. To do so, turn the calculator off, then press and hold down the . key while you press ;. Doing so again sets the calculator to use the original digit separators in the display.

Negative Numbers

To make a displayed number negative — either one that has just been keyed in or one that has resulted from a calculation — simply press Þ (change sign) . When the display shows a negative number — that is, the number is preceded by a minus sign — pressing Þ removes the minus sign from the display, making the number positive.

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 17 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

18 Section 1: Getting Started

Keying in Large Numbers

Since the display cannot show more than 10 digits of a number, numbers greater than 9,999,999,999 cannot be entered into the display by keying in all the digits in the number. However, such numbers can be easily entered into the display if the number is expressed in a mathematical shorthand called “scientific notation.” To convert a number into scientific notation, move the decimal point until there is only one digit (a nonzero digit) to its left. The resulting number is called the “mantissa” of the original number, and the number of decimal places you moved the decimal point is called the “exponent” of the original number. If you moved the decimal point to the left, the exponent is positive; if you moved the decimal point to the right (this would occur for numbers less than one), the exponent is negative. To key the number into the display, simply key in the mantissa, press Æ (enter exponent), then key in the exponent. If the exponent is negative, press Þ after pressing

For example, to key in $1,781,400,000,000, we move the decimal point 12 places to the left, giving a mantissa of 1.7814 and an exponent of 12:

Keystrokes Display

1.7814Æ12

Numbers entered in scientific notation can be used in calculations just like any other number.

1.7814 12

1,781,400,000,000 entered in scientific notation.

The CLEAR Keys

Clearing a register or the display replaces the number in it with zero. Clearing program memory replaces the instructions there with clearing operations on the hp 12c, as shown in the table below:

00. There are several

Key(s) Clears:

fCLEAR² Statistics registers (R1 through R6), stack registers, and

fCLEARÎ Program memory (only when pressed in Program mode).

fCLEARG Financial registers.

fCLEARH Data storage registers, financial registers, stack and LAST X

Display and X-register.

display.

registers, and display.

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 18 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

Section 1: Getting Started 19

Simple Arithmetic Calculations

Any simple arithmetic calculation involves two numbers and an operation — addition, subtraction, multiplication, or division. To do such a calculation on your hp 12c, you first tell the calculator the two numbers, then tell the calculator the operation to be performed. The answer is calculated when the operation key (+,-,§, or z) is pressed.

The two numbers should be keyed into the calculator in the order they would appear if the calculation were written down on paper left-to-right. After keying in the first number, press the \ key to tell the calculator that you have completed entering the number. Pressing \ separates the second number to be entered from the first number already entered.

In summary, to perform an arithmetic operation:

1. Key in the first number.

2. Press \ to separate the second number from the first.

3. Key in the second number.

4. Press +,-,§, or z to perform the desired operation.

For example to calculate 13 ÷ 2, proceed as follows:

Keystrokes Display

13.

13.00

6.50

Keys the first number into the calculator.

Pressing \ separates the second number from the first.

Keys the second number into the calculator.

Pressing the operation key calculates the answer.

Notice that after you pressed \, two zeroes appeared following the decimal point. This is nothing magical: the calculator’s display is currently set to show two decimal places of every number that has been entered or calculated. Before you pressed \, the calculator had no way of knowing that you had completed entering the number, and so displayed only the digits you had keyed in. Pressing

tells the calculator that you have completed entering the number: it terminates

digit entry. You need not press \ after keying in the second number because

the +,-,§ and z keys also terminate digit entry. (In fact, all keys terminate digit entry except for digit entry keys — digit keys, ., Þ, and Æ — and prefix keys — f, g, ?, :, and (.)

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 19 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

20 Section 1: Getting Started

Chain Calculations

Whenever the answer has just been calculated and is therefore in the display, you can perform another operation with this number by simply keying in the second number and then pressing the operation key: you need not press \ to separate the second number from the first. This is because when a number is keyed in after a function key (such as +,-,§, z, etc.) is pressed, the result of that prior calculation is stored inside the calculator — just as when the \ key is pressed.

The only time you must press the \ key to separate two numbers is when you are keying them both in, one immediately following the other.

The hp 12c is designed so that each time you press a function key in RPN mode, the calculator performs the operation then — not later — so that you see the results of all intermediate calculations, as well as the “bottom line.”

Example:

and you’ve just deposited your paycheck for $1,053.00 into your checking account. If your latest balance was $58.33 and the checks were written for $22.95, $13.70, and $10.14, what is the new balance?

Solution:

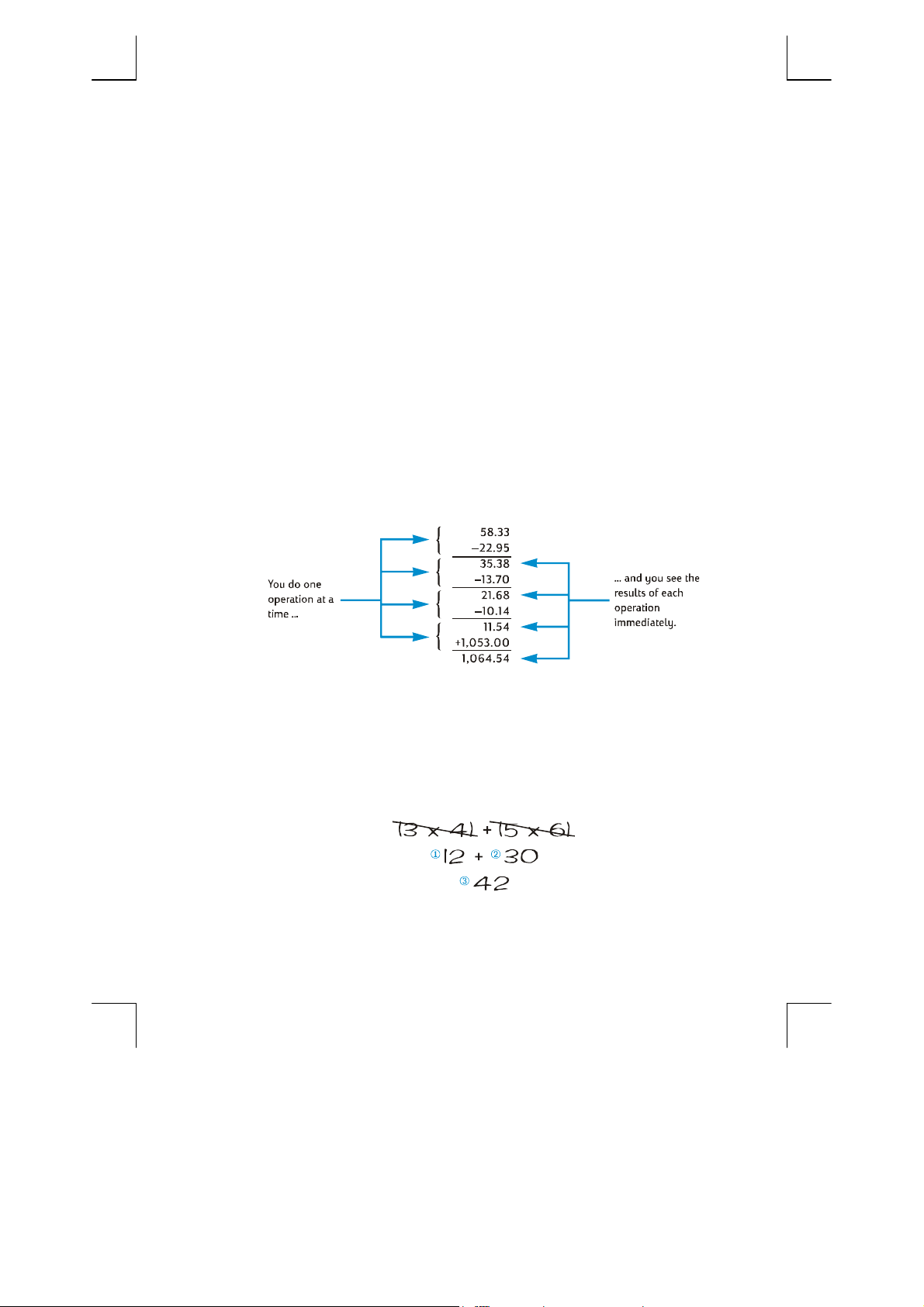
Keystrokes Display

58.33 \

22.95

13.70

Suppose you’ve written three checks without updating your checkbook,

When written down on paper, this problem would read

58.33 – 22.95 – 13.70 – 10.14 + 1053

58.33

22.95

35.38

13.70

Keys the first number.

Pressing \ separates the second number from the first.

Keys in the second number.

Pressing - subtracts the second number from the first. The calculator displays the result of this calculation, which is the balance after subtracting the first check.

Keys in the next number. Since a calculation has just been performed, do not press \; the next number entered (13.70) is automatically separated from the one previously in the display (35.38).

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 20 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

Section 1: Getting Started 21

Keystrokes Display

10.14-

1053+

The preceding example demonstrates how the hp 12c calculates just as you would using pencil and paper (except a lot faster!):

21.68

11.54

1,064.54

Pressing - subtracts the number just entered from the number previously in the display. The calculator displays the result of this calculation, which is the balance after subtracting the second check.

Keys in the next number and subtracts it from the previous balance. The new balance appears in the display. (It’s getting rather low!)

Keys in the next number — the paycheck deposited — and adds it to the previous balance. The new, current balance appears in the display.

Let’s see this happening in a different type of calculation — one that involves multiplying groups of two numbers and then adding the results. (This is the type of calculation that would be required to total up an invoice consisting of several items with different quantities and different prices.)

For example, consider the calculation of (3 × 4) + (5 × 6). If you were doing this on paper, you would first do the multiplication in the first parentheses, then the multiplication in the second parentheses, and finally add the results of the two multiplications:

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 21 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

22 Section 1: Getting Started

=+×

Your hp 12c calculates the answer in just the same way:

Keystrokes Display

3\4§

5\6§

Notice that before doing step 2, you did not need to store or write down the result of step 1: it was stored inside the calculator automatically. And after you keyed in the 5 and the 6 in step 2, the calculator was holding two numbers (12 and 5) inside for you, in addition to the 6 in the display. (The hp 12c can hold a total of three numbers inside, in addition to the number in the display.) After step 2, the calculator was still holding the 12 inside for you, in addition to the 30 in the display. You can see that the calculator holds the number for you, just as you would have them written on paper, and then calculates with them at the proper time, just as you would yourself.

down the results of an intermediate calculation, and you don’t even need to manually store it and recall it later.

By the way, notice that in step 2 you needed to press \ again. This is simply because you were again keying in two numbers immediately following each other, without performing a calculation in between.

To check your understanding of how to calculate with your hp 12c, try the following problems yourself. Although these problems are relatively simple, more complicated problems can be solved using the same basic steps. If you have difficulty obtaining the answers shown, review the last few pages.

12.00

30.00

42.00

But with the hp 12c, you don’t need to write

Step 1: Multiply the numbers in the first parentheses.

Step 2: Multiply the numbers in the second parentheses.

Step 3: Add the results of the two multiplications.

00.77)65()43(

)1427(

−

25.0

)3814(

21163

13.0

Although you don’t need to know just how these numbers are stored and brought back at just

the right time, if you’re interested you can read all about it in Appendix A. By gaining a more complete understanding of the calculator’s operation, you’ll use it more efficiently and confidently, yielding a better return on the investment in your hp 12c.

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 22 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

Section 1: Getting Started 23

Storage Registers

Numbers (data) in the hp 12c are stored in memories called “storage registers” or simply “registers.” (The singular term “ memory” is sometimes used in this handbook to refer to the entire collection of storage registers.) Four special registers are used for storing numbers during calculations (these “stack registers” are described in Appendix A), and another (called the “LAST X” register) is used for storing the number last in the display before an operation is performed. In addition to these registers into which numbers are stored automatically, up to 20 “data storage” registers are available for manual storage of numbers. These data storage registers are designated R are available for data storage if a program has been stored in the calculator (since the program is stored in some of those 20 registers), but a minimum of 7 registers is always available. Still other storage registers — referred to as the “financial registers” — are reserved for numbers used in financial calculations.

Storing and Recalling Numbers

To store the number from the display into a data storage register:

1. Press ? (store).

2. Key in the register number: 0 through 9 for registers R

through .9 for registers R

Similarly, to recall a number from a storage register into the display, press : (recall), then key in the register number. This copies the number from the storage register into the display; the number remains unaltered in the storage register. Furthermore, when this is done, the number previously in the display is automatically held inside the calculator for a subsequent calculation, just as the number in the display is held when you key in another number.

Example:

Before you leave to call on a customer interested in your personal computer, you store the cost of the computer ($3,250) and also the cost of a printer ($2,500) in data storage registers. Later, the customer decides to buy six computers and one printer. You recall the cost of the computer, multiply by the quantity ordered, and then recall and add the cost of the printer to get the total invoice.

Keystrokes Display

3250?1

2500?2 ;

through R9 and R.0 through R.9. Fewer registers

through R9, or .0

through R.9.

3,250.00

2,500.00

Stores the cost of the computer in R1.

Stores the cost of the printer in R2.

Turns the calculator off.

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 23 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

24 Section 1: Getting Started

Later that same day …

Keystrokes Display

;

6§

2,500.00

3,250.00

19,500.00

2,500.00

22,000.00

Turns the calculator back on.

Recalls the cost of the computer to the display.

Multiplies the quantity ordered to get the cost of the computers.

Recalls the cost of the printer to the display.

Total invoice.

Clearing Storage Registers

To clear a single storage register — that is, to replace the number in it with zero — merely store zero into it. You need not clear a storage register before storing data into it; the storing operation automatically clears the register before the data is stored.

To clear all storage registers at once — including the financial registers, the stack registers, and the LAST X register — press fCLEARH.

display.

All storage registers are also cleared when Continuous Memory is reset (as described on page 70).

This also clears the

Storage Register Arithmetic

Suppose you wanted to perform an arithmetic operation with the number in the display and the number in a storage register, then store the result back into the same register without altering the number in the display. The hp 12c enables you to do all this in a single operation:

1. Press ?.

2. Press +, -, §, or z to specify the desired operation.

3. Key in the register number.

When storage register arithmetic is performed, the new number in the register is determined according to the following rule:

CLEARH is not programmable.

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 24 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

Section 1: Getting Started 25

Storage register arithmetic is possible with only registers R0 through R

Example:

In the example on page 20, we updated the balance in your

checkbook. Let’s suppose that because data is stored indefinitely in your calculator’s Continuous Memory, you keep track of your checking account balance in the calculator. You could use storage register arithmetic to quickly update the balance after depositing or writing checks.

Keystrokes Display

58.33?0

22.95?-0

58.33

22.95

Stores the current balance in register

Subtracts the first check from the balance in R

. Note that the display

continues to show the amount subtracted; the answer is placed only in R

13.70?-0

10.14?-0

1053?+0

13.70

10.14

1,053.00

1,064.54

Subtracts the second check.

Subtracts the third check.

Adds the deposit.

Recalls the number in R0 to check the new balance.

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 25 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

Section 2

Percentage and Calendar

Functions

Percentage Functions

The hp 12c includes three keys for solving percentage problems: b, à, and Z. You don’t need to convert percentages to their decimal equivalents; this is done automatically when you press any of these keys. Thus, 4% need not be changed to

0.04; you key it in the way you see and say it: 4b.

Percentages

To find the amount corresponding to a percentage of a number:

1. Key in the base number.

2. Press \.

3. Key in the percentage.

4. Press b.

For example, to find 14% of $300:

Keystrokes Display

300

300.

300.00

14.

42.00

Keys in the base number.

Pressing \ separates the next number entered from the first number, just as when an ordinary arithmetic calculation is performed.

Keys in the percentage.

Calculates the amount.

If the base number is already in the display as a result of a previous calculation, you should not press \ before keying in the percentage — just as in a chain arithmetic calculation.

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 26 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

Section 2: Percentage and Calendar Functions 27

Net Amount

A net amount — that is, the base amount plus or minus the percentage amount — can be calculated easily with your hp 12c, since the calculator holds the base amount inside after you calculate a percentage amount. To calculate a net amount, simply calculate the percentage amount, then press = or -.

Example:

a discount of 8%, and the sales tax is 6%. Find the amount the dealer is charging you, then find the total cost to you, including tax.

Keystrokes Display

13250\

6b =

You’re buying a new car that lists for $13,250. The dealer offers you

13,250.00

1,060.00

12,190.00

731.40

12,921.40

Keys in the base amount and separates it from the percentage.

Amount of discount.

Base amount less discount.

Amount of tax (on $12,190).

Total cost: base amount less discount plus tax.

Percent Difference

To find the percent difference between two numbers:

1. Key in the base number.

2. Press \ to separate the other number from the base number.

3. Key in the other number.

4. Press à.

If the other number is greater than the base number, the percent difference will be positive. If the other number is less than the base number, the percent difference will be negative. Therefore, a positive answer indicates an increase, while a negative answer indicates a decrease.

If you are calculating a percent difference over time, the base number is typically the amount occurring first.

Example:

percent change?

Keystrokes Display

58.5\

53.25

Yesterday your stock fell from 58

58.50

53.25

–8.97

/2 to 531/4 per share. What is the

Keys in the base number and separates it from the other number.

Keys in the other number.

Nearly a 9% decrease.

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 27 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

28 Section 2: Percentage and Calendar Functions

The à key can be used for calculations of the percent difference between a wholesale cost and a retail cost. If the base number entered is the wholesale cost, the percent difference is called the markup; if the base number entered is the retail cost, the percent difference is called the margin. Examples of markup and margin calculations are included in the hp 12c Solutions Handbook.

Percent of Total

To calculate what percentage one number is of another:

1. Calculate the total amount by adding the individual amounts, just as in a chain arithmetic calculation.

2. Key in the number whose percentage equivalent you wish to find.

3. Press Z.

Example:

$2.36 million in Europe, and $1.67 million in the rest of the world. What percentage of the total sales occurred in Europe?

Keystrokes Display

3.92\

2.36+

1.67+

2.36

Last month, your company posted sales of $3.92 million in the U.S.,

3.92

6.28

7.95

2.36

29.69

Keys in the first number and separates it from the second.

Adds the second number.

Adds the third number to get the total. Keys in 2.36 to find what percentage

it is of the number in the display. Europe had nearly 30% of the total

sales.

The hp 12c holds the total amount inside after a percent of total is calculated. Therefore, to calculate what percentage another amount is of the total:

1. Clear the display by pressing O.

2. Key in that amount.

3. Press Z again.

For example, to calculate what percent of the total sales in the preceding example occurred in the U.S. and what percent occurred in the rest of the world:

Keystrokes Display

O3.92Z

O1.67 Z

49.31

21.01

The U.S. had about 49% of the total sales.

The rest of the world had about 21% of the total sales.

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 28 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

Section 2: Percentage and Calendar Functions 29

To find what percentage a number is of a total, when you already know the total number:

1. Key in the total number.

2. Press \ to separate the other number from the total number.

3. Key in the number whose percentage equivalent you wish to find.

4. Press Z.

For example, if you already knew in the preceding example that the total sales were $7.95 million and you wanted to find what percentage of that total occurred in Europe:

Keystrokes Display

7.95\

2.36

7.95

2.36

29.69

Keys in the total amount and separates it from the next number.

Keys in 2.36 to find what percentage it is of the number in the display.

Europe had nearly 30% of the total sales.

Calendar Functions

The calendar functions provided by the hp 12c — D and Ò — can handle dates from October 15, 1582 through November 25, 4046.

Date Format

For each of the calendar functions — and also for bond calculations (E and

)

the calculator uses one of two date formats. The date format is used to

—

interpret dates when they are keyed into the calculator as well as for displaying dates.

Month-Day-Year.

key in a date with this format in effect:

1. Key in the one or two digits of the month.

2. Press the decimal point key (.).

3. Key in the two digits of the day.

4. Key in the four digits of the year.

Dates are displayed in the same format.

For example, to key in April 7, 2004:

Keystrokes Display

4.072004

To set the date format to month-day-year, press

4.072004

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 29 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

gÕ

. To

30 Section 2: Percentage and Calendar Functions

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 30 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

Section 2: Percentage and Calendar Functions 31

Keystrokes Display

14.052004\

120gD

When D is executed as an instruction in a running program, the calculator pauses for about 1 second to display the result, then resumes program execution.

14.05

11,09,2004 6

Keys in date and separates it from number of days to be entered.

The expiration date is 11 September 2004, a Saturday.

Number of Days Between Dates

To calculate the number of days between two given dates:

1. Key in the earlier date and press \.

2. Key in the later date and press gÒ.

The answer shown in the display is the actual number of days between the two dates, including leap days (the extra days occurring in leap years), if any. In addition, the hp 12c also calculates the number of days between the two dates on the basis of a 30-day month. This answer is held inside the calculator; to display it, press ~. Pressing ~ again will return the original answer to the display.

Example:

of days or the number of days counted on the basis of a 30-day month. What would be the number of days counted each way, to be used in calculating the simple interest accruing from June 3, 2004 to October 14, 2005? Assume that you normally express dates in the month-day-year format.

Keystrokes Display

gÕ

6.032004\

10.142005gÒ

Simple interest calculations can be done using either the actual number

11.09

6.03

498.00

491.00

Sets date format to month-day-year. (Display shown assumes date remains from preceding example.)

Keys in earlier date and separates it from the later date.

Keys in later date. Display shows actual number of days.

Number of days counted on the basis of a 30-day month.

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 31 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

Section 3

Basic Financial Functions

The Financial Registers

In addition to the data storage registers discussed on page 23, the hp 12c has five special registers in which numbers are stored for financial calculations. These registers are designated n, i, PV, PMT, and FV. The first five keys on the top row of the calculator are used to store a number from the display into the corresponding register, to calculate the corresponding financial value and store the result into the corresponding register, or to display the number stored in the corresponding register.

Storing Numbers Into the Financial Registers

To store a number into a financial register, key the number into the display, then press the corresponding key (n, ¼, $, P, or M).

Displaying Numbers in the Financial Registers

To display a number stored in a financial register, press : followed by the corresponding key.

†

Which operation is performed when one of these keys is pressed depends upon the last

preceding operation performed: If a number was just stored into a financial register (using n, ¼, $, P, M, A, or C), pressing one of these five keys calculates the corresponding value and stores it into the corresponding register; otherwise pressing one of these five keys merely stores the number from the display into the corresponding register.

It’s good practice to press the corresponding key twice after :, since often you may want

†

to calculate a financial value right after displaying another financial value. As indicated in the preceding footnote, if you wanted to display FV and then calculate PV, for example, you should press :MM$. If you didn’t press M the second time, pressing $ would store FV in the PV register rather than calculating PV, and to calculate PV you would have to press $ again.

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 32 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

Section 3: Basic Financial Functions 33

Clearing the Financial Registers

Every financial function uses numbers stored in several of the financial registers. Before beginning a new financial calculation, it is good practice to clear all of the financial registers by pressing fCLEARG. Frequently, however, you may want to repeat a calculation after changing a number in only one of the financial registers. To do so, do not press fCLEARG; instead, simply store the new number in the register. The numbers in the other financial registers remain unchanged.

The financial registers are also cleared when you press fCLEARH and when Continuous Memory is reset (as described on page 70).

Simple Interest Calculations

The hp 12c simultaneously calculates simple interest on both a 360-day basis and a 365-day basis. You can display either one, as described below. Furthermore, with the accrued interest in the display, you can calculate the total amount (principal plus accrued interest) by pressing +.

1. Key in or calculate the number of days, then press n.

2. Key in the annual interest rate, then press ¼.

3. Key in the principal amount, then press Þ$.

4. Press fÏ to calculate and display the interest accrued on a 360-day

basis.

5. If you want to display the interest accrued on a 365-day basis, press

d~.

6. Press + to calculate the total of the principal and the accrued interest now

in the display.

The quantities n, i, and PV can be entered in any order.

Example 1:

requested that you lend him $450 for 60 days. You lend him the money at 7% simple interest, to be calculated on a 360-day basis. What is the amount of accrued interest he will owe you in 60 days, and what is the total amount owed?

Keystrokes Display

60n

Your good friend needs a loan to start his latest enterprise and has

60.00

Stores the number of days.

Pressing the $ key stores the principal amount in the PV register, which then contains the

present value of the amount on which interest will accrue. The Þ key is pressed first to change the sign of the principal amount before storing it in the PV register. This is required by the cash flow sign convention, which is applicable primarily to compound interest calculations.

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 33 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

34 Section 3: Basic Financial Functions

Keystrokes Display

7¼ 450Þ$

fÏ +

7.00

–450.00

5.25

455.25

Stores the annual interest rate.

Stores the principal.

Accrued interest, 360-day basis.

Total amount: principal plus accrued interest.

Example 2:

example, but asks that you compute it on a 365-day basis rather than a 360-day basis. What is the amount of accrued interest he will owe you in 60 days, and what is the total amount owed?

Keystrokes Display

60n 7¼ 450Þ$

fÏd~ +

Your friend agrees to the 7% interest on the loan from the preceding

60.00

7.00 –450.00

5.18

455.18

If you have not altered the numbers in the n, i, and PV registers since the preceding example, you may skip these keystrokes.

Accrued interest, 365-day basis. Total amount: principal plus accrued

interest.

Financial Calculations and the Cash Flow Diagram

The concepts and examples presented in this section are representative of a wide range of financial calculations. If your specific problem does not appear to be illustrated in the pages that follow, don’t assume that the calculator is not capable of solving it. Every financial calculation involves certain basic elements; but the terminology used to refer to these elements typically differs among the various segments of the business and financial communities. All you need to do is identify the basic elements in your problem, and then structure the problem so that it will be readily apparent what quantities you need to tell the calculator and what quantity you want to solve for.

An invaluable aid for using your calculator in a financial calculation is the cash flow diagram. This is simply a pictorial representation of the timing and direction of financial transactions, labeled in terms that correspond to keys on the calculator.

The diagram begins with a horizontal line, called a time line. It represents the duration of a financial problem, and is divided into compounding periods. For example, a financial problem that transpires over 6 months with monthly compounding would be diagrammed like this:

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 34 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

Section 3: Basic Financial Functions 35

The exchange of money in a problem is depicted by vertical arrows. Money you receive is represented by an arrow pointing up from the point in the time line when the transaction occurs; money you pay out is represented by an arrow pointing down.

Suppose you deposited (paid out) $1,000 into an account that pays 6% annual interest and is compounded monthly, and you subsequently deposited an additional $50 at the end of each month for the next 2 years. The cash flow diagram describing the problem would look like this:

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 35 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

36 Section 3: Basic Financial Functions

The form in which n is entered determines whether or not the calculator performs financial calculations in Odd-Period mode (as described on pages 50 through 53). If n is a noninteger (that is, there is at least one nonzero digit to the right of the decimal point), calculations of i, PV, PMT, and FV are performed in Odd-Period mode.

z i is the interest rate per compounding period. The interest rate shown in the

cash flow diagram and entered into the calculator is determined by dividing the annual interest rate by the number of compounding periods. In the problem illustrated above, i = 6% ÷ 12.

z PV — the present value — is the initial cash flow or the present value of a

series of future cash flows. In the problem illustrated above, PV is the $1,000 initial deposit.

z PMT is the period payment. In the problem illustrated above PMT is the $50

deposited each month. When all payments are equal, they are referred to as annuities. (Problems involving equal payments are described in this section under Compound Interest Calculations; problems involving unequal payments can be handled as described in under Discounted Cash Flow Analysis: NPV and IRR. Procedures for calculating the balance in a savings account after a series of irregular and/or unequal deposits are included in the hp 12c Solutions Handbook.)

z FV — the future value — is the final cash flow or the compounded value of a

series of prior cash flows. In the particular problem illustrated above, FV is unknown (but can be calculated).

Solving the problem is now basically a matter of keying in the quantities identified in the cash flow diagram using the corresponding keys, and then calculating the unknown quantity by pressing the corresponding key. In the particular problem illustrated in the cash flow diagram above, FV is the unknown quantity; but in other problems, as we shall see later, n, i, PV, or PMT could be the unknown quantity. Likewise, in the particular problem illustrated above there are four known quantities that must be entered into the calculator before solving for the unknown quantity; but in other problems only three quantities may be known — which must always include n or i.

The Cash Flow Sign Convention

When entering the PV, PMT, and FV cash flows, the quantities must be keyed into the calculator with the proper sign, + (plus) or – (minus), in accordance with …

The Cash Flow Sign Convention: Money received (arrow pointing up)

is entered or displayed as a positive value (+). Money paid out (arrow pointing down) is entered or displayed as a negative value (–).

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 36 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

Section 3: Basic Financial Functions 37

The Payment Mode

One more bit of information must be specified before you can solve a problem involving periodic payments. Such payments can be made either at the beginning of a compounding period (payments in advance, or annuities due) or at the end of the period (payments in arrears, or ordinary annuities). Calculations involving payments in advance yield different results than calculations involving payments in arrears. Illustrated below are portions of cash flow diagrams showing payments in advance (Begin) and payments in arrears (End). In the problem illustrated in the cash flow diagram above, payments are made in arrears.

Regardless of whether payments are made in advance or in arrears, the number of payments must be the same as the number of compounding periods.

To specify the payment mode:

z Press g× if payments are made at the beginning of the compounding

periods.

z Press gÂ if payments are made at the end of the compounding periods.

BEGIN

The is not lit, the payment mode is set to End.

The payment mode remains set to what you last specified until you change it; it is not reset each time the calculator is turned on. However, if Continuous Memory is reset, the payment mode will be set to End.

status indicator is lit when the payment mode is set to Begin. If

BEGIN

Generalized Cash Flow Diagrams

Examples of various kinds of financial calculations, together with the applicable cash flow diagrams, appear under Compound Interest Calculations later in this section. If your particular problem does not match any of those shown, you can solve it nevertheless by first drawing a cash flow diagram, then keying the quantities identified in the diagram into the corresponding registers. Remember always to observe the sign convention when keying in PV, PMT, and FV.

The terminology used for describing financial problems varies among the different segments of the business and financial communities. Nevertheless, most problems involving compound interest can be solved by drawing a cash flow diagram in one of the following basic forms. Listed below each form are some of the problems to which that diagram applies.

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 37 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

38 Section 3: Basic Financial Functions

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 38 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

Section 3: Basic Financial Functions 39

Compound Interest Calculations

Specifying the Number of Compounding Periods and the Periodic Interest Rate

Interest rates are usually quoted at the annual rate (also called the nominal rate): that is, the interest rate per year. However, in compound interest problems, the interest rate entered into i must always be expressed in terms of the basic compounding period, which may be years, months, days, or any other time unit. For example, if a problem involves 6% annual interest compounded quarterly for 5 years, n — the number of quarters — would be 5 × 4 = 20 and i — the interest rate per quarter — would be 6% ÷ 4 = 1.5%. If the interest were instead compounded monthly, n would be 5 × 12 = 60 and i would be 6% ÷ 12 = 0.5%.

If you use the calculator to multiply the number of years by the number of compounding periods per year, pressing n then stores the result into n. The same is true for i. Values of n and i are calculated and stored like this in Example 2 on page 47.

If interest is compounded monthly, you can use a shortcut provided on the calculator to calculate and store n and i:

z To calculate and store n, key the number of years into the display, then press

gA.

z To calculate and store i, key the annual rate into the display, then press

gC.

Note that these keys not only multiply or divide the displayed number by 12; they also automatically store the result in the corresponding register, so you need not press the n or ¼ key next. The A and C keys are used in Example 1 on page 46.

Calculating the Number of Payments or Compounding Periods

1. Press fCLEARG to clear the financial registers.

2. Enter the periodic interest rate, using ¼ or C.

3. Enter at least two of the following values:

z Present value, using $. z Payment amount, using P. z Future value, using M.

4. If a PMT was entered, press g× or gÂ to set the payment mode.

5. Press n to calculate the number of payments or periods.

Note:

Remember to observe

the cash flow sign convention.

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 39 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

40 Section 3: Basic Financial Functions

If the answer calculated is not an integer (that is, there would be nonzero digits to the right of the decimal point), the calculator rounds the answer up to the next higher integer before storing it in the n register and displaying it.

n were calculated as 318.15,

n is rounded up by the calculator to show the total number of payments needed: n–1 equal, full payments, and one final, smaller payment. The calculator does not

automatically adjust the values in the other financial registers to reflect n equal payments; rather, it allows you to choose which, if any, of the values to adjust.

Therefore, if you want to know the value of the final payment (with which you can calculate a balloon payment) or desire to know the payment value for n equal payments, you will need to press one of the other financial keys, as shown in the following two examples.

Example 1:

Your rich uncle offers you a $35,000 loan at 10.5% interest. If you make $325 payments at the end of each month, how many payments will be required to pay off the loan, and how many years will this take?

You’re planning to build a log cabin on your vacation property.

319.00

would be the displayed answer.

For example, if

†

Keystrokes Display

fCLEARG

10.5gC 35000$

325ÞP

gÂ n

0.88

35,000.00

–325.00

328.00

Calculates and stores i. Stores PV.

Stores PMT (with minus sign for cash paid out).

Sets the payment mode to End.

Number of payments required.

The calculator will round n down to the next lower integer if the fractional portion of n is less

than 0.005.

After calculating n, pressing ¼, $, P, or M will recalculate the value in the

†

corresponding financial register.

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 40 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

Section 3: Basic Financial Functions 41

Keystrokes Display

12z

Because the calculator rounds the calculated value of n up to the next higher integer, in the preceding example it is likely that — while 328 payments will be required to pay off the loan — only 327 full payments of $325 will be required, the next and final payment being less than $325. You can calculate the final, fractional, 328th payment as follows:

Keystrokes Display

328n

:P +

Alternatively, you could make the fractional payment together with the 327th payment. (Doing so will result in a somewhat smaller total of all payments, since you will not have to pay interest during the 328th payment period.) You can calculate this final, larger, 327th payment (essentially a balloon payment) as follows:

Keystrokes Display

327n M

:P +

27.33

328.00

181.89

–325.00

–143.11

327.00

–141.87

–325.00

–466.87

Twenty-seven years and four months.

Stores total number of payments.*

Calculates FV — which equals the overpayment if 328 full payments were made.

Recalls payment amount.

Final, fractional payment.

Stores number of full payments.

Calculates FV — which is the balance remaining after 327 full payments.

Recalls payment amount.

Final, balloon payment.

Instead of having a fractional (or balloon) payment at the end of the loan, you might wish to make 327 or 328 equal payments. Refer to “Calculating the Payment Amount” on page 46 for a complete description of this procedure.

You could skip this step, since 328 is already stored in the n register. If you do so, however,

you will need to press M twice in the next step (for the reason discussed in the first footnote on page 32; you would not have to press M twice if you had not pressed 12z after w in the example above.) We choose to show this and the following example in a parallel format so that the procedure is easy to remember: the number you key is the number of the final payment — either the fractional payment or the balloon payment — whose amount is to be calculated.

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 41 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

42 Section 3: Basic Financial Functions

Example 2:

with a $775 deposit. The account pays 6 If you make semimonthly deposits of $50 beginning next month, how long will it take for your account to reach $4000?

Keystrokes Display

fCLEARG

6.25\24z¼ 775Þ$

50ÞP

4000M

gÂ n

You’re opening a savings account today (the middle of the month)

0.26

–775.00

–50.00

4,000.00

58.00

29.00

/4% interest compounded semimonthly.

Calculates and stores i.

Stores PV (with minus sign for cash paid out).

Stores PMT (with minus sign for cash paid out).

Stores FV.

Sets the payment mode to End.

Number of semimonthly deposits.

Number of months.

As in Example 1, it is likely that only 57 full deposits will be required, the next and final deposit being less than $50. You can calculate this final, fractional, 58th deposit as in Example 1, except that for this example you must subtract the original FV. (In Example 1, the original FV was zero.) The procedure is as follows:

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 42 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

Section 3: Basic Financial Functions 43

Keystrokes Display

4,027.27

Calculates FV – which equals the balance in the account if 58 full

–50.00

3,977.27

deposits were made.

Recalls amount of deposits.

Calculates the balance in the account if 57 full deposits were made and interest accrued during the 58 month.†

4000-

–22.73

Calculates final, fractional, 58th deposit required to reach $4,000.

Calculating the Periodic and Annual Interest Rates

1. Press fCLEARG to clear the financial registers.

2. Enter the number of payments or periods, using n or A.

3. Enter at least two of the following values:

z Present value, using $. z Payment amount, using P. z Future value, using M.

Note:

Remember to observe the cash flow si convention.

4. If a PMT was entered, press g× or gÂ to set the payment mode.

5. Press ¼ to calculate the periodic interest rate.

6. To calculate the annual interest rate, key in the number of periods per year,

then press §.

In this example, M must be pressed twice, since the preceding key pressed was z. If we

had stored the number of deposits in n (as we did following Example 1), we would have to press M only once here, since the preceding key pressed would have been w (as it was following Example 1). Remember that it is not necessary to store the number of payments in n before calculating the amount of the final, fractional payment. (Refer to the preceding footnote.)

You might think that we could calculate the balance in the account after 57 full deposits were

†

made simply by storing that number in n and then calculating FV, as we did using the second method following Example 1. However, this balance would not include the interest accrued during the 58th month.

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 43 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

44 Section 3: Basic Financial Functions

Example:

8 years on an investment of $6,000 with quarterly compounding

Keystrokes Display

fCLEARG 8\4§w

6000Þ$

10000M ¼

4§

What annual interest rate must be obtained to accumulate $10,000 in

32.00

–6,000.00

10,000.00

1.61

6.44

Calculates and stores n.

Stores PV (with minus sign for cash paid out).

Stores FV.

Periodic (quarterly) interest rate.

Annual interest rate.

Calculating the Present Value

1. Press fCLEARG to clear the financial registers.

2. Enter the number of payments or periods, using n or A.

3. Enter the periodic interest rate, using ¼ or C.

4. Enter either or both of the following:

Note:

z Payment amount, using P. z Future value, using M.

5. If a PMT was entered, press g× or gÂ to set the payment mode.

6. Press $ to calculate the present value.

Remember to observe the cash flow si convention.

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 44 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

Section 3: Basic Financial Functions 45

Example 1:

that requires 15% interest compounded monthly over the 4-year term of the loan. If you can make payments of $150 at the end of each month and your down payment will be $1,500, what is the maximum price you can pay for the car? (Assume the purchase date is one month prior to the date of the first payment.)

Keystrokes Display

fCLEARG 4gA

15gC 150ÞP

gÂ $

1500+

Example 2:

condominiums with an annual net cash flow of $17,500. The expected holding period is 5 years, and the estimated selling price at that time is $540,000. Calculate the maximum amount the company can pay for the condominiums in order to realize at least a 12% annual yield.

You’re financing a new car purchase with a loan from an institution

48.00

1.25

–150.00

5,389.72

6,889.72

A development company would like to purchase a group of

Calculates and stores n.

Calculates and stores i.

Stores PMT (with minus sign for cash paid out).

Sets payment mode to End.

Maximum amount of loan.

Maximum purchase price.

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 45 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

46 Section 3: Basic Financial Functions

Keystrokes Display

fCLEARG 5n

12¼ 17500P

540000M

gÂ $

5.00

12.00

17,500.00

540,000.00

–369,494.09

Stores n. Stores i.

Stores PMT. Unlike in the previous problem, here PMT is positive since it represents cash received.

Stores FV.

Sets payment mode to End.

The maximum purchase price to provide a 12% annual yield. PV is displayed with a minus sign since it represents cash paid out.

Calculating the Payment Amount

1. Press fCLEARG to clear the financial registers.

2. Enter the number of payments or periods, using n or A.

3. Enter the periodic interest rate, using ¼ or C.

4. Enter either or both of the following:

Note:

z Present value, using $. z Future value, using M.

5. Press g× or gÂ to set the payment mode.

6. Press P to calculate the payment amount.

Example 1:

/4% annual interest.

Calculate the payment amount on a 29-year, $43,400 mortgage at

Remember to observe the cash flow si convention.

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 46 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

Section 3: Basic Financial Functions 47

Keystrokes Display

fCLEARG 29gA

14.25gC 43400$

gÂ P

348.00

1.19

43,400.00

–523.99

Calculates and stores n.

Calculates and stores i.

Stores PV.

Sets payment mode to End.

Monthly payment (with minus sign for cash paid out).

Example 2:

after 15 years by making deposits in an account that pays 9 compounded semiannually. You open the account with a deposit of $3,200 and intend to make semiannual deposits, beginning six months later, from your profit-sharing bonus paychecks. Calculate how much these deposits should be.

Keystrokes Display

fCLEARG 15\2µw

9.75\2z¼ 3200Þ$

60000M

gÂ P

Looking forward to retirement, you wish to accumulate $60,000

30.00

4.88

–3200.00

60,000.00

–717.44

Calculates and stores n. Calculates and stores i.

Stores PV (with minus sign for cash paid out).

Stores FV.

Sets payment mode to End.

Semiannual payment (with minus sign for cash paid out).

/4% interest

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 47 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

48 Section 3: Basic Financial Functions

Calculating the Future Value

1. Press fCLEARG to clear the financial registers.

2. Enter the number of payments or periods, using n or A.

3. Enter the periodic interest rate, using ¼ or C.

4. Enter either or both of the following:

Note:

z Present value, using $. z Payment amount, using P.

5. If a PMT was entered, press g× or gÂ to set the payment mode.

6. Press M to calculate the future value.

Example 1:

on a 29-year, $43,400 mortgage at 14 seller requests a balloon payment at the end of 5 years, what would be the amount of the balloon?

In Example 1 on page 46, we calculated that the payment amount

/4% annual interest is $523.99. If the

Remember to observe the cash flow si convention.

Keystrokes Display

fCLEARG 5gA

14.25gC 43400$

523.99ÞP

gÂ M

60.00

1.19

43,400.00

–523.99

–42,652.37

Calculates and stores n. Calculates and stores i.

Stores PV.

Stores PMT (with minus sign for cash paid out).

Sets payment mode to End.

Amount of balloon payment.

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 48 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

Section 3: Basic Financial Functions 49

Example 2:

new account that pays 6 you have in the account after 2 years?

Keystrokes Display

fCLEARG 2gA

6.25gC 50ÞP

g× M

Example 3:

of 2% per year. Assuming this trend continues, calculate the value in 6 years of property presently appraised at $32,000.

If you deposit $50 a month (at the beginning of each month) into a

Property values in an unattractive area are depreciating at the rate

/4% annual interest compounded monthly, how much will

24.00

0.52

–50.00

1,281.34

Calculates and stores n. Calculates and stores i.

Stores PMT (with minus sign for cash paid out).

Sets payment mode to Begin.

Balance after 2 years.

Keystrokes Display

fCLEARG 6n

6.00

Stores n.

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 49 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

50 Section 3: Basic Financial Functions

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 50 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

Section 3: Basic Financial Functions 51

You can calculate i, PV, PMT, and FV for transactions involving an odd period simply by entering a noninteger n. (A noninteger is a number with at least one nonzero digit to the right of the decimal point.) This places the calculator in Odd-Period mode.

The integer part of n (the part to the left of the decimal point)

specifies the number of full payment periods, and the fractional part (the part to the right of the decimal) specifies the length of the odd period as a fraction of a full period. The odd period, therefore, cannot be greater than one full period.

The fractional part of n can be determined using either the actual number of odd days or the number of odd days counted on the basis of a 30-day month.

function can be used to calculate the number of odd days either way. The

The

†

fractional part of n is a fraction of a payment period, so the number of odd days must be divided by the number of days in a period. If interest is compounded monthly, for this number you can use either 30, 365/12, or (if the odd period falls entirely within a single month) the actual number of days in that month. Usually, a monthly period is taken to be 30 days long.

At your option, the calculations of i, PV, PMT, and FV can be performed with either simple interest or compound interest accruing during the odd period. If the C status indicator in the display is not lit, simple interest is used. To specify compound interest, turn the C indicator on by pressing

?Æ

Pressing

‡

?Æ

again

turns the C indicator off, and calculations will then be performed using simple interest for the odd period.

Calculations of i, PMT, and FV are performed using the present value at the end of the odd

period. This is equal to the number in the PV register plus the interest accrued during the odd period. When calculating PV in Odd-Period mode, the calculator returns a value equal to the present value at the beginning of the odd period and stores it in the PV register.

After calculating i, PV, PMT, or FV in Odd-Period mode, you should not try to calculate n. If

you do, the calculator will switch out of Odd-Period mode and compute n without taking the odd period into account. The values in the other financial registers will correspond to the new n, but the original assumptions for the problem will be changed.

The two methods of counting odd days will yield slightly different answers. If you are

†

calculating i to determine the annual percentage rate (APR) for an odd-period transaction, the lower APR will result if the calculation uses the greater number of odd days determined using the two methods.

?Æ is not programmable.

‡

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 51 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

52 Section 3: Basic Financial Functions

Example 1:

percentage rate (APR), with the payments made at the end of each month. If interest begins accruing on this loan on February 15, 2004 (so that the first period begins on March 1, 2004), calculate the monthly payment, with the odd days counted on the basis of a 30-day month and compound interest used for the odd period.

Keystrokes Display

fCLEARG Clears financial registers. gÕ gÂ ?Æ

2.152004\

3.012004

gÒ ~

30z

36+n

15gC 4500$ P

A 36-month loan for $4,500 accrues interest at a 15% annual

Sets date format to month-day-year.

Sets payment mode to End.

Turns on the

so that compound interest will be used for the odd period.

2.15

3.012004

15.00

16.00

0.53

36.53

1.25

4,500.00

–157.03

Keys in the date interest begins accruing and separates it from the next date entered.

Keys in the date of the beginning of the first period.

Actual number of odd days.

Number of odd days counted on the basis of a 30-day month.

Divides by the length of a monthly period to get the fractional part of n.

Adds the fractional part of n to the number of complete payment periods, then stores the result in n.

Calculates and stores i.

Stores PV.

Monthly payment.

indicator in the display,

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 52 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

Section 3: Basic Financial Functions 53

Example 2:

2004, so that the first period began on August 1, 2004. Payments of $120 are made at the end of each month. Calculate the annual percentage rate (APR), using the actual number of odd days and simple interest for the odd period.

Keystrokes Display

fCLEARG ?Æ

7.192004\

8.012004

gÒ

30z

42+n

3950$

120ÞP

12§

A 42-month car loan for $3,950 began accruing interest on July 19,

7.19

8.012004

13.00

0.43

42.43

3,950.00

–120.00

1.16

13.95

Clears financial registers.

Turns off the Cindicator in the display, so that simple interest will be used for the odd period.

Keys in the date interest begins accruing and separates it from the next date entered.

Keys in the date of the beginning of the first period.

Actual number of odd days.

Divides by the length of a monthly period to get the fractional part of n.

Adds the fractional part of n to the number of complete payment periods, then stores the result in n.

Stores PV.

Stores PMT (with minus sign for cash paid out).

Periodic (monthly) interest rate.

Annual percentage rate (APR).

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 53 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

54 Section 3: Basic Financial Functions

Amortization

The hp 12c enables you to calculate the amounts applied toward principal and toward interest from a single loan payment or from several payments, and also tells you the remaining balance of the loan after the payments are made.

To obtain an amortization schedule:

1. Press fCLEARG to clear the financial registers.

2. Enter the periodic interest rate, using ¼ or C.

3. Enter the amount of the loan (the principal), using $.

4. Key in the periodic payment, then press ÞP (the sign of PMT must be

negative, in accordance with the cash flow sign convention).

5. Press g× or (for most direct reduction loans) gÂ to set the payment

mode.

6. Key in the number of payments to be amortized.

7. Press

to display the amount from those payments applied toward

interest.

8. Press ~ to display the amount from those payments applied toward the

principal.

9. To display the number of payments just amortized, press dd.

10. To display the remaining balance of the loan, press :$.

11.To display the total number of payments amortized, press :n.

Example:

for $50,000 at 13

For a house you’re about to buy, you can obtain a 25-year mortgage

/4% annual interest. This requires payments of $573.35 (at the end of each month). Find the amounts that would be applied to interest and to the principal from the first year’s payments.

Keystrokes Display

fCLEARG

13.25gC 50000$

1.10

50,000.00

Enters i.

Enters PV.

All amounts calculated when f! is pressed are automatically rounded to the number of

decimal places specified by the display format. (The display format is described in Section 5.) This rounding affects the number inside the calculator as well as how the number appears in the display. The amounts calculated on your hp 12c may differ from those on the statements of lending institutions by a few cents, since different rounding techniques are sometimes used. To calculate answers rounded to a different number of decimal places, press f followed by the number of decimal places desired before you press f!.

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 54 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

Section 3: Basic Financial Functions 55

Keystrokes Display

573.35ÞP

gÂ

12f!

:$ :n

–573.35

–6,608.89

–271.31

49,728.69

12.00

Enters PMT (with minus sign for cash paid out).

Sets payment mode to End.

Portion of first year’s payments (12 months) applied to interest.

Portion of first year’s payments applied to principal.

Balance remaining after 1 year.

Total number of payments amortized.

The number of payments keyed in just before payments following any that have already been amortized. Thus, if you now press

12 principal from the second year’s payments (that is, the second 12 months):

Keystrokes Display

12f!

dd :$ :n

Pressing did so after each of the last two calculations, you may have noticed that PV and n had been changed from their original values. The calculator does this so that you can easily check the remaining balance and the total number of payments amortized. But because of this, if you want to generate a new amortization schedule from the beginning, you must reset PV to its original value and reset n to

For example, suppose you now wanted to generate an amortization schedule for each of the first two months:

Keystrokes Display

50000$ 0n

, your hp 12c will calculate the amounts applied to interest and to the

–6,570.72

–309.48

12.00

49,419.21

24.00

displays the number in the PV or n register. When you

50,000.00

0.00

is pressed is taken to be the

Portion of second year’s payments applied to interest.

Portion of second year’s payments applied to principal.

Number of payments just amortized. Balance remaining after 2 years.

Total number of payments amortized.

Resets PV to original value.

Resets n to zero.

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 55 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

56 Section 3: Basic Financial Functions

Keystrokes Display

1f!

If you want to generate an amortization schedule but do not already know the monthly payment:

1. Calculate PMT as described on page 46.

2. Press 0n to reset n to zero.

3. Proceed with the amortization procedure listed on page 54 beginning with step 6.

Example:

mortgage for the same principal ($50,000) and at the same interest rate (13 as in the preceding example. Calculate the monthly payment, then calculate the amounts applied to interest and to the principal from the first month’s payment. Since the interest rate is not being changed, do not press fCLEARG; to calculate PMT, just enter the new value for n, reset PV, then press P.

Suppose you obtained a 30-year mortgage instead of a 25-year

–552.08

–21.27

–551.85

–21.50

2.00

Portion of first payment applied to interest.

Portion of first payment applied to principal.

Portion of second payment applied to interest.

Portion of second payment applied to principal.

Total number of payments amortized.

/4%)

Keystrokes Display

30gA 50000$ P

0n 1f!

360.00

50,000.00

–562.89

0.00

–552.08

–10.81

49,989.19

Enters n.

Enters PV.

Monthly payment.

Resets n to zero.

Portion of first payment applied to interest.

Portion of first payment applied to principal.

Remaining balance.

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 56 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

Section 4

Additional Financial

Functions

Discounted Cash Flow Analysis: NPV and IRR

The hp 12c provides functions for the two most widely-used methods of discounted cash flow analysis: l (net present value) and L (internal rate of return). These functions enable you to analyze financial problems involving cash flows (money paid out or received) occurring at regular intervals. As in compound interest calculations, the interval between cash flows can be any time period; however, the amounts of these cash flows need not be equal.

To understand how to use l and L, let’s consider the cash flow diagram for an investment that requires an initial cash outlay (CF (CF

) at the end of the first year, and so on up to the final cash flow (CF6) at the

end of the sixth year. In the following diagram, the initial investment is denoted by

, and is depicted as an arrow pointing down from the time line since it is cash

paid out. Cash flows CF represent projected cash flow losses.

and CF4 also point down from the time line, because they

) and generates a cash flow

NPV is calculated by adding the initial investment (represented as a negative cash flow) to the present value of the anticipated future cash flows. The interest rate, i, will be referred to in this discussion of NPV and IRR as the rate of return.

value of NPV indicates the result of the investment:

Other terms are sometimes used to refer to the rate of return. These include: required rate of

return, minimally acceptable rate of return, and cost of capital.

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 57 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

The

58 Section 4: Additional Financial Functions

z If NPV is positive, the financial value of the investor’s assets would be

increased: the investment is financially attractive.

z If NPV is zero, the financial value of the investor’s assets would not change:

the investor is indifferent toward the investment.

z If NPV is negative, the financial value of the investor’s assets would be

decreased: the investment is not financially attractive.

A comparison of the NPV’s of alternative investment possibilities indicates which of them is most desirable: the greater the NPV, the greater the increase in the financial value of the investor’s assets.

IRR is the rate of return at which the discounted future cash flows equal the initial cash outlay: IRR is the discount rate at which NPV is zero. The value of IRR relative to the present value discount rate also indicates the result of the investment:

z If IRR is greater than the desired rate of return, the investment is financially

attractive.

z If IRR is equal to the desired rate of return, the investor is indifferent toward

the investment.

z If IRR is less than the desired rate of return, the investment is not financially

attractive.

Calculating Net Present Value (NPV)

Calculating NPV for Ungrouped Cash Flows.

If there are no equal consecutive cash flows, use the procedure described (and then summarized) below. With this procedure, NPV (and IRR) problems involving up to 20 cash flows (in addition to the initial investment CF

) can be solved. If two or more consecutive

cash flows are equal — for example, if the cash flows in periods three and four are both $8,500 — you can solve problems involving more than 20 cash flows, or you can minimize the number of storage registers required for problems involving less than 20 cash flows, by using the procedure described next (under Calculating NPV for Grouped Cash Flows, page 61).

The amount of the initial investment (CF

key. Pressing

stores CF

) is entered into the calculator using the

in storage register R0 and also stores the

number 0 in the n register.

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 58 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

Section 4: Additional Financial Functions 59

The amounts of the subsequent cash flows are stored – in the order they occur – in the remaining storage registers: CF thru R

, respectively. If there is a CF20, that amount is stored in the FV register.*

Each cash flow (CF

, CF2, etc.) is designated CFj, where j takes on values from 1

thru CF9 in R1 thru R9, and CF10 thru CF19 in R.0

up to the number of the final cash flow. The amount of a cash flow is entered using the K key. Each time

is pressed, the amount in the display is stored in the next available storage register, and the number in the n register is increased by 1. This register therefore counts how many cash flow amounts (in addition to the initial investment CF

) have been entered.

Note: When entering cash flow amounts — including the initial investment

— remember to observe the cash flow sign convention by pressing Þ

after keying in a negative cash flow.

In summary, to enter the cash flow amounts:

1. Press fCLEARH to clear the financial and storage registers.

2. Key in the amount of the initial investment, press Þ if that cash flow is negative, then press gJ. If there is no initial investment, press 0gJ.

3. Key in the amount of the next cash flow, press Þ if the cash flow is negative, then press gK. If the cash flow amount is zero in the next period, press 0 gK.

4. Repeat step 3 for each cash flow until all have been entered.

With the amounts of the cash flows stored in the calculator’s registers, you can calculate NPV as follows:

1. Enter the interest rate, using ¼ or C.

2. Press fl.

The calculated value of NPV appears in the display and also is automatically stored in the PV register.

If you have stored a program in the calculator, the number of registers available for storing

cash flow amounts may be less than 21. (Storage registers are automatically allocated to program lines beginning with R pages 93 thru 95.) The maximum number of cash flow amounts (in addition to CF be stored is the number that appears at the right of the display when gN is pressed. If the maximum number of cash flow amounts is stored, the final cash flow amount is always stored in the FV register. For example, if N displays P-08 r-20, the last cash flow amount that can be stored – CF flow amount that can be stored – CF

– will be stored in FV. Similarly, if N displays P-22 r-18, the last cash

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 59 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

and proceeding in reverse order to R7, as described on

– will be stored in FV.

) that can

60 Section 4: Additional Financial Functions

Example:

would like a return of at least 13%. He expects to keep the duplex 5 years and then sell it for $130,000; and he anticipates the cash flows shown in the diagram below. Calculate NPV to determine whether the investment would result in a return or a loss.

Note that although a cash flow amount ($4,500) occurs twice, these cash flows are not consecutive. Therefore, these cash flows must be entered using the method described above.

Keystrokes Display

fCLEARH 80000ÞgJ

500ÞgK

4500gK

5500gK

4500gK

130000gK

13¼ fl

An investor has an opportunity to buy a duplex for $80,000 and

0.00

–80,000.00

–500.00

4,500.00

5,500.00

4,500.00

130,000.00

5.00

13.00

212.18

Clears financial and storage registers. Stores CF0 (with minus sign for a

negative cash flow). Stores CF1 (with minus sign for a

negative cash flow). Stores CF2.

Stores CF3.

Stores CF4.

Stores CF5.

Checks number of cash flow amounts entered (in addition to CF

Stores i.

NPV.

Since NPV is positive, the investment would increase the financial value of the investor’s assets.

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 60 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

Section 4: Additional Financial Functions 61

Calculating

amounts (in addition to the initial investment CF

NPV

for Grouped Cash Flows.

A maximum of 20 cash flow

) can be stored in the hp 12c.*

However, problems involving more than 20 cash flows can be handled if among the cash flows there are equal consecutive cash flows. For such problems, you merely enter along with the amounts of the cash flows the number of times — up to 99 — each amount occurs consecutively. This number is designated N corresponding to cash flow amount CF

, and is entered using the a key. Each Nj

is stored in a special register inside the calculator.

This method can, of course, be used for problems involving fewer than 20 cash flows — and it will require fewer storage registers than the method described above under Calculating NPV for Ungrouped Cash Flows. Equal consecutive cash flows can be entered using that method — provided there are enough storage registers available to accommodate the total number of individual cash flows. The facility of grouping equal consecutive cash flows is provided to minimize the number of storage registers required.

Note: When entering cash flow amounts — including the initial investment

— remember to observe the cash flow sign convention by pressing Þ

after keying in the amount for a negative cash flow.

In summary, to enter the amounts of the cash flows and the number of times they occur consecutively:

1. Press fCLEARH to clear the financial and storage registers.

2. Key in the amount of the initial investment, press Þ if that cash flow is negative, then press gJ. If there is no initial investment, press 0gJ.

3. If the initial investment consists of more than one cash flow of the amount entered in step 2, key in the number of those cash flows, then press ga. If ga is not pressed, the calculator assumes that N

is 1.

4. Key in the amount of the next cash flow, press Þ if that cash flow is negative, then press gK. If the cash flow amount is zero in the next period, press 0gK.

5. If the amount entered in step 4 occurs more than once consecutively, key in the number of times that cash flow amount occurs consecutively, then press ga. If ga is not pressed, the calculator assumes that N

is 1 for the CFj

just entered.

6. Repeat steps 4 and 5 for each CF

and Nj until all cash flows have been

entered.

With the amounts of the cash flows and the number of times they occur consecutively stored in the calculator, NPV can be calculated by entering the interest rate and pressing

, just as described earlier.

If you have stored a program in the calculator, the number of registers available for storing

cash flow amounts may be less than 21.

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 61 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

62 Section 4: Additional Financial Functions

Example:

$79,000; and he would like a 13 10 years for $100,000 and anticipates the yearly cash flows shown in the table below:

An investor has an opportunity to purchase a piece of property for

/2% return. He expects to be able to sell it after

Year Cash Flow Year Cash Flow

1 2 3 4 5

Since two cash flow amounts ($10,000 and $9,000) are repeated consecutively, we can minimize the number of storage registers required by using the method just described.

Keystrokes Display

fCLEARH

79000ÞgJ

14000gK 11000gK 10000gK 3ga

9100gK 9000gK 2ga

4500gK 100000gK :n

13.5¼ fl

$14,000 $11,000 $10,000 $10,000 $10,000

0.00

–79,000.00

14,000.00

11,000.00

10,000.00

3.00

9,100.00

9,000.00

2.00

4,500.00

100,000.00

7.00

13.50

907.77

6 7 8 9

Clears financial and storage registers.

Initial investment (with minus sign for a negative cash flow).

First cash flow amount.

Next cash flow amount.

Number of times this cash flow amount occurs consecutively.

Next cash flow amount.

Number of times this cash flow amount occurs consecutively.

Next cash flow amount.

Final cash flow amount.

Seven different cash flow amounts have been entered.

Stores i.

NPV.

$9,100 $9,000 $9,000 $4,500

$100,000

Since NPV is positive, the investment would increase the financial value of the investor’s assets by $907.77.

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 62 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

Section 4: Additional Financial Functions 63

Calculating Internal Rate of Return (IRR)

1. Enter the cash flows using either of the methods described above under Calculating Net Present Value.

2. Press fL.

The calculated value of IRR appears in the display and also is automatically stored in the i register.

Note: Remember that the L function may take a significant amount of

time to produce an answer, during which the calculator displays running.

Example:

that the actual rate of return (that is, the IRR) was greater than the 13 calculation. Find the IRR.

Assuming the cash flows are still stored in the calculator, we need only press

Keystrokes Display

Note that the value calculated by L is the periodic rate of return. If the cash flow periods are other than years (for example, months or quarters), you can calculate the nominal annual rate of return by multiplying the periodic IRR by the number of periods per year.

As noted above, the calculator may take several seconds or even minutes to produce an answer for IRR. This is because the mathematical calculations for finding IRR are extremely complex, involving a series of iterations — that is, a series of successive calculations. In each iteration, the calculator uses an estimate of IRR as the interest rate in a computation of NPV. The iterations are repeated until the computed NPV reaches about zero.

If you do not want to wait for the computation of IRR to be completed, press any key. This halts the computation of IRR and displays the estimated value of IRR being used in the current iteration.

calculating NPV using this estimate: if the estimate is close to IRR, the NPV calculated with it should be close to zero.* The values of IRR is put into the i register at the end of each iteration. Therefore, to check how good an estimate of IRR is after that estimate is in the display, just press

The NPV calculated in the preceding example was positive, indicating

13.72

You can then check how good this estimate is by

†

IRR is 13.72%.

/2 used in the

In practice, because the complex mathematical calculations inside the calculator are done

with numbers rounded to 10 digits, NPV may never reach exactly zero. Nevertheless, the interest rate that results in a very small NPV is very close to the actual IRR.

Provided the first iteration has been completed.

†

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 63 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

64 Section 4: Additional Financial Functions

The complex mathematical characteristics of the IRR computation have an additional ramification: Depending on the magnitudes and signs of the cash flows, the computation of IRR may have a single answer, multiple answers, a negative answer or no answer.

For additional information regarding L, refer to Appendix B. For an alternative method of calculating IRR, refer to Section 13.

Reviewing Cash Flow Entries

z To display a single cash flow amount, press :, then key in the number of

the register containing the cash flow amount to be displayed. Alternatively, store the number of that cash flow amount (that is, the value of j for the CF

desired) in the n register, then press :gK.

z To review all the cash flow amounts, press :g K repeatedly. This

displays the cash flow amounts in reverse order — that is, beginning with the final cash flow and proceeding to CF

z To display the number of times a cash flow amount occurs consecutively —

that is, to display the N

for a CFj — store the number of that cash flow

amount (that is, the value of j) in the n register, then press :ga.

z To review all the cash flow amounts together with the number of times each

cash flow amount occurs consecutively (that is, to review each CF pair), press :ga:gK repeatedly. This displays N

beginning with the final cash flow amount and proceeding to N0 and

and Nj

followed by

Note: Neither L nor l change the number in the n register. However,

each time :gK is pressed, the number in the n register is decreased by 1. If this is done, or if you manually change the number in the n register in order to display a single N

and/or CFj, be sure to reset the number in the

n register to the total number of cash flow amounts originally entered (not including the amount of the initial investment CF

). If this is not done, NPV

and IRR calculations will give incorrect results; also, a review of cash flow entries would begin with N

and CFn, where n is the number currently in the

n register.

For example, to display the fifth cash flow amount and the number of times that amount occurs consecutively:

Keystrokes Display

9,000.00

5.00

CF5

Stores the value of j in the n register.

In the case of multiple answers for IRR, the decision criteria listed on page 57 should be

modified accordingly.

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 64 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

Section 4: Additional Financial Functions 65

Keystrokes Display

:ga

To display all the cash flow amounts and the number of times they occur consecutively:

Keystrokes Display

:ga :gK :ga :gK :ga :gK

. . .

2.00

7.00

1.00

100,000.00

1.00

4,500.00

2.00

9,000.00

. . .

Resets the number in the n register to its original value.

N7 CF7 N6 CF6 N5 CF5

. . .

:ga :gK :ga :gK 7n

1.00

14,000.00

1.00

–79,000.00

7.00

N1 CF1 N0 CF0

Resets the number in the n register to its original value.

Changing Cash Flow Entries

z To change a cash flow amount:

1. Key the amount into the display.

2. Press ?.

3. Key in the number of the register containing the cash flow amount to be changed.

z To change the number of times a cash flow amount occurs consecutively —

that is, to change the N

1. Store the number of that cash flow amount (that is, j) in the n register.

2. Key the number of times the cash flow amount occurs consecutively into the display.

3. Press ga.

for a CFj:

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 65 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

66 Section 4: Additional Financial Functions

Note: If you change the number in the n register in order to change an Nj,

be sure to reset the number in the n register to the total number of cash flow amounts originally entered (not including the amount of the initial investment

). If this is not done, NPV and IRR calculations will give incorrect results.

Example 1:

$11,000 to $9,000, then calculate the new NPV for a 13

With the cash flows now stored in the calculator, change CF

/2% return.

from

Keystrokes Display

9000?2

13.5¼ fl

9,000.00

13.50

–644.75

Stores the new CF2 in R2.

Stores i.*

The new NPV.

Since this NPV is negative, the investment would decrease the financial value of the investor’s assets.

Example 2:

Change N

from 2 to 4, then calculate the new NPV.

Keystrokes Display

5n 4ga

5.00

4.00

7.00

Stores j in the n register.

Stores the new N5.

Resets the number in the n register to its original value.

–1,857.21

The new NPV.

Bond Calculations

The hp 12c enables you to solve for bond price (and the interest accrued since the last interest date) and the yield to maturity.

The E and S calculations are

†

done assuming a semiannual coupon payment and using an actual/actual basis (such as for U.S. Treasury bonds and U.S. Treasury notes). In accordance with market convention, prices are based on a redemption (par) value of 100.

This step is necessary in this example because we have calculated IRR since the first time we

calculated NPV. The IRR calculation replaced the 13.5 we keyed into i before calculating NPV with the result for IRR – 13.72.

All bond calculations are performed in accordance with. the Securities Industry Association’s

†

recommendations as contained in Spence, Graudenz, and Lynch, Standard Securities Calculation Methods, Securities Industry Association, New York, 1973.

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 66 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

Section 4: Additional Financial Functions 67

To calculate bond price and yield for a 30/360 bond (that is, using the basis of a 30day month and a 360-day year — such as for municipal bonds, corporate bonds, and state and local government bonds), and to calculate bond price for bonds with an annual coupon payment, refer to Section 16: Bonds.

Bond Price

1. Enter the desired yield to maturity (as a percentage), using ¼.

2. Enter the annual coupon rate (as a percentage), using P.

3. Key in the settlement (purchase) date (as described on page 29), then press

4. Key in the maturity (redemption) date.

5. Press fE.

The price is shown in the display and also is stored in the PV register. The interest accrued since the last interest date is held inside the calculator: to display the interest, press ~; to add the interest to the price, press +.

Example:

Treasury bond that matures on June 4, 2018, if you want a yield of 8 Assume that you normally express dates in the month-day-year format.

Keystrokes Display

8.25¼

6.75P gÕ

4.282004\

6.042018

fE +

What price should you pay on April 28, 2004 for a 6

8.25

6.75

4.28

6.042018

87.62

90.31

Enters yield to maturity.

Enters coupon rate.

Sets date format to month-day-year.

Enters settlement (purchase) date.

Enters maturity (redemption) date.

Bond price (as a percent of par).

Total price, including accrued interest.

/4% U.S.

/4%.

Bond Yield

1. Enter the quoted price (as a percent of par), using $.

2. Enter the annual coupon rate (as a percentage), using P.

3. Key in the settlement (purchase) date, then press \.

4. Key in the maturity (redemption) date.

5. Press fS.

The yield to maturity is shown in the display and also is stored in the i register.

Note: Remember that the S function may take a significant amount of

time to produce an answer, during which the calculator displays running.

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 67 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

68 Section 4: Additional Financial Functions

Example:

example. What yield will that provide?

Keystrokes Display

3\8z

88+$

6.75P

4.282004\

6.042018 fS

The market is quoting 88

0.38

88.38

6.75

4.28

6.042018

8.15

/8% for the bond described in the preceding

Calculates 3/8.

Enters quoted price.

Enters coupon rate.

Enters settlement (purchase) date.

Enters maturity (redemption) date.

Bond yield.

Depreciation Calculations

The hp 12c enables you to calculate depreciation and the remaining depreciable value (book value minus salvage value) using the straight-line, sum-of-the-years-digits, and declining-balance methods. To do so with any of these methods:

1. Enter the original cost of the asset, using $.

2. Enter the salvage value of the asset, using M. If the salvage value is zero, press 0M.

3. Enter the expected useful life of the asset (in years), using n.

4. If the declining-balance method is being used, enter the declining-balance factor (as a percentage), using ¼. For example, 1 rate — 125 percent declining-balance — would be entered as 125¼.

5. Key in the number of the year for which depreciation is to be calculated.

6. Press:

z fV for depreciation using the straight-line

/4 times the straight-line

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 68 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

Section 4: Additional Financial Functions 69

Example:

5 years. Its salvage value is estimated at $500. Find the depreciation and remaining depreciable value for the first 3 years of the machine’s life using the declining-balance method at double the straight-line rate (200 percent declining-balance).

Keystrokes Display

10000$ 500M 5n 200¼ 1f# ~

2f# ~

3f# ~

To calculate depreciation and the remaining depreciable value when the acquisition date of the asset does not coincide with the beginning of the fiscal accounting year, refer to the procedures in Section 13. That section also includes a procedure for depreciation calculations when changing from the declining-balance method to the straight-line method, and a procedure for calculating excess depreciation.

A metalworking machine, purchased for $10,000, is depreciated over

10,000.00

500.00

5.00

200.00

4,000.00

5,500.00

2,400.00

3,100.00

1,440.00

1,660.00

Enters original cost.

Enters salvage value.

Enters expected useful life.

Enters declining-balance factor.

Depreciation in first year.

Remaining depreciable value after first year.

Depreciation in second year.

Remaining depreciable value after second year.

Depreciation in third year.

Remaining depreciable value after third year.

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 69 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

Section 5

Additional Operating

Features

Continuous Memory

The calculator’s Continuous Memory contains the data storage registers, the financial registers, the stack and LAST X registers, program memory, and status information such as display format, date format, and payment mode. All information in Continuous Memory is preserved even while the calculator is turned off. Furthermore, information in Continuous Memory is preserved for a short time when the batteries are removed, so that you can change the batteries without losing your data and programs.

Continuous Memory may be reset if the calculator is dropped or otherwise traumatized, or if power is interrupted. You can also manually reset Continuous Memory as follows:

1. Turn the calculator off.

2. Hold down the - key, and press ;.

When Continuous Memory is reset:

z All registers are cleared. z Program memory consists of eight program lines, each containing the

instruction g(00.

z Display format is set to the standard format with two decimal places. z Date format is set to month-day-year. z Payment mode is set to End.

Whenever Continuous Memory has been reset, the display will show Pressing any key will clear this message from the display.

Pr Error

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 70 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

Section 5: Additional Operating Features 71

The Display

Status Indicators

Six indicators that appear along the bottom of the display signify the status of the calculator for certain operations. These status indicators are described elsewhere in this handbook where the relevant operation is discussed.

Number Display Formats

When the calculator is first turned on after coming from the factory or after Continuous Memory has been reset, answers are displayed with two decimal places.

Keystrokes Display

19.8745632\ 5-

Although you see only two decimal places, all calculations in your hp 12c are performed with full 10-digit numbers.

19.87

14.87

When only two decimal places are displayed, numbers are rounded to two decimal places: if the third digit is 5 through 9, the second digit is increased by one; if the third digit is 0 through 4, the second digit is not affected. Rounding occurs regardless of how many decimal places are displayed.

Several options are provided for controlling how numbers appear in the display. But regardless of which display format or how many displayed decimal places you specify, the number inside the calculator — which appears altered in the display — is not altered unless you use the B, !, V, Ý, or # functions.

Standard Display Format.

currently being displayed in the standard display format with two decimal places shown. To display a different number of decimal places, press f followed by a digit key (0 through 9) specifying the number of decimal places. In the following examples, notice how the displayed form of the number inside the calculator —

14.87456320 — is rounded to the specified number of digits.

The number 14.87 now in your calculator is

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 71 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

72 Section 5: Additional Operating Features

Keystrokes Display

f4 f1 f0 f9

The standard display format, plus the specified number of decimal places, remain in effect until you change them; they are not reset each time the calculator is turned on. However, if Continuous Memory is reset, when the calculator is next turned on numbers will be displayed in the standard display format with two decimal places shown.

If a calculated answer is either too small or too large to be displayed in the standard display format, the display format automatically switches to scientific notation (described below). The display returns to the standard display format for all numbers that can be displayed in that format.

14.8746

14.9

15.

14.87456320

Although nine decimal places were specified after f, only eight are displayed since the display can show a total of only 10 digits.

Scientific Notation Display Format

In scientific notation, a number is displayed with its mantissa at the left and a two-digit exponent at the right. The mantissa is simply the first seven digits in the number, and has a single, nonzero digit to the left of the decimal point. The exponent is simply how many decimal places you would move the decimal point in the mantissa before writing down the number in standard format. If the exponent is negative (that is, there is a minus sign between it and the mantissa), the decimal point should be moved to the left; this occurs for any number less than 1. If the exponent is positive (that is, there is a blank space between it and the mantissa), the decimal point should be moved to the right; this occurs for any number greater than or equal to 1.

To set the display format to scientific notation, press the display still shows

14.87456320

from the preceding example):

. For example (assuming

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 72 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

Section 5: Additional Operating Features 73

Keystrokes Display

1.487456 01

The exponent in this example indicates that the decimal point should be moved one decimal place to the right, giving the number 14.87456, which is the first seven digits of the number previously in the display.

To set the display back to standard display format, press f followed by the desired number of decimal places. Scientific notation display format remains in effect until you change to the standard display format; it is not reset each time the calculator is turned on. However, if Continuous Memory is reset, when the calculator is next turned on the standard display format, with two decimal places, will be used.

Mantissa Display Format.

Because both the standard display format and scientific notation display format often show only a few digits of a number, you may occasionally want to see all 10 digits — the full mantissa — of the number inside the calculator. To do so, press fCLEARX and hold down the X key. The display will show all 10 digits of the number as long as you hold down the

key; after you release the key, the number will again be displayed in the current display format. For instance, if the display still contains the result from the preceding example:

Keystrokes Display

fCLEARX

1487456320

All 10 digits of the number inside the calculator.

1.487456 01

Display returns to its former contents when the X key is released.

14.87

Returns display to standard format.

Special Displays

Running.

more to produce an answer. During these calculations, the word

Certain functions and many programs may take several seconds or

running

in the display to let you know that the calculator is running.

Overflow and Underflow.

magnitude is greater than 9.999999999 ×10 calculator displays

9.999999 99

If a calculation results in a number whose

(if the number is positive) or

, the calculation is halted and the

–9.999999 99

(if the number is negative).

If a calculation results in a number whose magnitude is less than 10 calculation is not halted, but the value 0 is used for that number in subsequent calculations.

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 73 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

flashes

–99

, the

74 Section 5: Additional Operating Features

Errors.

If you attempt an improper operation — such as division by zero — the

calculator will display the word

Error

the

Error

followed by a digit (0 through 9). To clear

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 74 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

Section 5: Additional Operating Features 75

Arithmetic Calculations With Constants

Example:

75, and 250. If the cost per fitting is $4.38, calculate the cost of each package.

Keystrokes Display

15\

4.38

250

Another method for doing arithmetic calculations with constants is described on page 177.

At Permex Pipes a certain pipe fitting is packaged in quantities of 15,

15.00

4.38

65.70

75.

4.38

328.50

250.

4.38

1,095.00

Keys first quantity into calculator.

Keys unit cost into display.

Cost of a package of 15.

Keys second quantity into display.

Recalls unit cost — which was last number in display before § was pressed — into display.

Cost of a package of 75.

Keys third quantity into display.

Recalls unit cost into display again.

Cost of a package of 250.

Recovering From Errors in Digit Entry

Example:

firm’s products (429,000) by the number of retail outlets (987) in order to calculate the average number distributed by each outlet. Unfortunately, you mistakenly key in the number of outlets as 9987 rather than as 987. It’s easy to correct:

Keystrokes Display

429000\

9987

429000\ 987z

Suppose you want to divide the total annual production for one of your

429,000.00

9,987.

42.96

9,987.00

429,000.00

434.65

You haven’t noticed your mistake yet.

About 43 products per outlet — but that seems too low!

Recalls to the display the number that was there before you press z. You see that you keyed it in wrong.

Begins the problem over.

The correct answer.

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 75 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

Section 6

Statistics Functions

Accumulating Statistics

The hp 12c can perform one- or two-variable statistical calculations. The data is entered into the calculator using the _ key, which automatically calculates and stores statistics of the data into storage registers R therefore referred to as the “statistics registers.”)

Before beginning to accumulate statistics for a new set of data, you should clear the statistics registers by pressing fclear².

In one-variable statistical calculations, to enter each data point — referred to as an “x-value” — key the x-value into the display, then press _.

In two-variable statistical calculations, to enter each data pair — referred to as the “x and y-values”:

1. Key the y-value into the display.

2. Press \.

3. Key the x-value into the display.

4. Press _.

Each time you press _, the calculator does the following:

z The number in R z The x-value is added to the number in R z The square of the x-value is added to the number in R z The y-value is added to the number in R z The square of the y-value is added to the number in R z The product of the x and y-values is added to the number in R

is increased by 1, and the result is copied into the display.

, through R6. (These registers are

This also clears the stack registers and the display.

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 76 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

Section 6: Statistics Functions 77

The table below shows where the accumulated statistics are stored.

R1 (and display) n: number of data pairs accumulated.

R2 Σx: summation of x-values.

R3 Σx2: summation of squares of x-values.

R4 Σy: summation of y-values.

R5 Σy2 summation of squares of y-values.

R6 Σxy: summation of products of x-values and y-values.

Correcting Accumulated Statistics

If you discover you have entered data incorrectly, the accumulated statistics can easily be corrected:

z If the incorrect data point or data pair has just been entered and _ has

been pressed, press gFg^.

z If the incorrect data point or data pair is not the most recent one entered, key

in the incorrect data point or data pair again as if it were new, but press g^ instead of _.

These operations cancel the effect of the incorrect data point or data pair. You can then enter the data correctly, using _, just as if it were new.

Mean

Pressing of the y-values ( pressed; to display the mean of the y-values, press ~.

Example:

the following hours a week and sell the following dollar volumes each month. How many hours does the average salesperson work each week? How much does the average salesperson sell each month?

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 77 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

gÖ

calculates the means (arithmetic averages) of the x-values (x) and

). The mean of the x-values appears in the display after Ö is

A survey of seven salespersons in your company reveals that they work

78 Section 6: Statistics Functions

Salesperson Hours/Week Hours/Week

1 32 $17,000

2 40 $25,000

3 45 $26,000

4 40 $20,000

5 38 $21,000

6 50 $28,000

7 35 $15,000

To find the average workweek and sales of this sample:

Keystrokes Display

fCLEAR² 32\

17000_ 40\

25000_ 45\

26000_ 40\

20000_ 38\

21000_ 50\

28000_ 35\

15000_

gÖ

0.00

32.00

1.00

40.00

2.00

45.00

3.00

40.00

4.00

38.00

5.00

50.00

6.00

35.00

7.00

21,714.29

40.00

Clears statistics registers.

First entry.

Second entry.

Third entry.

Fourth entry.

Fifth entry.

Sixth entry.

Total number of entries in the sample.

Mean dollar sales per month (x).

Mean workweek in hours (y).

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 78 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

Section 6: Statistics Functions 79

Standard Deviation

Pressing y-values (s

calculates the standard deviation of the x-values (sx) and of the

). (The standard deviation of a set of data is a measure of the dispersion

around the mean.) The standard deviation of the x-values appears in the display after v is pressed; to display the standard deviation of the y-values, press ~.

Example:

To calculate the standard deviations of the x-values and of the y-values

from the preceding example:

Keystrokes Display

gv ~

The formulas used in the hp 12c for calculating s

4,820.59

6.03

Standard deviation of sales.

Standard deviation of hours worked.

, and sy give best estimates of the

population standard deviation based on a sample of the population. Thus, current statistical convention calls them sample standard deviations. So we have assumed that the seven salespersons are a sample of the population of all salespersons, and our formulas derive best estimates of the population from the sample.

What if the seven salespersons constituted the whole population of salespersons. Then we wouldn’t need to estimate the population standard deviation. We can find the true population standard deviation (σ) when the data set equals the total population, using the following keystrokes.

Keystrokes Display

gÖ _ gv

21,714.29

8.00

4,463.00

5.58

Mean (dollars)

Number of entries + 1.

To continue summing data pairs, press

gÖg^

before entering more data.

It turns out that if you sum the mean of the population into the set itself and find the new s,

computed using the formulas on page 192, that s will be the population standard deviation, σ, of the original set.

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 79 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

80 Section 6: Statistics Functions

Linear Estimation

With two-variable statistical data accumulated in the statistics registers, you can

estimate a new y-value ( given a new y-value.

To calculate

1. Key in a new x-value.

2. Press gR.

To calculate

1. Key in a new y-value.

2. Press gQ.

Example:

the amount of sales delivered by a new salesperson working 48 hours per week.

Keystrokes Display

48gQ

The reliability of a linear estimate depends upon how closely the data pairs would, if plotted on a graph, lie in a straight line. The usual measure of this reliability is

the correlation coefficient, r. This quantity is automatically calculated whenever

or –1 indicates that the data pairs lie very close to a straight line. On the other hand, a correlation coefficient close to 0 indicates that the data pairs do not lie closely to a straight line; and a linear estimate using this data would not be very reliable.

Example:

displaying the correlation coefficient.

Keystrokes Display

Using the accumulated statistics from the preceding problem, estimate

is calculated; to display it, press ~. A correlation coefficient close to 1

Check the reliability of the linear estimate in the preceding example by

) given a new x-value, and estimate a new x-value (

28,818.93

0.90

Estimated sales for a 48 hour workweek.

The correlation coefficient is close to 1, so the sales calculated in the preceding example is a good estimate.

)

To graph the regression line, calculate the coefficients of the linear equation y = A + Bx.

1. Press 0gR to compute the y-intercept (A).

2. Press 1gR~d~- to compute the slope of the line (B).

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 80 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

Section 6: Statistics Functions 81

Example:

example.

Keystrokes Display

0gR

1 gR~d~-

The equation that describes the regression line is:

Compute the slope and intercept of the regression line in the preceding

15.55

0.001

y = 15.55 + 0.001x

y-intercept (A); projected value for x = 0.

Slope of the line (B); indicates the change in the projected values caused by an incremental chan the x value.

e in

Weighted Mean

You can compute the weighted mean of a set of numbers if you know the corresponding weights of the items in question.

1. Press fCLEAR².

2. Key in the value of the item and press \, then key in its weight and press _. Key in the second item’s value, press \, key in the second weight, and press _. Continue until you have entered all the values of the items and their corresponding weights. The rule for entering the data is “item \ weight _.”

3. Press g to calculate the weighted mean of the items.

Example:

four stations as follows: 15 gallons at $1.16 per gallon, 7 gallons at $1.24 per gallon, 10 gallons at $1.20 per gallon, and 17 gallons at $1.18 per gallon. You want to find the average cost per gallon of gasoline purchased. If you purchased the same quantity at each station, you could determine the simple arithmetic average or mean using the Ö key. But since you know the value of the item (gasoline) and its corresponding weight (number of gallons purchased), use the  key to find the weighted mean:

Suppose that you stop during a vacation drive to purchase gasoline at

Keystrokes Display

fCLEAR²

1.16\15_

1.24\7_

1.20\10_

1.18\17_

0.00

1.00

2.00

3.00

4.00

Clears statistics registers.

First item and weight.

Second item and weight.

Third item and weight.

Fourth item and weight.

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 81 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

82 Section 6: Statistics Functions

Keystrokes Display

g

A procedure for calculating the standard deviation and standard error (as well as the mean) of weighted or grouped data is included in the hp 12c Solutions Handbook.

1.19

Weighted mean cost per gallon.

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 82 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

Section 7

Mathematics and

Number-Alteration Functions

The hp 12c provides several keys for mathematical functions and for altering, numbers. These functions are useful for specialized financial calculations as well as for general mathematics calculations.

One-Number Functions

Most of the mathematics functions require that only one number be in the calculator (that is, the number in the display) before the function key is pressed. Pressing the function key then replaces the number in the display by the result.

Reciprocal.

that is, it divides 1 by the number in the display.

Square Root.

display.

Logarithm.

logarithm to the base e) of the number in the display. To calculate the common logarithm (that is, the logarithm to the base 10) of the number in the display, calculate the natural logarithm, then press 10

Exponential.

display — that is, it raises the base e to the number in the display.

Factorial.

that is, it calculates the product of the integers from 1 to n, where n is the number in the display.

Round.

inside the calculator is rounded when it appears in the display; but the display format alone does not affect the number itself inside the calculator. Pressing

version. Thus, to round a number in the display to a given number of decimal places, temporarily set the display format (as described on page 71) to show the desired number of decimal places, then press

Integer.

portion — that is, it replaces each digit to the right of the decimal point by 0. The number is changed inside the calculator as well as in the display. The original number can be recalled to the display by pressing

Pressing y calculates the reciprocal of the number in the display —

Pressing

The display format specifies to how many decimal places a number

, however, changes the number inside the calculator to match its displayed

Pressing

calculates the square root of the number in the

g°

calculates the natural logarithm (that is, the

g°z

calculates the exponential of the number in the

calculates the factorial of the number in the display —

gÑ

replaces the number in the display by its integer

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 83 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

84 Section 7: Mathematics and Number-Alteration Functions

Fractional.

portion — that is, it replaces all digits to the left of the decimal point by 0. Like

Ñ, T

version. The original number can be recalled to the display by pressing

All of the above functions are used basically in the same way. For example, to find the reciprocal of 0.258:

Keystrokes Display

.258 y

Any of the above functions can be done with a number in the display resulting from a previous calculation, as well as with a number you have just keyed in.

Keystrokes Display

fCLEARX

gÑ

Pressing

changes the number inside the calculator as well as its displayed

replaces the number in the display by its fractional

0.258

3.88

3875968992

3.88

3880000000

3.88

3.00

3.88

0.88

Keys the number into the display.

The reciprocal of 0.258, the original number.

Displays all 10 digits of the number inside the calculator.

Display returns to normal format when X key is released.

The number now in the display appears the same as before, but …

Displaying all 10 digits of the number inside the calculator shows

has changed the number to

match its displayed version.

Display returns to normal format.

The integer portion of the number previously displayed.

Recalls the original number to the display.

The fractional portion of the number previously displayed.

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 84 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

Section 7: Mathematics and Number-Alteration Functions 85

The Power Function

Pressing q calculates a power of a number — that is, yx. Like the arithmetic function +, q requires two numbers:

1. Key in the base number (which is designated by the y on the key).

2. Press \ to separate the second number (the exponent) from the first (the base).

3. Key in the exponent (which is designated by the x on the key).

4. Press q to calculate the power.

To Calculate Keystrokes Display

1.4

2\1.4q

–1.4

2\1.4Þq

(–2)3 2Þ\3q

1/3

or 2

2\3yq

2.64

0.38

–8.00

1.26

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 85 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

Part II

Programming

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 87 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

Section 8

Programming Basics

Why Use Programs?

A program is simply a sequence of keystrokes that is stored in the calculator. Whenever you have to calculate with the same sequence of keystrokes several times, you can save a great deal of time by incorporating these keystrokes in a program. Instead of pressing all the keys each time, you press just one key to start the program: the calculator does the rest automatically!

Creating a Program

Creating a program consists simply of writing the program, then storing it:

1. Write down the sequence of keystrokes that you would use to calculate the quantity or quantities desired.

2. Press fs to set the calculator to Program mode. When the calculator is in Program mode, functions are not executed when they are keyed in, but instead are stored inside the calculator. The PRGM status indicator in the display is lit when the calculator is in Program mode.

3. Press fCLEARÎ to erase any previous programs that may be stored inside the calculator. If you want to create a new program without erasing a program already stored, skip this step and proceed as described in Section 11, Multiple Programs.

4. Key in the sequence of keystrokes that you wrote down in step 1. Skip the beginning keystrokes that enter data, which would differ each time the program is used.

Example:

a program that calculates the net cost of an item after the discount is subtracted and the $5 handling charge is added.

First, we’ll manually calculate the net cost of an item listing for $200.

Keystrokes Display

200 \

25b

Your office supplies dealer is selling selected stock at 25% off. Create

200.

200.00

50.00

Keys in cost of item.

Separates cost of item from percentage to be keyed in next.

Amount of discount.

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 88 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

Section 8: Programming Basics 89

Keystrokes Display

5 +

Next, set the calculator to Program mode and erase any program(s) already stored:

Keystrokes Display

fCLEARÎ

Finally, press the keys that we used above to solve the problem manually. Do not key in 200; this number will vary each time the program is used. Don’t be concerned right now about what appears in the display as you press the keys; we’ll discuss that later in this section.

Keystrokes Display

5 +

150.00

155.00

00-

Price less discount.

Handling charge.

Net cost (price less discount plus handling charge).

Sets calculator to Program mode.

Clears program(s).

01- 36

02- 2

03- 5

04- 25

05- 30

06- 5

07- 40

Running a Program

To run (sometimes called “execute”) a program:

1. Press fs to set the calculator back to Run mode. If the calculator is

already in Run mode (that is, the PRGM status indicator in the display is not lit), skip this step.

2. Key any required data into the calculator, just as if you were calculating manually. When a program is run, it uses the data already keyed into the display and the registers inside the calculator.

3. Press t to begin program execution.

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 89 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

90 Section 8: Programming Basics

Example:

listing for $625 and an executive chair listing for $159.

Keystrokes Display

625 t

159 t

That’s all there is to creating and running simple programs! But if you want to use programs frequently, you’ll want to know more about programming — such as how to check what keystrokes are stored in program memory, how many keystrokes can be stored in program memory, how to correct or otherwise modify programs, how to skip keystrokes when running a program, and so on. Before you can understand these aspects of programming, we need to briefly discuss how keystrokes are treated by the calculator when they are stored in Program mode and when they are executed in Run mode.

Run the program created above to calculate the net cost of a typewriter

155.00

625.

473.75

159.

124.25

Sets calculator to Run mode. Display shows number previously calculated.

Keys in price of typewriter.

Net cost of typewriter.

Keys in list price of chair.

Net cost of chair.

Program Memory

Keystrokes entered into the calculator in Program mode are stored in program memory. Each digit, decimal point, or function key is called an instruction and is stored in one line of program memory — usually referred to simply as a program line. Keystroke sequences beginning with the f, g, ?, :, and i prefix

keys are considered to comprise a complete instruction and are stored in only one program line.

When a program is run, each instruction in program memory is executed — that is, the keystroke in that program line is performed, just as if you were pressing the key manually — beginning with the current line in program memory and proceeding sequentially with the higher-numbered program lines.

Whenever the calculator is in Program mode (that is, whenever the indicator in the display is lit), the display shows information about the program line to which the calculator is currently set. At the left of the display is the number of the program line within program memory. The remaining digits in the display comprise a code that indicates what instruction has been stored in that program line. No code is shown for program line 00, since no regular instruction is stored there.

PRGM

status

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 90 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

Section 8: Programming Basics 91

Identifying Instructions in Program Lines

Each key on the hp 12c keyboard — except for the digit keys 0 through 9 — is identified by a two-digit “keycode” that corresponds to the key’s position on the keyboard. The first digit in the keycode is the number of the key row, counting from row 1 at the top; the second digit is the number of the key in that row, counting from 1 for the first key in the row through 9 for the ninth key in the row and 0 for the tenth key in the row. The keycode for each digit key is simply the digit on the key. Thus, when you keyed the instruction b into program memory, the calculator displayed

04– 25

This indicates that the key for the instruction in program line 04 is in the second row on the keyboard and is the fifth key in that row: the b key. When you keyed the instruction + into program memory, the calculator displayed

07– 40

This indicates that the key for the instruction in program line 07 is in the fourth row on the keyboard and is the tenth key in that row: the + key. When you keyed the digit 5 into program memory, the keycode displayed was only the digit 5.

Since keystroke sequences beginning with f, g, ?, :, and i are stored in only one program line, the display of that line would show the keycodes for all the keys in the keystroke sequence.

Instruction Keycode

?=1 gi00

gÒ

nn- 43 26

nn- 44 40 1

nn- 43,33 00

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 91 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

92 Section 8: Programming Basics

Displaying Program Lines

Pressing line number and keycode for the program line to which the calculator is currently set.

Occasionally you’ll want to check several or all of the instructions stored in program memory. The hp 12c enables you to review program instructions either forward or backward through program memory:

For example, to display the first two lines of the program now stored in program memory, set the calculator to Program mode and press Ê twice:

Keystrokes Display

Ê Ê

to set the calculator from Run mode to Program mode displays the

z Pressing Ê (single step) while the calculator is in Program mode advances

the calculator to the next line in program memory, then displays that line number and the keycode of the instruction stored there.

z Pressing gÜ (back step) while the calculator is in Program mode sets the

calculator back to the previous line in program memory, then displays that line number and the keycode of the instruction stored there.

00-

01- 36

02- 2

Sets calculator to Program mode and displays current line of program memory

Program line 01: \

Program line 02: digit 2.

Pressing

Keystrokes Display

gÜ gÜ

If either the Ê key or the Ü key is held down, the calculator displays all of the lines in program memory. Press Ê again now, but this time hold it down until program line 07 is displayed.

Keystrokes Display

(Release Ê)

gÜ

does the reverse:

01- 36

00-

01- 36

. . .

07- 40

Program line 01.

Program line 00.

Program line 01

. . .

Program line 07

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 92 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

Section 8: Programming Basics 93

Program line 07 contains the last instruction you keyed into program memory. However, if you press Ê again, you’ll see that this is not the last line stored in program memory:

Keystrokes Display

As you should now be able to tell from the keycodes displayed, the instruction in program line 08 is

08- 43, 33 00

00.

Program line 08

The 00 Instruction and Program Line 00

Whenever you run the program now stored in program memory, the calculator executes the instruction in line 08 after executing the seven instructions you keyed in. This i00 instruction — as its name implies — tells the calculator to “go to” program line 00 and execute the instruction in that line. Although line 00 does not contain a regular instruction, it does contain a “hidden” instruction that tells the calculator to halt program execution. Thus, after each time the program is run, the calculator automatically goes to program line 00 and halts, ready for you to key in new data and run the program again. (The calculator is also automatically set to program line 00 when you press to Run mode.)

The i00 instruction was already stored in line 08 — in fact, in all program lines — before you keyed in the program. If no instructions have been keyed into program memory, if Continuous Memory is reset, or if fCLEARÎ is pressed (in Program mode), the instruction i00 is automatically stored in program lines 01 through 08. As you key each instruction into program memory, it replaces the

00 instruction in that program line.

If your program should consist of exactly eight instructions, there would be no

00 instructions remaining at the end of program memory. Nevertheless, after such a program is executed the calculator automatically returns to program line 00 and halts, just as if there were a i00 instruction following the program.

If you key in more than eight instructions, program memory automatically expands to accommodate the additional instructions.

to set the calculator from Program mode

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 93 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

94 Section 8: Programming Basics

Expanding Program Memory

If no instructions have been keyed into program memory, if Continuous Memory has been reset, or if fCLEARÎ has been pressed (in Program mode), program memory consists of 8 program lines, and there are 20 storage registers available for storage of data.

As you key in a ninth instruction, storage register R.9 is automatically converted into seven new lines of program memory. The instruction you key in is stored in program line 09, and the instruction i00 is automatically stored in program lines 10 through 15.

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 94 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

Section 8: Programming Basics 95

Program memory is automatically expanded like this whenever another seven instructions have been keyed into program memory — that is, when you key an instruction into program line 16, 23, 30 etc. In each case, the additional program lines made available are converted, seven lines at a time, from the last available data storage register (whether or not data has been stored in that register; if it has, it will be lost). Furthermore, the six new program lines (following the 16th, 23th etc.) will each contain the instruction i00.

To determine at any time how many program lines (including those containing

00) are currently in program memory and how many storage registers are

currently available for conversion to program lines or for data storage, press

(memory). The calculator will respond with a display like the following:

Up to 99 instructions can be stored in program memory. Doing so would require the conversion of 13 data storage registers (because 99 = 8 + [13 × 7]), leaving 7 storage registers — R

If you find yourself creating long programs, you should create your programs so that they don’t use up program lines unnecessarily, since program memory is limited to 99 program lines. One way to minimize program length is to replace numbers consisting of more than just one digit — like the number 25 in lines 02 and 03 of the program keyed in above — by a : instruction, and then storing the number in the designated storage register before running the program. In this case, this would save one program line, since the : instruction requires only one program line, not two as are required by the number 25. Of course, doing so uses up data storage registers that you might want to save for other data. As in many business and financial decisions, there is a trade off involved; here it is between program lines and data storage registers.

through R6 — available for data storage.

Setting the Calculator to a Particular Program Line

There will be occasions when you’ll want to set the calculator directly to a particular program line — such as when you’re storing a second program in program memory or when you’re modifying an existing program. Although you can set the calculator to any line by using Ç as described above, you can do so more quickly as follows:

z With the calculator in Program mode, pressing gi. followed by two

digit keys sets the calculator to the program line specified by the digit keys, and then displays that line number and the keycode of the instruction stored there.

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 95 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

96 Section 8: Programming Basics

z With the calculator in Run mode, pressing gi followed by two digit keys

sets the calculator to the program line specified by the digit keys. Since the calculator is not in Program mode, the line number and keycode are not displayed.

The decimal point is not necessary if the calculator is in Run mode, but it is necessary if the calculator is in Program mode.

For example, assuming the calculator is still in Program mode, you can set it to program line 00 as follows:

Keystrokes Display

gi.00

Executing a Program One Line at a Time

Pressing Ç repeatedly with the calculator in Program mode (as described earlier) enables you to verify that the program you have stored is identical to the program you wrote — that is, to verify that you have keyed the instructions in correctly. However, this does not ensure that the program you wrote calculates the desired results correctly: even programs created by the most experienced programmers often do not work correctly when they are first written.

To help you verify that your program works correctly, you can execute the program one line at a time, using the Ç key. Pressing Ç while the calculator is in Run mode advances the calculator to the next line in program memory, then displays that line’s number and the keycode of the instruction stored there, just as in Program mode. In Run mode, however, when the Ç key is released the instruction in the program line just displayed is executed and the display then shows the result of executing that line.

For example, to execute the program stored in the calculator one line at a time:

00-

Program line 00

Keystrokes Display

625

124.25

625.

01- 36

625.00

02- 2

Sets calculator to Run mode and to line 00 in program memory. (Display shown assumes results remain from previous calculation.)

Keys in price of typewriter.

Program line 01: \

Result of executing program line

01.

Program line 02: 2.

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 96 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

Section 8: Programming Basics 97

Keystrokes Display

03- 5

25.

04- 25

156.25

05- 30

468.75

06- 5

07- 40

473.75

Result of executing program line

02.

Program line 03: 5.

Result of executing program line

03.

Program line 04: b

Result of executing program line

04.

Program line 05: -

Result of executing program line

05.

Program line 06: 5

Result of executing program line

06.

Program line 07: +

Result of executing program line 07 (the last line of the program).

Pressing previous line in program memory, then displays that line’s number and the keycode of the instruction stored there, just as in Program mode. In Run mode, however, when the Ü key is released the display again shows the same number as it did before executed.

gÜ

while the calculator is in Run mode sets the calculator to the

gÜ

was pressed: no instruction in program memory is

Interrupting Program Execution

Occasionally you’ll want a program to stop executing so that you can see an intermediate result or enter new data. The hp 12c provides two functions for doing so: u (pause) and t (run/stop).

Pausing During Program Execution

When a running program executes a u instruction, program execution halts for about 1 second, then resumes. During the pause, the calculator displays the last result calculated before the u instruction was executed.

If you press any key during a pause, program execution is halted indefinitely. To resume program execution at the program line following that containing the u instruction, press t.

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 97 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

98 Section 8: Programming Basics

Example:

Create a program that calculates the entries in the AMOUNT, TAX, and TOTAL columns for each item on the jewelry distributor’s invoice shown on the next page, and also calculates the total in each of these columns for all items on the invoice. Assume the sales tax is 6

/4%.

To conserve lines of program memory, instead of keying in the tax rate before the

instruction we’ll store it in register R

and recall it before the b instruction.

Before storing the program in program memory, we’ll calculate the required amounts for the first item on the invoice manually. The keystroke sequence will use storage register arithmetic (described on page 24) in registers R

, R2, and R3 to

calculate the column sums. Since these registers are cleared when fCLEAR² is pressed, we’ll press those keys before beginning the manual calculation — and also later, before running the program — to ensure that the column sums are “initialized” to zero. (Pressing fCLEARH would clear registers R but would also clear R

, which will contain the tax rate.)

through R3,

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 98 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

Section 8: Programming Basics 99

Pressing the

keys is not necessary when we do the calculations manually, since in Run mode the result of every intermediate calculation is displayed automatically; but we’ll include u instructions in the program so that the intermediate results AMOUNT and TAX are automatically displayed when the program is executed.

Keystrokes Display

6.75?0

fCLEAR²

13 \

6.75

0.00

13.

13.00

Stores tax rate in R0.

Clears the registers in R1 through R

Keys in quantity of item.

Separates quantity of item from cost of item to be keyed in next.

68.5

?+1

:0 b

?+2

?+3

68.5

890.50

6.75

60.11

950.61

Keys in cost of item.

AMOUNT.

Adds AMOUNT to sum of AMOUNT entries in register R

Recalls tax rate to display.

TAX.

Adds TAX to sum of TAX entries in register R

TOTAL.

Adds TOTAL to sum of TOTAL entries in register R

Now, we’ll store the program in program memory. Do not key in the quantity and cost of each item; these numbers will vary each time the program is run.

Keystrokes Display

00-

Sets calculator to Program mode.

fCLEARÎ

§ gu

?+1 :0 b

00-

01- 20

02- 43 31

03- 44 40 1

04- 45 0

05- 25

Clears program memory.

Pauses to display AMOUNT.

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 99 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

100 Section 8: Programming Basics

Keystrokes Display

?+2 +

?+3

Now, to run the program:

Keystrokes Display

fCLEAR²

6.75?0 13\68.5

18\72.9

24\85

5\345

:1 :2 :3

06- 43 31

07- 44 40 2

08- 40

09- 44 40 3

950.61

0.00

68.5

890.50

60.11

950.61

72.9

1,312.20

88.57

1,400.77

85.

2,040.00

137.70

2,177.70

345.

1,725.00

116.44

1,841.44

5,967.70

402.82

6,370.52

Pauses to display TAX.

Sets calculator to Run mode.

Clears registers R1– R6.

Stores tax rate. Enters quantity and price of first

item on invoice.

AMOUNT for first item.

TAX for first item.

TOTAL for first item.

Enters quantity and price of second item on invoice.

AMOUNT for second item.

TAX for second item.

TOTAL for second item.

Enters quantity and price of third item on invoice.

AMOUNT for third item.

TAX for third item.

TOTAL for third item.

Enters quantity and price of fourth item on invoice.

AMOUNT for fourth item.

TAX for fourth item.

TOTAL for fourth item.

Sum of AMOUNT column.

Sum of TAX column.

Sum of TOTAL column.

File name: hp 12c_user's guide_English_HDPMBF12E44 Page: 100 of 209 Printered Date: 2005/7/29 Dimension: 14.8 cm x 21 cm

HP F2231AA User Manual

Specifications and Main Features

Frequently Asked Questions

User Manual