HP 38g User Manual

Download

User's Guide

WHSl HEWLETT»

mL'HM PACKARD

O CO

pLi

aplet views

aplet library -

Home -

for entering

Alpha shift

shift key (turquoise)

HEWLETT A

'Hm PACKARD

LI VIEWS NOTE SKETCH

_____

1 1 MODES ASIN ACOS ATAN x-1

1 1

1 1 ANSWER CHARS EEX

BIE^

a...z LIST

CLEAR NOTEPAD SPACE K LN

OFF PROGRAM

021 ■■ I

CANCEL

a a

7 ■ 8 ■ g ■ /

MATRIX [

1 ■ 2 I 3

G H

5 ■ 6 ■ ^

ABS

) LOG

___

]_ 10^

B38G

D-

'll—

-fi

The {{ok}} menu-key

label (when present in the display) acts the same as the | enter]

key.

Key Conventions-Examples:

■ [ANSWER] Means press the shift key followed by the | enter] key.

|a...z|A Means press the Alpha-shift key followed by the | home | key.

HP 38G Graphing Calculator

User’s Guide

HEWLETT®

PACKARD

HP Part No. FI 200-90013

Printed in Singapore

Notice

This manual and any examples contained herein are provided “as is” and are subject to change without notice. Hewlett-Packard Company makes no warranty of any kind with regard to this manual, including, but not limited to, the implied warranties of merchantability and fitness for a particular purpose. Hewlett-Packard Co. shall not be liable for any eiTors or for incidental or consequential damages in connection with the furnishing, performance, or use of this manual or the examples herein.

© Copyright Hewlett-Packard Company 1995. All rights reserved. Reproduction, adaptation, or translation of this manual is prohibited without prior written permission of Hewlett-Packard Company, except as allowed under the copyright laws.

The programs that control this product are copyrighted and all rights are reserved. Reproduction, adaptation, or translation of those programs without prior written permission of Hewlett-Packard Co. is also prohibited.

Hewlett-Packard Co. Australian Calculator Operation 347, Burwood Highway Burwood East Victoria 3151 Australia

Acknowledgments

Hewlett-Packard gratefully acknowledges the members of the Education Advisory Committee (Walter Bitz, Tom Dick, Mark Howell, Alice Kaseberg, Jim McManus, Carla Randall, Alison Warr, and Wade White) for their assistance in the development of this product.

Edition History

Edition 2

...............

.January 1998

Getting Started

Starting Out...........................................................................1-1

The Keyboard

The Display.............................................................................1-6

Display Modes Using Input Forms

Home History......................................................................1-9

Menu Lists........................................................................ 1-10

Aplets and Their Views.......................................................1-11

Aplets.................................................................................1-11

Views..................................................................................1-12

Exploring an Aplet View by View

Catalogs and Editors...........................................................1-16

Storing and Recalling Variables Notes and Sketches

Note View and Sketch View

The Notepad......................................................................1-23

Managing Aplets....................................................................1 -25

Sending and Receiving Aplets

Mathematical Calculations

How to Do Calculations........................................................2-1

Entering Expressions.........................................................2-1

Complex Numbers..............................................................2-4

Clearing Numbers..............................................................2-4

Using Previous Results.......................................................2-4

Storing in Variables...............................................................2-6

The VAR Menu......................................................................2-7

Symbolic Calculations

Using Math Functions.........................................................2-12

The MATH Menu.............................................................2-12

The Math Functions by Category...................................2-13

........................................................................

....................................................................

.............................................................

...................................

........................................

..............................................................

............................................

.........................................................

1-2

1-7 1-8

1 -14

1-17 1-18 1-18

1-27

2-10

Contents-1

Plotting and Exploring Functions

Defining a Problem

Select an Aplet

Define an Expression (Symbolic View)............................3-2

Evaluating Expressions Examples: Defining Expressions

Plotting....................................................................................3-7

Plot the Expression (Plot View) Examples: Plotting

Exploring the Plot

Tracing

..............................................................................

Zooming.............................................................................3-13

Other Views for Scaling and Splitting the Graph

Setting Up the Plot (Plot Setup)

Interactive Root-Finding Examples: Root-Finding with Plots

Using a Table of Numbers

Display a Table of Numbers (Numeric View) Exploring the Table of Numbers

Setting Up the Table (Numeric Setup)

Building Your Own Table of Numbers..........................3-26

More Examples

...............................................................

....................................................................

.....................................................

......................................

........................................

.............................................................

...............................................................

..........

.........................................

.................................................

...............................

..................................................

...............

....................................

...........................

....................................................................

Solve

Solving Equations..................................................................4-2

Define the Equation

Solve for the Unknown Variable Plotting the Equation

Interpreting Results...............................................................4-7

Plotting to Find Guesses........................................................4-8

About Variables...................................................................4-11

...........................................................

......................................

............................................................

3-1

3-2

3-5 3-6

3-7

3-8 3-11 3-12

3-16 3-18 3-19 3-21 3-23 3-23 3-24 3-25

3-28

4-2 4-4 4-6

Contents-2

Statistics

Example: Finding a Linear Equation to Fit Data

Entering Statistical Data.......................................................5-5

One-Variable Data

Two-Variable Data.............................................................5-9

Managing Statistical Data

Analyzing the Data

Defining a Regression Model (2VAR)............................5-14

Computing Statistics (IVAR and 2VAR)

Plotting..................................................................................5-19

Plot Types..........................................................................5-20

Fitting a Curve to 2VAR Data........................................5-21

Regression Coefficients Plot Settings Trouble-shooting

Exploring the Plot................................................................5-23

Calculating Predicted Values..........................................5-24

.............................................................

...............................................

..............................................................

...................................................

......................................................................

..............................................................

..............

....................

Using Matrices

Creating and Storing Matrices

Matrix Arithmetic..................................................................6-6

Solving Systems of Linear Equations

Matrix Functions....................................................................6-9

Examples...........................................................................6-13

............................................

...............................

5-2

5-6

5-12 5-14

5-16

5-21 5-22 5-22

6-1

6-8

Using Lists

Creating and Storing Lists

List Functions.........................................................................7-4

Finding Statistical Values for List Elements

...................................................

...................

7-1

7-7

Contents-3

Programming

The Contents of a Program...............................................8-1

Structured Programming

Using the Program Catalog..................................................8-1

Programming Commands

Aplet Commands..............................................................8-10

Branch Commands..........................................................8-11

Drawing Commands

Graphic Commands.........................................................8-15

Loop Commands Matrix Commands Print Commands Prompt Commands

Stat-One and Stat-two Commands.................................8-25

Storing and Retrieving Variables in Programs

The Variable Menu Plot-View Variables Symbolic-View Variables Numeric-View Variables Note Variables

Sketch Variables...............................................................8-39

Menu Maps of the VAR menu.............................................840

Home Variables................................................................8-40

Function Variables...........................................................8-40

Parametric Variables

Polar Vciriables................................................................8-41

Sequence Variables............................................................842

Solve Variables...................................................................842

Statistics Variables

..................................................................

.................................................

....................................................

........................................................

..............................................................

...........................................................

..............................................................

.........................................................

................

..........................................................

.........................................................

................................................

.................................................

......................................................

............................................................

8-1

8-9

8-13

8-17

8-18

8-20

8-21

8-26

8-28

8-35

8-37

8-39

8-41

843

Reference Information

Regulatory Information........................................................9-1

Limited One-Year Warranty Service

......................................................................................

Batteries..................................................................................9-7

Resetting the HP 38G............................................................9-8

Memory Specifications..........................................................9-8

Glossary..................................................................................9-9

Selected Status Messages....................................................9-11

...............................................

Content84

9-3

Getting Started

Read this chapter first! It will get you started using your HP 38G, from turning it on to running aplets.

Starting Out

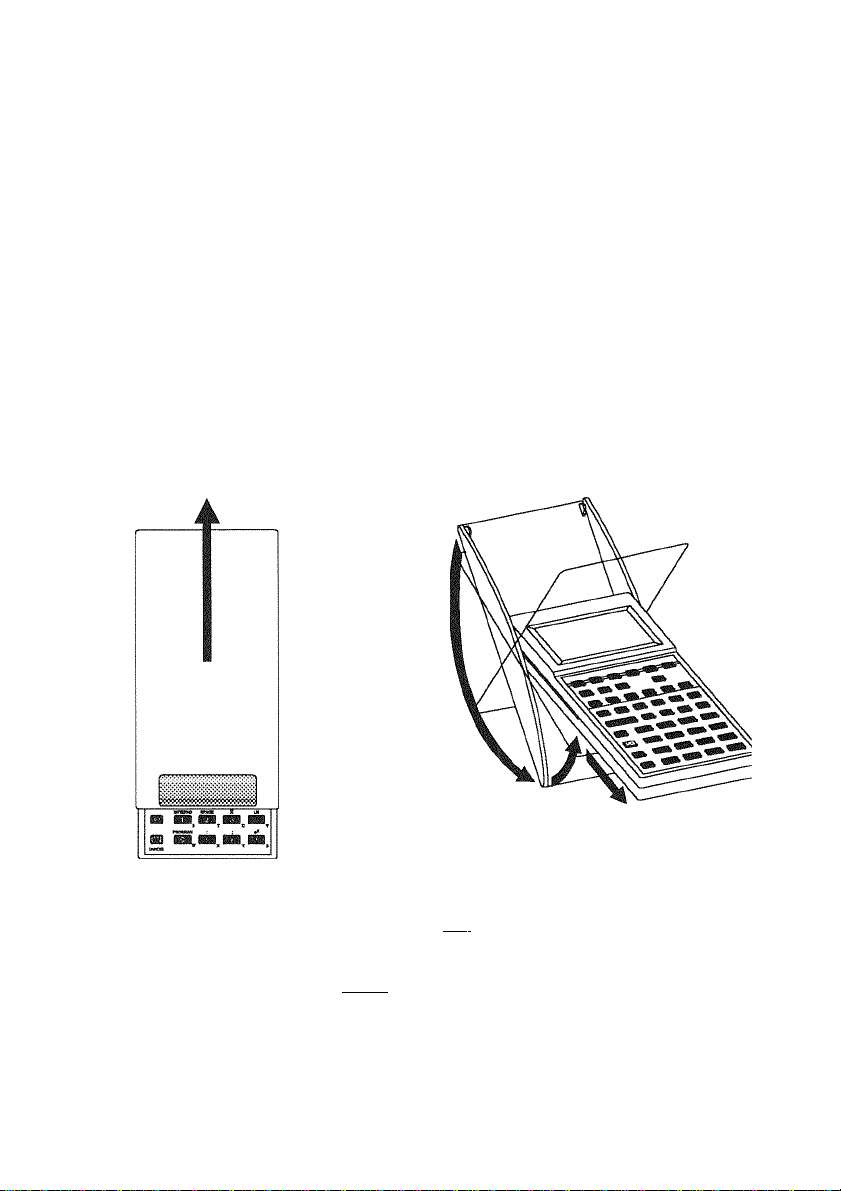
The Cover The protective cover swivels to provide a base for the

calculator. Be sure to protect the display by replacing the cover before transporting the calculator. Slide the cover gently so as not to hit the keys.

First push the cover away

from you until it

catches.

ON/CANCEL When the calculator is on, the |on| key cancels the current

operation.

OFF

Pressing ■ I ON I (that is, ■ [OFF]) turns the calculator off.

Then swivel the cover to the back and slide it towards you.

Getting Started 1-1

Demo

To see a demonstration of the HP 38G's features, type DEMO

into the edit line in Home. (Press | home | |a...z|D |a...z|E |A...z|M |A...z|0 I ENTER|.) To Stop the demo, press any key.

Home

Power

Home is the calculator’s home base. If you want to do calculations, or you want to quit the current activity (such as an aplet, a program, or an editor), press | home |.

To save power, the calculator turns itself off after several

minutes of inactivity. All stored and displayed information are

saved.

If you see the ((*)) annunciator or the Low Bat message, then the calculator needs fresh batteries. See chapter 9.

The Keyboard

Shifted The ■ (shift) key is a shifted keystroke that accesses the Keystrokes operation printed in turquoise above a key. For instance, to

® access the Modes screen, press ■, then | home |. (You do not

need to hold down the ■ .) This is depicted in this manual as “press ■[MODES] ."

To cancel a shift, press ■ again.

Alpha Shift The alphabetic keys are also shifted keystrokes. For instance,

l^ -^l to type z, press | A...Z | (T|. (The letters are printed in light

green to the lower right of each key.) To cancel Alpha, press | A...Z | again.

• For a lowercase letter, press ■ | A...Z |.

• For a string of letters, hold down | A...Z | while typing.

1-2 Getting Started

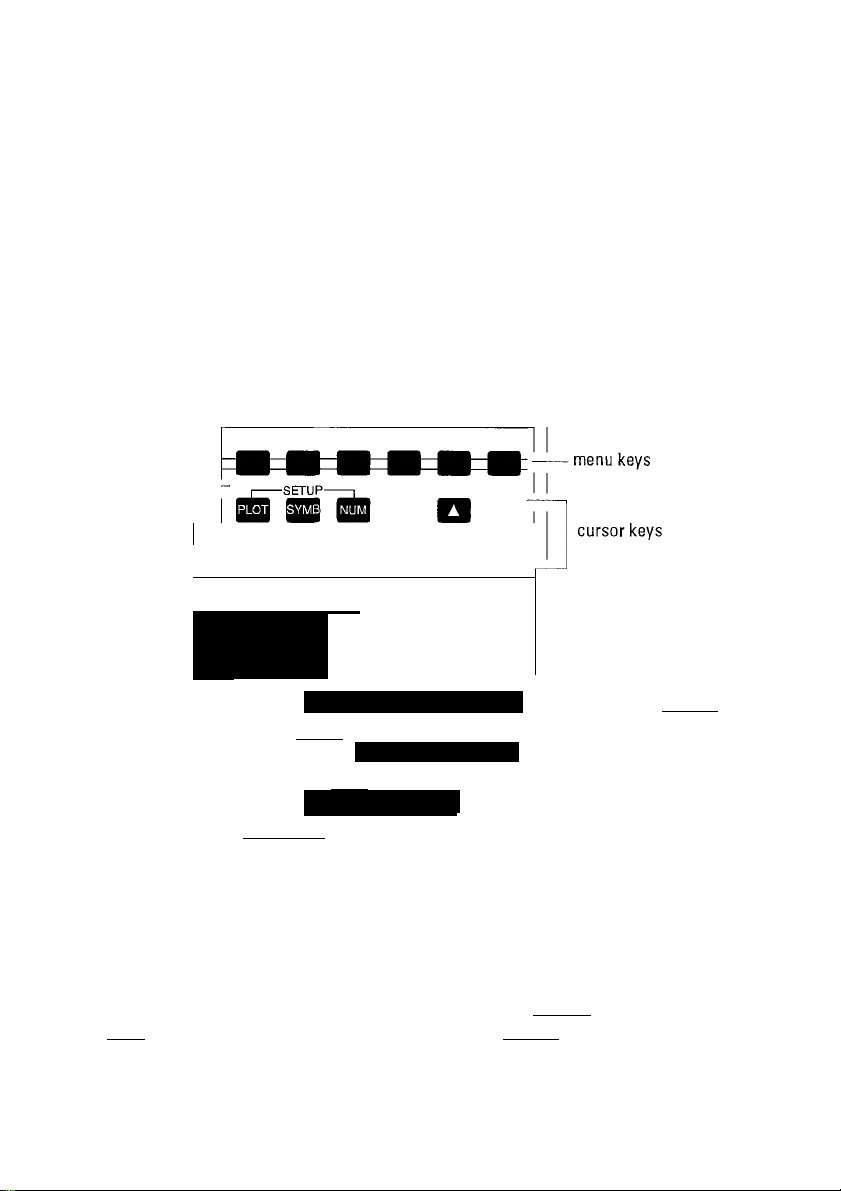
Menu Keys You can press fuBl to see this screen;

menu labels

menu keys

« The top-row keys are called menu keys because their

meanings depend on the context—that’s why their tops are blank.

• The bottom line of the display shows the labels for the menu keys’ current meanings, {{save}} is the label for the first menu key in this picture. “Press {{save}}’’ means to press the leftmost top-row key.

Parametric Polar Sequence Solve

Math Keys

Home (press | home |) is the place to do calculations.

• Keyboard keys. The most common arithmetic operations

P256

Getting Started 1-3

MATH menu. The | math | menu is a comprehensive menu

list of math operations that do not appear on the keyboard.

It also includes categories for all other functions and programmable commands. The functions are grouped by category, ranging in alphabetical order from Calculus to

Trigonometry.

Re.3l C CEILING

Stat-Tyo Symbolic

—

Tests ? FNROOT »

BDBSISiaiSI iHamBM

DEG+RFID FLOOR

The arrow keys scroll through the list (Q. ®) ^^d move

from the category list to the item list (0, Q). Press {{cancl}} to cancel the MATH menu. Pressing {{CMDS}} displays the list of Program Commands.

Pressing {{CONS}} displays the list of Program Constants. Pressing {{MTH}} displays the list of Math Functions.

1-4 Getting Started

Keys for Entry

and Editing

Key

(CANCEL)

Meanine

Pressing |ON| while the calculator is on

cancels the current operation. Pressing ■

first turns the calculator off.

■ (shift)

1 HOME 1

[M]

1 ENTER 1 Enters an input or executes an operation. In

[EEX] Enters an exponent of 10. To enter 5x10^

1 x,T,e 1

[MD

■ [CLEAR]

Accesses the function printed in turquoise color above a key.

Home base for calculations.

Alphabetic entry—press before a letter key.

calculations, 1 enter 1 acts like “=“ When

{{OK}} is present as a menu key, | enter] acts

the same as {{OK}}.

Starts a negative number. To enter -5, press 5.

you press 5 ■ [EEX] 9. This appears as

5E9 or, after pressing | enter],

5000000000.

Independent variable key. Types X, T, 0, or N into the display, depending on the current context.

Delete key. Backspaces if at the end of the

line.

Clear key. Clears all data on the screen except settings, which return to their default values.

0 B 0

■ [CHARS] Displays all available characters. To type

Inactive Keys If you press a key that does not operate in the current context,

a warning symbol like this A appears. There is no beep.

Cursor-movement (navigation) keys. Press

■ first to move far.

one, highlight it and press {{OK}}.

Getting Started 1-5

The Display

To adjust the contrast

The Parts of the Display

Annunciators

Simultaneously press decrease) the contrast

6*3

history

edit line

Mmsm

((•))

A T

RAD GRD DEG

8/5

17894

Shift in effect for next keystroke. To cancel, press ■ again.

Alpha in effect for next keystroke. To cancel, press 1 A...Z 1 again.

Low battery power. See chapter 9. Busy. Data is being transferred via infrared or cable.

There is more history in the Home display. Scroll up or down to see it.

Radians angle mode is set for Home. Grads angle mode is set for Home. Degrees angle mode is set for Home.

and 0 (or0) to increase (or

1.6

_ menu-key

labels

To clear the display

• Press

• Press ■ history.

1-6 Getting Started

to clear the edit line.

[CLEAR] to clear the edit line and the display

Display Modes

You can set the Home modes in ^ [MODES]. You make your selections using an input form. To fill out an input form, see “Using Input Forms,” after this table. The Decimal Mark

setting affects all aplets, as well as Home.

When you are done setting MODES, press | home | to return to the Home screen.

[MODES]

Setting

Angle Measure

Number Format

Decimal Mark

Title

Options Angle values are:

Degrees. 360 degrees in a circle. Radians. 2Tr radians in a circle. Grads. 400 grads in a circle.

Standard. Full-precision display.

Fbted. Displays results rounded to a number of decimal places. Example ; 123.456789 becomes

123.4568 in Fixed 4 format.

Scientific. Displays result with an exponent,

one digit to the left of the decimal point, and the specified number of decimal places. Example: 123.456789 becomes 1.23E2 in

Scientific 2 format.

Engineering. Displays result with an exponent that is a multiple of 3, and the specified number of significant digits beyond the first one.

Example: 123.456E7 becomes 1.23E9 in

Engineering 2 format. Fraction. Displays results as fractions based on the specified number of decimal places for

precision. Examples: 123.456789 becomes 123

in Fraction 2 format, and .333 becomes 1/3 and

29/1000 becomes 2/69.

Dot or Comma. Displays a number as 12456.98

(Dot mode) or as 12456,98 (Comma mode).

Dot mode uses commas to separate elements in

lists and matrices, and to separate function

arguments. Comma mode uses periods as separators in these contexts.

Customizes the title in the Home screen.

Getting Started 1-7

To display fractions

Set Fraction mode to display future results as fractions,

1. Press ■ [MODES], then press 0 to select number

FORMAT.

2. Press {{CHOOS}}, highlight Fraction, and press {{OK}}.

3. Press and enter a number for the precision of the fraction. The precision number determines how many

digits appear in the denominator. Press | enter |.

4. Press I HOME I to display Home.

To convert a result to a fraction

1. Set Fraction mode (as in the previous procedure).

2. In Home, press 0 to highlight the number in the history display that you want to convert.

3. Press ((COPY)) lENTERj.

Using Input Forms

An input form shows several fields of information for you to examine and specify. After highlighting the field to edit, you can enter or edit a number (or expression). You can also select options from a list ({{CHOOS}}). Some input forms include items to check ({{/CHK}}).

ANGLE MEASURE: [^PfiifeEH

NUMRER FORMAT; Standard

DECIMAL MARK; Dot < . > TITLE; HOME

CHOOSE ANGLE MEASURE

Example: Change the Angle Measure. Setting Modes

1. Press ■ {MODES} to open the MODES input form.

2. The cursor (highlight) should be on the first line, ANGLE

MEASURE. Press {{CHOOS}} to display a list of choices. Highlight Degrees, Radians, or Grads and press {{OK}}.

HOME MOPES I

3. When done, press | home | to return to Home.

1-8 Getting Started

Hint

Whenever an input form has a list of choices for a field, you can press (T) to cycle through them instead of using

{{CHOOS}}.

To reset values To reset the original, default value in an input form, press

I DEL |. To reset all values in the form, press ■ [CLEAR].

Home History

The Home display (press | home |) shows up to four lines of

history : the most recent input and output. Older lines scroll off the top of the display but are retained in memory; press

m to view them. Note that these examples are in Standard

display mode.

input —

last input-

edit line

— 5*77+4

When you highlight a previous input or result (pressing [Tl) the {{COPY}} and {{show}} menu labels appear. Pressing

{{COPY}} copies the highlighted value to the edit line.

HDME

1.41421356237

HOME

-result

■last result

1.41421356

5*77+1.414213562374

To copy a Highlight the line (press |T|) and press {{COPY}}. The number previous line (or expression) is copied into the edit line.

To repeat a To repeat the very last line, just press ( enter |. Otherwise,

previous line highlight the line (press |T1) first, and then press | enter). The

highlighted expression or number is re-entered.

Getting Started 1-9

To re-use a Press ■ [ANSWER] (last answer) to put the last result from previous result Home into an expression. Ans is a variable that is updated

each time you press [ enter |.

Example See how [ANSWER] retrieves and reuses the last result (50),

and I ENTER I updates Ans (from 50 to 75 to 100).

To display the

full number

Menu Lists

50 I ENTER I 25QH [ANSWER]

25+flns

1 enter! I enter!

You can use the last result as the first expression in the edit

line without pressing ■ [ANSWER]. Pressing 0, 0, or [7], (or other operators that require a preceding argument)

automatically enters Ans before the operator. You can reuse any other expression or value in the Home

display by highlighting the expression (using the arrow keys), then pressing {{copy}}.

If a number or expression is too long to appear on one line, then highlight it (press 0) and press {{SHOW}}. If it is still too long, press [0 to see more. When done, press {{OK}}.

A menu offers you a choice of items. The menu labels across the bottom of some displays are one kind of menu. A menu

list, which appears in one or two columns, is another kind.

FUNCTIONS

Plot-Table Overlay Plot fiuto Scale Decimal

Stat-Two DEG-»RflD Symbolic Tests V FNROOT w

CEILIHG FLOOR

100

• The ▼ arrow in the display means more items below.

• The A arrow in the display means more items above.

1-10 Getting Started

To search a menu list

® Press @ or 0 to scroll through the list. If you press

■ Q or ■ [^, you’ll go all the way to the end or the beginning of the list. Highlight the item you want to select, then press {{OK}} (or | enter |).

• If there are two columns, the left column shows general categories and the right column shows specific contents. Highlight the category on the left, then highlight the item on the right. The list on the right changes when a different category is highlighted. Press {{OK}} or [ enter |.

• To speed-search a list, type the first letter of the word. For example, to find the Matrix category in |math|, press M

(the g key).

• To go up a page, you can press ■ Q- To go down a page, press ■ .

To cancel a menu list

Press CANCEL or {{CANCL}}. This cancels the current

operation.

Aplets and Their Views

Aplets

The HP 38G provides built-in applications to solve specific kinds of math problems. These little applications, or aplets, are accessed from the Library (|lib|).

The library lists (and manages) all the aplets in the

calculator, whether they came with the calculator or were

added later. There are six types of math aplets built into the HP 38G :

Function

Parametric

Polar

• Real-valued, rectangular function y in terms of x. Example:

y = 2x-e3.

• Parametric functions x and y in terms of t. Example: x =

cos(0 and y = sin(f).

• Polar function r in terms of an angle 8.

Example: r = 2cos(40 ).

Getting Started 1-11

Sequence ® Sequence function i/in terms of n, or in terms of previous

terms in the sequence, such asUn~i and Example:

i/i = 0, f/2 = l,and a = +

Solve ® Finding the roots of an equation.

Example: x + 1 = -x-2.

Statistics e Analysis of one-variable (x) or two-variable (x and y)

statistical data.

Views

An aplet is represented in different ways. These views

compose an aplet problem and its solution. Here are illustrations of three major and six supporting aplet views.

SYMB

Symbolic view. The defining

equation(s) (in most aplets). The equation contains a

symbolic expression.

FUNCTION SVMtDLIC

^F10f>SIH<X)

F3<:x)=

F4<X>= F5<X>= ¥

PLOT

INUM!

Plot view. The graph of the

function(s).

Numeric view. Sampled

values of the function(s).

1-12 Getting Started

K: 0 FICH

.0ЦЦBЗЭH

.SRSSSOS .H7RH353

BHoai

: <! i8h:ih

■ [SETUPSYMB]

Symbolic Setup (■ |symb|). Sets parameters for the

symbolic expression.

FUMCTIDN SVMeOUC SETUP

ANGLE MEASURE:

CHMSE ANGLE MEASURE

Radian

■ [SETUPPLOT]

■ [SETUP-

NUM]

■ [VIEWS] Plot-Table

I [NOTE]

I [SKETCH]

Plot Setup (■ I PLOT I). Sets parameters to plot a graph.

Numeric Setup (■ | numQ. Sets parameters for building a table of numeric values.

Split Screen view. Two views side by side.

Note view. Text to

supplement an aplet.

Sketch view. Pictures to supplement an aplet.

^^^FONCIiDN PLDT KRNG: IMÜJiii VRNG; -3. 1 KTICK! 1 TTICK: 1 RES: Faster

ENTER MINIMUM HDRIZDNTAL VALUE

^^PUHCTIUN NUMERIC SETUP NUMSTART: ISHPBMBIlga NUMSTEP: . 1

NUMivPE: fiutomatic

NUMSBUM: 4

■ 6.5

3.2

ENTER STARTING VALUE FUR TAiLE

Changing Views

BannaHQi

BrjfaiinM

Each view is a separate “environment." To change the view,

press another view key. To change to Home, press | home |. You do not explicitly “close” the current view, you just enter another one-like passing from one room into another in a house.

Getting Started 1-13

Canceling To cancel an operation within a view, press |on| (the Operations CANCEL key). Pressing CANCEL will cancel pending

operations, but will not change the view.

Exploring an Aplet View by View

Example Use the Function aplet to explore the real function

y = sin(l/x)

using the Symbolic, Plot, and Numeric views. All the

information you enter is automatically saved

1. Open the Function aplet. Press

|lib|. If necessary, press 0 to

highlight Function.

Then press {{START}} to display the Symbolic view.

2. Enter the expression. (If necessary, highlight a new line or press I DEL I to clear the highlighted expression.)

Press

3. There are three Setup views. They are the shifted keystrokes for |symb|,

1 0 {{X}} {eñterI

I PLOT I, and |num|. Check that

Radians are set for Symbolic Setup; Press ■ [SETUP-SYMB] and choose Radians, if necessary.

Plot the graph. Press | plot |. The coordinates show that when .»=0, Kjk) is undefined.

(If your plot does not look like this, try resetting the default plot settings; Press ■ [SETUP-PLOT]

■ [CLEAR].)

Function

Parametric Polar Sequence Solye w

FUNCTION SVM6DÜC

F200 =

v<'FKH)=siHa^K>

F3(X)= F4<X)= F5<H)= w

FUNCTION SYMBOLIC SETUP

ANGLE MEASURE:

CHOOSE ANGLE MEASURE

............................

K; 0 FKK

Radian

: UNDEFINED IBiann

1-14 Getting Started

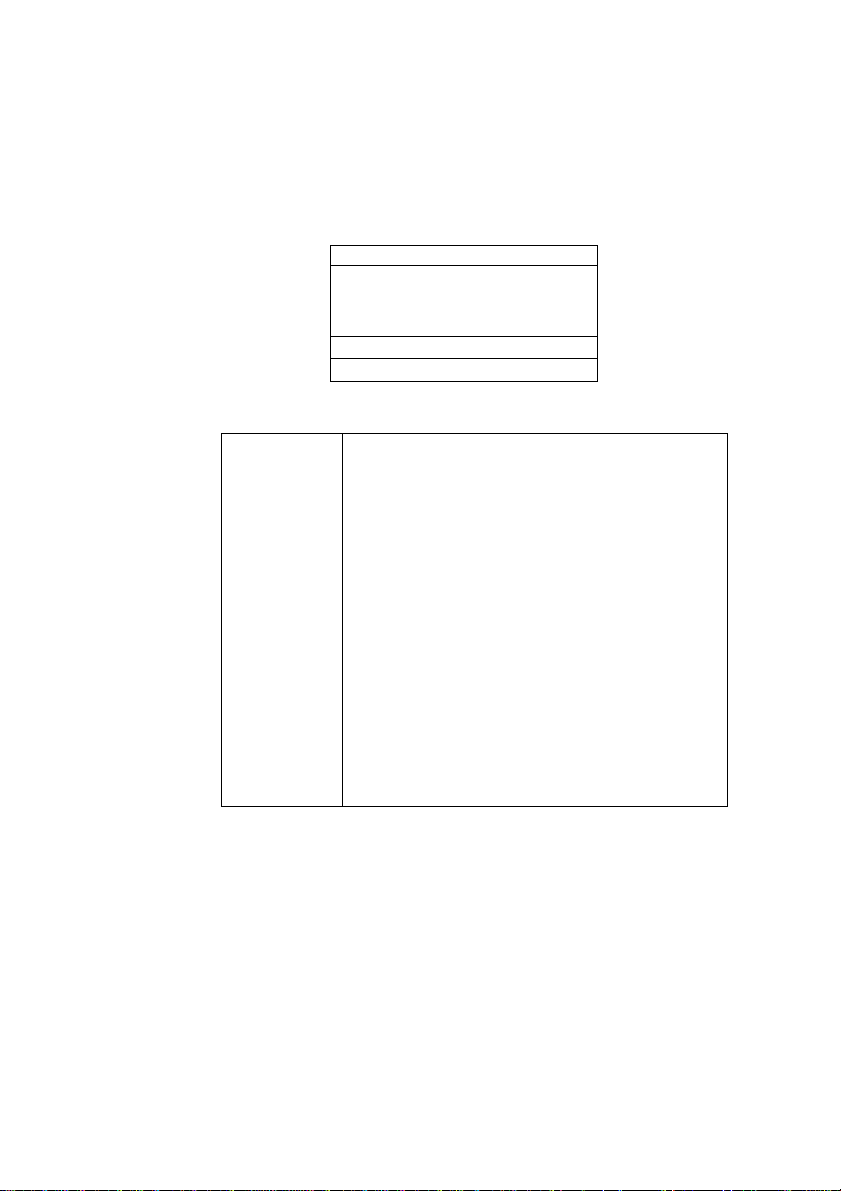
5. Trace the plot. Move the crosshairs

along the plot by pressing 0] and

B-

............................

i ' ' ' ' ' '

....,..

6. Zoom in and zoom out. Press

{{MENU}} {{ZOOM}}, highlight

In 4X4, and press {{OK}}.

To restore the original scale, select

{{ZOOM}} Un-zoom.

7. Display the numbers. To display a

table of data, press |num|. You see the independent (X) and dependent

(FI) variables listed with sampled

values.

(If your table does not look like this,

try resetting the default numeric settings : Press ■ [SETUP-NUM]

■ [CLEAR}.)

8. Split the screen. Press ■ [VIEWS],

then select Plot-Table {{OK}} to display these two views simultaneously.

K:1.3 FKK

i; .sissBas

K FI

-.60H3B -.HH?S3

-.HOSES

-.g03I3

s. HOSES

I.60H3P5

-.SEBBH

.SEBB35 .HH?535

Press I PLOT I to view the full-screen plot again.

Getting Started 1-15

Automatic With this example you have defined a new aplet-an aplet Saving containing data for the solution of y = sin(l/x). The data are

automatically saved in the Function aplet. If you want to create

another aplet based on Function, then you can give this one a new name in the Library ({{SAVE}}).

To keep as much memory available for storage as possible, delete aplets you no longer need.

Annotating The Note view (■ [NOTE}) attaches a note to the current

with Notes aplet. See “Notes and Sketches" later in this chapter. Annotating The Sketch view (■ [SKETCH]) attaches a picture to the

with Sketches current aplet. See “Notes and Sketches” later in this chapter.

Calculating in You can do calculations in aplets wherever you can enter

Aplets numbers or expressions. Use the math keys on the keyboard

or use operations from the | math | menu list. Chapter 2 discusses math calculations.

Catalogs and Editors

The HP 38G has several catalogs and editors. They access features and stored values (numbers or text or other items) that are not part of aplets. A catalog lists items, which you can delete or transmit. An editor lets you create or modify items and numbers.

Catalogs/Editors

Cataloe/Editor Contents Library ((051) Aplets. List (■ [UST]) Lists. In Home, lists are enclosed in {]. Matrix

One- and two-dimensional arrays. In

(■ [MATRIX]) Home, arrays are enclosed in [ ].

Notepad (■ [NOTEPAD])

Program (■ [PROGRAM])

Notes (short text entries).

Programs created by a user.

1-16 Getting Started

Storing £uid Recalling Variables

Variables are storage locations for numbers or values. The

HP 38G has different categories of variables for different kinds of data. The names for the variables are predefined. For real numbers, there are 27 variable names available, A through Z and 0. (Other categories and their names are in chapter 2.)

A variable holds just one value, so if you store a new number in it, any previous number is lost.

To store a

number

To recall a number

You can store a number from Home’s edit line into a named variable with the {{STO^}} (store) menu key. ({{STO^}} appears on a menu-key label whenever it is possible to store a value.) For example.

75{{STO^)} [TZzIA

ENTER

When you press | enter), the number 75 is stored into the

variable named A. To store the last answer, you don’t need to re-type the

number:

{{STO>}} [aIzIB

enter

This stores 75 (the last result) in B.

In Home, to recall a value from a stored variable back to the edit line, just type the name of the variable and press | enter].

i A...Z IA [enter! 75

7 5^A4

Ans ►Bi

Getting Started 1-17

“Deleting”

Variables

A variable always has a value in it, even if that value is zero. When you store another value into a variable, it overwrites the previous value. So you cannot delete a variable’s value, but you can overwrite it.

The predefined variable names (such as A through Z) always exist; you cannot change or delete them.

Home and Aplet Variables

Most variables are Home variables, which means they are shared throughout the different contexts of the calculator. Some variables are aplet variables, which means they apply

only to the current aplet. Aplet variables are data sets,

expressions, and settings made within an aplet.

Notes and Sketches

The HP 38G has compact text and picture editors for entering

notes and sketches.

® The Notepad is an independent collection of notes.

* Each aplet includes a Note view and a Sketch view for

that aplet only.

Note View and Sketch View

You can attach text to an aplet in its Note view (■ [NOTE]),

or attach pictures to it in its Sketch view (■ [SKETCH]).

To write a note 1. In an aplet, press ■ [NOTE] for the Note view. In Note view

2. Use the note editing keys shown below.

3. Set Alpha lock (([A...Z}}) for quick entry of letters. For

lowercase Alpha lock, press ■ ((A...Z}}.

® To type a single letter of the opposite case, press

■ letter.

4. Your work is automatically saved. When done, turn off

Alpha lock (by pressing ([A...Zh]}) if you want to go to

Home. (Otherwise, the | home | key will still type A.)

1-18 Getting Started

Note Editing Keys

Key Meaning

{{SPACE}} Space key for text entry. {{APACE}} Displays previous page of the note. {{PAGET}} {{A...Z}}

■ {{A...Z}} Lower-case Alpha-lock. {{BKSP}}

(HD

1 enter!

H {CLEAR] Erases the entire note.

1 VAR|

1 MATH 1

■ [CHARS] Displays special characters. To type one,

Displays next page of the note. Alpha-lock for letter entry.

Backspaces cursor and deletes character. Deletes current character. Starts a new line.

Menu for entering variable names, and contents of variables.

Menu for entering math operations, program commands, and constant names.

highlight it and press {{ECHO}}. Pressing

{{OK}} copies the character and closes the

CHARS screen.

To import a You can import a note from the Notepad into an aplet's Note

note view, and vice-versa.

1. Open the destination note in the Notepad or in the Note view of an aplet.

2. Press I var|.

* If the source note is in the Notepad, press {{HOME}},

highlight Notepad in the left-hand list, then highlight the name of the source note in the right-hand list.

* If the source note is part of the current aplet, press

{{APLET}}, highlight Note in the left-hand list, then

press 0 and highlight NoteText in the right-hand list.

3. Press {{VALUE}} {{OK}} to recall the contents of the source

note into the destination note.

Getting Started 1-19

Sketch Keys

To draw a sketch

Key Meanine

fPEH

■ [CLEAR] 0

1. In an aplet, press I

2. Press {{DRAW}}.

Stores the specified portion of the current sketch to a graphics variable (G1 through GO).

Adds a new, blank page to the current sketch set.

Displays previous sketch in the sketch set. Animates if held down.

Displays next sketch in the sketch set. Animates if held down.

Opens the edit line to type a text label.

Displays the menu-key labels for drawing (below).

Deletes the current sketch. Erases the entire sketch set.

Turns off the menu-key labels. Press any menu key to restore them.

[SKETCH] for the Sketch view.

3. Use the arrow keys to move the crosshairs (graphics cursor). To draw lines, boxes, or circles, use the menu keys (described next).

4. When done drawing, press {{OK}}. Your work is

automatically saved. Press any other view key or | home | to

exit the Sketch view.

1-20 Getting Started

To draw a line 1. In Sketch view, press {{DRAW}} and move the cursor to

where you want to start the line

2. Press {{LINE}}. This turns on line-drawing.

3. Move the cursor in any direction to the end point for the line.

4. Press {{OK}} to finish the line.

To draw a box 1. In Sketch view, press {{DRAW}} and move the cursor to

where you want any corner of the box to be.

2. Press {{BOX}}. This turns on box-drawing.

3. Move the cursor to mark the opposite corner for the box.

You can adjust the size of the box by moving the cursor.

4. Press {{OK}} to finish the box.

To draw a 1. In Sketch view, press {{DRAW}} and move the cursor to circle where you want the center of the circle to be.

2. Press {{CIRCL}}. This turns on circle-drawing.

3. Move the cursor the distance of the radius.

4. Press {{OK}} to draw the circle.

Getting Started 1-21

DRAW Keys

Key

Meaning

{{DOT-f}},

{{DOT-}} move. {{LINE}}

Dot on, dot off. Turns pixels on/off as crosshairs

Draws a line from the cursor’s starting position to the point at which you press {{ok}}. You can draw a line at any angle by moving the cursor.

Draws a box from the cursor's starting position to the point at which you press {{OK}}.

Draws a circle. The cursor’s starting position is the center of the circle. The cursor’s ending position (when you press {{ok}}) defines the radius.

To label parts 1. Press {{TEXT}} and type the text in the edit line. To lock of a sketch the Alpha shift on, press {{A...Z}} (for uppercase) or

■ {{A...Z}} (for lowercase).

2. To make the label a smaller character size, turn off

{{BIG«}}. (Pressing {{BIG}} turns on {{BIGh}} and vice-

versa.) The smaller character size cannot display lowercase letters.

3. Press {{OK}}. Use the arrow keys to position the label where you want it.

4. Press {{OK}} again to affix the label.

5. Press {{DRAW}} to continue drawing, or press | home | to

exit Sketch view.

To create a set You can create a sequence of up to ten sketches. This allows of sketches for simple animation.

« After making a sketch, press {{NEWP}} to add a new, blank

page that will follow the current page. You can now make a new sketch. The new image becomes part of the current set of sketches.

® To view the next sketch in an existing set, press

{{PAGET}}. Hold {{PAGET}} down for animation.

® To remove the current page in the current sketch series,

press [on |.

1-22 Getting Started

To store into a You can define a portion of a sketch inside a box, and then graphics store that graphic into a graphics variable.

variable

1. In the Sketch view, display the sketch you want to copy (store into a variable).

2. Press {{STO^}}. Highlight the variable name you want to use and press {{OK}}.

3. Draw a box around the whole screen or around the portion you want to copy: move the cursor to one corner, press {{OK}}, then move the cursor to another corner and press {{OK}}.

To recall a

graphics

variable

The Notepad

1. Open the Sketch view in the destination aplet.

2. Press I VAR I {{HOME}}. Highlight Graphic, then press

and highlight the name of the variable (G1, etc.).

3. Press {{VALUE}} {{OK}} to recall the contents of the

graphics variable.

4. Move the box to where you would like to copy the graphic,

then press {{ok}}.

You can store as many notes as you want in the Notepad

(■ {NOTEPAD}). These notes are independent of any aplet.

The Notepad catalog lists the existing entries by name . It does

not include notes that were created in Note view (■ {NOTE}).

IHDTE CBTftLDGi

TO DO PHONE NUMBERS

nMUzmii

Getting Started 1-23

To write a note 1. In the Notepad, press {{EDIT}} to modify the highlighted

in the Notepad note or press {{new}} to start a new note. For a new note,

type in a name and press {{OK}}.

2. This opens the note for you to write and edit. Use the Note editing keys as in Note view (see page 1-19).

3. When you are done, you can leave the Notepad by pressing I HOME I or an aplet view key. Your work is

automatically saved.

Notepad

Catalog Keys

Key

{{RECV}} (receive)

K [CLEAR]

Meaning

Opens the selected note for editing. Opens a new note, and asks for a

name.

Transmits the selected note to another HP 38G or a disk drive. See also page 1-27.

Receives a note being transmitted

from another HP 38G or a disk

drive. See also page 1-27. Deletes the selected note.

Deletes all notes in the catalog.

1-24 Getting Started

Managing Aplets

Once you have entered information into an aplet, you have defined a new version of an aplet. The information is automatically saved under the current aplet name, such as

“Function.” To create additional aplets of the same type, you

must give the current aplet a new name. The Library is where you go to manage your aplets. Press

jiiBl. Highlight (using the arrow keys) the name of the aplet

you want to act on.

currentaplet

names of aplets

The current aplet is highlighted.

tftPLET UERflRV

Function

Parametric Polar Sequence

Solue f

library Keys

To open an aplet

Key Meanine

{{RESET}} Resets the default values and

{{RECV}} (receive)

{{START}} (or 1 enter))

Press (LIB 1 to open the Library. Highlight the aplet and press {{START}} or I ENTER]. The aplet’s main view appears.

Instead of pressing {{START}}, you can press a view key (like I PLOT I, |symb|, or |num|) to immediately display that

view of the aplet.

Saves the highlighted apiet with a name.

settings in the highlighted aplet. Rearranges the aplet list. Transmits the highlighted aplet to

another HP 38G or a storage device. Receives the aplet being sent from

another HP 38G or storage device. Opens the highlighted aplet.

Getting Started 1-25

To name an aplet

1. Press I LIB I to open the Library. Highlight the aplet to name.

2. Press {{SAVE}} and enter a name. Press {{OK}} to confirm

it, {{CANCL}} to cancel it.

To create a new aplet

To delete an aplet

To clear an aplet

To sort the aplet list

You can create a new aplet based on an existing aplet.

1. Open the aplet you want to start from.

2. Enter or modify its information (equations, data, settings). This defines a new version of the aplet. All information is saved until you clear it or edit it.

3. To name the aplet for future access, use {{SAVE}} in the

Library.

Open the Library, highlight the custom (not built-in) aplet to

delete, and press |del|. To delete all custom aplets, press

■ {CLEAR}.

You cannot delete the built-in aplets. You can clear their data

and reset default settings using {{reset}}.

Resetting an aplet clears all data and resets all default settings.

® To reset an aplet, open the Library, select the aplet and

press {{RESET}}.

In the Library, press {{SORT}}. Select the sorting scheme and press I ENTER I.

e Chronologically produces a chronological order by

most recent use of the aplets. (The last-used aplet appears first, and so on.)

® Alphabetically produces an alphabetical order by

aplet name.

1-26 Getting Started

Sending and Receiving Aplets

A convenient way to distribute or share problems in class and

to turn in homework is to transmit (copy) aplets directly from one HP 38G to another. This takes place via the infrared port.

You can also send (copy) and receive aplets to/from a remote storage device (aplet disk drive or computer). This takes

place via a cable connection and requires an aplet disk drive or specialized software running on a PC or Mac (such as a connectivity kit).

To transmit an 1. Connect the storage device to the calculator by cable

aplet or

align the two calculators' infrared ports by matching up the triangle marks on the rims of the calculators. Place the calculators no more than 2 inches (5 cm) apart.

2. Sending calculator: Open the Library, highlight the aplet to send, and press {{send}}.

e You have two options : another HP 38G or a disk drive

(or a computer). Highlight your selection and press

{{OK}}.

e If transmitting to a disk drive (aplet disk drive or

computer), you have the options of sending to the current (default) directory or to another directory.

Getting Started 1-27

3. Receiving calculator : Open the Library and press

{{RECV}}.

* You have two options : another HP 38G or a disk drive

(or computer). Highlight your selection and press

{{OK}}.

If receiving from a remote storage device (aplet disk drive or computer), you will see a list of aplets in its current directory. You can choose a different directory to copy from. Check as many items as you would like to receive.

1-28 Getting Started

Mathematical Calculations

The most commonly used math operations are on the

keyboard. Access to the rest of the math functions is via the MATH menu (press |math|).

The MATH menu also contains commands to use for programming.

How to Do Calculations

Where to Start The home base for the calculator is Home (press |home |).

You can do all calculations here, and you can access all

[ MATH I operations.

Entering Expressions

Enter an expression into the HP 38G in the same left-toright order that you would write the expression.This is called algebraic entry.

To enter functions, select the key or MATH menu item for that function. You can also use Alpha keys to spell out a function's name.

Example

e Press I ENTER I to evaluate the expression you have in the

edit line (where the blinking cursor is). An expression can contain numbers, functions, and variables.

Calculate 23^-(14Vs)-!-(-3)ln45 with these keystrokes.

23 ■ [x^] □Ш14 0Ш 8ШШЕ1]30И[Ш] 45

m riiJiTFI 23a-14*T8/'-3*LNC45)

Ш LtNitKJ 579.245381391

Mathematical Calculations 2-1

Long Results

If the result is too long to fit in the display line, press 0 to highlight it and then press {{SHOW}}.

Negative Numbers

Scientific Notation powers of 10)

Type [^to start a negative number or to insert a negative

sign. If a negative number will be raised to a power, enclose it in

parentheses. For example, (—5)^= 25, whereas - 5^= - 25. A number like 5x10"' or 3.21x10"' is written in scientific

notation, that is, in terms of powers of ten. This is simpler to

work with than 50000 or 0.000000321. To enter numbers like these, use [EEX]. (This is easier than using fillOfx^.)

Example

Calculate ------------------------

4TEEXini3F]6

■ [EEX] 2 0 3® [EEX]

(4xl0"')(6xl0')

as shown :

3x10

4E-3*6E2x3E-5

FF|5 I ENTER I

Explicit and You should include the times sign where you expect Implicit multiplication in an expression. It is clearest to enter AS as Multiplication and A(B+C] as A* (B+c).

80000

Implied multiplication takes place when two operands appear

with no operator in between. If you enter AB, for example, the result is A* B.

Parentheses Parentheses are necessary to enclose arguments for

functions, such as SIN (4 5). You can omit the final parenthesis at the end of an edit line.

Parentheses are also important in specifying the order of operation. Mf/toui parentheses, the HP 38G calculates according to the order of algebraic precedence (the next topic). Following are some examples using parentheses.

2-2 Mathematical Calculations

Examples

Algebraic Precedence (Order of Evaluation)

Enterine...

[Ml 45 0 ■ [it] [Ml 45 eg 0 H [it] 1 Vx 1 85 01 9

[W1 B 55 0 9 Q]

Functions within an expression are evaluated in the following order of precedence. Functions with the same precedence are evaluated in order from left to right.

Expressions within parentheses. Nested parentheses are evaluated from inner to outer. Prefix functions, such as SIN and LOG. Postfix functions, such as ! Power function,NTHROOT. Negation, multiplication, and division.

6. Addition and subtraction.

7. AND and NOT.

OR and XOR.

9. Left argument of | (where).

10. Equals, =.

Calculates...

sin (45 -r tt) sin (45) + -IT

yfExQ

VS5x9

Fractions The HP 38G can display fractions of the form alb. To set

Fractions mode, select Fractions as the Number Format in Home Modes (■ [MODES]). Specify the number of decimal places to use for the denominator. For instance, in Fraction 2 format, 29/1000 becomes 2/69 .

To enter a fraction use the [7] key.

Largest and Smallest Numbers

The smallest number the HP 38G can represent is 1 xlO“®® (1E-499). A smaller result is displayed as zero. The largest number is 9.99999999999x10®’. A larger result is still displayed as this number.

Mathematical Calculations 2-3

Complex Numbers

Complex The HP 38G can return a complex number as a result for Results some math functions, A complex number appears as an

ordered pair (x, y), where x is the real part and y is the imaginary part. For example, entering returns (0,1).

To enter Enter the number in either of these forms, where x is the real complex part, y is the imaginary part, and i is the imaginary constant,

numbers ,JZ\-

e (X, y) or

e X + iy ,

To type i, press ■ | A...Z 11, or copy i from the Constant

category in the MATH menu.

Clearing Numbers

• I DEL I clears the character under the cursor (|). j backspaces when the cursor is after the last character.

® CANCEL (|ON|) clears the edit line.

• ■ [CLEAR] clears all input and output in the display, including the display history.

Using Previous Results

The Home display shows you four lines of input/output

history. An unlimited (except by memory) number of previous lines are available by scrolling. You can retrieve and reuse any of these values or expressions.

Last Answer You can reuse the last answer at any point in the edit line by ([ANSWER]) pressing ■ [ANSWER], This recalls the variable Ans (last

answer), the result from your last | enter].

The variable Ans is different from the numbers in Home's

display history, A value in Ans is stored internally with the full precision of the calculated result, whereas the displayed numbers match the display mode. When you retrieve a number from Ans, you obtain the result to its full precision. When you retrieve a number from Home’s display history, you obtain exactly what was displayed.

2-4 Mathematical Calculations

Note that pressing | enter] enters (or re-enters) the last input,

whereas pressing ■ [ANSWER] copies the last result into the edit line.

Continuing a You can continue calculating with your last result, Ans, Calculation simply by pressing an operator key.

50 [7] 3 I ENTER I

[+] 25 I ENTER I

50-^3 flns+25

^HDME

16.6666666667

41.6666666667

Accessing

the Display History

Pressing 1 ENTER 1 again updates the value of Ans and repeats the operation.

Pressing Q turns on the highlight bar in the display history. Key Meaning

S.E

{{COPY}} Copies the highlighted expression

{{SHOW}} Displays the current expression in

■ {CLEAR}

flns-E25

Scroll through the display history and highlight display lines.

to the position of the cursor in the edit line.

standard mathematical form.

Deletes the highlighted expression from the display history, unless

there is a cursor in the edit line. Clears all lines of display history

and the edit line.

»HDHE

16.6666666667

41.6666666667

66.6666666667

Mathematical Calculations 2-5

Clearing the Display History

It's a good habit to clear the display history (■ [CLEAR])

whenever you are done working in Home.

It saves calculator memory to clear the display history.

Remember that all your previous inputs and results are saved

until you clear them.

Clearing the Edit Line

* [ DEL I deletes single characters in the edit line.

(CANCEL) clears the entire edit line.

Storing in Variables

You can store numbers or expressions from any previous input or result into variables.

Numeric Precision

To store a value

A number stored in a variable is always stored as a 12-digit mantissa with a 3-digit exponent. Numeric precision in the display, however, depends on the display mode (Standard, Fbced, Scientific, Engineering, or Fraction). A displayed number has only the precision that is displayed.

Press {{STO>}} I letter I ENTER I, where letter represents the one-letter variable name for real numbers.

6 {{STO^}} [aIz] B

ENTER

You can store the last answer the same way:

13 Q 5 I ENTER I

{{STO^}} A fENTE^

BHai

la-'S

Hnsfrfl

mil

2.6

To store any previous value

To recall a value

If the value you want to store is somewhere else in the Home history, first copy it to the edit line: highlight the line (using arrow keys) and press {{COPY}}. Then store it.

Type the name of the variable and press | enter].

|A...Z|A I ENTER I 2.6

2-6 Mathematical Calculations

The VAR Menu

Another way to retrieve a variable is to use the VAR

(variables) menu. The VAR menu contains the Home variables, as well as the aplet variables for the current aplet.

The VAR menu is organized by category. For each category of

variables on the left, there is a list of variables on the right. The highlighted category is the current category.

current category

The {{HOME}} and {{APLET}} menu keys switch to Home and Aplet variables. The h symbol indicates what is "on": {{HOM*}} means that the Home variables are displayed.

«niTOWWWtWOWW« I

iComplex ■

Graphic Library Z3 List ¥ Z4 T

Z1 Z2

variable names

Home Variables

The Home variables are the ones you most commonly use while doing calculations in Home. Any value (or other data) you store must be stored in a variable of the correct type.

Cateeorv Complex Z1 through Z9 and ZO.

Graphic G1 through G9 and GO. Library List LI through L9 and ID.

Matrix Ml through M9 and MO.

Modes

Notepad User-provided. Program User-provided. Real A through Z and 6.

Available Names

aplets

The MODES screen (■ {MODES}) stores values in these variables.

Mathematical Calculations 2-7

Home variables retain their values regardless of context: Home, the aplets, and the editors recognize the Home

variables and retain whatever was last stored in them. This sharing allows you to work on the same problem in different places (such as Home and the Function aplet) without having

to update a variable whenever it is recalculated.

If you have not stored anything in a real variable, then it

contains the value zero. (It is never “empty.”)

To access a 1. Press | var | to display the VAR menu. Set {{HOMa}}, if Home variable necessary by pressing {{HOME}}.

2. Use 0 and 0 to scroll through the alphabetical list of

categories. To skip directly to a starting letter, press a letter key. To switch between the category list (left) and the variable list (right), use 0 and 0.

3. Highlight the name of the variable you want.

• To copy the name of the variable into the edit line,

press {{OK}}. (NAME is set: the menu label shows

{{NAM«}}).

To copy the value of the variable into the edit line, set VALUE

(press {{VALUE}} to make it {{VALU«}}) and press {{OK}}.

2-8 Mathematical Calculations

Aplet The variable types in the table below are aplet variables that Variables you use to define aplet functions and to store some kinds of

aplet data. They are usually found in the Symbolic view or the Numeric view of an aplet.

Aolet Cateeorv Function

Parametric XI, Y1 through X9, Y9 and XO,

Polar R1 through R9 and RO

Sequence U1 through U9 and UO

Solve El through E9 and EO

Statistical data Cl through C9 and CO

As you load new aplets in the HP 38G, their names and variables will be added to the VAR menu.

In addition, there are other aplet variables that are record settings, such as those in the Setup views. These types of variables (like NumStart and Xtick) are listed in chapter 8,

Programming, since you do not need to know their names

except when programming.

Available Names FI through P9 and FO

(Symbolic view)

YO (Symbolic view)

(Symbolic view)

(Numeric view)

Mathematical Calculations 2-9

To access an The {{APLET}} menu key in the VAR menu switches the menu aplet variable ¡¡st to aplet variables. The ■ symbol indicates what is "on":

{{APLEb}} means that aplet variables are displayed.

1. Open the aplet whose variable you want to recall.

2. Press I VAR I to display the VAR menu. Set {{apleb}}, if

necessary by pressing {{aplet}}.

I^^FUNCTIBN

Plot ■ fixes

Plot FCN Symbolic Numeric v

Connect Coord FastRes v

3. Highlight the view on the left side. If you’je not sure which view it’s in, just scroll through the view names and check

the names of the variables on the right.

4. Press {{OK}} or to switch to the list of variable names

on the right side.

5. Highlight the name of the variable you want. To copy its

name, turn on {{NAM»}}. To retrieve its value, turn on

{{valub}}. Press {{OK}}.

You can do this in Home if the aplet you want is current; that is, it was the last one open.

Symbolic Calculations

Formal Names

Note

A formal name acts as a placeholder—it does not represent a value, just a symbol. In Home or in a program, the expression

(s 1 * s 2) ^ always returns the expression (s 1 * s 2) ^. The real variables in {A*B) ^ on the pther hand, are evaluated to a number, the value of which depends on what is currently

stored in A and B.

Remember that there is always a value in a real variable, even if it is zero.

2-10 Mathematical Calculations

You can mix formal names and real variables. Evaluating

(A*s2) ^ will substitute a number for A but not for s2.

If you want to evaluate an expression like (sl*s2) ^ numerically, you can do so using the I (where} command, listed in the MATH menu under the Symbolic category. For instance, if you wanted si = 3 and s2 = 4, you would enter

(sl*s2) ''2 I (sl=3, s2=4). (The = symbol is in the CHARS

menu: press ■ [CHARS] {{OK}}).

Indeflnite

Integrals

Definite Integrals

Derivatives

To find the indefinite integral (with a symbolic rather than

numeric result), use formal variables (that is, sO through s5) for a limit of integration. For instance, to compute

I (6x - 5)dx ,

ehter the integration as / (0, si, 6*x'-5, X).

0 and si are the lower and upper limits, and X is the variable

of integration.

1. Enter the the integration expression in the Home edit line.

(The f symbol in the the CHARS menu.)

2. Press [ENTER], which produces an intermediate result.

3. Press 0 ([COPY]} [ENTER] to complete the evaluation.

The result of /(0,sl,6*X2-5,X) should be

-(5*sl)+6*(s 1^3/3), that is, 2x3-5x.Translators: in Comma

mode; change syntax to use periods. To find the definite integral (with a numeric result), use

numeric values (numbers or real variables containing numbers) for both the upper and lower limits. For instance, if

you enter J(-2,3,6*X2-5,X)and press [ENTER] , the result is

45.

To find the symbolic derivative of an expression, use a formal

variable (s 1, etc.) to define the derivative. For example, to find D/6x*-5x), enter 3sl (6*sl^- 5*sl) .The result is

6*(2*sl) -5, which is equal to 12x—5.

If you use real variables or numbers in the derivative, the calculator will find a numeric result.

Mathematical Calculations 2-11

Composition of You can define a function of another function using the Functions Function aplet (|lib| Function). That is, f(g(xy) can be

entered into the Symbolic view of Function as

F1(X) -expression!

F2 (X) = expression2 F3 (X) = FI {F2 (X) )

Using Math Functions

Selecting To enter a function, type it in or select its name from the Functions MATH menu.

The MATH Menu

The MATH menu provides access to Math Functions,

Programming Commands, and Programming Constants.

The MATH menu is organized by category. For each category

of functions on the left, there is a list of function names on the right. The highlighted category is the current category.

current category

Re.3l C

Stat-Two Symbolic FLOOR Tests ▼

»8»iopniTMMu;iai

• When you press | math |, you see the menu list of Math Functions. The menu key {{MTHa}} indicates that the Math Functions list is "on."

« To display the menu list of Program Commands, press

{{CMOS}}. To display the menu list of Program Constants,

press {{CONS}}. To re-display the Math Functions, press

{{MTH}}.

The programming commands and programming constants are discussed in chapter 8, Programming.

FUNCTIDNS^»|

CEILING

DEG-^RflD -J FNROOT T

•

IB3MIHII3Ì

functions

2-12 Mathematical Calculations

To copy a 1. Press | math | to display the MATH menu. The categories function appear in alphabetical order. Use 0 and 0 to scroll

through the categories. To skip directly to a starting letter, press a letter key.

2. The list of functions (on the right) applies to the currently highlighted category (on the left). Use 0 and 0 to

switch between the category list and the function list.

3. Highlight the name of the function you want and press

{{OK}}. This copies the function name (and an initial

parenthesis, if appropriate) to the edit line.

Function Categories

Calculus Complex

numbers Constant Hyperbolic trig Lists

Loop

Matrices

Polynomial Probability Real numbers

Statistics-Two Variable

Symbolic

Tests

Trigonometry

The Math Functions by Category

Following are definitions for all categories of functions except List, Matrbc, and Statistics, each of which appears in its own chapter. Except for the keyboard operations, which do not appear in the MATH menu, all other functions are listed by their category in the MATH menu.

Syntax Each function’s definition includes its syntax, that is, the exact

order and spelling of a function’s name, its delimiters (punctuation), and its arguments. Note that the syntax does

not include spaces.

Mathematical Calculations 2-13

Keyboard Functions

The most frequently used functions appear on the keyboard. The keyboard functions are the only math functions that do

not appear in the MATH menu. Many of the keyboard functions also accept complex numbers as arguments.

0.Q.0.0

Add, Subtract, Multiply, Divide. Also accept complex numbers.

value 1+ value2, etc.

m i e l

Natural exponential. Also accepts complex numbers.

e''value

■ [LN]

Natural logarithm. Also accepts complex numbers.

IM [value]

■ [101

Exponential (antilogarithm). Also accepts complex numbers.

10''value

■ [LOG]

Common logarithm. Also accepts complex numbers.

LOG [value]

|SIN|, |COS|, |TAN|

Sine, cosine, tangent. Inputs and outputs depend on the current angle format (Degrees, Radians, or Grads).

SIN(oo/ue)

COS [value]

TAN [value]

■ [ASIN] Arc sine : sin^'x Output ranges from -90° to 90°, -'ir/2 to tt/2, or -100 to 100 grads. Inputs and outputs depend on the current angle format.Also accepts complex numbers.

■ [ACOS]

ASIN(UO/ue)

Arc cosine: cos^'x. Output ranges from 0° to 180°, 0 to tt, or 0 to 200 grads. Inputs and outputs depend on the current angle format. Also accepts complex numbers.

ACOS [value]

2-14 Mathematical Calculations

[ATAN]

Arc tangent: tan^'x. Output ranges from -90° to 90°, -Tr/2 to

77/2, or -100 to 100 grads. Inputs and outputs depend on the current angle format. Also accepts complex numbers.

AT AN (oa/ue)

l[J^]

Square. Also accepts complex numbers.

value‘

Square root. Also accepts complex numbers.

V~value

[^]

K’]

Pi, a constant.

Multiplicative inverse (reciprocal). For a complex number, the

reciprocal is

X +y X +y

value''-!

Negation. Also accepts complex numbers.

-value

IZ]

Power (x raised toy). Also accepts complex numbers.

value'‘power

! [ABS] Absolute value. For a complex number, this is •/

ABS [value) ABS( (x,y) )

2 2

X +y .

I Takes the nth root of x.

roo/NTHROOTna/ue

Example: 3 B S/x 8 returns 2.

Mathematical Calculations 2-15

Calculus Functions

You will find the symbols for the calculus functions derivative

and integral in the CHARS menu (■ [CHARS]) as well as the MATH menu.

TAYLOR

Differentiates expression with respect to the variable of differentiation. Use a formal variable (si, etc.) for a non numeric result.

doariable(expression)

Example: asl (sl^+3*sl) returns 2*sl+3

Integrates expression from lower to upper limits with respect to the variable of integration. To find the definite (numeric) integral, both limits must have numeric values (that is, be numbers or real variables). To find the indefinite integral, one of the limits must be a formal variable (si, etc.).

/ {lower, upper, expression, variable') Example; /( 0, si, 2*X+3 , X) |ENTER| |T| ffCOPY}} |enter]

finds the indefinite result 3*sl+2*(sl''2/2)

Calculates the nth order Taylor’s polynomial of expression at the point where the given variable =0.

TAYLOR {expresslon,variable,n)

2-16 Mathematical Calculations

Complex-

Number

Functions

These functions are for complex numbers only. You can also

use complex numbers with all trigonometric and hyperbolic functions, and with some real-number and keyboard functions. Enter complex numbers in the form (x,y), where x is the real part and y is the imaginary part.

ARC

CONJ

Argument. Finds the angle defined by a complex number.

Inputs and outputs use the current angle format in Modes.

ARG{ ir,0) )

Complex conjugate. Conjugation is the negation (sign reversal) of the imaginary part of a complex number.

CONJ( lx,y) }

Imaginary part, y, of a complex number, (x,y).

IM ((x,y))

Real part x, of a complex number, (x,y).

RE ((X,y))

Mathematical Calculations 2-17

Constants

The HP 38G has an internal numeric representation for these constants.

MAXREAL

MINREAL

Natural logarithm base. Internally represented as

2.71828182846.

Imaginary value for , the complex number (0,1).

Maximum real number. Internally represented as

9.99999999999X10“.

MAXREAL

Minimum real number. Internally represented as 1 x 10 “

MINREAL

The ratio perimeter: diameter. Internally represented as

3.14159265359. TT

2-18 Mathematical Calculations

Hyperbolic Trigonometry

The hyperbolic trigonometry functions can also take complex

numbers as arguments.

ACOSH

Inverse hyperbolic cosine: cosh'r.

ACOsm value)

ALOG

Antilogarithm (exponential). This is more accurate than 10''x due to limitations of the power function.

ALOG [value]

ASINH

ATANH

COSH

Inverse hyperbolic sine : sinh''x.

ASINH (ua/ue)

Inverse hyperbolic tangent: tanh~'x. If the input is ± 1, an

Infinite Result occurs.

ATANH (ufl/ue)

Hyperbolic cosine: (e'4€^')/2.

COSH (value)

SINH

TANH

EXP Natural exponential. This is more accurate than e''x due to

Hyperbolic sine.

SlNH(oa/«e)

Hyperbolic tangent.

TANH(wa/iie)

limitations of the power function.

EXP (value)

EXPMl

LNPl Natural log plus 1 : ln(x+l). This is more accurate than LN

Exponent minus 1 : e'-1. This is more accurate than EXP when

X is close to zero.

EXPMl (value)

when X is close to zero.

LNPl (value)

Mathematical Calculations 2-19

List Functions These functions are for list data stored in list variables. See

chapter 7, Using Lists.

Loop Functions The loop functions display a result after evaluating an

expression a given number of times.

ITERATE Repeatedly (the specified dimes') evaluates an expression in

terms of variable. The value for variable is updated each time, starting with initialvalue.

ITERATE {expression, variable, initialvalue, ^imes)

RECURSE Provides a method of defining a sequence without using the

Symbolic view of the Sequence aplet.

RECURSE {sequencename, term-n, terml, term2)

Example: RECURSE (U,u (N-1) *N, 1,2) {{ST0^}}U1 (N) This produces the factorial ui(1)=1 Ul(2)=2 U1(N)=U1(N-1)*N

2 Summation. Finds the sum of expression with respect to variable

from initialvalue to finalvalue.

2 (variable=initialvalue, finalvalue, expression)

Example:2(C=l, 5,C^) returns55.

Matrix These functions are for matrix data stored in matrix variables. Functions See chapter 8, Using Matrices.

2-20 Mathematical Calculations

Polynomial

Functions

Polynomials are products of constants (coefficients) and variables raised to powers (terms).

POLYCOEF Polynomial coefficients. Returns the coefficients for the

polynomial with the specified roots.

POLYCOEF! [roofs] ) Example: to find the polynomial with roots 2,-3, 4, -5:

POLYCOEF ( [2,-3,4,-5]) returns [1,2 ,-25,-26,120], representing x%2з¿-25)¿-2%x+\ 20.

POLYEVAL Polynomial evaluation. Evaluates a polynomial with the

specified coefficients for the value of x.

POLYEVAL! [coefficients] , value) Example: for 25x^—26jc-rl20:

POLYEVAL! [1,2, -25, -25,120] , 8) returns 3432.

POLYFORM Polynomial form. Creates a polynomial in variable] from

expression. Can express the coefficients as a polynomial in variable2. (The coefficients of the coefficients can be expressed

as polynomials in variables, etc.) POLYFORM! expression, variable 1,.. .,variable-n)

Example: polyform! !x+1) ''2 + 1,x) returnsX''2+2*x+2 .

POLYROOT

Polynomial roots. Returns the roots for the nth-order polynomial

with the specified n+l coefficients.

polyroot! [coefficients])

Example: forx“-i-2x*-25x^-26x+120: POLYROOT! [1,2,-25,-26,120] ) returns [2,-3,4,-5].

Mathematical Calculations 2-21

Probability Functions

Probability functions are often used in statistical analyses.

COMB

PERM

RANDOM

UTPC

UTPF

Number of combinations (without regard to order) of n things taken rat a time, n!/(r!(n-r)).

COMB (n,r)

Factorial of a positive integer. For non-integers, ! = F(x + 1).

value !

Number of permutations (with regard to order) of n things taken rat a time, n\/ (_n-r)\.

PERM(n,r)

Random number (between zero and 1). Produced by a pseudo random number sequence. Becomes the seed for the next random number.You can set the seed using the command RANDSEED.

RANDOM

Upper-Tail Chi-Squared Probability given degrees of freedom,

evaluated at value. Returns the probablility that a random

variable is greater than value.

UTPC ( degrees, value )

Upper-Tail Snedecor’s F Probability given numerator degrees of

freedom and denominator degrees of freedom (of the F distribution), evaluated at value. Returns the probability that a

Snedecor's F random variable is greater than value.

UTPF {numerator, denominator, value)

UTPN

Upper-Tail Normal Probability given mean and variance,

evaluated at value. Returns the probability that a normal

random variable is greater than value for a normal distribution.

(The variance is the square of the standard deviation.)

UTPN ( mean, variance, value )

UTPT Upper-Tail Student's t Probability given degrees of freedom,

evaluated at value. Returns the probability that the Student's t

random variable is greater than value.

UTPT ( degrees, value )

2-22 Mathematical Calculations

Real-Number Functions

Some real-number functions can also take complex arguments.

CEIUNG

Smallest integer greater than, equal to value.

CEILING (oa/ue)

DEG->RAD Degrees to radians. Converts value from Degrees angle format

to Radians angle format.

DEG—>RA.D (VOltlB)

FLOOR

FNROOT

Greatest integer less than or equal to value.

FLOOR (value)

Function root-finder (like Solver aplet). Finds the value for the given variable at which expression most nearly evaluates to zero. Uses guess as initial estimate.

FNROOT (express/ou, variable, guess)

FRAG Fractional part.

FRAC (value)

HMS->

-^HMS

Hours-minutes-seconds to decimal. Converts a number or expression in H.MMSSs format (time or angle that can include fractions of a second) to x.x format (number of hours or degrees with a decimal fraction).

HMS-> ( H.MMSSs)

Decimal to hours-minutes-seconds. Converts a number or expression in x.x format (number of hours or degrees with a decimal fraction) to H.MMSSs format (time or angle up to fractions of a second).

—>HMS (x.x)

INT

MANX

Integer part.

INT (value)

Mantissa (significant digits) of value.

MANT (value)

Mathematical Calculations 2-23

MAX

Real-Number Functions, continued

Maximum. The greater of two values.

MAX (value!, value2)

MIN

MOD

%CHANGE

%TOTAL

RAD^DEG

ROUND

SIGN

Minimum. The lesser of two values.

MIN (value!, value2)

Modulo. The remainder of valueHualue2.

value! MOD value2

X percent of y; that is, Ay/100.

%(x,y)

Percent change from x toy, that is, 100(y-x)/x.

%CHANGE(X,y)

Percent total: (100)y/x What percentage of x isy.

%TOTAL(X,y)

Radians to degrees. Converts value from one angle format to another.

RAD-ADEG (value)

Rounds value to decimal places. Accepts complex numbers.

ROUND {value,places)

Sign of value. If positive, the result is +1. If negative, -1. If zero, result is zero. For a complex number, this is the unit vector in

the direction of the number

( ^

2 2 ’ I 2 T

X +y yx +y

.Y V

TRUNCATE

XPON

SIGN(ua/ue) SIGN( (x,y) )

Truncates value to decimal p/aces. Accepts complex numbers.

TRUNCATE (value, places)

Exponent of value.

XPON {value)

2-24 Mathematical Calculations

Statistics-Two

Symbolic Functions

These are functions for use with two-variable statistics. See

chapter 5, Statistics.

The symbolic functions are used for symbolic manipulations

of expressions. The variables can be formal or numeric, but the result is usually in symbolic form (not a number). You will find the symbols for the symbolic functions = and 1 (where) in the CHARS menu (|P [CHARS]) as well as the MATH menu.

= (equals')

ISOLATE

UNEAR?

QUAD

QUOTE

Sets an equality for an equation. This is not a logical operator. (See the Test category.)

expression 1 =expression2

Isolates the first occurrence of variable in expression and returns an equation, variable=value. The result is a general solution that represents multiple solutions by including the (formal) variables s7 to represent any sign and nl to represent any integer.

ISOLATE {expression, variable)

Tests whether expression is linear for the specified variable.

Returns 0 (false) or 1 (true).

LINEAR? [expression, variable)

Solves quadratic expression for variable and returns an equation, variable=newexpression. The result is a general solution that represents both positive and negative solutions by including the (formal) variable si to represent any sign, -r or - .

QUAD {expression, variable)

Encloses an expression that should not be evaluated numerically.

QUOTE (expression)

1 (where)

Evaluates expression where each given variable is set to the given value. Allows numeric evaluation of a symbolic expression.

expression \ (variable 1 =value 1,variable2=value2,...)

Mathematical Calculations 2-25

Test Functions The test functions are logical operators that always return

either a 1 (true') or a 0 (false).

<■ Less than. Returns 1 if true, 0 if false.

value Kaalue2

^ Less than or equal to. Returns 1 if true, 0 if false.

value l^value2

— — Equals (logical test). Returns 1 if true, 0 if false.

value 1 = =value2

Not equal to. Returns 1 if true, 0 if false. i=

value! i=value2

> Greater than. Returns 1 if true, 0 if false.

value I>value2

> Greater than or equal to. Returns 1 if true, 0 if false.

value! ^value2

AND

IFTE

NOT

XOR

Compcires value! and value2. Returns 1 if they cire both non zero, otherwise returns 0.

value! AND value2

If expression is true, do the trueclause; if not, do the falseclause.

IFTE (expression, trueclause, falseclause)

Example: IFTE(X>0,x^x’) Returns 1 if value is zero, otherwise returns 0.

NOT value

Returns 1 if either value! or value2 is non-zero, otherwise

returns 0.

value! OR value2

Exclusive OR. Returns 1 if either value! or value2 —but not both

of them—is non-zero, otherwise returns 0.

value! XOR value2

2-26 Mathematical Calculations

Trigonometry Functions

The trigonometry functions can also take complex numbers

as arguments. For SIN, COS, TAN, ASIN, ACOS, and ATAN, see the Keyboard category (all these functions have keys).

ACOT

ACSC

ASEC

COT

CSC

SEC

Arc cotangent.

ACOT (value)

Arc cosecant.

ACSC {value)

Arc secant.

ASEC {value)

Cotangent: cosx/sinx.

COT {value)

Cosecant: 1/sinx

CSC {value)

Secant: 1/cosx.

SEC {value)

Mathematical Calculations 2-27

Plotting and Exploring Functions

Types of Plots Graphing is at the heart of the HP 38G. All of the built-in aplets

do graphing. This chapter considers the four main built-in aplets:

« Function, ® Parametric, e Polar, and

9 Sequence,

The Solve aplet and Statistics aplet, which also include graphing, are covered in separate chapters.

Defining a Problem

You start with an aplet and a mathematical function to explore, like y = mx + h.

General Steps 1. From the Library (| lib |), open the aplet you want. This

determines the type of function you can enter and plot.

2. In the Symbolic view CIsymbQ, enter or select an expression. Check the angle units in the Symbolic Setup

(■ [SETUP-SYMB]).

3. In the Plot view (|plot1), display the graph. There are menu keys to explore by tracing and zooming. Optional: Specify graph settings in the Plot Setup (■ [SETUP-

PLOT]).

4. Explore a table of numeric values in the Numeric view (I NUM|). Optional: specify table settings in the Numeric

Setup (■ [SETUP-NUM]).

5. All information is automatically stored until you change it.

To preserve the complete aplet as you have set it up, use the Library to name and save the aplet (chapter 1).

Plotting and Exploring Functions 3-1

Select an Aplet

Select the aplet appropriate to your problem : Open the Library (|lib|), highlight the name of an aplet, and press {{START}} (or IENTErQ.

® Function . This aplet can define rectangular equations of

the form y = f(x) .

• Parametric . This aplet can define parametric expressions,

which define equations over time, t. They take the forms

jf = /'(0andy = g(0-

® Polar, This aplet can define polar expressions, which

graph equations in terms of an angle 0.

• Sequence. This aplet can define sequence functions,

which are defined in terms of n or in terms of the previous

terms in the sequence. Sequence plotting produces either

stairstep graphs (n .i/J or cobweb graphs (f/,U^.

® Other aplets . You can load or create other aplets besides

those that are built in. Those you create yourself will be based on an existing aplet, filled with data and then

named (if you like).

Define an Expression (Symbolic View)

The Symbolic view is the defining view for Function, Parametric, Polar, and Sequence aplets. The other views are derived from the symbolic expression.

You can define up to ten different functions for each Function, Parametric, Polar, and Sequence aplets. You can graph any number of functions (in the same aplet)

simultaneously by checkmarking them.

3-2 Plotting and Exploring Functions

To define the 1. Display the Symbolic view (| symb |). If the highlight is on expression an existing expression, scroll to an empty line—unless you

don’t mind writing over the expression. Or, clear one line

(I DEL I) or all lines (■ [CLEAR]).

2. Make sure your function is in the form “y = For example, given the equation 9x+y - 11=0, you would rearrange it to y = f(x) = -9x + 11. Type in just the expression (-9x+l 1) for the right side.

• For a Function definition, enter an expression to

define F(X). The only independent variable in the expression is X.

» For a Parametric definition, enter a pair of

expressions to define X(T) and Y(T). The only independent variable in the expressions is T.

® For a Polar definition, enter an expression to define

R(0). The only independent variable in the expression is 0.

e For a Sequence definition, enter the first, second, and

nth terms for U (U1, or...U9, or UO). Define a sequence function in terms of N or of the prior terms, U(N -1) and U(N -2). The expressions should produce real valued sequences with integer domains.

3. Press I ENTER I or {{OK}} to enter the expression into the list.

All checkmarked expressions mill be plotted.

Plotting and Exploring Functions 3-3

Symbolic View Keys

Key Meanine

{{EDIT}} Copies the highlighted expression to the edit

line for editing. Press {{OK}} when done.

{{^CHK}} Checks/unchecks the current expression (or

set of expressions). Only the checked expression(s) are evaluated in the Plot and

Numeric views.

{{X}}, {{T}}, {{0}}. {{N}}

{{U1}}...{{U9}}

{{EVAL}} Symbolically evaluates the variables of the

1 VAR| 1 MATH 1

■ {CHARS}

[M]

■ {CLEAR] Deletes all expressions in the list or clears the

Typing aids for the independent variable. Or, you can use the |xt6 | key on the keyboard.

Additional typing aids for variables in the Sequence aplet.

Displays the current expression in standard mathematical form.

current expression. Menus for entering variable names, contents

of variables, or math operations. Displays special characters. To type one,

place the cursor on it and press {{ok}}. Deletes the highlighted expression or the

current character in the edit line.

edit line (if it was in use).

Angle Measure For the Function, Parametric, Polar, and Sequence aplets, the Setup only setting for the Symbolic view is the angle measure. This

is significant only if any trigonometric function is used.

To check or change the angle measure, press ■ [SETUPSYMB]. The choices are Radians, Degrees, and Grads. This

setting can affect what the graph looks like, as well as what the numerical values are.

3-4 Plotting and Exploring Functions

Evaluating Expressions

In Aplets In the Symbolic view, a variable is a symbol only, and does

not represent one specific value. If a variable contains another variable in it, then {{EVAL}}

substitutes it as shown in this example.

In Function Symbolic view,

enter these three expressions.

Highlight F3.

FUNCTION SyHIDLIC MIEH

-^FKX>=R»X''2

F4<X>= F5<X) =

F1C-OH-F2'

I FUNCTION fVHEOLIC MIEH

-'FKX>=fl»X-'2

>^F2(X>=B

F4<X>= F5<X>=

■aata BBrnaiMMBiMgMiiaiiiiii lamw

In Home You can also evaluate any expression in Home by entering it

into the edit line and pressing | enter |. For example, in Home type F3 (X) i ENTER I to evaluate the above expression . This will fully evaluate the expression, substituting any stored values for A and B and X.

Plotting and Exploring Functions 3-5

Examples: Defining Expressions

Function Example

Define - 2x + 3 . Enter this expression as the right side of the equation in the

Symbolic view. In the Symbolic view of the Function aplet, highlight a line (or

clear the lines) and enter the expression.

I LIB I Select Function.

{{START}} {{X}} [ID 3 □ 2 0 {{X}} 0 3 I ENTER I

g FUNCTION SVMeOLIC VIEM^H

*'FKX>=X''3-2*X+3

F3CX)= F4<:x>= F5<X>=

i—HBnnniiUYIB

Remember that the equation that the HP 38G evaluates must be in the form /(x) = expression in terms of x.

Given this exoression...

3x + 2y - 4 = 0 y= -3/2x + 2

x^ + 7x+10 = 0 y = x' + 7x+]0

x^ = 2x+7

Rearrange it to...

y^ = 2x+7

y3 = y, -Y2

And enter...

-3/2*X+2

X''2 + 7*X+10

FI (X)=X''2, F2(X)=2*X+7,and F3(X)=F1 (X) -F2(X)

Parametric Define xQf) = 3 sinSi Example y(i) = 2 sin4i.

In the Symbolic view of the Parametric aplet, highlight a line (or clear the lines) and enter the expressions.

1 LIB I Select Parametric

3 0 I SIN I 3 0 {{T}} I ENTER I

2 0 I SIN I 4 0 {{T}} I ENTER I

3-6 Plotting and Exploring Functions

*FSR*METIilC SVHSnyC MIEW*

^X1<T)=3*SINC3*T>

''Yl(T>=2*SINC4sT)

Y2<T>= X3<T)=

BMEEaanii

iHiiiiBiranB

Polar Example Define r = 2 cos40.

In the Symbolic view of the Polar aplet, highlight a line (or clear the lines) and enter the expression.

I Select Polar

2 a 4 a {{0}}

ENTER

|PDL*f! SVHSDUC MIEW

^Rli0>=2*COSi;4*0>

R3<0>=

R4i;0>=

R5<0>=

■HihiBirang

Sequence Define the Fibonacci sequence, in which each term (after the Example first two) is the sum of the preceding two terms ;

( = 1, /j = 1, and /3 = (,_2 for /7 ss 3.

In the Symbolic view of the Sequence aplet, highlight a line (or clecir the lines) and enter the expressions.

I Select Sequence

1 I ENTER I 1 I ENTER I

{{Ul}} {{(N-1)}}Q {{Ul}}{{(N-2)}} [iNriWI

SEQUENCE SVMtDLIC VIEH

*^U1C2> = 1 '^ui<h>=ui<:h-i>+ui<n,

iMiiliiiS

U2<2>=

Plotting

Plot the Expression (Plot View)

After entering and selecting (checkmarking) the expression

in the Symbolic view, press| plot |. To adjust the appearance of the graph or the interval that is displayed, you can change the Plot Setup (page 3-18).

Compsiring

Plots

Pausing a Plot Press {{PAUSE}} or |on| to interrupt plotting. Press {{CONT}}

Erasing a Plot Press ■ [CLEAR] to erase a plot.

You can plot up to ten expressions at the same time. Simply

checkmark all those expressions you want to be plotted together.

to continue plotting. Press | plot | to start the plotting over.

Plotting and Exploring Functions 3-7

Undefined If, during plotting, a real value for the expression is not found, Points then that point is not plotted, and no line is connected

through it.

Tracing a Plot When a graph is nev/ly drawn, TRACE mode is on. Pressing a

cursor key will trace the crosshairs along the graph, displaying the coordinate values as they move.

Scrolling a Plot In Function and Sequence aplets, you can scroll left and right

beyond the edge of the window to see more of the graph.

Zooming

Press I PLOT [{{ZOOM}} for a choice of zooming options. To

switch to a predefined axis scaling (such as Trig or Integer),

press ■ [VIEWS].

Examples: Plotting

Function Plot the expression from the previous Function example, Example x' - 2x + 3 . In Plot Setup, specify YRNG ; -3.1 5 so

that you can see more of the graph (the default values are

-3.1 and 3.2). You can leave the other plot settings at their default values.

( Ob I Select Function {{START}}

Make sure the correct function

is highlighted and checked.

■ {SETUP-PLOT}

ryjfFlSfwriRl

I PLOT I

{F} 6 times (The cursor starts in the

center of the X -range and traces the plot.)

1^* FUNCTION

HRNG:

-6.5 6.5

VfiNQ:

-3.1 5

«TICK:

fiES:

Faster

ENTER HDRiZDNTAL TICK iPACIMS

mm\

,, j

«: . 6 FlC« i: E.OIS liil:t!lll

PLOT SETUPS*

VTICK: 1

3-8 Plotting and Exploring Fnnctions

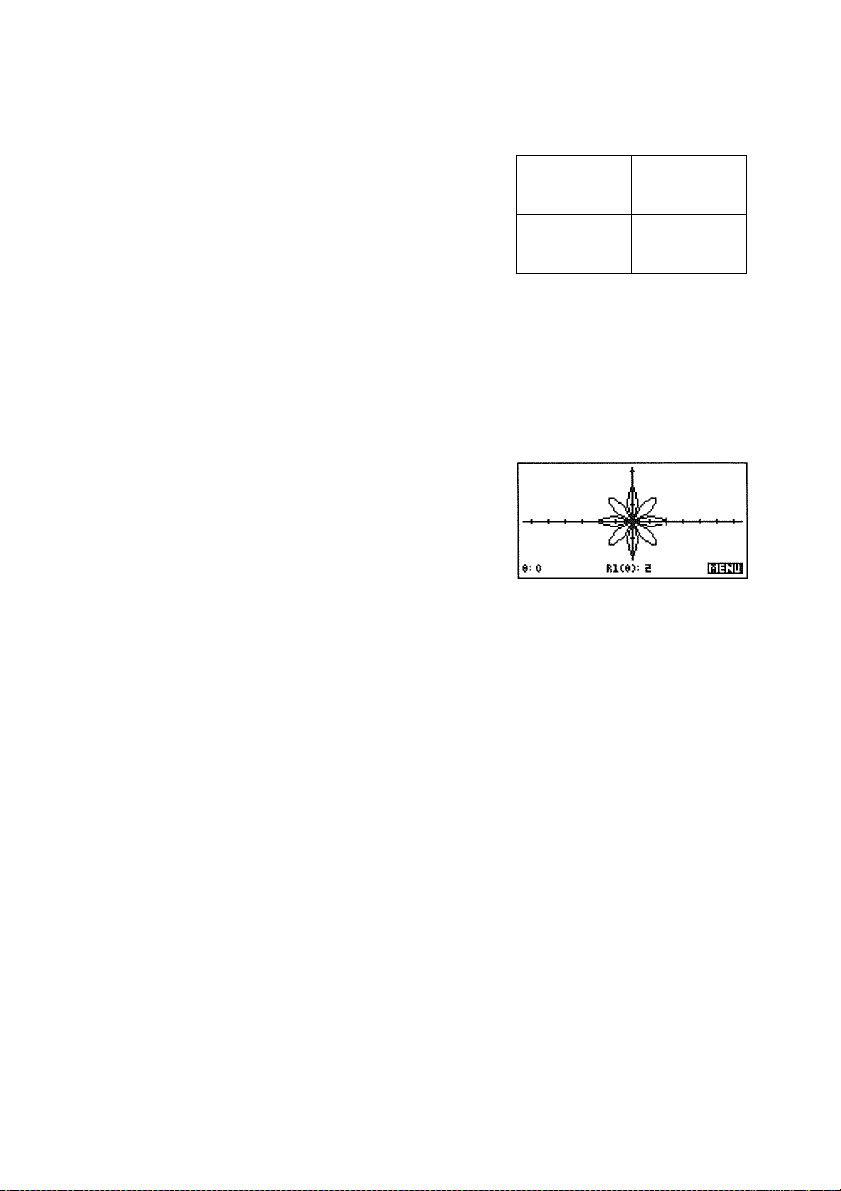
Parametric Example

Plot the expressions from the previous Parametric example,

x(f) = 3 sinSi and y(i) = 2 sin4f .Before plotting, however,

reset the default plot settings by clearing the Plot Setup view.

I Select Parametric

Make sure the correct function

is highlighted and checked,

m [SETUP-PLOT]

■ [CLEAR]

T: 0

ibn:ih

PLOT

Polar Example

Plot the expression from the previous Polar example,

r = 2 cos40. Before plotting, however, reset the default plot

settings by clearing the Plot Setup view.

j Select Polar

Make sure the correct function

is highlighted and checked.

■ [SETUP-PLOT]

■ [CLEAR]

PLOT

Plotting and Exploring Functions 3-9

Sequence Plot the Fibonacci sequence from the previous Sequence Example example, i/, = 1, = 1, and = i/„_, + . In Plot Setup,

first set the SEQPLOT to Stairstep, then try a Cobweb plot. Reset the default plot settings by clearing the Plot Setup view.

® A Stairstep graph plots n on the horizontal axis and t/ on

the vertical axis.

e A Cobweb graph plots on the horizontal axis and

on the vertical axis.

I LIB I Select Sequence

Make sure the correct function is highlighted and checked.

SEQUENCE PLOT SETUP SECFLDT: ISUEEfaSUEfS NRNQ: 1 XRNQ: -2 VRNG; -2

CHQD^E SEQUENCE PLOT TVPE

24 24

10.6

■ {SETUP-PLOT]

m [CLEAR]

PLOT

Now set SEQPLOT to Cobweb and see the difference.

m [SETUP-PLOT]

Select Cobweb

PLOT

3-10 Plotting and Exploring Functions

Exploring the Plot

Plot view (press [ plot | or ■ [VIEWS]) gives you a selection of menu keys to explore a graph further (for the checkmarked expressions in the Symbolic view). The options vary from

aplet to aplet.

PLOT View Keys

Key

■ [CLEAR]

■ [VIEWS]

■ a

■ 0

([ZOOM]}

([TRACE]}

({FCN}}

([DEFN]}

({MENU}}

Meaning

Erases the plot. Offers additional pre-defined views for

splitting the screen and for scaling

(“zooming") the axes. Moves cursor to far left or far right.

Displays ZOOM menu list. Turns Trace mode on/off. The ■ appears

when Trace mode is on ({{trac*}}). Displays the cursor’s coordinate position.

Press {{MENU}} to restore the menu. Function aplet only: Turns on menu list for

root-finding functions (see “Interactive Root-

Finding, ’’ later in this chapter}.

Displays the current, defining expression. Press {{MENU}} to restore the menu.

Turns menu-key labels on and off. When the

labels are off, any top-row key turns them back on.

Plotting and Exploring Functions 3-11

Tracing

Many aplets have a Trace mode. Trace mode is on when a plot has just been drawn. When Trace mode is on, the crosshairs cursor follows just the plotted points when you press the Q or @ keys. The cursor traces the function. The display also shows the current coordinate position (jc, y) of the cursor.

If there is more than one curve displayed, press (T| or [Yl to

move between curves.

Note that tracing might not appear to exactly follow your plot

if the resolution (in Plot Setup view) is set to Faster. This is because RES: FASTER plots in only every other column, whereas tracing always uses every column.

In Function and Sequence Aplets : You can also scroll (move the cursor) left or right beyond the edge of the display

window in Trace mode, giving you a view of more of the plot.

crosshairs cursor

coordinates.

: FSiinn

3-12 Plotting and Exploring Functions

To turn on e Trace mode and the coordinate display are automatically TRACE mode set when a plot is drawn. At other times, set Trace mode by

pressing {{TRACE}} to change the label to {{TRAC«}}. (If the menu labels are not displayed, press {{MENU}} first.)

• Turn off Trace mode by changing the menu label back to

{{TRACE}}.

To turn on e To turn On the display of the coordinates' values at the

coordinates current cursor position, press {{(X, Y)}}. To turn the

coordinate display off again, press {{MENU}}.

Zooming

One of the menu key options in PLOT is {{zoom}}. Zooming redraws the plot on a larger or smaller scale, or on a heightened or widened scale. It is a shortcut for changing the

Plot Setup, and it does change those settings.

With the Set Factors option you can specify the factors that

determine the extent of zooming, and whether the zoom is centered about the cursor.

Not all ZOOM options are available in all aplets.

Plotting and Exploring Functions 3-13

{{ZOOMI}

Options

Select an option and press {{OK}}. Option Meanine

Center Recenters the plot around the current

position of the crosshairs without changing the scale.

Box...

Lets you draw a box to define the zoom boundaries. Use the cursor keys to draw the box, and press {{OK}} to zoom in (see below).

In Divides horizontal and vertical scales by the

X-factor and Y-factor (in Set Factors, below).

For instance, if zoom factors are 4, then

zooming in results in 1/4 as many units

depicted per pixel.

Out Multiplies horizontal and vertical scales by

the X-factor and Y-factor (in Set Factors, below).

X-Zoom In Divides horizontal scale only, using X-factor. X-Zoom Out Multiplies horizontal scale only, using X-

factor.

Y-Zoom In Y-Zoom Out

Divides vertical scale only, using Y-factor. Multiplies vertical scale only, using Y-factor.

Square Changes the vertical scale to match the

horizontal scale.

Set Factors...

Sets the X-Zoom and Y-Zoom factors for zooming (multiplying for Zoom Out, dividing for Zoom In). Includes option to recenter the plot before zooming.

Un-zoom Returns the display to the previous zoom.

3-14 Plotting and Exploring Functions

To use Box The Box Zoom option lets you draw a box around the area Zoom you want to zoom in on.

1. If necessary, press {{MENU}} to turn on the menu-key

labels.

2. Press {{ZOOM}} and select Box.. .

3. Position the crosshairs into one corner of the box-to-be. Press {{OK}}.

4. Use the cursor keys (, etc.) to drag two sides of a box.

5. Press {{OK}} to zoom in on the boxed area.

Plotting and Exploring Functions 3-15

Other Views for Scaling and Splitting the Graph

Other Scales The preset viewing options (■ [VIEWS]) draw the plot using

certain pre-defined axis scales. This is a shortcut for changing Plot Setup. For instance, if you have defined a trigonometric function, then you could select Trig to plot your function on

a trigonometric scale.

[VIEWS]

Options

Select an option and press ([OK]). Option Meaninfi

Plot-Detail Splits the screen into the plot and a close-up

(see the next topic).

Plot-Table Splits the screen into the plot and the data

table (see page 3-24).

Overlay Plot Plots the current expression(s) without

erasing any pre-existing plot(s).

Auto Scale Rescales the axes using autoscaling. Decimal

Rescales both axes so each pixel = 0.1 unit. Resets default values for XRNG (-6.5 to 6.5) and YRNG (-3.1 to 3.2). (Not in Sequence or Statistics.)

Integer Rescales horizontal axis only, making each

pbcel =1 unit.(Not in Sequence or Statistics.)

Trig

Rescales horizontal axis so 1 pixel =Tr/24 radian, 7.5°, or 8.'/3 grads; rescales vertical axis so 1 pixel=0.1 unit. (Not in Sequence or Statistics.)

3-16 Plotting and Exploring Functions

Splitting the Screen

The Split Screen view can give you two simultaneous views of the plot.

1. Press ■ [VIEWS] . Select Plot-Detail and press {{OK}}.

The graph is plotted twice. You can now zoom in on the right side.

2. Press {{MENU}}{{ZOOM}} to choose the Zoom method and press {{OK}} or I ENTER ¡.This zooms the right side. Here is an example of split screen with zoom in.

The Plot menu keys are available as for the full plot (for tracing, coordinate display, equation display, and so

on).

■ 0] or ■ moves the cursor to the far left or far right of the full plot.

The {{<--}} left-arrow menu key will convert the base

plot (left side) to the scale of the zoomed plot (right

side). (It does so by resetting the variables’ minimum

and maximum values in the Plot Setup.)

Overlaying Plots

plot} . The left side takes over3. To un-split the screen, press

the whole screen.

If you would like to plot over an existing plot without erasing

that plot, then use ■ {VIEWS} Overlay Plot instead of

I PLOT I. Note that tracing follows only the current functions from the current aplet.

Plotting and Exploring Functions S-17

Setting Up the Plot (Plot Setup)

Press ■ [SETUP-PLOT] to define any of the settings shown in

the next two tables.

1. Use the arrow keys to move from field to field. Highlight the field to edit.

• If there is a number to enter, type it in and press | enter |

or {{OK}}.

• If there is an option to choose, press {{CHOOS}},

highlight your choice, and press | enter | or {{ok}}. As a shortcut to {{CHOOS}}, just highlight the field to change and press to display and select the different choices.

• If there is an option to turn on/off, press {{/CHK}} to

check or uncheck it.

2. Press {{PAGET}} to view more settings.

3. When done, press [plot] to view the new plot.

To reset settings

{SETUP-PLOT} Settings

To reset the default values for all plot settings, press

■ {CLEAR} in the Plot Setup view. Field

XRNG, YRNG. TRNG,

6RNG,

NRNG

RES

TSTEP , eSTEP

SEQPLOT

XTICK YTICK

Meaning For Function plot: Specifies the

minimum and maximum horizontal (X) and vertical (Y) values for the plotting window.

For Parametric, Polar, and Sequence plots: Specifies the time (T), angle (0), or index (N) values for the graph.

For Function plots: Resolution. "Faster" plots in alternate pixel columns; "More Detail" plots in every pixel column.

For Parametric and Polar plots: intervals at which to use the independent

variable to calculate the function.

For Sequence plots: Stairstep or Cobweb types.

Horizontal spacing for tickmarks.

Vertical spacing for tickmarks.

3-18 Plotting and Exploring Functions

Second-Page Those items with space for a checkmark are settings you can

turn on or off. Press {{PAGET}} to display the second page. SIMULT

INV. CROSS

CONNECT

LABELS Label the axes with XRNG and YRNG

AXES

GRID

Interactive Root-Finding

You can find roots, intersections, slopes, and areas for a

function in the Plot view of the Function aplet (and any Function-based aplets). The {{FCN}} operations act on the currently selected expression or on the graph being traced.

The results are saved in the variables Area, Extremum, Isect,

Root, and Slope, so you can do further calculations with these results in the aplet or in Home.

If more than one function is being plotted, plot them simultaneously (otherwise sequentially).

When the crosshairs cross the plot, invert those pixels that are overlapping.

Connect the plotted points. (Sequence always connects them.)

values. Draw the axes. Draw grid points using XTICK and YTICK

spacing.

To use a 1. In Symbolic view in a Function aplet, select the expression

{{FCN}} (for Intersect, two expressions) whose curve you want to operation study. Or trace the curve you want to study.

2. Position the cursor where you want it to be before pressing

{{FCN}}. If you cannot see the crosshairs, they might be on

the axes. Press 0 or 0 to move the cursor and make it visible.

3. Press {{FCN}}, then select an operation from the menu list and press {{OK}}.

4. To perform another operation, press {{MENU}} to turn the

menu-key labels back on.

Plotting and Exploring Functions S-19

To move the cursor

To change the starting position of the cursor after having selected an operation, press {{MENU}}, move the cursor, and

re-select the FCN operation.

To clear shading

To remove the shading produced by the AREA operation, press I PLOT I to re-draw the plot.

FCN Operations

Root Select Root to find the root x-value nearest the crosshairs. If

no root is found, but only an extremum, then the result is labeled EXTR: instead of root :. (The root-finder is also

used in the Solve aplet. See also “Interpreting Results,” in

chapter 4.) The resulting x-value is saved in a variable named

Root.

Extremum Select Extremum to find the maximum or minimum nearest

the crosshairs. This displays the coordinate values and moves the crosshairs to the extremum. (This uses the derivative.) The resulting value is saved in a variable named Extremum.

Slope Select slope to find the numeric derivative at the point

nearest the crosshairs. The result is saved in a variable named Slope.

Area Select Area to find the numeric integral. (If there are two or

more expressions checkmarked, then you will be asked to choose the second expression from a list that includes the x-

axis.) Select a starting point, then move the cursor to shade a

region between the curve and the x-axis (or another curve), and between the starting point and the current position. The shaded region will be between the two curves. The Area is

the signed value of the shaded area. Areas below the x-axis are negative. The result is saved in a variable named Area.

Intersection Select intersection to find the intersection of two graphs

nearest the crosshairs. (You need to have at least two selected

expressions in Symbolic view.) Displays the coordinate values

and moves the crosshairs to the intersection. (Uses Solve function.) The resulting x-value is saved in a variable named Isect.

3-20 Plotting and Exploring Functions

Examples: Root-Finding with Plots

These examples of the interactive root-finding operations use the expression f(x) = jc^-1 in the Function aplet with default plot settings.

Select the Function aplet.

SYMB

{{X}} ■ [^] □ 1 [¡EUR]

IFUNCTIDN fVHBDLIC VIEH

^FKX>=Xa-l

F2t;x> =

F3<X> = F4<X) = F5<X> =

ROOT

EXTREMUM

SLOPE

[SETUP-PLOT] [CLEAR]

PLOT

{{MENU}] {{FCN}}

Select Root {{OK}}

The crosshairs started at (0, -1). The root nearest the crosshairs is x = -1. The crosshairs have moved to ( -1,0).

5efeci Extremum {{OK}}

Sefeci Slope {{OK}}

■ VI

ftDDT: -1

,,,,vL/,,

EHTftM: <0,-D

,, ,v

The slope at the extremum (where the crosshairs are) is zero.

I8IJ!III

isuim

iaB;iii

Plotting and Exploring Functions 3-21

AREA

You move the cursor to the starting point first, then shade the area.

Select Area. . . {{OK}}

{{OK}} to set starting point

Q 10 times

The shaded area has a value of -0,666666666667 (to 12-digit accuracy). It is negative because the region lies below the x- axis.

Enter a second expression, f(x) = in Function aplet, and find the intersection of it with f(x) =x‘-l.

Select the Function aplet

SYMB

{{X}} 3 I enter)

,, ^

SELECT END POINT

...........................

^Fl<:x>=xa-1 ^F2CX>=X''3

F3(:x:)=

F4<x:>=

F5<X>=

Esnoanii

FUNCTION SVHiOLIC VIEM^

iHHiiBirang

RCTiroai

INTERSECT You must specify whether to find the intersection with the

second function or with the x-axis.

I PLOT I {{MENU}} {{FCN}}

Select Intersection

Select the function F(X)=X''3

(not the x-axis) {{ok}}.

3-22 Plotting and Exploring Functions

,.A|

l-SECT:

Using a Table of Numbers

Display a Table of Numbers (Numeric View)

After entering and selecting (checkmarking) the expression

in the Symbolic view, press | num| to view a table of data values for the independent (X, T, 0, or N) and dependent variables. To adjust the initial value or step size, change the Numeric Setup.

NUM View Keys

Key

Meaning

Displays ZOOM menu list.

Toggles between two character sizes.

Displays the defining function expression for the highlighted column. To cancel this display, press {{DEFb}}.

independent

variable

full display of

highlighted -

value

- X F3

.S .3 .4 .5

9.98334166-:

М||||81ИНМ1—1

---------------------------------

.3435303 .ЗВ4Ч1ВЭ .4744355

t68E-2

laatriaragran—

' dependent

variable

The table adds columns for each additional expression that is

checkmarked in the Symbolic view.

Press {{DEFN}} to display the expression that defines the function in the highlighted column.

X FI F2 F3

-1

-.44

-.46

-.41

-.ВЧ

-.75

.001

.008 .037 .064 .135

.3 .3 .4 .5

SINCX:)

Hililgl—

A ВЕЕПЕЕП

ТоткчУ

.3455303 .ЭВ441ВЗ .4744355

Automatic You can enter any new value in the X column for the Recalculation independent variable. When you then press | enter!. the

values for the dependent variables are recalculated, and the entire table is regenerated with a new interval between X values.

Plotting and Exploring Functions 3-23

Exploring the Table of Numbers

Zooming

Options

Zooming redraws the table of numbers in greater or lesser

detail.

Option

Meaning

Decreases the intervals for the independent variable so a narrower range is shown. Uses the NUMZOOM factor in Numeric Setup.

Out Increases the intervals for the independent

variable so that a wider range is shown. Uses the NUMZOOM factor in Numeric Setup.

Decimal Changes intervals for the independent

variable to 0.1 unit. Starts at zero. (Shortcut to changing NUMSTARTand NUMSTEP.)

Integer

Changes intervals for the independent variable to 1 unit. Starts at zero. (Shortcut to changing NUMSTEP.)

Trig

Changes intervals for independent variable to tt/24 radian or 7.5 degrees or 8V3 grads. Starts at zero.

Un-zoom Returns the display to the previous zoom.

The display on the right is a Zoom In of the display on the left.

X FI

^25 *

.15 .2

-.ццнз?s

-.цц

-.Ц7?5

-.Bfi

X FI

-.*i«îl311

-.RR

-.RBB?11

.1135

-.RB?3HH

.11B?5

-.RB5BRS

.135

-.RBR3?5

snnsii IB1HGS33I

3-24 Plotting and Exploring Functions

Splitting the

Screen

The Split Screen view gives you two simultaneous views.

1. In the Symbolic view of the appropriate aplet, make sure the function(s) you want are checkmarked.

2. Press ■[VIEWS}.

Select Plot-Table and press {{OK}}.

3. The Q and 0 cursor keys move the crosshairs along the plot; the view of the table adjusts itself. The Q and [V) cursor keys move the crosshairs from one graph to another.

4. To return to a full Numeric (or Plot) view, press | num| (or

I PLOT I).

Setting Up the Table (Numeric Setup)

Press ■ [SETUP-NUM] to define any of the settings shown in the table below. To reset the default values for all table

settings, press ■ [CLEAR].

1. Use the arrow keys to move from field to field. Highlight the field to edit.

• If there is a number to enter, type it in and press | enter | or {{OK}}. To modify an existing number, press

{{EDIT}}.

• If there is an option to choose, press {{CHOOS}}, highlight your choice, and press | enter] or {{OK}}.

• Shortcut: Press the {{PLOT>}} menu key to copy values from the Plot Setup into NUMSTART and

NUMSTEP.

Wli

/ 1

X FI

-.6BB66

-.BBHIE

-.10625

-!BiHi6

!hOEB5

.601575

IESHB13I1I

-.62B66

2. When done, press |num| to review the table of numbers.

To reset To reset the default values for all table settings, press settings ■[CLEAR}.

Plotting and Exploring Functions 3-25

SETUP-NUM

Screen

Field Meaning

NUMSTART

Where to start the independent variable’s first value.

NUMSTEP

The size of the increment from one

independent variable value to the next.

NUMTYPE

Type of numeric table: Automatic or

Build Your Own. To build your own table,

you must type each independent value

into the table yourself.

NUMZOOM

Zoom factor (multiplies the scale for Zoom Out, divides for Zoom In).

Building Your Own Table of Numbers

The default NUMTYPE is "Automatic", which fills the table with data for regular intervals of the independent (X, T, 0, or N) variable. With NUMTYPE "Build Your Own", you fill the table yourself by typing in the independent-variable values you want, and the dependent values are then calculated and displayed.

To format a 1. Start with an expression defined (in Symbolic view) in the table aplet of your choice.

2. In the Numeric Setup (■ [SETUP-NUM]), choose

NUMTYPE: Build Your Own.

3. Open the Numeric view (|num|). To clear existing data in the table, press ■ [CLEAR].

4. Enter the independent values in the left-hand column. Type in the number and press | enter |. You do not have to enter them in order, because the ([SORT]} function can rearrange them. To insert a number between two others, use ([INS]}.

You enter numbers into the X column.

The defining — X^-l expression |iHBMi:aBiiaiBBiEi33i

for FI.

ISS

FI entries are generated automatically.

3-26 Plotting and Exploring Functions

To clear data Press ■ [CLEAR] to erase the data from a table.

“Build Your

Own” Keys

Key

{{EDIT}} Puts the highlighted independent value (X, T,

{{BIG}} {{DEFN}} Displays the defining function expression for

Meanine

0, or N) into the edit line. After you edit the number, press |enter].

Inserts a row of zero values at the position of the highlight. Replace the zero by typing the number you want and pressing | enter 1.

Automatically rearranges the left-hand

column into values in ascending (getting larger) or descending (getting smaller) order.

Toggles between two character sizes.

the highlighted column.

Deletes the highlighted row.

■ {CLEAR} Clears all data from the table.

Plotting and Exploring Functions 3-27

More Examples

Function Example

Plot the circle, = 13. Rearrange the equation to

y = . This must be entered as two expressions,

y = ^(l3-x') and y = .

I LIB I Se/ect Function

SYMB

[^[D 13 □ {{X}} [x3 2Q]

I ENTER I

EU [S 0 13 □ {{X}} [13

IFUNCTIDN SVMeaUC MIEH

<^Fl<X)=>ra3-X'*'2> >/F2CX>=-Ta3-X''2>

F4CX>=

F5<X>= w

2Q] I ENTER I

■ [SETUP-PLOT]

(Check that the Plot settings

are the defaults—if not, press

■ [CLEAR] .J

FUNCTION PLOT SETUP KRNG: VRNG: -3. 1 ¡¡TICK: 1 VTICK: 1

RES: Faster

ENTER MINIMUM HURIZDNTRL VALUE

■ 6.5

3.2

PLOT

H: 0 FiiX

): 3.S0SSS1 li!M!ll|

The calculator plots the two expressions of the conic plot separately, sometimes producing a discontinuity in the graph. Specify a finer resolution to minimize these discontinuities.

(The gaps are due to the sampling interval.)

■ [SETUP-PLOT]

ESS {{cHoos}}

SelectMor& Detail

FUNCTIPN FLOT SETUP

!if!NG" ”6« 5 6*5

VRNa: -3.1 3.2

KTICK: 1 VTICK: 1

RES: legUCTM

CHUaSE PLOT RESULUTIDN

3-28 Plotting and Exploring Functions

Function Example, continued

PLOT

■ [SETUP-NUM]

(Check that the Numeric settings are the defaults—if not, press miClIAR].)

NUM

H: 0 FliK

^^FUNCTiDN NUMERIC fETUF NUMSTflfiT: 0 NUMSTEP: . 1 NUMTVPE: NUMZDDM: 4

X FI F2

3.fi05551

3.fiOH16H 3lS>130HB

3.5B3ERH

3.S?i?lH

■■ 3.S0SS51 i8n;iii

flut. omat i c

-3.S055S

-3.eoHifi

-3.6

-3.5330H

-3.3B3E>;

-3.5?i«?l

Plotting and Exploring Functions 3-29

Parametric Plot the two sets of equations below that describe the paths of Example two particles over time. Look at the interval between f = 0 and

i= 6.5 seconds.

I 5e/eci Parametric

■ [SETUP-SYMB]

Check that Radians is set.

*PftMMETIilC SVMEnUC SETUP» ANGLE MEASURE:

CHUDSE ANGLE MEASURE

1 SYMB I 16 Q 3 0 ® (Z1 3

0 {{T}} [enterI

4 0 {{T}} 0 5 fENTERl

2 0 H0 ■ [te] 0 2 0

{{T}} flNTE^

G0 3 0

W 02

^PARAMETRIC SVMRDLIC MIEH^^

-'XKT> = 16/'3-8-^3*T

^Yl(T)=4»T-5

^X2<T>=2*SIH<ir/2«T)

^ Y2 < T > =-3*C0S < ir^ 2»T :>

0 {{T}} [enterI

PLOT

\ 1

T: 0 CS.3333i3i3i3

Use the Numeric view to determine whether the particles ever collide (that is, whether their paths cross at the same moment

in time). Compare the T values when X1=X2 and when Y1=Y2. You can tell from the plot that the points of intersection are at or near X=2 and Y=3. If T is the same at these points, then the points collide.

NUM

Search for XI =2 and X2=2. Move the highlight to

Xl=l.866666.

T XI Yl X2

3.3

3.333333

!§

Z.666666

3.H

1.1

1.3

3.133333

1.3

1.86666666666 wiiiiaB»IM««Maa№gigTdiBHI—

3,-sj liSMilip

-l.B

-l.H

-1

-.6

-.3 .3

1.303113

1.3753?fi 3

1.375376

1.303113

1.7B3013

You can see that X2=2 when T=1. Use ZOOM to home in on Xl=2.

3-30 Plotting and Exploring Functions

Parametric Example, continued

{{ZOOM}} Select in {{ok}}

T XI Y1

1.1?5 2.2 -.3 I.REH'IIO

l.S

ill:

1.3 .2

-.2 1.R02113

2.133333

-.1

iTIl'iil'l

1.B763B2 l.BHPPSR I.BIBSBS

1.7B2013

1.99999999999

You can now see that Xl=2 when T=1.25, so the particles do not collide at X=2.

Now search for Yl=3 and Y2=3. You can use {{ZOOM}} Out to move more quickly through the columns, but {{ZOOM}} In again to find Y1=Y2=3.

0 0 B highlight the Y2

column

to highlight Y2=3

T Y1

1.B75

l.R

l.RES

1.R5 l.R?S

2 3

Hililill

2.5

2.?

1:1

.3R01B05 .312B5BR .2350?HB

.ISBRlBi .07BS1R5

-22-11

2.342356

2.463065

2.474205

2.440752

^u33£il£i

Since Y1 and Y2 intersect (when Y=3) at the same value for T,

the particles collide at T=2 seconds.

Plotting and Exploring Functions 3-31

Polar Example Plot the circle, r = 3 (sin^e + cos^0).

I Select Polar

■ [SETUP^YMB]

Check that Radians is set.

ISYMB13 g El

M[A 0 miA 0

I cos I

enter!

{{6}} 0

PLOT

(If your plot does not look this, check that the Plot Setup has the default settings.)

^RK6>=3*c:SIN<0>a+C...

R2(;0> =

R3C0>=

R4i;0>=

R5<0>=

naEBEMiaKiiE

S: 0

fVMEDLIC VIEH^M

>: 3 rararni

gHihisirama

NUM

(If your table does not look

like this, make sure the Numeric Setup has the default settings.)

HHlilülB

3 3 3 3 3 3

3-32 Plotting and Exploring Functions

Sequence Generate a sequence to calculate the square root of 2 using

Example the iterative relationship

) X ) = \{Ul, +a), where a = 2.

Define this sequence in the HP 38G as U1(N) = (Ul(N-iy + A)/(2*U1(N-1)) ,andstore2 in/t. The Sequence aplet finds the square root by evaluating this

expression with successive values of N until the value for U1 stops changing. In this case, the sequence converges at a value for -Jl starting with .

Start the sequence by setting U1 (1) and U1 (2) to 1.

I Select Sequence

11 ENTER I 1 [enter!

G]{{U1}}{{N-1}} ■ {X^} 0

^^SEOyENCE SYMEDLIC VIEM^

v^uia>=i

•/UK2>=1 v'Ul

usa:)=

U2<2>=

nail Banal

iBangmaB

0] 0 0 2 0 {{ui}}

{{N-1}} i)10^

Store the value 2 in the real variable A.

1 HOME I

2 {{STO^}} iA...Z|A I ENTER I

Set up a stairstep plot.

m {SETUP-PLOT] Check that the default values are set, including stairstep.

(Press ■ [CLEAR] to reset default values.)

Plotting and Exploring Functions 3-33

SEQUENCE nOT SETUP SEQPLDT: BWemWtggg NRNQ: 1 24 XRNG; -2 24

TRNGi -2 10.6

CHOOSE SEQUENCE PLOT TVPE

Sequence Example, continued

■ [VIEWS]

Select Auto Scale {{OK}} Explore the graph and the

values for N and Ul by

pressing g and [^.

As you trace the graph with the cursor keys, the crosshairs jump from N:1 to N:2 to N:3, and so on. The values for Ul

change by smaller and smaller amounts until they converge.

NUM

Scroll down to see that the values for U] remain the same

for N»6. Therefore, -Jl is

a 1.5 H 1.415557

l.HlHilS

I.HIHBIH

1.41421356237

1.41421356237 to 12 digits of

accuracy.

Compare the Stairstep plot (which plots N and Ul (N)) to a Cobweb plot (which plots Ul(N-l) and U1(N)). Use autoscaling for the plot. The coordinate values and the Numeric view are identical to the Stairstep plot.

■ {SETUP-PLOT} [3

Set SEQPLOT to Cobweb.

m {VIEWS}

Select Auto Scale {{OK}}

3-34 Plotting and Exploring Functions

Solve

The Solve aplet will solve an equation or an expression for its

unknown variable. You define an equation or expression in

Symbolic view, then supply values for all of the variables

except one in Numeric view. Then Solve will find the

remaining unknown. As a simple example, consider the equation

force = mass x acceleration (that is, f=m*a) in the Solve

Symbolic view.

SVMiaUC VliHS

^EliF=M*R

E3: E4! E5:

mia&sosi

If force is 600 N and acceleration is 9.8 m/sec^ then pressing

{{SOLV}} in the Solve Numeric view finds that the unknown

mass must be 61.22 kg.

1F: 600 1

ft: 9.8

NUMERIC SOLVE NUMERIC VIEW I

ft: 9.8

|F= 600 1

1.2244397959 ■

ENTER VALUE DR PRES! fDLVE

ENTER VALUE DR PRESS SOLVE

ntraimaTiHBaHHBBiTmnmTO

Furthermore, you can solve the equation for any one of its variables. You can solve the equation as many times as you want with new values and different unknowns.

Solve 4-1

Solving Equations

An equation contains an equals sign. Its solution is a value for the unkno^vn variable that makes both sides equal the same value.

An expression does not contain an equals sign. Its solution is a root, that is, a value for the unknown variable that makes the expression equal to zero.

Define the Equation

You can define up to ten equations (or expressions), named EO through E9. Each equation can contain up to 27 real variables, named A through Z or 6.

To define an equation

1. In the Library ((u^), select the Solve aplet.

Display the Symbolic view (|symb|). If the highlight is on

an existing equation, scroll to an empty line—unless you

don’t mind writing over the equation. Or, clear one line

(fpELl) or all lines (■ [CLEAR]).

Enter a complete equation, including the equals sign. (The

3. equals sign is available as a menu key.) Use only A through Z and 0 as variables’ names. Press | enter | or

{{OK}} to complete the equation. Only one equation at a

time can be checkmarked.

ISDLVE fVMiBLIC VIEH

^El;F=M*R

E3! E4! E5: *

A Solve variable (El through EO) can also be defined in terms of other Solve variables. For instance, you could define El to be the sum of E2 and E13.

4-2 Solve

HP 38g User Manual

Specifications and Main Features

Frequently Asked Questions

User Manual

B38G

Contents

Plotting and Exploring Functions

Getting Started

The Display

To adjust the contrast

The Parts of the Display

To clear the display

Display Modes

[MODES]

Using Input Forms

— 5*77+4

5*77+1.414213562374

Menu Lists

Aplets and Their Views

Aplets

Exploring an Aplet View by View

Catalogs and Editors

Storing £uid Recalling Variables

To store a

To recall a number

Notes and Sketches

Note View and Sketch View

The Notepad

Managing Aplets

Sending and Receiving Aplets

Mathematical Calculations

How to Do Calculations

Entering Expressions

Complex Numbers

Clearing Numbers

Using Previous Results

Storing in Variables

To store a value

The VAR Menu

Symbolic Calculations

Using Math Functions

The Math Functions by Category

Plotting and Exploring Functions

Defining a Problem

Select an Aplet

Define an Expression (Symbolic View)

Plotting

Plot the Expression (Plot View)

Zooming

Examples: Plotting

■ {SETUP-PLOT}

■ [CLEAR]

■ [SETUP-PLOT]

■ [CLEAR]

Exploring the Plot

Tracing

Zooming

Other Views for Scaling and Splitting the Graph

[VIEWS]

Setting Up the Plot (Plot Setup)

Interactive Root-Finding

Examples: Root-Finding with Plots

Using a Table of Numbers

Display a Table of Numbers (Numeric View)

Exploring the Table of Numbers

Setting Up the Table (Numeric Setup)

Building Your Own Table of Numbers

■ [SETUP-PLOT]

■ [SETUP-PLOT]

gHihisirama

Solve

Solving Equations

Define the Equation

To define an equation