HP 10B User Manual

Contents

Page 10 At a Glance

21 1: Getting Started 31 2: Business Percentages 35 3: Number Storage and Arithmetic 43 4: Picturing Financial Problems 51 5: Time Value of Money Calculations 75 6; Cash Flow Calculations 85 7: Statistical Calculations

95 8: Additional Examples 116 A; Assistance, Batteries, and Service 127 B: More About Calculations

133 Messages 136 Index

F.nglisli Hriiileil in Singapore

11/>-)4

(P)

HEWLETT PACKARD

00010-90037

HP-lOB

Who% HEWLETT

mLnM PACKARD

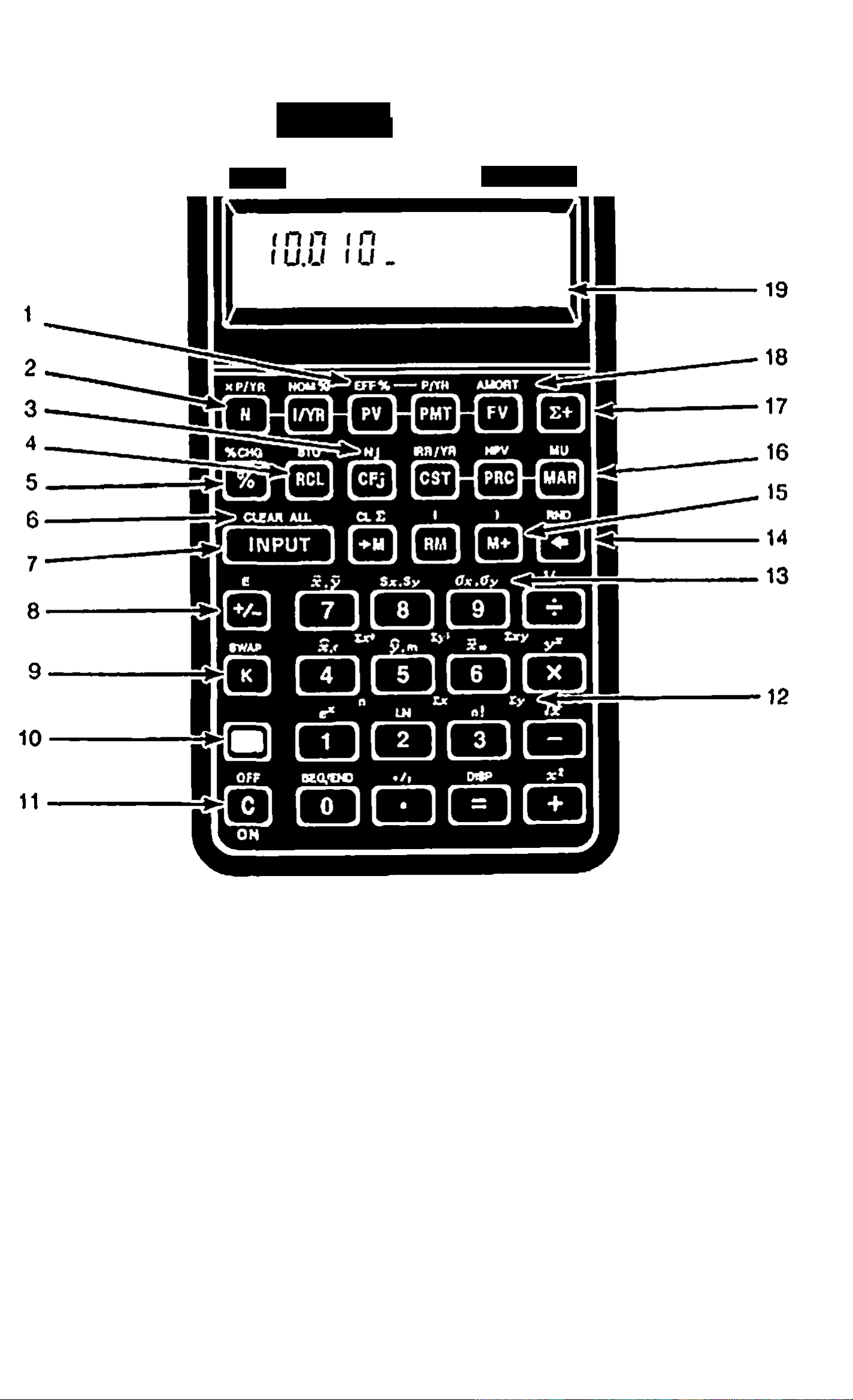
HfiWLBTT PACKAnO

Toe

BUSINESS

1. Interest conversion (page 71).

2. Time value of money (page 51).

3. Cash flows (page 75).

4. Store and recall (page 38).

5. Percent (page 31).

6. Clear all memory (page 23).

7. Separate two numbers (page 25),

8. Change sign (page 22).

9. Constant (page 35).

10. Shift: activate yellow labeled

functions (page 24).

11. On. clear display.cancel

operation (page 21).

12. n through Sxy: statistical summation

registers (page 89).

13. Statistical functions (page 88).

14. Backspace (page 23).

15. 3'key memory (page 37).

16. Margin and markup (page 33).

17. Accumulate statistical data

(page 86 and 87).

18. Amortization (page 66).

19. Annunciator line (page 24).

HP-1 OB Business Calculator

Owner’s Manual

HEWLETT

PACKARD

Edition 6 Pan Number 00010-^)0037

Notice

For warranly and regulatory information for this calculator, see pages 123 and 126.

This manual and any examples contained herein arc provided "as is" and

arc subject to change without notice. Hewlett-Packard Company makes no warranty of any kind with regard to this manual, including, but not limited to, the implied warranties of merchantability and fitness for a

particular purpose. Hewlett-Packard Co. shall not l>c liable for any

errors or for incidental or consequential damages in connection with the

furnishing, performance, or use of this manual or the keystroke programs contained herein.

o Hewlett-Packard Co. 1988. All rights rcscr\'cd. Reproduction,

adaptation, or translation of this manual is prohibited without prior written permission of Hewlett-Packard Company, except as allowed under

the copyright laws.

The programs that control your calculator arc copyrighted and all rights

arc reserved. Reproduction, adaptation, or translation of those programs without prior written permission of Hewlett-Packard Co. i.s also prohibited.

Corvallis Division 1000 N.E. Circle Blvd. Corvallis, OR 97330, U.S.A.

Printing History

Edition I Edition 2

Edition 3 Edition 4 Edition 6

October 1988

June 1989

June 1990

August 1992

November 1994

Welcome to the HP-1 OB

Your HP-lOB rcflccls ihc superior quality and attention to detail in

engineering and manufacturing that have distinguished Hewlett-Packard

products for 50 years. Hewlett-Packard stands behind this calculator —we

offer expertise to support its use (see inside the back cover) and world wide scr\icc.

Hewlett-Packard Quality

Our calculators arc made to excel and to be easy to use.

■ This calculator is designed to withstand (he drops, vibrations, pollu

tants (smog, ozone), temperature extremes, and humidity variations that it may encounter in everyday work life.

■ The calculator and its manual have been designed and tested for ease of use. We added many examples to highlight (he varied uses of the calculator. Advanced materials and permanent, molded key lettering

provide a long keyboard life and a positive feel to the keyboard.

■ CMOS (low-power) electronics and a liquid-crystal display allow data to be retained indefinitely and the batteries to last a long time.

■ The microprocessor has been optimized for fast and reliable compu tations using IS digits internally for precise results.

■ Extensive research has created a design that has minimized the adverse effects of static electricity, a potential cause of malfunctions

and data loss in calculators.

Welcome to the HP-10B

Features

The fc;iUircs of ihc HP-lOB and ihc manual reflect the needs and wishes

of many customers;

■ A large 12-charactcr display.

■ An At-a-Glancc section in the manual for quick reference.

■ Applications to solve business and financial tasks:

■ Time Value of Money. Loans, savings, leases, and amortiza

tion schedules.

m Interest Conversion. Nominal and effective rates.

■ Cash Flows. Net present value and internal rate of return.

■ Business Percentages. Percent change, markup, and margin

calculations.

■ Statistics. Mean, standard deviation, correlation cocITicicnt,

and linear regression forecasting, plus other statistical calcula tions.

■ Enough memory to store an initial cash flow and 14 cash flow groups,

with up to 99 cash flows per group.

■ Fifteen numbered storage registers.

■ Easy access to functions saves keystrokes and adds convenience.

■ Auto-incrcmcnt capability for amortization schedules.

■ Labels for amorti/;ilion and cash flows.

■ Automatic constant.

■ 3-key memory.

■ Many examples are included in the manual .so you can combine them

for your specific needs.

Welcome to the HP-10B

10 At a Glance...

10 Basics 11 Percentages

12 Memory Keys 13 Time Value of Money (TVM)

14 TVM Whal if... 15 Amort iziU ion

16 Interest Rale Conversion

17 IRR/YR and NPV

19 Statistics

21 Getting Started

21 Power On and Off 21 Adjusting the Display Contrast 21 Simple Arithmetic Calculations 23 Understanding the Display and Keyboard 23 Cursor 23 Clearing the Calculator 23 Clearing Memory 24 Annunciators 24 Shift Key 25 INPUT Key 25 SWAP Key

25 Math Functions

26 Display Formal of Numbers 27 Specifying Displayed Decimal Places

27 Scientific Notation 28 Displaying the Full Precision of Numbers

Contents

Interchanging the Period and Comma

28 29 29

Rounding Numbers

Messages Picturing Memory

31 Business Percentages 31 Percent Key 31 Finding a Percent

Adding or Subtracting a Percent

Percent Change

Margin and Markup Culculalinns

33 34 34

3 35

37 38 39

Margin Calculations Markup on Cost Calculations

Using Margin and Markup Together

Number Storage and Arithmetic

Using Stored Numbers in Calculations

Using Constants

Using the M Register Using Numbered Registers Doing Arithmetic Inside Registers

40 41 41

Doing Arithmetic Power Operator Using Parentheses in Calculations

Picturing Financial Problems 43 How to Approach a Financial Problem 44

Signs of Cash Flows

45 Periods and Cash Flows 45 45

Simple and Compound Interest

Simple Interest

Contenu

46 47 47 47 49

Compound Interest

Interest Rales

Two Types of Financial Problems

Recognizing a TVM Problem Recognizing a Cash Flow Problem

5 51

51 Using the TVM Application

53 Clearing TVM

53 Begin and End Modes

Time Value of Money Calculations

53 58

62 66

Loan Calculations

Savings Calculations

Lease Calculations

Amortization

71 Interest Rate Conversions 71

75 75

Investments With Different Compounding Periods Compounding and Payment Periods Differ

Cash Flow Calculations

How to Use the Cash Flow Application

NPV and IRR/YR: Discounting Cash Flows

77 Organizing Cash Flows 78 Entering Cash Flows 79 80

Viewing and Replacing Cash Flows Calculating Net Present Value

83 Calculating Internal Rate of Return 84 Automatic Storage of IRR/YR and NPV

85 Statistical Calculations

85 Clearing Statistical Data

86 Entering Statistical Data 86 One-Variable Statistics

86 Two-Variable Statistics and Weighted Mean

Correcting Statistical Data

87 Correcting One-Variable Data

Correcting Two-Variable Data

88 Summary of Slatislical Calculations 89 Mean, Standard Devaations, and Summation Statistics

91 Linear Regression and Estimation

Weighted Mean

Contents

Additional Examples

95 95 95 96 97 97 98 99

101 102

104 105

Business Applications

Setting a Sales Price

Forecasting Bused on History

Cost of Not Taking a Cash Discount

Loans and Mortgages

Simple Annual Interest

Continuous Compounding Yield of a Discounted (or Premium) Mortgage

Annual Percentage Rate for a Loan With Fees

Loan With a Partial (Odd) First Period Automobile Loan

Canadian Mortgages

106 107 107 109

111

112 112

114

116

What if ...TVM Calculations

Savings

Saving for College Costs

Gains That Go Untaxed Until Withdrawal Value of a Taxable Retirement Account

Cash Flow Examples

Wrap-Around Mortgages

Net Future Value

Assistance, Batteries, and Service 116 117

118 118

119

120 121

123 123 123

124 124

Answers (0 Comnu)a Questions

Environmental Limits

Power and Batteries

Low Power Annunciator Installing Batteries

Determining if the Calculator Requires Service

Confirming Calculator Operation — the Self-Test

Limited One-Year Warranty

What Is Covered What Is Not Covered Consumer Transactions in the United Kingdom

If the Calculator Requires Service

8 Contents

124 125

Obtaining Service

Service Charge

125 Shipping Instructions 126 Warranty on Service

126 Service Agreements 126 Regulatory lnform<ilion

127 More About Calculations

127 IRR/YR Calculations 127 Possible Outcomes of Calculating IRR/YR

128 Halting and Restarting IRR/YR 128 Entering a Guess for IRR/YR 129 Effect of Using S- to Correct Data 129 Range of Numbers 129 Equations 129 Margin and Markup Calculations

130 Time Value of Money (TVM) 130 Amortization 131 Interest Rate Conversions

131 Cash-Flow Calculations 132 Statistics

133 Messages 136 Index

Contents

At a Glance...

This section is designed Гог you if you're already familiar with calculator

operation or financial concepts. You can use it for quick reference. The rest of the manual is filled with explanations and examples of the concepts presented in this section.

Basics—At a Glance.

-------------

onoocju Qoaooo

mmmoom

ODOoa

oaaao

• aaoo

[■aaoaj >—

---------

Keys:

■

Display:

0.00 Turns calculator on.

0.00 Displays shift annuncia-

Description:

lor(.^).

■

123 0

■(cm

■(CLEAR ALLI

шт

10 At a Glance...

0.00

12_ Erases last character.

0.00

Discontinues shift.

Clears display. Clears statistics memory.

Clears all memory.

Turns calculator off.

Percentages—At a Glance...

— ' • OUOUDcl'

CDOOCCi

oaoco!.

Doaoc,

ooGOc:«

loonoci

Percent.

(CST)

i^ARl

Add 15% to $17.50.

Cost.

Price. Margin. Markup.

Keys:

17.50 0

Display:

17.50

Description:

Enters number.

15® 0

Find (he margin if the cost is $15.00 and

20.13

15 iesD 15.00

22 iP^ 22.00

fMM]

If the cost

20 (cUl 33IIMI

is $20.00 and the markup is 33%, what is the selling price?

31.82

20.00

33.00

Adds 15 %.

.selling price Ls $22.00.

Enters cost. Enters price.

Calculates margin.

Enters cost. Enters markup.

(PRC)

26.60

Calculates price.

At a Glance... 11

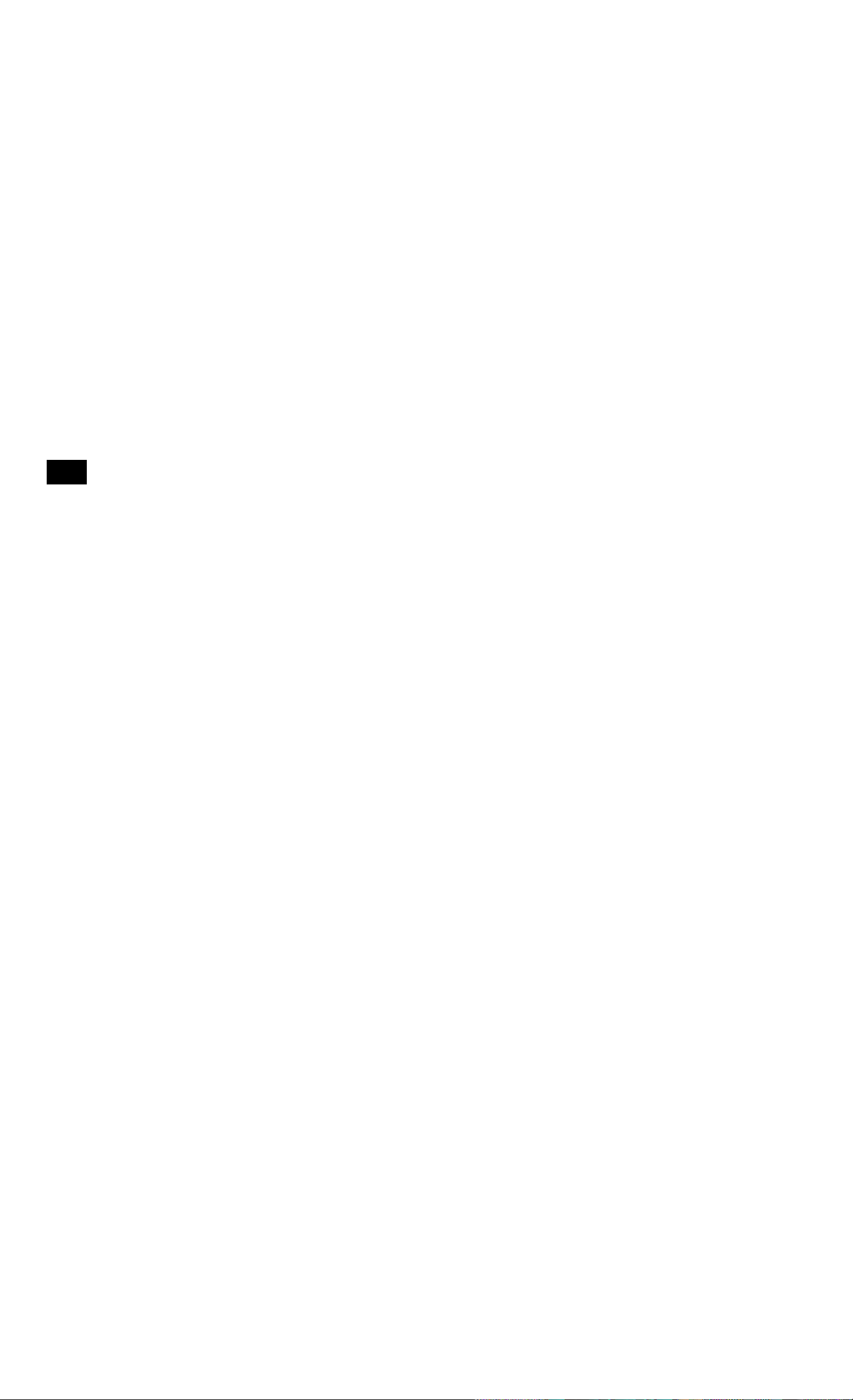
Memory Keys—At a Glance...

pooooo

paaaoo

xz=)aaao

□ oooo

• OCDOO

ooooa

Doaoa

Em)

Multiply 17, 22, and 25

Stores a constant operation.

Stores a value in the M register (memory location).

Recalls a value from the M register.

Adds a value to the number .stored in the M register.

Stores a value in a numbered register.

Recalls a value from a numbered register.

by 7, storing

“x

as a constant operation.

Keys:

170711

22 0 25 0

Store 519 in register 2, then recall it.

5191 ST012

Display: Description:

7.00 Stores “x 7” as a co

119.00

154.00 Multiplies 22x7.

175.00

519.00 Stores in register 2.

operation.

Multiplies 17

Multiplies 25x7.

iRCO 2

12 At a Glance...

0.00 Clears display.

519.00 Recalls register 2.

Time Value of Money (TVM)—At a Glance..

Ji’ Enter any four of the five values and solve for the fifth.

immmmc

DOOOOO

C3000C

{OOOOO

oooed oaac MOOC

A negative sign in the display represents money paid out;

money received is positive.

(N)

[iTyrI

iasfl

(Ey)

liPTYR]

Number of payments. Interest per year.

Present value.

Payment.

Future value.

Begin or End mode.

Number of payments per year mode.

If you borrow $14,000 for 360 months (N) at 10% interest (I/YR),

what is the monthly payment?

Set to End mode. Press

Keys:

12lfP7YR

360®

10 ii/YRl 14000 fPV]

1 lfiI3e?KiIill if BEGIN annunciator is displayed.

Display:

12.00

360.00

10.00 14,000.00

Description:

Sets payments per year.

Enters number of payments.

Enters interest per year. Enters present value.

(PM3

0.00

-122.86

Enters future value. Calculates payment if

paid at end of period.

At a Glance...

TVM What if...—At a Glance...

U is nol necessary to reenter TVM values Гог each example.

ommma

ooooool aoooo

ooooo; □ oooc

Qoaac:

OOOOC!;

Keys:

100 Ea

(pg

Using the values you just entered (page 13), how much can

you borrow if you want a payment of $100.00?

ши

Display:

-100.00

11.395.08

Description:

Enters new payment

amount. (Money paid out

is negative.)

Calculates amount you

How much can you borrow at a 9.5% interest rate?

9.5 IÌ7YRÌ (pg

lOfiTVRi

14000

[22

9.50 11,892.67

10.00

14,000.00

can borrow.

Enters new interest rate.

Calculates new present value for $100.00 pay

ment and 9.5% interest. Reenters original interest

rate. Reenters original present

ВШ

-122.86

value. Calculates original

payment.

14 At a Glance...

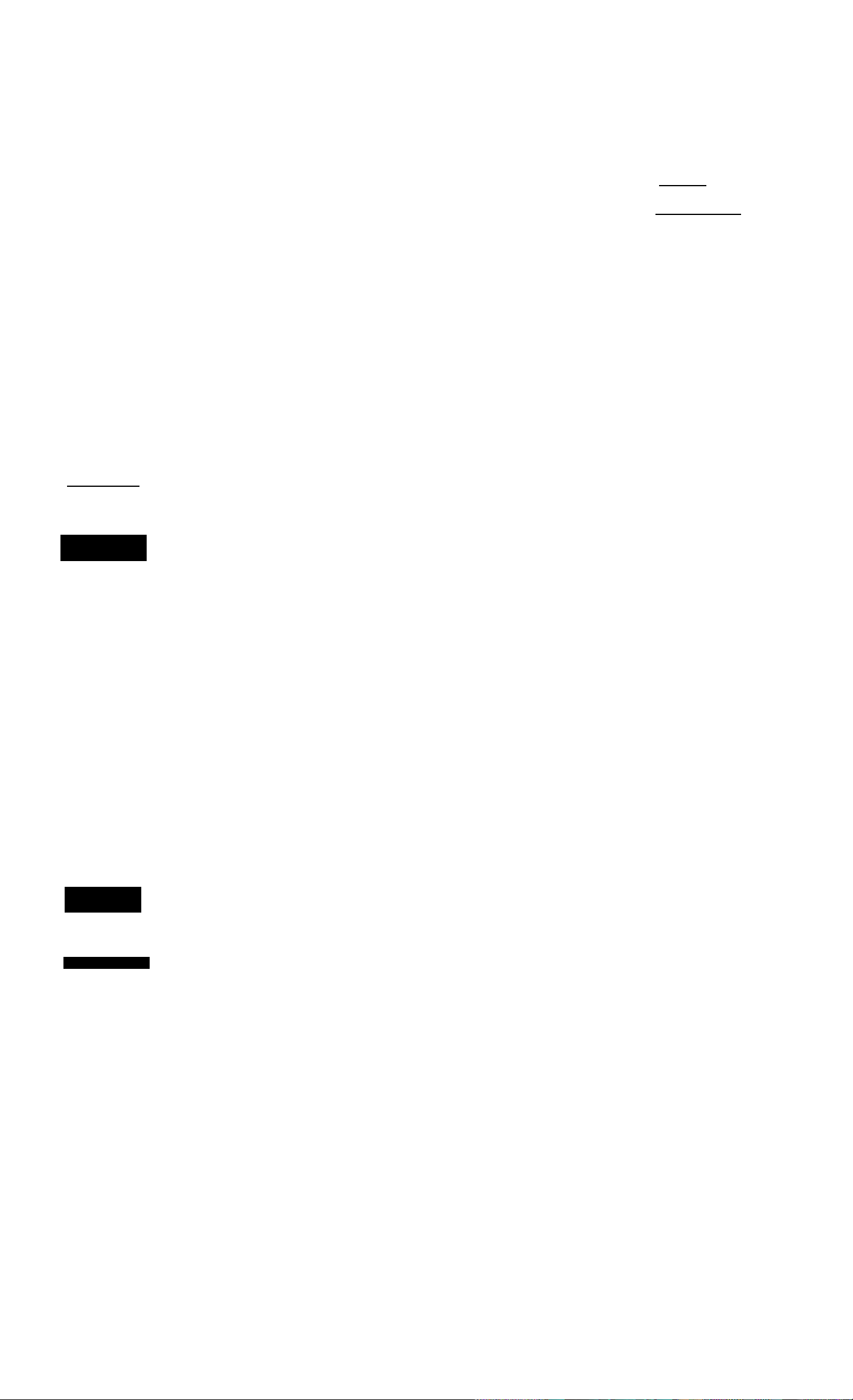
Amortization—At a Glance...

ooooao

oooooo

moooo

oaooo

□ oaoo

aoooD

□ OOMO

Amortize the 20th payment of the loan.

Keys:

20 lINPUTi

After calculating a payment using Time Value of Money

(TVM), enter the periods to amortize, then press BlAMORTI.

Using the previous TVM example (page 13), amortize a single payment and then a range of payments.

Display:

20.00

Description:

Enters payment to amortize.

msEo

PEr20- 20

Int

-115.61

Prin

-7.25

bAL

13,865.83

Amortize (he 1st through 12lh loan paymcnl.s.

Displays payment to

amortize.

Displays interest. (Money paid out is negative.)

Displays principal.

Displays balance.

QüjjQD

0 0

12_

PEr1 - 12

Int

-1.396.50

PrIn

-77.82

bAL

13,922.18

Enters range of payments to amortize.

Displays range of periods

(payments).

Displays interest. (Money paid out is negative.)

Displays principal.

Displays balance.

Ata Glano«... IS

Interest Rate Conversion—At a Glance...

To convert between nominal and cfTcctive interest rates,

ommmoo

oooooo

fCDOnOO

aooao nooao OOOCTO

UOOOf )

■FES

■ÎP7ŸR1

enter the known rale and the number of periods per year,

then solve for the unknown rate.

Nominal interest percent. Effective interest percent.

Periods per year.

Find the annual cfTcctive interest rate of 10% nominal interest com pounded monthly.

Keys:

12KEZŸH1

i(ËFF%

Display:

10.00

12.00

10.47

Description:

Enters nominal rate. Enters payments per

year. Calculates annual

cfTcclive interest.

16 At a Glance...

IRR/YR and NPV—At a Glance...

oooaoci

oommmzi

t300CC‘

ooDc:c

poncoc

nnc( K:i

C)i3Duc::|

V. -------------------

■rpTVRl [cRl

■(Nj]

onmoD

■I

If you have an initial cash outflow of $-40,(XX), followcii by monthly caslt inflows of $4,700. $7,OCX). $7,000, and $23,000. what is tlic IRR/YR? What is the IRR per month?

Number of periods per year (default is 12). Cash flows, up to 15 (“y“ identifies the cash flowii///?i/?cT), Number of consecutive times cash flow **y’* occurs.

Internal rale of return per year.

Net present value.

Keys:

ai CLEAR ALp

laliPTYRl

40000 ^ (CF]]

4700 pF]]

7000 fCFj]

Display:

0.00

12.00

CFO

- 40,000.00

CF 1 4,700.00

CF2

7,000.00

Description:

Clears all memorv. Sets payments ()cr year.

Enters initial outflow.

Enters first casli flow.

Enters second cash flow.

2|[^

2.00

Enters number of con-

sccutivc times cash flow occurs.

At a Glance... 17

23000 (cEB

CF3

23,000.00

Enters third cash flow.

onifili]

a 12 0

What is the NPy if the discount rate is 10%7

10 E

15.96

1.33

10.00

622.85

Calculates IRR/YR. Calculates IRR per

month.

Enters l/YR,

Calculates NPV.

18 At a Glance...

Statistics—At a Glance.

000008

OOOOOO

^•OOC

ommmc^

ocir joc:'

aaoocj

■fcm

number number BfZ^

numberl

number2 (|3 Enter two-variable statistical data.

Clear statistical registers. Enter one-variable statistical data.

Delete one-variable statistical data.

numberJ liNPUTi number! BO Delete two-variable statistical data.

WED Emm

Bd^

Mean of.v and}». Mean of.v weighted by>^.

BdEiD wmm BE5ZZ1 EMM

y-vatue BiEf] Bf§WÁPl x-value Bl?.ml

OBC® Bdffil

Sample standard deviation o(x andy.

Population standard deviation of.v and}». Estimate of.v and correlation coefficient. Estimate ofy.

y-interccpl and slope.

At a Glance... 19

Using the following data, find the mean of j; aiidy, the sample standard

deviation of at andy, and they-intcrcept and the slope of the linear regres sion forecast line. Then, use summation statistics to find n and Sty.

Keys:

■fern

2iiNPUTl50 4 fiNPDTl90

x-data

y-data

Display:

0.00

1.00

2.00

2 4

50 90 160

Description:

Clears stalistics registers.

Enters first .V,)» pair.

Enters second pair.

SfiNRJTl 160 IdiD

mna

■dim

0|[^

3.00

4.00

100.00

2.00

55.68

-10.00

Enters third pair.

Displays mean ofx.

Displays mean of>'. Displays .sample standard

deviation of.v. Displays sample standard

deviation ofy.

Displays j'-inlcrccpl of regression line (predicted

y value for.r *= 0).

iRCLl 4

27.50

3.00

1,420.00

Displays slope of regres

sion line.

Displays n, number of

data points entered.

Displays sum of the products ofjc- and

y-valucs.

20 At a Glance...

Getting Started

Power On and Off

To turn on your HP-lOB, press O (ihc key above ihe “ON

oocoao oooaoo

ki^ooon

□ DOOO

{oaooc

»oao loao

label). To turn the calculator off, press the yellow shift key (I )> then [§ (also written BIOPFI).

Since the calculator has continuous memory, turning it off

^ docs not affect the information you’ve stored. To conserve

energy, the calculator turns itself off approximately 10 minutes after you stop using it. The calculator’s three alkaline batteries last approximately one year. If you .see the low-battery symbol (CD) in the display, replace

the batteries. Refer to appendbe A for more information.

Adjusting the Display Contrast

To change the brightness of the display, hold down and press (T) or

Simple Arithmetic Calculations

Arithmetic Operators. The following examples demonstrate using the

arithmetic operators 0, 0, 0, and 0.

If you press more than one operator consecutively, for example 0 0 0 0 0, all are ignored except the last one.

1: GetUng Startod 21

If you make a typing mistake while entering a number, press [♦] to erase

the incorrect digits.

Keys:

24.71 0 62.47 0

When a calculation has been completed (by pressing 0), pressing a number key starts a new calculation.

19 0 12.68 0

If you press an operator key after completing a calculation, the calculation is continued.

0 115.5 0

Display:

87.18

240.92

356.42

Description:

Adds 24.71 and 62.47.

Calculates 19 x 12.68.

Completes calculation of

240.92 + 115.5.

You can do chain calculations without using 0 after each step.

6.9 0 5.35 0 36.92

.91 0

Chain calculations are interpreted in the order in which they arc entered. Calculate 4 + 9x3.

40.57

Pressing 0 displays intermediate result (6.9 x

5.35). Completes calculation.

4090 30

13.00

39.00

Adds 4 + 9.

Multiplies 13x3.

Negative Numbers. Enter the number and press I*/-! to change the

sign. Calculate -75 -f 3.

Keys:

030

Display:

-75_

-25.00

Description:

Changes the sign of 75.

Calculates result.

22 1: Getting Started

Understanding the Display and Keyboard

Cursor

The cursor (_) is visible when you arc entering a number.

Clearing the Calculator

oooooc

OOODOO

=JOOC«

oooac

aooooi

oonnr'.

ooeg

ill

When the cursor is on, 0 erases the last digit you entered. Otherwise, 0 clears the display and cancels the calculation.

While you arc entering a number, pressing (C) clears it to zero. Otherwise, (c) clears (he display of its current contents

and cancels the current calculation.

Clearing Messages. When the HP-lOB is displaying an error mes

sage, 0 or clears the message and restores the original contents of the

display. Refer Co “Messages,” on page 133 for a complete list of messages and meanings.

Clearing Memory

nooooo

DOOODO

^mooo

oaooc ooooo

ooooo! OOOOCj

Keys

Description

■ CLEAR ALLI

Clears all memory. Does not reset modes.* Clears statistical memory.

• Modoc on youf HP-10D aro number ol payments per year (page 52), Begin and

End (page and the display formats (page 26).

1: Getting Started 23

To dear all memory and reset calculator inodes, press and hold down O,

then press and hold down both and When you release all three,

all memory is cleared. The ALL CLr message is displayed.

Annunciators

Annunciators are symbols in the display that indicate the status of the calculator.

Annunciator Status

Shift Is active: when a key is pressed, the function labeled in yellow above the key, is executed

(below).

•

• liNPUTi has been oressed. or two values have

been entered or returned (page 25).

PEND

An arithmetic operator is pending ((+). for exam ple).

BEGIN

Begin mode is active (page 53). Battery power is low (page 118).

Shift Key

All of the HP-lOB keys have a second or “shifted” function

ooaoQu ooaoocH

dDOOOO

printed in yellow above the key. The yellow shift key (|) is used to access these functions.

ooooo

aaooo

• OOCDO

When you pres.s (he .shift annunciator is displayed

□ oooo

to indicate that the shifted functions arc active. To turn the

annunciator off, press

For example, press | followed by ED (also shov^n BED) to multiply a number in the display by itself.

again.

To perform consecutive shifted operations, hold down the shift key while

pressing the desired keys.

24 1: Getting Started

INPUT Key

The lINPUTI key is used lo separate two numbers when using

OOODOD

OOOOOO

BaOOG

ooooc

two-number functions or two-variable statistics.

The : annunciator is displayed if lINPUTI has been pressed. If

оооос

ooooa

a number is in the display, press [c] to erase the : annuncia

ooooo

tor and clear the display. If the cursor or an error message is

visible in the display, press O twice lo erase the :

annunciator.

SWAP Key

Pressing |{ exchanges the following:

OODOOO

OOOODO

IczDooao

ooooo

lOOOC

ooooc

aoooc

'S:

The last two numbers that you enlcrcd; for instance, to change the

order of division or subtraction.

The results of functions that return two values. The : annunciator

indicates that two results have been returned; press ■(SWAP) to sec the hidden result.

The X- and y-valucs when using .statistics.

Math Functions

One-Number Functions. Math functions involving one

ooooocj

OOOOOG CZDOOOOj

OCDOOI

ОООСЭС1 OCDOOI

looooc:

number use the number in the display.

1: Getting Sterted 25

Keys: Display; Description;

89.25 Ш{Щ\ 9.45

3.57 0 2.36 Ш\Ш} 0.42

a 3.99

Two-Number Functions. When a function requires two

DCOOOO

lOOCOO

■■nacD aDOCio

ooooa

оезооа

ooaoc

numbers, the numbers are entered like this: number I №UT

number2 followed by the operation. Pressing lINPUTi evalu

ates the current expression and displays the : annunciator. For example, the following keystrokes calculate the percent

change between 17 and 29.

Calculates square root.

1/2,36 is calculated first.

Adds 3.57 and 1/2.36.

Keys:

17IINPUTI

Display:

17.00

29 29_

■l%CHQ|

70.59

Display Format of Numbers

Description:

Enters number I y displays

: annunciator.

Enters number2. Calculates the percent

change.

When you turn on the HP-lOB for the first time, numbers

□QOOOQ aooooQ

[СЭОООО

oaooa

OOOOQ

are displayed with two decimal places and a period as the decimal point. The display format controls how many digits appear in the display.

ooaoQ

oaoaoi

If the result of a calculation is a number containing more

significant digits than can be displayed in the current display format, the

number is rounded to fit the current display setting.

Regardless of the current display format, each number is stored internally

as a signed, 12-digit number with a signed, three-digit exponent.

26 1: Getting Started

Specifying Displayed Decimal Places

To specify the number of displayed decimal places;

1. Press

2. Enter the number of digits (0 through 9) that you wish to appear

after the decimal point.

Keys:

та

45.6 0.1256 0

■в) 9

■fPiSPl 2

Display:

0.00

0.000

5.727

5.727360000

5.73

Description:

Clears display.

Displays three decimal places.

Displays nine decimal

places.

Restores two decimal places and rounds number in display.

When a number is too large or too small to be displayed in DISP format, it automatically displays in .scientific notation.

Scientific Notation

Scientific notation is used to represent numbers that are loo

OOOOOO

oooooo

iZ^OOOO

• oooo

ooooo □ aaoo

ooooo

large or too small to fit in the display. For example, if you

enter the number 10,000,000 0 10,000,000 0, the result

is 1.00E14, which means “one times ten to the fourteenth power” or “1.00 with the decimal point moved fourteen

places to the right.” You can enter this number by pressing

14. The E stands for “exponent of ten.”

Exponents can also be negative for very small numbers. The number

0.000000000004 is displayed as 4.00E-12, which means “four times ten to

the negative twelfth power” or “4.0 with the decimal point moved 12

places to the left.” You can enter this number by pressing 4 ШШ IV-112.

1: Getting Started 27

Displaying the Full Precision of Numbers

To SCI your calculator to display numbers as precisely as pos

ooQooa

□OOGOO

C3GOOO

oaooo oaaoo

cooao

ooMMc:

Start with two decimal places (|

Keys:

10 0 7 0

Esa

sible, press BlDlSPl 0 (trailing zeros arc not displayed.) To temporarily \aew all 12 digits of the number in the display

(regardless of the current display format setting), press

BloiSPl and hold 0* The number is displayed as long as you

continue holding 0. The decimal point is not shown.

Display:

1.43

142857142857

[■Ma

2).

Description:

Divides. Displays all 12 digits.

Interchanging the Period and Comma

To switch between the period and comma (United States and

ooaooo

ooooao

CZ5COOO

International display) used as the decimal point and digit

separator, press BEZD-

ooooo

oaaoo

ooaao

[QO«ao

For example, one million can be displayed as 1,000,000.00 or 1.000.000,00.

Rounding Numbers

GOGOGO OGGGOO

[aoool

ooooo ooooo ooooo

00000

The calculator stores and calculates using 12 digit numbers.

When 12 digit accuracy is not desirable, use BiRNDl to round the number to the displayed format before using it in a calcu

lation. Rounding numbers is useful when you want the actual (dollars and cents) monthly payment.

28 1: Gotting Started

Keys:

Display:

Description:

9.87654321

raiga

fiHSTl]

|(RND)

9.87654321

9.88

987654321000

9.88

Enters a number with more than Iwo non-zero decimal places.

Displays two decimal places.

Displays all digits without

the decimal while you

press 0. Rounds to two decimal

places (specified by pressing BiDISR 2).

988000000000

Shows rounded, stored number.

Messages

The HP-lOB displays messages about the status of the calculator or

informs you that you have attempted an incorrect operation. To clear a

message from the display, press (Cj or 0. Refer to ‘"Messages” on page 133 for a list of meanings.

Picturing Memory

The available memory in the HP-lOB consists of:

■ Ten business application registers.

■ A convenient M (memory) register.

■ Fifteen registers for storing numbers, cash flows, and summary

statistics.

1 : Getting Started 29

N l/YR

NOM%

PMT

CST

General Storage

and Cash Flows

PRC MAR

Ro Ri

R2 R3

«4

«8

P/YR

> Summation

Statistics

EFF%

R.0 R.1

R.2

R.3

R.4

Numbered Memory Registers

You can picture each memory register as a separate box (hat has a name and can hold one number at a time. If you store a number in a register,

you write over the number that was previously stored there.

Notice that I/YR and NOM% share the same register, and that MAR and

MU share the same register.

30 1: Getting Started

Business Percentages

You can U.SC (he HP-lOB to calculate simple percent, percent change,

cost, price, margin, and markup.

Percent Key

The key has two functions: finding a percent and adding

oooaoo

lOOOQO

CZJOOQO

oooao

ooocao

ooooo

OODOC

or subtracting a percent.

Finding a Percent

The @ key divides a number by 100 unless it is preceded by an addition

or subtraction sign.

Example. Find 25% of 200. Keys:

2000 200.00 Enters 200.

25®

Display:

0.25

50.00

Description:

Converts 25% to a decimal.

Multiplies 200 by 25%.

2: ButiiiMt Percentages 31

Adding or Subtracting a Percent

You can add or subtract a percent in one calculation.

Example. Decrease 200 by 25%. Keys:

200 0 200.00 Enters 200.

25 ® 50.00

Display:

150.00

Description:

Multiplies 200 by 0.25.

Subtracts 50 from 200.

Example. You borrow $1,2S0 from a relative, and you agree to repay the

loan in a year with 7% simple Interest. How much money will you owe?

Keys;

1250 07®

Display:

87.50

Description:

Calculates loan interest.

Percent Change

Calculate the percent change between two numbers (/ij and

onoODO

looaoD

BOOOO

ooooo

oacDoo

QOCDOO'

aoaao

/12, expressed as a percent of/t|) by entering/i| lINPUTi /I2,

then press ||

1.337.50

Adds $87.50 and

$1,250.00 to show repay

ment amount.

Example. Calculate the percent change between 291.7 and 316.8. Keys:

291.7

316.8 idCHQ)

n?ijm

Display:

291.70

8.60

Description:

Enters ni. Calculates percent

change.

32 2: Butinett PercenUget

Example. Calculate the percent change between (12 x S) and (65 + 18). Keys: Display: Description:

12 fx] 5 lINPUTI 60.00 Calculates and enters D|.

65 0 18 Bi%CHGl 38.33 Calculates percent

change.

Margin and Markup Calculations

The MP-lOB can calculate cost, selling price, margin, or markup.

Application

Margin

Markup

Keys

iesn. (PRÇ],

CŒID

(MS. (PRÇ].

Margin is markup expressed as a percent of price.

Markup calculations are expressed as a percent of cost.

Description

To see any value used by the Margin and Markup application, press

and then the key you wish to see. For example, to see the value stored as

[CSTI, press {RCL\ iCSfl. Margin and Markup share the same storage register. For example, if you store 20 in IMARI. then press [RCLI B(M3J>

you will sec 20.00 displayed.

Margin Calculations

Example. Kilowatt Electronics purchases televisions for $255. The tele

visions are sold for $300. What is the //iflrgi/i?

Keys:

Display: Description:

GHI

255 (EH)

300ÎPRC1

EM)

255.00 Stores cost in CST.

300.00 Stores selling price in

PRC.

15.00

Calculates margin.

2: Business Percentages

Markup on Cost Calculations

Example. The standard markup on costume jewelry at Kleiner’s

Knsmetique is 60%. They just received a shipment of chokers costing

$19.00 each. What is the retail price per choker?

Keys:

19 IC^

GIIS

Display:

19.00 Stores cost.

60.00

30.40 Calculates retail price.

Description:

Stores markup.

Using Margin and Markup Together

Example. A food cooperative buys eases of canned .soup with an invoice

cost of $9.60 per ease. If the co-op routinely uses a 15% markup, for what

price should it sell a case of soup? What is the margin?

Keys:

9.6[CST|

[¡I!]

Display:

9.60

15.00

11.04

13.04

Description:

Stores invoice cost. Stores markup.

Calculates the price on a case of soup.

Calculates mar^u.

34 2: Busines» Percentages

Number Storage and Arithmetic

Using Stored Numbers in Calculations

You can Store numbers, for reuse, in several different ways:

■ Use E) (Constant) to store a number and its operator for repetitive

operations.

■ Use 3 Key Memory [RMl. and (M+J) to store, recall, and sum

numbers with a single keystroke.

« Use mstQl and IRCLI to store and recall the 15 numbered registers.

Using Constants

oooooc oooooc

CTDOODO

OOQOCD

oaor^

PLjooc:

Use [K] to store a number and arithmetic operator for repeti tive calculations. Once the constant operation is stored, enter a number and press 0. The stored operation is performed on the number in the display.

3: Number Storage and Arithmetic 35

Keys

Operation

0 number (Q 0 0 number 0 0 Stores number" as constant. 0 number 0 0 0 number 0 0

KFl X value (K) 0 Stores *y * ” as constant.

0 number 0 0 0

0 number 0 0 0 0 number 0 0 0

Stores "+ number" as constant.

Stores “x number " as constant. Stores ‘‘-f number " as constant.

Stores “ + number %" as constant. Stores " - number %" as constant. Stores "x number %" as constant.

0 number 0 0 0 Stores number %” as constant.

Example. Calculate 5 + 2,6 + 2, and 7 + 2. Keys: Display:

5 0 2 (K) 2.00

0 7.00

6 0 8.00

7 0 9.00

Description:

Stores “+ 2” as constant.

Adds 5 + 2. Adds 6 + 2. Adds? + 2.

Example. Calculate 10 + 10%, 11 + 10%, and 25 + 10%. Keys:

10 0 io(D (K)

25 0

Display;

1.00

11.00

12.10

27.50

Description:

Stores “ + 10%” as con stant.

Adds 10% to 10. Adds 10% to 11. Adds 10% to 25.

36 3: Number Storage and Arithmetic

Example. Calculate 2^ and 4^.

Keys: Display:

2i(Z] 3 (K)

3.00

8.00 Calculates 2\

Description:

Stores as constant.

40 64.00 Calculates 4^

Using the M Register

The I-»ML IRMI. and keys perform memory operations

oooooo oooooa

l■ •0

00000 ooooa

oaaac) 000001

on a single storage register, called the M register. In most eases, it is unnecessary to clear the M register, since I-»Ml

replaces the previous contents. However, you can clear the M register by pressing 0 I-»Ml. To add a series of numbers

to the M register, use i-»MI to store the first number and IM+I

to add subsequent numbers. To subtract the displayed number from the number in the M register, press I•*•/-! followed by IM-t-l.

Description

Em]

Keys

Stores displayed number in the M register. Recalls number from the M register. Adds displayed number to the M register.

Example. Use the M register to add 17,14.25, and 16.95. Then subtract

4.65 and recall the re.sult.

Keys:

ITEM)

14.25 fi4+l

Display: Description:

17.00

Stores 17 in M register.

14.25 Adds 14.25 to M register.

16.95 (m3 16.95 Adds 16.95 to M register.

3: Number Storage and Arithmetic 37

4.65 Ea (M±]

-4.65

Adds -4.65 lo M

43.55

Using Numbered Registers

oooooo oaoooo

C300DD oasMO

The BiSTOI and IRCLI keys access storage registers Rq

through R9 and R 0 through R.4. (Refer to “Picturing Memory*' on page 29.) The BISTOI key is used to copy the

displayed number to a designated register. The IRCLI key is

used to copy a number from a register to the display.

Recalls contents of the M register.

To store or recall a number in two steps:

1- Press BlSTOl or [RCLl. (To cancel this step, press 0 or (§.)

2- Enter the register number (0 through 9 for registers Rq through R9

or 0 0 through 0 4 for registers R.o through R 4).

In the following example, two storage registers are used. Calculate the following:

Keys:

475.6 , 39,15

Display: Description:

560.1 + 475.6

39.15

475.6 ifSTO 1

m 39.15^8101 2

560.1 0 fRCLl 1 0 iRCLl2

475.60

39.15

12.15 Completes first

475.60

39.15

26.45

Stores 475.60 (displayed

number) in Rj.

Stores 39.15 in R2.

calculation.

Recalls R|. Recalls R2.

Completes second

calculation.

You can also use B(STO] and iRCLl for application registers. For exam ple, BdlO) il/YRI stores the number from the display in the [l7^ regis ter. iRCLl II/YRI copies the contents from Il/YRI to the display.

36 3: Number Storage and Arithmetic

In most cases, it is unnecessary to clear a storage register since storing a number replaces the previous contents. However, you can clear a sin^e

■l CLEAR ALD.

Doing Arithmetic Inside Registers

You can do arithmetic inside storage registers Rq through R9. The result is stored in the register.

Keys

B|STO| (+) register number

■|STO| □ register number B|STO| 0 register number

BjsTO] (±) register number

Old contents + displayed number Old contents - displayed number Old contents X displayed number

Old contents - displayed number

New Number in Register

Example. Store 45.7 in R3, multiply by 2.5, and store the result in R3. Keys:

45.7 ■ STÓ1 3

2.5 B STO] 0 3 2.50 Multiplies 45.7 in R3 by

fRCLl3

Display:

45.70 Stores 45.7 in R3.

114.25 Displays R3.

Description:

2.5 and stores result

(114.25) in R3.

3: Number Storage and Arithmetic 39

Doing Arithmetic

Math functions operate on the number in the display.

oooooo

□GOOD CZDOOOO

OOOO QOOO

ommm

jOOCDO

Example. Calculate Ihcn calculate + 47.2 + 1.1^.

Keys: Display:

4 loa

20 i(^

0 47.2 0

1.1 iE) 0

0.25

4.47

51.67

1.21

52.88

Description:

Calculates the reciprocal

of 4. Calculates

Calculates47.20. Calculates 1.1^.

Completes the calcula tion.

Example. Calculate natural logarithm (c^). Then calculate 790 + 4! Keys:

2.5 Id!) 12.18

790 0 4 |(ñ0

Display: Description:

2.50

24.00 Calculates 4 factorial.

814.00

Calculates e^-*. Calculates natural loga

rithm of the result.

Completes calculation.

40 3: Number Storage and Arithmetic

Power Operator

The power operator, B0> raises the preceding number (y-

oooooo

OOOOOOj

K=)OOOD

ooooo OQoai

oaoooj

ooooo

—■ ')

Example. Calculate 125^ then find the cube root of 125.

valuc) to the power of the following number (x-valuc).

Keys:

125i(Z)3tJ 1,953,125.00 1251(0 3100 (3 5.00

Display:

Description:

Calculates 125’. Calculates cube root of

125, which is the same as 125'/’.

Using Parentheses in Calculations

Use parentheses to postpone calculating an intermediate result until

you’ve entered more numbers. For example, suppose you want to

calculate

(85 - 12)

If you enter 30 0 85 0, the calculator displays the intermediate result,

0.35. This is because calculations without parentheses arc performed from

left to right, as you enter them. To delay the division until you’ve sub tracted 12 from 85, use parentheses. Closing parentheses at the end of the

expression can be omitted. For example, entering “25 -f (3 x (9 + 12 =”

is equivalent to “25 -r (3 x (9 + 12))

3: Number Storage and Arithmetic 41

Keys:

Display: Description:

30 0 10 85 0 85.00

12|(B

90 3.70 Multiplies the result by 9.

73.00 Calculates 85 - 12.

0.41

No calculation yet.

Calculates 30 *r 73.

42 3: Number Storage and Arithmetic

Picturing Financial Problems

How to Approach a Financial Problem

The financial vocabulary of the HP-lOB is simplified to apply to all finan

cial fields. For example, your profession may use the term balance, bal

loon payment, residual, maturity \^alue, or remaining amount to designate a

value that the HP-lOB knows as (E3 (future value).

The simplified terminology of the HP-lOB is based on cash flow diagrams.

Cash flow diagrams are pictures of financial problems that show cash flows over time. Drawing a cash flow diagram is the first step to solving a financial problem.

The following cash flow diagram represents investments in a mutual fund. The original investment was $7,000.00, followed by investments of

$5,000.00 and $6,000.00 at the end of the third and sixth months. At the end of the 11th month, $5,000.00 was withdrawn. At the end of the 16lh month, $16,567.20 was withdrawn.

4: Picturing Financial Problema 43

Up-arrows represent positive A cash flows (money received). ' * '

The horizontal line represents time. It is divided into regular

periods.

1 I 2 I 3 4 I 5 I 6

- 5,000.00

- 7.000.00

5,000.00

7 I 8 I 9 I 10i 11 12 113 114 115 116

\-\-r\

Down-arrows represent negative

cash flows (money paid out).

- 6.000.00

Any cash flow example can be represented by a cash flow diagram. As you draw a cash flow diagram, identify what is known and unknown about the

transaction.

Time is represented by a horizontal line divided into regular time periods.

Cash flows arc placed on the horizontal line when they occur. Where no arrows arc drawn, no cash flows occur.

Signs of Cash Flows

In cash flow diagrams, money invested is shown as negative and money

withdrawn is shown as positive. Cash flowing our isnegatiycy cash flowing

in IS positive.

For example, from the lender’s perspective, cash flows to customers for loans arc represented as negative. Likewise, when a lender receives money from cuslomcns, cash flows arc represented as positive. In contrast, from the borrower’s perspective, cash borrowed is positive while cash paid back IS negative.

44 4: Picturing Financial Problems

Periods and Cash Flows

In addition to the sign convention (cash flowing out is negative, cash flowing in is positive) on cash flow diagrams, there arc several more

considerations;

■ The time line is divided into equal time intervals. The most common period is a month, but days, quarters, and annual periods are also common. The period is normally defined in a contract and must be

known before you can begin calculating.

■ To solve a financial problem with the HP-lOB, all cash flows must occur at either the beginning or end of a period.

■ If more than one cash flow occurs at the same place on the cash flow diagram, they arc added together or netted. For example, a negative

cash flow of $-250.00 and a positive cash How of $750.00 occurring at the same time on the cash flow diagram arc entered as a $500.00 cash

flow (750 - 250 = 500).

■ A valid financial transaction must have at least one positive and one

negative cash flow.

Simple and Compound Interest

Financial calculations arc based on the fact that money earns interest over time. There arc two types of interest: simple intere.st and compound interest. The basis for Time Value of Money and cash flow calculations is compound interest.

Simple Interest

In simple-interest contracts, interest Lsa percent of the original principal. The interest and principal arc due at the end of the contract. For example, say you loan $500 to a f^riend for a year, and you want to be repaid with

10% simple interest. At the end of the year, your friend owes you $550.00 (50 is 10% of 500). Simple interest calculations arc done using the ® key on your HP-IOB. An example of a simple ¡nterc.st calculation is on page

97,

4: Picturing Financial Problema 4S

Compound Interest

A compound-interest contract is like a scries of simplc-intcrcst contracts that arc connected. The length of each simplc-intcrcst contract is equal to one compounding period. At the end of each period the interest earned on each simple-interest contract is added to the principal. For example, if you deposit $1,000.00 in a savings account that pays 6% annual interest,

compounded monthly, your earnings for the first month look like a

simplc-intcrcst contract written for 1 month at V2% (6% 12). At the

end of the first month the balance of the account is $1,005.00 (5 is V2% of

1,000).

The second month, the same process takes place on the new balance of

$1,005.00. The amount of interest paid at the end of the second month is

V2% of $1,005.00, or $5.03. The compounding process continues for the

third, fourth, and fifth months. The intermediate results in this illustration arc rounded to dollars and cents.

1,005.00

1,010.03

1,015.08

-1,000.00

1,020.16

-1,005.00

1,025.26

-1,010.03

-1,015.08

-1,020.16

The word compound in compound interest comes from the idea that

interest previously earned or owed is added to the principal. Thus, it can earn more interest. The Tmancial calculation capabilities on the HP-lOB arc based on compound interest.

4S 4: Picturing Financial Problema

Interest Rates

When you approach a financial problem, it is important to rccogni/e that the interest rate or rate of return can be described in at least three

different ways:

■ As a periodic rate. This is the rate that is applied to your money from

period to period.

■ As an annual nominal rate. This is the periodic rate multiplied by the

number of periods in a year.

■ As an annual effective rate. This is an annual rate that considers com pounding.

In the previous example of a $1,000.00 savings account, the periodic rate is

1/2% (per month), quoted as an annual nominal rate of 6% (I/2 ^ 12).

This same periodic rate could be quoted as an annual effective rate, which

considers compounding. The balance after 12 months of compounding is

$1,061.68, which means the annual effective interest rate is 6.168%.

Examples of converting between nominal and annual effective rates arc on pages 71 through 72.

Two Types of Financial Problems

The financial problems in this manual use compound interest unless specifically stated as simple interest calculations. Financial problems arc

divided into two groups: TVM problems and cash flow problems.

Recognizing a TVM Problem

If uniform cash flows occur between the first and last periods on the cash How diagram, the financial problem is a TVM (lime value of money) problem. There arc five main keys used to solve a TVM problem.

4; Picturing Financial Problems 47

Number of periods or payments.

шш

Ш]

(ЁУ)

You can calculate any value after entering the other four. Cash flow diagrams for loans, mortgages, leases, savings accounts, or any contract

Annual percentage interest rate (usually the annual nomi

nal rate). Present value (the cash flow at the beginning of the time

line).

Periodic payment.

Future value (the cash flow at the end of the cash flow

diagram, in addition to any regular periodic payment).

with regular cash flows of the same amount arc normally treated as TVM

problems. For example, following is a cash flow diagram, from the borrower’s perspective, for a 30-ycar, $75,000.00 mortgage, with a pay ment of $-684.07, at 10.5% annual interest, with a $5,000 balloon pay

ment.

One of the values for PV^ PA/T, FV can be zero. For example, following is

a cash flow diagram (from the saver’s perspective) for a savings account with a single deposit and a single withdrawal five years later. Interest compounds monthly. In this example, PA/r is zero.

4в 4: Picturing Financial Problems

l/YR = 8.00% PMT - 0.00

■ -I --i I ^ I ^ h • -I— I I ^ I ^

PV = -17,000.00

FV « 25,327.38

N « 60

Time value of money calculations arc described in the next chapter.

Recognizing a Cash Flow Problem

A financial problem that docs not have regular, uniform payments (some

times called uneven cash flows) is a cash flow problem rather than a TVM problem.

A cash flow diagram for an investment in a mutual fund follows. This is an example of a problem that is solved using either BiNPVl (Net Present

Value) or BlIRR/YRl (Internal Rate of Return per Year).

4: Picturing Financial Problems 49

5,000.00

16,567.20

1 I 2 1 3

1 1

^ -7,000.00

Cash flow problems arc described in chapter 6.

4 1 5 1 6

1 1 ■

•5,000.00

7 1 8 1 9 1 10 ill

1111

- 6.000.00

12|13|14|15

1 1 I

50 4: Picturing Financial Problama

Time Value of Money Calculations

Using the TVM Application

____

joooooo* ‘ ,, ,

eZDOODO

oaooo

ooooc

oaooc

ocaoowj

To use TVM, several prerequisites must be met:

■ The amount of each payment must be the same. If the payment amounts vary, use the procedures described in chapter 6, “Cash Flow Calculations.”

Bt Payments must occur at regular intervals.

i.i The time value of money (TVM) application is used for com-

pound interest calculations that involve regular, uniform cash

^ I , .

nows —called payments. Once the values arc entered you

can vary one value at a time, without entering all (he values again.

■ The payment period must coincide with the interest compounding period. (If it docs not, convert (lie inlercsl rate using the B|

BiEFF%l. and B(EZyr) keys described on page 71.)

o There must be at least one positive and one negative cash flow.

5: Time Value of Money Catculationt 51

Key Stores or Calculates

The number of payments or compounding

periods.

IE3

fp^

The annual nominal interest rate.

The present value of future cash flows. PV is

usually an initial Investment or loan amount and

always occurs at the beginning of the first period.

The amount of periodic payments. All payments

are equal, and none are skipped; payments can

occur at the beginning or end of each period.

The future value. FV is either a final cash flow or

compounded value of a series of previous cash

flows. FV occurs at the end of the last period.

■Eyr)

Stores the number of periods per year. The default

is 12. Reset only when you wish to change.

■(xPZ^ Optional shortcut for storing N: Number in display

is multiplied by the value in P/YR and stores result

in A/.

■IBEG/ENDI Switches between Begin and End mode. In Begin

mode, the begin annunciator is displayed.

■f AMORT 1 Calculates an amortization table.

To verify values, press (RlSL'l (R)> IRCLI li/VRl, IftCLI iPVi. IRCLI IPMTl. and

iRCLl (f3* Pressing IRCLI BixP/YRi recalls ihc lolal number of paymcnls in years and IRCLI B(EZXH) shows you ihc number of paymcnls per year.

Recalling these numbers docs noi change the content of the registers.

52 5: Time Value of Money Calcufatlont

Clearing TVM

Press BICLEAR ALLI lo dear the TVM registers. This sets N, f/YR, PV,

PMTy and FV to zero and briefly displays the current value in P/YR,

Begin and End Modes

OOODOQj OOOOOC' CZDOOOCii

OOOOCl ooooc^ oooac

{OBOOc:

To switch between modes, press BlBEG/ENDl. The BEGIN annunciator is

displayed when your calculator is in Begin mode. No annunciator is displayed when you arc in End mode.

Mortgages and loans typically use End mode. Leases and savings plans

Before you start a TVM calculation, identify whether the

first periodic payment occurs at the beginning or end of the first period. If the first payment occurs at the end of the first period, set your HP-lOB to End mode; if it occurs at the

beginning of the first period, set your calculator to Begin

mode.

typically use Begin mode.

Loan Calculations

Example: A Car Loan. You arc financing a new car with a three year

loan at 10.5% annual nominal interest, compounded monthly. The price

of the car is S7,250. Your down payment is $1,500.

Part 1. What arc your monthly payments at 10.5% interest? (Assume

your payments start one month after the purchase or at the end of the

first period.)

5: Time Value of Money Calculations S3

PV = 7,250-1,500

PMT = ? End Mode

Scl (o F.nd mode. Prc.s.s |

Keys:

12i(EZYR)

3 0 12®

10.5 [¡TYRI

7250 0 1500 (Py] 5,750.00

lIS7iiZBl

Display:

12.00

36.00

10.50

0 (pg 0.00

if BEGIN annuncialor is displayed.

Description:

Sets periods per year. Stores number of periods

in loan.

Stores annual nominal

interest rate.

Stores amount borrowed. Stores the amount left to

pay after 3 years.

-186.89

Calculates the monthly payment. The negative

sign indicates money paid out.

Part 2. At a price of $7,250.00, what interest rate is necessary to lower

your payment by $10.00, to -176.89?

0 10 (PMT

fiTTRl

-176.89

6.75

Decreases payment from

-186.89.

Calculates annual interest

54 5: Time Value of Money Catculatlona

rate for the reduced payment.

Part 3. If interest is 10.5%, what is the maximum you can spend on the

car to lower your car payment to $175.00?

10.5 flTYRl

175 m

01500 0

Slil

10.50

-175.00

5.384.21

6,884.21 Adds the down payment

Stores original interest

rate. Stores desired payment.

Calculates amount of

money to finance.

to the amount financed

for total price of the car.

Example: A Home Mortgage. You decide tha( the maximum

monthly mortgage payment you can afford is $630.00. You can make a $12,000 down payment, and annual interest rates arc currently 11.5%. If you obtain a 30 year mortgage, what is the maximum purchase price you

can afford?

A PV-?

I/YR - 11.5% N - 30x 12 P/YR = 12

• #

356

357

358

359

360

y y I Y

PMT - - 630.00 End Mode

Set tu End mode. Press |

Keys:

12lfP7YRl

Display:

12.00

y y y y y y

if BEGIN annunciator is displayed.

Description:

Sets periods per year.

5: Time Value of Money Calculations 55

30 WxP/YRI

360.00

Stores the length of the

mortgage (30 X 12).

11.5 n/YRl

630(S (PmT)

a 12000 a

0.00

11.50

-630.00

63,617.64

75,617.64

Pays mortgage off in 30

years. Stores interest rate.

Stores desired payment (money paid out is negative).

Calculates the loan you can afford with a $630 payment.

Adds $12,000 down

payment for the total purchase price.

Example: A Mortgage With a Balloon Payment. You’ve obtained

a 25 year, $72,500 mortgage at 13.8% annual interest. You anticipate (hat you will own the house for four years and then sell it, repaying the loan with a balloon payment. What will your balloon payment be?

Solve this problem using (wo steps:

1. Calculate (he loan payment using a 25 year term.

2. Calculate the remaining balance after 4 years.

Step 1. First calculate the loan payment using a 25 year term.

PV » 72.500

PMT - ? End Mode

56 5: Time Value of Money Calculationa

Set (o End mode. Press

if BEGIN annunciator is displayed.

Keys:

25 KxPZVr)

0 (FV)

72500 (PyJ

13.8 QZŸR]

Display:

12.00

300.00 Stores length of mortgage

0.00 Stores loan balance after

72,500.00

13.80 Stores annual interest

Description:

Sets periods per year.

(25 X 12 = 300 months).

25 years. Stores original loan

balance.

rate.

-861.65 Calculates monthly

payment.

Step 2. Since (he payment is at the end of the month, the last payment

and the balloon payment occur at the same time. The final payment is the

sum of PMT and FV,

PV = 72,500.00

l/YR - 13.8%

t Y Y Y

PMT = - 861.65 End Mode

N - 4x 12 P/YR - 12

45 46

Y Y I Y

47 48

FV = ?

5: Time Velue o( Money Calculations 57

The value in PMT should always be rounded lo two decimal

000*00

[OOOOOO

nOQC*

taoooo

boooo.

jOOOOC ^ooocjj

places when calculating FU'or PVio avoid small» accumula

tive discrepancies between non-rounded numbers and actual

(dollars and cents) payments. If the display is not set to two

decimal places» press BlDISPi 2.

Keys: Display: Description:

■ÍRÑDl ÍPMD

48®

-861.65 Rounds payment lo two decimal places, then stores.

48.00 Stores 4 year term (12 x

í+lÍRCLlfmR

4) that you expect to own

house.

-70,725.90

-71.587.55 Calculates total 4Slh

Calculates loan balance after 4 years.

payment (/^A//’and Fl'^

lo pay olTloan (money

paid out is negative).

Savings Calculations

Example: A Savings Account. If you deposit $2»000 in a savings

account that pays 7.2% annual interest compounded annually, and make

no other deposits to the account, how long will it take for the account to

grow to $3,000?

58 5: Time Value of Money Calculations

FV » 3.000.00

Since this account has no regular payments {PMT = 0), the payment

mode (End or Begin) is irrelevant.

Keys:

■I CLEAR ALLI 12 P Yr

Display:

o.oo”

1 liPTYRl

2000

1.00

-2,000.00

Description:

Displays a temporary

message and clears all

registers.

Sets P/YR to 1 since

interest is compounded annually.

Stores amount paid out

for first deposit.

3000 iFVl

7.2

i] 5.83 Calculates number of

3,000.00

7.20 Stores annual interest

Stores the amount you

wish to accumulate.

rate.

years it takes to reach $3,000.

5: Time Value of Money Calculations 59

Since (he calculated value of N is between S and 6, it will take six years of

annual compounding to achieve a balance of at least $3,000. Calculate the

actual balance at the end of six years.

6®

6.00

3,035,28

Sets ® to 6 years. Calculates amount you

can withdraw after 6 years.

Example: An Individual Retirement Account. You opened an

individual retirement account on April IS, 1985, ^^ith a deposit of $2,000.

Thereafter, you deposit $80.00 to the account at the end of each half

month. The account pays 8.3% annual interest compounded semimonthly.

How much will be in the account on April 15, 2000?

(Half-month periods)

Y t i i

FV =. ?

l/YR - 8.3% N - 360 (15 years x 24 half-months) P/YR » 24

« • •

360

Y Y Y Y Y Y

PMT = - 80.00

PV = -2,000.00

Set to End mode. Prcs,s BÍBÉG/ENDI if BEGIN annunciator i.s displayed.

Keys:

24 iEZYR]

2000FniPv|

Display:

24.00

- 2,000.00

Description:

Sets number of periods per year.

Stores initial deposit.

60 5: Time Value of Money Calculations

ши

-80.00 Stores regular semi monthly deposits.

8.3

15 lIxP/YRl

8.30

360.00

63.963.84

Stores interest rate.

Stores number of deposits.

Calculates balance.

Example: An Annuity Account. You opt Гог an early retirement

after a successful business career. You have accumulated a savings of

$400,000 that earns an average of 10% annual interest, compounded

monthly. What annuity (repetitive, uniform, withdrawal of funds) will you receive at the beginning of each month if you wish that savings account to

support you for the next 50 years?

pv = . 400,000.00

Begin Mode

PMT « ?

Set to Begin mode. Press |

Keys:

1211

400000 E3 (py)

[ШВ

шлш

Display:

12.00

-400,000.00

10.00

if annunciator is not displayed.

Description:

Sets payments per year. Stores your nest egg as

an outgoing deposit. Stores annual interest

rate you expect to earn.

5: 'Лтв Vatue of Mono, Catculations 61

50BxP/YRI

600.00

Stores number of

withdrawals.

0 (FV] 0.00

Ш)

3.328.68

Stores balance of account

after 50 years. Calculates amount that

you can withdraw at the beginning of each month.

Lease Calculations

A lease is a loan of valuable properly (Икс real estate, automobiles, or equipment) for a specific amount of lime, in exchange for regular pay*

mcnls. Some leases arc written as purchase agreements, with an option to buy at the end of the lca.se (sometimes for as little as Sl.OO). The defined future value (Fl^ of the property at the end of a lease is sometimes called

the “residual value” or “buy out value.'

All five TVM application keys can be used in lease calculations. There arc

two common lease calculations.

■ Finding the lease payment necessary to achieve a specified yield.

■ Finding the present value (capitalized value) of a lease.

The first payment on a lease usually occurs at the beginning of the first

period. Thus, most lca.se calculations use Begin mode.

Example: Calculating a Lease Payment. A customer wishes to

lease a $13,500 car for three years. The lease includes an option to buy the car for $7,500 at the end of the lease. The first monthly payment is due the day the customer drives the car off the lot. If you want to yield

14% annually, compounded monthly, what will the payments be? Calcu

late the payments from your (the dealer’s) point of view.

62 5: Tim« Vatu« of 1У1опеу Calculations

РМТ - ?

FV = 7,500.00

PV «■ -13,500.00

Begin Mode

Set to Begin mode.

ж Ж

I/YR - 14% N - 36 P/YR - 12

Money received by lessor is

if annunciator is not displayed.

positive.

Money paid out

by lessor is negative.

Keys: 12а[р7щ

14 [ITYRI

13500 Ea (pg

7500 7,500.00

36 (n]

[рШ1

Display:

12.00

14.00

-13,500.00

36.00

289.19 Calculates monthly lease

Description:

Sets payments per year. Stores desired annual

yield.

Stores lease price. Stores residual (buy out

value). Stores length of lease, in

month.s.

payment.

Notice that even if the customer chooses not to buy (he car, the lessor still includes a cash flow coming in at the end of the lease equal to the residual

value of the car. Whether the customer buys the car or it is sold on the

open market, the lessor expects to recover $7,500.

Example: Lease With Advance Payments. Your company, Quick-

Kit Pole Barns, plans to lease a forklift for the warehouse. The lease is written for a term of 4 years with monthly payments of $2,400. Payments arc due at the beginning of the month with the first and last payments due at the onset of the lease. You have an option to buy the forklift for $15,000 at the end of the leasing period.

5: Timo Value of Money CalculaUont S3

Ii‘ the annual interest rate is 18%, what is the capitalized value of the lease?

Begin Mode

PV = ?

This solution requires four steps.

1. Calculate the present value of the 47 monthly payments:

(4x12) -1 = 47.

2. Add the value of the additional advance payment.

3. Find the present value of the buy option.

4. Sum the values calculated in steps 2 and 3.

Step 1- Find the present value of the monthly payments.

Set to Begin mode. Press BIBEG/ENDI if annunciator is not displayed.

Keys:

121[P/Y~R1

47(H)

2400 (EMI

Display:

12.00

47.00

-2,400.00

Description:

Sets payments per year. Stores number of

payments.

Stores monthly payment.

64 5: Time Value of Money Calculations

oEy)

0.00

Stores FV for step 1.

18 il/YR

18.00

81.735.58

Stores interest rate.

Calculates present value of 47 monthly payments.

Step 2. Add the additional advance payment to PV. Store the answer.

m iRCLi iPMTi m

Fm]

84,135.58 84,135.58

Adds additional advance

payment. Stores result in M

Step 3. Find the present value of the buy option.

48 El

0 fPMTl

15000 m iFVI

48.00

0.00

-15,000.00

7,340.43

Step 4, Add the results of steps 2 and 3.

Keys:

Display:

Stores month when buy option occurs.

Stores zero payment for this step of solution.

Stores value to discount.

Calculates present value of last cash flow.

Description:

(±)[BM]0

91,476.00

Calculates present

(capitalized) value of lease. (Rounding discrepancies are

explained on page 58.)

5: Time Value of Money Calculations 65

Amortization

Amorlization is the process of dividing a payment into the

ooooaoi oooooo

^30000 ooooo

OOOQO

oooac

OOOOC3

amount that applies to interest and the amount that applies to principal. Payments near the beginning of a loan contribute more interest, and less principal, than payments

near the end of a loan.

TIME

The Miamorti key on the HP-lOB allows you to calculate.

■ The amount applied to interest in a range of payments.

m The amount applied to principal in a range of payments.

■ The loan balance after a specified number of payments are made.

66 5: Time Value of Money Calculations

The BlAMQRTI function assumes you have just calculated a payment or

you have stored the appropriate amortization values in I/YR^ FV, PMT^

wdP/YR.

msi

QQÛI

■iP/YRl

The numbers displayed for interest, principal, and balance arc rounded to

the current display setting.

Annual nominal interest rate. Starting balance.

Payment amount (rounded to the display format),

Number of payments per year.

To Amortize. To amortize a single payment, enter the period number

and press lINPUTi, then press BlAMORTl. The HP-lOB displays the message PEr followed by the starling and ending payments that will be

amortized.

Hold 0 down to display the label of the value that you are about to view.

Press 0 to see interest (Int). Press 0 again to sec the principal (Prin) and again to see the balance (bAL). Continue pressing 0 to cycle through the same values again.

To amortize a range of pajTOcnts, enter siarling period number I INPUT I

ending period number, then press BlAMORTl. The HP-lOB displays the

message PEr followed by the starting and ending payments that will be

amortized. Then press 0 repeatedly to cycle through interest, principal, and balance.

Press BiAMORTl again to move to the next set of periods. This autoincrement feature saves you the keystrokes of entering the new starling

and ending periods.

If you store, recall, or perform any other calculations during amorli/aliun, pressing 0 will no longer cycle through interest, principal, and balance.

To resume amortization with the same set of periods, press IRCLI

■ I

5: Time Value of Money Calculations 67

Exampio: Amortizing a Range of Paymanta. Calcuiate the first

tvb-o years of (he annual amortization schedule for a 30 year, $80,000 mortgage, at 9.75% annual interest with monthly payments.

Set to End mode. Press №B£0/ENDI if aEOIN annunciator is displayed.

Keya:

9.75

80000 fPVl

o(E3

[РЙТ1

Display:

12.00

360.00

9.75

80.000.00

0.00

-687.32

Deacrlption:

Sets payments per year.

Stores total number of

payments. Stores interest per year. Stores present value. Stores future value.

Calculates monthly

payment.

If you already know (he mortgage payment, you ean enter and store it just like you store (he other four values. Next, amortize the first year.

1 IINPUTI12

12_

PErl- 12 Displays range. Int

-7.779.42

Prin

-46842

Enters starting and

ending periods.

Displays label» then

interest paid the first

>'car.

Displays labcii then

principal paid the first

>*car.

The amount paid toward interest and principal (7,779.42 + 468.42 «

8.247.84) equals the total of 12 monthly payments (12 x 687Л2 >

8.247.84) . The remaining balance equals the initial mortgage, less the amount applied toward principal (80,000 - 468.42 = 79,531..58).

bAL

79.531.58

Displays label, then loan

balance after one year.

68 S: Tim* Vatu* of Money ColeuloUons

Amortize the !U:cond year;

РЕПЗ-24

The amount paid toward interest and principal (7,731,67 + 516.17 » 8,247JM) equals the total of 12 monthly payments (12 x 68732 *

Int

-7,731.67

Prin

-516.17

bAL Displays loan balance 79,015.41

Displa)*s next range of periods.

Displays interest paid in second year.

Displays principal paid in

second year.

after 24 payments.

8,24734). The remaining balance equals the initial mortgage less the amount applied toward principal (80,000 - 468.42 - 516.17 » 79,015.41).

More money is applied to principal during the second rather than (he first

>rar. The succeeding years continue in the same fashion.

Example: Amortizing a Single Payment. Amorti/c the 1st, 25ih,

and 54th payments of a five >%ar car lease. The lease amount is $14,250 and the interest rate is 11.5%. Payments arc monthly and begin immediately.

Set to Begin mode. Press

Key»:

Display:

if annunciator is not displayed.

Description:

i2i(EZXB)

5ШШШ

11.5 14250

та

12.00

60.00

11.50 14,250.00

0.00

-310.42

Sets payments per year. Stores number of

payments.

Stores interest per year.

Stores prc.scnt value.

Stores the future value. Calculates monthly

payment.

S: Tin. УЫи. «I М.П.У CrSculaUon. S9

Amortize the 1st, 2Sth, and 54tli payments.

25 lINPUTI

1.00

PEr 1 - 1

Int

Enters first payment.

Displays amortized payment period.

Displays interest.

0.00

Prin

-310.42 payment.

bAL Displays loan balance

13,939.58 after one payment.

25.00

Displays first principal

Enters payment to

■IamortI

54 IINPUTl

amortize.

PEr 25 - 25

Int Displays interest paid on

-90.21

Prin

-220.21 on 25th payment.

bAL

9,193.28 25lh payment.

54.00

Displays amortized payment period.

25th payment.

Displays principal paid

Displays balance after

Enters payment to

IfAMORfl

amortize.

PEr 54-54

Int Displays interest paid on

-20.05

Prin

-290.37

bAL

1,801.57

Displays amortized

payment period.

54lh payment.

Displays principal paid

on 54th payment.

Displays balance after

54lh payment.

70 5: Tima Vatu« of Money Calculationt

Interest Rate Conversions

The Inlcrcsl Conversion application uses three keys:

ommmoo

ooooon сэоооо □ ооосз! □ oooo

OODOO

□ ooao

If you know an annual nominal interest rale and you wish to solve for the

corresponding annual effective rate:

1. Enter the nominal rate and press BlNOM%l.

2. Enter the number of compounding periods and press BIP/YRI.

3. Calculate the cITcctive rate by pressing ЯШЕЕЭ*

BlNOM%l. BIEFF%L and Mp7yrI, They convert between

nominal and annual cfTective interest rates. Nominal and effective interest rates arc described on page 47.

To calculate a nominal rate from a known effective rate:

1. Enter the effective rate and press

2. Enter the number of compounding periods and press

3. Calculate the nominal rate by pressing

In the TVM application, BlNOM%l and ll/YRl share the same register.

Interest conversions are used primarily for two types of problems:

■ Comparing investments with different compounding periods.

■ Solving TVM problems where the payment period and the interest

period differ.

1Ш1ЕЗ

ШШ-

Investments With Different Compounding Periods

Example: Comparing Investments. You arc considering opening a

savings account in one of three banks. Which bank has the most favorable interest rale?

5: Time Value of Money Calculatlont 71

Firsl Bank

6.70% annual interest, compounded quarterly.

Second Bank Third Bank

First Bank. Keys:

6.7 4|

caflia

6.65% annual interest, compounded monthly.

6.63% annual interest, compounded 360 times per

year.

Display:

6.70

4.00

Description:

Stores nominal rate. Stores quarterly com

pounding periods.

Second Bank.

6.65

12i(PZ?S)

Third Bank.

6.87

6.65

12.00

Calculates annual effective rale.

Stores nominal rate. Stores monthly com

pounding periods.

6.86 Calculates annual

cfTcctivc rate.

6.63 360lfP7YRl

\mm

First Bank oQcrs a slightly better deal since 6.87 is greater than 6.86 and

6.85.

6.63 Stores nominal rate.

360.00

6.85

Stores compounding

periods. Calculates annual

cfTcctivc rale.

72 5: Time Value of Money Calculationt

Compounding and Payment Periods

The TVM application assumes that the compounding periods

•■■OOj

ooooo

oooo ooooo □ oooo

ooooo ooooo

To adjust an interest rate when the compounding period differs from (he

payment period complete the following steps:

and the payment periods are the some. Some loan install ments or savings deposits and withdrawals do not coincide with the bank's compounding periods. If the payment period

differs from the compounding period, adjust the interest rate to match the payment period before solving the problem.

1« Enter the nominal rate and press Enter the number of

compounding periods in a year and press BiP/YRi. Solve for the

effective rate by pressing BfEFP^,

2. Enter the number of payment periods in a year and press BlP/V^I.

Solve for (he adjusted nominal rate by pressing![ROMS.

Example: Monthly Payments, Daily Compounding. Starting

today, you make monthly deposits of S2S to an account paying 5% interest, compounded daily (using a 365 day year). What will the balance be in seven years?

Step 1. Calculate (he equivalent rate with monthly compounding.

Keys:

cBm

Display:

5.00 Stores nominal per

Description:

centage rate.

365 ■fPTTRl

|[EEES

12lfP7VR1

Since NOM% and l/YR share the same register, this value is ready for use

365.00

5.13

12.00 Stores monthly periods.

5.01

Stores bank’s compound

ing periods per year. Calculates annual

effective rate.

Calculates equivalent nominal percentage rate

for monthly compounding.

in the rest of the problem.

5: Time Value of Aloney Calculetlona 73

Step 2. Calculate the future value.

Set to Begin mode. Press B(BegZenQ if annunciator is not displayed.

0.00

25mipRm -25.00 Storc.s payment. 7llxP/YRI

84.00

2,519.61

Stores present value.

Stores number of pay

ments per year. Calculates balance after'

years.

74 5: Time Value of Money Caloutatlona

Cash Flow Calculations

How to Use the Cash Flow Application

The cash flow application is used to solve problems where

oaoaoo

daaasD

BOOOC

oaaoo

aooao

ODOOD

loooac

In general, these arc the steps for cash flow calculations on the HP-IOB.

1. Organize your cash flows on paper —a cash flow diagram is useful.

2. Clear the registers.

3. Enter the number of periods per year.

cash flows occur over regular intervals but arc of varying amounts. You can also use cash How calculations to solve problems with rcgtilar, equal, periodic cash flows, but these situations are handled more easily using TVM.

4. Enter the amount of the initial investment.

5. Enter the amount of the next cash flow.

6. If the amount entered in step 5 occurs more than once consecutively,

enter the number of times it occurs.

7. Repeat steps 5 and 6 for each cash flow and group.

8. To calculate net present value, enter the annual interest rate and

press il/YRI: then press BINPVI, Or, to calculate annual internal rale of return, press BlIRR/YRi.

Example: A Short Term Investment. The following cash flow

diagram represents an investment in stock over three months. Purchases were made at the beginning of each month, and the stock was sold at the end of the third month. Calculate the annual internal rate of return and the monthly rate of return.

6: Cash Flow Calculations 75

Flows received are positive.

Flows paid out

are negative.

Keys:

■Icl6Ar aLLI

12BiP7VR1

5000

2000 Ea

4000 iC^

Display:

0.00

12.00

CFO

-5,000.00

CF1

-2,000.00

CF2

Description:

Clears all registers. Stores periods per year.

Enters initial cash flow. Displays cash flow group numlrer while you hold down iCFlI.

Enters next cash flow.

Enters next cash ftow.

11765.29

Qm»aD

012Q

ISdl

-4,000.00

CF3

11,765.29

38.98

3.25

Enters final cash How.

Calculates annual nominal yield.

Monthly yield.

76 6: Cath Flow CatculaUona

NPV and IRR/YR: Discounting Cash Flows

Chapter 4 demonstrates the use of cash flow diagrams to clarify financial problems. This section describes discounted cash flows. The NPViund

¡RR/YR functions arc frequently referred to as discoutUed cash flow

functions.

When a cash flow is discounted, you calculate its present value. When multiple cash flows arc discounted, you calculate the present values and add them together.

The net present value {NPV) function finds the present value of a series

of cash flows. The annual nominal interest rate must be known to calculate NPV,

The internal rale of return {IRR/YR) function calculates the annual

nominal interest rate that is required to give a net present value of zero.

The utility of these two financial tools becomes dear after working a few

examples. The next two sections describe organizing and entering your

cash flows. Examples of NPV and IRR/YR calculations follow.

Organizing Cash Flows

The cash flow scries is organized into an initial cash flow (CF 0) and succeeding c^5/t fhwff’oups (up to 14 cash flows). CF 0 occurs at the

beginning of the first period. A cash flow group consists of a cash flow amount and the number of times it repeats.

For example, in the following cash flow diagram, the initial cash flow is

-$11,000. The next group of cash fiows consists of six flows of zero each,

followed by a group of three $1,000 cash flows. The final group consists of one $10,000 cash flow.

6: Cash Flow CalcutaUona 77

CF 3 « 10,000, N 3 » 1

Whenever you enter a series of cash ffows, it is important to account for

every period on the cash flow diagram, even periods with cash flows of zero.

Entering Cash Flows

The HP-lOB can store an initial cash flow plus 14 additional cash flow groups. Each cash flow group can have up to 99 cash flows. The cash flows

arc stored in registers Rq tlirough Ro and R o through R Enter cash flows using the following steps;

1. Press BiCLEAR all] to clear the registers.

2, Enter the number of periods per year and press BlP/YRl. 3, Enter the amount of the initial investment, then press iCFil. (The

‘7” stands for the casli flow ^'number,*' 0 through 14.)

4. Enter the amount of the next cash flow and press ICFil.

5- If the amount entered in step 4 occurs more than once conseatfivelyy

enter the number of times it occurs, and press BlNil.

6. Repeat steps 4 and 5 for each ICFil and |[N]] until all cash flows

have been entered.

78 6: Cash Flow CatculaUons

Example. Enter the cash flows from the preceding diagram and calcu

late the JRR/YR. Then calculate the effective interest rate. Assume there arc 12 periods per year.

Keys:

■l CLEAR ALLl

121íp7yr1

11000 m

[gdi

6|[ÑI]

Display:

0.00

12.00

CFO

-11,000.00

CF1

0.00

n 1

Description:

Clears all registers.

Sets Ip/YRI to 12.

Enters initial cash flow. Displays cash flow group number for as long as you hold down ICFjl.

Enters first cash flow

group amount.

Enters number of

1000 fCFH

10000

Q3iU2D

\Sil

6.00

CF2

1,000.00

3.00

CF3

10,000.00

21.22

repetitions. Enters second cash flow

group amount.

Enters number of repetitions.

Enters final cash flow.

Calculates annual nominal yield.

Viewing and Replacing Cash Flows

To view a cash flow list press the following:

1. IRCLl 0 to see the initial cash flow.

2. IRCLl ICFII to .see the next flow.

3. IRCLl KnI] to see the number of limes the cash flow occurs.

Repeat steps 2 and 3 until all cash flows are reviewed.

You can also view cash flows individually by pressing iRCLi. followed by a register number. Register numbers coincide with cash fbw numbers. For

example, press IRCLl 4 to see cash fbw 4, then iRCLl (N¡0 to see the

number of consecutive occurrences.

6: Cash Flow Calculations 79

To replace a cash flow, enter the new cash flow and press BiSTOl

followed by the cash flow (register) number.

To replace the number of limes a particular cash flow occurs, IRCLI the

cash flow whose number of occurrences will change. Then, enter (he number of times it occurs and press BfRIl.

To replace both the cash flow and number of times it occurs, enter the

new cash now, press BiSTOl followed by the cash flow (register) number.

Then enter the number of times it occurs and press

Since cash flows cannot be deleted or inserted, use BICLEAR ALU to start

over.

Calculating Net Present Value

The net present value (NPV) function is used to discount all cash flows to

the front of the time line using an annual nominal interest rate that you

supply.

These steps describe how to calculate

G!IjU

1. Press BiCLEAR^Lll. store number of periods per year in P/YR,

2. Enter the cash flows using tcfil and (N]].

3. Store the annual nominal intcre.st rate in I/YR and press BiNPVl.

Example: A Discounted Contract, Uneven Cash Flows. You

have an opportunity to purchase a contract with the following cash flows:

End Of Month

4 9

Amount

$ 5,000.00 $ 5,000.00

10 S 5,000.00

$ 7,500.00

25 $10,000.00

How much should you pay for the contract if you wish to yield a yearly

rate of 15% on your investment?

80 6: Cash Flow Calculations

I/YR = 15%

10.000

Keys:

■ICLEAR ALU 12BiP7YRl

0(CF])

o(cHj)

Display;

0,00

12.00

CFO

0.00

Description:

Clears registers. Sets payments per year.

Enters initial cash flow of

zero. The cash flow

number is displayed as long as you hold down the (CFil key.

CF1 Enters first cash flow.

0.00

n 1 Enters number of

3.00

5000 fCFil CF2

5,000.00

0(CFl)

4 mm

5000 fCF]l

CF3

0.00

4.00

CF4

5,000.00

occurrences.

Enters second cash flow.

Enters third cash flow.

Enters number of

occurrences.

Enters fourth cash flow.

n4 Enters number of

2.00 occurrences.

6: Cash Flow Calculations 81

0 fCFjl

CF5

0.00

Enters fifth cash flow.

4|[^

7500ÎCFJ1

0[çEB CF7

4.00 CF6

7,500.00

0.00

9|[^

10000 fcFil

9.00 CF8

10,000.00

Enters number of occurrences.

Enters sixth cash flow.

Enters seventh cash flow.

Enters number of

occurrences.

Enters next cash flow.

The cash flows thaï describe your prospective investment arc now in the calculator. You can press IRCLl 0, followed by IRCLl ÎCFII and IRCLI

BED, repeatedly to view the cash flows and number of times each occurs.

Now that you have entered the cash flows, store the interest rate and

calculate the net present value.

Keys:

ISfi/YRl

■iNPVl

Display:

15.00

27,199.92

Description:

Stores annual interest

rale.

Calculates net prc,senl value of stored cash

flows. (See rounding

example on page 58.)

This result shows that if you want a yield of 15% per year, you should pay

$27,199.92 for the contract. Notice that this amount is positive. The net present value is simply the summed (or netted) value of a series of cash

flows when they arc discounted to the front of the lime line.

82 6: Cash Flow Calculations

Calculating Internal Rate of Return

1. Press BICLEAR ALU, store number of periods per year in P/YR.

2. Enter the cash flows using (CF^ and (Nfl.

3. Press II

When you calculate ¡RR/YR^ you get llic annual nominal rate that gives an NPV of /его.

The following example uses the cash flows that were entered in the

previous example. More than one IRR/YR can exist. If you get the no SoLution message see

Appendbc В (page 127).

1шгдп

Example. If the seller of the contract in the previous example wants

$28,000 and you accept that price, what is your yield? This is an IRR/YR

calculation that requires a slight modification to the currently stored cash

flows.

6: Cash Flow Calculations $3

10.000

4-1-Ь

■b 1 M I 1 1 1 -b-

Y -28,000

5,000

7.500 '

5.000 ^ j к

к >

11 13 15 17 19 21 23 25

IRR/YR = ?

1 1 M I-I H-I -

Keys: 28000 ^

(ШШ

■

More examples (hat use NPV and IRR/YR calculations arc given in

chapters, “Additional Examples.”

0 -28.000.00

Display:

12.49

Description:

Changes initial cash How.

Calculates annual nomi nal yield.

Automatic Storage of IRR/YR and NPV

When you calculate NPVy the result is stored in PV Гог your convenience.

To recall that result, press [ЕЗ* If you haven’t changed the TVM

values from the last example using NPV (page 82), when you press IRCLI

(E3 Ihe result is 27,199.92. When you calculate IRR/YR^ the result is also stored in I/YR, For the

previous example, press IRCLI ll/YRI to display the annualized yield 12.49.

84 6: Cash Flow Calculatlont

Statistical Calculations

_______

*□ 00000 iwo-variablc statistics. Summation data is accumu-

<nnooo latcd in registers R.| through Rij. The register labels at the

c lower right of the keys indicate what statistical data is stored соаё^' register. Once you enter the data, you can use the

Mean and standard deviation. Linear regression statistics. Linear estimation and forecasting.

Weighted mean.

l! The (13 and ШШВ зге used to enlcr and delete data for

statistical functions to calculate the following;

Summation statistics: n, Ev, By, E^'^, and Evy.

Clearing Statistical Data

Clear the statistical registers before entering new data so that

OOOOOCi

oaooDo

ZDeOOD □ OCDCDO □ О CD CD C

oooac

caoac

R4 through R9 are zero when you begin. If you don’t clear the registers» data currently stored in R4 through R9 is auto matically included in the summation calculations. To clear

the statistical registers, press BlCL Zl. The display is also cleared.

7: Statistical Calculations 85

Entering Statistical Data

There is no limit to the number of values you can accumulate in the

statistical registers. *

One-Varfable Statistics

To enter jc data for one-variable statistics complete the following steps:

1. Clear the contents of through R9 by pressing BlcL zl.

2. Enter the first value and press (13. T'hc HP-lOB displays n, the

number of items accumulated.

3. Continue accumulating values by entering the numbers and pressing

d+). The n-valuc is incremented with each entry,

Two-Variable Statistics and Weighted Mean

To enter xj’ pairs of statistical data complete these steps:

1. Clear the contents of R4 through R9 by pressing BICL Zl.

2. Enter the first x-valuc and press lINPUTl. The HP-lOB displays the

x-valuc and the : annunciator appears in the display.

3. Enter the corrcspondingy-valuc and press (13. The HP-lOB

displays n, the number of pairs of items accumulated,

4. Continue cnlcringXjV pairs. The n-valuc is incremented with each

entry.

To enter data for calculating the weighted mean» enter each data value as

X, and its corresponding weight asy.

If siaiisiical data causes the value of a register to exceed ±9.99999999999 x 10 , the HI’-lOB displays a temporary o%erfk)tt’W'aming(OFLO).

86 7: Statistical Calculations

Correcting Statistical Data

Incorrect entries can be deleted using B[13- If either value of an is incorrect, you must delete and reenter both values.

Correcting One^Variable Data

To delete and reenter statistical data;

1. Key in the X-value to be deleted.

2. Press i(B to delete the value. The n-value is decreased by one.

3. Enter the correct value using [ZTI,

a:,v

oair

Correcting Two-Variable Data

To delete and reenter.pairs of statistical data:

1. Key in thcx-valuc, press lINPUTI and then key in ihcy-valuc.

2. Press B[13 to delete the values. The n-value is decreased by one.

3. Enter the correct pair using ilNPUT] and [|jj.

7: Statistical Calculations 87

Summary of Statistical Calculations

Some functions return two values. The : annunciator indicates that two values have been returned. Press BisWAPl to sec the hidden value.

Keys Description SIswAPi to Display

Mlerx,{ry\

Arithmetic mean (aver age) of the y-values.

Mean of the x-values weighted by the y-vaiues.

Sampie standard devia tion of the x-values.*

Popuiation standard devi ation of the x-values.*

Mean (average) of the y-values if you entered y-data.

Sample standard devia

tion of the y-values if you

entered y-data.*

Population standard devi

ation of the y-values if you entered y-data.*

y-value Idir]

y-value

Estimate of x for a given

value of y. Estimate of y for a given

value of X.

0|[Em|

y-intercept (b) of the cal

culated line.

* The sample standard deviation assumes that the data is a sampling of a larger,

Correlation coefficient.!

Slope (m) of calculated

line.

Slope (m) of the calcu

lated line.

complete set of data. The population standard deviation assumes that the data con

stitutes the entire population.

t The correlation coefficient is a number in the range * 1 through +1 that measures

how closety the data fits the calculated lino. A value of -f 1 indicates a perfect positive

correlation, and -1 indicates a perfect negative correlation. A value close to zero indicates the line is a poor fit.

88 7: Statistical Calculations

Keys

Description

(RCLl 4 (n) fRCLl5(E)i) Sum of the x-values.

(R^6(i:y)

RCL17(D<2)

(RcOsoy)

fRcqgiExy)

Number of data points entered.

Sum of the y-values. Sum of the squares of the x-values.

Sum of the squares of the y-values. Sum of the products of the x- and y-values.

Mean, Standard Deviations, and Summation

Statistics

You can calculate the mean (7), sample standard deviation

OOOOOl OOOOOO^

CZDOOOg

oSSSo

oooDc:

Example 1. A yacht captain wants to determine how long it takes to

(Sx), and population standard deviation and summation statistics, n, Ec, and Ev^ of.v-data. rorxy data, you can also calculate the mean, sample standard deviation, and popula tion standard deviation of they-data and the summation statistics X3y, Ey^, and Ety.

change a sail. She randomly chooses six members of her crew, observes them as they carry out the sail change, and records the number of minutes required: 4.5, 4,2, 3.25, 3.5, 3.75. Calculate the mean and sample standard deviation of the times. Also, calculate the root mean .square, u.sing the

formula V^Ex’V'» :

Keys:

■(cOl

Display:

0.00

Description:

Clears statistical registers.

7: Statistical Calculations 89

4.5 (1+)

1.00

Enters first time.

4d+)

2g±)

3.25 d±] 4.00

3.5 d3

3.75 d±]

■(M)

■EiSa

iRCp7

2.00

3.00

5.00

6.00

3.50

0.85 Calculates the sample

77.13

Enters second time.

Enters third time. Enters fourth time.

Enters fifth time. Enters sbah time. Calculates the mean.

.standard deviation.

Displays Ev^.

m iRCD4 Ql(^

1________1

QOOOOO

oooooo

CZDOOOO

aovao

• aacDo ooooa ooooo

..............

The standard deviations calculated bv lliS.v,Sy| and

■IS.r.Syl HlSWAPI are the sample standard deviations. Thev assume that the data is a sampling of a larger, complete set

of data.

ir the data constitutes the entire population, the true population standard deviations can be calculated by pressing

6.00

3.59

M\<rx,a-y\ and W\tTx,<ry\ HSWAPI.

Displays ;i.

Calculates the root mean square.

Example 2. The coach has four new players on the team with heights of

193,182,177, and 185 centimeters and weights of 90,81,83, and 77 kilo

grams. Find the mean and population standard deviation of both their

heights and weights, then sum they-data.

Keys:

liCL^

193

OSM]

90(13 1.00

81 d3

Display:

0.00

2.00

Description:

Clears .statistical registers.

Enters height and weight of player 1.

Enters heiglU and weight

90 7: Statistical Calculations

of player 2.

177 iINPUTi 83 fg»1 3.00

Enters liciglit and wciglit of player 3.

185 lINPUTI 77 (13 4.00

■diS

02E3a

M\cr_x,cry\

184.25

82.75

5.80

4.71

Enters height and weight of player 4..

Calculates mean of heights (r).

Displays mean of weights

O')-

Calculates population

standard delation for

heights (jtr). Displays population

standard dc\aation for

weights (y).

iRCOS

331.00

Displays the total of the

/s.

Linear Regression and Estimation

L oooooo

oooooo

CDOOnn

ooooo

IBSCDO

ooooc

oooac

Linear regression, is a statistical method for estimation and forecasting. It is used to find a straight line that best fits a set

cAxy data. There must be at least two differentpairs. The

straight line provides a relationship between thex- and

>»-variablcs:^ « nu* + b, where m is the slope and b is the >i-intcrccpt.

Linear Regression. Calculate m, b, and r (the correlation coefficient),

in three steps.

1. Enter thexj^ data using the instructions on page 86.

2. To display b (they-inlcrccpt), press 0 8Em). Then press ||

to display m (the slope of the line).

3. Press ■dZ) I(1Wa 0 to display r, the correlation coefficient.

7: SUtifttical Catculationt 91

Linear Estimation. The straight line calculated by linear regression

can be used to estimate ay-value for a given jc-valuc, or vice versa:

1. Enter the A;y-data using the instructions on page 86.

2. Enter the known x-valuc ory-valuc.

m To estimate X for the giveny, enter thcy-valuc, then press

■da.

■ To cstimalcy for the given x, enter thex-valuc, then press

l(£^.

Example: Forecasting. Ali's A/^ileus advertises on a local radio sta

tion. For the past six weeks, the manager has kept records of the number of minutes of advertising that were purchased, and the sales for that week.

Week Minutes of Advertising

(x-va lues)

Week 1

Week 2

Week 3 Week 4

Weeks

2 $1.400

1 $ 920

3 5 5

Sales

((/-values)

$1,100 $2.265

$2,890

Week 6 4 $2,200

What is they-intcrcepl, the slope, and the correlation coefficient?

92 7: Statistical Calculations

3.000,00

Sales in Dollars

2,000.00

1,000,00

/ •

“1

--------1-----1----0 12 3

Minutes of Advertising

• /•

m e 425.88

r 1

--------1-----1-----\-----

(forecasted)

1“

4 5 6 7 8

Keys: Display:

ШШИ

2 IINPUTI 1400 fZ+1

1 IlNPUTl 920 d+) 3 IINPUTI 1100 iZ+1 5 IINPUTI 2265 (Ё+1 5 IINPUTI 2890 fZ+1

0.00

1.00 Enters minutes and sales

2.00

3.00

4.00

5.00

Description:

Clears statistical registers.

for consecutive weeks.

4 IINPUTI 2200 i!+l

0Ш [Ш

■ISWAPI

■g^) ||SWAP| 0.90

Esiimalc what the level of sales would be if the businc.ss purchased 7 or 8

minutes of advertising.

6.00

376.25 Calculates y-inlcrccpl

(b).

425.88

Displays slope.

Calculates correlation

coefficient.

7: SUtJstlcal Calculations 93

3.357.38

Estimalcs sales if 7 minutes of advertising

were purchased.

3.783.25

How many minutes of advertising should Ali’s buy to attain sales of

$3,000?

3000 |[^ 6.16 Estimates minutes of

Estimates sales if 8 minutes were purchased.

advertising required for $3,000 in sales.

Weighted Mean

The following procedure calculates the weighted mean of data points.v¡,

^2,.. -tXn occurring with weights >»1,^2»* ••>yn-

1. Use IINPUTI and [|+] to enter pairs. Thcy-valucs arc the weights

of the.r-values.

2. Press Bl.rw!.

Example. A survey of 266 one*bedroom rental apartments reveals that

54 of them rent for $20() per month, 32 for $205,88 for $210, and 92 for $216. What is the average monthly rent?

Keys:

■icQ]

210

Düüüfl

Display:

0.00

54 f?Tl

1.00

32 gT] 2.00

88(13 3.00

92 g3 4.00

Description:

Clears statistics memory.

Enters first rent and its

weight,

EiUer.s second rent and

its weight. Enters third rent and its

weight.

Enters fourth rent and its

weight.

|[|^

94 7: Statistical Catculatlona

209.44

Calculates weighted

mean.

Additional Examples

Business Applications

Setting a Sales Price

One method for setting the per unit sales price is to determine the cost of

production per unit, and then multiply by the desired rale of return. For this method to be accurate, you must identify all costs associated with the product.

The following equation calculates unit price based on total cost and rate

of return: PRICE = TOTAL COST -r NUMBER OF UNITS x (1 + (%RTN -r 100))

Example. To produce 2,000 units, your co.st is $40,000. You want a 20%

rale of return. What price should you charge per unit?

Keys:

Display:

Description:

40000 0 40,000.00

2000 0

WD 1 [±]I(D 20 0

100 0

20.00

24.00

Enters cost.

Calculates unit cost. Calculates unit sales

price.

Forecasting Based on History

One method of forecasting sales, manufacturing rates, or expenses is reviewing historical trends. Once you have historical data, the data arc fit

to a curve that has lime on the j:-axis and quantity on they-axis.

8: Additional Examples 95

Example. Given the following sales data, what are the sales estimates

for years six and seven?

Year

3 4

Keys; Display:

Sales $

10,000

11,210

13,060

16,075

20,590

Description:

■iem 0.00

1 QnpDt] 10000 ШЗ 1.00

2QnpDT) 11210 d±] 2.00

3 QnpDT) 13060 Ё+]

4 fiNPPfl 16075 ШВ 5 lINPUTI 20590 Ш+]

ешш

3.00

4.00

5.00 22,000.50

Clears statistics registers. Enters first year and

sales for that year.

Enters .second year’s data.

Continues data entry.

Estimates .sales for year

.six.

7i(£^

24.605.00

Estimates sales for year

seven.

Cost of Not Taking a Cash Discount

A cash discount gives a buyer a reduction in price if the payment is made

within a specified time period. For example, "2/10, NET/30” means that

the buyer can deduct 2 percent if payment is made within 10 days. If pay

ment is not made within 10 days, the full amount must be paid by the 30th

day.

You can use the equation shown below to calculate the cost of failing to

take the cash discount. The cost is calculated as an annual interest rale

charged for delaying payment.

96 8: Additional Examples

DISC% X 360 X 100

COST% -

((100 - D1SC%) X (TOTAL DAYS - DISC DAYS))

DISC% is ihc discount percent if the payment is made early. TOTAL

DAYS is the total number of days until the bill must be paid. D/5C DAYS

is the number of days for which the discount is available.

Example. You receive a bill with the credit terms 2/10, NET/30. What

Is the cost of not taking the cash discount?

Keys:

2 0 360 (x) 100 (3 72,000.00

■Ш as 100 0 2

1Ш

0 аш 30 010 0

Display:

98.00 of calculation.

36.73

Description:

Calculates numerator in

equation.

Parentheses force order

Calculates, as an annual percentage rate, cost of not taking discount.

Loans and Mortgages

Simple Annual Interest

Example. Your good friend needs a loan to start his latest enterprise

and has requested that you lend him $450 for 60 days. You lend him the

money at 10% simple annual interest, to be calculated on a 365-day basis.

How much interest will he owe you in 60 days, and what is the total

amount owed?

This equation is used for calculating simple annual interest using a 365

day year:

INTEREST -

LOAN AMOUNT X INTEREST%x TERM OF LOAN (IN DAYS)

365

8: Additional Examples 97

HP 10B User Manual

Specifications and Main Features

Frequently Asked Questions

User Manual

Notice

Printing History

Welcome to the HP-1 OB

Hewlett-Packard Quality

Features

Contents

10 At a Glance...

21 Getting Started

Additional Examples

127 More About Calculations

133 Messages 136 Index

At a Glance...

Basics—At a Glance.

Percentages—At a Glance...

Memory Keys—At a Glance...

Time Value of Money (TVM)—At a Glance..

iasfl

TVM What if...—At a Glance...

Keys:

Display:

Description:

9.5 IÌ7YRÌ (pg

10.00

Amortization—At a Glance...

Keys:

Display:

20.00

Description:

msEo

QüjjQD

Interest Rate Conversion—At a Glance...

■FES

■ÎP7ŸR1

10.00

12.00

IRR/YR and NPV—At a Glance...

10.00

Statistics—At a Glance.

BdEiD wmm BE5ZZ1 EMM

y-vatue BiEf] Bf§WÁPl x-value Bl?.ml

Keys:

■fern

Display:

0.00

1.00

2.00

Description:

■dim

2.00

Getting Started

Power On and Off

Adjusting the Display Contrast

Simple Arithmetic Calculations

Keys:

Description:

Understanding the Display and Keyboard

Cursor

Clearing the Calculator

Clearing Memory

Annunciators

Shift Key

Math Functions

Display Format of Numbers

Specifying Displayed Decimal Places

Keys:

Display:

0.00

0.000

Description:

Scientific Notation

Displaying the Full Precision of Numbers

Keys:

Display:

Description:

Interchanging the Period and Comma

Rounding Numbers