Page 1

fx-50F PLUS
Guida dell’utilizzatore
http://world.casio.com/edu/
I
RCA502883-001V01
Page 2
Come iniziare
Congratulazioni per l’acquisto di questo prodotto CASIO.
Prima di usare la calcolatrice per la prima volta...
k
Capovolgere la calcolatrice e farla scorrere
fuori dalla custodia rigida come viene mostrato
nell’illustrazione. Successivamente, inserire la
custodia rigida sul retro della calcolatrice.
Dopo aver fi nito di usare la calcolatrice...
A
Rimuovere la custodia rigida dal retro della calcolatrice, e reinserirla sulla parte frontale.
Inizializzazione della calcolatrice ai valori iniziali di
k
default
Eseguire l’operazione riportata di seguito quando si desidera far ritornare l’impostazione
della calcolatrice ai suoi valori iniziali di default. Notare che questo procedimento annullerà
anche tutti contenuti presenti nella memoria (memoria indipendente, memoria di variabili,
memoria di risposte, dati campione del calcolo statistico, e dati di programmazione).
Per maggiori informazioni riguardo i modi di calcolo, le impostazioni di setup e i vari tipi di
memoria usati da questa calcolatrice, riferirsi alle seguenti sezioni.
k
(CLR)3(All)
9
!
• Modi di calcolo e impostazioni (pagina 7)
Annullamento del modo di calcolo e delle impostazioni di predisposizione (pagina 10)
• Operazioni con la memoria della calcolatrice (pagina 20)
• Calcoli statistici (SD/REG) (pagina 39)
• Modo di programmazione (PRGM) (pagina 64)
w
Informazioni sul manuale
• La maggior parte dei tasti eseguono funzioni multiple. Premendo ! o a e quindi un
altro tasto, si eseguirà la funzione alternativa di quel tasto. Le funzioni alternative sono
indicate sopra il tasto.
sin–1{D}
sin–1{D}
Funzione del tasto
Le operazioni con le funzioni alternative vengono annotate in questo manuale come viene
mostrato di seguito.
Esempio:
!s
–1
)
(sin
b
w
La notazione in parentesi indica la funzione eseguita dall’operazione precedente con i tasti.
s
s
I-1
Funzione alternativa
Page 3

• Di seguito viene mostrata la notazione utilizzata nel manuale per le voci di menu che
appaiono sul display (che vengono eseguite premendo un tasto numerico).
Esempio: b(Contrast)
La notazione in parentesi indica la voce di menu che è stata selezionata premendo il tasto
numerico.
• Il tasto cursore è contrassegnato con le frecce indicanti le direzioni, come
viene mostrato nell’illustrazione qui accanto. Le operazioni con il tasto
cursore vengono annotate in questo manuale con: f,c,d, e e.
• Le schermate e le illustrazioni (come pure i contrassegni dei tasti) mostrate nella presente
Guida dell’utilizzatore sono riportate al solo scopo illustrativo, e possono differire alquanto
dagli elementi reali che essere rappresentano.
• Il contenuto di questo manuale è soggetto a modifi che senza preavviso.
• In nessun caso la CASIO Computer Co., Ltd. sarà responsabile nei confronti di chiunque
per danni speciali, collaterali, incidentali o consequenziali, in relazione o derivanti
dall’acquisto o dall’uso di questo prodotto e degli elementi ad esso acclusi. Inoltre, la
CASIO Computer Co., Ltd. non sarà responsabile nei confronti di terze parti per qualsiasi
reclamo di qualunque specie derivante dall’uso di questo prodotto e degli elementi ad
esso acclusi.
REPLAYREPLAY
Precauzioni per la sicurezza
Assicurarsi si leggere le seguenti precauzioni per la sicurezza prima di usare questa
calcolatrice. Tenere questo manuale a portata di mano per futuri riferimenti.
Attenzione
Questo simbolo è utilizzato per indicare un’informazione che, se ignorata, può essere
causa di lesioni personali o danni materiali.
Pila
• Dopo la rimozione della pila dalla calcolatrice, riporla in un luogo sicuro, dove non
può essere presa in mano da bambini piccoli e inghiottita accidentalmente.
• Tenere le pile fuori dalla portata di mano dei bambini piccoli. Se vengono inghiottite
accidentalmente, consultare immediatamente un medico.
• Non ricaricare mai la pila, provare a smontarla o permettere che sia cortocircuitata.
Non esporre mai la pila a fonti di calore dirette o smaltirla nel fuoco.
• L’uso non corretto di una pila può causare la perdita del suo fl uido e un conseguente
danno agli elementi vicini, e inoltre può causare il rischio di incendio e lesioni
personali.
• Assicurarsi sempre che i terminali positivo
correttamente quando la si inserisce nella calcolatrice.
• Usare solo il tipo di pila specifi cato per questa calcolatrice nel presente manuale.
e negativo l della pila siano rivolti
k
I-2
Page 4

Smaltimento della calcolatrice
• Non smaltire mai la calcolatrice nel fuoco. In questo modo si può causare lo scoppio
improvviso di alcuni componenti, creando il rischio di incendio o lesioni personali.
Precauzioni d’uso
• Assicurarsi di premere il tasto O prima di usare la calcolatrice per la prima volta.
• Anche se la calcolatrice funziona normalmente, sostituire la pila almeno una volta
ogni tre anni.
Una pila esaurita può avere delle perdite, causando danni e malfunzionamento della
calcolatrice. Non lasciare mai una pila esaurita nella calcolatrice.
• La pila fornita in dotazione con questa unità si scarica leggermente durante il
trasporto e l’immagazzinamento. Pertanto, può richiedersi la sostituzione anticipata
rispetto alla normale aspettativa di durata della pila.
• Una pila con un basso livello di carica può causare la corruzione o la perdita
completa del contenuto della memoria. Tenere sempre copie scritte di tutti i dati
importanti.
• Evitare l’uso e la conservazione della calcolatrice in aree soggette a temperature
estreme.
Temperature molto basse possono causare una risposta lenta del display, la mancata
visualizzazione del display, e una durata abbreviata della pila. Evitare inoltre di lasciare la
calcolatrice esposta sotto i raggi solari diretti, vicino ad una fi nestra, vicino ad una fonte
di calore o in qualsiasi altro luogo che potrebbe essere esposto a temperature elevate. Il
calore può causare scoloramento o deformazione dell’involucro della calcolatrice, e danni
al circuito interno.
• Evitare l’uso e la conservazione della calcolatrice in luoghi soggetti ad eccessiva
umidità e polvere.
Fare attenzione a non lasciare mai la calcolatrice in luoghi dove potrebbe subire
schizzi d’acqua o essere esposta ad elevata umidità o polvere. Tali condizioni possono
danneggiare i circuiti interni.
• Non far cadere mai la calcolatrice o sottoporla altrimenti a forti urti.
• Non torcere o curvare la calcolatrice.
Evitare di trasportare la calcolatrice nella tasca dei pantaloni o in altro abbigliamento
aderente, dove potrebbe essere soggetta a torsione o piegatura.
• Non tentare mai di smontare la calcolatrice.
• Non premere mai i tasti della calcolatrice con una penna a sfera o altri oggetti
appuntiti.
• Per pulire la parte esterna della calcolatrice usare un panno morbido e asciutto.
Se la calcolatrice diviene molto sporca, strofi narla con un panno inumidito in una
soluzione diluita di acqua e detergente neutro delicato di tipo domestico. Strizzare il
panno per eliminare tutto il liquido in eccesso prima di pulire la calcolatrice. Non usare
mai solventi, benzene o altri agenti volatili per pulire la calcolatrice. In tal modo si possono
rimuovere i simboli stampati e danneggiare l’involucro.
I-3
Page 5

Indice
Come iniziare ............................................................................................1
Prima di usare la calcolatrice per la prima volta ... ............................................................. 1
Inizializzazione della calcolatrice ai valori iniziali di default ................................................ 1
Informazioni sul manuale ...................................................................................................1
Precauzioni per la sicurezza .................................................................... 2
Precauzioni d’uso .....................................................................................3
Prima di iniziare un calcolo... ..................................................................6
Accensione della calcolatrice .............................................................................................6
Etichette dei tasti ................................................................................................................ 6
Lettura del display ..............................................................................................................7
Modi di calcolo e impostazioni ................................................................ 7
Selezione di un modo di calcolo ......................................................................................... 7
Predisposizione della calcolatrice ......................................................................................8
Annullamento del modo di calcolo e delle impostazioni di predisposizione .....................10
Introduzione delle espressioni e dei valori di calcolo.........................10
Introduzione di un’espressione di calcolo (Introduzione naturale) ...................................10
Editazione di un calcolo ....................................................................................................12
Ritrovamento della posizione di un errore ........................................................................ 14
Calcoli fondamentali ..............................................................................14
Calcoli aritmetici ...............................................................................................................14
Frazioni ............................................................................................................................. 15
Calcoli di percentuali ........................................................................................................16
Calcoli di gradi, minuti e secondi (sessagesimali) ............................................................ 17
Memoria storica di calcolo e ripetizione ..............................................18
Accesso alla memoria storica di calcolo .......................................................................... 18
Uso di ripetizione .............................................................................................................. 19
Operazioni con la memoria della calcolatrice ...................................... 20
Uso della memoria di risposte (Ans) ...............................................................................20
Uso della memoria indipendente ...................................................................................... 22
Uso delle variabili .............................................................................................................23
Cancellazione dei contenuti di tutte le memorie ............................................................... 24
Uso di π,e, e costanti scientifi che ........................................................24
Pi greco ( π) e base- e dei logaritmi naturali ....................................................................... 24
Costanti scientifi che .........................................................................................................24
Calcoli di funzioni scientifi che .............................................................27
Funzioni trigonometriche e trigonometriche inverse ......................................................... 28
Conversione dell’unità angolare ....................................................................................... 28
Funzioni iperboliche e iperboliche inverse ........................................................................29
Funzioni esponenziali e logaritmiche ...............................................................................29
Funzioni di potenza e funzioni di radice di potenza ..........................................................30
I-4
Page 6

Conversione di coordinate (cartesiane ↔ polari) .............................................................30
Altre funzioni .....................................................................................................................32
Uso della notazione scientifi ca 103 (ENG) ............................................34
Esempi di calcolo scientifi co .............................................................................................34
Calcoli con numeri complessi (CMPLX) ...............................................35
Introduzione di numeri complessi ..................................................................................... 35
Visualizzazione del risultato di calcolo di numeri complessi ............................................35
Esempi di visualizzazione dei risultati di calcolo ..............................................................36
Numeri complessi coniugati (Conjg) .................................................................................37
Valore assoluto e argomento (Abs, arg) ...........................................................................38
Ridefi nizione del formato di visualizzazione di default di numeri complessi ..................... 38
Calcoli statistici (SD/REG) ....................................................................39
Dati campione di calcolo statistico ...................................................................................39
Esecuzione di calcoli statistici a variabile singola ............................................................39
Esecuzione di calcoli statistici a doppia variabile ............................................................ 43
Esempi di calcoli statistici ................................................................................................. 51
Calcoli in base- n (BASE) ........................................................................54
Esecuzione di calcoli in base-n .......................................................................................54
Conversione di un risultato visualizzato ad un’altra base numerica ................................. 55
Uso del menu LOGIC ....................................................................................................... 56
Specifi cazione di una base numerica per un valore particolare ....................................... 56
Esecuzione di calcoli usando operazioni logiche e valori binari negativi .........................57
Formule incorporate ............................................................................... 58
Uso delle formule incorporate ..........................................................................................58
Lista delle formule incorporate .........................................................................................60
Modo di programmazione (PRGM) ........................................................ 64
Panoramica sul modo di programmazione ....................................................................... 64
Creazione di un programma ............................................................................................. 65
Esecuzione di un programma ...........................................................................................66
Cancellazione di un programma .......................................................................................67
Comandi di introduzione ...................................................................................................67
Riferimento dei comandi ...................................................................................................68
Appendice ...............................................................................................74
Sequenza della priorità di calcolo..................................................................................... 74
Limitazioni di stack ...........................................................................................................75
Gamme di calcolo, numero di cifre e precisione ...............................................................76
Messaggi di errore ............................................................................................................77
Prima di ritenere che la calcolatrice abbia un malfunzionamento... ................................79
Requisiti di alimentazione .....................................................................79
Specifi che tecniche ................................................................................80
I-5
Page 7
Prima di iniziare un calcolo...
Accensione della calcolatrice
k
PremereO. La calcolatrice entrerà nel modo di calcolo (pagina 7) in cui essa era l’ultima
volta che è stata spenta.
Regolazione del contrasto del display
A
Se le fi gure che appaiono sul display divengono di diffi cile lettura, provare a regolare il
contrasto del display.
1. Premere
• Questo visualizza la schermata di regolazione del
contrasto.
2. Usare d e e per regolare il contrasto del display.
3. Dopo aver eseguito la regolazione nella maniera desiderata, premere A o
!
p
Nota
È anche possibile usare + e - per regolare il contrasto mentre il menu del modo di
calcolo che appare premendo il tasto , è sul display.
Importante!
Se la regolazione del contrasto del display non migliora la leggibilità del display stesso,
probabilmente sta a signifi care che la pila è scarica. Sostituire la pila.
Spegnimento della calcolatrice
A
Premere
!A
Le seguenti informazioni vengono mantenute in memoria quando si spegne la calcolatrice.
• Modi di calcolo e impostazioni (pagina 7)
• Contenuti della memoria di risposte (pagina 20), della memoria indipendente (pagina 22),
e della memoria di variabili (pagina 23)
Etichette dei tasti
k
!
N
(EXIT).
(SETUP)
(OFF).
(Contrasto).
b
d
M–
M
CL
DT
A
LIGHT DARK
LIGHT DARK
8
LOGIC
x
!
CASIO
CASIO
Funzione Colori Per eseguire la funzione
M+ Premere il tasto.
1
M– Testo: Ambra Premere ! e quindi premere il tasto.
2
MTesto: Rosso Premere a e quindi premere il tasto.
3
DT Testo: Blu Nel modo SD o REG, premere il tasto.
4
I-6
Page 8
Funzione Colori Per eseguire la funzione
2
×
(
5+4
)
–
2
×
-
3
24
2
×
(
5+4
)
–
2
×
-
3
24
CL Testo: Ambra
5
6
7
LOGIC Testo: Verde Nel modo BASE, premere il tasto.
8
Lettura del display
k
Introduzione delle espressioni e risultati di calcolo
A
Questa calcolatrice può visualizzare sia le espressioni introdotte che i risultati di calcolo
sulla stessa schermata.
Simboli sul display
A
I simboli descritti di seguito appaiono sul display della calcolatrice per indicare il modo
attuale di calcolo, le impostazioni della calcolatrice, i calcoli in corso, ed altro ancora. Nel
presente manuale, l’espressione “si attiva” è utilizzata per indicare che un simbolo appare
sul display, e “si disattiva” per indicare che il simbolo scompare.
La schermata di esempio riportata qui accanto mostra il
simbolo7 .
Il simbolo 7 si attiva quando viene selezionato gradi (Deg) per l’unità angolare di default
(pagina 8). Per maggiori informazioni sul signifi cato di ogni simbolo, vedere la sezione di
questo manuale che descrive ciascuna funzione.
Cornice: Blu
Testo: Ambra
∠
Cornice: Porpora
ATesto: Rosso
Cornice: Verde
Nel modo SD o REG, premere ! e quindi premere
il tasto.
Nel modo CMPLX, premere ! e quindi premere il
tasto.
Premerea e quindi premere il tasto (variabile A).
Nel modo BASE, premere il tasto.
Espressione introdotta
Risultato di calcolo
)
)
sin(30
sin(30
05
05
Modi di calcolo e impostazioni
Selezione di un modo di calcolo
k
La calcolatrice è dotata di sei “modi di calcolo”.
Selezione di un modo di calcolo
A
1. Premere ,.
• Questo visualizza il menu del modo di calcolo.
• Il menu del modo di calcolo comprende due schermate. Premere , per commutare
le schermate tra di loro. È anche possibile commutare le schermate di menu usando
e e.
d
I-7
Page 9

COMP CMPL X BA SE
1 2 3
2. Eseguire una delle seguenti operazioni per selezionare il modo di calcolo che si desidera.
Per selezionare questo modo di calcolo: Premere questo tasto:
COMP (Calcolo generale)
CMPLX (Numeri complessi)
n
BASE (BaseSD (Dati statistici a variabile singola)
REG (Dati statistici a doppia variabile)
PRGM (Programma)
• Premendo un tasto numerico da b a g si seleziona il modo applicabile,
indifferentemente da quale schermata di menu è attualmente visualizzata.
Predisposizione della calcolatrice
k
La predisposizione della calcolatrice può essere usata per confi gurare le impostazioni di
introduzione e di emissione, i parametri di calcolo e altre impostazioni. Le impostazioni
possono essere confi gurate utilizzando le schermate di predisposizione, alle quali si
accede premendo
possibile usare d e e per spostarsi tra di loro.
Specifi cazione dell’unità angolare
A
È possibile specifi care gradi, radianti o gradienti come unità angolare da applicare per i
calcoli di funzioni trigonometriche.
(90˚ =
Unità angolare Eseguire questa operazione con i tasti:
Gradi
Radianti
Gradienti
Specifi cazione delle cifre visualizzate
A
È possibile specifi care una qualsiasi delle tre impostazioni per le cifre di visualizzazione
dei risultati di calcolo: numero fi sso di posti decimali (da 0 a 9 posti), numero fi sso di cifre
signifi cative (da 1 a 10 cifre), o gamma di visualizzazione esponenziale (una scelta tra due
impostazioni).
)
!,
π
radianti = 100 gradienti)
2
(SETUP). Sono presenti sei schermate di predisposizione, ed è
SD REG PRGM
4 5 6
(COMP)
b
(CMPLX)
c
(BASE)
d
(SD)
e
(REG)
f
(PRGM)
g
(Deg)
b
!,
(Rad)
c
!,
(Gra)
d
!,
I-8
Page 10
Visualizzazione esponenziale Eseguire questa operazione con i tasti:
(Fix)
Numero di posti decimali
Cifre signifi cative
Gamma di visualizzazione esponenziale
!,e
a
!,e
b
!,e
b
b
(0) a j(9)
(Sci)
c
(1) a j(9),a(10)
(Norm)
d
(Norm1) o c(Norm2)
Di seguito viene spiegato come vengono visualizzati i risultati di calcolo a seconda delle
impostazioni da voi specifi cate.
• Vengono visualizzati da zero a nove posti decimali, a seconda del numero di posti
decimali (Fix) da voi specifi cato. I risultati di calcolo vengono arrotondati al numero di
cifre specifi cato.
Esempio: 100 ÷ 7 = 14,286 (Fix = 3)
14,29 (Fix = 2)
• Dopo aver specifi cato il numero di cifre signifi cative con Sci, i risultati di calcolo vengono
visulizzati utilizzando il numero di cifre signifi cative specifi cato e 10 alla potenza
applicabile. I risultati di calcolo vengono arrotondati al numero di cifre specifi cato.
Esempio: 1 ÷ 7 = 1,4286 × 10
1,429 × 10
–1
(Sci = 5)
–1
(Sci = 4)
• Selezionando Norm1 o Norm2 si commuta la visualizzazione alla notazione esponenziale
ogni volta che il risultato rientra nelle gamme defi nite sotto.
–2
Norm1: 10
Norm2: 10–9 >
x
>
x
Esempio: 100 ÷ 7 = 14,28571429 (Norm1 o Norm2)
1 ÷ 200 = 5, × 10
, x
, x
10
10
>
10
10
>
–3
(Norm1)
0,005 (Norm2)
Specifi cazione del formato di visualizzazione frazionario
A
È possibile specifi care il formato di frazioni improprie o di frazioni miste per visualizzare i
risultati di calcolo.
Formato frazionario Eseguire questa operazione con i tasti:
Frazioni miste
Frazioni improprie
!,ee
!,ee
b
c
(ab/c)
(d/c)
Specifi cazione del formato di visualizzazione di numeri
A
complessi
È possibile specifi care sia il formato in coordinate cartesiane che il formato in coordinate
polari per i risultati di calcolo di numeri complessi.
Formato di numeri complessi Eseguire questa operazione con i tasti:
i
Coordinate cartesiane
Coordinate polari
!,eee
!,eee
b
c
(
(
a+ b
r ∠Ƨ
)
)
I-9
Page 11
Specifi cazione dell’impostazione di frequenza statistica
A
Usare le operazioni con i tasti riportate sotto per attivare o disattivare la frequenza statistica
durante i calcoli con il modo SD e il modo REG.
Impostazione frequenza Eseguire questa operazione con i tasti:
Frequenza attivata
Frequenza disattivata
Annullamento del modo di calcolo e delle impostazioni
k
!,dd
!,dd
b
c
(FreqOn)
(FreqOff)
di predisposizione
Eseguire il procedimento descritto di seguito per annullare il modo attuale di calcolo e tutte
le impostazioni di predisposizione, e inizializzare la calcolatrice come segue.
Modo di calcolo ...................................COMP (calcolo generale)
Unità angolare .................................... Deg (gradi)
Visualizzazione esponenziale .............Norm1
Formato frazionario ............................ab/c (frazioni miste)
Formato di numeri complessi .............
Impostazione di frequenza .................FreqOn (frequenza attivata)
Eseguire le seguenti operazioni con i tasti per annullare il modo di calcolo e le impostazioni
di predisposizione.
Se non si desidera annullare le impostazioni della calcolatrice, premere A invece di
nell’operazione riportata sopra.
!
9
(CLR)2(Setup)
w
i
a+ b
(coordinate cartesiane)
w
Introduzione delle espressioni e
dei valori di calcolo
Introduzione di un’espressione di calcolo (Introduzione
k
naturale)
Il sistema di introduzione naturale della vostra calcolatrice vi permette di introdurre
un’espressione di calcolo esattamente come essa è scritta e di eseguirla premendo w.
La calcolatrice determina automaticamente la sequenza corretta della priorità di calcolo per
l’addizione, sottrazione, moltiplicazione, divisione, funzioni e parentesi.
Esempio: 2 × (5 + 4) – 2 × (–3) =
(
)
(
)
×
2*(5+4)-
2*-3
w
×
2
2
24
24
5+4
5+4
×
×
–
-
–
-
2
3
2
3
I-10
Page 12
Introduzione di funzioni scientifi che con parentesi (sin, cos,
A
, ecc.)
'
La calcolatrice supporta l’introduzione delle funzioni scientifi che con parentesi come
mostrato sotto. Notare che dopo l’introduzione dell’argomento, è necessario premere
per chiudere le parentesi.
sin(, cos(, tan(, sin–1(, cos–1(, tan–1(, sinh(, cosh(, tanh(, sinh–1(, cosh–1(, tanh–1(, log(, ln(,
e
^(, 10^(, '(,
Esempio: sin 30 =
Omissione del segno di moltiplicazione
A
È possibile omettere il segno di moltiplicazione nei casi seguenti.
• Immediatamente prima di una parentesi di apertura: 2 × (5 + 4)
• Immediatamente prima di una funzione scientifi ca con parentesi: 2 × sin(30), 2 ×'(3)
• Prima di un simbolo di prefi sso (escluso il segno meno): 2 × h123
• Prima del nome di una variabile, costante, o numero casuale: 20 × A, 2 × π, 2 ×
Parentesi fi nali di chiusura
A
È possibile omettere una o più parentesi di chiusura che si trovano alla fi ne di un calcolo,
immediatamente prima di premere il tasto w.
Esempio: (2 + 3) × (4 – 1) = 15
• Premere semplicemente w senza chiudere la parentesi. L’operazione riportata sopra
si applica soltanto alle parentesi di chiusura alla fi ne del calcolo. Il calcolo non produrrà
il risultato corretto se si dimentica di chiudere le parentesi che si richiedono prima della
conclusione.
Slittamento della schermata a sinistra e a destra
A
L’introduzione di un’espressione matematica con più di 16 caratteri, causerà
automaticamente lo slittamento della schermata, e una parte dell’espressione si sposterà
fuori del display. Il simbolo “b” sul bordo sinistro della schermata indica che sono presenti
dati addizionali fuori del lato sinistro del display.
• Mentre il simbolo b appare sulla schermata, è possibile usare il tasto d per spostare il
cursore a sinistra e scorrere la schermata.
• Slittando a sinistra, parte dell’espressione uscirà fuori del lato destro del display, che
verrà indicata dal simbolo \ sulla destra. Mentre il simbolo \ appare sulla schermata, è
possibile usare il tasto e per spostare il cursore alla destra e slittare la schermata.
• È anche possibile usare f per saltare all’inizio dell’espressione, o c per saltare alla
fi n e .
3
(, Abs(, Pol(, Rec(, arg(, Conjg(, Not(, Neg(, Rnd(
'
sin(30
30)
s
(2+3)*
(4-1
Espressione introdotta 12345 + 12345 + 12345
Espressione visualizzata
sin(30
w
05
05
(
)×(
(
)×(
2+3
2+3
w
15
15
345+12345+12345I 345+12345+12345I
Cursore
I-11
)
)
4–1
4–1
)
i
Page 13
Numero di caratteri introdotti (Byte)
A
Quando si introduce un’espressione matematica, essa viene salvata nella memoria
denominata “area di introduzione”, che ha una capacità di 99 byte. Questo sta ad indicare
che è possibile introdurre fi no a 99 byte per una singola espressione matematica.
Normalmente, il cursore che indica la posizione attuale di introduzione sul display viene
mostrato come una barra verticale lampeggiante (
capacità di memoria rimanente dell’area di introduzione è di otto byte o inferiore, il cursore
cambia alla forma di un rettangolo lampeggiante (
Se ciò accade, terminare l’introduzione dell’espressione attuale in qualche punto
conveniente e calcolarne il suo risultato.
Editazione di un calcolo
k
Modo di inserimento e modo di sovrascrittura
A
La calcolatrice è dotata di due modi di introduzione. Con il modo di inserimento, la vostra
introduzione viene inserita alla posizione del cursore, facendo slittare tutto quello che
è presente alla destra del cursore per creare spazio. Con il modo di sovrascrittura, si
sostituisce l’operazione con i tasti presente alla posizione del cursore, con la vostra
introduzione.
Espressione originale Premendo
Modo di inserimento
Modo di sovrascrittura
Un cursore verticale (|) indica il modo di inserimento, mentre un cursore orizzontale ( )
indica il modo di sovrascrittura.
Cursore
Cursore
) o barra orizzontale ( ). Quando la
|
).
k
+
1+2|34
1+2 3 4
1+2+ |34
1+2 + 4
Selezione di un modo di introduzione
L’impostazione iniziale di default del modo di introduzione, è il modo di inserimento.
Per cambiare al modo di sovrascrittura, premere:
Modifi ca di un’operazione con i tasti appena introdotta
A
Quando il cursore è posizionato alla fi ne dell’introduzione, premere D per cancellare
l’ultima operazione con i tasti da voi eseguita.
Esempio: Per correggere 369 × 13 in maniera che divenga 369 × 12
369*13
1
D
(INS).
D
2
369×13I369×13I
369×1I369×1I
369×12I369×12I
I-12
Page 14

Cancellazione di un’operazione con i tasti
A
Con il modo di inserimento, usare d e e per spostare il cursore alla destra
dell’operazione con i tasti che si desidera cancellare e quindi premere D. Con il modo di
sovrascrittura, spostare il cursore all’operazione con i tasti che si desidera cancellare, e
quindi premere D. Ogni pressione di D cancella un’operazione con i tasti.
Esempio: Per correggere 369 × × 12 in maniera che divenga 369 × 12
Modo di inserimento
Modo di sovrascrittura
Modifi ca di un’operazione con i tasti in un’espressione
A
Con il modo di inserimento, usare d e e per spostare il cursore alla destra dell’operazione con i tasti che si desidera modifi care, premere D per cancellarla, e quindi eseguire
l’operazione con i tasti corretta. Con il modo di sovrascrittura, spostare il cursore all’operazione con i tasti che si desidera correggere, e quindi eseguire l’operazione corretta.
Esempio: Per correggere cos(60) in maniera che divenga sin(60)
Modo di inserimento
Modo di sovrascrittura
369**12
dd
D
369**12
ddd
D
60)
c
dddD
s
60)
c
dddd
s
369××12I369××12I
369××I12369××I12
369×I12369×I12
369××12369××12
369××12369××12
369×12369×12
cos(60)Icos(60)I
)
I60)I60
sin(I60
sin(I60
cos(60
cos(60
cos(60
cos(60
sin(60
sin(60
)
)
)
)
)
)
)
)
I-13
Page 15
Inserimento di operazioni con i tasti in un’espressione
14÷0I×214÷0I×2
A
Assicurarsi di selezionare il modo di inserimento ogniqualvolta si desidera inserire
operazioni con i tasti in un’espressione. Usare d e e per spostare il cursore alla
posizione dove si desidera inserire le operazioni con i tasti, e quindi eseguirle.
Ritrovamento della posizione di un errore
k
Se la vostra espressione di calcolo non è corretta, apparirà un messaggio di errore sul
display quando si preme w per eseguirla. Dopo l’apparizione di un messaggio di errore,
premere il tasto d o e e quindi il cursore si porterà alla posizione nel calcolo che ha
causato l’errore, in modo che sia possibile correggerlo.
Esempio: Quando si introduce 14 ÷ 0 × 2 = invece di 14 ÷ 10 × 2 =
(Il seguente esempio usa il modo di inserimento.)
14/0*2
• Invece di premere e o d mentre viene visualizzato un messaggio di errore, è anche
possibile premere A per annullare il calcolo.
e
d
w
o
d
1
w
Mat h ERRORMat h ERROR
Posizione dell’errore
14÷1I0×214÷1I0×2
14÷10×2
14÷10×2
28
28
Calcoli fondamentali
A meno che diversamente citato, i calcoli riportati in questa sezione possono essere
eseguiti in uno qualsiasi dei modi di calcolo della calcolatrice, ad eccezione del modo
BASE.
Calcoli aritmetici
k
I calcoli aritmetici possono essere usati per eseguire l’addizione (+), sottrazione (-),
moltiplicazione (*) e divisione (/).
Esempio 1: 2,5 + 1 − 2 = 1,5
2.5+1-2
Esempio 2: 7 × 8 − 4 × 5 = 36
7*8-4*5
2.5+1–2
2.5+1–2
w
15
15
7×8–4×5
7×8–4×5
w
36
36
I-14
Page 16

• La calcolatrice determina automaticamente la sequenza della priorità di calcolo per
l’addizione, sottrazione, moltiplicazione e divisione. Per maggiori informazioni, vedere
“Sequenza della priorità di calcolo” a pagina 74.
Frazioni
k
Le frazioni vengono introdotte usando un simbolo separatore speciale ({).
Operazione con i tasti Visualizzazione
Frazioni
improprie
Frazioni
miste
Nota
• Con le impostazioni iniziali di default, le frazioni vengono visualizzate come frazioni miste.
• I risultati di calcolo di frazioni vengono sempre semplifi cati automaticamente prima di
essere visualizzati. Eseguendo 2 { 4 = ad esempio, si visualizzerà il risultato 1 { 2.
Esempi di calcoli con frazioni
A
Esempio 1: 3
Esempio 2: 4 – 3
Esempio 3:
Nota
• Se il numero totale di elementi (numero intero + numeratore + denominatore + simboli
separatori) di un risultato di calcolo di frazioni è superiore a 10, il risultato verrà
visualizzato in formato decimale.
• Se un calcolo introdotto include sia valori frazionari che valori decimali, il risultato sarà
visualizzato in formato decimale.
• È possibile introdurre numeri interi soltanto per gli elementi di una frazione. Introducendo
numeri non interi, si produrrà un risultato in formato decimale.
7$3
2$1$3
1
2
+ 1
= 4
4
3
1
1
=
2
2
2
1
7
+
=
3
(Formato di visualizzazione frazionario: d/c)
2
6
Numeratore Denominatore
Parte intera Numeratore Denominatore
11
1 2
3$1$4+
1$2$3
4-3$1$2
2$3+1$2
7{ 3
2{ 1 { 3
3{1{4+1{2{3
3{1{4+1{2{3
w
4{11{12
4{11{12
4–3{1{2
4–3{1{2
w
1{2
1{2
2{3+1{2
2{3+1{2
w
7{6
7{6
I-15
Page 17

Commutazione tra formato di frazione mista e frazione
A
impropria
Per convertire una frazione mista in una frazione impropria (o una frazione impropria in una
frazione mista), premere
Commutazione tra formato decimale e formato frazionario
A
Usare il procedimento riportato di seguito per scambiare un risultato di calcolo visualizzato
tra formato decimale e formato frazionario.
Esempio: 1,5 = 1
Nota
La calcolatrice non può commutare dal formato decimale al formato frazionario se il numero
totale degli elementi di frazione (numero intero + numeratore + denominatore + simboli
separatori) è superiore a 10.
Calcoli di percentuali
k
Introducendo un valore con un segno di percentuale (%) rende il valore una percentuale. Il
segno di percentuale (%) utilizza il valore immesso immediatamente prima ad esso come
argomento, il quale viene semplicemente diviso per 100 per ottenere il valore percentuale.
Esempi di calcoli di percentuali
A
Esempio 1: 2% = 0,02 (
Esempio 2: 150 × 20% = 30 (150 ×
Esempio 3: Quale percentuale di 880 è 660?
1
, 1
2
!$
1
= 1,5
2
2
1 0 0
(d/c).
)
20
)
1 0 0
660/880
1.5
w
15 15
$
L’impostazione corrente del formato di visualizzazione
frazionario determina se viene visualizzata una frazione
$
2%
2%
!
!
(
(
(%)
(%)
(%)
w
w
w
150×20%
150×20%
660÷880%
660÷880%
2!(
150*20
1{1{21{1{2
mista o impropria.
15 15
002
002
30
30
75
75
I-16
Page 18

Esempio 4: Incrementare 2500 del 15%.
2500+2500*
15!(
Esempio 5: Ridurre 3500 del 25%.
3500-3500*
25!(
Esempio 6: Ridurre la somma di 168, 98 e 734 del 20%.
168+98+734
-G*20!(
2500+2500×15%
2500+2500×15%
(%)
w
2875
2875
3500–3500×25%
3500–3500×25%
(%)
w
2625
2625
168+98+734
168+98+734
w
1000
1000
Ans–Ans×20%
Ans–Ans×20%
(%)
w
800
800
Esempio 7: Se 300 grammi vengono aggiunti ad un campione di prova che pesa all’origine
Esempio 8: Qual’è il cambio percentuale quando un valore viene incrementato da 40 a 46?
Modo di inserimento
k
È possibile eseguire i calcoli usando valori sessagesimali, ed è quindi possibile convertire
tali valori tra il formato sessagesimale e decimale.
A
Nel seguito è riportata la sintassi di base per l’introduzione di un valore sessagesimale.
Esempio: Per introdurre 2°30´30˝
500 grammi, quale è l’incremento percentuale in peso?
(
(
500+300
500+300
w
160
160
(
)
(
)
46–40
46–40
w
15
15
(
)
(
)
48–40
48–40
w
20
20
÷
÷
÷
÷
E quanto a 48?
(500+300)
/500!(
(46-40)/40
eeee
!
(
Y
(%)
(%)
8
Calcoli di gradi, minuti e secondi (sessagesimali)
Introduzione di valori sessagesimali
{Gradi} $ {Minuti} $ {Secondi}
$
2$30$30
I-17
$w
2˚30˚30
2˚30˚30
˚
˚
2˚30˚30
2˚30˚30
)
)
÷
÷
500%
500%
40%
40%
40%
40%
Page 19
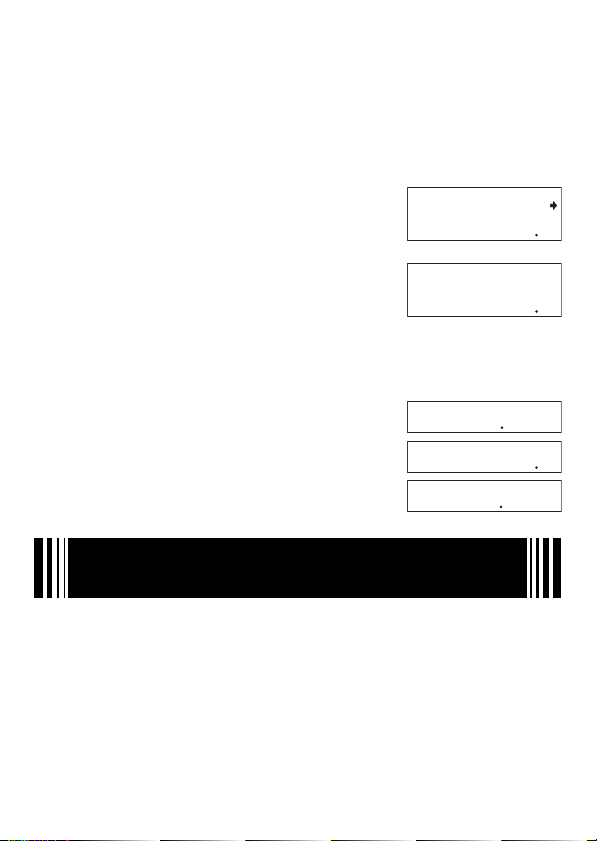
• Notare che si deve sempre introdurre qualche valore per i gradi e minuti, anche se essi
sono zero.
Esempio: Per introdurre 0°00´30˝, premere
Esempi di calcoli sessagesimali
A
I seguenti tipi di calcoli sessagesimali produrranno risultati sessagesimali.
• Addizione o sottrazione di due valori sessagesimali
• Moltiplicazione o divisione di un valore sessagesimale e un valore decimale
Esempio 1: 2°20´30˝ + 39´30˝ = 3°00´00˝
2$20$30$+
0$39$30
Esempio 2: 2°20´00˝ × 3,5 = 8°10´00˝
Conversione tra formato sessagesimale e decimale
A
Premendo$ mentre è visualizzato un risultato di calcolo, si commuta il valore tra il
formato sessagesimale e il formato decimale.
Esempio: Per convertire 2,255 a sessagesimale
0$0$30
$w
2$20$*
3.5
2.255
.
$
2˚20˚30
2˚20˚30
2˚20
2˚20
˚
w
w
$
˚
8˚10˚0
8˚10˚0
2255 2255
2˚15˚18 2˚15˚18
+
+
0˚39˚30
0˚39˚30
˚
˚
3˚0˚0
3˚0˚0
×
×
3. 5
3. 5
$
22552255
Memoria storica di calcolo e
ripetizione
La memoria storica di calcolo mantiene una registrazione di ciascun calcolo da voi eseguito,
incluse le espressioni introdotte e i risultati di calcolo. È possibile utilizzare la memoria
storica di calcolo nei modi COMP, CMPLX e BASE.
Accesso alla memoria storica di calcolo
k
Il simbolo ` nell’angolo in alto a destra del display indica che sono presenti dei dati
salvati nella memoria storica di calcolo. Per visualizzare i dati nella memoria storica di
calcolo, premere f. Ogni pressione di f farà scorrere verso l’alto (indietro) un calcolo,
visualizzando sia l’espressione di calcolo che il suo risultato.
I-18
Page 20
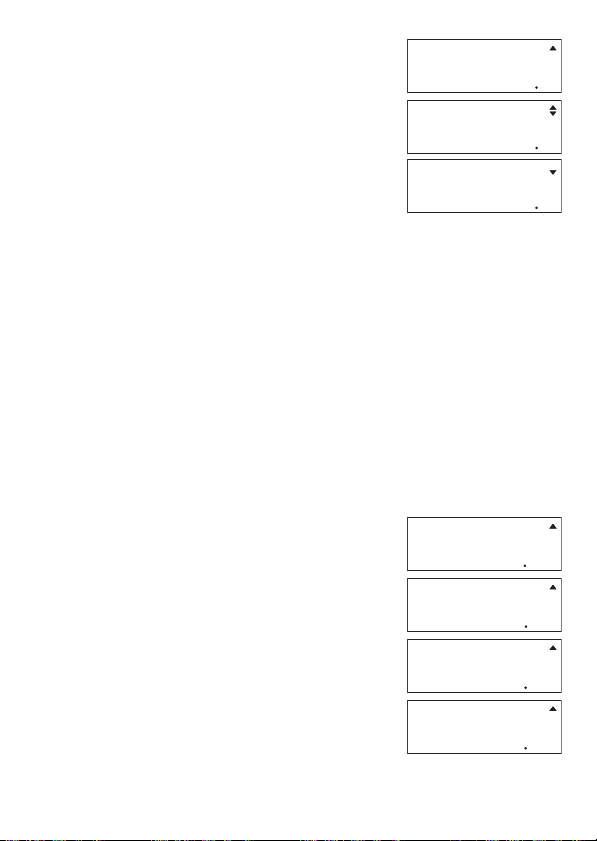
Esempio:
Durante lo scorrimento attraverso le registrazioni della memoria storica di calcolo, il simbolo
apparirà sul display, per indicare che sono presenti registrazioni sotto (più recenti di)
$
quella attuale. Quando è attivato questo simbolo, premere c per scorrere verso in basso (in
avanti) attraverso la memoria storica di calcolo.
Importante!
• Le registrazioni della memoria storica di calcolo vengono tutte cancellate ogni volta che si
premep, quando si cambia ad un differente modo di calcolo, o ogni volta che si esegue
qualsiasi operazione di azzeramento.
• La capacità della memoria storica di calcolo è limitata. Ogni volta che si esegue un nuovo
calcolo mentre la memoria storica di calcolo è piena, la registrazione storica più vecchia
viene automaticamente cancellata per creare spazio a quella nuova.
Uso di ripetizione
k
Mentre una memoria storica di calcolo appare sul display, premere d o e per
visualizzare il cursore ed entrare nel modo di edizione. Premendo e si visualizza il cursore
all’inizio dell’espressione di calcolo, mentre premendo d lo si visualizza alla fi ne. Dopo
aver eseguito le modifi che nella maniera desiderata, premere w per eseguire il calcolo.
Esempio: 4 × 3 + 2,5 = 14,5
4 × 3 – 7,1 = 4,9
1+1w2+2
3+3
4*3+2.5
w
w
f
f
w
d
3+363+3
2+242+2
1+121+1
4×3+2.5
4×3+2.5
4×3+2.5I
4×3+2.5I
6
4
2
145
145
145
145
DDDD
-7.1
I-19
w
4×3I
4×3I
4×3–7.1
4×3–7.1
145
145
49
49
Page 21

Operazioni con la memoria della
calcolatrice
La calcolatrice include i tipi di memoria descritti di seguito, che è possibile utilizzare per
salvare e richiamare i valori.
Nome di memoria Descrizione
Memoria di risposte
Memoria
indipendente
Var iabili
I tipi di memoria descritti sopra non vengono cancellati quando si preme il tasto A, si
cambia ad un altro modo, o si spegne la calcolatrice.
Uso della memoria di risposte (Ans)
k
Il risultato di un qualsiasi nuovo calcolo eseguito sulla calcolatrice viene automaticamente
salvato nella memoria di risposte (Ans).
Occasioni di aggiornamento e cancellazione della memoria di
A
risposte
Quando si usa la memoria di risposte in un calcolo, è importante tenere presente come e
quando cambia il suo contenuto. Annotare i seguenti punti.
• Il contenuto della memoria di risposte viene sostituito ogniqualvolta si esegue una
qualsiasi delle seguenti operazioni: calcolare un risultato di calcolo, aggiungere o sottrarre
un valore dalla memoria indipendente, assegnare un valore ad una variabile o richiamare
il valore di una variabile, oppure introdurre dati statistici nel modo SD o nel modo REG.
• Nel caso di un calcolo che produce più di un risultato (come per i calcoli di coordinate), il
valore che appare per primo sul display viene salvato nella memoria di risposte.
• Il contenuto della memoria di risposte non cambia se il calcolo attuale causa un errore.
• Quando si esegue un calcolo di numeri complessi nel modo CMPLX, sia la parte reale
che la parte immaginaria del risultato vengono salvate nella memoria di risposte. Notare,
tuttavia, che la parte immaginaria del valore viene cancellata se si cambia ad un altro
modo di calcolo.
Inserimento automatico di Ans nei calcoli consecutivi
A
Se si avvia un nuovo calcolo mentre appare ancora sul display il risultato di un calcolo
precedente, la calcolatrice inserirà automaticamente il valore di Ans nella posizione
applicabile del nuovo calcolo.
La memoria di risposte contiene il risultato dell’ultimo calcolo
eseguito.
La memoria indipendente può essere utilizzata in tutti i modi di
calcolo, eccetto per il modo SD e per il modo REG.
Sei variabili denominate A, B, C, D, X e Y possono essere utilizzate
per la memorizzazione temporanea di valori. Le variabili possono
essere usate in tutti i modi di calcolo.
I-20
Page 22
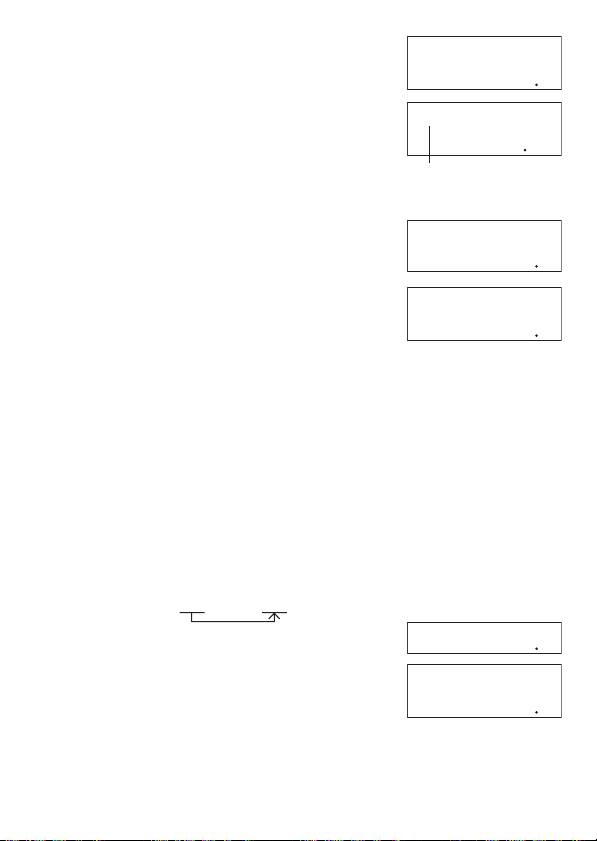
Esempio 1: Per dividere il risultato di 3 × 4 per 30
3*4
(Continuando)
Esempio 2: Per determinare la radice quadrata del risultato di 32 + 4
Nota
• Come negli esempi riportati sopra, la calcolatrice inserisce automaticamente il valore di
Ans come argomento di qualsiasi operatore di calcolo o di funzione scientifi ca introdotti
mentre appare un risultato di calcolo sul display.
• Nel caso di una funzione con argomento parentetico (pagina 11), Ans diviene
automaticamente l’argomento soltanto nel caso in cui si introduce la funzione singola e
quindi si preme w.
• Fondamentalmente, Ans viene inserito automaticamente solo quando il risultato del
calcolo precedente appare ancora sul display, immediatamente dopo aver eseguito
il calcolo che l’ha prodotto. Vedere la sezione successiva, per maggiori informazioni
sull’inserimento manuale di Ans in un calcolo con il tasto K.
Inserimento manuale di Ans in un calcolo
A
È possibile inserire Ans in un calcolo alla posizione attuale del cursore, premendo il tasto
.
K
Esempio 1: Per usare il risultato di 123 + 456 in un altro calcolo come mostrato sotto
123 + 456 = 579 789 – 579 = 210
123+456
/30
Premendo/ si introduce automaticamente Ans.
3x+4
w
w
xw
9w
w
3×4123×4
Ans÷30
Ans÷30
2
2
2
2
2
+
+
3
3
4
4
(
(
'
Ans
'
Ans
12
04
04
25
25
5
5
579579
789-
I-21
Kw
789–Ans
789–Ans
210
210
Page 23
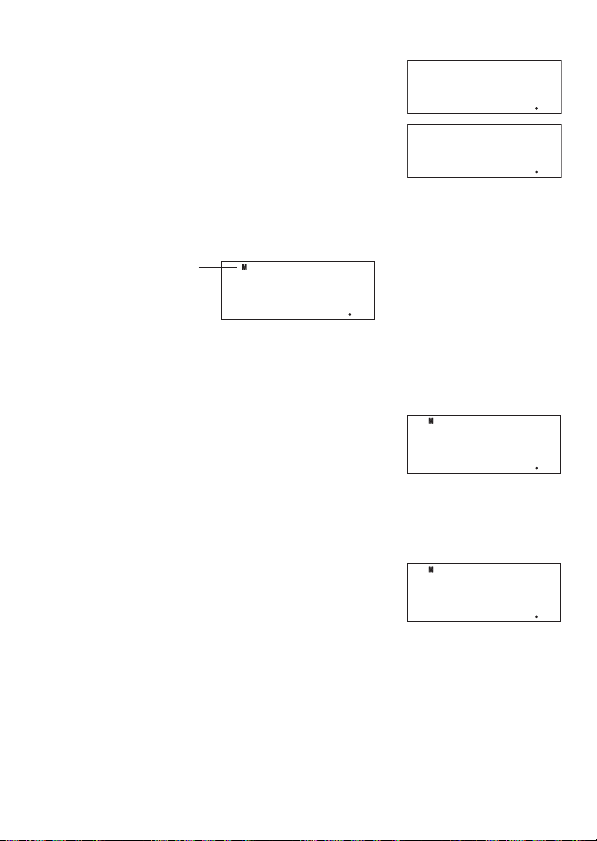
Esempio 2: Per determinare la radice quadrata di 32 + 42, e quindi aggiungere 5 al risultato
2
2
2
2
+
+
3
3
4
3x+4
9K
Uso della memoria indipendente
k
La memoria indipendente (M) viene usata per totali cumulativi di calcolo.
Se appare il simbolo M sul display, sta ad indicare che è presente un valore diverso da zero
nella memoria indipendente.
Addizione alla memoria indipendente
A
Mentre un valore da voi introdotto o il risultato di un calcolo appare sul display, premere
per aggiungerlo alla memoria indipendente (M).
Esempio: Per aggiungere il risultato di 105 ÷ 3 alla memoria indipendente (M)
Sottrazione dalla memoria indipendente
A
Mentre un valore da voi introdotto o il risultato di un calcolo appare sul display, premere
(M–) per sottrarlo dalla memoria indipendente (M).
1m
Esempio: Per sottrarre il risultato di 3 × 2 dalla memoria indipendente (M)
Nota
Premendom o
aggiungerà o sottrarrà dalla memoria indipendente.
Importante!
Il valore che appare sul display quando si preme m o
invece di w è il risultato del calcolo (che viene aggiunto o sottratto dalla memoria
indipendente). Esso non è il contenuto attuale della memoria indipendente.
Visualizzazione del contenuto della memoria indipendente
A
Premere
tm
Simbolo M
(M–) mentre un risultato di calcolo appare sul display, lo si
1m
(M).
10M
10M
+
+
105/3
3*2
xw
)+5
10
10
1m
1m
w
m
(M–)
4
25
25
(
)
(
)
+
+
'
Ans
'
Ans
5
5
10
10
+
+
105÷3M
105÷3M
35
35
–
–
3×2M
3×2M
6
6
(M–) alla fi ne di un calcolo
m
I-22
Page 24

Cancellazione del contenuto della memoria indipendente (a 0)
A
0
La cancellazione della memoria indipendente causerà la scomparsa del simbolo M.
A
Se il simbolo M viene visualizzato sulla schermata della calcolatrice, premere
0
eseguire la seguente operazione.
Esempio: 23 + 9 = 32
53 – 6 = 47
−) 45 × 2 = 90
99 ÷ 3 = 33
(Totale) 22
k
La calcolatrice supporta sei variabili denominate A, B, C, D, X e Y, che possono essere
utilizzate per memorizzare valori come richiesto.
A
(STO)m(M)
1t
Esempio di calcolo con l’uso della memoria indipendente
(STO)m(M) per cancellare il contenuto della memoria indipendente prima di
1t
23+9
53-6
45*2
99/3
(Richiama il valore di M.)
1m
tm
m
m
(M–)
m
(M)
Uso delle variabili
Assegnazione di un valore o di un risultato di calcolo ad una
variabile
Usare il procedimento mostrato sotto per assegnare un valore o un’espressione di calcolo
ad una variabile.
Esempio: Per assegnare 3 + 5 alla variabile A
A
Per visionare il valore assegnato ad una variabile, premere t e quindi specifi care il nome
della variabile.
Esempio: Per visionare il valore assegnato alla variabile A
A
È possibile usare le variabili nei calcoli, alla stessa maniera dell’uso dei valori.
Esempio: Per calcolare 5 + A
A
Esempio: Per cancellare la variabile A
3+5
Visione del valore assegnato ad una variabile
(A)
-
t
Uso di una variabile in un calcolo
5+
a-
Annullamento del valore assegnato ad una variabile (a 0)
0
1t
(STO)-(A)
1t
(A)
w
(STO)-(A)
I-23
Page 25

Esempio di calcolo con l’uso di variabili
π
A
Esempio: Per eseguire calcoli che assegnano i risultati alle variabili B e C, e quindi usare
k
Eseguire la seguente operazione con i tasti quando si desidera cancellare i contenuti della
memoria indipendente, della memoria di variabili, e della memoria di risposte.
le variabili per eseguire un altro calcolo
9× 6 + 3
9× 6 + 3
= 1,425
= 1,425
5× 8
5× 8
9*6+3
(STO)$(B)
1t
5*8
(STO)w(C)
1t
$
S
Sw
(B)
(C)
/
w
9×6+3→B
9×6+3→B
5×8→C
5×8→C
B÷C
B÷C
57
57
40
40
1425
1425
Cancellazione dei contenuti di tutte le memorie
(CLR)1(Mem)
9
1
• Se non si desidera annullare le impostazioni della calcolatrice, premere A invece di
nell’operazione riportata sopra.
w
w
Uso di
Pi greco ( π) e base-e dei logaritmi naturali
k
La calcolatrice supporta l’introduzione di pi greco ( π) e della base- e dei logaritmi naturali nei
calcoli. π e
valori che la calcolatrice applica per ciascuna delle costanti incorporate.
k
La vostra calcolatrice è dotata di 40 costanti scientifi che incorporate di uso frequente. Come
per π e
scientifi che sono supportate in tutti i modi, eccetto per il modo BASE.
e
sono supportati in tutti i modi, eccetto per il modo BASE. Il seguito mostra i
= 3,14159265358980 (
π
e
= 2,71828182845904 (
Costanti scientifi che
e
, ciascuna costante scientifi ca ha un simbolo unico di visualizzazione. Le costanti
, e, e costanti scientifi che
π
( π))
1e
( e))
Si
I-24
Page 26
Introduzione di una costante scientifi ca
A
1. Premere
• Questo visualizza la pagina 1 del menu delle costanti scientifi che.
mpmn ne m
1
(CONST).
7
μ
4321
• Sono presenti 10 schermate di menu di comandi scientifi ci, ed è possibile usare
ed per spostarsi tra loro. Per maggiori informazioni, vedere “Tabella delle costanti
scientifi che” a pagina 26.
2. Usare e e d per scorrere attraverso le pagine e visualizzare quella che contiene la
costante scientifi ca che si desidera.
3. Premere il tasto numerico (da 1 a 4) che corrisponde alla costante scientifi ca che si
desidera selezionare.
• Questo introdurrà il simbolo della costante scientifi ca che corrisponde al tasto numerico
da voi premuto.
mpmn ne m
• Premendo E in questo punto, si visualizzerà il valore della costante scientifi ca il cui
simbolo appare correntemente sulla schermata.
p
m
167262171
Calcoli di esempio che utilizzano costanti scientifi che
A
Esempio 1: Per introdurre la costante per la velocità della luce nel vuoto
–
μ
4321
27
mpI
\
1
dddd
(CONST)
7
4
0
C
0
C
(c
0
)
E
0
299792458
299792458
e
Esempio 2: Per calcolare la velocità della luce nel vuoto (
1/
(CONST)
7
1
ddd
I-25
c
= 1/ 0
0
9
(
ε
4
ε
µ
)
0
(
(
÷
÷
1
'
I
1
'
I
0
0
÷
÷
1
'(ε
0
I
1
'(ε
0
)
0
I
0
0
Page 27
)
)
'(ε0μ
0
I
'(ε0μ
0
I
0
0
)
)
'(ε0μ
0
'(ε0μ
0
299792458
299792458
Tabella delle costanti scientifi che
A
1
dd
(CONST)
7
1
÷
÷
1
1
ƫ
)
(
)
0
÷
÷
1
1
E
I numeri riportati nella colonna “No.” mostrano a sinistra il numero di pagina del menu delle
costanti scientifi che, e a destra il tasto numerico da premere per selezionare la costante
quando viene visualizzata la pagina esatta del menu.
No. Costante scientifi ca Simbolo Valore Unità
1-1 Massa del protone m
1-2 Massa del neutrone m
1-3 Massa dell’elettrone m
1-4 Massa del muone m
2-1 Raggio di Bohr a
p
n
e
ƫ
0
1,67262171×10
1,67492728×10
9,1093826×10
1,8835314×10
0,5291772108×10
2-2 Costante di Planck h 6,6260693×10
2-3 Magnetone nucleare
2-4 Magnetone di Bohr
µ
N
µ
B
5,05078343×10
927,400949×10
3-1 Costante di Planck, razionalizzata 1,05457168×10
3-2 Costante di struttura fi ne α 7,297352568×10
3-3 Raggio classico dell’elettrone r
3-4 Lunghezza d’onda di Compton
Rapporto giromagnetico del
4-1
protone
Lunghezza d’onda di Compton del
4-2
protone
Lunghezza d’onda di Compton del
4-3
neutrone
4-4 Costante di Rydberg R
λ
γ
λ
λ
e
c
p
cp
cn
∞
2,817940325×10
2,426310238×10
2,67522205×108s–1 T
1,3214098555×10
1,3195909067×10
10973731,568525 m
5-1 Costante di massa atomica u 1,66053886×10
5-2 Momento magnetico del protone
5-3 Momento magnetico dell’elettrone
5-4 Momento magnetico del neutrone
6-1 Momento magnetico del muone
µ
p
µ
e
µ
n
µ
ƫ
1,41060671×10
–928,476412×10
–0,96623645×10
–4,49044799×10
6-2 Costante di Faraday F 96485,3383 C mol
6-3 Carica elementare e 1,60217653×10
–27
kg
–27
kg
–31
kg
–28
kg
–10
m
–34
J s
–27
–26
–34
–15
–12
–15
–15
–27
–26
–26
–26
–26
–19
–1
J T
–1
J T
J s
–3
−
m
m
–1
m
m
–1
kg
–1
J T
–1
J T
–1
J T
–1
J T
–1
C
I-26
Page 28

No. Costante scientifi ca Simbolo Valore Unità
6-4 Costante di Avogadro N
A
7-1 Costante di Boltzmann k 1,3806505×10
7-2 Volume molare del gas ideale V
m
6,0221415×1023mol
–23
22,413996×10–3m3 mol
7-3 Costante del gas molare R 8,314472 J mol–1 K
7-4 Velocità della luce nel vuoto C
8-1 Prima costante di radiazione C
8-2 Seconda costante di radiazione C
0
1
2
8-3 Costante di Stefan-Boltzmann σ 5,670400×10
8-4 Costante elettrica
9-1 Costante magnetica
9-2 Quanto del fl usso magnetico
ε
0
µ
0
φ
0
9-3 Accelerazione di gravità standard g 9,80665 m s
9-4 Quanto di conduttanza G
10-1 Impedenza caratteristica del vuoto Z
0
0
299792458 m s
3,74177138×10
1,4387752×10
8,854187817×10
12,566370614×10–7N A
2,06783372×10
7,748091733×10
–16
–2
–8
–12
–15
–5
376,730313461
J K
W m
m K
W m–2 K
F m
Wb
S
Ω
–1
–1
–1
–1
2
–4
–1
–2
–2
10-2 Temperatura Celsius t 273,15 K
Costante di gravitazione
10-3
newtoniana
G 6,6742×10
–11m3
kg–1 s
10-4 Atmosfera standard atm 101325 Pa
• Fonte: Valori raccomandati da CODATA 2000
Calcoli di funzioni scientifi che
A meno che diversamente citato, le funzioni riportate in questa sezione possono essere
utilizzate in uno qualsiasi dei modi di calcolo della calcolatrice, eccetto per il modo BASE.
Precauzioni per il calcolo di funzioni scientifi che
• Quando si esegue un calcolo che include una funzione scientifi ca incorporata, potrebbe
richiedersi del tempo prima che appaia il risultato di calcolo. Non eseguire nessuna
operazione con i tasti fi nché non appare il risultato di calcolo.
• Per interrompere l’operazione di calcolo in corso, premere A.
Interpretazione della sintassi delle funzioni scientifi che
• Il testo che rappresenta un argomento della funzione viene racchiuso in parentesi graffe
({ }). Gli argomenti sono normalmente {valore} o {espressione}.
• Quando le graffe ({ }) sono racchiuse in parentesi tonde, sta ad indicare che l’introduzione
di tutto ciò che è presente all’interno delle parentesi è obbligatorio.
–1
–2
I-27
Page 29

Funzioni trigonometriche e trigonometriche inverse
k
sin(, cos(, tan(, sin–1(, cos–1(, tan–1(
Sintassi e introduzione
A
sin({ n}), cos({ n}), tan({ n}), sin–1({ n}), cos–1({ n}), tan–1({ n})
–1
Esempio: sin 30 = 0,5, sin
Note
A
• Queste funzioni possono essere utilizzate nel modo CMPLX, a condizione che non venga
usato un numero complesso nell’argomento. Ad esempio, un calcolo come
supportato, ma sin(1 +
• L’unità angolare che vi necessita usare in un calcolo, è quella che risulta attualmente
selezionata come unità angolare di default.
Conversione dell’unità angolare
k
È possibile convertire un valore che è stato introdotto con una determinata unità angolare,
ad un’altra unità angolare. Dopo aver introdotto un valore, premere
visualizzare la schermata di menu mostrata sotto.
DRG
DRG
312
312
Esempio: Per convertire entrambi
La seguente procedura presuppone che Deg (gradi) sia correntemente specifi cato come
unità angolare di default.
0,5 = 30 (Unità angolare: Deg)
s
–1
(sin
)
0.5)
s
1
) non lo è.
i
(D): Gradi
1
(R): Radianti
2
(G): Gradienti
3
π
radianti e 50 gradienti in gradi
2
(
1e
(DRG')2(R)
1G
50
1G
30)
( π)
/2)
(DRG')
(G)
3
w
w
E
E
sin(30
sin(30
–1
–1
(
(
sin
sin
1G
(
)
(
)
π
÷
π
÷
2
2
g
g
50
50
)
)
05
05
)
)
0.5
0.5
30
30
× sin(30) è
i
(DRG') per
r
r
90
90
45
45
I-28
Page 30

Funzioni iperboliche e iperboliche inverse
k
sinh(, cosh(, tanh(, sinh–1(, cosh–1(, tanh–1(
Sintassi e introduzione
A
sinh({ n}), cosh({ n}), tanh({ n}), sinh–1({ n}), cosh–1({ n}), tanh–1({ n})
Esempio: sinh 1 = 1,175201194
(sinh)
1)
s
w
Note
A
• Dopo aver premuto w per specifi care una funzione iperbolica, o
una funzione iperbolica inversa, premere s,c, o t.
• Queste funzioni possono essere utilizzate nel modo CMPLX, ma gli argomenti di numeri
complessi non sono supportati.
Funzioni esponenziali e logaritmiche
k
10^(, e^(, log(, ln(,
Sintassi e introduzione
A
10^({ n}) .......................... 10
n
}) ........................... log10{ n} (Logaritmo comune)
log({
m
log({
},{ n}) ..................... log
n
}) ............................. log e{ n} (Logaritmo naturale)
ln({
Esempio 1: log
Esempio 2: ln 90 (log e 90) = 4,49980967
Esempio 3:
16 = 4, log16 = 1,204119983
2
10
e
= 22026,46579
{ n}
(Lo stesso si applica a e^(.)
{ n} (Logaritmo in base { m})
{ m}
2,16)
l
l
Base 10 (logaritmo comune) viene assunta quando non è specifi cata nessuna base.
I
x
e
)
(
I
1
16)
90)
10)
E
E
E
E
E
)
)
sinh(1
sinh(1
1175201194
1175201194
per specifi care
1w
(
(
)
)
g
g
lo
2,16
lo
2,16
4
4
(
(
)
)
g
g
lo
16
lo
16
1204119983
1204119983
)
)
In(90
In(90
449980967
449980967
(10)
(10)
e
e
ˆ
ˆ
2202646579
2202646579
I-29
Page 31

Funzioni di potenza e funzioni di radice di potenza
k
2
3
–1
x
x
x
,
,
Sintassi e introduzione
A
2
x
{ n}
............................... { n}2 (Quadrato)
3
n} x
{
............................... { n}3 (Cubo)
–1
n} x
............................. { n}–1 (Reciproco)
{
m
)}^({ n}) ....................... { m}
{(
n
({
}) .......................... { n} (Radice quadrata)
'
3
({ n}) .........................3 { n} (Radice cubica)
'
x
m
})
({ n}) ..................
({
'
Esempio 1: (
Esempio 2: –2
Note
A
• Le funzioni
CMPLX. Per queste funzioni sono anche supportati gli argomenti di numeri complessi.
• ^(, '(,
numeri complessi non sono supportati per queste funzioni.
Conversione di coordinate (cartesiane ↔ polari)
k
La vostra calcolatrice è in grado di eseguire la conversione tra coordinate cartesiane e
coordinate polari.
2 + 1) ('2 – 1) = 1, (1 + 1)
'
2
3
= –1,587401052
2
3
x
x
,
, e
3
x
(,
( sono anche supportati nel modo CMPLX, tuttavia gli argomenti di
'
'
{ n}
(Elevamento a potenza)
{ m}
{ n} (Radice di potenza)
(92)-1)
(1+1)M2+2)
-2M2$
–1
x
possono essere utilizzate nei calcoli di numeri complessi nel modo
3
'
x
(,
'
3)
(
E
E
E
, ^(, '(,
2+2
= 16
(92)+1)
Pol(, Rec(
('(2)
)('(2)
('(2)
)('(2)
+
+
1
1
(
)ˆ(
(
(
)ˆ(
2{ 3
2{ 3
2+2
2+2
)
)
)
)
16
16
(
1+1
1+1
–
–
2
2
ˆ
ˆ
-
-
1587401052
1587401052
)
)
–
–
1
1
1
1
o
Coordinate cartesiane (Rec) Coordinate polari (Pol)
ooo
I-30
Page 32

Sintassi e introduzione
A
Conversione da coordinate cartesiane a coordinate polari (Pol)
x, y
)
Pol(
x
: Valore xdelle coordinate cartesiane
y
: Valore y delle coordinate cartesiane
Conversione da coordinate polari a coordinate cartesiane (Rec)
r,Ƨ
)
Rec(
r
: Valore r delle coordinate polari
Ƨ
: Valore θ delle coordinate polari
Esempio 1: Per convertire le coordinate cartesiane (
(Unità angolare: Deg)
(Per visionare il valore di
)
θ
+
1
,92))
2 ) in coordinate polari
'2,'
(Pol)
2)
9
,
t
E
(Y)
Pol
Pol
Y45Y
('(2)
('(2)
,
,
'
'
(2))
(2))
2
2
45
Esempio 2: Per convertire le coordinate polari (2, 30°) in coordinate cartesiane
(Unità angolare: Deg)
(Per visionare il valore di
(Rec)
-
1
y
)
2,
30)
,
t
Rec(2, 30
Rec(2, 30
E
1732050808
1732050808
Y1Y
(Y)
)
)
1
Note
A
• Queste funzioni possono essere utilizzate nei modi COMP, SD e REG.
• I risultati di calcolo mostrano soltanto il primo valore
r
• Il valore
• I valori ottenuti per
• Quando si esegue una funzione di conversione di coordinate all’interno di un’espressione
(o valore x) prodotto dal calcolo è assegnato alla variabile X, mentre il valore θ (o
y
) è assegnato alla variabile Y (pagina 23). Per visionare il valore θ(o il valore y),
valore
visualizzare il valore assegnato alla variabile Y, come mostrato nell’esempio.
sono compresi nella gamma da –180°<
di calcolo, il calcolo viene eseguito utilizzando il primo valore prodotto dalla conversione
r
(valore
Esempio: Pol (
o valore x).
'2,'
Ƨ
durante la conversione da coordinate cartesiane a coordinate polari
2 ) + 5 = 2 + 5 = 7
Ƨ
<
I-31
180°.
r
o il valore x .
Page 33

Altre funzioni
k
x
!, Abs(, Ran#, nP r, nC r, Rnd(
x!, nP r
Le funzioni
supportati gli argomenti di numeri complessi.
Fattoriale (!)
A
Sintassi: { n}! ({ n} deve essere un numero intero o 0.)
Esempio: (5 + 3)!
Valore assoluto (Abs)
A
Quando si sta eseguendo un calcolo con numeri reali, con Abs( si ottiene semplicemente
il valore assoluto. Questa funzione può essere utilizzata nel modo CMPLX per determinare
il valore assoluto (dimensione) di un numero complesso. Per maggiori informazioni, vedere
“Calcoli con numeri complessi” a pagina 35.
Sintassi: Abs({
Esempio: Abs (2 – 7) = 5
Numero casuale (Ran#)
A
Questa funzione genera un numero pseudo-casuale a tre cifre decimali (da 0,000 a
0,999). Essa non richiede un argomento, e può essere utilizzata alla stessa maniera di una
variabile.
Sintassi: Ran#
Esempio: Per usare 1000Ran# per ottenere numeri casuali a tre cifre.
, e nC r possono essere utilizzate nel modo CMPLX, tuttavia non sono
(
(
5+3)!
(5+3)
n
})
(Abs)
)
1
10001.
2-7)
1
(
X
(Ran#)
5+3)!
x
!)
E
Abs (2–7
Abs (2–7
E
5
5
1000Ran#
1000Ran#
E
287
287
40320
40320
)
)
1000Ran#
1000Ran#
E
613
613
1000Ran#
1000Ran#
E
118
118
• I valori riportati sopra sono forniti al solo scopo di esempio. I valori realmente prodotti
dalla vostra calcolatrice per questa funzione saranno differenti.
I-32
Page 34

Permutazione (
A
Sintassi: { n}P{ m}, { n}C{ m}
Esempio: Quante permutazioni e combinazioni di quattro persone sono possibili per un
A
È possibile usare la funzione di arrotondamento (Rnd) per arrotondare il valore,
l’espressione o il risultato di calcolo specifi cato dall’argomento. L’arrotondamento viene
eseguito al numero di cifre signifi cative concordemente con l’impostazione del numero di
cifre di visualizzazione.
Arrotondamento per Norm1 o Norm2
La mantissa viene arrotondata a 10 cifre.
Arrotondamento per Fix o Sci
Il valore viene arrotondato al numero di cifre specifi cato.
Esempio: 200 ÷ 7 × 14 = 400
(3 posti decimali)
(Il calcolo interno usa 15 cifre.)
gruppo di 10 persone?
Funzione di arrotondamento (Rnd)
)/Combinazione ( nC r)
nP r
101*
101/
200/7*14
1N
200/7
e
10P4
nP r
)
(
nC r
)
(
(Fix)
1
10P4
4
E
5040
5040
10C4
10C4
4
E
210
210
200÷7×14
200÷7×14
E
400
400
200÷7×14
200÷7×14
3
400000
400000
200÷7
200÷7
E
28571
28571
Ans×14
*14
Eseguire ora lo stesso calcolo usando la funzione di arrotondamento (Rnd).
200/7
I-33
Ans×14
E
400000
400000
200÷7
200÷7
E
28571
28571
Page 35

(Il calcolo usa il valore arrotondato.)
(Risultato arrotondato)
1
*14
0
(Rnd)
Rnd(Ans
Rnd(Ans
E
28571
28571
Ans×14
Ans×14
E
399994
399994
Uso della notazione scientifi ca
3
10
(ENG)
La notazione scientifi ca (ENG) esprime le quantità come un prodotto di un numero positivo
tra 1 e 10, e una potenza di 10 che è sempre un multiplo di tre. Sono possibili due tipi di
notazione scientifi ca, ENG/ e ENG,.
Funzione Operazione con i tasti
ENG
/
ENG
,
Esempi di calcolo scientifi co
k
Esempio 1: Per convertire 1234 in notazione scientifi ca usando ENG
Esempio 2: Per convertire 123 in notazione scientifi ca usando ENG
W
1W
(,)
1234
123
/
1234
1234
E
1234
1234
1234
1234
W
1234
1234
1234
1234
W
1234
1234
,
123
123
E
123
123
03
03
00
00
I-34
1W
123
123
(,)
0123
0123
03
03
Page 36

1W
0000123
0000123
06
06
123
123
(,)
Calcoli con numeri complessi
(CMPLX)
Per eseguire le operazioni di esempio riportate in questa sezione, selezionare prima
CMPLX (
Introduzione di numeri complessi
k
Introduzione di numeri immaginari ( i)
A
Nel modo CMPLX, il tasto W viene utilizzato per introdurre il numero immaginario i. Usare
) per introdurre numeri complessi che utilizzano il formato in coordinate cartesiane
(
i
W
a+ b
).
(
i
Esempio: Per introdurre 2 + 3
Introduzione di valori di numeri complessi usando il formato
A
in coordinate polari
I numeri complessi possono anche essere introdotti usando il formato in coordinate polari
r ∠Ƨ
(
Esempio: Per introdurre 5 ∠ 30
Importante!
Quando si introduce l’argomento Ƨ, immettere un valore che indica un angolo
concordemente con l’impostazione corrente dell’unità angolare di default della calcolatrice.
Visualizzazione del risultato di calcolo di numeri
k
complessi
Quando un calcolo produce un risultato in numero complesso, il simbolo R
nell’angolo in alto a destra del display, e appare per prima soltanto la parte reale. Per
commutare la visualizzazione tra la parte reale e la parte immaginaria, premere
1E
) come modo di calcolo.
2
N
).
(Re ⇔Im).
i
5
2+3
-
1
( ∠)
W
30
( i)
2+3 iI2+3 iI
5 30I
5 30I
I
si attiva
⇔
I-35
Page 37

Esempio: Per introdurre 2 + 1 i e visualizzare il suo risultato di calcolo
Prima di iniziare il calcolo, è necessario eseguire la seguente operazione per cambiare
l’impostazione di visualizzazione dei numeri complessi a “
Per selezionare il formato in coordinate cartesiane:
1
2+
a+ b
” come mostrato sotto.
i
(SETUP)
,
2+i
2+i
)
(
i
E
W
2
2
a+ b
(
1
eee
Visualizza la parte reale.
)
i
1E
(Re ⇔Im)
2+i12+i
1
si attiva durante la visualizzazione della parte
(Il simbolo
i
Formato di visualizzazione di default del risultato di calcolo di
A
numeri complessi
È possibile selezionare sia il formato in coordinate cartesiane che il formato in coordinate
polari, per i risultati di calcolo di numeri complessi.
Coordinate cartesiane Coordinate polari
Usare le schermate di predisposizione per specifi care il formato di visualizzazione di
default che si desidera. Per maggiori informazioni, vedere “Specifi cazione del formato di
visualizzazione di numeri complessi” (pagina 9).
Esempi di visualizzazione dei risultati di calcolo
k
Formato in coordinate cartesiane ( a+
A
,
1
Asse immaginario Asse immaginario
a + bi r
b
b
oo
oo
(SETUP)
eee
a + bi r
Asse reale Asse reale
a
a
a
b
+
)
(
i
1
Visualizza la parte immaginaria.
bi
)
/
/
u
u
immaginaria. )
I-36
Page 38

Esempio 1: 2 × ('3 + i) = 2'3 + 2 i = 3,464101615 + 2
2*(93)+
Esempio 2:
Formato in coordinate polari (
A
1
Esempio 1: 2 × (
Esempio 2: 1 + 1 i = 1,414213562 ∠ 45 (Unità angolare: Deg)
2 ∠ 45 = 1 + 1 i (Unità angolare: Deg)
'
,
(SETUP)
'
2
eee
3 + i) = 2'3 + 2 i = 4 ∠ 30
2*(93)+
9
r
)
(
∠
θ
1+1
i
( i)
)
W
(Re ⇔Im)
1E
2)
r ∠Ƨ
-
1
45
(Re ⇔Im)
1E
)
)
(
i
)
W
(Re ⇔Im)
1E
appare durante la visualizzazione del valore
∠
(
i
W
('(3)+i)
('(3)+i)
×
×
2
2
E
3464101615
3464101615
('(3)+i)
('(3)+i)
×
×
2
2
(2)
(2)
( ∠)
'
45
'
E
E
)
E
45
1
1
(2)
(2)
'
45
'
45
('(3)+i)
('(3)+i)
×
×
2
2
('(3)+i)
('(3)+i)
×
×
2
2
1+1 i
1+1 i
1414213562
1414213562
2
2
1
1
4
4
30
30
.
Ƨ
1E
(Re ⇔Im)
1+1 i451+1 i
45
Numeri complessi coniugati (Conjg)
k
È possibile eseguire l’operazione seguente per ottenere il numero complesso coniugato
¯ z
b
= a +
per il numero complesso z = a +
i
Esempio: Ottenere il numero complesso coniugato di 2 + 3
,
1
(Conjg)
b
.
i
2+3
I-37
W
i
(
)
(
)
jg
jg
Con
2+3 i
Con
(
)
i
)
E
2+3 i
2
2
Page 39

(
)
(
)
jg
jg
Con
2+3 i
Con
(Re ⇔Im)
1E
Valore assoluto e argomento (Abs, arg)
k
È possibile usare la procedura mostrata sotto per ottenere il valore assoluto (| z|) e
argomento (arg) sul piano gaussiano, per un numero complesso in formato
Esempio:
Per ottenere il valore assoluto e argomento di 2 + 2
(Unità angolare: Deg)
Valore assoluto:
(Abs)
)
(
(arg)
2+2
2+2
1
Argomento:
1
Ridefi nizione del formato di visualizzazione di default
k
i
(
W
(
W
Asse immaginario
Asse immaginario
b = 2
b = 2
o
o
)
i
)
E
)
i
)
E
2+3 i
-
-
3
3
z
b
= a +
.
i
Asse reale
Asse reale
a = 2
a = 2
)
g
g
(
(
2+2 i
2+2 i
)
)
)
45
45
Abs(2+2 i
Abs(2+2 i
2828427125
2828427125
ar
ar
di numeri complessi
È possibile usare le procedure descritte di seguito per ridefi nire il formato di visualizzazione
di default di numeri complessi, e specifi care un particolare formato di visualizzazione per il
calcolo che si sta introducendo correntemente.
Specifi cazione del formato in coordinate cartesiane per un
A
calcolo
Introdurre
Esempio: 2
a+ b
(
) alla fi ne del calcolo.
i
-
'
1
2 ∠ 45 = 2 + 2 i (Unità angolare: Deg)
'
292)
1
1
-
-
(2)
( ∠)
45
a+ b
(
)
i
'
E
(2)
2
'
45 a+bi
2
'
45 a+bi
2
2
I-38
1E
(Re ⇔Im)
(2)
(2)
2
'
45 a+bi
2
'
45 a+bi
2
2
Page 40

Specifi cazione del formato in coordinate polari per un calcolo
A
Introdurre
Esempio: 2 + 2
r ∠Ƨ
) alla fi ne del calcolo.
(
+
'
1
i
= 2'2 ∠ 45 = 2,828427125 ∠ 45 (Unità angolare: Deg)
2+2
r ∠Ƨ
(
+
'
1
(Re ⇔Im)
1E
(
)
i
W
2+2 ir
2+2 ir
)
E
2828427125
2828427125
2+2 ir
2+2 ir
θ
θ
θ
θ
45
45
Calcoli statistici (SD/REG)
Dati campione di calcolo statistico
k
Introduzione dei dati campione
A
È possibile introdurre i dati campione sia con la frequenza statistica attivata (FreqOn)
che disattivata (FreqOff). L’impostazione iniziale di default della calcolatrice è FreqOn. È
possibile selezionare il metodo di introduzione che si desidera utilizzare con l’impostazione
della schermata di predisposizione della frequenza statistica (pagina 10).
Numero massimo di elementi di dati di introduzione
A
Il numero massimo di elementi di dati che è possibile introdurre dipende dall’attivazione
(FreqOn) o disattivazione (FreqOff) della frequenza.
Modo di calcolo
Modo SD 40 elementi 80 elementi
Modo REG 26 elementi 40 elementi
Cancellazione dei dati campione
A
Tu tti i dati campione presenti correntemente nella memoria vengono cancellati ogniqualvolta
si cambia ad un altro modo di calcolo, e quando si cambia l’impostazione della frequenza
statistica.
Impostazione di frequenza
FreqOn FreqOff
Esecuzione di calcoli statistici a variabile singola
k
Per eseguire le operazioni di esempio riportate in questa sezione, selezionare prima SD
(
) come modo di calcolo.
4
N
I-39
Page 41

Introduzione dei dati campione
A
Frequenza attivata (FreqOn)
Il seguito mostra le operazioni con i tasti che si richiedono quando si introducono i valori di
x
x
classe
Nota
Se la frequenza di un valore di classe è soltanto una, è possibile introdurlo premendo solo
xn
{
}m(DT) (senza specifi care la frequenza).
Esempio: Per introdurre i seguenti dati
Valore di classe ( x) Frequenza (Freq)
xn
,
, ...
, e frequenza Freq1, Freq2, ... Freq n.
1
2
x
}
{
x
{
xn
{
(;) {Freq1}m(DT)
1
,
1
}
(;) {Freq2}m(DT)
2
,
1
}
(;) {Freq n}m(DT)
,
1
24,5 4
25,5 6
26,5 2
24.5;4I
24.5;4I
24.51,
(DT) indica alla calcolatrice che si è concluso il primo elemento di dati.
m
25.51,
26.51,
(;)
4
0
0
=
=
Line
Line
(DT)
m
(;)
6
m
(;)
2
m
1
1
=
=
Line
Line
(DT)
2
2
=
=
Line
Line
(DT)
3
3
Frequenza disattivata (FreqOff)
In questo caso, introdurre ciascun singolo elemento di dati come mostrato sotto.
x
{
1
Visione dei dati campione attuali
A
Dopo l’introduzione dei dati campione, è possibile premere c per scorrere i dati nella
sequenza in cui essi sono stati inseriti. Il simbolo $ indica che sono presenti dei dati sotto il
campione che appare attualmente sul display. Il simbolo ` indica che sono presenti dei dati
sopra.
}m(DT) {
x
}m(DT) ... {
2
xn
}m(DT)
I-40
Page 42

Esempio: Per visionare i dati da voi introdotti nell’esempio riportato in “Introduzione dei dati
Quando l’impostazione della frequenza statistica è FreqOn, i dati vengono visualizzati nella
sequenza:
nella sequenza:
direzione inversa.
A
Per modifi care un campione di dati, richiamarlo, introdurre il nuovo valore(i), e quindi
premereE.
Esempio: Per modifi care il campione di dati “Freq3” introdotto sotto “Introduzione dei dati
campione” a pagina 40 (Impostazione frequenza: FreqOn)
x
x
, Freq1,
1
Modifi ca di un campione di dati
campione” a pagina 40
, Freq2, e così via. Nel caso di FreqOff, essi vengono visualizzati
2
x
x
x
,
,
, e così via. È anche possibile usare f per scorrere nella
1
2
3
A
I
I
A
0
0
=
=
x 1
x 1
c
=
=
Freq 1
Freq 1
c
=
=
x 2
x 2
c
=
=
Freq 2
Freq 2
c
=
=
Freq 3
Freq 3
f
245
245
4
4
255
255
6
6
2
2
I-41
3
E
Freq 3
Freq 3
=
=
3
3
Page 43

Cancellazione di un campione di dati
A
Per cancellare un campione di dati, richiamarlo e quindi premere
Esempio: Per cancellare il campione di dati “
Nota
A
Eseguire la seguente operazione con i tasti per cancellare i dati di tutti i campioni.
Se non si desidera cancellare i dati di tutti i campioni, premere A invece di
nell’operazione riportata sopra.
A
Per eseguire un calcolo statistico, introdurre il comando applicabile e quindi premere E.
Per determinare il valore medio (o) dei dati campione introdotti correntemente, ad esempio,
eseguire l’operazione mostrata sotto.
campione” a pagina 40
• Il seguito mostra le immagini di come appaiono i dati prima e dopo l’operazione di
cancellazione.
• Quando l’impostazione della frequenza statistica è attivata (FreqOn), la coppia applicabile
di dati
Prima Dopo
x
: 24.5 Freq1: 4
1
x
: 25.5 Freq2: 6
2
x
: 26.5 Freq3: 2 Slittato verso l’alto.
3
x
e dati Freq viene cancellata.
Cancellazione dei dati di tutti i campioni
(CLR)1(Stat)
9
1
E
Calcoli statistici usando i dati campione introdotti
x
” introdotto in “Introduzione dei dati
2
ccc
A
(CL)
1m
x
1
x
2
(S-VAR)
2
1
(CL).
1m
=
=
x 2
x 2
255
255
=
=
Line
Line
2
2
: 24.5 Freq1: 4
: 26.5 Freq2: 2
E
x xσn xσn–
x xσn xσn–
12 3
12 3
1
1
x
x
1
E
2533333333
* Questo è un esempio dei possibili risultati di calcolo.
2533333333
I-42
Page 44

Riferimento dei comandi statistici nel modo SD
x
x
A
2
x
ƙ
Si ottiene la somma di quadrati dei dati
campione.
Σ
x
ƙ
Si ottiene la somma dei dati campione.
Σ
n
Si ottiene il numero di campioni.
n
= (numero di elementi di dati x)
¯ x
Si ottiene la media.
o
Esecuzione di calcoli statistici a doppia variabile
k
Per eseguire le operazioni di esempio riportate in questa sezione, selezionare prima REG
(
) come modo di calcolo.
5
N
Tipi di calcoli di regressione
A
Il modo REG vi consente di eseguire i sette tipi di regressione elencati sotto. Le fi gure in
parentesi mostrano le formule teoriche.
• Lineare ( y = a +
• Quadratica (
• Logaritmica (
• Esponenziale
• Esponenziale
• Elevamento a potenza (
• Inversa (
Ogni volta che si entra nel modo REG, si deve selezionare il tipo di calcolo di regressione
che si intende eseguire.
1
1
2
2
=
x
x
Σ
i
1
1
=
x
x
Σ
i
1
1
2
1
Σx
i
=
n
e
( y =
ab
( y =
(S-SUM)
(S-SUM)
(S-SUM)
(S-VAR)
y
y
y
y
1
2
3
1
bx
)
bx
= a+
+
= a + b ln x)
bx
ae
)
x
ab
)
b
ax
=
)
= a + b/ x)
σ
x
n
Si ottiene la deviazione standard della
popolazione.
σn
=
σ
x
–1
n
Si ottiene la deviazione standard del
campione.
σn–1
=
minX
Si determina il valore minimo dei campioni.
maxX
Si determina il valore massimo dei
campioni.
2
cx
)
1
1
1
Σ(x
1
Σ(x
2
2
2
– o)
i
n
2
– o)
i
n – 1
(S-VAR)
(S-VAR)
(S-VAR)
2
(S-VAR)
2
e
e
2
3
1
2
Selezione del tipo di calcolo di regressione
1. Premere
• Questo visualizza il menu iniziale per la selezione del calcolo di regressione. Il menu è
dotato di due schermate, ed è possibile usare d e e per spostarsi tra loro.
(REG) per entrare nel modo REG.
5
N
I-43
Page 45

Lin Log Exp Pwr
1234
2. Eseguire una delle seguenti operazioni per selezionare il calcolo di regressione che si
desidera.
Per selezionare questo tipo di
regressione:
Lineare
Logaritmica
Esponenziale
Elevamento a potenza
Inversa
Quadratica
Esponenziale
e
ab
Inv Quad AB–Ex
12 3
Premere questo tasto:
(Lin)
1
(Log)
2
(Exp)
3
(Pwr)
4
(Inv)
1
e
(Quad)
2
e
(AB-Exp)
3
e
p
Nota
È possibile commutare ad un altro tipo di calcolo di regressione rimanendo nel modo REG,
se lo si desidera. Premendo
menu simile a quella mostrata nel passo 1 riportato sopra. Eseguire la stessa operazione
come per la procedura riportata sopra, per selezionare il tipo di calcolo di regressione che
si desidera.
Introduzione dei dati campione
A
(S-VAR)3(TYPE) si visualizza una schermata di
2
1
Frequenza attivata (FreqOn)
Il seguito mostra le operazioni con i tasti che si richiedono quando si introducono i valori di
x
y
x
y
classe (
,
), (
1
1
x
y
},{
}
{
1
1
1
x
y
},{
}
{
2
2
1
xn
yn
{
},{
}
,
), ...(
2
2
(;) {Freq1} m(DT)
,
(;) {Freq2} m(DT)
,
(;) {Freq n}m(DT)
,
1
xn, yn
), e le frequenze Freq1, Freq2, ... Freq n.
Nota
Se la frequenza di un valore di classe è soltanto una, è possibile introdurlo premendo
xn
soltanto {
yn
},{
}m(DT) (senza specifi care la frequenza).
Frequenza disattivata (FreqOff)
In questo caso, introdurre ciascun elemento individuale di dati come mostrato sotto.
x
y
{
},{
}m(DT)
1
1
x
y
},{
}m(DT)
{
2
2
xn
yn
{
},{
}m(DT)
I-44
Page 46

Visione dei dati correnti del campione
A
Dopo l’introduzione dei dati del campione, è possibile premere c per scorrere i dati nella
sequenza in cui sono stati inseriti. Il simbolo $ indica che sono presenti dei dati sotto il
campione che appare correntemente sul display. Il simbolo ` indica che sono presenti dei
dati sopra.
Quando l’impostazione della frequenza statistica è FreqOn, i dati vengono visualizzati
nella sequenza:
visualizzati nella sequenza:
scorrere nella direzione inversa.
Modifi ca di un campione di dati
A
Per modifi care un campione di dati, richiamarlo, introdurre il nuovo valore(i), e quindi
premereE.
Cancellazione di un campione di dati
A
Per cancellare un campione di dati, richiamarlo e quindi premere
Cancellazione dei dati di tutti i campioni
A
Vedere “Cancellazione dei dati di tutti i campioni” (pagina 42).
Calcoli statistici usando i dati campione introdotti
A
Per eseguire un calcolo statistico, introdurre il comando applicabile e quindi premere E.
Per determinare il valore medio (
esempio, eseguire l’operazione mostrata sotto.
x
,
1
y
, Freq1,
1
x
y
,
, Freq2, e così via. Nel caso di FreqOff, essi vengono
2
2
x
y
x
y
x
,
2
1
,
2
1
2
y
,
, e così via. È anche possibile usare f per
3
3
1m
x xσn xσn–
(S-VAR)1(VAR)
2
1
(S-VAR)1(VAR)
x xσn xσn–
12 3
12 3
x
x
E
y
y
yσn yσn–
yσn yσn–
e
12 3
12 3
,
,
1
1
o p) dei dati campione introdotti correntemente, ad
o
(CL).
1
1
115
115
1
1
y14y
1
E
14
* Questo è un esempio dei possibili risultati di calcolo.
I-45
Page 47

Riferimento dei comandi statistici nel modo REG
x
x
x
A
Comandi di somma e numero di campioni (Menu S-SUM)
2
x
ƙ
Si ottiene la somma dei quadrati dei dati
dei campioni.
Σ
x
ƙ
Si ottiene la somma dei dati
Σ
n
Si ottiene il numero di campioni.
= (numero di elementi di dati x)
n
2
y
ƙ
Si ottiene la somma dei quadrati dei dati
dei campioni.
1
Σ
y
ƙ
Si ottiene la somma dei dati ydei campioni.
1
Σ
(S-SUM)
1
1
2
2
=
x
x
Σ
i
1
1
=
x
x
Σ
i
1
1
(S-SUM)
1
2
2
=
y
y
Σ
i
(S-SUM)
1
=
y
Σ
yi
1
(S-SUM)
2
x
dei campioni.
(S-SUM)
3
1
e
2
e
1
xy
ƙ
x
Si ottiene la somma dei prodotti dei dati
dei dati
2
y
x
ƙ
Si ottiene la somma dei quadrati dei dati
dei campioni moltiplicati per i dati y.
3
x
ƙ
Si ottiene la somma dei cubi dei dati
campioni.
y
4
x
ƙ
Si ottiene la somma alla quarta potenza dei
x
dei campioni.
dati
1
y
dei campioni.
xy
Σ
1
2
x
Σ
1
x
Σ
1
x
Σ
=
x
Σ
1
=
y
x
Σ
1
3
=
x
Σ
1
4
=
x
Σ
Comandi di media e deviazione standard (Menu VAR)
(S-VAR)1(VAR)
2
1
¯ x
x
Si ottiene la media dei dati
o
o
2
1
x
σ
n
Si ottiene la deviazione standard della
popolazione dei dati
σn
σn
=
=
dei campioni.
Σx
Σx
i
i
=
=
n
n
(S-VAR)1(VAR)
x
dei campioni.
2
2
Σ(x
– o)
Σ(x
– o)
i
i
n
n
1
2
x
–1
σ
n
Si ottiene la deviazione standard del
campione dei dati
1
¯ y
Si ottiene la media dei dati
(S-VAR)1(VAR)
2
1
x
dei campioni.
σn–1
=
(S-VAR)1(VAR)
2
=
=
p
p
Σ(x
Σy
Σy
n – 1
n
n
(S-SUM)
i y i
(S-SUM)
2
y
i
i
(S-SUM)
3
i
(S-SUM)
4
i
2
– o)
i
y
dei campioni.
i
i
e
d
d
d
e
3
1
2
x
3
3
1
dei
x
e
x
I-46
Page 48

(S-VAR)1(VAR)
y
y
2
1
y
σ
n
Si ottiene la deviazione standard della
popolazione dei dati
σn
σn
y
Σ (y
Σ (y
=
=
dei campioni.
i
i
n
n
– y)
– y)
e
2
2
2
y
σ
n
Si ottiene la deviazione standard del
campione dei dati
1
–1
yσn–1
(S-VAR)1(VAR)
2
y
dei campioni.
Σ (y
=
i
n – 1
– y)
3
e
2
Comandi del coeffi ciente di regressione e del valore stimato per la
regressione non quadratica (Menu VAR)
Il calcolo che viene effettuato quando si esegue uno di questi comandi, dipende dal tipo
di regressione correntemente selezionata. Per maggiori informazioni su ogni formula
di calcolo di regressione, vedere “Tabella delle formule di calcolo del coeffi ciente di
regressione e del valore stimato” (pagina 48).
(S-VAR)1(VAR)
2
a
Si ottiene il termine costante a di una formula di regressione.
b
Si ottiene il coeffi ciente b della formula di regressione.
r
Si ottiene il coeffi ciente di correlazione r.
ˆ x
Prendendo l’introduzione del valore immediatamente prima di questo comando come
y
, si ottiene il valore stimato di x basato sulla formula di regressione per il calcolo di
valore
regressione correntemente selezionato.
ˆ y
Prendendo l’introduzione del valore immediatamente prima di questo comando come
x
valore
, si ottiene il valore stimato di y basato sulla formula di regressione per il calcolo di
regressione correntemente selezionato.
1
1
1
2
2
1
1
(S-VAR)1(VAR)
(S-VAR)1(VAR)
(S-VAR)1(VAR)
2
(S-VAR)1(VAR)
2
ee
ee
ee
d
d
1
2
3
1
2
Comandi del coeffi ciente di regressione e del valore stimato per la
regressione quadratica (Menu VAR)
Per maggiori informazioni sulla formula che viene eseguita da ciascuno di questi comandi,
vedere “Tabella delle formule di calcolo del coeffi ciente di regressione e del valore stimato”
(pagina 48).
(S-VAR)1(VAR)
a
Si ottiene il termine costante a della formula di regressione.
I-47
1
2
ee
1
Page 49

(S-VAR)1(VAR)
2
b
Si ottiene il coeffi ciente b della formula di regressione.
c
Si ottiene il coeffi ciente c della formula di regressione.
ˆ x
1
Prendendo l’introduzione del valore immediatamente prima di questo comando come valore
y
, usa la formula a pagina 49 per determinare un valore stimato di x.
ˆ x
2
Prendendo l’introduzione del valore immediatamente prima di questo comando come valore
y
, usa la formula a pagina 49 per determinare un valore maggiormente stimato di x.
ˆ y
Prendendo l’introduzione del valore immediatamente prima di questo comando come valore
x
, usa la formula a pagina 49 per determinare un valore stimato di y.
1
1
2
1
1
1
(S-VAR)1(VAR)
(S-VAR)1(VAR)
2
(S-VAR)1(VAR)
2
(S-VAR)1(VAR)
2
ee
ee
d
d
d
2
3
1
2
3
Comandi di valore minimo e massimo (Menu MINMAX)
(S-VAR)2(MINMAX)
minX
Si ottiene il valore minimo dei dati
maxX
Si ottiene il valore massimo dei dati
minY
Si ottiene il valore minimo dei dati
maxY
Si ottiene il valore massimo dei dati
x
dei campioni.
x
dei campioni.
y
dei campioni.
y
dei campioni.
2
1
(S-VAR)2(MINMAX)
2
1
(S-VAR)2(MINMAX)
2
1
(S-VAR)2(MINMAX)
2
1
e
e
1
2
1
2
Tabella delle formule di calcolo del coeffi ciente di regressione
A
e del valore stimato
La seguente tabella mostra le formule di calcolo utilizzate dai comandi del coeffi ciente di
regressione e del valore stimato per ogni tipo di calcolo di regressione.
I-48
Page 50

Regressione lineare
i
x
)
m
m
n
2
Comando Formula di calcolo
Te r mine costante a della formula
di regressione
Coeffi ciente di regressione b
Coeffi ciente di correlazione r
Valore stimato
Valore stimato
m
ţ
Regressione quadratica
Comando Formula di calcolo
Te r mine costante a della formula
di regressione
Coeffi ciente di regressione b
Coeffi ciente di regressione c
Tuttavia,
Valore stimato
Valore stimato
Valore stimato
Sxx = Σx
Sxx = Σx
Sxy = Σxiy
Sxy = Σxiy
Comando Formula di calcolo
m
1
m
2
n
(Σxi)
(Σxi)
2
2
–
–
i
i
n
n
(Σx
(Σx
–
–
i
i
Σy
a =
n.Σx
b =
n.Σx
r =
{n
y – a
=
m
n = a + b
Σy
a = – b
n
Sxy.Sx
b =
Sx
c =
2
2
.
.
)
)
Σy
Σy
i
i
i
i
n
n
1 =
2 =
= a + bx + cx
.
– b
Σx
i
n
.
– Σx
Σy
iyi
i
2
)
–(Σx
i
i
n.Σx
iyi
2
.
Σx
i
–(Σx
)
i
b
Σx
i
i
– c
()
n
2x2
2
– Sx
2x2
Sxx.Sx
– (Sxx2)
2
.
y
Sxx – Sxy.Sxx
2x2
Sxx.Sx
– b +
2
2
Sxx
= Σx
Sxx
= Σx
2
2
Sx2x
= Σx
Sx2x
= Σx
Sx2y = Σx
Sx2y = Σx
2
b
– (Sxx2)
i
i
i
i
– 4c(a – y
2c
2
– 4c(a – y
b
– b –
2c
2
– Σx
2
}{n
y
3
3
–
–
4
4
i
i
2
2
y
y
.
i
Σx
(
Sxx
(Σx
(Σx
–
–
i
i
n
2
(Σx
(Σx
–
–
i
.
.
Σy
i
2
(Σx
(Σx
Σy
2
n
n
i
i
i
i
2
i
2
2
.
.
Σx
Σx
n
n
2)2
2)2
)
)
i
–(Σy
2
2
i
i
2
2
.
.
Σy
Σy
i
i
n
n
2
)
}
i
)
)
)
)
i
i
I-49
Page 51

Regressione logaritmica
i
x
)
x
}
x
Comando Formula di calcolo
Te r mine costante a della formula
di regressione
Coeffi ciente di regressione b
Coeffi ciente di correlazione r
Valore stimato
Valore stimato
m
n
– b.Σlnx
Σy
i
a =
(
ln
n.Σ
b =
n.Σ
r =
.
{n
Σ
y –a
b
m = e
n = a + bln
i
n
x
i)yi
(
x
ln
n.Σ
(
x
ln
2
)
i
2
)
i
– Σlnx
–(Σlnx
(
x
ln
i)yi
–(Σlnx
.
Σy
i
2
)
i
– Σlnx
)
i
2
}{n
.
Σy
i
i
2
i
–(Σy
2
)
}
i
.
Σy
Regressione esponenziale
Comando Formula di calcolo
Te r mine costante a della formula
di regressione
Coeffi ciente di regressione b
Coeffi ciente di correlazione r
Valore stimato
Valore stimato
m
n
Regressione esponenziale
Comando Formula di calcolo
Te r mine costante a della formula
di regressione
Coeffi ciente di regressione b
Coeffi ciente di correlazione r
Valore stimato
Valore stimato
m
n
e
.
lny
– b
Σ
Σx
i
ln
i
n
y
i
2
i
n.Σx
2
–(Σx
i
– Σx
–(Σx
i
.
Σ
lny
i
i
2
)
i
.
y
ln
– Σx
lny
i
}{n
Σ
i
i
2
.
(
)
ln
Σ
y
i
–(Σlny
2
)
}
i
i
2
)
i
a = exp
b =
r =
m =
n = ae
(
n.Σx
n.Σx
.
{n
Σx
lny – lna
b
b
ab
.
i
n.Σx
n.Σx
2
–(Σx
i
– lnb
n
y
ln
i
i
2
i
ln
i
– Σx
i
Σx
–(Σx
y
i
2
)
}{n
i
)
.
Σ
i
i
– Σx
.
Σ
lny
i
2
)
.
Σ
lny
i
i
2
(
)
ln
y
i
–(Σlny
2
)
i
Σ
lny
exp
a =
(
b= exp
r =
m =
n.Σx
()
.
{n
Σx
lny – lna
lnb
n = ab
I-50
Page 52

Regressione di potenza
)
Comando Formula di calcolo
Te r mine costante a della formula
di regressione
Coeffi ciente di regressione b
Coeffi ciente di correlazione r
Valore stimato
Valore stimato
m
n
Regressione inversa
Comando Formula di calcolo
Te r mine costante a della formula
di regressione
Coeffi ciente di regressione b
Coeffi ciente di correlazione r
Tuttavia,
Valore stimato
Valore stimato
Sxx = Σ(x
Sxx = Σ(x
Syy = Σy
Syy = Σy
Sxy = Σ(x
Sxy = Σ(x
Comando Formula di calcolo
m
n
–1)2
–1)2
i
i
(Σyi)
(Σyi)
2
2
–
–
i
i
–1
–1
)yi–
)yi–
i
i
–
–
n
n
a = exp
b =
r =
m = e
n = ax
a =
b =
r =
(Σx
(Σx
n
n
2
2
Σx
Σx
m =
n = a+
–1)2
–1)2
i
i
i
i
n.Σlnx
.
{n
ln y – ln a
Σy
Sxy
Sxx
Sxx.Syy
–1
–1
.
.
Σy
Σy
n
n
b
y – a
(
n.Σ
Σ
b
i
Sxy
i
i
x
b
Σ
(
ln
– b
n
b
lny
(
ln
i
ln
x
i
.
Σx
– b
i
n
y
– Σlnx
i
2
)
x
i
n.Σlnx
2
)
–(Σlnx
–1
i
.
Σ
lnx
–(Σlnx
ln
i
i
i
.
Σ
i
y
i
2
)
}{n
lny
2
)
i
– Σlnx
.
Σ
i
.
Σ
lny
i
i
2
(
)
ln
y
–(Σlny
i
2
)
}
i
Esempi di calcoli statistici
k
Questa sezione fornisce alcuni esempi reali di calcoli statistici, così come essi vengono
eseguiti sulla vostra calcolatrice.
I-51
Page 53

Esempio 1: La tabella accanto mostra i battiti cardiaci di
50 studenti che appartengono ad un liceo
maschile che ha un totale di 1000 studenti iscritti.
Determinare la media e la deviazione standard dei
dati campione.
Procedura operativa
Selezionare il modo SD:
Selezionare FreqOn per l’impostazione della frequenza statistica:
Introdurre i dati campione:
Si ottiene la media:
Si ottiene la deviazione standard del campione:
Esempio 2: I dati accanto mostrano il peso di un neonato a
Ottenere la formula di regressione e il coeffi ciente di
1
correlazione prodotti dalla regressione lineare dei dati.
Ottenere la formula di regressione e il coeffi ciente di
2
correlazione prodotti dalla regressione logaritmica dei dati.
Predire il peso dopo 350 giorni dalla nascita, basandosi sulla
3
formula di regressione che meglio si adatta all’andamento
dei dati conformemente con i risultati della regressione.
(SETUP)
1N
55
m
611,
651,
691,
731,
vari giorni dalla nascita.
4
N
dd
(DT)
571,
(;)
5
(;)
9
(;)
6
(;)
3
(SD)
m
m
m
m
1
(FreqOn)
1
(;)
(DT)
631,
(DT)
671,
(DT)
711,
(DT)
751,
1
(S-VAR)3(
2
(DT)
2
m
(S-VAR)1(o)
2
591,
(;)
8
m
(;)
8
m
(;)
4
m
(;)
2
m
E
x
)
σ
E
–1
n
Battito
cardiaco
54 – 56 1
56 – 58 2
58 – 60 2
60 – 62 5
62 – 64 8
64 – 66 9
66 – 68 8
68 – 70 6
70 – 72 4
72 – 74 3
74 – 76 2
(;)
(DT)
(DT)
(DT)
(DT)
x
x
xσn–
xσn–
4635444632
4635444632
Numero di
giorni
Studenti
(DT)
2
m
6568
6568
1
1
Peso
20 3150
50 4800
80 6420
110 7310
140 7940
170 8690
200 8800
230 9130
260 9270
290 9310
320 9390
(g)
I-52
Page 54

Procedura operativa
Entrare nel modo REG e selezionare la regressione lineare:
Selezionare FreqOff per l’impostazione della frequenza statistica:
Introdurre i dati campione:
Regressione lineare
1
Te r mine costante a della formula di regressione:
Coeffi ciente di regressione b:
Coeffi ciente di correlazione:
Regressione logaritmica
2
Selezionare la regressione logaritmica:
Te r mine costante a della formula di regressione:
Coeffi ciente di regressione b:
Coeffi ciente di correlazione:
Predizione del peso
3
Il valore assoluto del coeffi ciente di correlazione per la regressione logaritmica è più vicino
a 1, quindi eseguire il calcolo di predizione del peso utilizzando la funzione di regressione
logaritmica.
(REG)1(Lin)
5
N
(SETUP)
1N
20,3150
80,6420
140,7940
200,8800
260,9270
320,9390
1
1
1
A1
1
1
2
dd
m
m
(S-VAR)1(VAR)
2
(S-VAR)1(VAR)
2
(S-VAR)1(VAR)
2
(S-VAR)3(TYPE)2(Log)
2
1
(S-VAR)1(VAR)
2
(S-VAR)1(VAR)
2
(S-VAR)1(VAR)
2
(FreqOff)
(DT)
50,4800
(DT)
110,7310
(DT)
170,8690
m
(DT)
230,9130
m
(DT)
290,9310
m
(DT)
m
(a)
1
ee
(b)
2
ee
(r)
3
ee
(a)
1
ee
(b)
2
ee
(r)
3
ee
(DT)
m
(DT)
m
m
m
m
a
a
E
4446575758
4446575758
b
b
E
1887575758
1887575758
r
r
E
0904793561
0904793561
x
1
=
x
1
=
a
a
E
–
–
4209356544
4209356544
b
b
E
2425756228
2425756228
r
r
E
0991493123
0991493123
(DT)
(DT)
(DT)
20
20
I-53
Page 55

Ottenereţ quando x = 350:
y
(S-VAR)1(VAR)
2
1
350
2
d
(n)
E
y
350
350
1000056129
1000056129
Calcoli in base- n (BASE)
Per eseguire le operazioni di esempio riportate in questa sezione, selezionare prima BASE
(
) come modo di calcolo.
3
N
Esecuzione di calcoli in base-
k
Specifi cazione della base numerica di default
A
Usare i seguenti tasti per selezionare una base numerica di default.
x
DEC
' HEX
w
M
n
x
10xBIN
OCT ee
li
Per selezionare questa
base numerica:
Decimale
Esadecimale
Binaria
Ottale
Esempi di calcoli in base-
A
Esempio 1: Per selezionare binaria come base numerica e calcolare 12 + 1
Esempio 2: Per selezionare ottale come base numerica e calcolare 7
Premere questo tasto: Indicatore sullo schermo
(DEC) d
x
(HEX) H
M
(BIN) b
l
(OCT) o
i
1
1
1
1
Indicatore base numerica
b
b
n
1+1
E
E
1+1
7+1
7+1
8
+ 1
A
A
i
l
(BIN)
(OCT)
1+1
7+1
I-54
2
b
b
10
10
8
o
o
10
10
Page 56

• Introducendo un valore non valido si verifi ca un errore di sintassi (Syntax ERROR).
• Nel modo BASE, l’introduzione di valori frazionari (decimali) ed esponenziali non è
supportata. Qualsiasi valore alla destra del punto decimale dei risultati di calcolo viene
tagliato via.
Introduzione del valore esadecimale ed esempio di calcolo
A
Usare i seguenti tasti per introdurre i caratteri richiesti per i valori esadecimali (A, B, C, D, E,
F).
{}{A}e{B}w{C}ssin–1{D}ccos–1Ettan–1F
y
Esempio: Per selezionare esadecimale come base numerica e calcolare 1F16 + 1
1F+1
(HEX)
AM
Campi consentiti di calcolo
A
Base numerica Campo consentito
Binaria
Ottale
Decimale –2147483648
Esadecimale
Si verifi ca un errore matematico (Math ERROR) quando un risultato di calcolo è fuori del
campo applicabile per la base numerica corrente di default.
Conversione di un risultato visualizzato ad un’altra
k
Positivo: 0
Negativo: 1000000000
Positivo: 0
Negativo: 4000000000
Positivo: 0
Negativo: 80000000
x
111111111
<
<
x
3777777777
<
<
x
<
x
7FFFFFFF
<
<
1
t
x
<
<
x
<
<
2147483647
<
x
FFFFFFFF
<
<
(F)
+1
1111111111
7777777777
E
1F+1
base numerica
Premendox(DEC),M(HEX),l(BIN), o i(OCT) mentre viene visualizzato un risultato
di calcolo, si eseguirà la conversione del risultato alla base numerica corrispondente.
Esempio: Per convertire il valore decimale 30
al formato binario, ottale e esadecimale
10
30
Ax
(DEC)
30
E
30
16
20
20
30
30
H
H
d
d
I-55
l
(BIN)
30
30
11110
11110
b
b
Page 57

i
30
30
(HEX)
M
Uso del menu LOGIC
k
Nel modo BASE, il tasto X cambia la sua funzione, per divenire un tasto per visualizzare il
menu LOGIC. Il menu LOGIC è dotato di tre schermate, ed è possibile usare d e e per
spostarsi tra loro.
36
36
1E
1E
30
30
(OCT)
a n d o r x no r
123
Schermata1
o
o
H
H
d h b o
1234
Specifi cazione di una base numerica per un valore
k
x o r No t Ne
1 2 3
Schermata 2Schermata 3
g
particolare
È possibile specifi care una base numerica che sia differente dalla base numerica corrente
di default durante l’introduzione di un valore.
Specifi cazione della base numerica durante l’introduzione
A
L’introduzione di un valore decimale di 3, ad esempio, può essere eseguito usando la
seguente operazione con i tasti.
d
d
2
1
d
(h)
5
(d)
1
3
(d)
E
d3Id3I
d5+h5
d5+h5
n
1010
1010
(LOGIC)
X
Esempio di calcolo usando la specifi cazione base-
A
Esempio: Per eseguire il calcolo 510 + 516, e visualizzare il risultato in binario
(BIN)X(LOGIC)
A
l
(LOGIC)
5+
X
I-56
b
b
Page 58

Esecuzione di calcoli usando operazioni logiche e
k
valori binari negativi
La vostra calcolatrice può eseguire operazioni logiche binarie a 10 cifre (10 bit) e calcoli di
valori negativi. Tutti gli esempi mostrati di seguito sono stati eseguiti con l’impostazione BIN
(binario) come base numerica di default.
Prodotto logico (and)
A
Riporta il risultato di un prodotto bitwise.
Esempio: 1010
Somma logica (or)
A
Riporta il risultato di una somma bitwise.
Esempio: 1011
Somma logica esclusiva (xor)
A
Riporta il risultato di una somma logica esclusiva bitwise.
Esempio: 1010
Negazione somma logica esclusiva (xnor)
A
Riporta il risultato della negazione di una somma logica esclusiva bitwise.
Esempio: 1111
and 11002 = 1000
2
or 110102 = 11011
2
xor 11002 = 110
2
xnor 1012 = 1111110101
2
2
1010
2
1011
2
1010
1111
(LOGIC)1(and)
X
1100
(LOGIC)2(or)
X
11010
(LOGIC)
X
1100
2
(LOGIC)3(xnor)
X
101
e
1
1010and1100
1010and1100
E
1011o r 11010
1011o r 11010
E
1010xor 1100
1010xor 1100
(xor)
E
1111xnor 101
1111xnor 101
E
1111110101
1111110101
1000
1000
11011
11011
110
110
b
b
b
b
b
b
b
b
Complemento/Inversione (Not)
A
Riporta il complemento (inversione bitwise) di un valore.
Esempio: Not(1010
) = 1111110101
2
(LOGIC)
X
e
2
(Not)
2
1010)
I-57
No t(1010
No t(1010
E
1111110101
1111110101
)
)
b
b
Page 59

Negazione (Neg)
A
Riporta il complemento a due di un valore.
Esempio: Neg(101101
) = 1111010011
2
2
(LOGIC)
X
101101)
e
3
(
(
g
g
Ne
101101
Ne
(Neg)
E
101101
1111010011
1111010011
)
)
Formule incorporate
La calcolatrice è dotata di 23 formule incorporate per i matematici e fi sici, le quali possono
essere usate nel modo COMP.
Uso delle formule incorporate
k
Selezione di una formula incorporata tramite il suo numero di
A
formula
1. Premere G.
• Questo visualizzerà il messaggio “Formula No.?”.
2. Introdurre il numero a due cifre (da 01 a 23) della formula che si desidera richiamare.
• Per informazioni sulla lista delle formule e loro numeri, vedere “Lista delle formule
incorporate” (pagina 60).
Formula No.?
–06– 0
Selezione a scorrimento di una formula incorporata
A
1. Premere G.
2. Usare c e f per scorrere tra le formule incorporate, fi nché non appare sul display la
formula che si desidera richiamare.
Esecuzione di un calcolo con una formula incorporata
A
Il seguente esempio mostra come usare la formula di Heron per determinare l’area di un
triangolo quando si conoscono le lunghezze dei suoi tre lati (8, 5, 5).
Procedura operativa
Richiamare la formula di Heron:
Q
\
Gccc
03:Her onFormula03:Her onFormula
b
b
(Prompt per l’introduzione della variabile
I-58
E
a
a
)
0a0
Page 60

Introdurre 8 per la variabile a:
8
E
b
Introdurre 5 per la variabile
Introdurre 5 per la variabile
• Come viene mostrato sopra, il risultato di calcolo appare dopo aver assegnato i valori a
tutte le variabili richieste.
• Premendo E mentre appare sul display un risultato di calcolo, si rieseguirà la formula
dall’inizio.
Variabili speciali per le formule incorporate (Variabili di
A
b
:
5
E
c
c
:
5
E
s
s
03:Her onFormula
03:Her onFormula
0b0
0c0
12
12
formula)
Quando si esegue un calcolo utilizzando una formula incorporata, si assegnano valori alle
variabili della formula e si calcola quindi il risultato. In aggiunta alle variabili
abbiamo visto nella formula di Heron riportata sopra, ci sono anche variabili denominate
t, v
,
e Ƨ. Poiché queste variabili vengono utilizzate solo nelle formule incorporate, esse
ρ
vengono chiamate variabili di formula.
I valori che si assegnano alle variabili di formula quando si esegue un calcolo con una
formula incorporata, sono conservati in memoria fi nché non si cambia ad un altro modo di
calcolo, si esegue un’operazione di cancellazione della memoria (
o si ripristina la calcolatrice (
eseguire un calcolo incorporato diverse volte lasciando una o più variabili assegnate con gli
stessi valori come un’esecuzione precedente, se lo si desidera.
PremendoE dopo aver eseguito l’operazione riportata in “Esecuzione di un calcolo con
una formula incorporata”, si visualizza di nuovo la schermata per l’assegnazione delle
variabili, con i valori assegnati precedentemente come impostazione iniziale di default.
(CLR)3(All)). Questo sta a signifi care che è possibile
9
1
1
9
a, b
e c che
(CLR)1(Mem)),
r
,
Prompt per l’introduzione della variabile
Se si desidera lasciare il valore visualizzato assegnato alla variabile, premere E. In questo
caso, premendo E si lascerà 8 assegnato alla variabile
Nota
Anche se si seleziona una formula incorporata differente, tutte le variabili che hanno gli
stessi nomi come per la formula usata precedentemente, conserveranno i loro valori
correnti.
a
a
Valore assegnato precedentemente alla variabile
a
.
8a8
I-59
a
Page 61

Visualizzazione di una formula incorporata
A
Durante l’introduzione di valori per le variabili di una formula, è possibile visualizzare la
formula premendo
• Se la formula è troppo lunga per adattarsi al display, usare il tasto e per scorrere alla
destra e visionare la parte mancante.
• Per annullare la formula dal display, premere
Lista delle formule incorporate
k
No. 01 Soluzione di equazione quadratica
Risolve un’equazione quadratica utilizzando i valori da voi specifi cati per
2
2
ax
+ bx + c = 0
ax
+ bx + c = 0
No. 02 Teorema del coseno
Per un triangolo di cui si conoscono le lunghezze di due lati (
formato, determina la lunghezza del lato rimanente.
2
2
a = b
+ c2 − 2bc cos
a = b
+ c2 − 2bc cos
No. 03 Formula di Heron
Determina l’area (
S = s(s − a)(s − b)(s − c) , s=
S = s(s − a)(s − b)(s − c) , s=
(a + b > c > 0, b + c > a > 0, c + a > b > 0)
(a + b > c > 0, b + c > a > 0, c + a > b > 0)
No. 04 Funzione di probabilità normale P( x)
Usa la formula stimata di Hastings per determinare la probabilità di una distribuzione
normale standard P(
1
P(x) =
P(x) =
Importante!
Poiché questa è una formula stimata, potrebbe non essere conseguibile la precisione
esatta.
1
2π
2π
(0 ≦ x < 1 × 1050)
(0 ≦ x < 1 × 1050)
(LOOK).
G
1
(Schermata di introduzione valore)
G
1
(EXIT) o A.
1p
(a ≠ 0, b2− 4ac ≧0)
(a ≠ 0, b2− 4ac ≧0)
θ
θ
(b, c > 0, 0˚< 180˚)
(b, c > 0, 0˚< 180˚)
S
) di un triangolo, quando sono note le lunghezze dei suoi tre lati ( a, b, c).
(a + b + c)
(a + b + c)
2
2
x
) illustrata sotto, quando la variabile normalizzata ( x) è conosciuta.
2
2
t
t
x
x
−
−
2
2
edt
edt
∫
∫
−∞
−∞
x
x
P(x)
P(x)
a
(LOOK)
b
e c) e l’angolo (Ƨ) da essi
θ
θ
03:S
03:S
=
=
a, b
'
'
(s(
(s(
e c.
s–a)(s
s–a)(s
I-60
0a0
–
–
Page 62

No. 05 Funzione di probabilità normale Q( x)
Usa la formula stimata di Hastings per determinare la probabilità di una distribuzione
normale standard Q(
Q(x) = edt
Q(x) = edt
(0 ≦ x < 1 × 1050)
(0 ≦ x < 1 × 1050)
Importante!
Poiché questa è una formula stimata, potrebbe non essere conseguibile la precisione
esatta.
No. 06 Legge di Coulomb
Determina la forza (
r
.
di
F =
F =
4πε
4πε
No. 07 Resistenza di un conduttore
Determina la resistenza
l’area della sezione normale (
ρ
ρ
R =
R =
No. 08 Forza magnetica
Determina la forza motrice (
posizionato in un campo magnetico con forza magnetica uniforme di densità (
lunghezza del conduttore è
F = IB
F = IB
No. 09 Cambio nel voltaggio terminale di R in un circuito RC in serie
Determina il voltaggio (
quando viene applicato il voltaggio
VR = V•e
x
) illustrata sotto, quando la variabile normalizzata ( x) è conosciuta.
Q(x)
2
2
|x|
|x|
t
t
−
1
1
2π
2π
1
1
0
0
S
S
sin
sin
−t/CR
−
2
2
∫
∫
0
0
F
) tra due cariche elettriche di quantità Q e q, separate da una distanza
Qq
Qq
(r >0)
(r >0)
(
: costante dielettrica)
ε
2
2
r
r
R
di un conduttore, quando si conoscono la sua lunghezza ( ),
ρ
ρ
(S, ,
>0)
(S, ,
>0)
F
( >0, 0˚≦
( >0, 0˚≦
θ
θ
V
) dei terminali di R al momento t in un circuito RC in serie,
R
0
S
), e la resistenza ( ρ) del materiale componente.
) in un conduttore attraversato da una corrente elettrica ( I), e
e l’angolo formato dal conduttore e dal campo magnetico è Ƨ.
| |
| |
θ
θ
≦90˚)
≦90˚)
V
ad un circuito con resistenza R e capacità C.
(C, R, t >0)
Q(x)
x
x
Unità: : m, S: m2, ρ: Ω·m, R:
Unità: B: T, I: A, : m,
Unità: R: Ω, C: F, t: secondi, V e
Unità: Q, q: C, r m
B
), quando la
Ƨ
: ° (gradi), F: N
Ω
V
: V
R
I-61
Page 63

No. 10 Guadagno di voltaggio
Z
Z
Z
Z
G
Determina il guadagno in voltaggio (
E
ingresso (
Determina l’impedenza (
l’induttanza della bobina (
Determina l’impedenza (
resistenza (
Determina la frequenza di oscillazione armonica (
quando l’autoinduttanza (
Determina la distanza di caduta (
perpendicolarmente (direzione di gravità) alla velocità iniziale di
resistenza dell’aria).
) e il voltaggio in uscita (
G[dB] = 20 log10
No. 11 Impedenza in un circuito LRC in serie
2
2
= R
+ 2π f L−
= R
+ 2π f L−
()()
()()
No. 12 Impedenza in un circuito LRC in parallelo
R
), l’induttanza della bobina ( L), e la capacità ( C) sono conosciuti.
=
=
1
1
R
R
No. 13 Frequenza di oscillazione elettrica
1
1 =
f
2π LC
No. 14 Distanza di caduta
S = v1t + gt
S = v1t + gt
()
Z
) di un circuito LRC in serie di frequenza f, quando la resistenza ( R),
L
), e la capacità ( C) sono conosciuti.
2π f C
2π f C
(R, f, L, C> 0)
(R, f, L, C> 0)
Z
) di un circuito LRC in parallelo di frequenza f, quando la
1
1
+ 2
π f C−
π f C−
+ 2
(())
(())
L
) della bobina e la capacità ( C) sono conosciuti.
(L, C >0)
1
1
2
2
(g: accelerazione di gravità, t > 0)
(g: accelerazione di gravità, t > 0)
2
2
) di un circuito amplifi catore quando il voltaggio in
E´
) sono conosciuti.
'
E
[dB]
E
2
2
1
1
22
22
1
1
2π f L
2π f L
S
) dopo t secondi, di un oggetto lasciato cadere
/
'
(E
E >0)
2
2
= R
+ ωL −
= R
+ ωL −
()
()
Unità: f : Hz, L: H, C: F, R e Z:
(R, f, L, C> 0)
(R, f, L, C> 0)
Unità:
f
) di un circuito di risonanza in serie,
1
Unità:
Unità: E e
1
1
ω
ω
C
C
f
: Hz, C: F, L: H, R e Z:
Unità: L: H, C: F,
v
(senza considerare la
1
v
: m/s, t: secondi, S: m
1
E Ϣ
: V, G: dB
Ω
Ω
f
: Hz
1
I-62
Page 64

No. 15 Periodo di un pendolo semplice
Determina il periodo (
T = 2π
T = 2π
No. 16 Periodo di un pendolo a molla
Determina il periodo di oscillazione semplice (
m
del peso (
T = 2π
T = 2π
No. 17 Effetto Doppler
Determina la frequenza di oscillazione (
sonora e l’osservatore si stanno spostando, e quando la frequenza di oscillazione della
sorgente sonora (
v
) e la velocità di spostamento dell’osservatore ( u) sono conosciute.
sonora (
1
f = f1
= f1
f
No. 18 Equazione di stato del gas ideale
Determina la pressione (
e il volume (
nRT
nRT
P
=
P =
No. 19 Forza centrifuga
Determina la forza centrifuga (
v
in una traiettoria circolare di raggio r.
velocità
m
F =
T
) di un pendolo semplice con una corda di lunghezza .
(g: accelerazione di gravità, > 0)
(g: accelerazione di gravità, > 0)
g
g
T
) e la costante elastica della molla ( k) sono conosciuti.
m
m
(m, k > 0)
(m, k > 0)
k
k
f
), la velocità acustica ( v), la velocità di spostamento della sorgente
1
v− u
v− u
v− v1
v− v1
V
) sono conosciuti.
V
V
2
v
r
v ≠ v1, f1 > 0, (v− u)/( v− v1) > 0
v ≠ v1, f1 > 0, (v− u)/( v− v1) > 0
(
(
P
) di un gas quando il numero di moli ( n), la temperatura assoluta ( T),
(R: costante dei gas, n, T, V > 0)
(R: costante dei gas, n, T, V > 0)
F
) per un oggetto di massa m che si sta muovendo alla
(m, v, r > 0)
) di un pendolo a molla, quando la massa
f
) udita da un osservatore quando la sorgente
Unità: n: mol, T: K, V: m3, P: N/m
Unità: : m, T: secondi
Unità: m: kg, k: N/m, T: secondi
)
)
Unità: v,
Unità: m: kg, v: m/s, r: m, F: N
v
e u: m/s,
1
f
e
1
f
: Hz
3
No. 20 Energia elastica
Determina l’energia elastica (
lunghezza estesa (
U= Kx
U= Kx
1
1
2
2
x
) sono conosciute.
2
2
(K, x > 0)
(K, x > 0)
U
) di un oggetto, quando la sua costante elastica ( K) e
Unità: K: N/m, x: m, U: J
I-63
Page 65

No. 21 Teorema di Bernoulli
Determina il valore fi ssato (
incomprimibile) quando la velocità di fl usso (
e la pressione (
No. 22 Calcoli con una stadia (Altezza)
Determina la differenza in elevazione (
utilizzato un teodolite per leggere la lunghezza sull’asta graduata (
ed inferiore della stadia, e l’angolo di elevazione (
h =
h =
No. 23 Calcoli con una stadia (Distanza)
Determina la distanza orizzontale (
utilizzato un teodolite per leggere la lunghezza sull’asta graduata (
ed inferiore della stadia, e l’angolo di elevazione (
S = K cos
S = K cos
P
1
1
C =
C =
v
v
2
2
1
1
K sin2 + Csin
K sin2 + Csin
2
2
) sono conosciuti.
2
2
C
) di un fl uido non viscoso (fl usso costante, fl uido
P
P
++gz
++gz
ρ
ρ
θθ
θθ
2
2
+ Ccos
+ Ccos
θθ
θθ
(g: accelerazione di gravità, v, z,ρ, P > 0)
(g: accelerazione di gravità, v, z,ρ, P > 0)
v
), la posizione (altezza) ( z), il peso specifi co ( ρ),
Unità: v: m/s, z: m, ρ: kgf/m3, P: kgf/m2, C: m2/s
h
) dal teodolite all’asta graduata, dopo che è stato
Ƨ
).
( K e C: costanti della stadia, 0° <
S
) dal teodolite all’asta graduata, dopo che è stato
Ƨ
).
(K e C: costanti della stadia, 0° < θ< 90°, > 0)
(K e C: costanti della stadia, 0° < θ< 90°, > 0)
) tra le linee superiore
90°, > 0)
θ
<
Unità: : m, θ: ° (gradi), h: m
) tra le linee superiore
Unità: : m, θ: ° (gradi), S: m
Modo di programmazione (PRGM)
È possibile usare il modo PRGM (
che vi necessitano regolarmente. È possibile includere qualsiasi calcolo che può essere
eseguito nei modi COMP, CMPLX, BASE, SD o REG in una programma.
Panoramica sul modo di programmazione
k
Specifi cazione di un modo di esecuzione del programma
A
Sebbene i programmi vengano creati ed eseguiti nel modo PRGM, ogni programma ha
un “modo di esecuzione” che lo esegue. È possibile specifi care COMP, CMPLX, BASE,
SD o REG come modo di esecuzione del programma. Questo sta a signifi care che è
necessario rifl ettere su cosa si desidera far eseguire al programma, e selezionare il modo di
esecuzione più adatto.
) per creare e memorizzare programmi di calcolo
g
,
2
I-64
Page 66

Memoria di programma
A
La memoria di programma ha una capacità totale di 680 byte, che può essere condivisa fi no
a quattro programmi. Non è possibile memorizzare ulteriori programmi dopo che la memoria
è divenuta piena.
Creazione di un programma
k
Creazione di un nuovo programma
A
Esempio: Per creare un programma che converte pollici in centimetri (1 pollice = 2,54 cm)
? →A : A × 2.54
1. Premere
2. Premere b(EDIT).
EDIT Program
EDIT Program
P-1234 670
P-1234 670
3. Premere il tasto numerico che corrisponde ad un numero di area di programma
inutilizzata.
• Questo visualizza il menu di selezione del modo di esecuzione. Usare e e d per
commutare tra la schermata 1 e la schermata 2 del menu.
(PRGM) per entrare nel modo PRGM.
g
,
Aree di programma che contengono già dati di programma
(da P1 a P4)
Capacità rimanente della memoria di programma
EDIT RUN DEL
EDIT RUN DEL
123
123
MOD E:COMP CMPLX
12
Schermata 1 Schermata 2
4. Premere il tasto numerico che corrisponde al modo che si desidera assegnare come
modo di esecuzione del programma.
• Qui, selezionare b(COMP) sulla schermata 1. Questo
seleziona COMP come modo di esecuzione, e visualizza
la schermata di edizione del programma.
Importante!
Non è possibile cambiare il modo di esecuzione di un programma una volta che esso è
stato assegnato. Un modo di esecuzione può essere assegnato soltanto al momento della
creazione di un nuovo programma.
5. Introdurre il programma.
MOD E:BASE SD REG
I-65
345
I
I
?→A:A×2.54
?→A:A×2.54
000
000
010
010
Page 67

• Qui si introdurrà il programma mostrato sotto.
Programma ? → A : A × 2.54
(P-CMD)b(?)
d
Operazione con i tasti
•
(P-CMD) visualizza una schermata speciale per l’introduzione dei comandi del
d
!
programma. Per maggiori informazioni, vedere “Comandi di introduzione” a pagina 67.
6. Dopo l’introduzione del programma, premere A o
• Per eseguire il programma da voi appena creato, premere w qui per visualizzare la
schermata RUN Program di esecuzione del programma. Per maggiori informazioni,
vedere “Esecuzione di un programma” (riportato sotto).
• Per ritornare alla schermata normale di calcolo, premere
COMP.
Modifi ca di un programma esistente
A
1. Premere
modifi ca del programma.
2. Usare i tasti numerici da b a e per selezionare l’area di programma che contiene il
programma che si desidera modifi care.
3. Usare e e d per spostare il cursore all’interno del programma, ed eseguire le
operazioni che si richiedono per modifi care i contenuti del programma o aggiungere
nuovi contenuti.
• Premendo f si salta all’inizio del programma, mentre premendo c si salta alla fi ne.
4. Dopo aver terminato di modifi care il programma, premere A o
Esecuzione di un programma
k
È possibile eseguire un programma nel modo PRGM o da un altro modo.
Esecuzione di un programma dall’esterno del modo PRGM
A
1. Premere 5.
2. Usare i tasti numerici da b a e per selezionare un’area di programma ed eseguire il
suo programma.
Esecuzione di un programma nel modo PRGM
A
1. Premere
2. Premere c(RUN).
• Questo visualizzerà la schermata RUN Program di esecuzione del programma.
(PRGM)b(EDIT) per visualizzare la schermata EDIT Program di
g
,
(PRGM) per visualizzare la schermata iniziale del modo PRGM.
g
,
!
!~
a-
(STO)-(A)
(A)
*c.fe
w
!5
(EXIT).
per entrare nel modo
b
,
(EXIT).
!5
P1 P2 P3 P4
P1 P2 P3 P4
1 234
1 234
I-66
Page 68

Aree di programma che contengono già dati di programma
RUN P r ogram
RUN P r ogram
P-1234 670
P-1234 670
3. Usare i tasti numerici da b a e per selezionare l’area di programma che contiene il
programma che si desidera eseguire.
• Questo eseguirà il programma nell’area di programma selezionata.
Cosa fare se appare un messaggio di errore
A
Premered o e. Verrà visualizzata la schermata di modifi ca del programma, con
il cursore localizzato nella posizione dove è stato generato l’errore, in modo da poter
correggere il problema.
Cancellazione di un programma
k
È possibile cancellare un programma esistente specifi cando il suo numero di area di
programma.
Cancellazione del programma in un’area specifi cata di
A
programma
1. Premere
2. Premere d(DEL).
DELE TE Pr ogram
DELE TE Pr ogram
P-1234 670
P-1234 670
3. Usare i tasti numerici da b a e per selezionare l’area di programma di cui si desidera
cancellare il programma.
• Il simbolo successivo al numero dell’area di programma
che conteneva il programma da voi appena cancellato
si disattiverà, e il valore della capacità rimanente della
memoria di programma verrà incrementato.
Comandi di introduzione
k
Comandi speciali per l’introduzione del programma
A
1. Mentre appare sul display la schermata di edizione del programma, premere
(P-CMD).
• In questo modo si visualizza la pagina 1 del menu dei
comandi.
(PRGM) per visualizzare la schermata iniziale del modo PRGM.
g
,
(da P1 a P4)
Capacità rimanente della memoria di programma
Aree di programma che contengono già dati di programma
(da P1 a P4)
Capacità rimanente della memoria di programma
DELE TE Pr ogram
DELE TE Pr ogram
P-1234 680
P-1234 680
? →
? →
1234
1234
!
:
:
d
^
^
I-67
Page 69

2. Usare e e d per scorrere tra le pagine e visualizzare quella che contiene il comando
che si desidera.
3. Usare i tasti numerici da b a e per selezionare e introdurre il comando che si
desidera.
Nota
Per introdurre un simbolo separatore (:), premere w.
Funzioni che possono essere introdotte come comandi di
A
programma
È possibile introdurre come comandi di programma, le impostazioni e le altre operazioni che
vengono eseguite durante i calcoli normali. Per maggiori informazioni, vedere “Riferimento
dei comandi” riportato di seguito.
Riferimento dei comandi
k
Questa sezione fornisce i dettagli su ciascuno dei comandi che è possibile utilizzare nei
programmi. I comandi che hanno riportato
schermata che appare quando si preme
Comandi per le operazioni di base
A
? (Prompt di introduzione)
Sintassi ? → {variabile}
Funzione Visualizza il prompt di introduzione “{variabile}?” e assegna il valore di
Esempio ? → A
(Assegnazione della variabile)
→
Sintassi {espressione ; ?} → {variabile}
Funzione Assegna il valore ottenuto dall’elemento a sinistra, alla variabile a destra.
Esempio A+5 → A
: (Codice separatore)
Sintassi {istruzione} : {istruzione} : ... : {istruzione}
Funzione Separa le istruzioni. Non arresta l’esecuzione del programma.
Esempio ? → A : A
introduzione ad una variabile.
2
2
: Ans
nel titolo, possono essere introdotti sulla
g
(P-CMD) o 5.
d
!
g
(Comando di uscita)
^
Sintassi {istruzione} ^ {istruzione}
Funzione Mette in pausa l’esecuzione del programma e visualizza il risultato
Esempio ? → A : A
dell’esecuzione corrente. Il simbolo Q viene attivato mentre l’esecuzione
del programma è messa in pausa da questo comando.
2
2
Ans
^
I-68
Page 70

Comando di salto incondizionato
A
Goto ~ Lbl
Sintassi Goto
Funzione Esecuzione di salto incondizionato Goto
Esempio ? → A : Lbl 1 : ? → B : A × B ÷ 2 ^ Goto 1
Importante!
Si verifi ca un errore di sintassi (Syntax ERROR) se non è presente nessuna etichetta
corrispondente Lbl
incondizionato Goto
Comandi di salto condizionale ed espressioni condizionali
A
n
: .... : Lbl n o Lbl n : .... : Goto n ( n = numero intero da 0 a 9)
n
nello stesso programma dove è localizzato il comando di salto
n
.
g
n
all’etichetta Lbl n.
g
S
Sintassi
Funzione Comando di fl usso logico condizionale usato in combinazione con operatori
Sintassi 1: {istruzione1} viene eseguito se la condizione alla sinistra del
Sintassi 2: Un risultato di valutazione diverso da zero della condizione alla
Esempio Lbl 1 : ?
=, ≠, >, >, <, < (Operatori relazionali)
Sintassi {espressione} {operatore relazionale} {espressione}
Funzione Questi comandi valutano le espressioni su entrambi i lati, e ritornano
Esempio Vedere le annotazioni per il comando S (riportato sopra), istruzione If (pagina
Nota
Questi comandi valutano le espressioni su entrambi i lati, e ritornano a 1 se sono veri, e a 0
se sono falsi, e memorizzano il risultato nella memoria di risposte Ans.
{espressione} {operatore relazionale} {espressione} S {istruzione1} :
1
{istruzione2} : ....
{espressione} S {istruzione1} : {istruzione2} : ....
2
relazionali (=, ≠, >, >, <, <).
comandoS è vera, e quindi {istruzione2} e tutto ciò che è presente dopo di
esso viene eseguito in sequenza. {istruzione1} viene saltato se la condizione
alla sinistra del comando S è falsa, e quindi {istruzione2} e tutto ciò che è
presente dopo di esso viene eseguito.
sinistra del comando S viene interpretato come “vero”, e quindi {istruzione1}
viene eseguito, seguito da {istruzione2} e tutto ciò che è presente dopo di
esso in successione. Un risultato di valutazione zero della condizione alla
sinistra del comando S viene interpretato come “falso”, e quindi {istruzione1}
viene saltato, mentre {istruzione2} e tutto ciò che è presente dopo di esso
viene eseguito.
ad un valore di vero (1) o falso (0). Questi comandi vengono utilizzati in
combinazione con il comando di fl usso logico S, e quando si struttura la
{espressione condizionale} delle istruzioni If e istruzioni While.
70) e istruzione While (pagina 71).
A : A > 0
→
'
S
(A)^ Goto 1
I-69
Page 71

Comandi della struttura di controllo/Istruzione If
A
L’istruzione If viene usata per controllare il fl usso logico di esecuzione del programma a
seconda se la seguente espressione If (che rappresenta la condizione di fl usso logico) è
vera o falsa.
Avvertenze per l’istruzione If
• Un’istruzione If deve sempre essere accompagnata da un’istruzione Then. L’uso di If
senza un corrispondente Then determinerà un errore di sintassi (Syntax ERROR).
• Un’espressione, un comando Goto o un comando Break possono essere usati per la
{espressione*} che segue Then e Else.
If~Then (~Else) ~IfEnd
Sintassi If {espressione condizionale} : Then {espressione*} : Else {espressione*} :
Funzione • Le istruzioni che seguono Then vengono eseguite fi no a Else, e quindi le
• Else {espressione} può essere omesso.
• Includere sempre IfEnd:{istruzione}. Omettendolo non si determinerà un
Esempio 1 ? → A : If A < 10 : Then 10A ^ Else 9A ^ IfEnd : Ans×1.05
Esempio 2 ? → A : If A > 0 : Then A × 10 → A : IfEnd : Ans×1.05
Comandi di controllo struttura/Istruzione For
A
L’istruzione For ripete l’esecuzione delle istruzioni presenti tra For e Next per il tempo in cui
il valore assegnato alla variabile di controllo è compreso nella gamma specifi cata.
Avvertenze per l’istruzione For
Un’istruzione For deve essere sempre accompagnata da un’istruzione Next. L’uso di For
senza un corrispondente Next determinerà un errore di sintassi (Syntax ERROR).
For~To~Next
Sintassi For {espressione (valore iniziale)} → {variabile (variabile di controllo)} To
Funzione L’esecuzione delle istruzioni da For a Next ripete come la variabile di
Esempio For 1 → A To 10 : A
IfEnd : {istruzione} : ...
istruzioni che seguono IfEnd vengono eseguite se l’istruzione condizionale
che segue If è vera. Le istruzioni che seguono Else e quindi le istruzioni
che eseguono IfEnd vengono eseguite se l’istruzione condizionale che
segue If è falsa.
errore, tuttavia determinati contenuti del programma potrebbero causare
risultati di esecuzione inattesi per la parte restante che segue l’istruzione
If.
{espressione (valore fi nale)} : {istruzione} : ... {istruzione} : Next : ....
controllo è incrementata di 1 ad ogni esecuzione, iniziando dal valore iniziale.
Quando il valore di controllo raggiunge il valore fi nale, l’esecuzione salta
all’istruzione che segue Next. L’esecuzione del programma si arresta se non
c’è nessuna istruzione seguente a Next.
2
B : B ^ Next
→
g
g
I-70
Page 72

For~To~Step~Next
Sintassi For {espressione (valore iniziale)} → {variabile (variabile di controllo)} To
Funzione L’esecuzione delle istruzioni da For a Next ripete come la variabile di controllo
Esempio For 1 → A To 10 Step 0.5 : A
Comandi di controllo struttura/Istruzione While
A
While~WhileEnd
Sintassi While {espressione condizionale} : {istruzione} : ... {istruzione} : WhileEnd : ....
Funzione Le istruzioni da While a WhileEnd vengono ripetute mentre l’espressione
Esempio ? → A : While A < 10 : A
Nota
Se la condizione dell’istruzione While è falsa la prima volta che questo comando viene
eseguito, l’esecuzione salta direttamente all’istruzione che segue WhileEnd, senza eseguire
neanche una volta le istruzioni comprese da While a WhileEnd.
Comandi di controllo programma
A
Break
Sintassi .. : {Then ; Else ; S } Break : ..
Funzione Questo comando obbliga una rottura in un ciclo For o While, e salta al
Esempio ? → A : While A > 0 : If A > 2 : Then Break : IfEnd : WhileEnd : A
Comandi di predisposizione
A
Questi comandi funzionano alla stessa maniera delle impostazioni di varie predisposizioni
della calcolatrice. Per maggiori informazioni, vedere “Predisposizione della calcolatrice” a
pagina 8.
{espressione (valore fi nale)} Step {espressione (passo)} : {istruzione} : ...
{istruzione} : Next : ....
è incrementata dell’ammontare di passo con ogni esecuzione, iniziando dal
valore iniziale. Tranne ciò, questo comando è simile a For~To~Next.
2
B : B ^ Next
→
g
condizionale che segue While è vera (diversa da zero). Quando l’espressione
condizionale che segue While risulta falsa (0), viene eseguita l’istruzione che
segue WhileEnd.
2
A+1 → A : WhileEnd : A÷2
^
g
comando successivo. Normalmente, questo comando viene usato all’interno
di un’istruzione Then allo scopo di applicare una condizione Break.
^
Importante!
Con alcuni comandi di predisposizione, le impostazioni confi gurate rimangono effettive
anche dopo aver terminato l’esecuzione del programma.
Comandi di unità angolare
Deg, Rad, Gra (COMP, CMPLX, SD, REG)
Sintassi .. : Deg : ..
.. : Rad : ..
.. : Gra : ..
I-71
Page 73

Operazione
Funzione Questi comandi specifi cano l’impostazione dell’unità angolare.
Comando del formato di visualizzazione
Fix (COMP, CMPLX, SD, REG)
Sintassi .. : Fix {
Operazione
Funzione Questo comando fi ssa il numero di posti decimali (da 0 a 9) per l’emissione
Sci (COMP, CMPLX, SD, REG)
Sintassi .. : Sci {
Operazione
Funzione Questo comando fi ssa il numero di cifre signifi cative (da 1 a 10) per
Premendo
Norm (COMP, CMPLX, SD, REG)
Sintassi .. : Norm {1 ; 2} : ..
Operazione
Funzione Questo comando specifi ca sia Norm1 che Norm2 per l’emissione dei risultati
Comando di frequenza statistica
FreqOn, FreqOff (SD, REG)
Sintassi .. : FreqOn : ..
.. : FreqOff : ..
Operazione
Funzione Questo comando attiva (FreqOn) o disattiva (FreqOff) la frequenza statistica.
Comandi di cancellazione
A
ClrMemory (COMP, CMPLX, BASE)
Sintassi .. : ClrMemory : ..
Operazione
Funzione Questo comando riporta tutte le variabili (A, B, C, D, X, Y, M) a zero.
Nota
Per annullare una variabile specifi ca, usare 0 → {variabile}.
(SETUP)b(Deg)
!,
(SETUP)c(Rad)
!,
(SETUP)d(Gra)
!,
n
} : .. ( n = un numero intero da 0 a 9)
(SETUP)
!,
dei risultati di calcolo.
n
} : .. ( n = un numero intero da 0 a 9)
(SETUP)
!,
l’emissione dei risultati di calcolo.
signifi cative.
!,
di calcolo.
!,
!,
!
!,
(SETUP)
(SETUP)
(SETUP)
(CLR)b(Mem)
j
b
e
c
e
(SETUP)
d
e
b
d
c
d
(Fix)a a
(Sci)a a
e
(Norm)b o
(FreqOn)
(FreqOff)
j
j
(Sci) e quindi a specifi ca 10 cifre
c
c
I-72
Page 74

ClrStat (SD, REG)
Sintassi .. : ClrStat : ..
Operazione
Funzione Questo comando annulla tutti i dati del campione statistico presenti
Comandi della memoria indipendente
A
M+, M– (COMP, CMPLX, BASE)
Sintassi .. : {espressione} M+ : .. / .. : {espressione} M– : ..
Operazione l/
Funzione M+ aggiunge il valore dell’espressione alla memoria indipendente, mentre
Comando di arrotondamento (Rnd)
A
Rnd( (COMP, CMPLX, SD, REG)
Sintassi .. : {espressione} : Rnd(Ans : ..
Operazione
Funzione Questo comando arrotonda un risultato di calcolo a seconda del numero di
Comandi di base numerica
A
Dec, Hex, Bin, Oct (BASE)
Sintassi .. : Dec : .. / .. : Hex : .. / .. : Bin : .. / .. : Oct : ..
Operazione x(DEC)/M(HEX)/l(BIN)/I(OCT)
Funzione Questi comandi specifi cano la base numerica per i calcoli in base-
Comando di introduzione di dati statistici
A
DT (SD, REG)
Sintassi .. : {espressione (valore
.....................Modo SD, FreqOn
.. : {espressione (valore
..................Modo REG, FreqOn
.. : {espressione (valore
..................Modo REG, FreqOff
(CLR)b(Stat)
j
!
correntemente nella memoria.
(M–)
l
!
M– lo sottrae.
(Rnd)
a
!
cifre specifi cato dal formato di visualizzazione.
x
)} ; {espressione (valore Freq)} DT : ..
.. : {espressione (valore
(valore Freq)} DT : ..
x
)} DT : .. .....................Modo SD, FreqOff
x
)} , {espressione (valore y)} ; {espressione
x
)} , {espressione (valore y)} DT : ..
n
.
Importante!
Per introdurre un punto e virgola (;) nella sintassi riportata sopra, premere
introdurre una virgola (,), premere ,.
Operazione l(Introduce DT.)
Funzione Usare questo comando per introdurre una serie di dati campione. Il comando
DT funziona alla stessa maniera del tasto l (tasto DT ) nel modo SD e
modo REG.
!
,
(;). Per
I-73
Page 75

Funzioni non supportate nei programmi
A
Le seguenti funzioni non sono supportate all’interno di funzioni.
• Funzioni di conversione dei risultati di calcolo (ENG/, ENG,, Conversione
sessagesimale
• Commutazione visualizzazione (
calcolo di numeri complessi
• Ripristino (
• Cancellazione delle informazioni di predisposizione (
↔
decimale, Conversione frazione
!w
(CLR)d(All)w)
j
!
↔
decimale)
(Re⇔Im)) mentre è visualizzato un risultato di
j
!
(CLR)c(Setup)w)
Appendice
Sequenza della priorità di calcolo
k
La calcolatrice esegue i calcoli introdotti a seconda della sequenza della priorità mostrata sotto.
• Fondamentalmente, i calcoli vengono eseguiti da sinistra verso destra.
• Ai calcoli racchiusi in parentesi viene data la priorità.
Sequenza Tipo di operazione Descrizione
1 Funzioni con parentesi Pol(, Rec(
2 Funzioni precedute da valori
Potenza, Radice di potenza
Percentuale
3Frazioni
4Simboli di prefi sso (–) (segno meno)
5Calcoli di valori statistici stimatim,n,
6Permutazione, Combinazione
Simbolo di numero complesso
7Moltiplicazione, Divisione
Segno di moltiplicazione
omessa
8Addizione, Sottrazione +, −
9Operatori relazionali =, ≠, >, <, >,
10 Prodotto logico and
sin(, cos(, tan(, sin
tanh(, sinh
log(, ln(,
arg(, Abs(, Conjg(
Not(, Neg(, Rnd(
2
3
,
,
x
x
x
^(,
'
%
b
/
a
c
d, h, b, o (simbolo di base numerica)
,
m
1
nPr,nCr
∠
×, ÷
Il segno di moltiplicazione può essere omesso
immediatamente prima di π,
scientifi che (2 π, 5A, πA, 3mp, 2
con parentesi (2'(3), Asin(30), ecc.)
–1
(, cosh–1(, tanh–1(
^(, 10^(, '(,
e
–1
, x!, ° ´ ˝, °, r,
x
(
m
2
<
–1
(, cos–1(, tan–1(, sinh(, cosh(,
3
(
'
g
, variabili, costanti
e
, ecc.), e funzioni
i
I-74
Page 76

Sequenza Tipo di operazione Descrizione
= 4
or, xor, xnor
1
i
2
1
i
2
Stack numerico Stack dei comandi
Stack numerico Stack dei comandi
1
1
2
2
2
2
3
3
3
3
4
4
4
4
5
5
5
5
4
4
1
1
2
2
3
3
4
4
5
5
6
6
7
7
11 Prodotto logico, Somma logica
esclusiva, Somma logica
negativa esclusiva
Nota
• Se un calcolo contiene un valore negativo, potrebbe essere necessario racchiudere il valore
negativo in parentesi. Se si desidera elevare al quadrato il valore –2, ad esempio, è necessario
introdurre: (–2)
sopra), la cui priorità è maggiore rispetto al segno negativo, che rappresenta un simbolo di
prefi sso (priorità 4).
-cxw
(-c)
• Moltiplicazione e divisione, e moltiplicazione dove è omesso il segno, hanno la stessa priorità
(priorità 7), così queste operazioni vengono eseguite da sinistra a destra quando entrambi i tipi
sono riportati nello stesso calcolo. Racchiudendo un’operazione in parentesi si determina la sua
esecuzione per prima, in tal modo l’uso di parentesi può produrre risultati di calcolo differenti.
b
b$(c
Limitazioni di stack
k
Questa calcolatrice utilizza aree di memoria chiamate “stack” per memorizzare temporaneamente
valori, comandi e funzioni della sequenza di priorità di calcolo più bassa. Lo stack numerico ha 10
livelli e lo stack dei comandi ha 24 livelli, come viene mostrato nell’illustrazione sotto.
1
1
1 2 3 4 5 6
1 2 3 4 5 6
$
c
2
2
2
. Questo perché
.
3
3
2
è una funzione preceduta da un valore (priorità 2, riportato
x
(–2)
2
= –4
2
–2
xw
( i)w 1 { 2 i =
( i)
1 { (2 i) = –
)
.
w
45
45
7
7
Si verifi ca un errore Stack ERROR quando il calcolo che si sta eseguendo supera la capacità di
uno stack.
Nota
Quando si introduce un valore nel modo CMPLX, ogni valore richiede due livelli di stack: uno per
la parte reale e uno per la parte immaginaria. Questo sta a signifi care che lo stack numerico ha
soltanto cinque livelli nel modo CMPLX.
I-75
Page 77

Gamme di calcolo, numero di cifre e precisione
k
La tabella seguente mostra la gamma generale di calcolo (gamma dei valori di introduzione e
emissione), numero di cifre utilizzato per i calcoli interni, e precisione di calcolo.
Gamma di calcolo ±1×10
Calcolo interno 15 cifre
Precisione
Gamme di introduzione di funzioni di calcolo e precisione
A
Funzioni Gamma di introduzione
DEG 0
sin
RAD 0
x
GRA 0
DEG 0
cos
tan
sin
cos
tan
sinh
cosh
sinh
cosh
tanh
tanh
logx/lnx0 <
RAD 0
x
GRA 0
DEG Uguale come sinx, eccetto quando
RAD Uguale come sin
x
GRA Uguale come sin
–1
x
0
|x|
x
x
x
x
–1
x
–1
x
x
–1
x
x
<
0
|x|
<
0
|x|
<
0
|x|
<
1
<x<
0
|x|
<
0
|x|
<
<
x
–9,999999999×10
–9,999999999×10
0
< 1×10
<
x
< 1×10
|x|
–1
–1
10
x
e
'
x
2
x
–99
a ±9,999999999×1099 o 0
In generale, ±1 alla 10ª cifra per un singolo calcolo. L’errore nel caso
di un risultato di calcolo in formato esponenziale è ±1 all’ultima cifra
signifi cativa della mantissa. Nel caso di calcoli consecutivi, gli errori
sono cumulativi.
9
< 9×10
|x|
<
< 157079632,7
|x|
<
<
<
<
<
1
<
9,999999999×10
<
230,2585092
<
4,999999999×10
<
4,999999999×10
9,999999999×10
<
9,999999999×10
<
9,999999999×10
50
< 1×10
|
|
x
< 9×10
|x|
< 157079632,7
|x|
< 1×10
|
|
x
99
<x<
99
<x<
100
10
9
10
, eccetto quando
x
, eccetto quando
x
99
99
99
99
–1
99
99,99999999
230,2585092
= (2n–1)×90.
|x|
= (2n–1)×π/2.
|x|
= (2n–1)×100.
|x|
I-76
Page 78

Funzioni Gamma di introduzione
1/
|x|
x
3
|
'
x
!0
x
0
nPr
1< {
nCr
Pol(x,y)
Rec(r,θ)
0
1
|
0
θ
|
°’ ”
0
|x|
Conversione decimale ↔ sessagesimale
0°0´0
x
x
y
^(
)
x
x
Tu ttavia: –1×10
y
y
x
'
y
y
Tu ttavia: –1×10
Il totale di numeri interi, numeratore e denominatore devono essere di 10 cifre o
b
/
a
c
minori (inclusi i simboli di separatore)
• Le funzioni di tipo ^(
può avere come risultato l’accumulazione di errori che si verifi cano all’interno di ogni singolo
calcolo.
• Gli errori sono cumulativi e tendono ad aumentare in vicinanza di un punto singolare di funzione
e di un punto di infl essione.
100
< 1×10
;
G
x
100
< 1×10
|
x
69 (x è un numero intero)
<x<
< 1×1010, 0
<
n
!/(n–r)!} < 1×10
n
< 1×1010, 0
<
n
<
n!/r
|,|y|
x
2
2
+
x
y
<
<
r
: Uguale come sin
,b,c < 1×10
|
a
<
b,c
< 1×10
˝
> 0: –1×10
= 0: y > 0
< 0: y = n,
> 0:
x
= 0: x> 0
< 0: x= 2n+1,
y), x
x
<r<
<r<
100
! < 1×10
9,999999999×10
<
9,999999999×10
<
9,999999999×10
100
100
9999999°59´59
|x|
<
<
100
< ylogx < 100
m
2n+1
100
0, –1×10
G
2n+1
m
100
3
,
, x!, nP r, nC r richiedono il calcolo consecutivo interno, che
'
'
y
0
sono numeri interi)
n (n,r
100
sono numeri interi)
n (n,r
o 1
!/(n–r)! < 1×10
<
n
99
99
99
x
˝
sono numeri interi)
(
m,n
< ylog
< 100
|x|
100
< 1/xlogy < 100
(
0; m,n sono numeri interi)
G
m
< 1/xlog
|y|
< 100
100
Messaggi di errore
k
Se si esegue un calcolo che supera il limite della calcolatrice, o
si tenta di eseguire qualche operazione che non è consentita,
apparirà un messaggio di errore sulla schermata.
I-77
Mat h ERRORMat h ERROR
Esempio di messaggio di errore
Page 79

Ricupero da un messaggio di errore
A
È possibile ricuperare da un messaggio di errore eseguendo le operazioni con i tasti descritte sotto,
indifferentemente dal tipo di errore.
• Premere d o e per visualizzare la schermata di modifi ca per l’espressione di calcolo introdotta
immediatamente prima che si è verifi cato l’errore, con il cursore localizzato alla posizione che ha
causato l’errore. Per maggiori informazioni, vedere “Ritrovamento della posizione di un errore” a
pagina 14.
• Premendo A si cancellerà l’espressione di calcolo introdotta immediatamente prima del
verifi carsi dell’errore. Notare che un’espressione di calcolo che determina un errore non verrà
inclusa nella memoria storica di calcolo.
Riferimento del messaggio di errore
A
Questa sezione elenca tutti dei messaggi di errore che la calcolatrice visualizza, come anche le
loro cause e tutto ciò che è necessario eseguire per evitarli.
Math ERROR (Errore matematico)
Causa • Un risultato intermedio o fi nale del calcolo cade fuori della gamma di
Rimedio • Controllare i valori introdotti e ridurre il numero di cifre, se si richiede.
Per informazioni riguardo la gamma di introduzione del valore consentito, vedere “Gamme di
calcolo, numero di cifre e precisione” a pagina 76.
Stack ERROR (Errore di stack)
Causa Il calcolo ha superato la capacità dello stack numerico o dello stack dei
Rimedio • Semplifi care l’espressione di calcolo in modo che essa non ecceda la
Per informazioni riguardo le capacità degli stack, vedere “Limitazioni di stack” a pagina 75.
Syntax ERROR (Errore di sintassi)
Causa Il calcolo ha un problema di formato.
Rimedio Controllare la sintassi ed effettuare le correzioni richieste.
Arg ERROR (Errore di argomento)
Causa Il calcolo ha un problema con la modalità d’uso di un argomento.
Rimedio Controllare come sono utilizzati gli argomenti ed effettuare le correzioni
calcolo consentita.
• Un valore introdotto è fuori della gamma di introduzione consentita.
• Si sta tentando di eseguire un’operazione matematica non consentita
(come ad esempio una divisione per zero).
• Quando si usa la memoria indipendente o una variabile come argomento
di una funzione, assicurarsi che il valore della memoria o della variabile
sia all’interno della gamma consentita per la funzione.
comandi.
capacità degli stack.
• Tentare di suddividere il calcolo in due o più parti.
richieste.
I-78
Page 80

Data Full (Dati pieni)
Causa Si sta tentando di salvare i dati campione nel modo SD o nel modo REG
Rimedio Mantenere il numero di campioni di dati entro il limite consentito. Per
Go ERROR
Causa
Rimedio
Prima di ritenere che la calcolatrice abbia un malfunzionamento...
k
Eseguire i seguenti passi ogniqualvolta si verifi ca un errore durante un calcolo, o quando i risultati
di calcolo non sono quelli che ci si attende. Se il passo non corregge il problema, procedere al
passo seguente. Notare che è opportuno eseguire copie dei dati importanti prima dell’esecuzione
di questi passi.
Controllare l’espressione di calcolo, per assicurarsi che non includa nessun errore.
1
Assicurarsi che si sta utilizzando il modo corretto per il tipo di calcolo che si sta provando ad
2
eseguire.
Se i passi riportati sopra non ripristinano il funzionamento normale, premere il tasto p.
3
La calcolatrice eseguirà un autocontrollo del suo stato, come quando essa si avvia. Se
la calcolatrice rileva un problema, essa ritornerà al suo modo di calcolo e predisporrà le
impostazioni iniziali di default, e quindi cancellerà tutti i dati presenti correntemente in memoria.
Se il passo 3 non ripristina il funzionamento normale, inizializzare tutti i modi e le impostazioni
4
premendo
quando il numero di campioni di dati consentito è già registrato in memoria.
maggiori informazioni, vedere “Numero massimo di elementi di dati di
introduzione” a pagina 39.
Un programma (da voi creato nel modo PRGM) ha un comando “Goto
senza un’etichetta corrispondente “Lbl
Aggiungere un’etichetta “Lbl n” per il comando “Goto n”, o cancellare il
comando applicabile “Goto
(CLR)d(All)w.
j
!
”.
n
”.
n
”
n
Requisiti di alimentazione
La vostra calcolatrice ha un sistema TWO WAY POWER che combina una cella solare
con una pila a bottone (LR44). Differentemente dalle calcolatrici che funzionano solo
quando la luce è presente, una calcolatrice con sistema TWO WAY POWER mantiene il
funzionamento anche al buio. (Senza dubbio, per consentire la lettura del contenuto del
display sarà necessaria un’illuminazione suffi ciente.)
Sostituzione della pila
A
Se dopo l’accensione della calcolatrice i caratteri appaiono scuri, specialmente quando si
usa la calcolatrice dove l’illuminazione è scarsa, oppure la risposta della visualizzazione
è lenta, sta ad indicare che la pila a bottone è scarica. Sostituire la pila ogniqualvolta si
notano questi sintomi. Inoltre si deve sostituire regolarmente la pila almeno una volta ogni
tre anni, anche se la calcolatrice sta funzionando normalmente.
I-79
Page 81

Importante!
Rimuovendo la pila a bottone della calcolatrice, si causa la cancellazione dei contenuti della
memoria indipendente e dei valori assegnati alle variabili.
1. Premere
Per assicurarsi di non accendere accidentalmente la
calcolatrice durante la sostituzione della pila, slittare la
custodia rigida sulla parte frontale della calcolatrice.
2. Sul retro della calcolatrice, rimuovere la vite e il coperchio
del vano pila.
3. Rimuovere la pila esaurita.
4. Dopo aver strofi nato una nuova pila con un panno asciutto,
inserirla nel vano pila con il suo lato positivo k rivolto
verso l’alto (in modo da poterlo vedere).
5. Ricollocare il coperchio del vano pila e fi ssarlo al suo posto
con la vite.
6. Inizializzare la calcolatrice premendo
Accertarsi di eseguire questo passo! Non saltarlo!
Spegnimento automatico
A
La vostra calcolatrice si spegnerà automaticamente se non si esegue nessuna operazione
per circa 10 minuti. Se questo accade, premere il tasto p per accendere di nuovo la
calcolatrice.
(OFF) per spegnere la calcolatrice.
!A
!
j
(CLR)d(All)w.
ViteVite
Specifi che tecniche
Requisiti di alimentazione:
Cella solare: Incorporata sulla parte frontale della calcolatrice (fi ssa)
Pila a bottone: Tipo G13 (LR44) × 1
Durata della pila approssimativa:
3 anni (Sulla base di 1 ora di funzionamento al giorno)
Temperatura d’impiego: Da 0˚C a 40˚C
Dimensioni: 12,2 (A) × 80 (L) × 161 (P) mm
Peso approssimativo: 105 g inclusa la pila
Accessori in dotazione: Custodia rigida
I-80
Page 82

MEMO
I-81
Page 83

MEMO
I-82
Page 84

MEMO
I-83
Page 85

MEMO
I-84
Page 86

CASIO Europe GmbH
Bornbarch 10, 22848 Norderstedt,
Germany
Questo marchio vale soltanto nei paesi dell’UE.
Page 87

CASIO COMPUTER CO., LTD.
6-2, Hon-machi 1-chome
Shibuya-ku, Tokyo 151-8543, Japan
SA0603-A Printed in China
 Loading...
Loading...