Casio CLASSPAD II Quick Reference Manual

Download

Page 1

ClassPad II

Quick

Reference Guide

Press these keys for numbers, basic operations, and the most common variables

Tap any icon to select the application.

Tap m at any time to return to the menu screen.

Tap M at any time to return to the Main menu.

Tap to advance to the next page.

In any menu application, press k for the onscreen keyboard.

Press c to power on. Then press c to clear commands. Press Kc to power off.

Press these keys for numbers, basic operations, and the most common variables

Press E to execute commands.

Press these keys for numbers, basic operations, and the most common variables

Page 2

ClassPad II

Chapter 1 Main Menu ………….. ...............Page 3

Chapter 2 Numerical Solve Menu ……. ......Page 13

Chapter 3 Graph and Table Menu …… .......Page 15

Chapter 4 Conic Menu …….. .....................Page 25

Chapter 5 Statistics Menu …. .....................Page 32

Quick

Reference Guide

Author:

John Diehl Casio Teacher Advisory Council Editors: Nathan Austin, Amber Branch, Amy Chow Casio Education, Curriculum and Training Department

Page 3

Main Menu

If an object, such as a ball, is dropped from a initial height, c, the height, h, in feet, as a

function of time, t, in seconds, can be modeled by h = -16t

If the object is tossed upwards with an initial velocity, v, then the model becomes h = -16t2 + vt + c. These models ignore air resistance.

1. If a ball is dropped from a height of 120 feet, compute the height after 2 seconds.

Tap M for the Main menu.

Press: z16*2^2+120E.

+ c.

For a more mathematical display, the raised exponent template can be used from the Math1 Keyboard.

Press:

z16*2kO2:+120 E.

This expression can also be evaluated using a variable for substitution. A command in the form expression | variable = value means evaluate the expression with the given value(s) substituted for the variable(s).

Press

z16k_[)O2:+12 0-U_[=2E.

Getting Started with the Classpad II

Page 4

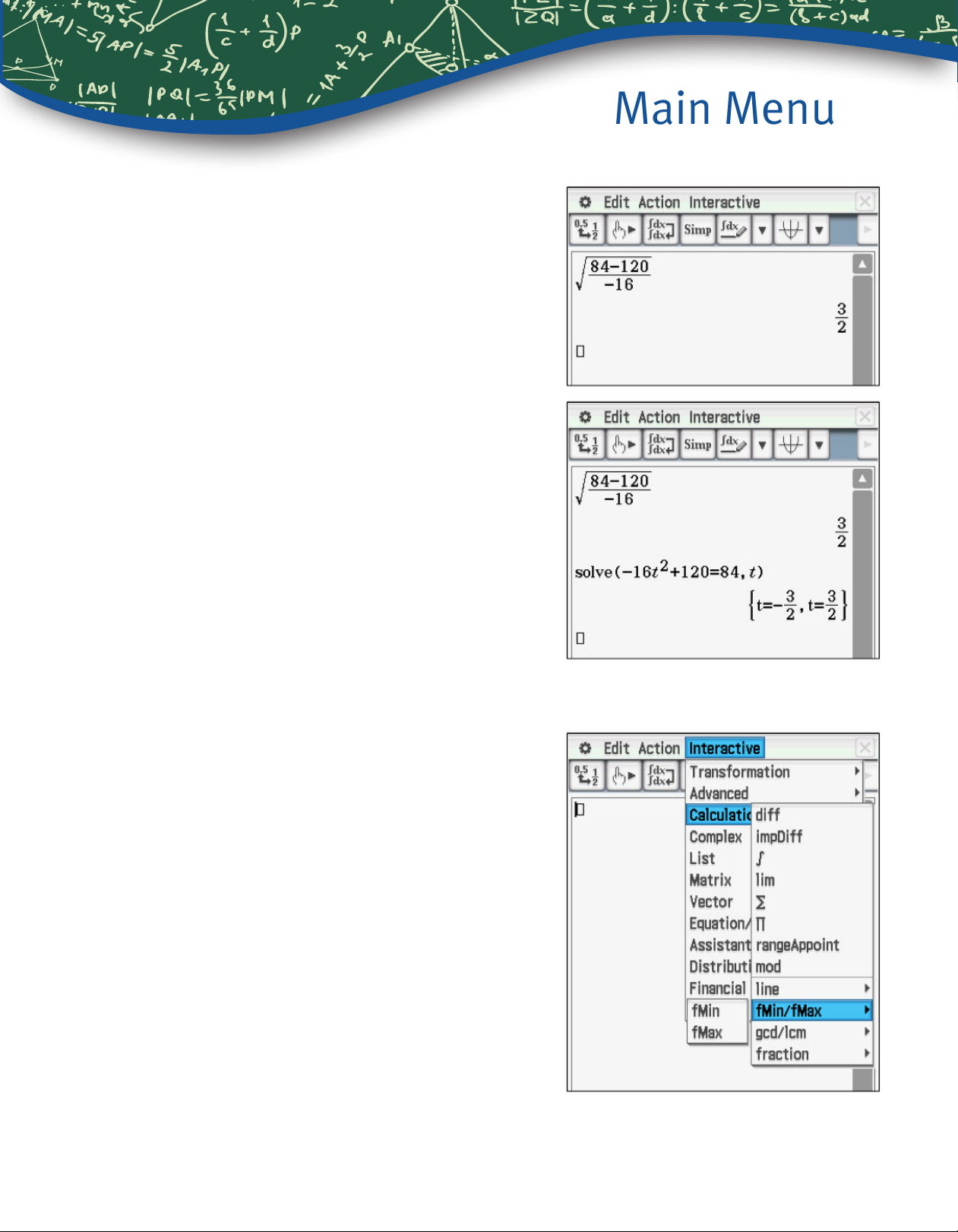
2. Compute the time when the height of the ball is 84 feet.

The value can be computed using the square root and fraction templates from Math1.

Tap

k5N84120Cz16E.

The value can also be computed using a solve command from Math1. The format is (equation,variable) even if there is only one variable in the equation.

Main Menu

Tap

)`z16_)O2 :+120=84,_ [)E.

3. A ball is tossed upwards with an initial velocity of 56 feet/second, from an initial height of 120 feet. Compute the time and the height when the ball is at a maximum height.

Commands such as fMax are found under the

Interactive and the Action menus. The Interactive commands open a dialogue box which gives

prompts for the input. The fMax command uses x as the default variable, but another variable such as t can be used.

Getting Started with the Classpad II

Page 5

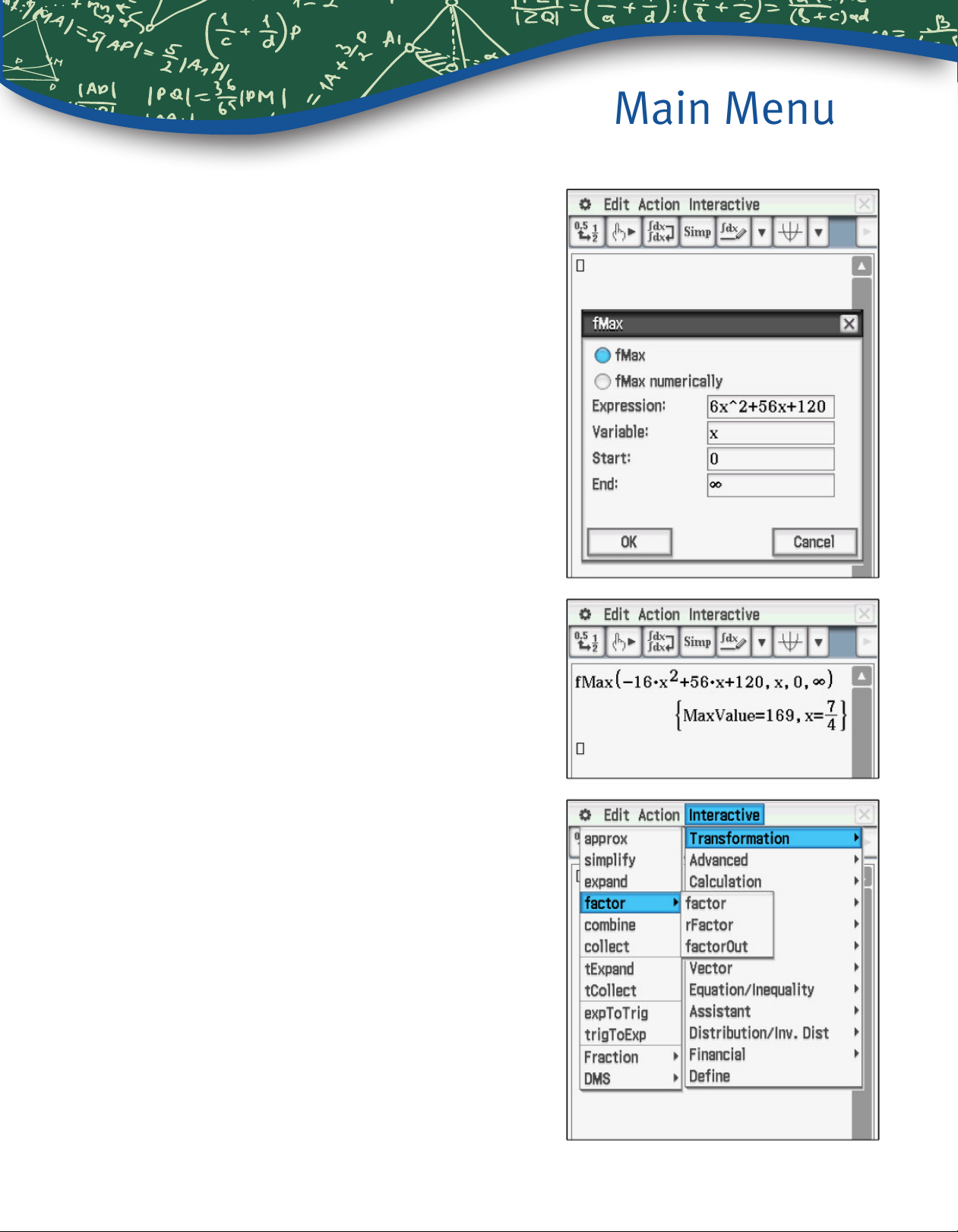
Tap Interactive, Calculation, fMin/fMax, fMax

and complete the inputs as shown. (Part of the rst coefcient, -16, has scrolled off the screen.)

Then tap OK.

Main Menu

4. Rewrite the expression from Question 3 in factored form.

Tap Interactive, Transformation, factor, factor.

Getting Started with the Classpad II

Page 6

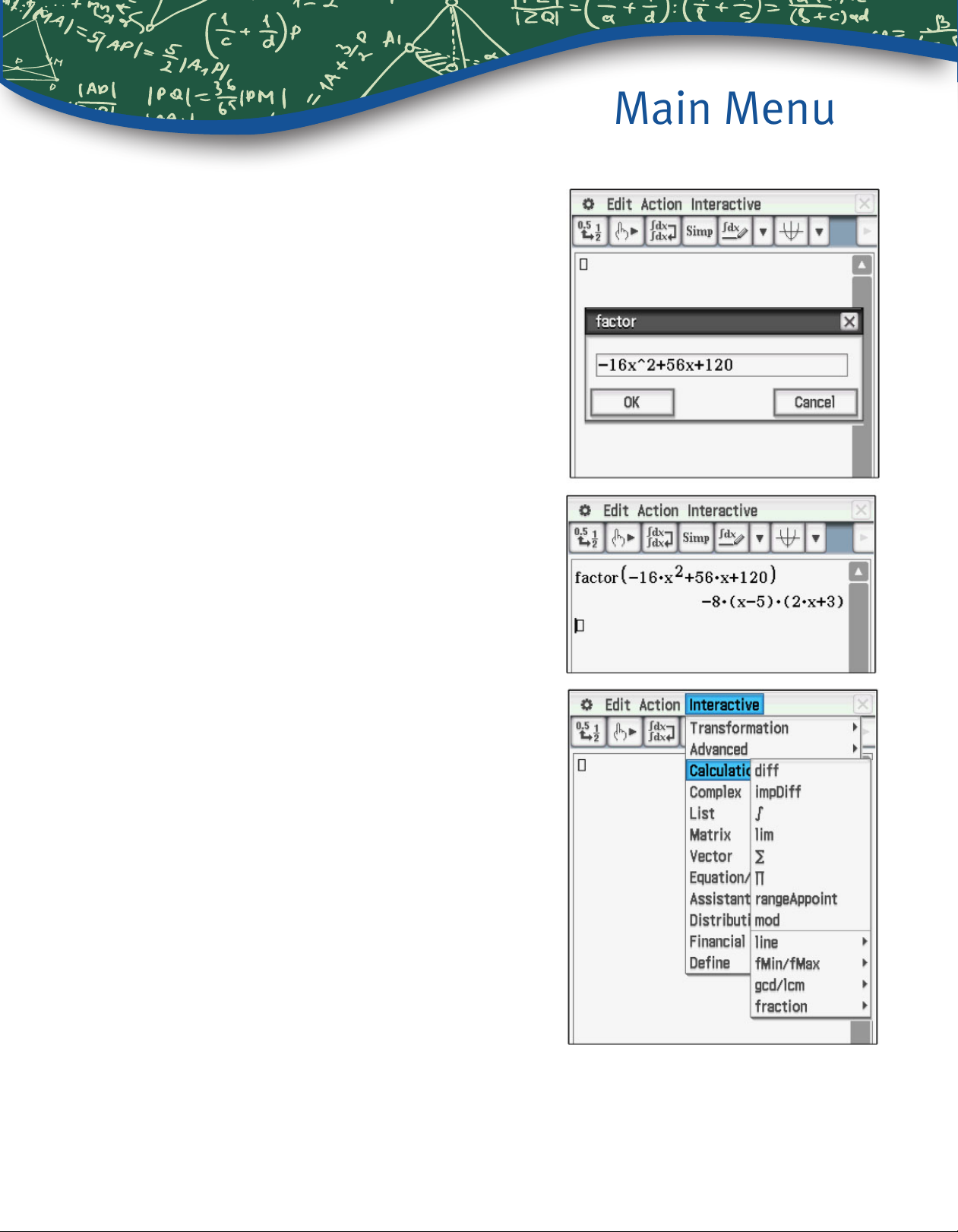
Enter the expression in the box. Then tap OK.

Main Menu

5. This model expresses height, or position, as a function of time. Construct a model for velocity as a function of time.

The velocity would be the derivative of the position function.

Tap Interactive, Calculation, diff.

Getting Started with the Classpad II

Page 7

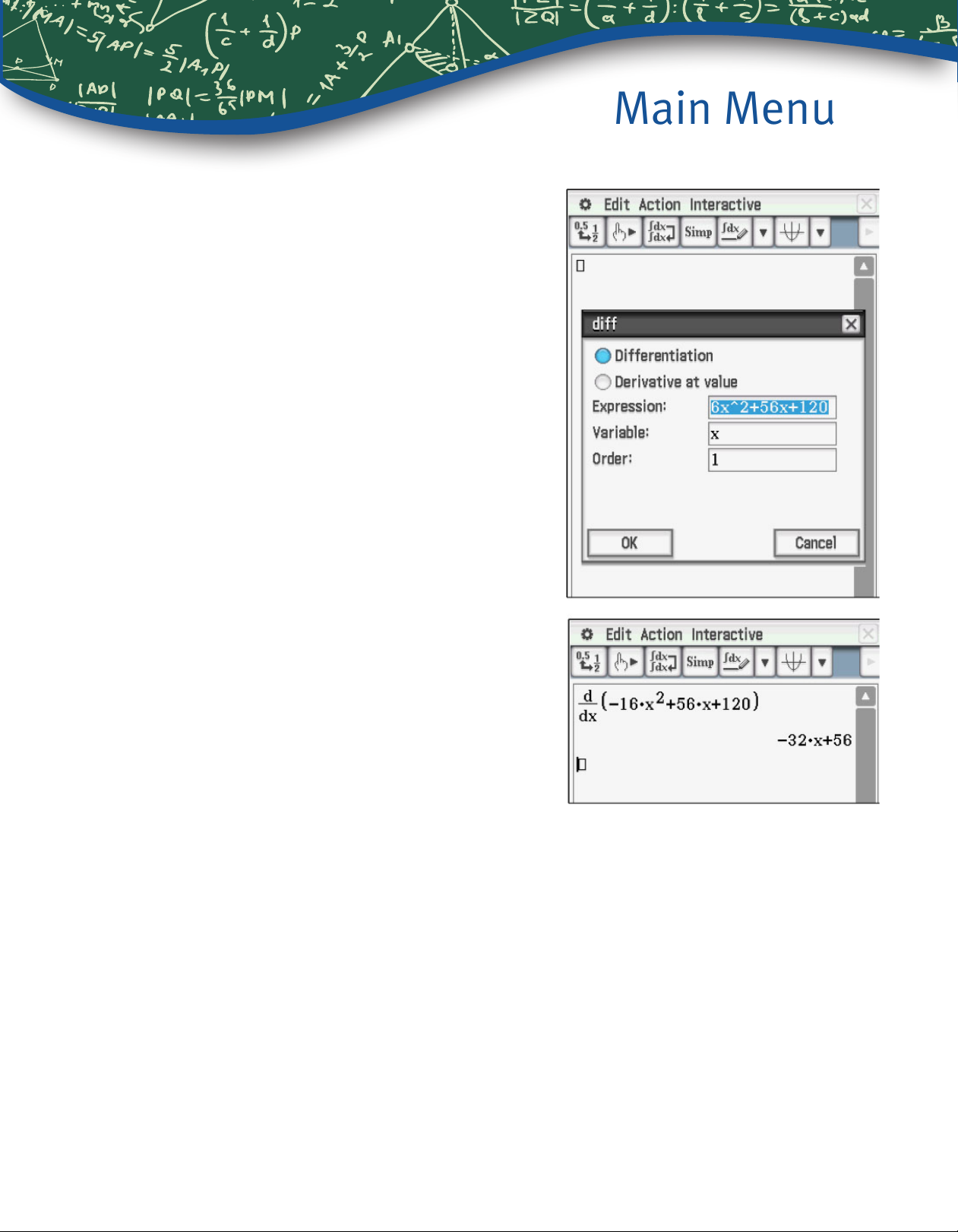
Enter the expression in the box. (Again, part of the

rst coefcient, -16, has scrolled off the screen.)

Then tap OK.

Main Menu

Alternately, the template for a derivative from Math2 can be used; the result will look the same.

Getting Started with the Classpad II

Page 8

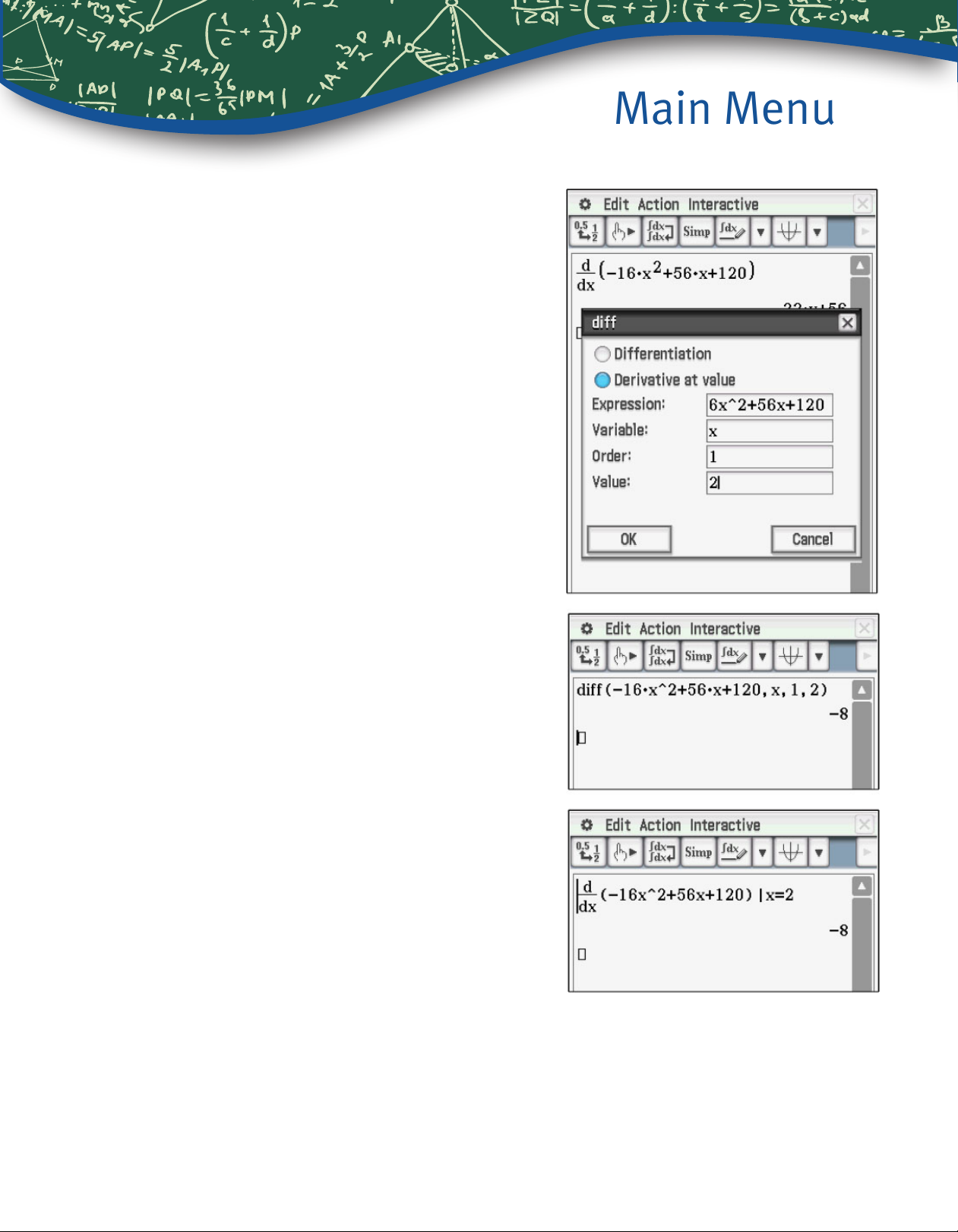
6. Compute the instantaneous velocity at time 2 seconds.

The only difference is to tap the bullet for Derivative at value, and to enter the value in the last box.

Main Menu

For a more intuitive display, use the derivative template from Math2 and the “with” ( on Math3.

U) command

Getting Started with the Classpad II

Page 9

7. Compute the total net distance that the ball travels.

The ball had an initial height of 120 and fell to height of 0, so the net distance should be -120.

For a calculus connection, integrate the velocity function.

Tap k9P.

Enter the integrand, the variable, and the limits. The variable t can be found at

9, then tap

Main Menu

8. Compute the total distance that the ball travels.

The initial height and the maximum height are known, so the total distance can be easily computed.

For another calculus connection, another integral can be used. The traditional approach is to use two integrals, but it is quicker to use the absolute value template. The template is also in

Getting Started with the Classpad II

Page 10

Main Menu

The ClassPad has a symbolic algebra system, sometimes called a computer algebra system, or CAS. An important distinction is a calculator using symbolic algebra can manipulate undeclared variables. The factoring example from Question 4 was an illustration. It is usually a good idea to tap Edit, then Clear All Variables to ensure that the variables do not have a value stored in memory. The next 2 questions illustrate additional symbolic algebra.

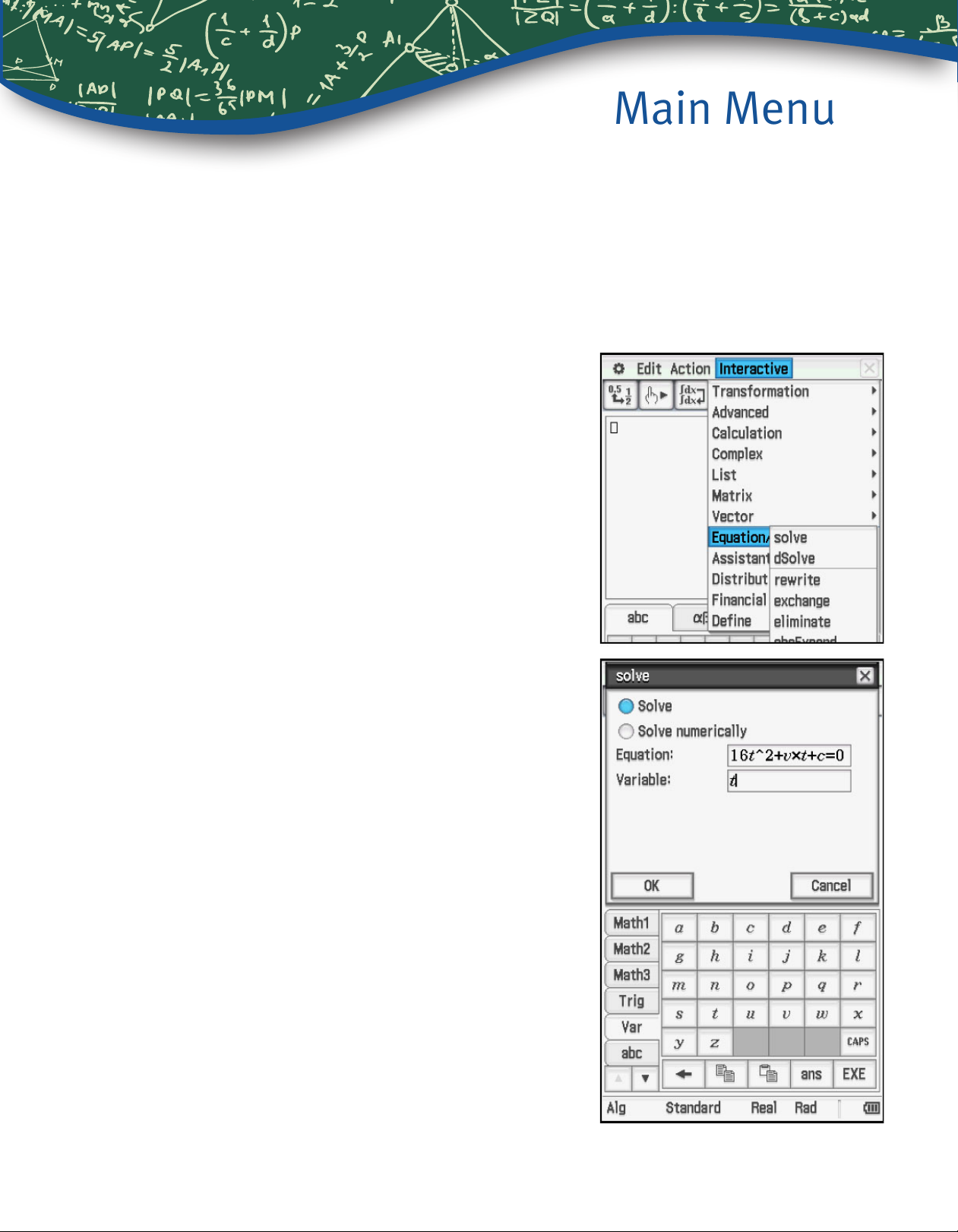
9. If a model for the height of a ball thrown upwards

as a function of time is given by h = -16t compute an expression for the time when the ball hits the ground.

Tap Interactive, Equation, solve.

+ vt + c,

Enter the equation in the box by pressing k and tap sign is to the left of 16 and has scrolled off.

Enter the variable in the second box and tap E, or press the

0 to view the variables. The negative

E key; then tap OK.

Getting Started with the Classpad II

Page 11

Both solutions are shown; the rst solution would be

negative and is not in the domain.

10. If a model for the height of a ball, thrown upwards, as a function of time, is given by

h = -16t velocity as a function of time.

+ vt + c, compute an expression for

Main Menu

Press

k and tap 9].

Enter the expression and the variable and tap E, or press the

E key.

Getting Started with the Classpad II

Page 12

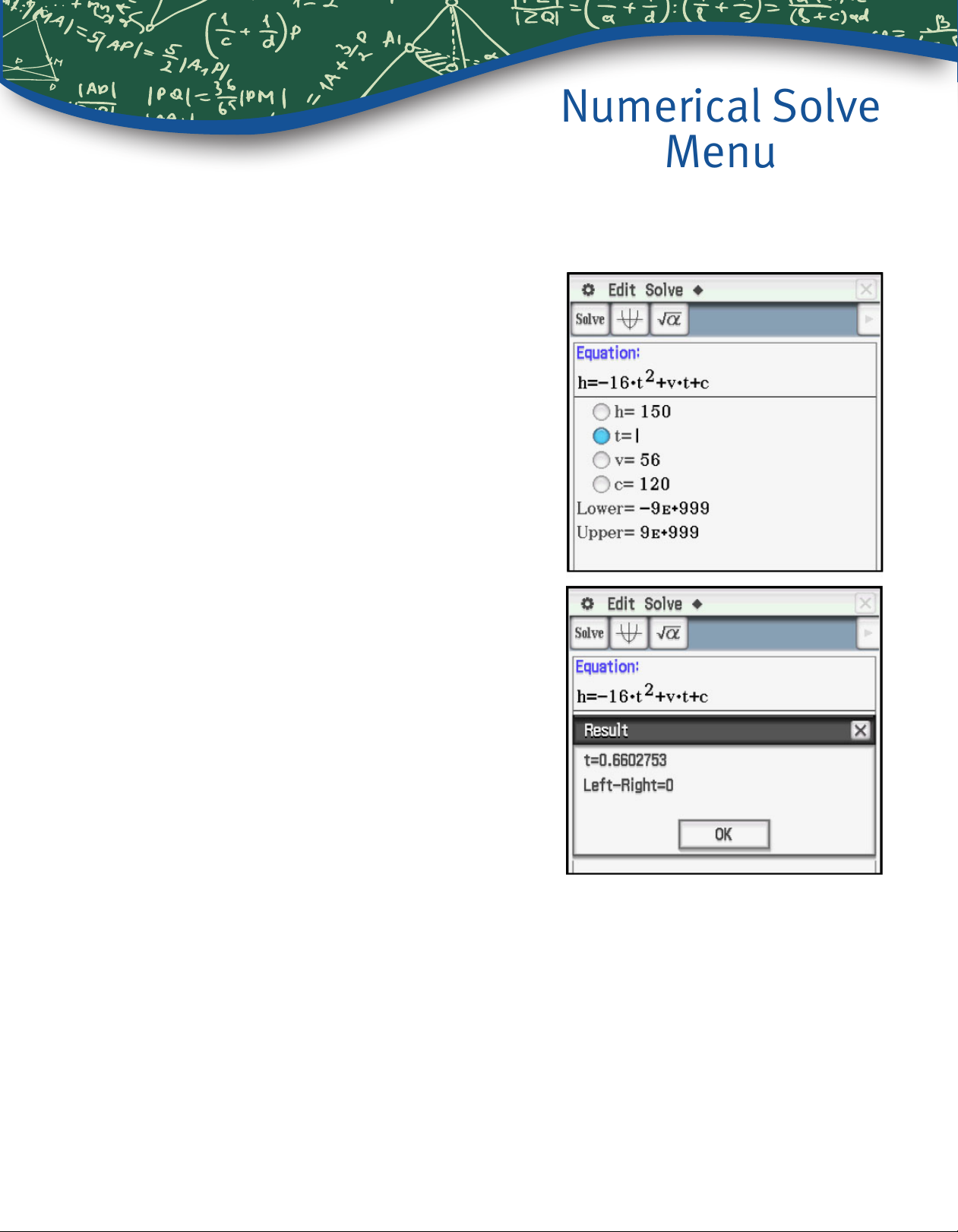
Numerical Solve

To use the Numerical Solve menu, tap the icon, enter the equation in the box, then enter values for the variables. Tap the bullet for the unknown variable and tap

1. If a ball is tossed upwards with an initial velocity of 56 ft/sec, from an initial height of 120 feet, compute the times when the ball is at height 150 feet.

Enter the equation. Note that a times symbol is needed between v and t to distinguish the product from a single variable named vt.

Enter the values of 150, 56, and 120, select the bullet for t and tap

Getting Started with the Classpad II

Page 13

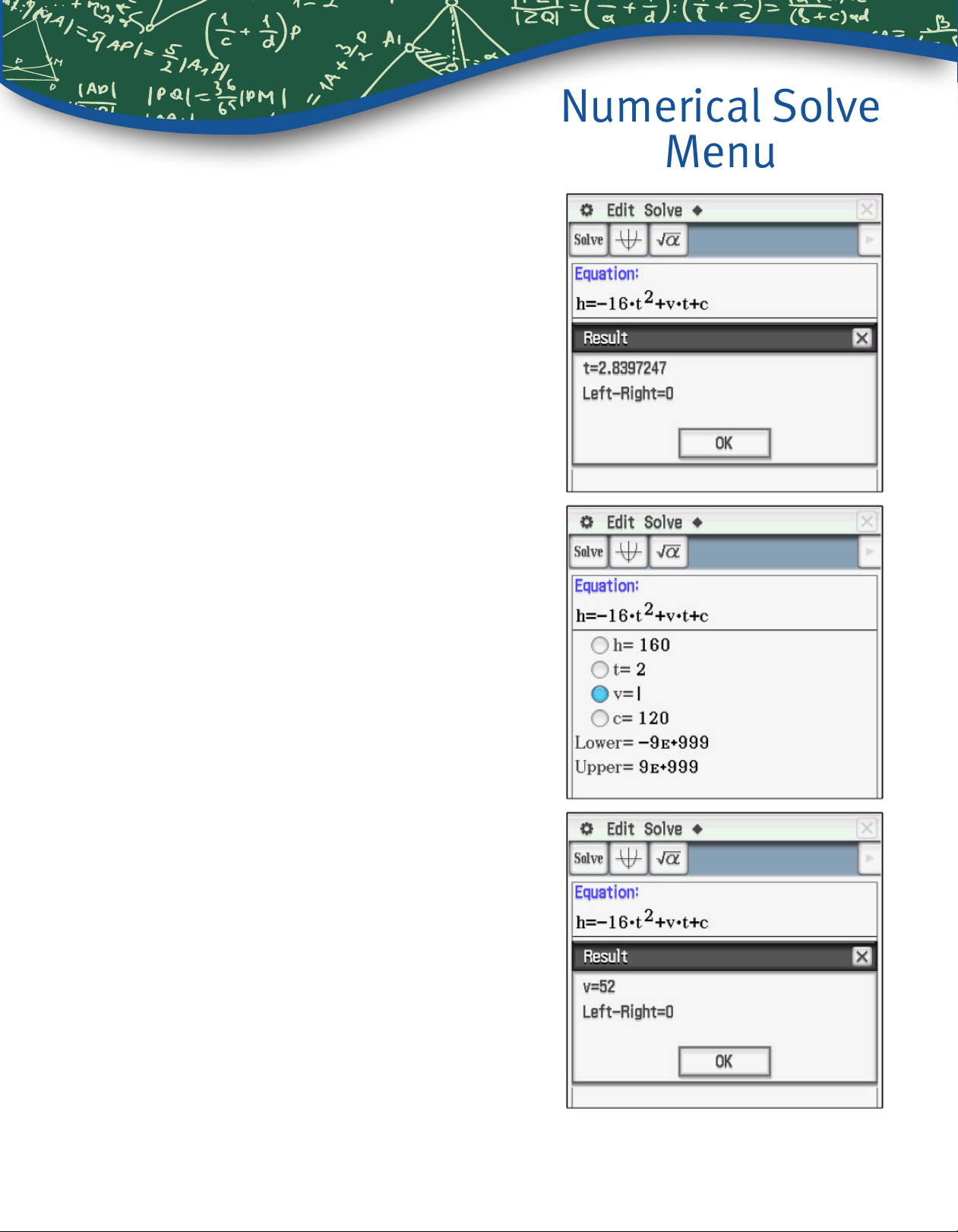
To compute the second value for t, enter an initial estimate, say 4, for t and tap

2. If a ball is tossed upwards from an initial height of 120 feet, and has height of 160 feet after 2 seconds,

Numerical Solve

compute the initial velocity.

Enter the values of 160, 2, and 120, select the bullet for v and tap

Getting Started with the Classpad II

Page 14

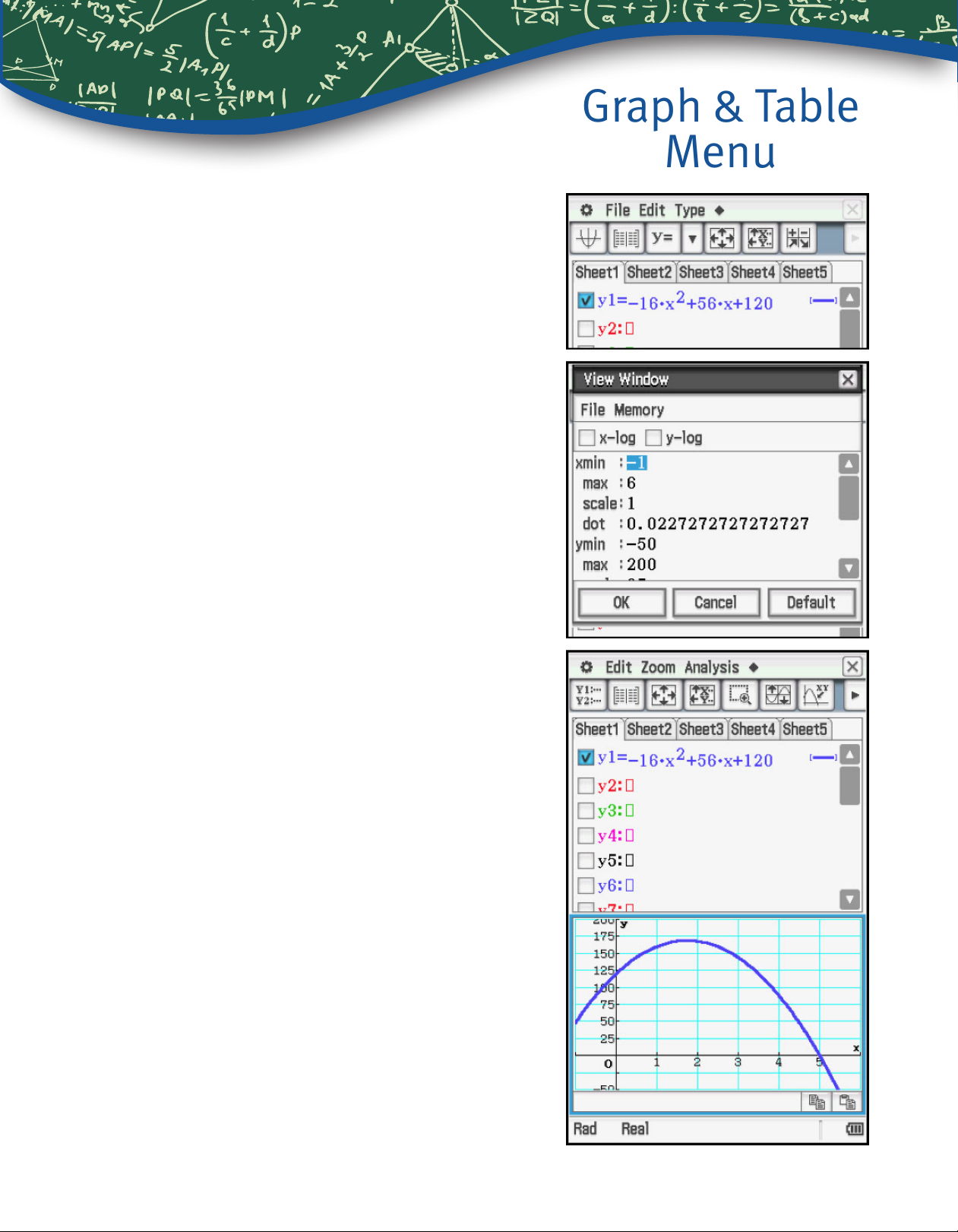
1. If a ball is tossed upwards with an initial velocity of 56 ft/sec from an initial height of 120 feet, graph the height of the ball, as a function of time.

From the Menu, select the Graph & Table icon.

Enter the function as y1.

To set a window tap 6, enter the values and tap OK.

Graph & Table

$ to graph.

Tap

Getting Started with the Classpad II

Page 15

Tap r to plot the graph in a full screen. To adjust the window, use the four directions, to zoom out.

#"23 to scroll in any of

+ to zoom in, and -

Graph & Table

2. Compute the height of the ball at time 4 seconds.

To trace, tap one of the number keys; this will open a dialogue box. Then tap OK.

=. To nd a specic value, press any

Getting Started with the Classpad II

Page 16

Graph & Table

Press coordinates on the display.

E to mark the point and keep the

Getting Started with the Classpad II

Page 17

3. Compute the times when the ball is at height 150 feet.

Tap Analysis, G-Solve, x-Cal/y-Cal, x-Cal.

Graph & Table

Enter the value for y and tap OK.

Getting Started with the Classpad II

Page 18

Press E to mark the point and keep the coordinates on the display.

Press 3 to move to the second point.

Graph & Table

4. Compute the time when the ball hits the ground.

To compute an x-intercept, tap the top of the screen, then tap

3 icon at the

Getting Started with the Classpad II

Page 19

5. Compute the coordinates of the maximum point.

Graph & Table

For a maximum point, tap the the screen, then tap

6. Construct a table of values for times

3 icon at the top of

{0, 1, 2, 3, 4, 5}.

To set the table, tap

Enter the values and tap OK.

Getting Started with the Classpad II

Page 20

To view the table, tap #.

Graph & Table

Getting Started with the Classpad II

Page 21

Graph & Table

These examples have used the coefcient of -16 for the t2 term. The value of that coefcient

could be different, based on conditions such as altitude. It would also be different on the moon or another planet, and of course, if different units for distance and/or time were used.

−

A more general equation for the model would be h =

the general quadratic y = ax

7. Explore the transformations of the graph of the function y = ax2 + bx + c as the coefcients a, b, c are changed.

Enter the function y1 = 1x2 + 0x + 0. The three

coefcients are needed, as explained later.

Set the window to Default.

+ bx + c.

gt2 + vt + c. This is an application of

Graph the equation.

Getting Started with the Classpad II

Page 22

Tap Analysis, Modify.

Enter 1 for the Step size and tap OK.

Graph & Table

The word Modify appears on the graph screen, the graph is thicker, and the function rule appears in a dialogue box at the bottom. To explore the

transformations, tap any one of the 3 coefcients

and highlight it. Tap on the graph screen. Now use 3 and 2 to increase or decrease the coefcient, respectively, and see the graph transform.

Getting Started with the Classpad II

Page 23

Alternately, to make changes without a step size, tap

any one of the 3 coefcients, highlight it, enter a new

value and press

Graph & Table

Getting Started with the Classpad II

Page 24

Conic Menu

The Conic Menu will graph conics in an (H, K) form, such as x = A(y – K )2 + H, a standard

form such as x = Ay The general form includes rotated conics. The easiest way to input the equation for the

relation is to insert a form, and edit the coefcients.

The G-Solve commands will display important features related to conics, such as a center, vertices, foci, and asymptotes.

1. Graph .

Tap m, then the Conics icon.

Tap

+ By + C, or the general form, Ax2 + Bxy + Cy2 + Dx + Ey + F = 0.

Select the form for this hyperbola, and tap OK.

Edit the coefcients A, B, H, and K. Highlight the letter and press the key for the number. For K, also change from subtraction to addition.

6 to set the window, or use shortcuts after

Tap graphing.

Getting Started with the Classpad II

Page 25

Tap ^ to graph.

Conic Menu

r to plot the graph in a full screen. You may

Tap wish to adjust the window.

The window can be easily changed by using #

"23

to scroll in any of the four directions,

+ to zoom in, and - to zoom out.

Getting Started with the Classpad II

Page 26

2. Display the vertices, foci, and asymptotes.

For vertices, tap Analysis, G-Solve, Vertex.

Conic Menu

Press nates on the display. Press vertex.

Use G-Solve in the same manner for foci and asymptotes.

E to mark the point and keep the coordi-

w to display the other

Getting Started with the Classpad II

Page 27

3. Convert the equation to a standard form.

Tap

r, then tap the equation window.

Tap

w, then select the bullet for general form, then

tap OK.

Conic Menu

Getting Started with the Classpad II

Page 28

4. Graph the rotated conic

– 3xy +4y2 – 5x + 6y – 7 = 0.

Tap

Tap the bullet for general form, then tap OK.

Conic Menu

Edit the coefcients and the signs. The addition sign

and the number can be highlighted together.

Getting Started with the Classpad II

Page 29

Tap ^ to graph.

Conic Menu

Again, you may tap screen.You may wish to adjust the window.

The window can be easily changed by using

#"23 to scroll in any of the four directions,

+ to zoom in, and- to zoom out.

r to plot the graph in a full

Getting Started with the Classpad II

Page 30

G-Solve commands may be used on rotated conics.

Conic Menu

Getting Started with the Classpad II

Page 31

Statistics Menu

Suppose one of the questions asked on a survey was “What type of pet do you have?”, and the results from 50 people are shown in this table.

Pet Category Dog Cat Fish Bird Other None Frequency 14 12 9 6 4 5

1. Construct a pie chart of these data.

It is easiest to work with categorical data from a spreadsheet. Tap

Enter the frequencies in the rst column. Press

to move to the next cell.

m, then the Spreadsheet icon.

To construct the chart, tap Column A so it is selected. If the graph icon is

Z, tap it. Otherwise tap the

# near the top-right to open the graph menu and

then tap

Z from the drop down list.

Getting Started with the Classpad II

Page 32

Statistics Menu

Tap any section of the chart to display the frequency.

Getting Started with the Classpad II

Page 33

Tap the chart and drag to Cell B1 to display the relative frequencies, shown as percents. (tap-anddrag is similar to click-and-drag with a mouse.)

Statistics Menu

2. Construct a bar chart for these data.

Select Column A again. Tap the # near the upperright corner to access the graph drop down menu.

Then tap H to construct a bar chart.

Getting Started with the Classpad II

Page 34

The bar graph is displayed.

Statistics Menu

Tap any bar to display the frequency.

Getting Started with the Classpad II

Page 35

Statistics Menu

Plots and statistics for quantitative data can be created in either the spreadsheet or statistics menu. The statistics menu will be used for this example.

The number of games won (out of 162) by a certain baseball team for the years 2002 – 2013 are shown in the table.

67 88 89 79 66 85 97 83 75 71 61 66

1. Construct a histogram for these data.

m, then the Statistics icon. Enter the frequen-

Tap cies in list1. Press

E to move to the next value.

Tap

G to setup the plot. Select On, and use the

drop down menus to select Histogram, list1, and 1 as shown. Then tap Set.

Getting Started with the Classpad II

Page 36

Tap y. Enter values for the starting value (HStart) and the step (Hstep), the width of each bin; then tap OK.

Statistics Menu

Getting Started with the Classpad II

Page 37

Tap Analysis, Trace to display the frequencies, using the directional pad to move through the data values.

Statistics Menu

Getting Started with the Classpad II

Page 38

2. Construct a box and whisker plot for these data.

Tap the list editor window.

Tap

G to setup the plot. Tap Off for StatGraph1,

then tap the 2 tab to select StatGraph2.

Select On, Medbox, list1, and 1 as shown. Tap the

Statistics Menu

box to Show Outliers and tap Set.

Getting Started with the Classpad II

Page 39

Tap y to view the box and whisker plot.

Statistics Menu

Tap Analysis, Trace and use the directional pad to

view the ve number summary.

Getting Started with the Classpad II

Page 40

3. Compute summary statistics for these data.

When the list editor window is selected (note the bold border) the Calc command is the second command. When the plot window is selected, the Calc command is the third command.

In either case, tap Calc, One-Variable.

Select list1 and 1, then tap OK.

Statistics Menu

One variable statistics are displayed; use the scroll bar to see additional information.

Getting Started with the Classpad II

Page 41