Low Cost, Low Power,
a
FEATURES
COMPUTES
True RMS Value
Average Rectified Value
Absolute Value
PROVIDES
200 mV Full-Scale Input Range
(Larger Inputs with Input Attenuator)
High Input Impedance of 10
Low Input Bias Current: 25 pA max
High Accuracy: 60.3 mV 60.3% of Reading
RMS Conversion with Signal Crest Factors Up to 5
Wide Power Supply Range: +2.8 V, –3.2 V to 616.5 V
Low Power: 200 mA max Supply Current
Buffered Voltage Output
No External Trims Needed for Specified Accuracy
AD737—An Unbuffered Voltage Output Version with
Chip Power Down Is Also Available
PRODUCT DESCRIPTION
The AD736 is a low power, precision, monolithic true
rms-to-dc converter. It is laser trimmed to provide a maximum
error of ±0.3 mV ±0.3% of reading with sine-wave inputs. Furthermore, it maintains high accuracy while measuring a wide
range of input waveforms, including variable duty cycle pulses
and triac (phase) controlled sine waves. The low cost and small
physical size of this converter make it suitable for upgrading the
performance of non-rms “precision rectifiers” in many applications. Compared to these circuits, the AD736 offers higher accuracy at equal or lower cost.
The AD736 can compute the rms value of both ac and dc input
voltages. It can also be operated ac coupled by adding one external capacitor. In this mode, the AD736 can resolve input signal levels of 100 µV rms or less, despite variations in
temperature or supply voltage. High accuracy is also maintained
for input waveforms with crest factors of 1 to 3. In addition,
crest factors as high as 5 can be measured (while introducing
only 2.5% additional error) at the 200 mV full-scale input level.
The AD736 has its own output buffer amplifier, thereby providing a great deal of design flexibility. Requiring only 200 µA of
power supply current, the AD736 is optimized for use in portable multimeters and other battery powered applications.
The AD736 allows the choice of two signal input terminals: a
high impedance (10
with high Z input attenuators and a low impedance (8 kΩ) input
12
Ω) FET input which will directly interface
12
V
True RMS-to-DC Converter
AD736
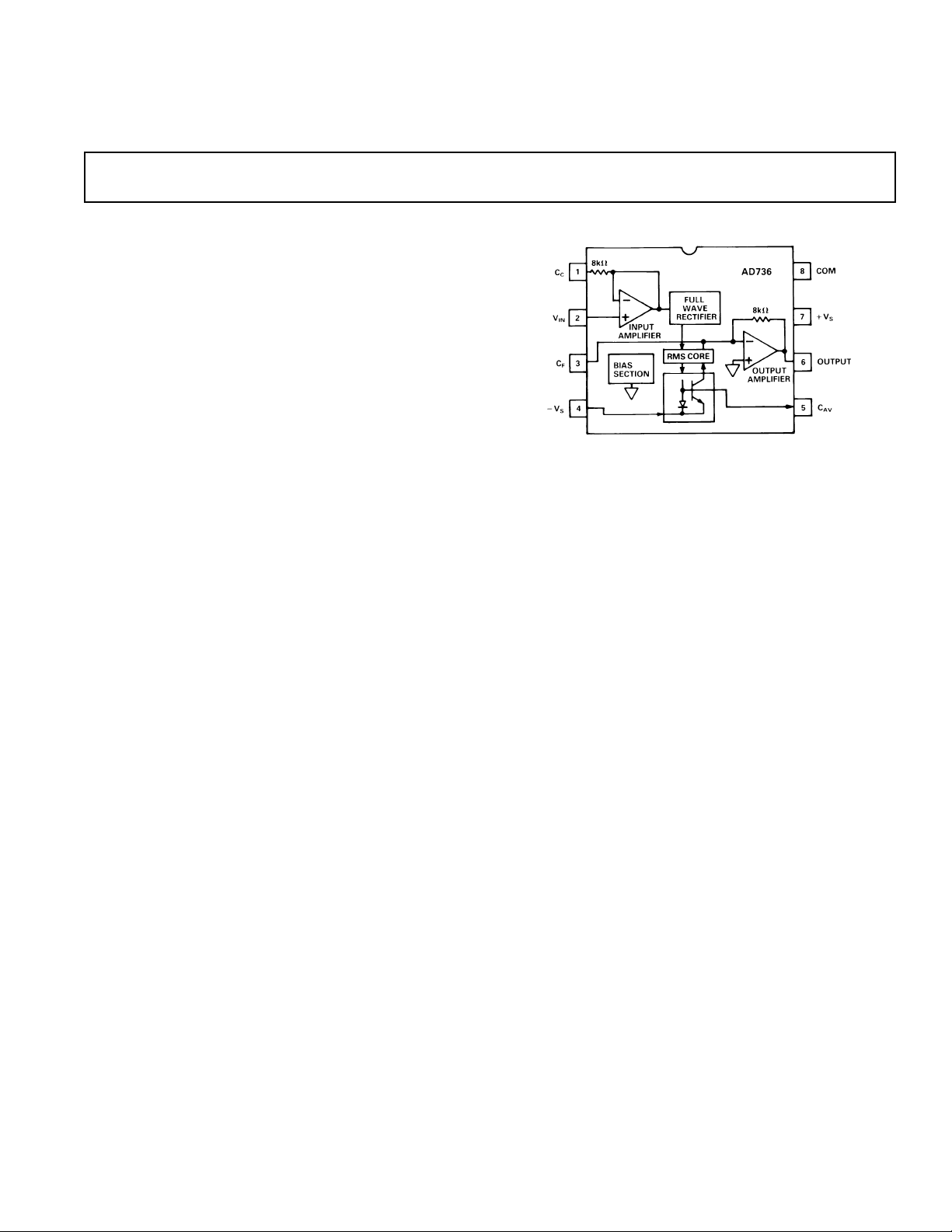
FUNCTIONAL BLOCK DIAGRAM
which allows the measurement of 300 mV input levels, while
operating from the minimum power supply voltage of +2.8 V,
–3.2 V. The two inputs may be used either singly or differentially.
The AD736 achieves a 1% of reading error bandwidth exceeding
10 kHz for input amplitudes from 20 mV rms to 200 mV rms
while consuming only 1 mW.
The AD736 is available in four performance grades. The
AD736J and AD736K grades are rated over the commercial temperature range of 0°C to +70°C. The AD736A and AD736B
grades are rated over the industrial temperature range of –40°C
to +85°C.
The AD736 is available in three low-cost, 8-pin packages: plastic
mini-DIP, plastic SO and hermetic cerdip.
PRODUCT HIGHLIGHTS
1. The AD736 is capable of computing the average rectified
value, absolute value or true rms value of various input
signals.
2. Only one external component, an averaging capacitor, is
required for the AD736 to perform true rms measurement.
3. The low power consumption of 1 mW makes the AD736
suitable for many battery powered applications.
4. A high input impedance of 10
external buffer when interfacing with input attenuators.
5. A low impedance input is available for those applications
requiring up to 300 mV rms input signal operating from low
power supply voltages.
12
Ω eliminates the need for an
REV. C
Information furnished by Analog Devices is believed to be accurate and
reliable. However, no responsibility is assumed by Analog Devices for its
use, nor for any infringements of patents or other rights of third parties
which may result from its use. No license is granted by implication or
otherwise under any patent or patent rights of Analog Devices.
One Technology Way, P.O. Box 9106, Norwood, MA 02062-9106, U.S.A.
Tel: 617/329-4700 Fax: 617/326-8703
(@ +258C 65 V supplies, ac coupled with 1 kHz sine-wave input applied unless
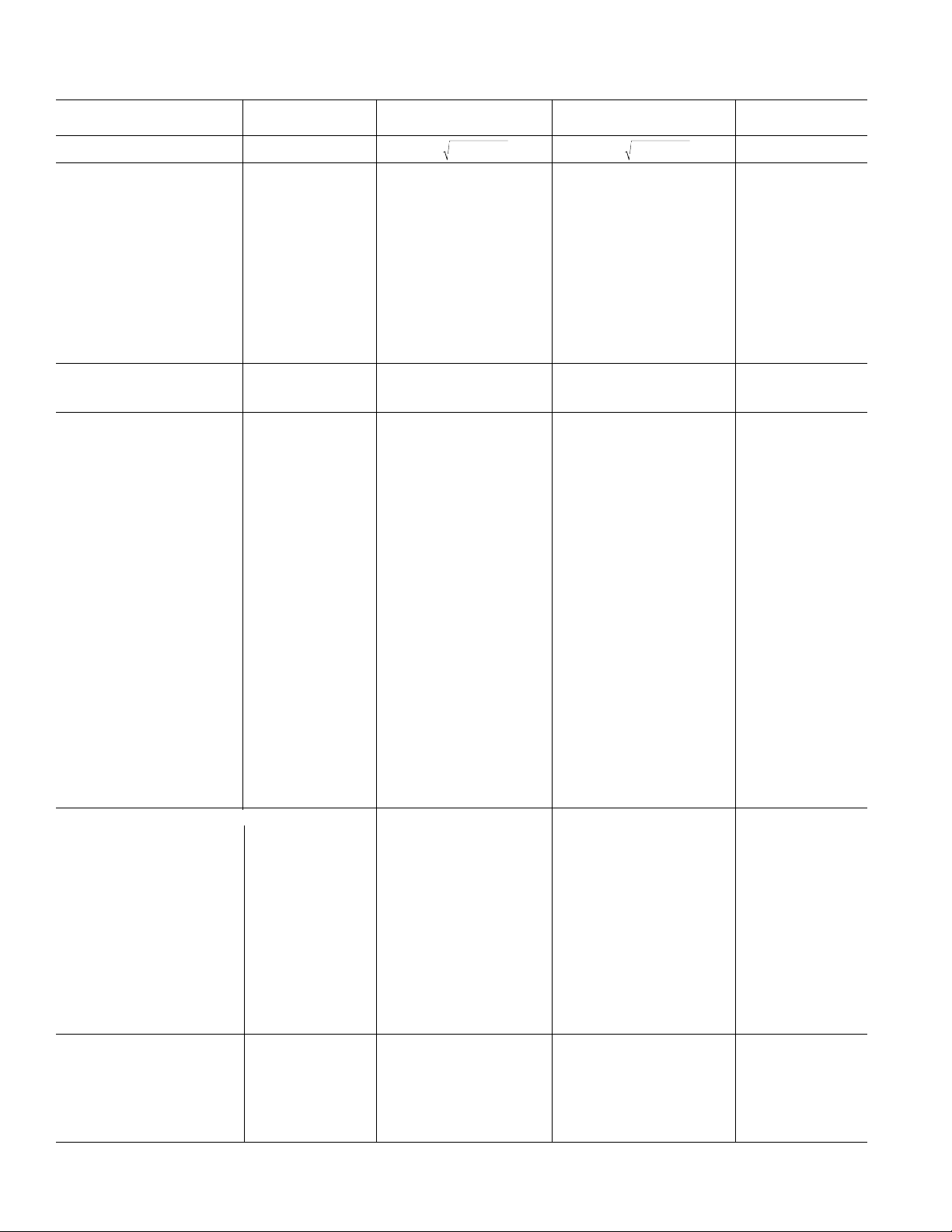
AD736–SPECIFICA TIONS
Model Conditions Min Typ Max Min Typ Max Units
TRANSFER FUNCTION
CONVERSION ACCURACY 1 kHz Sine Wave
Total Error, Internal Trim
All Grades 0–200 mV rms 0.3/0.3 0.5/0.5 0.2/0.2 0.3/0.3 ±mV/±% of Reading
T
MIN–TMAX
A&B Grades @ 200 mV rms 0.7/0.7 0.5/0.5 ±mV/±% of Reading
J&K Grades @ 200 mV rms 0.007 0.007 ±% of Reading/°C
vs. Supply Voltage
@ 200 mV rms Input V
@ 200 mV rms Input V
dc Reversal Error, dc Coupled @ 600 mV dc 1.3 2.5 1.3 2.5 % of Reading
Nonlinearity
2
, 0 mV–200 mV @ 100 mV rms 0 +0.25 +0.35 0 +0.25 +0.35 % of Reading
Total Error, External Trim 0–200 mV rms 0.1/0.5 0.1/0.3 ±mV/±% of Reading
ERROR vs. CREST FACTOR
Crest Factor 1 to 3 CAV, CF = 100 µF 0.7 0.7 % Additional Error
Crest Factor = 5 CAV, CF = 100 µF 2.5 2.5 % Additional Error
INPUT CHARACTERISTICS
High Impedance Input (Pin 2)
Signal Range
Continuous rms Level V
Continuous rms Level V
Peak Transient Input V
Peak Transient Input V
Peak Transient Input V
Input Resistance 10
Input Bias Current V
Low Impedance Input (Pin 1)
Signal Range
Continuous rms Level V
Continuous rms Level V
Peak Transient Input V
Peak Transient Input V
Peak Transient Input V
Input Resistance 6.4 8 9.6 6.4 8 9.6 kΩ
Maximum Continuous
Nondestructive Input All Supply Voltages ±12 ±12 V p-p
Input Offset Voltage
J&K Grades 63 63 mV
A&B Grades 63 63 mV
vs. Temperature 8 30 8 30 µV/°C
vs. Supply V
vs. Supply VS = ±5 V to ±3 V 80 80 µV/V
OUTPUT CHARACTERISTICS
Output Offset Voltage
J&K Grades ±0.1 60.5 ±0.1 60.3 mV
A&B Grades 60.5 60.3 mV
vs.Temperature 1 20 1 20 µV/°C
vs. Supply V
Output Voltage Swing
2 kΩ Load V
2 kΩ Load V
2 kΩ Load V
No Load V
Output Current 2 2 mA
Short-Circuit Current 3 3 mA
Output Resistance @ dc 0.2 0.2 Ω
FREQUENCY RESPONSE
High Impedance Input (Pin 2)
For 1% Additional Error Sine-Wave Input
V
= 1 mV rms 1 1 kHz
IN
V
= 10 mV rms 6 6 kHz
IN
V
= 100 mV rms 37 37 kHz
IN
VIN = 200 mV rms 33 33 kHz
1
ac Coupled Using C
200 mV–1 V rms –1.2 62.0 –1.2 62.0 % of Reading
= ±5 V to ±16.5 V 0 +0.06 +0.1 0 +0.06 +0.1 %/V
S
= ±5 V to ±3 V 0 –0.18 –0.3 0 –0.18 –0.3 %/V
S
3
= +2.8 V, –3.2 V 200 200 mV rms
S
= ±5 V to ±16.5 V 11V rms
S
= +2.8 V, –3.2 V 60.9 60.9 V
S
= ±5 V ±2.7 ±2.7 V
S
= ±16.5 V 64.0 64.0 V
S
= ±3 V to ±16.5 V 1 25 1 25 pA
S
= +2.8 V, –3.2 V 300 300 mV rms
S
= ±5 V to ±16.5 V l l V rms
S
= +2.8 V, –3.2 V ±1.7 ±1.7 V
S
= ±5 V ±3.8 ±3.8 V
S
= ±16.5 V ±11 ±11 V
S
4
ac Coupled
= ±5 V to ±16.5 V 50 150 50 150 µV/V
S
= ±5 V to ±16.5 V 50 130 50 130 µV/V
S
V
= ±5 V to ±3 V 50 50 µV/V
S
= +2.8 V, –3.2 V 0 to +1.6 +1.7 0 to +1.6 +1.7 V
S
= ±5 V 0 to +3.6 +3.8 0 to +3.6 +3.8 V
S
= ±16.5 V 0 to +4 +5 0 to +4 +5 V
S
= ±16.5 V 0 to +4 +12 0 to +4 +12 V
S
otherwise noted.)
AD736J/A AD736K/B
V
= Avg.(V
OUT
C
2
)
IN
12
V
OUT
= Avg.(V
10
2
)
IN
12
Ω
–2–
REV. C
AD736
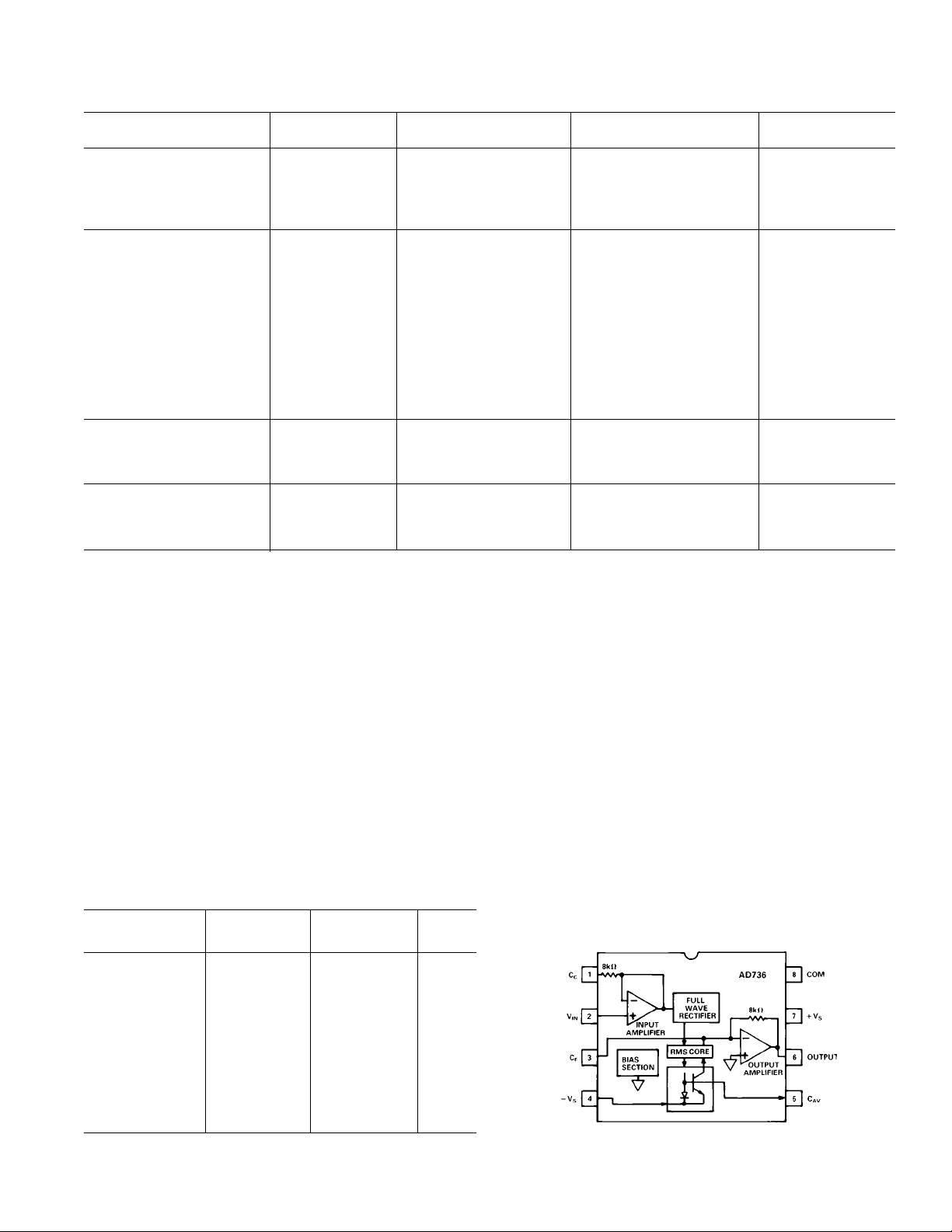
AD736J/A AD736K/B
Model Conditions Min Typ Max Min Typ Max Units
±3 dB Bandwidth Sine-Wave Input
= 1 mV rms 5 5 kHz
V
IN
V
= 10 mV rms 55 55 kHz
IN
V
= 100 mV rms 170 170 kHz
IN
VIN = 200 mV rms 190 190 kHz
FREQUENCY RESPONSE
Low Impedance Input (Pin 1)
For 1% Additional Error Sine-Wave Input
V
= 1 mV rms 1 1 kHz
IN
V
= 10 mV rms 6 6 kHz
IN
V
= 100 mV rms 90 90 kHz
IN
V
= 200 mV rms 90 90 kHz
IN
±3 dB Bandwidth Sine-Wave Input
V
= l mV rms 5 5 kHz
IN
V
= 10 mV rms 55 55 kHz
IN
V
= 100 mV rms 350 350 kHz
IN
VIN = 200 mV rms 460 460 kHz
POWER SUPPLY
OperatingVoltageRange +2.8, –3.2 ±5 ± 16.5 +2.8, –3.2 ±5 ± 16.5 Volts
Quiescent Current Zero Signal 160 200 160 200 µA
200 mV rms, No Load Sine-Wave Input 230 270 230 270 µA
TEMPERATURE RANGE
Operating, Rated Performance
Commercial (0°C to +70°C) AD736J AD736K
Industrial (–40°C to +85°C) AD736A AD736B
NOTES
l
Accuracy is specified with the AD736 connected as shown in Figure 16 with capacitor CC.
2
Nonlinearity is defined as the maximum deviation (in percent error) from a straight line connecting the readings at 0 and 200 mV rms. Output offset voltage is adjusted to zero.
3
Error vs. Crest Factor is specified as additional error for a 200 mV rms signal. C.F. = V
4
DC offset does not limit ac resolution.
Specifications are subject to change without notice.
Specifications shown in boldface are tested on all production units at final electrical test.
Results from those tests are used to calculate outgoing quality levels.
ABSOLUTE MAXIMUM RATINGS
Supply Voltage . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . ±16.5 V
Internal Power Dissipation
2
. . . . . . . . . . . . . . . . . . . . .200 mW
1
Input Voltage . . . . . . . . . . . . . . . . . . . . . . . ±V
Output Short-Circuit Duration . . . . . . . . . . . . . . . . . Indefinite
Differential Input Voltage . . . . . . . . . . . . . . . . . . +V
and –V
S
Storage Temperature Range (Q) . . . . . . –65°C to +150°C
Storage Temperature Range (N, R) . . . . . –65°C to +125°C
Operating Temperature Range
AD736J/K . . . . . . . . . . . . . . . . . . . . . . . . . . . 0°C to +70°C
AD736A/B . . . . . . . . . . . . . . . . . . . . . . . . . .–40°C to +85°C
/V rms.
PEAK
Lead Temperature Range (Soldering 60 sec) . . . . . . . . +300°C
ESD Rating . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .500 V
NOTES
1
Stresses above those listed under “Absolute Maximum Ratings” may cause
S
permanent damage to the device. This is a stress rating only and functional
operation of the device at these or any other conditions above those indicated in the
operational section of this specification is not implied. Exposure to absolute
S
maximum rating conditions for extended periods may affect device reliability .
2
8-Pin Plastic Package: θJA = 165°C/W
8-Pin Cerdip Package: θ
8-Pin Small Outline Package: θJA = 155°C/W
= 110°C/W
JA
ORDERING GUIDE
Temperature Package Package
Model Range Description Option
AD736JN 0°C to +70°C Plastic Mini-DIP N-8
AD736KN 0°C to +70°C Plastic Mini-DIP N-8
AD736JR 0°C to +70°C Plastic SOIC SO-8
AD736KR 0°C to +70°C Plastic SOIC SO-8
AD736AQ –40°C to +85°C Cerdip Q-8
AD736BQ –40°C to +85°C Cerdip Q-8
AD736JR-REEL 0°C to +70°C Plastic SOIC SO-8
AD736JR-REEL-7 0°C to +70°C Plastic SOIC SO-8
AD736KR-REEL 0°C to +70°C Plastic SOIC SO-8
AD736KR-REEL-7 0°C to +70°C Plastic SOIC SO-8
REV. C
PIN CONFIGURATION
8-Pin Mini-DIP (N-8), 8-Pin SOIC (R-8),
8-Pin Cerdip (Q-8)
–3–

AD736
–Typical Characteristics
Figure 1. Additional Error vs.
Supply Voltage
Figure 4. Frequency Response
Driving Pin 1
Figure 2. Maximum Input Level
vs. SupplyVoltage
Figure 5. Frequency Response
Driving Pin 2
Figure 3. Peak Buffer Output vs.
Supply Voltage
Figure 6. Additional Error vs.
Crest Factor vs. C
AV
Figure 7. Additional Error vs.
Temperature
Figure 8. DC Supply Current vs.
RMS lnput Level
–4–
Figure 9. –3 dB Frequency vs.
RMS Input Level (Pin2)
REV. C

Typical Characteristics–
AD736
Figure 10. Error vs. RMS Input
Voltage (Pin 2), Output Buffer Offset Is Adjusted To Zero
Figure 13. Pin 2 Input Bias Current
vs. Supply Voltage
CALCULATING SETTLING TIME USING FIGURE 14
The graph of Figure 14 may be used to closely approximate the
time required for the AD736 to settle when its input level is reduced in amplitude. The net time required for the rms converter
to settle will be the difference between two times extracted from
the graph – the initial time minus the final settling time. As an
example, consider the following conditions: a 33 µF averaging
capacitor, an initial rms input level of 100 mV and a final (reduced) input level of 1 mV. From Figure 14, the initial settling
time (where the 100 mV line intersects the 33 µF line) is around
80 ms.
Figure 11. C
Specified Averaging Error
Figure 14. Settling Time vs. RMS
Input Level for Various
Values of C
AV
AV
vs. Frequency for
The settling time corresponding to the new or final input level
of 1 mV is approximately 8 seconds. Therefore, the net time for
the circuit to settle to its new value will be 8 seconds minus
80 ms which is 7.92 seconds. Note that, because of the smooth
decay characteristic inherent with a capacitor/diode combination, this is the total settling time to the final value (i.e., not the
settling time to 1%, 0.1%, etc., of final value). Also, this graph
provides the worst case settling time, since the AD736 will settle
very quickly with increasing input levels.
Figure 12. RMS Input Level vs.
Frequency for Specified Averaging Error
Figure 15. Pin 2 Input Bias Current vs. Temperature
REV. C
–5–

AD736
TYPES OF AC MEASUREMENT
The AD736 is capable of measuring ac signals by operating as
either an average responding or a true rms-to-dc converter. As
its name implies, an average responding converter computes the
average absolute value of an ac (or ac and dc) voltage or current
by full wave rectifying and low-pass filtering the input signal;
this will approximate the average. The resulting output, a dc
“average” level, is then scaled by adding (or reducing) gain; this
scale factor converts the dc average reading to an rms equivalent
value for the waveform being measured. For example, the average absolute value of a sine-wave voltage is 0.636 that of V
the corresponding rms value is 0.707 times V
. Therefore,
PEAK
for sine-wave voltages, the required scale factor is 1.11 (0.707
divided by 0.636).
In contrast to measuring the “average” value, true rms measurement is a “universal language” among waveforms, allowing the
magnitudes of all types of voltage (or current) waveforms to be
compared to one another and to dc. RMS is a direct measure of
the power or heating value of an ac voltage compared to that of
dc: an ac signal of 1 volt rms will produce the same amount of
heat in a resistor as a 1 volt dc signal.
Mathematically, the rms value of a voltage is defined (using a
simplified equation) as:
V rms = Avg.(V2)
This involves squaring the signal, taking the average, and then
obtaining the square root. True rms converters are “smart rectifiers”: they provide an accurate rms reading regardless of the
type of waveform being measured. However, average responding
converters can exhibit very high errors when their input signals
deviate from their precalibrated waveform; the magnitude of the
error will depend upon the type of waveform being measured.
As an example, if an average responding converter is calibrated
to measure the rms value of sine-wave voltages, and then is used
to measure either symmetrical square waves or dc voltages, the
converter will have a computational error 11% (of reading)
higher than the true rms value (see Table I).
AD736 THEORY OF OPERATION
As shown by Figure 16, the AD736 has five functional subsec-
Table I. Error Introduced by an Average Responding Circuit When Measuring Common Waveforms
Waveform Type Crest Factor True rms Value Average Responding % of Reading Error*
1 Volt Peak (V
Amplitude Read rms Value of Responding Circuit
Undistorted 1.414 0.707 V 0.707 V 0%
Sine Wave
Symmetrical
Square Wave 1.00 1.00 V 1.11 V +11.0%
Undistorted
Triangle Wave 1.73 0.577 V 0.555 V –3.8%
Gaussian
Noise (98% of
Peaks <1 V) 3 0.333 V 0.295 V –11.4%
Rectangular 2 0.5 V 0.278 V –44%
Pulse Train 10 0.1 V 0.011 V –89%
SCR Waveforms
50% Duty Cycle 2 0.495 V 0.354 V –28%
25% Duty Cycle 4.7 0.212 V 0.150 V –30%
/V rms) Circuit Calibrated to Using Average
PEAK
*%of Reading Error =
;
PEAK
Average RespondingValue –True rmsValue
–6–
tions: input amplifier, full-wave rectifier, rms core, output amplifier and bias sections. The FET input amplifier allows
both a high impedance, buffered input (Pin 2) or a low impedance, wide-dynamic-range input (Pin 1). The high impedance
input, with its low input bias current, is well suited for use with
high impedance input attenuators.
The output of the input amplifier drives a full wave precision
rectifier, which in turn, drives the rms core. It is in the core that
the essential rms operations of squaring, averaging and square
rooting are performed, using an external averaging capacitor,
C
. Without CAV, the rectified input signal travels through the
AV
core unprocessed, as is done with the average responding connection (Figure 17).
A final subsection, an output amplifier, buffers the output from
the core and also allows optional low-pass filtering to be performed via external capacitor, C
, connected across the feed-
F
back path of the amplifier. In the average responding
connection, this is where all of the averaging is carried out. In
the rms circuit, this additional filtering stage helps reduce any
output ripple which was not removed by the averaging capacitor, C
AV
.
Figure 16. AD736 True RMS Circuit
Sine Waves Will Read
TruermsValue
×100%
REV. C

AD736
RMS MEASUREMENT – CHOOSING THE OPTIMUM
VALUE FOR C
AV
Since the external averaging capacitor, CAV, “holds” the rectified input signal during rms computation, its value directly affects the accuracy of the rms measurement, especially at low
frequencies. Furthermore, because the averaging capacitor appears across a diode in the rms core, the averaging time constant
will increase exponentially as the input signal is reduced. This
means that as the input level decreases, errors due to nonideal
averaging will reduce while the time it takes for the circuit to
settle to the new rms level will increase. Therefore, lower input
levels allow the circuit to perform better (due to increased averaging) but increase the waiting time between measurements.
Obviously, when selecting C
, a trade-off between computa-
AV
tional accuracy and settling time is required.
As shown, the dc error is the difference between the average of
the output signal (when all the ripple in the output has been
removed by external filtering) and the ideal dc output. The dc
error component is therefore set solely by the value of averaging
capacitor used-no amount of post filtering (i.e., using a very
large C
) will allow the output voltage to equal its ideal value.
F
The ac error component, an output ripple, may be easily removed by using a large enough post filtering capacitor, C
.
F
In most cases, the combined magnitudes of both the dc and ac
error components need to be considered when selecting appropriate values for capacitors C
and CF. This combined error,
AV
representing the maximum uncertainty of the measurement is
termed the “averaging error” and is equal to the peak value of
the output ripple plus the dc error.
As the input frequency increases, both error components decrease rapidly: if the input frequency doubles, the dc error and
ripple reduce to 1/4 and 1/2 their original values, respectively,
and rapidly become insignificant.
AC MEASUREMENT ACCURACY AND CREST FACTOR
The crest factor of the input waveform is often overlooked when
determining the accuracy of an ac measurement. Crest factor is
defined as the ratio of the peak signal amplitude to the rms amplitude (C.F. = V
/V rms). Many common waveforms, such
PEAK
as sine and triangle waves, have relatively low crest factors (≤2).
Other waveforms, such as low duty cycle pulse trains and SCR
waveforms, have high crest factors. These types of waveforms
require a long averaging time constant (to average out the long
time periods between pulses). Figure 6 shows the additional
error vs. crest factor of the AD736 for various values of C
AV
.
SELECTING PRACTICAL VALUES FOR INPUT
COUPLING (C
) CAPACITORS
(C
F
), AVERAGING (CAV) AND FILTERING
C
Table II provides practical values of CAV and CF for several
common applications.
Figure 17. AD736 Average Responding Circuit
RAPID SETTLING TIMES VIA THE AVERAGE
RESPONDING CONNECTION (FIGURE 17)
Because the average responding connection does not use the
C
averaging capacitor, its settling time does not vary with in-
AV
put signal level; it is determined solely by the RC time constant
of C
and the internal 8 kΩ resistor in the output amplifier’s
F
feedback path.
DC ERROR, OUTPUT RIPPLE, AND AVERAGING
ERROR
Figure 18 shows the typical output waveform of the AD736 with
a sine-wave input applied. As with all real-world devices, the
ideal output of V
= VIN is never exactly achieved; instead,
OUT
the output contains both a dc and an ac error component.
Figure 18. Output Waveform for Sine-Wave Input Voltage
Table II. AD737 Capacitor Selection Chart
Application rms Low Max C
Input Frequency Crest Time*
Level Cutoff Factor to 1%
(–3dB)
General Purpose 0–1 V 20 Hz 5 150 µF 10 µF 360 ms
rms Computation 200 Hz 5 15 µF1 µF 36 ms
0–200 mV 20 Hz 5 33 µF 10 µF 360 ms
200 Hz 5 3.3 µF1 µF 36 ms
General Purpose 0–1 V 20 Hz None 33 µF 1.2 sec
Average 200 Hz None 3.3 µF 120 ms
Responding
0–200 mV 20 Hz None 33 µF 1.2 sec
200 Hz None 3.3 µF 120 ms
SCR Waveform 0–200 mV 50 Hz 5 100 µF 33 µF 1.2 sec
Measurement 60 Hz 5 82 µF 27 µF 1.0 sec
0–100 mV 50 Hz 5 50 µF 33 µF 1.2 sec
60 Hz 5 47 µF 27 µF 1.0 sec
Audio
Applications
Speech 0–200 mV 300 Hz 3 1.5 µF 0.5 µF 18 ms
Music 0–100 mV 20 Hz 10 100 µF 68 µF 2.4 sec
*Settling time is specified over the stated rms input level with the input signal increasing
from zero. Settling times will be greater for decreasing amplitude input signals.
CFSettling
AV
REV. C
–7–

AD736
The input coupling capacitor, CC, in conjunction with the 8 kΩ
internal input scaling resistor, determine the –3 dB low frequency rolloff. This frequency, F
FL=
2π(8,000)(TheValue of C
, is equal to:
L
1
C
inFarads)
Applications Circuits
Figure 19. AD736 with a High Impedance Input Attenuator
Note that at FL, the amplitude error will be approximately
–30% (–3 dB) of reading. To reduce this error to 0.5% of reading, choose a value of C
that sets FL at one tenth the lowest
C
frequency to be measured.
In addition, if the input voltage has more than 100 mV of dc
offset, than the ac coupling network shown in Figure 21 should
be used in addition to capacitor C
Figure 22. Battery Powered Option
.
C
C1174a–10–9/88
Figure 20. Differential Input Connection
Figure 23. Low Z, AC Coupled Input Connection
OUTLINE DIMENSIONS
Dimensions shown in inches and (mm).
PRINTED IN U.S.A.
Figure 21. External Output VOS Adjustment
–8–
REV. C
 Loading...
Loading...