Victor Technology V12 User Manual

Owners Guide V12 Financial Calculator

VICTOR TECHNOLOGY

Preface

Congratulations on your purchase of the V12 financial calculator from Victor Technology. Victor has been serving customers since 1918. Today, Victor offers a complete line of printing, handheld, desktop, scientific, and financial calculators. For more information please see our website at www.victortech.com

Victor: The Choice of Professionals

or call us at 1-800-628-2420.

VICTOR TECHNOLOGY

Table of Contents

Chapter 1: Where to Start .................................. 6

Powering On and Off .............................................6

Controlling screen contrast .................................... 6

Keyboard Dynamics............................................... 6

Entering Digits .......................................................6

Decimal Placement................................................ 6

Entering Large Amounts ........................................7

Entering Small Amounts ........................................7

Changing the Sign of a Number............................. 7

Using the Clear Function .......................................8

ALG and RPN Setting Functions ...........................8

RPN method .......................................................... 9

Sequential Calculations in RPN method ................9

Storage Capacity and Recalling Entered Data....... 9

Chapter 2: The First Steps to Financial Functions11

Using the Financial Storage Registers.................11

Saving to a Register ............................................11

Resetting Saved Data.......................................... 11

Basic Interest Calculations................................... 11

Basic Financial Calculations ................................ 14

Positive and Negative Cash Flows ......................14

Payment Function................................................ 14

The special relationship between i. and n. ........ 15

Determining Interest Rate: Solving for i. ............ 15

Determining Present Value: Solving for PV ........16

VICTOR TECHNOLOGY

Determining Payment Amount: Solving for PMT 17

Determining Future Value: Solving for FV ......... 18

Determining Number of Periods: Solving for n.. 19

Loan With Balloon Payment................................. 19

Amortization Function ..........................................20

Chapter 3: Other Financial Calculations......... 22

NPV (Net Present Value)..................................... 22

Grouped Cash Flows ...........................................23

Replacing Current Cash Flow Value Data ...........25

Determining Values with Depreciation .................26

Determining Bond Values .................................... 28

Percentages......................................................... 30

Calendar Operations............................................ 32

Determining Number of Days Between Dates .....33

Chapter 4: Other Operational Features............ 35

Full Figure Display ...............................................37

Other Display Settings .........................................37

LST X...................................................................38

x ↔ y.................................................................... 39

Statistical Features and Functions....................... 39

Recovering Incorrectly Entered Statistical Data...40

Standard Deviation Entries .................................. 41

Mean Values........................................................ 41

Linear Estimates for x and y ................................42

Weighted Mean Values........................................43

Mathematical Features and Functions................. 44

Power Features in ALG method........................... 49

VICTOR TECHNOLOGY

Power Features in RPN method .......................... 49

Chapter 5: The Basics of Programming ........... 50

Creating Your Own Program................................ 50

Executing Your Own Program .............................53

Program Memory Basics...................................... 54

Determining Program Line Instructions................ 54

Program line 000 and the GTO 000 instruction:... 56

Performing a Program One Line at a Time ..........56

Setting the Calculator to a Specific Program Line 59

Interrupting a Program During Execution.............59

Stopping a Program During Execution................. 61

Chapter 6: Branch & Loop Programs ............... 63

Branching with Conditions ...................................63

Storing More Than One Program......................... 66

Chapter 7: Editing Your Programs ................... 67

Inserting Instructions Into a Program ...................68

Inserting Instructions at the End of a Program.....70

Chapter 8: Error Messages .............................. 72

VICTOR TECHNOLOGY

Chapter 1: Where to Start

Powering On and Off

Turn the unit on by touching the ON button. To turn the unit off, touch the ON button again. The calculator will automatically power off after 7 minutes if not used.

When the calculator is experiencing a low battery charge, a battery icon will appear in the top left corner of the display screen.

Controlling screen contrast

To change the contrast of the display screen for optimal viewing, hold down the

.b button and touch X or ÷ keys until desired contrast is reached.

Keyboard Dynamics

Most buttons perform multiple functions. The primary function is displayed on the center of the button, while alternative functions of the same button are imprinted on the bottom side of the button, below the button, or above the button. Alternate functions are obtainable by using one of two colored prefix buttons prior to entering the function desired. The colors of the prefix buttons match the alternative functions. The prefix buttons are b (blue) and r (red).

Entering Digits

To enter a digit, touch the number buttons and decimal place .. button in the same order as they would appear on paper.

Decimal Placement

On the display, digits are separated with commas left of the decimal place. To change the decimal point period icon to a comma and the comma icon to a decimal point, turn the V12 off, touch and hold the decimal point button . , and

touch the ON button. Repeat this process again to reset these placements to the standard display.

VICTOR TECHNOLOGY

Entering Large Amounts

The V12 displays numbers up to 10 digits. Scientific notation allows numbers

longer than 10 digits to be entered. To perform this function, enter the number with the decimal point moved to the left. Keep track of how many positions the decimal point moved. Next touch the EEX button and enter the number of positions the decimal point was moved. Touch the ENTER key to complete the entry.

Example

To enter a value of 7,894,300,000,000 the decimal place should move 12 spaces to the left leaving a mantissa of 7.8943 with an exponent of 12.

ENTRIES DISPLAY

7.8943 EEX 12

7.894300 12 Displays the figure in scientific notation.

These scientific notation numbers can be used in calculations the same as any number.

Entering Small Amounts

Scientific notation allows numbers more than 10 decimal places below zero to be entered. To perform this function, enter the number with the decimal point moved to the right. Keep track of how many positions the decimal point moved. Next touch the EEX button and enter the number of positions the decimal point

was moved. Touch the CHS key to make the number negative. Touch the ENTER key to complete the entry. For example, to enter the number .00000000047823456 we move the decimal point 10 positions. We enter

4.7823456, touch EEX, enter 10, touch CHS, and touch ENTER The display will show 4.782345 -10.

Changing the Sign of a Number

The CHS button allows a changing of the sign of a number. If a negative value is entered, or comes as a solution, touching the CHS button will make it a positive. Likewise, touching the CHS button after a positive value is displayed on the screen will change its sign to a negative.

VICTOR TECHNOLOGY

Using the Clear Function

Clearing replaces the displayed value with zero and replaces the previous instruction with the r GTO 000 instruction when programming. There are many ways of clearing data, outlined here:

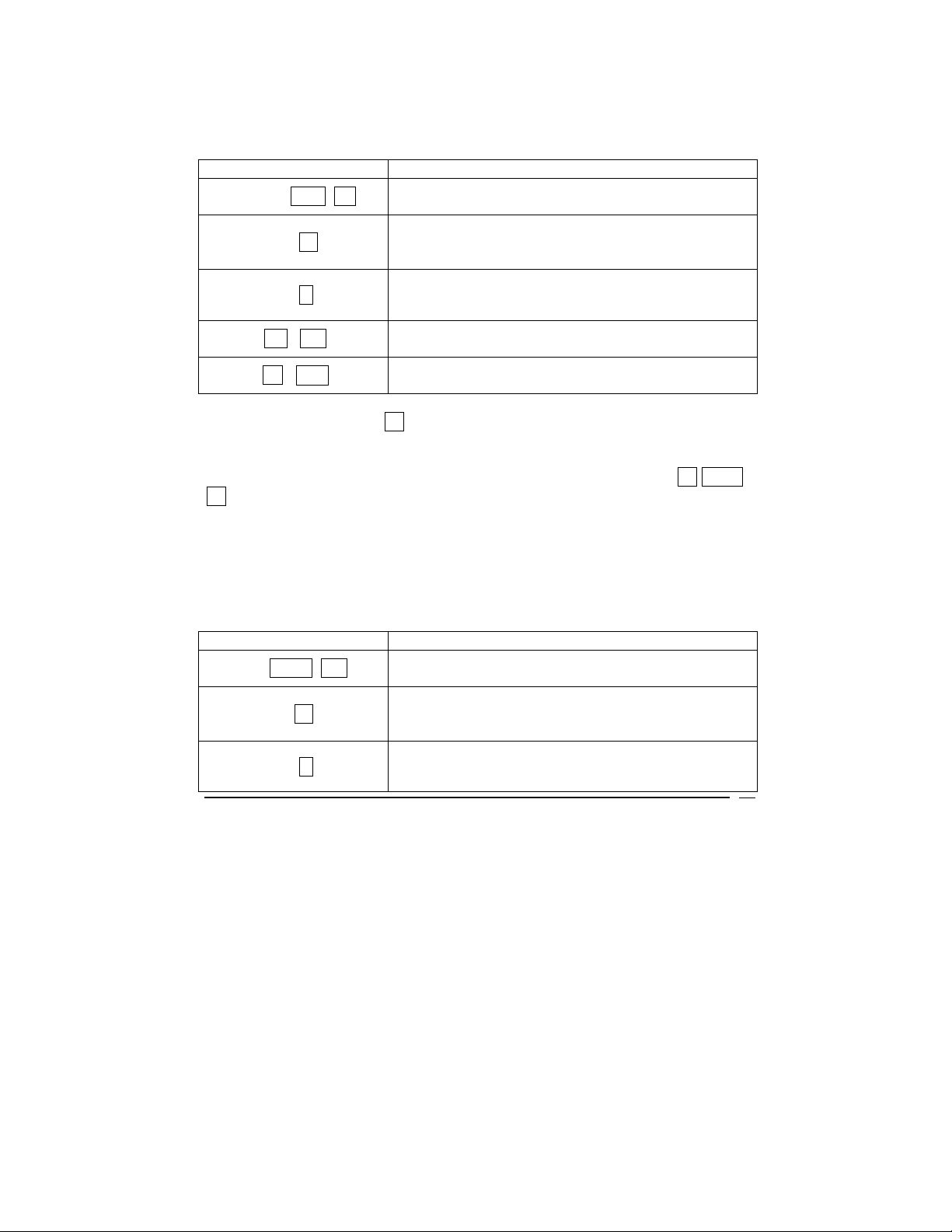
BUTTONS WILL CLEAR

.b CLEAR REG

.b CLEAR FIN

.b CLEAR ∑ 

.b CLEAR

PRGM

CLX

Storage registers, block and last x register, and display screen

Financial registers Statistical registers (121- R)

block registers and display screen Program memory (when touched in program

mode) Display screen and x register

ALG and RPN Setting Functions

RPN MODE ALG MODE

4 ENTER 2 X. 4 X 2 =

The ALG method enables calculations for addition, subtraction, multiplication, and division (with or without parentheses) in the standard method.

To select the ALG method. Touch b ALG , and the ALG icon will appear.

Sequential Calculations in ALG method

To complete a sequential calculation, touch = at the end of your entries and not after every entry.

Example: 5 X 2 + 3 – 4 ÷ 3 = 3.00

VICTOR TECHNOLOGY

RPN method

To select the RPN method, touch b RPN , and the RPN icon appears.

With RPN method enabled, you can perform basic calculations with two numbers and with multiplication, addition, division, or subtraction. It is necessary to enter both numbers in the equation, and then select the mathematical operation to be used.

Touching ENTER between number entries allows a separation of the different values within the calculator, and after entering the second value, selecting the mathematical operation completes the calculation.

Sequential Calculations in RPN method

Once a solution from a previous entry has been found and is on the display screen, enter the next value and select the mathematical operation to be performed.

Example: 5 ENTER 2 X 3 + 4 - 3 ÷ . Note: The display will show the answer: 3.00

Storage Capacity and Recalling Entered Data

Information entered into the calculator is stored to memory in different registers within the calculator. There are registers for data storage during calculations called blocks (covered later in this manual) and also a LST X register that stores the value last on the display screen before an operation when using the RPN method.

In addition to these storage registers, up to 20 more information registers are

available for storing values manually. The registers are called R0 through R9,

and R . 0 through R . 9 (with the decimal point in front of the number). Note: In this manual, .. represents the decimal point key.

To store numbers into a register, touch STO , and then touch the register number desired [either (0, 1, 2, 3, 4, 5, 6, 7, 8, or 9), or ( .. 0, . 1, . 2, . 3, . 4, . 5, . 6, . 7, . 8, . 9) ]. To recall a previously stored value, touch RCL , and similarly select the

desired stored value number, R0 through R9, and R ... 0 through R . 9.

VICTOR TECHNOLOGY

To delete stored values, enter zero, touch STO , and select the register to be

deleted, R0 through R9, and R .. 0 through R .. 9. (Note: Designating a new

value instead of 0 also replaces the old value set to the register)

VICTOR TECHNOLOGY

Chapter 2: The First Steps to Financial Functions

Using the Financial Storage Registers

Five specialty registers are used for financial calculations only. These are n ,

i , PV , PMT , and FV and are located along the top row of buttons. Saving data to these storage registers makes it possible to calculate financial problems such as loan payments.

Saving to a Register

To set the numbers into the registers, enter the number to be stored, and touch the button to which the number is to be stored. To recall the number, touch

RCL followed by the register you would like to recall ( n , i , PV , PMT , or

FV )

Resetting Saved Data

To replace current financial register values simply enter the new value and press the register key. To clear all financial registers at once, touch b clear

FIN. Financial storage registers are also reset when b REG is entered, or

when the continuous memory is reset.

Basic Interest Calculations

Simple interest can be calculated with either 365-day or 360-day cycles. Either can be displayed and the total amounts of principal plus the accrued interest

may be found by touching +. in RPN method, or +. x ↔ y = in ALG

method.

To perform this operation on a 365-day cycle, touch R↓ x ↔ y to find and

show interest accrued after determining the 360 day interest.

VICTOR TECHNOLOGY

Example Calculate the simple interest on a 100,000 amount with 12% annual interest for 180 days using the 360 day cycle and the 365 day cycle.

ENTRIES DISPLAY

100000 CHS PV

-100,000.00 Displays the amount.

180.00

180 n.

Displays the number of days for which interest will be calculated

12 i.

.b INT

R↓ x↔y

12.00 Displays the annual interest rate

6,000.00 Displays the simple interest on a 360 day basis 5,917.81 Displays the simple interest on a 360 day basis

In RPN method, touching + after the calculation places the total principal and interest accrued into the display.

To display total principal and interest accrued in ALG method, touch + x ↔ y

.= .

Example You take out a loan of $900, which you have 90 days to repay. You are lent the money at 4.3% simple interest, which is calculated on a 360-day cycle. You want to find the total amount of accrued interest you will owe in 90 days, the total amount you will owe including principal.

ENTRIES (ALG) DISPLAY

900 CHS PV

-900.00 Displays the amount.

90.00

90 n.

Displays the number of days for which interest will be calculated

4.3 i.

4.30 Displays the annual interest rate

VICTOR TECHNOLOGY

b INT

9.68 Displays the simple interest on a 360 day basis

909.68

.+ x ↔ y =

Displays the simple interest plus principal due on a 360 day basis

ENTRIES (RPN) DISPLAY

900 CHS PV

-900.00 Displays the amount.

90.00

90 n.

Displays the number of days for which interest will be calculated

4.3 i.

b INT

4.30 Displays the annual interest rate

9.68 Displays the simple interest on a 360 day basis

909.68

Displays the simple interest plus principal due on a 360 day basis

VICTOR TECHNOLOGY

Basic Financial Calculations

Before describing Basic Financial Calculations, it is important to review and understand five basic terms and keys used with the V12.

TERM /

KEY

DEFINITION

The number of periods in the financial loan, often

expressed in days, months, or years. The interest rate must be defined per period. The interest rate per period. Often an annual rate

is converted to monthly by dividing by 12, weekly by dividing by 52, or daily by dividing by 365. The initial cash value received or paid or the

present value of a series of future payments when discounted at an interest rate.

PMT

The payment made each period.

The final cash value received or paid or the future

value of a series of payments assuming an interest rate.

When using the V12, four of these five variables must be known to perform a calculation. The unknown variable can then be solved.

Positive and Negative Cash Flows

When performing financial calculations special care must be taken to enter values with the proper sign. A payment or outflow of cash must have a negative sign. A receipt of cash must have a positive sign. For example, the initial cash received in a loan is a positive amount. The payments are negative amounts.

Payment Function

Payments in compounding periods may be made either at the beginning of a period (such as payments in advance, and annuities due), or at the end of a period (such as regular annuities or payments in arrears).

VICTOR TECHNOLOGY

To select payment type: Touch r END if the payment will be made at the end of the period. Touch r BEG if the payment will be made at the beginning of the period. Most transactions utilize an End of the period payment. Note: This manual will only show examples using End of the period payments. If the BEGIN icon is not showing on the display, the payment function is set to END.

The special relationship between i. and n.

In compound interest problems, the interest rate entered into i must correlate

to the compounding period n in time (as in years, days, months, etc.)

Determining Interest Rate: Solving for i.

¾ Touch b CLEAR FIN to reset financial registers ¾ Enter the number of payment periods and touch n. ¾ Enter the present value of the loan and touch PV. ¾ Enter the payment value per period (a negative number) and touch

PMT.

¾ Enter the future value of the amount owed at the end of the payment

periods, touch CHS to make the number negative, and touch FV. Note: If the amount owed at the end of the loan period will be zero, this step can be skipped.

¾ Touch the i key to calculate the interest rate per period.

Example

ENTRIES (RPN) DISPLAY

b FIN

360 n.

400000 PV

2398.202 CHS PMT

0.00 Clears the financial registers.

360.00 Enters 360 months for a 30 year loan.

400,000.00 Enters the loan amount of $400,000.

-2,398.20 Displays the monthly payment

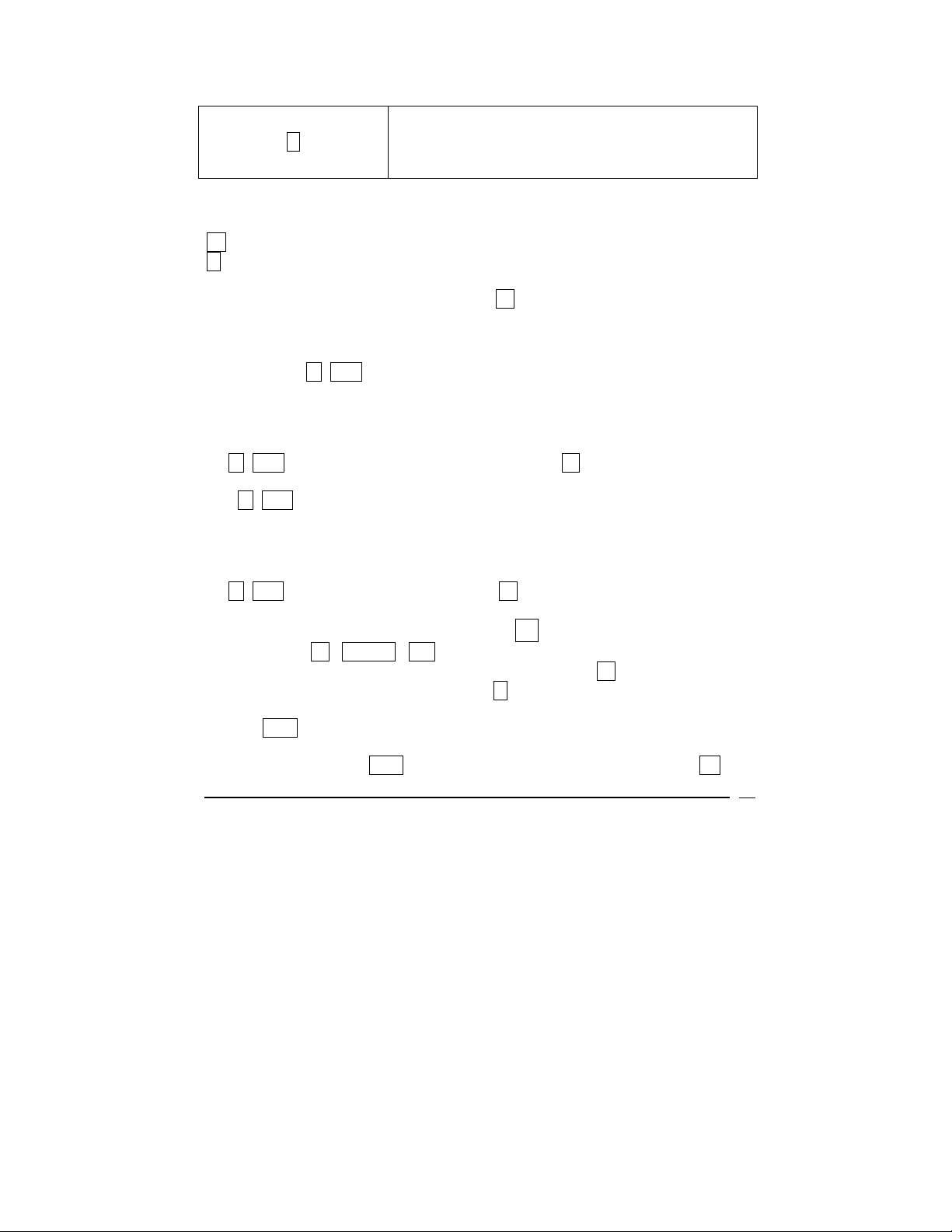
VICTOR TECHNOLOGY

------------

.i.

The V12 is calculating the value.

0.50 Displays the monthly interest rate.

Example

8 % annual interest, which is compounded quarterly for 3 years: n is number of quarters (3 * 4=12) i is interest rate per quarter (8% ÷ 4 = 0.02%)

If interest rate was compounded monthly, n would be 8% ÷ 12 =0.006

Since many financial calculations utilize an annual interest rate compounded monthly, the V12 has two functions to simplify the entry of interest rate and periods. The r 12÷ function will divide an annual interest rate by 12 and enter the result as the monthly interest rate.

Example

24% annual interest which is compounded monthly 24 r 12÷ will enter an interest rate of 2% into the i. register.

The r 12x function will multiply a number of years by 12 and enter the result as the number of monthly periods.

Example

30 year loan which is compounded monthly 30 r 12x will enter 360 periods into the n. register.

Determining Present Value: Solving for PV

¾ Touch b CLEAR FIN to reset financial registers ¾ Enter the number of payment periods and touch n. ¾ Enter the interest rate and touch i.. ¾ Enter the payment value per period (a negative number) and touch

PMT.

¾ Enter the future value of the amount owed at the end of the payment

periods, touch CHS to make the number negative, and touch FV.

VICTOR TECHNOLOGY

Note: If the amount owed at the end of the loan period will be zero, this step can be skipped.

¾ Touch the PV key to calculate the present value.

Example

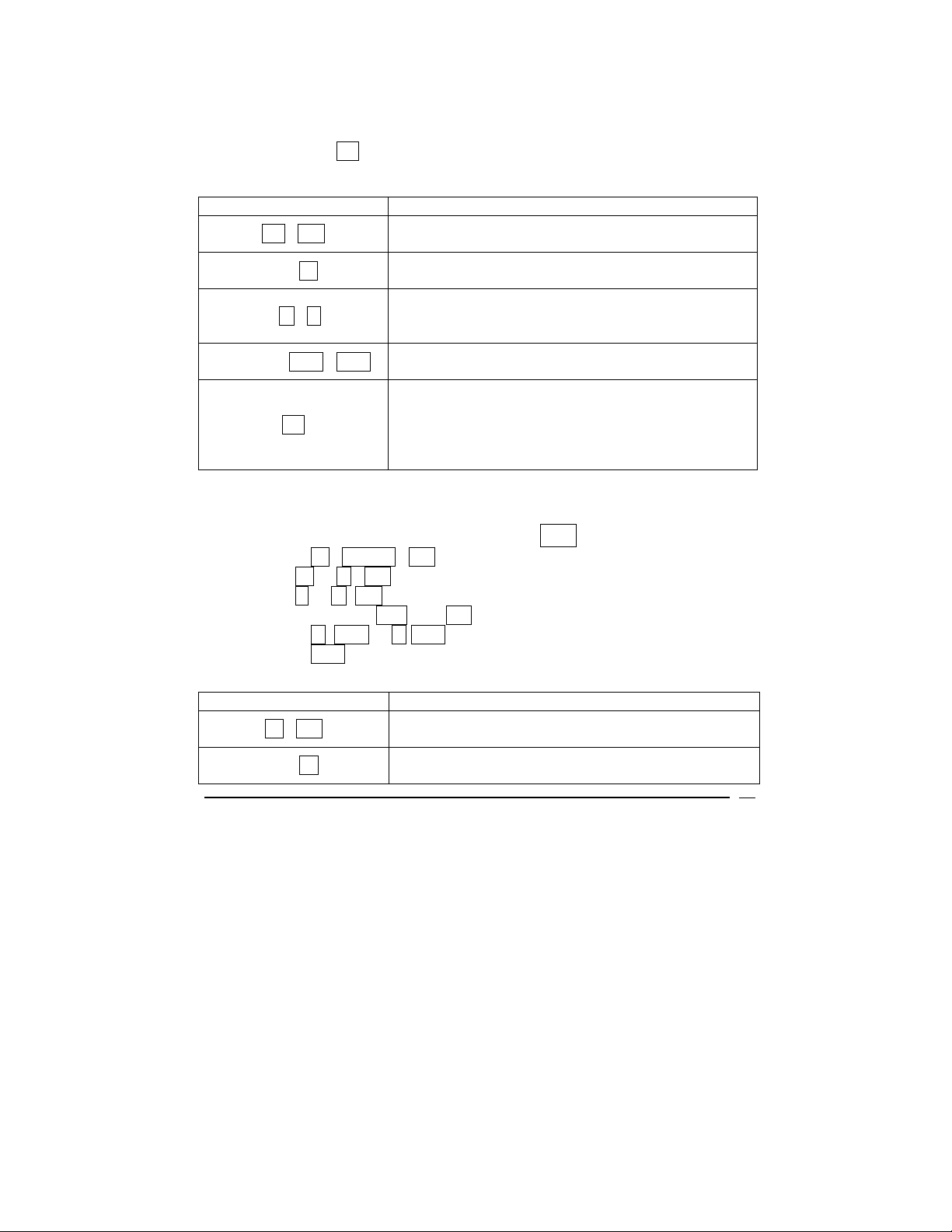
ENTRIES DISPLAY

.b FIN

360 n.

0.00 Clears the financial registers.

360.00 Displays 360 months for a 30 year loan.

0.50

6 r i.

Displays the interest rate of 6% per year or 0.5% per month.

2398.202 CHS PMT

-2,398.20 Displays the monthly payment

-----------The V12 is calculating the value.

400,000.00 Displays the loan amount or present value. Actual amount may vary slightly due to rounding

Determining Payment Amount: Solving for PMT

¾ Touch b CLEAR FIN to reset financial registers

¾ Use n or r 12x to enter number of periods or payments ¾ Use i or r 12÷ to enter periodic interest rate ¾ Enter values for PV and FV ¾ Touch r BEG or r END to select payment function

¾ Touch PMT to calculate the amount of the payment

Example

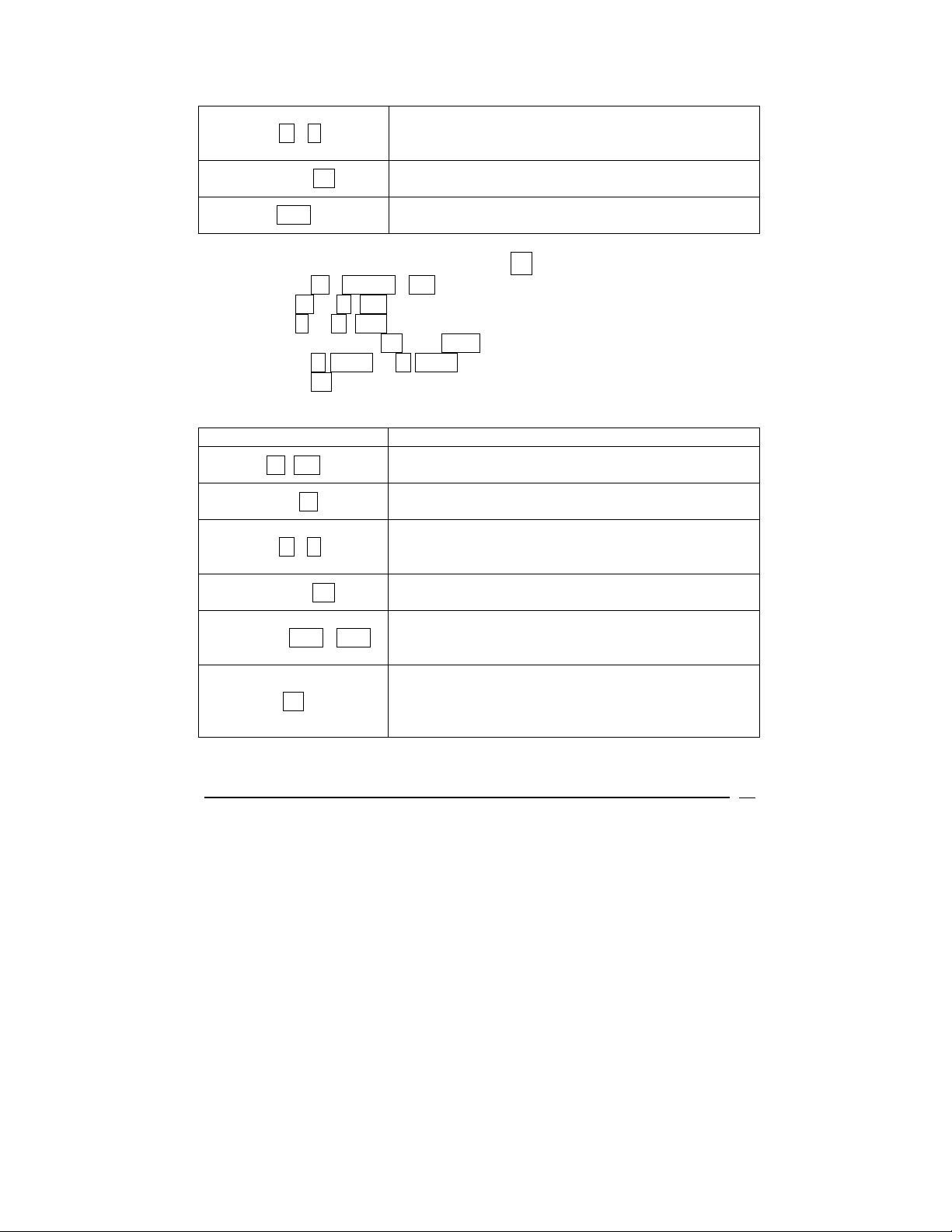
ENTRIES DISPLAY

b FIN

360 n.

0.00 Clears the financial registers.

360.00 Displays 360 months for a 30 year loan.

VICTOR TECHNOLOGY

0.50

6 r i.

Displays the interest rate of 6% per year or 0.5% per month.

400000 PV

PMT

400.000.00 Displays the loan amount or present value.

-2,398.20 Displays the monthly payment

Determining Future Value: Solving for FV

¾ Touch b CLEAR FIN to reset financial registers

¾ Use n or r 12x to enter number of periods or payments ¾ Use i or r 12÷ to enter annual interest rate ¾ Enter values for PV and PMT ¾ Touch r BEG or r END to select payment function ¾ Touch FV to calculate the future value

Example

ENTRIES (RPN) DISPLAY

b FIN

360 n.

0.00 Clears the financial registers.

360.00 Displays 360 months for a 30 year loan.

0.50

6 r i.

Displays the interest rate of 6% per year or 0.5% per month.

400000 PV

400.000.00 Displays the loan amount or present value.

-2,397.20

2397.202 CHS PMT

Displays the monthly payment. Notice the amount is reduced by $1 from previous examples.

-1,004.62

Displays the amount still owed at the end of the loan period. In this example, the payments over 30 years did not pay off the entire loan.

VICTOR TECHNOLOGY

Determining Number of Periods: Solving for n.

To determine the number of compounding periods and the number of payments:

¾ Touch b CLEAR FIN to reset financial registers

¾ Use i or r 12÷ to enter periodic interest rate.

¾ Enter values for PV(present value), PMT (amount of payment), FV

(future value)

¾ Select payment function by touching r BEG or r. END ¾ Touch n to calculate number of periods or payments

Example

ENTRIES (RPN) DISPLAY

b FIN

0.00 Clears the financial registers.

0.50

6 r i.

Displays the interest rate of 6% per year or 0.5% per month.

400000 PV

2398.202 CHS PMT

400.000.00 Displays the loan amount or present value.

-2,398.20 Displays the monthly payment.

360.00

Displays the number of periods (months) required to pay off the loan.

Loan With Balloon Payment

A common transaction is a loan with a balloon payment. In this case, the borrower makes a fixed payment each period until the end of the loan term. At the end of the term, the borrower makes one large final payment. The example below illustrates a $400,000 loan, at 6% annual interest paid monthly for 30 years with a balloon payment of $70,000.

VICTOR TECHNOLOGY

Example

ENTRIES (RPN) DISPLAY

b FIN

360 n.

0.00 Clears the financial registers.

360.00 Displays 360 months for a 30 year loan.

0.50

6 r i.

Displays the interest rate of 6% per year or 0.5% per month.

400000 PV

400.000.00 Displays the loan amount or present value.

-70,000.00

-70000 FV

Displays the future value required to pay off the loan (the balloon payment)

-2,328.52

PMT

Displays the monthly payment required to reach a $70.000 balloon payment.

Amortization Function

To Amortize is to liquidate a debt, such as a mortgage by installment payments. Amortization is the gradual elimination of a liability, such as a mortgage, in regular payments over a specified period of time. Such payments must be sufficient to cover both principal and interest. With the Amortization Function the V12 can calculate the total amount of principle (liability) and interest paid after a specified number of installments.

The following steps are required to determine the Amortization status of a loan:

• Push b CLEAR FIN first to reset financial registers of previous data

• Using i or r 12÷ , enter periodic interest rate

• Enter the principal using PV

• Enter the periodic payment, then push CHS PMT

• Select r BEG or r END to set the payment function

VICTOR TECHNOLOGY

• Enter the number of payments that will be amortized using n.

• Push b AMORT (will display amount from payments that will be

applied to interest)

• Push x↔y (will display amount from payments that will be applied to

principal)

• Push R↓ R↓ (will display number of payments to be amortized)

• Push RCL PV (will display remaining balance)

• Push RCL n (will display total number of payments amortized

If you repeat the Amortization function after an initial calculation, the V12 picks up where you left off. In other words, after you calculate the interest and principle paid after one year, the V12 resets the present value of the loan to the principle after one year. Calculation of Amortization will start from this point.

A common application of the Amortization function is to determine the amount of interest and principle paid on a mortgage for a given time period. The example below illustrates a 30 year loan with a principle of $400,000, a 6% annual interest rate, and monthly payment of $2,398.20. The task is to determine the interest and principle paid after 5 years or 60 months.

Example

ENTRIES (RPN) DISPLAY

.b FIN

6 r i.

400000 PV

2398.20 CHS PMT

60 b AMORT

x ↔ y

0.00 Clears the financial registers.

0.50 Displays the interest rate of 6% per year or 0.5% per month.

400.000.00 Displays the loan amount or present value.

-2,398.20 Displays the payment required to pay off the loan in 30 years (calculated in an earlier example)

-116,109.58 Displays the total interest paid after 60 months.

-27,782.42 Displays the total principle paid after 60 months

VICTOR TECHNOLOGY

372,217.58

RCL PV

RCL n

12 b AMORT

x ↔ y

Displays the remaining principle after 60 months of payments

60.00 Displays the number of payments amortized (60 months)

-22,152.81 Displays the amount of interest paid in the next 12 months of payments (after the initial 60 months already amortized)

-6,625.59 Displays the amount of principle paid in the next 12 months of payments (after the initial 60 months already amortized)

Chapter 3: Other Financial Calculations

NPV (Net Present Value)

b NPV (net present value) represents the value of a series of future cash

flows discounted at a specified rate of return to reflect the present value.

¾ When NPV is positive, financial value increases. ¾ When NPV is 0, financial value stays the same. ¾ When NPV is negative, financial value decreases.

Therefore, the greater the value of NPV, the greater the increase in financial value.

To find NPV, add the initial deposit (a negative cash flow) to present value of future cash flow. (Here, i will describe the rate of return, and NPV describes the result of the investment.)

Two keys not yet discussed in this manual are required to perform NPV calculations. The CFo key is used to store the initial cash flow. When touched, the contents of the x-register are stored in R0. The CFj key is used to store additional cash flows. When touched, the contents of the x-register are

VICTOR TECHNOLOGY

stored in R1. If used again in the same cash flow problem, the contents of the x-register are stored in first R

, then R3, R4, and so on.

Example

You want to buy a yacht for $23,000 and rent it to a skipper for a share of tour revenue. You expect cash flows of the initial cost ($23,000), ($5000) in the first year for repairs, +$10,000 in the second year from tours, +$15,000 in the third year, $17,000 in the fourth year, and then you expect to sell the yacht in the fifth year for $19,000. Your expected rate of return is 15%.

ENTRIES DISPLAY

b REG

23000 CHS r CF0

5000 CHS r CFj

10000 r CFj

15000 r CFj

17000 r CFj

19000 r CFj

0.00 Clears the x register

-23,000.00 Stores the initial cash outflow to buy the yacht

-5,000.00 Stores the first year cash flow 10,000.00 Stores the second year cash flow 15,000.00 Stores the third year cash flow 17,000.00 Stores the fourth year cash flow 19,000.00 Stores the final cash inflow at time of sale

5.00

RCL n.

Displays the number of cash flows entered after the initial

15 i.

b NPV

15.00 Stores the expected rate of return 9,242.52

Since NPV is positive, this investment would be attractive.

Grouped Cash Flows

It is possible to calculate NPV for 80 unique cash flows using the CFj key. In addition, the number of cash flows included in a calculation can go beyond 80

VICTOR TECHNOLOGY

when some of the cash flows are repetitive and consecutive. In these situations, the Nj key is invoked by entering the number of repeat cash flows followed by .r Nj . For example, if a cash flow of $1000 occurs 5 times in a row, the entries would be 5000 CHS r CFj 5 r Nj .

Example: A landlord buys and rents a building to a tenant for 8 years. The landlord pays $500,000 for the building and rents the building for a net cash flow of $60,000 for the first year, $100,000 per year for 3 years and $120,000 per year for the next 4 years. In the 9

year, the landlord expects to sell the property for $400,000. The landlord’s desired rate of return is 15% per year. What is the NPV of this investment?

Example

ENTRIES (RPN) DISPLAY

.b REG

500000 CHS r CFo

60000 r CFj

100000 r CFj

0.00 Clears the storage and financial registers.

-500,000.00 Displays -$500,000 as the initial cash flow.

60,000.00 Displays $60,000 as the year 1 cash flow.

100,000.00 Displays $100,000 as the year 2 cash flow.

3.00

3 r Nj

Displays the number of consecutive times the $100,000 cash flow will occur.

120000 r CFj

120,000.00 Displays $120,000 as the year 5 cash flow.

4.00

4 r Nj

Displays the number of consecutive times the $120,000 cash flow will occur.

400000 r CFj

15 i.

400,000.00 Displays $400,000 as the final cash flow amount

15.00 Displays the 15% desired rate of return

4.00

RCL n.

Displays the number of unique cash flow amounts entered

VICTOR TECHNOLOGY

60,301.37

b NPV

Displays the net present value of $60,301.37. Since the number is positive, this is an investment that exceeds the desired rate of return.

Replacing Current Cash Flow Value Data

Individual cash flow values stored in the V12 can be replaced. To replace a current cash flow value:

¾ Enter the amount ¾ Touch STO ¾ Enter the number of the CFj register to be replaced

Example

Starting from the previous example (A landlord buys and rents a building to a tenant for 8 years. The landlord pays $500,000 for the building, etc.), the landlord changes his assumptions. He now believes the net cash flow will be only $110,000 per year in years 5 through 8 instead of $120,000 per year.

ENTRIES (RPN) DISPLAY

110,000.00

110000 STO 3

Displays $110,000 as the new cash flow amount stored in the 3

43,977.94

b NPV

Displays the revised net present value of $43,977.94.

To replace the number of consecutive equal cash flows, (the Nj of a CF

¾ Touch RCL n to recall how many cash flow amounts are stored. ¾ Save the number of the cash flow value (the j) into the n register ¾ Enter the revised number of times the value occurs consecutively

¾ Touch r N

to store the revision

¾ Enter the original number of cash flows back into the n register

(otherwise the NPV calculation will be wrong)

VICTOR TECHNOLOGY

Example

Starting from the previous example, the landlord now believes the tenant will rent for 6 years instead of 4 at $110,000 per year (an additional 2 years).

ENTRIES (RPN) DISPLAY

4.00

RCL n.

Displays the number of unique cash flows entered. (This number will be required later)

3.00

3 n.

Displays the storage of 3 in the n register (because it is the 3

cash flow CF3 for which we will change

the frequency)

6 r Nj

6.00 Displays the new value of N

4.00

4 n.

Restores the original number of unique cash flows entered into the n register. 74,709.45

b NPV

Displays the revised net present value of $74,709.45

Determining Values with Depreciation

There are several ways of calculating depreciation including declining-balance, straight line, and sum-of-years numbers.

To calculate based on any of these types:

¾ Enter beginning cost with PV ¾ Enter salvage value with FV (if this value is 0, enter 0 FV) ¾ Enter expected life of asset (years) with n. ¾ For declining-balance calculations only: enter the percentage rate

followed by i . For example, 200% declining balance rate (double declining) is entered 200 .i.

¾ Enter the number of the year for which you wish to calculate the

depreciation

¾ Touch b DB for declining balance option ¾ Touch b SL for straight line option

VICTOR TECHNOLOGY

¾ Touch b SOYD for sum of years number option

No matter which depreciation method is used the remaining depreciated value

may be displayed by touching x ↔ y .

Example

Your company purchases a car for $3,500, which depreciates over 6 years. The salvage value is expected to be $900. Find the amount of depreciation and remaining depreciable value 1 year and after 4 years of car ownership using the declining-balance method at double the straight-line rate (200%).

ENTRIES DISPLAY

3,500.00

3500 PV

Stores the purchase price of $3,500 as the Present Value

900.00

900 FV

Stores the salvage value of $900 as the Future Value

6.00

6 n.

Stores 6 years as the number of periods for which depreciation will be calculated

200.00

200 i.

Stores 200% as the accelerated rate at which depreciation will be calculated.

1 b DB

1,1667.67 Displays the depreciation for year one 1,433.33

x ↔ y

Displays the amount left to be depreciated after one year

4 b DB

137.04 Displays the depreciation for year four

00.00

x ↔ y

Displays the amount left to be depreciated after four years

VICTOR TECHNOLOGY

Determining Bond Values

To calculate bond price and the interest accrued since its last interest date, as

well as its yield to maturity, use b PRICE and .b YTM functions.

Use these methods to calculate bond price and yield for 30/360 day bonds (municipal bonds, corporate bonds, and bonds with annual coupon payments.

To Calculate Standard Bond Price (.b PRICE )

¾ Enter coupon rate; touch PMT

¾ Enter desired yield to maturity; touch i.

¾ Enter purchase date (settlement date); touch ENTER ¾ Enter redemption date; touch b PRICE

The price displayed is the Bond Price as a percent of Part. This number is now stored to the PV register. The interest accrued since last interest date is also

stored, to show this touch x ↔ y To add the interest to the Bond Price in RPN method, touch + ; in ALG method,

touch + x ↔ y =.

Example

What Bond Price should you pay on September 17, 2009 for a 4.9% US Treasury Bond that matures on November 2, 2017 if you desire a yield of

6.65%?

ENTRIES DISPLAY

.b REG

4.9 PMT

0.00 Clears the registers

4.9 Enters coupon rate

6.65 i.

.r M.DY

6.65 Enters yield to maturity

6.65 Sets date format to month-day-year value

VICTOR TECHNOLOGY

9.172009 ENTER

11.022017 b PRICE

.+.

9.17 Enters purchase date

89.14 Enters maturity date and calculates bond price (as a % of Par)

90.98 Calculates total bond price including accrued interest

To Calculate Bond Yield to Maturity (.b YTM )

¾ Enter quoted Bond price (as a % of Par); touch PV ¾ Enter coupon rate; touch PMT ¾ Enter purchase date; touch ENTER ¾ Enter redemption date; touch .b YTM

Example

Using the Bond described above, what is the Yield to Maturity if the market quote for the Bond is 91.42?

ENTRIES DISPLAY

91.42 PV

4.9 PMT

9.172009 ENTER

11.022017 b YTM

91.42 Enters market quote

4.90 Enters coupon rate

9.17 Enters purchase date

6.26 Enters Maturity Date and calculates yield to maturity

To Calculate Bond Price and Yield for 30/360 Day Basis Bonds with a semiannual coupon, please reference V12 programming guide at

www.VictorV12.com

VICTOR TECHNOLOGY

To Calculate Price and Yield for Bonds with Annual Coupons, please reference V12 programming guide at www.VictorV12.com

Percentages

There are three buttons used for solving problems involving percents: Delta

Percentage Δ% ,Percentage % and Percent of Total %T.

Delta percentage calculates the percent difference between numbers using the first number as a base. To find the delta percentage ∆% of two values in both RPN and ALG method:

¾ Enter the base value ¾ Touch =. or ENTER ¾ Enter the second number ¾ Touch Δ%

Example

Calculate the percent difference between 100 and 25:

ENTRIES DISPLAY

100 ENTER/=

25 ∆%

100.00 Stores the base value

-75.00 Displays the result: 25 is 75% less than 100

To find the percentage % of a value in ALG method:

¾ Enter the base value ¾ Touch x. ¾ Enter the percentage ¾ Touch %. ¾ Touch =.

VICTOR TECHNOLOGY

Example

In ALG method, calculate 35% of $1,200:

ENTRIES (ALG) DISPLAY

CLX

1200

X 35 %.

00.00 Clears the display and x register

1200 Displays the base number

0.35 Displays the percent multiple

420.00 Displays the result

To find the percentage % of a value in RPN method:

¾ Enter the base value ¾ Touch ENTER ¾ Enter the percentage ¾ Touch %.

Example

In RPN method, calculate 35% of $1,200:

ENTRIES (RPN) DISPLAY

CLX

1200 ENTER

35 %.

00.00 Clears the display and x register

1200.00 Displays the base number

420.00 Displays the result

Percent of Total (%T) calculates what percent one number is of a second number using the first number as a base. To find the Percent of Total %T of two values in both RPN and ALG method:

¾ Enter the base value ¾ Touch =. or ENTER

VICTOR TECHNOLOGY

¾ Enter the second number ¾ Touch %T

Example

Calculate the Percent of Total for 200 and 50:

ENTRIES DISPLAY

200 ENTER/=

50 %T

200.00 Stores the base value

25.00 Displays the result: 50 is 25% less than 200

Calendar Operations

The V12 stores dates using two methods. The first is called Month-Day-Year and is set by touching r. M.DY. To enter a date in Month-Day-Year format:

¾ Enter the two digits of the month (01 to 12) ¾ Touch the decimal point key ¾ Enter the two digits of the day (01 to 31) ¾ Enter the four digits of the year ¾ Touch r M.DY

Example

Invoke the Month-Day-Year mode and enter the date January 5, 2001.

ENTRIES DISPLAY

01.052001 r M.DY

1.05 Stores the date

The second calendar method is called Day-Month-Year and is set by touching

.r. D.MY. To enter a date in Day-Month-Year format:

¾ Enter the two digits of the day (01 to 31) ¾ Touch the decimal point key ¾ Enter the two digits of the month (01 to 12) ¾ Enter the four digits of the year ¾ Touch r D.MY

VICTOR TECHNOLOGY

Example

Invoke the Day-Month-Year mode and enter the date January 5, 2001.

ENTRIES DISPLAY

05.012001 r D.MY

5.01 Stores the date

To calculate a date in the future or past:

¾ Enter the start date and touch r D.MY ¾ Enter number of days to be added or subtracted from the start date ¾ If subtracting days, don’t forget to use CHS

¾ Touch r DATE

Example

You have a time-share vacation starting on July 20, 2008, for 90 days. When will your stay be over? (Using day-month-year function)

ENTRIES DISPLAY

20.072008 r D.MY

90 r DATE

20.07 Stores the date 18,10,2008 6 Displays the result as the 18 month in year 2008 on the 6

day in the 10th

day of the week

(October 18, 2008 Saturday)

Determining Number of Days Between Dates

To calculate the number of days between a set of dates:

¾ Invoke your preferred calendar mode by touching r. M.DY or r

D.MY.

¾ Enter the start date and touch ENTER ¾ Enter the end date and touch ENTER ¾ Touch r ∆DYS

¾ To display the number of days based on a 360 day year press x ↔ y.

Example

With month-day-year function, the amount of simple interest accrued from January 15, 2008 through December 25, 2011 can be calculated with either

VICTOR TECHNOLOGY

actual amount of days between dates or by the 30-day month date function. You can calculate the amount of days each way.

ENTRIES DISPLAY

r M.DY

01.152008 ENTER

Puts the calculator in Month-Day-Year mode

1.15 Stores the date January 15, 2008 1,440.00

12.252011 r ∆DYS

Stores the date December 25, 2011 and displays the days between dates.

x ↔ y

1,420.00 Displays the result using a 360 day year

VICTOR TECHNOLOGY

Chapter 4: Other Operational Features

Another function of the V12 calculator is continuous memory of storage registers (financial. LSTx, block, and data), and information on the current status of the current function (display format, payment mode, and date format). Continuous memory is in effect even while the unit is off, and for a short amount of time while the batteries are out, to allow for battery replacement without losing data. Dropping or otherwise damaging the calculator may cause continuous memory to be reset.

Status Icons

There are nine icons on the lower portion of the display that notify calculator status during different operational procedures. RPN, ALG, r, b, BEGIN, D.MY, C, PRGM

Decimal Place Display Settings

To change the number of decimal places shown on the display screen, touch b and enter a value (0-9) to specify how many numbers will be displayed after the decimal. However many digits are displayed, they will be rounded for the display yet the entire number will be stored inside the calculator.

Example

ENTRIES DISPLAY

b. 2

5.7654368 ENTER

Sets the calculator to display two digits right of the decimal point

5.77 Stores the number with two decimal places

5.765

b. 3

Displays the figure with three digits to the right of the decimal point

5.76544

b. 5

Displays the figure with five digits to the right of the decimal point

VICTOR TECHNOLOGY

5.77

b. 2

Displays the figure with two digits to the right of the decimal point

The decimal place setting is kept until continuous memory is reset. Turning the unit off and on does not change the decimal place setting.

Scientific Notation Display Settings

With Scientific notation, the first non-zero digit of a value is moved the immediate left of the decimal point and all other digits are moved to the right. The resulting figure is called the mantissa. The number of decimal place movements required is called the exponent. For example, the figure 567.89 can be expressed in scientific notation as 5.6789 2 (with 5.6789 as the mantissa and 2 as the exponent since the decimal point was moved two positions). Likewise, the figure .056789 can be expressed in scientific notation as 5.6789 -2.

To convert a number to scientific notation:

¾ Enter the number ¾ Touch b ..

To exit scientific notation mode:

¾ Touch b followed by the number of decimal places you wish to

display

Example

Convert 567.89 to scientific notation and then set the display back to 2 decimal places

ENTRIES DISPLAY

567.89 ENTER

b ..

b 2

567.89 Displays the initial value

5.678900 02 Displays the figure in scientific notation

567.89 Displays the value using 2 decimal places

VICTOR TECHNOLOGY

Full Figure Display

To view all ten digits of a figure without decimal points touch b. PREFIX and hold down prefix as long as you wish to view the numbers.

Example

Convert 567.89 to scientific notation and then view the full figure with no decimal points.

ENTRIES DISPLAY

567.89 ENTER

b ..

b PREFIX

567.89 Displays the initial value

5.678900 02 Displays the figure in scientific notation 5678900000 Displays all 10 digits with no decimal point

Other Display Settings

Error Display

If an improper function or operation is entered the calculator will display ERROR on the screen, followed by a number (0-9). To clear the ERROR message from the display screen, touch any key to return calculator to state before improper command or entry was entered. The Errors are described in the appendix.

PR ERROR

When power to the calculator is disrupted and restored the display shows PR ERROR. This indicates continuous memory has been reset and all data, program and status information have been lost.

Underflow and Overflow Display If an value is calculated to be greater than 9.999999999 X 10

, the calculation is disrupted and the display will read 9.999999 99 or –9.999999 99 (for either positive or negative values)

VICTOR TECHNOLOGY

If an entered value is less than 10

-99

, the value of 0 is used in proceeding

equations. Running Display

Some programs and functions need an extended amount of time to complete.

During these times --------- will appear in the display.

LST X

To recall a value entered before an operation was executed, the LST X button is appropriate (RPN method only).

Example

You can purchase phone cards that are valid for 250 minutes, 500 minutes, or 1,000 minutes for 3 cents per minute. You can calculate how much each card would cost without re-entering .03.

ENTRIES DISPLAY

250 ENTER

250.00 Stores 250 minutes

.03 X.

7.50 Displays cost of 250 minutes at 3 cents per minute

500 .r. LST X

0.03 Stores 500 and recalls the cost of 3 cents per minute

.X.

15.00 Displays cost of 500 minutes

1000 .r. LST X

0.03 Stores 1000 and recalls the cost of 3 cents per minute

.X.

30.00 Displays cost of 1000 minutes

VICTOR TECHNOLOGY

x ↔ y

x ↔ y is the exchange key (RPN method only). It switches the values in the

x-register to the y-register and the value in the y-register to the x-register.

Example

You wish to calculate 2,520 ÷ 30 but you mistakenly enter 30 first and 2520 second which would give you the wrong answer. To correct this mistake, use

the x ↔ y button.

ENTRIES (RPN) DISPLAY

30.00

30 ENTER

Displays 30 as the first entry. The value is stored in the x register. 2,520.

2520

Displays the second value. At this time, you realize you entered the values in the reverse order for your desired division.

30.00

x↔y

Displays 30 because the Exchange key has swapped the value in the x-register with the value in the y-register.

÷.

84.00 Displays the result of 2520 ÷30

Statistical Features and Functions

Compiling Statistical Data

One and two variable statistical calculations are made possible with the ∑+

button which calculates and saves statistics into storage registers R1, R2, R3, R

, R5, and R6. The six calculations possible and the storage registers used

are summarized below:

STATISTICAL VALUE REGISTER UTILIZED

The number of data pairs entered: n R1

Sum of the x values: ∑x R2

VICTOR TECHNOLOGY

Sum of the square of the x values: ∑x2 R

Sum of the y values: ∑y R4

Sum of the square of the y values: ∑y2 R

Sum of the multiplication of x and y: ∑xy R6

Clearing the statistical registers before entering new data is necessary. Do this by touching

b. ∑+ (also resets block registers and the display screen).

One-variable statistical calculations contain only x-values (data points). To

enter only x-values, enter the value, and then touch ∑+.

Two variable statistical calculations contain both x and y values (data pairs). To enter these:

¾ Enter x value ¾ Touch ENTER ¾ Enter y value

¾ Touch ∑+

Every time ∑+ is touched, the calculator will:

¾ Increase the value in R1 by one, and display the value ¾ Add the x value to the number in R ¾ Add the square of the x value to R ¾ Add the y value to R

¾ Add the square of the y value to R ¾ Add the product of both x and y values to R

The values stored in the b registers can be retrieved by touching RCL and entering the number of the storage register.

Recovering Incorrectly Entered Statistical Data

The accumulated statistics can be modified if entered incorrectly.

Steps:

¾ Enter incorrect x and/or y values

VICTOR TECHNOLOGY

¾ Touch r ∑ -

¾ Enter new (correct) x and/or y values

¾ Touch r ∑+

Standard Deviation Entries

The button sequence r s will calculate the standard deviation (a measure of

the dispersion around the mean of the X and Y values) for both X and Y values.

Mean Values

The r x button sequence calculates the mean of the X and Y values. The product of the average (mean) of the X value is shown on the display screen

after touching r. x.. To show the average of the Y value, touch x↔y.

Example

A doctor measures the height and weight of 10 children with the same age. What is the standard deviation of the height and what is the standard deviation of the weight? What are the mean of the height and the mean of the weight?

The measurements are summarized below:

Child Height (Inches)

= y-values

Weight (lbs) = x-values

1 48 85 2 51 76 3 36 54 4 39 54 5 40 65 6 47 62 7 42 58 8 41 56 9 39 55

10 43 53

VICTOR TECHNOLOGY

ENTRIES DISPLAY

48 ENTER

48.00 Displays the first y value.

1.00

85 ∑+

Displays which entry has just been entered … the first data pair.

51 ENTER

51.00 Displays the second y value.

2.00

76 ∑+

Displays which entry has just been entered … the second data pair.

… etc. … etc. until all 10 data pairs have been entered.

10.77

r s.

Displays the standard deviation for the x values (Weight).

4.70

x↔y

Displays the standard deviation for the y values (Height).

r x.

x↔y

61.80 Displays the mean for the x values (Weight).

42.60 Displays the mean for the y values (Height).

Note: The above example provides the best estimates of the standard deviation assuming the data provided is a sample

of the population and not the

entire population.

Linear Estimates for x and y

When two-variable statistical information is stored in the statistical registers, an estimated y value can be calculated using a new x value or an estimated x value can be calculated using a new y value.

To estimate y:

¾ Enter the new x value

¾ Touch r y, r

To estimate x:

VICTOR TECHNOLOGY

¾ Enter the new y value

¾ Touch r x, r

The correlation coefficient, r, can be calculated by touching the x↔y key after calculating the estimate.

Example

Using the children’s height (y) and weight (x) values from above, estimate the height (y) of a child weighing 64 pounds (x) and determine the correlation coefficient. Note: Do not clear the registers after the prior example.

ENTRIES DISPLAY

43.34

64 r y, r

Displays the estimated height of a child weighting 64 pounds.

0.77

x↔y

Displays the correlation coefficient (r) of the data pairs.

Weighted Mean Values

A set of numbers and their weighted mean may be determined if you know the weights of the items to be calculated. To do this:

¾ Touch b clear ∑ 

¾ Enter value of item and touch ENTER

¾ Enter items’ weight and touch ∑+ ¾ Repeat until all values are entered, following the item ENTER weight

∑+ formula

¾ Touch r x w to calculate weighted mean of all values

Example

Over a 6-month period, you buy bricks on many occasions to lay a path through your garden.

• First month: 150 bricks at $0.68 a brick

• Second month: 200 bricks at $0.43 a brick

VICTOR TECHNOLOGY

• Third month: 50 bricks at $0.52 a brick

• Fourth month: 100 bricks at $0.61 a brick

• Fifth month: 250 bricks at $0.49 a brick

Find the weighted mean cost of the bricks.

ENTRIES DISPLAY

b ∑-

48.00 Displays the first x value.

1.00

.68 ENTER 150 ∑+

Displays which entry has just been entered … the first data pair.

2.00

.43 ENTER 100 ∑+

Displays which entry has just been entered … the second data pair.

3.00

.52 ENTER 50 ∑+

Displays which entry has just been entered … the third data pair.

4.00

.61 ENTER 100 ∑+

Displays which entry has just been entered … the fourth data pair.

5.00

.49 ENTER 250 ∑+

Displays which entry has just been entered … the fifth data pair.

0.55

r x w

Displays the weighted mean for the x values (price).

Mathematical Features and Functions

Most mathematical operations need only one number to be in the calculator (on the display screen) before a function button is touched. Touching the function button displays the result in the display screen in place of the originally entered number.

Fractional Values

VICTOR TECHNOLOGY

Touching r FRAC displays the fractional part of the value (all digits to the left of the decimal point are replaced by a 0.)

The use of r FRAC also changes the number inside the x register. In RPN method, the original number can be viewed again in the display screen by touching r LSTx .

Example

ENTRIES DISPLAY

99.12 ENTER

r FRAC

r LSTx

99.12 Displays the value.

0.12 Displays the fractional portion of the value.

99.12 Displays the original value.

Integer Values

Touching r INTG will replace the number on the display screen with its integer part (all digits to the right of the decimal point are replaced by 0)

Just like r FRAC , r INTG also changes the number inside the unit. In RPN method, the original number can be viewed again on the display screen by touching r LSTx.

Example

ENTRIES DISPLAY

99.12 ENTER

r INTG

r LST X

99.12 Displays the value.

99.00 Displays the integer portion of the value.

99.12 Displays the original value.

Rounded Values

VICTOR TECHNOLOGY

To round a number in the display screen to a specified number of decimal places, set the display format to show the exact number of decimal places desired. Each time a calculator function is performed, the value displayed will be rounded automatically. However, the value before rounding is actually stored in the register. To permanently round a value, touch b. RND. To see the full value of a number (without rounding) touch .b . PREFIX.

Example

ENTRIES DISPLAY

99.1266 ENTER

b PREFIX

b RND

99.13 Displays the rounded value.

99.126600000 Displays the entire value for a short pause.

99.13 Displays the original value.

99.130000000

b PREFIX

Displays the entire value for a short pause after permanent rounding.

Factorial Values

When r n! is touched, the factorial of the value on the display screen is calculated. (the product of the values of integers 1 to n, being the number on the display screen)

Example

ENTRIES DISPLAY

720.00

6 r n!

Displays the factorial value of 6 (1 X 2 X 3 X 4 X 5 X 6).

Exponential Values

When r e

is touched, the exponential of the value on the display screen is

calculated (raises the base number –e- to the number on the display screen)>

Example

VICTOR TECHNOLOGY

ENTRIES DISPLAY

3 r ex

20.09 Displays the exponential value of 3.

Logarithm Values

When r LN is touched, the natural logarithm (logarithm to the base of e) is calculated. Subsequently touching 10 r LN ÷. in RPN and ÷ 10 r LN = in ALG method calculates the common logarithm (logarithm to the base of 10 of

the number on the display screen).

Example

ENTRIES DISPLAY

9 r LN

2.20 Displays the natural logarithmic value of 9.

0.95

10 r LN ÷.

Displays the common logarithmic value of 9 (when in RPN mode)

0.95

÷ 10 r LN =

Displays the common logarithmic value of 9 (when in ALG mode)

Square Root Values

When r √x is touched, the square root of the value on the display screen will be calculated.

Example

ENTRIES DISPLAY

9 √x

3.00 Displays the square root of 9.

Squared Values

When r x

is touched, the square of the value on the display screen is

calculated.

VICTOR TECHNOLOGY

Example

ENTRIES DISPLAY

9 x2

81.00 Displays the square of 9.

Reciprocal Values

When 1/x is touched, the number on the display screen is divided into 1 (giving the reciprocal value).

Example

ENTRIES DISPLAY

5 1/x

0.20 Displays the reciprocal of 5.

VICTOR TECHNOLOGY

Power Features in ALG method

, the power of a value, may be calculated in ALG method as follows:

¾ Enter the y value ¾ Touch y

¾ Enter the x value (exponent value) ¾ Touch = to calculate number, the power of the value

Example

ENTRIES (ALG) DISPLAY

2 yx 3

8.00 Displays 2

(2 X 2 X 2 = 8).

Power Features in RPN method

, the power of a value, may be calculated in RPN method as follows:

¾ Enter the y value ¾ Touch ENTER ¾ Enter the x value ¾ Touch y

Example

ENTRIES (ALG) DISPLAY

2 ENTER 3 yx

8.00 Displays 2

(2 X 2 X 2 = 8).

VICTOR TECHNOLOGY

Chapter 5: The Basics of Programming

Programs are a sequence of button entries that are stored into the calculator. Calculations involving the same sequence of button entries are common, and saving them in a program can save time.

Creating Your Own Program To create a program, just write it and store it.

¾ Write out the sequence of operations you will use to calculate the value

or values you wish to find.

¾ Select the function option by touching either b ALG or .b RPN ¾ Note: Use programs made in ALG to perform operations while in ALG

METHOD only, and programs made in RPN METHOD to perform operations while in RPN METHOD only.

¾ Touch b P/R to enable program function. In program mode,

operations entered are not executed, but stored into the calculator. The PRGM icon will appear on the display screen while in program mode.

¾ Touch b clear PRGM to clear any previous programs stored into the

calculator

¾ Enter the sequence of operations you wrote down in the first step.

Example

Your online business is having a 30% off sale. You can make a program that will find the net price of each item after the discount and the $10.00 shipping and handling fee is added. Find the net price of a $150 item.

ENTRIES (RPN) DISPLAY

150

ENTER

150 Displays the regular price of $150 item

150.00 Prepares the number for further activity

30 %.

45.00 Computes the 30% discount.

VICTOR TECHNOLOGY

105.00 Displays the 30% off price plus $10.

10 Displays the shipping and handling fee

115.00 Displays the 30% off price plus $10.

In ALG method:

ENTRIES (ALG) DISPLAY

150

30 %.

150 Displays the regular price of $150 item

150.00 Prepares for number for further activity

45.00 Computes the 30% discount.

105.00 Displays amount after discount.

10 Displays the shipping and handling charge of $10

115.00 Displays the 30% off price plus $10.

After you calculate net cost, you can set the calculator to program function and erase any previously stored programs by:

ENTRIES DISPLAY

b P/R

Sets the calculator to program function

VICTOR TECHNOLOGY

b PRGM

000 Clears the program memory

To create a program, use the same buttons you used to solve for net cost manually. What is shown on the display screen in the next step will be further explained later.

In RPN method:

ENTRIES (RPN) DISPLAY

ENTER

001, 36

3 002, 3

0 003, 0

004, 25

005, 30

1 006, 1

0 007, 0

008, 40

In ALG method:

ENTRIES (ALG) DISPLAY

001, 30

3 002, 3

0 003, 0

004, 25

005, 40

VICTOR TECHNOLOGY

1 006, 5

0 007, 0

007, 36

Executing Your Own Program

Touch b P/R to put calculator back in run function. Enter all required input into the calculator the same as if you were calculating manually. (When a program is executed, the data already entered onto the display and into the registers inside the unit are used.)

Touch R/S to begin executing the program.

Use your program to now calculate the net cost of an $800 item and a $365 item. The program will work the same in both RPN and ALG method.

ENTRIES DISPLAY

b P/R

800

R/S

365

Puts the calculator in Run method

800.00 Displays the regular price of $800 item

570.00 Displays the 30% off price plus $10.

365.00 Displays the regular price of $365 item

R/S

265.50 Displays the 30% off price plus $10.

VICTOR TECHNOLOGY

Program Memory Basics

Program Memory stores a sequence of entries in calculator memory for re-use

at a later time. A program line is specific number, function key, or decimal

point. For example the ENTER button is a program line. Program lines that start with b , r , RCL, STO, or GTO buttons have two entries because the entry is incomplete without describing what comes after the first button.

When executing a program, all instructions therein are performed—all button sequences are carried out, just like touching the keys manually—and begin with the current program line proceeding through all the rest of the program lines.

When in program mode, the display screen holds data from the current program line. To the left of the display screen is the number of the program line in the program memory.

The rest of the digits describe a code that tells what instruction is stored within that program line. A program line set to 000 will show no code, because there is no instruction specified. To display a program line: touch b , P/R to set calculator to program mode instead of run mode, this will display the key code and line number for the calculator’s current program line.

To check some (or all) instruction stored within the program memory: touch SST (single step) in program mode to go to the next line of program memory and its instructional information. To see the prior line of program memory touch

.r BST which will back step the program one line at a time.

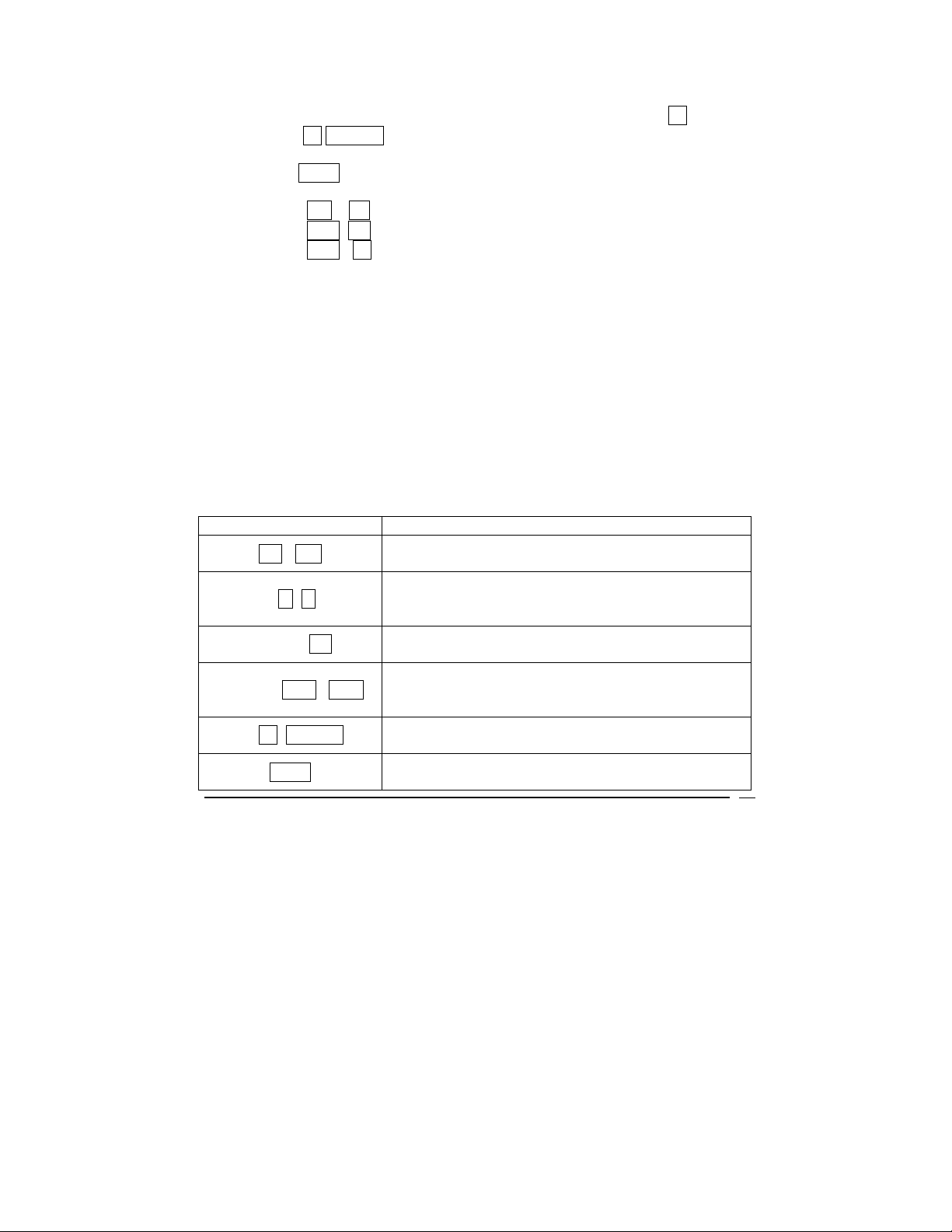
Determining Program Line Instructions

All keys besides the number 0-9 keys on the calculator are described by 2-digit key codes that correspond with that specific key’s location on the keyboard. The first number in the key code is the number of the key row, with the first row being 1-9, and 0 for the 10

key. The number keys 0-9 have key codes that correspond to their values (the number 3 button’s key code is only ‘3’), therefore storing the R↓ button to a program as an instruction into program memory displays a line number and key code of 001 33.

VICTOR TECHNOLOGY

1 2 3 4 5

Row 1

Row 2

Row 3

Row 4

Key Column

67890

Row, 3

= 33

Key

The illustration shows the button for the instruction in program line 001 is in the third row of the keyboard and is the third button within that row, the R↓ button. When the instruction ÷ is entered into the program memory it will be displayed as 002 10. This shows the button for the instruction in program line 2 within the program memory is in the first row and is the tenth key. When the instruction 3 is entered, the key code is displayed only as 3. The button sequences that begin with b , r , RCL , STO , and GTO are stored within one program line, and therefore the display of that line would show key codes for all keys within the button sequence.

Examples

ENTRIES DISPLAY

xxx, 43 7

r BEG

Displays the program line number, the position of the first key touched (43) and the position of the second key touched (7) xxx, 44 5

STO 5

Displays the program line number, the position of the first key touched (44) and the position of the second key touched (5)

VICTOR TECHNOLOGY

xxx, 42 15

b IRR

Displays the program line number, the position of the first key touched (42) and the position of the second key touched (15)

Program line 000 and the GTO 000 instruction:

The GTO 000 instruction tells the calculator to go to and execute program line

000. Line 000 contains no regular instruction, but holds a default instruction that tells the calculator to stop execution of the program. This means after you run the program, the calculator goes to program line 000 and stops, waiting for you to enter new data and run the program again. The calculator is also set to program line 000 when b., P/R is touched, or by touching b PRGM in run mode. The GTO 000 instruction is stored in every program line before beginning the program and is replaced by the instructions entered and moved into the next program line, all the way up to the 400

(maximum) program line. The calculator is set to hold eight lines of program memory, so if you had eight lines of programming, the calculator would automatically perform instruction GTO 000 after the eighth line was performed. Entering more that eight lines automatically expands to hold the additional instructions and program lines.

To find how many program lines (including r GTO 000) are in program memory, touch r MEM to prompt the display below where xx stands for the number of allocated program lines and yy stands for the number of available

registers:

P-xx r-yy

Performing a Program One Line at a Time

SST allows you to run a program a single step at a time and check that the program you wrote matches the program you stored. This does not mean that the program you wrote will correctly calculate your results. (Even skilled programmers’ programs don’t run correctly at first.)

VICTOR TECHNOLOGY

To ensure your program runs correctly, use the SST button while in RUN mode to move to the next line in the program and display its key code and line number. In RUN mode, releasing the SST button executes the program line instruction that was just displayed, and then displays the result of the execution of that line.

Example

Re-enter the program described earlier in this chapter: Your online business is having a 30% off sale. The program finds the net price of each item after the discount and the $10.00 shipping and handling fee is added. After entering the program, run the program with an initial price of $200 using SST.

ENTRIES (RPN) DISPLAY

b P/R

000, Sets calculator to program mode

ENTER

001, 36

3 002, 3

0 003, 0

004, 25

005, 30

1 006, 1

0 007, 0

008, 40

Program is now stored

b P/R

200

0.00 Sets calculator to run mode 200 Enters the initial price

VICTOR TECHNOLOGY

SST (Hold)

001, 36 Displays the first program line

200.00 Executes the first program line 002, 3 Displays the second program line

3. Executes the second program line 003, 0 Displays the third program line

30. Executes the third program line 004, 25 Displays the fourth program line

60.00 Executes the fourth program line 005, 30 Displays the fifth program line

140.00 Executes the fifth program line 006, 1 Displays the sixth program line 1 Executes the sixth program line 007, 0 Displays the seventh program line 10 Executes the seventh program line 008, 40 Displays the eighth program line 150 Executes the eighth program line

VICTOR TECHNOLOGY

Setting the Calculator to a Specific Program Line

Storing a second program or adjusting an existing program sometimes requires you to go to a specific line of programming. There are three alternative approaches:

1. Use the SST button to cycle through the program lines.

2. In PRGM mode press r. GTO . xxx with xxx being the desired program line. The display will next show the program line specified.

3. In run mode press r. GTO xxx with xxx being the desired program line. The display will not change however if the R/S key is touched the program will start executing from the specified program line.

Interrupting a Program During Execution

To disrupt a program during execution (to see a result or to enter new information) touch r , PSE (pause) or R/S (run/stop) buttons. Touching r PSE while running a program will stop the program for about one second and then continue. During the pause, the last result calculated before touching r PSE will be displayed. Touching any key during a pause stops the program execution completely. To resume executing the program of the program line following the r PSE instruction, touch R/S .

Example

Create a program that calculates the sale price of an item at both 10% off and 20% off. Display the results with a pause in between each figure. For example, if the regular price is $200, then 10% off would be $180 and 20% off would be $160.

ENTRIES (RPN) DISPLAY

b P/R

000, Puts the calculator in Program method

b PRGM

STO 0

Memory program is cleared.

001, 44 0 Program will store the entry into register 0 for later use

VICTOR TECHNOLOGY

002, 48 Decimal point

X-

r PSE

RCL 0

X-

003, 9 .9 = 90% or 10% off

004, 20 Multiply by 90% 005, 43 31 Pause 006, 45 0 Recall the original entry 007, 48 Decimal point 008, 8 .8 = 80% or 20% off 009, 20 Multiply by 80%

To run the program, exit the program mode, press b P/R., enter the regular price, and press R/S.

ENTRIES (RPN) DISPLAY

b P/R

200

Puts the calculator in Run method

200 Displays the regular price of $200

R/S

180.00 Displays the 10% off price

160.00 After a pause, displays the 20% off price. Note: If the pause is too short, additional pauses can be added by programming r. PSE more than once.

VICTOR TECHNOLOGY

Stopping a Program During Execution

Touching R/S during program execution automatically stops execution. To resume running the program from where it was stopped, touch R/S again.

A stop can be inserted into a program just like any other function or key.

Example

Create a program that calculates the sale price of an item at both 10% off and 20% off. Display the results with a stop in between each figure. For example, if the regular price is $200, then 10% off would be $180 and 20% off would be $160.

ENTRIES (RPN) DISPLAY

b P/R

000, Puts the calculator in Program method

b PRGM

STO 0

X-

R/S

RCL 0

Memory program is cleared.

001, 44 0 Program will store the entry into register 0 for later use

002, 48 Decimal point

003, 9 .9 = 90% or 10% off

004, 20 Multiply by 90% 005, 31 Stop program execution 006, 45 0 Recall the original entry 007, 48 Decimal point

VICTOR TECHNOLOGY

X-

008, 8 .8 = 80% or 20% off 009, 20 Multiply by 80%

To run the program, exit the program mode, press b P/R., enter the regular price, and press R/S.

ENTRIES (RPN) DISPLAY

b P/R

200

Puts the calculator in Run method

200 Displays the regular price of $200

R/S

180.00 Displays the 10% off price

160.00 After a stop, displays the 20% off price.

VICTOR TECHNOLOGY

Chapter 6: Branch & Loop Programs

Program instructions typically execute sequentially through program line numbers, but it is possible to transfer or ‘branch’ to a program line that is not the next line of program memory. Using the GTO instruction in a program will transfer an execution to any program line by using the designated three digit code of that line within the GTO command. After a branch, execution will resume sequentially as normal. For example, if program line 008 contains the command r GTO 004, then program line 004 will be executed after program line 008.

When the GTO instruction describes a lower number program line, the instructions contained within the lines between that line and the GTO instruction will be performed repeatedly. This is called ‘looping’.

To terminate the execution of a loop, insert a r x< instruction within the loop. Also, touching any key while executing the loop will stop the program.

Branching with Conditions

Sometimes you will need to branch to different lines of program memory, conditionally. There are two conditional test instructions used in program of conditional branching.

r x<

y determines whether the value in the x-register is less than or equal to the value in the y-register. The x-register holds the number currently displayed in run mode and the y-register holds the number in the display when you touched ENTER. (Touching 3 ENTER 9 would store 3 in the y-register and 9 in the x-register.)

r x=0 determines whether the value in the X register is equal to 0.

Using these instructions will either:

y , r x=0 , or R/S

VICTOR TECHNOLOGY

¾ Continue program execution sequentially to the next line of program

memory (if the tested condition was true when executed.)

¾ Skip instruction in the next line of programming and continue with the

following line (if the tested condition was false.)

Example

Create a program that determines the amount owed on a credit card after making $100 payments each month. The interest rate is 12% per year or 1% per month. Program a brief pause after showing each monthly amount. Stop the program when the amount owed is less than $0.

ENTRIES (RPN) DISPLAY

b P/R

000, Puts the calculator in Program method

b PRGM

Memory program is cleared.

001, 1 Digit 1 is the first program line

002, 25 Multiply by 1% to calculate monthly interest

003, 40 Add the 1% interest to the amount owed

004, 1 Digit 1 is the fourth program line 005, 0 Digit 0 is the fifth program line 006, 0 Digit 0 is the sixth program line 007, 30 Subtract $100 from the amount owed

VICTOR TECHNOLOGY

STO 0

r PSE

ENTER

008, 44 0 Store the value in register 0 009, 43 31 Pause 010, 43 31 Pause 011, 43 31 Pause 012, 43 31 Pause 013, 0 Digit 0 is the 13th program line 014, 36 Digit 0 is entered into the x register 015, 45 0

RCL 0

The value in register 0 is recalled into the x register and the value in the x register (zero) is moved to y register 016, 43 34

r x<

If x is less than or equal to y, then perform the next instruction, else skip the next instruction. 017, 43 33 000

r GTO 000

Go to program line 0 (halts program if the debt owed is less than or equal to $0) 018, 43 33 001

r GTO 001

Go to program line 1 (continues program if the debt owed is greater than $0)

To run the program, exit the program mode, press b P/R., enter the initial credit card debt, and press R/S. In the example below, we will use an initial debt of $300.

ENTRIES (RPN) DISPLAY

b P/R

Puts the calculator in Run method

VICTOR TECHNOLOGY

300

300.00 Displays the initial debt of $300

203.00

R/S

Executes the program and displays the amount owed after 1 month of interest at 1% and a $100 payment.

105.03 After a pause, displays the amount owed after the 2

month

6.08 After a pause, displays the amount owed after the next month

-93.86 After a pause, displays the amount owed after the next month. In this case, a $100 payment would create a balance less than zero and the program stops.

Note: With this example, if the program is halted before completion, the registers must be cleared by pressing b REG before running the program again.

Note: With this example, an initial debt of more than $10,000 will result in a growing credit card debt despite the $100 monthly payment.

Storing More Than One Program

More than one program may be created and stored if each program ends with

1) the R/S instruction to halt execution at program end and 2) the GTO instruction looping the program back to the starting line if it is to run again. To run a program that starts at a line other than 001, set the calculator to the first line in the program with a GTO instruction before you touch R/S.

VICTOR TECHNOLOGY

Chapter 7: Editing Your Programs

To change a single instruction in program memory, the following steps are followed:

¾ Touch b P/R to enter PROGRAM mode ¾ Touch SST , BST or GTO . buttons to find the program line

directly before the specific program line that contains the instruction you wish to change.

¾ Enter the new instruction.

Example

Re-enter the program described in chapter 5: Your online business is having a 30% off sale. The program finds the net price of each item after the discount and the $10.00 shipping and handling fee is added. After entering the program, change the program to reflect a 50% off sale. This will require a change to program line 002.

ENTRIES (RPN) DISPLAY

b P/R

b PRGM

000, Sets calculator to program mode 000, Clears all program lines

ENTER

001, 36

3 002, 3

0 003, 0

004, 25

005, 30

1 006, 1

0 007, 0

VICTOR TECHNOLOGY

008, 40

Program is now stored

b P/R

r GTO . 001

0.00 Sets calculator to run mode

0.00 Sets calculator to program mode 001, 36 Displays the first program line 002, 5

Displays the new information for program line 002: 3 has been replaced by 5 to enable the program to calculate a 50% discount instead of 30%.

b P/R

0.00 Sets calculator to run mode

If the program is run with a starting value of 100, the result should now be 60 (50% off of 100 plus 10).

Inserting Instructions Into a Program

To insert new instructions into a program, a branch must be created because the V12 does not have a mechanism to insert new program lines between existing program lines.

Branching will allow you to go to a new instruction added at the end of the program, then branch back and continue with the next program line after the branch.

To add by Branching Method:

¾ Touch b P/R to enter PROGRAM mode ¾ Touch r GTO . then the 3-digit program line number directly

before the point where the additional instructions will go.

¾ To specify the line number of the new branch, touch .r GTO and

the three-digit line number where the branch will start. Suggestion: Use the second line after the end of the program because the first

VICTOR TECHNOLOGY

line is reserved for the GTO 000 instruction. Therefore if the program ends on the 008 line, start the branch at line 010.

¾ Note: The replaced program line in the original program must be

replicated at the end of the new branch.

¾ Note: The last program line in your new branch must loop back to

the original program directly after the point where you wanted to insert the additional instructions. For example, if you branch out of the program in line 004, you must branch back to 005.

Example

Using the prior example for our online business, add a branch that will add 5% sales tax before adding the $10 shipping and handling charge. Program line 006 will be replaced with a branch.

ENTRIES (RPN) DISPLAY

b P/R

b PRGM

000, Sets calculator to program mode 000, Clears all program lines

ENTER

5 002, 5

0 003, 0

1 006, 1

0 007, 0

.r GTO 000

001, 36

004, 25

005, 30

008, 40

009,43,33,000 Instructs program to return to line 000 after execution. This is required if a branch is to follow.

VICTOR TECHNOLOGY

Program is now stored

b P/R

0.00 Sets calculator to run mode

0.00 Sets calculator to program mode 004, 25

.r GTO . 004

Go to and display the fourth program line. As a result, the next key strokes will be recorded on line 005. 005,43,33,010

.r GTO 010

Replaces and displays the contents of line 005 instructing the program to go to line 010 009,43,33,000

.r GTO . 009

Go to and display the ninth program line. As a result, the next key strokes will be recorded on line 010. 010, 30

.--

Places the minus key as the first line of the branch. This performs the function of the old line 005 which was replaced with the GTO function.

5 011, 5

.+-

.r GTO 006

b P/R

012, 25

013, 40

014,43,33,006 Instructs program to branch back to line 006

0.00 Sets calculator to run mode

If the program is run with a starting value of 100, the result should now be

62.50 (50% off of 100, add 5% tax, add 10 for shipping and handling). To see the execution one line at a time, use the SST key.

Inserting Instructions at the End of a Program

One or more instructions can be added at the end of a program with the following steps:

VICTOR TECHNOLOGY

¾ Touch b P/R to enter PROGRAM mode. ¾ Touch r GTO . and the three-digit line number of the last line

in the program.

¾ Enter new instructions.

VICTOR TECHNOLOGY

Chapter 8: Error Messages

Certain operational procedures prohibit the V12 from completing calculations causing an error message to appear on the display screen, along with a number 0-9 that corresponds with the particular error condition. These errors are summarized below:

ERROR CAUSE

2 A zero value is preventing statistical calculation

9 Service required. Contact Victor.

The operation included a zero value that prevented calculation. Example: 1 ÷ 0 The result is greater than the maximum possible number of

9.999999999 X 10

The IRR calculation can not be completed because more than one answer is possible. An estimate of IRR may need to be provided to overcome the error. Memory error caused by an attempt to enter more than the maximum number of program lines or go to a line that does not contain instructions. Error in calculating compound interest caused by entries such as improper values of zero or sets of input that have no solution. Example: n = 0 will not allow calculation of payments. Maximum register capacity has been exceeded or a storage register has been included in an operation that does not exist or is being used for program memory. For the inputs provided, no IRR can be calculated (often created when no negative cash flow is provided). Calendar error due to improper format or specification of dates out of range of the calculator.

VICTOR TECHNOLOGY

Thank you for purchasing a product from Victor Technology.

This product has been electronically tested. If you have problems using this product, please carefully refer to the instruction manual.

This product, except the battery, is warranted by Victor to the original purchaser to be free from defects in material and workmanship under normal use for a period of two years from the date of purchase. During the warranty period, and upon proof of purchase, the product will be repaired or replaced (with the same or a similar model) at Victor’s option, at a Victor Authorized Service Center, without any charge for either parts or labor.

This warranty will not apply if the product has been misused, abused, or altered. Without limiting the foregoing, battery leakage, bending of the unit, a broken display, a cracked housing, and cracks in the LCD display will be presumed to have resulted from misuse or abuse.

To obtain warranty service you must take or send the product, postage paid, with a copy of your sales receipt or other proof of purchase and the date of purchase, to a victor Authorized Service Center. Due to the possibility of damage or loss, it is recommended when sending product that you package the product securely and send it insured, return receipt requested.

NEITHER THIS WARRANTY NOR ANY OTHER WARRANTY, EXPRESS OR IMPLIED, INCLUDING ANY IMPLIED WARRANTY OF MERCHANTABILITY OR OF FITNESS FOR A PARTICULAR PURPOSE, SHALL EXTEND BEYOND THE WARRANTY PERIOD. NO RESPONSIBILITY IS ASSUMED FOR ANY INCIDENTAL OR CONSEQUENTIAL DAMAGES, INCLUDING WITHOUT LIMITATION DAMAGES RESULTING FROM MATHEMATICAL INACCURACY OF THE PRODUCT OR LOSS OF STORED DATA. SOME STATES DO NOT ALLOW LIMITATIONS ON HOW LONG AN IMPLIED WARRANTY LASTS AND SOME STATES DO NOT ALLOW THE EXCLUSION OR LIMITATION OF INCIDENTAL OR CONSEQUENTIAL DAMAGES, SO THE ABOVE LIMITATIONS OR EXCLUSIONS MAY NOT APPLY TO YOU. This warranty gives you specific rights and you may also have other rights which vary from state to state.

If your product needs repair, please call 1-800-

If for any reason this product is to be returned to the store where purchased, it must be packed in the original package. Thank you.

Victor Technology

V12 Calculator

Limited Warranty

628-2420 or visit us at www.VictorV12.com.

Victor Technology LLC

780 West Belden Ave.

Addison IL, 60101

Victor Technology V12 User Manual

Specifications and Main Features

Frequently Asked Questions

User Manual