Texas Instruments TI-Nspire CX CAS Reference Guide [pt]

TI-Nspire™CAS

Manual de Referência

Este manual do utilizador aplica-se ao software TI-Nspire™ versão 4.5. Para obter a versão mais recente da documentação, visite education.ti.com/go/download.

Informações importantes

Excepto se indicado expressamente na Licença que acompanha um programa, Texas Instruments não dá garantia, explícita ou implícita, incluindo mas não se limitando a quaisquer garantias de comercialização e adequação a um fim particular, relativamente a quaisquer programas ou materiais de documentação e disponibiliza estes materiais unicamente numa base “tal qual”. Em nenhum caso, a Texas Instruments será responsável perante alguém por danos especiais, colaterais, incidentais, ou consequenciais em ligação com a ou provenientes da compra ou utilização destas matérias, e a responsabilidade única e exclusiva da Texas Instruments, independentemente da forma de actuação, não excederá a quantia estabelecida na licença do programa. Além disso, a Texas Instruments não será responsável por qualquer queixa de qualquer tipo apresentada contra a utilização destes materiais por terceiros.

Licença

Consulte a íntegra da licença instalada em C:\ProgramFiles\TIEducation\<TI-Nspire™

Product Name>\license.

Índice

Informações importantes

Modelos de expressão 1

Lista alfabética 8

A B C D E F G I L M N O P Q R S T U V W X Z

17 21 48 61 72 82

93 102 119 127 137 140 149 152 168 196 212 213 214 216 217

iii

Símbolos 226

Elementos (nulos) vazios 253

Atalhos para introduzir expressões matemáticas 255

Hierarquia do EOS™ (Equation Operating System) 257

Constantes e valores 259

Mensagens e códigos de erros 260

Códigos de aviso e mensagens 269

Assistência e Suporte 271

Apoio técnico, manutenção e garantia dos produtos Texas Instruments

271

Índice remissivo 272

Modelos de expressão

Os modelos de expressão oferecem uma forma simples para introduzir expressões matemáticas em notação matemática padronizada. Quando introduzir um modelo, aparece na linha de entrada com pequenos blocos em posições em que pode introduzir elementos. Um cursor mostra o elemento que pode introduzir.

Utilize as teclas de setas ou prima e para mover o cursor para a posição de cada elemento e escreva um valor ou uma expressão para o elemento. Prima · ou

/· para avaliar a expressão.

Modelo de fracção

Nota: Consulte também / (dividir),

página 228.

Modelo de expoente

Nota: Escreva o primeiro valor, prima l e,

em seguida, escreva o expoente. Para colocar o cursor na base, prima a seta

direita ( ¢ ).

Nota: Consulte também ^ (potência),

página 229.

Modelo de raiz quadrada

Nota: Consulte também ‡() (raiz

quadrada), página 239.

Teclas /p

Exemplo:

Tecla l

Exemplo:

Teclas /q

Exemplo:

Modelos de expressão 1

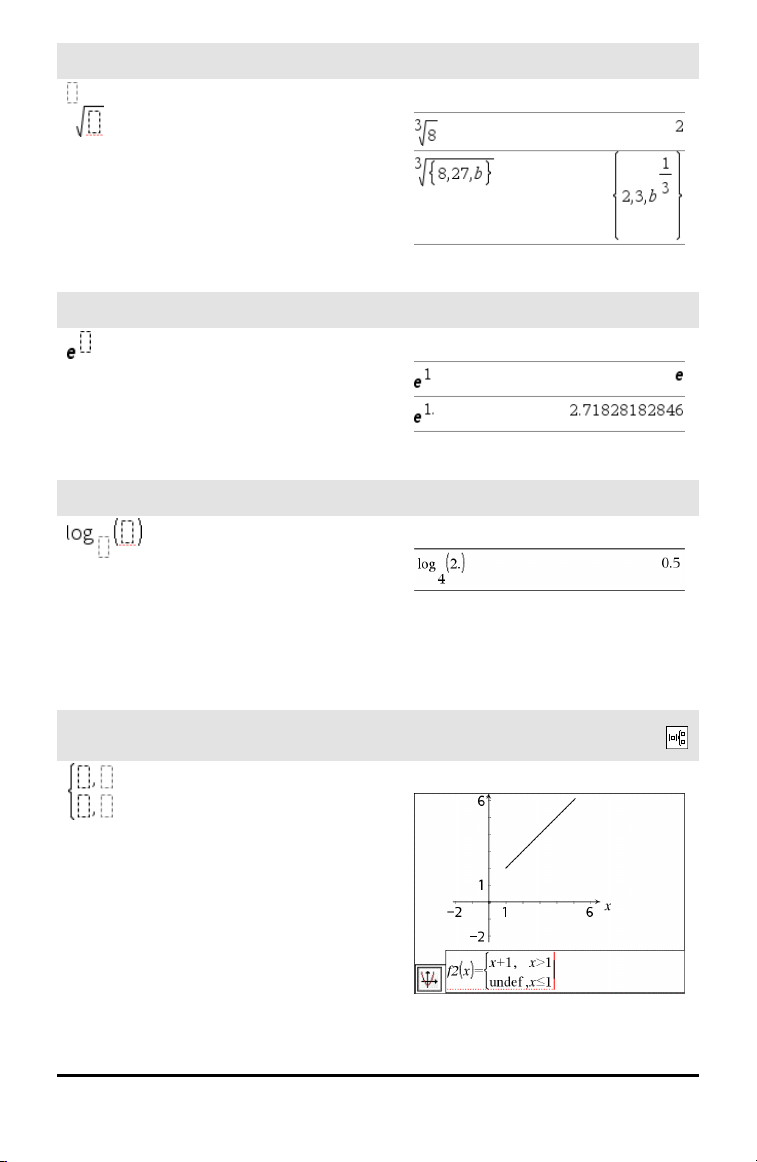
Modelo de raiz de índice N

Nota: Consulte também raiz(), página

165.

Teclas /l

Exemplo:

Modelo de expoente e

Exponencial natural e elevado à potência

Nota: Consulte também e ^(), página 61.

Modelo de log

Calcule o log para uma base especificada. Para uma predefinição de base 10, omita a base.

Nota: Consulte também log(), página 114.

Modelo de Função por ramos (2 ramos)

Permite criar expressões e condições para uma função por ramos de 2 ramos. Para adicionar um ramo, clique no modelo e repita o modelo.

Nota: Consulte também piecewise(), página

141.

Tecla u

Exemplo:

Teclas /s

Exemplo:

Catálogo>

Exemplo:

2 Modelos de expressão

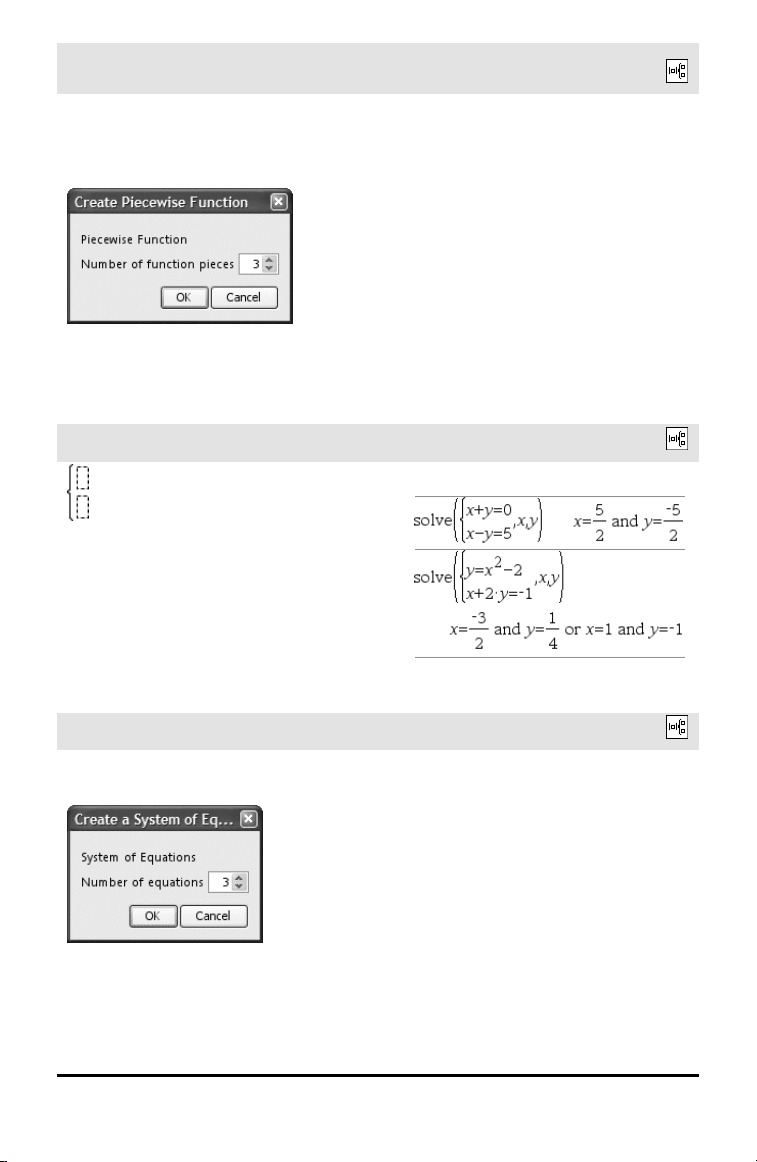
Modelo de Função por ramos (N ramos)

Permite criar expressões e condições para uma função por ramos de N -ramos. Para adicionar um ramo, clique no modelo e repita o modelo.

Nota: Consulte também piecewise(), página

141.

Catálogo>

Exemplo:

Consulte o exemplo para o modelo de Função por ramos (2 ramos).

Modelo do sistema de 2 equações

Cria um sistema de duas equações. Para adicionar uma linha a um sistema existente, clique no modelo e repita o modelo.

Nota: Consulte também sistema(), página

195.

Modelo do sistema de N equações

Permite criar um sistema de N equações. Pede N.

Nota: Consulte também sistema(), página

195.

Catálogo>

Exemplo:

Catálogo>

Exemplo:

Consulte o exemplo do modelo do sistema de equações (2equações).

Modelos de expressão 3

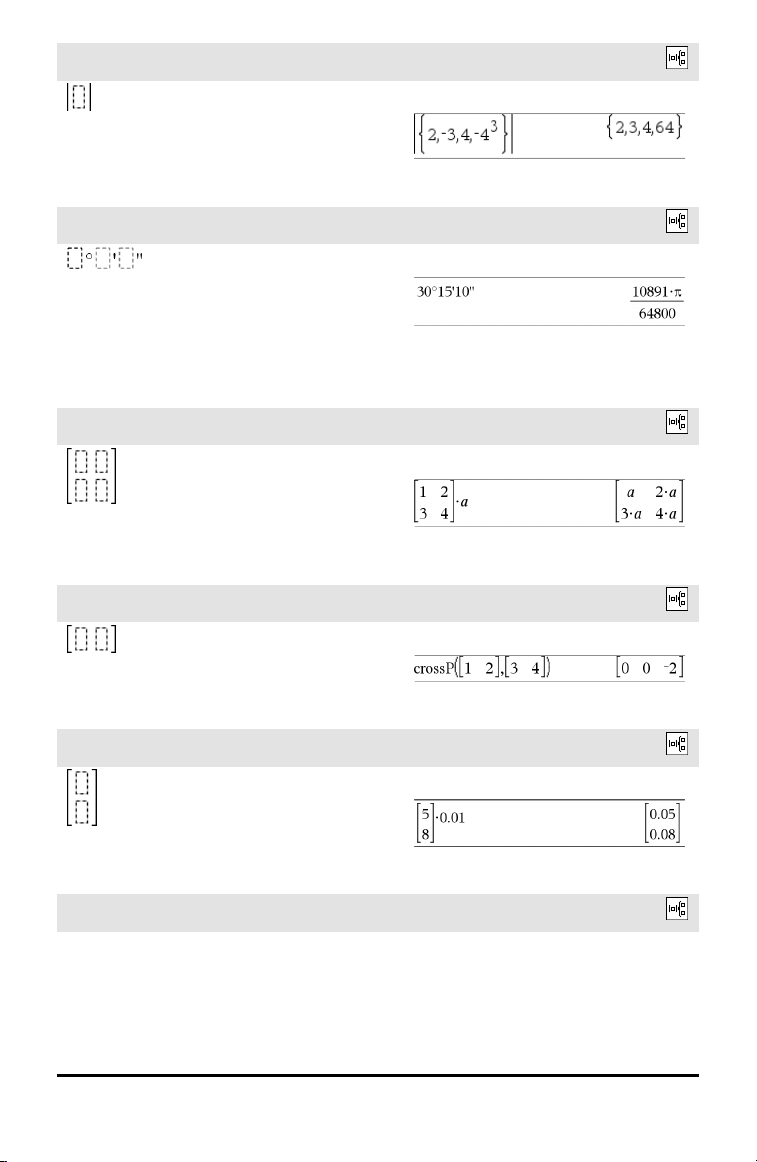
Modelo do valor absoluto

Nota: Consulte também abs(), página 8.

Catálogo>

Exemplo:

Modelo gg°mm’ss.ss’’

Permite introduzir ângulos na forma gg °

mm ’ ss.ss ’’, em que gg é o número de

graus decimais, mm é o número de minutos e ss.ss é o número de segundos.

Modelo da matriz (2 x 2)

Cria uma matriz 2 x 2.

Modelo da matriz (1 x 2)

Modelo da matriz (2 x 1)

Catálogo>

Exemplo:

Catálogo>

Exemplo:

Catálogo>

Exemplo:

Catálogo>

Exemplo:

Modelo da matriz (m x n)

O modelo aparece depois de lhe ser pedido para especificar o número de linhas e colunas.

4 Modelos de expressão

Catálogo>

Exemplo:

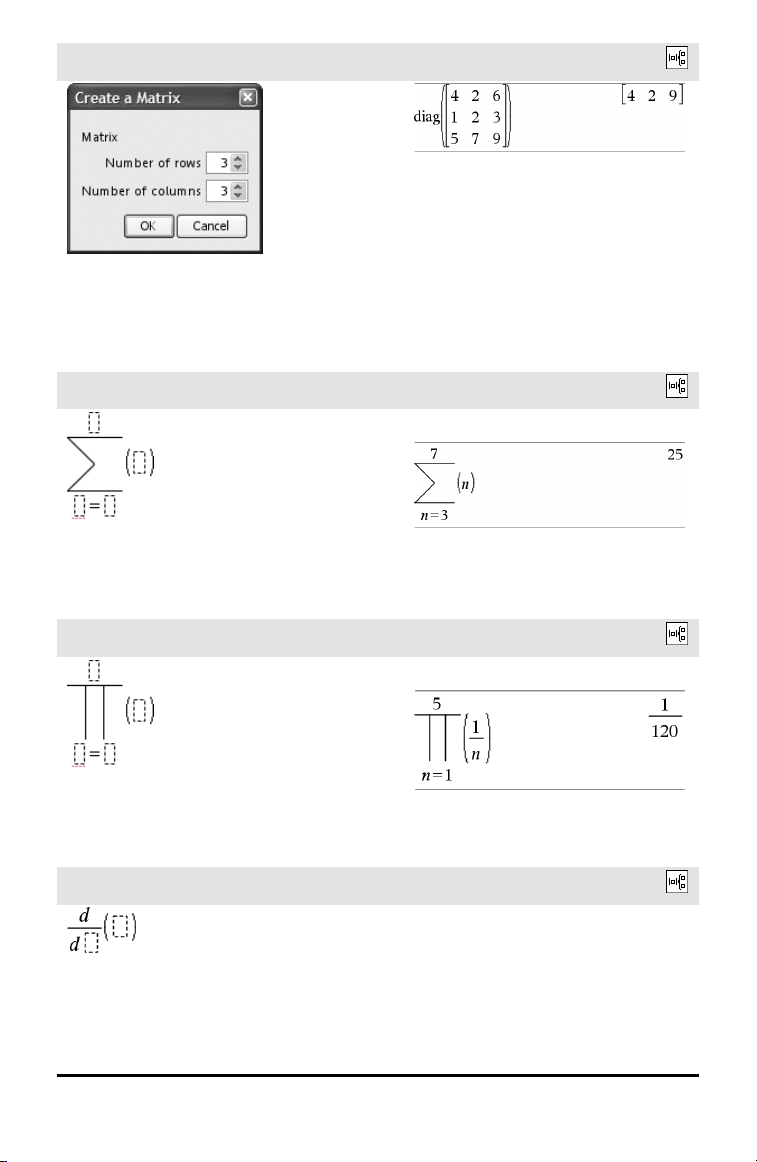
Modelo da matriz (m x n)

Nota: Se criar uma matriz com um grande

número de linhas e colunas, pode demorar alguns momentos a aparecer.

Catálogo>

Modelo da soma (G)

Nota: Consulte também G() (sumSeq),

página 241.

Modelo do produto (Π)

Nota: Consulte também Π () (prodSeq),

página 240.

Modelo da primeira derivada

Catálogo>

Exemplo:

Catálogo>

Exemplo:

Catálogo >

Exemplo:

Pode também utilizar o modelo da primeira derivada para calcular a primeira derivada num ponto.

Modelos de expressão 5

Modelo da primeira derivada

Nota: Consulte também d() (derivada) ,

página 237.

Catálogo >

Modelo da segunda derivada

Pode também utilizar o modelo da segunda derivada para calcular a segunda derivada num ponto.

Nota: Consulte também d() (derivada) ,

página 237.

Modelo da derivada de índice N

Pode utilizar o modelo da n-ésima derivada para calcular a derivada de ordem n.

Nota: Consulte também d() (derivada),

página 237.

Modelo do integral definido

Catálogo >

Exemplo:

Catálogo>

Exemplo:

Catálogo>

Exemplo:

Nota: Consulte também ‰() integral(), página 226.

6 Modelos de expressão

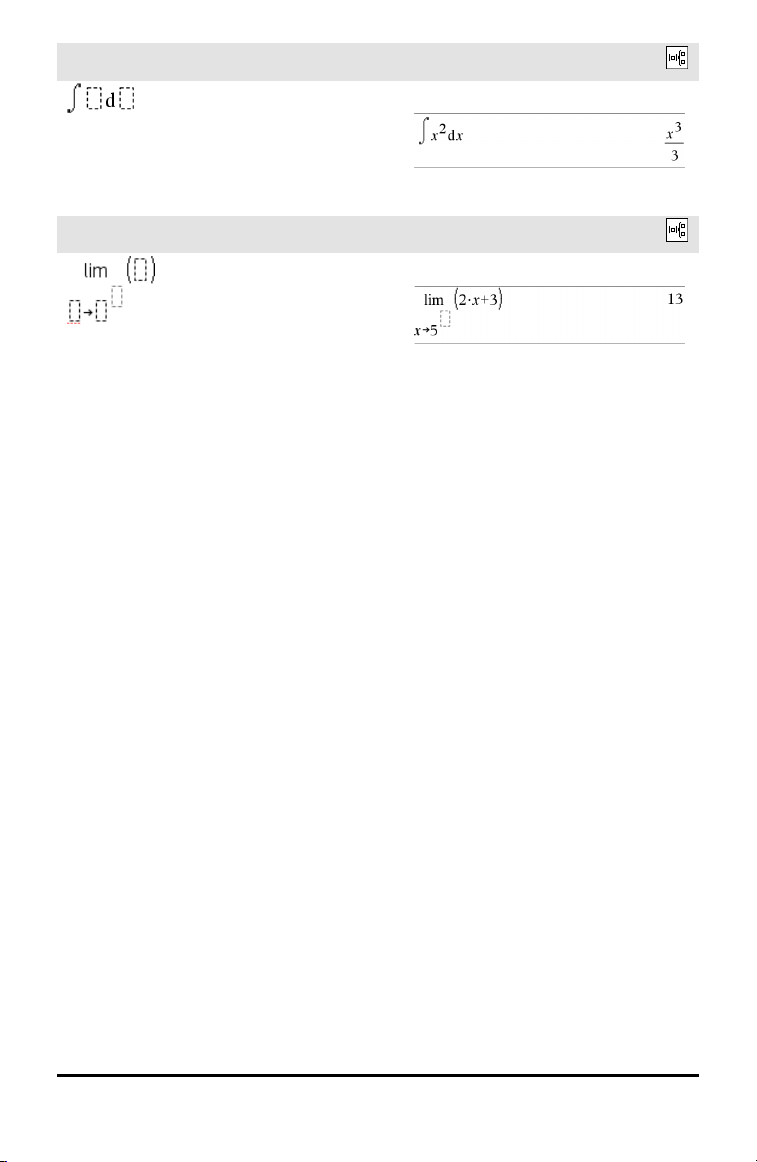
Modelo do integral indefinido

Nota: Consulte também ‰() integral(),

página 226.

Catálogo>

Exemplo:

Modelo do limite

Utilize N ou (N) para o limite esquerdo. Utilize + para o limite direito.

Nota: Consulte também limit(), página 104.

Catálogo>

Exemplo:

Modelos de expressão 7

Lista alfabética

Os itens cujos nomes não sejam alfabéticos (como +, !, e >) são listados no fim desta secção, começando (página 226). Salvo indicação em contrário, todos os exemplos desta secção foram efectuados no modo de reinicialização predefinido e todas as variáveis são assumidas como indefinidas.

abs()

abs(Expr1) ⇒expressão abs(Lista1) ⇒lista abs(Matriz1) ⇒matriz

Devolve o valor absoluto do argumento.

Nota: Consulte também Modelo do valor absoluto, página 4.

Se o argumento for um número complexo, devolve o módulo do número.

Nota: Todas as variáveis indefinidas são

tratadas como variáveis reais.

amortTbl()

amortTbl(NPmt, N, I, PV, [ Pmt ], [ FV ], [

PpY ], [ CpY ], [ PmtAt ], [ ValorArredondado ]) ⇒matriz

Função de amortização que devolve uma matriz como uma tabela de amortização para um conjunto de argumentos TVM.

NPmt é o número de pagamentos a incluir

na tabela. A tabela começa com o primeiro pagamento.

N, I, PV, Pmt, FV, PpY, CpY e PmtAt são

descritos na tabela de argumentos TVM, página 210.

• Se omitir Pmt, predefine-se para Pmt = tvmPmt (N, I, PV, FV, PpY, CpY,

PmtAt).

• Se omitir FV, predefine-se para FV =0.

• As predefinições para PpY, CpY e PmtAt

Catálogo >

8 Lista alfabética

amortTbl()

são iguais às predefinições para as funções TVM.

ValorArredondado especifica o número de

casas decimais para arredondamento. Predefinição=2.

As colunas da matriz de resultados são por esta ordem: Número de pagamentos, montante pago para juros, montante para capital e saldo.

O saldo apresentado na linha n é o saldo após o pagamento n.

Pode utilizar a matriz de saída como entrada para as outras funções de amortização G Int() e G Prn(), página 241 e

bal(), página 17.

Catálogo >

and

ExprBooleana1 and ExprBooleana2

⇒Expressão booleana

ListaBooleana1 and ListaBooleana2

⇒Lista booleana

MatrizBooleana1 and MatrizBooleana2

⇒Matriz booleana

Devolve falso, verdadeiro ou uma forma simplificada da entrada original.

Inteiro1 and Inteiro2 ⇒número inteiro

Compara dois números inteiros reais bit a bit com uma operação and. Internamente, ambos os números inteiros são convertidos para números binários de 64 bits assinados. Quando os bits correspondentes forem comparados, o resultado é 1 se ambos os bits forem 1; caso contrário, o resultado é

0. O valor devolvido representa os resultados dos bits e aparece de acordo com o modo base.

Catálogo >

No modo base Hex:

Importante: Zero, não a letra O.

No modo base Bin:

No modo base Dec:

Lista alfabética 9

and

Pode introduzir os números inteiros em qualquer base numérica. Para uma entrada binária ou hexadecimal, tem de utilizar o prefixo 0b ou 0h, respectivamente. Sem um prefixo, os números inteiros são tratados como decimais (base 10).

Se introduzir um número inteiro decimal muito grande para uma forma binária de 64 bits assinada, é utilizada uma operação de módulo simétrico para colocar o valor no intervalo adequado.

Catálogo >

Nota: Uma entrada binária pode ter até64

dígitos (não contando com o prefixo 0b). Uma entrada hexadecimalpode ter até 16 dígitos.

angle()

angle(Expr1) ⇒expressão

Devolve o ângulo do argumento, interpretando o argumento como um número complexo.

Nota: Todas as variáveis indefinidas são

tratadas como variáveis reais.

angle(Lista1) ⇒lista angle(Matriz1) ⇒matriz

Devolve uma lista ou matriz de ângulos dos elementos em Lista1 ou Matriz1, interpretando cada elemento como um número complexo que representa um ponto de coordenada rectangular bidimensional.

Catálogo >

No modo de ângulo Graus:

No modo de ângulo Gradianos:

No modo de ângulo Radianos:

ANOVA

ANOVA Lista1, Lista2 [, Lista3, ..., Lista20

10 Lista alfabética

Catálogo >

ANOVA

Catálogo >

][, Marcador]

Efectua uma análise de variação de uma via para comparar as médias de 2 a 20 populações. Um resumo dos resultados é guardado na variável stat.results (página

190).

Marcador =0 para Dados, Marcador =1

para Estatística

Variável de saída Descrição

stat.F Valor da estatística F

stat.PVal Menor nível de significância para o quala hipótese nulapodeser rejeitada

stat.df Graus deliberdade dos grupos

stat.SS Soma dos quadrados dos grupos

stat.MS Quadrados médios para os grupos

stat.dfError Graus deliberdade dos erros

stat.SSError Soma dos quadrados dos erros

stat.MSError Quadrado médio para os erros

stat.sp Desvio padrão associado

stat.xbarlist Médiada entrada daslistas

stat.CLowerList Intervalos de confiança de 95% para a média decada lista de entrada

stat.CUpperList Intervalos de confiança de 95%para a média de cada lista deentrada

ANOVA2way

ANOVA2way Lista1, Lista2 [, Lista3, …,

Lista10 ][, LinhaNiv]

Calcula uma análise de variação bidireccional através da comparação das médias de 2 a 10 populações. Um resumo dos resultados é guardado na variável

stat.results (página 190). LinhaNiv=0 para Bloco

Catálogo >

Lista alfabética 11

ANOVA2way

Catálogo >

LinhaNiv=2,3,...,Len-1, para Dois fatores,

em que Len=comprimento(Lista1) =comprimento(Lista2) = … = comprimento (Lista10) e Len / LinhaNiv ∈ {2,3,…}

Saídas: Design do bloco

Variável de saída Descrição

stat.F F estatística do factor dacoluna

stat.PVal Menor nível de significância para o quala hipótese nulapodeser rejeitada

stat.df Graus deliberdade do factor da coluna

stat.SS Soma dos quadrados do factor da coluna

stat.MS Quadrados médios para o factor da coluna

stat.FBloco F estatística para o factor

stat.PValBlock Menor probabilidadederejeição da hipótese nula

stat.dfBlock Graus deliberdade para factor

stat.SSBlock Soma dos quadrados para o factor

stat.MSBlock Quadrados médios para o factor

stat.dfError Graus deliberdade dos erros

stat.SSError Soma dos quadrados dos erros

stat.MSError Quadrados médios para os erro s

stat.s Desvio padrão do erro

Saídas do factor da coluna

Variável de saída Descrição

stat.Fcol F estatística do factor dacoluna

stat.PValCol Valor da probabilidade do factor da coluna

stat.dfCol Graus deliberdade do factor da coluna

stat.SSCol Soma dos quadrados do factor da coluna

stat.MSCol Quadrados médios para o factor da coluna

Saídas do factor da linha

12 Lista alfabética

Variável de saída Descrição

stat.FLinha F estatística do factor dalinha

stat.PValRow Valor da probabilidade do factor da linha

stat.dfRow Graus deliberdade do factor da linha

stat.SSRow Soma dos quadrados do factor da linha

stat.MSRow Quadrados médios para o factor da linha

Saídas de interacção

Variável de saída Descrição

stat.FInteragir Festatística da interacção

stat.PValInteract Valor da probabilidade da interacção

stat.dfInteract Graus deliberdade da interacção

stat.SSInteract Soma de quadrados da interacção

stat.MSInteract Quadrados médios para interacção

Saídas de erros

Variável de saída Descrição

stat.dfError Graus deliberdade dos erros

stat.SSError Soma dos quadrados dos erros

stat.MSError Quadrados médios para os erro s

s Desvio padrão do erro

Ans

Ans⇒valor

Devolve o resultado da expressão avaliada mais recentemente.

Teclas /v

Lista alfabética 13

approx()

approx(Expr1) ⇒expressão

Devolve a avaliação do argumentos como uma expressão com valores decimais, quando possível, independentemente do modo Auto ou Aproximado actual.

Isto é equivalente a introduzir o argumento e a introduzir / ·.

approx(Lista1) ⇒lista approx(Matriz1) ⇒matriz

Devolve uma lista ou uma matriz em que cada elemento foi avaliado para um valor decimal, quando possível.

Catálogo >

4approxFraction()

Expr 4approxFraction([Tol])⇒expressão Lista 4approxFraction([Tol])⇒lista Matriz 4 approxFraction([Tol])⇒matriz

Devolve a entrada como uma fracção com uma tolerância de Tol. Se omitir Tol, é utilizada uma tolerância de 5.E-14.

Nota: Pode introduzir esta função através

da escrita de @>approxFraction(...) no teclado do computador.

approxRational()

approxRational(Expr [ , Tol] )

⇒expressão

approxRational(Lista [ , Tol] ) ⇒lista approxRational(Matriz [ , Tol] ) ⇒matriz

Devolve o argumento como uma fracção com uma tolerância de Tol. Se omitir Tol, é utilizada uma tolerância de 5.E-14.

Catálogo >

14 Lista alfabética

arccos()

Consulte cos/(), página 33.

arccosh()

arccot()

arccoth()

arccsc()

arccsch()

arcLen()

arcLen(Expr1, Var, Início, Fim)

⇒expressão

Devolve o comprimento do arco de Expr1 do Início ao Fim em relação à variável

Var.

O comprimento do arco é calculado como um integral que assume uma definição do modo de função.

arcLen(Lista1, Var, Início, Fim) ⇒lista

Devolve uma lista dos comprimentos dos arcos de cada elemento de Lista1 do Início ao Fim em relação a Var.

Consulte cosh/(), página 35.

Consulte cot/(), página 36.

Consulte coth/(), página 37.

Consulte csc/(), página 39.

Consulte csch/(), página 40.

Catálogo >

arcsec()

Consulte sec/(), página 169.

Lista alfabética 15

arcsech()

Consulte sech/(), página 169.

arcsin()

arcsinh()

arctan()

arctanh()

augment()

augment(Lista1, Lista2) ⇒lista

Devolve uma nova lista que é a Lista2 acrescentada ao fim da Lista1.

augment(Matriz1, Matriz2) ⇒matriz

Devolve uma nova lista que é a Matriz2 acrescentada ao fim da Matriz1. Quando utilizar o carácter “,”, as matrizes têm de ter dimensões de colunas iguais, e a

Matriz2 é acrescentada à Matriz1 como

novas colunas. Não altere Matriz1 ou

Matriz2.

Consulte sin/(), página 180.

Consulte sinh/(), página 182.

Consulte tan/(), página 197.

Consulte tanh/(), página 198.

Catálogo >

16 Lista alfabética

avgRC()

avgRC(Expr1, Var [=Valor] [, Passo])

⇒expressão

avgRC(Expr1, Var [=Valor] [, Lista1])

⇒lista

avgRC(Lista1, Var [=Valor] [, Passo])

⇒lista

avgRC(Matriz1, Var [=Valor] [, Passo])

⇒matriz

Devolve o quociente de diferença de avanço (taxa de câmbio média).

Expr1 pode ser um nome de função

definido pelo utilizador (ver Func). Ao especificar o Valor, substitui qualquer

atribuição de variável anterior ou qualquer substituição atual “|” para a variável.

Passo é o valor do passo. Se omitir Passo,

predefine-se para 0,001.

Não se esqueça de que a função similar

centralDiff() utiliza o quociente de

diferença central.

Catálogo >

bal()

bal(NPmt, N, I, PV, [ Pmt ], [ FV ], [ PpY

], [ CpY ], [ PmtAt ], [ ValorArredondado ]) ⇒valor

bal(NPmt, TabelaDeDepreciação) ⇒valor

Função de amortização que calcula o saldo do plano após um pagamento especificado.

N, I, PV, Pmt, FV, PpY, CpY e PmtAt são

descritos na tabela de argumentos TVM, página 210.

NPmt especifica o número de pagamentos

a partir dos quais quer os dados calculados.

Catálogo >

Lista alfabética 17

bal()

N, I, PV, Pmt, FV, PpY, CpY e PmtAt são

descritos na tabela de argumentos TVM, página 210.

• Se omitir Pmt, predefine-se para Pmt = tvmPmt(N, I, PV, FV, PpY, CpY,

PmtAt).

• Se omitir FV, predefine-se para FV =0.

• As predefinições para PpY, CpY e PmtAt são iguais às predefinições para as funções TVM.

ValorArredondado especifica o número de

casas decimais para arredondamento. Predefinição=2.

bal(NPmt, TabelaDeDepreciação) calcula

o saldo após o número de pagamentos

NPmt, baseado na tabela de amortização TabelaDeDepreciação. O argumento TabelaDeDepreciação tem de ser uma

matriz no forma descrita em amortTbl(), página 8.

Nota: Consulte também G Int() e G Prn(),

página 241.

Catálogo >

4Base2

NúmeroInteiro1 4Base2 ⇒número inteiro

Nota: Pode introduzir este operador através

da escrita de @>Base2 no teclado do computador.

Converte NúmeroInteiro1 para um número binário. Os números binários ou hexadecimais têm sempre um prefixo 0b ou 0h, respectivamente. Zero, não a letra O, seguido por b ou h.

0b NúmeroBinário 0h NúmeroHexadecimal

Um número binário pode ter até 64 dígitos. Um número hexadecimal pode ter até 16 dígitos.

18 Lista alfabética

Catálogo >

4Base2

Sem um prefixo, NúmeroInteiro1 é tratado como decimal (base 10). O resultado aparece em binário, independentemente do modo base.

Os números negativos aparecem no formato de “complemento de dois”. Por exemplo,

N1 aparece como 0hFFFFFFFFFFFFFFFF no modo base Hex 0b111...111 (64 1’s) no modo base Binário

N263aparece como 0h8000000000000000 no modo base Hex 0b100...000 (63 zeros) no modo base Binário

Se introduzir um número inteiro na base 10 fora do intervalo de uma forma binária de 64 bits assinada, é utilizada uma operação de módulo simétrico para colocar o valor no intervalo adequado. Considere os seguintes exemplos de valores fora do intervalo.

263torna-se N263e aparece como 0h8000000000000000 no modo base Hex

0b100...000 (63 zeros) no modo base Binário

Catálogo >

264torna-se 0 e aparece como 0h0 no modo base Hex 0b0 no modo base Binário

N263N 1 torna-se 263N 1 e aparece como 0h7FFFFFFFFFFFFFFF no modo base Hex 0b111...111 (64 1’s) no modo base Binário

4Base10

NúmeroInteiro1 4Base10 ⇒número inteiro

Catálogo >

Lista alfabética 19

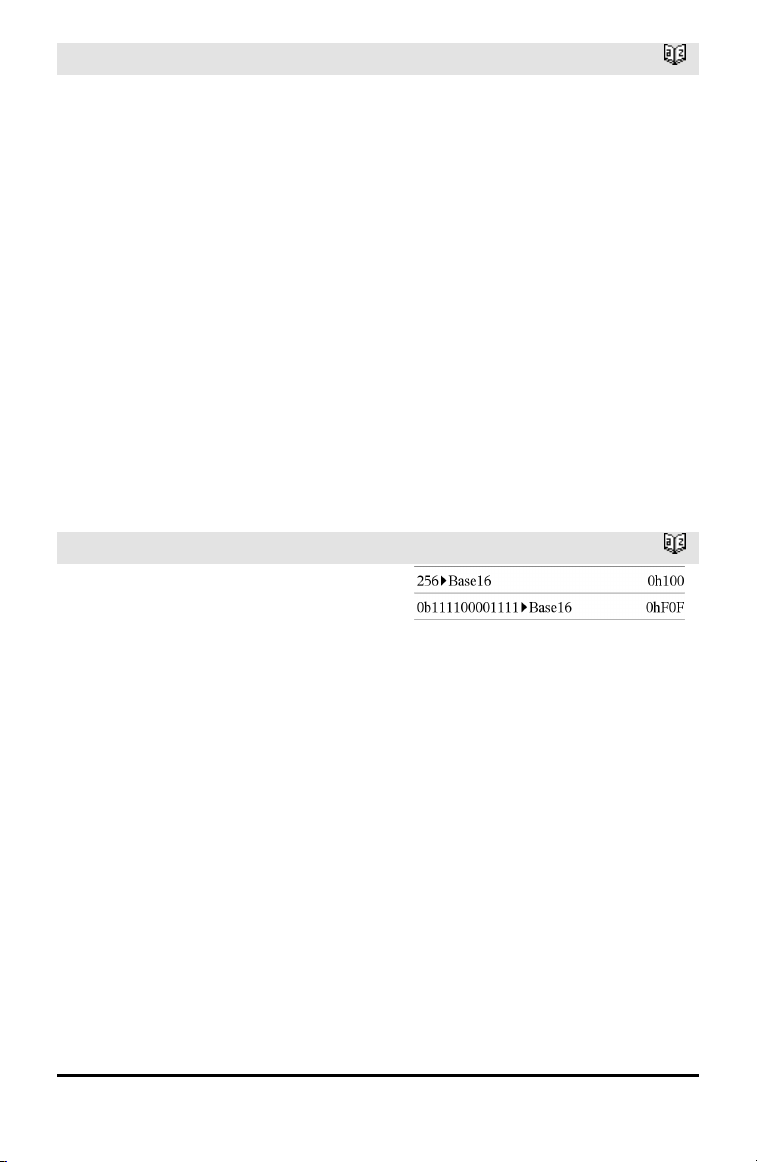
4Base10

Nota: Pode introduzir este operador através

da escrita de @>Base10 no teclado do computador.

Converte NúmeroInteiro1 para um número decimal (base 10). Uma entrada binária ou hexadecimal têm de ter sempre um prefixo 0b ou 0h, respectivamente.

0b NúmeroBinário 0h NúmeroHexadecimal

Zero, não a letra O, seguido por b ou h.

Um número binário pode ter até 64 dígitos. Um número hexadecimal pode ter até 16 dígitos.

Sem um prefixo, NúmeroInteiro1 é tratado como decimal. O resultado aparece em decimal, independentemente do modo base.

Catálogo >

4Base16

NúmeroInteiro1 4Base16 ⇒número inteiro

Nota: Pode introduzir este operador através

da escrita de @>Base16 no teclado do computador.

Converte NúmeroInteiro1 para um número hexadecimal. Os números binários ou hexadecimais têm sempre um prefixo 0b ou 0h, respectivamente.

0b NúmeroBinário 0h NúmeroHexadecimal

Zero, não a letra O, seguido por b ou h.

Um número binário pode ter até 64 dígitos. Um número hexadecimal pode ter até 16 dígitos.

Sem um prefixo, NúmeroInteiro1 é tratado como decimal (base 10). O resultado aparece em hexadecimal, independentemente do modo base.

20 Lista alfabética

Catálogo >

4Base16

Se introduzir um número inteiro na base 10 muito grande para uma forma binária de 64 bits assinada, é utilizada uma operação de módulo simétrico para colocar o valor no intervalo adequado. Para mais informações, consulte 4Base2, página 18.

Catálogo >

binomCdf()

binomCdf(n, p) ⇒lista binomCdf(n, p, LimiteInferior,

LimiteSuperior) ⇒ número se LimiteInferior e LimiteSuperior forem

números, lista se LimiteInferior e

LimiteSuperior forem listas

binomCdf(n,p,LimiteSuperior)para P(0{X {LimiteSuperior) ⇒ número se

LimiteSuperior for um número, lista se LimiteSuperior for uma lista

Calcula uma probabilidade cumulativa para a distribuição binomial discreta com n número de tentativas e a probabilidade p de sucesso de cada tentativa.

Para P(X { LimiteSuperior), defina

LimiteInferior=0

binomPdf()

binomPdf(n, p) ⇒lista binomPdf(n, p, ValX) ⇒número se ValX for

um número, lista se ValX for uma lista

Calcula uma probabilidade para a distribuição binomial discreta com o n número de tentativas e a probabilidade p de sucesso de cada tentativa.

Catálogo >

ceiling()

ceiling(Expr1) ⇒número inteiro

Catálogo >

Lista alfabética 21

ceiling()

Devolve o número inteiro mais próximo que é | o argumento.

O argumento pode ser um número complexo ou real.

Nota: Consulte também floor().

ceiling(Lista1) ⇒lista ceiling(Matriz1) ⇒matriz

Devolve uma lista ou matriz do ceiling de cada elemento.

Catálogo >

centralDiff()

centralDiff(Expr1,Var [=Valor][,Passo])

⇒expressão

centralDiff(Expr1,Var [,Passo]) |Var=Valor⇒expressão

centralDiff(Expr1,Var [=Valor][,Lista])

⇒lista

centralDiff(Lista1,Var [=Valor][,Passo])

⇒lista

centralDiff(Matriz1,Var [=Valor][,Passo])

⇒matriz

Devolve a derivada numérica com a fórmula do quociente da diferença central.

Ao especificar o Valor, substitui qualquer atribuição de variável anterior ou qualquer substituição atual “|” para a variável.

Passo é o valor do passo. Se omitir Passo,

predefine-se para 0,001. Quando utilizar Lista1 ou Matriz1 , a

operação é mapeada através dos valores da lista ou dos elementos da matriz.

Nota: Consulte também avgRC() e d().

Catálogo >

22 Lista alfabética

cFactor()

cFactor(Expr1 [, Var ]) ⇒expressão cFactor(Lista1 [, Var ]) ⇒lista cFactor(Matriz1 [, Var ]) ⇒matriz

cFactor(Expr1) devolve Expr1 decomposta

em factores em relação a todas as variáveis sobre um denominador comum.

Expr1 é decomposta o mais possível em

factores racionais lineares mesmo que isto introduza novos números não reais. Esta alternativa é adequada se quiser a factorização em relação a mais do que uma variável.

cFactor(Expr1, Var) devolve Expr1

decomposta em factores em relação à variável Var.

Expr1 é decomposta o mais possível em

factores que são lineares em Var, com talvez constantes não reais, mesmo que introduza subexpressões ou constantes irracionais que são irracionais noutras variáveis.

Os factores e os termos são ordenados com

Var como variável principal. As potências

similares de Var são recolhidas em cada factor. Inclua Var se a factorização for necessária em relação apenas a essa variável e estiver disposto a aceitar expressões irracionais em qualquer outra variável para aumentar a factorização em relação a Var. Pode existir alguma decomposição em factores incidental em relação a outras variáveis.

Catálogo >

Lista alfabética 23

cFactor()

Para a definição Auto do modo Auto ou

Aproximado, incluindo Var, permite

também a aproximação a coeficientes de pontos flutuantes em que os coeficientes irracionais não podem ser expressos explicitamente em termos das funções integradas. Mesmo quando exista apenas uma variável, incluindo Var, pode produzir a factorização mais completa.

Nota: Consulte também factor().

Catálogo >

Para ver o resultado completo, prima£ e, de seguida, utilize ¡ e ¢ para mover o cursor.

char()

char(Número inteiro) ⇒carácter

Devolve uma cadeia de caracteres com o carácter numerado Número inteiro a partir do conjunto de caracteres da unidade portátil. O intervalo válido para o Número

inteiro é 0–65535.

charPoly()

charPoly(MatrizQuadrada,Var)

⇒expressão polinomial

charPoly(MatrizQuadrada,Expr)

⇒expressão polinomial

charPoly(MatrizQuadrada1,Matriz2)

⇒expressão polinomial

Devolve o polinómio característico de

MatrizQuadrada. O polinómio

característico de n×n matriz A, indicado por

(l), é o polinómio definido por

(l) = det(l • I NA)

em que I indica a matriz identidade n×n.

MatrizQuadrada1 e MatrizQuadrada2 têm

de ter as dimensões iguais.

Catálogo >

2way

c22way MatrizObs

24 Lista alfabética

Catálogo >

2way

Catálogo >

chi22way MatrizObs

Calcula um teste c2para associação à tabela de contagens bidireccional na matriz observada MatrizObs. Um resumo dos resultados é guardado na variável

stat.results (página 190).

Para mais informações sobre o efeito dos elementos vazios numa matriz, consulte “Elementos (nulos) vazios” (página 253).

Variável de saída Descrição

stat.c

stat.PVal Menor nível de significância para o quala hipótese nulapodeser rejeitada

stat.df Graus deliberdade para a estatística do Quiquadrado

stat.ExpMat Matriz da tabela de contagem de elementos previsto, assumindo a hipótese

stat.CompMat Matriz de contribuições da estatística do Quiquadrado dos elementos

Estatísticado Quiquadrado: soma (observada - prevista)2/prevista

nula

Cdf()

c2Cdf(LimiteInferior,LimiteSuperior,df)

⇒número se LimiteInferior e

LimiteSuperior forem números, lista se LimiteInferior e LimiteSuperior forem

listas

chi2Cdf(LimiteInferior,LimiteSuperior,df)

⇒número se LimiteInferior e

LimiteSuperior forem números, lista se LimiteInferior e LimiteSuperior forem

listas

Calcula a probabilidade de distribuição c

entre LimiteInferior e LimiteSuperior para os graus de liberdade especificados df.

Para P(X { LimiteSuperior), defina

LimiteInferior = 0.

Para mais informações sobre o efeito dos elementos vazios numa lista, consulte “Elementos (nulos) vazios” (página 253).

Catálogo >

Lista alfabética 25

GOF

Catálogo >

c2GOF Lista obs, Lista exp, df

chi2GOF Lista obs, Lista exp, df

Efectua um teste para confirmar que os dados da amostra são de uma população que está em conformidade com uma distribuição especificada. Um resumo dos resultados é guardado na variável

stat.results (página 190).

Para mais informações sobre o efeito dos elementos vazios numa lista, consulte “Elementos (nulos) vazios” (página 253).

Variável de saída Descrição

stat.c

stat.PVal Menor nível de significância para o quala hipótese nulapodeser rejeitada

stat.df Graus deliberdade para a estatística do Quiquadrado

stat.CompList Matriz de contribuições da estatística do Qui quadrado dos elementos

Estatísticado Quiquadrado: soma((observada - prevista)2/prevista

Pdf()

Pdf(ValX,df)⇒número se ValX for um

número, lista se ValX for uma lista chi2Pdf(ValX,df)⇒número se ValX for um

número, lista se ValX for uma lista

Calcula a função de densidade de probabilidade (pdf) para a distribuição c num valor ValX especificado para os graus de liberdade especificados df.

Para mais informações sobre o efeito dos elementos vazios numa lista, consulte “Elementos (nulos) vazios” (página 253).

ClearAZ

Apaga todas as variáveis de um carácter no espaço do problema actual.

26 Lista alfabética

Catálogo >

ClearAZ

Se uma ou mais variáveis estiverem bloqueadas, este comando mostra uma mensagem de erro e só elimina as variáveis desbloqueadas. Consulte unLock, página

212.

Catálogo >

ClrErr

Apaga o estado de erro e define a variável do sistema errCode para zero.

A proposição Else do bloco Try...Else...EndTry deve utilizar ClrErr ou PassErr. Se tiver de processar ou ignorar o erro, utilize ClrErr. Se não souber o que fazer com o erro, utilize

PassErr para o enviar para a rotina de

tratamento de erros seguinte. Se não existirem mais rotinas de tratamento de erros Try...Else...EndTry pendente, a caixa de diálogo de erros aparecerá como normal.

Nota: Consulte também PassErr, página 141,

e Try, página 205.

Obs para introdução do exemplo: Para obter

instruções sobre como introduzir programas com várias linhas e definições de funções, consulte a secção Calculadora do manual do utilizador do produto.

colAugment()

colAugment(Matriz1, Matriz2) ⇒matriz

Devolve uma nova lista que é a Matriz2 acrescentada ao fim da Matriz1. As matrizes têm de ter dimensões de colunas iguais, e a Matriz2 é acrescentada à

Matriz1 como novas colunas. Não altere Matriz1 ou Matriz2.

Catálogo >

Para ver umexemplo deClrErr, consulteo exemplo 2 no comando Try, página 206.

Catálogo >

colDim()

colDim(Matriz) ⇒expressão

Catálogo >

Lista alfabética 27

colDim()

Devolve o número de colunas contidas em

Matriz.

Nota: Consulte também rowDim().

Catálogo >

colNorm()

colNorm(Matriz) ⇒expressão

Devolve o máximo das somas dos valores absolutos dos elementos nas colunas em

Matriz.

Nota: Os elementos da matriz indefinidos

não são permitidos. Consulte também

rowNorm().

comDenom()

comDenom(Expr1 [, Var ]) ⇒expressão comDenom(Lista1 [, Var ]) ⇒lista comDenom(Matriz1 [, Var ]) ⇒matriz

comDenom(Expr1) devolve uma fracção

simplificada com um numerador completamente expandido sobre um denominador completamente expandido.

comDenom(Expr1, Var) devolve um rácio

reduzido do numerador e do denominador expandidos em relação a Var. Os termos e os factores são ordenados com Var como variável principal. As potências similares de

Var são recolhidas. Pode existir alguma

decomposição em factores incidental dos coeficientes recolhidos. Comparada para omitir Var, esta poupa tempo frequentemente, memória e espaço no ecrã, enquanto torna a expressão mais compreensível. Torna também as operações subsequentes no resultado mais rápidas e poupa a memória.

Catálogo >

28 Lista alfabética

comDenom()

Se Var não ocorrer em Expr1, comDenom

(Expr1, Var) devolve uma fracção

simplificada com um numerador não expandido sobre um denominador não expandido. Estes resultados poupam geralmente mais tempo, memória e espaço no ecrã. Estes resultados decompostos parcialmente tornam também as operações subsequentes no resultado mais rápidas e poupam a memória.

Mesmo quando não exista um denominador, a função comden é frequentemente uma forma rápida para alcançar a factorização parcial se factor() for muito lento ou se esgotar a memória.

Sugestão: Introduza esta definição da

função comden() e experimente-a rotinamente como uma alternativamente para comDenom() e factor().

Catálogo >

completeSquare ()

completeSquare(ExprOrEqn, Var)

⇒expressão ou equação

completeSquare(ExprOrEqn, Var^Power)

⇒expressão ou equação

completeSquare(ExprOrEqn, Var1, Var2

[,...])⇒expressão ou equação

completeSquare(ExprOrEqn, {Var1, Var2

[,...]})⇒expressão ou equação

Converte uma expressão polinomial quadrática da forma a·x2+b·x+c para a forma a·(x-h)2+k

Converte uma equação do 2º grau da forma a·x2+b·x+c=d para a forma a·(x-h)2=k

O primeiro argumento tem de ser uma expressão quadrática ou equação na forma padrão, em relação ao segundo argumento.

Catálogo >

Lista alfabética 29

completeSquare ()

O segundo argumento tem de ser um único termo de uma só variável ou um único termo de uma só variável elevado a uma potência racional, por exemplo x, y2 ou z

(1/3)

A terceira e quarta expressões de sintaxe para concluir o quadrado nas variáveis

Var1, Var2 [,… ]).

Catálogo >

conj()

conj(Expr1) ⇒expressão conj(Lista1) ⇒lista conj(Matriz1) ⇒matriz

Devolve o conjugado complexo do argumento.

Nota: Todas as variáveis indefinidas são

tratadas como variáveis reais.

constructMat()

constructMat (Expr,Var1,Var2,NúmLinhas,NúmColunas)

⇒matriz

Devolve uma matriz de acordo com os argumentos.

Expr é uma expressão nas variáveis Var1 e Var2. Os elementos da matriz resultante

são formados através da avaliação de Expr para cada valor incrementado de Var1 e

Var2. Var1 é incrementada automaticamente de

1 a NúmLinhas. Em cada linha, Var2 é

incrementada de 1 a NúmColunas.

Catálogo >

30 Lista alfabética

CopyVar

CopyVar Var1, Var2

CopyVar Var1., Var2.

CopyVar Var1, Var2 copia o valor da

variável Var1 à variável Var2, criando

Var2, se for necessário. A variável Var1

tem de ter um valor. Se Var1 for o nome de uma função definida

pelo utilizador existente, copia a definição dessa função para a função Var2. A função

Var1 tem de ser definida. Var1 tem de cumprir os requisitos de

nomeação de variáveis ou tem de ser uma expressão indirecta que se simplifica para um nome de variável que cumpra os requisitos.

CopyVar Var1., Var2. copia todos os

membros da Var1. grupo de variáveis para a Var2. grupo, criando Var2. se for necessário.

Var1. tem de ser o nome de um grupo de

variáveis existentes, como, por exemplo, o da estatística stat.nn resultados ou variáveis criados com a função LibShortcut

(). Se Var2. já existe, este comando

substitui todos os membros comuns a ambos os grupos e adiciona os membros que já não existam. Se um ou mais membros de Var2. estiverem bloqueados, todos os membros de Var2. ficam inalteráveis.

Catálogo >

corrMat()

corrMat(Lista1, Lista2 [, …[, Lista20 ]])

Calcula a matriz de correlação para a matriz aumentada [ Lista1, Lista2, ..., Lista20 ].

4cos

Expr 4cos

Catálogo >

Lista alfabética 31

4cos

Nota: Pode introduzir este operador através

da escrita de @>cos no teclado do computador.

Representa Expr em função do co-seno. Este é um operador de conversão. Apenas pode ser utilizado no fim da linha de entrada.

4cos reduz todas as potências de sin(...) módulo 1Ncos(...)^2 para quaisquer polinómios residuais de potências de cos (...) tenham expoentes no intervalo [0, 2]. Por conseguinte, o resultado ficará livre de sin(...) se e só se sin(...) ocorrer na expressão fornecida apenas em potências pares.

Nota: Este operador de conversão não é

suportado nos modos de ângulos Graus ou Grados. Antes de o utilizar, certifique-se de que o modo Ângulo está definido para Radianos e que Expr não contém referências explícitas a ângulos em graus ou grados.

Catálogo >

cos()

cos(Expr1) ⇒expressão cos(Lista1) ⇒lista

cos(Expr1) devolve o co-seno do

argumento como uma expressão.

cos(Lista1) devolve uma lista de co-senos

de todos os elementos na Lista1.

Nota: O argumento é interpretado como

um ângulo express em graus, gradianos ou radianos, de acordo com a definição do modo de ângulo actual. Pode utilizar ¡, Gou R para substituir o modo de ângulo temporariamente.

32 Lista alfabética

Tecla µ

No modo de ângulo Graus:

No modo de ângulo Gradianos:

No modo de ângulo Radianos:

cos()

Tecla µ

cos(MatrizQuadrada1) ⇒Matriz quadrada

Devolve o co-seno da matriz da

MatrizQuadrada1. Isto não é o mesmo que

calcular o co-seno de cada elemento.

Quando uma função escalar f(A) operar na

MatrizQuadrada1 (A), o resultado é

calculado pelo algoritmo:

Calcule os valores próprios (li) e os vectores próprios (Vi) de A.

MatrizQuadrada1 tem de ser diagnolizável.

Também não pode ter variáveis simbólicas sem um valor.

Forme as matrizes:

A = X B X /e f(A) = X f(B) X /. Por exemplo, cos(A) = X cos(B) X / em que:

cos(B) =

No modo de ângulo Radianos:

Todos os cálculos são efectuados com a aritmética de ponto flutuante.

cos/()

cos/(Expr1) ⇒expressão cos/(Lista1) ⇒lista

Tecla µ

No modo de ângulo Graus:

Lista alfabética 33

cos/()

cos/(Expr1) devolve o ângulo cujo co-seno

é Expr1 como uma expressão.

cos/(Lista1) devolve uma lista de co-senos

inversos de cada elemento de Lista1.

Nota: O resultado é devolvido como um

ângulo expresso em graus, gradianos ou radianos, de acordo com a definição do modo de ângulo actual.

Nota: Pode introduzir esta função através

da escrita de arccos(...) no teclado.

cos/(MatrizQuadrada1) ⇒Matriz

quadrada

Devolve o co-seno inverso da matriz de

MatrizQuadrada1. Isto não é o mesmo que

calcular o co-seno inverso de cada elemento. Para mais informações sobre o método de cálculo, consulte cos().

MatrizQuadrada1 tem de ser diagnolizável.

O resultado contém sempre os números de ponto flutuante.

Tecla µ

No modo de ângulo Gradianos:

No modo de ângulo Radianos:

No modo de ângulo Radianos eFormato complexo rectangular:

Para ver o resultado completo, prima£ e, de seguida, utilize ¡ e ¢ para mover o cursor.

cosh()

cosh(Expr1) ⇒expressão cosh(Lista1) ⇒lista

cosh(Expr1) devolve o co-seno hiperbólico

do argumento como uma expressão.

cosh (Lista1) devolve uma lista dos co-

senos hiperbólicos de cada elemento de

Lista1.

cosh (MatrizQuadrada1) ⇒Matriz

quadrada

Devolve o co-seno hiperbólico da matriz de

MatrizQuadrada1. Isto não é o mesmo que

calcular o co-seno hiperbólico de cada elemento. Para mais informações sobre o método de cálculo, consulte cos().

34 Lista alfabética

Catálogo >

No modo de ângulo Graus:

No modo de ângulo Radianos:

cosh()

MatrizQuadrada1 tem de ser diagnolizável.

O resultado contém sempre os números de ponto flutuante.

Catálogo >

cosh/()

cosh/(Expr1) ⇒expressão cosh/(Lista1) ⇒lista

cosh/(Expr1) devolve o co-seno hiperbólico

inverso do argumento como uma expressão.

cosh/(Lista1) devolve uma lista dos co-

senos hiperbólicos inversos de cada elemento de Lista1.

Nota: Pode introduzir esta função através

da escrita de arccosh(...) no teclado.

cosh/(MatrizQuadrada1) ⇒Matriz

quadrada

Devolve o co-seno hiperbólico inverso da matriz de MatrizQuadrada1. Isto não é o mesmo que calcular o co-seno hiperbólico inverso de cada elemento. Para mais informações sobre o método de cálculo, consulte cos().

MatrizQuadrada1 tem de ser diagnolizável.

O resultado contém sempre os números de ponto flutuante.

Catálogo >

No modo de ângulo Radianos eFormato complexo rectangular:

Para ver o resultado completo, prima£ e, de seguida, utilize ¡ e ¢ para mover o cursor.

cot()

cot(Expr1) ⇒ expressão cot(Lista1) ⇒ lista

Devolve a co-tangente de Expr1 ou devolve uma lista das co-tangentes de todos os elementos em Lista1.

Tecla µ

No modo de ângulo Graus:

No modo de ângulo Gradianos:

Lista alfabética 35

cot()

Nota: O argumento é interpretado como

um ângulo expresso em graus, gradianos ou radianos, de acordo com a definição do modo de ângulo actual. Pode utilizar ¡, Gou R para substituir o modo de ângulo temporariamente.

Nota: Pode introduzir esta função através

da escrita de arccot(...) no teclado.

Tecla µ

No modo de ângulo Radianos:

cot/()

cot/(Expr1) ⇒expressão cot/(Lista1) ⇒lista

Devolve o ângulo cuja co-tangente é Expr1 ou devolve uma lista com as co-tangentes inversas de cada elemento de Lista1.

Nota: O resultado é devolvido como um

ângulo expresso em graus, gradianos ou radianos, de acordo com a definição do modo de ângulo actual.

coth()

coth(Expr1) ⇒expressão coth(Lista1) ⇒lista

Devolve a co-tangente hiperbólica de Expr1 ou devolve uma lista das co-tangentes hiperbólicas de todos os elementos de

List1.

Tecla µ

No modo de ângulo Graus:

No modo de ângulo Gradianos:

No modo de ângulo Radianos:

Catálogo >

36 Lista alfabética

coth/()

coth/(Expr1) ⇒expressão coth/(Lista1) ⇒lista

Devolve a co-tangente hiperbólica inversa de Expr1 ou devolve uma lista com as cotangentes hiperbólicas inversas de cada elemento de Lista1.

Nota: Pode introduzir esta função através

da escrita de arccoth(...) no teclado.

Catálogo >

count()

count(Valor1ouLista1 [, Valor2ouLista2

[,...]]) ⇒valor

Devolve a contagem acumulada de todos os elementos nos argumentos que se avaliam para valores numéricos.

Cada argumento pode ser uma expressão, valor, lista ou matriz. Pode misturar tipos de dados e utilizar argumentos de várias dimensões.

Para uma lista, matriz ou intervalo de dados, cada elemento é avaliado para determinar se deve ser incluído na contagem.

Na aplicação Listas e Folha de cálculo, pode utilizar um intervalo de células no lugar de qualquer argumento.

Os elementos (nulos) vazios são ignorados. Para mais informações sobre os elementos vazios, consulte página 253.

countif()

countif(Lista, Critérios) ⇒valor

Devolve a contagem acumulada de todos os elementos em Lista que cumpram os

critérios especificados. Critérios podem ser:

• Um valor, uma expressão ou uma cadeia.

Catálogo >

No último exemplo, apenas 1/2 e 3+4*i são contados. Os restantesargumentos, partindo do princípio que x é indefinido, não se avaliam para valores numéricos.

Catálogo >

Conta o número deelementos igual a3.

Conta o número deelementos igual a“def.”

Lista alfabética 37

countif()

Por exemplo, 3 conta apenas aqueles elementos em Lista que se simplificam para o valor 3.

• Uma expressão booleana com o símbolo ? como um identificador para cada elemento. Por exemplo, ?<5 conta apenas aqueles elementos em Lista inferiores a 5.

Na aplicação Listas e Folha de cálculo, pode utilizar um intervalo de células no lugar de

Lista.

Os elementos (nulos) vazios da lista são ignorados. Para mais informações sobre os elementos vazios, consulte página 253.

Nota: Consulte também sumIf(), página 194

e frequency(), página 80.

Catálogo >

Conta o número deelementos igual ax; este exemplo assume que avariável x é indefinida.

Conta 1e 3.

Conta 3, 5, e 7.

Conta 1, 3, 7 e9.

cPolyRoots()

cPolyRoots(Poli,Var)⇒lista cPolyRoots(ListaDeCoeficientes)⇒lista

A primeira sintaxe, cPolyRoots(Poly,Var), devolve uma lista de raízes complexas do polinómio Poly na variável Var.

Poly tem de ser um polinómio numa

variável.

A segunda sintaxe, cPolyRoots

(ListaDeCoeficientes), devolve uma lista

de raízes complexas para os coeficientes em ListaDeCoeficientes.

Nota: Consulte também polyRoots(), página

146.

38 Lista alfabética

Catálogo >

crossP()

crossP(Lista1, Lista2) ⇒lista

Devolve o produto cruzado de Lista1 e

Lista2 como uma lista. Lista1 e Lista2 têm de ter dimensões

iguais e a dimensão tem de ser 2 ou 3.

crossP(Vector1, Vector2) ⇒vector

Devolve um vector da linha ou coluna (dependendo dos argumentos) que é o produto cruzado de Vector1 e Vector2.

Vector1 e Vector2 têm de ser vectores de

linhas ou ambos têm de ser vectores de colunas. Ambos os vectores têm de ter dimensões iguais e a dimensão tem de ser 2 ou 3.

Catálogo >

csc()

csc(Expr1) ⇒expressão csc(Lista1) ⇒lista

Devolve a co-secante de Expr1 ou devolve uma lista com as co-secantes de todos os elementos em Lista1.

csc/()

csc/(Expr1) ⇒ expressão csc/(Lista1) ⇒ lista

Devolve o ângulo cuja co-secante é Expr1 ou devolve uma lista com as co-secantes inversas de cada elemento de Lista1.

Tecla µ

No modo de ângulo Graus:

No modo de ângulo Gradianos:

No modo de ângulo Radianos:

Tecla µ

No modo de ângulo Graus:

No modo de ângulo Gradianos:

Lista alfabética 39

csc/()

Nota: O resultado é devolvido como um

ângulo expresso em graus, gradianos ou radianos, de acordo com a definição do modo de ângulo actual.

Nota: Pode introduzir esta função através

da escrita de arccsc(...) no teclado.

Tecla µ

No modo de ângulo Radianos:

csch()

csch(Expr1) ⇒ expressão csch(Lista1) ⇒ lista

Devolve a co-secante hiperbólica de Expr1 ou devolve uma lista das co-secantes hiperbólicas de todos os elementos de

List1.

csch/()

csch/(Expr1) ⇒ expressão csch/(Lista1) ⇒ lista

Devolve a co-secante hiperbólica inversa de

Expr1 ou devolve uma lista com as co-

secantes hiperbólicas inversas de cada elemento de Lista1.

Nota: Pode introduzir esta função através

da escrita de arccsch(...) no teclado.

cSolve()

cSolve(Equação, Var) ⇒Expressão

booleana

Catálogo >

cSolve(Equação, Var=Tentativa)

⇒Expressão booleana cSolve(Desigualdade, Var) ⇒Expressão

booleana

40 Lista alfabética

cSolve()

Devolve as soluções complexas candidatas de uma equação ou desigualdade para Var. O objectivo é produzir candidatos para todas as soluções reais e não reais. Mesmo que Equação seja real, cSolve() permite resultados não reais no Formato complexo de resultados reais.

Apesar de todas as variáveis indefinidas que não terminam com um carácter de sublinhado (_) serem processadas como sendo reais, cSolve() pode resolver as equações polinomiais para soluções complexas.

cSolve() define temporariamente o domínio

para complexo durante a resolução mesmo que o domínio actual seja real. No domínio complexo, as potências fraccionárias que tenham denominadores ímpares utilizam o principal em vez da derivação real. Consequentemente, as soluções de solve() para equações que envolvam essas potências fraccionárias não são necessariamente um subconjunto dessas do

cSolve(). cSolve() começa com os métodos

simbólicos exactos. cSolve() utiliza também a decomposição polinomial complexa iterativa, se for necessária.

Nota: Consulte também cZeros(), solve() e zeros().

Nota: Se Equação for não polinomial com

funções, como abs(), angle(), conj(), real() ou imag(), deve colocar um carácter de

sublinhado (premir /_) no fim de

Var. Por predefinição, uma variável é

tratada como um valor real. Se utilizar var _, a variável é tratada como

complexa. Deve também utilizar var _ para qualquer

outra variável em Equação que pode ter valores não reais. Caso contrário, pode obter resultados imprevistos.

Catálogo >

No modo de visualização de dígitos deFix 2:

Para ver o resultado completo, prima£ e, de seguida, utilize ¡ e ¢ para mover o cursor.

Lista alfabética 41

cSolve()

cSolve(Eqn1andEqn2 [and…],

VarOuTentativa1, VarOuTentativa2 [, …

]) ⇒Expressãobooleana

cSolve(SistemaDeEquações,

VarOuTentativa1, VarOuTentativa2 [, …])

⇒Expressãobooleana

Devolve soluções complexas candidatas para as equações algébricas simultâneas, em que cada VarOuTentativa especifica uma variável que quer resolver.

Opcionalmente, pode especificar uma tentativa inicial para uma variável. Cada

varOuTentativa tem de ter a forma: variável

– ou –

variável = número real ou não real

Por exemplo, x é válido e logo é x=3+ i. Se todas as equações forem polinomiais e

se não especificar qualquer tentativa inicial,

cSolve() utiliza o método de eliminação

lexical Gröbner/Buchberger para tentar determinar todas as soluções complexas.

As soluções complexas podem incluir soluções reais e não reais, como no exemplo à direita.

Catálogo >

Nota: Os exemplos seguintes utilizam um

carácter desublinhado (premir /_) para que as variáveis sejamtratadas como

complexas.

As equações polinomiais simultâneas podem ter variáveis adicionais que não tenham valores, mas representam os valores numéricos dados que possam ser substituídos posteriormente.

42 Lista alfabética

Para ver o resultado completo, prima£ e, de seguida, utilize ¡ e ¢ para mover o cursor.

cSolve()

Pode também incluir variáveis de soluções que não aparecem nas equações. Estas soluções mostram como as famílias de soluções podem conter constantes arbitrárias da forma c k, em que k é um sufixo com valor inteiro de 1 a 255.

Para sistemas polinomiais, o tempo de cálculo ou o esgotamento da memória podem depender fortemente da ordem em que liste as variáveis das soluções. Se a escolha inicial esgotar a memória ou a sua paciência, tente reorganizar as variáveis nas equações e/ou na lista

varOuTentativa.

Se não incluir nenhuma tentativa e se a equação for não polinomial em qualquer variável, mas todas as equações forem lineares em todas as variáveis da solução,

cSolve() utiliza a eliminação Gaussian para

tentar determinar todas as soluções. Se um sistema não for polinomial em todas

as variáveis nem linear nas variáveis das soluções, cSolve() determina no máximo uma solução com um método iterativo aproximado. Para o fazer, o número de variáveis de soluções tem de ser igual ao número de equações e todas as outras variáveis nas equações têm de ser simplificadas para números.

Uma tentativa não real é frequentemente necessária para determinar uma solução não real. Para convergência, uma tentativa pode ter de ficar próxima a uma solução.

Catálogo >

Para ver o resultado completo, prima£ e, de seguida, utilize ¡ e ¢ para mover o cursor.

CubicReg

CubicReg X, Y[, [Freq] [, Categoria,

Incluir]]

Catálogo >

Lista alfabética 43

CubicReg

Calcula a regressão polinomial cúbicay = a·x3+b· x2+c·x+da partir das listas X e Y com a frequência Freq. Um resumo dos resultados é guardado na variável

stat.results (página 190).

Todas as listas têm de ter a mesma dimensão, excepto para Incluir.

X e Y são listas de variáveis independentes

e dependentes.

Freq é uma lista opcional de valores de

frequência. Cada elemento em Freq especifica a frequência de ocorrência para cada ponto de dados X e Y correspondente. O valor predefinido é 1. Todos os elementos têm de ser números inteiros | 0.

Categoria é uma lista de códigos de

categorias para os dados X e Y correspondentes.

Incluir é uma lista de um ou mais códigos

de categorias. Apenas os itens de dados cujo código de categoria está incluído nesta lista são considerados no cálculo.

Para mais informações sobre o efeito dos elementos vazios numa lista, consulte “Elementos (nulos) vazios” (página 253).

Catálogo >

Variável de saída

stat.RegEqn Equação deregressão: a · x3+b · x2+c · x+d

stat.a, stat.b, stat.c, stat.d

stat.R

stat.Resid Resíduos da regressão

stat.XReg

stat.YReg

stat.FreqReg

44 Lista alfabética

Descrição

Coeficientes de regressão

Coeficiente de determinação

Lista de pontos de dados naLista X modificada utilizada na regressão com base em restrições de Freq, Lista de categorias e Incluir categorias

Lista de pontos de dados naLista Y modificada utilizada na regressão com base nas restrições de Freq, Lista de categorias e Incluir categorias

Lista de frequências correspondentes a stat.XReg e stat.YReg

cumulativeSum()

cumulativeSum(Lista1)⇒lista

Devolve uma lista das somas acumuladas dos elementos em Lista1, começando no elemento 1.

cumulativeSum(Matriz1)⇒matriz

Devolve uma matriz das somas cumulativas dos elementos em Matriz1. Cada elemento é a soma cumulativa da coluna de cima a baixo.

Um elemento (nulo) vazio em Lista1 ou em

Matriz1 produz um elemento nulo na

matriz ou lista resultante. Para mais informações sobre os elementos vazios, consulte página 253.

Catálogo >

Cycle

Transfere o controlo imediatamente para a iteração seguinte do ciclo actual (For, While ou Loop).

Cycle não é permitido fora das três

estruturas em espiral (For, While ou Loop).

Obs para introdução do exemplo: Para obter

instruções sobre como introduzir programas com várias linhas e definições de funções, consulte a secção Calculadora do manual do utilizador do produto.

4Cylind

Vector 4 Cylind

Nota: Pode introduzir este operador através

da escrita de @>Cylind no teclado do computador.

Apresenta o vector da linha ou coluna em forma cilíndrica [r, ± q, z].

Vector tem de ter exactamente três

elementos. Pode ser uma linha ou coluna.

Catálogo >

Lista de funções que soma os números inteiros de 1a 100 ignorando 50.

Catálogo >

Lista alfabética 45

cZeros()

cZeros(Expr, Var) ⇒lista

Devolve uma lista de valores reais ou não reais candidatos de Var que torna Expr =0.

cZeros() faz isto, calculando exp4list(cSolve (Expr =0, Var), Var). Caso contrário, cZeros () é similar a zeros().

Nota: Consulte também cSolve(), solve() e zeros().

Nota: Se Expr for não polinomial com

funções, como abs(), angle(), conj(), real() ou imag(), deve colocar um carácter de

sublinhado (premir /_) no fim de

Var. Por predefinição, uma variável é

tratada como um valor real. Se utilizar var _, a variável é tratada como complexa.

Deve também utilizar var_ para qualquer outra variável em Expr que pode ter valores não reais. Caso contrário, pode obter resultados imprevistos.

cZeros({Expr1, Expr2 [, … ] }, {

VarOuTentativa1, VarOuTentativa2 [, … ]

}) ⇒matriz

Devolve posições candidatas em que as expressões são zero simultaneamente. Cada VarOuTentativa especifica um desconhecido cujo valor procura.

Opcionalmente, pode especificar uma tentativa inicial para uma variável. Cada

VarOuTentativa tem de ter a forma: variável

– ou –

variável = número real ou não real

Por exemplo, x é válido e logo é x=3+ i. Se todas as expressões forem polinomiais e

não especificar qualquer tentativa inicial,

cZeros() utiliza o método de eliminação

Gröbner/Buchberger lexical para tentar para determinar todos os zeros complexos.

Catálogo >

No modo de visualização de dígitos deFix 3:

Para ver o resultado completo, prima£ e, de seguida, utilize ¡ e ¢ para mover o cursor.

Nota: Os exemplos seguintes utilizam um

carácter desublinhado_ (premir /_) para que as variáveis sejamtratadas como

complexas.

46 Lista alfabética

cZeros()

Os zeros complexos podem incluir os zeros reais e não reais, como no exemplo à direita.

Cada linha da matriz resultante representa um zero alternativo com os componentes ordenados da mesma forma que na lista

VarOuTentativa. Para extrair uma linha,

indexe a matriz por [ linha ].

Os polinomiais simultâneos podem ter variáveis adicionais sem valores, mas representam valores numéricos dados que podem ser substituídos posteriormente.

Pode também incluir variáveis desconhecidas que não aparecem nas expressões. Estes zeros mostram como as famílias de zeros podem conter constantes arbitrárias da forma c k, em que k é um sufixo com valor inteiro de 1 a 255.

Para sistemas polinomiais, o tempo de cálculo ou o esgotamento da memória podem depender fortemente da ordem em que liste os desconhecidos. Se a escolha inicial esgotar a memória ou a sua paciência, tente reorganizar as variáveis nas expressões e/ou na lista

VarOuTentativa.

Se não incluir qualquer tentativa ou se qualquer expressão for não polinomial em qualquer variável, mas todas as expressões forem lineares em todos os desconhecidos,

cZeros() utiliza a eliminação Gaussiana

para tentar determinar todos os zeros.

Catálogo >

Extrair linha2:

Lista alfabética 47

cZeros()

Se um sistema não for polinomial em todas as variáveis nem linear nos desconhecidos,

cZeros() determina no máximo um zero

com um método iterativo aproximado. Para o fazer, o número de valores desconhecidos tem de ser igual ao número de expressões, e todas as outras variáveis nas expressões têm de ser simplificadas para números.

Uma tentativa não real é frequentemente necessária para determinar um zero não real. Para convergência, uma tentativa pode ter de ficar próxima a um zero.

Catálogo >

dbd()

dbd(data1,data2) ⇒valor

Devolve o número de dias entre data1 e

data2 com o método de contagem de dias

actual.

data1 e data2 podem ser números ou listas

de números no intervalo das datas no calendário padrão. Se data1 e data2 forem listas, têm de ter o mesmo comprimento.

data1 e data2 têm de estar entre os anos

1950 e 2049.

Pode introduzir as datas num de dois formatos. A colocação decimal diferenciase entre os formatos de data.

MM.AAAA (formato utilizado nos Estados Unidos)

DDMM.AA (formato utilizado na Europa)

4DD

Expr1 4 DD ⇒valor Lista1 4 DD ⇒lista Matriz1 4 DD ⇒matriz

Catálogo >

No modo de ângulo Graus:

48 Lista alfabética

4DD

Nota: Pode introduzir este operador através

da escrita de @>DD no teclado do computador.

Devolve o decimal equivalente do argumento expresso em graus. O argumento é um número, uma lista ou uma matriz que é interpretada pela definição do modo ângulo em gradianos, radianos ou graus.

Catálogo >

No modo de ângulo Gradianos:

No modo de ângulo Radianos:

4Decimal

Expressão1 4Decimal ⇒expressão Lista1 4 Decimal ⇒expressão Matriz1 4 Decimal ⇒expressão

Nota: Pode introduzir este operador através

da escrita de @>Decimal no teclado do computador.

Mostra o argumento em forma decimal. Este operador só pode ser utilizado no fim da linha de entrada.

Define

Define Var = Expressão

Define Função(Parâm1, Parâm2, ...) =

Expressão

Define a variável Var ou a função Função definida pelo utilizador.

Os parâmetros como, por exemplo,

Parâm1, fornecem marcadores para

argumentos de passagem para a função. Quando chamar uma função definida pelo utilizador, tem de fornecer os argumentos (por exemplo, valores ou variáveis) correspondentes aos parâmetros. Quando chamada, a função avalia a Expressão com os argumentos fornecidos.

Catálogo >

Lista alfabética 49

Define

Var e Função não podem ter o nome de

uma variável do sistema, um comando ou uma função integrada.

Nota: Esta forma de Define é equivalente à

execução da expressão: expressão &

Função(Parâm1,Parâm2).

Define Função(Parâm1, Parâm2, ...) = Func

Bloco

EndFunc

Define Programa(Parâm1, Parâm2, ...) = Prgm

Bloco

EndPrgm

Desta forma, o programa ou a função definida pelo utilizador pode executar um bloco de várias afirmações.

Bloco pode ser uma afirmação ou uma

série de afirmações em linhas separadas. O

bloco pode também incluir expressões e

instruções (como, por exemplo, If, Then,

Else e For).

Obs para introdução do exemplo: Para obter

instruções sobre como introduzir programas com várias linhas e definições de funções, consulte a secção Calculadora do manual do utilizador do produto.

Nota: Consulte também Define LibPriv,

página 50, e Define LibPub, página 51.

Catálogo >

Define LibPriv

Define LibPriv Var = Expressão

Define LibPriv Função(Parâm1, Parâm2, ...) = Expressão

Define LibPriv Função(Parâm1, Parâm2, ...)

50 Lista alfabética

Catálogo >

Define LibPriv

= Func

Bloco

EndFunc

Define LibPriv Programa(Parâm1, Parâm2, ...) = Prgm

Bloco

EndPrgm

Funciona da mesma forma que Define, excepto com um programa, uma função ou uma variável da biblioteca privada. As funções e os programas privados não aparecem no Catálogo.

Nota: Consulte também Define, página 49, e Define LibPub, página 51.

Catálogo >

Define LibPub

Define LibPub Var = Expressão

Define LibPub Função(Parâm1, Parâm2, ...) = Expressão

Define LibPub Função(Parâm1, Parâm2, ...) = Func

Bloco

EndFunc

Define LibPub Programa(Parâm1, Parâm2, ...) = Prgm

Bloco

EndPrgm

Funciona da mesma forma que Define, excepto com um programa, uma função ou uma variável da biblioteca pública. As funções e os programas públicos aparecem no Catálogo depois de guardar e actualizar a biblioteca.

Catálogo >

Lista alfabética 51

Define LibPub

Nota: Consulte também Define, página 49, e Define LibPriv, página 50.

Catálogo >

deltaList()

deltaTmpCnv()

DelVar

DelVar Var1[, Var2] [, Var3] ...

DelVar Var.

Elimina a variável ou o grupo de variáveis especificado da memória.

Se uma ou mais variáveis estiverem bloqueadas, este comando mostra uma mensagem de erro e só elimina as variáveis desbloqueadas. Consulte unLock, página

212.

DelVar Var. elimina todos os membros da

Var. grupo de variáveis (como, por

exemplo, as estatísticas stat.nn resultados ou variáveis criados com a função

LibShortcut()). O ponto (.) nesta forma do

comando DelVar limita-o à eliminação do grupo de variáveis; a variável simples Var não é afectada.

Consulte @List(), página 110.

Consulte @tmpCnv(), página

204.

Catálogo >

delVoid()

delVoid(Lista1)⇒lista

Devolve uma lista com o conteúdo de

Lista1 com todos os elementos (nulos)

vazios removidos.

52 Lista alfabética

Catálogo >

delVoid()

Para mais informações sobre os elementos vazios, consulte página 253.

Catálogo >

derivative()

deSolve()

deSolve(1ªOu2ªOrdemODE, Var, depVar)

⇒uma solução geral

Devolve uma equação que especifica explicita ou implicitamente uma solução geral para a equação diferencial ordinária (ODE) de 1ª ou 2ª ordem. Na ODE:

• Utilize um símbolo de apóstrofo (prima

º) para indicar a 1ª derivada da variável

dependente em relação à variável independente.

• Utilize dois símbolos de apóstrofo para indicar a segunda derivada correspondente.

O símbolo de apóstrofo é utilizado para derivadas apenas em deSolve(). Noutros casos, utilize d().

A solução geral de uma equação de 1ª ordem contém uma constante arbitrária da forma c k, em que k é um sufixo com valor inteiro de 1 a 255. A solução de uma equação de 2ª ordem contém duas constantes.

Aplique solve() numa solução implícita se a quiser tentar converter para uma ou mais soluções explícitas equivalentes.

Quando comparar os resultados com as soluções dos manuais, não se esqueça de que diferentes métodos introduzem constantes arbitrárias em diferentes pontos no cálculo, que pode produzir diferentes soluções gerais.

Consulte d(), página 237.

Catálogo >

Lista alfabética 53

deSolve()

deSolve(1ªOrdemODEandCondinic, Var,

depVar) ⇒uma solução específica

Devolve uma solução específica que satisfaz

1ªOrdemODE e Condinic. Esta é

geralmente mais simples do que determinar uma solução geral, substituir valores iniciais, resolver com constante arbitrária e, em seguida, substituir esse valor na solução geral.

Condinic é uma equação da forma: depVar (ValorIndependenteInicial) =

ValorDependenteInicial ValorIndependenteInicial e

ValorDependenteInicial podem ser

variáveis como, por exemplo, x0 e y0 que não tenham valores guardados. A diferenciação implícita pode ajudar a verificar as soluções implícitas.

deSolve (

2ªOrdemODEandCondinic1andCondinici2, Var, depVar)⇒uma solução específica

Devolve uma solução específica que satisfaz

2ª Ordem ODE e tem um valor

especificado da variável dependente e da primeira derivada num ponto.

Para Condinic1, utilize a forma:

depVar (ValorIndependenteInicial) = ValorDependenteInicial

Para Condinic2, utilize a forma:

depVar (ValorIndependenteInicial) = Valor1ªDerivadaInicial

deSolve (2ªOrdemODEandCondbnd1andCondbnd2,

Var, depVar)⇒uma solução específica

Apresenta uma solução particular

2ªOrdemODE e tem valores especificados

em dois pontos diferentes.

Catálogo >

54 Lista alfabética

deSolve()

Catálogo >

det()

det(MatrizQuadrada[, Tolerância])

⇒expressão

Apresenta o determinante de

MatrizQuadrada.

Opcionalmente, qualquer elemento da matriz é tratado como zero se o valor absoluto for inferior à Tolerância. Esta tolerância é utilizada apenas se a matriz tiver entradas de ponto flutuante e não contiver nenhuma variável simbólica sem nenhum valor atribuído. Caso contrário,

Tolerância é ignorada.

• Se utilizar /· ou definir o modo Auto ou Aproximado para Aproximado,

os cálculos são efectuados com a aritmética de ponto flutuante.

• Se Tolerância for omitida ou não utilizada, a tolerância predefinida é calculada da seguinte forma:

5EM14 ·max(dim(MatrizQuadrada))·

rowNorm(MatrizQuadrada)

diag()

diag(Lista) ⇒matriz

Catálogo >

diag(MatrizLinha) ⇒matriz diag(MatrizColuna) ⇒matriz

Devolve uma matriz com os valores da matriz ou da lista de argumentos na diagonal principal.

Lista alfabética 55

diag()

diag(MatrizQuadrada) ⇒MatrizLinha

Devolve uma matriz da linha com elementos da diagonal principal de

MatrizQuadrada. MatrizQuadrada tem de ser quadrada.

Catálogo >

dim()

dim(Lista) ⇒número inteiro

Devolve a dimensão de Lista.

dim(Matriz) ⇒lista

Devolve as dimensões da matriz como uma lista de dois elementos {linhas, colunas}.

dim(Cadeia) ⇒número inteiro

Devolve o número de caracteres contidos na cadeia de caracteres Cadeia.

Disp

Disp exprOuCadeia1 [, exprOuCadeia2 ]

...

Mostra os argumentos no histórico da

Calculadora. Os argumentos são

apresentados em sucessão com espaços pequenos como separadores.

Útil principalmente em programas e funções para garantir a visualização de cálculos intermédios.

Obs para introdução do exemplo: Para obter

instruções sobre como introduzir programas com várias linhas e definições de funções, consulte a secção Calculadora do manual do utilizador do produto.

Catálogo >

DispAt

DispAt int,expr1 [,expr2 ...] ...

56 Lista alfabética

Catálogo >

Exemplo

DispAt

DispAt permite-lhe especificar a linha

onde a expressão ou cadeia será apresentada no ecrã.

O número da linha pode ser especificado como uma expressão.

Tenha em atenção que o número da linha não se destina ao ecrã inteiro, mas à área imediatamente a seguir ao comando/programa.

Este comando permite uma apresentação de dados semelhante a um painel em que o valor de uma expressão ou de uma leitura de sensor é atualizado na mesma linha.

DispAte Disp podem ser utilizados no

mesmo programa.

Nota: o número máximo está definido

para 8, uma vez que esse número corresponde a um ecrã cheio de linhas no ecrã da unidade portátil - desde que as linhas não contenham expressões matemáticas 2D. O número exato de linhas depende do conteúdo da informação apresentada.

Exemplos ilustrativos:

Define z()= Prgm For n,1,3 DispAt 1,"N: ",n Disp "Olá" EndFor EndPrgm

Output z()

Catálogo >

Iteração 1:

Linha 1: N:1 Linha 2: Olá

Iteração 2:

Linha 1: N:2 Linha 2: Olá Linha 3: Olá

Iteração 3:

Linha 1: N:3 Linha 2: Olá Linha 3: Olá

Lista alfabética 57

DispAt

Define z1()= Prgm For n,1,3 DispAt 1,"N: ",n EndFor

For n,1,4 Disp "Olá" EndFor EndPrgm

Condições de erro:

Mensagem de erro Descrição

O número de linha DispAt deve situar-se entre 1 e 8

Poucos argumentos A função ou o comando não tem um ou

Nenhum argumento Igual à caixa de diálogo atual 'erro de

Demasiados argumentos Limitar argumento. Mesmo erro que

Tipo de dados inválido O primeiro argumento tem de ser um

Nulo: DispAt nulo O erro de tipo de dados "Olá mundo" é

Operador de conversão: DispAt 2_ft @> _m, "Olá mundo"

A expressão avalia o número de linha fora do intervalo 1-8 (inclusive)

mais argumentos.

sintaxe'

Disp.

número.

projetado para o nulo (se o callback estiver definido)

CAS: O erro de tipo de dados é projetado (se o callback estiver definido)

Numérico: A conversão será avaliada e, se o resultado for um argumento válido, DispAt imprime a cadeia na linha de resultados.

Catálogo >

Linha 4: Olá

z1()

Linha 1: N:3 Linha 2: Olá Linha 3: Olá Linha 4: Olá Linha 5: Olá

4DMS

Expr 4DMS

Lista 4DMS

58 Lista alfabética

Catálogo >

No modo de ângulo Graus:

4DMS

Matriz 4 DMS

Nota: Pode introduzir este operador através

da escrita de @>DMS no teclado do computador.

Interpreta o argumento como um ângulo e mostra o número DMS equivalente (DDDDDD ¡MM ' SS.ss ''). Consulte ¡, ', '' (página 245) para o formato DMS (grau, minutos, segundos).

Nota: 4DMS converterá de radianos para

graus quando utilizado em modo de radianos. Se a entrada for seguida por um símbolo de grau ¡, não ocorrerá nenhuma conversão. Pode utilizar o 4 DMS apenas no fim de uma linha de entrada.

Catálogo >

domain() (domínio)

domain(Expr1, Var)⇒expressão

Devolve o domínio de Expr1 em relação à

Var.

domain() pode ser utilizado para examinar

domínios e funções. Está limitado ao domínio real e finito.

Esta funcionalidade tem limitações devido a deficiências de simplificação algébrica computacional e a algoritmos de resolução.

Certas funções não podem ser utilizadas como argumentos para domain(), independentemente de aparecerem explicitamente ou em variáveis e funções definidas pelo utilizador. No exemplo seguinte, a expressão não pode ser simplificada porque ‰() é uma função não permitida.

Catálogo >

Lista alfabética 59

dominantTerm()

dominantTerm(Expr1, Var [, Ponto])

⇒expressão

dominantTerm(Expr1, Var [, Ponto]) |

Var>Ponto ⇒expressão

dominantTerm(Expr1, Var [, Ponto])

Var<Ponto ⇒expressão

Devolve o termo dominante de uma representação da série de potência deExpr1 aberta sobre Ponto. O termo dominante é aquele cuja magnitude cresce mais rapidamente junto a Var = Ponto. A potência resultante de (Var N Ponto) pode ter um expoente fraccionário e/ou negativo. O coeficiente desta potência pode incluir logaritmos de (Var N Ponto) e outras funções de Var que são dominadas por todas as potências de (Var N Ponto) com o mesmo sinal de expoente.

O Ponto predefine-se para 0. O Ponto

pode ser ˆ ou Nˆ, nestes casos, o termo dominante será o termo com o expoente maior de Var em vez do expoente menor de Var.

dominantTerm(…) devolve “dominantTerm (…)” se não for capaz de determinar essa

representação, como para singularidades essenciais, como, por exemplo, sin(1/z) a

1/z

z=0, e

a z=0, ou eza z = ˆ ou Nˆ.

Se a série ou um das derivadas tiver uma descontinuidade em Ponto, o resultado contém provavelmente subexpressões do sinal(…) ou abs(…) da forma para uma variável de expansão real ou (-1)

(…)…)

para uma variável de expansão

floor(…ângulo

complexa, que é uma que termina com “_”. Se quiser utilizar o termo dominante apenas para os valores num lado de Ponto, adicione ao dominantTerm(...), um valor adequado de “| Var > Ponto”, “| Var <

Ponto”, “| “Var | Ponto” ou “Var { Ponto” para obter um resultado mais

simples.

Catálogo >

60 Lista alfabética

dominantTerm()

dominantTerm() distribui-se pelas listas e

matrizes do 1º argumento.

dominantTerm() é útil quando quiser saber

a expressão mais simples possível que é assimptótica para outra expressão como

Var " Ponto. dominantTerm() é também

útil quando não for óbvio qual é o grau do primeiro termo não zero de uma série, e não quiser descobrir iterativamente de forma interactiva ou através de um ciclo do programa.

Nota: Consulte também série(), página 172.

Catálogo >

dotP()

dotP(Lista1, Lista2) ⇒expressão

Devolve o produto do “ponto” de duas listas.

dotP(Vector1, Vector2) ⇒expressão

Devolve o produto do “ponto” de dois vectores.

Ambos têm de ser vectores da linha ou da coluna.

e^()

e^(Expr1) ⇒expressão

Devolve e elevado à potência Expr1.

Nota: Consulte também e modelo do expoente, página 2.

Nota: Premir u para ver e ^( é diferente

de premir o carácter E no teclado.

Pode introduzir um número complexo na forma polar re forma apenas no modo de ângulo Radianos; causa um erro de domínio no modo de ângulo Graus ou Gradianos.

. No entanto, utilize esta

Catálogo >

Tecla u

Lista alfabética 61

e^()

e^(Lista1) ⇒lista

Devolve e elevado à potência de cada elemento em Lista1.

e^(MatrizQuadrada1) ⇒MatrizQuadrada

Devolve a matriz exponencial de

MatrizQuadrada1. Isto não é o mesmo que

calcular e elevado à potência de cada elemento. Para mais informações sobre o método de cálculo, consulte cos().

MatrizQuadrada1 tem de ser diagnolizável.

O resultado contém sempre os números de ponto flutuante.

Tecla u

eff()

eff(TaxaNominal,CpY) ⇒valor

Função financeira que converte a taxa de juro nominal TaxaNominal para uma taxa efectiva anual, dando CpY como o número de período compostos por ano.

TaxaNominal tem de ser um número real e CpY tem de ser um número real > 0.

Nota: Consulte também nom(), página 131.

eigVc()

eigVc(MatrizQuadrada) ⇒matriz

Devolve uma matriz com os vectores próprios para uma MatrizQuadrada real ou complexa, em que cada coluna do resultado corresponde a um valor próprio. Não se esqueça de que um vector próprio não é único; pode ser dimensionado por qualquer factor constante. Os vectores próprios são normalizados, significando que se V = [ x1, x2, …, xn]:

+ x

+ … + x

= 1

Catálogo >

No Formato complexo rectangular:

Para ver o resultado completo, prima£ e, de seguida, utilize ¡ e ¢ para mover o cursor.

62 Lista alfabética

eigVc()

MatrizQuadrada é primeiro equilibrada

com tranformações de similaridade até as normas das colunas e linhas estarem o mais perto possível do mesmo valor. A

MatrizQuadrada é reduzida para a forma

Hessenberg superior e os vectores próprios são calculados através de uma factorização Schur.

Catálogo >

eigVl()

eigVl(MatrizQuadrada) ⇒lista

Devolve uma lista dos valores próprios de uma MatrizQuadrada real ou complexa.

MatrizQuadrada é primeiro equilibrada

com tranformações de similaridade até as normas das colunas e linhas estarem o mais perto possível do mesmo valor. A

MatrizQuadrada é reduzida para a forma

Hessenberg superior e os valores próprios são calculados a partir da matriz Hessenberg superior.

Else

ElseIf

Se ExprBooleana1

Block1

ElseIf BooleanExpr2

Block2

Catálogo >

No modo de formato complexo rectangular:

Para ver o resultado completo, prima£ e, de seguida, utilize ¡ e ¢ para mover o cursor.

Consulte If, página 94.

Catálogo >

ElseIf ExprBooleanaN

BlockN

EndIf

Lista alfabética 63

ElseIf

Obs para introdução do exemplo: Para obter

instruções sobre como introduzir programas com várias linhas e definições de funções, consulte a secção Calculadora do manual do utilizador do produto.

Catálogo >

EndFor

EndFunc

EndIf

EndLoop

EndPrgm

EndTry

EndWhile

Consulte For, página 77.

Consulte Func, página 81.

Consulte If, página 94.

Consulte Loop, página 118.

Consulte Prgm, página 147.

Consulte Try, página 205.

Consulte While, página 216.

euler ()

euler(Expr, Var, depVar, {Var0, VarMax},

depVar0, VarStep [, eulerStep]) ⇒matriz

euler(SystemOfExpr, Var, ListOfDepVars,

64 Lista alfabética

Catálogo >

Equação diferencial:

y'=0.001*y*(100-y) e y(0)=10

euler ()

{Var0, VarMax}, ListOfDepVars0,

VarStep [, eulerStep]) ⇒matriz

euler(ListOfExpr, Var, ListOfDepVars, {Var0, VarMax}, ListOfDepVars0,

VarStep [, eulerStep]) ⇒matriz

Utiliza o método de Euler para resolver o sistema

com depVar(Var0)=depVar0 no intervalo [Var0,VarMax]. Apresenta uma matriz cuja primeira linha define os valores de saída

Var e cuja segunda linha define o valor da

primeira componente da solução nos valores Var correspondentes, e assim por diante.

Expr é o lado direito que define a equação

diferencial ordinária (EDO).

SystemOfExpr é o sistema de lados

direitos que definem o sistema de EDOs (corresponde à ordem de variáveis dependentes em ListOfDepVars).

ListOfExpr é uma lista de segundos

membros que definem o sistema de EDOs (corresponde à ordem de variáveis dependentes em ListOfDepVars).

Var é a variável independente. ListOfDepVars é uma lista de variáveis

dependentes. {Var0, VarMax} é uma lista de dois

elementos que informa a função para integrar de Var0 a VarMax.

ListOfDepVars0 é uma lista de valores

iniciais para variáveis dependentes.

Catálogo >

Para ver o resultado completo, prima£ e, de seguida, utilize ¡ e ¢ para mover o cursor.

Compare o resultado acimacom a solução exacta CAS obtida através de deSolve() e seqGen():

Sistema de equações:

com y1(0)=2 ey2(0)=5

Lista alfabética 65

euler ()

Catálogo >

VarStep é um número diferente de zero tal

como sign(VarStep) = sign(VarMax-Var0) e as soluções regressam a Var0+i·VarStep para todos os i=0,1,2,… tal como

Var0+i·VarStep está em [var0,VarMax]

(pode não existir um valor de solução em

VarMax). eulerStep é um número inteiro positivo

(passa para 1) que define o número de passos Euler entre os valores de saída. O tamanho de passo real utilizado pelo método Euler é VarStepàeulerStep.

eval () Menu Hub

eval(Expr) ⇒ cadeia

eval() só é válida no TI-Innovator™ Hub

argumento Comando dos comandos programados Get, GetStr e Send. O software avalia a expressão Expr e substitui a instrução eval() pelo resultado como cadeia de caracteres.

O argumento Expr tem de ser simplificado para um número real.

Definir o elemento azuldo LEDRGB para metade da intensidade.

Repor o elemento azulpara DESLIGADO.

O argumento eval() tem de ser simplificado para um número real.

66 Lista alfabética

Programar para aparecimento gradual do elemento vermelho.

Executar o programa.

eval () Menu Hub

Embora eval() não apresente o resultado, pode ver a cadeia de comando resultante do Hub após executar o comando inspecionando qualquer uma das variáveis especiais seguintes.

iostr.SendAns iostr.GetAns iostr.GetStrAns

Nota: Ver também Get(página 83), GetStr

(página 91) e Send(página 170).

exact()

exact(Expr1 [, Tolerância])⇒expressão exact(Lista1 [, Tolerância])⇒lista exact(Matriz1 [, Tolerância])⇒matriz

Utiliza o modo aritmético Exacto para apresentar, quando possível, o número racional equivalente do argumento.

Tolerância especifica a tolerância para a

conversão; a predefinição é 0 (zero).

Exit

Sai do bloco For, While ou Loop actual.

Exit não é permitido fora das três

estruturas circulares (For, While ou Loop).

Obs para introdução do exemplo: Para obter

instruções sobre como introduzir programas com várias linhas e definições de funções, consulte a secção Calculadora do manual do utilizador do produto.

Catálogo >

Listagemde funções:

Lista alfabética 67

4exp

Expr 4exp

Representa Expr em função do expoente natural e. Este é um operador de conversão. Apenas pode ser utilizado no fim da linha de entrada.

Nota: Pode introduzir este operador através

da escrita de @>exp no teclado do computador.

Catálogo >

exp()

exp(Expr1) ⇒expressão

Devolve e elevado à potência Expr1.

Nota: Consulte também e modelo do

expoente, página 2.

Pode introduzir um número complexo na forma polar re forma apenas no modo de ângulo Radianos; causa um erro de domínio no modo de ângulo Graus ou Gradianos.

exp(Lista1) ⇒lista

Devolve e elevado à potência de cada elemento em Lista1.

exp(MatrizQuadrada1) ⇒MatrizQuadrada

Devolve a matriz exponencial de

. No entanto, utilize esta

MatrizQuadrada1. Isto não é o mesmo que

calcular e elevado à potência de cada elemento. Para mais informações sobre o método de cálculo, consulte cos().

MatrizQuadrada1 tem de ser diagnolizável.

O resultado contém sempre os números de ponto flutuante.

Tecla u

exp4lista()

exp4lista(Expr, Var) ⇒lista

68 Lista alfabética

Catálogo >

exp4lista()

Examina Expr para equações separadas pela palavra “ ou,” e devolve uma lista com os lados direitos das equações da forma

Var=Expr. Isto fornece uma forma simples

para extrair alguns valores das soluções embebidos nos resultados das funções

solve(), cSolve(), fMin() e fMax().

Nota: exp4list() não é necessário com os zeros e as funções cZeros() porque

devolvem uma lista dos valores das soluções directamente.

Pode introduzir esta função através da escrita de exp@>list(...) no teclado.

Catálogo >

expand()

expand(Expr1 [, Var ]) ⇒expressão expand(Lista1 [, Var ]) ⇒lista expand(Matriz1 [, Var ]) ⇒matriz

expand(Expr1) devolve Expr1 expandido

em relação a todas as variáveis. A expansão é uma expansão polinomial para polinómios e a expansão de fracção parcial para expressões racionais.

O objectivo de expand() é transformar

Expr1 numa soma e/ou diferença de

termos simples. Pelo contrário, o objectivo de factor() é transformar Expr1 num produto e/ou quociente de factores simples.

expand (Expr1, Var) devolve Expr1

expandido em relação a Var. As potências similares de Var são recolhidas. Os termos e os factores são ordenados com Var como variável principal. Pode existir alguma decomposição de factores incidental ou a expansão dos coeficientes recolhidos. Comparada para omitir Var, esta poupa tempo frequentemente, memória e espaço no ecrã, enquanto torna a expressão mais compreensível.

Catálogo >

Lista alfabética 69

expand()

Mesmo quando exista apenas uma variável, a utilização de Var pode tornar a factorização do denominador utilizada para a expansão da fracção parcial mais completa.

Sugestão: Para expressões racionais,

propFrac() é mais rápida, mas uma

alternativa menos extrema para expand().

Nota: Consulte também comDenom() para

um numerador expandido sobre um denominador expandido.

expand (Expr1, [ Var ]) também distribui

potências fraccionárias e logaritmos, independentemente de Var. Para uma distribuição aumentada de potências fraccionárias e logaritmos, os limites das desigualdades podem ser necessários para garantir que alguns factores são não negativos.

expand (Expr1, [ Var ]) também distribui

valores absolutos, sign(), e exponenciais, independentemente de Var.

Nota: Consulte também tExpand() para a

soma de ângulos trigonométricos e a expansão de ângulos múltiplos.

Catálogo >

expr()

expr(Cadeia) ⇒expressão

Devolve a cadeia de caracteres contidos em

Cadeia como uma expressão e executa-a

imediatamente.

ExpReg

ExpReg X, Y [, [Freq][, Categoria,

Incluir]]

70 Lista alfabética

Catálogo >

ExpReg

Calcula a regressão exponencialy = a·(b)xa partir das listas X e Y com a frequência

Freq. Um resumo dos resultados é

guardado na variável stat.results (página

190).

Todas as listas têm de ter a mesma dimensão, excepto para Incluir.

X e Y são listas de variáveis independentes

e dependentes.

Freq é uma lista opcional de valores de

frequência. Cada elemento em Freq especifica a frequência de ocorrência para cada ponto de dados X e Y correspondente. O valor predefinido é 1. Todos os elementos têm de ser números inteiros 0.

Categoria é uma lista de códigos de

categorias para os dados X e Y correspondentes.

Incluir é uma lista de um ou mais códigos

de categorias. Apenas os itens de dados cujo código de categoria está incluído nesta lista são considerados no cálculo.

Para mais informações sobre o efeito dos elementos vazios numa lista, consulte “Elementos (nulos) vazios” (página 253).

Catálogo >

Variável de saída

stat.RegEqn Equação deregressão: a·(b)

stat.a, stat.b Parâmetros da regressão

stat.r

stat.r Coeficiente de correlação para dados transformados (x, ln(y))

stat.Resid Resíduos associados ao modelo exponencial

stat.ResidTrans Residuaisassociados ao ajuste linear dedados transformados

stat.XReg

stat.YReg

stat.FreqReg

Descrição

Coeficiente de determinação linear para dados transformados

Lista de pontos de dados naLista X modificada utilizada na regressão com base em restrições de Freq, Lista de categorias e Incluir categorias

Lista de pontos de dados naLista Y modificada utilizada na regressão com base nas restrições de Freq, Lista de categorias e Incluir categorias

Lista de frequências correspondentes a stat.XReg e stat.YReg

Lista alfabética 71

factor()

factor(Expr1 [, Var ]) ⇒expressão factor(Lista1 [, Var ]) ⇒lista factor(Matriz1 [, Var ]) ⇒matriz

factor(Expr1) devolve Expr1 decomposta

em relação a todas as variáveis sobre um denominador comum.

Expr1 é decomposta o mais possível em

factores racionais lineares sem introduzir novas subexpressões não reais. Esta alternativa é adequada se quiser a factorização em relação a mais de uma variável.

factor(Expr1, Var) devolve Expr1 decomposta em relação à variável Var.

Expr1 é decomposta o mais possível em

factores reais lineares em Var, mesmo que introduza constantes irracionais ou subexpressões irracionais noutras variáveis.

Os factores e os termos são ordenados com

Var como variável principal. As potências

similares de Var são recolhidas em cada factor. Inclua Var se a factorização for necessária em relação apenas a essa variável e estiver disposto a aceitar expressões irracionais em qualquer outra variável para aumentar a factorização em relação a Var. Pode existir alguma decomposição de factores incidental em relação a outras variáveis.

Para a definição Auto do modo Auto ou

Aproximado, incluindo Var, permite

Catálogo >

72 Lista alfabética

factor()

Nota: Consulte também comDenom() para

uma forma mais rápida para obter a decomposição de factores parcial quando

factor() não for suficientemente rápido ou

se a memória ficar esgotada.

Nota: Consulte também cFactor() para

decompor tudo para coeficientes complexos em busca de factores lineares.

factor(NúmeroRacional) devolve o número

racional em primos. Para números compostos, o tempo de cálculo cresce exponencialmente com o número de dígitos no segundo maior factor. Por exemplo, a decomposição em factores de um número inteiro de 30 dígitos pode demorar mais de um dia e a decomposição em factores de um número de 100 dígitos pode demorarar mais de um século.

Para parar um cálculo manualmente,

• Dispositivo portátil: Manter pressionada a tecla c e pressionar · repetidamente.

• Windows®: Manter pressionada a tecla F12 e pressionar Enter repetidamente.

• Macintosh®: Manter pressionada a tecla F5 e pressionar Enter repetidamente.

• iPad®: A aplicação apresenta um pedido. Pode continuar a aguardar ou pode cancelar.

Se quiser apenas determinar se um número é primo, utilize isPrime(). É muito mais rápido, em especial, se o NúmeroRacional não for primo e o segundo maior factor tiver mais de cinco dígitos.

Catálogo >

FCdf()

FCdf(LimiteInferior, LimiteSuperior,

dfNumer, dfDenom) ⇒número se LimiteInferior e LimiteSuperior forem

números, lista se LimiteInferior e

LimiteSuperior forem listas

Catálogo >

Lista alfabética 73

FCdf()

FCdf(LimiteInferior, LimiteSuperior,

dfNumer, dfDenom) ⇒número se LimiteInferior e LimiteSuperior forem

números, lista se LimiteInferior e

LimiteSuperior forem listas

Calcula a probabilidade da distribuição F entre LimiteInferior e LimiteSuperior para o dfNumer (graus de liberdade) e dfDenom especificados.

Para P(X { LimiteSuperior), definir

LimiteInferior = 0.

Catálogo >

Fill

Fill Expr, VarMatriz ⇒matriz

Substitui cada elemento na variável

VarMatriz por Expr. matrixVar já tem de existir.

Fill Expr, VarLista ⇒lista

Substitui cada elemento na variável

VarLista por Expr. VarLista já tem de existir.

FiveNumSummary

FiveNumSummary X[,[Freq]

[,Categoria,Incluir]]

Fornece uma versão abreviada da estatística de 1 variável na lista X. Um resumo dos resultados é guardado na variável

stat.results (página 190). X representa uma lista de dados. Freq é uma lista opcional de valores de

frequência. Cada elemento em Freq especifica a frequência de ocorrência para cada valor X correspondente. O valor predefinido é 1. Todos os elementos têm de ser números inteiros 0.

Catálogo >

74 Lista alfabética

FiveNumSummary

Categoria é uma lista de códigos de

categorias numéricos para os valores X correspondentes.

Incluir é uma lista de um ou mais códigos

de categorias. Apenas os itens de dados cujo código de categoria está incluído nesta lista são considerados no cálculo.

Um elemento (nulo) vazio em qualquer das listas X, Freq ou Category resulta num nulo para o elemento correspondente de todas essas listas. Para mais informações sobre os elementos vazios, consulte página 253.

Variável de saída Descriç ão

stat.MinX Mínimo dos valores x

stat.Q1X 1º quartilde x

stat.MedianX Mediana dex

stat.Q3X 3º quartilde x

stat.MaxX Máximo dos valores x

Catálogo >

floor()

floor(Expr1) ⇒número inteiro

Devolve o maior número inteiro que é { o argumento. Esta função é idêntica a int().

O argumento pode ser um número complexo ou real.

floor(Lista1) ⇒lista floor(Matriz1) ⇒matriz

Devolve uma lista ou matriz do floor de cada elemento.

Nota: Consulte também ceiling() e int().

Catálogo >

Lista alfabética 75

fMax()

fMax(Expr, Var) ⇒Expressão booleana

fMax(Expr, Var, LimiteInferior)

fMax(Expr, Var, LimiteInferior,

LimiteSuperior)

fMax(Expr, Var) | LimiteInferior {Var {LimiteSuperior

Devolve uma expressão booleana que especifica os valores candidatos de Var que maximiza Expr ou localiza o menor limite superior.

Pode utilizar o operador de limite (“|”) para limitar o intervalo da solução e/ou especificar outras restrições.

Para a definição Aproximado do modo Auto

ou Aproximado, fMax() procura

iterativamente um máximo local aproximado. Isto é frequentemente mais rápido, em especial, se utilizar o operador “|” para limitar a procura a um intervalo relativamente pequeno que contenha exactamente um máximo local.

Nota: Consulte também fMin() e max().

Catálogo >

fMin()

fMin(Expr, Var) ⇒Expressão booleana

fMin(Expr, Var, LimiteInferior)

fMin(Expr, Var, LimiteInferior,

LimiteSuperior)

fMin(Expr, Var) | LimiteInferior{Var {LimiteSuperior

Devolve uma expressão booleana que especifica os valores candidatos de Var que minimiza Expr ou localiza o maior limite inferior.

Pode utilizar o operador de limite (“|”) para limitar o intervalo da solução e/ou especificar outras restrições.

76 Lista alfabética

Catálogo >

fMin()

Para a definição Aproximado do modo Auto

ou Aproximado, fMin() procura

iterativamente um mínimo local aproximado. Isto é frequentemente mais rápido, em especial, se utilizar o operador “” para limitar a procura a um intervalo relativamente pequeno que contenha exactamente um mínimo local.

Nota: Consulte também fMax() e min().

Catálogo >

For

For Var, Baixo, Alto [, Passo ]

Bloco

EndFor

Executa as declarações em Bloco iterativamente para cada valor de Var, de

Baixo para Alto, em incrementos de Passo.

Var não tem de ser uma variável do

sistema.

Passo pode ser positivo ou negativo. O

valor predefinido é 1.

Bloco pode ser uma declaração ou uma

série de declarações separadas pelo carácter “:”.

Obs para introdução do exemplo: Para obter

instruções sobre como introduzir programas com várias linhas e definições de funções, consulte a secção Calculadora do manual do utilizador do produto.

Catálogo >

Lista alfabética 77

format()

format(Expr [, CadeiaFormato ])

⇒cadeia

Devolve Expr como uma cadeia de caracteres com base no modelo do formato.

Expr tem de ser simplificada para um

número.

CadeiaFormato é uma cadeia e tem de

estar na forma: “F[n]”, “S[n]”, “E[n]”, “G[n] [c]”, em que [ ] indica porções opcionais.

F[n]: Formato fixo. n é o número de dígitos para visualizar o ponto decimal.

S[n]: Formato científico. n é o número de dígitos para visualizar o ponto decimal.

E[n]: Formato de engenharia. n é o número de dígitos após o primeiro dígito significante. O exponente é ajustado para um múltiplo de três e o ponto decimal é movido para a direita zero, um ou dois dígitos.

G[n][c]: Igual ao formato fixo mas também separa os dígitos à esquerda da raiz em grupos de três. c especifica o carácter do separador de grupos e predefine para uma vírgula. Se c for um ponto, a raiz será apresentada como uma vírgula.

[Rc]: Qualquer um dos especificadores acima pode ser sufixado com o marcador de raiz Rc, em que c é um carácter que especifica o que substituir pelo ponto da raiz.

Catálogo >

fPart()

fPart(Expr1) ⇒expressão fPart(Lista1) ⇒lista fPart(Matriz1) ⇒matriz

Devolve a parte fraccionária do argumento.

78 Lista alfabética

Catálogo >

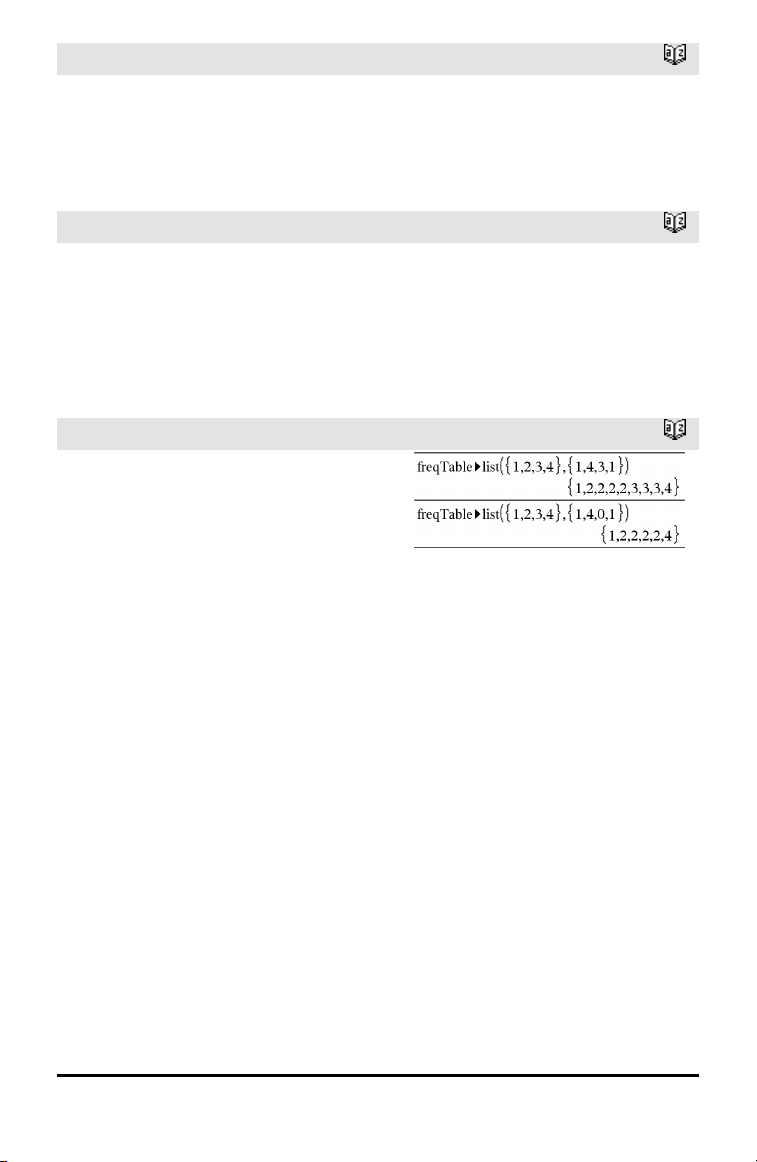
fPart()

Para uma lista ou matriz, devolve as partes fraccionárias dos elementos.

O argumento pode ser um número complexo ou real.

Catálogo >

FPdf()

FPdf(ValX, dfNumer, dfDenom) ⇒número

se ValX for um número, lista se ValX for uma lista

Calcula a probabilidade da distribuição F no

ValX para o dfNumer (graus de liberdade) e

o dfDenom especificados.

freqTable4list()

freqTable4list (Lista1,ListaNúmerosInteirosFreq)⇒lista

Apresenta uma lista com os elementos de

Lista1 expandida de acordo com as

frequências em

ListaNúmerosInteirosFreq. Esta função

pode ser utilizada para construir uma tabela de frequência para a aplicação Dados e Estatística.

Lista1 pode ser qualquer lista válida. ListaNúmerosInteirosFreq tem de ter a

mesma dimensão da Lista1 e só deve conter elementos de números inteiros não negativos. Cada elemento especifica o número de vezes que o elemento de Lista1 correspondente é repetido na lista de resultados. Um valor de zero exclui o elemento de Lista1 correspondente.

Nota: Pode introduzir esta função através

da escrita de freqTable@>list(...) no teclado do computador.

Os elementos (nulos) vazios são ignorados. Para mais informações sobre os elementos vazios, consulte página 253.

Catálogo >

Lista alfabética 79

frequency()

frequency(Lista1,Listabins) ⇒lista

Devolve uma lista que contém as contagens dos elementos em Lista1. As contagens são baseadas em intervalos (bins) definidos em Listabins.

Se Listabins for {b(1), b(2), …, b(n)}, os intervalos especificados são {?{ b(1), b(1)<? { b(2),…,b(n-1)<?{ b(n), b(n)>?}. A lista resultante é um elemento maior que

Listabins.

Cada elemento do resultado corresponde ao número de elementos de Lista1 que estão no intervalo desse lote. Expresso em termos da função countIf(), o resultado é { countIf(list, ?{ b(1)), countIf(lista, b(1)<?{ b (2)), …, countIf(lista, b(n-1)<?{ b(n)), countIf(lista, b(n)>?)}.

Elementos de Lista1 que não podem ser “colocados num lote” são ignorados.

Elementos de Lista1 que não podem ser “colocados num lote” são ignorados. Os elementos (nulos) vazios também são ignorados. Para mais informações sobre os elementos vazios, consulte página 253.

Na aplicação Listas e Folha de cálculo, pode utilizar um intervalo de células no lugar de ambos os argumentos.

Nota: Consulte também countIf(), página

37.

Catálogo >

Explicação do resultado:

2 elementos da Lista de dados são { 2.5

4 elementos da Lista de dados são >2.5 e

{ 4.5

3 elementos da Lista de dados são >4.5

O elemento “hello” é uma cadeia enão pode ser colocado em nenhumlotedefinido.

FTest_2Samp

FTest_2Samp Lista1, Lista2 [, Freq1 [,

Freq2 [, Hipótese ]]]

FTest_2Samp Lista1, Lista2 [, Freq1 [,

Freq2 [, Hipótese ]]]

(Entrada da lista de dados)

FTest_2Samp sx1, n1, sx2, n2 [, Hipótese]

80 Lista alfabética

Catálogo >

FTest_2Samp

Catálogo >

(Entrada estatística do resumo)

Efectua um teste F de duas amostras. Um resumo dos resultados é guardado na variável stat.results (página 190).

ou Ha: s1 > s2, defina Hipótese>0

Para Ha: s1 ƒ s 2 (predefinição), defina

Hipótese =0

Para Ha: s1 < s2, defina Hipótese<0

Para mais informações sobre o efeito dos elementos vazios numa lista, consulte “Elementos (nulos) vazios” (página 253).

Variável de saída Descrição

stat.F EstatísticaÛ calculada para a sequência de dados

stat.PVal Menor nível de significância para o quala hipótese nulapodeser rejeitada

stat.dfNumer grausde liberdadedo “numerador” = n1-1

stat.dfDenom graus de liberdade do “denominador”= n2-1

stat.sx1, stat.sx2

stat.x1_bar

stat.x2_bar

stat.n1, stat.n2 Tamanho dasamostras

Desvios padrão da amostra dassequências de dados emLista1 e Lista2

Médias daamostra das sequência dedados em Lista1 e Lista2

Func

Bloco

EndFunc

Modelo para criar uma função definida pelo utilizador.

Bloco pode ser uma declaração, uma série

de declarações separadas pelo carácter “:” ou uma série de declarações em linhas separadas. A função pode utilizar a função

Return para devolver um resultado

específicos.

Catálogo >

Definir umafunção por ramos:

Resultado do gráfico g(x)

Lista alfabética 81

Func

Obs para introdução do exemplo: Para obter

instruções sobre como introduzir programas com várias linhas e definições de funções, consulte a secção Calculadora do manual do utilizador do produto.

Catálogo >

gcd()

gcd(Valor1, Valor2) ⇒expressão

Devolve o máximo divisor comum dos dois argumentos. O gcd de duas fracções é o gcd dos numeradores divididos pelo lcm dos denominadores.

No modo Auto ou Aproximado, o gcd dos números do ponto flutuante fraccionária é

1.0.

gcd(Lista1, Lista2) ⇒lista

Devolve os máximos divisores comuns dos elementos correspondentes em Lista1 e

Lista2.

gcd(Matriz1, Matriz2) ⇒matriz

Devolve os máximos divisores comuns dos elementos correspondentes em Matriz1 e

Matriz2.

geomCdf()

geomCdf(p,LimiteInferior,LimiteSuperior)

⇒número se LimiteInferior e

LimiteSuperior forem números, lista se LimiteInferior e LimiteSuperior forem

listas

Catálogo >

geomCdf(p,LimiteSuperior)para P(1{ X

{LimiteSuperior) ⇒número se

LimiteSuperior for um número, lista se LimiteSuperior for uma lista

82 Lista alfabética

geomCdf()

Calcula uma probabilidade geométrica cumulativa do LimiteInferior ao

LimiteSuperior com a probabilidade de

sucesso especificada p. Para P(X { LimiteSuperior), defina

LimiteInferior = 1.

Catálogo >

geomPdf()

Catálogo >

geomPdf(p, ValX) ⇒número se ValX for

um número, lista se ValX for uma lista Calcula uma probabilidade em ValX, o

número da tentativa em que ocorre o primeiro sucesso, para a distribuição geométrica discreta com a probabilidade de sucesso especificada p.

Get Menu Hub

Get[promptString,]var[,statusVar]

Get[promptString,] func(arg1, ...argn)

[,statusVar]

Programar comando: Recupera um valor de um conectado TI-Innovator™ Hub e atribui o valor à variável var.

O valor tem de ser pedido:

• Com antecedência, através de um comando Send"READ..." .

— ou —

• Incorporando um pedido "READ..." como o argumento promptString opcional. Este método permite-lhe utilizar um único comando para pedir e recuperar o valor.

Ocorre uma simplificação implícita. Por exemplo, uma cadeia recebida como “123” é interpretada como um valor numérico. Para preservar a cadeia, usar GetStr em vez de Get.

Exemplo: pedir o valor atualdo sensor de nívelde luz incorporado no hub. Usar Get para recuperar o valor e atribuí-lo à variável

lightval.

Incorporar o pedido READ no comando

Get.

Lista alfabética 83

Get Menu Hub

Se incluir o argumento opcional statusVar, é atribuído um valor com base no êxito da operação. Um valor de zero significa que não foram recebidos dados.

Na segunda sintaxe, o argumento func() permite que o programa armazene a cadeia recebida como uma definição de função. Esta sintaxe funciona como se o programa executasse o comando:

Define func(arg1, ...argn) = cadeia

recebida

O programa pode então usar a função definida func().

Nota: pode usar o comando Get dentro de

um programa definido pelo utilizador mas não dentro de uma função.

Nota: ver também GetStr, página 91 e Send,

página 170.

getDenom()

getDenom(Expr1) ⇒expressão

Transforma o argumento numa expressão que tem um denominador comum simplificado e, em seguida, devolve o denominador.

getKey()

codeTouch([0|1]) ⇒ Cadeiadevolvida

Descrição:codeTouch() - permite a um

programa em TI Basic obter introduções com o teclado - portátil, computador de secretária e emulador no computador de secretária.

Exemplo:

• teclapremida := codeTouch() devolverá uma chave ou uma cadeia vazia se não tiver sido premida

84 Lista alfabética

Catálogo >

Exemplo:

getKey()

qualquer tecla. Esta chamada será devolvida de imediato.

• tecla premida := codeTouch(1) irá aguardar até ser premida uma tecla. Esta chamada irá colocar a execução do programa em pausa até ser premida uma tecla.

Catálogo >

Lista alfabética 85

Processar batimentos de teclas:

Dispositivo portátil/tecla do

emulador

Ambiente de trabalho Valor devolvido

Esc Esc "esc"

Touchpad - Clique superior N/D "cima"

Ligar N/D "nome"

Scratch apps N/D "rascunho"

Touchpad - Clique do lado

N/D "esquerda"

esquerdo

Touchpad - Clique central N/D "centro"

Touchpad - Clique do lado

N/D "direita"

direito

Doc N/D "doc"

Tab Tab "tab"

Touchpad - Clique inferior Seta para baixo "baixo"

Menu N/D "menu"

Ctrl Ctrl sem devolução

Deslocar Deslocar sem devolução

Var N/D "var"

Eliminar N/D "eliminar"

= = "="

trig N/D "trig"

0 a 9 0-9 "0" ... "9"

Modelos N/D "modelo"

Catálogo N/D "cat"

^ ^ "^"

X^2 N/D "quadrado"

/ (tecla de divisão) / "/"

* (tecla de multiplicação) * "*"

e^x N/D "exp"

86 Lista alfabética

Dispositivo portátil/tecla do

emulador

Ambiente de trabalho Valor devolvido

10^x N/D "à potência de 10"

+ + "+"

- - "-"

( ( "("

) ) ")"

. . "."

(-) N/D "-" (sinal de negação)

Enter Enter "enter"

ee N/D "E" (notação científica E)

a - z a-z alfa = letra premida

(minúsculas) ("a" - "z")

shift a-z shift a-z alfa = letra premida

"A" - "Z"

Nota: ctrl-shift ativa as maiúsculas

?! N/D "?!"

pi N/D "pi"

Marcador N/D sem devolução

, , ","

Return N/D "return"

Espaço Espaço " " (espaço)

Inacessível Caracteres especiais como

O carácter é devolvido

@,!,^, etc.

N/D Teclas de função Nenhum carácter devolvido

N/D Teclas de controlo do

Nenhum carácter devolvido ambiente de trabalho especiais

Inacessível As restantes teclas do

ambiente de trabalho que

O mesmo carácter que

obtém em Notas (e não

Lista alfabética 87

Dispositivo portátil/tecla do

emulador

Ambiente de trabalho Valor devolvido

não estão disponíveis na

numa caixa matemática) calculadora durante codeTouch() aguardam uma tecla pressionada. ({, },;, :, ...)

Nota: é importante salientar que a presença de codeTouch() num programa alterna a forma como alguns eventos são tratados pelo sistema. Alguns destes eventos são descritos em seguida.

Terminar programa e processar evento - Exatamente como se o utilizador abrisse o programa premindo a tecla ON

"Suporte" abaixo significa - O sistema funciona como previsto - o programa continua a ser executado.

Evento Dispositivo Ambiente de trabalho -

Consulta rápida Terminar programa,

processar evento

Software TI-Nspire™ do aluno

Da mesma forma que no portátil (TI-Nspire™ Student Software, TINspire™ Navigator™ NC Teacher Software apenas)

Gestão de ficheiros remota

(Incl. o envio do ficheiro 'Exit Press 2 Test' de outro portátil ou computador de secretária-portátil)

Terminar aula Terminar programa,

Terminar programa, processar evento

processar evento

Da mesma forma que no portátil.

(TI-Nspire™ Student Software, TI-Nspire™ Navigator™ NC Teacher Software apenas)

Suporte (TI-Nspire™ Student

Software, TI-Nspire™ Navigator™ NC Teacher Software apenas)

Evento Dispositivo Ambiente de trabalho - TI-

TI-Innovator™ Hub ligar/desligar

Suporte - Pode gerar comandos com êxito para

Nspire™ Todas as versões

Da mesma forma que no

portátil. TI-Innovator™ Hub. Depois de sair do programa, TIInnovator™ Hub ainda está a funcionar com o portátil.

88 Lista alfabética

getLangInfo()

getLangInfo()⇒abreviatura

Apresenta uma abreviatura do nome do idioma activo. Por exemplo, pode utilizá-lo num programa ou função para determinar o idioma actual.

Inglês = “en”

Dinamarquês = “da”

Alemão = “de”

Finlandês = “fi”

Francês = “fr”

Italiano = “it”

Holandês = “nl”

Flamengo = “nl_BE”

Norueguês = “no”

Português = “pt”

Espanhol = “es”

Sueco = “sv”

Catálogo >

getLockInfo()

getLockInfo(Var)⇒valor

Devolve o estado de bloqueio/desbloqueio actual da variável Var.

valor =0: Var está desbloqueada ou não

existe.

valor =1: Var está bloqueada e não pode

ser modificada nem eliminada.

Consulte Lock, página 114, eunLock, página

212.

Catálogo >

Lista alfabética 89

getMode()

getMode(NúmeroInteiroNomeModo)

⇒valor

getMode(0) ⇒lista

getMode(NúmeroInteiroNomeModo)

devolve um valor que representa a definição actual do modo

NúmeroInteiroNomeModo.

getMode(0) devolve uma lista com os pares

de números. Cada par é composto por um número inteiro do modo e um número inteiro da definição.

Para uma listagem dos modos e das definições, consulte a tabela abaixo.

Se guardar as definições com getMode(0) & var, pode utilizar setMode(var) num programa ou função para restaurar temporariamente as definições na execução da função ou do programa. Consulte setMode(), página 174.

Catálogo >

Nome do modo

Número inteiro do modo

Números inteiros da definição

Ver dígitos 1 1 =Flutuante, 2 =Flutuante1, 3 =Flutuante2, 4

=Flutuante3, 5 =Flutuante4, 6=Flutuante5, 7 =Flutuante6, 8 =Flutuante7, 9 =Flutuante8, 10 =Flutuante9, 11 =Flutuante10, 12 =Flutuante11,

13 =Flutuante12, 14 =Fixo0, 15 =Fixo1, 16 =Fixo2, 17 =Fixo3, 18 =Fixo4, 19 =Fixo5, 20 =Fixo6, 21

=Fixo7, 22 =Fixo8, 23 =Fixo9, 24 =Fixo10, 25 =Fixo11, 26 =Fixo12

Ângulo 2 1 =Radianos, 2 =Graus, 3 =Gradianos

Formato

3 1 =Normal, 2 =Científica, 3 =Engenharia

exponencial

Real ou

4 1 =Real, 2 =Rectangular, 3 =Polar

Complexo

Auto or

5 1 =Auto, 2 =Aproximado, 3 =Exacto

Aprox.

Formato

6 1 =Rectangular, 2 =Cilíndrico, 3 =Esférico

vectorial

Base 7 1 =Decimal, 2 =Hex, 3 =Binário

90 Lista alfabética

Nome do modo

Sistema de unidades

Número inteiro do modo

Números inteiros da definição

8 1 =SI, 2 =Eng/EUA

getNum()

Catálogo >

getNum(Expr1) ⇒expressão

Transforma o argumento numa expressão que tem um denominador comum simplificado e, em seguida, devolve o numerador.

GetStr Hub Menu

GetStr[promptString,] var[, statusVar]

GetStr[promptString,] func(arg1, ...argn)

[,statusVar]

Programar comando: funciona de forma idêntica ao comando Get, mas o valor recuperado é sempre interpretado como uma cadeia. Em contraste, o comando Get interpreta a resposta como uma expressão a não ser que esteja entre aspas ("").

Nota: ver também Get, página 83 e Send,

página 170.

getType()

getType(var)⇒cadeia de texto

Apresenta uma cadeia de texto que indica o tipo de dados da variável var.

Se var não tiver sido definido, apresenta a cadeia de texto "NENHUM".

Para exemplos, ver Get.

Catálogo >

Lista alfabética 91

getVarInfo()

getVarInfo()⇒matriz ou palavra

getVarInfo(CadeiaDoNomeDaBiblioteca)

⇒matriz ou palavra

getVarInfo() devolve uma matriz de

informações (nome da variável, tipo, acessibilidade da biblioteca e estado de bloqueio/desbloqueio) para todas as variáveis e os objectos da biblioteca definidos no problema actual.

Se não definir nenhuma variável, getVarInfo

() apresenta a palavra getVarInfo(NomeDaBiblioteca)apresenta

uma matriz com informações para todos os objectos da biblioteca definidos na biblioteca CadeiaDoNomeDaBiblioteca.

CadeiaDoNomeDaBiblioteca tem de ser

uma palavra (texto entre aspas) ou uma variável da frase.

Se a biblioteca

CadeiaDoNomeDaBiblioteca não existir,

ocorre um erro. Veja o exemplo do lado esquerdo, em que o

resultado de getVarInfo() é atribuído à variável vs. A tentar de apresentação da linha 2 ou da linha 3 de vs apresenta uma mensagem de erro de “Matriz ou lista inválida” porque pelo menos um dos elementos nessas linhas (variável b, por exemplo) reavalia-se para uma matriz.

Este erro pode também ocorrer quando utilizar Ans para reavaliar um resultado

getVarInfo().

O sistema apresenta o erro acima porque a versão actual do software não suporta uma estrutura de matriz generalizada em que um elemento de uma matriz pode ser uma matriz ou uma lista.

Catálogo >

92 Lista alfabética

Goto

Goto NomeDefinição

Transfere o controlo para a definição

NomeDefinição. NomeDefinição tem de ser definido na

mesma função com uma instrução Lbl.

Obs para introdução do exemplo: Para obter

instruções sobre como introduzir programas com várias linhas e definições de funções, consulte a secção Calculadora do manual do utilizador do produto.

Catálogo >

4Grad

Expr1 4 Grad ⇒expressão

Converte Expr1 para medição do ângulo de gradianos.

Nota: Pode introduzir este operador através

da escrita de @>Grad no teclado do computador.

identity ()

identity(Número inteiro) ⇒ matriz

Devolve a matriz identidade com uma dimensão de Número inteiro.

Número inteiro tem de ser um número

natural.

Catálogo >

No modo de ângulo Graus:

No modo de ângulo Radianos:

Catálogo >

Lista alfabética 93

If BooleanExpr

Declaração

If ExprBooleana Then

Bloco

EndIf

Se a ExprBooleana for avaliada como verdadeira, executa a declaração individual

Declaração ou o bloco de declarações Bloco antes de continuar a execução.

Se a ExprBooleana for avaliada como falsa, continua a execução sem executar a declaração ou o bloco de declarações.

Bloco pode ser uma declaração ou uma

sequência de declarações separadas pelo carácter ":" .

Obs para introdução do exemplo: Para obter

instruções sobre como introduzir programas com várias linhas e definições de funções, consulte a secção Calculadora do manual do utilizador do produto.

If ExprBooleana Then

Bloco1

Else

Bloco2

EndIf

Se a ExprBooleana for avaliada como verdadeira, executa o Bloco1 e ignora o

Bloco2.

Se a ExprBooleana for avaliada como falsa, ignora o Bloco1 , mas executa o

Bloco2. Bloco1 e Bloco2 podem ser uma

declaração única.

Catálogo >

94 Lista alfabética

If ExprBooleana1 Then

Bloco1

ElseIf ExprBooleana2 Then

Bloco2

⋮

ElseIf ExprBooleanaN Then

BlocoN

EndIf

Permite a derivação. Se a ExprBooleana1 for avaliada como verdadeira, executa o

Bloco1. Se a ExprBooleana1 for avaliada

como falsa, avalia a ExprBooleana2, etc.

Catálogo >

ifFn ()

ifFn(ExprBooleana, Value_If_true [,Value_If_false [,Value_If_unknown]]) ⇒

expressão, lista ou matriz

Avalia a expressão booleana ExprBooleana (ou cada elemento da ExprBooleana ) e produz um resultado com base nas seguintes regras:

• ExprBooleana pode testar um valor

individual, uma lista ou uma matriz.

• Se um elemento da ExprBooleana for

avaliado como verdadeiro, devolve o elemento correspondente de Value_If_

true.

• Se um elemento da ExprBooleana for

avaliada como falsa, devolve o elemento correspondente de Value_If_false. Se omitir Value_If_false, devolve undef.

• Se um elemento da ExprBooleana não

for verdadeiro nem falso, devolve o elemento correspondente Value_If_

unknown. Se omitir Value_If_unknown,

devolve undef.

• Se o segundo, o terceiro ou o quarto argumento da função ifFn() for uma expressão individual, o teste booleano é aplicado a todas as posições da

ExprBooleana.

Catálogo >

O valor do teste de 1é inferior a 2.5, por estarazão, o elemento

Value_If_True correspondentede 5 é

copiado para a lista de resultados.

O valor do teste de 2é inferior a 2.5, por estarazão, o elemento

Value_If_True correspondentede 6 é

copiado para a lista de resultados.

O valor do teste de 3não é inferior a 2.5, por estarazão, o elemento Value_If_

False correspondente de 10 é copiado para

a lista de resultados.

Value_If_true é um valor individual e

corresponde a qualquer posição seleccionada.

Lista alfabética 95

ifFn ()

Nota: Se a declaração ExprBooleana

simplificada envolver uma lista ou matriz, todos os outros argumentos da lista ou matriz têm de ter as mesmas dimensões e o resultado terá as mesmas dimensões.

Catálogo >

Value_If_falsenão é especificado. Undef é

utilizado.

Um elemento seleccionado de Value_If_

true. Um elemento seleccionado de Value_ If_unknown.

imag()

imag(Expr1) ⇒ expressão

Devolve a parte imaginária do argumento.

Nota: Todas as variáveis indefinidas são

tratadas como variáveis reais. Consulte também real(), page 156

imag(Lista1) ⇒ lista

Devolve uma lista de partes imaginárias dos elementos.

imag(Matriz1) ⇒ matriz

Devolve uma matriz das partes imaginárias dos elementos.

impDif()

impDif(Equação, Var, VarDependente

[,Ord]) ⇒ expressão em que a ordem Ord predefine-se para 1.

Calcula a derivada implícita para equações em que uma variável é definida implicitamente nos termos de outra.

Catálogo >

indirecta

96 Lista alfabética

Consultar #(), página 243.

Texas Instruments TI-Nspire CX CAS Reference Guide [pt]

Specifications and Main Features

Frequently Asked Questions

User Manual

Informações importantes

Modelos de expressão

Lista alfabética