Texas Instruments TI-Nspire CX CAS Reference Guide [fi]

TI-Nspire™CAS

Sovelluksen käsikirja

Tämä opas koskee TI-Nspire™-ohjelmiston versiota 4.5. Uusin versio asiakirjoista on saatavilla Internet-sivustolta education.ti.com/go/download.

Tärkeitä tietoja

Ellei muuten ilmoiteta ohjelman mukaan liitetyssä käyttöluvassa, Texas Instruments ei anna minkäänlaista suoraa tai välillistä takuuta mukaan lukien, mutta ei näihin rajoittuen, kaikki välilliset takuut, jotka koskevat kaikkien ohjelmien ja kirjojen myyntikelpoisuutta tai erityiseen tarkoitukseen sopivuutta, ja tarjoaa kyseisiä materiaaleja ainoastaan “sellaisina kuin ne ovat” -pohjalla. Texas Instruments ei ole missään tapauksessa vastuussa kenellekään mistään erityisistä, rinnakkaisista, tahattomista tai seurauksellisista vaurioista näiden materiaalien hankinnan tai käytön aiheuttamana, ja Texas Instruments:n yksinomainen ja eksklusiivinen vastuu toimintamuodosta riippumatta ei ylitä määrää, joka on asetettu käyttöluvassa ohjelmaa varten. Texas Instruments ei myöskään vastaa mistään vaateista, joita toinen osapuoli voi esittää aiheutuen näiden materiaalien käytöstä.

Lisenssi

Katso täydellinen lisenssi osoitteesta C:\ProgramFiles\TIEducation\<TI-Nspire™

Product N ame>\license.

Contents

Tärkeitä tietoja

Lausekemallit 1

Luettelo aakkosjärjestyksessä 8

A B C D E F G I L M N O P Q R S T U V W X Z

17 21 48 61 72 82

92 101 117 126 135 138 147 151 166 192 208 209 210 212 213

iii

Symbolit 222

Tyhjät elementit 250

Matemaattisten lausekkeiden syöttäminen pikavalintojen avulla 252

EOS-järjestelmän (yhtälökäyttöjärjestelmä) hierarkia 254

Vakiot ja arvot 256

Virhekoodit ja viestit 257

Varoituskoodit ja -viestit 264

Huolto ja Asiakastuki 266

TI-tuotteiden huolto- ja takuutietoa

266

Index 267

Lausekemallit

Lausekemallien avulla voit syöttää matemaattisia lausekkeita normaalissa matemaattisessa muodossa. Lisätessäsi mallin se näkyy syöterivillä siten, että elementtien syöttökohdissa on pienet ruudut. Kohdistin on syötettävän elementin kohdalla.

Voit siirtää kohdistimen kunkin elementin kohdalle nuolipainikkeilla tai painikkeella

e, jonka jälkeen voit kirjoittaa elementin arvon tai lausekkeen. Lauseke

sievennetään painamalla painikkeita · tai /·.

Murtolukumalli

Huomaa: Katso myös / (jakolasku), sivu

224.

Eksponenttimalli

Huomaa: Syötä ensimmäinen arvo, paina

l ja syötä sen jälkeen eksponentti. Voit

palauttaa kohdistimen perusviivalle painamalla oikealle osoittavaa nuolta (¢).

Huomaa: Katso myös ^ (potenssi), sivu 225.

Neliöjuurimalli

Huomaa: Katso myös ‡() (neliöjuuri),

sivu 236.

/p painikkeet

Esimerkki:

l painike

Esimerkki:

/q painikkeet

Esimerkki:

Lausekem allit 1

N:s juuri -malli

Huomaa: Katso myös root(), sivu 162.

/l painikkeet

Esimerkki:

e eksponenttimalli

e-kantainen eksponenttifunktio korotettuna

potenssiin

Huomaa: Katso myös e^(), sivu 61.

Logaritmimalli

Laskee määritetyn kantaisen logaritmin. 10kantaista logaritmia laskettaessa kantaluku jätetään pois.

Huomaa: Katso myös log(), sivu 113.

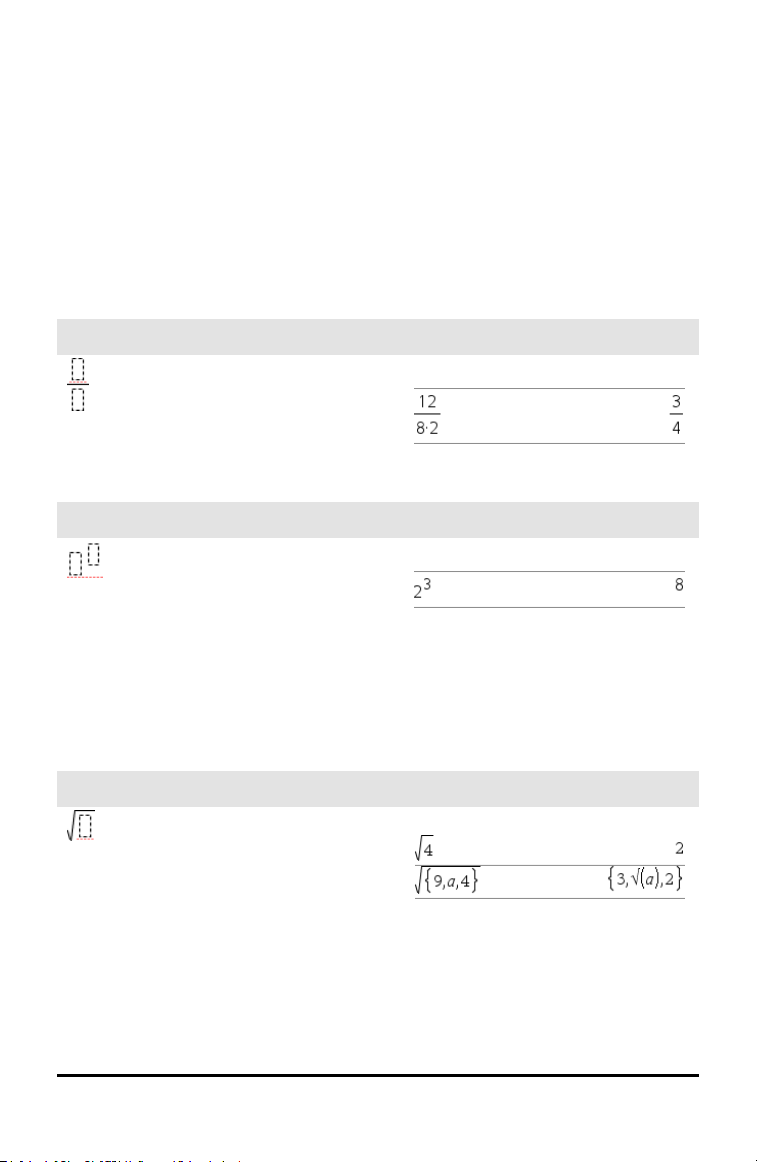
Paloittain määritellyn funktion malli (2-osainen)

Voit luoda lausekkeita ja ehtoja 2-osaiselle paloittain määritellylle funktiolle. Lisää osa napsauttamalla mallia ja toista malli.

Huomaa: Katso myös piecewise() , sivu 140.

u painikkeet

Esimerkki:

/s painike

Esimerkki:

Katalogi >

Esimerkki:

2 Lausekemallit

Paloittain määritellyn funktion malli (2-osainen)

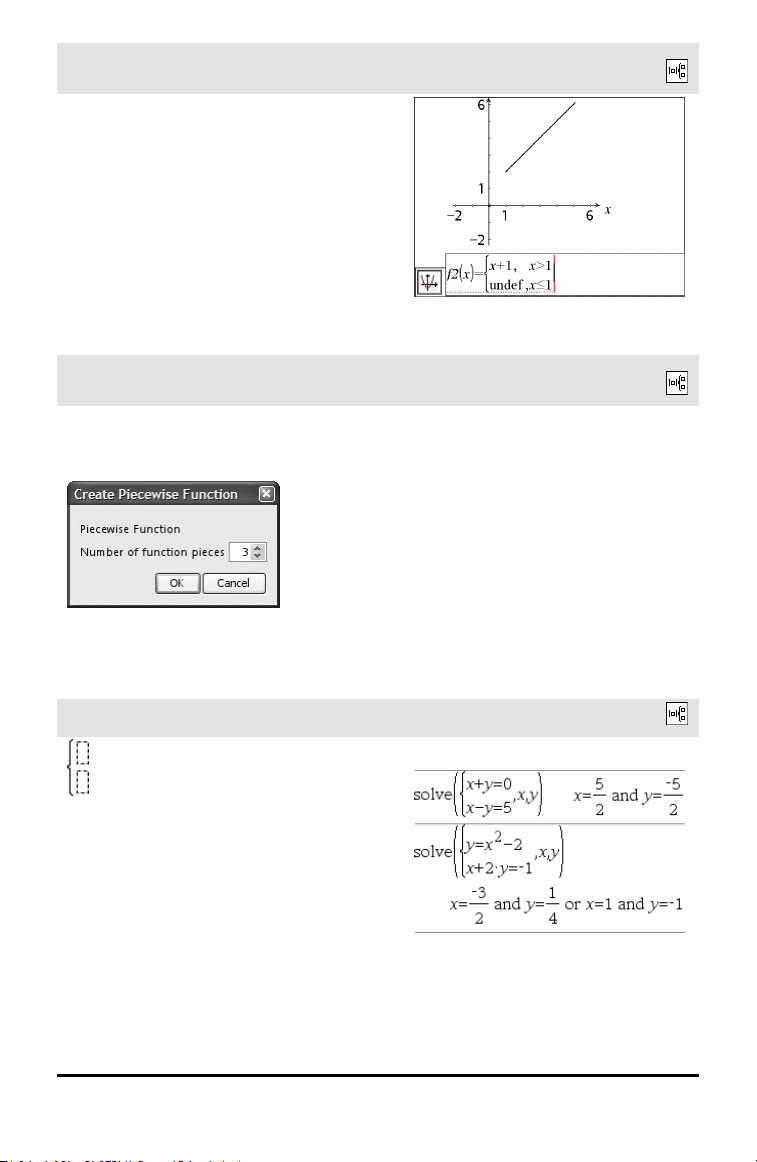
Paloittain määritellyn funktion malli (Nosainen)

Voit luoda lausekkeita ja ehtoja N--osaiselle paloittain määritellylle funktiolle. Laskin pyytää N:n arvoa.

Huomaa: Katso myös piecewise() , sivu 140.

Katalogi >

Esimerkki:

Katso paloittainmääritellynfunktion (2osaisen)mallinesimerkki.

Yhtälöparin malli

Luo kahden yhtälön ryhmän. Voit lisätä rivin olemassa olevaan yhtälöön napsauttamalla mallia ja toistamalla mallin.

Huomaa: Katso myös system(), sivu 192.

Katalogi >

Esimerkki:

Lausekem allit 3

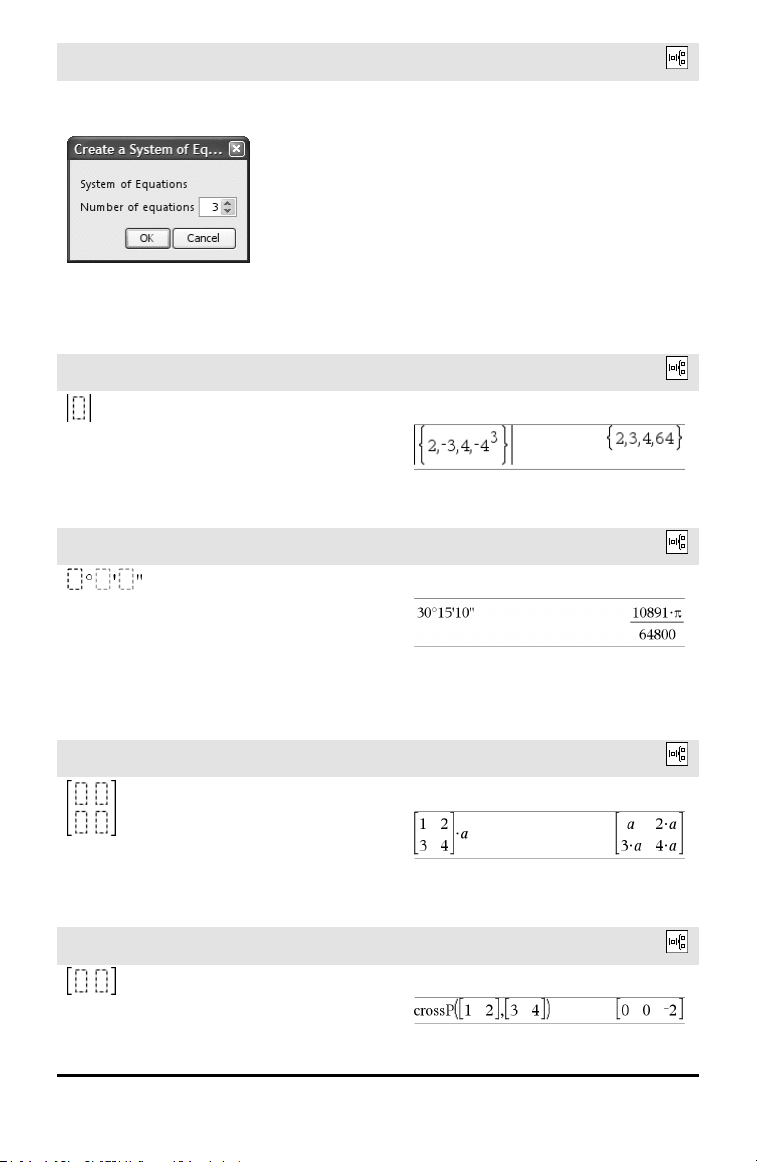
N-osaisen yhtälöryhmän malli

Voit luoda Nyhtälöä sisältävän yhtälöryhmän. Laskin pyytää N:n arvoa.

Huomaa: Katso myös system(), sivu 192.

Katalogi >

Esimerkki:

Katso yhtälöparin(2 yhtälöä) mallin esimerkki.

Itseisarvon malli

Huomaa: Katso myös abs( ), sivu 8.

dd°mm’ss.ss’’ -malli

Voit syöttää kulmia muodossa

dd°mm’ss.ss’’, jossa dd on

desimaaliasteiden lukumäärä, mm on minuuttimäärä, ja ss.ss on sekuntimäärä.

Matriisimalli (2 x 2)

Luo 2 x 2 -matriisin.

Matriisimalli (1 x 2)

Katalogi >

Esimerkki:

Katalogi >

Esimerkki:

Katalogi >

Esimerkki:

Katalogi >

Esimerkki:

4 Lausekemallit

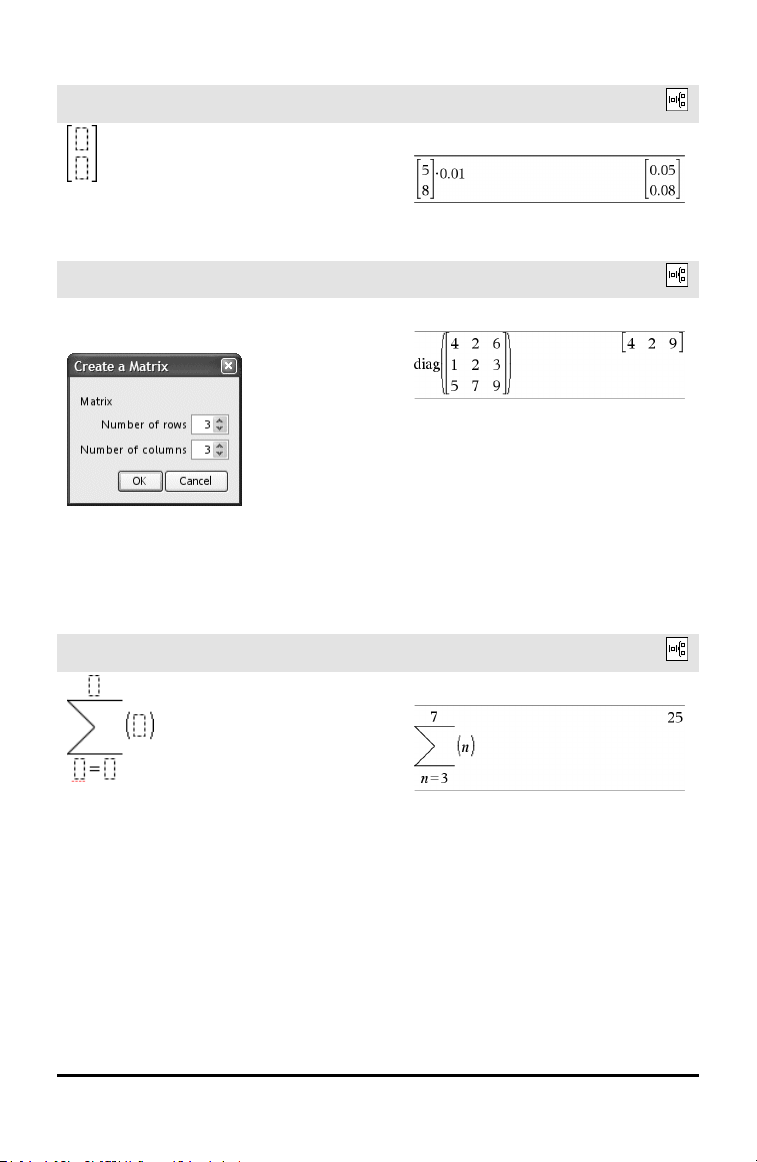
Matriisimalli (2 x 1)

Katalogi >

Esimerkki:

Matriisimalli (m x n)

Malli tulee näkyviin määritettyäsi rivien ja sarakkeiden lukumäärän syöttöruutuun.

Huomaa: Jos luot paljon rivejä ja sarakkeita

sisältävän matriisin, voi kestää jonkin aikaa, ennen kuin matriisi tulee näkyviin.

Summan malli (G)

Huomaa: Katso myös G() (sumSeq), sivu

237.

Katalogi >

Esimerkki:

Katalogi >

Esimerkki:

Lausekem allit 5

Tulon malli (Π)

Huomaa: Katso myös Π() (prodSeq), sivu

236.

Katalogi >

Esimerkki:

Ensimmäisen derivaatan malli

Ensimmäisen derivaatan mallia voi käyttää myös laskettaessa ensimmäinen derivaatta pisteessä.

Huomaa: Katso myös d() (derivaatta), sivu

233.

Toisen derivaatan malli

Toisen derivaatan mallia voi käyttää myös laskettaessa toinen derivaatta pisteessä.

Huomaa: Katso myös d() (derivaatta), sivu

233.

N:nnen derivaatan malli

Katalogi >

Esimerkki:

Katalogi >

Esimerkki:

Katalogi >

Esimerkki:

n:nnen derivaatan mallia voidaan käyttää

laskettaessa n:s derivaatta.

Huomaa: Katso myös d() (derivaatta), sivu

233.

6 Lausekemallit

Määrätyn integraalin malli

Huomaa: Katso myös ‰() integraali( ), sivu

222.

Katalogi >

Esimerkki:

määrittämättömän integraalin malli

Huomaa: Katso myös ‰() integral(), sivu 222.

Raja-arvon malli

Vasemman puolen raja-arvon saat painikkeella N tai (N). Oikean puolen rajaarvon saat painikkeella +.

Huomaa: Katso myös limit(), sivu 103.

Katalogi >

Esimerkki:

Katalogi >

Esimerkki:

Lausekem allit 7

Luettelo aakkosjärjestyksessä

Komennot, joiden nimiä ei voi järjestää aakkosjärjestykseen (esimerkiksi +, ! ja >), on esitetty tämän kappaleen lopussa alkaen sivulta (sivu 222). Ellei toisin ole mainittu, kaikki tämän kappaleen esimerkit on suoritettu laskimen oletustilassa, eikä mitään muuttujia ole määritetty.

abs()

abs(Laus1)⇒lauseke abs(Lista1)⇒lista

abs(Matriisi1)⇒matriisi

Laskee argumentin itseisarvon.

Huomaa: Katso myös Itseisarvon malli, sivu

Jos argumentti on kompleksiluku, määrittää luvun moduulin.

Huomaa: Kaikkia määrittämättömiä

muuttujia käsitellään reaalimuuttujina.

amortTbl()

amortTbl(NPmt,N,I,PV, [Pmt], [FV], [PpY], [CpY], [PmtAt], [pyörArvo])

⇒matriisi

Lainan lyhennysfunktio, joka laskee lyhennystaulukon tiettyjen TVMargumenttien perusteella.

NPmt on taulukon maksuerien lukumäärä.

Taulukko alkaa ensimmäisestä maksuerästä.

N, I, PV, Pmt, FV, PpY, CpY ja PmtAt on

kuvattu TVM-argumenttien taulukossa, sivu

206.

• Jos jätät argumentin Pmt pois, sen oletusarvoksi tulee Pmt=tvmPmt (N,I,PV,FV,PpY,CpY,PmtAt).

• Jos jätät argumentin FV pois, sen

Katalogi >

8 Luettelo aakkosjärjestyksessä

amortTbl()

oletusarvoksi tulee FV=0.

• Argumenttien PpY, CpY ja PmtAt oletusarvot ovat samat kuin TVMfunktioilla.

pyörArvo määrittää pyöristyksessä

käytettävien desimaalien määrän. Oletusarvo=2.

Tulosmatriisin sarakkeet ovat seuraavassa järjestyksessä: maksuerän numero, koron määrä, pääoman lyhennysmäärä ja velkasaldo.

Rivillä n näkyvä saldo on maksuerän n jälkeen jäljellä oleva velkasaldo.

Voit käyttää tulosmatriisia syötteenä muissa lyhennyslaskutoimituksissa GInt() ja GPrn(), sivu 237, sekä bal(), sivu 17.

Katalogi >

and

BoolenLaus1 and BoolenLaus2⇒Boolen

lausekeBoolenLista1

and BoolenLista2⇒Boolen

listaBoolenMatriisi1

and BoolenMatriisi2⇒Boolen matriisi

Määrittää totuusarvon tosi tai epätosi tai antaa vastauksena sievennetyn muodon alkuperäisestä syötteestä.

Kokonaisluku1

andKokonaisluku2⇒kokonaisluku

Vertaa kahta reaalikokonaislukua bitti bitiltä and-operaation avulla. Sisäisesti kumpikin kokonaisluku muunnetaan etumerkilliseksi, 64 bitin binaariluvuksi. Kun vastaavia bittejä verrataan, tulos on 1, jos kumpikin bitti on 1. Muussa tapauksessa tulos on 0. Laskettu arvo edustaa bittituloksia, ja se näkyy kantalukutilan mukaisesti.

Katalogi >

Heksadesimaalisessa kantalukutilassa:

Tärkeää: Nolla, ei O-kirjain.

Binaarisessa kantalukutilassa:

Desimaalisessa kantalukutilassa:

Luettelo aakkosjärjestyksessä 9

and

Kokonaisluvut voi syöttää minkä tahansa luvun kantalukuna. Binaarisen syötteen edelle tulee merkitä etumerkki 0b ja heksadesimaalisen syötteen edelle 0h. Jos etumerkkiä ei ole, kokonaislukuja käsitellään desimaalilukuina (kantaluku10).

Jos syötät desimaalikokonaisluvun, joka on liian suuri etumerkilliselle, 64 bitin binaarimuodolle, laskin käyttää symmetristä modulo-operaatiota, jotta arvo saadaan oikealle alueelle.

Katalogi >

Huomaa: Binaarisessa syötteessä voi olla

korkeintaan 64 numeroa (etuliitettä0b ei lasketa). Heksadesimaalisessasyötteessä voi ollakorkeintaan 16 numeroa.

angle()

angle(Laus1)⇒lauseke

Laskee argumentin kulman tulkiten argumentin kompleksiluvuksi.

Huomaa: Kaikkia määrittämättömiä

muuttujia käsitellään reaalimuuttujina.

angle(Lista1)⇒lista angle(Matriisi1)⇒matriisi

Laskee listan tai matriisin Lista1:n tai

Matriisi1:n elementtien kulmista tulkiten

jokaisen elementin kompleksiluvuksi, joka edustaa kaksiulotteista suorakulmakoordinaattipistettä.

Katalogi >

Astekulmatilassa:

Graadikulmatilassa:

Radiaanikulmatilassa:

ANOVA

ANOVA Lista1,Lista2[,Lista3,...,Lista20] [,Lippu]

10 Lue ttelo aakkosjärjestyksess ä

Katalogi >

ANOVA

Suorittaa yksisuuntaisen varianssianalyysin 2-20 perusjoukon keskiarvon vertailua varten. Tulosten yhteenveto tallentuu

stat.results-muuttujaan. (Katso sivu 187.)

Lippu=0 datalle, Lippu=1 tilastoille

Tulosmuuttuja Kuvaus

stat.F F-tilaston arvo

stat.PVal Alinmerkitsevyystaso, jolla nollahypoteesivoidaanhylätä

stat.df Ryhmienvapausasteet

stat.SS Ryhmienneliöiden summa

stat.MS Ryhmienkeskineliöt

stat.dfError Virheidenvapausasteet

stat.SSError Virheidenneliöiden summa

stat.MSError Virheidenkeskineliö

stat.sp Poolattukeskihajonta

stat.xbarlist Listojensyötteiden keskiarvo

stat.CLowerList 95 %:n luottamusvälit jokaisen syötelistankeskiarvolle

stat.CUpperList 95%:n luottamusvälitjokaisen syötelistankeskiarvolle

Katalogi >

ANOVA2way

ANOVA2way Lista1,Lista2

[,Lista3,…,Lista10][,TasoRivi]

Laskee kaksisuuntaisen varianssianalyysin 210 perusjoukon keskiarvojen vertaamiseksi. Tulosten yhteenveto tallentuu stat.resultsmuuttujaan. (Katso sivu 187.)

TasoRivi=0 lohkolle

TasoRivi=2,3,...,Pit-1, kahdelle tekijälle,

jossa Pit=pituus(List1)=pituus(List2) = … = pituus(List10) ja Pit/TasoRivi ∈ {2,3,…}

Tulokset: Lohkomuoto

Katalogi >

Luettelo aakkosjärjestyksessä 11

Tulosmuuttuja Kuvaus

stat.F F-tilasto, saraketekijänF-tilasto

stat.PVal Alinmerkitsevyystaso, jolla nollahypoteesivoidaanhylätä

stat.df Saraketekijänvapausasteet

stat.SS Saraketekijänneliöiden summa

stat.MS Saraketekijänkeskineliöt

stat.FBlock F-tilasto, tekijän F-tilasto

stat.PValBlock Pienintodennäköisyys, jolla nollahypoteesi voidaanhylätä

stat.dfBlock Tekijän vapausasteet

stat.SSBlock Tekijän neliöidensumma

stat.MSBlock Tekijän keskineliöt

stat.dfError Virheidenvapausasteet

stat.SSError Virheidenneliöiden summa

stat.MSError Virheidenkeskineliöt

stat.s Virheenkeskihajonta

SARAKETEKIJÄN tulokset

Tulosmuuttuja Kuvaus

stat.Fcol F-tilasto, saraketekijänF-tilasto

stat.PValCol Saraketekijäntodennäköisyysarvo

stat.dfCol Saraketekijänvapausasteet

stat.SSCol Saraketekijänneliöiden summa

stat.MSCol Saraketekijänkeskineliöt

RIVITEKIJÄN tulokset

Tulosmuuttuja Kuvaus

stat.FRow F-tilasto, rivitekijän F-tilasto

stat.PValRow Rivitekijäntodennäköisyysarvo

stat.dfRow Rivitekijänvapausasteet

stat.SSRow Rivitekijänneliöidensumma

stat.MSRow Rivitekijänkeskineliöt

12 Lue ttelo aakkosjärjestyksess ä

VUOROVAIKUTUKSEN tulokset

Tulosmuuttuja Kuvaus

stat.FInteract F -tilasto, vuorovaikutuksenF-tilasto

stat.PValInteract Vuorovaikutuksentodennäköisyysarvo

stat.dfInteract Vuorovaikutuksenvapausasteet

stat.SSInteract Vuorovaikutuksenneliöidensumma

stat.MSInteract Vuorovaikutuksenkeskineliöt

VIRHEIDEN tulokset

Tulosmuuttuja Kuvaus

stat.dfError Virheidenvapausasteet

stat.SSError Virheidenneliöiden summa

stat.MSError Virheidenkeskineliöt

s Virheenkeskihajonta

ans

ans⇒arvo

Näyttää viimeksi sievennetyn lausekkeen tuloksen.

approx()

approx(Laus1)⇒lauseke

Määrittää argumentin sievennetyn arvon lausekkeena, joka sisältää desimaaliarvoja, mikäli mahdollista, riippumatta nykyisestä

Automaattinen tai likimääräinen -tilasta.

Tämä vastaa argumentin syöttämistä ja painikkeen / · painamista.

approx(Lista1)⇒lista approx(Matriisi1)⇒matriisi

/v painikkeet

Katalogi >

Luettelo aakkosjärjestyksessä 13

approx()

Määrittää listan tai matriisin, jossa jokainen elementti on laskettu desimaaliarvoksi, mikäli mahdollista.

Katalogi >

4approxFraction()

Laus 4approxFraction([Tol])⇒lauseke Lista 4approxFraction([Tol])⇒lista Matriisi 4approxFraction([Tol])⇒matriisi

Laskee syötteen murtolukuna käyttäen toleranssia Tol. Jos operaattori Tol jätetään pois, laskin käyttää toleranssia 5.E-14.

Huomaa: Voit syöttää tämän funktion

tietokoneen näppäimistöltä kirjoittamalla

@>approxFraction(...).

approxRational()

approxRational(Laus[, tol])⇒lauseke approxRational(Lista[, tol])⇒lista approxRational(Matriisi[, tol])⇒matriisi

Laskee argumentin murtolukuna käyttäen toleranssia tol. Jos operaattori Tol jätetään pois, laskin käyttää toleranssia 5.E-14.

arccos()

Katalogi >

Katso cos/(), sivu 33.

arccosh()

arccot()

14 Lue ttelo aakkosjärjestyksess ä

Katso cosh/(), sivu 34.

Katso cot/(), sivu 35.

arccoth()

Katso coth/(), sivu 36.

arccsc()

arccsch()

arcLen()

arcLen(Laus1,Muutt,Alku,Loppu) ⇒lauseke

Laskee Laus1:n kaaren pituuden alusta Alku loppuun Loppu muuttujan Muutt suhteen.

Kaaren pituus lasketaan kokonaislukuna käyttäen oletuksena funktiotilan määritystä.

arcLen(Lista1,Muutt,Alku,Loppu)⇒lista

Laskee listan jokaisen Lista1:n elementin kaaren pituuden alusta Alku loppuun Loppu muuttujan Muutt suhteen.

arcsec()

Katso csc/(), sivu 39.

Katso csch/(), sivu 39.

Katalogi >

Katso sec/(), sivu 166.

arcsech()

arcsin()

Katso sech/(), sivu 167.

Katso sin/(), sivu 178.

Luettelo aakkosjärjestyksessä 15

arcsinh()

Katso sinh/(), sivu 179.

arctan()

arctanh()

augment()

augment(Lista1, Lista2)⇒lista

Luo uuden listan, joka on Lista2 liitettynä

Lista1:n loppuun.

augment(Matriisi1, Matriisi2)⇒matriisi

Luo uuden matriisin, joka on Matriisi2 liitettynä Matriisi1:een. Kun käytetään merkkiä “,”, matriiseiden rivimäärien on oltava samat, ja Matriisi2 liitetään

Matriisi1:een uusina sarakkeina. Ei muuta Matriisi1:ä eikä Matriisi2:a.

avgRC()

avgRC(Laus1, Muutt [=Arvo] [, Askel])

⇒lauseke

Katso tan/(), sivu 193.

Katso tanh/(), sivu 195.

Katalogi >

avgRC(Laus1, Muutt [=Arvo] [, Lista1])

⇒lista

avgRC(Lista1, Muutt [=Arvo] [, Askel])

⇒lista

avgRC(Matriisi1, Muutt [=Arvo] [, Askel])

⇒matriisi

Laskee erotusosamäärän eteenpäin (keskimääräisen muutosnopeuden).

Laus1 voi olla käyttäjän määrittämä

funktionimi (katso Func).

16 Lue ttelo aakkosjärjestyksess ä

avgRC()

Kun Arvo määritetään, se ohittaa mahdolliset aikaisemmat muuttujamääritykset tai mahdolliset muuttujan nykyiset “|” -sijoitukset.

Askel on askeleen arvo. Jos Askel jätetään

pois, sen oletusarvo on 0.001.

Huomaa, että samankaltaisessa funktiossa

centralDiff() käytetään

keskeiserotusosamäärää.

Katalogi >

bal()

bal(NPmt,N,I,PV ,[Pmt], [FV], [PpY], [CpY], [PmtAt], [pyörArvo])⇒arvo

bal(NPmt,amortTable)⇒arvo

Lyhennysfunktio, joka laskee määritetyn maksuerän jälkeen jäljellä olevan velkasaldon.

N, I, PV, Pmt, FV, PpY, CpY ja PmtAt on

kuvattu TVM-argumenttien taulukossa, sivu

206.

NPmt määrittää sen maksuerän numeron,

jonka jälkeen velkasaldo halutaan laskea.

N, I, PV, Pmt, FV, PpY, CpY ja PmtAt on

kuvattu TVM-argumenttien taulukossa, sivu

206.

• Jos jätät argumentin Pmt pois, sen oletusarvoksi tulee Pmt=tvmPmt (N,I,PV,FV,PpY,CpY,PmtAt).

• Jos jätät argumentin FV pois, sen oletusarvoksi tulee FV=0.

• Argumenttien PpY, CpY ja PmtAt oletusarvot ovat samat kuin TVMfunktioilla.

pyörArvo määrittää pyöristyksessä

käytettävien desimaalien määrän. Oletusarvo=2.

Katalogi >

Luettelo aakkosjärjestyksessä 17

bal()

bal(NPmt,amortTable) laskee

maksueränumeron NPmt jälkeen jäljellä olevan velkasaldon lyhennystaulukon

amortTable perusteella. amortTable-

argumentin on oltava matriisi, joka on kohdassa amortTbl() kuvatun muotoinen, katso sivu 8.

Huomaa: Katso myös GInt() ja GPrn(), sivu

237.

Katalogi >

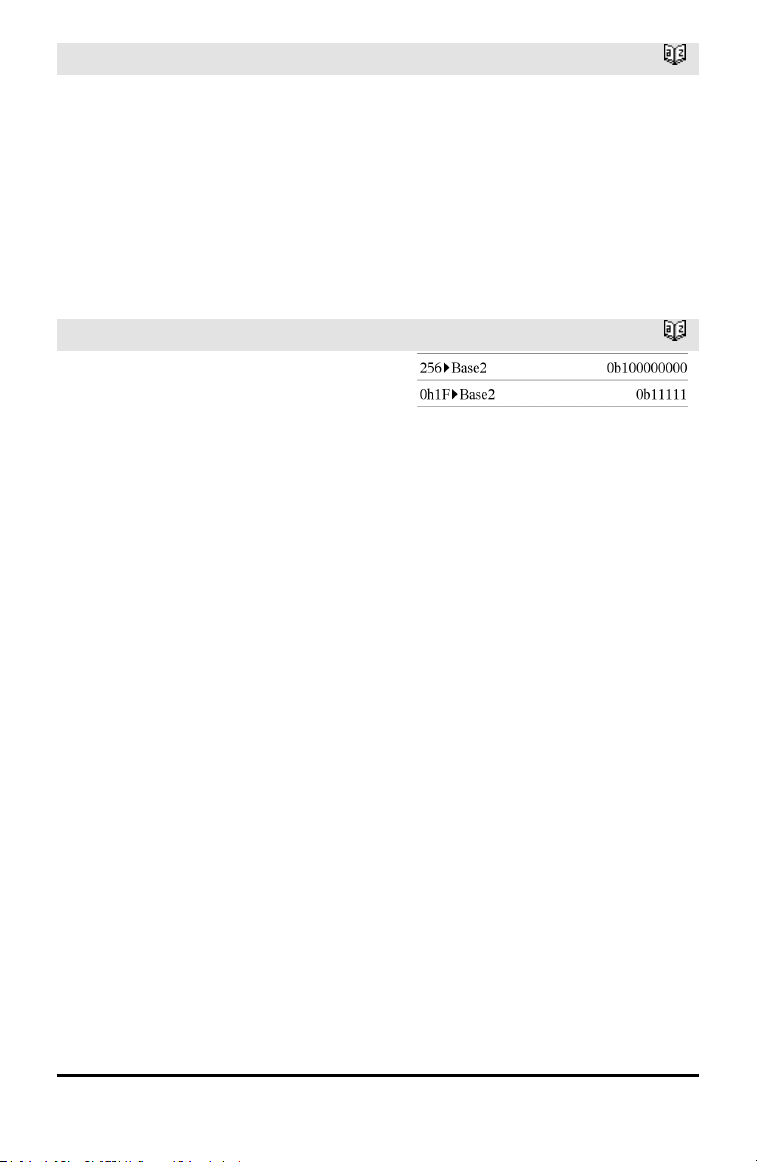
4Base2 (4Kantaluku2)

Kokonaisluku1 4Base2⇒kokonaisluku

Huomaa: Voit syöttää tämän operaattorin

tietokoneen näppäimistöltä kirjoittamalla

@>Base2.

Muuttaa Kokonaisluku1:n binaariluvuksi. Binaariluvuissa on aina etuliite 0b ja heksadesimaaliluvuissa etuliite 0h.

Ilman etuliitettä Kokonaisluku1:ä käsitellään desimaalilukuna (kantaluku10). Vastaus näkyy binaarilukuna kantalukutilasta riippumatta.

Negatiiviset luvut näytetään kahden komplementteina. Esimerkki:

N1näkyy muodossa 0hFFFFFFFFFFFFFFFFheksadesimaalisessa kantalukutilassa 0b111...111 (64ykköstä)binaarisessa kantalukutilassa

N263näkyy muodossa 0h8000000000000000heksadesimaalisessa kantalukutilassa 0b100...000 (63 zeros)binaarisessa kantalukutilassa

Katalogi >

18 Lue ttelo aakkosjärjestyksess ä

4Base2 (4Kantaluku2)

Jos syötät desimaalikokonaisluvun, joka on etumerkillisen, 64 bitin binaarimuodon lukualueen ulkopuolella, laskin käyttää symmetristä modulo-operaatiota, jotta arvo saadaan oikealle alueelle. Tarkastele seuraavassa esitettyjä esimerkkejä lukualueen ulkopuolella olevista arvoista.

263muuttuu muotoon N263ja näkyy muodossa 0h8000000000000000heksadesimaalisessa kantalukutilassa 0b100...000 (63 zeros)binaarisessa kantalukutilassa

264muuttuu muotoon 0 ja näkyy 0h0heksadesimaalisessa kantalukutilassa 0b0binaarisessa kantalukutilassa

N263N 1 muuttuu muotoon 263N 1 ja näkyy muodossa 0h7FFFFFFFFFFFFFFFheksadesimaalisessa kantalukutilassa 0b111...111 (64ykköstä)binaarisessa kantalukutilassa

Katalogi >

4Base10 (4Kantaluku10)

Kokonaisluku1 4Base10⇒kokonaisluku

Huomaa: Voit syöttää tämän operaattorin

tietokoneen näppäimistöltä kirjoittamalla

@>Base10.

Muuttaa Kokonaisluku1:n desimaaliluvuksi (kantaluku10). Binaarisen syötteen edellä tulee aina olla etumerkki 0b ja heksadesimaalisen syötteen edellä 0h.

0b binaariluku 0h heksadesimaaliluku

Nolla, ei O-kirjain, jonka perässä on b tai h.

Binaariluvussa voi olla enintään 64 numeroa. Heksadesimaaliluvussa voi olla enintään 16 numeroa.

Katalogi >

Luettelo aakkosjärjestyksessä 19

4Base10 (4Kantaluku10)

Ilman etuliitettä Kokonaisluku1:ä käsitellään desimaalilukuna. Vastaus näkyy desimaalilukuna kantalukutilasta riippumatta.

Katalogi >

4Base16 (4Kantaluku16)

Kokonaisluku1 4Base16⇒kokonaisluku

Huomaa: Voit syöttää tämän operaattorin

tietokoneen näppäimistöltä kirjoittamalla

@>Base16.

Muuttaa Kokonaisluku1:n heksadesimaaliluvuksi. Binaariluvuissa on aina etuliite 0b ja heksadesimaaliluvuissa etuliite 0h.

0b binaariluku 0h heksadesimaaliluku

Nolla, ei O-kirjain, jonka perässä on b tai h.

Binaariluvussa voi olla enintään 64 numeroa. Heksadesimaaliluvussa voi olla enintään 16 numeroa.

Ilman etuliitettä Kokonaisluku1:ä käsitellään desimaalilukuna (kantaluku10). Vastaus näkyy heksadesimaalilukuna kantalukutilasta riippumatta.

Jos syötät desimaalikokonaisluvun, joka on liian suuri etumerkilliselle, 64 bitin binaarimuodolle, laskin käyttää symmetristä modulo-operaatiota, jotta arvo saadaan oikealle alueelle.

Katalogi >

binomCdf()

binomCdf(n,p)⇒lista

20 Lue ttelo aakkosjärjestyksess ä

Katalogi >

binomCdf()

binomCdf(n,p,alaraja,yläraja)⇒luku, jos

alaraja ja yläraja ovat lukuja, lista, jos alaraja ja yläraja ovat listoja

binomCdf(n,p,yläraja)kun P(0{X{yläraja)

⇒luku, jos yläraja on luku, lista, jos

yläraja on lista

Laskee kumulatiivisen todennäköisyyden diskreetille binomiselle jakaumalle, jossa toistojen määrä on n ja jokaisen toiston onnistumistodennäköisyys on p.

Kun P(X { yläraja), aseta alaraja=0

Katalogi >

binomPdf()

binomPdf(n,p)⇒lista binomPdf(n,p,XVal)⇒luku, jos XVal on

luku, lista, jos XVal on lista

Laskee todennäköisyyden diskreetille binomiselle jakaumalle, jossa toistojen määrä on n ja jokaisen toiston onnistumistodennäköisyys on p.

ceiling()

ceiling(Laus1)⇒kokonaisluku

Laskee lähimmän kokonaisluvun, joka on | argumentti.

Argumentti voi olla reaali- tai kompleksiluku.

Huomaa: Katso myös floor() .

ceiling(Lista1)⇒lista ceiling(Matriisi1)⇒matriisi

Laskee listan tai matriisin jokaisen elementin ylärajasta.

Katalogi >

Luettelo aakkosjärjestyksessä 21

centralDiff()

centralDiff(Laus1,Muutt [=Arvo][,Askel])

⇒lauseke

centralDiff(Laus1,Muutt [,Askel]) |Muutt=Arvo⇒lauseke

centralDiff(Laus1,Muutt [=Arvo][,Lista])

⇒lista

centralDiff(Lista1,Muutt [=Arvo][,Askel])

⇒lista

centralDiff(Matriisi1,Muutt [=Arvo]

[,Askel])⇒matriisi

Laskee numeerisen derivaatan käyttäen keskeiserotusosamäärän kaavaa.

Kun Arvo määritetään, se ohittaa mahdolliset aikaisemmat muuttujamääritykset tai mahdolliset muuttujan nykyiset “|” -sijoitukset.

Askel on askeleen arvo. Jos Askel jätetään

pois, sen oletusarvo on 0.001.

Lista1:tä tai Matriisi1:tä käytettäessä

operaatio mapataan listan arvojen tai matriisin elementtien suhteen.

Huomaa: Katso myös avgRC() ja d().

Katalogi >

cFactor()

cFactor(Laus1[,Muutt])⇒lauseke cFactor(Lista1[,Muutt])⇒lista cFactor(Matriisi1[,Muutt])⇒matriisi

cFactor(Laus1) jakaa Laus1:n kaikki

muuttujat supistaen ne yhteisellä nimittäjällä.

Laus1:ä jaetaan tekijöihin mahdollisimman

paljon kohti lineaarisia rationaalitekijöitä, vaikka tästä saataisiin uusia ei-reaalilukuja. Tämä vaihtoehto on sopiva, jos haluat jakaa lausekkeen tekijöihin useamman kuin yhden muuttujan suhteen.

22 Lue ttelo aakkosjärjestyksess ä

Katalogi >

cFactor()

cFactor(Laus1,Muutt) jakaa Laus1:n

tekijöihin muuttujan Muutt suhteen.

Laus1:ä jaetaan tekijöihin mahdollisimman

paljon kohti tekijöitä, jotka ovat lineaarisia muuttujassa Muutt, sisältäen mahdollisesti ei-reaalisia vakioita, vaikka tästä saataisiin irrationaalisia vakioita tai alalausekkeita, joissa on muita irrationaalisia muuttujia.

Tekijät ja niiden termit lajitellaan siten, että Muutt on päämuuttuja. Muuttujan

Muutt samanlaiset potenssit kerätään

jokaisessa tekijässä. Muuttujan Muutt tulee olla mukana, jos vain kyseistä muuttujaa halutaan jakaa tekijöihin ja jos irrationaalilausekkeet ovat hyväksyttäviä kaikissa muissa muuttujissa, jotta muuttujaa Muutt voitaisiin jakaa enemmän tekijöihin. Toimenpiteessä voi esiintyä jonkin verran satunnaista muiden muuttujien tekijöihin jakamista.

Auto or Approximate (Automaattinen tai likimääräinen) -tilan Auto (Automaattinen)

-asetuksessa muuttujan Muutt mukanaolo sallii myös likiarvoistamisen liukulukuvakioilla, kun irrationaalisia kertoimia ei voida ilmaista täsmällisen tiiviisti sisäänrakennetuilla termeillä. Vaikka muuttujia olisi vain yksi, muuttujan

Muutt mukanaolo voi tuottaa

täydellisemmän tekijöihin jakamisen.

Huomaa: Katso myös factor().

Katalogi >

Jos haluat nähdä koko vastauksen, paina £ ja siirrä sen jälkeenosoitinta painikkeilla

¡ja¢.

char()

char(Kokonaisluku)⇒merkki

Näyttää vastauksena merkkijonon, joka sisältää kämmenlaitteen merkkisarjasta olevan merkin, jonka tunnusnumero on

Kokonaisluku. Kokonaisluvun Kokonaisluku

sallittu alue on 0–65535.

Katalogi >

Luettelo aakkosjärjestyksessä 23

charPoly()

charPoly(neliömatriisi,Muutt)

⇒polynomilauseke

charPoly(neliömatriisi,Laus)

⇒polynomilauseke

charPoly(neliömatriisi1,Matriisi2)

⇒polynomilauseke

Laskee neliömatriisin karakteristisen polynomin. Lausekkeen n×n matriisi A karakteristinen polynomi, merkitään pA(l), on polynomi, joka on määritetty lausekkeella

(l) = det(l• I NA)

jossa I tarkoittaa identtistä matriisia n×n.

neliömatriisi1:n ja neliömatriisi2:n on

oltava samankokoiset.

Katalogi >

2way

Katalogi >

c22way ObsMatriisi

chi22way ObsMatriisi

Laskee c2-testin tarkasteltavan matriisin

ObsMatriisi sisältämän kaksisuuntaisen

lukemataulukon arvojen välisestä assosiaatiosta. Tulosten yhteenveto tallentuu stat.results-muuttujaan. (Katso sivu 187.)

Lisätietoja matriisissa olevien tyhjien elementtien vaikutuksesta, katso Tyhjät elementitsivulla sivu 250.

Tulosmuuttuja Kuvaus

stat.c

stat.PVal Alinmerkitsevyystaso, jolla nollahypoteesivoidaanhylätä

stat.df Khinneliö -tilastojenvapausasteet

stat.ExpMat Odotetunelementtilukemataulukon matriisi, oletuksena nollahypoteesi

stat.Co mpMat Elementtien Khinneliö -tilastokontribuutioidenmatriisi

24 Lue ttelo aakkosjärjestyksess ä

Khinneliö -tilasto: summa (tarkasteltava - odotettu)2/odotettu

Cdf()

Cdf(alaraja,yläraja,df)⇒luku, jos alaraja

ja yläraja ovat lukuja, lista, jos alaraja ja

yläraja ovat listoja

chi2Cdf(alaraja,yläraja,df)⇒luku, jos

alaraja ja yläraja ovat lukuja, lista, jos alaraja ja yläraja ovat listoja

Laskee c2-jakauman todennäköisyyden

alarajan ja ylärajan väliltä määritetylle

vapausasteelle df.

Kun P(X { yläraja), aseta alaraja= 0.

Lisätietoja listassa olevien tyhjien elementtien vaikutuksesta, katso Tyhjät elementitsivulla sivu 250.

Katalogi >

GOF

c2GOF obsLista,expLista,df

chi2GOF obsLista,expLista,df

Suorittaa testin, jolla varmistetaan, että otoksen data on tiettyä jakaumaa vastaavasta perusjoukosta. obsList on lukemalista, ja sen tulee sisältää kokonaislukuja. Tulosten yhteenveto tallentuu stat.results-muuttujaan. (Katso sivu 187.)

Lisätietoja listassa olevien tyhjien elementtien vaikutuksesta, katso Tyhjät elementitsivulla sivu 250.

Tulosmuuttuja Kuvaus

stat.c

stat.PVal Alinmerkitsevyystaso, jolla nollahypoteesivoidaan hylätä

stat.df Khinneliö -tilastojenvapausasteet

stat.Co mpList Elementtien Khinneliö -tilastokontribuutiot

Khinneliö -tilasto: sum((tarkasteltava - odotettu)2/odotettu

Katalogi >

Luettelo aakkosjärjestyksessä 25

Pdf()

Pdf(XArvo,df)⇒luku, jos XArvo on luku,

lista, jos XArvo on lista

chi2Pdf(XArvo,df)⇒luku, jos XArvo on luku, lista, jos XArvo on lista

Laskee c2-jakauman todennäköisyystiheysfunktion (pdf) määritetyllä XArvon arvolla määritetylle vapausasteelle df.

Lisätietoja listassa olevien tyhjien elementtien vaikutuksesta, katso Tyhjät elementitsivulla sivu 250.

Katalogi >

clearAZ

Poistaa kaikki yksikirjaimiset muuttujat nykyiseltä tehtäväalueelta.

Jos yksi tai useampia muuttujia on lukittu, tämä komento aiheuttaa virheilmoituksen ja poistaa vain lukitsemattomat muuttujat. Katso unLock, sivu 209.

ClrErr

Poistaa virhetilan ja nollaa järjestelmän muuttujan errCode .

Else-lauseessa lohkossa Try...Else...EndTry

tulee käyttää komentoa ClrErr tai Pas sErr. Jos virhe on tarkoitus käsitellä tai jättää huomiotta, käytä komentoa ClrErr. Jos et tiedä, mitä tehdä virheen suhteen, lähetä se seuraavaan virheenkäsittelijään käyttämällä komentoa PassErr. Jos odottavia

Try...Else...EndTry-virheenkäsittelijöitä ei ole

enää, virheen valintaikkuna tulee näkyviin normaalisti.

Huomaa: Katso myös PassErr, sivu 139, ja Try, sivu 202.

Katalogi >

Esimerkki ClrErr-komennosta, katso esimerkki 2 Try-ko mennon kohdalla, sivu

202.

26 Lue ttelo aakkosjärjestyksess ä

ClrErr

Huomaa esimerkkiä syöttäessäsi: Ohjeet

monirivisten ohjelmien ja funktion määritysten syöttämisestä löytyvät tuotteen ohjekirjan Laskin-osiosta.

Katalogi >

colAugment()

colAugment(Matriisi1, Matriisi2)

⇒matriisi

Luo uuden matriisin, joka on Matriisi2 liitettynä Matriisi1:een. Matriiseiden sarakemäärän on oltava sama, ja Matriisi2 liitetään Matriisi1:een uusina riveinä. Ei muuta Matriisi1:ä eikä Matriisi2:a.

colDim()

colDim(Matriisi)⇒lauseke

Laskee Matriisin sisältämien sarakkeiden lukumäärän.

Huomaa: Katso myös rowDim().

colNorm()

colNorm(Matriisi)⇒lauseke

Laskee maksimiarvon Matriisin sarakkeissa olevien elementtien itseisarvojen summista.

Huomaa: Määrittämättömät

matriisielementit eivät ole sallittuja. Katso myös rowNorm().

Katalogi >

Luettelo aakkosjärjestyksessä 27

comDenom()

comDenom(Laus1[,Muutt])⇒lauseke comDenom(Lista1[,Muutt])⇒lista comDenom(Matriisi1[,Muutt])⇒matriisi

comDenom(Laus1) supistaa täydellisesti

lavennetun osoittajan täydellisesti lavennetulla nimittäjällä.

comDenom(Laus1,Muutt) supistaa

osoittajan ja nimittäjän, jotka on lavennettu muuttujalla Muutt. Termit ja niiden tekijät lajitellaan siten, että Muutt on päämuuttuja. Muuttujan Muutt samanlaiset potenssit kerätään. Toimenpiteessä voi esiintyä jonkin verran kerättyjen kertoimien satunnaista tekijöihin jakamista. Verrattuna siihen, että muuttuja Muutt jätettäisiin pois, tämä toiminto säästää usein aikaa, muistia ja näyttötilaa, ja samalla lausekkeesta tulee ymmärrettävämpi. Lisäksi tulokseen kohdistuvat seuraavat operaatiot ovat nopeampia eivätkä kuluta muistia yhtä todennäköisesti.

Jos muuttujaa Muutt ei ole Laus1:ssä,

comDenom(Laus1,Muutt) supistaa

laventamattoman osoittajan laventamattomalla nimittäjällä. Tällaiset tulokset säästävät yleensä vielä enemmän aikaa, muistia ja näyttötilaa. Tällaiset osittain tekijöihin jaetut tulokset nopeuttavat myös seuraavia tulokseen kohdistuvia operaatioita eivätkä kuluta muistia läheskään yhtä todennäköisesti.

Vaikka nimittäjää ei olisi, comden-funktio on usein nopea tapa suorittaa osittainen tekijöihin jako, mikäli factor() on liian hidas tai käyttää liikaa muistia.

Vinkki: Syötä tämä comden() -funktion

määritys ja kokeile sitä rutiininomaisesti vaihtoehtona funktioille comDenom() ja

factor().

Katalogi >

28 Lue ttelo aakkosjärjestyksess ä

completeSquare ()

completeSquare(ExprOrEqn, Var)

⇒lauseke tai yhtälö

completeSquare(ExprOrEqn, Var^Power)

⇒lauseke tai yhtälö

completeSquare(ExprOrEqn, Var1, Var2

[,...])⇒lauseke tai yhtälö

completeSquare(ExprOrEqn, {Var1, Var2

[,...]})⇒lauseke tai yhtälö

Muuntaa muotoa a·x2+b·x+c olevan toisen asteen polynomilausekkeen muotoon a·(xh)2+k

- tai -

Muuntaa muotoa a·x2+b·x+c olevan toisen asteen yhtälön muotoon a·(x-h)2+k

Ensimmäisen argumentin on oltava toisen asteen lauseke tai yhtälö vakiomuodossa toisen argumentin suhteen.

Toisen argumentin on oltava yhden muuttujan termi tai yhden muuttujan termi korotettuna rationaaliseen potenssiin x,y

(1/3)

taiz

Kolmas ja neljäs syntaksi yrittävät neliöksi täydentämisen muuttujien Var1, Var2 [,… ]) suhteen.

Katalogi >

conj()

conj(Laus1)⇒lauseke conj(Lista1)⇒lista

conj(Matriisi1)⇒matriisi

Laskee argumentin liittokompleksiluvun.

Huomaa: Kaikkia määrittämättömiä

muuttujia käsitellään reaalimuuttujina.

Katalogi >

Luettelo aakkosjärjestyksessä 29

constructMat()

constructMat (

Laus

,Muutt1,Muutt2,numRivit,numSarakkeet)

⇒matriisi

Laskee matriisin argumentteihin perustuen.

Laus on lauseke muuttujissa Muutt1 ja Muutt2. Tuloksena olevan matriisin

elementit muodostetaan sieventämällä

Laus jokaisella Muutt1:n ja Muutt2:n

lisätyllä arvolla.

Muutt1:ä lisätään automaattisesti välillä 1 - numRivit. Kullakin rivillä Muutt2:a lisätään

välillä 1 - numSarakkeet.

Katalogi >

CopyVar

CopyVar Muutt1, Muutt2

CopyVar Muutt1., Muutt2.

CopyVar Muutt1, Muutt2 kopioi muuttujan

Muutt1 arvon muuttujaan Muutt2 ja luo

tarvittaessa Muutt2:n. Muuttujalla Muutt1 on oltava arvo.

Jos Muutt1 on olemassa olevan käyttäjän määrittämän funktion nimi, kopioi kyseisen funktion määrityksen funktioon Muutt2. Funktio Muutt1 on määritettävä.

Muutt1:n on oltava muuttujien

nimeämissääntöjen mukainen tai epäsuora lauseke, joka sieventyy näitä vaatimuksia vastaavaksi muuttujan nimeksi.

CopyVar Muutt1., Muutt2. kopioi kaikki

Muutt1:n jäsenet. muuttujaryhmä Var2:een. ryhmä, Muutt2:n luominen.

tarvittaessa.

Katalogi >

30 Lue ttelo aakkosjärjestyksess ä

CopyVar

Muutt1. tulee olla olemassa olevan

muuttujaryhmän nimi, kuten tilastollinen

stat.nn vastausta tai muuttujaa, jotka on

luotu funktiolla LibShortcut(). Jos Muutt2. on jo olemassa, komento korvaa kaikki jäsenet, jotka ovat yhteisiä kummallekin ryhmälle, ja lisää jäsenet, joita ei vielä ole olemassa. Jos yksi tai useampia muuttujan

Muutt2. jäseniä on lukittu, kaikki muuttujan Var2. jäsenet pysyvät muuttumattomina.

Katalogi >

corrMat()

corrMat(Lista1,Lista2[,…[,Lista20]])

Laskee korrelaatiomatriisin laajennetulle matriisille [Lista1, Lista2, ..., Lista20].

4cos

Laus 4cos

Huomaa: Voit syöttää tämän operaattorin

tietokoneen näppäimistöltä kirjoittamalla

@>cos.

Näyttää Laus:n kulman kosinin. Tämä on näytön muunnosoperaattori. Sitä voidaan käyttää vain syöterivin lopussa.

4cos alentaa kaikkia lausekkeen sin(...) modulo 1Ncos(...)^2 potensseja, siten että jäljelle jäävien lausekkeen cos(...) potenssien eksponentit ovat alueella (0, 2). Tulos ei täten sisällä lauseketta sin(...), jos ja vain jos sin(...) esiintyy lausekkeessa korotettuna vain parillisiin potensseihin.

Huomaa: Tätä muunnosoperaattoria ei

tueta aste- eikä graadikulmatilassa. Ennen kuin käytät sitä, varmista, että kulmatila on asetettu radiaaneiksi ja että Laus ei sisällä eksplisiittisiä viittauksia aste- tai graadikulmiin.

Katalogi >

Luettelo aakkosjärjestyksessä 31

cos()

cos(Laus1)⇒lauseke cos(Lista1)⇒lista

cos(Laus1) määrittää argumentin kosinin

lausekkeena.

cos(Lista1) määrittää listan kaikkien

Lista1:n sisältämien elementtien

kosineista.

Huomaa: Argumentti tulkitaan aste-,

graadi- tai radiaanikulmaksi käytössä olevan kulmatila-asetuksen mukaisesti. Voit ohittaa kulmatilan väliaikaisesti painikkeilla ¡,Gtai R.

µ painike

Astekulmatilassa:

Graadikulmatilassa:

Radiaanikulmatilassa:

cos(neliömatriisi1)⇒neliömatriisi

Laskee neliömatriisi1:n matriisikosinin. Tämä ei ole sama kuin kunkin elementin kosinin laskeminen.

Kun skaalarista funktiota f(A) käytetään

neliömatriisi1:een (A), tulos lasketaan

algoritmilla:

Laske A:n ominaisarvot (li) ja ominaisvektorit (Vi).

neliömatriisi1:n on oltava

diagonalisoitavissa. Lisäksi siinä ei voi olla symbolisia muuttujia, joille ei ole määritetty arvoa.

32 Lue ttelo aakkosjärjestyksess ä

Radiaanikulmatilassa:

cos()

Matriiseista:

Tällöin A = X B X/ja f(A) = X f(B) X/. Esimerkiksi, cos(A) = X cos(B) X/, jossa:

cos(B) =

Kaikki laskut suoritetaan liukulukuaritmetiikalla.

µ painike

cos/()

cos/(Laus1)⇒lauseke cos/(Lista1)⇒lista

cos/(Laus1) määrittää lausekkeena

kulman, jonka kosini on Laus1.

cos/(Lista1) laskee listan Lista1:n jokaisen

elementin käänteiskosineista.

Huomaa: Vastaus lasketaan aste-, graadi-

tai radiaanikulmana käytössä olevan kulmatila-asetuksen mukaisesti.

Huomaa: Voit syöttää tämän funktion

näppäimistöltä kirjoittamalla arccos(...).

cos/(neliömatriisi1)⇒neliömatriisi

Laskee neliömatriisi1:n matriisin käänteiskosinin. Tämä ei ole sama kuin kunkin elementin käänteiskosinin laskeminen. Laskentamenetelmä on kuvattu kohdassa cos() .

µ painike

Astekulmatilassa:

Graadikulmatilassa:

Radiaanikulmatilassa:

Radiaanikulmatilassa ja suorakulmakompleksimuodossa:

Luettelo aakkosjärjestyksessä 33

cos/()

neliömatriisi1:n on oltava

diagonalisoitavissa. Vastaus sisältää aina liukulukuja.

µ painike

Jos haluat nähdä koko vastauksen, paina £ ja siirrä sen jälkeenosoitinta painikkeilla

¡ja¢.

cosh()

cosh(Laus1)⇒lauseke cosh(Lista1)⇒lista

cosh(Laus1) määrittää argumentin

hyperbolisen kosinin lausekkeena.

cosh(Lista1) määrittää listan Lista1:n

kunkin elementin hyperbolisista kosineista.

cosh(neliömatriisi1)⇒neliömatriisi

Laskee neliömatriisi1:n matriisin hyperbolisen kosinin. Tämä ei ole sama kuin kunkin elementin hyperbolisen kosinin laskeminen. Laskentamenetelmä on kuvattu kohdassa cos() .

neliömatriisi1:n on oltava

diagonalisoitavissa. Vastaus sisältää aina liukulukuja.

cosh/()

cosh/(Laus1)⇒lauseke cosh/(Lista1)⇒lista

cosh/(Laus1) määrittää argumentin

käänteisen hyperbolisen kosinin lausekkeena.

cosh/(Lista1) määrittää listan Lista1:n

kunkin elementin käänteisistä hyperbolisista kosineista.

Huomaa: Voit syöttää tämän funktion

näppäimistöltä kirjoittamalla arccosh

(...).

Katalogi >

Astekulmatilassa:

Radiaanikulmatilassa:

Katalogi >

34 Lue ttelo aakkosjärjestyksess ä

cosh/()

cosh/(neliömatriisi1)⇒neliömatriisi

Laskee neliömatriisi1:n matriisin käänteisen hyperbolisen kosinin. Tämä ei ole sama kuin kunkin elementin käänteisen hyperbolisen kosinin laskeminen. Laskentamenetelmä on kuvattu kohdassa

cos().

neliömatriisi1:n on oltava

diagonalisoitavissa. Vastaus sisältää aina liukulukuja.

Katalogi >

Radiaanikulmatilassa ja suorakulmakompleksimuodossa:

Jos haluat nähdä koko vastauksen, paina £ ja siirrä sen jälkeenosoitinta painikkeilla

¡ja¢.

cot()

cot(Laus1) ⇒ lauseke cot(Lista1) ⇒ lista

Laskee Laus1:n kotangentin tai määrittää listan Lista1:n kaikkien elementtien kotangenteista.

Huomaa: Argumentti tulkitaan aste-,

graadi- tai radiaanikulmaksi käytössä olevan kulmatila-asetuksen mukaisesti. Voit ohittaa kulmatilan väliaikaisesti painikkeilla ¡,Gtai R.

cot/()

cot/(Laus1)⇒lauseke cot/(Lista1)⇒lista

Laskee kulman, jonka kotangentti on Laus1, tai määrittää listan, joka sisältää Lista1:n kunkin elementin käänteiskotangentit.

Huomaa: Vastaus lasketaan aste-, graadi-

tai radiaanikulmana käytössä olevan kulmatila-asetuksen mukaisesti.

µ painike

Astekulmatilassa:

Graadikulmatilassa:

Radiaanikulmatilassa:

µ painike

Astekulmatilassa:

Graadikulmatilassa:

Radiaanikulmatilassa:

Luettelo aakkosjärjestyksessä 35

cot/()

Huomaa: Voit syöttää tämän funktion

näppäimistöltä kirjoittamalla arccot(...).

µ painike

coth()

coth(Laus1)⇒lauseke coth(Lista1)⇒lista

Laskee Laus1:n hyperbolisen kotangentin tai määrittää listan Lista1:n kaikkien elementtien hyperbolisista kotangenteista.

coth/()

coth/(Laus1)⇒lauseke coth/(Lista1)⇒lista

Laskee Laus1:n käänteisen hyperbolisen kotangentin tai määrittää listan, joka sisältää Lista1:n kaikkien elementtien käänteiset hyperboliset kotangentit.

Huomaa: Voit syöttää tämän funktion

näppäimistöltä kirjoittamalla arccoth

(...).

count()

count(Arvo1taiLista1 [,Arvo2taiLista2

[,...]])⇒arvo

Laskee elementtien kokonaismäärän argumenteille, jotka sieventyvät numeroarvoiksi.

Argumentit voivat olla lausekkeita, arvoja, listoja tai matriiseja. Argumenttien datatyypit voivat olla erilaisia, ja argumentit voivat olla erikokoisia.

Katalogi >

Viimeisessä esimerkissä lukumäärään lasketaan mukaan vain1/2 ja 3+4*i. Muut argumenteista, o lettaenettä x on määrittämätön, eivät sievenny numeroarvoiksi.

36 Lue ttelo aakkosjärjestyksess ä

count()

Listan, matriisin tai solualueen jokainen elementti sievennetään, jotta voidaan määrittää, kuuluuko se laskettavaan lukumäärään.

Listat & Taulukot -sovelluksessa voit käyttää solualueita argumenttien tilalla.

Tyhjiä elementtejä ei huomioida. Lisätietoja tyhjistä elementeistä, katso sivu 250.

Katalogi >

countif()

countif(Lista,Kriteerit)⇒arvo

Laskee niiden Listan sisältämien elementtien kokonaismäärän, jotka vastaavat määritettyjä kriteereitä

Kriteerit.

Kriteeri voi olla:

• Arvo, lauseke tai merkkijono. Jos kriteerinä käytetään esimerkiksi lukua 3, laskee lukumäärään vain ne Listan elementit, jotka sieventyvät arvoksi 3.

• Boolen lauseke, joka sisältää symbolin ? kunkin elementin paikanpitäjänä. Esimerkiksi lauseke ?<5 laskee lukumäärään vain ne Listan elementit, jotka ovat alle 5.

Listat & Taulukot -sovelluksessa voit käyttää solualueita Listan tilalla.

Listassa olevia tyhjiä elementtejä ei huomioida. Lisätietoja tyhjistä elementeistä, katso sivu 250.

Huomaa: Katso myös sumIf(), sivu 191, ja frequency() , sivu 80.

Katalogi >

Laskee niidenelementtien lukumäärän, jotka ovat yhtä kuin 3.

Laskee niidenelementtien lukumäärän, jotka ovat yhtä kuin "def".

Laskee niidenelementtien lukumäärän, jotka ovat yhtä kuin x; tässä esimerkissä oletetaan, että muuttuja x on määrittämätön.

Laskee lukumäärään 1:n ja 3:n.

Laskee lukumäärään 3:n, 5:n ja 7:n.

Laskee lukumäärään 1:n, 3:n, 7:n ja 9:n.

Luettelo aakkosjärjestyksessä 37

cPolyRoots()

cPolyRoots(Poly,Muutt)⇒lista cPolyRoots(Kertoinlista)⇒lista

Ensimmäinen syntaksi, cPolyRoots

(Poly,Muutt), laskee polynomin Poly

kompleksisten juurten listan muuttujan

Muutt suhteen.

Poly on oltava polynomi yhdessä

muuttujassa.

Toinen syntaksi, cPolyRoots(Kertoinlista), laskee kompleksisten juurten listan kertoimille, jotka sisältyvät Kertoinlistaan.

Huomaa: Katso myös polyRoots(), sivu 144.

Katalogi >

crossP()

crossP(Lista1, Lista2)⇒lista

Määrittää listan Lista1:n ja Lista2:n ristitulosta.

Lista1:n ja Lista2:n on oltava

samankokoiset, ja koon on oltava joko 2 tai

crossP(Vektori1, Vektori2)⇒vektori

Laskee rivi- tai sarakevektorin (argumenteista riippuen), joka on

Vektori1:n ja Vektori2:n ristitulo.

Sekä Vektori1:n että Vektori2:n on oltava rivivektoreita tai sarakevektoreita. Vektoreiden on oltava samankokoiset, ja koon tulee olla joko 2tai3.

csc()

csc(Laus1)⇒lauseke csc(Lista1)⇒lista

Laskee Laus1:n kosekantin tai määrittää listan, joka sisältää Lista1:n kaikkien elementtien kosekantit.

Katalogi >

µ painike

Astekulmatilassa:

Graadikulmatilassa:

38 Lue ttelo aakkosjärjestyksess ä

csc()

µ painike

Radiaanikulmatilassa:

csc/()

csc/(Laus1) ⇒ lauseke csc/(Lista1) ⇒ lista

Laskee kulman, jonka kosekantti on Laus1, tai määrittää listan, joka sisältää Lista1:n kunkin elementin käänteiskosekantit.

Huomaa: Vastaus lasketaan aste-, graadi-

tai radiaanikulmana käytössä olevan kulmatila-asetuksen mukaisesti.

Huomaa: Voit syöttää tämän funktion

näppäimistöltä kirjoittamalla arccsc(...).

csch()

csch(Laus1) ⇒ lauseke csch(Lista1) ⇒ lista

Laskee Laus1:n hyperbolisen kosekantin tai määrittää listan, joka sisältää Lista1:n kaikkien elementtien hyperboliset kosekantit.

µ painike

Astekulmatilassa:

Graadikulmatilassa:

Radiaanikulmatilassa:

Katalogi >

csch/()

csch/(Laus1) ⇒ lauseke csch/(Lista1) ⇒ lista

Katalogi >

Luettelo aakkosjärjestyksessä 39

csch/()

Laskee Laus1:n käänteisen hyperbolisen kosekantin tai määrittää listan, joka sisältää Lista1:n kaikkien elementtien käänteiset hyperboliset kosekantit.

Huomaa: Voit syöttää tämän funktion

näppäimistöltä kirjoittamalla arccsch

(...).

Katalogi >

cSolve()

cSolve(Yhtälö, Muutt)⇒Boolen lauseke cSolve(Yhtälö, Muutt=Arvaus)⇒Boolen

lauseke

cSolve(Epäyhtälö, Muutt)⇒Boolen

lauseke

Määrittää kompleksiyhtälön tai -epäyhtälön mahdollisia ratkaisuja muuttujalle Muutt. Tavoitteena on tuottaa kaikkien reaalisten ja ei-reaalisten ratkaisujen ehdotuksia. Vaikka Yhtälö olisi reaalinen, cSolve() sallii ei-reaaliset vastaukset reaalituloksen kompleksilukumuodossa.

Vaikka kaikkia määrittämättömiä muuttujia, joiden lopussa ei ole alaviivaa (_), käsiteltäisiin ikään kuin ne olisivat reaalisia, cSolve() pystyy laskemaan polynomiyhtälöiden kompleksilukuratkaisuja.

cSolve() asettaa määritysjoukon

väliaikaisesti kompleksilukumuotoon yhtälön ratkaisemisen ajaksi, vaikka nykyinen määritysjoukko olisi reaalinen. Kompleksilukujen määritysalueella murtolukueksponenteissa, joiden nimittäjä on pariton luku, käytetään perus- eikä reaalilukualuetta. Tämän vuoksi solve()funktion ratkaisut yhtälöille, joihin liittyy tällaisia murtopotensseja, eivät välttämättä ole cSolve()-funktion ratkaisujen alasarja.

Katalogi >

40 Lue ttelo aakkosjärjestyksess ä

cSolve()

cSolve()-funktion ratkaisu aloitetaan

eksakteilla symbolisilla menetelmillä.

cSolve() käyttää tarvittaessa myös

iteratiivista likimääräistä kompleksipolynomin tekijöihin jakamista.

Huomaa: Katso myös cZeros(), solve() ja zeros().

Huomaa: Jos Yhtälö on ei-polynominen

funktioilla, kuten abs(), angle(), conj(), real

() tai imag(), sijoita alaviiva (paina

/_) muuttujan Muutt:n loppuun.

Oletusarvoisesti muuttujaa käsitellään reaaliarvona.

Jos käytät merkintää muutt_ , muuttujaa käsitellään kompleksilukuna.

Merkintää muutt_ tulee käyttää myös kaikissa muissa Yhtälön muuttujissa, jotka voivat sisältää ei-reaaliarvoja. Muussa tapauksessa tulokset voivat olla väärin.

cSolve(Yht1andYht2 [and…],

MuuttTaiArvaus1, MuuttTaiArvaus2 [, …

]) ⇒Boolenlauseke

cSolve(Yhtälöryhmä, MuuttTaiArvaus1,

MuuttTaiArvaus2 [, …]) ⇒Boolenlauseke

Laskee mahdollisia kompleksiratkaisuja samanaikaisille algebrallisille yhtälöille, joissa jokainen MuuttTaiArvaus määrittää ratkaistavan muuttujan.

Voit halutessasi määrittää muuttujan ensimmäisen arvauksen. Jokaisen

muuttTaiArvaus-komennon on oltava

muodossa:

muuttuja

– tai –

muuttuja = reaaliluku tai ei-reaaliluku

Esimerkiksi x kelpaa ja samoin x=3+i .

Katalogi >

DesimaaliennäyttötilassaKiinteä 2:

Jos haluat nähdä koko vastauksen, paina £ ja siirrä sen jälkeenosoitinta painikkeilla

¡ja¢.

Luettelo aakkosjärjestyksessä 41

cSolve()

Jos kaikki yhtälöt ovat polynomeja, ja jos ET määritä yhtään ensimmäistä arvausta,

cSolve() käyttää leksikaalista

Gröbner/Buchbergerin eliminaatiomenetelmää yrittäessään määrittää kaikki kompleksiratkaisut.

Kompleksiratkaisut voivat sisältää sekä reaali- että ei-reaaliratkaisuja kuten oikealla olevassa esimerkissä.

Samanaikaisissa polynomiyhtälöissä voi olla ylimääräisiä muuttujia, joilla ei ole arvoja, vaan ne edustavat tiettyjä numeerisia arvoja, jotka voidaan korvata myöhemmin.

Voit ottaa mukaan myös ratkaisumuuttujia, jotka eivät esiinny yhtälöissä. Nämä ratkaisut osoittavat, miten ratkaisujen sarjat voivat sisältää mielivaltaisia vakioita, jotka ovat muotoa ck, jossa k on kokonaislukuliite väliltä 1-255.

Polynomisarjoissa laskun suoritusaika tai muistin käyttö voivat riippua merkittävästi ratkaisumuuttujien järjestyksestä. Jos ensimmäinen valintasi kuluttaa muistia, tai et jaksa odottaa vastausta, yritä järjestää muuttujat uudelleen yhtälöihin ja/tai

muuttTaiArvaus-listaan.

Jos et ota mukaan arvauksia, ja jos jokin yhtälöistä on ei-polynominen minkä tahansa muuttujan suhteen, mutta kaikki yhtälöt ovat lineaarisia kaikissa ratkaisumuuttujissa, cSolve() käyttää Gaussin eliminointia yrittäessään määrittää kaikki ratkaisut.

Katalogi >

Huomaa: Seuraavissa esimerkeissä

käytetäänalaviivaa (paina /_), jotta muuttujia käsitellään kompleksiarvoina.

Jos haluat nähdä koko vastauksen, paina £ ja siirrä sen jälkeenosoitinta painikkeilla

¡ja¢.

42 Lue ttelo aakkosjärjestyksess ä

cSolve()

Jos sarja ei ole polynominen kaikilta muuttujiltaan eikä lineaarinen ratkaisumuuttujiltaan, cSolve() määrittää korkeintaan yhden ratkaisun käyttäen likimääräistä iteratiivista menetelmää. Tässä ratkaisumuuttujien lukumäärän on oltava sama kuin yhtälöiden lukumäärä, ja kaikkien muiden yhtälöiden sisältämien muuttujien on sievennyttävä luvuiksi.

Ei-reaalinen arvaus on usein välttämätön ei-reaalisen ratkaisun määrittämiseksi. Suppenemista varten arvauksen on mahdollisesti oltava melko lähellä ratkaisua.

Katalogi >

Jos haluat nähdä koko vastauksen, paina £ ja siirrä sen jälkeenosoitinta painikkeilla

¡ja¢.

CubicReg

CubicReg X, Y[, [Frekv] [, Luokka,

Sisällytä]]

Laskee 3. asteen polynomiregressiony = a·x3+b· x2+c·x+dlistoista X ja Y frekvenssillä Frekv. Tulosten yhteenveto tallentuu stat.results-muuttujaan. (Katso sivu 187.)

Kaikkien listojen on oltava samankokoisia

Sisällytä-listaa lukuunottamatta.

X ja Y ovat riippumattomien ja riippuvien

muuttujien listoja.

Frekv on valinnainen frekvenssiarvojen lista.

Jokainen Frekv:n elementti määrittää kunkin vastaavan datapisteen X ja Y esiintymisfrekvenssin. Oletusarvo on 1. Kaikkien elementtien on oltava kokonaislukuja | 0.

Luokka on luokkakoodien lista vastaavalle X- ja Y -datalle.

Sisällytä on yhden tai usemman

luokkakoodin lista. Vain ne datayksiköt, joiden luokkakoodi sisältyy tähän listaan, ovat mukana laskutoimituksessa.

Katalogi >

Luettelo aakkosjärjestyksessä 43

CubicReg

Lisätietoja listassa olevien tyhjien elementtien vaikutuksesta, katso Tyhjät elementitsivulla sivu 250.

Tulosmuuttuja Kuvaus

stat.RegEqn Regressioyhtälö: a·x3+b·x2+c·x+d.

stat.a, stat.b, stat.c, stat.d

stat.R

stat.Resid Regressioyhtälön jäännökset

stat.XReg

stat.YReg

stat.FreqReg

Regressiokertoimet.

Määrityskerroin.

MuokatunX Lista:n sisältämä datapisteidenlista, jota käytetäänregressiossa komentojen Frekv, Luokkalista ja Sisällytä luokat rajoitusten mukaisesti.

MuokatunY Lista:n sisältämä datapisteiden lista, jota käytetäänregressiossa komentojen Frekv, Luokkalista ja Sisällytä luokat rajoitusten mukaisesti.

Komentoja stat.XReg ja stat.YReg vastaava frekvenssilista.

Katalogi >

cumulativeSum()

cumulativeSum(Lista1)⇒lista

Laskee listan Lista1:n sisältämien elementtien kumulatiivisista summista alkaen elementistä1.

cumulativeSum(Matriisi1)⇒matriisi

Laskee matriisin Matriisi1:n sisältämien elementtien kumulatiivisista summista. Jokainen elementti on ylhäältä alas ulottuvan sarakkeen kumulatiivinen summa.

Tyhjä elementti listassa Lista1 tai matriisissa Matriisi1 tuottaa tyhjän elementin tuloksena olevaan listaan tai matriisiin. Lisätietoja tyhjistä elementeistä, katso sivu 250.

Cycle

44 Lue ttelo aakkosjärjestyksess ä

Katalogi >

Funktio, joka laskee yhteenkoko naisluvut väliltä 1-100 ohittaen luvun50.

Cycle

Siirtää ohjauksen välittömästi nykyisen silmukan (For, While tai Loop) seuraavaan iteraatioon.

Cycle ei ole sallittu näiden kolmen

silmukkarakenteen (For, While tai Loop) ulkopuolella.

Huomaa esimerkkiä syöttäessäsi: Ohjeet

monirivisten ohjelmien ja funktion määritysten syöttämisestä löytyvät tuotteen ohjekirjan Laskin-osiosta.

Katalogi >

4Cylind

Vektori 4Cylind

Huomaa: Voit syöttää tämän operaattorin

tietokoneen näppäimistöltä kirjoittamalla

@>Cylind.

Näyttää rivi- tai sarakevektorin sylinterin muodossa [r,±q, z].

Vektorissa on oltava täsmälleen kolme

elementtiä. Se voi olla joko rivi tai sarake.

cZeros()

cZeros(Laus, Muutt)⇒lista

Määrittää listan muuttujan Muutt mahdollisista reaali- ja ei-reaaliarvoista, joiden tuloksena Laus=0. cZeros() suorittaa tämän seuraavasti:

exp4list(cSolve(Laus=0,Muutt),Muutt).

Muilta osin cZeros() on samanlainen kuin

zeros().

Huomaa: Katso myös cSolve(), solve() ja zeros().

Katalogi >

DesimaaliennäyttötilassaKiinteä 3:

Jos haluat nähdä koko vastauksen, paina £ ja siirrä sen jälkeenosoitinta painikkeilla

¡ja¢.

Luettelo aakkosjärjestyksessä 45

cZeros()

Huomaa: Jos Laus on ei-polynomiyhtälö

funktioilla, kuten abs(), angle(), conj(), real

() tai imag(), lisää alaviiva (paina /_)

muuttujan Muutt loppuun. Oletusarvoisesti muuttujaa käsitellään reaaliarvona. Jos käytät merkintää muutt_ , muuttujaa käsitellään kompleksiarvona.

Merkintää muutt_ on käytettävä kaikille muille Laus:n muuttujille, jotka voivat sisältää ei-reaaliarvoja. Muussa tapauksessa tulokset voivat olla väärin.

cZeros({Laus1, Laus2 [, … ] },

{MuuttTaiArvaus1,MuuttTaiArvaus2 [, …

] })⇒matriisi

Laskee mahdollisia kohtia, joissa lausekkeet ovat samanaikaisesti nolla. Jokainen

MuuttTaiArvaus määrittää ratkaistavan

tuntemattoman arvon. Voit halutessasi määrittää muuttujan

ensimmäisen arvauksen. Jokaisen

muuttTaiArvaus-komennon on oltava

muodossa:

muuttuja

– tai –

muuttuja = reaaliluku tai ei-reaaliluku

Esimerkiksi x kelpaa ja samoin x=3+i . Jos kaikki lausekkeet ovat polynomeja, ja ET

määritä ensimmäisiä arvauksia, cZeros() käyttää leksikaalista Gröbner/Buchbergerin eliminaatiomenetelmää yrittäessään määrittää kaikki kompleksiset nollakohdat.

Kompleksiset nollakohdat voivat sisältää sekä reaalisia että ei-reaalisia nollakohtia, kuten oikealla olevassa esimerkissä.

Jokainen tulosmatriisin rivi edustaa vaihtoehtoista nollakohtaa, jossa komponentit on järjestetty samalla tavalla kuin MuuttTaiArvaus-listassa. Jos haluat määrittää rivin juuren, indeksoi matriisi [riveittäin].

Katalogi >

Huomaa: Seuraavissa esimerkeissä

käytetäänalaviivaa _ (paina /_) , jotta muuttujia käsitellään kompleksiarvoina.

Määritä rivin2 juuri:

46 Lue ttelo aakkosjärjestyksess ä

cZeros()

Samanaikaisissa polynomeissa voi olla ylimääräisiä muuttujia, joilla ei ole arvoja, vaan ne edustavat tiettyjä numeerisia arvoja, jotka voidaan korvata myöhemmin.

Voit ottaa mukaan myös tuntemattomia muuttujia, jotka eivät esiinny lausekkeissa. Nämä nollakohdat osoittavat, miten nollakohtien sarjat voivat sisältää mielivaltaisia vakioita, jotko ovat muotoa

ck, jossa k on kokonaislukuliite väliltä 1-255.

Polynomisarjoissa laskutoimituksen suoritusaika tai muistin käyttö voivat riippua merkittävästi tuntemattomien muuttujien järjestyksestä. Jos ensimmäinen valintasi kuluttaa muistia, tai et jaksa odottaa vastausta, yritä järjestää muuttujat uudelleen lausekkeisiin ja/tai

MuuttTaiArvaus-listaan.

Jos et ota mukaan arvauksia, ja jokin lausekkeista on ei-polynominen missä tahansa muuttujassa, mutta kaikki muuttujat ovat lineaarisia kaikissa tuntemattomissa muuttujissa, cZeros() käyttää Gaussin eliminointia yrittäessään määrittää kaikki nollakohdat.

Jos sarja ei ole polynominen kaikilta muuttujiltaan eikä lineaarinen tuntemattomilta muuttujiltaan, cZeros() määrittää korkeintaan yhden nollakohdan käyttäen likimääräistä iteratiivista menetelmää. Tässä tuntemattomien muuttujien lukumäärän on oltava sama kuin lausekkeiden lukumäärä, ja kaikkien muiden lausekkeiden sisältämien muuttujien on sievennyttävä luvuiksi.

Katalogi >

Luettelo aakkosjärjestyksessä 47

cZeros()

Ei-reaalinen arvaus on usein välttämätön ei-reaalisen nollakohdan määrittämiseksi. Suppenemista varten arvauksen on mahdollisesti oltava melko lähellä nollakohtaa.

Katalogi >

dbd()

dbd(pvm1,pvm2)⇒arvo

Laskee pvm1:n ja pvm2:n välissä olevien päivien lukumäärän käyttäen todellisten päivien laskentamenetelmää.

pvm1 ja pvm2 voivat olla lukuja tai

lukulistoja, jotka ovat vakiokalenterin päivämääräalueen sisällä. Jos sekä pvm1 että pvm2 ovat listoja, niiden on oltava samanpituiset.

pvm1:n ja pvm2:n on oltava vuosien 1950 ja

2049 välillä.

Voit syöttää päivämäärät kahdessa eri muodossa. Desimaalipisteen paikka on erilainen näissä päivämäärien esitystavoissa.

MM.DDYY (Yhdysvalloissa yleisesti käytetty esitystapa) DDMM.YY (Euroopassa yleisesti käytetty esitystapa)

4DD

Laus1 4DD⇒arvoLista1

4DD⇒listaMatriisi1 4DD⇒matriisi

Huomaa: Voit syöttää tämän operaattorin

tietokoneen näppäimistöltä kirjoittamalla

@>DD.

Katalogi >

Astekulmatilassa:

48 Lue ttelo aakkosjärjestyksess ä

Graadikulmatilassa:

4DD

Laskee vastaavan desimaaliluvun asteina ilmaistulle argumentille. Argumentti on luku, lista tai matriisi, jonka kulmatilaasetus tulkitsee graadeina, radiaaneina tai asteina.

Katalogi >

Radiaanikulmatilassa:

4Decimal

Lauseke14Decimal⇒lauseke Lista1 4Decimal⇒lauseke Matriisi1 4Decimal⇒lauseke

Huomaa: Voit syöttää tämän operaattorin

tietokoneen näppäimistöltä kirjoittamalla

@>Decimal.

Näyttää argumentin desimaalimuodossa. Tätä operaattoria voi käyttää ainoastaan syöterivin lopussa.

Define (Määritä)

Define Muutt = Lauseke Define Funktio(Param1, Param2, ...) =

Lauseke

Määrittää muuttujan Muutt tai käyttäjän määrittämän funktion Funktio.

Parametrit, kuten Param1, toimivat paikanpitäjinä argumenttien syöttämiseksi funktioon. Kun haet käyttäjän määrittämän funktion, sinun on annettava parametreja vastaavat argumentit (esimerkiksi arvoja tai muuttujia). Kun funktio haetaan, se sieventää Lausekkeen annettujen argumenttien perusteella.

Muutt ja Funktio eivät voi olla järjestelmän

muuttujan tai sisäänrakennetun funktion tai komennon nimenä.

Katalogi >

Luettelo aakkosjärjestyksessä 49

Define (Määritä)

Huomaa: Seuraava Define-funktion muoto

on vastaava kuin lausekkeen sieventäminen:

lauseke & Funktio(Param1,Param2).

Define Funktio(Param1, Param2, ...) = Func

  Lohko

EndFunc

Define Ohjelma(Param1, Param2, ...) = Prgm

  Lohko

EndPrgm

Tässä muodossa käyttäjän määrittämä funktio tai ohjelma voi suorittaa useista lausekkeista koostuvan lohkon.

Lohko voi olla joko yksi lauseke tai eri

riveillä olevien lausekkeiden sarja. Lohko voi sisältää myös lausekkeita ja ohjeita (kuten If, Then, Else ja For).

Huomaa esimerkkiä syöttäessäsi: Ohjeet

monirivisten ohjelmien ja funktion määritysten syöttämisestä löytyvät tuotteen ohjekirjan Laskin-osiosta.

Huomaa: Katso myös Define LibPriv, sivu 50,

ja Define LibPub, sivu 51.

Katalogi >

Define LibPriv (Määritä LibPriv)

Define LibPriv Muutt = Lauseke Define LibPriv Funktio(Param1, Param2,

...) = Lauseke

Define LibPriv Funktio(Param1, Param2,

...) = Func

  Lohko

EndFunc

Define LibPriv Ohjelma(Param1, Param2, ...) = Prgm

  Lohko

EndPrgm

50 Lue ttelo aakkosjärjestyksess ä

Katalogi >

Define LibPriv (Määritä LibPriv)

Tämä komento toimii muuten samalla tavalla kuin Define paitsi, että se määrittää yksityisen kirjastomuuttujan, -funktion tai ohjelman. Yksityiset funktiot ja ohjelmat eivät ole katalogissa.

Huomaa: Katso myös Define, sivu 49, ja Define LibPub, sivu 51.

Katalogi >

Define LibPub (Määritä LibPub)

Define LibPub Muutt = Lauseke Define LibPub Funktio(Param1, Param2, ...) = Lauseke

Define LibPub Funktio(Param1, Param2, ...) = Func

  Lohko

EndFunc

Define LibPub Ohjelma (Param1, Param2, ...) = Prgm

  Lohko

EndPrgm

Tämä komento toimii muuten samalla tavalla kuin Define paitsi, että se määrittää julkisen kirjastomuuttujan, -funktion tai ohjelman. Julkiset funktiot ja ohjelmat näkyvät katalogissa sen jälkeen, kun kirjasto on tallennettu ja näyttö on päivitetty.

Huomaa: Katso myös Define, sivu 49, ja Define LibPriv, sivu 50.

deltaList()

Katalogi >

Katso @List(), sivu 109.

deltaTmpCnv()

Katso @tmpCnv(), sivu 200.

Luettelo aakkosjärjestyksessä 51

DelVar

DelVar Muutt1[, Muutt2] [, Muutt3] ...

DelVar Muutt.

Poistaa määritetyn muuttujan tai muuttujaryhmän muistista.

Jos yksi tai useampia muuttujia on lukittu, tämä komento aiheuttaa virheilmoituksen ja poistaa vain lukitsemattomat muuttujat. Katso unLock, sivu 209.

DelVar Muutt. poistaa kaikki Muutt:n jäsenet. muuttujaryhmä (kuten tilastollinen

stat.nn tulosta tai muuttujaa, jotka on luotu

funktiolla LibShortcut()). Piste (.) tässä

DelVar-komennon muodossa rajoittaa

funktion muuttujaryhmän poistamiseen; komento ei vaikuta yksinkertaiseen muuttujaan Muutt.

Katalogi >

delVoid()

delVoid(Lista1)⇒lista

Antaa tuloksena listan, jossa on listan

Lista1 sisältö, ja kaikki tyhjät elementit on

poistettu.

Lisätietoja tyhjistä elementeistä, katso sivu

250.

derivative()

52 Lue ttelo aakkosjärjestyksess ä

Katalogi >

Katso d(), sivu 233.

deSolve()

deSolve(1.astTai2.astODE, Muutt,

riippuvaMuutt)⇒yleinen ratkaisu

Ratkaisee yhtälön, joka määrittää eksplisiittisesti tai implisiittisesti yleisratkaisun 1. tai 2. asteen tavalliselle differentiaaliyhtälölle (ODE). ODE:ssa:

• Käytä jaottoman merkkiä (näppäin º) viittaamaan riippuvan muuttujan 1.

derivaattaan riippumattomaan muuttujaan nähden.

• Käytä kahta jaottoman merkkiä viittaamaan vastaavaan toiseen derivaattaan.

Jaottoman merkkiä käytetään vain deSolve()

-funktion derivaatoissa. Muissa tapauksissa käytetään merkintääd().

1. asteen yhtälön yleisratkaisu sisältää mielivaltaisen vakion muotoa ck, jossa k on kokonaislukuliite väliltä 1-255. 2. asteen yhtälön ratkaisu sisältää kaksi tällaista vakiota.

Käytä s olve()-funktiota implisiittisessä ratkaisussa, jos haluat yrittää muuntaa sen yhdeksi tai useammaksi ekvivalenttiseksi eksplisiittiseksi ratkaisuksi.

Kun vertaat vastauksia oppikirjan tai käsikirjan ratkaisuihin, huomaa, että erilaisiset menetelmät tuovat mielivaltaisia vakioita eri kohtiin laskutoimituksessa, mistä voi olle tuloksena erilaisia yleisratkaisuja.

deSolve(1.astODEandalkuehto, Muutt,

riippuvaMuutt) ⇒tietty ratkaisu

Laskee tietyn ratkaisun, joka täyttää

1.astODE:n ja alkuehdon vaatimukset.

Tämä on yleensä helpompaa kuin yleisratkaisun määrittäminen, alkuarvojen korvaaminen, mielivaltaisen vakion ratkaiseminen ja sen jälkeen arvon korvaaminen yleisratkaisuun.

alkuehto on yhtälö, joka on muotoa:

Katalogi >

Luettelo aakkosjärjestyksessä 53

deSolve()

riippuvaMuutt (riippumatonAlkuarvo) = riippuvaAlkuarvo

riippumatonAlkuarvo ja riippuvaAlkuarvo

voivat olla muuttujia, kuten x0 ja y0, joilla ei ole tallennettuja arvoja. Implisiittinen derivointi voi helpottaa implisiittisten ratkaisujen tarkistamista.

deSolve (2.astODEandalkuehto1andalkuehto2,

Muutt, riippuvaMuutt) ⇒tietty ratkaisu

Antaa tietyn ratkaisun, joka sopii 2. ast

ODE:hen ja jolla on määritetty riippuvan

muuttujan arvo ja sen ensimmäinen derivaatta yhdessä pisteessä.

Käytä alkuehto1:lle muotoa:

riippuvaMuutt (riippumatonAlkuarvo) = riippuvaAlkuarvo

Käytä alkuehto2:lle muotoa:

riippuvaMuutt (riippumatonAlkuarvo) =

1.derivaatanAlkuarvo

deSolve(2.astODEandreunaehto1and

reunaehto2, Muutt, riippuvaMuutt)⇒tietty

ratkaisu

Laskee tietyn ratkaisun, joka sopii

2.astODE:lle ja jolla on määritetyt arvot

kahdessa eri pisteessä.

Katalogi >

54 Lue ttelo aakkosjärjestyksess ä

det()

det(neliömatriisi[, Toleranssi])⇒lauseke

Laskee neliömatriisin determinantin.

Valinnaisesti kaikkia matriisielementtejä käsitellään nollana, jos niiden itseisarvo on pienempi kuin Toleranssi. Tätä toleranssia käytetään vain, jos matriisissa on liukulukusyötteitä eikä se sisällä symbolisia muuttujia, joille ei ole määritetty arvoa. Muussa tapauksessa Tolerassia ei huomioida.

• Jos käytät painikkeita /· tai Automaattinen tai likimääräinen -tilan

valintaa Approximate (Likimääräinen), laskut suoritetaan liukulukuaritmetiikalla.

• Jos Toleranssi jätetään pois tai sitä ei käytetä, oletusarvoinen toleranssi lasketaan seuraavasti:

5EM14 ·max(dim(neliömatriisi))·

rowNorm(neliömatriisi)

Katalogi >

diag()

diag(Lista)⇒matriisi diag(rivimatriisi)⇒matriisi diag(sarakematriisi)⇒matriisi

Laskee matriisin, joka sisältää arvot argumenttilistassa tai matriisin sen päälävistäjässä.

diag(neliömatriisi)⇒rivimatriisi

Laskee rivimatriisin, joka sisältää elementit

neliömatriisin päälävistäjästä.

neliömatriisi:n on oltava neliö.

dim()

dim(Lista)⇒kokonaisluku

Laskee Listan mitat.

Katalogi >

Luettelo aakkosjärjestyksessä 55

dim()

dim(Matriisi)⇒lista

Laskee matriisin mitat kahden elementin listana {rivit, sarakkeet}.

dim(Merkkijono)⇒kokonaisluku

Laskee merkkijonon Merkkijono sisältämien merkkien lukumäärän.

Katalogi >

Disp

Disp lausTaiMerkkijono1 [,

lausTaiMerkkijono2] ...

Näyttää Laskin-sovelluksen historiatietojen sisältämät argumentit. Argumentit näytetään peräkkäin, ja erotinmerkkeinä käytetään ohuita välilyöntejä.

Käyttökelpoisia pääasiassa ohjelmissa ja funktioissa, jotta välilaskutoimitusten näyttäminen voidaan varmistaa.

Huomaa esimerkkiä syöttäessäsi: Ohjeet

monirivisten ohjelmien ja funktion määritysten syöttämisestä löytyvät tuotteen ohjekirjan Laskin-osiosta.

DispAt

DispAt int,lauseke1 [,lauseke2 ...] ...

Komennolla DispAt voidaan määritellä

rivi, jolla määrätty lauseke tai merkkijono näytetään ruudulla.

Rivinumero voidaan määritellä lausekkeeksi.

Huomaa, että rivin numero ei viittaa koko ruutuun vaan alueeseen, joka seuraa välittömästi komentoa/ohjelmaa.

Katalogi >

Esimerkki

56 Lue ttelo aakkosjärjestyksess ä

DispAt

Tämä komento mahdollistaa ohjauspaneelin kaltaisen tuotoksen ohjelmista, joissa lausekkeen arvo tai anturin lukema päivitetään samalle riville.

Komentoja DispAtja Disp voidaan käyttää samassa ohjelmassa.

Huomaa: Suurin sallittu numero on

asetettu luvuksi 8, koska se vastaa koko näyttöä täynnä rivejä kannettavassa laitteessa – kunhan riveillä ei ole kaksiulotteisia matemaattisia lausekkeita. Rivien täsmällinen määrä riippuu näytetyn tiedon sisällöstä.

Havainnollistavia esimerkkejä:

Define z()= Prgm For n,1,50 DispAt 1,"N: ",n Disp "Hello" EndFor EndPrgm

Define z1()= Prgm For n,1,50 DispAt 1,"N: ",n EndFor

For n,1,50 Disp "Hello" EndFor EndPrgm

Ulostulo z()

Iteraatio 1:

Iteraatio 2:

z1()

Katalogi >

Rivi 1: N:1

Rivi 2: Hello

Rivi 1: N:2 Rivi 1: Hello Rivi 3: Hello

Rivi 1: N:3 Rivi 2: Hello Rivi 3: Hello Rivi 4: Hello

Rivi 1: N:3 Rivi 2: Hello Rivi 3: Hello Rivi 4: Hello Rivi 5: Hello

Luettelo aakkosjärjestyksessä 57

DispAt

Virhetilat:

Virheviestit Kuvaus

DisplAt-rivinumeron on oltava lukujen 1 ja 8 välillä

Liian vähän argumentteja Toiminnosta tai komennosta puuttuu yksi

Ei argumentteja Sama kuin nykyinen "syntaksivirhe" -

Liian monta argumenttia Rajoita argumenttia. Sama virhe kuin

Virheellinen tietotyyppi Ensimmäisen argumentin on oltava

Mitätön: DispAt mitätön "Hello World" Datatyyppivirhe on

Muunnosoperaattori: DispAt 2_ft @> _m, "Hello World

Lauseke arvioi rivinumeron välin 1–8 (mukaan lukien) ulkopuolella

tai useampi argumentti

dialogi

Disp.

numero.

mitätöity (jos soittopyyntö on määritelty)

CAS: Datatyyppi Virhe annetaan (jos takaisinkutsu on määritetty)

Numeerinen Tulos arvioidaan ja jos tulos on kelpuutettu argumentti, DispAt tulostaa merkkijonon tuloslinjalla.

Katalogi >

4DMS

Laus 4DMS

Arvo 4DMS

Huomaa: Voit syöttää tämän operaattorin

tietokoneen näppäimistöltä kirjoittamalla

@>DMS.

Tulkitsee argumentin kulmana ja näyttää vastaavan DMS-luvun (DDDDDD¡MM'SS.ss''). DMS-muoto (asteet, minuutit, sekunnit) on kuvattu kohdissa ¡, ', '' sivulla sivu 242 .

Huomaa: 4DMS muuntaa radiaanit asteiksi,

kun sitä käytetään radiaanitilassa. Jos syötteen perässä on asteen merkki ¡, muunnosta ei suoriteta. Voit käyttää komentoa 4DMS ainoastaan syöterivin lopussa.

58 Lue ttelo aakkosjärjestyksess ä

Katalogi >

Astekulmatilassa:

domain()

domain(Laus1, Muut)⇒lauseke

Antaa vastauksena Laus1 määrittelyjoukon verrattuna Muut.

domain() voi käyttää funktioiden

arvoalueiden tarkasteluun. Se on rajattu todelliseen ja äärelliseen määrittelyjoukkoon.

Tällä toiminnolla on rajoituksia johtuen tietokonealgebran sieventämis- ja ratkaisualgoritmien puutteista.

Tiettyjä funktioita ei voi käyttää argumentteina domain(), -funktiolle riippumatta siitä, ilmaantuvatko ne eksplisiitisti tai käyttäjän määrittämien muuttujien ja funktioiden puitteissa. Seuraavassa esimerkissä lauseketta ei voi sieventää, sillä ‰() on kielletty funktio.

Luettelo >

dominantTerm()

dominantTerm(Laus1, Muutt [, Piste])

⇒lauseke

dominantTerm(Laus1, Muutt [, Piste]) |

Muutt>Piste ⇒lauseke

dominantTerm(Laus1, Muutt [, Piste]) |

Muutt<Piste ⇒lauseke

Katalogi >

Luettelo aakkosjärjestyksessä 59

dominantTerm()

Laskee dominanttitermin Laus1:n potenssisarjaesityksestä, kun lauseke on lavennettu Pisteellä. Dominanttitermi on se, jonka suuruus kasvaa nopeimmin lähellä arvoa Muutt = Piste. Lausekkeen (Muutt N

Piste) tuloksena olevalla potenssilla voi olla

negatiivinen ja/tai murtolukueksponentti. Tämän potenssin kertoin voi sisältää lausekkeen (Muutt N Piste) logaritmeja ja muita Muutt:n funktioita, joita hallitsevat kaikki lausekkeen (Muutt N Piste) potenssit, joilla on sama eksponentin etumerkki.

Pisteen oletusarvo on 0. Piste voi olla ˆ tai

Nˆ, jolloin dominanttitermi on termi, jolla

on suurin Muutt:n eksponentti eikä pienin

Muutt:n eksponentti.

dominantTerm(…) antaa tuloksena

“dominantTerm(…)”, ellei se pysty määrittämään tällaista esitystä, kuten olennaisille erikoispisteille, esim. sin(1/z), kun z=0, e

1/z

, kun z=0, tai ez, kun z = ˆtai

Nˆ.

Jos sarjassa tai yhdellä sen derivaatoista on hyppyepäjatkuvuus kohdassa Piste, tulos sisältää todennäköisesti alalausekkeita, jotka ovat muotoa sign(…) tai abs(…) reaaliselle kehitelmän muuttujalle tai (-1)

floor(…angle(…)…)

kompleksille kehitelmän muuttujalle, joka on merkkiin “_” päättyvä muuttuja. Jos tarkoituksesi on käyttää dominanttitermiä vain Pisteen toisella puolella oleville arvoille, siinä tapauksessa liitä funktioon dominantTerm(...) sopiva lauseke, “| Muutt > Piste”, “| Muutt <

Piste”, “| “Muutt | Piste” tai “Muutt { Piste”, jotta saat yksinkertaisemman

vastauksen.

dominantTerm() jakautuu 1. argumentin

listoihin ja matriiseihin.

Katalogi >

60 Lue ttelo aakkosjärjestyksess ä

dominantTerm()

dominantTerm() on hyödyllinen funktio, kun

haluat selvittää mahdollisimman yksinkertaisen lausekkeen, joka on asymptoottinen toisen lausekkeen suhteen, esim. Muutt " Piste. dominantTerm() on hyödyllinen myös silloin, kun sarjan ensimmäisen ei-nolla-termin astetta ei tiedetä, etkä halua arvailla iteratiivisesti tai interaktiivisesti ohjelmasilmukan avulla.

Huomaa: Katso myös series(), sivu 170.

Katalogi >

dotP()

dotP(Lista1, Lista2)⇒lauseke

Laskee kahden listan “pistetulon”.

dotP(Vektori1, Vektori2)⇒lauseke

Laskee kahden vektorin “pistetulon”.

Kummankin on oltava rivivektoreita, tai kummankin on oltava sarakevektoreita.

e^()

e^(Laus1)⇒lauseke

Laskee e:n arvon korotettuna Laus1:n potenssiin.

Huomaa: Katso myös e eksponenttimalli,

sivu 2.

Huomaa: Painikkeen u painaminen, jotta

näkyviin saadaan e^(, on eri asia kuin näppäimistön merkin E painaminen.

Voit syöttää kompleksiluvun re polaarisessa muodossa. Käytä tätä muotoa kuitenkin vain radiaanikulmatilassa; astetai graadikulmatilassa se aiheuttaa määritysjoukkovirheen (Domain).

Katalogi >

u painike

Luettelo aakkosjärjestyksessä 61

e^()

e^(Lista1)⇒lista

Laskee e:n arvon korotettuna Lista1:n jokaisen elementin potenssiin.

e^(neliömatriisi1)⇒neliömatriisi

Laskee neliömatriisi1:n matriisieksponentin. Tämä ei ole sama kuin laskettaessa e korotettuna kunkin elementin mukaiseen potenssiin. Laskentamenetelmä on kuvattu kohdassa

cos().

neliömatriisi1:n on oltava

diagonalisoitavissa. Vastaus sisältää aina liukulukuja.

u painike

eff()

eff(nimelliskorko,CpY)⇒arvo

Talouslaskentatoiminto, joka muuntaa nimelliskorkokannan nimelliskorko efektiiviseksi vuosikoroksi, kun CpY määritetään korkojaksojen lukumääräksi vuodessa.

nimelliskoron on oltava reaaliluku, ja CpY:n on oltava reaaliluku > 0.

Huomaa: Katso myös nom(), sivu 130.

eigVc()

eigVc(neliömatriisi)⇒matriisi

Laskee matriisin, joka sisältää ominaisvektorit reaaliselle tai kompleksiselle neliömatriisille, jossa jokainen vastauksen sarake vastaa ominaisarvoa. Huomaa, että ominaisvektori ei ole yksilöllinen; sitä voidaan skaalata millä tahansa vakiokertoimella. Ominaisvektorit ovat normaalimuotoisia, mikä tarkoittaa, että, jos V = [x1, x2, … , xn], tällöin:

Katalogi >

Suorakulmakompleksimuodossa:

62 Lue ttelo aakkosjärjestyksess ä

eigVc()

+x

+ … +x

= 1

neliömatriisia tasapainotetaan ensin

similaarimuunnoksilla, kunnes rivi- ja sarakenormit ovat mahdollisimman lähellä samaa arvoa. Sen jälkeen neliömatriisi sievennetään Hessenbergin ylämatriisimuotoon ja ominaisvektorit lasketaan Schurin tekijöihin jaon menetelmällä.

Katalogi >

Jos haluat nähdä koko vastauksen, paina £ ja siirrä sen jälkeenosoitinta painikkeilla

¡ja¢.

eigVl()

eigVl(neliömatriisi)⇒lista

Laskee listan reaalisen tai kompleksisen

neliömatriisin ominaisarvoista.

neliömatriisia tasapainotetaan ensin

Else

ElseIf

If BoolenLaus1 Then

  Lohko1

ElseIf BoolenLaus2 Then

  Lohko2

©

ElseIf BoolenLausN Then

  LohkoN

EndIf

Katalogi >

Suorakulmakompleksimuodossa:

Jos haluat nähdä koko vastauksen, paina £ ja siirrä sen jälkeenosoitinta painikkeilla

¡ja¢.

Katso If, sivu 93.

Katalogi >

Luettelo aakkosjärjestyksessä 63

ElseIf

Huomaa esimerkkiä syöttäessäsi: Ohjeet

monirivisten ohjelmien ja funktion määritysten syöttämisestä löytyvät tuotteen ohjekirjan Laskin-osiosta.

Katalogi >

EndFor

EndFunc

EndIf

EndLoop

EndPrgm

EndTry

Katso For, sivu 77.

Katso Func, sivu 81.

Katso If, sivu 93.

Katso Loop, sivu 116.

Katso Prgm, sivu 145.

Katso Try, sivu 202.

EndWhile

64 Lue ttelo aakkosjärjestyksess ä

Katso While, sivu 212.

euler ()

euler(Expr, Var, depVar, {Var0, VarMax},

depVar0, VarStep

[, eulerStep]) ⇒matriisi

euler(SystemOfExpr, Var, ListOfDepVars, {Var0, VarMax},   ListOfDepVars0,

VarStep [, eulerStep]) ⇒matriisi

euler(ListOfExpr, Var, ListOfDepVars, {Var0, VarMax},

ListOfDepVars0, VarStep [, eulerStep])

⇒matriisi

Käyttää Eulerin menetelmää järjestelmän ratkaisuun

muuttujalla depVar(Var0)=depVar0 välillä [Var0,VarMax]. Laskee matriisin, jonka ensimmäinen rivi määrittelee Var tulosarvot ja jonka toinen rivi määrittelee ensimmäisen ratkaisukomponentin arvon vastaavilla Var-arvoilla jne.

Expr on oikea puoli, joka määrittelee

tavallisen differentiaaliyhtälön (ODE).

SystemOfExpr on oikeiden puolten ryhmä,

joka määrittelee ODE-yhtälöiden ryhmän (vastaa riippuvien muuttujien järjestystä kohdassa ListOfDepVars).

ListOfExpr on oikeiden puolten luettelo,

joka määrittelee ODE-yhtälöiden ryhmän (vastaa riippuvien muuttujien järjestystä kohdassa ListOfDepVars).

Var on riippumaton muuttuja.

ListOfDepVars on riippuvien muuttujien

luettelo.

{Var0, VarMax} on kahden elementin lista, joka määrittää funktion integroinnin muuttujasta Var0 muuttujaan VarMax.

ListOfDepVars0 on riippuvien muuttujien

alkuehtojen luettelo.

Katalogi >

Differentiaaliyhtälö: y'=0.001*y*(100-y) ja y(0)=10

Jos haluat nähdä koko vastauksen, paina £ ja siirrä sen jälkeenosoitinta painikkeilla

¡ja¢.

Vertaile yllä olevaa tulostaCAS:n tarkkaan tulokseen, joka on saatukäyttämällä deSolve()-ja seqGEN()-funktioita:

Yhtälöryhmä:

kun y1(0)=2 ja y2(0)=5

Luettelo aakkosjärjestyksessä 65

euler ()

Katalogi >

VarStep nollasta eroava numero niin, että

sign(VarStep) = sign(VarMax-Var0) ja

ratkaisut lasketaan Var0+i·VarStep kaikille i=0,1,2,… niin, että Var0+i·VarStep on alueella [var0,VarMax] (muuttujalla

VarMax ei ehkä ole ratkaisuarvoa).

eulerStep on positiivinen kokonaisluku

(oletus 1), joka määrittelee Eulerin vaiheiden määrän tulosarvojen välillä. Eulerin menetelmän käyttämä varsinainen vaihemäärä on VarStepàeulerStep.

eval() Laitevalikko

eval(Expr) ⇒ string

eval() on validi vain TI-Innovator™ Hub

ohjelmointikomentojen komentoargumenteissa Get, GetStr, ja Send. Ohjelmisto käsittelee lausekkeen Expr ja korvaa eval()-ilmauksen lopputuloksella merkkijoukkona

Argumentin Expr on sievennyttävä reaaliluvuksi.

AsetaRGB-ledinsininenväri puolelle intensiteetille.

Palauta sininenväri OFF-tilaan.

eval()-argumentino n sievennyttävä reaaliluvuksi.

66 Lue ttelo aakkosjärjestyksess ä

Ohjelmoi punainen väri voimistumaan

Suorita ohjelma.

eval() Laitevalikko

Vaikka eval() ei näytä tulostaan,voi tuloksena saatavaa laitekomentojonoa katsoa komennon suorittamisen jälkeen tarkastamalla jonkin seuraavista erikoismuuttujista.

iostr.SendAns iostr.GetAns iostr.GetStrAns

Huomio: Katso myös Get (sivu 83), GetStr

(sivu 90), ja Send(sivu 168).

exact()

exact(Laus1 [, Toleranssi])⇒lauseke exact(Lista1 [, Toleranssi])⇒lista exact(Matriisi1 [, Toleranssi])⇒matriisi

Laskee täsmällisen tilan aritmetiikalla argumentin vastaavan rationaaliluvun, mikäli mahdollista.

Toleranssi määrittää muunnoksen

toleranssin; oletusarvo on 0 (nolla).

Exit

Poistuu nykyisestä For-, While- tai Looplohkosta.

Exit-komento ei ole sallittu näiden kolmen

silmukkarakenteen (For, While tai Loop) ulkopuolella.

Huomaa esimerkkiä syöttäessäsi: Ohjeet

monirivisten ohjelmien ja funktion määritysten syöttämisestä löytyvät tuotteen ohjekirjan Laskin-osiosta.

Katalogi >

Funktion listaus:

Luettelo aakkosjärjestyksessä 67

4exp

Laus 4exp

Näyttää Laus:n e:n luonnollisen eksponentin arvolla. Tämä on näytön muunnosoperaattori. Sitä voidaan käyttää vain syöterivin lopussa.

Huomaa: Voit syöttää tämän operaattorin

tietokoneen näppäimistöltä kirjoittamalla

@>exp.

Katalogi >

exp()

exp(Laus1)⇒lauseke

Laskee e:n arvon korotettuna Laus1:n potenssiin.

Huomaa: Katso myös e eksponenttimalli,

sivu 2.

Voit syöttää kompleksiluvun re polaarisessa muodossa. Käytä tätä muotoa kuitenkin vain radiaanikulmatilassa; astetai graadikulmatilassa se aiheuttaa määritysjoukkovirheen (Domain).

exp(Lista1)⇒lista

Laskee e:n arvon korotettuna Lista1:n jokaisen elementin potenssiin.

exp(neliömatriisi1)⇒neliömatriisi

Laskee neliömatriisi1:n matriisieksponentin. Tämä ei ole sama kuin laskettaessa e korotettuna kunkin elementin mukaiseen potenssiin. Laskentamenetelmä on kuvattu kohdassa

cos().

neliömatriisi1:n on oltava

diagonalisoitavissa. Vastaus sisältää aina liukulukuja.

u painike

68 Lue ttelo aakkosjärjestyksess ä

exp4lista()

exp4list(Laus,Muutt)⇒lista

Tutkii, onko lausekkeessa Laus yhtälöitä, jotka on erotettu sanalla “or”, ja laskee listan, joka sisältää yhtälöiden oikeat puolet, jotka ovat muotoa Muutt=Laus. Tällä tavoin voit saada helpolla tavalla joitakin ratkaisuarvoja, jotka on upotettu funktioiden solve(), cSolve(), fMin() ja fMax

() vastauksiin.

Huomaa: exp4list() ei ole välttämätön

funktioiden zeros ja cZeros() kanssa, koska ne laskevat suoraan ratkaisulistan.

Voit syöttää tämän funktion näppäimistöltä kirjoittamalla exp@>list(...).

Katalogi >

expand()

expand(Laus1 [, Muutt])⇒lauseke expand(Lista1 [,Muutt])⇒lista expand(Matriisi1 [,Muutt])⇒matriisi

expand(Laus1) laskee Laus1:n arvon

lavennettuna kaikkien muuttujiensa suhteen. Lavennus on polynomilavennus polynomeille ja osamurtolukulavennus rationaalilukulausekkeille.

Funktion expand() tehtävä on muuntaa

Laus1 yksinkertaisten termien summaksi

ja/tai erotukseksi. Funktion factor() tehtävä sen sijaan on muuntaa Laus1 yksinkertaisten tekijöiden tuloksi ja/tai osamääräksi.

expand(Laus1,Muutt) laskee Laus1:n arvon

lavennettuna muuttujan Muutt suhteen. Muuttujan Muutt samanlaiset potenssit kerätään. Termit ja niiden tekijät lajitellaan siten, että Muutt on päämuuttuja. Kerättyjen kertoimien satunnaista tekijöihin jakamista tai laventumista voi esiintyä jonkin verran. Verrattuna siihen, että muuttuja Muutt jätettäisiin pois, tämä toiminto säästää usein aikaa, muistia ja näyttötilaa, ja samalla lausekkeesta tulee ymmärrettävämpi.

Katalogi >

Luettelo aakkosjärjestyksessä 69

expand()

Vaikka muuttujia olisi vain yksi, muuttujan

Muutt käytön ansiosta nimittäjää voidaan

mahdollisesti jakaa täydellisemmin tekijöihinsä lavennettaessa murtolukua osittain.

Vinkki: Rationaalilausekkeissa propFrac() on nopeampi, mutta vähemmän äärimmäinen vaihtoehto kuin expand().

Huomaa: Katso myös comDenom(), jossa

käsitellään lavennetulla nimittäjällä lavennettua osoittajaa.

expand(Laus1,[Muutt]) jakaa myös

logaritmit ja murtopotenssit muuttujasta

Muutt riippumatta. Jos logaritmeja ja

murtopotensseja halutaan jakaa enemmän, tarvitaan mahdollisestä epäyhtälöehtoja, jotta voidaan varmistaa, että jotkin tekijät ovat ei-negatiivisia.

expand(Laus1, [Muutt]) jakaa myös

itseisarvot, sign(), ja eksponentit muuttujasta Muutt riippumatta.

Huomaa: Katso myös tExpand(), jossa

käsitellään trigonometrista kulma-summaja monikulmalavennusta.

Katalogi >

expr()

expr(Merkkijono)⇒lauseke

Määrittää Merkkijonon sisältämän merkkijonon lausekkeena ja suorittaa toimenpiteen välittömästi.

ExpReg

ExpReg X, Y [, [Frekv][, Luokka,

Sisällytä]]

70 Lue ttelo aakkosjärjestyksess ä

Katalogi >

ExpReg

Laskee eksponentiaalisen regressiony = a· (b)xlistoista X ja Y frekvenssillä Frekv. Tulosten yhteenveto tallentuu stat.resultsmuuttujaan. (Katso sivu 187.)

Kaikkien listojen on oltava samankokoisia

Sisällytä-listaa lukuunottamatta.

X ja Y ovat riippumattomien ja riippuvien

muuttujien listoja.

Frekv on valinnainen frekvenssiarvojen lista.

Jokainen Frekv:n elementti määrittää kunkin vastaavan datapisteen X ja Y esiintymisfrekvenssin. Oletusarvo on 1. Kaikkien elementtien on oltava kokonaislukuja | 0.

Luokka on luokkakoodien lista vastaavalle X- ja Y -datalle.

Sisällytä on yhden tai usemman

luokkakoodin lista. Vain ne datayksiköt, joiden luokkakoodi sisältyy tähän listaan, ovat mukana laskutoimituksessa.

Lisätietoja listassa olevien tyhjien elementtien vaikutuksesta, katso Tyhjät elementitsivulla sivu 250.

Katalogi >

Tulosmuuttuja Kuvaus

stat.RegEqn Regressioyhtälö: a·(b)

stat.a, stat.b Regressiokertoimet

stat.r

stat.r Muunnettujen tietojen korrelaatiokerroin (x, ln(y))

stat.Resid Eksponentiaalimalliinliittyvät jäännökset

stat.ResidTrans Muunnettujen tietojen lineaariseensovitukseen liittyvät jäännökset

stat.XReg

stat.YReg

stat.FreqReg

Muunnettujen tietojen lineaarimäärittelyn kerroin

MuokatunX Lista:n sisältämä datapisteidenlista, jota käytetäänregressiossa komentojen Frekv, Luokkalista ja Sisällytä luokat rajoitusten mukaisesti

MuokatunY Lista:n sisältämä datapisteiden lista, jota käytetäänregressiossa komentojen Frekv, Luokkalista ja Sisällytä luokat rajoitusten mukaisesti

Komentoja stat.XReg ja stat.YReg vastaava frekvenssilista

Luettelo aakkosjärjestyksessä 71

factor()

factor(Laus1[, Muutt])⇒lauseke factor(Lista1[,Muutt])⇒lista factor(Matriisi1[,Muutt])⇒matriisi

factor(Laus1) jakaa Laus1:n kaikki

muuttujat tekijöihin yhteisen nimittäjän suhteen.

Laus1 :ä jaetaan tekijöihin mahdollisimman

paljon lineaaristen rationaalilukutekijöiden suuntaan ilman, että uusia ei-reaalisia alalausekkeita syntyy. Tämä vaihtoehto on sopiva, jos haluat jakaa lausekkeen tekijöihin useamman kuin yhden muuttujan suhteen.

factor(Laus1,Muutt) laskee Laus1:n jaettuna tekijöihin muuttujan Muutt suhteen.

Laus1 :ä jaetaan mahdollisimman paljon

kohti reaalisia tekijöitä, jotka ovat lineaarisia muuttujassa Muutt, vaikka tästä syntyisi irrationiaalisia vakioita tai alalausekkeita, jotka ovat irrationaalisia muissa muuttujissa.

Tekijät ja niiden termit lajitellaan siten, että Muutt on päämuuttuja. Muuttujan

Muutt samanlaiset potenssit kerätään

Katalogi >

72 Lue ttelo aakkosjärjestyksess ä

factor()

Auto or Approximate (Automaattinen tai likimääräinen) -tilan Auto (Automaattinen)

-asetuksessa muuttujan Muutt mukanaolo sallii likiarvoistamisen liukulukukertoimilla, kun irrationaalisia kertoimia ei voida ilmaista täsmällisen tiiviisti sisäänrakennetuilla termeillä. Vaikka muuttujia olisi vain yksi, muuttujan Muutt mukanaolo voi tuottaa täydellisemmän tekijöihin jakamisen.

Huomaa: Katso myös comDenom(), jossa on

kuvattu nopea tapa suorittaa osittainen tekijöihin jako, kun factor() ei ole tarpeeksi nopea tai käyttää liikaa muistia.

Huomaa: Katso myös cFactor(), jossa on

kuvattu täydellinen tekijöihin jako kompleksikertoimiksi etsittäessä lineaarisia tekijöitä.

factor(rationaaliluku) laskee

rationaaliluvun, joka on jaettu jaottomiin tekijöihin. Sekalukujen kohdalla laskentaaika pitenee eksponentiaalisesti toiseksi suurimman tekijän sisältämien numeroiden määrän suhteen. Esimerkiksi 30numeroisen kokonaisluvun tekijöihin jakaminen voi kestää pitempään kuin vuorokauden ja 100-numeroisen luvun pitempään kuin vuosisadan.

Pysäytä laskenta käsin,

Katalogi >

• Kämmenlaite: Pidä c-painiketta painettuna ja paina toistuvasti ·-

painiketta.

• Windows®: Pidä F12-näppäintä pohjassa ja paina toistuvasti Enter.

• Macintosh®: Pidä F5-näppäintä pohjassa ja paina toistuvasti Enter.

• iPad®: Sovellus näyttää kehotuksen. Voit jatkaa odottamista tai peruuttaa.

Luettelo aakkosjärjestyksessä 73

factor()

Jos haluat pelkästään määrittää, onko jokin luku jaoton, käytä sen sijaan komentoa

isPrime(). Se on paljon nopeampi, erityisesti

jos rationaaliluku ei ole jaoton, ja jos toiseksi suurimmassa tekijässä on enemmän kuin viisi numeroa.

Katalogi >

FCdf()

FCdf(alaraja,yläraja,dfOsoitt,dfNimitt)

⇒luku, jos alaraja ja yläraja ovat lukuja,

lista, jos alaraja ja yläraja ovat listoja

FCdf(alaraja,yläraja,dfOsoitt,dfNimitt)

⇒luku, jos alaraja ja yläraja ovat lukuja,

lista, jos alaraja ja yläraja ovat listoja

Laskee F-jakauman todennäköisyydenalarajan ja ylärajan välillä määritellylle dfOsoittajalle (vapausaste) ja dfNimittäjälle.

Aseta P(X { yläraja):lle alaraja = 0.

Fill

Fill Laus, matriisiMuutt⇒matriisi

Korvaa muuttujan matriisiMuutt jokaisen elementin lausekkeella Laus.

matriisiMuuttujan on oltava valmiiksi

olemassa.

Fill Laus, listaMuutt⇒lista

Korvaa muuttujan listaMuutt jokaisen elementin lausekkeella Laus.

listaMuuttujan on oltava valmiiksi

olemassa.

Katalogi >

FiveNumSummary

FiveNumSummary X[,[Frekv] [,Luokka,Sisällytä]]

74 Lue ttelo aakkosjärjestyksess ä

Katalogi >

FiveNumSummary

Antaa lyhennetyn version 1 muuttujan tilastoista listalle X. Tulostenyhteenveto tallentuu stat.results-muuttujaan. (Katso sivu 187.)

X edustaa datan sisältävää listaa.

Frekv on valinnainen frekvenssiarvojen lista.

Jokainen Frekv:n elementti määrittää kunkin vastaavan X:n arvon esiintymisfrekvenssin. Oletusarvo on 1. Kaikkien elementtien on oltava kokonaislukuja 0.

Luokka on numeeristen luokkakoodien lista

vastaaville X:n arvoille.

Sisällytä on yhden tai usemman

luokkakoodin lista. Vain ne datayksiköt, joiden luokkakoodi sisältyy tähän listaan, ovat mukana laskutoimituksessa.

Tyhjä elementti jossakin listassa X, Frekv tai Luokka saa aikaan, että kaikkien listojen vastaava elementti on tyhjä. Lisätietoja tyhjistä elementeistä, katso sivu 250.

Tulosmuuttuja Kuvaus

stat.MinX x:n arvo jenminimi

stat.Q1X x:n ensimmäinenneljännes

stat.MedianX x:n mediaani

stat.Q3X x:n kolmasneljännes

stat.MaxX x:n arvo jenmaksimi

Katalogi >

floor()

floor(Laus1)⇒kokonaisluku

Laskee suurimman kokonaisluvun, joka on { argumentti. Tämä funktio on identtinen funktion int() kanssa.

Argumentti voi olla reaali- tai kompleksiluku.

Katalogi >

Luettelo aakkosjärjestyksessä 75

floor()

floor(Lista1)⇒lista floor(Matriisi1)⇒matriisi

Määrittää listan tai matriisin jokaisen elementin alarajasta.

Huomaa: Katso myös ceiling() ja int().

Katalogi >

fMax()

fMax(Laus, Muutt)⇒Boolen lauseke

fMax(Laus, Muutt,alaraja)

fMax(Laus, Muutt,alaraja,yläraja)

fMax(Laus, Muutt) | alaraja{Muutt

{yläraja

Laskee Boolen lausekkeen, joka määrittää mahdollisia arvoja muuttujalle Muutt, joilla saadaan suurin lausekkeen Laus arvo tai jotka määrittävät sen pienimmän ylärajan.

Voit käyttää sijoitusoperaattoria (“|”) rajoittaaksesi ratkaisuväliä ja/tai määrittääksesi muita ehtoja.

Auto or Approximate (Automaattinen tai likimääräinen) -tilan Approximate

(Likimääräinen) -asetuksessa fMax() etsii iteratiivisesti yhtä likimääräistä paikallista maksimiarvoa. Tämä on usein nopeampi menetelmä, erityisesti jos rajoitat haun operaattorilla “|” suhteellisen pienelle välille, joka sisältää täsmälleen yhden paikallisen maksimin.

Huomaa: Katso myös fMin() ja max().

Katalogi >

fMin()

fMin(Laus, Muutt)⇒Boolen lauseke

fMin(Laus, Muutt,alaraja)

fMin(Laus, Muutt,alaraja,yläraja)

fMin(Laus, Muutt) | alaraja{Muutt

{yläraja

76 Lue ttelo aakkosjärjestyksess ä

Katalogi >

fMin()

Laskee Boolen lausekkeen, joka määrittää mahdollisia arvoja muuttujalle Muutt, joilla saadaan pienin lausekkeen Laus arvo tai jotka määrittävät sen suurimman alarajan.

Voit käyttää sijoitusoperaattoria (“|”) rajoittaaksesi ratkaisuväliä ja/tai määrittääksesi muita ehtoja.

Auto or Approximate (Automaattinen tai likimääräinen) -tilan Approximate

(Likimääräinen) -asetuksessa fMin() etsii iteratiivisesti yhtä likimääräistä paikallista minimiarvoa. Tämä on usein nopeampi menetelmä, erityisesti jos rajoitat haun operaattorilla “|” suhteellisen pienelle välille, joka sisältää täsmälleen yhden paikallisen minimin.

Huomaa: Katso myös fMax() ja min().

Katalogi >

For

For Muutt, Matala, Korkea [, Askel]

  Lohko

EndFor

Suorittaa Lohkon sisältämät lausekkeet iteratiivisesti jokaiselle muuttujan Muutt arvolle, Matalasta Korkeaaan kohdassa

Askel määritetyin portain.

Muutt ei saa olla järjestelmän muuttuja.

Askel voi olla positiivinen tai negatiivinen.

Oletusarvo on 1.

Lohko voi olla joko yksi lauseke tai sarja

lausekkeita, jotka on erotettu toisistaan kaksoispisteellä (:).

Huomaa esimerkkiä syöttäessäsi: Ohjeet

monirivisten ohjelmien ja funktion määritysten syöttämisestä löytyvät tuotteen ohjekirjan Laskin-osiosta.

Katalogi >

Luettelo aakkosjärjestyksessä 77

format()

format(Laus[, muotoMerkkijono])

⇒merkkijono

Määrittää lausekkeen Laus merkkijonona muotoilumallin perusteella.

Laus on voitava sieventää luvuksi.

muotoMerkkijono on merkkijono, ja sen

tulee olla muodossa: “F[n]”, “S[n]”, “E[n]”, “G[n][c]”, jossa [] ilmaisevat valinnaisia osia.

F[n]: Kiinteä muoto. n on desimaalipisteen jälkeen näytettävien numeroiden lukumäärä.

S[n]: Kymmenpotenssimuoto. n on desimaalipisteen jälkeen näytettävien numeroiden lukumäärä.

E[n]: Tekninen esitystapa. n on ensimmäisen merkitsevän numeron jälkeen näytettävien numeroiden lukumäärä. Eksponentti säätyy kolmella kerrolliseksi, ja desimaalipiste siirtyy 0, 1 tai 2 numeroa oikealle.

G[n][c]: Muuten sama kuin kiinteä muoto, mutta erottaa myös juuren vasemmalla puolella olevat numerot kolmen ryhmiin. c määrittää ryhmän erotusmerkin, ja sen oletusarvo on pilkku. Jos c on piste, juuri näytetään pilkkuna.

[Rc]: Mihin tahansa edellä mainituista määrittäjistä voidaan liittää Rc-juurilippu, jossa c on yksi merkki, joka määrittää korvauksen kohteen juuripisteestä.

Katalogi >

fPart()

fPart(Laus1)⇒lauseke fPart(Lista1)⇒lista fPart(Matriisi1)⇒matriisi

Laskee argumentin murtolukuosan.

Kun kyseessä on lista tai matriisi, laskee elementtien murtolukuosat.

78 Lue ttelo aakkosjärjestyksess ä

Katalogi >

fPart()

Argumentti voi olla reaali- tai kompleksiluku.

Katalogi >

FPdf()

FPdf(XArvo,dfOsoitt,dfNimitt)⇒luku, jos

XArvo on luku, lista, jos XArvo on lista

Laskee F-jakauman todennäköisyyden

XArvon kohdalle määritetyille dfOsoittajalle (vapausasteet) ja dfNimittäjälle.

freqTable4list()

freqTable4list

(Lista1,frekvKokonaislukuLista)⇒lista

Laskee listan, joka sisältää Lista1:n elementit lavennettuina

frekvKokonaislukuListan määrittämien

frekvenssien mukaisesti. Tätä funktiota voidaan käyttää laadittaessa frekvenssitaulukkoa Data & Tilastot sovelluksessa.

Lista1 voi olla mikä tahansa kelvollinen

lista.

frekvKokonaislukuListan on oltava

samankokoinen kuin Lista1 ja sen tulee sisältää ainoastaan ei-negatiivisia kokonaislukuelementtejä. Jokainen elementti määrittää kuinka monta kertaa

Lista1-elementti toistetaan tuloslistassa.

Nolla-arvo sulkee pois vastaavan Lista1elementin.

Huomaa: Voit syöttää tämän funktion

tietokoneen näppäimistöltä kirjoittamalla

freqTable@>list(...).

Tyhjiä elementtejä ei huomioida. Lisätietoja tyhjistä elementeistä, katso sivu 250.

Katalogi >

Luettelo aakkosjärjestyksessä 79

frequency()

frequency(Lista1,lokerotLista)⇒lista

Luo listan, joka sisältää Lista1:n elementtien lukumäärät. Lukumäärät perustuvat alueisiin (lokeroihin), jotka määritetään kohtaan lokerotLista.

Jos lokerotLista on {b(1), b(2), …, b(n)}, määritetyt alueet ovat {?{b(1), b(1)<?{b (2),…,b(n-1)<?{b(n), b(n)>?}. Tuloksena oleva lista on yhden elementin pitempi kuin

lokerotLista.

Jokainen vastauksen elementti vastaa niiden Lista1:n elementtien lukumäärää, jotka ovat kyseisen lokeron alueella. Funktion countIf() termeillä ilmaistuna vastaus on {countIf(list, ?{b(1)), countIf (list, b(1)<?{b(2)), …, countIf(list, b(n-1)<? {b(n)), countIf(list, b(n)>?)}.

Niitä Lista1:n elementtejä, joita ei voi “lokeroida”, ei huomioida. Tyhjiä elementtejä ei myöskään huomioida. Lisätietoja tyhjistä elementeistä, katso sivu

250.

Listat & Taulukot -sovelluksessa voit käyttää solualueita kummankin argumentin tilalla.

Huomaa: Katso myös countIf() , sivu 37.

Katalogi >

Vastauksen selitys:

2 Datalistan elementtiä on {2.5

4 Datalistan elementtiä on >2.5 ja {4.5

3 Datalistan elementtiä on >4.5

Elementti"hei" on merkkijono, jota ei voi sijoittaamihinkäänmääritetyistä lokeroista.

FTest_2Samp

FTest_2Samp Lista1,Lista2[,Frekv1

[,Frekv2[,Hypot]]]

FTest_2Samp Lista1,Lista2[,Frekv1

[,Frekv2[,Hypot]]]

(Datalistan syöte)

FTest_2Samp sx1,n1,sx2,n2[,Hypot]

(Yhteenvetotilaston syöte)

80 Lue ttelo aakkosjärjestyksess ä

Katalogi >

FTest_2Samp

Suorittaa kahden otoksen F-testin. Tulosten yhteenveto tallentuu stat.resultsmuuttujaan. (Katso sivu 187.)

Kun Ha: s1 > s2, aseta Hypot>0 Kun Ha: s1 ƒ s2 (oletus), aseta Hypot =0 Kun Ha: s1 < s2, aseta Hypot<0

Lisätietoja listassa olevien tyhjien elementtien vaikutuksesta, katso Tyhjät elementitsivulla sivu 250.

Tulosmuuttuja Kuvaus

stat.F

stat.PVal Alinmerkitsevyystaso, jolla nollahypoteesivoidaanhylätä

stat.dfNumer osoittajan vapausasteet = n1-1

stat.dfDenom nimittäjän vapausasteet = n2-1

stat.sx1, stat.sx2

stat.x1_bar stat.x2_bar

stat.n1, stat.n2 Otostenkoko

LaskettuÛ-tilasto datasekvenssille

Otoksen keskihajonnat Lista1:n ja Lista2:n sisältämilledatasekvensseille

Otoksen keskiarvot Lista1:n ja Lista2:n sisältämille datasekvensseille

Katalogi >

Func

  Lohko

EndFunc

Malli käyttäjän määrittämän funktion luomista varten.

Lohko voi olla yksi lauseke tai sarja

lausekkeita, jotka on erotettu toisistaan kaksoispisteellä (:), tai sarja eri riveillä olevia lausekkeita. Funktio voi käyttää

Return-ohjetta tietyn vastauksen

laskemiseen.

Huomaa esimerkkiä syöttäessäsi: Ohjeet

monirivisten ohjelmien ja funktion määritysten syöttämisestä löytyvät tuotteen ohjekirjan Laskin-osiosta.

Katalogi >

Määritä paloittainmääritelty funktio:

Funktion g(x) kuvaajanpiirtämisen tulos

Luettelo aakkosjärjestyksessä 81

Func

Katalogi >

gcd()

gcd(Arvo1, Arvo2)⇒lauseke

Laskee kahden argumentin suurimman yhteisen jakajan. Kahden murtoluvun gcd on niiden osoittajien gcd jaettuna nimittäjien

lcm:llä.

Auto or Approximate (Automaattinen tai likimääräinen) -tilassa murtoluvun liukulukujen gcd on 1.0.

gcd(Lista1, Lista2)⇒lista

Laskee Lista1:n ja Lista2:n toisiaan vastaavien elementtien suurimmat yhteiset jakajat.

gcd(Matriisi1, Matriisi2)⇒matriisi

Laskee Matriisi1:n ja Matriisi2:n toisiaan vastaavien elementtien suurimmat yhteiset jakajat.

geomCdf()

geomCdf(p,alaraja,yläraja)⇒luku, jos

alaraja ja yläraja ovat lukuja, lista, jos alaraja ja yläraja ovat listoja

geomCdf(p,yläraja)kun P(1{X{yläraja)

⇒luku, jos yläraja on luku, lista, jos

yläraja on lista

Katalogi >

82 Lue ttelo aakkosjärjestyksess ä

geomCdf()

Laskee kumulatiivisen geometrisen todennäköisyyden alarajalta ylärajalle määritetyllä onnistumistodennäköisyydellä

Kun P(X { yläraja), aseta alaraja = 1.

Katalogi >

geomPdf()

Katalogi >

geomPdf(p,XArvo)⇒luku, jos XArvo on

luku, lista, jos XArvo on lista

Laskee diskreetin jakauman todennäköisyyden XArvo:n, eli ensimmäisen onnistuneen kokeen järjestysnumeron kohdalla, määritetyllä onnistumistodennäköisyyllä p.

Get Laitevalikko

Get [kehotemerkkijono,] var[, statusVar]

Get [kehotemerkkijono,] func(arg1,

...argn)[,statusVar]

Ohjelmointikomento: Noutaa arvon liitetystä TI-Innovator™ Hub ja sijoittaa arvon muuttujaan var.

Arvo täytyy kysyä:

• Etukäteen Send "READ ..." - komennolla.

— tai —

• Upottamalla "READ ..." kysy valinnaisena

Esimerkki: Kysy laitteensisäänrakennetun valaistusanturin tämänhetkinenarvo. Käytä komentoa Get noutaaksesi arvon ja sijoittaaksesi se muuttujaanlightval.

Upota READ-kysely ko mentoon Get.

kehotemerkkijonoargumenttina. Tämä

menetelmä antaa sinun käyttää yksittäistä komentoa kysyäksesi arvoa ja hakeaksesi sen.

Tapahtuu implisiittinen yksinkertaistus. Esimerkiksi vastaanotettu merkkijono "123" tulkitaan numeeriseksi arvoksi. Säilyttääksesi merkkijonon käytä toimintoa

GetStr toiminnon Get sijaan.

Luettelo aakkosjärjestyksessä 83

Get Laitevalikko

Jos sisällytät valinnaisen argumentin

statusVar, sille määrätään arvo

toimenpiteen onnistumisen perusteella. Arvo nolla merkitsee, ettei tietoa ole vastaanotettu.

Järjestyksessä toisessa syntaksissa func()argumentti sallii ohjelman tallentaa vastaanotetun merkkijonon funktiomääritelmänä. Tämä syntaksi toimii ikään kuin ohjelma suorittaisi komennon:

Määrittele func(arg1, ...argn) =

vastaanotettu merkkijono

Sen jälkeen ohjelma voi käyttää määriteltyä funktiota func().

Huomio: Komentoa Get voi käyttää

käyttäjän määrittelemän ohjelman sisällä, mutta ei funktion sisällä.

Huomio: Katso myös GetStr, sivu 90 ja Send

sivu 168.

getDenom()

getDenom(Laus1)⇒lauseke

Muuttaa argumentin lausekkeeksi, jolla on sievennetty yhteinen nimittäjä, ja laskee sen jälkeen lausekkeen nimittäjän.

getKey()

getKey([0|1]) ⇒ returnString

Kuvaus:getKey() – mahdollistaa TI-Basic

-ohjelmalle näppäimistön – kannettava laite, pöytätietokone ja emulaattori pöytätietokoneella.

Esimerkki:

• alas painettu näppäin := getKey() palauttaa näppäimen tai tyhjän

84 Lue ttelo aakkosjärjestyksess ä

Katalogi >

Esimerk ki:

getKey()

merkkijonon, jos mitään näppäintä ei ole painettu. Tämä komento palaa välittömästi.

• alas painettu näppäin := getKey(1) odottaa, kunnes jotakin näppäintä painetaan. Tämä komento pysäyttää ohjelman suorituksen, kunnes jotakin näppäintä on painettu.

Näppäimen pitäminen painettuna:

Kannettava

laite/Emulaattorinäppäin

Esc Esc "esc"

Kosketuslevy – Yläpainallus N/A "ylös"

Päällä N/A "päävalikko"

Scratchapps N/A muistilehtiö

Kosketuslevy – Vasen painallus

Kosketuslevy – Keskipainallus

Kosketuslevy – Oikea painallus

Doc N/A "doc"

Pöytätietokone Palauta arvo

N/A "vasen"

N/A "keskus"

N/A "oikea"

Katalogi >

Tabulaattori Tabulaattori "Tabulaattori"

Kosketuslevy – Alapainallus Nuoli alaspäin "alas"

Päävalikko N/A "päävalikko"

Ctrl Ctrl ei palautusta

Vaihto Vaihto ei palautusta

Var N/A "var"

Poista N/A "poista"

= = "="

Luettelo aakkosjärjestyksessä 85

Kannettava

laite/Emulaattorinäppäin

Pöytätietokone Palauta arvo

Trigonometria N/A Trigonometria

0:sta 9:ään 0-9 "0" ... 9

Sapluunat N/A "sapluuna"

Lista N/A "lista"

^ ^ "^"

X^2 N/A "neliö"

/ (jakonäppäin) / "/"

* (kertonäppäin) * "*"

e^x N/A "eksponentti"

10^x N/A "10voima"

+ + "+"

- - "-"

( ( "("

) ) ")"

. . "."

(-) N/A "-" (negatiivinen merkki)

Syötä Syötä "syötä"

ee N/A "E" (tieteellinen merkintä E)

a – z a–z alfa = kirjainmerkki painettu

(pieni kirjain) ("a" – "z")

vaihto a–z vaihto a–z alfa = kirjainmerkki painettu

"A" - "Z"

Huomaa: Ctrl-vaihto lukitsee isot kirjaiment

?! N/A "?!"

pii N/A "pii"

Lippu N/A ei palautusta

86 Lue ttelo aakkosjärjestyksess ä

Kannettava

laite/Emulaattorinäppäin

Pöytätietokone Palauta arvo

, , ","

Palautus N/A Palautus

Välilyönti Välilyönti Välilyönti

Ei pääsyä Näppäimet erikoismerkeille,

Kirjainmerkki on palautettu

kuten @,!,^, etc.

N/A Toimintonäppäimet Kirjainmerkkejä ei ole

palautettu

N/A Erityiset näytön

kontrollinäppäimet

Ei pääsyä Muita näytön näppäimiä,

jotka eivät ole käytettävissä laskimessa, kun getkey()

Kirjainmerkkejä ei ole palautettu

Sama kirjainmerkki, jonka saat Notesista (ei

matemaattisessa kentässä) odottaa näppäimen painallusta. ({, },;, :, ...)

Huomaa: On tärkeää huomata, että ohjelman getKey () läsnäolo muuttaa ohjelmaa tiettyjen tapahtumien käsittelyä. Joitakin näistä kuvataan jäljempänä.

Lopeta ohjelma ja käsittele tapahtuma – aivan kuin jos käyttäjä poistuisi ohjelmasta painamalla ON -näppäintä

"Tuki " jäljempänä tarkoittaa – Järjestelmä toimii odotetusti – ohjelma jatkuu.

Tapahtuma laite Työpöytä – TI-Nspire ™

Pikakysely Lopeta ohjelma, käsittele

tapahtuma

Ohjelmisto opiskelijoille

Sama kuin kannettava laite (TI-Nspire™ Student Software, TI-Nspire™ Navigator™ NC Teacher Software – vain)

Etätiedoston hallinta

(Sisältää lähetyksen "Exit Press 2 Test" -tiedoston toisesta kämmenlaitteesta

Lopeta ohjelma, käsittele tapahtuma

Sama kuin kannettava laite. (TI-Nspire™ Student

Software, TI-Nspire™ Navigator™ NC Teacher Software-vain)

tai työpöydän kannettavasta laitteesta)

Lopeta oppitunti Lopeta ohjelma, käsittele

tapahtuma

Tuki (TI-Nspire™ Student

Software, TI-Nspire™ Navigator™ NC Teacher Software-vain)

Luettelo aakkosjärjestyksessä 87

Tapahtuma Laite Työpöytä – TI-Nspire ™

TI-Innovator™ Hub Yhdistä / katkaise

Tuki – onnistuu komennolla TI-Innovator™ Hub. Kun olet lopettanut ohjelman, TI-Innovator™ Hub työskentelee edelleen kämmenlaitteen kanssa.

Kaikki versiot

Sama kuin kannettava laite

getLangInfo()

getLangInfo()⇒merkkijono

Antaa merkkijonon, joka vastaa parhaillaan käytössä olevan kielen lyhyttä nimeä. Voit käyttää sitä esimerkiksi ohjelmassa tai funktiossa nykyisen kielen määrittämiseen.

englanti = “en” tanska = “da” saksa = “de” suomi = “fi” ranska = “fr” italia = “it” hollanti = “nl” flaami = “nl_BE” norja = “no” portugali = “pt” espanja = “es” ruotsi = “sv”

getLockInfo()

getLockInfo(Muutt)⇒arvo

Määrittää muuttujan Muutt nykyisen lukittu/lukitsematon-tilan.

arvo =0: Muutt on lukitsematon tai sitä ei

ole olemassa.

arvo =1: Muutt on lukittu eikä sitä voi

muuttaa tai poistaa.

Katso Lock, sivu 112, ja unLock, sivu 209.

Katalogi >

88 Lue ttelo aakkosjärjestyksess ä

getMode()

getMode(TilanNimiKokonaisluku)⇒arvo getMode(0)⇒lista

getMode(TilanNimiKokonaisluku) laskee

arvon, joka vastaa TilanNimiKokonaislukutilan nykyistä asetusta.

getMode(0) laskee listan, joka sisältää

lukupareja. Jokainen pari koostuu tilaa kuvaavasta kokonaisluvusta ja asetusta kuvaavasta kokonaisluvusta.

Tilat ja niiden asetukset on esitetty alla olevassa taulukossa.

Jos tallennat asetukset komennolla

getMode(0) & muutt, voit käyttää

komentoa setMode(muutt) funktiossa tai ohjelmassa ja tallentaa asetukset näin väliaikaisesti pelkästään funktion tai ohjelman suorituksen ajaksi. Katso setMode

(), sivu 172.

Katalogi >

Tilan nimi

Näytettävät numerot

Tilaa vastaava kokonaisluku

Asetuksia vastaavat kokonaisluvut

1 1=Liukuva, 2=Liukuva1, 3=Liukuva2,

4=Liukuva3, 5=Liukuva4, 6=Liukuva5, 7=Liukuva6, 8=Liukuva7, 9=Liukuva8, 10=Liukuva9, 11=Liukuva10, 12=Liukuva11, 13=Liukuva12, 14=Kiinteä0, 15=Kiinteä1, 16=Kiinteä2, 17=Kiinteä3, 18=Kiinteä4, 19=Kiinteä5, 20=Kiinteä6, 21=Kiinteä7, 22=Kiinteä8, 23=Kiinteä9, 24=Kiinteä10, 25=Kiinteä11, 26=Kiinteä12

Kulma 2 1=Radiaani, 2=Aste, 3=Graadi

Eksponenttimuoto 3 1=Normaali, 2=Kymmenpotenssi,

3=Tekninen

Reaali- tai

4 1=Reaali, 2=Suorakulma, 3=Polaarinen

kompleksiluku

Automaattinen tai likimääräinen.

5 1=Automaattinen, 2=Likimääräinen,

3=Täsmällinen

Vektorimuoto 6 1=Suorakulma, 2=Sylinteri, 3=Pallo

Luettelo aakkosjärjestyksessä 89

Tilan nimi

Tilaa vastaava kokonaisluku

Asetuksia vastaavat kokonaisluvut

Kantaluku 7 1=Desimaali, 2=Heksagonaalinen,

3=Binaarinen

Yksikköjärjestelmä 8 1=SI, 2=Eng/US

getNum()

Katalogi >

getNum(Laus1)⇒lauseke

Muuttaa argumentin lausekkeeksi, jolla on sievennetty yhteinen nimittäjä, ja laskee sen jälkeen lausekkeen osoittajan.

GetStr Hub-valikko

GetStr [kehotemerkkijono,] var[,

Katso esimerkitkohdasta Get.

statusVar]

GetStr [kehotemerkkijono,] func(arg1,

...argn)[,statusVar]

Ohjelmointikomento: Toimii samalla tavalla kuin Get-komento, mutta vastaanotettu arvo tulkitaan aina merkkijonoksi. Get-komento kuitenkin tulkitsee vastauksen lausekkeeksi, jollei sitä merkitä lainausmerkkien ("") sisään.

Huomio: Katso myös Get, sivu 83 ja Send sivu

168.

getType()

Katalogi >

getType(var)⇒merkkijono

Antaa tulokseksi merkkijonon, joka ilmoittaa muuttujan var datatyypin.

Jos muuttujaa var ei ole määritelty, tulokseksi tulee merkkijono "EI MITÄÄN".

90 Lue ttelo aakkosjärjestyksess ä

getVarInfo()

getVarInfo()⇒matriisi tai merkkijono getVarInfo(LibNameString)⇒matriisi tai

merkkijono

getVarInfo() laskee tietomatriisin

(muuttujan nimi, tyyppi, kirjaston käytettävyys ja lukittu/lukitsematon-tila) kaikille nykyisessä tehtävässä määritetyille muuttujille ja kirjasto-objekteille.

Jos yhtään muuttujaa ei ole määritetty,

getVarInfo() antaa vastauksena merkkijonon

"NONE".

getVarInfo(KirjNimiMerkkijono)antaa

tuloksena tietomatriisin kaikista kirjastossa

KirjNimiMerkkijono määritetyistä

kirjasto-objekteista. KirjNimiMerkkijonon on oltava merkkijono (lainausmerkkien sisällä oleva teksti) tai merkkijonomuuttuja.

Jos kirjastoa KirjNimiMerkkijono ei ole olemassa, esiintyy virhe.

Huomaa vasemmanpuoleinen esimerkki, jossa funktion getVarInfo() vastaus on määritetty muuttujaan vs. Jos muuttujan vs riviä 2 tai riviä 3 yritetään näyttää, tuloksena on “Kelpaamaton lista tai matriisi” -virhe, koska vähintään yksi näiden rivien elementeistä (esimerkiksi muuttuja

b) sieventyy uudelleen matriisiksi.

Tämä virhe voi esiintyä myös käytettäessä

Ans-muuttujaa funktion getVarInfo()

tuloksen uudelleenlaskennassa.

Järjestelmä antaa edellä mainitun virheen, koska ohjelmiston nykyinen versio ei tue yleistettyä matriisirakennetta, jossa matriisin elementti voi olla joko matriisi tai lista.

Katalogi >

Luettelo aakkosjärjestyksessä 91

Goto

Goto tunnusnimi

Siirtää ohjauksen tunnukseen tunnusnimi.

tunnusnimi on määritettävä samassa

funktiossa käyttäen Lbl-ohjetta.

Huomaa esimerkkiä syöttäessäsi: Ohjeet

monirivisten ohjelmien ja funktion määritysten syöttämisestä löytyvät tuotteen ohjekirjan Laskin-osiosta.

Katalogi >

4Grad

Laus1 4 Grad⇒lauseke

Muuttaa Laus1:n graadikulmaan.

Huomaa: Voit syöttää tämän operaattorin

tietokoneen näppäimistöltä kirjoittamalla

@>Grad.

identity()

identity(kokonaisluku) ⇒ matriisi

Laskee identiteettimatriisin, jonka koko on

kokonaisluku.

Kokonaisluvun on oltava positiivinen

kokonaisluku.

Katalogi >

Astekulmatilassa:

Radiaanikulmatilassa:

Luettelo >

92 Lue ttelo aakkosjärjestyksess ä

Jos

JosBoolenLaus

Ilmaisut

Jos BoolenLaus Niin

Lohko

EndIf

Jos BoolenLaus on tosi, suorittaa yhden lausekkeen Lauseke tai lausekkeiden lohkon

Lohko ennen suorituksen jatkamista.

Jos BoolenLaus on epätosi, jatkaa suoritusta suorittamatta lauseketta tai lausekkeiden lohkoa.

Lohko voi olla joko yksi lauseke tai sarja lausekkeita, jotka on erotettu toisistaan kaksoispisteellä (:) merkki.

Huomaa esimerkkiä syöttäessäsi: Ohjeet

monirivisten ohjelmien ja funktion määritysten syöttämisestä löytyvät tuotteen ohjekirjan Laskin-osiosta.

Jos BoolenLaus, niin

  Lohko1

Tai

  Lohko2

EndIf

Jos BoolenLauson tosi, suorittaa Lohko1:n ja sen jälkeen jättää väliin Lohko2:n.

Jos BoolenLaus on epätosi, ohittaa

Lohko1:n, mutta suorittaa Lohko2:n.

Lohko1 ja Lohko2 voivat olla yksi lauseke.

Luettelo >

Luettelo aakkosjärjestyksessä 93

Jos

Jos BoolenLaus1, niin

  Lohko1

Jos taas BoolenLaus2, niin

  Lohko2

⋮

Jos taas BoolenLausN, niin

  LohkoN

EndIf

Sallii haarautumisen Jos BoolenLaus1 on tosi, suorittaa Lohko1:n Jos BoolenLaus1 on epätosi, laskee BoolenLaus2:n jne.

Luettelo >

ifFn()

ifFn(BoolenLaus,Arvo_Jos_tosi [,Arvo_

Jos_epätosi [,Arvo_Jos_tuntematon]]) ⇒ lauseke, lista tai matriisi

Laskee BoolenLaus (jokaiselle BoolenLaus

) elementille) ja antaa tuloksen

noudattaen seuraavia sääntöjä:

• BoolenLaus voi testata yksittäisen arvon, listan tai matriisin.

• Jos jokin BoolenLaus elementti on tosi, laskee vastaavan elementin lausekkeesta

Arvo_Jos_tosi.

• Jos jokin BoolenLaus elementti on epätosi, laskee vastaavan elementin lausekkeesta Arvo_Jos_epätosi. Jos jätät pois lausekkeen Arvo_Jos_epätosi, laskee määrittelemättömäksi.

• Jos BoolenLaus elementti ei ole tosi eikä epätosi, laskee vastaavan elementin

Arvo_If_unknown. Jos jätät pois Arvo_ If_unknown, laskee

määrittelemättömäksi.

• Jos funktion josFn() toinen, kolmas tai neljäs argumentti on yksi lauseke, Boolen testiä sovelletaan jokaiseen sijaintiin Boolen lausekkeessaBoolenLaus.

Luettelo >

1:n testiarvo on alle 2.5, joten sen vastaava

Arvo_Jos_tosi -elementtiarvolle5

kopioidaanvastaustenlistaan.

2:n testiarvo on alle 2.5, joten sitä vastaava

Arvo_Jos_tosi-elementtiarvolle 6

kopioidaanvastaustenlistaan.

3:n testiarvo ei ole alle 2.5, joten sitä

vastaava Arvo_Jos_epätosi-elementti 10 kopioidaanvastaustenlistaan.

Arvo_Jos_tosi on yksittäinen arvo ja

vastaa mitä tahansa valittuasijaintia.

Arvoa Arvo_Jos_epätosi ei ole määritelty. Käytetäänmerkintää EiMäär

94 Lue ttelo aakkosjärjestyksess ä

ifFn()

Huomaa: Jos sievennetty BoolenLaus

ilmaisu sisältää listan tai matriisin, kaikkien muiden lista- tai matriisiargumenttien on oltava samansuuruisia, ja myös tuloksen on oltava samansuuruinen.

Luettelo >

Yksi elementti valittulausekkeestaArvo_

Jos_tosi. Yksi elementti valittu lausekkeesta Arvo_Jos_epätosi.

imag()

imag(Expr1) ⇒ lauseke

Laskee argumentin imaginaarisen osan.

Huomaa: Kaikkia määrittelemättömiä

muuttujia käsitellään reaalimuuttujina. Katso myös real(), page 154

imag(Lista1) ⇒ lista

Laskee listan alkutekijöiden imaginaarisista osista.

imag(Matriisi1) ⇒ matriisi

Laskee matriisin alkutekijöiden imaginaarisista osista.

impDif()

impDif(Yhtälö, Muutt, riippuvaMuutt

[,Aste]) ⇒ lauseke

jossa luokan Aste oletusarvo on 1

Laskee implisiittisen derivaatan yhtälöille, joissa yksi muuttuja määritellään implisiittisesti toisen suhteen

Luettelo >

Epäsuora operaattori

inString()

inString(srcMerkkijono, alaMerkkijono[,

Alku]) ⇒ kokonaisluku

Katso #(), sivu 239.

Luettelo >

Luettelo aakkosjärjestyksessä 95

inString()

Laskee merkin paikan merkkijonossa

srcMerkkijono, jossa merkkijonon alaMerkkijono ensimmäinen esiintyminen

alkaa.

Alku, jos se sisältyy, määrää merkin paikan

siinä merkkijonossa srcMerkkijono, josta haku alkaa. Oletusarvo = 1 (srcMerkkijonon ensimmäinen merkki).

Jos srcMerkkijono ei sisällä

alaMerkkijonoa tai Alku on srcMerkkijonon pituus, vastaus on nolla.

Luettelo >

int()

int(Laus) ⇒ kokonaisluku

int(Lista1) ⇒ lista int(Matriisi1) ⇒ matriisi

Laskee suurimman kokonaisluvun, joka on pienempi tai yhtä suuri kuin argumentti. Tämä funktio on identtinen funktion pohjan

floor() kanssa.

Argumentti voi olla reaali- tai kompleksiluku.

Kun kyseessä on lista tai matriisi, laskee kunkin elementin suurimman kokonaisluvun.

intDiv()

intDiv(Luku1, Luku2) ⇒ kokonaisluku intDiv(Lista1, Lista2) ⇒ lista intDiv(Matriisi1, Matriisi2) ⇒ matriisi

Laskee lausekkeen Luku1 ÷ Luku2) etumerkillisen kokonaislukuosan.

Laskee sarjoille ja matriiseille lausekkeen (argumentti1÷argumentti2) etumerkillisen kokonaislukuosan kullekin elementtiparille.

Luettelo >

96 Lue ttelo aakkosjärjestyksess ä

Texas Instruments TI-Nspire CX CAS Reference Guide [fi]

Specifications and Main Features

Frequently Asked Questions

User Manual

Tärkeitä tietoja

Lausekemallit

Luettelo aakkosjärjestyksessä