Texas Instruments TI-Nspire CX CAS Reference Guide [es]

TI-Nspire™CAS

Guía de Referencia

Esta guía corresponde a la versión 4.5 del software TI-Nspire™. Para obtener la versión más reciente de la documentación, visite el sitio education.ti.com/go/download

Información importante

Excepto por lo que se establezca expresamente en contrario en la Licencia que se incluye con el programa, Texas Instruments no otorga ninguna garantía, ni expresa ni implícita, incluidas pero sin limitarse a cualquier garantía implícita de comerciabilidad e idoneidad con un propósito en particular, en relación con cualquier programa o material impreso, y hace dichos materiales disponibles únicamente "tal y como se encuentran". En ningún caso Texas Instruments será responsable en relación con ninguna persona de daños especiales, colaterales, incidentales o consecuenciales en conexión con o que surjan de la compra o el uso de estos materiales, y la responsabilidad única y exclusiva de Texas Instruments, independientemente de la forma de acción, no excederá la cantidad estipulada en la licencia para el programa. Asimismo, Texas Instruments no será responsable de ninguna reclamación de ningún tipo en contra del uso de estos materiales por parte de cualquier otro individuo.

Licencia

Favor de ver la licencia completa instalada en

C:\ProgramFiles\TIEducation\<TI-Nspire™ Product Name>\license.

Índice de contenido

Información importante

Plantillas de expresiones 1

Listado alfabético 8

A B C D E F G I L M N O P Q R S T U V W X Z

17 21 48 62 72 82

93 102 119 128 138 140 150 153 169 196 212 213 214 216 217

iii

Símbolos 226

Elementos vacíos (inválidos) 253

Accesos directos para ingresar expresiones matemáticas 255

Jerarquía de EOS™ (Sistema Operativo de Ecuaciones) 257

Constantes y valores 259

Códigos y mensajes de error 260

Códigos y mensajes de advertencia 269

Soporte y Servicio 271

Soporte y Servicio de Texas Instruments

271

Índice alfabético 272

Plantillas de expresiones

Las plantillas de expresiones ofrecen una manera fácil de ingresar expresiones matemáticas en una notación matemática estándar. Cuando se inserta una plantilla, ésta aparece en la línea de ingreso con pequeños bloques en las posiciones donde se pueden ingresar elementos. Un cursor muestra cuál elemento se puede ingresar.

Use las teclas de flechas o presione e para mover el cursor a cada posición del elemento, y escriba un valor o una expresión para el elemento. Presione · o

/· para evaluar la expresión.

Plantilla de fracciones

Nota: Vea también / (dividir), página

228.

Plantilla de exponentes

Nota: Escriba el primer valor, presione l y

después escriba el exponente. Para regresar el cursor a la línea base, presione la flecha

derecha (¢).

Nota: Vea también ^ (potencia), página

229.

Plantilla de raíz cuadrada

Nota: Vea también ‡() (raíz cuadrada),

página 239.

/p teclas

Ejemplo:

l teclas

Ejemplo:

/q teclas

Ejemplo:

Plantilla de raíz enésima

Nota: Vea también root(), página 165.

/l teclas

Ejemplo:

Plantillas de expresiones 1

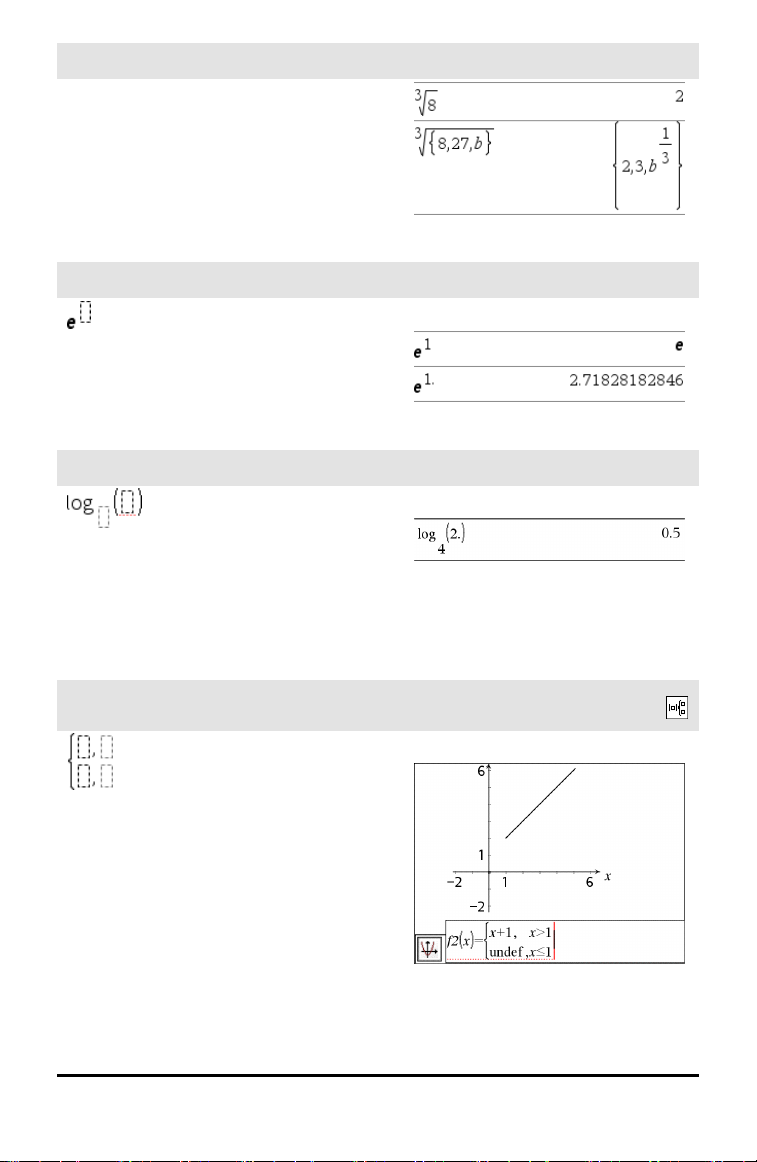
Plantilla de raíz enésima

/l teclas

e plantilla de exponentes

Exponecial natural e elevado a una potencia

Nota: Vea también e^(), página 62.

Plantilla de logística

Calcula la logística para una base especificada. Para un predeterminado de base 10, omitir la base.

Nota: Vea también logístic(), página 115.

Plantilla de compuesto de variables (2 piezas)

Permite crear expresiones y condiciones para una función de compuesto de variables de dos-piezas. Para agregar una pieza, haga clic en la plantilla y repita la plantilla.

Nota: Vea también piecewise(), página 142.

u tecla

Ejemplo:

/s tecla

Ejemplo:

Catálogo >

Ejemplo:

2 Plantillas de expresiones

Plantilla de compuesto de variables (N piezas)

Permite crear expresiones y condiciones para una función de compuesto de variables de N-piezas. Indicadores para N.

Nota: Vea también piecewise(), página 142.

Catálogo >

Ejemplo:

Vea elejemplo de plantilla de compuesto de variables(2 piezas).

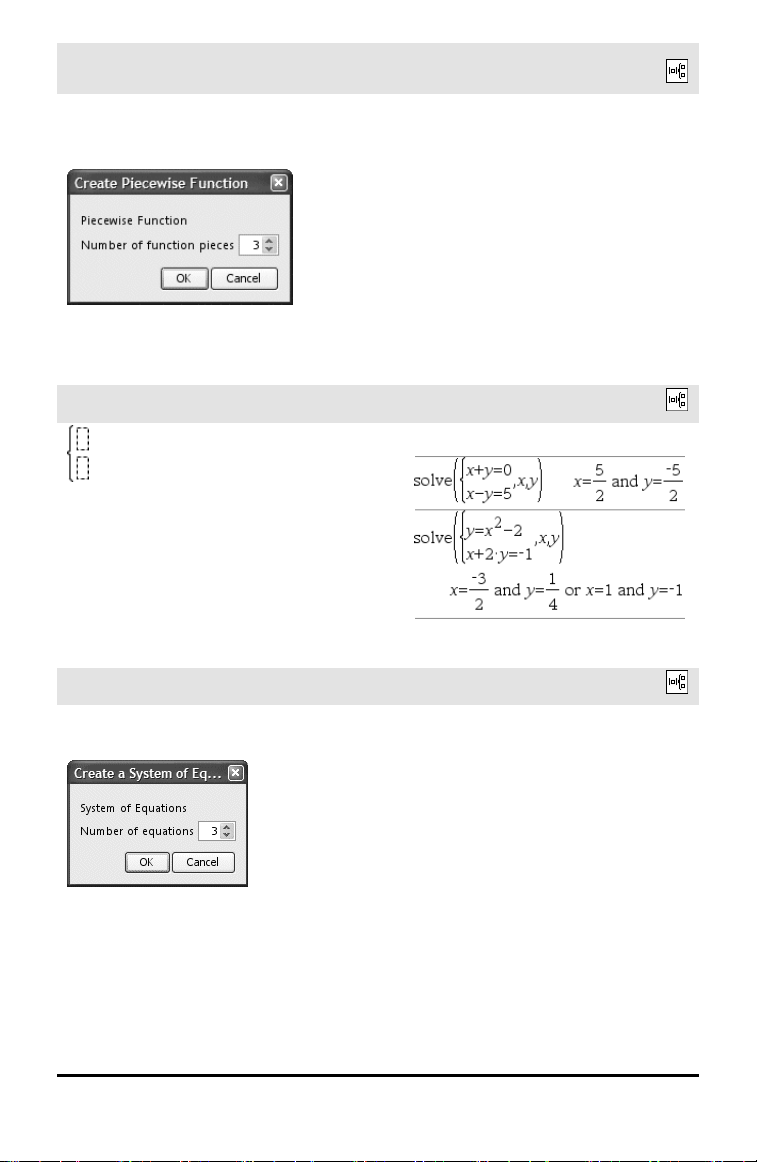
Sistema de plantilla de 2 ecuaciones

Crea un sistema de dos lineales. Para agregar una fila a un sistema existente, haga clic en la plantilla y repita la plantilla.

Nota: Vea también system(), página 195.

Sistema de plantilla de N ecuaciones

Permite crear un sistema de Nlineales. Indicadores para N.

Nota: Vea también system(), página 195.

Catálogo >

Ejemplo:

Catálogo >

Ejemplo:

Vea elejemplo de Sistema de plantilla de ecuaciones (2piezas).

Plantillas de expresiones 3

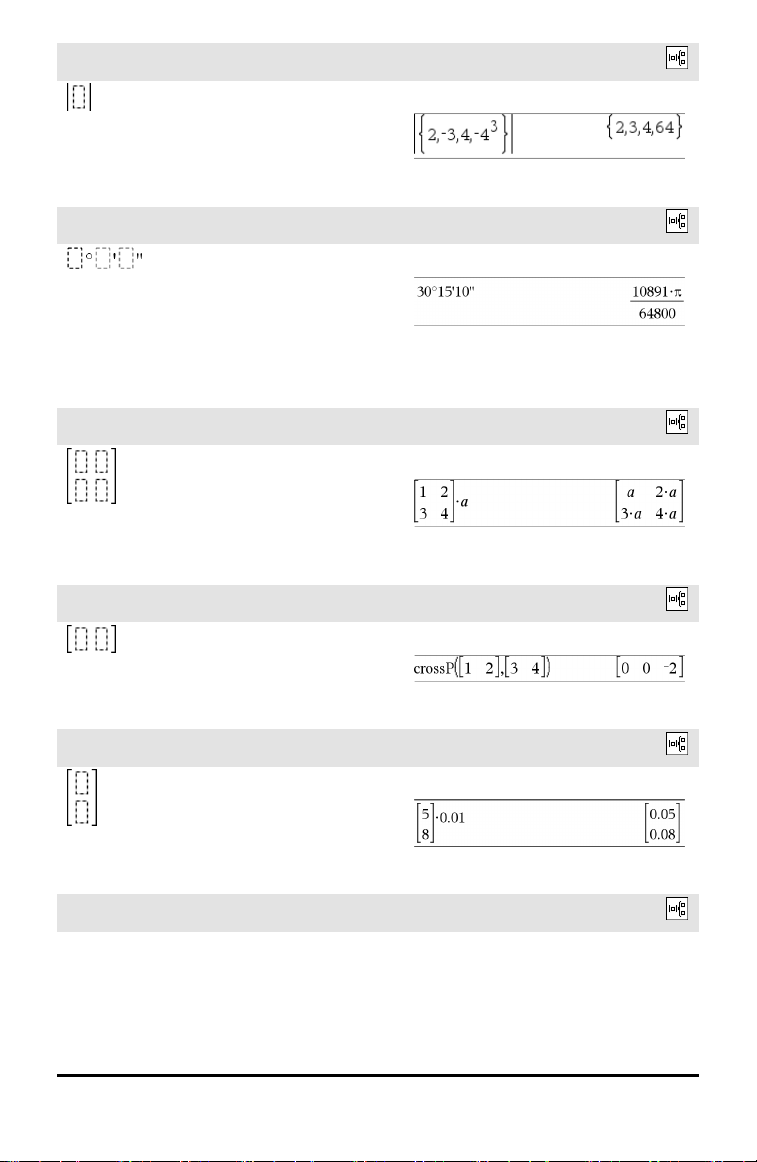
Plantilla de valor absoluto

Nota: Vea también abs(), página 8.

Catálogo >

Ejemplo:

plantilla gg°mm’ss.ss’’

Permite ingresar ángulos en el formato

gg°mm’ss.ss’’, donde gg es el número de

grados decimales, mm es el número de minutos y ss.ss es el número de segundos.

Plantilla de matriz (2 x 2)

Crea una matriz de 2 x 2

Plantilla de matriz (1 x 2)

Plantilla de matriz (2 x 1)

Catálogo >

Ejemplo:

Catálogo >

Ejemplo:

Catálogo >

Ejemplo:

Catálogo >

Ejemplo:

Plantilla de matriz (m x n)

La plantilla aparece después de que se le indica especificar el número de filas y columnas.

4 Plantillas de expresiones

Catálogo >

Ejemplo:

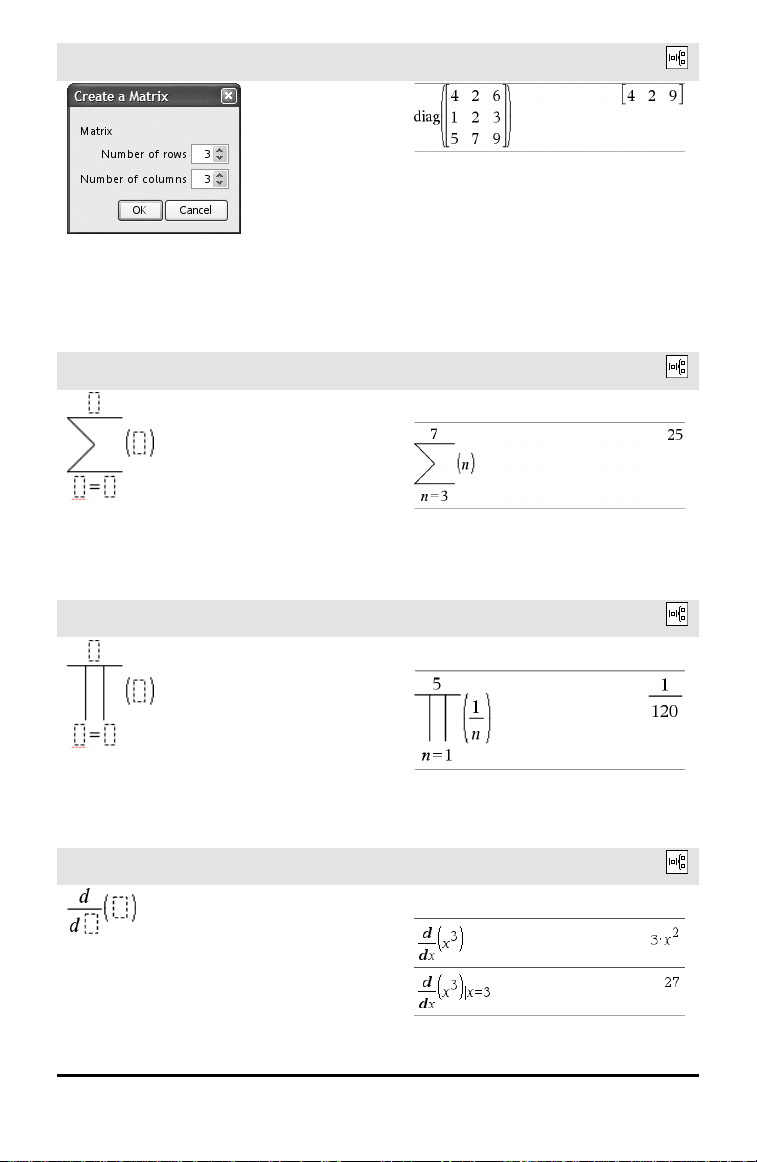
Plantilla de matriz (m x n)

Nota: Si se crea una matriz con un número

grande de filas y columnas, puede llevarse unos cuantos segundos en aparecer.

Catálogo >

Plantilla de suma (G)

Nota: Vea también G() (sumaSec), página

241.

Plantilla de producto (Π)

Nota: Vea también Π() (prodSec), página

240.

Plantilla de primera derivada

Catálogo >

Ejemplo:

Catálogo >

Ejemplo:

Catálogo >

Ejemplo:

La plantilla de primera derivada también se puede usar para calcular la primera derivada en un punto.

Plantillas de expresiones 5

Plantilla de primera derivada

Nota: Vea también d() (derivada), página

237.

Catálogo >

Plantilla de segunda derivada

La plantilla de segunda derivada también se puede usar para calcular la segunda derivada en un punto.

Nota: Vea también d() (derivada), página

237.

Plantilla de enésima derivada

La plantilla de enésima derivada se puede usar para calcular la enésima derivada.

Nota: Vea también d() (derivada), página

237.

Plantilla de integral definida

Catálogo >

Ejemplo:

Catálogo >

Ejemplo:

Catálogo >

Ejemplo:

Nota: Vea también ‰() integral(), página

238.

Plantilla de integral indefinida

Nota: Vea también ‰() integral(), página

238.

6 Plantillas de expresiones

Catálogo >

Ejemplo:

Plantilla de límite

Use N o (N) para el límite de la izquierda. Use + para el límite de la derecha.

Nota: Vea también limit(), página 104.

Catálogo >

Ejemplo:

Plantillas de expresiones 7

Listado alfabético

Los elementos cuyos nombres no son alfabéticos (como +, ! y >) se enumeran al final de esta sección, comenzando (página 226). A menos que se especifique lo contrario, todos los ejemplos en esta sección se realizaron en el modo de reconfiguración predeterminado, y se supone que todas las variables no están definidas.

abs()

abs(Expr1)⇒expresión abs(Lista1)⇒lista abs(Matriz1)⇒matriz

Entrega el valor absoluto del argumento.

Nota: Vea también Plantilla de valor absoluto, página 4.

Si el argumento es un número complejo, entrega el módulo del número.

Nota: Todas las variables indefinidas se

tratan como variables reales.

amortTbl() (tablaAmort)

amortTbl(NPgo,N,I,VP, [Pgo], [VF], [PpA], [CpA], [PgoAl], [valorRedondo])

⇒matriz

La función de amortización que entrega una matriz como una tabla de amortización para un conjunto de argumentos de TVM.

NPgo es el número de pagos a incluirse en

la tabla. La tabla comienza con el primer pago.

N, I, VP, Pgo, VF, PpA, CpA, and PgoAl

se describen en la tabla de argumentos de VTD, página 210.

• Si se omite Pgo, se predetermina a

Pgo=tvmPmt

(N,I,VP,VF,PpA,CpA,PgoAl).

• Si se omite VF, se predetermina a VF=0.

• Los predeterminados para PpA, CpAy

Catálogo >

8 Listado alfabético

amortTbl() (tablaAmort)

PgoAl son los mismos que para las

funciones de TVM.

valorRedondo especifica el número de

lugares decimales para el redondeo. Predeterminado=2.

Las columnas en la matriz de resultado están en este orden: Número de pago, cantidad pagada a interés, cantidad pagada a capital y balance.

El balance desplegado en la fila n es el balance después del pago n.

Se puede usar la matriz de salida como entrada para las otras funciones de amortización GInt() y GPrn(), página 241y

bal(), página 17.

Catálogo >

and (y)

ExprBooleana1 and ExprBooleana2⇒expresión Booleana

ListaBooleana1 and ListaBooleana2⇒Lista Booleana

MatrizBooleana1 and MatrizBooleana2⇒Matriz Booleana

Entrega verdadero o falso o una forma simplificada del ingreso original.

Entero1andEntero2⇒entero

Compara dos enteros reales bit por bit usando una operación y . En forma interna, ambos enteros se convierten en números binarios de 64 bits firmados. Cuando se comparan los bits correspondientes, el resultado es 1 si ambos bits son 1; de otro modo, el resultado es 0. El valor producido representa los resultados de los bits, y se despliega de acuerdo con el modo de Base.

Catálogo >

En modo de base hexadecimal:

Importante: Cero, no la letra O.

En modo de base binaria:

En modo de base decimal:

Listado alfabético 9

and (y)

Se pueden ingresar enteros en cualquier base de números. Para un ingreso binario o hexadecimal, se debe usar el prefijo 0b ó 0h, respectivamente. Sin un prefijo, los enteros se tratan como decimales (base10).

Catálogo >

Nota: Un ingreso binario puede tener hasta

64 dígitos (sincontar el prefijo 0b). Un ingreso hexadecimalpuede tener hasta 16 dígitos.

angle()

angle(Expr1)⇒expresión

Entrega el ángulo del argumento, interpretando el argumento como un número complejo.

Nota: Todas las variables indefinidas se

tratan como variables reales.

angle(Lista1)⇒lista angle(Matriz1)⇒matriz

Entrega una lista o matriz de ángulos de los elementos en Lista1 o Matriz1, interpretando cada elemento como un número complejo que representa un punto de coordenada bidimensional o rectangular.

Catálogo >

En modo de ángulo enGrados:

En modo de ángulo enGradianes:

En modo de ángulo enRadianes:

ANOVA

ANOVA Lista1,Lista2[,Lista3,...,Lista20] [,Bandera]

10 Listado alfabético

Catálogo >

ANOVA

Catálogo >

Realiza un análisis unidireccional de la varianza para comparar las medias de dos a 20 poblaciones. Un resumen de resultados se almacena en la variable stat.results (página 190).

Bandera=0 para Datos, Bandera=1 para

Estadísticas

Variable de salida Descripción

stat.F Valor de F estadístico

stat.ValP Nivel más bajo de significanciaen el cual la hipótesis nulase puederechazar

stat.df Grados de libertadde los grupos

stat.SS Suma de cuadrados de los grupos

stat.MS Cuadrados medios de los grupos

stat.dfError Grados de libertadde los errores

stat.SSError Suma de cuadrados de los erro res

stat.MSError Cuadrado medio de los errores

stat.sp Desviación estándar agrupada

stat.xbarlista Mediade la entrada de las listas

stat.ListaCBajo 95%de intervalos de confianzapara la mediade cada lista de entrada

stat.ListaCAlto 95%de intervalos de confianzapara la mediade cada lista de entrada

ANOVA2way (ANOVA2vías)

ANOVA2way Lista1,Lista2

[,Lista3,…,Lista10][,LevRow]

Genera un análisis bidireccional de la varianza para comparar las medias de dos a 10 poblaciones. Un resumen de resultados se almacena en la variable stat.results (página 190).

LevRow=0 para bloque LevRow=2,3,...,Len-1, para factor dos,

donde Len=largo(Lista1)=largo(Lista2) = … = largo(Lista10) y Len/LevRow ∈ {2,3,…}

Salidas: Diseño de bloque

Catálogo >

Listado alfabético 11

Variable de salida Descripción

stat.F F estadístico del factor de columna

stat.ValP Nivel más bajo de significanciaen el cual la hipótesis nulase puederechazar

stat.df Grados de libertaddel factor de columna

stat.SS Suma de cuadrados delfactor decolumna

stat.MS Cuadrados medios para el factor de columna

stat.BloqF F estadístico para el factor

stat.BloqValP Probabilidad más baja a la cual la hipótesis nula se puederechazar

stat.dfBloque Grados delibertaddelfactor

stat.SSBloque Suma de cuadrados para elfactor

stat.MSBloque Cuadrados medios para el factor

stat.dfError Grados de libertadde los errores

stat.SSError Suma de cuadrados de los erro res

stat.MSError Cuadrados medios para los errores

stat.s Desviación estándar delerror

Salidas del FACTOR DE COLUMNA

Variable de salida Descripción

stat.Fcol F estadístico del factor de columna

stat.ValPCol Valor de probabilidaddelfactor decolumna

stat.dfCol Grados de libertaddel factor de columna

stat.SSCol Suma de cuadrados delfactor decolumna

stat.MSCol Cuadrados medios para el factor de columna

Salidas del FACTOR DE FILAS

Variable de salida Descripción

stat.FFila F estadístico del factor de fila

stat.ValPFila Valor deprobabilidad del factor de fila

stat.dfFila Grados de libertaddel factor de fila

stat.SSFila Suma de cuadrados delfactor defila

stat.MSFila Cuadrados medios para el factor de fila

12 Listado alfabético

Salidas de INTERACCIÓN

Variable de salida Descripción

stat.FInterac F estadístico de la interacción

stat.ValPInterac Valor de probabilidadde la interacción

stat.dfInterac Grados de libertad de la interacción

stat.SSInterac Suma de cuadrados de la interacción

stat.MSInterac Cuadrados medios para la interacción

Salidas de ERROR

Variable de salida Descripción

stat.dfError Grados de libertad de los errores

stat.SSError Suma de cuadrados de los errores

stat.MSError Cuadrados medios para los errores

s Desviación estándar delerror

Ans

Ans⇒valor

Entrega el resultado de la expresión evaluada más recientemente.

approx()

approx(Expr1)⇒expresión

Entrega la evaluación del argumento como una expresión que contiene valores decimales, cuando es posible, independientemente del modo Auto o

Aproximado actual.

Esto es equivalente a ingresar el argumento y presionar /·.

approx(Lista1)⇒lista approx(Lista1)⇒lista

/v teclas

Catálogo >

Listado alfabético 13

approx()

Entrega una lista o matriz donde cada elemento se ha evaluado a un valor decimal, cuando es posible.

Catálogo >

4approxFraction()

Expr 4approxFraction([Tol])⇒expresión Lista 4approxFraction([Tol])⇒lista Matriz 4approxFraction([Tol])⇒matriz

Entrega la entrada como una fracción, usando una tolerancia de Tol. Si Tol se omite, se usa una tolerancia de 5.E-14.

Nota: Se puede insertar esta función desde

el teclado de la computadora al escribir

@>approxFraction(...).

approxRational()

approxRational(Expr[, Tol])⇒expresión approxRational(Lista[, Tol])⇒lista approxRational(Matriz[, Tol])⇒matriz

Entrega el argumento como una fracción usando una tolerancia de Tol. Si Tol se omite, se usa una tolerancia de 5.E-14.

arccos()

Catálogo >

Vea cos/(), página 33.

arccosh()

arccot()

14 Listado alfabético

Vea cosh/(), página 34.

Vea cot/(), página 35.

arccoth()

Vea coth/(), página 36.

arccsc()

arccsch()

arcLen()

arcLen(Expr1,Var,Iniciar,Terminar)

⇒expresión

Entrega la longitud de arco de Expr1 desde

Iniciar a Terminar con respecto de la

variable Var.

La longitud de arco se calcula como una integral suponiendo una definición de modo de función.

arcLen(Lista1,Var,Iniciar,Terminar)

⇒lista

Entrega una lista de longitudes de arco de cada elemento de Lista1 desde Iniciar hasta Terminar con respecto de Var.

arcsec()

Vea csc/(), página 39.

Vea csch/(), página 39.

Catálogo >

Vea sec/(), página 169.

arcsech()

arcsin()

Vea sech(), página 170.

Vea sin(), página 180.

Listado alfabético 15

arcsinh()

Vea sinh(), página 181.

arctan()

arctanh()

augment()

augment(Lista1, Lista2)⇒lista

Entrega una nueva lista que es Lista2 adjuntada al final de Lista1.

augment(Matriz1, Matriz2)⇒matriz

Entrega una nueva matriz que es Matriz2 adjuntada a Matriz2. Cuando se usa el caracter “,” las matrices deben tener dimensiones de fila iguales, y Matriz2 se adjunta a Matriz1 como nuevas columnas. No altera Matriz1 o Matriz2.

avgRC()

avgRC(Expr1, Var [=Valor] [, Paso])

⇒expresión

Vea tan(), página 197.

Vea tanh(), página 198.

Catálogo >

avgRC(Expr1, Var [=Valor] [, Lista1])

⇒lista

avgRC(Lista1, Var [=Valor] [, Paso])

⇒lista

avgRC(Matriz1, Var [=Valor] [, Paso])

⇒matriz

Entrega el cociente diferencial progresivo (tasa de cambio promedio).

Expr1 puede ser un nombre de función

definido por el usuario (vea Func).

16 Listado alfabético

avgRC()

Cuando se especifica el Valor, se eliminan todas las asignaciones anteriores de la variable o cualquier sustitución "|" para la variable.

Paso es el valor del paso. Si se omite Paso

se predetermina a 0.001.

Tome en cuenta que la función similar

centralDiff() usa el cociente diferencial

central.

Catálogo >

bal()

bal(NPgo,N,I,VP ,[Pgo], [VF], [PpA], [CpA], [PgoAl], [valorRedondo])⇒valor

bal(NPgo,tablaAmort)⇒valor

Función de amortización que calcula el balance del programa después de un pago especificado.

N, I, VP, Pgo, VF, PpA, CpAy PgoAl se

describen en la tabla de argumentos de VTD, página 210.

NPgo especifica el número de pago

después del cual usted desea que los datos se calculen.

N, I, VP, Pgo, VF, PpA, CpAy PgoAl se

describen en la tabla de argumentos de VTD, página 210.

• Si se omite Pgo, se predetermina a

Pgo=tvmPmt

(N,I,VP,VF,PpA,CpA,PgoAl).

• Si se omite VF, se predetermina a VF=0.

• Los predeterminados para PpA, CpAy

PgoAl son los mismos que para las

funciones de VTD.

valorRedondo especifica el número de

lugares decimales para el redondeo. Predeterminado=2.

Catálogo >

Listado alfabético 17

bal()

bal(NPgo,tablaAmort) calcula el balance

después del número de pago NPgo, basado en la tabla de amortización tablaAmort. El argumento tablaAmort debe ser una matriz en la forma descrita bajo amortTbl(), página 8.

Nota: Vea también GInt() y GPrn(), página

241.

Catálogo >

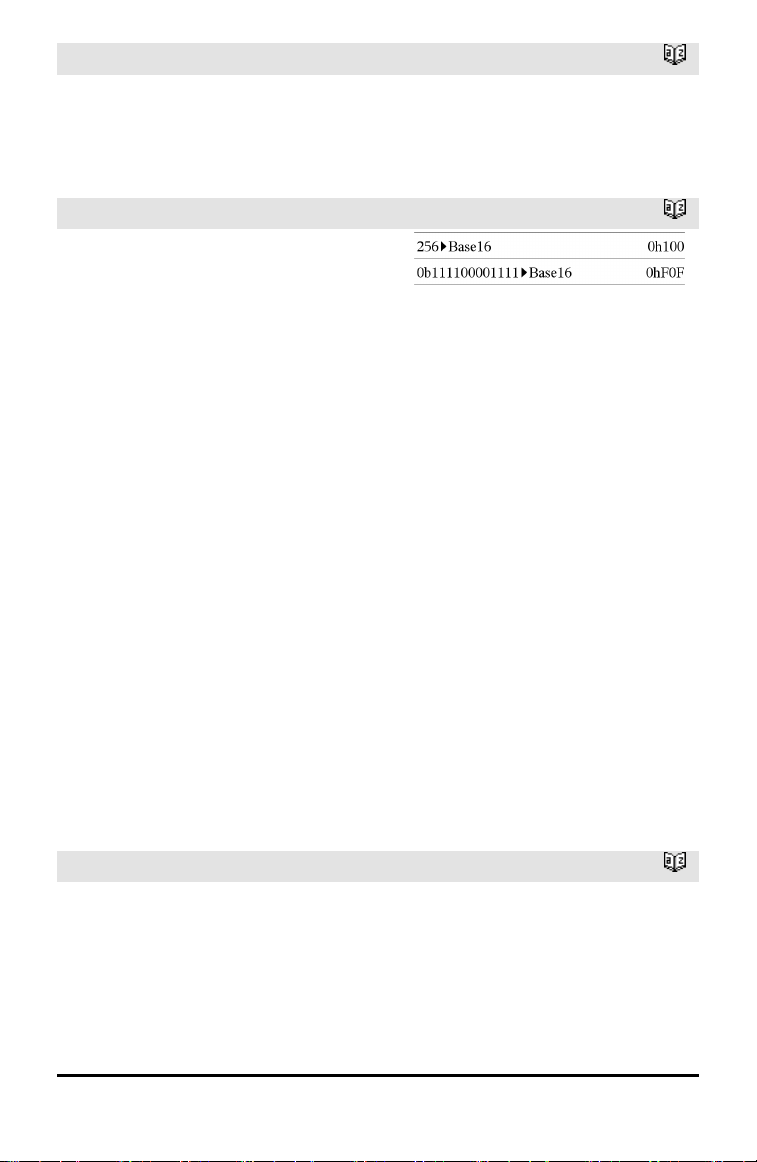
4Base2

Entero1 4Base2⇒entero

Nota: Se puede insertar este operador

desde el teclado de la computadora al escribir @>Base2.

Convierte Entero1 en un número binario. Los número binarios o hexadecimales siempre tienen un prefijo 0b ó 0h, respectivamente. Cero, no la letra O, seguida de b o de h.

0b númeroBinario 0h númeroHexadecimal

Un número binario puede tener hasta 64 dígitos. Un número hexadecimal puede tener hasta 16.

Sin un prefijo, Entero1 se trata como decimal (base10). El resultado se despliega en binario, independientemente del modo de la Base.

Los números negativos se despliegan en forma de "complemento de dos". Por ejemplo:

N1se despliega como 0hFFFFFFFFFFFFFFFFen modo de base Hexadecimal 0b111...111 (641’s)en modo de base Binaria

N263se despliega como 0h8000000000000000en modo de base Hexadecimal 0b100...000 (63 ceros)en modo de base Binaria

Catálogo >

18 Listado alfabético

4Base2

Si se ingresa un entero decimal que está fuera del rango de una forma binaria de 64 bits firmada, se usa una operación de módulo simétrico para llevar el valor al rango apropiado. Considere los siguientes ejemplos de valores fuera del rango.

263se convierte en N263y se despliega como 0h8000000000000000en modo de base Hexadecimal 0b100...000 (63 ceros) en modo de base Binaria

264se convierte en 0 y se despliega como 0h0en modo de base Hexadecimal 0b0en modo de base Binaria

N263N 1 se convierte en 263N 1 y se despliega como 0h7FFFFFFFFFFFFFFFen modo de base Hexadecimal 0b111...111 (641’s)en modo de base Binaria

Catálogo >

4Base10

Entero1 4Base10⇒entero

Nota: Se puede insertar este operador

desde el teclado de la computadora al escribir @>Base10.

Convierte Integer1 en un número decimal (base10). El ingreso binario o hexadecimal siempre debe tener un prefijo 0b ó 0h, respectivamente.

0b númeroBinario 0h númeroHexadecimal

Cero, no la letra O, seguida de b o de h.

Un número binario puede tener hasta 64 dígitos. Un número hexadecimal puede tener hasta 16.

Catálogo >

Listado alfabético 19

4Base10

Sin un prefijo, Integer1 se trata como decimal. El resultado se despliega en decimal, independientemente del modo de la Base.

Catálogo >

4Base16

Entero1 4Base16⇒entero

Nota: Se puede insertar este operador

desde el teclado de la computadora al escribir @>Base16.

Convierte Entero1 en un número hexadecimal. Los número binarios o hexadecimales siempre tienen un prefijo 0b ó 0h, respectivamente.

0b númeroBinario 0h númeroHexadecimal

Cero, no la letra O, seguida de b o de h.

Un número binario puede tener hasta 64 dígitos. Un número hexadecimal puede tener hasta 16.

Sin un prefijo, Integer1 se trata como decimal (base10). El resultado se despliega en hexadecimal, independientemente del modo de la Base.

Si se ingresa un entero decimal que es demasiado grande para una forma binaria de 64 bits firmada, se usa una operación de módulo simétrico para llevar el valor al rango apropiado. Para obtener más información, vea 4Base2, página 18.

Catálogo >

binomCdf()

binomCdf(n,p)⇒lista

binomCdf (n,p,límiteInferior,límiteSuperior)

⇒número si límiteInferior y

límiteSuperior son números, lista si límiteInferior y límiteSuperior son listas

20 Listado alfabético

Catálogo >

binomCdf()

binomCdf(n,p,límiteSuperior)para P(0{X

{límiteSuperior)⇒número si

límiteSuperior es un número, lista si límiteSuperior es una lista

Genera una probabilidad acumulativa para la distribución binómica discreta con n número de pruebas y probabilidad p de éxito en cada prueba.

Para P(X { límiteSuperior), configure

límiteInferior=0

Catálogo >

binomPdf()

binomPdf(n,p)⇒lista binomPdf(n,p,XVal)⇒número si XVal es un

número, lista si XVal es una lista

Genera una probabilidad para la distribución binómica discreta con n número de pruebas y probabilidad p de éxito en cada prueba.

ceiling() (techo)

ceiling(Expr1)⇒entero

Entrega el entero más cercano que es | el argumento.

El argumento puede ser un número real o complejo.

Nota: Vea también floor().

ceiling(Lista1)⇒lista ceiling(Matriz1)⇒matriz

Entrega una lista o matriz del techo de cada elemento.

Catálogo >

Listado alfabético 21

centralDiff()

centralDiff(Expr1,Var [=Valor][,Paso])

⇒expresión

centralDiff(Expr1,Var [,Paso]) |Var=Valor⇒expresión

centralDiff(Expr1,Var [=Valor][,Lista])

⇒lista

centralDiff(Lista1,Var [=Valor][,Paso])

⇒lista

centralDiff(Matriz1,Var [=Valor][,Paso])

⇒matriz

Entrega la derivada numérica usando la fórmula del cociente diferencial central.

Cuando se especifica el Valor, se eliminan todas las asignaciones anteriores de la variable o cualquier sustitución "|" para la variable.

Paso es el valor del paso. Si se omite Paso

, se predetermina a 0.001. Al usar Lista1 o Matriz1, la operación se

mapea a lo largo de los valores en la lista y a lo largo de los elementos de la matriz.

Nota: Vea también avgRC() y d().

Catálogo >

cFactor()

cFactor(Expr1[,Var])⇒expresión cFactor(Lista1[,Var])⇒lista cFactor(Matriz1[,Var])⇒matriz

cFactor(Expr1) entrega Expr1 factorizado

con respecto de todas sus variables sobre un denominador común.

22 Listado alfabético

Catálogo >

cFactor()

Expr1 se factoriza tanto como es posible

hacia los factores racionales lineales, incluso si esto introduce nuevos número no reales Esta alternativa es apropiada si se desea una factorización con respecto de más de una variable.

cFactor(Expr1,Var) entrega Expr1

factorizado con respecto de la variable Var.

Expr1 se factoriza tanto como es posible

hacia factores que son lineales en Var, quizá con constantes no reales, incluso si esto introduce constantes irracionales o subexpresiones que son irracionales en otras variables.

Los factores y sus términos se clasifican con

Var como la variable principal. Se recopilan

potencias similares de Var en cada factor. Incluya Var si se necesita la factorización con respecto de sólo esa variable y usted está dispuesto a aceptar expresiones irracionales en otras variables para incrementar la factorización con respecto de Var. Podría haber cierta factorización incidental con respecto de otras variables.

Para la configuración automática del modo

Auto o Aproximado , incluyendo Var ,

también permite la aproximación con coeficientes de punto flotante, donde los coeficientes irracionales no se pueden expresar en forma explícita concisamente en términos de funciones integradas. Incluso cuando hay sólo una variable, incluyendo Var , puede producir una factorización más completa.

Nota: Vea también factor().

Catálogo >

Para ver elresultado completo, presione £ y después use¡ y ¢ para mover el cursor.

char()

char(Entero)⇒caracter

Entrega una cadena de caracteres que contiene el caracter numerado Entero desde el conjunto de caracteres del dispositivo portátil. El rango válido para

Entero es 0–65535.

Catálogo >

Listado alfabético 23

charPoly()

charPoly(matrizCuadrada,Var)⇒expresión

polinómica

charPoly(matrizCuadrada,Expr)

⇒expresión polinómica

charPoly(matrizCuadrada1,Matriz2)

⇒expresión polinómica

Entrega el polinomio característico de

matrizCuadrada. El polinomio

característico de n×n matriz A, denotado por pA(l), es el polinomio definido por

(l) = det(l• I NA)

donde I denota la matriz de identidad n×n .

matrizCuadrada1 y matrizCuadrada2

deben tener dimensiones iguales.

Catálogo >

2way

Catálogo >

c22way matrizObs

chi22way matrizObs

Resuelve una prueba c2para la asociación en la tabla bidireccional de conteos en la matriz observada matrizObs. Un resumen de resultados se almacena en la variable

stat.results (página 190).

Para obtener información sobre el efecto de los elementos vacíos en una matriz, vea “Elementos vacíos (inválidos)” (página 253).

Variable de salida Descripción

stat.c

stat.ValP Nivel más bajo de significancia enel cual la hipótesis nulase puede rechazar

stat.df Grados de libertadpara las estadísticas cuadradasde ji

stat.ExpMat Matriz de tablade conteo elementalesperada, suponiendo una hipótesis nula

stat.CompMat Matriz de contribuciones deestadísticas cuadradasde ji elementales

Estadísticascuadradas de Ji: suma (observada - esperada)2/esperada

24 Listado alfabético

Cdf()

c2Cdf(límiteInferior,límiteSuperior,df)

⇒número si límiteInferior y

límiteSuperior son números, lista si límiteInferior y límiteSuperior son listas

chi2Cdf(límiteInferior,límiteSuperior,df)

⇒número si límiteInferior y

límiteSuperior son números, lista si límiteInferior y límiteSuperior son listas

Genera la probabilidad de distribución c

entre límiteInferior y límiteSuperior para grados específicos de libertad df.

Para P(X { límiteSuperior), configure

límiteInferior = 0.

Para obtener información sobre el efecto de los elementos vacíos en una lista, vea “Elementos vacíos (inválidos)” (página 253).

Catálogo >

GOF

Catálogo >

c2GOF listaObs,listaExp,df

chi2GOF listaObs,listaExp,df

Realiza una prueba para confirmar que los datos de la muestra son de una población que cumple con una distribución especificada. listaObs es una lista de conteos y debe contener enteros. Un resumen de resultados se almacena en la variable stat.results (página 190).

Para obtener información sobre el efecto de los elementos vacíos en una lista, vea “Elementos vacíos (inválidos)” (página 253).

Variable de salida Descripción

stat.c

stat.ValP Nivel más bajo de significanciaen el cual la hipótesis nulase puederechazar

stat.df Grados de libertadpara las estadísticas cuadradasde ji

stat.ListaComp Contribuciones de estadísticas cuadradas dejielementales

Estadísticascuadradas de Ji: suma((observada - esperada)2/esperada

Listado alfabético 25

Pdf()

Pdf(XVal,df)⇒número si XVal es un

número, lista si XVal es una lista chi2Pdf(XVal,df)⇒número si XVal es un

número, lista si XVal es una lista

Genera la función de densidad de probabilidad (pdf) para la distribución c2a un valor especificado XVal para los grados de libertad especificados df.

Para obtener información sobre el efecto de los elementos vacíos en una lista, vea “Elementos vacíos (inválidos)” (página 253).

Catálogo >

ClearAZ (LimpiarAZ)

ClearAZ

Limpia todas las variables de caracter único en el espacio del problema actual.

Si una o más de las variables están bloqueadas, este comando despliega un mensaje de error y borra únicamente las variables no bloqueadas. Vea unLock,

página 212.

ClrErr (LimpErr)

ClrErr

Limpia el estado del error y configura

Codigerr de la variable del sistema a cero.

La cláusula Else del bloque Try...Else...EndTry debe usar ClrErr o PassErr. Si el error se debe procesar o ignorar, use ClrErr. Si no se sabe qué hacer con el error, use PassErr para enviarlo al siguiente manipulador de errores. Si no hay ningún otro manipulador de errores Try...Else...EndTry pendiente, el cuadro de diálogo de error se desplegará como normal.

Nota: Vea también PasErr, página 141, y Try,

página 205.

Catálogo >

Para consultar unejemplo de ClrErr, vea el Ejemplo 2 bajo el comando Try , página

206.

26 Listado alfabético

ClrErr (LimpErr)

Nota para introducir el ejemplo: Para

obtener instrucciones sobre cómo introducir las definiciones de programas y funciones en varias líneas, consulte la sección Calculadora de la guía del producto.

Catálogo >

colAugment()

colAugment(Matriz1, Matriz2)⇒matriz

Entrega una nueva matriz que es Matriz2 adjuntada a Matriz2. Las matrices deben tener dimensiones de columna iguales, y

Matriz2 se adjunta a Matriz1 como nuevas

filas. No altera Matriz1 o Matriz2.

colDim()

colDim(Matriz)⇒expresión

Entrega el número de columnas contenidas en Matriz.

Nota: Vea también rowDim().

colNorm()

colNorm(Matriz)⇒expresión

Entrega el máximo de las sumas de los valores absolutos de los elementos en las columnas en Matriz.

Nota: Los elementos de matriz indefinida

no están permitidos. Vea también rowNorm

().

Catálogo >

comDenom()

comDenom(Expr1[,Var])⇒expresión comDenom(List1[,Var])⇒lista comDenom(Matriz1[,Var])⇒matriz

Catálogo >

Listado alfabético 27

comDenom()

comDenom(Expr1) entrega una proporción

reducida de un numerador completamente expandido sobre un denominador completamente expandido.

comDenom(Expr1,Var) entrega una

proporción reducida del numerador y el denominador expandidos con respecto de

Var. Los términos y sus factores se

clasifican con Var como la variable principal. Se recopilan potencias similares de Var . Puede haber cierta factorización incidental de los coeficientes recopilados. Se compara para omitir Var, con frecuencia esto ahorra tiempo, memoria y espacio de pantalla, mientras que hace la expresión más comprensible. También hace que las operaciones subsiguientes en el resultado sean más rápidas y que haya menos probabilidad de que se agote la memoria.

Si Var no ocurre en Expr1, comDenom

(Expr1,Var) entrega una proporción

reducida de un numerador no expandido sobre un denominador no expandido. Por lo general, dichos resultados incluso ahorran más tiempo, memoria y espacio de pantalla. Tales resultados parcialmente factorizados también hacen que las operaciones subsiguientes en el resultado sean más rápidas y que haya mucho menos probabilidad de que se agote la memoria.

Incluso cuando no hay ningún denominador, la función comden es con frecuencia una manera rápida de lograr la factorización parcial si factor() es demasiado lento o si se agota la memoria.

Sugerencia: Ingrese esta definición de la

función comden() y pruébela en forma rutinaria como una alternativa para

comDenom() y factor().

Catálogo >

completeSquare ()

completeSquare(ExprOEcn, Var)

expresión o ecuación ⇒

completeSquare(ExprOEcn,

28 Listado alfabético

Catálogo >

completeSquare ()

Var^Potencia) expresión o ecuación ⇒

completeSquare(ExprOEcn, Var1, Var2

[,...])expresión o ecuación ⇒

completeSquare(ExprOEcn, {Var1, Var2

[,...]})expresión o ecuación ⇒

Convierte una expresión polinomial cuadrática de la forma a·x2+b·x+c en la forma a·(x-h)2+k

- o -

Convierte una ecuación cuadrática de la forma a·x2+b·x+c=d en la forma a·(x-h)2=k

El primer argumento debe ser una expresión o ecuación cuadrática en forma estándar con respecto del segundo argumento.

El Segundo argumento debe ser un término de una variable sencilla o un término de una variable sencilla elevado a una potencia racional, por ejemplo x, y2o z

La tercera y cuarta sintaxis intentan completar el cuadrado con respecto de las variables Var1, Var2 [,… ]).

(1/3)

Catálogo >

conj()

conj(Expr1)⇒expresión conj(Lista1)⇒lista conj(Matriz1)⇒matriz

Entrega el complejo conjugado del argumento.

Nota: Todas las variables indefinidas se

tratan como variables reales.

Catálogo >

Listado alfabético 29

constructMat()

constructMat (Expr,Var1,Var2,numFilas,numCols)

⇒matriz

Entrega una matriz basada en los argumentos.

Expr es una expresión en las variables Var1 y Var2. Los elementos en la matriz

resultante se forman al evaluar Expr para cada valor incrementado de Var1 y Var2.

Var1 se incrementa automáticamente

desde 1 a numFilas. Dentro de cada fila,

Var2 se incrementa desde 1 a numCols.

Catálogo >

CopyVar

CopyVar Var1, Var2

CopyVar Var1., Var2.

CopyVar Var1, Var2 copia el valor de la

variable Var1 a la variable Var2, creando

Var2 si es necesario. La variable Var1 debe

tener un valor. Si Var1 es el nombre de una función

existente definida por el usuario, copia la definición de esa función a la función Var2. La función Var1 se debe definir.

Var1 debe cumplir con los requisitos de

nombramiento de la variable o debe ser una expresión de indirección que se simplifica a un nombre de variable que cumple con los requisitos.

CopyVar Var1., Var2. copia todos los

miembros del grupo de la variable Var1. al grupo Var2. , creando Var2. si es necesario.

Catálogo >

30 Listado alfabético

CopyVar

Var1. debe ser el nombre de un grupo de

variables existente, como los resultados de las estadísticas stat.nn o las variables creadas usando la función LibShortcut() . Si

Var2. ya existe, este comando reemplaza

todos los miembros que son comunes para ambos grupos y agrega los miembros que no existen todavía. Si uno o más miembros de Var2. están bloqueados, todos los miembros de Var2. se dejan sin cambios.

Catálogo >

corrMat()

corrMat(Lista1,Lista2[,…[,Lista20]])

Genera la matriz de correlación para la matriz aumentada [Lista1, Lista2, ...,

Lista20].

4cos

Expr 4cos

Nota: Se puede insertar este operador

desde el teclado de la computadora al escribir @>cos.

Representa Expr en términos de coseno. Este es un operador de conversión de despliegue. Se puede usar únicamente al final de la línea de ingreso.

4cos reduce todas las potencias de sin(...) módulo 1Ncos(...)^2 de manera que cualquier potencia restante de cos(...) tiene exponentes en el rango (0, 2). Entonces, el resultado estará libre de sin(...) si y sólo si sin(...) ocurre en la expresión dada únicamente para potencias iguales.

Nota: Este operador de conversión no está

soportado en los modos de Ángulo en Grados o Gradianes. Antes de usarlo, asegúrese de que el modo de Ángulo está configurado a Radianes y que Expr no contiene referencias explícitas para ángulos en grados o gradianes.

Catálogo >

Listado alfabético 31

cos()

cos(Expr1)⇒expresión cos(Lista1)⇒lista

cos(Expr1) entrega el coseno del

argumento como una expresión.

cos(Lista1) entrega una lista de cosenos de

todos los elementos en Lista1.

Nota: El argumento se interpreta como un

ángulo en grados, gradianes o radianes, de acuerdo con la configuración del modo del ángulo actual. Se puede usar ¡,Go Rpara anular el modo de ángulo en forma temporal.

µ tecla

En modo de ángulo enGrados:

En modo de ángulo enGradianes:

En modo de ángulo enRadianes:

cos(matrizCuadrada1)⇒matrizCuadrada

Entrega el coseno de la matriz de

matrizCuadrada1. Esto no es lo mismo que

calcular el coseno de cada elemento.

Cuando una función escalar f(A) opera en

matrizCuadrada1 (A), el resultado se

calcula por medio del algoritmo:

Compute los valores propios (li) y los vectores propios (Vi) de A.

matrizCuadrada1 debe ser diagonalizable.

Asimismo, no puede tener variables simbólicas a las que no se ha asignado un valor.

Forme las matrices:

32 Listado alfabético

En modo de ángulo enRadianes:

cos()

Luego A = X B X/y f(A) = X f(B) X/. Por ejemplo, cos(A) = X cos(B) X/ donde:

cos(B) =

Todos los cálculos se realizan usando aritmética de punto flotante.

µ tecla

cos/()

cos/(Expr1)⇒expresión cos/(Lista1)⇒lista

cos/(Expr1) entrega el ángulo cuyo coseno

es Expr1 como una expresión.

cos/(Lista1) entrega una lista de cosenos

inversos de cada elemento de Lista1.

Nota: El resultado se entrega como un

ángulo en grados, gradianes o radianes, de acuerdo con la configuración del modo del ángulo actual.

Nota: Se puede insertar esta función desde

el teclado al escribir arccos(...).

cos/(matrizCuadrada1)⇒matrizCuadrada

Entrega el coseno inverso de la matriz de

matrizCuadrada1. Esto no es lo mismo que

calcular el coseno inverso de cada elemento. Para obtener información acerca del método de cálculo, consulte cos().

µ tecla

En modo de ángulo enGrados:

En modo de ángulo enGradianes:

En modo de ángulo enRadianes:

En el modo de ángulo enRadianes y el Formato Complejo Rectangular:

Listado alfabético 33

cos/()

matrizCuadrada1 debe ser diagonalizable.

El resultado siempre contiene números de punto flotante.

µ tecla

Para ver elresultado completo, presione £ y después use¡ y ¢ para mover el cursor.

cosh()

cosh(Expr1)⇒expresión cosh(Lista1)⇒lista

cosh(Expr1) entregael coseno hiperbólico del argumento como una expresión.

cosh(Lista1) entrega una lista de cosenos

hiperbólicos de cada elemento de Lista1.

cosh(matrizCuadrada1)⇒matrizCuadrada

Entrega el coseno hiperbólico de la matriz de matrizCuadrada1. Esto no es lo mismo que calcular el coseno hiperbólico de cada elemento. Para obtener información acerca del método de cálculo, consulte cos().

matrizCuadrada1 debe ser diagonalizable.

El resultado siempre contiene números de punto flotante.

cosh/()

cosh/(Expr1)⇒expresión cosh/(Lista1)⇒lista

Catálogo >

En modo de ángulo enGrados:

En modo de ángulo enRadianes:

Catálogo >

cosh/(Expr1) entrega el coseno hiperbólico

inverso del argumento como una expresión.

cosh/(Lista1) entrega una lista de cosenos

hiperbólicos inversos de cada elemento de

Lista1.

Nota: Se puede insertar esta función desde

el teclado al escribir arccosh(...).

cosh/(matrizCuadrada1)

⇒matrizCuadrada

34 Listado alfabético

En el modo de ángulo enRadianes y enel Formato Complejo Rectangular:

cosh/()

Entrega el coseno hiperbólico inverso de la matriz de matrizCuadrada1. Esto no es lo mismo que calcular el coseno hiperbólico inverso de cada elemento. Para obtener información acerca del método de cálculo, consulte cos().

matrizCuadrada1 debe ser diagonalizable.

El resultado siempre contiene números de punto flotante.

Catálogo >

Para ver elresultado completo, presione £ y después use¡ y ¢ para mover el cursor.

cot()

cot(Expr1) ⇒ expresión cot(Lista1) ⇒ lista

Entrega la cotangente de Expr1 o entrega una lista de cotangentes de todos los elementos en Lista1.

Nota: El argumento se interpreta como un

ángulo en grados, gradianes o radianes, de acuerdo con la configuración del modo del ángulo actual. Se puede usar ¡,Go R para anular el modo de ángulo en forma temporal.

cot/()

cot/(Expr1)⇒expresión cot/(Lista1)⇒lista

Entrega el ángulo cuya cotangente es

Expr1 o entrega una lista que contiene las

cotangentes inversas de cada elemento de

Lista1.

Nota: El resultado se entrega como un

ángulo en grados, gradianes o radianes, de acuerdo con la configuración del modo del ángulo actual.

Nota: Se puede insertar esta función desde

el teclado al escribir arccot(...).

µ tecla

En modo de ángulo enGrados:

En modo de ángulo enGradianes:

En modo de ángulo enRadianes:

µ tecla

En modo de ángulo enGrados:

En modo de ángulo enGradianes:

En modo de ángulo enRadianes:

Listado alfabético 35

coth()

coth(Expr1)⇒expresión coth(Lista1)⇒lista

Entrega la cotangente hiperbólica de Expr1 o entrega una lista de cotangentes hiperbólicas de todos los elementos de

Lista1.

Catálogo >

coth/()

coth/(Expr1)⇒expresión coth/(Lista1)⇒lista

Entrega la cotangente hiperbólica inversa de Expr1 o entrega una lista que contiene las cotangentes hiperbólicas inversas de cada elemento de Lista1.

Nota: Se puede insertar esta función desde

el teclado al escribir arccoth(...).

count()

count(Valor1oLista1 [,Valor2oLista2

[,...]])⇒valor

Entrega el conteo acumulado de todos los elementos en los argumentos que se evalúan a valores numéricos.

Cada argumento puede ser una expresión, valor, lista o matriz. Se puede mezclar tipos de datos y usar argumentos de varias dimensiones.

Para una lista, matriz o rango de celdas, cada elemento se evalúa para determinar si se debe incluir en el conteo.

Dentro de la aplicación Listas y Hoja de Cálculo, se puede usar un rango de celdas en lugar de cualquier argumento.

Los elementos vacíos (anulados) se ignoran. Para obtener más información sobre elementos vacíos, vea página 253.

Catálogo >

En el último ejemplo, sólo 1/2 y 3+4*i se cuentan. Los argumentos restantes, suponiendo que x no está definida, no se evalúana valores numéricos.

36 Listado alfabético

countif() (conteoSi)

countif(Lista,Criterios)⇒valor

Entrega el conteo acumulado de todos los elementos en Lista que cumplen con los

Criteriosespecificados. Los criterios pueden ser:

• Un valor, una expresión o una cadena. Por ejemplo, 3 cuenta sólo aquellos elementos en Lista que se simplifican al valor 3.

• Una expresión Booleana que contiene el símbolo ? como un marcador de posición para cada elemento. Por ejemplo, ?<5 cuenta sólo aquellos elementos en Lista que son menos de 5.

Dentro de la aplicación Listas y Hoja de Cálculo, se puede usar un rango de celdas en lugar de Lista.

Los elementos vacíos (anulados) en la lista se ignoran. Para obtener más información sobre elementos vacíos, vea página 253.

Nota: Vea también sumIf(), página 194, y frequency(), página 80.

Catálogo >

Cuenta elnúmero de elementos iguales a 3.

Cuenta elnúmero de elementos iguales a “dif.”

Cuenta elnúmero de elementos iguales a x; esteejemplo suponequela variablex es indefinida.

Cuenta 1y 3.

Cuenta 3, 5 y 7.

cPolyRoots() (RaícesPoliC)

cPolyRoots(Poli,Var)⇒lista cPolyRoots(ListaDeCoefs)⇒lista

La primera sintaxis, cPolyRoots(Poli,Var), entrega una lista de raíces complejas del polinomio Poli con respecto de la variable

Var. Poli debe ser un polinomio en una variable.

Cuenta 1, 3, 7 y 9.

Catálogo >

Listado alfabético 37

cPolyRoots() (RaícesPoliC)

La segunda sintaxis, cPolyRoots

(ListaDeCoefs), entrega una lista de raíces

complejas para los coeficientes en

ListaDeCoefs.

Nota: Vea también polyRoots(), página 146.

Catálogo >

crossP()

crossP(Lista1, Lista2)⇒lista

Entrega el producto cruzado de Lista1 y

Lista2 como una lista. Lista1 y Lista2 deben tener una dimensión

igual, y la dimensión debe ser 2 ó 3.

crossP(Vector1, Vector2)⇒vector

Entrega un vector de fila o columna (dependiendo de los argumentos) que es el producto cruzado de Vector1 y Vector2.

Tanto Vector1 como Vector2 deben ser vectores de fila, o ambos deben ser vectores de columna. Ambos vectores deben tener una dimensión igual, y la dimensión debe ser 2ó3.

csc()

csc(Expr1)⇒expresión csc(Lista1)⇒lista

Entrega la cosecante de Expr1 o entrega una lista que contiene las cosecantes de todos los elementos en Lista1.

Catálogo >

µ tecla

En modo de ángulo enGrados:

En modo de ángulo enGradianes:

38 Listado alfabético

En modo de ángulo enRadianes:

csc/()

csc/(Expr1) ⇒ expresión csc/(Lista1) ⇒ lista

Entrega el ángulo cuya cosecante es Expr1 o entrega una lista que contiene las cosecantes inversas de cada elemento de

Lista1.

Nota: El resultado se entrega como un

ángulo en grados, gradianes o radianes, de acuerdo con la configuración del modo del ángulo actual.

Nota: Se puede insertar esta función desde

el teclado al escribir arccsc(...).

µ tecla

En modo de ángulo enGrados:

En modo de ángulo enGradianes:

En modo de ángulo enRadianes:

csch()

csch(Expr1)⇒expresión csch(Lista1) ⇒ lista

Entrega la cosecante hiperbólica de Expr1 o entrega una lista de cosecantes hiperbólicas de todos los elementos de

Lista1.

csch/()

csch/(Expr1) ⇒ expresión csch/(Lista1) ⇒ lista

Entrega la cosecante hiperbólica inversa de

Expr1 o entrega una lista que contiene las

cosecantes hiperbólicas inversas de cada elemento de Lista1.

Nota: Se puede insertar esta función desde

el teclado al escribir arccsch(...).

Catálogo >

Listado alfabético 39

cSolve() (solucionC)

cSolve(Ecuación, Var)⇒expresión

Booleana

cSolve(Ecuación, Var=Cálculo)

⇒expresión Booleana cSolve(Desigualdad, Var)⇒expresión

Booleana

Entrega soluciones complejas posibles de una ecuación o desigualdad para Var. La meta es producir posibles para todas las soluciones reales y no reales. Incluso si la

Ecuación es real, cSolve() permite

resultados no reales en Formato Complejo de resultado Real.

Aunque todas las variables no definidas que no cSolve con un guión bajo (_) se procesan como si fueran reales, cSolve() puede solucionar ecuaciones polinómicas para soluciones complejas.

cSolve() configura temporalmente el

dominio para complejas durante la solución, incluso si el dominio actual es real. En el dominio complejo, las potencias fraccionarias que tienen denominadores nones usan el principal en lugar del ramal real En consecuencia, las soluciones de

solve() para las ecuaciones que incluyen

dichas potencias fraccionarias no son necesariamente un subconjunto de aquellas de cSolve().

cSolve() comienza con métodos simbólicos

exactos. cSolve() también usa factorización polinómica compleja aproximada iterativa, de ser necesario

Nota: Vea también cZeros(), solve() y zeros ().

Catálogo >

En modo de Dígitos de Desplieguede Fijo 2:

40 Listado alfabético

Para ver elresultado completo, presione £ y después use¡ y ¢ para mover el cursor.

cSolve() (solucionC)

Nota: Si la Ecuación no es polinómica con

funciones como abs(), angle(), conj(), real() o imag(), usted debe poner un guión bajo

(presione /_) al final de Var. De manera predeterminada, una variable se trata como un valor real.

Si se usa var_ , la variable se trata como complejo.

También se debe usar var_ para cualquier otra variable en la Ecuación que pudiera tener valores irreales. De otro modo, usted puede recibir resultados inesperados.

cSolve(Ecn1andEcn2 [and…],

VarOCálculo1, VarOCálculo2 [, … ])

⇒expresiónBooleana

cSolve(SistemaDeEcns, VarOCálculo1,

VarOCálculo2 [, …])

⇒expresiónBooleana

Entrega soluciones complejas posibles para las ecuaciones algebraicas simultáneas, donde cada varOCálculo especifica una variable que usted desea solucionar.

De manera opcional, se puede especificar un cálculo inicial para una variable. Cada

varOCálculo debe tener la forma: variable

– o –

variable = número real o irreal

Por ejemplo, x es válida y también lo es x=3+i.

Si todas las ecuaciones son polinomios y usted NO especifica cualquier cálculo inicial, cSolve() usa el método de eliminación de léxico Gröbner/Buchberger para intentar determinar todas las soluciones complejas.

Catálogo >

Nota: Los siguientes ejemplos usan un guión

bajo (presione/_) demanera que las variablesse tratarán como complejas.

Listado alfabético 41

cSolve() (solucionC)

Las soluciones complejas pueden incluir soluciones tanto reales como irreales, como en el ejemplo de la derecha.

Las ecuaciones polinómicas simultáneas pueden tener variables extras que no tienen ningún valor, aunque representan valores numéricos dados que podrían sustituirse más adelante.

También se pueden incluir variables de solución que no aparecen en las ecuaciones. Estas soluciones muestran cómo las familias de soluciones podrían contener constantes arbitrarias de la forma ck, donde k es un sufijo de entero desde 1 hasta 255.

Para sistemas polinómicos, el tiempo de cálculo o el agotamiento de memoria pueden depender ampliamente del orden en el cual se enumeran las variables de solución. Si su elección inicial agota la memoria o su paciencia, intente volver a arreglar las variables en las ecuaciones y/o en la lista varOCálculo .

Si usted no incluye ningún cálculo y si cualquier ecuación no es polinómica en cualquier variable, pero todas las ecuaciones son lineales en todas las variables de solución, cSolve() usa la eliminación Gausiana para tratar de determinar todas las soluciones.

Si un sistema no es ni polinómico en todas sus variables ni lineal en sus variables de solución, cSolve() determina como máximo una solución usando un método iterativo aproximado. Para hacer esto, el número de variables de solución debe igualar el número de ecuaciones, y todas las demás variables en las ecuaciones deben simplificarse a números.

Catálogo >

Para ver elresultado completo, presione £ y después use¡ y ¢ para mover el cursor.

42 Listado alfabético

cSolve() (solucionC)

Con frecuencia es necesario un cálculo irreal para determinar una solución irreal. Por convergencia, un cálculo podría tener que ser más bien cercano a una solución.

Catálogo >

Para ver elresultado completo, presione £ y después use¡ y ¢ para mover el cursor.

CubicReg

CubicReg X, Y[, [Frec] [, Categoría,

Incluir]]

Resuelve la regresión polinómica cúbicay = a·x3+b· x2+c·x+den listas X y Y con frecuencia Frec. Un resumen de resultados se almacena en la variable stat.results (página 190).

Todas las listas deben tener una dimensión igual, excepto por Incluir.

X y Y son listas de variables independientes

y dependientes.

Frec es una lista opcional de valores de

frecuencia. Cada elemento en Frec especifica la frecuencia de la ocurrencia para cada punto de datos X y Y correspondientes. El valor predeterminado es 1. Todos los elementos deben ser enteros | 0.

Categoría es una lista de códigos de

categoría para los datos X y Y correspondientes.

Incluir es una lista de uno o más códigos de

categoría. Sólo aquellos elementos de datos cuyo código de categoría está incluido en esta lista están incluidos en el cálculo.

Para obtener información sobre el efecto de los elementos vacíos en una lista, vea “Elementos vacíos (inválidos)” (página 253).

Catálogo >

Variable de salida

stat.EcnReg Ecuación deregresión: a·x3+b·x2+c·x+d

Descripción

Listado alfabético 43

Variable de salida

stat.a, stat.b, stat.c, stat.d

stat.R

stat.Resid Residualesde la regresión

stat.XReg

stat.YReg

stat.FrecReg

Descripción

Coeficientesde regresión

Coeficientede determinación

La lista de puntos de datos enLista X modificada se usa dehecho enla regresión con baseen las restriccionesde las Categorías Frec, Lista de Categoríae Incluir

La lista de puntos de datos enLista Y modificada se usa de hecho en la regresión con baseen las restriccionesde las Categorías Frec, Lista de Categoríae Incluir

Lista de frecuencias correspondientes a stat.XReg y stat.YReg

cumulativeSum()

cumulativeSum(Lista1)⇒lista

Entrega una lista de sumas acumulativas de los elementos en List1comenzando en el elemento1.

cumulativeSum(Matriz1)⇒matriz

Entrega una matriz de sumas acumulativas de los elementos en Matriz1. Cada elemento está en la suma acumulativa de la columna desde la parte superior hasta ha parte inferior.

Un elemento vacío (anulado) en Lista1 o

Matriz1 produce un elemento anulado en la

lista o matriz resultante. Para obtener más información sobre elementos vacíos, vea página 253.

Cycle

Transfiere el control de inmediato a la siguiente iteración del bucle actual (For,

While, o Loop).

Cycle no está permitido afuera de las tres

estructuras de bucles ((For, While, o Loop).

Catálogo >

Lista de funciones que suma los enteros desde 1 hasta 100, saltándose 50.

44 Listado alfabético

Cycle

Nota para introducir el ejemplo: Para

obtener instrucciones sobre cómo introducir las definiciones de programas y funciones en varias líneas, consulte la sección Calculadora de la guía del producto.

Catálogo >

4Cylind

Vector 4Cylind

Nota: Se puede insertar este operador

desde el teclado de la computadora al escribir @>Cylind.

Despliega el vector de fila o columna en forma cilíndrica [r,±q, z].

Vector debe tener exactamente tres

elementos. Puede ser una fila o una columna.

cZeros()

cZeros(Expr, Var)⇒lista

Entrega una lista de valores reales e irreales posibles de Var que hacen Expr=0.

cZeros() hace esto al calcular exp4list(cSolve (Expr=0,Var),Var). De otro modo, cZeros()

es similar a zeros().

Nota: Vea también cSolve(), solve() y zeros ().

Nota: Si Expr no es polinómica con

funciones como abs(), angle(), conj(), real() o imag(), usted debe poner un guión bajo

(presione /_) al final de Var. De manera predeterminada, una variable se trata como un valor real. Si se usa var_, la variable se trata como complejo.

Catálogo >

En modo de Dígitos de Desplieguede Fijo 3:

Para ver elresultado completo, presione £ y después use¡ y ¢ para mover el cursor.

Listado alfabético 45

cZeros()

También se debe usar var_ para cualquier otra variable en Expr que pudiera tener valores irreales. De otro modo, usted puede recibir resultados inesperados.

cZeros({Expr1, Expr2 [, … ] }, {VarOcálculo1,VarOCálculo2 [, … ] })

⇒matriz

Entrega las posibles posiciones donde las expresiones son cero en forma simultánea. Cada VarOcálculo especifica un desconocido cuyo valor usted busca.

De manera opcional, se puede especificar un cálculo inicial para una variable. Cada

VarOcálculo debe tener la forma: variable

– o –

variable = número real o irreal

Por ejemplo, x es válida y también lo es x=3+i.

Si todas las expresiones son polinomios y usted NO especifica cualquier cálculo inicial, cZeros() usa el método de eliminación de léxico Gröbner/Buchberger para intentar determinar todos los ceros complejos.

Los ceros complejos pueden incluir ceros tanto reales como irreales, como en el ejemplo de la derecha.

Cada fila de la matriz resultante representa un cero alterno, con los componentes ordenados igual que la lista VarOCálculo lista. Para extraer una fila, index de la matriz con [fila].

Catálogo >

Nota: Los siguientes ejemplos usan un guión

bajo (presione/_) demanera que las variablesse tratarán como complejas.

Extraer la fila 2:

46 Listado alfabético

cZeros()

Los polinomios simultáneos pueden tener variables extras que no tienen ningún valor, aunque representan valores numéricos dados que podrían sustituirse más adelante.

Usted también puede incluir variables desconocidas que no aparecen en las expresiones. Estos ceros muestran cómo las familias de ceros podrían contener constantes arbitrarias de la forma ck, donde k es un sufijo de entero desde 1 hasta 255.

Para sistemas polinómicos, el tiempo de cálculo o el agotamiento de memoria pueden depender ampliamente del orden en el cual se enumeran los desconocidos. Si su elección inicial agota la memoria o su paciencia, intente volver a arreglar las variables en las expresiones y/o en la lista

VarOCálculo .

Si usted no incluye ningún cálculo y si cualquier expresión no es polinómica en cualquier variable, pero todas las expresiones son lineales en todos los desconocidos, cZeros() usa la eliminación Gausiana para tratar de determinar todos los ceros.

Si un sistema no es ni polinómico en todas sus variables ni lineal en sus desconocidos,

cZeros() determina como máximo un cero

usando un método iterativo aproximado. Para hacer esto, el número de desconocidos debe igualar el número de expresiones, y todas las demás variables en las expresiones deben simplificarse a números.

Con frecuencia es necesario un cálculo irreal para determinar un cero irreal. Por convergencia, un cálculo podría tener que ser más bien cercano a un cero.

Catálogo >

Listado alfabético 47

dbd()

dbd(fecha1,fecha2)⇒valor

Entrega el número de días entre fecha1 y

fecha2 usando el método de conteo de días

reales.

fecha1 y fecha2 pueden ser números

dentro del rango de las fechas en el calendario estándar. Si tanto fecha1 como

fecha2 son listas, deberán tener la misma

longitud.

Tanto fecha1 como fecha2 deben estar

entre los años 1950 a 2049.

Usted puede ingresar las fechas en uno de dos formatos. La colocación decimal se diferencia entre los formatos de fecha.

MM.DDAA (formato que se usa de manera común en los Estados Unidos) DDMM.AA (formato que se usa de manera común en Europa)

4DD

Expr1 4DD⇒valor Lista1 4DD⇒lista

Catálogo >

En modo de ángulo enGrados:

Matriz1 4DD⇒matriz

Nota: Usted puede insertar este operador

desde el teclado de la computadora al escribir @>DD.

Entrega el decimal equivalente del argumento expresado en grados. El argumento es un número, lista o matriz que se interpreta por medio de la configuración del modo de Ángulo en gradianes, radianes o grados.

48 Listado alfabético

En modo de ángulo enGradianes:

En modo de ángulo enRadianes:

4Decimal

Expresión1 4Decimal⇒expresión Lista1 4Decimal⇒expresión Matriz1 4Decimal⇒expresión

Nota: Usted puede insertar este operador

desde el teclado de la computadora al escribir @>Decimal.

Despliega el argumento en forma decimal. Este operador se puede usar únicamente al final de la línea de ingreso.

Catálogo >

Define (Definir)

Define Var = Expresión

Define Función(Param1, Param2, ...) =

Expresión

Define la variable Var o la función definida por el usuario Función.

Los parámetros, como Param1, proporcionan marcadores de posición para pasar argumentos a la función. Cuando llame a una función definida por el usuario, usted deberá suministrar argumentos (por ejemplo, valores o variables) que correspondan a los parámetros. Cuando se llama, la función evalúa la Expresión usando los argumentos provistos.

Var y Función no pueden ser el nombre de

una variable de sistema o de una función o un comando integrado.

Nota: Esta forma de Define es equivalente

a ejecutar la expresión: expresión&

Función(Param1,Param2).

Define Función(Param1, Param2, ...) = Func

Bloque

EndFunc

Catálogo >

Define Programa(Param1, Param2, ...) = Prgm

Bloque

EndPrgm

Listado alfabético 49

Define (Definir)

En esta forma, la función o el programa definido por el usuario puede ejecutar un bloque de varias sentencias.

Bloque puede ser una sentencia sencilla o

una serie de sentencias en líneas separadas. Bloque también puede incluir expresiones e instrucciones (como If, Then,

Else, y For).

Nota para introducir el ejemplo: Para

obtener instrucciones sobre cómo introducir las definiciones de programas y funciones en varias líneas, consulte la sección Calculadora de la guía del producto.

Nota: Vea también Define LibPriv, página

50y Define LibPub, página 50.

Catálogo >

Define LibPriv

Define LibPriv Var = Expresión

Define LibPriv Función(Param1, Param2,

...) = Expresión

Define LibPriv Función(Param1, Param2,

...) = Func

Bloque

EndFunc

Define LibPriv Programa(Param1, Param2, ...) = Prgm

Bloque

EndPrgm

Opera igual que Define, excepto porque define una variable de librería privada, función o programa. Las funciones y los programas privados no aparecen en el Catálogo.

Nota: Vea también Define, página 49 y Define LibPub, página 50.

Define LibPub

Define LibPub Var = Expresión

Catálogo >

50 Listado alfabético

Define LibPub

Define LibPub Función(Param1, Param2,

...) = Expresión

Define LibPub Función(Param1, Param2,

...) = Func

Bloque

EndFunc

Define LibPub Programa(Param1, Param2, ...) = Prgm

Bloque

EndPrgm

Opera igual que Define, excepto porque define una variable de librería pública, función o programa. Las funciones y los programas públicos aparecen en el Catálogo después de que la librería se ha guardado y actualizado.

Nota: Vea también Define, página 49 y Define LibPriv, página 50.

Catálogo >

deltaList()

deltaTmpCnv()

DelVar

DelVar Var1[, Var2] [, Var3] ...

DelVar Var.

Borra la variable o el grupo de variables especificado de la memoria.

Si una o más de las variables están bloqueadas, este comando despliega un mensaje de error y borra únicamente las variables no bloqueadas. Vea unLock,

página 212.

Vea @List(), página 111.

Vea @tmpCnv(), página 204.

Catálogo >

Listado alfabético 51

DelVar

DelVar Var. borra todos los miembros del

grupo de variables Var. (como las estadísticas stat.nn los resultados o las variables que se crean con el uso de

LibShortcut() función). El punto (.) en esta

forma de comando DelVar lo limita a borrar un grupo de variables; la variable sencilla

Var no se ve afectada.

Catálogo >

delVoid() (borrInválido)

delVoid(Lista1)⇒lista

Entrega una lista que tiene el contenido de

Lista1 con todos los elementos (nulos)

vacíos eliminados.

Para obtener más información sobre elementos vacíos, vea página 253.

derivative()

deSolve() (resolverEd)

deSolve(EDO1erO2oGrado, Var, depVar)

⇒una solución general

Entrega una ecuación que especifica en forma explícita o implícita una solución general para la ecuación diferencial ordinaria (EDO) de 1er o 2o grado. En la EDO:

• Use un símbolo primo (presione º) para denotar la 1a derivada de la variable

dependiente con respecto de la variable independiente.

• Use dos símbolos primos para denotar la segunda derivada correspondiente.

El símbolo primo se usa para las derivadas dentro de resolverEd() únicamente. En otros casos, used().

Catálogo >

Vea d(), página 237.

Catálogo >

52 Listado alfabético

deSolve() (resolverEd)

La solución general de una ecuación de 1er grado contiene una constante arbitraria de la forma ck, donde k es un sufijo de entero desde 1 hasta 255. La solución de una ecuación de 2o grado contiene dos constantes.

Aplique solve() para una solución implícita si desea tratar de convertirla en una o más soluciones explícitas equivalentes.

Cuando compare sus resultados con las soluciones del libro de texto o del manual, tome en cuenta que los diferentes métodos introducen constantes arbitrarias en distintos puntos en el cálculo, lo que puede producir soluciones generales diferentes.

deSolve(EDO1erGradoandcondInic, Var,

depVar) ⇒una solución particular

Entrega una solución particular que satisface la EDO1erGrado y la condInic. Por lo general esto es más fácil que determinar una solución general, al sustituir los valores iniciales, solucionar la constante arbitraria y luego sustituir ese valor en la solución general.

condInic es una ecuación de la forma: depVar (valorInicialIndependiente) =

valorInicialDependiente

El valorIinicialIndependiente y el

valorInicialDependiente pueden ser

variables como x0 y y0 que no tienen ningún valor almacenado. La diferenciación implícita puede ayudar a verificar las soluciones implícitas.

Catálogo >

Listado alfabético 53

deSolve() (resolverEd)

deSolve (EDO2oGradoandcondIinic1andcondInic2,

Var, depVar)⇒una solución particular

Entrega una solución particular que satisface la EDO de 2o Grado y tiene un valor especificado de la variable dependiente y su primera derivada en un punto.

Para condInic1, use la forma:

depVar (valorInicialIndependiente) = valorInicialDependiente

Para condIinic2, use la forma:

depVar (valorInicialIndependiente) = valorInicial1aDerivada

deSolve (EDO2oGradoandbndCond1andcondBnd2,

Var, depVar)⇒una solución particular

Entrega una solución particular que satisface la EDO2oGrado y tiene valores especificados en dos puntos diferentes.

Catálogo >

54 Listado alfabético

det()

det(matrizCuadrada[, Tolerancia])

⇒expresión

Entrega la determinante de

matrizCuadrada.

De manera opcional, cualquier elemento de matriz se trata como cero si su valor absoluto es menor que la Tolerancia. Esta tolerancia se usa sólo si la matriz tiene ingresos de punto flotante y no contiene ninguna variable simbólica a la que no se le haya asignado un valor. De otro modo, la

Tolerancia se ignora.

• Si usted usa /· o configura el modo Auto o Aproximado para

aproximar, los cálculos se realizan al usar la aritmética de punto flotante.

• Si la Tolerancia se omite o no se usa, la tolerancia predeterminada se calcula como:

5EM14 ·max(dim(matrizCuadrada))

·rowNorm(matrizCuadrada)

Catálogo >

diag()

diag(Lista)⇒matriz diag(matrizFila)⇒matriz diag(matrizColumna)⇒matriz

Entrega una matriz con los valores en la lista o matriz de argumentos en su diagonal principal.

diag(matrizCuadrada)⇒matrizFila

Entrega una matriz de filas que contiene los elementos de la diagonal principal de

matrizCuadrada. matrizCuadrada debe ser cuadrada.

Catálogo >

Listado alfabético 55

dim()

dim(Lista)⇒entero

Entrega la dimensión de Lista.

dim(Matriz)⇒lista

Entrega las dimensiones de la matriz como una lista de dos elementos {filas, columnas}.

dim(Cadena)⇒entero

Entrega el número de caracteres contenidos en la cadena de caracteres Cadena.

Catálogo >

Disp

Disp exprOCadena1 [, exprOCadena2] ...

Despliega los argumentos en el historial de la Calculadora . Los argumentos se despliegan en sucesión, con espacios pequeños como separadores.

Es útil principalmente con programas y funciones para asegurar en despliegue de cálculos intermedios.

Nota para introducir el ejemplo: Para

obtener instrucciones sobre cómo introducir las definiciones de programas y funciones en varias líneas, consulte la sección Calculadora de la guía del producto.

DispAt

DispAt int,expr1 [,expr2 ...] ...

DispAt permite especificar la línea en la

que se mostrará en la pantalla la expresión o cadena de caracteres especificada.

El número de línea se puede especificar como una expresión.

Tenga en cuenta que el número de línea no es para toda la pantalla, sino para el área inmediatamente después del comando/programa.

Catálogo >

Ejemplo

56 Listado alfabético

DispAt

Este comando permite tener salidas tipo tablero de instrumentos de programas donde el valor de una expresión o de una lectura de sensor se actualiza en la misma línea.

DispAty Disp pueden utilizarse dentro

del mismo programa.

Nota: El número máximo se establece

en 8 ya que coincide con una pantalla llena de líneas en la pantalla del dispositivo portátil, siempre y cuando las líneas no tengan expresiones matemáticas en 2D. El número exacto de líneas depende del contenido de la información mostrada.

Ejemplos ilustrativos:

Define z()= Prgm For n,1,3 DispAt 1, "N: ",

n Disp "Hello" EndFor EndPrgm

Salida z()

Catálogo >

Iteration 1:

Line 1: N:1

Line 2: Hello

Iteration 2:

Line 1: N:2 Line 2: Hello Line 3: Hello

Define z1()= Prgm For n,1,3 DispAt 1, "N: ",

n EndFor

For n,1,3 Disp "Hello"

Iteration 3:

Line 1: N:3 Line 2: Hello Line 3: Hello Line 4: Hello

z1()

Line 1: N:3 Line 2: Hello Line 3: Hello Line 4: Hello Line 5: Hello

Listado alfabético 57

DispAt

EndFor EndPrgm

Condiciones de error:

Mensaje de error Descripción

El número de línea de DispAt debe ser entre 1 y 8

Muy pocos argumentos Le falta uno o más argumentos a la

No hay argumentos Igual que el cuadro de diálogo actual

Demasiados argumentos Limite los argumentos. Mismo error que

Tipo de datos no válido El primer argumento debe ser un

Anular: anular DispAt Un tipo de error datatype "Hello World"

Operador de conversión: DispAt 2_ft @> _m, "Hello World"

La expresión evalúa el número de línea fuera del rango 1 a 8 (inclusive)

función o al comando.

'error de sintaxis'

en Disp.

número.

se produce para la anulación (si se define la devolución de llamada)

CAS: Se produce un tipo de error datatype "Hello World" para la anulación (si se define la devolución de llamada)

Numérico: La conversión se evaluará y si el resultado es un argumento válido, DispAt imprime la cadena en la línea de resultados.

Catálogo >

4DMS (4GMS)

Expr 4DMS

Lista 4DMS

Matriz 4DMS

Nota: Usted puede insertar este operador

desde el teclado de la computadora al escribir @>DMS.

Interpreta el argumento como un ángulo y despliega el número GMS (GGGGGG¡MM'SS.ss'') equivalente. Vea ¡, ', '' (página 245) para el formato GMS (grado, minutos, segundos).

58 Listado alfabético

Catálogo >

En modo de ángulo enGrados:

4DMS (4GMS)

Nota: 4DMS se convertirá de radianes a

grados cuando se use en el modo de Radián. Si la entrada va seguida de un símbolo de grados ¡ , no ocurrirá ninguna conversión. Usted puede usar 4DMS sólo al final de una línea de ingreso.

Catálogo >

domain() (dominio)

domain(Expr1, Var)⇒expresión

Devuelve el dominio de Expr1con respecto a Var.

domain() puede utilizarse para examinar

los dominios de las funciones. Se restringe a un dominio real y finito.

Esta funcionalidad presenta limitaciones debido a defectos en los algoritmos de simplificación algebráicos para computadora y algoritmos solucionadores.

Algunas funciones no pueden ser utilizadas como argumentos para domain(), sin importar si aparecen explícitamente o dentro de las variables y funciones definidas por el usuario: En el siguiente ejemplo, la expresión no puede simplificarse porque ‰() no es una función permitida.

Catálogo >

Listado alfabético 59

dominantTerm()

dominantTerm(Expr1, Var [, Punto])

⇒expresión

dominantTerm(Expr1, Var [, Punto]) |

Var>Punto ⇒expresión

dominantTerm(Expr1, Var [, Punto]) |

Var<Punto ⇒expresión

Entrega el término dominante de la representación de una serie de potencia de

Expr1 expandida alrededor de Punto. El

término dominante es aquel cuya magnitud crece con más rapidez cerca de Var =

Punto. La potencia resultante de (Var N Punto) puede tener un exponente negativo

y/o fraccional. El coeficiente de esta potencia puede incluir logaritmos de (Var N

Punto) y otras funciones de Var que están

dominadas por todas las potencias de (Var N Punto) teniendo el mismo signo de exponente.

Punto se predetermina a 0. Punto puede

ser ˆ o Nˆ, en cuyos casos el término dominante será el término que tiene el exponente más grande de Var en lugar del exponente más pequeño de Var.

dominantTerm(…) entrega “dominantTerm (…)” si no puede determinar tal

representación, como para singularidades esenciales como sin(1/z) en z=0, e z=0, o ezen z = ˆ o Nˆ.

1/z

Catálogo >

60 Listado alfabético

dominantTerm()

Si la serie o una de sus derivadas tiene una discontinuidad de salto en un Punto, es probable que el resultado contenga subexpresiones del signo de forma(…) o abs (…) para una variable de expansión real o (-

piso(…angle(…)…)

para una variable de expansión compleja, que es una que termina con “_”. Si usted pretende usar el término dominante sólo para valores en un lado de Punto, entonces anexe a

dominantTerm(...) el apropiado de “| Var >

Punto”, “| Var < Punto”, “| “Var | Punto”

o “Var { Punto” para obtener un resultado más simple.

dominantTerm() se distribuye sobre listas y

matrices del 1er argumento.

dominantTerm() es útil cuando usted desea

conocer la expresión más simple posible que sea asintótica para otra expresión como Var " Punto. dominantTerm() también es útil cuando no es obvio cuál será el grado del primer término no-cero de una serie, y usted no desea calcular iterativamente, ya sea de manera interactiva o por medio de un bucle de programa.

Nota: Vea también series(), página 173.

Catálogo >

dotP() (pPunto)

dotP(Lista1, Lista2)⇒expresión

Entrega el producto "punto" de dos listas.

dotP(Vector1, Vector2)⇒expresión

Entrega el producto punto" de dos vectores.

Ambos deben ser vectores de fila, o ambos deben ser vectores de columna.

Catálogo >

Listado alfabético 61

e^()

e^(Expr1 )⇒expresión

Entrega e elevado a la potencia de Expr1 .

Nota: Vea también plantilla de exponente e, página 2.

Nota: Presionar u para desplegar e^(es

diferente de presionar el caracter E en el teclado.

Usted puede ingresar un número complejo en la forma polar re esta forma sólo en el modo de ángulo en Radianes; esto causa un error de Dominio en el modo de ángulo en Grados o en Gradianes.

e^(Lista1)⇒lista

Entrega e elevado a la potencia de cada elemento en Lista1.

e^(matrizCuadrada1)⇒matrizCuadrada

Entrega el exponencial de la matriz de

. Sin embargo, use

matrizCuadrada1. Esto no es lo mismo que

calcular e elevado a la potencia de cada elemento. Para obtener información acerca del método de cálculo, consulte cos().

matrizCuadrada1 debe ser diagonalizable.

El resultado siempre contiene números de punto flotante.

u tecla

eff()

eff(tasaNominal,CpA)⇒valor

Función financiera que convierte la tasa de interés nominal tasaNominal en una tasa efectiva anual, donde CpA se da como el número de periodos de capitalización por año.

tasaNominal debe ser un número real y CpA debe ser un número real > 0.

62 Listado alfabético

Catálogo >

eff()

Nota: Vea también nom(), página 132.

Catálogo >

eigVC() (vcProp)

eigVc(matrizCuadrada)⇒matriz

Entrega una matriz que contiene los vectores propios para una

matrizCuadradareal o compleja, donde

cada columna en el resultado corresponde a un valor propio. Tome en cuenta que un vector propio no es único; puede escalarse por medio de cualquier factor constante. Los vectores propios se normalizan, lo que significa que si V = [x1, x2, … , xn], entonces:

+x

+ … +x

= 1

matrizCuadrada se balancea primero con

transformaciones de similaridad hasta que las normas de fila y columna están tan cerca del mismo valor como es posible. La

matrizCuadrada se reduce entonces a una

forma de Hessenberg superior y los vectores propios se generan o se obtienen por medio de la factorización de Schur.

eigVl() (vlProp)

eigVl(matrizCuadrada)⇒lista

Entrega una lista de valores propios de una

matrizCuadradareal o compleja. matrizCuadrada se balancea primero con

transformaciones de similaridad hasta que las normas de fila y columna están tan cerca del mismo valor como es posible. La

matrizCuadrada se reduce entonces a una

forma de Hessenberg superior y los vectores propios se generan o se obtienen por medio de la matriz de Hessenberg superior.

Catálogo >

En Formato Complejo Rectangular:

Para ver elresultado completo, presione £ y después use¡ y ¢ para mover el cursor.

Catálogo >

En modo de formato complejo Rectangular:

Para ver elresultado completo, presione £ y después use¡ y ¢ para mover el cursor.

Else (Más)

Vea If, página 93.

Listado alfabético 63

ElseIf (MásSi)

If ExprBooleana1 Then

Bloque1

ElseIf ExprBooleana2 Then

Bloque2

ElseIf ExprBooleanaN Then

BloqueN

EndIf

Nota para introducir el ejemplo: Para

obtener instrucciones sobre cómo introducir las definiciones de programas y funciones en varias líneas, consulte la sección Calculadora de la guía del producto.

Catálogo >

EndFor (TerminarPara)

EndFunjc (TerminarFunc)

EndIf (TerminarSi)

EndLoop (TerminarBucle)

EndPrgm (TerminarPrgm)

EndTry (TerminarIntentar)

EndWhile (TerminarMientras)

Vea For, página 78.

Vea Func, página 82.

Vea If, página 93.

Vea Loop, página 118.

Vea Prgm, página 148.

Vea Try, página 205.

Vea While, página 216.

64 Listado alfabético

euler ()

euler(Expr, Var, varDep, {Var0,

VarMax}, var0Dep, PasoVar [, pasoEuler]) matriz ⇒

euler(SistemaDeExpr, Var,

ListaDeVarsDep, {Var0, VarMax}, ListaDeVars0Dep, PasoVar [, pasoEuler]) matriz ⇒

euler(ListaDeExpr, Var,

ListaDeVarsDep, {Var0, VarMax}, ListaDeVars0Dep, PasoVar [, pasoEuler]) matriz ⇒

Use el método de Euler para resolver el sistema

con varDep(Var0)=var0Dep en el intervalo [Var0,VarMax]. Entrega una matriz cuya primera fila define los valores del resultado de Var y cuya segunda fila define el valor del primer componente de solución a los valores de Var correspondientes, y así sucesivamente.

Expr es el lado derecho que define la

ecuación diferencial ordinaria (EDO).

SistemaDeExpr es el sistema de lados

derechos que define el sistema de EDOs (corresponde al orden de variables dependientes en ListaDeVarsDep).

ListaDeExpr es una lista de lados

derechos que define el sistema de EDOs (corresponde al orden de variables dependientes en ListaDeVarsDep).

Var es la variable independiente. ListaDeVarsDep es una lista de variables

dependientes. {Var0, VarMax} es una lista de dos

elementos que le dice a la función que se integre de Var0 a VarMax.

Catálogo >

Ecuacióndiferencial:

y'=0.001*y*(100-y) y y(0)=10

Para ver elresultado completo, presione £ y despuésuse ¡ y ¢ para mover el cursor.

Compare el resultado anterior con la solución exacta de CAS obtenido al usar deResolver() y genSec():

Sistema de ecuaciones:

con y1(0)=2y y2(0)=5

Listado alfabético 65

euler ()

Catálogo >

ListaDeVars0Dep es una lista de valores

iniciales para variables dependientes.

PasoVar es un número distinto de cero de

manera que sign(PasoVar) = sign

(VarMax-Var0) y las soluciones se

entregan a Var0+i·PasoVar para todos i=0,1,2,… de tal manera que

Var0+i·PasoVar está en [var0,VarMax]

(puede que no haya un valor de solución en

VarMax). pasoEuler es un entero positivo

(predeterminado a 1) que define el número de pasos de Euler entre los valores de resultado. El tamaño del paso real utilizado por el método de Euler es

PasoVaràpasoEuler.

eval () Menú del Concentrador

eval(Expr) ⇒ cadena

eval() solo es válida en el [[[Undefined

variable MyVariables.HubFullName]]] argumento del comando de los comandos de programación Get, GetStr y Send. El software evalúa la expresión Expr y reemplaza el enunciado eval() con el resultado como cadena de caracteres.

El argumento Expr se debe simplificar a un número real.

Establezca elelemento azulde LED RGB a una intensidad media.

Restablezca elelemento azula APAGADO.

El argumento eval()se debe simplificar a un número real.

66 Listado alfabético

Programe el elemento rojo a que aparezca gradualmente

eval () Menú del Concentrador

Ejecute el programa.

Aunque eval() no muestra el resultado, puede ver la cadena de comandos del Concentrador después de ejecutar el comando al inspeccionar cualquiera de las siguientes variables especiales.

iostr.SendAns iostr.GetAns iostr.GetStrAns

Nota: Consulte además Get(página 84), GetStr(página 91) y Send(página 170).

exact()

exact(Expr1 [, Tolerancia])⇒expresión exact(Lista1 [, Tolerancia])⇒lista exact(Matriz1 [, Tolerancia])⇒matriz

Usa aritmética de modo Exacto para producir, cuando es posible, el equivalente de número racional del argumento.

Tolerancia especifica la tolerancia para la

conversión; la predeterminada es 0 (cero).

Exit (Salir)

Exit

Sale del bloque For, While, o Loop .

Exit no está permitido afuera de las tres

estructuras de bucles (For, While, o Loop).

Nota para introducir el ejemplo: Para

obtener instrucciones sobre cómo introducir las definiciones de programas y funciones en varias líneas, consulte la sección Calculadora de la guía del producto.

Catálogo >

Listado de funciones:

Listado alfabético 67

4exp

Expr 4exp

Representa la Expr en términos del exponencial natural e. Este es un operador de conversión de despliegue. Se puede usar únicamente al final de la línea de ingreso.

Nota: Usted puede insertar este operador

desde el teclado de la computadora al escribir @>exp.

Catálogo >

exp()

exp(Expr1)⇒expresión

Entrega e elevado a la potencia de Expr1 .

Nota: Vea también la plantilla exponencial

e , página 2.

Usted puede ingresar un número complejo en la forma polar re esta forma sólo en el modo de ángulo en Radianes; esto causa un error de Dominio en el modo de ángulo en Grados o en Gradianes.

exp(Lista1)⇒lista

Entrega e elevada a la potencia de cada elemento en Lista1.

exp(matrizCuadrada1)⇒matrizCuadrada

Entrega el exponencial de la matriz de

. Sin embargo, use

matrizCuadrada1. Esto no es lo mismo que

calcular e elevado a la potencia de cada elemento. Para obtener información acerca del método de cálculo, consulte cos().

matrizCuadrada1 debe ser diagonalizable.

El resultado siempre contiene números de punto flotante.

u tecla

exp4list()

exp4list(Expr,Var)⇒lista

68 Listado alfabético

Catálogo >

exp4list()

Examina la Expr para las ecuaciones que están separadas por la palabra “or”, y entrega una lista que contiene los lados derechos de las ecuaciones de la forma

Var=Expr. Esto le brinda una forma fácil

de extraer algunos valores de solución incrustados en los resultados de las funciones solve(), cSolve(), fMin(), y fMax() .

Nota: exp4list() no es necesaria con las

funciones zeros() y cZeros() porque entregan una lista de valores de solución en forma directa.

Usted puede insertar esta función desde el teclado al escribir exp@>list(...).

Catálogo >

expand() (expandir)

expand(Expr1 [, Var])⇒expresión expand(Lista1 [,Var])⇒lista expand(Matriz1 [,Var])⇒matriz

expand(Expr1) entrega Expr1 expandida

con respecto de todas sus variables. La expansión es una expansión polinómica para los polinomios y una expansión de fracción parcial para las expresiones racionales.

La meta de expand() es transformar Expr1 en una suma y/o diferencia de términos sencillos. En contraste, la meta de factor() es transformar Expr1 en un producto y/o cociente de factores sencillos.

Catálogo >

Listado alfabético 69

expand() (expandir)

expand(Expr1,Var) entrega Expr1

expandida con respecto de Var. Se recopilan potencias similares de Var . Los términos y sus factores se ordenan con Var como la variable principal. Puede haber cierta factorización o expansión incidental de los coeficientes recopilados. Se compara para omitir Var, con frecuencia esto ahorra tiempo, memoria y espacio de pantalla, mientras que hace la expresión más comprensible.

Incluso cuando hay sólo una variable, al usar Var se puede hacer la factorización del denominador que se usa para la expansión de la fracción parcial más completa.

Sugerencia: Para expresiones racionales,

propFrac() es una alternativa más rápida

aunque menos extrema para expand().

Nota: Vea también comDenom() para un

numerador expandido sobre un denominador expandido.

expand(Expr1,[Var]) también distribuye

logaritmos y potencias fraccionales independientemente de Var. Para una distribución incrementada de logaritmos y potencias fraccionales, podrían ser necesarias restricciones de desigualdad para garantizar que algunos factores son no negativos.

expand(Expr1, [Var]) también distribuye

valores absoluto, sign(), y exponenciales, independientemente de Var.

Nota: Vea también tExpand() para suma de

ángulo trigonométrico y expansión de ángulo múltiple.

Catálogo >

70 Listado alfabético

expr()

expr(Cadena)⇒expresión

Entrega la cadena de caracteres contenida en Cadena como una expresión y la ejecuta de inmediato.

Catálogo >

ExpReg

ExpReg X, Y [, [Frec] [, Categoría,

Incluir]]

Genera la regresión exponencialy = a·(b)xen listas X y Y con frecuencia Frec. Un resumen de resultados se almacena en la variable stat.results (página 190).

Todas las listas deben tener una dimensión igual, excepto por Incluir.

X y Y son listas de variables independientes

y dependientes.

Frec es una lista opcional de valores de

frecuencia. Cada elemento en Frec especifica la frecuencia de la ocurrencia para cada punto de datos X y Y correspondientes. El valor predeterminado es 1. Todos los elementos deben ser enteros | 0.

Categoría es una lista de códigos de

categoría para los datos X y Y correspondientes.

Incluir es una lista de uno o más códigos de

categoría. Sólo aquellos elementos de datos cuyo código de categoría está incluido en esta lista están incluidos en el cálculo.

Para obtener información sobre el efecto de los elementos vacíos en una lista, vea “Elementos vacíos (inválidos)” (página 253).

Catálogo >

Variable de salida

stat.EcnReg Ecuaciónde regresión: a·(b)

Descripción

Listado alfabético 71

Variable de salida

stat.a, stat.b Coeficientes de regresión

stat.r

stat.r Coeficientede correlaciónpara datos transformados (x, ln(y))

stat.Resid Residuales asociados con el modelo exponencial

stat.TransResid Residualesasociadascon elajuste lineal de datos transformados

stat.XReg

stat.YReg

stat.FrecReg

Descripción

Coeficientede determinación lineal para datos transformados

La lista de puntos de datos enLista X modificada se usa dehecho enla regresión con base enlas restricciones delas Categorías Frec, Lista de Categoríae Incluir

La lista de puntos de datos enLista Y modificada se usa de hecho en la regresión con base enlas restricciones delas Categorías Frec, Lista de Categoríae Incluir

Lista de frecuencias correspondientes a stat.XReg y stat.YReg

factor()

factor(Expr1[, Var])⇒expresión factor(Lista1[,Var])⇒lista factor(Matriz1[,Var])⇒matriz

factor(Expr1) entrega Expr1 factorizado

con respecto de todas sus variables sobre un denominador común.

Expr1 se factoriza tanto como es posible

hacia los factores racionales lineales sin introducir nuevas subexpresiones no reales. Esta alternativa es apropiada si se desea una factorización con respecto de más de una variable.

factor(Expr1,Var) entrega Expr1

factorizado con respecto de la variable Var.

Expr1 se factoriza tanto como es posible

hacia factores reales que son lineales en

Var, incluso si introduce constantes

irracionales o subexpresiones que son irracionales en otras variables.

Catálogo >

72 Listado alfabético

factor()

Los factores y sus términos se clasifican con

Var como la variable principal. Se recopilan

Para la configuración Automática del modo

Auto o Aproximado , incluyendo Var

permite la aproximación con coeficientes de punto flotante, donde los coeficientes irracionales no se pueden expresar en forma explícita concisamente en términos de funciones integradas. Incluso cuando hay sólo una variable, incluyendo Var, puede producir una factorización más completa.

Nota: Vea también comDenom() para

obtener una forma rápida de lograr una factorización parcial cuando factor() no es lo suficientemente rápido o si agota la memoria.

Nota: Vea también cFactor() para factorizar

hasta los coeficientes complejos en busca de factores lineales.

factor(númeroRacional) entrega el número

racional factorizado en primos. Para números compuestos, el tiempo de cómputo aumenta exponencialmente con el número de dígitos en el segundo factor más grande. Por ejemplo, factorizar un entero de 30 dígitos podría llevarse más de un día, y factorizar un número de 100 dígitos podría llevarse más de un siglo.

Para detener el cálculo manualmente:

• Dispositivo portátil: Mantenga

presionada la tecla c y presione

· varias veces.

• Windows®: Mantenga presionada la tecla F12 y presione Intro varias veces.

Catálogo >

Listado alfabético 73

factor()

• Macintosh®: Mantenga presionada la tecla F5 y presione Intro varias veces.

• iPad®: La aplicación muestra un indicador. Puede seguir esperando o cancelar.

Si usted simplemente desea determinar si un número es primo, use isPrime() en su lugar. Es mucho más rápido, en particular si

númeroRacional no es primo y si el

segundo factor más grande tiene más de cinco dígitos.

Catálogo >

FCdf()

FCdf

(

límiteInferior

,límiteSuperior,númerodf,denomdf)

⇒número si límiteInferior y

límiteSuperior son números, lista si límiteInferior y límiteSuperior son listas

FCdf (

límiteInferior

,límiteSuperior,númerodf,denomdf)

⇒número si límiteInferior y

límiteSuperior son números, lista si límiteInferior y límiteSuperior son listas

Calcula la probabilidad de la distribución F entre el Liminte inferior y Limite Superior para los grados de libertad dfNumer y

dfDenom especificados.

Para P(X { Limite superior), establecer

Limite Inferior=0.

Fill (Llenar)

Fill Expr, varMatriz⇒matriz

Reemplaza cada elemento en la variable

varMatriz con Expr. varMatriz ya debe existir.

Catálogo >

74 Listado alfabético

Fill (Llenar)

Fill Expr, varLista⇒lista

Reemplaza cada elemento en la variable

varLista con Expr. varLista ya debe existir.

FiveNumSummary (ResumenNúmCinco)

FiveNumSummary X[,[Frec]

[,Categoría,Incluir]]

Proporciona una versión abreviada de las estadísticas de 1 variable en la lista X. Unresumen de resultados se almacena en la variable stat.results (página 190).

X representa una lista que contiene los

datos.

Frec es una lista opcional de valores de

frecuencia. Cada elemento en Frec especifica la frecuencia de la ocurrencia para cada punto de datos X y Y correspondientes. El valor predeterminado es 1.

Categoría es una lista de códigos de

categoría numérica para los datos X correspondientes.

Incluir es una lista de uno o más códigos de

categoría. Sólo aquellos elementos de datos cuyo código de categoría está incluido en esta lista están incluidos en el cálculo.

Un elemento (inválido) vacío en cualquiera de las listas X, Frec, o Categoría da como resultado un inválido para el elemento correspondiente de todas esas listas. Para obtener más información sobre elementos vacíos, vea página 253.

Catálogo >

Variable de salida Descripción

stat.MínX Mínimo devalores x.

stat.C1X 1er Cuartil de x.

Listado alfabético 75

Variable de salida Descripción

stat.MedianaX Mediana de x.

stat.C3X 3er Cuartil de x.

stat.MaxX Máximo de valores x.

floor() (piso)

floor(Expr1)⇒entero

Entrega el entero más grande que es { el argumento. Esta función es idéntica a int().

El argumento puede ser un número real o complejo.

floor(Lista1)⇒lista floor(Matriz1)⇒matriz

Entrega una lista o matriz del piso de cada elemento.

Nota: Vea también ceiling() e int().

fMax()

fMax(Expr, Var)⇒expresión Booleana

fMax(Expr, Var,límiteInferior)

fMax(Expr,

Var,límiteInferior,límiteSuperior)

fMax(Expr, Var) | límiteInferior{Var {límiteSuperior

Entrega una expresión Booleana que especifica valores candidatos de Var que maximizan Expr o ubican su límite superior menor.

Puede utilizar el operador restrictivo ("|") para restringir el intervalo de solución o especificar otras restricciones.

Catálogo >

76 Listado alfabético

fMax()

Para la configuración aproximada del modo

Auto o Aproximado, fMax() busca

iterativamente un máximo local aproximado. Con frecuencia esto es más rápido, en particular si usted usa el operador “|” para restringir la búsqueda a un intervalo relativamente pequeño que contiene exactamente un máximo local.

Nota: Vea también fMín() y Max().

Catálogo >

fMín()

fMín(Expr, Var)⇒expresión Booleana

fMín(Expr, Var,límiteInferior)

fMín(Expr,

Var,límiteInferior,límiteSuperior)

fMín(Expr, Var) | límiteInferior{Var {límiteSuperior

Entrega una expresión Booleana que especifica valores candidatos de Var que minimizan Expr o ubican su límite inferior mayor.

Puede utilizar el operador restrictivo ("|") para restringir el intervalo de solución o especificar otras restricciones.

Para la configuración aproximada del modo

Auto o Aproximado, fMín() busca

iterativamente un mínimo local aproximado. Con frecuencia esto es más rápido, en particular si usted usa el operador “|” para restringir la búsqueda a un intervalo relativamente pequeño que contiene exactamente un mínimo local.

Nota: Vea también fMax() y mín().

Catálogo >

Listado alfabético 77

For (Para)

For Var, Bajo, Alto [, Paso]

Bloque

EndFor

Ejecuta las sentencias en Bloque iterativamente para cada valor de Var, desde Bajo hasta Alto, en incrementos de

Paso. Var no debe ser una variable de sistema. Paso puede ser positivo o negativo. El valor

predeterminado es 1.

Bloque puede ser una sentencia sencilla o

una serie de sentencias separadas con el caracter ":".

Nota para introducir el ejemplo: Para

obtener instrucciones sobre cómo introducir las definiciones de programas y funciones en varias líneas, consulte la sección Calculadora de la guía del producto.

Catálogo >

format()

format(Expr[, cadenaFormato])⇒cadena

Entrega Expr como una cadena de caracteres con base en la plantilla de formato.

Expr debe simplificarse a un número. cadenaFormato es una cadena y debe ser

en la forma: “F[n]”, “S[n]”, “E[n]”, “G[n] [c]”, donde [] indican porciones adicionales.

F[n]: Formato fijo. n es el número de dígitos a desplegar después del punto decimal.

S[n]: Formato científico. n es el número de dígitos a desplegar después del punto decimal.

78 Listado alfabético

Catálogo >

format()

E[n]: Formato de ingeniería. n es el número de dígitos después del primer dígito significativo. El exponente se ajusta a un múltiplo de tres, y el punto decimal se mueve hacia la derecha por cero, uno o dos dígitos.

G[n][c]: Igual que el formato fijo, pero también separa los dígitos hacia la izquierda de la raíz en grupos de tres. c especifica el caracter del separador del grupo y se predetermina a una coma. Si c es un punto, la raíz se mostrará como una coma.

[Rc]: Cualquiera de los especificadores anteriores puede tener un sufijo con la bandera de la raíz Rc, donde c es un caracter sencillo que especifica qué sustituir para el punto de la raíz.

Catálogo >

fPart() (parteF)

fPart(Expr1)⇒expresión fPart(Lista1)⇒lista fPart(Matriz1)⇒matriz

Entrega la parte fraccional del argumento.

Para una lista o matriz, entrega las partes fraccionales de los elementos.

El argumento puede ser un número real o complejo.

FPdf()

FPdf(XVal,númerodf,denomdf)⇒número si

XVal es un número, lista si XVal es una

lista

Resuelve la probabilidad de distribución F en

XVal para los númerodf (grados de libertad)

y denomdfespecificados.

Catálogo >

Listado alfabético 79

freqTable4list()

freqTable4list(Lista1,listaEnteroFrec)

⇒lista

Entrega una lista que contiene los elementos desde Lista1 expandida de acuerdo con las frecuencias en

listaEnteroFrec. Esta función se puede

usar para construir una tabla de frecuencia para la aplicación de Datos y Estadísticas.

Lista1 puede ser cualquier lista válida. listaEnteroFrec debe tener la misma

dimensión que Lista1 y debe contener sólo elementos enteros no negativos. Cada elemento especifica el número de veces que el elemento de Lista1 correspondiente se repetirá en la lista de resultados. Un valor de cero excluye el elemento de Lista1 correspondiente.

Nota: Usted puede insertar esta función

desde el teclado de la computadora al escribir freqTable@>list(...).

Los elementos vacíos (anulados) se ignoran. Para obtener más información sobre elementos vacíos, vea página 253.

Catálogo >

frequency (frecuencia)

frequency(Lista1,listaCajones)⇒lista

Entrega una lista que contiene los conteos de los elementos en Lista1. Los conteos se basan en los rangos (cajones) que usted define en listaCajones.

Si listaCajones es {b(1), b(2), …, b(n)}, los rangos especificados son {?{b(1), b(1)<?{b (2),…,b(n-1)<?{b(n), b(n)>?}. La lista resultante es un elemento más largo que

listaCajones.

80 Listado alfabético

Catálogo >

Explicación del resultado:

2 elementos de listaDatos son {2.5

4 elementos de listaDatos son >2.5 y {4.5

3 elementos de listaDatos son >4.5

El elemento "hola" esuna cadena y no se puedecolocar en ninguno de los cajones definidos.

frequency (frecuencia)

Cada elemento del resultado corresponde al número de elementos de Lista1 que están en el rango de ese cajón. Expresado en términos de la función countIf() , el resultado es {conteoSi(lista, ?{b(1)), conteoSi(lista, b(1)<?{b(2)), …, conteoSi (lista, b(n-1)<?{b(n)), conteoSi(lista, b(n) >?)}.

Los elementos de Lista1 que no pueden estar “colocados en un cajón” se ignoran. Los elementos (inválidos) vacíos también se ignoran. Para obtener más información sobre elementos vacíos, vea página 253.

Dentro de la aplicación Listas y Hoja de Cálculo, usted puede usar un rango de celdas en lugar de ambos argumentos.

Nota: Vea también countIf(), página 37.

Catálogo >

FTest_2Samp

FTest_2Samp Lista1,Lista2[,Frec1[,Frec2

[,Hipot]]]

FTest_2Samp Lista1,Lista2[,Frec1[,Frec2

[,Hipot]]]

(Entrada de lista de datos)

FTest_2Samp sx1,n1,sx2,n2[,Hipot]

(Entrada de estadísticas de resumen)

Realiza una prueba Fde dos muestras. Un resumen de resultados se almacena en la variable stat.results (página 190).

Para Ha: s1 > s2, configurar Hipot>0

Para Ha: s1 ƒ s2 (predeterminado), configurar Hipot =0

Para Ha: s1 < s2, configurar Hipot<0

Para obtener información sobre el efecto de los elementos vacíos en una lista, vea “Elementos vacíos (inválidos)” (página 253).

Catálogo >

Listado alfabético 81

Variable de salida

stat.F EstadísticaÛ calculada para la secuenciade datos

stat.ValP Nivel más bajo de significancia enel cual la hipótesis nulase puede rechazar

stat.númerodf grados de libertad del numerador = n1-1

stat.denomdf grados delibertaddel denominador = n2-1

stat.sx1, stat.sx2

stat.x1_bar

stat.x2_bar

stat.n1, stat.n2 Tamaño de las muestras

Descripción

Desviacionesestándar demuestra de lassecuencias de datos enLista1 y

Lista2

Muestra significa las secuencias de datos enLista1 y Lista2

Func

Bloque

EndFunc

Plantilla para crear una función definida por el usuario.

Bloque puede ser una sentencia sencilla,

una serie de sentencias separadas con el caracter ":" o una serie de sentencias en líneas separadas. La función puede usar la instrucción Return para producir un resultado específico.

Nota para introducir el ejemplo: Para

obtener instrucciones sobre cómo introducir las definiciones de programas y funciones en varias líneas, consulte la sección Calculadora de la guía del producto.

gcd() (mcd)

gcd(Número1, Número2)⇒expresión

Catálogo >

Defina una función de compuesto de variables:

Resultado de graficar g(x)

Catálogo >

82 Listado alfabético

gcd() (mcd)

Entrega el máximo común divisor de los dos argumentos. El gcd de dos fracciones es el

gcd de sus numeradores dividido entre el lcm de sus denominadores.

En el modo de Auto o Aproximado, el gcd de los números de punto flotante es 1.0.

gcd(Lista1, Lista2)⇒lista

Entrega los máximos comunes divisores de los elementos correspondientes en Lista1 y

Lista2.

gcd(Matriz1, Matriz2)⇒matriz

Entrega los máximos comunes divisores de los elementos correspondientes en

Matriz1y Matriz2.

Catálogo >

geomCdf()

geomCdf(p,límiteInferior,límiteSuperior)

⇒número si límiteInferior y

límiteSuperior son números, lista si límiteInferior y límiteSuperior son listas

geomCdf(p,límiteSuperior)para P(1{X {límiteSuperior)⇒número si

límiteSuperior es un número, lista si límiteSuperior es una lista

Resuelve una probabilidad geométrica acumulativa desde límiteInferior hasta

límiteSuperior con la probabilidad de éxito pespecificada.

Para P(X { límiteSuperior), configure

límiteInferior =1.

geomPdf()

geomPdf(p,XVal)⇒número si XVal es un

número, lista si XVal es una lista Resuelve una probabilidad en XVal, el

número de la prueba en la que ocurre el primer éxito, para la distribución geométrica discreta con la probabilidad de éxito p.

Catálogo >

Listado alfabético 83

Get Menú del Concentrador

Get[promptString,]var[,statusVar]

Get[promptString,] func(arg1, ...argn)

[,statusVar]

Comando de programación: Recupera un valor de uno conectado [[[Undefined variable MyVariables.HubFullName]]] y asigna el valor a var variable.

El valor se debe solicitar:

• Por adelantado, a través de un comando

Send"READ..." .

— o bien —

• Mediante la inserción de una solicitud

"READ..." como argumento

Ejemplo: Soliciteel valor actual del sensor de nivelde luz incorporado delconcentrador. Use Get para recuperar el valor y asignarlo a lightval variable.

Inserte la solicitudREAD dentro del comando Get.

promptString opcional. Este método le

permite usar un solo comando para solicitar el valor y recuperarlo.

Se lleva a cabo una simplificación implícita. Por ejemplo, una cadena recibida de "123" se interpreta como valor numérico. Para conservar la cadena, use GetStr en lugar de

Get.

Si incluye el argumento opcional statusVar, se le asigna un valor que se basa en el éxito de la operación. Un valor de cero significa que no se recibieron datos.

En la segunda sintaxis, el argumento func() permite a un programa almacenar la cadena recibida como una definición de la función. La sintaxis opera como si el programa ejecutara el comando:

Se define func(arg1, ...argn) = received

string

Entonces el programa puede usar la función

func() definida.

Nota: Puede usar el comando Get dentro de

un programa definido por el usuario pero no dentro de una función.

84 Listado alfabético

Get Menú del Concentrador

Nota: Consulte además GetStr, página 91 y Send, página 170.

getDenom()

getDenom(Expr1)⇒expresión

Transforma el argumento en una expresión que tiene un denominador común reducido, y después entrega su denominador.

getKey()

getKey ([0 | 1]) ⇒ returnString

Descripción:getKey(): permite a un

programa de TI-Basic obtener entradas de teclado, dispositivo portátil, computadora y emulador en la computadora.

Ejemplo:

• keypressed:= getKey(): devolverá una tecla o una cadena vacía si no se ha presionado ninguna tecla. Esta llamada volverá inmediatamente.

• keypressed := getKey(1) esperará hasta que se presione una tecla. Esta llamada hará una pausa en la ejecución del programa hasta que se presione una tecla.

Catálogo >

Ejemplo:

Manejo de teclas presionadas:

Tecla de dispositivo

portátil/emulador

Esc Esc "esc"

Tableta sensible al tacto: clic superior

Activado n/a "home"

Computadora Valor devuelto

n/a "up"

Listado alfabético 85

Tecla de dispositivo

portátil/emulador

Computadora Valor devuelto

Scratchapps n/a "scratchpad"

Tableta sensible al tacto: clic

n/a "left"

izquierdo

Tableta sensible al tacto: clic

n/a "center"

en el centro

Tableta sensible al tacto: clic

n/a "right"

derecho

Doc n/a "doc"

Tabulación Tabulación "tab"

Tableta sensible al tacto: clic

Flecha hacia abajo "down"

inferior

Menú n/a "menu"

Ctrl Ctrl sin devolución

Mayús Mayús sin devolución

Variable n/a "var"

Supr n/a "del"

= = "="

trigonometría n/a "trig"

0 a 9 0 a 9 "0" ... "9"

Plantillas n/a "template"

Catálogo n/a "cat"

^ ^ "^"

X^2 n/a "square"

/ (tecla de división) / "/"

* (tecla de multiplicación) * "*"

e^x n/a "exp"

10^x n/a "10power"

+ + "+"

86 Listado alfabético

Tecla de dispositivo

portátil/emulador

Computadora Valor devuelto

- - "-"

( ( "("

) ) ")"

. . "."

(-) n/a "-" (signo de resta)

Intro Intro "enter"

ee n/a "E" (notación científica E)

a - z a-z alfa = letra presionada

(minúsculas) ("a" - "z")

mayús a-z mayús a-z alfa = letra presionada

"A" - "Z"

Nota: ctrl-mayús sirve para bloquear mayúsculas

?! n/a "?!"

pi n/a "pi"

Bandera n/a sin devolución

, , ","

Devolver n/a "return"

Espacio Espacio " " (espacio)

Inaccesible Teclas de caracteres

Se devuelve el carácter especiales como @, !, ^, etc.

n/a Teclas de funciones Ningún carácter devuelto

n/a Teclas especiales de control

Ningún carácter devuelto de la computadora

Inaccesible Otras teclas de computadora

que no están disponibles en la calculadora mientras

El mismo carácter que se

obtiene en Notas (no en un

cuadro de matemáticas) getkey() está esperando que se presione una tecla. ({, },;,

Listado alfabético 87

Tecla de dispositivo

portátil/emulador

Computadora Valor devuelto

:, ...)

Nota: Es importante señalar que la presencia de getKey() en un programa cambia cómo se manejan ciertos eventos en el sistema. Algunos de estos se describen a continuación.

Terminar el programa y manejar el evento: exactamente como si el usuario saliera del programa al presionar la tecla ENCENDER.

"Compatibilidad" a continuación significa que el sistema funciona como se espera y que el programa continúa ejecutándose.

Evento Dispositivo Computadora: TI-Nspire™

Encuesta rápida Terminar programa,

manejar evento

Student Software

Igual que en el dispositivo portátil (TI-Nspire™ Student Software, TINspire™ Navigator™ NC Teacher Software, solamente)

Admin. de archivos remotos

Terminar programa, manejar evento

Igual que en el dispositivo portátil.

(TI-Nspire™ Student

(Incluye enviar el archivo 'Exit Press 2 Test' desde otro dispositivo portátil o

Software, TI-Nspire™ Navigator™ NC Teacher Software solamente)

computadora)

Terminar clase Terminar programa,

manejar evento

Compatibilidad (TI-Nspire™ Student

Software, TI-Nspire™ Navigator™ NC Teacher Software solamente)

Evento Dispositivo Computadora: todas las

TI-Innovator™ Hub : conectar/desconectar

Compatibilidad: puede emitir comandos

versiones de TI-Nspire ™

Igual que en el dispositivo

portátil correctamente al TIInnovator™ Hub. Después de salir del programa, el TI-Innovator™ Hub sigue funcionando con el dispositivo portátil.

88 Listado alfabético

getLangInfo() (obtInfoIdioma)

getLangInfo()⇒cadena

Entrega una cadena que corresponde al nombre corto del idioma activo actualmente. Por ejemplo, usted puede usarlo en un programa o una función para determinar el idioma actual.

Inglés = “en”

Danés = “da”

Alemán = “de”

Finlandés = “fi”

Francés = “fr”

Italiano = “it”

Holandés = “nl”

Holandés belga = “nl_BE”

Noruego = “no”

Portugués = “pt”

Español = “es”

Sueco = “sv”

Catálogo >

getLockInfo()

getLockInfo(Var)⇒valor

Entrega el estado de bloqueada/desbloqueada actual de la variable Var.

valor =0: Var está desbloqueada o no

existe.

valor =1: Var está bloqueada y no se puede

modificar ni borrar.

Vea Lock, página 114 yunLock, página 212.

Catálogo >

Listado alfabético 89

getMode()

getMode(EnteroNombreModo)⇒valor getMode(0)⇒lista

getMode(EnteroNombreModo) entrega un

valor que representa la configuración actual del modo EnteroNombreModo .

getMode(0) entrega una lista que contiene

pares de números. Cada par consiste en un entero de modo y un entero de configuración.

Para obtener un listado de modos y sus configuraciones, consulte la tabla de abajo.

Si usted guarda las configuraciones con

getMode(0) & var, podrá usar setMode (var) en una función o un programa para

restaurar temporalmente las configuraciones dentro de la ejecución de la función o el programa únicamente. Vea

setMode(), página 174.

Catálogo >

Modo Nombre

Desplegar dígitos

Modo Entero

Cómo configurar enteros

1 1=Flotante, 2=Flotante1, 3=Flotante2, 4=Flotante3,

5=Flotante4, 6=Flotante5, 7=Flotante6, 8=Flotante7, 9=Flotante8, 10=Flotante9, 11=Flotante10, 12=Flotante11, 13=Flotante12, 14=Fijo0, 15=Fijo1, 16=Fijo2, 17=Fijo3, 18=Fijo4, 19=Fijo5, 20=Fijo6, 21=Fijo7, 22=Fijo8, 23=Fijo9, 24=Fijo10, 25=Fijo11, 26=Fijo12

Ángulo 2 1=Radián, 2=Grado, 3=Gradián

Formato

3 1=Normal, 2=Científico, 3=Ingeniería

exponencial

Real o

4 1=Real, 2=Rectangular, 3=Polar

Complejo

Auto o

5 1=Auto, 2=Aproximado, 3=Exacto

Aprox.

Formato de

6 1=Rectangular, 2=Cilíndrico, 3=Esférico

Vector

Base 7 1=Decimal, 2=Hexagonal, 3=Binario

Sistema de

8 1=SI, 2=Ing/EEUU

unidad

90 Listado alfabético

getNum()

getNum(Expr1)⇒expresión

Transforma el argumento en una expresión que tiene un denominador común reducido, y después entrega su numerador.

Catálogo >

GetStr Menú del Concentrador

GetStr[promptString,] var[, statusVar]

GetStr[promptString,] func(arg1, ...argn)

[,statusVar]

Comando de programación: Opera de forma idéntica que el comando Get, excepto que el valor recuperado siempre se interpreta como una cadena. En contraste, el comando

Get interpreta la respuesta como una

expresión a menos que esté entre comillas ("").

Nota: Consulte además Get, página 84 y Send, página 170.

Para ver ejemplos, consulte Get.

getType()

getType(var) cadena ⇒

Entrega una cadena que indica el tipo de datos de la variable var.

Si var no se ha definido, entrega la cadena "NINGUNA".

Catálogo >

Listado alfabético 91

getVarInfo()

getVarInfo()⇒matriz o cadena getVarInfo(CadenaNombreLib)⇒matriz o

cadena

getVarInfo() entrega una matriz de

información (nombre de variable, tipo, accesibilidad de librería y estado de bloqueada/desbloqueada) para todas las variables y los objetos de librería definidos en el problema actual.

Si no hay ninguna variable definida,

getVarInfo() entrega la cadena "NINGUNA". getVarInfo(CadenaNombreLib)entrega una

matriz de información para todos los objetos de librería definidos en la librería

CadenaNombreLib. CadenaNombreLib

debe ser una cadena (texto encerrado entre comillas) o una variable de cadena.

Si la librería CadenaNombreLib no existe, ocurrirá un error.

Tome en cuenta el ejemplo de la izquierda, en el cual el resultado de getVarInfo() se asigna a la variable vs. Intentar desplegar la fila 2 ó la fila 3 de vs entrega un error de “Lista o matriz inválida” porque al menos uno de los elementos en esas filas (variable

b, por ejemplo) se revalúa a una matriz.

Este error también podría ocurrir cuando se usa Ans para reevaluar un resultado de

getVarInfo() .

El sistema arroja el error anterior porque la versión actual del software no soporta una estructura de matriz generalizada donde un elemento de una matriz puede ser una matriz o una lista.

Catálogo >

92 Listado alfabético

Goto (IrA)

Goto nombreEtiqueta

Transfiere el control a la etiqueta

nombreEtiqueta. nombreEtiqueta se debe definir en la

misma función al usar una instrucción Lbl .

Nota para introducir el ejemplo: Para

obtener instrucciones sobre cómo introducir las definiciones de programas y funciones en varias líneas, consulte la sección Calculadora de la guía del producto.

Catálogo >

4Grad

Expr1 4Grad⇒expresión

Convierte Expr1 para la medida de ángulo en gradianes.

Nota: Usted puede insertar este operador

desde el teclado de la computadora al escribir @>Grad.

identity()

identity(Entero) ⇒ matriz

Produce la matriz de identidad con una dimensión de Entero.

Entero debe ser un entero positivo.

Si BooleanExpr

Enunciado

SiBooleanExprEntonces

Bloque

EndIf

Catálogo >

En modo de ángulo enGrados:

En modo de ángulo enRadianes:

Catálogo >

Listado alfabético 93

Si BooleanExpr evalúa si es verdadero, ejecuta el enunciado simple Enunciado o el bloque de enunciados Bloque antes de proceder a ejecutar.

Si BooleanExpr evalúa si es falso, procede a ejecutar sin ejecutar el enunciado o bloque de enunciados.

El Bloque puede ser un solo enunciado o una secuencia de enunciados separados por el caracter ":".

Nota para introducir el ejemplo: Para

obtener instrucciones sobre cómo introducir las definiciones de programas y funciones en varias líneas, consulte la sección Calculadora de la guía del producto.

SiBooleanExprEntonces

Bloque1

Else

Bloque2

EndIf

Si BooleanExpr evalúa si es verdadero, ejecuta Bloque1 y pasa al Bloque2.

Si BooleanExpr evalúa si es falso, pasa a

Bloque1 pero ejecuta Bloque2. Bloque1 y Bloque2 pueden ser un solo

enunciado.

SiBooleanExpr1Entonces

Bloque1

ElseIf BooleanExpr2Entonces

Bloque2

⋮

ElseIf BooleanExprNEntonces

BlockN

EndIf

Permite ramificar. Si BooleanExpr1 evalúa si es verdadero, ejecuta Block1. Si

BooleanExpr1 evalúa si es falso, evalúa BooleanExpr2, y así sucesivamente.

Catálogo >

94 Listado alfabético

ifFn()

ifFn(BooleanExpr,Value_If_true [,Value_

If_false [,Value_If_unknown]]) ⇒ expresión, lista, o matriz

Evalúa la expresión booleana BooleanExpr (o cada elemento de BooleanExpr ) y genera un resultado en base a las reglas siguientes:

• BooleanExpr puede probar un solo

valor, una lista, o una matriz.

• Si un elemento de BooleanExpr evalúa

si es verdadero, produce el elemento correspondiente de Value_If_true.

• Si un elemento de BooleanExpr evalúa

si es falso, produce el elemento correspondiente de Value_If_false. Si omite Value_If_false, produce indef.

• Si un elemento de BooleanExpr no es

ni verdadero ni falso, produce el elemento correspondiente Value_If_

unknown. Si omite Value_If_unknown,

produce indef.

• Si el segundo, tercero, o cuarto argumento de la función ifFn() es expresión sencilla, la prueba booleana se aplica a cada posición en BooleanExpr.

Nota: Si el enunciado simplificado

BooleanExpr involucra una lista o matriz,

todos los demás argumentos de la lista o matriz deben tener las mismas dimensiones, y el resultado tendrá también las mismas dimensiones.

Catálogo >

El valor de pruebade 1 es menor a 2,5; por lo que el correspondiente

El elemento Value_If_True de 5 se copiaa la lista de resultados.

El valor de pruebade 2 es menor a 2,5; por lo que el correspondiente

El elemento Value_If_True de 6 se copiaa la lista de resultados.

El valor de pruebade 3 no es menor a 2,5; por que suelemento Value_If_False correspondiente de10 se copia a la listade resultados.

Value_If_true es un valor sencillo y

corresponde a cualquier posición seleccionada.

Value_If_false no está especificado. Se

utiliza Indef.

Se selecciona un elemento de Value_If_

true. Se selecciona un elemento de Value_ If_unknown.

Listado alfabético 95

imag()

imag(Expr1) ⇒ expresión

Produce la parte imaginaria del argumento.

Nota: Todas las variables indefinidas son

tratadas como variables reales. Ver también real(), page 157

imag(List1) ⇒ lista

Produce una lista de las partes imaginarias de los elementos.

imag(Matrix1) ⇒ matriz

Produce una matriz de las partes imaginarias de los elementos.

Catálogo >

impDif()

impDif(Ecuación, Var, dependVar[,Ord])

⇒ expresión

donde el orden Ord es 1 de forma predeterminada.

Calcula la derivada implícita para las ecuaciones en las que una de las variables se define implícitamente en términos de otra.

Indirección

inString()

inString(srcString, subString[, Arrancar])

⇒ entero

Produce la posición del caracter en la serie

srcString en la cual inicia la primera

ocurrencia de la serie subString.

Arrancar, si se incluye, específica la

posición del caracter dentro de srcString en dónde inicia la búsqueda. Predeterminado = 1 (el primer caracter de srcString).

Catálogo >

Consulte #(), página 243.

Catálogo >

96 Listado alfabético

Texas Instruments TI-Nspire CX CAS Reference Guide [es]

Specifications and Main Features

Frequently Asked Questions

User Manual

Información importante

Plantillas de expresiones

Listado alfabético