Texas Instruments TI-Nspire CX CAS Reference Guide [de]

TI-Nspire™CAS

Referenzhandbuch

Dieser Leitfaden îst gültig für die TI-Nspire™ Software-Version 4.5. Die aktuellste
Version der Dokumentation finden Sie unter education.ti.com/go/download

Wichtige Informationen

Außer im Fall anderslautender Bestimmungen der Lizenz für das Programm gewährt
Texas Instruments keine ausdrückliche oder implizite Garantie, inklusive aber nicht
ausschließlich sämtlicher impliziter Garantien der Handelsfähigkeit und Eignung für
einen bestimmten Zweck, bezüglich der Programme und der schriftlichen
Dokumentationen, und stellt dieses Material nur im „Ist-Zustand“ zur Verfügung. Unter
keinen Umständen kann Texas Instruments für besondere, direkte, indirekte oder
zufällige Schäden bzw. Folgeschäden haftbar gemacht werden, die durch Erwerb oder
Benutzung dieses Materials verursacht werden, und die einzige und exklusive Haftung
von Texas Instruments, ungeachtet der Form der Beanstandung, kann den in der
Programmlizenz festgesetzten Betrag nicht überschreiten. Zudem haftet Texas
Instruments nicht für Forderungen anderer Parteien jeglicher Art gegen die Anwendung
dieses Materials.

Lizenz

Bitte lesen Sie die vollständige Lizenz im Verzeichnis

C:\ProgramFiles\TIEducation\<TI-Nspire™ Product Name>\license.

© 2006 - 2017 Texas Instruments Incorporated

ii

Inhaltsverzeichnis

Wichtige Informationen

Vorlagen für Ausdrücke 1

Alphabetische Auflistung 8

A
B
C
D
E
F
G
I
L
M
N
O
P
Q
R
S
T
U
V
W
X
Z

17
22
50
64
75
86

97
106
123
132
142
145
155
158
174
202
219
219
221
223
224

ii

8

iii

Sonderzeichen 233

Leere (ungültige) Elemente 261

Tastenkürzel zum Eingeben mathematischer Ausdrücke 263

Auswertungsreihenfolge in EOS™ (Equation Operating System) 265

Konstanten und Werte 267

Fehlercodes und -meldungen 268

Warncodes und -meldungen 277

Allgemeine Hinweise 279

Hinweise zu TI Produktservice und Garantieleistungen

279

Index 280

iv

Vorlagen für Ausdrücke

Vorlagen für Ausdrücke bieten Ihnen eine einfache Möglichkeit, mathematische
Ausdrücke in der mathematischen Standardschreibweise einzugeben. Wenn Sie eine
Vorlage eingeben, wird sie in der Eingabezeile mit kleinen Blöcken an den Positionen
angezeigt, an denen Sie Elemente eingeben können. Der Cursor zeigt, welches Element
eingegeben werden kann.

Verwenden Sie die Pfeiltasten oder drücken Sie e, um den Cursor zur jeweiligen
Position der Elemente zu bewegen, und geben Sie für jedes Element einen Wert oder

Ausdruck ein. Drücken Sie · oder /·, um den Ausdruck auszuwerten.

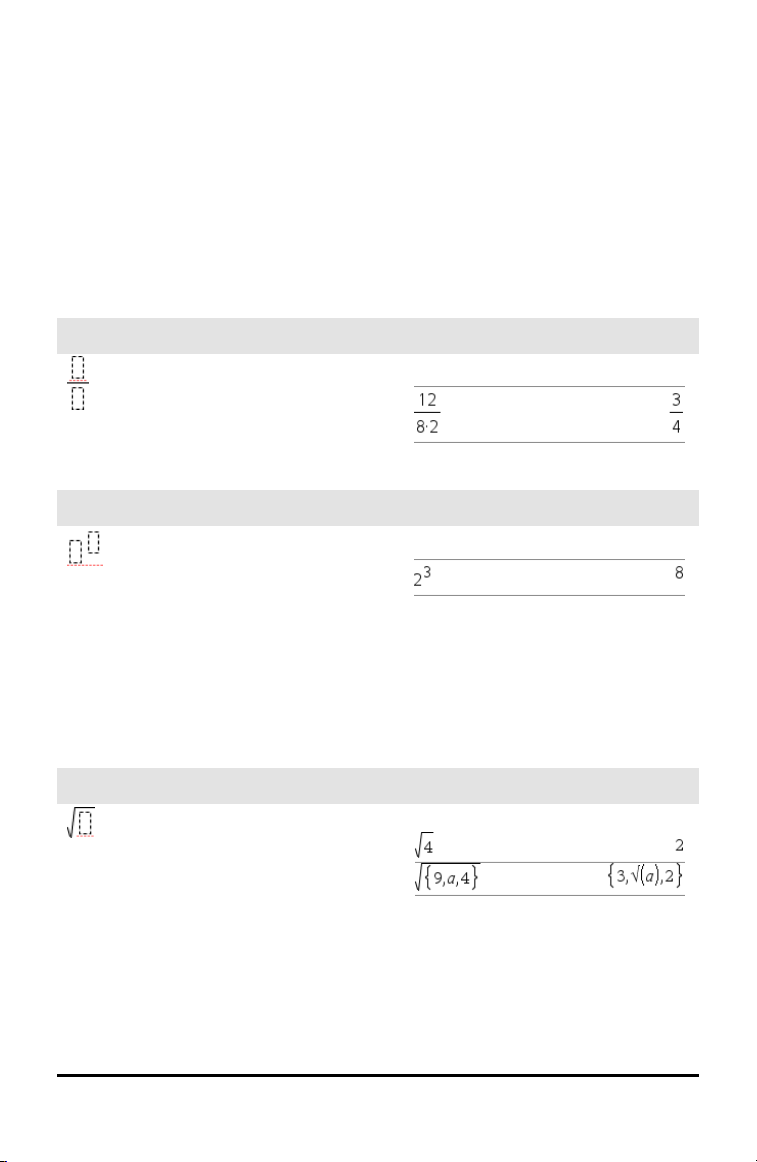
Vorlage Bruch

Hinweis: Siehe auch / (Dividieren), Seite

235.

Vorlage Exponent

Hinweis: Geben Sie den ersten Wert ein,

drücken Sie l und geben Sie dann den
Exponenten ein. Um den Cursor auf die
Grundlinie zurückzusetzen, drücken Sie die

rechte Pfeiltaste (¢).

Hinweis: Siehe auch ^ (Potenz), Seite 236.

Vorlage Quadratwurzel

Hinweis: Siehe auch ‡()

(Quadratwurzel), Seite 247.

/p Tasten

Beispiel:

l Taste

Beispiel:

/q Tasten

Beispiel:

Vorlagen für A usdrücke 1

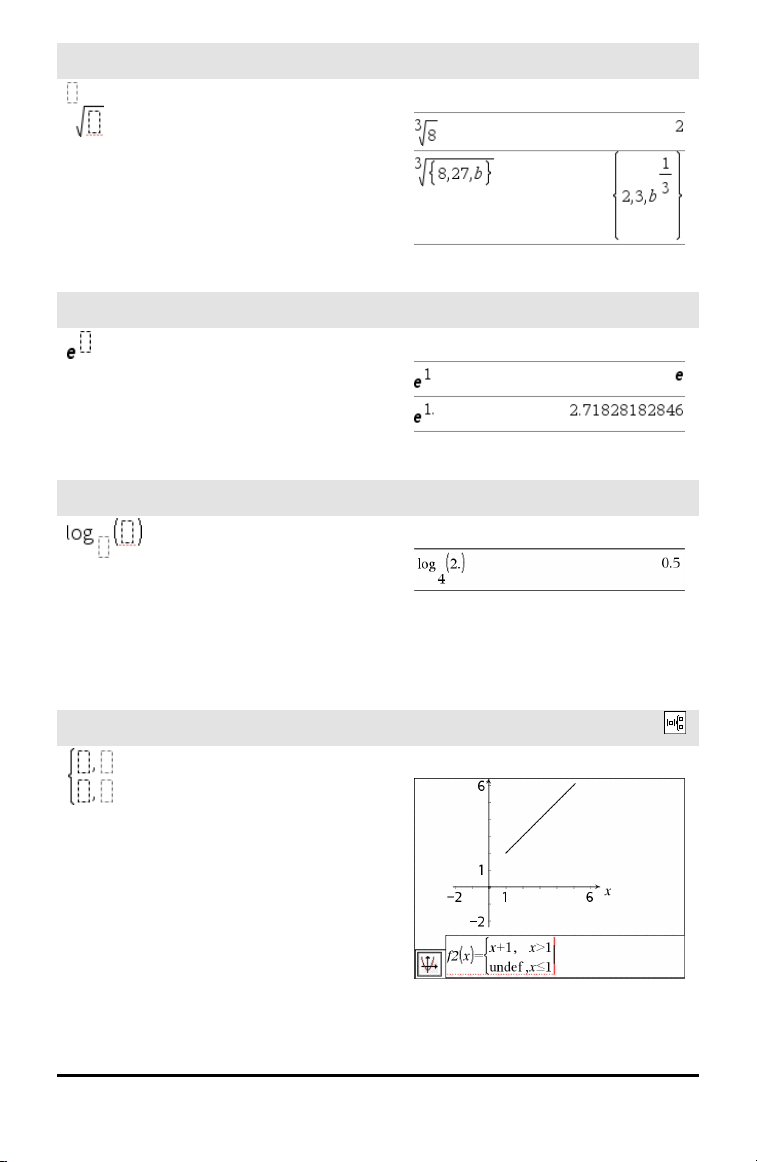
Vorlage n-te Wurzel

Hinweis: Siehe auch root(), Seite 170.

/l Tasten

Beispiel:

Vorlage e Exponent

Potenz zur natürlichen Basis e

Hinweis: Siehe auch e^(), Seite 64.

Vorlage Logarithmus

Berechnet den Logarithmus zu einer
bestimmten Basis. Bei der Standardbasis
10 wird die Basis weggelassen.

Hinweis: Siehe auch log(), Seite 119.

Vorlage Stückweise (2 Teile)

Ermöglicht es, Ausdrücke und Bedingungen
für eine stückweise definierte Funktion aus
zwei-Stücken zu erstellen. Um ein Stück
hinzuzufügen, klicken Sie in die Vorlage und
wiederholen die Vorlage.

Hinweis: Siehe auch piecewise(), Seite 147.

u Tasten

Example:

/s Taste

Beispiel:

Katalog >

Beispiel:

2 Vorlagen für Ausdrücke

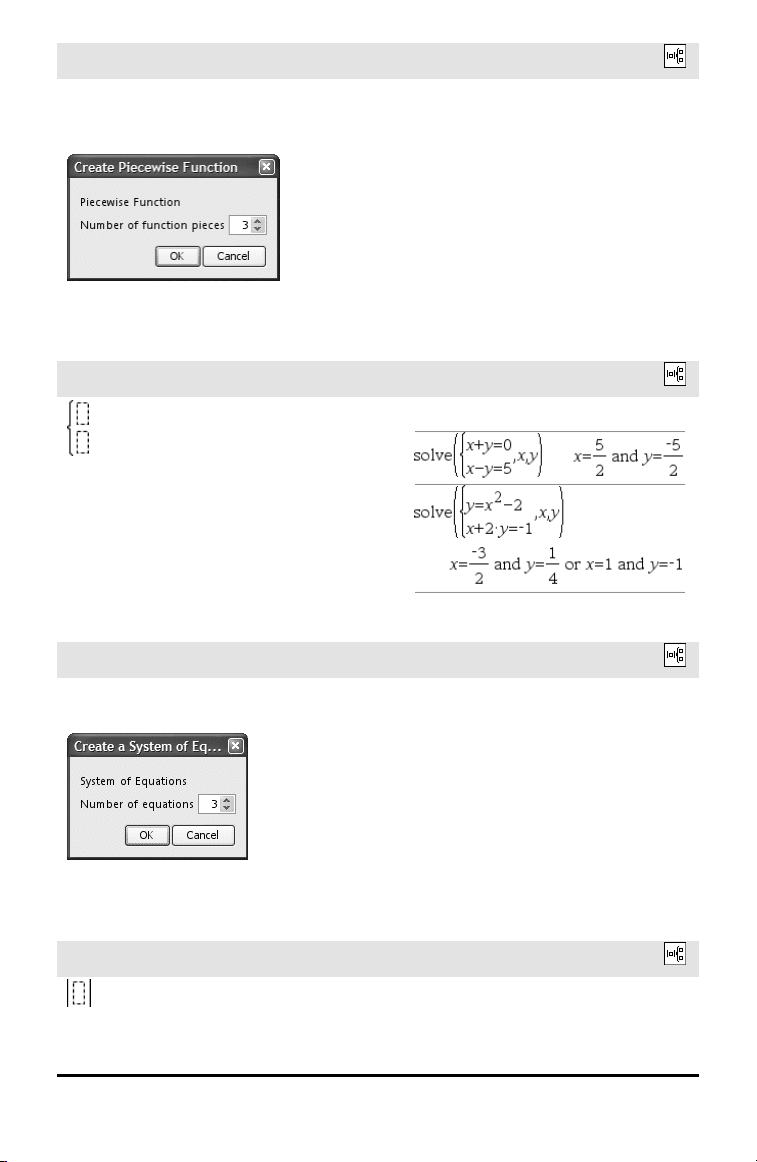
Vorlage Stückweise (n Teile)

Ermöglicht es, Ausdrücke und Bedingungen
für eine stückweise definierte Funktion aus

n-Teilen zu erstellen. Fragt nach n.

Hinweis: Siehe auch piecewise(), Seite 147.

Katalog >

Beispiel:

SieheBeispielfür die Vorlage Stückweise(2
Teile).

Vorlage System von 2 Gleichungen

Erzeugt ein System aus zwei Gleichungen.
Um einem vorhandenen System eine Zeile
hinzuzufügen, klicken Sie in die Vorlage und
wiederholen die Vorlage.

Hinweis: Siehe auch system(), Seite 202.

Vorlage System von n Gleichungen

Ermöglicht es, ein System aus NGleichungen
zu erzeugen. Fragt nach N.

Hinweis: Siehe auch system(), Seite 202.

Vorlage Absolutwert

Hinweis: Siehe auch abs(), Seite 8.

Katalog >

Beispiel:

Katalog >

Beispiel:

SieheBeispielfür die Vorlage
Gleichungssystem(2 Gleichungen).

Katalog >

Beispiel:

Vorlagen für A usdrücke 3

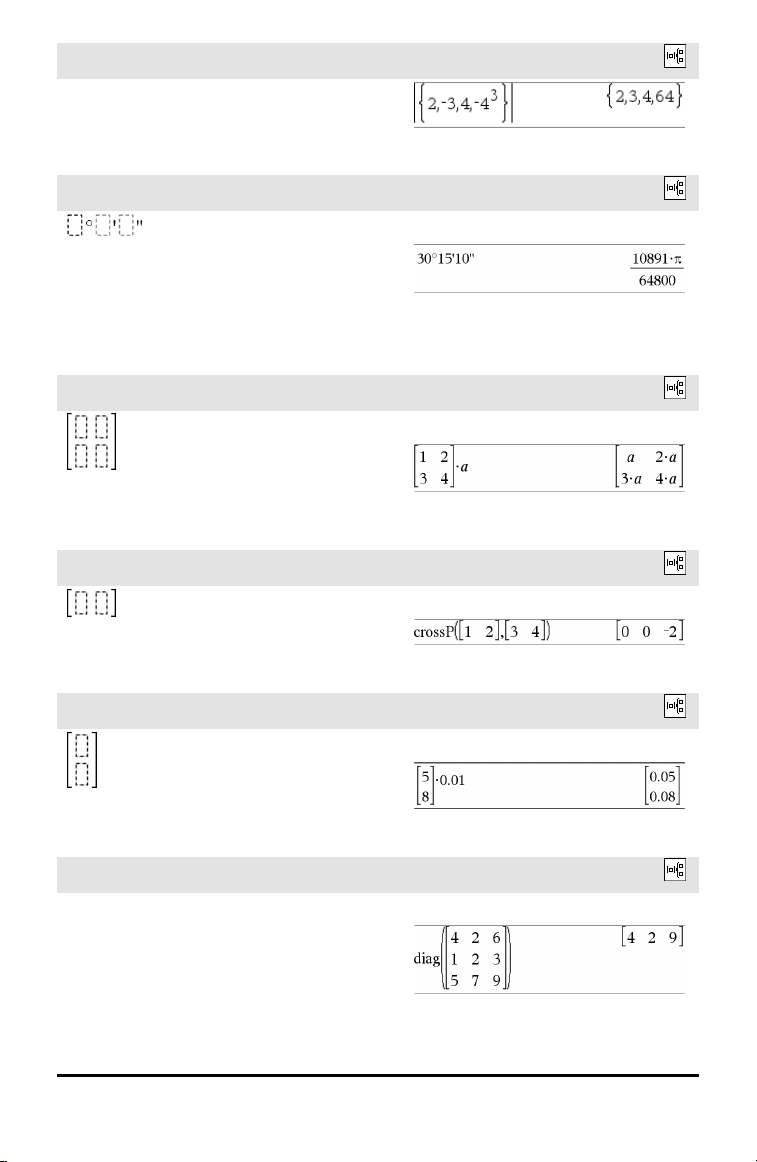
Vorlage Absolutwert

Katalog >

Vorlage dd°mm’ss.ss’’

Ermöglicht es, Winkel im Format

dd°mm’ss.ss’’ einzugeben, wobei dd für den

Dezimalgrad, mm die Minuten und ss.ss die
Sekunden steht.

Vorlage Matrix (2 x 2)

Erzeugt eine 2 x 2 Matrix.

Vorlage Matrix (1 x 2)

.

Vorlage Matrix (2 x 1)

Katalog >

Beispiel:

Katalog >

Beispiel:

Katalog >

Beispiel:

Katalog >

Beispiel:

Vorlage Matrix (m x n)

Die Vorlage wird angezeigt, nachdem Sie
aufgefordert wurden, die Anzahl der Zeilen
und Spalten anzugeben.

4 Vorlagen für Ausdrücke

Katalog >

Beispiel:

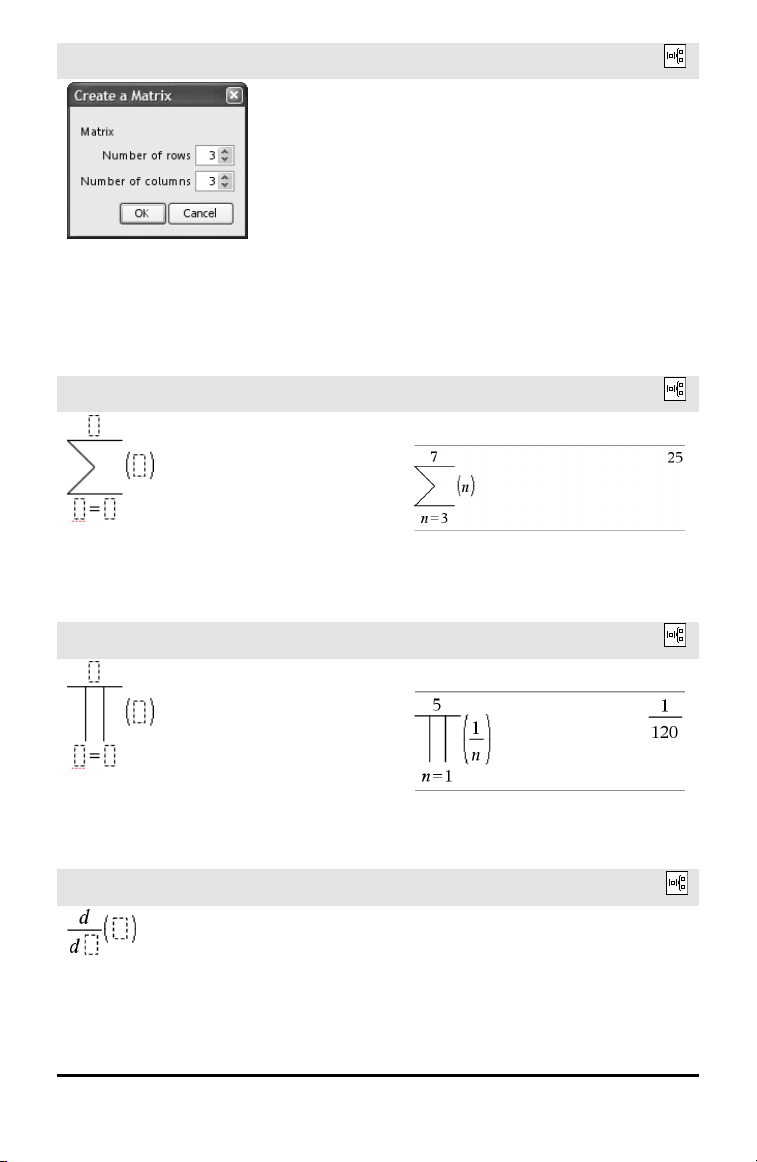
Vorlage Matrix (m x n)

Hinweis: Wenn Sie eine Matrix mit einer

großen Zeilen- oder Spaltenanzahl
erstellen, dauert es möglicherweise einen
Augenblick, bis sie angezeigt wird.

Katalog >

Vorlage Summe (G)

Hinweis: Siehe auch G() (sumSeq), Seite

248.

Vorlage Produkt (Π)

Hinweis: Siehe auch Π() (prodSeq), Seite

248.

Vorlage Erste Ableitung

Katalog >

Beispiel:

Katalog >

Beispiel:

Katalog >

Beispiel:

Mit der Vorlage „Erste Ableitung“ können
Sie auch die erste Ableitung an einem Punkt
berechnen.

Vorlagen für A usdrücke 5

Vorlage Erste Ableitung

Hinweis: Siehe auch d() (Ableitung), Seite

245.

Katalog >

Vorlage Zweite Ableitung

Mit der Vorlage „Zweite Ableitung“ können
Sie auch die zweite Ableitung an einem
Punkt berechnen.

Hinweis: Siehe auch d() (Ableitung), Seite

245.

Vorlage n-te Ableitung

Mit der Vorlage „n-te Ableitung“ können Sie
die n-te Ableitung.

Hinweis: Siehe auch d() (Ableitung), Seite

245.

Vorlage Bestimmtes Integral

Katalog >

Beispiel:

Katalog >

Beispiel:

Katalog >

Beispiel:

Hinweis: Siehe auch ‰() integral(), Seite 233.

Vorlage Unbestimmtes Integral

6 Vorlagen für Ausdrücke

Katalog >

Beispiel:

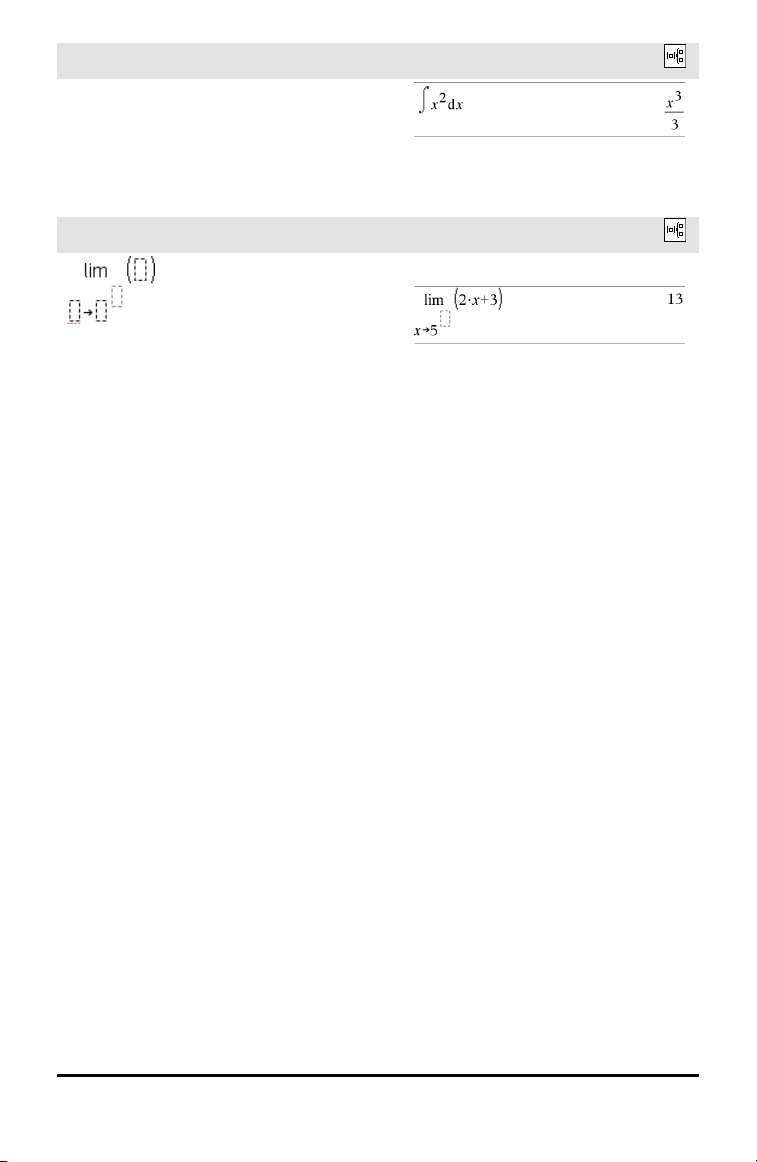
Vorlage Unbestimmtes Integral

Hinweis: Siehe auch ‰() integral(), Seite 233.

Katalog >

Vorlage Limes

Verwenden Sie N oder (N) für den
linksseitigen Grenzwert. Verwenden Sie +
für den rechtsseitigen Grenzwert.

Hinweis: Siehe auch limit(), Seite 108.

Katalog >

Beispiel:

Vorlagen für A usdrücke 7

Alphabetische Auflistung

Elemente, deren Namen nicht alphabetisch sind (wie +, !, und >) finden Sie am Ende
dieses Abschnitts (Seite 233). Wenn nicht anders angegeben, wurden sämtliche
Beispiele im standardmäßigen Reset-Modus ausgeführt, wobei alle Variablen als nicht
definiert angenommen wurden.

A

abs() (Absolutwert)

abs(Ausdr1)⇒Ausdruck
abs(Liste1)⇒Liste
abs(Matrix1)⇒Matrix

Gibt den Absolutwert des Arguments
zurück.

Hinweis: Siehe auch Vorlage Absolutwert,

Seite 3.

Ist das Argument eine komplexe Zahl, wird
der Betrag der Zahl zurückgegeben.

Hinweis: Alle undefinierten Variablen

werden als reelle Variablen behandelt.

amortTbl()

amortTbl(NPmt,N,I,PV, [Pmt], [FV],
[PpY], [CpY], [PmtAt], [WertRunden])

⇒Matrix

Amortisationsfunktion, die eine Matrix als
Amortisationstabelle für eine Reihe von
TVM-Argumenten zurückgibt.

NPmt ist die Anzahl der Zahlungen, die in

der Tabelle enthalten sein müssen. Die
Tabelle beginnt mit der ersten Zahlung.

N, I, PV, Pmt, FV, PpY, CpY und PmtAt

werden in der TVM-Argumentetabelle
(Seite 216) beschrieben.

• Wenn Sie Pmt nicht angeben, wird
standardmäßig Pmt=tvmPmt
(N,I,PV,FV,PpY,CpY,PmtAt)
eingesetzt.

Katalog >

Katalog >

8 Alphabetische Auflistung

amortTbl()

• Wenn Sie FV nicht angeben, wird
standardmäßig FV=0 eingesetzt.

• Die Standardwerte für PpY, CpY und

PmtAt sind dieselben wie bei den TVM-

Funktionen.

WertRunden (roundValue) legt die Anzahl

der Dezimalstellen für das Runden fest.
Standard=2.

Die Spalten werden in der Ergebnismatrix in
der folgenden Reihenfolge ausgegeben:
Zahlungsnummer, Zinsanteil,
Tilgungsanteil, Saldo.

Der in Zeile n angezeigte Saldo ist der Saldo
nach Zahlung n.

Sie können die ausgegebene Matrix als
Eingabe für die anderen
Amortisationsfunktionen GInt() und GPrn(),
Seite 249, und bal(), Seite 17, verwenden.

Katalog >

and (und)

Boolescher Ausdr1 and Boolescher
Ausdr2⇒Boolescher Ausdruck

Boolesche Liste1 and Boolesche Liste2

⇒Boolesche Liste

Boolesche Matrix1 and Boolesche
Matrix2⇒Boolesche Matrix

Gibt „wahr“ oder „falsch“ oder eine
vereinfachte Form des ursprünglichen
Terms zurück.

Ganzzahl1andGanzzahl2⇒Ganzzahl

Vergleicht zwei reelle ganze Zahlen mit
Hilfe einer and-Operation Bit für Bit. Intern
werden beide ganzen Zahlen in binäre 32­Bit-Zahlen mit Vorzeichen konvertiert. Beim
Vergleich der sich entsprechenden Bits ist
das Ergebnis dann 1, wenn beide Bits 1
sind; anderenfalls ist das Ergebnis 0. Der
zurückgegebene Wert stellt die Bit­Ergebnisse dar und wird im jeweiligen
Basis-Modus angezeigt.

Katalog >

Im Hex-Modus:

Wichtig: Null, nicht BuchstabeO.

Im Bin-Modus:

Alphabetische Auflistung 9

and (und)

Sie können die ganzen Zahlen in jeder Basis
eingeben. Für eine binäre oder
hexadezimale Eingabe ist das Präfix 0b
bzw. 0h zu verwenden. Ohne Präfix werden
ganze Zahlen als dezimal behandelt
(Basis 10).

Geben Sie eine dezimale ganze Zahl ein,
die für eine 32-Bit-Dualform mit Vorzeichen
zu groß ist, dann wird eine symmetrische
Modulo-Operation ausgeführt, um den
Wert in den erforderlichen Bereich zu
bringen.

Katalog >

Im Dec-Modus:

Hinweis: Eine binäre Eingabe kann bis zu 64

Stellenhaben (das Präfix 0bwirdnicht
mitgezählt). Einehexadezimale Eingabekann
biszu 16 Stellen aufweisen.

angle() (Winkel)

angle(Ausdr1)⇒Ausdruck

Gibt den Winkel des Arguments zurück,
wobei das Argument als komplexe Zahl
interpretiert wird.

Hinweis: Alle undefinierten Variablen

werden als reelle Variablen behandelt.

angle(Liste1)⇒Liste
angle(Matrix1)⇒Matrix

Gibt als Liste oder Matrix die Winkel der
Elemente aus Liste1 oder Matrix1 zurück,
wobei jedes Element als komplexe Zahl
interpretiert wird, die einen
zweidimensionalen kartesischen
Koordinatenpunkt darstellt.

Katalog >

Im Grad-Modus:

Im Neugrad-Modus:

Im Bogenmaß-Modus:

10 A lphabetische Auflistung

ANOVA

Katalog >

ANOVA Liste1,Liste2[,Liste3,...,Liste20]

[,Flag]

Führt eine einfache Varianzanalyse durch,
um die Mittelwerte von zwei bis maximal 20
Grundgesamtheiten zu vergleichen. Eine
Zusammenfassung der Ergebnisse wird in
der Variable stat.results gespeichert. (Seite

196)

Flag=0 für Daten, Flag=1 für Statistik

Ausgabevariable Beschreibung

stat.F Wert der F Statistik

stat.PVal Kleinste Signifikanzebene, beider die Nullhypothese verworfen werdenkann

stat.df Gruppen-Freiheitsgrade

stat.SS Summe der Fehlerquadrate zwischenden Gruppen

stat.MS Mittlere Quadrateder Gruppen

stat.dfError Fehler-Freiheitsgrade

stat.SSError Summe der Fehlerquadrate

stat.MSError MittleresQuadratfür die Fehler

stat.sp VerteilteStandardabweichung

stat.xbarlist Mittelwerte der Eingabelisten

stat.CLowerList 95 % Konfidenzintervalle für den Mittelwert jeder Eingabeliste

stat.CUpperList 95% Konfidenzintervalle für denMittelwertjeder Eingabeliste

ANOVA2way (ANOVA 2fach)

ANOVA2way Liste1,Liste2

[,Liste3,…,Liste10][,LevZei]

Berechnet eine zweifache Varianzanalyse,
um die Mittelwerte von zwei bis maximal 10
Grundgesamtheiten zu vergleichen. Eine
Zusammenfassung der Ergebnisse wird in
der Variable stat.results gespeichert. (Seite

196)

LevZei=0 für Block

Katalog >

Alphabetische Auflistung 11

ANOVA2way (ANOVA 2fach)

Katalog >

LevZei=2,3,...,Len-1, für Faktor zwei, wobei
Len=length(Liste1)=length(Liste2) = … =

length(Liste10) und Len / LevZei ∈
{2,3,…}

Ausgaben: Block-Design

Ausgabevariable Beschreibung

stat.F F Statistik desSpaltenfaktors

stat.PVal Kleinste Signifikanzebene, beider die Nullhypothese verworfen werdenkann

stat.df Freiheitsgradedes Spaltenfaktors

stat.SS Summe der Fehlerquadratedes Spaltenfaktors

stat.MS Mittlere Quadratefür Spaltenfaktor

stat.FBlock F Statistik für Faktor

stat.PValBlock Kleinste Wahrscheinlichkeit, beider dieNullhypothese verworfenwerdenkann

stat.dfBlock Freiheitsgrade für Faktor

stat.SSBlock Summe der Fehlerquadrate für Faktor

stat.MSBlock Mittlere Quadratefür Faktor

stat.dfError Fehler-Freiheitsgrade

stat.SSError Summeder Fehlerquadrate

stat.MSError Mittlere Quadratefür die Fehler

stat.s Standardabweichung des Fehlers

Ausgaben des SPALTENFAKTORS

Ausgabevariable Beschreibung

stat.Fcol F Statistik des Spaltenfaktors

stat.PValCol Wahrscheinlichkeitswert des Spaltenfaktors

stat.dfCol Freiheitsgradedes Spaltenfaktors

stat.SSCol Summe der Fehlerquadrate des Spaltenfaktors

stat.MSCol Mittlere Quadratefür Spaltenfaktor

Ausgaben des ZEILENFAKTORS

12 A lphabetische Auflistung

Ausgabevariable Beschreibung

stat.Frow F Statistik des Zeilenfaktors

stat.PValRow Wahrscheinlichkeitswert des Zeilenfaktors

stat.dfRow Freiheitsgrade des Zeilenfaktors

stat.SSRow Summe der Fehlerquadrate des Zeilenfaktors

stat.MSRow Mittlere Quadratefür Zeilenfaktor

INTERAKTIONS-Ausgaben

Ausgabevariable Beschreibung

stat.FInteract F Statistik der Interaktion

stat.PValInteract Wahrscheinlichkeitswert der Interaktion

stat.dfInteract Freiheitsgrade der Interaktion

stat.SSInteract Summe der Fehlerquadrate der Interaktion

stat.MSInteract Mittlere Quadratefür Interaktion

FEHLER-Ausgaben

Ausgabevariable Beschreibung

stat.dfError Fehler-Freiheitsgrade

stat.SSError Summe der Fehlerquadrate

stat.MSError Mittlere Quadratefür die Fehler

s Standardabweichung des Fehlers

Ans (Antwort)

Ans⇒Wert

Gibt das Ergebnis des zuletzt
ausgewerteten Ausdrucks zurück.

/v Taste

Alphabetische Auflistung 13

approx() (Approximieren)

approx(Ausdr1)⇒Ausdruck

Gibt die Auswertung des Arguments
ungeachtet der aktuellen Einstellung des
Modus Auto oder Näherung als
Dezimalwert zurück, sofern möglich.

Gleichwertig damit ist die Eingabe des
Arguments und Drücken von /·.

approx(Liste1)⇒Liste
approx(Matrix1)⇒Matrix

Gibt, sofern möglich, eine Liste oder Matrix
zurück, in der jedes Element dezimal
ausgewertet wurde.

Katalog >

4approxFraction()

Ausdr 4approxFraction([Tol])⇒Ausdruck

Liste 4approxFraction([Tol])⇒Liste
Matrix 4approxFraction([Tol])⇒Matrix

Gibt die Eingabe als Bruch mit der Toleranz

Tol zurück. Wird tol weggelassen, so wird

die Toleranz 5.E-14 verwendet.

Hinweis: Sie können diese Funktion über die

Tastatur Ihres Computers eingeben, indem
Sie @>approxFraction(...) eintippen.

approxRational()

approxRational(Ausdr[, Tol])⇒Ausdruck
approxRational(Liste[, Tol])⇒Liste
approxRational(Matrix[, Tol])⇒Matrix

Gibt das Argument als Bruch mit der
Toleranz Tol zurück. Wird tol weggelassen,
so wird die Toleranz 5.E-14 verwendet.

Katalog >

Katalog >

14 A lphabetische Auflistung

arccos()

Siehe cos/(), Seite 35

arccosh()

arccot()

arccoth()

arccsc()

arccsch()

arcLen() (Bogenlänge)

arcLen(Ausdr1,Var,Start,Ende)

⇒Ausdruck

Gibt die Bogenlänge von Ausdr1 von Start
bis Ende bezüglich der Variablen Var
zurück.

Die Bogenlänge wird als Integral unter
Annahme einer Definition im Modus
Funktion berechnet.

arcLen(Liste1,Var,Start,Ende)⇒Liste

Gibt eine Liste der Bogenlängen für jedes
Element von Liste1 zwischen Start und

Ende bezüglich der Variablen Var zurück.

Siehe cosh/(), Seite 36.

Siehe cot/(), Seite 37.

Siehe coth/(), Seite 38.

Siehe csc/(), Seite 40.

Siehe csch/(), Seite 41.

Katalog >

arcsec()

Siehe sec/(), Seite 174.

Alphabetische Auflistung 15

arcsech()

Siehe sech/(), Seite 175.

arcsin()

arcsinh()

arctan()

arctanh()

augment() (Erweitern)

augment(Liste1, Liste2)⇒Liste

Gibt eine neue Liste zurück, die durch
Anfügen von Liste2 ans Ende von Liste1
erzeugt wurde.

augment(Matrix1, Matrix2)⇒Matrix

Gibt eine neue Matrix zurück, die durch
Anfügen von Matrix2 an Matrix1 erzeugt
wurde. Wenn das Zeichen “,” verwendet
wird, müssen die Matrizen gleiche
Zeilendimensionen besitzen, und Matrix2
wird spaltenweise an Matrix1 angefügt.
Verändert weder Matrix1 noch Matrix2.

Siehe sin/(), Seite 186.

Siehe sinh/(), Seite 187.

Siehe tan/(), Seite 203.

Siehe tanh/(), Seite 205.

Katalog >

16 A lphabetische Auflistung

avgRC() (Durchschnittliche
Änderungsrate)

avgRC(Ausdr1, Var [=Wert] [, Schritt])

⇒Ausdruck

avgRC(Ausdr1, Var [=Wert] [, Liste1])

⇒Liste

avgRC(Liste1, Var [=Wert] [, Schritt])

⇒Liste

avgRC(Matrix1, Var [=Wert] [, Schritt])

⇒Matrix

Gibt den rechtsseitigen
Differenzenquotienten zurück
(durchschnittliche Änderungsrate).

Ausdr1 kann eine benutzerdefinierte

Funktion sein (siehe Func).

Wenn Wert angegeben ist, setzt er jede
vorausgegangene Variablenzuweisung oder
jede aktuelle „|“ Ersetzung für die Variable
außer Kraft.

Schritt ist der Schrittwert. Wird Schritt

nicht angegeben, wird als Vorgabewert
0,001 benutzt.

Beachten Sie, dass die ähnliche Funktion

centralDiff() den zentralen

Differenzenquotienten benutzt.

Katalog >

B

bal()

bal(NPmt,N,I,PV,[Pmt], [FV], [PpY],
[CpY], [PmtAt], [WertRunden])⇒Wert

bal(NPmt,AmortTabelle)⇒Wert

Amortisationsfunktion, die den Saldo nach
einer angegebenen Zahlung berechnet.

N, I, PV, Pmt, FV, PpY, CpY und PmtAt

werden in der TVM-Argumentetabelle
(Seite 216) beschrieben.

Katalog >

Alphabetische Auflistung 17

bal()

NPmt bezeichnet die Zahlungsnummer,

nach der die Daten berechnet werden
sollen.

N, I, PV, Pmt, FV, PpY, CpY und PmtAt

werden in der TVM-Argumentetabelle
(Seite 216) beschrieben.

• Wenn Sie Pmt nicht angeben, wird
standardmäßig Pmt=tvmPmt
(N,I,PV,FV,PpY,CpY,PmtAt)
eingesetzt.

• Wenn Sie FV nicht angeben, wird
standardmäßig FV=0 eingesetzt.

• Die Standardwerte für PpY, CpY und

PmtAt sind dieselben wie bei den TVM-

Funktionen.

WertRunden (roundValue) legt die Anzahl

der Dezimalstellen für das Runden fest.
Standard=2.

bal(NPmt,AmortTabelle) berechnet den

Saldo nach jeder Zahlungsnummer NPmt
auf der Grundlage der Amortisationstabelle

AmortTabelle. Das Argument
AmortTabelle (amortTable) muss eine

Matrix in der unter amortTbl(), Seite 8,
beschriebenen Form sein.

Hinweis: Siehe auch GInt() und GPrn(), Seite

249.

Katalog >

4Base2

Ganzzahl1 4Base2⇒Ganzzahl

Hinweis: Sie können diesen Operator über

die Tastatur Ihres Computers eingeben,
indem Sie @>Base2 eintippen.

Konvertiert Ganzzahl1 in eine Binärzahl.
Dual- oder Hexadezimalzahlen weisen stets
das Präfix 0b bzw. 0h auf. Null (nicht
Buchstabe O) und b oder h.

0b binäre_Zahl

0h hexadezimale_Zahl

18 A lphabetische Auflistung

Katalog >

4Base2

Eine Dualzahl kann bis zu 64 Stellen haben,
eine Hexadezimalzahl bis zu 16.

Ohne Präfix wird Ganzzahl1 als
Dezimalzahl behandelt (Basis 10). Das
Ergebnis wird unabhängig vom Basis­Modus binär angezeigt.

Negative Zahlen werden als
Binärkomplement angezeigt. Beispiel:

N1 wird angezeigt als

0hFFFFFFFFFFFFFFFF im Hex-Modus

0b111...111 (64 Einsen) im Binärmodus

N263wird angezeigt als

0h8000000000000000 im Hex-Modus

0b100...000 (63 Nullen) im Binärmodus

Geben Sie eine dezimale ganze Zahl ein,
die außerhalb des Bereichs einer 64-Bit­Dualform mit Vorzeichen liegt, dann wird
eine symmetrische Modulo-Operation
ausgeführt, um den Wert in den
erforderlichen Bereich zu bringen. Die
folgenden Beispiele verdeutlichen, wie
diese Anpassung erfolgt:

Katalog >

263wird zu N263und wird angezeigt als

0h8000000000000000 im Hex-Modus

0b100...000 (63 Nullen) im Binärmodus

264wird zu 0 und wird angezeigt als

0h0 im Hex-Modus

0b0 im Binärmodus

N263N 1 wird zu 263N 1 und wird angezeigt
als

Alphabetische Auflistung 19

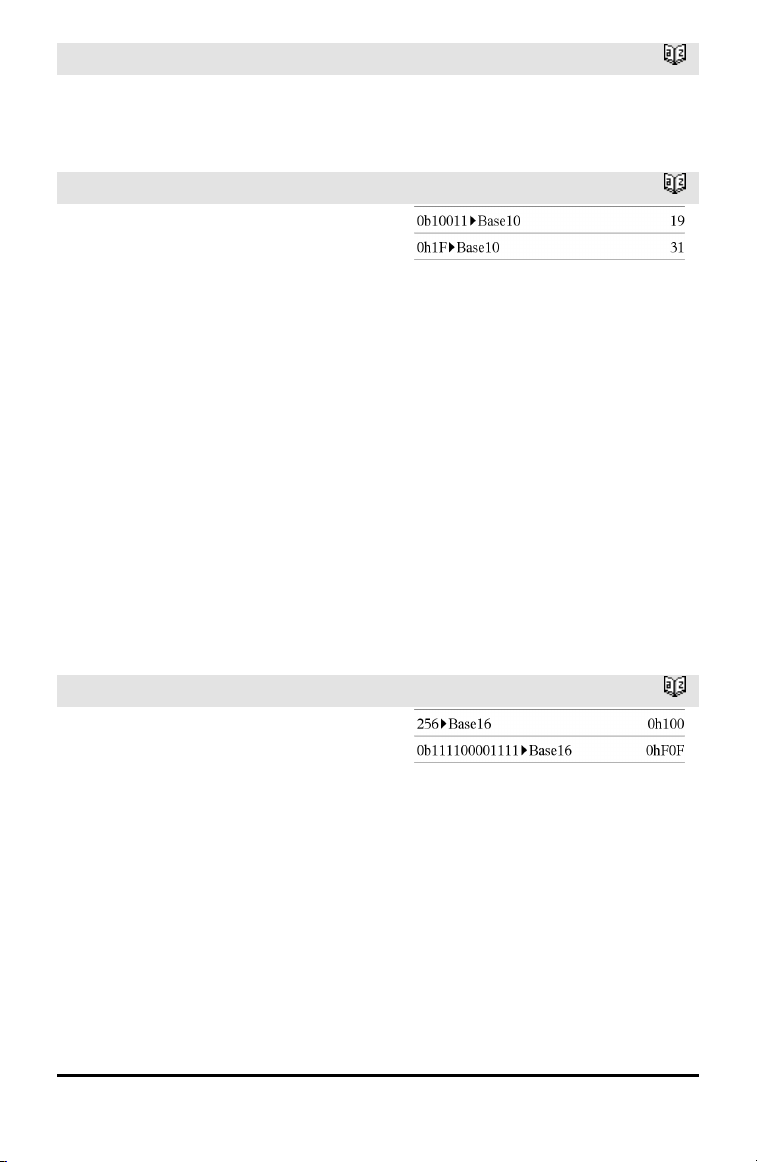
4Base2

0h7FFFFFFFFFFFFFFF im Hex-Modus

0b111...111 (64 1’s) im Binärmodus

Katalog >

4Base10

Ganzzahl1 4Base10⇒Ganzzahl

Hinweis: Sie können diesen Operator über

die Tastatur Ihres Computers eingeben,
indem Sie @>Base10 eintippen.

Konvertiert Ganzzahl1 in eine Dezimalzahl
(Basis 10). Ein binärer oder hexadezimaler
Eintrag muss stets das Präfix 0b bzw. 0h
aufweisen.

0b binäre_Zahl

0h hexadezimale_Zahl

Null (nicht Buchstabe O) und b oder h.

Eine Dualzahl kann bis zu 64 Stellen haben,
eine Hexadezimalzahl bis zu 16.

Ohne Präfix wird Ganzzahl1 als
Dezimalzahl behandelt. Das Ergebnis wird
unabhängig vom Basis-Modus dezimal
angezeigt.

4Base16

Ganzzahl1 4Base16⇒Ganzzahl

Hinweis: Sie können diesen Operator über

die Tastatur Ihres Computers eingeben,
indem Sie @>Base16 eintippen.

Wandelt Ganzzahl1 in eine
Hexadezimalzahl um. Dual- oder
Hexadezimalzahlen weisen stets das Präfix
0b bzw. 0h auf.

0b binäre_Zahl

0h hexadezimale_Zahl

Null (nicht Buchstabe O) und b oder h.

Katalog >

Katalog >

20 A lphabetische Auflistung

4Base16

Eine Dualzahl kann bis zu 64 Stellen haben,
eine Hexadezimalzahl bis zu 16.

Ohne Präfix wird Ganzzahl1 als
Dezimalzahl behandelt (Basis 10). Das
Ergebnis wird unabhängig vom Basis­Modus hexadezimal angezeigt.

Geben Sie eine dezimale ganze Zahl ein,
die für eine 64-Bit-Dualform mit Vorzeichen
zu groß ist, dann wird eine symmetrische
Modulo-Operation ausgeführt, um den
Wert in den erforderlichen Bereich zu
bringen. Weitere Informationen finden Sie
unter 4Base2, Seite 18.

Katalog >

binomCdf()

binomCdf(n,p)⇒Liste

binomCdf(n,p,untereGrenze,obereGrenze)

⇒Zahl, wenn untereGrenze und

obereGrenze Zahlen sind, Liste, wenn
untereGrenze und obereGrenze Listen sind

binomCdf(n,p,obereGrenze)für P(0{X
{obereGrenze) ⇒Zahl, wenn obereGrenze

eine Zahl ist, Liste, wenn obereGrenze eine
Liste ist

Berechnet die kumulative
Wahrscheinlichkeit für die diskrete
Binomialverteilung mit n Versuchen und der
Wahrscheinlichkeit p für einen Erfolg in
jedem Einzelversuch.

Für P(X { obereGrenze) setzen Sie

untereGrenze=0

binomPdf()

binomPdf(n,p)⇒Liste
binomPdf(n,p,XWert)⇒Zahl, wenn XWert

eine Zahl ist, Liste, wenn XWert eine Liste
ist

Katalog >

Katalog >

Alphabetische Auflistung 21

binomPdf()

Berechnet die Wahrscheinlichkeit an einem

XWert für die diskrete Binomialverteilung

mit n Versuchen und der Wahrscheinlichkeit

p für den Erfolg in jedem Einzelversuch.

C

Katalog >

ceiling() (Obergrenze)

ceiling(Ausdr1)⇒Ganzzahl

Gibt die erste ganze Zahl zurück, die | dem
Argument ist.

Das Argument kann eine reelle oder eine
komplexe Zahl sein.

Hinweis: Siehe auch floor().

ceiling(Liste1)⇒Liste
ceiling(Matrix1)⇒Matrix

Für jedes Element einer Liste oder Matrix
wird die kleinste ganze Zahl, die größer
oder gleich dem Element ist,
zurückgegeben.

centralDiff()

centralDiff(Ausdr1,Var [=Wert][,Schritt])

⇒Ausdruck

centralDiff(Ausdr1,Var [,Schritt])
|Var=Wert⇒Ausdruck

centralDiff(Ausdr1,Var [=Wert][,Liste])

⇒Liste

Katalog >

Katalog >

centralDiff(Liste1,Var [=Wert][,Schritt])

⇒Liste

centralDiff(Matrix1,Var [=Wert][,Schritt])

⇒Matrix

Gibt die numerische Ableitung unter
Verwendung des zentralen
Differenzenquotienten zurück.

22 A lphabetische Auflistung

centralDiff()

Wenn Wert angegeben ist, setzt er jede
vorausgegangene Variablenzuweisung oder
jede aktuelle „|“ Ersetzung für die Variable
außer Kraft.

Schritt ist der Schrittwert. Wird Schritt

nicht angegeben, wird als Vorgabewert
0,001 benutzt.

Wenn Sie Liste1 oder Matrix1 verwenden,
wird die Operation über die Werte in der
Liste oder die Matrixelemente abgebildet.

Hinweis: Siehe auch und d().

Katalog >

cFactor() (Komplexer Faktor)

cFactor(Ausdr1[,Var])⇒Ausdruck
cFactor(Liste1[,Var])⇒Liste
cFactor(Matrix1[,Var])⇒Matrix

cFactor(Ausdr1) gibt Ausdr1 nach allen

seinen Variablen über einem gemeinsamen
Nenner faktorisiert zurück.

Ausdr1 wird soweit wie möglich in lineare

rationale Faktoren zerlegt, selbst wenn dies
die Einführung neuer nicht-reeller Zahlen
bedeutet. Diese Alternative ist
angemessen, wenn Sie die Faktorisierung
bezüglich mehr als einer Variablen
vornehmen möchten.

cFactor(Ausdr1,Var) gibt Ausdr1 nach der

Variablen Var faktorisiert zurück.

Ausdr1 wird soweit wie möglich in

Faktoren zerlegt, die linear in Var sind, mit
möglicherweise nicht-reellen Konstanten,
selbst wenn irrationale Konstanten oder
Unterausdrücke, die in anderen Variablen
irrational sind, eingeführt werden.

Katalog >

Alphabetische Auflistung 23

cFactor() (Komplexer Faktor)

Die Faktoren und ihre Terme werden mit

Var als Hauptvariable sortiert. Gleichartige

Potenzen von Var werden in jedem Faktor
zusammengefasst. Beziehen Sie Var ein,
wenn die Faktorisierung nur bezüglich
dieser Variablen benötigt wird und Sie
irrationale Ausdrücke in anderen Variablen
akzeptieren möchten, um die Faktorisierung
bezüglich Var so weit wie möglich
vorzunehmen. Es kann sein, dass als
Nebeneffekt in gewissem Umfang eine
Faktorisierung nach anderen Variablen
auftritt.

Bei der Einstellung Auto für den Modus

Auto oder Näherung ermöglicht die

Einbeziehung von Var auch eine Näherung
mit Gleitkommakoeffizienten in Fällen, wo
irrationale Koeffizienten nicht explizit
bezüglich der integrierten Funktionen
ausgedrückt werden können. Selbst wenn
es nur eine Variable gibt, kann das
Einbeziehen von Var eine vollständigere
Faktorisierung ermöglichen.

Hinweis: Siehe auch factor().

Katalog >

Um dasganze Ergebniszu sehen, drücken
Sie £undverwendendann¡ und ¢, umden
Cursor zu bewegen.

char() (Zeichenstring)

char(Ganzzahl)⇒Zeichen

Gibt ein Zeichenstring zurück, das das
Zeichen mit der Nummer Ganzzahl aus
dem Zeichensatz des Handhelds enthält.
Der gültige Wertebereich für Ganzzahl ist
0–65535.

charPoly()

charPoly(Quadratmatrix,Var)

⇒Polynomausdruck

charPoly(Quadratmatrix, Ausdr)

⇒Polynomausdruck

charPoly(Quadratmatrix1,Matrix2)

⇒Polynomausdruck

24 A lphabetische Auflistung

Katalog >

Katalog >

charPoly()

Gibt das charakteristische Polynom von

Quadratmatrix zurück.

Das charakteristische Polynom einer n×n
Matrix A, gekennzeichnet durch pA(l), ist
das durch

p

(l) = det(l• I NA)

A

definierte Polynom, wobei I die n×n­Einheitsmatrix kennzeichnet.

Quadratmatrix1 und Quadratmatrix2

müssen dieselbe Dimension haben.

Katalog >

c

2

2way

Katalog >

c22way BeobMatrix

chi22way BeobMatrix

Berechnet eine c2Testgröße auf Grundlage
einer beobachteten Matrix BeobMatrix.
Eine Zusammenfassung der Ergebnisse wird
in der Variable stat.results gespeichert.
(Seite 196.)

Informationen zu den Auswirkungen leerer
Elemente in einer Matrix finden Sie unter
“Leere (ungültige) Elemente” (Seite 261).

Ausgabevariable Beschreibung

2

stat.c

stat.PVal Kleinste Signifikanzebene, beider die Nullhypothese verworfen werdenkann

stat.df Freiheitsgrade der Chi-Quadrat-Testgröße

stat.ExpMat Berechnete Kontingenztafelder erwarteten HäufigkeitenbeiAnnahme der

stat.CompMat BerechneteMatrix der Chi-Quadrat-Summandenin der Testgröße

2

c

Cdf()

Chi-Quadrat-Testgröße: sum(beobachtet- erwartet)2/erwartet

Nullhypothese

Katalog >

c2Cdf

(untereGrenze,obereGrenze,Freigrad)

⇒Zahl, wenn untereGrenze und

obereGrenze Zahlen sind, Liste, wenn
untereGrenze und obereGrenze Listen sind

Alphabetische Auflistung 25

2

c

Cdf()

chi2Cdf
(

untereGrenze,obereGrenze,Freiheitsgrad)

⇒Zahl, wenn untereGrenze und

obereGrenze Zahlen sind, Liste, wenn
untereGrenze und obereGrenze Listen sind

Berechnet die Verteilungswahrscheinlichkeit

c2zwischen untereGrenze und

obereGrenze für die angegebenen

Freiheitsgrade FreiGrad.

Für P(X { obereGrenze) setzen Sie

untereGrenze= 0.

Informationen zu den Auswirkungen leerer
Elemente in einer Liste finden Sie unter
“Leere (ungültige) Elemente” (Seite 261).

Katalog >

2

c

GOF

Katalog >

c2GOF BeobListe,expListe,FreiGrad

chi2GOF BeobListe,expListe,FreiGrad

Berechnet eine Testgröße, um zu
überprüfen, ob die Stichprobendaten aus
einer Grundgesamtheit stammen, die einer
bestimmten Verteilung genügt. obsList ist
eine Liste von Zählern und muss Ganzzahlen
enthalten. Eine Zusammenfassung der
Ergebnisse wird in der Variablen stat.results
gespeichert. (Seite 196)

Informationen zu den Auswirkungen leerer
Elemente in einer Liste finden Sie unter
“Leere (ungültige) Elemente” (Seite 261).

Ausgabevariable Beschreibung

2

stat.c

stat.PVal Kleinste Signifikanzebene, beider die Nullhypothese verworfen werdenkann

stat.df Freiheitsgradeder Chi-Quadrat-Testgröße

stat.CompList Liste der Chi-Quadrat-Summanden in der Testgröße

Chi-Quadrat-Testgröße: sum((beobachtet -erwartet)2/erwartet

26 A lphabetische Auflistung

2

c

Pdf()

2

c

Pdf(XWert,FreiGrad)⇒Zahl, wenn

Xwert eine Zahl ist, Liste, wenn XWert eine

Liste ist
chi2Pdf(XWert,FreiGrad)⇒Zahl, wenn

XWert eine Zahl ist, Liste, wenn XWert

eine Liste ist

Berechnet die
Wahrscheinlichkeitsdichtefunktion (Pdf)
einer c2-Verteilung an einem bestimmten

XWert für die vorgegebenen Freiheitsgrade
FreiGrad.

Informationen zu den Auswirkungen leerer
Elemente in einer Liste finden Sie unter
“Leere (ungültige) Elemente” (Seite 261).

Katalog >

ClearAZ (LöschAZ)

ClearAZ

Löscht alle Variablen mit einem Zeichen im
aktuellen Problembereich.

Wenn eine oder mehrere Variablen
gesperrt sind, wird bei diesem Befehl eine
Fehlermeldung angezeigt und es werden
nur die nicht gesperrten Variablen gelöscht.
Siehe unLock, Seite 219

ClrErr (LöFehler)

ClrErr

Löscht den Fehlerstatus und setzt die
Systemvariable FehlerCode (errCode) auf
Null.

Katalog >

Katalog >

EinBeispiel für ClrErr finden Sie alsBeispiel
2 im AbschnittzumBefehlVersuche (Try),

Seite 212.

Alphabetische Auflistung 27

ClrErr (LöFehler)

Das Else im Block Try...Else...EndTry muss

ClrErr oder PassErr (ÜbgebFehler)

verwenden. Wenn der Fehler verarbeitet
oder ignoriert werden soll, verwenden Sie

ClrErr. Wenn nicht bekannt ist, was mit dem

Fehler zu tun ist, verwenden Sie PassErr, um
ihn an den nächsten Error Handler zu
übergeben. Wenn keine weiteren

Try...Else...EndTry Error Handler unerledigt

sind, wird das Fehlerdialogfeld als normal
angezeigt.

Hinweis: Siehe auch PassErr, Seite 146, und
Try, Seite 212.

Hinweis zum Eingeben des Beispiels:

Anweisungen für die Eingabe von
mehrzeiligen Programm- und
Funktionsdefinitionen finden Sie im
Abschnitt „Calculator“ des
Produkthandbuchs.

Katalog >

colAugment() (Spaltenerweiterung)

colAugment(Matrix1, Matrix2)⇒Matrix

Gibt eine neue Matrix zurück, die durch
Anfügen von Matrix2 an Matrix1 erzeugt
wurde. Die Matrizen müssen gleiche
Spaltendimensionen haben, und Matrix2
wird zeilenweise an Matrix1 angefügt.
Verändert weder Matrix1 noch Matrix2.

colDim() (Spaltendimension)

colDim(Matrix)⇒Ausdruck

Gibt die Anzahl der Spalten von Matrix
zurück.

Hinweis: Siehe auch rowDim().

colNorm() (Spaltennorm)

colNorm(Matrix)⇒Ausdruck

28 A lphabetische Auflistung

Katalog >

Katalog >

Katalog >

colNorm() (Spaltennorm)

Gibt das Maximum der Summen der
absoluten Elementwerte der Spalten von

Matrix zurück.

Hinweis: Undefinierte Matrixelemente sind

nicht zulässig. Siehe auch rowNorm().

Katalog >

comDenom() (Gemeinsamer Nenner)

comDenom(Ausdr1[,Var])⇒Ausdruck
comDenom(Liste1[,Var])⇒Liste
comDenom(Matrix1[,Var])⇒Matrix

comDenom(Ausdr1) gibt den gekürzten

Quotienten aus einem vollständig
entwickelten Zähler und einem vollständig
entwickelten Nenner zurück.

comDenom(Ausdr1,Var) gibt einen

gekürzten Quotienten von Zähler und
Nenner zurück, der bezüglich Var
entwickelt wurde. Die Terme und Faktoren
werden mit Var als der Hauptvariablen
sortiert. Gleichartige Potenzen von Var
werden zusammengefasst. Es kann sein,
dass als Nebeneffekt eine Faktorisierung
der zusammengefassten Koeffizienten
auftritt. Verglichen mit dem Weglassen von

Var spart dies häufig Zeit, Speicherplatz

und Platz auf dem Bildschirm und macht
den Ausdruck verständlicher. Außerdem
werden anschließende Operationen an
diesem Ergebnis schneller, und es wird
weniger wahrscheinlich, dass der
Speicherplatz ausgeht.

Katalog >

Alphabetische Auflistung 29

comDenom() (Gemeinsamer Nenner)

Wenn Var nicht in Ausdr1 vorkommt, gibt

comDenom(Ausdr1,Var) einen gekürzten

Quotienten eines nicht entwickelten Zählers
und eines nicht entwickelten Nenners
zurück. Solche Ergebnisse sparen meist
sogar noch mehr Zeit, Speicherplatz und
Platz auf dem Bildschirm. Solche partiell
faktorisierten Ergebnisse machen ebenfalls
anschließende Operationen mit dem
Ergebnis schneller und das Erschöpfen des
Speicherplatzes weniger wahrscheinlich.

Sogar wenn kein Nenner vorhanden ist, ist
die Funktion comden häufig ein gutes Mittel
für das partielle Faktorisieren, wenn factor

() zu langsam ist oder den Speicherplatz

erschöpft.

Tipp: Geben Sie diese Funktionsdefinition
comden() ein, und verwenden Sie sie

regelmäßig als Alternative zu comDenom()
und factor().

Katalog >

completeSquare ()

completeSquare(AusdrOdGl, Var)

⇒Ausdruck oder Gleichung

completeSquare(AusdrOdGl, Var^Potenz)

⇒Ausdruck oder Gleichung

completeSquare(AusdrOdGl, Var1, Var2

[,...])⇒Ausdruck oder Gleichung

completeSquare(AusdrOdGl, {Var1, Var2

[,...]})⇒Ausdruck oder Gleichung

Konvertiert einen quadratischen
Polynomausdruck der Form a·x2+b·x+c in die
Form a·(x-h)2+k

- oder -

Konvertiert eine quadratische Gleichung der
Form a·x2+b·x+c=d in die Form a·(x-h)2=k

Das erste Argument muss ein quadratischer
Ausdruck oder eine Gleichung im
Standardformat bezüglich des zweiten
Arguments sein.

30 A lphabetische Auflistung

Katalog >

completeSquare ()

Das zweite Argument muss ein einzelner
univariater Term bzw. ein einzelner
univariater Term hoch einer rationalen
Potenz sein, z. B. x, y2 oder z

Die dritte und vierte Syntax versuchen, das
Quadrat mit Bezug auf Var1, Var2 [,… ]) zu
vervollständigen.

(1/3)

.

Katalog >

conj() (Komplex Konjugierte)

conj(Ausdr1)⇒Ausdruck
conj(Liste1)⇒Liste
conj(Matrix1)⇒Matrix

Gibt das komplex Konjugierte des
Arguments zurück.

Hinweis: Alle undefinierten Variablen

werden als reelle Variablen behandelt.

constructMat()

constructMat
(Ausdr,Var1,Var2,AnzZeilen,AnzSpalten)

⇒Matrix

Gibt eine Matrix auf der Basis der
Argumente zurück.

Ausdr ist ein Ausdruck in Variablen Var1

und Var2. Die Elemente in der
resultierenden Matrix ergeben sich durch
Berechnung von Ausdr für jeden
inkrementierten Wert von Var1 und Var2.

Var1 wird automatisch von 1 bis AnzZeilen

inkrementiert. In jeder Zeile wird Var2
inkrementiert von 1 bis AnzSpalten.

Katalog >

Katalog >

Alphabetische Auflistung 31

CopyVar

CopyVar Var1, Var2

CopyVar Var1., Var2.

CopyVar Var1, Var2 kopiert den Wert der

Variablen Var1 auf die Variable Var2 und
erstellt ggf. Var2. Variable Var1 muss
einen Wert haben.

Wenn Var1 der Name einer vorhandenen
benutzerdefinierten Funktion ist, wird die
Definition dieser Funktion nach Funktion

Var2 kopiert. Funktion Var1 muss definiert

sein.

Var1 muss die Benennungsregeln für

Variablen erfüllen oder muss ein indirekter
Ausdruck sein, der sich zu einem
Variablennamen vereinfachen lässt, der den
Regeln entspricht.

CopyVar Var1., Var2. kopiert alle

Mitglieder der Var1. -Variablengruppe auf
die Var2. -Gruppe und erstellt ggf. Var2..

Var1. muss der Name einer bestehenden

Variablengruppe sein, wie die
Statistikergebnisse stat. nn oder Variablen,
die mit der Funktion LibShortcut() erstellt
wurden. Wenn Var2. schon vorhanden ist,
ersetzt dieser Befehl alle Mitglieder, die zu
beiden Gruppen gehören, und fügt die
Mitglieder hinzu, die noch nicht vorhanden
sind. Wenn einer oder mehrere Teile von

Var2. gesperrt ist/sind, wird kein Teil von
Var2. geändert.

Katalog >

corrMat() (Korrelationsmatrix)

corrMat(Liste1,Liste2[,…[,Liste20]])

Berechnet die Korrelationsmatrix für die
erweiterte Matrix [Liste1 Liste2 . . .

Liste20].

4cos

Ausdr 4cos

32 A lphabetische Auflistung

Katalog >

Katalog >

4cos

Hinweis: Sie können diesen Operator über

die Tastatur Ihres Computers eingeben,
indem Sie @>cos eintippen.

Drückt Ausdr durch Kosinus aus. Dies ist ein
Anzeigeumwandlungsoperator. Er kann nur
am Ende der Eingabezeile verwendet
werden.

4cos reduziert alle Potenzen von

sin(...) modulo 1Ncos(...)^2,

so dass alle verbleibenden Potenzen von cos
(...) Exponenten im Bereich (0, 2) haben.
Deshalb enthält das Ergebnis dann und nur
dann kein sin(...), wenn sin(...) im
gegebenen Ausdruck nur bei geraden
Potenzen auftritt.

Hinweis: Dieser Umrechnungsoperator wird

im Winkelmodus Grad oder Neugrad (Gon)
nicht unterstützt. Bevor Sie ihn verwenden,
müssen Sie sicherstellen, dass der
Winkelmodus auf Radian eingestellt ist und

Ausdr keine expliziten Verweise auf Winkel

in Grad oder Neugrad enthält.

Katalog >

cos() (Kosinus)

cos(Ausdr1)⇒Ausdruck
cos(Liste1)⇒Liste

cos(Ausdr1) gibt den Kosinus des

Arguments als Ausdruck zurück.

cos(Liste1) gibt in Form einer Liste für

jedes Element in Liste1 den Kosinus zurück.

Hinweis: Der als Argument angegebene

Winkel wird gemäß der aktuellen
Winkelmoduseinstellung als Grad, Neugrad
oder Bogenmaß interpretiert. Sie können
¡, Goder R benutzen, um den Winkelmodus
vorübergend aufzuheben.

µ Taste

Im Grad-Modus:

Im Neugrad-Modus:

Im Bogenmaß-Modus:

Alphabetische Auflistung 33

cos() (Kosinus)

µ Taste

cos(Quadratmatrix1)⇒Quadratmatrix

Gibt den Matrix-Kosinus von

Quadratmatrix1 zurück. Dies ist nicht

gleichbedeutend mit der Berechnung des
Kosinus jedes einzelnen Elements.

Wenn eine skalare Funktion f(A) auf

Quadratmatrix1 (A) angewendet wird,

erfolgt die Berechnung des Ergebnisses
durch den Algorithmus:

Berechnung der Eigenwerte (li) und
Eigenvektoren (Vi) von A.

Quadratmatrix1 muss diagonalisierbar

sein. Sie darf auch keine symbolischen
Variablen ohne zugewiesene Werte
enthalten.

Bildung der Matrizen:

Dann ist A = X B X/und f(A) = X f(B) X/.
Beispiel: cos(A) = X cos(B) X/, wobei:

cos (B) =

Im Bogenmaß-Modus:

Alle Berechnungen werden unter
Verwendung von Fließkomma-Operationen
ausgeführt.

34 A lphabetische Auflistung

cos/() (Arkuskosinus)

cos/(Ausdr1)⇒Ausdruck
cos/(Liste1)⇒Liste

µ Taste

Im Grad-Modus:

cos/(Ausdr1) gibt den Winkel, dessen

Kosinus Ausdr1 ist, als Ausdruck zurück.

cos/(Liste1) gibt in Form einer Liste für

jedes Element aus Liste1 den inversen
Kosinus zurück.

Hinweis: Das Ergebnis wird gemäß der

aktuellen Winkelmoduseinstellung in Grad,
in Neugrad oder im Bogenmaß
zurückgegeben.

Hinweis: Sie können diese Funktion über die

Tastatur Ihres Computers eingeben, indem
Sie arccos(...) eintippen.

cos/(Quadratmatrix1)⇒Quadratmatrix

Gibt den inversen Matrix-Kosinus von

Quadratmatrix1 zurück. Dies ist nicht

gleichbedeutend mit der Berechnung des
inversen Kosinus jedes einzelnen Elements.
Näheres zur Berechnungsmethode finden
Sie im Abschnitt cos().

Quadratmatrix1 muss diagonalisierbar

sein. Das Ergebnis enthält immer
Fließkommazahlen.

Im Neugrad-Modus:

Im Bogenmaß-Modus:

Im Winkelmodus Bogenmaß undKomplex­Formatmodus “kartesisch”:

Um dasganze Ergebniszu sehen, drücken
Sie £undverwendendann¡ und ¢, umden
Cursor zu bewegen.

cosh() (Cosinus hyperbolicus)

cosh(Ausdr1)⇒Ausdruck
cosh(Liste1)⇒Liste

cosh(Ausdr1) gibt den Cosinus hyperbolicus

des Arguments als Ausdruck zurück.

cosh(Liste1) gibt in Form einer Liste für

jedes Element aus Liste1 den Cosinus
hyperbolicus zurück.

cosh(Quadratmatrix1)⇒Quadratmatrix

Katalog >

Im Grad-Modus:

Im Bogenmaß-Modus:

Alphabetische Auflistung 35

cosh() (Cosinus hyperbolicus)

Gibt den Matrix-Cosinus hyperbolicus von

Quadratmatrix1 zurück. Dies ist nicht

gleichbedeutend mit der Berechnung des
Cosinus hyperbolicus jedes einzelnen
Elements. Näheres zur
Berechnungsmethode finden Sie im
Abschnitt cos().

Quadratmatrix1 muss diagonalisierbar

sein. Das Ergebnis enthält immer
Fließkommazahlen.

Katalog >

cosh/() (Arkuskosinus hyperbolicus)

cosh/(Ausdr1)⇒Ausdruck
cosh/(Liste1)⇒Liste

cosh/(Ausdr1) gibt den inversen Cosinus

hyperbolicus des Arguments als Ausdruck
zurück.

cosh/(Liste1) gibt in Form einer Liste für

jedes Element aus Liste1 den inversen
Cosinus hyperbolicus zurück.

Hinweis: Sie können diese Funktion über die

Tastatur Ihres Computers eingeben, indem
Sie arccosh(...) eintippen.

cosh/(Quadratmatrix1)⇒Quadratmatrix

Gibt den inversen Matrix-Cosinus
hyperbolicus von Quadratmatrix1 zurück.
Dies ist nicht gleichbedeutend mit der
Berechnung des inversen Cosinus
hyperbolicus jedes einzelnen Elements.
Näheres zur Berechnungsmethode finden
Sie im Abschnitt cos().

Quadratmatrix1 muss diagonalisierbar

sein. Das Ergebnis enthält immer
Fließkommazahlen.

Katalog >

Im Winkelmodus Bogenmaß undKomplex­Formatmodus “kartesisch”:

Um dasganze Ergebniszu sehen, drücken
Sie £undverwendendann¡ und ¢, umden
Cursor zu bewegen.

cot() (Kotangens)

cot(Ausdr1) ⇒ Ausdruck

36 A lphabetische Auflistung

µ Taste

Im Grad-Modus:

cot() (Kotangens)

cot(Liste1) ⇒ Liste

Gibt den Kotangens von Ausdr1 oder eine
Liste der Kotangens aller Elemente in

Liste1 zurück.

Hinweis: Der als Argument angegebene

Winkel wird gemäß der aktuellen
Winkelmoduseinstellung als Grad, Neugrad
oder Bogenmaß interpretiert. Sie können
¡, Goder R benutzen, um den Winkelmodus
vorübergend aufzuheben.

µ Taste

Im Neugrad-Modus:

Im Bogenmaß-Modus:

cot/() (Arkuskotangens)

cot/(Ausdr1)⇒Ausdruck
cot/(Liste1)⇒Liste

Gibt entweder den Winkel, dessen
Kotangens Ausdr1 ist, oder eine Liste der
inversen Kotangens aller Elemente in

Liste1 zurück.

Hinweis: Das Ergebnis wird gemäß der

aktuellen Winkelmoduseinstellung in Grad,
in Neugrad oder im Bogenmaß
zurückgegeben.

Hinweis: Sie können diese Funktion über die

Tastatur Ihres Computers eingeben, indem
Sie arccot(...) eintippen.

coth() (Kotangens hyperbolicus)

coth(Ausdr1)⇒Ausdruck
coth(Liste1)⇒Liste

Gibt den hyperbolischen Kotangens von

Ausdr1 oder eine Liste der hyperbolischen

Kotangens aller Elemente in Liste1 zurück.

µ Taste

Im Grad-Modus:

Im Neugrad-Modus:

Im Bogenmaß-Modus:

Katalog >

Alphabetische Auflistung 37

coth/() (Arkuskotangens hyperbolicus)

coth/(Ausdr1)⇒Ausdruck
coth/(Liste1)⇒Liste

Gibt den inversen hyperbolischen Kotangens
von Ausdr1 oder eine Liste der inversen
hyperbolischen Kotangens aller Elemente in

Liste1 zurück.

Hinweis: Sie können diese Funktion über die

Tastatur Ihres Computers eingeben, indem
Sie arccoth(...) eintippen.

Katalog >

count() (zähle)

count(Wert1oderListe1 [,Wert2oderListe2

[,...]])⇒Wert

Gibt die kumulierte Anzahl aller Elemente
in den Argumenten zurück, deren
Auswertungsergebnisse numerische Werte
sind.

Jedes Argument kann ein Ausdruck, ein
Wert, eine Liste oder eine Matrix sein. Sie
können Datenarten mischen und Argumente
unterschiedlicher Dimensionen verwenden.

Für eine Liste, eine Matrix oder einen
Zellenbereich wird jedes Element daraufhin
ausgewertet, ob es in die Zählung
eingeschlossen werden soll.

Innerhalb der Lists & Spreadsheet
Applikation können Sie anstelle eines
beliebigen Arguments auch einen
Zellenbereich verwenden.

Leere (ungültige) Elemente werden
ignoriert. Weitere Informationen zu leeren
Elementen finden Sie (Seite 261).

countIf()

countIf(Liste,Kriterien)⇒Wert

Gibt die kumulierte Anzahl aller Elemente
in der Liste zurück, die die festgelegten

Kriterien erfüllen.

Katalog >

Im letzten Beispiel werdennur 1/2 und3+4*i
gezählt. Die übrigen Argumente ergeben
unter der Annahme, dassx nicht definiert ist,
keinenumerischenWerte.

Katalog >

Zähltdie Anzahlder Elemente, die 3
entsprechen.

38 A lphabetische Auflistung

countIf()

Kriterien können sein:

• Ein Wert, ein Ausdruck oder eine
Zeichenfolge. So zählt zum Beispiel 3 nur
Elemente in der Liste, die vereinfacht
den Wert 3 ergeben.

• Ein Boolescher Ausdruck, der das
Sonderzeichen ? als Platzhalter für jedes
Element verwendet. Beispielsweise zählt

?<5 nur die Elemente in der Liste, die

kleiner als 5 sind.

Innerhalb der Lists & Spreadsheet
Applikation können Sie anstelle der Liste
auch einen Zellenbereich verwenden.

Leere (ungültige) Elemente in der Liste
werden ignoriert. Weitere Informationen zu
leeren Elementen finden Sie (Seite 261).

Hinweis: Siehe auch sumIf(), Seite 201, und
frequency(), Seite 84.

Katalog >

Zähltdie Anzahlder Elemente, die “def.”
entsprechen

Zähltdie Anzahlder Elemente, die x
entsprechen; dieses Beispiel nimmt an, dass
dieVariablex nichtdefiniert ist.

Zählt1 und3.

Zählt3, 5 und 7.

Zählt1, 3, 7 und9.

cPolyRoots()

cPolyRoots(Poly,Var)⇒Liste
cPolyRoots(KoeffListe)⇒Liste

Die erste Syntax cPolyRoots(Poly,Var) gibt
eine Liste mit komplexen Wurzeln des
Polynoms Poly bezüglich der Variablen Var
zurück.

Poly muss dabei ein Polynom in einer

Variablen sein.

Die zweite Syntax cPolyRoots(KoeffListe)
liefert eine Liste mit komplexen Wurzeln
für die Koeffizienten in KoeffListe.

Hinweis: Siehe auch polyRoots(), Seite 151.

Katalog >

Alphabetische Auflistung 39

crossP() (Kreuzprodukt)

crossP(Liste1, Liste2)⇒Liste

Gibt das Kreuzprodukt von Liste1 und

Liste2 als Liste zurück.

Liste1 und Liste2 müssen die gleiche

Dimension besitzen, die entweder 2 oder 3
sein muss.

crossP(Vektor1, Vektor2)⇒Vektor

Gibt einen Zeilen- oder Spaltenvektor
zurück (je nach den Argumenten), der das
Kreuzprodukt von Vektor1 und Vektor2 ist.

Entweder müssen Vektor1 und Vektor2
beide Zeilenvektoren oder beide
Spaltenvektoren sein. Beide Vektoren
müssen die gleiche Dimension besitzen, die
entweder 2 oder 3 sein muss.

Katalog >

csc() (Kosekans)

csc(Ausdr1)⇒Ausdruck
csc(Liste1)⇒Liste

Gibt den Kosekans von Ausdr1 oder eine
Liste der Konsekans aller Elemente in

Liste1 zurück.

csc/() (Inverser Kosekans)

csc/(Ausdr1) ⇒ Ausdruck
csc/(Liste1) ⇒ Liste

µ Taste

Im Grad-Modus:

Im Neugrad-Modus:

Im Bogenmaß-Modus:

µ Taste

Im Grad-Modus:

Im Neugrad-Modus:

40 A lphabetische Auflistung

csc/() (Inverser Kosekans)

Gibt entweder den Winkel, dessen
Kosekans Ausdr1 entspricht, oder eine Liste
der inversen Kosekans aller Elemente in

Liste1 zurück.

Hinweis: Das Ergebnis wird gemäß der

aktuellen Winkelmoduseinstellung in Grad,
in Neugrad oder im Bogenmaß
zurückgegeben.

Hinweis: Sie können diese Funktion über die

Tastatur Ihres Computers eingeben, indem
Sie arccsc(...) eintippen.

µ Taste

Im Bogenmaß-Modus:

csch() (Kosekans hyperbolicus)

csch(Ausdr1) ⇒ Ausdruck
csch(Liste1) ⇒ Liste

Gibt den hyperbolischen Kosekans von

Ausdr1 oder eine Liste der hyperbolischen

Kosekans aller Elemente in Liste1 zurück.

csch/() (Inverser Kosekans
hyperbolicus)

csch/(Ausdr1) ⇒ Ausdruck
csch/(Liste1) ⇒ Liste

Gibt den inversen hyperbolischen Kosekans
von Ausdr1 oder eine Liste der inversen
hyperbolischen Kosekans aller Elemente in

Liste1 zurück.

Hinweis: Sie können diese Funktion über die

Tastatur Ihres Computers eingeben, indem
Sie arccsch(...) eintippen.

cSolve() (Komplexe Lösung)

cSolve(Gleichung, Var)⇒Boolescher

Ausdruck

Katalog >

Katalog >

Katalog >

cSolve(Gleichung, Var=Schätzwert)

⇒Boolescher Ausdruck

Alphabetische Auflistung 41

cSolve() (Komplexe Lösung)

cSolve(Ungleichung, Var)⇒Boolescher

Ausdruck

Gibt mögliche komplexe Lösungen einer
Gleichung oder Ungleichung für Var zurück.
Das Ziel ist, Kandidaten für alle reellen und
nicht-reellen Lösungen zu erhalten. Selbst
wenn Gleichung reel ist, erlaubt cSolve()
nicht-reelle Lösungen im reellen Modus.

Obwohl alle undefinierten Variablen, die
mit einem Unterstrich (_) enden, so
verarbeitet werden, als wären sie reell,
kann cSolve() Polynomgleichungen für
komplexe Lösungen lösen.

cSolve() setzt den Bereich während der

Berechnung zeitweise auf komplex, auch
wenn der aktuelle Bereich reell ist. Im
Komplexen benutzen Bruchexponenten mit
ungeradem Nenner den Hauptzweig und
sind nicht reell. Demzufolge sind Lösungen
mit solve() für Gleichungen, die solche
Bruchexponenten besitzen, nicht unbedingt
eine Teilmenge der mit cSolve() erzielten
Lösungen.

cSolve() beginnt mit exakten symbolischen

Verfahren. Außer im Modus Exakt benutzt

cSolve() bei Bedarf auch die iterative

näherungsweise polynomische
Faktorisierung.

Hinweis: Siehe auch cZeros(), solve() und
zeros().

Hinweis: Enthält Gleichung Funktionen wie

beispielsweise abs(), angle(), conj(), real()
oder imag(), ist sie also kein Polynom,

sollten Sie einen Unterstrich (/_
drücken) hinter Var setzen. Standardmäßig
wird eine Variable als reeller Wert
behandelt.

Bei Verwendung von var_ wird die Variable
als komplex behandelt.

Katalog >

Im ModusAngezeigte Ziffern auf Fix 2:

Um dasganze Ergebniszu sehen, drücken
Sie £undverwendendann¡ und ¢, umden
Cursor zu bewegen.

42 A lphabetische Auflistung

cSolve() (Komplexe Lösung)

Sie sollten var_ auch für alle anderen
Variablen in Gleichung verwenden, die
nicht-reelle Werte haben könnten.
Anderenfalls erhalten Sie möglicherweise
unerwartete Ergebnisse.

cSolve(Glch1andGlch2 [and…],

VarOderSchätzwert1,
VarOderSchätzwert2 [, … ])

⇒Boolescher Ausdruck

cSolve(Gleichungssystem,

VarOderSchätzwert1,
VarOderSchätzwert2 [, …])

⇒Boolescher Ausdruck

Gibt mögliche komplexe Lösungen eines
algebraischen Gleichungssystems zurück, in
dem jede VarOderSchätzwert eine
Variable darstellt, nach der Sie die
Gleichungen auflösen möchten.

Sie haben die Option, eine
Ausgangsschätzung für eine Variable
anzugeben. VarOderSchätzwert muss
immer die folgende Form haben:

Variable

– oder –

Variable = reelle oder nicht-reelle Zahl

Beispiel: x ist gültig und x=3+i ebenfalls.
Wenn alle Gleichungen Polynome sind und

Sie KEINE Anfangsschätzwerte angeben,
dann verwendet cSolve() das
lexikalischeGröbner/Buchbergersche
Eliminationsverfahren beim Versuch, alle
komplexen Lösungen zu bestimmen.

Komplexe Lösungen können, wie aus
nebenstehendem Beispiel hervorgeht,
sowohl reelle als auch nicht-reelle
Lösungen enthalten.

Katalog >

Hinweis: In folgendenBeispielen wird ein

Unterstrich(/_ drücken)verwendet,
damit die Variablenals komplex behandelt

werden.

Um dasganze Ergebniszu sehen, drücken
Sie £undverwendendann¡ und ¢, umden
Cursor zu bewegen.

Alphabetische Auflistung 43

cSolve() (Komplexe Lösung)

Gleichungssysteme, die aus Polynomen
bestehen, können zusätzliche Variablen
ohne Wert aufweisen, die aber für
numerische Werte stehen, welche später
eingesetzt werden können.

Sie können auch Lösungsvariablen angeben,
die in der Gleichung nicht erscheinen. Diese
Lösungen verdeutlichen, dass
Lösungsfamilien willkürliche Konstanten der
Form ck enthalten können, wobei k ein
ganzzahliger Index im Bereich 1 bis 255 ist.

Bei Gleichungssystemen aus Polynomen
kann die Berechnungsdauer oder
Speicherbelastung stark von der
Reihenfolge abhängen, in welcher Sie die
Lösungsvariablen angeben. Übersteigt Ihre
erste Wahl die Speicherkapazität oder Ihre
Geduld, versuchen Sie, die Variablen in der
Gleichung und/oder VarOderSchätzwert­Liste umzuordnen.

Wenn Sie keine Schätzwerte angeben und
eine Gleichung in einer Variablen nicht­polynomisch ist, aber alle Gleichungen in
allen Lösungsvariablen linear sind, so
verwendet cSolve() das Gaußsche
Eliminationsverfahren beim Versuch, alle
Lösungen zu bestimmen.

Wenn ein System weder in all seinen
Variablen polynomial noch in seinen
Lösungsvariablen linear ist, dann bestimmt

cSolve() mindestens eine Lösung anhand

eines iterativen näherungsweisen
Verfahrens. Hierzu muss die Anzahl der
Lösungsvariablen gleich der
Gleichungsanzahl sein, und alle anderen
Variablen in den Gleichungen müssen zu
Zahlen vereinfachbar sein.

Zur Bestimmung einer nicht-reellen Lösung
ist häufig ein nicht-reeller Schätzwert
erforderlich. Für Konvergenz sollte ein
Schätzwert ziemlich nahe bei einer Lösung
liegen.

Katalog >

Um dasganze Ergebniszu sehen, drücken
Sie £undverwendendann¡ und ¢, umden
Cursor zu bewegen.

44 A lphabetische Auflistung

CubicReg (Kubische Regression)

CubicReg X, Y[, [Häuf] [, Kategorie, Mit]]

Berechnet die kubische polynomiale
Regressiony = a·x3+b· x2+c·x+dauf Listen X
und Y mit der Häufigkeit Häuf. Eine
Zusammenfassung der Ergebnisse wird in
der Variablen stat.results gespeichert.
(Seite 196.)

Alle Listen außer Mit müssen die gleiche
Dimension besitzen.

X und Y sind Listen von unabhängigen und

abhängigen Variablen.

Häuf ist eine optionale Liste von

Häufigkeitswerten. Jedes Element in Häuf
gibt die Häufigkeit für jeden entsprechenden
Datenpunkt X und Y an. Der Standardwert
ist 1. Alle Elemente müssen Ganzzahlen | 0
sein.

Kategorie ist eine Liste von Kategoriecodes

für die entsprechenden X und Y Daten.

Mit ist eine Liste von einem oder mehreren

Kategoriecodes. Nur solche Datenelemente,
deren Kategoriecode in dieser
Liste enthalten ist, sind in der Berechnung
enthalten.

Informationen zu den Auswirkungen leerer
Elemente in einer Liste finden Sie unter
“Leere (ungültige) Elemente” (Seite 261).

Katalog >

Ausgabevariable Beschreibung

stat.RegEqn Regressionsgleichung: a·x3+b·x2+c·x+d

stat.a, stat.b,
stat.c, stat.d

2

stat.R

stat.Resid Residuenvon der Regression

stat.XReg

Regressionskoeffizienten

Bestimmungskoeffizient

Liste der Datenpunktein der modifiziertenX List, die schließlich in der
Regression mit denBeschränkungenfür Häufigkeit, Kategorieliste undMit

Kategorien verwendetwurde

Alphabetische Auflistung 45

Ausgabevariable Beschreibung

stat.YReg

stat.FreqReg

Liste der Datenpunktein der modifiziertenY List, die schließlichin der
Regression mit denBeschränkungenfür Häufigkeit, Kategorieliste undMit

Kategorien verwendetwurde

Liste der Häufigkeiten für stat.XReg und stat.YReg

cumulativeSum() (kumulierteSumme)

cumulativeSum(Liste1)⇒Liste

Gibt eine Liste der kumulierten Summen
der Elemente aus Liste1 zurück, wobei bei
Element 1 begonnen wird.

cumulativeSum(Matrix1)⇒Matrix

Gibt eine Matrix der kumulierten Summen
der Elemente aus Matrix1 zurück. Jedes
Element ist die kumulierte Summe der
Spalte von oben nach unten.

Ein leeres (ungültiges) Element in Liste1
oder Matrix1 erzeugt ein ungültiges
Element in der resultierenden Liste oder
Matrix. Weitere Informationen zu leeren
Elementen finden Sie (Seite 261).

Cycle (Zyklus)

Cycle (Zyklus)

Übergibt die Programmsteuerung sofort an
die nächste Wiederholung der aktuellen
Schleife (For, While oder Loop).

Cycle ist außerhalb dieser drei

Schleifenstrukturen (For, While oder Loop)
nicht zulässig.

Hinweis zum Eingeben des Beispiels:

Anweisungen für die Eingabe von
mehrzeiligen Programm- und
Funktionsdefinitionen finden Sie im
Abschnitt „Calculator“ des
Produkthandbuchs.

Katalog >

Katalog >

Funktionslisting, das die ganzenZahlenvon 1
bis100summiert unddabei 50 überspringt.

46 A lphabetische Auflistung

4Cylind (Zylindervektor)

Vektor 4Cylind

Hinweis: Sie können diesen Operator über

die Tastatur Ihres Computers eingeben,
indem Sie @>Cylind eintippen.

Zeigt den Zeilen- oder Spaltenvektor in
Zylinderkoordinaten [r,±q, z] an.

Vektor muss genau drei Elemente besitzen.

Er kann entweder ein Zeilen- oder
Spaltenvektor sein.

Katalog >

cZeros() (Komplexe Nullstellen)

cZeros(Ausdr, Var)⇒Liste

Gibt eine Liste möglicher reeller und nicht­reeller Werte für Var zurück, die Ausdr=0
ergeben. cZeros() tut dies durch Berechnung
von

exp4list(cSolve(Ausdr=0,Var),Var).

Ansonsten ist cZeros() ähnlich wie zeros().

Hinweis: Siehe auch cSolve(), solve() und
zeros().

Hinweis: Ist Ausdr nicht-polynomial mit

Funktionen wie beispielsweise abs(), angle

(), conj(), real() oder imag(), sollten Sie

einen Unterstrich (/_ drücken) hinter

Var setzen. Standardmäßig wird eine

Variable als reeller Wert behandelt. Bei
Verwendung von var_ wird die Variable als
komplex behandelt.

Sie sollten var_ auch für alle anderen
Variablen in Ausdr verwenden, die nicht­reelle Werte haben könnten. Anderenfalls
erhalten Sie möglicherweise unerwartete
Ergebnisse.

cZeros({Ausdr1, Ausdr2 [, … ] },
{

VarOderSchätzwert1

,VarOderSchätzwert2 [, … ] })⇒Matrix

Katalog >

Im ModusAngezeigte Ziffern auf Fix 3:

Um dasganze Ergebniszu sehen, drücken
Sie £undverwendendann¡ und ¢, umden
Cursor zu bewegen.

Alphabetische Auflistung 47

cZeros() (Komplexe Nullstellen)

Gibt mögliche Positionen zurück, in welchen
die Ausdrücke gleichzeitig Null sind. Jeder

VarOderSchätzwert steht für eine

Unbekannte, deren Wert Sie suchen.
Sie haben die Option, eine

Ausgangsschätzung für eine Variable
anzugeben. VarOderSchätzwert muss
immer die folgende Form haben:

Variable

– oder –

Variable = reelle oder nicht-reelle Zahl

Beispiel: x ist gültig und x=3+i ebenfalls.
Wenn alle Ausdrücke Polynome sind und Sie

KEINE Anfangsschätzwerte angeben, dann
verwendet cZeros() das lexikalische
Gröbner/Buchbergersche
Eliminationsverfahren beim Versuch, alle
komplexen Nullstellen zu bestimmen.

Komplexe Nullstellen können, wie aus
nebenstehendem Beispiel hervorgeht,
sowohl reelle als auch nicht-reelle
Nullstellen enthalten.

Jede Zeile der sich ergebenden Matrix stellt
eine alternative Nullstelle dar, wobei die
Komponenten in derselben Reihenfolge wie
in der VarOderSchätzwert-Liste
angeordnet sind. Um eine Zeile zu erhalten
ist die Matrix nach [Zeile] zu indizieren.

Katalog >

Hinweis: In folgendenBeispielen wird ein

Unterstrich_ (/_ drücken)
verwendet, damit dieVariablenals komplex

behandeltwerden.

Zeile2 extrahieren:

Gleichungssysteme, die aus Polynomen
bestehen, können zusätzliche Variablen
haben, die zwar ohne Werte sind, aber
gegebene numerische Werte darstellen, die
später eingesetzt werden können.

48 A lphabetische Auflistung

cZeros() (Komplexe Nullstellen)

Sie können auch unbekannte Variablen
angeben, die nicht in den Ausdrücken
erscheinen. Diese Nullstellen verdeutlichen,
dass Nullstellenfamilien willkürliche
Konstanten der Form ck enthalten können,
wobei k ein ganzzahliger Index im Bereich 1
bis 255 ist.

Bei polynomialen Gleichungssystemen kann
die Berechnungsdauer oder
Speicherbelastung stark von der
Reihenfolge abhängen, in der Sie die
Unbekannten angeben. Übersteigt Ihre
erste Wahl die Speicherkapazität oder Ihre
Geduld, versuchen Sie, die Variablen in den
Ausdrücken und/oder der

VarOderSchätzwert-Liste umzuordnen.

Wenn Sie keine Schätzwerte angeben und
ein Ausdruck in einer Variablen nicht­polynomial ist, aber alle Ausdrücke in allen
Unbekannten linear sind, so verwendet

cZeros() das Gaußsche

Eliminationsverfahren beim Versuch, alle
Nullstellen zu bestimmen.

Wenn ein System weder in all seinen
Variablen polynomial noch in seinen
Unbekannten linear ist, dann bestimmt

cZeros() mindestens eine Nullstelle anhand

eines iterativen Näherungsverfahrens.
Hierzu muss die Anzahl der Unbekannten
gleich der Ausdruckanzahl sein, und alle
anderen Variablen in den Ausdrücken
müssen zu Zahlen vereinfachbar sein.

Zur Bestimmung einer nicht-reellen
Nullstelle ist häufig ein nicht-reeller
Schätzwert erforderlich. Für Konvergenz
muss ein Schätzwert ziemlich nahe bei der
Nullstelle liegen.

Katalog >

Alphabetische Auflistung 49

D

dbd()

dbd(Datum1,Datum2)⇒Wert

Zählt die tatsächlichen Tage und gibt die
Anzahl der Tage zwischen Datum1 und

Datum2 zurück.

Datum1 und Datum2 können Zahlen oder

Zahlenlisten innerhalb des Datumsbereichs
des Standardkalenders sein. Wenn sowohl

Datum1 als auch Datum2 Listen sind,

müssen sie dieselbe Länge haben.

Datum1 und Datum2 müssen innerhalb der

Jahre 1950 und 2049 liegen.

Sie können Datumseingaben in zwei
Formaten vornehmen. Die Datumsformate
unterscheiden sich in der Anordnung der
Dezimalstellen.

MM.TTJJ (üblicherweise in den USA
verwendetes Format)

TTMM.JJ (üblicherweise in Europa
verwendetes Format)

4DD (Dezimalwinkel)

Zahl 4DD⇒Wert

Katalog >

Katalog >

Im Grad-Modus:

Liste1 4DD⇒Liste
Matrix1 4DD⇒Matrix

Hinweis: Sie können diesen Operator über

die Tastatur Ihres Computers eingeben,
indem Sie @>DD eintippen.

Gibt das Dezimaläquivalent des Arguments
zurück. Das Argument ist eine Zahl, eine
Liste oder eine Matrix, die gemäß der
Moduseinstellung als Neugrad, Bogenmaß
oder Grad interpretiert wird.

50 A lphabetische Auflistung

Im Neugrad-Modus:

Im Bogenmaß-Modus:

4Decimal (Dezimal)

Ausdr1 4Decimal⇒Ausdruck
Liste1 4Decimal⇒Ausdruck
Matrix1 4Decimal⇒Ausdruck

Hinweis: Sie können diesen Operator über

die Tastatur Ihres Computers eingeben,
indem Sie @>Decimal eintippen.

Zeigt das Argument in Dezimalform an.
Dieser Operator kann nur am Ende der
Eingabezeile verwendet werden.

Katalog >

Definie

Define Var = Expression

Define Function(Param1, Param2, ...) =

Expression

Definiert die Variable Var oder die
benutzerdefinierte Funktion Function.

Parameter wie z.B. Param1 enthalten
Platzhalter zur Übergabe von Argumenten
an die Funktion. Beim Aufrufen
benutzerdefinierter Funktionen müssen Sie
Argumente angeben (z.B. Werte oder
Variablen), die zu den Parametern passen.
Beim Aufruf wertet die Funktion Ausdruck

(Expression) unter Verwendung der

übergebenen Parameter aus.

Var und Funktion (Function) dürfen nicht

der Name einer Systemvariablen oder einer
integrierten Funktion / eines integrierten
Befehls sein.

Hinweis: Diese Form von Definiere (Define)

ist gleichwertig mit der Ausführung
folgenden Ausdrucks: expression &

Function(Param1,Param2).

Katalog >

Alphabetische Auflistung 51

Definie

Define Function(Param1, Param2, ...) =
Func

Block

EndFunc

Define Program(Param1, Param2, ...) =
Prgm

Block

EndPrgm

In dieser Form kann die benutzerdefinierte
Funktion bzw. das benutzerdefinierte
Programm einen Block mit mehreren
Anweisungen ausführen.

Block kann eine einzelne Anweisung oder

eine Serie von Anweisungen in separaten
Zeilen sein. Block kann auch Ausdrücke und
Anweisungen enthalten (wie If, Then, Else
und For).

Hinweis zum Eingeben des Beispiels:

Anweisungen für die Eingabe von
mehrzeiligen Programm- und
Funktionsdefinitionen finden Sie im
Abschnitt „Calculator“ des
Produkthandbuchs.

Hinweis: Siehe auch Definiere LibPriv
(Define LibPriv), Seite 52, und Definiere
LibPub (Define LibPub), Seite 53.

Katalog >

Definiere LibPriv (Define LibPriv)

Define LibPriv Var = Expression

Define LibPriv Function(Param1, Param2,
...) = Expression

Define LibPriv Function(Param1, Param2,
...) = Func

Block

EndFunc

Define LibPriv Program(Param1, Param2,
...) = Prgm

Block

EndPrgm

52 A lphabetische Auflistung

Katalog >

Definiere LibPriv (Define LibPriv)

Funktioniert wie Define, definiert jedoch
eine Variable, eine Funktion oder ein
Programm für eine private Bibliothek.
Private Funktionen und Programme werden
im Katalog nicht angezeigt.

Hinweis: Siehe auch Definiere (Define), Seite

51, und Definiere LibPub (Define LibPub),
Seite 53.

Katalog >

Definiere LibPub (Define LibPub)

Define LibPub Var = Expression

Define LibPub Function(Param1, Param2,
...) = Expression

Define LibPub Function(Param1, Param2,
...) = Func

Block

EndFunc

Define LibPub Program(Param1, Param2,
...) = Prgm

Block

EndPrgm

Funktioniert wie Definiere (Define), definiert
jedoch eine Variable, eine Funktion oder ein
Programm für eine öffentliche Bibliothek.
Öffentliche Funktionen und Programme
werden im Katalog angezeigt, nachdem die
Bibliothek gespeichert und aktualisiert
wurde.

Hinweis: Siehe auch Definiere (Define), Seite

51, und Definiere LibPriv (Define LibPriv),
Seite 52.

deltaList()

Katalog >

Siehe @List(), Seite 115.

deltaTmpCnv()

Siehe @tmpCnv(), Seite 210.

Alphabetische Auflistung 53

DelVar

DelVar Var1[, Var2] [, Var3] ...

DelVar Var.

Löscht die angegebene Variable oder
Variablengruppe im Speicher.

Wenn eine oder mehrere Variablen
gesperrt sind, wird bei diesem Befehl eine
Fehlermeldung angezeigt und es werden
nur die nicht gesperrten Variablen gelöscht.
Siehe unLock, Seite 219.

DelVar Var. löscht alle Mitglieder der

Variablengruppe Var. (wie die
Statistikergebnisse stat.nn oder Variablen,
die mit der Funktion LibShortcut() erstellt
wurden). Der Punkt (.) in dieser Form des
Befehls DelVar begrenzt ihn auf das
Löschen einer Variablengruppe; die
einfache Variable Var ist nicht davon
betroffen.

Katalog >

delVoid()

delVoid(Liste1)⇒Liste

Gibt eine Liste mit dem Inhalt von Liste1
aus, wobei alle leeren (ungültigen)
Elemente entfernt sind.

Weitere Informationen zu leeren
Elementen finden Sie (Seite 261).

derivative()

54 A lphabetische Auflistung

Katalog >

Siehe d(), Seite 245.

deSolve() (Lösung)

deSolve(ODE1.Oder2.Ordnung, Var,

abhängigeVar) ⇒eine allgemeine Lösung

Ergibt eine Gleichung, die explizit oder
implizit eine allgemeine Lösung für die
gewöhnliche Differentialgleichung erster
oder zweiter Ordnung (ODE) angibt. In der
ODE:

• Verwenden Sie einen Ableitungsstrich
(drücken Sie º), um die erste Ableitung
der abhängigen Variablen gegenüber der

unabhängigen Variablen zu kennzeichnen.

• Kennzeichnen Sie die entsprechende
zweite Ableitung mit zwei Strichen.

Das Zeichen ' wird nur für Ableitungen
innerhalb von deSolve() verwendet.
Verwenden Sie für andere Fälle d().

Die allgemeine Lösung einer Gleichung
erster Ordnung enthält eine willkürliche
Konstante der Form ck, wobei k ein
ganzzahliger Index im Bereich 1 bis 255 ist.
Die Lösung einer Gleichung zweiter Ordnung
enthält zwei derartige Konstanten.

Wenden Sie solve() auf eine implizite
Lösung an, wenn Sie versuchen möchten,
diese in eine oder mehrere äquivalente
explizite Lösungen zu konvertieren.

Beachten Sie beim Vergleich Ihrer
Ergebnisse mit Lehrbuch- oder
Handbuchlösungen bitte, dass die
willkürlichen Konstanten in den
verschiedenen Verfahren an
unterschiedlichen Stellen in der Rechnung
eingeführt werden, was zu
unterschiedlichen allgemeinen Lösungen
führen kann.

Katalog >

Alphabetische Auflistung 55

deSolve() (Lösung)

deSolve
(ODE1.OrdnungandAnfangsbedingung,

Var, abhängigeVar) ⇒eine spezielle

Lösung

Ergibt eine spezielle Lösung, die

ODE1.Ordnung und Anfangsbedingung

erfüllt. Dies ist in der Regel einfacher, als
eine allgemeine Lösung zu bestimmen,
Anfangswerte einzusetzen, nach der
willkürlichen Konstanten aufzulösen und
dann diesen Wert in die allgemeine Lösung
einzusetzen.

Anfangsbedingung ist eine Gleichung der

Form

abhängigeVar (unabhängigerAnfangswert)

= abhängigerAnfangswert

Der unabhängigeAnfangswert und

abhängigeAnfangswert können Variablen

wie beispielsweise x0 und y0 ohne
gespeicherte Werte sein. Die implizite
Differentiation kann bei der Prüfung
impliziter Lösungen behilflich sein.

deSolve
(

ODE2.Ordnung

and

Anfangsbedingung1

andAnfangsbedingung2, Var,

abhängigeVar)⇒eine spezielle Lösung

Ergibt eine spezielle Lösung, die

ODE2.Ordnung erfüllt und in einem Punkt

einen bestimmten Wert der abhängigen
Variablen und deren erster Ableitung
aufweist.

Verwenden Sie für Anfangsbedingung1 die
Form

abhängigeVar (unabhängigerAnfangswert)

= abhängigerAnfangswert

Verwenden Sie für Anfangsbedingung2 die
Form

Katalog >

56 A lphabetische Auflistung

deSolve() (Lösung)

abhängigeVar (unabhängigerAnfangswert)

= anfänglicher1.Ableitungswert

deSolve
(

ODE2.Ordnung

andRandbedingung1andRandbedingung2,

Var, abhängigeVar)⇒eine spezielle

Lösung

Ergibt eine spezielle Lösung, die

ODE2.Ordnung erfüllt und in zwei

verschiedenen Punkten angegebene Werte
aufweist.

Katalog >

det() (Matrixdeterminante)

det(Quadratmatrix[, Toleranz])

⇒Ausdruck

Gibt die Determinante von Quadratmatrix
zurück.

Jedes Matrixelement wird wahlweise als 0
behandelt, wenn sein Absolutwert kleiner
als Toleranz ist. Diese Toleranz wird nur
dann verwendet, wenn die Matrix
Fließkommaelemente aufweist und
keinerlei symbolische Variablen ohne
zugewiesene Werte enthält. Anderenfalls
wird Toleranz ignoriert.

• Wenn Sie /· verwenden oder den
Modus Autom. oder Näherung auf

'Approximiert' einstellen, werden
Berechnungen in Fließkomma-Arithmetik
durchgeführt.

• Wird Toleranz weggelassen oder nicht
verwendet, so wird die Standardtoleranz
folgendermaßen berechnet:

5EM14 ·max(dim(Quadratmatrix))·

Katalog >

Alphabetische Auflistung 57

det() (Matrixdeterminante)

rowNorm(Quadratmatrix)

Katalog >

diag() (Matrixdiagonale)

diag(Liste)⇒Matrix
diag(Zeilenmatrix)⇒Matrix
diag(Spaltenmatrix)⇒Matrix

Gibt eine Matrix mit den Werten der
Argumentliste oder der Matrix in der
Hauptdiagonalen zurück.

diag(Quadratmatrix)⇒Zeilenmatrix

Gibt eine Zeilenmatrix zurück, die die
Elemente der Hauptdiagonalen von

Quadratmatrix enthält.

Quadratmatrix muss eine quadratische

Matrix sein.

dim() (Dimension)

dim(Liste)⇒Ganzzahl

Gibt die Dimension von Liste zurück.

dim(Matrix)⇒Liste

Gibt die Dimensionen von Matrix als Liste
mit zwei Elementen zurück {Zeilen,
Spalten}.

dim(String)⇒Ganzzahl

Gibt die Anzahl der in der Zeichenkette

String enthaltenen Zeichen zurück.

Katalog >

Katalog >

58 A lphabetische Auflistung

Disp (Zeige)

Disp AusdruckOderString1 [,

AusdruckOderString2] ...

Zeigt die Argumente im Calculator
Protokoll an. Die Argumente werden
hintereinander angezeigt, dabei werden
Leerzeichen zur Trennung verwendet.

Dies ist vor allem bei Programmen und
Funktionen nützlich, um die Anzeige von
Zwischenberechnungen zu gewährleisten.

Hinweis zum Eingeben des Beispiels:

Anweisungen für die Eingabe von
mehrzeiligen Programm- und
Funktionsdefinitionen finden Sie im
Abschnitt „Calculator“ des
Produkthandbuchs.

Katalog >

DispAt

DispAt int,Term1 [,Term2 …] …

Mit DispAt können Sie die Zeile
festlegen, in der der angegebene Term
oder die angegebene Zeichenkette auf
dem Bildschirm angezeigt wird.

Die Zeilennummer kann als Term
angegeben werden.

Beachten Sie, dass die Zeilennummer
nicht für den gesamten Bildschirm
gedacht ist, sondern für den Bereich
unmittelbar nach dem
Befehl/Programm.

Dieser Befehl ermöglicht die dashboard­ähnliche Ausgabe von Programmen, bei
denen der Wert eines Terms oder von
einer Sensormessung in der gleichen
Zeile aktualisiert wird.

DispAtund Disp können im gleichen

Programm verwendet werden.

Katalog >

Beispiel

Alphabetische Auflistung 59

DispAt

Hinweis: Die maximale Anzahl ist auf 8

eingestellt, da diese Zahl einem
Bildschirm voller Zeilen auf dem
Handheld-Bildschirm entspricht –
soweit die Zeilen über keine
mathematischen 2D-Ausdrücke
verfügen. Die genaue Anzahl der Zeilen
hängt vom Inhalt der angezeigten
Informationen ab.

Erläuternde Beispiele:

Define z()=
Prgm
For n,1,3
DispAt 1,„N:

“,n
Disp „Hallo“
EndFor
EndPrgm

Define z1()=
Prgm
For n,1,3
DispAt 1,„N:

“,n
EndFor

Beenden von
z()

z1()

Katalog >

Iteration 1:

Zeile 1: N:1

Zeile 2: Hallo

Iteration 2:

Zeile 1: N:2
Zeile 2: Hallo
Zeile 3: Hallo

Iteration 3:

Zeile 1: N:3
Zeile 2: Hallo
Zeile 3: Hallo
Zeile 4: Hallo

Zeile 1: N:3
Zeile 2: Hallo
Zeile 3: Hallo
Zeile 4: Hallo
Zeile 5: Hallo

For n,1,4
Disp „Hallo“
EndFor
EndPrgm

Fehlermeldungen:

Fehlermeldung Beschreibung

DispAt Zeilennummer muss zwischen 1 und 8
liegen

Zu wenig Argumente Der Funktion oder dem Befehl fehlen ein

Keine Argumente Entspricht dem aktuellen Dialog

Zu viele Argumente Argument eingrenzen. Gleicher Fehler

60 A lphabetische Auflistung

Term bewertet die Zeilennummer
außerhalb des Bereichs 1-8 (inklusive)

oder mehr Argumente.

'Syntaxfehler'

Fehlermeldung Beschreibung

wie Disp.

Ungültiger Datentyp Erstes Argument muss eine Zahl sein.

Ungültig: DispAt ungültig „Hallo Welt“ Datentypfehler für die

Konvertierungsoperator: DispAt 2_ft @> _m,
„Hallo Welt“

Lücke wird verworfen (falls die
Rückmeldung definiert ist)

CAS: Datentypfehler wird verworfen (falls
die Rückmeldung definiert ist)

Numerisch: Umrechnung wird bewertet
und falls das Ergebnis ein gültiges
Argument ist, druckt DispAt die
Zeichenkette an der Ergebniszeile aus.

4DMS (GMS)

Ausdr 4DMS

Liste 4DMS

Matrix 4DMS

Hinweis: Sie können diesen Operator über

die Tastatur Ihres Computers eingeben,
indem Sie @>DMS eintippen.

Interpretiert den Parameter als Winkel und
zeigt die entsprechenden GMS-Werte (engl.
DMS) an (GGGGGG¡MM'SS.ss''). Siehe ¡, ',
'' (Seite 253) zur Erläuterung des DMS­Formats (Grad, Minuten, Sekunden).

Hinweis: 4DMS wandelt Bogenmaß in Grad

um, wenn es im Bogenmaß-Modus benutzt
wird. Folgt auf die Eingabe das Grad­Symbol ¡, wird keine Umwandlung
vorgenommen. Sie können 4DMS nur am
Ende einer Eingabezeile benutzen.

Katalog >

Im Grad-Modus:

Alphabetische Auflistung 61

domain()

domain(Ausdr1, Var) ⇒Ausdruck

Gibt den Definitionsbereich von Ausdr1 in
Bezug auf Var zurück.

domain() kann verwendet werden, um

Definitionsbereiche von Funktionen zu
erkunden. Es ist auf reelle und endliche
Bereiche beschränkt.

Diese Funktionalität ist aufgrund von
Schwächen von Computer-Algebra­Vereinfachungs- und Lösungsalgorithmen
eingeschränkt.

Bestimmte Funktionen können nicht als
Argumente für domain() verwendet
werden, unabhängig davon, ob sie explizit
oder innerhalb von benutzerdefinierten
Variablen und Funktionen auftreten. In dem
folgenden Beispiel kann der Ausdruck nicht
vereinfacht werden weil ‰() eine nicht
zulässige Funktion ist.

Katalog >

dominanterTerm (), dominantTerm()

dominantTerm(Expr1, Var [, Point])

⇒expression

dominantTerm(Expr1, Var [, Point]) |

Var>Point⇒ expression

dominantTerm(Expr1, Var [, Point]) |

Var<Point ⇒expression

62 A lphabetische Auflistung

Katalog >

dominanterTerm (), dominantTerm()

Gibt den dominanten Term einer
Potenzreihendarstellung von Expr1
entwickelt um Point zurück. Der dominante
Term ist derjenige, dessen Betrag nahe Var
= Point am schnellsten anwächst. Die
resultierende Potenz von (Var N Point)
kann einen negativen und/oder
Bruchexponenten haben. Der Koeffizient
dieser Potenz kann Logarithmen von (Var N

Point) und andere Funktionen von Var

enthalten, die von allen Potenzen von (Var
N Point) dominiert werden, die dasselbe
Exponentenzeichen haben.

Point ist vorgegeben als 0. Point kann ˆ

oder Nˆ sein; in diesen Fällen ist der
dominante Term eher derjenige mit dem
größten Exponenten von Var als der mit
dem kleinsten Exponenten von Var.

dominantTerm(…) gibt “dominantTerm(…)”

zurück, wenn es keine Darstellung
bestimmen kann wie für wesentliche
Singularitäten wie z.B. sin(1/z) bei z=0,

1/z

N

e

bei z=0 oder ezbei z = ˆ oder Nˆ.

Wenn die Folge oder eine ihrer Ableitungen
eine Sprungstelle bei Point hat, enthält das
Ergebnis wahrscheinlich Unterausdrücke
der Form sign(…) oder abs(…) für eine
reelle Expansionsvariable oder (-1)

(…angle(…)…)

für eine komplexe

floor

Expansionsvariable, die mit “_” endet.
Wenn Sie beabsichtigen, den dominanten
Term nur für Werte auf einer Seite von

Point zu verwenden, hängen Sie an

dominantTerm(...) je nach Bedarf “| Var >

Point”, “| Var < Point”, “| “Var | Point”

oder “Var { Point” an, um ein einfacheres
Ergebnis zu erhalten.

dominantTerm() wird über Listen und

Matrizen mit erstem Argument verteilt.

Katalog >

Alphabetische Auflistung 63

dominanterTerm (), dominantTerm()

dominantTerm() können Sie verwenden,

wenn Sie den einfachsten möglichen
Ausdruck wissen möchten, der
asymptotisch zu einem anderen Ausdruck
wie Var " Point ist. dominantTerm() ist
ebenfalls hilfreich, wenn nicht klar
ersichtlich ist, welchen Grad der erste Term
einer Folge haben wird, der nicht Null ist
und Sie nicht iterativ interaktiv oder mit
einer Programmschleife schätzen möchten.

Hinweis: Siehe auch series(), Seite 178.

Katalog >

dotP() (Skalarprodukt)

dotP(Liste1, Liste2)⇒Ausdruck

Gibt das Skalarprodukt zweier Listen zurück.

dotP(Vektor1, Vektor2)⇒Ausdruck

Gibt das Skalarprodukt zweier Vektoren
zurück.

Es müssen beide Zeilenvektoren oder beide
Spaltenvektoren sein.

E

e^()

e^(Ausdr1)⇒Ausdruck

Gibt e hoch Ausdr1 zurück.

Hinweis: Siehe auch Vorlage e Exponent,

Seite 2.

Hinweis: Das Drücken von u zum Anzeigen

von e^( ist nicht das gleiche wie das
Drücken von E auf der Tastatur.

Sie können eine komplexe Zahl in der
polaren Form re
Sie diese aber nur im Winkelmodus
Bogenmaß, da die Form im Grad- oder
Neugrad-Modus einen Bereichsfehler
verursacht.

i

q

eingeben. Verwenden

Katalog >

u Taste

64 A lphabetische Auflistung

e^()

e^(Liste1)⇒Liste

Gibt e hoch jedes Element der Liste1
zurück.

e^(Quadratmatrix1)⇒Quadratmatrix

Ergibt den Matrix-Exponenten von

Quadratmatrix1. Dies ist nicht

gleichbedeutend mit der Berechnung von e
hoch jedes Element. Näheres zur
Berechnungsmethode finden Sie im
Abschnitt cos().

Quadratmatrix1 muss diagonalisierbar

sein. Das Ergebnis enthält immer
Fließkommazahlen.

u Taste

eff()

eff(Nominalzinssatz, CpY)⇒Wert

Finanzfunktion, die den Nominalzinssatz

Nominalzinssatz in einen jährlichen

Effektivsatz konvertiert, wobei CpY als die
Anzahl der Verzinsungsperioden pro Jahr
gegeben ist.

Nominalzinssatz muss eine reelle Zahl sein

und CpY muss eine reelle Zahl > 0 sein.

Hinweis: Siehe auch nom(), Seite 136.

eigVc() (Eigenvektor)

eigVc(Quadratmatrix)⇒Matrix

Ergibt eine Matrix, welche die
Eigenvektoren für eine reelle oder komplexe

Quadratmatrix enthält, wobei jede Spalte

des Ergebnisses zu einem Eigenwert
gehört. Beachten Sie, dass ein Eigenvektor
nicht eindeutig ist; er kann durch einen
konstanten Faktor skaliert werden. Die
Eigenvektoren sind normiert, d. h. wenn V =
[x1, x2, …, xn], dann:

2

2

x

+ x

+ … + x

1

2

2

= 1

n

Katalog >

Katalog >

Im Komplex-Formatmodus“kartesisch”:

Um dasganze Ergebniszu sehen, drücken
Sie £undverwendendann¡ und ¢, umden
Cursor zu bewegen.

Alphabetische Auflistung 65

eigVc() (Eigenvektor)

Quadratmatrix wird zunächst mit

Ähnlichkeitstransformationen bearbeitet,
bis die Zeilen- und Spaltennormen so nahe
wie möglich bei demselben Wert liegen.
Die Quadratmatrix wird dann auf die obere
Hessenberg-Form reduziert, und die
Eigenvektoren werden mit einer Schur­Faktorisierung berechnet.

Katalog >

eigVl() (Eigenwert)

eigVl(Quadratmatrix)⇒Liste

Ergibt eine Liste von Eigenwerten einer
reellen oder komplexen Quadratmatrix.

Quadratmatrix wird zunächst mit

Ähnlichkeitstransformationen bearbeitet,
bis die Zeilen- und Spaltennormen so nahe
wie möglich bei demselben Wert liegen.
Die Quadratmatrix wird dann auf die obere
Hessenberg-Form reduziert, und die
Eigenwerte werden aus der oberen
Hessenberg-Matrix berechnet.

Else

ElseIf

If Boolescher Ausdr1 Then

   Block1

ElseIf Boolescher Ausdr2 Then

   Block2

©

ElseIf Boolescher AusdrN Then

   BlockN

EndIf

©

Hinweis zum Eingeben des Beispiels:

Anweisungen für die Eingabe von
mehrzeiligen Programm- und
Funktionsdefinitionen finden Sie im
Abschnitt „Calculator“ des
Produkthandbuchs.

Katalog >

Im Komplex-Formatmodus“kartesisch”:

Um dasganze Ergebniszu sehen, drücken
Sie £undverwendendann¡ und ¢, umden
Cursor zu bewegen.

Siehe If, Seite 97.

Katalog >

66 A lphabetische Auflistung

EndFor

Siehe For, Seite 81.

EndFunc

EndIf

EndLoop

EndWhile

EndPrgm

EndTry

euler ()

euler(Ausdr, Var, abhVar, {Var0,

VarMax}, abhVar0, VarSchritt [,
eulerSchritt]) ⇒Matrix

Siehe Func, Seite 85.

Siehe If, Seite 97.

Siehe Loop, Seite 122.

Siehe While, Seite 223.

Siehe Prgm, Seite 153.

Siehe Try, Seite 212.

Katalog >

Differentialgleichung:

y'=0.001*y*(100-y) undy(0)=10

euler(AusdrSystem, Var, ListeAbhVar,
{Var0, VarMax}, ListeAbhVar0,

VarSchritt [, eulerSchritt]) ⇒Matrix

euler(AusdrListe, Var, ListeAbhVar,
{Var0, VarMax},ListeAbhVar0,

VarSchritt [, eulerSchritt]) ⇒Matrix

Verwendet die Euler-Methode zum Lösen
des Systems

Um dasganze Ergebniszu sehen, drücken
Sie £undverwendendann¡ und ¢, umden
Cursor zu bewegen.

Alphabetische Auflistung 67

euler ()

mit abhVar(Var0)=abhVar0 auf dem
Intervall [Var0,VarMax]. Gibt eine Matrix
zurück, deren erste Zeile die Ausgabewerte
von Var definiert und deren zweite Zeile
den Wert der ersten Lösungskomponente
an den entsprechenden Var-Werten
definiert usw.

Ausdr ist die rechte Seite, die die

gewöhnliche Differentialgleichung (ODE)
definiert.

AusdrSystem ist das System rechter Seiten,

welche das ODE-System definieren
(entspricht der Ordnung abhängiger
Variablen in ListeAbhVar).

AusdrListe ist eine Liste rechter Seiten,

welche das ODE-System definieren
(entspricht der Ordnung abhängiger
Variablen in ListeAbhVar).

Var ist die unabhängige Variable.

ListeAbhVar ist eine Liste abhängiger

Variablen.

{Var0, VarMax} ist eine Liste mit zwei
Elementen, die die Funktion anweist, von

Var0 zu VarMax zu integrieren.

ListeAbhVar0 ist eine Liste von

Anfangswerten für abhängige Variablen.

VarSchritt ist eine Zahl ungleich Null,

sodass sign(VarSchritt) = sign

(VarMax-Var0) und Lösungen an

Var0+i·VarSchritt für alle i=0,1,2,…

zurückgegeben werden, sodass

Var0+i·VarSchritt in [var0,VarMax] ist

(möglicherweise gibt es keinen
Lösungswert an VarMax).

Katalog >

VergleichenSie das vorstehende Ergebnis
mitder exakten CAS-Lösung, die Sie
erhalten, wennSie deSolve() undseqGen()
verwenden:

Gleichungssystem:

mity1(0)=2undy2(0)=5

68 A lphabetische Auflistung

euler ()

Katalog >

eulerSchritt ist eine positive ganze Zahl

(standardmäßig 1), welche die Anzahl der
Euler-Schritte zwischen Ausgabewerten
bestimmt. Die tatsächliche von der Euler­Methode verwendete Schrittgröße ist

VarSchrittàeulerSchritt.

eval () Hub-Menü

eval(Expr) ⇒Zeichenfolge

eval() ist nur im TI-Innovator™ Hub

Befehlsargument von Programmierbefehlen

Get, GetStr und Send gültig. Die Software

wertet den Ausdruck Expr aus und ersetzt
die Anweisung eval() mit dem Ergebnis als
Zeichenfolge.

Das Argument Expr muss zu einer reellen
Zahl vereinfachbar sein.

StellenSie das blaueElementvon RGB LED
auf halbe Intensitätein.

SetzenSie das blaueElementauf AUS
zurück.

Argument eval() musszu einer reellenZahl
vereinfachbar sein.

Programm zum Einblendendesroten
Elements

FührenSie das Programm aus.

Alphabetische Auflistung 69

eval () Hub-Menü

Obwohl eval() sein Ergebnis nicht anzeigt,
können Sie die resultierende Hub­Zeichenfolge nach Ausführen des Befehls
durch Prüfung einer beliebigen der
folgenden speziellen Variablen anzeigen.

iostr.SendAns
iostr.GetAns
iostr.GetStrAns

Hinweis: Siehe auch Get(Seite 87), GetStr

(Seite 94) und Send(Seite 175).

exact() (Exakt)

exact(Ausdr1 [, Toleranz])⇒Ausdruck
exact(Liste1 [, Toleranz])⇒Liste
exact(Matrix1 [, Toleranz])⇒Matrix

Benutzt den Rechenmodus 'Exakt' und gibt
nach Möglichkeit die rationale Zahl zurück,
die dem Argument äquivalent ist.

Toleranz legt die Toleranz für die

Umwandlung fest, wobei die Vorgabe 0
(null) ist.

Exit (Abbruch)

Exit (Abbruch)

Beendet den aktuellen For, While, oder Loop
Block.

Exit ist außerhalb dieser drei

Schleifenstrukturen (For, While oder Loop)
nicht zulässig.

Hinweis zum Eingeben des Beispiels:

Anweisungen für die Eingabe von
mehrzeiligen Programm- und
Funktionsdefinitionen finden Sie im
Abschnitt „Calculator“ des
Produkthandbuchs.

Katalog >

Katalog >

Funktionslisting:

70 A lphabetische Auflistung

4exp

Ausdr 4exp

Drückt Ausdr durch die natürliche
Exponentialfunktion e aus. Dies ist ein
Anzeigeumwandlungsoperator. Er kann nur
am Ende der Eingabezeile verwendet
werden.

Hinweis: Sie können diesen Operator über

die Tastatur Ihres Computers eingeben,
indem Sie @>exp eintippen.

Katalog >

exp() (e hoch x)

exp(Ausdr1)⇒Ausdruck

Gibt e hoch Ausdr1 zurück.

Hinweis: Siehe auch Vorlage e Exponent,

Seite 2.

Sie können eine komplexe Zahl in der
polaren Form rei q eingeben. Verwenden
Sie diese aber nur im Winkelmodus
Bogenmaß, da die Form im Grad- oder
Neugrad-Modus einen Bereichsfehler
verursacht.

exp(Liste1)⇒Liste

Gibt e hoch jedes Element der Liste1
zurück.

exp(Quadratmatrix1)⇒Quadratmatrix

Ergibt den Matrix-Exponenten von

Quadratmatrix1. Dies ist nicht

gleichbedeutend mit der Berechnung von e
hoch jedes Element. Näheres zur
Berechnungsmethode finden Sie im
Abschnitt cos().

Quadratmatrix1 muss diagonalisierbar

sein. Das Ergebnis enthält immer
Fließkommazahlen.

u Taste

Alphabetische Auflistung 71

exp4list() (Ausdruck in Liste)

exp4list(Ausdr,Var)⇒Liste

Untersucht Ausdr auf Gleichungen, die
durch das Wort “or” getrennt sind und gibt
eine Liste der rechten Seiten der
Gleichungen in der Form Var=Ausdr
zurück. Dies erlaubt Ihnen auf einfache
Weise das Extrahieren mancher
Lösungswerte, die in den Ergebnissen der
Funktionen solve(), cSolve(), fMin() und

fMax() enthalten sind.

Hinweis: exp4list() ist für die Funktionen
zeros und cZeros() unnötig, da diese direkt

eine Liste von Lösungswerten zurückgeben.

Sie können diese Funktion über die Tastatur
Ihres Computers eingeben, indem Sie

exp@>list(...) eintippen.

Katalog >

expand() (Entwickle)

expand(Ausdr1 [, Var])⇒Ausdruck
expand(Liste1 [,Var])⇒Liste
expand(Matrix1 [,Var])⇒Matrix

expand(Ausdr1) gibt Ausdr1 bezüglich

sämtlicher Variablen entwickelt zurück. Die
Entwicklung ist eine Polynomentwicklung
für Polynome und eine
Partialbruchentwicklung für rationale
Ausdrücke.

expand() versucht Ausdr1 in eine Summe

und/oder eine Differenz einfacher
Ausdrücke umzuformen. Dagegen versucht

factor() Ausdr1 in ein Produkt und/oder

einen Quotienten einfacher Faktoren
umzuformen.

72 A lphabetische Auflistung

Katalog >

expand() (Entwickle)

expand(Ausdr1,Var) entwickelt Ausdr1

bezüglich Var. Gleichartige Potenzen von

Var werden zusammengefasst. Die Terme

und Faktoren werden mit Var als der
Hauptvariablen sortiert. Es kann sein, dass
als Nebeneffekt in gewissem Umfang eine
Faktorisierung oder Entwicklung der
zusammengefassten Koeffizienten auftritt.
Verglichen mit dem Weglassen von Var
spart dies häufig Zeit, Speicherplatz und
Platz auf dem Bildschirm und macht den
Ausdruck verständlicher.

Selbst wenn es nur eine Variable gibt, kann
das Einbeziehen von Var eine
vollständigere Faktorisierung des Nenners,
die für die Partialbruchentwicklung benutzt
wird, ermöglichen.

Tipp: Für rationale Ausdrücke ist propFrac()
eine schnellere, aber weniger weitgehende
Alternative zu expand().

Hinweis: Siehe auch comDenom() zu einem

Quotienten aus einem entwickelten Zähler
und entwickeltem Nenner.

expand(Ausdr1,[Var]) vereinfacht auch

Logarithmen und Bruchpotenzen
ungeachtet von Var. Für weitere
Zerlegungen von Logarithmen und
Bruchpotenzen können Einschränkungen
notwendig werden, um sicherzustellen,
dass manche Faktoren nicht negativ sind.

expand(Ausdr1, [Var]) vereinfacht auch

Absolutwerte, sign() und Exponenten
ungeachtet von Var.

Hinweis: Siehe auch tExpand() zur

trigonometrischen Entwicklung von
Winkelsummen und -produkten.

Katalog >

Alphabetische Auflistung 73

expr() (String in Ausdruck)

expr(String)⇒Ausdruck

Gibt die in String enthaltene Zeichenkette
als Ausdruck zurück und führt diesen sofort
aus.

Katalog >

ExpReg (Exponentielle Regression)

ExpReg X, Y [, [Häuf][, Kategorie, Mit]]

Berechnet die exponentielle Regressiony =
a·(b)xauf Listen X und Y mit der Häufigkeit

Häuf. Eine Zusammenfassung der

Ergebnisse wird in der Variablen stat.results
gespeichert. (Seite 196.)

Alle Listen außer Mit müssen die gleiche
Dimension besitzen.

X und Y sind Listen von unabhängigen und

abhängigen Variablen.

Häuf ist eine optionale Liste von

Häufigkeitswerten. Jedes Element in Häuf
gibt die Häufigkeit für jeden entsprechenden
Datenpunkt X und Y an. Der Standardwert
ist 1. Alle Elemente müssen Ganzzahlen | 0
sein.

Kategorie ist eine Liste von Kategoriecodes

für die entsprechenden X und Y Daten.

Mit ist eine Liste von einem oder mehreren

Kategoriecodes. Nur solche Datenelemente,
deren Kategoriecode in dieser Liste
enthalten ist, sind in der Berechnung
enthalten.

Informationen zu den Auswirkungen leerer
Elemente in einer Liste finden Sie unter
“Leere (ungültige) Elemente” (Seite 261).

Katalog >

Ausgabevariable Beschreibung

stat.RegEqn Regressionsgleichung: a·(b)

stat.a, stat.b Regressionskoeffizienten

74 A lphabetische Auflistung

x

Ausgabevariable Beschreibung

2

stat.r

stat.r Korrelationskoeffizient für transformierte Daten(x, ln(y))

stat.Resid MitdemexponentiellenModellverknüpfte Residuen

stat.ResidTrans Residuumfür die lineare Anpassung der transformiertenDaten.

stat.XReg

stat.YReg

stat.FreqReg

Koeffizient der linearenBestimmtheit für transformierte Daten

Liste der Datenpunktein der modifiziertenX List, die schließlich in der
Regression mit denBeschränkungenfür Häufigkeit, Kategorieliste undMit

Kategorien verwendetwurde

Liste der Datenpunktein der modifiziertenY List, die schließlichin der
Regression mit denBeschränkungenfür Häufigkeit, Kategorieliste undMit

Kategorien verwendetwurde

Liste der Häufigkeiten für stat.XReg und stat.YReg

F

factor() (Faktorisiere)

factor(Ausdr1[, Var])⇒Ausdruck
factor(Liste1[,Var])⇒Liste
factor(Matrix1[,Var])⇒Matrix

factor(Ausdr1) gibt Ausdr1 nach allen
seinen Variablen bezüglich eines
gemeinsamen Nenners faktorisiert zurück.

Ausdr1 wird soweit wie möglich in lineare

rationale Faktoren aufgelöst, selbst wenn
dies die Einführung neuer nicht-reeller
Unterausdrücke bedeutet. Diese Alternative
ist angemessen, wenn Sie die
Faktorisierung bezüglich mehr als einer
Variablen vornehmen möchten.

factor(Ausdr1,Var) gibt Ausdr1 nach der
Variablen Var faktorisiert zurück.

Ausdr1 wird soweit wie möglich in reelle

Faktoren aufgelöst, die linear in Var sind,
selbst wenn dadurch irrationale Konstanten
oder Unterausdrücke, die in anderen
Variablen irrational sind, eingeführt
werden.

Katalog >

Alphabetische Auflistung 75

factor() (Faktorisiere)

Die Faktoren und ihre Terme werden mit

Var als Hauptvariable sortiert. Gleichartige

Potenzen von Var werden in jedem Faktor
zusammengefasst. Beziehen Sie Var ein,
wenn die Faktorisierung nur bezüglich
dieser Variablen benötigt wird und Sie
irrationale Ausdrücke in anderen Variablen
akzeptieren möchten, um die Faktorisierung
bezüglich Var so weit wie möglich
vorzunehmen. Es kann sein, dass als
Nebeneffekt in gewissem Umfang eine
Faktorisierung nach anderen Variablen
auftritt.

Bei der Einstellung Auto für den Modus

Auto oder Näherung ermöglicht die

Einbeziehung von Var auch eine Näherung
mit Gleitkommakoeffizienten in Fällen, wo
irrationale Koeffizienten nicht explizit
bezüglich der integrierten Funktionen
ausgedrückt werden können. Selbst wenn
es nur eine Variable gibt, kann das
Einbeziehen von Var eine vollständigere
Faktorisierung ermöglichen.

Hinweis: Siehe auch comDenom() zu einer

schnellen partiellen Faktorisierung, wenn

factor() zu langsam ist oder den

Speicherplatz erschöpft.

Hinweis: Siehe auch cFactor() zur

kompletten Faktorisierung bis zu komplexen
Koeffizienten, um lineare Faktoren zu
erhalten.

factor(RationaleZahl) ergibt die rationale

Zahl in Primfaktoren zerlegt. Bei
zusammengesetzten Zahlen nimmt die
Berechnungsdauer exponentiell mit der
Anzahl an Stellen im zweitgrößten Faktor
zu. Das Faktorisieren einer 30-stelligen
ganzen Zahl kann beispielsweise länger als
einen Tag dauern und das Faktorisieren
einer 100-stelligen Zahl mehr als ein
Jahrhundert.

So halten Sie eine Berechnung manuell an:

Katalog >

• Handheld: Halten Sie die Taste c

76 A lphabetische Auflistung

factor() (Faktorisiere)

gedrückt und drücken Sie mehrmals

·.

• Windows®: Halten Sie die Taste F12
gedrückt und drücken Sie mehrmals die
Eingabetaste.

• Macintosh®: Halten Sie die Taste F5
gedrückt und drücken Sie mehrmals die
Eingabetaste.

• iPad®: Die App zeigt eine
Eingabeaufforderung an. Sie können
weiter warten oder abbrechen.

Möchten Sie hingegen lediglich feststellen,
ob es sich bei einer Zahl um eine Primzahl
handelt, verwenden Sie isPrime(). Dieser
Vorgang ist wesentlich schneller,
insbesondere dann, wenn RationaleZahl
keine Primzahl ist und der zweitgrößte
Faktor mehr als fünf Stellen aufweist.

Katalog >

FCdf()

FCdf

(

UntGrenze

,

ObGrenze

,FreiGradZähler,FreiGradNenner)⇒Zahl,

wenn UntGrenze und ObGrenze Zahlen
sind, Liste, wenn UntGrenze und

ObGrenze Listen sind

FCdf
(

UntGrenze

,

ObGrenze

,FreiGradZähler,FreiGradNenner)⇒Zahl,

wenn UntGrenze und ObGrenze Zahlen
sind, Liste, wenn UntGrenze und

ObGrenze Listen sind

Berechnet die F
Verteilungswahrscheinlichkeit zwischen

UntereGrenze und ObereGrenze für die

angegebenen FreiGradZähler
(Freiheitsgrade) und FreiGradNenner.

Katalog >

Alphabetische Auflistung 77

FCdf()

Für P(X { ObereGrenze), UntGrenze =0
setzen.

Katalog >

Fill (Füllen)

Fill Ausdr, MatrixVar⇒Matrix

Ersetzt jedes Element in der Variablen

MatrixVar durch Ausdr.

MatrixVar muss bereits vorhanden sein.

Fill Ausdr, ListeVar⇒Liste

Ersetzt jedes Element in der Variablen

ListeVar durch Ausdr.

ListeVar muss bereits vorhanden sein.

FiveNumSummary

FiveNumSummary X[,[Häuf]

[,Kategorie,Mit]]

Bietet eine gekürzte Version der Statistik
mit 1 Variablen auf Liste X.
Eine Zusammenfassung der Ergebnisse wird
in der Variablen stat.results gespeichert.
(Seite 196.)

X stellt eine Liste mit den Daten dar.

Häuf ist eine optionale Liste von

Häufigkeitswerten. Jedes Element in Häuf
gibt die Häufigkeit für jeden entsprechenden

X-Wert an. Der Standardwert ist 1. Alle

Elemente müssen Ganzzahlen | 0 sein.

Kategorie ist eine Liste von Kategoriecodes

für die entsprechenden X Daten.

Mit ist eine Liste von einem oder mehreren

Kategoriecodes. Nur solche Datenelemente,
deren Kategoriecode in dieser Liste
enthalten ist, sind in der Berechnung
enthalten.

Katalog >

Katalog >

78 A lphabetische Auflistung

FiveNumSummary

Ein leeres (ungültiges) Element in einer der
Listen X, Freq oder Kategorie führt zu
einem Fehler im entsprechenden Element
aller dieser Listen. Weitere Informationen zu
leeren Elementen finden Sie (Seite 261).

Ausgabevariable Beschreibung

stat.MinX Minimum der x-Werte

stat.Q1X 1. Quartilvon x

stat.MedianX Median von x

stat.Q3X 3. Quartilvon x

stat.MaxX Maximumder x-Werte

Katalog >

floor() (Untergrenze)

floor(Ausdr1)⇒Ganzzahl

Gibt die größte ganze Zahl zurück, die {
dem Argument ist. Diese Funktion ist
identisch mit int().

Das Argument kann eine reelle oder eine
komplexe Zahl sein.

floor(Liste1)⇒Liste

floor(Matrix1)⇒Matrix

Für jedes Element einer Liste oder Matrix
wird die größte ganze Zahl, die kleiner oder
gleich dem Element ist, zurückgegeben.

Hinweis: Siehe auch ceiling() und int().

fMax() (Funktionsmaximum)

fMax(Ausdr, Var)⇒Boolescher Ausdruck

fMax(Ausdr, Var,UntereGrenze)

fMax(Ausdr,

Var,UntereGrenze,ObereGrenze)

fMax(Ausdr, Var) | UntereGrenze{Var
{ObereGrenze

Katalog >

Katalog >

Alphabetische Auflistung 79

fMax() (Funktionsmaximum)

Gibt einen Booleschen Ausdruck zurück, der
mögliche Werte von Var angibt, welche

Ausdr maximieren oder seine kleinste

obere Grenze angeben.
Sie können den womit-Operator („|“) zur

Beschränkung des Lösungsintervalls
und/oder zur Angabe anderer
Einschränkungen verwenden.

Ist der Modus Auto oder Näherung auf
Approximiert eingestellt, sucht fMax()
iterativ nach einem annähernden lokalen
Maximum. Dies ist oft schneller,
insbesondere, wenn Sie den Operator “|”
benutzen, um die Suche auf ein relativ
kleines Intervall zu beschränken, das genau
ein lokales Maximum enthält.

Hinweis: Siehe auch fMin() und max().

Katalog >

fMin() (Funktionsminimum)

fMin(Ausdr, Var)⇒Boolescher Ausdruck

fMin(Ausdr, Var,UntereGrenze)

fMin(Ausdr,

Var,UntereGrenze,ObereGrenze)

fMin(Ausdr, Var) | UntereGrenze{Var
{ObereGrenze

Gibt einen Booleschen Ausdruck zurück, der
mögliche Werte von Var angibt, welche

Ausdr minimieren oder seine kleinste

untere Grenze angeben.

Sie können den womit-Operator („|“) zur
Beschränkung des Lösungsintervalls
und/oder zur Angabe anderer
Einschränkungen verwenden.

Katalog >

80 A lphabetische Auflistung

fMin() (Funktionsminimum)

Ist der Modus Auto oder Näherung auf
Approximiert eingestellt, sucht fMin()
iterativ nach einem annähernden lokalen
Minimum. Dies ist oft schneller,
insbesondere, wenn Sie den Operator “|”
benutzen, um die Suche auf ein relativ
kleinesIntervall zu beschränken, das genau
ein lokales Minimum enthält.

Hinweis: Siehe auch fMax() und min().

Katalog >

For

For Var, Von, Bis [, Schritt]

Block

EndFor

Führt die in Block befindlichen
Anweisungen für jeden Wert von Var
zwischen Von und Bis aus, wobei der Wert
bei jedem Durchlauf um Schritt
inkrementiert wird.

Var darf keine Systemvariable sein.

Schritt kann positiv oder negativ sein. Der

Standardwert ist 1.

Block kann eine einzelne Anweisung oder

eine Serie von Anweisungen sein, die durch
“:” getrennt sind.

Hinweis zum Eingeben des Beispiels:

Anweisungen für die Eingabe von
mehrzeiligen Programm- und
Funktionsdefinitionen finden Sie im
Abschnitt „Calculator“ des
Produkthandbuchs.

format() (Format)

format(Ausdr[, FormatString])⇒String

Gibt Ausdr als Zeichenkette im Format der
Formatvorlage zurück.

Ausdr muss zu einer Zahl vereinfachbar

sein.

Katalog >

Katalog >

Alphabetische Auflistung 81

format() (Format)

FormatString ist eine Zeichenkette und

muss diese Form besitzen: “F[n]”, “S[n]”,
“E[n]”, “G[n][c]”, wobei [ ] optionale Teile
bedeutet.

F[n]: Festes Format. n ist die Anzahl der
angezeigten Nachkommastellen (nach dem
Dezimalpunkt).

S[n]: Wissenschaftliches Format. n ist die
Anzahl der angezeigten Nachkommastellen
(nach dem Dezimalpunkt).

E[n]: Technisches Format. n ist die Anzahl
der Stellen, die auf die erste signifikante
Ziffer folgen. Der Exponent wird auf ein
Vielfaches von 3 gesetzt, und der
Dezimalpunkt wird um null, eine oder zwei
Stellen nach rechts verschoben.

G[n][c]: Wie Festes Format, unterteilt
jedoch auch die Stellen links des
Dezimaltrennzeichens in Dreiergruppen. c
ist das Gruppentrennzeichen und ist auf
“Komma” voreingestellt. Wenn c auf
“Punkt” gesetzt wird, wird das
Dezimaltrennzeichen zum Komma.

[Rc]: Jeder der vorstehenden
Formateinstellungen kann als Suffix das
Flag Rc nachgestellt werden, wobei c ein
einzelnes Zeichen ist, das den Dezimalpunkt
ersetzt.

Katalog >

fPart() (Funktionsteil)

fPart(Ausdr1)⇒Ausdruck
fPart(Liste1)⇒Liste
fPart(Matrix1)⇒Matrix

Gibt den Bruchanteil des Arguments zurück.

Bei einer Liste bzw. Matrix werden die
Bruchanteile aller Elemente zurückgegeben.

Das Argument kann eine reelle oder eine
komplexe Zahl sein.

82 A lphabetische Auflistung

Katalog >

FPdf()

FPdf

(XWert,FreiGradZähler,FreiGradNenner)

⇒Zahl, wenn XWert eine Zahl ist, Liste,
wenn XWert eine Liste ist

FPdf
(XWert,FreiGradZähler,FreiGradNenner)

⇒Zahl, wenn XWert eine Zahl ist, Liste,
wenn XWert eine Liste ist

Berechnet die F
Verteilungswahrscheinlichkeit bei XWert für
die angegebenen FreiGradZähler
(Freiheitsgrade) und FreiGradNenner.

Katalog >

freqTable4list()

freqTable4list(Liste1,HäufGanzzahlListe)

⇒Liste

Gibt eine Liste zurück, die die Elemente von

Liste1 erweitert gemäß den Häufigkeiten in
HäufGanzzahlListe enthält. Diese Funktion

kann zum Erstellen einer Häufigkeitstabelle
für die Applikation 'Data & Statistics'
verwendet werden.

Liste1 kann eine beliebige gültige Liste

sein.

HäufGanzzahlListe muss die gleiche

Dimension wie Liste1 haben und darf nur
nicht-negative Ganzzahlelemente
enthalten. Jedes Element gibt an, wie oft
das entsprechende Liste1-Element in der
Ergebnisliste wiederholt wird. Der Wert 0
schließt das entsprechende Liste1-Element
aus.

Hinweis: Sie können diese Funktion über die

Tastatur Ihres Computers eingeben, indem
Sie freqTable@>list(...) eintippen

Leere (ungültige) Elemente werden
ignoriert. Weitere Informationen zu leeren
Elementen finden Sie (Seite 261).

Katalog >

Alphabetische Auflistung 83

frequency() (Häufigkeit)

frequency(Liste1,binsListe)⇒Liste

Gibt eine Liste zurück, die die Zähler der
Elemente in Liste1 enthält. Die Zähler
basieren auf Bereichen (bins), die Sie in

binsListe definieren.

Wenn binsListe {b(1), b(2), …, b(n)} ist,
sind die festgelegten Bereiche {?{b(1), b(1)
<?{b(2),…,b(n-1)<?{b(n), b(n)>?}. Die
Ergebnisliste enthält ein Element mehr als
die binsListe.

Jedes Element des Ergebnisses entspricht
der Anzahl der Elemente aus Liste1, die im
Bereich dieser bins liegen. Ausgedrückt in
Form der countIf() Funktion ist das Ergebnis
{ countIf(Liste, ?{b(1)), countIf(Liste, b(1)<?
{b(2)), …, countIf(Liste, b(n-1)<?{b(n)),
countIf(Liste, b(n)>?)}.

Elemente von Liste1, die nicht “in einem
bin platziert” werden können, werden
ignoriert. Leere (ungültige) Elemente
werden ebenfalls ignoriert. Weitere
Informationen zu leeren Elementen finden
Sie (Seite 261).

Innerhalb der Lists & Spreadsheet
Applikation können Sie für beide Argumente
Zellenbereiche verwenden.

Hinweis: Siehe auch countIf(), Seite 38.

Katalog >

Erklärung des Ergebnisses:

2 Elementeaus Datenliste (Datalist) sind

{2.5

4 Elementeaus Datenliste sind>2.5 und

{4.5

3 Elementeaus Datenliste sind>4.5

Das Element“Hallo” ist eineZeichenfolge
und kann nichtineinem der definiertenbins
platziert werden.

FTest_2Samp (Zwei-Stichproben F-

Test)

FTest_2Samp Liste1,Liste2[,Häufigkeit1
[,Häufigkeit2[,Hypoth]]]

FTest_2Samp Liste1,Liste2[,Häufigkeit1
[,Häufigkeit2[,Hypoth]]]

(Datenlisteneingabe)

FTest_2Samp sx1,n1,sx2,n2[,Hypoth]

FTest_2Samp sx1,n1,sx2,n2[,Hypoth]

(Zusammenfassende statistische Eingabe)

84 A lphabetische Auflistung

Katalog >

FTest_2Samp (Zwei-Stichproben F-

Test)

Führt einen F -Test mit zwei Stichproben
durch. Eine Zusammenfassung der
Ergebnisse wird in der Variable stat.results
gespeichert. (Seite 196.)

Für Ha: s1 > s2 setzen Sie Hypoth>0

Für Ha: s1 ƒ s2 (Standard) setzen Sie

Katalog >

Hypoth =0

Für Ha: s1 < s2 setzen Sie Hypoth<0

Informationen zu den Auswirkungen leerer
Elemente in einer Liste finden Sie unter
“Leere (ungültige) Elemente” (Seite 261).

Ausgabevariable Beschreibung

Statistik.F Berechnete Û Statistik für die Datenfolge

stat.PVal Kleinste Signifikanzebene, beider die Nullhypothese verworfen werdenkann

stat.dfNumer Freiheitsgrade des Zählers =n1-1

stat.dfDenom Freiheitsgradedes Nenners =n2-1

stat.sx1, stat.sx2

stat.x1_bar

stat.x2_bar

stat.n1, stat.n2 Stichprobenumfang

Stichproben-Standardabweichungen der Datenfolgen in Liste1 undListe2

Stichprobenmittelwerte der Datenfolgen in Liste1 undListe2

Func

Func

   Block

EndFunc

Vorlage zur Erstellung einer
benutzerdefinierten Funktion.

Block kann eine einzelne Anweisung, eine

Reihe von durch das Zeichen “:”
voneinander getrennten Anweisungen oder
eine Reihe von Anweisungen in separaten
Zeilen sein. Die Funktion kann die
Anweisung Zurückgeben (Return)
verwenden, um ein bestimmtes Ergebnis
zurückzugeben.

Katalog >

Definieren Sie einestückweise definierte
Funktion:

Ergebnis der graphischen Darstellung g(x)

Alphabetische Auflistung 85

Func

Hinweis zum Eingeben des Beispiels:

Anweisungen für die Eingabe von
mehrzeiligen Programm- und
Funktionsdefinitionen finden Sie im
Abschnitt „Calculator“ des
Produkthandbuchs.

G

Katalog >

gcd() (Größter gemeinsamer Teiler)

gcd(Zahl1, Zahl2)⇒Ausdruck

Gibt den größten gemeinsamen Teiler der
beiden Argumente zurück. Der gcd zweier
Brüche ist der gcd ihrer Zähler dividiert
durch das kleinste gemeinsame Vielfache
(lcm) ihrer Nenner.

In den Modi Auto oder Approximiert ist der

gcd von Fließkommabrüchen 1,0.

gcd(Liste1, Liste2)⇒Liste

Gibt die größten gemeinsamen Teiler der
einander entsprechenden Elemente von

Liste1 und Liste2 zurück.

gcd(Matrix1, Matrix2)⇒Matrix

Gibt die größten gemeinsamen Teiler der
einander entsprechenden Elemente von

Matrix1 und Matrix2 zurück.

geomCdf()

geomCdf(p,untereGrenze,obereGrenze)

⇒Zahl, wenn untereGrenze und

obereGrenze Zahlen sind, Liste, wenn
untereGrenze und obereGrenze Listen sind

Katalog >

Katalog >

geomCdf(p,obereGrenze)für P(1{X

{obereGrenze)⇒Zahl, wenn obereGrenze
eine Zahl ist, Liste, wenn obereGrenze eine
Liste ist

86 A lphabetische Auflistung

geomCdf()

Berechnet die kumulative geometrische
Wahrscheinlichkeit von UntereGrenze bis

ObereGrenze mit der angegebenen

Erfolgswahrscheinlichkeit p.

Für P(X { obereGrenze) setzen Sie

untereGrenze = 1.

Katalog >

geomPdf()

Katalog >

geomPdf(p,XWert)⇒Zahl, wenn XWert

eine Zahl ist, Liste, wenn XWert eine Liste
ist

Berechnet die Wahrscheinlichkeit an einem

XWert, die Anzahl der Einzelversuche, bis

der erste Erfolg eingetreten ist, für die
diskrete geometrische Verteilung mit der
vorgegebenen Erfolgswahrscheinlichkeit p.

Get Hub-Menü

Get[EingabeString,]Var[,statusVar]

Get[EingabeString,] Fkt(arg1, ...argn)

[,statusVar]

Programmierbefehl: Ruft einen Wert von
einem verbundenen TI-Innovator™ Hub ab
und weist den Wert der Variablen var zu.

Der Wert muss angefordert werden:

• Im Voraus durch einen Befehl

Send"READ..." .

– oder –

• Durch Einbetten einer Anforderung

"READ..." als optionales Argument von

Beispiel: Fordern SiedenaktuellenWert des
integrierten Lichtpegelsensors des Huban.
VerwendenSie Get, um denWert abzurufen,
und weisen Sie ihnder Variablenlightval zu.

Betten Sie die Anforderung READinden
BefehlGet ein.

promptString. Bei dieser Methode

können Sie einen einzelnen Befehl
verwenden, um den Wert anzufordern
und abzurufen.

Alphabetische Auflistung 87

Get Hub-Menü

Implizite Vereinfachung findet statt. Zum
Beispiel wird eine empfangene
Zeichenfolge „123“ als numerischer Wert
interpretiert. Um die Zeichenfolge
beizubehalten, verwenden Sie GetStr statt

Get.

Wenn Sie das optionale Argument von

statusVar einbeziehen, wird ihm ein Wert

auf Basis des Erfolgs der Operation
zugewiesen. Ein Wert von null bedeutet,
dass keine Daten empfangen wurden.

In der zweiten Synthax ermöglicht das
Argument von Fkt() es einem Programm,
die empfangene Zeichenfolge als
Funktionsdefinition zu speichern. Diese
Syntax verhält sich so, als hätte das
Programm den folgenden Befehl
ausgeführt:

Definiere Fkt(arg1, ...argn) = empfanger

String

Anschließend kann das Programm die so
definierte Funktion Fkt() nutzen.

Hinweis: Sie können den Befehl Get in

einem benutzerdefinierten Programm, aber
nicht in einer Funktion verwenden.

Hinweis: Siehe auch GetStr, Seite 94 und
Send, Seite 175.

getDenom() (Nenner holen)

getDenom(Ausdr1)⇒Ausdruck

Transformiert das Argument in einen
Ausdruck mit gekürztem gemeinsamem
Nenner und gibt dann den Nenner zurück.

getKey()

getKey([01]) ⇒ returnString

88 A lphabetische Auflistung

Katalog >

Katalog >

Beispiel:

getKey()

Beschreibung:getKey() – ermöglicht ein

TI-Basic-Programm zum Holen von
Tastatureingaben – Handheld, Desktop
und Emulator auf Desktop.

Beispiel:

• gedrückteTaste := getKey() gibt eine
Taste oder eine leere Zeichenkette
zurück, wenn keine Taste gedrückt
wurde. Dieser Aufruf wird umgehend
zurückgegeben.

• gedrückteTaste := getKey(1) wartet
bis eine Taste gedrückt wird. Dieser
Aufruf pausiert die Ausführung des
Programms, bis eine Taste gedrückt
wird.

Handhabung von Tastenbetätigungen:

Handheld/Emulatortaste Desktop Rückgabewert

Esc Esc „Esc“

Touchpad – Oben klicken – „nach oben“

Ein – „Hauptmenü“

Scratch Apps – „Scratchpad“

Touchpad – Linksklick – „links“

Touchpad – Mittig klicken – „Mittelpunkt“

Touchpad – Rechtsklick – „rechts“

Dok – „Dok“

Katalog >

Tab Tab „Tab“

Touchpad – Unten klicken Abwärtspfeil „nach unten“

Menü – „Menü“

Strg Strg keine Rückgabe

Verschieben (Shift) Verschieben (Shift) keine Rückgabe

Var – „var“

Entf – „del“

Alphabetische Auflistung 89

Handheld/Emulatortaste Desktop Rückgabewert

= = "="

Trigonometrie – „Trigonometrie“

0 bis 9 0-9 „0“ …“9“

Vorlagen – „Vorlage“

Katalog – „cat“

^ ^ "^"

X^2 – „Quadrat“

/ (Divisionstaste) / "/"

* (Multiplikationstaste) * "*"

e^x – „Ausdr“

10^x – „10power“

+ + "+"

- - "-"

( ( "("

) ) ")"

. . "."

(-) – „-“ (Negativ-Zeichen)

Eingabetaste Eingabetaste „Eingabe“

Osteuropa – „E“ Exponentialform

(wissenschaftliche
Schreibweise E)

a – z a-z Alpha = Buchstabe gedrückt

(Kleinschreibung)
(„a“ – „z“)

Umschalt a-z Umschalt a-z Alpha = Buchstabe gedrückt

„A“ – „Z“

Hinweis: Strg-Umschalt
ergibt Feststelltaste

?! – "?!"

90 A lphabetische Auflistung

Handheld/Emulatortaste Desktop Rückgabewert

pi – „pi“

Flag – keine Rückgabe

, , ","

Return – „Rückgabe“

Leerzeichen Leerzeichen „ “ (Leerzeichen)

Unzugänglich Tasten für Sonderzeichen

wie @,!,^ etc.

Das Zeichen wird
zurückgegeben

– Funktionstasten Kein zurückgegebenes

Zeichen

– Besondere Desktop-

Bedientasten

Unzugänglich Sonstige Desktop-Tasten, die

nicht auf dem Calculator zur
Verfügung stehen, während

Kein zurückgegebenes
Zeichen

Gleiches Zeichen wie in
Notes (nicht in einem math.

Feld)
getKey() auf eine
Tastenbetätigung wartet. ({,
},;, :, …)

Hinweis: Es ist wichtig zu beachten, dass das Vorhandensein von getKey() in einem
Programm die Art und Weise ändert, wie sicher Ereignisse durch das System gehandhabt
werden. Einige davon werden unten beschrieben.

Programm beenden und Ereignis handhaben – Auf gleiche Art als sollte der Benutzer das
Programm verlassen, indem er die EIN-Taste drückt

„Support“ unten bedeutet – System arbeitet wie erwartet – Programm läuft weiter.

Ereignis Handheld-Gerät Desktop – TI-Nspire™

Schnellumfrage Programm beenden,

Ereignis handhaben

Schülersoftware

Entspricht dem Handheld
(nur TI-Nspire™ Student
Software, TI-Nspire™
Navigator™ NC Teacher
Software)

Verwaltung Remote-Datei

(Einschl. Versenden der
Datei 'Press-to-Test
verlassen' von einem

Programm beenden,
Ereignis handhaben

Entspricht dem Handheld.
(nur TI-Nspire™ Student

Software, TI-Nspire™
Navigator™ NC Teacher
Software)

anderen Handheld oder
Desktop-Handheld)

Klasse beenden Programm beenden, Support

Alphabetische Auflistung 91

Ereignis Handheld-Gerät Desktop – TI-Nspire™

Ereignis handhaben (nur TI-Nspire™ Student

Schülersoftware

Software, TI-Nspire™
Navigator™ NC Teacher
Software)

Ereignis Handheld-Gerät Desktop – TI-Nspire™ Alle

TI-Innovator™ Hub
verbinden/trennen

Support – Kann erfolgreich
Befehle an den TI­Innovator™ Hub geben.
Nachdem Sie das
Programm verlassen
haben, arbeitet der TI­Innovator™ Hub noch mit
dem Handheld weiter.

getLangInfo()

Versionen

Entspricht dem Handheld

Katalog >

getLangInfo()⇒Zeichenkette

Gibt eine Zeichenkette zurück, die der
Abkürzung der gegenwärtig aktiven Sprache
entspricht. Sie können den Befehl zum
Beispiel in einem Programm oder einer
Funktion zum Bestimmen der aktuellen
Sprache verwenden.

Englisch = “en”

Dänisch = “da”

Deutsch = “de”

Finnisch = “fi”

Französisch = “fr”

Italienisch = “it”

Holländisch = “nl”

Holländisch (Belgien) = “nl_BE”

Norwegisch = “no”

Portugiesisch = “pt”

Spanisch = “es”

92 A lphabetische Auflistung

getLangInfo()

Schwedisch = “sv”

Katalog >

getLockInfo()

getLockInfo(Var)⇒Wert

Gibt den aktuellen Gesperrt/Entsperrt­Status der Variablen Var aus.

Wert =0: Var ist nicht gesperrt oder ist

nicht vorhanden.

Wert =1: Var ist gesperrt und kann nicht

geändert oder gelöscht werden.

Siehe Lock, Seite 118, undunLock, Seite 219.

getMode()

getMode(ModusNameGanzzahl)⇒Wert
getMode(0)⇒Liste

getMode(ModusNameGanzzahl) gibt einen

Wert zurück, der die aktuelle Einstellung
des Modus ModusNameGanzzahl darstellt.

getMode(0) gibt eine Liste mit

Zahlenpaaren zurück. Jedes Paar enthält
eine Modus-Ganzzahl und eine
Einstellungs-Ganzzahl.

Eine Auflistung der Modi und ihrer
Einstellungen finden Sie in der
nachstehenden Tabelle.

Wenn Sie die Einstellungen mit getMode(0)
& var speichern, können Sie setMode(var)
in einer Funktion oder in einem Programm
verwenden, um die Einstellungen nur
innerhalb der Ausführung dieser Funktion
bzw. dieses Programms vorübergehend
wiederherzustellen. Siehe setMode(), Seite

179.

Katalog >

Katalog >

Alphabetische Auflistung 93

Modus
Name

Modus
Ganzzahl Einstellen von Ganzzahlen

Angezeigte Ziffern 1 1=Fließ, 2=Fließ 1, 3=Fließ 2, 4=Fließ 3, 5=Fließ 4,

6=Fließ 5, 7=Fließ 6, 8=Fließ 7, 9=Fließ 8, 10=Fließ

9, 11=Fließ 10, 12=Fließ 11, 13=Fließ 12, 14=Fix 0,

15=Fix 1, 16=Fix 2, 17=Fix 3, 18=Fix 4, 19=Fix 5,
20=Fix 6, 21=Fix 7, 22=Fix 8, 23=Fix 9, 24=Fix 10,
25=Fix 11, 26=Fix 12

Winkel 2 1=Bogenmaß, 2=Grad, 3=Neugrad

Exponentialformat 3 1=Normal, 2=Wissenschaftlich, 3=Technisch

Reell oder

4 1=Reell, 2=Kartesisch, 3=Polar

komplex

Auto oder Approx. 5 1=Auto, 2=Approximiert, 3=Exakt

Vektorformat 6 1=Kartesisch, 2=Zylindrisch, 3=Sphärisch

Basis 7 1=Dezimal, 2=Hex, 3=Binär

Einheitensystem 8 1=SI, 2=Eng/US

getNum() (Zähler holen)

Katalog >

getNum(Ausdr1)⇒Ausdruck

Transformiert das Argument in einen
Ausdruck mit gekürztem gemeinsamem
Nenner und gibt dann den Zähler zurück.

GetStr Hub-Menü

GetStr[EingabeString,] Var[, statusVar]

GetStr[EingabeString,] Fkt(arg1, ...argn)

[,statusVar]

Programmierbefehl: Verhält sich genauso
wie der Befehl Get, der abgerufene Wert
wird aber immer als Zeichenfolge
interpretiert. Der Befehl Get interpretiert die
Antwort hingegen als Ausdruck, es sei denn,
sie ist in Anführungszeichen ("") gesetzt.

Hinweis: Siehe auch Get, Seite 87 und Send,

Seite 175.

ZumBeispiel sieheGet.

94 A lphabetische Auflistung

getType()

getType(var)⇒String

Gibt eine Zeichenkette zurück, die den
Datentyp einer Variablen var anzeigt.

Wenn var nicht definiert ist, wird die
Zeichenkette „NONE" zurückgegeben.

Katalog >

getVarInfo()

getVarInfo()⇒Matrix oder String
getVarInfo(BiblioNameString)⇒Matrix

oder String

getVarInfo() gibt eine Informationsmatrix

(Name, Typ, Erreichbarkeit einer Variablen
in der Bibliothek und Gesperrt/Entsperrt­Status) für alle Variablen und
Bibliotheksobjekte zurück, die im aktuellen
Problem definiert sind.

Wenn keine Variablen definiert sind, gibt

getVarInfo() die Zeichenfolge "KEINE"

(NONE) zurück.

getVarInfo(BiblioNameString)gibt eine

Matrix zurück, die Informationen zu allen
Bibliotheksobjekten enthält, die in der
Bibliothek BiblioNameString definiert sind.

BiblioNameString muss eine Zeichenfolge

(in Anführungszeichen eingeschlossener
Text) oder eine Zeichenfolgenvariable sein.

Wenn die Bibliothek BiblioNameString
nicht existiert, wird ein Fehler angezeigt.

Katalog >

Alphabetische Auflistung 95

getVarInfo()

Beachten Sie das Beispiel links, in dem das
Ergebnis von getVarInfo() der Variablen vs
zugewiesen wird. Beim Versuch, Zeile 2
oder Zeile 3 von vs anzuzeigen, wird der
Fehler “Liste oder Matrix ungültig”
zurückgegeben, weil mindestens eines der
Elemente in diesen Zeilen (Variable b zum
Beispiel) eine Matrix ergibt.

Dieser Fehler kann auch auftreten, wenn

Ans zum Neuberechnen eines getVarInfo()-

Ergebnisses verwendet wird.

Das System liefert den obigen Fehler, weil
die aktuelle Version der Software keine
verallgemeinerte Matrixstruktur
unterstützt, bei der ein Element einer
Matrix eine Matrix oder Liste sein kann.

Katalog >

Goto (Gehe zu)

Goto MarkeName

Setzt die Programmausführung bei der
Marke MarkeName fort.

MarkeName muss im selben Programm

mit der Anweisung Lbl definiert worden
sein.

Hinweis zum Eingeben des Beispiels:

Anweisungen für die Eingabe von
mehrzeiligen Programm- und
Funktionsdefinitionen finden Sie im
Abschnitt „Calculator“ des
Produkthandbuchs.

4Grad (Neugrad)

Ausdr1 4Grad⇒Ausdruck

Wandelt Ausdr1 ins Winkelmaß Neugrad
um.

Hinweis: Sie können diesen Operator über

die Tastatur Ihres Computers eingeben,
indem Sie @>Grad eintippen.

Katalog >

Katalog >

Im Grad-Modus:

Im Bogenmaß-Modus:

96 A lphabetische Auflistung