Texas Instruments TI-Nspire CX CAS Reference Guide [da]

TI-Nspire™CAS

Opslagsvejledning

Denne vejledning gælder TI-Nspire™ software version 4.5. Du kan få den nyeste version af dokumentationen ved at gå til education.ti.com/go/download

Vigtige oplysninger

Medmindre andet udtrykkeligt angives i den Licens, der følger med et program, stiller Texas Instruments ingen garantier, hverken udtrykkeligt eller underforstået, herunder men ikke begrænset til underforståede garantier om salgbarhed og egnethed til et bestemt formål, for programmer eller skriftligt materiale, og Texas Instruments stiller udelukkende sådant materiale til rådighed, som det foreligger. Texas Instruments kan under ingen omstændigheder holdes ansvarlig for særlige, indirekte, hændelige eller følgeskader i forbindelse med eller som følge af køb eller brug af dette materiale, og hele Texas Instruments' erstatningsansvar kan, uanset søgsmålets art, ikke overstige det beløb, der fremgår af programlicensen. Derudover kan Texas Instruments ikke holdes ansvarlig for nogen form for krav som følge af en anden parts brug af dette materiale.

Licens

Se hele licensen der er installeret i C:\ProgramFiles\TIEducation\<TI-Nspire™ Product Name>\license.

Indholdsfortegnelse

Vigtige oplysninger

Udtryksskabeloner 1

Alfabetisk oversigt 8

A B C D E F G I L M N O P Q R S T U V W X Z

17 21 47 60 70 80 91

99 115 125 132 135 144 147 162 187 203 204 205 207 208

iii

Symboler 217

Tomme (ugyldige) elementer 244

Genveje til indtastning af matematiske udtryk 246

Hierarkiet i EOS™ ligningsoperativsystemet (Equation Operating System) 248

Konstanter og værdier 250

Fejlkoder og fejlmeddelelser 251

Fejlkoder og -meddelelser 259

Generelle oplysninger 261

Oplysninger om TI-produktservice og garanti

261

Indeks 262

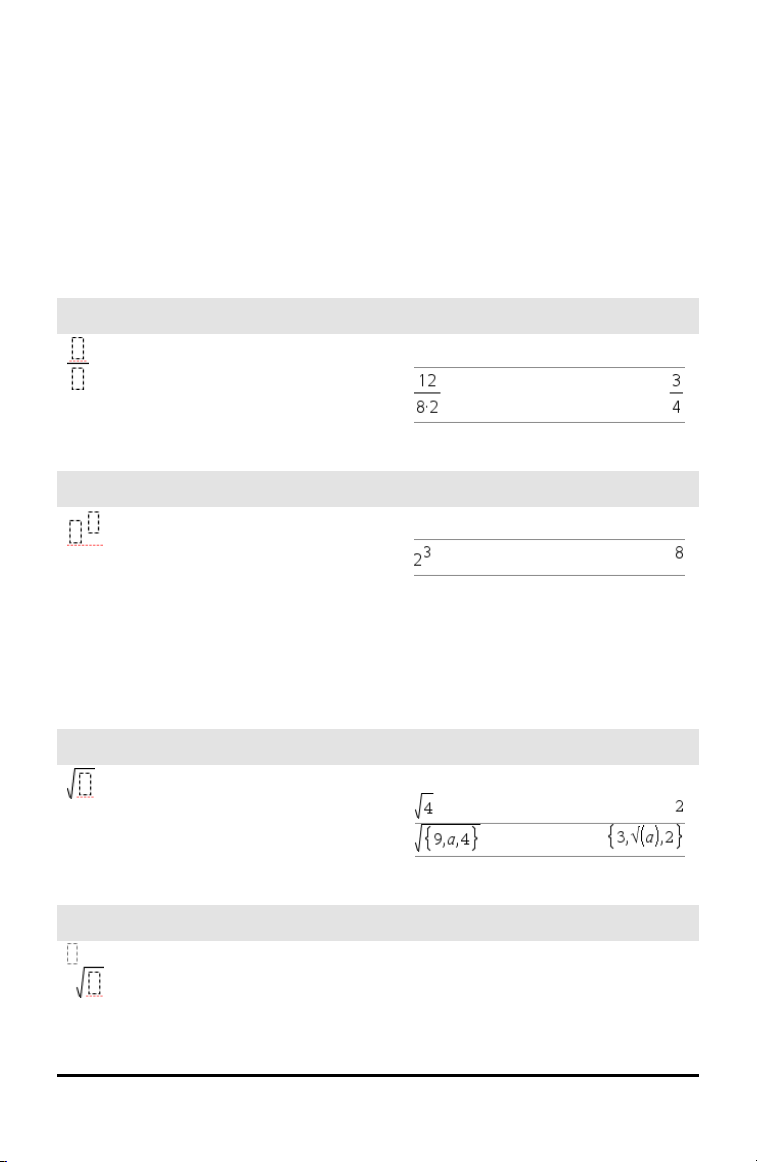
Udtryksskabeloner

Udtryksskabeloner er en nem metode til at indsætte matematiske udtryk i matematisk standardnotation. Når du indsætter en skabelon, optræder den i indtastningslinjen med små blokke på positioner, hvor du kan indsætte elementer. En markør viser, hvilket element, du kan indsætte.

Anvend piletasten eller tryk på e for at flytte markøren til hvert elements position, og skriv en værdi eller et udtryk for hvert element. Tryk på · eller /· for at

beregne udtrykket.

Brøkskabelon

Bemærk: Se også / (divider), side 219.

Eksponentskabelon

Bemærk: Skriv første værdi, tryk på l, og

skriv derefter eksponenten. Tryk på højrepilen (¢) for at hente markøren tilbage

til basislinjen.

Bemærk: Se også ^ (potens), side 220.

Kvadratrodsskabelon

Bemærk: Se også ‡() (kvadratrod), side

230.

/p-taster

Eksempel:

l-tast

Eksempel:

/q-taster

Eksempel:

Nte rod-skabelon

Bemærk: Se også root(), side 158.

/l-taster

Eksempel:

Udtryksskabeloner 1

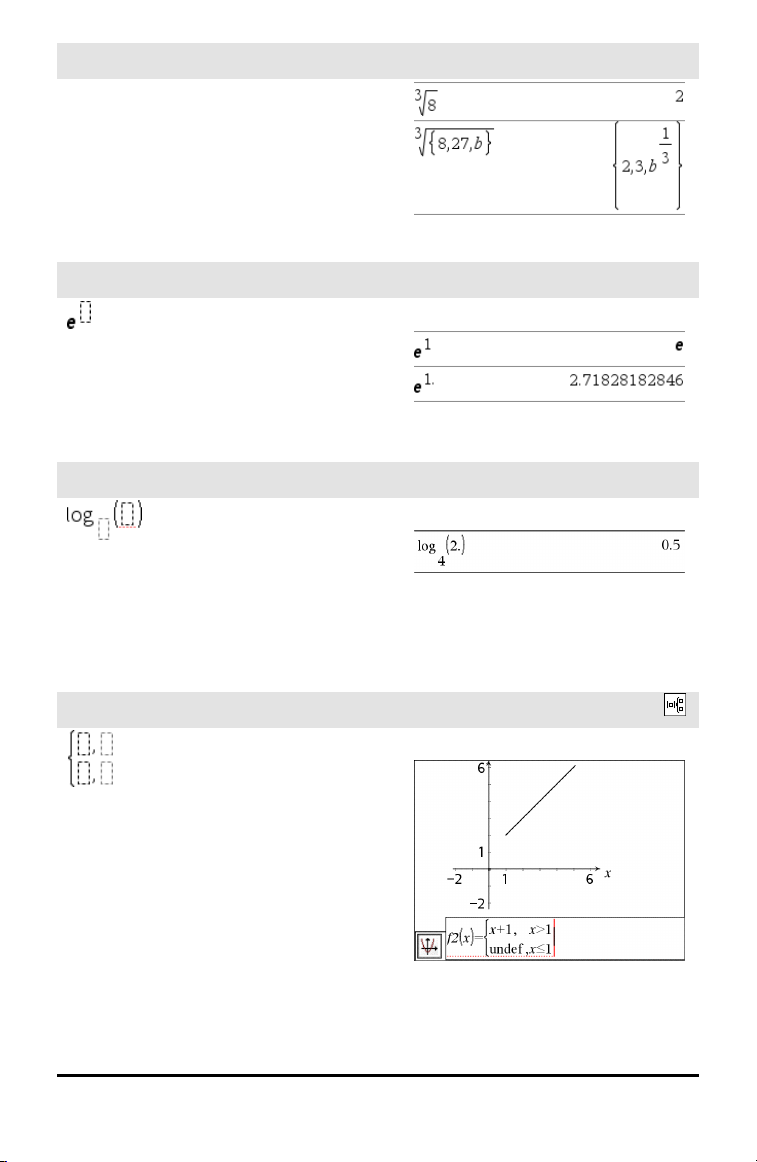
Nte rod-skabelon

/l-taster

e ekponentskabelon

Den naturlige eksponentialfunktion e opløftet til en potens

Bemærk: Se også e^(), side 60.

Log-skabelon

Beregner logaritmen med et angivet grundtal. Ved 10-talslogaritmen, der er standard, udelades grundtallet.

Bemærk: Se også log(), side 111.

Stykkevis-skabelon (2 stykker)

Gør det muligt at oprette udtryk og betingelser for en stykkevis funktion med to stykker.- Du kan tilføje et stykke ved at klikke på skabelonen og gentage skabelonen.

Bemærk: Se også piecewise(), side 136.

u-taster

Eksempel:

/s-tasten

Eksempel:

Katalog >

Eksempel:

2 Udtryksskabeloner

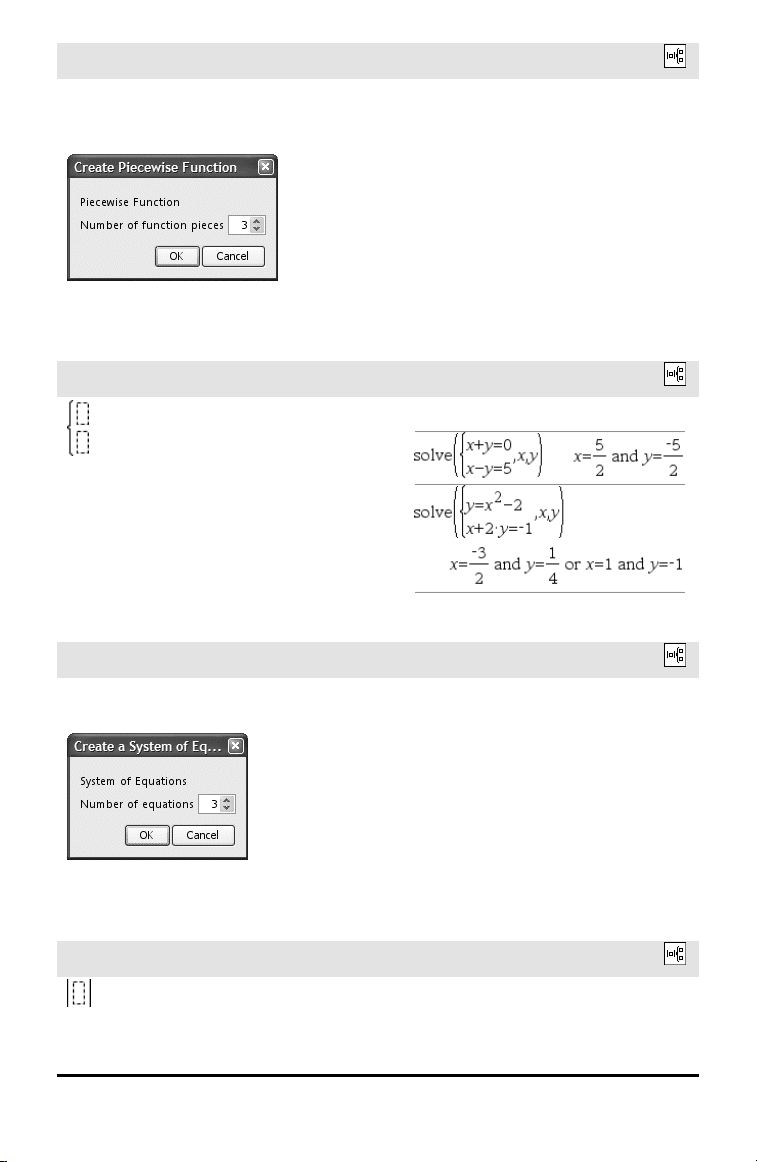
Stykkevis-skabelon (N stykker)

Gør det muligt at oprette udtryk og betingelser for en stykkevis funktion med Nstykker. Beder om N.

Bemærk: Se også piecewise(), side 136.

Katalog >

Eksempel:

Se eksempletmedstykkevis-skabelonen(2 stykker).

Skabelon til system med 2 ligninger

Opretter et ligningssystem med to ligninger. Du kan tilføje en række i et eksisterende system ved at klikke i skabelonen og gentage skabelonen.

Bemærk: Se også system(), side 187.

Skabelon til system med N ligninger

Gør det muligt at oprette et system af

Nligninger Beder om N.

Bemærk: Se også system(), side 187.

Absolut værdi-skabelon

Bemærk: Se også abs(), side 8.

Katalog >

Eksempel:

Katalog >

Eksempel:

Se eksempletmed ligningssystemskabelonen(2-ligninger).

Katalog >

Eksempel:

Udtryksskabeloner 3

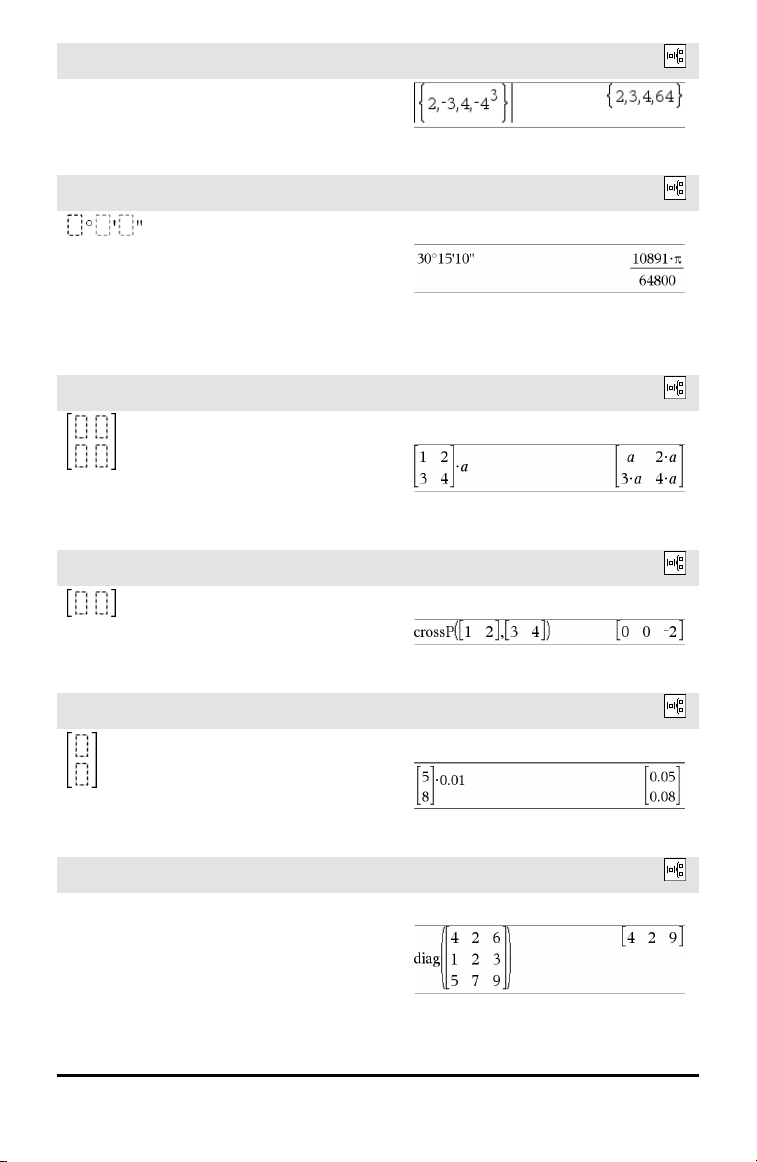
Absolut værdi-skabelon

Katalog >

dd°mm’ss.ss’’-skabelon

Her kan du indtaste vinkler i gg°mm’ss.ss’’ format, hvor gg er antallet af decimalgrader, mm er antallet af minutter, og ss.ss antallet af sekunder.

Matrix-skabelon (2 x 2)

Opretter en matrix 2 x 2.

Matrix-skabelon (1 x 2)

Matrix-skabelon (2 x 1)

Katalog >

Eksempel:

Katalog >

Eksempel:

Katalog >

Eksempel:

Katalog >

Eksempel:

Matrix-skabelon (m x n)

Skabelonen vises, efter at du er blevet bedt om at angive antallet af rækker og kolonner.

4 Udtryksskabeloner

Katalog >

Eksempel:

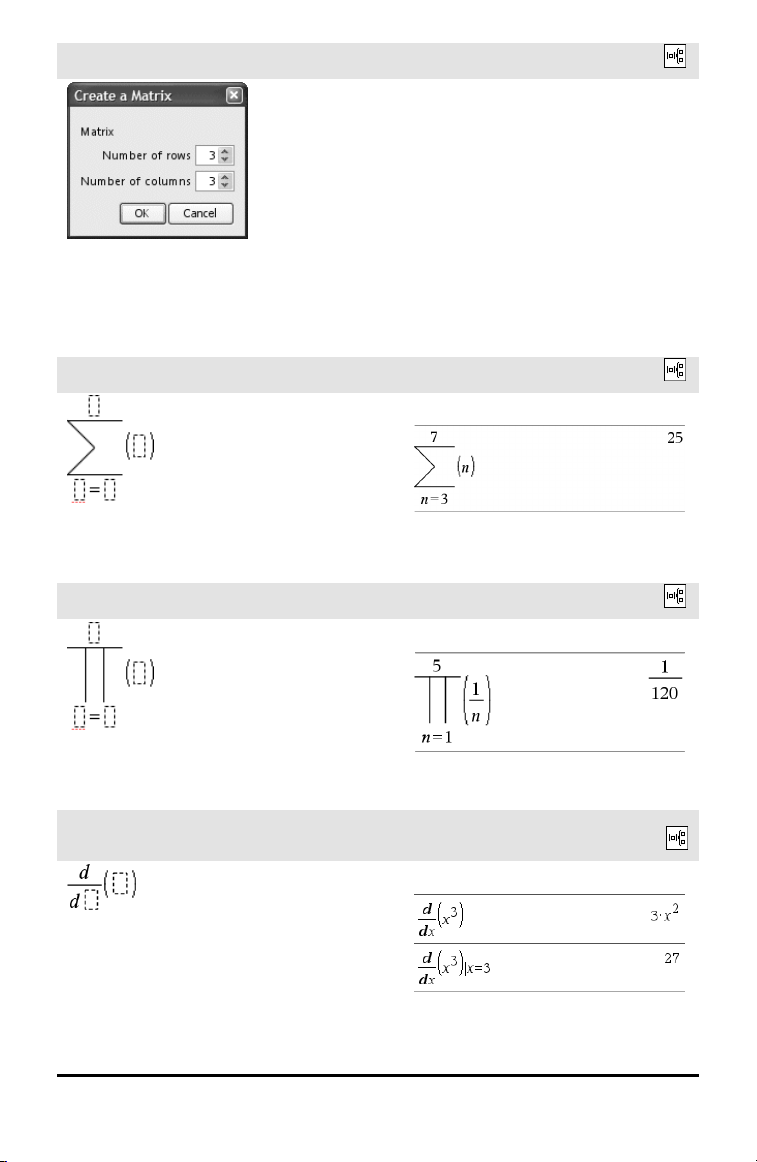
Matrix-skabelon (m x n)

Bemærk: Hvis du opretter en matrix med

mange rækker og kolonner, kan det tage et øjeblik, før den kommer frem.

Katalog >

Sum-skabelon (G)

Bemærk: Se også G() (sumSeq), side 232.

Produkt-skabelon (Π)

Bemærk: Se også Π() (prodSeq), side 231.

Skabelon til differentialkvotient af første orden

Skabelonerne til differentialkvotienter af første orden kan også anvendes til at beregne differentialkvotienten af første orden i et punkt.

Katalog >

Eksempel:

Katalog >

Eksempel:

Katalog >

Eksempel:

Udtryksskabeloner 5

Skabelon til differentialkvotient af første orden

Bemærk: Se også d() (differentialkvotient),

side 228.

Skabelon til differentialkvotient af anden orden

Skabelonerne til differentialkvotienter af anden orden kan også anvendes til at beregne differentialkvotienten af anden orden i et punkt.

Bemærk: Se også d() (differentialkvotient),

side 228.

Skabelon til differentialkvotient af Nte orden

Skabelonen til differentialkvotienten af nte orden kan anvendes til at beregne differentialkvotienten af nte orden.

Bemærk: Se også d() (differentialkvotient),

side 228.

Katalog >

Eksempel:

Katalog >

Eksempel:

Bestemt integral skabelon

Bemærk: Se også ‰() integral(), side 217.

Ubestemt integralskabelon

6 Udtryksskabeloner

Katalog >

Eksempel:

Katalog >

Eksempel:

Ubestemt integralskabelon

Bemærk: Se også ‰() integral(), side 217.

Katalog >

Grænseværdi skabelon

Anvend N eller (N) til grænseværdi fra venstre. Anvend + til grænseværdi fra højre.

Bemærk: Se også limit(), side 101.

Katalog >

Eksempel:

Udtryksskabeloner 7

Alfabetisk oversigt

Elementer, hvis navne ikke er alfabetiske (som f.eks. +, ! og >), er anført sidst i dette afsnit, startende (side 217). Medmindre andet er angivet, udføres alle eksempler i dette afsnit i standard nulstillingstilstand, og alle variable antages at være ikkedefineret.

abs()

abs(Udtr1)⇒udtryk abs(Liste1)⇒liste abs(Matrix1)⇒matrix

Returnerer den absolutte værdi af argumentet.

Bemærk: Se også Absolut værdi-skabelon,

side 3.

Hvis argumentet er et komplekst tal, returneres tallets modulus.

Bemærk: Alle udefinerede variable

behandles som reelle variable.

amortTbl()

amortTbl(NPmt,N,I,PV, [Pmt], [FV], [PpY], [CpY], [PmtAt], [afrundVærdi])

⇒matrix

Amortiseringsfunktion, der returnerer en matrix som en amortiseringstabel for et sæt af TVM-argumenter.

NPmt er antallet af betalinger, der skal

inkluderes i tabellen. Tabellen starter med den første betaling.

N, I, PV, Pmt, FV, PpY, CpY og PmtAt er

beskrevet i tabellen over TVM-argumenter (side 201).

• Hvis du udelader Pmt, sættes den som standard til Pmt=tvmPmt (N,I,PV,FV,PpY,CpY,PmtAt).

• Hvis du udelader FV, sættes FV=0 som

Katalog >

8 Alfabetisk oversigt

amortTbl()

standard.

• Standardværdierne for PpY, CpY og

PmtAt er de samme som for TVM-

funktionerne.

afrundVærdi angiver antallet af decimaler

til afrunding. Standardværdi=2.

Kolonnerne i resultatmatricen er i denne rækkefølge: Betalingsnummer, beløb betalt til renter, beløb betalt til hovedstol og saldo.

Saldoen, der vises i række n, er saldoen efter betaling n.

Du kan bruge outputmatricen som input for de andre amortiseringsfunktioner GInt() og GPrn(), side 232 og bal(), side 17.

Katalog >

and

Boolsk Udtr1 and Boolsk Udtr2 ⇒Boolsk

udtryk

Boolsk Liste1 and Boolsk Liste2⇒Boolsk

liste

Boolsk Matrix1 and Boolsk

Matrix2⇒Boolsk matrix

Returnerer true eller false eller en forenklet form af den oprindelige indtastning.

Heltal1andHeltal2⇒heltal

Sammenligner to heltal bit for bit med en

and-operation. Internt konverteres begge

heltal til 64-bit binære tal med fortegn. Når de tilsvarende bits sammenlignes, er resultatet 1, hvis begge bits er 1. Ellers er resultatet 0. Den returnerede værdi repræsenterer bit-resultaterne og vises i overensstemmelse med den valgte talsystemtilstand.

Katalog >

I hexadecimaltilstand:

Vigtigt: Talletnul, ikke bogstavetO.

I binær tilstand:

I decimaltilstand:

Alfabetisk oversigt 9

and

Du kan indtaste heltallene i ethvert talsystem. Til binære eller hexadecimale indtastninger skal du som præfiks benytte henholdsvis 0b eller 0h. Uden præfiks behandles heltallene som decimaltal (10talssystem).

Hvis du indtaster et decimalt heltal, der er for stort til en 64-bit binær form med fortegn, anvendes en symmetrisk modulooperation til at bringe værdien ind i det korrekte område.

Katalog >

Bemærk: En binær indtastning kan have o p

til64 cifre (præfikset0b ikke medregnet). En hexadecimal indtastning kan have op til16 cifre.

angle()

angle(Udtr1)⇒udtryk

Returnerer vinklen på argumentet og fortolker argumentet som et komplekst tal.

Bemærk: Alle udefinerede variable

behandles som reelle variable.

angle(Liste1)⇒liste angle(Matrix1)⇒matrix

Returnerer en liste eller matrix med vinkler af elementerne i Liste1 eller matrix1, hvor hvert element fortolkes som et komplekst tal, der repræsenterer et todimensionalt rektangulært koordinatpunkt.

Katalog >

I vinkeltilstandenGrader:

I vinkeltilstandenNygrader:

I vinkeltilstandenRadian:

ANOVA

ANOVA Liste1,Liste2[,Liste3,...,Liste20]

10 A lfabetisk oversigt

Katalog >

ANOVA

Katalog >

[,Flag]

Udfører envejsanalyse af varians til sammenligning af middelværdier for to til 20 populationer. En sammenfatning af resultaterne lagres i variablen stat.results. (side 182.)

Flag=0 for data, Flag=1 for statistik

Output-variabel Beskrivelse

stat.F Værdienfor F-statistik

stat.PVal Mindstesignifikansniveau, ved hvilketnul-hypotesenkan forkastes

stat.df Frihedsgrader i grupperne

stat.SS Kvadratsum i grupperne

stat.MS Middelkvadratfor grupperne

stat.dfError Frihedsgrader for fejl

stat.SSError Kvadratsum for fejlene

stat.MSError Middelkvadratfor fejlene

stat.sp Puljetstandardafvigelse

stat.xbarlist Gennemsnit af inputfor listerne

stat.CLowerList 95%konfidensintervaller for middelværdien for hver inputliste

stat.CUpperList 95%konfidensintervaller for middelværdienfor hver inputliste

ANOVA2-way

ANOVA2way Liste1,Liste2

[,Liste3…,Liste10][,levRow]

Beregner en tovejsanalyse af varians til sammenligning af middelværdier for to til ti populationer. En sammenfatning af resultaterne lagres i variablen stat.results. (side 182.)

LevRow=0 for Blok

LevRow=2,3,…,Len-1, for to-faktor, hvor Len=length(List1)=length(List2) = … =

length(List10) og Len / LevRow Î {2,3,…}

Output: Blokdesign

Katalog >

Alfabetisk oversigt 11

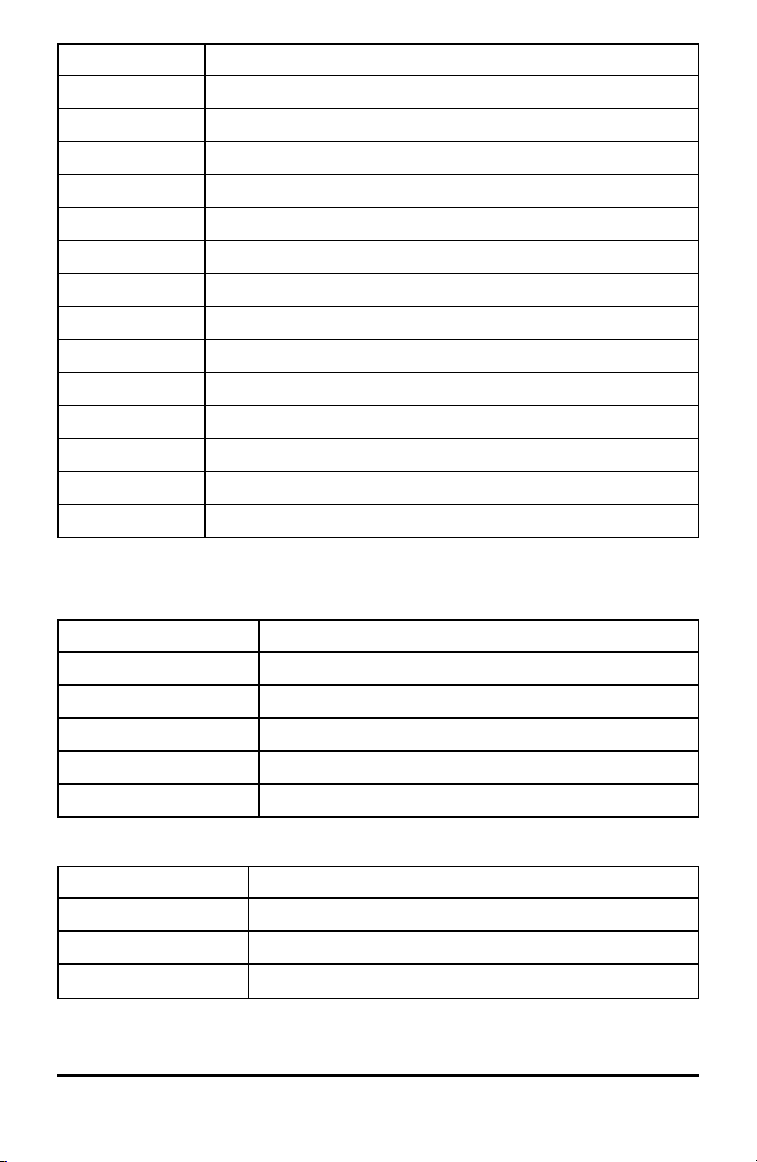
Output-variabel Beskrivelse

stat.F F statistik for kolonnefaktor

stat.PVal Mindstesignifikansniveau, ved hvilketnul-hypotesenkan forkastes

stat.df Frihedsgrader i kolonnefaktoren

stat.SS Kvadratsum for kolonnefaktoren

stat.MS Middelkvadratfor kolonnefaktoren

stat.FBlok F statistik for faktor

stat.PValBlock Mindstesandsynlighed, ved hvilken nul-hypotesen kan forkastes

stat.dfBlock Frihedsgrader for faktoren

stat.SSBlock Kvadratsumfor faktoren

stat.MSBlock Middelkvadratfor faktoren

stat.dfError Frihedsgrader for fejl

stat.SSError Kvadratsum for fejlene

stat.MSError Middelkvadratfor fejlene

stat.s Standardafvigelse for fejlen

KOLONNEFAKTOR Output

Output-variabel Beskrivelse

stat.Fcol F statistik for kolonnefaktor

stat.PValCol Sandsynlighedsværdifor kolonnefaktoren

stat.dfCol Frihedsgrader i kolonnefaktoren

stat.SSCol Kvadratsum for kolonnefaktoren

stat.MSCol Middelkvadratfor kolonnefaktoren

RÆKKEFAKTOR Output

Output-variabel Beskrivelse

stat.Frow F statistik for rækkefaktoren

stat.PValRow Sandsynlighedsværdifor rækkefaktoren

stat.dfRow Frihedsgrader for rækkefaktoren

12 A lfabetisk oversigt

Output-variabel Beskrivelse

stat.SSRow Kvadratsum for rækkefaktoren

stat.MSRow Kvadraternes middelværdifor rækkefaktoren

INTERAKTION-output

Output-variabel Beskrivelse

stat.FInteract F statistik for interaktionen

stat.PValInteract Sandsynlighedsværdi for interaktionen

stat.dfInteract Frihedsgrader for interaktionen

stat.SSInteract Kvadratsumfor interaktionen

stat.MSInteract Middelkvadratfor interaktionen

FEJL-output

Output-variabel Beskrivelse

stat.dfError Frihedsgrader for fejl

stat.SSError Kvadratsum for fejlene

stat.MSError Middelkvadratfor fejlene

s Standardafvigelse for fejlen

Ans

Ans⇒værdi

Returnerer resultatet af de sidst beregnede udtryk.

/v-tasten

Alfabetisk oversigt 13

approx()

approx(Udtr1)⇒udtryk

Returnerer beregningen af argumentet som et udtryk med decimale værdier, når det er muligt, uanset den aktuelle indstilling af

Autoellertilnærmet.

Dette svarer til at indtaste argumentet og trykke på /·.

approx(Liste1)⇒liste approx(Matrix1)⇒matrix

Returnerer en liste eller matrix, hvor hvert element er beregnet til en decimalværdi, hvor det er muligt.

Katalog >

4approxFraction()

Expr 4approxFraction([Tol])⇒udtryk List 4approxFraction([Tol])⇒liste Matrix 4approxFraction([Tol])⇒matrix

Returnere inputtet som en brøk mede en tolerance på Tol. Hvis Tol udelades, anvendes en tolerance på 5.E-14.

Bemærk: Du kan indsætte denne funktion

fra computerens tastatur ved at skrive

@>approxFraction(...).

approxRational()

approxRational(Udtryk[, Tol])⇒udtryk approxRational(Liste[, Tol])⇒liste approxRational(Matrix[, Tol])⇒matrix

Returnerer argumentet som en brøk med en tolerance på Tol. Hvis Tol udelades, anvendes en tolerance på 5.E-14.

Katalog >

14 A lfabetisk oversigt

arccos()

Se cos/(), side 32.

arccosh()

arccot()

arccoth()

arccsc()

arccsch()

arcLen()

arcLen(Udtr1,Var,Start,S) ⇒udtryk

Returnerer buelængden for Udtr1 fra Start til Slut med hensyn til variablen Var.

Buelængden beregnes som et integral, der forudsætter er funktionsdefinition.

arcLen(Liste1,Var,Start,Slut)⇒liste

Returnerer en liste med buelængder for hvert element i Liste1 fra Start til Slut med hensyn til Var.

Se cosh/(), side 34.

Se cot/(), side 35.

Se coth/(), side 36.

Se csc/(), side 38.

Se csch/(), side 39.

Katalog >

arcsec()

Se sec/(), side 162.

Alfabetisk oversigt 15

arcsech()

Se sech/(), side 163.

arcsin()

arcsinh()

arctan()

arctanh()

augment()

augment(Liste1, Liste2)⇒liste

Returnerer en ny liste, der er liste2 føjet til enden af Liste1.

augment(Matrix1, Matrix2)⇒matrix

Returnerer en ny matrix, der er Matrix2 føjet til Matrix1. Når tegnet “,” anvendes, skal matricerne have lige store rækkedimensioner, og Matrix2 føjes til

Matrix1 som nye kolonner. Ændrer ikke Matrix1 eller Matrix2.

Se sin/(), side 173.

Se sinh/(), side 174.

Se tan/(), side 188.

Se tanh/(), side 190.

Katalog >

16 A lfabetisk oversigt

avgRC()

avgRC(Udtryk1, Var [=Værdi] [, Trin])

⇒udtryk

avgRC(Udtryk1, Var [=Værdi] [, Liste1])

⇒liste

avgRC(Liste1, Var [=Værdi] [, Trin])

⇒liste

avgRC(Matrix1, Var [=Værdi] [, Trin])

⇒matrix

Returnerer den fremadrettede differenskvotient (gennemsnitlig ændringshastighed).

Udtr1 kan være et brugerdefineret

funktionsnavn (se Func).

Når Værdi er angivet, tilsidesætter den alle forudgående variabeltildelinger og alle nuværende “|” substitutioner for variablen.

Trin er trinværdien. Hvis Trin udelades, er

standardværdien 0.001.

Bemærk, at den lignende funktion

centralDiff() anvender den centrale

differenskvotient.

Katalog >

bal()

bal(NPmt,N,I,PV,[Pmt], [FV], [PpY], [CpY], [PmtAt], [afrundVærdi])⇒værdi

bal(NPmt,amortTabel)⇒værdi

Amortiseringsfunktion, der beregner saldo efter en angivet betaling.

N, I, PV, Pmt, FV, PpY, CpY og PmtAt er

beskrevet i tabellen over TVM-argumenter (side 201).

NPmt angiver betalingsnummeret,

hvorefter du vil have dataene beregnet.

Katalog >

Alfabetisk oversigt 17

bal()

N, I, PV, Pmt, FV, PpY, CpY og PmtAt er

beskrevet i tabellen over TVM-argumenter (side 201).

• Hvis du udelader Pmt, bliver den som standard Pmt=tvmPmt (N,I,PV,FV,PpY,CpY,PmtAt).

• Hvis du udelader FV, bliver den som standard FV=0.

• Standardværdierne for PpY, CpY og

PmtAt er de samme som for TVM-

funktionerne.

afrundVærdi angiver antallet af decimaler

til afrunding. Standardværdi=2.

bal(NPmt,amortTabel) beregner saldoen

efter betaling nummer NPmt, baseret på amortiseringstabel amortTabel.

amortTabel-argumentet skal være en

matrix i formen beskrevet under amortTbl(), side 8.

Bemærk: Se også GInt() og GPrn(), side 232.

Katalog >

4Base2

Heltal1 4Base2⇒heltal

Bemærk: Du kan indsætte denne operator

fra computerens tastatur ved at skrive

@>Base2.

Konverterer Heltal1 til et binært tal. Binære eller hexadecimale tal har altid henholdsvis 0b eller 0h som præfiks. Tallet nul, ikke bogstavet O, efterfulgt af b eller h.

0b binærtTal

0h hexadecimaltTal Et binært tal kan have op til 64 cifre. Et

hexadecimalt tal kan have op til 16.

Uden præfiks behandles Heltal1 som decimaltal (10-talssystem). Resultatet vises som binært uanset tilstanden for talsystem.

18 A lfabetisk oversigt

Katalog >

4Base2

Negative tal vises på “2-komplement” form. For eksempel:

N1vises som

0hFFFFFFFFFFFFFFFFi det hexadecimale talsystem 0b111...111 (641-taller)i det binære talsystem

N263vises som

0h8000000000000000i det hexadecimale talsystem 0b100...000 (63 nuller)i det binære talsystem

Hvis du indtaster et decimalt heltal, der ligger uden området for en 64-bit binær form med fortegn, anvendes en symmetrisk modulo-operation til at bringe værdien ind i det korrekte område. Undersøg følgende eksempler på værdier uden for området.

263bliver N263og vises som

0h8000000000000000på hexadecimal form 0b100...000 (63 nuller). På binær form bliver

Katalog >

264til 0 og vises som

0h0på hexadecimal form

0b0på binær form.

N263N 1 bliver 263N 1 og vises som

0h7FFFFFFFFFFFFFFFhexadecimal form 0b111...111 (641’s)på binær form

4Base10

Heltal1 4Base10⇒heltal

Bemærk: Du kan indsætte denne operator

fra computerens tastatur ved at skrive

@>Base10.

Katalog >

Alfabetisk oversigt 19

4Base10

Konverterer Heltal1 til et decimaltal (i titalssystemet).Binære eller hexadecimale indtastninger skal altid have hhv. 0b eller 0h som præfiks.

0b binærtTal

0h hexadecimaltTal

Tallet nul, ikke bogstavet O, efterfulgt af b eller h.

Et binært tal kan have op til 64 cifre. Et hexadecimalt tal kan have op til 16.

Uden præfiks behandles Heltal1 som decimaltal. Resultatet vises som decimaltal uanset tilstanden for talsystem.

Katalog >

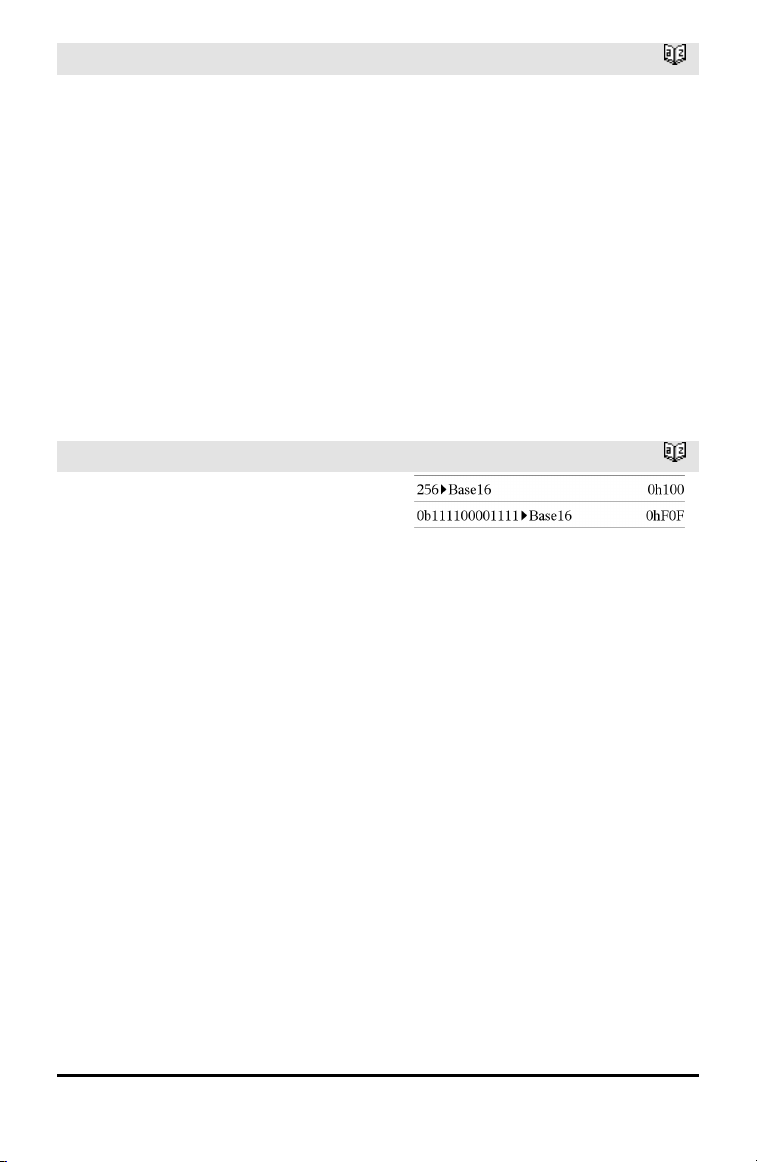
4Base16

Heltal1 4Base16⇒heltal

Bemærk: Du kan indsætte denne operator

fra computerens tastatur ved at skrive

@>Base16.

Konverterer Heltal1 til et hexadecimalt tal. Binære eller hexadecimale tal har altid henholdsvis 0b eller 0h som præfiks.

0b binærtTal

0h hexadecimaltTal

Tallet nul, ikke bogstavet O, efterfulgt af b eller h.

Et binært tal kan have op til 64 cifre. Et hexadecimalt tal kan have op til 16.

Uden præfiks behandles Heltal1 som decimaltal (10-talssystem). Resultatet vises som hexadecimalt uanset tilstanden for talsystem.

Hvis du indtaster et decimalt heltal, der er for stort til en 64-bit binær form med fortegn, anvendes en symmetrisk modulooperation til at bringe værdien ind i det korrekte område. Yderligere oplysninger findes under 4Base2, side 18.

Katalog >

20 A lfabetisk oversigt

binomCdf()

binomCdf(n,p)⇒liste

binomCdf(n,p,nedreGrænse,øvreGrænse)

⇒tal hvis nedreGrænse og øvreGrænse er tal, liste if nedreGrænse og øvreGrænse er lister

binomCdf(n,p,øvreGrænse)for P(0{X {øvreGrænse)⇒tal hvis øvreGrænse er et

tal, liste hvis øvreGrænse er en liste

Beregner den kumulerede sandsynlighed for den diskrete binomialfordeling med n antal forsøg og sandsynligheden p for succes ved hvert forsøg.

For P(X { øvreGrænse), sæt

nedreGrænse=0

Katalog >

binomPdf()

binomPdf(n,p)⇒liste binomPdf(n,p[,XVærdi])⇒tal hvis XVærdi

er et tal, liste hvis XVærdi er en liste

Beregner en sandsynlighed ved XVærdi for den diskrete binomialfordeling med n antal forsøg og sandsynligheden p for succes ved hvert forsøg.

ceiling()

ceiling(Udtr1)⇒heltal

Returnerer det nærmeste heltal, der er | argumentet.

Argumentet kan være et reelt eller komplekst tal.

Bemærk: Se også floor().

ceiling(Liste)⇒liste ceiling(Matrix1)⇒matrix

Katalog >

Alfabetisk oversigt 21

ceiling()

Returnerer en liste eller matrix med oprunding anvendt på hvert element.

Katalog >

centralDiff()

centralDiff(Udtr1,Var [=Værdi][,Trin])

⇒udtryk

centralDiff(Udtr1,Var [,Trin]) |Var=Værdi⇒udtryk

centralDiff(Udtr1,Var [=Værdi][,])⇒liste centralDiff(1,Var [=Værdi][,Trin])⇒liste

centralDiff(Matrix1,Var [=Værdi][,Trin])

⇒matrix

Returnerer den numeriske differentialkvotient udregnet med formlen for den centrale differenskvotient.

Når Værdi er angivet, tilsidesætter den alle forudgående variabeltildelinger og alle nuværende “|” substitutioner for variablen.

Trin er trinværdien. Hvis Trin udelades, er

standardværdien 0,001.

Ved anvendelse af Liste1 eller Matrix1 bliver operationen mappet på tværs af værdierne i listen eller på tværs af matrixelementerne.

Bemærk: Se også og d().

Katalog >

cFactor()

cFactor(Udtr1[,Var])⇒udtryk cFactor(Liste1[,Var])⇒liste cFactor(Matrix1[,Var])⇒matrix

cFactor(Udtr1) returnerer Udtr1 opløst i

faktorer med hensyn til alle dens variable over en fællesnævner.

22 A lfabetisk oversigt

Katalog >

cFactor()

Udtr1 opløses så meget som muligt i

faktorer af 1. grad, også selvom dette indfører nye ikke-relle tal. Denne mulighed er velegnet, hvis du ønsker opløsning i faktorer med hensyn til mere end en variabel.

cFactor(Udtr1,Var) returnerer Udtr1 opløst

i faktorer med hensyn til variablen Var.

Udtr1 opløses så meget som muligt i

faktorer mod faktorer af 1. grad i Var, med mulige ikke-reelle konstanter, også selvom det indfører irrationale konstanter eller deludtryk, der er irrationale i andre variable.

Faktorerne og deres led sorteres med Var som hovedvariabel. Ens potenser af var samles i hver faktor. Medtag Var, hvis opløsning i faktorer kun er nødvendig med hensyn til den pågældende variabel, og du er villig til at acceptere irrationale udtryk i alle andre variable for at øge opløsningen i faktorer med hensyn til Var. Der kan forekomme en uforudset faktoropløsning med hensyn til andre variable.

For automatisk indstilling af

Autoellertilnærmet-tilstanden tillader

medtagningen af Var også en approksimation med koefficienter med flydende decimal, hvor irrationale koefficienter ikke kan udrykkes eksplicit og koncist med de indbyggede funktioner. Også når der kun er en variabel, kan en medtagelse af Var give en mere komplet opløsning i faktorer.

Bemærk: Se også factor().

Katalog >

Dukan se heleresultatetved at trykke på £ og derefter bruge ¡ og ¢ tilat bevæge markøren.

char()

char(Heltal)⇒tegn

Returnerer en tegnstreng med tegnet nummereret Heltal fra grafregnerens tegnsæt. Det gyldige område for Heltal er 0–65535.

Katalog >

Alfabetisk oversigt 23

charPoly()

charPoly(kvadratMatrix,Var)

⇒polynomielt udtryk

charPoly(kvadratMatrix,Udtr)

⇒polynomielt udtryk charPoly(kvadratMatrix1,Matrix2)⇒

polynomium udtryk

Returnerer det karakteristiske polynomium af kvadratMatrix. Det karakteristiske polynomium af en n×n matrix A, betegnet ved pA(l), er polynomiet defineret ved

(l) = det(l• I NA)

hvor I betegner n×n identitetsmatrixen.

kvadratMatrix1 og kvadratMatrix2 skal

have de samme dimensioner.

Katalog >

2way

Katalog >

c22way obsMatrix

chi22way obsMatrix

Beregner en c2test til association på tovejstabellen med tællinger i den observerede matrix obsMatrix. En sammenfatning af resultaterne lagres i variablen stat.results. (side 182.)

Oplysninger om effekten af tomme elementer i en matrix findes “Tomme (ugyldige) elementer,” side 244.

Output-variabel Beskrivelse

stat.c

stat.PVal Mindstesignifikansniveau, ved hvilketnul-hypotesenkan forkastes

stat.df Frihedsgrader for Chi-kvadrat stat

stat.ExpMat Matrix medforventetelementtællingstabel, der antager nulhypotese

stat.CompMat Matrix med bidrag til chi-kvadratelementbidrag

Chi-kvadratstat: sum (observeret - forventet)2/forventet

24 A lfabetisk oversigt

Cdf()

Cdf(nedreGrænse,øvreGrænse,df)⇒tal

hvis nedreGrænse og øvreGrænse er tal,

liste hvis nedreGrænse og øvreGrænse er

lister

chi2Cdf(nedreGrænse,øvreGrænse,df)⇒tal

hvis nedreGrænse og øvreGrænse er tal,

liste hvis nedreGrænse og øvreGrænse er

lister

Beregn c2sandsynlighedsfordelingen mellem nedreGrænse og øvreGrænse for de angivne frihedsgrader df.

For P(X { øvreGrænse), sæt

nedreGrænse=0.

Oplysninger om effekten af tomme elementer i en liste findes “Tomme (ugyldige) elementer,” side 244.

Katalog >

GOF

Katalog >

c2GOF obsListe,forvListe,fg

chi2GOF obsListe,forvListe,fg

Udfører en test for at bekræfte, at måledataene er fra en population, der er i overensstemmelse med en angivet distribution. obsList er en liste med antal, og skal indeholde heltal. En sammenfatning af resultaterne lagres i stat.results variable. (side 182.)

Oplysninger om effekten af tomme elementer i en liste findes “Tomme (ugyldige) elementer,” side 244.

Output-variabel Beskrivelse

stat.c

stat.PVal Mindstesignifikansniveau, ved hvilketnul-hypotesenkan forkastes

stat.df Frihedsgrader for Chi-kvadrat stat

stat.CompList Bidrag til chi-kvadratelementbidrag

Chi-kvadratstat: sum((observeret- forventet)2/forventet

Alfabetisk oversigt 25

Pdf()

Pdf(XVal,df)⇒tal hvis XVal er et tal,

liste hvis XVal er en liste

chi2Pdf(XVal,df)⇒tal hvis XVal er et tal,

liste, hvis XVal er en liste

Beregner tæthedsfunktionen (pdf) for c

fordelingen ved en angivet XVal-værdi for den angivne frihedsgrad df.

Oplysninger om effekten af tomme elementer i en liste findes “Tomme (ugyldige) elementer,” side 244.

Katalog >

ClearAZ

Katalog >

ClearAZ

Sletter alle enkelttegnsvariable i det aktuelle opgaverum.

Hvis en eller flere af variablene er låst, viser denne kommando en fejlmeddelelse og sletter kun de ulåste variable. Se unLock, side 204.

ClrErr Katalog

ClrErr

Sletter fejlstatus og indstiller systemvariabel

Se eteksempel på ClrErr, i Eksempel2 under Tr y-kommandoen, side 197.

errCode til nul.

Else betingelsen i Try...Else...EndTry-blokken

bør anvende ClrErr eller PassErr. Brug ClrErr, hvis fejlen skal behandles eller ignoreres. Brug PassErr, hvis det ikke er kendt, hvad der skal gøres ved fejlen, for at sende den til den næste fejlhåndtering. Hvis der ikke er flere ventende Try...Else...EndTry-fejlhåndteringer, vises fejldialogboksen som normalt.

Bemærk: Se også PassErr, side 136, og Try,

side 197.

Bemærk indtastning af eksemplet: For

instruktioner til at indtaste programmer over flere linjer og definering af funktioner se Beregninger-afsnittet i din produktvejledning.

26 A lfabetisk oversigt

colAugment()

colAugment(Matrix1, Matrix2)⇒matrix

Returnerer en ny matrix, der er Matrix2 føjet til Matrix1. Matricerne skal have lige store kolonnedimensioner, og Matrix2 føjes til Matrix1 som nye rækker. Ændrer ikke

Matrix1 eller Matrix2.

Katalog >

colDim()

colDim(Matrix)⇒udtryk

Returnerer antallet af kolonner i Matrix.

Bemærk: Se også rowDim().

colNorm()

colNorm(Matrix)⇒udtryk

Returnerer maksimum for summerne af de absolutte værdier for elementerne i kolonnerne i Matrix.

Bemærk: Udefinerede matrixelementer er

ikke tilladt. Se også rowNorm().

comDenom()

comDenom(Udtr1[,Var])⇒udtryk comDenom(Liste1[,Var])⇒liste comDenom(Matrix1[,Var])⇒matrix

comDenom(Udtryk1) returnerer en forkortet

brøk af en fuldt udviklet tæller over en fuldt udviklet nævner.

Katalog >

Alfabetisk oversigt 27

comDenom()

comDenom(Udtr1,Var) returnerer en brøk

med fuldt udviklet tæller og nævner med hensyn til Var. Leddene og deres faktorer sorteres med Var som hovedvariabel. Ens potenser af Var samles. Der kan være tilfældige opløsninger i faktorer i de samlede koefficienter. Sammenlignet med at at udelade Var sparer dette ofte tid, hukommelse og skærmplads, samtidig med, at det gør udtrykket mere læseligt. Det gør også de efterfølgende operationer på resultatet hurtigere og giver mindre risiko for at fylde hukommelsen op.

Hvis Var ikke forekommer i Udtr1,

comDenom(Udtr1, returnerer Var) en brøk

med uudviklet tæller og nævner. Sådanne resultater sparer normalt endnu mere tid, hukommelse og skærmplads. Sådanne resultater, der er delvist opløst i faktorer, gør også de efterfølgende operationer på resultatet hurtigere og mindre tilbøjelige til at fylde hukommelsen op.

Selv hvis der ikke er en nævner, er comdenfunktionen ofte et hurtigt middel til en delvis faktoropløsning, hvis factor() er for langsom eller bruger hele hukommelsen.

Tip: Indsæt denne comden()-

funktionsdefinition og prøv den rutinemæssigt som et alternativ til

comDenom() og factor().

Katalog >

completeSquare ()

completeSquare(ExprOrEqn, Var)

⇒udtryk eller ligning

completeSquare(ExprOrEqn, Var^Power)

⇒udtryk eller ligning

completeSquare(ExprOrEqn, Var1, Var2

[,...])⇒udtryk eller ligning

completeSquare(ExprOrEqn, {Var1, Var2

[,...]})⇒udtryk eller ligning

28 A lfabetisk oversigt

Katalog >

completeSquare ()

Konverterer et kvadratisk, polynomielt udtryk af formen a·x2+b·x+c til formen a·(xh)2+k

— eller —

Konverterer en kvadratisk ligning af formen a·x2+b·x+c=d til formen a·(x-h)2=k

Det første argument skal være et kvadratisk udtryk eller en ligning på standardform med hensyn til det andet argument.

Det andet argument skal være en enkelt variabel eller en enkelt variabel opløftet til en rationel potens, f.eks. x,y2ellerz

Den tredje eller fjerde del af syntaksen forsøger at kvadratetkomplettere med hensyn til variable Var1, Var2 [,… ]).

(1/3)

Katalog >

conj()

conj(Udtr1)⇒udtryk conj(Liste1)⇒liste conj(Matrix1)⇒matrix

Returnerer kompleks konjugerede af argumentet.

Bemærk: Alle udefinerede variable

behandles som reelle variable.

constructMat()

constructMat (Udtr,Var1,Var2,antalRækker,antalKol)

⇒matrix

Returnerer en matrix baseret på argumenter.

Udtr er et udtryk i variablerne Var1 og Var2. Elementer i den resulterende matrix

er dannet ved beregning af Udtr for hver forøget værdi af Var1 og Var2.

Katalog >

Alfabetisk oversigt 29

constructMat()

Var1 er automatisk forøget fra 1 til antalRækker. Inden for hver række, Var2 er

forøget fra 1 til antalKol.

Katalog >

CopyVar

CopyVar Var1, Var2

CopyVar Var1., Var2.

CopyVar Var1, Var2 kopierer værdien af

variablen Var1 til variabelen Var2, og opretter Var2 hvis nødvendigt. Variablen

Var1 skal have en værdi

Hvis Var1 er navnet på en eksisterende brugerdefineret funktion, kopieres definitionen af denne funktion til funktionen

Var2. Funktionen Var1 skal defineres.

Var1 skal opfylde kravene til navngivning af

variable, eller være et indirekte udtryk, der kan reduceres til et variabelnavn, der opfylder betingelserne.

CopyVar Var1., Var2. kopierer alle

elementer af Var1. variabelgruppen til

Var2. gruppen, og opretter Var2. hvis

nødvendigt.

Var1. skal være navnet på en eksisterende

variabelgruppe, så som statistikken stat.nn resultater eller variable dannet ved brug af

LibShortcut()-funktionen. Hvis Var2.

allerede eksisterer, vil denne kommando udskifte alle elementer, der er fælles i begge grupper, og tilføje de elementer, som ikke allerede eksisterer. Hvis et eller flere elementer i Var2. er låst, efterlades alle elementer i Var2. uændret.

Katalog >

corrMat()

corrMat(Liste1,Liste2[,…[,Liste20]])

Beregner korrelationsmatricen for den udvidede matrix [Liste1 Liste2 . . . Liste20].

30 A lfabetisk oversigt

Katalog >

4cos

Udtr 4cos

Bemærk: Du kan indsætte denne operator

fra computerens tastatur ved at skrive

@>cos.

Repræsentrer Expr i termer af cosinus. Det er en konverteringsoperator for visning. Denne operator kan kun anvendes ved slutningen af indtastningslinjen.

4cos reducerer alle potenser af

sin(...) modulo 1Ncos(...)^2

således, at alle tilbageværende potenser af cos(...) har eksponenter i området (0, 2). Således vil resultatet være uden sin(...) hvis, og kun hvis sin(...) ku optræder i det givne udtryk med lige potenser.

Bemærk: Konverteringsoperatorer

understøttes ikke i vinkeltilstandene Grader eller Nygrader. Før brug skal man sikre at vinkeltilstanden er indstillet til radianer, og at Udtr ikke indeholder eksplicit reference til grader eller nygrader.

Katalog >

cos()

cos(Udtr1)⇒udtryk

cos(Liste1)⇒list

cos(Udtr1) returnerer cosinus af

argumentet som et udtryk.

cos(Liste1) returnerer en liste med cosinus

til alle elementer i Liste1.

Bemærk: Argumentet fortolkes som en

vinkel målt i grader, nygrader eller radianer afhængigt af den aktuelt indstillede vinkeltilstand. Du kan bruge ¡,Geller Rtil midlertidigt at ignorere vinkeltilstanden.

µ-tast

I vinkeltilstandenGrader:

I vinkeltilstandenNygrader:

I vinkeltilstandenRadian:

Alfabetisk oversigt 31

cos()

µ-tast

cos(kvadratMatrix1)⇒kvadratMatrix

Returnerer matrixcosinus af

kvadratMatrix1. Dette er ikke det samme

som at beregne cosinus for hvert element.

Når en skalær funktion f(A) opererer på

kvadratMatrix1 (A), beregnes resultatet

efter algoritmen:

Beregn egenværdierne (li) og egenvektorer (Vi) af A.

KvadratMatrix1 skal være diagonaliserbar.

Den må heller ikke have symbolske variable, der ikke er tildelt en værdi.

Dan matricerne:

Derefter A = X B X/og f(A) = X f(B) X/. For eksempel cos(A) = X cos(B) X/, hvor:

cos (B) =

I vinkeltilstandenRadian:

Alle beregninger udføres aritmetisk med flydende komma.

cos/()

cos/(Udtr1)⇒udtryk cos/(Liste1)⇒liste

32 A lfabetisk oversigt

µ-tast

I vinkeltilstandenGrader:

cos/()

µ-tast

cos/(Udtr1) returnerer den vinkel, hvis

cosinus er Udtr1 som et udtryk.

cos/(Liste1) returnerer en liste med de

inverse cosinusværdier for hvert element af

Liste1.

Bemærk: Resultatet returneres som en

vinkel i grader eller radianer afhængigt af den aktuelle vinkeltilstand.

Bemærk: Du kan indsætte denne funktion

fra computerens tastatur ved at skrive

arccos(...).

cos/(kvadratMatrix1)⇒kvadratMatrix

Returnerer den matrixinverse cosinus af

kvadratMatrix1. Dette er ikke det samme

som at beregne den inverse cosinus for hvert element. Oplysninger om beregningsmetoden findes i cos().

KvadratMatrix1 skal være diagonaliserbar.

Resultatet indeholder altid tal med flydende decimaler.

cosh()

cosh(Udtr1)⇒udtryk

I vinkeltilstandenNygrader:

I vinkeltilstandenRadian:

I vinkeltilstandenradianog rektangulært komplekstformat:

Dukan se heleresultatetved at trykke på £ og derefter bruge ¡ og ¢ tilat bevæge markøren.

Katalog >

I vinkeltilstandenGrader:

cosh(Liste1)⇒liste

cosh(Udtr1) returnerer den hyperbolske

cosinus af argumentet som et udtryk.

cosh(Liste1) returnerer en liste med

hyperbolsk cosinus for hvert element i

Liste1.

cosh(kvadratMatrix1)⇒kvadratMatrix

I vinkeltilstandenRadian:

Alfabetisk oversigt 33

cosh()

Returnerer matrix hyperbolsk cosinus af

kvadratMatrix1. Dette er ikke det samme

som at beregne den hyperbolske cosinus for hvert element. Oplysninger om beregningsmetoden findes i cos().

KvadratMatrix1 skal være diagonaliserbar.

Resultatet indeholder altid tal med flydende decimaler.

Katalog >

cosh/()

cosh/(Udtr1)⇒udtryk cosh/(Liste1)⇒liste

cosh/(Udtr1) returnerer den inverse

hyperbolske cosinus af argumentet som et udtryk.

cosh/(Liste1) returnerer en liste med de

inverse hyperbolske cosinusværdier for hvert element i Liste1.

Bemærk: Du kan indsætte denne funktion

fra computerens tastatur ved at skrive

arccosh(...).

cosh/(kvadratMatrix1)⇒kvadratMatrix

Returnerer den matrixinverse hyperbolske cosinus af kvadratMatrix1. Dette er ikke det samme som at beregne den inverse hyperbolske cosinus for hvert element. Oplysninger om beregningsmetoden findes i cos().

KvadratMatrix1 skal være diagonaliserbar.

Resultatet indeholder altid tal med flydende decimaler.

Katalog >

I vinkeltilstandenRadianog i rektangulært komplekstformat:

Dukan se heleresultatetved at trykke på £ og derefter bruge ¡ og ¢ tilat bevæge markøren.

cot()

cot(Udtr1) ⇒ udtryk

34 A lfabetisk oversigt

µ-tast

I vinkeltilstandenGrader:

cot()

cot(Liste1) ⇒ liste

Returnerer cotangens til Udtr1 eller returnerer en liste med cotangens til alle elementer i Liste1.

Bemærk: Argumentet fortolkes som en

vinkel målt i grader, nygrader eller radianer afhængigt af den aktuelt indstillede vinkeltilstand. Du kan bruge ¡,Geller Rtil midlertidigt at ignorere vinkeltilstanden.

µ-tast

I vinkeltilstandenNygrader:

I vinkeltilstandenRadian:

cot/()

cot/(Udtr1)⇒udtryk cot/(Liste1)⇒liste

Returnerer den vinkel, hvis cotangens er

Udtr1, eller returnerer en liste med den

inverse cotangens til hvert element i

Liste1.

Bemærk: Resultatet returneres som en

vinkel i grader eller radianer afhængigt af den aktuelle vinkeltilstand.

Bemærk: Du kan indsætte denne funktion

fra computerens tastatur ved at skrive

arccot(...).

coth()

coth(Udtr1)⇒udtryk coth(Liste1)⇒liste

Returnerer den hyperbolske cotangens til

Udtr1 eller returnerer en liste med den

hyperbolske cotangens til alle elementer i

Liste1.

µ-tast

I vinkeltilstandenGrader:

I vinkeltilstandenNygrader:

I vinkeltilstandenRadian:

Katalog >

Alfabetisk oversigt 35

coth/()

coth/(Udtr1)⇒udtryk coth/(Liste1)⇒liste

Returnerer den inverse hyperbolske cotangens til Udtr1 eller returnerer en liste med den inverse hyperbolske cotangens til alle elementer i Liste1.

Bemærk: Du kan indsætte denne funktion

fra computerens tastatur ved at skrive

arccoth(...).

Katalog >

count()

count(Værdi1ellerListe1

[,Værdi2ellerListe2 [,...]])⇒værdi

Returnerer det akkumulerede antal af alle elementer i argumenterne, der evalueres til numeriske værdier.

Hvert argument kan være et udtryk, en værdi, en liste eller en matrix. Du kan blande datatyper og anvende argumenter med forskellige dimensioner.

For lister, matricer eller celleområder evalueres hvert element for at bestemme, om det skal inkluderes i tællingen.

I applikationen Lister og regneark kan du anvende et celleområde i stedet for ethvert argument.

Tomme (ugyldige) elementer ignoreres. Yderligere oplysninger om tomme elementer findes på side 244.

countif()

countif(Liste,Kriterie)⇒værdi

Returnerer det akkumulerede antal af alle elementer i Liste, der opfylder de angivne

Kriterie.

Kriterie kan være:

• En værdi, et udtryk eller en streng. For

Katalog >

I detsidste eksempeltælles kun 1/2 og 3+4*i. De resterendeargumenter evalueres ikke til numeriske værdier, hvis det antages at x er udefineret.

Katalog >

Tæller antalletaf elementer lig med 3.

Tæller antalletaf elementer lig med “def.”

36 A lfabetisk oversigt

countif()

eksempel tæller 3 kun de elementer i

Liste, der reduceres til værdien 3.

• Et Boolsk udtryk, der indeholder symbolet ? som pladsholder for hvert element. For eksempel ?<5 tæller kun de elementer i Liste, der er mindre end 5.

I applikationen Lister og regneark kan du anvende et celleområde i stedet for Liste.

Tomme (ugyldige) elementer i listen ignoreres. Yderligere oplysninger om tomme elementer findes på side 244.

Bemærk: Se også sumIf() , side 186, og frequency() , side 78.

Katalog >

Tæller antalletaf elementer lig med x; dette eksempel antager, at variablen x er udefineret.

Tæller 1 og 3.

Tæller 3, 5 og 7.

Tæller 1, 3, 7 og 9.

cPolyRoots()

cPolyRoots(Poly,Var)⇒liste cPolyRoots(ListeAfKoeff)⇒liste

Den første syntaks, cPolyRoots(Poly,Var), returnerer en liste med komplekse rødder af polynomiet Poly med hensyn til variablen Var.

Poly skal være et polynomium i en variabel.

Den anden syntaks, cPolyRoots(OfCoeffs), returnerer en liste med komplekse rødder for koefficienterne i ListeAfKoeff.

Bemærk: Se også polyRoots(), side 141.

Katalog >

Alfabetisk oversigt 37

crossP()

crossP(Liste1, Liste2)⇒liste

Returnerer vektorproduktet af Liste1 og

liste2 som en liste.

Liste1 og Liste2 skal have ens dimension,

og dimensionen skal være 2 eller 3.

crossP(Vektor1, Vektor2)⇒vektor

Returnerer en række eller kolonnevektor (afhængigt af argumenterne), der er vektorproduktet af Vektor1 og Vektor2.

Både Vektor1 og Vektor2 skal være rækkevektorer, eller begge skal være kolonnevektorer. Begge vektorer skal have ens dimension, og dimensionen skal være enten 2eller3.

Katalog >

csc()

csc(Udtr1)⇒udtryk csc(Liste1)⇒liste

Returnerer cosecansen til Udtr1 eller returnerer en liste med cosecansen til alle elementer i Liste1.

csc/()

csc/(Udtr1) ⇒ udtryk csc/(Liste1) ⇒ liste

Returnerer den vinkel, hvis cosecans er

Udtr1, eller returnerer en liste med den

inverse cosecans til de enkelte elementer på Liste1.

µ-tast

I vinkeltilstandenGrader:

I vinkeltilstandenNygrader:

I vinkeltilstandenRadian:

µ-tast

I vinkeltilstandenGrader:

I vinkeltilstandenNygrader:

38 A lfabetisk oversigt

csc/()

Bemærk: Resultatet returneres som en

vinkel i nygrader eller radianer afhængigt af den aktuelle vinkeltilstand.

Bemærk: Du kan indsætte denne funktion

fra computerens tastatur ved at skrive

arccsc(...).

µ-tast

I vinkeltilstandenRadian:

csch()

csch(Udtr1) ⇒ udtryk csch(Liste1) ⇒ liste

Returnerer den hyperbolske cosecans til

Udtr1 eller returnerer en liste med den

hyberbolske cosecans til alle elementer i

Liste1.

csch/()

csch/(Udtr1) ⇒ udtryk csch/(Liste1) ⇒ liste

Returnerer den hyperbolske cosecans til

Udtr1 eller returnerer en liste med den

inverse hyperbolske cosecans til hvert element i Liste1.

Bemærk: Du kan indsætte denne funktion

fra computerens tastatur ved at skrive

arccsch(...).

cSolve()

cSolve(Ligning, Var)⇒Boolsk udtryk

Katalog >

cSolve(Ligning, Var=Gæt)⇒Boolesk

udtryk

cSolve(Ulighed, Var)⇒Boolsk udtryk

Alfabetisk oversigt 39

cSolve()

Returnerer komplekse løsninger til en ligning eller ulighed for Var. Målet er at finde alle reelle og ikke-reelle løsninger. Også selvom Ligning er reel, tillader cSolve

() ikke-reelle resultater i den reelle tilstand.

Selvom alle udefinerede variable, der ikke ender med en understregning (_) behandles, som reelle, kan cSolve() løse polynomielle ligninger for komplekse løsninger.

cSolve() indstiller midlertidigt til det

komplekse domæne under løsningen, også selvom det aktuelle domæne er det reelle. I det komplekse domæne anvender brøkpotenser med ulige nævnere hovedområdet i stedet for det reelle område. Som følge heraf er løsninger fra

solve() af ligninger med sådanne

brøkpotenser ikke nødvendigvis en delmængde af løsningerne fra cSolve().

cSolve() starter med eksakte symbolske

metoder. Med undtagelse af Eksakt tilstand anvender cSolve() om nødvendigt også en iterativ tilnærmet kompleks polynnomiel faktoropløsning.

Bemærk: Se også cZeros(), solve(), og zeros ().

Bemærk: Hvis Ligning er ikke-polynomiel

med funktioner som abs(), angle(), conj(),

real() eller imag(), skal du placere en

understregning (tryk på /_) ved enden af var. Som standard behandles en variabel som en reel værdi.

Hvis du anvender var_, behandles variablen som kompleks.

Du bør også anvende var_ til andre variable i Ligning, der kan indeholde ikke-reelle værdier. Ellers kan du få utilsigtede resultater.

cSolve(Eqn1and Eqn2 [and…],

Katalog >

I Vis cifre-tilstandfor Fast 2:

Dukan se heleresultatetved at trykke på £ og derefter bruge ¡ og ¢ tilat bevæge markøren.

VarEllerGæt1, VarEllerGæt2 [, … ])

40 A lfabetisk oversigt

cSolve()

⇒Booleskudtryk

cSolve(SystemAfLign, VarEllerGæt1,

VarEllerGæt2 [, …]) ⇒Booleskudtryk

Returnerer mulige komplekse løsninger til de sammenhørende algebraiske ligninger, hvor hvertvarEllerGæt angiver en variabel, du vil løse for.

Du kan også vælge at angive et initielt gæt til en variabel. Hvert varEllerGæt skal have formen:

variabel

– eller –

variabel = reelt eller ikke-reelt tal

For eksempel er x gyldig, og det er x=3+iogså.

Hvis alle ligningerne er polynomier, og hvis du IKKE angiver nogle initielle gæt, benytter

cSolve() den leksikale Gröbner/Buchberger

eliminationsmetode som forsøg på at bestemme alle komplekse løsninger.

Komplekse løsninger kan omfatte både reelle og ikke-reelle løsninger som i eksemplet til højre.

Katalog >

Bemærk: I de følgendeeksempler anvendes

enunderstregning (tryk på /_) så variablene kan behandles som komplekse.

Sammenhørende polynomielle ligninger kan have ekstra variable, der ikke har nogen værdier men repræsenterer givne numeriske værdier, der kan substitueres efterfølgende.

Dukan se heleresultatetved at trykke på £ og derefter bruge ¡ og ¢ tilat bevæge markøren.

Alfabetisk oversigt 41

cSolve()

Du kan også medtage løsningsvariable, der ikke optræder i ligningerne. Disse løsninger viser, hvordan løsningsfamilier kan indeholde arbitrære konstanter af formen

ck, hvor k er et heltalssuffix fra 1 til og med

255.

For polynomielle systemer afhænger beregningstiden eller hukommelsesforbrug stærkt af den rækkefølge løsningsvariablene angives i. Hvis det initielle valg kræver for meget hukommelse eller tålmodighed, skal du prøve at omarrangere variablene i ligningerne og/eller varEllerGæt listen.

Hvis du ikke medtager nogen gæt, og hvis en ligning er ikke-polynomiel i en variabel, men alle ligninger er lineære i alle løsningsvariable, anvender cSolve() en Gauss-eliminering i et forsøg på at bestemme alle løsninger.

Hvis et system hverken er polynomielt i alle variable eller lineært i sine løsningsvariable, bestemmer cSolve() højst en løsning med en iterativ approksimationsmetode. Dette gøres ved at lade antallet af løsningsvariable være lig med antallet af ligninger og reducere alle andre variable i ligningerne til tal.

Et ikke-reelt gæt er ofte nødvendigt for at bestemme en ikke-reel løsning. For at opnå konvergens skal et gæt være meget tæt på en løsning.

Katalog >

Dukan se heleresultatetved at trykke på £ og derefter bruge ¡ og ¢ tilat bevæge markøren.

CubicReg

CubicReg X, Y[, [Frekv] [, Kategori,

Medtag]]

Beregner polynomiel tredjegradsregression y = a·x3+b· x2+c·x+dpå listerne X og Y med frekvens Frekv. En sammenfatning af resultaterne lagres i stat.resultat variable. (side 182.)

42 A lfabetisk oversigt

Katalog >

CubicReg

Alle lister skal have samme dimension med undtagelse af Medtag.

X og Y er lister med uafhængige og

afhængige variable.

Frekv er en valgfri liste med hyppigheder.

Hvert element i Frekv angiver hyppigheden af hvert tilsvarende X og Y datapunkt. Standardværdien er 1. Alle elementer skal være heltal | 0.

Kategory er en liste, der indeholder

kategorikoder for X og Y data.

Medtag er en liste med en eller flere af

kategorikoderne. Kun de dataelementer hvis kategorikode er medtaget i denne liste, er medtaget i beregningen.

Oplysninger om effekten af tomme elementer i en liste findes “Tomme (ugyldige) elementer,” side 244.

Katalog >

Outputvariabel

stat.RegEqn Regressionsligning: a·x3+b·x2+c·x+d

stat.a, stat.b, stat.c, stat.d

stat.r

stat.Resid Residualer fra regressionen

stat.XReg

stat.YReg

stat.FreqReg

Beskrivelse

Regressionskoefficienter

Forklaringsgraden

Liste af datapunkter i denmodificeredeX-liste, der faktisk brugesi regressionenud fra begrænsninger af Hyppighed, Kategoriliste, og Medtag kategorier

Liste af datapunkter i denmodificeredeY-liste, der faktisk bruges i regressionenud fra begrænsninger af Hyppighed, Kategoriliste, og Medtag kategorier

Liste med hyppigheder, der svarer til stat.XReg og stat.YReg

cumulativeSum()

cumulativeSum(Liste1)⇒liste

Returnerer en liste med de kumulerede summer af elementerne i Liste1, startende ved element1.

Katalog >

Alfabetisk oversigt 43

cumulativeSum()

cumulativeSum(Matrix1)⇒matrix

Returnerer en matrix af de kumulerede summer af elementerne i Matrix1. Hvert element er den kumulerede sum af kolonnen fra top til bund.

Et tomt (ugyldigt) element i Liste1 eller

Matrix1 giver et ugyldigt element i den

resulterende liste eller matrix. Yderligere oplysninger om tomme elementer findes på side 244.

Katalog >

Cycle

Cyklus

Overfører kontrol direkte til næste iteration i den aktuelle løkke (For, While eller Loop).

Cycle må ikke ikke benyttes uden for (For, While eller Loop).

Bemærk indtastning af eksemplet: For

instruktioner til at indtaste programmer over flere linjer og definering af funktioner se Beregninger-afsnittet i din produktvejledning.

4Cylind

Vektor 4Cylind

Bemærk: Du kan indsætte denne operator

fra computerens tastatur ved at skrive

@>Cylind.

Viser række- eller kolonnevektoren i cylindrisk form [r±q, z].

Vektor skal have nøjagtig tre elementer.

Det kan være en række eller en kolonne.

Katalog >

Funktionsliste, der adderer heltallenefra 1 til 100og udelader 50.

Katalog >

cZeros()

cZeros(Udtr, Var)⇒liste

44 A lfabetisk oversigt

Katalog >

I Vis cifre-tilstandmedFast 3:

cZeros()

Returnerer en liste med mulige reelle og ikke-reelle værdier for Var som løser

Udtr=0. cZeros() gør dette ved at beregne

exp4liste(cSolve(Udtr=0,Var),Var). Ellers

ligner cZeros() zeros().

Bemærk: Se også cSolve(), solve() og zeros ().

Bemærk: Hvis Udtr er ikke-polynomiel med

funktioner som abs(), angle(), conj(), real() , eller imag(), skal du sætte en

understregning (tryk på /_) i enden af

var. Som standard behandles en variabel

som en reel værdi. Hvis du anvender var_, behandles variablen som kompleks.

Du bør også anvende Var_ til andre variable i udtryk, der kunne have ikke-reelle værdier. Ellers kan du få utilsigtede resultater.

cZeros({Udtr1, Udtr2 [, … ] }, {varEllerGæt1,varEllerGæt2 [, … ] })

⇒matrix

Returnerer mulige positioner, hvor udtrykkene samtidigt er nul. Hver

varEllerGæt angiver en ubekendt, hvis

værdi du søger. Du kan også vælge at angive et initielt gæt

til en variabel. Hvert varEllerGæt skal have formen:

variabel

– eller –

variabel = reelt eller ikke-reelt tal

For eksempel er x gyldig, og det er x=3+iogså.

Hvis alle ligningerne er polynomier, og hvis du IKKE angiver nogle initielle gæt, benytter

cZeros() den leksikale Gröbner/Buchberger

eliminationsmetode som forsøg på at bestemme alle komplekse nulpunkter.

Katalog >

Dukan se heleresultatetved at trykke på £ og derefter bruge ¡ og ¢ tilat bevæge markøren.

Bemærk: I de følgendeeksempler anvendes

enunderstregning _ (tryk på /_) så variablene kan behandles som komplekse.

Alfabetisk oversigt 45

cZeros()

Komplekse nulpunkter kan omfatte både reelle og ikke-reelle nulpunkter som i eksemplet til højre.

Hver række i den resulterende matrix repræsenterer et nulpunkt med komponenterne arrangeret på samme måde som varEllerGæt-listen. Du kan udtrække en række og indeksere matricen efter [række].

Sammenhørende polynomier kan have ekstra variable, der ikke har nogen værdier men repræsenterer givne numeriske værdier, der kan substitueres efterfølgende.

Du kan også medtage ubekendte variable, der ikke optræder i udtrykkene. Disse nulpunkter viser, hvordan nulpunktsfamilier kan indeholde arbitrære konstanter af formen ck, hvor k er et heltalssuffiks fra 1 til og med 255.

For polynomielle systemer afhænger beregningstiden eller hukommelsesforbruget stærkt af den rækkefølge, de ubekendte angives i. Hvis det initielle valg kræver for meget hukommelse eller tålmodighed, skal du prøve at omarrangere variablene i udtrykkene og/eller varEllerGæt listen.

Hvis du ikke medtager nogen gæt, og hvis en ligning er ikke-polynomiel i en variabel, men alle udtryk er lineære i alle ubekendte, anvender cZeros() en Gauss-eliminering i et forsøg på at bestemme alle nulpunkter.

Katalog >

Udtræk række 2:

46 A lfabetisk oversigt

cZeros()

Hvis et system hverken er polynomielt i alle variable eller lineært i sine ubekendte, bestemmer cZeros() højst et nulpunkt med en iterativ approksimationsmetode. Dette gøres ved at lade antallet af ubekendte være lig med antallet af udtryk og forkorte alle andre variable i udtrykkene til tal.

Et ikke-reelt gæt er ofte nødvendigt for at bestemme ikke-reelle nulpunkter. For at opnå konvergens skal et gæt være meget tæt på et nulpunkt.

Katalog >

dbd()

dbd(dato1,dato2)⇒værdi

Returnerer antallet af dage mellem dato1 og dato2 med tælling af faktiske dage.

dato1 og dato2 kan være tal eller lister med

tal inden for området af datoer i en standardkalender. Hvis både dato1 og dato2 er lister, skal de have samme længde.

dato1 og dato2 skal ligge mellem årene

1950 til 2049.

Du kan indtaste datoerne i to formater. Placeringen af decimaler er forskellen mellem datoformaterne.

MM.DDÅÅ (almindeligt format i USA)

DDMM.ÅÅ (almindeligt format i Europa)

4DD

Tal 4DD⇒værdi Liste1 4DD⇒liste Matrix1 4DD⇒matrix

Bemærk: Du kan indsætte denne operator

fra computerens tastatur ved at skrive

@>DD.

Katalog >

I vinkeltilstandenGrader:

Alfabetisk oversigt 47

4DD

Returnerer den decimale ækvivalent til argumentet udtrykt i grader. Argumentet er et tal, en liste eller matrix, som efter den indstillede tilstand af Vinkel tolkes i grader, nygrader eller radianer.

Katalog >

I vinkeltilstandenNygrader:

I vinkeltilstandenRadian:

4Decimal

Udtr1 4Decimal⇒udtryk Liste1 4Decimal⇒udtryk Matrix1 4Decimal⇒udtryk

Bemærk: Du kan indsætte denne operator

fra computerens tastatur ved at skrive

@>Decimal.

Viser argumentet i decimal form. Denne operator kan kun anvendes ved slutningen af indtastningslinjen.

Define

Define Var = Udtryk

Define Funktion(Param1, Param2, ...) =

Udtryk

Definerer variablen Var eller den brugerdefinerede funktion Funktion.

Parametre som Param1 er pladsholdere til at sætte argumenter ind i funktionen. Ved kald af en brugerdefineret funktion skal du angive argumenter (for eksempel værdier eller variable), der svarer til parametrene. Når den kaldes, evaluerer funktionen

Udtryk med de angivne argumenter.

Var og Funktion kan ikke være navnet på

en systemvariabel eller en integreret funktion eller kommando.

Katalog >

48 A lfabetisk oversigt

Define

Bemærk: Denne form for Define svarer til at

eksekvere udtrykket: udtryk & Funktion (Param1,Param2).

Define Funktion(Param1, Param2, ...) = Func

Blok

EndFunc

Define Program(Param1, Param2, ...) = Prgm

Blok

EndPrgm

I denne form kan den brugerdefinerede funktion eller programmet eksekvere en blok med flere sætninger.

Blok kan en være en enkelt sætning eller en

række sætninger på separate linjer. Blok kan også rumme udtryk og kommandoer (som f.eks. If, Then, Else og For).

Bemærk indtastning af eksemplet: For

instruktioner til at indtaste programmer over flere linjer og definering af funktioner se Beregninger-afsnittet i din produktvejledning.

Bemærk: Se også Define LibPriv, side 49 og Define LibPub, side 50.

Katalog >

Define LibPriv

Define LibPriv Var = Udtryk

Define LibPriv Funktion(Param1, Param2, ...) = Udtryk

Define LibPriv Funktion(Param1, Param2, ...) = Func

Blok

EndFunc

Define LibPriv Program(Param1, Param2, ...) = Prgm

Blok

EndPrgm

Katalog >

Alfabetisk oversigt 49

Define LibPriv

Fungerer på samme måde som Define med den undtagelse, at den definerer en privat biblioteksvariabel, funktion, eller et program. Private funktioner og programmer optræder ikke i Katalog.

Bemærk: Se også Define, side 48, og Define LibPub, side 50.

Katalog >

Define LibPub

Define LibPub Var = Udtryk

Define LibPub Funktion(Param1, Param2, ...) = Udtryk

Define LibPub Funktion(Param1, Param2, ...) = Func

Blok

EndFunc

Define LibPub Program(Param1, Param2, ...) = Prgm

Blok

EndPrgm

Fungerer på samme måde som Define med den undtagelse, at den definerer en offentlig biblioteksvariabel, funktion, eller et program. Offentlige funktioner og programmer optræder i Katalog, når biblioteket er gemt eller opdateret.

Bemærk: Se også Define, side 48 og Define LibPriv, side 49.

deltaList()

Katalog >

Se @List(), side 107.

deltaTmpCnv()

50 A lfabetisk oversigt

Se @tmpCnv(), side 195.

DelVar

DelVar Var1[, Var2] [, Var3] ...

DelVar Var.

Sletter de angivne variable, eller variabelgruppe fra hukommelse.

Hvis en eller flere af variablene er låst, viser denne kommando en fejlmeddelelse og sletter kun de ulåste variable. Se unLock, side 204

DelVar Var. sletter alle elementer i Var.

variabelgruppe(så som statistikken stat.nn resultater, eller variable dannet ved brug af

LibShortcut()-funktionen). Punktummet (.) i

denne form af DelVar -kommandoen begrænser den til at slette en variabelgruppe: den simple variabel Var berøres ikke.

Katalog >

delVoid()

delVoid(Liste1)⇒liste

Returnerer en liste med indholdet i Liste1 med alle tomme (ugyldige) elementer fjernet.

Yderligere oplysninger om tomme elementer findes på side 244.

derivative()

Catalog >

Se d(), side 228.

Alfabetisk oversigt 51

deSolve()

deSolve(1.Eller2.OrdenODE, Var, afhVar)

⇒en generel løsning

Returnerer en ligning, der eksplicit eller implicit angiver en generel løsning til en 1. eller anden ordens ordinær differentialligning (ODE). IODE'en:

• Anvend et mærketegn (tryk på º) for at betegne differentialkvotienten af første

orden af den afhængige variabel med hensyn til den uafhængige variable

• Anvend to mærketegn for at betegne den tilsvarende anden afledede.

Mærketegnet ' anvendes kun til differentialkvotienter i deSolve(). Iandre tilfælde anvendesd().

Den generelle løsning til en 1. grads ligning indeholder en arbitrær konstant af formen

ck, hvor k er et heltalssuffiks fra 1 til og med

255. Løsningen af en 2. ordens differentialligning indeholder to af disse konstanter.

solve() anvendes på en implicit løsning, hvis

du vil prøve at omregne den til en eller flere ækvivalente eksplicitte løsninger.

Ved sammenligning af dine resultater med tekstbogen eller manuelt frembragte løsninger skal du være opmærksom på, at forskellige metoder indfører arbitrære konstanter på forskellige steder i beregningen, hvilket kan frembringe forskellige generelle løsninger.

deSolve(1.OrdenODEandstartBeting, Var,

afhVar) ⇒en partikulær løsning

Returnerer en partikulær løsning, som opfylder 1.OrdenODE og startBeting. Dette er normalt nemmere end at bestemme en generel løsning, substituere startværdier, løse for den arbitrære konstant og derefter substituere denne værdi ind i den generelle løsning.

startBeting er en ligning på formen:

Katalog >

52 A lfabetisk oversigt

deSolve()

afhVar (uafhængigStartværdi) = afhængigStartværdi

uafhængigStartværdiog afhængigStartværdi kan være variable som

f.eks. x0 og y0, der ikke har nogen lagrede værdier. Implicit differentiation kan hjælpe med at verificere implicitte løsninger.

deSolve (

2.OrdensODE

andstartBeting1andstartBeting2, Var,

depVa)⇒ en partikulær løsning

Returnerer en partikulær løsning, der opfylder 2. ordens ODE og har en angivet værdi for den afhængige variable og dens første afledede i et punkt.

For startBeting1, brug formen:

depVar (uafhængigStartværdi) = afhængigStartværdi

For startBeting2, brug formen:

afhVar (uafhængigStartværdi) = start

1.afledede

deSolve (

2.OrdensODE

andbegrBeting1andbegrBeting2, Var,

depVar)⇒ en partikulær løsning

Returnerer en partikulær løsning, der opfylder 2. ordens ODE og har angivne værdier i to forskellige punkter.

Katalog >

Alfabetisk oversigt 53

det()

det(kvadratMatrix[, Tolerance])⇒udtryk

Returnerer determinanten af

kvadratMatrix.

Ethvert matrixelement kan valgfrit behandles som nul, hvis den absolutte værdi er mindre end Tolerance. Denne tolerance anvendes kun, hvis matricen har elementer med flydende decimaler og ikke indeholder symbolske variable, der ikke er tildelt en værdi. Ellers, Tolerance ignoreres.

• Hvis du anvender /· eller indstiller Autoellertilnærmet -tilstanden

til Approximate, foretages beregningerne med aritmetik med flydende komma.

• Hvis Tolerance udelades eller ikke anvendes, beregnes standardtolerancen som:

5EM14 ·max(dim(kvadratMatrix))?

rowNorm(kvadratMatrix)

Katalog >

diag()

diag(List)⇒matrix diag(rækkeMatrix)⇒matrix diag(kolonneMatrix)⇒matrix

Returnerer en matrix med værdierne i argumentlisten eller matricen i hoveddiagonalen.

diag(kvadratMatrix)⇒rækkeMatrix

Returnerer en rækkematrix, der indeholder elementerne fra hoveddiagonalen i

kvadratMatrix.

kvadratMatrix skal være kvadratisk.

dim()

dim(Liste)⇒heltal

54 A lfabetisk oversigt

Katalog >

dim()

Returnerer dimensionen af liste.

dim(matrix)⇒liste

Returnerer dimensionerne af matricen som en liste med to elementer {rækker, kolonner}.

dim(Streng)⇒heltal

Returnerer det antal tegn, der er indeholdt i tegnstrengen Streng.

Katalog >

Disp

Disp udtrykEllerStreng1 [,

udtrykEllerStreng2] ...

Viser argumenterne i Calculator historikken. Argumenterne vises efter hinanden med små mellemrum som separator.

Anvendes hovedsagelig i programmer og funktioner til at sikre at mellemregninger vises.

Bemærk indtastning af eksemplet: For

instruktioner til at indtaste programmer over flere linjer og definering af funktioner se Beregninger-afsnittet i din produktvejledning.

DispAt

DispAt int,expr1 [,expr2 ...] ...

DispAt tillader dig at angive den linje,

hvor det specificerede udtryk eller streng vil blive vist på skærmen.

Linjeantallet kan angives som et udtryk.

Vær opmærksom på, at linjenummeret ikke gælder hele skærmen, men for området umiddelbart efter kommando/program.

Katalog >

Eksempel

Alfabetisk oversigt 55

DispAt

Denne kommando tillader dashboardlignende output fra programmer, hvor værdien af et udtryk eller fra en sensoraflæsning bliver opdateret på den samme linje.

DispAtog Disp kan bruges indenfor det

samme program.

Bemærk: Det maksimale antal er sat til

8, idet det passer til en hel skærm af linjer på den håndholdte skærm sålænge linjerne ikke har 2Dmatematiske udtryk. Det præcise antal linjer afhænger af indholdet af den viste information.

Konkrete eksempler:

Define z()= Prgm For n,1,3 DispAt 1,"N:

",n Disp "Hallo" EndFor EndPrgm

Katalog >

Output z()

Iteration 1:

Linje 1: N:1

Linje 2: Hallo

Iteration 2:

Linje 1: N:2 Linje 2: Hallo Linje 3: Hallo

56 A lfabetisk oversigt

Define z1()= Prgm For n,1,3 DispAt 1,"N:

",n EndFor

For n,1,4 Disp "Hallo"

Iteration 3:

Linje 1: N:3 Linje 2: Hallo Linje 3: Hallo Linje 4: Hallo

z1()

Linje 1: N:3 Linje 2: Hallo Linje 3: Hallo Linje 4: Hallo Linje 5: Hallo

DispAt

EndFor EndPrgm

Fejlbetingelser:

Fejlmeddelelse Beskrivelse

DispAt linjeantal skal være mellem 1 og 8 Udtryk evaluerer linjeantallet udenfor

For få argumenter Funktionen eller kommandoen mangler

Ingen argumenter Samme som aktuel syntaksfejl-dialog For mange argumenter Begræns argument. Samme fejl som Disp. Ugyldig datatype Første argument skal være et tal. Ugyldig: DispAt ugyldig "Hallo verden" datatypefejl er fundet

Konverteringsoperator: DispAt 2_ft @> _m, "Hallo verden"

rækken 1-8 (inklusive)

et eller flere argumenter.

ugyldig (hvis tilbagekald er defineret) CAS: Datatypefejl er fundet ugyldig (hvis

tilbagekald er defineret) Numerisk: Konverteringen vil blive

evalueret, og hvis resultatet er et gyldigt argument, vil DispAt printe strengen på resultatlinjen.

Katalog >

4DMS

Udtr 4DMS

List 4DMS

Matrix 4DMS

Bemærk: Du kan indsætte denne operator

fra computerens tastatur ved at skrive

@>DMS.

Tolker argumentet som en vinkel og viser tilsvarende tal for grader (D), minutter (M) og sekunder (S/s) (DDDDDD¡MM'SS.ss''). Se mere om DMS-formatet for grader, minutter og sekunder ¡, ', '' på side 236.

Katalog >

I vinkeltilstandenGrader:

Alfabetisk oversigt 57

4DMS

Bemærk: 4DMS konverterer fra radianer til

grader ved anvendelse i radiantilstanden. Hvis inputtet følges af et grader-symbol ¡, sker der ingen konvertering. Du kan kun anvende 4DMS ved slutningen af en indtastningslinje.

Katalog >

domain()

domain(udtryk1, Var)⇒udtryk

Beregner definitionsmængden forudtryk1 med hensyn til Var.

domain() kan bruges til at undersøge

definitionsmængden for funktioner. Den er begrænset til de reelle tal og til et endeligt antal intervaller.

Denne funktionalitet har begrænsninger pga. mangler i computeralgebraens reduktions- og ligningsløsningsalgoritmer.

Visse funktioner kan ikke bruges som argumenter for domain(), hvad enten de forekommer eksplicit eller inden for brugerdefinerede variable og funktioner. I det følgende eksempel kan udtrykket ikke reduceres, fordi ‰() ikke er en tilladt funktion.

Katalog >

58 A lfabetisk oversigt

dominantTerm()

dominantTerm(Udtr1, Var [, Punkt])

⇒udtryk

dominantTerm(Udtr1, Var [, Punkt]) |

Var>Punkt⇒ udtryk

dominantTerm(Udtr1, Var [, Punkt])

Var<Punkt ⇒udtryk

Returnerer det dominerende led i potensrækkeudviklingen af Udtr1 udviklet omkringPunkt. Det dominerende led er det led, hvis der vokser hurtigst nær Var =

Punkt. Den resulterende potens af (Var N Punkt) kan have en negativ og/eller

brøkeksponent. Koefficienten af denne potens kan indeholde logaritmer af (Var N

Punkt) og andre funktioner af Var, der

domineres af alle potenser af (Var N

Punkt) med samme eksponentfortegn.

Punkt er som standard 0. Punkt kan være

ˆ eller Nˆ, i hvilke tilfælde det dominerende led vil være det led, der har den største eksponent af Var frem for den mindste eksponent for Var.

dominantTerm(…) returnerer

“dominantTerm(…)” hvis den ikke kan bestemme en sådan repræsentation, for eksempel for væsentlige singulariteter som

sin(1/z) ved z=0, e

z = ˆ eller Nˆ.

Hvis rækken eller en af dens afledte afbrydes af et spring ved Punkt, indeholder resultatet sandsynligvis deludtryk på formen sign(…) eller abs(…) for en reel udviklingsvariabel eller (-1) for en kompleks udviklingsvariabel, der slutter med “_”. Hvis du kun vil bruge det dominerende led til værdier på den ene af

1/z

ved z=0, eller ezved

floor(…angle(…)…)

Punkt, skal du til dominantTerm(...) tilføje

den korrekte af funktionerne “| Var >

Punkt”, “| Var < Punkt”, “| “Var | Punkt”,

eller “Var { Punkt” for at opnå et enklere resultat.

Katalog >

Alfabetisk oversigt 59

dominantTerm()

dominantTerm() distribuerer over 1.

argument lister og matricer.

dominantTerm() er nyttig, når du vil have

det enklest mulige udtryk, der nærmer sig asymptotisk til et andet udtryk som

Var " Punkt. dominantTerm() er også

nyttig, når det ikke er klart, hvad graden af det første ikke-nul-led i en række vil være, og du ikke ønsker en række interaktive iterative gæt eller med en programløkke.

Bemærk: Se også series(), side 166.

Katalog >

dotP()

dotP(Liste1, Liste2)⇒udtryk

Returnerer “prik” produktet af to lister.

dotP(Vektor1, Vektor2)⇒udtryk

Returner “prik” produktet af to vektorer.

Begge skal være rækkevektorer, eller begge skal være kolonnevektorer.

e^()

e^(Udtr1)⇒udtryk

Returnerer e opløftet til potensen Udtr1.

Bemærk: Se også e Eksponentskabelon, side

Bemærk: At trykke /u for at vise e^(er

ikke det samme som at trykke på tegnet E på tastaturet.

Du kan indtaste et komplekst tal i re polær form. Anvend dog kun denne form i vinkeltilstanden Radian. Den forårsager en domænefejl i vinkeltilstandene Grader eller Nygrader.

e^(Liste1)⇒liste

Katalog >

u-tast

60 A lfabetisk oversigt

e^()

Returnerer e opløftet til potensen af hvert element i Liste1.

e^(kvadratMatrix1)⇒kvadratMatrix

Returnerer matrix eksponentialfunktion af

kvadratMatrix1. Dette er ikke det samme

som at beregne e opløftet til potensen af hvert element. Oplysninger om beregningsmetoden findes i cos().

KvadratMatrix1 skal være diagonaliserbar.

Resultatet indeholder altid tal med flydende decimaler.

u-tast

eff()

eff(nominelRente,CpY)⇒værdi

Finansfunktion, der omregner den nominelle rente nominelRente til en effektiv årlig rente, hvor CpY er antallet af rentetilskrivninger per år.

nominelRente skal være et reelt tal, og CpY skal være et reelt tal > 0.

Bemærk: Se også nom(), side 128.

eigVc()

eigVc(kvadratMatrix)⇒matrix

Returnerer en matrix med egenvektorerne for en reel eller kompleks kvadratMatrix, hvor hver kolonne i resultatet svarer til en egenværdi. Bemærk, at en egenvektor ikke er unik. Den kan skaleres af enhver konstantfaktor. Egenvektorerne er normaliseret, dvs. at hvis V = [x1, x2, …, xn], så:

+x

+ … +x

= 1

Katalog >

I rektangulært komplekstformat:

Dukan se heleresultatetved at trykke på £ og derefter bruge ¡ og ¢ tilat bevæge markøren.

Alfabetisk oversigt 61

eigVc()

kvadratMatrix balanceres først med

similaritetstransformationer, til række- og kolonnenormer er så tæt som muligt på samme værdi. KvadratMatrix reduceres derefter til øvre Hessenberg form, og egenvektorerne beregnes via en Schur faktorisering.

Katalog >

eigVl()

eigVl(kvadratMatrix)⇒liste

Returnerer en liste med egenværdier af en reel eller kompleks kvadratMatrix.

kvadratMatrix balanceres først med

similaritetstransformationer, til række- og kolonnenormer er så tæt som muligt på samme værdi. KvadratMatrix reduceres derefter til øvre Hessenberg form, og egenværdierne beregnes fra øvre Hessenberg-matricen.

Else

ElseIf

If Boolsk Udtr1 Then

  Blok1

ElseIf Boolsk Udtr2 Then

  Blok2

©

ElseIf Boolsk UdtrN Then

  BlokN

EndIf

Katalog >

I rektangulær kompleks formattilstand:

Dukan se heleresultatetved at trykke på £ og derefter bruge ¡ og ¢ tilat bevæge markøren.

Se If, side 91.

Katalog >

©

Bemærk indtastning af eksemplet: For

instruktioner til at indtaste programmer over flere linjer og definering af funktioner se Beregninger-afsnittet i din produktvejledning.

62 A lfabetisk oversigt

EndFor

Se For, side 76.

EndFunc

EndIf

EndLoop

EndPrgm

EndTry

EndWhile

euler ()

euler(Expr, Var, depVar, {Var0, VarMax},

depVar0, VarStep [, eulerStep]) ⇒matrix

euler(SystemOfExpr, Var, ListOfDepVars, {Var0, VarMax},  ListOfDepVars0,

VarStep [, eulerStep]) ⇒matrix

Se Func, side 80.

Se If, side 91.

Se Loop, side 114.

Se Prgm, side 142.

Se Try, side 197.

Se While, side 207.

Katalog >

Differentialligning:

y'=0.001*y*(100-y) og y(0)=10

euler(ListOfExpr, Var, ListOfDepVars, {Var0, VarMax},ListOfDepVars0,

VarStep [, eulerStep]) ⇒matrix

Anvender Euler-metoden til at løse systemet

Dukan se heleresultatetved at trykke på £ og derefter bruge ¡ og ¢ tilat bevæge markøren.

Alfabetisk oversigt 63

euler ()

med depVar(Var0)=depVar0 i intervallet [Var0,VarMax]. Returnerer en matrix, hvor første række definerer Varoutputværdierne, og anden række definerer værdien af første løsningskomponent ved de tilsvarende Var-værdier, osv.

Expr er højresiden, som definerer den

ordinære differentialligning (ODE - ordinary differential equation).

SystemOfExpr er systemet af højresider,

der definerer ODE'erne (svarer til rækkefølgen af afhængige variable i

ListOfDepVars).

ListOfExpr er en liste af højresider, der

definerer systemet af ODE'er (svarer til rækkefølgen af afhængige variable i

ListOfDepVars).

Var er den uafhængige variable.

ListOfDepVars er en liste med afhængige

variable.

{Var0, VarMax} er en liste med to elementer, der informerer funktionen om, at integrere fra Var0 til VarMax.

ListOfDepVars0 er en liste med

startværdier for afhængige variable.

VarStep er et tal forskelligt fra nul, således

at sign(VarStep) = sign(VarMax-Var0) og løsninger returneres i Var0+i·VarStep for alle i=0,1,2,… således at Var0+i·VarStep er i [var0,VarMax] (der vil muligvis ikke være en løsningsværdi ved VarMax).

eulerStep er et positivt heltal (som

standard er 1), der definerer antallet af euler-trin mellem outputværdier. Den faktiske trinstørrelse, som euler-metoden anvender, er VarStepàeulerStep.

Katalog >

Sammenlignresultatet ovenfor medden eksakte CAS løsning opnåetvedbrug af deSolve() og seqGen():

System af ligninger:

medy1(0)=2 og y2(0)=5

64 A lfabetisk oversigt

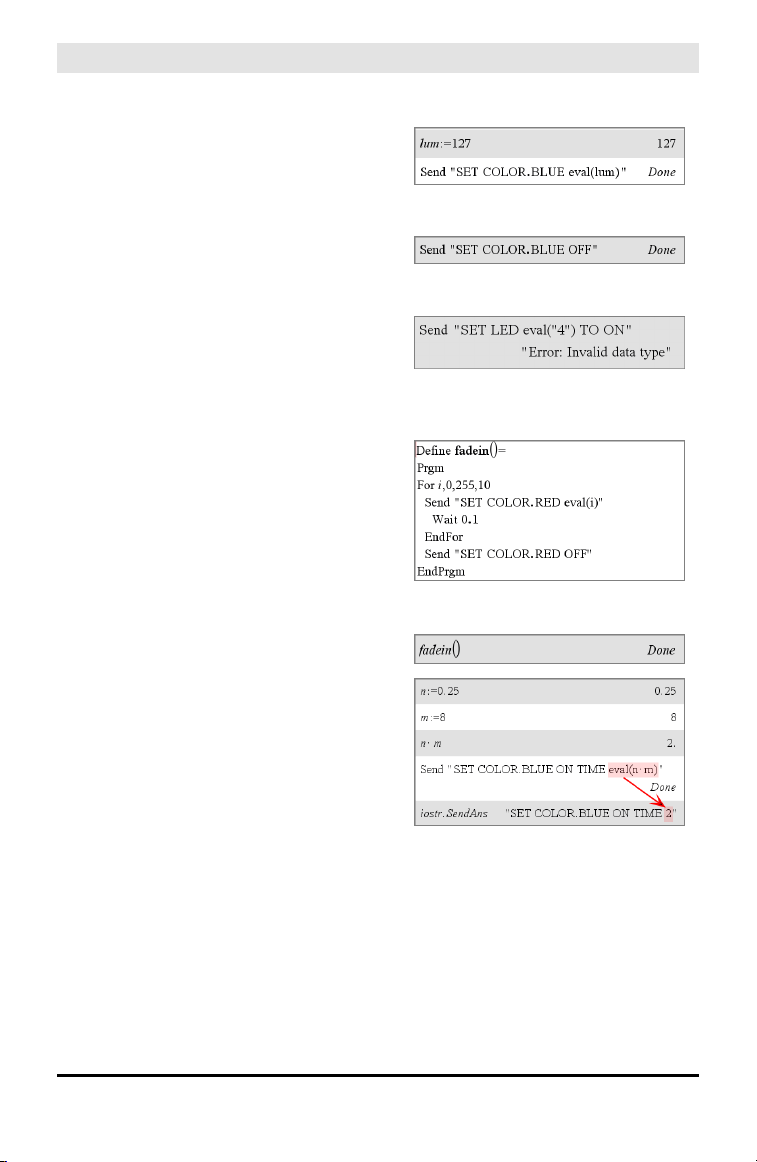
eval () Hub-menu

eval(Expr) ⇒ string

eval() er kun gyldig i TI-Innovator™ Hub

Kommandoargument for programmeringskommandoerne Get, GetStr og Send. Softwaren evaluerer udtrykket

Sæt det blå element i RGB LEDtilhalv intensitet.

Expr og udskifter eval()-udsagnet med

resultatet som en tekststreng.

Nulstildetblå elementtil OFF.

Argumentet Expr skal blot være et reelt tal.

eval()-argumentskal blot være etreelt tal.

Programmet villangsomtindføre detrøde element

Kør programmet.

Selvom eval() ikke viser et resultat, kan du se den resulterende Hub-kommandostreng, efter at du har udført kommandoen ved at inspicere en af følgende specielle variable.

iostr.SendAns iostr.GetAns iostr.GetStrAns

Bemærk: Se også Get(side 81), GetStr(side

88), og Send(side 163).

Alfabetisk oversigt 65

exact()

exact(Udtr1 [, Tolerance])⇒udtryk exact (Liste1 [, Tolerance])⇒liste exact (Matrix1 [, Tolerance])⇒matrix

Anvender Eksakt-tilstandens aritmetik til at returnere det rationale talækvivalent til argumentet, hvis det er muligt.

Tolerance angiver tolerancen for

konverteringen; standardindstillingen er 0 (nul).

Katalog >

Exit

Afslutter den aktuelle For, While, eller Loopblok.

Exit er ikke tilladt uden for de tre

løkkestrukturer (For, While, eller Loop).

Bemærk indtastning af eksemplet: For

instruktioner til at indtaste programmer over flere linjer og definering af funktioner se Beregninger-afsnittet i din produktvejledning.

4exp

Udtr 4exp

Repræsenterer Udtr i termer af den naturlige eksponentialfunktion e. Det er en konverteringsoperator til visning. Denne operator kan kun anvendes ved slutningen af indtastningslinjen.

Bemærk: Du kan indsætte denne operator

fra computerens tastatur ved at skrive

@>exp.

Katalog >

Funktionsliste:

Katalog >

66 A lfabetisk oversigt

exp()

exp(Udtr1)⇒udtryk

Returnerer e opløftet til potensen Udtr1.

Returnerer e opløftet til potensen Værdi1.

Bemærk: Se også e eksponentskabelon, side

Du kan indtaste et komplekst tal i reI q polær form. Anvend dog kun denne form i vinkeltilstanden Radian. Den forårsager en domænefejl i vinkeltilstandene Grader eller Nygrader.

exp(Liste1)⇒liste

Returnerer e opløftet til potensen af hvert element i Liste1.

exp(kvadratMatrix1)⇒kvadratMatrix

Returnerer matrix eksponentialfunktion af

kvadratMatrix1. Dette er ikke det samme

som at beregne e opløftet til potensen af hvert element. Oplysninger om beregningsmetoden findes i cos().

KvadratMatrix1 skal være diagonaliserbar.

Resultatet indeholder altid tal med flydende decimaler.

u-tast

exp4liste()

exp4list(Udtr,Var)⇒liste

Undersøger Udtr for ligninger, der er adskilt af ordet “or”, og returnerer en liste med ligningernes højresider på formen

Var=udtryk. Dette er en nem metode til at

udtrække løsningsværdier, der er indlejret i resultaterne af funktionerne solve(), cSolve

(), fMin() , og fMax().

Bemærk: exp4lis t() er ikke nødvendig med

funktionerne zeros og cZeros(), da de direkte returnerer en liste med løsningsværdier.

Du kan indsætte denne funktion fra computerens tastatur ved at skrive

exp@>list(...).

Katalog >

Alfabetisk oversigt 67

expand()

expand(Udtr1 [, Var])⇒udtryk expand(Liste1 [,Var])⇒liste expand(Matrix1 [,Var])⇒matrix

expand(Udtr1) returnerer Udtr1 på ledform

med hensyn til alle variable. Ledformen er en polynomiumsudvikling for polynomier og en udvikling i partialbrøker for polynomiumsbrøker.

Målet for expand() er at transformere

Udtr1 til en sum og/eller differens for

simple led. Som modsætning er målet for

factor() at transformere Udtr1 til et

produkt og/eller kvotient af simple faktorer.

expand(,Udtr1,Var) returnerer Udtr1 på

ledform med hensyn til Var. Ens potenser af Var samles. Leddene og deres faktorer sorteres med Var som hovedvariabel. Der kan opstå en vis utilsigtet faktoropløsning eller udvikling af de reducerede koefficienter. Sammenlignet med at udelade Var sparer dette ofte tid, hukommelse og skærmplads, samtidig med, at det gør udtrykket mere læseligt.

Selv når der kun er en variabel, kan anvendelsen af Var gøre faktoropløsningen af nævneren til delvis udvikling af brøker mere fuldstændig.

Tip: For rationale udtryk er propFrac() et hurtigere men mindre vidtgående alternativ til expand().

Bemærk: Se også comDenom() vedrørende

en tæller på ledform over en nævner på ledform.

Katalog >

68 A lfabetisk oversigt

expand()

expand(Udtr1,[Var]) distribuerer også

logaritmer og brøkpotenser, uanset Var. For øget distribution af logaritmer og brøkpotenser kan grænser for uligheder være nødvendige for at garantere, at visse faktorer er ikke-negative.

expand(Udtr1, [Var]) distribuerer også

absolutte værdier, sign() og eksponentialfunktioner uanset Var.

Bemærk: Se også tExpand() vedrørende

trigonometriske additionsformler og formler for multipel vinkel.

Katalog >

expr()

expr(Streng)⇒udtryk

Returnerer den tegnstreng, der er indeholdt i Streng som et udtryk og og eksekverer den straks.

ExpReg

ExpReg X, Y [, [Frekv][, Kategori,

Medtag]]

Beregner polynomielle tredjegradsregression y = a·(b)xpå listerne X og Y med hyppighed Frekv. En sammenfatning af resultaterne lagres i

stat.results variable. (side 182.)

Alle lister skal have ens dimensioner med undtagelse af Medtag.

X og Y er lister med uafhængige og

afhængige variable.

Frekv er en valgfri liste med hyppigheder.

Hvert element i Frekvangiver hyppigheden af hændelse for hver tilsvarende

XogYdatapunkt. Standardværdien er 1.

Alle elementer skal væreheltal | 0.

Katalog >

Alfabetisk oversigt 69

ExpReg

Kategory er en liste, der indeholder

kategorikoder for X og Y data.

Medtag er en liste med en eller flere af

kategorikoderne. Kun de dataelementer, hvis kategorikode er medtaget i denne liste, er medtaget i beregningen.

Oplysninger om effekten af tomme elementer i en liste findes “Tomme (ugyldige) elementer,” side 244.

Katalog >

Outputvariabel

stat.RegEqn Regressionsligning: a·(b)

stat.a, stat.b Regressionskoefficienter

stat.r

stat.r Korrelationskoefficient tiltransformerededata(x, ln(y))

stat.Resid Residualer af kurvetilpasningen= y - a·(b)

stat.ResidTrans Residualer associeret med lineær tilpasning af transformerededata

stat.XReg

stat.YReg

stat.FreqReg

Beskrivelse

Koefficientaf enlineær forklaringsgradtiltransformerededata

Liste af datapunkter i denmodificeredeX-liste, der faktisk brugesi regressionenud fra begrænsninger af Hyppighed, Kategoriliste og Medtag kategorier

Liste af datapunkter i denmodificeredeY-liste, der faktisk bruges i regressionenud fra begrænsninger af Hyppighed, Kategoriliste og Medtag kategorier

Liste med hyppigheder, der svarer til stat.XReg og stat.YReg

factor()

factor(Udtr1[, Var])⇒udtryk factor(Liste1[,Var])⇒liste factor(Matrix1[,Var])⇒matrix

factor(Udtr1) returnerer Udtr1 opløst i faktorer med hensyn til alle dens variable over en fællesnævner.

Katalog >

70 A lfabetisk oversigt

factor()

Udtr1 opløses mest muligt mod lineære

rationale faktorer uden at indføre nye ikkereelle deludtryk. Denne mulighed er velegnet, hvis du ønsker opløsning i faktorer med hensyn til mere end en variabel.

factor(Udtr1,Var) returnerer Udtr1 opløst i faktorer med hensyn til variablen Var.

Udtr1 opløses mest muligt i faktorer, der er

lineære i Var, også hvis den indfører irrationale konstanter eller deludtryk, der er irrationale i andre variable.

Faktorerne og deres led sorteres med Var som hovedvariabel. Ens potenser af Var samles i hver faktor. Medtag Var, hvis opløsning i faktorer kun er nødvendig med hensyn til den pågældende variabel, og du er villig til at acceptere irrationale udtryk i alle andre variable for at øge opløsningen i faktorer med hensyn til Var. Der kan forekomme en uforudset faktoropløsning med hensyn til andre variable.

For Auto-indstillingen af

Autoellertilnærmet tilstanden muliggør

medtagelsen af Var også en approksimering med koefficienter med flydende decimaler, hvor irrationale koefficienter ikke kan udtrykkes med de indbyggede funktioner. Også når der kun er en variabel, kan en medtagelse af Var give en mere komplet opløsning i faktorer.

Bemærk: Se også comDenom() for en hurtig

metode til at opnå partiel faktoropløsning, når factor() ikke er hurtig nok, eller den bruger hele hukommelsen.

Bemærk: Se også cFactor() om

faktoropløsning med komplekse koefficienter for at opnå lineære faktorer.

Katalog >

Alfabetisk oversigt 71

factor()

factor(rationaltTal) returnerer det

rationale tal opløst i primtal. Ved sammensatte tal øges beregningstiden eksponentielt med antallet af cifre i den næststørste faktor. Opløsning af et 30-cifret heltal kan for eksempel vare længere end en dag, og opløsning af et 100-cifret tal kan vare længere end et århundrede.

Sådan stopper du en beregning manuelt,

• Håndholdt: Hold tasten c nede, mens du gentagne gange trykker på ·.

• Windows®: Hold tasten F12 nede, mens du gentagne gange trykker på Enter.

• Macintosh®: Hold tasten F5 nede, mens du gentagne gange trykker på Enter.

• iPad®: App'en viser en meddelelse. Du kan fortsat vente eller annullere.

Hvis du kun vil bestemme, om et tal er et primtal, skal du anvende isPrime() i stedet. Det er meget hurtigere, især hvis

RationaltTal ikke er et primtal, og den

næststørste faktor har mere end fem cifre.

Katalog >

FCdf()

FCdf

(

nedreGrænse

,øvreGrænse,fgTæller,fgNævner)⇒tal hvis

nedreGrænse og øvreGrænse er tal, liste

hvis nedreGrænse og øvreGrænse er lister

FCdf (

nedreGrænse

,øvreGrænse,fgTæller,fgNævner)⇒tal hvis

nedreGrænse og øvreGrænse er tal, liste

hvis nedreGrænse og øvreGrænse er lister

Beregner sandsynligheden hørende tilFfordelingen for intervallet mellem

nedreGrænse og øvreGrænse med de

angivne frihedsgraderdfTællerog

dfNævner.

72 A lfabetisk oversigt

Katalog >

FCdf()

For den kumulerede fordeling P(X {

øvreGrænse) skal du sætte nedreGrænse =

Katalog >

Fill

Fill Udtr, matrixVar⇒matrix

Erstatter hvert element i variablen

matrixVar med Udtr.

matrixVar skal eksistere i forvejen.

Fill Udtr, listeVar⇒liste

Erstatter hvert element i variablen Listevar med Udtr.

Listevar skal eksistere i forvejen.

FiveNumSammendrag

FiveNumSummary X[, [Frekvv][

Kategori,Medtag]]

Frembringer en forkortet version af 1variabelstatistikken på listen X. Ensammenfatning af resultaterne lagres i

stat.results variable. (side 182.)

X repræsenterer en liste med dataene.

Frekv er en valgfri liste med hyppigheder.

Hvert element i Frekv¨angiver hyppigheden af hver tilsvarende X værdi. Standardværdien er 1. Alle elementer skal være heltal | 0.

Kategori er en liste med numeriske

kategorikoder for tilsvarende Xværdier.

Medtag er en liste med en eller flere af

kategorikoderne. Kun de dataelementer, hvis kategorikode er medtaget i denne liste, er medtaget i beregningen.

Katalog >

Alfabetisk oversigt 73

FiveNumSammendrag

Et tomt (ugyldigt) element i en af listerne X,

Freq eller Category resulterer i at det

tilsvarende element i alle disse lister bliver ugyldigt. Yderligere oplysninger om tomme elementer findes på side 244

Output-variabel Beskrivelse

stat.MinX Minimum af x-værdier

stat.Q1X 1. kvartil af x

stat.MedianX Median af x

stat.Q3X 3. kvartil af x

stat.MaxX Maksimum af x-værdier

Katalog >

floor()

floor(Udtr1)⇒heltal

Returnerer det største heltal, der er { argumentet. Denne funktion er identisk med int().

Argumentet kan være et reelt eller komplekst tal.

floor(Liste1)⇒liste

floor(Matrix1)⇒matrix

Returnerer en liste eller matrix med nedrunding af hvert element.

Bemærk: Se også ceiling() og int() .

fMax()

fMax(Udtr, Var)⇒Boolsk udtryk

fMax(Udtr, Var,nedreGrænse)

fMax(Udtr,

Var,nedreGrænse,øvreGrænse)

fMax(Udtr, Var) | nedreGrænse{Var {øvreGrænse

Katalog >

74 A lfabetisk oversigt

fMax()

Returnerer et Boolsk udtryk, der angiver mulige værdier for Var, der maksimerer

udtryk eller finder dets mindste øvre

grænse. Med (“|”) betingelses-operatoren kan du

indskrænke løsningsintervallet og/eller angive andre begrænsninger.

I Tilnærmet-indstillingen af

Autoellertilnærmet-tilstanden søger fMax () iterativt efter et tilnærmet lokalt

maksimum. Dette er ofte hurtigere, især hvis du anvender “|”-operatoren til at begrænse søgningen til et relativt lille interval, der indeholder nøjagtigt et lokalt maksimum.

Bemærk: Se også fMin() og max().

Katalog >

fMin()

fMin(Udtr, Var)⇒Boolsk udtryk

fMin(Udtr, Var,nedreGrænse)

fMin(Udtr, Var,nedreGrænse,øvreGrænse)

fMin(Udtr, Var) | nedreGrænse{Var

{øvreGrænse

Returnerer et Boolsk udtryk, der angiver mulige værdier for var, der minimerer Udtr eller finder dets største nedre grænse.

Med (“|”) betingelses-operatoren kan du indskrænke løsningsintervallet og/eller angive andre begrænsninger.

Til Approx-indstillingen af

Autoellertilnærmet tilstanden søger fMin()

iterativt for et enkelt tilnærmet lokalt minimum. Dette er ofte hurtigere, især hvis du anvender “|”-operatoren til at begrænse søgningen til et relativt lille interval, der indeholder nøjagtigt et lokalt minimum.

Bemærk: Se også fMax() og min().

Katalog >

Alfabetisk oversigt 75

For

For Var, Lav, Høj [, Trin]

Blok

EndFor

Eksekverer sætningerne i blok iterativt for hver værdi af Var fra Lav til Høj i intervaller på Trin.

Var må ikke være en systemvariabel.

Trin kan være positiv eller negativ.

Standardværdien er 1.

Blok kan enten være en enkelt sætning

eller en serie sætninger adskilt med kolon.

Bemærk indtastning af eksemplet: For

instruktioner til at indtaste programmer over flere linjer og definering af funktioner se Beregninger-afsnittet i din produktvejledning.

Katalog >

format()

format(Udtr[, formatStreng])⇒streng

Returnerer Udtr som en tegnstreng baseret på formatskabelonen.

Udtr skal kunne omregnes til et tal.

formatStreng er en streng og skal være på

formen: “F[n]”, “S[n]”, “E[n]”, “G[n][c]”, hvor [] angiver valgfrie dele.

F[n]: Fast format. n er det antal cifre, der vises efter decimalpunktet.

S[n]: Videnskabeligt format. n er det antal cifre, der vises efter decimalpunktet.

E[n]: Teknisk format. n er antallet af cifre efter det betydende ciffer. Eksponenter er justeret til et multiplum af tre, og decimalpunktet flyttes til højre med nul, en eller to pladser.

Katalog >

76 A lfabetisk oversigt

format()

G[n][c]: Samme som fast format men skiller også cifrene til venstre for decimalpunktet i grupper på tre. c angiver gruppeskilletegnet og er som standard et komma. Hvis c er et punktum, vises grundtallet som et komma.

[Rc]: Alle ovennævnte angivelser kan udvides med Rc-grundtalflaget, hvor c er et enkelt tegn, der angiver, hvad der skal substitueres for grundtalspunktet.

Katalog >

fPart()

fPart(Udtr1)⇒udtryk fPart(Liste1)⇒liste fPart(Matrix1)⇒matrix

Returnerer decimaldelen af argumentet.

For en liste eller matrix returneres decimaldelen af elementerne.

Argumentet kan være et reelt eller komplekst tal.

FPdf()

FPdf(XVærdi,dfTæller,dfNævner)

Beregner F sandsynlighedsfordelingen på

XVal for den angivne dfTæller

(frihedsgrader i tælleren) og dfNævner (frihedsgrader i nævneren).

freqTable4list()

freqTable4liste(Liste1,frekvHeltalListe)

⇒liste

Katalog >

Alfabetisk oversigt 77

freqTable4list()

Returnerer en liste indeholdende elementerne fra Liste1 udvidet i henhold til hyppighederne i frekvHeltalListe. Denne funktion kan anvendes til at danne en frekvenstabel for Data- & Statistikapplikationerne.

Liste1 kan være enhver gyldig liste.

frekvHeltalListe skal have den samme

dimension som Liste1 og må kun indeholde ikke-negative heltalselementer. Hvert element angiver det antal gange det tilsvarende Liste1 element vil blive gentaget i resultatlisten. En nul-værdi udelukker det tilsvarende Liste1 element.

Bemærk: Du kan indsætte denne funktion

fra computerens tastatur ved at skrive

freqTable@>list(...).

Tomme (ugyldige) elementer ignoreres. Yderligere oplysninger om tomme elementer findes på side 244.

Katalog >

frequency()

frequency(Liste1,binsListe)⇒liste

Returnerer en liste, der indeholder optælling af elementerne i Liste1. Antallene er baseret på områder (bins), som du definerer i binsListe.

Hvis binsListe er {b(1), b(2), …, b(n)}, er de specificerede områder {?{b(1), b(1)<?{b (2),…,b(n-1)<?{b(n), b(n)>?}. Den resulterende liste er et element længere end binsListe.

Hvert element af resultatet svarer til antallet af elementer fra Liste1, der er i dette område. Udtrykt med countIf()funktionen er resultatet {countIf(liste, ?{b (1)), countIf(liste, b(1)<?{b(2)), …, countIf (liste, b(n-1)<?{b(n)), countIf(liste, b(n)>?)}.

78 A lfabetisk oversigt

Katalog >

Forklaring af resultatet:

2 elementer fra Dataliste er {2.5

4 elementer fra Dataliste er >2,5 og {4,5

3 elementer fra Dataliste er >4,5

Elementet"hello" er enstreng og kan ikke placeres i nogen af de definerede områder.

frequency()

Elementer i Liste1, der ikke kan “placeres i en størrelse” ignoreres. Tomme (ugyldige) elementer ignoreres også. Yderligere oplysninger om tomme elementer findes på side 244.

I applikationen Lister og regneark kan du anvende et celleområde i stedet for begge argumenter.

Bemærk: Se også countIf(), side 36.

Katalog >

FTest_2Samp

Katalog >

FTest_2Samp Liste1,Liste2[,Hyppighed1 [,Hyppighed2[,Hypot]]]

(Datalisteinput)

FTest_2Samp sx1,n1,sx2,n2[,Hypot]

(Sammenfatning, stat input)

Udfører en Ftest med to målinger. En sammenfatning af resultaterne lagres i variablen stat.results. (side 182.)

eller Ha: s1 > s2, sæt Hypot>0

Til Ha: s1 ƒ s2 (standard), sæt Hypot =0

Til Ha: s1 < s2, sæt Hypot<0

Oplysninger om effekten af tomme elementer i en liste findes “Tomme (ugyldige) elementer,” side 244.

Output-variabel Beskrivelse

stat.F Beregnet Û statistik for datasekvensen

stat.PVal Mindstesignifikansniveau, ved hvilketnul-hypotesenkan forkastes

stat.dfTæller frihedsgrader for tæller = n1-1

stat.dfNævner tæller, frihedsgrader = n2-1

stat.sx1, stat.sx2

Stikprøve standardafvigelse for datasekvensernei Liste1 og Liste2

Alfabetisk oversigt 79

Output-variabel Beskrivelse

stat.x1_bar

stat.x2_bar

stat.n1, stat.n2 Størrelsepå stikprøverne

Middelværdiaf stikprøver for datasekvenserne i Liste1 og Liste2

Func

  Blok

EndFunc

Skabelon til oprettelse af en brugerdefineret funktion.

Blok kan være en enkelt sætning,

en serie sætninger adskilt med kolon eller en serie sætninger på separate linjer. Funktionen kan anvende Return-instruktionen til at returnere et specifikt resultat.

Bemærk indtastning af eksemplet:

For instruktioner til at indtaste programmer over flere linjer og definering af funktioner se Beregninger-afsnittet i din produktvejledning.

gcd()

gcd(Værdi1, Værdi2)⇒udtryk

Returnerer den største fælles divisor af to argumenter. Gcd for to brøker er gcd af deres tællere divideret med lcm af deres nævnere.

I Autoellertilnærmet- tilstand er gcd af flydende decimalbrøker 1.0.

gcd(Liste1, Liste2)⇒liste

Katalog >

Definitionaf enstykvis funktion:

Tegnetresultataf grafen g(x)

Katalog >

80 A lfabetisk oversigt

gcd()

Returnerer de største fælles divisorer af de tilsvarende elementer i Liste1 og Liste2.

gcd(Matrix1, Matrix2)⇒matrix

Returnerer de største fælles divisorer af de tilsvarende elementer i Matrix1og

Matrix2.

Katalog >

geomCdf()

geomCdf(p,nedreGrænse,øvreGrænse)

⇒tal, hvis nedreGrænse og øvreGrænse er tal, liste, hvis nedreGrænse og øvreGrænse er lister

geomCdf(p,øvreGrænse)for P(1{X {øvreGrænse)⇒tal hvis øvreGrænse er et

tal, liste, hvis øvreGrænse er en liste

Beregner den kumulerede geometriske sandsynlighed fra nedreGrænse til

øvreGrænse med den angivne

sandsynlighed for succes p.

For P(X { øvreGrænse), sæt nedreGrænse=

geomPdf()

geomPdf(p,XVærdi)⇒tal hvis XVærdi er et

tal, liste hvis XVærdi er en liste

Beregner sandsynligheden i XVærdi, nummeret på den forsøgsgang hvor den første succes forekommer, for den diskrete geometrisk distribution med den angivne sandsynlighed for succes, p.

Katalog >

Get Hub-menu

Get[promptString,]var[,statusVar]

Get[promptStreng,] func(arg1, ...argn)

[,statusVar]

Eksempel: Anmod om dennuværendeværdi for hubbens indbyggede lysniveausensor. Brug Get for at modtageværdien, og tildel dentil den variable lightval.

Alfabetisk oversigt 81

Get Hub-menu

Programmeringskommando: Henter en værdi fra en tilsluttet TI-Innovator™ Hub og tildeler værdien til den variable var.

Der skal anmodes om værdien:

• i forvejen gennem en Send "READ ..." kommando.

Indlejr READ-anmodningenmed Getkommandoen.

—eller—

• ved at indlejre en "READ..." anmodning som det valgfrie promptStringargument. Med denne metode kan du bruge en enkelt kommando til at anmode om værdien og modtage den.

Implicit reduktion finder sted. For eksempel fortolkes en modtaget streng på "123" som en numerisk værdi. Brug GetStr i stedet for

Get for at bevare strengen.

Hvis du inkluderer det valgfrie argument

statusVar, tildeles det en værdi baseret på

operationens succes. En værdi på nul betyder, at ingen data blev modtaget.

I den anden syntaks lader argumentet func () et program gemme den modtagne streng som en funktionsdefinition. Denne syntaks virker, ligesom hvis programmet udførte kommandoen:

Define func(arg1, ...argn) = modtaget

streng

Så kan programmet bruge den definerede funktion func().

Bemærk: Du kan bruge kommandoen Get i

et brugerdefineret program, men ikke i en funktion.

Bemærk: Se også GetStr, side 88 og Send,

side 163.

82 A lfabetisk oversigt

getDenom()

getDenom(Udtr1)⇒udtryk

Transformerer argumentet til et udtryk med en forkortet fællesnævner og returnerer derefter dens nævner.

Katalog >

getKey()

getKey([0|1]) ⇒ returnString

Beskrivelse:getKey() - tillader et TI-

Basic-program at få tastaturinput håndholdt, stationær og emuleret på stationær.

Eksempel:

• tasttrykket := getKey() vil returnere en tast eller en tom streng, hvis ingen tast blev trykket. Denne kommando vil straks returnere.

• tasttrykket := getKey(1) venter til en tast bliver trykt ned. Denne kommando vil sætte udførelsen af programmet på pause, indtil en tast er trykket ned.

Håndtering af tasttryk:

Håndholdte

enheder/emulatortast

Esc Esc "esc" Touchpad - klik øverst n/a "op" Til n/a ”til top”

Eksempel:

Skrivebord Returværdi

Katalog >

Scratchapps n/a ”kladde” Touchpad - venstreklik n/a ”venstre” Touchpad - klik i midten n/a ”midten” Touchpad - højreklik n/a ”højre” Dok n/a ”dok”

Alfabetisk oversigt 83

Håndholdte

enheder/emulatortast

Skrivebord Returværdi

Tabulator Tabulator ”tabulator” Touchpad - klik nederst Ned pil ”ned” menu n/a ”menu”

Ctrl Ctrl ingen retur Skift Skift ingen retur Var n/a ”var” Del n/a "del"

= = "=" trigonometri n/a ”trigonometri” 0 til 9 0-9 "0" ... "9" Skabeloner n/a ”skabelon” Katalog n/a ”kat”

^ ^ "^" X^2 n/a ”kvadrat” / (divisionstast) / "/" * (gangetast) * "*" e^x n/a ”eksp” 10^x n/a "10potens" + + "+"

- - "-"

( ( "(" ) ) ")" . . "." (-) n/a ”-” (negativ fortegn) Indtast Indtast ”indtast”

ee n/a ”E” (eksponentiel notation

84 A lfabetisk oversigt

Håndholdte

enheder/emulatortast

Skrivebord Returværdi

a - z a - z alpha = bogstav trykket ned

(lille bogstav) ("a" - "z")

skift a - z skift a - z alpha = bogstav trykket ned

"A" - "Z" Bemærk: ctrl-shift fungerer

som lock-caps

?! n/a "?!"

pi n/a ”pi” Flag n/a ingen retur

, , "," Return n/a ”retur” mellemrum mellemrum ” ” (mellemrum)

Utilgængelig Specielle tegntaster som

Tegnet returneres

@,!^, osv. n/a Funktionstaster Ingen returnerede tegn n/a Specielle

Ingen returnerede tegn

skrivebordskontroltaster Utilgængelig Andre skrivebordstaster,

som ikke er tilgængelige på

Samme tegn du får i noter

(ikke i et matematik-felt) beregneren, når getkey () venter på et tastetryk. ({, },;, :, ...)

Bemærk: Det er vigtigt at være opmærksom på, at tilstedeværelsen af getKey() i et program ændrer, hvordan visse hændelser, bliver håndteret af systemet. Nogle af disse er beskrevet nedenfor.

Afslut program og håndter hændelse - Præcis som hvis en bruger ville afbryde et program ved at trykke på tasten ON

"Support" nedenfor betyder - system fungerer som forventet - program kører stadig.

Hændelse Enhed Skrivebord - TI-Nspire™

Hurtigsvar Afslut program, håndter

hændelse

Student Software

Samme som den håndholdte (TI-Nspire™ Student Software, TINspire™ Navigator™ NC

Alfabetisk oversigt 85

Hændelse Enhed Skrivebord - TI-Nspire™

Fjern fil mgmt

(Inkl. afsendelse af ”exit tryk 2 test” fil fra en anden håndholdt eller skrivebordshåndholdt)

Afslut klasse Afslut program, håndter

Afslut program, håndter hændelse

hændelse

Student Software

Teacher Software-kun)

Samme som den håndholdte.

(TI-Nspire™ Student Software, TI-Nspire™ Navigator™ NC Teacher Software-kun)

Support (TI-Nspire™ Student

Software, TI-Nspire™ Navigator™ NC Teacher Software-kun)

Hændelse Enhed Skrivebords - TI-Nspire™

TI-Innovator™ Hub forbind/afbryd

Support - kan med held udstede kommandoer til TI-Innovator™ Hub. Når du går ud af programmet, arbejder TI-Innovator™ Hub stadig med den håndholdte.

getLangInfo()

alle versioner

Samme som den håndholdte

Katalog >

getLangInfo()⇒streng

Returnerer en streng, som svarer til det korte navn af det aktuelle aktive sprog. Man kan, for eksempel, bruge det i et program eller funktion til at bestemme det aktuelle sprog.

86 A lfabetisk oversigt

getLangInfo()

Engelsk = “en” Dansk = “da” Tysk = “de” Finsk = “fi” Fransk = “fr” Italiensk = “it” Hollandsk = “nl” Belgisk Hollandsk = “nl_BE” Norsk = “no” Portugisisk = “pt” Spansk = “es” Svensk = “sv”

Katalog >

getLockInfo()

getLockInfo(Var)⇒værdi

Returnerer den aktuelle låste/oplåste tilstand på variablen Var.

værdi =0: Var er ulåst eller findes ikke.

værdi =1: Var er låst og kan ikke

ændres eller slettes.

Se Lock, side 110, ogunLock, side 204.

getMode()

getMode(TilstandNavnHeltal)⇒værdi getMode(0)⇒liste

getMode(TilstandNavnHeltal) returnerer

en værdi, der repræsenterer den aktuelle indstilling for tilstanden

TilstandNavnHeltal.

getMode(0) returnerer en liste, der

indeholder talpar. Hvert par består af et tilstandsheltal og et indstillingsheltal.

Se tabellen nedenfor for en oversigt over tilstande og deres indstillinger.

Catalog >

Katalog >

Alfabetisk oversigt 87

getMode()

Hvis du gemmer indstillingerne med

getMode(0) & var, kan du anvende setMode( var) i en funktion eller et program

for midlertidigt at gendanne indstillingerne under eksekveringen af funktionen eller programmet. Se setMode(), side 167.

Katalog >

Tilstandsnavn

Viste cifre

Vinkel Eksponentielt

Tilstandsheltal Indstil lingsheltal

1=Float, 2=Float1, 3=Float2, 4=Float3, 5=Float4, 6=Float5, 7=Float6, 8=Float7, 9=Float8, 10=Float9, 11=Float10, 12=Float11, 13=Float12, 14=Fix0, 15=Fix1, 16=Fix2, 17=Fix3, 18=Fix4, 19=Fix5, 20=Fix6, 21=Fix7, 22=Fix8, 23=Fix9, 24=Fix10, 25=Fix11, 26=Fix12

1=Radian, 2=Grader, 3=Gradian 1=Normal, 2=Videnskabelig, 3=Teknisk

format Reel eller

1=Reel, 2=Rektangulær, 3=Polær

kompleks Auto eller

1=Auto, 2=Tilnærmet, 3=Eksakt

tilnærmet Vektorformat Talsystem Enhedssystem

1=Rektangulær, 2=Cylindrisk, 3=Sfærisk 1=Decimal, 2=Hex, 3=Binær 1=SI, 2=Eng/US

getNum()

getNum(Udtr1)⇒udtryk

Transformerer argumentet til et udtryk med en forkortet fællesnævner og returnerer derefter dens tæller.

Katalog >

GetStr Hub-menu

GetStr[promptStreng,] var[, statusVar]

GetStr[promptStreng,] func(arg1, ...argn) [,statusVar]

88 A lfabetisk oversigt

Se Get for eksempler.

GetStr Hub-menu

Programmeringskommando: Fungerer identisk med kommandoen Get, bortset fra at den hentede værdi altid fortolkes som en streng. I modsætning hertil fortolker kommandoen Get svarene som et udtryk, medmindre det er omsluttet af citationstegn ("").

Bemærk: Se også Get, side 81 og Send, side

163.

getType()

getType(var)⇒streng

Returnerer en streng, som angiver datatypen for variablen var.

Hvis var ikke er defineret, returneres strengen "NONE".

getVarInfo()

getVarInfo()⇒matrix eller streng getVarInfo(BibNavnStreng) ⇒matrix eller

streng

getVarInfo() returnerer en matrix med

informationer (variabelnavn, type, bibliotekets tilgængelighed og låst/ulåststatus) for alle variable og biblioteksobjekter defineret i den aktuelle opgave.

Hvis der ikke er defineret nogen variable, returnerer getVarInfo() strengen "NONE"

getVarInfo(Biblioteksnavnestreng)

returnerer en matrix med oplysninger for alle biblioteksobjekter, der er defineret i biblioteket BibNavnStreng. BibNavnStreng skal være en streng (tekst omsluttet af citationstegn) eller en strengvariabel.

Hvis biblioteket BibNavnStreng ikke findes, opstår der en fejl.

Katalog >

Alfabetisk oversigt 89

getVarInfo()

Bemærk eksemplet til venstre, i hvilket resultatet af getVarInfo() er tilknyttet til variabel vs. Forsøg på at vise række 2 eller række 3 af vs returnerer en “ugyldig liste eller matrix” fejl, fordi mindst et af elementerne i disse rækker (variable b, f.eks) reevaluerer til en matrix.

Denne fejl kan også opstå, når Ans bruges til at evaluere et getVarInfo() resultat.

Systemet giver den ovenfor nævnte fejl, fordi den aktuelle version af softwaren ikke understøtter en generaliseret matrixstruktur, hvor et element i en matrix enten kan være en matrix eller en liste.

Katalog >

Goto

Goto etiketnavn

Overfører kontrol til etiketten etiketnavn.

Etiketnavn skal defineres i den samme

funktion med en Lbl-kommando.

Bemærk indtastning af eksemplet: For

instruktioner til at indtaste programmer over flere linjer og definering af funktioner se Beregninger-afsnittet i din produktvejledning.

4Grad

Udtr1 4 Grad⇒udtryk

Konverterer Udtr1 til vinkelmål i nygrader.

Bemærk: Du kan indsætte denne operator

fra computerens tastatur ved at skrive

@>Grad.

Katalog >

I vinkeltilstandenGrader:

I vinkeltilstandenRadian:

90 A lfabetisk oversigt

identitet()

identitet(heltal) ⇒ matrix

Returnerer identitetsmatrixen med en dimension af heltal.

Heltal skal være et positivt heltal.

If BooleanExpr

Statement

If BooleanExpr Then

Block

EndIf

Hvis BooleanExpr evalueres som sand, eksekveres enkeltsætningen Statement eller sætningsblokken Block, før eksekveringen fortsættes.

Hvis BooleanExpr evalueres som falsk, fortsættes eksekveringen uden eksekvering af sætningen eller sætningsblokken.

Block kan enten være en enkelt sætning

eller en række sætninger adskilt af":"- tegn

Bemærk indtastning af eksemplet: For

instruktioner til at indtaste programmer over flere linjer og definering af funktioner se Beregninger-afsnittet i din produktvejledning.

If BooleanExpr Then

  Block1

Else

  Block2

EndIf

Hvis BooleanExpr evalueres som sand, eksekveres Block1, og Block2 springes over.

Hvis BooleanExpr evalueres som falsk, springes over Block1, men Block2 eksekveres.

Katalog >

Alfabetisk oversigt 91

Block1 og Block2 kan være en enkelt

sætning.

If BooleanExpr1 Then

  Block1

ElseIf BooleanExpr2 Then

  Block2

⋮

ElseIf BooleanExprN Then

  BlockN

EndIf

Muliggør en forgrening. Hvis BooleanExpr1 evalueres som sand, eksekveres Block1. Hvis BooleanExpr1 evalueres som falsk, evalueres BooleanExpr2, og så videre.

Katalog >

ifFn()

ifFn(BooleanExpr,Value_If_true [,Value_

If_false [,Value_If_unknown]]) ⇒ udtryk, liste eller matrix

Beregner det boolske udtryk BooleanExpr (eller hvert element i BooleanExpr ) og giver et resultat baseret på følgende regler:

• BooleanExpr kan teste en enkelt værdi, en liste eller en matrix.

• Hvis et element i BooleanExpr evaluerer sandt, returneres det tilsvarende element fra Value_If_true.

• Hvis et element i BooleanExpr evaluerer falsk, returneres det tilsvarende element fra Value_If_false. Hvis du udelader Value_If_false, returneres undef.

• Hvis et element i BooleanExpr hverken er sandt eller falsk, returneres det tilsvarende element Value_If_unknown. Hvis du udelader Value_If_unknown, returneres undef.

• Hvis det andet, tredje eller fjerde argument i ifFn()-funktionen er et enkelt udtryk, udføres den Boolske test på hver position i BooleanExpr.

Katalog >

Testværdienfor 1 er mindre end2,5, så dens tilsvarende

Value_If_True-elementpå 5 kopieres til

resultatlisten.

Testværdienfor 2 er mindre end2,5, så dens tilsvarende

Value_If_True-elementpå 6 kopieres til

resultatlisten.

Testværdienfor 3 er ikke mindre end2,5, så dettilhørende Value_If_False-element på

10 kopieres tilresultatlisten.

Value_If_True er en enkelt værdiog

svarer til enhver valgtposition.

92 A lfabetisk oversigt

ifFn()

Bemærk: Hvis den reducerede

BooleanExpr-sætning indeholder en liste

eller matrix, skal alle andre liste- eller matrixargumenter have de samme dimensioner, og resultatet vil have de samme dimensioner.

Katalog >

Value_If_False er ikke specificeret. Undef

anvendes.

Ét elementvalgt fra Value_If_True. Ét elementvalgtfra Value_If_unknown.

imag()

imag(Expr1) ⇒ udtryk

Returnerer imaginærdelen af argumentet.

Bemærk: Alle udefinerede variable

behandles som reelle variable. Se også reel (), page 150

imag(List1) ⇒ liste

Returnerer en liste med imaginærdelen af elementerne.

imag(Matrix1) ⇒ matrix

Returnerer en matrix med imaginærdelene af elementerne.

impDif()

impDif(Equation, Var, dependVar[,Ord])

⇒ udtryk

hvor ordenen Ord som standard er 1.

Beregner den implicitte differentialkvotient til ligninger, hvor en variabel defineres implicit ud fra en anden.

Katalog >

Henvisning

Se #(), side 234.

Alfabetisk oversigt 93

inString()

inString(srcString, subString[, Start]) ⇒

heltal

Returnerer tegnpositionen i strengen

srcString, hvor første forekomst af

strengen subString begynder.

Start, hvis medtaget, angiver den position i srcString, hvor søgningen begynder.

Standard = 1 (første tegn i srcString).

Hvis srcString ikke indeholder subString, eller Start er > længden på srcString, returneres nul.

Katalog >

int()

int(Expr) ⇒ heltal

int(List1) ⇒ liste int(Matrix1) ⇒ matrix

Returnerer det største heltal, der er mindre end eller lig med argumentet. Denne funktion identisk med floor().

Argumentet kan være et reelt eller komplekst tal.

For lister og matrixer returneres det største heltal mindre end eller lig med hvert element.

intDiv()

intDiv(Number1, Number2) ⇒ heltal intDiv(List1, List2) ⇒ liste intDiv(Matrix1, Matrix2) ⇒ matrix

Returnerer den heltalsdel med fortegn, der er en del af (Number1 ÷ Number2).

Returnerer for lister og matricer heltalsdelen med fortegn, der er en del af (argument1÷argument2), for hvert elementpar.

Katalog >

94 A lfabetisk oversigt

integral

See ∫(), side 229.

interpoler ()

interpoler(xValue, xList, yList,

yPrimeList) ⇒ liste

Denne funktion gør følgende:

Givet xList, yList=f(xList) og

yPrimeList=f'(xList) for en ukendt funktion

f anvendes en kubisk interpolation til at

approksimere funktionen f ved xValue. Det antages, at xList er en liste med monotont voksende eller aftagende tal, men denne funktion kan returnere en værdi selvom det ikke er tilfældet. Denne funktion gennemløber xList i søgningen efter et interval [xList[i], xList[i+1]] der indeholder

xValue. Hvis den finder et sådan interval,

returnerer den en interpoleret værdi for f

(xValue); i modsat fald returnerer den undef.

xList, yList og yPrimeList skal have

samme dimension ≥ 2 og indeholde udtryk, der reducerer til tal.

xValue kan være en ikke-defineret variabel,

et tal eller en liste af tal.

invχ2()

invχ2(Areal,df)

Katalog >

Differentialligning:

y'=-3•y+6•t+5og y(0)=5

Dukan se heleresultatetved at trykke på £ og derefter bruge ¡ og ¢ tilat bevæge markøren.

Brug funktioneninterpolate()tilat beregne funktionsværdierne for listenmedxværdier:

Katalog >

invChi2(Areal,df)

Beregner den inverse kumulerede χ2(chikvadrat) sandsynlighedsfunktion angivet ved frihedsgrad, fg for et givet Areal under kurven.

invF()

invF(Areal,dfNumer,dfDenom)

invF(Area,dfNumer,dfDenom)

Katalog >

Alfabetisk oversigt 95

invF()

Beregner den inverse kumulerede F fordelingsfunktion angivet ved dfNumer og

dfDenom for et givet Areal under kurven.

Katalog >

invBinom()

invBinom (CumulativeProb,NumTrials,Prob,

OutputForm)⇒ skalar eller matrix

Givet antallet af forsøg (NumTrials) og sandsynligheden for succes i hvert forsøg (Prob) vil denne funktion returnere det minimale antal successer, k, således at den kumulerede sandsynlighed for k succeser er større end eller lig med den givne kumulerede sandsynlighed (CumulativeProb).

OutputForm=0, viser resultatet som en

skalar (standard).

OutputForm=1, viser resultatet som en

matrix.

invBinomN()

invBinomN(CumulativeProb,Prob,

NumSuccess,OutputForm)⇒ skalar eller

matrix

Givet sandsynligheden for succes i hvert forsøg (Prob) og antallet af succeser (NumSuccess) vil denne funktion returnere det minimale antal forsøg, N, således at den kumulerede sandsynlighed for x succeser er mindre end eller lig med den givne kumulerede sandsynlighed (CumulativeProb).

OutputForm=0, viser resultatet som en

skalar (standard).

OutputForm=1, viser resultatet som en

matrix.

Katalog >

Eksempel: Mary og Kevinspiller et spil terninger. Mary skal gættedetmaksimale antal gange, der rulles ensekser i 30 slag. Hvis der rulles en sekser så mange eller færre gange, vinder Mary. Desudenvinder hun mere, jo mindre dettal, hungætter på, er. Hvad er det mindstetal, Mary kan gætte på, hvishunvilhave ensandsynlighedfor at vinde på over 77 %?

Katalog >

Eksempel: Mo nique øver sig i målskudi kurvebold. Hunved fra erfaring, at hendes chancefor at ramme måletved et kast er 70 %. Hun har tænktsig at øve, til hunhar fået 50 mål. Hvor mange skud skal hunforsøge for at være sikker på, at sandsynligheden for at få mindst 50 målerstørre end0,99?

96 A lfabetisk oversigt

Texas Instruments TI-Nspire CX CAS Reference Guide [da]

Specifications and Main Features

Frequently Asked Questions

User Manual

Vigtige oplysninger

Udtryksskabeloner

Alfabetisk oversigt