Suunto 1520, PM5 User Manual

EN | FR | DE | ES | IT | FI | SV

PM-5 / PM-5/1520

CUSTOMER SERVICE CONTACTS

COORDONNÉES DU SERVICE CLIENTS, KUNDENDIENSTE, DATOS DE CONTACTO DE ATENCION AL CLIENTE, NUMERI UTILI PER IL SERVIZIO CLIENTI, KLANTENSERVICE, ASIAKASPALVELUN YHTEYSTIEDOT, KUNDSERVICE, KONTAKTER

Global Help Desk +358 2 284 11 60 Suunto USA Phone +1 (800) 543-9124 Canada Phone +1 (800) 776-7770 Suunto website

This publication and its contents are proprietary to Suunto Oy.

While we have taken great care to ensure that information contained in this documentation is both comprehensive and accurate, no warranty of accuracy is expressed or implied. Its content is subject to change at any time without notice.

www.suunto.com

Suunto PM-5, PM-5/1520 USER'S GUIDE

TABLE OF CONTENTS

PM-5/1520 ................................................................................................................ 4

OPTICAL HEIGHT METER ................................................................................4

INSTRUCTIONS FOR USE ...............................................................................4

MEASUREMENT OF HEIGHT ...........................................................................5

INSTRUCTIONS FOR USE OF NOMOGRAM ..................................................6

ESTABLISHING THE BASIC DISTANCE .......................................................... 6

PM-5 ......................................................................................................................... 8

OPTICAL READING CLINOMETER ..................................................................8

AVAILABLE PM-5 VERSIONS ...........................................................................9

INSTRUCTIONS FOR USE ............................................................................. 10

NOMOGRAPHICAL HEIGHT CORRECTION .................................................. 15

INSTRUMENT BODY COVER FOR SUUNTO KB-14 AND PM-5 ...................16

PM-5/1520

OPTICAL HEIGHT METER

Suunto Height Meter PM-5/1520 is an instrument for measuring heights, especially heights of trees, with great accuracy and speed. The body of the instrument is corrosion-resistant anodized aluminium-alloy. The scale card runs on a special bearing in a hermetically sealed plastic container filled with a liquid which guarantees that it runs freely and stops quickly. The liquid will not freeze, retains full damping properties in working conditions and eliminates irritating scale vibrations.

INSTRUCTIONS FOR USE

When measured from distances of 15 m a nd 20 m, tree heights can be read straight off the instrument’s scales. The readings should be doubled when measuring from distances of 30 m and 40 m. The Suunto Height Meter can also be used to determine the angle of a gradient. This is done by taking a sighting along the line of a gradient using the 20 m scale on the left of the instrument. The reading obtained can be checked in the conversion table on the back of the instrument to obtain the angle.

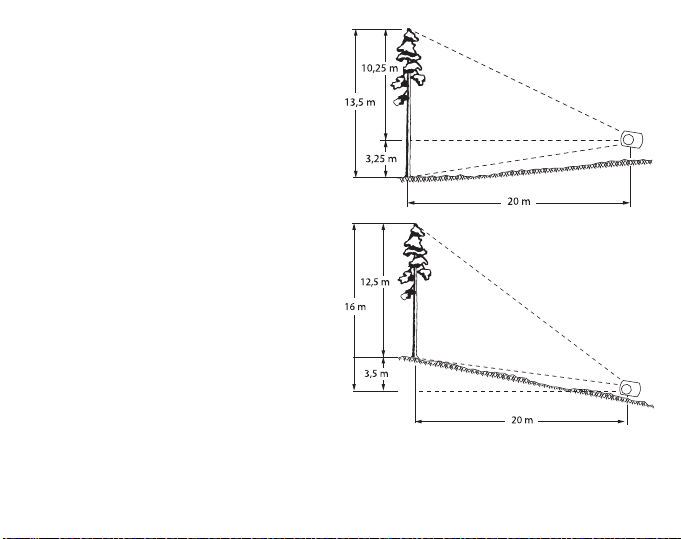
MEASUREMENT OF HEIGHT

The actual measurement of the height of the tree should be done from the distance measured in the following way: the observer sights the top of the tree with both eyes open. The object sighted, the hair line and the scale will all be simultaneously visible in the instrument`s field of vision. As soon as the hairline coincides with the top of the tree, the tree height can be read off (in this example, from the 20 m scale on the left of the instrument). The reading obtained is the height of the tree measured from the eye level of the observer. The base of the tree remains to be sighted. If this is situated below the eye level of the observer, then the actual height of the tree is obtained by adding the two readings together. If it is above the observer`s eye level, the tree height is obtained by taking the difference between the two readings. In fact, in the latter case the distance cannot be measured horizontally. Thus, to get

exactly correct result you have to proceed as stated below. On level ground, the tree top readings is usually sufficient: one only has to add the height of the observer`s eye level (1.60 m in this case), which is already known.

INSTRUCTIONS FOR USE OF NOMOGRAM

If the distance, because of very uneven ground, cannot de determined horizontally as stated above, the nomogram on page 7 should be used.

ESTABLISHING THE BASIC DISTANCE

Because this instrument does not incorporate a prism, the basic distance e.g. 15 m has to be determined using a tape measure along the ground. Take the top and base readings and add or subtract them to get the apparent height. On the nomogram on page 7, locate the apparent height on the right hand scale. On the double scale on the left, locate the reading obtained from sighting the base of the tree. Note that readings for falling and rising gradients should be taken from different sides of the scale. Connect these two points of the nomogram with a straight line. The centre scale of the nomogram now indicates the true height of the tree.

Important notice

Uphill

Base reading

Apparent height

Corrected height

L-20

Downhill

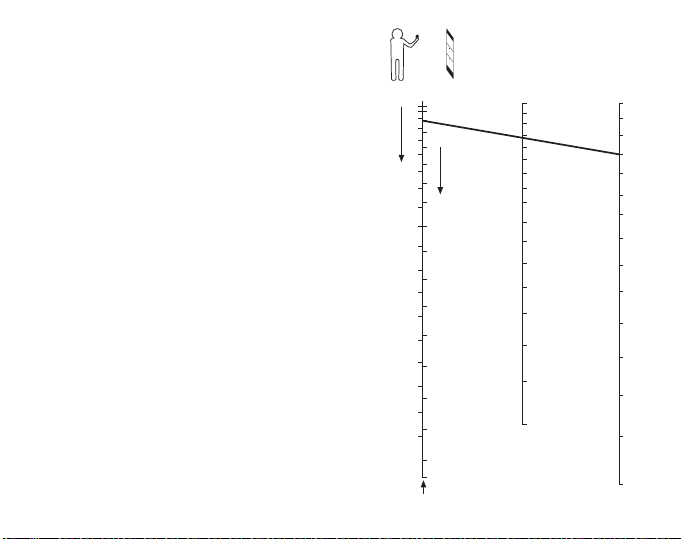
The axes of the eyes of some people are not parallel, a condition called heterophoria. This can even vary in time and be dependent on different factors too. Therefore, in order to be sure that said phenomenon does not affect the accuracy of readings, it is suggested that the user checks this possibility before taking the actual readings as follows: Take a reading with both eyes open and then close the free eye. If the reading does not change appreciably there is no disalignment of the eye axes, and both eyes can be kept open. Should there be a difference in the readings, keep the other eye closed and sight halfway to the side of the instrument body. This will create an optical illusion whereby the hairline continues past the instrument body and is seen against the target.

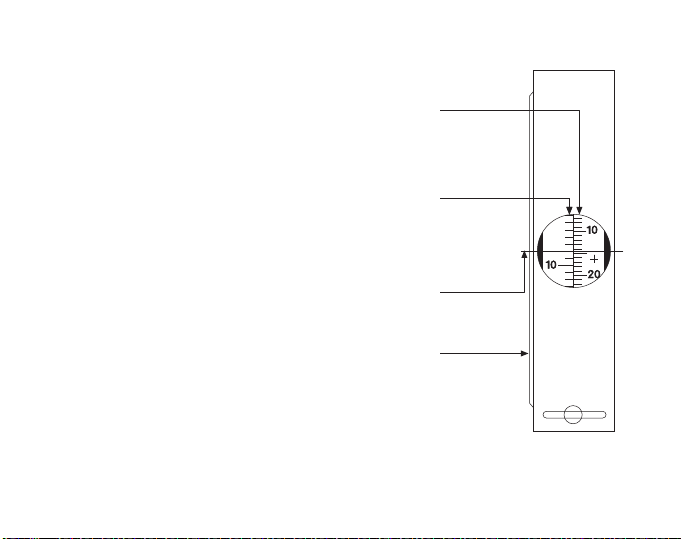
PM-5

+ and – ft. scales

Additional degree scale in side window

Cross-hair extended by optical illusion

+ and – degree scales

OPTICAL READING CLINOMETER

The sturdy pocket-size construction renders the SUUNTO CLINOMETER most suitable for every type of work. Easy for rapid reading through a parallax-free lens is incorporated into the design.

Sighting and scale reading are done simultaneously. There are no screws to turn, no bubbles to center, and nothing to adjust.

Where space is limited, as in geological and mineralogical work, the inclination of strata and other formations can be read placing the instrument along the contour or surface of the formation and reading the angle directly through the side window.

Construction features

The framework is of corrosion resistant light-weight aluminum.

The scale card is supported by a jewel bearing assembly and all moving parts are immersed in a damping liquid inside a high strength hermetically sealed plastic container. The liquid dampens all undue scale vibrations and permits a smooth shockless movement of the scale card.

The material of the container is not attacked by sunlight or water. The liquid does not freeze in the arctic or evaporate in the tropics.

Specifications

Weight: 120 g / 4.2 oz. Dimensions: 74 x 52 x 15 mm / 2 3/4" x 2" x 5/8". The optical scales are graduated in degrees from 0° to ±90°, and 0 % to ±150 %.

A table of cosines is imprinted on the back of the instrument.

Resolution

Can be read directly to one degree or one per cent. Can be estimated to 10 minutes or 1/5 of 1 per cent, the latter naturally applying to readings around the zero level.

AVAILABLE PM-5 VERSIONS

The basic PM-5/360 PC has been modified by fitting it with different scale combinations for special uses. Thus there is available a version with a ”new degree” or grade scale. Here, instead of the normal 360-degree division, the full circle is divided into 400 grades (g). The per cent scale there alongside is normal. The model is PM-5/400 PC.

INSTRUCTIONS FOR USE

Readings are usually taken with the right eye. Owing to differences in the keenness of the sight of the eyes and because of personal preferences the use of the left eye is sometimes easier. It is of prime importance that both eyes are kept open. The supporting hand must not obstruct the vision of the other eye.

The instrument is held before the reading eye so that the scale can be read through the optics, and the round side-window faces to the left. The instrument is aimed at the object by raising or lowering it until the hairline is sighted against the point to be measured. At the same time the position of the hair line against the scale gives the reading. Owing to an optical illusion the hair line (crosshair) seems to continue outside the frame and is thus easily observed against the terrain or the object.

The left-hand scale gives the slope angle in degrees from the horizontal plane at eye level. The right-hand scale gives the height of the point of sight from the same horizontal eye level, and it is expressed in per cent of the horizontal distance. The following example illustrates the procedure:

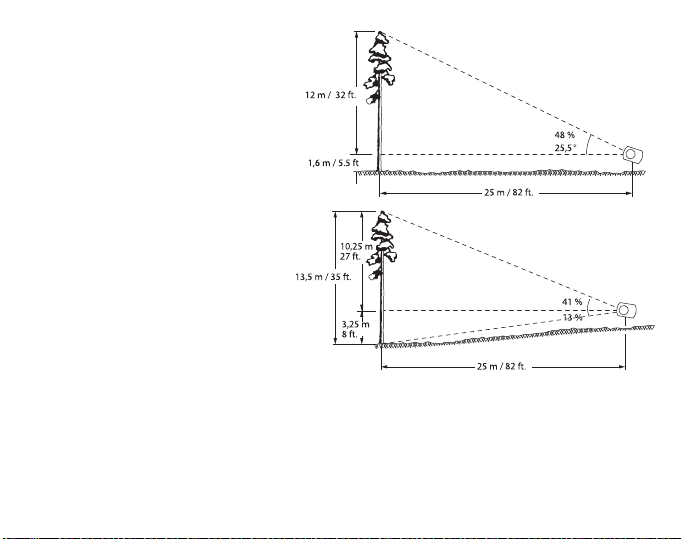
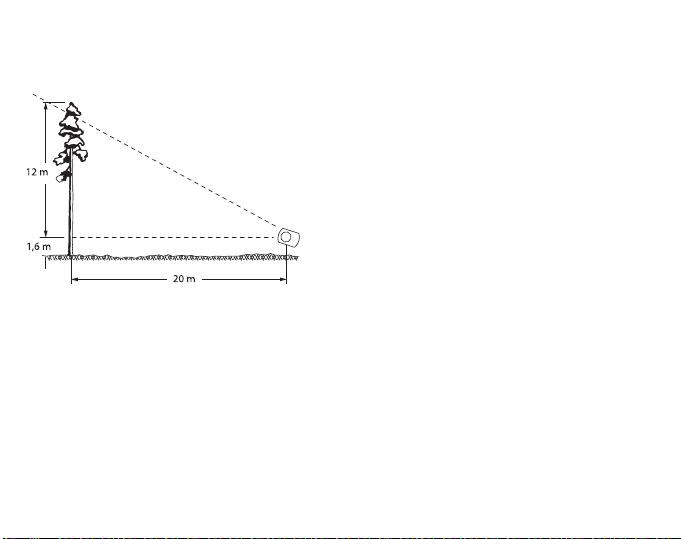
The task is to measure the height of a tree at a distance of 25 m / 82 ft. on level ground. The instrument is tilted so that the hair line is seen against the tree-top (apex). The reading obtained will be 48 per cent (ca

25.5°). As the distance is 25 m / 82 ft. the height of the tree is 48 / 100 x 25 m = ca. 12 m or equally 48 / 100 x 25 m = ca. 12 m or equally 48 / 100 x 82 ft. = ca. 39 ft. To this must be added the eye’s height from the ground, e.g. 1.6 m or 5 ½ ft. Their sum is 13.6 m or 44 ½ ft, the height of the tree.

In very exact measurements, and particularly on sloping ground two readings are taken, one to the top, the other to the base of the trunk. When the trunk base is below eye level the percentages obtained are added. The total height is the sum percentage of the horizontal distance. For example, it the apex reading is 41 % and the ground reading 13 %, the total height of the tree measured from a distance of 25 m / 82 ft. is (41 + 13) / 100 x 25 m = 54 / 100 x 25 m = ca. 13.5 m or equally in feet (41 + 13) / 100 x 82 ft = 54 / 100 x 82 ft = ca. 44 ½ ft.

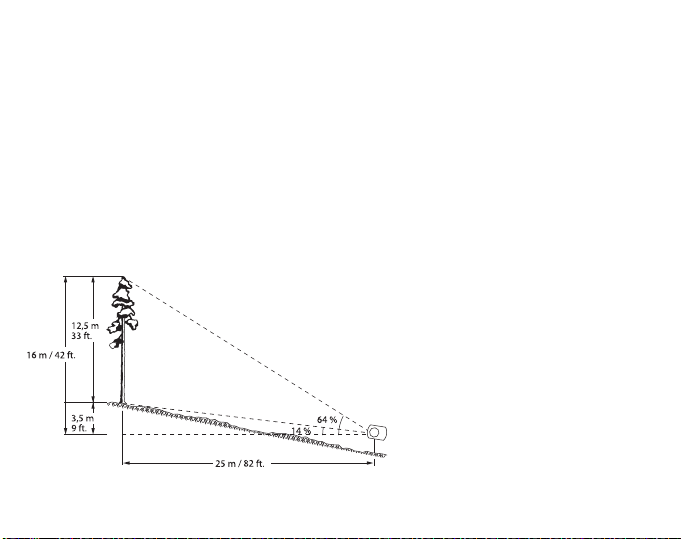
When the trunk base is above eye level, the base reading is subtracted from the apex reading, and the total height is the difference percentage of the horizontal distance.

For example, if the apex reading is 65 % and the base reading 14 %, the total height is (64 – 14) / 100 x 25 m = 50 / 10 0 x 25 m = 12.5 m or equally in feet (64 – 14) / 100 x 82 ft = 50 / 100 x 82 ft = 41 ft. When calculations are made mentally it is advisable to use measuring distance of 50, 100 or 200 m / ft. for the sake of simplicity.

All readings of the percentage scale are based on the horizontal distance. This means that if the distance on sloping terrain is measured along the ground an error is introduced, and this must be corrected for accurate results. The error is insignificant for most purposes at small ground slope angles but increases progressively as the angle increases.

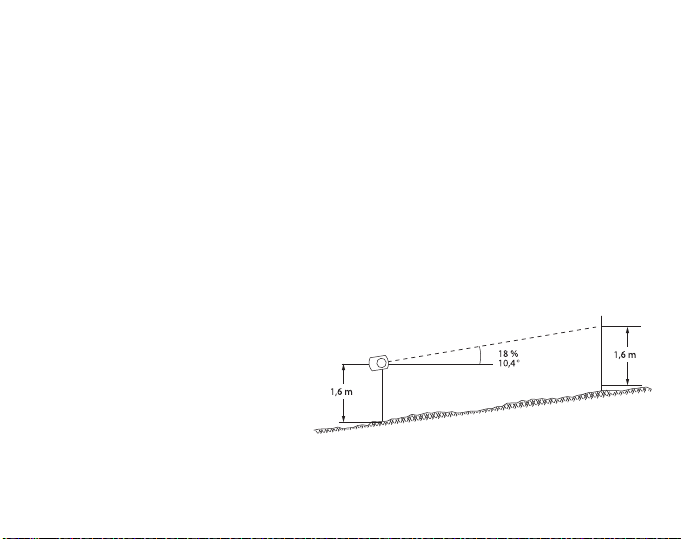
The trigonometrical correlation is

H = h x cos

Where H is the true or corrected height, h is the observed height and α (alpha) is the ground slope angle. With the aid of the above equation the correction can also be made in the distance. In this case h means the distance measured along the ground and H is the horizontal distance sought. If the corrected distance is used no correction in the height observed is needed. When calculating the horizontal distance by using the ground distance and the slope, it must be pointed out that an error is introduced if the slope is measured from eye level to the trunk base. Measuring the slope along the ground would be cumbersome and inconvenient. No error is introduced, however, when the slope angle is measured from eye level to sighting mark made or placed on the trunk at eye level whereby the two lines of measurement become parallel. The true angle of slope is 9 degrees.

The example shown in the following figure illustrates both methods of calculation.

Method 1. Measure the ground distance. This is found to be 25 m / 82 ft. Then measure the slope angle. This is 9 degrees. Read percentages of top and ground points. These are 29 and 23 per cent.

Calculate:

100

-------- -

100

-------- -

100

-------- -=+

100

-------- -

24 6m 12 8m,=,×

100

-------- -

80 9ft 42ft=,×

Take 52 per cent of 25 m / 82 ft. This is 13 m / 42.6 ft. Multiply this by the cosine of 9 degrees.

0.987 x 13 m = 12.8 m or equally in feet 0.987 x 42.6 ft. = 42 ft. Method 2. Multiply the ground distance by the slope angle cosine.

0.987 x 25 m = 24.6 m or equally in feet 0.987 x 82 ft. = 80.9 ft. Add percentage readings as above and take the sum percentage of the corrected

distance.

or equally in feet

This example shows that a slope angle of 9 degrees causes a correction of only

2.3 per cent but when the slope angle is 35 degrees the correction means a reduction of about 18 per cent in the observed height.

NOMOGRAPHICAL HEIGHT CORRECTION

When the nomogram is used, all correction calculation becomes unnecessary. Only a ruler or some other convenient object with a straight edge is nee ded to obtain the nomographical solution. The nomogram is used by placing the ruler so that its edge intersects the angle scale on the left at the slope angle point and the observed height scale (on the right) at the pertinent point. The corrected height (or distance) is read at the point where the edge intersects the corrected height scale in the middle. When using a measuring distance of 100 m / ft. along the ground the corr ection procedure becomes very simple. No slope angle measurement is then necessary. One needs only the reading of the top point and that of the ground point. Depending on the situation their sum or difference gives the apparent height directly in feet. This is then corrected as follows: First, find on the right-hand scale in the nomogram the point indicating the apparent height. Secondly find on the left-hand double scale the point indicating the ground point reading. Thirdly, connect these points. The corrected reading will be found from the pertinent middle scale at the point of intersection. In this procedure the slope angle can be neglected as the left-hand ground point scale has been constructed so that slope angle and the average eye level height of 1.6 m /

5.5 ft. have been taken into account.

INSTRUMENT BODY COVER FOR SUUNTO KB-14 AND PM-5

The instrument body cover is suited to the following KB and PM models: KB-14 (all models) and PM-5.

Suunto PM-5, PM-5/1520 GUIDE DE L'UTILISATEUR

TABLE DES MATIÈRES

PM-5/1520 ................................................................................................................ 4

ALTIMÈTRE OPTIQUE ...................................................................................... 4

MODE D’EMPLOI ............................................................................................... 4

MESURE DES HAUTEURS ............................................................................... 5

MODE D’EMPLOI DU NOMOGRAMME ............................................................ 6

DÉTERMINATION DE LA DISTANCE DE BASE .............................................. 6

PM-5 ......................................................................................................................... 8

CLINOMÈTRE À LECTURE OPTIQUE ............................................................. 8

VERSIONS DE PM-5 DISPONIBLES ................................................................9

MODE D’EMPLOI ............................................................................................. 10

CORRECTION DE LA HAUTEUR NOMOGRAPHIQUE .................................. 15

PROTECTION DU CORPS DES KB-14 ET PM-5 DE SUUNTO ..................... 16

PM-5/1520

ALTIMÈTRE OPTIQUE

L’altimètre PM-5/1520 de Suunto est un instrument destiné à mesurer des hauteurs et plus particulièrement des hauteurs d’arbres, avec précision et rapidité. Le corps de l’instrument est en aluminium anodisé résistant à la corrosion. Le disque gradué repose sur un palier spécial dans une capsule en plastique étanche et toutes les parties mobiles sont immergées dans un liquide, ce qui permet au cadran de se déplacer librement et de s'arrêter rapidement. Le liquide ne gèle pas, conserve l’ensemble de ses propriétés d’amortissement dans des conditions de travail et élimine les vibrations irritantes de la calamine.

MODE D’EMPLOI

En cas de mesure d’une hauteur à une distance de 15 ou 20 mètres, trois hauteurs peuvent être lues directement sur l’échelle de l’altimètre. En cas de mesure d’une hauteur à une distance de 30 ou 40 mètres, le chiffre obtenu doit être doublé. L’altimètre de Suunto peut également être utilisé pour déterminer l’angle d’une pente. Pour ce faire, il convient de visualiser la ligne de la pente à l’aide de l’échelle de 20 mètres à gauche de l’instrument. Le relevé obtenu perme ttant d’obtenir l’angle peut être comparé aux chiffres indiqués dans le tableau de conversion situé à l’arrière de l’instrument.

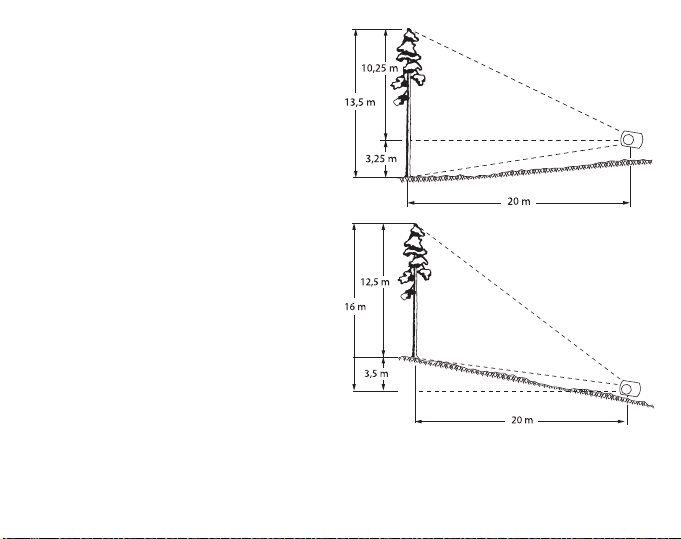
MESURE DES HAUTEURS

La mesure réelle de la hauteur de l’arbre doit être réalisée depuis la distance mesurée comme suit : l'observateur vise la cime de l’arbre en gardant les deux yeux ouverts. L’objet observé, le réticule et l’échelle apparaissent simultanément dans le champ de vision de l’instrument. Dès que le réticule coïncide avec la cime de l’arbre, la hauteur de ce dernier peut être lue (dans cet exemple, à partir de l’échelle de 20 m à gauche de l'instrument). La lecture obtenue correspond à la hauteur de l’arbre mesurée à hauteur des yeux de l’observateur. La base de l’arbre n’est pas observée. Si elle se trouve sous la hauteur des yeux de l’observateur, la hauteur réelle de l’arbre est obtenue en cumulant les deux relevés. Si elle se trouve au-dessus de la hauteur des yeux de l’observateur, la hauteur de l’arbre est obtenue en calculant la différence entre les deux relevés. En fait, dans le

dernier cas, la distance ne peut pas être mesurée horizontalement. Par conséquent, pour obtenir le résultat exact, il convient de procéder comme suit : sur un sol plat, les lectures supérieures de l’arbre suffisent généralement : il suffit d’ajouter la hauteur au niveau des yeux de l’observateur (1,60 m dans ce cas), qui est déjà connue.

MODE D’EMPLOI DU NOMOGRAMME

Si, en raison d’un terrain irrégulier, la distance ne peut pas être déterminée horizontalement comme indiqué ci-dessus, le nomogramme de la page 7 doit être utilisé.

DÉTERMINATION DE LA DISTANCE DE BASE

Étant donné que cet instrument ne comporte pas de prisme, la distance de base, par exemple 15 mètres, doit être mesurée à l’aide d’un ruban d’arpenteur. Prendre les lectures du sommet et du pied et additionner ou soustraire ces valeurs pour obtenir la hauteur apparente. Sur le nomogramme de la page 7, chercher la hauteur apparente sur l’échelle de droite. Sur l´échelle double de gauche, chercher la lecture obtenue en visant le pied de l´arbre. Noter que les lectures des gradients doivent être prises de côtés différents de l’échelle. Relier ces deux points du nomogramme par une ligne droite. L’échelle centrale du nomogramme indique désormais la hauteur réelle de l'arbre.

Remarque importante

L-20

Terrain mountant

Lecture à la base

Hauteur corrigée

Hauteur apparente

Terrain déclinant

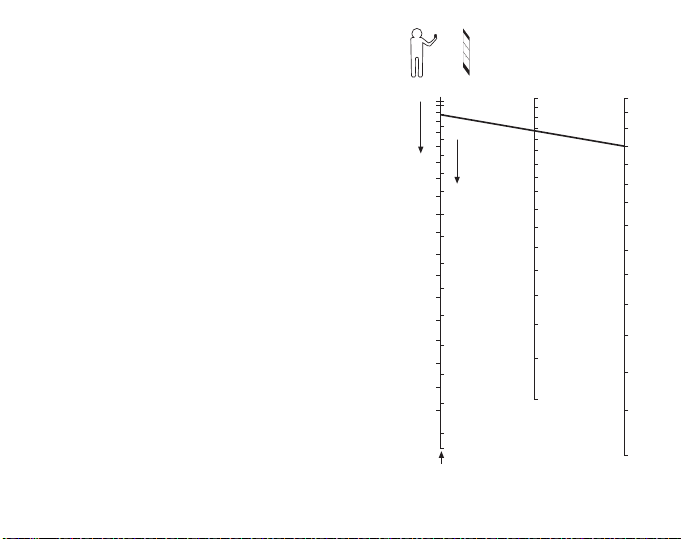
Les axes optiques des yeux de certaines personnes ne sont pas parallèles. Ce phénomène s’appelle hétérophorie. Il peut varier avec le temps et dépend également de plusieurs facteurs. Par conséquent, afin de s´assurer que ce phénomène n’affectera pas la précision des lectures, il est conseillé à l’utilisateur de contrôler sa vue, avant la lecture, en faisant le petit test suivant : commencer par effectuer une lecture en gardant les deux yeux ouverts, puis fermer l’œil libre. Si les lectures ne divergent pas considérablement, c’est que les axes optiques sont alignés, et les deux yeux peuvent donc être tenus ouverts pour prendre des lectures. Si les lectures diffèrent, tenir l’autre œil fermé et viser à mi-chemin en direction du côté du corps de l´instrument, afin de créer une illusion optique, grâce à laquelle le réticule se prolonge au-delà du corps de l'instrument et est visible contre l'objectif.

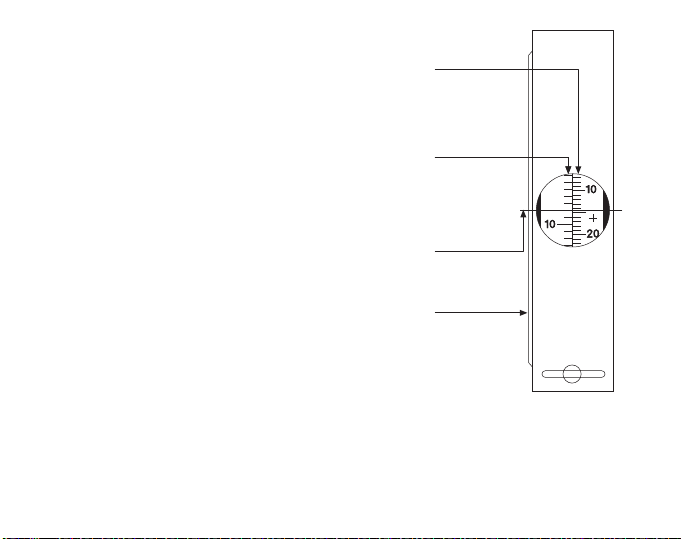
PM-5

Graduation en % +/-

Graduation en degrés +/-

Prolongement du réticule dû à l'illusion optique

Graduation complémentaire en degrés de la fenêtre latérale

CLINOMÈTRE À LECTURE OPTIQUE

Le CLINOMÈTRE de poche SUUNTO est solide, ce qui permet de l’utiliser pour tout type de travail. Grâce à sa lentille exempte de parallaxe intégrée au design, il permet une lecture facile et rapide.

La visée et la lecture s’effectuent simultanément. L’instrument ne comporte ni vis de fixation, ni niveau, ni besoin de réglage.

En cas d’espace restreint, comme dans les travaux géologiques et minéralogiques, les déclivités et autres formations peuvent être déterminées en plaçant l’instrument le long du contour ou de la surface de la formation ; l’angle est ensuite lu directement à travers la fenêtre latérale.

Caractéristiques de la construction

La structure est en aluminium léger résistant à la corrosion.

Le disque gradué est soutenu par un ensemble de paliers à rubis et toutes les pièces mobiles sont immergées dans une capsule en plastique hermétique et très solide remplie de liquide amortisseur. Le liquide amortit toutes les vibrations excessives de l’échelle et permet un mouvement en douceur et sans à-coups du disque gradué.

Le matériau du conteneur n’est pas agressé par le soleil ou l'eau. Le liquide ne gèle pas dans les conditions arctiques et ne s'évapore pas sous les tropiques.

Caractéristiques techniques

Poids : 120 g Dimensions : 74 x 52 x 15 mm. Les échelles optiques sont graduées en degrés, de 0° à ±90° et de 0 % à ±150 %.

Une table de cosinus est imprimée au dos de l’instrument.

Résolution

Elle peut être lue directement selon une précision de 1 degré ou 1 %. Elle peut être estimée avec une précision de 10 minutes ou env. 1/5 de 1 %, ce dernier chiffre s’appliquant naturellement aux lectures autour de zéro.

VERSIONS DE PM-5 DISPONIBLES

Le PM-5/360 PC de base a été développé en plusieurs variantes dotées de différentes combinaisons de graduation pour des usages spéciaux. Par conséquent, une version comportant une graduation de ”nouveaux degrés” ou grades est maintenant disponible. Ici, plutôt que d’observer la division normale en 360 degrés, le cercle complet est divisé en 400 grades (g). La graduation en pourcentage est normale. Le modèle concerné est le PM-5/400 PC.

MODE D’EMPLOI

Les mesures s’effectuent généralement à l’aide de l’œil droit. En raison des différences d’acuité visuelle et des préférences personnelles, il est parfois plus facile d’utiliser l’œil gauche. Il est de la plus haute importance de garder les deux yeux ouverts. La main soutenant l’instrument ne doit pas gêner la vision de l’autre œil.

Tenir l’instrument devant l’œil qui effectue la lecture, de sorte que la graduation soit lisible à travers l’optique et que la fenêtre latérale ronde soit orientée vers la gauche. Orienter l’instrument vers l’objet en le soulevant ou en l’abaissant jusqu’à ce que le réticule soit visible sur le point à mesurer. Parallèlement, lire la position du réticule sur l’échelle pour obtenir la mesure. En raison de l’illusion optique, le réticule (pointeur en croix) semble se prolonger au-delà du cadre et peut donc être observé facilement sur le terrain ou l’objet.

La graduation à gauche indique l’angle de la pente en degrés depuis le plan horizontal à la hauteur des yeux. La graduation de droite indique la hauteur de l’objectif depuis la même hauteur horizontale des yeux et elle est exprimée en pourcentage de la distance horizontale. L’exemple suivant illustre la procédure.

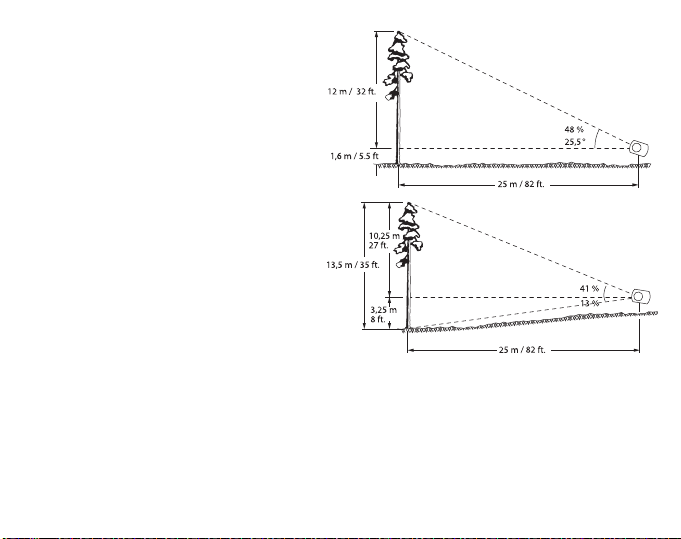
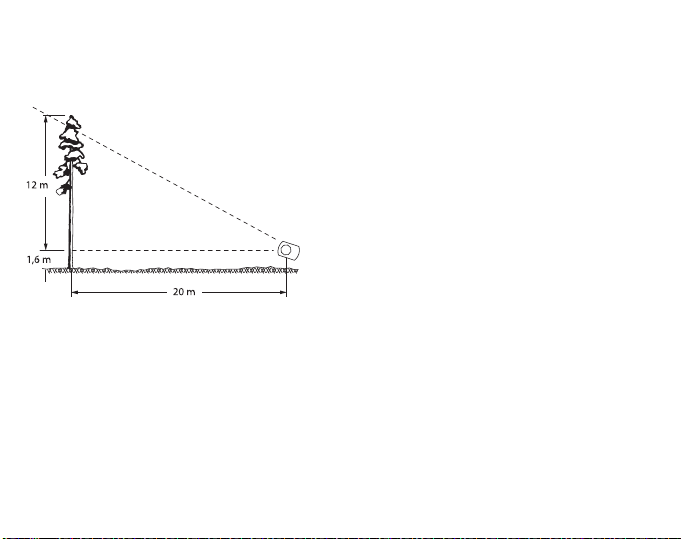
La tâche consiste à mesurer la hauteur d’un arbre situé à une distance de 25 m / 82 pi. sur un sol plat. L’instrument est incliné, de sorte que le réticule soit visible contre la cime de l’arbre (sommet). La lecture obtenue est 48 % (environ 25,5°). Comme la distance est de 25 m / 82 pi., la hauteur de l’arbre est de 48 / 100 x 25 m = env. 12 m, soit 48 / 100 x 25 m = env. 12 m, soit 48 / 100 x 82 pi. = env. 39 pi. À ce chiffre doit être ajoutée la hauteur des yeux depuis le sol, par ex. 1,6 m ou 5 pi.½. La somme de ces chiffres est 13,6 m, soit 44 pi. ½, ce qui correspond à la hauteur de l’arbre.

En cas de mesures très précises et en particulier sur un sol en pente, deux relevés sont réalisés, le premier au sommet et l'autre à la base du tronc. Lorsque la base du tronc se trouve sous la hauteur des yeux, les pourcentages obtenus sont ajoutés. La hauteur totale correspond au pourcentage total de la distance horizontale. Par exemple, si la lecture du sommet est 41 % et la lecture du sol 13 %, la hauteur totale de l’arbre mesurée à une distance de 25 m / 82 pi. est (41 + 13) / 100 x 25 m = 54 / 100 x 25 m = env. 13.5 m, soit (41 + 13) / 100 x 82 pi. = 54 / 100 x 82 pi. = env. 44 ½ pi.

Lorsque la base du tronc se situe au-dessus de la hauteur des yeux, la lecture de la base est soustraite de la lecture du sommet et la hauteur totale correspond à la différence en pourcentage de la distance horizontale.

Par exemple, si la lecture du sommet est 65 % et la lecture de la base 14 %, la hauteur totale est (64 – 14) / 100 x 25 m = 50 / 100 x 25 m = 12,5 m, soit (64 – 14) / 100 x 82 pi. = 50 / 100 x 82 pi. = 41 pi. Pour des raisons de simplicité, lorsque les calculs sont réalisés mentalement, il est conseillé d’utiliser une distance de 50, 100 ou 200 m / pi.

Tous les relevés sur l’échelle des pourcentages sont effectués à partir de la distance horizontale. Cela signifie que si la distance d’un terrain en pente est mesurée au sol, une erreur est insérée et doit être corrigée pour que les résultats soient corrects. Cette erreur est peu importante dans la plupart des cas lorsque les angles sont faibles mais elle augmente progressivement lorsque l’angle s’accentue.

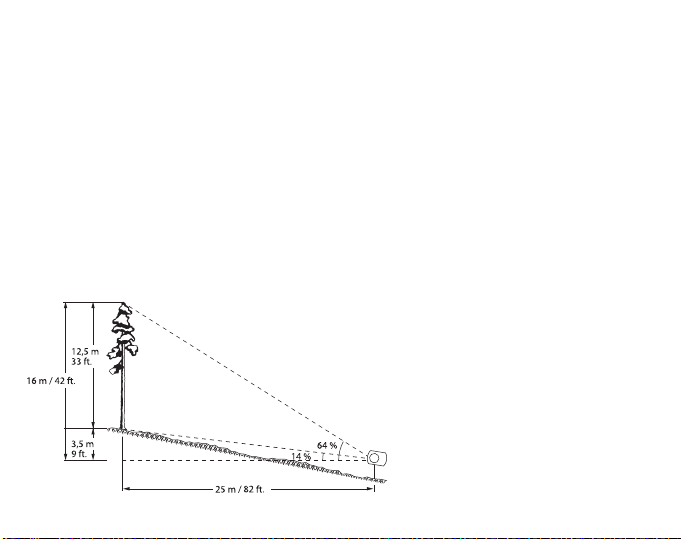
La corrélation trigonométrique est la suivante :

H = h x cos

où H est la hauteur réelle ou corrigée, h la hauteur observée et α (alpha) l’angle de la pente au sol. À l’aide de l’équation précédente, il est également possible de procéder à la correction à distance. Dans ce cas, h correspond à la distance mesurée au sol et H à la distance horizontale recherchée. Si la distance corrigée est utilisée, il n’est pas nécessaire de corriger la hauteur observée. Lors du calcul de la distance horizontale à l’aide de la distance au sol et de la pente, il convient de préciser qu’une erreur est insérée si la pente est mesurée depuis la hauteur des yeux jusqu’à la base du tronc. Il serait gênant et non pratique de mesurer la pente au sol. Toutefois, aucune erreur n’est insérée lorsque l’angle de la pente est mesuré depuis la hauteur des yeux jusqu’au repère indicateur réalisé ou placé sur le tronc à la hauteur des yeux, les deux lignes de la mesure devenant parallèles. L’angle réel de la pente est de 9 degrés.

L’exemple indiqué sur la figure suivante illustre les deux méthodes de calcul.

1ère méthode : mesurer la distance au sol. Elle est égale à 25 m / 82 pi. Ensuite, mesurer l’angle de la pente. Il est de 9 degrés. Lire les pourcentages des points situés au niveau de la cime et du sol. Ils sont de 29 et 23 %.

Calculer :

100

-------- -

100

-------- -

100

-------- -=+

100

-------- -

24 6m 12 8m,=,×

100

-------- -

80 9ft 42ft=,×

Prendre 52 % de 25 m / 82 pi. Cela correspond à 13 m / 42,6 pi. Multiplier ce chiffre par le cosinus de 9 degrés.

0,987 x 13 m = 12,8 m, soit 0,987 x 42,6 pi. = 42 pi. 2ème méthode : multiplier la distance au sol par le cosinus de l’angle de la pente. 0,987 x 25 m = 24,6 m, soit 0,987 x 82 pi. = 80,9 pi. Ajouter le relevé des pourcentages comme indiqué ci-dessus et prendre la somme

des pourcentages de la distance corrigée.

soit

Cet exemple indique qu’un angle de 9 degrés entraîne une correction de 2,3 % seulement mais lorsque l’angle est de 35 degrés, la correction correspond à une réduction d’environ 18 % de la hauteur observée.

+ 78 hidden pages