Sharp W Series User Manual
SCIENTIFIC
SCIENTIFIC
CALCULATOR
CALCULATOR
OPERATION GUIDE
OPERATION GUIDE
<W Series>
C O N TENTS
HOW TO OPERATE
Read Before Using
Key layout/Reset switch 2
Display pattern
Display format 3
Exponent display 4
Angular unit 5
Function and Key Operation
O N /O FF, entry correction keys 6
Data entry keys 7
Random key
Modify key
Basic arithmetic keys, parentheses 10
Percent 11
Inverse, square, cube, xth power of y,
square root, cube root, xth root of y
10 to the power of x, common logarithm 13
e to the power of x, natural logarithm 14
Factorials 15
Permutations, combinations 16
3
8
9
12
Time calculation 17
Fractional calculations 18
Memor y calculations 19
Last answer memory 20
Trigonometric functions 21
Arc trigonometric functions 22
Hyperbolic functions 23
C oordinate conversion 24
Binary, pental, octal, decimal, and
hexadecimal operations (N-base)
STATISTICS FUNCTION
Data input and correction
“AN S” keys for 1-variable statistics
“AN S” keys for 2-variable statistics
1
~
25
26
27
31
H ow to O pe ra te
≈Read B efore Using≈
This operation guide has been written based on the EL-531W , EL-509W , and EL-531W H
models. Some functions described here are not featured on other models. In addition,
key operations and symbols on the display may differ according to the model.
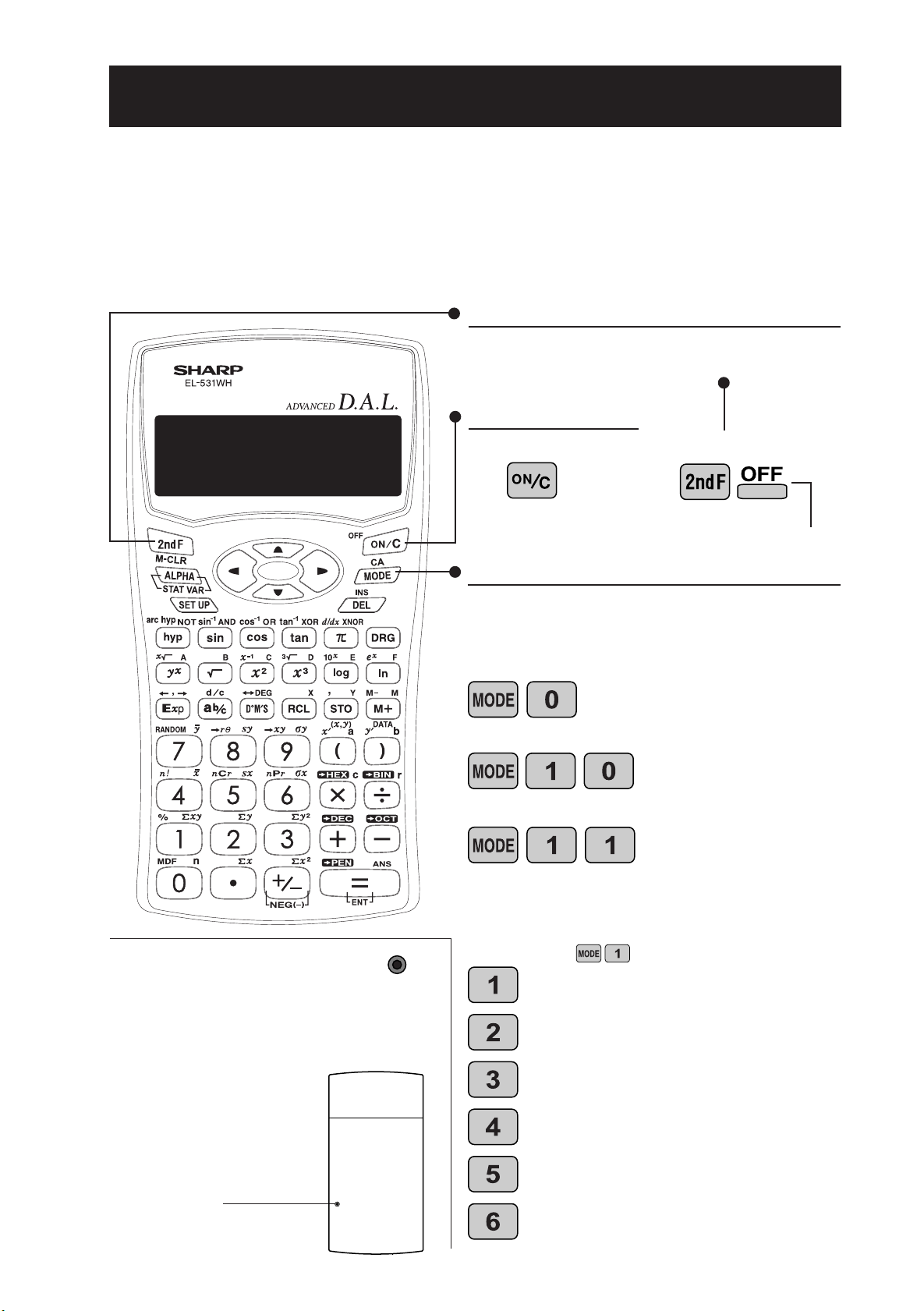
1 . K E Y L AY O U T
2nd function key
Pressing this key will enable the functions
written in orange above the calculator
buttons.
ON/C, OFF key
2 . R E S E T S W I T C H
If the calculator fails to operate normally,
press the reset switch on the back to
reinitialise the unit. The display format
and calculation mode will return to their
initial settings.
RESET
D irect function
<Power on>
Mode key
This calculator can operate in three different
modes as follows.
<Example>
[Normal mode]
[STAT-0 mode]
[STAT-1–6 mode]
W hen changing to the statistical sub-mode,
press the corresponding number key after
performing the operation to select the statistics
mode (press ).
(LINE): Linear regression calculation
(Q UAD): Q uadratic regression calculation
(EX P): Exponential regression calculation
2nd function
<Power off>
W ritten in orange above
the O N/C key
•Mode = 0; normal mode for
performing nor mal arithmetic
and function calculations.
•Mode = 1; STAT- 0 mode for
performing 1-variable statistical calculations.
•Mode = 1; STAT -1–6 mode
for performing 2-variable
statistical calculations.
N O T E :
Pressing the reset switch
will erase any data stored
in memory.
Reset switch
(LOG): Logarithmic regression calculation
(PW R): Power regression calculation
RESET
(IN V): Inverse regression calculation
2
3 . DI S P L AY P AT T E R N
DEG
DEG
DEGFIX
The actual display does not appear like this.
This illustration is for explanatory purposes only.
4 . DI S P L AY F O R M AT A N D
D E C I M A L S E T T I N G F U N C T I O N
For convenient and easy operation, this model can be used in one of four display modes.
The selected display status is shown in the upper part of the display (Format Indicator).
N ote: If more 0’s (zeros) than needed are displayed when the O N /C key is pressed, check
whether or not the calculator is set to a Special D isplay Format.
• Floating decimal point format (no symbol is displayed)
Valid values beyond the maximum range are displayed in the form of a [10-digit
(mantissa) + 2-digit (exponent)]
• Fixed decimal point format (FIX is displayed)
Displays the fractional part of the calculation result according to the specified
number of decimal places.
• Scientific notation (SCI is displayed)
Frequently used in science to handle extremely small or large numbers.
• Engineering scientific notation (ENG is displayed)
C onvenient for converting between different units.
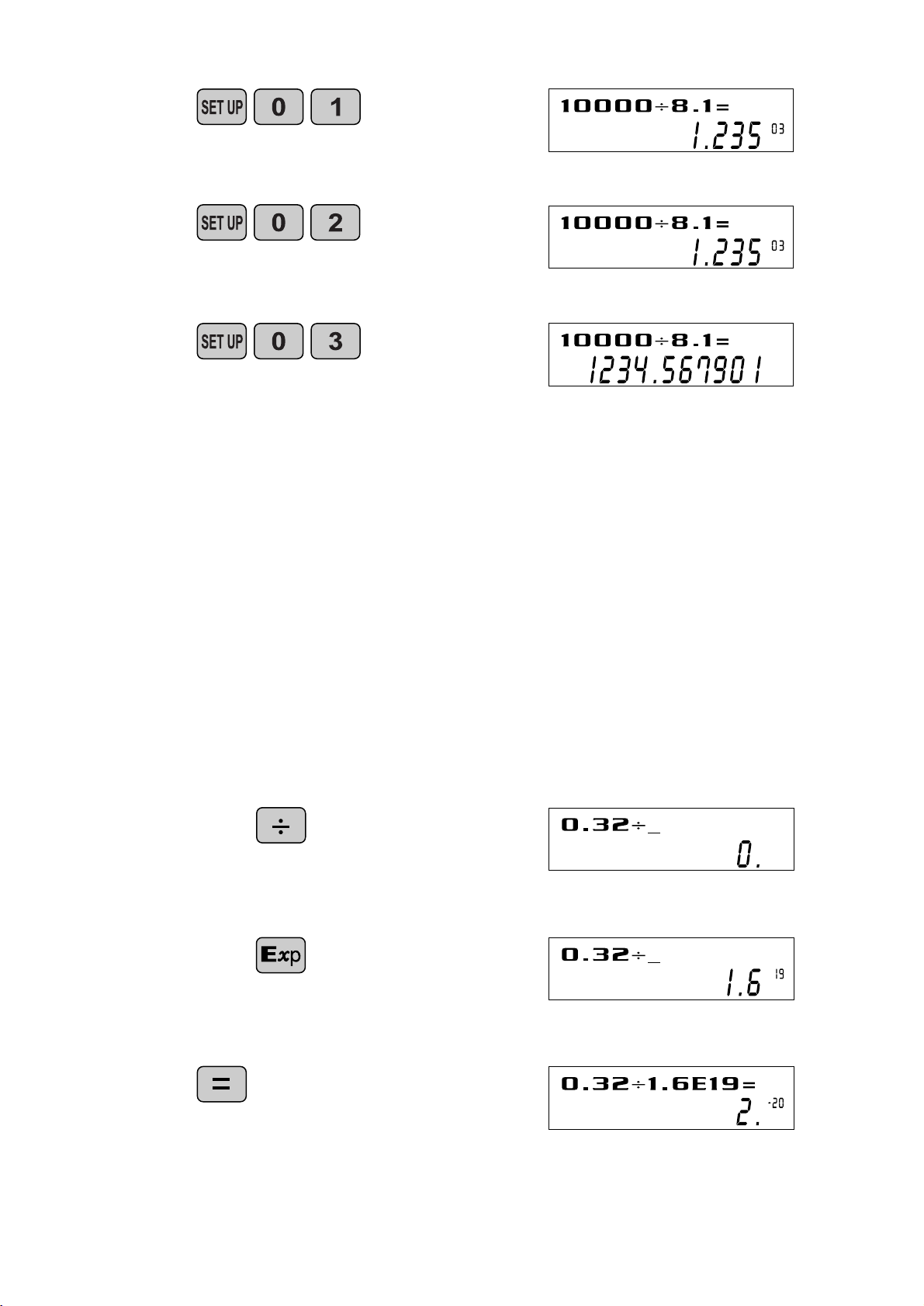
<Example>
Let’s compare the display result of
[10000 8. 1 =] in each display format.
(specifies normal mode)
Initial display
N ote: The calculator has two settings for displaying a
floating point number: N O RM1 (default setting) and
N O RM2. In each display setting, a number is
automatically displayed in scientific notation outside a
preset range:
• N ORM1: 0.000000001 x 9999999999
• N ORM2: 0.01 x 9999999999
10000 8.1
(normal mode)
(FIX mode TAB = 3)
3
SCI DEG
X10
(SC I mode)
ENG DEG
X10
(EN G mode)
DEG
(normal mode)
5 . E X P O N E N T D I S P L AY
The distance from the earth to the sun is approx. 150,000,000 (1.5 x 108) km. Values
such as this with many zeros are often used in scientific calculations, but entering the
zeros one by one is a great deal of work and it’s easy to make mistakes.
In such a case, the numerical values are divided into mantissa and exponent portions,
displayed and calculated.
<Example>
0.32
W hat is the number of electronics flowing in a conductor when
the electrical charge across a given cross-section is 0.32 cou-
DEG
DEG
-19
coulombs).
lombs. (T he charge on a single electron = 1.6 x 10
191.6
X10
DEG
X10
4
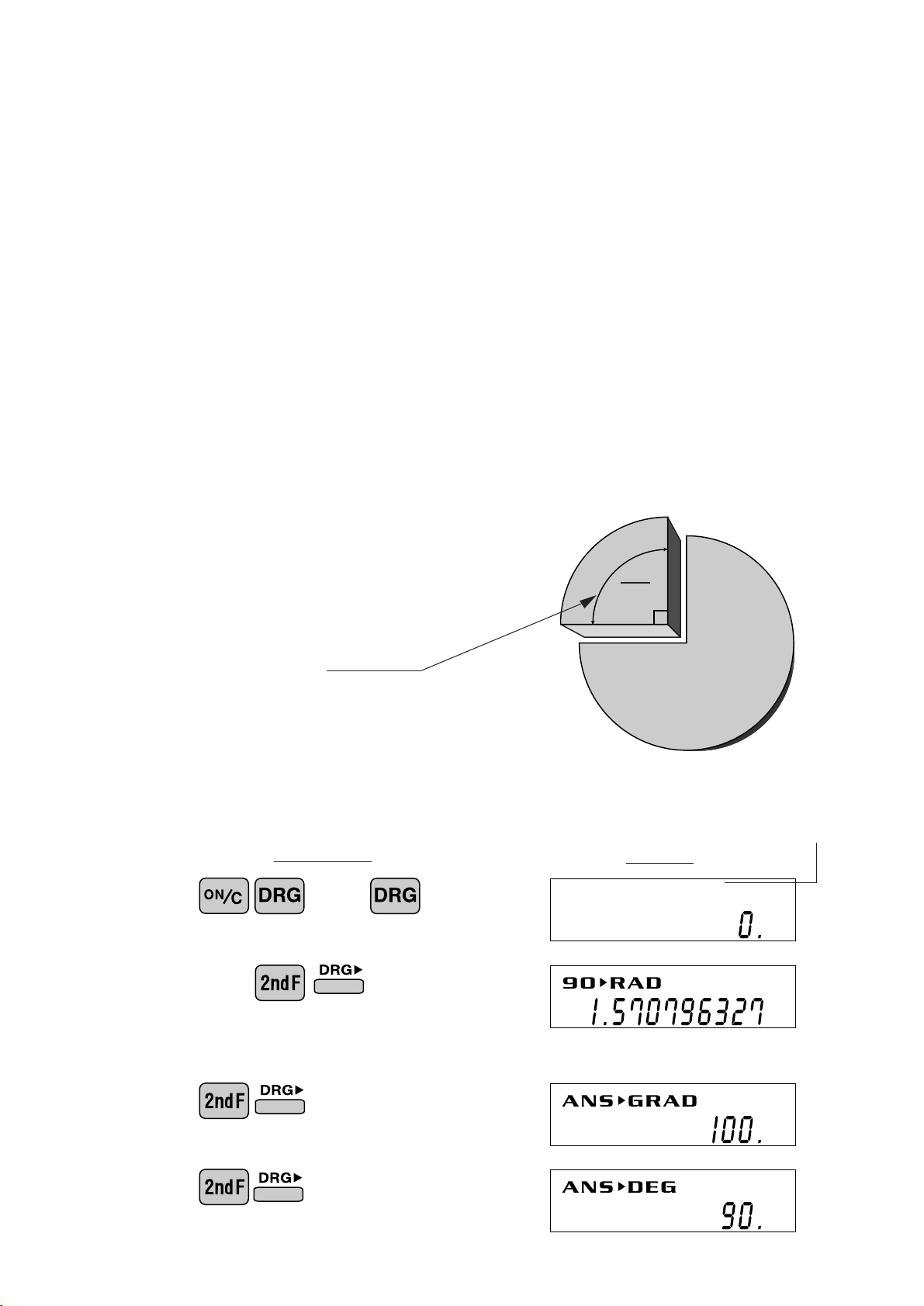
6 . A N G U L A R U N I T
Angular values are converted from D EG to RAD to G RAD with each push of the DRG
key. This function is used when doing calculations related to trigonometric functions or
coordinate geometry conversions.
D egrees ( D E G is shown at the top of the display)
A commonly used unit of measure for angles. The angular measure of a circle
is expressed as 360°.
R adians (R A D is shown at the top of the display)
Radians are different than degrees and express angles based on the circumference of a circle. 180° is equivalent to π radians. Therefore, the angular measure of a circle is 2π radians.
G r ads (G R A D is shown at the top of the display)
Grads are a unit of angular measure used in Europe, particularly in France. An
angle of 90 degrees is equivalent to 100 grads.
The relationships between the three types
of angular units can be expressed as right:
90° (DEG) =
π/2 (RAD) =
100 (GRAD) =
π
2
<Example>
O per ation
(in D EG mode)
90
C heck to confirm 90 degrees equaling π/2 radians
equaling 100 grads. (π=3.14159...)
Angular indicator
D isplay
DEG
••• •••••
RAD
( π /2)
GRAD
DEG
5
≈F unction and K ey Operation≈
ON/OFF, Entry
Correction Keys
Turns the calculator on or clears the data. It also clears the contents of the
calculator display and voids any calculator command; however, coefficients in 3-variable linear equations and statistics, as well as values stored
in the independent memory in normal mode, are not erased.
Turns the calculator off.
C lears all internal values, including coefficients in 3-variable linear equations and
statistics. Values stored in memory in normal mode are not erased.
These arrow keys are useful for Multi-Line playback, which lets you
scroll through calculation steps one by one. (refer to page 8)
These keys are useful for editing equations. The key moves the
cursor to the left, and the key moves the cursor to the right. T he
key deletes the symbol/number at the cursor.
key inserts the symbol/number at the cursor.
6
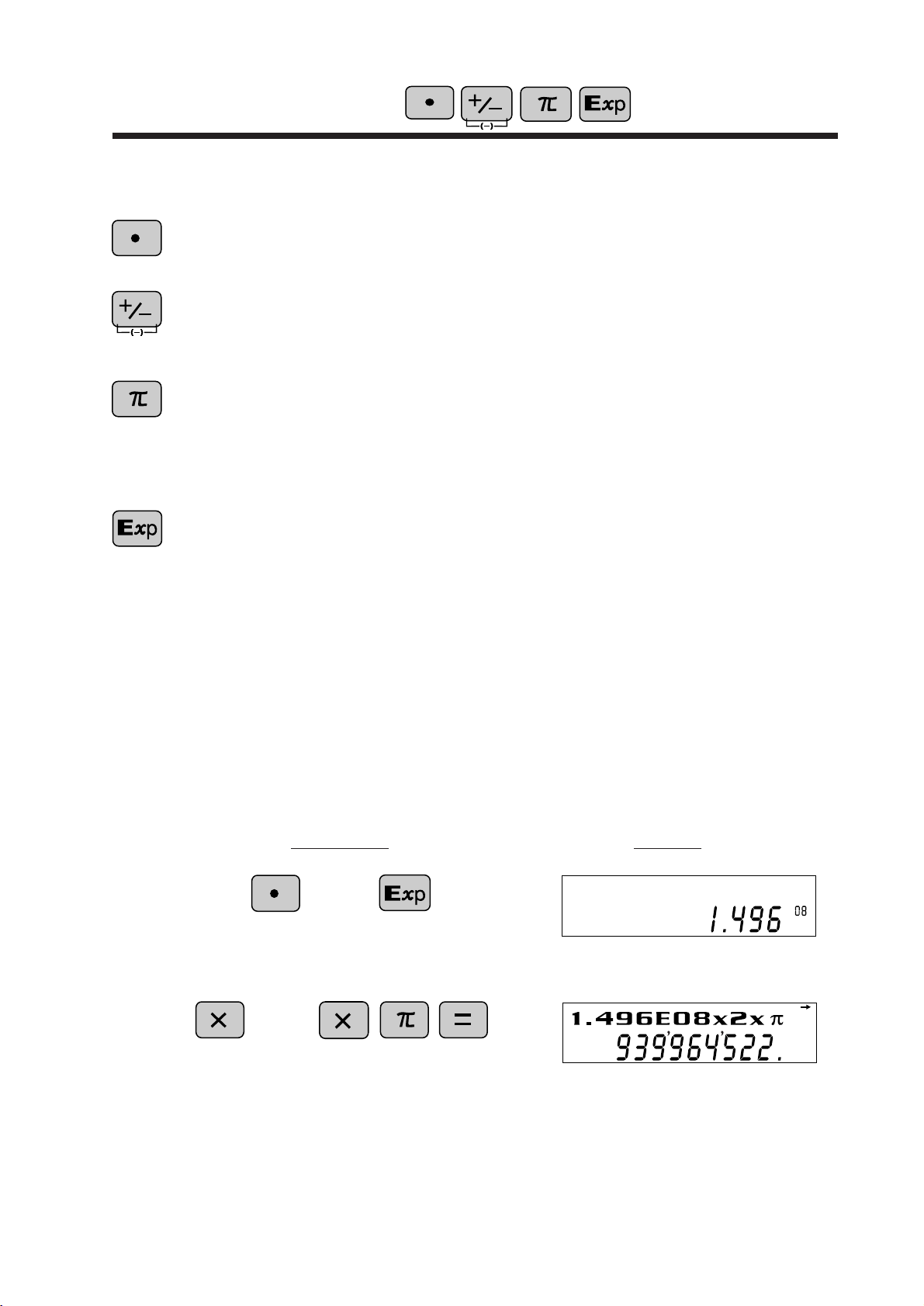
Data Entry Keys
0 to 9
N umeric keys for entering data values.
Decimal point key. Enters a decimal point.
Enters minus symbol or sign change key.
C hanges positive numbers to negative and negative numbers to positive.
Pressing π automatically enters the value for π (3.14159...).
The constant π, used frequently in function calculations, is the ratio of the
circumference of a circle to its diameter.
Pressing this key switches to scientific notation data entr y.
<Example>
Provided the earth is moving around the sun in a circular orbit,
how many kilometers will it travel in a year?
1
* The average distance between the earth and the sun being
1.496 x 10
C ircumference equals diameter x π; therefore,
1.496 x 10
O per ation D isplay
496
8
km.
8
x 2 x π
8
2
DEG
X10
DEG
7
Random
Generates random numbers.
Random numbers are three-decimal-place values between 0.000 and 0.999. Using this
function enables the user to obtain unbiased sampling data derived from random
values generated by the calculator.
<Example>
[ R andom D ice]
To simulate a die-rolling, a random integer between 1 and 6 can be generated by
pressing . T o generate the next random dice number, press .
[ R andom C oin]
To simulate a coin flip, 0 (heads) or 1 (tails) can be randomly generated by pressing
[ R andom Integer]
An integer between 0 and 99 can be generated randomly by pressing .
To generate the next random integer, press .
0. * * * (A random number has been generated. )
. To generate the next random coin number, press .
A PP L IC AT I O N S:
Building sample sets for statistics or research.
8
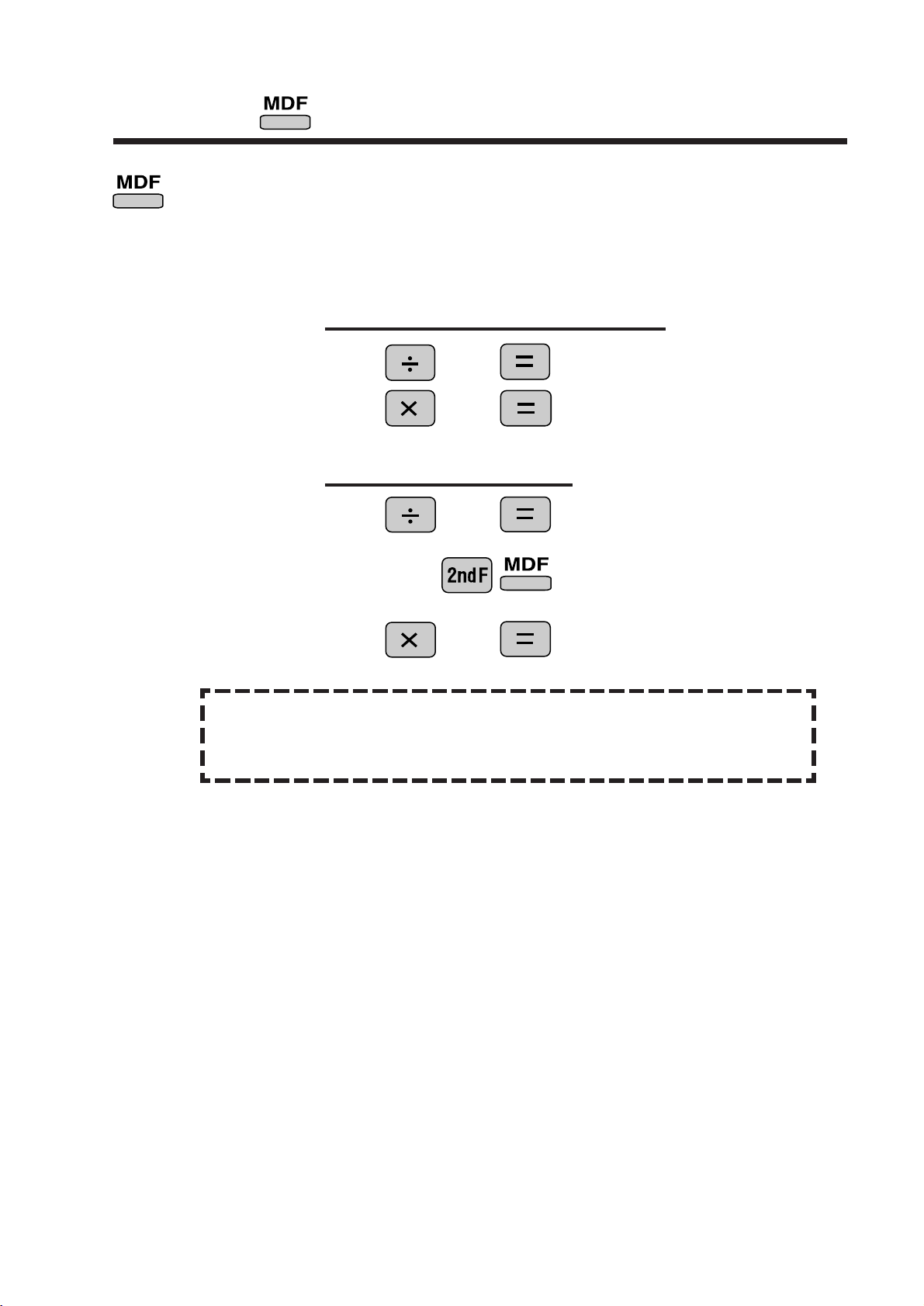
Modify
Function to round calculation results.
Even after setting the number of decimal places on the display, the calculator performs calculations using a larger number of decimal places than that which appears
on the display. By using this function, internal calculations will be performed using
only the displayed value.
<Example>
A PPL IC AT IO N S:
Frequently used in scientific and technical fields, as well as business,
when performing chained calculations.
FIX mode TAB = 1 (normal calculation)
0.6
5
9
9
Rounded calculation (MDF)
5 9
9
(internally, 0 . 6 )
(internally, 0. 5 55 5 ... )
5.0
0.6
(internally, 0 . 5 55 5 ... )
5.4
9
Loading...