Sharp EL-531RHB Operation Manual

SCIENTIFIC CALCULATOR

TEACHER’S GUIDE

EL-531RH

Contents

Introduction………………………………………………………………………………………………p .2
How to Operate…………………………………………………………………………………p.3
Number of Bowling…………………………………………………………………………………p.4
Down to One…………………………………………………………………………………p.6
Reverse the Order…………………………………………………………………………………p.8
Different Products…………………………………………………………………………………p.10
Sums and Products…………………………………………………………………………………p .12
Target 100……………………………………………………………………………………p.14
Ordering Fractions…………………………………………………………………………………p.16
Addting Fractions…………………………………………………………………………………p.18
Halfway Between…………………………………………………………………………………p.20
Near Integers…………………………………………………………………………………p.22
Reshaping Cuboids…………………………………………………………………………………p.24
Function Tables…………………………………………………………………………………p .26
Palindromes…………………………………………………………………………………p.28
Trial and Improvement………………………………………………………………………p.30
Last Digits…………………………………………………………………………………p.32
A Question and Interest……………………………………………………………………p.34
Getting Even…………………………………………………………………………………p.37

1

Introduction

The use of calculators as a classroom teaching tool is becoming more and more
popular. Contrary to the belief that their use encourages dependency and inhibits
the development of mental skills, research has proven that calculators are highly
unlikely to harm achievement in mathematics and using them can actually improve
the students’ performance and attitude.* Calculators allow students to quickly gen­erate large amounts of data from which patterns can be spotted, and predictions can
be made and tested. This is an important aspect of the dev elopment of mental meth­ods of calculation. Therefore, priority must be given to create new ways to exploit
the potential of the calculator as an effective learning tool in the classroom.

This Teacher’s Guide presents several classroom activities that make use of Sharp
scientific calculators. The purpose of these activities is not to introduce the calcula­tor as a device to relieve the burden of performing difficult calculations, but rather
to develop the students understanding of mathematical concepts and explore areas
of mathematics that would otherwise be inaccessible. Mental methods should al­ways be considered as a first resort when tackling calculations introduced in these
activities. The development of trial and improvement methods ar e supported by the
activities as well. We hope you will find them interesting and useful for reinforcing
your students’ understanding of mathematical concepts.

* Mike Askew & Dylan Williams (1995) Recent Research in Mathematics Education HMSO

2

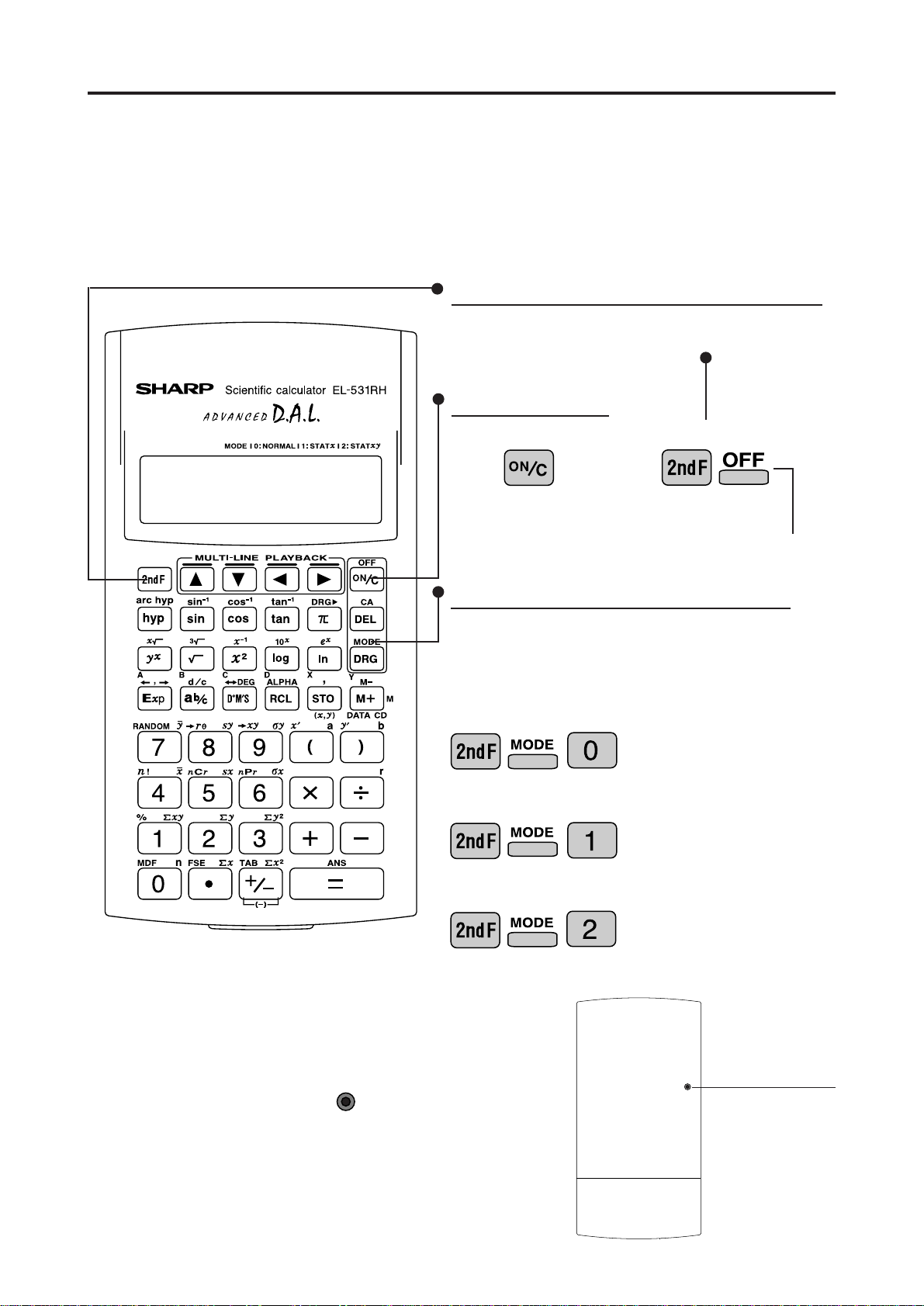
≈Read Before Using≈

1. KEY LAY OUT

How to Operate

2nd function ke y

Pressing this key will enable the functions written
in yellow above the calculator buttons.

ON/C, OFF key
Direct function

<Power on>

2nd function

<Power off>

Written in yellow
above the ON/C key

Mode ke y

This calculator can operate in three different
modes as follows.

<Example>

[Normal mode]

[STAT-1 mode]

•Mode = 0; normal mode for
performing normal arithmetic
and function calculations.

•Mode = 1; STAT-1 mode for
performing 1-variable
statistical calculations.

[STAT-2 mode]

RESET

2. RESET SWITCH

If the calculator fails to operate normally, press the reset
switch on the back to reinitialise the unit. The display format
and calculation mode will return to their initial settings.

NO TE:

Pressing the reset switch will erase any data stored in memory.

3

•Mode = 2; STAT-2 mode for
performing 2-variable
statistical calculations.

Reset switch

RESET

Number Bowling

Junior high school

•••••••• •••••••••••••Objective •••••••• •••••••••••••

Read whole numbers and understand that the position of a digit signifies its value.
Understand and use the concept of place value in whole numbers.

• •••••••• ••••••Explanation of the activity ••••• •••••••••

Think of a 3-digit number and enter it into your calculator.
Pretend each digit is a “bowling pin.”
Knock down each pin one at a time, so that your calculator display shows 0.

A: Using subtraction
B: Using addition

• •••• • ••••• ••• •••Using the calculator • • • •••••••• • • ••••

Calculator functions used: Subtraction, addition, last answer memory

A: Using subtraction

Press the following buttons and then start operation.

(1) Enter a 3-digit number.

638

(2) Knock down one digit, or “pin”; i.e. change the last

digit to a 0.

8

(3) Knock down the next pin; i.e. change the tens column

digit to 0.

30

638=

ANS-8=

ANS-30=

DEG

DEG

DEG

(4) Knock down the pin of the hundreds column.

600

4

ANS-600=

DEG

Number Bowling

B: Using addition

Press the following buttons and then start operation.

Junior high school

(1) Enter a 3-digit number.

638

(2) Knock down one digit, or pin; i.e. change the last digit

to a 0, except this time, do so by adding a number to
the last digit to make it 0.

2

(3) Knock down the next pin; i.e. change the tens column

digit to 0.

60

(4) Knock down the pin of the hundreds column.

300

638=

DEG

DEG

ANS+2=

DEG

ANS+60=

DEG

ANS+300=

• • • • • • • • • • • Using the activity in the classroom • • • • • • • • • • •

This activity is a good game for students to play in pairs.
One student enters a number in the calculator, and the other student has to knock each digit, or
“pin,” down.

Example:

638 - 8 = 630
630 - 30 = 600
600 - 600 = 0

•••• ••• ••• ••• ••Points for students to discuss • • • ••••• •• ••••

It is important for students to talk about what they are doing and use the appropriate language, for
example: “six hundred and thirty, minus thirty, equals six hundred.” Students should be challenged
to vary the starting point; i.e. sometimes starting with the hundreds digit and sometimes with the
tens digit.

Further Ideas

• Play the game using 2-, 4-, or 5-digit numbers according to the ability of the students.

5

Down to One

Junior high school

•••••••• •••••••••••••Objective •••••••• •••••••••••••

Develop a variety of mental methods of computation.
Develop the use of the four operations to solve problems.
Use sequence methods of computation when appropriate to a problem.
Estimate and approximate solutions to problems.

• •••••••• ••••••Explanation of the activity ••••• •••••••••

Use the calculator to generate a 3-digit random number.
The aim is to get the calculator to display the n umber 1.
Players can use any of the numbers 1 – 9 together with any of the keys below:

, , , , , ,

You cannot put numbers together to make 2- or 3-digit numbers.
You can use each number only once.
The first player to get his/her calculator display to show 1 scores five points.
If after an agreed time limit no player has reached 1, the player who is closest scores two points.

While working on this activity, students should develop their skills of mental mathematics and their
fluency with numerical calculations.

• •••• • ••••• ••• •••Using the calculator • • • •••••••• • • ••••

Calculator functions used: Subtraction, division, last answer memory

Press the following buttons and then start operation.

Suppose the random number you generate is 567.

Example A:

567 9

567÷9=

7

ANS÷7=

DEG

DEG

8

The answer is 1 and the game is finished.

ANS-8=

DEG

6

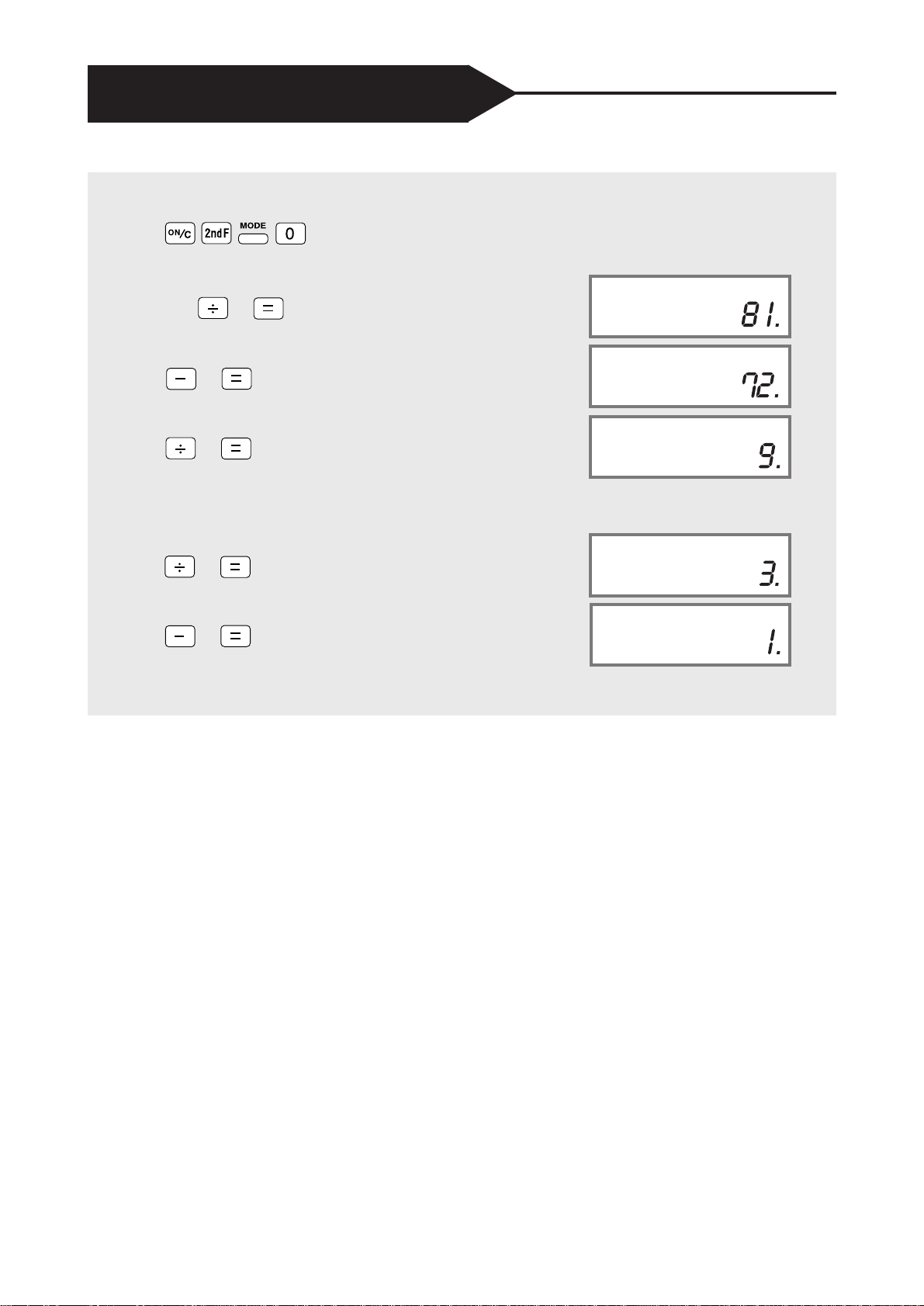
Down to One

Press the following buttons and then start operation.

Junior high school

Example B:

DEG

567÷7=

567 7

ANS-9=

DEG

9

ANS÷8=

DEG

8

You want to subtract 8 from 9, but you cannot since you have already used 8 once.
So...

ANS÷3=

DEG

3

ANS-2=

DEG

2

The calculator displays 1 and the game is finished.

• • • • • • • • • • • Using the activity in the classroom • • • • • • • • • • •

Students should be encouraged to estimate the results of calculations and think about the appro­priate operations and numbers to use during the game. Let’s start with 864, for example. This
number is divisible by 9, 6, 3 and 2. The equation 846 ÷ 9 could therefore be a possible first step.
This will prompt students to test the divisibility of numbers. Students should also be encouraged to
think about the various strategies they use.

The game could be played between small group of students.

•••• ••• ••• ••• ••Points for students to discuss • • • ••••• •• ••••

For some students, it may be more appropriate to start with a 2-digit number. In this case, the calcula­tor should be set to fixed decimal place mode by pressing the [2ndF] key once and then pressing the
[ . ] key, which has FSE written in yellow above it, until FIX is displayed at the top of the calculator
screen. And press [2ndF] [TAB] and [0] keys. Doing this will round answers to 0 decimal places. The
starting number can then be generated by multiplying a random number by 100.

Further Ideas

• Play the game using decimal starting numbers.

• Give the students a shuffled set of cards numbered from 1 to 9 and a shuffled set of
cards numbered 10, 20, 30, 40, 50. Students choose five cards from the first set, and
two cards from the second set. The calculator is then used to generate a random three
digit integer, and the students have to make this total by using the numbers on the cards.

7

Reverse the Order

Junior high school

•••••••• •••••••••••••Objective •••••••• •••••••••••••

Develop a variety of mental methods of computation.
Estimate and approximate solutions to problems.

• •••••••• ••••••Explanation of the activity ••••• •••••••••

Enter any 2-digit number into the calculator.
Reverse the order of the digits through simple calculator operations.

While working on this activity, students should develop their skills of mental mathematics.
They should also be interpreting and generalizing their answers.

• •••• • ••••• ••• •••Using the calculator • • • •••••••• • • ••••

Calculator functions used: Addition, subtraction

Press the following buttons and then start operation.

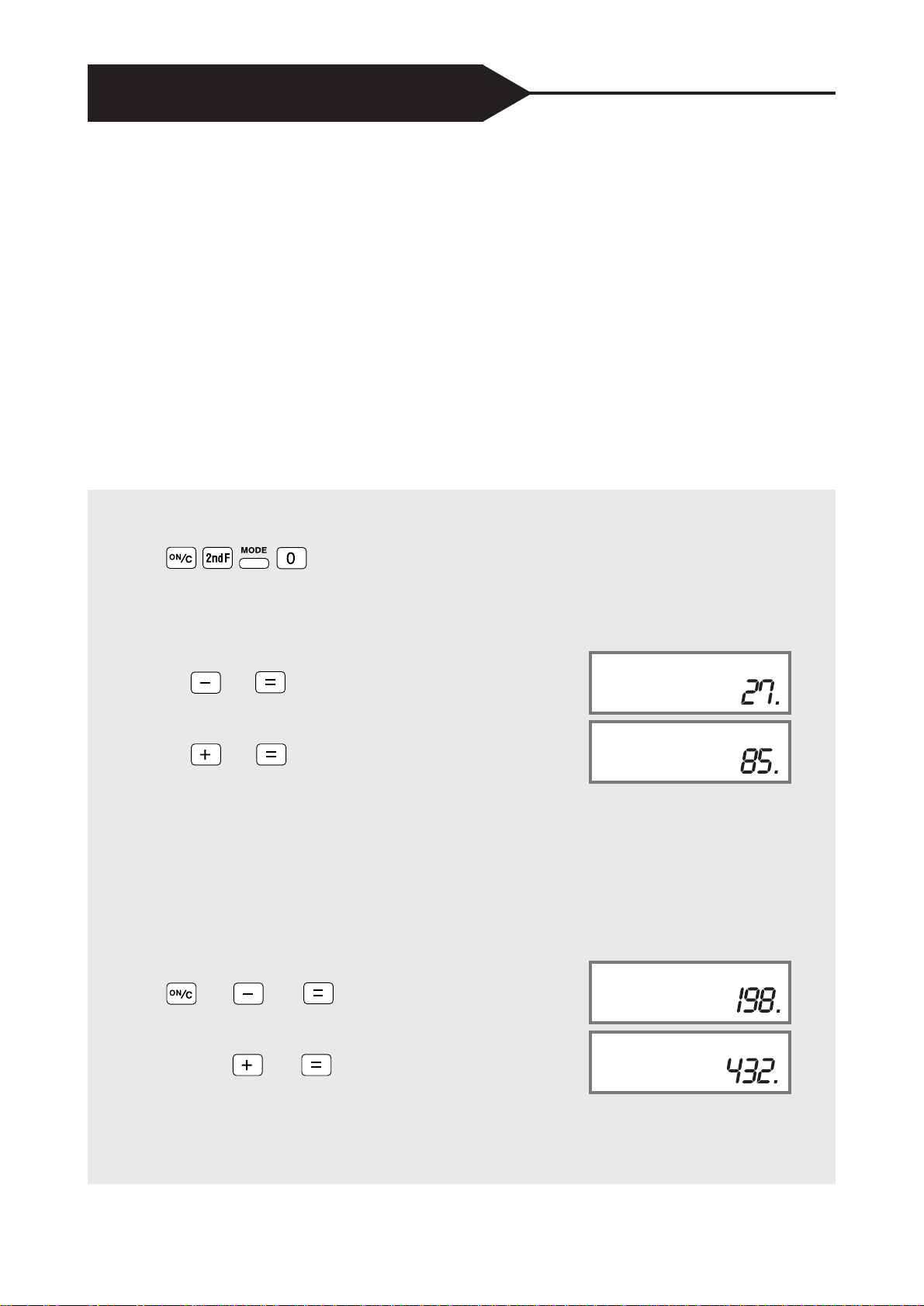
Example A:

To reverse the order of 58:

85

58

58 27

Solution: Add 27 to 58 to get 85.
Now try using a 3-digit number.

Example B:

Enter 432 into the calculator

432

234

234

1

98

85-58=

DEG

DEG

58+27=

DEG

432+234=

DEG

234+198=

Solution: Add 198 to 234 to get 432.

8

Reverse the Order

Junior high school

• • • • • • • • • • • Using the activity in the classroom • • • • • • • • • • •

This activity is probably best introduced orally to a group of students. Ask the students to enter
any two digit number into their calculators. Then, ask them to find a simple way to reverse the
order of the digits of these numbers. Students may do this by using inverse operations.

•••• ••• ••• ••• ••Points for students to discuss • • • ••••• •• ••••

After trying an example, the students can talk about the operations and numbers that they used.
This discussion should lead to the generalization that one way to reverse the order of the digits is
to add or subtract a multiple of 9. More able students could be asked to try and prove this gener­alization:

(10a + b) + N = (10b + a)
N = (10b + a) - (10a + b)
N = 9b - 9a = 9(b - a)

Further Ideas

Try using the activity with 3-digit numbers, 4-digit numbers, etc.
Choose any 2-digit number, reverse it, and then add the reversed number to the original.
What happens? Try this with 3-digit numbers or 4-digit numbers, etc.

9

Different Products

Junior high school

•••••••• •••••••••••••Objective •••••••• •••••••••••••

Estimate and approximate solutions to problems.

• •••••••• ••••••Explanation of the activity ••••• •••••••••

Have the class make up multiplication problems using the digits 1, 2, 3 and 4. Each digit can only be
used once. Find out what the largest product among the possible answers will be.

While working on this activity, students should practice their skills of mental estimation. They
should also be interpreting and generalizing their answers.

• •••• • ••••• ••• •••Using the calculator • • • •••••••• • • ••••

Calculator functions used: Multiplication

Press the following buttons and then start operation.

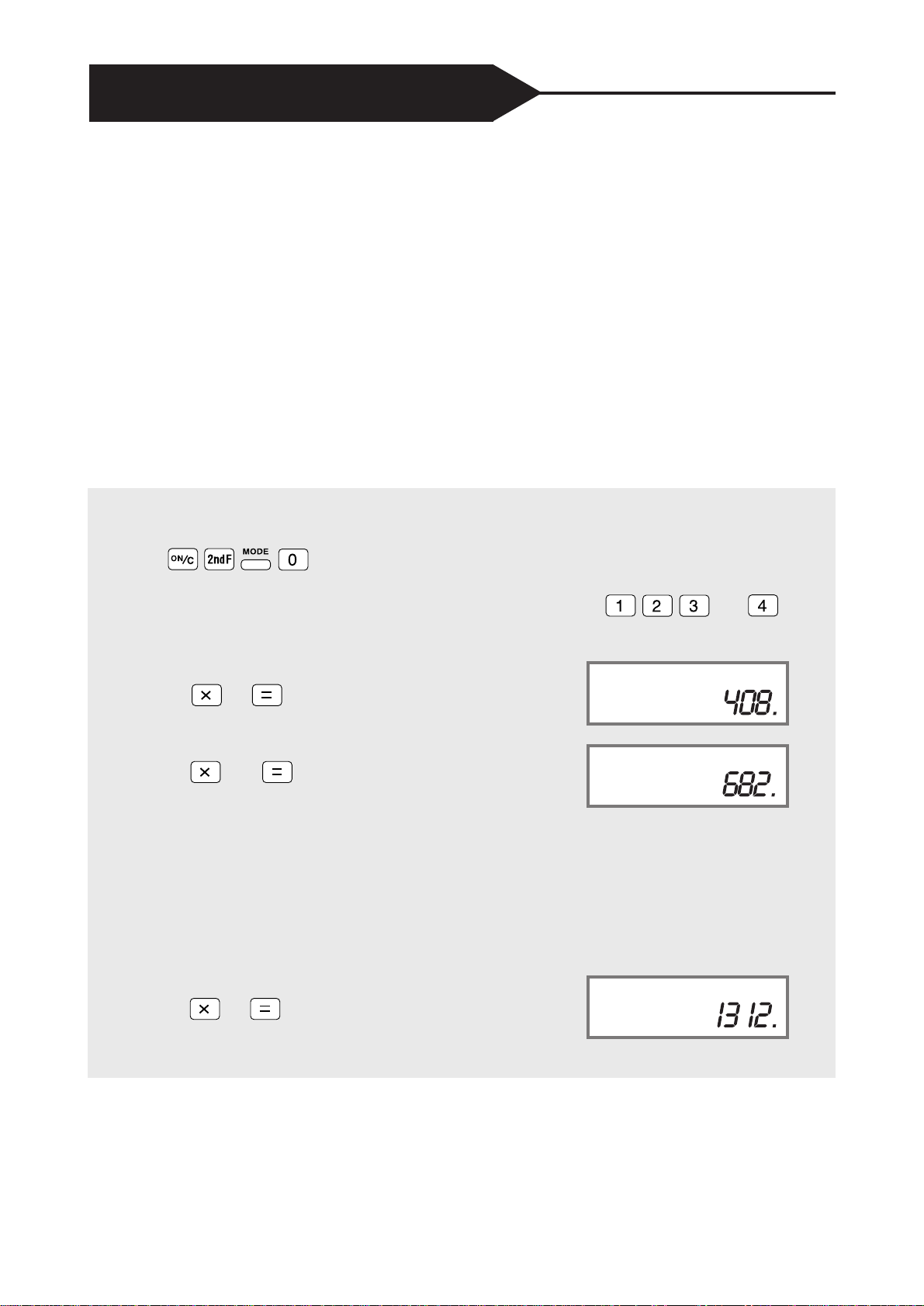
What is the largest number you can make by pressing the keys and
once and only once?

Example:

DEG

DEG

DEG

1

2 34

2 341

Can you make a larger number?
Using algebra, for any four digits a, b, c, d, where
a < b < c < d, the largest product is given by:
(10d + a) x (10c + b).

Ans: The largest product is given by

41 32

12X34=

2X341=

41X32=

10

Different Products

Junior high school

• • • • • • • • • • • Using the activity in the classroom • • • • • • • • • • •

This activity could be introduced to the whole class by asking students to individually make up any
multiplication using only the digits 1, 2, 3 and 4. The different multiplication problems and their
answers can then be compar ed and students can be set the task of finding the largest product.
Students should be encouraged to estimate the answers to the various multiplication problems.

•••• ••• ••• ••• ••Points for students to discuss • • • ••••• •• ••••

Students can explore other sets of four numbers, generalizing the rule to find the largest product
using words or symbols. After generalizing, explain the rule that for any four digits a, b, c, d, where
a < b < c < d, the largest product is given by:

(10d + a) x (10c + b).
If the investigation is extended to the five digits 1, 2, 3, 4, 5, then the largest product is given by:
431 x 52 = 22412.
For some students it may be appropriate to begin with only three digits.

Further Ideas

• Find the largest product for any number of digits.

• Find the smallest product for any number of digits.

• Find the different sums that can be made by adding the digits 1, 2 and 3 once and only
once. For example 12 + 3 = 15. What happens for other sets of 3-digit numbers?

11

Sums and Products

Junior high school

•••••••• •••••••••••••Objective •••••••• •••••••••••••

Calculate with decimals and understand the results.
Select suitable sequences of operations and methods of computation, including trial-and-improve­ment methods, to solve problems involving integers and decimals.

• •••••••• ••••••Explanation of the activity ••••• •••••••••

Choose two numbers whose sum is 10.
Find out what the product of those two numbers would be.
Find the products of other pairs of numbers whose sum is 10.
Find out which number pair gives the largest possible product.

This activity helps to reinforce students’ understanding of the mathematical terms ‘sum’ and ‘prod­uct’ and develops trial-and-improvement methods.

• •••• • ••••• ••• •••Using the calculator • • • •••••••• • • ••••

Calculator functions used: Addition, multiplication, subtraction, parentheses

Press the following buttons and then start operation.

Try to find the largest product of any two numbers whose sum is 10.

Example:

2 8

2 8

You can also calculate this as 2 x (10 - 2) = 16.

2 10 2

What two numbers give the largest product?
Try multiplying various combinations of numbers whose sum is 10.

Ans: 5 x 5 = 25

2+8=

2X8=

2X(10-2)=

DEG

DEG

DEG

12

Sums and Products

Junior high school

• • • • • • • • • • • Using the activity in the classroom • • • • • • • • • • •

This activity could be introduced orally.
The largest product is 25, given by 5 x 5. Some students may need to be encouraged to consider
decimal numbers to verify that the largest product is 25. More able students should be encouraged
to try and prove that this is the largest product.
One method of using the calculator is to enter the product as two numbers that can be edited.
Some students may prefer to enter the product as an expression such as 2 x (10 - 2), which can be
edited.

•••• ••• ••• ••• ••Points for students to discuss • • • ••••• •• ••••

Students could be encouraged to devise similar problems to give to each other involving numbers
with different sums.

Further Ideas

• Investigate products of 3, 4, 5... numbers which have the same sum. This could be explored
graphically.
(Generally, for two numbers whose sum is n, the largest product is given by (n/2)2, for three
numbers whose sum is n, the largest product is given by (n/3)3... The nearest integer to (n/e)
where e = 2.718 is the number of numbers which will give the maximum product.)

• The problem of finding two numbers whose product is a given total can be turned into a
game where students score points according to the number of trials they perform to
identify the solution. For example: The sum of two numbers is 10 and their product is

1

9.71. What are the two numbers?

Ans: The two numbers whose product is 19.71 are 7.3 and 2.7.

13

Target 100

Junior high school

•••••••• •••••••••••••Objective •••••••• •••••••••••••

Understand and use the concept of place value in whole numbers and decimals, relating this to
computation.
Calculate with decimals and understand the results; e.g. multiplying by numbers between 0 and 1.
Mentally estimate and approximate solutions to numerical calculations.

• •••••••• ••••••Explanation of the activity ••••• •••••••••

A game for two players.

• Player 1 enters any 2-digit number into the calculator.

• Player 2 then multiplies this by another number so that the answer is as close as possible to 100.

• Players score points according to how close they are to 100:
within 10 = 1 point
within 5 = 2 points
within 1 = 5 points
exactly 100 = 10 points

• Player 2 then enters a number and the game continues.

• The first player to score 20 points wins.

While working on this activity, students will be extending their understanding of decimals and
improving their estimation skills.

• •••• • ••••• ••• •••Using the calculator • • • •••••••• • • ••••

Calculator functions used: Multiplication

Press the following buttons and then start operation.

Example:

Player 1 enters 28.

28

Player 2 multiplies this by 3.5.

3.5

28X3.5=

DEG

DEG

Player 2 scores two points.
The game continues until one player reaches 20 points.

14

Target 100

Junior high school

• • • • • • • • • • • Using the activity in the classroom • • • • • • • • • • •

This activity could be given to students with little introduction from the teacher. Alternatively, the
game could initially be played between the teacher and a large group of students. It is important
that students are encouraged to think carefully about the numbers they choose and that the
teacher focuses on the students’ mental skills. Most benefit is obtained from the activity when
students are playing together in small teams, discussing their choices of a number to multiply by.

•••• ••• ••• ••• ••Points for students to discuss • • • ••••• •• ••••

At the end of the activity, students’ strategies should be discussed and compared.

Further Ideas

• Play the game with different target numbers. For example, students could multiply or divide

a random number to reach a target of 1.

• The first player multiplies a random number to aim for a target of 100. The second player

then multiplies this answer to try and get even closer to 100. The player who gets the
calculator to display a number between 99 and 101 wins.

15

Ordering Fractions

Junior high school/

Elementary school

(upper grades)

•••••••• •••••••••••••Objective •••••••• •••••••••••••

Understand and use fractions.
Understand the interrelationship between fractions and decimals.

• •••••••• ••••••Explanation of the activity • • • • • •••••••••

Estimate where a given fraction would be located on a numerical line.
Check the answer using the calculator.
While working on this activity, students will be developing their understanding of the relative sizes of
common fractions. The activity suggests an approach to teaching equivalence of common fractions.

• •••• • ••••• ••• •••Using the calculator • • • •••••••• • • ••••

Calculator functions used: Addition, division, fractional calculation

Press the following buttons and then start operation.

You will need a 0 – 2 number line.
Estimate where the following common fractions should be placed on the number line

and then record estimates.

, , , , , , , , ,

Use a calculator and a ruler to check your estimates.

Example A:

Find the value of the fraction .
Using division:

1 2

0

1

2

DEG

1÷2=

Using fractional calculation:

1

2 on the calculator display means .

1 2=

DEG

1 2

Convert to decimal notation.

1 2=

DEG

Example B:

Try the fraction .
Using division:

1 2 5

0

1

2

DEG

1+2÷5=

Using fractional calculation:
To input the fraction :

1

2 5 on the calculator display means .

Convert to decimal notation.

1 2 5

1 2 5=

DEG

16

Ordering Fractions

Junior high school/

Elementary school

(upper grades)

DEG

Convert to a common fraction.

1 2 5=

Try checking these decimal fractions against the estimates you put on the number line.

DEG

1 2 5=

Example C:

Try .
Using division:

0

4 8

Convert to a fraction.
Using fractional calculation, input .

4 8

You can see that = .

Convert to decimal notation.

1

2

DEG

4÷8=

4 8=

DEG

4 8=

DEG

• • • • • • • • • • • Using the activity in the classroom • • • • • • • • • • •

This activity may be introduced orally. The number line could be copied onto an overhead projec­tor transparency or written on the board. Divide students into small groups and give each group a
fraction card. Have the groups discuss where to place their given fraction on the line. Groups then
take turns marking their fractions on the number line. Solutions can be discussed, together with
methods of checking the solutions. This should lead into converting common fractions to
decimal notation, and students can be shown how to do this on the calculator. It is important
that students are aware of the general method of converting common fractions into decimal
notation (dividing the numerator by the denominator), as well as the use of the fraction key
on the calculator.

•••• ••• ••• ••• ••Points for students to discuss • • • ••••• •• ••••

It will be discovered that some of the fractions are equivalent to each other and this leads into the
second part of the activity. When the fraction 4/6 is entered into the calculator, pressing ‘=’ simpli­fies the fraction to 2/3. Students should explore the results of entering different fractions, thus
generating sets of equivalent fractions. It is important that students are encouraged to understand
the concept of equivalence.

Further Ideas

Small groups of students are given a pack of cards with a different fraction on each card. The
group has to sort the cards into sets, so that all the cards in each set are equivalent to each
other.

17

Adding Fractions

Junior high school/

Elementary school

(upper grades)

•••••••• •••••••••••••Objective •••••••• •••••••••••••

Understand and use fractions.
Calculate with fractions and understand the results.

• •••••••• ••••••Explanation of the activity ••••• •••••••••

Using the calculator, find the sum of two given fractions each having 1 in the numerator.
Look for patterns to help understand how to add the fractions without using the calculator.
This activity suggests an approach to teaching addition of common fractions.

• •••• • ••••• ••• •••Using the calculator • • • •••••••• • • ••••

Calculator functions used: Addition, fractional calculation

Press the following buttons and then start operation.

Example:

Using fractional calculation, find the sum of and .

1

2 1 3

+ = on the calculator display means .

Convert to decimal notation.

0.83333··· on the calculator display means .
Find the sums of other common fractions.

1

5 1 7

1 2+1 3=

DEG

DEG

1 2+1 3=

DEG

1 5+1 7=

DEG

1 5+1 7=

18

Adding Fractions

Junior high school/

Elementary school

(upper grades)

• • • • • • • • • • • Using the activity in the classroom • • • • • • • • • • •

This activity should be presented after studying equivalence of common fractions.
The activity is best introduced orally. Ensure that the students know how to add two common

fractions on the calculator. Ask them to add 1/2 and 1/3 and record the answer (5/6). Ask the
students if they can see any connection between the answer and the original two fractions. Stu­dents may note that 2 + 3 = 5 and 2 x 3 = 6. Allow students to explore other unit fractions and
encourage them to generalize. Students should be asked to try and explain what is happening. It
should be noted that the pattern may appear to break down when fractions with a common
denominator are added.

•••• ••• ••• ••• ••Points for students to discuss • • • ••••• •• ••••

Students can then explore what happens when other common fractions are added. For some
students, it may be appropriate to begin by considering a pair of fractions that includes one unit
fraction.

It is important that students are encouraged to understand what is happening, and that reference
is made to equivalent fractions.

Further Ideas

•Investigate subtracting, multiplying or dividing common fractions.

•The Babylonians mostly used fractions which had 1 as the numerator. For example, 5/6

could be written as 1/2 + 1/3. Investigate Babylonian fractions.

19

Halfway Between

Junior high school/

Elementary school

(upper grades)

•••••••• •••••••••••••Objective •••••••• •••••••••••••

Understand and use fractions.
Calculate with fractions and understand the results.

• •••••••• ••••••Explanation of the activity ••••• •••••••••

Use the calculator to find the fraction that is exactly halfway between two other fractions.
Look for patterns to help understand how to find the answer without using the calculator.

This activity reinforces addition of common fractions and considers the result of dividing
common fractions by integers. By working on the activity, students should also develop an
increasing feel for the relative sizes of fractions.

• •••• • ••••• ••• •••Using the calculator • • • •••••••• • • ••••

Calculator functions used: Addition, division, multiplication, fraction, calculation

Press the following buttons and then start operation.

Example A:

Find the fraction that is halfway between and .
Using fractional calculation, obtain the sum of and .

1

2 1 3

Half of this fraction is the number you are looking for, so
divide this fraction by 2.

2

Or after <Display 1>, multiply by .

1 2

1 2+1 3=

DEG

<Display 1>

DEG

ANS÷2=

DEG

ANSX1 2=

Example B:

Find the fraction that is halfway between and .
Using fractional calculation, obtain the sum of and .

1

3 1 4

20

1 3+1 4=

DEG

<Display 2>

Halfway Between

Half of this fraction is the number you are looking for,
so divide this fraction by 2.

2

Junior high school/

Elementary school

(upper grades)

DEG

ANS÷2=

Or after <Display 2>, multiply by .

1 2

Continue the activity using other common fractions.

ANSX1 2=

DEG

• • • • • • • • • • • Using the activity in the classroom • • • • • • • • • • •

This activity could follow the study of addition of common fractions.
The activity is best introduced orally. Ask the students to give different fractions that lie between 5/

1

2 and 2/3. One possibility is to arrange these on a fraction line. It is important that students are
challenged to justify their answers and, in some cases, it may be appropriate to consider decimal
equivalents. The students should then be asked to identify the common fraction that is halfway
between 5/12 and 8/12, justifying their answer.

•••• ••• ••• ••• ••Points for students to discuss • • • ••••• •• ••••

Furthering the activity, students can be asked to give fractions that lie between 1/2 and 1/3 and
identify the common fraction that is halfway between them. At this stage it may be necessary to
discuss methods for finding a number that is halfway between two numbers. Students can then use
their calculators to identify fractions that are halfway between other unit fractions. This can be
extended to non-unit fractions. It is important that students are encouraged to understand what is
happening.

Further Ideas

• Find fractions that lie 1/3 of the way between two fractions, or 1/4 of the way between two
fractions, etc.

21

Near Integers

Junior high school

•••••••• •••••••••••••Objective •••••••• •••••••••••••

Understand and use the concept of place value in decimals.
Understand and use decimals and fractions while comprehending the interrelationship between
them.
Use some common properties of numbers, including multiples.
Give solutions in the context of the problem, selecting the appropriate degree of accuracy and
interpreting the display on a calculator.

• •••••••• ••••••Explanation of the activity ••••• •••••••••

Use the calculator to find fractions that are near integers in decimal form.
While working on this activity, students will be developing their understanding of decimals,

particularly their relationship with fractions.

• •••• • ••••• ••• •••Using the calculator • • • •••••••• • • ••••

Calculator functions used: Multiplication, division

Press the following buttons and then start operation.

The 35th multiple of 0.314 is 10.99.
35 x 0.314 = 10.99

35 0.314

1

0.99 is a ‘near integer’; it is nearly 11.

Using fractional calculation, input .

11 35

Convert to decimal notation.

Using division, divide 11 by 35.
The fraction has a decimal value close to 0.314.

11

35

35X0.314=

DEG

DEG

11 35=

DEG

11 35=

DEG

11÷35=

22

Near Integers

Junior high school

• • • • • • • • • • • Using the activity in the classroom • • • • • • • • • • •

This activity is probably best introduced orally. Students could use the sequence function of the
calculator to generate the multiples of some integers, and could then begin to investigate the
multiples of some decimals.

•••• ••• ••• ••• ••Points for students to discuss • • • ••••• •• ••••

The teacher could ask the students to generate the multiples of 0.314, challenging them to find a
multiple that is nearly an integer. Students can then begin to investigate the situation further.

Further Ideas

• Use this idea to investigate different approximations for π. For example, 22/7 = 3.142857,

whereas π ≈ 3.141593. However, 179/57 = 3.140351.

• Investigate approximations for , or , etc.

23

Reshaping Cuboids

Junior high school

•••••••• •••••••••••••Objective •••••••• •••••••••••••

Reinforce students’ understanding of the equivalence of shapes in various alignments and how this
relates to multiplication within a practical context.
Develop mental skills involving factors, divisors, and systematic thinking.

• •••••••• ••••••Explanation of the activity ••••• •••••••••

1

2 cubes, each with a volume of 1 cm3, may be placed together to create any of four cuboids, each

having a volume of 12 cm3.
Find the equivalent equations for each of the cuboids; for example,

1

x 1 x 12 = 12,2 x 2 x 3 = 12, etc.

• •••• • ••••• ••• •••Using the calculator • • • •••••••• • • ••••

Calculator functions used: Multiplication, Multi-line Playback

Press the following buttons and then start operation.

Introduce students to the calculator’s Multi-line playback feature, which will be useful to
display sets of solutions for each “volume” number.

1X1X12=

DEG

1

1 12

DEG

DEG

2 2 3

1

3 4 etc.

2X2X3=

1X3X4=

Each press of a key takes you one calculation step forward or backward.

1X1X12=

DEG

Display the first calcualtion
with

DEG

2X2X3=

24

1X3X4=

DEG

Reshaping Cuboids

Find the five calculations that represent
cuboids that each have a volume of 30 cm3.

e.g. 1 1 30 etc.
In a similar way, find the twelve calculations for

cuboids each having a volume of 96 cm3.
How many similar calculations must there be

for 180 cm3?
Which of these cuboids is nearest to looking
like a cube?

For volumes betw een 150 cm3 and 200 cm3,
which particular ones can be represented by at
least 16 cuboids each? Which volumes have
the smallest number of cuboids each?

Junior high school

1

x 1 x 12 = 121 x 2 x 6 = 12

2 x 2 x 3 = 12

1

x 3 x 4 = 12

• • • • • • • • • • • Using the activity in the classroom • • • • • • • • • • •

Students may benefit from the use of actual blocks that can be stacked to form the different cubic
combinations. An OHP calculator could also be used to collect solutions from the entire class.

•••• ••• ••• ••• ••Points for students to discuss • • • ••••• •• ••••

The number of divisors for a number expressed as pa x qb x rc (where p, q, and r are all prime) is
(a + 1) (b + 1) (c +1). For example, 360 = 23 x 32 x 51. Here, a = 3, b = 2, and c = 1, so the number
of divisors is given by the expression (3 + 1) (2 + 1) (1 + 1) = 24. Therefore, 360 has 24 divisors.

Further Ideas

•Use trial and improvement to find the side of a cube having a volume of 180 cm3.

•Move into “four (or more) dimensions” as a means of finding the factors of a number.

For example, 6006 = 77 x 78 = (7 x 11) x (6 x 13) = 2 x 3 x 7 x 11 x 13. All stages can
be displayed using the replay function.

25

Function T ables

Junior high school

•••••••• •••••••••••••Objective •••••••• •••••••••••••

Understand and use calculator functions.
Understand and apply functional relationships.
Enable speedy plotting of graphs.

• •••••••• ••••••Explanation of the activity ••••• •••••••••

Use the calculator to calculate the y values for a given function using a set range of values for x.
Record the values on a table and use them to plot a graph.

• •••• • ••••• ••• •••Using the calculator • • • •••••••• • • ••••

Calculator functions used: Multiplication, editing, Multi-line Playback

Press the following buttons and then start operation.

x -5 -4 -3 -2 -1... 5
y -25 -2

1-17-1

3 -9 ...15

Enter the y values for the function y = 4x - 5 using the values from -5 to +5 f or x.
Use the calculator’s playback function to calculate the functions efficiently. After calcu­lating the values, use them to plot the graph of y = 4x - 5.

4X(-5)-5=

DEG

4 5 5

DEG

DEG

DEG

4

4X(-5)-5=

4X(-4)-5=

4X(-4)-5=

4X(-5)-5=

DEG

In the same way, find the values for
x = -3, -2, 1, 0,...5.

Each press of a key takes you
one calculation step forward or backward.

Display the first calcualtion with

26

4X(-4)-5=

...

4X(4)-5=

4X(5)-5=

...

DEG

DEG

DEG

...

...

Function T ables

Junior high school

Return to the calculation for x = 5 and redo the calculation for the equation y = 4x - 3.
Add another line to the table and calculate the values of y for the new equation.
Plot the second graph with the first on the same axis.

What do you notice about the graphs and the numbers in the table?
What do you think will happen if you try another similar equation such as y = 4x - 1,

y = 4x + 1, or y = 4x + 4?
Can you explain the number pattern and the picture you have produced?

• • • • • • • • • • • Using the activity in the classroom • • • • • • • • • • •

This activity should be introduced after practicing substitution.
Start the activity as a whole class so the students can gain confidence in using the calculator and

see the advantages of calculating first and then recording the results to speed up the process of
making the graph table. The students can calculate the y values for the second equation themselves
and quickly continue with other suggested equations using multi-line playback to go directly from
the (x, y) values to the graph without needing to record the result in a table. This enables the
families of graphs to be compared rapidly. Try extending the activity by using graphs with different
gradients to establish the parallel nature of the graphs, and then try keeping the intercept constant
and varying the gradient.

•••• ••• ••• ••• ••Points for students to discuss • • • ••••• •• ••••

The idea of using the playback function as a rapid way to calculate function values can be applied to
a wide range of equations including polynomials, trigonometric functions, etc. Students can do
calculations in one sequence and then use the playback function to go back through the answers
and record or plot them all at once.

Further Ideas

Investigations on graphs can be done more quickly if the playback function is used so each
function does not have to be retyped at every entry. Demonstrate this by using the following
suggestions:

•Solve a quadratic function such as ax2 + bx + c = 0 for varying values of a, b, and c.

•Use the calculator to generate values of a trigonometric function and enter the results

directly onto a graph using the playback function.

27

Palindromes

Junior high school

•••••••• •••••••••••••Objective •••••••• •••••••••••••

Understand and use the concept of place value in whole numbers.
Explore a variety of situations that lead to the expression of relationships.
Construct and interpret formulas and expr essions.
Manipulate algebraic expressions.

• •••••••• ••••••Explanation of the activity ••••• •••••••••

A word that reads the same forwards and backwards, such as “mom” and “level”, is called a palin­drome. A palindromic number is exactly the same; the number has the same value whichever way
you write the digits. For Example, 212, 34543 and 10001.

• •••• • ••••• ••• •••Using the calculator • • • •••••••• • • ••••

Calculator functions used: Division

Press the following buttons and then start operation.

Write down some 4-digit palindromes and use the calculator to divide each of them by 11.

Example:

2332÷11=

2332 11

5665÷K=

5665 11 etc.

Do you notice a pattern?
The use of the playback function will speed up the calculations and enable students to

compare results to look for a pattern.
Make up some more 4-digit palindromes and divide each of them by 11.

Have students compare their results until they notice a pattern.

DEG

DEG

28

Palindromes

Junior high school

• • • • • • • • • • • Using the activity in the classroom • • • • • • • • • • •

This is an activity that can first be given to students to work on and the results later discussed as a
group. The object is to discover a pattern in the results—the pattern being that the answer will
always be a whole number.

•••• ••• ••• ••• ••Points for students to discuss • • • ••••• •• ••••

The pattern may be too obvious for the students to mention, so it may be necessary to give them
the following hint:
Try writing the number in its long form; for example,

2332 = 2 x 1000 + 3 x 100 + 3 x 10 + 2

Further Ideas

• Try to explain the problem using algebra. You could start off by giving the class just the first
line of the calculation below and let them work on the rest individually or in groups.

a b b a = a x 1000 + b x 100 + b x 10 + a

= a x 1000 + a + b x 100 + b x 10
= a (1000 + 1) + b (100 + 10)
= a x 1001 + b x 110
= a 91 x 11 + b x 10 x
= 11 (91a + 10b)

11

• Try the activity using 6-digit palindromes.
Have the class prove that not all 5-digit palindromes are exactly divisible by 11.

29

Trial and Impro vement

Junior high school

•••••••• •••••••••••••Objective •••••••• •••••••••••••

Mentally estimate and approximate solutions to numerical calculations.
Understand and use the concept of place value in decimals and relate it to computation.

• •••••••• ••••••Explanation of the activity ••••• •••••••••

Use “trial and improvement” to find the length of the side of a cube-shaped box that can hold 100
cm3 of ice cream.
The two mental calculations 4 x 4 x 4 = 64 and 5 x 5 x 5 = 125 should suggest a possible starting
calculation such as 4.5 x 4.5 x 4.5 = 91, which can be shortened to 4.53 = 91.
This activity gives students the opportunity to enhance their understanding of decimals and im­prove their skills in estimation.

• •••• • ••••• ••• •••Using the calculator • • • •••••••• • • ••••

Calculator functions used: Multiplication, FSE, TAB

Press the following buttons and then start operation.

Set the calculator to “fixed point” notation with a TAB
value of 0.
(Doing this will display answers to the nearest whole number.)
Adjust the TAB setting to 1 and then continue to improve
the accuracy of the answer

1

4 4 4

5 5 5

4.9 4.9 4.9

•

•

•

4.7 4.7 4.7

DEG

FIX DEG

FIX DEG

4X4X4=

5X5X5=

FIX DEG

4.9X4.9X4.9=

FIX DEG

•

•

•

FIX DEG

4.7X4.7X4.7=

4.6 4.6 4.6

From this we can see the answer lies between 4.6 and

4.7. Continue to search for the answer repeating this
operation.

30

4.6X4.6X4.6=

FIX DEG

FIX DEG

4.642X4.642X

Trial and Impro vement

Junior high school

Switch FSE and TAB to normal display for further operation.

DEG

Press FSE until FIX, SCI, or ENG are not shown on the display.

• • • • • • • • • • • Using the activity in the classroom • • • • • • • • • • •

This activity may be given to students with little introduction or, with the use of the OHP unit, this
or a similar task may be introduced to the whole class followed by individual work on one or more
of the extension activities. The use of the multi-line playback function will be of practical benefit in
tackling questions involving trial and improvement.

•••• ••• ••• ••• ••Points for students to discuss • • • ••••• •• ••••

It will be necessary to familiarize the students with the FSE and TAB keys in order to understand,
for example, why 4.6413 and 4.6423 both have the value 100 to the nearest unit. In the context of
similar problems, students will need to consider what degrees of accuracy are appropriate; in the
case of cubic centimeters of ice cream, possibly only to one decimal place.

Further Ideas

• Find the side of a cubical carton whose volume is 1/2 liter. It may be necessary to remind
students of the equivalence of 500 ml (fluid measure) and 500 cm3 (solid measure).

• Find the dimensions of a fruit juice carton whose sides are in the proportion 1 : 2 : 3 and
whose capacity is 1 liter.

• Find the Golden Ratio x by trial and improvement of the relation

Guess x (Guess + 1) =

Use the playback function on the calculator to show that

x = 1 / (1 + x) and that x = .

1

All metric paper has the same shape (except golden). If A0 has an area of 1 m2 and the longer
side is times bigger than the smaller side, find these dimensions. What are the dimensions
of A4? Have the students confirm their calculations by measuring a sheet.

31

Last Digits

Junior high school

•••••••• •••••••••••••Objective •••••••• •••••••••••••

Use last digits as a means of checking the output of a calculator.
Practice estimation and observe patterns.
Reinforce the concept of prime numbers.

• •••••••• ••••••Explanation of the activity ••••• •••••••••

Perform a series of multiplication equations keeping the last digit of each of the multipliers con­stant; for example, 3 x 7, 13 x 7, 3 x 17, etc.

• •••• • ••••• ••• •••Using the calculator • • • •••••••• • • ••••

Calculator functions used: Multiplication

Press the following buttons and then start operation.

Enter the following equations into the calculator:

3 7

1

3 7

3 17

Find other last digit combinations that give answers ending in 1.
Which of the numbers in the following set can be made from the product of two numbers?

(excluding equations using 1 multiplied by the number itself)
21, 41, 51, 61, 71, 81, 91, 101,
Which of the numbers can be made in more than one way?
Make a collection of your calculations so that they can be displayed in order of answer size.

111, 121, 131, 141, 151, 161, 171, 181, 191

3X7=

13X7=

3X17=

DEG

DEG

DEG

, 20

1

Name the type of numbers that cannot be made.

32

Last Digits

Junior high school

• • • • • • • • • • • Using the activity in the classroom • • • • • • • • • • •

It is probably best to first introduce the activity as a class to give the students an opportunity to
make estimates before using their calculators. Once the class has shared their initial ideas, they can
be given time to inv estigate any patterns they discover.

•••• ••• ••• ••• ••Points for students to discuss • • • ••••• •• ••••

After investigating patterns on their own, students should share their discoveries with the rest of
the class.

Further Ideas

• Examine the first 20 prime numbers. Except for the number 2, they all end with an odd last
digit. Repeat the procedure for the last digits of 3, 7, and 9. Find all the prime numbers

between 1 and 201.

• Find the last digits to:

1

. the answers to the multiplication tables.

2. the square numbers.

3. other number sequences such as the cube numbers and triangle numbers.

• Find the two consecutive numbers whose product is 6006.

33

A Question of Interest

Junior high school

•••••••• •••••••••••••Objective •••••••• •••••••••••••

Understand, use and calculate with percentages.
Select suitable sequences of operations and methods of computation, including trial-and-improve­ment methods, to solve problems involving integers, decimals and percentages.
Give solutions in the context of the problem, selecting an appropriate degree of accuracy, and
interpret the display on a calculator.

• •••••••• ••••••Explanation of the activity ••••• •••••••••

Use the calculator to find solutions to problems involving interest rates.
While working on this activity, students will develop their understanding of percentages within the
context of compound interest situations.

• •••• • ••••• ••• •••Using the calculator • • • •••••••• • • ••••

Calculator functions used: % calculation, multiplication

Press the following buttons and then start operation.

If you invest money at a certain level of interest, by how much will your money grow?

Example:

$100 is invested at 0.1% annual interest.
Using multiplication: Multiply the principal $100 by 1.001.

1

00 1.001

For the total after two years, multiply the previous answer
again by 1.001.

1.001

After three years...

100X1.001=

ANSX1.001=

ANSX1.001=

DEG

DEG

DEG

After four years...

After 10 years, you have approximately $101.

34

ANSX1.001=

DEG

DEG

ANSX1.001=

A Question of Interest

Using the % calculation key: After one year, you should have 0.1% of your
$100.

1

00 0.1

You now have $100.10.

100+0.1%

Junior high school

DEG

DEG

DEG

After two years, you have 0.1% more. 0.1

After three years...

ANS+0.1%

ANS+0.1%

After 10 years...

You have approximately $101.

ANS+0.1%

DEG

• • • • • • • • • • • Using the activity in the classroom • • • • • • • • • • •

This activity is probably best introduced orally. After a discussion about investments and interest
rates, the teacher can use the sequence function of the calculator to generate sequences showing
how an initial capital sum grows for a fixed interest rate. Students can be asked to find the annual
interest rate that ensures their money is doubled in 10 years.
Students can then investigate the annual interest rates that would double their money for different
numbers of years. These interest rates could be plotted on a graph.

5 years

1

0 years 7.2%

1

5 years 4.7%

20 years 3.6%
25 years 2.8%

1

4.9%

•••• ••• ••• ••• ••Points for students to discuss • • • ••••• •• ••••

It may be useful to show students how to generate sequences on the calculator.

Further Ideas

•Investigate interest rates that would triple an investment, or...

•From 1970 to 1980 prices tripled. What was the average rate of inflation?

35

A Question of Interest

Junior high school

For High school Students

How much will your investment be worth in n years?
Let’s make an equation.

The original amount of money invested, called the principal, multiplies each year by the
amount x.
Let’s use this equation to see how much money we have after 100 years.

Press the following buttons and then start operation.

The original amount, or principal, is $100; so a = 100.
The number of years is 100; so n = 100.
The interest is 0.1%; so x = 1.001.

100X1.001^10

1

00 1.001 100

DEG

You have $110.50 after 100 years.
How many years would it take for the money to double?

Let’s make an equation.
The money invested multiplies each year by the amount x.
After n years the money doubles, so...

axn = 2a

Divide both sides by ‘a’ xn = 2
Calculates the ‘log’ of both sides log xn = log2

nlogx = log2
n = log2/logx

If ‘a’ is the money deposited, the savings would double.

2 1.001

It takes approximately 694 years for your money to double.

log2÷log1.00

DEG

36

Getting Even

Elementary school

(upper grade)

•••••••• •••••••••••••Objective •••••••• •••••••••••••

Use some common properties of numbers.
Explore a variety of situations that lead to the expression of relationships.

• •••••••• ••••••Explanation of the activity ••••• •••••••••

A game of chance to compare the relationship between odd and even numbers.
By working on this activity, students will reinforce their understanding of odd and even
numbers. More able students could develop their skills in using algebra to prove generaliza­tions.

• •••• • ••••• ••• •••Using the calculator • • • •••••••• • • ••••

Calculator functions used: Addition

Press the following buttons and then start operation.

A game for two players
The first player enters any number into his/her calculator

without showing it to the other player.
For example, 298.

The second player then enters a number into his/her
calculator without showing it to the other player.
For example, 55.

The players then show each other their numbers and add
them. If the answer is even the first player scores 1 point; if
the answer is odd, the second player scores 1 point.

298 55

The first player to score 10 points is the winner.

DEG

DEG

DEG

298+55=

37

Getting Even

Elementary school

(upper grade)

• • • • • • • • • • • Using the activity in the classroom • • • • • • • • • • •

The game is best played between pairs or small groups of students. It could be introduced by the
teacher playing the game against some students.
While playing the game, students should be encouraged to reflect on whether the game is fair, and
also try and think about the reasons for their conjectures.

Odd + Even = Odd
Even + Odd = Odd
Odd + Odd = Even
Even + Even = Even

•••• ••• ••• ••• ••Points for students to discuss • • • ••••• •• ••••

More able students could try to formally prove their conjectures.
The idea can be extended by students thinking about the conditions for obtaining even or odd
answers when three numbers are added, or four numbers, or...

Further Ideas

More able students could try to formally prove their conjectures.
The idea can be extended by students thinking about the conditions for obtaining even
or odd answers when three numbers are added, or four numbers, or...

38

©SHARP CORP. (MAR. ’99) 0.5E Printed in Japan