PASCO WA-9611, WA-9613 User Manual

Download

Includes

Teacher's Notes

and

Typical

Experiment Results

Instruction Manual and Experiment Guide for the PASCO scientific Model WA-9611, and 9613

SONOMETER

012-03489E

5/95

WA-9613

DRIVER

WA-9611

SONOMETER

WA-9613

DETECTOR

KEEP WEIGHTS AS NEAR TO FLOOR

AS POSSIBLE IN THE EVENT THE

SONOMETER WIRE SHOULD BREAK

CAUTION!

1.75 kg MAXIMUM LOAD ON LEVER

100.5 Hz

012-03489E Sonometer

T able of Contents

Section Page

Introduction ......................................................................................................1

Equipment ........................................................................................................1

Setup and Operation..........................................................................................2

Using the Sonometer and the WA-9613 Driver/Detector Coils:

Sonometer w/WA-9613, Driver/Detector Coils ...........................................3

Sonometer and Driver/Detector w/PASCO Computer Interface ...................4

Power Amplifier w/Series 6500 Computer Interface .................................... 4

Power Amplifier w/CI-6550 or CI-6565 Computer Interface .......................4

Function Generator w/Series 6500 Computer Interface ................................ 5

Function Generator w/CI-6550 or CI-6565 Computer Interface ...................6

Replacing Sonometer Strings ............................................................................7

Theory of Waves on a Stretched String..............................................................8

Experiments:

Experiment 1: Resonance Modes of a Stretched String ........................ 11

Experiment 2: Velocity of Wave Propagation ......................................13

Suggested Research Topics ..............................................................................16

Teacher’s Guide...............................................................................................17

Technical Support ....................................................................Inside Back Cover

Sonometer 012-03489E

Please—Feel free to duplicate this manual subject to the copyright restrictions below.

The PASCO scientific Model WA-9611 Sonometer manual is copyrighted and all rights reserved. However, permission is granted to non-profit educational institutions for reproduction of any part of this manual providing the reproductions are used only for their laboratories and are not sold for profit. Reproduction under any other circumstances, without the written consent of PASCO scientific, is prohibited.

Limited Warranty

PASCO scientific warrants this product to be free from defects in materials and workmanship for a period of one year from the date of shipment to the customer. PASCO will repair or replace, at its option, any part of the product which is deemed to be defective in material or workmanship. This warranty does not cover damage to the product caused by abuse or improper use. Determination of whether a product failure is the result of a manufacturing defect or improper use by the customer shall be made solely by PASCO scientific. Responsibility for the return of equipment for warranty repair belongs to the customer. Equipment must be properly packed to prevent damage and shipped postage or freight prepaid. (Damage caused by improper packing of the equipment for return shipment will not be covered by the warranty.) Shipping costs for returning the equipment, after repair, will be paid by PASCO scientific.

Equipment Return

Should the product have to be returned to PASCO scientific for any reason, notify PASCO scientific by letter, phone, or fax BEFORE returning the product. Upon notification, the return authorization and shipping instructions will be promptly issued.

NOTE: NO EQUIPMENT WILL BE

ACCEPTED FOR RETURN WITHOUT AN AUTHORIZATION FROM PASCO.

When returning equipment for repair, the units must be packed properly. Carriers will not accept responsibility for damage caused by improper packing. To be certain the unit will not be damaged in shipment, observe the following rules:

➀ The packing carton must be strong enough for the

item shipped.

➁ Make certain there are at least two inches of

packing material between any point on the apparatus and the inside walls of the carton.

➂ Make certain that the packing material cannot shift

in the box or become compressed, allowing the instrument come in contact with the packing carton.

Credits

This manual authored by: Clarence Bakken This manual edited by: Dave Griffith Teacher’s guide written by: Eric Ayars

Address: PASCO scientific

10101 Foothills Blvd. Roseville, CA 95747-7100

Phone: (916) 786-3800 FAX: (916) 786-3292 email: techsupp@pasco.com web: www.pasco.com

012-03489E Sonometer

Introduction

The PASCO scientific Model WA-9611 Sonometer is an enhanced version of the classic sonometer. You can perform the standard, qualitative sonometer experiments, varying the tension, length, and linear density of the string and observing the effects on the pitch of the plucked string. Also, you can perform quantitative experiments, verifying the equations for wave motion on a string by adding the WA-9613 Driver/Detector Coils, a function generator capable of delivering 0.5 A of current, and an oscilloscope (or a computer interface and power amplifier) where,

l = wavelength L = length of string

Equipment

The WA-9611 Sonometer comes with the following equipment (see Figure 1):

• Sonometer base with tensioning lever

• Two bridges

• 10 wires (guitar strings), 2 each of the following diameters (linear densities):

— 0.010" (0.39 gm/m) — 0.014" (0.78 gm/m) — 0.017" (1.12 gm/m) — 0.020" (1.50 gm/m) — 0.022" (1.84 gm/m)

Additional Equipment

To perform qualitative experiments, you will also need a mass hanger and no more than 1.75 kg of mass to hang from the tensioning lever.

Bridge

WA-9613

DRIVER

String

WA-9611

SONOMETER

WA-9613

DETECTOR

KEEP WEIGHTS AS NEAR TO FLOOR

AS POSSIBLE IN THE EVENT THE

SONOMETER WIRE SHOULD BREAK

n = number of antinodes V = velocity of wave propagation T = string tension m = linear density of string n = frequency of wave

The driver and detector coil can be placed anywhere along the string. The driver coil drives string vibrations at any frequency your function generator (or computer-compatible power amplifier) will produce. The detector coil allows you to view the vibration of the string on your oscilloscope or computer interface. With a dual trace oscilloscope or a computer interface, you can examine phase differences between the driving frequency and the string vibrations.

Recommended Equipment

If you wish to accurately measure the frequency and wavelength of the string vibrations, you will also need:

• WA-9613 Driver/Detector coils

• CI-6550 or CI-6565 Computer Interface and a Power Amplifier (CI-6552)

• Series 6500 Computer Interface, CI-6508 Input Adapter Box, and a function generator capable of producing 0.5 A

• dual trace oscilloscope and a function generator capable of producing 0.5 A

Optional Equipment (for use with function generator)

• banana plug patch cords and BNC-to-banana adapter (for connecting the function generator to the BNC connector on an oscilloscope)

Tensioning

lever

CAUTION!

1.75 kg MAXIMUM LOAD ON LEVER

Sonometer base

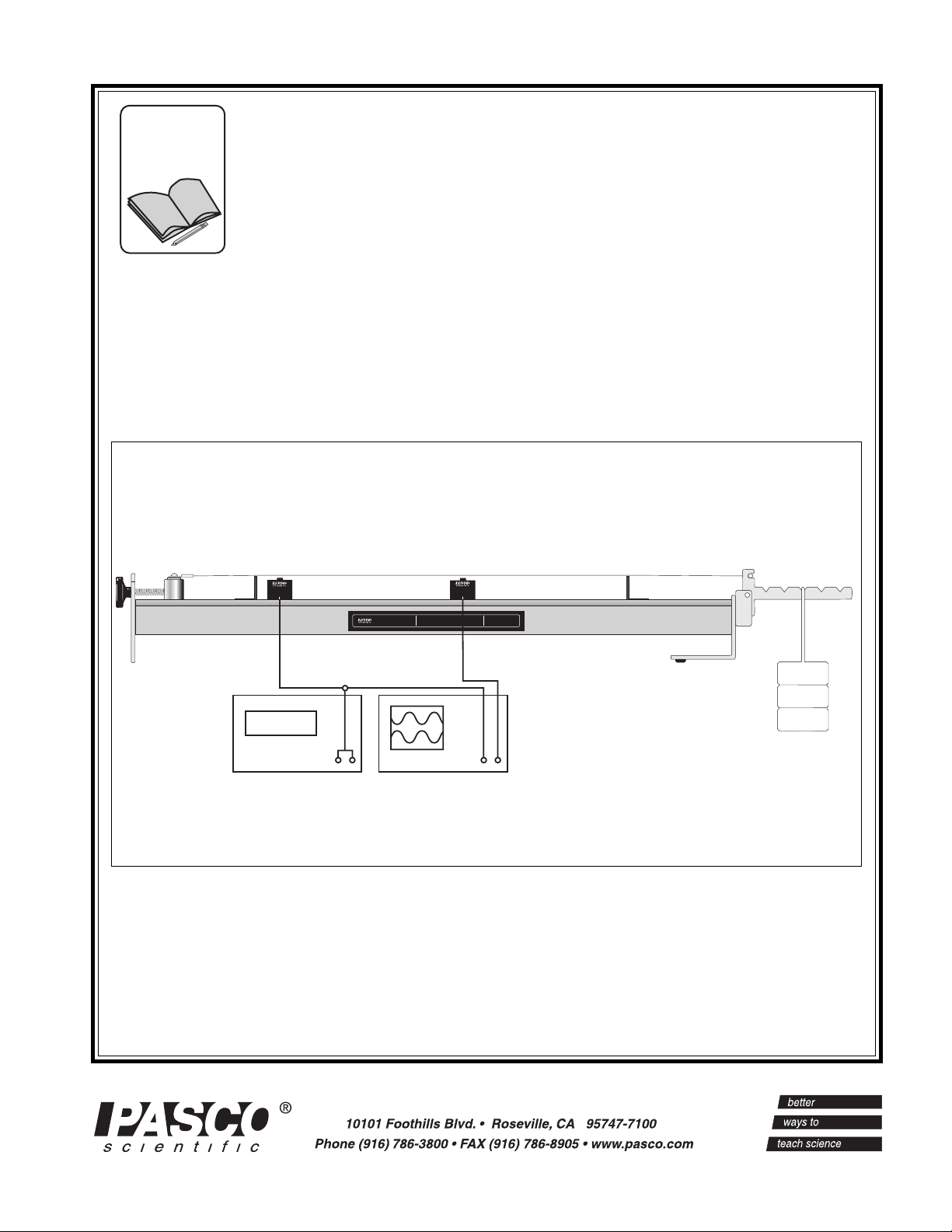
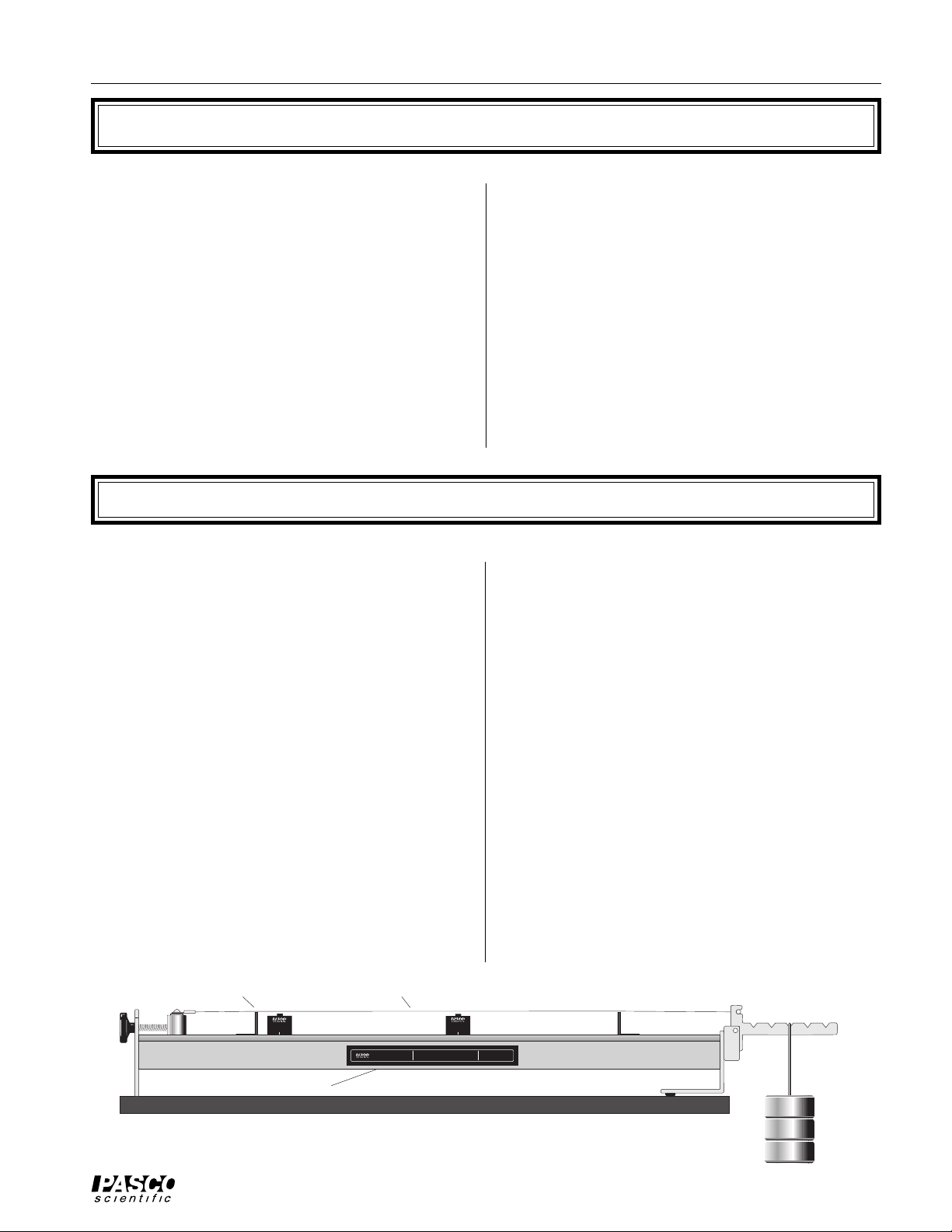
Figure 1 The Sonometer and Suggested Accessories

Sonometer 012-03489E

Setup and Operation

To setup the sonometer (see Figure 2):

➀ Choose one of the ten strings and place the brass

string retainer into the slot on the tensioning lever.

➁ Loosen the string adjustment screw and place the

crimped lug that is attached to the other end of the string over the screw head, as shown.

Crimped lug

Brass string retainer

➂ Tighten the string adjustment screw until the

tensioning lever hangs level.

➃ Place the bridges in any locations you wish, to deter-

mine the length of the string.

➄ Hang a mass (approximately 1 kg) from the tensioning

lever to produce the desired tension, then adjust the string adjustment screw as needed so that the tensioning lever is level. See Figure 3. (The lever must be level to accurately determine the string tension from the hanging mass.)

String tension is determined as shown in Figure 3. If you hang a mass “M” from slot one of the lever, the tension of the string is equal to Mg, where g is the gravitational constant (9.8 m/s

). If you hang the mass from slot two, the tension equals 2Mg; if you hang it from slot three, the tension is 3 Mg, etc.

➅ You can now:

- Vary the tension of the string by hanging the mass from different slots in the tensioning lever. (Always adjust the string adjustment screw so the lever remains level.)

String adjustment screw

Figure 2 Sonometer Setup

String tension (T)

Slot 1 2 3 4 5

Figure 3 Setting the Tension

Tensioning lever

Bridges

5Mg

4Mg

3Mg

2Mg

1Mg

Hanging

Mass

(mass = M)

(weight = Mg)

- Vary the length of the string by adjusting the distance between the bridges.

- Vary the linear density of the string by changing strings.

- Pluck the string to observe how each of these variables effects the resonant frequency.

End plate

String

Adjustment

screw

Aluminum Cylinder

Figure 4 Reversing the End Plates

End plate

012-03489E Sonometer

➤NOTE: At some lab stations, you may want the tensioning lever to hang over the left end of the table instead of the right (see Figure 4). In this case, you can switch the end plates so that, when performing the experiment, the metric scale will still be right side up. To switch the endplates:

➀ Loosen the string adjustment screw and remove

the string.

➁ Unscrew the two screws that hold each end plate

onto the sonometer and remove the end plates.

➂ Slide the aluminum cylinder out of the slot. ➃ Slide the cylinder into the slot on the other end

of the sonometer, then switch the end plates.

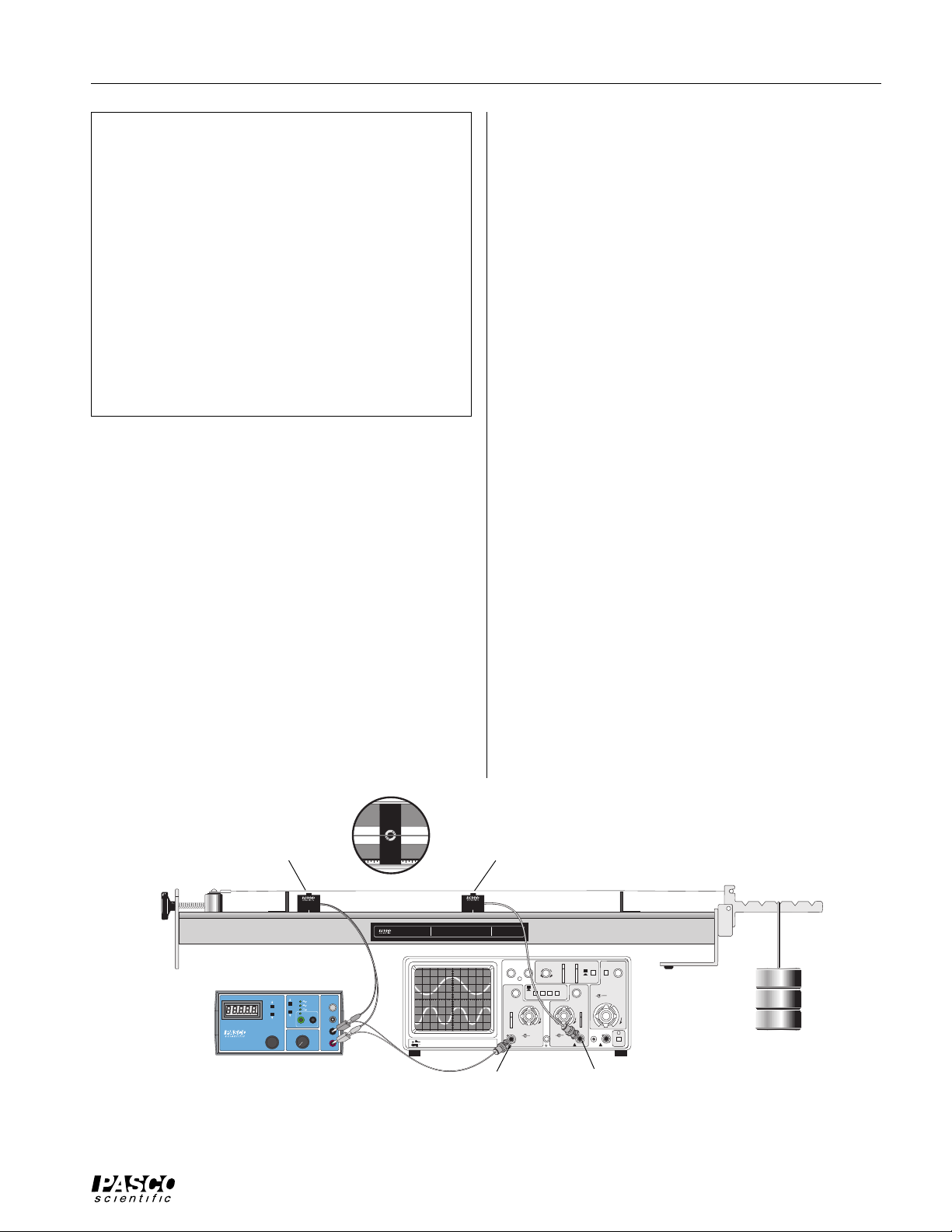
Using the Sonometer and the WA-9613 Driver/Detector Coils:

Sonometer and Driver/Detector Coils with a function generator and oscilloscope:

➀ Connect the Driver and Detector Coils to the function

generator and oscilloscope as shown in the diagram. Connect the driver coil directly to the output of the PASCO PI-9587B Digital Function Generator. Connect the detector coil directly to channel two of an oscilloscope that has a BNC connector. You can use banana plug patch cords and a BNC-to-banana plug adapter to connect the output of the function generator to channel one of an oscilloscope that has a BNC connector. (If you are using a single trace oscilloscope, connect only the detector coil to the oscilloscope.)

➁ Position the driver coil approximately 5 cm from one

of the bridges. Depending on the wave pattern you are trying to pro-

duce, you might want to place the driver at some other position. It will drive the string best if it is placed at an antinode of the wave pattern. However, if you place it near one of the bridges, it will work reasonably well for most frequencies.

➂ Position the detector midway between the bridges ini-

tially, though for some patterns you may want to reposition it to best pick up the signal. As with the driver coil, it works best when positioned near an antinode of the wave pattern.

➃ Set the gain on channel-one of the oscilloscope to 5

mV/cm. Adjust the oscilloscope so it triggers on the signal from the function generator.

➄ Set the function generator to produce a sine wave. Set

the frequency to a value between 100 and 200 Hz. Adjust the amplitude to about 5 V (approximately half of maximum). Slowly vary the frequency of the function generator output. When you reach a resonant frequency, you should see the motion of the string and the sound produced by the vibrating string should be a maximum. The wave pattern shown on the oscilloscope should become a clean sine wave. If you can’t see or hear the string, raise the amplitude of the function generator output slightly and try again.

Driver coil Detector coil

WA-9613

DRIVER

FREQUEN

HE RTZ

PI-9587B DIGITAL FUNCTION GENERATOR AMPLIFIER

WAVEFO

RA NGE

EXTERN

INPUTG

AMPLITU

ADJU

Function generator

WA-9611

SONOMETER

OUTP

TT L

Ω

G ND

Ω

WA-9613

DETECTOR

KEEP WEIGHTS AS NEAR TO FLOOR

AS POSSIBLE IN THE EVENT THE

SONOMETER WIRE SHOULD BREAK

200 Mhz OSCILLISCOPE

BK PRECISION

Channel 1 (trigger) Channel 2

Figure 5 Using the Driver and Detector Coils

CAUTION!

1.75 kg MAXIMUM LOAD ON LEVER

INTENSITY

TRACE NOTATION

POS

CH 1

∞

400V

MODEL

MAX

2120

Oscilloscope

FOCUS

TRIG LEVEL

MANUAL AUTO

NORM

CH1

EXT

CH2

VERTICAL MODE

CH 1 VOLTZ/DIV

CAL

VAR VAR

PULL XS PULL XS

T XY

T XY LINE

CH1 CH2

CH 2 VOLTZ/DIV

COUPLE SOURCE

CH1

X-POS

λ - Y

SLOPE

CH2

ALT EXT

POSNORM

TIME/DI V

VAR SWEEP

CAL

CH4

CAL EXT

CH 2

∞

200V

POWER

400V

MAX

Sonometer 012-03489E

Table 1

Computer Interface Device to drive coil Software FFT? Apple II AI-6501 Power Amplifier Power Amplifier (Apple II) no

Apple II AI-6501 function generator Data Monitor (Apple II) no DOS - PC CI-6500 Power Amplifier Power Amplifier (MS-DOS) no DOS - PC CI-6500 function generator Data Monitor (MS-DOS) yes Macintosh CI-6550 Power Amplifier Science Workshop (Mac) yes Macintosh CI-6550 function generator Science Workshop (Mac) yes Windows - PC CI-6565 Power Amplifier Science Workshop (Windows) yes Windows - PC CI-6565 function generator Science Workshop (Windows) yes Windows - PC CI-6500 function generator Data Monitor (Windows) yes

Sonometer and Driver/Detector Coils with a PASCO Computer Interface

There are several ways to use a PASCO Computer Interface with the sonometer. The method you use depends on the kind of computer, the interface (e.g., CI-6500, CI6550, etc.), the device to control the coil, and whether you wish to do frequency analysis (Fast Fourier Transform or FFT) of the standing waves. See Table 1.

Using the Power Amplifier with a Series 6500 Computer Interface:

➀ Connect the Power Amplifier DIN plug to channel C

of the interface. Connect the Sonometer Driver Coil to the output of the Power Amplifier.

➤ CAUTION: Do not turn on the power amplifier until you have set the output amplitude from within the program.

➁ Connect the BNC plug on the Sonometer Detector

Coil to the BNC jack on the CI-6508 Input Adapter Box, and the DIN plug on the Adapter Box to channel A of the interface. Turn the amplification select switch on the CI-6508 to 100X. (See Figure 5.1.)

➂ Start the Power Amplifier program and set the output

to a 3-5 V sine wave; then turn on the power amplifier. Show channel A and channel C on the screen, so you can see both the driving force and the resultant motion of the wire.

➤ NOTE: The Power Amplifier program does not have a frequency analysis feature (Fast Fourier Transform or FFT).

Using the Power Amplifier with a CI-6550 or CI-6565 Computer Interface:

The Science Workshop program that comes with the CI- 6550 or CI-6565 interface allows you to do frequency analysis (Fast Fourier Transform, or FFT) of the standing waves. This can be used for an in-depth analysis of the harmonics present in a standing wave, analysis of noise, or observation of multiple simultaneous resonances.

➀ Connect the Power Amplifier DIN plug to channel C

of the interface. Connect the Sonometer Driver Coil to the output of the Power Amplifier.

➤ CAUTION: Do not turn on the power amplifier until you have set the output amplitude from within the program.

CI-6502

POWER AMPLIFIER

FOR USE WITH PASCO SERIES 6500 INTERFACES

CAUTION!

PASCO

SERIES

WHEN LIGHT IS ON WAVEFORM IS DISTORTED.

6500

INTERFACE

DECREASE AMPLITUDE!

SYSTEM

Power Amplifier

KEEP WEIGHTS AS NEAR TO FLOOR

AS POSSIBLE IN THE EVENT THE

SONOMETER WIRE SHOULD BREAK

Interface

A ▲

GAIN = 1,10,100

ISOLATED

WA-9613

DETECTOR

ANALOG CHANNELS

B ■ C ●

GAIN

ISOLATED

GAIN = 1

REF TO GND

CAUTION!

1.75 kg MAXIMUM LOAD ON LEVER

ANALOG INPUT

PASCO

SERIES

6500

INTERFACE SYSTEM

INPUT ADAPTOR

FOR USE WITH PASCO SERIES 6500 INTERFACES

(±10V MAX)

Model CI-6508

GAIN SELECT

X 100

X 10

X 1

NOTE: SWITCH

FUNTIONS ONLY WHEN

ADAPTOR IS

CONNECTED TO INPUT MARKED ▲ ON THE SIGNAL INTERFACE

SIGNAL OUTPUT

0 to ±10 V 1 A MAX

WA-9613

DRIVER

WA-9611

SONOMETER

CI-6510

SIGNAL INTERFACE

FOR USE WITH PASCO SERIES 6500 SENSORS

DIGITAL CHANNELS

1234

PASCO

SERIES

6500

INTERFACE SYSTEM

Adapter Box

Figure 5.1 Using the Power Amplifier and Series 6500 Interface

012-03489E Sonometer

➁ Connect the BNC plug on the Sonometer Detector

Coil to the BNC adapter that is included with the Driver/Detector Coils. Connect the banana plugs of a CI-6503 Voltage Sensor to the BNC adapter. Connect the DIN plug of the Voltage Sensor to channel A of the interface.

➂ Start the Science Workshop program. In the Experi-

ment Setup window, click-and-drag the analog sensor plug icon to channel C. Select “Power Amplifier” from the list of sensors. Set the Signal Generator output to a 3-5 V sine wave. Click on “Auto ON/OFF” (so the output signal will begin when you start your measurements) and switch on the power amplifier.

➄ In the Scope, use the input menu for the second chan-

nel to select “Analog A” so the Scope will show both the driving signal and the detected motion of the wire. Set the sensitivity for the Analog A channel to about

0.005 v/div.

For frequency analysis, select “New FFT” from the Display menu. Click on “MON” in the Setup window (or commandM on the keyboard) when you are ready to begin.

➃ In the Experiment Setup window, click-and-drag the

analog sensor plug icon to channel A. Select “Sound Sensor” from the list of sensors. Click-and-drag a Scope display to the Output channel icon in the Setup window.

WA-9613

DRIVER

WA-9611

SONOMETER

WAVEFO

FREQUEN

RA NGE

HE RTZ

ADJU

PI-9587B DIGITAL FUNCTION GENERATOR AMPLIFIER

PI-4587C Function Generator

OUTP

TT L

EXTERN

Ω

INPUTG

AMPLITU

Ω

CI-6510

FOR USE WITH PASCO SERIES 6500 SENSORS

DIGITAL CHANNELS

1234

PASCO

SERIES

6500

INTERFACE SYSTEM

SIGNAL INTERFACE

Figure 5.2 Using a Function Generator and the Series 6500

WA-9613

DETECTOR

KEEP WEIGHTS AS NEAR TO FLOOR

AS POSSIBLE IN THE EVENT THE

SONOMETER WIRE SHOULD BREAK

CI-6500

A ▲

GAIN = 1,10,100

ISOLATED

Using a Function Generator with the Series 6500 Computer Interface:

The MS-DOS and Windows™ versions of the Data Monitor program allow you to do frequency analysis

(Fast Fourier Transform or FFT) of the standing waves. This can be used for an in-depth analysis of the harmonics present in a standing wave, analysis of noise, or observation of multiple simultaneous resonances.

➀ Connect the BNC plug on the Sonometer Detector

Coil to the BNC jack on the CI-6508 Input Adapter Box, and the DIN plug on the Adapter Box to channel A of the Series-6500. Turn the amplification select switch on the CI-6508 to 100X.

➁ If you have a CI-6503 Voltage Sensor, use it to link

the function generator to channel B of the CI-6500 interface. (This step is optional; it allows you to use the function generator for triggering, with slightly improved results.) See Figure 5.2.

CAUTION!

1.75 kg MAXIMUM LOAD ON LEVER

Model CI-6508

INPUT ADAPTOR

ANALOG CHANNELS

B ■ C ●

GAIN

ISOLATED

GAIN = 1

REF TO GND

FOR USE WITH PASCO SERIES 6500 INTERFACES

ANALOG INPUT

(±10V MAX)

PASCO

SERIES

6500

INTERFACE SYSTEM

CI-6508

GAIN SELECT

X 100

X 10

X 1

NOTE: SWITCH

FUNTIONS ONLY WHEN

ADAPTOR IS

CONNECTED TO INPUT MARKED ▲ ON THE SIGNAL INTERFACE

Sonometer 012-03489E

➂ Set the function generator to produce a sine wave. Set

For the Data Monitor (MS-DOS) Program:

Start the program. Select “Oscilloscope” from the Main Menu. Set triggering to automatic on channel B. Show channels A and B on the screen, and find the resonances you are interested in. If you wish, turn on the frequency analysis option (FFT) and observe the frequencies that are contributing to the standing wave.

For the Data Monitor (Windows™) Program:

Start the program. Choose “Select Channels” from the Experiment menu and turn off channel C. Select “Replace Window” from the Window menu, and change the Plotter/Graph window to an Oscilloscope window. Repeat the process to change the Data Table window to the FFT window. Click on “Trigger” to set the triggering for channel B.

Using a Function Generator with a CI-6550 or CI6565 Computer Interface:

➀ Connect the BNC plug on the Sonometer Detector

Coil to the BNC adapter that is included with the Driver/Detector Coils. Connect the banana plugs of a

CI-6503 Voltage Sensor to the BNC adapter. Connect the DIN plug of the Voltage Sensor to channel A of the interface.

If you have another CI-6503 Voltage Sensor, use it to link the function generator to channel B of the computer interface. (This step is optional; it allows you to use the function generator for triggering, with slightly improved results.)

➁ Start the Science Workshop program. In the Experi-

ment Setup window, click-and-drag the analog sensor plug icon to channel A. Select “Sound Sensor” from the list of sensors. If you have connected a Voltage Sensor from the function generator to channel B, click-and-drag the analog sensor plug icon to channel B and select “Voltage Sensor” from the list of sensors.

➂ To view the data, click-and-drag a Scope display to

the Sound Sensor icon. (If you have connected a Voltage Sensor from the function generator to channel B, use the input menu of the first channel on the Scope to switch the input to “Analog B”. Use the input menu of the second channel on the Scope to select “Analog A”. This will allow you to use the function generator for triggering.) Set the sensitivity for the Analog A channel to about 0.005 v/div. Click on “MON” to begin measuring data.

➃ Set the function generator to produce a sine wave. Set

012-03489E Sonometer

➤NOTES:

➀ The frequency observed on the wire may not be

the frequency of the driver. Usually it is twice the driver frequency, since the driver electromagnet exerts a force on the wire twice during each cycle. It is theoretically possible for the wire to form standing waves at the driver frequency, and at any even integer multiple of the driver frequency; although the highest multiple observed on this equipment so far has been six.

➁ If the detector is placed too close to the driver, it

will pick up some interference. You can check for this interference by observing the waveform from the detector on an oscilloscope; when they are too close, the trace will change shape. For best results, keep the detector at least 10 cm from the driver.

➂ You will occasionally see higher and lower fre-

quencies superimposed on the primary waveform. It is possible for multiple standing waves to form. For example, the wire may vibrate at the driver frequency and twice the driver frequency at the same time, thus causing two sets of “nodes” (see figure below).

At the points where only one wave has a node, instead of complete extinction you will see the waveform change from a combined wave to a single wave of the lower frequency. Complete extinction will occur only at the nodal points for both waves. This does somewhat complicate things; if you wish to avoid this problem, you may do so by using higher frequencies whenever possible. (Since higher frequencies damp faster, the doubled-frequency standing wave will not have a significant amplitude—compared to the normal wave—at high frequencies.) A full analysis of this effect would make an excellent experiment for sophomore- or junior-level physics or engineering students.

Replacing Sonometer Strings

You can use standard steel or electric guitar strings to replace lost or broken strings. However, you will need to attach a spade lug to the end of the wire to mount it on the Sonometer. To ensure that the connection between the wire and the lug is secure, wrap the wire around the spade lug, then crimp and/or solder the wire into the lug (see Figure 7).

Nodes for higher frequency, but not lower. Nodes for both frequencies.

Wrap wire around lug, then

crimp and/or solder.

Standard steel or

Spade lug

Figure 7 Adapting Guitar Strings for the

Sonometer

electric guitar string

Sonometer 012-03489E

Theory of Waves on a Stretched String

Standing Waves

A simple sine wave traveling along a taut string can be described by the equation y1 = ym sin 2π (x/λ - t/n). If the string is fixed at one end, the wave will be reflected back when it strikes that end. The reflected wave will then interfere with the original wave. The reflected wave can be described by the equation y2 = ym sin 2π (x/λ + t/n). Assuming the amplitudes of these waves are small enough so that the elastic limit of the string is not exceeded, the resultant waveform will be just the sum of the two waves:

y = y

+ y2 = ym sin 2π (x/λ - t/λ) + ym sin 2π (x/λ + t/λ).

Using the trigonometric identity:

sin A + sin B = 2 sin1/2(A + B) cos1/2(B - A),

this equation becomes:

y = 2y

This equation has some interesting characteristics. At a fixed time, t

, the shape of the string is a sine wave with a

maximum amplitude of 2ym cos (2πt0/λ). At a fixed position on the string, x0, the string is undergoing simple harmonic motion, with an amplitude of 2ym sin (2πx0/λ). Therefore, at points of the string where x0 = l/4, 3l/4, 5l/4, 7l/4, etc., the amplitude of the oscillations will be a maximum. At points of the string where x0 = l/2, l, 3l/2, 2l, etc., the amplitude of the oscillations will be zero.

This waveform is called a standing wave because there is no propagation of the waveform along the string. A time exposure of the standing wave would show a pattern something like the one in Figure 8. This pattern is called the envelope of the standing wave. Each point of the string oscillates up and down with its amplitude determined by the envelope. The points of maximum amplitude are called antinodes. The points of zero amplitude are called nodes.

Antinode

Node

Figure 8 The Envelope of a Standing Wave Pattern

sin (2πx/λ) cos (2πt/λ).

Antinode

Node

Antinode

Node

Antinode

Node

Resonance

The analysis above assumes that the standing wave is formed by the superposition of an original wave and one reflected wave. In fact, if the string is fixed at both ends, each wave will be reflected every time it reaches either end of the string. In general, the multiply reflected waves will not all be in phase, and the amplitude of the wave pattern will be small. However, at certain frequencies of oscillation, all the reflected waves are in phase, resulting in a very high amplitude standing wave. These frequencies are called resonant frequencies.

In Experiment 1, the relationship between the length of the string and the frequencies at which resonance occurs is investigated. It is shown that the conditions for resonance are more easily understood in terms of the wavelength of the wave pattern, rather than in terms of the frequency. In general, resonance occurs when the wavelength (λ) satisfies the condition:

λ = 2L/n; n = 1, 2, 3, 4,…

Another way of stating this same relationship is to say that the length of the string is equal to an integral number of half wavelengths. This means that the standing wave is such that a node of the wave pattern exists naturally at each fixed end of the string.

Velocity of Wave Propagation

Assuming a perfectly flexible, perfectly elastic string, the velocity of wave propagation (V) on a stretched string depends on two variables: the mass per unit length or linear density of the string (m) and the tension of the string (T). The relationship is given by the equation:

V =

Without going into the derivation of this equation, its basic form can be appreciated. The equation is analogous to Newton’s Second law, providing a relationship between a measure of force, a measure of inertia, and a quantity of motion. With this analogy in mind, it makes sense that the velocity should depend on the tension and linear density of the string. That the form of the two equations is not exactly the same is to be expected. The motion of the string is considerably different than the motion of a simple rigid body acted on by a single force. (It could be asked whether velocity, rather than acceleration, is the right measure of motion to focus on. Since the waves on the string do not accelerate, this is at least a reasonable assumption.)

012-03489E Sonometer

If the analogy with Newton’s Law is accepted, and it is assumed that the wave velocity depends only on tension and linear density, dimensional analysis shows that the form of the equation must be as it is. There is no other way to combine tension (with units of MLT -2) with linear density (ML-1) to get velocity (LT -1).

Of course, the equation must be verified experimentally. This is done in Experiment 2, in which the linear density of the string is varied by using different strings. The tension is varied using hanging weights on a lever arm. The wavelength is then measured by adjusting the frequency until a resonance pattern develops. The velocity can then be calculated using the relationship

V = λν, and the effects of tension and linear density on velocity can be determined.

Experiments

The two experiments are:

• Resonance Modes of a Stretched String

• Velocity of Wave Propagation Both can be done with a function generator and dual-trace

oscilloscope OR with a computer interface (such as the CI-6550) and power amplifier.

Sonometer 012-03489E

Notes:

012-03489E Sonometer

Experiment 1: Resonance Modes of a Stretched String

EQUIPMENT NEEDED:

– WA-9611 Sonometer – Mass and mass hanger – WA-9613 Driver/Detector Coils – Dual trace oscilloscope – Function generator capable of delivering 0.5 amp

Procedure

➀ Set up the Sonometer as shown in Figure 1.1.

Start with the bridges 60 cm apart. Use any of the included strings and hang a mass of approximately 1 kg from the tensioning lever. Adjust the string adjustment knob so that the tensioning lever is horizontal. Position the driver coil approximately 5 cm from one of the bridges and position the detector near the center of the wire. Record the length, tension (mg), and linear density of the string in Table 1.1.

String

adjustment

knob

FREQUEN

RTZ

PI-9587B DIGITAL FUNCTION GENERATOR AMPLIFIER

Frequency generator

Driver coil

RA NGE

ADJU

Detector coil

60 cm

KEEP WEIGHTS AS NEAR TO FLOOR

AS POSSIBLE IN THE EVENT THE

SONOMETER WIRE SHOULD BREAK

BK PRECISION

WA-9613

DETECTOR

MODEL

200 Mhz OSCILLISCOPE

2120

Oscilloscope

CAUTION!

1.75 kg MAXIMUM LOAD ON LEVER

INTENSITY FOCUS

TRACE NOTATI ON

CH 1

MANUAL AUTO

POS POSNORM

CH 1 VOLTZ/DIV

∞

400V

PULL XS PULL XS

MAX

COUPLE SOURCE

AC CH1

TRIG LEVEL

T X-

-++Y

T XY LINE

CH1

NORM

CH1

EXT

CH2

EXT

CH2

VERTICAL MODE

CH 2 VOLTZ/DIV

CAL

VAR VAR

X-POS

SLOPE - Y

CH2

ALT

EXT

TIME/DI V

VAR SWEEP

CAL

mVV

CAL

∞

CH 2

CAL EXT CH4

200V

400V

MAX

POWER

Channel 2 (detector coil) Channel 1 (driver coil)

WA-9613

DRIVER

WA-9611

SONOMETER

OUTP

WAVEFO

TT L

EXTERN

INPUTG

Ω

G ND

AMPLITU

Ω

Figure 1.1 Equipment Setup

➁ Set the signal generator to produce a sine wave and set the gain of the oscilloscope to approxi-

mately 5 mV/cm.

➂ Slowly increase the frequency of the signal to the driver coil, starting at approximately 25 Hz.

Listen for an increase in the volume of the sound from the sonometer and/or an increase in the size of the detector signal on the oscilloscope screen. Frequencies that result in maximum string vibration are resonant frequencies. Determine the lowest frequency at which resonance occurs. This is resonance in the first, or fundamental, mode. Measure this frequency and record it in Table 1.1.

Tensioning

lever

1 kg

➃ Start with the detector as close as you can get it to one of the bridges. Watch the oscilloscope as

you slide the detector slowly along the string. Locate and record the locations of each node and antinode. Record your results in Table 1.1.

➄ Continue increasing the frequency to find successive resonant frequencies (at least five or six).

Record the resonance frequency for each mode, and the locations of nodes and antinodes in Table 1.1.

Sonometer 012-03489E

Vibrating Waveform

Driving

Waveform

Oscilliscope Screen

➤ NOTE: The driving frequency of the signal generator may not be

the frequency at which the wire is vibrating. By using a dual trace oscilloscope, you can determine if the two frequencies are the same, or if the vibrating frequency is a multiple of the driving frequency, as shown in Figure 1.2.

➅ From your results, determine and record the wavelength of each

resonance pattern you discovered. (➤ Note that adjacent nodes are one half wavelength apart.)

➆ Change the string length by moving one or both of the bridges.

Construct a new data table and repeat your measurements for at least

Figure 1.2 String Vibrations at a

Multiple of the Driving Frequency

three different string lengths.

Analysis

Using your data, determine the shape of the successive resonance waveforms as the frequency is increased. How do the wave shapes depend on the length of the string? Sketch the resonance waveforms for an arbitrary string length. What relationship holds between the wavelength of the wave and the string length when resonance occurs? Can you state this relationship mathematically?

For each string length, inspect the frequencies at which resonance occurred. Determine a mathematical relationship between the lowest resonant frequency (the fundamental frequency) and the higher frequencies (overtones) at which resonance occurred.

Optional

➀ Change the string tension by hanging the weight from a different notch. Experiment as needed to

answer the following questions. Do the frequencies at which resonance occurs depend on the tension of the wire? Do the shapes of the resonance patterns (locations of nodes and antinodes) depend on the tension of the wire?

➁ Change the linear density of the string by changing strings. Do the frequencies at which resonance

occurs depend on the linear density of the wire? Do the shapes of the resonance patterns (locations of nodes and antinodes) depend on the linear density of the wire?

Table 1.1

String length:________________ String tension:_______________ Wire diameter:_______________

Resonant Amplitude Maxima Amplitude Minima

Mode Frequencies (Antinodes) (Nodes)

012-03489E Sonometer

Experiment 2: Velocity of Wave Propagation

EQUIPMENT NEEDED:

– WA-9611 Sonometer – WA-9613 Driver/Detector Coils – Function generator capable of delivering 0.5 amp – Dual trace oscilloscope – Mass and mass hanger

Procedure

➀ Set up the Sonometer as shown in Figure 2.1.

Set the bridges 60 cm apart. Use any of the included strings and hang a mass of approximately 1 kg from the tensioning lever. Adjust the string adjustment knob so that the tensioning lever is horizontal. Position the driver coil approximately 5 cm from one of the bridges and position the detector near the center of the wire.

➁ Set the signal generator to produce a sine wave and set the gain of the oscilloscope to approxi-

mately 5 mV/cm.

➂ Slowly increase the frequency of the signal driving the driver coil, starting with a frequency of

around 1 Hz. Determine the lowest frequency at which resonance occurs. Record this value in Table 2.1.

WA-9613

DETECTOR

KEEP WEIGHTS AS NEAR TO FLOOR

AS POSSIBLE IN THE EVENT THE

SONOMETER WIRE SHOULD BREAK

200 Mhz OSCILLISCOPE

MODEL 2120

CAUTION!

1.75 kg MAXIMUM LOAD ON LEVER

INTENSITY

CH 1

400V MAX

FOCUS

TRACE NOTATION

POS

CH 1 VOLTZ/DIV

∞

VAR VAR

PULL XS PULL XS

TRIG LEVEL

MANUAL AUTO

CH1

EXT

CH2

VERTICAL MODE

CAL

NORM EXT

CH 2 VOLTZ/DIV

COUPLE SOURCE

T XY T XY

LINE

CH1 CH2

CH1

CH2

ALT EXT

CAL

X-POS

λ - Y

SLOPE

POSNORM

TIME/DI V

VAR SWEEP

CAL

CH4

CAL EXT

∞

CH 2

200V

POWER

400V

MAX

FREQUEN

HE RTZ

PI-9587B DIGITAL FUNCTION GENERATOR AMPLIFIER

WA-9613

DRIVER

WA-9611

SONOMETER

WAVEFO

NGE

ADJU

OUTP

TT L

EXTERN

Ω

INPUTG

AMPLITU

Ω

BK PRECISION

Figure 2.1 Equipment Setup

➤ NOTE: To be sure you have found the lowest resonant frequency, slide the detector coil the

length of the string. The wave pattern should have just a single antinode located midway between the two bridges.

Sonometer 012-03489E

➃ In Table 2.1, record the string tension (T) and the linear

density of the string (µ). The tension is determined as shown in Figure 2.2. Just

multiply the weight of the hanging mass by one, two, three, four, or five, depending on which notch of the tensioning lever the mass is hanging from. The linear density of the strings are given in the front of this manual (see your teacher, if necessary).

➄ Change the string tension by hanging the mass from a

different notch. Repeat steps 3 and 4 for five different values of the string tension.

➅ Set the string tension to a midrange value. Then repeat

your measurements of steps 3 and 4 using each of the five different strings.

Table 2.1 Data and Calculations

Tension Linear Density Fundamental Wave

(T) (µ) Frequency Velocity

String tension

(T)

2Mg

1Mg

15234Slot

5Mg

4Mg

3Mg

(mass = M)

(weight = Mg)

Figure 2.2 Setting the Tension

Hanging

Mass

012-03489E Sonometer

Analysis

➀ Use your measured string length, the fundamental frequency, and the equation V = λν to determine the velocity

of the wave on the string for each value of tension and linear density that you used.

➁ Determine the functional relationship between the speed of the wave (V) and the wire tension (T). This can be

accomplished using either of the following three methods. If you are not familiar with these procedures, you might want to try all three.

➤ NOTE: Options A and B are easily performed using a computer with graphical analysis

software.

A. Plot a graph of V versus T, with V on the y-axis. If the graph is not a straight line, try plotting V versus some

power of T (such as T

B. Assume that the functional relationship is of the form V = kT

1/2

, T

, etc.), until you get a straight line.

. Then ln V = p ln T + ln k, where p and k are unknown constants. Then, if lnV is plotted against the independent variable lnT, a straight line will be obtained having a slope p, where p is lnV/ lnT and ln k is the y-intercept.

C. Many calculators have the ability to do power regressions or linear regressions on the logarithms of V and T.

This will accomplish essentially what the graph of method B did.

➂ Using one of the methods above, determine the functional relationship of the speed of the wave (V) to the linear

density of the string (µ).

Conclusions

Characterize the resonant modes of a vibrating wire. That is:

➀ Determine a mathematical relationship that describes the wavelengths of the waves that form standing wave

patterns in a wire of length L (see Experiment 1).

➁ Use your answer to question 1, and the expression V = λν, to determine the resonant frequencies of a wire of

length L.

➂ Use your experimental results to write an expression for the resonant frequencies of a vibrating wire in terms of

T, µ, and L.

Sonometer 012-03489E

Suggested Research T opics

The following are a few suggestions for further experimentation with the Sonometer. ➀ Obtain two wires of the same linear density (mass per unit length), one that is wound and one that

is not wound (a plain wire). Investigate the effects of the winding on the mathematical relationships of wave propagation.

➁ Use a harmonic analyzer to analyze the effects of placing the Driver Coil at different places along

the wire. Also investigate the effects of placing the Detector Coil at different places along the wire. You can also investigate the effects of plucking, strumming, and bowing the string.

➂ By devising a method to measure string stretch, you can use this apparatus to investigate the

Hooke's Law relationship for a wire placed under tension. Possible investigations include:

a. Strain versus Stress (Stretch versus Applied Load) b. Strain versus Diameter of Wire (Constant Stress) c. Strain versus Type of Wire (Constant Diameter)

➃ Obtain wires made of different materials, but with the same linear density. Investigate the speed

of wave propagation in these wires when the same tension is applied to e

ach.

012-03489E Sonometer

T eacher’s Guide

Experiment 1: Resonance Modes of a Stretched String

Note

To avoid cross-talk between the detector and driver, keep the detector coil at least 10 cm from the driver coil during measurements.

Notes on Analysis

Wavelength v. String Length

0.3

f(x) = 4.000000E-1*x + 1.084202E-19 R^2 = 10.000000E-1

0.25

n = 5 (constant) This verifies that wavelength = 2L/n

0.2

0.15

0.1

Wavelength (m)

0.05

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7

String Length (m)

There is a linear relationship between resonant wavelength and string length.

The overtones are all multiples of the fundamental frequency.

Optional

➀

Frequency v. Tension

1600 1400 1200 1000

800 600

Frequency (Hz)

400 200

0 5 10 15 20 25 30 35 40 45 50

1200

1000

800

600

400

Frequency (Hz)

200

0.0002 0.0007 0.0012 0.0017 0.0022 0.0027

f(µ) = 2.163996E+1 * (µ^-5.088207E-1 ) R^2 = 9.991369E-1

This verifies that f ` µ

f(T) = 2.105721E+2 * (T^5.045696E-1 ) R^2 = 9.994170E-1

This verifies that f ` T

Tension (N)

Frequency v. Mass/Length

µ (kg/m)

1/2

-1/2

Sonometer 012-03489E

Note

To avoid cross-talk between the detector and driver, keep the detector coil at least 10 cm from the driver coil during measurements.

Analysis

➁

400 350 300 250 200 150

Velocity (m/s)

100

0 5 10 15 20 25 30 35 40 45 50

➂

Velocity v. Tension

f(x) = 5.053730E+1 * (x^5.045696E-1 ) R^2 = 9.994170E-1 µ = 0.00039 kg/m Theoretical: 50.637 Experimental constant is 0.2% low.

This verifies that V ` T

1/2

Tension (N)

Notes on Conclusions

➀ As shown in Experiment 1, l = 2L/n. ➂ From the Analysis section, V = sqrt(T/µ). Since

l = 2L/n, substituting and rearranging gives us

n = (n/2L)*sqrt(T/µ)

The graphs below verify this equation.

Frequency v. n

1400

f(x) = 1.357518E+2*x + -5.901176E+0 R^2 = 9.995529E-1

1200

T = 9.8 N; µ = 0.00039 kg/m; L = 0.60 m Theoretical slope: 1/2L * sqrt(T/µ) = 132.099

1000

Experimental value 2.8% above theoretical.

800

600

Frequency (Hz)

400

200

012345678910

300

Velocity v. Mass/Length

250

200

150

f(x) = 5.193590E+0 * (x^-5.088207E-1 ) R^2 = 9.991369E-1

Velocity (m/s)

100

T = 29.4 N Theoretical: 5.4222

Experimental constant is 4.2% low. This verifies that V ` µ

-1/2

0.0002 0.0007 0.0012 0.0017 0.0022 µ (kg/m)

Frequency v. Tension

1600 1400 1200 1000

800 600

Frequency (Hz)

400

f(T) = 2.105721E+2 * (T^5.045696E-1 ) R^2 = 9.994170E-1 Theoretical: (n/2L)*sqrt(1/µ) = 210.99

200

Experimental constant is 0.2% low.

0 5 10 15 20 25 30 35 40 45 50

Tension (N)

012-03489E Sonometer

T echnical Support

Feed-Back

If you have any comments about this product or this manual please let us know. If you have any suggestions on alternate experiments or find a problem in the manual please tell us. PASCO appreciates any customer feed-back. Your input helps us evaluate and improve our product.

To Reach PASCO

For Technical Support call us at 1-800-772-8700 (tollfree within the U.S.) or (916) 786-3800.

Internet: techsupp@PASCO.com Tech Support Fax: (916)786-3292

Contacting Technical Support

Before you call the PASCO Technical Support staff it would be helpful to prepare the following information:

• If your problem is with the PASCO apparatus, note: Title and Model number (usually listed on the label). Approximate age of apparatus.

A detailed description of the problem/sequence of events. (In case you can't call PASCO right away, you won't lose valuable data.)

If possible, have the apparatus within reach when calling. This makes descriptions of individual parts much easier.

• If your problem relates to the instruction manual,

note: Part number and Revision (listed by month and year

on the front cover).

Have the manual at hand to discuss your questions.

PASCO WA-9611, WA-9613 User Manual

Specifications and Main Features

Frequently Asked Questions

User Manual