Page 1
Includes
Teacher's Notes
and
Typical
Experiment Results
THERMAL EFFICIENCY
Instruction Manual and
Experiment Guide for
the PASCO scientific
Model TD-8564
APPARATUS
012-05443A
3/94
12.9
12.9
12.4
12.4
12.0
12.0
11.6
11.6
11.2
11.2
10.8
10.8
10.4
10.4
KΩ
KΩ
scientific
5Ω±1%
5Ω±1%
12 VDC MAX
12 VDC MAX
T
°C
°C
KΩ
KΩ
75
75
9.12
9.12
76
76
8.81
8.81
77
77
8.52
8.52
78
78
8.24
8.24
79
79
7.96
7.96
80
80
7.70
7.70
81
81
7.45
7.45
Cold
Reservoir
c
°C
°C
KΩ
KΩ
°C
°C
85
85
6.53
6.53
95
95
86
86
6.33
6.33
96
96
87
87
6.12
6.12
97
97
88
88
5.93
5.93
98
98
89
89
5.74
5.74
99
99
90
90
5.56
5.56
100
100
91
91
5.39
5.39
101
101
Hot
Reservoir
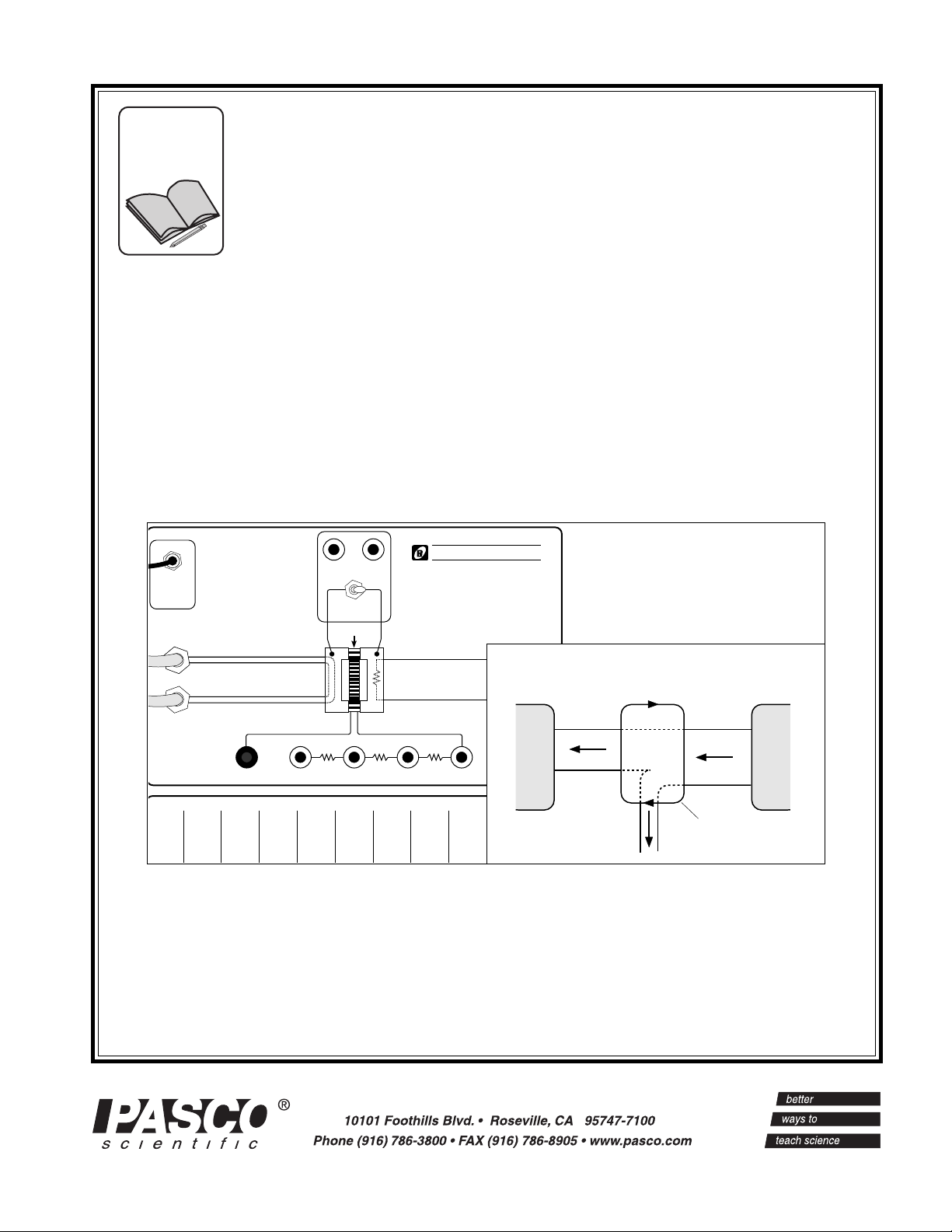
Q
c
W
Q
h
Heat
Engine
T
h
WATER
WATER
PUMP
PUMP
7.5 - 12 VDC
7.5 - 12 VDC
@500mA
@500mA
KΩ
KΩ
°C
°C
461
461
-5
-5
436
436
-4
-4
413
413
-3
-3
391
391
-2
-2
370
370
-1
-1
351
351
0
0
332
332
1
1
PASCO
Model TD-8564
Model TD-8564
THERMAL EFFICIENCY
THERMAL EFFICIENCY
APPARATUS
27.4
27.4
26.4
26.4
25.3
25.3
24.4
24.4
23.4
23.4
22.5
22.5
21.7
21.7
KΩ
KΩ
°C
°C
55
55
56
56
57
57
58
58
59
59
60
60
61
61
APPARATUS
HEATER
2.0Ω2.0Ω1.0Ω1.0Ω0.5Ω0.5Ω
KΩ
KΩ
°C
°C
18.6
18.6
65
65
17.9
17.9
66
66
17.3
17.3
67
67
16.6
16.6
68
68
16.0
16.0
69
69
15.5
15.5
70
70
14.9
14.9
71
71
THERMISTOR
THERMISTOR
SELECT
SELECT
PELTIER
PELTIER
DEVICE
DEVICE
COOLING
COOLING
WATER
WATER
THERMISTOR TABLETHERMISTOR TABLE
KΩ
KΩ
°C
KΩ
KΩ
°C
°C
KΩ
KΩ
°C
°C
KΩ
KΩ
°C
°C
KΩ
269
269
5
5
161
161
15
255
255
242
242
230
230
218
218
207
207
197
197
15
6
6
153
153
16
16
7
7
146
146
17
17
8
8
139
139
18
18
9
9
133
133
19
19
10
10
126
126
20
20
11
11
120
120
21
21
95.4
95.4
91.1
91.1
87.0
87.0
83.1
83.1
79.4
79.4
75.9
75.9
KΩ
100
100
25
25
63.4
63.4
26
26
60.7
60.7
27
27
58.1
58.1
28
28
55.6
55.6
29
29
53.2
53.2
30
30
51.0
51.0
31
31
48.9
48.9
°C
°C
°C
41.2
41.2
45
45
35
35
39.6
39.6
46
46
36
36
37.9
37.9
47
47
37
37
36.4
36.4
48
48
38
38
34.9
34.9
49
49
39
39
33.5
33.5
50
50
40
40
32.2
32.2
51
51
41
41
© 1991 PASCO scientific $10.00
Page 2

Page 3

012-05443A Thermal Efficiency Apparatus
T able of Contents
Copyright, Warranty and Equipment Return...................................................ii
Introduction .....................................................................................................1
Quick Start.......................................................................................................2
Theory ............................................................................................................. 3
HEAT ENGINE:
Introduction ...............................................................................................3
Actual Efficiency.......................................................................................3
Carnot Efficiency.......................................................................................3
Adjusted Efficiency ...................................................................................3
HEAT PUMP (REFRIGERATOR):
Introduction ...............................................................................................4
Actual Coefficient of Performance............................................................ 4
Maximum Coefficient of Performance...................................................... 4
Adjusted Coefficient of Performance ........................................................4
MEASUREMENTS USING THE THERMAL EFFICIENCY APPARATUS:
Direct Measurements.................................................................................5
Temperatures .......................................................................................5
Power Delivered to the Hot Reservoir (PH) ......................................... 6
Power Dissipated by the Load Resistor (PW)....................................... 6
Indirect Measurements ..............................................................................6
Internal Resistance...............................................................................6
Heat Conduction and Radiation...........................................................6
Heat Pumped from the Cold Reservoir................................................7
EXPERIMENTS:
1 — Heat Engine and Temperature Difference ......................................... 9
2 — Heat Engine Efficiency (Detailed Study) .........................................13
3 — Heat Pump Coefficient of Performance............................................17
4 — Thermal Conductivity.......................................................................20
5 — Load for Optimum Performance.......................................................21
Teacher’s Guide..............................................................................................25
Technical Support................................................................. Inside Back Cover
i
Page 4
Thermal Efficiency Apparatus 012-05443A
Copyright, Warranty and Equipment Return
Please—Feel free to duplicate this manual
subject to the copyright restrictions below.
Copyright Notice
The PASCO scientific Model TD-8564 Thermal Efficiency Apparatus manual is copyrighted and all rights
reserved. However, permission is granted to non-profit
educational institutions for reproduction of any part of
this manual providing the reproductions are used only for
their laboratories and are not sold for profit. Reproduction under any other circumstances, without the written
consent of PASCO scientific, is prohibited.
Limited Warranty
PASCO scientific warrants this product to be free from
defects in materials and workmanship for a period of one
year from the date of shipment to the customer. PASCO
will repair or replace, at its option, any part of the product
which is deemed to be defective in material or workmanship. This warranty does not cover damage to the product
caused by abuse or improper use. Determination of
whether a product failure is the result of a manufacturing
defect or improper use by the customer shall be made
solely by PASCO scientific. Responsibility for the return
of equipment for warranty repair belongs to the customer.
Equipment must be properly packed to prevent damage
and shipped postage or freight prepaid. (Damage caused
by improper packing of the equipment for return shipment will not be covered by the warranty.) Shipping
costs for returning the equipment, after repair, will be
paid by PASCO scientific.
Equipment Return
Should the product have to be returned to PASCO
scientific for any reason, notify PASCO scientific by
letter, phone, or fax BEFORE returning the product.
Upon notification, the return authorization and
shipping instructions will be promptly issued.
ä
NOTE: NO EQUIPMENT WILL BE
ACCEPTED FOR RETURN WITHOUT AN
AUTHORIZATION FROM PASCO.
When returning equipment for repair, the units
must be packed properly. Carriers will not accept
responsibility for damage caused by improper
packing. To be certain the unit will not be
damaged in shipment, observe the following rules:
➀ The packing carton must be strong enough for the
item shipped.
➁ Make certain there are at least two inches of
packing material between any point on the
apparatus and the inside walls of the carton.
➂ Make certain that the packing material cannot shift
in the box or become compressed, allowing the
instrument come in contact with the packing
carton.
Credits
This manual authored by: Ann Hanks
This manual edited by: Ann Hanks and Eric Ayars
Teacher’s Guide written by: Eric Ayars
Address: PASCO scientific
10101 Foothills Blvd.
Roseville, CA 95747-7100
Phone: (916) 786-3800
FAX: (916) 786-3292
email: techsupp@pasco.com
web: www.pasco.com
ii
Page 5
012-05443A Thermal Efficiency Apparatus
Introduction
The Thermal Efficiency Apparatus can be used as a
heat engine or a heat pump. When used as a heat
engine, heat from the hot reservoir is used to do work
by running a current through a load resistor. The
actual efficiency of this real heat engine can be obtained and compared to the theoretical maximum
efficiency . When used as a heat pump to transfer heat
from the cold reservoir to the hot reservoir, the actual
coefficient of performance and the theoretical maximum coefficient of performance can be obtained.
The apparatus is built around a thermoelectric converter called a Peltier device. To simulate the theoretical heat engines found in textbooks which have infinite
hot and cold reservoirs, one side of the Peltier device
is maintained at a constant cold temperature by pumping ice water through the block and the other side of
the Peltier device is maintained at a constant hot
temperature using a heater resistor imbedded in the
block. The temperatures are measured with thermistors which are imbedded in the hot and cold blocks.
Additional Equipment Needed
Then, in 1834, Jean-Charles-Athanase Peltier discovered the opposite of the Seebeck Effect, that a current
flowing through a junction of dissimilar metals causes
heat to be absorbed or freed, depending on the direction in which the current is flowing.
2
Since the Thermal Efficiency Apparatus is operated in this manner
the thermoelectric converter is called a Peltier device.
However, the Thermal Efficiency Apparatus also
exhibits the Seebeck Effect because the two sides of
the device are maintained at different temperatures.
Today the Seebeck Effect is achieved using pn junctions. The arrangement of the dissimilar semiconductors is as seen in Figure 1. If the left side of the device
is maintained at a higher temperature than the right
side, then holes generated near the junction drift across
the junction into the p region and electrons drift into
the n region. At the cold junction on the right side, the
same process occurs but at a slower rate so the net
effect is a flow of electrons in the n region from the
hot side to the cold side. Thus there is a current from
the cold side to hot side in the n region.
3
To perform the experiments in this manual, you will
need the following equipment in addition to the
Thermal Efficiency Apparatus.
• 1 DC power supply capable of 2.5A at 12V
(SF-9584)
• 3 kg (7 lbs) ice and a bucket for the ice-water bath
• Ohmmeter (SB-9624)
• 1 Ammeter (up to 3A) (SB-9624A)
• 2 Voltmeters (SB-9624A)
• Patch Cords (SE-9750-51)
History
The principle upon which the Thermal Efficiency
Apparatus operates has been known since the 1800’s
but has only become practical since the recent development of semiconductors.
In 1821 the Russian-German physicist Thomas Johann
Seebeck discovered that when a junction of dissimilar
metals is heated, a current is produced.
enon is now known as the Seebeck Effect and is the
basis of the thermocouple.
1
This phenom-
Cold
)
(T
Hot
(Th)
p
n
p
n
Copper
Figure 1: Arrangement of Thermocouples
1
Timetables of Science, by Alexander Hellemans and
c
I
I
I
I
I
Load resistor
Bryan Bunch, Simon & Schuster, NY, 1988, p.281.
2
IBID, p.301.
3
Circuits, Devices, and Systems, 3rd ed., by Ralph J.
Smith, Wiley, 1976, p.543.
1
Page 6

Thermal Efficiency Apparatus 012-05443A
Quick Start
The following sections of this manual are essential to
operate the Thermal Efficiency Apparatus and will
give the user the minimum amount of information
necessary to get started quickly:
Theory
Heat Engine
• Introduction
• Actual Efficiency
• Carnot Efficiency
Measurements Using the Thermal
Efficiency Apparatus
Direct Measurements
• Temperatures
• Power to the Hot Reservoir
• Power Used by the Load Resistor
Experiment — 1: Heat Engine Efficiency
and Temperature Difference
The other portions of the manual provide a more
detailed explanation of the operation of the Thermal
Efficiency Apparatus in other modes as well as the
heat engine mode.
2
Page 7
012-05443A Thermal Efficiency Apparatus
Theory
Heat Engine
Introduction
A heat engine uses the temperature difference between
a hot reservoir and a cold reservoir to do work. Usually the reservoirs are assumed to be very large in size
so the temperature of the reservoir remains constant
regardless of the amount of heat extracted or delivered
to the reservoir. This is accomplished in the Thermal
Efficiency Apparatus by supplying heat to the hot side
using a heating resistor and by extracting heat from the
cold side using ice water.
In the case of the Thermal Efficiency Apparatus, the
heat engine does work by running a current through a
load resistor. The work is ultimately converted into
heat which is dissipated by the load resistor (Joule
heating).
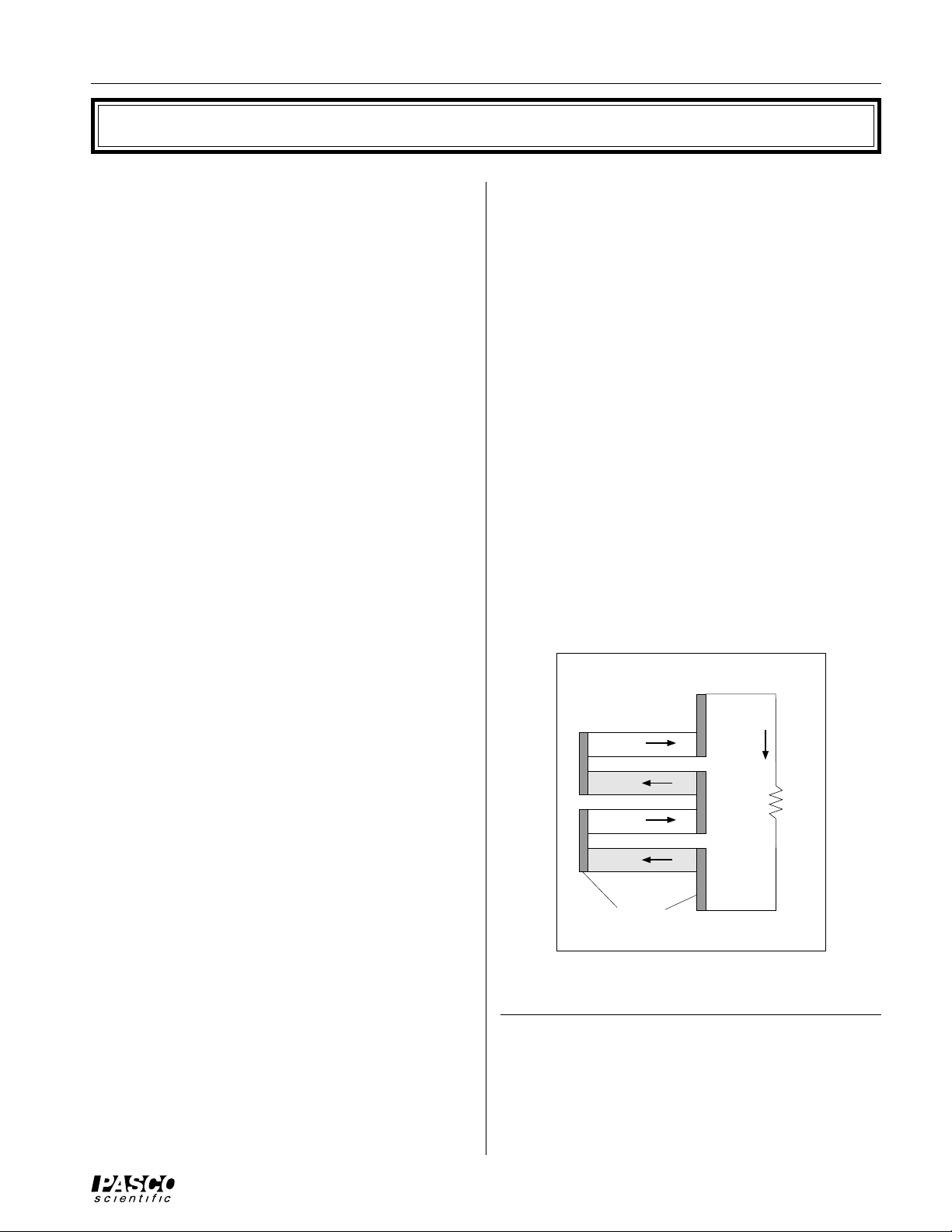
A heat engine can be represented by a diagram (Figure
2). The law of Conservation of Energy (First Law of
Thermodynamics) leads to the conclusion that
Q
= W + QC, the heat input to the engine equals the
H
work done by the heat engine on its surroundings plus
the heat exhausted to the cold reservoir.
Cold
Reservoir
Q
c
Q
Hot
Reservoir
h
➤ NOTE: Since you will be measuring the rates
at which energy is transferred or used by the
Thermal Efficiency Apparatus all measurements
will be power rather than energy. So
P
= dQH/dt and then the equation
H
QH = W + QC becomes PH=PW+PC and the
efficiency becomes
P
W
e =
P
H
Carnot Efficiency
Carnot showed that the maximum efficiency of a heat
engine depends only on the temperatures between
which the engine operates, not on the type of engine.
– T
T
H
e
=
Carnot
where the temperatures must be in Kelvin. The only
engines which can be 100% efficient are ones which
operate between TH and absolute zero. The Carnot
efficiency is the best a heat engine can do for a given
pair of temperatures, assuming there are no energy
losses due to friction, heat conduction, heat radiation,
and Joule heating of the internal resistance of the
device.
C
T
H
T
c
W
Figure 2: Heat Engine
Heat
Engine
T
h
Actual Efficiency
The efficiency of the heat engine is defined to be the
work done divided by the heat input
W
e =
Q
H
So if all the heat input was converted to useful work,
the engine would have an efficiency of one (100%
efficient). Thus, the efficiency is always less than one.
Adjusted Efficiency
Using the Thermal Efficiency Apparatus, you can
account for the energy losses and add them back into
the powers PW and PH. This shows that, as all losses
are accounted for, the resulting adjusted efficiency
approaches the Carnot efficiency, showing that the
maximum efficiency possible is not 100%.
3
Page 8
Thermal Efficiency Apparatus 012-05443A
W
Heat Pump (Refrigerator)
Introduction
A heat pump is a heat engine run in reverse. Normally,
when left alone, heat will flow from hot to cold. But a
heat pump does work to pump heat from the cold reservoir to the hot reservoir, just as a refrigerator pumps heat
out of its cold interior into the warmer room or a heat
pump in a house in winter pumps heat from the cold
outdoors into the warmer house.
In the case of the Thermal Efficiency Apparatus, heat is
pumped from the cold reservoir to the hot reservoir by
running a current into the Peltier device in the direction
opposite to the direction in which the Peltier device will
produce a current.
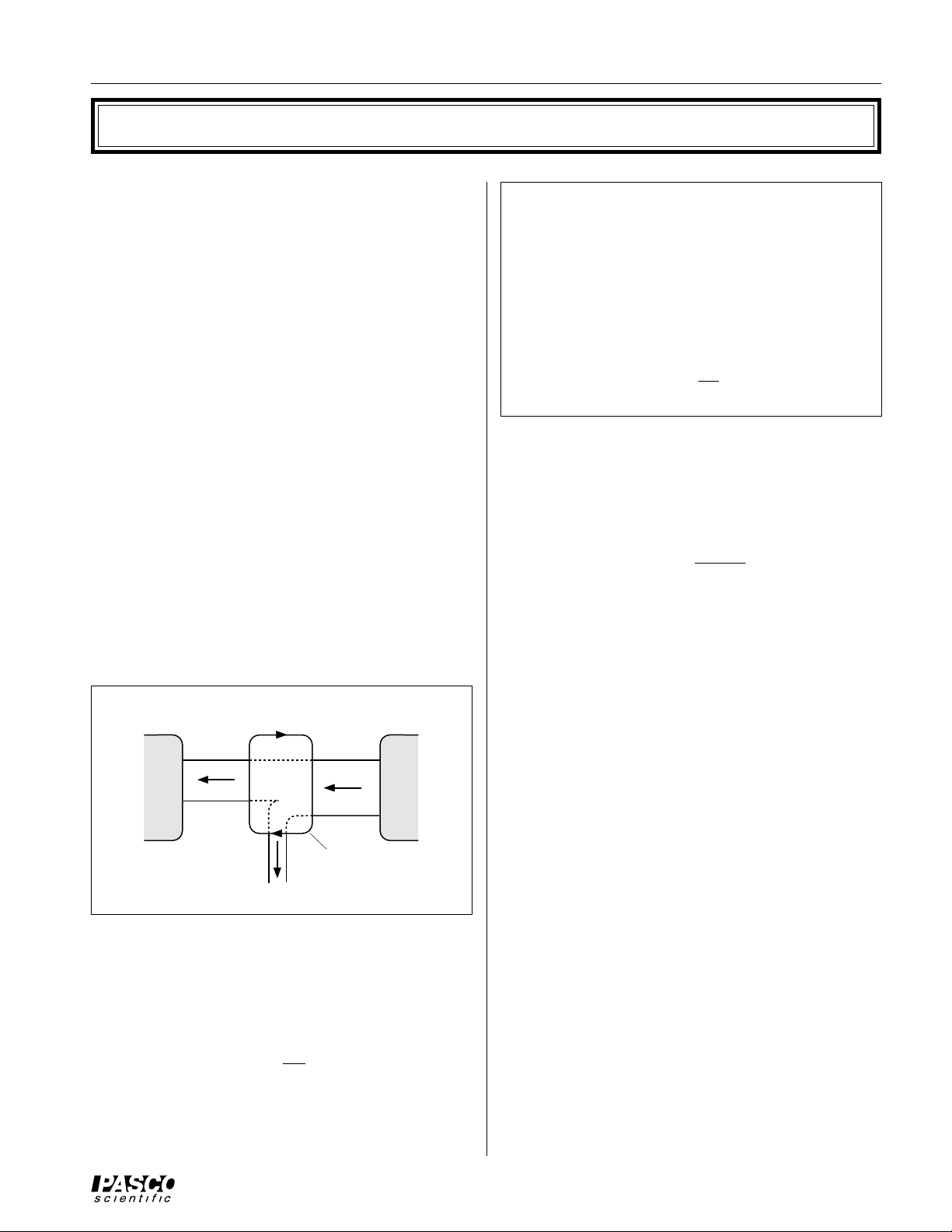
A heat pump is represented in a diagram such as Figure 3.
➤NOTE: The arrows are reversed compared to the
heat in Figure 2. By conservation of energy,
Q
+ W = QH,
or in terms of power
C
PC+PW=PH.
This is similar to efficiency because it is the ratio of
what is accomplished to how much energy was expended to do it. Notice that although the efficiency is
always less than one, the COP is always greater than
one.
Maximum Coefficient of Performance
As with the maximum efficiency of a heat engine, the
maximum COP of a heat pump is only dependent on
the temperatures.
T
=
TH– T
C
C
κ
max
where the temperatures are in Kelvin.
Adjusted Coefficient of Performance
If all losses due to friction, heat conduction, radiation,
and Joule heating are accounted for, the actual COP
can be adjusted so it approaches the maximum COP.
Ohmmeter
Ω
h
Hot
Reservoir
T
h
Cold
Reservoir
T
c
Q
c
W
Q
Heat
Pump
Figure 3: Heat Pump
Actual Coefficient of Performance
Instead of defining an efficiency as is done for a heat
engine, a coefficient of performance (COP) is defined
for a heat pump. The COP is the heat pumped from the
cold reservoir divided by the work required to pump it
P
κ
= COP =
C
.
P
9V Power
Supply In
Rubber
Hoses
WATER
PUMP
7.5 - 12 VDC
@500mA
In
COOLING
WATER
THERMISTOR
SELECT
PELTIER
DEVICE
Out
THERMISTOR TABLE
KΩ
°C
KΩ
°C
KΩ
°C
KΩ
°C
KΩ
°C
461
-5
269
5
436
413
391
370
351
332
315
298
283
161
-4
255
6
153
-3
242
7
146
-2
230
8
139
-1
218
9
133
0
207
10
126
1
197
11
120
2
187
12
115
3
178
13
109
4
169
14
104
KΩ
15
100
25
63.4
16
95.4
26
60.7
17
91.1
27
58.1
18
87.0
28
55.6
19
83.1
29
53.2
20
79.4
30
51.0
21
75.9
31
48.9
22
72.5
32
46.8
23
69.3
33
44.9
24
66.3
34
43.0
KΩ
°C
41.2
45
27.4
35
39.6
46
26.4
36
37.9
47
25.3
37
36.4
48
24.4
38
34.9
49
23.4
39
33.5
50
22.5
40
32.2
51
21.7
41
30.9
52
20.9
42
29.7
53
20.1
43
28.5
54
19.3
44
Figure 4: Thermal Efficiency Apparatus
scientific
PASCO
Model TD-8564
THERMAL EFFICIENCY
APPARATUS
HEATE R
°C
55
56
57
58
59
60
61
62
63
64
5Ω±1%
12 VDC MAX
2.0Ω1.0Ω0.5Ω
KΩ
°C
KΩ
°C
18.6
65
12.9
75
17.9
66
12.4
76
17.3
67
12.0
77
16.6
68
11.6
78
16.0
69
11.2
79
15.5
70
10.8
80
14.9
71
10.4
81
14.4
72
10.1
82
13.8
73
9.76
83
13.4
74
9.43
84
KΩ
°C
KΩ
°C
9.12
85
6.53
95
8.81
86
6.33
96
8.52
87
6.12
97
8.24
88
5.93
98
7.96
89
5.74
99
7.70
90
5.56
100
7.45
91
5.39
101
7.21
92
5.22
102
6.98
93
5.06
103
6.75
94
4.91
104
4
Page 9
012-05443A Thermal Efficiency Apparatus
C
Measurements Using the Thermal Efficiency Apparatus
Direct Measurements
Three quantities may be directly measured with the
Thermal Efficiency Apparatus: temperatures, the power
delivered to the hot reservoir, and the power dissipated by
the load resistors. The details of how these measurements
are made follow.
Temperatures
The temperatures of the hot and cold reservoirs are
determined by measuring the resistance of the thermistor
imbedded in the hot or cold block. To do this, connect an
ohmmeter to the terminals located as shown in Figure 4.
The switch toggles between the hot side and the cold side.
The thermistor reading can be converted to a temperature
Table 1: Resistance to Temperature Conversion Chart
kΩ °C kΩ °C kΩ °C kΩ °C kΩ °C
461 -5
436 -4
413 -3
146 17
139 18
133 19
53.2 39
51.0 40
48.9 41
by using the chart located on the front of the Thermal
Efficiency Apparatus and in Table 1. Notice that as the
temperature increases, the thermistor resistance decreases
(100 kΩ is a higher temperature than 200 kΩ).
➤ NOTE: To get the exact temperature reading
the user must interpolate between numbers on the
chart. For example, suppose the ohmmeter reads
118.7 kΩ. This reading lies between
120 kΩ = 21°C and 115 kΩ = 22°C. The reading is
120-118.7 = 1.3 kΩ above 21°C which is
1.3kΩ×
1°C
120 – 115kΩ
= 0.26°
Therefore 118.7 kΩ is 21.26°C.
21.7 61
20.9 62
20.1 63
9.76 83
9.43 84
9.12 85
391 -2
370 -1
351 0
332 1
315 2
298 3
283 4
269 5
255 6
242 7
230 8
218 9
207 10
197 11
187 12
178 13
169 14
161 15
126 20
120 21
115 22
109 23
104 24
100 25
95.4 26
91.1 27
87.0 28
83.1 29
79.4 30
75.9 31
72.5 32
69.3 33
66.3 34
63.4 35
60.7 36
58.1 37
46.8 42
44.9 43
43.0 44
41.2 45
39.6 46
37.9 47
36.4 48
34.9 49
33.5 50
32.2 51
30.9 52
29.7 53
28.5 54
27.4 55
26.4 56
25.3 57
24.4 58
23.4 59
19.3 64
18.6 65
17.9 66
17.3 67
16.6 68
16.0 69
15.5 70
14.9 71
14.4 72
13.8 73
13.4 74
12.9 75
12.4 76
12.0 77
11.6 78
11.2 79
10.8 80
10.4 81
8.81 86
8.52 87
8.24 88
7.96 89
7.70 90
7.45 91
7.21 92
6.98 93
6.75 94
6.53 95
6.33 96
6.12 97
5.93 98
5.74 99
5.56 100
5.39 101
5.22 102
5.06 103
153 16
55.6 38
22.5 60
5
10.1 82
4.91 104
Page 10
Thermal Efficiency Apparatus 012-05443A
Power Delivered to the Hot Reservoir (PH)
The hot reservoir is maintained at a constant temperature
by running a current through a resistor. Since the resistance changes with temperature, it is necessary to measure the current and the voltage to obtain the power input.
Then P
= IHVH.
H
Power Dissipated by the Load Resistor (PW)
The power dissipated by the load resistor is determined
by measuring the voltage drop across the known load
resistance and using the formula
2
V
PW=
.
R
The load resistors have a tolerance of 1%.
2
V
➤ NOTE: We may use the equation
PW=
for
R
measuring the power in the load resistor because
the temperature (and therefore resistance) of this
resistor does not change significantly. We may not
use this equation to measure power in the heating
resistor, since its temperature (and resistance)
changes.
When the Thermal Efficiency Apparatus is operated as a
heat pump rather than as a heat engine, the load resistors
are not used so it is necessary to measure both the current
and the voltage. So the current into the Peltier device is
measured with an ammeter, and the voltage across the
Peltier device is measured with a voltmeter and the power
input is calculated with the formula P
= IWVW.
W
Indirect Measurements
It will be necessary to know three additional quantities in
the experiments:
device;
➁ The amount of heat conducted through the
device and the amount radiated away;
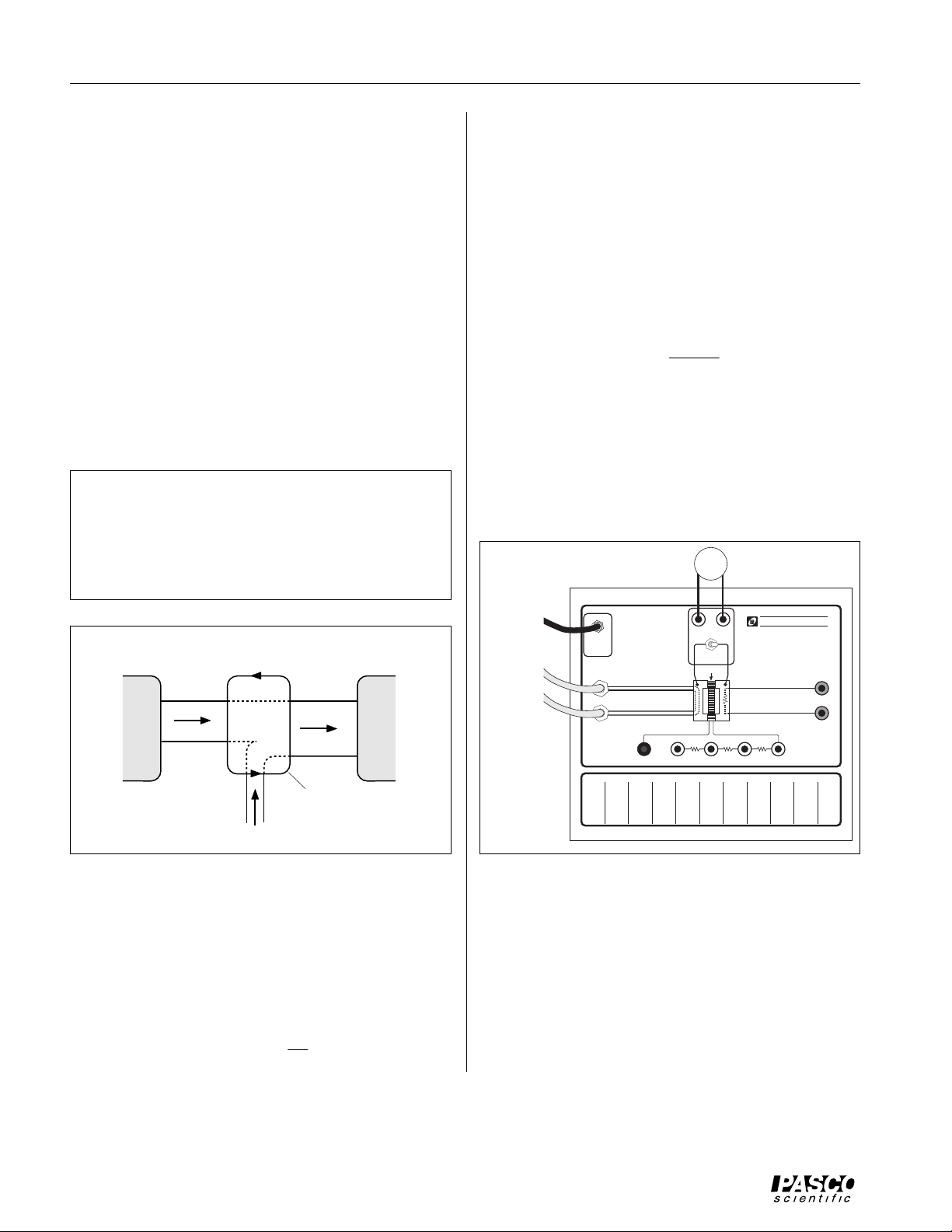
Figure 5: Procedure for Finding Internal Resistance
➀ The internal resistance of the Peltier
➂ The amount of
Peltier Device
R
r
V
l
l
V
s
heat pumped from the cold reservoir. These quantities
may be determined indirectly with the Thermal Efficiency Apparatus in the following ways.
Internal Resistance
Before the adjusted efficiency can be calculated, it is
necessary to calculate the internal resistance. This is
accomplished by measuring the voltage drop across the
Peltier device when an external load is applied.
First run the Thermal Efficiency Apparatus with a load
resistor (R) as in figure 6. The electrical equivalent of this
setup is shown in figure 5. Kirchoff’s Loop Rule gives
VS– Ir – IR =0
Next, run the Thermal Efficiency Apparatus with no load,
as in Figure 7. Since there is no current flowing through
the internal resistance of the Peltier Device, the voltage
drop across the internal resistance is zero and the voltage
measured will just be VS.
Since we have measured V
rather than I in the heat
w
engine mode, the equation above becomes
V
w
Vs–
r – Vw=0
R
Solving this for the internal resistance gives us
– V
V
s
r =
w
R
V
.
w
You may also find the resistance by measuring the
currents for two different load resistors and then solving
the resulting loop rule equations simultaneously.
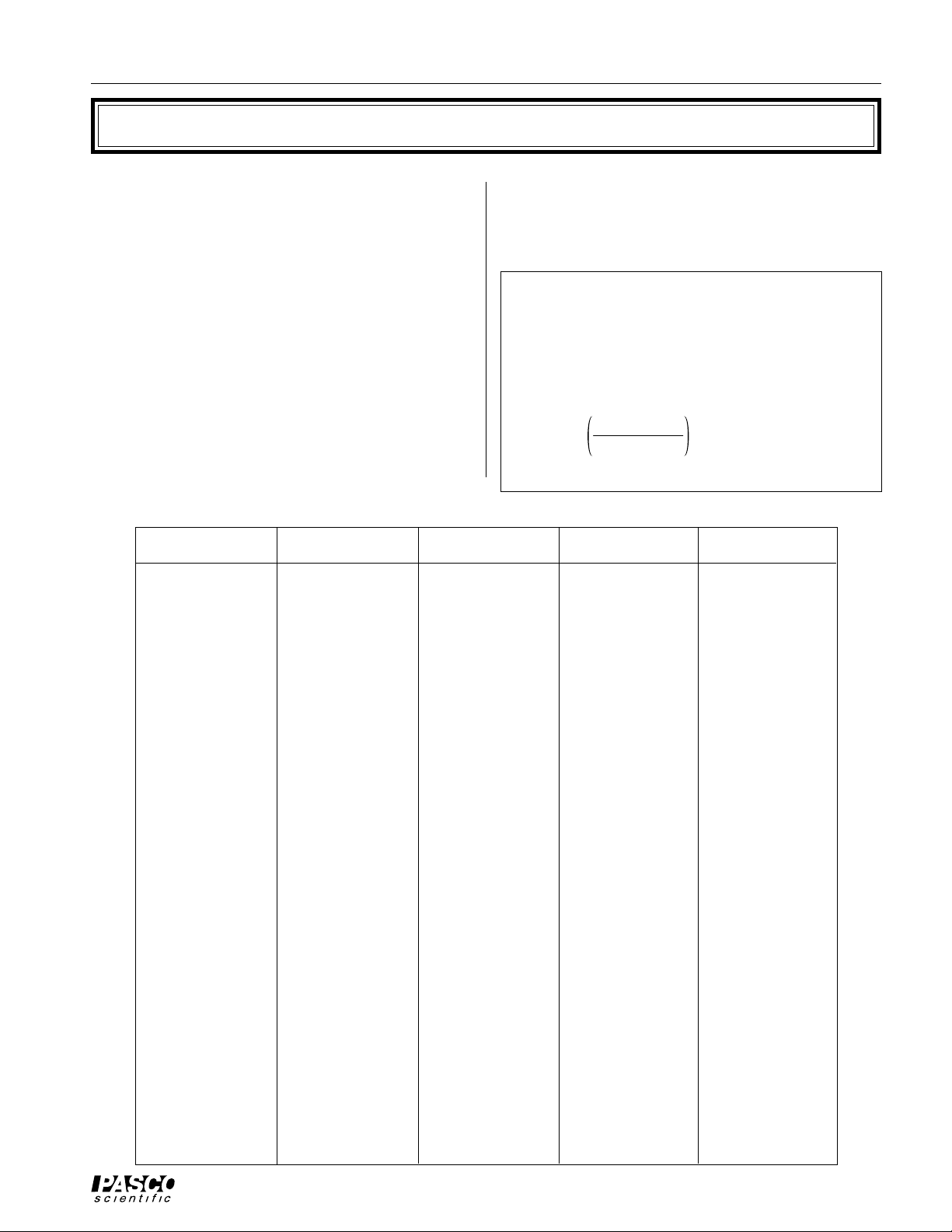
Heat Conduction and Radiation
The heat that leaves the hot reservoir goes two places:
part of it is actually available to be used by the heat
engine to do work while the other part bypasses the
engine either by being radiated away from the hot
reservoir or by being conducted through the Peltier device
to the cold side. The portion of the heat which bypasses
the engine by radiation and conduction would be transferred in this same manner whether or not the device is
connected to a load and the heat engine is doing work.
The Thermal Efficiency Apparatus is run with a load
connected to measure P
disconnected and the power input into the hot reservoir is
adjusted to maintain the temperatures (less power is needed
when there is no load since less heat is being drawn from
the hot reservoir). See Figure 7. P
(Figure 6) and then the load is
H
is the power input
H(open)
6
Page 11
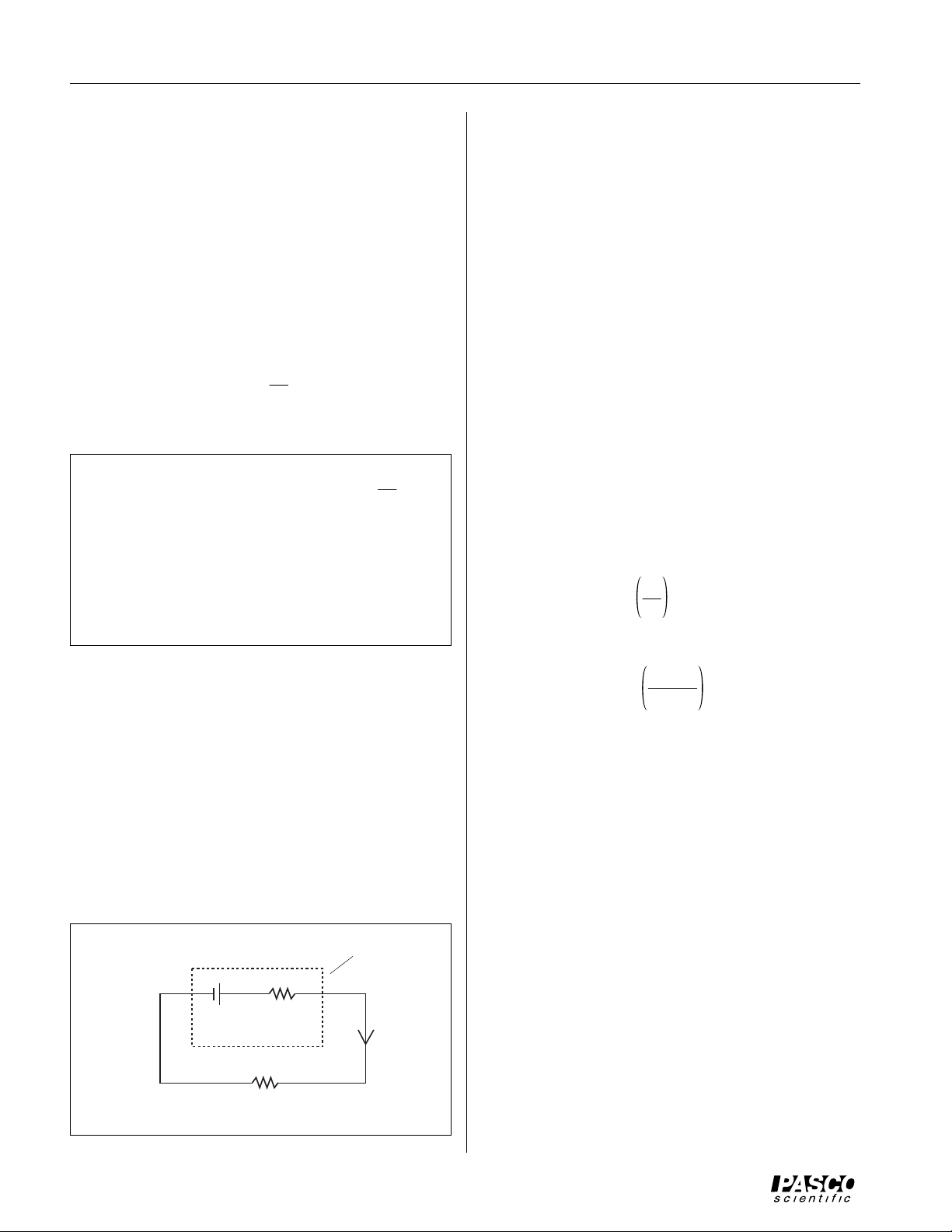
012-05443A Thermal Efficiency Apparatus
to the hot reservoir when no load is present. Since, while
there is no load, the hot reservoir is maintained at an
equilibrium temperature, the heat put into the hot reservoir by the heating resistor must equal the heat radiated
and conducted away from the hot reservoir. So measuring
the heat input when there is no load determines the heat
loss due to radiation and conduction. It is assumed this
loss is the same when there is a load and the heat engine
is operating.
Heat Pumped from the Cold Reservoir
When the Thermal Efficiency Apparatus is operated as a
heat pump, conservation of energy yields that the rate at
which heat is pumped from the cold reservoir, PC, is equal
to the rate at which heat is delivered to the hot reservoir,
PH, minus the rate at which work is being done, P
W
(Figure 3).
Ω
The work can be measured directly but the heat delivered
to the hot reservoir has to be measured indirectly. Notice
that when the heat pump is operating, the temperature of
the hot reservoir remains constant. Therefore, the hot
reservoir must be in equilibrium and the heat delivered to
it must equal the heat being conducted and radiated away.
So a measurement of the heat conducted and radiated
away at a given temperature difference will also be a
measurement of the heat delivered to the hot reservoir.
The heat conducted and radiated is measured by running
the device with no load and measuring the heat input
needed to maintain the temperature of the hot side
(Figure 7).
T
H
Conducted
Power
V
Engine
Ω
A
Power
Supply
V
Figure 6: Heat Engine With A Load
V
A
Conducted
Power
PH (open)
Power
Supply
P
W
T
C
T
H
V
Figure 7: No Load
7
T
C
Page 12

Thermal Efficiency Apparatus 012-05443A
Copy-Ready Experiments
The following experiments are written in worksheet form.
Feel free to photocopy them for use in your lab.
➤ NOTE: The first paragraph in each experiment lists all the equipment needed
to perform the experiment. Be sure to read this equipment list first, as the requirements vary with each experiment.
8
Page 13

012-05443A Thermal Efficiency Apparatus
Experiment 1: Heat Engine and T emperature Difference
EQUIPMENT NEEDED:
— Thermal Efficiency Apparatus — DC power supply capable of 2.5 A at 12 V
— ohmmeter — ammeter (up to 3 A)
— patch cords — 2 voltmeters
— 3 kg (7 lbs) ice and a bucket for the ice-
water bath
Introduction
In this experiment the user will determine the actual efficiency and the Carnot efficiency of the
heat engine as a function of the operating temperatures.
Setup
➀ Prepare the ice-water bath and immerse both rubber tubes from the Thermal Efficiency Appara-
tus into the bath (Figure 4).
➁ Plug the 9V transformer into the wall socket and into the pump on the Thermal Efficiency
Apparatus. You should now hear the pump running and water should be coming out of the
rubber hose marked “out”.
➂ Plug the ohmmeter into the thermistor terminals.
➃ Connect a DC power supply and a voltmeter and ammeter to the heater block terminals. Adjust
the voltage to about 11 V.
➤ NOTE: This is just a suggested value chosen to make the hot temperature nearly at the
maximum allowed. Any voltage less than 12 V is suitable. The Thermal Efficiency
Apparatus should not be run for more than 5 minutes with the hot side above 80°C. A
thermal switch will automatically shut off the current to the heater block if it exceeds
93°C to prevent damage to the device.
Ω
V
A
Power
Supply
0.5Ω
1Ω
2Ω
Figure 1.1
V
9
Page 14

Thermal Efficiency Apparatus 012-05443A
➄ Connect the 2Ω load resistor with a short patch cord as shown in Figure 1.1. Connect a voltmeter
across the load resistor. The choice of the 2Ω load resistor is arbitrary. Any of the load resistances may be used.
Procedure
➀ Allow the system to come to equilibrium so that the hot and cold temperatures are constant.
This may take 5 to 10 minutes, depending on the starting temperatures. To speed up the
process, increase the voltage across the heating resistor momentarily and then return it to
the original setting. If it is desired to cool the hot side, the voltage can be momentarily
decreased. Remember that the thermistor resistance goes down as the temperature increases.
➁ Measure the temperature resistances of the hot side and the cold side by using the toggle
switch to switch the ohmmeter to each side. Record the readings in Table 1.1. Convert the
resistances to temperatures using the chart on the front of the device or Table 1 as explained
in the Measurements section and record these temperatures in Table 1.2.
➂ Record the voltage (V
the load resistor (V
) across the heating resistor, the current (IH), and the voltage across
H
) in Table 1.1.
W
➃ Lower the voltage across the heating resistor by about 2 V.
➄ Repeat Steps 1 through 4 until data for five different hot temperatures have been taken.
Table 1.1 Data for Heat Engine
Trial TH (kΩ)Tc (kΩ)TH (°C) TH (°C) V
1
2
3
4
5
H
I
H
V
w
Calculations
➀ For each of the data runs, calculate the power supplied to the hot reservoir, P
power used by the load resistor, P
, and record these in Table 1.2.
W
, and the
H
➁ Calculate the temperature difference for each trial and record it in Table 1.2.
➂ Calculate the actual efficiencies from the powers and record in Table 1.2.
➃ Calculate the Carnot (maximum) efficiencies from the temperatures and record in Table 1.2.
10
Page 15

012-05443A Thermal Efficiency Apparatus
Table 1.2 Calculated Values
Trial P
1
2
3
4
5
H
P
w
Analysis and Questions
To compare the actual efficiency to the Carnot efficiency, construct a graph.
Plot the Carnot efficiency vs. ∆T and also plot the actual efficiency vs. ∆T. This may be
done on the same graph.
➤ NOTE: We are assuming by doing this that T
TH (k) Tc (k) ∆T (k) e
was nearly constant.
c
actual
e
Carnot
➀ The Carnot efficiency is the maximum efficiency possible for a given temperature differ-
ence. According to the graph, is the actual efficiency always less than the Carnot efficiency?
➁ Does the Carnot efficiency increase or decrease as the temperature difference increases?
➂ Does the actual efficiency increase or decrease as the temperature difference increases?
➃ The Carnot efficiency represents the best that a perfect heat engine can do. Since this heat
engine is not perfect, the actual efficiency is a percentage of the Carnot efficiency. The
overall (actual) efficiency of a real heat engine represents the combination of the engine’s
ability to use the available energy and the maximum energy available for use. From the data
taken, what is the percentage of available energy used by this heat engine?
➄ The actual efficiency of this heat engine is very low and yet heat engines of this type are
used extensively in remote areas to run things. How can such an inefficient device be of
practical use?
11
Page 16

Thermal Efficiency Apparatus 012-05443A
Notes:
12
Page 17

012-05443A Thermal Efficiency Apparatus
Ω
V
V
A
Power
Supply
0.5Ω
1Ω
2Ω
Experiment 2: Heat Engine Efficiency (Detailed Study)
EQUIPMENT NEEDED:
— Thermal Efficiency Apparatus — 1 DC power supply capable of 2.5 A at 12 V
— ohmmeter — patch cords
— ammeter (up to 3 A) — 2 voltmeters
— 3 kg — (7 lbs) ice and a bucket for the ice-
water bath
Introduction
In this experiment the user will determine the actual efficiency and the Carnot efficiency of
the heat engine and then compensate for the energy losses to show that the compensated
actual efficiency approaches the Carnot efficiency.
Initial Setup
➀ Prepare the ice-water bath and immerse both rubber tubes from the Thermal Efficiency
Apparatus into the bath (Figure 4).
➁ Plug the 9V transformer into the wall socket and into the pump on the Thermal Efficiency
Apparatus. You should now hear the pump running and water should be coming out of the
rubber hose marked “out”.
➂ Plug the ohmmeter into the thermistor terminals.
Modes of Operation:
To obtain all the necessary data for the heat engine it is necessary to run the Thermal
Efficiency Apparatus in two different modes. The Heat Engine Mode determines the actual
efficiency of the Peltier device. The Open Mode determines the losses due to conduction
and radiation. Data from both modes is used to calculate internal resistance and the Carnot
Efficiency.
➀ Heat Engine
A. Connect a DC power supply and a voltmeter and ammeter to the heater block terminals.
Turn on the voltage to about 11 V.
➤ NOTE: This is just a suggested value
chosen to make the hot temperature nearly
at the maximum allowed. Any voltage less
than 12 V is suitable. The Thermal
Efficiency Apparatus should not be run
for more than 5 minutes with the hot side
above 80°C. A thermal switch will
automatically shut off the current to the
heater block if it exceeds 93°C to prevent
damage to the device.
Figure 2.1
13
Page 18

Thermal Efficiency Apparatus 012-05443A
W
B. Connect the 2 Ω load resistor with a short patch cord as shown in Figure 2.1. Connect a
voltmeter across the load resistor.
C. Allow the system to come to equilibrium so that the hot and cold temperatures are
constant. This may take 5 to 10 minutes, depending on the starting temperatures. To
speed up the process, increase the voltage across the heating resistor momentarily and
then return it to 11 V. If it is desired to cool the hot side, the voltage can be momentarily
decreased. Remember that the thermistor resistance goes down as the temperature
increases.
D. Measure the temperature resistances of the hot side and the cold side by using the toggle
switch to switch the ohmmeter to each side. Record the readings in Table 3. Convert the
resistances to temperatures using the chart on the front of the device or Table 1 as
explained in the Measurements section.
E. Record the voltage (V
) across the heating resistor, the current (IH), and the voltage
H
across the load resistor (VW) in Table 2.1.
➁ Open
A. Disconnect the patch cord from the load resistor so no current is flowing through the
load and thus no work is being done. Now all the power delivered to the heating resistor
is either conducted to the cold side or radiated away. Leave the voltmeter attached so
that the Seebeck voltage (Vs) can be measured. (see figure 7)
B. Decrease the voltage applied to the hot side so that the system comes to equilibrium at
the same hot temperature as in the Heat Engine Mode. Since the temperature difference
is the same as when the heat engine was doing work, the same amount of heat is now
being conducted through the device when there is no load as when there is a load.
(It may not be possible to exactly match the previous cold temperature.)
C. Record the resistances in Table 2.1 and convert them to degrees.
Also record V
, IH and Vp.
H
Calculations for the Heat Engine
➀ Actual Efficiency: Calculate the actual efficiency using
P
W
e =
,
P
H
2
PW=
V
and PH = IHVH.
R
Table 2.1 Data
where
Record the powers in Table 2.2 and the efficiency in Table 2.3.
Mode TH (kΩ)Tc (kΩ)TH (°C) Tc (°C) V
Engine
Open
H
I
H
V
w
V
S
14
Page 19

012-05443A Thermal Efficiency Apparatus
r
I
Table 2.2 Calculated Values
Internal Resistance = r = ________________
Mode Th (K) Tc (K) P
Engine
(2Ω load)
Open
Table 2.3 Results
Actual Adjusted % Difference
Efficiency
h
Maximum
(Carnot)
P
w
I
w
➁ Maximum Efficiency: Convert the temperatures to Kelvin and record in Table 2.2. Calcu-
late the Carnot efficiency using the temperatures and record in Table 2.3.
➂ Adjusted Efficiency: The purpose of the following calculations is to account for all the
energy losses and adjust the actual efficiency so that it matches the Carnot efficiency.
2
A. First, the work done in the actual efficiency calculation only includes
dissipated by the load resistor R but, to account for total work done by the device, it
2
should also include I
r for the power dissipated by the internal resistance, r, of the
device. This Joule heating of the Peltier device is not counted in the actual efficiency
because it is not useful work. Thus, in the adjusted efficiency, the total work done in
terms of power is
V
for the power
R
2
V
P
where
′
= PW+ I
W
=
W
V
W
. Calculate IW for the 2Ω load and record in Table 4.
R
W
2
r =
W
2
+ I
W
R
B. Second, the heat input must be adjusted. The heat that leaves the hot reservoir goes two
places. Part of it is actually available to be used by the heat engine to do work while the
other part bypasses the engine either by being radiated away from the hot reservoir or by
being conducted through the Peltier device to the cold side. The portion of the heat
which bypasses the engine by radiation and conduction would be transferred in this
same manner whether or not the device is connected to a load and the heat engine is
doing work. Therefore this heat can be considered to not be available to do work and
should not be included in the heat input in the adjusted efficiency.
′
P
= available heat = PH– P
H
H open
15
Page 20

Thermal Efficiency Apparatus 012-05443A
′
R
The Thermal Efficiency Apparatus is run with a load connected to measure PH (Figure
6) and then the load is disconnected and the power input into the hot reservoir is adjusted to maintain the temperatures (less power is needed when there is no load since
less heat is being drawn from the hot reservoir). See Figure 7. P
H(OPEN)
is the power
input to the hot reservoir when no load is present. Since, while there is no load, the hot
reservoir is maintained at an equilibrium temperature, the heat put into the hot reservoir
by the heating resistor must equal the heat radiated and conducted away from the hot
reservoir. So measuring the heat input when there is no load determines the heat loss
due to radiation and conduction. It is assumed this loss is the same when there is a load
and the heat engine is operating.
Having accounted for the obvious energy losses, the adjusted efficiency should match
the Carnot efficiency which assumes no energy loss. The adjusted efficiency is
′
e
adjusted
P
W
=
=
′
P
P
H
H
P
W
– P
2
+ I
W
H open
r
Calculate the internal resistance, r, using the equation
– V
V
P
r =
W
V
W
which is derived in the Indirect Measurement section. Record this resistance in Table
2.2. Then calculate the adjusted efficiency and record the result in Table 2.3.
Calculate the percent difference between the adjusted efficiency and the Carnot (maxi-
mum) efficiency
–
e
e
max
% Difference =
e
max
adjusted
× 100%
and record in Table 2.3.
Questions
➀ If the difference between the temperature of the hot side and the cold side was decreased,
would the maximum efficiency increase or decrease?
➁ The actual efficiency of this heat engine is very low and yet heat engines of this type are
used extensively in remote areas to run things. How can such an inefficient device be of
practical use?
➂ Calculate the rate of change in entropy for the system which includes the hot and cold
reservoirs. Since the reservoirs are at constant temperature, the rate of change in entropy is
∆Q / ∆t
∆S
=
∆t
T
for each reservoir. Is the total change in entropy positive or negative? Why?
P
=
T
16
Page 21

012-05443A Thermal Efficiency Apparatus
Experiment 3: Heat Pump Coefficient of Performance
EQUIPMENT NEEDED:
— Thermal Efficiency Apparatus — 1 DC power supplies capable of 2.5 A at 12 V
— patch cords — ohmmeter
— ammeter (up to 3 A) — voltmeter
— 3 kg — (7 lbs) ice and a bucket for the
ice-water bath
➤ NOTE: Before doing this experiment, it is necessary to perform the HEAT ENGINE
EFFICIENCY experiment to get the data necessary to determine the internal resistance of
the Peltier device.
To complete the measurements for this experiment, use the following instructions to run the
apparatus as a heat pump (pumping heat from the cold side to the hot side):
Setup
➀ Prepare the ice-water bath and immerse both rubber tubes from the Thermal Efficiency
Apparatus into the bath (Figure 4).
for measuring temperatures
to AC supply
to ice water
tub
Ω
–
Power
Supply
+
for driving the Peltier device
V
for measuring V
Figure 3.1 Heat Pump Mode
17
A
for measuring I
w
Pw = VwI
w
w
Page 22

Thermal Efficiency Apparatus 012-05443A
W
W
➁ Plug the 9V transformer into the wall socket and into the pump on the Thermal Efficiency
Apparatus. You should now hear the pump running and water should be coming out of the
rubber hose marked “out”.
➂ Disconnect the power supply to the hot side. Connect the power supply directly across the
Peltier device with no load resistance. See Figure 3.1
➃ Connect an ammeter and a voltmeter to the power supply.
Procedure
➀ Increase the voltage until equilibrium is reached at the same hot temperature as in the
previous experiment. The hot side is now being heated by heat pumped from the cold side
rather than the heater resistor.
➁ Record the resistances and convert them to degrees. Also record the voltage (V
current (I
) in Table 3.1.
W
Analysis
➀ Actual Coefficient of Performance: Calculate the actual COP using the data taken in the
Heat Engine experiment.
P
P
C
W
=
H (OPEN)
κ
=
P
– P
P
W
Record this result in Table 3.1.
➁ Maximum Coefficient of Performance: Calculate the maximum COP using
T
=
TH– T
C
C
κ
MAX
and record this result in Table 3.1.
➂ Adjusted Coefficient of Performance: Part of the power being applied to the Peltier device
is being dissipated in the Joule heating of the internal resistance of the device rather than
being used to pump the heat from the cold reservoir. Therefore, to adjust for this, I
be subtracted from the power input to the Peltier device. Then the COP becomes the heat
pumped from the cold reservoir divided by work done to pump the heat, rather than dividing by the work done to pump the heat and heat the internal resistance. In terms of the
power,
) and the
W
2
r must
κ
ADJUSTED
P
=
H (OPEN)
PW– I
– P
2
W
r
Record this result in Table 3.1. Calculate the percent difference between the adjusted COP
and maximum COP:
% Difference =
MAX
ADJUSTED
κ
MAX
× 100%
κ
–
κ
and record in Table 3.1.
18
Page 23

012-05443A Thermal Efficiency Apparatus
Table 3.1 Heat Pump Data and Results
COP COP COP
(kΩ)TC(kΩ)TH(K) T
T
H
C
(K) V
I
W
P
W
actual max adj % diff
W
Questions
➀ If the difference between the temperature of the hot side and the cold side was decreased,
would the maximum COP increase or decrease?
➁ Calculate the rate of change in entropy for the system which includes the hot and cold
reservoirs. Since the reservoirs are at constant temperature, the rate of change in entropy is
∆Q / ∆t
∆S
∆t
=
T
P
=
T
for each reservoir. Is the total change in entropy positive or negative? Why?
19
Page 24

Thermal Efficiency Apparatus 012-05443A
Experiment 4: Thermal Conductivity
Introduction
The rate at which heat is conducted through a material of thickness x and cross-sectional
area A depends on the difference in temperature between the sides (∆T) and the thermal
conductivity (k) of the material.
Power =
Heat
Time
kA (∆T)
=
x
For the Thermal Efficiency Apparatus, the Peltier device has 71 couples and each couple
consists of 2 elements, so there is a total of 142 elements which conduct heat (Figure 9).
Each element has a length to area ratio of 8.460 cm
-1
. So
x
=
A
8.460cm
142
–1
. Use the data taken
in Experiment 2 for the Open Mode to calculate the thermal conductivity of the Peltier
device:
k =
P
H (OPEN)
(x / A)
∆T
Question
➀ How does the thermal conductivity of the Peltier device compare with the thermal conduc-
tivity of copper?
Copper
P
N
Figure 4.1 One Couple Equals Two Elements
20
Page 25

012-05443A Thermal Efficiency Apparatus
Experiment 5: Load for Optimum Performance
EQUIPMENT NEEDED:
Theory
— Thermal Efficiency Apparatus
— DCpower supply capable of 2.5 A at 12 V
V
s
r
— 3 kg (7 lbs) ice and a bucket for the ice-water bath
— ohmmeter
— ammeter (up to 3 A)
R
— 2 voltmeters
— patch cords
Figure 5.1 Peltier device connected
to a load resistor
This experiment finds the load resistor which maximizes the power output of the heat
engine. The power delivered to the load resistor, R, is P = I2R. The amount of current that
flows through the load resistor varies as the load is varied. From Figure
10, VS = I(r+R) where VS is the Seebeck voltage and r is the internal resistance of the
Peltier device.
So the power can be expressed in terms of the Seebeck voltage, the internal resistance, and
the load resistance:
2
V
P =
s
r + R
R
Assuming the Seebeck voltage remains constant if the temperatures of the hot and cold
reservoirs are constant, the power can be maximized with respect to the load resistance by
taking the derivative and setting it equal to zero:
V
l
dP
dR
=
S
(r + R)
=0
3
2
(r – R)
V
This shows that when the load resistance is equal to the internal resistance of the Peltier
device, the power delivered to the load will be a maximum.
Connect to appropriate AC supply
(powers pump to circulate ice water)
Ω
V
Place ends
of tubing in
ice water
tub
0.5Ω
2 Ω1 Ω
A
V
Figure 5.2 Connecting the 0.5Ω load resistor
Power
supply
21
Page 26

Thermal Efficiency Apparatus 012-05443A
Procedure
➀ Connect a DC power supply and a voltmeter and ammeter to the heater block terminals.
Turn on the voltage to about 11 V.
➤ NOTE: This is just a suggested value chosen to make the hot temperature nearly at the
maximum allowed. Any voltage less than 12 V is suitable. The Thermal Efficiency
Apparatus should not be run for more than 5 minutes with the hot side above 80°C. A
thermal switch will automatically shut off the current to the heater block if it exceeds
93°C to prevent damage to the device.
➁ Connect the 0.5W load resistor with a short patch cord as shown in Figure 11. Connect a
voltmeter across the load resistor.
➤ NOTE: Alternatively, a variable power resistor (rheostat) may be used in place of the load
resistors supplied with the Thermal Efficiency Apparatus. This has the advantage of being
able to continuously vary the load resistance. However, it will be necessary to measure
the resistance of the load.
➂ Allow the system to come to equilibrium so that the hot and cold temperatures are constant.
This may take 5 to 10 minutes, depending on the starting temperatures. To speed up the
process, increase the voltage across the heating resistor momentarily and then return it to 11
V. If it is desired to cool the hot side, the voltage can be momentarily decreased. Remember
that the thermistor resistance goes down as the temperature increases.
➃ Measure the temperature resistances of the hot side and the cold side by using the toggle
switch to switch the ohmmeter to each side. Record the readings in Table 5.1. Convert the
resistances to temperatures using the chart on the front of the device or Table 1 as explained
in the Measurements section.
➄ Record the voltage (V
the load resistor (V
R(Ω)TH(kΩ)TC(kΩ)TH(°K) T° (°K) V
0.5
1.0
1.5
2.0
2.5
3.0
) across the heating resistor, the current (IH), and the voltage across
H
) in Table 5.1.
W
Table 5.1: Heat Engine Data and Results
I
H
V
H
P
W
P
H
L
e
3.5
22
Page 27

012-05443A Thermal Efficiency Apparatus
➅ Calculate the power input to the hot side, P
2
V
resistor,
PL=
W
. Calculate the efficiency,
R
= IHVH, and the power dissipated by the load
H
P
L
e =
. Record all these values in Table 5.1.
P
H
➆ Adjust the power input to the hot side to keep the temperature of the hot reservoir at the
same temperature as it was for the 0.5 Ω resistor while Steps 1 through 6 are repeated for the
other possible load resistances: 1, 1.5, 2, 2.5, 3, and 3.5 ohms.
Questions
➀ For which load resistor is the efficiency a maximum?
➁ If you have done experiment 2: How does the load resistance for optimum efficiency
compare with the internal resistance measured in that experiment?
23
Page 28

Thermal Efficiency Apparatus 012-05443A
Notes:
24
Page 29

012-05443A Thermal Efficiency Apparatus
H
T eacher’s Guide
Experiment 1: Heat Engine and Temperature Difference
Notes on Setup
➁ It may be necessary to prime the pump by sucking
on the output line briefly.
Notes on Calculations
2
V
W
➀ Use the equations
P
➂
efficiency =
➃
e
Carnot
W
P
H
– T
T
H
=
C
T
H
PH= VHI
and
PW=
R
Notes on Analysis and Questions
0.2
0.18
0.16
0.14
0.12
0.1
0.08
Efficiency (%)
0.06
0.04
0.02
0
0 10203040506070
Carnot Efficiency
B
Actual Efficiency
J
B
B
J
J
Temperature Difference (°C)
B
B
B
B
J
J
J
J
B
J
➀ Yes.
➁,➂ Both Carnot and actual efficiency increase with
increasing temperature difference. (for a constant
cold temperature)
➃ In these trials, 11-12% of the available energy was
used.
➄ Although the efficiency is low, the reliability is ex-
tremely high. (There are no moving parts in the
Peltier device.) One practical application of these
devices is in satellite power supplies. A small piece
of radioactive material is used as a source of heat,
and a radiation fin is used as a heat sink. Another
similar application is to use the temperature difference between a nuclear isotope and arctic weather
to run a remote unmanned weather station. Any application where the thermal mass of the available
sources is large, the power requirements are small,
and the required reliability is high is good for the
Peltier device.
25
Page 30

Thermal Efficiency Apparatus 012-05443A
Experiment 2: Heat Engine Efficiency (Detailed Study)
Notes on Setup
➁ It may be necessary to prime the pump by sucking
on the output line briefly.
Sample Data
Mode Th (°C) Tc (°C) V
Engine 57.9 3.5 10.00 2.02 0.890
Open 57.9 3.3 8.99 1.815 1.495
h
I
h
V
w
V
Calculated Values
Mode Th (K) Tc (K) P
Engine 330.9 276.5 20.2 0.40 0.45
Open 330.9 276.3 16.3
Internal Resistance: r = 1.36Ω
h
P
w
I
w
Results
Actual Adjusted Maximum
(Carnot)
Efficiency 1.96% 17.13% 16.44% -4.23%
Note that these results were obtained using slightly
lower initial voltage than recommended in the lab.
In general, mid-range temperatures give better
results than extremely large or small temperature
differences.
% Difference
s
Answers to Questions
➀ If the temperature difference was decreased, the ef-
ficiency would also decrease.
➁ See experiment 1, question 5.
➂ For the hot reservoir, ∆S/∆t was -0.061. For the
cold reservoir, it was 0.073. The total change in entropy is positive. In any non-reversible process, the
entropy will increase.
26
Page 31

012-05443A Thermal Efficiency Apparatus
Experiment 3: Heat Pump Coefficient of Performance
Typical Results
Note that values of Ph and r were taken from
experiment 2.
Th (K) Tc (K) V
330.9 275.5 3.64 1.63 5.93 1.75 4.97 4.48 9.9%
w
I
w
P
w
COP COP
max
COP
adj
Answers to Questions
➀ The COP increases when the difference in tempera-
ture decreases.
➁ For the hot reservoir, ∆S/∆t = +0.018. For the cold
reservoir, it is – 0.0215. The net change in entropy
is negative. Work is done by the heat pump to decrease the entropy.
Experiment 4: Thermal Conductivity
Answer to Questions
➀ The thermal conductivity, based on the data taken
in experiment 2 of this guide, is 1.79 Watt/mK. By
comparison, the thermal conductivity of copper (at
273 K) is 401 Watt/mK.
% diff
The Peltier device is made of Bismuth Telluride,
which has an accepted thermal conductivity of
approximately 1.6 Watt/mK
27
Page 32

Thermal Efficiency Apparatus 012-05443A
Experiment 5: Load for Optimum Performance
Notes on Sample Data
2.4
2.3
2.2
2.1
% Efficiency
2
1.9
1
00.511.522.533.5
1
1
Load Resistance ( )
Answer to Question
The efficiency is a maximum when the 1.5Ω resistance
is used. This is close to the value of the internal
1
1
1
resistance determined in experiment 2, as well.
28
Page 33

012-05443A Thermal Efficiency Apparatus
T echnical Support
Feed-Back
If you have any comments about this product or this
manual please let us know. If you have any suggestions on alternate experiments or find a problem in the
manual please tell us. PASCO appreciates any customer feed-back. Your input helps us evaluate and
improve our product.
To Reach PASCO
For Technical Support call us at 1-800-772-8700 (tollfree within the U.S.) or (916) 786-3800.
Contacting Technical Support
Before you call the PASCO Technical Support staff it
would be helpful to prepare the following information:
• If your problem is with the PASCO apparatus, note:
Title and Model number (usually listed on the label).
Approximate age of apparatus.
A detailed description of the problem/sequence of
events. (In case you can't call PASCO right away,
you won't lose valuable data.)
If possible, have the apparatus within reach when
calling. This makes descriptions of individual parts
much easier.
• If your problem relates to the instruction manual,
note:
Part number and Revision (listed by month and year
on the front cover).
Have the manual at hand to discuss your questions.
29
Page 34

 Loading...
Loading...