Page 1
Includes
Teacher's Notes
and
Typical
Experiment Results
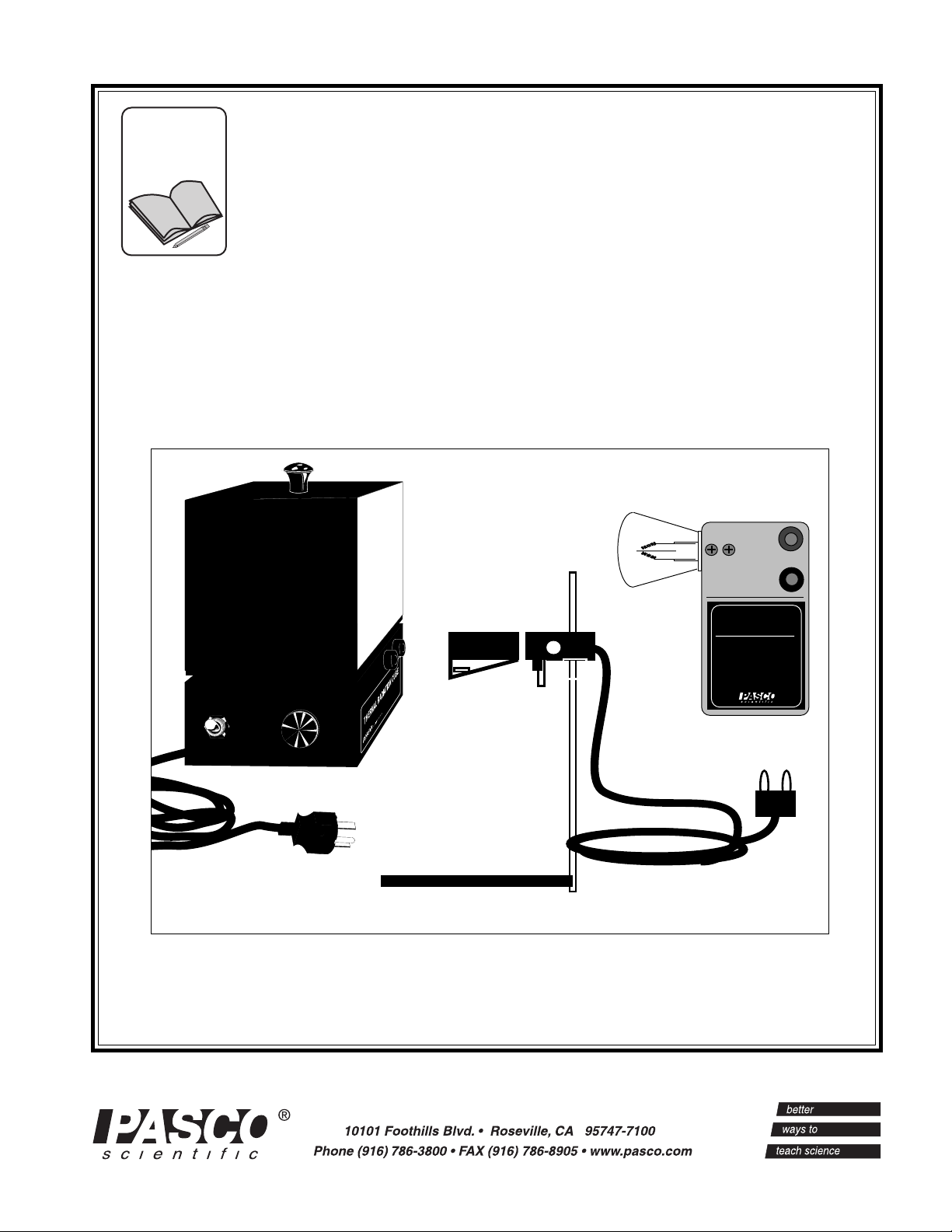
RADIATION SYSTEM
Instruction Manual and
Experiment Guide for the
PASCO scientific
Model TD-8553/8554A/8555
THERMAL
TD-8554A Radiation Cube
(Leslie's Cube)
012-04695D
03/99
TD-8555
STEFAN-BOLTZMAN
LAMP
CAUTION
13 VDC MAX LAMP VOLTAGE
FOR MAXIMUM ACCURACY,
MEASURE VOLTAGE AT
BINDING POSTS
USE NO.1196 BULB
TD-8555 Stefan
Boltzman Lamp
CAUTION: HOT!
ON
OFF
4
5
3
2
1
LOW HIGH
R
O
T
IS
M
R
E
N
H
T
IO
T
A
4
!
5
U
5
T
A
-8
D
O
100W
T
C
l
e
H
d
o
BULB
M
MAX.
6
7
8
(LESLIE'S CUBE)
TD-8553 Radiation Sensor
© 1988 PASCO scientific $5.00
Page 2
Thermal Radiation 012-04695D
The lightning flash with arrowhead,
within an equilateral triangle, is intended
to alert the user of the presence of
uninsulated “dangerous voltage” within
the product’s enclosure that may be of
sufficient magnitude to constitute a risk
of electric shock to persons.
CAUTION
RISK OF ELECTRIC SHOCK
DO NOT OPEN
CAUTION:
TO PREVENT THE RISK OF
ELECTRIC SHOCK, DO NOT
REMOVE BACK COVER. NO USER
SERVICEABLE PARTS INSIDE.
REFER SERVICING TO QUALIFIED
SERVICE PERSONNEL.
The exclamation point within an equilateral triangle is intended to alert the
user of the presence of important
operating and maintenance (servicing) instructions in the literature accompanying the appliance.
2
Page 3

012-04695D Thermal Radiation System
T able of Contents
Section...................................................................................................... Page
Copyright and Warranty, Equipment Return.................................................. ii
Introduction .....................................................................................................1
Radiation Sensor..............................................................................................1
Thermal Radiation Cube (Leslie’s Cube)........................................................2
Stefan-Boltzmann Lamp..................................................................................3
Experiments:
Experiment 1: Introduction to Thermal Radiation ...................................5
Experiment 2: Inverse Square Law ..........................................................9
Experiment 3: Stefan-Boltzmann Law (high temperature) .....................13
Experiment 4: Stefan-Boltzmann Law (low temperature) .....................17
Teacher’s Guide.............................................................................................19
Technical Support................................................................Inside Back Cover
i
Page 4
Thermal Radiation System 012-04695D
Copyright, Warranty, and Equipment Return
Please—Feel free to duplicate this manual
subject to the copyright restrictions below.
Copyright Notice
The PASCO scientific Model TD 8553/
8554A/8555 Thermal Radiation System manual is
copyrighted and all rights reserved. However, permission is granted to non-profit educational institutions for
reproduction of any part of the manual providing the
reproductions are used only for their laboratories and
are not sold for profit. Reproduction under any other
circumstances, without the written consent of PASCO
scientific, is prohibited.
Limited Warranty
PASCO scientific warrants the product to be free from
defects in materials and workmanship for a period of
one year from the date of shipment to the customer.
PASCO will repair or replace at its option any part of
the product which is deemed to be defective in material
or workmanship. The warranty does not cover damage
to the product caused by abuse or improper use.
Determination of whether a product failure is the result
of a manufacturing defect or improper use by the
customer shall be made solely by PASCO scientific.
Responsibility for the return of equipment for warranty
repair belongs to the customer. Equipment must be
properly packed to prevent damage and shipped postage or freight prepaid. (Damage caused by improper
packing of the equipment for return shipment will not
be covered by the warranty.) Shipping costs for returning the equipment after repair will be paid by PASCO
scientific.
Credits
Equipment Return
Should the product have to be returned to PASCO
scientific for any reason, notify PASCO scientific by
letter, phone, or fax BEFORE returning the product.
Upon notification, the return authorization and shipping instructions will be promptly issued.
ä
NOTE: NO EQUIPMENT WILL BE
ACCEPTED FOR RETURN WITHOUT AN
AUTHORIZATION FROM PASCO.
When returning equipment for repair, the units must be
packed properly. Carriers will not accept responsibility
for damage caused by improper packing. To be certain
the unit will not be damaged in shipment, observe the
following rules:
➀ The packing carton must be strong enough for the
item shipped.
➁ Make certain there are at least two inches of pack-
ing material between any point on the apparatus and
the inside walls of the carton.
➂ Make certain that the packing material cannot shift
in the box or become compressed, allowing the
instrument come in contact with the packing carton.
Address: PASCO scientific
10101 Foothills Blvd.
Roseville, CA 95747-7100
Phone: (916) 786-3800
FAX: (916) 786-3292
email: techsupp@pasco.com
web: www.pasco.com
This manual authored by: Bruce Lee
Teacher’s guide written by: Eric Ayres
ii
Page 5
012-04695D Thermal Radiation System
Introduction
The PASCO Thermal Radiation System includes three
items: the TD-8553 Radiation Sensor, the TD-8554A
Radiation Cube (Leslie's Cube), and the TD-8555
Stefan-Boltzmann Lamp. This manual contains
operating instructions for each of these items plus
instructions and worksheets for the following four
experiments:
① Introduction to Thermal Radiation,
② Inverse Square Law,
③ Stefan-Boltzmann Law* (at high temperatures),
④ Stefan-Boltzmann Law* (at low temperatures).
* The Stefan-Boltzmann law states that the radiant
energy per unit area is proportional to the fourth
power of the temperature of the radiating surface.
Radiation Sensor
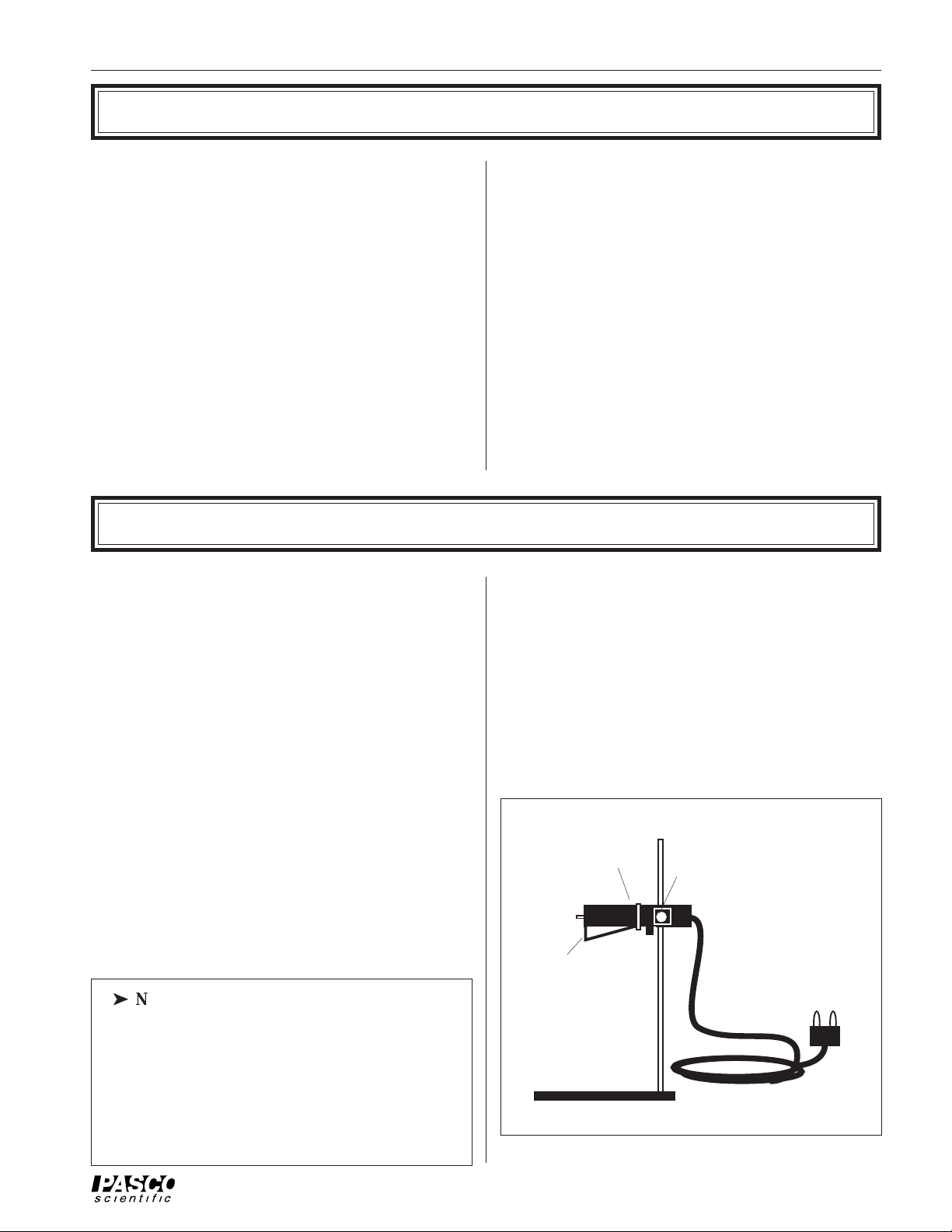
The PASCO TD-8553 Radiation Sensor (Figure 1)
measures the relative intensities of incident thermal
radiation. The sensing element, a miniature thermopile, produces a voltage proportional to the intensity of
the radiation. The spectral response of the thermopile
is essentially flat in the infrared region (from 0.5 to 40
µm), and the voltages produced range from the microvolt range up to around 100 millivolts. (A good
millivolt meter is sufficient for all the experiments
described in this manual. See the current PASCO
catalog for recommended meters.)
In addition to the equipment in the radiation system,
several standard laboratory items, such as power
supplies and meters are needed for most experiments.
Check the experiment section of this manual for
information on required equipment.
If you don't have all the items of the radiation system,
read through the operating instructions for the equipment you do have, then check the experiment section
to determine which of the experiments you can perform. (A radiation sensor is required for all the
experiments.)
The two posts extending from the front end of the
Sensor protect the thermopile and also provide a
reference for positioning the sensor a repeatable
distance from a radiation source.
Specifications
Temperature Range: -65 to 85 °C.
Maximum Incident Power: 0.1 Watts/cm2.
Spectral Response: .6 to 30µm.
Signal Output: Linear from 10-6 to 10-1 Watts/cm2.
The Sensor can be hand held or mounted on its stand
for more accurate positioning. A spring-clip shutter is
opened and closed by sliding the shutter ring forward
or back. During experiments, the shutter should be
closed when measurements are not actively being
taken. This helps reduce temperature shifts in the
thermopile reference junction which can cause the
sensor response to drift.
ä
NOTE: When opening and closing the
shutter, it is possible you may inadvertently
change the sensor position. Therefore, for
experiments in which the sensor position is
critical, such as Experiment 3, two small sheets
of opaque insulating foam have been provided.
Place this heat shield in front of the sensor when
measurements are not actively being taken.
Shutter Ring: Slide
forward to open
shutter
Shutter
1
Thumbscrew: Loosen to
reposition Sensor or to
remove Sensor from stand
Banana Connectors:
Connect to millivolt meter
Figure 1 Radiation Sensor
Page 6

Thermal Radiation System 012-04695D
Thermal Radiation Cube (Leslie’s Cube)
The TD-8554A Radiation Cube (Figure 2) provides
four different radiating surfaces that can be heated
from room temperature to approximately 120 °C. The
cube is heated by a 100 watt light bulb. Just plug in
the power cord, flip the toggle switch to “ON”, then
turn the knob clockwise to vary the power.
Measure the cube temperature by plugging your
ohmmeter into the banana plug connectors labeled
THERMISTOR. The thermistor is embedded in one
corner of the cube. Measure the resistance, then use
Table 1, below, to translate the resistance reading into a
temperature measurement. An abbreviated version of
this table is printed on the base of the Radiation Cube.
ä
NOTE: For best results, a digital ohmmeter
should be used. (See the current PASCO catalog
for recommended meters.)
ä
IMPORTANT: When replacing the light
bulb, use a 100-Watt bulb. Bulbs of higher
power could damage the cube.
CAUTION: Cube may be HOT!
Flip toggle
switch to
“ON” to turn
on power.
CAUTION: HOT!
ON
OFF
Figure 2 Radiation Cube (Leslie's Cube)
Turn knob
clockwise to
increase
temperature.
100W
BULB
4
5
MAX.
3
6
2
7
1
8
LOW HIGH
To 115
IST
N
THERM
O
I
T
!
U
T
A
O
T
C
l
e
H
d
o
M
E
I
L
S
E
L
(
or
200
VAC
Banana
OR
-8
D
'S
A
4
5
5
)
E
B
U
C
Connectors:
Measure
thermistor
resistance.
Use table on
back to
determine
cube
temperature.
Therm. Temp.
Res. (Ω) (°C)
207,850 10
197,560 11
187,840 12
178,650 13
169,950 14
161,730 15
153,950 16
146,580 17
139,610 18
133,000 19
126,740 20
120,810 21
115,190 22
109,850 23
104,800 24
100,000 25
95,447 26
91,126 27
87,022 28
83,124 29
79,422 30
75,903 31
72,560 32
69,380 33
Table 1
Resistance versus Temperature for the Thermal Radiation Cube
Therm. Temp.
Res. (Ω) (°C)
66,356 34
63,480 35
60,743 36
58,138 37
55,658 38
53,297 39
51,048 40
48,905 41
46,863 42
44,917 43
43,062 44
41,292 45
39,605 46
37,995 47
36,458 48
34,991 49
33,591 50
32,253 51
30,976 52
29,756 53
28,590 54
27,475 55
26,409 56
25,390 57
Therm. Temp.
Res. (Ω) (°C)
24,415 58
23,483 59
22,590 60
21,736 61
20,919 62
20,136 63
19,386 64
18,668 65
17,980 66
17,321 67
16,689 68
16,083 69
15,502 70
14,945 71
14,410 72
13,897 73
13,405 74
12,932 75
12,479 76
12,043 77
11,625 78
11,223 79
10,837 80
10,467 81
Therm. Temp.
Res. (Ω) (°C)
10,110 82
9,767.2 83
9,437.7 84
9,120.8 85
8,816.0 86
8,522.7 87
8,240.6 88
7,969.1 89
7,707.7 90
7,456.2 91
7,214.0 92
6,980.6 93
6,755.9 94
6,539.4 95
6,330.8 96
6,129.8 97
5,936.1 98
5,749.3 99
5,569.3 100
5,395.6 101
5,228.1 102
5,066.6 103
4,910.7 104
4,760.3 105
Therm. Temp.
Res. (Ω) (°C)
4,615.1 106
4,475.0 107
4,339.7 108
4,209.1 109
4,082.9 110
3,961.1 111
3,843.4 112
3,729.7 113
3,619.8 114
3,513.6 115
3,411.0 116
3,311.8 117
3,215.8 118
3,123.0 119
3,033.3 120
2,946.5 121
2,862.5 122
2,781.3 123
2,702.7 124
2,626.6 125
2,553.0 126
2,481.7 127
2,412.6 128
2,345.8 129
Therm. Temp.
Res. (Ω) (°C)
2,281.0 130
2,218.3 131
2,157.6 132
2,098.7 133
2,041.7 134
1,986.4 135
1,932.8 136
1,880.9 137
1,830.5 138
1,781.7 139
1,734.3 140
1,688.4 141
1,643.9 142
1,600.6 143
1,558.7 144
1,518.0 145
1,478.6 146
1,440.2 147
1,403.0 148
1,366.9 149
1,331.9 150
2
Page 7
012-04695D Thermal Radiation System
Stefan-Boltzmann Lamp
IMPORTANT: The voltage into the lamp
should NEVER exceed 13 V. Higher voltages
will burn out the filament.
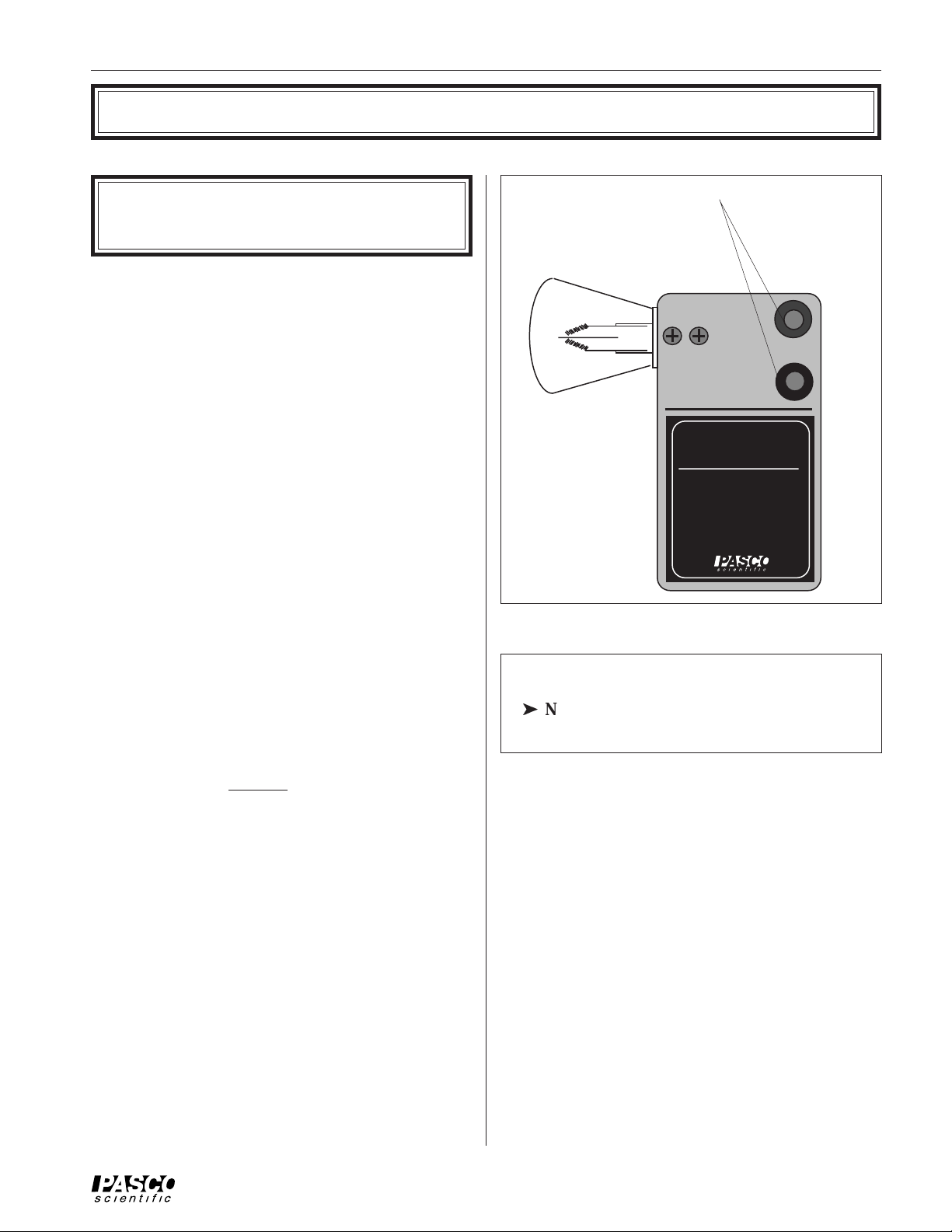
The TD-8555 Stefan-Boltzmann Lamp (Figure 3) is a
high temperature source of thermal radiation. The
lamp can be used for high temperature investigations
of the Stefan-Boltzmann Law. The high temperature
simplifies the analysis because the fourth power of the
ambient temperature is negligibly small compared to
the fourth power of the high temperature of the lamp
filament (see Experiments 3 and 4). When properly
oriented, the filament also provides a good approximation to a point source of thermal radiation. It therefore
works well for investigations into the inverse square
law.
By adjusting the power into the lamp (13 Volts max, 2
A min, 3 A max), filament temperatures up to approximately 3,000 °C can be obtained. The filament
temperature is determined by carefully measuring the
voltage and current into the lamp. The voltage divided
by the current gives the resistance of the filament.
Banana Connectors:
Connect to Power
Supply – 13 V MAX,
(2 A min, 3 A max)
TD-8555
STEFAN-BOLTZMAN
LAMP
CAUTION
13 VDC MAX LAMP VOLTAGE
FOR MAXIMUM ACCURACY,
PASCO scientific
MEASURE VOLTAGE AT
BINDING POSTS
USE NO.1196 BULB
Figure 3 Stefan-Boltzmann Lamp
Equipment Recommended
AC/DC LV Power Supply (SF-9584) or equivalent
capable of 13 V @ 3 A max
R - R
aR
ref
ref
ref
ref
T = + T
For small temperature changes, the temperature of
the tungsten filament can be calculated using a, the
temperature coefficient of resistivity for the filament:
where,
T = Temperature
R = Resistance at temperature T
T
= Reference temperature (usually room temp.)
ref
R
= Resistance at temperature T
ref
a = Temperature coefficient of resistivity for the
filament (α = 4.5 x 10-3 K-1 for tungsten)
For large temperature differences, however, a is not
constant and the above equation is not accurate.
REPLACEMENT BULB: GE Lamp No. 1196,
available at most auto parts stores.
ä
NOTE: When replacing the bulb, the leads
should be soldered to minimize resistance.
For large temperature differences, therefore, determine the temperature of the tungsten filament as
follows:
① Accurately measure the resistance (R
) of the tung-
ref
sten filament at room temperature (about 300 °K).
Accuracy is important here. A small error in R
ref
will result in a large error in your result for the filament temperature.
② When the filament is hot, measure the voltage and
current into the filament and divide the voltage by
the current to measure the resistance (R
③ Divide R
(RT/R
by R
T
).
ref
to obtain the relative resistance
ref
).
T
④ Using your measured value for the relative resistiv-
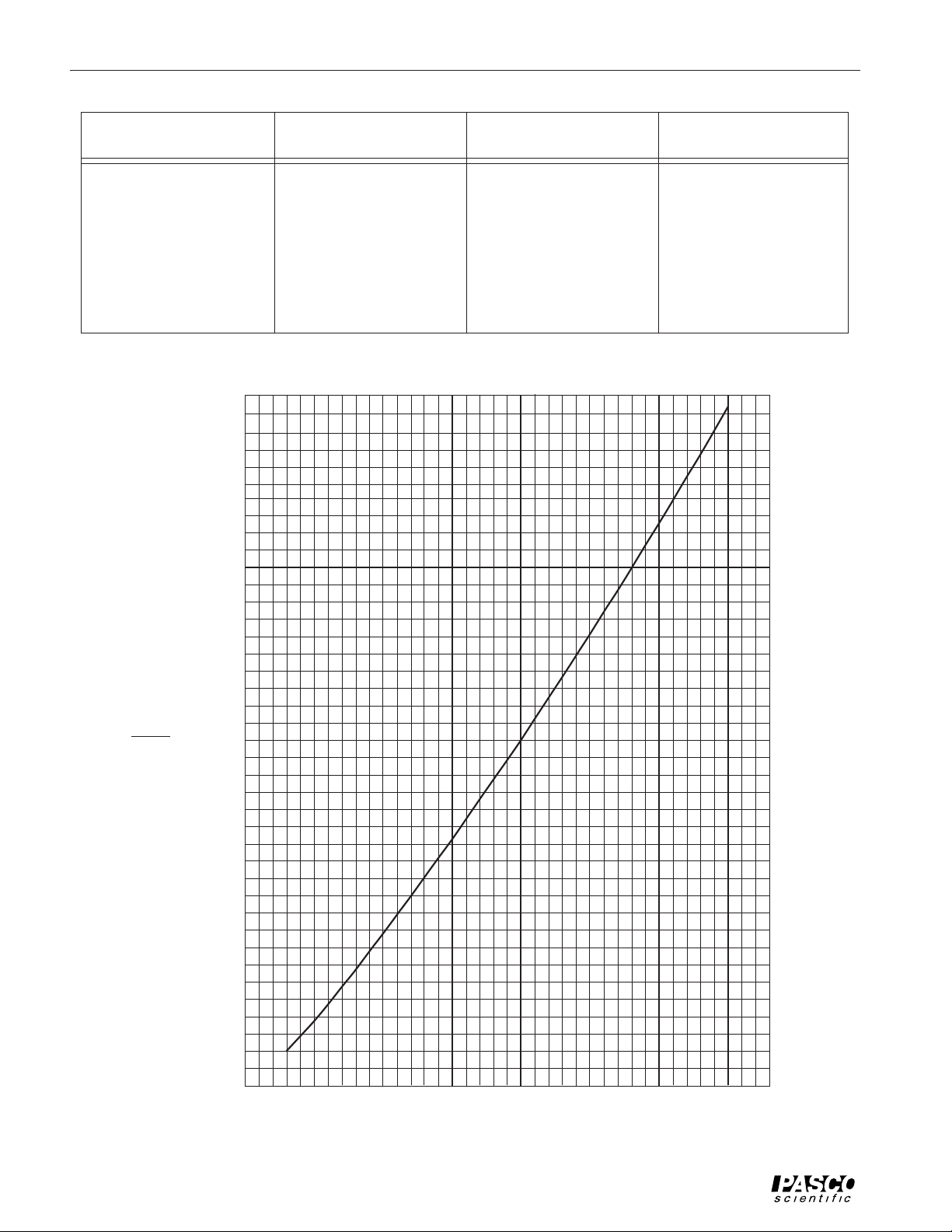
ity of the filament at temperature T, use Table 2 on
the following page, or the associated graph, to determine the temperature of the filament.
3
Page 8
Thermal Radiation System 012-04695D
Table 2 Temperature and Resistivity for Tungsten
Temp
R/R
300K
°K
Resistivity
µΩ cm
R/R
300K
Temp
°K
Resistivity
µΩ cm
R/R
300K
Temp
°K
Resistivity
µΩ cm
R/R
300K
Temp
°K
Resistivity
µΩ cm
1.0
1.43
1.87
2.34
2.85
3.36
3.88
4.41
4.95
300
400
500
600
700
800
900
1000
1100
5.65
8.06
10.56
13.23
16.09
19.00
21.94
24.93
27.94
20
19
18
17
16
15
14
5.48
6.03
6.58
7.14
7.71
8.28
8.86
9.44
10.03
1200
1300
1400
1500
1600
1700
1800
1900
2000
30.98
34.08
37.19
40.36
43.55
46.78
50.05
53.35
56.67
10.63
11.24
11.84
12.46
13.08
13.72
14.34
14.99
15.63
2100
2200
2300
2400
2500
2600
2700
2800
2900
60.06
63.48
66.91
70.39
73.91
77.49
81.04
84.70
88.33
Temperature versus Resistivity for Tungsten
16.29
16.95
17.62
18.28
18.97
19.66
26.35
3000
3100
3200
3300
3400
3500
3600
92.04
95.76
99.54
103.3
107.2
111.1
115.0
Relative
Resistivity
R
T
R
300K
13
12
11
10
9
8
7
6
5
4
3
2
1
0
0 500 1000 1500 2000 2500 3000 3500
Temperature (Kelvin)
4
Page 9
012-04695D Thermal Radiation System
Experiment 1: Introduction to Thermal Radiation
EQUIPMENT NEEDED:
— Radiation Sensor, Thermal Radiation Cube — Window glass
— Millivoltmeter — Ohmmeter.
ä
NOTES:
① If lab time is short, it's helpful to preheat the cube at a setting of 5.0 for 20 minutes before
the laboratory period begins. (A very quick method is to preheat the cube at full power
for 45 minutes, then use a small fan to reduce the temperature quickly as you lower the
power input. Just be sure that equilibrium is attained with the fan off.)
② Part 1 and 2 of this experiment can be performed simultaneously. Make the measure-
ments in Part 2 while waiting for the Radiation Cube to reach thermal equilibrium at each
of the settings in Part 1.
③ When using the Radiation Sensor, always shield it from the hot object except for the few
seconds it takes to actually make the measurement. This prevents heating of the thermopile which will change the reference temperature and alter the reading.
Radiation Rates from Different Surfaces
Part 1
① Connect the Ohmmeter and Millivoltmeter as shown in Figure 1.1.
② Turn on the Thermal Radiation Cube and set
the power switch to “HIGH”. Keep an eye on
the ohmmeter reading. When it gets down to
about 40 kΩ, reset the power switch to 5.0. (If
the cube is preheated, just set the switch to 5.0.)
③ When the cube reaches thermal equilibrium—
the ohmmeter reading will fluctuate around a
relatively fixed value—use the Radiation
Sensor to measure the radiation emitted from
each of the four surfaces of the cube. Place
the Sensor so that the posts on its end are in
contact with the cube surface (this ensures that
the distance of the measurement is the same for
all surfaces). Record your measurements in the
appropriate table on the following page. Also
measure and record the resistance of the thermistor. Use the table on the base of the cube to
determine the corresponding temperature.
CAUTION: HOT!
ON
OFF
A
100W
C
H
BULB
4
5
MAX.
3
6
2
7
1
8
LOW HIGH
Ohmmeter
R
O
T
IS
M
R
E
N
H
T
O
I
T
A
4
!
5
U
5
T
8
-
D
O
T
l
e
d
o
M
)
E
B
U
C
'S
IE
L
S
E
(L
Millivoltmeter
④ Increase the power switch setting, first to
6.5, then to 8.0, then to “HIGH”. At each
Figure 1.1 Equipment Setup
setting, wait for the cube to reach thermal equilibrium, then repeat the measurements
of step 1 and record your results in the appropriate table.
5
Page 10

Thermal Radiation System 012-04695D
Part 2
Use the Radiation Sensor to examine the relative magnitudes of the radiation emitted from
various objects around the room. On a separate sheet of paper, make a table summarizing your
observations. Make measurements that will help you to answer the questions listed below.
Absorption and Transmission of Thermal Radiation
① Place the Sensor approximately 5 cm from the black surface of the Radiation Cube and record
the reading. Place a piece of window glass between the Sensor and the bulb. Does window
glass effectively block thermal radiation?
② Remove the lid from the Radiation Cube (or use the Stefan-Boltzmann Lamp) and repeat the
measurements of step 1, but using the bare bulb instead of the black surface. Repeat with other
materials.
Radiation Rates from Different Surfaces
Data and Calculations
Power Setting 5.0
Therm. Res. Therm. Res.
Temperature
Sensor
Surface
Black
White
Polished
Aluminum
Dull
Aluminum
Reading
(mV)
Power Setting 6.5
Therm. Res.
Ω
°C
Temperature Temperature
Sensor
Surface
Black
White
Polished
Aluminum
Dull
Aluminum
Reading
(mV)
Power Setting 8.0 Power Setting 10.0
Ω
°C
Surface
Black
White
Polished
Aluminum
Dull
Aluminum
Sensor
Reading
(mV)
Ω
°C
Therm. Res.
Temperature
Surface
Black
White
Polished
Aluminum
Dull
Aluminum
Ω
°C
Sensor
Reading
(mV)
6
Page 11

012-04695D Thermal Radiation System
Questions (Part 1)
① List the surfaces of the Radiation Cube in order of the amount of radiation emitted. Is the order
independent of temperature?
② It is a general rule that good absorbers of radiation are also good emitters. Are your measure-
ments consistent with this rule? Explain.
Questions (Part 2)
① Do different objects, at approximately the same temperature, emit different amounts of radiation?
② Can you find materials in your room that block thermal radiation? Can you find materials that
don't block thermal radiation? (For example, do your clothes effectively block the thermal
radiation emitted from your body?)
Absorption and Transmission of Thermal Radiation
Questions
① What do your results suggest about the phenomenon of heat loss through windows?
② What do your results suggest about the Greenhouse Effect?
7
Page 12

Thermal Radiation System 012-04695D
Notes
8
Page 13

012-04695D Thermal Radiation System
Experiment 2: Inverse Square Law
EQUIPMENT NEEDED:
— Radiation Sensor
— Stefan-Boltzmann Lamp, Millivoltmeter
— Power Supply (12 VDC; 3 A), meter stick.
Align axes of filament and Sensor
Top View
X
Power Supply
(13 V MAX!)
Millivoltmeter
Meter Stick
Align zero-point of meter stick
with center of filament
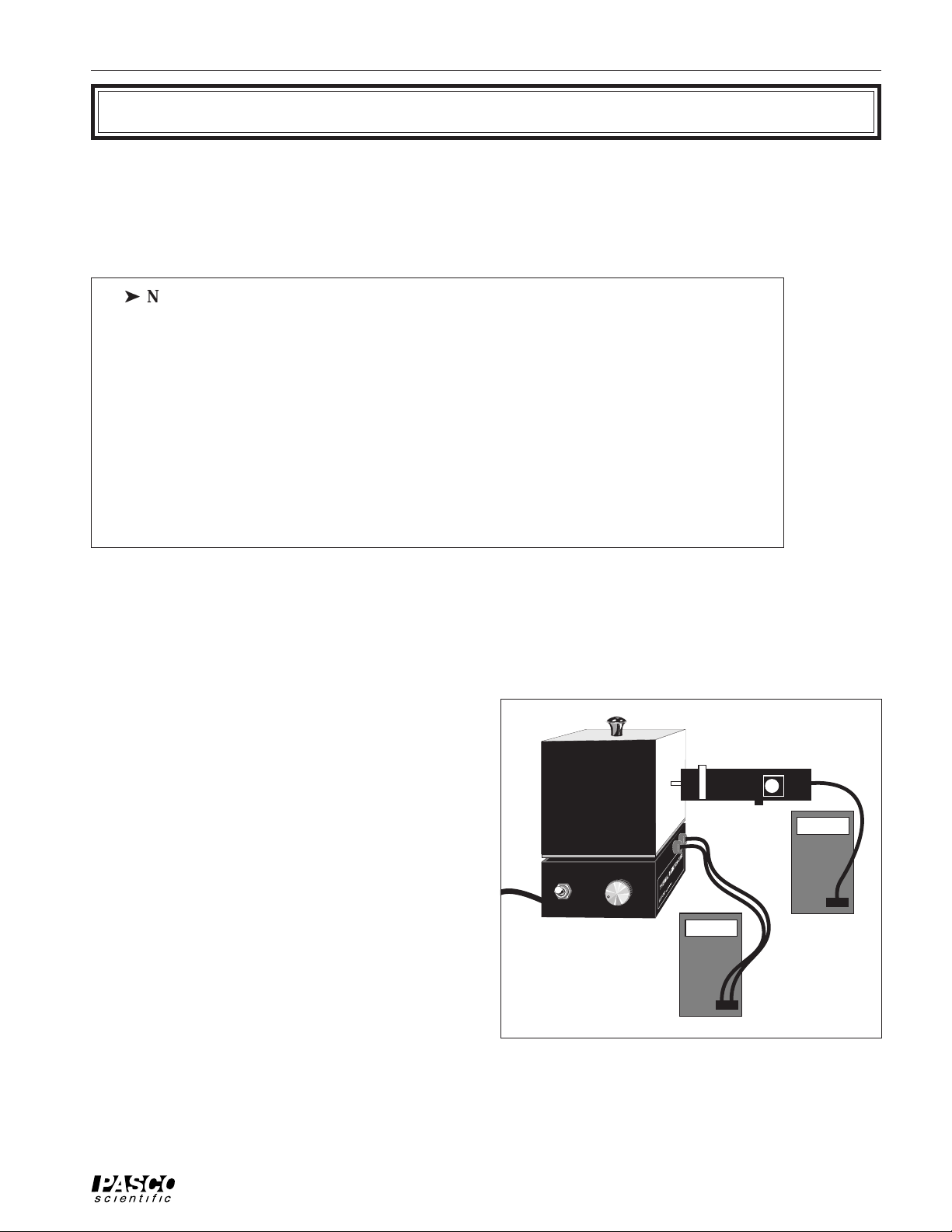
Figure 2.1 Equipment Setup
① Set up the equipment as shown in Figure 2.1.
a. Tape a meter stick to the table.
b. Place the Stefan-Boltzmann Lamp at one end of the meter stick as shown. The zero-
point of the meter stick should align with the center of the lamp filament.
c. Adjust the height of the Radiation Sensor so it is at the same level as the filament of the
Stefan-Boltzmann Lamp.
d. Align the lamp and sensor so that, as you slide the Sensor along the meter stick, the axis
of the lamp aligns as closely as possible with the axis of the Sensor.
e. Connect the Sensor to the millivoltmeter and the lamp to the power supply as indicated
in the figure.
② With the lamp OFF, slide the sensor along the meter stick. Record the reading of the
millivolt-meter at 10 cm intervals. Record your values in Table 2.1 on the following page.
Average these values to determine the ambient level of thermal radiation. You will need to
subtract this average ambient value from your measurements with the lamp on, in order to
determine the contribution from the lamp alone.
③ Turn on the power supply to illuminate the lamp. Set the voltage to approximately 10 V.
9
Page 14

Thermal Radiation System 012-04695D
ä
IMPORTANT: Do not let the voltage to the lamp exceed 13 V.
④ Adjust the distance between the Sensor and the lamp to each of the settings listed in Table 2.2.
At each setting, record the reading on the millivoltmeter.
ä
IMPORTANT: Make each reading quickly. Between readings, move the Sensor away
from the lamp, or place the reflective heat shield between the lamp and the Sensor, so that
the temperature of the Sensor stays relatively constant.
X Ambient Radiation Level
(cm) (mV)
10
20
30
40
50
60
70
80
90
100
Average Ambient
Radiation Level =
Table 2.1
Ambient Radiation Level
X Rad 1/X
(cm) (mV) (cm-2) (mV)
2.5
3.0
3.5
4.0
4.5
5.0
6.0
7.0
8.0
9.0
10.0
12.0
14.0
16.0
2
Rad - Ambient
Table 2.2
Radiation Level versus Distance
18.0
20.0
25.0
30.0
35.0
40.0
45.0
50.0
60.0
70.0
80.0
90.0
100.0
10
Page 15

012-04695D Thermal Radiation System
Calculations
① For each value of X, calculate 1/X2. Enter your results in Table 2.2.
② Subtract the Average Ambient Radiation Level from each of your Rad measurements in
Table 2.2. Enter your results in the table.
③ On a separate sheet of paper, make a graph of Radiation Level versus Distance from Source,
using columns one and four from Table 2.2. Let the radiation level be the dependent (y) axis.
④ If your graph from part 3 is not linear, make a graph of Radiation Level versus 1/X
2
, using
columns three and four from table 2.2.
Questions
① Which of the two graphs is more linear? Is it linear over the entire range of measurements?
② The inverse square law states that the radiant energy per unit area emitted by a point source
of radiation decreases as the square of the distance from the source to the point of detection.
Does your data support this assertion?
③ Is the Stefan-Boltzmann Lamp truly a point source of radiation? If not, how might this
affect your results? Do you see such an effect in the data you have taken?
11
Page 16

Thermal Radiation System 012-04695D
Notes
12
Page 17

012-04695D Thermal Radiation System
W
Experiment 3:
EQUIPMENT NEEDED:
— Radiation Sensor — Stefan-Boltzmann Lamp
— Ohmmeter — Ammeter (0-3 A)
— Voltmeter (0-12 V) — Millivoltmeter
— Ohmmeter — Thermometer.
Introduction
The Stefan-Boltzmann Law relates R, the power per unit area radiated by an object, to T, the
absolute temperature of the object. The equation is:
In this experiment, you will make relative measurements of the power per unit area emitted
from a hot object, namely the Stefan-Boltzmann Lamp, at various temperatures. From your
data you will be able to test whether the radiated power is really proportional to the fourth
power of the temperature.
Stefan-Boltzmann Law (high temperature)
R = σ T4; σ =5.6703 x 10
–8
m2K
4
Most of the thermal energy emitted by the lamp comes from the filament of the lamp. The
filament temperature can be determined using the procedure given on pages 3 and 4 of this
manual.
Power Supply
(13 V MAX!)
Millivoltmeter
+
–
6 cm
Figure 3.1 Equipment Setup
Ammeter
–+
Voltmeter
13
Page 18

Thermal Radiation System 012-04695D
Procedure
ä
IMPORTANT: The voltage into the lamp should NEVER exceed 13 V. Higher voltages
will burn out the filament.
① BEFORE TURNING ON THE LAMP, measure T
Kelvin, (K=°C + 273) and R
, the resistance of the filament of the Stefan-Boltzmann Lamp
ref
, the room temperature in degrees
ref
at room temperature. Enter your results in the spaces on the following page.
② Set up the equipment as shown in Figure 3.1. The voltmeter should be connected directly to
the binding posts of the Stefan-Boltzmann Lamp. The Sensor should be at the same height as
the filament, with the front face of the Sensor approximately 6 cm away from the filament.
The entrance angle of the thermopile should include no close objects other than the lamp.
③ Turn on the power supply. Set the voltage, V, to each of the settings listed in Table 3.1 on
the following page. At each voltage setting, record I, the ammeter reading, and Rad, the
reading on the millivoltmeter.
ä
IMPORTANT: Make each Sensor reading quickly. Between readings, place both sheets
of insulating foam between the lamp and the Sensor, with the silvered surface facing the
lamp, so that the temperature of the Sensor stays relatively constant.
14
Page 19

012-04695D Thermal Radiation System
Data and Calculations
① Calculate R, the resistance of the filament at each of the voltage settings used (R = V/I).
Enter your results in Table 3.1.
② Use the procedure on pages 3 and 4 of this manual to determine T, the temperature of the
lamp filament at each voltage setting. Enter your results in the table.
③*Calculate T
④*On a separate sheet of paper, construct a graph of Rad versus T
4
for each value of T and enter your results in the table.
4
. Use Rad as your dependent
variable (y-axis).
*In place of calculations ① and , some may prefer to perform a power regression on Rad
versus T to determine their relationship, or graph on log-log paper and find the slope.
Questions
① What is the relationship between Rad and T? Does this relationship hold over the entire
range of measurements?
② The Stefan-Boltzmann Law is perfectly true only for ideal, black body radiation. A black body is
any object that absorbs all the radiation that strikes it. Is the filament of the lamp a true black
body?
③ What sources of thermal radiation, other than the lamp filament, might have influenced your
measurements? What affect would you expect these sources to have on your results?
a = 4.5 x 10
T
(room temperature) = _______ K (K = °C + 273)
ref
R
(filament resistance at T
ref
-3 K-1
) = ________ Ω
ref
Table 3.1
Data Calculations
V I Rad R T T
(Volts) (Amps) (mV) (Ohms) (K) (K4)
1.00
2.00
3.00
4.00
5.00
4
6.00
7.00
8.00
9.00
10.00
11.00
12.00
15
Page 20

Thermal Radiation System 012-04695D
Notes
16
Page 21

012-04695D Thermal Radiation System
Experiment 4:
EQUIPMENT NEEDED:
— Radiation Sensor — Thermal Radiation Cube
— Millivoltmeter — Ohmmeter.
Introduction
In experiment 3, you investigated the Stefan-Boltzmann Law (R
temperatures attained by an incandescent filament. At those high temperatures (approximately 1,000 to 3,000 K), the ambient temperature is small enough that it can be neglected
in the analysis. In this experiment you will investigate the Stefan-Boltzmann relationship at
much lower temperatures using the Thermal Radiation Cube. At these lower temperatures,
the ambient temperature can not be ignored.
If the detector in the Radiation Sensor were operating at absolute zero temperature, it would
produce a voltage directly proportional to the intensity of the radiation that strikes it. However, the detector is not at absolute zero temperature so it is also radiating thermal energy.
According to the Stefan-Boltzmann
law, it radiates at a rate, R
4
sT
. The voltage produced by the
det
sensor is proportional to the radiation striking the detector minus the
radiation leaving it. Mathematically, the sensor voltage is proportional to R
4
T
). As long as you are careful to
det
shield the Radiation Sensor from
the Radiation Cube when measurements are not being taken, T
be very close to room temperature
(Trm).
net
= R
rad
– R
Stefan-Boltzmann Law (low temperature)
= sT4) for the high
rad
=
det
= s(T4 -
det
Ohmmeter
det
will
Millivoltmeter
CAUTION: HOT!
ON
OFF
4
5
3
2
1
LOW HIGH
R
O
T
IS
M
R
E
N
H
T
O
I
T
A
4
!
5
U
5
T
8
A
-
D
O
100W
T
C
l
e
H
d
o
BULB
M
)
E
B
U
MAX.
C
S
'
E
I
6
L
S
E
L
(
7
8
Heat Shield
(reflective side
toward cube)
Procedure
Figure 4.1 Equipment Setup
① Set up the equipment as shown in
Figure 4.1. The Radiation Sensor should be pointed directly at the center of one of the
better radiating surfaces of the cube (the black or white surface). The face of the Sensor
should be parallel with the surface of the cube and about 3 to 4 cm away.
② With the Thermal Radiation Cube off, measure R
, the resistance of the thermistor at room
rm
temperature. Enter this data in the space on the following page.
③ Shield the sensor from the cube using the reflecting heat shield, with the reflective side of
the shield facing the cube.
④ Turn on the Radiation Cube and set the power switch to 10.
⑤ When the thermistor resistance indicates that the temperature is about 12 C° above room
temperature, turn the power down so the temperature is changing slowly. Read and record
R, the ohmmeter reading, and Rad, the millivoltmeter reading. The readings should be
taken as nearly simultaneously as possible while briefly removing the heat shield. Record
these values in Table 4.1.
17
Page 22

Thermal Radiation System 012-04695D
ä
IMPORTANT: Make each reading quickly, removing the heat shield only as long as it
takes to make the measurement. Take care that the position of the sensor with respect to the
cube is the same for all measurements.
⑥ Replace the heat shield, and turn the cube power to 10. When the temperature has risen an
additional 12-15 C°, repeat the measurements of step 5. Repeat this procedure at about 12-15°
intervals until the maximum temperature of the cube is reached.
Data and Calculations
Room Temperature: Rrm = ________ Ω
Trm = ____ °C = _____ K
Table 4.1
Data Calculations
R Rad T
c
T
k
4
T
k
(ý) (mV) (°C) (K) (K4)(K
4
T
4
- T
k
rm
4
)
① Using the table on the base of the Thermal Radiation Cube, determine Tc, the temperature in
degrees Centigrade corresponding to each of your thermistor resistance measurements. For
each value of Tc, determine Tk, the corresponding value in degrees Kelvin (K = °C + 273).
Enter both sets of values in Table 4.1, above. In the same manner, determine the room temperature, Trm.
4
② CalculateT
③ Calculate T
④ On separate sheet of paper, construct a graph of Rad versus T
for each value of Tk and record the values in the table.
k
4
4
- T
k
for each value of Tk and record your results in the table.
rm
4
k
4
- T
. Use Rad as the depen-
rm
dent variable (y-axis).
Questions
① What does your graph indicate about the Stefan-Boltzmann law at low temperatures?
② Is your graph a straight line? Discuss any deviations that exist.
18
Page 23

012-04695D Thermal Radiation System
Teacher’s Guide
Experiment 1: Introduction to Thermal Radiation
Notes on Questions
Part 1
① In order of decreasing emissivity, the surfaces are
Black, White, Dull Aluminum, and Polished Aluminum. This order is independent of temperature; and
within the temperature range tested, the ratio of
emissions between sides is almost constant. The
normalized percentages are as follows: (Black is
defined as 100%)
Surface
Normalized
Emissions
Black 100
White 96.86 ±1.21%
Dull 20.23 ±2.17%
Polished 7.38 ±1.82%
② Measurements are consistent with the rule. The bet-
ter reflectors (poorer absorbers) are poor emitters.
Standard
Error
Notes on Questions
Part 2
① Yes. All sides of the Leslie’s Cube are at the same
temperature, but the polished side emits less than
10% as much radiation as the black side.
② Materials that block thermal radiation well include
aluminum foil, styrofoam, etc. Materials that do not
block radiation as well include air, clothing, etc. All
materials will block radiation to some degree, but
there are strong differences in how much is
blocked.
Notes on Questions
Absorbtion and Transmission of Thermal Radiation
① Heat loss through (closed) windows is primarily
conductive. Although the glass tested transmitted
some infrared, most was blocked.
② A greenhouse allows light in, but does not allow
much heat to escape. This phenomenon is used to
grow tropical plants in cold climates.
Calculations
③
30
1
25
1
20
1
15
1
1
1
10
Radiation (mV)
1
1
5
0
1
1
1
0 102030405060
f(x) = 2.060229E+2 * (x^-1.815646E+0 )
R^2 = 9.822989E-1
1
1
1
1
1
1
1
1
Distance (cm)
11
11
Experiment 2: Inverse Square Law
③
30
Radiation (mV)
19
25
20
15
1
10
1
5
1
1
1
1
1
1
1
1
1
1
11
11
0
0 0.02 0.04 0.06 0.08 0.1 0.12 0.14 0.16
1
1
1
1
1
1/x^2
1
1
Page 24

Thermal Radiation System 012-04695D
Notes on Questions
① The graph of Radiation versus 1/x2 is more linear,
but not over the entire range. There is a distinct
falloff in intensity at the nearer distances, due to the
non-point characteristics of the lamp. (A graph of
2
Radiation versus 1/x
using only data points from
10cm or more is nearly linear.)
② If we use data from distances that are large com-
pared to the size of the lamp filament—so that the
filament is effectively a “point”—then this data supports the hypothesis.
③ The Stefan-Boltzmann Lamp is not truly a point
source. If it were not, then there would be a falloff
in light level for measurements taken close to the
lamp. This falloff can be seen in our data.
Experiment 3: Stefan-Boltzmann Law (at high temperatures)
Suggestion:
The largest part of the error in this lab is due to the
non-point nature of the Stefan-Boltzmann Lamp.
You can approximate a much better “point” source
with a laser and a converging lens.
Laser
For best results, use a short-focal-length lens and
make sure that the sensor is always completely
within the beam.
"Point" S ource
Notes on Procedure
Part 1
③ Between readings, place the insulating material be-
tween the lamp and the sensor. For best results use
both sheets, with the aluminum sides facing away
from each other. Remove the sheets for only
enough time to take each measurement.
Calculations
③/④
14
f(x) = 5.521363E-14 * (x^4.363707E+0 )
12
R^2 = 9.979700E-1
10
8
6
4
Radiation Sensor Voltage
2
0
0 200 400 600 800 1000 1200 1400 1600 1800 2000
1
1
Temperature (K)
1
1
1
1
1
1
1
1
1
Notes on Questions
① A power regression of our data shows a power of
4.36. However, an analysis of only those points
with temperature greater than 1500° shows a power
of 4.01. This inaccuracy in the low-temperature
points is due to absorbtion of the infrared by the
glass lamp bulb. (See experiment 1) This absorbtion
is more significant at the lower temperatures, where
the infrared makes up a larger percentage of the entire output.
1
100
f(x) = 5.521363E-14 * (x^4.363707E+0 )
R^2 = 9.979700E-1
f(x) = 8.141230E-13 * (x^4.006331E+0 )
R^2 = 9.974766E-1
10
1
Radiation sensor Voltage
0.1
100 1000 10000
First fit uses all data points,
second uses only those 1500K or higher.
X
X
X
X
X
X
X
X
X
X
X
X
Temperature (K)
20
Page 25

012-04695D Thermal Radiation System
1
1
1
1
1
1
1
0
2
4
6
8
10
12
14
16
18
0
2000000000
4000000000
6000000000
8000000000
10000000000
12000000000
14000000000
Radiation (mV)
Difference in T^4
f(x) = 1.235365E-9*x + -1.396775E-1
R^2 = 9.881626E-1
② The lamp filament is not a true black body. If it
were, it would be completely and totally black at
room temperature. It is a fairly good approximation,
though, as long as the temperature is high enough
that the emitted light is much greater than the incident light.
Experiment 4: Stefan-Boltzmann Law (at low temperatures)
Notes on Procedure
③ Make sure that the Thermal Radiation Cube has
been off for enough time to be at equilibrium with
the room before making this measurement. If the
cube has been turned on recently, use another thermometer to make the measurement.
⑤ Use ridiculous precautions with this experiment. It
is impossible to have too much insulation between
the cube and the sensor between measurements. For
our experiments, we use two foam sheets covered
with aluminum tape, and an air gap between the
sheets. We never removed this heat shield for more
than 5 seconds while taking a measurement.
③ Any other thermal source in the room would influ-
ence the results, including the warm body of the experimenter and the room itself. These introduce
some error, but it is small as long as the temperature of the lamp is high compared to the temperature of these other sources.
Calculations
Notes on Questions
① The linearity of this graph indicates that the Stefan-
Boltzmann equation is correct, even at low temperatures.
② The graph should be straight, with some statistical
variations.
21
Page 26

Thermal Radiation System 012-04695D
Notes
22
Page 27

012-04695D Thermal Radiation System
Technical Support
Feed-Back
If you have any comments about this product or this
manual please let us know. If you have any suggestions on alternate experiments or find a problem in the
manual please tell us. PASCO appreciates any customer feed-back. Your input helps us evaluate and
improve our product.
To Reach PASCO
For Technical Support call us at 1-800-772-8700 (tollfree within the U.S.) or (916) 786-3800.
Contacting Technical Support
Before you call the PASCO Technical Support staff it
would be helpful to prepare the following information:
• If your problem is computer/software related, note:
Title and Revision Date of software.
Type of Computer (Make, Model, Speed).
Type of external Cables/Peripherals.
• If your problem is with the PASCO apparatus, note:
Title and Model number (usually listed on the label).
Approximate age of apparatus.
A detailed description of the problem/sequence of
events. (In case you can't call PASCO right away,
you won't lose valuable data.)
If possible, have the apparatus within reach when
calling. This makes descriptions of individual parts
much easier.
• If your problem relates to the instruction manual,
note:
Part number and Revision (listed by month and year
on the front cover).
Have the manual at hand to discuss your questions.
23
Page 28

 Loading...
Loading...