PASCO ME-9341 User Manual

Download

Includes

Teacher's Notes

and

Typical

Experiment Results

Instruction Manual and Experiment Guide for

012-03051F

3/95

the PASCO scientific Model ME-9341

INTRODUCTORY

ROTATIONAL APPARATUS

012-03051F Introductory Rotational Apparatus

T able of Contents

Section........................................................................................................Page

Introduction .....................................................................................................1

Equipment........................................................................................................2

Setup .............................................................................................................4

Timing with a Photogate..................................................................................6

Five Copy-Ready Experiments:.......................................................................7

Experiment 1: Angular Acceleration—1..................................................9

Experiment 2: Angular Acceleration—2.................................................11

Experiment 3: Gravitational - Rotational Energy....................................15

Experiment 4: Frictional Torque .............................................................17

Experiment 5: Rotational Collisions........................................................19

Teacher's Guide ..............................................................................................23

Appendix ........................................................................................................33

Technical Support.................................................................................... back cover

Introductory Rotational Apparatus 012-03051F

Please—Feel free to duplicate this manual subject to the copyright restrictions below.

The PASCO scientific Model ME-9341 Introductory Rotational Apparatus manual is copyrighted and all rights reserved. However, permission is granted to non-profit educational institutions for reproduction of any part of this manual providing the reproductions are used only for their laboratories and are not sold for profit. Reproduction under any other circumstances, without the written consent of PASCO scientific, is prohibited.

Limited Warranty

PASCO scientific warrants this product to be free from defects in materials and workmanship for a period of one year from the date of shipment to the customer. PASCO will repair or replace, at its option, any part of the product which is deemed to be defective in material or workmanship. This warranty does not cover damage to the product caused by abuse or improper use. Determination of whether a product failure is the result of a manufacturing defect or improper use by the customer shall be made solely by PASCO scientific. Responsibility for the return of equipment for warranty repair belongs to the customer. Equipment must be properly packed to prevent damage and shipped postage or freight prepaid. (Damage caused by improper packing of the equipment for return shipment will not be covered by the warranty.) Shipping costs for returning the equipment, after repair, will be paid by PASCO scientific.

Equipment Return

Should the product have to be returned to PASCO scientific for any reason, notify PASCO scientific by letter, phone, or fax BEFORE returning the product. Upon notification, the return authorization and shipping instructions will be promptly issued.

NOTE: NO EQUIPMENT WILL BE

ACCEPTED FOR RETURN WITHOUT AN AUTHORIZATION FROM PASCO.

When returning equipment for repair, the units must be packed properly. Carriers will not accept responsibility for damage caused by improper packing. To be certain the unit will not be damaged in shipment, observe the following rules:

➀ The packing carton must be strong enough for the

item shipped.

➁ Make certain there are at least two inches of

packing material between any point on the apparatus and the inside walls of the carton.

➂ Make certain that the packing material cannot shift

in the box or become compressed, allowing the instrument come in contact with the packing carton.

Credits

This manual authored by: Ed Pitkin This manual edited by: Dave Griffith Teacher’s guide written by: Dave Griffith

Address: PASCO scientific

10101 Foothills Blvd. Roseville, CA 95747-7100

Phone: (916) 786-3800 FAX: (916) 786-3292 email: techsupp@pasco.com web: www.pasco.com

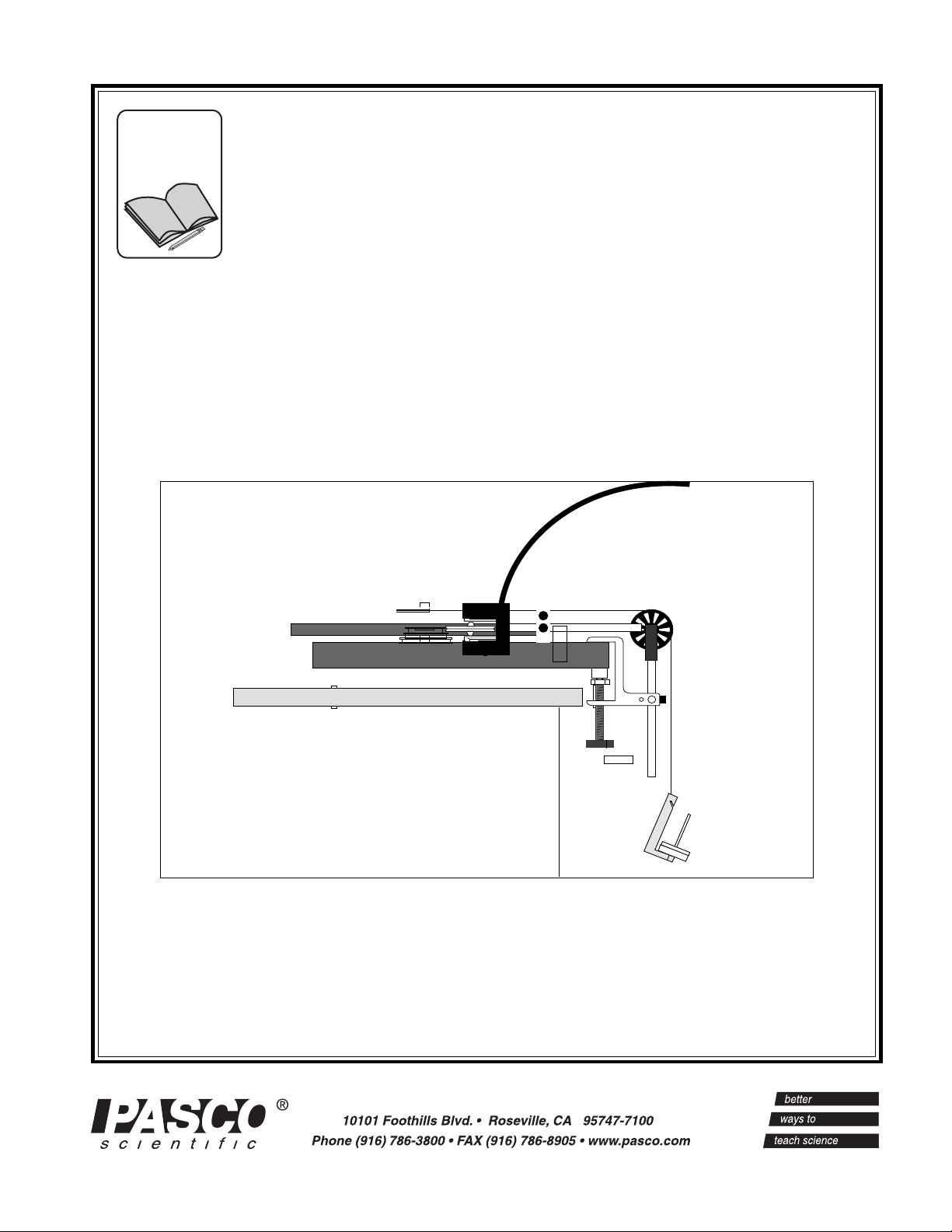
012-03051F Introductory Rotational Apparatus

Introduction

With the PASCO ME-9341 Introductory Rotational Apparatus, your students can perform a variety of experiments in rotational mechanics, including investigations into torque, angular acceleration, moment of inertia, and conservation of angular momentum.

Setup is quick and operation is simple. As shown in Figure 1, a platter spins on low-friction ball bearing supports. Torques can be applied to the platter with various torque arms and forces, and the angular velocity of the platter can be monitored over time to determine angular acceleration. The moment of inertia of the rotating system can be varied by adding a second platter, a steel ring, or a steel block.

The motion of the platter is described mathematically by Newton's Second Law in its rotational form: t = Ia, where t is the applied torque, I is the moment of inertia of the spinning platter, and a is the angular acceleration of the platter.

τ = r x F = Ια

Timing with the Smart Pulley

The Smart Pulley (see Figure 1) connects to your Apple II computer (II+, IIe, IIc, or IIGS), or IBM PC or compatible, providing automatic data collection, analysis, and graphing. As the platter spins, the pulley is held lightly against the rim of the platter, and therefore spins with the platter. The Smart Pulley photogate monitors the rotation of the pulley, sending its signals to the computer for timing and analysis. The software for the Smart Pulley includes options designed specifically for use with the Introductory Rotational Apparatus, producing tables and graphs showing angular displacement, velocity, and acceleration as a function of time.

The Smart Pulley is more than just a computer timer for the Rotational Apparatus. When used with an Apple II or IBM PC computer and standard laboratory equipment such as an air track or dynamics carts, the Smart Pulley provides a complete introductory lab in linear mechanics. See the PASCO catalog for more information about the Smart Pulley System, or Smart Pulley Timer and Accessories.

Smart Pulley with photogate

(not included)

Figure 1 Rotational Diagram

Timing the Rotational Motion

A variety of timing systems can be used to measure the motion of the Introductory Rotational Apparatus. The most versatile option is the PASCO Smart Pulley. However, standard photogate timers such as the PASCO model ME-9206A or ME-9215A can also be used.

➤ NOTE: The original 3-hole Smart Pulley has been

replaced . The new PASCO Smart Pulley has 10 spokes and less friction than the 3-hole pulley. If you currently have 3-hole pulleys and wish to replace them with 10-spoke pulleys an upgrade kit is available from PASCO. The upgrade kit includes software that allows use of either the 3-hole or 10-spoke pulleys. This manual makes reference to both pulleys.

➤ IMPORTANT: If you are using the Smart Pulley to time the motion of the Rotational Apparatus, you should begin by familiarizing yourself with the setup and operation of the Smart Pulley. See the Smart Pulley manual and the Smart Pulley Timer Software Manual.

Timing with a Standard Photogate

Timing for the Rotational Apparatus can also be performed using a standard photogate timer, such as PASCO model ME-9206A or ME-9215A. The five ready-to-use experiments in this manual assume you are using the Smart Pulley to time your experiments with the Rotational Apparatus. However, each of these experiments can be modified for standard photogate timing. See the section, "Timing with a Photogate." For more information about photogate timers, see the current PASCO catalog.

Introductory Rotational Apparatus 012-03051F

Equipment

The following equipment is included with the ME-9341 Introductory Rotational Apparatus (see Figure 2):

– Base with leveling supports and main bearing – Spindle – Main platter with step pulley – Pulley clamp – Tensioning screw – Level – Photogate clamp – Steel bar – Auxiliary platter – Steel ring – Instruction manual and experiments guide

You will also need either:

A PASCO Smart Pulley System (Model ME-9420 or ME-9421) or one of the Smart Pulley Timers (ME9382, ME-9384, ME-9386, or ME-9388) - (Please see the PASCO catalog for complete details.) - and an Apple II or IBM PC (or compatible) computer.

➂ To measure the radius of the Smart Pulley outer cir-

cumference, roll the Smart Pulley over a smooth, flat surface. Measure the distance, L, over which you pull the pulley for a predetermined number, n, of LED flashes. Again, the radius of the outer circumference of the pulley is r = 3L/2 n for a 3-hole pulley or r = 10L/2 n for a 10-spoke pulley. (You can draw a mark on the edge of the rim of the Smart Pulley to use as a reference mark for measuring L.)

➤NOTE: If you would rather not make the measurements yourself, use the values in the box below. They should be valid to within 10 percent for your Rotational Apparatus.

Main platter: Mass = 991 gm; Radius = 12.7 cm;

-3

Moment of inertia = 7.50 x 10

kgm

Step pulley: Radii = (1.50 cm, 2.00 cm, 2.50 cm) Auxiliary platter: Mass = 894 gm; Radius = 12.7

-3

cm; Moment of inertia = 7.22 x 10

kgm

A photogate timing system such as PASCO Model ME-9206A or ME-9215A.

Measuring Equipment Parameters

In experiments with the Rotational Apparatus, you will often be comparing experimentally determined values, such as moment of inertia or angular acceleration, with calculated values based on theory. These listed, precalculated values may be helpful in those calculations. For best results, however, we recommend that you make the necessary measurements yourself. The following suggestions may be helpful in making certain measurements accurately:

➀ To measure the radii of the step pulley, use calipers

to determine the diameter, then divide by two.

➁ To measure the radius of the Smart Pulley groove,

observe the LED on the top of the photogate as you pull a string over the pulley. Measure the distance, L, through which you pull the string for a predetermined number, n, of LED flashes. The radius of the pulley groove is then r = 3L/2 n for a 3-hole pulley or r = 10L/2 n for a 10-spoke pulley.

Steel bar: Mass = 690 gm; Dimensions = 22.2 x

5.1 cm; Moment of inertia = 2.98 x 10-3 kgm

Steel ring: Mass = 701 gm; Outer radius = 6.4 cm;

Inner radius = 5.4 cm; Moment of inertia =2.46 x 10-3 kgm

Smart Pulley: 3-hole 10-spoke

radius inside groove 2.29 cm 2.38 cm radius outside circum. 2.51 cm 2.54 cm moment of inertia 15.3x10-7kgm

18.6x10-7kgm

Note: Platters of the earlier versions of the ME9341 were made from masonite. Their mass and moment of inertia are given below.

Main platter: Mass = 776 gm; Radius = 12.7 cm;

-3

Moment of inertia = 6.01 x 10

kgm

Auxiliary platter: Mass = 694 gm; Radius = 12.7

cm; Moment of inertia = 5.82 x 10-3 kgm

012-03051F Introductory Rotational Apparatus

Bearing

Leveling supports

Spindle

Step pulley

Base

Pulley clamp

Tensioning screws (2)

Bubble level

Steel ring

Photogate

clamp

Main platter

Steel bar

Figure 2 Rotational Apparatus Equipment

Auxiliary platter

Introductory Rotational Apparatus 012-03051F

Setup

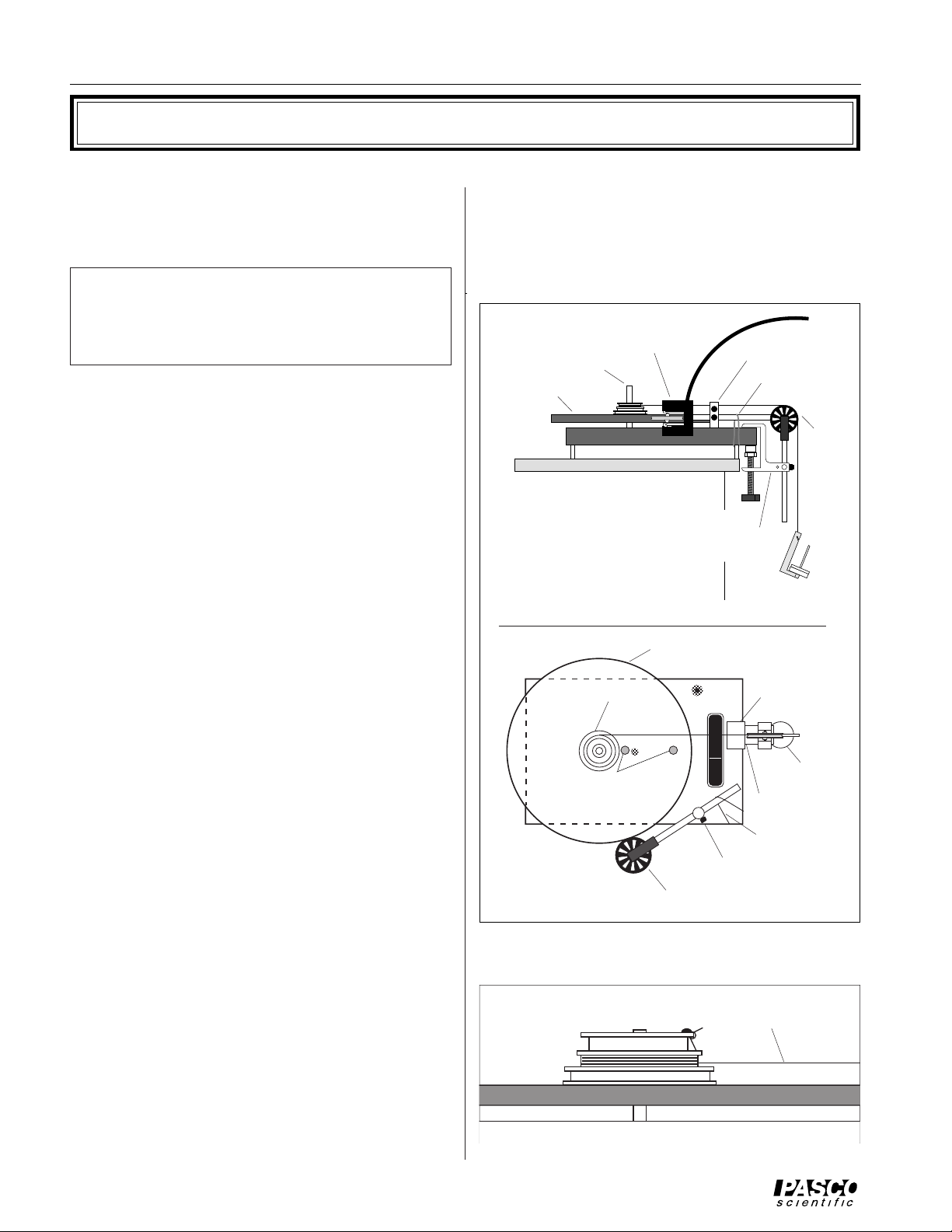
➀ Place the base on a flat table. Place the bubble

level on top of the base, then adjust the leveling supports until the top of the base is level.

➤ NOTE: Leveling the base is important. Not only does it ensure the accuracy of your experimental results, it also prevents uneven wear on the bearings.

➁ Slide the spindle into the bushing of the bearing

assembly. Either end of the spindle can face up, but you will want the long end facing up if you plan on using the auxiliary platter, the ring, or the bar.

➂ Place the Main Platter over the spindle. The step

pulley can face up or down, but should face down if you plan on using the auxiliary platter, the ring, or the bar.

If you are using a standard photogate timer:

➃ See the "Timing with a Photogate" section.

If you are using the Smart Pulley:

➄ Slide the stem of the Smart Pulley clamp into ei-

ther of the two bushings near the edge of the base.

➅ Place the Smart Pulley rod through the hole in the

Smart Pulley clamp, level the pulley, and tighten the screw. (Use the upper hole in the clamp if the Step pulley is facing down, the lower hole if the step pulley is facing up.)

➆ If you wish, attach a rubber band (not included)

over the rod of the Smart Pulley and a leg under the base, as shown in Figure 3. This can be useful in collision experiments, in which an extra "hand" may be needed to keep the Smart Pulley in contact with the platter.

➇ See the Smart Pulley System manual for connect-

ing and using the Smart Pulley. For most experiments using the rotational apparatus, you will want to use Option M – MOTION TIMER from the Smart Pulley main menu. When you are ready to begin timing, just press the Smart Pulley lightly against the edge of the platter.

If you are applying torque with a hanging mass:

➉ Thread the thread through the holes in the step pul-

ley to the desired level. (For instance, thread it through one hole if you are using the smallest pulley, two holes if you are using the medium size pulley, etc.)

Smart Pulley

Spindle

Main platter

(SIDE VIEW)

Main platter

Spindle

Tensioning Screws

(TOP VIEW)

Figure 3 Setting Up the Rotational Apparatus

Smart Pulley

Smart Pulley clamp

Rubber band

Pulley

Universal

Clamp

Hanging

Mass

Universal

Clamp

Hanging

Mass

Pulley Rubber band

Smart Pulley clamp

Thread parallel to platter.

➈ Attach a piece of thread to the step pulley using the

screw to hold the thread, or tying it to the hole in the smallest pulley (see Figure 4).

Figure 4 Threading the Step Pulley

012-03051F Introductory Rotational Apparatus

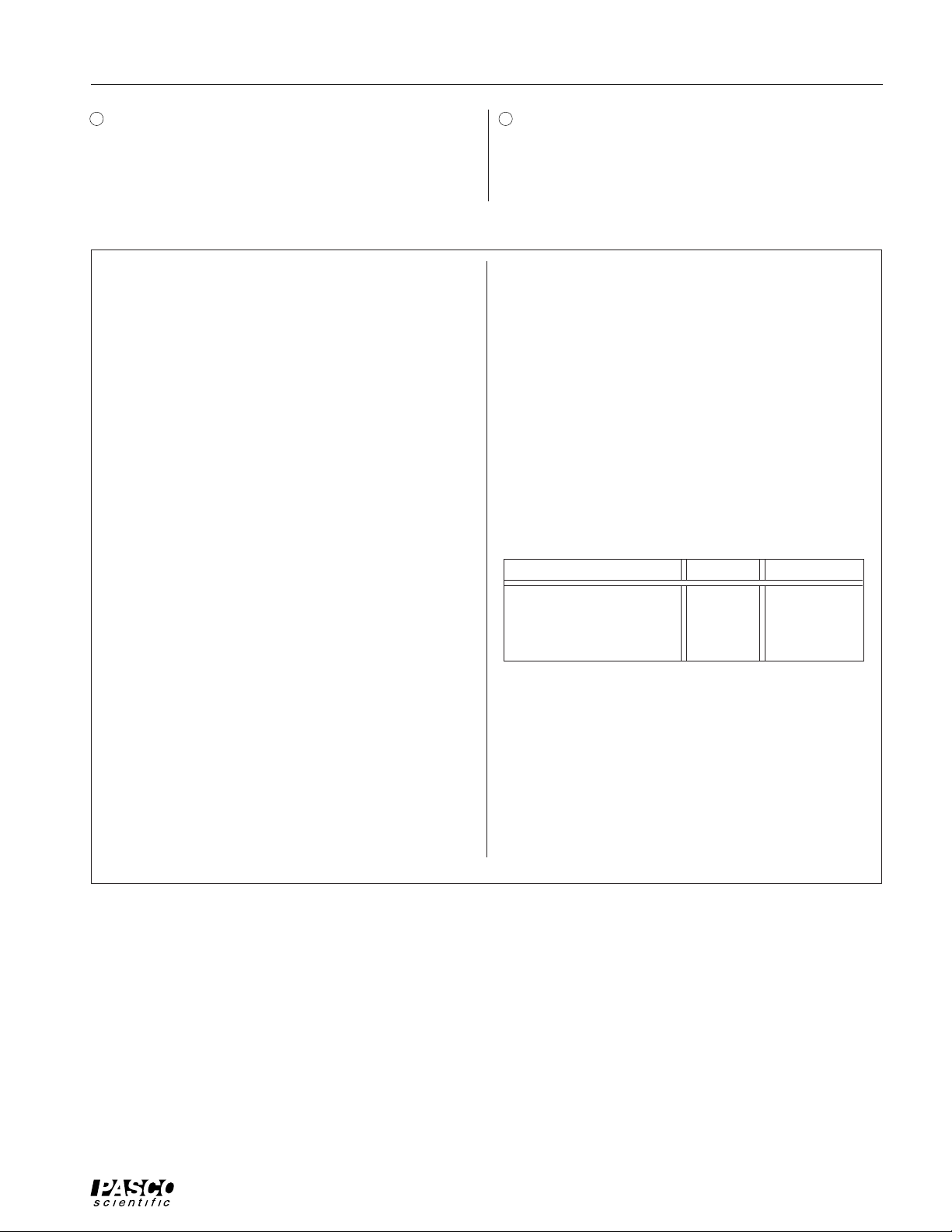
11 Attach a pulley to the base of the apparatus using

the Smart Pulley table clamp as shown in Figure 3. If you don't have the table clamp, a pulley mounted to a ring stand can be used, as long as the height and angle of the pulley are adjustable.

NOTE: When using a falling mass to accelerate the platter, there are two setup options.

Option a—This option requires the Smart Pulley and a second pulley, set up as shown in Figure 3. This method is slightly less accurate than option b, but conceptually simpler. When entering the graphing mode of the Smart Pulley software, you will be asked to identify the type of device being used to interrupt the photogate. If you are using the version of Smart Pulley Timer software that functions with either 10-spoke or 3-hole pulleys, simply choose ROTATIONAL APPARATUS. If you are using an older version of Smart Pulley Timer and a 3-hole pulley, choose ROTATIONAL APPARATUS. However, if you are using an older version of Smart Pulley Timer software and a 10-spoke pulley, choose OTHER (ANGULAR MEASUREMENT). The computer will ask you to enter the angle in radians between the spokes. Enter 0.125 [calculated by using θ = 2π/10 (R

SMART PULLEY/RMAIN PLATTER)]. The computer

will then automatically convert the measured times to determine the angular displacement, velocity, and acceleration of the platter. The slight decrease in accuracy results from the friction caused by the pressure of the Smart Pulley on the rim of the spinning platter.

12 Pass the thread over the pulley and adjust the pulley

angle and height so the thread is parallel with the platter surface and with the groove in the pulley.

Option b—In this option, use the Smart Pulley as the pulley that supports the hanging weight. No other pulley is needed. When asked by the computer to identify the type of device being used to interrupt the photogate, select option F— OTHER (ANGULAR MEASUREMENT). You will then be asked to enter the angle between openings. Enter one of the values shown below, depending on which tier of the step pulley you are using and the type of Smart Pulley you have (these values are the angle, in radians, through which the platter turns for each signal sent to the computer by the Smart Pulley).

Tier of step pulley used 3-hole 10-spoke

Smallest 3.20 1.00

Middle 2.49 0.75 Largest 1.92 0.60

These values can be calculated using the formula:

θ = 2 /3 (Rp/Rsp) for a 3-hole pulley

or θ = 2 /10 (Rp/Rsp) for a 10-spoke pulley

where Rp is the radius of the Smart Pulley groove, and Rsp is the radius of the tier of the step pulley that is being used.

Introductory Rotational Apparatus 012-03051F

Timing with a Photogate

If you don't have the Smart Pulley system, a PASCO photogate can be used to time the Rotational Apparatus. Other photogates can be used as well. The Rotational Apparatus includes a mounting clamp that should work with most photogates.

To Use a Photogate:

➀ Mount the photogate in the photogate clamp, and

mount the photogate clamp in the pulley clamp, as shown in Figure 5.

➁ Tape a piece of cardboard to the top of the platter

to trigger the photogate. The shape of the cardboard depends on which of the following timing techniques you choose.

PASCO photogates have three timing modes: Pulse, Gate, and Pendulum. If your photogate has these timing modes, any of the following four timing techniques can be used:

1. PULSE MODE (Method 1)—In pulse mode, the

photogate will be triggered each time the leading edge of the cardboard interrupts the photogate beam (see Figure 5). The times displayed will therefore show the time for one full revolution of the platter. Experimenters will then have one revolution to record the time before a new time is displayed. (Just divide 2 by the measured time to determine the angular velocity of the platter in radians/second.)

2. PULSE MODE (Method 2)—Tape two pieces of

cardboard to the main platter (see Figure 6). If the cardboard pieces are accurately placed so the leading edges are along a single diameter of the platter, the timing resolution is twice as good as with a single cardboard piece. The displayed times will show the time per 1/2 revolution of the platter.

Cardboard

Photogate

Figure 5 Pulse Mode (Method 1) and Pendulum

Mode

Figure 6 Pulse Mode (Method 2)

Pulley clamp

Photogate clamp

3. GATE MODE—Tape a one radian sector of card-

board to the top of the main platter (see Figure 7). In gate mode, for each revolution of the platter, the timer will display the time during which the cardboard interrupted the photogate. The reciprocal of the measured times will therefore give the angular velocity in radians/second. (See the Appendix for a one radian sector that you can copy and use as a template for cutting the cardboard.)

One Radian

Sector

Figure 7 Gate Mode

012-03051F Introductory Rotational Apparatus

4. PENDULUM MODE—If the rotational speed is

too great to record the times as they are displayed, use a single cardboard piece, as in Figure 5, and set the photogate to pendulum mode. The timer will display the time for two full revolutions of the platter, allowing one revolution time for reading and recording the value.

Five Copy-Ready Experiments

The following five experiments are written in worksheet form. Feel free to photocopy them for use in your lab.

Some precautions will help keep your data as accurate as possible:

5. Alternative Methods

• Use the PASCO Model AI-6577A Apple Com-

patible Photogate System. This system offers many of the same advantages as Smart Pulley timing. However, since it was not designed specifically for the Rotational Apparatus, experiments will have to be adapted somewhat.

➀ Before conducting any experiment, always level the base as

accurately as possible.

➁ When using a thread to apply a torque to the platter, keep the

thread as parallel to the platter as possible.

➂ When measuring the radius of a tier of the step pulley, use

calipers to measure the diameter, then divide by two.

➤ NOTE: For more information about each of these labs, including relevant equations and suggested alternatives, see the LAB NOTES section, near the end of this manual.

Introductory Rotational Apparatus 012-03051F

Notes:

012-03051F Introductory Rotational Apparatus

Experiment 1: Angular Acceleration - 1

EQUIPMENT NEEDED:

- Introductory Rotational Apparatus with auxiliary platter, ring, steel bar, and bubble level

- Smart Pulley with table clamp and software - 2.5-newton spring balance

- Apple II or IBM PC or compatible computer - thread When a force causes an object to rotate, the angular acceleration of the object depends upon

four factors: (1) the magnitude of the force, (2) the direction of the force, (3) the point on the object at which the force is applied, and (4) the rotational inertia of the object. In this lab you will investigate the quantitative relationship between these four factors and the angular acceleration of a rotating system. A spring balance will be used to apply the force.

Procedure

➀ Set up the apparatus as shown in

Figure 1.1. Place the main platter on the shaft so that the step pulley is on top. Use the bubble level to level the apparatus.

➁ Insert the Smart Pulley Timer soft-

Pull with constant force.

ware disk into your computer disk drive and start up the computer.

[Note: Please refer to the Smart

Figure 1.1 Equipment Setup

Pulley Timer manual.]

➂ Attach a 2-3 meter piece of thread to your spring balance. Attach the other end to the step

pulley and wind it up on the smallest of the three spindles. Hold the Smart Pulley lightly against the edge of the platter. If the LED on the Smart Pulley photogate is OFF, rotate the platter slightly until it comes ON.

➃ Now select MOTION TIMER from the main menu. Pull the thread with a constant force of

0.4 newton while the Smart Pulley monitors the motion of the platter. Just runs out, push <RETURN> to stop the timing.

➄ When the computer finishes calculating the times, examine the data table. If you think your

run was good, press <RETURN>, then select GRAPH DATA to move to the graphing program. You will be asked to identify the type of device used to interrupt the photogate. See Option a on page 4. Select ROTATIONAL APPARATUS or OTHER (ANGULAR MEASUREMENT) depending on which style of Smart Pulley you are using. Then select VELOCITY VS TIME for a velocity-time graph.

➅ For the graph style, select STATISTICS, so the computer will do a statistical analysis of

your data (press the S-key, then press the space bar so a check appears to the left of your selection). When the graph is constructed, there will be three sets of numbers at the top. "M" is the slope of the graph, which is the angular acceleration of the platter in rad/sec

➆ In Table 1.1, record the angular acceleration, the force you applied with the spring balance,

and the radius of the spindle of the step pulley around which the thread was wrapped.

➇ Go back to step 4 and repeat the experiment using the same force, but use the next largest

spindle on the step pulley. Repeat again using the largest spindle.

Smart Pulley

before the thread

➈ Go back to step 4, use the smallest spindle again, but now use 0.8, 1.2, 1.6 and 2.0 newtons

of force.

Introductory Rotational Apparatus 012-03051F

➉ Turn the platter over. Go back to step 4. Use the smallest spindle and 0.4 newton of force.

Place the auxiliary platter on top of the main platter, and repeat the experiment. If you have additional platters, repeat again using two or three platters on top of the main platter. Now repeat the experiment first with the ring and then the steel bar on top of the main platter.

Analysis

Draw a graph of angular acceleration versus the step pulley radius, given a constant applied force. Draw a second graph of angular acceleration versus the applied force for a constant step pulley radius. The angular acceleration of an object (a) depends upon the torque (τ) applied to it and the moment of inertia (I) of the object: a = τ/I. Torque equals the applied force times the perpendicular distance from the axis of rotation to the point of application of the force, τ = d⊥ F (see Figure 1.2).

In step 8 of the procedure, the applied force remained constant while the distance d changed (d⊥ is the step pulley radius). In your first graph, you should see that the angular acceleration is directly proportional to d⊥.

In step 9 of the procedure, d

remained constant while the applied force was changed. There-

⊥

fore, your second graph should show that angular acceleration is directly proportional to the applied force.

Finally, the angular acceleration is inversely proportional to the moment of inertia, given a constant torque. The moment of inertia of an object depends on its mass and on how that mass is distributed. In the first part of step 10, you increased the mass but kept the distribution the same. What affect did the increased mass have on the acceleration? What affect did it have on the moment of inertia?

The auxiliary platter, the ring, and the bar have approximately the same mass. Based on your acceleration data, rank them from greatest to least in terms of their moments of inertia. Be prepared to explain your logic for ranking them as you did in your Discussion. Do your results agree with theory?

⊥

τ = d⊥ F

α = τ/Ι

Figure 1.2 The Geometry of Torque

was

⊥

Report

Your report should include PURPOSE, PROCEDURE, DATA, and DISCUSSION. Your discussion should include your Analysis. Compare rotational dynamics with linear dynamics in your discussion.

Name: Date: Group:

Table 1.1 Data

Description of Applied Force Step Pulley Radius Angular Acceleration

Rotating Object (F)(d⊥)(α)

012-03051F Introductory Rotational Apparatus

Experiment 2: Angular Acceleration—2

EQUIPMENT NEEDED:

- Introductory Rotational Apparatus with auxiliary platter, ring, steel bar, and bubble level

- Smart Pulley with table clamp and software - thread

- A second pulley with rod - mass hanger with mass set

- Apple II or IBM PC or compatible computer, When a force causes an object to rotate, the angular acceleration of the object depends upon

Procedure

➀ Set up the apparatus as shown in Figure 2.1.

Then use the bubble level to level the apparatus.

➁ Insert the Smart Pulley Timer software disk into

your computer disk drive and start up the computer.

[Note: See Smart Pulley manual.]

➂ Attach a 2-meter piece of thread to the step

pulley and wind it up on the smallest of the three spindles. Attach the mass holder to the other end of the thread by wrapping 4-5 turns around it. Add masses to a total of 40 grams (remember, the mass of the hanger is 5 grams).

➃ Hold the Smart Pulley lightly against the edge of

the platter. If the LED is OFF, rotate the platter

Figure 2.1 Equipment Setup

slightly until it lights up. Now select MOTION TIMER from the main menu. Release the mass so it falls while the Smart Pulley monitors the motion of the platter. Just

before the mass

hits the floor or the thread runs out, push <RETURN> to stop the timing.

➄ When the computer finishes calculating the times, examine the data table. If you think your

run was good, press <RETURN>, then select GRAPH DATA to move to the graphing program. When asked to identify the type of device you used to interrupt the photogate, select ROTATIONAL APPARATUS. Then select VELOCITY VS TIME for a velocity-time graph.

➅ For the graph style, select STATISTICS, so the computer will do a statistical analysis of your

data (press the S-key, then press the space bar so a check appears to the left of your selection). When the graph is constructed, there will be three sets of numbers at the top. "M" is the slope of the graph, which is the angular acceleration of the platter in rad/sec

➆ In Table 2.1, record the angular acceleration, the mass you used, and the radius of the step

pulley spindle around which the thread was wrapped.

➇ Repeat steps 4-7 with the same mass but the next largest spindle of the step pulley. Then

repeat again using the largest spindle.

➈ Repeat again, using the smallest spindle, but use masses of 80, 120, 160, and 200 grams.

Introductory Rotational Apparatus 012-03051F

➉ Turn the platter over and place the auxiliary platter on top. Go back to step 4. Use the

smallest spindle and 40 grams total mass. Repeat the measurements using two and then three auxiliary platters, if you have them. Now try the experiment first with the ring and then with the steel bar on top of the main platter.

Analysis

Graph angular acceleration versus step pulley radius, given a constant value for the falling mass. Also graph angular acceleration versus the value of the falling mass for a constant step pulley radius. The angular acceleration of an object (a) depends upon the torque (τ) applied to it and the moment of inertia (I) of the object: a = τ/I. Torque equals the applied force times the perpendicular distance from the axis of rotation to the point of application of the force, τ = Fd⊥.

In this case, the applied force is the tension, T, in the string. T must be less than mg, the weight of the falling mass, since m must experience a net downward force in order to accelerate downward. However, for m less than 40 grams, the step pulley radii are small enough that the approximation T=mg results in a less than 1% error in the angular acceleration (see Lab Note on Experiment 2, page 17, for details). Thus, as an approximation, use mg as the applied force.

⊥

τ = d⊥ F

α = τ/Ι

Figure 2.2 The Geometry of Torque

Report

Beyond

In step 8 of the procedure, the applied force (mg) remained constant while the distance, d

⊥

changed (d⊥ is the step pulley radius). In your first graph, you should see that the angular acceleration is directly proportional to d⊥.

In step 9 of the procedure, d

remained constant. Therefore, your second graph should

⊥

show that angular acceleration is directly proportional to the applied force. Finally, the angular acceleration is inversely proportional to the moment of inertia, given a

constant torque. The moment of inertia of an object depends on its mass and on how that mass is distributed. In the first part of step 10, you increased the mass but kept the distribution the same. What affect did the increased mass have on the acceleration? What affect did it have on the moment of inertia?

The platter, the ring, and the bar have approximately the same mass. Based on your acceleration data, rank them from greatest to least in terms of their moments of inertia. Be prepared to explain your reasoning. Do your results agree with theory?

Your report should include Purpose, Procedure, Data, and Discussion. Your Discussion should include your analysis. Compare rotational dynamics with linear dynamics in your Discussion.

In the Analysis above, the effect of the acceleration of the falling mass was neglected. If your instructor wishes, include this effect and analyze this more complex situation in your discussion and analysis.

012-03051F Introductory Rotational Apparatus

Name: Date: Group:

Table 2.1 Data

Description of Applied Force Step Pulley Radius Angular Acceleration

Rotating Object (F)(d⊥)(α)

Introductory Rotational Apparatus 012-03051F

Notes:

012-03051F Introductory Rotational Apparatus

Experiment 3: Gravitational - Rotational Energy

EQUIPMENT NEEDED:

- Introductory Rotational Apparatus - mass hanger and mass set

- Smart Pulley with table clamp and software, - second pulley with rod

- meter stick - thread

- Apple II or IBM PC or compatible computer

Introduction

In this experiment, you will use a falling mass to apply a constant torque to a rotating platter. As the mass falls, it loses gravitational potential energy. This lost energy is gained by the platter as rotational kinetic energy. By measuring the energy lost by the mass and the energy gained by the platter, you will be able to determine if energy is conserved.

Procedure

➀ Set up the apparatus as shown in

Figure 3.1, with the step pulley facing up. Use the bubble level to level the apparatus.

➁ Insert the Smart Pulley software

disk into your computer disk drive and start up the computer.

[Note: See Smart Pulley manual.]

➂ Measure r, the radius of the

smallest spindle, and record the value in Table 3.1. Attach a 1.5-meter piece of thread to the step pulley and wind it up on the smallest of the three spindles. Attach the mass hanger to the thread, high enough on the thread so the masses will not hit the floor at the lowest part of their fall. Add masses to the holder, so the total mass is approximately 50 grams. Record the total mass as m in the data table. Also measure and record h

, the distance of the hanging mass from the floor.

➃ Hold the Smart Pulley lightly against the edge of the platter. Select

MOTION TIMER from the main menu. Allow the mass to fall while the Smart Pulley monitors the motion of the platter. Allow the

Figure 3.1 Equipment Setup

mass to reach its maximum drop and begin its rise, then push <RETURN> to stop the timing.

➄ When the computer finishes calculating the times, select GRAPH DATA to move to the

graphing program, selecting ROTATIONAL APPARATUS so the computer knows you are using the Rotational Apparatus, and then VELOCITY VS TIME for a velocity-time graph.

➅ Examining the graph, you should note that there is a point of maximum velocity, corre-

sponding to the point where the gravitational potential energy reached a minimum and the rotational kinetic energy reached a maximum. Press <RETURN>, then choose DISPLAY TABLE OF DATA to see a table of the data. Determine the maximum angular velocity of the platter, given in rad/sec. Record this value as ω

max

in Table 3.1.

Introductory Rotational Apparatus 012-03051F

➆ Now let the mass hang with the thread fully extended. Measure the distance between the mass

and the floor, and record this value as h2.

➇ Repeat your measurements at least three times, keeping h

constant. Repeat more times if your

data shows any inconsistencies between trials.

➈ Repeat steps 4-9, but change the mass to 100, 150, and then 200 grams. ➉ Further experimentation can be done with different spindles of the step pulleys and with

different numbers of platters. Follow your instructor's direction.

Analysis

For each trial, calculate GPE ( mg h ), the gravitational potential energy lost by the falling mass. Also calculate RKE ( 1/2 I ω disk. (For your disk, the value for I is 7.75 x 10-3 kgm2.) Was energy conserved?

Part of the gravitational energy also went into the kinetic energy, KE (1/2 mv mass. To determine this quantity, calculate v pulley over which the thread passes. Calculate the translational kinetic energy and add it to the rotational kinetic energy. Is energy conserved now?

), the rotational kinetic energy gained by the rotating

max

= rω

, where r is the radius of the step

max

Report

Your report should include Purpose, Procedure, Data, and Discussion.

, of the falling

Name: Date: Group:

Table 3.1

Data

Trial r m h

max

GPE RKE KE RKE + KE

Calculations

012-03051F Introductory Rotational Apparatus

Experiment 4: Frictional Torque

EQUIPMENT NEEDED:

- Introductory Rotational Apparatus

- Smart Pulley with rod and table clamp (another pulley will work, the photogate is not needed)

- Mass hanger with mass set

- Thread

- Meter stick.

Introduction

In order to apply Newton's equations of motion, all the forces acting on the system under investigation must be known. In any mechanical system, however, there are usually unmeasured frictional forces, so it often appears as if the motion of the system is not in complete accord with Newton's laws.

In this lab, you will use a falling mass to provide a torque that will rotate a platter. The energy lost by the falling mass will supply the rotational kinetic energy of the spinning platter. Then, as the mass is pulled back up by the platter, the platter will again slow down, its kinetic energy transformed back into the gravitational potential energy of the rising mass. However, the mass will not rise all the way to its original height, because some energy has been lost due to friction. By assuming that energy is conserved in this system, you will determine the amount of frictional torque acting in the Introductory Rotational Apparatus.

Procedure

➀ Set up the apparatus as

shown in Figure 4.1, with the step pulley on top. Then use the bubble level to level the apparatus.

Note: In this experiment the Smart Pulley should be mounted on the lab table far enough from the apparatus to keep the tread angle from the spindle to the pulley as small as possible. If the angle is too great the thread will snap as the mass is pulled back by the platter and the thread rewinds on the spindle.

➁ Attach a 1.5 meter piece of thread to the step pulley and wind it

up on the smallest of the three spindles. Measure and record r, the radius of the spindle, in Table 3.1. Attach the mass hanger so that when the thread is fully extended the hanger will not reach the floor. Extend the thread and measure h from the floor to the mass hanger.

, the distance

Figure 4.1 Equipment Setup

➂ Place 100 grams on the hanger, and record the total mass, m, in the data table.

Introductory Rotational Apparatus 012-03051F

➃ Now raise the mass to a starting height of approximately 1 meter. Measure this height care-

fully and record it as h1. Release the mass so it falls, reaches it lowest point, then rises again. Measure and record, h2, the greatest height that the mass hanger rises to in its ascent.

➄ Repeat your measurement three times, starting from the same h

, and recording the value of h2.

➅ Repeat steps 3-5, changing the mass on the hanger, first to 150 grams, then to 200 grams. If

instructed, try the same mass with another pulley. If instructed, repeat the measurements with two platters. In each case, record the same five values in Table 4.1.

Analysis

Average the final heights, h2, for each set of three trials that were performed under identical conditions. For each trial, determine the amount of gravitational potential energy lost ( GPE) by the mass in falling from h1 to h2avg: GPE = mg(h2 – h1).

Determine the total distance that the mass moved, d = [(h

– h 0) + (h2 – ho)] = h1 + h2 – 2ho.

From this value, and the radius of the step pulley spindle, determine the angular distance, in radians, that the platter moved: θ = d/r.

Now calculate the magnitude of the frictional torque, τ

, using the relationship τf θ = GPE.

Compare your results for τf under the different experimental conditions that you tried.

Report

Your report should include Purpose, Procedure, Data, and Discussion. Include your Analysis in the Discussion.

Name: Date: Group:

Table 4.1 Data

Trial r m h

Table 4.2 Calculations

Trial h2 (avg) GPE d θτ

012-03051F Introductory Rotational Apparatus

Experiment 5: Rotational Collisions

EQUIPMENT NEEDED:

- Introductory Rotational Apparatus

- Smart Pulley with table clamp and software

- Auxiliary platter

- An Apple II or IBM PC or compatible computer

Introduction

A rotating platter has rotational kinetic energy, RKE, and angular momentum, L. In a collision between two platters, the sum of the angular momentums (L1 + L2) following the collision will be equal to the sum of the angular momentums before the collision. In this lab, you will investigate this relationship in a particular case—that in which one of the platters has no initial angular momentum.

Procedure

➀ Set up the apparatus as shown in Figure 5.1.

Mount the main platter so the step pulley is facing

Auxiliary platter

downward. Level the apparatus.

➁ Insert the Smart Pulley software disk into your

Main platter

computer disk drive and start up the computer. [Note: See Smart Pulley manual.]

➂ Hold the Smart Pulley just off the edge of the

platter. Select MOTION TIMER from the main menu.

Figure 5.1 Equipment Setup

➃ Hold the auxiliary platter just above the main

platter of your Introductory Rotational Apparatus. Give the main platter a spin using your hand. Push the Smart Pulley lightly against the spinning platter, and after about 25 data points have been taken, drop the auxiliary platter onto the spinning one.

➄ Hold the Smart Pulley against the platter until it has taken about 50 data points, then push

<RETURN> to stop the timing.

➅ When the computer finishes calculating the times, select GRAPH DATA to move to the

graphing program, selecting ROTATIONAL APPARATUS so the computer knows you are using the Rotational Apparatus, and then VELOCITY VS TIME for a velocity-time graph.

➆ Examining the graph, you should note that there are two sections that are straight lines,

showing the platter slowing down. They are joined by a region where the platter abruptly slowed down due to the second platter colliding with it. Press <RETURN> then choose DISPLAY TABLE OF DATA to see a table of the angular velocities. Determine the angular velocity immediately before the collision (ω

) and immediately after (ωf). Record

these values in Table 5.1.

➇ Repeat this process a total of three times, recording your data each time. ➈ If you have additional platters try dropping two platters on one, or one on two. Also, if

directed, use the ring as the second, or dropping, object. Then use the steel bar. When dropping the ring, be careful to center it over the platter and drop it with the pins up.

Introductory Rotational Apparatus 012-03051F

Analysis

Angular momentum L is equal to the moment of inertia I times the angular velocity ω. Calculate L momentum before each collision, and L momentum after the collision. For I, use 1/2 MR the platters (the step pulley can be safely neglected),

for the ring, and 1/12 M(A2 + B2) for the bar (see

Figure 5.2). Check the conservation of angular momentum by calculating the percentage difference between L and Lf in each case.

If instructed, calculate the initial and final rotational kinetic energy, showing your results in Table 5.2. Was RKE conserved in the collisions?

Report

Your report should include Purpose, Procedure, Data, and Discussion.

Name: Date: Group:

Moving Dropping %

Trial Object Object ω

, the angular

Table 5.1

for

I = 1/12 M(A

+ B2)

Figure 5.2 Calculating the Moment of

Inertia for the Bar

Difference

1 2 3 4 5 6 7 8 9

012-03051F Introductory Rotational Apparatus

Table 5.2

Trial

RKE

% Difference

2 3 4 5 6 7 8 9

Introductory Rotational Apparatus 012-03051F

Notes:

012-03051F Introductory Rotational Apparatus

Teacher's Guide

Exp 1 – Angular Acceleration - 1

Introduction

Applying torque with a spring balance ensures that the applied force is simple to understand, as opposed to using a falling mass, as in Experiment 2. The disadvantage is the inherent inaccuracy of using a hand-pulled device. Students measure the force and the torque arm, each of which can be independently varied, so the effects of each on acceleration can be examined. Moment of inertia can also be qualitatively investigated, yielding relative values.

Alternatives

➀ Larger forces than those listed in the lab sheet can be used. However, the speeds increase and the difficulty in

maintaining a constant torque also increases.

➁ For a shorter lab period, all students could do steps 1-7. The class can then be split into three groups to carry

out steps 8, 9, and 10.

Notes – on Procedure

➂ For best results on all of these labs, use a fine thread and make sure that the thread is wound evenly around the

spindle without overlapping.

➃ It is difficult to maintain a constant

force on the string. We found that the best results were obtained when the data was taken for a short time (about 1 second) rather than for the entire length of the string.

➇ The larger spindles are proportion-

ally more difficult to maintain at a constant force, due to the higher acceleration.

➈ The higher forces are also harder to

maintain, for the same reason.

Object Force (N) R (m) alpha (rad/s/s) base plate: 0.4000 0.0150 0.9724

1.0000 0.0150 2.3181

2.0000 0.0150 4.5086

0.4000 0.0200 1.5984

1.0000 0.0200 2.7110

0.4000 0.0250 1.5645

1.0000 0.0250 3.7425

B.P. + ring 0.4000 0.0150 0.8913

1.0000 0.0150 1.7716

1.8000 0.0150 2.9834

2.0000 0.0150 3.2425

average

B.P. + disk 0.4000 0.0150 0.5763

1.0000 0.0150 1.2496

2.0000 0.0150 2.0803

B.P. + bar 0.4000 0.0150 0.7808

1.0000 0.0150 1.5346

2.0000 0.0150 3.7007

Introductory Rotational Apparatus 012-03051F

Notes – on Analysis

Acceleration vs. Radius

Force = 1.0 N

The acceleration is directly proportional to the radius for a constant force.

3.5 3

2.5 2

1.5 1

Angular Acceleration

0.5 0

0 0.005 0.01 0.015 0.02 0.025 0.03

Force = 1.0 N

●

Radius

Acceleration vs. Force

Radius = 1.5 cm

The acceleration is directly proportional to the force for a constant radius.

Increasing the mass by adding another disk increased the rotational inertia and decreased the acceleration.

4.5 4

3.5 3

2.5 2

1.5

Angular Acceleration

0.5 0

0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2

Base plate alone

●

❍

With added disk

Applied Force

●

❍

Ranking the three objects in increasing order of inertia would give: ring, bar, then disk. This is misleading, because for objects of the same mass and radius the ring would have the highest inertia. The lower inertia of the ring is due to its smaller radius, not its shape.

Using the spring scale as a constant-force apparatus is good in a way because it allows the student to directly see that the acceleration is proportional to the force, without messing around with the falling masses as in experiment

2. Its accuracy is limited, however, by the difficulty in maintaining a constant force on the scale. For this reason, I would consider experiment 2 to be preferable to experiment 1 for anything but the most basic introductory course.

012-03051F Introductory Rotational Apparatus

Exp 2 – Angular Acceleration - 2

Introduction

In its simplest form, the principles in this lab are very clear, the setup is easy, and the variables are easy to control. However, in its simplest form, the lab assumes that the mass exerts a constant force of F = mg on the platter. Since the mass is accelerated along with the platter, the tension (T) on the thread must be less than the mass. An accurate analysis of the motion must take into account that T, not F, is the force that accelerates the platter. The following equations and diagram derive the rotational acceleration, a, using T as the force that causes the platter to rotate.

mg - T = ma = mrα τ = Tr = Iα a = rα

→ T = mg - mrα

τ = mgr - mr2α = Iα mgr = Iα + mr2α α = (mgr)/(I + mr2)

For large masses or for large values of r, the mr2 term in the denominator may have a significant impact. For a mass of 200 grams and a radius of 1.5 cm, the mr2 term reduces the rotational acceleration only by 0.8%. Therefore, the decision to neglect this factor does not detract significantly from the final results. However, students can be given the option of trying to prove the theoretical results as given above.

Alternatives

➀ See Experiment 1: Angular Acceleration - 1. ➁ For a more accurate, but somewhat less straightfor-

ward method, see "Option b" in the note on page 4.

Radius of step pulley spindle = r

I = Moment of inertia of the platter = MR2 for a cylinder. τ = Torque = r x T

Experiment 2: Diagram of Relevant Variables

(Tension)

F = mg

Notes – on Procedure

➂ Using a lighter mass than 40 grams will give good results, as long as it is heavy enough that the frictional

torque may be ignored.

➃ Use a lightweight rubber band to hold the smart pulley against the platter. The pulley should be held with just

enough tension to keep it from slipping; any extra tension will add to the friction of the system.

➈ Using the heavier masses will introduce significant errors due to the linear acceleration of the mass. These er-

rors are negligible when lighter masses are used.

Introductory Rotational Apparatus 012-03051F

average

Object Mass (g) Force (N) R (m) alpha (rad/s/s) Base Plate 25.5700 0.2506 0.015 0.4111

46.3500 0.4542 0.015 0.8646

87.2300 0.8549 0.015 1.6976

117.4100 1.1506 0.015 2.3157

157.7600 1.5460 0.015 3.1756

191.7200 1.8789 0.015 3.8850 B.P. + ring 25.5700 0.2506 0.015 0.2858 B.P. + disk 25.5700 0.2506 0.015 0.1917 B.P. + bar 25.5700 0.2506 0.015 0.2694 B.P. 25.5700 0.2506 0.015 0.4472

25.5700 0.2506 0.020 0.6253

25.5700 0.2506 0.025 0.7704

Notes – on Analysis

The acceleration is directly proportional to the radius for a constant force.

The acceleration is directly proportional to the force for a constant radius.

Increasing the mass by adding another disk increased the rotational inertia and decreased the acceleration.

Ranking the three objects in increasing order of inertia would give: ring, bar, then disk. This is misleading, because for objects of the same mass and

radius the ring would have the highest inertia. The lower inertia of the ring is due to its smaller radius, not its shape.

Notes

The assumption that the force on the turntable equals mg is valid only for small masses and acceleratons. Using larger masses will lessen your accuracy in this experiment. If the masses used are too small, then the friction in the device may be proportionally large enough that it causes errors as well. Generally, keep the falling mass between about 20 and 200 grams.

With the assumption mentioned, this lab is essentially identical to experiment 1.

Angular Acceleration v. Radius

0.8

0.6

0.4

0.2

angular acceleration

0 0.005 0.01 0.015 0.02 0.025 0.03

3.5

2.5

1.5

angular acceleration

0.5

0 20 40 60 80 100 120 140 160 180 200

mass = 25.57g

●

radius (cm)

Acceleration vs. Mass

radius = 1.5 cm

●

mass (g)

●

012-03051F Introductory Rotational Apparatus

Exp 3 – Gravitational-Rotational Energy

Introduction

In this lab, results should verify conservation of energy to within 2% or better. Loss of energy will occur in the bearings of the Rotational Apparatus, and in the pulley. This loss should remain relatively constant for various masses pulling the thread. Therefore, for heavier falling masses, since the total energy exchange is greater, the percentage error will be less. (This can be a useful point for student discussion.)

Alternatives

This experiment might be included in a laboratory in which different student groups carry out different experiments, all related to energy conservation.

Notes – on Procedure

➂ Make sure that the thread is wound evenly—without overlapping itself—for best results. ➆ h

will change as the thread unwinds and stretches. Measure it in each trial for maximum accuracy.

smallest step used: r = 0.015

g = 9.8 h1 = 0.651

Average Average Average

Mass (g) Force (N) h

46.35 0.4542 0.0880 8.1307 0.1220 0.8883

96.74 0.9481 0.0840 11.9843 0.1798 1.8756

147.01 1.4407 0.0810 14.7693 0.2215 2.8722

197.22 1.9328 0.0790 17.3205 0.2598 3.9055

ω max max wt. vel. alpha

Notes – on Analysis

I = 7.75E-3

mgh 1/2 I ω

0.2557 0.2562 0.0003 0.2565 0.17% 0.31%

0.5375 0.5565 0.0016 0.5581 3.53% 3.82%

0.8212 0.8453 0.0036 0.8489 2.93% 3.37%

1.1055 1.1625 0.0067 1.1692 5.15% 5.75%

1/2 m v

Note that in each case the final energy of the system (RKE+ KE) is greater than the original energy (mgh). This is rather unsettling... (not to mention wrong!) As near as I can tell, the actual moment of inertia of the platter is less than the value listed in the manual. You can experimentally check the moment of inertia of your own platter (they vary some due to manufacturing differences) by assuming conservation of energy and then solving for I:

mgh = 1/2 I ω

+ 1/2 m v

RKE + KE % error (1) % error (2)

where w is the angular velocity and v is the linear velocity of the mass m.Using this method, I found the moment of inertia to be 7.50x10-3 ± 3%. This value for I gives me much better results, although the energy is still too high.

Introductory Rotational Apparatus 012-03051F

I = 7.50E—3

mgh 1/2 I ω

1/2 m v

RKE + KE % error (1) % error (2)

0.2557 0.2480 0.0003 0.2484 -3.02% -2.89%

0.5375 0.5388 0.0016 0.5404 0.23% 0.52%

0.8212 0.8183 0.0036 0.8219 -0.35% 0.09%

1.1055 1.1255 0.0067 1.1321 1.80% 2.40%

012-03051F Introductory Rotational Apparatus

Exp 4 – Frictional Torque - Notes and Data

Introduction

This lab is easy and requires no sophisticated electronic equipment. The greatest source of error in this experiment is in measuring the highest point reached by the hanging mass when the spinning platter pulls it back up. Resist attempts to talk about the friction of the system, unless you also attempt to identify the effective radius at which the frictional force is applied.

Alternatives

The students give the platter a spin and measure an initial angular velocity. They then count the number of revolutions until the platter comes to a stop. From the total angle through which the platter rotated, θ, they could determine the torque using τθ = RKE , where RKE = 1/2 Iω2 = the rotational kinetic energy of the platter.

Notes – on Procedure

➀ Setting up the apparatus with the spindles down will allow you to test the frictional torque with different

masses if desired. Make sure that the pulley is at an appropriate height so that the string will wind onto the desired step automatically.

➃ The frictional torque has been shown to be somewhat dependent on the angular velocity of the base plate.

Since the difference in height that the weight drops affects this velocity, the original height of the weight will affect the frictional torque measured.

➅ Again, because the friction is dependent on velocity, the mass used will affect the measured friction. The mass

will also affect the friction of the pulley used for support. The greater the mass used, the greater the magnitude of the measured frictional torque.

Notes – on Analysis

Data

DataData

Data

DataData

Mass (kg) r (m) h0 (m) h1 (m) h2 (m) h2 (m) h2 (m)

B.P. + pulley 0.02523 0.015 0.12 0.651 0.505 0.495 0.430

0.07548 0.015 0.115 0.651 0.572 0.562 0.572

0.12586 0.015 0.112 0.651 0.594 0.595 0.595

0.17610 0.015 0.106 0.651 0.602 0.602 0.604

0.19674 0.015 0.103 0.651 0.605 0.600 0.603

B.P. only 0.09662 0.015 0.115 0.651 0.575 0.575 0.575

0.14683 0.015 0.113 0.651 0.582 0.580 0.581

0.19722 0.015 0.082 0.651 0.598 0.600 0.600

B.P. + disk 0.19722 0.015 0.102 0.651 0.595 0.595 0.595

Introductory Rotational Apparatus 012-03051F

Calculations frictional average

h2 (avg) GPE (J) d (m) theta (rad) torque (Nm) torque

B.P. + pulley 0.477 -0.043 0.888 59.18 -0.00073

0.569 -0.061 0.990 65.98 -0.00092 compare

0.595 -0.069 1.022 68.11 -0.00102 -0.00104 with

0.603 -0.083 1.042 69.44 -0.00120 below

0.603 -0.093 1.048 69.84 -0.00133

B.P. only 0.575 -0.072 0.996 66.40 -0.00108

0.581 -0.101 1.006 67.07 -0.00150 -0.00132

0.599 -0.100 1.086 72.42 -0.00138

B.P. + disk 0.595 -0.108 1.042 69.47 -0.00156 -0.00156

A second method of measuring the friction was used for comparison. The falling mass and attatched string were removed and the super pulley was used with the Motion Timer program. The base plate was initially spun by hand, and the frictional deceleration was measured as the slope of the velocity vs. time graph. (see graph) The frictional torque was calculated from this deceleration and the known rotational inertia of the base plate.

I = 0.01

alpha torque average

B.P. + pulley 6.3575 -0.11244 -0.00084

6.4890 -0.11504 -0.00086

2.8102 -0.10378 -0.00078

2.2213 -0.12181 -0.00091

2.2008 -0.08772 -0.00066 -0.00080

1.2787 -0.10370 -0.00078

0.6177 -0.09142 -0.00069

2.2157 -0.10252 -0.00077

1.7819 -0.12055 -0.00090

3.7205 -0.11370 -0.00085

There is a 23% difference in the measured friction with these two methods; mostly due to the fact that the second method does not include the friction of the pulley used to hold up the dropping mass.

Notes

Expect a fairly wide spread of results on this

0.25

M = -0.007076 ± 0.00001571

VELOCITY VS. TIME

B = 0.2472 ± 0.0001405

R = -0.9997

lab. The friction of the system depends on many factors which may not be completely controlled, and a 10% variation between successive identical measurements is not uncommon.

VELOCITY

0.2

(M/S)

0.15

510

15 20

TIME (SEC)

012-03051F Introductory Rotational Apparatus

Exp 5 – Rotational Collisions

Introduction

This lab lets students verify the conservation of angular momentum. In practice, the graphs that emerge help students to see that the changes in rotational speed are not instantaneous. Applications of this principle abound, such as the decrease in an engine's speed as the clutch is engaged, or the temporary slowing down of a phonograph turntable as a new record drops onto it.

Alternatives

➀ This type of experiment can be used to investigate

the moment of inertia of an object. The calculations are left to the instructor, but in practice, rather than dropping disks onto disks, the ring or the steel bar can be dropped.

➁ A second type of collision can be created using two

rotational apparatuses. Each platter is given an initial rotational velocity, then the two platters are butted up against each other as shown below, so they have a common final rotational velocity. A rim on one of the disks that permits minimal slipping would help to increase the accuracy of the lab.

➂ With a few do-it-yourself accessories, the Introduc-

tory Rotational Apparatus can be used to demonstrate the conservation of angular momentum as in the spinning ice skater example. You will need:

1. A piece of U-channel with an inside width of about 1.2 cm and a length of about 25 cm.

2. A cross-hole spindle as shown in the illustration below.

3. Equal masses of 100-500 grams that will slide in the channel (the PASCO masses that come with the Smart Pulley will work).

4. Double-stick tape, thread.

Drill a 1 cm (3/8"+) hole in the center of the U-channel and attach the spindle as shown in the illustration below. Attach the U-channel to the platter with double-stick tape.

Place masses of 100-500 grams on each side of the channel, and run a piece of thread down the center hole and out the sides of the cross-hole spindle. Attach each end of the thread to a mass. Give the platter a spin. Pull on the thread to vary the distances of the masses from the center, obtaining a corresponding increase or decrease in angular velocity.

Experiment 5: Alternative Method for Collisions

ThreadSpindle

Weight

U-channel

Main platter

Close-up of spindle

Experiment 5: Conservation of Momentum

Demonstration

Weight

Thread

Introductory Rotational Apparatus 012-03051F

Notes – on Procedure

➂-➄ Rather than go through the process of releasing and engaging the smart pulley each time, I found it easier to

hold the pulley against the platter with a rubber band all the time. Either way works fine, though.

➈ I did not get consistent results when dropping the ring on the disk, due to the difficulty in centering the ring

each time.

Notes – on Analysis

object ω

% dif. RKE

RKE

disk on B.P. 4.30 2.16 0.00750 0.01453 0.032 0.031 2.68% 0.069 0.033

4.00 1.92 0.00750 0.01453 0.030 0.027 7.00% 0.060 0.026

6.75 3.45 0.00750 0.01453 0.050 0.050 0.98% 0.170 0.086

4.06 2.01 0.00750 0.01453 0.030 0.029 4.08% 0.061 0.029

7.20 3.39 0.00750 0.01453 0.054 0.049 8.78% 0.194 0.083

5.14 2.73 0.00750 0.01453 0.038 0.039 -2.89% 0.099 0.054

Bar on B.P. 3.62 2.45 0.00750 0.01052 0.027 0.025 5.06% 0.049 0.031

2.88 2.02 0.00750 0.01052 0.021 0.021 1.61% 0.031 0.021

2.35 1.54 0.00750 0.01052 0.017 0.016 8.08% 0.020 0.012

1.88 1.34 0.00750 0.01052 0.014 0.014 0.02% 0.013 0.009

Bar on B.P.+disk 2.80 2.33 0.01453 0.01755 0.040 0.040 -0.51% 0.056 0.047

3.14 2.60 0.01453 0.01755 0.045 0.045 -0.01% 0.071 0.059

5.48 4.41 0.01453 0.01755 0.079 0.077 2.79% 0.218 0.170

2.24 1.87 0.01453 0.01755 0.032 0.032 -0.83% 0.036 0.030

Angular momentum is conserved, kinetic energy is not. There is a bit of delay time between when the objects first touch and when they equalize their velocities, and it has

been suggested that friction in the bearings during this delay is a source of error. To investigate this, a rubber band was placed on top of the base plate and the first part of the experiment was repeated.

This method was found to greatly decrease the delay time, and there is some improvement on the actual results. (The angular momentum of the rubber band was neglected.)

object ω

Disk on B.P. 2.86 1.50 0.00750 0.01453 0.021 0.021 -1.60% 0.031 0.016 (rubber band) 4.01 1.93 0.00750 0.01453 0.030 0.028 6.76% 0.060 0.027

3.01 1.56 0.00750 0.01453 0.022 0.022 -0.41% 0.034 0.018

5.47 2.83 0.00750 0.01453 0.041 0.041 -0.23% 0.112 0.058

% dif. RKE

RKE

Another method of analysis, which almost entirely eliminates frictional problems, is to extrapolate both linear regions of the velocity graph completely across the graph, then measure the instantaneous distance between these two lines as the difference in velocity before and after the collision.

012-03051F Introductory Rotational Apparatus

Appendix

1-Radian Sector

➤ NOTE: This one radian sector can be photocopied to provide a template for constructing photogate triggers out of cardboard. See the "Timing with a Photogate" section in this manual.

Introductory Rotational Apparatus 012-03051F

Notes

Technical Support

Feedback

If you have any comments about the product or manual, please let us know. If you have any suggestions on alternate experiments or find a problem in the manual, please tell us. PASCO appreciates any customer feedback. Your input helps us evaluate and improve our product.

To Reach PASCO

For technical support, call us at 1-800-772-8700 (toll-free within the U.S.) or (916) 786-3800.

fax: (916) 786-3292 e-mail: techsupp@PASCO.com web: www.pasco.com

Contacting Technical Support

Before you call the PASCO Technical Support staff, it would be helpful to prepare the following information:

➤ If your problem is with the PASCO apparatus, note:

- Title and model number (usually listed on the

label);

- Approximate age of apparatus;

- A detailed description of the problem/sequence

of events. (In case you can’t call PASCO right away, you won’t lose valuable data.);

- If possible, have the apparatus within reach

when calling to facilitate description of individual parts.

➤ If your problem relates to the instruction manual, note:

- Part number and revision (listed by month and

year on the front cover);

- Have the manual at hand to discuss your ques-

tions.

PASCO ME-9341 User Manual

Specifications and Main Features

Frequently Asked Questions

User Manual