PASCO ME-8950A User Manual

Download

012-05293F Complete Rotational System

Instruction Manual and

012-05293F

01/09

Experiment Guide for the PASCO scientific Model ME-8950A

COMPLETE ROTATIONAL

SYSTEM

Complete Rotational System 012-05293F

012-05293F Complete Rotational System

Table of Contents

Section Page

Introduction...................................................................................................... 1

• Description

• About this Manual

• Computer Timing

Equipment ....................................................................................................... 2

Miscellaneous Supplies ................................................................................... 3

Assembly

ME-8951 Rotating Platform ......................................................................4

ME-8952 Centripetal Force Accessory ..................................................... 6

ME-8953 Rotational Inertia Accessory ..................................................... 8

Experiments Using the ME-8951 Rotating Platform

Exp 1 Conservation of Angular Momentun (Projectile Version)........ 9

Exp 2 Rotational Inertia of a Point Mass............................................ 15

Experiments Using the ME-8952 Centripetal Force Accesory

Exp 3 Centripetal Force...................................................................... 19

Exp 4 Conservation of Angular Momentum Using Point Mass.........25

Experiments Using the ME-8953 Rotational Inertia Accessory

Exp 5 Rotational Inertia of Disk and Ring ......................................... 31

Exp 6 Rotational Inertia of Disk Off-Axis (Fixed/Rotating).............. 37

Exp 7 Conservation of Angular Momentum Using Disk and Ring.... 41

Technical Support........................................................................................... 45

Complete Rotational System 012-05293F

Please—Feel free to duplicate this manual subject to the copyright restrictions below.

The PASCO scientific Model ME-8950A Complete Rotational System manual is copy right ed and all rig hts reserved. However, per mis si on i s gr anted to non-profit educational institutions for reproduction of any part of this manual providing the reproductions are used only for their laboratories and are not sold for profit. Reproduction under any other circumstances, wi thout the written consent of PASCO scientific, is prohibited.

Limited Warranty

PASCO scientific warrant s thi s produc t to be fre e from defects in material s and workmanship for a period o f one year from the date of shipment to the customer. PASCO will repair or replace, at its opti on, any part of the product which is deemed to be defecti ve in material or workmanship. This warranty does not cov er damage to the product caused by abuse or improper use. Determination of whether a product failur e is the result of a manufacturing defect or improper use by the customer shall be made solely by PASCO scientif ic. Responsibility for the retur n of equipment for warranty repair belongs to the customer. Equipment must be properly packed to prevent damage and shipped postage or freight prepaid. (Damage caused by improp er packing of the equipment fo r return shipment will not be covered by the war ranty.) Shipping costs for returning the eq uipment, after repair, will be paid by PASCO scientific.

Equipment Return

Should this product have to be returned to PASCO scientific, for whate ver reason, not ify PASCO scientifi c by letter or phone BEFORE returning the product. Upon notification, the return authorization and shipping instructions will be promptly issued.

NOTE: NO EQUIPMENT WILL BE

ACCEPTED FOR RETURN WITHOUT AN AUTHORIZATION.

When returning equipment for repair, the units must be packed properly. Carriers will not accept responsibility for damage caused by improper packing. To be certain the unit will not be damaged in shipment, observe the following ru les:

1. The carton must be strong enough for the item shipped.

2. Make certain there is at least two inches of packing material between any poi nt on the appa rat us and the inside walls of the carton.

3. Make cer tain that the packing material can not shift in the box, or become co mpressed, thus letting the instrument come in contact wit h th e edge of the box.

Address:PASCO scientific

10101 Foothills Blvd. P.O. Box 619011

Credits

This manual authored by: Ann and Jon Hanks This manual edited by: Ann and Jon Hanks

Roseville, CA 95678-9011

Phone: (916) 786-3800 FAX: (916) 786-8905 email: techsupp@pasco.com web: www.pasco.com

012-05293F Complete Rotational System

Introduction

PASCO’s Complete Rotational System provides a full range of experiments in centripetal force and rotational dynamics. The system consists of three separate components:

Description

The ME-8951 Rotating Platform consists of a sturdy 4 kg base with low friction bearings and a rotating arm which serves as a versatile base for rotation experiments. This platform is a general purpose base upon which you may mount anything (having a mass under 3 kg) you wish to rotate. The T-slots in the track supply a convenient way to mount objects to the track using thumbscrews and square nuts. To use the Centripetal Force Accessory (ME-

8952) or the Rotational Inertia Accessory (ME-8953), each must be mounted on this base. A photogate/pulley mount and two 300 g masses are also included.

The ME-8952 Centripetal Force Accessory is comprised of two vertical posts which can be mounted to the Rotating Platform with thumbscrews. These posts are adjustable and can be positioned virtually anywhere along the length of the platform. The radius indicator is at the center of the apparatus so it can be clearly seen while the apparatus is rotating. This accessory requires the Rotating Platform (ME-8951) to operate. The PASCO Centripetal Force Accessory can be used to experiment with centripetal force and conservation of angular momentum. For the centripetal force experiments it is possible to vary the mass and radius to see the resulting change in the centripetal force. The force can also be held constant while other quantities are varied. The Centripetal Force Accessory is powered by hand and the rate of rotation can be counted manually or read by a computer. Variable hanging masses are included.

The ME-8953 Rotational Inertia Accessory includes a disk and a metal ring. The disk can be mounted to the rotating base in a variety of positions and at any radius. This accessory requires the Rotating Platform (ME-8951) to operate. The Rotational Inertia Accessory allows you to perform rotational inertia experiments and conservation of angular momentum experiments.

About This Manual

The following Equipment section describes each component in detail and the subsequent Assembly section provides instructions for component assembly and setup.

The Experiment section contains several experiments that can illustrate some of the basic theory of centripetal force, rotational inertia, etc.

Computer Timing

You can use a PASCO computer interface with a PASCO Photogate Head to measure the motion of the apparatus. Some of the experiments describe how to use DataStudio, the software program that supports every PASCO computer interface.

If you are using a computer interface such as a Science- Workshop 750 or ScienceWorkshop 500, you can connect the cable of the Photogate Head directly into the interface.

If you are using a PASPORT interface such as a USB Link, PowerLink, Xplorer, or Xplorer GLX, you will need to use a PASPORT Digital Adapter (PS-2159) to connect the Photogate Head to the interface.

See the PASCO web site at www.pasco.com for more information on PASCO interfaces, sensors, and software.

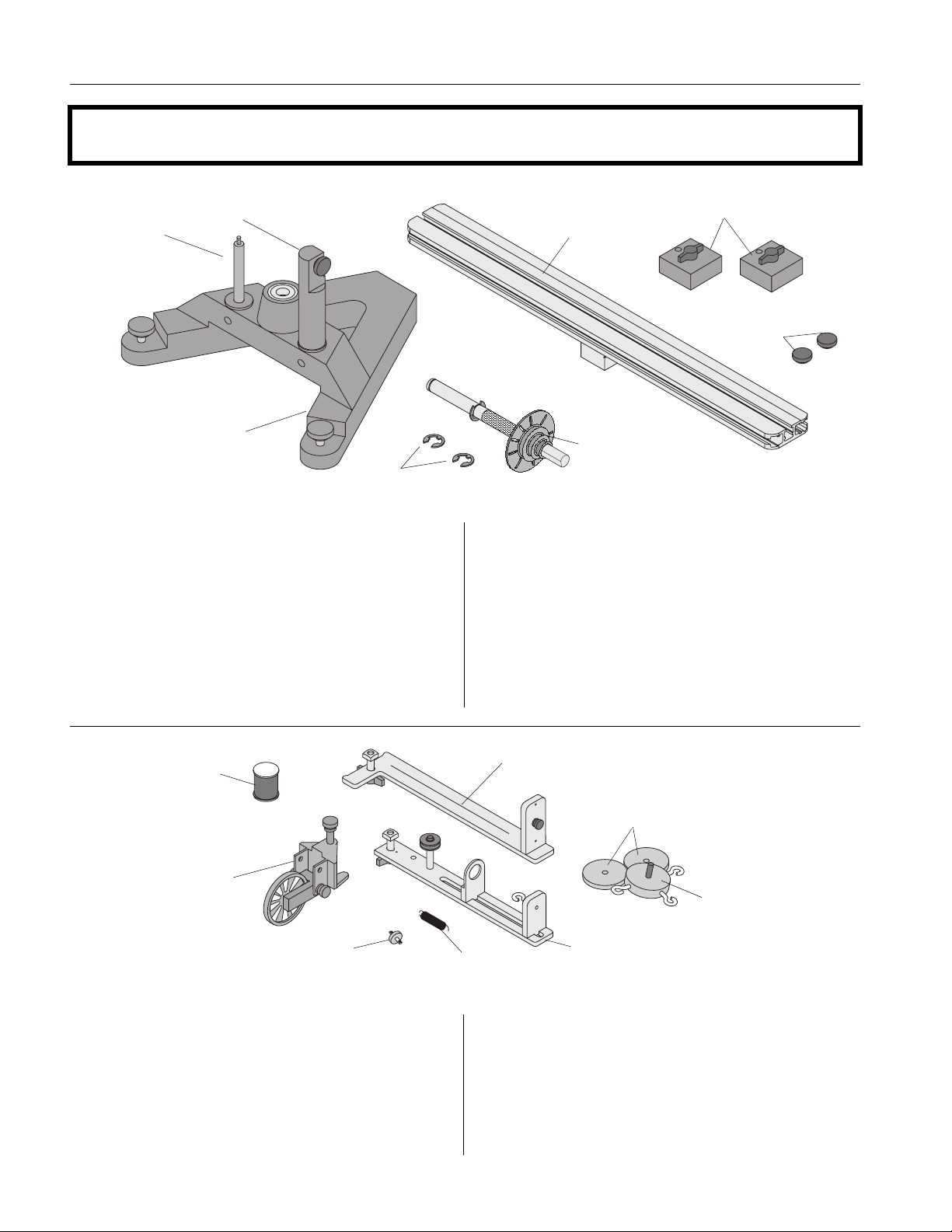
Complete Rotational System 012-05293F

Equipment

300g square mass (2) with thumbscrews and

square nuts

low-profile thumb-

screw assemblies (2)

photogate

mounting rod

accessory

mounting rod

aluminum rotating

platform

cast iron "A" base

"E" rings (2, 1 extra)

ME-8951 Rotating Platform Equipment

The ME-8951 Rotating Platform includes the following:

- PASCO cast iron “A” base with rotating shaft and pulley with 10 holes

- aluminum track

- two square masses (about 300 g) with thumb screw and square nut

spool of thread

clamp-on

pulley

rotating vertical shaft

with 10-hole pulley

- two additional low-profile screws and square nuts to act as stops for the square mass in the Conservation of Angular Momentum experiment

- accessory mounting rod for mounting a 10-spoke pulley with or without the optional PASCO Photogate Head

- photogate mounting rod for mounting a PASCO Photogate Head (ME-9498A)

side post

50g masses (2)

100g mass with 3 open

hooks

plastic

indicator disk

ME-8952 Centripetal Force Accessory Equipment

The ME-8952 Centripetal Force Accessory includes:

- center post that supports an indicator mechanism which consists of a small pulley, a movable spring holder, a movable indicator, a spring, and a plastic indicator disk

spring

center post

- side post for hanging hooked mass

- mass (100 g) with 3 open hooks

- 2 additional 50 gram masses

- clamp-on pulley

- 1 spool of thread

012-05293F Complete Rotational System

mass ring

(12.7 cm outside

diameter)

rotational disk

(25.4 cm diameter)

ACCESSORY

ROTATIONAL INERTIA

Super Pulley and rod

rotating platform

adapter

ME-8953 Rotational Inertia Accessory Equipment

The ME-8953 Rotational Inertia Accessory includes:

- disk with bearings in the center

- ring (12.7 cm diameter)

- adapter to connect disk to platform

- 10-spoke pulley and rod

Other Equipment Needed:

The following is a list of equipment recommended for the experiments described in this manual. See the PASCO catalog for more information.

- Projectile Launcher

- Projectile Collision Accessory

- Photogate Head (and a compatible PASCO computer interface)

- Mass and Hanger Set

- Stopwatch

- String

- Balance (for measuring mass)

- Calipers

-Meter Stick

Miscellaneous Supplies:

- graph paper

- carbon paper

- white paper

- rubber bands

- paper clips

Compatible PASCO Computer Interfaces:

The Photogate Head connects directly to a

ScienceWorkshop interface (such as the

ScienceWorkshop 500), and connects through a Digital

Adapter (PS-2159) to a PASPORT interface (such as a

USB Link, PowerLink, Xplorer, or Xplorer GLX).

Complete Rotational System 012-05293F

Assembly

ME-8951 Rotating Platform

Assembling the Rotating Platform

1. Insert the cylindrical end of the shaft into the bearings on the top-side of the A-shaped iron base. Secure the shaft in place by inserting the "E" ring in the slot at the bottom of the shaft. See Figure 1.

2. Mount the track to the shaft and tighten the thumb screw against the flat side of the “D” on the shaft. See Figure 1.

rotating platform

thumbscrew

flat of vertical shaft

vertical shaft

"A" base

"E" ring

Figure 1: Attaching the Vertical Shaft to the Base and Rotating Platform Assembly

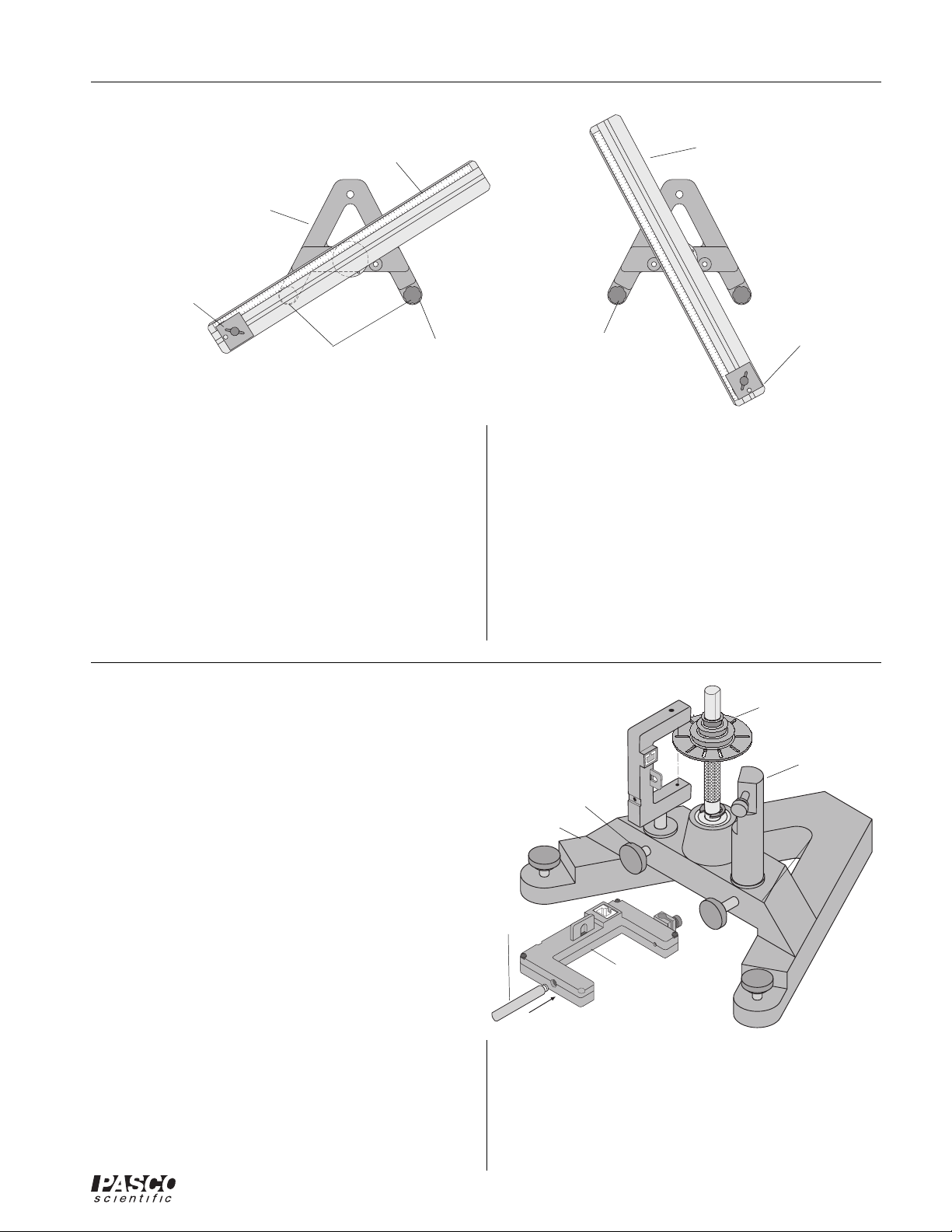
012-05293F Complete Rotational System

rotating plat-

form

191817161514131211 24232221

300g square

mass

Leveling the Base

"A" base

111213141516171819212224

leveling feet

010

123456789

987654321

adjust this foot

Figure 2: Leveling the Base

Some experiments (such as the Centripetal Force experiments) require the apparatus to be extremely level. If the track is not level, the uneven performance will affect the results. To level the base, perform the following steps:

1. Purposely make the apparatus unbalanced by attaching the 300 g square mass onto either end of the aluminum track. Tighten the screw so the mass will not slide. If the hooked mass is hanging from the side post in the centripetal force accessory, place the square mass on the same side.

2. Adjust the leveling screw on one of the legs of the

rotating platform

(rotated 90° as shown)

010

123456789

111213141516171819212224

first

191817161514131211 24232221

then adjust this

foot

987654321

base until the end of the track with the square mass is aligned over the leveling screw on the other leg of the base. See Figure 2.

3. Rotate the track 90 degrees so it is parallel to one side of the “A” and adjust the other leveling screw until the track will stay in this position.

4. The track is now level and it should remain at rest regardless of its orientation.

300g square

mass

Using an Optional Photogate Head

The optional Photogate Head (ME-9498A) can be mounted to the Rotating Platform in two ways:

• Photogate Mount Rod can be used to mount the Photogate Head directly to the base as shown in Figure 3.

• Accessory Mounting Rod can to be used to mount a Pulley Mounting rod and a Super Pulley along with the Photogate Head to the base in order to run a string over the Super Pulley. See Figure 4.

To Mount the Photogate Head Only:

1. Mount the Photogate Head on the threaded end of the photogate mount rod.

2. Remove the swivel clamp from the top of the Photogate Head.

3. Slide the non-threaded end of the photogate mount rod into a hole in the A-base and clamp it in place with the thumbscrew.

4. Adjust the Photogate Head so that its infrared beam can be interrupted by the 10 spoke pulley on the vertical shaft as the shaft turns.

10-spoke pulley on vertical shaft

accessory

mounting rod

thumbscrew

"A" base

photogate mount rod

Photogate Head

(optional)

Figure 3: Using the Photogate Mount Rod With the

Photogate Head

Make sure that the Photogate Head does not rub against

the 10 spoke pulley or any other part of the apparatus.

5. Connect the cable to the Photogate Head and a PASCO interface.

Complete Rotational System 012-05293F

6. When the Photogate Head is powered by a computer interface, you can tell when the photogate is blocked by watching the LED indicator on the photogate.

10-spoke pulley on

vertical

shaft

nylon thumb-

screw

To use the Super Pulley and Photogate Head with the Pulley Mounting Rod:

1. Attach the Super Pulley -- and the Photogate Head if needed -- to the Pulley Mounting Rod.

2. Insert the pulley mounting rod into the hole in the Accessory Mounting Rod and tighten the thumb screw. See Figure 4.

accessory

mounting rod

3. Rotate the accessory mounting rod so that a string from the pulley on the center shaft will be aligned with the groove on the Super

"A" base

Pulley.

4. Adjust the position of the base so the string passing over the Super Pulley will clear the edge of the table.

Figure 4: Using the Accessory Mounting Rod With the Pulley

Mounting Rod, Super Pulley, and Photogate Head

pulley

mounting rod

Super Pulley

Photogate Head

(optional)

ME-8952 Centripetal Force Accessory

Center Post Assembly

Assemble the center post as shown in Figure 5:

1. Attach one end of the spring to the spring bracket and connect the indicator disk to the other end of the spring. Insert the spring bracket into the slot on the center post and tighten the thumb screw.

2. Tie one end of a string (about 30 cm long) to the bottom of the indicator disk and tie a loop in the other end of the string.

3. Insert the indicator bracket into the slot on the center post, placing it below the spring bracket. Tighten the thumb screw.

4. Attach the pulley in the higher of the two holes on the center bracket.

5. Insert the thumb screw at the bottom of the center post and attach the square nut.

spring

bracket

spring

pulley

reference mark (center of post)

square nut

Figure 5: Center Post Assembly

center

post

indicator

disk

indicator

bracket

thumbscrew

012-05293F Complete Rotational System

holes for

thread

nylon thumbscrew

Side Post Assembly

Assemble the side post as shown in Figure 6:

1. Insert the thumb screw at the bottom of the side post and attach the square nut.

single length

of thread

(30cm long)

side post

2. Using a string about 30 cm long, tie the string around the screw head on the top of the side post. Then thread the other end of the string down through one of the holes in the top of the side post and then back up through the other hole. Do not pull the string taut.

3. Loosen the screw on the top of the side post and wrap

100g mass

the loose end of the string around the threads of the screw and tighten the screw.

square nut

Figure 6: Side Post Assembly

thumbscrew

Threading the Centripetal Force Accessory

1. Mount the center post in the T-slot on the side of the track that has the rule. Align the line on the center post with the zero mark on the rule and tighten the thumb screw to secure it in place. Then mount the side post on the same side of the track. See Figure 7.

2. Hang the 100 g mass from the string on the side post and adjust the height of the mass so the string coming from the center post will be level when the mass is hanging straight down.

rotating

platform

100g mass

thread

zero mark

of rule

side post

indicator

disk

indicator

bracket

center post

pulley

reference mark (center of post)

Figure 7: Threading the Centripetal Force Accessory

Complete Rotational System 012-05293F

bearing of

"D" hole on top sur-

face of rotational

ACCESSORY

ROTATIONAL INERTIA

rotational disk

square

nut

platform

adapter

rotational disk

platform

adapter

rotating platform

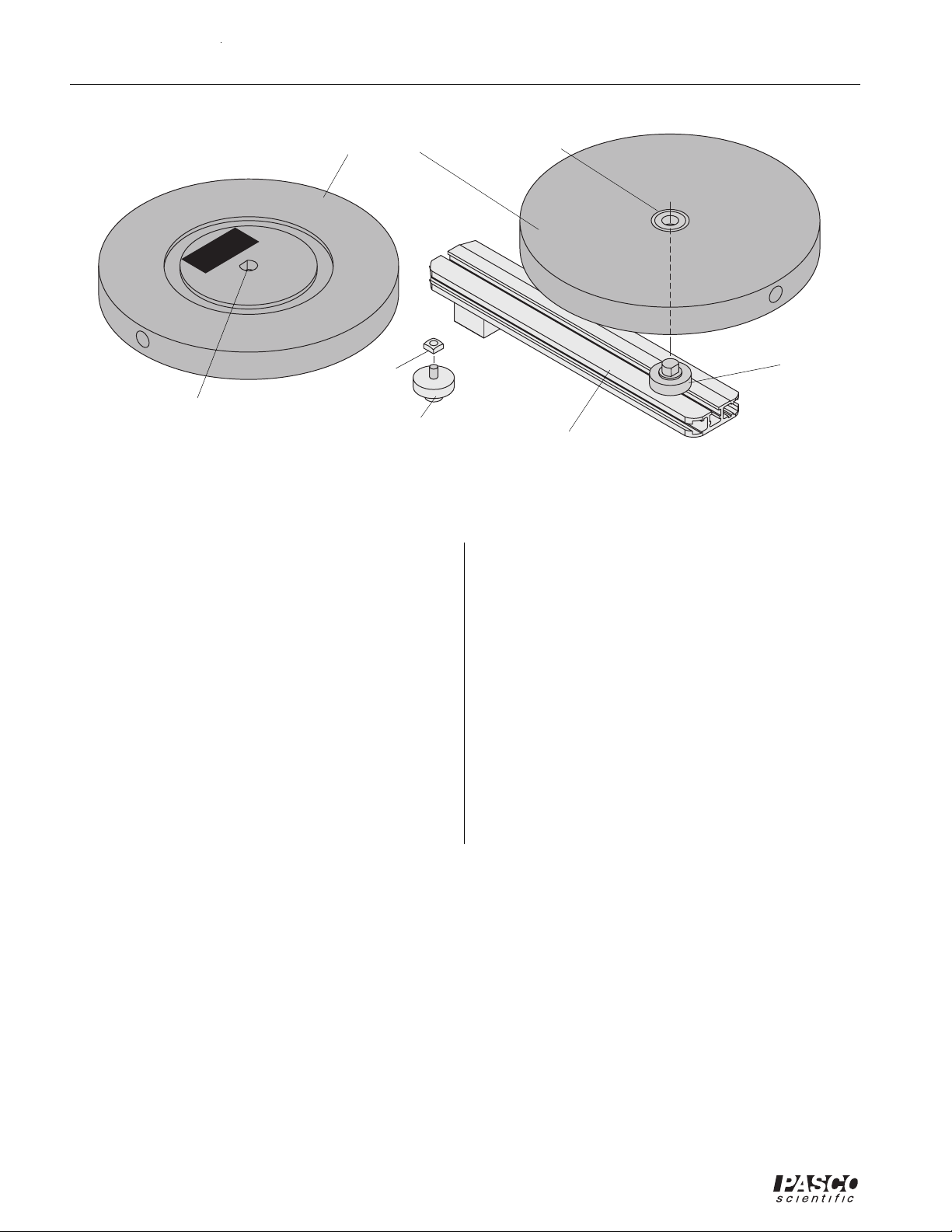
Figure 8: Rotational Inertia Accessory Including Platform Adapter Assembly

ME-8953 Rotational Inertia Accessory

Rotational Inertia Accessory Assembly

Little assembly is required to use the Rotational Inertia Accessory. The rotational disk can be placed directly onto the axle of the rotating base or can be used with the rotating platform via the included platform adapter.

Platform Adapter Assembly

1. Attach the square nut (supplied with the Rotational Inertia Accessory) to the platform adapter.

2. Position the platform adapter at the desired radius as shown in Figure 8.

3. Grip the knurled edge of the platform adapter and tighten.

The rotating disk can be mounted in a variety of positions using any of the four holes on the rotation disk.

• Two “D” holes exist on the edge of the disk, located at 180° from one another.

• One “D” hole is located at the center on the top surface (the surface with the metal ring channel and the PASCO label) of the disk.

• One hole is located at the center on the bottom surface of the disk and is actually the inner race of a bearing. This enables the rotational disk to rotate (in either direction) in addition to other rotating motions applied to your experiment setup.

012-05293F Complete Rotational System

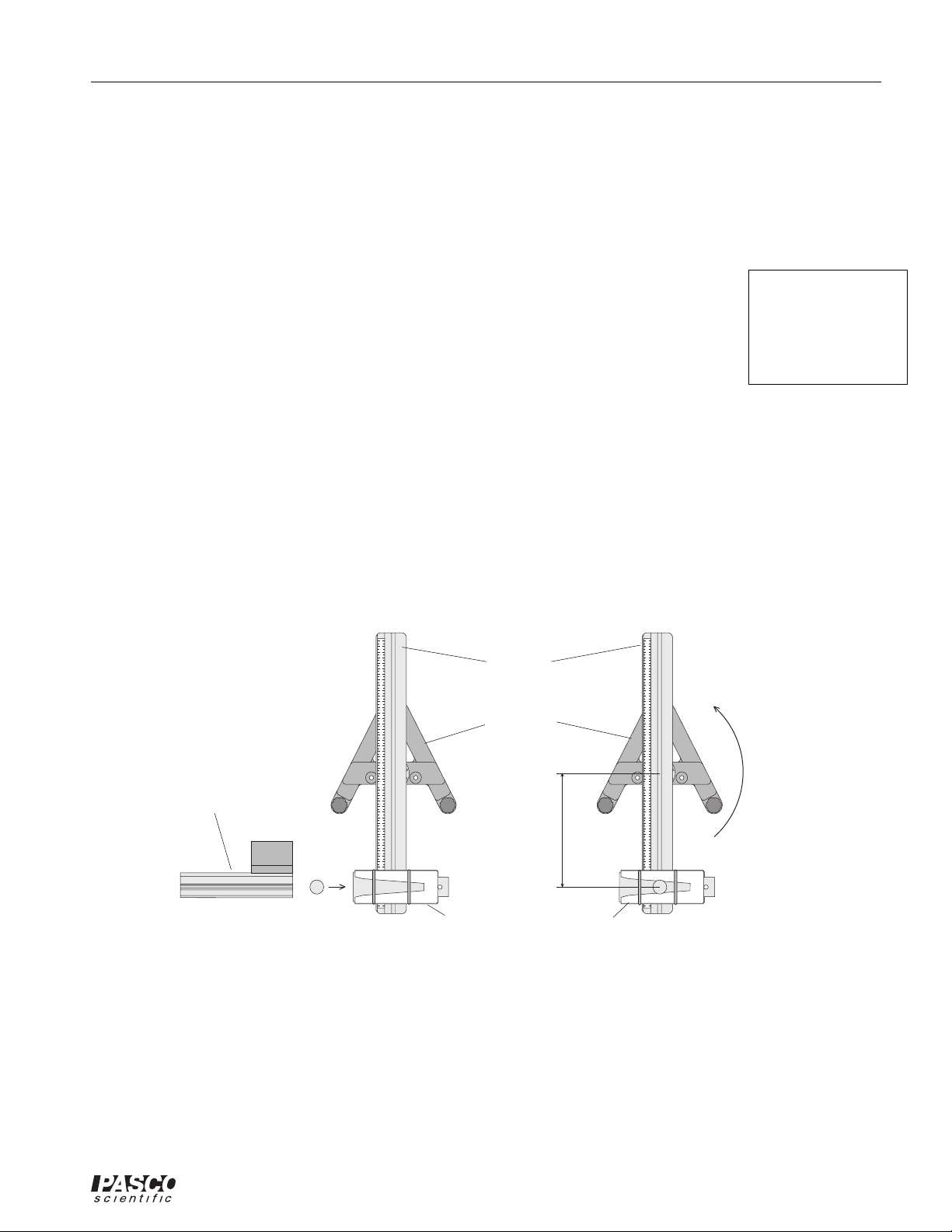
Experiment 1: Conservation of Angular Momentum

(Projectile Version)

EQUIPMENT NEEDED

- Rotating Platform (ME-8951) - Rubber band

- Projectile Launcher (ME-6800) - White paper and carbon paper

- Projectile Collision Accessory (ME-6815) - Thread

- Photogate/Pulley System (ME-6838) - Meter Stick (SE-6895)

- DataStudio Software - Mass and Hanger Set (ME-8967)

- PASCO Interface (see Note) - Calipers (SF-8711)

Purpose

The muzzle velocity of the Projectile Launcher can be determined by shooting the ball into the catcher mounted on the platform and conserving angular momentum during the collision. This result can be checked by finding the muzzle velocity of the Launcher by shooting the ball horizontally off the table.

Note: If you are using a PASPORT interface, you will also need a Digital Adapter (PS-2159)

Theory

A ball is launched horizontally and embeds in the catcher mounted on the platform. The platform then rotates. See Figure 1.1.

Angular momentum is conserved during the collision but energy is not conserved. The angular

Projectile Launcher

Rotating Platform

"A" base

Projectile Collision Accessory

("catcher")

Figure 1.1 Conservation of Angular Momentum

momentum before the collision is equal to the angular momentum after the collision:

Lmbv0RIω==

3 2

7 1

where m

is the mass of the ball, vo is the muzzle velocity of the ball, R is the distance between the ball

and the axis of rotation, I is the rotational inertia of the catcher, ball, and rotating platform after the collision, and ω is the angular velocity of the system immediately after the collision.

Solving for the muzzle velocity of the ball gives:

Complete Rotational System 012-05293F

Iω

----------

To find the rotational inertia experimentally, a known torque is applied to the object and the resulting angular acceleration is measured. Since τ = Iα,

---

where α is the angular acceleration which is equal to a/r and τ is the torque caused by the weight hanging from the thread which is wrapped around the base of the apparatus, and

τ rT=

where r is the radius of the step pulley about which the thread is wound and T is the tension in the thread when the apparatus is rotating.

Applying Newton’s Second Law for the hanging mass, m, gives (See Figure 1.2):

ΣFmgT– ma==

Rotating Platform

"A" base

hanging

mass

Figure 1.2: Rotational Apparatus and Free-Body Diagram

Solving for the tension in the thread gives:

Tmga–()=

Once the linear acceleration of the mass (m) is determined, the torque and the angular acceleration can be obtained for the calculation of the rotational inertia.

For comparison, the initial speed (muzzle velocity) of the ball is determined by shooting the ball horizontally off the table onto the floor and measuring the vertical and horizontal distances through which the ball travels.

For a ball shot horizontally off a table with an initial speed, v

ball is given by x = v

t, where t is the time the ball is in the air. No air friction is assumed.

The vertical distance the ball drops in time t is given by .

, the horizontal distance traveled by the

---

The initial velocity of the ball can be determined by measuring x and y. The time of flight of the ball can be found using:

------=

and then the muzzle velocity can be found using v

= x/t.

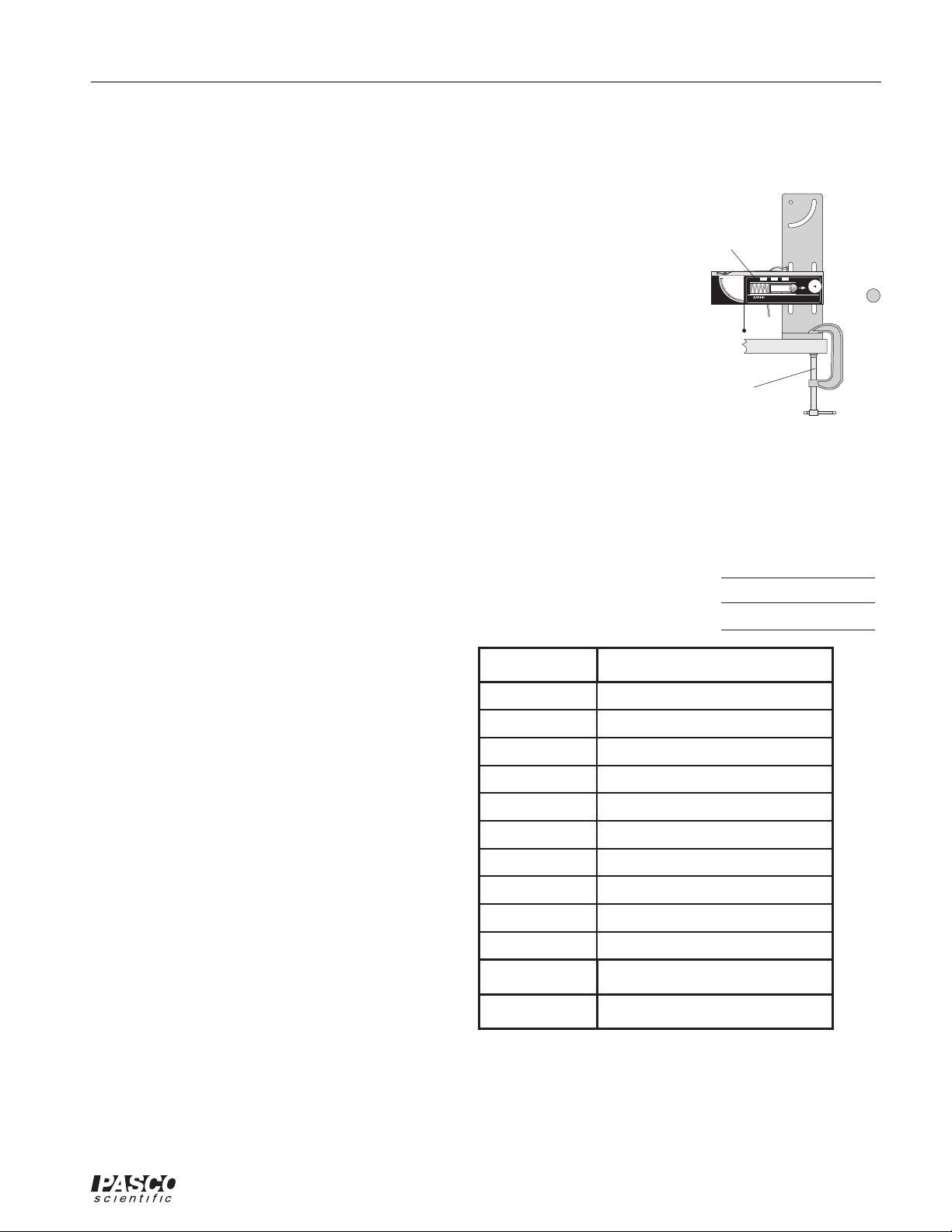
012-05293F Complete Rotational System

Part I: Determining the initial velocity of the ball

Setup

Projectile Launcher

1. Clamp the Projectile Launcher to a sturdy table near one end of the table.

2. Adjust the angle of the Projectile Launcher to zero degrees so the ball will be shot off horizontally. See Figure 1.3.

WEAR SAFETY GLASSES WHEN IN USE.

6 0

5 0

4 0

3 0

2 0

ME-6800

Procedure

1. Put the ball into the Projectile Launcher and cock it to the long range position. Fire one shot to locate where the ball hits the floor. At this position, tape a piece of white paper to the floor. Place a piece of carbon paper (carbon-side down) on top of this paper and tape it down. When the ball hits the floor, it will leave a mark on the white paper.

2. Fire about ten shots.

3. Measure the vertical distance from the bottom of the ball as it leaves the barrel (this position is marked on the side of the barrel) to the floor. Record this distance in Table 1.1.

Table 1.1 Determining the Initial Velocity

4. Use a plumb bob to find the point on the floor that is directly beneath the release point on the barrel. Measure the horizontal distance along the floor from the release

Horizontal distance to edge of paper =

Vertical distance =

Initial velocity =

point to the leading edge of the paper. Record in Table 1.1.

5. Measure from the leading edge of the paper

Trial Number

to each of the ten dots and record these distances in Table 1.1.

6. Find the average of the ten distances and record in Table 1.1.

7. Using the vertical distance and the average

horizontal distance, calculate the time of flight and the initial velocity of the ball. Record in Table 1.1 and Table 1.4.

clamp

Figure 1.3 Projectile

Launcher Setup

Distance

LONG

MEDIUM

RANGE

CAUTION!

DO NOT LOOK

DO NOT LOOK DOWN BARREL!

DOWN BARREL!

DOWN THE BARREL.

PROJECTILE LAUNCHER

CAUTION!

SHORT RANGE

Yellow Band in Window Indicates Range.

Launch

Use 25 mm

Position of Ball

balls ONLY!

Alternate Method: Determining the Muzzle Velocity with Photogates

1. Attach the photogate bracket to the

Launcher and attach two Photogates to the bracket. Plug the Photogates into a computer or other timer.

Average

Total Distance

2. Put the ball into the Projectile Launcher and cock it to the long range position.

3. Run the DataStudio program. Set it to measure the time between the ball blocking the two Photogates as it comes out of the Launcher.

4. Shoot the ball three times and take the average of these times. Record in Table 1.2.

Complete Rotational System 012-05293F

Trial Number

Time

Average Time

Initial Velocity

Table 1.2 Initial Speed Using Photogates

5. The distance between the Photogates is 10 cm. Calculate the initial speed and record it in Table

1.2 and Table 1.4.

Part II: Conservation of Angular Momentum

Setup

rubber band

end view of

rotating platform

side view of

rotating platform

rubber band

tab of "catcher"

against platform

Figure 1.4: Attaching the Catcher to the Track

"catcher"

1. Find the mass of the ball and record it in Table 1.3.

2. Attach the ball catcher to the track using a rubber band as shown in Figure 1.4.

3. With the Projectile Launcher mounted as it was in Part I, aim the launcher directly down the middle of the ball catcher using the sights inside the projectile launcher. Clamp the launcher to the table.

4. Attach the Photogate Head to the base. Connect the Photogate Head to a computer and run the DataStudio program.

5. Set up the program so that it measures and displays angular speed.

Procedure

1. Level the rotating platform.

2. Load the Launcher with the steel ball on the long range setting.

3. Make sure the rotating platform is at rest and fire the ball into the catcher. Record the angular speed of the platform in Table

1.3. Repeat for a total of five shots.

4. Measure the distance from the axis of rotation to the ball in the catcher and record in Table 1.3.

Distance from axis of rotation, R =

Trial Trial

Angular Speed Angular Speed

Table 1.3 Angular Speed

Mass of ball =

Avg.

012-05293F Complete Rotational System

Part III: Determining the Rotational Inertia

Setup

1. Attach a Photogate with a pulley and mounting rod to the base using the black rod.

2. Connect the Photogate to a PASCO interface and connect the interface to a computer.

3. Wind a thread around the middle step pulley on the center shaft and pass the thread over the pulley.

Procedure

Accounting For Friction

Because the theory used to find the rotational inertia experimentally does not include friction, it will be compensated for in this experiment by finding out how much mass over the pulley it takes to overcome kinetic friction and allow the mass to drop at a constant speed. Then this “friction mass” will be subtracted from the mass used to accelerate the apparatus.

1. Start the DataStudio program. Select ’Smart Pulley (Linear)’ and set up a Digits display to show velocity with three significant figures.

2. Hang a small amount of mass such as a few paper clips on the end of the thread that is over the pulley.

3. Start monitoring data, and then give the Rotating Platform a tap to get it started moving.

4. Watch the Digits display to see the velocity.

5. If the velocity increases or decreases as the Rotating Platform turns, stop monitoring data, stop the Rotating Platform, and adjust the amount of mass on the thread by adding or removing a paper clip.

6. Repeat the process until the velocity stays constant.

7. Measure the mass on the end of the thread and record it as the ’Friction Mass’ in Table 1.4.

Projectile

Catcher

step pulley

Photogate with pulley

Finding the Acceleration of the Apparatus

To find the acceleration, put about 30 g - record the exact hanging mass in Table 1.4 - over the pulley. In the DataStudio program, set up a Graph display of Velocity versus Time.

1. Wind the thread up and hold the Rotating Platform.

2. Let the Rotating Platform begin to turn and at the same time, start recording data.

3. Let the mass descend toward the floor but STOP recording data just before the mass hits the floor.

4. Examine your Graph display of Velocity versus Time. The slope of the best fit line for your data is the acceleration of the apparatus.

5. Record the slope in Table 1.4.

Table 1.4 Rotational Inertia Data

Friction Mass

Hanging Mass

Slope

Radius

Complete Rotational System 012-05293F

Measure the Radius

1. Using calipers, measure the diameter of the step pulley about which the thread is wrapped and calculate the radius.

2. Record the radius in Table 1.4.

Analysis

1. Calculate the average of the angular speeds in Table 1.3 and record the result in Table 1.5.

2. Calculate the rotational inertia:

• Subtract the “friction mass” from the hanging mass used to accelerate the apparatus to determine the mass, m, to be used in the equations.

• Calculate the experimental value of the rotational inertia and record it in Table 1.5.

Table 1.5 Results

Average Angular Speed

Rotational Inertia

Calculated Initial Velocity, v

Measured Initial Velocity

% Difference

3. Using the average angular speed, the rotational inertia, and the distance, r, calculate the muzzle velocity of the ball and record it in Table 1.5.

4. Calculate the percent difference between the muzzle velocities found in Parts I and II. Record in Table 1.5.

Questions

1. What percentage of the kinetic energy is lost in the collision? Use the masses and velocities to calculate this percentage.

%Lost

----------------------------------------------

before

–

before

after

x100 %=

012-05293F Complete Rotational System

Experiment 2: Rotational Inertia of a Point Mass

EQUIPMENT NEEDED

- DataStudio Software

- PASCO Interface (see Note) - Mass and Hanger Set

- Paper clips (for masses < 1 g) - Photogate/Pulley System

- Balance - Calipers

Purpose

The purpose of this experiment is to find the rotational inertia of a point mass experimentally and to verify that this value corresponds to the calculated theoretical value.

Theory

Theoretically, the rotational inertia, I, of a point mass is given by I = MR2, where M is the mass, R is the distance the mass is from the axis of rotation.

To find the rotational inertia experimentally, a known torque is applied to the object and the resulting angular acceleration is measured. Since τ = Iα,

---

where α is the angular acceleration which is equal to a/r and τ is the torque caused by the weight hanging from the thread which is wrapped around the step pulley below the rotating platform, and

τ rT=

Note: If you are using a PASPORT interface, you will also need a Digital Adapter (PS-2159)

where r is the radius of the step pulley about which the thread is wound and T is the tension in the thread when the apparatus is rotating.

Applying Newton’s Second Law for the hanging mass, m, gives (see Figure 2.1).

ΣFmgT– ma==

rotating

platform

"A" base

hanging

mass

Figure 2.1: Rotational Apparatus and Free-Body Diagram

Solving for the tension in the thread gives:

Tmga–()=

Complete Rotational System 012-05293F

Once the linear acceleration of the mass (m) is determined, the torque and the angular acceleration can be obtained for the calculation of the rotational inertia.

Setup

1. Level the rotating platform.

2. Attach the square mass (point mass) to the track on the rotating platform at any radius you wish.

3. Mount the Photogate/Pulley system to the base and connect the photogate through an interface to a computer. See Figure 2.2.

4. Attach a thread to the middle step of the step pulley and hang the thread over the 10-spoke pulley. Allow the string to reach to the floor.

300g mass

rotating

platform

"A" base

10-spoke pulley with

photogate head

Figure 2.2: Rotational inertia of a point mass

Procedure

Part I: Measurements For the Theoretical Rotational Inertia

1. Weigh the square mass to find the mass M and record in Table 2.1. Why is it possible to assume that the square mass acts the same as a point mass?

2. Measure the distance from the axis of rotation to the center of the square mass and record this radius in Table 2.1.

Table 2.1: Theoretical Rotational Inertia

Mass, M

Radius, R

Part II: Measurement For the Experimental Method

Accounting For Friction

1. Start the DataStudio program. Select ’Smart Pulley (Linear)’ and set up a Digits display to show velocity with three significant figures.

2. Hang a small amount of mass - such as a few paper clips - on the end of the thread that is over the pulley.

3. Start monitoring data, and then give the Rotating Platform a tap to get it started moving.

4. Watch the Digits display to see the velocity.

012-05293F Complete Rotational System

5. If the velocity increases or decreases as the platform turns, stop monitoring data, stop the platform, and adjust the amount of mass on the thread by adding or removing a paper clip.

6. Repeat the process until the velocity stays constant as the mass falls.

7. Measure the mass on the end of the thread and record it as the ’Friction Mass’ in Table 2.2.

Finding the Acceleration of the Point Mass and Apparatus

To find the acceleration, put about 50 g - measure the exact mass and record it in Table 2.2 - on the end of the thread over the pulley. In DataStudio, set up a Graph display of Velocity versus Time.

1. Wind the thread up and hold the Rotating Platform.

2. Let the platform begin to turn and at the same time, start recording data.

3. Let the mass fall toward the floor but STOP recording data just before the mass hits the floor.

4. Examine your Graph display of Velocity versus Time. The slope of the best ’Linear Fit’ for your data is the acceleration of the apparatus.

5. Record the slope in Table 2.2.

Table 2.2: Rotational Inertia Data

Point Mass and Apparatus Apparatus Alone

Friction Mass

Hanging Mass

Slope

Radius, r

Measure the Radius

1. Using calipers, measure the diameter of the step pulley about which the thread is wrapped and calculate the radius.

2. Record the radius in Table 2.2.

Finding the Acceleration of the Apparatus Alone

Since in Finding the Acceleration of the Point Mass and Apparatus the apparatus is rotating as well as the point mass, it is necessary to determine the acceleration, and the rotational inertia, of the apparatus by itself so this rotational inertia can be subtracted from the total, leaving only the rotational inertia of the point mass.

1. Take the point mass off the rotational apparatus and repeat Finding the Acceleration of the Point Mass and Apparatus for the apparatus alone.

NOTE: that it will take less “friction mass” to overcome the new kinetic friction and it is only necessary to put about 20 g on the end of the thread over the pulley.

2. Record the data in Table 2.2.

Calculations

1. Subtract the “friction mass” from the hanging mass used to accelerate the apparatus to determine the mass, m, to be used in the equations.

2. Calculate the experimental value of the rotational inertia of the point mass and apparatus together and record in Table 2.3.

3. Calculate the experimental value of the rotational inertia of the apparatus alone. Record in Table 2.3.

Complete Rotational System 012-05293F

4. Subtract the rotational inertia of the apparatus from the combined rotational inertia of the point mass and apparatus. This will be the rotational inertia of the point mass alone. Record in Table

2.3.

5. Calculate the theoretical value of the rotational inertia of the point mass. Record in Table 2.3.

6. Use a percent difference to compare the experimental value to the theoretical value. Record in Table 2.3.

Table 2.3: Results

Rotational Inertia for Point Mass

and Apparatus Combined

Rotational Inertia for

Apparatus Alone

Rotational Inertia for Point Mass

(experimental value)

Rotational Inertia for Point Mass

(theoretical value)

% Difference

012-05293F Complete Rotational System

Experiment 3: Centripetal Force

EQUIPMENT NEEDED

- Centripetal Force Accessory (ME-8952) - Rotating Platform (ME-8951)

- Stopwatch - Balance

- Graph paper (2 sheets) - Mass and Hanger Set

- String

Purpose

The purpose of this experiment is to study the effects of varying the mass of the object, the radius of the circle, and the centripetal force on an object rotating in a circular path.

Theory

When an object of mass m, attached to a string of length r, is rotated in a horizontal circle, the centripetal force on the mass is given by:

---------

mrω

where v is the tangential velocity and ω is the angular speed (v = r ω). To measure the velocity, the time for one rotation (the period, T) is measured. Then:

2πr

---------

and the centripetal force is given by:

4π

----------------

Setup

Level the "A" base and rotating platform as described in the ME-8951 assembly section in the introduction to this manual.

Procedure

Part I: Vary Radius (constant force and mass)

1. The centripetal force and the mass of the hanging object will be held constant for this part of the experiment. Weigh the object and record its mass in Table 3.1. Hang the object from the side post and connect the string from the spring to the object. The string must pass under the pulley on the center post. See Figure 3.1.

Complete Rotational System 012-05293F

clamp-on

pulley

hanging

mass

side post

assembly

Figure 3.1: Centripetal Force Apparatus

string

center post

assembly

rotating

platform

"A" base

2. Attach the clamp-on pulley to the end of the track nearer to the hanging object. Attach a string to the hanging object and hang a known mass over the clamp-on pulley. Record this mass in Table

3.1. This establishes the constant centripetal force.

3. Select a radius by aligning the line on the side post with any desired position on the measuring tape. While pressing down on the side post to assure that it is vertical, tighten the thumb screw on the side post to secure its position. Record this radius in Table 3.1.

4. The object on the side bracket must hang vertically: On the center post, adjust the spring bracket vertically until the string from which the object hangs on the side post is aligned with the vertical line on the side post.

5. Align the indicator bracket on the center post with the orange indicator.

6. Remove the mass that is hanging over the pulley and remove the pulley.

7. Rotate the apparatus by hand, increasing the speed until the orange indicator is centered in the indicator bracket on the center post. This indicates that the string supporting the hanging object is once again vertical and thus the hanging object is at the desired radius.

Table 3.1: Varying the Radius

8. Maintaining this speed, use a stopwatch to time ten revolutions. Divide the time by ten and record the period in Table 3.1.

9. Move the side post to a new radius and repeat

Mass hanging over the pulley =

Mass of the object =

Slope from graph =

the procedure. Do this for a total of five radii.

Radius Period (T) T

Analysis

1. The weight of the mass hanging over the pulley is equal to the centripetal force applied by the spring. Calculate this force by multiplying the mass hung over the pulley by “g” and record this force at the top of Table 3.2.

2. Calculate the square of the period for each trial and record this in Table 3.1.

3. Plot the radius versus the square of the period. This will give a straight line since:

-------------

⎛⎞

4π2m

⎝⎠

4. Draw the best-fit line through the data points and measure the slope of the line. Record the slope in Table 3.1.

012-05293F Complete Rotational System

5. Calculate the centripetal force from the slope

Table 3.2: Results (varying raduis)

and record in Table 3.2.

6. Calculate the percent difference between the two values found for the centripetal force

Centripetal Force = mg

Centripetal Force From Slope

and record in Table 3.2.

Percent Difference

Part II: Vary Force (constant radius and mass)

The radius of rotation and the mass of the hanging object will be held constant for this part of the experiment.

1. Weigh the object and record its mass in Table 3.3. Hang the object from the side post and connect the string from the spring to the object. The string must pass under the pulley on the center post.

2. Attach the clamp-on pulley to the end of the track nearer to the hanging object. Attach a string to the hanging object and hang a known mass over the clamp-on pulley. Record this mass in Table

3.3. This determines the centripetal force.

5. Align the indicator bracket on the center post with the orange indicator.

6. Remove the mass that is hanging over the pulley and remove the pulley.

7. Rotate the apparatus, increasing the speed until the orange indicator is centered in the indicator bracket on the center post. This indicates that the string supporting the hanging object is once again vertical and thus the hanging object is at the desired radius.

8. Maintaining this speed, use a stopwatch to time ten revolutions. Divide the time by ten and record the period in Table 3.3.

9. To vary the centripetal force, clamp the pulley to the track again and hang a different mass over the pulley. Keep the radius constant and repeat the procedure from Step #4. Do this for a total of five different forces.

Analysis

1. The weight of the mass hanging over the pulley is equal to the centripetal force applied by the spring. Calculate this force for each trial by multiplying the mass hung over the pulley by “g” and record the results in Table 3.3.

2. Calculate the inverse of the square of the period for each trial and record this in Table 3.3.

3. Plot the centripetal force versus the inverse square of the period. This will give a straight line since:

4π

----------------

4. Draw the best-fit line through the data points and measure the slope of the line. Record the slope in Table 3.3.

Complete Rotational System 012-05293F

Table 3.3: Varying the Centripetal Force

Mass of the object =

Radius =

Slope from graph =

Mass Over Pulley

Centripetal Force = mg Period (T)

5. Calculate the mass of the object from the slope and record in Table 3.4.

6. Calculate the percent difference between the two values found for

Table 3.4: Results (varying the centripetal force)

the mass of the object and record in Table 3.4.

Mass of Object (from scale)

Mass of Object (from slope)

Percent Difference

Part III: Vary Mass (constant radius and force)

The centripetal force and the radius of rotation will be held constant for this part of the experiment.

1. Weigh the object with the additional side masses in place. Record its mass in Table 3.5. Hang the object from the side post and connect the string from the spring to the object. The string must pass under the pulley on the center post.

2. Attach the clamp-on pulley to the end of the track nearer to the hanging object. Attach a string to the hanging object and hang a known mass over the clamp-on pulley. Record this mass in Table

3.5. This establishes the constant centripetal force.

5. Align the indicator bracket on the center post with the orange indicator.

6. Remove the mass that is hanging over the pulley and remove the pulley.

8. Maintaining this speed, use a stopwatch to time ten revolutions. Divide the time by ten and record the period in Table 3.5.

9. Vary the mass of the object by removing the side masses. Keep the radius constant and measure the new period. Weigh the object again and record the mass and period in Table 3.5.

012-05293F Complete Rotational System

Table 3.5: Varying the Mass of the Object

Mass hanging over pulley =

Centripetal Force = mg =

Radius =

Mass of Object % Difference

Period (T)

Calculated

Centripetal Force

Analysis

2. Calculate the centripetal force for each trial using:

4π

----------------

and record this in Table 3.5.

3. Calculate the percent difference between the calculated centripetal force for each trial and mg. Record in Table 3.5.

Questions

1. When the radius is increased, does the period of rotation increase or decrease?

2. When the radius and the mass of the rotating object are held constant, does increasing the period increase or decrease the centripetal force?

3. As the mass of the object is increased, does the centripetal force increase or decrease?

Complete Rotational System 012-05293F

Notes:

012-05293F Complete Rotational System

---

rT=

FmgT– ma==

Tmga–

Experiment 4: Conservation of Angular Momentum

Using a Point Mass

EQUIPMENT REQUIRED

- DataStudio Program - Rotating Platform (ME-8951)

- PASCO Interface (see Note) - Photogate/Pulley System

- Rotational Inertia Accessory (ME-8953) - Balance

Purpose

A mass rotating in a circle is pulled in to a smaller radius and the new angular speed is predicted using conservation of angular momentum.

Theory

Angular momentum is conserved when the radius of the circle is changed

Note: If you are using a PASPORT interface, you will also need a Digital Adapter (PS-2159)

where I

iωiIf

is the initial rotational inertia and ωi is the initial angular speed. So the final rotational

speed is given by:

-- -

To find the rotational inertia experimentally, a known torque is applied to the object and the resulting angular acceleration is measured. Since τ = Iα,

where α is the angular acceleration which is equal to a/r and τ is the torque caused by the weight hanging from the thread which is wrapped around the base of the apparatus.

where r is the radius of the cylinder about which the thread is wound and T is the tension in the thread when the apparatus is rotating.

Applying Newton’s Second Law for the hanging mass, m, gives (See Figure 4.1)

Solving for the tension in the thread gives:

()

Once the linear acceleration of the mass (m) is determined, the torque and the angular acceleration can be obtained for the calculation of the rotational inertia.

Complete Rotational System 012-05293F

rotating

platform

"A" base

hanging

mass

Figure 4.1: Rotational Apparatus and Free-Body Diagram

Part I: Conservation of Angular Momentum

Setup

1. Level the apparatus using the square on the track as shown in the leveling instructions in the Assembly Section.

2. Slide a thumb screw and square nut into the T-slot on the top of the track and tighten it down at about the 5 cm mark. This will act as a stop for the sliding square mass. See Figure 4.2.

string

300g mass

center post

rotating

stop screws (2)

"A" base

platform

Figure 4.2: Set-up for conservation of angular momentum

3. With the side of the square mass that has the hole oriented toward the center post, slide the square mass onto the trac k by ins er ti ng i ts square nut into the T-slot, bu t d o not tighten the thumb screw; the square mass should be free to slide in the T-slot.

4. Slide a second thumb screw and square nut into the T-slot and tighten it down at about the 20 cm mark. Now the square mass is free to slide between the two limiting stops.

5. Move the pulley on the center post to its lower position. Remove the spring bracket from the center post and set it aside.

6. Attach a string to the hole in the square mass and thread it around the pulley on the center post and pass it through the indicator bracket.

7. Mount the Photogate on the rod on the base and position it so it straddles the holes in the pulley on the center rotating shaft.

8. Start the DataStudio program. Connect the Photogate to a PASCO int er fa ce a nd c onnect the interface to a computer (if needed).

012-05293F Complete Rotational System

Procedure

1. Select ’Smart Pulley (Rotationa l)’ as t he t ype of sen sor. Set up a Graph disp lay o f Velocity (rad/s) versus time.

2. Hold the string just above the center post. With the square mass against the outer stop, give the track a spin using your hand.

3. Click ’Start’ to begin recording data. After about 20 data points have been taken, pull up on the string to cause the square mass to slide from the outer stop to the inner stop.

4. Continue to hold the string up and take about 20 data points after pulling up on the string. Click ’Stop’ to end recording dat a.

5. Examine the Graph display of Velocity (rad/s) versus time. The graph shows the angular speed before and after the square mass is pulled toward the inner stop. Rescale the graph if necessary.

6. Use the Smart Cursor tool to determine the angular speed immediately before and immediately after pulling the string. Record these values in Table 4.1.

7. Repeat the experiment a total of thr ee times with diffe rent initial angular speeds . Record these values in Table 4.1.

Trial Number

Table 4.1: Data

Angular Speeds

Initial Final

Part II: Determining the Rotational Inertia

Measure the rotational inertia of th e apparatus twice: once with the squ are mass in its initial position and once with it in its final position.

Setup

1. Attach a Photogate with Pulley to a mounting rod and attach the mounting rod to the black support rod on the base.

2. Wind a thread aro und the pulley on the cen ter shaft and pass the thread over the Pulley. See Figure 4.3.

string

300g mass

stop screws (2)

center post

rotating

platform

10-spoke pulley with

photogate head

"A" base

Figure 4.3: Set-up for determining rotational inertia

hanging mass

Complete Rotational System 012-05293F

Procedure

Accounting For Friction

Because the theory used to find the rotational inertia experimentally does not include friction, it will be compensated for in this exp er iment by fi ndi ng out how much mass over the pulley it takes to overcome kinetic fricti on an d allo w the mass t o dr op at a consta nt spee d. Then th is “fricti on mass” wil l be subtracted from the mass used to accelerate the apparatus.

1. Start the DataStudio program. Select ’Smart Pulley (L inear)’ and set up a Digits display to how velocity with three significant figures.

2. Hang a small amount of mass (such as a few paper clips) on the end of the thread that is over the pulley. Make sure that the thread is wound around the step pulley.

3. Start monitoring data, and then give the Rotating Platform a tap to get it started moving.

4. Watch the Digits display to see the velocity.

5. If the velocity increases or decreases as the platform turns, stop monitoring data, stop the platform, and adjust the amount of mass on the end of the thread.

6. Repeat the process until the velocity stays constant.

7. Measure the mass on the end of the thread and record it as ’Friction Mass’ in Table 4.2..

Finding the Acceleration of the Apparatus

T o fi nd the accele rati on, put about 30 g - recor d the exac t hang ing mass in Table 4.2 - over the pulley. In the DataStudio program, set up a Graph display of Velocity versus Time.

1. Wind the thread up and hold the Rotating Platform.

2. Let the Rotating Platform begin to turn and at the same time, START recording d ata.

3. Let the mass descend toward the floor but STOP re cordi ng data ju st befor e the mass hits the floor.

4. Examine your graph of velocity versus time. The slope ("m") of the best fit line for your data is the acceleration (use F it>Linear Fit). Record the slope in Table 4.2.

Repeat the procedure for the mass at the inner stop. Record results in Table 4.2.

Measure Radius

1. Using calipers, measure the diameter of the step pulley about which the thread is wrapped and calculate the radius.

2. Record the radius in Table 4.2.

Table 4.2 Rotational Inertia Data

Mass at Outer Stop Mass at Inner Stop

Friction Mass

Hanging Mass

Slope

Radius

Rotational Inertia

012-05293F Complete Rotational System

Analysis

1. Calculate the rotational inertias:

• Subtract the “friction mass” from the hanging mass used to accelerate the apparatus to determine the mass, m, to be used in the equations.

• Calculate the experimental values of the rotational inertia and record it in Table 4.3.

2. Calculate the expected (theoretical) values for the final angular velocity and record these values in Table 4.3.

Table 4.3: Results

Trial #1 Trial #2

Trial #3

Theoretical Angular Speed

% Difference

3. For each trial, calculate the percent difference between the experimental and the theoretical values of the final angular velocity and record these in Table 4.3.

Questions

Calculate the rotational kinetic energy before the string was pulled.

-- -

Then calculate the rotational kinetic energy after the string was pulled.

1. Which kinetic energy is greater?

2. Why?

-- -

Complete Rotational System 012-05293F

Notes:

012-05293F Complete Rotational System

---

Experiment 5: Rotational Inertia of Disk and Ring

EQUIPMENT REQUIRED

- DataStudio Program - Mass and Hanger Set

- PASCO Interface (see Note) - Paper Clips (for masses < 1 g)

- Rotational Inertia Accessory (ME-8953) - Balance

- Photogate/Pulley System - Calipers

Purpose

The purpose of t his experiment is to fin d the rotational inertia of a ring and a disk expe rimentally and to verify that these values correspond to the calculated theoretical values.

Theory

Theoretically, the rotati onal inerti a, I, of a rin g about its center o f mass is given by:

-- -

+()=

Note: If you are using a PASPORT interface, you will also need a Digital Adapter (PS-2159)

where M is the mass of the ring, R

is the inner radius of the r in g, and R2 is the

outer radius of the ring. See Figure 5.1. The rotational inertia of a disk about its center of mass is given by:

Figure 5.1: Ring

-- -

where M is the mass of the disk and R is the radius of the disk. The rotati onal ine rtia of a disk about its diameter is given by:

-- -

Disk about center of Mass Disk about Diameter

Figure 5.2:

To find the rotational inertia experimentally, a known torque is applied to the object and the resulting angular acceleration is measured. Since τ = Iα,

Complete Rotational System 012-05293F

rT=

FmgT– ma==

Tmga–

where α is the angular acceleration which is equal to a/r and τ is the torque caused by the weight hanging from the thread which is wrapped around the base of the apparatus.

where r is the radius of the cylinder about which the thread is wound and T is the tensi on in the thread when the apparatus is rotating.

Applying Newton’s Second Law for the hanging mass, m, gives (See Figure 5.3)

rotational disk

"A" base

Figure 5.3: Rotational Apparatus and Free-Body Diagram

Solving for the tension in the thread gives:

()

Once the linear acceleration of the mass (m) is determined, the torque and the angular acceleration can be obtained for the calculation of the rotational inertia.

Setup

1. Remove the track from the Rotating Platform and place the disk directly on t he cent er sh aft a s shown i n Figur e 5.4. Th e side of the disk that has the indentation for the ring should be up.

2. Place the ring on the disk, seating it in this indentation.

3. Mount the Photogate/Pulley System to the base and connect it to a PASCO interface.

4. Attach a thread to the top step of the three- step pulley on the Rotational Apparatus shaft and suspend the string over the pulley of the Photogate/ Pulle y System. At tach a ha nger and mass to the en d of the thread.

5. Start the DataStudio program.

hanging

mass

mass ring

rotational

disk

"A" base

10-spoke pulley with

photogate head

Figure 5.4: Set-up for Disk and Ring

mass and

hanger

Procedure

Measurements for the Theoretical Rotational Inertia

1. Weigh the ring and disk to find their masses and record these masses in Table 5.1.

2. Measure the inside and outside diameters of the ring and calculate the radii R Table 5.1.

3. Measure the diameter of the disk and calculate the radius R and record it in Table 5.1.

and R2. Record in

012-05293F Complete Rotational System

Table 5.1: Theoretical Rotational Inertia

Mass of Ring

Mass of Disk

Inner Radius of Ring

Outer Radius of Ring

Radius of Disk

Measurements for the Experimental Method

Accounting For Friction

Because the theory used to find the rotational inertia experimentally does not include friction, it will be compensated for in this ex periment by finding out how much mass over the pulley it takes to overcome kinetic frictio n and allow the mass to drop at a cons tant speed. Then this “frictio n mass” will be subtracted from the mass used to accelerate the apparatus.

1. In the DataStudio program, select ’Smart Pulley (Linear)’ and set up a Digits display to show velocity with three significant figures.

2. Hang a small amount of mass such as a few paper clips on the end of the thread that is over the pulley.

3. Start monitoring data, and then give the Rotational Disk a tap to get it started moving.

4. Watch the Digits display to see the velocity.

5. If the velocity increases or decreases as the Rotational Disk turns, stop monitoring data, stop the Rotational Disk, and adjust the amount of mass on the thread by adding or removing a paper clip.

6. Repeat the process until the velocity stays constant.

7. Measure the mass on the end of the thread and record it as the ’Friction Mass’ in Table 5.2.

Table 5.2: Rotational Inertia Data

Ring and Disk

Combined

Disk Alone

Disk Vertical

Friction Mass

Hanging Mass

Slope

Radius

Finding the Acceleration of Ring and Disk

To find the acc elerati on, put about 50 g - r ecord the exact hangi ng ma ss i n Table 5.2 - o ver t he pul ley. In the DataStudio program, set up a Graph display of Velocity versus Time.

1. Wind the thread up and hold the Rotati ng Platform.

2. Let the Rotating Platform begin to turn and at the same time, start recording data.

3. Let the mass descend toward the floor but STOP re cordi ng data ju st befo re the mass hits the floor.

4. Examine your Graph display of Velocity versus Time. The slope of the best fit line for your data is the acceleration of the apparatus.

5. Record the slope in Table 5.2.

Complete Rotational System 012-05293F

Measure t he Radius

1. Using calipers, measure the diameter of the cyl inder about which t he th read i s wrapp ed and cal culate the rad ius. Record i n Table 5.2.

Finding the Acceleration of the Disk Alone

Since in Finding the Acceleration of Ring and Disk the disk is rotating as well as the ring, it is necessary to determine the acceleration, and the rotational inertia, of the disk by itself so this rotational in ertia can be subtract ed from the total, le aving only the rota tional inert ia of the ring.

1. To do this, take the r ing off the rotationa l app aratu s a nd re peat Findi ng the Accelera tion of Ring

and Disk for the disk alone.

NOTE: that it will take less “f riction mass” to overcome the new kinetic friction and i t is only necessary to put about 30 g over the pulley in Finding the Acceleration of the Disk

Alone.

Disk Rotating on an Axis Through Its Diameter

Remove the disk from the shaft and rot ate it up on its side. Mount the disk vertically by inse rting the shaft in one of the two “D”-shaped holes on the edge of the disk. See Figure 5.5.

WARNING! Never mount the disk vertically using the adapter on the track. The adapter is too short for this purpose and the disk might fall over while being rotated.

Repeat steps Measure the Radius and Finding the Acceleration of the Disk Alone to determine the rotational inertia of the disk about its diameter. Record the data in Table 5.2.

rotational disk

"D" hole of

rotational disk

rotating shaft

"A" base

Figure 5.5: Disk mounted vertically

Calculations

Record the results of the following calculations in Table 5. 3.

1. Subtract the “friction mass” from the hanging mass used to acc el er ate the apparatus to determine the mass, m, to be used in the equations.

2. Calculate the experimental value of the rotational inertia of the ring and disk together.

3. Calculate the experimental value of the rotational inertia of the disk alone.

4. Subtract the rotational inertia of the disk from the total rotational inertia of the ring and disk.

This will be the rotational inertia of the ring alone.

5. Calculate the experimental value of the rotational inertia of the disk about its diameter.

6. Calculat e the theoretical value of the rotational inerti a of the ring.

012-05293F Complete Rotational System

7. Calculate the theoretical value of the rotational inertia of the disk about its center of mass and about its diameter.

8. Use a percent difference to compare the experimental values to the theoretical values.

Table 5.3: Results

Rotational Inertia for Ring and

Disk Combined

Rotational Inertia for Disk Alone

(experimental value)

Rotational Inertia for Ring

(experimental value)

Rotational Inertia for Vertical Disk

(experimental value)

Rotational Inertia for Disk

(theoretical value)

Rotational Inertia for Ring

(theoretical value)

Rotational Inertia for Vertical Disk

(theoretical value)

% Difference for Disk

% Difference for Ring

% Difference for Vertical Disk

Complete Rotational System 012-05293F

Notes:

012-05293F Complete Rotational System

--rT=

Experiment 6: Rotational Inertia of Disk Off-Axis

(Fixed/Rotating)

EQUIPMENT REQUIRED

- DataStudio Program - Calipers

- PASCO Interface (See Note) - Mass and Hanger Set

- Rotational Inertia Accessory (ME-8953) - Paper Clips (for masses < 1 g)

- Photogate/Pulley System - Balance

Purpose

The purpose of this exper ime nt i s to f ind the r otational inertia of a disk about an axi s parallel to the center of mass axis.

Theory

Theoretically, the rota tional inertia, I, of a disk about a perpendicular axis through its center of mass is given by:

-- -

Note: If you a re using a PASPORT interface, y ou will also need a Digital Adapter (PS-2159)

where M is the mass of the disk and R is the radius of the di sk. The rot ation al iner tia of a disk about an axis parallel to the center of mass axis is given by:

IcmMd2+=

where d is the distance between the two axes. In one part of this experiment, the disk is mounted on its ball bearing side which allows the

disk to free ly rotate relative to the track. So as the track is rotated, the di sk does not rotate relative to its center of mass . Since th e disk is not rota ting a bout i ts ce nter o f mass, it act s as a point mass rather than an extende d object and its rotational inerti a reduces fr om:

IcmMd2 to I+ Md

To find the rotational inertia experimentally, a known torque is applied to the object and the resulting angular acceleration is measured. Since τ = Iα;

where α is the angular acceleration which is equal to a/r and τ is the torque caused by the weight hanging f rom the thread which is wrapped ar oun d t he three step pulley on the shaft of the apparatus.

where r is the radius of the st ep pulley ab out which the thread is wound and T is the tension in the thread when the apparatus is rotating.

Complete Rotational System 012-05293F

FmgT– ma==

Tmga–

Applying Newton’s Second Law for the hanging mass, m, gives (See Figure 6.1)

rotating plat-

form

rotational disk

platform

adapter

"A" base

hanging

mass

Figure 6.1: Rotational Apparatus and Free-Body Diagram

Solving for the tension in the thread gives:

()

Once the linear acceleration of the mass (m) is determined, the torque and the angular acceleration can be obtained for the calculation of the rotational inertia.

Setup

1. Set up the Rotational Accessory as shown in Figure 6.2. Mount the disk with its bearing side up. Use the platform adapter to fasten the disk to the track at a large radius.

2. Mount two square masses on the opposite end of the platform to act as a counterweight. Be sure to tighten the screws.

3. Mount the Photogate/Pulley System to the base and connect it to an interface.

4. Run the DataStudio program.

rotational disk

platform adapter

"A" base

Figure 6.2: Set-up for Disk Off-Axis

rotating

platform

10-spoke pulley with

photogate head

hanging

mass

Measurements For the Theoretical Rotational Inertia

Record these measurements in Table 6.1.

1. Weigh the disk to find the mass M.

2. Measure the diameter and calculate the radius R.

3. Measure the distance, d, from the axis of rotation to the center of the disk.

012-05293F Complete Rotational System

Table 6.1: Theoretical Rotational Inertia

Mass of Disk

Radius of Disk

Distance Between

Parallel Axis

Measurements For the Experimental Method

Accounting For Friction

Because the theory used to find the rotational inertia experimentally does not include friction, it will be compensated for in this ex periment by finding out how much mass over the pulley it take s to overcome kinetic friction and allow the mass to drop at a constant speed. Then this “friction mass” will be subtracted from the mass used to accelerate the apparatus.

1. In the DataStudio program, select ’Smart Pulley (Linear)’ and set up a Digits display to show velocity with three significant figures.

2. Hang a small amount of mass such as a few paper clips on the end of the thread that is over the pulley.

3. Start monitoring data, and then give the Rotational Disk a tap to get it started moving.

4. Watch the Digits display to see the velocity.

5. If the velocity increases or decreases as the Rotational Disk turns, stop monitoring data, stop the Rotational Disk, and adjust the amount of mass on the thread by adding or removing a paper clip.

6. Repeat the process until the velocity stays constant.

7. Measure the mass on the end of the thread and record it as the ’Friction Mass’ in Table 6.2.

Finding the Acceleration of Disk and Track

Table 6.2: Rotational Inertia Data

Fixed Disk and

Track Combined

Track Alone

Rotating Disk and

Track Combined

Friction Mass

Hanging Mass

Slope

Radius

To find the acceleration , put about 50 g - rec ord the exact hanging mass in Tabl e 5.2 - over the pull ey. In the DataStudio program, set up a Graph display of Velocity versus Time.

1. Wind the thread up and hold the Rotati ng Platform.

2. Let the Rotating Platform begin to turn and at the same time, start recording data.

3. Let the mass descend toward the floor but STOP reco rdi ng data j ust bef ore the mas s hits t he floor.

4. Examine your Graph display of Velocity versus Time. The slope of the best fit line for your data is the acceleration of the apparatus.

5. Record the slope in Table 6.2.

Complete Rotational System 012-05293F

Measure t he Radius

1. Using calipers, measure the diameter of the c ylind er about which t he thr ead is wrappe d a nd cal culate the rad ius. Record i n Table 6.2.

Finding the Acceleration of Track Alone

Since in Finding the Acc eleration of Dis k and Track the track is rotating as well as the disk, it is necessary to determine the acceleration, and the rotational inertia, of the track by itself so this rotational inertia can be subtracted from the total, leaving only the rotational inertia of the disk.

1. To do this, ta ke the dis k of f t he rot atio nal appara tus a nd repe at Findi ng the Acceleration of Disk

and Track for the track alone.

NOTE: It will take less “friction mass” to overcome the new kinetic friction and it is only

necessary to put about 30 g over the pulley in Finding the Acceleration of Track Alone.

Disk Using Ball Bearings (Free Disk)

Mount the disk upside- down at the same radius as before. Now the ball bearings a t the center of the disk will allow t he disk t o rota te relativ e to the tr ack. Repea t Account ing For Friction and Finding the Acceleration of Disk and Track for this case and record the data in Table 6.2.

Calculations

Record the results of the following calculations in Table 6.3.

1. Subtract the “friction mass” from the hanging mass used to accelerate the apparatus to determine the mass, m, to be used in the equations.

2. Calculate the experimental value of the rotational inertia of the fixed disk and track combined.

3. Calculate the experimental value of the rotational inertia of the track alone.

4. Subtract the rotational inertia of the track f rom the rotational inertia of the fixed disk and track. This will be the rotational inertia of the fixed disk alone.

5. Calculate the experimental value of the rotat ional inerti a of the fixed disk and track combined.

6. Subtract the rotational inertia of the track from the rotational inertia of the free disk and track. This will be the rotational inertia of the free disk alone.

7. Calculate the theoretical value of the rotational inertia of the fixed disk off axis.

8. Calculate the theoretical value of a point mass having the mass of the disk.

9. Use a percent difference to compare the experimental values to the theoretical values.

Rotational Inertia for Fixed Disk

and Track Combined

Rotational Inertia for Track Alone

Rotational Inertia for Fixed Disk

Off-Axis (experimental value)

Rotational Inertia for Free Disk

and Track Combined

Rotational Inertia for Free Disk

Alone (experimental value)

Rotational Inertia for Fixed Disk

Off-Axis (theoretical value)

Rotational Inertia for Point Mass

(theoretical value)

% Difference for Fixed

% Difference for Free Disk

Table 6.3: Results

012-05293F Complete Rotational System

Experiment 7: Conservation of Angular

Momentum

EQUIPMENT REQUIRED

- DataStudio Program - PASCO Interface

- Rotational Inertia Accessory (ME-8953) - Balance

- Rotating Platform (ME-8951) - Photogate/Pulley System

Purpose

A non-rotating ring is dropped onto a rotating disk and the final angular speed of the system is compared with the value predicted using conservation of angular momentum.

Theory

When the ring is dropped ont o the r otati ng dis k, ther e is no n et tor que on t he syst em since the torque on the ring is equal an d opposite to the torque on the disk. Therefore, there is no change in angular momentum. Angular momentum is conserved

where I inertia is that of a disk

and the final rotational inertia of the combined disk and ring is

Note: If you are using a PASPORT interface, you will also need a Digital Adapter (PS-2159)

iωiIf

is the initia l rot atio nal iner tia a nd ωi is the initial angular speed. The initial rotational

-- -

2r1

+()+=

-- -

So the final rotational speed is given by

M1R

-------------------------------------------------

M1R2M2r

+()+

Setup

1. Level the apparatus using the square mass on the track.

2. Assemble the Rotational Inertia Accessory as shown in Figure

7.1. The side of th e disk with the indentatio n f or the ring should be up.

3. Mount the Photogate on the metal rod on the base and posit ion it so it straddles the holes in the pulley on the center rotating shaft.

4. Start the DataStudio program. Select ’Smart Pulley (Rotational)’ as the sensor.

5. Set up a Graph display of Velocity (rad/s) versus Time (s).

Rotational Disk

(indentation up)

"A"-base

Figure 7.1: Assembly for Dropping

Ring onto Disk

Complete Rotational System 012-05293F

Procedure

1. Hold the ring just above the center of the disk. Give the disk a spin using your hand.

2. Start recording data. After about 25 data points have been taken, drop the ring onto the spinning disk. See Figure 7.2.

3. Continue to take data after the collision for a few seconds and then stop recording data.

dropped ring

photogate head

rotational disk

"A" base

Figure 7.2: Experiment Setup

4. Examine the Graph display of the rotational speed versus time. Use the Autoscale tool to resize the axes if necessary.

5. In the Graph display, use the Smart Tool to determine the angular velocity immed iately befo re and immediately after the collision. Record these values in Table 7.1.

6. Weigh the disk and ring and measure the radii. Record these values in Table 7.1.

Analysis

1. Calculate the expected (theoretical) value for the final angular velocity and record this value in Table 7.1.

2. Calculate the percent difference between the experimental and the theoretical values of the final angular velocity and record in Table 7.1.

Table 7.1: Data and Results

Initial Angular Speed

Final Angular Speed (experimental value)

Mass of Disk

Mass of Ring

Inner Radius of Ring

Outer Radius of Ring

Radius of Disk

Final Angular Speed

(theoretical value)

% Difference Between Final

Angular Speeds

% KE Lost

012-05293F Complete Rotational System

----

Questions

1. Does the experimental result fo r the angul ar speed agr ee with the theory?

2. What percentage of the rotational kinetic energy is lost during the collision? Calculate this and record the results in Table 7.1.

KE Lost

-- 2

------------------------------

-- -

–

iωi

-- -

iωi

Complete Rotational System 012-05293F

Notes:

012-05293F Complete Rotational System

Technical Support

Feed-Back

If you have any comments about this product or this manual please let u s know. If you have any sugge st ion s on alternate experi ments or find a pr oblem in the manual please tell us. PASCO appreciates any customer feedback. Your input helps us evaluate and improve our product.

To Reach PASCO

For Technical Support call us at 1-800-772-8700 (tollfree within the U.S.) or (916) 786-3800.

email: techsupp@PASCO.com Tech support fax: (916) 786-3292

Contacting Technical Support

Before you call the PASCO Technical Support staff it would be helpful to prepare the following information:

• If your problem is computer/software related, note: Title and Revision Date of software. Type of Computer (Make, Model, Speed). Type of external Cables/Peripherals.

• If your problem is with the PASCO apparatus, note: Title and Model number (usually listed on the label). Approximate age of apparatus.

A detailed description of the problem/sequence of events. (In case you can't call PASCO right aw ay, you won't lose valuable data.)

If possible, have the apparatus within reach when calling. This makes descript io ns of i ndi vidual parts much easier.

• If your problem relat es to t he ins truct ion manu al, not e:

Part number and Revision (li sted by month and year on the front cover).

Have the manual at hand to discuss your questions.

PASCO ME-8950A User Manual

Specifications and Main Features

Frequently Asked Questions

User Manual