JBL SOUND SYSTEM DESIGN User Manual

Sound System Design Reference Manual

Table of Contents

Preface ............................................................................................................................................. i

Chapter 1: Wave Propagation........................................................................................................ 1-1

Wavelength, Frequency, and Speed of Sound ................................................................................. 1-1

Combining Sine Waves .................................................................................................................... 1-2

Combining Delayed Sine Waves ...................................................................................................... 1-3

Diffraction of Sound .......................................................................................................................... 1-5

Effects of Temperature Gradients on Sound Propagation ................................................................ 1-6

Effects of Wind Velocity and Gradients on Sound Propagation........................................................ 1-6

Effect of Humidity on Sound Propagation......................................................................................... 1-7

Chapter 2: The Decibel................................................................................................................... 2-1

Introduction....................................................................................................................................... 2-1

Power Relationships......................................................................................................................... 2-1

Voltage, Current, and Pressure Relationships.................................................................................. 2-2

Sound Pressure and Loudness Contours......................................................................................... 2-4

Inverse Square Relationships........................................................................................................... 2-6

Adding Power Levels in dB............................................................................................................... 2-7

Reference Levels.............................................................................................................................. 2-7

Peak, Average, and RMS Signal Values........................................................................................... 2-8

Chapter 3: Directivity and Angular Coverage of Loudspeakers ................................................ 3-1

Introduction....................................................................................................................................... 3-1

Some Fundamentals ........................................................................................................................ 3-1

A Comparison of Polar Plots, Beamwidth Plots, Directivity Plots, and Isobars ................................ 3-3

Directivity of Circular Radiators ........................................................................................................ 3-4

The Importance of Flat Power Response ......................................................................................... 3-6

Measurement of Directional Characteristics..................................................................................... 3-7

Using Directivity Information............................................................................................................. 3-8

Directional Characteristics of Combined Radiators .......................................................................... 3-8

Chapter 4: An Outdoor Sound Reinforcement System............................................................... 4-1

Introduction....................................................................................................................................... 4-1

The Concept of Acoustical Gain ....................................................................................................... 4-2

The Influence of Directional Microphones and Loudspeakers on System Maximum Gain .............. 4-3

How Much Gain is Needed?............................................................................................................. 4-4

Conclusion........................................................................................................................................ 4-5

Chapter 5: Fundamentals of Room Acoustics............................................................................. 5-1

Introduction....................................................................................................................................... 5-1

Absorption and Reflection of Sound ................................................................................................. 5-1

The Growth and Decay of a Sound Field in a Room ........................................................................ 5-5

Reverberation and Reverberation Time............................................................................................ 5-7

Direct and Reverberant Sound Fields .............................................................................................. 5-12

Critical Distance................................................................................................................................ 5-14

The Room Constant ......................................................................................................................... 5-15

Statistical Models and the Real World.............................................................................................. 5-20

Sound System Design Reference Manual

Table of Contents (cont.)

Chapter 6: Behavior of Sound Systems Indoors ......................................................................... 6-1

Introduction....................................................................................................................................... 6-1

Acoustical Feedback and Potential System Gain............................................................................. 6-2

Sound Field Calculations for a Small Room ..................................................................................... 6-2

Calculations for a Medium-Size Room ............................................................................................. 6-5

Calculations for a Distributed Loudspeaker System......................................................................... 6-8

System Gain vs. Frequency Response ............................................................................................ 6-9

The Indoor Gain Equation ................................................................................................................ 6-9

Measuring Sound System Gain........................................................................................................ 6-10

General Requirements for Speech Intelligibility................................................................................ 6-11

The Role of Time Delay in Sound Reinforcement ............................................................................ 6-16

System Equalization and Power Response of Loudspeakers .......................................................... 6-17

System Design Overview ................................................................................................................. 6-19

Chapter 7: System Architecture and Layout................................................................................ 7-1

Introduction....................................................................................................................................... 7-1

Typical Signal Flow Diagram ............................................................................................................ 7-1

Amplifier and Loudspeaker Power Ratings ...................................................................................... 7-5

Wire Gauges and Line Losses ......................................................................................................... 7-5

Constant Voltage Distribution Systems (70-volt lines)...................................................................... 7-6

Low Frequency Augmentation—Subwoofers ................................................................................... 7-6

Case Study A: A Speech and Music System for a Large Evangelical Church.................................. 7-9

Case Study B: A Distributed Sound Reinforcement System for a Large Liturgical Church .............. 7-12

Case Study C: Specifications for a Distributed Sound System Comprising a Ballroom,

Small Meeting Space, and Social/Bar Area ............................................................................... 7-16

Bibliography

Sound System Design Reference Manual

Preface to the 1999 Edition:

This third edition of JBL Professional’s Sound System Design Reference Manual is presented in a new graphic format that makes for easier reading and study. Like its predecessors, it presents in virtually their original 1977 form George Augspurger’s intuitive and illuminating explanations of sound and sound system behavior in enclosed spaces. The section on systems and case studies has been expanded, and references to JBL components have been updated.

The fundamentals of acoustics and sound system design do not change, but system implementation improves in its effectiveness with ongoing developments in signal processing, transducer refinement, and front-end flexibility in signal routing and control.

As stated in the Preface to the 1986 edition: The technical competence of professional dealers and sound contractors is much higher today than it was when the Sound Workshop manual was originally introduced. It is JBL’s feeling that the serious contractor or professional dealer of today is ready to move away from simply plugging numbers into equations. Instead, the designer is eager to learn what the equations really mean, and is intent on learning how loudspeakers and rooms interact, however complex that may be. It is for the student with such an outlook that this manual is intended.

John Eargle

January 1999

Sound System Design Reference Manual

Chapter 1: Wave Propagation

Sound System Design Reference Manual

Wavelength, Frequency, and Speed of Sound

Sound waves travel approximately 344 m/sec (1130 ft/sec) in air. There is a relatively small velocity dependence on temperature, and under normal indoor conditions we can ignore it. Audible sound covers the frequency range from about 20 Hz to 20 kHz. The wavelength of sound of a given frequency is the distance between successive repetitions of the waveform as the sound travels through air. It is given by the following equation:

wavelength = speed/frequency

or, using the common abbreviations of c for speed

for frequency, and λ for wavelength:

λ = c/f

Period

(T) is defined as the time required for

one cycle of the waveform. T = 1/f.

For f = 1 kHz, T = 1/1000, or 0.001 sec, and

λ = 344/1000, or .344 m (1.13 ft.)

The lowest audible sounds have wavelengths on the order of 10 m (30 ft), and the highest sounds have wavelengths as short as 20 mm (0.8 in). The range is quite large, and, as we will see, it has great bearing on the behavior of sound.

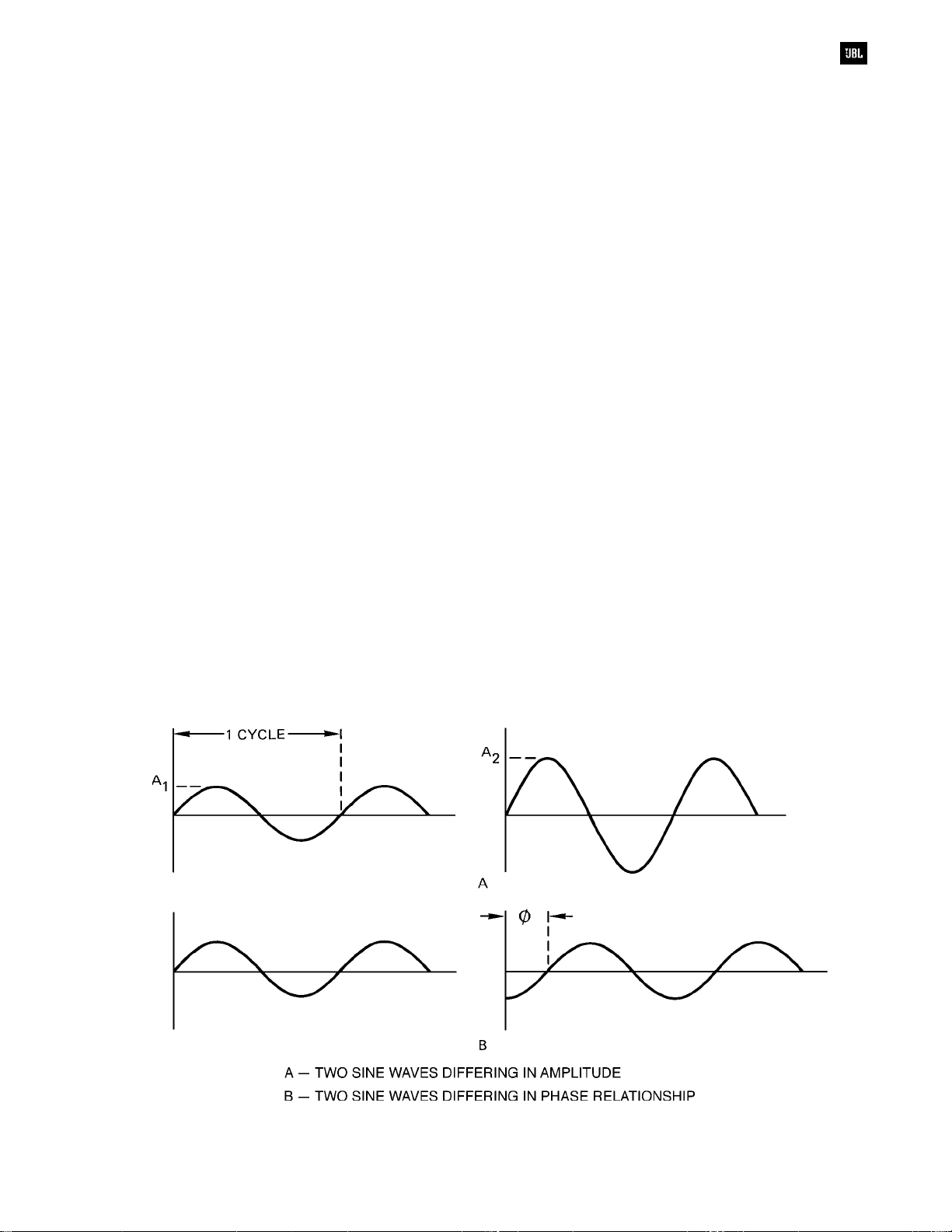
The waves we have been discussing are of course speech and music signals. Figure 1-1 shows some of the basic aspects of sine waves. Note that waves of the same frequency can differ in both amplitude and in phase angle. The amplitude and phase angle relationships between sine waves determine how they combine, either acoustically or electrically.

sine waves

, those basic building blocks of all

Figure 1-1. Properties of sine waves

1-1

Sound System Design Reference Manual

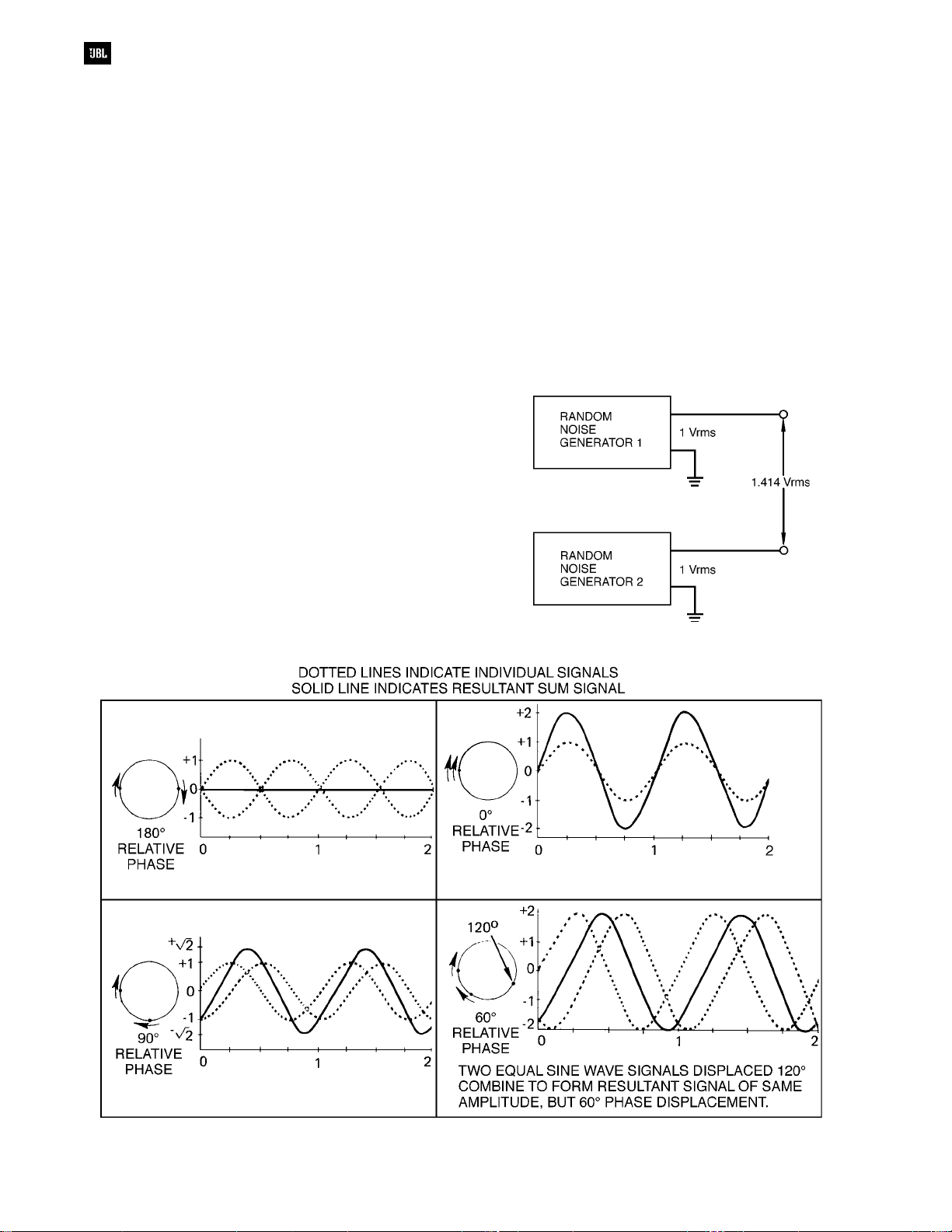
Combining Sine Waves

Referring to Figure 1-2, if two or more sine wave signals having the same frequency and amplitude are added, we find that the resulting signal also has the same frequency and that its amplitude depends upon the phase relationship of the original signals. If there is a phase difference of 120°, the resultant has exactly the same amplitude as either of the original signals. If they are combined in phase, the resulting signal has twice the amplitude of either original. For phase differences between l20° and 240°, the resultant signal always has an amplitude less than that of either of the original signals. If the two signals are exactly 180° out of phase, there will be total cancellation.

In electrical circuits it is difficult to maintain identical phase relationships between all of the sine components of more complex signals, except for the special cases where the signals are combined with a 0° or 180° phase relationship. Circuits which maintain some specific phase relationship (45°, for example) over a wide range of frequencies are fairly complex. Such wide range, all-pass phase-shifting networks are used in acoustical signal processing.

When dealing with complex signals such as music or speech, one must understand the concept of

coherence

through a high quality amplifier. Apart from very small amounts of distortion, the output signal is an exact

. Suppose we feed an electrical signal

replica of the input signal, except for its amplitude. The two signals, although not identical, are said to be highly coherent. If the signal is passed through a poor amplifier, we can expect substantial differences between input and output, and coherence will not be as great. If we compare totally different signals, any similarities occur purely at random, and the two are said to be non-coherent.

When two non-coherent signals are added, the

rms

(root mean square) value of the resulting signal can be calculated by adding the relative powers of the two signals rather than their voltages. For example, if we combine the outputs of two separate noise generators, each producing an rms output of 1 volt, the resulting signal measures 1.414 volts rms, as shown in Figure 1-3.

Figure 1-3. Combining two random noise generators

1-2

Figure 1-2. Vector addition of two sine waves

Sound System Design Reference Manual

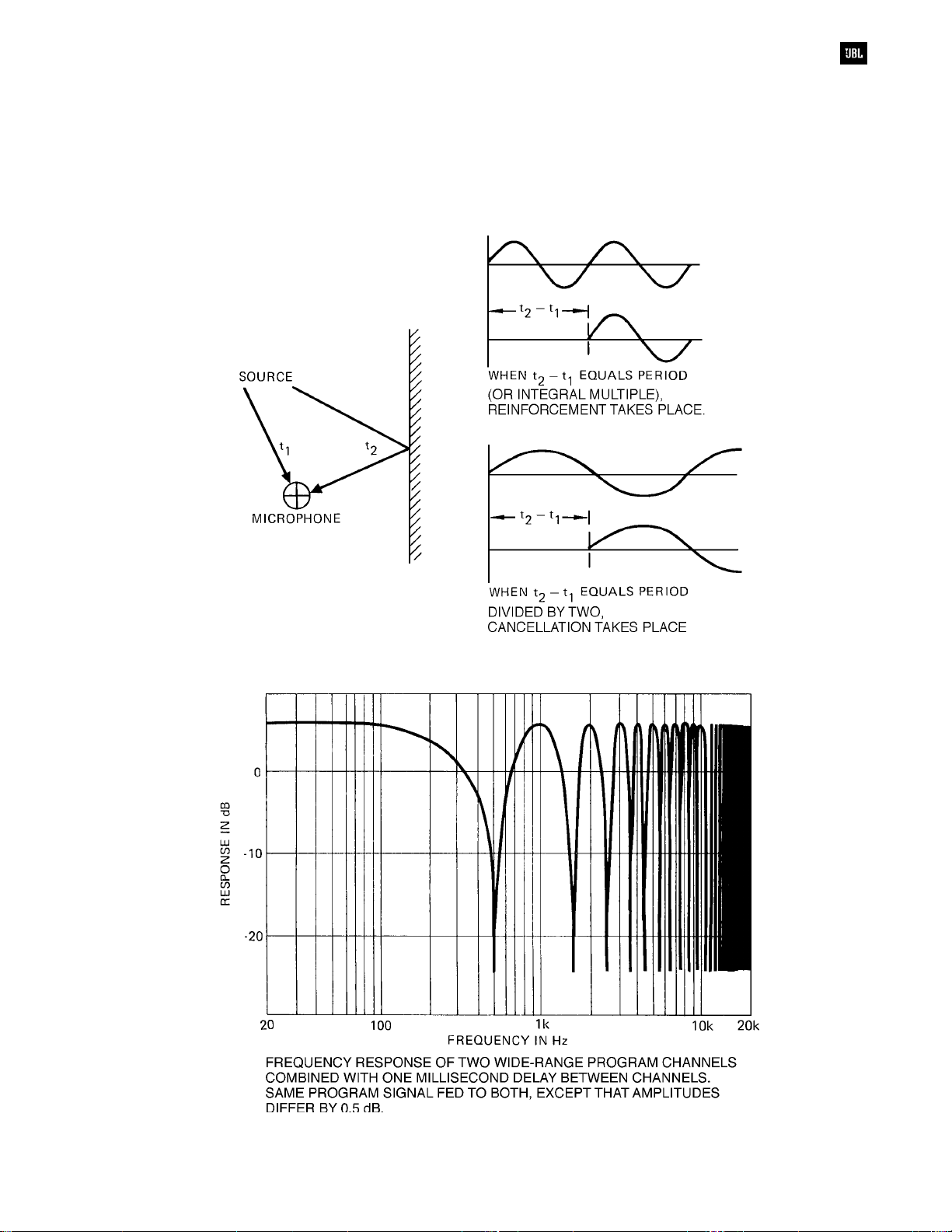
Combining Delayed Sine Waves

If two coherent wide-range signals are combined with a specified time difference between them rather than a fixed phase relationship, some frequencies will add and others will cancel. Once the delayed signal arrives and combines with the original signal, the result is a form of “comb filter,” which

alters the frequency response of the signal, as shown in Figure 1-4. Delay can be achieved electrically through the use of all-pass delay networks or digital processing. In dealing with acoustical signals in air, there is simply no way to avoid delay effects, since the speed of sound is relatively slow.

Figure 1-4A. Combining delayed signals

Figure 1-4B. Combining of coherent signals with constant time delay

1-3

Sound System Design Reference Manual

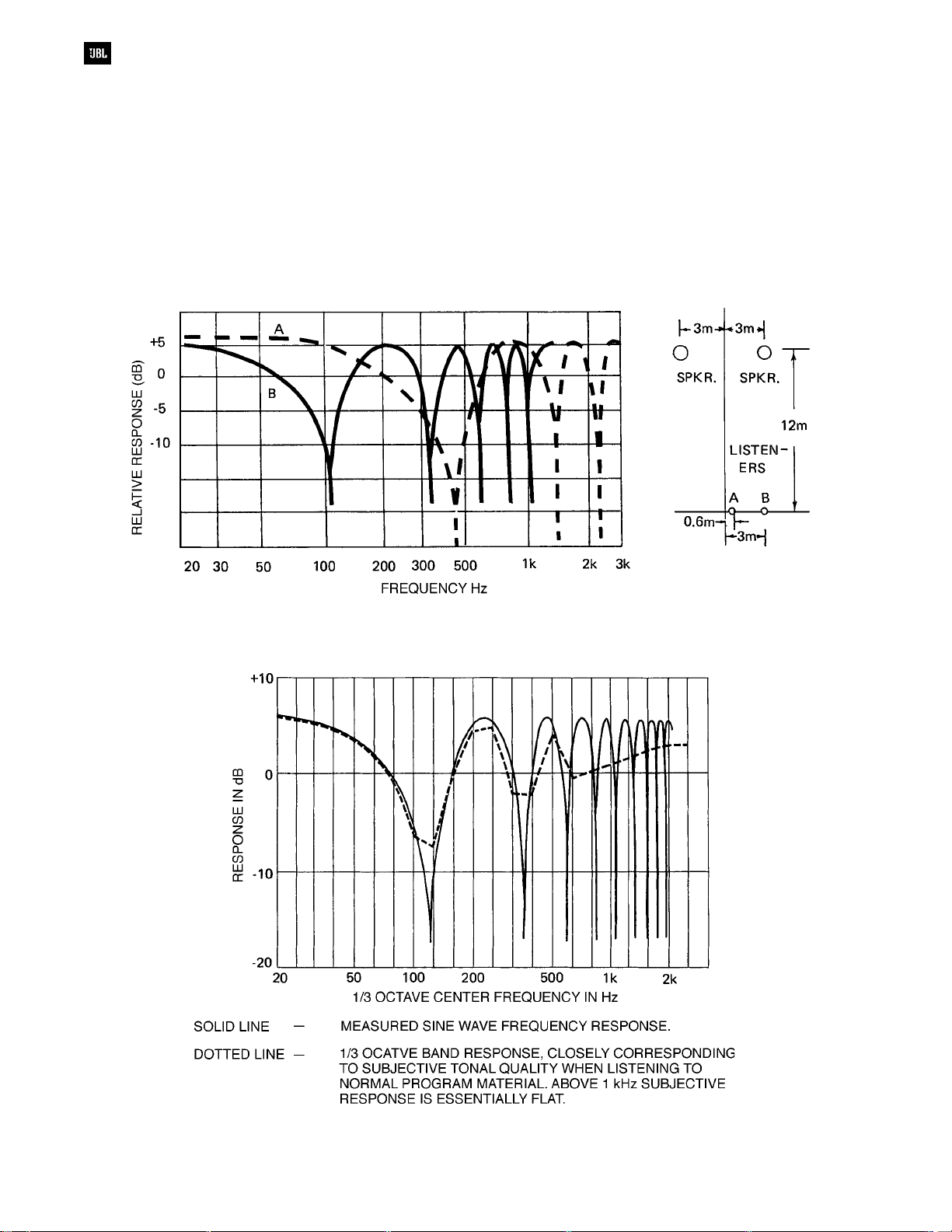
A typical example of combining delayed coherent signals is shown in Figure 1-5. Consider the familiar outdoor PA system in which a single microphone is amplified by a pair of identical separated loudspeakers. Suppose the loudspeakers in question are located at each front corner of the stage, separated by a distance of 6 m (20 ft). At any distance from the stage along the center line, signals from the two loudspeakers arrive simultaneously. But at any other location, the distances of the two loudspeakers are unequal, and sound from one must

arrive slightly later than sound from the other. The illustration shows the dramatically different frequency response resulting from a change in listener position of only 2.4 m (8 ft). Using random noise as a test signal, if you walk from Point B to Point A and proceed across the center line, you will hear a pronounced swishing effect, almost like a siren. The change in sound quality is most pronounced near the center line, because in this area the response peaks and dips are spread farther apart in frequency.

Figure 1-5. Generation of interference effects (comb filter response) by a split array

1-4

Figure 1-6. Audible effect of comb filters shown in Figure 1-5

Sound System Design Reference Manual

Subjectively, the effect of such a comb filter is not particularly noticeable on normal program material as long as several peaks and dips occur within each one-third octave band. See Figure 1-6. Actually, the controlling factor is the “critical bandwidth.” In general, amplitude variations that occur within a critical band will not be noticed as such. Rather, the ear will respond to the signal power contained within that band. For practical work in sound system design and architectural acoustics, we can assume that the critical bandwidth of the human ear is very nearly one-third octave wide.

In houses of worship, the system should be suspended high overhead and centered. In spaces which do not have considerable height, there is a strong temptation to use two loudspeakers, one on either side of the platform, feeding both the same program. We do not recommend this.

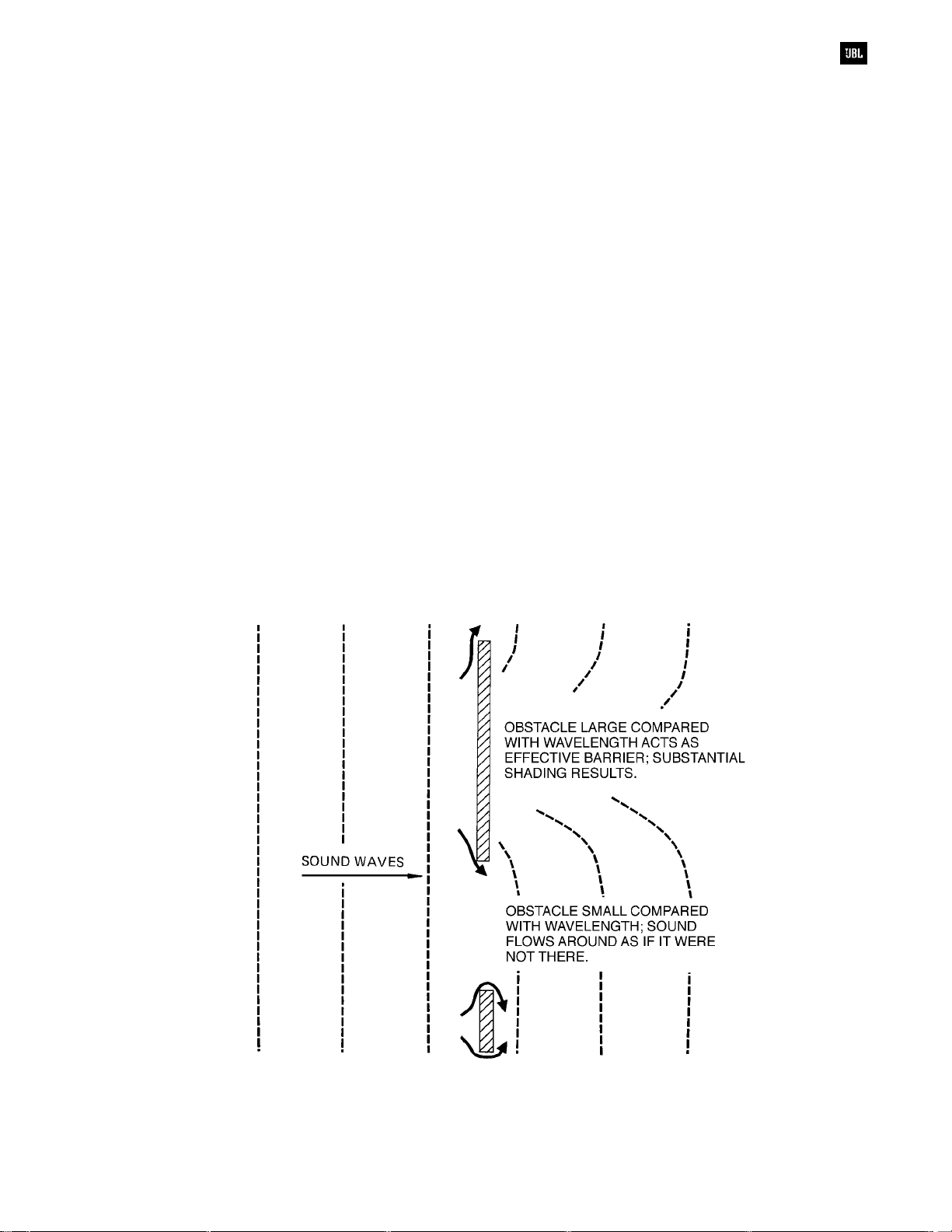
Diffraction of Sound

Diffraction refers to the bending of sound waves as they move around obstacles. When sound strikes a hard, non-porous obstacle, it may be reflected or

diffracted, depending on the size of the obstacle relative to the wavelength. If the obstacle is large compared to the wavelength, it acts as an effective barrier, reflecting most of the sound and casting a substantial “shadow” behind the object. On the other hand, if it is small compared with the wavelength, sound simply bends around it as if it were not there. This is shown in Figure 1-7.

An interesting example of sound diffraction occurs when hard, perforated material is placed in the path of sound waves. So far as sound is concerned, such material does not consist of a solid barrier interrupted by perforations, but rather as an open area obstructed by a number of small individual objects. At frequencies whose wavelengths are small compared with the spacing between perforations, most of the sound is reflected. At these frequencies, the percentage of sound traveling through the openings is essentially proportional to the ratio between open and closed areas.

At lower frequencies (those whose wavelengths are large compared with the spacing between perforations), most of the sound passes through the openings, even though they may account only for 20 or 30 percent of the total area.

Figure 1-7. Diffraction of sound around obstacles

1-5

Sound System Design Reference Manual

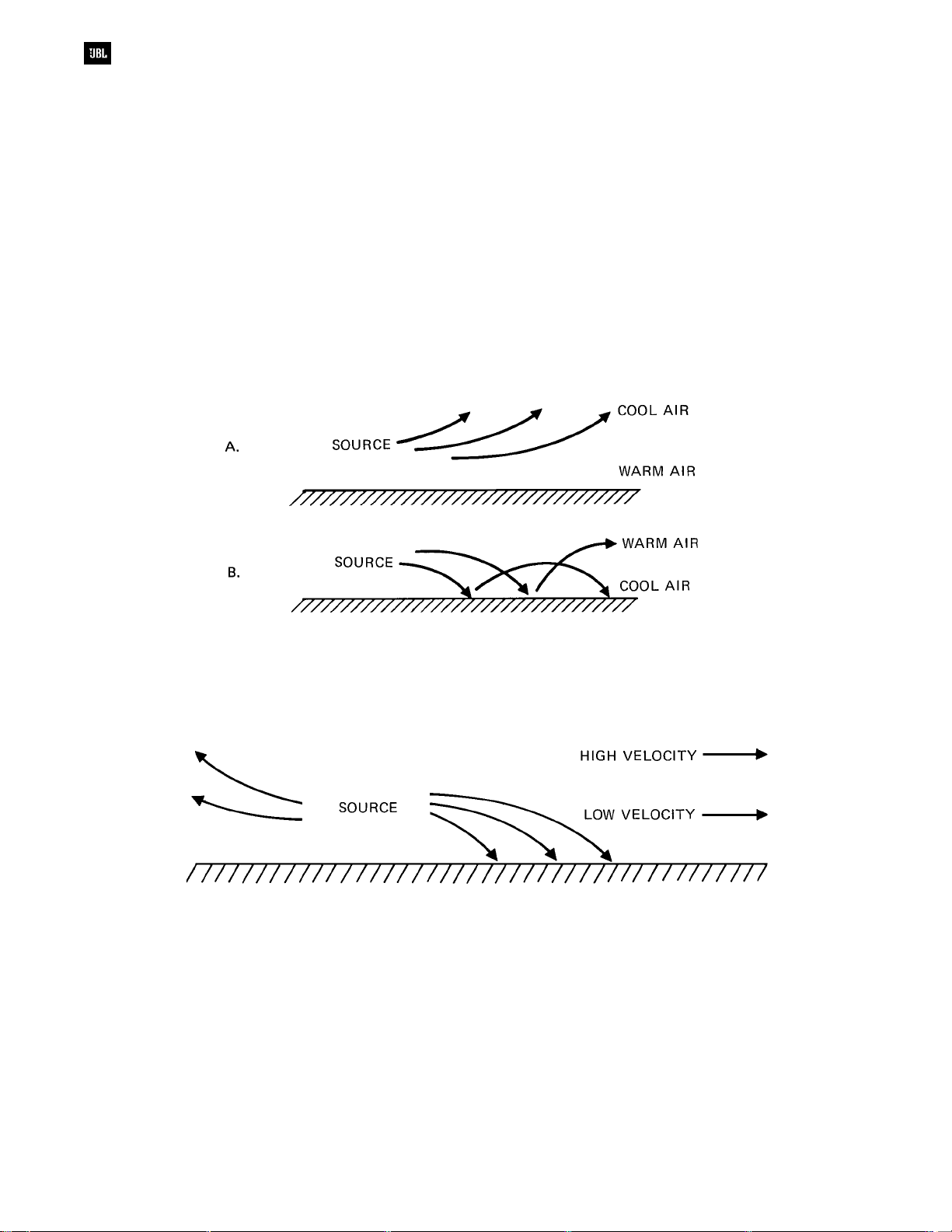
Effects of Temperature Gradients on Sound Propagation

If sound is propagated over large distances out of doors, its behavior may seem erratic. Differences (gradients) in temperature above ground level will affect propagation as shown in Figure 1-8. Refraction of sound refers to its changing direction as its velocity increases slightly with elevated temperatures. At Figure 1-8A, we observe a situation which often occurs at nightfall, when the ground is still warm. The case shown at B may occur in the morning, and its “skipping” characteristic may give rise to hot spots and dead spots in the listening area.

Effects of Wind Velocity and Gradients on Sound Propagation

Figure 1-9 shows the effect wind velocity gradients on sound propagation. The actual velocity of sound in this case is the velocity of sound in still air plus the velocity of the wind itself. Figure 1-10 shows the effect of a cross breeze on the apparent direction of a sound source.

The effects shown in these two figures may be evident at large rock concerts, where the distances covered may be in the 200 - 300 m (600 - 900 ft) range.

Figure 1-8. Effects of temperature gradients on sound propagation

Figure 1-9. Effect of wind velocity gradients on sound propagation

1-6

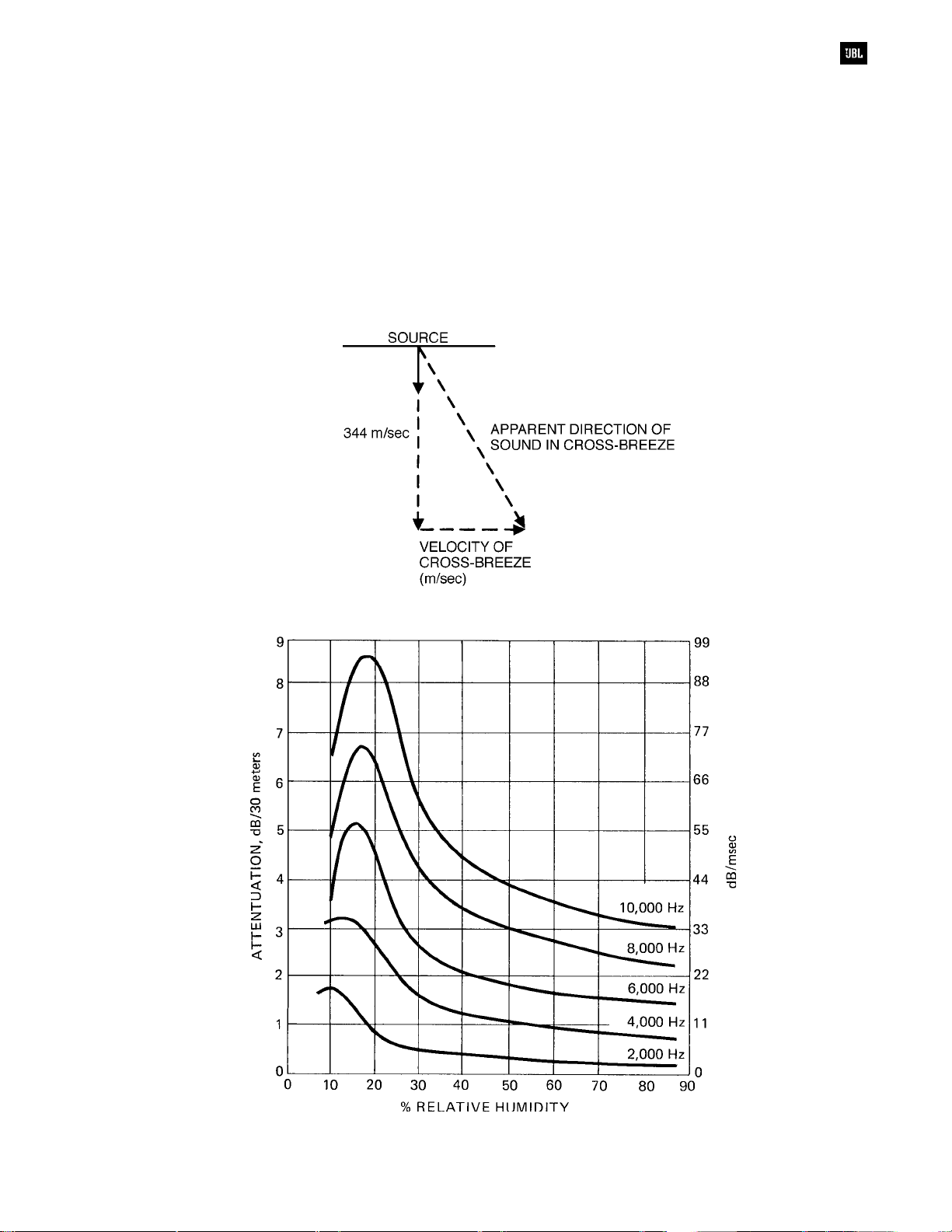
Effects of Humidity on Sound Propagation

Contrary to what most people believe, there is more sound attenuation in dry air than in damp air. The effect is a complex one, and it is shown in Figure 1-11. Note that the effect is significant only at frequencies above 2 kHz. This means that high frequencies will be attenuated more with distance than low frequencies will be, and that the attenuation will be greatest when the relative humidity is 20 percent or less.

Sound System Design Reference Manual

Figure 1-10. Effect of cross breeze on apparent direction of sound

Figure 1-11. Absorption of sound in air vs. relative humidity

1-7

Sound System Design Reference Manual

Chapter 2: The Decibel

Sound System Design Reference Manual

Introduction

In all phases of audio technology the decibel is used to express signal levels and level differences in sound pressure, power, voltage, and current. The reason the decibel is such a useful measure is that it enables us to use a comparatively small range of numbers to express large and often unwieldy quantities. The decibel also makes sense from a psychoacoustical point of view in that it relates directly to the effect of most sensory stimuli.

Power Relationships

Fundamentally, the common logarithm of a power ratio:

For convenience, we use the one-tenth bel. Thus:

decibel = 10 log (P1/P0)

The following tabulation illustrates the usefulness of the concept. Letting P0 = 1 watt:

bel

is defined as the

bel = log (P1/P0)

decibel

, which is simply

signal. The convenience of using decibels is apparent; each of these power ratios can be expressed by the same level, 10 dB. Any 10 dB level difference, regardless of the actual powers involved, will represent a 2-to-1 difference in subjective loudness.

We will now expand our power decibel table:

P1 (watts) Level in dB

1.25 1

1.60 2 23

2.5 4

3.15 5 46 57

6.3 8 89

10 10

This table is worth memorizing. Knowing it, you can almost immediately do mental calculations, arriving at power levels in dB above, or below, one watt.

P1 (watts) Level in dB

10 10

100 20

1000 30 10,000 40 20,000 43

Note that a 20,000-to-1 range in power can be expressed in a much more manageable way by referring to the powers as levels in dB above one watt. Psychoacoustically, a ten-times increase in power results in a level which most people judge to be “twice as loud.” Thus, a 100-watt acoustical signal would be twice as loud as a 10-watt signal, and a 10-watt signal would be twice as loud as a 1-watt

Here are some examples:

1. What power level is represented by 80 watts? First, locate 8 watts in the left column and note that the corresponding level is 9 dB. Then, note that 80 is Thus:

2. What power level is represented by 1 milliwatt? 0.1 watt represents a level of minus 10 dB, and 0.01 represents a level 10 dB lower. Finally,

0.001 represents an additional level decrease of 10 dB. Thus:

10 times

–10 – 10 – 10 =

8, giving another 10 dB.

9 + 10 =

19 dB

–30 dB

2-1

Sound System Design Reference Manual

3. What power level is represented by 4 milliwatts? As we have seen, the power level of 1 milliwatt is –30 dB. Two milliwatts represents a level increase of 3 dB, and from 2 to 4 milliwatts there is an additional 3 dB level increase. Thus:

–30 + 3 + 3 =

–24 dB

4. What is the level difference between 40 and 100 watts? Note from the table that the level corresponding to 4 watts is 6 dB, and the level corresponding to 10 watts is 10 dB, a difference of 4 dB. Since the level of 40 watts is 10 dB greater than for 4 watts, and the level of 80 watts is 10 dB greater than for 8 watts, we have:

6 – 10 + 10 – 10 =

–4 dB

We have done this last example the long way, just to show the rigorous approach. However, we could simply have stopped with our first observation, noting that the dB level difference between 4 and 10 watts, .4 and 1 watt, or 400 and 1000 watts will always be the same, 4 dB, because they all represent the same power ratio.

The level difference in dB can be converted back to a power ratio by means of the following equation:

Power ratio = 10

dB/10

For example, find the power ratio of a level difference of 13 dB:

Power ratio = 10

13/10

= 10

1.3

= 20

Voltage, Current, and Pressure Relationships

The decibel fundamentally relates to power ratios, and we can use voltage, current, and pressure ratios as they relate to power. Electrical power can be represented as:

P = EI

P = I2Z

P = E2/Z

Because power is proportional to the square of the voltage, the effect of

quadruple

the power:

As an example, let E = 1 volt and Z = 1 ohm. Then, P = E2/Z = 1 watt. Now, let E = 2 volts; then, P = (2)2/1 = 4 watts.

The same holds true for current, and the following equations must be used to express power levels in dB using voltage and current ratios:

dB level = 10 log

doubling

the voltage is to

(2E)2/Z = 4(E)2/Z





20 log





















 



20 log



, and

















The reader should acquire a reasonable skill in dealing with power ratios expressed as level differences in dB. A good “feel” for decibels is a qualification for any audio engineer or sound contractor. An extended nomograph for converting power ratios to level differences in dB is given in Figure 2-1.

Figure 2-1. Nomograph for determining power ratios directly in dB

2-2

Sound pressure is analogous to voltage, and

levels are given by the equation:





dB level = 20 log









Sound System Design Reference Manual

The normal reference level for voltage, E0, is one volt. For sound pressure, the reference is the extremely low value of 20 x 10

-6

newtons/m2. This reference pressure corresponds roughly to the minimum audible sound pressure for persons with normal hearing. More commonly, we state pressure in

pascals

(Pa), where 1 Pa = 1 newton/m2. As a convenient point of reference, note that an rms pressure of 1 pascal corresponds to a sound pressure level of 94 dB.

We now present a table useful for determining levels in dB for ratios given in voltage, current, or sound pressure:

Voltage, Current or

Pressure Ratios Level in dB

1.25 2

1.60 4 26

2.5 8

3.15 10 412 514

6.3 16 818

10 20

This table may be used exactly the same way as the previous one. Remember, however, that the reference impedance, whether electrical or acoustical, must remain fixed when using these ratios to determine level differences in dB. A few examples are given:

If we simply compare input and output voltages,

we still get 0 dB as our answer. The

voltage gain

is in fact unity, or one. Recalling that decibels refer primarily to power ratios, we must take the differing input and output impedances into account and actually compute the input and output powers.

Input power =

Output power =

T 10 log

  

600



= 10 log 40 = 16 dBhus,

 

600

watt

Fortunately, such calculations as the above are not often made. In audio transmission, we keep track of operating levels primarily through voltage level calculations in which the voltage reference value of

0.775 volts has an assigned level of 0 dBu. The value of 0.775 volts is that which is applied to a 600ohm load to produce a power of 1 milliwatt (mW). A power level of 0 dBm corresponds to 1 mW. Stated somewhat differently, level values in dBu and dBm will have the same numerical value only when the load impedance under consideration is 600 ohms.

The level difference in dB can be converted back to a voltage, current, or pressure ratio by means of the following equation:

Ratio = 10

dB/20

1. Find the level difference in dB between 2

volts and 10 volts. Directly from the table we observe

20 – 6 =

14 dB

2. Find the level difference between 1 volt and 100 volts. A 10-to-1 ratio corresponds to a level difference of 20 dB. Since 1-to-100 represents the product of

two

such ratios (1-to-10 and 10-to-100),

the answer is

20 + 20 = 40 dB.

3. The signal input to an amplifier is 1 volt, and the input impedance is 600 ohms. The output is also 1 volt, and the load impedance is 15 ohms. What is the gain of the amplifier in dB? Watch this one carefully!

For example, find the voltage ratio

corresponding to a level difference of 66 dB:

voltage ratio = 10

66/20

= 10

3.3

= 2000.

2-3

Sound System Design Reference Manual

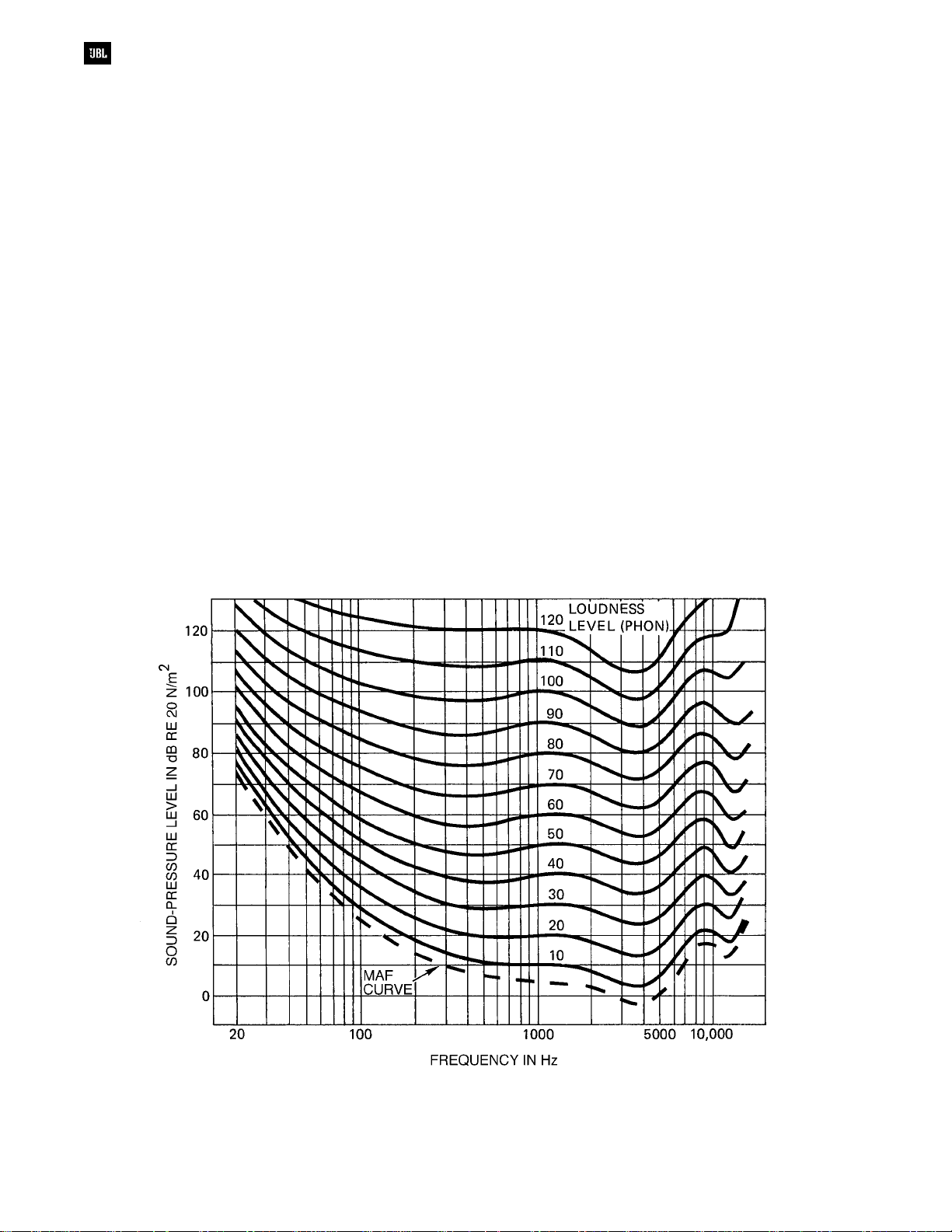
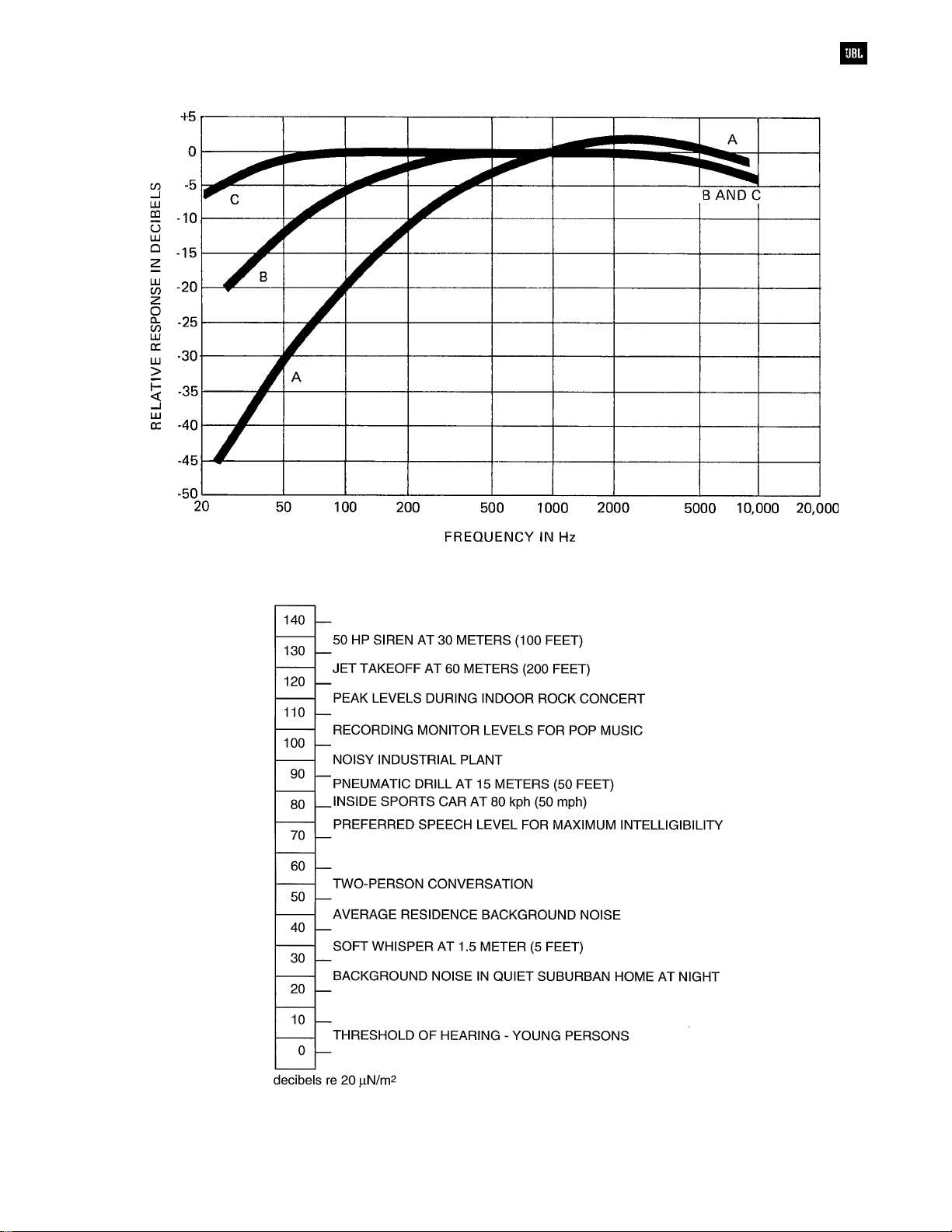
Sound Pressure and Loudness Contours

We will see the term dB-SPL time and again in professional sound work. It refers to sound pressure levels in dB above the reference of 20 x 10-6 N/m2. We commonly use a measure SPL. Loudness and sound pressure obviously bear a relation to each other, but they are not the same thing. Loudness is a subjective sensation which differs from the measured level in certain important aspects. To specify loudness in scientific terms, a different unit is used, the Phons and decibels share the same numerical value only at 1000 Hz. At other frequencies, the phon scale deviates more or less from the sound level scale, depending on the particular frequency and the sound pressures; Figure 2-2 shows the relationship between phons and decibels, and illustrates the well-known Robinson-Dadson equal loudness contours. These show that, in general, the ear becomes less sensitive to sounds at low frequencies as the level is reduced.

sound level meter

(SLM) to

phon

When measuring sound pressure levels, weighted response may be employed to more closely approximate the response of the ear. Working with sound systems, the most useful scales on the sound level meter will be the A-weighting scale and the linear scale, shown in Figure 2-3. Inexpensive sound level meters, which cannot provide linear response over the full range of human hearing, often have no linear scale but offer a C-weighting scale instead. As can be seen from the illustration, the C-scale rolls off somewhat at the frequency extremes. Precision sound level meters normally offer in addition to linear response. Measurements made with a sound level meter are normally identified by noting the weighting factor, such as: dB(A) or dB(lin).

Typical levels of familiar sounds, as shown in Figure 2-4, help us to estimate dB(A) ratings when a sound level meter is not available. For example, normal conversational level in quiet surrounds is about 60 dB(A). Most people find levels higher than 100 dB(A) uncomfortable, depending on the length of exposure. Levels much above 120 dB(A) are definitely dangerous to hearing and are perceived as painful by all except dedicated rock music fans.

A, B,

and C scales

2-4

Figure 2-2. Free-field equal loudness contours

Sound System Design Reference Manual

Figure 2-3. Frequency responses for SLM weighting characteristics

Figure 2-4. Typical A-weighted sound levels

2-5

Sound System Design Reference Manual

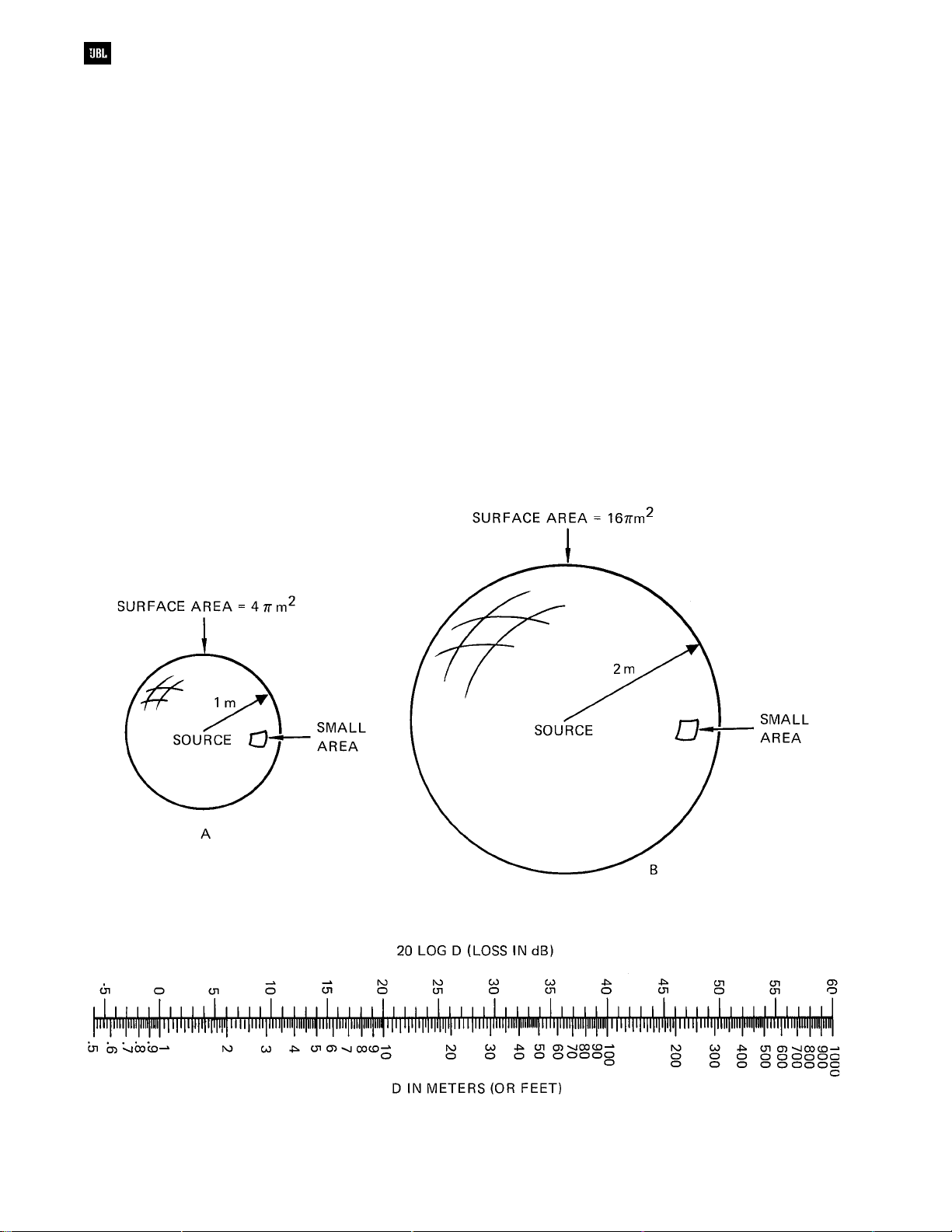
Inverse Square Relationships

When we move away from a

sound out of doors, or in a

free field

SPL falls off almost exactly 6 dB for each doubling of distance away from the source. The reason for this is shown in Figure 2-5. At A there is a sphere of radius one meter surrounding a point source of sound P representing the SPL at the surface of the sphere. At B, we observe a sphere of twice the radius, 2 meters. The area of the larger sphere is smaller one, and this means that the acoustical power passing through a small area on the larger sphere will be

one-fourth

that passing through the same small area on the smaller sphere. The 4-to-1 power ratio represents a level difference of 6 dB, and the corresponding sound pressure ratio will be 2-to-1.

A convenient nomograph for determining inverse square losses is given in Figure 2-6. Inverse square calculations depend on a theoretical point source in a free field. In the real world, we can

point source

, we observe that

four times

that of the

closely approach an ideal free field, but we still must take into account the factors of finite source size and non-uniform radiation patterns.

Consider a horn-type loudspeaker having a rated sensitivity of 100 dB, 1 watt at 1 meter. One meter from where? Do we measure from the mouth of the horn, the throat of the horn, the driver diaphragm, or some indeterminate point in between? Even if the measurement position is specified, the information may be useless. Sound from a finite source does not behave according to inverse square law at distances close to that source. Measurements made in the “near field” cannot be used to estimate performance at greater distances. This being so, one may well wonder why loudspeakers are rated at a distance of only 1 meter.

The method of rating and the accepted methods of measuring the devices are two different things. The manufacturer is expected to make a number of measurements at various distances under free field conditions. From these he can establish

2-6

Figure 2-5. Inverse square relationships

Figure 2-6. Nomograph for determining inverse square losses

Sound System Design Reference Manual

that the measuring microphone is far enough away from the device to be in its calculate the imaginary point from which sound waves diverge, according to inverse square law. This point is called the accurate field measurements have been made, the results are converted to an equivalent one meter rating. The rated sensitivity at one meter is that SPL which would be measured if the inverse square relationship were actually maintained that close to the device.

Let us work a few exercises using the

nomograph of Figure 2-6:

1. A JBL model 2360 horn with a 2446 HF driver produces an output of 113 dB, 1 watt at 1 meter. What SPL will be produced by 1 watt at 30 meters? We can solve this by inspection of the nomograph. Simply read the difference in dB between 1 meter and 30 meters: 29.5 dB. Now, subtracting this from 113 dB:

2. The nominal power rating of the JBL model 2446 driver is 100 watts. What maximum SPL will be produced at a distance of 120 meters in a free field when this driver is mounted on a JBL model 2366 horn?

There are three simple steps in solving this problem. First, determine the inverse square loss from Figure 2-6; it is approximately 42 dB. Next, determine the level difference between one watt and 100 watts. From Figure 2-1 we observe this to be 20 dB. Finally, note that the horn-driver sensitivity is 118 dB, 1 watt at 1 meter. Adding these values:

Calculations such as these are very commonplace in sound reinforcement work, and qualified sound contractors should be able to make them easily.

acoustic center

113 – 29.5 = 83.5 dB

118 – 42 + 20 = 96 dB-SPL

far field

, and he can also

of the device. After

Adding Power Levels in dB

Quite often, a sound contractor will have to add power levels expressed in dB. Let us assume that two sound fields, each 94 dB-SPL, are combined. What is the resulting level? If we simply add the levels numerically, we get 188 dB-SPL, clearly an absurd answer! What we must do in effect is convert the levels back to their actual powers, add them, and then recalculate the level in dB. Where two levels are involved, we can accomplish this easily with the data of Figure 2-7. Let D be the difference in dB between the two levels, and determine the value N corresponding to this difference. Now, add N to the original values.

As an exercise, let us add two sound fields, 90 dB-SPL and 84 dB-SPL. Using Figure 2-7, a D of 6 dB corresponds to an N of about 1 dB. Therefore, the new level will be 91 dB-SPL.

Note that when two levels differ by more than about 10 dB, the resulting summation will be substantially the same as the higher of the two values. The effect of the lower level will be negligible.

higher

of the two

Reference Levels

Although we have discussed some of the common reference levels already, we will list here all of those that a sound contractor is likely to encounter.

In acoustical measurements, measured relative to 20 x 10-6 Pa. An equivalent expression of this is .0002 dynes/cm2.

In broadcast transmission work, power is often expressed relative to 1 milliwatt (.001 watt), and such levels are expressed in

The designation one watt. Thus, 0 dBW = 30 dBm.

In signal transmission diagrams, the designation .775 volts.

dBu

indicates voltage levels referred to

dBm

dBW

refers to levels relative to

SPL

is always

Figure 2-7. Nomograph for adding levels expressed in dB.

Summing sound level output of two sound sources where D is their output difference in dB.

N is added to the higher to derive the total level.

2-7

Sound System Design Reference Manual

In other voltage measurements,

dBV

refers to

levels relative to 1 volt.

Rarely encountered by the sound contractor will be acoustical power levels. These are designated dB-PWL, and the reference power is 10

-12

watts. This is a very small power indeed. It is used in acoustical measurements because such small amounts of power are normally encountered in acoustics.

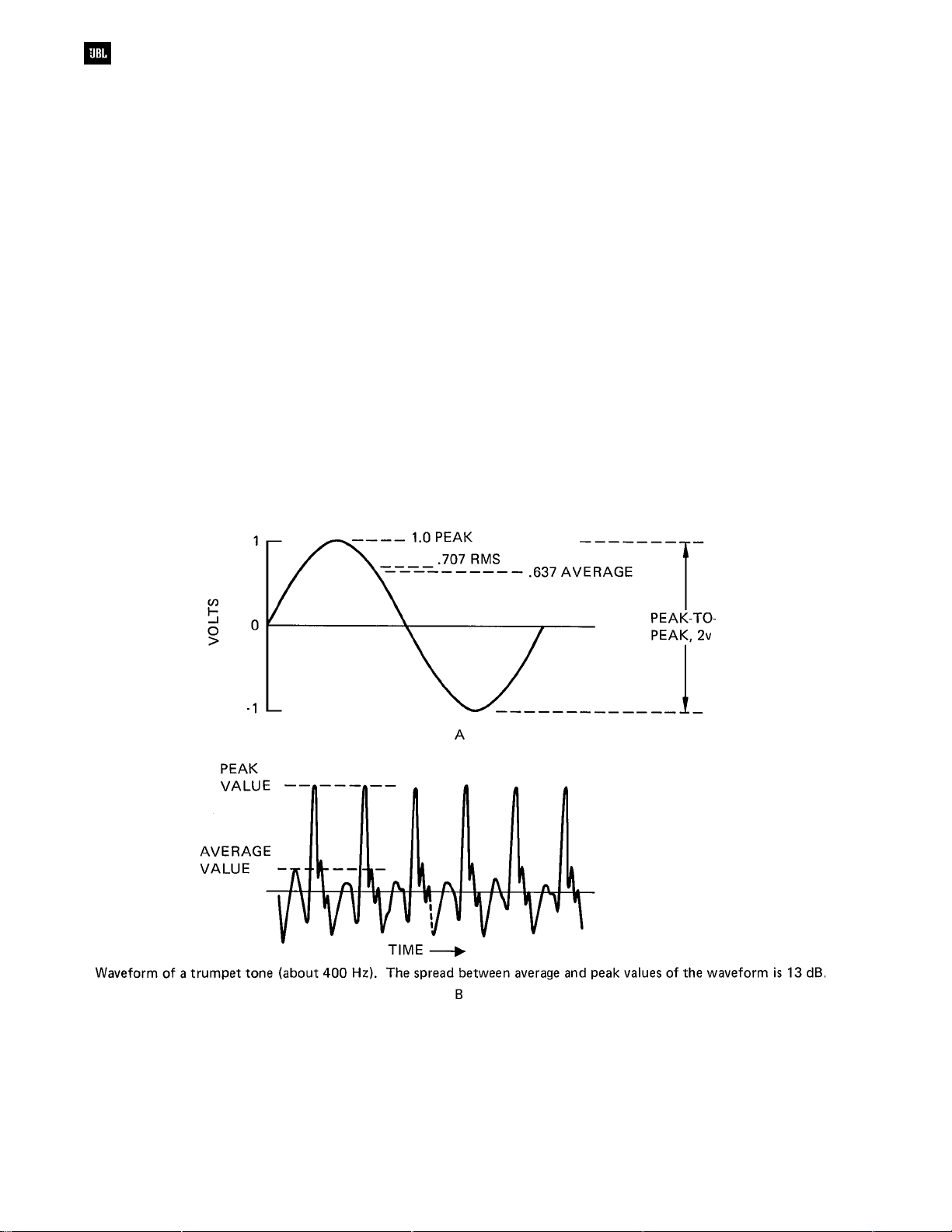
Peak, Average, and

rms

Signal Values

Most measurements of voltage, current, or sound pressure in acoustical engineering work are given as

rms

(root mean square) values of the waveforms. The rms value of a repetitive waveform equals its equivalent DC value in power transmission. Referring to Figure 2-8A for a sine wave with a peak value of one volt, the rms value is .707 volt, a 3 dB difference. The average value of the waveform is .637 volt.

For more complex waveforms, such as are found in speech and music, the peak values will be considerably higher than the average or rms values. The waveform shown at Figure 2-8B is that of a trumpet at about 400 Hz, and the spread between peak and average values is 13 dB.

In this chapter, we have in effect been using rms values of voltage, current, and pressure for all calculations. However, in all audio engineering applications, the time-varying nature of music and speech demands that we consider as well the instantaneous values of waveforms likely to be encountered. The term

headroom

refers to the extra margin in dB designed into a signal transmission system over its normal operating level. The importance of headroom will become more evident as our course develops.

2-8

Figure 2-8. Peak, average, and rms values.

Sinewave (A); complex waveform (B).

Sound System Design Reference Manual

Chapter 3: Directivity and Angular

Coverage of Loudspeakers

Introduction

Proper coverage of the audience area is one of the prime requirements of a sound reinforcement system. What is required of the sound contractor is not only a knowledge of the directional characteristics of various components but also how those components may interact in a multi-component array. Such terms as directivity index (DI), directivity factor (Q), and beamwidth all variously describe the directional properties of transducers with their associated horns and enclosures. Detailed polar data, when available, gives the most information of all. In general, no one has ever complained of having too much directivity information. In the past, most manufacturers have supplied too little; however, things have changed for the better in recent years, largely through data standardization activities on the part of the Audio Engineering Society.

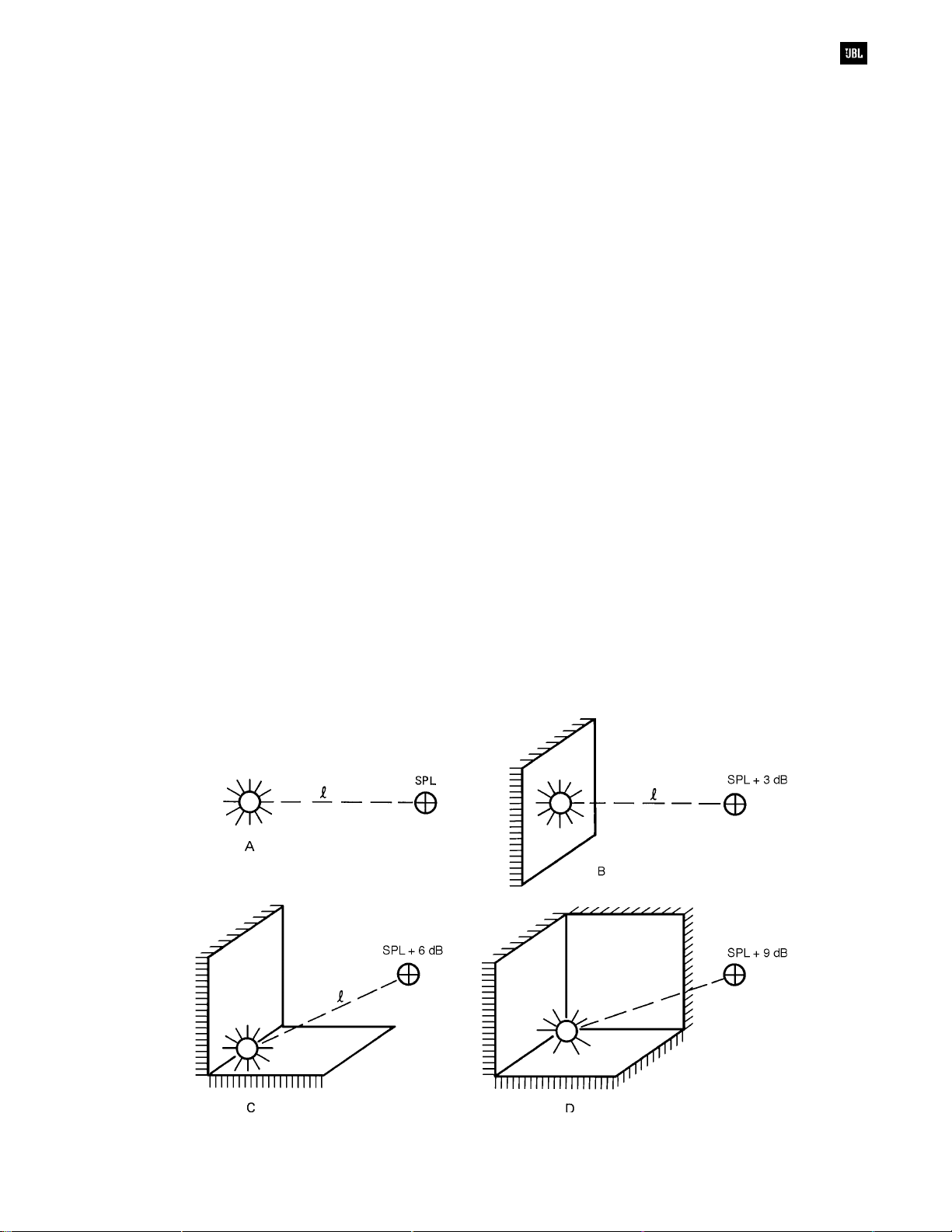
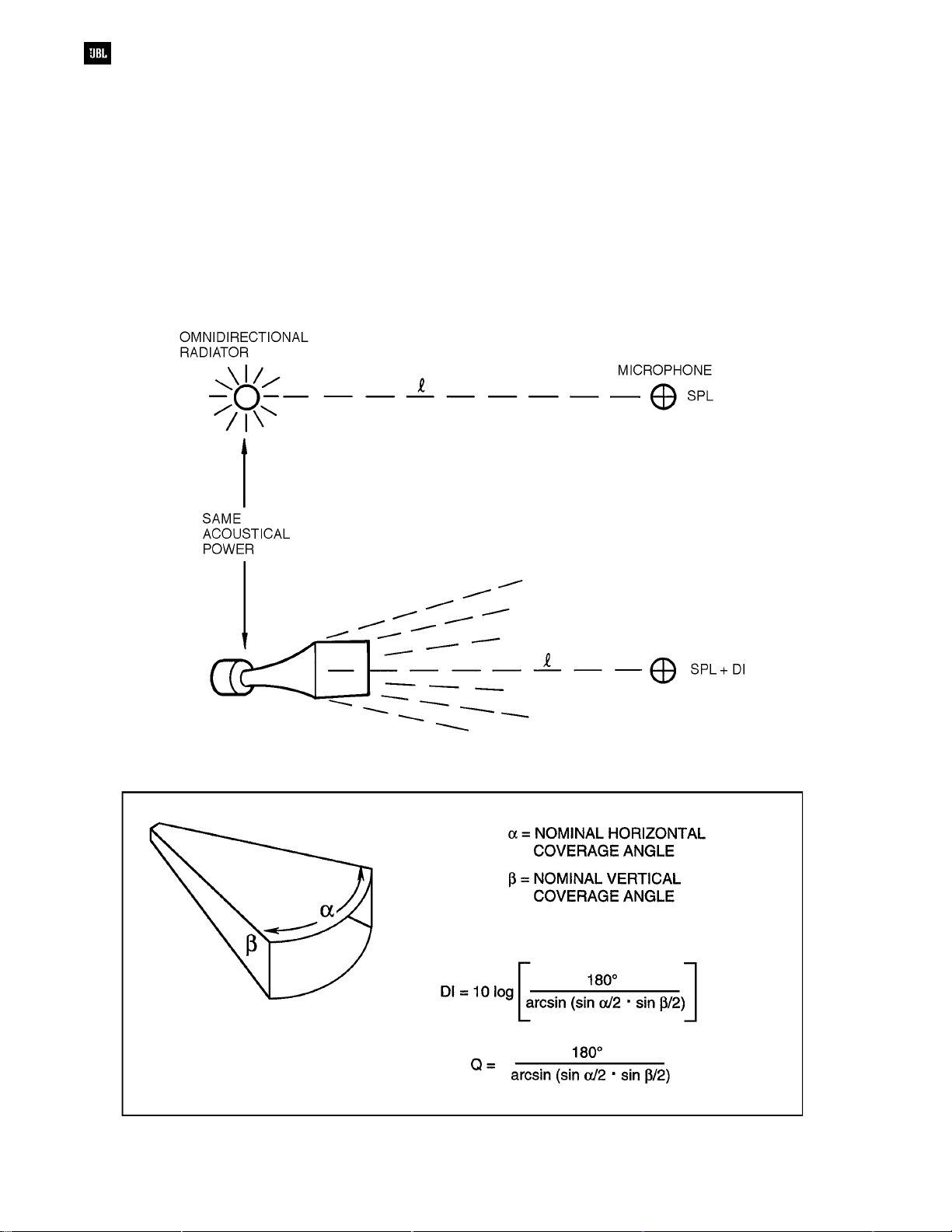
Some Fundamentals

Assume that we have an omnidirectional radiator located in free space and that there is a microphone at some fixed distance from it. This is shown in Figure 3-1A. Let the power radiated from the loudspeaker remain constant, and note the SPL at the microphone. Now, as shown in B, let us place a large reflecting boundary next to the source and again note the SPL at the microphone. At high frequencies (those whose wavelengths are small compared to the size of the reflecting boundary), the increase in SPL will be 3 dB. The power that was radiating into full space is now confined to half space; thus, the doubling of power at the microphone. Moving on to the example at C, we place a dihedral (2-sided) corner next to the source. Power that was confined to half-space now radiates into quarter-space, and the SPL at the microphone

Figure 3-1. Directivity and angular coverage

3-1

Sound System Design Reference Manual

increases another 3 dB. Continuing on at D, we place the sound source in a trihedral (3-sided) corner, and we note an additional 3 dB increase as sound power is radiated into one-eighth-space.

We could continue this exercise further, but our point has already been made. In going from A to D in successive steps, we have increased the

index

3 dB at each step, and we have doubled the

directivity factor

at each step.

directivity

We will now define these terms: Directivity index is the level difference in intensity along a given

axis, and at a given distance, from a sound radiator compared to the intensity that would be produced at the same distance by an omnidirectional point source radiating the same power. Directivity factor is the ratio of the two intensities. Details are shown in Figure 3-2. Directivity index (DI) and directivity factor (Q) are related as follows:

DI = l0 log Q

DI/10

Q = 10

3-2

Figure 3-2. Directivity index and directivity factor

Figure 3-3. Illustration of Molloy’s equation

Sound System Design Reference Manual

The data of Figure 3-1 was generalized by Molloy (7) and is shown in Figure 3-3. Here, note that Dl and Q are related to the solid angular coverage of a hypothetical sound radiator whose horizontal and vertical coverage angles are specified. Such ideal sound radiators do not exist, but it is surprising how closely these equations agree with measured Dl and Q of HF horns that exhibit fairly steep cut-off outside their normal coverage angles.

As an example of this, a JBL model 2360 Bi-Radial horn has a nominal 900-by-400 pattern measured between the 6 dB down points in each plane. If we insert the values of 90° and 40° into Molloy’s equation, we get DI = 11 and Q = 12.8. The published values were calculated by integrating response over 360° in both horizontal and vertical planes, and they are Dl = 10.8 and Q = 12.3. So the estimates are in excellent agreement with the measurements.

For the JBL model 2366 horn, with its nominal 6 dB down coverage angles of 40° and 20°, Molloy’s equation gives Dl = 17.2 and Q = 53. The published values are Dl = 16.5 and Q = 46. Again, the agreement is excellent.

Is there always such good correlation between the 6 dB down horizontal and vertical beamwidth of a horn and its calculated directivity? The answer is no. Only when the response cut-off is sharp beyond the

6 dB beamwidth limits and when there is minimal radiation outside rated beamwidth will the correlation be good. For many types of radiators, especially those operating at wavelengths large compared with their physical dimensions, Molloy’s equation will not hold.

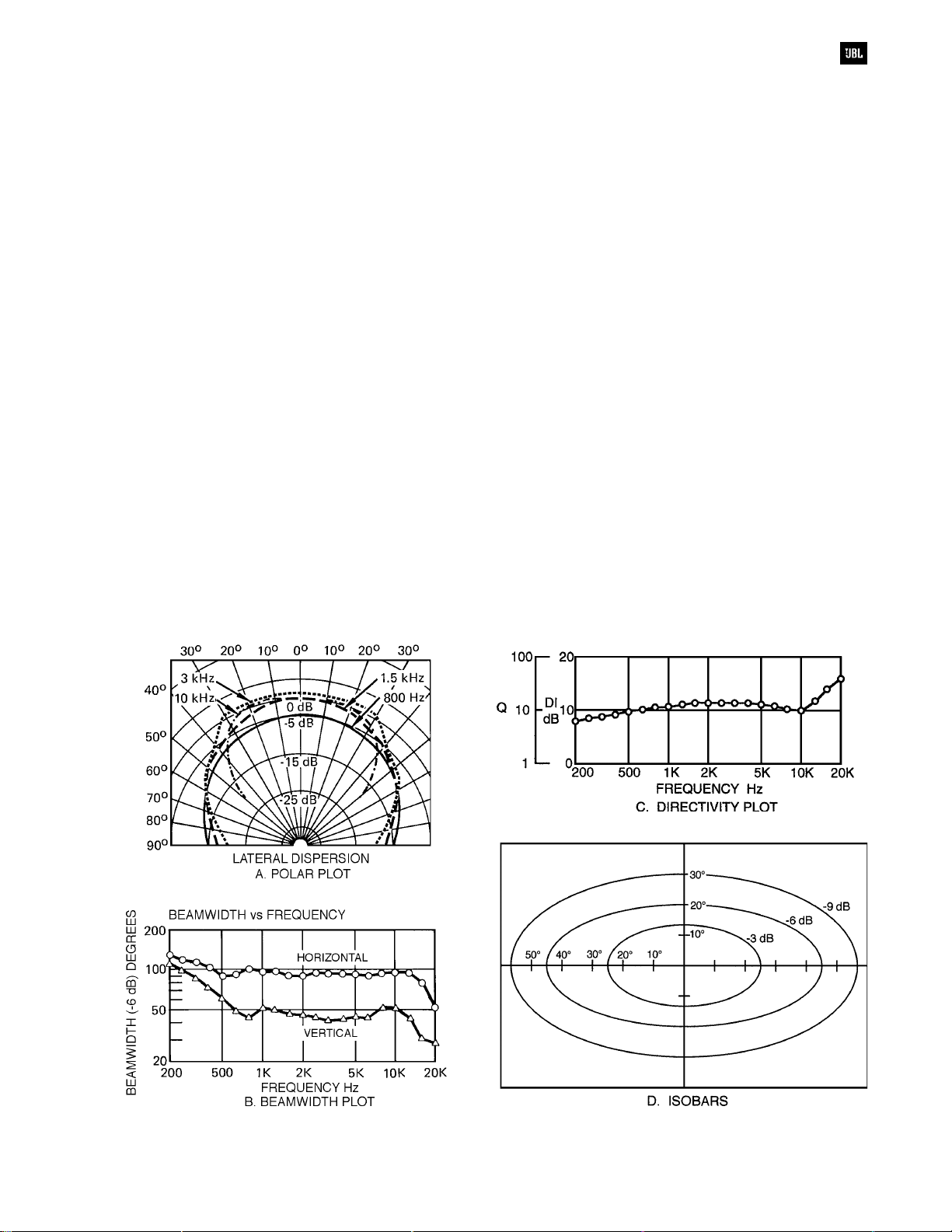
A Comparison of Polar Plots, Beamwidth Plots, Directivity Plots, and Isobars

There is no one method of presenting directional data on radiators which is complete in all regards. Polar plots (Figure 3-4A) are normally presented in only the horizontal and vertical planes. A single polar plot covers only a single frequency, or frequency band, and a complete set of polar plots takes up considerable space. Polars are, however, the only method of presentation giving a clear picture of a radiator’s response outside its normal operating beamwidth. Beamwidth plots of the 6 dB down coverage angles (Figure 3-4B) are very common because considerable information is contained in a single plot. By itself, a plot of Dl or Q conveys information only about the on-axis performance of a radiator (Figure 3-4C). Taken together, horizontal and vertical beamwidth plots and Dl or Q plots convey sufficient information for most sound reinforcement design requirements.

Figure 3-4. Methods of presenting directional information

3-3

Sound System Design Reference Manual

Isobars have become popular in recent years. They give the angular contours in spherical coordinates about the principal axis along which the response is -3, -6, and -9 dB, relative to the on-axis maximum. It is relatively easy to interpolate visually between adjacent isobars to arrive at a reasonable estimate of relative response over the useful frontal solid radiation angle of the horn. Isobars are useful in advanced computer layout techniques for determining sound coverage over entire seating areas. The normal method of isobar presentation is shown in Figure 3-4D.

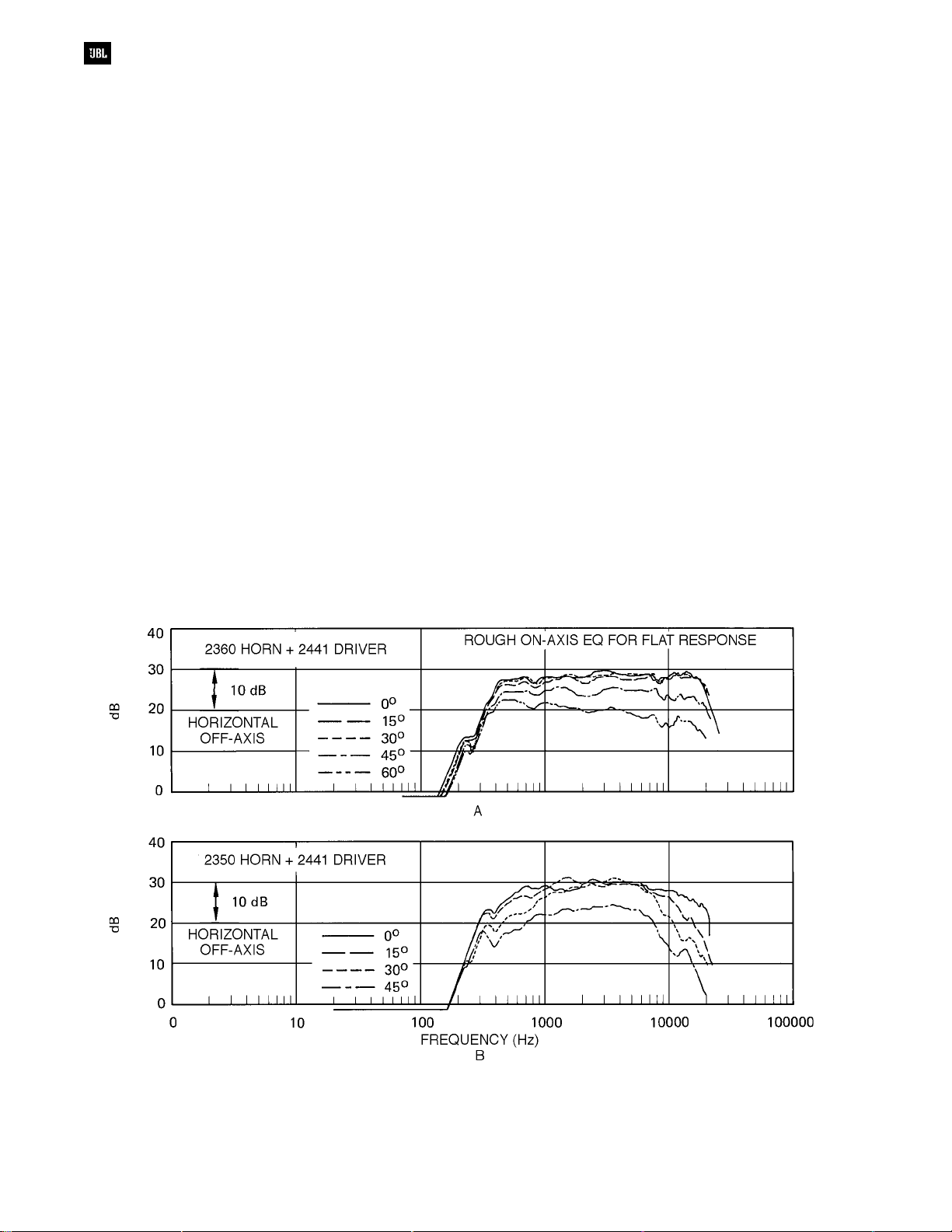
Still another way to show the directional characteristics of radiators is by means of a family of off-axis frequency response curves, as shown in Figure 3-5. At A, note that the off-axis response curves of the JBL model 2360 Bi-Radial horn run almost parallel to the on-axis response curve. What this means is that a listener seated off the main axis will perceive smooth response when a Bi-Radial constant coverage horn is used. Contrast this with the off-axis response curves of the older (and obsolete) JBL model 2350 radial horn shown at B. If this device is equalized for flat on-axis response, then listeners off-axis will perceive rolled-off HF response.

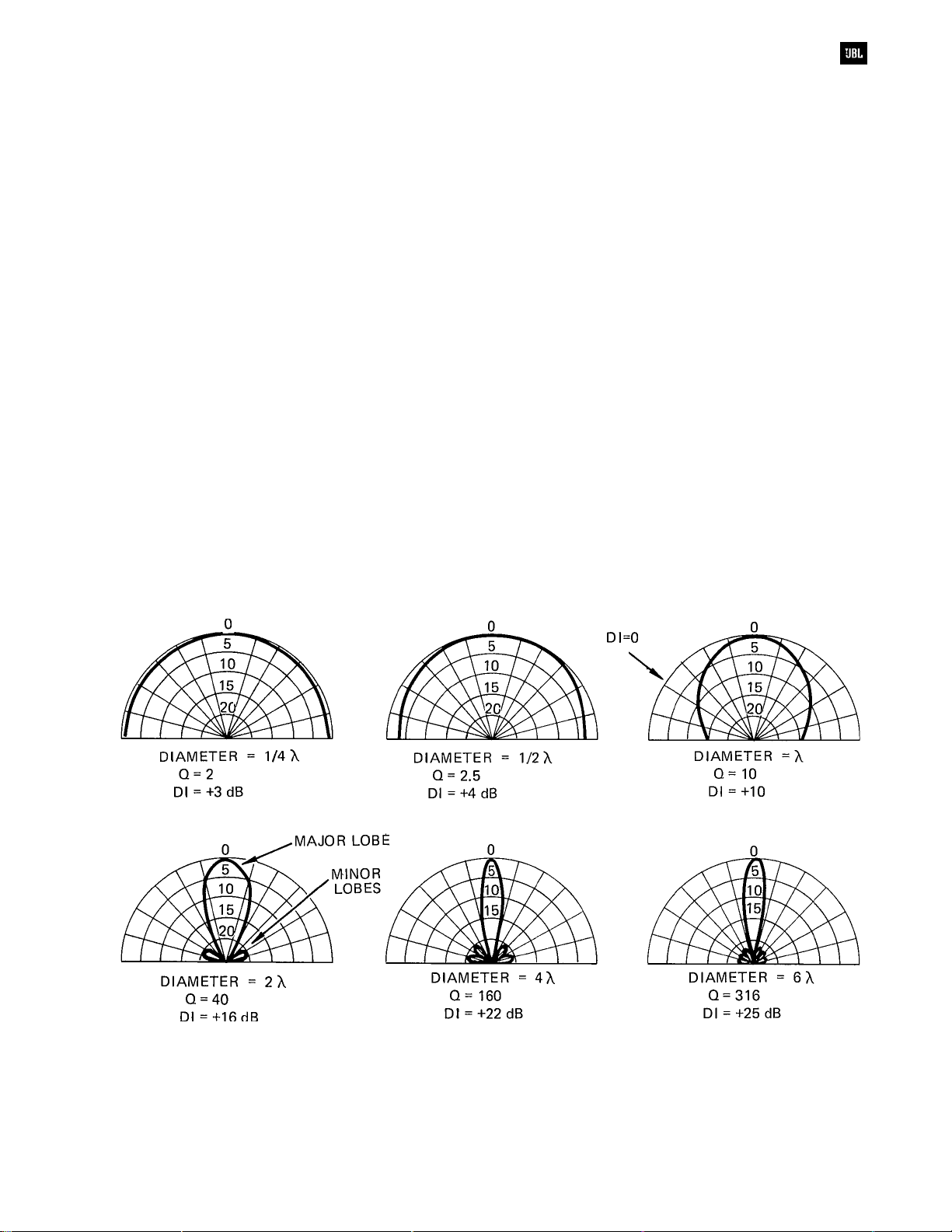
Directivity of Circular Radiators

Any radiator has little directional control for frequencies whose wavelengths are large compared with the radiating area. Even when the radiating area is large compared to the wavelength, constant pattern control will not result unless the device has been specifically designed to maintain a constant pattern. Nothing demonstrates this better than a simple radiating piston. Figure 3-6 shows the sharpening of on-axis response of a piston mounted in a flat baffle. The wavelength varies over a 24-to-1 range. If the piston were, say a 300 mm (12”) loudspeaker, then the wavelength illustrated in the figure would correspond to frequencies spanning the range from about 350 Hz to 8 kHz.

Among other things, this illustration points out why “full range,” single-cone loudspeakers are of little use in sound reinforcement engineering. While the on-axis response can be maintained through equalization, off-axis response falls off drastically above the frequency whose wavelength is about equal to the diameter of the piston. Note that when the diameter equals the wavelength, the radiation pattern is approximately a 90° cone with - 6 dB response at ±45°.

3-4

Figure 3-5. Families of off-axis frequency response curves

Sound System Design Reference Manual

The values of DI and Q given in Figure 3-6 are the on-axis values, that is, along the axis of maximum loudspeaker sensitivity. This is almost always the case for published values of Dl and Q. However, values of Dl and Q exist along

any

axis of the radiator, and they can be determined by inspection of the polar plot. For example, in Figure 3-6, examine the polar plot corresponding to Diameter = λ. Here, the on-axis Dl is 10 dB. If we simply move off-axis to a point where the response has dropped 10 dB, then the Dl along that direction will be 10 - 10, or 0 dB, and the Q will be unity. The off-axis angle where the response is 10 dB down is marked on the plot and is at about 55°. Normally, we will not be concerned with values of Dl and Q along axes other than the principal one; however, there are certain calculations involving interaction of microphones and loudspeakers where a knowledge of off-axis directivity is essential.

Omnidirectional microphones with circular diaphragms respond to on- and off-axis signals in a manner similar to the data shown in Figure 3-6. Let us assume that a given microphone has a diaphragm about 25 mm (1”) in diameter. The frequency corresponding to λ/4 is about 3500 Hz, and the response will be quite smooth both on and off axis. However, by the time we reach 13 or 14 kHz, the diameter of the diaphragm is about equal to λ, and the Dl of the microphone is about 10 dB. That is, it will be 10 dB more sensitive to sounds arriving on axis than to sounds which are randomly incident to the microphone.

Of course, a piston is a very simple radiator — or receiver. Horns such as JBL’s Bi-Radial series are complex by comparison, and they have been designed to maintain constant HF coverage through attention to wave-guide principles in their design. One thing is certain: no radiator can exhibit much pattern control at frequencies whose wavelengths are much larger than the circumference of the radiating surface.

Figure 3-6. Directional characteristics of a circular-piston source

mounted in an infinite baffle as a function of diameter and λ.

3-5

Sound System Design Reference Manual

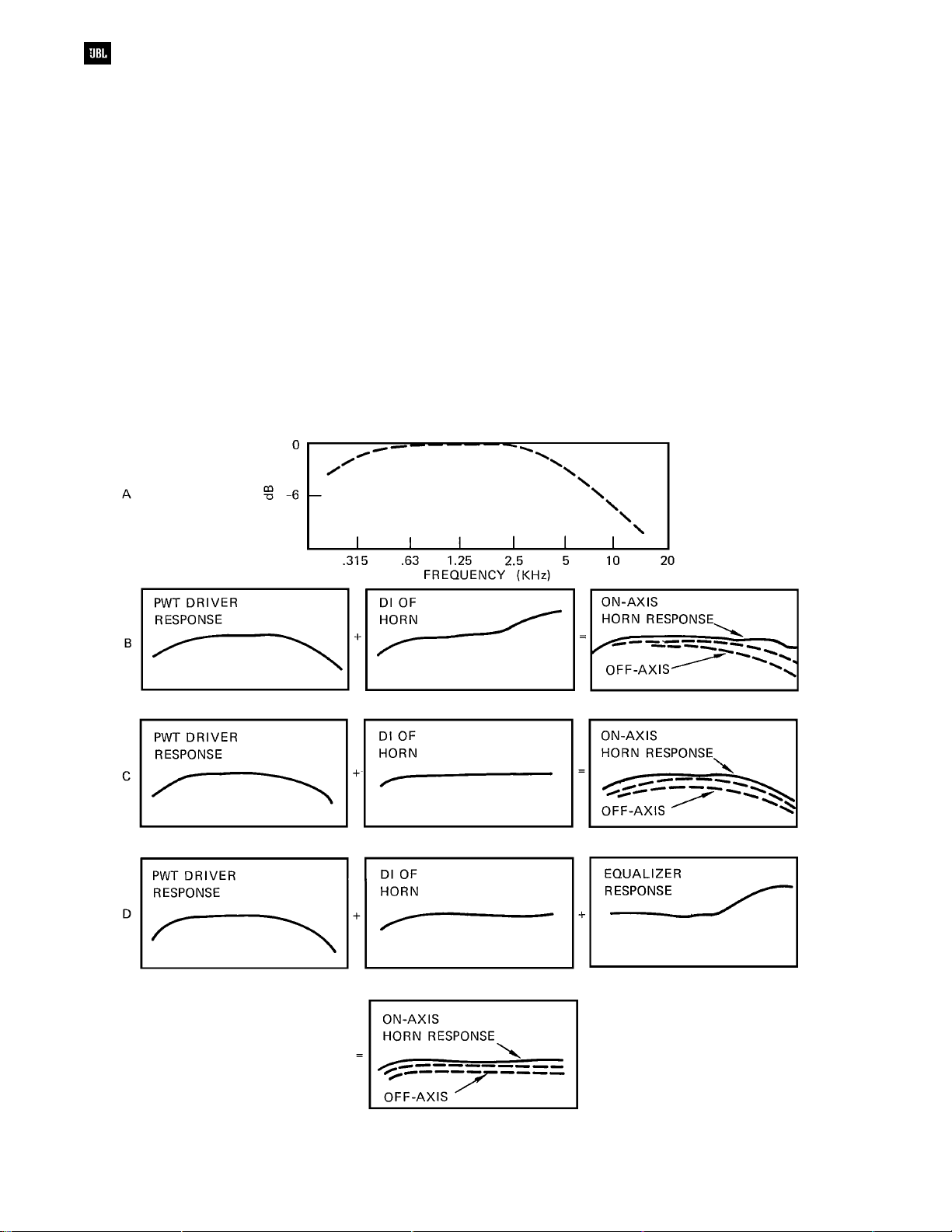
The Importance of Flat Power Response

If a radiator exhibits flat power response, then the power it radiates, integrated over all directions, will be constant with frequency. Typical compression drivers inherently have a rolled-off response when measured on a Figure 3-7A. When such a driver is mounted on a typical radial horn such as the JBL model 2350, the on-axis response of the combination will be the sum of the PWT response and the Dl of the horn. Observe at B that the combination is fairly flat on axis and does not need additional equalization. Off-axis response falls off, both vertically and horizontally, and the total power response of the combination will be the same as observed on the PWT; that is, it rolls off above about 3 kHz.

plane wave tube

(PWT), as shown in

Now, let us mount the same driver on a BiRadial uniform coverage horn, as shown at C. Note that both on-and off-axis response curves are rolled off but run parallel with each other. Since the Dl of the horn is essentially flat, the on-axis response will be virtually the same as the PWT response.

At D, we have inserted a HF boost to compensate for the driver’s rolled off power response, and the result is now flat response both on and off axis. Listeners anywhere in the area covered by the horn will appreciate the smooth and extended response of the system.

Flat power response makes sense only with components exhibiting constant angular coverage. If we had equalized the 2350 horn for flat power response, then the on-axis response would have been too bright and edgy sounding.

3-6

Figure 3-7. Power response of HF systems

Sound System Design Reference Manual

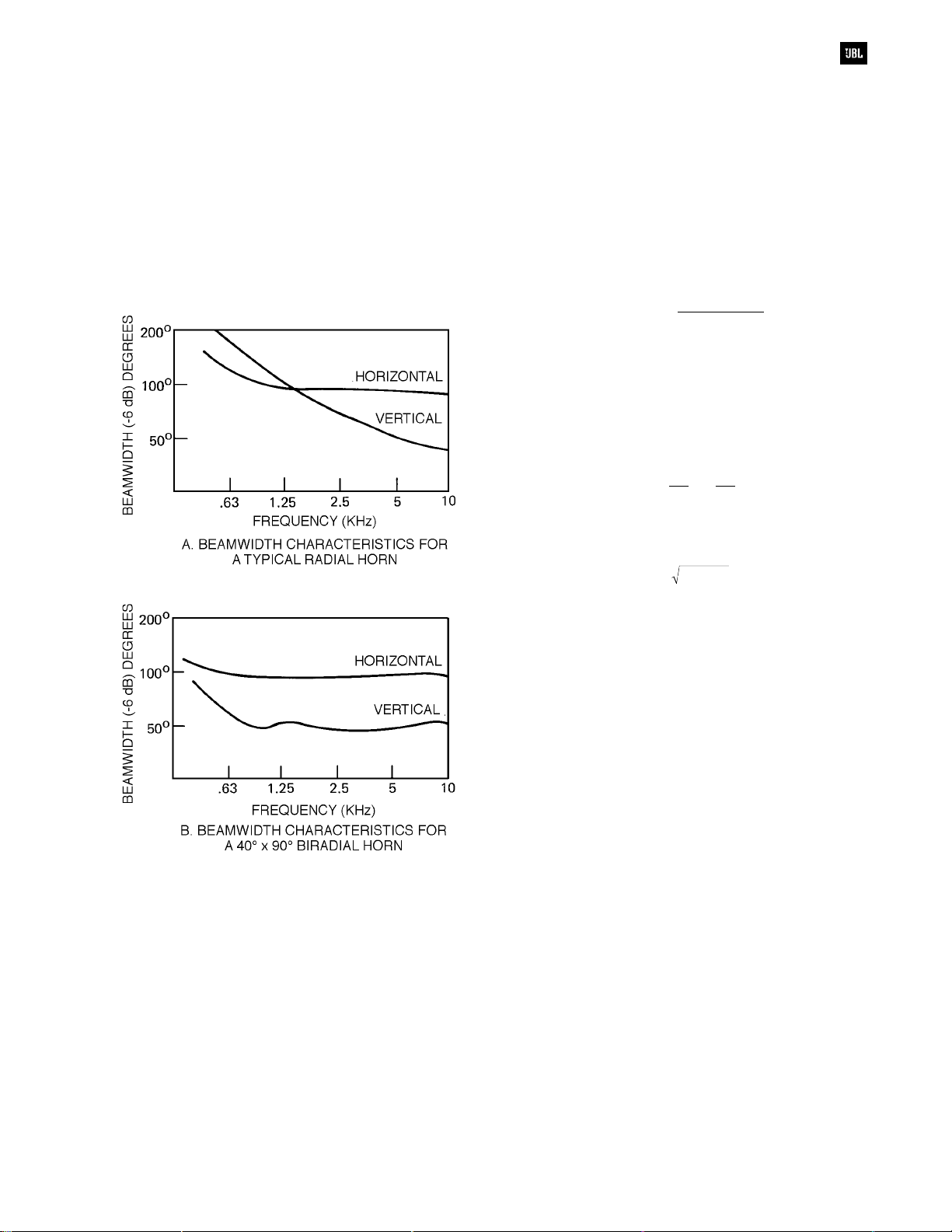
The rising DI of most typical radial horns is accomplished through a narrowing of the vertical pattern with rising frequency, while the horizontal pattern remains fairly constant, as shown in Figure 3-8A. Such a horn can give excellent horizontal coverage, and since it is “self equalizing” through its rising DI, there may be no need at all for external equalization. The smooth-running horizontal and vertical coverage angles of a Bi-Radial, as shown at Figure 3-8B, will always require power response HF boosting.

Measurement of Directional Characteristics

Polar plots and isobar plots require that the radiator under test be rotated about several of its axes and the response recorded. Beamwidth plots may be taken directly from this data.

DI and Q can be calculated from polar data by integration using the following equation:

sin d

θθ

    



 

DI = 10 log

is taken as unity, and θ is taken in 10° increments.

  



∫

(

)

The integral is solved for a value of DI in the horizontal plane and a value in the vertical plane. The resulting DI and Q for the radiator are given as:

DI =

and

Figure 3-8. Increasing DI through narrowing

vertical beamwidth

Q = Q Q

⋅

(Note: There are slight variations of this method, and of course all commonly use methods are only approximations in that they make use of limited polar data.)

3-7

Sound System Design Reference Manual

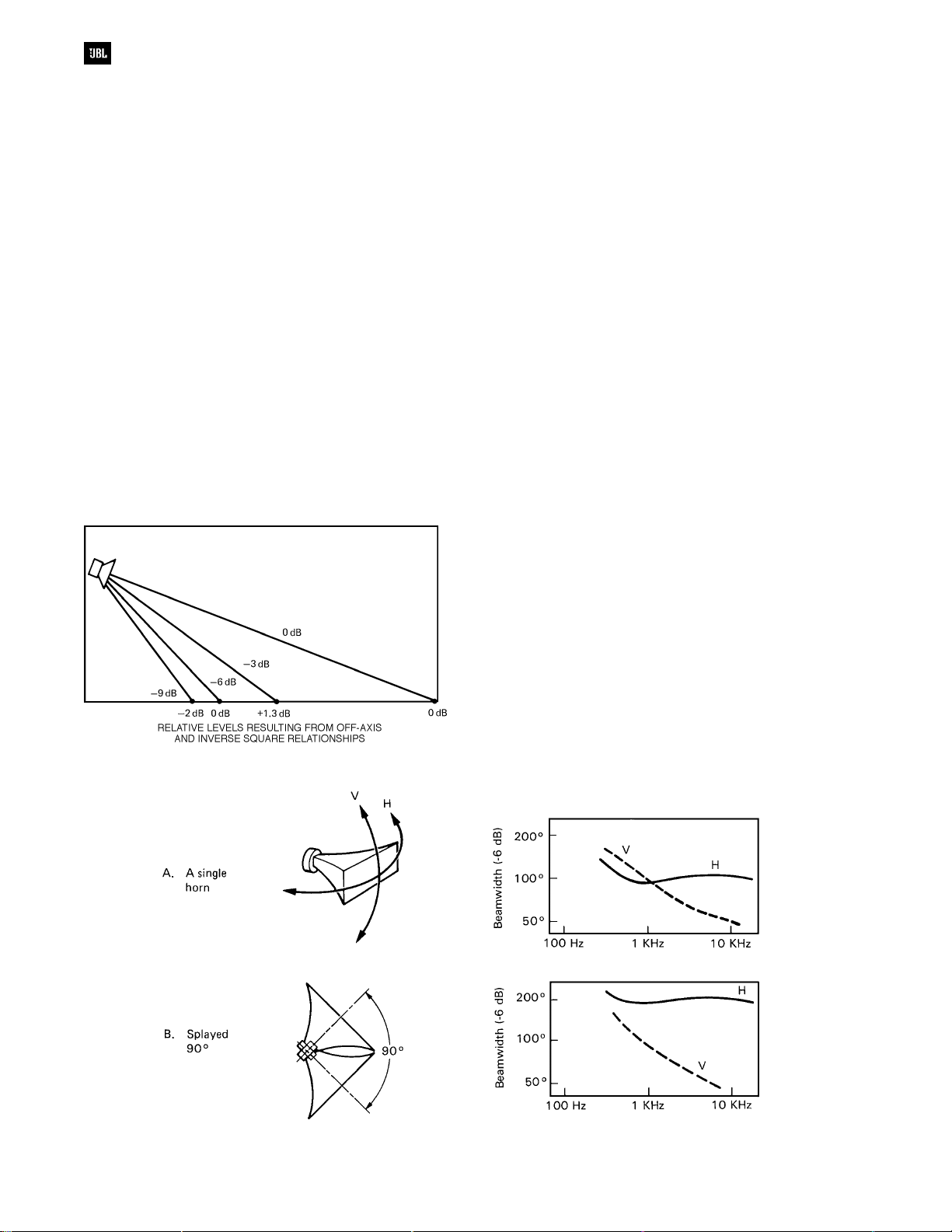
Using Directivity Information

A knowledge of the coverage angles of an HF horn is essential if the device is to be oriented properly with respect to an audience area. If polar plots or isobars are available, then the sound contractor can make calculations such as those indicated in Figure 3-9. The horn used in this example is the JBL 2360 Bi-Radial. We note from the isobars for this horn that the -3 dB angle off the vertical is 14°. The -6 dB and -9 dB angles are 23° and 30° respectively. This data is for the octave band centered at 2 kHz. The horn is aimed so that its major axis is pointed at the farthest seats. This will ensure maximum reach, or “throw,” to those seats. We now look at the -3 dB angle of the horn and compare the reduction in the horn’s output along that angle with the inverse square advantage at the closer-in seats covered along that axis. Ideally, we would like for the inverse square advantage to exactly match the horn’s off-axis fall-off, but this is not always possible. We similarly look at the response along the -6 and -9 dB axes of the horn,

Figure 3-9. Off-axis and inverse square calculations

comparing them with the inverse square advantages afforded by the closer-in seats. When the designer has flexibility in choosing the horn’s location, a good compromise, such as that shown in this figure, will be possible. Beyond the -9 dB angle, the horn’s output falls off so rapidly that additional devices, driven at much lower levels, would be needed to cover the front seats (often called “front fill” loudspeakers).

Aiming a horn as shown here may result in a good bit of power being radiated toward the back wall. Ideally, that surface should be fairly absorptive so that reflections from it do not become a problem.

Directional Characteristics of Combined Radiators

While manufacturers routinely provide data on their individual items of hardware, most provide little, if any, data on how they interact with each other. The data presented here for combinations of HF horns is of course highly wavelength, and thus size, dependent. Appropriate scaling must be done if this data is to be applied to larger or smaller horns.

In general, at high frequencies, horns will act independently of each other. If a pair of horns are properly splayed so that their -6 dB angles just overlap, then the response along that common axis should be smooth, and the effect will be nearly that of a single horn with increased coverage in the plane of overlap. Thus, two horns with 60° coverage in the horizontal plane can be splayed to give 120° horizontal coverage. Likewise, dissimilar horns can be splayed, with a resulting angle being the sum of the two coverage angles in the plane of the splay. Splaying may be done in the vertical plane with similar results. Figure 3-10 presents an example of horn splaying in the horizontal plane.

3-8

Figure 3-10. Horn splaying for wider coverage

+ 74 hidden pages