Hp 49G+ User Manual [pt]

Download

hp 49g+ calculadora gráfica

manual do usuário

Edição 2 Número de peça HP F2228-90004

Aviso

REGISTRO SEU PRODUTO EM : www.register.hp.com

ESTE MANUAL E TODOS OS EXEMPLOS CONTIDOS AQUI SÃO FORNECIDOS “DO JEITO QUE ESTÃO” E ESTÃO SUJEITOS À MUDANÇAS SEM AVISO PRÉVIO. A COMPAINHA HEWLETTPACKARD NÃO FAZ GARANTIA DE NENHUM TIPO COM RESPEITO A ESTE MANUAL OU OS EXEMPLOS CONTIDOS AQUI, INCLUINDO, MAS NÃO SE LIMITANDO ÀS GARANTIAS IMPLÍCITAS DE COMERCIABILIDADE, NÃO-VIOLAÇÃO E APTIDÃO PARA UM PROPÓSITO PARTICULAR.

HEWLETT-PACKARD CO. NÃO SERÁ RESPONSÁVEL POR QUAISQUER ERROS OU POR DANOS ACIDENTAIS OU CONSEQUENCIAIS RELACIONADOS COM O FORNECIMENTO, DESEMPENHO, OU USO DESTE MANUAL OU OS EXEMPLOS CONTIDOS AQUI.

© Copyright 2003 Hewlett-Packard Development Company, L.P. Reprodução, adaptação, ou tradução deste manual é proibido sem permissão prévia por escrito de Hewlett-Packard Company, exceto quando permitido pelas leis de direitos autorais.

Hewlett-Packard Company 4995 Murphy Canyon Rd, Suite 301 San Diego,CA 92123

Histórico da Tiragem

Edição 2 Dezembro 2003

Prefácio

Você tem em suas mãos um computador numérico e simbólico compacto que facilitará o cálculo e a análise matemática de problemas em uma variedade de assuntos, da matemática elementar até a engenharia avançada e disciplinas científicas.

O manual contém exemplos que ilustram o uso das funções e operações básicas da calculadora. Os capítulos neste manual de Bolso estão organizados por assunto, em ordem de dificuldade: da configuração dos modos da calculadora, até os cálculos com números reais e complexos, operações com listas, vetores e matrizes, gráficos, aplicações de cálculo, análise vetorial, equações diferenciais, probabilidade e estatística.

Para as operações simbólicas, a calculadora inclui um Sistema Algébrico de Computador (CAS) poderoso, que permite selecionar diferentes modos de operação, como por exemplo: números complexos ou reais, nos modos exato (simbólico) ou aproximado (numérico). O visor pode ser ajustado para fornecer expressões na forma de texto, que podem ser úteis em trabalhos com matrizes, vetores, frações, somatórios, derivadas e integrais. Os gráficos de alta velocidade da calculadora são muito convenientes para gerar quadros complexos em muito pouco tempo.

Graças à porta infravermelha e ao cabo USB disponíveis com a calculadora, você poderá conectar-se a outras calculadoras ou computadores. A conexão em alta velocidade através de infravermelho ou USB permite a troca eficiente e rápida de programas e dados com outras calculadoras ou computadores. A calculadora está equipada com uma porta para cartão de memória flash que facilita o armazenamento e intercâmbio de dados com outros usuários.

Esperamos que esta calculadora torne-se uma companheira fiel para suas aplicações escolares ou profissionais.

Índice

Capítulo 1 – Introdução

Operações básicas, 1-1 Baterias, 1-1 Ligando e desligando a calculadora, 1-2 Ajustando o contraste do visor, 1-2 Conteúdo do visor da calculadora, 1-3 Menus, 1-3 O menu TOOL(FERRAMENTA), 1-4 Configurando hora e data, 1-4 Apresentando o teclado da calculadora, 1-5 Selecionando os modos de calculadora, 1-6 Modo de operação, 1-7 Formato de número e ponto ou vírgula decimais, 1-11 Formato padrão, 1-11 Formato fixo com decimais, 1-12 Formato científico, 1-13 Formato de engenharia, 1-13 Vírgula ou ponto decimais, 1-14 Medida do ângulo, 1-15 Sistema de coordenadas, 1-16 Selecionar as configurações CAS, 1-16 Explicação das configurações CAS, 1-18 Selecionando os modos de exibição,1-19 Selecionando a fonte do visor, 1-20 Selecionando as propriedades do editor de linha, 1-20 Selecionando as propriedades da pilha, 1-21 Selecionando as propriedades do equation writer (EQW), 1-22 Referências, 1-23

Capítulo 2 – Apresentação da calculadora

Objetos da calculadora, 2-1 Editando as expressões na pilha, 2-1 Criando expressões aritméticas, 2-1

, 1-1

, 2-1

Página TOC-1

Criando expressões algébricas, 2-4 Usando o Equation Writer (EQW) para criar expressões, 2-5 Criando expressões aritméticas, 2-5 Criando expressões algébricas, 2-8 Organizando dados na calculadora, 2-9 O diretório HOME, 2-9 Subdiretórios, 2-9 Variáveis, 2-10 Digitando os nomes das variáveis, 2-10 Criando variáveis, 2-11 Modo Algébrico, 2-12 Modo RPN, 2-13 Verificando os conteúdos das variáveis, 2-14 Modo Algébrico, 2-14 Modo RPN, 2-14

Use a tecla shift direita‚ seguida pelo item do menu de tecla de

função, 2-15 Listando o conteúdos de todas as variáveis no visor, 2-15 Excluindo variáveis, 2-16 Usando a função PURGE na pilha no modo Algébrico, 2-16 Usando a função PURGE na pilha no modo RPN, 2-17 Funções UNDO e CMD, 2-17 CHOOSE boxes x MENU de tecla de função, 2-17 Referências, 2-20

Capítulo 3 – Cálculos com números reais, 3-1

Exemplos de cálculos com números reais, 3-1 Usando potências de 10 ao inserir dados, 3-4 Funções com números reais no menu MTH, 3-6 Usando os menus da calculadora, 3-6 Funções hiperbólicas e seus inversos, 3-7 Operações com unidades, 3-8 O menu UNITS, 3-9 Unidades disponíveis, 3-11 Anexando as unidades aos números, 3-11 Prefixos de unidades, 3-12

Página TOC-2

Operações com unidades, 3-13 Conversão de unidades, 3-14 Constantes física na calculadora, 3-15 Definindo e usando funções, 3-17 Referências, 3-19

Capítulo 4 – Cálculos com números complexos

Definições, 4-1 Configurando a calculadora para o modo COMPLEX, 4-1 Inserindo números complexos, 4-2 A representação polar de um número complexo, 4-2 Operações Simples com números complexos, 4-4 Os menus CMPLX, 4-4 Menu CMPLX através do menu MTH, 4-4 Menu CMPLX no teclado, 4-5 Funções aplicadas a números complexos, 4-6 Função DROITE: equação de uma linha reta, 4-7

Referências, 4-7

, 4-1

Capítulo 5 – Operações algébricas e aritméticas, 5-1

Inserindo objetos algébricos, 5-1 Operações simples com objetos algébricos, 5-2 Funções no menu ALG, 5-4 Operações com funções transcendentais, 5-6 Expansão e fatoração usando as funções log-exp, 5-6 Expansão e fatoração usando as funções trigonométricas, 5-6 Funções no menu ARITHMETIC, 5-7 Polinômios, 5-8 A função HORNER, 5-9 A variável VX, 5-9 A função PCOEF, 5-9 A função PROOT , 5-10 As funções QUOT e REMAINDER, 5-10 A função PEVAL , 5-10 Frações, 5-10 A função SIMP2 , 5-11

Página TOC-3

A função PROPFRAC, 5-11 A função PARTFRAC, 5-11 A função FCOEF , 5-12 A função FROOTS, 5-12 Operações passo a passo com polinômios e frações, 5-13 Referências, 5-14

Capítulo 6 –Solucionando equações, 6-1

Solução simbólica de equações algébricas, 6-1 Função ISOL, 6-1 Função SOLVE, 6-2 Função SOLVEVX, 6-4 Função ZEROS, 6-4 Menu Numerical Solver, 6-5 Equações polinomiais, 6-6 Encontrando as soluções de uma equação polinomial, 6-6 Gerando os coeficientes de um polinômio dadas suas raízes, 6-7 Gerando a expressão algébrica de um polinômio, 6-8 Cálculos financeiros, 6-9 Resolvendo equações de uma incógnita usando o NUM.SLV, 6-9 Função STEQ, 6-9 Solucionando equações simultâneas com MSLV, 6-11 Referências, 6-12

Capítulo 7 – Operações com listas

Criando e armazenando listas, 7-1 Operações com listas numéricas, 7-1 Alterarando sinais, 7-1 Adição, subtração, multiplicação e divisão, 7-2 Funções aplicadas a listas, 7-3 Listas de números complexos, 7-4 Listas de objetos algébricos, 7-4 O menu MTH/LIST, 7-5 A função SEQ, 7-6 A função MAP, 7-6 Referências, 7-7

, 7-1

Página TOC-4

Capítulo 8 – Vetores, 8-1

Inserindo vetores, 8-1 Digitando vetores na pilha, 8-1 Armazenando os vetores em variáveis na pilha, 8-2 Usando o Matrix Writer (MTRW) para inserir vetores, 8-2 Operações simples com vetores, 8-5 Alterando os sinais, 8-5 Adição e subtração, 8-5 Multiplicação e divisão por um escalar, 8-6 Função de valor absoluto, 8-6 O menu MTH/VECTOR, 8-7 Magnitude, 8-7 Produto ponto, 8-7 Produto cruzado, 8-8 Referências, 8-9

Capítulo 9 – Matrizes e álgebra linear, 9-1

Inserindo matrizes na pilha, 9-1 Usando o Matrix Writer, 9-1 Digitando a matriz diretamente na pilha, 9-2 Operações com matrizes, 9-3 Adição e subtração, 9-4 Multiplicação, 9-4 Multiplicação por um escalar, 9-4 Multiplicação matriz-vetor, 9-4 Multiplicação de matrizes, 9-5 Multiplicação termo a termo, 9-5 A matriz identidade, 9-6 A matriz inversa, 9-6 Caracterizando uma matriz (o menu NORM da matriz), 9-7 Função DET, 9-7 Função TRACE, 9-7 Solução de sistemas lineares, 9-8 Usando o solucionador numérico para sistemas lineares, 9-8 Solução com a matriz inversa, 9-10

Página TOC-5

Solução pela "divisão” de matrizes, 9-10 Referências, 9-11

Capítulo 10 – Gráficos, 10-1

As opções gráficas na calculadora, 10-1 Plotando uma expressão da forma y = f(x), 10-2 Gerando uma tabela de valores para uma função, 10-4 Plotagens rápidas em 3D, 10-6 Referências, 10-8

Capítulo 11 – Aplicações em Cálculo

O menu CALC (Cálculus), 11-1 Limites e derivadas, 11-1 Função lim, 11-1 Funções DERIV e DERVX, 11-2 Antiderivadas e integrais, 11-3 Funções INT, INTVX, RISCH, SIGMA e SIGMAVX, 11-3 Integrais definidas, 11-4 Séries infinitas, 11-5 Funções TAYLR, TAYLR0 e SERIES, 11-5 Referências, 11-7

, 11-1

Capítulo 12 – Aplicações em Cálculos com multiplas variáveis, 12-1

Derivadas parciais, 12-1 Integrais múltiplas, 12-2 Referências, 12-2

Capítulo 13 –Aplicações em Análise Vetorial, 13-1

O operador del, 13-1 Gradiente, 13-1 Divergência, 13-2 Rotacional, 13-2 Referências, 13-2

Página TOC-6

Capítulo 14 – Equações Diferenciais, 14-1

O menu CALC/DIFF, 14-1 Solução para equações lineares e não-lineares, 14-1 Função LDEC, 14-2 Função DESOLVE, 14-3 A variável ODETYPE, 14-4 Transformadas de Laplace, 14-5 A transformada de Laplace e sua inversa na calculadora, 14-5 Série de Fourier, 14-6 Função de FOURIER, 14-6 Série de Fourier para uma função quadrática, 14-7 Referências, 14-8

Capítulo 15 – Distribuições de probabilidade, 15-1

O submenu MTH/PROBABILITY – 1ª parte, 15-1 Fatoriais, combinações e permutações, 15-1 Números aleatórios, 15-2 O submenu MTH/PROB.. –2ª parte, 15-3 A distribuição normal, 15-3 A distribuição de Student, 15-4 A distribuição Qui-quadrada, 15-4 A distribuição F, 15-4 Referências, 15-4

Capítulo 16 – Aplicações estatísticas, 16-1

Inserindo dados, 16-1 Calculando estatísticas de variável única, 16-2 Obtendo as distribuições de freqüência, 16-3 Ajustando os dados para uma função y = f(x), 16-5 Obtendo estatísticas adicionais de resumo, 16-6 Intervalos de confiança, 16-8 Teste de hipóteses, 16-10 Referências, 16-12

Capítulo 17 – Números com Bases Diferentes, 17-1

Página TOC-7

O menu BASE, 17-1 Escrevendo números não-decimais, 17-2

Referências, 17-2

Capítulo 18 – Usando cartões SD, 18-1

Armazenando objetos no cartão SD, 18-1 Restaurando um objeto do cartão SD, 18-2 Excluindo um objeto do cartão SD, 18-2

Garantia Limitada –

Serviço de atendimento ao cliente, G-2 Informações sobre regulamentação, G-4

G-1

Página TOC-8

Capítulo 1 Introdução

Este capítulo fornece informações básicas sobre a operação de sua calculadora. Os exercícios têm por objetivo familiarizá-lo com as operações e configurações básicas, antes de procederaos cálculos.

Operações básicas

Os seguintes exercícios pretendem dar-lhe uma idéia geral sobre o hardware de sua calculadora.

Baterias

A calculadora usa 3 baterias AAA(LR03) como alimentação principal e uma bateria de lítio CR2032 para memória de segurança. Antes de usar a calculadora, instale as baterias de acordo com o seguinte procedimento.

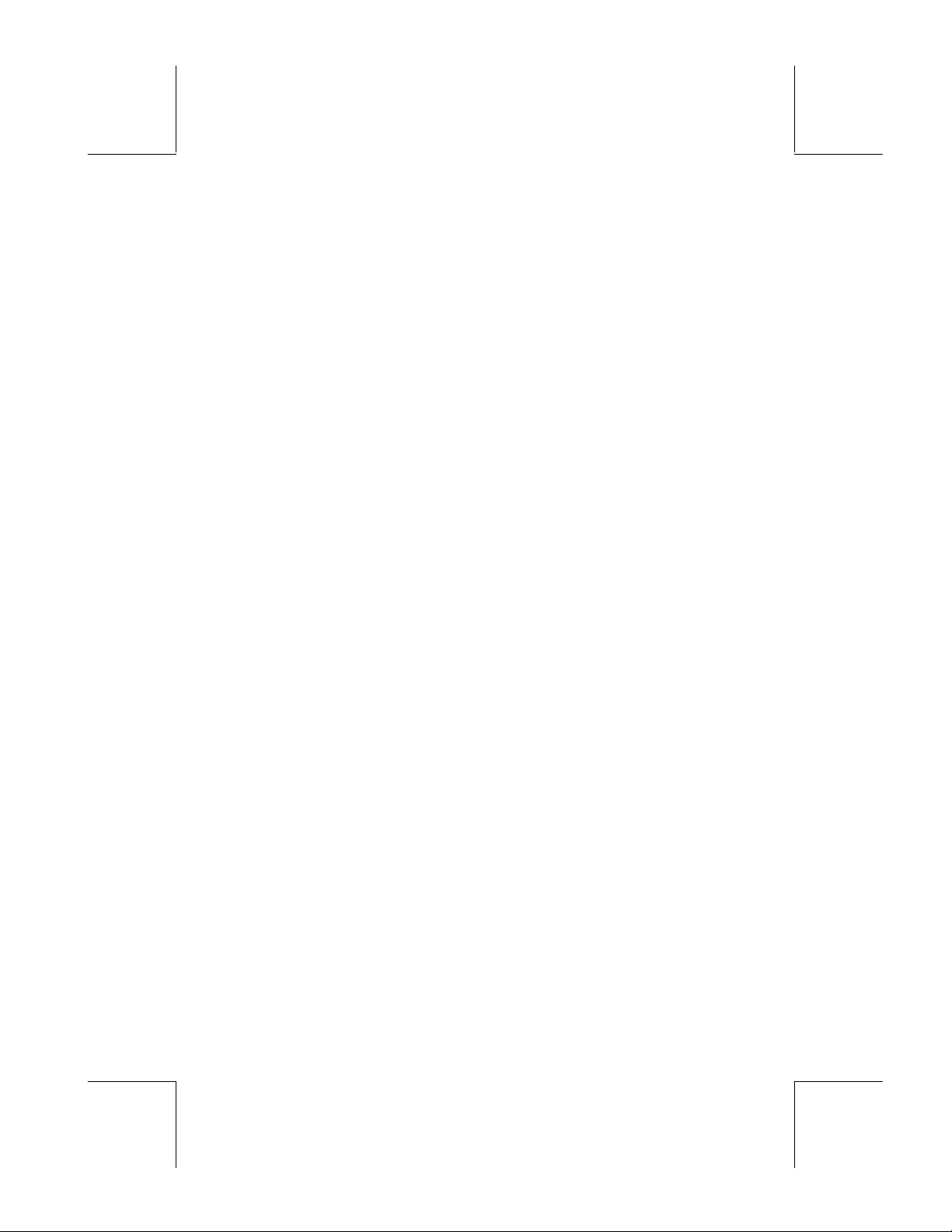
Para instalar as baterias a. Certifique-se de que a calculadora esteja desligada. Deslize a tampa do

compartimento da bateria confome a figura abaixo.

b. Insira 3 baterias AAA(LR03) novas no compartimento principal. Certifique-

se de que cada bateria seja inserida no sentido indicado.

Para instalar as baterias de segurança

a. Certifique-se de que a calculadora esteja desligada. Pressione o prendedor

da tampa. Empurre a tampa no sentido indicado e levante-a.

Página 1-1

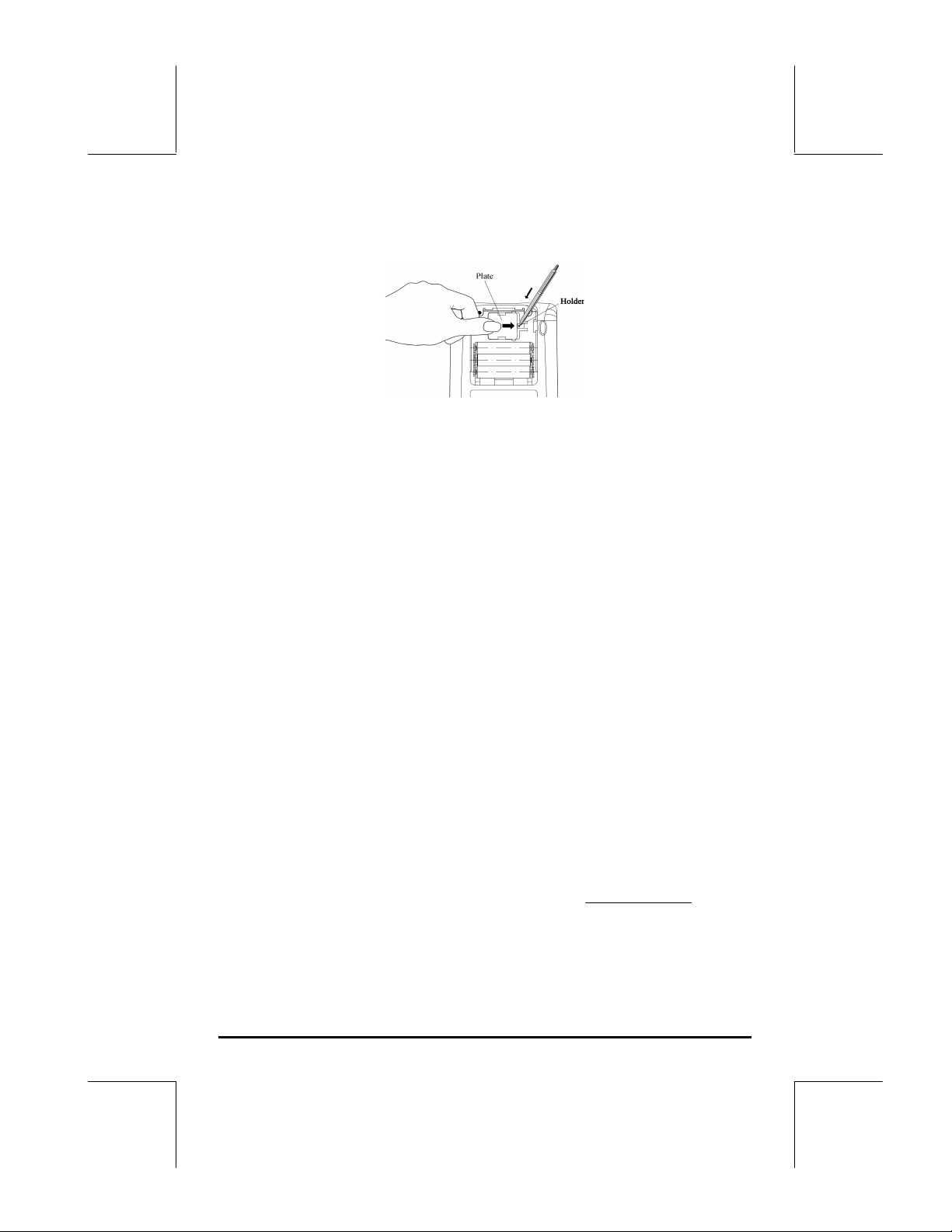
b. Insira uma bateria de lítio CR2032. nova. Certifique-se de que o lado

positivo (+) esteja voltado para cima. c. Recoloque a tampa e encaixe-a no local original. Depois de instalar as baterias, pressione [ON] para ligar a alimentação. Aviso: Quando o ícone de bateria com carga baixa for exibido, é necessário substituir as baterias logo que possível. Entretanto, evite remover a bateria de segurança e as baterias principais ao mesmo tempo para evitar perda de dados.

Ligando e desligando a calculadora

A tecla $ está localizada no canto inferior esquerdo do teclado. Pressionea uma vez para ligar a calculadora. Para desligar a calculadora, pressione a tecla de deslocamento para a direita @ (primeira tecla da segunda linha na base do teclado), seguida da tecla $. Observe que a tecla $ possui um símbolo OFF impresso no canto superior direito como lembrete do comando OFF.

Ajustando o contraste do visor

Você poderá ajustar o contraste do visor mantendo a tecla $ pressionado, enquanto pressiona a tecla + ou -.

A combinação da tecla $(manter) + produz um visor mais escuro

A combinação da tecla $(manter) - produz um visor mais claro

Página 1-2

Conteúdo do visor da calculadora

Ligue a calculadora novamente. No topo do visor encontrará duas linhas de informações que descrevem as configurações da calculadora. A primeira linha mostrará os caracteres:

RAD XYZ HEX R= 'X'

Para obter detalhes sobre essas especificações, consulte o capítulo 2 do guia do usuário da calculadora.

A segunda linha mostra os caracteres:

{ HOME }

indicando que o diretório HOME é o diretório atual do arquivo na memória da calculadora.

Na base do visor aparecerão vários símbolos, a saber,

@EDIT @VIEW @@ RCL @@ @@STO@ !PURGE !CLEAR

associados às seis teclas do menu, F1 até F6:

ABCDEF

Os seis símbolos exibidos na parte inferior do visor serão alterados, dependendo de qual menu estiver sendo exibido. Mas A sempre estará associado ao primeiro símbolo exibido, B ao segundo símbolo exibido, e assim por diante.

Menus

Os seis símbolos associados às teclas A até F fazem parte de um menu de funções. Dado que a calculadora possui apenas seis teclas, apenas 6 símbolos são exibidos de cada vez. Portanto, um menu pode ter mais de seis entradas. Cada grupo de 6 entradas é chamado de página do Menu. Para mover para a próxima página do menu (se estiver disponível), pressione a

Página 1-3

tecla L (menu NeXT). Esta tecla é a terceira da esquerda, na terceira fileira de teclas do teclado.

O menu TOOL (FERRAMENTA)

As teclas para o menu padrão, conhecido como menu TOOL , são associadas às operações relacionadas à manipulação de variáveis (consulte a seção sobre variáveis neste capítulo):

@EDIT A Edita o conteúdo de uma variável (consulte o capítulo 2 neste guia e o capítulo 2 e apêndice L no guia do usuário, para obter mais informações sobre edição).

@VIEW B Visualiza o conteúdo de uma variável @RCL@@ C Reproduz o conteúdo de uma variável @STO@ D Armazena o conteúdo de uma variável @PURGE E Elimina uma variável @CLEAR F Limpa o visor ou pilha.

Estas seis funções constituem a primeira página do menu TOOL. Este menu possui, na verdade, seis entradas dispostas em duas páginas. A segunda página torna-se disponível ao pressionar-se a tecla L (menu NeXT ). Esta tecla é a terceira da esquerda, na terceira fileira de teclas no teclado.

Neste caso, apenas as duas primeiras teclas estão associadas aos comandos. Esses comandos são:

@CASCM A CASCMD: CAS CoMmanD (Comando CAS), usado para

lançar um comando a partir do CAS selecionado da lista

@HELP B o recurso HELP descrevendo os comandos disponíveis na

calculadora.

Ao pressionar-ser a tecla L, aparecerá o menu TOOL original. Outra forma de recuperar o menu TOOL é pressionar a tecla I (terceira tecla da esquerda na segunda fileira de teclas do topo do teclado).

Configurando hora e data

Consulte o capítulo 1 no guia do usuário da calculadora para configurar a hora e a data.

Página 1-4

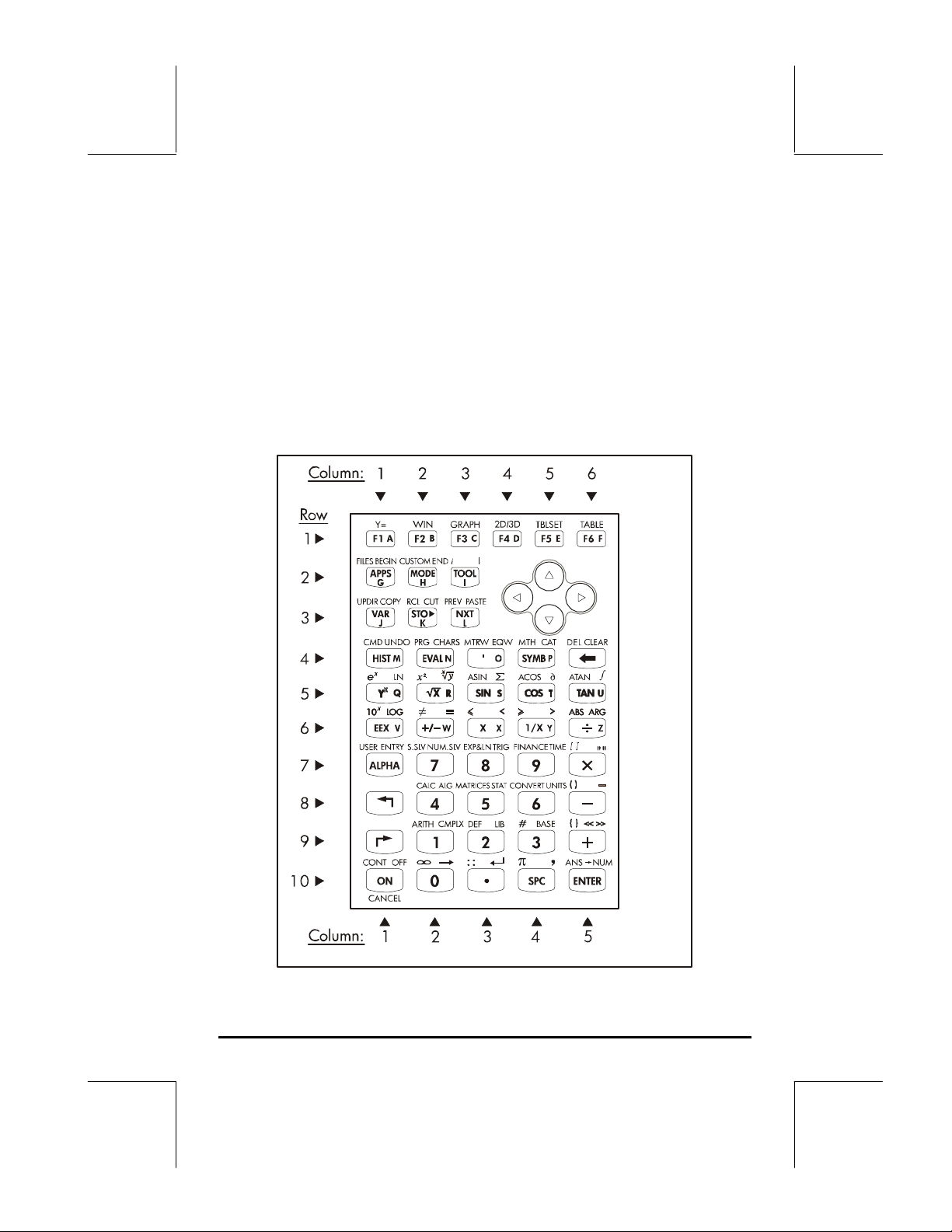
Apresentando o teclado da calculadora

A figura abaixo mostra um diagrama do teclado da calculadora com a numeração de suas linhas e colunas. Cada tecla possui três, quatro ou cinco funções. A função principal da tecla corresponde ao símbolo mais proeminente na tecla. Além disso, a tecla shift esquerda verde, key (8,1), a tecla shift direita vermelha, key (9,1) e a tecla ALPHA azul, key (7,1), podem ser combinadas com algumas das outras teclas para ativar as funções alternativas mostradas no teclado.

Página 1-5

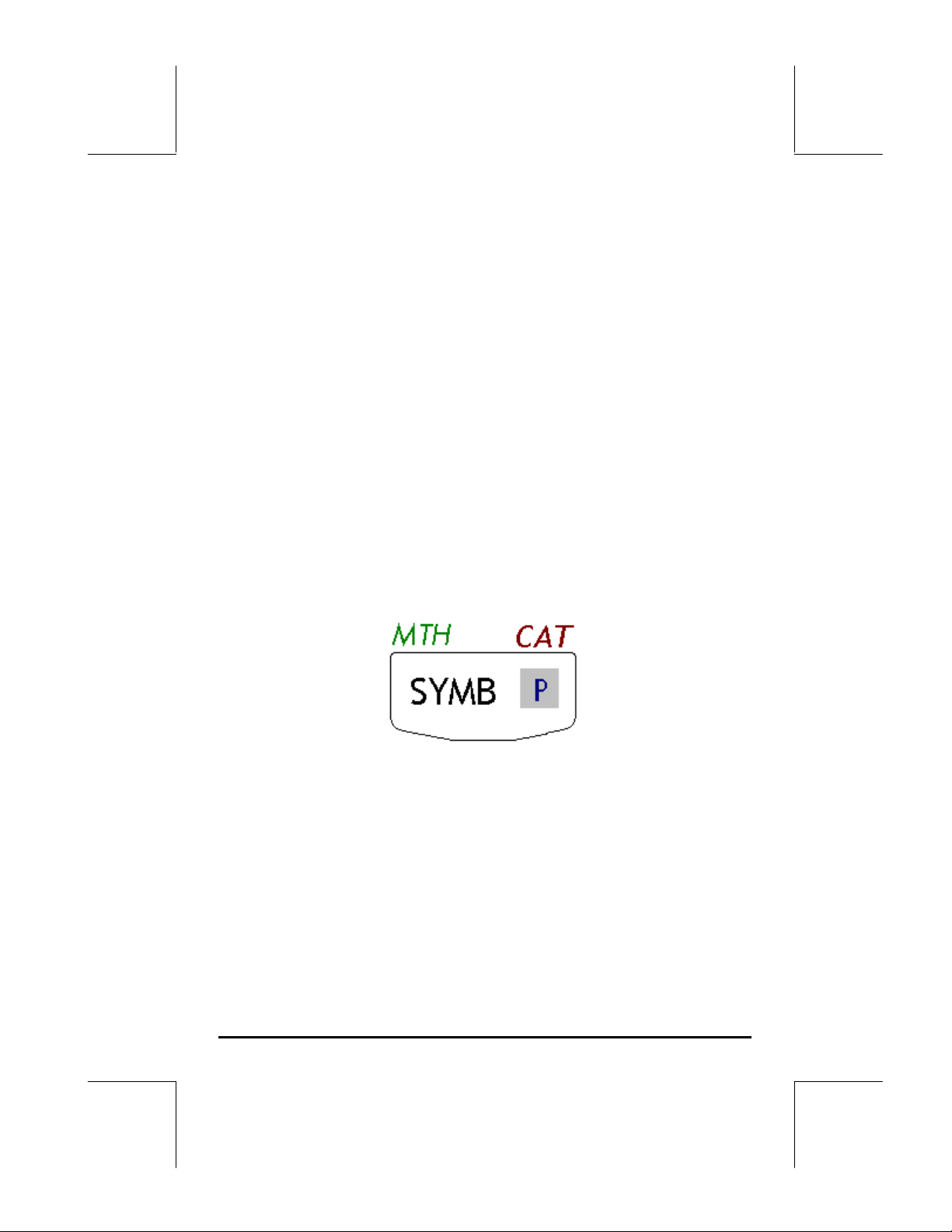
Por exemplo, a tecla P, key(4,4), está associada às seis funções descritas a seguir:

P Função Principal, para ativar o menu SYMBolic „´ Função Shift esquerda, para ativar o menu MTH (Matemática) …N Função Shift direita, para ativar a função CATalog ~p Função ALPHA, para inserir a letra P maiúscula ~„p Função ALPHA, Shift esquerda, para inserir a letra p

minúscula

~…p Função ALPHA, Shift direita, para inserir o símbolo π

Das seis funções associadas à tecla apenas a primeira das quatro são mostradas no próprio teclado. A figura na próxima página mostra esses quatro símbolos para a tecla P. Observe que a cor e a posição dos símbolos na tecla, a saber, SYMB, MTH, CAT e P, indicam qual é a função principal (SYMB) e qual das outras três funções está associada às teclas shift esquerda „(MTH), shift direita … (CAT ) e ~ (P).

Para obter informações detalhadas sobre a operação do teclado da calculadora, consulte o apêndice A do Guia do Usuário.

Selecionando os modos de calculadora

Esta seção presume que até este momente vocêesteja, pelo menos em parte, familiariazado com o uso de caixas de seleção e de diálogo (se não estiver, consulte o apêndice A do guia do usuário).

Página 1-6

Pressione o botão H (segunda tecla da esquerda na segunda fileira de teclas a partir do topo) para mostrar o seguinte formulário de entrada dos CALCULATOR MODES (MODOS DE CALCULADORA):

Pressione a tecla !!@@OK#@ ( F) para retornar ao modo de exibição normal. Exemplos de seleção de direfentes modos de calculadora são apresentados a seguir.

Modo de operação

A calculadora oferece dois modos de operação: o modo Algébrico e o modo Reverse Polish Notation (RPN- notação polonesa invertida). O modo padrão é

o modo Algébrico (conforme indicado na figura acima), contudo, os usuários das calculadoras HP anteriores podem estar familiarizados com o modo RPN.

Para selecionar um modo de operação, abra primeiro o formulário de entrada CALCULATOR MODES pressionando o botão H. O campo

Operating Mode será realçado. Selecione o modo de operação Algébrico ou RPN, usando a tecla \ (segunda da esquerda, na quinta fileira a partir da

basedo teclado) ou pressionando o tecla @CHOOS do menu ( B). Se optar pela última abordagem, use as teclas com as setas para cima e para baixo, —˜, para selecionar o modo e pressione a tecla !!@@OK#@ para completar a operação.

Para ilustrar a diferença entre esses dois modos de operação, calcularemos a seguinte expressão em ambos os modos:



0.50.3

−⋅

 

0.23

 

0.30.3

⋅



5.2

Página 1-7

Para digitar essa expressão na calculadora, usaremos primeiro o equation writer, ‚O. Identifique as seguintes teclas no teclado, além das teclas

numéricas:

!@.#*+-/R

Q¸Ü‚Oš™˜—`

O equation writer é um modo de exibição no qual você pode construir expressões matemáticas usando notações matemáticas que inclúam frações, derivadas, integrais, raízes, etc. Para usar o equation writer para escrever a expressão mostrada acima, use as seguintes teclas:

‚OR3.*!Ü5.-

1./3.*3. —————

/23.Q3™™+!¸2.5`

Depois de pressionar `a calculadora exibirá a expressão:

√ (3.*(5.-1/(3.*3.))/23.^3+EXP(2.5))

Pressionar `novamente fornecerá o valor seguinte (aceita Aprox., modo ligado, se solicitado, pressionando !!@@OK#@):

Você também poderá digitar a expressão diretamente no visor sem usar o equation writer, conforme segue:

R!Ü3.*!Ü5.-

1/3.*3.™

/23.Q3+!¸2.5`

para obter o mesmo resultado.

Página 1-8

Altere o modo de operação para RPN pressionando primeiro o botão H. Selecione o modo de operação RPN usando a tecla \ ou ou pressionando a tecla @CHOOS. Pressione a tecla !!@@OK#@ ( F) para completar a operação. O visor no modo RPN será como a figura a seguir:

Observe que o visor mostra diversos níveis de saídas marcadas, da base ao topo, como 1, 2, 3, etc. Isto é chamado de pilha da calculadora. Os diferentes níveis são chamados de níveis de pilha , ex. nível de pilha 1, nível de pilha 2, etc.

Basicamente, RPN significa que, em vez de escrever uma operação como 3 + 2, na calculadora usando

3+2`

escrevemos primeiro os operandos na ordem correta e então o operador, ou seja.,

3`2`+

Ao inserir os operandos, eles ocuparão diferentes níveis de pilha. Inserir

3`coloca o número 3 no nível de pilha 1. Depois, inserir 2`pressiona o 3 para cima ocupando o nível de pilha 2. Finalmente,

pressionando +estamos requisitando que a calculadora aplique o operador , ou programa, + aos objetos que ocupam os níveis 1 e 2. O resultado, 5, é então colocado no nível 1.

Tentemos algumas das operações mais simples antes de tentar a expressão mais complicada usada anteriormente para o modo de operação algébrica:

123/32 123`32/

4`2Q

√(√27) 27`R3@»

Página 1-9

Observe a posição do y e do x nas duas últimas operações. A base na operação exponencial é y (nível de pilha 2) enquanto o expoente é x (nível de pilha 1) antes que a tecla Q seja pressionada. De forma similar, na operação de raiz cúbica, y (nível de pilha 2) é a grandeza abaixo do sinal de raiz, e x (nível de pilha 1) é a raiz.

Tente o seguinte exercício, o qual envolve 3 fatores: (5 + 3) × 2

5`3`+ Calcula (5 +3) primeiro. 2X Conclui o cálculo.

Tentemos agora a expressão proposta anteriormente:



 



−⋅



⋅



5.2

3` Insira 3 no nível 1. 5` Insira 5 no nível 1, 3 move-se para o nível 2. 3` Insira 3 no nível 1, 5 move-se para o nível 2, 3 para

nível 3

3* Coloque 3 e multiplique, 9 aparece no nível 1 Y 1/(3×3), último valor no nível 1; 5 no nível 2; 3 no

nível 3

- 5 - 1/(3×3) , ocupa o nível 1 agora; 3 no nível 2 * 3× (5 - 1/(3×3)), ocupa nível 1 agora. 23` Insira 23 no nível 1, 14,66666 move-se para o nível

3Q Insira 3, calcule 23 / 3× (5 -1/(3×3)))/23

no nível 1. 14,666 no nível. 2.

no nível 1.

2.5 Insira 2,5 no nível 1. !¸ e

2.5

, vai para o nível 1, nível 2 mostra o valor

anterior.

+ (3× (5 -1/(3×3)))/23

2.5

= 12,18369 no nível. 1.

Página 1-10

R √((3× (5 - 1/(3×3)))/23

2.5

) = 3,4905156, em 1.

Para selecionar entre os modos de operação ALG ou RPN, você pode configurar também configurar/limpar o sinalizador do sistema 95 através da seguinte seqüência de teclado:

H @)FLAGS —„—„—„— @@CHK@@

Formato de número e ponto ou vírgula decimais

Alterar o formato do número permite que você personalize a forma em que números reais são exibidos pela calculadora. Verá que esta característica é extremamente útil nas operações com potências de dez ou para limitar o número de decimais em um resultado.

Para selecionar um modo de operação, abra primeiro o formulário de entrada CALCULATOR MODES pressionando o botão H. Depois, use a tecla com a seta para baixo, ˜, para selecionar a opção Number format. O valor default é Std, ou formato Standard (Padrão). No formato padrão, a calculadora mostrará os números de ponto de flutuação sem divisão decimal e com a máxima precisão permitida pela calculadora (12 dígitos significativos). Para obter mais informações sobre números reais, consulte o capítulo 2 do guia do usuario. Para ilustrar isto e outros formatos de números tente os exercícios seguintes:

• Formato padrão: Este modo é o modo mais usado, pois mostra os números nas notações mais familiares. Pressione a tecla !!@@OK#@ , com Number format definido para Std, para retornar ao visor da calculadora. Digite o número

123.4567890123456 (com 16 números de dígitos significativos). Pressione a tecla `. O número é arredondado para o máximo de 12 dígitos significativos e é exibido conforme segue:

Página 1-11

• Formato fixo com decimais: Pressione o botão H. Em seguida, use a tecla com a seta para baixo, ˜, para selecionar a opção Number format. Pressione a tecla @CHOOS ( B) e selecione a opção Fixed com a tecla de seta para baixo ˜.

Pressione a tecla com a seta para a direita, ™, para ressaltar o zero na frente da opção Fix. Pressione a tecla @CHOOS e, usando as teclas com as setas para cima e para baixo, —˜ selecione, digamos, 3 decimais.

Pressione a tecla !!@@OK#@ para concluir a seleção:

Pressione a tecla do menu !!@@OK#@ retornar para o visor da calculadora. O número agora é mostrado como:

Página 1-12

Observe como o número é arredondado, não truncado. Assim, o número 123,4567890123456, para esta configuração, é exibido como 123,457, e não como 123,456, porque o dígito após o dígito após 6 é > 5.

• Formato científico Para configurar este formato, comece pressionando o botão H. Depois, use a tecla com a seta para baixo, ˜, para selecionar a opção Number format. Pressione a tecla @CHOOS ( B) do menu de tecla de função e selecione a opção Scientific com a tecla com a seta para baixo ˜. Mantenha o número 3 na frente de Sci. (Esse número poderá ser alterado da mesma forma que alteramos o número Fixed de decimais no exemplo acima).

Pressione a tecla !!@@OK#@ retornar para o visor da calculadora. O número agora é mostrado como:

Esse resultado, 1.23E2, é a versão da notação de potência de dez na calculadora, ou seja,1,235 × 10

. Nessa assim chamada notação científica, o número 3 na frente do formato de número Sci (mostrado anteriormente) representa o número de dígitos significativos depois do ponto decimal. A notação científica inclui sempre um número inteiro, conforme mostrado acima. Para esse caso, portanto, o número de dígitos significativos é quatro.

• Formato de engenharia

Página 1-13

O formato de engenharia é muito similar ao formato científico, exceto que as potências de dez são múltiplos de três. Para configurar esse formato, comece pressionando o botão H. Depois, use a tecla com a seta para baixo, ˜, para selecionar a opção Number format. Pressione a tecla @CHOOS ( B) e selecione a opção Fixed com a tecla com a seta para baixo ˜. Mantenha o número 3 na frente do Eng. (Esse número pode ser alterado da mesma forma que alteramos o número Fixed de decimais em um exemplo anterior).

Pressione a tecla !!@@OK#@ para etornar ao visor da calculadora. O número agora é mostrado como:

Dado que esse número possui três dígitos na parte inteira, é mostrado com quatro dígitos significativos e uma potência de dez igual a zero, enquanto usa o formato de engenharia. Por exemplo, o número 0,00256, será mostrado como:

• Vírgula ou ponto decimais

Os pontos decimais nos números com ponto flutuante podem ser substituídos por vírgula, se o usuário estiver mais familiarizado com tal notação. Para substituir os pontos por vírgulas, altere a opção FM na tela de entrada CALCULATOR MODES para vírgulas, conforme segue (observe que alteramos Number Format para Std):

Página 1-14

• Pressione o botão H. Em seguida, use a tecla da seta para baixo, ˜, uma vez e a tecla de seta para a direita, ™,para realçar a opção__FM,. Para selecionar vírgulas, pressione a tecla @CHK@@ do menu de função(ou seja. a tecla B). A tela de entrada será como a mostrada abaixo:

• Pressione a tecla !!@@OK#@ para retornar ao visor da calculadora: O número

123.456789012, inserido anteriormente, agora é mostrado como:

Medida do ângulo

As funções trigonométricas, por exemplo, exigem argumentos que representem os ângulos planos. A calculadora fornece três modos Angle Measure diferentes para trabalhar com ângulos, a saber:

• Degrees: Existem 360 graus (360

• Radians: Existem 2π radianos (2π

• Grades: Existem 400 gradoss (400

A medida do ângulo afeta as funções trigonométricas como SIN, COS, TAN e funções associadas.

Para alterar o modo de medida do ângulo, use o seguinte procedimento:

• Pressione o botão H. Em seguida, use a tecla de seta para baixo, ˜, duas vezes. Selecione o modo Angle Measure usando a tecla \ (segunda da esquerda na quinta fileira a partir da base teclado) ou

) numa circunferência completa.

Página 1-15

pressionando o tecla virtual de menu @CHOOS ( B). Se optar pela última abordagem, use as teclas de seta para cima e para baixo, —˜, para selecionar o modo e pressione !!@@OK#@ ( F) para completar a operação. Por exemplo, na tela seguinte, o modo Radians é selecionado:

Sistema de coordenadas

A seleção do sistema de coordenadas afeta a forma pela qual os vetores e números complexos são exibidos e inseridos. Para saber mais sobre os números e vetores complexos, consulte os capítulos 4 e 8, respectivamente, neste guia. Existem três sistemas de coordenadas disponíveis na calculadora: o Retangular (RECT), o Cilíndrico (CYLIN) e o Esférico (SPHERE). Para alterar o sistema de coordenadas:

• Pressione o botão H. Em seguida, use a tecla com a seta para baixo, ˜, três vezes. Selecione o modo Coord System usando a tecla \

(segunda da esquerda na quinta fileira a partir da base do teclado) ou pressionando a tecla @CHOOS ( B). Se optar pela última abordagem, use as teclas de seta para cima e para baixo, —˜, para selecionar o modo preferido e pressione a tecla !!@@OK#@ (F) para completar a operação. Por exemplo, na tela seguinte, o modo de coordenada Polar está selecionado:

Selecionar as configurações CAS

Página 1-16

CAS significa Sistema Algébrico do Computador (Computer Algebraic System). Este é o centro matemático da calculadora onde as operações e funções matemáticas simbólicas são programadas. O CAS oferece várias configurações que podem ser ajustadas de acordo com o tipo de operação exigida. Para consultar as configurações CAS opcionais use o seguinte procedimento:

• Pressione o botão H para ativar a tela de entrada CALCULATOR MODES.

• Para alterar as configurações CAS pressione a tecla @@ CAS@@. Os valores default da configuração CAS são mostrados abaixo:

• Para navegar através das diversas opções na tela de entrada do CAS MODES, use as teclas com setas: š™˜—.

• Para selecionar ou alterar a seleção de qualquer uma das configurações mostradas acima, selecione o sublinhado antes da opção de interesse e alterne a tecla @CHK@@ até que a configuração correta seja alcançada. Quando uma opção for selecionada, a marca de verificação será mostrada no sublinhado (p. ex., as opções Rigorous e Simp Non-Rational acima). As opções desmarcadas não mostrarão nenhuma marca de verificação sublinhada precendendo as opções de interesse (p.ex., as opções _Numeric, _Approx, _Complex, _Verbose, _Step/Step, _Incr Pow acima).

Página 1-17

• Depois de selecionar e desmarcar todas as opções que você deseja na tela de entrada CAS MODES, pressione a tecla @@@OK@@@. Isso lhe fará voltar à tela de entrada CALCULATOR MODES. Para retornar ao visor normal da calculadora nesta altura, pressione a tecla @@@OK@@@ novamente.

Explicação das configurações CAS

• Indep. var: A variável independente para os aplicativos CAS. Tipicamente, VX = ‘X’.

• Modulo módulo ou módulos do anel aritmético (consulte o capítulo 5 no guia do usuário da calculadora).

• Numeric ponto de flutuação ou numérico nos cálculos.

• Approx resultados numéricos nos cálculos. Se for desmarcado, o CAS está no modo Exact, que produz resultados simbólicos nos cálculos algébricos.

• Complex ativas. Se for desmarcar o CAS no modo Real, ex. os cálculos de números reais são o padrão por definição. Consulte o capítulo 4 para verificar operações com números complexos.

• Verbose certas operações CAS.

• Step/Step para certas operações CAS. Útil para ver etapas intermediárias em operações de resumos, derivadas, integrais e operações de polinômios (ex. divisão sintética) e de matriz.

• Incr Pow termos polinomiais são mostrados na ordem de aumento das potências da variável independente.

• Rigorous |X| para X.

• Simp Non-Rational não racionais tanto quanto possível.

: Para operações na aritmética modular esta variável mantém o

: Se for configurada, a calculadora produz um resultado de

: Se for configurado, o Modo Approximate usado para os

: Se for configurado, as operações complexas de números estão

: Se for configurado, fornece as informações detalhadas em

: Se for configurado, fornece os resultados etapa por etapa

: Aumentar a potência significa que, se for configurada, os

: Se for configurada, não simplifica a função absoluta do valor

: Se for configurada, tentará simplificar as expressões

Página 1-18

Selecionando os modos de exibição

O visor da calculadora pode ser personalizado com suas preferências selecionando diferentes modos de exibição. Para ver as configurações de exibição opcionais, faça o seguinte:

• Pressione o botão H para ativar a tela de entrada CALCULATOR MODES. Dentro da tela de entrada CALCULATOR MODES, pressione a tecla @@DISP@ (D) para exibir a tela de entrada DISPLAY MODES.

• Para navegar através de diversas opções na tela de entrada DISPLAY MODES, use as teclas de setas: š™˜—.

• Para selecionar ou alterar a seleção de qualquer uma das configurações mostradas acima, selecione o sublinhado antes da opção de interesse e alterne a tecla @CHK@@ até que a configuração correta seja alcançada. Quando uma opção for selecionada, a marca de verificação será mostrada no sublinhado (p.ex., a opção Textbook no Stack: da linha acima). Opções desmarcadas não mostrarão as marcas de verificação no sublinhado precedento a opção de interesse (p.ex., a opção _Small, _Full page, e _Indent no Edit: da linha acima).

• Para selecionar a fonte para exibição, realce o campo na frente da opção Font: na tela de entrada DISPLAY MODES e use a tecla @CHOOS (B).

• Depois de selecionar e desmarcar todas as opções que você desejar na tela de entrada DISPLAY MODES, pressione a tecla @@@OK@@@. Isso o levará de volta à tela de entrada CALCULATOR MODES. Para retornar ao visor normal da calculadora nesa altura, pressione a tecla @@@OK@@@ novamente.

Página 1-19

Selecionando a fonte do visor

Pressione o botão H para ativar a tela de entrada CALCULATOR MODES. Dentro da tela de entrada CALCULATOR MODES, pressione o tecla @@DISP@ (D) para exibir a tela de entrada DISPLAY MODES. O campo Font: é realçado e a opção Ft8_0:system 8 é selecionada. Esse é o valor default da fonte do visor. Ao pressionar a tecla @CHOOS (B), aparecerá uma lista de fontes disponíveis do sistema, conforme mostrado abaixo:

As opções disponíveis são três System Fonts padrão (tamanhos 8, 7 e 6) e a opção Browse... A última permitirá que você navegue na memória da calculadora para visualizar as fontes adicionais que possa ter criado (consulte o capítulo 23) ou instalado através de download na calculadora.

Pratique alterando as fontes do visor entre os tamanhos 7 e 6. Pressione a tecla do menu de função OK para efetuar a seleção. Quando a seleção tiver sido concluída, pressione a tecla de função @@@OK@@@ para retornar à tela de entrada CALCULATOR MODES. Para retornar ao visor normal da calculadora à essa altura, pressione a tecla @@@OK@@@ novamente e veja como o visor da pilha é alterado para acomodar a fonte diferente.

Selecionando as propriedades do editor de linha

Primeiramente, pressione o botão H para ativar a tela de entrada CALCULATOR MODES. Dentro da tela de entrada CALCULATOR MODES, pressione o tecla @@DISP@ (D) para exibir a tela de entrada DISPLAY MODES. Pressione a tecla com a seta para baixo, ˜, uma vez para ir para a linha Edit. Esta linha mostra três propriedades que podem ser alteradas. Quando essas propriedades são selecionadas (marcadas), os seguintes efeitos são ativados.

_Small Altera o tamanho da fonte para pequeno

Página 1-20

_Full page Permite que você coloque o cursor depois do final da linha. _Indent Avanço automático do cursor ao introduzir mudança de linha

Instruções para uso do editor de linha são apresentadas no capítulo 2 do guia do usuário.

Selecionando as propriedades da pilha

Pressione o botão H para ativar a tela de entrada CALCULATOR MODES. Dentro do formulário de entrada CALCULATOR MODES, pressione o tecla @@DISP@ (D) para exibir a tela de entrada DISPLAY MODES. Pressione a tecla com a seta para baixo, ˜, uma vez para obter a linha Edit. Esta linha mostra três propriedades que podem ser alteradas. Quando essas propriedades são selecionadas (marcadas) os seguintes efeitos são ativados.

_Small Altera o tamanho da fonte para pequeno. Isso maximiza o

volume de informações exibidas no visor. Observe que esta selecção substitui a seleção de fonte para a exibição da pilha.

_Textbook Exibe as expressões matemáticas na notação matemática

gráfica.

Para ilustrar essas configurações, tanto no modo RPN como no modo algébrico, use o equation writer para digitar a seguinte integral definitiva:

‚O…Á0™„è™„¸\x™x`

No modo algébrico, a tela a seguir mostra os resultados dessas teclas pressionadas quando nem _Small nem _Textbook estão selecionados:

Página 1-21

Com apenas a opção _Small marcada, o visor exibe o seguinte:

Com a opção _Textbook selecionada (valor default), independente se a opção _Small for selecionada ou não, o visor mostra o seguinte resultado:

Selecionando as propriedades do equation writer (EQW)

Primeiramente, pressione o botão H para ativar a tela de entrada CALCULATOR MODES. Dentro da tela de entrada CALCULATOR MODES, pressione o tecla @@DISP@ (D) para exibir a tela de entrada DISPLAY MODES. Pressione a tecla com a seta para baixo, ˜, três vezes, para obter a linha EQW (Equation Writer). Esta linha mostra duas propriedades que podem ser alteradas. Quando estas propriedades são selecionadas (marcadas), os seguintes efeitos são ativados.

_Small Altera o tamanho da fonte para pequeno (small) ao

usar o equation editor.

_Small Stack Disp Mostra a fonte pequena na pilha depois de usar o

equation editor.

Instruções detalhadas sobre o uso do equation editor (EQW) são apresentas neste guia.

∞

−

Para ver um exemplo da integral

_Small Stack Disp na linha EQW da tela de entrada DISPLAY MODES exibe o seguinte:

dXe

∫

, apresentada acima, selecionar

Página 1-22

Referências

Referências adicionais sobre os assuntos mencionados neste capítulo podem ser encontradas no Capítulo 1 e no Apêndice C do guia do usuário da calculadora.

Página 1-23

Capítulo 2 Apresentação da calculadora

Neste capítulo apresentamos uma série de operações básicas da calculadora incluindo o uso do Equation Writer e a manipulação de objetos de dados na calculadora. Estude os exemplos neste capítulo para ter uma boa idéia da capacidade da calculadora para aplicações futuras.

Objetos da calculadora

Alguns dos objetos mais usados são: reais (números reais, escritos com um ponto decimal, p. ex, -0.0023, 3.56), inteiros (números inteiros, escritos sem um ponto decimal, p. ex., 1232, -123212123), números complexos (escritos como um par ordenado, p. ex., (3,-2)), listas, etc. Os objetos da calculadora são descritos nos Capítulos 2 e 24, no Guia do Usuário da calculadora.

Editando as expressões na pilha

Nesta seção apresentamos exemplos de edição de expressões diretamente no visor ou pilha da calculadora.

Criando expressões aritméticas

Para este exemplo, selecionamos o modo de operação Algébrico e um formato Fix com 3 decimais para o visor. Vamos agora inserir a expressão aritmética:

0.1

0.5

⋅

Para inserir esta expressão, pressione as seguintes teclas:

5.*„Ü1.+1/7.5™/ „ÜR3.-2.Q3

A expressão resultante é: 5*(1+1/7.5)/( ƒ3-2^3).

5.7

0.20.3

−

Página 2-1

Pressione ` para obter a expressão no visor, como segue:

Observe que, se seu CAS for configurado para EXACT (consulte Apêndice C no Guia do Usuário) e você inserir sua expressão usando os números inteiros para os valores inteiros, o resultado é uma grandeza simbólica, p. ex.,

5*„Ü1+1/7.5™/

„ÜR3-2Q3

Antes de produzir um resultado, você será solicitado a mudar para o modo Approximate. Aceite a alteração para obter o seguinte resultado (mostrado no modo Fix com três casas decimais – consulte o Capítulo 1):

Neste caso, quando a expressão for inserida diretamente na pilha, logo que pressionar `, a calculadora tentará calcular um valor para a expressão. Entretanto, se a expressão for inserida entre aspas, a calculadora reproduzirá a expressão tal como foi inserida. Por exemplo:

³5*„Ü1+1/7.5™/

„ÜR3-2Q3`

O resultado será mostrado como segue:

Página 2-2

Para solucionar a expressão podemos usar a função EVAL, como segue:

µ„î`

Se o CAS for definido para Exact, você será solicitado a aprovar a alteração das configurações CAS para Approx. Logo que isto for feito, você obterá o mesmo resultado de antes.

Uma forma alternativa de solucionar a expressão inserida anteriormente entre aspas é usando a opção …ï.

Vamos inserir agora a expressão usada acima quando a calculadora for definida para o modo de operação RPN. Definimos também o CAS para Exact e o visor para Textbook. As teclas usadas para inserir a expressão entre aspas são as mesmas usadas anteriormente, ou seja:

³5*„Ü1+1/7.5™/

„ÜR3-2Q3`

Resultando em

Pressione ` novamente para manter duas cópias da expressão disponíveis na pilha para cálculo. Calculamos primeiro a expressão usando a função EVAL e a seguir usando a função NUM: µ.

Página 2-3

Esta expressão é semi-simbólica no sentido de que existem componentes de ponto flutuante para o resultado, como também uma √3. Depois, alternamos os locais na pilha (usando ™) e calculamos usando a função NUM, ou seja, ™…ï.

Este último resultado é puramente numérico, de forma que os dois resultados na pilha, embora representem a mesma expressão, parecem diferentes. Para verificar se não são, subtraímos os dois valores e calculamos esta diferença usando a função EVAL: -µ. O resultado é zero (0.).

Para obter informações adicionais sobre a edição de expressões aritméticas no visor ou na pilha, consulte o Capítulo 2 no guia do usuário da calculadora.

Criando expressões algébricas

As expressões algébricas incluem não apenas números, mas também nomes de variáveis. Como exemplo, vamos inserir a seguinte expressão algébrica:

L212

Definimos o modo de operação da calculadora para Algébrico, o CAS para Exact e o visor para Textbook. Para inserir esta expressão algébrica pressionamos as seguintes teclas:

³2*~l*R„Ü1+~„x/~r™/ „ Ü ~r+~„y™+2*~l/~„b

Pressione ` para obter o seguinte resultado:

Página 2-4

A forma de inserção desta expressão, com a calculadora definida no modo RPN, é exatamente a mesma deste exercício, feito no modo Algébrico.

Para obter informações adicionais sobre a edição de expressões algébricas no visor ou na pilha, consulte o Capítulo 2 no Guia do Usuário da calculadora.

Usando o Equation Writer (EQW) para criar expressões

O Equation Writer é uma ferramenta poderosa que não apenas permite que você insira ou visualize uma equação, mas também permite que você modifique e trabalhe/aplique funções em toda a equação ou em parte dela.

O Equation Writer é iniciado pressionando-se a combinação de teclas ‚ O (a terceira tecla na quarta fileira da parte superior do teclado). A tela resultante é a seguinte. Pressione L para visualizar a segunda página do menu:

Os seis ítens do menu de tecla de função para o Equation Writer ativa as funções EDIT, CURS, BIG, EVAL, FACTOR, SIMPLIFY, CMDS e HELP. Informações detalhadas sobre estas funções são fornecidas no Capítulo 3 do Guia do Usuário da calculadora.

Criando expressões aritméticas

O ato de Inserir expressões aritméticas no Equation Writer é muito similar ao de inserir uma expressão aritmética entre aspas na pilha: A principal diferença é que no Equation Writer as expressões produzidas são escritas no estilo “textbook” em vez de um estilo de entrada linear. Por exemplo, tente pressionar as seguintes teclas na tela do Equation Writer:

5/5+2

O resultado é a expressão

Página 2-5

O cursor é mostrado como uma tecla para a esquerda. O cursor indica o local atual de edição. Por exemplo, para o cursor no local indicado acima, digite agora:

*„Ü5+1/3

A expressão editada é similar à seguinte:

Suponha que você deseje substituir o valor entre parênteses no denominador (ou seja, 5+1/3) por (5+π para excluir a expressão atual 1/3 e então substituímos esta fração por π

/2). Primeiro, usamos a tecla de exclusão (ƒ)

/2,

como segue:

ƒƒƒ„ìQ2

Quando chegarmos a este ponto, a tela será similar à seguinte:

Para inserir o denominador 2 na expressão, precisamos realçar a expressão

inteira. Fazemos isso pressionando a tecla com a seta para a direita (™)

uma vez. Nesta altura, pressionamos as seguintes teclas:

Página 2-6

A expressão editada é agora similar à seguinte:

Suponha que agora você queira adicionar a fração 1/3 a toda esta expressão, ou seja, você quer inserir a expressão:

+⋅+

5(25

)

Primeiramente, precisamos realçar inteiramente o primeiro termo usando a tecla da seta para a direita ( ™) ou a seta para cima (—), repetidamente, até que a expressão inteira seja realçada, ou seja, sete vezes, produzindo:

OBSERVAÇÃO: Alternativamente, da posição original do cursor (para a direita de 2 no denominador de π2/2), podemos pressionar a combinação de teclas ‚—, interpretada como (‚ ‘ ).

Assim que a expressão for realçada conforme mostrado acima, digite +1/3 para adicionar a fração 1/3. Resultando em:

Página 2-7

Criando expressões algébricas

Uma expressão algébrica é muito similar a uma expressão aritmética, exceto pelo fato de que as letras dos alfabetos latino e grego podem ser incluídas. O processo de criação de uma expressão algébrica, portanto, segue a mesma idéia de criar uma expressão aritmética, exceto pelo fato de que também se usa o teclado alfabético..

Como ilustração do uso do Equation Writer para inserir uma equação algébrica, usaremos o seguinte exemplo. Suponha que desejemos inserir a expressão:

∆⋅+

−

⋅+

LNe

Pressione as seguintes teclas:

2 / R3 ™™* ~‚n + „¸\ ~‚m

™™*‚¹ ~„x + 2 * ~‚m * ~‚c

~„y ——— / ~‚t Q1/3

Isto resulta no seguinte:

 



 

3/1



Neste exemplo usamos diversas letras latinas em minúsculo, p. ex., (~„x), diversas letras gregas, p. ex., λ (~‚n), e até uma combinação de letras gregas e latinas, a saber, ∆y (~‚c

Página 2-8

~„y). Lembre-se de que para inserir letra latina em minúsculo, é necessário usar a combinação: ~„ seguida pela letra que você deseja inserir. Além disso, você pode sempre copiar os caracteres especiais usando o menu CHARS (…±) se você não memorizar a combinação de teclas pressionadas que a produziu. Uma lista de combinações de teclas ~‚ mais usadas está relacionada no Apêndice D do guia do usuário.

Para obter informações adicionais sobre edição, avaliação, fatoração e simplificação de expressões algébricas, consulte o Capítulo 2 do guia do usuário da calculadora.

Organizando dados na calculadora

Você pode organizar dados na calculadora armazenando as variáveis numa árvore de diretório. A base da árvore de diretórios da calculadora é o diretório HOME descrito a seguir.

O diretório HOME

Para ir ao diretório HOME, pressione a função UPDIR („§),repetindo conforme necessário, até que a especificação {HOME} seja mostrada na segunda linha do cabeçalho do visor. Alternativamente, use „ (mantendo pressionado) §. Para este exemplo, o diretório HOME contém somente o CASDIR. Ao pressionar-se J serão mostradas as variáveis no menu de tecla de função:

Subdiretórios

Para armazenar dados em uma árvore de diretório bem organizado você pode desejar criar os subdiretórios sob o diretório HOME e mais subdiretórios dentro de subdiretórios, numa hierarquia de diretórios similar à de pastas nos computadores modernos. Os subdiretórios receberão nomes que podem refletir os

Página 2-9

conteúdos de cada subdiretório ou qualquer nome arbitrário que você resolver dar. Para obter detalhes sobre a manipulação de diretórios, consulte o Capítulo 2 do guia do usuário da calculadora.

Variáveis

As variáveis são similares aos arquivos em um disco rígido de computador. Uma variável pode armazenar um objeto (valores numéricos, expressões algébricas, listas, vetores, matrizes, programas, etc). As variáveis são chamadas pelos seus nomes, que podem ser qualquer combinação de caracteres alfabéticos ou numéricos, iniciando com uma letra (latina ou grega). Alguns caracteres não-alfabéticos, tais como uma seta (→) podem ser usados em um nome de variável, se combinado com um caractere alfabético. Assim, ‘→A’ é um nome válido de variável, mas ‘→’ não é. Entre exemplos válidos de nomes de variáveis estão: ‘A’, ‘B’, ‘a’, ‘b’, ‘α’, ‘β’, ‘A1’, ‘AB12’, ‘A12’, ’Vel’, ’Z0’, ’z1’, etc.

Uma variável não pode ter o mesmo nome de uma função da calculadora. Os nomes das variáveis da calculadora reservados são os seguintes: ALRMDAT, CST, EQ, EXPR, IERR, IOPAR, MAXR, MINR, PICT, PPAR, PRTPAR, VPAR, ZPAR, der_, e, i, n1,n2, …, s1, s2, …, ΣDAT, ΣPAR, π, ∞

As variáveis podem ser organizadas em subdiretórios (consulte o Capítulo 2 no Guia do Usuário da calculadora).

Digitando os nomes das variáveis

Para nomear as varáveis, você terá que digitar a série de letras de uma vez, que pode ou não ser combinada com números. Para digitar séries de caracteres você pode bloquear o teclado alfabético como segue:

~~ bloqueia o teclado alfabético em maiúsculas. Quando bloqueado desta forma, ao pressionar-se „ antes de uma tecla de letra produz minúsculas, enquanto que ao pressionar-se a tecla ‚ ao mesmo tempo que a tecla da letra produz um caractere especial. Se o teclado alfabético já está bloqueado em maísculas e deseja-se bloqueá-lo em minúsculas, digite

„~

Página 2-10

Digite ~~„~ para bloquear o teclado alfabético em minúsculas. Quando bloqueado desta forma, pressionar „ antes da tecla de letra para produzir uma letra em maiúscula. Para desbloquear em minúsculas, pressione „~

Para desbloquear o teclado bloqueado para maiúsculas, pressione ~

Tente executar os seguintes exercícios:

³~~math` ³~~m„a„t„h` ³~~m„~at„h`

O visor da calculadora mostrará o seguinte (o lado esquerdo está no modo Algébrico e o lado direito no modo RPN):

Criando variáveis

A forma mais simples de criar uma variável é usando K. Os exemplos seguintes são usados para armazenar as variáveis relacionadas na tabela a seguir (pressione J se necessário, para ver o menu de variáveis):

Nome Conteúdo Tipo

A12 3×105 real

Q ‘r/(m+r)' algébrico

R [3,2,1] vetor z1 3+5i complexo p1 « → r 'π*r^2' » programa

-0.25 real

Página 2-11

• Modo Algébrico Para armazenar o valor de –0.25 na variável α:

0.25\ K ~‚a. Nesta altura, a tela será similar à seguinte:

Pressione ` para criar a variável. A variável é agora mostrada como um item do menu de tecla de função:

A seguir estão as teclas necessárias para inserir as variáveis restantes:

A12: 3V5K~a12`

Q: ³~„r/„Ü

~„m+~„r™™K~q`

R: „Ô3‚í2‚í1™K~r`

z1: 3+5*„¥ K~„z1` (Aceitar a alteração para o modo Complex, se solicitado).

p1: ‚å‚é~„r³„ì* ~„rQ2™™™K~„p1`..

A tela, nesta altura, é similar à seguinte:

Página 2-12

Você verá seis das sete variáveis listadas na parte inferior do visor: p1, z1, R, Q, A12, α.

• Modo RPN (Use H\@@OK@@ para mudar para o modo RPN). Use as seguintes teclas para armazenar o valor de –0.25 na variável α:

0.25\` ~‚a`. A tela, nesta altura, é similar à seguinte:

Esta expressão significa que o valor –0.25 está pronto para ser armazenado em α. Pressione K para criar a variável. A variável é agora mostrada como um item do menu de tecla de função:

Para inserir o valor 3×10

em A12, podemos usar uma versão mais

curta do procedimento: 3V5³~a12` K

Aqui está uma forma de inserir o conteúdo de Q.

Q: ³~„r/„Ü ~„m+~„r™™³~q` K

Para inserir o valor de R, podemos usar uma versão ainda mais curta do procedimento:

Página 2-13

R: „Ô3#2#1™³K

Observe que para separar os elementos de um vetor no modo RPN podemos usar a tecla de espaço (#), em vez da vírgula (‚í ), que foi usada acima no modo Algébrico.

z1: ³3+5*„¥ ³~„z1 K

p1: ‚å‚é~„r³„ì* ~„rQ2™™™³ ~„p1™` K.

A tela, nesta altura, é similar à seguinte:

Você verá seis das sete variáveis listadas na parte inferior do visor: p1, z1, R, Q, A12, α.

Verificando o conteúdo das variáveis

A forma mais simples de verificar um conteúdo de variável é pressionando-se o item do menu de tecla de função para a variável. Por exemplo, para as variáveis listadas acima, pressione as seguintes teclas para ver os conteúdos das variáveis:

Modo Algébrico

Digite estas teclas: J@@z1@@ ` @@@R@@ `@@@Q@@@ `. A tela, nesta altura, é similar à seguinte:

Modo RPN

Página 2-14

No modo RPN, é necessário apenas pressionar o item do menu de tecla de função correspondente para obter o conteúdo da variável numérica ou algébrica. Para o caso em estudo, podemos tentar observar as variáveis z1, R, Q, A12, α, criadas acima, como segue: J@@z1@@ @@@R@@ @@@Q@@ @@A12@@ @@ª@@

A tela, nesta altura, é similar à seguinte:

Use a tecla shift direita‚ seguida pelo item do menu de tecla de função.

Este acesso para visualizar os conteúdos de uma variável funciona da mesma forma em ambos os modos, Algébrico e RPN. Tente os seguintes exemplos em ambos os modos:

J‚@@p1@@ ‚ @@z1@@ ‚ @@@R@@ ‚@@@Q@@ ‚ @@A12@@

Isto produz as seguintes telas (modo Algébrico à esquerda, RPN à direita)

Observe que desta vez o conteúdo do programa p1 é listado no visor. Para ver as variáveis restantes neste diretório, use:

@@@ª@@ L ‚ @@@A@@

Listando os conteúdos de todas as variáveis no visor

Use a combinação de teclas ‚˜ para listar os conteúdos de todas as variáveis no visor. Por exemplo:

Página 2-15

Pressione $ para retornar ao visor normal da calculadora.

Excluindo variáveis

A forma mais simples de excluir as variáveis é usando a função PURGE. Esta função pode ser acessada diretamente usando o menu TOOLS (I) ou usando o menu FILES „¡@@OK@@ .

Usando a função PURGE (Apagar) na pilha no modo Algébrico

Nossa lista de variáveis contém as variáveis p1, z1, Q, R, e α. Usaremos o comando PURGE para excluir a variável p1. Pressione I @PURGE@ J@@p1@@ `. O visor mostrará agora a variável p1 removida:

Você pode agora usar o comando PURGE para apagar mais do que uma variável colocando seus nomes em uma lista no argumento do PURGE. Por exemplo, se quisermos agora apagar as variáveis R e Q, simultaneamente, podemos tentar o seguinte exercício. Pressione:

I @PURGE@ „ä³ J@@@R!@@ ™‚í ³ J@@@Q!@@

Nesta altura, a tela mostrará o seguinte comando pronto para ser executado:

Para terminar de excluir as variáveis, pressione `. O visor mostrará agora as variáveis restantes:

Página 2-16

Usando a função PURGE na pilha no modo RPN

Presumindo que a lista de variáveis contenha as variáveis p1, z1, Q, R, e α, usaremos o comando PURGE para excluir a variável p1. Pressione ³@@p1@@ ` I @PURGE@. O visor mostrará agora a variável p1 removida:

Para excluir duas variáveis simultaneamente, digamos as variáveis R e Q, primeiro crie uma lista (no modo RPN, não é necessário separar os elementos da lista por vírgulas como no modo Algébrico):

J „ä³ @@@R!@@ ™ ³ @@@Q!@@ `

Depois, pressione I@PURGE@ para apagar as variáveis.

Informações adicionais sobre a manipulação da variáveis estão disponíveis no Capítulo 2 do guia do usuário da calculadora.

Funções UNDO e CMD

As funções UNDO e CMD são úteis para recuperar os comandos recentes ou para reverter uma operação se for cometido um erro. Estas funções estão associadas à tecla HIST: UNDO resulta da seqüência de teclas ‚¯, enquanto o CMD resulta da seqüência de teclas „®.

CHOOSE boxes x MENU de tecla de função

Em alguns exercícios apresentados neste capítulo vimos menus com listas de comando exibidas na tela. Estas listas de menu são chamadas de Menus de lista de opções (CHOOSE boxes). Aqui indicamos a maneira de mudar de

Página 2-17

menu de lista de opções para menu de tecla de função (Soft Menu) e viceversa, através de um exercício.

Embora não seja aplicado a um exemplo específico, o presente exercício mostra as duas opções para os menus na calculadora (menu de lista de opções e menu de tecla de função). Neste exercício, para acessarmos o comando ORDER com o objetivo de reordenar as variáveis em um diretório, usamos, no modo ALG.

„°˜ Mostre a lista de opções PROG e selecione

MEMORY

@@OK@@ ˜˜˜˜ Mostre a lista de opções MEMORY e selecione

O menu UNITS

O menu Units é ativado pela combinação de teclas ‚Û(associadas com a tecla 6). Com o sinalizador do sistema 117 configure para CHOOSE boxes, o resultado é o seguinte menu:

Opção 1. Tools.. contém funções usadas para operar sobre as unidades (discutidas mais tarde). Opções de 2. Length. até 17.Viscosity.. contém menus com várias unidades para cada uma das grandezas descritas. Por exemplo, selecionando-se a opção 8. Force são mostrados os seguintes menus de unidade:

O usuário reconhecerá a maioria destas unidades (alguns, p. ex., dina, não são usados freqüentemente hoje em dia) de suas aulas de física: N = newtons, dyn = dinas, gf = gramas-força (para distingüir de grama-massa ou

Página 3-9

apenas grama, uma unidade de massa), kip = quilo-libra (1000 libras), lbf = libra-força (para distinguir da libra, unidade de massa), pdl = libra.

Para anexar um objeto de unidade a um número, o número deve ser seguido de um sinal de sublinhado. Assim a força de 5 N será inserida como 5_N.

Para operações abrangentes com unidades, o menu SOFT fornece uma forma mais conveniente de anexar as unidades. Altere o sinalizador do sistema 117 para menus SOFT (consulte o Capítulo 2) e use a combinação de teclas ‚Û para obter os seguintes menus. Pressione L para mudar para a próxima página do menu.

Ao pressionar-se a tecla de função correta será aberto o submenu das unidades para esta seleção em particular. Por exemplo, para o submenu @)SPEED, as seguintes unidades estão disponíveis:

Pressionando a tecla de função @)UNITS o levará de volta para o menu UNITS.

Lembre-se de que você pode sempre listar todos os símbolos dos menus no visor usando ‚˜, p. ex., para o conjunto @)ENRG de unidades os seguintes símbolos serão listados:

Página 3-10

Observação: Use a tecla L ou a sequência de teclas „«para navegar através dos menus.

Unidades disponíveis

Para obter uma lista completa de unidades, consulte o Capítulo 3 no Guia do Usuário da calculadora.

Anexando as unidades aos números

Para anexar um objeto de unidade a um número, o número deve ser seguido por um sinal de sublinhado (‚Ý, tecla(8,5)). Assim a força de 5 N será inserida como 5_N.

Aqui está a seqüência de etapas para inserir este número no modo ALG, o sinalizador do sistema 117 configurado para CHOOSE boxes:

5‚Ý ‚Û 8@@OK@@ @@OK@@ `

Observação: Se esquecer o sublinhado, o resultado é a expressão 5*N, onde N aqui representa um nome possível de variável e não Newtons.

Para inserir este mesmo valor com a calculadora no modo RPN, use as seguintes teclas:

5‚Û8@@OK@@ @@OK@@

Observe que o sublinhado é inserido automaticamente quando o modo RPN estiver ativo.

Página 3-11

As seqüências de teclas para inserir as unidades quando a opção SOFT menu estiver selecionada, em ambos os modos RPN e ALG, são ilustradas a

seguir. Por exemplo, no modo ALG, para inserir o valor 5_N use:

5‚Ý ‚ÛL @)@FORCE @ @@N@@ `

A mesma grandeza, inserida no modo RPN usa a seguinte seqüência de teclas:

5‚ÛL @)@FORCE @ @@N@@

Observação: Você pode inserir uma grandeza com unidades digitando o sublinhado e as unidades com a tecla ~, p. ex., 5‚Ý~n produzirá a entrada: 5_N

Prefixos de unidades

Você pode inserir os prefixos para as unidades de acordo com a seguinte tabela de prefixos do sistema SI: A abreviação do prefixo é mostrada primeiro, seguida de seu nome e pelo expoente x no fator 10

correspondente a cada prefixo:

____________________________________________________ Prefixo Nome x Prefixo Nome x ____________________________________________________ Y yotta +24 d deci -1 Z zetta +21 c centi -2 E exa +18 m milli -3 P peta +15 µ micro -6 T tera +12 n nano -9 G giga +9 p pico -12 M mega +6 f femto -15 k,K kilo +3 a atto -18 h,H hecto +2 z zepto -21 D(*) deka +1 y yocto -24 _____________________________________________________

Página 3-12

(*) No sistema SI, este prefixo é da em vez de D. Entretando, use D para deka na calculadora.

Para inserir esses prefixos, digite apenas o prefixo usando o teclado ~. Por exemplo, para inserir 123 pm (1 picômetro), use:

123‚Ý~„p~„m

Ao usar UBASE para (digite o nome) converter para a unidade default (1 m) o resultado é:

Operações com unidades

Aqui estão alguns exemplos de cálculos usando o modo de operação ALG. Observe que, ao multiplicar ou dividir as grandezas com unidades, é necessário incluir cada valor com suas unidades entre parênteses). Assim, para inserir, por exemplo, o produto 12.5m × 5.2 jd, digite-o assim (12.5_m)*(5.2_jd) `:

que resulta em 65_(m⋅jd). Para converter para unidades do sistema SI, use a função UBASE (encontre-a usando o catálogo de comandos, ‚ N):

Página 3-13

Observação: Lembre-se de que a variável ANS(1) está disponível através da combinação de teclas „î(associada com a tecla `).

Para calcular uma divisão, digamos, 3250 mi / 50 h, insira-a como

(3250_mi)/(50_h) `

que transformada nas unidades SI com a função UBASE, produz:

Adição e subtração podem ser feitas, no modo ALG, sem utilizar os parênteses, p. ex., 5 m + 3200 mm, pode ser inserido apenas como

5_m + 3200_mm `.

Expressões mais complicadas exigem o uso de parênteses, p. ex.,

(12_mm)*(1_cm^2)/(2_s) `:

Cálculos na pilha no modo RPN, não requerem que você inclua os diferentes termos nos parênteses, p. ex.,

12 @@@m@@@ 1.5 @@yd@@ *

3250 @@mi@@ 50 @@@h@@@ /

Estas operações produzem o seguinte resultado:

Conversão de unidades

O menu UNITS contém um submenu TOOLS que oferece as seguintes funções:

CONVERT(x,y): converte do objeto de unidade x para a unidade de

objeto y

Página 3-14

UBASE(x): converte objeto de unidade x em unidades SI UVAL(x): extrai o valor da unidade de objeto x UFACT(x,y): fatora uma unidade x do objeto de unidade y UNIT(x,y): combina o valor de x com unidades de y

Exemplos da função CONVERT são mostrados abaixo. Exemplos de outras funções UNIT/TOOLS estão disponíveis no Capítulo 3 do guia do usuário da calculadora. Por exemplo, para converter 33 watts para BTUs, use uma das seguintes entradas:

CONVERT(33_W,1_hp) `

CONVERT(33_W,11_hp) `

Constantes físicas na calculadora

As constantes físicas da calculadora estão contidas em constants library (biblioteca de constantes) ativadas com o comando CONLIB. Para ativar este comando você pode simplesmente digitá-lo na pilha: ~~conlib` ou você pode selecionar o comando CONLIB do catálogo de comandos, como segue: Primeiro, abra o catálogo usando: ‚N~c. Depois, use as teclas com setas para cima e para baixo —˜ para selecionar CONLIB. Finalmente, pressione a tecla de função F(@@OK@@). Pressione `, se necessário. Use as setas para cima e para baixo (—˜) para navegar através da lista de constantes na sua calculadora.

As teclas de função correspondentes à tela CONSTANTS LIBRARY incluem as seguintes funções:

SI quando selecionado, os valores das constantes são

mostrados em unidades SI (*)

ENGL quando selecionado, os valores das constantes são

mostrados em unidades inglesas (*)

UNIT quando selecionado, as constantes são mostradas com as

unidades anexadas (*)

Página 3-15

VALUE quando selecionado, as constantes são mostradas sem

unidades STK copia valores (com ou sem unidades) para a pilha QUIT sai da biblioteca de constantes

(*) Ativada apenas se a opção VALUE estiver selecionada.

Este é o modo com que a parte superior da tela CONSTANTS LIBRARY se parece quando a opção VALUE é selecionada (unidades no sistema SI):

Para ver os valores das constantes no sistema inglês (ou Imperial), pressione a opção @ENGL:

Se desmarcarmos a opção UNITS (pressione @UNITS ) apenas os valores são mostrados (Unidades inglesas selecionadas neste caso):

Para copiar os valores de Vm para a pilha, selecione o nome da variável e pressione !²STK, e depois pressione @QUIT@. Para a calculadora definida para ALG, a tela parecerá desta forma:

Página 3-16

O visor mostra o que é chamado de valor identificado, Vm:359.0394. Aqui, Vm, é o identificador deste resultado. Qualquer operação aritmética com este número ignorará o identificador. Tente, por exemplo:

‚¹2*„î `

que produz:

A mesma operação no modo RPN exigirá as seguintes teclas (depois do valor de Vm ser extraído da biblioteca de constantes):

2`*‚¹

Definindo e usando funções

Os usuários podem definir suas próprias funções usando o comando DEFINE disponível através da sequência de teclas „à (associada com a tecla

2). A função deve ser inserida no seguinte formato:

Nome_da função(arguments) = expressão_contendo_argumentos

Por exemplo, podemos definir uma função simples

H(x) = ln(x+1) + exp(-x)

Suponha que você precisa solucionar esta função para um número de valores discretos e, portanto, você deseja pressionar um único botão e obter o resultado desejado sem ter que digitar a expressão no lado direito para cada valor separado. No exemplo seguinte, presumimos que você definiu sua calculadora para o modo ALG. Insira a seguinte seqüência de teclas:

„à³~h„Ü~„x™‚Å

Página 3-17

‚¹~„x+1™+„¸~„x`

O visor deverá ser similar a este:

Pressione a tecla J e perceberá que existe uma nova variável no seu menu de teclas de função (@@@H@@). Para ver o conteúdo desta variável pressione ‚@@@H@@. O visor mostrará agora:

Assim, a variável H contém um programa definido por:

<<  x ‘LN(x+1) + EXP(x)’ >>

Este é um programa simples na linguagem de programação default da HP 48G série e também incorporado à série HP 49 G. Esta linguagem de programação é chamada de UserRPL (Consulte os Capítulos 20 e 21 no Guia do Usuário da calculadora). O programa mostrado acima é relativamente simples e consiste de duas partes, contidas entre os recipientes do programa << >>:

• Entrada:  x  x

• Processo ‘LN(x+1) + EXP(x) ‘

Isto deve ser interpretado como se dissesse: insira um valor que é temporariamente atribuído ao nome x (mencionado como uma varável local), solucione a expressão entre aspas que contém esta variável local e mostre a solução da expressão.

Página 3-18

Para ativar a função no modo ALG, digite o nome da função seguida pelo argumento entre parênteses, p. ex., @@@H@@@ „Ü2`. Alguns exemplos são mostrados a seguir:

No modo RPN, para ativar a função insira o argumento primeiro, depois pressione a tecla de função correspondente ao nome da variável @@@H@@@ . Por exemplo, você poderia tentar: 2`@@@H@@@ . Os outros exemplos mostrados acima podem ser inseridos usando: 1.2`@@@H@@@ , 2`/3`@@@H@@@ .

Referências

Informações adicionais sobre operações com números reais com a calculadora estão descritos no capítulo 3 do guia do usuário.

Página 3-19

Capítulo 4 Cálculos com números complexos

Este capítulo mostra exemplos de cálculos e aplicações de funções para números complexos.

Definições

Um número complexo z é escrito como z = x + iy, (forma cartesiana) onde x e y são números reais e i é a unidade imaginária definida por i número tem uma parte real, x = Re(z) e uma parte imaginária, y = Im(z). A

forma polar de um número complexo é z = re

|z| =

yx + é o módulo do número complexo z e θ = Arg(z) =

= r⋅cosθ + i r⋅sinθ, onde r =

arctan(y/x) é o argumento do número complexo z. O conjugado complexo

de um número complexo z = x + iy = re

de z, –z = -x-iy = - re

, pode ser visto como a reflexão de z sobre a origem.

, éz = x – iy = re

= -1. O

-i

. O negativo

Configurando a calculadora para modo COMPLEX

Para trabalhar com números complexos, selecione o modo complexo de CAS:

H)@@CAS@ ˜˜™@CHK@@

O modo COMPLEX será selecionado se a tela CAS MODES mostrar a opção _Complex marcada, ou seja,

Pressione @@OK@@ duas vezes para retornar à pilha.

Página 4-1

Inserindo números complexos

Os números complexos podem ser inseridos na calculadora em uma das duas representações cartesianas, a saber, x+iy ou (x,y). Os resultados na calculadora serão mostrados no formado par ordenado, ou seja (x,y). Por exemplo, com a calculadora no modo ALG, o número complexo (3.5,-1.2), é inserido como:

„Ü3.5‚í\1.2`

Um número complexo pode também ser inserido na forma x+iy. Por exemplo, no modo ALG, 3.5-1.2i é inserido como (aceita alteração de modo) :

3.5 -1.2*„¥`

No modo RPN, estes números serão inseridos pressionando-se as seguintes teclas:

„Ü3.5‚í1.2\`

(Observe que a tecla de alteração de sinal é inserida depois do número 1.2, na ordem oposta ao do exercício no modo ALG) e

³3.5 -1.2*„¥`

(Observe que é necessário inserir um apóstrofo antes de digitar o número

3.5-1.2i no modo RPN).

Para inserir a unidade de número imaginário digite: „¥(a tecla I).

A representação polar de um número complexo

A representação polar do número complexo 3.5-1.2i, inserida acima, é obtida alterando o sistema de coordenadas para cilíndrico ou polar (usando a função CYLIN). Você pode encontrar esta função no catálogo (‚N). Você também poderá alternar a coordenada para POLAR usando a tecla H. Alternando para coordenada polar com a medida angular em radianos, produz o resultado:

Página 4-2

O resultado mostrado acima representa uma magnitude, 3.7, e um ângulo de

0.33029…. O símbolo do ângulo (∠) é mostrado na frente da medida do ângulo.

Retorne para as coordenadas retangulares ou cartesianas usando a função RECT (disponível no catálogo, ‚N). Um número complexo na

representação polar é escrito como z = r⋅e

. Você pode inserir este número complexo na calculadora usando um par ordenado da forma (r, ∠θ). O símbolo do ângulo (∠) pode ser inserido como ~‚6. Por exemplo, o número complexo z = 5.2e

1.5i

, pode ser inserido conforme a seguir (as

imagens mostram a pilha RPN antes e depois de inserir o número):

Dado que o sistema da calculadora é definido para retangular (ou cartesiano), a calculadora converte automaticamente o número inserido para coordenadas cartesianas, p. ex., x = r cos θ, y = r sin θ, resultando, neste caso, em (0.3678…, 5.18…).

Por outro lado, se o sistema de coordenada for definido para coordenadas cilíndricas (use CYLIN), a inserção um número complexo (x,y), onde x e y são números reais, produzirá uma representação polar. Por exemplo, nas coordenadas cilíndricas, insira o número (3.,2.). A figura abaixo mostra a pilha RPN, antes e depois de inserir este número:

Página 4-3

Operações Simples com números complexos

Números complexos podem ser combinados usando as quatro operações fundamentais (+-*/). O resultado segue as normas da álgebra com a ressalva de que i similares àquelas com números reais. Por exemplo, com a calculadora no modo ALG e o CAS configurado para Complex, tente as seguintes operações:

= -1. As operações com números complexos são

(3+5i) + (6-3i) = (9,2);

(5-2i) - (3+4i) = (2,-6)

(3-i)(2-4i) = (2,-14);

(5-2i)/(3+4i) = (0.28,-1.04)

1/(3+4i) = (0.12, -0.16) ;

-(5-3i) = -5 + 3i

OS menus CMPLX

Existem dois menus CMPLX (números CoMPLeXos) disponíveis nesta calculadora. Um está disponível através do menu MTH (apresentado no Capítulo 3) e outro diretamente no teclado (‚ß). Os dois menus CMPLX são apresentados a seguir.

Menu CMPLX através do menu MTH

Presumindo que o sinalizador do sistema 117 esteja configurado para CHOOSE boxes (consulte o capítulo 2), o submenu CMPLX dentro do menu MTH será acessado usando: „´9 @@OK@@ . As funções disponíveis são as seguintes:

O primeiro menu (opções de 1 a 6) mostra as seguintes funções:

Página 4-4

RE(z) : Parte real de um número complexo IM(z) : Parte imaginária de um número complexo

C→R(z) : Separa um número complexo em suas partes real e imaginária R→C(x,y) : Forma o número complexo (x,y) dos números reais x e y

ABS(z) : Calcula a magnitude de um número complexo. ARG(z) : Calcula o argumento de um número complexo. SIGN(z) : Calcula um número complexo de magnitude unitária como z/|z|. NEG(z) : Altera o sinal de z CONJ(z) : Produz o conjugado complexo de z Exemplos das aplicações destas funções são mostradas a seguir em coordenadas RECT. Lembre-se que, para o modo ALG, a função deve preceder o argumento, enquanto no modo RPN você insere o argumento primeiro e depois seleciona a função. Alem disso, lembre-se de que você pode obter estas funções como símbolos do menu de tecla de funções alterando as configurações do sinalizador do sistema 117 (consulte o capítulo 2).

Menu CMPLX no teclado

O segundo menu CMPLX é acessível usando a tecla shift direita associada com a tecla 1, p. ex., ‚ß. Com o sinalizador do sistema 117 configurado para CHOOSE boxes, o menu CMPLX do teclado aparece como as telas a seguir:

Página 4-5

O menu resultante inclui algumas das funções já introduzidas na seção anterior, a saber, ARG, ABS, CONJ, IM, NEG, RE e SIGN. Inclui também a função i que tem a mesma finalidade que a combinação de teclas „¥.

Funções aplicadas a números complexos

Muitas das funções baseadas no teclado e nas funções do menu MTH definidas no capítulo 3 para os números reais (p. ex.: SQ,LN, e podem ser aplicadas aos números complexos. O resultado é outro número complexo, como ilustrado nos seguintes exemplos.

, etc.),

Observação: Ao usar as funções trigonométricas e seus inversos com os números complexos os argumentos não são mais ângulos. Portanto, a medida

Página 4-6

angular selecionada para a calculadora não tem validade nestas funções com argumentos complexos.

Função DROITE: equação de uma linha reta

A função DROITE tem como argumento dois números complexos, digamos, x

+iy e x2+iy2, e retorna a equação da linha reta, digamos, y = a+bx, que

contém os pontos (x e B(6,2) pode ser encontrada como segue (exemplo no modo Algébrico):

A função DROITE é encontrada no catálogo de comandos (‚N). Se a calculadora estiver em modo APPROX, o resultado será Y = 5.*(X-5.)-3.

) e (x2,y2). Por exemplo, a linha entre os pontos A(5,-3)

1,y1

Referências

Informações adicionais sobre operações com números complexos podem ser obtidas no Capítulo 4 do guia do usuário da calculadora.

Página 4-7

Capítulo 5 Operações algébricas e aritméticas

Um objeto algébrico é qualquer número, nome de variável ou expressão algébrica que possa sofrer operações, manipulações e combinações de acordo com as normas algébricas. Exemplos de objetos algébricos são descritos a seguir:

• Um número: 12.3, 15.2_m, ‘π’, ‘e’, ‘i’

• Um nome de variável: ‘a’, ‘ux’, ‘width’, etc.

• Uma expressão: ‘p*D^2/4’,’f*(L/D)*(V^2/(2*g))’,

• Uma equação: ‘p*V=n*R*T’, ‘Q=(Cu/n)*A(y)*R(y)^(2/3)*√So’

Inserindo objetos algébricos

Os objetos algébricos podem ser criados digitando-se o objeto entre aspas simples diretamente no nível 1 da pilha usando-se o Equation Writer [EQW]. Por exemplo, para inserir o objeto algébrico ‘π*D^2/4’ diretamente no nível 1 da pilha use:

³„ì*~dQ2/4`

Um objeto algébrico pode também ser construído no Equation Writer e depois enviado à pilha ou manipulado no próprio Equation Writer. A operação do Equation Writer foi descrita no capítulo 2. Como exercício, construa o seguinte objeto algébrico no Equation Writer:

Pagina 5-1

Depois de construir o objeto, pressione ` para exibi-lo na pilha (modos ALG e RPN mostrados abaixo):

Operações simples com objetos algébricos

Os objetos algébricos podem ser adicionados, subtraídos, multiplicados e divididos (exceto por zero), elevados a uma potência e usados como argumentos por várias funções-padrão (exponencial, logarítmica, trigonométrica, hiperbólica, etc), como se fossem números reais ou complexos. Para demonstrar as operações básicas com os objetos algébricos, criaremos alguns objetos, digamos ‘π*R^2’ e ‘g*t^2/4’ que serão armazenados nas variáveis A1 e A2 (consulte o capítulo 2 para aprender como criar variáveis e armazenar valores nelas). Aqui estão as teclas para armazenar a variável A1 no modo ALG.

³„ì*~rQ2™K ~a1 `

resultando em:

As teclas correspondentes ao modo RPN são:

„ì~r`2Qx ~a1 K

Depois de armazenar a variável A2 e pressionar a tecla, a tela mostrará a variável como segue:

Pagina 5-2

No modo ALG, as seguintes teclas mostrarão uma série de operações com os objetos algébricos contidos nas variáveis @@A1@@ e @@A2@@ (pressione J para recuperar o menu de variáveis):

@@A1@@ + @@A2@@ ` @@A1@@ - @@A2@@ `

@@A1@@ * @@A2@@ ` @@A1@@ / @@A2@@ `

‚¹@@A1@@ „¸v @@A2@@

@@A1@ ` @@A2@@ + @@A1@@ ` @@A2@@ -

@@A1@@ ` @@A2@@ * @@A1@@ ` @@A2@@ /

Pagina 5-3

@@A1@@ ` ‚¹ @@A2@@ ` „¸

Funções no menu ALG

O menu ALG (Algébrico) está disponível através da sequência de teclas ‚× (associadas com a tecla 4). Com o sinalizador do sistema 117 configurado para CHOOSE boxes, o menu ALG mostra as seguintes funções:

Em vez de listar a descrição de cada função neste Guia, o usuário está convidado a buscar a descrição usando a ajuda da calculadora: I L @)HELP@ ` . Para localizar uma função em particular, digite a primeira letra desta função. Por exemplo, para a função COLLECT digitamos ~c, depois usamos as teclas com as setas para cima e para baixo, —˜, para localizar COLLECT dentro da janela de ajuda.

Para concluir a operação pressione @@OK@@. Aqui está o visor de ajuda para a função COLLECT:

Observamos que, na parte inferior do visor, a linha See: EXPAND FACTOR sugere ligações com outras entradas de ajuda, as funções EXPAND e FACTOR. Para passar diretamente para estas entradas, pressione a tecla virtual @SEE1! para EXPAND e @SEE2! para FACTOR. Pressionando @SEE1!, por exemplo, mostra a seguinte informação para EXPAND, enquanto @SEE2! mostra a informação para FACTOR:

Pagina 5-4

Copie os exemplos fornecidos na sua pilha pressionando @ECHO!. Por exemplo, para a entrada EXPAND mostrada acima, pressione a tecla de função @ECHO! para copiar o seguinte exemplo na pilha (pressione ` para executar o comando):

Assim, deixamos para o usuário explorar as aplicações das funções no menu ALG. Esta é a lista de comandos:

Por exemplo, para a função SUBST, encontramos a seguinte CAS entrada da ajuda:

Observação: Lembre-se de que, para usar essas ou quaisquer outras funções no modo RPN, é necessário inserir o argumento primeiro e depois a função. Por exemplo, TEXPAND, no modo RPN será definifo como:

Pagina 5-5

Nesta altura, selecione a função TEXPAND do menu ALG (ou diretamente do catálogo ‚N), para concluir a operação.

³„¸+~x+~y`

Operações com funções transcendentais

A calculadora oferece diversas funções que podem ser usadas para substituir as expressões contendo as funções logarítmicas e exponenciais („Ð), como também as funções trigonométricas (‚Ñ).

Expansão e fatoração usando as funções log-exp

A seqüência de teclas „Ð produz o seguinte menu:

Informações e exemplos destes comandos estão disponíveis na ajuda da calculadora. Por exemplo, a descrição de EXPLN é mostrada no lado esquerdo e o exemplo da ajuda é mostrado a direita:

Expansão e fatoração usando as funções trigonométricas

O menu TRIG, acessado usando ‚Ñ, mostra as seguintes funções:

Pagina 5-6

Estas funções permitem simplificar as expressões substituindo algumas categorias de funções trigonométricas por outras. Por exemplo, a função ACOS2S permite substituir a função arccosine (acos(x)) por sua expressão em termos de arcsine (asin(x)).

A descrição desses comandos e exemplos de suas aplicações estão disponíveis na ajuda da calculadora (IL@HELP). O usuário está convidado a explorar essa ajuda para encontrar as informações sobre os comandos do menu TRIG.

Funções no menu ARITHMETIC

O menu ARITHMETIC é iniciado através da combinação de teclas „Û (associada à tecla 1). Com o sinalizador do sistema 117 configurado para CHOOSE boxes, „Þ, o resultado é o seguinte menu:

Desta lista de menu, as opções de 5 a 9 (DIVIS, FACTORS, LGCD, PROPFRAC, SIMP2) correspondem às funções comuns que se aplicam a números inteiros ou a polinômios. As opções restantes (1. INTEGER, 2.

Pagina 5-7

POLYNOMIAL, 3. MODULO e 4. PERMUTATION) são, na verdade, submenus de funções que se aplicam a objetos matemáticos específicos. Quando o sinalizador do sistema 117 for configurado para SOFT menus, o menu ARITHMETIC („Þ) produzirá:

A seguir, apresentamos as entradas da ajuda para as funções FACTORS e SIMP2 no menu ARITHMETIC:

FACTORS: SIMP2:

As funções associadas aos submenus ARITHMETIC: INTEGER, POLYNOMIAL, MODULO e PERMUTATION são apresentadas em detalhe no Capítulo 5 do guia do usuário da calculadora. As seções a seguir mostram algumas aplicações para polinômios e frações.

Polinômios

Polinômios são expressões algébricas que consistem em um ou mais termos contendo potências decrescentes de uma dada variável. Por exemplo, ‘X^3+2*X^2-3*X+2’ é um polinômio de terceira ordem em X, ao passo que ‘SIN(X)^2-2’ é um polinômio de segunda ordem em SIN(X). As funções COLLECT e EXPAND podem ser usadas com polinômios, como anteriormente mostrado. Outras aplicações de funções polinomiais são apresentadas a seguir:

Pagina 5-8

A função HORNER

A função HORNER („Þ, POLYNOMIAL, HORNER) produz a divisão Horner ou divisão sintética de um polinômio P(X) pelo fator (X-a), ou seja, HORNER(P(X),a) = {Q(X), a, P(a)}, onde P(X) = Q(X)(X-a)+P(a). Por exemplo,

HORNER(‘X^3+2*X^2-3*X+1’,2) = {X^2+4*X+5 2 11}

i.e., X

+2X2-3X+1 = (X2+4X+5)(X-2)+11. Também,

HORNER(‘X^6-1’,-5)=

{ X^5-5*X^4+25*X^3-125*X^2+625*X-3125 -5 15624}

ou seja, X

-1 = (X5-5*X4+25X3-125X2+625X-3125)(X+5)+15624.

A variável VX

A maior parte dos exemplos com polinômios acima foi escrita usando a variável X. Isto porque uma variável chamada VX existe no diretório da calculadora {HOME CASDIR} que aceita, como padrão, o valor de ‘X’. Este é o nome da variável independente para as aplicações algébricas e de cálculo. Evite usar a variável VX nos seus programas ou equações, para não ficar confuso com a VX do CAS. Para obter informações adicionais sobre a variável do CAS, consulte o Apêndice C no guia do usuário da calculadora.

A função PCOEF

Dado um conjunto que contém as raízes de um polinômio, a função PCOEF gera uma série de combinações contendo os coeficientes do polinômio correspondente. Os coeficientes correspondem a ordem decrescente da variável independente. Por exemplo:

PCOEF([-2, –1, 0 ,1, 1, 2]) = [1. –1. –5. 5. 4. –4. 0.],

que representa o polinômio X

6-X5

-5X4+5X3+4X2-4X.

Pagina 5-9

A função PROOT

Dada uma série contendo os coeficientes de um polinômio, na ordem decrescente, a função PROOT fornece as raízes do polinômio. Exemplo, para

+5X+6 =0, PROOT([1,–5,6]) = [2. 3.].

As funções QUOT e REMAINDER

As funções QUOT e REMAINDER fornecem, respectivamente, o coeficiente Q(X) e o resto R(X), resultantes da divisão de dois polinômios, P Em outras palavras,s eles fornecem os valores de Q(X) e R(X) de P Q(X) + R(X)/P

Assim podemos escrever: (X

Observação: você poderia obter o último resultado usando PARTFRAC:

(X). Por exemplo:

QUOT(‘X^3-2*X+2’, ‘X-1’) = ‘X^2+X-1’

REMAINDER(‘X^3-2*X+2’, ‘X-1’) = 1.

-2X+2)/(X-1) = X2+X-1 + 1/(X-1).

PARTFRAC(‘(X^3-2*X+2)/(X-1)’) = ‘X^2+X-1 + 1/(X-1)’.

(X) e P2(X).

(X)/P2(X) =

A função PEVAL

A função PEVAL (Polynomial EVALuation) pode ser usada para solucionar um polinômio

p(x) = a

⋅xn+a

dado um conjunto de coeficientes [a resultado é a solução p(x

). A função PEVAL não está disponível no menu

ARITHMETIC, em seu lugar use o Menu CALC/DERIV&INTEG. Exemplo: PEVAL([1,5,6,1],5) = 281.

Informações adicionais sobre aplicações das funções polinomiais são apresentadas no Capítulo 5 do guia do usuário da calculadora.

n-1

⋅x

+ …+ a2⋅x2+a1⋅x+ a0,

n-1

, a

, … a2, a1, a0] e um valor de x0. O

n-1

Frações

As frações podem ser expandidas e fatoradas usando-se as funções EXPAND e FACTOR, do menu ALG (‚×). Por exemplo:

Pagina 5-10

EXPAND(‘(1+X)^3/((X-1)(X+3))’) = ‘(X^3+3*X^2+3*X+1)/(X^2+2*X-3)’ EXPAND(‘(X^2*(X+Y)/(2*X-X^2)^2’) = ‘(X+Y)/(X^2-4*X+4)’

FACTOR(‘(3*X^3-2*X^2)/(X^2-5*X+6)’) = ‘X^2*(3*X-2)/((X-2)*(X-3))’ FACTOR(‘(X^3-9*X)/(X^2-5*X+6)’ ) = ‘X*(X+3)/(X-2)’

A função SIMP2

A função SIMP2 no menu ARITHMETIC considera como argumentos dois números ou polinômios, representando o numerador e o denominador de uma fração racional, e retorna o numerador e o denominador simplificados. Por exemplo:

SIMP2(‘X^3-1’,’X^2-4*X+3’) = { ‘X^2+X+1’,‘X-3’}

A função PROPFRAC

A função PROPFRAC converte uma fração racional em uma fração “própria”, ou seja, uma parte inteira adicionada a uma parte fracionária, se tal decomposição for possível. Por exemplo:

PROPFRAC(‘5/4’) = ‘1+1/4’

PROPFRAC(‘(x^2+1)/x^2’) = ‘1+1/x^2’

A função PARTFRAC

A função PARTFRAC decompõe uma fração racional nas frações parciais que produzem a fração original. Por exemplo:

PARTFRAC(‘(2*X^6-14*X^5+29*X^4-37*X^3+41*X^2-16*X+5)/(X^57*X^4+11*X^3-7*X^2+10*X)’) = ‘2*X+(1/2/(X-2)+5/(X-5)+1/2/X+X/(X^2+1))’

Pagina 5-11

A função FCOEF

A função FCOEF, disponível através do menu ARITHMETIC/POLYNOMIAL, é usada para obter uma fração racional, dadas as raízes e pólos da fração.

Observação: Se a fração racional for dada como F(X) = N(X)/D(X), as raízes da fração resultam da solução da equação N(X) = 0, enquanto os pólos resultam da solução da equação D(X) = 0.

A entrada para a função é um vetor que lista as raízes seguidas pela multiplicidade (ou seja, quantas vezes uma dada raiz é repetida) e os pólos seguidos pela multiplicidade representados por um número negativo. Por exemplo, se quisermos criar uma fração tendo raízes: 2 com multiplicidade 1, 0 com multiplicidade de 3 e -5 com a multiplicidade 2 e pólos: 1 com multiplicidade 2 e –3 com multiplicidade 5, use:

FCOEF([2,1,0,3,–5,2,1,-2,-3,-5]) = ‘(X--5)^2*X^3*(X-2)/(X--3)^5*(X-1)^2’

Se você pressionar µ„î(ou, simplesmente µ no modo RPN) você irá obter:

‘(X^6+8*X^5+5*X^4-50*X^3)/(X^7+13*X^6+61*X^5+105*X^4-45*X^3297*X62-81*X+243)’

A função FROOTS

A função FROOTS, do menu ARITHMETIC/POLYNOMIAL, obtém as raízes e pólos de uma fração. Como exemplo, ao aplicar a função FROOTS ao resultado produzido acima, obteremos: [1 –2. –3 –5. 0 3. 2 1. –5 2.]. O resultado mostra os pólos seguidos de sua multiplicidade como um número negativo e as raízes seguidas de sua multiplicidade como um número positivo. Neste caso, os pólos são (1, -3) com multiplicidades (2, 5) respectivamente e as raízes são (0, 2, -5) com multiplicidades (3, 1, 2), respectivamente.

Outro exemplo é: FROOTS(‘(X^2-5*X+6)/(X^5-X^2)’) = [0 –2. 1 –1. 3 1. 2

1.], ou seja, pólos = 0 (2), 1(1) e raízes = 3(1), 2(1). Se tivesse sido selecionado o modo Complex, então os resultados seriam:

Pagina 5-12

[0 –2. 1 –1. ‘-((1+i*√3)/2’ –1. ‘-((1-i*√3)/2’ –1.)

Operações passo a passo com polinômios e frações

Ao configurar os modos CAS para Step/step a calculadora mostrará as simplificações de frações ou operações com polinômios da forma passo a passo. Isso é muito útil para visualizar os passos de uma divisão sintética. O exemplo da divisão

−

é mostrado em detalhe no Apêndice C do Guia do Usuário da calculadora. O seguinte exemplo mostra uma divisão sintética mais longa (DIV2 está disponível no menu ARITH/POLYNOMIAL):

−

235

−+−

XXX

Pagina 5-13

Referências

Informações, definições e exemplos adicionais de operações algébricas e aritméticas são apresentados no Capítulo 5 do guia do usuário da calculadora.

Pagina 5-14

Capítulo 6 Solucionando equações

Associados à tecla 7 existem dois menus de funções de solução de equações, o Symbolic SoLVer („Î) para soluções simbólicas e o NUMerical SoLVer (‚Ï) para soluções numéricas. A seguir, apresentamos algumas das funções contidas nesses menus.

Solução simbólica de equações algébricas

Aqui descrevemos algumas das funções do menu Symbolic Solver. Ative o menu usando a combinação de teclas „Î. Com o sinalizador do sistema 117 configurado para CHOOSE boxes, a seguinte lista será apresentada:

As funções ISOL e SOLVE podem ser usadas para encontrar qualquer incógnita em uma equação polinomial. A função SOLVEVX resolve equações polinomiais onde a incógnita é o VX da variável CAS default (tipicamente configurado para ‘X’). Finalmente, a função ZEROS fornece os zeros, ou raízes, de um polinômio.

Função ISOL:

A função ISOL(Equação, variável) encontrará a(s) solução(ões) para Equação isolando uma variável. Por exemplo, com a calculadora configurada no modo ALG, para isolar t na equação at

-bt = 0, podemos usar o seguinte:

Página 6-1

Ao usar o modo RPN, a solução é conseguida inserindo-se a equação na pilha, seguida da variável, antes de inserir a função ISOL. Logo antes da execução da função ISOL, a pilha RPN deve ser similar à figura da esquerda. Depois de aplicar ISOL, o resultado é mostrado na figura da direita:

O primeiro argumento da função ISOL pode ser uma expressão, conforme mostrado acima, ou uma equação. Por exemplo, no modo ALG, tente:

Observação: Para digitar o sinal de igual (=) na equação, use ‚Å (associado à tecla \).

O mesmo problema pode ser resolvido no modo RPN, conforme ilustrado abaixo (as figuras mostram a pilha RPN antes e depois da aplicação da função ISOL):

Função SOLVE

A função SOLVE usa a mesma sintaxe da função ISOL, exceto que SOLVE também pode ser usada para resolver um conjunto de equações polinomiais. O recurso auxiliar de inserção da função SOLVE, com a solução para a equação X^4 – 1 = 3 , é mostrado a seguir:

Página 6-2

Os seguintes exemplos mostram o uso da função SOLVE nos modos ALG e RPN (Use o modo Complex no CAS):

A tela mostrada acima exibe duas soluções. Na primeira, β SOLVE não encontra uma solução { }. Na segunda, β

-5β =125,

- 5β = 6, SOLVE encontra quatro soluções, mostradas na última linha de resultado. A última solução não é visível porque o resultado ocupa mais caracteres do que a largura do visor da calculadora. Entretanto, você poderá visualizar todas as soluções usando a seta para baixo (˜), que ativa o editor de linha (esta operação pode ser usada para acessar qualquer linha de resultado mais larga do que o visor da calculadora):

As telas RPN correspondentes a esses dois exemplos, antes e depois da aplicação da função SOLVE, são mostradas a seguir:

Página 6-3

Função SOLVEVX

A função SOLVEVX resolve uma equação utilizando a variável CAS default indicada pela variável reservada VX. Por definição, esta variável está configurada para ‘X’. Exemplos, usando o modo ALG com VX = ‘X’, são mostrados abaixo:

No primeiro caso SOLVEVX não encontrou soluções. No segundo, SOLVEVX encontrou somente uma solução, X = 2.

As seguintes telas mostram a pilha RPN para resolver os dois exemplos mostrados acima (antes e depois da aplicação de SOLVEVX):

Função ZEROS

A função ZEROS encontra as soluções de uma equação polinomial, sem mostrar suas multiplicidades. A função requer como entrada a expressão da

Página 6-4

equação e o nome da variável a ser isolada. Exemplos no modo ALG são mostrados a seguir:

Para usar a função ZEROS no modo RPN, entre primeiro com a expressão polinomial, depois com a variável a ser isolada e então com a função ZEROS. As seguintes telas mostram a pilha RPN antes e depois da aplicação da função ZEROS para os dois exemplos acima (Use o modo Complex no CAS):

As funções do Symbolic Solver apresentadas até aqui produzem soluções para as equações racionais (principalmente, equações polinomiais). Se a equação a ser resolvida tiver todos os coeficientes numéricos, uma solução numérica é possível utilizando os recursos do Numerical Solver da calculadora.

Menu Numerical Solver

A calculadora oferece um ambiente muito poderoso para a solução de equações algébricas ou transcendentes. Para acessar este ambiente iniciamos o solucionador numérico (NUM.SLV) usando a combinação de teclas ‚Ï. Será apresentado um menu suspenso com as seguintes opções:

Página 6-5

A seguir, descrevemos as aplicações dos itens: 3. Solve poly.., 5. Solve finance, e 1. Solve equation, nesta ordem. O Apêndice 1-A, no Guia do

Usuário, contém as instruções sobre como usar as telas de entrada com exemplos para as aplicações do solucionador numérico. O item 6. MSLV (Multiple equation SoLVer -Solucionador de múltiplas equações) será apresentado mais adiante Página 6-10.

Observações:

1. Sempre que for possível encontrar um valor nas aplicações do NUM.SLV, o valor encontrado será colocado na pilha. Isto é útil nos casos em que se desejamanter este valor disponível para outras operações.

2. Uma ou mais variáveis serão criadas a cada vez que alguns dos aplicativos do menu NUM.SLV forem ativados.

Equações polinomiais

Ao usar a opção Resolver poly… no ambiente SOLVE da calculadora você poderá:

(1) encontrar as soluções para uma equação polinomial. (2) obter os coeficientes do polinômio conhecendo suas raízes e (3) obter a expressão algébrica de um polinômio como uma função de X.

Encontrando as soluções de uma equação polinomial

Uma equação polinomial é uma equação da forma: a + a

= 0. Por exemplo, para resolver a equação: 3s4 + 2s3 - s + 1 = 0.

xn + a

Queremos colocar os coeficientes da equação num vetor: [3,2,0,-1,1]. Para resolver esta equação polinomial usando a calculadora, tente o seguinte:

‚Ï˜˜@@OK@@ Selecione Solve poly…

n-1

+ …+ a1x

Página 6-6

Hp 49G+ User Manual [pt]

Specifications and Main Features

Frequently Asked Questions

User Manual

Baterias

Ligando e desligando a calculadora

Ajustando o contraste do visor

Menus

O menu TOOL (FERRAMENTA)

Configurando hora e data

Apresentando o teclado da calculadora

Selecionando os modos de calculadora

• Formato fixo com decimais: Pressione o botão H. Em seguida, use a tecla com a seta para baixo, ˜, para selecionar a opção Number format. Pressione a tecla @CHOOS ( B) e selecione a opção Fixed com a tecla de seta para baixo ˜.

• Formato de engenharia

Sistema de coordenadas

Selecionando a fonte do visor

Selecionando as propriedades do editor de linha

Selecionando as propriedades da pilha

Selecionando as propriedades do equation writer (EQW)

Objetos da calculadora

Organizando dados na calculadora

• Modo RPN (Use H\@@OK@@ para mudar para o modo RPN). Use as seguintes teclas para armazenar o valor de –0.25 na variável α:

Modo RPN

O menu UNITS

Prefixos de unidades

Configurando a calculadora para modo COMPLEX

OS menus CMPLX

Menu CMPLX no teclado

Menu Numerical Solver