Hp 49G+ User Manual [de]

Download

hp 49g+ grafikfähiger Taschenrechner

Benutzerhandbuch

2. Ausgabe HP Artikel-Nr. F2228-90002

Hinweis

REGISTRIEREN Sie IHRES PRODUKT AN : www.register.hp.com

FÜR DIESES HANDBUCH UND ALLE DARIN ENTHALTENEN BEISPIELE WIRD KEINE GEWÄHR ÜBERNOMMEN. ÄNDERUNGEN SIND VORBEHALTEN. HEWLETT–PACKARD ÜBERNIMMT WEDER AUSDRÜCKLICH NOCH STILLSCHWEIGEND IRGENDWELCHE HAFTUNG FÜR DIE IN DIESEM HANDBUCH ENTHALTENEN INFORMATIONEN EINSCHLIESSLICH, ABER NICHT BESCHRÄNKT AUF DIE FUNKTIONSFÄHIGKEIT DES GERÄTS NOCH DESSEN NICHTVERLETZUNG EIGNUNG FÜR EINEN BESTIMMTEN ZWECK.

HEWLETT–PACKARD HAFTET NICHT FÜR DIREKTE ODER INDIREKTE SCHÄDEN IM ZUSAMMENHANG MIT ODER ALS FOLGE DER LIEFERUNG, BENUTZUNG ODER LEISTUNG DER PROGRAMME ODER DER VERWENDUNG DIESES HANDBUCHS UND DER DARIN ENTHALTENEN BEISPIELE.

© Copyright 2003 Hewlett-Packard Development Company, L.P. Die Vervielfältigung, Adaptierung oder Übersetzung dieses Handbuchs ist, wenn sie nicht durch die Urheberrechtsgesetze zulässig sind, ohne die vorherige schriftliche Genehmigung von Hewlett–Packard untersagt.

Hewlett-Packard Company 4995 Murphy Canyon Rd, Suite 301 San Diego,CA 92123

Druckgeschichte

2. Ausgabe Dez. 2003

Vorwort

Sie haben einen kompakten Computer für numerische und symbolische Anwendungen erworben, der die Berechnung und mathematische Analyse von Problemen in zahlreichen Bereichen unterstützt, von elementarer Mathematik bis zu fortgeschrittenen technischen und wissenschaftlichen Themen.

Die Anleitung enthält Beispiele, die die grundlegenden Funktionen und Operationen des Taschenrechners veranschaulichen. Die Kapitel dieser Bedienungsanleitung sind nach Schwierigkeitsstufe themenbezogen geordnet: vom Einstellen der Modi des Taschenrechners über die Berechnung reeller und komplexer Zahlen, Operationen mit Listen, Vektoren und Matrizen bis zu Anwendungen der Infinitesimalrechnung, Vektorrechnung, Differenzialgleichungen, Wahrscheinlichkeitsrechnung und Statistik.

Für Operationen mit Symbolen enthält der Rechner ein leistungsstarkes computergestütztes algebraisches System (CAS), das Ihnen die Auswahl unterschiedlicher Betriebsmodi ermöglicht, z. B. komplexe Zahlen oder reelle Zahlen und exakter (symbolischer) Modus oder Näherungsmodus (numerischer Modus). Die Anzeige kann so eingestellt werden, dass Ausdrücke wie in einem Texteditor eingegeben werden können. Dies bietet sich für die Arbeit mit Matrizen, Vektoren, Brüchen, Additionen, Ableitungen und Integrale an. Die schnellen Grafikfunktionen des Taschenrechners ermöglichen ein komfortables Erstellen komplexer Abbildungen in sehr kurzer Zeit.

Mithilfe der Infrarotschnittstelle und des für den Taschenrechner verfügbaren USB-Kabels können Sie diesen mit anderen Taschenrechnern oder Computern verbinden. Die Hochgeschwindigkeitsverbindung über Infrarot oder USB ermöglicht den schnellen und effizienten Austausch von Programmen und Daten mit anderen Taschenrechnern oder Computern. Der Taschenrechner enthält eine Flash-Speicherkarte für das Speichern von Daten und ihren Austausch mit anderen Benutzern.

Wir hoffen, dass Ihnen der Taschenrechner ein zuverlässiger Begleiter für Ihre schulischen oder beruflichen Anwendungen sein wird.

Inhaltsverzeichnis

Kapitel 1 – Einführung, 1-1

Grundlegende Operationen, 1-1 Batterien, 1-1 Ein- und Ausschalten des Taschenrechners, 1-2 Einstellen des Displaykontrastes, 1-2 Inhalt des Taschenrechnerdisplays, 1-3 Menüs, 1-3 Das Menü TOOL, 1-4 Einstellen von Datum und Uhrzeit, 1-4

Einführung in die Tastatur des Taschenrechners, 1-5 Auswählen der Taschenrechnermodi, 1-7

Betriebsmodus, 1-7 Zahlenformat und Dezimalpunkt oder -komma, 1-11 Standardformat, 1-12 Festes Format für Dezimalzahlen, 1-12 Wissenschaftliches Format, 1-13 Technisches Format, 1-14 Dezimalkomma und Dezimalpunkt, 1-15 Winkelmaß, 1-16 Koordinatensystem, 1-17 Auswählen der CAS-Einstellungen, 1-18 Erklärung der CAS-Einstellungen, 1-19 Auswählen der verschiedenen Display-Modi, 1-20 Auswählen der Schriftart für die Anzeige, 1-21 Auswählen der Eigenschaften des Zeileneditors, 1-22 Auswählen der Eigenschaften des Stacks, 1-22 Auswählen der Eigenschaften für den EquationWriter (EQW), 1-23 Weitere Informationen, 1-24

Kapitel 2 – Einführung in den Taschenrechner, 2-1

Objekte des Taschenrechners, 2-1 Bearbeiten der Ausdrücke im Stack, 2-1

Erstellen von arithmetischen Ausdrücken, 2-1

Seite TOC-1

Erstellen von algebraischen Ausdrücken, 2-4 Verwenden des EquationWriters (EQW) zum Erstellen von Ausdrücken, 2-5 Erstellen von arithmetischen Ausdrücken, 2-5 Erstellen von algebraischen Ausdrücken, 2-8 Strukturieren der Daten im Taschenrechner, 2-9 Das Verzeichnis HOME, 2-9 Unterverzeichnisse, 2-10 Variablen, 2-10 Eingeben von Variablennamen, 2-11 Erstellen von Variablen, 2-12 Algebraischer Modus, 2-12 RPN-Modus, 2-13 Überprüfen des Inhalts von Variablen, 2-15 Algebraischer Modus, 2-15 RPN-Modus, 2-15

Drücken der Nach-Rechts-Taste und anschließend der

entsprechenden Softmenütastenbeschriftungen, 2-15 Auflisten des Inhalts aller Variablen auf dem Bildschirm, 2-16 Löschen von Variablen, 2-16

Verwenden der Funktion PURGE im Stack im algebraischen

Modus, 2-16 Anwenden der Funktion PURGE im Stack im RPN-Modus, 2-17

Die Funktionen UNDO und CMD, 2-18 CHOOSE boxes und Soft MENU, 2-18 Weitere Informationen, 2-21

Kapitel 3 – Berechnungen mit reellen Zahlen, 3-1

Beispiele für Berechnungen mit reellen Zahlen, 3-1 Verwenden von Zehnerpotenzen bei der Dateneingabe, 3-5 Funktionen mit reellen Zahlen im Menü MTH, 3-6 Verwenden der Menüs des Taschenrechners, 3-7 Hyperbolische Funktionen und ihre Inversen, 3-7 Operationen mit Einheiten, 3-9 Das Menü UNITS, 3-9 Verfügbare Einheiten, 3-11 Zuordnen von Einheiten zu Zahlen, 3-11

Seite TOC-2

Vorzeichen für Einheiten , 3-12 Operationen mit Einheiten, 3-13 Konvertierung von Einheiten , 3-15

Physikalische Konstanten im Taschenrechner, 3-15 Definieren und Verwenden von Funktionen, 3-18 Weitere Informationen, 3-19

Kapitel 4 – Berechnungen mit komplexen Zahlen, 4-1

Definitionen, 4-1 Einstellen des Modus COMPLEX am Taschenrechner, 4-1

Eingeben von komplexen Zahlen, 4-2 Polare Darstellung von komplexen Zahlen, 4-2

Einfache Operationen mit komplexen Zahlen, 4-4 Die CMPLX-Menüs, 4-4

Menü CMPLX über das Menü MTH, 4-4 Menü CMPLX auf der Tastatur, 4-6

Auf komplexe Zahlen angewendete Funktionen, 4-6 Funktion DROITE: Gleichung einer Geraden, 4-7 Weitere Informationen, 4-7

Kaptitel 5 – Algebraische und arithmetische Operationen, 5-1

Eingabe von algebraischen Objekten, 5-1 Einfache Operationen mit algebraischen Objekten, 5-2

Funktionen im Menü ALG, 5-4 Operationen mit transzendenten Funktionen, 5-6

Erweitern und faktorisieren mit Hilfe der log-exp Funktionen, 5-6 Erweitern und faktorisieren anhand trigonometrischer Funktionen, 5-6

Funktionen im Menü ARITHMETIC, 5-7 Polynome, 5-8

Funktion HORNER, 5-9 Variable VX, 5-9 Funktion PCOEF, 5-9 Funktion PROOT, 5-10 Funktionen QUOT und REMAINDER, 5-10 Funktion PEVAL, 5-10

Seite TOC-3

Brüche, 5-11 Funktion SIMP2, 5-11 Funktion PROPFRAC, 5-11 Funktion PARTFRAC, 5-11 Funktion FCOEF, 5-12 Funktion FROOTS, 5-12

Step-by-Step Operationen mit Polynomen und Brüchen, 5-13 Weitere Informationen, 5-14

Kapitel 6 – Lösung für Gleichungen, 6-1

Symbolische Lösung algebraischer Gleichungen, 6-1 Funktion ISOL, 6-1 Funktion SOLVE, 6-3 Funktion SOLVEVX, 6-4 Funktion ZEROS, 6-5 Menü numerischer Löser (Numerical solver), 6-6 Polynomgleichungen, 6-6 Lösungen einer Polynomgleichung finden, 6-7

Erzeugen von Polynom-Koeffizienten, wenn die Nullstellen des

Polynoms bekannt sind, 6-8 Erstellen eines algebraischen Ausdrucks für das Polynom, 6-8 Finanzmathematische Berechnungen, 6-9 Lösen von Gleichungen mit einer Unbekannten über NUM.SLV, 6-10 Funktion STEQ, 6-10

Lösung von Simultansystemen mit MSLV, 6-11 Weitere Informationen, 6-13

Kapitel 7 –Operationen mit Listen, 7-1

Erstellen und speichern von Listen, 7-1 Operationen mit Zahlenlisten, 7-1

Änderung des Vorzeichens, 7-1 Addition, Subtraktion, Multiplikation, Division, 7-2 Auf Listen anwendbare Funktionen, 7-3

Listen von komplexen Zahlen, 7-4 Listen von algebraischen Objekten, 7-4 Das Menü MTH/LIST, 7-5

Seite TOC-4

Die Funktion SEQ, 7-6 Die Funktion MAP, 7-6 Weitere Informationen, 7-7

Kapitel 8 – Vektoren, 8-1

Eingabe von Vektoren, 8-1 Eingebe von Vektoren in den Stack, 8-1 Speichern von Vektoren in Variablen im Stack, 8-2 Eingabe von Vektoren mit Hilfe des MatrixWriters (MTRW), 8-2 Einfache Operationen mit Vektoren, 8-5 Änderung des Vorzeichens, 8-6 Addition, Subtraktion, 8-6 Multiplikation und Division mit einem Skalar, 8-6 Funktion Absolutbetrag, 8-7 Das Menü MTH/VECTOR, 8-7 Magnitude (Betrag), 8-7 Skalarprodukt, 8-8 Kreuzprodukt, 8-8 Weitere Informationen, 8-9

Kapitel 9 – Matrizen und lineare Algebra, 9-1

Eingaben von Matrizen in den Stack, 9-1 Verwendung des MatrixWriters , 9-1 Die Matrix direkt in den Stack eingeben, 9-2 Operationen mit Matrizen, 9-3 Addition und Subtraktion, 9-4 Multiplikation, 9-4 Multiplikation mit einem Skalar, 9-4 Matrix-Vektor Multiplikation, 9-5 Matrix Multiplikation, 9-5 Glied-für-Glied Multiplikation, 9-6 Die Identitätsmatrix, 9-6 Die Umkehrmatrix, 9-6 Charakterisieren einer Matrix (Das Matrixmenü NORM), 9-7 Funktion DET, 9-7 Funktion TRACE, 9-7

Seite TOC-5

Lösungen für lineare Systeme, 9-8

Verwendung des numerischen Lösers für lineare Systeme, 9-8 Lösung mit der Umkehrmatrix, 9-10 Lösung durch "dividieren" der Matrix, 9-11 Weitere Informationen, 9-11

Kapitel 10 – Grafiken, 10-1

Grafikoptionen des Rechners, 10-1 Plotten eines Ausdrucks y= f(x), 10-2 Erstellen einer Wertetabelle für eine Funktion, 10-4 Schnelle 3D Plots, 10-6 Weitere Informationen, 10-9

Kapitel 11 – Analysis-Anwendungen, 11-1

Das Menü CALC (Calculus), 11-1 Grenzwerte und Ableitungsfunktionen, 11-1

Funktion lim, 11-2 Funktionen DERIV und DERVX, 11-2 Stammfunktionen und Integrale, 11-3 Funktionen INT, INTVX, RISCH, SIGMA und SIGMAVX, 11-3 Bestimmte Integrale, 11-4 Unendliche Reihen, 11-5 Funktionen TAYLR, TAYLR0 und SERIES, 11-5 Weitere Informationen, 11-7

Kapitel 12 –Multivariate Analysis-Anwendungen, 12-1

Partielle Ableitungen, 12-1 Mehrfachintegrale, 12-2 Weitere Informationen, 12-3

Kapitel 13 –Anwendungen der Vektorrechnung, 13-1

Der del-Operator, 13-1 Gradient, 13-1 Divergenz, 13-2 Rotation, 13-2

Seite TOC-6

Weitere Informationen, 13-3

Kapitel 14 – Differentialgleichungen, 14-1

Das Menü CALC/DIFF, 14-1 Lösung für lineare und nichtlineare Gleichungen, 14-1

Die Funktion LDEC, 14-2 Die Funktion DESOLVE, 14-3 Die Variable ODETYPE, 14-4 Laplace-Transformationen, 14-5 Laplace-Transformation und Inverse im Rechner, 14-5 Fouriersche Reihe, 14-6 Funktion FOURIER, 14-7 Fouriersche Reihe für eine quadratische Funktion, 14-7 Weitere Informationen, 14-8

Kaptitel 15 – Wahrscheinlichkeitsverteilungen, 15-1

Das Untermenü MTH/PROBABILITY.. – Teil 1, 15-1

Fakultäten, Kombinationen und Permutationen, 15-1 Zufallszahlen, 15-2 Das Menü MTH/PROBABILITY.. – Teil 2, 15-3 Die Normalverteilung, 15-3 Die Studentsche t-Verteilung, 15-4 Die Chi-Quadrat-Verteilung, 15-4 Die F-Verteilung, 15-4 Weitere Informationen, 15-5

Kapitel 16 – Statistische Anwendungen, 16-1

Dateneingabe, 16-1 Berechnen von univariaten Statistiken, 16-2 Ermitteln von Häufigkeitsverteilungen, 16-3 Daten an eine Funktion y=f(x) angleichen(Regression), 16-5 Ermitteln von zusätzlichen Summenstatistiken, 16-6 Konfidenzintervalle, 16-7 Testen von Hypothesen, 16-10 Weitere Informationen, 16-12

Seite TOC-7

Kapitel 17 – Zahlen mit unterschiedlicher Basis, 17-1

Das Menü BASE, 17-1 Schreiben nichtdezimaler Zahlen, 17-1 Weitere Informationen, 17-2

Kapitel 18 –Verwenden von SD-Karten, 18-1

Speichern von Objekten auf der SD-Karte, 18-1 Laden eines Objekts von der SD-Karte, 18-2 Löschen eines Objekts von der SD-Karte, 18-2

Beschränkte Garantie – G-1

Service, G-3

Hinweise und Bestimmungen, G-4

Seite TOC-8

Kapitel 1 Einführung

Dieses Kapitel soll Grundkenntnisse zur Bedienung Ihres Taschenrechners vermitteln. Die Übungen dienen dazu, Sie mit der grundlegenden Bedienung und den wichtigsten Einstellungen des Taschenrechners vertraut zu machen, bevor Sie mit den eigentlichen Berechnungen beginnen.

Grundlegende Operationen

Die folgenden Übungen sind dazu gedacht, Sie mit der Hardware des Taschenrechners vertraut zu machen.

Batterien

Für den Taschenrechner werden 3 AAA(LR03)-Batterien zur Hauptstromversorgung und eine CR2032 Lithiumbatterie für das Sichern des Speichers benötigt. Bevor Sie den Taschenrechner in Betrieb nehmen, setzen Sie die Batterien wie folgt ein:

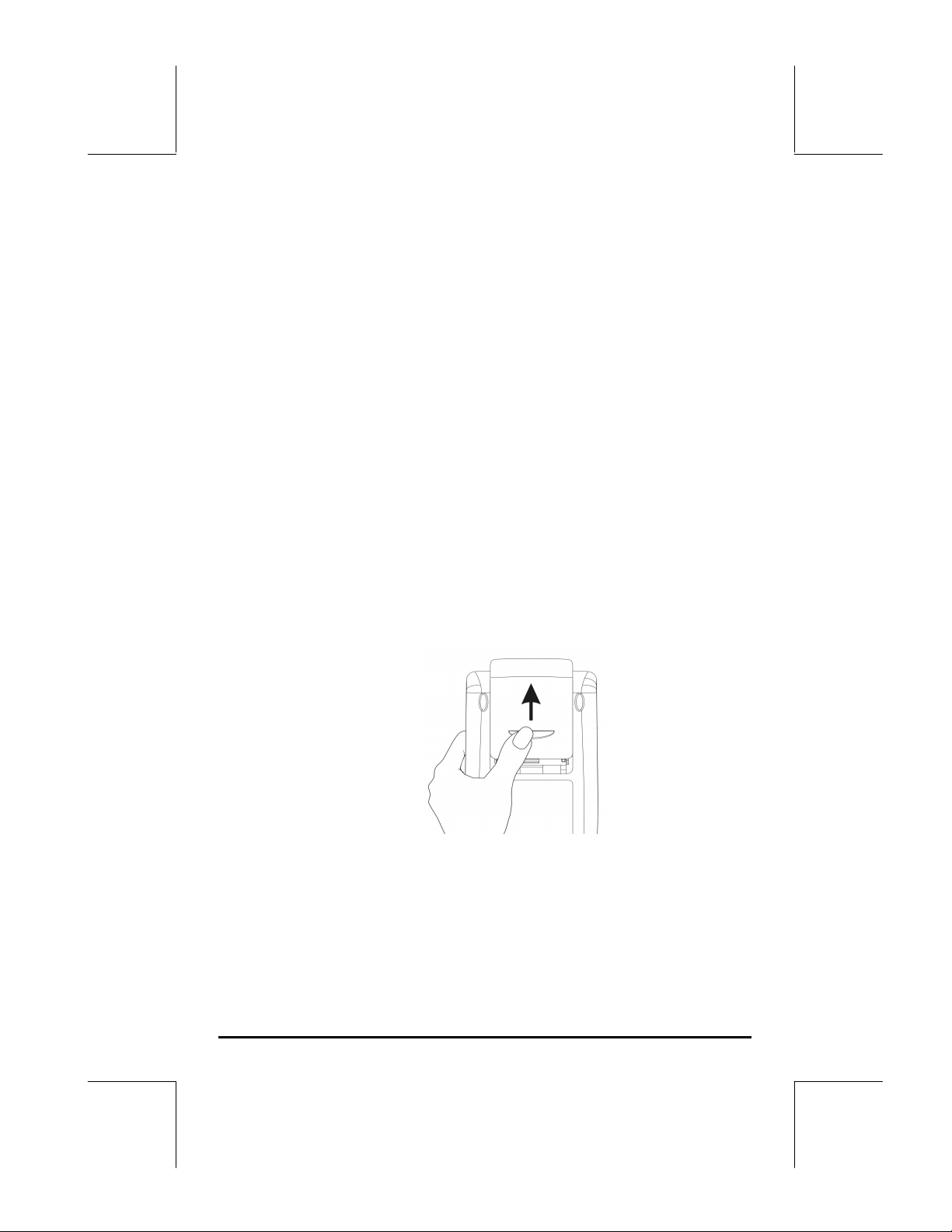
So installieren Sie die Hauptbatterien

a. Stellen Sie sicher, daß der Rechner ausgeschaltet ist. Schieben Sie die

Abdeckung des Batteriefachs wie abgebildet nach oben.

b. Legen Sie 3 neue AAA(LR03)-Batterien in das Hauptfach. Stellen Sie sicher,

dass jede Batterie in der angegebenen Richtung eingelegt wird.

So installieren Sie die Batterie für das Backup des Speichers

a. Stellen Sie sicher, daß der Rechner ausgeschaltet ist. Drücken Sie die

Halterung nach unten. Schieben Sie den Deckel in die angegebene Richtung, und heben Sie ihn an.

Seite 1-1

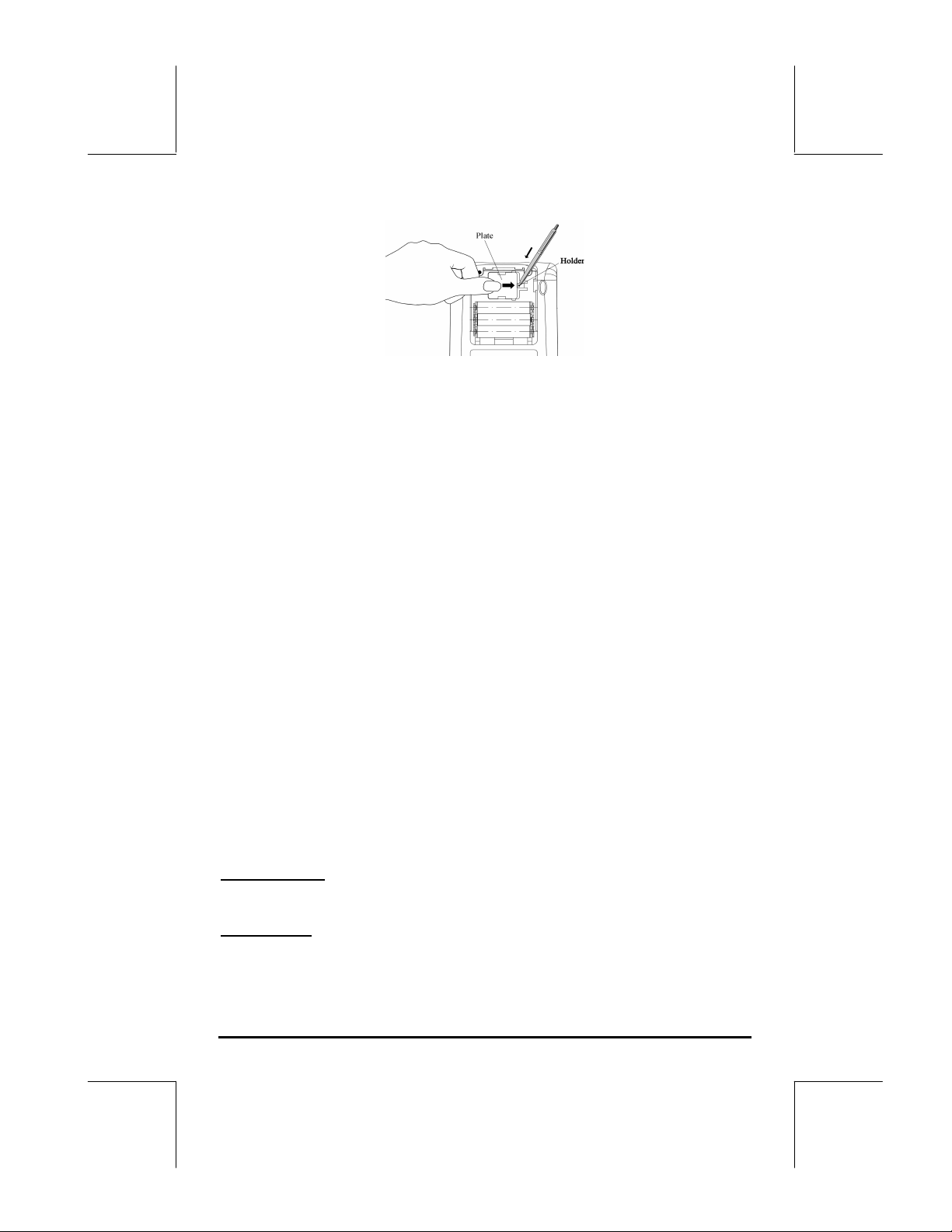
b. Setzen Sie eine neue CR2032-Lithiumbatterie ein. Stellen Sie sicher, dass

die positive (+) Seite nach oben zeigt.

c. Setzen Sie den Deckel wieder ein, und schieben Sie ihn an die

ursprüngliche Position. Nachdem Sie die Batterien installiert haben, drücken Sie [ON], um den Taschenrechner einzuschalten. Warnung: Sobald das Symbol für eine niedrige Batterieladung angezeigt wird, müssen Sie die Batterien so schnell wie möglich austauschen. Wechseln Sie jedoch , um einen Datenverlust zu vermeiden,nicht die Backup-Batterie und die Hauptbatterien gleichzeitig aus.

Ein- und Ausschalten des Taschenrechners

Die Taste $ befindet sich auf der Tastatur links unten. Drücken Sie diese Taste einmal, um den Taschenrechner einzuschalten. Um den Taschenrechner auszuschalten, drücken Sie die rote Nach-Rechts-Taste @ (die erste Taste in der zweiten Reihe von unten) und anschließend die Taste $. Beachten Sie, dass sich in der rechten oberen Ecke der Taste $ eine rote Markierung OFF als Hinweis auf den Befehl OFF befindet.

Einstellen des Displaykontrastes

Der Displaykontrast kann mit den Tasten + und - bei gleichzeitig gedrückter Taste $ eingestellt werden.

Durch gleichzeitiges Drücken der Tasten $ (Hold) und + wird das Display dunkler

Durch gleichzeitiges Drücken der Tasten $ (Hold) und - wird das Display heller

eingestellt.

Seite 1-2

Inhalt des Taschenrechnerdisplays

Schalten Sie den Taschenrechner erneut ein. Im oberen Teil des Displays werden zwei Zeilen mit den Einstellungen des Taschenrechners angezeigt. Die erste Zeile enthält folgende Zeichen:

RAD XYZ HEX R= 'X'

Informationen über die Bedeutung dieser Angaben erhalten Sie in Kapitel 2 der Bedienungsanleitung.

In der zweiten Zeile werden die Zeichen

{ HOME }

angezeigt, die das Verzeichnis HOME als aktuelles Verzeichnis für die Dateien im Speicher des Taschenrechners ausweisen.

Am unteren Rand des Displays befinden sich die Beschriftungen

@EDIT @VIEW @@ RCL @@ @@STO@ ! PURGE !CLEAR

Diese sind den Softmenütasten F1 bis F6 zugeordnet:

Die sechs Beschriftungen am unteren Rand des Bildschirms ändern sich je nach angezeigtem Menü. Doch die Softmenütaste A ist stets der ersten angezeigten Beschriftung zugeordnet, B der zweiten Beschriftung usw.

Menüs

Die sechs den Tasten A bis F zugeordneten Beschriftungen sind Teil eines Menüs insgesamt 6 Softmenütasten besitzt, werden jeweils nur 6 Beschriftungen auf einmal angezeigt. Ein Menü kann jedoch mehr als sechs Einträge besitzen. Eine Gruppe von 6 Einträgen wird als Menüseite bezeichnet. Um zur nächsten Menüseite zu gelangen (falls vorhanden), drücken Sie die Taste L (NeXT = nächstes Menü). Auf der Tastatur ist dies die dritte Taste von links in der dritten Reihe der Tastatur.

mit unterschiedlichen Funktionen. Da der Taschenrechner nur

Seite 1-3

Das Menü TOOL

Die Softmenütasten für das Standardmenu, das als Menü TOOL bezeichnet wird, sind den Operationen zum Ändern von Variablen zugeordnet (siehe den Abschnitt über Variablen in diesem Kapitel):

@EDIT A EDIT (Bearbeiten) des Inhalts einer Variablen (weitere Informationen über das Bearbeiten finden Sie in Kapitel 2 dieses Handbuchs und in Kapitel 2 und Anhang L des Bedienungsanleitung)

@VIEW B VIEW (Anzeigen) des Inhalts von Variablen @@ RCL @@ C ReCaLl (Abrufen) des Inhalts von Variablen @@STO@ D STOre (Speichern) des Inhalts von Variablen PURGE E PURGE (Löschen) einer Variablen CLEAR F CLEAR (Löschen) des Displays oder Stacks

Diese sechs Funktionen bilden die erste Seite des Menüs TOOL. Eigentlich besitzt dieses Menü acht Einträge, aufgeteilt auf zwei Seiten. Die zweite Seite ist verfügbar, wenn Sie die Taste L (NeXT = nächstes Menü) drücken. Dies ist die dritte Taste von links in der dritten Reihe der Tastatur.

In diesem Fall sind nur den ersten beiden Softmenütasten Befehle zugeordnet. Diese Befehle lauten sind:

@CASCM A CASCMD: Der Befehl CAS CoMmanD, der verwendet wird,

um einen Befehl aus dem CAS-Modul durch Auswahl aus einer Liste zu starten

@HELP B HELP: Die Hilfefunktion, in der die im Taschenrechner

vorhandenen Befehle beschrieben sind

Wenn Sie die Taste L drücken, wird das ursprüngliche Menü TOOL wieder angezeigt. Eine weitere Möglichkeit, zum Menü TOOL zurückzukehren, besteht im Drücken der Taste I (die dritte Taste von links in der zweiten Reihe von oben der Tastatur).

Einstellen von Datum und Uhrzeit

Informationen über das Einstellen von Uhrzeit und Datum finden Sie in Kapitel 1 der Bedienungsanleitung für den Taschenrechner.

Seite 1-4

Einführung in die Tastatur des Taschenrechners

In der folgenden Abbildung ist die Tastatur des Taschenrechners mit nummerierten Zeilen und Spalten dargestellt. Jede Taste besitzt drei, vier oder fünf Funktionen. Die Hauptfunktion der Taste entspricht der auf der Taste hervorgehobenen Beschriftung. Außerdem können die grüne Nach-Links-Taste, Taste (8,1), die rote Nach-Rechts-Taste, Taste (9,1), und die blaue ALPHATaste, Taste (7,1), mit anderen Tasten kombiniert werden, um die auf der Tastatur angezeigten alternativen Funktionen zu aktivieren.

Seite 1-5

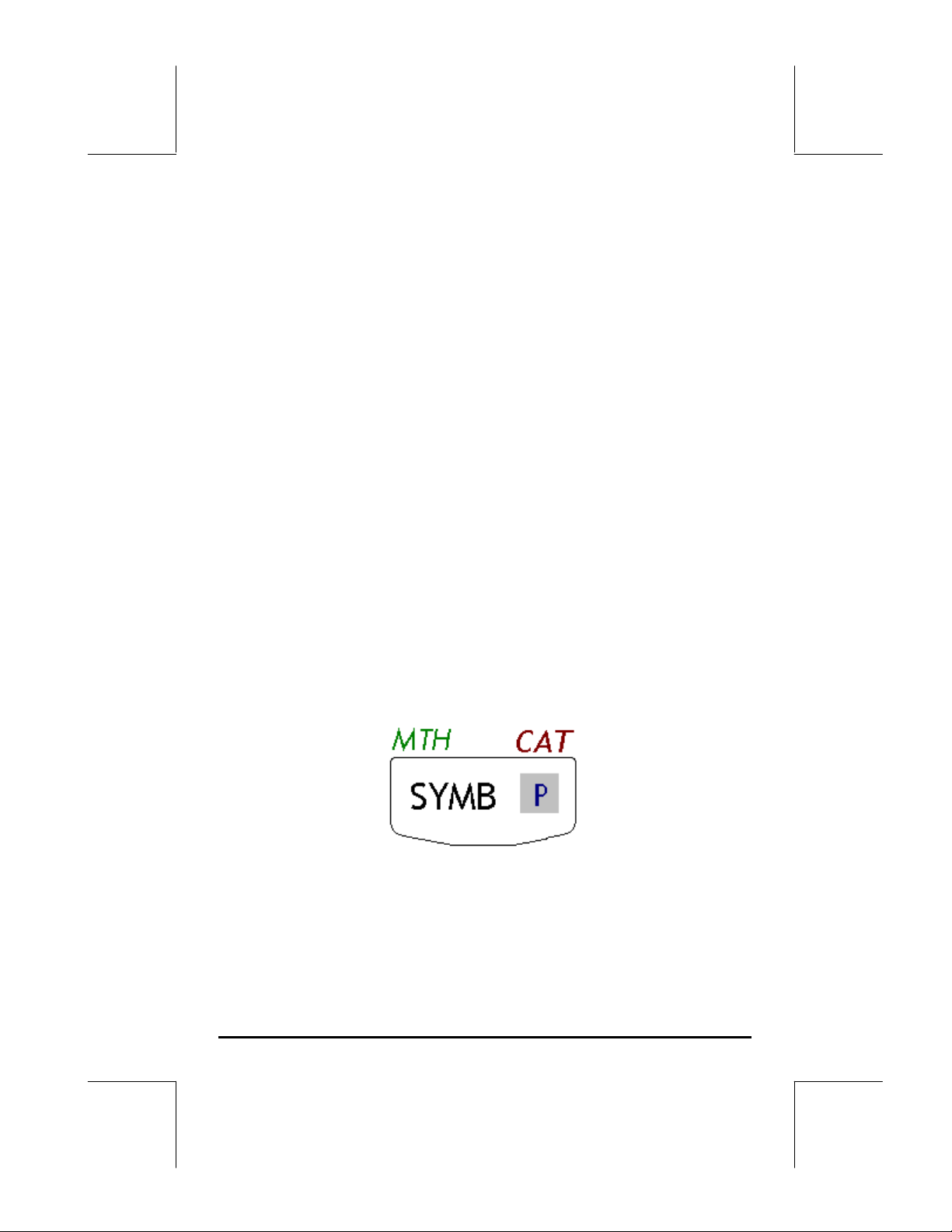
Beispielsweise sind der Taste P, Taste (4,4), die folgenden sechs Funktionen zugeordnet:

P Hauptfunktion zum Starten des Menüs SYMB (SYMBolic) „´ Tastenkombination mit Nach-Links-Taste zum Starten des

Menüs MTH (Mathematik) …N Tastenkombination mit Nach-Rechts-Taste zum Starten der Funktion CATalog (Katalog) ~p Tastenkombination mit ALPHA-Taste zum Einfügen des Großbuchstabens P ~„p Kombination von ALPHA- und Nach-Links-Taste zum Einfügen

des Kleinbuchstabens p

~…p Kombination von ALPHA- und Nach-Rechts-Taste zum

Einfügen des Symbols π

Von den sechs dieser Taste zugeordneten Funktionen werden nur die ersten vier auf der Tastatur selbst angezeigt. Die Abbildung auf der nächsten Seite enthält diese vier Beschriftungen für die Taste P. Beachten Sie, dass durch Farbe und Position der Beschriftungen auf der Taste, und zwar SYMB, MTH, CAT und P, bestimmt wird, bei welcher Funktion es sich um die Hauptfunktion (SYMB) handelt und welche der drei weiteren Funktionen der jeweiligen Tastenkombination zugeordnet ist: Nach-Links-Taste „(MTH), Nach-RechtsTaste …(CAT ) und ~ (P).

Ausführliche Informationen über die Verwendung der Tastatur des Taschenrechners finden Sie in Anhang B der Bedienungsanleitung für den Taschenrechner.

Seite 1-6

Auswählen der Taschenrechnermodi

In diesem Abschnitt wird vorausgesetzt, dass Sie nun zumindest grob mit der Verwendung von Auswahl- und Dialogfeldern vertraut sind (wenn dies nicht der Fall ist, schauen Sie bitte in Anhang A der Bedienungsanleitung für den Taschenrechner nach).

Drücken Sie die Taste H (zweite Taste von links in der zweiten Reihe von oben), um die folgende Eingabemaske CALCULATOR MODES (Taschenrechner-Modi) anzuzeigen:

Drücken Sie die Softmenütaste !!@@OK#@ ( F) , um zum normalen Display zurückzukehren. Es folgen einige Beispiele für das Auswählen verschiedener Taschenrechnermodi.

Betriebsmodus

Der Taschenrechner bietet zwei verschiedene Betriebsmodi: den Modus Algebraic (algebraisch) und den Modus Reverse Polish Notation (RPN). (umgekehrte polnische Notation) Der Modus Algebraic ist der Standardmodus (wie in der obigen Abbildung gezeigt), doch Anwender früherer Taschenrechner von HP sind eventuell mit dem RPN-Modus besser vertraut.

Um einen Betriebsmodus auszuwählen, rufen Sie zunächst die Eingabemaske CALCULATOR MODES auf, indem Sie die Taste H drücken. Das Feld Operating Mode (Betriebsmodus) wird hervorgehoben. Wählen Sie nun den Modus Algebraic oder RPN, indem Sie die Taste \ (zweite Taste von links in der fünften Reihe von unten) oder die Softmenütaste @CHOOS ( B) drücken. Wenn Sie die letzte Methode wählen, verwenden Sie die Nach-Unten- und Nach-Oben-Taste —˜ zur Auswahl des entsprechenden Modus und drücken anschließend die Softmenütaste !!@@OK#@ , um den Vorgang abzuschließen.

Seite 1-7

Um den Unterschied zwischen diesen beiden Betriebsmodi zu veranschaulichen, berechen wir den folgenden Ausdruck in beiden Modi:



0.50.3

−⋅

 

0.23

Um diesen Ausdruck in den Taschenrechner einzugeben, verwenden wir zunächst den EquationWriter ‚O. Beachten Sie außer den numerischen Tasten die folgenden Tasten auf der Tastatur:

!@.#*+-/R

Q¸Ü‚Oš™˜—`

Beim EquationWriter handelt es sich um einen Anzeigemodus, in dem Sie mathematische Ausdrücke unter Verwendung einer expliziten mathematischen Notation, z. B. mit Brüchen, Ableitungen, Integralen, Wurzeln usw., erstellen können. Verwenden Sie zur Eingabe des oben angegebenen Ausdrucks mit dem EquationWriter folgende Tastenkombinationen:

‚OR3.*!Ü5.-

1./3.*3. —————

/23.Q3™™+!¸2.5`

Nach Drücken der Taste ` wird folgender Ausdruck angezeigt:

√ (3.*(5.-1/(3.*3.))/23.^3+EXP(2.5))

Durch erneutes Drücken von ` wird folgender Wert ausgegeben (akzeptieren Sie im Fall einer entsprechenden Meldung die Aktivierung des Modus Approx. (Rundungswerte), indem Sie !!@@OK#@ drücken):

 

0.30.3

⋅



5.2

Seite 1-8

Sie können den Ausdruck aber auch ohne den EquationWriter wie folgt direkt eingeben:

R!Ü3.*!Ü5.-

1/3.*3.™

/23.Q3+!¸2.5`

Sie erhalten das gleiche Ergebnis.

Ändern Sie nun den Modus in RPN, indem Sie zunächst die Taste H drücken. Wählen Sie den RPN-Modus entweder mit der Taste \ oder durch Drücken der Softmenütaste @CHOOS. Drücken Sie die Softmenütaste !!@@OK#@ ( F), um den Vorgang abzuschließen. Im RPN-Modus wird das Display wie folgt dargestellt:

Beachten Sie, dass das Display unterschiedliche Ausgabeebenen aufweist, die von unten nach oben mit 1, 2, 3 usw. beschriftet sind. Dies wird als Stack des Taschenrechners bezeichnet. Die verschiedenen Ebenen werden als Stack- Ebenen bezeichnet, also Stack-Ebene 1, Stack-Ebene 2 usw.

Im Grunde bedeutet RPN nur, dass eine Operation, z. B. 3 + 2, nicht mit

3+2`

in den Taschenrechner eingegeben wird, sondern dass zuerst die Operanden in der richtigen Reihenfolge und anschließend der Operator wie folgt eingegeben werden:

Seite 1-9

3`2`+

Wenn Sie die Operanden eingeben, befinden sich diese auf unterschiedlichen Ebenen des Stacks. Durch die Eingabe von 3` wird die Zahl 3 auf Stack-Ebene 1 abgelegt. Durch die anschließende Eingabe von 2` wird die Zahl 3 eine Stack-Ebene nach oben in Stack-Ebene 2 verschoben. Wenn Sie schließlich die Taste + drücken, wird der Taschenrechner angewiesen, den Operator bzw. das Programm + auf die Objekte auf Stack-Ebene 1 und 2 anzuwenden. Das Ergebnis 5 wird dann auf Stack-Ebene 1 platziert.

Wir führen zunächst einige weitere einfache Operationen durch, bevor wir uns dem komplizierteren Ausdruck zuwenden, der zuvor für den algebraischen Modus verwendet wurde:

123/32 123`32/

4`2Q

√(√27) 27`R3@»

Beachten Sie die Position von y und x in den letzten beiden Operationen. Bevor die Taste Q gedrückt wird, ist y die Basis der Exponentialoperation (Stack-Ebene 2), während der Exponent x (Stack-Ebene 1) ist. Analog hierzu ist in der Quadratwurzeloperation y (Stack-Ebene 2) die Zahl unter dem Wurzelzeichen, und x (Stack-Ebene 1) stellt die Wurzel dar.

Probieren Sie folgendes Beispiel mit 3 Faktoren aus: (5 + 3) × 2

5`3`+ Berechnet zunächst (5 + 3). 2X Schließt die Berechnung ab.

Berechnen wir nun den weiter oben dargestellten Ausdruck:

Seite 1-10



 



−⋅



⋅



5.2

3` Geben Sie 3 in Ebene 1 ein 5` Geben Sie 5 in Ebene 1 ein. 3 wird in Ebene 2 zwei

verschoben 3` Geben Sie 3 in Ebene 1 ein. 5 wird in Ebene 2 und 3 in Ebene 3 verschoben 3* Geben Sie 3 und das Multiplikationszeichen ein. 9 wird in Ebene 1 angezeigt Y 1/(3x3), letzter Wert auf Ebene 1; 5 auf Ebene 2, 3

auf Ebene 3

- 5 - 1/(3×3) belegt nun Ebene 1. 3 ist auf Ebene 2 * 3× (5 - 1/(3×3)) belegt nun Ebene 1. 23` Geben Sie 23 auf Ebene 1 ein. 14,66666 wird in

Ebene 2 verschoben. 3Q Geben Sie 3 ein, berechnen Sie 23

auf Ebene 1. 14,666 befindet sich auf Ebene 2. / (3× (5-1/(3×3)))/23

auf Ebene 1

2.5 Geben Sie 2,5 in Ebene 1 ein !¸ e

2,5

ist auf Ebene 1, auf Ebene 2 wird der

vorangegangene Wert angezeigt.

+ (3× (5 - 1/(3×3)))/23 R √((3× (5 - 1/(3×3)))/23

2,5

= 12,18369, in Ebene 1.

2,5

) = 3,4905156, in

Ebene 1.

Um zwischen den Modi ALG und RPN zu wählen, können Sie auch Systemflag 95 mit folgender Tastenfolge setzen/löschen:

H @)FLAGS —„—„—„— @@CHK@@

Zahlenformat und Dezimalpunkt oder -komma

Durch das Ändern des Zahlenformats können Sie die Anzeige reeller Zahlen im Taschenrechner anpassen. Sie werden diese Funktion bei Operationen mit

Seite 1-11

Zehnerpotenzen oder zum Begrenzen der Dezimalstellen in einem Ergebnis äußerst nützlich finden.

Um ein Zahlenformat auszuwählen, öffnen Sie zunächst die Eingabemaske CALCULATOR MODES durch Drücken der Taste H. Verwenden Sie anschließend die Nach-Unten-Taste ˜, um die Option Number format (Zahlenformat) auszuwählen. Der Standardwert ist Std order Standardformat. Im Standardformat werden Fließkommazahlen ohne feste Dezimalstelle und mit der maximalen Genauigkeit des Taschenrechners (12 signifikante Stellen) angezeigt. Weitere Informationen über reelle Zahlen finden Sie in Kapitel 2 dieser Bedienungsanleitung. Berechnen Sie zur Veranschaulichung dieses und weiterer Zahlenformate die folgenden Übungsbeispiele:

• Standardformat:

Dies ist der am häufigsten verwendete Modus, da in diesem die Zahlen in der vertrautesten Notation angezeigt werden. Drücken Sie die Softmenütaste !!@@OK#@ , wobei Number format (Zahlenformat) auf Std gesetzt ist, um zum Display des Taschenrechners zurückzukehren. Geben Sie die Zahl 123,4567890123456 (mit 16 signifikanten Stellen) ein. Drücken Sie die Taste `. Die Zahl wird auf die maximalen 12 signifikanten Stellen gerundet und wie folgt angezeigt:

• Festes Format für Dezimalzahlen:

Drücken Sie die Taste H. Verwenden Sie anschließend die Nach-UntenTaste ˜, um die Option Number format auszuwählen. Drücken Sie die Softmenütaste @CHOOS ( B), und wählen Sie mit der Nach-Unten-Taste ˜ die Option Fix aus.

Seite 1-12

Drücken Sie die Nach-Rechts-Taste ™, um die Null vor der Option Fix hervorzuheben. Drücken Sie anschließend die Softmenütaste @CHOOS und wählen Sie mit der Nach-Oben- und Nach-Unten-Taste —˜ 3 Dezimalstellen aus.

Drücken Sie die Softmenütaste !!@@OK#@ , um die Auswahl abzuschließen:

Drücken Sie die Softmenütaste !!@@OK#@ , um zum Display des Taschenrechners zurückzukehren. Die Zahl wird nun wie folgt angezeigt:

Beachten Sie, dass die Zahl gerundet und nicht abgeschnitten ist. Somit wird die Zahl 123,4567890123456 in dieser Einstellung als 123,457 und nicht als 123,456 angezeigt, da die Ziffer nach 6 > 5 ist.

• Wissenschaftliches Format

Seite 1-13

Zum Einstellen dieses Formates drücken Sie zunächst die Taste H. Verwenden Sie anschließend die Nach-Unten-Taste ˜, um die Option Number format auszuwählen. Drücken Sie die Softmenütaste @CHOOS ( B), und wählen Sie mit der Nach-Unten-Taste ˜ die Option Scientific (wissenschaftlich) aus. Belassen Sie die Zahl 3 vor Sci . (Diese Zahl kann auf dieselbe Weise geändert werden, wie wir die feste Anzahl von Dezimalstellen im vorherigen Beispiel geändert haben.)

Drücken Sie die Softmenütaste !!@@OK#@ , um zum Display des Taschenrechners zurückzukehren. Die Zahl wird nun wie folgt angezeigt:

Bei dem Ergebnis 1,23E2 handelt es sich um die Darstellung des Taschenrechners von Zehnerpotenzen, d. h. 1,235 × 10

. In dieser so genannten wissenschaftlichen Notation stellt die Sci vorangestellte Ziffer 3 (wie vorher gezeigt) die Anzahl der signifikanten Stellen nach dem Komma dar. Die wissenschaftliche Darstellung umfasst immer eine Ganzzahl, wie oben gezeigt. Deshalb ist in diesem Fall die Anzahl der signifikanten Stellen vier.

• Technisches Format

Das technische Format ähnelt sehr dem wissenschaftlichen Format, mit der Ausnahme, dass die Zehnerpotenzen ein Vielfaches von drei sind. Zum Einstellen dieses Formates, drücken Sie die Taste H. Verwenden Sie anschließend die Nach-Unten-Taste ˜, um die Option Number format (Zahlenformat) auszuwählen. Drücken Sie die Softmenütaste @CHOOS (B), und wählen Sie mit der Nach-Unten-Taste ˜ die Option Engineering

Seite 1-14

(technisch) aus. Behalten Sie die Zahl 3 vor Eng bei. (Diese Zahl kann auf dieselbe Weise geändert werden, wie wir dies im Zahlenformat Fixed mit den Dezimalstellen in einem vorangegangenen Beispiel durchgeführt haben.)

Drücken Sie die Softmenütaste !!@@OK#@ , um zum Display des Taschenrechners zurückzukehren. Die Zahl wird nun wie folgt angezeigt:

Da diese Zahl drei Ziffern vor dem Komma enthält, wird sie im technischen Format mit vier signifikanten Stellen und der Zehnerpotenz Null angegeben. Daher wird beispielsweise die Zahl 0,00256 wie unten angezeigt:

• Dezimalkomma und Dezimalpunkt

Dezimalpunkte in Gleitkommazahlen können durch ein Komma ersetzt werden, wenn der Benutzer mit dieser Notation besser vertraut ist. Um Dezimalpunkte durch Kommas zu ersetzen, ändern Sie in der Eingabemaske CALCULATOR MODES die Option FM wie folgt in Kommas (beachten Sie, dass wir das Zahlenformat in Std geändert haben):

• Drücken Sie die Taste H. Drücken Sie anschließend einmal die Nach- Unten-Taste ˜, und die Nach-Rechts-Taste ™, um die Option __FM

Seite 1-15

zu markieren. Um Kommas auszuwählen, drücken Sie die Softmenütaste @CHK@@ (d. h. die Taste B). Die Eingabemaske wird wie folgt aussehen:

• Drücken Sie die Softmenütaste !!@@OK#@ , um zum Display des Taschenrechners zurückzukehren. Die Zahl 123,4567890123456, die Sie bereits zuvor eingegeben haben, wird nun wie folgt angezeigt:

Winkelmaß

Trigonometrische Funktionen erfordern beispielsweise Argumente, die Flächenwinkel darstellen. Der Taschenrechner enthält drei Angle MeasureModi (Winkelmaß) zum Arbeiten mit Winkeln, und zwar:

• Degrees: 360 Grad (360

• Radians: 2π-Radianten (2π

• Grades: 400 Zentesimalgrad (400

Kreisumfang.

Das Winkelmaß wirkt sich auf die trigonometrischen Funktionen wie SIN, COS, TAN und damit verbundene Funktionen aus.

Um den Winkelmaßmodus zu ändern, gehen Sie wie folgt vor:

• Drücken Sie die Taste H. Drücken Sie anschließend zweimal die Nach- Unten-Taste ˜. Wählen Sie nun den Angle Measure-Modus entweder durch Drücken der Taste \ (zweite Taste von links in der fünften Reihe von unten) oder durch Drücken der Softmenütaste @CHOOS ( B) aus.

) ergeben einen vollständigen Kreisumfang.

) ergeben einen vollständigen

Seite 1-16

Verwenden Sie bei der zweiten Methode die Nach-Unten- und NachOben-Taste —˜ zur Auswahl des gewünschten Modus, und drücken Sie anschließend die Softmenütaste !!@@OK#@ ( F), um den Vorgang abzuschließen. Im folgenden Beispiel ist der Modus Radians ausgewählt:

Koordinatensystem

Das Koordinatensystem wirkt sich auf die Darstellung von Vektoren und komplexen Zahlen aus. Weitere Informationen über komplexe Zahlen und Vektoren finden Sie in Kapitel 4 bzw. 8 dieser Anleitung. Im Taschenrechner stehen drei Koordinatensysteme zur Verfügung: Rechtwinklig (RECT), zylindrisch (CYLIN) und sphärisch (SPHERE). So ändern Sie das Koordinatensystem:

• Drücken Sie die Taste H. Drücken Sie anschließend dreimal die Nach- Unten-Taste ˜. Wählen Sie nun den Modus Coord System aus, indem Sie die Taste \ (zweite Taste von links in der fünften Reihe von unten) oder die Softmenütaste @CHOOS ( B) drücken. Verwenden Sie bei der zweiten Methode die Nach-Unten- und Nach-Oben-Taste —˜ zur Auswahl des gewünschten Modus, und drücken Sie anschließend die Softmenütaste !!@@OK#@ ( F), um den Vorgang abzuschließen. Auf dem unten abgebildeten Bildschirm ist beispielsweise der Koordinatenmodus Polar ausgewählt:

Seite 1-17

Auswählen der CAS-Einstellungen

CAS steht für Computer Algebraic System (algebraisches Computersystem). Dies ist das mathematische Herzstück des Taschenrechners, in dem die Operationen mit mathematischen Symbolen und Funktionen programmiert sind. Das CAS-Modul bietet eine Reihe von Einstellungen, die an die Art der gewünschten Operation angepasst werden können. So zeigen Sie die optionalen CAS-Einstellungen an:

• Drücken Sie die Taste H, um die Eingabemaske CALCULATOR MODES aufzurufen.

• Um die CAS-Einstellungen zu ändern, drücken Sie die Softmenütaste @@ CAS@@. Die Standardwerte der CAS-Einstellungen sind unten dargestellt:

• Um zwischen den einzelnen Optionen der Eingabemaske CAS MODES zu navigieren, verwenden Sie die Pfeiltasten: š™˜—.

• Um eine der obigen Einstellungen auszuwählen oder die Auswahl aufzuheben, wählen Sie zuerst den Unterstrich vor der gewünschten Option aus und verwenden die Softmenütaste @CHK@@, bis die gewünschte Einstellung vorgenommen wurde. Sobald eine Option ausgewählt wurde, wird über dem Unterstrich ein Häkchen angezeigt (im obigen Beispiel bei den Optionen Rigorous und Simp Non-Rational). Nicht ausgewählte Optionen weisen kein Häkchen über dem Unterstrich vor der Option auf

Seite 1-18

• (im obigen Beispiel die Optionen _Numeric, _Approx, _Complex, _Verbose, _Step/Step, _Incr Pow in der Zeile Edit).

• Nachdem Sie in der Eingabemaske CAS MODES alle gewünschten Optionen ausgewählt (bzw. die Auswahl aufgehoben) haben, drücken Sie die Softmenütaste @@@OK@@@. Damit kehren Sie zur Eingabemaske CALCULATOR MODES zurück. Um an dieser Stelle zum normalen Display des Taschenrechners zurückzukehren, drücken Sie erneut die Taste @@@OK@@@ .

Erklärung der CAS-Einstellungen

• Indep var: Die unabhängige Variable für CAS-Anwendungen. Normalerweise VX = ‘X’.

• Modulo den Modulo-Wert des arithmetischen Ringes (siehe Kapitel 5 im Bedienungsanleitung für den Taschenrechner).

• Numeric ein Ergebnis im numerischen oder Fließkommaformat.

• Approx numerische Ergebnisse verwendet. Wenn nicht ausgewählt, ist das CASModul im Modus Exact, in dem in Berechnungen symbolische Ergebnisse ausgegeben werden.

• Complex aktiviert. Wenn nicht ausgewählt, ist das CAS-Modul im Modus Real, d. h., in der Standardeinstellung erfolgen Berechnungen mit reellen Zahlen. Informationen über Berechnungen mit komplexen Zahlen finden Sie in Kapitel 4.

• Verbose ausführliche Information bereitgestellt.

• Step/Step Berechnungen schrittweise angezeigt. Dies bietet sich zum Anzeigen der Zwischenschritte in Summenberechnungen, Ableitungen, Integralen, Polynomoperationen (z. B. bei der Polynomdivision durch Linearfaktoren) und Matrixoperationen an.

• Incr Pow aufsteigender Reihenfolge der Potenzen unabhängiger Variablen angezeigt.

: Für Operationen der modularen Arithmetik enthält diese Variable

: Wenn festgelegt, erzeugt der Taschenrechner bei Berechnungen

: Wenn festgelegt, werden für Berechnungen im Näherungsmodus

: Wenn festgelegt, sind Berechnungen mit komplexen Zahlen

: Wenn festgelegt, werden bei bestimmten CAS-Operationen

: Wenn festgelegt, werden die Ergebnisse für bestimmte CAS-

: Wenn festgelegt, werden die Faktoren des Polynoms in

Seite 1-19

• Rigorous: Wenn festgelegt, vereinfacht der Taschenrechner nicht die Funktion für den Absolutbetrag |X| durch X.

• Simp Non-Rational irrationale Ausdrücke so weit wie möglich zu vereinfachen.

: Wenn festgelegt, versucht der Taschenrechner,

Auswählen der verschiedenen Display-Modi

Durch die Auswahl der einzelnen Anzeigemodi kann das Display des Taschenrechners Ihren Wünschen angepasst werden. So zeigen Sie die möglichen Display-Einstellungen an:

• Drücken Sie die Taste H zu aktivieren. Drücken Sie in der Eingabemaske CALCULATOR MODES die Softmenütaste @@DISP@ (D), um die Eingabemaske DISPLAY MODES anzuzeigen.

• Verwenden Sie die Pfeiltasten š™˜—, um zwischen den einzelnen Optionen der Eingabemaske DISPLAY MODES zu navigieren.

• Um eine der obigen Einstellungen, die ein Häkchen erfordern, auszuwählen oder die Auswahl aufzuheben, markieren Sie zunächst den Unterstrich vor der gewünschten Option, und betätigen Sie die Softmenütaste @CHK@@, bis die gewünschte Einstellung erreicht ist. Sobald eine Option ausgewählt wurde, wird über dem Unterstrich ein Häkchen angezeigt (im obigen Beispiel in der Zeile Stack die Option Textbook ). Nicht ausgewählte Optionen weisen kein Häkchen über dem Unterstrich vor der betreffenden Option auf (z. B. die Optionen _Small, _Full page und _Indent in der Zeile bei Edit:).

, um die Eingabemaske CALCULATOR MODES

Seite 1-20

• Um die Schriftart für das Display auszuwählen, markieren Sie das Feld vor der Option Font: in der Eingabemaske DISPLAY MODES, und verwenden Sie die Softmenütaste @CHOOS ( B).

• Nachdem Sie in der Eingabemaske DISPLAY MODES alle gewünschten Optionen ausgewählt (bzw. die Auswahl aufgehoben) haben, drücken Sie die Softmenütaste @@@OK@@@. Damit kehren Sie zur Eingabemaske CALCULATOR MODES zurück. Um an dieser Stelle zum normalen Display des Taschenrechners zurückzukehren, drücken Sie erneut die Taste @@@OK@@@ .

Auswählen der Schriftart für die Anzeige

Drücken Sie zunächst die Taste H MODES aufzurufen. Drücken Sie in der Eingabemaske CALCULATOR MODES die Softmenütaste @@DISP@ (D), um die Eingabemaske DISPLAY MODES anzuzeigen. Das Feld Font: ist markiert und die Option Ft8_0:system 8 ist ausgewählt. Dies ist der Standardwert für die Anzeigeschriftart Wenn Sie die Softmenütaste @CHOOS (B) drücken, wird eine Liste aller im System vorhandenen Schriftarten angezeigt, wie unten dargestellt:

, um die Eingabemaske CALCULATOR

Zur Auswahl stehen die drei Standardschriftarten System Fonts (Größe 8, 7 und 6) und Browse (Suchen). Mit dieser Option können Sie den Speicher des Taschenrechners nach weiteren Schriftarten durchsuchen, die Sie eventuell selbst erstellt oder auf den Taschenrechner heruntergeladen haben.

Üben Sie das Ändern der Schriftart in die Schriftgrößen 7 und 6. Drücken Sie die Softmenütaste OK, um die Auswahl zu übernehmen. Nachdem Sie eine Schriftart ausgewählt haben, drücken Sie die Softmenütaste @@@OK@@@, um zur Eingabemaske CALCULATOR MODES zurückzukehren. Um an dieser Stelle zum normalen Display des Taschenrechners zurückzukehren, drücken Sie die

Seite 1-21

Softmenütaste @@@OK@@@ erneut, und beachten Sie, wie sich die Anzeige des Stacks entsprechend der neuen Schriftart ändert.

Auswählen der Eigenschaften des Zeileneditors

Drücken Sie zunächst die Taste H, um die Eingabemaske CALCULATOR MODES zu aktivieren. Drücken Sie in der Eingabemaske CALCULATOR MODES die Softmenütaste @@DISP@ (D), um die Eingabemaske DISPLAY MODES anzuzeigen. Drücken Sie einmal die Nach-Unten-Taste ˜, um zur Zeile Edit zu gelangen. Diese Zeile weist drei Eigenschaften auf, die geändert werden können. Wenn diese Eigenschaften ausgewählt (mit einem Häkchen versehen) sind, sind folgende Effekte aktiviert:

_Small Die Schriftgröße wird verkleinert _Full page Ermöglicht das Verschieben des Cursors an das

Zeilenende _Indent Automatischer Zeileneinzug des Cursors, wenn eine Zeilenumbruch erfolgt

Anweisungen zur Verwendung des Zeileneditors finden Sie in Kapitel 2 des Bedienungsanleitung.

Auswählen der Eigenschaften des Stacks

Drücken Sie zunächst die Taste ,H um die Eingabemaske CALCULATOR MODES zu aktivieren. Drücken Sie in der Eingabemaske CALCULATOR MODES die Softmenütaste @@DISP@ (D), um die Eingabemaske DISPLAY MODES anzuzeigen Drücken Sie einmal die Nach-Unten-Taste ˜, um zur Zeile Stack zu gelangen.Diese Zeile weist zwei Eigenschaften auf, die geändert werden können. Wenn diese Eigenschaften ausgewählt (mit einem Häkchen versehen) sind, sind folgende Effekte aktiviert:

_Small Die Schriftart wird verkleinert. Hierdurch wird der Umfang

der auf dem Bildschirm angezeigten Informationen erhöht. Beachten Sie, dass durch diese Auswahl die Auswahl für die Anzeige der Schriftart des Stacks aufgehoben wird.

Seite 1-22

_Textbook Zeigt mathematische Ausdrücke in grafischer mathematischer

Notation an.

Um diese Einstellungen zu veranschaulichen, geben Sie im EquationWriter im algebraischen oder RPN-Modus das folgende bestimmte Integral ein:

‚O… Á0™„è™„¸\x™x`

Wenn weder _Small noch _Textbook ausgewählt ist, wird diese Eingabe im algebraischen Modus wie folgt dargestellt:

Wenn nur die Option _Small ausgewählt ist, wird die Eingabe wie folgt dargestellt:

Wenn jedoch die Option _Textbook ausgewählt (Standardwert) ist, wird die Eingabe unabhängig davon, ob die Option _

Small ausgewählt ist, wie folgt

dargestellt:

Auswählen der Eigenschaften für den EquationWriter (EQW)

Seite 1-23

Zeile EQW (EquationWriter = Gleichungseditor) zu gelangen. Diese Zeile weist zwei Eigenschaften auf, die geändert werden können. Wenn diese Eigenschaften ausgewählt (mit einem Häkchen versehen) sind, sind folgende Effekte aktiviert:

_Small Verkleinert die Schriftart während der Verwendung

des Gleichungseditors

_Small Stack Disp Zeigt nach der Verwendung des Gleichungseditors

eine kleine Schriftart im Stack an

Ausführliche Anweisungen zur Verwendung des Gleichungseditors (EQW) finden Sie in diesem Handbuch an anderer Stelle.

∞

−

dXe

Wenn für das oben als Beispiel dargestellte Integral

Eingabemaske DISPLAY MODES in der Zeile EQW die Option _Small Stack Disp ausgewählt wird, wird die Eingabe wie folgt dargestellt:

∫

in der

Weitere Informationen

Weitere Informationen über die in diesem Kapitel behandelten Themen finden Sie in Kapitel 1 und Anhang C des Bedienungsanleitung für den Taschenrechner.

Seite 1-24

Kapitel 2 Einführung in den Taschenrechner

In diesem Kapitel wird eine Anzahl von Basisoperationen des Rechners erläutert, einschließlich der Anwendung des EquationWriters und der Manipulation von Datenobjekten im Rechner. Studieren Sie die Beispiele in diesem Kapitel genau, um die Möglichkeiten des Rechners für zukünftige Anwendungen genau zu begreifen.

Objekte des Taschenrechners

Einige der am häufigsten verwendeten Objekte sind: reals (reelle Zahlen, dargestellt mit Dezimalzeichen, z. B. -0,0023, 3,56), integers (Ganzzahlen, ohne Dezimalzeichen, z. B. 1232, -123212123), complex numbers (komplexe Zahlen, als geordnete Paare dargestellt, (z. B. 3,-2)), lists (Listen) usw. Eine Beschreibung der Objekte des Taschenrechners finden Sie in den Kapiteln 2 und 24 der Bedienungsanleitung.

Bearbeiten der Ausdrücke im Stack

Dieser Abschnitt enthält Beispiele für das Bearbeiten von Ausdrücken direkt im Display oder im Stack des Taschenrechners.

Erstellen von arithmetischen Ausdrücken

Für dieses Beispiel verwenden wir den algebraischen Modus und ein festes (Fix)Format mit 3 Dezimalstellen für das Display. Wir geben den folgenden arithmetischen Ausdruck ein:

0.1

0.5

⋅

Um diesen Ausdruck einzugeben, verwenden Sie folgende Tastenkombination:

5.*„Ü1.+1/7.5™/ „ÜR3.-2.Q3

5.7

0.20.3

−

Seite 2-1

Der fertige Ausdruck lautet: 5*(1+1/7,5)/( ƒ3-2^3).

Drücken Sie die Taste `, um den Ausdruck wie folgt anzuzeigen:

Beachten Sie, dass bei der Einstellung EXACT des CAS-Moduls (siehe Anhang C in der Bedienungsanleitung) und der Eingabe von Ganzzahlen das Ergebnis als Formel angezeigt wird, z. B.:

5*„Ü1+1/7.5™/

„ÜR3-2Q3

Bevor ein Ergebnis ausgegeben wird, werden Sie gebeten, den Modus in Approx (Rundungswerte) zu ändern. Übernehmen Sie die Änderung, um folgendes Ergebnis zu erhalten (angezeigt im Dezimalmodus Fix mit drei Dezimalstellen – siehe Kapitel 1):

Wenn in diesem Fall der Ausdruck direkt in den Stack eingegeben wird, versucht der Taschenrechner einen Wert zu berechnen, sobald Sie die Taste ` drücken. Wird der Ausdruck aber in Apostrophe eingegeben, gibt der Taschenrechner den Wert entsprechend der Eingabe aus. Beispiel:

³5*„Ü1+1/7.5™/

„ÜR3-2Q3`

Das Ergebnis wird wie folgt angezeigt:

Seite 2-2

Um den Ausdruck zu berechnen, können wir die Funktion EVAL wie folgt verwenden:

µ„î`

Wenn das CAS-Modul auf Exact gesetzt ist, werden Sie gebeten, das Ändern der CAS-Einstellung in Approx zu bestätigen. Wenn dies erfolgt ist, erhalten Sie das gleiche Ergebnis wie zuvor.

Eine andere Möglichkeit zur Berechnung des zuvor in Anführungszeichen eingegebenen Ausdrucks ist die Verwendung der Option …ï.

Wir geben nun den oben verwendeten Ausdruck ein, während der Taschenrechner im RPN-Modus ist. Wir setzen das CAS-Modul auf Exact das Display auf Textbook und das Zahlenformat auf Standard. Die Tastenkombination zur Eingabe des Ausdrucks zwischen Anführungszeichen ist die gleiche wie zuvor, d. h.

³5*„Ü1+1/7.5™/

„ÜR3-2Q3`

Dies ergibt die folgende Ausgabe:

Seite 2-3

Drücken Sie die Taste ` erneut, um zwei Kopien des Ausdrucks fur die Berechnung im Stack zu behalten. Zunächst berechnen wir den Ausdruck mit der Funktion EVAL und anschließend mit der Funktion NUM: µ.

Dieser Ausdruck ist semi-symbolisch, da das Ergebnis sowohl Fließkommakomponenten als auch√3 enthält. Anschließend verwenden wir eine andere Position [mit ™]im Stack und führen die Berechnung mit der Funktion NUM, d. h., ™ …ï durch.

Das letzte Ergebnis ist rein numerisch, so dass die Ergebnisse im Stack unterschiedlich aussehen, obwohl sie den gleichen Ausdruck darstellen. Um sicherzustellen, dass die beiden Ergebnisse gleich sind, subtrahieren wir den einen Wert vom anderen und berechnen diese Differenz mit der Funktion EVAL: -µ. Das Ergebnis ist Null (0).

Weitere Informationen über das Bearbeiten arithmetischer Ausdrücke im Display oder Stack finden Sie in Kapitel 2 der Bedienungsanleitung.

Erstellen von algebraischen Ausdrücken

Algebraische Ausdrücke enthalten nicht nur Zahlen, sondern auch Namen von Variablen. Als Beispiel geben wir folgenden algebraischen Ausdruck ein:

L212

Wir setzen den Betriebsmodus des Taschenrechners auf Algebraic, CAS auf Exact und das Display auf Textbook. Um diesen algebraischen Ausdruck

einzugeben, verwenden wir folgende Tastenkombination:

³2*~l*R„Ü1+~„x/~r™/„ Ü ~r+~„y™+2*~l/~„b

Drücken Sie `, um folgendes Ergebnis zu erhalten:

Seite 2-4

Die Eingabe dieses Ausdrucks im RPN-Modus ist mit dieser Übung im Modus Algebraic identisch.

Weitere Informationen über die Bearbeitung algebraischer Ausdrücke im Display oder Stack finden Sie in Kapitel 2 der Bedienungsanleitung.

Verwenden des EquationWriters (EQW) zum Erstellen von Ausdrücken

Der EquationWriter ist ein äußerst leistungsstarkes Werkzeug, mit dem Sie nicht nur Gleichungen eingeben und anzeigen, sondern auch Funktionen ändern und auf einen Teil der Gleichung oder die ganze Gleichung anwenden können.

Der EquationWriter wird durch Drücken der Tastenkombination ‚O aufgerufen (die dritte Taste in der vierten Reihe von oben). Das Display wird anschließend wie folgt dargestellt. Drücken Sie die Taste L, um die zweite Menüseite anzuzeigen.

Mit den sechs Softmenütasten für den EquationWriter werden die Funktionen EDIT, CURS, BIG, EVAL, FACTOR, SIMPLIFY, CMDS und HELP aktiviert. Ausführliche Informationen über diese Funktionen finden Sie in Kapitel 3 der Bedienungsanleitung.

Erstellen von arithmetischen Ausdrücken

Die Eingabe von arithmetischen Ausdrücken in den EquationWriter ist fast mit der Eingabe von arithmetischen Ausdrücken in Anführungszeichen in den

Seite 2-5

Stack identisch. Der Hauptunterschied besteht darin, dass die in den EquationWriter eingegebenen Ausdrücke wie im Stil von „textbook“ und nicht wie im Zeileneditor eingegeben werden. Probieren Sie beispielsweise die Eingabe folgender Tastenkombination auf dem Bildschirm des EquationWriters aus: 5/5+2

Das Ergebnis ist der Ausdruck

Der Cursor wird als ein nach links gerichteter Pfeil angezeigt. Der Cursor zeigt die derzeitige Bearbeitungsposition an. Geben Sie beispielsweise an der oben abgebildeten Cursorposition Folgendes ein:

*„Ü5+1/3

Der bearbeitete Ausdruck wird wie folgt dargestellt:

Angenommen, Sie möchten den in Klammern stehenden Ausdruck im Nenner ändern, also (5+1/3) durch (5+π

/2) ersetzen. Zunächst verwenden wir die Löschtaste (ƒ), um den Ausdruck 1/3 zu löschen, und ersetzen anschließend diesen Bruch durch π

/2:

ƒƒƒ„ìQ2

Nun wird das Display wie folgt dargestellt:

Seite 2-6

Um den Nenner 2 in den Ausdruck einzufügen, müssen wir den gesamten Ausdruck π An dieser Stelle fügen wir folgende Tastenkombination ein:

Der Ausdruck wird nun wie folgt dargestellt:

markieren. Hierzu drücken wir einmal die Nach-Rechts-Taste (™).

Angenommen, Sie möchten dem gesamten Ausdruck den Bruch 1/3 hinzufügen, d. h., Sie möchten folgenden Ausdruck eingeben:

5(25

+⋅+

)

Zunächst müssen wir den gesamten ersten Ausdruck markieren. Dazu verwenden wir wiederholt die Nach-Rechts-Taste (™) oder der Nach-ObenTaste (—), bis der gesamte Ausdruck markiert ist, also siebenmal. Das Ergebnis sieht wie folgt aus:

Seite 2-7

Anmerkung: Stattdessen können wir auch, ausgehend von der ursprünglichen Cursorposition (rechts von der 2 im Nenner von π2/2), die Tastenkombination ‚— verwenden, die als (‚ ‘ ) interpretiert wird.

Sobald der Ausdruck wie oben dargestellt markiert ist, geben Sie +1/3 ein, um den Bruch 1/3 hinzuzufügen. Das Ergebnis sieht wie folgt aus:

Erstellen von algebraischen Ausdrücken

Ein algebraischer Ausdruck ähnelt einem arithmetischen Ausdruck, mit dem Unterschied, dass lateinische oder griechische Buchstaben enthalten sein können. Algebraische Ausdrücke werden wie arithmetische Ausdrücke erstellt, mit der Ausnahme, dass auch eine alphabetische Tastatur verwendet wird.

Wir veranschaulichen die Verwendung des EquationWriters zum Eingeben eines algebraischen Ausdrucks mit dem nachstehenden Beispiel. Angenommen, wir möchten folgenden Ausdruck eingeben:

∆⋅+

−

⋅+

LNe

Verwenden Sie dazu folgende Tastenkombination:

2 / R3 ™™* ~‚n + „¸\ ~‚m

™™*‚¹ ~„x + 2 * ~‚m * ~‚c

~„y ——— / ~‚t Q1/3

Dies ergibt die folgende Ausgabe:

 



 

3/1



Seite 2-8

In diesem Beispiel haben wir mehrere lateinische Kleinbuchstaben verwendet, z. B. x (~„x), mehrere griechische Buchstaben, z. B. λ (~‚n), aber auch eine Kombination aus lateinischen und griechischen Buchstaben, nämlich ∆y (~‚c~„y). Beachten Sie, dass Sie die Tastenkombination ~„, gefolgt vom einzugebenden Buchstaben, verwenden müssen, um einen lateinischen Kleinbuchstaben einzugeben. Sie können stattdessen auch stets mithilfe des Menüs CHARS (…±) Sonderzeichen eingeben, wenn Sie die erforderliche Tastenkombination nicht auswendig lernen möchten. In Anhang D der Bedienungsanleitung finden Sie eine Auflistung häufig verwendeter Tastenkombinationen mit ~….

Weitere Informationen über das Ändern, Berechnen, Faktorisieren und Vereinfachen von algebraischen Ausdrücken finden Sie in Kapitel 2 der Bedienungsanleitung.

Strukturieren der Daten im Taschenrechner

Sie können Daten im Taschenrechner strukturieren, indem Sie Variablen in einem Verzeichnisbaum speichern. Die Basis des Verzeichnisbaums des Taschenrechners ist das Verzeichnis HOME, das im Anschluss beschrieben wird.

Das Verzeichnis HOME

Um das Verzeichnis HOME aufzurufen, drücken Sie die Funktion UPDIR („§), und wiederholen Sie diesen Vorgang ggf., bis in der zweiten Zeile des Displays {HOME} angezeigt wird. Stattdessen können Sie auch „ (gedrückt halten) § verwenden. In diesem Beispiel enthält das Verzeichnis HOME nur das Verzeichnis CASDIR. Durch Drücken der Taste J werden die Variablen auf den Softmenütasten angezeigt:

Seite 2-9

Unterverzeichnisse

Um Ihre Daten in einem gut strukturierten Verzeichnisbaum zu speichern, können Sie im Verzeichnis HOME Unterverzeichnisse anlegen und weitere Unterverzeichnisse in diesen Unterverzeichnissen, so dass Sie eine mit Verzeichnissen moderner Computer vergleichbare Hierarchie erstellen. Die Namen der Unterverzeichnisse sollten Aufschluss über ihren Inhalt geben, Sie können aber auch willkürliche Namen verwenden. Weitere Informationen über das Bearbeiten von Verzeichnissen finden Sie in Kapitel 2 der Bedienungsanleitung.

Variablen

Variablen sind mit Dateien auf der Festplatte eines Computers vergleichbar. In einer Variablen wird ein einziges Objekt gespeichert (numerische Werte, algebraische Ausdrücke, Listen, Vektoren, Matrizen, Programme usw.). Variablen werden über ihre Namen aufgerufen, die aus einer beliebigen Kombination von Buchstaben und Zahlen bestehen können, doch das erste Zeichen muss ein Buchstabe (lateinisch oder griechisch) sein. Einige nichtalphabetische Zeichen, z. B. der Pfeil (→), können im Variablennamen verwendet werden, wenn sie mit einem alphabetischen Zeichen kombiniert werden. Somit ist ‘→A’ ein gültiger Name für eine Variable, ‘→’ hingegen nicht. Gültige Variablennamen sind beispielsweise ‘A’, ‘B’, ‘a’, ‘b’, ‘α’, ‘β’, ‘A1’, ‘AB12’, ‘A12’,’Vel’,’Z0’,’z1’ usw.

Variablen dürfen nicht denselben Namen wie eine Funktion des Taschenrechners besitzen. Einige der reservierten Variablennamen des Taschenrechners lauten: ALRMDAT, CST, EQ, EXPR, IERR, IOPAR, MAXR, MINR, PICT, PPAR, PRTPAR, VPAR, ZPAR, der_, e, i, n1,n2, …, s1, s2, …, ΣDAT, ΣPAR, π, ∞

Variablen können in Unterverzeichnissen angeordnet werden (siehe Kapitel 2 der Bedienungsanleitung).

Seite 2-10

Eingeben von Variablennamen

Um Namen für Variablen festzulegen, müssen Sie eine Buchstabenfolge auf einmal eingeben, die mit Zahlen kombiniert werden kann. Um Buchstabenfolgen einzugeben, arretieren Sie die alphabetische Tastatur wie folgt:

~~ arretiert die Großschreibung für die alphabetische Tastatur. Wenn die Tastatur auf diese Weise arretiert ist, können Sie Kleinbuchstaben eingeben, indem Sie die Taste „ vor Eingabe des Buchstabens drücken. Durch Drücken der Taste ‚ vor Eingabe des Buchstabens geben Sie Sonderzeichen ein. Wenn die Großschreibung für die alphabetische Tastatur bereits arretiert ist, können Sie mit der Tastenkombination „~ die Kleinschreibung arretieren.

~~„~ arretiert die Kleinschreibung für die alphabetische Tastatur. Wenn die Tastatur auf diese Weise arretiert ist, können Sie Großbuchstaben eingeben, indem Sie die Taste „ vor Eingabe des Buchstabens drücken. Um die Arretierung der Kleinschreibung aufzuheben, drücken Sie „~.

Um die Arretierung der Großschreibung aufzuheben, drücken Sie ~.

Führen Sie folgende Übungen durch:

³~~math` ³~~m„a„t„h` ³~~m„~at„h`

Auf dem Bildschirm des Taschenrechners wird Folgendes angezeigt (links Modus Algebraic, rechts RPN-Modus):

Seite 2-11

Erstellen von Variablen

Variablen werden am einfachsten mit der Taste K erstellt. In den folgenden Beispielen werden die in der Tabelle unten aufgelisteten Variablen gespeichert (Drücken Sie ggf. die Taste J, um das Variablenmenü anzuzeigen):

Name Inhalt Typ

A12 3×105 reell

Q ‘r/(m+r)' algebraisch

R [3,2,1] Vektor z1 3+5i komplex p1 « → r 'π*r^2' » Programm

• Algebraischer Modus

Um den Wert -0,25 in einer Variablen α zu speichern:

0.25\ K ~‚a. An dieser Stelle sieht das Display wie folgt aus:

-0.25 reell

Drücken Sie `, um die Variable zu erstellen. Der Variablenname wird nun als Softmenütastenbeschriftung angezeigt:

Im Folgenden werden die Tastenkombinationen zur Eingabe der restlichen Variablen dargestellt:

Seite 2-12

A12: 3V5K~a12`

Q: ³~„r/„Ü

~„m+~„r™™K~q`

R: „Ô3‚í2‚í1™K~r`

z1: 3+5*„¥ K~„z1` (Bestätigen Sie im Fall einer entsprechenden Meldung das Wechseln in den Modus Complex).

p1: ‚å‚é~„r³„ì* ~„rQ2™™™K~„p1`..

An dieser Stelle sieht das Display wie folgt aus:

Sechs der sieben Variablen werden um unteren Rand des Bildschirms angezeigt: p1, z1, R, Q, A12, α.

• RPN-Modus

(Drücken Sie H\@@OK@@, um in den RPN-Modus zu wechseln). Drücken Sie folgende Tastenkombination, um den Wert -0,25 in einer Variablen α zu speichern: 0.25\` ~‚a`. An dieser Stelle sieht das Display wie folgt aus:

Dieser Ausdruck bedeutet, dass der Wert -0,25 in α gespeichert werden kann. Drücken Sie die Taste K, um die Variable zu

Seite 2-13

erstellen. Der Variablenname wird nun als Softmenütastenbeschriftung angezeigt.

Zur Eingabe des Wertes 3×10

in die Variable A12 kann auch ein

kürzeres Verfahren verwendet werden:

3V5³~a12` K

Es folgt eine Methode zur Eingabe des Inhalts von Q:

Q: ³~„r/„Ü ~„m+~„r™™³~q` K

Zur Eingabe eines Wertes für R kann auch ein noch kürzeres Verfahren verwendet werden:

R: „Ô3#2#1™³K

Beachten Sie, dass im RPN-Modus die Elemente eines Vektors durch die Leertaste (#) und nicht durch das im algebraischen Modus verwendete Komma (‚í ) getrennt werden.

z1: ³3+5*„¥ ³~„z1 K

p1: ‚å‚é~„r³„ì* ~„rQ2™™™³ ~„p1™ ` K.

An dieser Stelle sieht das Display wie folgt aus:

Sechs der sieben Variablen werden um unteren Rand des Bildschirms angezeigt: p1, z1, R, Q, A12, α.

Seite 2-14

Überprüfen des Inhalts von Variablen

Der Inhalt einer Variablen wird am einfachsten durch Drücken der Softmenütastenbeschriftung für diese Variable angezeigt. Für die oben aufgelisteten Variablen können Sie beispielsweise die folgenden Tasten drücken, um den Inhalt der Variablen anzuzeigen:

Algebraischer Modus

Drücken Sie die Tastenkombination: J@@z1@@ ` @@@R@@ `@@@Q@@@ `. An dieser Stelle sieht der Bildschirm wie folgt aus:

RPN-Modus Im RPN-Modus müssen Sie nur die entsprechende Softmenütaste drücken, um den Inhalt einer numerischen oder algebraischen Variablen abzurufen. Im vorliegenden Fall können wir den Inhalt der oben erstellten Variablen z1, R, Q, A12, α, wie folgt anzeigen: J@@z1@@ @@@R@@ @@@Q@@ @@A12@@ @@ª@@

An dieser Stelle sieht das Display wie folgt aus:

Drücken der Nach-Rechts-Taste und anschließend der entsprechenden Softmenütastenbeschriftungen

Diese Methode zum Anzeigen des Variableninhalts ist im algebraischen und RPN-Modus identisch. Führen Sie die folgenden Beispiele in beiden Modi aus:

J‚@@p1@@ ‚ @@z1@@ ‚ @@@R@@ ‚@@@Q@@ ‚ @@A12@@

Seite 2-15

Nach obiger Eingabe sieht der Bildschirm wie folgt aus (algebraischer Modus links und RPN-Modus rechts):

Beachten Sie, dass in diesem Fall der Inhalt des Programms p1 angezeigt wird. Um die noch verbleibenden Variablen in diesem Verzeichnis anzuzeigen, gehen Sie folgendermaßen vor:

@@@ª@@ L ‚ @@@A@@

Auflisten des Inhalts aller Variablen auf dem Bildschirm

Verwenden Sie die Tastenkombination ‚˜ um den Inhalt aller Variablen auf dem Bildschirm aufzulisten. Beispiel:

Drücken Sie die Taste $, um zum normalen Display des Taschenrechners zurückzukehren.

Löschen von Variablen

Variablen werden am einfachsten mit der Funktion PURGE gelöscht. Auf diese Funktion wird direkt über das Menü TOOLS (I) oder das Menü FILES „¡@@OK@@ zugegriffen.

Verwenden der Funktion PURGE im Stack im algebraischen Modus

Unsere Variablenliste enthält die Variablen p1, z1, Q, R und α. Wir löschen die Variable p1 mit dem Befehl PURGE. Drücken Sie I @PURGE@ J@@p1@@

Seite 2-16

`. Auf dem Bildschirm wird nun angezeigt, dass Variable p1 entfernt wurde:

Mit dem Befehl PURGE können Sie mehrere Variablen löschen, indem Sie deren Namen in einer Liste in das Argument von PURGE einfügen. Wenn wir beispielsweise die Variablen R und Q gleichzeitig löschen möchten, können wir folgendes Verfahren verwenden. Geben Sie ein:

I @PURGE@ „ä³ J@@@R!@@ ™‚í ³ J@@@Q!@@

Auf dem Bildschirm wird nun folgender Befehl angezeigt, der ausgeführt werden kann:

Um den Löschvorgang für die Variable abzuschließen, drücken Sie `. Auf dem Bildschirm werden nun die restlichen Variablen angezeigt:

Anwenden der Funktion PURGE im Stack im RPN-Modus

Angenommen, unsere Liste enthält die Variablen p1, z1, Q, R und α. Wir verwenden den Befehl PURGE, um die Variable p1 zu löschen. Drücken Sie ³@@p1@@ ` I @PURGE@. Auf dem Bildschirm wird nun angezeigt, dass Variable p1 entfernt wurde.

Seite 2-17

Um zwei Variablen gleichzeitig zu löschen, z. B. die Variablen R und Q, erstellen Sie zunächst eine Liste (im RPN-Modus müssen die Elemente der Liste nicht wie im algebraischen Modus durch Kommas getrennt werden):

J „ä³ @@@R!@@ ™³ @@@Q!@@ `

Drücken Sie anschließend I@PURGE@ , um die Variablen zu löschen.

Weitere Informationen über das Bearbeiten von Variablen finden Sie in Kapitel 2 der Bedienungsanleitung.

Die Funktionen UNDO und CMD

Die Verwendung der Funktionen UNDO und CMD bietet sich an, wenn Sie kürzlich gelöschte Befehle wiederherstellen oder im Fall eines Fehlers eine Operation rückgängig machen möchten. Diese Funktionen sind der Taste HIST zugeordnet: UNDO wird durch die Tastenkombination ‚¯ aufgerufen, während CMD durch die Tastenkombination „® aufgerufen wird.

CHOOSE boxes und Soft MENU

In einigen Beispielen dieses Kapitels wurden Menülisten mit Befehlen auf dem Bildschirm angezeigt. Diese Menülisten werden als CHOOSE boxes (Auswahlfelder) bezeichnet. Im Folgenden wird anhand eines Beispiels das Wechseln zwischen CHOOSE boxes und Soft MENU veranschaulicht.

Wenn auch nicht auf ein bestimmtes Beispiel bezogen, enthält die vorliegende Übung die beiden Optionen für Menüs im Taschenrechner (CHOOSE boxes und Soft MENU). In diesem Beispiel wenden wir den Befehl ORDER an, um die Variablen in einem Verzeichnis neu anzuordnen, im ALG-Modus:

„°˜ Menüliste PROG anzeigen und MEMORY auswählen

Seite 2-18

@@OK@@ ˜˜˜˜ Menüliste MEMORY anzeigen und DIRECTORY

auswählen

@@OK@@ —— Menüliste DIRECTORY anzeigen und ORDER

auswählen

@@OK@@ Befehl ORDER aktivieren

Eine andere Methode für den Zugriff auf diese Menüs über die Tasten von Soft MENU steht zur Verfügung,wenn das Systemflag 117 gesetzt ist. (Weitere Informationen über Flags finden Sie in Kapitel 2 und 24 der Bedienungsanleitung.) Um dieses Flag zu setzen, geben Sie Folgendes ein:

H @FLAGS! ———————

Auf dem Bildschirm ist Flag 117 nicht gesetzt (CHOOSE boxes):

Drücken Sie die Softmenütaste @CHK@@ um Flag 117 auf Soft MENU zu setzen. Auf dem Bildschirm wird diese Änderung angezeigt:

Seite 2-19

Drücken Sie die Taste @@OK@@ zweimal, um zum normalen Display des Taschenrechners zurückzukehren.

Nun versuchen wir, den Befehl ORDER mit einer ähnlichen Eingabe wie der oben verwendeten aufzurufen, d. h., wir beginnen mit „°. Beachten Sie, dass anstelle einer Menüliste Softmenütastenbeschriftungen mit den verschiedenen Optionen für das Menü PROG angezeigt werden, d. h

Drücken Sie B, um das Softmenü MEMORY ()@@MEM@@) auszuwählen. Das Display enthält nun folgende Elemente:

Drücken Sie E, um das Softmenü DIRECTORY ()@@DIR@@) auszuwählen.

Der Befehl ORDER wird auf diesem Bildschirm nicht angezeigt. Wir suchen ihn mithilfe der Taste L:

Seite 2-20

Um den Befehl ORDER zu aktivieren, drücken wir die Softmenütaste C (@ORDER).

Weitere Informationen

Weitere Informationen über die Eingabe und Bearbeitung von Ausdrücken im Display oder im EquationWriter finden Sie in Kapitel 2 des Bedienungsanleitung. Informationen über die Einstellungen des CAS-Moduls (Computer Algebraic System, algebraisches Computersystem) finden Sie im Anhang C der Bedienungsanleitung. Weitere Informationen über Flags finden Sie in Kapitel 24 der Bedienungsanleitung.

Seite 2-21

Kapitel 3 Berechnungen mit reellen Zahlen

In diesem Kapitel wird die Verwendung des Taschenrechners für Operationen und Funktionen im Zusammenhang mit reellen Zahlen erläutert. Der Benutzer sollte mit der Tastatur vertraut sein, um bestimmte über die Tastatur verfügbare Funktionen erkennen zu können (z. B. SIN, COS, TAN usw.). Es wird auch vorausgesetzt, dass der Benutzer weiß, wie der Betriebsmodus des Taschenrechners geändert (Kapitel 1), Menüs verwendet und Felder ausgewählt (Kapitel 1) werden und wie mit Variablen gearbeitet wird (Kapitel 2).

Beispiele für Berechnungen mit reellen Zahlen

Um Berechnungen mit reellen Zahlen durchzuführen, sollte das CAS-Modul auf den Modus Real (und nicht Complex) gesetzt sein. Der Modus Exact ist der Standardmodus für die meisten Berechnungen. Deshalb sollten Sie die Berechnungen in diesem Modus beginnen. Im Folgenden werden einige Operationen mit reellen Zahlen veranschaulicht:

• Verwenden Sie die Taste \, um das Vorzeichen einer Zahl zu ändern.

Beispiel für den ALG-Modus: \2.5` Beispiel für den RPN-Modus: 2.5\

• Verwenden Sie die Taste Y, um den Kehrwert einer Zahl zu berechnen.

Beispiel für den ALG-Modus: Y2`. Beispiel für den RPN-Modus: 4`Y.

• Verwenden Sie für Addition, Subtraktion, Multiplikation und Division

die jeweils entsprechende Operatortaste, und zwar + - * /.

Beispiele für den ALG-Modus:

3.7 + 5.2 `

6.3 - 8.5 `

Seite 3-1

4.2 * 2.5 `

2.3 / 4.5 `

Beispiele für den RPN-Modus:

3.7` 5.2 +

6.3` 8.5 -

4.2` 2.5 *

2.3` 4.5 /

Im RPN-Modus können Sie stattdessen auch die Operanden durch ein Leerzeichen (#) trennen, bevor Sie die Operatortaste drücken. Beispiele:

3.7#5.2 +

6.3#8.5 -

4.2#2.5 *

2.3#4.5 /

• Mit Klammern („Ü) können Sie Operationen in Gruppen zusammenfassen oder auch Funktionsargumente einschließen. Im ALG-Modus:

„Ü5+3.2™/„Ü7-

2.2`

Im RPN-Modus sind Klammern nicht erforderlich, die Berechnung erfolgt direkt im Stack:

5`3.2`+7`2.2`-/

Wenn Sie im RPN-Modus den Ausdruck in einfachen Apostrophen, können Sie ihn wie im algebraischen Modus eingeben:

³„Ü5+3.2™/

„Ü7-2.2`µ

Sowohl im ALG-Modus als auch im RPN-Modus kann der EquationWriter verwendet werden:

Seite 3-2

‚O5+3.2™/7-2.2

Der Ausdruck kann im EquationWriter berechnet werden, indem Sie Folgendes eingeben:

————@EVAL@ oder, ‚—@EVAL@

• Die Funktion für den Absolutbetrag ABS kann über „Ê aufgerufen werden. Beispiel für den ALG-Modus:

„Ê \2.32`

Beispiel für den RPN-Modus:

2.32\„Ê

• Die Quadratfunktion SQ kann über „º aufgerufen werden. Beispiel für den ALG-Modus:

„º\2.3`

Beispiel für den RPN-Modus:

2.3\„º

Die Quadratwurzelfunktion √ kann über die Taste R aufgerufen werden. Bei Stack-Berechnungen im ALG-Modus geben Sie die Funktion vor dem Argument ein, z. B.:

R123.4`

Im RPN-Modus geben Sie zuerst die Zahl und dann die Funktion ein, z. B.:

123.4R

Seite 3-3

• Die Potenzfunktion ^ wird über die Taste Q aufgerufen. Bei Stack- Berechnungen im ALG-Modus geben Sie die Basis (y) ein, drücken anschließend die Taste Q, und geben dann den Exponenten (x) ein, z. B.:

5.2Q1.25`

• Im RPN-Modus geben Sie zuerst die Zahl und dann die Funktion ein, z. B.:

5.2`1.25Q

• Die Wurzelfunktion XROOT(y,x) kann über die Tastenkombination

‚» aufgerufen werden. Bei Stack-Berechnungen im ALG-Modus geben Sie die Funktion XROOT und anschließend die Argumente (y,x) durch Komma getrennt ein, z. B.:

‚»3‚í 27`

Im RPN-Modus geben Sie zunächst das Argument y, dann x und anschließend den Funktionsaufruf ein, z. B.:

27`3‚»

• Logarithmen mit der Basis 10 werden mit der Tastenkombination ‚Ã (Funktion LOG) berechnet, während die Umkehrfunktion (ALOG oder Antilogarithmus) mit der Tastenkombination „Â berechnet wird. Im ALG-Modus wird die Funktion vor dem Argument eingegeben:

‚Ã2.45` „Â\2.3`

Im RPN-Modus wird das Argument vor der Funktion eingegeben:

2.45 ‚Ã

2.3\ „Â

Seite 3-4

Verwenden von Zehnerpotenzen bei der Dateneingabe

Zehnerpotenzen, d. h. Zahlen im Format –4,5×10-2 usw., werden mit der Taste V eingegeben. Beispiel für den ALG-Modus:

\4.5V\2`

Oder im RPN-Modus:

4.5\V2\`

• Natürliche Logarithmen werden mit ‚¹ (Funktion LN) berechnet, während die Exponentialfunktion (EXP) mit „¸ berechnet wird. Im ALG-Modus wird die Funktion vor dem Argument eingegeben:

‚¹2.45` „¸\2.3`

Im RPN-Modus wird das Argument vor der Funktion eingegeben:

2.45` ‚¹

2.3\` „¸

• Drei trigonometrische Funktionen können einfach über die Tastatur aufgerufen werden: Sinus (S), Cosinus (T) und Tangens (U). Argumente dieser Funktionen sind Winkel in Grad, Zentesimalgrad oder im Bogenmaß. In den folgenden Beispielen werden die Winkel in Grad (DEG) angegeben:

Im ALG-Modus:

S30` T45`

U135`

Im RPN-Modus:

30S 45T

135U

• Die über die Tastatur verfügbaren inversen trigonometrischen Funktionen sind Arcussinus („¼), Arcuscosinus („¾), und

Seite 3-5

Arcustangens („À). Das Ergebnis dieser Funktionen wird im gewählten Winkelmaß (DEG, RAD, GRD) ausgegeben. Einige Beispiele sind nächst gezeigt:

Im ALG-Modus:

„¼0.25` „¾0.85` „À1.35`

Im RPN-Modus:

0.25„¼

0.85„¾

1.35„À

Alle oben aufgeführten Funktionen, und zwar ABS, SQ, √, ^, XROOT, LOG, ALOG, LN, EXP, SIN, COS, TAN, ASIN, ACOS, ATAN, können mit den grundlegenden Operationen (+-*/) kombiniert werden, um komplexere Ausdrücke zu erstellen. Der EquationWriter, dessen Operationen in Kapitel 2 beschrieben wurden, ist für diese Ausdrücke unabhängig vom Betriebsmodus des Taschenrechners hervorragend geeignet.

Funktionen mit reellen Zahlen im Menü MTH

Das Menü MTH („´) enthält eine Reihe von mathematischen Funktionen, die zum Großteil für reelle Zahlen geeignet sind. Mit der Standardeinstellung CHOOSE Boxes für Systemflag 117 (siehe Kapitel 2) enthält das Menü MTH folgende Funktionen:

Die Funktionen sind nach Argumenttyp angeordnet ( 1. Vektoren, 2. Matrizen,

3. Listen, 7. Wahrscheinlichkeit, 9. komplexe Zahlen) oder nach Funktionstyp (4. hyperbolisch, 5. reell, 6. Basis, 8. schnelle Fourier-Transformationen, FFT). Das Menü enthält auch einen Eintrag für die im Taschenrechner verfügbaren mathematischen Konstanten (Eintrag 10).

Seite 3-6

Im Allgemeinen sollten Sie die Anzahl und Anordnung der für jede Funktion erforderlichen Argumente beachten und in Erinnerung behalten, dass im ALGModus zunächst die Funktion und dann das Argument eingegeben wird, während im RPN-Modus erst das Argument in den Stack eingegeben und anschließend die Funktion ausgewählt wird.

Verwenden der Menüs des Taschenrechners:

1. In diesem Abschnitt beschreiben wir ausführlich die Verwendung des

Menüs 4. HYPERBOLIC, um die allgemeine Funktionsweise der Taschenrechnermenüs zu erläutern. Beachten Sie insbesondere die Vorgehensweise beim Auswählen unterschiedlicher Optionen.

2. Um die nummerierten Optionen der Menüliste (oder des CHOOSE box) schnell auswählen zu können, drücken Sie einfach die Taste für die Nummer der gewünschten Option. Um beispielsweise im Menü MTH die Option 4. HYPERBOLIC.. auszuwählen, drücken Sie einfach die Taste

Hyperbolische Funktionen und ihre Inversen

Um das Menü für hyperbolische Funktionen aufzurufen, wählen Sie im Menü MTH die Option 4. HYPERBOLIC.. aus und drücken anschließend die Taste @@OK@@.

Um beispielsweise im ALG-Modus die Funktion tanh(2,5) zu berechnen, geben Sie Folgendes ein:

„´4 @@OK@@ 5 @@OK@@ 2.5`

Im RPN-Modus ist für diese Berechnung folgende Eingabe erforderlich:

Seite 3-7

2.5`„´4 @@OK@@ 5 @@OK@@

Die oben dargestellten Operationen setzen voraus, dass Sie die Standardeinstellung für Systemflag 117 (CHOOSE boxes) verwenden. Wenn Sie die Einstellung dieses Flags in Soft MENU (siehe Kapitel 2) geändert haben, wird das Menü MTH wie folgt angezeigt (links ALG-Modus, rechts RPN-Modus):

Wenn Sie die Taste L drücken, werden die restlichen Optionen angezeigt:

Um z. B. das Menü für die hyperbolischen Funktionen in diesem Menüformat auszuwählen, drücken Sie die Taste )@@HYP@ , folgender Bildschirm erscheint:

Um abschließend z.B. den Tangens hyperbolicus (atanh) auszuwählen, drücken Sie einfach @@TANH@.

Anmerkung: Um weitere Optionen dieser Softmenüs anzuzeigen, drücken Sie die Taste L oder die Tastenkombination „«.

Um z. B. tanh(2,5) im ALG-Modus zu berechnen, wenn statt CHOOSE boxes die Einstellung Soft MENU verwendet wird, geben Sie Folgendes ein:

„´@@HYP@ @@TANH@ 2.5`

Seite 3-8

Denselben Wert berechnen Sie im RPN-Modus wie folgt:

2.5`„´)@@HYP@ @@TANH@

Überprüfen Sie zum Üben der Anwendung hyperbolischer Funktionen die folgenden Werte:

SINH (2.5) = 6.05020.. ASINH (2.0) = 1.4436… COSH (2.5) = 6.13228.. ACOSH (2.0) = 1.3169… TANH (2.5) = 0.98661.. ATANH (0.2) = 0.2027… EXPM (2.0) = 6.38905…. LNP1 (1.0) = 0.69314….

Operationen mit Einheiten

Den Zahlen des Taschenrechners können unterschiedliche Einheiten zugeordnet sein. Daher können Sie Ergebnisse mit einem konsistenten System von Einheiten berechnen und die Ergebnisse mit der entsprechenden Kombination von Einheiten ausgeben lassen.

Das Menü UNITS

Das Menü UNITS wird über die Tastenkombination ‚Û (der Taste 6 zugeordnet) aufgerufen. Wenn das Systemflag 117 auf CHOOSE boxes gesetzt ist, wird das folgende Menü angezeigt:

Seite 3-9

Option 1. Tools.. enthält Funktionen für Operationen mit Einheiten (Erläuterung weiter unten). Die Optionen 2. Length. (Länge). bis 17.Viscosity (Viskosität).. enthalten Menüs mit einer Reihe von Einheiten für jede der beschriebenen Größen. Wenn Sie beispielsweise das Menü 8. Force (Kraft).. auswählen, wird das folgende Menü für Einheiten angezeigt:

Sie werden die meisten Einheiten (einige Einheiten, z. B. Dyne, werden heute nur noch selten verwendet) aus dem Physikunterricht kennen: N = Newton, dyn = Dyne, gf = Gramm – Kraft (zur Unterscheidung von Gramm-Masse oder einfach Gramm als Einheit für Masse), kip = Kilopound (1000 engl. Pound), lbf = Pound – Kraft (zur Unterscheidung von Pound – Masse), pdl = Poundal.

Um einer Zahl eine Einheit zuzuordnen, muss auf diese Zahl ein Unterstrich folgen. Somit wird eine Kraft von 5 N als 5_N eingegeben.

Für ausführliche Berechnungen mit Einheiten bieten die Optionen von Soft MENU eine komfortablere Methode zum Zuordnen von Einheiten. Ändern Sie das Systemflag 117 in Soft MENU (siehe Kapitel 2), und verwenden Sie die Tastenkombination ‚Û, um folgende Menüs aufzurufen. Drücken Sie die Taste L, um zur nächsten Menüseite zu navigieren.

Seite 3-10

Wenn Sie die entsprechende Softmenütaste drücken, wird ein Untermenü für die Einheiten zu dieser Auswahl angezeigt. Beispielsweise sind für das Untermenü @)SPEED folgende Einheiten verfügbar:

Wenn Sie die Softmenütaste @)UNITS drücken, kehren Sie zum Menü UNITS zurück.

Beachten Sie, dass Sie mit ‚˜ jederzeit die vollständige Liste der Menüeinträge auf dem Bildschirm anzeigen können. Beispielsweise werden für die mithilfe von @)ENRG aufgerufene Gruppe von Einheiten folgende Einträge aufgelistet:

Anmerkung: Verwenden Sie die Taste L oder die Tastenkombination „«, um in den einzelnen Menüs zu navigieren.

Verfügbare Einheiten

Eine vollständige Liste der verfügbaren Einheiten finden Sie in Kapitel 3 der Bedienungsanleitng.

Zuordnen von Einheiten zu Zahlen

Um einer Zahl eine Einheit zuzuordnen, muss auf die Zahl ein Unterstrich folgen (‚Ý, Taste(8,5)). Somit wird eine Kraft von 5 N als 5_N eingegeben.

Seite 3-11

Dies ist die Tastenkombination, die im ALG-Modus mit Systemflag 117 auf CHOOSE boxes gesetzt eingegeben werden muss:

5‚Ý ‚Û 8@@OK@@ @@OK@@ `

Anmerkung: Wenn Sie den Unterstrich auslassen, ist das Ergebnis der Ausdruck 5*N, wobei N einen möglichen Variablennamen, nicht aber die Einheit Newton darstellt.

Verwenden Sie folgende Eingabe, um dieselbe Größe im RPN-Modus einzugeben:

5‚Û8@@OK@@ @@OK@@

Beachten Sie dabei, dass bei aktiviertem RPN-Modus der Unterstrich automatisch eingefügt wird.

Im Folgenden wird die Eingabe von Einheiten bei ausgewählter Option Soft MENU im ALG- und im RPN-Modus dargestellt: Im ALG-Modus geben Sie beispielweise die Größe 5_N wie folgt ein:

5‚Ý ‚ÛL @)@FORCE @ @@N@@ `

Für dieselbe Größe wird im RPN-Modus folgende Eingabe verwendet:

5‚ÛL @)@FORCE @ @@N@@

Anmerkung: Sie können einen Ausdruck mit Einheiten eingeben, indem Sie den Unterstrich und die Einheiten mit der Taste ~ eingeben. Beispielsweise ergibt 5‚Ý~n den Eintrag 5_N.

Vorzeichen für Einheiten

Vorzeichen für Einheiten können Sie entsprechend der folgenden Tabelle aus dem SI-System eingeben. In der ersten Spalte ist die Abkürzung des Vorzeichens aufgeführt, anschließend der Name, gefolgt vom Exponenten x im Faktor 10

, der dem jeweiligen Vorzeichen entspricht:

Seite 3-12

____________________________________________________ Vorzeichen Name x Vorzeichen Name x ____________________________________________________ Y Zotta +24 d Dezi -1 Z Zetta +21 c Centi -2 E Exa +18 m Milli -3 P Peta +15 µ Mikro -6

T Tera +12 n Nano -9 G Giga +9 p Piko -12 M Mega +6 f Femto -15

k,K Kilo +3 a Atto -18 h,H Hekto +2 z Zepto -21 D(*) Deka +1 y Yocto -24 _____________________________________________________

(*) Im SI-System lautet dieses Vorzeichen da und nicht D. Verwenden Sie jedoch am Taschenrechner für Deka das D.

Um diese Vorzeichen einzugeben, tippen Sie einfach das Vorzeichen mit der Taste ~ ein. Um z. B. 123 pm (Picometer) einzugeben, verwenden Sie folgende Eingabe:

123‚Ý~„p~„m

Mit UBASE (geben Sie den Namen ein) wandeln Sie das Ergebnis in die Standardeinheit (1 m) um:

Operationen mit Einheiten

Es folgen einige Rechenbeispiele im ALG-Modus. Beachten Sie, dass bei der Multiplikation und Division von Größen mit Einheiten jede Größe zusammen mit der zugehörigen Einheit eingeklammert werden muss. Um beispielsweise

Seite 3-13

das Produkt 12,5 m × 5,2 yd einzugeben, muss daher Ihre Eingabe (12,5_m)*(5,2_yd) `lauten:

Diese wird dann als 65_(m⋅yd) angezeigt. Zur Umwandelung in Einheiten des SI-Systems, verwenden Sie die Funktion UBASE (die Sie im Befehlskatalog über ‚N finden):

Anmerkung: Beachten Sie, dass die Variable ANS(1) über die Tastenkombination „î (der Taste ` zugeordnet) aufgerufen wird.

Um eine Division durchzuführen, z. B. 3250 mi / 50 h, geben Sie

(3250_mi)/(50_h) `

ein. Die Umwandlung in SI-Einheiten mit der Funktion UBASE ergibt Folgendes:

Die Addition und Subtraktion kann im ALG-Modus ohne Klammern durchgeführt werden, z. B. kann 5 m + 3200 mm einfach wie folgt eingegeben werden:

5_m + 3200_mm `.

Kompliziertere Ausdrücke erfordern jedoch Klammern, z. B.

(12_mm)*(1_cm^2)/(2_s) `:

Seite 3-14

Bei Stack-Berechnungen im RPN-Modus müssen die einzelnen Ausdrücke nicht in Klammern eingeschlossen werden. Beispiel:

12 @@@m@@@ 1.5 @@yd@@ *

3250 @@mi@@ 50 @@@h@@@ /

Diese Operationen ergeben folgende Ausgabe:

Konvertierung von Einheiten

Das Menü UNITS enthält das Untermenü TOOLS, das folgende Funktionen enthält:

CONVERT(x,y): konvertiert Einheit der Objektes x in die Einheit von y

UBASE(x): konvertiert Einheit von Objekt x in SI-Einheiten

UVAL(x): extrahiert den Wert von Objekt x

UFACT(x,y): trennt eine Einheit x vom Objekt y ab

UNIT(x,y): kombiniert den Wert von x mit der Einheit von y

Beispiele für die Funktion CONVERT sind unten dargestellt. Beispiele für die anderen Funktionen von UNIT/TOOLS finden Sie in Kapitel 3 der Bedienungsanleitung. Um beispielsweise 33 Watt in BTUs (British Thermal Unit) umzuwandeln, können Sie einen der beiden Einträge verwenden:

CONVERT(33_W,1_hp) `

CONVERT(33_W,11_hp) `

Physikalische Konstanten im Taschenrechner

Die physikalischen Konstanten des Taschenrechners befinden sich in der constants library (Konstantenbibliothek), die mit dem Befehl CONLIB aufgerufen wird. Um diesen Befehl zu starten, können Sie einfach ~~conlib` in den Stack eingeben, oder wählen Sie im

Seite 3-15

Befehlskatalog den Befehl CONLIB wie folgt aus: Rufen Sie zunächst den Katalog mit ‚N~c auf. Verwenden Sie dann die Nach-Unten- und Nach-Oben-Tasten —˜, um CONLIB auszuwählen. Drücken Sie schließlich die Softmenütaste F(@@OK@@). Drücken Sie erforderlichenfalls `. Verwenden Sie die Nach-Unten- und Nach-Oben-Tasten (—˜) zur Navigation in der Konstantenliste des Taschenrechners.

Die Softmenütasten für den Bildschirm CONSTANTS LIBRARY umfassen folgende Funktionen:

SI wenn ausgewählt, werden die Werte der Konstanten in SI-

Einheiten angezeigt

ENGL wenn ausgewählt, werden die Werte der Konstanten in

traditionellen britischen Maßeinheiten angezeigt

UNIT wenn ausgewählt, werden die Konstanten mit den

zugeordneten Einheiten angezeigt

VALUE wenn ausgewählt, werden die Konstanten ohne Einheiten

angezeigt STK kopiert den Wert (mit oder ohne Einheiten) in den Stack QUIT schließt die Anzeige der Konstantenbibliothek

(*) nur aktiviert, wenn die Option VALUE ausgewählt wurde.

Der oberste Abschnitt des Bildschirms CONSTANTS LIBRARY sieht wie folgt aus, wenn die Option VALUE ausgewählt wurde (Einheiten im SI-System):

Um die Werte der Konstanten in traditionellen britischen Maßeinheiten anzuzeigen, drücken Sie die Option @ENGL :

Seite 3-16

Wenn die Auswahl der Option UNITS aufgehoben wird (drücken Sie @UNITS), werden nur die Werte angezeigt (in diesem Fall wurden traditionelle britische Maßeinheiten ausgewählt):

Um den Wert von Vm in den Stack zu kopieren, wählen Sie den Variablennamen aus, und drücken Sie zunächst die Taste !²STK und anschließend @QUIT@. Wenn sich der Taschenrechner im ALG-Modus befindet, sieht der Bildschirm wie folgt aus:

Der Bildschirm weist einen so genannten gekennzeichneten Wert (tagged value) auf, Vm:359.0394. In diesem Fall ist Vm die Kennzeichnung (tag) des Ergebnisses. Bei jeder arithmetischen Operation mit dieser Zahl wird das Tag ignoriert. Geben Sie beispielsweise

‚¹2*„î `

ein. Sie erhalten folgendes Ergebnis:

Für die gleiche Operation im RPN-Modus ist die folgende Eingabe erforderlich (nachdem der Wert von Vm aus der Konstantenbibliothek abgerufen wurde):

Seite 3-17

2`*‚¹

Definieren und Verwenden von Funktionen

Benutzer können mit dem Befehl DEFINE, der über die Tastenkombination „à aufgerufen wird (der Taste 2 zugeordnet), eigene Funktionen definieren. Die Funktion muss im folgenden Format eingegeben werden:

Funktionsname(Argumente) = Ausdruck_mit_den_Argumenten

So können wir z. B. eine einfache Funktion definieren:

H(x) = ln(x+1) + exp(-x)

Angenommen, Sie müssen diese Funktion für eine Zahl von diskreten Werten berechnen und möchten daher nur eine einzige Taste verwenden, um das gewünschte Ergebnis zu erhalten, ohne für jeden einzelnen Wert den Ausdruck auf der rechten Seite einzugeben. Im folgenden Beispiel wird vorausgesetzt, dass sich der Taschenrechner im ALG-Modus befindet. Geben Sie folgende Tastenkombinationen ein:

„à³~h„Ü~„x™‚Å

‚¹~„x+1™+„¸~„x`

Auf dem Bildschirm wird Folgendes angezeigt:

Drücken Sie die Taste J, und Sie werden feststellen, dass die Softmenü taste (@@@H@@) eine neue Variable enthält. Um den Inhalt dieser Variablen anzuzeigen, drücken Sie ‚@@@H@@. Auf dem Bildschirm wird nun Folgendes angezeigt:

Seite 3-18

Somit enthält die Variable H ein Programm, das durch folgenden Ausdruck definiert ist:

<<  x ‘LN(x+1) + EXP(x)’ >>

Dies ist ein einfaches Programm in der Standard-Programmiersprache der HP 48 G-Serie, die auch in der HP 49 G-Serie enthalten ist. Diese Programmiersprache heißt UserRPL (siehe Kapitel 20 und 21 des Bedienungsanleitung für den Taschenrechner). Das oben dargestellte Programm ist relativ einfach und besteht aus zwei Teilen, die sich zwischen den Programm-Containern << >> befinden:

• Eingabe:  x  x

• Verarbeitung: ‘LN(x+1) + EXP(x) ‘

Dies wird so interpretiert: Trage einen Wert ein, der temporär dem Namen x (als lokale Variable bezeichnet) zugeordnet wird, berechne den Ausdruck zwischen den Anführungszeichen, der die lokale Variable enthält, und zeige den berechneten Ausdruck an.

Um die Funktion im ALG-Modus aufzurufen, geben Sie den Namen der Funktion ein, gefolgt vom Argument in Klammern, z. B. @@@H@@@ „Ü2`. Es folgen einige Beispiele:

Im RPN-Modus müssen Sie zum Aufrufen der Funktion zunächst das Argument eingeben und dann die dem Variablennamen entsprechende Softmenütaste @@@H@@@ drücken. Sie können z. B. 2`@@@H@@@ eingeben. Die anderen oben aufgeführten Beispiele können wie folgt eingegeben werden:

1.2`@@@H@@@ , 2`3/@@@H@@@ .

Weitere Informationen

Weitere Informationen über Operationen des Taschenrechners mit reellen Zahlen finden Sie in Kapitel 3 des Bedienungsanleitung.

Seite 3-19

Kapitel 4 Berechnungen mit komplexen Zahlen

Dieses Kapitel enthält Beispiele zum Rechnen mit und Anwenden von Funktionen au komplexe Zahlen.

Definitionen

Eine komplexe Zahl z wird als z = x + iy, (Kartesische Form) angegeben, wobei x und y reelle Zahlen sind und i die imaginäre Einheit, definiert durch

= -1, darstellt. Die Zahl hat einen reellen Teil x = Re(z) und einen

imaginären Teil y = Im(z). Die polare Form einer komplexen Zahl lautet z = re

r⋅cosθ + i r⋅sinθ, wobei r = |z| =

yx + den Betrag der komplexen Zahl z

und θ = Arg(z) = arctan(y/x) das Argument der komplexen Zahl z darstellt.

Die konjugiert komplexe Zahl einer komplexen Zahl z = x + iy = re x – iy = re

-i

. Der negative Wert von z, –z = -x-iy = - re

, kann als

istz =

Spiegelung von z am Ursprung betrachtet werden.

Einstellen des Modus COMPLEX am Taschenrechner

Zum Arbeiten mit komplexen Zahlen wählen Sie den CAS-Modus COMPLEX aus:

H)@@CAS@ ˜˜™ @CHK@@

Der Modus COMPLEX ist ausgewählt, wenn auf dem Bildschirm CAS MODES die Option _Complex mit einem Häkchen versehen ist:

Drücken Sie zweimal @@OK@@, um zum Stack zurückzukehren.

Seite 4-1

Eingeben von komplexen Zahlen

Komplexe Zahlen können in einer der beiden Kartesischen Darstellungsarten in den Taschenrechner eingegeben werden, entweder mit x+iy oder (x,y). Die Ergebnisse des Taschenrechners werden als geordnete Paare dargestellt, d. h. (x,y). Im ALG-Modus wird beispielsweise die komplexe Zahl (3,5; -1,2) wie folgt eingegeben:

„Ü3.5‚í\1.2`

Eine komplexe Zahl kann aber auch als x+iy eingegeben werden. Im ALGModus wird 3,5-1,2i beispielsweise wie folgt eingegeben(Modusänderungen übernehmen):

3.5 -1.2*„„¥`

Im RPN-Modus können diese Zahlen mit folgenden Tastenkombinationen eingegeben werden:

„Ü3.5‚í1.2\`

(Beachten Sie, dass die Taste zum Ändern des Vorzeichens nach der Zahl 1,2 eingegeben wird, also in der umgekehrten Reihenfolge wie im Beispiel für den ALG-Modus) und

³3.5 -1.2*„„¥`

(Beachten Sie, dass im RPN-Modus vor Eingabe der Zahl 3,5-1,2i ein Hochkomma eingegeben werden muss.)

Um die imaginäre Einheit der Zahl einzugeben, verwenden Sie „¥ (die Taste l).

Polare Darstellung von komplexen Zahlen

Sie erhalten die polare Darstellung der oben verwendeten komplexen Zahl 3,5-1,2i, indem Sie das Koordinatensystem von zylindrisch in polar ändern (mit der Funktion CYLIN). Sie finden diese Funktion im Katalog (‚N). Sie können auch mithilfe von H das Koordinatensystem in POLAR ändern. Nach

Seite 4-2

dem Einstellen des polaren Koordinatensystems und Ändern des Winkelmaßes in Bogenmaß (RAD) erhalten Sie folgendes Ergebnis:

Das oben dargestellte Ergebnis weist den Betrag 3,7 und den Winkel 0,33029... auf. Das Winkelsymbol (∠) wird vor dem Winkelmaß angezeigt.

Wechseln Sie wieder zur Darstellung in kartesischen bzw. rechtwinkligen Koordinaten, indem Sie die Funktion RECT verwenden (im Katalog ‚N

verfügbar). In der polaren Darstellung wird eine komplexe Zahl als z = r⋅e

angegeben. Sie können diese komplexe Zahl als komplexes Paar der Form (r, ∠θ) in den Taschenrechner eingeben. Das Winkelsymbol (∠) kann als ~‚6 eingegeben werden. Beispielsweise kann die komplexe Zahl z = 5,2e

1,5i

wie folgt eingegeben werden (die Abbildungen stellen den RPN

Stack vor und nach Eingabe der Zahl dar):

Da das Koordinatensystem auf rechtwinklige (bzw. kartesische) Darstellung eingestellt ist, wandelt der Taschenrechner die eingegeben Zahl automatisch in kartesische Koordinaten um, d. h. x = r cos θ, y = r sin θ, in diesem Fall mit dem Ergebnis (0,3678…, 5,18…).

Wenn andererseits das zylindrische Koordinatensystem eingestellt ist (über die Funktion CYLIN), erhalten Sie bei der Eingabe einer komplexen Zahl (x,y), wobei x und y reelle Zahlen sind, eine polare Darstellung. Geben Sie z. B. bei der Verwendung zylindrischer Koordinaten die Zahl (3.,2.) ein. In der folgenden Abbildung ist der RPN-Stack vor und nach Eingabe dieser Zahl dargestellt:

Seite 4-3

Einfache Operationen mit komplexen Zahlen

Komplexe Zahlen können mit den vier Grundrechenarten (+-*/) kombiniert werden. Die Ergebnisse werden nach algebraischen Regeln berechnet, mit der Ausnahme, dass i Zahlen sind mit Operationen mit reellen Zahlen vergleichbar. Führen Sie mit dem Taschenrechner im ALG-Modus und der CAS-Einstellung Complex die folgenden Operationen durch:

(5-2i)/(3+4i) = (0,28;-1,04)

1/(3+4i) = (0,12; -0,16);

= -1 ist. Operationen mit komplexen

(3+5i) + (6-3i) = (9;2);

(5-2i) - (3+4i) = (2;-6)

(3-i)(2-4i) = (2;-14);

-(5-3i) = -5 + 3i

Die CMPLX-Menüs

Im Taschenrechner stehen zwei CMPLX-Menüs (CoMPLeXe Zahlen) zur Verfügung. Ein Menü kann über das Menü MTH (in Kapitel 3 vorgestellt) und das andere direkt über die Tastatur (‚ß) aufgerufen werden. Im Folgenden werden die beiden CMPLX-Menüs vor vorgestellt.

Menü CMPLX über das Menü MTH

Wenn das Systemflag 117 auf CHOOSE boxes (siehe Kapitel 2) gesetzt ist, wird das Untermenü CMPLX im Menü MTH wie folgt aufgerufen: „´9 @@OK@@. Folgende Funktionen sind verfügbar:

Seite 4-4

Der erste Abschnitt des Menüs (Optionen 1 bis 6) weist folgende Funktionen auf: RE(z) : Realteil einer komplexen Zahl IM(z) : Imaginärteil einer komplexen Zahl

C→R(z) : teilt eine komplexe Zahl in ihre reellen und imaginären

Komponenten auf

R→C(x,y) : Bildet die komplexe Zahl (x,y) aus den reellen Zahlen x und y

ABS(z) : Berechnet den Betrag einer komplexen Zahl. ARG(z) : Berechnet das Argument einer komplexen Zahl. SIGN(z) : Berechnet eine komplexe Zahl mit Einheitsbetrag als z/|z|. NEG(z) : Ändert das Vorzeichen von z CONJ(z) : Erzeugt die konjugiert komplexe Zahl von z Im Folgenden finden Sie Anwendungsbeispiele dieser Funktionen mit RECTKoordinaten. Beachten Sie, dass im ALG-Modus das Argument der Funktion vorangestellt werden muss, während im RPN-Modus erst das Argument eingegeben und dann die Funktion ausgewählt wird. Beachten Sie auch, dass Sie diese Funktionen über die Softmenütasten aufrufen können, indem Sie die Einstellung des Systemflags 117 ändern (siehe Kapitel 2).

Seite 4-5

Menü CMPLX auf der Tastatur

Ein zweites Menü CMPLX kann über die Tastatur aufgerufen werden, indem Sie die Nach-Rechts-Taste zusammen mit der Taste 1 verwenden, also ‚ß. Wenn das Systemflag 117 auf CHOOSE boxes gesetzt ist, wird das Menü CMPLX wie folgt angezeigt:

Dieses Menü enthält einige bereits im vorangegangenen Abschnitt vorgestellte Funktionen, und zwar ARG, ABS, CONJ, IM, NEG, RE und SIGN. Weiterhin enthält es auch die Funktion i, die der Tastenkombination „¥ entspricht.

Auf komplexe Zahlen angewendete Funktionen

Viele Tastaturfunktionen und Funktionen des Menüs MTH, die in Kapitel 3 für reelle Zahlen definiert wurden (z. B. SQ, ,LN, e komplexe Zahlen angewendet werden. Das Ergebnis ist eine weitere komplexe Zahl, wie in den folgenden Beispielen dargestellt.

, usw.) können auch auf

Seite 4-6

Anmerkung: Wenn Sie trigonometrische Funktionen und deren Inverse mit komplexen Zahlen verwenden, sind die Argumente keine Winkel mehr. Deshalb hat das für den Taschenrechner ausgewählte Winkelmaß bei der Berechnung dieser Funktionen mit komplexen Argumenten keine Auswirkung.

Funktion DROITE: Gleichung einer Geraden

Die Funktion DROITE akzeptiert als Argument zwei komplexe Zahlen, z. B.

+iy1 und x2+iy2, und gibt die Gleichung einer Geraden zurück, z. B. y =

a+bx, die die Punkte (x zwischen den Punkten A(5,-3) und B(6,2) wie folgt ermittelt werden (Beispiel im algebraischen Modus):

) und (x2,y2) enthält. Beispielsweise kann die Linie

1,y1

Die Funktion DROITE wird über den Befehlskatalog (‚N) aufgerufen. Wenn der Taschenrechner im Modus APPROX ist, lautet das Ergebnis Y =

5.*(X-5.)-3.

Weitere Informationen

Weitere Informationen über Operationen mit komplexen Zahlen finden Sie in Kapitel 4 des Bedienungsanleitung.

Seite 4-7

Kapitel 5 Algebraische und arithmetische Operationen

Ein algebraisches Objekt , oder einfach, Algebraik, kann jede Zahl, Variable oder jeder algebraische Ausdruck sein, der nach den Regeln der Algebra berechnet, manipuliert oder kombiniert werden kann. Beispiele von algebraischen Objekten sind:

• Eine Zahl: 12,3, 15,2_m, ‘π’, ‘e’, ‘i’

• Der Name einer Variablen: ‘a’, ‘ux’, ‘width’, usw.

• Ein Ausdruck: ‘p*D^2/4’,’f*(L/D)*(V^2/(2*g))’,

• Eine Gleichung: ‘p*V = n*R*T’, ‘Q=(Cu/n)*A(y)*R(y)^(2/3)*√So’

Eingabe von algebraischen Objekten

Algebraische Objekte können mit Hilfe von einfachen Anführungszeichen (') direkt in den Stack, Ebene 1 oder über den EquationWriter [EQW] eingegeben werden. Hier ein Beispiel wie Sie das algebraische Objekt ‘π*D^2/4’ direkt in den Stack, Ebene 1 eingeben können:

³„ì*~dQ2/4`

Ein algebraisches Objekt kann auch mit dem EquationWriter erzeugt und dann in den Stack verschoben oder im EquationWriter selbst berechnet werden. Die Handhabung des EquationWriters wurde in Kapitel 2 beschrieben. Als Übung erstellen Sie folgendes algebraisches Objekt im EquationWriter:

Seite 5-1

Nachdem Sie das Objekt erzeugt haben, drücken Sie `um dieses im Stack anzuzeigen (nachfolgend im ALG und RPN Modus dargestellt)

Einfache Operationen mit algebraischen Objekten

Algebraische Objekte können, genau wie jede reelle oder komplexe Zahl addiert, subtrahiert, multipliziert, dividiert (ausgenommen durch Null), potenziert und als Argumente für eine Reihe von Standardfunktionen (exponential, logarithmisch, trigonometrisch, hyperbolisch usw.) verwendet werden. Um die Grundoperationen mit algebraischen Objekten zu veranschaulichen, erstellen wir einige Objekte, sagen wir ‘π*R^2’ and ‘g*t^2/4’ und speichern diese in den Variablen A1 und A2 (siehe Kapitel 2, zum Erstellen von Variablen und Speichern von Werten in denselben). Nachfolgend die Tastenfolge um die Variable A1 im ALG-Modus zu speichern:

³„ì*~rQ2™ K ~a1 `

Das Resultat sieht dann so aus:

Die Tastenfolge für den RPN-Modus sieht so aus:

„ì~r`2Qx ~a1 K

Nachdem Sie nun die Variable A2 gespeichert und die Taste gedrückt haben, erscheinen die Variablen in der Anzeige wie folgt:

Seite 5-2

Im ALG-Modus zeigen die folgenden Tastenkombinationen eine Anzahl von Operationen mit den algebraischen Objekten, die in den Variablen @@A1@@ und @@A2@@ enthalten sind (drücken Sie J, um zum Variablen-Menü zurückzukehren)

@@A1@@ + @@A2@@ ` @@A1@@ - @@A2@@ `

@@A1@@ * @@A2@@ ` @@A1@@ / @@A2@@ `

‚¹@@A1@@ „¸@@A2@@

Zum gleichen Ergebnis kommen Sie, wenn Sie im RPN-Modus die nachstehenden Tastenfolgen verwenden:

@@A1@ ` @@A2@@ + @@A1@@ ` @@A2@@ -

Seite 5-3

@@A1@@ ` @@A2@@ * @@A1@@ ` @@A2@@ /

@@A1@@ ` ‚¹ @@A2@@ ` „¸

Funktionen im Menü ALG

Das Menü ALG (algebraisch) erreicht man über die Tastenfolge ‚× (der Taste 4 zugeordnet). Mit dem Systemflag 117 auf CHOOSE boxes gesetzt, zeigt das Menü ALG folgende Funktionen an:

Wir wollen hier keine Beschreibung jeder einzelnen Funktion auflisten, sondern empfehlen dem Anwender, sich diese mit der Hilfefunktion des Rechners selbst anzeigen zu lassen: I L @)HELP@ ` . Um eine bestimmte Funktion auszuwählen, geben Sie den ersten Buchstaben der Funktion ein. Geben Sie beispielsweise für die Funktion COLLECT, ~c ein und verwenden Sie anschließend die Pfeiltasten —˜, um COLLECT im Hilfefenster zu lokalisieren.

Um den Vorgang abzuschließen, drücken Sie auf @@OK@@. Nachfolgend die Hilfeansicht für die Funktion COLLECT:

Am unteren Rand der Anzeige bemerken wir nun die Zeile „See: EXPAND FACTOR“, welche uns auf andere Hilfe-Einträge zu den Funktionen EXPAND und FACTOR hinweist. Um direkt zu diesen Einträgen zu gelangen, drücken Sie die Funktionstaste @SEE1! für EXPAND und @SEE2! für FACTOR. Wenn Sie

Seite 5-4

z.B. @SEE1! drücken, erhalten Sie folgende Informationen zu EXPAND, drücken Sie auf @SEE2! erhalten Sie Informationen zur Funktion FACTOR:

Kopieren Sie die bereitgestellten Beispiele, durch Drücken der Taste @ECHO! in den Stack. Um z.B. das Beispiel für den obigen Eintrag zu EXPAND in den Stack zu kopieren, drücken Sie die Funktionstaste @ECHO! (drücken Sie `, um den Befehl auszuführen):

Nun, überlassen wir es dem Benutzer die Anwendung dieser Funktionen im ALG Menü selbst zu ergründen. Dies ist eine Liste der Befehle:

Für die Funktion SUBST, z.B. finden wir den folgenden CAS Hilfeeintrag:

Anmerkung: Merken Sie sich: im RPN-Modus, muss das jeweilige Argument der Funktion vorangestellt werden, erst dann wird die Funktion

Seite 5-5

selbst ausgewählt. Beispielsweise müssen Sie für TEXPAND im RPN-Modus wie folgt vorgehen:

³„¸+~x+~y`

Wählen Sie an dieser Stelle die Funktion TEXPAND aus dem Menü ALG (oder direkt aus dem Katalog ‚N), um die Operation abzuschließen.

Operationen mit transzendenten Funktionen

Der Rechner bietet eine Anzahl von Funktionen, welche Ausdrücke, die logarithmische oder Exponentialfunktionen („Ð), aber auch trigonometrische Funktionen (‚Ñ) enthalten, ersetzen können.

Erweitern und faktorisieren mit Hilfe der log-exp Funktionen

Mit „Ð erhalten Sie nachfolgendes Menü:

Informationen und Beispiele zu diesen Befehlen erhalten Sie über die Hilfe des Rechners. Als Beispiel wird die Beschreibung EXPLN auf der linken Seite und das Beispiel dazu aus dem Hilfeeintrag auf der rechten Seite angezeigt:

Erweitern und faktorisieren anhand trigonometrischer Funktionen

Seite 5-6

Das Menü TRIG wird über die Tastenkombination ‚Ñ aufgerufen und enthält folgende Funktionen:

Mit Hilfe dieser Funktionen können Ausdrücke, durch Austauschen einer bestimmten trigonometrischen Kategorie mit einer anderen, vereinfacht werden. So z.B. erlaubt die Funktion ACOS2S das Ersetzen der Funktion Arcuscosinus (acos(x)) ,indem sie mithilfe des Arcussinus (asin(x)) in anderer Form dargestellt wird.

Beschreibungen dieser Befehle und Beispiele, sowie Beispiele zu deren Anwendung finden Sie über die Hilfefunktion des Rechners (IL@HELP). Der Anwender wird dazu aufgefordert diese Hilfe nach Informationen zu den Befehlen im Menü TRIG zu durchsuchen.

Funktionen im Menü ARITHMETIC

Das ARITHMETIC-Menü wird über die Tastenkombination „Þ (der Taste 1 zugeordnet) gestartet. Ist das Systemflag 117 auf CHOOSE boxes gesetzt, erscheint über „Þ das nachfolgende Menü:

Seite 5-7

Die Optionen 5 bis 9 (DIVIS, FACTORS, LGCD, PROPFRAC, SIMP2) aus dieser Liste, entsprechen den allgemeinen Funktionen für Ganzzahlen und Polynome. Die verbliebenen Optionen (1. INTEGER, 2. POLYNOMIAL,

3. MODULO, und 4. PERMUTATION) sind eigentlich Untermenüs mit Funktionen, welche bestimmten mathematischen Objekten zugeordnet sind. Wenn das Systemflag 117 auf SOFT menus steht, erscheint im ARITHMETIC-Menü („Þ) folgende Anzeige:

Nachfolgend sind die Hilfe-Einträge für die Funktionen FACTORS und SIMP2 im ARITHMETIC Menü dargestellt:

FACTORS: SIMP2:

Die den Untermenüs von ARITHMETIC zugeordneten Funktionen INTEGER, POLYNOMIAL, MODULO und PERMUTATION werden in Kapitel 5 der Bedienungsanleitung detailliert vorgestellt. Die folgenden Abschnitte enthalten einige Anwendungen für Polynome und Brüche.

Polynome

Polynome sind algebraische Ausdrücke, die aus einem oder mehreren Gliedern in abfallender Höhe der Potenz einer gegebenen Variablen bestehen. So z.B. ist ‘X^3+2*X^2-3*X+2’ ein Polynom dritten Grades in X, während ‘SIN(X)^2-2’ ein Polynom zweiten Grades in SIN(X) darstellt. Die bereits dargestellten Funktionen COLLECT und EXPAND können für Polynome verwendet werden. Weitere Anwendungen von Polynomfunktionen werden im Folgenden vorgestellt:

Seite 5-8

Funktion HORNER

Die Funktion HORNER („Þ, POLYNOMIAL, HORNER) erzeugt die Horner oder synthetische Division eines Polynoms P(X) mit dem Faktor (X-a), d.h. HORNER(P(X),a) = {Q(X), a, P(a)} wobei P(X) = Q(X)(X-a)+P(a) ist. So zum Beispiel:

HORNER(‘X^3+2*X^2-3*X+1’,2) = {X^2+4*X+5 2 11}

d. h., X

+2X2-3X+1 = (X2+4X+5)(X-2)+11. Auch,

HORNER(‘X^6-1’,-5)=

{ X^5-5*X^4+25*X^3-125*X^2+625*X-3125 -5 15624}

d.h., X

-1 = (X5-5*X4+25X3-125X2+625X-3125)(X+5)+15624.

Variable VX

Für die meisten der oben dargestellten Beispielpolynome wurde die Variable X verwendet. Der Grund hierfür ist, dass im Verzeichnis {HOME CASDIR} des Taschenrechners eine Variable VX vorhanden ist, die standardmäßig den Wert von ‘X’ annimmt. Dies ist der bevorzugte Name für die unabhängige Variable in algebraischen und Analysis Anwendungen. Vermeiden Sie in Ihren Programmen oder Gleichungen eine Variable VX zu benennen, um diese nicht mit der CAS Variablen VX zu verwechseln. Zusätzliche Informationen zur CAS Variablen finden Sie in Anhang C der Bedienungsanleitung.

Funktion PCOEF

Haben Sie ein Array, welches die Nullstellen eines Polynoms enthält, erzeugt die Funktion PCOEF ein Array mit den Koeffizienten des entsprechenden Polynoms. Die Koeffizienten entsprechen der abfallenden Reihenfolge der unabhängigen Variablen. So zum Beispiel:

PCOEF([-2, –1, 0 ,1, 1, 2]) = [1. –1. –5. 5. 4. –4. 0.],

Seite 5-9

welches das Polynom X

6-X5

-5X4+5X3+4X2-4X darstellt.

Funktion PROOT

Bei einem Array, das die Koeffizienten eines Polynoms in abfallender Reihenfolge enthält, stellt die Funktion PROOT die Nullstellen dieses Polynoms bereit. Bespiel, aus dem Polynom X

+5X+6 =0 erhalten Sie über PROOT([1,–

5,6]) = [2. 3.].

Funktionen QUOT und REMAINDER

Die Funktionen QUOT und REMAINDER stellen, den Quotienten Q(X) bzw. den Rest R(X) bereit, der sich aus der Division der Polynome P ergibt. Mit anderen Worten erhalten Sie die Werte Q(X) und R(X) aus P

(X)/P2(X) = Q(X) + R(X)/P2(X) So zum Beispiel:

QUOT(‘X^3-2*X+2’, ‘X-1’) = ‘X^2+X-1’

REMAINDER(‘X^3-2*X+2’, ‘X-1’) = 1.

So können wir schreiben: (X

Anmerkung: Das letzte Ergebnis können Sie auch durch die Funktion PARTFRAC erhalten:

PARTFRAC(‘(X^3-2*X+2)/(X-1)’) = ‘X^2+X-1 + 1/(X-1)’.

-2X+2)/(X-1) = X2+X-1 + 1/(X-1).

(X) und P2(X)

Funktion PEVAL

Die Funktion PEVAL (EVALuation (Auswertung) eines Polynoms) wird dazu verwendet ein Polynom auszuwerten,

p(x) = a

⋅xn+a

wobei das Array der Koeffizienten [a gegeben sein müssen. Das Ergebnis ist die Auswertung p(x PEVAL steht im Menü ARITHMETIC nicht zur Verfügung. Verwenden Sie stattdessen das Menü CALC/DERIV&INTEG. Beispiel: PEVAL([1,5,6,1],5) = 281.

Zusätzliche Anwendungen von Polynom Funktionen finden Sie in Kapitel 5 der Bedienungsanleitung.

n-1

⋅x

+ …+ a2⋅x2+a1⋅x+ a0,

n-1

, a

, … a2, a1, a0] und ein Wert x0

n-1

). Die Funktion

Seite 5-10

Brüche

Brüche können mit den Funktionen EXPAND und FACTOR aus dem ALG Menü (‚×), erweitert bzw. faktorisiert werden. So zum Beispiel:

EXPAND(‘(1+X)^3/((X-1)*(X+3))’) = ‘(X^3+3*X^2+3*X+1)/(X^2+2*X-3)’ EXPAND(‘(X^2*(X+Y)/(2*X-X^2)^2’) = ‘(X+Y)/(X^2-4*X+4)’

FACTOR(‘(3*X^3-2*X^2)/(X^2-5*X+6)’) = ‘X^2*(3*X-2)/((X-2)*(X-3))’ FACTOR(‘(X^3-9*X)/(X^2-5*X+6)’ ) = ‘X*(X+3)/(X-2)’

Funktion SIMP2

Die Funktion SIMP2 (im ARITHMETIC-Menü) benötigt als Argumente zwei Zahlen eines Polynoms, die den Zähler und den Nenner eines rationalen Bruches darstellen und gibt den vereinfachten Zähler und Nenner zurück. Zum Beispiel:

Funktion PROPFRAC

Die Funktion PROPFRAC wandelt einen rationalen in einen echten Bruch um, d.h. zieht den ganzzahligen Anteil aus dem Bruch, falls eine derartige Zerlegung möglich ist. Zum Beispiel:

Funktion PARTFRAC

Die Funktion PARTFRAC zerlegt einen rationalen Bruch in Teilbrüche, die zusammen den ursprünglichen Bruch bilden. Zum Beispiel:

PARTFRAC(‘(2*X^6-14*X^5+29*X^4-37*X^3+41*X^2-16*X+5)/(X^57*X^4+11*X^3-7*X^2+10*X)’) =

SIMP2(‘X^3-1’,’X^2-4*X+3’) = { ‘X^2+X+1’,‘X-3’}

PROPFRAC(‘5/4’) = ‘1+1/4’

PROPFRAC(‘(x^2+1)/x^2’) = ‘1+1/x^2’

Seite 5-11

‘2*X+(1/2/(X-2)+5/(X-5)+1/2/X+X/(X^2+1))’

Funktion FCOEF

Mit Hilfe der Funktion FCOEF, die über das Menü ARITHMETIC /POLYNOMIAL aufgerufen werden kann, erhält man einen rationalen Bruch, wenn dessen NullstellenWurzeln und Polstellen bekannt sind.

Anmerkung: Angenommen wir haben den rationalen Bruch F(X) = N(X)/D(X), dann werden die Nullstellen des Bruches über die Gleichung N(X) = 0 und die Polstellen über die Gleichung D(X) = 0 errechnet.

Die Eingabe für die Funktion ist ein Vektor der die Nullstellen, gefolgt von deren Vielfachheit (d.h. wie oft kommt eine Nullstelle vor) und die Polstellen gefolgt von deren Vielfachheit als negative Zahl. Wenn wir z.B. einen Bruch mit den Nullstellen 2, Vielfachheit 1, 0 Vielfachheit 3,und -5 mit Vielfachheit 2, sowie den Polstellen 1, Vielfachheit 2, und -3, Vielfachheit 5, erzeugen wollen, verwenden wir:

FCOEF ([2,1,0,3,–5,2,1,-2,-3,-5]) = ‘(X--5)^2*X^3*(X-2)/(X--3)^5*(X-1)^2’

Wenn Sie µ„ î(oder einfach µ im RPN-Modell) drücken, wird Folgendes angezeigt:

‘(X^6+8*X^5+5*X^4-50*X^3)/(X^7+13*X^6+61*X^5+105*X^4-45*X^3297*X62-81*X+243)’

Funktion FROOTS

Mit der Funktion FROOTS im Menü ARITHMETIC/POLYNOMIAL erhalten Sie beispielsweise die Null- und Polstellen eines Bruches. Wenn Sie beispielsweise die Funktion FROOTS auf das oben erzielte Ergebnis anwenden, erhalten Sie: [1 –2. –3 –5. 0 3. 2 1. –5 2.]. Das Ergebnis zeigt Pole gefolgt von deren Vielfachheit als negative Zahl und Nullstellen gefolgt von deren Vielfachheit als positive Zahl. In diesem Fall sind das die Pole (1, -3) mit zugehöriger Vielfachheit (2,5) und die Nullstellen (0, 2, -5) mit zugehöriger Vielfachheit (3, 1, 2).

Seite 5-12

Ein weiteres Beispiel: FROOTS(‘(X^2-5*X+6)/(X^5-X^2)’) = [0 –2. 1 –1. 3 1. 2 1.], d. h. Polstellen = 0 (2), 1(1) und Nullstellen = 3(1), 2(1). Wenn der Modus Complex ausgewählt wurde, lautet das Ergebnis: [0 –2. 1 –1. ‘-((1+i*√3)/2)’ –1. ‘-((1-i*√3)/2)’ –1].

Step-by-Step Operationen mit Polynomen und Brüchen

Stellen Sie den CAS-Modus auf Step/step, zeigt der Rechner die Vereinfachungen von Brüchen oder Polynomoperationen schrittweise an. Dies ist sehr nützlich, um die Schritte einer Horner-Division zu sehen. Eine genaue Beschreibung einer derartigen Division

−

wird in Anhang C der Bedienungsanleitung aufgezeigt. Im folgenden Beispiel wird eine umfangreichere Polynomdivision veranschaulicht (DIV2 kann über das Menü ARITH/POLYNOMIAL aufgerufen werden):

−

235

−+−

XXX

Seite 5-13

Weitere Informationen

Zusätzliche Informationen, Definitionen und Beispiele von algebraischen und arithmetischen Operationen finden Sie in Kapitel 5 der Bedienungsanleitung.

Seite 5-14

Kapitel 6 Lösung für Gleichungen

Der Taste 7 sind zwei Gleichungs-Lösungs-Menüs zugeordnet, der symbolische SOLVer (Löser) („Î) und der NUMerische SoLVer (Löser) (‚Ï). Nachfolgend werden einige Funktionen aus diesen Menüs beschrieben.

Symbolische Lösung algebraischer Gleichungen

Nachfolgend werden einige Funktionen aus dem Menü Symbolic Solver (symbolischer Löser) beschrieben. Aktivieren Sie das Menü über die Tastenkombination „Î. Mit dem Systemflag 117 auf CHOOSE boxes gesetzt, werden folgende Menü-Einträge aufgelistet:

Die Funktionen ISOL und SOLVE können zur Lösung der Unbekannten in einer Polynom-Gleichung verwendet werden. Die Funktion SOLVEX löst eine Polynomgleichung, in welcher die Standard CAS Variable VX (standardmäßig 'X') die Unbekannte ist. Abschließend gibe es noch die Funktion ZEROS, welche Nullen eines ein Polynoms bereitstellt.

Funktion ISOL

Mit der Funktion ISOL (Gleichung, Variable) erhalten Sie dieLösung(en) für Gleichung durch Isolierung der Variablen. Um beispielsweise t in der Gleichung at wie folgt vorgehen:

-bt = 0, mit dem Rechner im ALG-Modus, zu finden, können wir

Seite 6-1

Im RPN-Modus erhalten wir das gleiche Ergebnis, wenn wir die Gleichung, gefolgt von der Variablen, in den Stack schreiben und anschließend die Funktion ISOL eingeben. Bevor Sie die Funktion ISOL ausführen, sollte die Anzeige im RPN-Modus wie in der Abbildung auf der linken Seite aussehen. Nachdem Sie die Funktion ISOL ausgeführt haben, sieht lhre Anzeige so wie in der rechten Abbildung aus:

Das erste Argument in ISOL kann ein Ausdruck – wie oben aufgeführt – oder eine Gleichung sein. Versuchen Sie z.B. im ALG-Modus:

Anmerkung: Um das Gleichheitszeichen (=) in einer Gleichung zu schreiben, verwenden Sie die Tastenfolge ‚Å (der Taste \ zugeordnet).

Das gleiche Problem kann im RPN-Modus, wie unten dargestellt gelöst werden (Abbildungen zeigen den RPN-Stack vor und nachdem die Funktion ISOL angewendet wurde):

Seite 6-2

Funktion SOLVE

Die Funktion SOLVE hat die gleiche Syntax wie die Funktion ISOL, nur dass SOLVE auch zur Lösung einer Gruppe von Polynom-Gleichungen verwendet werden kann. Untenstehend sehen Sie den Hilfetext für die Funktion SOLVE, mit der Lösung der Gleichung X^4 – 1 = 3:

Nachfolgende Beispiele zeigen die Funktion SOLVE im ALG und RPN-Modus (Verwenden Sie im CAS den Modus COMPLEX):

Die obige Abbildung zeigt zwei Lösungen. In der ersten, β SOLVE keine Lösungen { }. In der zweiten Abbildung hingegen, β

-5β =125 findet

- 5β = 6, findet SOLVE gleich vier Lösungen, welche in der letzten Ausgabezeile angegeben sind. Die letzte Lösung ist nicht sichtbar, weil die Anzahl der Buchstaben der Lösung größer als die Breite des Displays ist. Sie können aber alle Lösungen, mit Hilfe der Pfeiltaste (˜) ansehen, welche von einer Zeile des Zeileneditors in die andere umschaltet (dieser Vorgang kann jederzeit benutzt werden, wenn die Ausgabezeile länger als die Breite des Rechner-Displays ist):

Seite 6-3

Die entsprechenden Anzeigen im RPN-Modus für diese beiden Beispiele, jeweils vor und nach der Anwendung der Funktion SOLVE, sind nachstehend zu sehen:

Funktion SOLVEVX

Die Funktion SOLVEVX löst eine Gleichung für die Standard CAS-Variable in der reservierten Variablen VX. Standardmäßig ist der Wert dieser Variablen auf 'X' gesetzt. Nachfolgend finden sich einige Beispiele, im ALG-Modus mit VX = 'X':

Im ersten Fall konnte SOLVEVX keine Lösung finden. Im zweiten Fall, hat SOLVEVX eine einzige Lösung gefunden, X = 2.

Nachfolgend die Anzeigen der beiden Beispiele im RPN Stack (vor und nach Anwendung der Funktion SOLVEVX):

Seite 6-4

Hp 49G+ User Manual [de]

Specifications and Main Features

Frequently Asked Questions

User Manual

Inhaltsverzeichnis

Grundlegende Operationen

Batterien

Ein- und Ausschalten des Taschenrechners

Einstellen des Displaykontrastes

Inhalt des Taschenrechnerdisplays

Einstellen von Datum und Uhrzeit

Betriebsmodus

Zahlenformat und Dezimalpunkt oder -komma

• Wissenschaftliches Format

• Technisches Format

• Dezimalkomma und Dezimalpunkt

Koordinatensystem

Weitere Informationen

Objekte des Taschenrechners

Strukturieren der Daten im Taschenrechner

Das Verzeichnis HOME

Unterverzeichnisse

Variablen

Eingeben von Variablennamen

Erstellen von Variablen

• Algebraischer Modus

• RPN-Modus

Algebraischer Modus

Auflisten des Inhalts aller Variablen auf dem Bildschirm

Verwenden der Funktion PURGE im Stack im algebraischen Modus

Anwenden der Funktion PURGE im Stack im RPN-Modus

Die Funktionen UNDO und CMD

CHOOSE boxes und Soft MENU

Weitere Informationen

Kapitel 3 Berechnungen mit reellen Zahlen

Verwenden von Zehnerpotenzen bei der Dateneingabe

Hyperbolische Funktionen und ihre Inversen

Operationen mit Einheiten

Zuordnen von Einheiten zu Zahlen

Operationen mit Einheiten

Konvertierung von Einheiten

Physikalische Konstanten im Taschenrechner

Definieren und Verwenden von Funktionen

Weitere Informationen

Kapitel 4 Berechnungen mit komplexen Zahlen

Definitionen

Einstellen des Modus COMPLEX am Taschenrechner

Eingeben von komplexen Zahlen

Polare Darstellung von komplexen Zahlen

Einfache Operationen mit komplexen Zahlen

Auf komplexe Zahlen angewendete Funktionen

Funktion DROITE: Gleichung einer Geraden

Weitere Informationen

Kapitel 5 Algebraische und arithmetische Operationen

Eingabe von algebraischen Objekten

Einfache Operationen mit algebraischen Objekten

Operationen mit transzendenten Funktionen

Erweitern und faktorisieren mit Hilfe der log-exp Funktionen

Erweitern und faktorisieren anhand trigonometrischer Funktionen

Polynome

Funktion HORNER

Variable VX

Funktion PCOEF

Funktion PROOT

Funktionen QUOT und REMAINDER

Funktion PEVAL

Funktion SIMP2

Funktion PROPFRAC

Funktion PARTFRAC

Funktion FCOEF

Funktion FROOTS

Weitere Informationen

Funktion ISOL

Funktion SOLVE

Funktion SOLVEVX