HP 48 SX, 48S User Manual [fr]

Download

hp 48gII calculatrice graphique

manuel de l’utilisateur

Édition 2 Référence HP F2226-90003

Avis

ENREGISTRER VOTRE PRODUIT A: www.register.hp.com

CE MANUEL ET LES EXEMPLÉS STIPULES DANS LES PRÉSENTES SONT FOURNIS TELS QUELS ET PEUVENT ÊTRE MODIFIÉS SANS PRÉAVIS. HEWLETT-PACKARD COMPANY N’OFFRE AUCUNE GARANTIE CONCERNANT CE MANUEL, Y COMPRIS MAIS NON LIMITÉE AUX GARANTIES IMPLICITES DE COMMERCIALISATION, DE NON-VIOLATION ET DE D’APTITUDE À UN EMPLOI PARTICULIER.

HEWLETT-PACKARD CO. N’ENDOSSE AUCUNE RESPONSABILITÉ QUANT AUX ERREURS OU DOMMAGES INDIRECTS OU ACCESSOIRES LIÉS À L’APPROVISIONNEMENT, LA PERFORMANCE OU L’EMPLOI DE CE MANUEL OU DES EXEMPLES QU’IL CONTIENT.

© Copyright 2003 Hewlett-Packard Development Company, L.P. Toute reproduction, adaptation ou traduction dudit manuel est interdite à moins d’avoir obtenu au préalable le consentement écrit de Hewlett-Packard Company, sauf conformément aux lois de droits d’auteur.

Hewlett-Packard Company 4995 Murphy Canyon Rd, Suite 301 San Diego,CA 92123

Historique d’impression

Édition 2 Décembre 2003

Table des matières

Chapitre 1 – Pour commencer

Prise en main, 1-1 Piles, 1-1 Allumer et éteindre la calculatrice, 1-2 Ajuster le contraste de l’écran, 1-2 Description de l’écran de la calculatrice, 1-2 Menus, 1-3 Le menu TOOL, 1-4 Régler la date et l’heure, 1-4 Le clavier de la calculatrice, 1-5 Choisir les modes d’opération de la calculatrice, 1-6 Mode d’opération, 1-7 Format numérique et point décimal ou virgule, 1-11 Format standard, 1-12 Format fixe avec décimales, 1-12 Format scientifique 1-13 Format ingénierie, 1-14 Virgule et point décimal, 1-15 Mesure d’angle, 1-15 Système de coordonnées, 1-16

Sélectionner les paramètres CAS

Explication des paramètres du CAS, 1-18 Choix du mode d’affichage,1-19 Choisir la police d’affichage, 1-20 Choisir les propriétés de l’éditeur de ligne, 1-21 Choisir les propriétés de la pile, 1-21

Choisir les propriétés de l’éditeur d’équations (EQW), 1-23

Références, 1-23

Chapitre 2 – Présentation de la calculatrice

Objets, 2-1

Ecrire des expressions dans la pile

Créer des expressions arithmétiques, 2-1

, 1-1

, 1-17

, 2-1

Page TDM-1

Créer des expressions algébriques, 2-4 Utiliser l’Editeur d’équations (EQW) pour écrire des expressions, 2-5 Créer des expressions arithmétiques, 2-6 Créer des expressions algébriques, 2-8 Organiser les données dans la calculatrice, 2-9 Le répertoire HOME, 2-9 Sous-répertoires, 2-10 Les variables, 2-10 Taper un nom de variable, 2-11 Créer des variables, 2-12 Mode algébrique, 2-12 Mode RPN, 2-13 Vérifier le contenu des variables, 2-15 Mode algébrique. 2-15 Mode RPN, 2-15 Utiliser la touche right-shift‚ suivie des touches de menu, 2-15 Afficher le contenu de toutes les variables à l’écran, 2-16 Effacer des variables, 2-16 Utiliser la fonction PURGE dans la pile en mode algébrique, 2-16 Utiliser la fonction PURGE dans la pile, mode RPN, 2-17 Les fonctions UNDO et CMD , 2-18

CHOOSE-boxes ou Soft MENU

, 2-18

Références, 2-21

Chapitre 3 – Calculs avec des nombres réels, 3-1

Exemples de calculs avec des nombres réels, 3-1 Entrer des données avec des puissances de 10, 3-4 Les fonctions réelles dans le menu MTH, 3-6 Utiliser les menus de la calculatrice, 3-7 Fonctions hyperboliques et leurs inverses, 3-7 Opérations sur les unités, 3-9 Le menu des unités (UNITS), 3-9 Unités disponibles, 3-11 Associer des unités à des nombres, 3-11 Les préfixes d’unités, 3-12 Opérations sur les unités, 3-13

Page TDM-2

Les conversions d’unités, 3-14 Constantes physiques de la calculatrice, 3-15 Définir et utiliser des fonctions, 3-17 Référence, 3-19

Chapitre 4 – Calculs avec des nombres complexes

Définitions, 4-1 Paramétrer la calculatrice en mode COMPLEX, 4-1 Saisie de nombres complexes, 4-2 Représentation d’un nombre complexe, 4-2 Opérations simples avec des nombres complexes, 4-4

Les menus CMPLX

Menu CMPLX en passant par le menu MTH, 4-4 Menu CMPLX accessible sur le clavier, 4-5 Fonctions appliquées aux nombres complexes, 4-6 Fonction DROITE: équation d’une ligne droite, 4-7 Référence, 4-7

, 4-4

Chapitre 5 – L’algèbre et les opérations mathématiques

Saisie des objets algébriques, 5-1 Opérations simples avec les objets algébriques, 5-2 Fonctions du menu ALG, 5-4 Opérations avec les fonctions transcendantales, 5-6 Développement et mise en facteur en utilisant les fonctions log-exp, 5-6

Développement et mise en facteur en utilisant les fonctions trigonométriques, 5-7

Fonctions du menu ARITHMETIC, 5-7

Polynômes

La fonction HORNER, 5-9 La variable VX, 5-9 La fonction PCOEF, 5-10 La fonction PROOT, 5-10 Les fonctions QUOT et REMAINDER, 5-10 La fonction PEVAL, 5-10 Fractions, 5-11 La fonction SIMP2, 5-11

, 5-8

, 4-1

, 5-1

Page TDM-3

La fonction PROPFRAC, 5-11 La fonction PARTFRAC, 5-12 La fonction FCOEFF, 5-12 La fonction FROOTS, 5-13 Opérations étape par étape avec des polynômes et des fractions, 5-13 Référence, 5-14

Chapitre 6 – Résolution d’équations

Résolution symbolique des équations algébriques, 6-1 Fonction ISOL, 6-1 Fonction SOLVE, 6-3 Fonction SOLVEVX, 6-4 Fonction ZEROS, 6-5 Menu de Résolution numérique, 6-6 Equations polynomiales, 6-7 Trouver les solutions d’une équation polynomiale, 6-7 Générer des coefficients polynomiaux à partir des racines polynomiales, 6-8 Générer une expression algébrique pour le polynôme, 6-8 Calculs financiers, 6-9 Résoudre des équations à une inconnue avec NUM.SLV, 6-10 Fonction STEQ, 6-10 Résoudre des équations simultanées avec MSLV, 6-11 Référence, 6-12

, 6-1

Chapitre 7 – Opérations avec des listes

Créer et enregistrer des listes , 7-1

Opérations avec des listes de nombres

Changement de signe, 7-1 Addition, soustraction, multiplication, division, 7-2 Fonctions appliquées à des listes, 7-4 Listes de nombres complexes, 7-4 Listes d’objets algébriques, 7-4 Le menu MTH/LIST, 7-5 La fonction SEQ, 7-6 La fonction MAP, 7-7

, 7-1

Page TDM-4

Référence, 7-7

Chapitre 8 – Vecteurs

Saisie de vecteurs, 8-1 Saisir des vecteurs dans la pile, 8-1 Enregistrer des vecteurs dans les variables de la pile, 8-2 Utiliser l’Editeur de matrice (MTRW) pour saisir les vecteurs, 8-2 Opérations simples avec des vecteurs, 8-5 Changement de signe, 8-5 Addition, soustraction, 8-6 Multiplication et division par un scalaire, 8-6 Fonction valeur absolue, 8-7 Le menu MTH/VECTOR, 8-7 Magnitude, 8-7 Produit scalaire, 8-8 Produit croisé, 8-8 Référence , 8-9

Chapitre 9 – Matrices et algèbre linéaire

Saisie de matrices dans la pile, 9-1 Utilisation de l’Editeur de Matrice, 9-1 Saisir la matrice directement dans la pile, 9-2 Opérations avec des matrices, 9-3 Addition et soustraction, 9-4 Multiplication, 9-4 Multiplication par un scalaire, 9-4 Multiplication Matrice-vecteur, 9-4 Multiplication de matrices, 9-5 Multiplication terme par terme, 9-5 La matrice identité, 9-6 La matrice inversée, 9-6 Caractérisation d’une matrice (Menu NORM de matrice), 9-7 Fonction DET, 9-7 Fonction TRACE, 9-7 Résolutions des systèmes linéaires, 9-8

, 8-1

, 9-1

Page TDM-5

Utilisation de la résolution numérique pour les systèmes linéaires, 9-8 Résolution avec la matrice inversée, 9-10 Résolution par “division” de matrices, 9-10 Références, 9-11

Chapitre 10 – Graphiques

Options graphiques de la calculatrice, 10-1 Tracé d’une expression de forme y = f(x), 10-2 Générer une table de valeurs pour une fonction, 10-4 Graphiques rapides 3D, 10-6 Référence, 10-9

, 10-1

Chapitre 11 – Applications infinitésimales

Le menu CALC (Calculus), 11-1 Limites et dérivées, 11-1 Fonction lim, 11-2 Fonctions DERIV et DERVX, 11-2 Primitives et intégrales, 11-3 Fonctions INT, INTVX, RISCH, SIGMA et SIGMAVX, 11-3 Intégrées définies, 11-4 Séries infinies, 11-5 Fonctions TAYLR, TAYLR0 et SERIES, 11-5 Référence, 11-7

Chapitre 12 – Applications infinitésimales à plusieurs variables

12-1 Dérivées partielles, 12-1 Intégrales multiples, 12-2 Référence, 12-3

Chapitre 13 – Applications d’analyse vectorielle

L'opérateur del, 13-1 Gradient, 13-1 Divergence, 13-2 Boucle, 13-2

, 11-1

, 13-1

Page TDM-6

Référence, 13-3

Chapitre 14 – Equations différentielles

Le menu CALC/DIFF, 14-1 Solution des équations linéaires et non linéaires, 14-1 Fonction LDEC, 14-2 Fonction DESOLVE,14-3 La variable ODETYPE, 14-4 Transformations de Laplace, 14-5

Transformation de Laplace et transformation inverse sur la calculatrice,

14-5 Séries de Fourier, 14-6 Fonction de FOURIER, 14-7 Séries de Fourier pour une équation quadratique, 14-7 Référence, 14-8

, 14-1

Chapitre 15 – Distributions de probabilités, 15-1

ère

Sous-menu MTH/PROBABILITY.. – 1 Factorielles, combinaisons et permutations, 15-1 Nombres aléatoires, 15-2 Menu MTH/PROB - – 2

ème

partie, 15-3

La Distribution Normale, 15-3 La distribution t de Student, 15-4 La distribution chi-carré, 15-4 La distribution de la fonction F, 15-4 Référence, 15-4

Chapitre 16 – Applications statistiques

Saisie de données, 16-1 Calcul de statistiques à une seule variable, 16-2 Obtenir des distributions de fréquence, 16-3 Adapter les données à une fonction y = f(x), 16-5 Obtenir des statistiques de résumé additionnelles, 16-6 Intervalles de confiance, 16-8

partie, 15-1

, 16-1

Page TDM-7

Test d’hypothèses, 16-10 Référence, 16-12

Chapitre 17 – Nombres dans différentes bases, 17-1

Le menu BASE, 17-1 Ecrire des nombres non décimaux, 17-2 Référence, 17-2

Garantie limltée –

Entretien, G-2 Informations de réglementation, G-4

G-1

Page TDM-8

Chapitre 1 Pour commencer

Le présent chapitre a pour but de vous fournir les informations de base nécessaires à l’utilisation de votre calculatrice. Les exercices vous permettront de vous familiariser avec le fonctionnement et les opérations de base avant d’effectuer un vrai calcul.

Prise en main

Le but des exercices suivants est de vous familiariser avec le boîtier de votre calculatrice.

Piles

La calculatrice utilise 3 piles AAA(LR03) comme source d’alimentation et une pile CR2032 au lithium comme pile de secours pour la mémoire. Avant d’utiliser la calculatrice, veuillez installer les piles de la manière suivante :

Pour installer les piles principales

a. Vérifiez que le calculateur est éteint.

comme illustré ci-dessous.

Ouvrez le compartiment des piles

b. Insérez 3 piles neuves AAA(LR03) dans le compartiment. Faites attention à

ce qu’elles soient installées dans la bonne direction.

Pour installer l’alimentation de secours

a. Vérifiez que le calculateur est éteint. Appuyez sur le support, poussez

ensuite sur la platine dans la direction indiquee sur l'illustration, puis soulevez-la.

Page 1-1

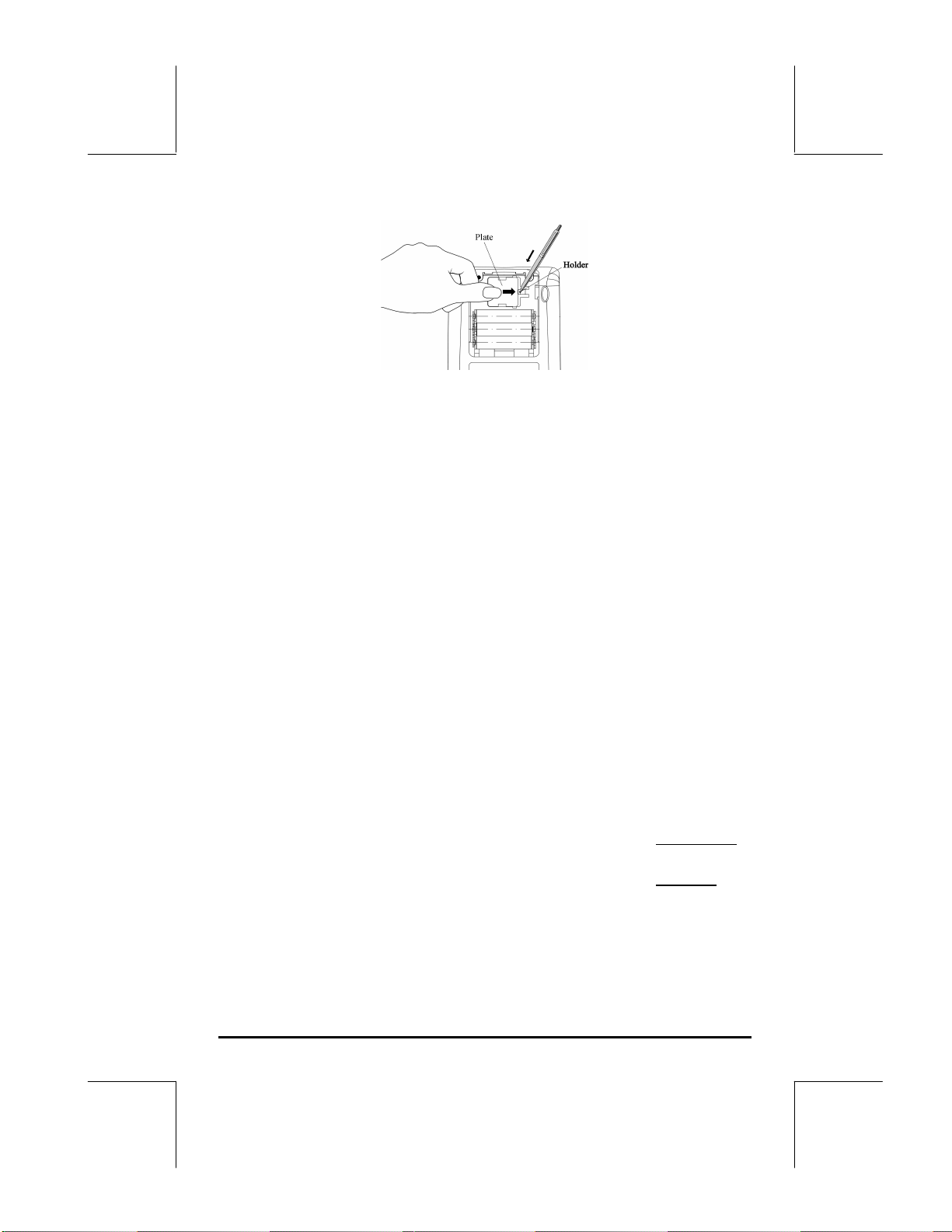
b. Insérez une nouvelle pile CR2032 au lithium. Faites attention à ce que le

signe positif (+) soit en haut.

c. Remettez le compartiment et appuyez jusqu’à ce qu’il soit retourné en

position originale. Après avoir installé les piles, appuyez sur [ON] pour allumer la calculatrice. Attention : Si un message apparaît à l’écran vous signalant de changer cette pile, remplacez-la au plus tôt. Par contre, évitez d’enlever la pile de secours en même temps que les piles principales, afin de ne pas perdre de données.

Allumer et éteindre la calculatrice

La touche $ est situee en bas a gauche du clavier. Appuyez une seule fois pour allumer votre calculatrice. Pour éteindre la calculatrice, appuyez sur le bouton rouge @ (première touche de la deuxième ligne à partir du bas sur le clavier) puis sur la touche $. Notez que le mot OFF est indiqué en rouge dans le coin supérieur droit de la touche $, pour rappeler l’utilisation de la commande OFF.

Ajuster le contraste de l’écran

Vous pouvez ajuster le contraste de l’écran en maintenant la touche $ enfoncée tout en appuyant sur les touches + ou - .

La combinaison $ (maintenue enfoncée) et + rend l’écran plus sombre

La combinaison $ (maintenue enfoncée) et - rend l’écran plus clair

Description de l’écran de la calculatrice

Page 1-2

Rallumez une nouvelle fois votre calculatrice. Deux lignes decrivant les parametres de configuration de la calculatrice sont affichees en haut de l'ecran. La première ligne contient les caractères :

RAD XYZ HEX R= 'X'

Pour plus d'informations sur la signification de ces informations, consultez le Chapitre 2 du guide de l’utilisateur de la calculatrice.

La seconde ligne contient les caractères

{ HOME }

ce qui indique que le répertoire HOME est le répertoire actuel dans la mémoire de la calculatrice.

En bas de l’écran se trouvent une série d’indicateurs, avec les noms suivants,

@EDIT @VIEW @@ RCL @@ @@STO@ ! PURGE !CLEAR

qui sont associés aux six touches de menu système, F1 à F6:

ABCDEF

Les six indicateurs affichés en bas de l’écran changeront suivant le menu affiché. Cependant, A sera toujours associé avec le premier indicateur, B avec le deuxième indicateur, et ainsi de suite.

Menus

Les six indicateurs associés avec les touches A à F constituent le menu des fonctions. Comme la calculatrice ne comporte que 6 touches de menu, seulement 6 indicateurs peuvent être affichés au même moment. Cependant, un menu peut comporter plus de six choix. Chaque groupe de 6 choix est appelé une Page menu. Pour afficher la Page menu suivante (si elle existe), appuyez sur la touche L (NeXT menu). Cette touche est la troisième touche en partant de la gauche dans la troisième ligne des touches du clavier.

Page 1-3

Le menu TOOL

Les touches de menu pour le menu par défault, appelé menu TOOL sont associées avec les opérations liées à la manipulation de variables (voir la section sur les variables dans ce Chapitre): @EDIT A EDIT Pour afficher le contenu d’une variable (voir Chapitre 2

de ce guide et Chapitre 2 et Appendice L dans le guide de l’utilisateur pour plus d’informations sur l’affichage)

@VIEW B VIEW – Pour voir le contenu d’une variable @@ RCL @@ C ReCaLl – Pour rappeler le contenu d’une variable @@STO@ D STOre – Pour mémoriser le contenu d’une variable ! PURGE E PURGE – Pour effacer une variable de la mémoire CLEAR F CLEAR – Pour effacer l’écran ou la pile

Ces six fonctions constituent la première page du menu TOOL. Ce menu comporte en fait huit choix disposés en deux pages. La deuxième page devient visible en appuyant sur la touche L . Cette touche est la troisième touche en partant de la gauche dans la troisième ligne des touches du clavier.

Dans ce cas, seules les deux premières touches de menu sont associées à des commandes. Ces commandes sont :

@CASCM A CASCMD: CAS CoMmanD, à utiliser pour lancer une commande depuis le CAS en choisissant dans une liste @HELP B HELP – Commande d’aide qui décrit les commandes

disponibles de la calculatrice

En appuyant sur la touche L , on fait réapparaître le menu TOOL de départ. En appuyant sur la touche I (troisième touche en partant de la gauche dans la deuxième ligne des touches du clavier), on dispose d’une autre façon de faire réapparaître le menu TOOL.

Régler la date et l’heure

Reportez-vous au Chapitre 1 du guide de l’utilisateur de la calculatrice pour apprendre à régler l’heure et la date.

Page 1-4

Le clavier de la calculatrice

La figure ci-dessous représente un schéma du clavier de la calculatrice et indique les numéros des lignes et des colonnes. Chaque touche dispose de trois, quatre ou cinq fonctions. La fonction principale de la touche correspond au caractère le plus important sur la touche. De plus, il est possible de combiner la touche verte, touche (8,1), la touche rouge, touche (9,1), et la touche bleue ALPHA, touche (7,1), avec les autres touches pour activer les autres fonctionnalités indiquées sur le clavier.

Page 1-5

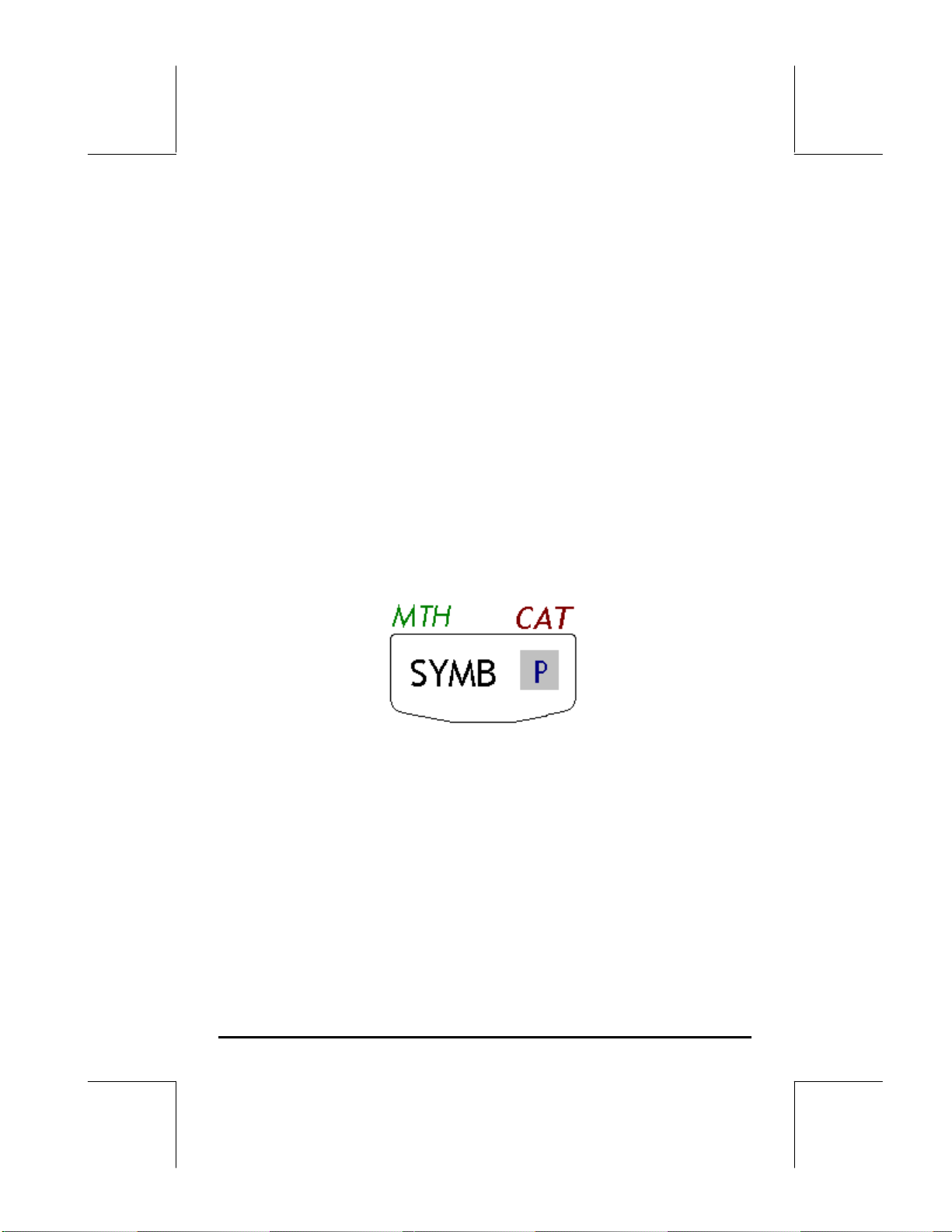
Par exemple, la touche P, touche(4,4), est associée aux six fonctions suivantes :

P Fonction principale, pour activer le menu SYMBolique „´ Fonction <lefft-shift>, pour activer le menu MTH (Math) … N Fonction <right-shift>, pour activer la fonction CATalogue ~p Fonction ALPHA, pour entrer la lettre P majuscule ~„p Fonction ALPHA-Left-Shift, pour entrer la lettre P minuscule ~…p Fonction ALPHA-Right-Shift, pour entrer la lettre minuscule π

Des six fonctions associées à une touche, seules les quatre premières sont indiquées sur le clavier. La figure de la page suivante vous montre ces quatre indicateurs pour la touche P. Vous remarquerez que la couleur et la position des indicateurs sur la touche, c’est-à-dire, SYMB, MTH, CAT et P, indiquent quelle est la fonction principale (SYMB), et quelles sont les trois autres fonctions respectivement associées à la touche <left-shift> „(MTH), <right-shift> … (CAT ), et ~ (P).

Pour plus d’informations sur l’utilisation du clavier de la calculatrice, reportezvous à l’Appendice B du guide de l’utilisateur de la calculatrice.

Choisir les modes d’opération de la calculatrice

Dans ce paragraphe, nous supposons que vous êtes maintenant familiarisé, au moins en partie, avec l’utilisation des boîtes de choix et de dialogue (si vous ne l’êtes pas, veuillez vous reporter à l’appendice A du guide de l’utilisateur).

Page 1-6

Appuyez sur la touche H (deuxième touche en partant de la gauche sur la deuxième ligne de touches en partant du haut) pour afficher la fenêtre CALCULATOR MODES suivante :

Appuyez sur la touche !!@@OK#@ ( F) pour revenir en mode d’affichage normal. Des exemples de sélection des différent modes de la calculatrice sont expliqués ci-dessous.

Mode d’opération

La calculatrice comporte deux modes d’opération : le mode Algebraic, et le mode Reverse Polish Notation (RPN). Le mode par défaut est le mode Algébrique (comme indiqué sur la figure ci-dessus), mais, les utilisateurs des calculatrices HP précédentes sont certainement davantage habitués au mode RPN.

Pour sélectionner un mode d’opération, ouvrez d’abord la fenêtre CALCULATOR MODES, en appuyant sur la touche H. Le champ Operating Mode apparaît surligné. Sélectionnez le mode Algebraic ou RPN soit en utilisant la touche \ (deuxième touche en partant de la gauche de la cinquième ligne depuis le bas du clavier), soit en appuyant sur la touche menu @CHOOS ( B). Si vous utilisez cette dernière méthode, activez les touches flèches vers le bas et vers le haut, — ˜, pour sélectionner le mode avant d’appuyer sur la touche menu !!@@OK#@ pour valider l’opération.

Pour illustrer la différence entre ces deux modes d’opération, nous allons calculer l’expression suivante dans les deux modes :

Page 1-7



0.50.3

−⋅

 

0.23

Pour entrer cette expression dans la calculatrice, nous allons d’abord utiliser l’éditeur d’équation, ‚O. Veuillez identifier les touches suivantes sur le clavier, à côté des touches du clavier numérique :

!@.#*+-/R

Q¸Ü‚Oš™˜—`

L’éditeur d’équation est un mode d’affichage dans lequel vous pouvez construire des expressions mathématiques en utilisant les notations mathématiques explicites comme, notamment, les fractions, les dérivées, les intégrales, les racines, etc. Pour utiliser l’éditeur d’équation pour écrire l’expression évoquée plus haut, faites appel à la séquence de touches suivante :

‚OR3.*!Ü5.-

1./3.*3. —————

/23.Q3™™+!¸2.5`

Après avoir appuyé sur `, la calculatrice affiche l’expression suivante :

√ (3.*(5.-1/(3.*3.))/23.^3+EXP(2.5))

En appuyant à nouveau sur ` la valeur suivante s’affichera (acceptez le mode Approx, si on vous le propose, en appuyant sur !!@@OK#@) :

 

0.30.3

⋅



5.2

Vous pouvez également entrer l’expression directement à l’affichage, sans utiliser l’éditeur d’équation, de la manière suivante, :

Page 1-8

R!Ü3.*!Ü5.-

1/3.*3.™

/23.Q3+!¸2.5`

pour obtenir le même résultat.

Passez en mode d’opération RPN en appuyant d’abord sur la touche H. Sélectionner le mode RPN soit en utilisant la touche \, soit en appuyant sur la touche de menu @CHOOS. Appuyez sur la touche de menu !!@@OK#@ ( F) pour compléter l'opération. Pour le mode RPN, l’écran suivant s’affiche :

Vous remarquerez qu’il apparaît plusieurs niveaux de sortie numérotés 1, 2, 3, etc.…, de bas en haut. On appelle cela la pile de la calculatrice. Les différents niveaux sont appelés les niveaux de la pile, et ainsi on a le niveau de pile 1, le niveau de pile 2, etc.

En fait, RPN signifie que, plutôt que d’écrire une opération telle que 3 + 2, dans la calculatrice en tapant

3+2`

on écrit d’abord les opérandes,, dans l’ordre exact avant d’ajouter l’opérateur, c’est-à-dire,

3`2`+

Au fur et à mesure que vous entrez les opérandes, ils occupent des niveaux de pile différents. En entrant 3` on place le chiffre 3 dans le niveau de pile 1. Ensuite, en entrant 2` on pousse le nombre 3 vers le haut pour occuper le niveau de pile 2. Enfin, en appuyant sur +, on indique à la calculatrice d’appliquer l’opérateur ou programme + aux objets qui occupent les niveaux 1 et 2. Le résultat, 5, est alors placé dans le niveau 1.

Page 1-9

Essayons d’autres opérations simples avant d’essayer l’expression plus compliquée que nous avons utilisée plus haut pour le mode d’opération algébrique :

123/32 123`32/

4`2Q

√(√27) 27`R3@»

Vous remarquerez la position du y et du x dans les deux dernières expressions. Dans l’expression exponentielle, la base est y (niveau de pile 2) alors que l’exposant est x (niveau de pile 1) avant d’appuyer sur la touche Q . De la même façon, dans l’opération de racine cubique, y (niveau de pile 2) est le nombre en dessous du signe racine, et x (niveau de pile 1) est la racine.

Essayez l’exercice suivant qui implique 3 facteurs : (5 + 3) × 2

5`3`+ Calcule (5 +3) d’abord. 2X Termine le calcul.

Essayons maintenant l’expression proposée plus haut :



 

3` Entrez 3 dans le niveau 1 5` Entrez 5 dans le niveau 1, 3 monte au niveau 2 3` Entrez 3 dans le niveau 1, 5 monte au niveau 2, 3

monte au niveau 3

3* Tapez 3 et multipliez, 9 apparaît dans le niveau 1 Y 1/(3×3), dernière valeur dans le niv. 1; 5 dans le

niveau 2; 3 dans le niveau 3



−⋅



⋅



5.2

Page 1-10

- 5 - 1/(3×3) , occupe maintenant le niveau 1; 3 dans

le niveau 2

* 3× (5 - 1/(3×3)), occupe maintenant le niveau 1. 23` Entrez 23 dans le niveau 1, 14.66666 monte au

niveau 2.

3Q Entrez 3, calculez 23

dans le niveau 1. 14.666

dans niv. 2.

/ (3× (5-1/(3×3)))/23

dans le niveau 1

2.5 Entrez 2.5 dans le niveau 1 !¸ e

2.5

, arrive au niveau 1, le niveau 2 contient la

valeur précédente.

+ (3× (5 - 1/(3×3)))/23 R √((3× (5 - 1/(3×3)))/23

2.5

= 12.18369, dans 1.

2.5

) = 3.4905156, dans 1

Pour basculer entre les modes d’opération ALG et RPN, vous pouvez aussi activer/désactiver l’indicateur système 95 par la séquence de touches suivante :

H @)FLAGS —„—„—„—@CHK@@

Format numérique et point décimal ou virgule

Changer le format numérique vous permet de personnaliser la façon dont les nombres réels sont affichés par la calculatrice. Vous trouverez cette fonctionnalité très utile pour les opérations qui manipulent des puissances de dix ou pour limiter le nombre de décimales dans un résultat.

Pour sélectionner un format numérique, ouvrez d’abord la fenêtre CALCULATOR MODES en appuyant sur la touche H. Ensuite, utilisez la flèche vers le bas, ˜, pour sélectionner l’option Number format. La valeur par défaut est Std, ou format Standard. Dans le format standard, la calculatrice affiche les nombres à virgule sans décimale fixe et avec la précision maximale supportée par la calculatrice (12 chiffres significatifs). Pour en savoir plus sur les réels, reportez vous au chapitre 2 du guide de l’utilisateur. Pour illustrer ceci ainsi que les autres formats numériques, essayez les exercices suivants :

Page 1-11

• Format standard :

Ce mode est le mode le plus utilisé car il affiche les nombres dans leur notation la plus fréquente. Appuyez sur la touche menu !!@@OK#@ avec le paramètre Number format dans l’état Std, pour revenir à l’affichage de la calculatrice. Entrez le nombre 123.4567890123456 (avec 16 chiffres significatifs). Appuyez sur la touche `. Le nombre est arrondi avec le maximum de 12 chiffres significatifs et s’affiche comme indiqué cidessous :

• Format fixe avec décimales :

Appuyez sur la touche H. Ensuite, utilisez la flèche vers le bas ˜, pour sélectionner l’option Number format. Appuyez sur le menu @CHOOS et la touche ( B), puis sélectionnez l’option Fixed avec la touche de flèche vers le bas ˜.

Appuyez sur la touche flèche vers la droite, ™, pour surligner le zéro en face de l’option Fix. Appuyez sur la touche de menu @CHOOS et, en utilisant les touches de flèches vers le haut et vers le bas, —˜, sélectionnez, disons, 3 décimales.

Page 1-12

Appuyez sur la touche de menu !!@@OK#@ pour terminer la sélection :

Appuyez sur la touche de menu !!@@OK#@ pour revenir à l’affichage normal de la calculatrice. Le nombre apparaît maintenant ainsi :

Vous noterez que le nombre est arrondi et non tronqué. Ainsi, le nombre

123.4567890123456, pour cet exemple, devient 123.457 à l’affichage et non pas 123.456 car le chiffre après 6 est supérieur à 5.

• Format scientifique:

Pour activer ce format, commencez par appuyer sur la touche H. Ensuite, utilisez la flèche vers le bas ˜, pour sélectionner l’option Number format. Appuyez sur le menu @CHOOS et la touche ( B), puis sélectionnez l’option Scientific avec la touche de flèche vers le bas ˜. Gardez le nombre 3 en face de Sci. (On peut changer ce nombre de la même manière qu’on a pu changer le nombre de décimales de l’option Fixed dans l'exemple ci-dessus).

Appuyez sur la touche de menu !!@@OK#@ pour revenir à l’affichage normal de la calculatrice. Le nombre apparaît maintenant ainsi :

Page 1-13

Ce résultat, 1.23E2, est la notation de la calculatrice pour les puissances de dix, et est équivalent à 1.235 × 10

. Dans cette prétendue notation scientifique, le nombre 3 en face du format numérique Sci (indiqué cidessus) représente le nombre de chiffres significatifs après la virgule. La notation scientifique comprend toujours un nombre entier, comme indiqué ci-dessus. Donc, dans ce cas-ci, le nombre de chiffres significatifs est quatre.

• Format ingénierie

Le format ingénierie est très proche du format scientifique, mais les puissances de dix y sont des multiples de trois. Pour activer ce format, commencez par appuyer sur la touche H. Ensuite, utilisez la flèche vers le bas ˜ pour sélectionner l’option Number format. Appuyez sur le menu @CHOOS et la touche ( B) et sélectionnez l’option Engineering avec la touche de flèche vers le bas ˜. Gardez le nombre 3 en face de Eng. (On peut changer ce nombre de la même manière qu’on a pu changer le nombre de décimales de l’option Fixed dans l’un des exemples précédents).

Appuyez sur la touche de menu !!@@OK#@ pour revenir à l’affichage normal de la calculatrice. Le nombre apparaît maintenant ainsi :

Page 1-14

Comme ce nombre comporte trois chiffres dans sa partie entière, il est affiché avec quatre chiffres significatifs et zéro puissances de dix, dans le format ingénierie. Par exemple, le nombre 0.00256 sera affiché ainsi :

• Virgule et point décimal

Pour les nombres décimaux, le point décimal peut être remplacé par une virgule, si l’utilisateur est familiarisé davantage avec cette notation. Pour remplacer les points décimaux par des virgules, sélectionnez l’option FM dans la fenêtre CALCULATOR MODES pour virgule, comme indiqué cidessous (Vous noterez que nous avons changé l’option de format numérique en Std) :

• Appuyez sur la touche H. Ensuite, appuyez une seule fois sur la touche

de flèche vers le bas, ˜, et appuyez à deux reprises sur la touche de flèche vers la droite, ™, pour surligner l'option __FM,. Pour sélectionner les virgules, appuyez sur la touche de menu @CHK@@ (c’est-à-dire la touche B). La fenêtre apparaît comme suit :

• Appuyez sur la touche de menu !!@@OK#@ pour revenir à l’affichage normal

de la calculatrice. Le nombre 123.4567890123456, qui a été entré précédemment, est maintenant affiché ainsi :

Mesure d’angle

Page 1-15

Les fonctions trigonométriques, par exemple, nécessitent l’emploi d’arguments qui représentent des angles plans. La calculatrice fournit trois modes différents, appelés modes de Mesure d’angle pour travailler avec les angles :

• Degrés: Il y a 360 degrés (360

• Radians: Il y a 2π radians (2π

• Grades: Il y a 400 grades (400

) dans une circonférence.

La mesure d’angle affecte les fonctions trigonométriques telles que SIN, COS, TAN et les fonctions qui leurs sont associées.

Pour changer le mode de mesure d’angle, suivez la procédure suivante :

• Appuyez sur la touche H. Ensuite, appuyez à deux reprises sur la

touche de flèche vers le bas, ˜. Sélectionnez le mode de Mesure d’Angle soit en utilisant la touche \ (deuxième à partir de la gauche dans la cinquième ligne depuis le bas du clavier), soit en appuyant sur la touche de menu @CHOOS ( B). Si vous utilisez cette dernière méthode, utilisez les touches de flèches vers le haut et vers le bas, —˜, pour sélectionner le mode choisi, et appuyez sur la touche de menu !!@@OK#@ (F) pour terminer l’opération. Par exemple, sur l’écran suivant, le mode Radians a été sélectionné :

Système de coordonnées

Le système de coordonnées affecte la manière dont les vecteurs et les nombres complexes sont affichés et saisis. Pour en savoir plus sur les nombres complexes et les vecteurs, reportez vous respectivement aux Chapitres 4 et 8 du présent guide. La calculatrice propose trois systèmes de coordonnées : Rectangulaire (RECT), Cylindrique (CYLIN), et Sphérique (SPHERE). Pour changer de système de coordonnées :

Page 1-16

• Appuyez sur la touche H. Ensuite, appuyez à trois reprises sur la

touche de flèche vers le bas, ˜. Sélectionnez le mode Coord System soit en utilisant la touche \ (deuxième à partir de la gauche dans la cinquième ligne depuis le bas du clavier), soit en appuyant sur la touche de menu @CHOOS ( B). Si vous utilisez cette dernière méthode, utilisez les touches de flèches vers le haut et vers le bas, —˜, pour sélectionner le mode choisi, et appuyez sur la touche de menu !!@@OK#@ ( F) pour terminer l’opération. Par exemple, on voit sur l’écran suivant, que le mode de coordonnées polaires a été sélectionné :

Sélectionner les paramètres CAS

CAS est l’acronyme de Computer Algebraic System. Il s’agit du noyau mathématique de la calculatrice, dans lequel sont programmées les opérations et fonctions mathématiques symboliques. Le CAS comprend un certain nombre de paramètres qui peuvent être ajustés suivant le type d’opération choisi. Pour afficher les paramètres optionnels du CAS suivez les indications ci-dessous :

• Appuyez sur la touche H pour activer la fenêtre CALCULATOR MODES.

• Pour modifier les paramètres du CAS appuyez sur la touche de menu

@@ CAS@@. Les valeurs par défaut des paramètres du CAS sont affichées cidessous :

Page 1-17

• Pour vous déplacer parmi ces nombreuses options dans la fenêtre CAS

MODES, utilisez les touches de flèches : š™˜—.

• Pour sélectionner ou désélectionner l’un des paramètres ci-dessus,

choisissez le symbole ‘souligné’ qui précède l’option en question, et appuyez sur la touche de menu @CHK@@ jusqu’à ce que le paramètre désiré apparaisse. Lorsqu’une option est sélectionnée, un signe de validation apparaît sur le symbole ‘souligné’ (c’est le cas pour les options Rigorous et de Simp Non-Rational dans l'exemple ci-dessus). Les options non sélectionnées n’auront pas de signe de validation associé à leur symbole ‘souligné’ (comme c’est le cas pour les options _Numeric, _Approx, _Complex, _Verbose, _Step/Step, _Incr Pow dans l'exemple ci-dessus).

• Après avoir sélectionné et désélectionné toutes les options désirées dans

la fenêtre CAS MODES, appuyez sur la touche de menu @@@OK@@@. Cela vous ramènera à la fenêtre CALCULATOR MODES. Pour revenir en mode d’affichage normal de la calculatrice à ce moment-là, appuyez encore une fois sur la touche de menu @@@OK@@@.

Explication des paramètres du CAS

• Indep var: La variable indépendante pour les applications CAS.

Typiquement, VX = ‘X’.

• Modulo

contient le module ou le modulo de l’anneau arithmétique (voir le Chapitre 5 du guide de l’utilisateur de la calculatrice).

• Numeric

résultat de calcul numérique, ou décimal.

• Approx

utilisé dans les résultats de calcul. Sinon, le CAS est dans le mode Exact, qui produit des résultats symboliques pour les calculs algébriques.

: Pour les opérations en arithmétique des modules, cette variable

: Lorsque ce paramètre est activé, la calculatrice produit un

: Lorsque ce paramètre est activé, le mode d’approximation est

Page 1-18

• Complex: Lorsque ce paramètre est activé, les opérations sur les nombres

complexes sont actives. Sinon, le CAS est en mode Réel et les calculs sont effectués pour les nombres réels par défaut. Voir le Chapitre 4 pour les opérations sur les nombres complexes.

• Verbose

fournies à propos de certaines opérations du CAS.

• Step/Step

pas-à-pas pour certaines opérations du CAS. Il est utile pour voir les étapes de calcul intermédiaires pour les sommes, les dérivées, les intégrales, les opérations de polynômes (par exemple pour la division synthétique) et les opérations matricielles.

• Incr Pow

activé, les termes polynomiaux sont affichés dans l’ordre croissant de puissance de la variable indépendante.

• Rigorous

la fonction de valeur absolue |X| par X.

• Simp Non-Rational

essaiera de simplifier au maximum les expressions irrationnelles.

: Lorsque ce paramètre est activé, des informations détaillées sont

: Lorsque ce paramètre est activé, il fournit les résultats en mode

: Puissance croissante, ce qui signifie que, si ce paramètre est

: Lorsque ce paramètre est activé, la calculatrice ne simplifie pas

: Lorsque ce paramètre est activé, la calculatrice

Choix du mode d’affichage

Vous pouvez personnaliser l’affichage de la calculatrice en sélectionnant différents modes d’affichage. Pour voir les différents paramètres de cette option, procédez comme suit :

• D'abord, appuyez sur la touche H pour activer la fenêtre

CALCULATOR MODES. Dans la fenêtre CALCULATOR MODES, appuyez sur la touche de menu @@DISP@ (D) pour afficher la fenêtre DISPLAY MODES.

Page 1-19

• Pour naviguer parmi les différentes options de la fenêtre DISPLAY MODES,

utiliser les touches de flèches : š™˜—.

• Pour sélectionner ou désélectionner l’un des paramètres affichés ci-dessus,

qui nécessite une marque de validation, sélectionnez le symbole ‘souligné’ devant l’option en question, et appuyez sur les touches @CHK@@ jusqu’à ce que le paramètre désiré apparaisse. Lorsqu’une option est sélectionnée, un signe de validation apparaît sur le symbole ‘souligné’ (c’est le cas des options Textbook dans la ligne Stack: ). Les options non sélectionnées n’auront pas de signe de validation associé à leur symbole ‘souligné’ (comme c’est le cas pour les options _Small, _Full page, et _Indent de l'exemple ci-dessus Edit:).

• Pour sélectionner la police d’affichage, surlignez le champ en face de

l’option Font: dans la fenêtre DISPLAY MODES et utilisez la touche @CHOOS (B).

• Après avoir sélectionné et désélectionné toutes les options voulues dans la

fenêtre DISPLAY MODES, appuyez sur la touche de menu @@@OK@@@. Cela vous ramènera à la fenêtre CALCULATOR MODES. Pour revenir en mode d’affichage normal de la calculatrice à ce moment-là, appuyez encore une fois sur la touche de menu @@@OK@@@.

Choisir la police d’affichage

D'abord, appuyez sur la touche H pour activer la fenêtre CALCULATOR MODES. Dans la fenêtre CALCULATOR MODES, appuyez sur la touche de menu @@DISP@ (D) pour afficher la fenêtre DISPLAY MODES. Le champ Font: est surligné, et l’option Ft8_0:system 8 est sélectionnée. C’est la valeur par défaut de la police d’affichage. En appuyant sur la touche de menu @CHOOS (B), vous obtiendrez la liste des polices disponibles dans le système, comme indiqué ci-dessous :

Page 1-20

Les options disponibles sont trois System Fonts standards (taille 8, 7, et 6) et l’option Browse. Cette dernière vous permettra de parcourir la mémoire de la calculatrice pour y chercher des polices supplémentaires que vous avez pu créer ou télécharger dans la calculatrice.

Essayez de modifier la taille de la police en tailles 7 et 6. Appuyez sur la touche de menu OK pour valider la sélection. Lorsque vous en avez terminé avec le choix de la police, appuyez sur la touche de menu @@@OK@@@ pour revenir à la fenêtre CALCULATOR MODES. Pour repasser en mode d’affichage normal à ce moment-là, appuyez encore une fois sur la touche de menu @@@OK@@@ et vous pourrez constater que le mode d’affichage de la pile a changé pour s’accorder avec cette nouvelle police.

Choisir les propriétés de l’éditeur de ligne

D'abord, appuyez sur la touche H pour activer la fenêtre CALCULATOR MODES. Dans la fenêtre CALCULATOR MODES, appuyez sur la touche de menu @@DISP@ (D) pour afficher la fenêtre DISPLAY MODES. Appuyez une seule fois sur la touche de flèche vers le bas, ˜, pour accéder à la ligne Edit. Cette ligne comporte trois propriétés qui peuvent être modifiées. Lorsque ces propriétés sont sélectionnées (validées), cela active les effets suivants :

_Small Réduit la taille de la police _Full page Autorise le placement du curseur en fin de ligne _Indent Autoindexation du curseur après un retour à la ligne

Les instructions d’utilisation de l’éditeur de ligne sont présentées dans le Chapitre 2 de ce guide de l’utilisateur.

Choisir les propriétés de la pile

Page 1-21

D'abord, appuyez sur la touche H pour activer la fenêtre CALCULATOR MODES. Dans la fenêtre CALCULATOR MODES, appuyez sur la touche de menu @@DISP@ (D) pour afficher la fenêtre DISPLAY MODES. Appuyez une seule fois sur la touche de flèche vers le bas, ˜, pour accéder à la ligne Edit. Cette ligne comporte trois propriétés qui peuvent être modifiées. Lorsque ces propriétés sont sélectionnées (validées), cela active les effets suivants :

_Small Réduit la taille de la police. Ceci permet de maximiser la

quantité d’informations affichée à l’écran. Notez que ce choix annule le choix de la police d’affichage de la pile.

_Textbook Affiche les expressions mathématiques en notation

mathématique graphique.

Pour illustrer ces paramètres, en mode algébrique ou en mode RPN, utilisez l’éditeur d’équation pour entrer l’intégrale infinie suivante :

‚O…Á0™„è™„¸\x™x`

En mode algébrique, l’écran suivant montre le résultat de cette combinaison de touches, alors qu’aucune des options _Small ou _Textbook n'est sélectionnée :

Avec uniquement l’option _Small activée, l’affichage apparaît comme suit :

Avec l'option _Textbook activée (valeur par défaut), que l’option _Small soit active ou non, le résultat suivant est affiché :

Page 1-22

Choisir les propriétés de l’éditeur d’équation (Equation writer EQW)

D'abord, appuyez sur la touche H pour activer la fenêtre CALCULATOR MODES. Dans la fenêtre CALCULATOR MODES, appuyez sur la touche de menu @@DISP@ (D) pour afficher la fenêtre DISPLAY MODES. Appuyez à trois reprises sur la touche de flèche vers le bas, ˜, pour accéder à la ligne EQW (Equation Writer). Cette ligne comporte deux propriétés qui peuvent être modifiées. Lorsque ces propriétés sont sélectionnées (validées), cela active les effets suivants :

_Small Réduit la taille de la police pour l’éditeur d’équation _Small Stack Disp Affiche la police de petite taille dans la pile après

Les instructions détaillées sur l’utilisation de l’éditeur d’équation (Equation Writer – EQW) sont présentées dans une autre partie de ce manuel.

Pour l’exemple de l’intégrale

l’option _Small Stack Disp sur la ligne EQW de la fenêtre DISPLAY MODES produira l’affichage suivant :

avoir utilisé l’éditeur d’équation

∞

−

dXe

∫

, présenté ci-dessus, sélectionner

Références

On pourra trouver des références supplémentaires à propos des sujets traités dans ce Chapitre dans le Chapitre 1 et dans l’Appendice C du guide de l’utilisateur de la calculatrice.

Page 1-23

Chapitre 2 Présentation de la calculatrice

Dans ce chapitre nous présentons les fonctionnalités de base de la calculatrice, notamment l’utilisation de l’éditeur d’équations et la manipulation de données dans la calculatrice. Etudiez les exemples de ce chapitre pour acquérir une bonne connaissance des capacités de la calculatrice pour vos applications futures.

Objets

Les objets les plus fréquemment rencontrés sont : les réels (nombres réels, écrits en notation décimale, par exemple : -0.0023, 3.56), les entiers (nombres entiers, sans virgule, par exemple : 1232, -123212123), les nombres complexes (écrits sous la forme d’une paire ordonnée, par exemple : (3,-2)), les listes, etc. Les objets de la calculatrice sont décrits dans les Chapitres 2 et 24 du guide de l’utilisateur de la calculatrice.

Ecrire des expressions dans la pile

Dans cette section nous présentons des exemples d’écriture directe d’expressions dans l’afficheur de la calculatrice aussi appelé pile.

Créer des expressions arithmétiques

Dans cet exemple, nous sélectionnons le mode Algébrique et choisissons le format Fix avec 3 décimales pour l’affichage. Nous allons entrer l’expression arithmétique suivante :

0.1

0.5

⋅

Pour entrer cette expression, utilisez la séquence de touches suivante :

5.*„Ü1.+1/7.5™/ „ÜR3.-2.Q3

5.7

0.20.3

−

Page 2-1

L’expression obtenue est : 5*(1+1/7.5)/( ƒ3-2^3).

Appuyez sur ` pour obtenir l’affichage suivant à l’écran :

Remarquez que, si votre CAS est en mode EXACT (voir l’Appendice C du guide de l’utilisateur) et si vous entrez votre expression en utilisant des nombres entiers pour des valeurs entières, le résultat est une quantité symbolique, par exemple :

5*„Ü1+1/7.5™/

„ÜR3-2Q3

Avant de donner un résultat, on vous demandera de passer en mode Approximate. Acceptez ce changement pour obtenir le résultat suivant (donné ici en mode décimal Fix avec trois décimales – voir Chapitre 1) :

Dans le cas présent, lorsque vous entrez l’expression directement dans la pile, dès que vous appuyez sur `, la calculatrice va essayer de calculer le résultat de l’expression. Cependant, si l’expression est saisie entre deux apostrophes, la calculatrice va reproduire l’expression telle quelle. Par exemple :

³5*„Ü1+1/7.5™/

„ÜR3-2Q3`

Page 2-2

Le résultat apparaîtra comme indiqué ci-dessous :

Pour calculer l’expression, nous pouvons utiliser la function EVAL, comme suit :

µ„î`

Si le CAS est en mode Exact, on vous demandera de valider le passage du CAS en mode Approx . Une fois que ce changement est réalisé, vous obtiendrez le même résultat que précédemment.

Une autre méthode pour calculer l’expression entrée plus haut entre apostrophes consiste à utiliser l’option

…ï.

Nous allons maintenant entrer l’expression utilisée ci-dessus lorsque la calculatrice est en mode d’opérations RPN. Nous avons également placé le CAS en mode Exact et l'affichage en mode Textbook. La séquence de touches pour entrer l’expression entre apostrophes est la même que précédemment, c’est-à-dire :

³5*„Ü1+1/7.5™/

„ÜR3-2Q3`

Ce qui donne le résultat

Page 2-3

Appuyez encore une fois sur ` pour garder deux copies disponibles de l’expression dans la pile, afin d’en effectuer le calcul. Nous calculerons l’expression en utilisant d’abord la fonction EVALpuis la fonction NUM: µ.

Cette expression est semi-symbolique puisque le résultat contient des composantes décimales ainsi qu’une racine √3. Ensuite, nous échangeons les positions dans la pile [utilisant ™] et nous calculons l’expression en utilisant la fonction NUM, par exemple, ™…ï.

Ce dernier résultat étant purement numérique, les deux résultats dans la pile paraissent différents, bien qu’ils représentent tous les deux le calcul d’une même expression. Pour vérifier qu’ils sont bien égaux, nous soustrayons les deux résultats et nous calculons cette différence en utilisant la fonction EVAL:

-µ. Le résultat est zéro (0.).

Pour obtenir un complément d’information sur l’écriture d’expressions arithmétiques sur l’écran ou dans la pile, reportez-vous au Chapitre 2 du guide de l’utilisateur de la calculatrice.

Créer des expressions algébriques

Les expressions algébriques comportent non seulement des nombres mais aussi des noms de variables. Comme exemple, nous allons entrer l’expression algébrique suivante :

L212

Nous plaçons la calculatrice en mode d’opération Algébrique, le CAS en mode Exact et l'affichage en mode Textbook. Pour entrer cette expression algébrique, nous utilisons la séquence de touches suivante :

³2*~l*R„Ü1+~„x/~r™/ „ Ü ~r+~„y™+2*~l/~„b

Page 2-4

Appuyez sur ` pour obtenir le résultat suivant :

Entrer cette expression lorsque la calculatrice est en mode RPN revient exactement au même que d’utiliser le mode Algébrique dans cet exercice.

Pour obtenir des informations complémentaires sur l’écriture d’expressions algébriques sur l’écran ou dans la pile de la calculatrice, reportez-vous au Chapitre 2 du guide de l’utilisateur de la calculatrice.

Utiliser l’Editeur d’équation (EQW) pour écrire des expressions

L’éditeur d’équation est un outil extrêmement puissant, qui non seulement vous permet d’entrer et de visualiser une équation mais vous permet aussi de modifier et d’appliquer des fonctions à l’équation ou à une partie de l’équation.

Le démarrage de l’éditeur d’équation se fait par la combinaison de touches ‚O (troisième touche de la quatrième ligne du clavier). L’écran suivant apparaît. Appuyez sur L pour afficher la deuxième page du menu :

Pour l’éditeur d’équation, les six touches de menu activent les fonctions EDIT, CURS, BIG, EVAL, FACTOR, SIMPLIFY, CMDS et HELP. Vous pourrez trouver des informations détaillées à propos de ces fonctions dans le Chapitre 3 du guide de l’utilisateur de la calculatrice.

Page 2-5

Créer des expressions arithmétiques

La méthode pour saisir des expressions arithmétiques avec l’éditeur d’équation est très similaire à la façon dont on entre des expressions arithmétiques entre apostrophes dans la pile. Seule grande différence : les expressions produites avec l’éditeur d’équation apparaissent en style “textbook” au lieu d’apparaître comme une ligne d’écriture. Par exemple, essayez la séquence de touches suivante dans l’éditeur d’équations :

5/5+2

Il en résulte l’expression

Le curseur, prenant la forme d’un triangle qui pointe vers la gauche, indique la position d’écriture actuelle. Par exemple, avec le curseur en position indiquée ci-dessus, tapez maintenant :

*„Ü5+1/3

L’expression inscrite apparaît comme suit :

Supposons que vous vouliez remplacer la quantité entre parenthèses dans le dénominateur (c’est-à-dire : 5+1/3) par (5+π

/2). Tout d’abord, nous

utiliserons la touche effacer (ƒ) pour effacer l’expression 1/3, ensuite, nous remplacerons cette fraction par π

/2, comme indiqué ci-dessous :

ƒƒƒ„ìQ2

Page 2-6

A ce moment-là, l’affichage est le suivant :

Pour insérer le dénominateur 2 dans l’expression, nous devons surligner l’expression π touche de flèche vers la droite (™). A ce moment-là, nous entrons la séquence suivante :

L’expression apparaît maintenant ainsi :

dans sa totalité. Pour cela, nous cliquons une seule fois sur la

Supposons alors que vous vouliez ajouter la fraction 1/3 à cette expression, c’est-à-dire entrer l’expression :

5(25

+⋅+

)

Tout d’abord, nous devons surligner la totalité du premier terme en utilisant la touche de flèche vers la droite (™) ou la touche de flèche vers le haut (—) de façon répétée jusqu’à ce que toute l’expression soit surlignée, ce qui donne donc :

Page 2-7

NOTE: On peut aussi utiliser, à partir de la position initiale du curseur (à la droite du 2 dans le dénominateur de π2/2), la combinaison de touches suivante ‚—, qui sera interprétée comme (‚ ‘ ).

Une fois que l’expression est surlignée comme indiqué ci-dessus, tapez +1/3 pour ajouter la fraction 1/3. Cela donne :

Créer des expressions algébriques

Une expression algébrique est très similaire à une expression arithmétique, mise à part le fait qu’elle peut inclure des lettres des alphabets latins et grecs. La procédure pour créer une expression algébrique suit donc la même idée que l’écriture d’une expression arithmétique, sauf qu’on utilise en plus le clavier alphabétique.

Pour illustrer l’utilisation de l’éditeur d’équation pour entrer une expression algébrique, nous allons utiliser l’exemple suivant. Supposons que nous voulions entrer l’expression :

∆⋅+

−

⋅+

LNe

On utilise la séquence de touches suivante :

 



 

3/1



Page 2-8

2 / R3 ™™ * ~‚n + „¸\ ~‚m

™™ * ‚¹ ~„x + 2 * ~‚m * ~‚c

~„y ——— / ~‚t Q1/3

Ce qui donne le résultat :

Dans cet exemple, nous avons utilisé un certain nombre de minuscules latines, x (~„x), quelques lettres grecques, λ (~‚n) et même une combinaison de lettres latines et grecques, ∆y (~‚c~„y). Souvenez-vous que pour entrer une lettre minuscule, il faut utiliser la combinaison : ~„ suivie de la lettre que vous voulez saisir. De plus, vous pouvez toujours écrire des caractères spéciaux en utilisant le menu CHARS (…±) si vous ne voulez pas avoir à mémoriser la combinaison de touches qui permet de les obtenir. Une liste des combinaisons de touches ~‚ les plus fréquemment utilisées se trouve dans l’Appendice D du guide de l’utilisateur.

Pour obtenir des informations supplémentaires sur l’édition, le calcul, la factorisation et la simplification d’expressions algébriques, reportez-vous au Chapitre 2 du guide de l’utilisateur de la calculatrice.

Organiser les données dans la calculatrice

Vous avez la possibilité d’organiser les données dans votre calculatrice en mémorisant les variables dans un arbre de répertoires. La base de l’arbre des répertoires de la calculatrice est le répertoire HOME, qui est décrit ci-dessous.

Le répertoire HOME

Pour atteindre le répertoire HOME, appuyez sur la fonction UPDIR („§)

-- autant de fois que nécessaire, jusqu’à ce que le symbole {HOME} apparaisse sur la deuxième ligne de l’en-tête de l’afficheur. Vous pouvez aussi utiliser „ (maintenu) §. Dans cet exemple, le répertoire HOME contient

Page 2-9

uniquement le CASDIR. En appuyant sur J, les variables apparaissent sur les touches de menu :

Sous-répertoires

Pour enregistrer vos données dans un arbre de répertoires bien organisé, vous pouvez créer des sous-répertoires dans le répertoire HOME et d’autres sousrépertoires à l’intérieur de ces sous-répertoires, construisant ainsi une hiérarchie de répertoires similaire à l’organisation des fichiers dans les ordinateurs modernes. Les sous-répertoires auront des noms qui, en général, sont symboliques du contenu de chaque sous-répertoire ou tout autre nom que vous désirerez. Pour plus de détails sur la manipulation des répertoires, reportez-vous au Chapitre 2 du guide de l’utilisateur de la calculatrice.

Les variables

Les variables fonctionnent comme les fichiers sur le disque dur d’un ordinateur. Une variable peut contenir un objet (des valeurs numériques, des expressions algébriques, des listes, des vecteurs, des matrices, des programmes, etc.). On se réfère aux variables par leurs noms, qui peuvent être une combinaison de caractères alphanumériques, commençant toujours par une lettre (latine ou grecque). On peut utiliser certains symboles, comme la flèche (→), dans un nom de variable, à condition de les combiner avec un caractère alphabétique. Ainsi, ‘→A’ est un nom de variable valide, mais ‘→’ ne l’est pas. Comme exemples de noms de variables valides, on a : ‘A’, ‘B’, ‘a’, ‘b’, ‘α’, ‘β’, ‘A1’, ‘AB12’, ‘A12’,’Vel’,’Z0’,’z1’, etc.

Une variable ne peut pas avoir le même nom qu’une fonction dans la calculatrice. Les noms de variables réservés par la calculatrice sont les suivants : ALRMDAT, CST, EQ, EXPR, IERR, IOPAR, MAXR, MINR, PICT, PPAR, PRTPAR, VPAR, ZPAR, der_, e, i, n1,n2, …, s1, s2, …, ΣDAT, ΣPAR, π, ∞

Page 2-10

Il est possible d’organiser les variables en sous-répertoires (voir le Chapitre 2 du guide de l’utilisateur de la calculatrice).

Taper un nom de variable

Pour nommer les variables, vous devrez taper les chaînes de caractères en une fois, qu’elles soient ou non combinées avec des nombres. Pour taper les chaînes de caractères, vous pouvez forcer le clavier en mode alphabétique de la façon suivante :

~~ bloque le clavier alphabétique en mode majuscule. Dans ce mode, appuyer sur „ avant une touche de caractère donne une lettre minuscule et appuyer sur la touche ‚ avant une touche de caractère crée un caractère spécial. Si le clavier alphabétique est déjà bloqué en position majuscule, pour le bloquer en position minuscule, tapez, „~

~~„~ bloque le clavier alphabétique en mode minuscule. Dans ce mode, appuyer sur „ avant une touche de caractère donne une lettre majuscule. Pour désactiver le mode minuscule, appuyez sur „~

Pour désactiver le clavier bloqué en mode majuscule, appuyez sur ~

Essayez les exercices suivants :

³~~math` ³~~m„a„t„h` ³~~m„~at„h`

Sur l’écran de la calculatrice, on verra l’affichage suivant (à gauche pour le mode algébrique, à droite pour le mode RPN) :

Page 2-11

Créer des variables

La façon la plus simple de créer une variable est d’utiliser le K . Les exemples ci-dessous permettent d’enregistrer les variables de la table suivante (Appuyez sur J si nécessaire pour afficher le menu des variables) :

Nom Contenu Type

A12 3×105 réel

Q ‘r/(m+r)' algébrique

R [3,2,1] vecteur

z1 3+5i complexe

p1 « → r 'π*r^2' » programme

• Mode algébrique

Pour mémoriser la valeur –0.25 dans la variable α:

0.25\ K ~‚a. L’écran est alors le suivant :

-0.25 réel

Appuyez sur ` pour créer la variable. La variable apparaît maintenant sur les indicateurs des touches de menu :

Pour entrer les variables restantes, utilisez les séquences de touches suivantes :

A12: 3V5K~a12`

Page 2-12

Q: ³~„r/„Ü ~„m+~„r™™ K~q`

R: „Ô3‚í2‚í1™ K~r`

z1: 3+5*„¥ K~„z1` (Acceptez le passage en mode Complex si on vous le demande).

p1: ‚å‚é~„r³„ì* ~„rQ2™™™ K~„p1`..

L’affichage est alors le suivant :

Vous verrez six des sept variables affichées en bas de l’écran : p1, z1, R, Q, A12, α.

• Mode RPN

(Utilisez la touche H\@@OK@@ pour passer en mode RPN). Utilisez la séquence de touches suivante pour enregistrer la valeur –0.25 dans la variable α: 0.25\` ~‚a`. L’écran est alors le suivant :

Cette expression signifie que la valeur –0.25 est prête à être enregistrée dans α. Appuyez sur K pour créer la variable. La variable apparaît maintenant sur les indicateurs des touches de menu :

Page 2-13

Pour entrer la valeur 3×10

dans la variable A12, on peut utiliser une

méthode raccourcie : 3V5³~a12` K

Voici la séquence à suivre pour enregistrer le contenu de Q :

Q: ³~„r/„Ü ~„m+~„r™™ ³~q` K

Pour entrer la valeur de R, nous pouvons utiliser une méthode encore plus rapide :

R: „Ô3#2#1™ ³K

Vous remarquerez que pour séparer les éléments d’un vecteur en mode RPN, on peut utiliser la touche espace (#), plutôt que la virgule (‚í ) utilisée plus haut en mode algébrique.

z1: ³3+5*„¥ ³~„z1 K

p1: ‚å‚é~„r³„ì* ~„rQ2™™™ ³ ~„p1™` K.

L’affichage est alors le suivant :

Vous verrez six des sept variables affichées en bas de l’écran : p1, z1, R, Q, A12, α.

Page 2-14

Vérifier le contenu des variables

La manière la plus simple de vérifier le contenu d’une variable est d’appuyer sur la touche de menu de la variable. Par exemple, pour les variables affichées précédemment, appuyez sur les touches suivantes pour afficher le contenu des variables :

Mode algébrique

Tapez ces séquences de touches : J@@z1@@ ` @@@R@@ `@@@Q@@@ `. L’affichage est alors le suivant :

Mode RPN En mode RPN, il suffit d’appuyer sur la touche de menu correspondante pour obtenir le contenu d’une variable numérique ou algébrique. Dans le cas présent, on peut essayer d’afficher les variables z1, R, Q, A12, α, créées plus haut, de la façon suivante : J@@z1@@ @@@R@@ @@@Q@@ @@A12@@ @@ª@@

L’affichage est alors le suivant :

Utiliser la touche right-shift suivie des touches de menu

Cette méthode de visualisation des variables fonctionne de la même façon pour les modes algébrique et RPN. Essayez les exemples suivants dans l’un de ces modes :

J‚@@p1@@ ‚ @@z1@@ ‚ @@@R@@ ‚@@@Q@@ ‚ @@A12@@

Page 2-15

Cela donne le résultat suivant (mode algébrique à gauche, mode RPN à droite) :

Vous remarquerez que cette fois le contenu du programme p1 est affiché à l’écran. Pour visualiser les autres variables de ce répertoire, composez :

@@@ª@@ L ‚ @@@A@@

Afficher le contenu de toutes les variables à l’écran

Utilisez la combinaison de touches ‚˜ pour afficher le contenu de toutes les variables à l’écran. Par exemple :

Appuyez sur $ pour retourner en mode d’affichage normal.

Effacer des variables

La façon la plus simple d’effacer des variables est d’utiliser la fonction PURGE. On peut accéder à cette fonction directement en utilisant le menu TOOLS (I), ou en utilisant le menu FILES „¡@@OK@@ .

Utiliser la fonction PURGE dans la pile en mode algébrique

Notre liste de variables contient les variables p1, z1, Q, R, et α. Nous allons utiliser la commande PURGE pour effacer la variable p1. Appuyez sur I @PURGE@ J@@p1@@ `. L’affichage indique maintenant que la variable p1 a été effacée :

Page 2-16

Vous pouvez utiliser la commande PURGE pour effacer plus d’une variable en plaçant leurs noms dans une liste dans l’argument de PURGE. Par exemple, si nous voulons maintenant effacer simultanément les variables R et Q, nous pouvons essayer la méthode suivante. Composez :

I @PURGE@ „ä³ J@@@R!@@ ™ ‚í ³ J@@@Q!@@

L’écran indique alors la commande suivante, qui est prête à être exécutée :

Pour terminer la destruction des variables, appuyez sur `. L’affichage indique maintenant les variables restantes :

Utiliser la fonction PURGE dans la pile en mode RPN

Notre liste de variables contient les variables p1, z1, Q, R, et α. Nous allons utiliser la commande PURGE pour effacer la variable p1. Appuyez sur ³@@p1@@ ` I @PURGE@. L’affichage indique maintenant que la variable p1 a été effacée :

Page 2-17

Pour effacer simultanément deux variables, par exemple les variables R et Q, créez tout d’abord une liste (en mode RPN, il n’est pas nécessaire de séparer les éléments d’une liste par des virgules, contrairement au mode algébrique) :

J „ä³ @@@R!@@ ™ ³ @@@Q!@@ `

Ensuite, appuyez sur I@PURGE@ pour effacer les variables.

Vous trouverez des informations supplémentaires sur la manipulation des variables au Chapitre 2 du guide de l’utilisateur de la calculatrice.

Les fonctions UNDO et CMD

Les fonctions UNDO et CMD sont utiles pour récupérer des commandes récentes ou pour annuler une opération si une erreur a été commise. Ces fonctions sont associées à la touche HIST : la séquence de touches ‚¯, donne accès à la fonction UNDO, tandis que la commande CMD est accessible par la combinaison „®.

CHOOSE-boxes ou Soft MENU

Dans un certain nombre d’exercices présentés dans ce chapitre nous avons pu voir des menus de commandes affichés à l’écran. Ces menus sont appelées CHOOSE-boxes. Nous indiquons ci-dessous comment passer des CHOOSEboxes aux Soft MENUs et inversement, par le biais d’un exercice.

Bien qu’il ne s’applique pas à un exemple particulier, l’exercice proposé présente les deux options de menus de la calculatrice (CHOOSE-boxes et Soft MENU). Pour cet exercice, nous utilisons la commande ORDER pour réordonner les variables d’un répertoire en mode ALG:

„°˜ Affiche le menu PROG et sélectionne MEMORY

Page 2-18

@@OK@@ ˜˜˜˜ Affiche le menu MEMORY et sélectionne DIRECTORY

@@OK@@ —— Affiche le menu DIRECTORY et sélectionne ORDER

@@OK@@ Active la commande ORDER

Un autre moyen d’accéder à ces menus par les touches de MENU est d’activer l’indicateur système 117 (pour de plus amples informations sur les indicateurs système, reportez-vous au Chapitres 2 et 24 du guide de l’utilisateur de la calculatrice). Pour activer cet indicateur, procédez comme suit :

H @FLAGS! ———————

L’écran indique que l’indicateur 117 n’est pas activé (CHOOSE boxes), comme indiqué ci-dessous :

Appuyez sur la touche de menu @CHK@@ pour activer l’indicateur 117 en mode soft MENU. L’écran indique que ce changement est effectif :

Page 2-19

Appuyez deux fois pour revenir en mode d’affichage normal. Appuyez deux fois sur @@OK@@ pour revenir en mode d’affichage normal de la calculatrice.

Maintenant, nous allons essayer de trouver la commande ORDER en utilisant les mêmes séquences de touches que précédemment, c’est-à-dire en commençant par „°. Vous remarquerez qu’à la place d’un menu, nous obtenons des indicateurs de menu avec les différentes options du menu PROG, c’est-à-dire :

Appuyez sur B pour sélectionner le menu MEMORY ()@@MEM@@). L’affichage est alors :

Appuyez sur E pour sélectionner le menu DIRECTORY ()@@DIR@@)

La commande ORDER apparaît maintenant à l’écran. Utilisons la touche L pour y accéder :

Page 2-20

Pour activer la commande ORDER, appuyez sur la touche de menu C(@ORDER).

Références

Pour obtenir des informations supplémentaires sur l’écriture et la manipulation d’expressions à l’affichage ou dans l’éditeur d’équation, reportez-vous au Chapitre 2 du guide de l’utilisateur de la calculatrice. Pour les paramètres CAS (Computer Algebraic System), consultez l’Appendice C du guide de l’utilisateur de la calculatrice. Pour obtenir des informations sur les indicateurs système, consultez le Chapitre 24 du guide de l’utilisateur de la calculatrice.

Page 2-21

Chapitre 3 Calculs avec des nombres réels

Ce chapitre explique comment utiliser la calculatrice pour effectuer des opérations ou pour utiliser des fonctions sur les nombres réels. L’utilisateur devra être familier avec le clavier pour identifier certaines de ses fonctions (par exemple, SIN, COS, TAN, etc.). De plus, on suppose que le lecteur sait gérer les modes de fonctionnement de la calculatrice, c’est-à-dire sélectionner le mode opératoire (voir Chapitre 1), utiliser les menus et les CHOOSE-boxes (voir Chapitre 1) et travailler avec les variables (voir Chapitre 2).

Exemples de calculs avec des nombres réels

Pour effectuer des calculs sur les nombres réels, il vaut mieux mettre le CAS en mode Real (et non Complex). Le mode Exact est le mode par défaut pour la plupart des opérations. Et donc, vous pouvez commencer vos calculs dans ce mode.

Quelques calculs avec des nombres réels sont illustrés ci-dessous :

• Utilisez la touche \ pour changer le signe.

Par exemple, en mode ALG, essayer \2.5`. En mode RPN, essayer 2.5\.

• Utilisez la touche Y pour calculer l'inverse d'un chiffre.

Par exemple, en mode ALG, essayer Y2`. En mode RPN, utiliser 4`Y.

• Pour les additions, les soustractions, multiplications et divisions,

utilisez la touche d’opération appropriée, + - * /.

Exemples en mode ALG :

3.7 + 5.2 `

6.3 - 8.5 `

4.2 * 2.5 `

2.3 / 4.5 `

Page 3-1

Exemples en mode RPN :

3.7` 5.2 +

6.3` 8.5 -

4.2` 2.5 *

2.3` 4.5 /

En mode RPN, vous pouvez également séparer les opérandes avec un espace (#) avant d’appuyez sur la touche de l’opérateur. Exemples :

3.7#5.2 +

6.3#8.5 -

4.2#2.5 *

2.3#4.5 /

• On utilise des parenthèses („Ü) pour grouper des opérations et

aussi pour entrer les arguments des fonctions. En mode ALG:

„Ü5+3.2™/„Ü7-

2.2`

En mode RPN, les parenthèses sont inutiles, le calcul est effectué directement sur la pile :

5`3.2`+7`2.2`-/

En mode RPN, vous pouvez entrer une expression comme dans le mode algébrique, en tapant l’expression entre apostrophes :

³„Ü5+3.2™/

„Ü7-2.2`µ

Pour les deux modes ALG et RPN et en utilisant l’éditeur d’équation :

‚O5+3.2™/7-2.2

L’expression peut être calculée dans l’éditeur d’équation, en utilisant :

Page 3-2

————@EVAL@ ou, ‚—@EVAL@

• La fonction valeur absolue, ABS, est accessible par la combinaison de

touches : „Ê. Exemple en mode ALG :

„Ê \2.32`

Exemple en mode RPN :

2.32\„Ê

• La fonction carré, SQ, est accessible par la combinaison de touches

„º. Exemple en mode ALG :

„º\2.3`

Exemple en mode RPN :

2.3\„º

La fonction racine carrée, √, est accessible par la touche R. Lorsque vous effectuez le calcul dans la pile en mode ALG, entrez la fonction avant d’entrer l’argument, c’est-à-dire :

R123.4`

En mode RPN, entrez d’abord le nombre et ensuite la fonction, c’està-dire :

123.4R

• La fonction puissance, ^, est accessible par la touche Q . Lorsque

vous effectuez le calcul dans la pile en mode ALG, entrez la base (y) suivie par la touche Q et entrez ensuite l’exposant (x), c’est-à-dire :

Page 3-3

5.2Q1.25`

En mode RPN, entrez d’abord le nombre, et ensuite la fonction, c’està-dire :

5.2`1.25Q

• La fonction racine, XROOT(y,x), est accessible par la combinaison de

touches ‚». Lorsque vous effectuez le calcul dans la pile en mode ALG, entrez la fonction XROOT suivie des arguments (y,x), séparés par des virgules, c’est-à-dire :

‚»3‚í 27`

En mode RPN, entrez d’abord l’argument y, ensuite x, et enfin la fonction, c’est-à-dire :

27`3‚»

• Les logarithmes en base 10 sont calculés par la combinaison de

touches ‚Ã (fonction LOG), alors que la fonction inverse (ALOG, ou anti-logarithme) est calculée en utilisant „Â. En mode ALG, on entre la fonction avant l’argument :

‚Ã2.45` „Â\2.3`

En mode RPN, on entre l’argument avant la fonction :

2.45 ‚Ã

2.3\ „Â

Entrer des données avec des puissances de 10

On entre les puissances de dix, c’est-à-dire les nombres de la forme -4.5×10-2, etc., en utilisant la touche V . Par exemple, en mode ALG :

\4.5V\2`

Ou, en mode RPN :

4.5\V2\`

Page 3-4

• Les logarithms sont calculés en utilisant ‚¹ (fonction LN) alors

que la fonction exponent (EXP) est calculée en utilisant „¸. En mode ALG, on entre la fonction avant l’argument :

‚¹2.45` „¸\2.3`

En mode RPN, on entre l’argument avant la fonction

2.45` ‚¹

2.3\` „¸

• Trois fonctions trigonométriques sont accessibles directement sur le

clavier : le sinus (S), le cosinus (T), et la tangente (U). Les arguments de ces fonctions sont des angles, en degrés, radians ou grades. Les exemples suivants utilisent des angles en degrés (DEG) :

En mode ALG:

S30` T45`

U135`

En mode RPN:

30S 45T

135U

• Les fonctions trigonométriques inverses disponibles sur le clavier sont

arc sinus („¼), arc cosinus („¾) et arc tangente („À). Le résultat de ces fonctions sera donné dans l’unité de mesure d’angles sélectionnée (DEG, RAD, GRD). Des exemples sont donnés ci-dessous :

En mode ALG :

„¼0.25` „¾0.85` „À1.35`

Page 3-5

En mode RPN :

0.25„¼

0.85„¾

1.35„À

Toutes les fonctions décrites ci-dessus, ABS, SQ, √, ^, XROOT, LOG, ALOG, LN, EXP, SIN, COS, TAN, ASIN, ACOS, ATAN peuvent être combinées avec les opérateurs fondamentaux (+-*/) pour former des expressions plus complexes. L’éditeur d’équation, dont le fonctionnement est décrit au Chapitre 2, est l’outil idéal pour construire ce type d’expressions, quel que soit le mode d’opération de la calculatrice.

Les fonctions réelles dans le menu MTH

Le menu MTH („´) contient un certain nombre de fonctions mathématiques, dont la plupart sont applicables à des nombres réels. Avec le paramètre par défaut en position de CHOOSE-boxes pour l’indicateur système 117 (voir Chapitre 2), le menu MTH est affiché sous la forme du menu suivant :

Les fonctions sont groupées selon le type d'argument (1. vecteurs, 2. matrices,

3. listes, 7. probabilité, 9. complexes) ou selon la fonction (4. hyperbolique,

5. réel, 6. base, 8. fft). Il existe aussi une donnée pour les constantes mathématiques, donnée 10.

De façon générale, pour appliquer ces fonctions, vous devez connaître le nombre et l’ordre des arguments nécessaires et vous souvenir que, en mode ALG, vous devez d’abord sélectionner la fonction et ensuite entrer l’argument, alors qu’en mode RPN, vous devez d’abord entrer l’argument dans la pile avant de sélectionner la fonction.

Page 3-6

Utiliser les menus de la calculatrice:

1. Nous allons décrire en détail l'utilisation du menu 4. HYPERBOLIC.. dans le but de décrire le fonctionnement général des menus de la calculatrice. Faites bien attention à la méthode de sélection des différentes options.

2. Pour sélectionner rapidement l’une des nombreuses options dans un menu (ou dans une de CHOOSE-boxes), cliquez simplement sur le numéro de l’option au clavier. Par exemple, pour sélectionner l’option 4. HYPERBOLIC.. dans le menu MTH, appuyez simplement sur 4.

Fonctions hyperboliques et leurs inverses

En choisissant l’option 4. HYPERBOLIC.. , dans le menu MTH et en appuyant sur @@OK@@, on obtient le menu de fonctions hyperboliques suivant :

Par exemple, en mode ALG, la séquence de touches qui permet de calculer tanh(2.5), est la suivante :

„´4 @@OK@@ 5 @@OK@@ 2.5`

En mode RPN, la séquence de touches qui permet ce calcul est la suivante :

2.5`„´4 @@OK@@ 5 @@OK@@

Les opérations décrites ci-dessus supposent que vous utilisez le paramètre par défaut pour l’indicateur système 117 (CHOOSE-boxes). Si vous avez changé l’état de cet indicateur (voir Chapitre 2) en état SOFT menu, le menu MTH apparaîtra comme indiqué ci-dessous (en mode ALG à gauche, et en mode RPN à droite) :

Page 3-7

En appuyant sur L, on affiche le reste des options :

Ainsi, pour sélectionner, par exemple, le menu des fonctions hyperboliques, avec ce format de menu, appuyez sur )@@HYP@ , ce qui donne :

Enfin, pour sélectionner, par exemple, la fonction tangente hyperbolique (tanh), appuyez simplement sur @@TANH@.

Note: Pour afficher des options supplémentaires sur ces touches de menu, appuyez sur la touche L ou sur la séquence de touches „«.

Par exemple, pour calculer tanh(2.5), en mode ALG, en utilisant les SOFT menus plutôt que les CHOOSE-boxes, procédez ainsi :

„´@@HYP@ @@TANH@ 2.5`

En mode RPN, on calcule la même valeur en utilisant :

2.5`„´)@@HYP@ @@TANH@

A titre d’exercice d’application des fonctions hyperboliques, vérifiez les valeurs suivantes :

SINH (2.5) = 6.05020.. ASINH(2.0) = 1.4436…

Page 3-8

COSH (2.5) = 6.13228.. ACOSH (2.0) = 1.3169… TANH(2.5) = 0.98661.. ATANH(0.2) = 0.2027… EXPM(2.0) = 6.38905…. LNP1(1.0) = 0.69314….

Opérations sur les unités

Il est possible d’associer des unités aux nombres de la calculatrice. Ainsi, il est possible de calculer des résultats qui impliquent un système d’unités cohérent et de produire un résultat avec la combinaison d’unités appropriée.

Le menu des unités (UNITS)

On lance le menu des unités par la combinaison de touches ‚Û (associée à la touche 6). Avec l’indicateur système 117 configuré sur les CHOOSE-boxes, vous obtenez le menu suivant :

Option 1. Tools.. contient des fonctions d’opérations sur les unités (sera présenté plus loin). Options 2. Length.. jusqu’à 17.Viscosity.. contiennent des menus avec un certain nombre d’unités pour chacune des quantités décrites. Par exemple, choisir l'option 8. Force.. affiche le menu des unités suivant :

Page 3-9

L’utilisateur reconnaîtra la plupart de ces unités (certaines d’entre elles, comme le dyne, ne sont pas très utilisées de nos jours) vues en cours de physique : N = newtons, dyn = dynes, gf = grammes – force (pour les distinguer des grammes-masse, une unité de masse), kip = kilo-livres (1000 livres), lbf = livre-force (pour les distinguer des livres-masse), pdl = poundal.

Pour affecter une unité à un nombre, le nombre doit être suivi d’un symbole ‘souligné’. Ainsi, une force de 5 N sera entrée en tant que 5_N.

Pour effectuer des opérations plus complètes sur les unités, les touches menu SOFT permettent d’associer des unités de façon plus pratique. Changez l’indicateur système 117 en menu SOFT (voir Chapitre 2), et utilisez la combinaison de touches ‚Û pour obtenir les menus suivants. Appuyer sur L pour afficher la page de menu suivante.

En appuyant sur les touches de menu, on pourra ouvrir des sous-menus d’unités de la section en question. Par exemple, pour le sous-menu @)SPEED, les unités suivantes sont disponibles :

En appuyant sur les touches de menu @)UNITS, on revient au menu des UNITES.

Page 3-10

Souvenez-vous que vous pouvez à tout moment afficher tous les composants du menu à l’écran en tapant ‚˜, et ainsi, pour l’ensemble des unités @)ENRG les indicateurs suivants apparaîtront :

Note: Utilisez la touche L ou la séquence de touches „« pour naviguer dans les menus.

Unités disponibles

Pour plus de détails sur les unités, reportez vous au Chapitre 3 du guide de l’utilisateur de la calculatrice.

Associer des unités à des nombres

Pour affecter une unité à un nombre, le nombre doit être suivi d’un symbole ‘souligné (‚Ý, key(8,5)). Ainsi, une force de 5 N sera entrée en tant que 5_N.

Voici la séquence à suivre pour entrer ce nombre en mode ALG, avec l’indicateur système 117 en position CHOOSE-boxes.

5‚Ý ‚Û 8@@OK@@ @@OK@@ `

Note: Si vous oubliez le symbole souligné, le résultat est l’expression 5*N, et N représente ici un nom de variable et non des Newtons.

Pour entrer la même quantité, en mode RPN, utilisez la séquence de touches suivante :

5‚Û8@@OK@@ @@OK@@

Page 3-11

Vous remarquerez que le symbole souligné apparaît automatiquement, lorsque le mode RPN est actif.

Les séquences de touches utilisées pour entrer les unités, lorsque l’option SOFT menu est sélectionnée, sont décrites ci-dessous, pour les modes ALG et RPN. Par exemple, en mode ALG, pour entrer la quantité 5_N, utilisez la séquence suivante :

5‚Ý ‚ÛL @)@FORCE @ @@N@@ `

Pour la même quantité, en mode RPN, utilisez la séquence suivante :

5‚ÛL @)@FORCE @ @@N@@

Note: Vous pouvez entrer une quantité avec ses unités en entrant le symbole souligné et les unités avec le ~ du clavier. Par exemple, 5‚Ý~n donnera le résultat : 5_N

Les préfixes d’unités

Vous pouvez utiliser les préfixes d’unités selon la table des préfixes du SI Système International qui suit. L’abréviation du préfixe est indiquée et est suivie du nom et de l’exposant x de la puissance de 10

correspondant à

chaque préfixe :

____________________________________________________ Préfixe Nom x Préfixe Nom x ____________________________________________________ Y iotta +24 d deci -1 Z zetta +21 c centi -2 E exa +18 m milli -3 P peta +15 µ micro -6 T tera +12 n nano -9 G giga +9 p pico -12 M mega +6 f femto -15 k,K kilo +3 a atto -18 h,H hecto +2 z zepto -21 D(*) deca +1 y yocto -24 _____________________________________________________

Page 3-12

(*) Dans le système SI, ce préfixe est da et non D. Cependant, dans la calculatrice, on utilisera D pour deca.

Pour entrer ces préfixes, tapez simplement le préfixe en utilisant la touche ~ sur le clavier. Par exemple, pour entrer 123 pm (picomètres), utilisez la séquence :

123‚Ý~„p~„m

En utilisant UBASE (tapez le nom) pour convertir ce nombre en unités par défaut (1 m), on obtient::

Opérations sur les unités

Voici quelques exemples de calculs en mode ALG. Faites attention lorsque vous multipliez ou divisez des quantités avec unités, vous devez entrer chaque quantité et ses unités entre parenthèses. Ainsi, pour entrer le produit 12.5m ×

5.2_yd, par exemple, tapez (12.5_m)*(5.2_yd) `:

ce qui donne 65_(m⋅yd). Pour convertir en unités du SI, utilisez la fonction UBASE (elle se trouve dans le catalogue de commande, ‚N):

Page 3-13

Note: Souvenez-vous que la variable ANS(1) est accessible par la combinaison de touches „î(associée à la touche `).

Pour effectuer une division, par exemple, 3250 mi / 50 h, entrez

(3250_mi)/(50_h) `

ce qui, une fois transformé en unités SI avec la fonction UBASE, donne :

Les additions et les soustractions peuvent être effectuées en mode ALG sans utiliser les parenthèses ; par exemple, on peut entrer 5 m + 3200 mm, simplement sous la forme

5_m + 3200_mm `.

Une expression plus compliquée nécessiterait des parenthèses, comme dans le cas de

(12_mm)*(1_cm^2)/(2_s) `:

Les calculs de pile en mode RPN ne nécessitent pas de parenthèses et on a, par exemple,

12 @@@m@@@ 1.5 @@yd@@ *

3250 @@mi@@ 50 @@@h@@@ /

Ces opérations donnent les résultats suivants :

Les conversions d’unités

Le menu UNITS a un sous-menu TOOLS (outils), qui contient les fonctions suivantes :

Page 3-14

CONVERT(x,y) : convertit un objet à unités x en un objet à unités y UBASE(x) : convertit un objet à unités x en unités du SI UVAL(x) : extrait la valeur de l’objet à unités x UFACT(x,y) : factorise l’unité y de l’objet à unités x UNIT(x,y) : combine la valeur de x avec les unités de y

Quelques exemples de la fonction CONVERT sont présentés ci-dessous : Des informations complémentaires sur les autres fonctions du UNIT/TOOLS sont présentées au Chapitre 3 du présent guide de l’utilisateur. Par exemple, pour convertir 33 watts en btu, utilisez l'une des deux méthodes ci-dessous :

CONVERT(33_W,1_hp) `

CONVERT(33_W,11_hp) `

Constantes physiques de la calculatrice

Ces constantes physiques sont mémorisées dans une bibliothèque des constantes accessible avec la commande CONLIB. Pour lancer ces

commandes, vous pouvez les taper dans la pile ~~conlib`, ou vous pouvez utiliser la commande CONLIB dans le catalogue de commande, comme suit : En premier, lancer le catalogue avec : ‚N~c. Utilisez ensuite les flèches vers le haut et vers le bas —˜ pour sélectionner CONLIB. Enfin, appuyez sur la touche de menu F(@@OK@@) . Appuyez sur `, si nécessaire. Utilisez ensuite les flèches vers le haut et vers le bas —˜ pour voir les constantes.

Les touches de menu correspondant à cette bibliothèque de constantes (CONSTANTS LIBRARY) contiennent les fonctions suivantes :

SI lorsqu’elle est active, les constantes sont affichées en unités

du SI (*)

ENGL lorsqu’elle est active, les constantes sont affichées en unités

impériales (*)

UNIT lorsqu’elle est active, les constantes sont affichées avec leurs

unités (*)

Page 3-15

VALUE lorsqu’elle est active, les constantes sont affichées sans unités STK copie la valeur (avec ou sans unités) dans la pile QUIT sort de la bibliothèque des constantes

(*) uniquement si l’option VALUE est sélectionnée.

Lorsque l’option VALUE est active (unités du SI), le haut de la bibliothèque des constantes s’affiche ainsi :

Pour afficher les valeurs des constantes en unités (ou impériales), appuyez sur l’option @ENGL :

Si nous désactivons l’option UNITS (en appuyant sur @UNITS ), seules les valeurs seront affichées (les unités impériales étant sélectionnées dans ce cas) :

Pour copier la valeur de Vm dans la pile, sélectionner le nom de la variable avant d’appuyer sur !²STK; cliquez ensuite sur @QUIT@. Si le mode de calcul est ALG, l’affichage est le suivant :

Page 3-16

L’affichage montre ce que l’on appelle une valeur étiquetée, Vm:359.0394. Dans ce cas, Vm, est l’étiquette de ce résultat. Toute opération arithmétique utilisant ce nombre ignorera l’étiquette. Essayer, par exemple,

‚¹2*„î `

ce qui donne :

La même opération en mode RPN s’effectue par la combinaison de touches suivante (une fois que la valeur de Vm a été extraite de la bibliothèque de constantes) :

2`*‚¹

Définir et utiliser des fonctions

Les utilisateurs peuvent définir leurs propres fonctions en utilisant la commande DEFINE accessible par la séquence de touches „à (associée à la touche

2). La fonction doit être entrée dans le format suivant :

Nom_de_la_fonction(arguments) = expression_qui_contient_les_argumenteurs.

Par exemple, on peut définir une fonction simple

H(x) = ln(x+1) + exp(-x)

Supposons que vous ayez besoin de calculer cette fonction pour un certain nombre de valeurs discrètes et que, par conséquent, vous souhaitiez n’appuyer que sur une seule touche pour obtenir le résultat sans devoir retaper l’expression pour chacune des valeurs. Dans l’exemple suivant, nous

Page 3-17

supposons que vous êtes en mode ALG. Composez la combinaison de touches suivante :

„à³~h„Ü~„x™‚Å

‚¹~„x+1™+„¸~„x`

L’affichage est le suivant :

Appuyez sur la touche J, et vous remarquerez qu’une nouvelle variable apparaît sur la touche de menu (@@@H@@). Pour afficher le contenu de cette variable, appuyez sur ‚@@@H@@. Cela donne alors :

Ainsi, la variable H contient un programme défini par :

<<  x ‘LN(x+1) + EXP(x)’ >>

Ceci est un programme simple qui est écrit dans le langage de programmation par défaut de la série HP 48 G et est également inclus dans la série HP 49 G. Ce langage de programmation s'appelle UserRPL (voir Chapitres 20 et 21 du guide de l’utilisateur de la calculatrice). Le programme ci-dessus est relativement simple et est constitué de deux parties, incluses entre les délimiteurs du programme << >>:

• Entrées :  x  x

• Calcul : ‘LN(x+1) + EXP(x) ‘

Ceci est interprété de la façon suivante : on entre une valeur qui est temporairement affectée à la variable x (appelée variable locale), on calcule

Page 3-18

l’expression entre guillemets qui contient la variable locale et on affiche l’expression calculée.

Pour activer la fonction en mode ALG, tapez le nom de la fonction suivi de l’argument entre parenthèses, par exemple, @@@H@@@ „Ü2`. Des exemples sont affichés ci-dessous :

En mode RPN, pour activer la fonction, entrez d’abord l’argument et appuyez ensuite sur la touche de menu correspondant au nom de la variable @@@H@@@ . Par exemple, vous pouvez essayer d’entrer : 2`@@@H@@@ . Les autres exemples ci-dessus peuvent être entrés en utilisant : 1.2`@@@H@@@ , 2`3/@@@H@@@ .

Référence

De plus amples détails sur les calculs avec des nombres réels sont présentés dans le Chapitre 3 du guide de l’utilisateur de la calculatrice.

Page 3-19

Chapitre 4 Calculs avec des nombres complexes

Ce chapitre montre des exemples de calculs et d’applications de fonctions à des nombres complexes.

Définitions

Une nombre complexe z s’écrit as z = x + iy, (forme cartésienne) où x et y sont des nombres réels et i l’unité imaginaire définie par i une partie réelle, x = Re(z) et une partie imaginaire, y = Im(z). La forme

polaire d’un nombre complexe est z = re

yx + est le module du nombre complexe z et θ = Arg(z) = arctan(y/x)

= r⋅cosθ + i r⋅sinθ, où r = |z|

représente l’argument du nombre complexe z. Le complexe conjugué d’un

nombre complexe z = x + iy = re

= -x-iy = - re

, peut être considéré comme la réflexion de z sur l’origine.

estz = x – iy = re

= -1. Le nombre a

-i

. L’opposé de z, –z

Paramétrer la calculatrice en mode COMPLEX

Pour travailler avec des nombres complexes, sélectionner le mode complexe du CAS :

H)@@CAS@ ˜˜™ @CHK@@

Le mode COMPLEX sera sélectionné si l’écran des MODES CAS affiche l’option _Complex cochée, c'est-à-dire:

Appuyer sur @@OK@@ , deux fois, afin de retourner à la pile.

Page 4-1

Saisie de nombres complexes

On peut saisir des nombres complexes dans la calculatrice dans l’une des deux représentations cartésiennes, à savoir, x+iy ou (x,y). Les résultats seront affichés sur la calculatrice sous le format de paire ordonnée, c’est-à-dire (x,y). Par exemple, si la calculatrice est en mode ALG mode, le nombre complexe (3.5,-1.2) est saisi de la façon suivante :

„Ü3.5‚í\1.2`

Un nombre complexe peut aussi être saisi sous la forme x+iy. Par exemple, en mode ALG mode, 3.5-1.2i est saisi de la façon suivante (acceptez les changements de mode):

3.5 -1.2*„„¥`

En mode RPN, ces nombres peuvent être saisis en composant la séquence de touches suivantes:

„Ü3.5‚í1.2\`

(Remarquez que l’on appuie sur la touche de changement de signe après avoir saisi le nombre 1.2, dans l’ordre opposé à celui employé pour l’exercice en mode ALG), et

³3.5 -1.2*„„¥`

(Remarquez la nécessité de saisir une apostrophe avant de taper le nombre

3.5-1.2i en mode RPN).

Pour saisir le nombre imaginaire de l’unité, appuyer sur : „¥(la touche I).

Représentation d’un nombre complexe

La représentation polaire du nombre complexe 3.5-1.2i, saisi ci-dessus, est obtenue en changeant le système coordonné de cylindrique à polaire (en utilisant la fonction CYLIN). Vous pouvez trouver cette fonction dans le catalogue (‚N). Vous pouvez aussi basculer les coordonnées sur

Page 4-2

POLAR en utilisant la touche H . Le basculement sur coordonnées polaires avec des mesures angulaires en radians produit le résultat suivant:

Le résultat illustré ci-dessus représente une magnitude, 3.7, et un angle

0.33029…. Le symbole angulaire (∠) s’affiche devant la mesure d’angle.

Retourner aux coordonnées cartésiennes ou rectangulaires en utilisant la fonction RECT (présente dans le catalogue ‚N). Un nombre complexe en

représentation polaire s’écrit z = r⋅e

. Vous pouvez saisir ce nombre dans la calculatrice en utilisant une paire ordonnée de forme (r, ∠θ). Le symbole angulaire (∠) est saisi de la façon suivante ~‚6. Par exemple, le nombre complexe z = 5.2e

1.5i

peut être saisi comme suit (les illustrations

montrent la pile RPN avant et après avoir saisi le nombre) :

Parce que le système coordonné est configuré sur rectangulaire (ou cartésien), la calculatrice convertit automatiquement le nombre saisi en coordonnées cartésiennes, c'est-à-dire x = r cos θ, y = r sin θ, égal, dans ce cas, à (0.3678…, 5.18…).

D’un autre côté, si le système coordonné est paramétré sur coordonnées cylindriques (utiliser CYLIN), la saisie d’un nombre complexe (x,y), où x et y sont des nombres réels, produira une représentation polaire. Par exemple, en coordonnées polaires, saisir le nombre (3.,2.). Les illustrations montrent la pile RPN avant et après avoir saisi le nombre :

Page 4-3

Opérations simples avec des nombres complexes

Les nombres complexes peuvent être combinés en utilisant les quatre opérations de base (+-*/). Les résultats suivent les règles de l’algèbre avec l’avertissement suivant i complexes sont similaires à celles avec des nombres réels. Par exemple, lorsque la calculatrice est en mode ALG et la CAS est paramétrée sur Complex, essayez les opérations suivantes :

(3+5i) + (6-3i) = (9,2);

(5-2i) - (3+4i) = (2,-6)

(3-i)(2-4i) = (2,-14);

(5-2i)/(3+4i) = (0.28,-1.04)

1/(3+4i) = (0.12, -0.16) ;

= -1. Les opérations avec des nombres

-(5-3i) = -5 + 3i

Les menus CMPLX

Il existe deux menus CMPLX (Nombres CoMPLeX) sur la calculatrice. L’un est disponible en passant par le menu MTH (expliqué au chapitre 3) et l’autre reste directement accessible par le clavier (‚ß). Les deux menus CMPLX sont présentés ci-dessous.

Menu CMPLX en passant par le menu MTH Supposant que l’indicateur système 117 est paramétré sur CHOOSE-boxes (voir Chapitre 2), on accède au sous-menu CMPLX au sein du menu MTH en utilisant : „´9 @@OK@@ . Les fonctions disponibles sont les suivantes :

Le premier menu (options 1 à 6) indique les fonctions suivantes :

Page 4-4

RE(z) : Partie réelle d’un nombre complexe IM(z) : Partie imaginaire d’un nombre complexe

C→R(z) : Sépare un nombre complexe en sa partie réelle et sa partie

imaginaire

R→C(x,y) : Forme le nombre complexe (x,y) à partir des nombres réels x et y

ABS(z) : Calcule la magnitude d’un nombre complexe ARG(z) : Calcule l’argument d’un nombre complexe SIGN(z) : Calcule un nombre complexe de magnitude d’unité z/|z|. NEG(z) : Change le signe de z CONJ(z) : Produit le complexe conjugué de z

Des exemples d’applications de ces fonctions sont illustrés ci-dessous en coordonnées RECT. Se souvenir que, pour le mode ALG, la fonction doit précéder l’argument, alors qu’en mode RPN, vous devez d’abord saisir l’argument avant de sélectionner la fonction. N’oubliez pas non plus que vous pouvez afficher ces fonctions sous forme d’onglets de menu logiciels en changeant les paramètres de l’indicateur système 117 (Voir Chapitre 2). [Remarque : Certaines des lignes ne seront pas visible dans les exercices affichés dans les dessins ci-dessous.]

Menu CMPLX accessible sur le clavier

Page 4-5

On peut accéder à un second menu CMPLX en utilisant l’option de la touche shift de droite associée à la touche 1, c’est-à-dire, ‚ß. En paramétrant l’indicateur système 117 sur CHOOSE-boxes, le menu CMPLX accessible par le clavier s’affiche comme sur les écrans suivants :

Le menu en résultant comprend certaines des fonctions déjà introduites dans les sections précédentes, à savoir ARG, ABS, CONJ, IM, NEG, RE, et SIGN. Il comprend aussi la fonction i qui sert à la même fonction que la combinaison de touches „¥.

Fonctions appliquées aux nombres complexes

Une grand nombre des fonctions clavier et des fonctions du menu MTH définies au Chapitre 3 pour les nombres réels (c’est-à-dire : SQ, ,LN, e peuvent être appliquées aux nombres complexes. Le résultat est un autre nombre complexe, comme l’illustrent les exemples suivants : [Remmarque : Certaines des lignes ne seront pas visible sur l’écran de la calculatrice avec les exercices affichés dans les dessins ci-dessous.]

, etc.)

Page 4-6

Note: Lorsque l’on utilise des fonctions trigonométriques et leurs opposées avec des nombres complexes, les arguments ne sont plus des angles. Par conséquent, la mesure angulaire sélectionnée pour la calculatrice n’a pas d’incidence dans la calcul de ces fonctions avec des arguments complexes.

Fonction DROITE: équation d’une ligne droite

La fonction DROITE prend pour argument deux nombre complexes (par ex. : x

+iy1 et x2+iy2) et retourne l’équation de la ligne droite (par ex. : y = a+bx),

qui contient les points (x points A(5,-3) et B(6,2) peut être trouvée en procédant comme suit (en mode algébrique) :

) et (x2,y2). Par exemple, la ligne passant entre les

1,y1

La fonction DROITE se trouve dans le catalogue de commandes (‚N). Si la calculatrice est configurée en mode APPROX, le résultat sera Y = 5.*(X-5.)-3.

Référence

De plus amples informations sur les nombres complexes sont présentées au Chapitre 4 du guide de l’utilisateur de la calculatrice.

Page 4-7

Chapitre 5 L’algèbre et les opérations mathématiques

Un objet algébrique ou plus simplement un élément d’algèbre est n’importe quel nombre, n’importe quelle variable ou n’importe quelle expression algébrique sur lesquels on peut effectuer des opérations, des manipulations et des combinaisons suivant les règles de l’algèbre. Voici ci-dessous quelques exemples d’objets algébriques :

• Un nombre : 12.3, 15.2_m, ‘π’, ‘e’, ‘i’

• Une variable : ‘a’, ‘ux’, ‘largeur’, etc.

• Une expression: ‘p*D^2/4’,’f*(L/D)*(V^2/(2*g))’,

• Une équation: ‘p*V = n*R*T’, ‘Q=(Cu/n)*A(y)*R(y)^(2/3)*√So’

Saisie des objets algébriques

Les objets algébriques peuvent être saisis en tapant l’objet entre guillemets directement dans la pile niveau 1 ou en utilisant l’éditeur d’équation [EQW]. Par exemple, pour entrer l’objet algébrique ‘π*D^2/4’ directement dans la pile niveau 1, utilisez :

³„ì*~dQ2/4`

Un objet algébrique peut aussi être construit dans l’éditeur d’équation puis envoyé dans la pile où l’on peut effectuer des opérations sur cet objet directement dans l’éditeur d’équation. Le fonctionnement de l’éditeur d’équation est décrit au Chapitre 2. En guise d’exercice, construire l’objet algébrique suivant dans l’éditeur d’équation :

Page 5-1

Après avoir construit l’objet, appuyez sur `pour l’afficher dans la pile (l’affichage en mode ALG et RPN est illustré ci-dessous):

Opérations simples avec les objets algébriques

Les objets algébriques peuvent être additionnés, soustraits, multipliés ou divisés (à part le zéro), élevés à une puissance, utilisés comme arguments dans de nombreuses fonctions courantes (fonctions exponentielle, logarithmique, trigonométrique, hyperbolique etc.), comme on peut le faire avec n’importe quel nombre réel ou complexe. Afin de faire une démonstration des opérations de base avec des objets algébriques, nous allons créer deux objets(par ex. : ‘π*R^2’ et ‘g*t^2/4’) et les enregistrer dans les variables A1 et A2 (Voir le Chapitre 2 pour apprendre comment créer des variables et y enregistrer des valeurs). Voici la combinaison de touches permettant de stocker les variables A1 en mode ALG :

³„ì*~rQ2™ K ~a1 `

Ce qui nous donne :

La combinaison de touches correspondante en mode RPN est la suivante :

„ì~r`2Qx ~a1 K

Après avoir stocké la variable A2 et appuyé sur la touche, l’écran affiche les variables comme suit :

Page 5-2

En mode ALG, la combinaison de touches suivante affichera une série d’opérations avec les éléments d’algèbre contenus dans les variables @@A1@@ et

@@A2@@ (appuyer sur J pour retourner au menu variable) :

@@A1@@ + @@A2@@ ` @@A1@@ -@@A2@@ `

@@A1@@ *@@A2@@ ` @@A1@@ / @@A2@@ `

‚¹@@A1@@ „¸@@A2@@

On peut obtenir le même résultat en mode RPN en utilisant la combinaison de touches suivante :

Page 5-3

@@A1@ ` @@A2@@ + @@A1@@ ` @@A2@@ -

@@A1@@ ` @@A2@@ * @@A1@@ ` @@A2@@ /

@@A1@@ ` ‚¹ @@A2@@ ` „¸

Fonctions du menu ALG

Le menu ALG (Algébrique) est accessible en utilisant la séquence de touches ‚× (associé à la touche 4). En paramétrant l’indicateur système 117 sur CHOOSE-boxes, le menu ALG affiche les fonctions suivantes :

Plutôt que de faire une liste de descriptions de chaque fonction dans ce manuel, nous invitons l’utilisateur à consulter la description en utilisant la fonction d’aide de la calculatrice: I L @)HELP@ ` . Afin de localiser une fonction particulière, saisir d’abord la première lettre de la fonction. Par exemple, pour la fonction COLLECT, nous saisissons ~c, puis utilisons les flèches haut et bas, —˜, pour localiser COLLECT dans la fenêtre d’aide.

Pour terminer l’opération, appuyer sur @@OK@@. Voici le menu d’aide pour la fonction COLLECT:

Remarquez que, en bas de l’écran, la ligne See: EXPAND FACTOR suggère des liens vers d’autres entrées de la fonction d’aide, ici les fonctions EXPAND et FACTOR. Pour aller directement à ces entrées, appuyez sur l’onglet du menu logiciel @SEE1! pour EXPAND, et @SEE2! pour FACTOR. En

Page 5-4

appuyant sur @SEE1!, par exemple, l’information suivante sur EXPAND s’affiche, tandis qu’en choisissant @SEE2@, l’information suivante sur FACTOR apparaît :

Copiez les exemples fournis dans la pile en appuyant sur @ECHO!. Par exemple, pour l’entrée EXPAND illustrée ci-dessus, appuyez sur l’onglet du menu logiciel @ECHO! pour copier l’exemple suivant dans la pile (appuyez sur ` pour exécuter):

Par la suite, nous laissons le lecteur explorer les applications des fonctions dans le menu ALG. Voici une liste des commandes :

Par exemple, pour la fonction SUBST, nous trouvons les entrées d’aide du CAS suivantes :

Page 5-5

Note: Rappelez-vous que, pour utiliser ces fonctions ou n’importe quelle autre fonction dans le mode RPN, vous devez d’abord saisir l’argument avant la fonction. Ainsi, l’exemple pour TEXPAND sera saisi en mode RPN comme suit :

³„¸+~x+~y`

A ce stade, sélectionnez la fonction TEXPAND du menu ALG (ou directement dans le catalogue ‚N), pour terminer l’opération.

Opérations avec les fonctions transcendantales

La calculatrice propose toute une série de fonctions qui peuvent être utilisées pour remplacer des expressions contenant des fonctions logarithmiques ou exponentielles („Ð) ainsi que des fonctions trigonométriques (‚Ñ).

Développement et mise en facteur en utilisant les fonctions logexp

La commande „Ð affiche le menu suivant :

Des informations et des exemples sur ces commandes sont disponibles dans la fonction d’aide de la calculatrice. Par exemple, la description de EXPLN est illustrée ici dans la colonne de gauche et l’exemple extrait de la fonction d’aide s’inscrit à droite :

Page 5-6

Développement et mise en facteur en utilisant les fonctions trigonométriques

Le menu TRIG, auquel on accède en utilisant ‚Ñ, affiche les fonctions suivantes :

Ces fonctions permettent de simplifier des expressions en remplaçant certaines catégories de fonctions trigonométriques par d’autres. Par exemple, la fonction ACOS2S permet de remplacer la fonction (acos(x)) par son expression en termes de arcsine (asin(x)).

La description de ces commandes ainsi que des exemples de leurs applications sont disponibles dans la fonction d’aide de la calculatrice (IL@HELP). Nous invitons l’utilisateur à explorer cette fonction pour trouver des informations sur les commandes du menu TRIG.

Fonctions du menu ARITHMETIC

Le menu ARITHMETIC est accessible en utilisant la séquence de touches „Þ (associée à la touche 1). Une fois l’indicateur système 117 paramétré sur CHOOSE-boxes, en appuyant sur la commande „Þ menu suivant s’affiche :

, le

Page 5-7

Dans cette liste du menu, les options 5 à 9 (DIVIS, FACTORS, LGCD, PROPFRAC, SIMP2) correspondent aux fonctions habituelles qui

s’appliquent aux nombres entiers ou aux polynômes. Les options restantes (1. INTEGER, 2. POLYNOMIAL, 3. MODULO, et 4. PERMUTATION) sont en fait des sous-menus de fonctions qui s’appliquent à des objets mathématiques spécifiques. Lorsque l’indicateur système 117 est paramétré sur SOFT menus, le menu ARITHMETIC („Þ) se présente comme suit :

Nous présentons ci-dessous les entrées de la fonction d’aide pour les fonctions FACTORS et SIMP2 du menu ARITHMETIC :

FACTORS: SIMP2:

Les fonctions associées aux sous-menus de ARITHMETIC : INTEGER, POLYNOMIAL, MODULO et PERMUTATION presentées au Chapitre 5 du guide de l’utilisateur. Les paragraphes suivants présentent quelques applications sur des polynômes et des fractions.

Polynômes

Page 5-8

Les polynômes sont des expressions algébriques consistant en un ou plusieurs termes contenant des puissances décroissantes d’une variable donnée. Par exemple, ‘X^3+2*X^2-3*X+2’ est un polynôme de troisième degré de X, tandis que ‘SIN(X)^2-2’ est un polynôme de deuxième degré de SIN(X). Les fonctions COLLECT et EXPAND peuvent être utilisées sur les polynômes, comme cela a été expliqué précédemment. Nous vous présentons ci-dessous d’autres applications des fonctions polynomiales :

La fonction HORNER

La fonction HORNER („Þ, POLYNOMIAL, HORNER) effectue la division de Horner, ou division artificielle, d’un polynôme P(X) par la facteur (X-a), c'est-à-dire, HORNER(P(X),a) = {Q(X), a, P(a)}, où P(X) = Q(X)(X-a)+P(a). Par exemple,

HORNER(‘X^3+2*X^2-3*X+1’,2) = {X^2+4*X+5 2 11}

c’est-à-dire : X

+2X2-3X+1 = (X2+4X+5)(X-2)+11. Ainsi,

HORNER(‘X^6-1’,-5)=

{ X^5-5*X^4+25*X^3-125*X^2+625*X-3125 -5 15624}

c’est-à-dire : X

-1 = (X5-5*X4+25X3-125X2+625X-3125)(X+5)+15624.

La variable VX

La plupart des exemples de polynômes ci-dessus utilisent une variable X. En effet, une variable, appelée VX existe dans le répertoire de la calculatrice {HOME CASDIR}. Elle prend, par défaut, la valeur de ‘X’. Elle prend, par défaut, la valeur de ‘X’. Il s’agit du nom de la variable indépendante la plus fréquemment utilisée pour les applications algébriques et infinitésimales. Evitez d’utiliser la variable VX dans vos programmes ou équations afin de ne pas confondre avec le VX du CAS’. Pour des informations complémentaires sur la variable CAS, voir l’Annexe C du guide de l’utilisateur de la calculatrice.

Page 5-9

La fonction PCOEF

Dans une série contenant les racines d’un polynôme, la fonction PCOEF génère une série contenant les coefficients du polynôme correspondant. Les coefficients correspondent à la valeur, dans l’ordre décroissant, de la variable indépendante. Par exemple :

PCOEF([-2, –1, 0 ,1, 1, 2]) = [1. –1. –5. 5. 4. –4. 0.],

représente le polynôme X

6-X5

-5X4+5X3+4X2-4X.

La fonction PROOT

Dans une série contenant les coefficients d’un polynôme, dans l’ordre décroissant, la fonction PROOT fournit les racines du polynôme. Par exemple, à partir de X

+5X+6 =0, PROOT([1,–5,6]) = [2. 3.].

Les fonctions QUOT et REMAINDER

Les fonctions QUOT et REMAINDER fournissent, respectivement, le quotient Q(X) et le reste R(X) résultant de la division de deux polynômes, P En d’autres termes, elles fournissent les valeurs de Q(X) et R(X) à partir de P

(X)/P2(X) = Q(X) + R(X)/P2(X). Par exemple :

QUOT(‘X^3-2*X+2’, ‘X-1’) = ‘X^2+X-1’

REMAINDER(‘X^3-2*X+2’, ‘X-1’) = 1.

Par conséquent, nous pouvons écrire : (X

Note : Vous pourriez obtenir le même résultat en utilisant PARTFRAC:

PARTFRAC(‘(X^3-2*X+2)/(X-1)’) = ‘X^2+X-1 + 1/(X-1)’.

(X) et P2(X).

-2X+2)/(X-1) = X2+X-1 + 1/(X-1).

La fonction PEVAL

La fonction PEVAL (Polynomial EVALuation) peut être utilisée pour évaluer un polynôme

p(x) = a

⋅xn+a

n-1

⋅x

+ …+ a2⋅x2+a1⋅x+ a0,

n-1

Page 5-10

dans une série de coefficients [an, a Le résultat de l’évaluation est p(x

, … a2, a1, a0] avec une valeur de x0.

n-1

). La fonction PEVAL n’étant pas disponible

dans le menu ARITHMETIC, utilisez à la place le menu CALC/DERIV&INTEG. Exemple : PEVAL([1,5,6,1],5) = 281.

Des applications supplémentaires des fonctions polynomiales sont présentées au Chapitre 5 du guide de l’utilisateur de la calculatrice.

Fractions

Les fractions peuvent être développées et mises en facteur en utilisant les fonctions EXPAND et FACTOR dans le menu ALG (‚×). Par exemple :

EXPAND(‘(1+X)^3/((X-1)*(X+3))’) = ‘(X^3+3*X^2+3*X+1)/(X^2+2*X-3)’ EXPAND(‘(X^2*(X+Y)/(2*X-X^2)^2’) = ‘(X+Y)/(X^2-4*X+4)’

FACTOR(‘(3*X^3-2*X^2)/(X^2-5*X+6)’) = ‘X^2*(3*X-2)/((X-2)*(X-3))’ FACTOR(‘(X^3-9*X)/(X^2-5*X+6)’ ) = ‘X*(X+3)/(X-2)’

La fonction SIMP2

La fonction SIMP2 du menu ARITHMETIC prend pour argument deux nombres ou polynômes représentant le numérateur et le dénominateur d’une fraction rationnelle et calcule le numérateur et le dénominateur simplifiés. Par exemple :

SIMP2(‘X^3-1’,’X^2-4*X+3’) = { ‘X^2+X+1’,‘X-3’}

La fonction PROPFRAC

La fonction PROPFRAC convertit une fraction rationnelle en fraction ”correcte“, c'est-à-dire en un entier additionné à une fraction, si une telle décomposition est possible. Par exemple :

PROPFRAC(‘5/4’) = ‘1+1/4’

PROPFRAC(‘(x^2+1)/x^2’) = ‘1+1/x^2’

Page 5-11

La fonction PARTFRAC

La fonction PARTFRAC décompose une fraction rationnelle en fractions partielles qui produisent la fraction originale. Par exemple :

PARTFRAC(‘(2*X^6-14*X^5+29*X^4-37*X^3+41*X^2-16*X+5)/(X^57*X^4+11*X^3-7*X^2+10*X)’) = ‘2*X+(1/2/(X-2)+5/(X-5)+1/2/X+X/(X^2+1))’

La fonction FCOEF

La fonction FCOEF, disponible dans le menu ARITHMETIC/POLYNOMIAL est utilisée pour obtenir une fraction rationnelle à partir des racines et des pôles de la fraction.

Note: Si une fraction rationnelle est produite sous forme F(X) = N(X)/D(X), les racines de la fraction sont données par la résolution de l’équation N(X) = 0, tandis que les pôles sont donnés par la résolution de l’équation D(X) = 0.

La base de la fonction est un vecteur faisant la liste des racines suivies de leur multiplicité (c’est-à-dire combien de fois une racine donnée est répétée), et les pôles suivis de leur multiplicité représentée comme un nombre négatif. Par exemple, si vous voulez créer une fraction de racines 2 avec multiplicité 1, 0 de multiplicité 3, et -5 de multiplicité 2, et des pôles 1 de multiplicité 2 et –3 de multiplicité 5, utilisez :

FCOEF([2,1,0,3,–5,2,1,-2,-3,-5]) = ‘(X--5)^2*X^3*(X-2)/(X--3)^5*(X-1)^2’

Si vous appuyez sur µ„î(or, simplement µ, en mode RPN) vous obtenez:

‘(X^6+8*X^5+5*X^4-50*X^3)/(X^7+13*X^6+61*X^5+105*X^4-45*X^3297*X62-81*X+243)’

Page 5-12

La fonction FROOTS

La fonction FROOTS du menu ARITHMETIC/POLYNOMIAL calcule les racines et les pôles d’une fraction. A titre d’exemple, si l’on applique la fonction FROOTS au résultat obtenu ci-dessus, on obtient : [1 –2. –3 –5. 0 3. 2

1. –5 2.]. Le résultat indique les pôles suivis de leur multiplicité sous forme de nombre négatif et les racines suivies de leur multiplicité sous forme de nombre positif. Dans ce cas, les pôles sont (1, -3) avec les multiplicités respectives (2,5) et les racines sont (0, 2, -5) avec les multiplicité respectives (3, 1, 2).

Autre exemple : FROOTS(‘(X^2-5*X+6)/(X^5-X^2)’) = [0 –2. 1 –1. 3 1. 2

1.], C’est-à-dire : pôles = 0 (2), 1(1), et racines = 3(1), 2(1). Si vous sélectionniez le mode Complex, le résultat serait le suivant : [0 –2. 1 –1. ‘-((1+i*√3)/2’ –1. ‘-((1-i*√3)/2’ –1.].

Opérations étape par étape avec des polynômes et des fractions

En paramétrant les modes du CAS sur étape par étape, la calculatrice affiche les simplifications des fractions ou les opérations avec des polynômes étape par étape. Cela est très utile pour visualiser les étapes d’une division synthétique. L’exemple de la division

−

est illustré en détail en Annexe C du guide de l’utilisateur de la calculatrice. L’exemple suivant illustre une division synthétique plus longue (DIV2 est aussi disponible dans le menuARITH/POLYNOMIAL).

−

235

−+−

XXX

Page 5-13

Référence

De plus amples informations, accompagnées de définitions et d’exemples d’opérations algébrique et arithmétique, font l’objet du Chapitre 5 du guide de l’utilisateur de la calculatrice.

Page 5-14

Chapitre 6 Résolution d’équations

Deux menus de fonctions de résolution d’équations sont associés à la touche 7, le menu de résolution symbolique Symbolic SOLVer („Î), et le menu de résolution numérique NUMerical SoLVer (‚Ï). Nous vous présentons ci-dessous certaines des fonctions contenues dans ces menus.

Résolution symbolique des équations algébriques

Nous décrivons ici certaines des fonctions du menu de résolution symbolique Symbolic Solver. Activer le menu en utilisant la combinaison de touches „Î. Si l’indicateur système 117 est paramétré sur CHOOSE-boxes, les listes de menu suivantes s’affichent :

Les fonctions ISOL et SOLVE peuvent être utilisées pour toute inconnue dans une équation polynomiale. La fonction SOLVZVX résout une équation polynomiale où l’inconnue est la variable par défaut du CAS VX (paramétré généralement comme ‘X’). Finalement, la fonction ZEROS calcule les zéros, ou racines, des polynômes.

Fonction ISOL

La fonction ISOL (Equation, variable) donnera la ou les solution(s) à une Equation en isolant une variable. Par exemple, avec la calculatrice paramétrée en mode ALG, pour trouver t dans l’équation at pouvons procéder comme suit :

-bt = 0 nous

Page 6-1

En utilisant le mode RPN, on trouvera la solution en saisissant l’équation dans la pile, suivie de la variable, avant d’entrer dans la fonction ISOL. Juste avant d’exécuter la fonction ISOL, la pile RPN doit ressembler à l’illustration de gauche. Après avoir appliqué la fonction ISOL, le résultat s’affiche comme dans l’illustration de droite :

Le premier argument dans ISOL peut être une expression, comme illustré cidessus, ou une équation. Par exemple, en mode ALG, essayer :

Note: Pour saisir le signe égale (=) dans une équation, utiliser ‚Å (associée à la touche \ ).

Le même problème peut être résolu en mode RPN de la façon présentée cidessous (les illustrations montrent la pile RPN avant et après l’application de la fonction ISOL) :

Page 6-2

Fonction SOLVE

La fonction SOLVE utilise la même syntaxe que la fonction ISOL, sauf que SOLVE peut aussi être utilisée pour résoudre des équations polynomiales. L’entrée de la fonction d’aide de la calculatrice pour la fonction SOLVE, présentant la solution de l’équation X^4 – 1 = 3, est illustrée ci-dessous :

Les exemples suivants montrent comment utiliser la fonction SOLVE en mode ALG et RPN (Utilisez le mode Complex du CAS). [Remarque : Certaines des lignes ne seront pas visible dans les exercices affichés dans les dessins cidessous.]

La saisie d’écran ci-dessus affiche deux solutions. Pour la première, β =125, SOLVE n’a pas trouvé de solution { }. Pour la seconde, β

-5β

- 5β = 6,

SOLVE a trouvé quatre solutions, affichées à la dernière ligne. La toute dernière solution n’est pas visible car l’affichage du résultat nécessite plus de caractères que la largeur d’écran ne le permet. Cependant, vous pouvez toujours voir toutes les solutions en utilisant la flèche bas (˜), qui enclenche l’éditeur de ligne (cette opération peut être utilisée pour accéder à n’importe quelle ligne de résultat dépassant la largeur de la calculatrice) :

Page 6-3

Les écrans RPN correspondants à ces deux exemples, avant et après application de la fonction SOLVE, sont illustrés ci-dessous :

Fonction SOLVEVX

La fonction SOLVEVX résout une équation avec la variable par défaut du CAS contenue dans la variable réservée nommée VX. Par défaut, cette variable est paramétrée comme ‘X’. Des exemples utilisant le mode ALG avec VX = ‘X’ sont présentés ci-dessous :

Dans le premier cas, SOLVEVX n’a pas trouvé de solution. Dans le deuxième cas, SOLVEVX a trouvé une seule solution, X = 2.

Les écrans suivants montrent la pile RPN pour la résolution des deux exemples ci-dessus (avant et après application de la SOLVEVX):

Page 6-4

Fonction ZEROS

La fonction ZEROS trouve les solutions d’équations polynomiales sans indiquer leur multiplicité. Cette fonction nécessite de saisir l’expression de l’équation et le nom de la variable qui doit être trouvée. Des exemples en mode ALG sont présentés ci-dessous:

Pour utiliser la fonction ZEROS en mode RPN, saisir d’abord l’expression polynomiale, puis la variable à trouver, puis la fonction ZEROS. Les saisies d’écran suivantes montrent la pile RPN avant et après application de la fonction ZEROS aux deux exemples ci-dessus (utilisez le mode Complexe du CAS):

Page 6-5

Les fonctions du menu de résolution symbolique Symbolic Solver présentées cidessus donnent des solutions à des équations rationnelles (essentiellement des équations polynomiales). Si l’équation à résoudre est affectée de coefficients numériques, il est possible de trouver une solution numérique en utilisant les options de résolution numérique de la calculatrice.

Menu de Résolution numérique

La calculatrice offre un environnement très puissant pour résoudre des équations algébriques simples ou des équations transcendantales. Pour accéder à cet environnement, vous devez lancer la résolution numérique numerical solver (NUM.SLV) en utilisant ‚Ï. Cela fait s’afficher un menu déroulant qui présente les options suivantes :

Nous vous présentons ci-dessous les applications des options 3. Solve poly..,

5. Solve finance, et 1. Solve equation.., dans cet ordre. L’Annexe 1-A, du présent guide de l’utilisateur contient des instructions sur la façon d’utiliser les formulaires de saisie avec des exemples pour les applications de la résolution numérique. L’option 6. MSLV (Multiple equation SoLVer) sera présentée sur la page 6-11.

Notes:

1. Chaque fois que vous résolvez une équation pour une valeur donnée dans les applications NUM.SLV, la valeur trouvée est placée dans la pile. Cela est pratique si vous avez besoin de conserver cette valeur pour d’autres opérations.

2. Une ou plusieurs variables seront créées chaque fois que vous activez certaines des applications du menu NUM.SLV.

Page 6-6

HP 48 SX, 48S User Manual [fr]

Specifications and Main Features

Frequently Asked Questions

User Manual

Prise en main

Piles

Menus

Le menu TOOL

Le clavier de la calculatrice

Mesure d’angle

Choix du mode d’affichage

Choisir la police d’affichage

Objets

Ecrire des expressions dans la pile

Les variables

Taper un nom de variable

• Mode RPN

Utiliser la touche right-shift suivie des touches de menu

Effacer des variables

Utiliser la fonction PURGE dans la pile en mode RPN

Les fonctions UNDO et CMD

CHOOSE-boxes ou Soft MENU

Fonctions hyperboliques et leurs inverses

Constantes physiques de la calculatrice

Saisie de nombres complexes

Les menus CMPLX

Menu CMPLX en passant par le menu MTH Supposant que l’indicateur système 117 est paramétré sur CHOOSE-boxes (voir Chapitre 2), on accède au sous-menu CMPLX au sein du menu MTH en utilisant : „´9 @@OK@@ . Les fonctions disponibles sont les suivantes :

Menu CMPLX accessible sur le clavier

Fonctions du menu ALG

Fonctions du menu ARITHMETIC

La fonction HORNER

La variable VX

La fonction PCOEF

La fonction PROOT

Les fonctions QUOT et REMAINDER

La fonction PEVAL

Fractions

La fonction SIMP2

La fonction PROPFRAC

La fonction PARTFRAC

La fonction FCOEF

La fonction FROOTS

Fonction ISOL

Fonction SOLVE

Fonction SOLVEVX

Fonction ZEROS