Hp 48GII User Manual [nl]

hp 48gII grafische rekenmachine

gebruiksaanwijzing

H

Editie 2
HP artikelnummer F2226-90013

Mededeling

Het REGISTER JE PRODUCT AAN: www.register.hp.com

DE INHOUD VAN DEZE HANDLEIDING EN DE HIERIN VERVATTE
FICTIEVE PRAKTIJKVOORBEELDEN KUNNEN ZONDER
AANKONDIGING VERANDERD WORDEN. HEWLETT–PACKARD
COMPANY GEEFT GEEN GARANTIE AF VAN WELKE AARD DAN
OOK MET BETREKKING TOT DEZE HANDLEIDING, WAARONDER
OOK STILZWIJGENDE GARANTIES VAN VERHANDELBAARHEID,
GESCHIKTHEID VOOR EEN BEPAALD DOEL EN GEEN INBREUK
VORMEND VAN TOEPASSING ZIJN, MAAR DIE HIER NIET TOT
BEPERKT ZIJN.

HEWLETT–PACKARD CO. KAN NIET AANSPRAKELIJK WORDEN
GESTELD VOOR ENIGERLEI FOUTEN OF VOOR INCIDENTELE OF
GEVOLGSCHADE IN VERBAND MET LEVERING, PRESTATIE OF
GEBRUIK VAN DEZE HANDLEIDING OF DE HIERIN VERVATTE
VOORBEELDEN.

© Copyright 2003 Hewlett-Packard Development Company, L.P.
Vermenigvuldiging, aanpassing, of vertaling van deze handleiding is,
behalve zoals toegestaan onder de auteurswet, niet toegestaan zonder eerder
schriftelijke toestemming van Hewlett-Packard Company.

Hewlett-Packard Company
4995 Murphy Canyon Rd,
Suite 301
San Diego,CA 92123

Oplage

Editie 2 December 2003

Inhoudsopgave

Hoofdstuk 1 – Beginnen

Basisbediening, 1-1

Batterijen , 1-1
De rekenmachine in- en uitschakelen, 1-2
Het contrast van het beeldscherm instellen, 1-2
Inhoud van het beeldscherm van de rekenmachine, 1-3
Menu’s, 1-3
Het menu TOOL, 1-4
De tijd en datum instellen, 1-4

Toetsenbord van de rekenmachine, 1-5
Modi van de rekenmachine selecteren, 1-6

Bedieningsmodus, 1-7
Getalopmaak en punt of komma als decimaalteken, 1-11
Standaardopmaak:, 1-11
Vaste opmaak met decimalen, 1-12
Wetenschappelijke opmaak:, 1-13
Technische opmaak:, 1-14
Komma’s en punten, 1-14
Hoekmeting, 1-15
Coördinatenstelsel, 1-16

CAS-instellingen selecteren,

Uitleg van de CAS-instellingen, 1-18
Beeldschermmodi selecteren, 1-19
Lettertype van het beeldscherm selecteren, 1-20
Eigenschappen van de regeleditor selecteren, 1-21
Eigenschappen van het Stapelgeheugen selecteren, 1-21

Eigenschappen van de vergelijkingenschrijver (EQW) selecteren,
1-22

Referenties, 1-23

Hoofdstuk 2 – Introductie van de rekenmachine

Objecten van de rekenmachine,
Uitdrukkingen in het stapelgeheugen bewerken, 2-1

, 1-1

1-17

2-1

, 2-1

Blz. TOC-1

Rekenkundige uitdrukkingen maken, 2-1
Algebraïsche uitdrukkingen maken, 2-4

De vergelijkingenschrijver (EQW) gebruiken om uitdrukkingen te maken,

2-5
Rekenkundige uitdrukkingen maken, 2-6
Algebraïsche uitdrukkingen maken, 2-8

Gegevens organiseren in de rekenmachine, 2-9

De HOME-directory, 2-9

Subdirectory's, 2-10
Variabelen, 2-10

Variabelen maken, 2-12
De Algebraic-modus, 2-12
De RPN-modus, 2-13
Inhoud van variabelen controleren, 2-15
De Algebraic-modus, 2-15
De RPN-modus, 2-15
Toets rechts-shift gevolgd door labels van softmenutoetsen
gebruiken, 2-15
Inhoud van alle variabelen op het scherm weergeven, 2-16
Variabelen verwijderen, 2-16

De functies UNDO en CMD, 2-18
CHOOSE- boxes en Soft-MENU, 2-18
Referenties, 2-21

Variabelennamen invoeren,, 2-11

De functie PURGE gebruiken in het stapelgeheugen in de
Algebraic-modus, 2-16
De functie PURGE gebruiken in het stapelgeheugen in de RPN­modus, 2-17

Hoofdstuk 3 – Berekeningen met reële getallen

Voorbeelden van berekeningen met reële getallen, 3-1

Tiende machten gebruiken om gegevens in te voeren, 3-4
Functies voor reële getallen in het menu MTH, 3-6
Rekenmachinemenu’s gebruiken, 3-6
Hyperbolische functies en de tegenwaarden, 3-7
Handelingen met eenheden, 3-9

, 3-1

Blz. TOC-2

Het menu UNITS, 3-9
Beschikbare eenheden, 3-11
Eenheden aan getallen koppelen, 3-11
Eenheidprefixen, 3-12
Handelingen met eenheden, 3-13
Eenheidconversies, 3-15

Fysische constanten in de rekenmachine, 3-15
Functies definiëren en gebruiken, 3-17
Referentie, 3-19

Hoofdstuk 4 – Berekeningen met complexe getallen

Definities,
De rekenmachine in de modus COMPLEX instellen, 4-1

Complexe getallen invoeren, 4-2
Polaire weergave van een complex getal, 4-2

Eenvoudige handelingen met complexe getallen, 4-4
De menu’s CMPLX, 4-4

Menu CMPLX via het menu MTH, 4-4
Menu CMPLX via het toetsenbord, 4-5

Functies toegepast op complexe getallen, 4-6
Functie DROITE: vergelijking van een rechte lijn, 4-7
Referentie,

4-1

4-7

, 4-1

Hoofdstuk 5 – Algebraïsche en rekenkundige handelingen, 5-1

Algebraïsche objecten invoeren, 5-1
Eenvoudige handelingen met algebraïsche objecten, 5-2

Functies in het menu ALG, 5-4
Handelingen met transcendente functies, 5-6
Uitbreiding en factorisering met log-exp-functies, 5-6
Uitbreiding en factorisering met trigonometrische functies, 5-6

Functies in het menu ARITHMETIC, 5-7
Polynomen, 5-8

De functie HORNER, 5-9
De variabele VX, 5-9
De functie PCOEF, 5-9
De functie PROOT, 5-10

Blz. TOC-3

De functies QUOT en REMAINDER, 5-10
De functie PEVAL, 5-10
Breuken, 5-11
De functie SIMP2, 5-11
De functie PROPFRAC, 5-11
De functie PARTFRAC, 5-11
De functie FCOEF, 5-12
De functie FROOTS, 5-12

Stapsgewijze handelingen met polynomen en breuken, 5-13
Referentie, 5-14

Hoofdstuk 6 – Het oplossen van vergelijkingen, 6-1

Symbolische oplossing van algebraïsche vergelijkingen, 6-1

De functie ISOL, 6-1
De functie SOLVE, 6-2
De functie SOLVEVX, 6-4
De functie ZEROS, 6-5
Menu van de Numerieke solver, 6-5
Polynome Vergelijkingen, 6-6
De oplossingen voor een polynome vergelijking vinden, 6-7

Polynome coëfficiënten genereren waarbij de wortels van de

polynoom zijn gegeven, 6-8
Een algebraïsche expressie genereren voor de polynomen, 6-8
Financiële berekeningen, 6-9
Vergelijkingen met één onbekende oplossen m.b.v. NUM.SLV, 6-10
De functie STEQ, 6-10

Oplossing voor gelijktijdige vergelijkingen met MSLV,
Referentie, 6-12

6-11

Hoofdstuk 7 – Bewerkingen met lijsten

Lijsten aanmaken en opslaan, 7-1
Bewerkingen met getallenlijsten, 7-1

Veranderend teken, 7-1
Optellen, aftrekken, vermenigvuldigen, delen, 7-2
Functies toegepast op lijsten, 7-3

, 7-1

Blz. TOC-4

Lijsten van complexe getallen, 7-4
Lijsten van algebraïsche objecten, 7-4
Het menu MTH/LIST, 7-5
De functie SEQ, 7-6
De functie MAP, 7-6
Referentie, 7-7

Hoofdstuk 8 – Vectoren

Vectoren invoeren, 8-1

Vectoren in het stapelgeheugen invoeren, 8-1
Vectoren opslaan in variabelen in het stapelgeheugen, 8-2
De Matrixschrijver (MTRW) gebruiken om vectoren in te voeren, 8-2
Eenvoudige bewerkingen met vectoren, 8-5
Veranderend teken, 8-5
Optellen, aftrekken, 8-5
Vermenigvuldigen met een scalair en delen door een scalair, 8-6
De functie absolute waarde, 8-6
Het menu MTH/VECTOR, 8-7
Grootte, 8-7
Scalair product, 8-7
Vectorieel product, 8-8

Referentie,

8-9

, 8-1

Hoofdstuk 9 – Matrices en lineaire algebra, 9-1

Matrices in het stapelgeheugen invoeren, 9-1

Met de Matrixschrijver, 9-1
De Matrix direct in het stapelgeheugen invoeren, 9-2
Bewerkingen met matrices, 9-3
Optellen en aftrekken, 9-4
Vermenigvuldiging, 9-4
Vermenigvuldiging met een scalair, 9-4
Matrix-vectorvermenigvuldiging, 9-4
Matrixvermenigvuldiging, 9-5
Term-voor-term vermenigvuldiging, 9-5
De identiteitsmatrix, 9-6
De inverse matrix, 9-6

Blz. TOC-5

Een matrix karakteriseren (Het menu matrix NORM), 9-7
De functie DET, 9-7
De functie TRACE, 9-7
Oplossing van lineaire systemen, 9-8
De numerieke solver gebruiken voor lineaire systemen, 9-8
Oplossing met de inverse matrix, 9-10
Oplossing door “deling” van matrices, 9-11

Referenties, 9-11

Hoofdstuk 10 – Grafieken

Grafische opties in de rekenmachine, 10-1
Een uitdrukking van de vorm
Een tabel genereren van waarden voor een functie, 10-4
Snelle 3D-grafieken, 10-6
Referentie, 10-8

, 10-1

y = f(x)

plotten, 10-2

Hoofdstuk 11 – Calculustoepassingen

Het menu CALC (Calculus), 11-1
Limieten en afgeleiden, 11-1

De functie Lim, 11-1
De Functies DERIV en DERVX, 11-2
Anti-afgeleiden en integralen, 11-3
De functies INT, INTVX, RISCH, SIGMA en SIGMAVX, 11-3
Eindige integralen, 11-4
Oneindige series, 11-4
De Functies TAYLR, TAYLR0 en SERIES, 11-5
Referentie, 11-7

, 11-1

Hoofdstuk 12 – Multivariant Calculustoepassingen, 12-1

Partiële afgeleiden, 12-1
Meervoudige integralen, 12-2
Referentie, 12-2

Hoofdstuk 13 – Toepassingen van vectoranalyse, 13-1

De del-operator, 13-1

Blz. TOC-6

Gradiënt, 13-1
Divergentie, 13-2
Rotatie, 13-2
Referentie, 13-2

Hoofdstuk 14 – Differentiaalvergelijkingen

Het menu CALC/DIFF, 14-1
Oplossing voor lineaire en niet-lineaire vergelijkingen, 14-1

De functie LDEC, 14-2
De functie DESOLVE, 14-3
De variabele ODETYPE, 14-4

Laplace-transformaties,

Laplace-transformaties en inversies in de rekenmachine, 14-5
Fourier-reeksen, 14-6
De functie FOURIER, 14-6
Fourier-reeks voor een kwadratische functie, 14-7

Referentie, 14-8

Hoofdstuk 15 – Kansverdelingen

Het submenu MTH/PROBABILITY..– deel 1, 15-1

Faculteiten, combinaties en permutaties, 15-1
Willekeurige getallen, 15-2
Het menu MTH/PROBABILITY.. – deel 2, 15-3
De normale verdeling, 15-3
De Student-t-verdeling, 15-4
De Chi-kwadraat verdeling, 15-4
De F-verdeling, 15-4
Referentie, 15-4

14-5

, 15-1

, 14-1

Hoofdstuk 16 – Statistische Toepassingen, 16-1

Gegevens invoeren, 16-1
Statistieken met één variabele berekenen, 16-2
Frequentieverdelingen verkrijgen,
Gegevens in een functie y = f(x) plaatsen, 16-5
Aanvullende samenvattende statistieken verkrijgen, 16-6
Betrouwbaarheidsintervallen, 16-7

16-3

Blz. TOC-7

Hypotheses testen, 16-10
Referentie, 16-12

Hoofdstuk 17 – Getallen in Verschillende Grondtallen, 17-1

Het menu BASE, 17-1
Niet-decimale getallen schrijven,
Referentie, 17-2

17-1

Beperkte Garantie –

Service, G-2
Regelgeving, G-4

G-1

Blz. TOC-8

Hoofdstuk 1
Beginnen

Dit hoofdstuk beschrijftde basisinformatie over het gebruik van uw
rekenmachine. De doelstelling van de oefeningen is dat u vertrouwd raakt met
de basisfuncties en instellingen voordat u daadwerkelijk een berekening
maakt .

Basisbediening

De volgende oefeningen zijn bedoeld om de hardware van uw rekenmachine
beter te leren kennen.

Batterijen

De rekenmachine gebruikt 3 AAA(LR03)-batterijen als hoofdvoeding en een
CR2032 lithiumbatterij voor geheugenbackup.
Plaats de batterijen volgens de onderstaande procedure alvorens de
rekenmachine te gebruiken.

De hoofdbatterijen plaatsen

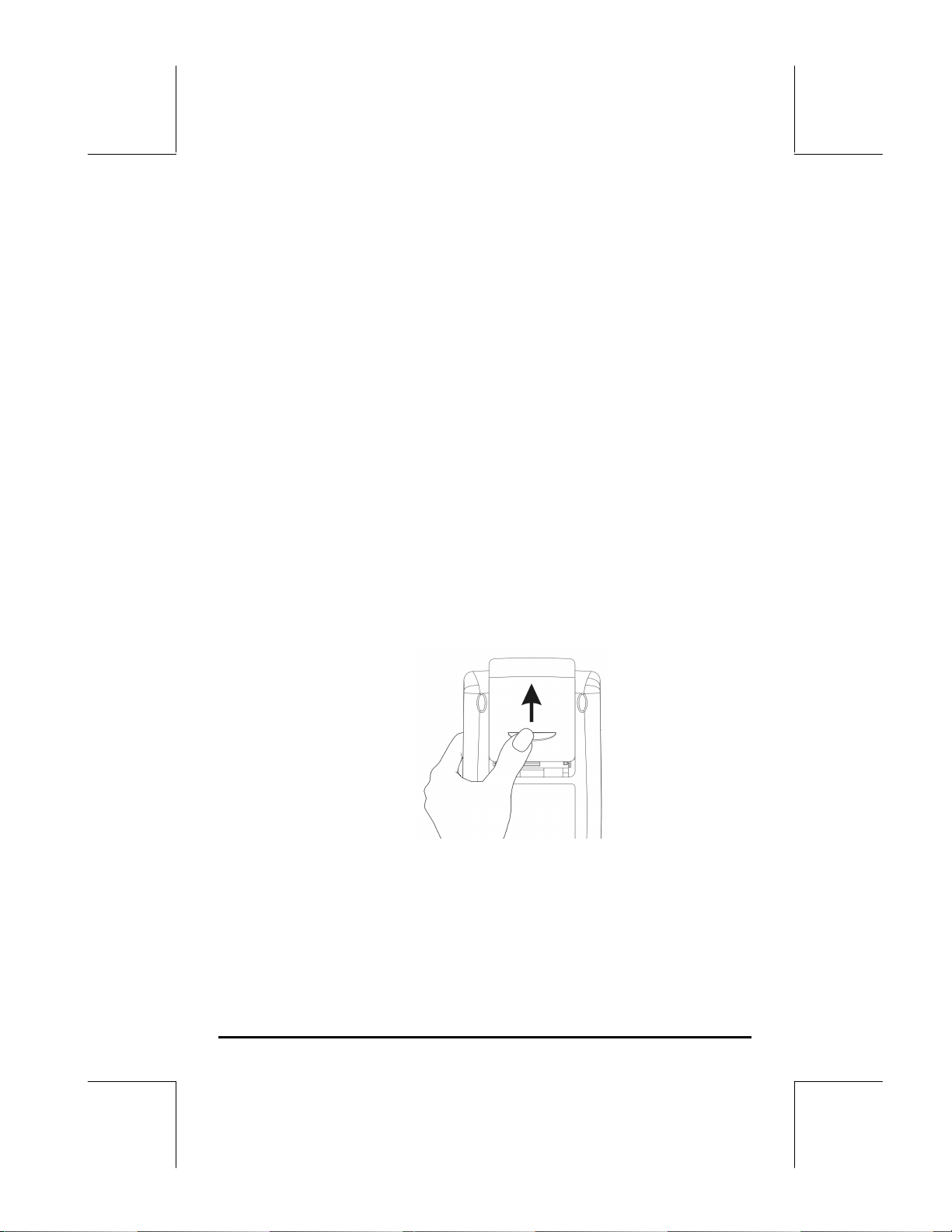
a. Zorg ervoor dat de calculator uitgeschakeld is. Schuif het deksel van de

batterijhouder omhoog zoals in de afbeelding.

b. Plaats 3 nieuwe AAA(LR03)-batterijen in het batterijgedeeltevenster. Zorg

ervoor dat elke batterij in de juiste richting wordt geplaatst.

De backupbatterij plaatsen

a. Zorg ervoor dat de calculator uitgeschakeld is. Druk de houder naar

beneden. Duw het afdekplaatje in de getoonde richting en til het op.

Blz. 1-1

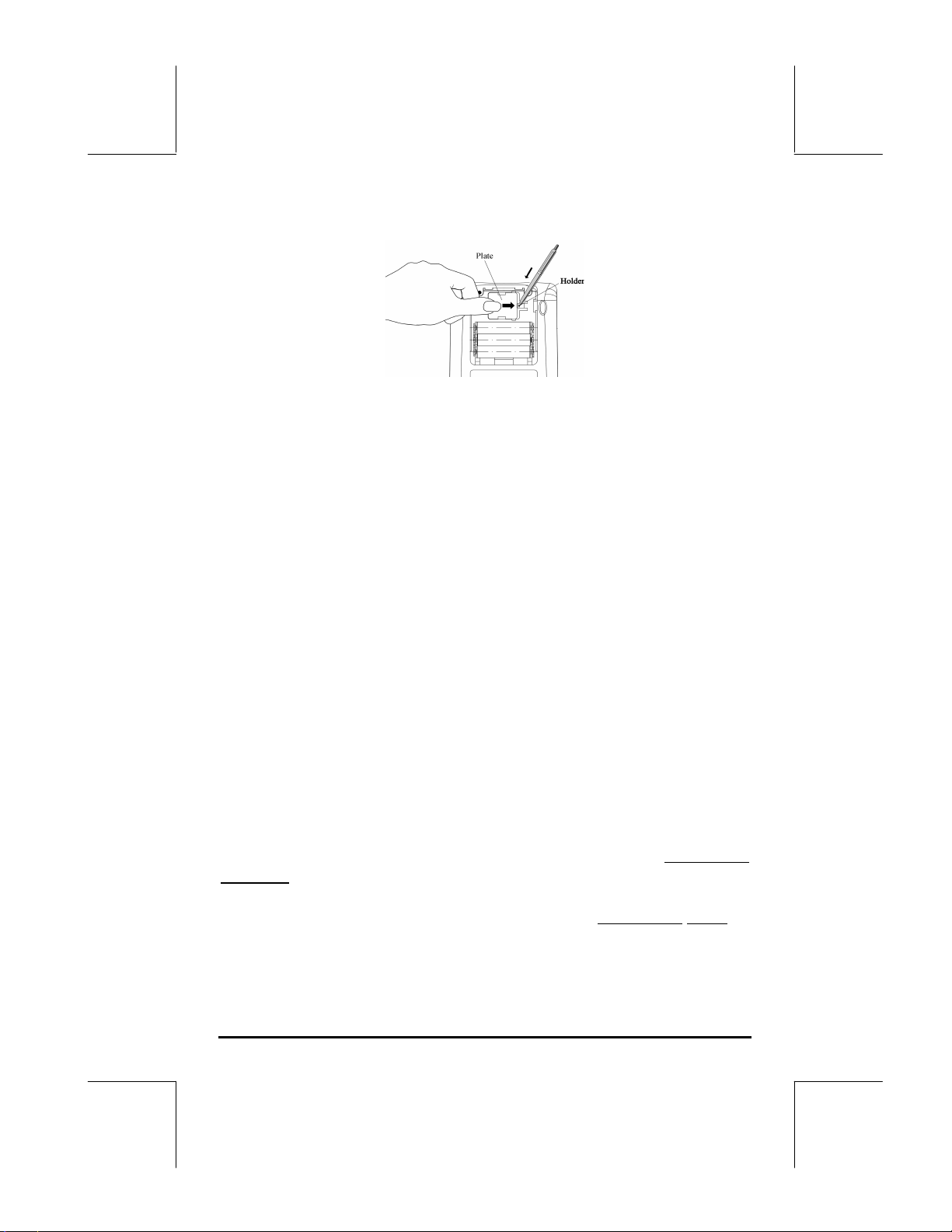
b. Plaats een nieuwe CR2032 lithiumbatterij. Zorg ervoor dat de positieve

kant (+) naar boven is geplaatst.
c. Plaats het afdekplaatje terug en duw het in de beginpositie.
Druk, nadat de batterijen zijn geplaatst, op [ON] om de rekenmachine in te
schakelen.
Waarschuwing: als de pictogram van een zwakke batterij op het beeldscherm
verschijnt, dienen de batterijen zo spoedig mogelijk vervangen te worden. De
backupbatterij en de hoofdbatterijen echter nooit tegelijkertijd verwijderen om
gegevensverlies te voorkomen.

De rekenmachine in- en uitschakelen

De toets $ bevindt zich in de linkeronderhoek van het toetsenbord. Druk
één keer op deze toets om de rekenmachine in te schakelen. Druk, om de
rekenmachine uit te schakelen, op de rechter rode shifttoets @ (eerste toets
in de tweede rij vanaf de onderzijde van het toetsenbord) en daarna op $.
De toets $ is in de rechterbovenhoek voorzien van een rode OFF-markering,
als geheugensteuntje voor de OFF-functie van de rekenmachine.

Het contrast van het beeldscherm instellen

U kunt het beeldschermcontrast instellen door tegelijkertijd op de toets $ en
de toetsen +of - te drukken.

De toetscombinatie $(vasthouden) en +maken het beeldscherm
donkerder

De toetscombinatie $(vasthouden) en -maken het beeldscherm

lichter

Blz. 1-2

Inhoud van het beeldscherm van de rekenmachine

Zet uw rekenmachine weer aan. Boven in het beeldscherm staan twee
informatieregels die de instellingen van de rekenmachine beschrijven. In de
eerste regel staan de volgende tekens:

RAD XYZ HEX R= 'X'

Raadpleeg hoofdstuk 2 in de gebruikshandleiding van de rekenmachine voor
meer informatie over de betekenis van deze specificaties.

In de tweede regel staan de volgende tekens

{ HOME }

Dit betekent dat de HOME-directory de huidige bestandsdirectory in het
geheugen van de rekenmachine is.

Onder in het beeldscherm staan enkele labels, te weten:

@EDIT @VIEW @@ RCL @@ @@STO@ ! PURGE !CLEAR

die bij de zes softmenutoetsen, F1 tot en met F6, horen:

ABCDEF

De zes labels die in onder in het scherm worden weergegeven, kunnen
veranderen als er een ander menu wordt getoond. A hoort altijd bij het
eerste weergegeven label en B altijd bij het tweede label, enz.

Menu’s

De zes labels die bij de toetsen A tot en met F horen, maken deel uit
van een menu
softmenutoetsen heeft, worden er maar 6 labels per keer weergegeven. Een
menu kan echter uit meer dan zes invoeren bestaan. Elke groep van 6
invoeren wordt een menupagina genoemd. Druk op de toets L(Volgende

met functies. Omdat de rekenmachine slechts zes

Blz. 1-3

menu) wanneer u naar de volgende menupagina wilt (indien beschikbaar).
Dit is de derde toets van links in de derde toetsenrij van het toetsenbord.

Het menu TOOL

De softmenutoetsen van het weergegeven menu, het menu TOOL, zijn voor het
bewerken van variabelen (zie de paragraaf over variabelen in dit hoofdstuk).

@EDIT A EDIT: bewerken van de inhoud van een variabele (zie

hoofdstuk 2 in deze handleiding en hoofdstuk 2 en Bijlage L in
de gebruikshandleiding voor meer informatie over bewerken)

@VIEW B VIEW: bekijken van de inhoud van een variabele
@@ RCL @@ C ReCaLl: oproepen van de inhoud van een variabele
@@STO@ D STOre: opslaan van de inhoud van een variabele
! PURGE E PURGE: verwijderen van een variabele
CLEAR F CLEAR: wissen van het beeldscherm of het stapelgeheugen

Deze zes functies vormen de eerste pagina van het menu TOOL. Dit menu
heeft in totaal acht invoeren die over twee pagina’s zijn verdeeld. Door op de
toets L (volgende menu) te drukken, komt u op de tweede pagina. Dit is de
derde toets van links in de derde toetsenrij van het toetsenbord.

Nu hebben alleen de eerste twee softmenutoetsen specifieke commando’s.
Deze commando’s zijn:

@CASCM A CASCMD: CAS CoMmanD, wordt gebruikt om een commando

te starten van de CAS door uit een lijst te selecteren

@HELP B HELP-functie die de commando’s beschrijft in de rekenmachine

Door op de toets L te drukken, verschijnt het originele menu TOOL. Het
menu TOOL kan ook worden verkregen door op de toets I te drukken (dit
is de derde toets van links in de tweede toetsenrij boven in het toetsenbord).

De tijd en datum instellen

Raadpleeg hoofdstuk 1 in de gebruikshandleiding van de rekenmachine voor
het instellen van de tijd en de datum.

Blz. 1-4

Toetsenbord van de rekenmachine

In onderstaande afbeelding ziet u een weergave van het toetsenbord van de
rekenmachine met genummerde rijen en kolommen. Elke toets heeft drie, vier
of vijf functies. De hoofdfunctie van een toets heeft de meest zichtbare
markering op de toets. De groene linkershifttoets, toets (8,1), de rode
rechtershifttoets, toets (9,1) en de blauwe toets ALPHA, toets (7,1) kunnen
worden gecombineerd met enkele andere toetsen om de andere functies in
het toetsenbord te activeren.

Zo kan met toets P, toets(4,4), de volgende zes functies worden uitgevoerd:

P Hoofdfunctie: het activeren van het menu SYMBolic

Blz. 1-5

„´ Functie links-shift: het activeren van het menu MTH
(wiskundig)

…N Functie rechts-shift: het activeren van de functie CATalog
~p functie ALPHA: het invoeren van de hoofdletter P
~„p functie ALPHA-Links-shift: het invoeren van de kleine letter p
~…p functie ALPHA-Rechts-shift: het invoeren van het symbool π

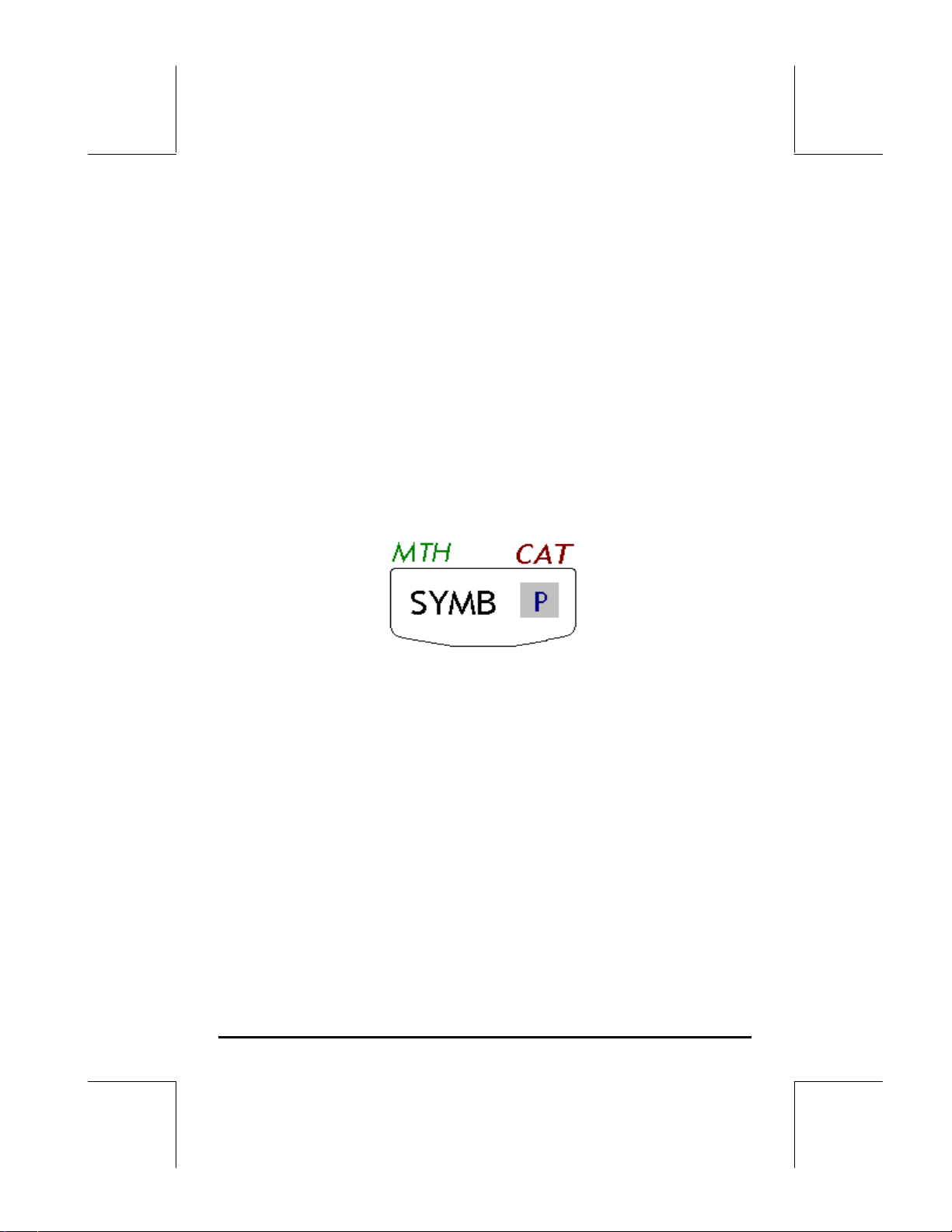
Van de zes functies die met een toets kunnen worden uitgevoerd, worden
alleen de eerste vier op het toetsenbord weergegeven. De afbeelding op de
volgende pagina geeft de vier labels voor de toets P weer. -De kleur en de
plaats van de markeringen op de toets, namelijk SYMB, MTH, CAT en P,
geven aan wat de hoofdfunctie is (SYMB) en welke drie andere functies
kunnen worden uitgevoerd met de toetsen links-shift „(MTH), rechts­shift …(CAT ) en ~(P).

Raadpleeg Bijlage B in de gebruikshandleiding van de rekenmachine voor
meer informatie over het gebruik van het toetsenbord van de rekenmachine.

Modi van de rekenmachine selecteren

In deze paragraaf gaan we er vanuit dat u al een beetje bekend bent met het
gebruik van de kies- en dialoogvensters (Raadpleeg Bijlage A in de
gebruikshandleiding wanneer dit niet het geval is).

Druk op de toets H (tweede toets van links in de tweede toetsenrij boven in
het toetsenbord) om het volgende invoervenster voor CALCULATOR MODES
weer te geven:

Blz. 1-6

Druk op de softmenutoets !!@@OK#@ ( F) om terug te keren naar het normale
beeldscherm. Hier volgen enkele voorbeelden voor het selecteren van
verschillende rekenmachinemodi.

Bedieningsmodus

De rekenmachine bevat twee bedieningsmodi: de modus Algebraic en de
modus Reverse Polish Notation (RPN). De rekenmachine staat standaard in de
modus Algebraic (zoals in de bovenstaande afbeelding te zien is), maar
gebruikers van oudere modellen van HP-rekenmachines zijn misschien meer
bekend met de RPN-modus.

Als u een bedieningsmodus wilt selecteren, moet u eerst het invoervenster
CALCULATOR MODES openen met de toets H. Het Veld Operating Mode
wordt gemarkeerd. Selecteer de bedieningsmodus Algebraic of RPN met de
toets \ (tweede van links in de vijfde rij onder in het toetsenbord) of door
op de softmenutoets @CHOOS ( B) te drukken. Bij de tweede methode kunt u
de pijltjes omhoog en omlaag, —˜, gebruiken om de modus te selecteren.
Druk daarna op de softmenutoets !!@@OK#@ om de handeling te voltooien.

Om het verschil aan te geven tussen deze twee bedieningsmodi, voeren we
de volgende uitdrukking op beide manieren uit:

1



0.50.3

−⋅




3

0.23

Om deze uitdrukking in de rekenmachine in te voeren, gebruiken we eerst de
vergelijkingenschrijver, ‚O. Zoek de volgende toetsen op het
toetsenbord, samen met de numerieke toetsen.




0.30.3

⋅



5.2

e+

Blz. 1-7

!@.#*+-/R

Q¸Ü‚Oš™˜—`

De vergelijkingenschrijver is een beeldschermmodus waarmee u wiskundige
uitdrukkingen kunt opstellen met expliciet wiskundige aanduidingen, zoals
breuken, afgeleiden, integralen, wortels, enz. Gebruik de volgende toetsen
als u de vergelijkingenschrijver wilt gebruiken voor het opstellen van de
hierboven weergegeven uitdrukking:

‚OR3.*!Ü5.-

1./3.*3.
—————

/23.Q3™™+!¸2.5`

Als u op ` drukt, geeft de rekenmachine de volgende uitdrukking weer:

√ (3.*(5.-1/(3.*3.))/23.^3+EXP(2.5))

Als u opnieuw op ` drukt, krijgt u de volgende waarde (accepteer modus
Approx. aan als u hierom wordt gevraagd door op !!@@OK#@ te drukken):

U kunt de uitdrukking ook als volgt rechtstreeks in het beeldscherm typen
zonder de vergelijkingenschrijver te gebruiken:

R!Ü3.*!Ü5.-

1/3.*3.™

/23.Q3+!¸2.5`

Zo krijgt u hetzelfde resultaat.

Verander de bedieningsmodus in RPN door eerst op de toets H te drukken.
Selecteer de bedieningsmodus RPN met de toets \ of door op de

Blz. 1-8

softmenutoets @CHOOS te drukken. Druk op de softmenutoets !!@@OK#@ ( F) om de
handeling te voltooien. Het beeldscherm ziet er bij de RPN-modus als volgt uit:

U ziet dat het beeldscherm meerdere niveaus van de uitkomst heeft
genummerd met van onder naar boven 1, 2, 3, enz. Dit wordt het
stapelgeheugen van de rekenmachine genoemd. De verschillende niveaus
worden stapelgeheugenniveaus genoemd, dus stapelgeheugenniveau 1,
stapelgeheugenniveau 2, etc.

RPN wil dus eigenlijk zeggen dat u een handeling zoals 3 + 2 niet in de
rekenmachine invoert met

3+2`

maar eerst de operanden in de juiste volgorde invoert en daarna de operator,
dus

3`2`+

De operanden nemen bij het invoeren verschillende stapelgeheugenniveaus
in gebruik. Als u 3` invoert, wordt het getal 3 in stapelgeheugenniveau
1 ingevoerd. Als u daarna 2` invoert, gaat het getal 3 naar naar
stapelgeheugenniveau 2. Door vervolgens op + te drukken, vertellen we de
rekenmachine dat hij de operator of het programma + moet toepassen op
de objecten in niveaus 1 en 2. De uitkomst, 5, wordt vervolgens in niveau 1
geplaatst.

We proberen eerst enkele eenvoudige handelingen voordat we de moeilijkere
uitdrukking uitproberen die eerder is gebruikt bij de algebraïsche modus.

123/32 123`32/

2

4

4`2Q

3

√(√27) 27`R3@»

Blz. 1-9

Let op de posities van de y en de x in de laatste twee handelingen. De basis
in de exponentiële handeling is y (stapelgeheugenniveau 2), terwijl het
exponent x is (stapelgeheugenniveau 1) voordat de toets Q wordt ingedrukt.
In de derdemachtswortel is y (stapelgeheugenniveau 2) het getal onder het
wortelteken en x (stapelgeheugenniveau 1) de wortel.

Probeer de volgende oefening met de volgende 3 factoren: (5 + 3) × 2

5`3`+ Berekent eerst (5 +3).
2X Voltooit de berekening.

Probeer nu de eerder genoemde uitdrukking:

1



53




23

3` Voer 3 in op niveau 1
5` Voer 5 in op niveau 1, 3 gaat naar niveau 2
3` Voer 3 in op niveau 1, 5 gaat naar niveau 2, 3 naar

niveau 3
3* Voer 3 in en vermenigvuldig, 9 verschijnt op niveau

1
Y 1/(3×3), laatste waarde op niv. 1; 5 op niveau 2; 3
op niveau 3

- 5 - 1/(3×3) , staat nu op niveau 1; 3 op niveau 2

* 3× (5 - 1/(3×3)), staat nu op niveau 1.
23` Voer 23 in op niveau 1, 14.66666 gaat naar

niveau 2.
3Q Voer 3 in, bereken 23

2.

/ (3× (5-1/(3×3)))/23

2.5 Voer 2.5 in niveau 1



−⋅



33

⋅



5.2

3

e+

3

op niveau 1. 14.666 op niv.

3

naar niveau 1

Blz. 1-10

!¸ e

2.5

, gaat naar niveau 1, niveau 2 geeft de vorige

waarde weer.

3

+ (3× (5 - 1/(3×3)))/23

1.
R √((3× (5 - 1/(3×3)))/23

2.5

e

= 12.18369, naar niv.

+

3

2,5

e

) = 3.4905156, naar

+

1.

Om te wisselen tussen de bedieningsmodi ALG en RPN kunt u ook
systeemvlag 95 wissen/verwijderen door op de volgende toetsen te drukken:

H @)FLAGS —„—„—„—@@CHK@@

Getalopmaak en punt of komma als decimaalteken

Door de getalopmaak te wijzigen, kunt u de manier aanpassen waarop reële
cijfers worden weergegeven door de rekenmachine. Deze functie is bijzonder
handig bij handelingen met tiende machten of om het aantal decimalen van
een uitkomst te beperken.

Om een getalopmaak te selecteren, moet u eerst het invoervenster
CALCULATOR MODES openen door op de toets H te drukken. Gebruik
daarna de toets pijltje omlaag, ˜, om de optie Number format te selecteren.
De standaardwaarde is Std, oftewel Standaardopmaak. In de
standaardopmaak geeft de rekenmachine getallen met zwevende komma
weer met geen ingestelde decimalen en met de maximaal door de
rekenmachine toegestane precisie (12 significante cijfers). U leest meer over
reële getallen in hoofdstuk 2 van deze gebruikshandleiding. Probeer ter
verduidelijking van bovengenoemde en andere getalopmaken de volgende
oefeningen:

• Standaardopmaak:
Deze modus wordt het meeste gebruikt, omdat de cijfers in de meest
bekende notatie worden weergegeven. Druk op de softmenutoets !!@@OK#@ ,
met Number format ingesteld op Std, om terug te keren naar het
beeldscherm van de rekenmachine. Voer het getal

123.4567890123456 in (met 16 significante cijfers). Druk op de toets

Blz. 1-11

`. Het getal wordt afgerond op maximaal 12 significante cijfers en
wordt als volgt weergegeven:

• Vaste opmaak met decimalen: Druk op de toets H. Selecteer daarna met de toets pijltje omlaag, ˜, de optie . Druk op de softmenutoets @CHOOS ( B) en selecteer de optie Fixed met de toets pijltje omlaag ˜.

Druk op de toets pijltje rechts, ™, om de nul voor de optie Fix te
markeren. Druk op de softmenutoets @CHOOS en selecteer bijvoorbeeld 3
decimalen met de toetsen pijltje omhoog en omlaag, —˜.

Druk op de softmenutoets !!@@OK#@ om de selectie te voltooien:

Blz. 1-12

Druk op de softmenutoets !!@@OK#@ om terug te keren naar het beeldscherm
van de rekenmachine. Het getal wordt nu weergegeven als:

U ziet dat het getal is afgerond en niet afgekapt. Het getal

123.4567890123456 wordt voor deze instelling dus weergegeven als

123.457 en niet als 123.456, omdat het cijfer na 6 > 5 is

• Wetenschappelijke opmaak U stelt deze opmaak in door op de toets H te drukken. Selecteer daarna met de toets pijltje omlaag, ˜, de optie Number format. Druk op de softmenutoets @CHOOS ( B) en selecteer de optie Scientific met de toets pijltje omlaag ˜. Het getal 3 moet voor Sci blijven staan. (Dit getal kan op dezelfde manier worden gewijzigd als het Fixed aantal decimalen in het bovenstaande voorbeeld).

Druk op de softmenutoets !!@@OK#@ om terug te keren naar het beeldscherm
van de rekenmachine. Het getal wordt nu weergegeven als:

De uitkomst, 1.23E2, is de rekenmachineversie van de notatie voor tiende
machten, dus 1.235 × 10

2

. In deze zogenaamde wetenschappelijke
notatie geeft het getal 3 voor de getalopmaak Sci (zoals eerder getoond)
het aantal significante cijfers na de komma weer. De wetenschappelijke

Blz. 1-13

notatie heeft altijd één geheel getal, zoals hierboven. In dit geval is het
aantal significante cijfers dus vier.

• Technische opmaak

De technische opmaak (Engineering) lijkt sterk op de wetenschappelijke
opmaak, maar de tiende machten zijn hier meervouden van drie. U stelt
deze opmaak in door op de toets H te drukken. Selecteer daarna met
de toets pijltje omlaag, ˜, de optie Number format . Druk op de
softmenutoets @CHOOS ( B) en selecteer de optie Engineering met de toets
pijltje omlaag ˜. Het getal 3 moet voor Eng blijven staan. (Dit getal
kan op dezelfde manier worden gewijzigd als het Fixed aantal decimalen
in het bovenstaande voorbeeld.)

Druk op de softmenutoets !!@@OK#@ om terug te keren naar het beeldscherm
van de rekenmachine. Het getal wordt nu weergegeven als:

Omdat er bij dit getal drie cijfers in het gehele getal staan, wordt het
weergegeven met vier significante cijfers en een tiende macht van nul in
de Technische opmaak. Het getal 0.00256 wordt bijvoorbeeld als volgt
weergegeven:

• Komma’s en punten

De punten in cijfers met zwevende punten kunnen worden vervangen
door komma's als de gebruiker hier liever mee werkt. Om de punten te

Blz. 1-14

vervangen door komma's wijzigt u de optie FM in CALCULATOR MODES
als volgt naar komma's (U ziet dat we Number Format hebben gewijzigd
in Std):

• Druk op de toets H. Druk daarna een keer op de toets pijltje omlaag,
˜, en keer op het pijltje rechts, ™, om de optie __FM, te markeren.

Om komma’s te selecteren, drukt u op de softmenutoets @CHK@@ (dus de
toets B). Het invoerscherm ziet er als volgt uit:

• Druk op de softmenutoets !!@@OK#@ om terug te keren naar het beeldscherm
van de rekenmachine. Het getal 123.4567890123456, dat we eerder
hebben ingevoerd, wordt nu weergegeven als:

Hoekmeting

Bij trigonometrische functies moet u bijvoorbeeld argumenten invoeren voor
vlakke hoeken. De rekenmachine heeft drie verschillende modi voor
Hoekmetingen die u bij hoeken kunt gebruiken:

• Graden: Er zitten 360 graden (360

• Radialen: Er zitten 2π radialen (2π

• Decimale graden: Er zitten 400 decimale graden (400

omtrek.

De hoekmeting is van invloed op trigonometrische functies als SIN, COS, TAN
en de bijbehorende functies.

o

) in een complete omtrek.

r

) in een complete omtrek.

g

) in een complete

Blz. 1-15

U kunt de modi voor hoekmetingen als volgt wijzigen:

• Druk op de toets H. Druk daarna twee keer op de toets pijltje omlaag,
˜. Selecteer de modus Hoekmeting met de toets \ (tweede van links

in de vijfde rij onder in het toetsenbord) of door op de softmenutoets
@CHOOS ( B) te drukken. Bij de tweede methode kunt u de pijltjes
omhoog en omlaag, —˜, gebruiken om de gewenste modus te
selecteren. Druk daarna op de softmenutoets !!@@OK#@ ( F) om de
handeling te voltooien. In het volgende scherm is bijvoorbeeld de modus
Radians geselecteerd:

Coördinatenstelsel

Als u het coördinatenstelsel selecteert, heeft dit invloed op de manier waarop
vectoren en complexe getallen worden weergegeven en ingevoerd.
Raadpleeg hoofdstuk 4 en 8 in deze handleiding voor meer informatie over
respectievelijk complexe getallen en vectoren . De rekenmachine beschikt over
drie soorten coördinatenstelsels: Rechthoekig (RECT), Cilindrisch (CYLIN) en
bolvormig (SPHERE). Zo wijzigt u het coördinatenstelsel:

• Druk op de toets H. Druk daarna drie keer op de toets pijltje omlaag,
˜. Selecteer de modus Coord System door op de toets \ (tweede

van links in de vijfde rij onder in het toetsenbord) of doorop de
softmenutoets @CHOOS ( B) te drukken. Bij de tweede methode kunt u de
pijltjes omhoog en omlaag, —˜, gebruiken om de gewenste modus
te selecteren. Druk daarna op de softmenutoets !!@@OK#@ ( F) om de
handeling te voltooien. In het volgende scherm is bijvoorbeeld het
coördinatenstelsel Polar geselecteerd:

Blz. 1-16

CAS-instellingen selecteren

CAS is een afkorting van Computer Algebraic System, oftewel algebraïsch
computersysteem. Dit is het wiskundige hart van de rekenmachine waar de
symbolische wiskundige handelingen en functies zijn geprogrammeerd. Het
CAS biedt een aantal instellingen die kunnen worden aangepast aan de
gewenste handeling. Zo krijgt u de mogelijke CAS-instellingen te zien:

• Druk op de toets H om het invoervenster CALCULATOR MODES te
openen.

• Druk op de softmenutoets@@ CAS@@ om de CAS-instellingen te wijzigen. Hier
volgen de standaardwaarden van de CAS-instellingen:

• Met de pijltjestoetsen kunt u door de vele opties van het invoervenster
CAS MODES navigeren: š™˜—.

• Als u een van de bovenstaande instellingen wilt selecteren of deselecteren,
moet u het onderliggende streepje voor de gewenste optie selecteren en
op de softmenutoets @CHK@@ drukken totdat u de gewenste instelling ziet.

Blz. 1-17

Als er een optie is geselecteerd, verschijnt er een vinkje op het
onderliggende streepje (bijvoorbeeld de bovenstaande opties Rigorous en
Simp Non-Rational). De niet-geselecteerde opties hebben geen vinkje op
het onderliggende streepje voor de gewenste optie (zoals de
bovenstaande opties _Numeric, _Approx, _Complex, _Verbose,
_Step/Step, _Incr Pow ).

• Druk op de softmenutoets @@@OK@@@ als u alle gewenste opties in het
invoervenster CAS MODES heeft geselecteerd en gedeselecteerd . U keert
nu terug naar het invoervenster CALCULATOR MODES. Druk nogmaals
op de softmenutoets @@@OK@@@ om weer naar het normale beeldscherm van de
rekenmachine terug te keren.

Uitleg van de CAS-instellingen

• Indep var: de onafhankelijke variabele voor CAS-toepassingen. Meestal
VX = ‘X’.

• Modulo
de coëfficiënt of modulo van de rekenkundige ring (raadpleeg hoofdstuk
5 van de gebruikshandleiding van de rekenmachine).

• Numeric
numerieke uitkomst of een uitkomst met zwevende komma bij
berekeningen.

• Approx
numerieke uitkomsten bij berekeningen. Als deze niet is aangevinkt, staat
de CAS in de modus Exact, die symbolische uitkomsten in algebraïsche
berekeningen geeft.

• Complex
complexe getallen actief. Als deze niet is aangevinkt, staat de CAS in de
modus Real, d.w.z. dat de standaardwaarde dus berekeningen met reële
getallen zijn. Raadpleeg hoofdstuk 4 voor handelingen met complexe
getallen.

• Verbose
bij bepaalde CAS-handelingen gegeven.

• Step/Step
stap gegeven voor bepaalde CAS-handelingen. Dit kan handig zijn om
de tussenliggende stappen in sommeringen, afgeleiden, integralen,

: voor handelingen in modulaire rekenkunde heeft deze variabele

: als deze waarde is ingesteld, produceert de rekenmachine een

: als deze waarde is ingesteld, gebruikt de modus Approximate

: als deze waarde is ingesteld, zijn de handelingen voor

: als deze waarde is ingesteld, wordt er gedetailleerde informatie

: als deze waarde is ingesteld, worden de uitkomsten stap voor

Blz. 1-18

polynome handelingen (bijvoorbeeld synthetische delingen) en
matrixhandelingen te bekijken.

• Incr Pow
waarde is ingesteld, polynome termen worden weergegeven in
oplopende volgorde van de machten van de onafhankelijke variabele.

• Rigorous
waardefunctie |X| niet vereenvoudigen naar X.

• Simp Non-Rational
rekenmachine niet-rationele uitdrukkingen zoveel mogelijk te
vereenvoudigen.

: Increasing Power (Oplopende machten) betekent dat als deze

: als deze waarde is ingesteld, zal de rekenmachine de absolute

: als deze waarde is ingesteld, probeert de

Beeldschermmodi selecteren

Het beeldscherm van de rekenmachine kan naar wens worden aangepast
door verschillende beeldschermmodi te selecteren. Zo krijgt u de mogelijke
beeldscherminstellingen te zien:

• Druk eerst op de toets H om het invoervenster CALCULATOR MODES
te activeren. Druk in het invoervenster CALCULATOR MODES op de
softmenutoets @@DISP@ (D) om het invoervenster DISPLAY MODES weer te
geven.

• Met de pijltjestoetsen kunt u door de vele opties van het invoervenster
DISPLAY MODES navigeren: š™˜—.

• Als u een van de bovenstaande aan te vinken instellingen wilt selecteren
of deselecteren, moet u het onderliggende streepje voor de gewenste
optie selecteren en op de softmenutoets @CHK@@ drukken totdat u de
gewenste instelling krijgt. Als er een optie is geselecteerd, verschijnt er
een vinkje op het onderliggende streepje (bijvoorbeeld de bovenstaande
optie Textbook in de Stapelgeheugen:-regel). De ongeselecteerde opties

Blz. 1-19

hebben geen vinkje op het onderliggende streepje voor de gewenste
optie (bijvoorbeeld de bovenstaande opties _Small, _Full page, en
_Indent ) in de bovenstaande Edit:-regel).

• Als u het lettertype voor het beeldscherm wilt selecteren, markeert u het
veld voor de optie Font: in het invoerveld DISPLAY MODES en drukt u op
de softmenutoets @CHOOS (B).

• Druk op de softmenutoets @@@OK@@@ als u alle gewenste opties in het invoervenster
DISPLAY MODES heeft geselecteerd en gedeselecteerd. U keert nu terug naar
het invoervenster CALCULATOR MODES. Druk nogmaals op de softmenutoets
@@@OK@@@ om weer terug te keren naar het normale rekenmachinebeeldscherm.

Lettertype van het beeldscherm selecteren

Druk eerst op de toets H om het invoervenster CALCULATOR MODES te
activeren. Druk in het invoervenster CALCULATOR MODES op de softmenutoets
@@DISP@ (D) om het invoervenster DISPLAY MODES weer te geven. Het veld
Font: is gemarkeerd en de optie Ft8_0:system 8 is geselecteerd. Dit is de
standaardwaarde voor het lettertype van het beeldscherm. Door op de
softmenutoets @CHOOS (B) te drukken, krijgt u een lijst met alle beschikbare
systeemlettertypen, zie hieronder:

De beschikbare opties zijn drie standaard System Fonts (grootten 8, 7 en 6)
en een optie Browse... Met deze laatste optie kunt u door het geheugen van
de rekenmachine bladeren voor extra lettertypen die u heeft aangemaakt (zie
hoofdstuk 23) of in de rekenmachine heeft gedownload.

Oefen in het wijzigen van het lettertype van het beeldscherm van grootte 7
naar 6. Druk op de softmenutoets OK om de selectie te bevestigen. Druk op
de softmenutoets @@@OK@@@ als u een lettertype heeft geselecteerd om terug te

Blz. 1-20

keren naar het invoervenster CALCULATOR MODES. , Druk nogmaals op de
softmenutoets @@@OK@@ om weer terug te keren naar het normale
rekenmachinebeeldscherm. De stapelgeheugenweergave wijzigt en u ziet een
ander lettertype.

Eigenschappen van de regeleditor selecteren

Druk eerst op de toets H om het invoervenster CALCULATOR MODES te
activeren. Druk in het invoervenster CALCULATOR MODES op de
softmenutoets @@DISP@ (D) om het invoervenster DISPLAY MODES weer te
geven. Druk een keer op de toets pijltje omlaag, ˜, om naar de Edit-regel
te gaan. In deze regel staan drie eigenschappen die kunnen worden
aangepast. Als deze eigenschappen zijn geselecteerd (aangevinkt), worden
de volgende effecten actief:

_Small Het lettertype wordt gewijzigd naar klein
_Full page De cursor wordt aan het eind van de regel geplaatst
_Indent Automatische inspringing van de cursor als er een

regelterugloop wordt ingevoerd

In hoofdstuk 2 van deze handleiding vindt u aanwijzingen over het gebruik
van de regeleditor.

Eigenschappen van het stapelgeheugen selecteren

Druk eerst op de toets H om het invoervenster CALCULATOR MODES te
activeren. Druk in het invoervenster CALCULATOR MODES op de
softmenutoets @@DISP@ (D) om het invoervenster DISPLAY MODES weer te
geven. Druk een keer op de toets pijltje omlaag, ˜, om naar de Edit-regel
te gaan. In deze regel staan drie eigenschappen die kunnen worden
aangepast. Als deze eigenschappen zijn geselecteerd (aangevinkt), worden
de volgende effecten actief:

_Small Het lettertype wordt gewijzigd naar klein. Zo staat er zoveel

mogelijk informatie op het scherm. Let op, deze selectie
overschrijft het lettertype voor de stapelgeheugen-weergave.

Blz. 1-21

_Textbook De wiskundige uitdrukkingen worden in grafische wiskundige

notatie weergegeven.

Ter illustratie van deze instellingen, zowel in de algebraïsche modus als de
RPN-modus, kunt u de vergelijkingenschrijver gebruiken om de volgende
definitieve integraal in te voeren:

‚O…Á0™ „è™ „¸\x™ x`

In de algebraïsche modus toont het volgende scherm het resultaat van deze
toetsencombinaties terwijl _Small en _Textbook beide niet zijn geselecteerd:

Als alleen de optie _Small is geselecteerd, ziet het beeldscherm er als volgt uit:

Als de optie _Textbook is geselecteerd (standaardwaarde), ongeacht of de
optie _Small is geselecteerd, geeft het beeldscherm het volgende resultaat
weer:

Eigenschappen van de vergelijkingenschrijver (EQW) selecteren

Druk eerst op de toets H om het invoervenster CALCULATOR MODES te
activeren. Druk in het invoervenster CALCULATOR MODES op de
softmenutoets @@DISP@ (D) om het invoervenster DISPLAY MODES weer te
geven. Druk drie keer op de toets pijltje omlaag, ˜, om naar de regel

Blz. 1-22

EQW (Vergelijkingenschrijver) te gaan. In deze regel staan twee
eigenschappen die kunnen worden aangepast. Als deze eigenschappen zijn
geselecteerd (aangevinkt), worden de volgende effecten actief:

_Small De grootte van het lettertype wordt gewijzigd naar

klein tijdens het gebruik van de vergelijkingeneditor

_Small Stack Disp Een klein lettertype wordt in het stapelgeheugen

weergegeven na het gebruik van de
vergelijkingeneditor

Elders in deze handleiding vindt u uitgebreide aanwijzingen over het gebruik
van de vergelijkingeneditor (EQW).

∞

−

In het bovenstaande voorbeeld van de integraal

volgende resultaat als u _Small Stack Disp selecteert in de EQW-regel van het
invoervenster DISPLAY MODES:

X

dXe

∫

0

krijgt u het

Referenties

Raadpleeg hoofdstuk 1 en Bijlage C in de gebruikshandleiding van de
rekenmachine voor extra verwijzingen naar de onderwerpen die in dit
hoofdstuk zijn besproken .

Blz. 1-23

Hoofdstuk 2
Introductie van de rekenmachine

In dit hoofdstuk laten wij u een aantal basishandelingen van de rekenmachine
zien, waaronder het gebruik van de Vergelijkingenschrijver en het bewerken
van gegevensobjecten in de rekenmachine. Bestudeer de voorbeelden in dit
hoofdstuk goed zodat u de functies van de rekenmachine in de toekomst
optimaal kunt gebruiken.

Objecten van de rekenmachine

De meest gebruikte objecten zijn: reële getallen (echte getallen, geschreven
met een punt, bijvoorbeeld –0.0023, 3.56), hele getallen (geschreven zonder
punt, bijvoorbeeld 1232, -123212123), complexe getallen (geschreven als
een geordend paar, bijvoorbeeld (3,-2)), lijsten, enz. Raadpleeg hoofdstuk 2
en 24 in de gebruikshandleiding van de rekenmachine voor meer informatie
over rekenmachineobjecten.

Uitdrukkingen in het stapelgeheugen bewerken

In deze paragraaf behandelen we voorbeelden van uitdrukkingen die direct
in het beeldscherm van de rekenmachine of in het stapelgeheugen kunnen
worden bewerkt.

Rekenkundige uitdrukkingen maken

Voor dit voorbeeld selecteren we de bedieningsmodus Algebraic en
selecteren we de opmaak Fix met 3 decimalen voor het beeldscherm. We
voeren de volgende rekenkundige uitdrukking in:

0.1

0.1

+

0.5

⋅

Voer deze uitdrukking in met de volgende toetsencombinaties:

5.*„Ü1.+1/7.5™/
„ÜR3.-2.Q3

5.7

3

0.20.3

−

Blz. 2-1

U krijgt dan de volgende uitdrukking: 5*(1+1/7.5)/(ƒ3-2^3).

Druk op ` om de uitdrukking als volgt in het beeldscherm te krijgen:

U ziet dat als het CAS is ingesteld op EXACT (zie Bijlage C in de
gebruikshandleiding) en u de uitdrukking met hele getallen invoert, het
resultaat een symbolische hoeveelheid is, bijvoorbeeld:

5*„Ü1+1/7.5™/

„ÜR3-2Q3

Voordat de uitkomst wordt berekend, wordt u gevraagd de modus
Approximate in te stellen. Accepteer de wijziging om de volgende uitkomst te
krijgen (weergegeven met de decimalenmodus Fix met drie decimalen – zie
hoofdstuk 1):

Als de uitdrukking rechtstreeks in het stapelgeheugen wordt ingevoerd, zal de
rekenmachine in dit geval een waarde voor de uitdrukking proberen te
berekenen als u op ` drukt. Als de uitdrukking tussen apostrofen wordt
ingevoerd, zal de rekenmachine de uitdrukking echter weergeven zoals hij is
ingevoerd. Bijvoorbeeld:

³5*„Ü1+1/7.5™/

„ÜR3-2Q3`

Blz. 2-2

Het resultaat ziet er als volgt uit:

Om de uitdrukking te evalueren, kunnen we de EVAL-functie als volgt
gebruiken:

µ„î`

Als het CAS is ingesteld op Exact, wordt u gevraagd de wijziging van de
CAS-instelling naar Approx goed te keuren. Als dit is gedaan, krijgt u
hetzelfde resultaat als voorheen.

U kunt de uitdrukking tussen aanhalingstekens die eerder is ingevoerd ook
evalueren door de optie

…ï

gebruiken

.

We voeren nu de bovenstaande uitdrukking in als de rekenmachine is
ingesteld op de bedieningsmodus RPN. We stellen de CAS ook in op Exact,
het beeldscherm op Textbook en de getallenweergave op Standaard. De
toetsencombinaties waarmee u de uitdrukking tussen aanhalingstekens kunt
invoeren, zijn dezelfde als die we eerder hebben gebruikt, dus:

³5*„Ü1+1/7.5™/

„ÜR3-2Q3`

Het resultaat ziet er als volgt uit:

Blz. 2-3

Druk een keer op ` om twee kopieën van de uitdrukking in het
stapelgeheugen op te slaan voor evaluatie. We evalueren eerst de uitdrukking
met de functie EVAL en vervolgens met de functie NUM: µ.

Deze uitdrukking is semi-symbolisch, omdat er onderdelen met zwevende
punten in de uitkomst staan, net als een √3. Daarna wijzigen we de locaties
van het stapelgeheugen [d.m.v. ™] en evalueren we met de functie NUM,
bijv., ™…ï.

De laatste uitkomst is puur numeriek, zodat de twee resultaten in het
stapelgeheugen er anders uitzien, hoewel ze voor dezelfde uitdrukking staan.
Om te controleren of ze inderdaad hetzelfde zijn, trekken we de twee
waarden van elkaar af en evalueren we dit verschil met de functie EVAL: ­µ. De uitkomst is nul (0.).

Raadpleeg hoofdstuk 2 in de gebruikshandleiding van de rekenmachine voor
meer informatie over het bewerken van wiskundige uitdrukkingen in het
beeldscherm of in het stapelgeheugen van de rekenmachine.

Algebraïsche uitdrukkingen maken

Algebraïsche uitdrukkingen omvatten niet alleen getallen, maar ook
variabelennamen. Als voorbeeld voeren we de volgende algebraïsche
uitdrukking in de rekenmachine in:

L212

We stellen de bedieningsmodus van de rekenmachine in op Algebraic, het
CAS op Exact en het beeldscherm op Textbook. Voer deze algebraïsche
uitdrukking in met de volgende toetsencombinaties:

³2*~l*R„Ü1+~„x/~r™/
„Ü~r+~„y™+2*~l/~„b

Druk op ` voor het volgende resultaat:

x

+

R

yR

+

L

+

b

Blz. 2-4

Het invoeren van deze uitdrukking terwijl de rekenmachine is ingesteld op de
RPN-modus, gebeurt op dezelfde manier als wanneer de rekenmachine in de
modus Algebraic staat.

Raadpleeg hoofdstuk 2 in de gebruikshandleiding van de rekenmachine voor
meer informatie over het bewerken van algebraïsche uitdrukkingen in het
beeldscherm of in het stapelgeheugen van de rekenmachine.

De vergelijkingenschrijver (EQW) gebruiken om uitdrukkingen te maken

De vergelijkingenschrijver is een bijzonder handige voorziening waarmee u
niet alleen een vergelijking kunt invoeren of bekijken, maar waarmee u
functies ook kunt aanpassen en gebruiken/toepassen op de gehele
vergelijking of delen daarvan.

U start de vergelijkingenschrijver door op de toetsencombinatie ‚O (de
derde toets in de vierde rij boven in het toetsenbord) te drukken. Het scherm
wordt als volgt weergegeven. Druk op L voor de tweede menupagina:

De zes softmenutoetsen voor de vergelijkingenschrijver activeren de functies
EDIT, CURS, BIG, EVAL, FACTOR, SIMPLIFY, CMDS en HELP. Deze functies
worden uitvoerig beschreven in hoofdstuk 3 in de gebruikshandleiding van de
rekenmachine.

Blz. 2-5

Rekenkundige uitdrukkingen maken

De manier waarop rekenkundige uitdrukkingen in de vergelijkingenschrijver
worden ingevoerd, lijkt erg op de manier waarop een rekenkundige
uitdrukking in het stapelgeheugen tussen aanhalingstekens wordt ingevoerd.
Het grootste verschil is dat in de vergelijkingenschrijver de uitdrukkingen in de
stijl “textbook” worden geschreven en niet in een regelinvoerstijl. Voer
bijvoorbeeld de volgende toetsencombinaties in het scherm van de
vergelijkingenschrijver: 5/5+2

De volgende uitdrukking wordt weergegeven:

De cursor wordt weergegeven als een pijltje naar links. De cursor geeft de
huidige bewerkingslocatie aan. Typ bijvoorbeeld bij de cursor op de
bovenstaande locatie:

*„Ü5+1/3

De bewerkte uitdrukking ziet er als volgt uit:

Stel dat u de getallen tussen de haakjes in de noemer wilt vervangen (dus
5+1/3) door (5+π

2

/2). We gebruiken eerst de deletetoets (ƒ) om de
huidige uitdrukking 1/3 te wissen en daarna vervangen we die breuk als
volgt door π

2

/2:

ƒƒƒ„ìQ2

Blz. 2-6

Het scherm ziet er dan als volgt uit:

Om de noemer 2 in de uitdrukking in te voegen moeten we de volledige
uitdrukking π
(™) te drukken. We voeren vervolgens de volgende toetsencombinatie in:

De uitdrukking ziet er nu als volgt uit:

2

markeren. Dat doen we door een keer op de toets pijltje rechts

/2

Stel dat u nu de breuk 1/3 wilt toevoegen aan de gehele uitdrukking. U wilt
dus de volgende uitdrukking invoeren:

5

π

5(25

+⋅+

1

+

2

3

)

2

We moeten eerst de volledige eerste term markeren door het pijltje rechts
( ™) of het pijltje omhoog ( —) herhaaldelijk in te drukken, totdat de
gehele uitdrukking is gemarkeerd. In totaal moet u dus zeven keer drukken.
Dat geeft het volgende resultaat:

Blz. 2-7

N.B.: een andere manier is om vanuit de oorspronkelijke positie van de
cursor (rechts van de 2 in de noemer van π2/2) de toetsencombinatie
‚—, geïnterpreteerd als (‚‘) in te drukken.

Als de uitdrukking is gemarkeerd zoals hierboven, voert u +1/3
in om de breuk 1/3 toe te voegen. Het resultaat is:

Algebraïsche uitdrukkingen maken

Een algebraïsche uitdrukking lijkt sterk op een rekenkundige uitdrukking,
alleen kunnen er Nederlandse en Griekse letters in voorkomen. Het maken
van een algebraïsche uitdrukking volgt daarom dezelfde lijn als die van het
maken van een rekenkundige uitdrukking, alleen wordt er een alfabetisch
toetsenbord gebruikt.

We gebruiken het volgende voorbeeld om het gebruik van de
vergelijkingenschrijver voor het invoeren van een algebraïsche vergelijking te
illustreren. Stel dat we de volgende uitdrukking willen invoeren:

∆⋅+

2

−

µ

λ

⋅+

LNe

3

Gebruik de volgende toetsencombinaties:

2

µ

yx




θ






3/1



Blz. 2-8

2 / R3 ™™ * ~‚n + „¸\ ~‚m

™™ * ‚¹ ~„x + 2 * ~‚m * ~‚c

~„y ——— / ~‚t Q1/3

uitkomst:

In dit voorbeeld gebruiken we meerdere kleine Nederlandse letters,
bijvoorbeeld x (~„x), enkele Griekse letters, bijvoorbeeld λ
(~‚n) en zelfs een combinatie van Griekse en Nederlandse letters,
namelijk ∆y (~‚c~„y). Om een kleine letter in te voeren, moet u
de combinatie ~„ gebruiken gevolgd door de letter die u wilt invoeren .
U kunt speciale tekens ook kopiëren door het menu CHARS (…±) te
gebruiken als u de betreffende toetsencombinaties niet uit uw hoofd wilt leren.
In Appendix D van de gebruikshandleiding vindt u een lijst met veel gebruikte
toetsencombinaties met ~‚.

Raadpleeg hoofdstuk 2 in de gebruikshandleiding van de rekenmachine voor
meer informatie over het bewerken, evalueren, factoriseren en
vereenvoudigen van algebraïsche uitdrukkingen.

Gegevens organiseren in de rekenmachine

U kunt de gegevens in de rekenmachine organiseren door variabelen in een
directory-structuur op te slaan. De basis van de directory-structuur van de
rekenmachine is de HOME-directory die we hierna zullen bespreken.

De HOME-directory

U komt in de HOME-directory door – zo vaak als nodig – op de functie UPDIR
(„§) te drukken, totdat {HOME} in de tweede regel van de kop van het
beeldscherm verschijnt. U kunt ook op „ (vasthouden) §drukken. In dit
voorbeeld bevat de HOME-directory alleen de CASDIR. Door op J te
drukken, verschijnen de variabelen in de softmenutoetsen:

Blz. 2-9

Subdirectory's

Als u de gegevens in een goedgeorganiseerde directory-structuur wilt opslaan,
kunt u subdirectory’s aanmaken onder de HOME-directory, en meer
subdirectory’s binnen de subdirectory’s. Deze hiërarchie van directory’s lijkt
op de mapstructuur in een computer. U kunt de subdirectory’s namen geven
die weergeven wat er in elke subdirectory staat, of een andere willekeurige
naam. Raadpleeg hoofdstuk 2 in de gebruikshandleiding van de
rekenmachine voor meer informatie over het bewerken van directory’s.

Variabelen

Variabelen lijken op de bestanden in de harde schijf van een computer. Een
variabele kan een object (numerieke waarden, algebraïsche uitdrukkingen,
lijsten, vectoren, matrices, programma’s, enz.) opslaan. Variabelen hebben
namen die kunnen bestaan uit elke combinatie van alfabetische en numerieke
tekens, maar die moeten beginnen met een letter (Nederlands of Grieks). De
naam van een variabele mag ook enkele niet-alfabetische tekens bevatten,
zoals het pijltje (→), maar deze moeten wel met een alfabetisch teken worden
gecombineerd. ‘→A’ is dus een geldige variabelennaam, maar ‘→’ niet.
Geldige voorbeelden van variabelennamen zijn: ‘A’, ‘B’, ‘a’, ‘b’, ‘α’, ‘β’,
‘A1’, ‘AB12’, ‘A12’,’Vel’,’Z0’,’z1’, enz.

Een variabele kan niet dezelfde naam krijgen als een functie van de
rekenmachine. De volgende namen zijn gereserveerd voor de rekenmachine:
ALRMDAT, CST, EQ, EXPR, IERR, IOPAR, MAXR, MINR, PICT, PPAR, PRTPAR,
VPAR, ZPAR, der_, e, i, n1,n2, …, s1, s2, …, ΣDAT, ΣPAR, π, ∞.

Variabelen kunnen worden georganiseerd in subdirectory’s (raadpleeg
hoofdstuk 2 in de gebruikshandleiding van de rekenmachine).

Blz. 2-10

Variabelennamen invoeren

Als u variabelen wilt benoemen, moet u strings van letters achter elkaar
invoeren, mogelijk in combinatie met getallen. Om strings met tekens in te
voeren, kunt u het alfabetische toetsenbord als volgt vergrendelen:

~~ vergrendelt het alfabetische toetsenbord voor hoofdletters. Als het
toetsenbord op deze manier is vergrendeld, moet u op „ drukken voor
kleine letters, terwijl u op ‚ moet drukken om met een lettertoets een
speciaal teken te krijgen. Als het alfabetische toetsenbord al voor hoofdletters
is vergrendeld, kunt u het voor kleine letters vergrendelen met „~

~~„~ vergrendelt het toetsenbord voor kleine letters. Als het
toetsenbord op deze manier is vergrendeld, moet u op „ drukken om met
een lettertoets een hoofdletter te kunnen typen. Om de kleine letters te
ontgrendelen, drukt u op „~

Om de hoofdletters te ontgrendelen, drukt u op ~

Probeer de volgende oefeningen:

³~~math`
³~~m„a„t„h`
³~~m„~at„h`

de rekenmachine geeft het volgende weer (links de Algebraic-modus, rechts
de RPN-modus):

Blz. 2-11

Variabelen maken

De eenvoudigste manier om een variabele te maken is met K. De volgende
voorbeelden worden gebruikt om de variabelen in de volgende tabel op te
slaan (druk op J om het variabelenmenu te bekijken):

Naam Inhoud Type

α

A12 3×105 reëel

Q ‘r/(m+r)' algebraïsch

R [3,2,1] vector
z1 3+5i complex
p1 « → r 'π*r^2' » programma

• De Algebraic-modus

Zo slaat u de waarde –0.25 op in variabele α:

0.25\K~‚a. Het scherm ziet er als volgt zo
uit:

-0.25 reëel

Druk op ` om de variabele te maken. De variabele wordt nu
weergegeven in de labels van de softmenutoets:

Dit zijn de toetsencombinaties voor de overgebleven variabelen:

A12: 3V5K~a12`

Blz. 2-12

Q: ³~„r/„Ü
~„m+~„r™™K~q`

R: „Ô3‚í2‚í1™K~r`

z1: 3+5*„¥K~„z1` (Accepteer
wijziging naar de modus Complex als hierom wordt gevraagd).

p1: ‚å‚é~„r³„ì*
~„rQ2™™™K~„p1`..

Het scherm ziet er nu als volgt uit:

U ziet zes van de zeven variabelen die onder in het scherm worden
vermeld: p1, z1, R, Q, A12, α.

• De RPN-modus

(Gebruik H\@@OK@@ om naar de RPN-modus te wijzigen). Gebruik
de volgende toetsencombinaties om de waarde –0.25 in variabele α
op te slaan: 0.25\`~‚a`. Het scherm
ziet er nu als volgt uit:

Deze uitdrukking betekent dat de waarde –0.25 kan worden
opgeslagen in α. Druk op K om de variabele op te slaan. De
variabele wordt nu weergegeven in de labels van de softmenutoets:

Blz. 2-13

We kunnen de waarde 3×10

5

op een snellere manier invoeren in

A12: 3V5³~a12`K

Zo kunt u de inhoud van Q invoeren:

Q: ³~„r/„Ü
~„m+~„r™™³~q`K

We kunnen de waarde R nog sneller invoeren:

R: „Ô3#2#1™³K

De spatietoets (#) kan gebruikt worden om de elementen van een
vector in de RPN-modus van elkaar te scheiden in plaats van met een
komma (‚í die in de Algebraic-modus in het bovenstaande
voorbeeld is gebruikt.

z1: ³3+5*„¥³~„z1K

p1: ‚å‚é~„r³„ì*
~„rQ2™™™³~„p1™`K.

Het scherm ziet er nu als volgt uit:

U ziet zes van de zeven variabelen die onder in het scherm worden
vermeld: p1, z1, R, Q, A12, α.

Blz. 2-14

Inhoud van variabelen controleren

De eenvoudigste manier om de inhoud van een variabele te controleren, is
door op het label van de softmenutoets voor de variabele te drukken. Druk
bijvoorbeeld voor de variabelen die hierboven worden vermeld op de
volgende toetsen om de inhoud van de variabelen te bekijken:

De Algebraic-modus

Voer deze toetsencombinaties in: J@@z1@@ ` @@@R@@ `@@@Q@@@`. Het scherm
ziet er nu als volgt uit:

De RPN-modus In de RPN-modus hoeft u alleen op het label van de bijbehorende softmenutoetsen te drukken om de inhoud van een numerieke of algebraïsche variabele te bekijken. In dit geval kunnen we proberen of we de inhoud van de variabelen z1, R, Q, A12 en α kunnen bekijken, die we hierboven hebben aangemaakt:: J@@z1@@ @@@R@@ @@@Q@@ @@A12@@ @@ª@@

Het scherm ziet er nu als volgt uit:

Toets rechts-shift gevolgd door labels van softmenutoetsen gebruiken

Deze manier voor het bekijken van de inhoud van een variabele werkt precies
hetzelfde in de modi Algebraic en RPN. Probeer het volgende voorbeeld in
beide modi:

J‚@@p1@@ ‚ @@z1@@ ‚ @@@R@@ ‚@@@Q@@ ‚ @@A12@@

Blz. 2-15

Het scherm ziet er nu als volgt uit (links staat de Algebraic-modus, rechts de
RPN-modus)

U ziet dat de inhoud van programma p1 nu op het scherm worden
weergegeven. U kunt de overgebleven variabelen in deze directory zien met:

@@@ª@@ L ‚ @@@A@@

Inhoud van alle variabelen op het scherm weergeven

Met de toetsencombinaties ‚˜ kunt u de inhoud van alle variabelen op
het scherm weergeven. Bijvoorbeeld:

Druk op $ om naar het normale beeldscherm van de rekenmachine terug te
keren.

Variabelen verwijderen

De eenvoudigste manier om een variabele te verwijderen, is met de functie
PURGE. Deze functie is direct toegankelijk via het menu TOOLS (I) of via
het menu FILES „¡@@OK@@ .

De functie PURGE gebruiken in het stapelgeheugen in de Algebraic-modus

Onze lijst met variabelen bevat de variabelen p1, z1, Q, R en α. Met het
commando PURGE wordt variabele p1 verwijderd. Druk op

Blz. 2-16

I@PURGE@J@@p1@@ `. Het scherm laat nu zien dat variabele p1 is
verwijderd:

U kunt het commando PURGE gebruiken om meerdere variabelen te
verwijderen door de namen in een lijst in het argument van PURGE te
plaatsen. Als we bijvoorbeeld variabelen R en Q tegelijkertijd willen
verwijderen, kunnen we de volgende oefening proberen. Druk op:

I@PURGE@ „ä³J@@@R!@@ ™ ‚í³J@@@Q!@@

Het scherm geeft nu het volgende commando weer dat kan worden
uitgevoerd:

Druk op ` om het verwijderen van de variabelen te voltooien. Het scherm
geeft nu de overgebleven variabelen weer:

De functie PURGE gebruiken in het stapelgeheugen in de RPN­modus

We gaan er vanuit dat onze lijst met variabelen de variabelen p1, z1, Q, R
en α bevat. Met het commando PURGE wordt variabele p1 verwijderd. Druk
op ³@@p1@@ `I@PURGE@. Het scherm laat nu zien dan variabele p1 is
verwijderd:

Blz. 2-17

Om twee variabelen tegelijkertijd te verwijderen, bijvoorbeeld variabelen R
en Q, maken we eerst een lijst (in de RPN-modus hoeven de elementen in de
lijst niet te worden gescheiden door komma’s zoals in de Algebraic-modus).

J„ä³@@@R!@@ ™³@@@Q!@@ `

Druk vervolgens op I@PURGE@ om de variabelen te verwijderen.

Raadpleeg hoofdstuk 2 in de gebruikshandleiding van de rekenmachine voor
meer informatie over het bewerken van variabelen.

De functies UNDO en CMD

De functies UNDO en CMD zijn handig voor het oproepen van recent
gebruikte commando’s of om een handeling terug te draaien als er een fout is
gemaakt. Deze functies zitten onder de HIST-toets: UNDO wordt uitgevoerd
met de toetsen ‚¯, terwijl CMD wordt uitgevoerd met de
toetsencombinatie „®.

CHOOSE boxes en Soft-MENU

In sommige oefeningen in dit hoofdstuk hebben we menulijsten met
commando’s op het scherm gezien. Deze menulijsten noemen we ook wel
CHOOSE boxes. De volgende oefening is bedoeld om u te laten zien u hoe u
van CHOOSE boxes naar Soft-MENU’s en andersom kunt wijzigen.

Hoewel we geen specifiek voorbeeld gebruiken, laat deze oefening de twee
opties voor menu’s in de rekenmachine zien (CHOOSE boxes en soft­MENU’s). We gebruiken in deze oefening het commando ORDER om de
variabelen te sorteren in een directory. Dit wordt als volgt gedaan in ALG­modus:

„°˜ Toon menulijst PROG en selecteer MEMORY

Blz. 2-18

@@OK@@˜˜˜˜ Toon menulijst MEMORY en selecteer DIRECTORY

@@OK@@ —— Toon menulijst DIRECTORY en selecteer ORDER

@@OK@@ Activeer het commando ORDER

Er bestaat een andere manier om deze menu’s te openen met soft-MENU-
toetsen: door systeemvlag 117 in te stellen. (Raadpleeg hoofdstuk 2 en 24 in
de gebruikshandleiding van de rekenmachine voor meer informatie over
vlaggen). Probeer deze vlag als volgt in te stellen:

H @FLAGS! ———————

Het scherm geeft weer dat vlag 117 niet is ingesteld (CHOOSE boxes), zoals
u hier kunt zien:

Blz. 2-19

Druk op de softmenutoets @CHK@@ om vlag 117 in te stellen op soft MENU. U
ziet deze wijziging op het scherm:

Tweemaal op @@OK@@ drukken om naar het normale beeldscherm van de
rekenmachine terug te keren.

We proberen nu het commando ORDER te zoeken door gelijkwaardige
toetsencombinaties te gebruiken zoals hierboven. We beginnen met „°.
In plaats van een menulijst verschijnen er softmenulabels met verschillende
opties in het menu PROG:

Druk op B om softmenu MEMORY ()@@MEM@@) te selecteren. Het beeldscherm
zier er nu als volgt uit:

Druk op E om softmenu DIRECTORY )@@DIR@@) te selecteren.

Blz. 2-20

Het commando ORDER verschijnt niet in het scherm. We gebruiken de toets
L om het commando te zoeken:

We activeren het commando ORDER met de softmenutoets C(@ORDER).

Referenties

Raadpleeg hoofdstuk 2 in de gebruikshandleiding van de rekenmachine voor
meer informatie over het invoeren en bewerken van uitdrukkingen in het
beeldscherm of in de vergelijkingenschrijver. Raadpleeg Bijlage C in de
gebruikshandleiding van de rekenmachine voor CAS-instellingen (Computer
Algebraic System). Raadpleeg hoofdstuk 24 in de gebruikshandleiding van
de rekenmachine voor meer informatie over vlaggen.

Blz. 2-21

Hoofdstuk 3
Berekeningen met reële getallen

In dit hoofdstuk laten we het gebruik van de rekenmachine voor handelingen
en functies met betrekking tot reële getallen zien. We gaan er vanuit dat de
gebruiker bekend is met het toetsenbord zodat hij bepaalde functies op het
toetsenbord herkent (bijvoorbeeld SIN, COS, TAN, enz.). We gaan er ook
vanuit dat de lezer weet hoe hij het besturingssysteem van de rekenmachine
kan wijzigen (hoofdstuk 1), menu’s en kiesvakjes kan gebruiken (hoofdstuk 1)
en met variabelen kan werken (hoofdstuk 2).

Voorbeelden van berekeningen met reële getallen

Bij berekeningen met reële getallen kan het CAS het beste worden ingesteld
op de modus Real (en niet Complex). De modus Exact is de standaardmodus
voor de meeste handelingen. U kunt uw berekeningen dus het beste op deze
manier starten.
Hierna worden enkele handelingen met reële getallen geïllustreerd:

• Gebruik de toets \ om het merkteken van een getal te wijzigen.
Bijvoorbeeld in de ALG-modus, \2.5`.
In de RPN-modus bijvoorbeeld 2.5\.

• Gebruik de toets Y om de inversie van een getal te wijzigen.
Bijvoorbeeld in de ALG-modus Y2`.
Gebruik in de RPN-modus 4`Y.

• Gebruik voor optellen, aftrekken, vermenigvuldigingen en delingen

de juiste toets, namelijk +-*/.

Voorbeelden in de ALG-modus:

3.7+5.2`

6.3-8.5`

4.2*2.5`

2.3/4.5`

Blz. 3-1

Voorbeelden in de RPN-modus:

3.7` 5.2+

6.3` 8.5-

4.2` 2.5*

2.3` 4.5/

Daarnaast kunt u in de RPN-modus de operanden scheiden met een
spatie (#) voordat u op de operatortoets drukt. Voorbeelden:

3.7#5.2+

6.3#8.5-

4.2#2.5*

2.3#4.5/

• U kunt haakjes („Ü) gebruiken om handelingen te groeperen, of

om argumenten van functies in te sluiten.
In de ALG-modus:

„Ü5+3.2™/„Ü7-

2.2`

In de RPN-modus hoeft u geen haakjes te gebruiken, de berekening
wordt meteen in het stapelgeheugen uitgevoerd:

5`3.2`+7`2.2`-/

Door de uitdrukking tussen aanhalingstekens in te voeren, kunt u in de
RPN-modus de uitdrukking op dezelfde manier invoeren als in de
Algebraic-modus invoeren:

³„Ü5+3.2™/

„Ü7-2.2`µ

Voor zowel de ALG- als de RPN-modus kunt u de vergelijkingenschrijver
gebruiken:

‚O5+3.2™/7-2.2

Blz. 3-2

De uitdrukking kan worden geëvalueerd binnen de vergelijkingenschrijver
door het gebruik van:

————@EVAL@ of ‚—@EVAL@

• De absolute waardefunctie, ABS, wordt verkregen via „Ê.

Voorbeeld in de ALG-modus:

„Ê\2.32`

Voorbeeld in de RPN-modus:

2.32\„Ê

• De kwadraatfunctie, SQ, wordt verkregen via „º.

Voorbeeld in de ALG-modus:

„º\2.3`

Voorbeeld in de RPN-modus:

2.3\„º

De vierkantswortelfunctie, √, wordt verkregen via toets R. Bij het
berekenen van de stapel in de ALG-modus, moet u de functie voor het
argument invoeren. Bijvoorbeeld:

R123.4`

In de RPN-modus voert u eerst het getal in en daarna de functie.
Bijvoorbeeld:

123.4R

• De machtfunctie, ^, wordt verkregen via toets Q. Bij het berekenen

van de stapel in de ALG-modus, voert u de basis (y) in gevolgd door
de toets Q en daarna de exponent (x). Bijvoorbeeld:

Blz. 3-3

5.2Q1.25`

In de RPN-modus voert u eerst het getal in en daarna de functie.
Bijvoorbeeld:

5.2`1.25Q

• De wortelfunctie, XROOT(y,x), wordt verkregen via de

toetsencombinatie ‚». Bij het berekenen van de stapel in de
ALG-modus, moet u de functie XROOT gevolgd door de argumenten
(y,x) en gescheiden door komma’s invoeren. Bijvoorbeeld:

‚»3‚í27`

In de RPN-modus voert u eerst het argument y in, daarna x en als
laatste de functie. Bijvoorbeeld:

27`3‚»

• Logaritmen met natuurlijk grondtal 10 worden berekend met de

toetsencombinatie ‚Ã (functie LOG) terwijl de inverse functie
(ALOG of antilogaritme) wordt berekend met „Â. In de ALG­modus wordt de functie ingevoerd voor het argument:

‚Ã2.45`
„Â\2.3`

In de RPN-modus wordt het argument ingevoerd voor de functie:

2.45‚Ã

2.3\„Â

Tiende machten gebruiken om gegevens in te voeren

Tiende machten, dus getallen in de vorm –4,5×10-2, enz. worden ingevoerd
met de toets V. Voorbeeld in de ALG-modus:

\4.5V\2`

Of in de RPN-modus:

4.5\V2\`

Blz. 3-4

• Natuurlijke logaritmen worden berekend met ‚¹ (functie LN)

terwijl de exponentiële functie (EXP) wordt berekend met „¸. In
de ALG-modus wordt de functie voor het argument ingevoerd:

‚¹2.45`
„¸\2.3`

In de RPN-modus wordt het argument voor de functie ingevoerd:

2.45`‚¹

2.3\`„¸

• Er zijn drie trigonometrische functies in het toetsenbord beschikbaar:

sinus (S), cosinus (T) en tangens (U). De argumenten van
deze functies zijn hoeken in graden, radialen en decimale graden.
De volgende voorbeelden gebruiken hoeken in graden (DEG):

In de ALG-modus:

S30`
T45`

U135`

In de RPN-modus:

30S
45T

135U

• De inverse trigonometrische functies in het toetsenbord zijn de

boogsinus („¼), boogcosinus („¾) en boogtangens
(„À). Het antwoord van deze functies wordt gegeven in de
geselecteerde hoekmeting (DEG, RAD, GRD). Hieronder worden
enkele voorbeelden gegeven:

In de ALG-modus:

„¼0.25`
„¾0.85`
„À1.35`

Blz. 3-5

In de RPN-modus:

0.25„¼

0.85„¾

1.35„À

Alle functies die hierboven worden beschreven, ABS, SQ, √, ^, XROOT, LOG,
ALOG, LN, EXP, SIN, COS, TAN, ASIN, ACOS, ATAN, kunnen worden
gecombineerd met de fundamentele handelingen (+-*/) om zo
meer complexe uitdrukkingen te vormen. De vergelijkingenschrijver, die in
hoofdstuk 2 wordt beschreven, is ideaal voor het maken van deze
uitdrukkingen, ongeacht de bedieningsmodus van de rekenmachine.

Functies voor reële getallen in het menu MTH

Het menu MTH („´) bevat een aantal wiskundige functies die vooral
toepasbaar zijn op reële getallen. Met systeemvlag 117 ingesteld op de
standaardinstelling CHOOSE boxes (zie hoofdstuk 2), geeft het menu MTH de
volgende functies weer:

De functies zijn geordend op het argumenttype (1. vectoren, 2. matrices, 3.
lijsten, 7. waarschijnlijkheid, 9. complex) of op het functietype (4. hyperbolen,

5. reëel, 6. basis, 8. fft). Het bevat ook een invoer voor de wiskundige
constanten die beschikbaar zijn in de rekenmachine, invoer 10.

Let over het algemeen goed op het getal en de volgorde van de argumenten
die nodig zijn voor elke functie. Vergeet ook niet dat in de ALG-modus u eerst
de functie moet selecteren en daarna pas het argument moet invoeren. In de
RPN-modus moet u daarentegen eerst het argument in de stapel invoeren en
daarna de functie selecteren.

Rekenmachinemenu’s gebruiken:

Blz. 3-6

1. We bespreken hier uitvoerig het gebruik van het menu 4. HYPERBOLIC..
om zo de algemene werking van de rekenmachinemenu’s te laten zien.
Let goed op bij de procedure voor het selecteren van verschillende opties.

2. Om snel een van de genummerde opties in een menulijst (of CHOOSE
box) te selecteren, kunt u eenvoudig op het nummer voor de optie op het
toetsenbord drukken. Druk op 4 als u bijvoorbeeld optie 4.
HYPERBOLIC.. in het menu MTH wilt selecteren .

Hyperbolische functies en de tegenwaarden

Als u optie 4. HYPERBOLIC.. selecteert in het menu MTH en daarna op @@OK@@
drukt, verschijnt het menu voor hyperbolische functies:

In de ALG-modus is de toetsencombinatie voor bijvoorbeeld tanh(2.5) de
volgende:

„´4@@OK@@ 5@@OK@@ 2.5`

In de RPN-modus zijn de toetsencombinaties voor deze berekening de
volgende:

2.5`„´4@@OK@@ 5@@OK@@

De bovenstaande handelingen gaan er vanuit dat u de standaardinstelling
voor systeemvlag 117 (CHOOSE boxes) gebruikt. Als u de instelling van deze
vlag heeft gewijzigd (zie hoofdstuk 2) naar SOFT menu, wordt het menu MTH
als volgt weergegeven (links in de ALG-modus, rechts in de RPN-modus):

Blz. 3-7

Als u op L drukt, worden de overgebleven opties weergegeven:

Als u bijvoorbeeld het menu voor hyperbolische functies wilt selecteren, drukt
u met deze menuopmaak op )@@HYP@ en dan krijgt u:

Als u tenslotte bijvoorbeeld de functie hyperbolische tangens (tanh) wilt
selecteren, drukt u op @@TANH@.

N.B.: als u meer opties in deze softmenu’s wilt bekijken, drukt u op de toets
L of gebruikt u de toetsencombinatie „«.

Als u bijvoorbeeld tanh(2.5) in de ALG-modus wilt berekenen met de SOFT-
menu’s in plaats van de CHOOSE boxes, gaat u als volgt te werk:

„´@@HYP@ @@TANH@ 2.5`

In de RPN-modus wordt dezelfde waarde berekend met:

2.5`„´)@@HYP@ @@TANH@

Controleer als oefening van de toepassingen van hyperbolische functies de
volgende waarden:

SINH (2.5) = 6.05020.. ASINH(2.0) = 1.4436…
COSH (2.5) = 6.13228.. ACOSH (2.0) = 1.3169…
TANH(2.5) = 0.98661.. ATANH(0.2) = 0.2027…
EXPM(2.0) = 6.38905…. LNP1(1.0) = 0.69314….

Blz. 3-8

Handelingen met eenheden

De getallen in de rekenmachine kunnen worden ingesteld op eenheden. Het
is dus mogelijk om uitkomsten te berekenen met een consistent
eenhedensysteem en een uitkomst te produceren met de juiste
eenhedencombinatie.

Het menu UNITS

Het menu Units wordt geactiveerd met de toetsencombinatie
‚Û(behorend bij de toets 6). Als systeemvlag 117 is ingesteld op
CHOOSE boxes, wordt het volgende menu weergegeven:

Optie 1. Tools.. bevat functies die op eenheden werken (dit wordt later
besproken). Opties 2. Length.. tot en met 17.Viscosity.. bevatten menu’s met
een aantal eenheden voor de beschreven hoeveelheden. Als u bijvoorbeeld
optie 8. Force.. selecteert, wordt het volgende eenhedenmenu weergegeven:

Blz. 3-9

De gebruiker herkent de meeste eenheden (sommige eenheden, bijvoorbeeld
dyne, worden tegenwoordig niet meer vaak gebruikt) uit de lessen
natuurkunde. N = newton, dyn = dyne, gf = gramkracht (als onderscheid van
grammassa of gewoon gram, een massa-eenheid), kip = kilopond (1000
pond), lbf = pondkracht (als onderscheid van pondmassa), pdl = poundal.

Om een eenheidobject aan een getal te koppelen, moet het getal worden
gevolgd door een onderliggend streepje. Een kracht van 5 N wordt dus
ingevoerd als 5_N.

Voor uitgebreide handelingen met eenheden bieden SOFT-menu’s een
handigere manier voor het koppelen van eenheden. Wijzig systeemvlag 117
naar SOFT-menu’s (zie hoofdstuk 2) en gebruik de toetsencombinatie ‚Û
voor de volgende menu’s. Druk op L om naar de volgende menupagina te
bladeren.

Door op de juiste softmenutoets te drukken, wordt het submenu geopend met
eenheden voor die specifieke selectie. Voor het submenu @)SPEED zijn
bijvoorbeeld de volgende eenheden beschikbaar:

Door op de softmenutoets @)UNITS te drukken, keert u terug naar het menu
UNITS.

Blz. 3-10

We hebben al gezien dat u alle menulabels op het scherm kunt weergegeven
door middel van ‚˜. Voor de @)ENRG-verzameling eenheden worden de
volgende eenheden weergegeven:

N.B.: gebruik de toets L van de toetsencombinatie „«om door de
menu’s te bladeren.

Beschikbare eenheden

Raadpleeg hoofdstuk 3 in de gebruikshandleiding van de rekenmachine voor
een volledige lijst met beschikbare eenheden.

Eenheden aan getallen koppelen

Om een eenheidobject aan een getal te koppelen, moet het getal worden
gevolgd door een onderliggend streepje (‚Ý, toets (8,5)). Een kracht
van 5 N wordt dus ingevoerd als 5_N.

Hier de procedure om dit getal in te voeren in de ALG-modus, waarbij
systeemvlag 117 is ingesteld op CHOOSE boxes:

5‚Ý‚Û 8@@OK@@ @@OK@@ `

N.B.: als u het onderliggende streepje vergeet, bestaat het resultaat uit de
uitdrukking 5*N, waarbij N staat voor een mogelijke variabelennaam en niet
Newton.

Als u dezelfde hoeveelheid wilt invoeren met de rekenmachine in de RPN­modus, gebruikt u de volgende toetsencombinatie:

5‚Û8@@OK@@ @@OK@@

Blz. 3-11

Het onderliggende streepje wordt automatisch ingevoegd als de RPN-modus
actief is.

We laten u nu de toetsencombinatie zien voor het invoeren van eenheden
terwijl de optie SOFT-menu is geselecteerd. Deze combinatie geldt zowel voor
de ALG- als de RPN-modus. Gebruik bijvoorbeeld in de ALG-modus voor het
invoeren van de hoeveelheid 5_N:

5‚Ý‚ÛL @)@FORCE @ @@N@@`

Voor dezelfde hoeveelheid in de RPN-modus wordt de volgende
toetsencombinatie gebruikt:

5‚ÛL @)@FORCE @ @@N@@

N.B.: u kunt een hoeveelheid met eenheden invoeren door het onderliggende
streepje en de eenheden in te voeren met het ~-toetsenbord,
5‚Ý~n zal bijvoorbeeld het volgende opleveren: 5_N

Eenheidprefixen

U kunt prefixen invoeren voor eenheden aan de hand van de volgende tabel
met prefixen uit het SI-systeem. De afkorting van het prefix wordt eerst
gegeven, gevolgd door de naam en de exponent x in de factor 10

x

overeenkomstig elke prefix.

____________________________________________________
Prefix Naam x Prefix Naam x
____________________________________________________
Y yotta +24 d deci -1
Z zetta +21 c centi -2
E exa +18 m milli -3
P peta +15 µ micro -6
T tera +12 n nano -9
G giga +9 p pico -12
M mega +6 f femto -15

Blz. 3-12

k,K kilo +3 a atto -18
h,H hecto +2 z zepto -21
D(*) deka +1 y yocto -24
_____________________________________________________

(*) In het SI-systeem is dit prefix da en geen D. Gebruik D echter voor deka in
de rekenmachine.

Om deze prefixen in te voeren, typt u het prefix met het ~-toetsenbord in.
Gebruik bijvoorbeeld voor 123 pm (picometer):

123‚Ý~„p~„m

Als u UBASE (voer de naam in) gebruikt om te converteren naar de
standaardeenheid (1 m), krijgt u:

Handelingen met eenheden

Hier volgen enkele voorbeelden van berekeningen met de ALG-modus. Let er
wel op dat u bij vermenigvuldigingen en delingen met eenheden elke
hoeveelheid met de eenheden tussen haakjes moet zetten. Het product 12.5m
× 5.2 yd, moet als volgt worden ingevoerd: (12.5_m)*(5.2_yd) `

dit wordt weergegeven als 65_(m⋅yd). Als u eenheden wilt omzetten naar het
SI-systeem, moet u de functie UBASE gebruiken (u vindt deze functie met de
commandocatalogus, ‚N):

Blz. 3-13

N.B.: Let op: de variabele ANS(1) is beschikbaar via de toetsencombinatie

„î (behorend bij de toets `).

Als u een deling wilt berekenen, bijvoorbeeld 3250 mi / 50 h, voert u dit als
volgt in

(3250_mi)/(50_h) `

Omgezet in SI-eenheden, met de functie UBASE, geeft dit:

Optellen en aftrekken kan in de ALG-modus worden uitgevoerd zonder
haakjes te gebruiken. 5 m + 3200 mm kan bijvoorbeeld worden ingevoerd
als:

5_m + 3200_mm `.

Bij ingewikkeldere uitdrukkingen moet u wel haakjes gebruiken, bijvoorbeeld:

(12_mm)*(1_cm^2)/(2_s) `:

Bij stapelberekeningen in de RPN-modus hoeft u de verschillende termen niet
tussen haakjes te zetten. Bijvoorbeeld:

12 @@@m@@@ 1.5 @@yd@@ *

3250 @@mi@@ 50 @@@h@@@ /

Deze handelingen geven de volgende uitkomst:

Blz. 3-14

Eenheidconversies

Het menu UNITS bevat een submenu TOOLS met de volgende functies:

CONVERT(x,y): zet eenheidobject x om in eenheden van object y
UBASE(x): zet eenheidobject x om in SI-eenheden
UVAL(x): trekt de waarde van eenheidobject x af
UFACT(x,y): factoriseert eenheid y van eenheidobject x
UNIT(x,y): combineert de waarde van x met de eenheden van y

Voorbeelden van de functie CONVERT worden hieronder weergegeven.
Voorbeelden van de andere functies UNIT/TOOLS staan in hoofdstuk 3 van
de gebruikshandleiding van de rekenmachine.
Om bijvoorbeeld 33 watt om te zetten in calorie kunt u een van de volgende
invoeren gebruiken:

CONVERT(33_W,1_hp) `

CONVERT(33_W,11_hp) `

Fysische constanten in de rekenmachine

De fysische constanten van de rekenmachine staan in een constants library,
die met het commando CONLIB kan worden geactiveerd. Om dit commando
te activeren, voert u het volgende in het stapelgeheugen:
~~conlib` of u kunt het commando CONLIB als volgt uit de
commandocatalogus selecteren: Open eerst de catalogus met: ‚N~c.
Gebruik daarna de pijltjes omhoog en omlaag —˜ om CONLIB te
selecteren. Druk tenslotte op de softmenutoets F(@@OK@@). Druk indien nodig
op `. Gebruik de pijltjes omhoog en omlaag (—˜) om door de lijst
constanten in uw rekenmachine te bladeren.

De softmenutoetsen die bij het scherm CONSTANTS LIBRARY behoren,
bestaan onder meer uit de volgende functies:

Blz. 3-15

SI als deze functie is geselecteerd, worden de waarden van de
constanten in SI-eenheden weergegeven (*)
ENGL als deze functie is geselecteerd, worden de waarden van de
constanten in Engelse eenheden weergegeven (*)
UNIT als deze functie is geselecteerd, worden de constanten met
gekoppelde eenheden weergegeven (*)
VALUE als deze functie is geselecteerd, worden de constanten
zonder eenheden weergegeven
STK kopieert de waarde (met of zonder eenheden) naar de stapel
QUIT sluit de constantenbibliotheek af

(*) Wordt alleen geactiveerd als de optie VALUE is geselecteerd.

Zo ziet het bovenste deel van het scherm van de CONSTANTS LIBRARY eruit
als de optie VALUE is geselecteerd (eenheden in het SI-systeem):

, Druk op de optie @ENGL als u de waarden van de constanten in het Engelse
(Imperiaal) systeem wilt bekijken:

Als we de optie UNITS deselecteren (druk op @UNITS), worden alleen de
waarden weergegeven (in dit geval zijn de Engelse eenheden geselecteerd):

Blz. 3-16

Als u de waarde van Vm naar het stapelgeheugen wilt kopiëren, selecteert u
de naam van de variabele en drukt u op ²STK en daarna op @QUIT@. Als de
rekenmachine is ingesteld op ALG, ziet het scherm er als volgt uit:

Het beeldscherm geeft de zogenaamde gelabelde waarde weer,
Vm:359.0394. Hier is Vm de tag van deze uitkomst. Elke rekenkundige
handeling met dit getal zal de tag negeren. Probeer bijvoorbeeld:

‚¹2*„î `

dat geeft het volgende:

Voor dezelfde handeling in de RPN-modus is de volgende toetsencombinatie
vereist (nadat de waarde van Vm uit de constantenbibliotheek is opgehaald):

2`*‚¹

Functies definiëren en gebruiken

Gebruikers kunnen hun eigen functies definiëren door het commando DEFINE
te gebruiken dat via de toetsencombinatie „à wordt opgeroepen
(behorende bij de toets 2). De functie moet op de volgende manier worden
ingevoerd.

Functie_naam(argumenten) = uitdrukking_met_argumenten

Blz. 3-17

We kunnen bijvoorbeeld een eenvoudige functie definiëren

H(x) = ln(x+1) + exp(-x)

Stel dat u deze functie moet evalueren voor een aantal discrete waarden en u
wilt daarom het resultaat met een enkele toets kunnen oproepen, zonder dat u
de uitdrukking aan de rechterzijde voor elke afzonderlijke waarde hoeft in te
voeren. In het volgende voorbeeld gaan we er vanuit dat uw rekenmachine in
de ALG-modus staat. Voer de volgende toetsencombinatie in:

„à³~h„Ü~„x™‚Å

‚¹~„x+1™+„¸~„x`

Het scherm ziet er nu als volgt uit:

Door op de toets J te drukken, ziet u dat er een nieuwe variabele in uw
softmenutoets (@@@H@@) staat. Druk op ‚@@@H@@ als u de inhoud van deze
variabele wilt bekijken. Het scherm ziet er nu als volgt uit:

De variabele H bevat een programma dat wordt gedefinieerd door:

<<  x ‘LN(x+1) + EXP(x)’ >>

Dit is een eenvoudig programma in de standaard programmeertaal van de
serie HP 48 G, dat ook in de serie HP 49 G is opgenomen. Deze
programmeertaal heet UserRPL (zie hoofdstuk 20 en 21 in de
gebruikshandleiding van de rekenmachine). Het bovenstaande programma is
vrij eenvoudig en bestaat uit twee delen tussen de programmacontainers
<< >>:

Blz. 3-18

• Invoer:  x  x

• Proces: ‘LN(x+1) + EXP(x) ‘

Dit kan worden geïnterpreteerd als: voer een waarde in die tijdelijk de
aanduiding x krijgt (een zogenaamde lokale variabele), evalueer de
uitdrukking tussen aanhalingstekens die die locale variabele bevat en toon de
geëvalueerde uitdrukking.

U activeert de functie in de ALG-modus door de naam van de functie in te
voeren, gevolgd door het argument tussen haakjes, bijvoorbeeld
@@@H@@@ „Ü2`. Hieronder worden enkele voorbeelden weergegeven:

In de RPN-modus moet u het argument eerst invoeren om de functie te
activeren en daarna op de softmenutoets drukken die bij de variabelennaam
hoort @@@H@@@ . Probeer bijvoorbeeld het volgende: 2`@@@H@@@ . De andere
bovenstaande voorbeelden kunnen als volgt worden ingevoerd:

1.2`@@@H@@@ , 2`3/@@@H@@@ .

Referentie

Raadpleeg hoofdstuk 3 in de gebruikshandleiding voor meer informatie over
reële getallen met de rekenmachine.

Blz. 3-19

Hoofdstuk 4
Berekeningen met complexe getallen

In dit hoofdstuk laten wij voorbeelden zien van berekeningen en toepassingen
van functies voor complexe getallen.

Definities

Een complex getal z wordt geschreven als z = x + iy, (Cartesische vorm)
waarbij x en y reële getallen zijn en i de denkbeeldige eenheid is die wordt
gedefinieerd door i

denkbeeldig deel, y = Im(z). De polaire vorm van een complex getal is z = re
= r⋅cosθ + i r⋅sinθ, waarbij r = |z| =

2

= -1. Het getal heeft een reëel deel, x = Re(z) en een

22

yx + de modulus van het complexe

θ

i

getal z is, en θ = Arg(z) = arctan(y/x) het argument van het complexe getal z
is. De complexe geconjugeerde grootheid van een complex getal z = x + iy

θ

i

= re

, bestaat uitz = x – iy = re

θ

i

- re

, kan worden gezien als een weergave van z over de oorsprong.

θ

-i

. De negatieve waarde van z, –z = -x-iy =

De rekenmachine in de modus COMPLEX instellen

Om met complexe getallen te werken, moet u de modus CAS complex
selecteren.

H)@@CAS@˜˜™@CHK@@

De modus COMPLEX wordt geselecteerd als in het scherm CAS MODES de
optie _Complex aangevinkt is, dus

Druk twee keer op @@OK@@ om terug te keren naar de stapel.

Blz. 4-1

Complexe getallen invoeren

Complexe getallen kunnen in de rekenmachine op een van de twee
Cartesische weergaven worden ingevoerd, namelijk x+iy of (x,y). De
resultaten in de rekenmachine worden weergegeven in de opmaak geordend
paar, dus (x,y). Als de rekenmachine bijvoorbeeld in de ALG-modus staat,
wordt het complexe getal (3.5,-1.2) ingevoerd als:

„Ü3.5‚í\1.2`

Een complex getal kan ook worden ingevoerd in de vorm x+iy. In de ALG­modus wordt 3.5-1.2i ingevoerd als (accepteer moduswijzigingen):

3.5-1.2*„¥`

In de RPN-modus kunt u deze getallen invoeren met de volgende
toetsencombinatie:

„Ü3.5‚í1.2\`

(U ziet dat de toets verander-teken wordt ingevoerd na het cijfer 1.2. Dit is
dus anders dan bij de oefening in de ALG-modus) en

³3.5-1.2*„¥`

(U ziet dat u een apostrof moet invoeren voordat u het getal 3.5-1.2i in de
RPN-modus invoert).

Gebruik voor het invoeren van het denkbeeldige getal van de
eenheid :„¥(de toets I).

Polaire weergave van een complex getal

De polaire weergave van het complexe getal 3.5-1.2i, dat hierboven werd
ingevoerd, krijgt u door het coördinatenstelsel te wijzigen naar cilindrisch of
polair (met de functie CYLIN). U vindt deze functie in de catalogus (‚N).
U kunt de coördinaat ook naar POLAIR veranderen met H. Als u naar polaire

Blz. 4-2

coördinaat verandert met de hoekmeting in radialen, wordt het resultaat als
volgt weergegeven:

Het bovenstaande resultaat geeft een grootte, 3.7, en een hoek, 0.33029…
aan. Het hoeksymbool (∠) wordt voor de hoekmeting gegeven.

U keert terug naar Cartesische of rechthoekige coördinaten met de functie
RECT (deze staan in de catalogus, ‚N). Een complex getal in de polaire

θ

weergave wordt geschreven als z = r⋅e

i

. U kunt dit complexe getal in de
rekenmachine invoeren door een geordend paar in de vorm (r, ∠θ) te
gebruiken. Het hoeksymbool (∠) kan worden ingevoerd als ~‚6.
Het complexe getal z = 5.2e

1.5i

, kan als volgt worden ingevoerd (de
afbeeldingen geven het RPN-stapelgeheugen weer, voordat en nadat het getal
is ingevoerd):

Omdat het coördinatenstelsel is ingesteld op rechthoekig (of Cartesisch), zet
de rekenmachine het getal automatisch om in Cartesische coördinaten, dus x
= r cos θ, y = r sin θ, wat in dit geval resulteert in (0.3678…, 5.18…).

Als echter het coördinatenstelsel is ingesteld op cilindrische coördinaten (met
CYLIN), dan zal het invoeren van een complex getal (x,y), waarbij x en y
reële getallen zijn, een polaire weergave opleveren. Voer bijvoorbeeld in de
cilindrische coördinaten het getal (3.,2.) in. In de onderstaande afbeelding
ziet u het RPN-stapelgeheugen, voordat en nadat dit getal is ingevoerd.

Blz. 4-3

Eenvoudige handelingen met complexe getallen

Complexe getallen kunnen worden gecombineerd met vier fundamentele
handelingen (+-*/). De resultaten volgen de algebraregels onder
voorbehoud dat i
handelingen met reële getallen. Met de rekenmachine bijvoorbeeld in de
ALG-modus en het CAS ingesteld op Complex, kunt u de volgende oefening
uitvoeren:

2

= -1. Handelingen met complexe getallen lijken op

(3+5i) + (6-3i) = (9,2);

(5-2i) - (3+4i) = (2,-6)

(3-i)(2-4i) = (2,-14);

(5-2i)/(3+4i) = (0.28,-1.04)

1/(3+4i) = (0.12, -0.16) ;

-(5-3i) = -5 + 3i

De menu’s CMPLX

De rekenmachine bevat twee CMPLX-menu’s (CoMPLeXe getallen). Een is
toegankelijk via het menu MTH (zie hoofdstuk 3) en de ander is direct
toegankelijk via het toetsenbord (‚ß). Hierna worden de twee CMPLX­menu’s toegelicht.

Menu CMPLX via het menu MTH

We gaan er vanuit dat systeemvlag 117 is ingesteld op CHOOSE-boxes
(zie hoofdstuk 2). Het submenu CMPLX in het menu MTH wordt geactiveerd
met „´9@@OK@@. Dit zijn de beschikbare functies:

Het eerste menu (opties 1 tot en met 6) heeft de volgende functies:

Blz. 4-4

RE(z) : Reëel deel van een complex getal
IM(z) : Denkbeeldig deel van een complex getal

C→R(z) : Scheid een complex getal in het reële en het denkbeeldige deel
R→C(x,y) : Vormt het complexe getal (x,y) uit de reële getallen x en y

ABS(z) : Berekent de grootte van een complex getal.
ARG(z) : Berekent het argument van een complex getal.
SIGN(z) : Berekent een complex getal met eenheidgrootte als z/|z|.
NEG(z) : Wijzigt het merkteken van z
CONJ(z) : Produceert de complexe geconjugeerde grootheid van z
Hieronder volgen voorbeelden van toepassingen van deze functies in RECT­coördinaten. Vergeet niet dat in de ALG-modus de functie voor het argument
moet staan, terwijl in de RPN-modus het argument eerst moet worden
ingevoerd en daarna de functie moet worden geselecteerd. Deze functies kunt
u ook als softmenulabels krijgen door de instelling van systeemvlag 117 te
wijzigen (zie hoofdstuk 2). [Opmerking: niet alle lijnen zullen zichtbaar zijn
wanneer u klaar bent met de oefeningen in de volgende afbeeldingen.]

Menu CMPLX via het toetsenbord

Er kan een tweede CMPLX-menu geactiveerd worden via de optie rechts-shift
samen met de toets 1, dus ‚ß. Als systeemvlag 117 is ingesteld op
CHOOSE-boxes , verschijnt het toetsenbordmenu CMPLX als volgt op het
scherm:

Blz. 4-5

Het menu bevat enkele functies die we al ial eerder zijn behandeld, namelijk
ARG, ABS, CONJ, IM, NEG, RE en SIGN. Er is ook nog een functie i die
dezelfde functie heeft als de toetsencombinatie „¥.

Functies toegepast op complexe getallen

Veel functies via het toetsenbord en functies via het menu MTH die in
hoofdstuk 3 voor reële getallen zijn behandeld (bijvoorbeeld SQ, LN, e
enz.), kunnen worden toegepast op complexe getallen. Het resultaat is een
ander complex getal, zoals in de volgende voorbeelden wordt weergegeven.
[Opmerking: niet alle lijnen zullen zichtbaar zijn op het scherm van uw
rekenmachine wanneer u de oefeningen in de volgende afbeeldingen af hebt.]

x

,

Blz. 4-6

N.B.: Als u trigonometrische functies en hun tegenwaarden met complexe
getallen gebruikt, zijn de argumenten geen hoeken meer. De hoekmeting die
voor de rekenmachine is geselecteerd, heeft dus geen invloed meer op de
berekeningen van deze functies met complexe argumenten.

Functie DROITE: vergelijking van een rechte lijn

De functie DROITE heeft als argument twee complexe getallen, bijvoorbeeld
x

+iy1 en x2+iy2, en geeft de vergelijking van een rechte lijn, bijvoorbeeld y =

1

a+bx, die de punten (x
en B(6,2) kan bijvoorbeeld als volgt worden gevonden (voorbeeld in de
Algebraïsche modus):

) en (x2,y2) bevat. De lijn tussen de punten A(5,-3)

1,y1

U vindt de functie DROITE in de commandocatalogus (‚N). Met de
rekenmachine in APPROX-modus is het resultaat Y = 5.*(X-5.)-3.

Referentie

Raadpleeg hoofdstuk 4 in de gebruikshandleiding van de rekenmachine voor
meer informatie over handelingen met complexe getallen.

Blz. 4-7

Hoofdstuk 5
Algebraïsche en rekenkundige handelingen

Een algebraïsch object is elk getal, variabelennaam of algebraïsche
uitdrukking die behandeld, bewerkt en gecombineerd kan worden volgens de
regels van de algebra. Hier volgen voorbeelden van algebraïsche objecten:

• Een getal: 12.3, 15.2_m, ‘π’, ‘e’, ‘i’

• Een variabelennamen: ‘a’, ‘ux’, ‘breedte’, enz.

• Een uitdrukking: ‘p*D^2/4’,’f*(L/D)*(V^2/(2*g))’,

• Een vergelijking: ‘p*V = n*R*T’, ‘Q=(Cu/n)*A(y)*R(y)^(2/3)*√So’

Algebraïsche objecten invoeren

Algebraïsche objecten kunnen worden gemaakt door het object tussen enkele
aanhalingstekens direct in stapelniveau 1 te zetten of door de
vergelijkingenschrijver [EQW] te gebruiken. Met de volgende toetsencombinaties
wordt het algebraïsche object ‘π*D^2/4’ rechtstreeks in stapelniveau 1
ingevoerd:

³„ì*~dQ2/4`

Een algebraïsch object kan ook in de vergelijkingenschrijver worden gemaakt
en daarna naar het stapelgeheugen worden gestuurd of in de
vergelijkingenschrijver zelf worden berwerkt. WHet gebruik van de
vergelijkingenschrijver is in hoofdstuk 2 besproken. Bouw bij wijze van
oefening het volgende algebraïsche object op in de vergelijkingenschrijver:

Blz. 5-1

Druk nadat het object is aangemaakt op ` zodat het in het stapelgeheugen
wordt weergegeven (zowel de ALG- als RPN-modus worden weergegeven):

Eenvoudige handelingen met algebraïsche objecten

Algebraïsche objecten kunnen worden opgeteld, afgetrokken,
vermenigvuldigd, gedeeld (behalve door nul), tot een macht worden verheven,
als argumenten voor een aantal standaardfuncties worden gebruikt
(exponentieel, logaritme, trigonometrie, hyperbolisch, enz.), net als bij elk reël
of complex getal. Om de basishandelingen met algebraïsche objecten te laten
zien, maken we een aantal objecten, bijvoorbeeld ‘π*R^2’ en ‘g*t^2/4’, en
slaan we zo op in variabelen A1 en A2 (zie hoofdstuk 2 over het aanmaken
van variabelen en het opslaan van waarden in variabelen). Dit zijn de
toetsencombinaties voor het opslaan van variabelen A1 in de ALG-modus:

³„ì*~rQ2™K~a1`

Het resultaat:

De toetsencombinaties voor de RPN-modus zijn:

„ì~r`2Qx ~a1 K

Als u de variabele A2 heeft opgeslagen en op de toets heeft gedrukt, geeft
het scherm de variabelen als volgt weer:

Blz. 5-2

In de ALG-modus laat de volgende toetsencombinatie een aantal handelingen
zien met de algebraïsche functies behorende bij variabelen @@A1@@en@@A2@@ (druk
op J voor het variabelenmenu):

@@A1@@ + @@A2@@ ` @@A1@@ - @@A2@@ `

@@A1@@ * @@A2@@ ` @@A1@@ / @@A2@@ `

‚¹@@A1@@ „¸@@A2@@

U krijgt dezelfde resultaten in de RPN-modus als u de volgende
toetsencombinaties gebruikt:

Blz. 5-3

@@A1@ ` @@A2@@ + @@A1@@ ` @@A2@@ -

@@A1@@ ` @@A2@@ * @@A1@@ ` @@A2@@ /

@@A1@@ ` ‚¹ @@A2@@ ` „¸

Functies in het menu ALG

Het menu ALG (Algebraïsch) wordt geactiveerd met de toetsencombinatie
‚×(behorend bij de toets 4). Met systeemvlag 117 ingesteld op de
CHOOSE-boxes biedt het menu ALG de volgende functies:

We zullen niet alle beschrijvingen van de functies in deze handleiding geven.
De gebruiker kan deze vinden in de helptekst van de rekenmachine. I
L @)HELP@ ` . Voer de eerste letter van de functie in als u een bepaalde
functie zoekt. Voor de functie COLLECT moet bijvoorbeeld ~c ingevoerd
worden. Daarna gebruiken we de pijltjes omhoog en omlaag, —˜, om
COLLECT in het helpvenster te zoeken.

Druk op @@OK@@ om de handeling te voltooien. Dit is het helpscherm voor de
functie COLLECT:

U ziet onder in het scherm de regel See EXPAND FACTOR staan, hier worden
de koppelingen naar andere helpteksten en de functies EXPAND en FACTOR
weergegeven. Als u meteen naar deze items wilt, drukt u op softmenutoets
@SEE1! voor EXPAND en @SEE2! voor FACTOR. Als u bijvoorbeeld op @SEE1! drukt,

Blz. 5-4

krijgt u de volgende informatie voor EXPAND, terwijl @SEE2! informatie voor
FACTOR geeft:

Kopieer de voorbeelden naar uw stapelgeheugen door op @ECHO! te drukken.
Voor EXPAND hierboven drukt u op softmenutoets @ECHO! om het volgende
voorbeeld naar het stapelgeheugen te kopiëren (druk op ` om het
commando uit te voeren):

Verder laten we de gebruiker zelf de toepassingen van de functies in het
menu ALG verkennen. Dit is een lijst met de commando’s:

Voor de functie SUBST vinden we de volgende CAS-helptekst:

Blz. 5-5

N.B.: als u deze of andere functies in de RPN-modus gebruikt, moet u het
argument eerst invoeren en daarna de functie. Het voorbeeld voor
TEXPAND wordt in de RPN-modus als volgt ingevoerd:

³„¸+~x+~y`

Selecteer nu functie TEXPAND uit menu ALG (of direct uit de catalogus
‚N) om de handeling te voltooien.

Handelingen met transcendente functies

De rekenmachine biedt een aantal functies die kunnen worden gebruikt om
uitdrukkingen met logaritmische & exponentiële functies („Ð) en
trigonometrische functies (‚Ñ) te vervangen.

Uitbreiding en factorisering met log-exp-functies

De toets „ Ð geeft het volgende menu weer:

Informatie over en voorbeelden van deze commando’s staan in de helptekst
van de rekenmachine. De beschrijving van EXPLN wordt bijvoorbeeld aan de
linkerzijde weergegeven en het voorbeeld van de helptekst aan de
rechterzijde:

Uitbreiding en factorisering met trigonometrische functies

Blz. 5-6

Het menu TRIG, dat wordt opgeroepen met ‚Ñ, geeft de volgende
functies weer:

Met deze functies kunt u uitdrukkingen vereenvoudigen door de ene categorie
trigonometrische functies te vervangen door een andere. Met de functie
ACOS2S kunt u bijvoorbeeld de functie boogcosinus (acos(x)) vervangen
door de uitdrukking van boogsinus (asin(x)).

De beschrijving van deze commando’s en voorbeelden van hun toepassingen
staan in de helptekst van de rekenmachine (IL@HELP). De gebruiker kan
deze helpteksten gebruiken voor informatie over de commando’s in het menu
TRIG.

Functies in het menu ARITHMETIC

Het menu ARITHMETIC wordt geactiveerd met de toetsencombinatie „Þ
(behorend bij de toets 1). Met systeemvlag 117 ingesteld op CHOOSE-
boxes, wordt met „Þ het volgende menu weergegeven:

Blz. 5-7

In deze menulijst komen opties 5 tot en met 9 (DIVIS, FACTORS, LGCD,
PROPFRAC, SIMP2) overeen met veelgebruikte functies die van
toepassing zijn op hele getallen of op polynomen. De andere opties (1.
INTEGER, 2. POLYNOMIAL, 3. MODULO en 4. PERMUTATION) zijn

eigenlijk submenu's van functies die van toepassing zijn op specifieke
wiskundige objecten. Met systeemvlag 117 ingesteld op SOFT-menu’s,
wordt het menu ARITHMETIC („Þ) als volgt weergegeven:

In het volgende voorbeeld wordt de helptekst voor de functies FACTORS en
SIMP2 in het menu ARITHMETIC weergegeven.

FACTOREN: SIMP2:

De functies van de submenu’s ARITHMETIC: INTEGER, POLYNOMIAL,
MODULO en PERMUTATION, worden behandeld in Hoofdstuk 5 van de
gebruikshandleiding van de rekenmachineDe volgende secties laten enige
toepassingen op polynomen en breuken zien.

Polynomen

Polynomen zijn algebraïsche uitdrukkingen die uit een of meer termen bestaan
met afnemende machten van een bepaalde variabele. ‘X^3+2*X^2-3*X+2’ is
bijvoorbeeld een polynoom van de derde orde in X, terwijl ‘SIN(X)^2-2’ een
polynoom van de tweede orde SIN(X) is. De functies COLLECT en EXPAND
kunnen worden toegepast voor polynomen, zoals we eerder lieten zien.
Andere toepassingen van de polynome functies worden hieronder
weergegeven:

Blz. 5-8

De functie HORNER

De functie HORNER („Þ, POLYNOMIAL, HORNER) geeft de Horner­deling, of de synthetische deling, van een polynoom P(X) met de factor (X-a),
dus HORNER(P(X),a) = {Q(X), a, P(a)}, waarbij P(X) = Q(X)(X-a)+P(a).
Bijvoorbeeld:

HORNER(‘X^3+2*X^2-3*X+1’,2) = {X^2+4*X+5 2 11}

3

dus, X

+2X2-3X+1 = (X2+4X+5)(X-2)+11. Ook,

HORNER(‘X^6-1’,-5)=

{ X^5-5*X^4+25*X^3-125*X^2+625*X-3125 -5 15624}

dus, X

6

-1 = (X5-5*X4+25X3-125X2+625X-3125)(X+5)+15624.

De variabele VX

De meeste polynome voorbeelden hierboven zijn geschreven met variabele X.
De reden hiervoor is dat een variabele VX bestaat in de directory {HOME
CASDIR}van de rekenmachine die die standaard de waarde van ‘X’
aanneemt. Dit is de naam van de gewenste onafhankelijke variabele voor
algebraïsche en calculustoepassingen Gebruik de variabele VX liever niet in
uw programma’s of vergelijkingen, om niet in de war te raken met de CAS’
VX. Raadpleeg bijlage C in de gebruikshandleiding van de rekenmachine
voor meer informatie over de CAS-variabele.

De functie PCOEF

Bij een reeks met de wortels van een polynoom zal de functie PCOEF een
reeks genereren met de coëfficiënten van de bijbehorende polynomen. De
coëfficiënten komen overeen met de aflopende volgorde van de
onafhankelijke variabele. Bijvoorbeeld:

PCOEF([-2, –1, 0 ,1, 1, 2]) = [1. –1. –5. 5. 4. –4. 0.],

Blz. 5-9

welke de polynoom X6-X5-5X4+5X3+4X2-4X weergeeft.

De functie PROOT

Bij een reeks met de coëfficiënten van een polynoom, in aflopende volgorde,
zal de functie PROOT de wortels van de polynoom geven. Voorbeeld van

2

X

+5X+6 =0, PROOT([1, –5, 6]) = [2. 3.].

De functies QUOT en REMAINDER

De functies QUOT en REMAINDER geven respectievelijk het quotiënt Q(X) en
de rest R(X), het resultaat van de deling van twee polynomen, P
Ze leveren met andere woorden de waarden Q(X) en R(X) van P
Q(X) + R(X)/P

Dat kunnen we als volgt schrijven: (X

N.B.: u kunt het laatste resultaat krijgen met PARTFRAC:

(X). Bijvoorbeeld:

2

QUOT(‘X^3-2*X+2’, ‘X-1’) = ‘X^2+X-1’

REMAINDER(‘X^3-2*X+2’, ‘X-1’) = 1.

PARTFRAC(‘(X^3-2*X+2)/(X-1)’) = ‘X^2+X-1 + 1/(X-1)’.

(X) en P2(X).

1

(X)/P2(X) =

1

3

-2X+2)/(X-1) = X2+X-1 + 1/(X-1).

De functie PEVAL

De functie PEVAL (Polynome EVALuatie) kan worden gebruikt om een
polynoom te evalueren

p(x) = a

⋅xn+a

n

met een reeks coëfficiënten [a
resultaat is de evaluatie p(x

0

menu ARITHMETIC, gebruik in plaats daarvan het CALC/DERIV&INTEG-Menu.
Voorbeeld: PEVAL([1,5,6,1],5) = 281.
Raadpleeg hoofdstuk 5 in de gebruikshandleiding van de rekenmachine voor
aanvullende toepassingen van polynome functies.

n-1

⋅x

+ …+ a2⋅x2+a1⋅x+ a0,

n-1

, a

, … a2, a1, a0] en een waarde van x0. Het

n

n-1

). De functie PEVAL is niet beschikbaar in het

Blz. 5-10

Breuken

Breuken kunnen worden uitgebreid en gefactoriseerd met de functies EXPAND
en FACTOR uit het menu ALG (‚×). Bijvoorbeeld:

EXPAND(‘(1+X)^3/((X-1)*(X+3))’) = ‘(X^3+3*X^2+3*X+1)/(X^2+2*X-3)’
EXPAND(‘(X^2*(X+Y)/(2*X-X^2)^2’) = ‘(X+Y)/(X^2-4*X+4)’

FACTOR(‘(3*X^3-2*X^2)/(X^2-5*X+6)’) = ‘X^2*(3*X-2)/((X-2)*(X-3))’
FACTOR(‘(X^3-9*X)/(X^2-5*X+6)’ ) = ‘X*(X+3)/(X-2)’

De functie SIMP2

De functie SIMP2 In het menu ARITHMETIC neemt als argumenten twee
getallen of polynomen die de teller en de noemer van een rationele breuk
weergeven en geeft een vereenvoudigde teller en noemer. Bijvoorbeeld:

De functie PROPFRAC

De functie PROPFRAC zet een rationele breuk om in een “echte” breuk, d.w.z.
er wordt een integer deel toegevoegd aan een breukdeel als deze
decompositie mogelijk is. Bijvoorbeeld:

De functie PARTFRAC

De functie PARTFRAC splitst een rationele breuk op in gedeeltelijke breuken
die de originele breuk vormen. Bijvoorbeeld:

PARTFRAC(‘(2*X^6-14*X^5+29*X^4-37*X^3+41*X^2-16*X+5)/(X^5­7*X^4+11*X^3-7*X^2+10*X)’) =
‘2*X+(1/2/(X-2)+5/(X-5)+1/2/X+X/(X^2+1))’

SIMP2(‘X^3-1’,’X^2-4*X+3’) = { ‘X^2+X+1’,‘X-3’}

PROPFRAC(‘5/4’) = ‘1+1/4’

PROPFRAC(‘(x^2+1)/x^2’) = ‘1+1/x^2’

Blz. 5-11

De functie FCOEF

De functie FCOEF, beschikbaar via het ARITHMETIC/POLYNOMIAL-menu
wordt gebruikt om een rationele breuk te krijgen met de wortels en polen van
de breuk.

N.B.: als een rationele breuk wordt gegeven als F(X) = N(X)/D(X), zijn de
wortels van de breuk het resultaat van de oplossing van de vergelijking N(X)
= 0, terwijl de polen het resultaat zijn van de vergelijking D(X) = 0.

De invoer voor de functie is een vector met de wortels gevolgd door hun
veelvoud (d.w.z. hoe vaak een bepaalde wortel wordt herhaald), en de polen
gevolgd door hun veelvoud die als een negatief getal wordt weergegeven.
Als we bijvoorbeeld een breuk willen maken die wortels heeft van 2 met
veelvoud 1, 0 met veelvoud 3 en -5 met veelvoud 2, en polen 1 met veelvoud
2 en –3 met veelvoud 5, gebruiken we:
FCOEF([2,1,0,3,–5,2,1,-2,-3,-5]) = ‘(X--5)^2*X^3*(X-2)/(X--3)^5*(X-1)^2’

Als u drukt op µ„ î (of simpelweg µ, in RPN modus), krijgt u:

‘(X^6+8*X^5+5*X^4-50*X^3)/(X^7+13*X^6+61*X^5+105*X^4-45*X^3­297*X62-81*X+243)’

De functie FROOTS

De functie FROOTS, in het ARITHMETIC/POLYNOMIAL-menu, bevat de
wortels en polen van een breuk. Als we bijvoorbeeld de functie FROOTS
zouden toepassen op het bovenstaande resultaat, zouden we het volgende
krijgen:[1 –2. –3 –5. 0 3. 2 1. –5 2.]. Het resultaat laat de polen gevolgd
door hun veelvoud zien als een negatief getal, en de wortels gevolgd door
hun veelvoud als een positief getal. In dit geval zijn de polen (1, -3) met de
respectievelijke veelvouden (2,5) en de wortels zijn (0, 2, -5) met de
respectievelijke veelvouden (3, 1, 2).

Een ander voorbeeld: FROOTS(‘(X^2-5*X+6)/(X^5-X^2)’) = [0 –2. 1 –1. 3 1.
2 1.], dus polen = 0 (2), 1(1), en wortels = 3(1), 2(1). Als de modus Complex
was geselecteerd, zouden de resultaten als volgt zijn:

Blz. 5-12

[0 –2. 1 –1. ‘-((1+i*√3)/2’ –1. ‘-((1-i*√3)/2’ –1.].

Stapsgewijze handelingen met polynomen en breuken

Als we de CAS-modi instellen op Stap/stap, geeft de rekenmachine
vereenvoudigde breuken of handelingen met polynomen stap voor stap weer.
Dit is bijzonder handig bij het bekijken van de stappen van een synthetische
deling. Het voorbeeld van de volgende deling.

23

2

−

X

wordt in detail weergegeven in bijlage C in de gebruikshandleiding van de
rekenmachine. Het volgende voorbeeld geeft een langere synthetische deling
weer(DIV2 is beschikbaar in het ARITH/POLYNOMIAL-menu):

9

1

−

X

2

1

−

X

235

−+−

XXX

Blz. 5-13

Referentie

Raadpleeg hoofdstuk 5 in de gebruikshandleiding van de rekenmachine voor
meer informatie, definities en voorbeelden van algebraïsche en rekenkundige
handelingen.

Blz. 5-14

Hoofdstuk 6
Het oplossen van vergelijkingen

Aan de 7 toets zijn twee functiemenu's verbonden voor het oplossen van
vergelijkingen. De Symbolische SOLVer („Î) en de NUMerieke SoLVer
(‚Ï). Hieronder laten we enkele van de functies in deze menu’s zien.

Symbolische oplossing van algebraïsche vergelijkingen

Hier beschrijven we enkele van de functies van het Symbolische Solver-menu.
Activeer het menu met de toetsaanslagcombinatie „Î. Met systeemvlag
117 ingesteld op de CHOOSE-boxes zijn de volgende menulijsten
beschikbaar:

De functies ISOL en SOLVE kunnen worden gebruikt om elke onbekende
parameter in een polynome vergelijking op te lossen. De functie SOLVEXX lost
een polynome vergelijking op waarin de onbekende parameter de standaard
CAS variabele VX is (meestal ingesteld als ‘X’). De functie ZEROS tenslotte
verschaft de nullen, of wortels, van een polynome vergelijking.

De functie ISOL

De functie ISOL (vergelijking, variabele) geeft de oplossing(en) voor een
Vergelijking door de variabele te isoleren. Voorbeeld: met de rekenmachine
in de ALG-modus, kunnen we het volgende gebruiken om t in de vergelijking

3

at

-bt = 0 op te lossen:

Blz. 6-1

In de RPN-modus wordt de oplossing bereikt door de vergelijking in het
stapelgeheugen in te voeren gevolgd door de variabele, alvorens de ISOL
functie te activeren. Net voor de uitvoering van ISOL dient het RPN­stapelgeheugen er net als in de linkerafbeelding uit te zien. Na het toepassen
van de functie ISOL wordt het resultaat zoals in de rechterafbeelding:

Het eerste argument in ISOL kan een uitdrukking zijn, zoals hierboven, of een
vergelijking. Probeer bijvoorbeeld het volgende in de ALG-modus:

N.B.: gebruik ‚Å (verbonden aan de toets \) om het isgelijkteken (=)
in een vergelijking in te voeren.

Hetzelfde probleem kan worden opgelost in de RPN-modus zoals in de
onderstaande afbeelding (de afbeeldingen tonen het RPN-stapelgeheugen
voor en na toepassing van de functie ISOL):

De functie SOLVE

De functie SOLVE heeft dezelfde samenstelling als de functie ISOL, behalve
dat SOLVE ook kan worden gebruikt om een reeks polynome vergelijkingen

Blz. 6-2

op te lossen. De helptekst voor de functie SOLVE, met de oplossing op de
vergelijking X^4 – 1 = 3 wordt hieronder weergegeven:

De volgende voorbeelden laten het gebruik van de functie SOLVE in de RPN­en ALG-modi zien (Gebruik de Complexe modus in de CAS). [Opmerking:
niet alle lijnen zullen zichtbaar zijn wanneer u klaar bent met de oefeningen
in de volgende afbeeldingen.]

De schermweergave hierboven geeft twee oplossingen weer. In de eerste, β
5β =125, geeft SOLVE geen oplossingen { }. In de tweede, β

4

- 5β = 6, geeft

4

-

SOLVE vier oplossingen in de laatste uitvoerregel. De allerlaatste oplossing is
niet zichtbaar omdat het resultaat langer is dan de breedte van het scherm
van de rekenmachine. Maar u kunt alle oplossingen bekijken door de pijltoets
naar beneden (˜) te gebruiken. Deze activeert de regeleditor (deze
bewerking kan gebruikt worden om uitvoerregels te zien die breder zijn dan
het scherm van de rekenmachine):

De corresponderende RPN-schermen voor deze twee voorbeelden, voor en na
toepassing van de functie SOLVE, ziet u hieronder:

Blz. 6-3

De functie SOLVEVX

De functie SOLVEVX lost een vergelijking voor de standaard CAS-variabele
op in de voor de variabele gereserveerde naam VX. Standaard is deze
variabele ingesteld op ‘X’. Voorbeelden waarin de ALG-modus met VX=’X’
wordt gebruikt, ziet u hieronder:

In het eerste geval kon SOLVEVX geen oplossing vinden. In het tweede geval
vond SOLVEVX één oplossing, X=2.

De volgende schermen tonen het RPN-stapelgeheugen voor het oplossen van
de hierboven getoonde voorbeelden (voor en na toepassing van SOLVEVX):

Blz. 6-4

De functie ZEROS

De functie ZEROS vindt de oplossingen van een polynome vergelijking
zonder de veelvoud te tonen. De functie vereist als invoer de uitdrukking voor
de vergelijking en de naam van de variabele die opgelost moet worden.
Voorbeelden in de ALG-modus ziet u hieronder:

Voer eerste de polynome uitdrukking in, dan de op te lossen variabele en
vervolgens de functie ZEROS om deze functie in de RPN-modus te gebruiken.
De volgende schermweergaven geven het RPN-stapelgeheugen weer voor en
na toepassing van ZEROS op de twee voorbeelden hierboven (Gebruik
Complex-modus in de CAS):

De Symbolische Solver-functies hierboven geven oplossingen voor rationele
vergelijkingen (voornamelijk polynome vergelijkingen). Indien de op te lossen
vergelijking alleen numerieke coëfficiënten heeft, is een numerieke oplossing
mogelijk met behulp van de Numerieke Solver van de rekenmachine.

Menu van de Numerieke solver

De rekenmachine biedt een zeer krachtige omgeving voor het oplossen van
enkele algebraïsche of transcendente vergelijkingen. Voor toegang tot deze

Blz. 6-5

omgeving activeren we de numerieke solver (NUM.SLV) met ‚Ï. Nu
verschijnt een drop-downmenu met de volgende opties:

Hieronder laten we achtereenvolgens de toepassing zien van de items 3.
Solve poly.., 5. Solve finance en 1. Solve equation... Appendix 1-A in de
gebruikshandleiding van de rekenmachine bevat instructies voor het gebruik
van invoerschermen met voorbeelden voor de numerieke solvertoepassingen.
Item 6. MSLV (Meervoudige vergelijking SoLVer) wordt verderop op pagina
6-10 behandeld.

N.B.:

1. Wanneer een oplossing wordt gevonden voor een waarde m.b.v. de
NUM.SLV-toepassingen, wordt deze geplaatst in het stapelgeheugen. Dit is
handig indien u die waarde nodig heeft voor andere bewerkingen.

2. Er zullen een of meer variabelen aangemaakt worden wanneer u enkele
van de toepassingen in het NUM.SLV-menu activeert.

Polynome Vergelijkingen

Met de Solve poly… -optie in de SOLVE-omgeving van de rekenmachine kunt
u:

(1) de oplossingen voor een polynome vergelijking vinden
(2) de coëfficiënten van de polynoom met een gegeven aantal wortels krijgen,

en

(3) een algebraïsche uitdrukking voor de polynoom als een functie van X

krijgen

Blz. 6-6