GE 6000 User Manual

Download

GE Consumer & Industrial

ISO9001:2000

Multilin

EPM 6000 Multi-function Power

Metering System

Chapter 1:

EPM 6000 Instruction Manual

Software Revision: 4.5

Manual P/N: 1601-0215-A4 Manual Order Code: GEK-106558C

GE Multilin

215 Anderson Avenue, Markham, Ontario

Canada L6E 1B3

Tel: (905) 294-6222 Fax: (905) 201-2098

Internet:

*1601-0215-A4*

http://www.GEmultilin.com

LISTED

GE Multilin's Quality

Management System is

registered to ISO9001:2000

QMI # 005094

Table of Contents

1: OVERVIEW INTRODUCTION ................................................................................................................................ 1-1

ESCRIPTION ........................................................................................................................ 1-1

IGHLIGHTS ......................................................................................................................... 1-1

FEATURES ............................................................................................................................................ 1-3

NIVERSAL VOLTAGE INPUTS ............................................................................................ 1-3

URRENT INPUTS ................................................................................................................. 1-3

TILITY PEAK DEMAND .......................................................................................................1-3

EASURED VALUES ............................................................................................................ 1-4

ORDERING ........................................................................................................................................... 1-5

RDER CODES ..................................................................................................................... 1-5

SPECIFICATIONS ............................................................................................................................... 1-6

NPUTS/OUTPUTS ................................................................................................................ 1-6

ETERING ............................................................................................................................. 1-6

NVIRONMENTAL ................................................................................................................. 1-7

OMMUNICATIONS .............................................................................................................. 1-7

ECHANICAL PARAMETERS ................................................................................................ 1-7

PPROVALS ........................................................................................................................... 1-8

2: ELECTRICAL BACKGROUND

THREE-PHASE POWER MEASUREMENT .................................................................................2-1

ESCRIPTION ........................................................................................................................ 2-1

THREE-PHASE SYSTEM CONFIGURATIONS ........................................................................... 2-2

ESCRIPTION ........................................................................................................................ 2-2

YE CONNECTION .............................................................................................................. 2-2

ELTA CONNECTION ........................................................................................................... 2-4

LONDELL'S THEOREM AND THREE-PHASE MEASUREMENT ........................................2-5

POWER, ENERGY, AND DEMAND .............................................................................................. 2-8

ESCRIPTION ........................................................................................................................ 2-8

OWER .................................................................................................................................. 2-8

NERGY ................................................................................................................................. 2-8

EMAND ...............................................................................................................................2-10

REACTIVE ENERGY AND POWER FACTOR ............................................................................. 2-12

EAL, REACTIVE, AND APPARENT POWER ........................................................................ 2-12

OWER FACTOR ................................................................................................................... 2-13

HARMONIC DISTORTION ..............................................................................................................2-14

ARMONICS OF A NON-SINUSOIDAL WAVEFORM ......................................................... 2-14

NDUCTIVE AND CAPACITIVE IMPEDANCE ......................................................................... 2-15

OLTAGE AND CURRENT MONITORING ............................................................................ 2-15

AVEFORM CAPTURE .........................................................................................................2-16

POWER QUALITY .............................................................................................................................. 2-17

ESCRIPTION ........................................................................................................................ 2-17

3: INSTALLATION MECHANICAL INSTALLATION .....................................................................................................3-1

IMENSIONS ......................................................................................................................... 3-1

D ANSI I

NSTALLATION STEPS ............................................................................................... 3-2

DIN I

NSTALLATION STEPS .................................................................................................. 3-3

ELECTRICAL INSTALLATION ......................................................................................................... 3-5

EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE TOC–1

INSTALLATION CONSIDERATIONS ....................................................................................... 3-5

CT L

EADS TERMINATED TO METER ...................................................................................3-6

CT L

EADS PASS-THROUGH (NO METER TERMINATION) ................................................ 3-6

UICK CONNECT CRIMP CT TERMINATIONS ................................................................... 3-7

OLTAGE AND POWER SUPPLY CONNECTIONS .............................................................. 3-7

ROUND CONNECTIONS ....................................................................................................3-8

WIRING DIAGRAMS .........................................................................................................................3-9

ESCRIPTION ........................................................................................................................ 3-9

YE, 4-WIRE WITH NO PTS AND 3 CTS, 3 ELEMENT ..................................................3-10

YE, 4-WIRE WITH NO PTS AND 3 CTS, 2.5 ELEMENT .............................................. 3-11

YE, 4-WIRE WITH 3 PTS AND 3 CTS, 3 ELEMENT .................................................... 3-12

YE, 4-WIRE WITH 2 PTS AND 3 CTS, 2.5 ELEMENT ................................................. 3-13

ELTA, 3-WIRE WITH NO PTS AND 2 CTS ..................................................................... 3-14

ELTA, 3-WIRE WITH 2 PTS AND 2 CTS ........................................................................ 3-15

URRENT-ONLY MEASUREMENT (THREE-PHASE) .......................................................... 3-16

URRENT-ONLY MEASUREMENT (DUAL-PHASE) ............................................................ 3-17

URRENT-ONLY MEASUREMENT (SINGLE-PHASE) ......................................................... 3-18

COMMUNICATIONS SETUP .......................................................................................................... 3-19

ESCRIPTION ........................................................................................................................ 3-19

RDA COM1 PORT .............................................................................................................3-19

RS485 COM2 P

ORT ......................................................................................................... 3-19

4: USING THE METER FRONT PANEL INTERFACE ............................................................................................................ 4-1

ESCRIPTION ........................................................................................................................ 4-1

D F

ACEPLATE ELEMENTS ........................................................................................................ 4-1

ACEPLATE BUTTONS .......................................................................................................... 4-2

ERCENTAGE OF LOAD BAR ...............................................................................................4-3

ATT-HOUR ACCURACY TESTING (VERIFICATION) ........................................................ 4-4

CONFIGURING THE METER VIA THE FRONT PANEL .......................................................... 4-5

VERVIEW ............................................................................................................................ 4-5

TART UP .............................................................................................................................. 4-5

AIN MENU ......................................................................................................................... 4-6

ESET MODE AND PASSWORD ENTRY .............................................................................4-6

CHANGING SETTINGS IN CONFIGURATION MODE ...........................................................4-9

ESCRIPTION ........................................................................................................................ 4-9

ONFIGURING THE SCROLL FEATURE ............................................................................... 4-9

ROGRAMMING THE CONFIGURATION MODE SCREENS ................................................ 4-10

ONFIGURING THE CT SETTING ........................................................................................ 4-11

ONFIGURING THE PT SETTING ........................................................................................4-12

ONFIGURING THE CONNECTION SETTING ...................................................................... 4-13

ONFIGURING THE COMMUNICATION PORT SETTING .................................................... 4-14

OPERATING MODE ...........................................................................................................................4-17

ESCRIPTION ........................................................................................................................ 4-17

5: COMMUNICATIONS MODBUS COMMUNICATIONS ..................................................................................................... 5-1

EMORY MAP DESCRIPTION ............................................................................................. 5-1

M M

EMORY MAP ......................................................................................................................5-1

ODBUS MEMORY MAP NOTES .......................................................................................5-7

ODBUS MEMORY MAP DATA FORMATS ........................................................................5-9

DNP POINT MAPPING ..................................................................................................................... 5-10

DNP P

OINT MAPS ..............................................................................................................5-10

DNP P

OINT MAP NOTES ...................................................................................................5-12

TOC–2 EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE

DNP IMPLEMENTATION ................................................................................................................. 5-13

VERVIEW ............................................................................................................................ 5-13

ATA LINK LAYER ................................................................................................................ 5-13

RANSPORT LAYER .............................................................................................................. 5-13

PPLICATION LAYER ............................................................................................................5-14

DNP OBJECTS AND VARIATIONS ............................................................................................... 5-15

ESCRIPTION ........................................................................................................................ 5-15

INARY OUTPUT STATUS (OBJECT 10, VARIATION 2) ...................................................5-15

ONTROL RELAY OUTPUT (OBJECT 12, VARIATION 1) .................................................. 5-15

32-B

IT BINARY COUNTER WITHOUT FLAG (OBJECT 20, VARIATION 4) .................... 5-16

16-B

IT ANALOG INPUT WITHOUT FLAG (OBJECT 30, VARIATION 5) ......................... 5-16

LASS 0 DATA (OBJECT 60, VARIATION 1) ..................................................................... 5-17

NTERNAL INDICATIONS (OBJECT 80, VARIATION 1) ...................................................... 5-17

6: MISCELLANEOUS NAVIGATION MAPS .........................................................................................................................6-1

NTRODUCTION .....................................................................................................................6-1

I M

AIN MENU SCREENS ........................................................................................................ 6-2

PERATING MODE SCREENS ............................................................................................. 6-3

ESET MODE SCREENS ....................................................................................................... 6-4

ONFIGURATION MODE SCREENS .................................................................................... 6-5

REVISION HISTORY .......................................................................................................................... 6-6

ELEASE DATES ...................................................................................................................6-6

HANGES TO THE MANUAL ............................................................................................... 6-6

WARRANTY ......................................................................................................................................... 6-8

GE M

ULTILIN WARRANTY .................................................................................................. 6-8

EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE TOC–3

TOC–4 EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE

GE Consumer & Industrial

Multilin

1.1 Introduction

EPM 6000 Multi-function Power

Metering System

Chapter 1: Overview

Overview

1.1.1 Description

1.1.2 Highlights

The EPM 6000 is a multifunction power meter designed to be used in electrical substations, panel boards and as a power meter for OEM equipment. The unit provides multifunction measurement of electrical parameters.

The unit is designed with advanced measurement capabilities, allowing it to achieve high performance accuracy. The EPM 6000 is specified as a 0.2% class energy meter for billing applications as well as a highly accurate panel indication meter.

The EPM 6000 provides a host of additional capabilities, including standard RS485 Modbus Protocol and an IrDA port remote interrogation.

The following EPM 6000 features are detailed in this manual:

• 0.2% class revenue certifiable energy and demand metering

• Meets ANSI C12.20 (0.2%) and IEC 687 (0.2%) classes

• Multifunction measurement including voltage, current, power, frequency, energy

• Percentage of load bar for analog meter perception

• Easy-to-use faceplate programming

• IrDA port for PDA remote read

• RS485 Modbus communications

EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE 1–1

FIGURE 1–1: EPM 6000 Highlights

CHAPTER 1: OVERVIEW

1–2 EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE

CHAPTER 1: OVERVIEW

1.2 Features

1.2.1 Universal Voltage Inputs

1.2.2 Current Inputs

Voltage Inputs allow measurement to 416 V line-to-neutral and 721 V line-to-line. This insures proper meter safety when wiring directly to high voltage systems. One unit will perform to specification on 69 V, 120 V, 230 V, 277 V, and 347 V systems.

The EPM 6000 current inputs use a unique dual input method.

• Method 1 – CT Pass Through: The CT passes directly through the meter without

any physical termination on the meter. This insures that the meter cannot be a point of failure on the CT circuit. This is preferable for utility users when sharing relay class CTs. No burden is added to the secondary CT circuit.

• Method 2 – Current “Gills”: This unit additionally provides ultra-rugged

termination pass-through bars that allow CT leads to be terminated on the meter. This, too, eliminates any possible point of failure at the meter. This is a preferred technique for insuring that relay class CT integrity is not compromised (the CT will not open in a fault condition).

FIGURE 1–2: Current Input Connections

1.2.3 Utility Peak Demand

The EPM 6000 provides user-configured Block (fixed) or Rolling window demand. This feature allows you to set up a customized demand profile. Block window demand is demand used over a user-defined demand period (usually 5, 15, or 30 minutes). Rolling window demand is a fixed window demand that moves for a user-specified subinterval period. For example, a 15-minute demand using 3 subintervals and providing a new demand reading every 5 minutes, based on the last 15 minutes.

EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE 1–3

Utility demand features can be used to calculate kW, kvar, kVA and PF readings. All other parameters offer maximum and minimum capability over the user-selectable averaging period. Voltage provides an instantaneous maximum and minimum reading which displays the highest surge and lowest sag seen by the meter.

1.2.4 Measured Values

The EPM 6000 provides the following measured values all in real time and some additionally as average, maximum, and minimum values.

Measured Values Real Time Average Maximum Minimum

Voltage L-N XXX

Voltage L-L XXX

Current per phase XXXX

Watts XXXX

CHAPTER 1: OVERVIEW

Table 1–1: EPM 6000 Measured Values

vars XXXX

VA XXXX

Power Factor (PF) XXXX

Positive watt-hours X

Negative watt-hours X

Net watt-hours X

Positive var-hours X

Negative var-hours X

Net var-hours X

VA-hours X

Frequency XXX

%THD XXX

Voltage angles X

Current angles X

% of load bar X

1–4 EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE

CHAPTER 1: OVERVIEW

1.3 Ordering

1.3.1 Order Codes

The order codes for the EPM 6000 are indicated below.

Table 1–2: EPM 6000 Order Codes

PL6000 – * – * – *

Base Unit System

Frequency

Current Input

THD and Pulse Output

For example, to order an EPM 6000 for 60 Hz system with a 1 A secondary CT input and no THD or pulse output option, select order code PL6000-6-1A-0. The standard unit includes display, all current/voltage/power/frequency/energy counters, percent load bar, RS485, and IrDA communication ports.

PL6000 || |

5 | | 6 | |

1A | 5A |

EPM 6000 Power Metering System 50 Hz AC frequency system 60 Hz AC frequency system 1 A secondary CT 5 A secondary CT No THD or pulse output option

THD, limit alarms, and 1 KYZ pulse output

THD

EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE 1–5

1.4 Specifications

1.4.1 Inputs/Outputs

CHAPTER 1: OVERVIEW

POWER SUPPLY

Range:..................................................................D2 Option: Universal, 90 to 265 V AC at 50/60Hz, or 100 to

370 V DC D Option: 18 to 60 V DC

Power consumption:.....................................5 VA, 3.5 W

VOLTAGE INPUTS (MEASUREMENT CATEGORY III)

Range:..................................................................Universal, Auto-ranging up to 416 V AC L-N, 721 V AC L-L

Supported hookups:......................................3-element Wye, 2.5-element Wye, 2-element Delta,

4-wire Delta

Input impedance:...........................................1 MOhm/phase

Burden:................................................................0.0144 VA/phase at 120 Volts

Pickup voltage: ................................................10 V AC

Connection:.......................................................Screw terminal (see Voltage Connection on page 3–8)

Maximum input wire gauge: ....................AWG #12 / 2.5 mm

Fault withstand: ..............................................Meets IEEE C37.90.1

Reading:..............................................................Programmable full-scale to any PT ratio

1.4.2 Metering

CURRENT INPUTS

Class 10:..............................................................5 A nominal, 10 A maximum

Class 2: ................................................................1 A nominal, 2 A maximum

Burden:................................................................0.005 VA per phase maximum at 11 A

Pickup current:.................................................0.1% of nominal

Connections:.....................................................O or U lug (see CT Leads Terminated to Meter on page 3–

6);

Pass-through wire, 0.177" / 4.5 mm maximum diameter

(see Pass-Through Wire Electrical Connection on page 3–7); Quick connect, 0.25" male tab

(see Quick Connect Electrical Connection on page 3–7)

Fault Withstand:..............................................100 A / 10 seconds, 300 A / 3 seconds, 500 A / 1 second

Reading:..............................................................Programmable full-scale to any CT ratio

MEASUREMENT METHODS

Voltage and current:.....................................true RMS

Power:..................................................................sampling at 400+ samples/cycle on all channels

measured; readings simultaneously

A/D conversion:...............................................6 simultaneous 24-bit analog-to-digital converters

UPDATE RATE

Watts, vars, and VA: ......................................100 ms (10 times per second)

All other parameters:....................................1 second

1–6 EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE

CHAPTER 1: OVERVIEW

ACCURACY

Measured Parameters Display Range Accuracy

Voltage L-N 0 to 9999 kV or scalable 0.1% of reading Voltage L-L 0 to 9999 V or kV scalable 0.1% of reading Current 0 to 9999 A or kA 0.1% of reading +/– Watts 0 to 9999 W, kW, or MW 0.2% of reading +/– Wh 5 to 8 digits (programmable) 0.2% of reading +/– vars 0 to 9999 vars, kvars, Mvars 0.2% of reading +/– varh 5 to 8 digits (programmable) 0.2% of reading VA 0 to 9999 VA, kVA, MVA 0.2% of reading VAh 5 to 8 digits (programmable) 0.2% of reading Power Factor (PF) ±0.5 to 1.0 0.2% of reading Frequency 45 to 65 Hz 0.01 Hz % THD 0 to 100% 2.0% F.S. % Load Bar 10 digit resolution scalable 1 to 120% of reading

NOTE: Typical results are more accurate.

1.4.3 Environmental

TEMPERATURE AND HUMIDITY

Storage:...............................................................–40 to 85°C

Operating:..........................................................–30 to 70°C

Humidity:............................................................up to 95% RH, non-condensing

Faceplate rating: ............................................NEMA 12 (water resistant), mounting gasket included

1.4.4 Communications

COMMUNICATIONS FORMAT

Types:...................................................................RS485 port through back plate

COMMUNICATIONS PORTS

Protocol:..............................................................Modbus RTU, Modbus ASCII, DNP 3.0

Baud rate: ..........................................................9600 to 57600 bps

Port address: ....................................................001 to 247

Data format:.....................................................8 bits, no parity

1.4.5 Mechanical Parameters

DIMENSIONS

Size:.......................................................................4.25" × 4.82" × 4.85" (L × W × H)

Mounting:...........................................................mounts in 92 mm square DIN or ANSI C39.1 4-inch round

Weight:................................................................2 pounds / 0.907 kg

Shipping..............................................................ships in 6-inch / 152.4 mm cube container

IrDA port through face plate

105.4 mm × 123.2 mm × 123.2 mm (L × W × H)

cut-out

EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE 1–7

1.4.6 Approvals

CHAPTER 1: OVERVIEW

TYPE TESTING

IEC 687 (0.2% accuracy) ANSI C12.20 (0.2% accuracy)

ANSI (IEEE) C37.90.1: ....................................Surge Withstand

ANSI C62.41 (burst)

IEC 1999-4-2: ...................................................ESD

IEC 1000-4-3: ...................................................Radiated Immunity

IEC 1000-4-4: ...................................................Fast Transient

IEC 1000-4-5: ...................................................Surge Immunity

COMPLIANCE

ISO: ........................................................................manufactured to an ISO9001 registered program

UL:..........................................................................UL listed (file E250818)

CSA:.......................................................................Certified per: C22.2 No.1010.1 Electrical and Electronic

Measuring and Testing Equipment

CE:..........................................................................conforms to EN 55011 / EN 50082

1–8 EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE

GE Consumer & Industrial

Multilin

EPM 6000 Multi-function Power

Metering System

Chapter 2: Electrical Background

Electrical Background

2.1 Three-Phase Power Measurement

2.1.1 Description

This introduction to three-phase power and power measurement is intended to provide only a brief overview of the subject. The professional meter engineer or meter technician should refer to more advanced documents such as the EEI Handbook for Electricity Metering and the application standards for more in-depth and technical coverage of the subject.

EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE 2–1

2.2 Three-Phase System Configurations

2.2.1 Description

Three-phase power is most commonly used in situations where large amounts of power will be used because it is a more effective way to transmit the power and because it provides a smoother delivery of power to the end load. There are two commonly used connections for three-phase power, a wye connection or a delta connection. Each connection has several different manifestations in actual use. When attempting to determine the type of connection in use, it is a good practice to follow the circuit back to the transformer that is serving the circuit. It is often not possible to conclusively determine the correct circuit connection simply by counting the wires in the service or checking voltages. Checking the transformer connection will provide conclusive evidence of the circuit connection and the relationships between the phase voltages and ground.

2.2.2 Wye Connection

The wye connection is so called because when you look at the phase relationships and the winding relationships between the phases it looks like a wye (Y). The following figure depicts the winding relationships for a wye-connected service. In a wye service the neutral (or center point of the wye) is typically grounded. This leads to common voltages of 208/ 120 and 480/277 (where the first number represents the phase-to-phase voltage and the second number represents the phase-to-ground voltage).

CHAPTER 2: ELECTRICAL BACKGROUND

Van

FIGURE 2–1: Three-Phase Wye Winding

Vbn

Vcn

The three voltages are electrically separated by 120°. Under balanced load conditions with unity power factor, the currents are also separated by 120°. However, unbalanced loads and other conditions can cause the currents to depart from the ideal 120° separation.

Three-phase voltages and currents are usually represented with a phasor diagram. A phasor diagram for the typical connected voltages and currents is shown below.

2–2 EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE

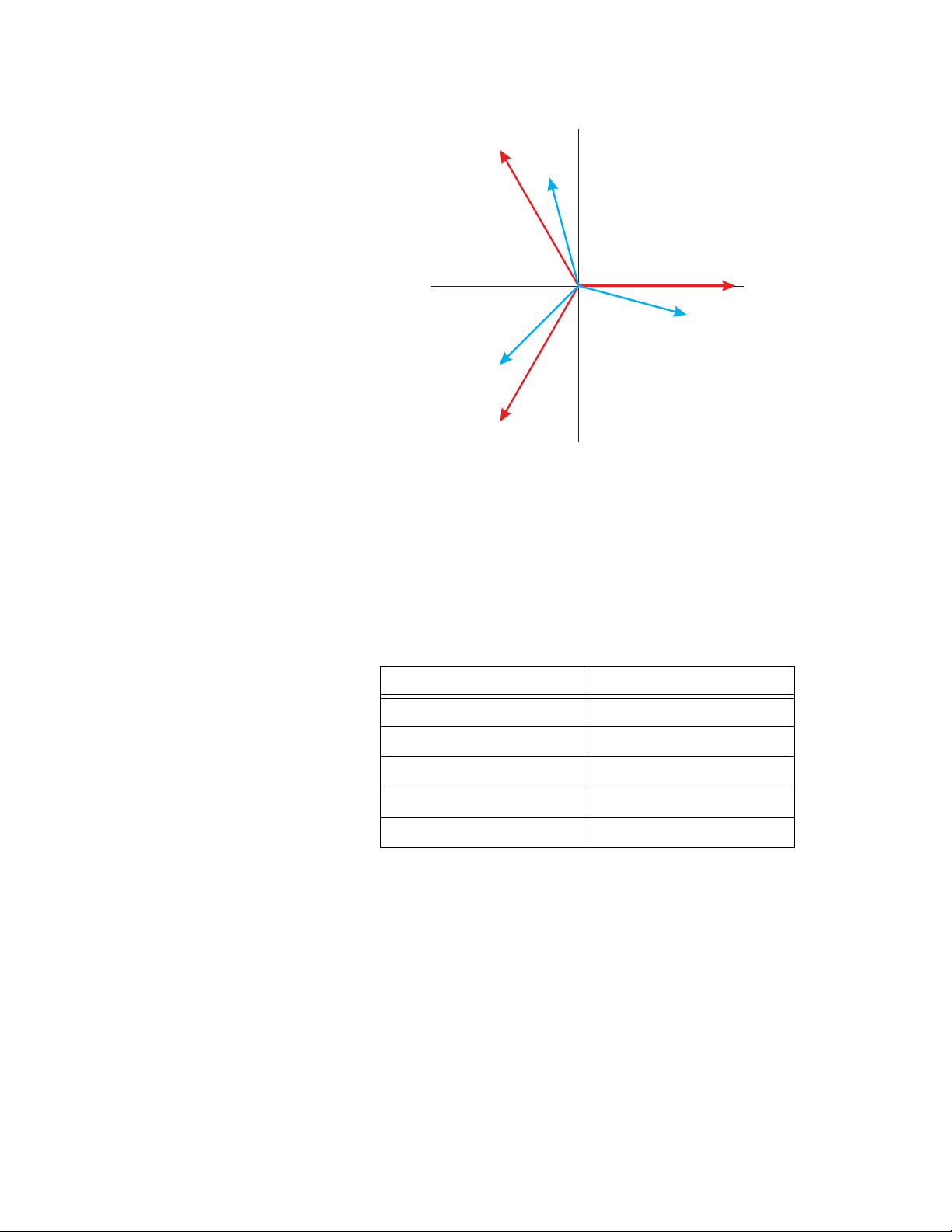
CHAPTER 2: ELECTRICAL BACKGROUND

The phasor diagram shows the 120° angular separation between the phase voltages. The phase-to-phase voltage in a balanced three-phase wye system is 1.732 times the phaseto-neutral voltage. The center point of the wye is tied together and is typically grounded. The following table indicates the common voltages used in the United States for wyeconnected systems.

Vcn

Van

Vbn

FIGURE 2–2: Three-Phase Voltage and Current Phasors for Wye Winding

Table 2–1: Common Phase Voltages on Wye Services

Phase-to-Ground Voltage Phase-to-Phase Voltage

120 volts 208 volts

277 volts 480 volts

2400 volts 4160 volts

7200 volts 12470 volts

7620 volts 13200 volts

Usually, a wye-connected service will have four wires: three wires for the phases and one for the neutral. The three-phase wires connect to the three phases. The neutral wire is typically tied to the ground or center point of the wye (refer to the Three-Phase Wye Winding diagram above).

In many industrial applications the facility will be fed with a four-wire wye service but only three wires will be run to individual loads. The load is then often referred to as a deltaconnected load but the service to the facility is still a wye service; it contains four wires if you trace the circuit back to its source (usually a transformer). In this type of connection the phase to ground voltage will be the phase-to-ground voltage indicated in the table above, even though a neutral or ground wire is not physically present at the load. The transformer is the best place to determine the circuit connection type because this is a location where the voltage reference to ground can be conclusively identified.

EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE 2–3

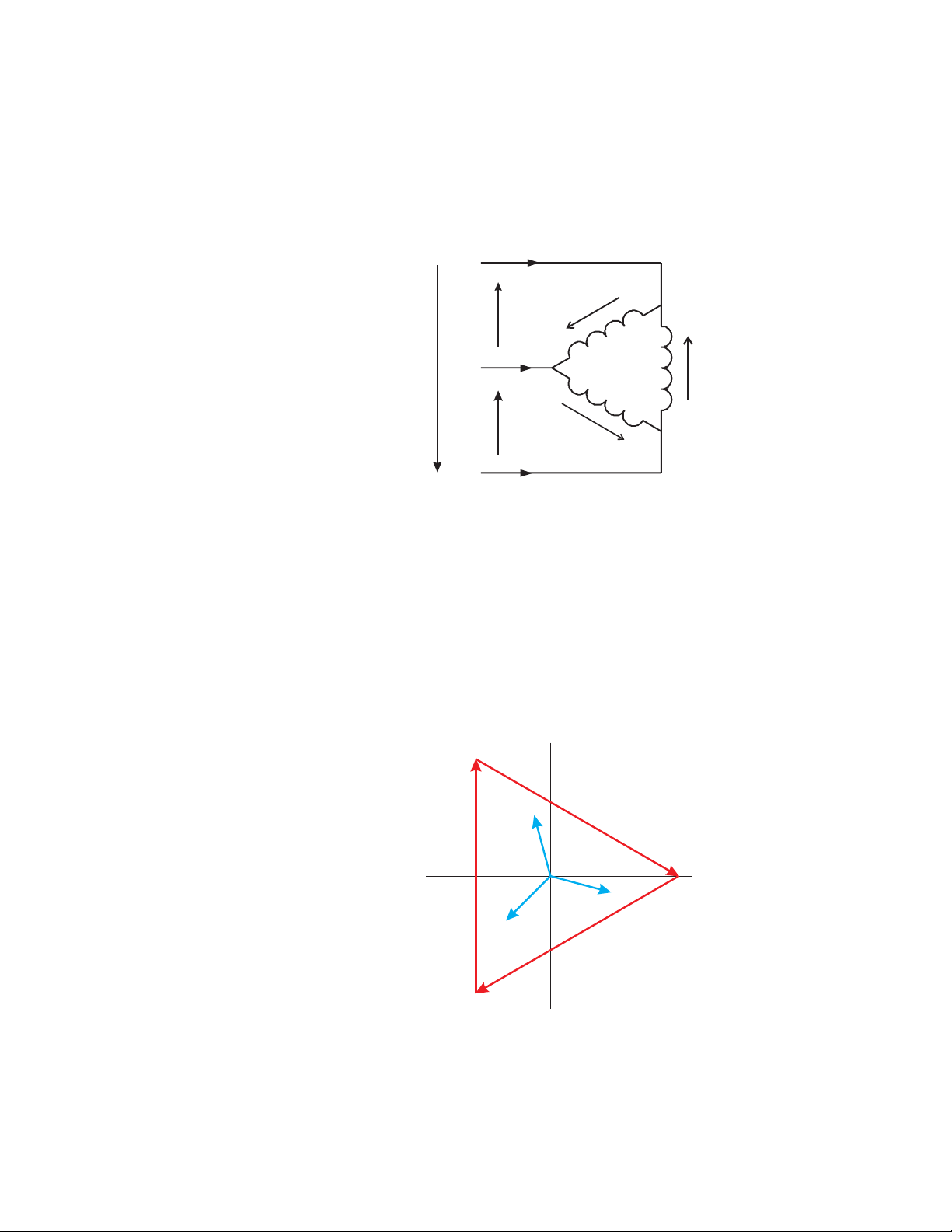
2.2.3 Delta Connection

Delta connected services may be fed with either three wires or four wires. In a three-phase delta service the load windings are connected from phase-to-phase rather than from phase-to-ground. The following figure shows the physical load connections for a delta service.

CHAPTER 2: ELECTRICAL BACKGROUND

Iab

Vab

Vca

Vbc

Ica

Ibc

FIGURE 2–3: Three-Phase Delta Winding Relationship

In this example of a delta service, three wires will transmit the power to the load. In a true delta service, the phase-to-ground voltage will usually not be balanced because the ground is not at the center of the delta.

The following diagram shows the phasor relationships between voltage and current on a three-phase delta circuit.

In many delta services, one corner of the delta is grounded. This means the phase to ground voltage will be zero for one phase and will be full phase-to-phase voltage for the other two phases. This is done for protective purposes.

Vca

Vbc

Vab

FIGURE 2–4: Three-Phase Voltage and Current Phasors for Delta Winding

2–4 EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE

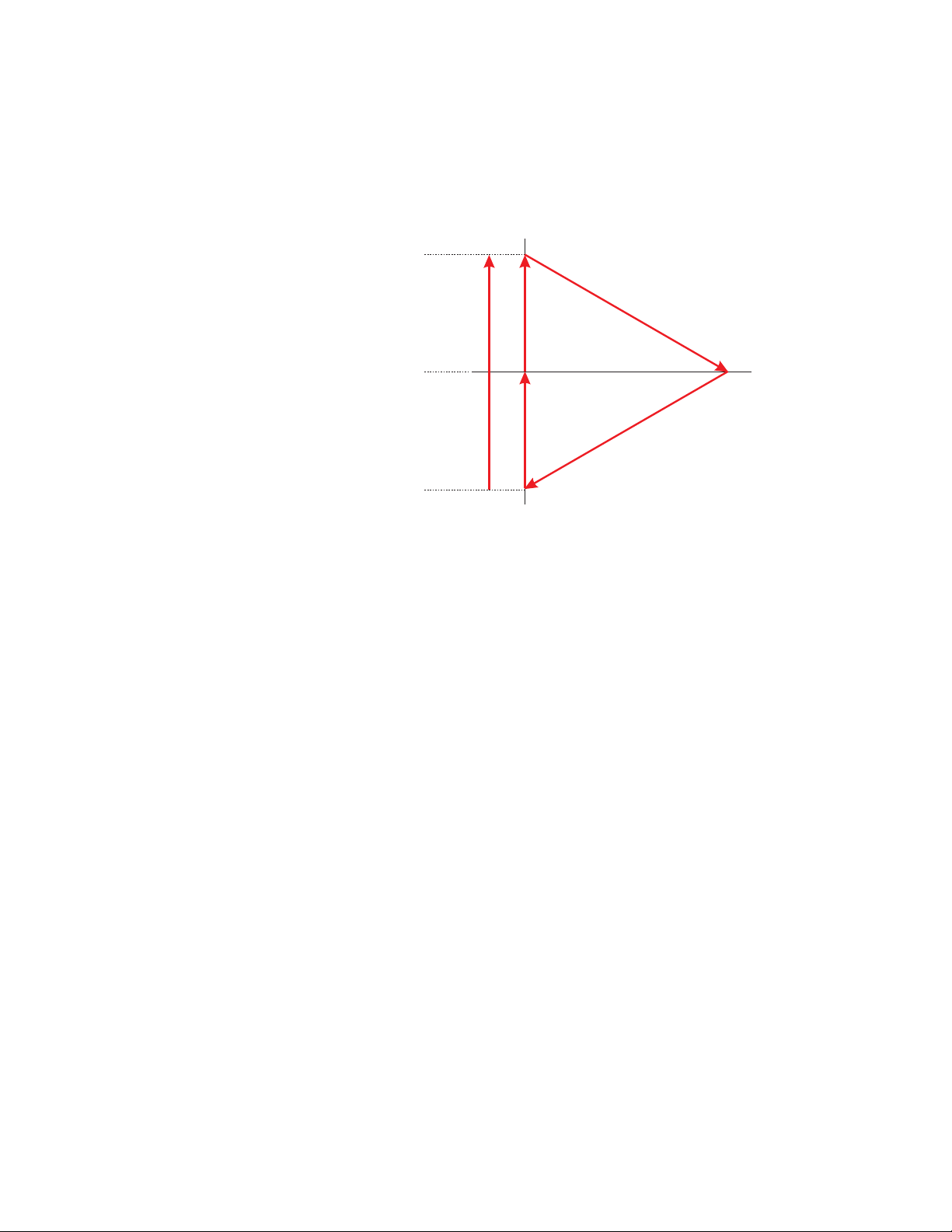
CHAPTER 2: ELECTRICAL BACKGROUND

Another common delta connection is the four-wire, grounded delta used for lighting loads. In this connection the center point of one winding is grounded. On a 120/240 volt, fourwire, grounded delta service the phase-to-ground voltage would be 120 volts on two phases and 208 volts on the third phase. The phasor diagram for the voltages in a threephase, four-wire delta system is shown below.

120 V

Vbc

120 V

FIGURE 2–5: Three-Phase, Four-Wire Delta Phasors

Vnc

Vbn

2.2.4 Blondell's Theorem and Three-Phase Measurement

In 1893 an engineer and mathematician named Andre E. Blondell set forth the first scientific basis for poly phase metering. His theorem states:

If energy is supplied to any system of conductors through N wires, the total power in the system is given by the algebraic sum of the readings of N watt-meters so arranged that each of the N wires contains one current coil, the corresponding potential coil being connected between that wire and some common point. If this common point is on one of the N wires, the measurement may be made by the use of N-1 wattmeters.

Vca

Vab

The theorem may be stated more simply, in modern language:

In a system of N conductors, N – 1 meter elements will measure the power or energy taken provided that all the potential coils have a common tie to the conductor in which there is no current coil.

Three-phase power measurement is accomplished by measuring the three individual phases and adding them together to obtain the total three phase value. In older analog meters, this measurement was made using up to three separate elements. Each element combined the single-phase voltage and current to produce a torque on the meter disk. All three elements were arranged around the disk so that the disk was subjected to the combined torque of the three elements. As a result the disk would turn at a higher speed and register power supplied by each of the three wires.

According to Blondell's Theorem, it was possible to reduce the number of elements under certain conditions. For example, a three-phase, three-wire delta system could be correctly measured with two elements (two potential coils and two current coils) if the potential coils were connected between the three phases with one phase in common.

EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE 2–5

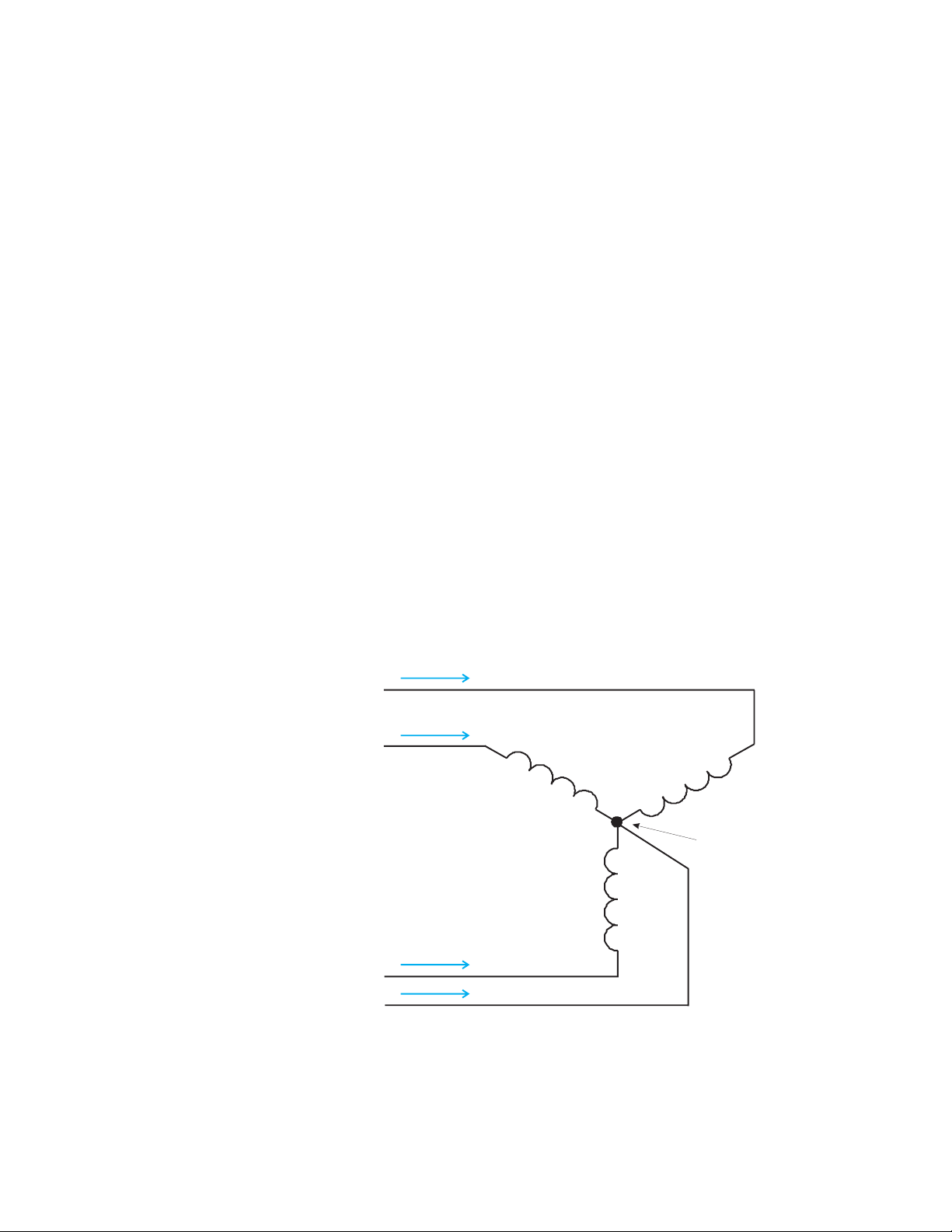
CHAPTER 2: ELECTRICAL BACKGROUND

In a three-phase, four-wire wye system it is necessary to use three elements. Three voltage coils are connected between the three phases and the common neutral conductor. A current coil is required in each of the three phases.

In modern digital meters, Blondell's Theorem is still applied to obtain proper metering. The difference in modern meters is that the digital meter measures each phase voltage and current and calculates the single-phase power for each phase. The meter then sums the three phase powers to a single three-phase reading.

Some digital meters calculate the individual phase power values one phase at a time. This means the meter samples the voltage and current on one phase and calculates a power value. Then it samples the second phase and calculates the power for the second phase. Finally, it samples the third phase and calculates that phase power. After sampling all three phases, the meter combines the three readings to create the equivalent three-phase power value. Using mathematical averaging techniques, this method can derive a quite accurate measurement of three-phase power.

More advanced meters actually sample all three phases of voltage and current simultaneously and calculate the individual phase and three-phase power values. The advantage of simultaneous sampling is the reduction of error introduced due to the difference in time when the samples were taken.

Blondell's Theorem is a derivation that results from Kirchhoff's Law. Kirchhoff's Law states that the sum of the currents into a node is zero. Another way of stating the same thing is that the current into a node (connection point) must equal the current out of the node. The law can be applied to measuring three-phase loads. The figure below shows a typical connection of a three-phase load applied to a three-phase, four-wire service. Kirchhoff's Laws hold that the sum of currents A, B, C and N must equal zero or that the sum of currents into Node “n” must equal zero.

Phase B

Phase C

Node "n"

Phase A

FIGURE 2–6: Three-Phase Load Illustrating Kirchhoff’s Law and Blondell’s Theorem

2–6 EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE

CHAPTER 2: ELECTRICAL BACKGROUND

If we measure the currents in wires A, B and C, we then know the current in wire N by Kirchhoff's Law and it is not necessary to measure it. This fact leads us to the conclusion of Blondell's Theorem that we only need to measure the power in three of the four wires if they are connected by a common node. In the circuit of Figure 1.6 we must measure the power flow in three wires. This will require three voltage coils and three current coils (a three element meter). Similar figures and conclusions could be reached for other circuit configurations involving delta-connected loads.

EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE 2–7

2.3 Power, Energy, and Demand

2.3.1 Description

It is quite common to exchange power, energy, and demand without differentiating between the three. Because this practice can lead to confusion, the differences between these three measurements will be discussed.

2.3.2 Power

Power is an instantaneous reading. The power reading provided by a meter is the present flow of watts. Power is measured immediately just like current. In many digital meters, the power value is actually measured and calculated over a one-second interval, since it takes some amount of time to calculate the RMS values of voltage and current. However, this time interval is kept small to preserve the instantaneous nature of power.

2.3.3 Energy

CHAPTER 2: ELECTRICAL BACKGROUND

Energy is always based upon some time increment – it is the integration of power over a defined time increment. Energy is an important value because almost all electric bills are based, in part, on the amount of energy consumed.

Typically, electrical energy is measured in units of kilowatt-hours (kWh). A kilowatt-hour represents a constant load of 1000 watts (1 kW) for 1 hour. Stated another way, if the power delivered (instantaneous watts) is measured as 1000 W, and the load was served for a one-hour time interval, then the load would have absorbed 1 kWh of energy. A different load may have a constant power requirement of 4000 W. If this load were served for one hour, it would absorb 4 kWh of energy. Likewise, if it were served for 15 minutes, it would absorb ¼ of that total, or 1 kWh.

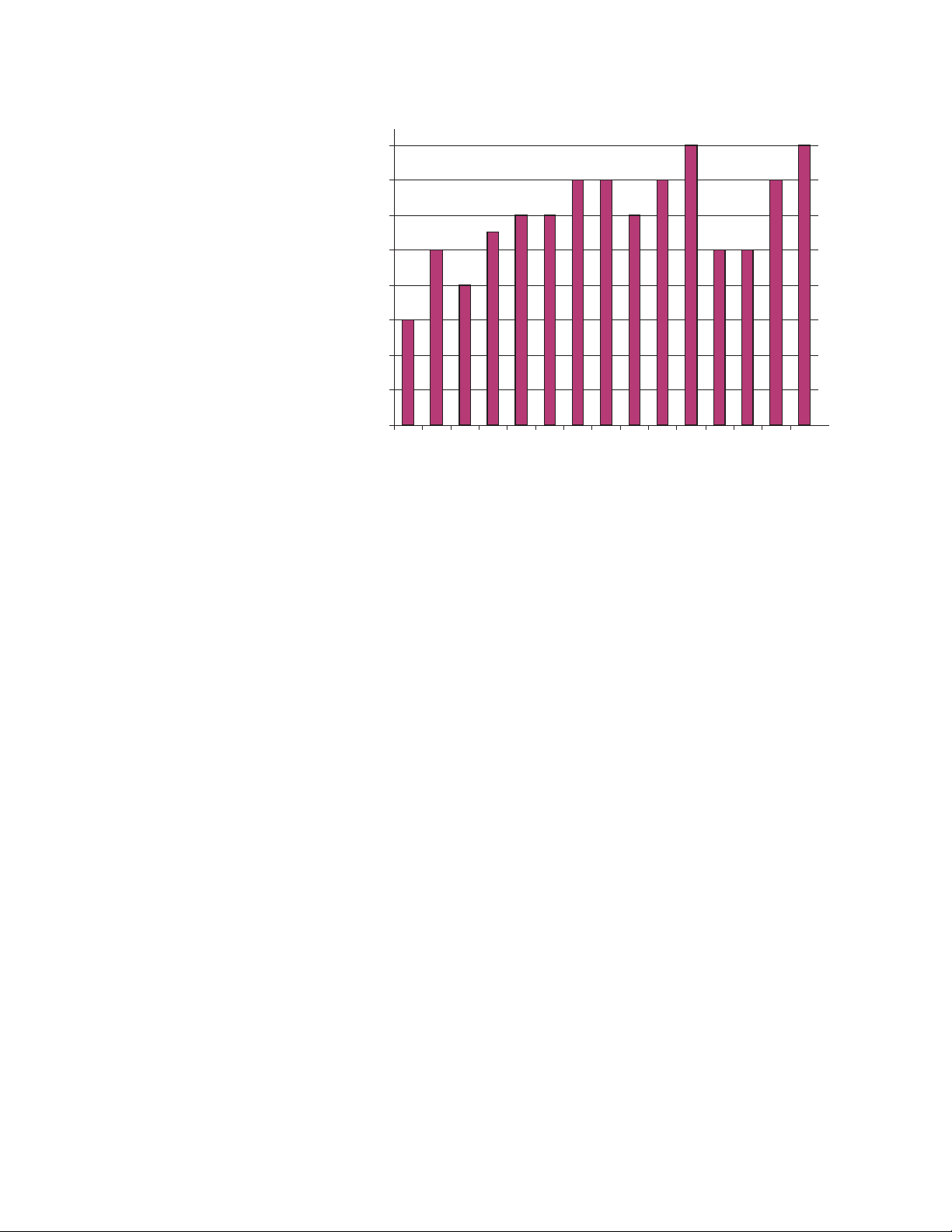
The following figure shows a graph of power and the resulting energy that would be transmitted as a result of the illustrated power values. For this illustration, it is assumed that the power level is held constant for each minute when a measurement is taken. Each bar in the graph represents the power load for the one-minute increment of time. In real life, the power values are continually moving.

2–8 EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE

CHAPTER 2: ELECTRICAL BACKGROUND

kilowatts

123456789101112131415

Time (minutes)

FIGURE 2–7: Power Use Over Time

The data in the above figure is reproduced in the following table to illustrate the calculation of energy. Since the time increment of the measurement is one minute, and since we specified a constant load over that minute, the power reading can be converted to an equivalent consumed energy reading by multiplying the power reading by 1/60 (converting the time base from minutes to hours).

EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE 2–9

CHAPTER 2: ELECTRICAL BACKGROUND

Table 2–2: Power and Energy Relationship Over Time

Time Interval Power Energy Accumulated

Energy

1 minute 30 kW 0.50 kWh 0.50 kWh

2 minutes 50 kW 0.83 kWh 1.33 kWh

3 minutes 40 kW 0.67 kWh 2.00 kWh

4 minutes 55 kW 0.92 kWh 2.92 kWh

5 minutes 60 kW 1.00 kWh 3.92 kWh

6 minutes 60 kW 1.00 kWh 4.92 kWh

7 minutes 70 kW 1.17 kWh 6.09 kWh

8 minutes 70 kW 1.17 kWh 7.26 kWh

9 minutes 60 kW 1.00 kWh 8.26 kWh

10 minutes 70 kW 1.17 kWh 9.43 kWh

11 minutes 80 kW 1.33 kWh 10.76 kWh

12 minutes 50 kW 0.83 kWh 12.42 kWh

13 minutes 50 kW 0.83 kWh 12.42 kWh

14 minutes 70 kW 1.17 kWh 13.59 kWh

2.3.4 Demand

15 minutes 80 kW 1.33 kWh 14.92 kWh

As shown in the above table, the accumulated energy for the power load profile of the data in Power Use Over Time on page 2–9 is 14.92 kWh.

Demand is also a time-based value. The demand is the average rate of energy use over time. The actual label for demand is kilowatt-hours/hour but this is normally reduced to kilowatts. This makes it easy to confuse demand with power. But demand is not an instantaneous value. To calculate demand it is necessary to accumulate the energy readings (as illustrated in Power Use Over Time on page 2–9) and adjust the energy reading to an hourly value that constitutes the demand.

In the example, the accumulated energy is 14.92 kWh. But this measurement was made over a 15-minute interval. To convert the reading to a demand value, it must be normalized to a 60-minute interval. If the pattern were repeated for an additional three 15minute intervals the total energy would be four times the measured value or 59.68 kWh. The same process is applied to calculate the 15-minute demand value. The demand value associated with the example load is 59.68 kWh/hour or 59.68 kWd. Note that the peak instantaneous value of power is 80 kW, significantly more than the demand value.

2–10 EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE

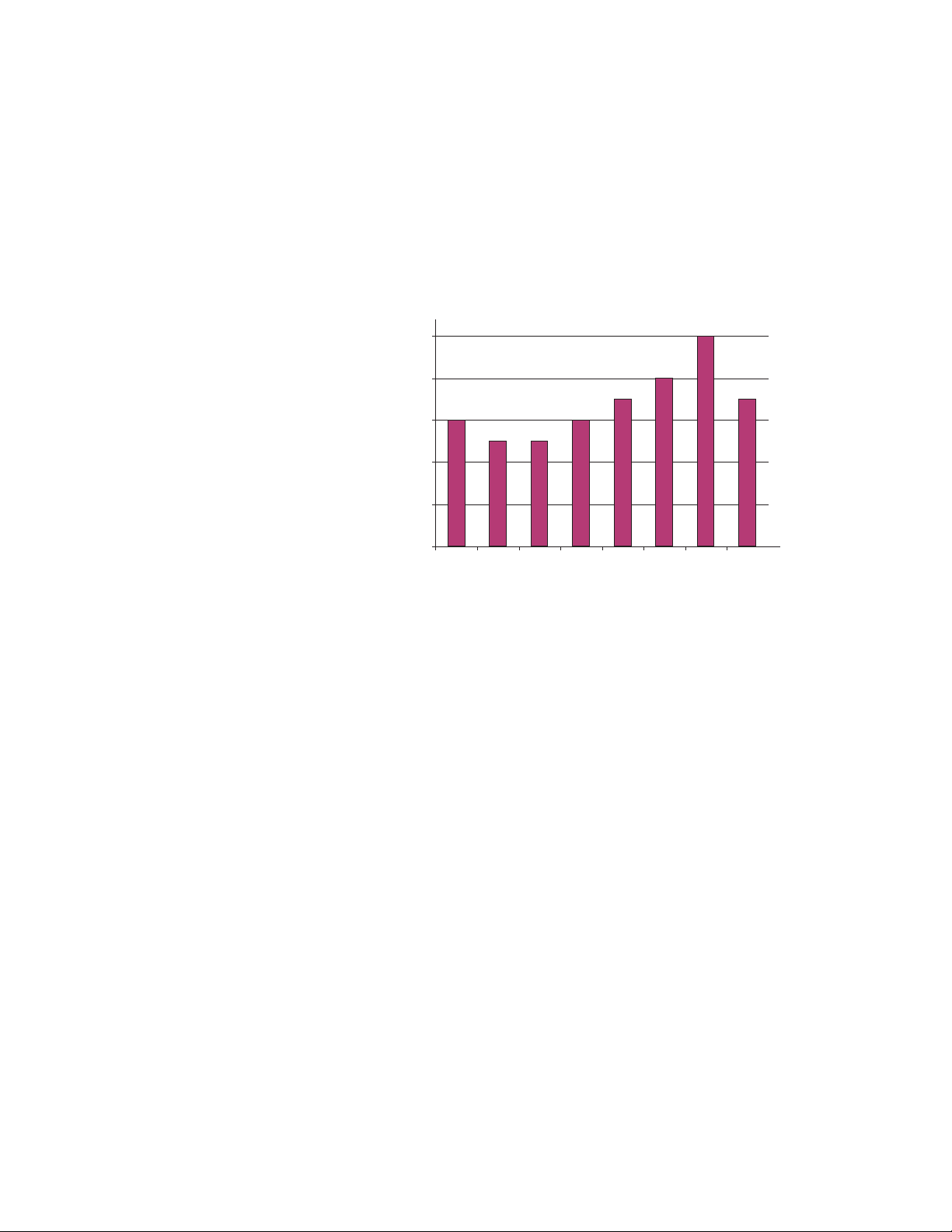
CHAPTER 2: ELECTRICAL BACKGROUND

The following figure illustrates another example of energy and demand. In this case, each bar represents the energy consumed in a 15-minute interval. The energy use in each interval typically falls between 50 and 70 kWh. However, during two intervals the energy rises sharply and peaks at 100 kWh in interval #7. This peak of usage will result in setting a high demand reading. For each interval shown the demand value would be four times the indicated energy reading. So interval 1 would have an associated demand of 240 kWh/hr. Interval #7 will have a demand value of 400 kWh/hr. In the data shown, this is the peak demand value and would be the number that would set the demand charge on the utility bill.

100

kilowatt-hours

12345678

FIGURE 2–8: Energy Use and Demand Intervals

Intervals (15 mins.)

As seen in this example, it is important to recognize the relationships between power, energy and demand in order to effectively control loads or to correctly monitor use.

EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE 2–11

2.4 Reactive Energy and Power Factor

2.4.1 Real, Reactive, and Apparent Power

The real power and energy measurements discussed in the previous section relate to the quantities that are most used in electrical systems. But it is often not sufficient to only measure real power and energy. Reactive power is a critical component of the total power picture because almost all real-life applications have an impact on reactive power. Reactive power and power factor concepts relate to both load and generation applications. However, this discussion will be limited to analysis of reactive power and power factor as they relate to loads. To simplify the discussion, generation will not be considered.

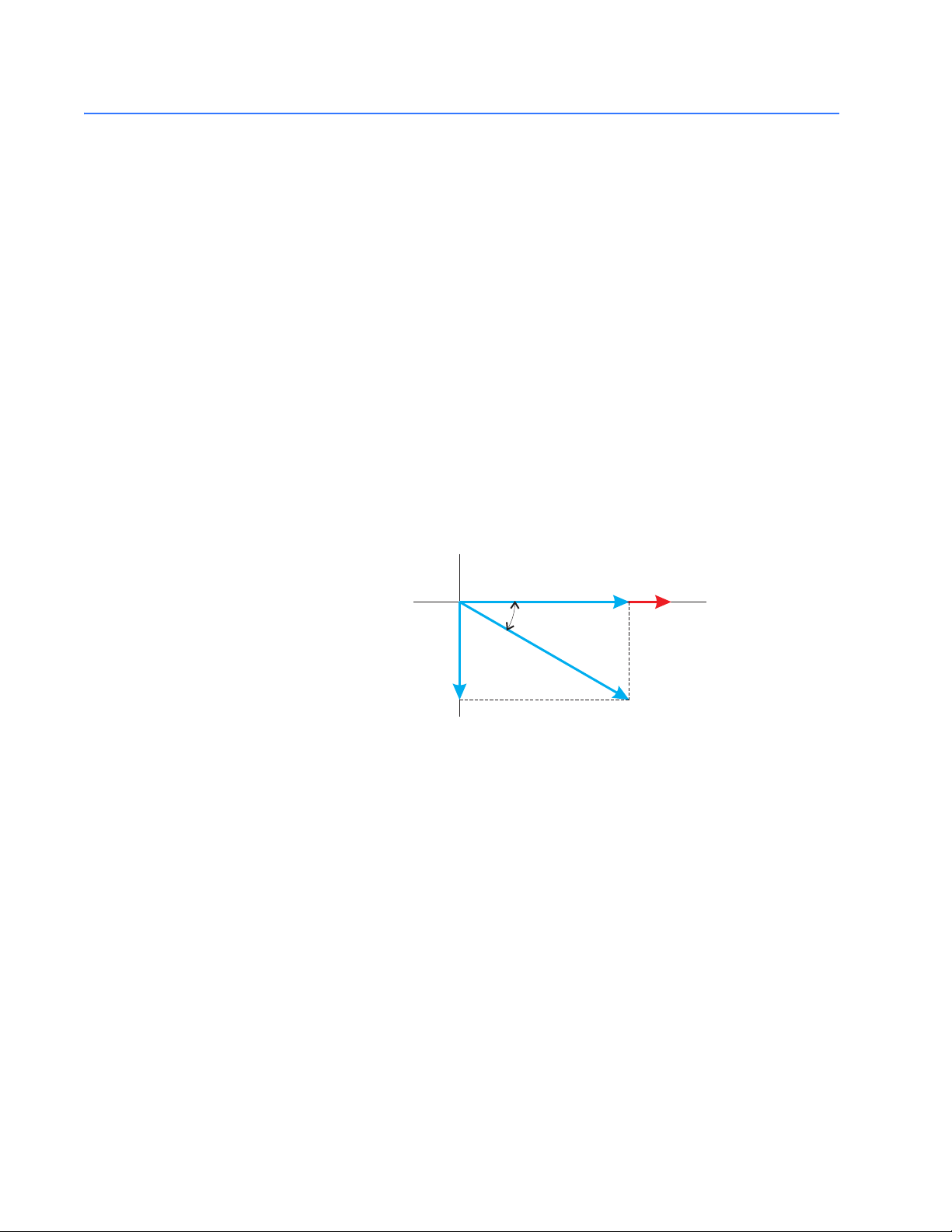
Real power (and energy) is the component of power that is the combination of the voltage and the value of corresponding current that is directly in phase with the voltage. However, in actual practice the total current is almost never in phase with the voltage. Since the current is not in phase with the voltage, it is necessary to consider both the in-phase component and the component that is at quadrature (angularly rotated 90° or perpendicular) to the voltage. The following figure shows a single-phase voltage and current and breaks the current into its in-phase and quadrature components.

CHAPTER 2: ELECTRICAL BACKGROUND

FIGURE 2–9: Voltage and Complex Current

The voltage (V) and the total current (I) can be combined to calculate the apparent power or VA. The voltage and the in-phase current (I watts. The voltage and the quadrature current (I

) are combined to produce the real power or

) are combined to calculate the reactive

power.

The quadrature current may be lagging the voltage (as shown above) or it may lead the voltage. When the quadrature current lags the voltage the load is requiring both real power (watts) and reactive power (vars). When the quadrature current leads the voltage the load is requiring real power (watts) but is delivering reactive power (vars) back into the system; that is VARs are flowing in the opposite direction of the real power flow.

Reactive power (vars) is required in all power systems. Any equipment that uses magnetization to operate requires vars. Usually the magnitude of vars is relatively low compared to the real power quantities. Utilities have an interest in maintaining VAR requirements at the customer to a low value in order to maximize the return on plant invested to deliver energy. When lines are carrying vars, they cannot carry as many watts.

2–12 EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE

CHAPTER 2: ELECTRICAL BACKGROUND

So keeping the var content low allows a line to carry its full capacity of watts. In order to encourage customers to keep VAR requirements low, most utilities impose a penalty if the var content of the load rises above a specified value.

2.4.2 Power Factor

A common method of measuring reactive power requirements is power factor. Power factor can be defined in two different ways. The more common method of calculating power factor is the ratio of the real power to the apparent power. This relationship is expressed in the following formula:

Total PF

real power

----------------------------------------

apparent power

watts

------------- -==

(EQ 2.1)

This formula calculates a power factor quantity known as Total Power Factor. It is called Total PF because it is based on the ratios of the power delivered. The delivered power quantities will include the impacts of any existing harmonic content. If the voltage or current includes high levels of harmonic distortion the power values will be affected. By calculating power factor from the power values, the power factor will include the impact of harmonic distortion. In many cases this is the preferred method of calculation because the entire impact of the actual voltage and current are included.

A second type of power factor is Displacement Power Factor. Displacement PF is based on the angular relationship between the voltage and current. Displacement power factor does not consider the magnitudes of voltage, current or power. It is solely based on the phase angle differences. As a result, it does not include the impact of harmonic distortion. Displacement power factor is calculated using the following equation:

Displacement PF θcos=

(EQ 2.2)

where θ is the angle between the voltage and the current (see FIGURE 2–9: Voltage and Complex Current on page 2–12).

In applications where the voltage and current are not distorted, the Total Power Factor will equal the Displacement Power Factor. But if harmonic distortion is present, the two power factors will not be equal.

EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE 2–13

2.5 Harmonic Distortion

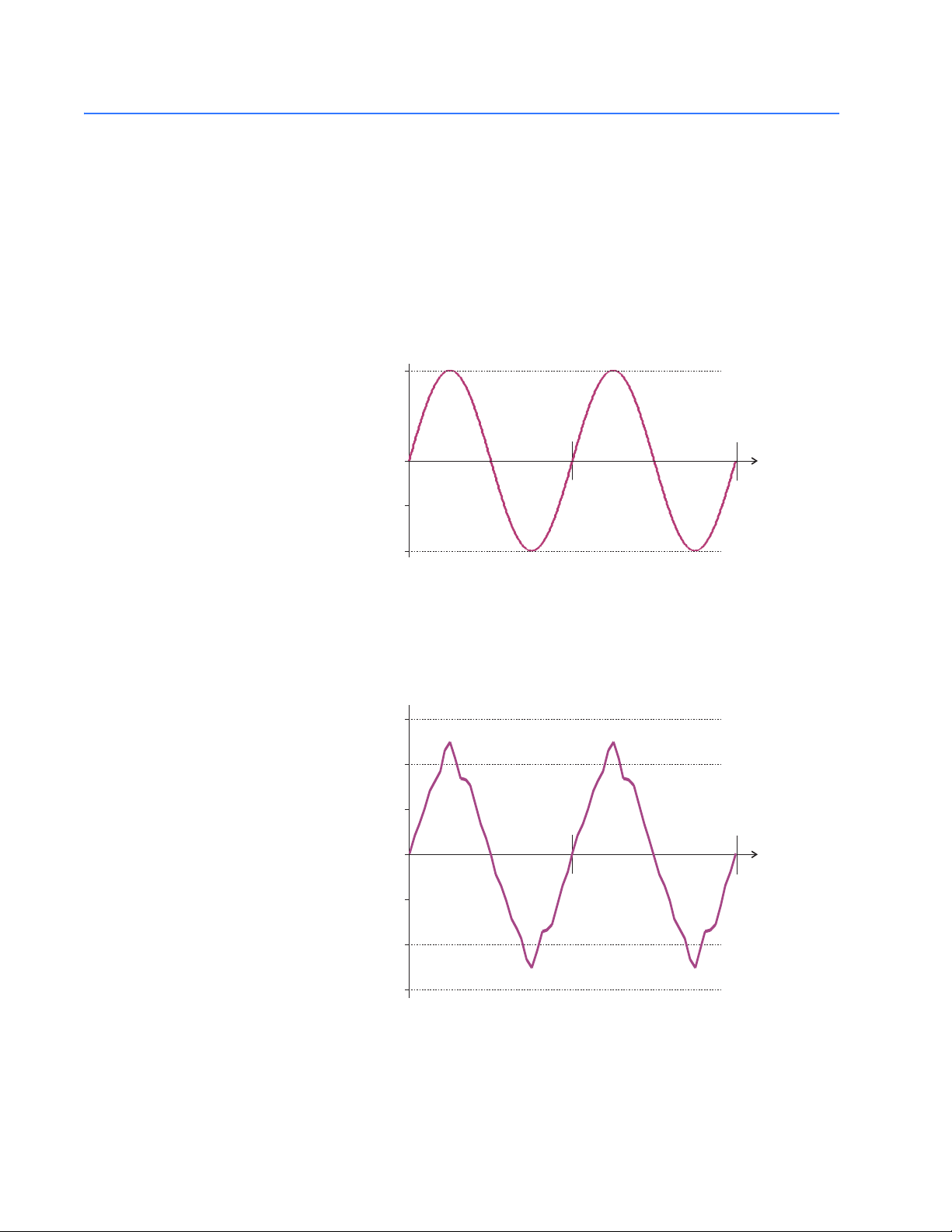
2.5.1 Harmonics of a Non-Sinusoidal Waveform

Harmonic distortion is primarily the result of high concentrations of non-linear loads. Devices such as computer power supplies, variable speed drives and fluorescent light ballasts make current demands that do not match the sinusoidal waveform of AC electricity. As a result, the current waveform feeding these loads is periodic but not sinusoidal. The following figure shows a normal, sinusoidal current waveform with a period of a. This example has no distortion.

CHAPTER 2: ELECTRICAL BACKGROUND

1000

500

Current (amps)

–500

–1000

FIGURE 2–10: Non-Distorted Current Waveform

The figure below shows a current waveform with a slight amount of harmonic distortion. The waveform is still periodic and is fluctuating at the normal 60 Hz frequency (a = 1/60 second). However, the waveform is not the smooth sinusoidal form seen above.

1500

1000

500

Current (amps)

–500

–1000

–1500

FIGURE 2–11: Distorted Current Waveform

The distortion above can be modeled as the sum of several sinusoidal waveforms of frequencies that are multiples of the fundamental 60 Hz frequency. This modeling is performed by mathematically reducing the distorted waveform into a collection of higher

2–14 EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE

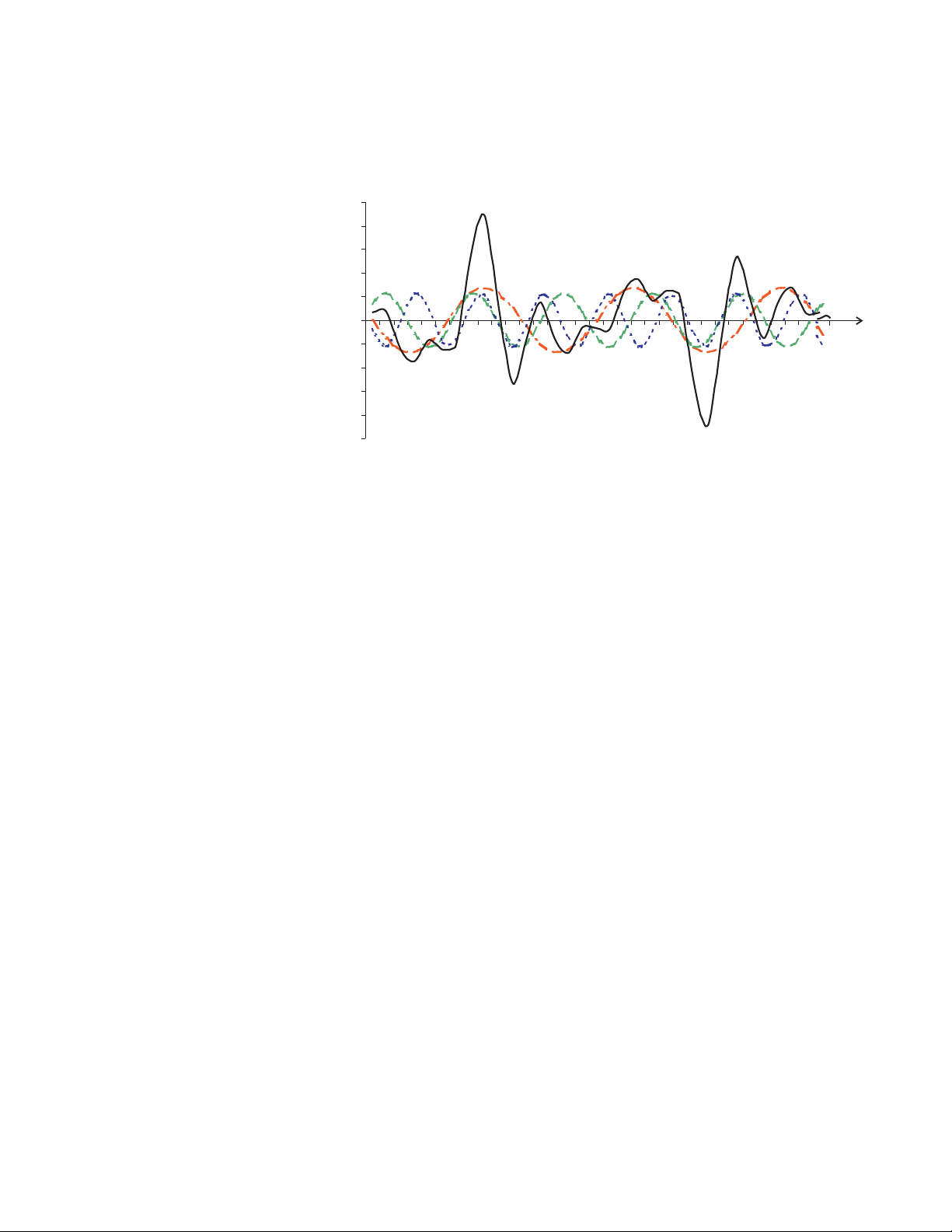
CHAPTER 2: ELECTRICAL BACKGROUND

frequency waveforms. These higher frequency waveforms are referred to as harmonics. The following figure shows the content of the harmonic frequencies that comprise one cycle of the distorted portion of the above waveform.

250

200

150

100

-50

Current (amps)

-100

-150

-200

-250

FIGURE 2–12: Harmonics for Distorted Current Waveform

The waveforms above provide an indication of the impact of combining multiple harmonic frequencies together. The broken lines represent the 3rd, 5th, and 7th current harmonics. The solid line represents the sum of the three harmonics.

When harmonics are present, it is important to remember that they are operating at higher frequencies. As such, they do not always respond in the same manner as 60 Hz values.

2.5.2 Inductive and Capacitive Impedance

Inductive and capacitive impedance are present in all power systems. We are accustomed to thinking about these impedances as they perform at 60 Hz. However, these impedances are subject to frequency variation.

XLjω L and XC1 jωC⁄==

At 60 Hz, ω = 377; but at 300 Hz (5th harmonic) ω = 1885. As frequency changes, the impedance changes and system impedance characteristics that are normal at 60 Hz may be entirely different in the presence of higher order harmonic waves.

Traditionally, the most common harmonics have been the low order odd frequencies, such as the 3rd, 5th, 7th, and 9th. However newer, new-linear loads are introducing significant quantities of higher order harmonics.

(EQ 2.3)

2.5.3 Voltage and Current Monitoring

Since much voltage monitoring and almost all current monitoring is performed using instrument transformers, the higher order harmonics are often not visible. Instrument transformers are designed to pass 60 Hz quantities with high accuracy. These devices, when designed for accuracy at low frequency, do not pass high frequencies with high

EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE 2–15

accuracy; at frequencies above about 1200 Hz they pass almost no information. So when instrument transformers are used, they effectively filter out higher frequency harmonic distortion making it impossible to see.

However, when monitors can be connected directly to the measured circuit (such as direct connection to 480 V bus) the user may often see higher order harmonic distortion. An important rule in any harmonics study is to evaluate the type of equipment and connections before drawing a conclusion. Not being able to see harmonic distortion is not the same as not having harmonic distortion.

2.5.4 Waveform Capture

It is common in advanced meters to perform a function commonly referred to as waveform capture. Waveform capture is the ability of a meter to capture a present picture of the voltage or current waveform for viewing and harmonic analysis. Typically a waveform capture will be one or two cycles in duration and can be viewed as the actual waveform, as a spectral view of the harmonic content, or a tabular view showing the magnitude and phase shift of each harmonic value. Data collected with waveform capture is typically not saved to memory. Waveform capture is a real-time data collection event.

Waveform capture should not be confused with waveform recording that is used to record multiple cycles of all voltage and current waveforms in response to a transient condition.

CHAPTER 2: ELECTRICAL BACKGROUND

2–16 EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE

CHAPTER 2: ELECTRICAL BACKGROUND

2.6 Power Quality

2.6.1 Description

Power quality can mean several different things. The terms power quality and power quality problem have been applied to all types of conditions. A simple definition of power quality problem is any voltage, current or frequency deviation that results in misoperation

or failure of customer equipment or systems. The causes of power quality problems vary widely and may originate in the customer equipment, in an adjacent customer facility or with the utility.

In his book Power Quality Primer, Barry Kennedy provided information on different types of power quality problems. Some of that information is summarized in the following table.

Table 2–3: Typical Power Quality Problems

Cause Disturbance Type Source(s)

Impulse transient

Oscillatory transient with decay

Sag/swell

Interruptions

Undervoltage/ Overvoltage

Voltage flicker

Harmonic distortion

It is often assumed that power quality problems originate with the utility. While it is true that may power quality problems can originate with the utility system, many problems originate with customer equipment. Customer-caused problems may manifest themselves inside the customer location or they may be transported by the utility system to another adjacent customer. Often, equipment that is sensitive to power quality problems may in fact also be the cause of the problem.

Transient voltage disturbance, sub-cycle duration

Transient voltage, sub-cycle duration

RMS voltage, multiple cycle duration

RMS voltage, multiple second or longer duration

RMS voltage, steady state, multiple second or longer duration

RMS voltage, steady state, repetitive condition

Steady-state current or voltage, long term duration

Lightning; Electrostatic discharge; Load switching; Capacitor switching

Line/cable switching; Capacitor switching; Load switching

Remote system faults

System protection; Circuit breakers; Fuses; Maintenance

Motor starting; Load variations; Load dropping

Intermittent loads; Motor starting; Arc furnaces

Non-linear loads; System resonance

If a power quality problem is suspected, it is generally wise to consult a power quality professional for assistance in defining the cause and possible solutions to the problem.

EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE 2–17

CHAPTER 2: ELECTRICAL BACKGROUND

2–18 EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE

GE Consumer & Industrial

Multilin

EPM 6000 Multi-function Power

Chapter 3: Installation

Installation

3.1 Mechanical Installation

Metering System

3.1.1 Dimensions

The EPM 6000 meter can be installed using a standard ANSI C39.1 (4" round) or an IEC 92 mm DIN (square) form. In new installations, simply use existing DIN or ANSI punches. For existing panels, pull out old analog meters and replace with the EPM 6000. The various models use the same installation. See Wiring Diagrams on page 3–9 for various Wye and Delta wiring diagrams.

FIGURE 3–1: Bezel, Side, and Back Dimensions

EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE 3–1

3.1.2 ANSI Installation Steps

Mount the meter in a dry location free from dirt and corrosive substances. The meter is designed to withstand harsh environmental conditions (see the Environmental specifications in Chapter 2 for additional details).

CHAPTER 3: INSTALLATION

FIGURE 3–2: ANSI and DIN Mounting Panel Cutouts

Use the following steps to install the meter:

Z Insert the four threaded rods by hand into the back of the meter.

Twist until secure.

Z Slide the ANSI 12 mounting gasket onto the back of the meter with

the rods in place.

Z Slide the meter with the mounting gasket into the panel.

Z Secure from the back of the panel with a lock washer and nut on

each threaded rod. Use a small wrench to tighten – do not overtighten.

3–2 EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE

CHAPTER 3: INSTALLATION

NEMA12 mounting

gasket

threaded rods

lock washer

and nut

FIGURE 3–3: ANSI Mounting Procedure

3.1.3 DIN Installation Steps

Use the following steps to install the meter:

Z Slide the meter with NEMA 12 mounting gasket into panel.

EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE 3–3

CHAPTER 3: INSTALLATION

Z From back of the panel, slide 2 DIN mounting brackets into the

grooves on the top and bottom of the meter housing, then snap into place.

Z Secure meter to panel with a lock washer and #8 screw through

each of the two mounting brackets. Tighten with a #2 Phillips screwdriver – do not overtighten.

DIN mounting bracket

top-mounting bracket groove

bottom mounting bracket groove

#8 screw

EPM 6000 meter with NEMA 12 mounting gasket

FIGURE 3–4: DIN Mounting Procedure

3–4 EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE

CHAPTER 3: INSTALLATION

3.2 Electrical Installation

3.2.1 Installation Considerations

Installation of the EPM 6000 Power Metering System must be performed by only qualified personnel who follow standard safety precautions during all procedures. Those personnel should have appropriate training and experience with high voltage devices. Appropriate safety gloves, safety glasses and protective clothing is recommended.

During normal operation of the EPM 6000, dangerous voltages flow through many parts of the meter, including: Terminals and any connected CTs (current transformers) and PTs (potential transformers), all input/output modules and their circuits. All primary and secondary circuits can, at times, produce lethal voltages and currents. Avoid contact with any current-carrying surfaces.

Do not use the meter or any I/O output device for primary protection or in an energylimiting capacity. The meter can only be used as secondary protection. Do not use the meter for applications where failure of the meter may cause harm or death. Do not use the meter for any application where there may be a risk of fire.

All meter terminals should be inaccessible after installation.

Do not apply more than the maximum voltage the meter or any attached device can withstand. Refer to meter and/or device labels and to the Specifications for all devices before applying voltages. Do not hi-pot/dielectric test any outputs, inputs or communications terminals.

GE recommends the use of shorting blocks and fuses for voltage leads and power supply to prevent hazardous voltage conditions or damage to CTs, if the meter needs to be removed from service. CT grounding is optional.

If the equipment is used in a manner not specified by the manufacturer, the protection provided by the equipment may be impaired.

Note

There is no required preventive maintenance or inspection necessary for safety. however, any repair or maintenance should be performed by the factory.

DISCONNECT DEVICE: The following part is considered the equipment disconnect device.

A switch or circuit-breaker must be included in the end-use equipment or building installation. The switch shall be in close proximity to the equipment and within easy reach of the operator. The switch shall be marked as the disconnecting device for the equipment.

EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE 3–5

3.2.2 CT Leads Terminated to Meter

The EPM 6000 is designed to have current inputs wired in one of three ways. The figure below shows the most typical connection, where CT Leads are terminated to the meter at the current gills. This connection uses nickel-plated brass studs (current gills) with screws at each end. This connection allows the CT wires to be terminated using either an “O” or a “U” lug. Tighten the screws with a #2 Phillips screwdriver.

Current gills (nickel-plated brass stud)

CHAPTER 3: INSTALLATION

FIGURE 3–5: CT Leads Terminated to Meter

Wiring diagrams are detailed in Wiring Diagrams on page 3–9. Communications connections are detailed in Communications Setup on page 3–19.

3.2.3 CT Leads Pass-Through (No Meter Termination)

The second method allows the CT wires to pass through the CT Inputs without terminating at the meter. In this case, remove the current gills and place the CT wire directly through the CT opening. The opening will accommodate up to 0.177" / 4.5 mm maximum diameter CT wire.

3–6 EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE

CHAPTER 3: INSTALLATION

3.2.4 Quick Connect Crimp CT Terminations

CT wire passing through the meter

Current gills removed

FIGURE 3–6: Pass-Through Wire Electrical Connection

For quick termination or for portable applications, a quick connect crimp CT connection can also be used.

Crimp CT terminations

FIGURE 3–7: Quick Connect Electrical Connection

3.2.5 Voltage and Power Supply Connections

Voltage Inputs are connected to the back of the unit via a optional wire connectors. The connectors accommodate up to AWG#12 / 2.5 mm wire.

EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE 3–7

3.2.6 Ground Connections

The EPM 6000 ground terminals ( ) should be connected directly to the installation's protective earth ground. Use 2.5 mm wire for this connection.

Power supply inputs

Voltage inputs

CHAPTER 3: INSTALLATION

RS485 outputs (do not place voltage on these terminals!)

FIGURE 3–8: Voltage Connection

GE recommends the use of fuses on each of the sense voltages and on the control power, even though the wiring diagrams in this chapter do not show them.

• Use a 0.1 A fuse on each voltage input.

• Use a 3 A fuse on the power supply.

3–8 EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE

CHAPTER 3: INSTALLATION

3.3 Wiring Diagrams

3.3.1 Description

Choose the diagram that best suits your application and maintains the CT polarity.

These diagrams are indicated in the sections following.

1. Three-phase, four-wire system Wye with direct voltage, 3 element.

2. Three-phase, four-wire system Wye with direct voltage, 2.5 element.

3. Three-phase, four-wire Wye with PTs, 3 element.

4. Three-phase, four-wire Wye with PTs, 2.5 element.

5. Three-phase, three-wire Delta with direct voltage.

6. Three-phase, three-wire Delta with PTs.

7. Current-only measurement (three-phase).

8. Current-only measurement (dual-phase).

9. Current-only measurement (single-phase).

EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE 3–9

3.3.2 Wye, 4-Wire with no PTs and 3 CTs, 3 Element

For this wiring type, select 3ELWYE (3-element Wye) in the meter programming setup.

CHAPTER 3: INSTALLATION

FIGURE 3–9: 4-Wire Wye with no PTs and 3 CTs, 3 Element

3–10 EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE

CHAPTER 3: INSTALLATION

3.3.3 Wye, 4-Wire with no PTs and 3 CTs, 2.5 Element

For this wiring type, select 2.5EL WYE (2.5-element Wye) in the meter programming setup.

FIGURE 3–10: 4-Wire Wye with no PTs and 3 CTs, 2.5 Element

EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE 3–11

3.3.4 Wye, 4-Wire with 3 PTs and 3 CTs, 3 Element

For this wiring type, select 3ELWYE (3-element Wye) in the meter programming setup.

CHAPTER 3: INSTALLATION

FIGURE 3–11: 4-Wire Wye with 3 PTs and 3 CTs, 3 Element

3–12 EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE

CHAPTER 3: INSTALLATION

3.3.5 Wye, 4-Wire with 2 PTs and 3 CTs, 2.5 Element

For this wiring type, select 2.5EL WYE (2.5-element Wye) in the meter programming setup.

FIGURE 3–12: 4-Wire Wye with 2 PTs and 3 CTs, 2.5 Element

EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE 3–13

3.3.6 Delta, 3-Wire with no PTs and 2 CTs

For this wiring type, select 2CtdEL (2 CT Delta) in the meter programming setup.

CHAPTER 3: INSTALLATION

FIGURE 3–13: 3-Wire Delta with no PTs and 2 CTs

3–14 EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE

CHAPTER 3: INSTALLATION

3.3.7 Delta, 3-Wire with 2 PTs and 2 CTs

For this wiring type, select 2CtdEL (2 CT Delta) in the meter programming setup.

FIGURE 3–14: 3-Wire Delta with 2 PTs and 2 CTs

EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE 3–15

3.3.8 Current-Only Measurement (Three-Phase)

For this wiring type, select 3ELWYE (3 Element Wye) in the meter programming setup.

CHAPTER 3: INSTALLATION

Note

Even if the meter is used only for current measurement, the unit requires a AN volts reference. Please ensure that the voltage input is attached to the meter. AC control power can be used to provide the reference signal.

3–16 EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE

CHAPTER 3: INSTALLATION

3.3.9 Current-Only Measurement (Dual-Phase)

For this wiring type, select 3ELWYE (3 Element Wye) in the meter programming setup.

Note

EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE 3–17

3.3.10 Current-Only Measurement (Single-Phase)

For this wiring type, select 3ELWYE (3 Element Wye) in the meter programming setup.

CHAPTER 3: INSTALLATION

Note

3–18 EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE

CHAPTER 3: INSTALLATION

3.4 Communications Setup

3.4.1 Description

The EPM 6000 Power Metering System provides two independent communication ports. The first port, COM1, is an optical IrDA port . The second port, COM2, provides RS485 communication via the Modbus protocol.

3.4.2 IrDA COM1 Port

The COM1 IrDA port is located on the meter faceplate. The IrDA port allows the unit to be set up and programmed using a remote laptop without the need for a communication cable. Just point at the meter with an IrDA-equipped computer to configure it.

Use the GE Communicator software package that works with the EPM 6000 IrDA port to configure the port and poll readings. Refer to the GE Communicator User Manual for details on programming and accessing readings.

Wireless Communication

Settings for the COM1 IrDA port are configured using GE Communicator software. This port communicates via the Modbus ASCII protocol only.

3.4.3 RS485 COM2 Port

The EPM 6000 COM2 port uses standard 2-wire, half-duplex RS485 communications. The RS485 connector is located on the back face of the meter. A connection can easily be established to a master device or to other slave devices, as indicated below.

Direct PC Interface

FIGURE 3–15: Simultaneous Dual Communications Paths

Modbus Serial RS485

Master Host

EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE 3–19

CHAPTER 3: INSTALLATION

FIGURE 3–16: RS485 Communications Installation

The EPM 6000 COM2 port can be programmed through the faceplate or with software. The standard RS485 port settings are:

Address: 001 to 247 Baud rate: 9.6, 19.2, 38.4, or 57.6 kbps Protocol: Modbus RTU, Modbus ASCII, or DNP 3.0

3–20 EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE

GE Consumer & Industrial

Multilin

EPM 6000 Multi-function Power

Chapter 4: Using the Meter

Using the Meter

4.1 Front Panel Interface

Metering System

4.1.1 Description

The EPM 6000 Power Metering System can be configured and a variety of functions can be accomplished simply by using the elements and the buttons on the meter faceplate. This chapter will review front panel navigation. Complete navigation maps can be found in Navigation Maps on page 6–1.

4.1.2 Faceplate Elements

The meter faceplate elements are described below.

• Reading Type Designator: indicates type of reading.

• IrDA Communication Port: COM1 port for wireless communications.

• % of Load Bar: graphic display of current as a percentage of the load.

• Parameter Designator: indicates the reading displayed.

• Watt-Hour Pulse: energy pulse output to test accuracy.

• Scale Selector: “kilo” or “mega” multiplier of displayed readings.

EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE 4–1

CHAPTER 4: USING THE METER

4.1.3 Faceplate Buttons

The following functions can be performed using the MENU, ENTER, DOWN and RIGHT buttons:

• View meter information

•Enter display modes

• Configure parameters (password protected)

• Perform resets

• Perform LED checks

• Change settings

• View parameter values

• Scroll parameter values

•View limit states

Reading

type indicator

IRDA communications

port

% of Load Bar

Parameter designator

Watt-hour pulse

FIGURE 4–1: EPM 6000 Faceplate Elements

The faceplate buttons function as follows:

• Enter button: Press and release the ENTER button to select one of four display modes: operating mode (default), reset mode (press ENTER once, followed by DOWN), settings mode (press ENTER twice, followed by DOWN), and configuration mode (press ENTER three times, followed by DOWN).

• Menu button: Press and release to navigate the configuration menu and again to return to the main menu.

• Right button: Press the RIGHT button to enter the menus for the operate, reset , settings, and configuration mode.

• Down button: Press the DOWN button to scroll through the menus for each of the modes.

In operating mode (default), the faceplate buttons are used to view parameter values. In reset mode, the buttons are used to restore maximum and minimum values. In settings mode, the buttons are used to view settings parameters and change the scroll setting. In configuration mode, the buttons are used to change meter configuration (in this case, they can be password protected).

4–2 EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE

CHAPTER 4: USING THE METER

4.1.4 Percentage of Load Bar

The 10-segment LED bar graph at the bottom of the EPM 6000 front panel provides a graphic representation of current. The segments illuminate according to the load shown in the table below. When the load is greater than 120% of full-load, all segments flash “ON” for 1.5 seconds and “OFF” for 0.5 seconds.

button

DOWN button

ENTER button

RIGHT button

FIGURE 4–2: EPM 6000 Faceplate Buttons

Table 4–1: % of Load Bar Segments

Segments Load ≥ % Full Load

none no load

11%

1 to 2 15%

1 to 3 30%

1 to 4 45%

1 to 5 60%

1 to 6 72%

1 to 7 84%

1 to 8 96%

1 to 9 108%

1 to 10 120%

all blinking >120%

EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE 4–3

4.1.5 Watt-Hour Accuracy Testing (Verification)

To be certified for revenue metering, power providers and utility companies have to verify that the billing energy meter will perform to the stated accuracy. To confirm the meter's performance and calibration, power providers use field test standards to ensure that the unit's energy measurements are correct. Since the EPM 6000 is a traceable revenue meter, it contains a utility grade test pulse that can be used to gate an accuracy standard. This is an essential feature required of all billing grade meters.

CHAPTER 4: USING THE METER

FIGURE 4–3: Using the Watt-Hour Test Probe

The following table lists the watt-hour pulse constants for accuracy testing.

Table 4–2: EPM 6000 Accuracy Test Constants

Voltage Level Class 10 Models Class 2 Models

Below 150 V 0.2505759630 0.0501151926

Above 150 V 1.0023038521 0.2004607704

4–4 EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE

CHAPTER 4: USING THE METER

4.2 Configuring the Meter via the Front Panel

4.2.1 Overview

The EPM 6000 front panel can be used to configure the meter. The EPM 6000 has three modes: operating mode (default), IrDA reset mode, and configuration mode. The MENU, ENTER, DOWN and RIGHT buttons navigate through the modes and navigate through all the screens in each mode.

A typical setup will be demonstrated in this section; other settings are possible. Complete navigation maps for the display modes are shown in Navigation Maps on page 6–1. The meter can also be configured through software.

4.2.2 Start Up

Upon power-up, the meter will display a sequence of screens. The sequence includes the following screens:

Lamp test screen where all LEDs are lighted; Lamp test screen where all digits are lighted; Firmware screen showing build number; Error screen (if an error exists).

The EPM 6000 will then auto-scroll the parameter designators on the right side of the front panel. Values are displayed for each parameter. The KILO or MEGA LED will illuminate, showing the scale for the Wh, varh and VAh readings.

An example of a Wh reading is shown below.

FIGURE 4–4: Typical Wh Reading

The EPM 6000 will continue to scroll through the parameter designators, providing readings until one of the buttons on the front panel is pushed, causing the meter to enter one of the other modes.

EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE 4–5

4.2.3 Main Menu

CHAPTER 4: USING THE METER

The following procedure describes how the navigate the main menu.

Z Push the MENU button from any of the auto-scrolling readings to

display the main menu screens. The string for reset mode (

rSt) will be blinking in the “A” Screen.

Z Press the DOWN key to scroll the menu and display the

configuration mode string (

CFG) in the “A” screen.

Z Press the DOWN key again to scroll the menu and display the

operating mode string in the “A” screen.

Z Press the DOWN key again to scroll back to reset mode (

Z Press ENTER from the main menu to enter the mode displayed on

the “A” screen. See Main Menu Screens on page 6–2 for navigation details.

4.2.4 Reset Mode and Password Entry

The following procedure describes how the navigate the reset mode menu.

Z Press ENTER while the “A” screen is in reset mode (i.e., the “A”

screen displays The resets all maximum and minimum values.

rSt).

FIGURE 4–5: Main Menu Screens

rSt).

rSt ALL? no message will appear. The rSt ALL? function

Z Press ENTER to continue scrolling through the main menu.

The DOWN button does not change the screen.

4–6 EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE

CHAPTER 4: USING THE METER

Z Press the RIGHT button to display the rSt ALL? YES message.

Resetting the maximum and minimum value requires entry of a four-digit password, if enabled in software.

Z Press ENTER to display the password screen.

If password is enabled in the software, the screen displays the

PASS message in the “A”

screen and 4 dashes in the “B” screen, with the left-most digit flashing.

Z Using the DOWN button, select 0 to 9 for the flashing digit.

Z When the desired number appears, use the RIGHT button to select

it and move to the next digit.

Z When all four password digits have been selected, press ENTER.

If the correct password has been entered, the

rSt ALL donE message appears and the

screen returns to auto-scroll the parameters.

EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE 4–7

CHAPTER 4: USING THE METER

If an incorrect password has been entered, the PASS ---- FAIL message appears and the screen returns to the

rSt ALL? YES message.

4–8 EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE

CHAPTER 4: USING THE METER

4.3 Changing Settings in Configuration Mode

4.3.1 Description

The following procedure describes how the navigate the configuration mode menu.

Z Press the MENU Button from any of the auto-scrolling readings.

Z Press DOWN to display the configuration mode (

w Press ENTER to scroll through the configuration parameters,

Z Push the DOWN Button to scroll all the parameters: scroll, CT, PT,

4.3.2 Configuring the Scroll Feature

Use the following procedure to configure the scroll feature.

CFG) in the “A”

screen.

starting at the

connection ( The active parameter is always flashing and displayed in the “A” screen.

SCrL Ct Pt screen.

Cnct) and port.

Z Press the ENTER button to display the

Z Press the RIGHT button to change the display to

shown below.

FIGURE 4–6: Scroll Mode Configuration

EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE 4–9

SCrL no message.

SCrL YES as

CHAPTER 4: USING THE METER

When in scroll mode, the unit scrolls each parameter for 7 seconds on and 1 second off. The meter can be configured through software to only display selected screens. In this case, it will only scroll the selected displays.

Z Push ENTER to select

Z Scroll to the CT parameters screen.

4.3.3 Programming the Configuration Mode Screens

Use the following procedure to program the screen for configuration mode.

Z Press the DOWN or RIGHT button (for example, from the

message below) to display the password screen, if enabled in the software.

Z Use the DOWN and RIGHT buttons to enter the correct password

(refer to Reset Mode and Password Entry on page 4–6 for steps on password entry).

Z Once the correct password is entered, push ENTER.

The

Ct-n message will reappear, the PRG faceplate LED will flash,

and the first digit of the “B” screen will also flash.

YES or no.

Ct-n

Z Use the DOWN button to change the first digit.

Z Use the RIGHT button to select and change the successive digits.

Z When the new value is entered, push ENTER twice.

This will display the

Z Use the RIGHT button to scroll to change the value from

Z When the

Stor ALL? YES message is displayed, press ENTER to

Stor ALL? no screen.

no to YES.

change the setting.

4–10 EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE

CHAPTER 4: USING THE METER

4.3.4 Configuring the CT Setting

The Stor ALL donE message will appear and the meter will reset.

Use the following procedure to program the CT setting.

Z Push the DOWN Button to scroll through the configuration mode

parameters.

Press ENTER when

Ct is the active parameter (i.e. it is in the “A” screen and flashing).

This will display the and the

Z Press ENTER again to change to display the

screen.

Ct-n (CT numerator) screen.

Ct-d (CT denominator)

The Ct-d value is preset to a 1 or 5 A at the factory and cannot be changed.

EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE 4–11

CHAPTER 4: USING THE METER

Z Press ENTER again to select the to Ct-S (CT scaling) value.

The

Ct-S value can be “1”, “10”, or “100”. Refer to Programming the Configuration Mode

Screens on page 4–10 for instructions on changing values.

Note

The value for amps is a product of the Ct-n and the Ct-S values.

Example settings for the

200/5 A: set the 800/5 A: set the 2000/5 A: set the 10000/5 A: set the

Ct-S value are shown below:

Ct-n value for “200” and the Ct-S value for “1” Ct-n value for “800” and the Ct-S value for “1”

Ct-n value for “2000” and the Ct-S value for “1”.

Ct-n value for “1000” and the Ct-S value for “10”.

Z Press ENTER to scroll through the other

CFG parameters.

Pressing DOWN or RIGHT displays the password screen (see Reset Mode and Password Entry on page 4–6 for details).

Z Press MENU to return to the main configuration menu.

Note

Ct-n and Ct-S are dictated by primary current. Ct-d is secondary current.

4.3.5 Configuring the PT Setting

Use the following procedure to program the PT setting.

Z Push the DOWN Button to scroll through the configuration mode

parameters.

Z Press ENTER when

Pt is the active parameter (i.e. it is in the “A”

screen and flashing).

4–12 EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE

CHAPTER 4: USING THE METER

This will display the and the Pt-n (PT numerator) screen.

Z Press ENTER again to change to display the

Pt-d (PT denominator)

screen.

Z Press ENTER again to select the to Pt-S (PT scaling) value.

The

Pt-S value can be “1”, “10”, or “100”. Refer to Programming the Configuration Mode

Screens on page 4–10 for instructions on changing values.

Example settings for the

• 14400/120 V (reads 14400 V): set

Pt-n, Pt-d, and Pt-S values are shown below:

Pt-n to “1440”, Pt-d to “120”, and Pt-S

to “10”

• 138000/69 V (reads 138000 V): set

Pt-n to “1380”, Pt-d to “69”, and Pt-S

to “100”

• 345000/115 V (reads 347000 V): set

Pt-S to “100”

Z Press ENTER to scroll through the other

Pt-n to “3450”, Pt-d to “115”, and

CFG parameters.

Z Press DOWN or RIGHT to display the password screen (see Reset

Mode and Password Entry on page 4–6 for details).

Z Press MENU to return to the main configuration menu.

Note

Pt-n and Pt-S are dictated by primary voltage. Pt-d is secondary voltage.

4.3.6 Configuring the Connection Setting

Use the following procedure to program the connection (Cnct) setting.

EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE 4–13

CHAPTER 4: USING THE METER

Z Push the DOWN Button to scroll through the configuration mode

parameters.

This will display the 3-element Wye (

3 EL WYE), 2.5-element Wye (2.5EL WYE), and 2 CT Delta (2CtdeL), as

shown below.

3-Element Wye 2.5-Element Wye

Z Press ENTER when

Cnct is the active parameter (i.e. it is in the “A”

screen and flashing).

Cnct (connection) screen. The possible connection configurations are

2 CT Delta

Z Press ENTER to scroll through the other

CFG parameters.

Z Press DOWN or RIGHT to display the password screen (see Reset

Mode and Password Entry on page 4–6 for details).

Z Press MENU to return to the main configuration menu.

4.3.7 Configuring the Communication Port Setting

Use the following procedure to program the communication port (POrt) settings.

Z Push the DOWN Button to scroll through the configuration mode

parameters.

Z Press ENTER when

screen and flashing).

The following parameters can be configured through the

• The meter address (

• The baud rate ( 38400, and 57600 kbps, respectively.

• The communications protocol (

Adr, a 3-digit number).

bAUd). Select from “9600”, “19.2”, “38.4”, and “57.6” for 9600, 19200,

POrt is the active parameter (i.e. it is in the “A”

POrt menu

Prot).

4–14 EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE

CHAPTER 4: USING THE METER

Z Select “rtU” for Modbus RTU, “ASCI” for Modbus ASCII, and “dnP” for

the DNP 3.0 protocol.

•The first

POrt screen is meter address (Adr). The current address appears on the

screen.

Z Select three-digit number for the address.

Refer to Programming the Configuration Mode Screens on page 4– 10 for details on changing values.

Address 005

• The next

POrt screen is the baud rate (bAUd). The current baud rate is displayed

on the “B” screen. Refer to Programming the Configuration Mode Screens on page 4–10 for details on changing values. The possible baud rate screens are shown below.

• The final

POrt screen is the communications protocol (Prot).

The current protocol is displayed on the “B” screen. Refer to Programming the Configuration Mode Screens on page 4–10 for details on changing values. The three protocol selections are shown below.

EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE 4–15

CHAPTER 4: USING THE METER

Z Press ENTER to scroll through the other CFG parameters.

Z Press DOWN or RIGHT to display the password screen (see Reset

Mode and Password Entry on page 4–6 for details).

Z Press MENU to return to the main configuration menu.

4–16 EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE

CHAPTER 4: USING THE METER

4.4 Operating Mode

4.4.1 Description

Operating mode is the EPM 6000 meter’s default mode. If scrolling is enabled, the meter automatically scrolls through these parameter screens after startup. The screen changes every 7 seconds. Scrolling is suspended for 3 minutes after any button is pressed.

Push the DOWN button to scroll all the parameters in operating mode. The active parameter has the indicator light next to it on the right face of the meter. Push the RIGHT button to view additional displays for that parameter. A table of the possible displays in the operating mode is below. Refer to Operating Mode Screens on page 6–3 for a detailed navigation map of the operating mode.

Table 4–3: Operating Mode Parameter Readings

Parameter designator

VOLTS L-N VOLTS_LN

VOLTS L-L VOLTS_LL

Possible display readings

VOLTS_LN_ MAX

VOLTS_LL_ MAX

VOLTS_LN_ MIN

VOLTS_LL_ MIN

VOLTS_LN_ THD

AMPS AMPS_MAX AMPS_MIN AMPS_THD

W/VAR/PF W_VAR_PF

VA/Hz VA_FREQ

W_VAR_PF _MAX_POS

VA_FREQ_ MAX

W_VAR_PF _MIN_POS

VA_FREQ_ MIN

W_VAR_PF _MAX_NEG

Wh KWH_REC KWH_DEL KWH_NET

VARh KVARH_ POS KVARH_ NEG KVARH_ NET

VAh KVAH

Note

Readings or groups of readings are skipped if not applicable to the meter type or hookup, or if explicitly disabled in the programmable settings.

EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE 4–17

CHAPTER 4: USING THE METER

4–18 EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE

GE Consumer & Industrial

Multilin

EPM 6000 Multi-function Power

Chapter 5: Communications

Communications

5.1 Modbus Communications

Metering System

5.1.1 Memory Map Description

The Modbus memory map is divided into four primary sections:

1. Fixed data registers: addresses 0001 to 0021.

2. Meter data registers: addresses 1000 to 5003.

The meter data registers read as “0” until the first readings are available or if the meter is not in operating mode. Writes to these registers will be accepted but will have no effect on the register.

3. Command registers: addresses 20000 to 26011.

The command registers always read as “0”. The may be written only when the meter is in a suitable mode. The registers return an illegal data address exception if a write is attempted in an incorrect mode.

4. Programmable settings registers: addresses 30000 to 30026.

All registers explicitly listed in the table read as “0”. Writes to these registers will be accepted but won’t actually the register, since it doesn’t exist.

5.1.2 Memory Map

The Modbus memory map is shown below. Additional notes indicated in the memory map (“See Note ...”) are located at the end of the table, as well as a description of the format codes.

EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE 5–1

CHAPTER 5: COMMUNICATIONS

HEX

ADDRESS

DESCRIPTION

FORMAT RANGE

UNITS OR

RESOLUTION

COMMENTS # REG

FIXED DATA SECTION Identification Block

0000 - 0007 Meter Name ASCII 16 char none

0008 - 000F Meter Serial Number ASCII 16 char none

0010 - 0010 Meter Type UINT16 bit-mapped -------t -----vvv

0011 - 0012 Firmware Version ASCII 4 char none

0013 - 0013 Map Version UINT16 0 to 65535 none

0014 - 0014 Meter Configuration UINT16 bit-mapped -------- --ffffff ffffff = calibration frequency (50 or 60)

0015 - 0015 ASIC Version UINT16 0-65535 none

0016 - 0026 Reserved

0027 - 002E GE Part Number ASCII 16 char none

METER DATA SECTION

Primary Readings Block, 6 cycles (IEEE Floating Point)

0383 - 0384 Watts, 3-Ph total FLOAT -9999 M to +9999 M watts 0385 - 0386 VARs, 3-Ph total FLOAT -9999 M to +9999 M VARs 0387 - 0388 VAs, 3-Ph total FLOAT -9999 M to +9999 M VAs

read-only

t = transducer model (1=yes, 0=no), vvv = V-switch(1 to 4)

Block Size:

read-only

Block Size:

8 8 1

2 1 1

2 2 2 6

Primary Readings Block, 60 cycles (IEEE Floating Point)

03E7 - 03E8 Volts A-N FLOAT 0 to 9999 M volts

03E9 - 03EA Volts B-N FLOAT 0 to 9999 M volts

03EB - 03EC Volts C-N FLOAT 0 to 9999 M volts

03ED - 03EE Volts A-B FLOAT 0 to 9999 M volts

03EF - 03F0 Volts B-C FLOAT 0 to 9999 M volts

03F1 - 03F2 Volts C-A FLOAT 0 to 9999 M volts

03F3 - 03F4 Amps A FLOAT 0 to 9999 M amps

03F5 - 03F6 Amps B FLOAT 0 to 9999 M amps

03F7 - 03F8 Amps C FLOAT 0 to 9999 M amps

03F9 - 03FA Watts, 3-Ph total FLOAT -9999 M to +9999 M watts

03FB - 03FC VARs, 3-Ph total FLOAT -9999 M to +9999 M VARs

03FD - 03FE VAs, 3-Ph total FLOAT -9999 M to +9999 M VAs

03FF - 0400 Power Factor, 3-Ph total FLOAT -1.00 to +1.00 none

0401 - 0402 Frequency FLOAT 0 to 65.00 Hz

0403 - 0404 Neutral Current FLOAT 0 to 9999 M amps

Primary Energy Block

044B - 044C W-hours, Received SINT32

044D - 044E W-hours, Delivered SINT32

044F - 0450 W-hours, Net SINT32 -99999999 to 99999999 Wh per energy format

0451 - 0452 W-hours, Total SINT32 0 to 99999999 Wh per energy format * 5 to 8 digits

0453 - 0454 VAR-hours, Positive SINT32 0 to 99999999 VARh per energy format

0455 - 0456 VAR-hours, Negative SINT32 0 to -99999999 VARh per energy format

0457 - 0458 VAR-hours, Net SINT32 -99999999 to 99999999 VARh per energy format

0 to 99999999 or 0 to

-99999999

0 to 99999999 or 0 to

-99999999

Wh per energy format

read-only

Block Size:

read-only

* Wh received & delivered always have opposite signs

* Wh received is positive for "view as load", delivered is positive for "view as generator"

* decimal point implied, per energy format

* resolution of digit before decimal point = units, kilo, or mega, per energy format

2 2 2 2 2 2 2 2 2 2 2 2 2 2 2

2 2 2

2 2

5–2 EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE

CHAPTER 5: COMMUNICATIONS

HEX

ADDRESS

0459 - 045A VAR-hours, Total SINT32 0 to 99999999 VARh per energy format

045B - 045C VA-hours, Total SINT32 0 to 99999999 VAh per energy format * see note 10

DESCRIPTION

FORMAT RANGE

Primary Demand Block (IEEE Floating Point)

07CF - 07D0 Amps A, Average FLOAT 0 to 9999 M amps

07D1 - 07D2 Amps B, Average FLOAT 0 to 9999 M amps

07D3 - 07D4 Amps C, Average FLOAT 0 to 9999 M amps

07D5 - 07D6

07D7 - 07D8

07D9 - 07DA

07DB - 07DC

07DD - 07DE VAs, 3-Ph, Average FLOAT -9999 M to +9999 M VAs

07DF - 07E0 Positive PF, 3-Ph, Average FLOAT -1.00 to +1.00 none

07E1 - 07E2

Positive Watts, 3-Ph, Average Positive VARs, 3-Ph, Average Negative Watts, 3-Ph, Average Negative VARs, 3-Ph, Average

Negative PF, 3-PF, Average

FLOAT -9999 M to +9999 M watts

FLOAT -9999 M to +9999 M VARs

FLOAT -9999 M to +9999 M watts

FLOAT -9999 M to +9999 M VARs

FLOAT -1.00 to +1.00 none

Primary Minimum Block (IEEE Floating Point)

0BB7 - 0BB8 Volts A-N, Minimum FLOAT 0 to 9999 M volts

0BB9 - 0BBA Volts B-N, Minimum FLOAT 0 to 9999 M volts

0BBB - 0BBC Volts C-N, Minimum FLOAT 0 to 9999 M volts

0BBD - 0BBE Volts A-B, Minimum FLOAT 0 to 9999 M volts

0BBF - 0BC0 Volts B-C, Minimum FLOAT 0 to 9999 M volts

0BC1 - 0BC2 Volts C-A, Minimum FLOAT 0 to 9999 M volts

0BC3 - 0BC4

0BC5 - 0BC6

0BC7 - 0BC8

0BC9 - 0BCA

0BCB - 0BCC

0BCD - 0BCE

0BCF - 0BD0

0BD1 - 0BD2

0BD3 - 0BD4

0BD5 - 0BD6

0BD7 - 0BD8 Frequency, Minimum FLOAT 0 to 65.00 Hz

Amps A, Minimum Avg Demand Amps B, Minimum Avg Demand Amps C, Minimum Avg Demand Positive Watts, 3-Ph, Minimum Avg Demand Positive VARs, 3-Ph, Minimum Avg Demand Negative Watts, 3-Ph, Minimum Avg Demand Negative VARs, 3-Ph, Minimum Avg Demand VAs, 3-Ph, Minimum A vg Demand Positive Power Factor, 3Ph, Minimum Avg Demand Negative Power Factor, 3Ph, Minimum Avg Demand

FLOAT 0 to 9999 M amps

FLOAT 0 to +9999 M watts

FLOAT 0 to +9999 M VARs

FLOAT 0 to +9999 M watts

FLOAT 0 to +9999 M VARs

FLOAT -9999 M to +9999 M VAs

FLOAT -1.00 to +1.00 none

UNITS OR

RESOLUTION

COMMENTS # REG

Block Size:

read-only

Block Size:

read-only

Block Size:

2 2

2 2 2 2

2 2 2

2 2 2 2 2 2 2

Primary Maximum Block (IEEE Floating Point)

0C1B - 0C1C Volts A-N, Maximum FLOAT 0 to 9999 M volts

0C1D - 0C1E Volts B-N, Maximum FLOAT 0 to 9999 M volts

0C1F - 0C20 Volts C-N, Maximum FLOAT 0 to 9999 M volts

0C21 - 0C22 Volts A-B, Maximum FLOAT 0 to 9999 M volts

0C23 - 0C24 Volts B-C, Maximum FLOAT 0 to 9999 M volts

0C25 - 0C26 Volts C-A, Maximum FLOAT 0 to 9999 M volts

0C27 - 0C28

0C29 - 0C2A

0C2B - 0C2C

0C2D - 0C2E

Amps A, Maximum Avg Demand Amps B, Maximum Avg Demand Amps C, Maximum Avg Demand Positive Watts, 3-Ph, Maximum Avg Demand

FLOAT 0 to 9999 M amps

FLOAT 0 to +9999 M watts

read-only

2 2 2 2 2 2 2

EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE 5–3

CHAPTER 5: COMMUNICATIONS

HEX

ADDRESS

0C2F - 0C30

0C31 - 0C32

0C33 - 0C34

0C35 - 0C36

0C37 - 0C38

0C39 - 0C3A

0C3B - 0C3C Frequency, Maximum FLOAT 0 to 65.00 Hz

THD Block

0F9F - 0F9F Volts A-N, %THD UINT16 0 to 9999, or 65535 0.1%

0FA0 - 0FA0 Volts B-N, %THD UINT16 0 to 9999, or 65535 0.1%

0FA1 - 0FA1 Volts C-N, %THD UINT16 0 to 9999, or 65535 0.1%

0FA2 - 0FA2 Amps A, %THD UINT16 0 to 9999, or 65535 0.1%

0FA3 - 0FA3 Amps B, %THD UINT16 0 to 9999, or 65535 0.1%

0FA4 - 0FA4 Amps C, %THD UINT16 0 to 9999, or 65535 0.1%

0FA5 - 0FA5

0FA6 - 0FA6

0FA7 - 0FA7

0FA8 - 0FA8

0FA9 - 0FA9

0FAA - 0FAA

0FAB - 0FAB

0FAC - 0FAC

0FAD - 0FAD

0FAE - 0FAE

0FAF - 0FAF

0FB0 - 0FB0

0FB1 - 0FB8 0FB9 - 0FBC 0FBD - 0FC4 0FC5 - 0FC8

DESCRIPTION

Positive VARs, 3-Ph, Maximum Avg Demand Negative Watts, 3-Ph, Maximum Avg Demand Negative VARs, 3-Ph, Maximum Avg Demand VAs, 3-Ph, Maximum Avg Demand Positive Power Factor, 3Ph, Maximum Avg Demand Negative Power Factor, 3Ph, Maximum Avg Demand

7, 13

Phase A Current 0th harmonic magnitude Phase A Current 1st harmonic magnitude Phase A Current 2nd harmonic magnitude Phase A Current 3rd harmonic magnitude Phase A Current 4th harmonic magnitude Phase A Current 5th harmonic magnitude Phase A Current 6th harmonic magnitude Phase A Current 7th harmonic magnitude Phase A Voltage 0th harmonic magnitude Phase A Voltage 1st harmonic magnitude Phase A Voltage 2nd harmonic magnitude Phase A Voltage 3rd harmonic magnitude Phase B Current

Phase B Voltage Phase C Current Phase C Voltage

FORMAT RANGE

FLOAT 0 to +9999 M VARs

FLOAT 0 to +9999 M watts

FLOAT 0 to +9999 M VARs

FLOAT -9999 M to +9999 M VAs

FLOAT -1.00 to +1.00 none

UINT16 0 to 65535 none

same as Phase A Current 0th to 7th harmonic magnitudes same as Phase A Voltage 0th to 3rd harmonic magnitudes same as Phase A Current 0th to 7th harmonic magnitudes same as Phase A Voltage 0th to 3rd harmonic magnitudes

UNITS OR

RESOLUTION

Block Size:

read-only

Block Size:

COMMENTS # REG

1 1 1 1 1 1 1

8 4 8 4

Phase Angle Block

1003 - 1003 Phase A Current SINT16 -1800 to +1800 0.1 degree

1004 - 1004 Phase B Current SINT16 -1800 to +1800 0.1 degree

1005 - 1005 Phase C Current SINT16 -1800 to +1800 0.1 degree

1006 - 1006 Angle, Volts A-B SINT16 -1800 to +1800 0.1 degree

1007 - 1007 Angle, Volts B-C SINT16 -1800 to +1800 0.1 degree

1008 - 1008 Angle, Volts C-A SINT16 -1800 to +1800 0.1 degree

read-only

Block Size:

1 1 1 1 1 1 6

5–4 EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE

CHAPTER 5: COMMUNICATIONS

HEX

ADDRESS

DESCRIPTION

FORMAT RANGE

Status Block

1387 - 1387 Meter Status UINT16 bit-mapped --exnpch ssssssss

1388 - 1388

1389 - 138A Time Since Reset UINT32 0 to 4294967294 4 msec wraps around after max count

Limits Status

COMMANDS SECTION

Resets Block

4E1F - 4E1F Reset Max/Min Blocks UINT16

4E20 - 4E20

Reset Energy Accumulators

UINT16 bit-mapped 87654321 87654321

password

UINT16

password

Meter Programming Block

55EF - 55EF

55F0 - 55F0

55F1 - 55F1

55F2 - 55F2

55F3 - 55F3

Initiate Programmable Settings Update

Terminate Programmable Settings Update

Calculate Programmable Settings Checksum

Programmable Settings Checksum

Write New Password

UINT16

UINT16 any value

UINT16

UINT16 0000 to 9999 write-only register; always reads zero

password

UNITS OR

RESOLUTION

COMMENTS # REG

read-only

exnpch = EEPROM block OK flags (e=energy, x=max, n=min, p=programmable settings, c=calibration, h=header), ssssssss = state (1=Run, 2=Limp, 10=Prog Set Update via buttons, 11=Prog Set Update via IrDA, 12=Prog Set Update via COM2)

high byte is setpt 1, 0=in, 1=out low byte is setpt 2, 0=in, 1=out

Block Size:

write-only

Block Size:

read/conditional write

meter enters PS update mode

meter leaves PS update mode via reset

meter calculates checksum on RAM copy of PS block

read/write checksum register; PS block saved in EEPROM on write

2 4

1 1

59D7 - 59D7

Initiate Meter Firmware Reprogramming

UINT16

Other Commands Block

61A7 - 61A7 Force Meter Restart UINT16

Encryption Block

658F - 659A

Perform a Secure Operation

UINT16

password

Block Size:

read/write

causes a watchdog reset, always reads 0

Block Size:

read/write

encrypted command to read password or change meter type

Block Size:

PROGRAMMABLE SETTINGS SECTION Basic Setups Block

752F - 752F

7530 - 7530 CT numerator UINT16 1 to 9999 none

7531 - 7531 PT numerator UINT16 1 to 9999 none

CT multiplier & denominator

UINT16 bit-mapped

EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE 5–5

dddddddd mmmmmmmm

write only in PS update mode

high byte is denominator (1 or 5, readonly), low byte is multiplier (1, 10, or 100)

1 1

CHAPTER 5: COMMUNICATIONS

HEX

ADDRESS

7532 - 7532 PT denominator UINT16 1 to 9999 none

7533 - 7533 PT multiplier & hookup UINT16 bit-mapped

7534 - 7534 Averaging Method UINT16 bit-mapped --iiiiii b----sss

7535 - 7535 Power & Energy Format UINT16 bit-mapped pppp--nn -eee-ddd

7536 - 7536

7537 - 753D Reserved

753E - 753E User Settings Flags UINT16 bit-mapped ---g--nn srp--wf-

DESCRIPTION

Operating Mode Screen Enables

FORMAT RANGE

UINT16 bit-mapped 00000000 eeeeeeee

UNITS OR

RESOLUTION

mmmmmmmm MMMMhhhh

COMMENTS # REG

MMMMmmmmmmmm is PT multiplier (1, 10, 100, 1000), hhhh is hookup enumeration (0 = 3 element wye[9S], 1 = delta 2 CTs[5S], 3 = 2.5 element wye[6S])

iiiiii = interval (5,15,30,60) b = 0-block or 1-rolling sss = # subintervals (1,2,3,4)

pppp = power scale (0-unit , 3-kilo, 6mega, 8-auto) nn = number of energy digits (5-8 --> 0-3) eee = energy scale (0-unit, 3-kilo, 6mega) ddd = energy digits after decimal point (0-6) See note 10.

eeeeeeee = op mode screen rows on(1) or off(0), rows top to bottom are bits low order to high order

g = enable alternate full scale bargraph current (1=on, 0=off ) nn = number of phases for voltage & current screens (3=ABC, 2=AB, 1=A, 0=ABC) s = scroll (1=on, 0=off) r = password for reset in use (1=on, 0=off) p = password for configuration in use (1=on, 0=off) w = pwr dir (0-view as load, 1-view as generator) f = flip power factor sign (1=yes, 0=no)

1 1

7 1

753F - 753F

7540 - 7547 Meter Designation ASCII 16 char none

7548 - 7548 COM1 setup UINT16 bit-mapped ----dddd -0100110

7549 - 7549 COM2 setup UINT16 bit-mapped ----dddd -ppp-bbb

754A - 754A COM2 address UINT16 1 to 247 none

754B - 754B Limit #1 Identifier UINT16 0 to 65535

754C - 754C

754D - 754D Limit #1 In High ThresholdSINT16 -200.0 to +200.0 0.1% of full scale

754E - 754E Limit #1 Out Low SetpointSINT16 -200.0 to +200.0 0.1% of full scale

754F - 754F Limit #1 In Low Threshold SINT16 -200.0 to +200.0 0.1% of full scale

Full Scale Current (for load % bargraph)

Limit #1 Out High Setpoint

UINT16 0 to 9999 none

SINT16 -200.0 to +200.0 0.1% of full scale

If non-zero and user settings bit g is set, this value replaces CT numerator in the full scale current calculation.

dddd = reply delay (* 50 msec) ppp = protocol (1-Modbus RTU, 2Modbus ASCII, 3-DNP) bbb = baud rate (1-9600, 2-19200, 438400, 6-57600)

use Modbus address as the identifier (see notes 7, 11, 12)

Setpoint for the "above" limit (LM1), see notes 11-12.

Threshold at which "above" limit clears; normally less than or equal to the "above" setpoint; see notes 11-12.

Setpoint for the "below" limit (LM2), see notes 11-12.

Threshold at which "below" limit clears; normally greater than or equal to the "below" setpoint; see notes 11-

12.

8 1

1 1

5–6 EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE

CHAPTER 5: COMMUNICATIONS

HEX

ADDRESS

7550 - 7554 Limit #2 SINT16

7555 - 7559 Limit #3 SINT16

755A - 755E Limit #4 SINT16

755F - 7563 Limit #5 SINT16

7564 - 7568 Limit #6 SINT16

7569 - 756D Limit #7 SINT16

756E - 7572 Limit #8 SINT16

DESCRIPTION

FORMAT RANGE

same as Limit #1 same as Limit #1 same as Limit #1

UNITS OR

RESOLUTION

COMMENTS # REG

Block Size:

SECONDARY READINGS SECTION Secondary Block

9C40 - 9C40 System Sanity Indicator UINT16 0 or 1 none 0 indicates proper meter operation

9C41 - 9C41 Volts A-N UINT16 2047 to 4095 volts 2047= 0, 4095= +150

9C42 - 9C42 Volts B-N UINT16 2047 to 4095 volts

9C43 - 9C43 Volts C-N UINT16 2047 to 4095 volts

9C44 - 9C44 Amps A UINT16 0 to 4095 amps 0= -10, 2047= 0, 4095= +10

9C45 - 9C45 Amps B UINT16 0 to 4095 amps

9C46 - 9C46 Amps C UINT16 0 to 4095 amps

9C47 - 9C47 Watts, 3-Ph total UINT16 0 to 4095 watts 0= -3000, 2047= 0, 4095= +3000

9C48 - 9C48 VARs, 3-Ph total UINT16 0 to 4095 VARs watts, VARs, VAs = 9C49 - 9C49 VAs, 3-Ph total UINT16 2047 to 4095 VAs 3000 * (register - 2047) / 2047

9C4A - 9C4A Power Factor, 3-Ph total UINT16 1047 to 3047 none

9C4B - 9C4B Frequency UINT16 0 to 2730 Hz

9C4C - 9C4C Volts A-B UINT16 2047 to 4095 volts 2047= 0, 4095= +300

9C4D - 9C4D Volts B-C UINT16 2047 to 4095 volts

9C4E - 9C4E Volts C-A UINT16 2047 to 4095 volts

9C4F - 9C4F CT numerator UINT16 1 to 9999 none

9C50 - 9C50 CT multiplier UINT16 1, 10, 100 none

9C51 - 9C51 CT denominator UINT16 1 or 5 none

9C52 - 9C52 PT numerator UINT16 1 to 9999 none 9C53 - 9C53 PT multiplier UINT16 1, 10, 100 none 9C54 - 9C54 PT denominator UINT16 1 to 9999 none 9C55 - 9C56 W-hours, Positive UINT32 0 to 99999999 Wh per energy format * 5 to 8 digits

9C57 - 9C58 W-hours, Negative UINT32 0 to 99999999 Wh per energy format

9C59 - 9C5A VAR-hours, Positive UINT32 0 to 99999999 VARh per energy format

9C5B - 9C5C VAR-hours, Negative UINT32 0 to 99999999 VARh per energy format

9C5D - 9C5E VA-hours UINT32 0 to 99999999 VAh per energy format * see note 10

9C5F - 9C5F Neutral Current UINT16 0 to 4095 amps see Amps A/B/C above

9C60 - 9CA2 Reserved N/A N/A none

9CA3 - 9CA3

Reset Energy Accumulators

UINT16

password

read-only except as noted

volts = 150 * (register - 2047) / 2047

amps = 10 * (register - 2047) / 2047

1047= -1, 2047= 0, 3047= +1 pf = (register - 2047) / 1000

0= 45 or less, 2047= 60, 2730= 65 or more freq = 45 + ((register / 4095) * 30)

volts = 300 * (register - 2047) / 2047

CT = numerator * multiplier / denominator

PT = numerator * multiplier / denominator

* decimal point implied, per energy format

* resolution of digit before decimal point = units, kilo, or mega, per energy format

write-only register; always reads as 0

Block Size:

5 5 5 5 5 5 5

1 1 1 1 1 1 1 1 1 1

1 1 1 1 1 1 1 1

1 2

2 2 2 1

100

5.1.3 Modbus Memory Map Notes

The memory map notes are indicated by number below.

1. All registers not explicitly listed in the table read as 0. Writes to these registers will be

accepted but won't actually change the register (since it doesn't exist).

EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE 5–7

CHAPTER 5: COMMUNICATIONS

2. Meter Data Section items read as 0 until first readings are available or if the meter is not in operating mode. Writes to these registers will be accepted but won't actually change the register.

3. Register valid only in programmable settings update mode. In other modes these registers read as 0 and return an illegal data address exception if a write is attempted.

4. Meter command registers always read as 0. They may be written only when the meter is in a suitable mode. The registers return an illegal data address exception if a write is attempted in an incorrect mode.

5. If the password is incorrect, a valid response is returned but the command is not executed. Use 5555 for the password if passwords are disabled in the programmable settings.

6. M denotes a 1,000,000 multiplier.

7. Not applicable to Shark 100, V-Switch 1, 2, or 3

8. Writing this register causes data to be saved permanently in EEPROM. If there is an error while saving, a slave device failure exception is returned and programmable settings mode automatically terminates via reset.

9. Reset commands make no sense if the meter state is LIMP. An illegal function exception will be returned.

10. Energy registers should be reset after a format change.

11. Entities to be monitored against limits are identified by Modbus address. Entities occupying multiple Modbus registers, such as floating point values, are identified by the lower register addrress. If any of the 8 limits is unused, set its identifier to zero. If the indicated Modbus register is not used or is a non-sensical entity for limits, it will behave as an unused limit .

12. There are 2 setpoints per limit, one above and one below the expected range of values. LM1 is the "too high" limit, LM2 is "too low". The entity goes "out of limit" on LM1 when its value is greater than the setpoint. It remains "out of limit" until the value drops below the in threshold. LM2 works similarly, in the opposite direction. If limits in only one direction are of interest, set the in threshold on the "wrong" side of the setpoint. Limits are specified as % of full scale, where full scale is automatically set appropriately for the entity being monitored:

current FS = CT numerator * CT multiplier

voltage FS = PT numerator * PT multiplier

power FS = CT numerator * CT multiplier * PT numerator * PT multiplier * 3 [ *

SQRT(3) for delta hookup]

frequency FS = 60 (or 50)

power factor FS = 1.0

percentage FS = 100.0

angle FS = 180.0

13. THD not available shows 65535 (=0xFFFF) in all THD and harmonic magnitude registers for the channel when V-switch=4. THD may be unavailable due to low V or I amplitude, or delta hookup (V only).

5–8 EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE

CHAPTER 5: COMMUNICATIONS

5.1.4 Modbus Memory Map Data Formats

14. All 3 voltage angles are measured for Wye and Delta hookups. For 2.5 Element, Vac is

measured and Vab & Vbc are calculated. If a voltage phase is missing, the two voltage angles in which it participates are set to zero. A and C phase current angles are measured for all hookups. B phase current angle is measured for Wye and is zero for other hookups. If a voltage phase is missing, its current angle is zero.

The date format codes indicated in the Format column of the Modbus memory map are described below:

ASCII: ASCII characters packed 2 per register in high, low order and without any termination characters. For example, "Shark100" would be 4 registers containing 0x5378, 0x6172, 0x6B31, 0x3030.

SINT16 / UINT16: 16-bit signed / unsigned integer. SINT32 / UINT32: 32-bit signed / unsigned integer spanning 2 registers. The lower-addressed register

is the high order half. FLOAT: 32-bit IEEE floating point number spanning 2 registers. The lower-addressed register is the high order half (i.e., contains the exponent).

EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE 5–9

CHAPTER 5: COMMUNICATIONS

5.2 DNP Point Mapping

5.2.1 DNP Point Maps

The DNP point mappings (DNP-11 to DNP-22) for the EPM 6000 Power Metering System shows the client-server relationship in GE Multilin’s use of the DNP protocol. The notes are listed after the table.

Table 5–1: DNP Point Mapping (Sheet 1 of 2)

Object Var Point Description Format Range/units Multiplier Comments

Binary output states (Read via Class 0 only)

10 2

Control Relay Outputs

12 1

Binary Counters (Primary; read via Class 0 only)

0 Reset energy counters BYTE 0 N/A

1 Change to Modbus RTU protocol BYTE 0 N/A

0 Reset energy counters N/A N/A N/A See note 1

1 Change to Modbus RTU protocol N/A N/A N/A See note 2

0 Positive watt-hours UINT32 0 to 99999999 Wh See note 3 See note 4

1 Negative watt-hours UINT32 0 to 99999999 Wh See note 3 See note 4

20 4

Analog Inputs (Secondary; read via Class 0 only)

30 5 0 Meter health SINT16 0 or 1 N/A 0 = OK

2 Positive var-hours UINT32 0 to 99999999 varh See note 3 See note 4

3 Negative var-hours UINT32 0 to 99999999 varh See note 3 See note 4

4 Total VA-hours UINT32 0 to 99999999 VAh See note 3 See note 4

1 Voltage A-N SINT16 0 to 32767 V (150/32768) See note 5

2 Voltage B-N SINT16 0 to 32767 V (150/32768) See note 5

3 Voltage C-N SINT16 0 to 32767 V (150/32768) See note 5

4 Phase voltage A-B SINT16 0 to 32767 V (300/32768) See note 6

5 Phase voltage B-C SINT16 0 to 32767 V (300/32768) See note 6

6 Phase voltage C-A SINT16 0 to 32767 V (300/32768) See note 6

7 Phase A current SINT16 0 to 32767 A (10/32768) See note 7

8 Phase B current SINT16 0 to 32767 A (10/32768) See note 7

9 Phase C current SINT16 0 to 32767 A (10/32768) See note 7

10 Total three-phase real power SINT16 –32768 to +32767 W (4500/32768)

11 Total three-phase reactive power SINT16 –32768 to +32767 var (4500/32768)

12 Total three-phase apparent power SINT16 0 to 32767 VA (4500/32768)

13 Total three-phase power factor SINT16 –1000 to 1000 0.001

14 Frequency SINT16 0 to 9999 Hz 0.01

5–10 EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE

CHAPTER 5: COMMUNICATIONS

Table 5–1: DNP Point Mapping (Sheet 2 of 2)

Object Var Point Description Format Range/units Multiplier Comments

Maximum average positive three-phase

real power demand

Maximum average positive three-phase

reactive power demand

Maximum average negative three-phase

real power demand

Maximum average negative three-phase

reactive power demand

Maximum average three-phase apparent

power demand

30 5 20 Phase A current angle SINT16 –1800 to 1800° 0.1

21 Phase B current angle SINT16 –1800 to 1800° 0.1

22 Phase C current angle SINT16 –1800 to 1800° 0.1

23 Phase A-B voltage angle SINT16 –1800 to 1800° 0.1

24 Phase B-C voltage angle SINT16 –1800 to 1800° 0.1

25 Phase C-A voltage angle SINT16 –1800 to 1800° 0.1

26 CT numerator SINT16 1 to 9999 N/A See note 8

SINT16 –32768 to +32767 W (4500/32768)

SINT16 –32768 to +32767 var (4500/32768)

SINT16 –32768 to +32767 W (4500/32768)

SINT16 –32768 to +32767 var (4500/32768)

SINT16 –32768 to +32767 VA (4500/32768)

27 CT multiplier SINT16 1, 10, or 100 N/A

28 CT denominator SINT16 1 or 5 N/A

29 PT numerator SINT16 1 to 9999 N/A See note 9

30 PT multiplier SINT16 1, 10, or 100 N/A

31 PT denominator SINT16 1 to 9999 N/A

Internal Indication

80 1 0 Device restart bit N/A N/A N/A See note 10

EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE 5–11

5.2.2 DNP Point Map Notes

1. Responds to Function 5 (direct operate), Qualifier Code 7 or 8, Control Code 3, Count 0, On 1 ms, Off 0 ms ONLY.

2. Responds to Function 6 (direct operate - no acknowledge), Qualifier Code 7, Control Code 3, Count 0, On 1 ms, Off 0 ms ONLY.

3. The multiplier = 10 6 per energy format scale and d = number of decimal places.

CHAPTER 5: COMMUNICATIONS

(n–d)

, where n and d are derived from the energy format. n = 0, 3, or

4. Example: If energy format = 7.2 K and watt-hours counter = 1234567, with n=3 (kscale) and d = 2 (2 digits after decimal point), then multiplier = 10

(3–2)

= 10, so the

energy is 1234567 × 10 Wh, or 12345.67 kWh.

5. Values greater than 150 V secondary read 32767.

6. Values greater than 300 V secondary read 32767.

7. Values greater than 10 A secondary read 32767. For the 1 A model, the multiplier is (2/

32768) and values above 2 A secondary read 32767.

8. CT ratio = (numerator × multiplier) / denominator.

9. PT ratio = (numerator × multiplier) / denominator.

10. Clear via Function 2 (write), Qualifier Code 0.

5–12 EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE

CHAPTER 5: COMMUNICATIONS

5.3 DNP Implementation

5.3.1 Overview

The EPM 6000 meter is capable of using RS485 as the physical layer. This is accomplished by connecting a PC to the meter with the RS485 connection on the back face.

RS485 provides multi-drop network communication capabilities. Multiple meters may be placed on the same bus, allowing for a master device to communicate with any of the other devices. Appropriate network configuration and termination should be evaluated for each installation to insure optimal performance.

The EPM 6000 communicates in DNP 3.0 using the following communications settings: 8 data bits, no parity, and 1 stop bit. The EPM 6000 can be programmed to use several standard baud rates, including: 9600, 19200, 38400, and 57600 bps.

5.3.2 Data Link Layer

The Data Link Layer as implemented on the EPM 6000 is subject to the following considerations.

The control byte contains several bits and a function code. Communications directed to the meter should be primary master messages (DIR = 1, PRM = 1). Responses will be primary non-master messages (DIR = 0, PRM = 1). Acknowledgment will be secondary nonmaster messages (DIR = 0, PRM = 0).

The EPM 6000 supports all of function codes for DNP 3.0:

• Reset of Data Link (function 0): Before confirmed communication with a master

device, the data link layer must be reset. This is necessary after a meter has been restarted, either by applying power or reprogramming the meter. The meter must receive a RESET command before confirmed communication may take place. Unconfirmed communication is always possible and does not require a RESET command.

• User Data (function 3): After receiving a request for USER DATA, the meter will

generate a data link CONFIRMATION, signaling the reception of that request, before the actual request is processed. If a response is required, it will also be sent as UNCONFIRMED USER DATA.

• Unconfirmed User Data (function 4): After receiving a request for UNCONFIRMED

USER DATA, a response will be sent as UNCONFIRMED USER DATA if required.

DNP 3.0 allows for addresses from 0 to 65534 (0000h to FFFEh) for individual device identification, with the address 65535 (FFFFh) defined as an all stations address. Addresses are programmable from 0 to 247 (0000h to 00F7h), and recognize address 65535 (FFFFh) as the all stations address.

5.3.3 Transport Layer

Multiple-frame messages are not allowed for the EPM 6000. Each transport header should indicate it is both the first frame (FIR = 1) and the final frame (FIN = 1)

EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE 5–13

5.3.4 Application Layer

The application layer contains a header (request or response header, depending on direction) and data.

Application headers contain the application control field and the function code. For the application control field, multiple-fragment messages are not allowed for EPM 6000. Each application header should indicate it is both the first fragment (FIR = 1) as well as the final fragment (FIN = 1). Application-level confirmation is not used for the EPM 6000.

The following function codes are implemented on the EPM 6000.

• Read (function 1): Objects supporting the READ function are Binary Outputs (object 10), Counters (object 20), Analog Inputs (object 30), and Class (object 60). These Objects may be read either by requesting a specific variation available as listed in DNP Point Mapping on page 5–10, or by requesting variation 0. A READ request for variation 0 of an object will be fulfilled with the variation listed in the DNP points table.

• Write (function 2): The Internal Indications object (object 80), supports the WRITE function.

• Direct Operate (function 5): The Control Relay Output object (object 12) supports the DIRECT OPERATE function.

CHAPTER 5: COMMUNICATIONS

• Direct Operate - No Acknowledgment (function 6): the Change to Modbus RTU protocol (object 12, point 1) supports the DIRECT OPERATE - NO ACKNOWLEDGMENT function.

• Response (function 129): Application responses from the EPM 6000 use the RESPONSE function.

5–14 EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE

CHAPTER 5: COMMUNICATIONS

5.4 DNP Objects and Variations

5.4.1 Description

Application Data contains information about the object and variation, as well as the qualifier and range. The following objects and variations are supported:

• Binary Output Status (object 10, variation 2)

• Control Relay Output Block (object 12, variation 1)

• 32-Bit Binary Counter Without Flag (object 20, variation 4)

• 16-Bit Analog Input Without Flag (object 30, variation 5)

• Class 0 Data (object 60, variation 1)

• Internal Indications (object 80, variation 1)

Read requests for variation 0 will be honored on the Binary Output Status, 32-Bit Binary Counter Without Flag, 16-Bit Analog Input Without Flag, and Class 0 Data variations.

5.4.2 Binary Output Status (Object 10, Variation 2)

The Binary Output Status supports the Read function (function 1). A READ request for Variation 0 will be responded to with Variation 2.

The Binary Output Status is used to communicate the following metered data:

• Energy Reset State (point 0): EPM 6000 meters accumulate power generated or

consumed over time as hour readings, which measure positive VAh and positive and negative Wh and varh. These readings may be reset using the Control Relay Output object (object 12). This Binary Output Status point reports whether the energy readings are in the process of being reset or if they are accumulating. Normally, readings are being accumulated and the state of this point is read as “0”. If the readings are in the process of being reset, the state of this point is read as “1”.

• Change to Modbus RTU Protocol State (point 1): EPM 6000 meters are capable of

switching from the DNP protocol to the Modbus RTU protocol. This enables the user to update the device profile of the meter. This feature does not change the protocol setting, as reset returns the meter to DNP. A status reading of “1” equals open (or deenergized); a reading of “0” equals closed (or energized).

5.4.3 Control Relay Output (Object 12, Variation 1)

The Control Relay Output Block supports the following functions: Direct Operate (function 5) and Direct Operate - No Acknowledgment (function 6).

The Control Relay Output Block is used for the following purposes:

• Energy Reset (point 0): EPM 6000 meters accumulate power generated or consumed

over time as hour readings, which measure positive VAh and positive and negative Wh and varh. These readings may be reset using Point 0.

The Direct Operate (function 5) function will operate only with the settings of Pulsed ON (Code = 1 of Control Code field) once (Count =01h) for ON 1 ms and OFF 0 ms.

EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE 5–15

• Change to Modbus RTU Protocol (point 1): EPM 6000 meters are capable of switching from the DNP Protocol to the Modbus RTU Protocol. This enables the user to update the device profile of the meter. This does not change the protocol setting, as a reset returns the meter back to DNP.

The Direct Operate - No Acknowledge (function 6) function will operate only with the settings of Pulsed ON (Code = 1 of the Control Code field) once (Count = 01h) for ON 1 ms and OFF 0 ms.

5.4.4 32-Bit Binary Counter Without Flag (Object 20, Variation 4)

The counters support the Read function (function 1). A read request for Variation 0 will be responded to with Variation 4.

Counters are used to communicate the hour readings measured by the EPM 6000 meter. Refer to DNP Point Mapping on page 5–10 for details. These readings may be cleared by using the Control Relay Output Block.

5.4.5 16-Bit Analog Input Without Flag (Object 30, Variation 5)

CHAPTER 5: COMMUNICATIONS

The analog inputs support the Read function (function 1). A read request for Variation 0 will be responded to with Variation 5.

Refer to DNP Point Mapping on page 5–10 for details on the data measured by the analog inputs.

• Health Check (point 0): The health check point indicates problems detected by the EPM 6000. A value of zero (0000h) indicates the meter does not detect a problem; nonzero values indicate a detected anomaly.

• Phase-to-Neutral Voltages (points 1 to 3): These points are formatted as two's complement fractions. They represent a fraction of a 150 V secondary input. Inputs greater than 150 V secondary will be pinned at 150 V secondary.

• Phase-to-Phase Voltages (points 4 to 6): These points are formatted as two's complement fractions. They represent a fraction of a 300 V secondary input. Inputs greater than 300 V secondary will be pinned at 300 V secondary.

• Phase Currents (points 7 to 9): These points are formatted as two's complement fractions. They represent a fraction of a 10 A secondary input. Inputs greater than 10 A secondary will be pinned at 10 A secondary.

• Total Real and Reactive Power (points 10 and 11): These points are formatted as two's complement fractions. They represent a fraction of 4500 W secondary in normal operation or 3000 W secondary in open delta operation. Inputs above/below ±4500 or ±3000 W secondary will be pinned at ±4500 or ±3000 W secondary, respectively.

• Total Apparent Power (point 12): This point is formatted as a two's complement fraction. It represents a fraction of 4500 W secondary in normal operation or 3000 W secondary in open delta operation. Inputs above/below ±4500 or ±3000 W secondary will be pinned at ±4500 or ±3000 W secondary, respectively.

• Power Factor (point 13): This point is formatted as a two's complement integer. It represents power factors from –1.000 (0FC18h) to +1.000 (003E8h). When in open delta operation, the total power factor (point 13) is always zero.

5–16 EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE

CHAPTER 5: COMMUNICATIONS

• Frequency (point 14): This point is formatted as a two's complement fraction. It

represents the frequency as measured on phase A voltage in units of cHz (centiHertz, 1/100 Hz). Inputs below 45.00 Hz are pinned at 0 (0000h), while inputs above 75.00 Hz are pinned at 9999 (270Fh).

• Maximum Demands of Total Power (points 15 to 19): These points are formatted as

two's complement fractions. They represent a fraction of 4500 W secondary in normal operation or 3000 W secondary in open delta operation. Inputs above/below ±4500 or ±3000 W secondary will be pinned at ±4500 or ±3000 W secondary, respectively.

• Phase Angles (points 20 to 25): These points are formatted as two's complement

integers. They represent angles from –180.00 (0F8F8h) to +180.00 (00708h).

• CT and PT Ratios (points 26 to 31): These points are formatted as two's complement

integers. They can be used to convert from units in terms of the secondary of a CT or PT into units in terms of the primary of a CT or PT. The ratio of numerator divided by denominator is the ratio of primary to secondary. The EPM 6000 typically uses full scales relating primary current to 5 A and primary voltage to 120 V. However, these full scales can range from mAs to thousands of kAs, or mVs to thousands of kVs. Example settings are as follows:

CT example settings:

200 A: Set the 800 A: Set the

Ct-n value for “200” and the Ct-S value for “1”. Ct-n value for “800” and the Ct-S value for “1”.

2000 A: Set the 10000 A: Set the

PT example settings:

120 V (reads 14400 V):

Set the

Pt-n value to “1440”, Pt-d to “120”, and Pt-S to “10”.

69 V (reads 138000 V):

Set the

Pt-n value to “1380”, Pt-d to “69”, and Pt-S to “100”.

115 V (reads 345000 V):

Set the

Pt-n value to “3450”, Pt-d to “115”, and Pt-S to “100”.

5.4.6 Class 0 Data (Object 60, Variation 1)

The Class 0 Data object supports the Read (function 1) function. A request for Class 0 Data from an EPM 6000 returns three object headers. Specifically, it returns 16-Bit Analog Input Without Flags (object 30, variation 5) points 0 to 31, followed by 32-Bit Counters Without Flags (object 20, variation 4) points 0 to 4, followed by Binary Output Status (object 10, variation 2), points 0 to 1. There is NO Object 1.

A request for Object 60, Variation 0 will be treated as a request for Class 0 Data.

Ct-n value for “2000” and the Ct-S value for “1”.

Ct-n value for “1000” and the Ct-S value for “10”.

5.4.7 Internal Indications (Object 80, Variation 1)

The Internal Indications object support the Write function (function 2). Internal Indications may be indexed by Qualifier Code 0.

The Device Restart (point 0) bit is set whenever the meter has reset. The polling device may clear this bit by writing (function 2) to Object 80, Point 0.

EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE 5–17

CHAPTER 5: COMMUNICATIONS

5–18 EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE

GE Consumer & Industrial

Multilin

EPM 6000 Multi-function Power

Chapter 6: Miscellaneous

Miscellaneous

6.1 Navigation Maps

Metering System

6.1.1 Introduction

The EPM 6000 meter can be configured and a variety of functions performed using the buttons on the meter faceplate. An overview of the elements and buttons on the faceplate can be found in Chapter 4. The meter can also be programmed using software such as GE Communicator.

The navigation maps show in detail how to move from one screen to another and from one display mode to another using the buttons on the meter faceplate. All display modes will automatically return to operating mode after 10 minutes of no user activity.

EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE 6–1

6.1.2 Main Menu Screens

The main menu navigation map is shown below.

CHAPTER 6: MISCELLANEOUS

FIGURE 6–1: Main Menu Navigation

6–2 EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE

CHAPTER 6: MISCELLANEOUS

6.1.3 Operating Mode Screens

The operating mode navigation map is shown below.

FIGURE 6–2: Operating Mode Navigation

EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE 6–3

6.1.4 Reset Mode Screens

The reset mode navigation map is shown below.

CHAPTER 6: MISCELLANEOUS

FIGURE 6–3: Reset Mode Navigation

6–4 EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE

CHAPTER 6: MISCELLANEOUS

6.1.5 Configuration Mode Screens

The configuration mode navigation map is shown below.

FIGURE 6–4: Reset Mode Navigation

EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE 6–5

6.2 Revision History

6.2.1 Release Dates

CHAPTER 6: MISCELLANEOUS

Table 6–1: Release Dates

MANUAL GE PART NO. EPM 6000

GEK-106558 1601-0215-A1 1.0x 24 January 2004

GEK-106558A 1601-0215-A2 1.0x 08 April 2005

GEK-106558B 1601-0215-A3 1.0x 06 September 2005

GEK-106558C 1601-0215-A4 1.0x 14 February 2007

6.2.2 Changes to the Manual

SECT

(A3)

Title Title Update Manual part number to 1601-0215-A4

1.4.2 1.4.2 Update %THD Accuracy Changed

4.1.5 4.1.5 Update Fig 4-3 updated

4.3.5 4.3.5 Update

SECT

(A4)

REVISION

RELEASE DATE

Table 6–2: Major Updates for 1601-0215-A4

CHANGE DESCRIPTION

PT Settings example values changed to be more reflective of actual customer values

5.4.5 5.4.5 Update

PT Settings example values changed to align with above values

6.1.1 6.1.1 Update Added mention of GE Communicator software.

Table 6–3: Major Updates for 1601-0215-A3

PAGE

(A2)

PAGE

(A3)

CHANGE DESCRIPTION

Title Title Update Manual part number to 1601-0215-A3

3-4 3-4 Update Updated ELECTRICAL INSTALLATION section

3-16 3-16 Update

6–6 EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE

Updated RS485 COMMUNICATIONS INSTALLATION diagram

CHAPTER 6: MISCELLANEOUS

Table 6–4: Major Updates for 1601-0215-A2

PAGE

(A1)

PAGE

(A2)

CHANGE DESCRIPTION

Title Title Update Manual part number to 1601-0215-A2

2-3 2-3 Update Updated ORDER CODES section

2-3 --- Delete Removed ACCESSORIES section

2-4 2-4 Update Updated INPUTS/OUTPUTS specifications

--- 3-13 Add

--- 3-14 Add

--- 3-15 Add

Added CURRENT ONLY MEASUREMENT (THREEPHASE) section

Added CURRENT ONLY MEASUREMENT (DUAL-PHASE) section

Added CURRENT ONLY MEASUREMENT (SINGLEPHASE) section

4-9 4-9 Update Updated CONFIGURING THE CT SETTING section

4-10 4-10 Update Updated CONFIGURING THE PT SETTING section

--- 5-7 Add Added DNP COMMUNICATIONS section

EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE 6–7

6.3 Warranty

6.3.1 GE Multilin Warranty

CHAPTER 6: MISCELLANEOUS

General Electric Multilin (GE Multilin) warrants each device it manufactures to be free from defects in material and workmanship under normal use and service for a period of 24 months from date of shipment from factory.

In the event of a failure covered by warranty, GE Multilin will undertake to repair or replace the device providing the warrantor determined that it is defective and it is returned with all transportation charges prepaid to an authorized service centre or the factory. Repairs or replacement under warranty will be made without charge.

Warranty shall not apply to any device which has been subject to misuse, negligence, accident, incorrect installation or use not in accordance with instructions nor any unit that has been altered outside a GE Multilin authorized factory outlet.

GE Multilin is not liable for special, indirect or consequential damages or for loss of profit or for expenses sustained as a result of a device malfunction, incorrect application or adjustment.

For complete text of Warranty (including limitations and disclaimers), refer to GE Multilin Standard Conditions of Sale.

6–8 EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE

Index

ACCURACY......................................................................................................................................................1–7, 4–4

BAUD RATE ................................................................................................................................................4–14, 4–15

BLONDELL’S THEOREM .......................................................................................................................................2–5

CATALOG NUMBERS.............................................................................................................................................1–5

CHANGES TO MANUAL..............................................................................................................................6–6, 6–7

CHANGING SETTINGS..........................................................................................................................................4–9

COMMUNICATIONS

description .................................................................................................................................................. 3–19

IrDA................................................................................................................................................................. 3–19

memory map ......................................................................................................................................5–1, 5–2

Modbus............................................................................................................................................................5–1

RS485............................................................................................................................................................. 3–19

settings ......................................................................................................................................................... 4–14

specifications................................................................................................................................................1–7

COMPLIANCE...........................................................................................................................................................1–8

CONFIGURATION MODE

changing settings.......................................................................................................................................4–9

description .....................................................................................................................................................4–5

navigation.......................................................................................................................................................6–5

programming............................................................................................................................................. 4–10

CONNECTION SETTING..................................................................................................................................... 4–13

CT SETTING............................................................................................................................................................ 4–11

CURRENT INPUTS

connections...................................................................................................................................................1–3

settings ......................................................................................................................................................... 4–11

specifications................................................................................................................................................1–6

DELTA CONNECTION

3-wire, 2 PTs, 3 CTs.................................................................................................................................. 3–15

3-wire, no PTs, 3 CTs............................................................................................................................... 3–14

background ...................................................................................................................................................2–4

phasors..................................................................................................................................................2–4, 2–5

setting............................................................................................................................................................ 4–13

DEMAND................................................................................................................................................................. 2–10

DIMENSIONS..................................................................................................................................................1–7, 3–1

DOWN BUTTON......................................................................................................................................................4–2

ENERGY......................................................................................................................................................... 2–8, 2–12

ENTER BUTTON.......................................................................................................................................................4–2

EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE INDEX–1

INDEX

ENVIRONMENTAL SPECIFICATIONS...............................................................................................................1–7

FACEPLATE BUTTONS..........................................................................................................................................4–2

FACEPLATE ELEMENTS........................................................................................................................................4–2

FEATURES..................................................................................................................................................................1–1

FUSES..........................................................................................................................................................................3–8

GROUND CONNECTION......................................................................................................................................3–8

INSTALLATION

CT leads pass-through .............................................................................................................................3–6

CT leads terminated to meter...............................................................................................................3–6

electrical..........................................................................................................................................................3–5

mechanical ....................................................................................................................................................3–1

precautions....................................................................................................................................................3–5

quick connect ...............................................................................................................................................3–7

voltage connections..................................................................................................................................3–7

wiring................................................................................................................................................................3–9

IRDA

communications paths ......................................................................................................................... 3–19

description................................................................................................................................................... 3–19

LOAD BAR..................................................................................................................................................................4–3

MAIN MENU

description......................................................................................................................................................4–6

navigation.......................................................................................................................................................6–2

MEASURED VALUES..............................................................................................................................................1–4

MEMORY MAP..........................................................................................................................................................5–1

MENU BUTTON........................................................................................................................................................4–2

METER ADDRESS................................................................................................................................................. 4–14

METERING .......................................................................................................................................................1–4, 1–6

MODBUS

memory map ......................................................................................................................................5–1, 5–2

settings ......................................................................................................................................................... 4–15

MOUNTING

ANSI panel......................................................................................................................................................3–2

DIN panel ........................................................................................................................................................3–3

panel cutouts................................................................................................................................................3–2

NAVIGATION MAPS ...............................................................................................................................................6–1

INDEX–2 EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE

OPERATING MODE

navigation.......................................................................................................................................................6–3

programming............................................................................................................................................. 4–17

ORDER CODES.........................................................................................................................................................1–5

PANEL CUTOUTS....................................................................................................................................................3–2

PASSWORD ENTRY......................................................................................................................................4–7, 4–8

POWER .......................................................................................................................................................................2–8

POWER FACTOR ..................................................................................................................................................2–13

POWER QUALITY ................................................................................................................................................. 2–17

POWER SUPPLY

connection .....................................................................................................................................................3–8

specifications................................................................................................................................................1–6

PROTOCOL............................................................................................................................................................. 4–16

PT SETTING ............................................................................................................................................................ 4–12

QUICK CONNECT....................................................................................................................................................3–7

REGISTER MAP ........................................................................................................................................................5–1

RESET MODE

description .....................................................................................................................................................4–6

navigation.......................................................................................................................................................6–4

REVENUE METERING............................................................................................................................................4–4

REVISION HISTORY................................................................................................................................................6–6

RIGHT BUTTON .......................................................................................................................................................4–2

RS485

specifications................................................................................................................................................1–7

wiring............................................................................................................................................................. 3–19

SCROLL FEATURE...................................................................................................................................................4–9

SPECIFICATIONS.....................................................................................................................................................1–6

STARTUP ....................................................................................................................................................................4–5

TYPE TESTING..........................................................................................................................................................1–8

UTILITY PEAK DEMAND .......................................................................................................................................1–3

VOLTAGE INPUTS

connections...................................................................................................................................................3–8

EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE INDEX–3

INDEX

description......................................................................................................................................................1–3

settings ......................................................................................................................................................... 4–12

specifications................................................................................................................................................1–6

WARRANTY...............................................................................................................................................................6–8

WATT-HOUR ACCURACY TEST.........................................................................................................................4–4

WAVEFORM CAPTURE ......................................................................................................................................2–16

WIRING

current-only, dual-phase...................................................................................................................... 3–17

current-only, single-phase...................................................................................................................3–18

current-only, three-phase....................................................................................................................3–16

delta ...................................................................................................................................................3–14, 3–15

description......................................................................................................................................................3–9

wye............................................................................................................................ 3–10, 3–11, 3–12, 3–13

WYE CONNECTION

4-wire, 2 PTs, 3 CTs, 2.5 element.......................................................................................................3–13

4-wire, 3 PTs, 3 CTs, 3 element .......................................................................................................... 3–12

4-wire, no PTs, 3 CTs, 2.5 element.................................................................................................... 3–11

4-wire, no PTs, 3 CTs, 3 element........................................................................................................3–10

background....................................................................................................................................................2–2

phasors............................................................................................................................................................2–3

setting............................................................................................................................................................ 4–13

INDEX–4 EPM 6000 MULTI-FUNCTION POWER METERING SYSTEM – USER GUIDE

GE 6000 User Manual

Specifications and Main Features

Frequently Asked Questions

User Manual