Danfoss Selection of Driveline Components User guide

Download

Applications Manual

Selection of Driveline Components

powersolutions.danfoss.com

Applications Manual

Selection of Driveline Components

Revision history Table of revisions

Date Changed Rev

July 2015 Minor edits 0304

April 2015 Minor edits CC

December 2014 Corrections to the equations CB

November 2013 Major rewrite - Danfoss layout CA

July 1997 Second edition B

2 | © Danfoss | July 2015 BLN-9885 | BC00000245en-US0304

Applications Manual

Selection of Driveline Components

Introduction

Applications Manuals......................................................................................................................................................................4

Selection of Driveline Components

Introduction........................................................................................................................................................................................5

Design Goal.........................................................................................................................................................................................5

Sizing Procedure...............................................................................................................................................................................5

Machine Corner Power (CP)..........................................................................................................................................................6

Variable or Fixed Motor..................................................................................................................................................................8

Motor Selection.................................................................................................................................................................................9

Final Drive Selection..................................................................................................................................................................... 11

Input Gearing...................................................................................................................................................................................13

Pump Selection...............................................................................................................................................................................14

Continuous Pressure.....................................................................................................................................................................16

System Sizing Flow Chart............................................................................................................................................................17

Sizing Flow Chart...................................................................................................................................................................... 19

Equations.......................................................................................................................................................................................... 23

Definition of Terms........................................................................................................................................................................25

Tractive Effort

Tractive Effort.................................................................................................................................................................................. 26

Acceleration

Acceleration.....................................................................................................................................................................................30

Charge Pump Sizing

Introduction.....................................................................................................................................................................................33

Charge Pump Considerations....................................................................................................................................................33

Charge Pump Sizing Worksheet...............................................................................................................................................36

Danfoss | July 2015 BLN-9885 | BC00000245en-US0304 | 3

Applications Manual

Selection of Driveline Components

Introduction

Applications Manuals

Content included in these manuals

These applications manuals provide design theory and detailed calculations for building hydraulically powered machines.

The original document was written as one manual with four sections. The current set of manuals includes the four documents listed below. The section numbers from the

original document are listed in parenthesis after the current document title.

•

Selection of Driveline Components BLN-9885 (originally Section 1)

•

Pressure and Speed Limits for Hydrostatic Units BLN-9884 (originally Section 2)

•

Transmission Circuit Recommendations BLN-9886 (originally Section 4)

•

Fluids and Lubricants 520L0463 (originally Section 3)

Other Reference Manuals

•

Hydraulic Fan Drive Systems Technical Information 520L0824

•

Hydraulic Fan Drive Systems Design Guidelines 520L0926

4 | © Danfoss | July 2015 BLN-9885 | BC00000245en-US0304

Applications Manual

Selection of Driveline Components

Introduction

This section presents a method of sizing driveline components for typical closed loop hydrostatic transmissions. Although the method was developed for propel systems, it may be used for winch, or reel, applications, or other circuits with very slight modifications. The terminology used in this procedure also tends to reflect off-highway mobile applications.

It is assumed that the specific functional requirements of the application have been defined, and that the fundamental design parameters have been established for each mode of operation. These typically include vehicle speed, gradability, useful life, vehicle weight, and drive configuration. It is also assumed that required engine power has been established.

Design Goal

The goal of this design method is to optimize the performance and cost of the driveline system by selecting appropriate driveline components. Smaller hydraulic components cost less than larger components, but they have lower torque capability.

Hydraulic unit life is highly dependent on system pressure. Establish maximum and continuous pressure based on the required life of the driveline. Danfoss document Pressure and Speed Limits for Hydrostatic Units BLN-9884 covers this subject in detail.

The figure below Driveline Element Selection shows the components typically found in a closed loop hydrostatic drive system as well as the design parameters and degree of design flexibility associated with each component. Because driveline design includes so many variables (each dependent on the others), and because final component selection is ultimately limited by product availability, several iterations of this procedure may be required before arriving at the optimum system.

Sizing Procedure

The sizing procedure starts with values for the machine maximum torque and required speed. From these values, a hydraulic motor size can be selected. This motor selection is then made compatible with ratings of available output gear drives. From a motor size, a pump size can be established. The pump must be capable of accepting the required input power, and it must be compatible with the pump drive mechanisms. It must also be large enough to provide sufficient flow to the drive motor to attain the required speed.

Danfoss | July 2015 BLN-9885 | BC00000245en-US0304 | 5

Driving

Element

Design

Parameter

Design

Flexibility

Power Speed

Engine

SometimesRatio

Gearing

Yes

Size

Pressure

Speed

Pump

Size

Pressure

Speed

Yes

Motor

Rati

o U

suallyGearing

Speed

Weight

Load

Driveline Element Selection

Applications Manual

Selection of Driveline Components

Machine Corner Power (CP)

Optimizing the size of the hydraulic units depends on selecting the correct gear ratios. By matching machine corner power with motor corner power, the required unit sizes can be quickly determined. The gear ratios can usually be adjusted to provide some optimization of hydraulic unit component size.

Along with the equations presented throughout this document, a sizing flowchart is included to assist with sizing. The flowchart details the sizing procedure and includes numerous design check steps to validate the calculated sizing values.

Design limits for associated mechanical components are not identified.

Machine designers should verify that the design parameters are met for all driveline components. The steps outlined in this manual are designed to guide you in component selection. For further

assistance, contact your Danfoss representative for help interpreting and verifying your results.

The first step in the sizing process is to determine the value referred to as Machine Corner Power (CP). The concept of Corner Power is abstract and is normally not an attainable value of transmission power. It is useful in the design process because it provides an indication of transmission component size and ratio requirements. Corner Power is representative of the maximum torque and the maximum speed (at full load) that the machine is required to have. These two values of maximum speed and maximum torque (or Tractive Effort) never happen at the same time, but the purpose of Corner Power is to capture both values to define an operating envelope for the machine and to aid in the selection of the hydraulic motor. Refer to the Machine Corner Power graph below for an illustration of the concept.

The concept of Corner Power also applies to hydraulic motors. As demonstrated in the topic Motor

Selection on page 9, the maximum corner power of a hydraulic motor represents the maximum torque

and maximum continuous speed capabilities of that product. Equations are provided in the Motor Selection topic that allow you to select the appropriate motor based on the machine’s corner power.

The equations for calculating Corner Power are provided below. For rotary drives (work function), the input values to the equation are the required maximum output torque and the maximum output speed

6 | © Danfoss | July 2015 BLN-9885 | BC00000245en-US0304

Max System Pressure

HP Out

(Approx. 0.70 HP In)

Output

Torque

Output Speed

Rated Speed

Part Load Speed

No Load, High Idle Speed (NLHI)

Full Load Speed

BLN-9885-4

CP = machine corner power kW (hp) TQ = maximum drive output torque Nm (in lbf) ND = maximum drive output design speed rpm

SI System US System Description

Rotary Drives

TE = maximum vehicle tractive effort N (lbf) S = maximum vehicle design speed kph (mph)

Propel Drives

Machine CP =

TQ • ND

63 025

Machine CP =

TQ • ND

9549

Machine CP =

TE • S

375

Machine CP =

3600

TE • S

Applications Manual

Selection of Driveline Components

(at full load) of the machine. For propel drives, the input values are maximum tractive effort and maximum vehicle speed (at full load).

For multi-speed drives (e.g. work mode and travel mode), corner power must be calculated for all ranges.

Tractive Effort

Tractive Effort refers to the amount of force available at the wheel or wheels of the vehicle and represents the maximum possible pull a vehicle could exert, if it had no resistance to movement.

Ideally, tractive effort or output torque requirements should be derived from actual tests of the machine. However, for establishing tractive effort design values, an analytical approach based on machine parameters and functional modes of operation has been used successfully.

The topic Tractive Effort on page 26 describes tractive effort in more detail.

Machine Corner Power

Machine Corner Power (CP) is determined by estimating the maximum torque and maximum output speed required. It is normally greater than actual transmission output power. Maximum output speed is assumed to be at engine rated speed. However, under part load conditions slightly higher speed may be obtained.

Warning

Protect yourself from injury. Use proper safety equipment, including safety glasses, at all times.

Warning

Check to ensure that maximum motor speed is NOT exceeded under dynamic braking conditions, when engine speed can exceed No Load High Idle (NLHI) ratings.

Danfoss | July 2015 BLN-9885 | BC00000245en-US0304 | 7

Applications Manual

Selection of Driveline Components

Variable or Fixed Motor

Because the machine corner power is an expression of maximum torque (tractive effort) and maximum vehicle speed, it can be used to establish the effective Transmission Ratio (TR) required to satisfy system demands.

The effective Transmission Ratio (TR) is the ratio of the required vehicle corner power divided by the available power from the machine’s prime mover (engine). This ratio is similar to the ratio spread of a similarly sized mechanical transmission and indicates the amount of hydrostatic ratio which is required.

Systems with high transmission ratios normally benefit from variable, or two-position, drive motors.

For drives with variable load cycles, determine the normal input power (available power) to the transmission by deducting the average power dedicated to other functions from the maximum engine power available to the drive.

A Transmission Ratio (TR) greater than 1.0 means that there is not enough engine power available to meet all of the operating requirements at the same time.

•

Typically, machines with high transmission ratios have high torque (Tractive Effort) requirements at low speed and high speed requirements at low torque (Tractive Effort). In this case, a large fixed motor would satisfy the high torque requirements, but operating the same motor to meet the maximum speed requirement could exceed the speed limit of the motor and require a large displacement pump. For high transmission ratios, use a variable displacement motor; it can be used at high displacement to satisfy the maximum torque requirement and then shifted to a smaller displacement to satisfy the machine’s maximum speed requirement. A fixed motor could be used with a multi-ratio gearbox for machines with a high transmission ratio, but usually a variable motor will be the most cost effective solution.

•

If the transmission ratio is low, that means that there is probably enough engine power available to achieve the maximum torque and speed requirements simultaneously. In those cases, a fixed motor is suitable for the task.

•

In cases of extremely high transmission ratio, a variable motor may not satisfy the need. In these cases, a multi-speed gearbox may also be required. Some applications use 2-speed, 3-speed, or 4speed gearboxes to meet the vehicle requirements; but a 2-speed gearbox is most common.

The rule for selecting a fixed or variable drive motor is as follows:

•

If TR is greater than 4, use a variable motor,

•

If TR is less than 2, use a fixed motor,

•

If TR is between 2 and 4, evaluate both variable and fixed motors for suitability,

•

If TR is greater than 14, use a multi-ratio gear box between the motor and the final drive.

There is no direct relationship between transmission ratio and final drive ratio. The final drive ratio is calculated based on the displacement of the motor that has been chosen, the maximum pressure, the loaded radius of the wheels, and the required maximum tractive effort.

The transmission ratio is only used to help determine the motor type, not the motor size. Refer to the topic Final Drive Selection on page 11 to calculate the Final Drive Ratio (FD).]

8 | © Danfoss | July 2015 BLN-9885 | BC00000245en-US0304

TR < 2, use fixed displacement motor

TR > 4, use variable displacement motor

SI / US System Description

TR = effective transmission ratio

HP = normal input power kW (hp)

2) TR =

Machine CP

TR > 14, use multi-ratio gearbox

HP = 0.7

Available prime mover power

Applications Manual

Selection of Driveline Components

Motor Selection

Calculate the required motor corner power from machine corner power and driveline efficiency using equation (3) Required Motor CP. This establishes the minimum motor size capable of meeting the power requirement of the machine. For multi-speed drives, use the largest corner power for each of the operating ranges.

For transmission circuits using multiple drive motors, the required motor corner power should be interpreted as the required corner power at each motor.

Use equation (4) Maximum Motor CP to calculate the maximum motor corner power based on the design maximum pressure and the design maximum speed and the desired life of the motor.

Design maximum pressure is the maximum pressure at which the motor is intended to operate to meet the required life. The design maximum pressure may or may not be the same as the maximum pressure rating published in the product literature. Published ratings for maximum pressure assume the pressure will occur for only a small percentage of the operating time, usually less than 2% of the total, and will result in “normal” life. For applications in which the maximum pressure will occur over a significant portion of the duty cycle, or applications in which additional life is required, the design maximum pressure should be assigned a value less than the published rating for maximum pressure.

Design maximum speed is the maximum speed at which the motor is intended to operate to meet the required life. Although speed has less effect on life than pressure, lower operating speeds will have the effect of increasing life. The value for the design maximum speed must never exceed the maximum speed rating published in the product literature; and will usually be less, to allow for motor speed increases as a result of reduced-load, or no-load, conditions (see Machine Corner Power graph).

Danfoss document Pressure and Speed Limits for Hydrostatic Units BLN-9884, provides additional information concerning pressure and speed limits with respect to component life.

Ideally, values for the design maximum pressure and design maximum speed would be used in Equation (4) Maximum Motor CP to determine motor CP capability. However, this is difficult at this stage of the sizing process because both the motor displacement and final drive ratio are unknown. Despite this limitation, the next step is to choose a logical motor displacement based on the required motor CP. The table Hydrostatic Motor Corner Power Chart can be used as an aid in preliminary motor selection. You

Danfoss | July 2015 BLN-9885 | BC00000245en-US0304 | 9

should choose a motor with a motor CP at least as large as the required motor CP calculated using Equation (3) Required Motor CP.

Equation (A) Design Check serves as a design check to ensure that a motor with sufficient corner power capability is selected. Motor selection based on corner power results in the smallest motor capable of transmitting the required machine power while achieving system life requirements.

Design Check: Maximum Motor CP ≥ Required Motor CP

)

Required Motor CP =

Machine CP

E • #

Required Motor CP =

Machine CP

E • #

Maximum Motor CP =

DM • NM • PM

396 000

Maximum Motor CP =

DM • NM • PM

600 000

SI System

US System Description

# = number of motors

CP = corner power E = final drive efficiency

DM = maximum motor displacement NM = design maximum speed PM = design maximum pressure

cc [in

]/rev rpm bar [psi]

kW [hp] (%/100)

Applications Manual

Selection of Driveline Components

For variable motor systems, the transmission CP is determined only by the motor. For various pump sizes, actual applied motor CP may be varied by adjusting the minimum motor angle.

For fixed motor systems, the transmission CP is ultimately determined by the pump speed and displacement. Although the fixed motor CP must be large enough to accommodate the maximum load and speed, the pump must be large enough to drive the motor at the required design speed.

An additional sizing exercise may be required for fixed motor systems after pump selection has been made.

For either variable or fixed motor systems, it may be necessary to increase the motor size if proper output gearing is not available. Gearing must accommodate both the desired transmission ratio and maximum motor speed, in addition to meeting the torque requirements.

10 | © Danfoss | July 2015 BLN-9885 | BC00000245en-US0304

Series 15 4500 4350 ---- 4000 --- - --- - 42 31 ---- ---- Series 40 - M25 5000 4350 ---- 4000 ---- ---- 77 57 ---- ---Series 40 - M35 5000 4350 ---- 3600 5300 4200 97 72 113 84 Series 40 - M44 5000 4350 ---- 3300 4850 3900 112 83 132 99 Series 40 - M46 5000 4350 ---- 3600 5000 4500 128 95 160 119

LV/LC25 6000 ---- ---- 5000 4400 --- - --- - 102 76 LV/LC30 5000 ---- ---- 5150 4450 --- - --- - 103 77

LV/LC35 4350 ---- ---- 5300 4500 --- - --- - 106 79 KV/KC38 6000 ---- --- - 5200 4650 --- - --- - 163 122 KV/KC45 5000 ---- --- - 5050 4500 --- - --- - 156 116

Series 90 - 55cc 7000 4250 3900 5100 4600 231 173 273 204

Series 90 - 75cc 7000 3950 3600 4700 4250 291 217 344 256 Series 90 - 100cc 7000 3650 3300 356 266 --- - --- Series 90 - 130cc 7000 3400 3100 435 324 --- - --- -

H1B060 7000 6525 ---- 7250 5900 --- - --- - 382 285 H1B080 7000 6525 ---- 6600 5300 --- - --- - 457 341 H1B110 7000 6525 ---- 5950 4800 --- - --- - 570 425 H1B160 7000 6525 ---- 5250 4250 --- - --- - 734 547 H1B250 7000 6525 ---- 4500 3650 --- - --- - 985 734 51V060 7000 7000 5600 --- - --- - 363 270 51V080 7000 6250 5000 --- - --- - 432 322 51V110 7000 5600 4500 --- - --- - 534 398 51V160 7000 5000 4000 --- - --- - 691 515 51V250 7000 4250 3400 --- - --- - 917 684

Hydrostatic Motor Corner Power Chart

Fixed Variable

Motor

Max

Pressure

(psid)

Max Working Pressure

(psid)

Max

Speed

at Max

Angle

(rpm)

Cont Speed at

Max Angle

(rpm)

Max Speed at

Min Ang le

(rpm)

Cont Speed

at Min Angle

(rpm)

Corner Power

(HP)

Corner Power

(kW)

Corner Power

(HP)

Corner Power

(kW)

Applications Manual

Selection of Driveline Components

These values for corner power capability are based on maximum pressure and maximum speed ratings.

Refer to Pressure and Speed Limits for Hydrostatic Units BLN-9884 for detailed information on ratings of units and expected life.

Final Drive Selection

Danfoss | July 2015 BLN-9885 | BC00000245en-US0304 | 11

After the motor is initially sized, calculate the required final drive ratio. One of two approaches can be taken to determine this ratio. Both take into account the design maximum and continuous pressures allowed to meet the life requirements of the machine (see Pressure and Speed Limits for Hydrostatic Units BLN-9884).

The two methods are as follows:

Applications Manual

Selection of Driveline Components

1. Using the Sizing Flow Chart on page 19, size the final drive ratio using the design maximum pressure

and the maximum torque requirement. Use equation (5) Required FD on the following page for this calculation. After the pump is sized and all speed conditions have been met, estimate the continuous pressure, using the Sizing Flow Chart on page 19, and compare it with the maximum design continuous pressure.

2. As an alternate method, calculate the final drive ratio required for all modes of operation (travel

mode, work mode, etc.). Calculate the final drive ratio from the assumed pressure and torque requirements for each operating mode. For worst case or intermittent modes of operation, use the design maximum pressure along with the tractive effort or torque requirement to obtain a value for the final drive ratio. Use the design continuous pressure for typical or continuous modes of operation, and calculate required final drive ratios for these modes as well. Select the largest final drive ratio from the values calculated for the various operating modes.

For variable or two-position motors, only final drive ratios from those modes utilizing maximum motor displacement can be calculated, since the motor minimum displacement is not yet known.

The next step is to check motor speed limits using the limits obtained from Pressure and Speed Limits for Hydrostatic Units BLN-9884, or the respective Technical Information manual.

Motor speed will usually be satisfactory unless the final drive ratio is significantly higher than required (Gearbox limits must also be met). Equation (6) NMR=FD•NMD is used to determine the required motor speed at maximum motor displacement based on the final drive ratio calculated in equation (5) Required FD. For fixed displacement motors, the maximum motor displacement referred to in the equation is simply the displacement of the motor. For variable motors, use the displacement at the maximum swashplate angle. Use design check (C) NMR ≤ NML to ensure that the speed limit of the motor is not exceeded. If a variable motor is specified, use equation (7) NVR=FD•NMD and design check (D) NVR ≤ NVL to determine if the speed required at the minimum motor displacement exceeds the maximum reduced angle speed limit. As explained in Pressure and Speed Limits for Hydrostatic Units BLN-9884, the maximum speed limit of a variable motor increases with decreasing angle, up to a certain value (the maximum reduced angle speed limit or cutoff point on the speed/angle curve). At low swashplate angles (i.e., below the angle cutoff point), a decrease in angle does not result in a greater maximum speed limit.

Note that reduced angle speed limits cannot be checked until the pump displacement and minimum motor displacement have been established. (This will be done in subsequent steps of this procedure.) However, if the speed exceeds the limit associated with the smallest possible swashplate angle (i.e., at the cutoff point of the speed/angle curve), then increase the motor’s maximum displacement and recalculate the final drive ratio.

Refer to Pressure and Speed Limits for Hydrostatic Units BLN-9884 for more information concerning speed limits.

Both SM (vehicle speed required at max angle) and SV (vehicle speed required at min angle) are customer defined conditions

12 | © Danfoss | July 2015 BLN-9885 | BC00000245en-US0304

SI System US System Description

Rotary Drives

DM = max motor displacement cc (in

)/rev E = final drive efficiency (%)/100 FD = final drive ratio

LR = wheel loaded radius mm (in) NMD NML = motor speed limit at max angle rpm NMR = req'd motor speed at max angle rpm NVD = non-propel design speed at min angle rpm NVR = req'd motor speed at min angle rpm NVL = motor speed limit at min angle rpm PM = maximum pressure bar (psid) SM = vehicle speed req'd at max angle kph (mph) SV = vehicle speed req'd at min angle kph (mph) TE = vehicle tractive effort N (lbf) TQ = max drive output torque Nm (in•lbf) # = number of motors

Propel Drives

Design Check: FD ≥ Required FD

Propel Drives

Rotary Drives

Design Check: NMR ≤ NML

Propel Drives

Rotary Drives

Design Check: NVR ≤ NVL

NMR = FD • NMDNMR = FD • NMD

NVR = FD • NVDNVR = FD • NVD

Required FD =

DM • PM • E • EM

Torque • 20

Required FD =

DM • PM • E • EM • #

TE • LR • 20

Required FD =

Torque • 2

FD • SM • 2650

NMR =

FD • SM • 168

NMR =

FD • SV • 2650

NVR =

FD • SV • 168

NVR =

DM • PM • E • EM

Torque • 2

d’less

E = motor mechanical efficiencyM (%)/100

= non-propel design speed at max angle rpm

DM • PM • E • EM • #

Applications Manual

Selection of Driveline Components

Input Gearing

The use of input gearing is usually customer defined and determined by the machine configuration. For vehicles with multiple hydraulic systems, use of an input splitter box is common. Splitter boxes are usually available with various ratios to accommodate pump speed requirements. For machines with only a single hydrostatic system (or machines utilizing tandem pumps) a direct drive pump may be appropriate, in which case the pump speed is the same as the prime mover speed.

Use equation (8) NP = NE•IR to determine the relationship between the prime mover speed, pump speed, and input gear ratio.

Danfoss | July 2015 BLN-9885 | BC00000245en-US0304 | 13

NP = NE • IR8)

SI / US System Description

NP = maximum pump design speed rpm NE = prime mover design speed rpm IR = pump input ratio

Applications Manual

Selection of Driveline Components

Pump Selection

Pump sizing consists of selecting a pump that will meet the flow (speed) requirements of the motor, or motors, in the system.

Use equation (9) to determine the required pump displacement. This calculation is based on an assumed pump input speed. Select a pump displacement at least as large as the calculated displacement. Also, check that the desired pump speed does not exceed the rated maximum speed for the pump. If the rated speed limit is exceeded, choose a different pump and calculate the input speed required and the corresponding input ratio using equations (10) and (11).

With a pump displacement selected, calculate the actual motor speed. The actual speed will usually be slightly higher than the required motor speed because the pump that is selected will usually have a displacement slightly greater than the calculated displacement.

Fixed Motor

For a fixed motor, determine the actual motor speed and compare with its rated maximum speed using equation (12) and design check (G). Note that equation (12) includes a calculation for an overrunning condition. An overrunning condition is characterized by a speed increase at the pump (and consequently the motors), typically by as much as 15%. The condition is especially common during downhill operation. Not only is there an increase in pump speed, but during either downhill operation or vehicle deceleration using hydrostatic braking; the motor becomes the pump and the pump becomes the motor. The net result is that the motor will turn faster for any given pump speed than what would be experienced during normal propel operation.

A 15% increase in engine speed is just an estimate; check with the engine manufacturer for specific details concerning the engine’s ability to provide dynamic braking and its maximum, or [not-to-exceed] operating speed.

14 | © Danfoss | July 2015 BLN-9885 | BC00000245en-US0304

SI / US System Description

Design Check: DP ≥ DPR

Design Check: NP ≤ NPL

DM = max motor displacement DP = max pump displacement DPR = required max pump displacement

rpm rpm rpm rpm rpm rpm rpm

IR = pump input ratio NMR = required motor speed at max angle NE = prime mover design speed NM = design maximum speed NML = motor speed limit at max angle NP = max pump design speed NPL = pump speed limit at max angle NPR = required pump speed

# = number of motors

10)

DPR = NMR • DM • #

•NP

NPR = DM • NMR • #

11)

IR = NPR

12)

Without Overrunning Condition:

With Overrunning Condition:

G) Design Check:

NM ≤ NML

NM = DP • NE • IR •

DM • #

NM = DP • NE • IR • 1.15

• DM • #

EVP • EVM

•DP EVP • EVM

EVP • EVM

)/rev

cc (in

)/rev

cc (in

)/rev

cc (in

EVP = pump volumetric efficiency EVM = motor volumetric efficiency

%/100 %/100

Assume EVP = EVM = 95% for first pass thru the sizing exercise

dimensionless

Applications Manual

Selection of Driveline Components

Variable Motor

For a variable motor, the procedure for assuring that the rated maximum speed is not exceeded is somewhat more involved.

The steps are as follows:

1. Determine if the rated maximum speed is exceeded using the method above, reference equation

(12).

2. Determine the minimum motor displacement using equation (13).

3. Calculate the angle associated with this displacement using equation (14). Select an available

minimum swashplate angle using design check (H) and determine the actual motor speed using equation (15).

4. Determine the reduced swashplate angle speed from Pressure and Speed Limits for Hydrostatic Units

BLN-9884, or by using equation (16). Use design check (I) to ensure that the minimum angle speed limit is not exceeded.

The Sizing Flowchart below details the above procedure.

Danfoss | July 2015 BLN-9885 | BC00000245en-US0304 | 15

13)

SI / US System

AV = min angle for a variable motor degrees DM = max motor displacement DP = max pump displacement DPR = req'd max pump displacemnt DV = min motor displacement IR = pump input ratio NE = prime mover design speed NM = motor speed at max angle NML = motor speed limit at max angle NMR = req'd motor speed at max angle NV = motor speed at min angle NVL = motor speed limit at min angle NVR = req'd motor speed at min angle NP = max pump design speed NPL = pump speed limit at max angle SINM = sine of motor at max angle SINV = sine of motor at min angle SV = vehicle speed req'd at min angle TANM= tangent of motor at max angle TANV = tangent of motor at min angle

# = number of motors

Description

All Swashplate Motors:

All H1B andSeries 51 Bent-Axis Motors:

All Swashplate Motors:

Series 51 Bent-Axis Motors:

H) Design Check:

AV Min Available

With Overrunning Condition:

• NE • IR • NVR • #

EVP • EVM

Note: Sin 32º = 0.53, 32º = Maximum angle of H1B and S51 bent axis motors

IF “YES”, then proceed; IF “NO”, increase pump displacement in Equation 13

NOTE: 1.15 is an estimate of engine max speed capability, contact engine supplier for additional information

DV =

ARCTAN (TANV)

AV =

TANM • (DV / DM)

TANV =

SINV =

0.53 • (DV / DM)

ARCSIN (SINV)AV =

14)

≥

NVL Max Reduced Angle ValueDesign Check:

IF “YES”, then proceed

≤

15) Without Overrunning Condition: DP

• NE

• IR •

DV • #

EVP • EVM

NV =

• NE

• IR • (1.15)

• DV • #

EVP • EVM

16) NVL =

NML • DM / DV

• (0.53 / SINV)NML NVL =

dimensionless

dimensionless dimensionless

EVP = pump volumetric efficiency EVM = motor volumetric efficiency

%/100 %/100

Assume EVP = EVM = 95% for first pass thru the sizing exercise

kph (mph)

rpm rpm rpm rpm rpm rpm rpm rpm rpm

dimensionless dimensionless

)/rev

cc (in

)/rev

cc (in

)/rev

cc (in

)/rev

cc (in

Applications Manual

Selection of Driveline Components

Continuous Pressure

16 | © Danfoss | July 2015 BLN-9885 | BC00000245en-US0304

The final (but crucial) step in the procedure is to estimate the continuous pressure based on the components selected.

The Pump Selection graph below shows the relationship between system pressure and system flow for a hydrostatic pump. The figure shows that the continuous system pressure usually occurs near maximum pump flow and normal input power.

The Sizing Flow Chart on page 19 equations provide a check to ensure that the continuous pressure is below the pressure required to meet the design life.

Full Load Speed

System Pressure Line

NLHI

Continuous

Max

System Pressure

Output Flow

Rated

Pump Selection

Defined by Engine Power

17)

SI System US System Description

DP = max pump displacement cc (in3)/rev FD = final drive ratio HP = normal power input to drive kW (hp) IR = pump input ratio LR = wheel loaded radius mm (inch) NE = prime mover design speed rpm NMD = non-propel speed at max angle rpm NML = motor speed limit at max angle rpm NVD = non-propel speed at min angle rpm PC = estimated continuous pressure bar (psid) SM = vehicle speed req'd at max angle kph (mph) SV = vehicle speed req'd at min angle kph (mph)

18)

Propel, Motor at Max Angle

Non-Propel, Motor at Max Angle

FD = NML • LR

168 • SM

FD = NML • LR

2650 • SM

PC = HP • 600 000

DP • NE • IR

PC = HP • 396 000

DP • NE • IR

FD = NML

NMD

FD = NML

NMD

Propel, Motor at Min Angle

Non-Propel, Motor at Min Angle

FD = NML • LR

168 • SV

FD = NML • LR

2650 • SV

FD = NML

NVD

FD = NML

NVD

Applications Manual

Selection of Driveline Components

Continuous system pressure at maximum pump flow may be estimated from the normal input power to the drive. For many systems, the continuous pressure determined in this manner is a good indicator of typical system pressure experienced in the drive.

System Sizing Flow Chart

The flowchart is designed to be used as a sizing algorithm to assist in the selection of system

Danfoss | July 2015 BLN-9885 | BC00000245en-US0304 | 17

components. It provides a concise step-by-step run-through of the sizing process. It is intended to accompany the previous sections and to expand the equations presented with the text.

The symbols used in the flowchart are explained in the box below. The equations used to calculate the quantities are included following the flowchart, along with the definitions of the symbols.

Be aware that the flowchart does not consider any torque/speed limits associated with various mechanical components, e.g., pump drives or final drive gearboxes.

Use the flowchart on the following pages to assist in sizing a hydrostatic transmission. The number of the equation required to complete this calculation is shown at the lower right corner of the boxes (X). This equation can be found in the tables following the flowchart.

(X)

X = Number of equation required to

Y = Flow chart reference numbers (numbers that jump to other reference points on the flowchart).

complete this calculation A list of equations follows the Sizing Flow Chart

Applications Manual

Selection of Driveline Components

18 | © Danfoss | July 2015 BLN-9885 | BC00000245en-US0304

Determine

TE or Torque

Multi-speed

Drive?

Calculate

Machine CP

Calculate

Transmission

Ratio

TR > 4?

TR < 2?

Calculate

Machine CP

for All Speeds

Select

Largest CP

Value

Use MV

Use MF

Try both

MF and MV

Calculate Required Motor CP

Yes

(1)

(2)

(3)

(1)

Begin by calculating the required effort or torque.

For multi-speed drives, machine corner (CP) power must be calculated for each drive.

Transmission Ratio (TR) indicates the need for a fixed or variable motor.

Sizing begins at the motor. First, determine the required motor corner power.

FDR

Yes

1.0

“Direct Drive”

LSHT

Yes

Applications Manual

Selection of Driveline Components

Sizing Flow Chart

Danfoss | July 2015 BLN-9885 | BC00000245en-US0304 | 19

(7)

Select a

Motor

Size (DM)

Calculate Motor CP

CP ≥ Required?

Determine

Required Final

Drive Ratio (FD)

Select FD

≥ Required

Calculate Required

Motor Speed (NMR)

at Max. Angle

Yes

NMR ≥ NML?

Increase

Motor

Size

MV?

Calculate Required

Motor Speed (NVR)

at Min. Angle

Establish

Pump Speed

(NP)

NVR ≥ NVL

at Smallest Possible

Angle?

Yes

(6)

(8)

(4)

(5)

Select a likely motor displacement and either calculate its corner power capability or use the Motor Power Capabilities table. If this value is less than the required corner power, select a larger motor.

Select a

Motor

Size (DM)

Calculate Motor CP

CP ≥ Required?

Yes

(4)

(5)

Determine the final drive ratio (FD) required. This calculation is based on the maximum motor displacement.

Calculate the required motor speed at maximum angle and compare with the maximum speed limit allowed.

Calculate Required

Motor Speed (NMR)

at Max. Angle

(6)

Establish

Pump Speed

For variable motors, calculate the required motor speed at the minimum angle and compare with the maximum speed limit at the smallest possible motor angle. Note that at this point in the sizing procedure, the required minimum angle is unknown, so the reduced angle speed limit is also unknown. However, the unknown speed limit will be less than the speed limit at the smallest possible motor angle.

Increase

Motor

NMR ≥ NML?

Yes

(NP)

Size

FDR

1.0

Applications Manual

Selection of Driveline Components

20 | © Danfoss | July 2015 BLN-9885 | BC00000245en-US0304

Yes

Calculate Pump Disp.

Req'd (DPR) for Motor

Max. Angle Speed

Choose Pump

Disp. (DP) ≥

Required (DPR)

Overrunning

Condition?

Increase

NP by 15%

NP ≥ NPL?

Choose

Different

Pump Size

Calculate Required

Pump Speed

Determine

New Pump

Drive Ratio

Yes

Calculate Actual

Motor Speed (NM)

at Motor Max. Angle

NM ≥ NML?

Increase

Motor Size

MV?

Calculate Motor Min. Disp. (DV)

Calculate

Actual

Motor Speed

(NV) at Motor

Min. Angle

Determine Min. Motor Angle (AV)

AV ≤ Min.

Available?

Determine Speed Limit for Reduced Angle

Increase

Pump

Disp.

NV ≥ NVL?

Increase

Motor

Size

(10) (11)

(12)

(13)

(15)

(14)

(16)

(9)

Yes

S elect

Convenient Angle ≤ AV

Determine Pump Displacement.

Check for the possibility of a overrunning condition (e.g., vehicle in downhill mode). If so, increase speed by 15%.

Using the displacement for the pump selected, determine the actual motor speed and compare with the rating. This step is required since the pump selected usually has a displacement slightly higher than the displacement required.

Applications Manual

Selection of Driveline Components

Danfoss | July 2015 BLN-9885 | BC00000245en-US0304 | 21

Estimate Continuous Press. (PC)

Increase

Motor Size

CP ≥ Continuous

Limit?

Can FD be Increased?

Calculate

Maximum

Choose

FD ≤ Maximum

Yes

(18)

Yes

END

(17)

Continuous pressure can be estimated based on the input horsepower.

If the final drive can be increased to reduce pressure, calculate the largest final drive that will keep motor speed under limits. Reselect a final drive no larger than this value.

Applications Manual

Selection of Driveline Components

22 | © Danfoss | July 2015 BLN-9885 | BC00000245en-US0304

stnemmoCderiuqeR snoitauqEpetS

metsyS SUmetsyS cirteM

1 Machine CP = TE • S Machine CP = TE • S Propel Drive

573 0063

Machine CP = TQ • ND Machine CP = TQ • ND Non-Propel Drive

520369459

emaSPC enihcaM = RT2

0.7 • Available power

emaSPC enihcaM = PC rotoM deriuqeR3

E • #

4 Motor CP = 0.95 • DM • NM • PM Motor CP = 0.95 • DM • NM • PM

000 693 000 006

5 Required FD = TE • LR • 0.02

Required FD = TE • LR • 2π Propel Drive

0.95 • DM • PM • E • 59.0# • DM • PM • E • #

Required FD = TQ • 20 π Required FD = TQ • 2 π Non-Propel Drive

0.95 • DM • PM • 59.0E • DM • PM • E

6 NMR = FD • SM • 2650 NMR = FD • S • evirD leporP861

RLRL

NMR = FD • evirD leporP-noNemaSMDN

7 NVR = FD • SV • 2650 NVR = FD • SV • evirD leporP861

RLRL

NVR = FD • evirD leporP-noNemaSVDN

8 NP = NE • emaSRI

9 DPR = NMR • DM • emaS#

(0.95)

• NP

10 NPR = DM • NMR • emaS#

DP • (0.95)

(choose DP ≥ DPR)

emaSRPN = RI11

Applications Manual

Selection of Driveline Components

Equations

Danfoss | July 2015 BLN-9885 | BC00000245en-US0304 | 23

stnemmoCderiuqeR snoitauqEpetS

metsyS SUmetsyS cirteM

12 NM = DP • NE • IR • (0.95)

noitarepO lamroNemaS

DM • #

NM = DP • NE • IR • snoitidnoC gninnurrevOemaS51.1

(0.95)

• DM • #

13 DV = DP • NE • IR • (0.95)

Same

NVR • #

15 NV = DP • NE • IR • (0.95)

noitarepO lamroNemaS

DV • #

NV = DP • NE • IR • snoitidnoCgninnurrevOemaS51.1

(0.95)

• DV • #

16 NVL = NML • (DM / DV)

1/2

srotoM etalphsawS llAemaS

NVL = emaS

NVL ≥ Reduced Angle Value

17 PC = HP • 600 000 PC = HP • 396 000

DP • NE • PDRI • NE • IR

18 FD = NML • LR FD = NML • LR Propel,

2650 • 861MS • SM Motor at Max Angle

,leporP-noNemaSLMN=DF

elgnA xaM ta rotoMDMN

FD = NVL • LR FD = NVL • LR Propel,

2650 • 861VS • SV Motor at Min Angle

,leporP-noNemaSLVN=DF

elgnA niM ta rotoMDVN

14 TANV = TANM • ( srotoM etalphsawS llAemaS)MD / VD

AV = Arctan (TANV)

Bent Axis Motors

emaS

AV = Refer to Technical

Information manual

H1B & Series 51

Refer to Technical Information manual

Bent Axis Motors

H1B & Series 51

Applications Manual

Selection of Driveline Components

24 | © Danfoss | July 2015 BLN-9885 | BC00000245en-US0304

Applications Manual

Selection of Driveline Components

Definition of Terms

The following list of terms describe the variables used in the sizing equations:

AV Minimum angle for a variable motor Degrees CP Corner power kW [hp] DM Maximum motor displacement cc [in3]/rev DV Minimum motor displacement cc [in3]/rev DP Maximum pump displacement cc [in3]/rev DPR Required maximum pump displacement cc [in3]/rev E Final drive efficiency % FD Final drive ratio — HP Normal power input to drive kW [hp] IR Input ratio (pump speed /prime mover speed) — LR Wheel loaded radius (rolling radius) mm [inch] ND Design speed for non-propel rpm — NMD Non-propel design speed at motor max angle rpm NVD Non-propel design speed at motor min angle rpm NE Prime mover input speed (engine, electric motor) rpm NML Motor speed limit at maximum angle rpm NPL Pump speed limit rpm NVL Motor speed limit at minimum angle rpm NM Motor speed at maximum angle rpm NP Pump speed rpm NV Motor speed at minimum angle rpm NMR Required motor speed at maximum angle rpm NPR Required pump speed rpm NVR Required motor speed at minimum angle rpm PC Estimated continuous pressure bar [psid] PM Maximum system pressure bar [psid] S Maximum vehicle speed kph [mph] SM Vehicle speed required with motor at max angle kph [mph] SINM Sine of motor maximum angle — SINV Sine of motor minimum angle — SV Vehicle speed required with motor at min angle kph [mph] TE Tractive effort requirement N [lbf] TANM Tangent of motor maximum angle — TQ Torque requirement (non-propel) Nm [in lbf] TR Transmission ratio — TANV Tangent of motor minimum angle —

Danfoss | July 2015 BLN-9885 | BC00000245en-US0304 | 25

Applications Manual

Selection of Driveline Components

Tractive Effort

For vehicle propel drives, motion resistance and required tractive efforts are directly related to vehicle weight. For a particular class or type of vehicle, the ratio of tractive effort to vehicle weight is relatively constant. This term is commonly called a pull ratio and it is a convenient design parameter.

The elements constituting a particular class or type of vehicle are machine function, drive configuration, grade, and terrain. Values for motion resistance contributing to pull ratio requirements have been estimated and are listed in the table Pull Ratio Requirements for Vehicle Propel Drives below. To establish the required pull ratio, sum the motion resistance values for machine function, drive configuration, grade and rolling resistance. Calculate required tractive effort from pull ratio and vehicle weight.

PR = MF + DC + GR + RR

where: PR = Pull ratio MF = Machine function motion resistance DC = Drive configuration motion resistance GR = Grade motion resistance RR = Rolling resistance

TE = (PR) (WT)

where: TE = Vehicle tractive effort (lb) WT = Vehicle weight (lb) The tractive effort to weight ratio, or pull ratio, is the sum of all expected demands on vehicle motion

resistance. We recommend verifying the calculated tractive effort values by testing an actual vehicle. To determine Machine Function (MF) motion resistance, consider all functions and modes of operation

separately. Usually, the functions performed in the worst ground conditions predominate. For transmissions with multi-speed mechanical gearboxes, designers should consider the functions performed for each speed range. This usually requires examining several possible work situations and selecting the one with the highest rolling resistance and/or grade.

The pull ratio listed for propel forces main work drive in the table Pull Ratio Requirements for Vehicle Propel Drives below is approximate. For propel drives which interact with work functions (cutters, planers, etc.), make an accurate determination of the required motion resistance by testing a working machine.

Transport mode should be used only for specific modes of operation in which traveling or carrying is the only requirement. It is assumed that the vehicle operates at a relatively constant speed in the transport mode.

The component of pull ratio due to Drive Configuration (DC) results from geometry effects when steering. The particular form of drive for the vehicle affects motion resistance. Skid steer configurations imply turning with differential side-to-side torque and no variable geometry. Dual path variable steer

geometry configurations are usually wheeled machines with a single trailing pivot or caster wheel. Single path track or single path wheel configurations imply a geometry adjustment of the ground

engaging elements to achieve steering. Grade motion Resistance (GR), or Gradability, is a function of terrain slope. Select the maximum grade at

which the particular machine function is performed. The maximum grade is assumed to be intermittent, with the average grade one-half to two-thirds of maximum.

Rolling Resistance (RR) affects motion resistance depending on the condition of the terrain. Rolling resistance values listed here are typical and may vary depending on location, particular conditions and

26 | © Danfoss | July 2015 BLN-9885 | BC00000245en-US0304

Pull Ratio Requirements for

Vehicle Propel Drives

Machine Function MF

Dozing (All Wheel / Track Drive) .90 Drawbar (All Wheel / Track Drive) .80 Drawbar (Single Axle Drive) .60 Dig and Load (All Wheel / Track Drive) .50 Propel Forces Main Work Drive .30 (Typ) Stop and Go Shuttle .15 Transport (No Work Interaction) .00

Drive Configuration DC

04.kcarT reetS dikS

03.leehW reetS dikS Dual Path Variable Steer Geometry .20 Single Path Track .10 Single Path Wheel .00

Grade (Intermittent) GR

01.edarG %01

02.edarG %02

92.edarG %03

73.edarG %04

54.edarG %05

15.edarG %06

Rolling Resistance RR

52.dnaS

02.duM ,lioS teW Fresh Deep Snow .16 Loose Soil, Gravel .12 Grassy Field, Dry Cropland .08 Packed Soil, Dirt Roadway .05

20.tnemevaP Steel on Steel Rails .004

Applications Manual

Selection of Driveline Components

Tractive Effort

drive configuration. These may be adjusted with more specific data. These values apply for typical rubber tired vehicles. High flotation tires and tracked crawlers may show somewhat lower values in poor terrain.

Vehicle weight (WT) is the maximum weight for the function being considered. For most vehicles, this is the loaded weight. Empty weight may be appropriate for some transport modes. For shuttle and transport vehicles, maximum weight is the gross combined weight of the power unit plus any towed trailer or wagon. For drawbar vehicles, maximum weight is only the weight of the power unit.

Simulating a trailer load: If we make the assumption that the coefficient of rolling resistance is the same for the vehicle and the trailer, then the weight of the trailer and its load can be added to the weight of the vehicle. If the coefficient of rolling resistance is different, then pro-rate the trailer weight before adding it to the vehicle weight with the following formula:

Typical minimum design values of pull ratio for some common vehicles have been determined and are listed in the Minimum Tractive Efforts Requirements table below. These values may be useful for checking intended tractive effort requirements. Vehicle performance testing is highly recommended to verify suitability in an actual working environment.

Danfoss | July 2015 BLN-9885 | BC00000245en-US0304 | 27

Pull ratio may be used to determine tractive effort in vehicle propel drives. Pull ratios are based on working vehicle weight. In general, this is loaded weight. For vehicles having a separate transport mode, empty weight may be appropriate.

Minimum Tractive Effort Requirements

Assumed Operating Conditions Minimum Pull Ratio

Vehicle Type Function and Terrain Working Grade Loaded Empty (Ref)

Crane, Tracked Transport in Wet Soil 30% .89 Crane, Wheeled Transport in Wet Soil 30% .49 Crawler Dozer Dozing, Wet Soil 10% 1.60 Crawler Loader Dig and Load, Loose Soil 10% 1.12 1.30 Excavator, Tracked Transport in Wet Soil 40% .97 Farm Tractor, 2WD Plow in Loose Dirt 15% .82 Farm Tractor, 4WD Plow in Loose Dirt 15% 1.02 Garbage Packer Crane, Wheeled 15% .27 Grader Grading Wet Soil 15% .65 Harvesting Machine High Speed, Grassy Field 15% .23 Harvesting Machine Low Speed, Mud 15% .35

54.elcatsbO bmilCenihcaM gnitsevraH Commercial Lawn Mower Mow on Grassy Field 30% .37 Lift Truck, Cushion Tire Stop and Go, Pavement 5% .22 Lift Truck, Pneumatic Tire Stop and Go, Gravel 5% .32 Lift Truck, Rough Terrain Stop and Go, Loose Soil 25% .52 Locomotive, Switcher Shuttle Rail Cars 3% .19 Log Feller, Dual Path Steer Accelerate With Load, Wet Soil 10 % .65 Log Forwarder, Wheeled Transport in Wet Soil 30 % .49 Mining Scoop, Wheeled Scoop in Gravel, Rock 10 % .72

54.% 01lioS mriF no gnivaPrevaP

25.% 01yawhgiH enalPrenalP daoR

03.% 01lioS dekcaP lloRrelloR Skid Steer Loader Dig and Load, Loose Soil 10 % 1.02 1.25 Snow Groomer Grooming Snow on Steep Slope 60 % 1.07 Soil Stabilizer Stabilize Wet Soil 15% .65 Street Sweeper Dump Load in Loose Soil 10% .22

49.% 03llihpU gnidalBrotcapmoC hsarT Wheel Loader, Articulated Dig and Load, Loose Soil 0 % .62 .80

Applications Manual

Selection of Driveline Components

Tractive Effort

Pull ratio and tractive effort requirements are based on typical vehicles being operated in normal fashion. Specific requirements may vary. Vehicle testing is recommended to verify that performance is satisfactory and that sufficient life of the driveline components will be obtained.

Pull Ratio

28 | © Danfoss | July 2015 BLN-9885 | BC00000245en-US0304

( )

(

( )

( )( )

( ) ( )

( )

−+±

−+−±

=++−−

−

−+=

−==

+=+=

−

WT*RR1

TERR1*WTTE*RR

CosTan *100θTan *100% y,Gradabilit

1**

*1*2

**1*4***4***2

:X""for Equation Quadratic Solve

0**1****2

1***

X1θSin θ, CosXLet

θSin *WTθ Cos*WT*RRF2RTE

:downhill forces balances uphill force when occursy Gradabilit Maximum

(lbf) N θ, Cos*WT*RRF1*RRRForce, Resistance Rolling

(lbf) N θ,Sin *WTF2 Force, Tangential

(lbf) N θ, Cos*WTF1 Force, Normal

degrees Angle,y Gradabiltiθ

:Find

lessd' ,Resistance Rolling oft CoefficienRR

(lbf) N Vehicle, ofWeight WT

(lbf) N Vehicle, of Force TractiveTE

:Given

222

2222222

22222

WTRR

TERRWTTERR

WTRR

WTTEWTRRWTRRTEWTRRTE

XWTRRXWTRRTEWTTE

) ( )

( )

−= 1*

XWTWTRRTE

XWTXWTRRTE

* X

Applications Manual

Selection of Driveline Components

Tractive Effort

Derivation of Maximum Gradability

Danfoss | July 2015 BLN-9885 | BC00000245en-US0304 | 29

Applications Manual

Selection of Driveline Components

Acceleration

Vehicle acceleration and deceleration times are often ignored during a vehicle transmission sizing proposal. This data is important to know especially for high inertia vehicles. An acceptable tractive force for steady state running may be inadequate for calculating acceleration time. Tractive force minus rolling resistance is the force left for calculating acceleration on level terrain.

A simple formula for calculating average acceleration or deceleration time on level terrain is: t = (W) (V) (g) (F) t = time (seconds) W = Vehicle weight (lbs.) V = Vehicle velocity (ft. per sec.) V = (MPH) (1.467) g = Gravity (32.2 ft. per sec. per sec.) F = Drawbar pull (lbs.) (tractive force minus rolling resistance) Available tractive force will change with vehicle speed due to engine power and/or pump and motor

displacement and power train ratio. Calculating acceleration time requires a summation of forces as they change with vehicle speed. For example, air resistance may be a factor at high vehicle speeds.

Rolling resistance will have an effect on any vehicle’s ability to accelerate as well as the ability to transmit all available force to the wheel before wheel slip.

Deceleration time is calculated by this same method, if only engine dynamic braking is used. Tractive force will vary with pump displacement and the capability of the engine to absorb torque.

Large centrifugal type loads or long conveyor belt drives may also have acceleration time requirements and should not be overlooked during the equipment selection stage.

An example is attached using computer generated (P-Cubed) performance data.

30 | © Danfoss | July 2015 BLN-9885 | BC00000245en-US0304

Prime Mover Speed (rpm): 2800 Limiting Pressure (psid): 5500

Input Power (hp): 200 Charge Pressure (psid): 348

Delta System Pressure (psid) 5500 5500 5500 4961 4012 3356 2871 2477 2000 1800

Pump 1 H1P165 - H1, 10.07cir, 18deg Max Angle, 1.59cir charge pump

Pump Drive Ratio: 1.00 Pump Drive Efficiency (%): 100 Swashplate Angle (deg) 2.8 5.0 7.4 9.5 11.7 13.8 15.9 18.0 18.0 18.0 Displacement (cir) 1.50 2.70 4.00 5.20 6.40 7.60 8.80 10.07 10.07 10.07 Displacement (cc ) 24.6 44.2 65.5 85.2 104.9 124.5 144.2 165.0 165.0 165.0 Input Shaft Speed (rpm) 2800 2800 2800 2800 2800 2800 2800 2800 2800 2800 Torque at Shaft (in-lb) 1646 2718 3877 4502 4502 4502 4502 4502 3724 3398 Actual Flow (gpm) 10.3 24.8 40.5 55.8 71.5 87.0 102.3 118.6 119.2 119.5 Power Loss (hp) 33.7 34.8 35.9 32.2 26.1 23.3 22.2 22.2 20.0 19.1 Charge Pump Loss (hp) 6.44 6.44 6.44 6.44 6.44 6.44 6.44 6.44 6.44 6.44 Volumet ric Efficiency (%) 57 76 84 88 92 94 96 97 98 98 Torque Efficiency (%) 87 92 94 94 94 93 92 91 90 89 Overall Efficiency (%) 49 70 78 83 87 88 89 89 87 87

Tot al Pump Flow (gpm) 10.3 24.8 40.5 55.8 71.5 87.0 102.3 118.6 119.2 119.5

Final Drive Case 1 Motor 1 90M100 - Series 90, 6.1cir, 17deg Max Angle, AxialPiston

Rolling Radius (in): 15.00 Coeff. Rolling Resistance: 0.02 Final Drive Ratio: 6.5

Weight Carried by Motor/Wheel (lb): 17500 Rolling Resistance (lb): 350 Final Drive Efficiency (%): 95 Swashplate Angle (deg) 17.0 17.0 17.0 17.0 17.0 17.0 17.0 17.0 17.0 17.0 Displacement (cir) 6.10 6.10 6.10 6.10 6.10 6.10 6.10 6.10 6.10 6.10 Displacement (cc ) 100.0 100.0 100.0 100.0 100.0 100.0 100.0 100.0 100.0 100.0 Shaft Speed (rpm) 162 432 726 1015 1317 1610 1900 2207 2226 2234 Torque at Motor Shaft (in-lb) 5047 5085 5121 4634 3743 3119 2650 2261 1794 1598 Power Loss (hp) 3.5 4.9 5.9 6.0 5.5 5.5 5.8 6.5 6.2 6.1 Volumet ric Efficiency (%) 83 92 95 96 97 98 98 98 99 99 Torque Efficiency (%) 95 95 96 96 96 96 95 94 92 91 Overall Efficiency (%) 79 88 91 93 93 94 93 92 91 90 Torque at Wheel (in-lb) 31162 31401 31619 28613 23113 19260 16367 13962 11078 9865 Wheel Speed (rpm) 25 67 112 156 203 248 292 340 342 344 Trac tive Force (lb) 2077 2093 2108 1908 1541 1284 1091 931 739 658

Motor 2 90M100 - Series 90, 6.1cir, 17deg Max Angle, AxialPiston

Rolling Radius (in): 15.00 Coeff. Rolling Resistance: 0.02 Final Drive Ratio: 6.5

Total Vehicle Performance

Vehicle Weight (lb): 35000 Coeff . Rolling Resistanc e: 0.02 Rolling Resistance (lb): 700 Input Power (hp) 73.1 120.8 172.3 200.0 200.0 200.0 200.0 200.0 165.5 151.0 Output Power (hp) 26.0 69.8 118.0 149.3 156.4 159.4 159.8 158.4 126.7 113.2 Power Loss (hp) 47.2 51.0 54.3 50.7 43.6 40.6 40.2 41.6 38.7 37.7 System Efficiency (%) 36 58 69 75 78 80 80 79 77 75 Trac tive Force (lb) 4155 4187 4216 3815 3082 2568 2182 1862 1477 1315 Vehicle Speed (mph) 2.228 5.938 9.971 13.943 18.085 22.106 26.091 30.305 30.564 30.670 Vehicle Speed (fpm) 196 523 877 1227 1591 1945 2296 2667 2690 2699 Drawbar Pull @ 0% Grade (lb) 3455 3487 3516 3115 2382 1868 1483 1162 777 616 Gradeabilit y (%) 9.94 10.03 10.11 8.95 6.83 5.35 4.24 3.32 2.22 1.76

Applications Manual

Selection of Driveline Components

Acceleration

Danfoss | July 2015 BLN-9885 | BC00000245en-US0304 | 31

Drawbar pull Speed Speed

Time to

accel

Cumulative

Tim

(lb) (mph) (ft/sec) (sec ) (sec) (ft/sec2) g's 3455 0.000 0.000 0.000 0.000 0.000 0.000 3455 2.228 3.267 1.028 1.028 3.179 0.099 3487 5.938 8.709 1.704 2.732 3.208 0.100 3516 9.971 14.625 1.836 4.568 3.235 0.100 3115 13.943 20.449 1.909 6.477 2.866 0.089 2382 18.085 26.525 2.403 8.880 2.192 0.068 1868 22.106 32.422 3.016 11.896 1.719 0.053 1483 26.091 38.266 3.791 15.687 1.364 0.042 1162 30.305 44.447 5.081 20.768 1.069 0.033

777 30.564 44.827 0.425 21.193 0.715 0.022

616 30.670 44.983 0.244 21.437 0.567 0.018

Assumes average force between two speeds

Accel

Applications Manual

Selection of Driveline Components

Acceleration

32 | © Danfoss | July 2015 BLN-9885 | BC00000245en-US0304

Applications Manual

Selection of Driveline Components

Charge Pump Sizing

Introduction

The charge pump is a critical component of the hydrostatic transmission. Without charge flow and charge pressure, the transmission will cease to function.

The primary function of the charge pump is to replenish fluid lost through leakage. In closed circuit hydrostatic systems, continual internal leakage of high pressure fluid is inherent in the design of the components used in such a system, and will generally increase as the displacement of the system’s pumps and motors increase. This make-up fluid from the charge pump is added to the low pressure side of the closed circuit to keep the lines full of fluid and avoid cavitation at the pump.

In addition to the primary function of replenishing fluid, another major function of the charge pump is to provide charge pressure to help return the pistons and keep the slippers against the swashplate.

Another function of the charge pump includes providing fluid for servo pistons on those systems having servo-controlled transmissions. If an Electronic Displacement Control (EDC) is used, the charge pump provides flow for the operation of a pressure control pilot valve (PCP). Charge flow also provides a transfer medium for heat dissipation. If the charge pump is used for auxiliary functions, then it must also be sized to provide this additional flow.

The Charge Pump Functions illustration shows the functions that the charge pump may be required to provide in a given application.

Charge Pump Considerations

As a rule of thumb, the charge flow requirement for a simple hydrostatic circuit is approximately 10% of the total displacement of all units in the system. However, this guideline is only an approximation for a simple system containing high speed piston components. The best way to size a charge pump is to individually consider each demand imposed on the charge pump. Many of these requirements do not occur in a simple hydrostatic circuit.

To properly size a charge pump, each of the following factors must be taken into account:

Danfoss | July 2015 BLN-9885 | BC00000245en-US0304 | 33

Applications Manual

Selection of Driveline Components

Charge Pump Sizing

•

System Pressure, and rate-of-change of system pressure (ΔP)

•

Input Speed

•

Minimum operational input speed

•

Line size, length, and Effective Bulk Modulus of the fluid

•

Control requirements

•

Non-Danfoss components

•

Type of loading

The System Leakage graph shows how system pressure and input speed affect leakage in the system. The graph shows that leakage increases with both higher system pressure and higher input speed. Changes in pressure have a greater effect on leakage than changes in speed. However, the affects due to changes in speed are greater at higher system pressures.

The Charge Flow and Leakage graph shows why it is important to also know the “minimum pump input speed”. In addition to the curves showing leakage, the figure includes curves for two charge pump sizes and their respective flows. (Charge pump #1 has the larger displacement.) The figure shows that for a given system pressure and charge pump size, system leakage varies at a rate different than that for charge flow. .

Disregarding for the moment all other charge pump requirements, other than leakage; for a given speed and pressure (and temperature) a charge pump has a flow curve which intersects the system leakage curve. At low speeds and high pressures, the potential system leakage may exceed the flow that the

34 | © Danfoss | July 2015 BLN-9885 | BC00000245en-US0304

Applications Manual

Selection of Driveline Components

Charge Pump Sizing

charge pump is capable of providing. Furthermore, the charge pump’s Volumetric Efficiency decreases with decreasing speed. Therefore, even though leakage rate may be greater at high pump input speeds, the largest charge pump displacement may be required at a reduced input speed. Both extremes of speed need to be checked for charge flow requirements. In many cases, the low input speed operational requirement will predominate in the final charge pump size selection.

If a larger charge pump displacement is selected due to a low input speed, then the case flow rate at the higher speeds will be greater and larger case drain lines may be required to keep case pressure within limits.

Make sure that all components with potential leakage are considered. Any component connected to the charge flow (i.e., connected to the low pressure side of the hydrostatic loop) must have its leakage value included in the total available charge flow. In addition, if these same components also create large drops in pressure, additional charge flow may be required for cooling.

The maximum flow required for the “control requirements” for servo-controlled pumps is dependent on the stroke rate and the servo volume. Normally, the flow required is in the range of 2 to 8 lpm [1/2 to 2 gpm]. In any case, servo flow must be included in the charge pump sizing requirement when applicable.

If an Electrical Displacement Control (EDC) is also used, a small amount of additional charge flow is required, usually 2 to 4 lpm [1/2 to 1 gpm]. This flow rate is needed for operation of the Pressure Control Pilot Valve (PCP), which regulates the position of the control spool of the displacement control. This additional flow requirement does not apply to hydraulic or manual displacement controls.

In some applications, special considerations for “cooling flow” requirements are not necessary. Charge pump flow necessary to make up for leakage may be sufficient for cooling. More often, additional cooling flow is required and a loop flushing shuttle valve is specified. The charge pump displacement must then accommodate this additional requirement for charge flow.

The “type of loading” can also require additional charge flow. Particularly, if the load is erratic or cyclical, a bulk modulus effect can occur. Bulk modulus is the inverse of a material property, Compressibility, which is defined as the amount that a fluid compresses for a given pressure increase. At low pressures, the amount of this fluid compression is small, and for this reason fluids are usually thought of as being “incompressible”. The pressures that can occur in hydrostatic systems, however, are of a magnitude that the influence of fluid compressibility can be significant. .

The bulk modulus effect occurs when rapid system pressure spikes compress the fluid in the high pressure side of the system. This results in an instantaneous reduction of the return flow rate into the low pressure side of the system. This reduction of return flow rate must be provided by the charge system, in order to maintain proper charge pressure in the low pressure side of the system.

The degree of bulk modulus effect in a given system will depend on several factors. These are, the length and diameter of the pressure conduits (which determine the volume of fluid subjected to the high pressure spikes), the rate of rise of the pressure spike, the magnitude of the pressure spike, and the bulk modulus of the fluid.

Because the bulk modulus effect is so easily overlooked, and because it often results in a tremendous increase in required charge flow, a section has been included in Fluids and Lubricants 520L0463. An example calculation is provided below to bring special attention to this topic.

Danfoss | July 2015 BLN-9885 | BC00000245en-US0304 | 35

Applications Manual

Selection of Driveline Components

Charge Pump Sizing

The required charge pump displacement is the one which is able to provide flow for all of the above requirements. If the required charge flow exceeds the capability of all available charge pump displacements, then a gear pump (or some additional charge flow source) must be used. Most Danfoss pumps include an auxiliary pad to mount gear pumps of various displacements.

After the charge pump displacement is selected, a system must be tested to be certain that charge flow and pressure requirements are met.

Use the Charge Pump Sizing Worksheet below to size a charge pump. Each of the charge flow requirements is included. The sum of the required charge flows represents the total flow required if all charge flow demands need to be met simultaneously. In reality, this is usually not the case. For example, it may be that for a particular system, a bulk modulus effect may never occur while an auxiliary function is active. Each application needs to be reviewed carefully to determine how much charge flow is required.

Charge Pump Sizing Worksheet

Leakage: "Pump" refers to hydrostatic pump, not the charge pump. Actually, only a portion of all inefficiencies can

be attributed to crossport leakage between high and low system loops. Since the charge pump needs to replace only fluid leaking past the rotating kits (i.e. case flow), the calculations below are conservative. If case flow values are available, they should be used instead of the equations below.

36 | © Danfoss | July 2015 BLN-9885 | BC00000245en-US0304

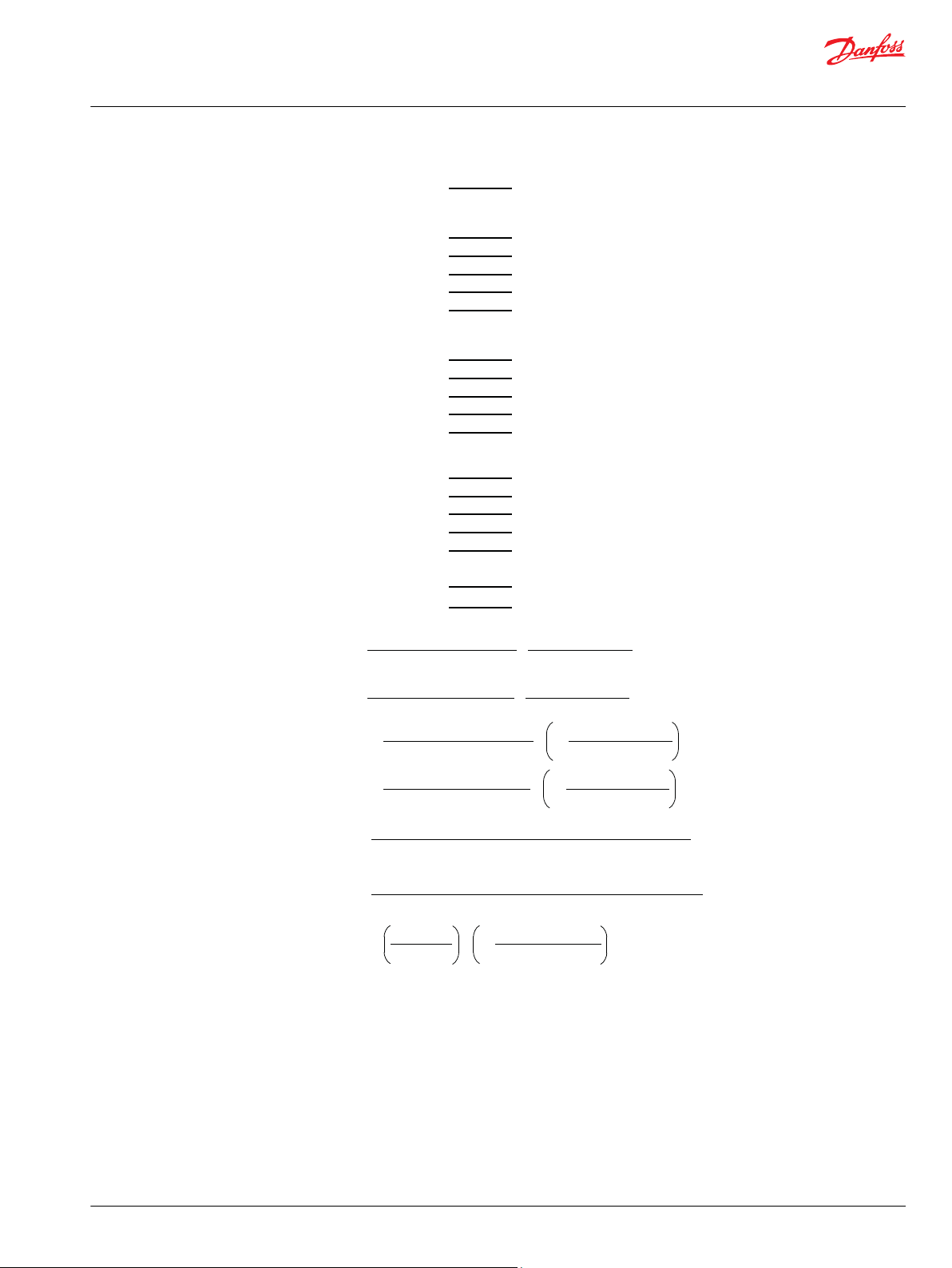
System Pressure psi

Pump

Series Frame Size

MPRdeepS

Volumetric Efficiency %

mpgegakaeL

Motor #1

Series Frame Size

MPRdeepS

Volumetric Efficiency %

mpgegakaeL

Motor #2

Series Frame Size

MPRdeepS

Volumetric Efficiency %

mpgegakaeL

Total Leakage gpm

lpm

( )

(

)

( )

(

)

( )

(

)

( )

(

)

.Efficiency Volumetric of for values

bulletinsn informatio chnicalproduct teConsult :Note

(lpm) gpm ,

100

% ,EfficiencyMotor

Motors #

Flow Pump

geMotorLeaka

Motors # * /rev

cmDisp,Motor

%/100 ,EfficiencyMotor /3cm 1000* lpm Flow, Pump

SpeedMotor

Motors # * /rev

inDisp,Motor

%/100 ,EfficiencyMotor /3in 231* gpm Flow, Pump

SpeedMotor

lpm ,

100

% ,Efficiency Pump

cc/liter 1000

RPM Pump*cc Disp, Pump

Leakage Pump

gpm ,

100

% ,Efficiency Pump

/gal

in 231

RPM Pump*cir Disp, Pump

Leakage Pump

lpm ,

100

% ,Efficiency Pump

cc/liter 1000

RPM Pump*cc Disp, Pump

Flow Pump

gpm ,

100

% ,Efficiency Pump

/gal

in 231

RPM Pump*cir Disp, Pump

Flow Pump

−=

RPM

liter

RPM

gal

Applications Manual

Selection of Driveline Components

Charge Pump Sizing

Danfoss | July 2015 BLN-9885 | BC00000245en-US0304 | 37

Applications Manual

Selection of Driveline Components

Charge Pump Sizing

Applications Manual

Selection of Driveline Components

Charge Pump Sizing

Danfoss | July 2015 BLN-9885 | BC00000245en-US0304 | 39

w/o

1.2 mm0.8 mm0.6

w/o 1.2 mm 0.8 mm 0.6 mm

Max  Min (s) Max  Min (s)

(100%  20%) (100%  20%)

Min  Max (s) Min  Max (s)

(20%  100%) (20%  100%)

Max  Min (s) Max  Min (s)

(100%  20%) (100%  20%)

Min  Max (s) Min  Max (s)

(20%  100%) (20%  100%)

Max  Min (s) Max  Min (s)

(100%  20%) (100%  20%)

Min  Max (s) Min  Max (s)

(20%  100%) (20%  100%)

w/o

1.2 mm0.8 mm0.6

w/o 1.2 mm 0.8 mm 0.6 mm

Max  Min (s) Max  Min (s)

(100%  20%) (100%  20%)

Min  Max (s) Min  Max (s)

(20%  100%) (20%  100%)

Max  Min (s) Max  Min (s)

(100%  20%) (100%  20%)

Min  Max (s) Min  Max (s)

(20%  100%) (20%  100%)

Max  Min (s) Max  Min (s)

(100%  20%) (100%  20%)

Min  Max (s) Min  Max (s)

(20%  100%) (20%  100%)

w/o 1.2 mm 0.8 mm 0.6 mm

Max  Min (s)

(100%  20%)

Min  Max (s)

(20%  100%)

Max  Min (s)

(100%  20%)

Min  Max (s)

(20%  100%)

Max  Min (s)

(100%  20%)

Min  Max (s)

(20%  100%)

60cc

Orifice diame ter

0.40

0.71

1.50

2.70

0.14

0.30

0.74

1.32

0.30

0.61

1.50

2.80

0.19

0.34

0.73

1.16

0.11

0.23

0.57

1.00

210 bar

0.21

0.52

1.00

1.56

210 bar

0.14

0.26

0.58

0.85

30 bar

0.22

0.47

1.13

400 bar

0.14

0.27

0.54

0.90

110cc

Orifice diame ter

0.20

0.33

0.51

80cc

Orifice diame ter

30 bar

0.15

0.25

0.45

0.71

400 bar

0.13

0.21

0.46

0.65

0.15

1.70

30 bar

0.56

1.40

1.94

3.60

0.44

1.13

1.89

3.59

210 bar

0.22

0.45

0.80

1.38

0.21

0.41

0.92

1.67

400 bar

0.22

0.33

0.58

0.97

0.22

0.31

0.69

1.25

160cc

Orifice diame ter

30 bar

0.48

1.32

2.62

4.36

0.50

1.30

3.03

4.92

210 bar

0.27

0.68

1.25

2.10

0.28

0.71

1.61

2.57

400 bar

0.31

0.50

0.90

1.47

0.24

0.56

1.24

2.04

250cc

Orifice diame ter

30 bar

0.55

1.56

3.28

5.59

0.62

1.46

3.52

5.94

210 bar

0.32

0.72

1.38

2.21

0.31

0.72

1.64

2.73

400 bar

0.33

0.53

0.97

1.50

0.25

0.55

1.24

2.03

P108905

2 Position Control: Step Response, seconds

Step response has been tested with a 2-Position control (de-energized max. angle) at delta p = 30 bar. 210 bar and 400 bar and orifices for Servo M4 & M5 For Max. to Min., current went from zero to max, then back to zero current.

Applications Manual

Selection of Driveline Components

Charge Pump Sizing

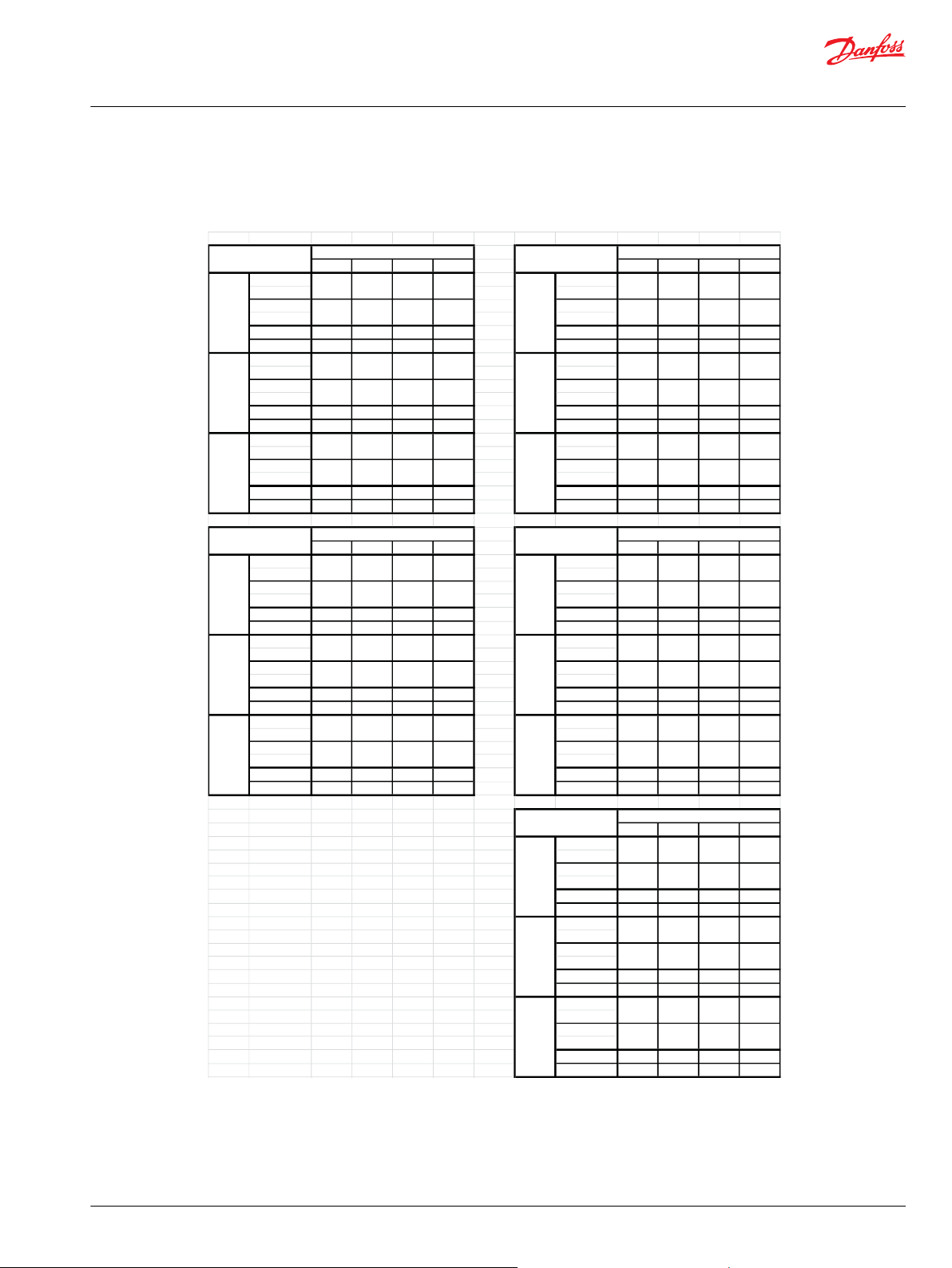
w/o 1.2 mm 0.8 mm 0.6 m m w/o 1.2 mm 0.8 mm 0.6 m m

Max  Min (s) Max  Min (s)

(100%  20%) (100%  20%)

Min  Max (s) Min  Max (s)

(20%  100%) (20%  100%)

50%  20% (s) 0.20 0.25 0.43 0.68 50%  20% (s) 0.20 0.34 0.69 1.11

20%  50% (s) 0.21 0.27 0.42 0.62 20%  50% (s) 0.18 0.34 0.68 1.16

Max  Min (s) Max  Min (s)

(100%  20%) (100%  20%)

Min  Max (s) Min  Max (s)

(20%  100%) (20%  100%)

50%  20% (s) 0.20 0.19 0.27 0.39 50%  20% (s) 0.18 0.16 0.29 0.45

20%  50% (s) 0.20 0.20 0.24 0.32 20%  50% (s) 0.19 0.20 0.37 0.61

Max  Min (s) Max  Min (s)

(100%  20%) (100%  20%)

Min  Max (s) Min  Max (s)

(20%  100%) (20%  100%)

50%  20% (s) 0.23 0.21 0.24 0.33 50%  20% (s) 0.33 0.31 0.21 0.33

20%  50% (s) 0.21 0.20 0.22 0.27 20%  50% (s) 0.24 0.18 0.33 0.56

w/o 1.2 mm 0.8 mm 0.6 m m w/o 1.2 mm 0.8 mm 0.6 m m

Max  Min (s) Max  Min (s)

(100%  20%) (100%  20%)

Min  Max (s) Min  Max (s)

(20%  100%) (20%  100%)

50%  20% (s) 0.17 0.30 0.50 0.89 50%  20% (s) 0.27 0.48 0.84 1.45

20%  50% (s) 0.16 0.37 0.53 0.95 20%  50% (s) 0.35 0.48 0.90 1.52

Max  Min (s) Max  Min (s)

(100%  20%) (100%  20%)

Min  Max (s) Min  Max (s)

(20%  100%) (20%  100%)

50%  20% (s) 0.18 0.18 0.20 0.34 50%  20% (s) 0.43 0.31 0.45 0.67

20%  50% (s) 0.17 0.20 0.25 0.43 20%  50% (s) 0.49 0.38 0.53 0.81

Max  Min (s) Max  Min (s)

(100%  20%) (100%  20%)

Min  Max (s) Min  Max (s)

(20%  100%) (20%  100%)

50%  20% (s) 0.17 0.20 0.15 0.24 50%  20% (s) 0.56 0.39 0.35 0.50

20%  50% (s) 0.13 0.20 0.19 0.33 20%  50% (s) 0.57 0.43 0.45 0.68

w/o 1.2 mm 0.8 mm 0.6 m m

Max  Min (s)

(100%  20%)

Min  Max (s)

(20%  100%)

50%  20% (s) 0.28 0.53 0.98 1.63

20%  50% (s) 0.23 0.48 1.00 1.76

Max  Min (s)

(100%  20%)

Min  Max (s)

(20%  100%)

50%  20% (s) 0.42 0.43 0.46 0.66

20%  50% (s) 0.55 0.92

Max  Min (s)

(100%  20%)

Min  Max (s)

(20%  100%)

50%  20% (s) 0.55 0.50 0.35 0.49

20%  50% (s) 0.48 0.78

060cc

Orifice di ameter

30 bar

0.30

0.47

0.96

1.59

0.04

0.50

0.95

1.37

210 bar

0.24

0.31

0.53

0.84

0.23

0.32

0.46

0.65

400 bar

0.28

0.27

0.43

0.65

0.24

0.26

0.38

0.49

080cc

Orifice di ameter

30 bar

0.36

0.78

1.39

2.28

0.30

0.59

1.45

2.35

210 bar

0.16

0.40

0.56

0.97

0.27

0.31

0.67

1.16

400 bar

0.19

0.34

0.40

0.69

0.32

0.25

0.50

0.86

110cc

Orifice di ameter

30 bar

0.51

1.27

1.76

3.27

0.40

1.03

1.72

3.26

210 bar

0.20

0.41

0.73

1.25

0.19

0.37

0.84

1.52

400 bar

0.20

0.30

0.53

0.88

0.20

0.28

0.63

1.14

160cc

Orifice di ameter

30 bar

0.52

1.15

2.08

3.58

0.42

1.03

2.12

3.74

210 bar

0.40

0.58

1.05

1.64

0.28

0.58

1.15

1.91

400 bar

0.53

0.49

0.75

1.18

0.24

0.46

0.87

1.43

250cc

Orifice di ameter

30 bar

0.58

1.29

3.12

4.68

0.50

1.14

2.89

4.93

210 bar

0.24

0.55

1.12

1.74

0.24

0.56

1.27

2.27

400 bar

0.19

0.41

0.82

1.24

0.19

0.43

0.97

1.72

P108906

Proportional Control: Step Response, seconds

Step response has been tested with a Proportional control (de-energized max. angle) at delta p = 30 bar. 210 bar and 400 bar and orifices for Servo M4 & M5 For Max. to Min., current went from zero to max, then back to zero current.

Applications Manual

Selection of Driveline Components

Charge Pump Sizing

Danfoss | July 2015 BLN-9885 | BC00000245en-US0304 | 41

Applications Manual

Selection of Driveline Components

Charge Pump Sizing

Applications Manual

Selection of Driveline Components

Charge Pump Sizing

Danfoss | July 2015 BLN-9885 | BC00000245en-US0304 | 43

Danfoss Power Solutions GmbH & Co. OHG

Krokamp 35 D-24539 Neumünster, Germany Phone: +49 4321 871 0

Danfoss Power Solutions ApS

Nordborgvej 81 DK-6430 Nordborg, Denmark Phone: +45 7488 2222

Danfoss Power Solutions (US) Company

2800 East 13th Street Ames, IA 50010, USA Phone: +1 515 239 6000

Danfoss Power Solutions Trading (Shanghai) Co., Ltd.

Building #22, No. 1000 Jin Hai Rd Jin Qiao, Pudong New District Shanghai, China 201206 Phone: +86 21 3418 5200

Products we offer:

Comatrol

www.comatrol.com

Turolla

www.turollaocg.com

Hydro-Gear

www.hydro-gear.com

Daikin-Sauer-Danfoss

www.daikin-sauer-danfoss.com

Bent Axis Motors

•

Closed Circuit Axial Piston

•

Pumps and Motors Displays

•

Electrohydraulic Power

•

Steering Electrohydraulics

•

Hydraulic Power Steering

•

Integrated Systems

•

Joysticks and Control

•

Handles Microcontrollers and

•

Software Open Circuit Axial Piston

•

Pumps Orbital Motors

•

PLUS+1® GUIDE

•

Proportional Valves

•

Sensors

•

Steering

•

Transit Mixer Drives

•

Danfoss Power Solutions is a global manufacturer and supplier of high-quality hydraulic and electronic components. We specialize in providing state-of-the-art technology and solutions that excel in the harsh operating conditions of the mobile off-highway market. Building on our extensive applications expertise, we work closely with our customers to ensure exceptional performance for a broad range of off-highway vehicles.

We help OEMs around the world speed up system development, reduce costs and bring vehicles to market faster.

Danfoss – Your Strongest Partner in Mobile Hydraulics.

Go to www.powersolutions.danfoss.com for further product information.

Wherever off-highway vehicles are at work, so is Danfoss. We offer expert worldwide support for our customers, ensuring the best possible solutions for outstanding performance. And with an extensive network of Global Service Partners, we also provide comprehensive global service for all of our components.

Please contact the Danfoss Power Solution representative nearest you.

Local address:

Danfoss can accept no responsibility for possible errors in catalogues, brochures and other printed material. Danfoss reserves the right to alter its products without notice. This also applies to products already on order provided that such alterations can be made without changes being necessary in specifications already agreed. All trademarks in this material are property of the respective companies. Danfoss and the Danfoss logotype are trademarks of Danfoss A/S. All rights reserved.

Danfoss | July 2015 BLN-9885 | BC00000245en-US0304

Danfoss Selection of Driveline Components User guide

Specifications and Main Features

Frequently Asked Questions

User Manual

Contents

Introduction

Applications Manuals

Selection of Driveline Components

Introduction

Design Goal

Sizing Procedure

Machine Corner Power (CP)

Variable or Fixed Motor

Motor Selection

Final Drive Selection

Input Gearing

Pump Selection

Continuous Pressure

System Sizing Flow Chart

Sizing Flow Chart

Equations

Definition of Terms

Tractive Effort

Tractive Effort

Acceleration

Acceleration

Charge Pump Sizing

Introduction

Charge Pump Considerations

Charge Pump Sizing Worksheet