Page 1

GRAPH 95/GRAPH 75/GRAPH 35+
GRAPH 85 SD/GRAPH 85 (Mise à jour OS 2.00)
CONNECTABLE
Logiciel version 2.00
MANUEL DE L’UTILISATEUR
DEXXON DATAMEDIA
Page 2
• Le contenu de ce manuel est susceptible d’être modifié sans préavis.
• Aucune partie de ce manuel ne peut être reproduite sous quelque forme que ce soit sans la
permission écrite du fabricant.
• Les options décrites dans le chapitre 13 de ce manuel ne sont pas disponibles dans certaines
zones géographiques. Demandez à votre distributeur ou au revendeur CASIO le plus proche
quelles sont les options qui sont disponibles dans votre pays.
• Conservez la documentation à portée de main pour toute référence future.
i
Page 3

Contenu
Familiarisation — A lire en premier!
Chapitre 1 Opérations de base
1. Touches ........................................................................................................................ 1-1
2. Affichage ....................................................................................................................... 1-2
3. Saisie et édition de calculs ........................................................................................... 1-6
4. Utilisation du mode d’écriture mathématique .............................................................1-10
5. Menu d’options (OPTN) .............................................................................................. 1-22
6. Menu de données de variables (VARS) ..................................................................... 1-23
7. Menu de programmation (PRGM) .............................................................................. 1-26
8. Utilisation de l’écran de configuration ......................................................................... 1-27
9. Capture d’écran .......................................................................................................... 1-30
10. En cas de problème persistant… ...............................................................................1-31
Chapitre 2 Calculs manuels
1. Calculs de base ............................................................................................................2-1
2. Fonctions spéciales ...................................................................................................... 2-6
3. Spécification de l’unité d’angle et du format d’affichage .............................................2-10
4. Calculs de fonctions ...................................................................................................2-11
5. Calculs numériques .................................................................................................... 2-20
6. Calculs avec nombres complexes ..............................................................................2-30
7. Calculs binaire, octal, décimal et hexadécimal avec entiers ...................................... 2-33
8. Calculs matriciels ........................................................................................................ 2-36
9. Calculs de conversion métrique .................................................................................2-48
Chapitre 3 Listes
1. Saisie et édition d’une liste ...........................................................................................3-1
2. Traitement des données d’une liste ..............................................................................3-5
3. Calculs arithmétiques à partir de listes ....................................................................... 3-10
4. Changement de fichiers de listes ...............................................................................3-14
Chapitre 4 Calcul d’équations
1. Équations linéaires simultanées ...................................................................................4-1
2. Équations d’ordre supérieur, du 2
3. Solveur numérique d’équations ....................................................................................4-4
ème
au 6
ème
degré ...................................................... 4-2
Chapitre 5 Représentation graphique de fonctions
1. Exemples de graphes ................................................................................................... 5-1
2. Contrôle des paramètres apparaissant sur un écran graphique ..................................5-3
3. Tracé d’un graphe ........................................................................................................5-6
4. Stockage d’un graphe dans la mémoire d’images ......................................................5-11
5. Tracé de deux graphes sur le même écran ................................................................ 5-11
6. Représentation graphique manuelle ...........................................................................5-13
7. Utilisation de tables ....................................................................................................5-15
8. Représentation graphique dynamique ........................................................................5-20
9. Représentation graphique d’une formule de récurrence ............................................ 5-23
10. Tracé du graphe d’une section conique .....................................................................5-27
11. Changement de l’aspect d’un graphe ......................................................................... 5-28
12. Analyse de fonctions ..................................................................................................5-30
ii
Page 4

Chapitre 6 Graphes et calculs statistiques
1. Avant d’effectuer des calculs statistiques ..................................................................... 6-1
2. Calcul et représentation graphique de données statistiques à variable unique ...........6-4
3. Calcul et représentation graphique de données statistiques à variable double ...........6-9
4. Exécution de calculs statistiques ................................................................................ 6-16
5. Tests ........................................................................................................................... 6-23
6. Intervalle de confiance ................................................................................................6-36
7. Lois de probabilité ......................................................................................................6-40
8. Termes des tests d’entrée et sortie, intervalle de confiance et loi de probabilité ....... 6-52
9. Formule statistique ..................................................................................................... 6-55
Chapitre 7 Calculs financiers (TVM)
1. Avant d’effectuer des calculs financiers .......................................................................7-1
2. Intérêt simple ................................................................................................................ 7-2
3. Intérêt composé ............................................................................................................ 7-3
4. Cash-flow (Évaluation d’investissement) ...................................................................... 7-5
5. Amortissement .............................................................................................................. 7-7
6. Conversion de taux d’intérêt ......................................................................................... 7-9
7. Coût, prix de vente, marge ......................................................................................... 7-10
8. Calculs de jours/date ..................................................................................................7-11
9. Dépréciation ............................................................................................................... 7-12
10. Calculs d’obligations ................................................................................................... 7-14
11. Calculs financiers en utilisant des fonctions ...............................................................7-17
Chapitre 8 Programmation
1. Étapes élémentaires de la programmation ................................................................... 8-1
2. Touches de fonction du modeTouches de fonction du mode PRGM .......................................................................... 8-2
3. Édition du contenu d’un programme .............................................................................8-4
4. Gestion de fichiers ........................................................................................................ 8-5
5. Guide des commandes .................................................................................................8-7
6. Utilisation des fonctions de la calculatrice dans un programme ................................. 8-22
7. Liste des commandes du modeListe des commandes du mode PRGM ...................................................................... 8-39
8. Bibliothèque de programmes ......................................................................................8-44
Chapitre 9 Feuille de Calcul
1. Notions fondamentales du Tableur et le menu de fonctions ........................................9-1
2. Opérations fondamentales du Tableur ......................................................................... 9-2
3. Utilisation des commandes spéciales du mode S • SHT ............................................. 9-14
4. Traçage de graphes statistiques et calculs statistiques et de régression ...................9-16
5. Mémoire du mode S • SHT .......................................................................................... 9-20
Chapitre 10 L’eActivity
1. Aperçu de l’application eActivity .................................................................................10-1
2. Menus de fonctions de l’application eActivity ............................................................. 10-2
3. Opérations sur les fichiers eActivity ............................................................................10-3
4. Saisie et édition de données ......................................................................................10-4
Chapitre 11 Gestionnaire de la mémoire
1. Utilisation du gestionnaire de mémoire ......................................................................11-1
Chapitre 12 Menu de réglages du système
1. Utilisation du menu de réglages du système .............................................................. 12-1
2. Réglages du système .................................................................................................12-1
iii
Page 5

Chapitre 13 Communication de données
1. Connexion de deux calculatrices ................................................................................ 13-1
2. Connexion de la calculatrice à un ordinateur personnel .............................................13-1
3. Communication des données .....................................................................................13-2
4. Précautions lors la communication de données .........................................................13-5
5. Envoi de l’image d’écran ..........................................................................................13-11
Chapitre 14 Utilisation des cartes de mémoire flash (SD)
(GRAPH 95 seulement)
1. Utilisation d’une carte SD ........................................................................................... 14-1
2. Formatage d’une carte SD .........................................................................................14-3
3. Précautions d’utilisation de la carte SD ......................................................................14-3
Appendice
1. Tableau des messages d’erreur ...................................................................................A-1
2. Plages d’introduction ....................................................................................................A-5
E-CON2 Application (English)
1 E-CON2 Overview
2 Using the Setup Wizard
3 Using Advanced Setup
4 Using a Custom Probe
5 Using the MULTIMETER Mode
6 Using Setup Memory
7 Using Program Converter
8 Starting a Sampling Operation
9 Using Sample Data Memory
10 Using the Graph Analysis Tools to Graph Data
11 Graph Analysis Tool Graph Screen Operations
12 Calling E-CON2 Functions from an eActivity
iv
Page 6

Familiarisation — A lire en premier!
I A propos du manuel de l’utilisateur
• Différences spécifiques au modèle pour les fonctions et les écrans
Ce manuel de l’utilisateur recouvre des multiples modèles de calculatrice. Notez que
certaines fonctions décrites ici peuvent ne pas être disponibles sur tous les modèles couverts
par ce document. Dans ce manuel, toutes les captures d’écran montrent l’écran de la GRAPH
95 et l’aspect des écrans des autres modèles peut varier légèrement.
• Saisie et affichage naturel des données mathématiques
Sous le paramétrage initial par défaut, la calculatrice est configuré pour utiliser le « mode
d’écriture mathématique » ce qui active la saisie et l’affichage naturel des expressions
mathématiques. Cela signifie que vous pouvez définir des fractions, des racines carrées,
des différentiels et autres expressions comme si on les écrivait à la main. Dans le « mode
d’écriture mathématique », la plupart des résultats des calculs sont visualisés avec cet
affichage naturel.
Pour saisir et afficher des expressions de calcul sur une seule ligne vous pouvez sélectionner
aussi le « mode d’écriture linéaire ». Avec la calculatrice le mode d’écriture mathématique est
configuré comme paramétrage initial par défaut.
0
Les exemples montrés dans ce manuel de l’utilisateur sont présentés principalement en
utilisant le mode d’écriture linéaire. Si vous utilisez la calculatrice notez les points suivants :
• Pour obtenir de l’information concernant le basculement entre le mode d’écriture
mathématique et le mode d’écriture linéaire, voir l’explication sur le paramètre « Input/
Output » (mode d’entrée/sortie) dans « Utilisation de l’écran de configuration » (page 1-27).
• Pour obtenir de l’information concernant l’entrée et l’affichage de données avec le mode
d’écriture mathématique, voir « Utilisation du mode d’écriture mathématique » (page 1-10).
S V()
Cette suite de touches indique que vous devez appuyer sur puis sur V pour écrire
le symbole . Toutes les opérations qui nécessitent l’utilisation de plusieurs touches sont
indiquées de cette façon. Les indications sur les touches proprement dites sont suivies du
caractère ou de la commande à saisir entre parenthèses.
S K EQUA
Cette suite de touches indique que vous devez appuyer d’abord sur K, utiliser les touches
du pavé directionnel D, A, B, C pour sélectionner le mode EQUA et appuyer ensuite
sur U. Les opérations qu’il faut effectuer pour accéder à un mode depuis le menu principal
sont toutes indiquées de cette façon.
S Touches de fonction et menus
• Un certain nombre d’opérations effectuées par la calculatrice peuvent être exécutées en
utilisant les touches de fonction à . L’opération affectée à chaque touche de fonction
dépend du mode dans lequel se trouve la calculatrice, et les opérations disponibles sont
indiquées sur les menus de fonctions qui apparaissent au bas de l’écran.
• Dans ce manuel, l’opération en cours affectée à une touche de fonction est indiquée entre
parenthèses après le nom de la touche. (Comp), par exemple, indique que par une
pression sur vous sélectionnez {Comp}, qui apparaît aussi sur le menu de fonctions.
v
Page 7
• Quand (E) est indiqué sur le menu de fonctions pour la touche , ce symbole signifie
qu’en appuyant sur vous afficherez la page suivante ou précédente des options de ce
menu.
S Titres des menus
• Les titres des menus dans le manuel indiquent l’opération de touches nécessaire pour
afficher le menu expliqué. L’opération d’un menu affiché en appuyant sur * puis {LIST}
apparaîtra comme suit : [OPTN]-[LIST].
• L’utilisation de la touche (E) pour le changement de page d’un menu n’est pas indiquée
dans les titres des menus.
S Liste de commandes
La liste des commandes du mode PRGM (page 8-39) fournit un organigramme des différents
menus correspondant aux touches de fonction. EIle vous indique comment accéder au menu
de commandes souhaité.
Exemple : L’opération suivante affiche Xfct : [VARS]-[FACT]-[Xfct]
S E-CON2
Ce manuel n’aborde pas le mode E-CON2. Pour plus d’infomation sur le mode E-CON2,
téléchargez le manuel E-CON2 du site : http://edu.casio.com (version disponible seulement
en anglais).
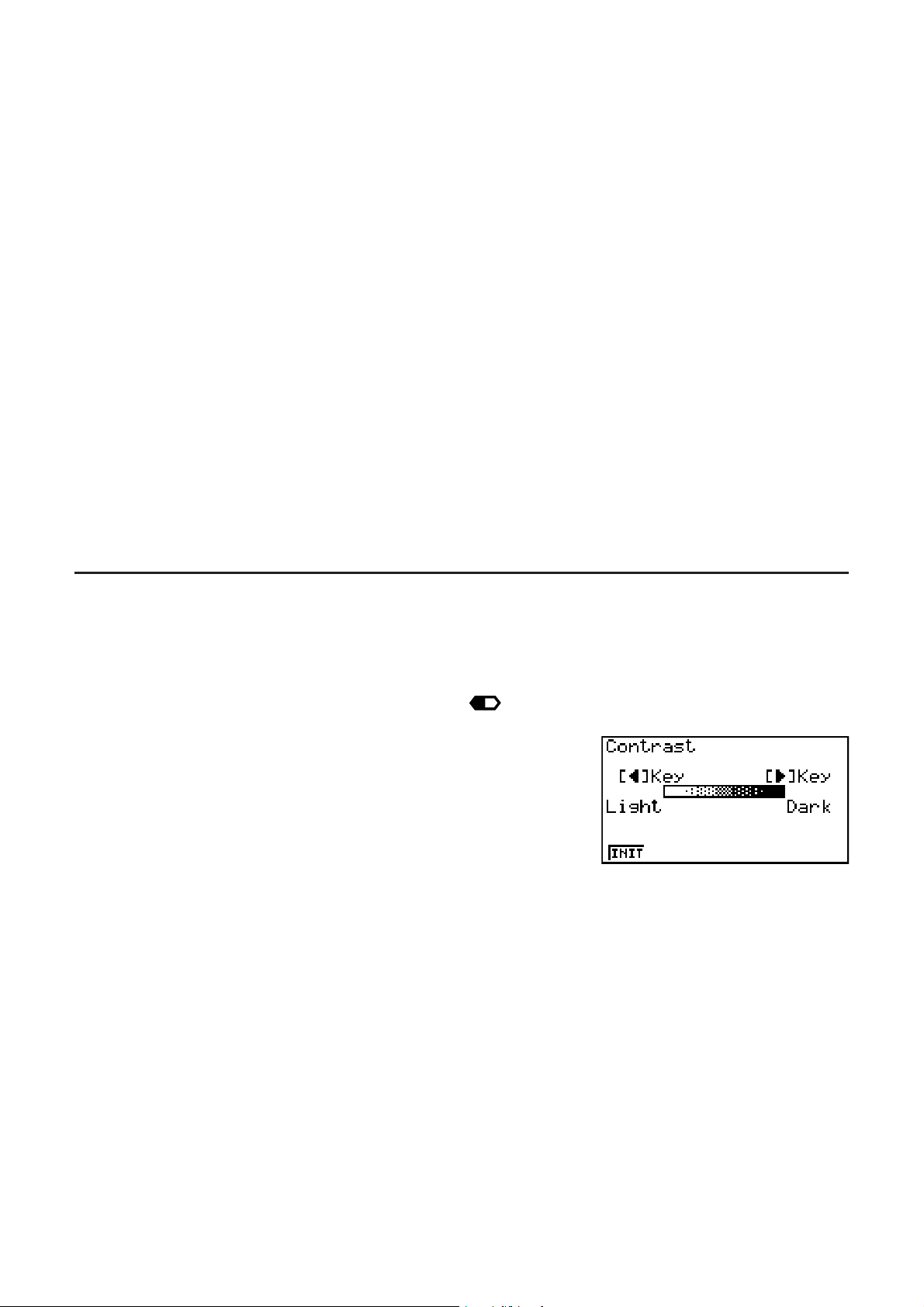
I Réglage du contraste
Réglez le contraste chaque fois que les objets affichés paraissent sombres ou sont difficiles à
distinguer.
1. Utilisez les touches du pavé directionnel (D, A, B ou C) pour sélectionner l’icône
SYSTEM et appuyez sur U, puis sur (
contraste.
2. Ajustez le contraste.
• La touche du pavé directionnel C rend le contraste plus sombre.
• La touche du pavé directionnel B rend le contraste moins sombre.
• (INIT) rétablit le contraste initial.
3. Pour quitter l’écran de réglage du contraste, appuyez sur K.
) pour afficher l’écran de réglage du
vi
Page 8
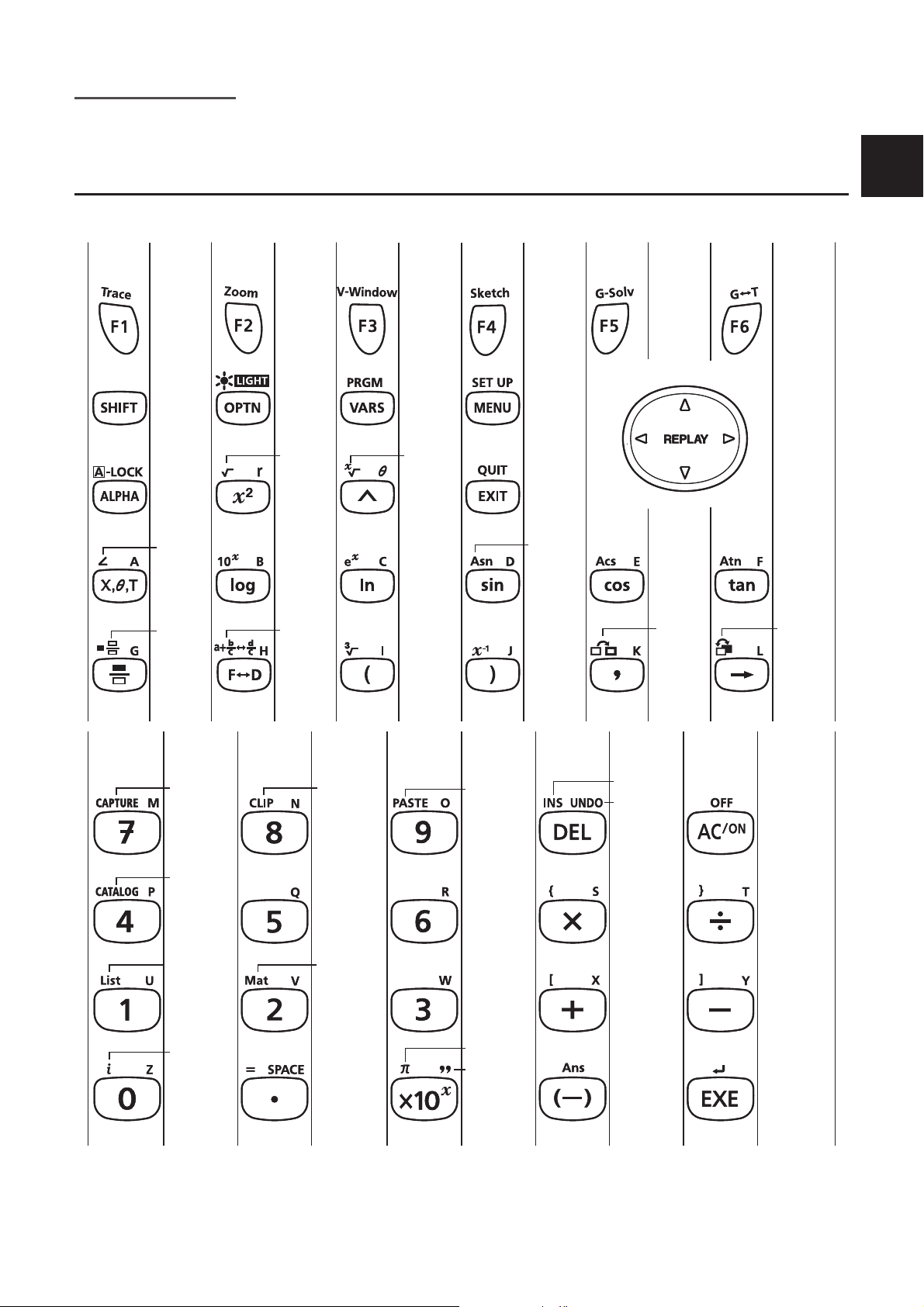
Chapitre 1 Opérations de base
1. Touches
I Table des touches
Page Page Page Page Page Page
Page Page Page Page Page Page
1
5-30 5-5 5-3
5-30 5-5 5-3
1-26 1-27
1-26 1-27
1-2 1-22 1-23 1-3
1-2 1-22 1-23 1-3
1-19,
2-14
2-7
2-7
1-2
1-2
2-30
2-30
1-11 2-19
1-11 2-19
1-12
1-12
1-19
1-19
2-19
2-19
2-14
2-14 2-14
2-14 2-14
2-14
2-14
1-19
1-19
2-19
2-19
1-19,
2-14
2-14
2-1
2-1
5-29 5-31 5-1
5-29 5-31 5-1
2-13
2-13
2-13 2-13
2-13 2-13
2-1 2-6
2-1 2-6
5-24
5-24
10-11 10-10
10-11 10-10
Page Page Page Page Page
Page Page Page Page Page
1-6, 1-14
1-30
1-30
1-9
1-9
3-2 2-41
3-2 2-41
2-30
2-30
Les fonctions listées ci-dessus ne sont pas toutes disponibles sur tous les modèles couverts
par ce manuel. Selon le modèle de votre calculatrice, certaines des touches dessinées cidessus peuvent être absentes du clavier.
1-8
1-8
1-9
1-9
2-13
2-13
2-7
2-7
1-6, 1-14
1-16
1-16
1-6
1-6
2-1
2-1
2-1
2-1
2-9
2-9
2-12-1
2-12-1
2-1
2-1
1-1
Page 9
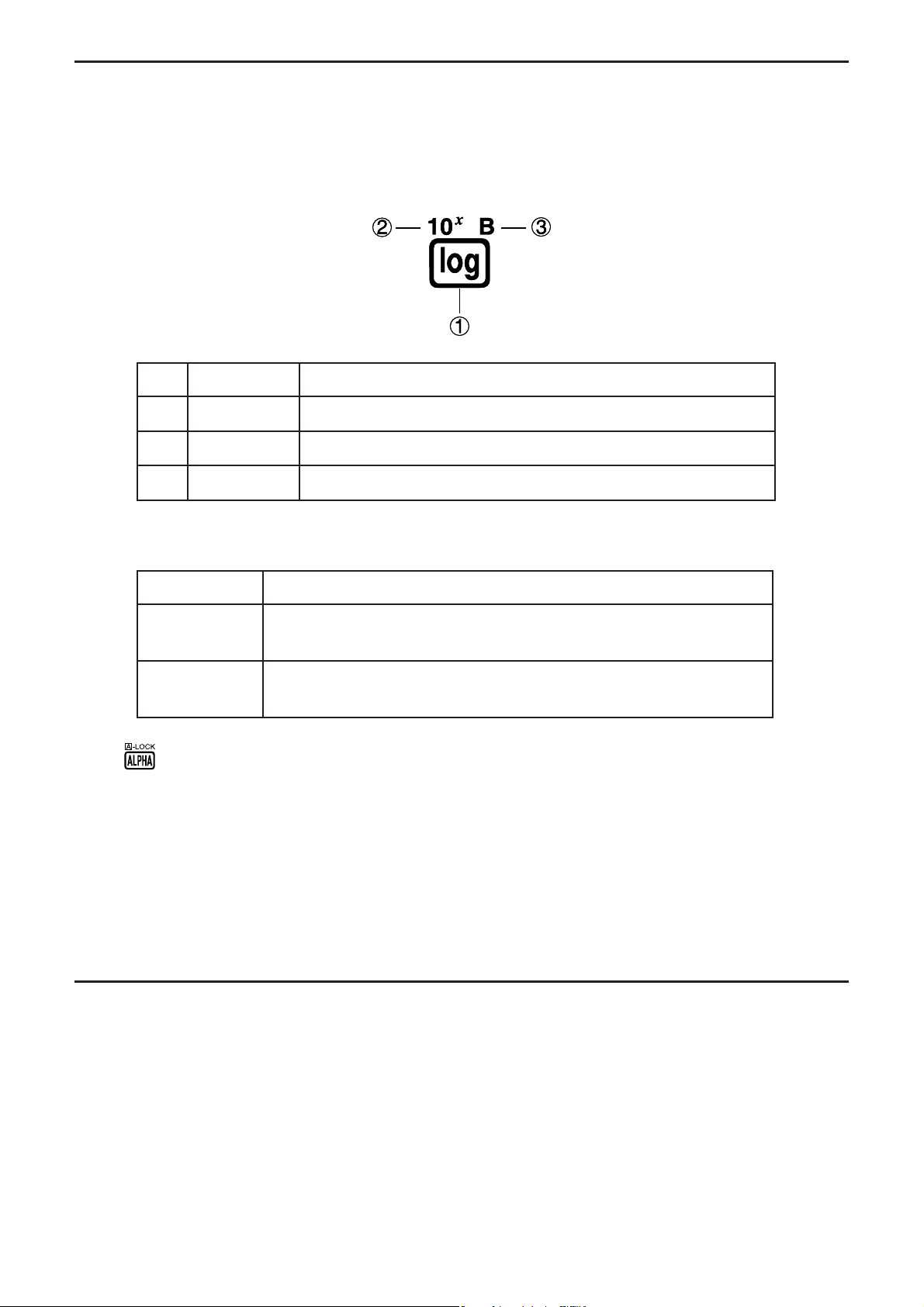
I Marquage des touches
De nombreuses touches de la calculatrice servent à exécuter plus d’une fonction. Les
fonctions marquées sur le clavier sont codées par couleur pour vous aider à trouver
rapidement et aisément celle dont vous avez besoin.
Fonction Touches utilisées
Le codage couleur utilisé pour le marquage des touches est le suivant.
Couleur Touches utilisées
Jaune
Rouge
Verrouillage alpha
•
Normalement, après avoir appuyé sur ? puis sur une touche pour saisir un caractère
alphabétique, le clavier revient immédiatement à ses fonctions primaires.
Si vous appuyez sur puis sur ?, le clavier se verrouillera sur l’entrée alphabétique
jusqu’à ce que vous appuyiez de nouveau sur ?.
log
10
B
x
J
J
?J
Appuyez sur puis sur la touche pour exécuter la fonction
indiquée.
Appuyez sur ? puis sur la touche pour exécuter la fonction
indiquée.
2. Affichage
I Sélection d’une icône
Ce paragraphe décrit comment sélectionner une icône sur le menu principal pour entrer dans
le mode souhaité.
1-2
Page 10
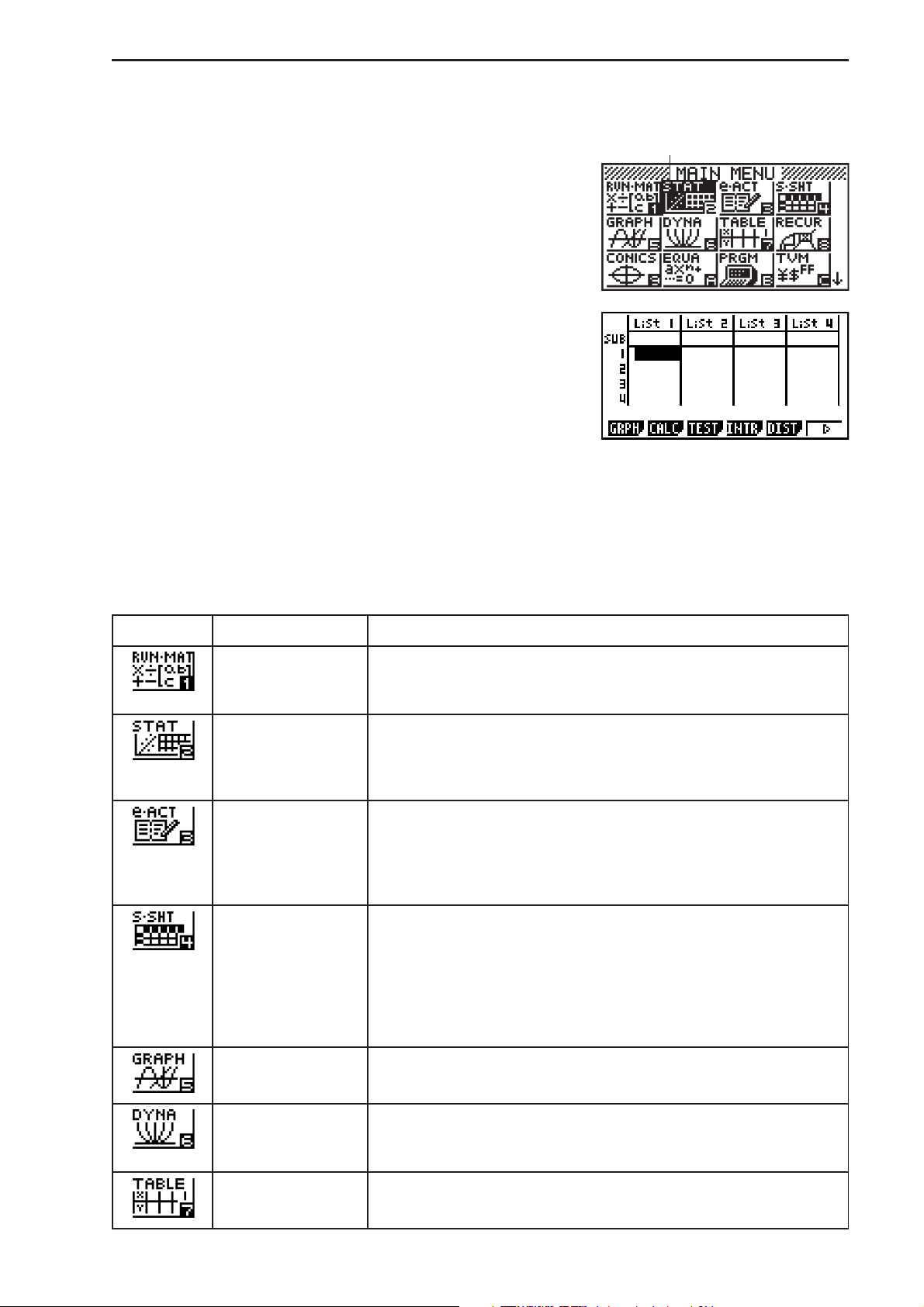
S Pour sélectionner une icône
1. Appuyez sur K pour afficher le menu principal.
2. Utilisez les touches du pavé directionnel (B, C, D,
Icône actuellement sélectionnéeIcône actuellement sélectionnée
A) pour mettre l’icône souhaitée en surbrillance.
3. Appuyez sur U pour afficher l’écran initial du mode
correspondant à l’icône sélectionnée. Ici nous
choisissons le mode STAT.
• Vous pouvez aussi accéder à un mode sans mettre l’icône en surbrillance dans le menu
principal en entrant le nombre ou la lettre indiqué dans le coin inférieur droit de l’icône.
• Utilisez uniquement les procédures décrites ci-dessus pour accéder à un mode. Sinon, vous
vous trouverez dans un mode différent de celui que vous pensiez avoir sélectionné.
La signification de chaque icône est la suivante.
Icône Nom de mode Description
RUN • MAT
(exécution
matrices)
STAT
(statistiques)
e • ACT*
(eActivity)
S • SHT*
(tableur)
·
Utilisez ce mode pour les calculs arithmétiques et les calculs
de fonction, ainsi que pour les calculs impliquant des valeurs
binaires, octales, décimales et hexadécimales et des matrices.
Utilisez ce mode pour effectuer des calculs statistiques à
variable unique (écart-type) ou à variable double (régression),
pour effectuer des tests, analyser des données et pour tracer
des graphes statistiques.
eActivity permet de saisir du texte, des expressions
mathématiques et d’autres données comme sur un portable.
Utilisez ce mode pour sauvegarder du texte ou des formules,
ou les données des applications de la calculatrice sous forme
de fichier.
Utilisez ce mode pour les calculs sur les feuilles de calculs.
Chaque fichier contient une feuille de 26 colonnes et 999
lignes. Dans ce mode vous pouvez non seulement utiliser
les commandes de la calculatrice et les commandes du
mode S • SHT, mais aussi effectuer des calculs statistiques
et représenter des statistiques de la même façon que dans le
mode STAT.
GRAPH
(graphe)
DYNA
(graphe
dynamique)
TABLE Utilisez ce mode pour stocker des fonctions, créer un tableau
Utilisez ce mode pour stocker des fonctions graphiques et pour
tracer des graphes à partir de ces fonctions.
Utilisez ce mode pour stocker des fonctions graphiques et pour
tracer plusieurs graphes en changeant les valeurs affectées
aux paramètres d’une fonction.
de valeurs et tracer le graphe.
1-3
Page 11
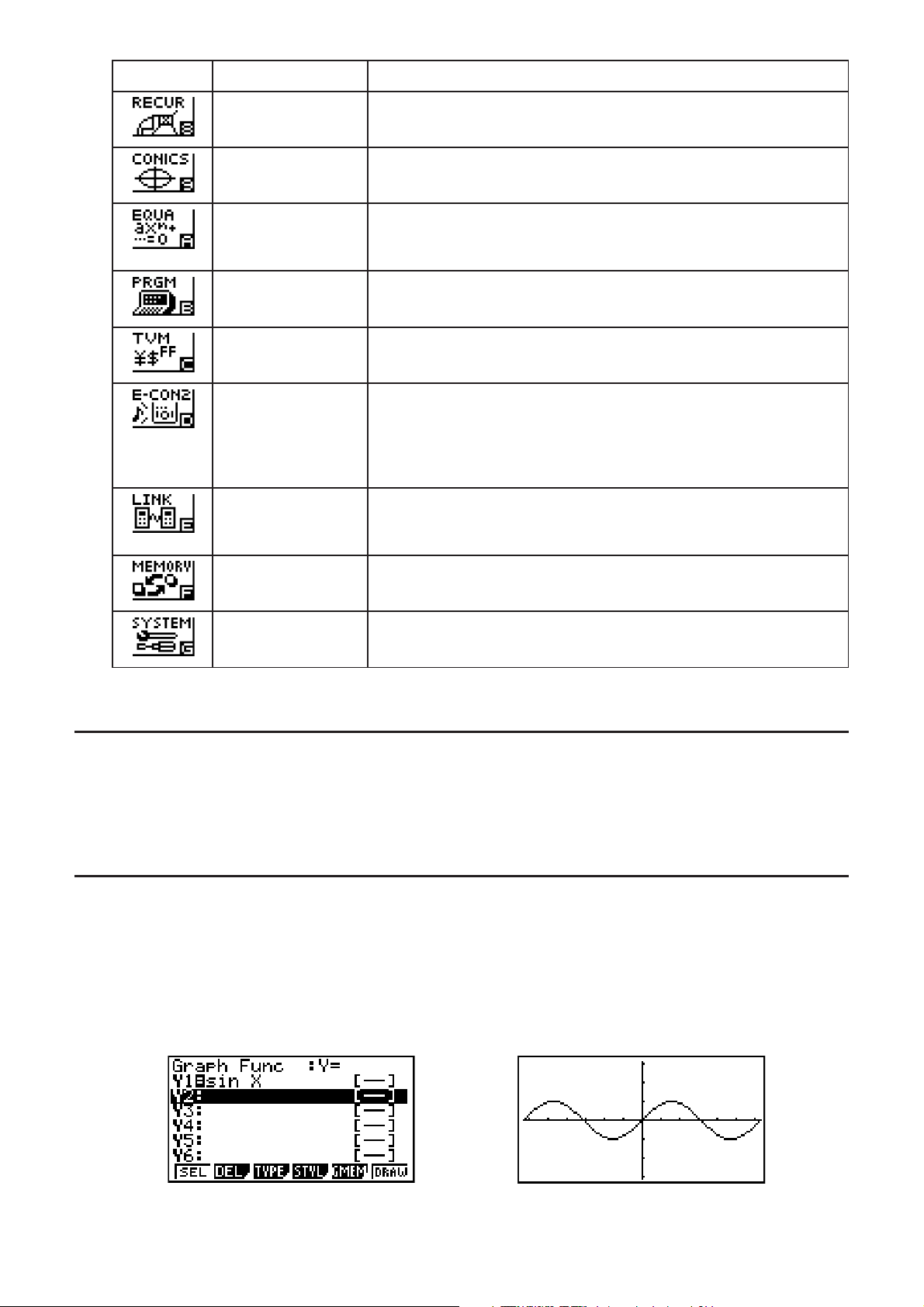
Icône Nom de mode Description
RECUR
(récurrence)
CONICS
(coniques)
EQUA
(équation)
PRGM
(programme)
TVM
(finance)
E-CON2 Utilisez ce mode pour contrôler l’analyseur de données
LINK
(liaison)
Utilisez ce mode pour stocker les formules de récurrence,
créer un tableau de valeurs mumériques et tracer les graphes.
Utilisez ce mode pour tracer des graphes de sections
coniques.
Utilisez ce mode pour résoudre des équations linéaires de
deux à six inconnues et des équations d’ordre supérieur du
ème
2
Utilisez ce mode pour stocker des programmes dans la zone
de programmes et lancer des programmes.
Utilisez ce mode pour effectuer des calculs financiers et tracer
des graphes de cash-flow et d’autres types de graphes.
optionnel EA-200.
Pour plus d’information sur le mode E-CON2, téléchargez
le manuel E-CON2 du site : http://edu.casio.com (version
disponible seulement en anglais).
Utilisez ce mode pour transférer le contenu de la mémoire
ou des données de sauvegarde sur une autre machine ou un
ordinateur.
au 6
ème
degré.
MEMORY
(mémoire)
SYSTEM
(système)
Utilisez ce mode pour travailler sur des données stockées
dans la mémoire.
Utilisez ce mode pour initialiser la mémoire, ajuster le contraste
et effectuer d’autres réglages du système.
* Ne sont pas inclus sur la GRAPH 35+.
I A propos du menu de fonction
Utilisez les touches de fonction ( à ) pour accéder aux menus et commandes dans
la barre de menu au bas de l’écran. Les menus et les commandes se différencient par leur
aspect.
I A propos des écrans
La calculatrice emploie deux types d’écrans : un écran de texte et un écran graphique. L’écran
de texte peut contenir 21 caractères sur une ligne et 8 lignes, y compris la ligne inférieure
utilisée pour le menu de touches de fonction. L’écran graphique utilise une zone de 127 points
(l) × 63 points (h).
Écran de texte Écran graphique
1-4
Page 12
I Affichage normal
La calculatrice affiche normalement des valeurs jusqu’à 10 chiffres de long. Les valeurs qui
dépassent cette limite sont converties automatiquement et affichées en format exponentiel.
S Comment interpréter le format exponentiel
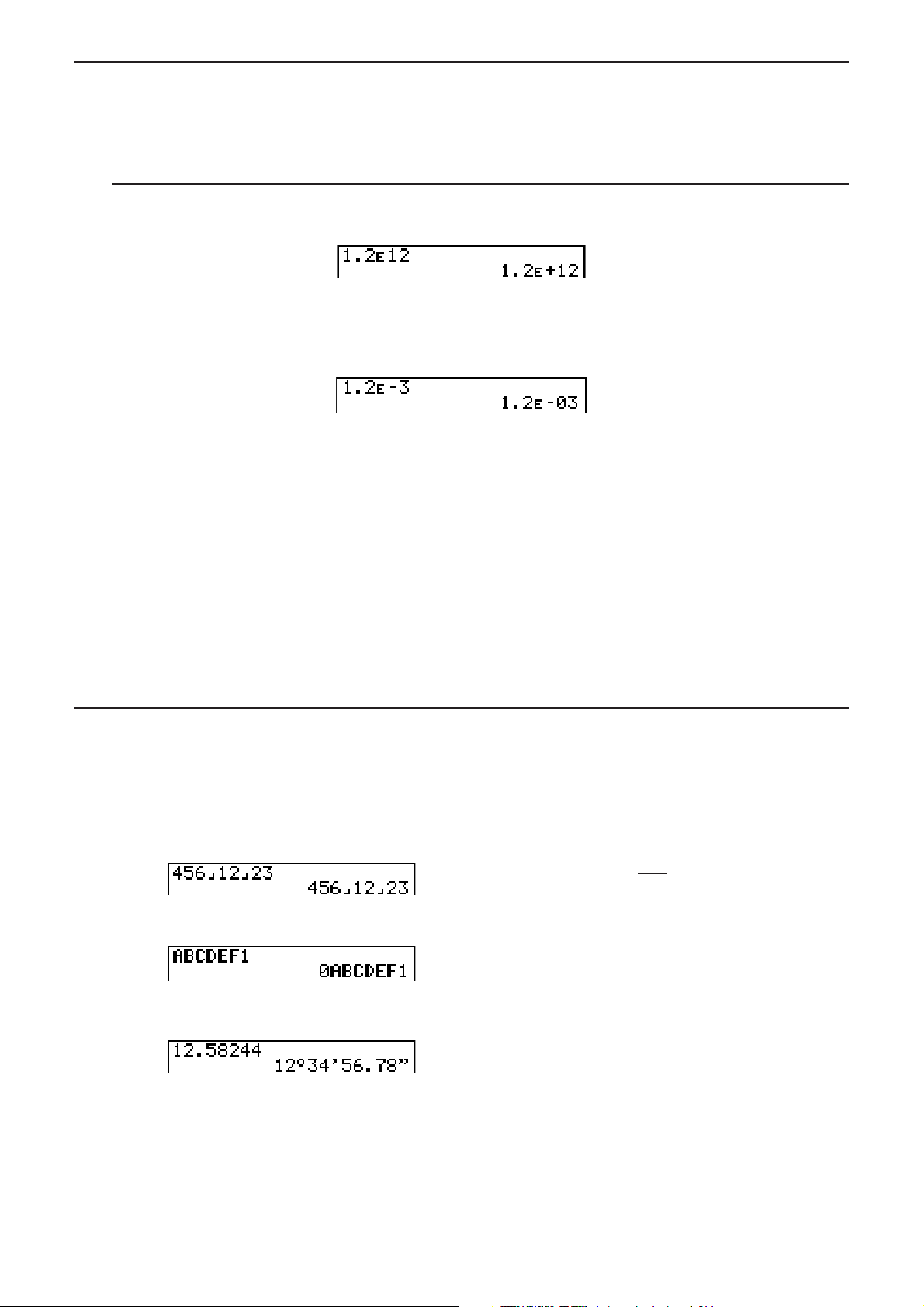
1.2E+12 indique que le résultat est égal à 1,2 × 1012. Cela signifie que vous devez déplacer la
virgule des décimales dans 1,2 de douze rangs vers la droite, puisque l’exposant est positif.
Le résultat est 1.200.000.000.000.
–03 indique que le résultat est égal à 1,2 × 10–3. Cela signifie que vous devez déplacer la
1.2
E
virgule des décimales dans 1,2 de trois rangs vers la gauche, puisque l’exposant est négatif.
Le résultat est 0,0012.
Vous pouvez choisir une des deux plages pour l’affichage automatique normal.
Norm 1 ................... 10
–2
(0,01) > |x|, |x| 10
Norm 2 ................... 10–9 (0,000000001) > |x|, |x| 10
10
10
Tous les exemples de calculs dans ce manuel affichent des résultats avec Norm 1.
Voir page 2-11 pour les détails sur la commutation entre Norm 1 et Norm 2.
I Formats d’affichage spéciaux
Cette calculatrice emploie des formats d’affichage spéciaux pour indiquer les fractions, les
valeurs hexadécimales et les valeurs exprimées en degrés/minutes/secondes.
S Fractions
(10)
12
23
, qui est égal à
(16)
S Valeurs hexadécimales
................... Indique : 456 +
................... Indique : 0ABCDEF1
180150001
S Valeurs en degrés/minutes/secondes
................... Indique : 12° 34’ 56,78”
• Outre ces formats spéciaux, la calculatrice utilise aussi d’autres indicateurs et symboles qui
sont décrits dans chaque paragraphe concerné de ce manuel.
1-5
Page 13

3. Saisie et édition de calculs
I Saisie de calculs
Lorsque vous êtes prêt à saisir un calcul, appuyez d’abord sur la touche pour effacer
l’affichage. Introduisez ensuite vos formules de calcul, exactement comme elles sont écrites,
de gauche à droite et appuyez sur U pour obtenir le résultat.
Exemple 2 + 3 – 4 + 10 =
ABC@?U
I Édition de calculs
Utilisez les touches B et C pour amener le curseur sur la position à changer, puis effectuez
une des opérations décrites ci-dessous. Après avoir édité le calcul, vous pouvez l’exécuter
en appuyant sur U. Vous pouvez aussi utiliser C pour aller à la fin du calcul et continuer à
saisir des données.
• Pour la saisie de données vous pouvez sélectionner soit le mode d’insertion ou le mode
1
surécriture.*
Vous pouvez basculer entre les modes d’insertion et surécriture en effectuant les opérations
suivantes : #(INS). Le curseur a l’aspect « I » pour l’insertion et l’aspect « » pour
surécriture.
1
Le basculement entre insertion et surécriture est possible seulement quand le mode
*
d’écriture linéaire (page 1-27) a été sélectionné préalablement.
Dans ce mode, le texte saisi remplace le texte dans la position du curseur.
S Pour changer un pas
Exemple Changer cos60 en sin60
AE?
BBB
#
Q
S Pour effacer un pas
Exemple Remplacer 369 s s 2 par 369 s 2
BEHA
B#
Dans le mode d’insertion, la touche # sert de touche de retour en arrière.
1-6
Page 14

S Pour insérer un pas
Exemple Remplacer 2,362 par sin2,36
2
ABEV
BBBBB
Q
I Utilisation de la mémoire de répétition
Le dernier calcul est toujours stocké dans la mémoire de répétition. Le contenu de la mémoire
de répétition peut être rappelé par une pression sur B ou C.
Lorsque vous appuyez sur C, le calcul apparaît avec le curseur au début. Une pression
sur B permet de faire apparaître le curseur à la fin du calcul. Vous pouvez effectuer des
changements dans le calcul, puis le réexécuter.
• La mémoire de répétition est activé seulement dans le mode d’écriture linéaire. Dans le
mode d’écriture mathématique, la fonction historique est utilisée à la place de la mémoire de
répétition. Pour plus de détails, voir « Fonction historique » (page 1-17).
Exemple 1 Effectuer les deux calculs suivants
4,12 s 6,4 = 26,368
4,12 s 7,1 = 29,252
C@AECU
BBBB
#(INS)
F@
U
Une fois que vous avez appuyé sur , vous pouvez appuyer sur D ou sur A pour
rappeler des calculs précédents, dans l’ordre, en commençant par le plus récent pour finir par
le plus ancien (Fonction de multi-répétitions). Vous pouvez utiliser C et B pour déplacer le
curseur dans un calcul et faire des changements pour créer un nouveau calcul.
Exemple 2
@ABCDEU
ABCDEFU
D (Un calcul précédent)
D (Deux calculs précédents)
1-7
Page 15
• Un calcul reste sauvegardé dans la mémoire de répétition jusqu’à ce que vous en réalisiez
un nouveau.
• Le contenu de la mémoire de répétition n’est pas effacé lorsque vous appuyez sur la touche
, vous pouvez donc rappeler et exécuter un calcul même après avoir appuyé sur la
touche .
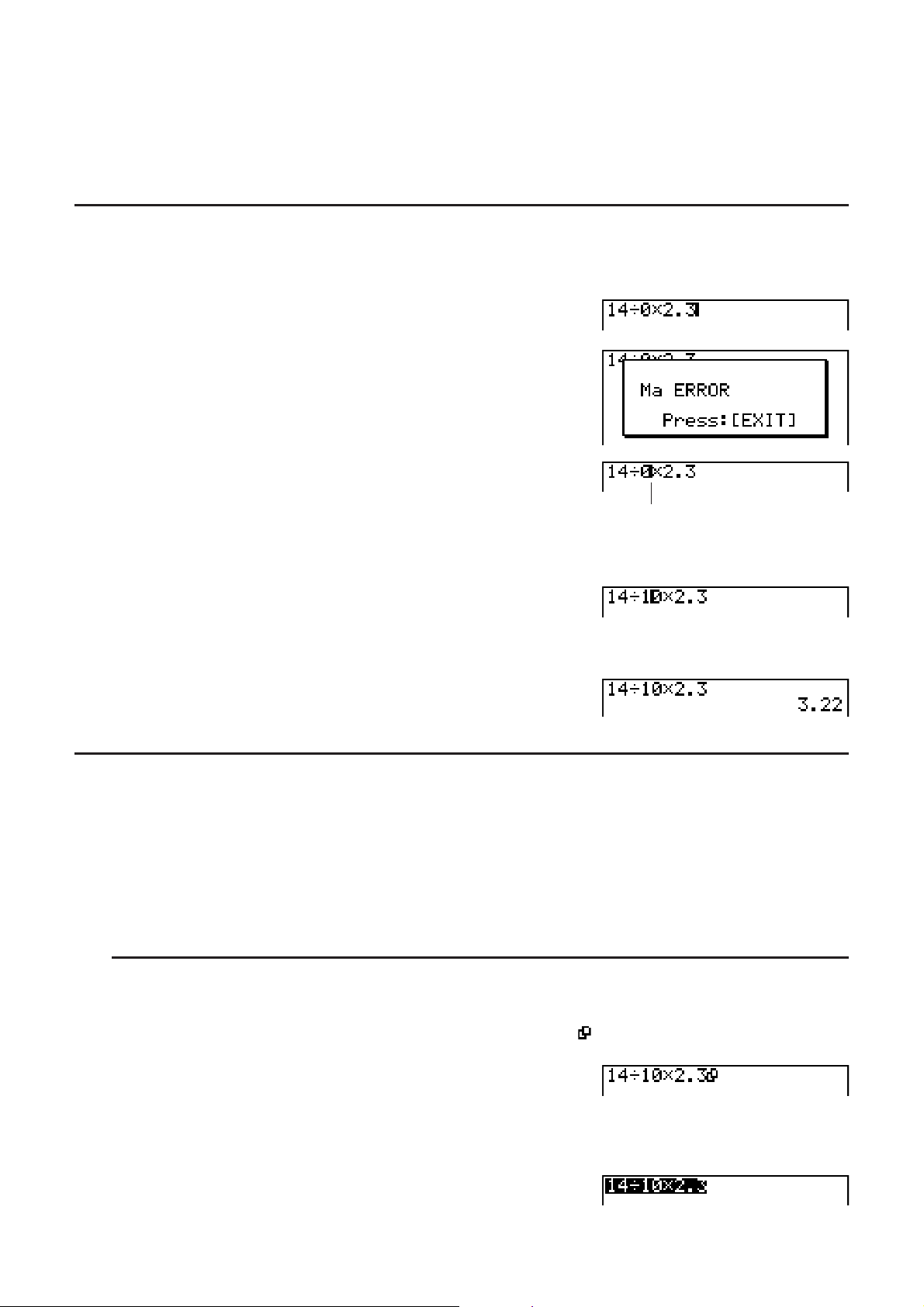
I Pour faire des corrections dans le calcul d’origine
Exemple 14 w 0 s 2,3 tapé par erreur à la place de for 14 w 10 s 2,3
@C?AB
U
Appuyez sur ).
Le curseur se met automatiquement à
l’emplacement de la cause de l’erreur.
Faites les changements nécessaires.
B@
Réexécutez le calcul.
U
I Emploi du presse-papier pour le copier et le coller
Vous pouvez copier (ou couper) une fonction, une commande ou tout autre terme saisi dans
le presse-papier puis collez le contenu du presse-papier à un autre endroit.
• Toutes les procédures décrites ici utilisent le mode d’écriture linéaire. Pour plus de détails
concernant les opérations copier et coller lorsque le mode d’écriture mathématique est
sélectionné, voir « Utilisation du presse-papier pour copier et coller avec le mode d’écriture
mathématique » (page 1-18).
S Pour définir le texte à copier
1. Amenez le curseur (I) au début ou à la fin du texte que vous voulez copier, puis appuyez
sur la touche G(CLIP). Le curseur prend la forme «
».
2. Utilisez les touches du pavé directionnel pour amener le curseur sur le texte et mettre en
surbrillance le texte que vous voulez copier.
1-8
Page 16

3. Appuyez sur (COPY) pour copier le texte en surbrillance dans le presse-papiers, puis
sortez du mode de sélection de texte.
Les caractères sélectionnés ne
disparaissent pas lorsque vous les copiez.
Pour annuler la surbrillance sans copier le texte, appuyez sur la touche ).
S Pour couper le texte
1. Amenez le curseur (I) au début ou à la fin du texte que vous voulez couper, puis appuyez
sur la touche G(CLIP). Le curseur prend la forme « ».
2. Utilisez les touches du pavé directionnel pour amener le curseur sur le texte et mettre en
surbrillance le texte que vous voulez couper.
3. Appuyez sur (CUT) pour couper le texte en surbrillance dans le presse-papiers.
Les caractères coupés disparaissent de
l’écran.
S Collage du texte
Amenez le curseur à l’endroit où vous voulez coller le texte et appuyez sur H(PASTE).
Le contenu du presse-papiers est collé à la position du curseur.
H(PASTE)
I Fonction de catalogue
Le catalogue est une liste alphabétique de toutes les commandes présentes dans la
calculatrice. Vous pouvez saisir une commande en affichant le catalogue et en sélectionnant
cette commande.
S Utilisation du catalogue pour entrer une commande
1. Pour afficher un catalogue alphabétique des commandes, appuyez sur C(CATALOG).
• L’écran qui s’affiche en premier est le dernier ayant été utilisé pour l’entrée de
commandes.
1-9
Page 17

2. Pour afficher la liste de catégories, appuyez sur
(CTGY).
• Si vous le désirez, vous pouvez sauter cette étape
et aller directement à l’étape 5.
3. Pour mettre en surbrillance la catégorie de commande voulue utilisez les touches du pavé
directionnel (D, A) et appuyez ensuite sur (EXE) ou sur U.
• Ceci provoque l’affichage d’une liste de commandes de la catégorie sélectionnée.
4. Saisissez la première lettre de la commande que vous voulez entrer. Ceci provoquera
l’affichage de la première commande qui commence par cette lettre.
5. Pour mettre en surbrillance la commande que vous voulez entrer, utilisez les touches du
pavé directionnel (D, A) et appuyez ensuite sur (INPUT) ou sur U.
Exemple Utiliser le catalogue pour saisir la commande ClrGraph
C(CATALOG)((C)A~AU
Le catalogue se ferme par une pression sur ) ou )(QUIT).
4. Utilisation du mode d’écriture mathématique
La sélection de « Math » pour le paramètre du mode d’écriture « Input/Output » dans l’écran
de configuration (page 1-27) active le mode d’écriture mathématique. Ce mode de entrée/
sortie permet la saisie et l’affichage naturel de certaines fonctions, telles qu’elles sont écrites
dans votre manuel scolaire.
• Les opérations de cette section s’effectuent toutes dans le mode d’écriture mathématique.
- Le paramétrage initial par défaut de la GRAPH 95/GRAPH 75/GPRAH 35+ est le mode
d’écriture mathématique. Si vous avez basculé vers le mode d’écriture linéaire, revenez
sur le mode d’écriture mathématique avant d’effectuer les opérations de cette section.
Pour plus d’information sur le changement de modes, voir « Utilisation de l’écran de
configuration » (page 1-27).
- Le paramètre initial par défaut de la GRAPH 85 SD/GRAPH 85 est le mode d’écriture
lineaire. Avant d’effectuer les opérations de cette section, basculez vers le mode d’écriture
mathématique. Pour plus d’information sur le basculement entre les modes d’écriture,
consultez « Utilisation de l’écran de configuration » (page 1-27).
• Dans le mode d’écriture mathématique, toute saisie se fait en mode d’insertion (et pas en
mode d’écrasement). Notez que l’opération de touches #(INS) (page 1-6) que vous
utilisez en mode d’écriture linéaire afin de basculer vers le mode d’insertion, en mode
d’écriture mathématique elle réalise une fonction complètement différente. Pour obtenir plus
d’information, voir « Utilisation de valeurs et d’expressions comme arguments » (page 1-14).
• Sauf indication en contraire, toutes les opérations de cette section s’effectuent dans le mode
RUN • MAT.
1-10
Page 18
I Saisie d’opérations dans le mode d’écriture mathématique
S Fonctions et symboles utilisés dans le mode d’écriture mathématique
Les fonctions et symboles figurant dans la liste suivante peuvent être utilisés pour l’écriture
naturelle dans le mode d’écriture mathématique. La colonne « Octets » indique le nombre
d’octets utilisés dans la mémoire pour la saisie dans le mode d’écriture mathématique.
Fonction/Symbole Touches utilisées Octets
Fraction en notation française
Fraction en notation anglo-saxonne*
Puissance
Carré
Puissance négative (Réciproque)
Racine cubique
Racine de puissance
x
e
x
10
Logarithme de base
a
1
()
,
V
(
–1
x
)
V()
3
(
)
,(x)
((ex)
J(10x)
(Saisie par le menu MATH*2)7
Abs (Valeur absolue) (Saisie par le menu MATH*
Différentielle linéaire*
Différentielle quadratique*
Intégrale*
Calcul de 3*
3
4
3
3
(Saisie par le menu MATH*2)7
(Saisie par le menu MATH*2)7
(Saisie par le menu MATH*2)8
(Saisie par le menu MATH*2)11
Matrice (Saisie par le menu MATH*
9
14
4
4
5
6
9
9
6
6
2
)6
2
) 14*
5
Parenthèses
Accolades (utilisées lors de la saisie de
listes)
Crochets (utilisées lors de la saisie de
matrices)
1
Les fractions en notations anglo-saxonne ne sont possibles que dans le mode d’écriture
*
et
( { ) et ( } )
( [ ) et ( ] )
1
1
1
mathématique.
2
Pour le détail sur la saisie de fonctions par le menu de fonctions MATH, reportez-vous à
*
« Utilisation du menu MATH » indiqué ci-dessous.
3
La tolérance ne peut pas être spécifiée dans le mode d’écriture mathématique. Si vous
*
voulez la spécifier, utilisez le mode d’écriture linéaire.
4
Pour le calcul de 3 dans le mode d’écriture mathématique, l’incrément est toujours 1. Si
*
vous voulez utiliser un autre incrément, utilisez le mode d’écriture linéaire.
5
C’est le nombre d’octets pour une matrice de 2 s 2.
*
1-11
Page 19

S Utilisation du menu MATH
x
Dans le mode RUN
Vous pouvez utiliser ce menu pour l’écriture naturelle de matrices, de différentielles,
d’intégrales, etc.
• {MAT} ... {affiche le sous-menu MAT, pour l’écriture naturelle des matrices suivantes}
• {2s2} ... {saisit une matrice de 2 s 2}
• {3s3} ... {saisit une matrice 3 s 3}
msn} ... {saisit une matrice de m lignes et n colonnes (6 s 6 au maximum)}
• {
•
MAT, le menu MATH suivant s’affiche par une pression de (MATH).
• {log
• {Abs} ... {permet l’écriture naturelle d’une valeur absolue |X|}
• {
• {
• {°
• {3(} … {permet l’écriture naturelle du calcul de
b} ... {permet l’écriture naturelle d’un logarithme en base a}
a
d/dx} ... {permet l’écriture naturelle d’une différentielle linéaire
2
d
/dx2} ... {permet l’écriture naturelle d’une différentielle quadratique
B
3
=A
b
f(x)dx
a
}
f(x
)
A
dx} … {permet l’écriture naturelle d’une intégrale
dx
}
d
(x)
f
x
=
a
}
2
d
f(x
)
x
=
a
dx
2
}
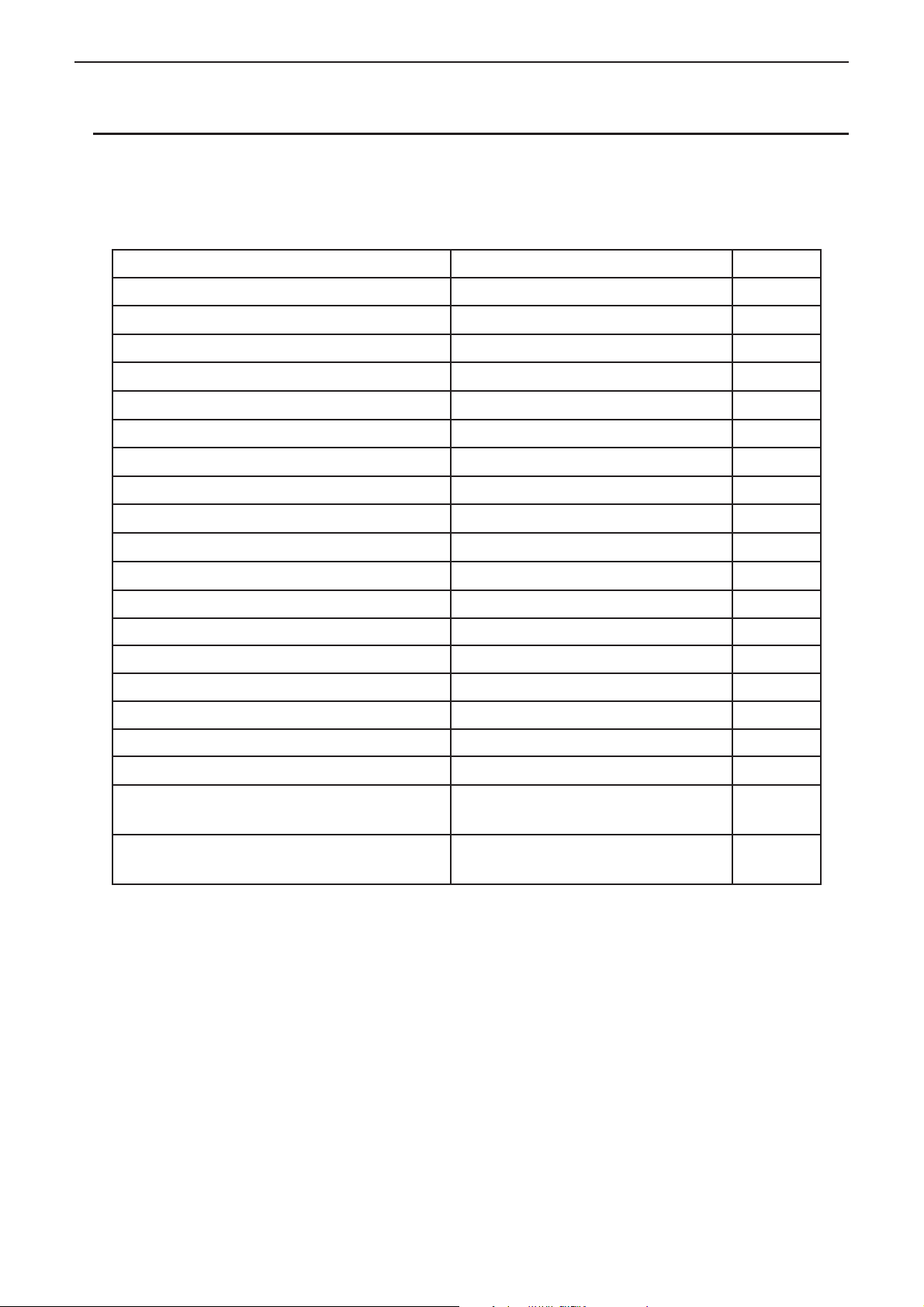
S Exemples de saisie dans le mode d’écriture mathématique
Les exemples suivants montrent comment utiliser le menu de fonctions MATH et les autres
touches lors de l’écriture naturelle dans le mode d’écriture mathématique. Faites bien attention
à la position du curseur lorsque vous saisissez des valeurs et des données.
3
Exemple 1 Ecrire 2
A,
+ 1
B
C
@
U
Exemple 2 Ecrire
@
1+
(
2
2
)
5
1-12
Page 20
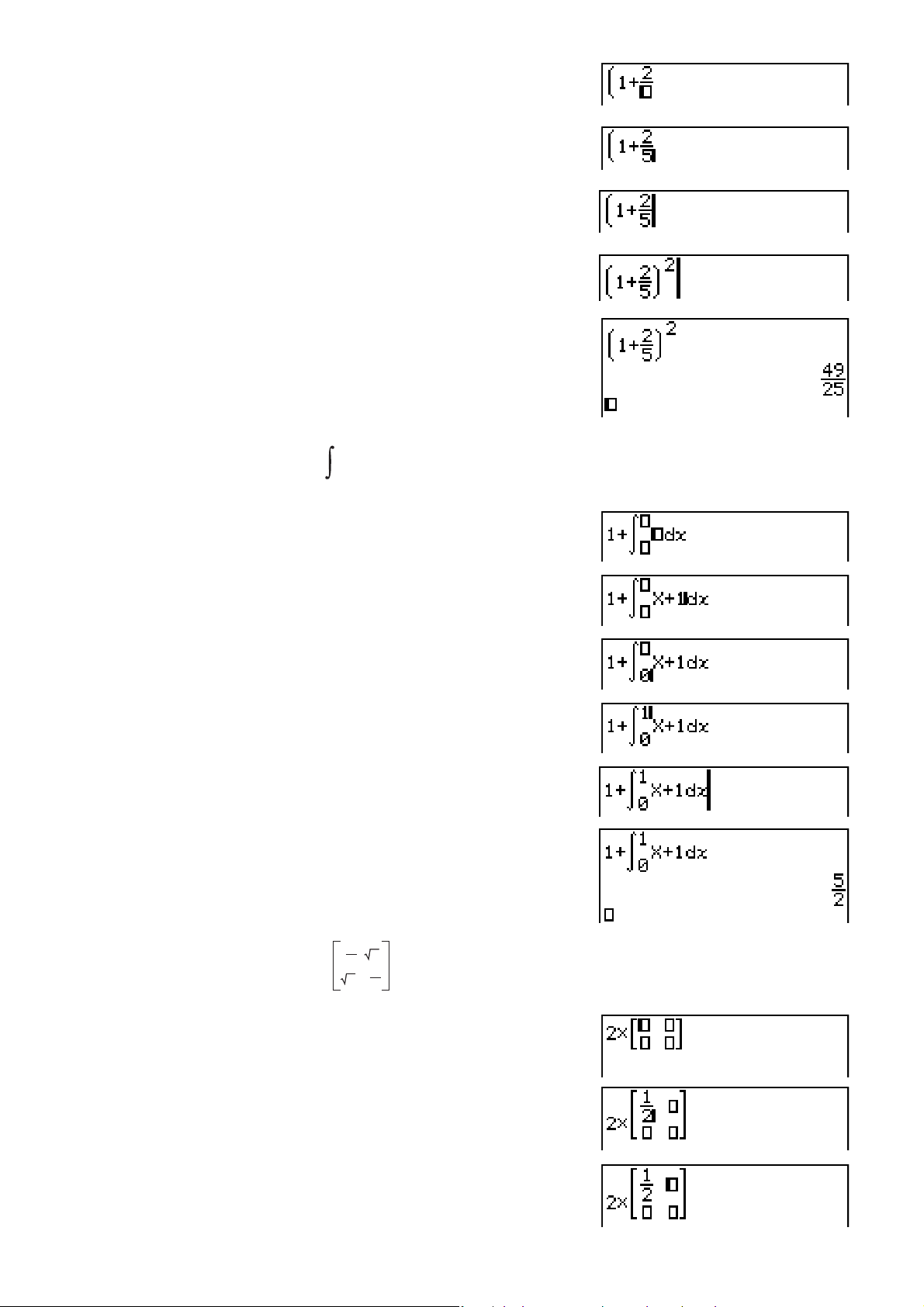
AA
D
C
V
U
Exemple 3 Ecrire
1
1+ x + 1dx
0
@(MATH)(E)(
T@
C?
D@
C
U
1
2
Exemple 4 Ecrire
2 ×
2
1
2
2
°
dx
)
A(MATH)(MAT)(2×2)
@AA
CC
1-13
Page 21
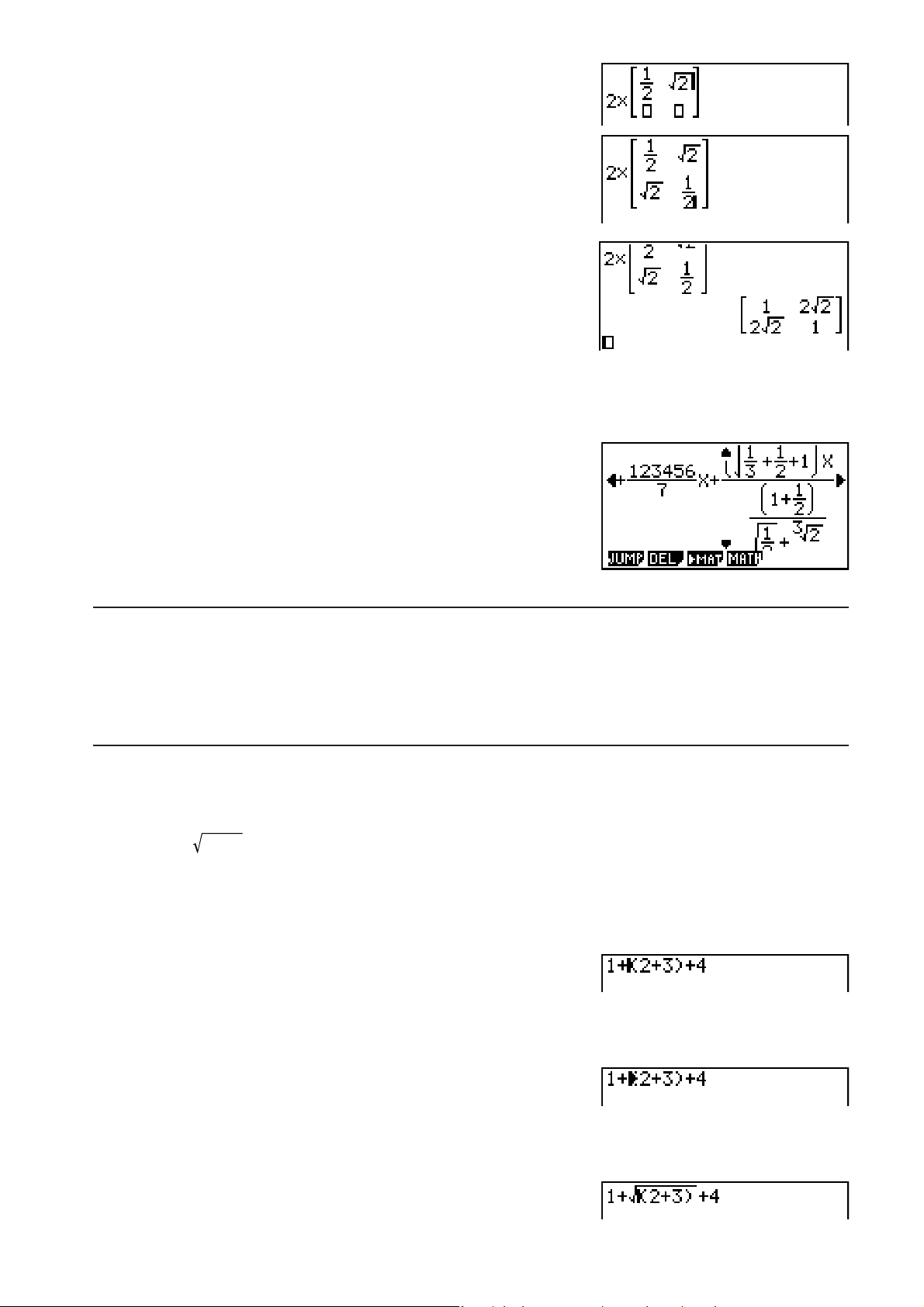
V()AC
CV()ACC@AA
U
S Si le calcul est trop long pour s’afficher complètement dans la fenêtre
d’affichage
Une flèche apparaît à la gauche, à la droite, au haut
ou au bas de l’affichage pour indiquer que le calcul
continue dans le sens indiqué.
Lorsqu’une flèche apparaît, vous pouvez utiliser les
touches du pavé directionnel pour faire défile le contenu
de l’écran et voir les autres termes du calcul.
S Restrictions de saisie dans le mode d’écriture mathématique
Avec certains types d’expressions la hauteur d’une formule peut être supérieure à la ligne
d’affichage. La hauteur d’une formule ne doit pas être supérieure à deux écrans d’affichage
(120 points). Il n’est pas possible de saisir une expression qui dépasse cette limite.
S Utilisation de valeurs et d’expressions comme arguments
Une valeur ou une expression déjà saisie peut être utilisée comme argument d’une fonction.
Après avoir saisi, par exemple, « (2+3) », vous pouvez le faire devenir l’argument de , avec
le résultat
Exemple
1. Déplacez le curseur pour le placer juste à la gauche de la partie de l’expression qui doit
devenir l’argument de la fonction que vous voulez insérer.
(2+3)
.
2. Appuyez sur #(INS).
• Le curseur prend la forme du curseur d’insertion ().
3. Appuyez sur V() pour insérer la fonction .
• La fonction est insérée et l’expression entre parenthèses devient l’argument.
1-14
Page 22

Tel que montré ci-dessus, après l’appui sur #(INS), la valeur ou expression à droite du
curseur devient l’argument de la fonction spécifiée immédiatement après. La plage comprise
comme argument correspond à tout ce qui se trouve à la droite du curseur jusqu’à la première
parenthèse ouvrante, s’il y en a une, ou jusqu’à la première fonction (sin(30), log2(4), etc.).
Cette possibilité peut s’utiliser avec les fonctions suivantes :
Fonction Touches utilisées
Fraction en notation
française
Puissance
Racine cubique
Racine de puissance
x
e
x
10
Logarithme de base a
Valeur absolue
Différentielle linéaire
Différentielle
quadratique
Intégrale
Calcul de 3
,
V()
3
(
,(
)
x
)
((ex)
J(10x)
(MATH)(logab)
(MATH)(Abs)
(MATH)(
(MATH)(
d/dx)
2
d
/dx2)
(MATH)(E)
(°
dx)
(MATH)(E)
(3( )
Expression
originale
Expression après
l’insertion
• Dans le mode d’écriture linéaire, il faut appuyer sur #(INS) pour passer au mode
d’insertion. Voir page 1-6 pour le détail.
S Édition de calculs dans le mode d’écriture mathématique
L’édition de calculs dans le mode d’écriture mathématique s’effectue en principe de la même
façon que dans le mode d’écriture linéaire. Pour le détail, reportez-vous à « Édition de
calculs » (page 1-6).
Notez toutefois les différences suivantes entre le mode d’écriture mathématique et le mode
d’écriture linéaire.
• La saisie en mode d’écrasement, disponible dans le mode d’écriture linéaire n’est pas
disponible dans le mode d’écriture mathématique. Dans ce mode, les termes écrits
s’insèrent toujours à la position du curseur.
• Dans le mode d’écriture mathématique, la touche # sert toujours à faire un retour en
arrière.
• Vous pouvez déplacer le curseur de la façon suivante lors de la saisie de calculs sous mode
d’écriture mathématique.
Pour faire ceci :
Faire revenir le curseur au début du calcul lorsqu’il est à la fin
Faire passer le curseur à la fin du calcul lorsqu’il est au début
Appuyez sur cette touche :
C
B
1-15
Page 23
I Utilisation des opérations UNDO pour défaire et refaire
Lors de la saisie d’expressions de calcul en mode d’écriture mathématique, vous pouvez
utiliser les procédures suivantes (jusqu’à ce que vous appuyez sur la touche U) pour défaire
la dernière opération de touche et pour refaire l’opération de touche que vous venez de
réaliser.
- Pour défaire la dernière opération de touche, appuyez sur: ?#(UNDO).
- Pour refaire une opération de touche que vous venez de défaire, appuyez encore sur :
?#(UNDO).
• Vous pouvez utiliser UNDO pour annuler une opération de touche . Après avoir appuyé
sur pour effacer une expression que vous venez d’entrer, l’appui sur ?#(UNDO)
restaure ce qui se trouvait sur l’écran avant d’appuyer sur .
• Vous pouvez utiliser aussi UNDO pour annuler une opération de touche du pavé
directionnel. Si vous appuyez sur C pendant la saisie et puis vous appuyez sur ?#
(UNDO), le curseur retourne à la position où il se trouvait avant d’appuyer sur C.
• L’opération UNDO est désactivée lorsque le clavier est verrouillé en alpha-locked. L’appui
sur ?#(UNDO) lorsque le clavier est verrouillé en alpha-locked effectue la même
opération d’effacement que la touche # seule.
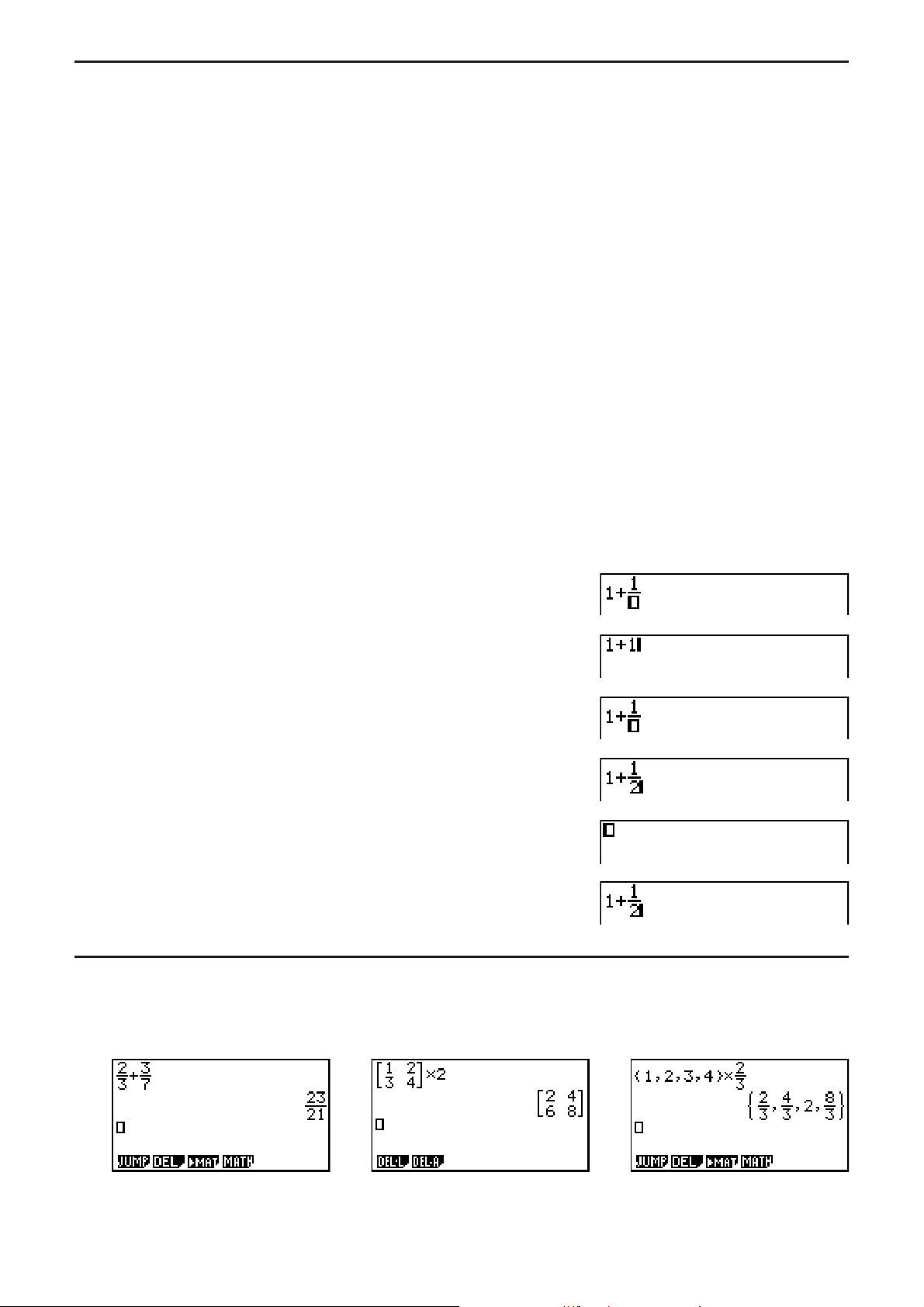
Exemple
@@C
#
?#(UNDO)
A
?#(UNDO)
I Affichage des résultats de calculs en mode d’écriture mathématique
Les fractions, les matrices et les listes produites lors de calculs en mode d’écriture
mathématique s’affichent sous forme naturelle, telles qu’elles apparaissent dans les livres.
Exemples d’affichage de résultats de calculs
1-16
Page 24

• Les fractions s’affichent soit en notation française soit en notation anglo-saxonne, selon le
réglage effectué pour « Frac Result » sur l’écran de configuration. Pour le détail, reportezvous à « Utilisation de l’écran de configuration » (page 1-27).
• Les matrices apparaissent sous forme naturelle, jusqu’à 6 s 6. Une matrice de plus de six
lignes fois six colonnes s’affichera sur l’écran MatAns, c’est-à-dire sur le même écran que
celui qui est utilisé dans le mode d’écriture linéaire.
• Les listes s’affichent sous forme naturelle jusqu’à 20 éléments. Une liste de plus de 20
éléments s’affichera sur l’écran ListAns, c’est-à-dire sur le même écran que celui qui est
utilisé dans le mode d’écriture linéaire.
• Des flèches apparaissent à la gauche, à la droite, au haut et au bas de l’affichage pour vous
indiquer qu’il existe d’autres données sur l’écran dans le sens indiqué.
Vous pouvez utiliser les touches du pavé directionnel pour faire défiler l’écran et voir les
données souhaitées.
• Le résultat d’un calcul et le calcul s’effacent par une pression de (DEL)(DEL
lorsqu’un résultat est sélectionné.
• Le signe de multiplication ne peut pas être omis tout de suite devant une fraction en notation
anglo-saxonne ou française. Dans ce cas, mettez toujours un signe de multiplication.
2
2 ×
Exemple :
5
AAD
–1
x
• L’opération avec les touches ,, V, ou (
d’une autre opération avec les mêmes touches ,, V, ou (
) ne peut pas être suivie immédiatement
–1
x
). Dans ce cas,
utilisez des parenthèses pour séparer ces deux opérations.
2)–1
Exemple : (3
BV(x–1)
I Fonction historique
La fonction historique permet de conserver les expressions de calculs et leurs résultats en
mode d’écriture mathématique. Plus de 30 expressions peuvent être mémorisées avec leurs
résultats.
@AU
•
L)
AU
Les expressions de calculs enregistrées dans l’historique peuvent être modifiées et
recalculées. Toutes les expressions suivant l’expression qui a été modifiée seront alors
recalculées.
1-17
Page 25

Exemple Remplacer « 1+2 » par « 1+3 » et recalculer l’expression.
Effectuez les opérations suivantes pour l’exemple précédent.
DDDDB#BU
• La valeur enregistrée dans la mémoire de dernier résultat dépend toujours du résultat
obtenu lors du dernier calcul. Si le contenu de l’historique comprend des opérations utilisant
la mémoire de dernier résultat, la modification d’un calcul peut se répercuter sur la valeur
enregistrée dans la mémoire de dernier résultat et sur les calculs suivants.
- Si une série de calculs utilise la mémoire de dernier résultat pour inclure le résultat du
dernier calcul dans le calcul suivant, le changement d’un calcul aura une influence sur les
résultats de tous les calculs suivants.
- Lorsque le premier calcul de l’historique comprend des éléments de la mémoire de dernier
résultat, la valeur de la mémoire de dernier résultat est « 0 » parce qu’il n’y a pas de calcul
avant le premier de l’historique.
I Utilisation du presse-papier pour copier et coller avec le mode
d’écriture mathématique
Vous pouvez copier une fonction, une commande ou autre saisie vers le presse-papier et
coller ensuite le contenu du presse-papier à un autre endroit.
• Dans le mode d’écriture mathématique, vous ne pouvez spécifier qu’une seule ligne comme
plage pour la copie.
• L’opération CUT n’est supportée que par le mode d’écriture linéaire. Elle n’est pas supportée
par le mode d’écriture mathématique.
S Pour copier du texte
1. Utilisez les touches du pavé directionnel pour positionner le curseur sur la ligne que vous
voulez copier.
2. Appuyez sur G(CLIP). Le curseur changera à «
•
3. Appuyez sur (CPY
L) pour copier le texte mis en surbrillance vers le presse-papier.
S Pour coller du texte
Déplacez le curseur à la position où vous voulez coller le texte et appuyez ensuite sur
H(PASTE). Le contenu du presse-papier est collé à la position du curseur.
».
I Opérations de calcul dans le mode d’écriture mathématique
Cette section présente des exemples de calcul en mode d’écriture mathématique.
• Pour plus de détails sur les opérations de calcul, voir « Chapitre 2 Calculs manuels ».
1-18
Page 26

S Réalisation de calculs de fonctions avec le mode d’écriture mathématique
i
Exemple Opération
3
=
4×5610
645U
cos
( )
3
log
8 = 3
2
7
123 = 1,988647795
2 + 3 ×
3
4
2
+ 3 =
5
1,5 + 2,3
d
3
x
( )
dx
5
2
2
+ 3x + 4
x
1
1
(Angle: Rad)
=
2
3
64 − 4 = 10
= 0,1249387366log
1
73
4
20
3
=
i
2
2
+ 4
+ x − 6
x
+
dx
23
10
x = 3
=
= 52
404
3
A
(MATH)(logab) 2C8U
,(
23,(
(MATH)(Abs)J34U
25C3()1C4U
1.52.3?(
(MATH)(d/dx)T,3C4
TVT6C3U
(MATH)(E)(°dx) 2TV3T4C1
C5U
9(P)3CU
x
) 7C123U
x
) 3C64C4U
i)U,
6
2
− 3k + 5) = 55
k
(
∑
k
=2
(MATH)(E)(3)?(K)V3?(K)
5C?(K)C2C6U
I Exécution de calculs de matrices en utilisant l’écriture naturelle
S Pour spécifier les dimensions (la taille) d’une matrice
1. Dans le mode RUN
2. Appuyez sur (MATH) pour afficher le menu MATH.
3. Appuyez sur (MAT) pour afficher le menu suivant.
• {2s2} … {saisit une matrice 2 s 2}
• {3s3} … {saisit une matrice 3 s 3}
msn} … {saisit une matrice de m lignes s n colonnes (jusqu’à 6 s 6)}
• {
Exemple Créer une matrice de 2 lignes s 3 colonnes
•
MAT, appuyez sur K(SET UP)(Math)).
(
Spécifiez le nombre de lignes.
AU
msn)
1-19
Page 27
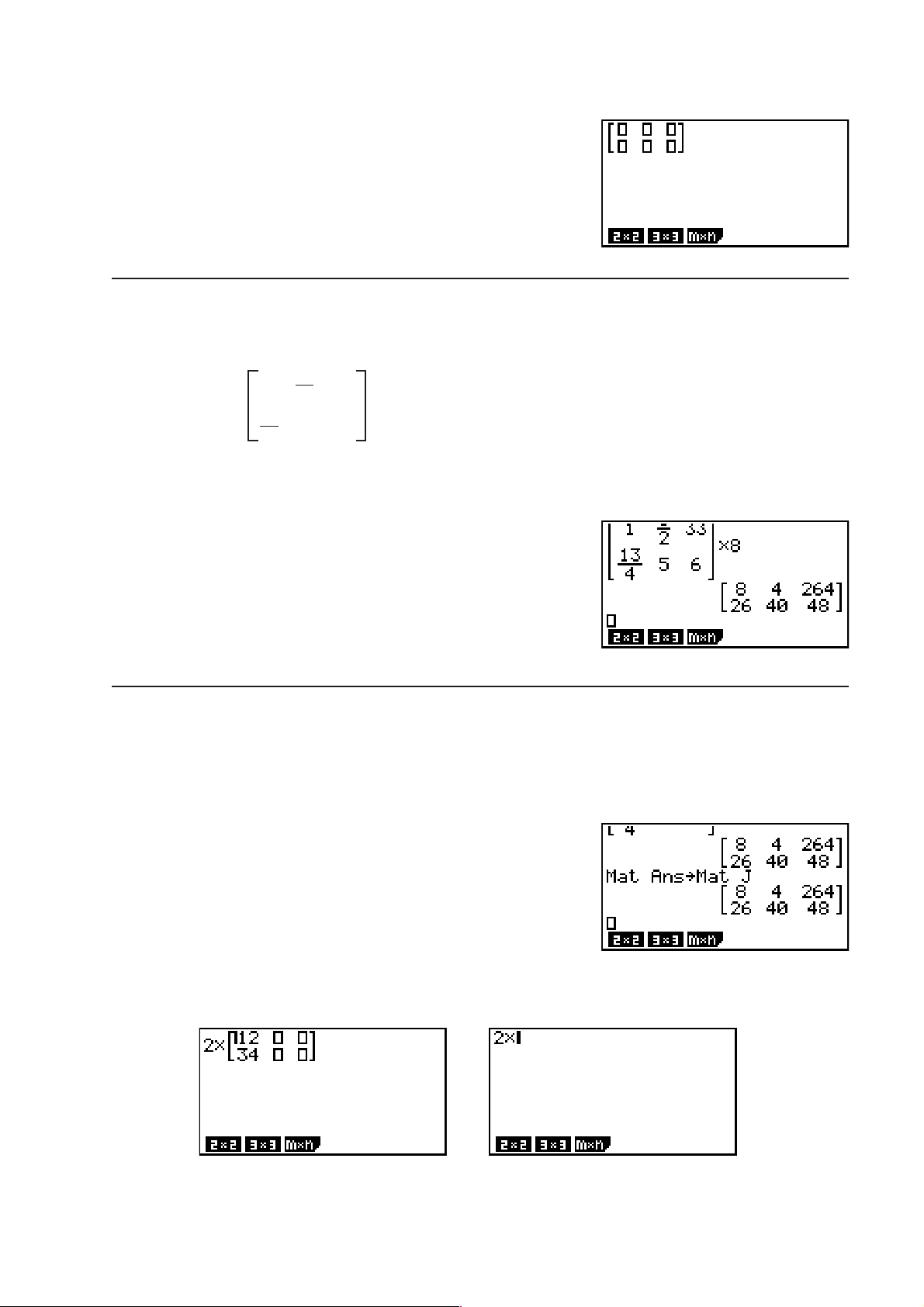
Spécifiez le nombre de colonnes.
BU
U
S Pour saisir les valeurs des cellules
Exemple Effectuer le calcul suivant
1
1
1
1
13
13
4
4
L’opération suivante est la suite du calcul cité en exemple à la page précédente.
33
33
2
2
× 8
× 8
65
65
@C@ACCBBC
@BCCCD
CECGU
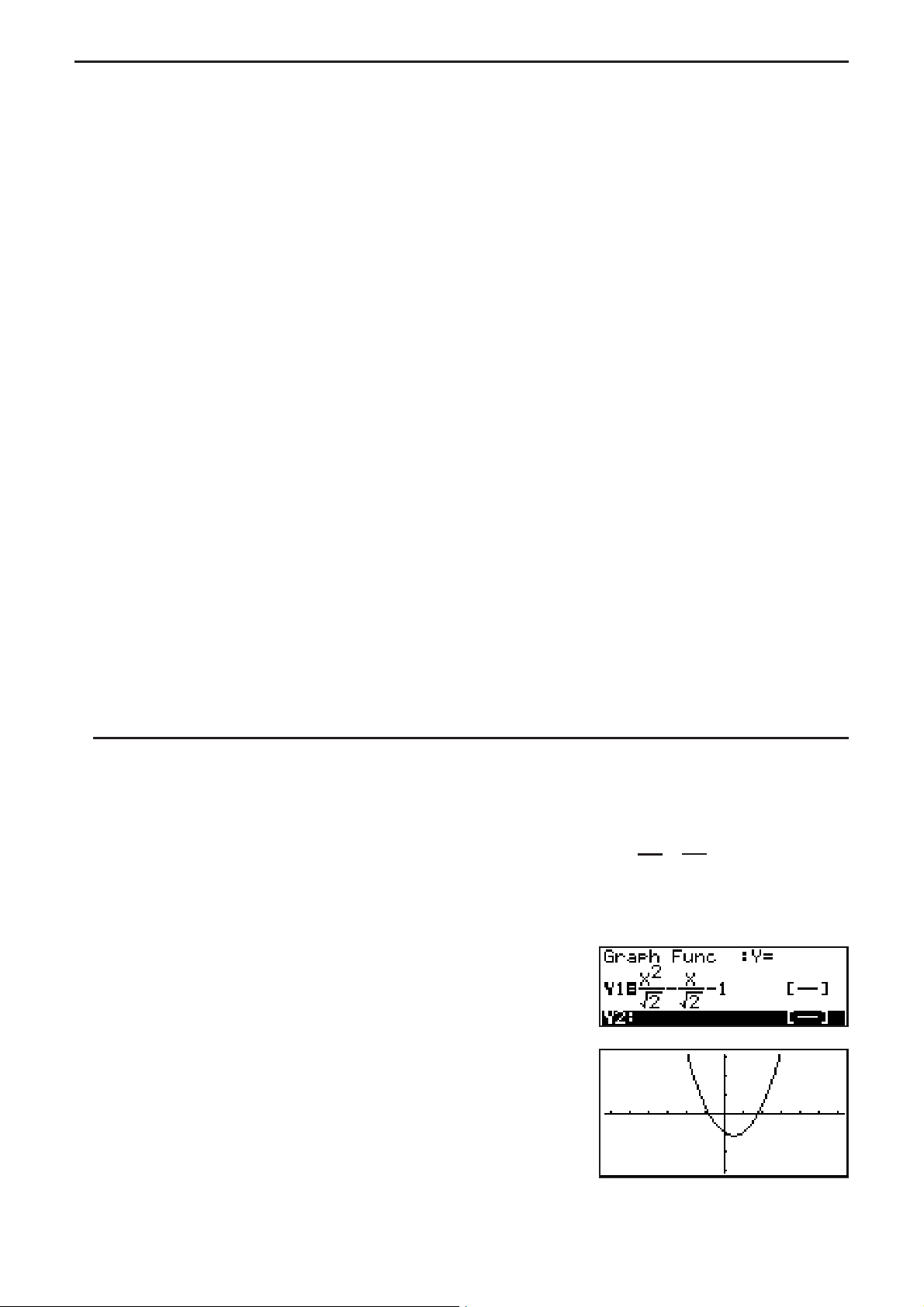
S Pour affecter une matrice créée à l’aide de l’écriture naturelle à une matrice
du mode MAT
Exemple Affecter le résultat du calcul à la matrice J
A(Mat)(Ans)?
A(Mat)?(J)U
• La matrice complète se supprime par une pression sur la touche # lorsque le curseur est
dans la partie supérieure (en haut à gauche) de la matrice.
#
1-20
Page 28
I Utilisation de mode GRAPH et du mode EQUA avec le mode d’écriture
mathématique
L’utilisation du mode d’écriture mathématique avec tous les modes indiqués ci-dessous vous
permet la saisie d’expressions telles qu’elles sont écrites dans votre manuel scolaire, ainsi
que la visualisation des résultats des calculs dans format d’affichage naturel.
Modes que supportent la saisie d’expressions telle qu’elles sont écrites dans les manuels
scolaires :
RUN • MAT, e • ACT, GRAPH, DYNA, TABLE, RECUR, EQUA (SOLV)
Modes qui supportent le format d’affichage naturel :
RUN • MAT, e • ACT, EQUA
Les expressions suivantes montrent des opérations en mode d’écriture mathématique dans
les modes GRAPH, DYNA, TABLE, RECUR et EQUA, ainsi que l’affichage naturel de
résultats de calculs dans le mode EQUA.
• Pour plus de détails sur cette opération, voir la section dédiée à chaque calcul.
• Pour plus de détails sur les opérations de saisie et sur les affichages de résultats de calculs
dans le mode RUN • MAT en mode d’écriture mathématique, voir « Saisie d’opérations dans
le mode d’écriture mathématique » (page 1-11) et « Opérations de calcul dans le mode
d’écriture mathématique » (page 1-18).
Les opérations de saisie et d’affichage des résultats du mode e • ACTsont les mêmes que
ceux du mode RUN • MAT. Pour plus d’information sur les opérations du mode e • ACT,
consultez « Chapitre 10 L’eActivity ».
Important !
• Sur un modèle dont le système d’exploitation a été mis à jour avec l’OS 2.00 à partir d’une
version plus ancienne, la saisie et l’affichage de résultats en mode d’écriture mathématique
ne sont pas supportés dans aucun mode, à l’exception des modes RUN • MAT et e • ACT.
S Mode d’écriture mathématique dans le mode GRAPH
Vous pouvez utiliser le mode d’écriture mathématique pour saisir des expressions de graphe
dans les modes GRAPH, DYNA, TABLE et RECUR.
2
Exemple 1 Dans le mode GRAPH, saisissez la fonction
tracez son graphe.
Assurez-vous que les paramètres initiaux par défaut sont configurés
sur la fenêtre d’affichage.
KGRAPHTVV()A\
CCTV()ACC\
x
=
y
'
x
−−1
2
2
'
et puis
@U
(DRAW)
1-21
Page 29
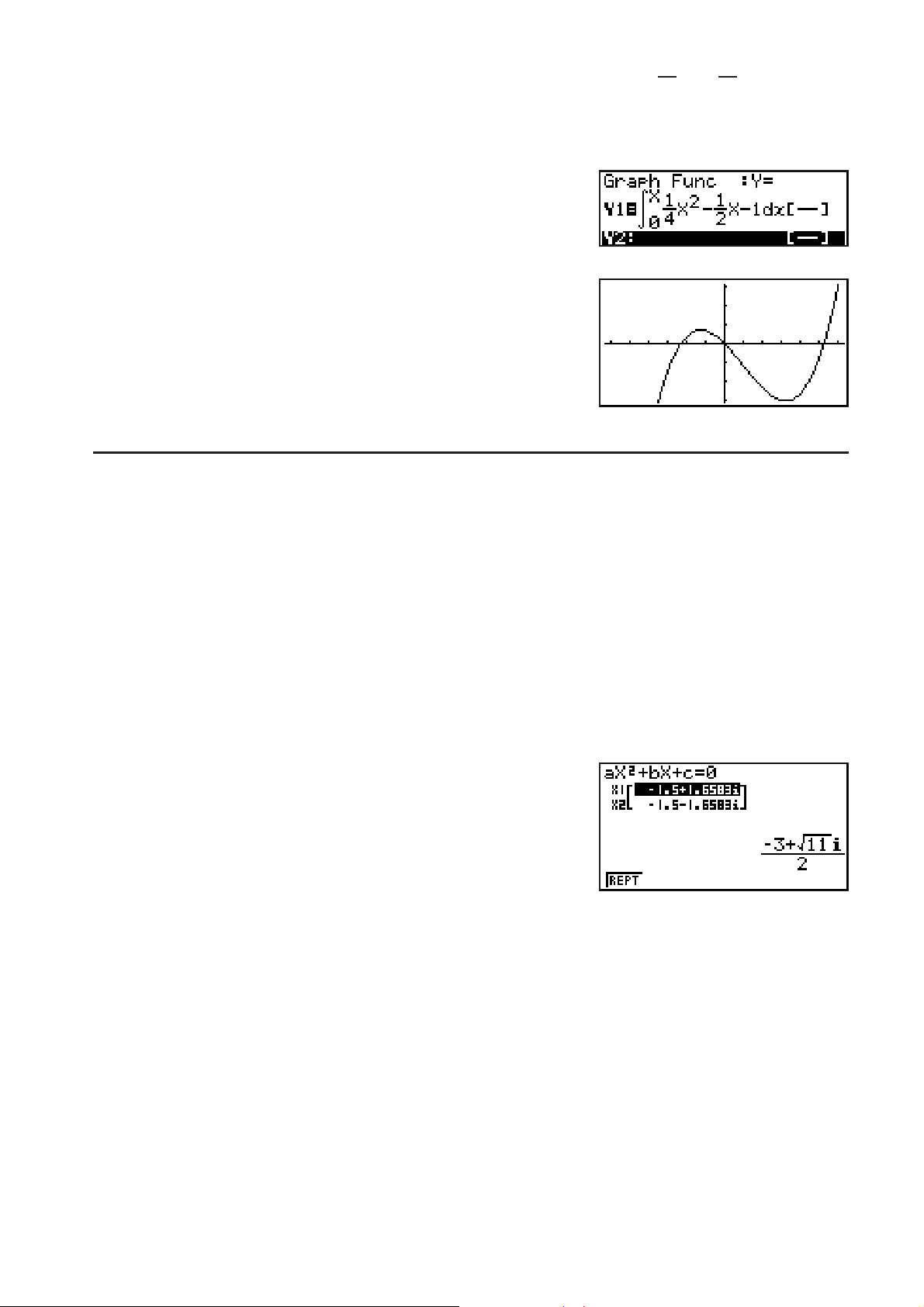
Exemple 2 Dans le mode GRAPH, saisissez la fonction
puis tracez son graphe.
Assurez-vous que les paramètres initiaux par défaut sont configurés
sur la fenêtre d’affichage.
x
1
=
y
0
4
1
2
−
x
x−1dx
2
et
KGRAPH*(CALC)(°
@CCTV@AC
T@C?CTU
(DRAW)
dx)
• Saisie et affichage de résultats du mode d’écriture mathématique dans le
mode EQUA
Vous pouvez utiliser le mode d’écriture mathématique dans le mode EQUA pour saisir et
afficher, comme indiqué ci-dessous :
• Dans le cas des équations simultanées ((SIML)) et des équations d’ordre supérieur
((POLY)), dans tous les cas où cela est possible la sortie des solutions se fait en format
d’affichage naturel (fractions, , P sont affichés en format naturel).
• Dans le cas de la résolution d’équations avec le solveur ((SOLV)), vous pouvez utiliser
I’écriture naturelle du mode d’écriture mathématique.
Exemple Pour résoudre l’équation quadratique
EQUA
KEQUAK(SET UP)
AAAA(Complex Mode)
(a+b
(POLY)(2)@UBUDUU
i))
2
x
+ 3x + 5 = 0 dans le mode
5. Menu d’options (OPTN)
Le menu d’options vous permet d’accéder aux fonctions scientifiques et autres fonctionnalités
qui ne sont pas indiquées sur le clavier de la calculatrice. Le contenu du menu d’options varie
en fonction du mode dans lequel est la calculatrice quand vous appuyez sur la touche *.
• Lorsque le système numérique par défaut est configuré pour les modes binaire, octal,
décimal ou hexadécimal, quand vous appuyez sur * le menu des options ne s’affiche pas.
• Pour plus de détails concernant les commandes comprises dans le menu des options
(OPTN), voir le paragraphe « touche * » dans « Liste des commandes du mode PRGM »
(page 8-39).
• Les significations des éléments du menu des options sont décrites dans les sections qui
traitent de chaque mode.
1-22
Page 30

La liste suivante montre le menu qui s’affiche quand on sélectionne le mode RUN • MAT ou le
mode PRGM.
• {LIST} ... {menu de fonctions de listage}
• {MAT} ... {menu d’opérations matricielles}
• {CPLX} ... {menu de calculs avec nombres complexes}
• {CALC} ... {menu d’analyse de fonctions}
• {STAT} ... {menu pour la valeur statistiquement estimée de variables appariées, la
distribution, l’écart-type, la variance et les fonctions de test}
• {CONV} ... {menu de conversion métrique}
• {HYP} ... {menu de calculs hyperboliques}
• {PROB} ... {menu des calculs de probabilité/distribution}
• {NUM} ... {menu de calculs numériques}
• {ANGL} ... {menu pour la conversion d’angles/coordonnées, entrée/conversion
sexagésimale}
• {ESYM} ... {menu de symboles d’ingénierie}
• {PICT} ... {menu sauvegarde/rappel du graphe}
• {FMEM} ... {menu de mémoires de fonctions}
• {LOGIC} ... {menu d’opérateurs logiques}
• {CAPT} ... {menu de capture d’écran}
• {TVM} ... {menu de calculs financiers}
• Lorsque « Math » est sélectionné comme « Input/Output » dans l’écran de configuration, les
éléments PICT, FMEM et CAPT ne sont pas affichés.
6. Menu de données de variables (VARS)
Pour rappeler des données de variables, appuyez sur ) pour afficher le menu de données
de variables.
{V-WIN}/{FACT}/{STAT}/{GRPH}/{DYNA}/{TABL}/{RECR}/{EQUA}/{TVM}/{Str}
• Notez que les éléments EQUA et TVM apparaissent pour les touches de fonction (
et ) uniquement lorsque vous accédez au menu de données de variables du mode
RUN • MAT ou PRGM.
• Le menu de données de variables n’apparaît pas si vous appuyez sur ) lorsque le
système binaire, octal, décimal ou hexadécimal est défini par défaut.
• Selon le modèle de calculatrice, certains éléments du menu peuvent ne pas être disponibles.
• Pour plus de détails concernant les commandes comprises dans le menu des données de
variable (VARS), voir le paragraphe « touche ) » dans « Liste des commandes du mode
PRGM » (page 8-39).
S V-WIN — Rappel des valeurs de la fenêtre d’affichage
• {X}/{Y}/{T,θ} ... {menu de l’axe x}/{menu de l’axe y}/{menu de T,θ}
{R-X}/{R-Y}/{R-T,θ} ... {menu de l’axe x}/{menu de l’axe y}/{menu de T, θ} pour le côté
•
droit de l’écran double
• {min}/{max}/{scal}/{dot}/{ptch} ... {valeur minimale}/{valeur maximale}/{graduation}/
1
{valeur de points*
}/{incrément}
1-23
Page 31

1
La valeur de points indique la plage d’affichage (valeur Xmax – valeur Xmin) divisée
*
par le pas des points (126). Cette valeur est normalement calculée automatiquement à
partir des valeurs maximales et minimales. Le changement de la valeur des points se
répercute automatiquement sur le maximum.
S FACT — Rappel des facteurs de zoom
• {Xfct}/{Yfct} ... {facteur de l’axe x}/{facteur de l’axe y}
S STAT — Rappel de données statistiques
• {X} … {données x à variable unique, variable double}
• {
n}/{¯x}/{3x}/{3x
{somme}/{somme des carrés}/{écart-type sur une population}/{écart-type sur un
échantillon}/{valeur minimale}/{valeur maximale}
{Y} ... {données y à variable double}
•
• {
ӯ}/{3y}/{3y
carrés}/{somme des produits de données
population}/{écart-type sur un échantillon}/{valeur minimale}/{valeur maximale}
{GRPH} ... {menu de données de graphes}
•
• {a}/{b}/{c}/{d}/{e} ... {coefficient de régression et coefficients polynomiaux}
2
• {r}/{r
} ... {coefficient de corrélation}/{coefficient de détermination}
2
}/{σx}/{sx}/{minX}/{maxX} ... {nombre de données}/{moyenne}/
2
}/{3xy}/{σy}/{sy}/{minY}/{maxY} ... {moyenne}/{somme}/{somme des
x et de données y}/{écart-type sur une
• {MSe} ... {carrés des moyennes des erreurs}
• {Q
}/{Q3} ... {premier quartile}/{troisième quartile}
1
• {Med}/{Mod} ... {médiane}/{mode} des données saisies
• {Strt}/{Pitch} ... {division initiale}/{pas} de l’histogramme
•
{PTS} ... {menu de données de points récapitulatifs}
• {x1}/{y1}/{x2}/{y2}/{x3}/{y3} ... {coordonnées de points récapitulatifs}
{INPT} ... {valeurs d’entrée pour les calculs statistiques}
•
• {n}/{¯x}/{sx}/{n1}/{n2}/{¯x1}/{¯x2}/{s
x
}/{s
}/{sp} ... {taille de l’échantillon}/{moyenne
x
1
2
de l’échantillon}/{écart-type de l’échantillon}/{taille de l’échantillon 1}/{taille de
l’échantillon 2}/{moyenne de l’échantillon 1}/{moyenne de l’échantillon 2}/{écart-type
de l’échantillon 1}/{écart-type de l’échantillon 2}/{écart-type de l’échantillon p}
{RESLT} ... {valeurs de sortie des calculs statistiques}
•
• {TEST} ... {résultats des calculs des tests}
• {
p}/{z}/{t}/{Chi}/{F}/{ ˆp}/{ ˆp
}/{ ˆp2}/{df}/{se}/{r}/{r 2}/{pa}/{Fa}/{Adf}/{SSa}/{MSa}/{pb}/{Fb}/
1
{Bdf}/{SSb}/{MSb}/{pab}/{Fab}/{ABdf}/{SSab}/{MSab}/{Edf}/{SSe}/{MSe}
... {valeur-
p}/{note-Z }/{note-t}/{valeur C
2
}/{valeur F}/{effectif estimé de l’échantillon}/
{effectif estimé de l’échantillon 1}/{effectif estimé de l’échantillon 2}/{degrés de
liberté}/{erreur standard }/{coefficient de corrélation}/{coefficient de détermination}/
{valeur-p du facteur A}/{valeur F du facteur A }/{degrés de liberté du facteur A}/
{somme des carrés du facteur A} /{carré moyen du facteur A}/{valeur-
p du facteur
B}/{valeur F du facteur B }/{degrés de liberté du facteur B}/{somme des carrés
du facteur B} /{carré moyen du facteur B}/{valeur-
p du facteur AB}/{valeur F du
facteur AB }/{degrés de liberté du facteur AB}/{somme des carrés du facteur AB}/
{carré moyen du facteur AB}/{degrés de liberté de l’erreur}/{somme des carrés de
l’erreur}/{carré moyen de l’erreur}
• {INTR} ... {résultats des calculs de l’intervalle de confiance}
ˆp}/{ ˆp
• {Left}/{Right}/{
}/{ ˆp2}/{df} ... {limite inférieure (bord gauche) de l’intervalle de
1
confiance}/{limite supérieure (bord droit) de l’intervalle de confiance}/{effectif estimé
de l’échantillon}/{effectif estimé de l’échantillon 1}/{effectif estimé de l’échantillon 2}/
{degrés de liberté}
1-24
Page 32

• {DIST} ... {résultats des calculs de distribution}
• {
p}/{xInv}/{x1Inv}/{x2Inv}/{zLow}/{zUp}/{tLow}/{tUp} ... {résultat de la distribution de
probabilité ou de la distribution cumulative (valeur-p)}/{résultat de la distribution
cumulative inverse t de Student, C2, F, binomial, de Poisson, géométrique ou
hypergéométrique}/{limite supérieure (bord droit) ou limite inférieure (bord gauche)
de la distribution normale cumulative inverse}/{limite supérieure (bord droit) de la
distribution normale cumulative inverse}/{limite inférieure (bord gauche) de la
distribution normale cumulative}/{limite supérieure (bord droit) de la distribution
normale cumulative}/{limite inférieure (bord gauche) de la distribution
t de Student
cumulative}/{limite supérieure (bord droit) de la distribution t de Student cumulative}
S GRPH — Rappel des fonctions graphiques
• {Y}/{r} ... {fonction à coordonnées rectangulaires ou d’inégalité}/{fonction à coordonnées
polaires}
• {Xt}/{Yt} ... fonction de graphe paramétrique {Xt}/{Yt}
• {X} ... {fonction de graphe avec constante = X}
• Appuyez sur ces touches avant d’entrer une valeur pour désigner la zone de mémoire.
S DYNA — Rappel des données de configuration de graphes dynamiques
• {Strt}/{End}/{Pitch} ... {valeur initiale de la plage de coefficient}/{valeur finale de la plage
de coefficient}/{incrément du coefficient}
S TABL — Rappel des données de configuration et du contenu de tables
• {Strt}/{End}/{Pitch} ... {valeur initiale de la plage de la table}/{valeur finale de la plage de
la table}/{incrément des valeurs de la table}
1
• {Reslt*
1
Le paramètre Reslt n’apparaît que si le menu TABL est affiché dans les modes
*
} ... {matrice du contenu de la table}
RUN • MAT et PRGM.
S RECR — Rappel des données de formules de récurrence*1, de plages de
tables et du contenu de tables
• {FORM} ... {menu de données de formules de récurrence}
a
}/{a
}/{a
• {
n
{b
+1
n
}/{cn}/{c
+2
n
}/{bn}/{b
+2
n
+1
n
}/{c
• {RANG} ... {menu de données de plages de tables}
• {Strt}/{End} ... {valeur initiale}/{valeur finale} de la plage d’une table
a
• {
• {
}/{a1}/{a2}/{b0}/{b1}/{b2}/{c0}/{c1}/{c2} ... valeur {a0}/{a1}/{a2}/{b0}/{b1}/{b2}/{c0}/{c1}/{c2}
0
a
St}/{bnSt}/{cnSt} ... origine du graphe de convergence/divergence d’une formule de
n
récurrence {an}/{bn}/{cn} (graphe WEB)
2
• {Reslt*
} ... {matrice du contenu d’une table*3}
}/{b
+1
n
}
+2
n
}/{cn}/{c
+2
n
}/{c
+1
n
} ... expressions {an}/{a
+2
n
}/{a
+1
n
}/{bn}/{b
+2
n
}/
+1
n
*1 Une erreur se produit s’il n’y a pas de fonction ni de table numérique de formules de
récurrence dans la mémoire.
2
« Reslt » n’est disponible que dans les modes RUN • MAT et PRGM
*
3
Le contenu d’une table est automatiquement stocké dans la mémoire de réponse
*
matricielle (MatAns).
S EQUA — Rappel des coefficients et des solutions d’équations*1 *
2
• {S-Rlt}/{S-Cof} ... matrice de {solutions}/{coefficients} pour les équations linéaires de
deux à six inconnues*
3
1-25
Page 33

• {P-Rlt}/{P-Cof} ... matrice de {solutions}/{coefficients} pour les équations quadratriques ou
cubiques
1
*
Les coefficients et les solutions sont automatiquement stockés dans la mémoire de
réponse matricielle (MatAns).
2
*
Dans les cas suivants, une erreur se produit:
- Aucun coefficient n’a été saisi pour l’équation.
- Aucune solution n’a été obtenue pour l’équation.
3
*
Le coefficient et la solution mémorisés d’une équation linéaire ne peuvent pas être
rappelés en même temps.
S TVM — Rappel des données de calculs financiers
• {n}/{I%}/{PV}/{PMT}/{FV} ... {périodes de paiement (versements)}/{taux d’intérêt annuel}/
{valeur presénte}/{paiement}/{valeur future}
P/Y}/{C/Y} ... {périodes de versement par année}/{périodes de composition par année}
• {
S Str — commande Str
• {Str} ... {mémoire de chaînes}
7. Menu de programmation (PRGM)
Pour afficher le menu de programmation (PRGM), accédez d’abord au mode RUN • MAT
ou PRGM à partir du menu principal, puis appuyez sur )(PRGM). Les sélections
disponibles dans le menu de programmation (PRGM) sont les suivantes.
• {COM} ...... {menu de commandes de programmation}
• {CTL} ....... {menu de commandes de contrôle de programmation}
• {JUMP} ..... {menu de commande de saut}
• {?} ............ {commande de saisie}
• {<} .......... {commande d’affichage}
• {CLR} ....... {menu de commande de suppression}
• {DISP} ...... {menu de commande d’affichage}
• {REL} ....... {menu d’opérateurs relationnels avec saut conditionnel}
• {I/O} ......... {menu de commande de contrôle/transfert d’entrée/sortie}
• {:} ............. {commande d’instructions multiples}
• {STR} ....... {commande de chaîne}
Le menu de touches de fonction suivant apparaît si vous appuyez sur )(PRGM) dans
le mode RUN • MAT ou le mode PRGM quand le système numérique par défaut est binaire,
octal, décimal ou hexadécimal.
• {Prog} ....... {rappel de programme}
• {JUMP}/{?}/{<}/{REL}/{:}
Les fonctions attribuées aux touches de fonction sont identiques à celles du mode Comp.
Pour les détails sur les commandes disponibles dans les différents menus auxquels vous avez
accès à partir du menu de programmation, voir « Chapitre 8. Programmation ».
1-26
Page 34

8. Utilisation de l’écran de configuration
L’écran de configuration de mode indique l’état en cours des réglages de mode et permet
d’effectuer les changements souhaités. Vous pouvez changer les réglages d’un mode de la
façon suivante.
S Pour changer la configuration d’un mode
1. Sélectionnez l’icône souhaitée et appuyez sur U pour acceder au mode et en afficher
l’écran initial. Ici nous choisissons le mode RUN • MAT.
2. Appuyez sur K(SET UP) pour afficher l’écran de
configuration de ce mode.
• Cet écran de configuration est utilisé à titre d’exemple.
Le contenu de l’écran peut être différent en fonction du
mode dans lequel vous êtes et des réglages actuels de
ce mode.
3. Utilisez les touches du pavé directionnel D et A pour mettre le paramètre dont vous
voulez changer le réglage en surbrillance.
4. Appuyez sur la touche de fonction ( to ) qui indique le réglage que vous voulez faire.
5. Quand vous avez fait les changements nécessaires, appuyez sur ) pour sortir de l’écran
de configuration.
I Menus de touches de fonction sur l’écran de configuration
Cette partie détaille les réglages que vous pouvez effectuer à l’aide des touches de fonction
de l’écran de configuration.
indique le réglage par défaut.
S Input/Output (mode d’entrée/sortie)
• {Math}/{Line}*1 ... mode d’écriture {mathématique}/{linéaire}
1
Le paramètre initial par défaut de la GRAPH 85 SD (OS 2.00)/GRAPH 85 (OS 2.00) est
*
le mode d’écriture linéaire (« Line »).
S Mode (calcul/mode binaire, octal, décimal, hexadécimal)
• {Comp} ... {mode de calcul arithmétique}
• {Dec}/{Hex}/{Bin}/{Oct} ... {décimal}/{hexadécimal}/{binaire}/{octal}
S Frac Result (format d’affichage du résultat d’une fraction)
• {d/c}/{ab/c} ... fraction {en notation française}/{en notation anglo-saxonne}
S Func Type (type de fonction graphique)
Une pression sur une des touches de fonction suivantes commute aussi la fonction de la
touche T.
1-27
Page 35

• {Y=}/{r=}/{Parm}/{X=} ... graphe à {coordonnées rectangulaires (type Y
{coordonnées polaires}/{paramétriques}/{coordonnées rectangulaires (type X=f(y))}
=f(x))}/
• {Y>}/{Y<}/{YP}/{YO} ... graphe de l’inéquation {
• {X>}/{X<}/{XP}/{XO} ... graphe de l’inéquation {
y>f(x)}/{y<f(x)}/{yrf(x)}/{ybf(x)}
x>f(y)}/{x<f(y)}/{xrf(y)}/{xbf(y)}
S Draw Type (méthode de tracé du graphe)
• {Con}/{Plot} ... {par points connectés}/{par points séparés}... {par points connectés}/{par points séparés}
S Derivative (affichage de la valeur de la dérivée)
• {On}/{Off} ... {affichage activé}/{affichage désactivé} pendant l’utilisation de graphe à
table, de graphe et table et de Trace.
S Angle (unité par défaut de l’unité d’angle)
• {Deg}/{Rad}/{Gra} ... {degrés}/{radians}/{grades}
S Complex Mode
• {Real} ... {calcul dans la plage des nombres réels seulement}
• {
a+bi}/{rθ} ... {affichage d’un calcul complexe à {format rectangulaire}/{format polaire}
S Coord (affichage des coordonnées du pointeur graphique)
• {On}/{Off} ... {affichage activé}/{affichage désactivé}
S Grid (affichage de la trame du graphe)
• {On}/{Off} ... {affichage activé}/{affichage désactivé}
S Axes (affichage de l’axe du graphe)
• {On}/{Off} ... {affichage activé}/{affichage désactivé}
S Label (affichage du nom de l’axe graphique)
• {On}/{Off} ... {affichage activé}/{affichage désactivé}
S Display (format d’affichage)
• {Fix}/{Sci}/{Norm}/{Eng} ... {nombre de décimales défini}/{nombre de chiffres significatifs}/
{réglage d’affichage normal}/{mode Ingénieur}
S Stat Wind (méthode de réglage de la fenêtre d’affichage de graphes
statistiques)
• {Auto}/{Man} ... {automatique}/{manuel}
S Resid List (calcul résiduel)
• {None}/{LIST} ... {pas de calcul}/{spécification de la liste pour les données résiduelles
calculées}
S List File (réglage d’affichage de fichier de listes)
• {FILE} ... {réglage du fichier de liste affiché}
S Sub Name (nom liste)
• {On}/{Off} ... {affiché}/{non affiché}
1-28
Page 36

S Graph Func (affichage de la fonction pendant le tracé d’un graphe et
l’affichage des coordonnées d’un point)
• {On}/{Off} ... {affichage activé}/{affichage désactivé}
S Dual Screen (état du mode écran double)
• {G+G}/{GtoT}/{Off} ... {tracé graphique sur les deux côtés de l’écran double}/{graphe sur
un côté et table numérique de l’autre côté de l’écran double}/{écran double désactivé}
S Simul Graph (mode de graphe simultané)
• {On}/{Off} ... {tracé de graphes simultanés activé (tous les graphes sont tracés
simultanément)}/{tracé de graphes simultanés désactivé (tous les graphes sont tracés
les uns après les autres)}
S Background (arrière-plan d’affichage de graphe)
• {None}/{PICT} ... {pas d’arrière-plan}/{désignation de l’image en arrière-plan du graphe}
S Sketch Line (type de ligne superposée)
• { }/{ }/{ }/{ } ... {normal}/{épais}/{discontinu}/{points}
S Dynamic Type (type de graphe dynamique)
• {Cnt}/{Stop} ... {sans arrêt (continu)}/{arrêt automatique après 10 tracés}
S Locus (mode de lieu de graphe dynamique)
• {On}/{Off} ... {lieu identifié}/{lieu non identifié}
S Y=Draw Speed (vitesse de tracé dynamique de courbes)
• {Norm}/{High} ... {normal}/{rapide}
S Variable (réglages pour la génération de tables et le tracé de graphes)
• {RANG}/{LIST} ... {utilisation de la plage d’une table}/{utilisation des données d’une liste}
S 3 Display (affichage de la valeur 3 dans une table de récurrence)
• {On}/{Off} ... {affichage activé}/{affichage désactivé}
S Slope (affichage de la dérivée à la position actuelle du pointeur dans un
graphe de section conique)
• {On}/{Off} ... {affichage activé}/{affichage désactivé}
S Payment (désignation d’une période de paiement)
• {BGN}/{END} ... désignation {du début}/{de la fin} de la période de paiement
S Date Mode (désignation du nombre de jours par année)
• {365}/{360} ... calcul des intérêts pour {365}*1/{360} jours par année
1
Il faut utiliser l’année de 365 jours pour les calculs de dates en mode TVM , sinon une
*
erreur se produit.
S Periods/YR. {spécification de l’intervalle de paiement}
• {Annu}/{Semi} ... {annuel}/{semestriel}
1-29
Page 37

S Ineq Type (spécification de remplissage de l’inéquation)
• {AND}/{OR} ... Lors du traçage d’inéquations multiples, {remplissage des aires où toutes
les conditions de l’inéquation sont satisfaites}/{remplissage des aires où chaque
condition de l’inéquation est satisfaite}
S Simplify (spécification de la réduction automatique/manuelle du calcul)
• {Auto}/{Man} ... {réduction et affichage automatiques}/{affichage sans réduction}
S Q1Q3 Type (formules de calcul de Q1/Q3)
• {Std}/{OnData} ... {Division de la population totale au point central, entre les groupes
supérieurs et inférieurs, avec la médiane du groupe inférieur Q1 et la médiane du
groupe supérieur Q3}/{Calcule la valeur de l’élément dont le taux d’effectif cumulatif
est supérieur à 1/4 et le plus proche de 1/4 Q1, et la valeur de l’élément dont le taux
d’effectif cumulatif est supérieur à 3/4 et le plus proche de 3/4 Q3}
Pour une calculatrice GRAPH 85 Series ayant été mise à jour avec l’OS 2.00 à partir d’une
version d’OS antérieure, le paramètre initial par défaut est « Std ».
Les éléments suivants ne sont pas inclus dans la GRAPH 35+.
S Auto Calc (calcul auto sur les feuilles de calculs)
• {On}/{Off} ... {exécute}/{n’exécute pas} les formules automatiquement
S Show Cell (mode d’affichage des cellules sur les feuilles de calculs)
• {Form}/{Val} ... {formule}*1/{valeur}
S Move (sens du curseur de cellule sur les feuilles de calculs)*
• {Low}/{Right} ... {déplacement vers le bas}/{déplacement vers la droite}
1
*
Lorsque « Form » (formule) est sélectionné, une formule apparaît dans la cellule.
« Form » n’affecte pas les données de la cellule qui ne sont pas une formule.
2
Spécifie le sens dans lequel le curseur de cellule se déplace lorsque vous appuyez
*
sur la touche U pour enregistrer les données introduites dans les cellules, lorsque la
commande Suite crée une table numérique et lorsque vous rappelez des données de la
mémoire de listes.
2
9. Capture d’écran
Vous pouvez capturer une image de l’écran affiché et l’enregistrer dans la mémoire d’écrans à
n’importe quel moment lorsque vous utilisez la calculatrice.
S Pour capturer l’image d’un écran
1. Mettez la calculatrice en marche et affichez l’écran que vous voulez capturer.
2. Appuyez sur A(CAPTURE).
• Une boîte de dialogue de sélection de zone mémoire
s’affiche.
1-30
Page 38

3. Saisissez une valeur de 1 à 20 et appuyez sur U.
• L’image de l’écran est capturée et sauvegardée dans une zone de la mémoire d’écrans
nommée « Capt
• Vous ne pouvez pas capturer l’image d’écran d’un message indiquant qu’une opération ou la
transmission de données est en cours.
• Une erreur « Memory ERROR » se produit si la capacité de la mémoire principale n’est pas
suffisante pour enregistrer l’écran capturé.
n » ( n = la valeur spécifiée).
S Pour rappeler une image d’écran de la mémoire d’écrans
Cette opération n’est possible qu’avec le mode d’écriture linéaire sélectionné au préalable.
1. Dans le mode RUN • MAT, appuyez sur *(E)
(E)(CAPT)(RCL).
2. Spécifiez un numéro de 1 à 20 de la mémoire d’écrans et appuyez sur U.
• Ceci affiche l’image stockée dans la mémoire de capture d’écran que vous avez spécifiée.
3. Appuyez sur ) pour sortir de l’affichage de l’image et revenir à l’écran de départ de
l’étape 1.
• Vous pouvez aussi utiliser la commande RclCapt dans un programme pour rappeler une
image d’écran de la mémoire d’écrans.
10. En cas de problème persistant…
Si vous rencontrez un problème pendant que vous effectuez une opération, effectuez les
opérations suivantes avant de supposer que la calculatrice ne fonctionne pas.
I Rétablissement des réglages de modes initiaux de la calculatrice
1. Depuis le menu principal, accédez au mode SYSTEM.
2. Appuyez sur (RSET).
3. Appuyez sur (STUP) et sur (Yes).
4. Appuyez sur )K pour revenir au menu principal.
Accédez maintenant au mode correct et effectuez à nouveau votre calcul en vérifiant les
résultats sur l’écran.
I Redémarrage et réinitialisation
S Redémarrage (RESTART)
Si la calculatrice commence à se comporter de manière anormale vous pouvez la redémarrer
en appuyant sur le bouton RESTART (bouton P). Notez néanmoins, que vous devez utiliser le
bouton RESTART seulement comme dernier recours.
1-31
Page 39

Normalement, l’appui sur le bouton RESTART réinitialise le système d’exploitation de la
calculatrice mais préserve les programmes, les fonctions graphiques et d’autres données
stockées dans la mémoire.
Bouton RESTART
Bouton RESTART
Bouton P
Bouton P
GRAPH 95/GRAPH 75 GRAPH 35+ GRAPH 85 SD
GRAPH 95/GRAPH 75 GRAPH 35+ GRAPH 85 SD
GRAPH 85
GRAPH 85
Important !
Quand vous éteignez l’alimentation, la calculatrice sauvegarde les données de l’utilisateur
(mémoire principale). Au rallumage de l'alimentation, la calculatrice récupère les données
sauvegardées.
Chaque fois que vous appuyez sur le bouton RESTART, la calculatrice redémarre et charge
les données sauvegardées précédemment.
Cela signifie que si vous appuyez sur le bouton RESTART après avoir édité un programme,
tracé le graphe d’une fonction ou traité d’autres données, toute donnée non encore
sauvegardée sera perdue.
S Réinisialisation
Utilisez la réinitialisation quand vous voulez effacer toutes les données courantes stockées
dans la mémoire de la calculatrice et reconfigurer tous les paramètres des modes à leur
valeurs par défaut.
Avant d’effectuer l’opération de réinitialisation, faites d’abord une copie par écrit de toutes les
données importantes.
Pour plus de détails, voir « Réinitialisation » (page 12-3).
I Message de faible tension des piles
Si le message suivant apparaît à l’écran, éteignez immédiatement la calculatrice et remplacez
les piles de la façon indiquée.
Si vous continuez d’utiliser la calculatrice sans remplacer les piles, l’alimentation sera
automatiquement coupée afin de protéger le contenu de la mémoire. Le cas échéant, il sera
impossible de remettre la calculatrice sous tension et le contenu de la mémoire risque d’être
vérolé ou entièrement perdu.
• Vous ne pouvez effectuer aucun transfert de données après l’apparition du message de
faible tension des piles.
1-32
Page 40

Chapitre 2 Calculs manuels
1. Calculs de base
I Calculs arithmétiques
• Introduisez les calculs arithmétiques comme ils sont écrits, de gauche à droite.
• Utilisez la touche pour entrer le signe moins devant une valeur négative.
• Les calculs sont effectués internement avec une mantisse de 15 chiffres. Le résultat est
arrondi à une mantisse de 10 chiffres avant d’être affiché.
• Pour les calculs arithmétiques mixtes, la multiplication et la division ont priorité sur l’addition
et la soustraction.
Exemple Opération
2
56 × (–12) ÷ (–2,5) = 268,8
(2 + 3) × 10
2 + 3 × (4 + 5) = 29
6
= 0,3
4 × 5
1
*
Les fermetures de parenthèses (immédiatement avant une opération de la touche U)
peuvent être omises, quel qu’en soit le nombre.
2
= 500
56122.5U
2312U
2345U*
645U
1
I Nombre de décimales, nombre de chiffres significatifs, plage
d’affichage normal
• Même après que le nombre de décimales ou le nombre de chiffres significatifs a été défini,
les calculs internes sont effectués avec une mantisse de 15 chiffres et les valeurs affichées
sont enregistrées avec une mantisse de 10 chiffres. Utilisez Rnd du menu de calculs
numériques (NUM) (page 2-12) pour arrondir la valeur affichée au nombre de décimales et
de chiffres significatifs spécifié.
• Le réglage du nombre de décimales (Fix) et de chiffres significatifs (Sci) reste valide tant que
vous ne les changez pas ou tant que vous ne changez pas le réglage d’affichage normal
(Norm).
[SET UP]- [Display]
-
[Fix]
/
[Sci] / [Norm]
Exemple 1 100 w 6 = 16,66666666...
Condition Opération Affichage
4 décimales
5 chiffres significatifs
Annule la spécification
1
Les valeurs affichées sont arrondies à la décimale spécifiée.
*
K(SET UP) DD
(Fix)CU)U
K(SET UP) DD
(Sci)DU)U
K(SET UP) DD
(Norm))U
2-1
1006U
16.66666667
16.6667
1
*1*
1.6667E+01
16.66666667
1
*1*
Page 41

Exemple 2 200 w 7 s 14 = 400
Condition Opération Affichage
200714U
3 décimales
K(SET UP) DD
(Fix)BU)U
Le calcul continue en
2007U
utilisant l’affichage de 10
chiffres.
• Si le même calcul est effectué avec le nombre de chiffres spécifié:
2007U
La valeur enregistrée est
*(E)(NUM)(Rnd)U
arrondie au nombre de
décimales spécifié sur
l’écran de configuration.
2007U
Vous pouvez aussi spécifier
(E)(RndFi)(Ans)2
le nombre de décimales pour
l’arrondi des valeurs internes
pour un calcul particulier.
(Exemple : Spécifier un
arrondi à deux décimales)
14U
14U
U
14U
400
400.000
28.571
Ans s
I
400.000
28.571
28.571
Ans s
I
399.994
28.571
RndFix(Ans,2)
28.570
Ans s
I
399.980
I Séquence de priorité de calcul
Cette calculatrice emploie la vraie logique algébrique pour calculer les parties d’une formule
dans l’ordre suivant :
Fonctions de type A
• Transformation de coordonnées Pol (
x, y), Rec (r,
• Fonctions comportant des parenthèses (telles que des dérivées, intégrales, 3, etc.)
d/dx, d
2
/dx2, °dx, 3, Solve, FMin, FMax, ListmMat, Fill, Seq, SortA, SortD, Min, Max,
Median, Mean, Augment, MatmList, P(, Q(, R(, t(, RndFix, logab
• Fonctions composées*
1
, List, Mat, fn, Yn, rn, Xtn, Ytn, Xn
Fonctions de type B
Avec ces fonctions, la valeur est introduite, puis la touche de fonction enfoncée.
2
x
, x–1, x!, ° ’ ”, symboles ENG, unité d’angle °, r,
Puissance/Racine ^(xy), x
Fractions
a +
b
/
c
Format de multiplication abrégé devant P, nom de mémoire ou nom de variable.
2P, 5A, Xmin, F Start, etc.
Fonctions de type C
Avec ces fonctions, la touche de fonction est enfoncée, puis la valeur introduite.
,
3
, log, In, ex, 10x, sin, cos, tan, Asn, Acs, Atn, sinh, cosh, tanh, sinh–1, cosh–1, tanh–1,
(–), d, h, b, o, Neg, Not, Det, Trn, Dim, Identity, Ref, Rref, Sum, Prod, Cuml, Percent, List,
Abs, Int, Frac, Intg, Arg, Conjg, ReP, ImP
Q
)
g
2-2
Page 42

Format de multiplication abrégé devant les fonctions de type A, les fonctions de type C et
les parenthèses.
23, A log2, etc.
Permutation, combinaison
nPr, nCr
Commandes de conversion métrique
s, ÷, Int÷, Rnd
+, –
Opérateurs relationnels =, x, >, <, r, b
And (opérateur logique), and (opérateur des bits)
Or, Xor (opérateur logique), or, xor, xnor (opérateur des bits)
1
*
Vous pouvez combiner le contenu de plusieurs endroits de la mémoire de fonctions (fn)
ou de la mémoire de graphes (Yn, rn, Xtn, Ytn, Xn) en fonctions composées. Par exemple,
lorsque vous spécifiez fn1 (fn2), vous obtiendrez la fonction composée fn1°fn2 (voir page
5-7). Une fonction composée peut comprendre jusqu’à cinq fonctions.
Exemple 2 + 3 s (log sin2P
6
6
5
5
3
3
2
+ 6,8) = 22,07101691 (unité d’angle = Rad)
1
1
2
2
4
4
• Vous ne pouvez pas utiliser d’expression avec calcul de différentielle, différentielle
quadratique, intégration, 3, valeur maximale/minimale, résolution, RndFix ou logab à
l’intérieur d’un terme du calcul de RndFix.
• Lorsque des fonctions ayant la même priorité sont utilisées en série, l’exécution est effectuée
de droite à gauche.
x
e
In 120 m ex{In( 120)}
Sinon, l’exécution se fait de gauche à droite.
• Les fonctions composées sont exécutées de droite à gauche.
• Tout ce qui se trouve entre parenthèses a la plus grande priorité.
I Affichage des résultats des calculs comme nombres irrationnels
(GRAPH 95/GRAPH 75/GRAPH 35+ seulement)GRAPH 95/GRAPH 75/GRAPH 35+ seulement) seulement)
Vous pouvez configurer la calculatrice pour afficher les résultats des calculs dans le format
des nombres irrationnels (y compris ou P) en sélectionnant « Math » (mathématique)
comme « Input/Output » (entrée/sortie).
Exemple 2 + 8 = 32 (Input/Output : Math)
V()ACV()GU
2-3
Page 43

S Plage d’affichage des résultats de calculs avec
L’affichage du résultat d’un calcul en format est supporté pour un résultat qui comporte
jusqu’à deux termes. Les résultats des calculs en format adoptent une des formes
suivantes :
p
• Voici les plages pour chacun des coefficients (a, b, c, d, e, f) qui peuvent être affichés en
format de calcul avec :
1
0
• Dans les cas montrés ci-dessous, le résultat d’un calcul peut être affiché en format ,
même si ses coefficients (
Un résultat de calcul en format utilise un dénominateur commun.
Puisque le résultat du calcul utilise un dénominateur commun, il peut encore être affiché en
format , même si les coefficients (
coefficients (a, c, d).
Exemple :
ab, p b p ab, p
a < 100, 1 < b < 1000, 1 c < 100
d < 100, 0 e < 1000, 1 f < 100
a'b
'
11
b'e
+
c
3
'
+
10
m
f
10'3 + 11'2
2
=
a'b
a, c, d) sont en dehors des plages indiquées.
´
b
a
'
110
b'e
p
c
+ d´
´
c
f
e
'
* c´ est le plus petit commun multiple de c et f.
a´, c´, d´) sont en dehors de la correspondante plage de
Exemples de calculs
Ce calcul : Produit ce type d’affichage :
2 s (3 – 25) = 6 – 45 format
352 s 3 = 148,492424 (=
150'2
23 s (5 – 23) = 35,32566285 (=
2 + 3 + 8 = 3 + 32 format
'
1
Format décimal parce que les valeurs sont en dehors de la plage.
*
2
Format décimal parce que le résultat du calcul a trois termes.
*
• Le résultat du calcul est affiché en format décimal même si un résultat intermédiaire atteint
plus de deux termes.
= 8,485281374*
25
2 + '3 + '6
= 5,595754113*
1
105
2)*
115
2
– 463)*
1
1
format décimal
format décimal
format décimal
Exemple : (1 + 2 + 3) (1 – 2 – 3) (= – 4 – 26)
= –8,898979486
• Si la formule du calcul contient un terme avec et un terme qui ne peut être affiché
comme une fraction, le résultat du calcul sera affiché en format décimal.
Exemple : log3 + 2 = 1,891334817
2-4
Page 44

S Plage d’affichage des résultats de calculs avec P
Le résultat d’un calcul est affiché en format P dans les cas suivants.
• Lorsque le résultat du calcul peut être affiché sous la forme
n est un nombre entier jusqu’à |10
• Lorsque le résultat du calcul peut être affiché sous la forme
Cependant, {nombre de chiffres de
doit être inférieur ou égal à 9 lorsque la précédente expression
Également, trois est le nombre maximum de chiffres attribuables à c.*
*1 Lorsque c < b, le nombre de chiffres de a, b et c sont comptés quand la fraction est
convertie d’une fraction impropre (
2
Lorsque dans l’écran de configuration le paramètre « Simplify » a été spécifié à
*
« Manual », le résultat du calcul peut être affiché en format décimal, même si ces
conditions sont remplies.
Exemples de calculs
Ce calcul : Produit ce type d’affichage :
78Ps 2 = 156P format P
123456P s 9 = 3490636,164 (=
6
|.
a + nombre de chiffres de b + nombre de chiffres de c}
b
) en une fraction mixte (
c
11111104
P)*
3
format décimal
n P
a
+
a
a
+
b
P ou
c
+
b
P
c
b
b
ou
c
2
b
).
c
est réduite.*1*2
c
105 +
2 +
*
*
568
P = 105 +
824
258
3238
3
Format décimal parce que la partie entière du résultat du calcul est supérieure ou égale à
|106|.
4
Format décimal parce que, pour la forme
est supérieur ou égal à quatre.
6.533503684
P =
71
103
P
129
1619
4
*
2 +
a
+
format P
format décimal
b
P, le nombre de chiffres du dénominateur
c
I Opérations de multiplication sans signe de multiplication
Vous pouvez omettre le signe de multiplication (s) dans toutes les opérations suivantes.
• Devant les fonctions de type A ( à la page 2-2) et les fonctions de type C ( à la page
2-2), sauf pour les signes négatifs
'
Exemple 1 2sin30, 10log1,2, 2
• Devant les constantes et les noms de variables et de mémoires
3
, 2Pol(5, 12), etc.
Exemple 2 2P, 2AB, 3Ans, 3Y
• Devant une ouverture de parenthèses
Exemple 3 3(5 + 6), (A + 1)(B – 1), etc.
1, etc.
2-5
Page 45

I Dépassement de capacité et erreurs
Le dépassement d’une plage de calcul ou de définition spécifiée, ou une tentative d’entrée
invalide entraîne l’apparition d’un message d’erreur sur l’affichage. Toute autre opération est
impossible quand un message d’erreur est affiché. Pour plus de détails, voir « Tableau des
messages d’erreur » à la page A-1.
• Lorsqu’un message d’erreur est affiché, la plupart des touches de la calculatrice sont
inopérantes. Appuyez sur ) pour effacer l’erreur et revenir à l’opération normal.
I Capacité de la mémoire
Chaque fois que vous appuyez sur une touche, un octet ou deux octets de mémoire sont
utilisés. Les fonctions qui n’utilisent qu’un octet sont les suivantes : @, A, B, sin, cos, tan,
log, In, et P. Les fonctions nécessitant deux octets sont d/dx(, Mat, Xmin, If, For, Return,
DrawGraph, SortA(, PxIOn, Sum et a
• Le nombre d’octets requis pour entrer des fonctions et des commandes est différent dans les
modes d’écriture linéaire et dans le mode d’écriture mathématique. Pour plus de détails sur
le nombre d’octets requis pour chaque fonction dans le mode d’écriture mathématique, voir
page 1-11.
.
n
+1
2. Fonctions spéciales
I Calculs avec variables
Exemple Opération Affichage
193,2 ÷ 23 = 8,4
193,2 ÷ 28 = 6,9
I Mémoire
S Variables (mémoire alphabétique)
Cette calculatrice est dotée de 28 variables en standard. Vous pouvez utiliser les variables
pour sauvegarder les valeurs à utiliser à l’intérieur des calculs. Les variables sont identifiées
par des noms d’une lettre, correspondant aux 26 lettres de l’alphabet plus
maximale des valeurs que vous pouvez affecter aux variables est de 15 chiffres pour la
mantisse et 2 chiffres pour l’exposant.
193.2??T(A)U
?T(A)23U
?T(A)28U
r et
Q
. La taille
193.2
8.4
6.9
• Le contenu des variables est retenu même lorsque la calculatrice est mise hors tension.
S Pour affecter une valeur à une variable
[valeur] ? [nom de la variable] U
2-6
Page 46

Exemple 1 Affecter 123 à la variable A
@AB??T(A)U
Exemple 2 Ajouter 456 à la variable A et sauvegarder le résultat dans la variable B
?T(A)CDE?
?J(B)U
S Pour affecter la même valeur à plus d’une variable
[valeur]? [premier nom de la variable]?(~) [dernier nom de la variable]U
• Vous ne pouvez pas utiliser «
Exemple Affecter la valeur 10 aux variables A à F
@???T(A)
?(~)?R(F)U
r » ou «
Q
» comme nom de variable.
S Mémoire de stockage des chaînes
Dans la mémoire de stockage des chaînes vous pouvez stocker jusqu’à 20 chaînes (nommées
Str1 à Str20). Les chaînes stockées peuvent être affichées ou utilisées dans les fonctions et
les commandes qui acceptent des arguments de type chaîne.
Pour plus de détails sur les opérations avec des chaînes, voir « Chaînes » (page 8-19).
Exemple Affecter la chaîne « ABC » à Str1 et puis afficher la variable Str1
A
?(
J(B)((C)(”)?(Relâche Alpha-Lock.)
?)(E)(Str)@U
-LOCK)(”)T(A)
(Str)@U
La chaîne s’affiche justifiée à gauche.
• Effectuez l’opération ci-dessus dans le mode d’écriture linéaire. Elle ne peut s’effectuer en
mode d’écriture mathématique.
S Mémoire de fonctions [OPTN]-[FMEM]
La mémoire de fonctions est pratique pour le stockage provisoire d’expressions souvent
utilisées. Pour le stockage d’expressions à long terme, il est conseillé d’utiliser le mode
GRAPH pour les expressions et le mode PRGM pour les programmes.
• {STO}/{RCL}/{fn}/{SEE} ... {sauvegarde de la fonction}/{rappel de la fonction}/{spécification
de la zone de la fonction comme nom de variable dans une expression}/{liste des
fonctions}
2-7
Page 47

S Pour stocker une fonction
Exemple Sauvegarder la fonction (A+B) (A–B) dans la mémoire de fonctions 1
?T(A)?J(B)
?T(A)?J(B)
*(E)(E)(FMEM)
(STO)@U
)))
• Si le numéro de mémoire de fonctions où vous sauvegardez une fonction contient déjà une
fonction, celle-ci sera remplacée par la nouvelle.
• Vous pouvez aussi utiliser ? pour enregistrer une
fonction dans la mémoire de fonctions à l’intérieur
d’un programme. Dans ce cas, vous devrez mettre la
fonction entre guillemets.
S Pour rappeler une fonction
Exemple Rappeler le contenu de la mémoire de fonctions 1
*(E)(E)(FMEM)
(RCL)@U
• La fonction rappelée apparaît à l’emplacement actuel du curseur sur l’écran.
S Pour rappeler une fonction comme variable
B??T(A)U
@??J(B)U
*(E)(E)(FMEM)(fn)
@AU
S Pour afficher une liste des fonctions disponibles
*(E)(E)(FMEM)
(SEE)
2-8
Page 48

S Pour supprimer une fonction
Exemple Effacer le contenu de la mémoire de fonctions 1
*(E)(E)(FMEM)
(STO)@U
• L’exécution d’une sauvegarde quand l’affichage est vierge supprime la fonction de la
mémoire de fonctions spécifiée.
I Fonction de réponse
La fonction de réponse stocke le dernier résultat calculé automatiquement en appuyant sur
U (à moins que l’opération de touche U résulte en une erreur). Le résultat est sauvegardé
dans la mémoire de dernier résultat.
• La valeur la plus élevée que peut contenir la mémoire de dernier résultat est 15 chiffres pour
la mantisse et 2 chiffres pour l’exposant.
• Le contenu de la mémoire de dernier résultat n’est pas effacé lorsque la touche est
enfoncée ou l’appareil mis hors tension.
S Pour utiliser le contenu de la mémoire de dernier résultat dans un calcul
Exemple 123 + 456 = 579
789 – 579 = 210
@ABCDEU
FGH(Ans)U
Utilisateurs de la GRAPH 35+ ...
• Le contenu de la mémoire de réponse n’est pas modifié par une opération qui affecte des
valeurs à la mémoire Alpha (telles que : D??J(B)U).
Utilisateurs des GRAPH 95/GRAPH 75 ...
• Dans le mode d’écriture mathématique, l’opération pour rappeler le contenu de la mémoire
de réponse est différente de l’opération requise dans le mode d’écriture linéaire. Pour plus
de détails, voir « Fonction historique » (page 1-17).
• Lors de la réalisation d’une opération qui affecte une valeur à une mémoire Alpha (tel que
D??J(B)U), le contenu de la mémoire de réponse est mis à jour dans le mode
d’écriture mathématique mais pas dans le mode d’écriture linéaire.
I Exécution de calculs continus
La mémoire de réponse permet d’utiliser le résultat d’un calcul comme argument dans le
calcul suivant.
2-9
Page 49

Exemple 1 w 3 =
1 w 3 s 3 =
@BU
(En continuant)BU
Les calculs continus peuvent également être utilisés avec les fonctions de type B (
la page 2-2), +, –, ^(
y
x
), x, ° ’ ”, etc.
2
x
, x–1, x!, à
3. Spécification de l’unité d’angle et du format d’affichage
Avant d’effectuer un calcul pour la première fois, vous devez définir l’unité d’angle et le format
d’affichage sur l’écran de configuration.
I Pour définir l’unité d’angle [SET UP]- [Angle]
1. Sur l’écran de configuration, mettez « Angle » en surbrillance.
2. Appuyez sur la touche de fonction correspondant à l’unité d’angle que vous voulez spécifier,
puis appuyez sur ).
• {Deg}/{Rad}/{Gra} ... {degré}/{radian}/{grade}
• La relation entre les degrés, les grades et les radians est la suivante.
360° = 2P radians = 400 grades
90° = P/2 radians = 100 grades
I Pour définir le format d’affichage [SET UP]- [Display]
1. Sur l’écran de configuration, mettez « Display » en surbrillance.
2. Appuyez sur la touche de fonction correspondant au paramètre que vous voulez spécifier,
puis appuyez sur ).
• {Fix}/{Sci}/{Norm}/{Eng} ... {nombre de décimales défini}/{nombre de chiffres significatifs}/
{affichage normal}/{mode d’ingénierie}
S Pour définir le nombre de chiffres après la virgule (Fix)
Exemple Définir deux chiffres après la virgule
(Fix)AU
Appuyez sur la touche numérique qui correspond au nombre de chiffres après la virgule que
vous souhaitez (
n = 0 à 9).
• Les valeurs affichées sont arrondies au nombre de chiffres après la virgule que vous avez
spécifié.
2-10
Page 50

S Pour définir le nombre de chiffres significatifs (Sci)
Exemple Définir trois chiffres significatifs
(Sci)BU
Appuyez sur la touche numérique qui correspond au nombre de chiffres significatifs que vous
souhaitez (
n = 0 à 9). Si vous spécifiez 0, le nombre de chiffres significatifs sera 10.
• Les valeurs affichées sont arrondies au nombre de chiffres significatifs que vous avez
spécifié.
S Pour définir l’affichage normal (Norm 1/Norm 2)
Appuyez sur (Norm) pour alterner entre les deux plages, Norm 1 et Norm 2.
–2
Norm 1: 10
(0,01) > |x|, |x| 10
Norm 2: 10–9 (0,000000001) > |x|, |x| 10
10
10
S Pour définir l’affichage en notation d’ingénierie (mode Eng)
Appuyez sur (Eng) pour alterner entre la notation d’ingénierie et la notation normale.
L’indicateur « /E » apparaît sur l’écran quand la notation d’ingénierie est validée.
Vous pouvez utiliser les symboles suivants pour convertir les valeurs en notation d’ingénierie,
3
comme 2.000 (= 2 × 10
E (exa)
P (péta)
T (téra)
G (giga)
M (méga)
k (kilo)
) m 2k.
s 10
s 10
s 10
s 10
s 10
s 10
18
15
12
9
6
3
m (milli)
M (micro) s 10
n (nano)
p (pico)
f (femto)
s 10
s 10
s 10
s 10
–3
–6
–9
–12
–15
• La calculatrice sélectionne automatiquement le symbole d’ingénierie qui fait rentrer la valeur
de la mantisse dans la plage de 1 à 1000 quand la notation d’ingénierie est validée.
4. Calculs de fonctions
I Menus de fonctions
La calculatrice comprend cinq menus de fonctions pour l’accès aux fonctions scientifiques qui
ne sont pas indiquées sur le clavier.
• Le contenu de chaque menu de fonctions varie selon le mode que vous avez choisi sur le
menu principal avant d’avoir appuyé sur la touche *. Les exemples suivants indiquent les
menus de fonctions qui apparaissent dans le mode RUN • MAT ou PRGM.
2-11
Page 51

S Calculs hyperboliques (HYP) [OPTN]-[HYP]
• {sinh}/{cosh}/{tanh} ... {sinus}/{cosinus}/{tangente} hyperbolique
• {sinh
–1
}/{cosh–1}/{tanh–1} ... {sinus}/{cosinus}/{tangente} hyperbolique inverse
S Calculs de probabilité/répartition (PROB) [OPTN]-[PROB]
x!} ... {appuyez après avoir saisie une valeur pour obtenir la factorielle de cette valeur}
• {
nPr}/{nCr} ... {permutation}/{combinaison}
• {
• {RAND} ... {génération de nombre aléatoire}
• {Ran#}/{Int}/{Norm}/{Bin}/{List} ... {génération de nombre réel aléatoire (0 à 1)}/
{génération de nombre entier aléatoire}/{génération de nombre aléatoire conforme
à une distribution normale basée sur la moyenne
nombre aléatoire conforme à une distribution binomiale basée sur le nombre d’essais
et la probabilité
dans ListAns}
p}/{génération de nombre réel aléatoire (0 à 1) et stockage des résultats
μ et l’écart-type σ}/{génération de
n
• {P(}/{Q(}/{R(} ... calcul de la valeur {P(
t(} ... {valeur de la variante réduite t(x)}
• {
t)}/{Q(t)}/{R(t)} avec la loi normale centrée réduite
S Calculs numériques (NUM) [OPTN]-[NUM]
• {Abs} ... {sélectionnez cette rubrique et entrez une valeur pour obtenir la valeur absolue de
cette valeur}
• {Int}/{Frac} ... sélectionnez le paramètre et saisissez une valeur pour extraire la partie
{entière}/{fractionnaire}
• {Rnd} ... {arrondit la valeur utilisée pour les calculs internes à 10 chiffres significatifs (en
fonction de la valeur enregistrée dans la mémoire de dernier résultat), ou au nombre de
décimales (Fix) et au nombre de chiffres significatifs (Sci) que vous avez définis}
• {Intg} ... {sélectionnez ce paramètre et saisissez une valeur pour obtenir le plus grand entier
qui n’est pas supérieur à cette valeur}
• {RndFi} ... {arrondit la valeur utilisée pour les calculs internes aux chiffres spécifiés (0 à 9)
(voir page 2-2).}
• {GCD} ... {le plus grand commun diviseur de deux valeurs}
• {LCM} ... {le plus petit commun multiple de deux valeurs}
• {MOD} ... {reste d’une division (le reste obtenu quand
•
• {MOD
E} ... {reste d’une division sur une valeur de puissance (le reste obtenu quand n est
élévé à la puissance p et ensuite divisé par m)}
n est divisé par m)}
S Unités d’angle, conversion de coordonnées, opérations en notation
sexagésimale (ANGL)
• {°}/{r}/{g} ... {degré}/{radian}/{grade} pour une valeur saisie particulière
• {° ’ ”} ... {définit les degrés (heures), minutes, secondes lors de la saisie de valeurs
exprimées en degrés, minutes ou secondes}
• {
• Les opérations de menus {
• {Pol(}/{Rec(} ... conversion de coordonnées {rectangulaires en polaires}/{polaires en
} ... {convertit la valeur décimale en degrés/minutes/secondes}
° ’ ”
} ne sont disponibles que si un résultat de calcul est affiché.
° ’ ”
rectangulaires}
2-12
[OPTN]-[ANGL]
Page 52

• {DMS} ... {convertit une valeur décimale en valeur sexagésimale}
S Symbole d’ingénierie (ESYM) [OPTN]-[ESYM]
• {m}/{
μ}/{n}/{p}/{f} ... {milli (10
• {k}/{M}/{G}/{T}/{P}/{E} ... {kilo (10
{exa (10
18
)}
–3
)}/{micro (10–6)}/{nano (10–9)}/{pico (10
3
)}/{méga (106)}/{giga (109)}/{téra (1012)}/{péta (1015)}/
• {ENG}/{ENG} ... déplace la virgule des décimales de la valeur affichée de trois chiffres vers
la {gauche}/{droite} et {réduit}/{augmente} l’exposant de trois.
Quand vous utilisez la notation d’ingénierie, le symbole d’ingénierie change en
conséquence.
• Les opérations de menus {ENG} et {ENG} ne sont disponibles que si un résultat de calcul
est affiché.
–12
)}/{femto (10
–15
)}
I Unités d’angle
• Veillez à spécifier Comp pour Mode sur l’écran de configuration.
Exemple Opération
Convertir 4,25 radians en degrés:
243,5070629
47,3° + 82,5rad = 4774,20181°
2°20´30˝ + 39´30˝ = 3°00´00˝
K(SET UP)AAAAAA(Deg))
4.25*(E)(ANGL)(r)U
47.382.5*(E)(ANGL)(r)U
2*(E)(ANGL)(° ’ ”) 20(° ’ ”) 30
(° ’ ”)0(° ’ ”)39(° ’ ”) 30(° ’ ”)U
2,255° = 2°15´18˝
(
2.255*(E)(ANGL)(E)(DMS)U
° ’ ”
)
I Fonctions trigonométriques et trigonométriques inverses
• Toujours régler l’unité d’angle avant d’effectuer des calculs de fonction trigonométrique et de
fonction trigonométrique inverse.
(90° = ––– radians = 100 grades)
(90° = ––– radians = 100 grades)
2
2
• Veillez à spécifier Comp pour Mode sur l’écran de configuration.
Exemple Opération
cos (
2
rad) = 0,5
3
•
sin 45° s cos 65° = 0,5976724775
K(SET UP)AAAAAA(Rad))
A(P)3U
K(SET UP)AAAAAA(Deg))
2Q45A65U*
Asn 0,5 = 30°
Q(Asn) 0.5*
(x quand sinx = 0,5)
1
peut être omis.
*
2
*
La saisie du zéro initial n’est pas nécessaire.
2-13
2
U
1
Page 53

I Fonctions logarithmiques et exponentielles
• Veillez à spécifier Comp pour Mode sur l’écran de configuration.
Exemple Opération
log 1,23 (log
log
8 = 3
2
4
= (–3) s (–3) s (–3) s (–3) = 81
(–3)
7
123 (= 123
1,23) = 0,08990511144
10
1
7
) = 1,988647795
J1.23U
*(CALC)(E)(log
3,4U
7,(
x
)123U
b) 28U
a
• Les modes d’écriture linéaire et mathématique produisent des résultats différents lorsque
deux puissances ou plus sont entrées en série, telles que : 2 , 3 , 2.
2
3
Mode d’écriture linéaire : 2^3^2 = 64 Mode d’écriture mathématique :
2
= 512
Ceci est dû au fait que, en interne, le mode d’écriture mathématique traite la saisie ci-dessus
dans l’ordre : 2^(3^(2)).
I Fonctions hyperboliques et hyperboliques inverses
• Veillez à spécifier Comp pour Mode sur l’écran de configuration.
Exemple Opération
sinh 3,6 = 18,28545536
*(E)(HYP)(sinh)3.6U
cosh
= 0,7953654612
15
*(E)(HYP)(cosh
20
–1
I Autres fonctions
• Veillez à spécifier Comp pour Mode sur l’écran de configuration.
Exemple Opération
2 + 5 = 3,65028154
2
= (–3) s (–3) = 9
(–3)
8! (= 1 s 2 s 3 s .... s 8) = 40320
Quelle est la partie entière de –3,5?
V()2V()5U
3VU
8*(E)(PROB)(
*(E)(NUM)(Int)3.5U
–3
I Génération de nombres aléatoires (RAND)
–1
)2015U
x!)U
S Génération de nombre réel aléatoire (entre 0 et 1) (Ran#, RanList#)
Ran# et RanList# génèrent des nombres réels aléatoires de 10 chiffres significatifs entre 0 et
1, soit de façon aléatoire ou de façon séquentielle. Ran# retourne un nombre aléatoire unique,
tandis que RanList# retourne des nombres aléatoires multiples sous forme de liste. Les lignes
suivantes montrent les syntaxes de Ran# et de RanList# :
2-14
Page 54

Ran# [a] 1
a 9
RanList# (n [,a]) 1
•
n correspond au nombre d’essais. RanList# génère la quantité de nombres aléatoires
spécifiée par
valeur pour
• «
a » correspond à la séquence de répartition aléatoire. Si « a » n’est pas spécifiée, la
fonction retourne des nombres aléatoires. En spécifiant «
fonction retourne le nombre aléatoire séquentiel correspondant.
• L’exécution de la fonction Ran# 0 entraîne l’initialisation des séquences des deux fonctions,
aussi bien de Ran# que de RanList#. La séquence est initialisée aussi quand on utilise Ran#
ou RanList#, lors de la génération d’un nombre aléatoire séquentiel avec une séquence
différente à celle de l’exécution précédente ou bien quand on génère un nombre aléatoire.
Exemples de Ran#
Ran#
(Génère un nombre aléatoire.)
(A chaque pression sur U, un nouveau
nombre aléatoire est généré.)
n et affiche l’ensemble dans l’écran ListAns. Il est obligatoire d’entrer une
n.
Exemple Opération
n 999
a » par un entier entre 1 et 9, la
*(E)(PROB)(RAND)
(Ran#)U
U
U
Ran# 1
(Génère le premier nombre aléatoire de la
séquence 1.)
(Génère le second nombre aléatoire de la
séquence 1.)
Ran# 0
(Initialise la séquence.)
Ran# 1
(Génère le premier nombre aléatoire de la
séquence 1.)
Exemples de RanList#
Exemple Opération
RanList# (4)
(Génère quatre nombres aléatoires et affiche
le résultat dans l’écran ListAns.)
*(E)(PROB)(RAND)
(Ran#) 1U
U
(Ran#) 0U
(Ran#) 1U
*(E)(PROB)(RAND)(List) 4
U
RanList# (3, 1)
(Génère les trois premiers nombres
aléatoires, du premier au troisième, de la
séquence 1 et affiche le résultat dans l’écran
ListAns.)
(Ensuite, génère les trois nombres aléatoires
suivants, du quatrième au sixième, de la
séquence 1 et affiche le résultat dans l’écran
ListAns.)
2-15
)*(E)(PROB)(RAND)
(List) 31U
)U
Page 55

Ran# 0
(Initialise la séquence.)
)(Ran#) 0U
RanList# (3, 1)
(Régénère les trois premiers nombres
aléatoires, du premier au troisième, de la
séquence 1 et affiche le résultat dans l’écran
ListAns.)
(List) 31U
S Génération de nombres entiers aléatoires (RanInt#)
RanInt# génère des nombres entiers aléatoires appartenant à l’intervalle entre deux nombres
entiers spécifiés.
RanInt# (A, B [,n]) A < B |A|,|B| < 1
• A correspond à la valeur initiale et B à la valeur finale de l’intervalle. L’omision de la valeur
n provoque la génération et le retour d’un nombre aléatoire unique. La spécification de la
de
valeur de n provoque le retour du nombre spécifié de valeurs aléatoires sous forme de liste.
Exemple Opération
RanInt# (1, 5)
(Génère un nombre entier aléatoire entre 1
et 5.)
E10 B – A < 1E10 1 n 999
*(E)(PROB)(RAND)(Int) 1
5U
RanInt# (1, 10, 5)
(Génère cinq nombres entiers aléatoires
entre 1 et 10 et affiche le résultat dans
l’écran ListAns.)
*(E)(PROB)(RAND)(Int) 1
105U
S Génération de nombres aléatoires suivant une distribution normale
(RanNorm#)
Cette fonction génère un nombre aléatoire de 10 chiffres significatifs en conformité avec une
distribution normale basée sur les valeurs d’une moyenne μ et d’un écart-type σ spécifiés.
RanNorm# (
• L’omision de la valeur de
La spécification de la valeur de
sous forme de liste.
RanNorm# (8, 68)
(Produit de façon aléatoire la valeur d’une
taille corporelle qui suit une distribution
normale de la taille corporelle dans un
groupe d’enfants de moins d’un an avec une
moyenne de 68 cm et un écart-type de 8.)
σ, μ [,n]) σ > 0 1 n 999
n provoque la génération et le retour d’un nombre aléatoire unique.
n provoque le retour du nombre spécifié de valeurs aléatoires
Exemple Opération
*(E)(PROB)(RAND)(Norm)
868U
RanNorm# (8, 68, 5)
(Produit de façon aléatoire les tailles
corporelles de cinq enfants de l’exemple cidessus et affiche les résultats dans une liste.)
2-16
*(E)(PROB)(RAND)(Norm)
8685U
Page 56

S Génération de nombres aléatoires suivant une distribution binomiale
(RanBin#)
Cette fonction génère des nombres entiers aléatoires en conformité avec une distribution
binomiale basée sur les valeurs spécifiés du nombre d’essais n et de la probabilité p.
RanBin# (n, p [,m]) 1
• L’omision de la valeur de
unique. La spécification de la valeur de m provoque le retour du nombre spécifié de valeurs
aléatoires sous forme de liste.
Exemple Opération
RanBin# (5, 0,5)
(Produit de façon aléatoire le nombre
de « faces » qu’on peut espérer de cinq
tirages « pile ou face », en conformité avec
la distribution binomiale où la probabilité
d’obtenir « face » est de 0,5.)
RanBin# (5, 0,5, 3)
(Effectue trois fois la même séquence de
tirages de l’exemple précédent et affiche les
résultats dans une liste.)
n 100000 1 m 999 0 p 1
m provoque la génération et le retour d’un nombre aléatoire
I Conversion de coordonnées
*(E)(PROB)(RAND)(Bin) 5
0.5U
*(E)(PROB)(RAND)(Bin) 5
0.53U
S Coordonnées rectangulaires S Coordonnées polaires
• Avec les coordonnées polaires, θ peut être calculé et affiché dans une plage de
–180°< θ 180° (les radians et les grades ont la même plage).
• Veillez à spécifier Comp pour Mode sur l’écran de configuration.
Exemple Opération
Calculer
1 24,98924,98979792 (r)
1 24,98924,98979792 (r)
2 55,928 55,92839019 ( )
2 55,928 55,92839019 ( )
Calculer
1 13,97913,97982259 (x)
1 13,97913,97982259 (x)
2 20,725 20,72593931 (y)
2 20,725 20,72593931 (y)
r et θ° lorsque x = 14 et y = 20,7
x et y lorsque r = 25 et θ = 56°
K(SET UP)AAAAAA
(Deg))
*(E)(ANGL)(E)(Pol()
1420.7U)
(Rec() 2556U
2-17
Page 57

I Permutation et combinaison
S Permutation S Combinaison
n
n
!
=
=
!
n–r
n–r
nCr
)!
)!
nCr
nPr
nPr
(
(
• Veillez à spécifier Comp pour Mode sur l’écran de configuration.
Exemple 1 Calculer le nombre possible d’arrangements différents quand 4
éléments sont sélectionnés parmi 10 éléments
Formule Opération
=
=
r!(n–r
r!(n–r
n
n
!
!
)!
)!
10P4 = 5040
10*(E)(PROB)(
nPr) 4U
Exemple 2 Calculer le nombre possible de combinaisons différentes de 4 éléments
qu’on peut sélectionner parmi 10 éléments
Formule Opération
10C4 = 210
10*(E)(PROB)(
nCr) 4U
I Plus grand commun diviseur (GCD), plus petit commun multiple (LCM)
Exemple Opération
Pour déterminer le plus grand commun
diviseur de 28 et 35
(GCD (28, 35) = 7)
Pour déterminer le plus petit commun
multiple de 9 et 15
(LCM (9, 15) = 45)
*(E)(NUM)(E)(GCD) 2835
U
*(E)(NUM)(E)(LCM) 915
U
I Reste d’une division (MOD), reste d’une division exponentielle (MOD
Exp)
Exemple Opération
Pour déterminer le reste de la division de
137 par 7
(MOD (137, 7) = 4)
Pour déterminer le reste de la division de
3
5
par 3
(MOD • E (5, 3, 3) = 2)
*(E)(NUM)(E)(MOD) 1377
U
•
*(E)(NUM)(E)(MOD
E) 53
3U
2-18
Page 58

I Fractions
–
–
–
–
• Dans le mode d’écriture mathématique, la méthode de saisie des fractions est différente de
celle décrite ci-dessous. Pour consulter les opérations de saisie de fractions dans le mode
d’écriture mathématique, voir page 1-11.
• Veillez à spécifier Comp pour Mode sur l’écran de configuration.
Exemple Opération
2 1 73
–+3––=––
5 4 20
= 3,65 (Conversion en valeur décimale)*
1 1
–––– + –––––
2578 4572
1
s 0,5 = 0,25*
–
2
1
*
Les fractions peuvent être converties en valeurs décimales et vice versa.
2
*
Lorsque le nombre total de caractères, y compris le nombre entier, le numérateur, le
= 6,066202547 s 10
3
–4 *2
25314U
1
,
1257814572U
12.5U
dénominateur et le séparateur, dépasse 10, la fraction est automatiquement convertie en
décimale.
3
Les calculs contenant à la fois des fractions et des décimales sont effectués sous forme
*
décimale.
• Pour permuter entre la notation anglo-saxonne et la notation française, il faut appuyer sur les
touches ,(
).
I Calculs en notation d’ingénierie
Introduisez les symboles d’ingénierie sur le menu de notation d’ingénierie.
• Veillez à spécifier Comp pour Mode sur l’écran de configuration.
Exemple Opération
999k (kilo) + 25k (kilo)
= 1,024M (méga)
9 w 10 = 0,9 = 900m (milli)
= 0,9
= 0,0009k (kilo)
= 0,9
= 900m
K(SET UP)DD(Eng))999*(E)(E)
(ESYM)(E)(k)25(k)U
910U
*(E)(E)(ESYM)(E)(E)(ENG)*
(ENG)*
(ENG)*
(ENG)*
1
2
2
1
*1 Convertit la valeur affichée à l’unité ingénieur supérieure suivante, en déplaçant la virgule
décimale de trois unités vers la droite.
2
*
Convertit la valeur affichée à l’unité ingénieur inférieure suivante, en déplaçant la virgule
décimale de trois unités vers la gauche.
2-19
Page 59

I Opérateurs logiques (AND, OR, NOT, XOR) [OPTN]-[LOGIC]
Le menu Opérateur logique fournit une sélection d’opérateurs logiques.
• {And}/{Or}/{Not}/{Xor} ... {op. logique AND}/{op. logique OR}/{op. logique NOT}/{op. logigue
XOR}
• Veillez à spécifier Comp pour Mode sur l’écran de configuration.
Exemple Quel est l’opérateur logique AND de A et B lorsque A = 3 et B = 2 ?
A AND B = 1
Opération Affichage
3??T(A)U
2??J(B)U
?T(A)*(E)(E)
(LOGIC)(And)?J(B)U
S A propos des opérations logiques
• Une opération logique produit toujours un résultat de 0 ou 1.
1
• La table suivante montre tous les résultats possibles produits par les opérateurs AND, OR et
XOR.
Valeur ou expression A Valeur ou expression B A AND B A OR B A XOR B
A x 0B x 0
A x 0
A = 0
A = 0 B = 0 0 0 0
• La table suivante montre les résultats produits par l’opérateur NOT.
Valeur ou expression A NOT A
A x 0
A = 0 1
B = 0 0 1 1
B x 0
0
110
011
5. Calculs numériques
Ce qui suit explique les opérations de calcul numérique comprises dans le menu de fonctions
affiché quand vous appuyez sur *(CALC). On peut effectuer les calculs suivants :
• {Int÷}/{Rmdr}/{Simp} ... {quotient}/{reste}/{simplification}
• {Solve}/{
• {FMin}/{FMax}/{3(}/{log
d/dx}/{d
quadratique}/{intégration}/{solution de fonction f(x)}
logab}
2
/dx2}/{°dx}/{SolvN} ... {solution d’équation}/{différentielle}/{différentielle
b} ... {valeur minimale}/{valeur maximale}/{sommes 3}/{logarithme
a
2-20
Page 60

I Quotient d’entier divisé par entier [OPTN]-[CALC]-[Int÷]
La fonction « Int÷ » peut être utilisée pour déterminer le quotient quand on divise un nombre
entier par un autre entier.
Exemple Calculer le quotient de 107 divisé par 7
@?F*(CALC)(E)(E)
(Int÷)F
U
I Reste d’entier divisé par entier [OPTN]-[CALC]-[Rmdr]
La fonction « Rmdr » peut être utilisée pour déterminer le reste quand on divise un nombre
entier par un autre entier.
Exemple Calculer le reste de 107 divisé par 7
@?F*(CALC)(E)(E)
(Rmdr)F
U
I Simplification [OPTN]-[CALC]-[Simp]
La fonction « Simp » peut être utilisée pour simplifier manuellement des fractions. Les
opérations suivantes peuvent être utilisées pour effectuer des simplifications quand des
résultats non simplifiés sont affichés à l’écran.
• {Simp} U ... Cette fonction simplifie automatiquement le calcul affiché en utilisant le plus
petit nombre premier disponible. Le nombre premier utilisé et le résultat simplifié sont
affichés à l’écran.
• {Simp}
Dans sa configuration initiale de paramètres par défaut, cette calculatrice simplifie
automatiquement les résultats des calculs de fractions avant de les afficher. Avant d’essayer
les exemples suivants, utilisez l’écran de configuration pour changer le paramètre « Simplify »
de « Auto » vers « Manual » (page 1-30).
n U ... Cette fonction effectue la simplification en utilisant le diviseur n spécifié
• Lorsque dans l’écran de configuration le paramètre « Complex Mode » a été spécifié à
i » ou « r
« a+b
l’affichage, même si le paramètre « Simplify » a été spécifié à « Manual ».
• Si vous voulez simplifier les fractions manuellement (Simplify : Manual), assurez vous que
« Real » soit sélectionnée pour le paramètre « Complex Mode ».
Q
», les résultats des calculs de fractions sont toujours simplifiés avant
2-21
Page 61

Exemple 1 Simplifier
@DE?U
*(CALC)(E)(E)(Simp)U
(Simp)U
15
60
15
60
5
==
2014
La valeur « F= » correspond au diviseur.
Exemple 2 Simplifier
AFEBU*(CALC)
(E)(E)(Simp)HU
• Une erreur se produit si la simplification ne peut s’effectuer avec le diviseur spécifié.
• L’exécution de Simp lors de l’affichage d’une valeur que ne peut être simplifiée, retourne la
valeur originale, sans afficher « F= ».
27
en spécifiant le diviseur 9
63
27
63
3
=
7
I Calcul de résolution [OPTN]-[CALC]-[Solve]
La syntaxe requise pour l’utilisation de la fonction de résolution dans un programme est la
suivante.
Solve(
f(x), n, a, b) (a : limite inférieure, b : limite supérieure, n : valeur initiale estimée)
Deux méthodes différentes peuvent être utilisées pour le calcul de résolution : l’affectation
directe et l’introduction d’une table de variables.
Avec l’affectation directe (méthode décrite ici), vous attribuez directement des valeurs aux
variables. Cette méthode est identique à celle qui est utilisée avec la commande de résolution
dans le mode PRGM.
L’introduction d’une table de variables est utilisée avec la fonction de résolution du mode
EQUA. Cette méthode est recommandée pour la saisie de la plupart des fonctions de
résolution ordinaires.
Une erreur « Time Out » se produit lorsqu’il n’y a pas de convergence dans la solution.
Pour le détail sur les calculs de résolution, voir page 4-4.
• Vous ne pouvez pas utiliser une valeur de différentielle quadratique, 3, valeur maximale/
minimale ou une expression de calcul de résolution dans les fonctions ci-dessus.
• Le fait d’appuyer sur pendant le calcul de résolution (lorsque le curseur n’est pas affiché
à l’écran) interrompt le calcul.
2-22
Page 62

I Résolution d’une fonction f(x) [OPTN]-[CALC]-[SolvN]
Vous pouvez utiliser SolvN pour résoudre une fonction
syntaxe de saisie est la suivante :
SolveN (terme partie gauche [= terme partie droite] [, variable] [, limite inférieure, limite
supérieure])
• On peut omettre le terme de la partie droite, la variable, ainsi que les limites inférieures et
supérieures.
• L’expression « terme partie gauche[=terme partie droite] » correspond à l’expression à
résoudre. Les variables supportées vont de A jusqu’à Z,
droite est omis, la résolution est efectuée avec terme partie droite = 0.
• La variable spécifie sur quelle variable dans l’expression doit se porter la résolution (de A à
r,
Q
Z,
de la variable X.
• Les limites inférieure et supérieure spécifient la plage de la solution. Vous pouvez saisir une
valeur ou une expression comme plage.
• Les fonctions suivantes ne peuvent être utilisées dans aucun des arguments.
Solve(,
On peut afficher simultanément dans le format de ListAns les résultats de jusqu’à 10 calculs.
). L’omission de la spécification de la variable à résoudre provoque l’utilisation d’office
2
d
/dx2, FMin(, FMax(, 3(
f(x) en utilisant l’analyse numérique. La
r et
Q
. Quand le terme de la partie
• Quand il n’y a pas de solution, s’affiche le message « No Solution ».
• Le message « More solutions may exist. » (plus de solutions sont possibles.) s’affiche quand
il est possible l’existence d’autres solutions que celles affichées par SolvN.
Exemple Résoudre
*(CALC)(SolvN)
TVDTEU
)
2
x
– 5x – 6 = 0
I Calculs de différentielles [OPTN]-[CALC]-[d/dx]
Pour effectuer des calculs de différentielles, affichez d’abord le menu d’analyse de fonctions,
puis saisissez les valeurs en utilisant la syntaxe suivante.
*(CALC)(
a : point pour lequel la dérivée doit être déterminée, tol : tolérance)
(
d/dx
d/dx
(f
(f
d/dx) f(x)atol
d
d
f
f
(a)
(x)
(x)
a
a
)
)
,
,
dx
dx
(a)
2-23
Page 63

La différentiation pour ce type de calcul est définie par :
f(a
'
'
f (a
f (a
) = lim
) = lim
f(a
–––––––––––––
–––––––––––––
x
x
0
0
A
A
+
+
A
A
x)–f(a
x)–f(a
x
x
A
A
)
)
Dans cette définition, infinitésimal est remplacé par suffisamment petit x, avec la valeur aux
f
'
environs de
'
'
f (a
f (a
(a) calculée par :
x)–f(a
+
+
A
A
x)–f(a
x
x
A
A
f(a
f(a
)
)
–––––––––––––
–––––––––––––
)
)
Afin d’offrir la meilleure précision possible, la machine emploie la différence moyenne pour
réaliser les calculs différentiels.
Exemple Déterminer la dérivée au point
x = 3 pour la fonction y = x
3
+ 4x2 + x – 6,
avec pour tolérance « tol » = 1E – 5
Introduisez la fonction f(x).
*(CALC)(
Indiquez le point
x = a pour lequel vous voulez déterminer la dérivée.
d/dx)T,BCTVTE
B
Indiquez la valeur de tolérance.
@DU
Utilisation d’un calcul différentiel dans une fonction graphique
• L’omission de la valeur de tolérance (tol) lorsque la commande différentielle est utilisée à
l’intérieur d’une fonction graphique simplifie le calcul pour le tracé du graphe. Dans ce cas,
la précision est sacrifiée pour obtenir un tracé plus rapide. La valeur de tolérance est définie
et le graphe est tracé avec la précision que vous obtenez lors de l’exécution d’un calcul
différentiel.
• Vous pouvez aussi omettre le point de dérivée en utilisant la formule de graphe
différentiel suivante: Y2=
d/dx(Y1). Dans ce cas, la valeur de la variable X est utilisée comme
point de dérivée.
Précautions des calculs différentiels
• Dans la fonction f(x), seule X peut être utilisée comme variable dans les expressions. Les
autres variables (A à Z sans X,
cette variable est appliquée au cours du calcul.
• La valeur de tolérance (
tol) et la fermeture de parenthèses peuvent être omises. Si vous
omettez la valeur de tolérance (
comme valeur.
• Indiquez la valeur 1
E–14 ou une valeur supérieure comme tolérance (tol). Une erreur (Time
Out) se produira si aucune solution satisfaisant la valeur de tolérance ne peut être obtenue.
r, θ) sont traitées comme constantes, et la valeur affectée à
tol) la calculatrice utilisera automatiquement tol = 1E–10
• Le fait d’appuyer sur pendant le calcul de différentielle (lorsque le curseur n’est pas
affiché à l’écran) interrompt le calcul.
• Les résultats inexacts et les erreurs peuvent être causés par les problèmes suivants :
- Points discontinus dans les valeurs
- Changements extrêmes des valeurs de
x
x
- Inclusion d’un point maximal local et d’un point minimal local dans les valeurs x
- Inclusion d’un point d’inflexion dans les valeurs x
2-24
Page 64

- Inclusion de points non différentiables dans les valeurs x
–
–
f
f
- Résultat de calculs différentiels proche de zéro
• Utilisez toujours le radian (mode Rad) comme unité d’angle pour effectuer des différentielles
trigonométriques.
• Vous ne pouvez pas utiliser d’expression avec calcul de différentielle, différentielle
quadratique, intégration, 3, valeur maximale/minimale, résolution, RndFix ou log
b à
a
l’intérieur d’un terme du calcul différentiel.
• Dans le mode d’écriture mathématique, la tolérance est fixée à 1
E–10 et ne peut pas être
changée.
I Calculs de différentielles quadratiques [OPTN]-[CALC]-[d2/dx
Après avoir affiché le menu d’analyse de fonctions, vous pouvez saisir des différentielles
quadratiques en utilisant la syntaxe suivante.
2
d
*(CALC)(
(
a : point de coefficient différentiel, tol : tolérance)
2
2
d
d
f(x), a
f(x), a
–– (
–– (
2
2
dx
dx
Les calculs de différentielles quadratiques produisent une valeur différentielle approximative
avec la formule de différentielle de second ordre suivante qui se base sur l’interprétation
polynomiale de Newton.
2 f(a + 3h) – 27 f(a + 2h) + 270 f(a + h) – 490 f(a) + 270 f(a – h) – 27 f(a –2h) + 2 f(a – 3h)
''(a) =
''(a) =
2 f(a + 3h) – 27 f(a + 2h) + 270 f(a + h) – 490 f(a) + 270 f(a – h) – 27 f(a –2h) + 2 f(a – 3h)
/dx2) f(x)atol
2
2
d
d
f(a
–––
–––
dx
dx
f(a
)
)
2
2
)
)
180h
180h
2
2
2
]
Dans cette expression, les valeurs pour les « incréments suffisamment petits de
h » sont
utilisées pour obtenir une valeur proche de f"(a).
Exemple Déterminer le coefficient différentiel quadratique au point où
x = 3 pour
la fonction y = x3 + 4x2 + x – 6
Ici nous utiliserons tol = 1E – 5 comme tolérance
Introduisez la fonction f(x).
*(CALC)(
Saisissez 3 comme point
a qui est un point de coefficient différentiel.
2
d
/dx2) T,BCTVTE
B
Indiquez la valeur de tolérance.
@D
U
Précautions des calculs de différentielles quadratiques
• Dans la fonction f(x), seule X peut être utilisée comme variable dans les expressions.
Toutes les autres variables (A à Z sans X, r, θ) sont traitées comme constantes et la valeur
actuellement attribuée à cette variable est utilisée pendant le calcul.
• La valeur de tolérance (
tol) et la fermeture de parenthèses peuvent être omises.
2-25
Page 65

• Indiquez la valeur 1E–14 ou une valeur supérieure comme tolérance (tol). Une erreur (Time
x
x
Out) se produira si aucune solution satisfaisant la valeur de tolérance ne peut être obtenue.
• Les règles valides pour le calcul de différentielle linéaire sont aussi valides lorsqu’un calcul
de différentielle quadratique est utilisé pour la formule d’une courbe (voir page 2-24).
• Les résultats inexacts et les erreurs peuvent être causés par les problèmes suivants :
- Points discontinus dans les valeurs
- Changements extrêmes des valeurs de x
- Inclusion d’un point maximal local et d’un point minimal local dans les valeurs x
- Inclusion d’un point d’inflexion dans les valeurs x
- Inclusion de points non différentiables dans les valeurs x
- Résultat de calculs différentiels proche de zéro
• Vous pouvez interrompre un calcul de différentielle quadratique en cours en appuyant sur la
touche .
• Utilisez toujours les radians (mode Rad) comme unité d’angle quand vous effectuez des
différentielles quadratiques trigonométriques.
• Vous ne pouvez pas utiliser d’expression avec calcul de différentielle, différentielle
quadratique, intégration, 3, valeur maximale/minimale, résolution, RndFix ou log
l’intérieur d’un terme du calcul de différentielle quadratique.
• Dans les calculs de différentielles quadratiques, la précision des calculs est de cinq chiffres
pour la mantisse.
• Dans le mode d’écriture mathématique, la tolérance est fixée à 1
changée.
x
b à
a
E–10 et ne peut pas être
I Calculs d’intégrations [OPTN]-[CALC]-[°dx]
Pour effectuer des calculs d’intégration, affichez d’abord le menu d’analyse de fonctions, puis
entrez les valeurs en utilisant la syntaxe suivante.
*(CALC)(°
: point initial, b : point final,
(
a
f(x),a
f(x),a
dx) f(x) a b tol
tol
b
b
f(x)d
b, tol
b, tol
,
,
)
)
f(x)d
a
a
: tolérance)
Zone calculée par
b
f(x)dx
a
Comme indiqué sur l’illustration ci-dessus, les calculs d’intégration sont exécutés en calculant
les valeurs intégrales de
zone ombrée sur l’illustration est ainsi calculée.
a à b pour la fonction y = f (x) quand a x b et f (x) 0. L’aire de la
2-26
Page 66

Exemple Effectuer un calcul d’intégration pour la fonction indiquée ci-dessous
avec une tolérance de “
5
5
(2x2 + 3x + 4) dx
(2x2 + 3x + 4) dx
1
1
Introduisez la fonction f (x).
tol” = 1E – 4
*(CALC)(°
Indiquez le point initial et le point final.
@D
Indiquez la valeur de tolérance.
@CU
Notez les points suivants pour obtenir de bonnes valeurs d’intégration.
(1) Lorsque les fonctions cycliques pour les valeurs d’intégration deviennent positives ou
négatives pour différentes divisions, effectuez le calcul pour des cycles uniques ou divisez
entre négatif et positif, puis ajoutez les résultats.
Partie
positive (
dx)ATVBTC
)
S
Partie négative (
)
S
b
b
f(x)dx =
f(x)dx =
a
a
Partie positive (S) Partie négative (S)
(2) Lorsque des changements minimes dans les divisions d’intégration donnent des
changements importants dans les valeurs d’intégration, calculez séparément les divisions
d’intégration (divisez les grandes zones de changement en zones plus petites), puis
ajoutez les résultats.
x
x
1
a
a
1
f(x)dx
f(x)dx
b
b
f(x)dx =
f(x)dx =
a
a
• Le fait d’appuyer sur pendant le calcul d’une intégrale (lorsque le curseur n’est pas
affiché à l’écran) interrompt le calcul.
+
+
c
c
f(x)dx
f(x)dx
a
a
x
x
x
x
2
2
f(x)dx
f(x)dx
1
1
+ (–
+ (–
+.....+
+.....+
b
b
f(x)dx
f(x)dx
c
c
x
x
)
)
b
b
f(x)dx
f(x)dx
4
4
• Utilisez toujours le radian (mode Rad) comme unité d’angle pour effectuer des intégrations
trigonométriques.
• Une erreur « Time Out » se produira si aucune solution satisfaisant la valeur de tolérance ne
peut être obtenue.
2-27
Page 67

Précautions des calculs d’intégration
• Dans la fonction f(x), seule X peut être utilisée comme variable dans les expressions. Les
autres variables (A à Z sans X, r, θ) sont traitées comme constantes, et la valeur affectée à
cette variable est utilisée au cours du calcul.
• Il est inutile d’indiquer la valeur «
tol » et de fermer la parenthèse. Si vous n’indiquez pas la
valeur « tol », la calculatrice utilisera automatiquement 1E–5 comme valeur par défaut.
• Les calculs d’intégration peuvent prendre un certain temps.
• Vous ne pouvez pas utiliser d’expression avec calcul de différentielle, différentielle
quadratique, intégration, 3, valeur maximale/minimale, résolution, RndFix ou log
b à
a
l’intérieur d’un terme du calcul d’intégration.
• Dans le mode d’écriture mathématique, la tolérance est fixée à 1
E–5 et ne peut pas être
changée.
I Calculs de sommes 3 [OPTN]-[CALC]-[3(]
Pour effectuer des calculs de 3, affichez d’abord le menu d’analyse de fonctions, puis entrez
les valeurs en utilisant la syntaxe suivante.
*(CALC)(E)(3( )
k
k
,
,
(
,
(
,
a
a
k
k
(
n : distance entre les partitions)
,
,
n
n
)
)
,
,
=
=
k =
k =
k
k
a
a
ak k
+
+
+1
+1
a
a
a
a
=
=
A
B n
+........+
+........+
a
a
Exemple Effectuer le calcul suivant :
6
6
2
2
(
–3k+5)
(
–3k+5)
k
k
k = 2
k = 2
Utilisez
n = 1 comme distance entre les partitions.
*(CALC)(E)(3( )?(K)
VB?(K)D
?(K)AE@U
Précautions des calculs de 3
• La valeur de la variable spécifiée change pendant un calcul de 3. Pensez à noter les valeurs
des variables spécifiées dont vous pouvez avoir besoin plus tard avant d’effectuer un calcul.
• Vous pouvez utiliser seulement une variable dans cette fonction comme suite
A
• Saisissez des nombres entiers seulement pour le terme initial (
) de la suite ak et le dernier
terme (B) de la suite ak.
• La saisie de
calculatrice utilisera automatiquement
• La valeur utilisée comme terme final
n et la fermeture de parenthèses peuvent être omises. Si vous omettez n, la
n = 1.
B
doit être supérieure à la valeur utilisée comme terme
initial A. Sinon, une erreur se produit.
ak.
• Pour interrompre un calcul de 3 en cours (indiqué par l’absence de curseur sur l’écran),
appuyez sur la touche .
• Vous ne pouvez pas utiliser d’expression avec calcul de différentielle, différentielle
quadratique, intégration, 3, valeur maximale/minimale, résolution, RndFix ou log
b à
a
l’intérieur d’un terme du calcul de 3.
2-28
Page 68

• Dans le mode d’écriture mathématique, la distance entre les partitions (n) est fixée à 1 et ne
peut pas être changée.
I Calculs de valeurs maximale/minimale [OPTN]-[CALC]-[FMin]/[FMax]
Après avoir affiché le menu d’analyse de fonctions, vous pouvez effectuer des calculs de
valeurs maximale/minimale en utilisant les formats suivants et trouver le maximum et le
minimum d’une fonction dans un intervalle tel que
S Valeur minimale
*(CALC)(E)(FMin) f (x) a b n
a : point initial de l’intervalle, b : point final de l’intervalle, n : précision (n = 1 à 9))
(
S Valeur maximum
*(CALC)(E)(FMax) f (x) a b n
(
a : point initial de l’intervalle, b : point final de l’intervalle, n : précision (n = 1 à 9))
Exemple Déterminer la valeur minimale dans l’intervalle défini par le pointinitial
a = 0 et point final b = 3, avec une précision n = 6 de la fonction
2
y = x
– 4x + 9
Saisisssez f (x).
a x b.
*(CALC)(E)(FMin)TVCTH
Saisissez l’intervalle
?B
Saisissez la précision
EU
• Dans la fonction
autres variables (A à Z sans X,
cette variable est appliquée au cours du calcul.
• La saisie de
• Les points ou sections discontinus soumis à des grandes fluctuations peuvent affecter la
précision du calcul ou même provoquer une erreur.
• La saisie d’une valeur plus grande pour
temps de calcul requis.
• Le point final de l’intervalle (
Sinon, une erreur se produit.
n et la fermeture de parenthèses peuvent être omises.
a = 0, b = 3.
n = 6.
f
(x), seule X peut être utilisée comme variable dans les expressions. Les
r, θ) sont traitées comme constantes, et la valeur affectée à
n augmente la précision du calcul, mais aussi le
b) doit avoir une valeur supérieure à celle du point initial (a).
• Vous pouvez interrompre un calcul de valeurs maximale/minimale en cours en appuyant sur
la touche .
• Vous pouvez utiliser un entier de 1 à 9 comme valeur de
cette plage cause une erreur.
• Vous ne pouvez pas utiliser d’expression avec calcul de différentielle, différentielle
quadratique, intégration, 3, valeur maximale/minimale, résolution, RndFix ou log
l’intérieur d’un terme du calcul des valeurs maximale et minimale.
2-29
n. L’utilisation d’une valeur hors de
b à
a
Page 69

6. Calculs avec nombres complexes
Vous pouvez effectuer des calculs avec addition, soustraction, multiplication, division, des
calculs de fonctions, parenthèses et des calculs à partir de la mémoire avec les nombres
complexes comme vous le faites avec les calculs manuels décrits aux pages 2-1 à 2-14.
Vous pouvez sélectionner le mode de calcul de nombre complexe en sélectionnant un des
réglages suivants comme paramètre « Complex Mode » sur l’écran de configuration.
• {Real} ... Calcul dans la plage des nombres réels seulement*
• {a+bi} ... Exécution d’un calcul de nombre complexe et affichage des résultats par des
coordonnées rectangulaires
• {
rθ} ... Exécution d’un calcul de nombre complexe et affichage des résultats par des
coordonnées polaires*
*1 Lorsque l’argument contient un nombre imaginaire, cependant, le calcul du nombre
complexe est effectué et le résultat est affiché avec des coordonnées rectangulaires.
Exemples:
i = 0,6931471806 + 1,570796327i
ln 2
ln 2i + ln (– 2) = (Non-Real ERROR)
2
La plage d’affichage de θ dépend de l’unité d’angle désigné sur l’écran de configuration.
*
• Deg ... –180 <
• Rad ... – P <
• Gra ... –200 <
Appuyez sur *(CPLX) pour afficher le menu de calcul de nombre complexe, qui contient
les paramètres suivants.
θ 180
θ P
θ 200
2
1
• {
i} ... {entrée de l’unité imaginaire i}
• {Abs}/{Arg} ... obtention de {la valeur absolue}/{l’argument}
• {Conj} ... {calcul du conjugué}
• {ReP}/{ImP} ... extraction de la partie {réelle d’un nombre}/{imaginaire d’un nombre}
• {rθ}/{a+bi} ... convertit le résultat sous forme {polaire}/{algébrique}
• Vous pouvez aussi utiliser ?(
• Les solutions obtenues par les modes Real,
puissance (xy) lorsque x < 0 et y = m/n quand n est un nombre impair.
x
Exemple: 3
= 1 + 1,732050808i (a+bi)
= 260 (rθ)
• Pour saisir l’opérateur « » dans l’expression à coordonnées polaires (
T().
(–8) = –2 (Réel)
i) au lieu de *(CPLX)(i).
a+bi et rθ sont différentes pour les calculs de
rθ), appuyez sur
I Opérations arithmétiques [OPTN]-[CPLX]-[i]
Les opérations arithmétiques sont les mêmes que celles que vous utilisez dans les calculs
manuels. Vous pouvez même utiliser les parenthèses et la mémoire.
2-30
Page 70

Exemple (1 + 2i) + (2 + 3i)
*(CPLX)
@A(
AB(
i)
i)U
I Inverses, racines carrées et carrés
Exemple (3 + i)
*(CPLX)
V()B(
i)U
I Format de nombres complexes sous forme polaire
Exemple 230 s 345 = 675
K(SET UP)AAAAAA
(Deg)A(
rθ))
AT()B?B
T()CDU
I Valeur absolue (module) et argument [OPTN]-[CPLX]-[Abs]/[Arg]
La machine considère un nombre complexe dans le format
sur un plan de Gauss et calcule la valeur absolue²Z ²et l’argument (arg).
Exemple Calculer la valeur absolue (
i, avec le degré comme unité d’angle
3 + 4
Axe imaginaire
Axe réel
r) et l’argument (θ) pour le nombre complexe
a + bi comme des coordonnées
*(CPLX)(Abs)
BC(
(Calcul de la valeur absolue)
*(CPLX)(Arg)
BC(
(Calcul de l’argument)
i)U
i)U
2-31
Page 71

• Le résultat du calcul de l’argument change selon l’unité d’angle (degré, radian, grade)
sélectionnée.
I Nombres complexes conjugués [OPTN]-[CPLX]-[Conj]
Un nombre complexe de format
Exemple Calculer le nombre complexe conjugué pour le nombre complexe 2 + 4
*(CPLX)(Conj)
AC(
a + bi devient un nombre complexe conjugué de format a – bi.
i)U
I Extraction des parties réelle et imaginaire d’un nombre
[OPTN]-[CPLX]-[ReP]/[lmP]
Utilisez la méthode suivante pour extraire la partie réelle
nombre complexe de format
Exemple Extraire les parties réelle et imaginaire du nombre complexe 2 + 5
*(CPLX)(E)(ReP)
AD(E)(
(Extraction de la partie réelle)
*(CPLX)(E)(ImP)
a + bi.
i)U
a et la partie imaginaire b d’un
i
i
AD(E)(
(Extraction de la partie imaginaire)
i)U
I Forme polaire et transformation sous forme rectangulaire (algébrique)
[OPTN]-[CPLX]-[rθ]/[a+bi]
Procédez de la façon suivante pour transformer un nombre complexe affiché sous forme
rectangulaire en forme polaire, et inversement.
Exemple Transformer la forme rectangulaire du nombre complexe 1 + 3
sa forme polaire
K(SET UP)AAAAAA
(Deg)A(
@V()B
*(CPLX)(
AT()E?
*(CPLX)(E)(
a+bi))
i)(E)(r
a+bi)U
Q
)U
i sous
• La plage d’entrée/sortie des nombres complexes est normalement de 10 chiffres pour la
mantisse et de deux chiffres pour l’exposant.
• Lorsqu’un nombre complexe a plus de 21 chiffres, la partie réelle et la partie imaginaire du
nombre sont affichées sur deux lignes séparées.
2-32
Page 72

• Les fonctions suivantes peuvent être utilisées avec les nombres complexes.
,
ENG, ° ’ ”,
2
x
, x–1, ^(xy), 3, x, In, log, logab, 10x, ex, Int, Frac, Rnd, Intg, RndFix(, Fix, Sci, ENG,
b
,
a +
° ’ ”
/c, d/c
7. Calculs binaire, octal, décimal et hexadécimal avec entiers
Vous pouvez utilisez le mode RUN • MAT et les réglages de système binaire, octal, décimal
et hexadécimal pour effectuer des calculs qui contiennent des valeurs binaires, octales,
décimales et hexadécimales. Vous pouvez aussi convertir les systèmes numériques entre eux
et effectuer des opérations sur les bits.
• Vous ne pouvez pas utiliser de fonctions scientifiques dans les calculs binaires, octaux,
décimaux et hexadécimaux.
• Vous ne pouvez utiliser que des entiers dans les calculs binaires, octaux, décimaux et
hexadécimaux, ce qui signifie que les valeurs fractionnaires ne sont pas admises.
Si vous introduisez une valeur qui comprend une partie décimale, la calculatrice élimenera
automatiquement la partie décimale.
• Si vous essayez d’introduire une valeur invalide pour le système de notation (binaire, octale,
décimale, hexadécimale) utilisé, la calculatrice affichera un message d’erreur. Voici les
chiffres qui peuvent être utilisés dans chaque système de notation.
Binaire : 0, 1
Octale : 0, 1, 2, 3, 4, 5, 6, 7
Décimale : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Hexadécimale : 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
• Les valeurs binaires, octales et hexadécimales négatives sont produites en utilisant le
complément de deux de la valeur d’origine.
• La capacité d’affichage de chacun des systèmes de notation est la suivante.
Système numérique Binaire Octal Décimal Hexadécimal
Capacité d’affichage 16 chiffres 11 chiffres 10 chiffres 8 chiffres
• Les caractères alphabétiques utilisés dans la notation hexadécimale apparaissent
différemment sur l’écran pour les distinguer des caractères de texte.
Texte normal ABCDEF
Valeurs hexadécimales
Touches
• Les plages de calcul pour chacun des systèmes de notation sont les suivantes.
Valeurs binaires
Positive : 0
x 111111111111111
STUVW X
TJ(QAR
Négative : 1000000000000000
Valeurs octales
Positive : 0
Négative : 20000000000
x 17777777777
x 37777777777
x 1111111111111111
2-33
Page 73

Valeurs décimales
Positive : 0
x 2147483647
Négative : –2147483648
Valeurs héxadécimales
Positive : 0
Négative : 80000000
x 7FFFFFFF
x –1
x FFFFFFFF
S Pour effectuer des calculs binaires, octaux, décimaux, ou héxadécimaux
[SET UP]-[Mode]-[Dec]/[Hex]/[Bin]/[Oct]
1. Sur le menu principal, sélectionnez RUN • MAT.
2. Appuyez sur K(SET UP). Appuyez sur A pour surligner « Mode », puis définissez
le système numérique par défaut en appuyant sur (Dec), (Hex), (Bin) ou (Oct)
pour le réglage de Mode.
3. Appuyez sur ) pour changer d’écran pour la saisie du calcul. Un menu de fonctions
apparaît avec les paramètres suivants.
• {d~o}/{LOG}/{DISP} ... menu de {désignation du système numérique}/
{opérations à un bit}/{conversion décimale/hexadécimale/binaire/octale}
I Sélection du système numérique
Vous pouvez spécifier le système décimal, hexadécimal, binaire ou octal sur l’écran de
configuration.
S Pour définir un système numérique pour la saisie d’une valeur seulement
Vous pouvez définir un système numérique pour chaque valeur que vous entrez. Appuyez sur
(d~o) pour afficher un menu de symboles représentant les systèmes numériques. Appuyez
sur la touche de fonction correspondant au symbole que vous voulez sélectionner et indiquez
la valeur souhaitée.
• {d}/{h}/{b}/{o} ... {décimal}/{hexadécimal}/{binaire}/{octal}
S Pour saisir des valeurs dans différents systèmes numériques
Exemple Saisir 12310, quand le système numérique par défaut est le système
hexadécimal
K(SET UP)
Appuyez sur A pour surligner « Mode »,
puis appuyez sur (Hex)).
(d~o)(d)@ABU
I Valeurs négatives et opérations sur les bits
Appuyez sur (LOG) pour afficher un menu de négations ou d’opérateurs des bits.
• {Neg} ... {négation}*
• {Not}/{and}/{or}/{xor}/{xnor} ... {NOT}*2/{AND}/{OR}/{XOR}/{XNOR}*
1
3
2-34
Page 74

*1 complément de deux
2
*
complément de un (complément des bits)
3
*
AND des bits, OR des bits, XOR des bits, XNOR des bits
S Valeurs négatives
Exemple Déterminer la valeur négative de 1100102
K(SET UP)
Appuyez sur A pour surligner « Mode »,
puis appuyez sur (Bin)).
(LOG)(Neg)
@@??@?U
• Les valeurs binaires, octales et hexadécimales négatives sont obtenues en prenant le
complément binaire de deux et en renvoyant le résultat à la base de numération originale.
Dans le cas de la base décimale, les valeurs négatives sont pourvues du signe moins.
S Opérations sur les bits
Exemple Saisir et exécuter « 12016 and AD16 »
K(SET UP)
Appuyez sur A pour surligner « Mode »,
puis appuyez sur (Hex)).
@A?(LOG)
(and) #U
I Transformation du système numérique
Appuyez sur (DISP) pour afficher un menu des fonctions de transformation du système
numérique.
Dec}/{Hex}/{Bin}/{Oct} ... transformation de la valeur affichée en son équivalent
• {
{décimal}/{hexadécimal}/{binaire}/{octal}
S Pour convertir une valeur affichée d’un système numérique dans un autre
Exemple Convertir 2210 (système numérique par défaut) dans sa valeur binaire
ou octale correspondante
K(SET UP)
Appuyez sur A pour surligner « Mode »,
puis appuyez sur (Dec)).
(d~o)(d)AAU
)(DISP)(Bin)U
(Oct)U
2-35
Page 75

8. Calculs matriciels
Depuis le menu principal, accédez au mode RUN • MAT et appuyez (MAT) pour effectuer
des calculs matriciels.
Vous pouvez effectuer les opérations suivantes grâce aux 26 mémoires matricielles (Mat A à
Mat Z) et à la mémoire matricielle de dernier résultat (MatAns).
• Addition, soustraction, multiplication, division
• Calculs de produits des valeurs
• Calculs de déterminant
• Transposition d’une matrice
• Inversion d’une matrice
• Élévation d’une matrice au carré
• Élévation d’une matrice à une puissance
• Calculs de valeur absolue, extraction de la partie entière, extraction de la partie
fractionnaire d’un nombre, nombre entier maximal
• Saisir des nombres complexes dans les éléments d’une matrice et utilisation de fonctions
relatives aux nombres complexes
• Modification de matrices à l’aide des commandes de matrice
Le nombre maximal de lignes pouvant être spécifiées pour une matrice est 999 et le nombre
maximal de colonnes est également 999.
Au sujet de la mémoire matricielle de dernier résultat (MatAns)
• La calculatrice stocke automatiquement les résultats de calculs matriciels dans la mémoire
matricielle. Il faut noter les points suivants concernant la mémoire matricielle de dernier
résultat.
• Quand vous effectuez un calcul avec matrice, le contenu de la mémoire matricielle est
remplacé par le nouveau résultat. Le contenu précédent est effacé et ne peut pas être
récupéré.
• L’introduction de valeurs dans une matrice n’affecte pas le contenu de la mémoire matricielle
de dernier résultat.
I Saisie et édition de calculs matriciels
Appuyez sur (MAT) pour afficher l’écran de l’éditeur de matrices. Utilisez cet écran pour
saisir et éditer des matrices.
None… Aucune matrice définie
• {DEL}/{DEL•A} ... suppression {d’une matrice particulière}/{de toutes les matrices}
• {DIM} ... {définit les dimensions de la matrice (nombre d’éléments)}
m s n … Matrice de m (lignes) s n (colonnes)
2-36
Page 76

S Création d’une matrice
Pour créer une matrice, vous devez définir ses dimensions (sa taille) dans l’éditeur de
matrices. Vous pouvez ensuite introduire des valeurs dans la matrice.
S Pour spécifier les dimensions (la taille) d’une matrice
Exemple Créer une matrice de 2 lignes s 3 colonnes dans la zone nommée Mat B
Mettez Mat B en surbrillance.
A
(DIM) (Cette étape peut être omise.)
Spécifiez le nombre de lignes.
AU
Spécifiez le nombre de colonnes.
BU
U
• Tous les éléments de la nouvelle matrice contiennent la valeur 0.
• Le changement de dimensions d’une matrice aura pour effet d’en supprimer le contenu.
• Si « Memory ERROR » reste à côté du nom de la zone de matrice après l’introduction des
dimensions, c’est que la mémoire n’est pas suffisante pour créer la matrice souhaitée.
S Pour saisir les valeurs d’éléments
Exemple Introduire les données suivantes dans la matrice B :
1 2 3
1 2 3
4 5 6
4 5 6
L’opération suivante est la suite du calcul cité en exemple à la page précédente.
@UAUBU
CUDUEU
(La donnée est introduite dans l’élément
en surbrillance. A chaque pression sur U,
l’élément suivant de droite est mis en
surbrillance.)
• Les valeurs affichées des éléments indiquent des nombres entiers positifs de six chiffres
au maximum et des nombres entiers négatifs de cinq chiffres (un chiffre est utilisé pour le
signe négatif). Les valeurs exponentielles sont indiquées avec au plus deux chiffres pour
l’exposant. Les valeurs fractionnaires ne sont pas affichées.
2-37
Page 77

S Suppression d’une matrice
Vous pouvez supprimer une matrice particulière ou toutes les matrices en mémoire.
S Pour supprimer une matrice particulière
1. Quand l’éditeur de matrices est à l’écran, utilisez D et A pour mettre la matrice que vous
voulez supprimer en surbrillance.
2. Appuyez sur (DEL).
3. Appuyez sur (Yes) pour supprimer la matrice ou sur (No) pour abandonner
l’opération sans rien supprimer.
S Pour supprimer toutes les matrices
1. Quand l’éditeur de matrices est à l’écran, appuyez sur (DEL • A).
2. Appuyez sur (Yes) pour supprimer toutes les matrices de la mémoire ou sur (No)
pour abandonner l’opération sans rien supprimer.
I Opérations sur les éléments d’une matrice
Procédez de la manière suivante pour préparer une matrice avant d’effectuer une opération.
1. Quand l’éditeur de matrices est à l’écran, utilisez D et A pour mettre le nom de la
matrice que vous voulez utiliser en surbrillance.
Vous pouvez sauter à une matrice particulière en indiquant la lettre du nom de la matrice. Si
vous indiquez ?G(N), par exemple, vous sauterez à la matrice N.
Pour accéder la mémoire de matrice, appuyez sur (Ans).
2. Appuyez sur U pour faire apparaître le menu de fonctions contenant les paramètres
suivants.
• {R-OP} ... {menu d’opérations sur les lignes}
• {ROW}
• {DEL}/{INS}/{ADD} ... {suppression}/{insertion}/{addition} de lignes
• {COL}
• {DEL}/{INS}/{ADD} ... {suppression}/{insertion}/{addition} de colonnes
• {EDIT} ... {écran d’édition d’éléments}
Tous les exemples précédents utilisent la matrice A.
S Calculs sur les lignes
Le menu suivant apparaît si vous appuyez sur (R-OP) quand une matrice que vous avez
rappelée est à l’écran.
• {Swap} ... {échange de lignes}
• {sRw} ... {produit des valeurs d’une ligne donnée par un nombre}
• {sRw+} ... {addition du produit des valeurs d’une ligne donnée par un nombre et les valeurs
d’une autre ligne}
• {Rw+} ... {addition d’une ligne désignée et d’une autre ligne}
2-38
Page 78

S Pour échanger deux lignes
Exemple Échanger les lignes deux et trois de la matrice suivante :
Tous les exemples d’opération sont réalisés avec la matrice suivante.
1 2
Matrice A =
(R-OP)(Swap)
Indiquez le numéro des lignes que vous voulez échanger.
AUBUU
3 4
5 6
S Pour calculer le produit des valeurs d’une ligne par un nombre
Exemple Calculer le produit des valeurs de la ligne 2 en multipliant par 4
(R-OP)(sRw)
Indiquez la valeur du multiplicateur.*
CU
Spécifiez le numéro de la ligne.
AUU
* Un nombre complexe peut être saisi aussi en tant que valeur de multiplicateur (k).
S Pour calculer le produit des valeurs d’une ligne par un nombre et ajouter le
résultat à une autre ligne
Exemple Calculer le produit des valeurs de la ligne 2 en multipliant par 4 et
ajouter le résultat à ligne 3
(R-OP)(sRw+)
Indiquez la valeur du multiplicateur.*
CU
Spécifiez le numéro de la ligne dont le produit des valeurs doit être calculé.
AU
Spécifiez le numéro de la ligne dont le résultat doit être ajouté.
BUU
* Un nombre complexe peut être entré aussi en tant que
valeur de multiplicateur (k).
S Pour additionner deux lignes
Exemple Ajouter la ligne 2 à la ligne 3
(R-OP)(Rw+)
Spécifiez le numéro de la ligne que vous ajoutez.
AU
2-39
Page 79

Spécifiez le numéro de la ligne à laquelle vous ajoutez la
première ligne.
BUU
S Opérations sur les lignes
• {DEL} ... {suppression d’une ligne}
• {INS} ... {insertion d’une ligne}
• {ADD} ... {addition d’une ligne}
S Pour supprimer une ligne
Exemple Supprimer la ligne 2
(ROW)A
(DEL)
S Pour insérer une ligne
Exemple Insérer une nouvelle ligne entre les lignes une et deux
(ROW)A
(INS)
S Pour ajouter une ligne
Exemple Ajouter une nouvelle ligne 2 sous la ligne 3
(ROW)AA
(ADD)
S Opérations sur les colonnes
• {DEL} ... {suppression d’une colonne}
• {INS} ... {insertion d’une colonne}
• {ADD} ... {addition d’une colonne}
2-40
Page 80

S Pour supprimer une colonne
Exemple Supprimer la colonne 2
(COL)C
(DEL)
I Modification de matrices à l’aide des commandes de matrice
[OPTN]-[MAT]
S Pour afficher les commandes de matrice
1. Depuis le menu principal, accédez au mode RUN • MAT.
2. Appuyez sur * pour afficher le menu d’options.
3. Appuyez sur (MAT) pour afficher le menu de commandes de matrice.
Vous trouverez ici seulement les paramètres du menu de commandes qui sont utilisés pour la
création d’une matrice et pour l’introduction de données dans cette matrice.
• {Mat} ... {commande Mat (spécification de a matrice)}
• {MmL} ... {Commande MamList (affectation du contenu de la colonne sélectionnée à un
fichier liste)}
• {Aug} ... {commande Augment (liaison de deux matrices)}
• {Iden} ... {commande Identity (entrée de matrice unité)}
• {Dim} ... {commande Dim (contrôle de dimensions)}
• {Fill} ... {commande Fill (valeurs d’éléments identiques)}
• Vous pouvez aussi utiliser A(Mat) au lieu de *(MAT)(Mat).
S Format d’introduction des données dans une matrice [OPTN]-[MAT]-[Mat]
Voici le format que vous devez utiliser quand vous introduisez des données pour créer une
matrice à l’aide de la commande Mat.
a11 a
a11 a
a21 a
a21 a
am1 a
am1 a
...
...
12
12
22
22
...
...
m2
m2
...
...
...
...
... a
... a
a1n
a1n
a2n
a2n
mn
mn
...
...
= [ [a
, a12, ..., a
11
] [a21, a22, ..., a
n
1
] .... [a
n
2
, a
1
, ..., amn] ]
m
2
m
m Mat [lettre de A à Z]
Exemple Introduisez les données suivantes comme matrice A :
( [ )( [ )@BD
( ] )( [ )ACE
( ] )( ] )?*(MAT)
(Mat)?T(A)
U
Nom de la matrice
2-41
1 3 5
1 3 5
2 4 6
2 4 6
Page 81

• La valeur maximale de m et n est 999.
• Une erreur se produit si la mémoire est pleine quand vous introduisez des données.
• Vous pouvez aussi utiliser le format précédent à l’intérieur d’un programme qui introduit des
données de matrice.
S Pour créer une matrice unité [OPTN]-[MAT]-[Iden]
Utilisez la commande Identity pour créer une matrice unité.
Exemple Créer une matrice unité 3 s 3 comme matrice A
*(MAT)(E)(Iden)
B?(E)(Mat)?T(A)U
Nombre de lignes et colonnes
S Pour contrôler les dimensions d’une matrice [OPTN]-[MAT]-[Dim]
Utilisez la commande Dim pour contrôler les dimensions d’une matrice existante.
Exemple 1 Contrôler les dimensions de la matrice A
*(MAT)(E)(Dim)
(E)(Mat)?T(A)U
L’écran montre que la matrice A consiste de deux lignes et trois colonnes.
Puisque le résultat de la commande Dim apparaît sous forme de liste, il est sauvegardé dans
la mémoire ListAns.
Vous pouvez aussi utiliser {Dim} pour définir les dimensions d’une matrice.
Exemple 2 Définir une matrice de 2 lignes et de 3 colonnes pour la matrice B
( H )AB( J )?
*(MAT)(E)(Dim)
(E)(Mat)?J(B)U
S Modification d’une matrice à l’aide des commandes de matrice
Vous pouvez aussi utiliser les commandes de matrice pour affecter des valeurs à une matrice
et rappeler des valeurs d’une matrice existante, remplir tous les éléments d’une matrice
existante par la même valeur, combiner deux matrices en une seule matrice et affecter le
contenu d’une matrice à une liste.
S Pour affecter ou rappeler des valeurs d’une matrice existante
Utilisez le format suivant avec la commande Mat pour spécifier l’élément auquel ou duquel
une valeur sera affectée ou rappelée.
Mat X [
X = nom de la matrice (A à Z, ou Ans)
m, n]
2-42
[OPTN]-[MAT]-[Mat]
Page 82

m = numéro de la ligne
n = numéro de la colonne
Exemple 1 Affecter 10 à l’élément correspondant à la ligne 1 et à la colonne 2 de la
matrice suivante :
1 2
Matrice A =
@??*(MAT)(Mat)
?T(A)( F )@A
( G )U
Exemple 2 Multiplier par 5 la valeur de l’élément correspond à la ligne 2 et à la
colonne 2 de la matrice précédente
*(MAT)(Mat)
?T(A)( F )AA
( G )DU
3 4
5 6
S Pour remplir une matrice par des valeurs identiques et combiner deux
matrices en une seule
Utilisez la commande Fill pour remplir tous les éléments d’une matrice existante par une
valeur identique ou la commande Augment pour combiner deux matrices existantes en une
seule.
[OPTN]-[MAT]-[Fill]/[Aug]
Exemple 1 Remplir tous les éléments de la matrice A par la valeur 3
*(MAT)(E)(Fill)
B(E)(Mat)?T(A)U
(Mat)?T(A)U
Exemple 2 Combiner les deux matrices suivantes :
1
A =
A =
*(MAT)(Aug)
(Mat)?T(A)
(Mat)?J(B)U
• Les deux matrices que vous combinez doivent avoir le même nombre de lignes. Une erreur
se produit si vous essayez de combiner deux matrices qui ont un nombre de lignes différent.
• Vous pouvez utiliser la mémoire matricielle de dernier résultat pour affecter les résultats de
l’entrée précédente et effectuer des changements sur une variable de matrice. Pour ce faire,
utilisez la syntaxe suivante.
Fill (
Augment (Mat
n, Mat
A
)
A
1
2
2
, Mat B) m Mat
B =
B =
3
3
4
4
G
Ici, A, B, et G sont des noms de variables A à Z et n est une valeur quelconque.
L’opération précédente n’affecte pas le contenu de la mémoire matricielle de dernier résultat.
2-43
Page 83

S Pour affecter le contenu d’une colonne à une liste [OPTN]-[MAT]-[MmL]
Utilisez le format suivant avec la commande MatmList pour affecter une colonne à une liste.
Mat m List (Mat X,
X = nom de la matrice (A à Z)
Exemple Affecter le contenu de la colonne 2 de la matrice suivante à la liste 1 :
Matrice A =
*(MAT)(MmL)
(Mat)?T(A)A
?*(LIST)(List)@U
(List)@U
m = numéro de la colonne
n = numéro de la liste
m) m List n
1 2
3 4
5 6
I Calculs matriciels [OPTN]-[MAT]
Utilisez le menu de commandes de matrice pour effectuer des calculs matriciels.
S Pour afficher les commandes de matrice
1. Depuis le menu principal, accédez au mode RUN • MAT.
2. Appuyez sur * pour afficher le menu d’options.
3. Appuyez sur (MAT) pour afficher le menu de commandes de matrice.
Seules les commandes de matrice qui sont utilisées pour les opérations arithmétiques sont
décrites ici.
• {Mat} ... {commande Mat (spécification de la matrice)}
• {Det} ... {commande Det (commande de déterminant)}
• {Trn} ... {commande Trn (commande de transposition de matrice)}
• {Iden} ... {commande Identity (entrée de matrice unité)}
• {Ref} ... {commande Ref (commande de forme échelonnée par rapport aux lignes)}
• {Rref} ... {commande Rref (commande de forme échelonnée réduite par rapport aux
lignes)}
Tous les exemples suivants présupposent que les données matricielles sont déjà enregistrées
dans la mémoire.
S Opérations arithmétiques avec matrices [OPTN]-[MAT]-[Mat]/[Iden]
Exemple 1 Additionner les deux matrices suivantes (matrice A + matrice B) :
1
1
A =
A =
1
1
2 1
2 1
B =
B =
2 3
2 3
2 1
2 1
2-44
Page 84

*(MAT)(Mat)?T(A)
(Mat)?J(B)U
Exemple 2 Multiplier les deux matrices de l’exemple 1 (matrice A s matrice B)
*(MAT)(Mat)?T(A)
(Mat)?J(B)U
• Les deux matrices doivent avoir les mêmes dimensions pour que vous puissiez les
additionner ou les soustraire. Une erreur se produit si vous essayez d’additionner ou de
soustraire des matrices de dimensions différentes.
• Pour la multiplication (matrice 1 s matrice 2) le nombre de colonnes de la matrice 1 doit être
égal au nombre de lignes de la matrice 2, sinon une erreur se produit.
S Déterminant [OPTN]-[MAT]-[Det]
Exemple Obtenir le déterminant de la matrice suivante :
1 2 3
Matrice A =
4 5 6
−1 −2 0
*(MAT)(Det)(Mat)
?T(A)U
• Les déterminants ne peuvent être obtenus que pour les matrices carrées (même nombre de
lignes et de colonnes). Si vous essayez d’obtenir un déterminant pour une matrice qui n’est
pas carrée, une erreur se produira.
• Le déterminant de la matrice 2 s 2 est calculé comme indiqué ci-dessous.
a11a
| A | =
a
21a22
12
=a11a22–a12a
21
• Le déterminant de la matrice 3 s 3 est calculé comme indiqué ci-dessous.
|A| =
a11a12a
a21a22a
a31a32a
13
23
= a11a22a33 + a12a23a31 + a13a21a
33
32
– a
11a23a32
– a12a21a33 – a13a22a
31
S Transposition de matrice [OPTN]-[MAT]-[Trn]
Une matrice est transposée quand ses lignes deviennent les colonnes et ses colonnes
deviennent les lignes.
Exemple Transposer la matrice suivante :
1 2
Matrice A =
3 4
5 6
*(MAT)(Trn)(Mat)
?T(A)U
2-45
Page 85

S Forme échelonnée par rapport aux lignes [OPTN]-[MAT]-[Ref]
Cette commande utilise l’algorithme d’élimination gaussien pour trouver la forme échelonnée
d’une matrice.
Exemple Trouver la forme échelonnée par rapport aux lignes de la matrice
suivante :
1 2 3
1 2 3
Matrice A =
4 5 6
4 5 6
*(MAT)(E)(Ref)
(E)(Mat)?T(A)U
S Forme échelonnée réduite par rapport aux lignes [OPTN]-[MAT]-[Rref]
Cette commande permet de trouver la forme échelonnée réduite d’une matrice.
Exemple Trouver la forme échelonnée réduite par rapport aux lignes de la matrice
suivante :
2 −1 3 19
2 −1 3 19
1 1 −5 −21
Matrice A =
1 1 −5 −21
0 4 3 0
0 4 3 0
*(MAT)(E)(Rref)
(E)(Mat)?T(A)U
• Les calculs de forme échelonnée et de forme échelonnée réduite peuvent ne pas produire
de résultats précis en raison de la chute de chiffres.
S Inversion d’une matrice [x
Exemple Inverser la matrice suivante :
–1
]
1 2
1 2
Matrice A =
3 4
3 4
*(MAT)(Mat)
–1
x
?T(A)(
)U
• Seules les matrices carrées (même nombre de lignes et de colonnes) peuvent être
inversées. Si vous essayez d’inverser une matrice qui n’est pas carrée, une erreur se
produira.
2-46
Page 86

• Une matrice dont le déterminant est égale à zéro ne peut pas être inversée. Si vous essayez
d’inverser une matrice dont le déterminant est égale à zéro, une erreur se produira.
• La précision du calcul est affectée pour les matrices dont le déterminant est proche de zéro.
• Une matrice inversée doit remplir les conditions suivantes.
A A–1 = A–1 A = E =
1 0
0 1
Voici la formule utilisée pour inverser la matrice A en matrice inverse A–1.
a b
c d
1
ad – bc
d–b
–c a
A =
A–1=
Notez que ad – bc x 0.
S Élévation d’une matrice au carré [x
Exemple Élever la matrice suivante au carré :
1 2
1 2
Matrice A =
*(MAT)(Mat)?T(A)VU
3 4
3 4
2
]
S Élévation d’une matrice à une puissance [^]
Exemple Élever la matrice suivante à la puissance 3 :
1 2
1 2
Matrice A =
3 4
3 4
*(MAT)(Mat)?T(A)
,BU
• Pour les calculs matriciels avec puissance, le calcul est possible jusqu’à la puissance de
32766.
S Détermination de la valeur absolue, de la partie entière, de la partie
fractionnaire et de l’entier maximal d’une matrice
Exemple Déterminer la valeur absolue de la matrice suivante :
1 –2
1 –2
Matrice A =
–3 4
–3 4
[OPTN]-[NUM]-[Abs]/[Frac]/[Int]/[Intg]
*(E)(NUM)(Abs)
*(MAT)(Mat)?T(A)U
2-47
Page 87

S Calcul de nombres complexes avec une matrice
Exemple Déterminer la valeur absolue d’une matrice avec les éléments de
nombres complexes suivants :
i
–1 + i 1 +
–1 + i 1 +
Matrice D =
*(E)(NUM)(Abs)
*(MAT)(Mat)?Q(D)U
• Les fonctions de nombres complexes suivantes sont supportées pour les matrices :
i, Abs, Arg, Conjg, ReP, ImP, a+bi, r
Notez, cependant, que « a+bi » et « r Q » ne peuvent être utilisées dans le mode
d’écriture linéaire.
1 + i –2 + 2
1 + i –2 + 2
Précautions des calculs matriciels
i
i
i
Q
• Les déterminants et les matrices inverses sont sujets à erreur à cause des chiffres tronqués.
• Les opérations sur une matrice sont effectuées séparément pour chaque élément, si bien
que les calculs peuvent prendre un temps considérable pour aboutir au résultat.
• La précision de calcul des résultats affichés pour les calculs matriciels est de p1 au chiffre le
moins significatif.
• Si le résultat d’un calcul matriciel est trop long pour entrer dans la mémoire matricielle de
dernier résultat, une erreur se produira.
• Vous pouvez utiliser l’opération suivante pour transférer le contenu de la mémoire matricielle
de dernier résultat dans une autre matrice (ou quand la mémoire de réponse matricielle
contient un déterminant pour une variable).
MatAns m Mat
Ici, A est un nom de variable de A à Z. L’opération précédente n’affecte pas le contenu de la
mémoire matricielle de dernier résultat.
A
9. Calculs de conversion métrique
Vous pouvez convertir des valeurs exprimées dans une unité de mesure vers d’autres unités.
Les unités de mesure sont classées selon les 11 catégories suivantes : Les indicateurs
dans la colonne d’affichage « Nom d’écran » montrent le texte qui s’affiche dans le menu de
fonction de la calculatrice.
Nom d’écran Catégorie Nom d’écran Catégorie Nom d’écran Catégorie
LENG Longueur TMPR Température PRES Pression
AREA Surface VELO Vitesse ENGY Énergie/Travail
VLUM Volume MASS Masse PWR Puissance
TIME Temps FORC Force/Poids
2-48
Page 88

Vous pouvez convertir toute unité d’une catégorie vers une autre unité de la même catégorie.
• Une tentative de conversion d’une unité d’une catégorie (telle que « AREA ») vers une unité
d’une autre catégorie (telle que « TIME ») se traduit par l’erreur « Conversion ERROR ».
• Pour obtenir de l’information sur les unités comprises dans chaque catégorie, voir la « Liste
de commande conversion d’unité » (page 2-50).
I Réalisation d’un calcul de conversion d’unité [OPTN]-[CONV]
Pour effectuer un calcul de conversion d’unité, entrez la valeur que vous allez convertir et les
commandes montrées ci-dessous :
{valeur à convertir}{commande de conversion 1} {commande de conversion 2}
• Utilisez {commande de conversion 1} pour spécifier l’unité à partir de laquelle se fera la
conversion et {commande de conversion 2} pour spécifier l’unité vers laquelle la valeur sera
converti.
• correspond à une commande qui lie les deux commandes de conversion. Cette
commande est toujours disponible sous () dans le menu de conversion.
• Des nombres réels ou une liste qui contient seulement des nombres réels comme éléments
peuvent être utilisés comme valeurs à convertir. Quand les valeurs à convertir sont saisies
dans une liste (ou quand une mémoire de liste est spécifiée), le calcul de conversion est
effectué sur chaque élément de la liste et les résultats du calcul sont retournés en format de
liste (écran ListAns).
• Un nombre complexe ne peut être utilisé comme valeur à convertir. Une erreur se produit,
même si un seul élément d’une liste utilisée comme valeur à convertir contient un nombre
complexe.
Exemple 1 Convertir 50 cm en pouces (inches)
D?*(E)(CONV)(LENG)
D(cm)()(LENG)CA(in)U
Exemple 2 Convertir {175, 162, 180} centimètres en pieds (feet)
( { )@FD@EA
@G?( } )
2
*(E)(CONV)(AREA)A(m
)
()(AREA)B(ha)U
2-49
Page 89

I Liste de commande conversion d’unité
Cat. Nom à l’écran Unité Cat. Nom à l’écran Unité
Longueur
fm fermi
cm
3
centimètre cubique
Å angstrom mL millilitre
M
m
mm millimètre m
cm centimètre in
m mètre ft
micromètre L litre
3
3
3
mètre cubique
pouce cubique
pied cubique
km kilomètre fl_oz(UK) once (Royaume Uni)
AU unité astronomique fl_oz(US)
l.y. année-lumière gal(US) gallon (États Unis)
Volume
once liquide
(États Unis)
pc parsec gal(UK) gallon (Royaume Uni)
Mil 1/1000 pouce pt chopine (pint)
in pouce (inch) qt pinte (quart)
ft pied (foot) tsp
cuillère à thé
(teaspoon)
Surface
yd verge (yard) tbsp
cuillerée à table
(tablespoon)
fath brasse (fathom) cup tasse (cup)
rd perche (rod)
mile mille terrestre
n mile
2
cm
2
m
ha hectare h heure
2
km
2
in
2
ft
2
yd
mille marin
(nautical mile)
centimètre carré s seconde
mètre carré min minute
Temps
kilomètre carré day jour
pouce carrée week semaine
pied carré yr année
verge carrée s-yr année sidérale
ns nanoseconde
M
s
microseconde
ms milliseconde
acre acre t-yr année tropique
mile
2
mille terrestre carrée
2-50
Page 90

Cat. Nom à l’écran Unité Cat. Nom à l’écran Unité
Température
Vitesse
°C degrés Celsius
Pa Pascal
K degrés Kelvin kPa kilo Pascal
°F degrés Fahrenheit mmH
O millimètre d’eau
2
°R degrés Rankine mmHg millimètre de Mercure
m/s mètre par seconde atm atmosphère
km/h kilomètre par heure inH
O pouce d’eau
2
Pression
knot noeud (knot) inHg pouce de Mercure
ft/s pied par seconde lbf/in
2
livre par pouce carrée
mile/h mille par heure bar bar
u
unité de masse
atomique
mg milligramme
kgf/cm
2
eV électron-Volt
kilogramme de force
par centimètre carré
g gramme J Joule
kg kilogramme cal
th
calorie
th
Masse
Force/ Poids
mton tonne métrique cal
oz once (avoirdupois) cal
lb
slug
ton(short)
ton(long)
livre de masse
(pound mass)
barreau de
combustible
tonne courte
(2000lbm)
tonne anglaise
(2240lbm)
Énergie/ Travail
15
IT
kcal
th
kcal
15
kcal
IT
l-atm litre atmosphère
calorie (15°C)
calorie
kilocalorie
kilocalorie (15°C)
kilocalorie
N newton kW•h kilowatt heure
•
lbf livre de force ft
lbf pied-livre (foot-pound)
unité thermique
tonf tonne de force Btu
(Royaume Uni)
(British thermal unit)
dyne dyne erg erg
IT
th
IT
kgf kilogramme de force kgf
2-51
•
m
kilogramme de force
mètre
Page 91

Cat. Nom à l’écran Unité
W watt
/s calorie par seconde
cal
th
cheval de vapeur
(horsepower)
pied-livre par
seconde
Puissance
ft
hp
•
lbf/s
Unité thermique par
Btu/min
minute (Royaume
Uni)
Source: NIST Special Publication 811 (1995)
(N. d. T. : Office de la langue française)
2-52
Page 92

Chapitre 3 Listes
Une liste est un lieu de stockage de données multiples.
Cette calculatrice peut contenir au maximum 6 fichiers de 26 listes chacun. Les listes pourront être
utilisées dans des calculs arithmétiques et statistiques ou pour le graphisme.
Numéro d’élément Plage d’affichage Elément Colonne
List 1 List 2 List 3 List 4 List 5 List 26
List 1 List 2 List 3 List 4 List 5 List 26
SUB
SUB
1
1
2 37 2 75 6 0 0
2 37 2 75 6 0 0
3 21 4 122 2.1 0 0
3 21 4 122 2.1 0 0
4 69 8 87 4.4 2 0
4 69 8 87 4.4 2 0
5 40 16 298 3 0 0
5 40 16 298 3 0 0
648 32 48 6.8 3 0
648 32 48 6.8 3 0
7 93 64 338 2 9 0
7 93 64 338 2 9 0
8 30 128 49 8.7 0 0
8 30 128 49 8.7 0 0
•
•
•
•
•
•
• •••••
• •••••
56 1 107 3.5 4 0
56 1 107 3.5 4 0
••••••
••••••
••••••
••••••
••••••
••••••
•
•
Nom de la
liste
Nom
secondaire
Ligne
1. Saisie et édition d’une liste
Lorsque vous accédez au mode STAT, l’éditeur de liste apparaît en premier. Vous pouvez
l’utiliser pour saisir des données dans une liste et utiliser les données de la liste dans diverses
opérations.
3
S Pour introduire des valeurs une à une
Utilisez les touches du pavé directionnel pour mettre la
surbrillance sur le nom, le nom secondaire ou l’élément
de la liste que vous voulez sélectionner. Notez que A ne
déplace pas le surlignage sur un élément ne contenant pas
de valeur.
L’écran défile automatiquement quand la surbrillance atteint l’une ou l’autre extrémité de
l’écran.
Dans l’opération suivante, on part de l’élément 1 de la liste 1, qui a été mis en surbrillance.
1. Saisissez une valeur et appuyez sur U pour la stocker
dans la liste.
BU
• La surbrillance va automatiquement sur l’élément
suivant.
2. Saisissez la valeur 4 dans le second élément, puis le
résultat de 2 + 3 dans l’élément suivant.
CUABU
3-1
Page 93

• Vous pouvez aussi introduire le résultat d’une expression ou un nombre complexe dans un
élément.
• Des valeurs peuvent être écrites dans 999 éléments d’une seule liste au maximum.
S Pour saisir une série de valeurs simultanément
1. Utilisez les touches du pavé directionnel pour amener la
surbrillance sur une autre liste.
2. Appuyez sur ( { ), puis entrez vos valeurs, en
appuyant sur entre chacune d’elles. Appuyez sur
( } ) après avoir saisi la dernière valeur.
( { )EFG( } )
3. Appuyez sur U pour stocker toutes les valeurs dans
votre liste.
U
• Souvenez-vous qu’une virgule sépare des valeurs. Il ne faut donc pas mettre de virgule
après la dernière valeur.
bon : {34, 53, 78}
Mauvais : {34, 53, 78,}
Vous pouvez aussi utiliser des noms de listes dans une expression mathématique pour
introduire des valeurs dans un autre élément. L’exemple suivant indique comment ajouter les
valeurs de chaque ligne des listes 1 et 2, et comment transférer le résultat dans la liste 3.
1. Utilisez les touches du pavé directionnel pour amener
la surbrillance sur le nom de la liste où vous voulez
introduire le résultat du calcul.
2. Appuyez sur la touche * et introduisez l’expression.
*(LIST)(List)@
*(LIST)(List)AU
• Vous pouvez aussi utiliser @(List) au lieu de *(LIST)(List).
I Édition des valeurs d’une liste
S Pour changer la valeur d’un élément
Utilisez les touches du pavé directionnel pour amener la surbrillance sur l’élément dont vous
voulez changer la valeur. Introduisez la nouvelle valeur et appuyez sur U pour remplacer
l’ancienne valeur par la nouvelle.
3-2
Page 94

S Pour éditer la valeur d’un élément
1. Utilisez les touches du pavé directionnel pour amener la surbrillance sur l’élément dont vous
voulez éditer le contenu.
2. Appuyez sur (E)(EDIT).
3. Changez les données souhaitées.
S Pour supprimer un élément
1. Utilisez les touches du pavé directionnel pour amener la surbrillance sur l’élément que vous
voulez effacer.
2. Appuyez sur (E)(DEL) pour supprimer l’élément sélectionné et faire remonter toutes
les valeurs qui se trouvent en dessous.
• La suppression d’un élément n’affecte pas les éléments des autres listes. Si la donnée de
la liste dont vous avez supprimé un élément est en relation avec des données de listes
voisines, la suppression d’un élément peut causer un mauvais alignement des valeurs
correspondantes.
S Pour supprimer tous les éléments d’une liste
Procédez comme suit pour supprimer toutes les données d’une liste.
1. Utilisez les touches du pavé directionnel pour amener la surbrillance sur un élément
quelconque de la liste dont vous voulez supprimer les données.
2. En appuyant sur (E)(DEL
3. Appuyez sur (Yes) pour supprimer tous les éléments de la liste sélectionnée ou sur
(No) pour abandonner l’opération sans rien supprimer.
•
A) un message de confirmation apparaît.
S Pour insérer un nouvel élément
1. Utilisez les touches du pavé directionnel pour amener la surbrillance à l’endroit où vous
voulez insérer un nouvel élément.
2. Appuyez sur (E)(INS) pour insérer un nouvel élément, qui contient la valeur 0. Tout
ce qui se trouve en dessous est décalé vers le bas.
• L’insertion d’un élément n’affecte pas les éléments des autres listes. Si la donnée de la
liste où vous avez inséré un élément est en relation avec des données de listes voisines,
l’insertion d’un élément peut être à l’origine d’un mauvais alignement des valeurs
correspondantes.
I Désignation d’une liste
Vous pouvez désigner les listes 1 à 26 par des « noms secondaires » de huit octets chacun.
S Pour désigner une liste
1. Accédez à l’écran de configuration, surlignez « Sub Name » et appuyez sur (On)).
3-3
Page 95

2. Utilisez les touches du pavé directionnel pour déplacer le surlignement sur la cellule SUB
de la liste que vous voulez désigner.
3. Tapez le nom et appuyez sur U.
• Pour taper un nom avec les caractères alphabétiques, appuyez sur ? pour accéder
au mode ALPHA-LOCK.
Exemple: YEAR
(Y)A(E)T(A)E(R)U
•
• Pour afficher un nom secondaire dans le mode RUN
suivantes.
@(List)
n = numéro de liste de 1 à 26)
(
• Bien qu’un nom secondaire de 8 octets puisse être saisi, seuls les caractères rentrant dans
la cellule de l’éditeur de liste apparaîtront.
• La cellule SUB de l’éditeur de liste n’apparaît pas lorsque « Off » est sélectionné pour « Sub
Name » sur l’écran de configuration.
n( [ )?( ] )U
MAT, effectuez les opérations
I Tri des valeurs d’une liste
Les valeurs d’une liste peuvent être triées par ordre ascendant ou descendant. La surbrillance
peut se trouver sur n’importe quel élément de la liste.
S Pour trier une seule liste
Ordre ascendant
•
1. Lorsque les listes sont affichées, appuyez sur (E)(TOOL)(SRT
2. Le message « How Many Lists?: » apparaît pour vous demander combien de listes vous
voulez trier. Nous indiquons ici 1 car une seule liste doit être triée.
@U
3. Répondez au message « Select List List No: » en indiquant le numéro de la liste qui doit
être triée.
@U
3-4
A).
Page 96

Ordre descendant
Procédez de la même façon que pour le tri dans l’ordre ascendant. Mais vous devez appuyer
sur (SRT
•
D) à la place de (SRT
•
A).
S Pour trier plusieurs listes
Vous pouvez mettre en relation plusieurs listes pour les trier de sorte que tous leurs éléments
soient arrangés en fonction d’une liste servant de référence. La liste de référence est triée
dans l’ordre ascendant ou descendant, et les éléments des listes qui sont en relation sont mis
en ordre mais de manière à maintenir le lien qui existe entre toutes les lignes.
Ordre ascendant
•
1. Lorsque les listes sont affichées, appuyez sur (E)(TOOL)(SRT
2. Le message « How Many Lists?: » apparaît pour vous demander combien de listes vous
voulez trier. Nous allons trier une liste de référence en relation avec une autre liste, donc
nous indiquons 2.
AU
3. Répondez au message « Select Base List List No: » en indiquant le numéro de la liste qui
doit être triée dans l’ordre ascendant. Ici nous désignons la liste 1.
A).
@U
4. Répondez au message « Select Second List List No: » en indiquant le numéro de la liste
que vous voulez mettre en relation. Ici nous désignons la liste 2.
AU
Ordre descendant
Procédez de la même façon que pour le tri dans l’ordre ascendant. Mais vous devez appuyer
sur (SRT
•
D) à la place de (SRT
•
A).
• Vous pouvez spécifier une valeur de 1 à 6 pour le nombre de listes à trier.
• Si vous spécifiez plus d’une fois une liste pour un seul tri, une erreur se produira.
Une erreur se produira également si les listes devant être triées n’ont pas le même nombre
de valeurs (lignes).
2. Traitement des données d’une liste
Les données des listes peuvent être utilisées dans les calculs arithmétiques et de fonctions.
Différentes fonctions permettent de traiter facilement et rapidement les données des listes.
Vous pouvez utiliser les fonctions de traitement de données de listes dans les modes RUN •
MAT, STAT, TABLE, EQUA et PRGM.
I Accès au menu de fonctions
Tous les exemples suivants sont exécutés à partir du mode RUN • MAT.
Appuyez sur * puis sur (LIST) pour afficher le menu de traitement des données de listes
qui contient les paramètres suivants.
• {List}/{LmM}/{Dim}/{Fill}/{Seq}/{Min}/{Max}/{Mean}/{Med}/{Aug}/{Sum}/{Prod}/{Cuml}/
{%}/{ }
3-5
Page 97

Notez que toutes les fermetures de parenthèses à la fin des opérations suivantes peuvent être
omises.
S Pour transférer le contenu de la liste dans la mémoire matricielle de dernier
résultat
*(LIST)(LmM)(List) <numéro de liste 1-26> (List) <numéro de liste 1-26>
... (List) <numéro de liste 1-26> U
• Vous pouvez omettre (List) dans la partie de l’opération précédente.
• Toutes les listes doivent contenir le même nombre d’éléments de données. Si ce n’est pas le
cas, une erreur se produira.
Exemple: List m Mat (1, 2)U
Exemple Transférer le contenu de la liste 1 (2, 3, 6, 5, 4) dans la colonne 1 et le
contenu de la liste 2 (11, 12, 13, 14, 15) dans la colonne 2 de la mémoire
de rappel de matrice
*(LIST)(LmM)
(List)@(List)AU
[OPTN]-[LIST]-[LmM]
S Pour compter le nombre d’éléments de données dans une liste
*(LIST)(Dim)(List) <numéro de liste 1 - 26> U
• Le nombre d’éléments d’une liste désigne sa « dimension ».
Exemple Compter le nombre de valeurs dans la liste 1 (36, 16, 58, 46, 56)
*(LIST)(Dim)
(List)@U
[OPTN]-[LIST]-[Dim]
S Pour créer une liste en spécifiant le nombre d’éléments de données
Procédez de la façon suivante pour spécifier le nombre de données dans l’instruction
d’affectation et créer une liste.
<nombre de données
(n = 1 - 999)
Exemple Créer cinq données (chacune d’elles contenant 0) dans la liste 1
n>?*(LIST)(Dim)(List) <numéro de liste 1 - 26>U
[OPTN]-[LIST]-[Dim]
D?*(LIST)(Dim)
(List)@U
Vous pouvez voir la liste créée en accédant au mode STAT.
3-6
Page 98

S Pour remplacer toutes les données par la même valeur [OPTN]-[LIST]-[Fill]
*(LIST)(Fill) <valeur>(List) <numéro de liste 1 - 26>U
Exemple Remplacer toutes les valeurs de la liste 1 par le nombre 3
*(LIST)(Fill)
B(List)@U
Voici le nouveau contenu de la liste 1.
S Pour créer une suite de nombres [OPTN]-[LIST]-[Seq]
*(LIST)(Seq) <expression> <nom de la variable> <valeur initiale>
<valeur finale> <incrément> U
• Le résultat de cette opération est sauvegardé dans la mémoire ListAns.
Exemple Introduire la suite numérique 1
fonction f(x) = X2. Utiliser 1 comme valeur initiale, 11 comme valeur
finale et 5 comme incrément.
*(LIST)(Seq)TV
T@@@DU
Si vous définissez 12, 13, 14 ou 15 comme valeur finale, le résultat sera le même que celui
indiqué ci-dessus, car toutes les valeurs sont inférieures à la valeur produite par l’incrément
suivant (16).
2
, 62, 112, dans une liste en utilisant la
S Pour trouver la valeur minimale d’une liste [OPTN]-[LIST]-[Min]
*(LIST)(E)(Min)(E)(E)(List) <numéro de liste 1 - 26> U
Exemple Trouver la valeur minimale dans la liste 1 (36, 16, 58, 46, 56)
*(LIST)(E)(Min)
(E)(E)(List)@U
S Pour trouver parmi deux listes celle qui contient la plus grande valeur
*(LIST)(E)(Max)(E)(E)(List) <numéro de liste 1 - 26> (List)
<numéro de liste 1 - 26>U
• Les deux listes doivent contenir le même nombre d’éléments de données. Si ce n’est pas le
cas, une erreur se produira.
• Le résultat de cette opération est sauvegardé dans la mémoire ListAns.
3-7
[OPTN]-[LIST]-[Max]
Page 99

Exemple Trouver si la liste 1 (75, 16, 98, 46, 56) ou la liste 2 (35, 59, 58, 72, 67)
contient la plus grande valeur
*(LIST)(E)(Max)
(E)(E)(List)@
(List)AU
S Pour calculer la moyenne des données d’une liste [OPTN]-[LIST]-[Mean]
*(LIST)(E)(Mean)(E)(E)(List) <numéro de liste 1 - 26>U
Exemple Calculer la moyenne des données de la liste 1 (36, 16, 58, 46, 56)
*(LIST)(E)(Mean)
(E)(E)(List)@U
S Pour calculer la médiane des données d’un effectif particulier
[OPTN]-[LIST]-[Med]
Cette opération utilise deux listes : une qui contient des valeurs et l’autre qui indique l’effectif
de chaque valeur. L’effectif des données de l’élément 1 de la première liste est indiqué par la
valeur de l’élément 1 de la seconde liste, etc.
• Les deux listes doivent contenir le même nombre d’éléments de données. Si ce n’est pas le
cas, une erreur se produira.
*(LIST)(E)(Med)(E)(E)(List) <numéro de liste 1 - 26 (donnée)> \
(List) <numéro de liste 1 - 26 (effectif)>U
Exemple Calculer la médiane des données de la liste 1 (36, 16, 58, 46, 56), dont
l’effectif est indiqué dans la liste 2 (75, 89, 98, 72, 67)
*(LIST)(E)(Med)
(E)(E)(List)@
(List)AU
S Pour combiner des listes [OPTN]-[LIST]-[Aug]
• Vous pouvez combiner deux listes différentes en une seule liste. La liste obtenue sera
stockée dans la mémoire ListAns.
*(LIST)(E)(Aug)(E)(E)(List) <numéro de liste 1 - 26> (List)
<numéro de liste 1 - 26>U
Exemple Combiner la liste 1 (–3, –2) et la liste 2 (1, 9, 10)
*(LIST)(E)(Aug)
(E)(E)(List)@
(List)AU
3-8
Page 100

S Pour calculer la somme des données d’une liste [OPTN]-[LIST]-[Sum]
*(LIST)(E)(E)(Sum)(E)(List) <numéro de liste 1 - 26>U
Exemple Calculer la somme des données de la liste 1 (36, 16, 58, 46, 56)
*(LIST)(E)(E)(Sum)
(E)(List)@U
S Pour calculer le produit des valeurs d’une liste [OPTN]-[LIST]-[Prod]
*(LIST)(E)(E)(Prod)(E)(List) <numéro de liste 1 - 26>U
Exemple Calculer le produit des valeurs de la liste 1 (2, 3, 6, 5, 4)
*(LIST)(E)(E)(Prod)
(E)(List)@U
S Pour calculer les effectifs cumulés de chaque donnée [OPTN]-[LIST]-[Cuml]
*(LIST)(E)(E)(Cuml)(E)(List) <numéro de liste 1 - 26>U
• Le résultat de cette opération est sauvegardé dans la mémoire ListAns.
Exemple Calculer les effectifs cumulés de chaque donnée de la liste 1 (2, 3, 6, 5,
4)
*(LIST)(E)(E)(Cuml)
(E)(List)@U
2+3=
2+3=
2+3+6=
2+3+6=
2+3+6+5=
2+3+6+5=
2+3+6+5+4=
2+3+6+5+4=
S Pour calculer le pourcentage représenté par chaque donnée
*(LIST)(E)(E)(%)(E)(List) <numéro de liste 1 - 26>U
[OPTN]-[LIST]-[%]
• L’opération précédente calcule le pourcentage de chaque donnée par rapport au total de la
liste.
• Le résultat de cette opération est sauvegardé dans la mémoire ListAns.
Exemple Calculer le pourcentage représenté de chaque donnée de la liste 1 (2, 3,
6, 5, 4)
3-9
 Loading...
Loading...