Page 1

ClassPad II
fx-CP400
Mode d’emploi
F
URL du site web CASIO Education
http://edu.casio.com
Téléchargez la version d’essai gratuite du logiciel et le logiciel d’aide
http://edu.casio.com/dl/
Des manuels sont disponibles en plusieurs langues à
http://world.casio.com/manual/calc
Page 2

Conservez toujours des copies de toutes les données importantes !
Une décharge des piles ou un mauvais remplacement des piles qui alimentent le ClassPad peut entraîner une
destruction ou une perte définitive des données sauvegardées. Les données sauvegardées peuvent aussi être
affectées par une charge électrostatique ou un choc violent. Vous devez vous protéger contre de telles pertes
en faisant des copies.
Sauvegarde de données
Il est possible de convertir les données du ClassPad au format VCP ou XCP et de stocker les fichiers convertis
sur un ordinateur. Pour plus de détails, voir « 19-2 Transfert de données entre le ClassPad et un ordinateur
personnel».
• Conservez la documentation à portée de main pour toute référence future.
• Les écrans modèles représentés dans ce manuel servent à titre de référence. Ils peuvent être différents
des écrans réellement produits par le ClassPad.
• Le contenu de ce manuel est susceptible d’être modifié sans préavis.
• Aucune partie de ce manuel ne peut être reproduite sous quelque forme que ce soit sans la permission
écrite du fabricant.
• CASIO Computer Co., LTD. décline toute responsabilité quant aux dommages spéciaux, collatéraux,
directs ou indirects liés à ou résultant de l’utilisation de ces matériaux. CASIO Computer Co., LTD.
décline aussi toute responsabilité quant aux plaintes de tiers, quelle qu’en soit la nature, résultant de
l’emploi de ces matériaux.
• Windows® est soit une marque commerciale soit une marque déposée de Microsoft Corporation aux
États-Unis et/ou dans d’autres pays.
• Mac OS, OS X et macOS sont soit des marques commerciales soit des marques déposées d’Apple Inc.
aux États-Unis et/ou dans d’autres pays.
• Fugue © 1999 – 2012 Kyoto Software Research, Inc. Tous droits réservés.
• Les noms des entreprises et des produits mentionnés dans ce manuel peuvent être des marques de
commerce ou des marques déposées de leurs propriétaires respectifs.
• Remarque que le logo pour une marque de commerce ™ et le logo pour une marque déposée ® ne sont
pas utilisées dans le texte de ce manuel.
2
Page 3

Table des matières
A propos de ce mode d’emploi .................................................................................................................10
Chapitre 1 : Bases ................................................................................................................11
1-1 Aperçu ......................................................................................................................................11
Aperçu des fonctions du ClassPad ..........................................................................................................11
Mise sous ou hors tension........................................................................................................................12
1-2 Alimentation ............................................................................................................................12
1-3 Fonctionnement de base des applications internes ...........................................................13
Emploi du menu d’applications .................................................................................................................13
Applications internes ................................................................................................................................13
Compléments d’applications ...................................................................................................................14
Fenêtre d’application ................................................................................................................................ 15
Emploi du menu O ..................................................................................................................................16
Informations de la barre d’état..................................................................................................................16
Suspension et arrêt d’une opération ........................................................................................................16
1-4 Saisie .......................................................................................................................................17
Emploi du clavier tactile ............................................................................................................................17
Jeux de touches du clavier tactile ............................................................................................................17
Saisie de base ..........................................................................................................................................19
Différentes opérations du clavier tactile ...................................................................................................21
1-5 Données du ClassPad ............................................................................................................26
Types de données et emplacements de stockage (Zones de mémoire) ..................................................26
Types de données de la mémoire principale ............................................................................................27
Dossiers de la mémoire Principale ...........................................................................................................28
Emploi du gestionnaire de variables ........................................................................................................28
Gestion des fichiers d’application .............................................................................................................31
1-6 Création et emploi de variables .............................................................................................33
Création d’une nouvelle variable .............................................................................................................. 33
Exemple d’emploi de variables .................................................................................................................33
Variables du dossier « library » ................................................................................................................ 34
Règles d’accès aux variables ...................................................................................................................34
1-7 Paramétrage du format des applications .............................................................................35
Format des applications ...........................................................................................................................36
Initialisation de tous les réglages de format des applications ..................................................................42
1-8 En cas de problème persistant… ..........................................................................................42
Chapitre 2 : Application Principale .................................................................................... 44
Boutons et menus spécifiques de l’application Principale ........................................................................44
2-1 Calculs de base .......................................................................................................................44
Calculs arithmétiques et calculs entre parenthèses ................................................................................. 44
Emploi de la touche e.........................................................................................................................45
Omission du signe de multiplication ......................................................................................................... 45
Emploi de la variable de dernier résultat (ans) .........................................................................................45
Affectation d’une valeur à une variable ....................................................................................................45
Ordre de priorité des calculs ....................................................................................................................46
Modes de calcul .......................................................................................................................................46
2-2 Emploi de l’historique des calculs ........................................................................................48
2-3 Calculs de fonctions ...............................................................................................................48
2-4 Calculs de listes ......................................................................................................................58
Saisie des données de listes dans la zone de travail ...............................................................................58
Opérations sur les éléments d’une variable LIST .....................................................................................58
Emploi d’une liste dans un calcul .............................................................................................................58
Utilisation d’une liste pour affecter des valeurs différentes à plusieurs variables ....................................58
3
Page 4

2-5 Calculs de matrices et de vecteurs .......................................................................................58
Saisie de données dans une matrice .......................................................................................................58
Réalisation de calculs matriciels ..............................................................................................................59
Utilisation d’une matrice pour affecter des valeurs différentes à plusieurs variables ............................... 60
2-6 Spécification d’une base numérique ....................................................................................60
Limites d’un calcul binaire, octal, décimal et hexadécimal ....................................................................... 60
Sélection d’une base numérique .............................................................................................................. 61
Opérations arithmétiques .........................................................................................................................61
Manipulation de bits .................................................................................................................................61
Utilisation de la fonction baseConvert (Transformation du système numérique) ..................................... 62
2-7 Emploi du menu Action ..........................................................................................................62
Abréviations et ponctuation utilisées dans cette partie du manuel ...........................................................62
Exemples d’écrans ................................................................................................................................... 63
Emploi du sous-menu Transformation .....................................................................................................63
Emploi du sous-menu Avancé ..................................................................................................................65
Emploi du sous-menu Calcul ....................................................................................................................68
Emploi du sous-menu Complexe .............................................................................................................71
Emploi du sous-menu Création-Liste .......................................................................................................72
Emploi des sous-menus Statistiques-Liste et Calcul-Liste .......................................................................73
Emploi du sous-menu Création-Matrice ................................................................................................... 76
Emploi des sous-menus Calcul-Matrice et Ligne&Colonne-Matrice ........................................................77
Emploi du sous-menu Vecteur .................................................................................................................80
Emploi du sous-menu Équation/Inégalité ................................................................................................83
Emploi du sous-menu Assistant ............................................................................................................... 86
Emploi du sous-menu Distribution/Distribution inverse ............................................................................ 86
Emploi du sous-menu Finances ............................................................................................................... 92
Emploi du sous-menu Commande ........................................................................................................... 92
2-8 Emploi du menu Interactif .....................................................................................................93
Exemple du menu Interactif......................................................................................................................93
Emploi de la commande « apply » ...........................................................................................................93
2-9 Emploi de l’application Principale en combinaison avec d’autres applications ..............94
Emploi de la fenêtre d’une autre application ............................................................................................94
Emploi de la fenêtre de l’éditeur de statistiques .......................................................................................95
Utilisation de la fenêtre géométrique ........................................................................................................95
2-10 Utilisation de la fonction Vérifier .........................................................................................96
2-11 Emploi de Probabilité ...........................................................................................................97
2-12 Exécution d’un programme dans l’application Principale ................................................98
Chapitre 3 : Application Graphe & Table ........................................................................... 99
Boutons et menus spécifiques de l’application Graphe & Table ..............................................................99
3-1 Sauvegarde de fonctions .....................................................................................................101
Emploi des feuilles de l’éditeur de graphes ............................................................................................101
Sauvegarde d’une fonction.....................................................................................................................101
Représentation graphique d’une fonction mémorisée ............................................................................102
Hachurage de la région reliée par deux expressions ............................................................................. 103
Superposition de deux inégalités dans un point d’intersection / point d’union .......................................103
Sauvegarde des informations de l’éditeur de graphes dans la mémoire de graphes ............................104
3-2 Emploi de la fenêtre graphique ...........................................................................................104
Fenêtre d’affichage pour le paramétrage de la fenêtre d’affichage graphique .......................................105
Mémorisation de la fenêtre d’affichage ..................................................................................................107
Déplacement de la fenêtre graphique ....................................................................................................107
Défilement de la fenêtre graphique ........................................................................................................107
Zoom de la fenêtre graphique ................................................................................................................108
Zoom rapide ...........................................................................................................................................108
Emploi des fonctions intégrées pour la représentation graphique .........................................................109
4
Page 5

Sauvegarde du cliché d’une courbe ....................................................................................................... 109
Réglage de la luminosité (Fade I/O – fondu enchaîné) de l’image d’arrière-plan de la
fenêtre graphique ...................................................................................................................................110
3-3 Emploi des tables et graphes .............................................................................................. 110
Génération d’une table numérique ......................................................................................................... 110
Affichage des écrans liés des coordonnées de la table numérique et des coordonnées du graphe
(Liaison du suivi de courbe) ...................................................................................................................112
Génération des valeurs d’une table numérique à partir de la courbe .....................................................112
Génération d’un tableau récapitulatif......................................................................................................112
3-4 Suivi de courbe ..................................................................................................................... 114
Suivi de courbe et relevé de coordonnées ............................................................................................. 114
3-5 Emploi du menu de dessin ..................................................................................................115
Emploi des commandes du menu Sketch .............................................................................................. 115
3-6 Analyse d’une fonction représentée graphiquement ........................................................ 116
Exemples d’utilisation des commandes du menu G-Solve ....................................................................116
Emploi des commandes du menu G-Solve ............................................................................................ 117
3-7 Modification d’une courbe ................................................................................................... 118
Modifier une seule courbe (Direct Modify) ..............................................................................................118
Modifier simultanément plusieurs courbes (Dynamic Modify) ................................................................ 118
Chapitre 4 : Application Coniques ................................................................................... 121
Boutons et menus spécifiques de l’application Coniques ......................................................................121
4-1 Saisie d’équations ................................................................................................................122
4-2 Représentation graphique d’une conique ..........................................................................122
Représentation graphique d’une parabole .............................................................................................122
Représentation graphique d’un cercle ....................................................................................................123
Représentation graphique d’une ellipse ................................................................................................. 123
Représentation graphique d’une hyperbole ...........................................................................................123
Représentation graphique à partir de l’équation générale .....................................................................123
4-3 Emploi de G-Solve et analyse de la courbe d’une conique ..............................................123
Exemples d’utilisation des commandes du menu G-Solve ....................................................................123
Emploi des commandes du menu G-Solve ............................................................................................ 124
4-4 Modification d’une courbe (Dynamic Modify) ....................................................................124
Chapitre 5 : Application Graphes d’équations différentielles ....................................... 125
Boutons et menus spécifiques des fenêtres de l’éditeur d’équations différentielles ..............................125
Boutons et menus spécifiques de la fenêtre graphique d’équation différentielle ...................................125
5-1 Représentation graphique d’une équation différentielle ..................................................126
Représentation graphique d’une équation différentielle du premier ordre .............................................126
Représentation graphique d’une équation différentielle du second ordre .............................................. 127
Représentation graphique d’une équation différentielle d’ordre
Configuration et modification des conditions initiales .............................................................................128
Configuration des paramètres de la fenêtre d’affichage graphique d’équation différentielle ..................129
n .......................................................... 128
5-2 Tracé de graphes d’une fonction de type f ( x) et de graphes d’une fonction
paramétrique .........................................................................................................................131
5-3 Visualisation des coordonnées d’un graphe .....................................................................131
5-4 Représentation graphique d’une expression ou valeur en la déposant dans la fenêtre
graphique d’équation différentielle .....................................................................................132
Chapitre 6 : Application Suites ........................................................................................ 133
Boutons et menus spécifiques de l’application Suites ............................................................................133
6-1 Forme récurrente et explicite d’une suite ..........................................................................134
Génération d’une table numérique ......................................................................................................... 134
Détermination du terme général d’une expression récurrente ............................................................... 135
Calcul de la somme d’une suite .............................................................................................................135
5
Page 6

6-2 Représentation graphique d’une suite ...............................................................................135
Chapitre 7 : Application Statistiques ............................................................................... 136
7-1 Emploi de l’éditeur de statistiques .....................................................................................136
Emploi de base des listes.......................................................................................................................136
Menus et boutons utilisés pour l’édition de liste ..................................................................................... 138
Emploi de fichiers CSV ...........................................................................................................................138
7-2 Représentation graphique de statistiques .........................................................................139
Flux opérationnel jusqu’à la représentation graphique de statistiques ...................................................140
Représentation graphique de données statistiques à une variable ........................................................141
Représentation graphique de données statistiques à deux variables .................................................... 142
Superposition d’une courbe de régression à un diagramme à nuages de points ..................................144
Superposition de la courbe d’une fonction à un graphique statistique ................................................... 145
Boutons et menus de la fenêtre de graphique statistique ......................................................................145
7-3 Exécution de calculs statistiques de base .........................................................................146
Calcul de valeurs statistiques .................................................................................................................146
Exécution de calculs de régression ........................................................................................................149
Visualisation des résultats des derniers calculs statistiques effectués (DispStat) .................................150
7-4 Exécution de calculs statistiques avancés ........................................................................150
Exécution de calculs de test, d’intervalle de confiance et de probabilité à l’aide de l’assistant .............150
Tests.......................................................................................................................................................152
Intervalles de confiance..........................................................................................................................154
Distributions............................................................................................................................................155
Termes de saisie et d’affichage ..............................................................................................................159
Chapitre 8 : Application Géométrie ................................................................................. 161
Boutons et menus spécifiques de l’application Géométrie .....................................................................161
Paramétrage de la fenêtre d’affichage de géométrie .............................................................................162
À propos de la boîte de dialogue du format Géométrie ..........................................................................162
8-1 Tracé de figures ....................................................................................................................162
Représentation graphique d’une figure ..................................................................................................162
Insertion d’un texte sur l’écran ...............................................................................................................166
Rattachement d’une mesure d’angle à une figure ..................................................................................166
Affichage des mesures d’une figure ....................................................................................................... 166
Affichage du résultat d’un calcul utilisant les mesures indiquées sur l’écran ......................................... 167
Emploi du sous-menu Special Polygon ..................................................................................................167
Emploi du sous-menu Construct ............................................................................................................168
8-2 Édition de figures .................................................................................................................172
Sélection et désélection de figures.........................................................................................................172
Déplacement et copie de figures ............................................................................................................173
Punaiser une annotation sur la fenêtre géométrique .............................................................................173
Spécification du format numérique d’une mesure .................................................................................. 173
Spécification de la couleur et du type de ligne d’un objet affiché ...........................................................174
Modification de la priorité d’affichage des objets ....................................................................................174
8-3 Emploi de la case de mesure ...............................................................................................175
Visualisation des mesures d’une figure ..................................................................................................175
Spécification et contrainte d’une mesure d’une figure ............................................................................176
Utiliser les loquets ..................................................................................................................................177
Changement d’une étiquette ou ajout d’un nom à un élément ...............................................................179
8-4 Travail avec animations .......................................................................................................179
Emploi des commandes d’animation ......................................................................................................179
8-5 Emploi de l’application Géométrie avec d’autres applications ........................................182
Glisser-déposer ......................................................................................................................................182
Copier et coller .......................................................................................................................................183
6
Page 7

Chapitre 9 : Application Résolution numérique ............................................................. 184
Boutons et menus spécifiques de l’application Résolution numérique ...................................................184
Saisie d’une équation ............................................................................................................................. 184
Résolution d’une équation ......................................................................................................................184
Chapitre 10 : Application eActivity .................................................................................. 186
Boutons et menus spécifiques de l’application eActivity ........................................................................186
10-1 Création d’une eActivity .....................................................................................................186
Opérations de base pour la création d’une eActivity .............................................................................. 186
Insertion de données dans une eActivity................................................................................................187
Insertion d’un bandeau de données d’application .................................................................................. 188
Insertion d’une ligne de lien géométrique ...............................................................................................190
10-2 Transfert de fichiers eActivity ...........................................................................................191
Compatibilité des fichiers .......................................................................................................................191
Transfert de fichiers eActivity entre un ClassPad et un ordinateur ........................................................191
Transfert de fichiers eActivity entre deux ClassPad ...............................................................................191
Chapitre 11 : Application Finances .................................................................................. 192
11-1 Fonctionnement de base de l’application Finances ........................................................192
Opérations de page ................................................................................................................................193
Configuration des réglages de l’application Finances ............................................................................ 194
11-2 Exécution de calculs financiers ........................................................................................195
11-3 Formules des calculs .........................................................................................................196
Intérêt simple ..........................................................................................................................................196
Intérêt composé......................................................................................................................................196
Marge brute d’autofinancement..............................................................................................................197
Amortissement .......................................................................................................................................197
Conversion d’intérêts..............................................................................................................................198
Coût/Vente/Marge ..................................................................................................................................198
Dépréciation ...........................................................................................................................................198
Calculs d’obligations...............................................................................................................................199
Seuil de rentabilité ..................................................................................................................................200
Marge de sécurité...................................................................................................................................200
Levier financier ....................................................................................................................................... 200
Levier d’exploitation................................................................................................................................200
Levier combiné ....................................................................................................................................... 200
Conversion de quantité ..........................................................................................................................200
11-4 Fonctions de calculs financiers ........................................................................................200
11-5 Noms des champs de saisie et d’affichage ......................................................................202
Chapitre 12 : Application Programme ............................................................................. 203
Boutons et menus spécifiques de l’application Programme ...................................................................203
12-1 Création et Exécution d’un programme ...........................................................................204
Création d’un programme .......................................................................................................................204
Exécution d’un programme ....................................................................................................................206
Arrêt de l’exécution d’un programme .....................................................................................................207
Création d’un fichier texte.......................................................................................................................207
Emploi de fichiers de texte .....................................................................................................................208
Conversion d’un fichier de texte en un fichier de programme ................................................................ 208
Conversion d’un fichier de programme en un fichier exécutable ...........................................................208
12-2 Débogage d’un programme ...............................................................................................209
Débogage après l’apparition d’un message d’erreur ..............................................................................209
Débogage d’un programme en cas de résultats imprévus .....................................................................209
Édition d’un programme .........................................................................................................................209
7
Page 8

12-3 Fonctions définies par l’utilisateur ...................................................................................210
Création d’une nouvelle fonction définie par l’utilisateur ........................................................................210
Exécution d’une fonction définie par l’utilisateur ....................................................................................211
Édition d’une fonction définie par l’utilisateur .........................................................................................211
12-4 Commandes de programmation ........................................................................................212
Emploi de cette référence ......................................................................................................................212
Conventions de syntaxe ......................................................................................................................... 212
Liste des Commandes............................................................................................................................213
12-5 Inclusion de fonctions du ClassPad dans les programmes ...........................................233
Inclusion de fonctions graphiques dans un programme .........................................................................233
Inclusion de fonctions Graphe & Table dans un programme .................................................................233
Inclusion des fonctions de table et graphe de récurrence dans un programme .....................................233
Inclusion de fonctions graphiques et de calculs statistiques dans un programme .................................233
Inclusion de fonctions de calculs financiers dans un programme .......................................................... 234
Chapitre 13 : Application Spreadsheet ............................................................................ 235
Boutons et menus spécifiques de la fenêtre de la feuille de calcul ........................................................ 235
Changement de la largeur d’une colonne ..............................................................................................236
Options de réglage ................................................................................................................................. 237
13-1 Saisie et Édition du contenu des cellules ........................................................................237
Sélection de cellules...............................................................................................................................237
Saisie de données dans une cellule .......................................................................................................238
Saisie d’une formule ...............................................................................................................................239
Saisie d’une référence à une cellule ......................................................................................................239
Types de données pour une cellule (données de texte et données de calcul) ......................................240
Saisie d’une constante dans une cellule à données de calcul ...............................................................241
Emploi de la fenêtre de visualisation des cellules .................................................................................. 242
Changement de la couleur du texte et de la couleur de remplissage de cellules spécifiques ...............243
Copier ou couper des cellules et les coller dans un autre emplacement ............................................... 243
Recalculer les expressions d’une feuille de calcul .................................................................................244
Transfert de données entre une feuille de calcul et des fichiers CSV ....................................................244
Importation et exportation de valeurs de variables .................................................................................245
13-2 Représentation graphique .................................................................................................247
Opérations de base ............................................................................................................................... 247
Série de colonnes et série de lignes ......................................................................................................247
Couleurs de graphes et Color Link .........................................................................................................248
Boutons et menus spécifiques de la fenêtre graphique de la feuille de calcul ....................................... 249
Menu Graph et exemples de graphiques ...............................................................................................250
Opérations sur les graphiques de régression (Lissage) .........................................................................252
Autres opérations sur la fenêtre graphique ............................................................................................254
13-3 Calculs statistiques ............................................................................................................255
Calculs statistiques à une variable, à deux variables et de régression .................................................. 255
Calculs de test et d’intervalle ..................................................................................................................256
Calculs de distribution ............................................................................................................................259
À propos de la commande DispStat .......................................................................................................259
13-4 Calculs avec les cellules et les listes ...............................................................................260
Emploi des fonctions de calculs de cellules ...........................................................................................260
Emploi des fonctions de calculs de listes ............................................................................................... 260
Chapitre 14 : Application Graphe 3D ............................................................................... 261
Boutons et menus spécifiques de l’application Graphe 3D .................................................................... 261
14-1 Saisie d’une expression .....................................................................................................262
Emploi des feuilles de l’éditeur de graphes 3D ......................................................................................262
Sauvegarde d’une fonction.....................................................................................................................262
Représentation graphique d’une fonction mémorisée ............................................................................263
8
Page 9

14-2 Emploi de la fenêtre graphique 3D ....................................................................................264
Paramétrage de la fenêtre d’affichage de graphe 3D ............................................................................264
Afficher et masquer les axes et les noms ...............................................................................................265
Rotation du graphe .................................................................................................................................266
Exemple de graphes 3D .........................................................................................................................266
Visualisation des coordonnées d’un graphe ...........................................................................................266
Insertion d’un texte dans la fenêtre graphique 3D ..................................................................................267
Calcul d’une valeur
z pour des valeurs x et y, ou des valeurs s et t particulières ................................... 267
Chapitre 15 : Application Plot Image ............................................................................... 268
Boutons et menus spécifiques de l’application Plot Image ....................................................................269
15-1 Emploi de la fonction Plot ..................................................................................................270
Lancer une opération Plot Image ...........................................................................................................270
Tracé de points dans un fichier image c2p .............................................................................................270
Tracé de points dans un fichier image c2b .............................................................................................271
Modifier des tracés sur une image en arrière-plan .................................................................................272
Superposer un graphe sur des tracés d’une image en arrière-plan ....................................................... 272
G-Solve ..................................................................................................................................................274
Défilement de la fenêtre Plot Image ....................................................................................................... 275
15-2 Emploi de la liste des tracés ..............................................................................................275
Emploi de la fenêtre de la liste des tracés pour modifier des tracés ...................................................... 275
Enregistrement/Importation de données vers/depuis une feuille de calcul ............................................ 276
Exportation/Importation de données d’un tracé vers/depuis une variable ..............................................276
15-3 Affichage des tracés aux coordonnées t-y ou t-x ............................................................276
15-4 Fichiers de l’application Plot Image ..................................................................................277
Chapitre 16 : Application Calcul différentiel interactif ................................................... 278
Boutons et menus spécifiques de la fenêtre de la table DiffCalc ...........................................................278
16-1 Connaitre les tangentes en utilisant l’onglet [Tangent] ..................................................279
16-2 Dérivation de la dérivée à l’aide de l’onglet [Deriv] .........................................................280
16-3 Génération d’une table numérique et représentation graphique de la première
et de la seconde dérivées à l’aide de l’onglet [D Trace] ..................................................282
Chapitre 17 : Application Physium .................................................................................. 284
Menus et boutons de l’application Physium ...........................................................................................284
17-1 Tableau périodique .............................................................................................................285
17-2 Constantes physiques fondamentales .............................................................................287
17-3 Précautions .........................................................................................................................288
Chapitre 18 : Application Système .................................................................................. 290
18-1 Gestion de l’utilisation de la mémoire ..............................................................................290
Emploi de la feuille de stockage .............................................................................................................290
Emploi de la feuille de mémoire principale et de la feuille eActivity ....................................................... 291
18-2 Configuration des paramètres Système ...........................................................................292
Menus et boutons de l’application Système ........................................................................................... 292
Configuration des paramètres Système ................................................................................................. 293
Chapitre 19 : Communication de données ...................................................................... 296
19-1 Aperçu de la communication de données ........................................................................296
Emploi de l’application Communication du ClassPad ............................................................................ 296
Boîte de dialogue de sélection du mode de raccordement ....................................................................297
19-2 Transfert de données entre le ClassPad et un ordinateur personnel ............................297
Raccordement et débranchement avec un ordinateur en mode USB Flash .......................................... 298
Transfert de données entre le ClassPad et un ordinateur personnel .....................................................299
Installer un complément d’application ...................................................................................................300
Importation automatique de fichiers VCP ...............................................................................................300
9
Page 10

Règles concernant les fichiers et les dossiers du ClassPad .................................................................. 300
Opérations sur les fichiers VCP et XCP ................................................................................................. 300
19-3 Communication de données entre deux ClassPad .........................................................302
Raccordement à un autre ClassPad ......................................................................................................302
Transfert de données entre deux ClassPad ...........................................................................................302
Attente de communication ......................................................................................................................304
Interruption d’une opération de communication de données en cours ...................................................304
19-4 Raccordement du ClassPad à un enregistreur de données ...........................................304
Raccordement du ClassPad à un enregistreur de données ...................................................................304
19-5 Raccordement du ClassPad à un projecteur ...................................................................305
Projection du contenu de l’écran ClassPad depuis un projecteur .......................................................... 305
Précautions lors du raccordement ..........................................................................................................305
Appendice .......................................................................................................................... 306
Tableau des codes de caractères ...............................................................................................306
Tableau des variables système ..................................................................................................310
Types de graphes et fonctions exécutables..............................................................................314
Tableaux des messages d’avertissement et d’erreur ...............................................................315
Tableau des messages d’erreur ............................................................................................................315
Tableau de messages d’avertissement ..................................................................................................319
Erreur de mémoire insuffisante ..............................................................................................................319
Réinitialisation et initialisation du ClassPad ............................................................................320
Nombre de chiffres et précision .................................................................................................321
Nombre de chiffres ................................................................................................................................. 321
Précision.................................................................................................................................................321
Luminosité de l’affichage et durée de vie des piles .................................................................321
Luminosité de l’affichage ........................................................................................................................321
Durée de vie des piles ............................................................................................................................322
Fiche technique ...........................................................................................................................322
Mode Examen .................................................................................................................... 324
Application Communication - Menu du Mode Examen ..........................................................................324
Accéder au Mode Examen ..................................................................................................................... 324
Fonctionnement du ClassPad en Mode Examen ................................................................................... 325
Quitter le Mode Examen.........................................................................................................................326
Affichage de l’aide du Mode Examen .....................................................................................................327
A propos de ce mode d’emploi
• Les numéros d’exemple à quatre chiffres en caractères gras (comme 0201 ) qui apparaissent dans
les Chapitres 2 à 14 indiquent des exemples de fonctionnement que vous pouvez trouver dans le livret
« Exemples » séparé. Vous pouvez utiliser le livret « Exemples » conjointement à ce manuel en vous référant
aux numéros de l’exemple qui s’applique.
• Dans ce manuel, le fonctionnement du pavé directionnel est représenté par f, c, d, e (1-1 Aperçu).
10
Page 11
Chapitre 1 : Bases
Ce chapitre fournit un aperçu général du fonctionnement du ClassPad et des ses applications, aussi bien que
des informations concernant les opérations de saisie, la manipulation des données (variables et dossiers), les
opérations sur les fichiers, et la manière de configurer des réglages de format d’application.
1-1 Aperçu
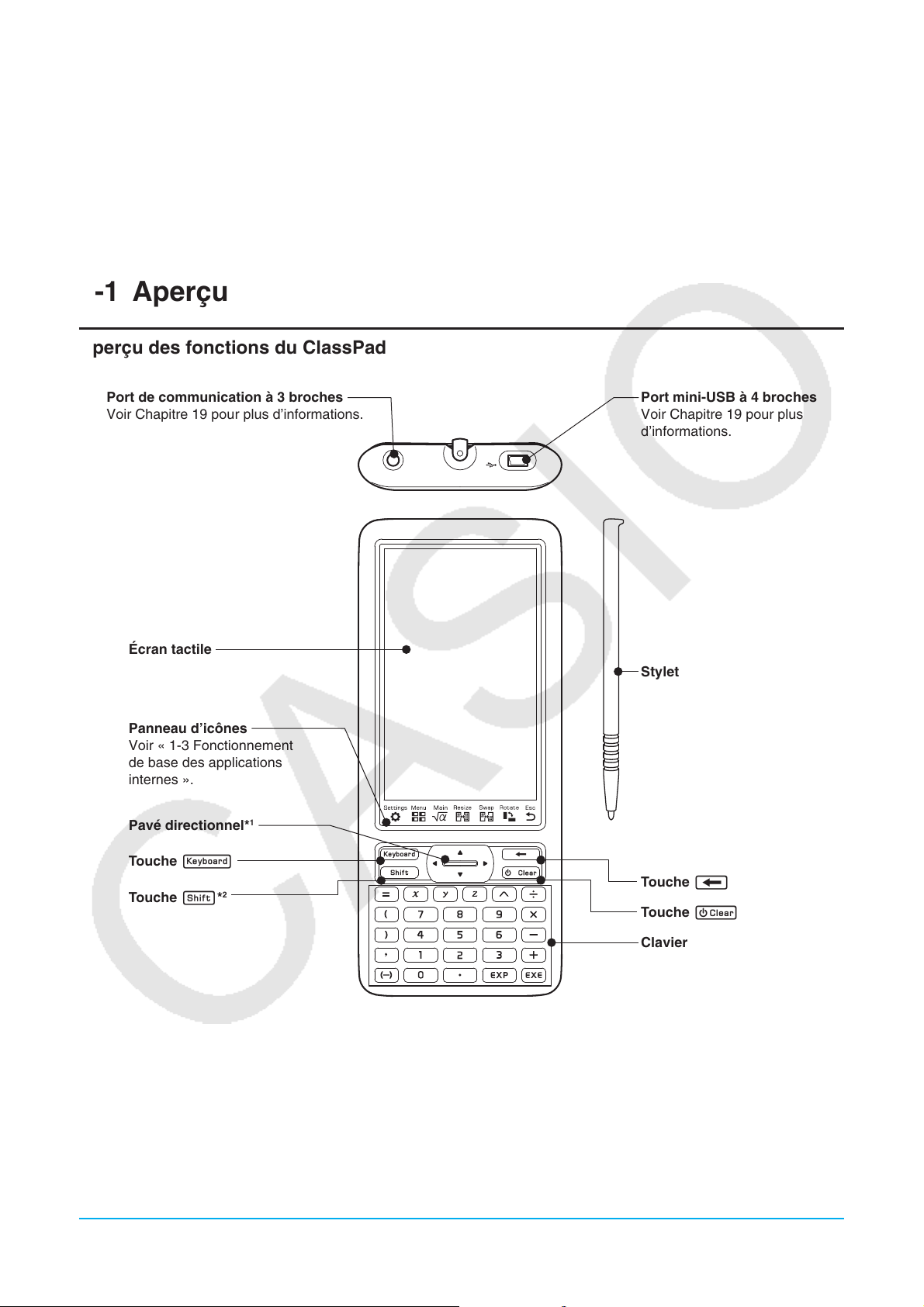
Aperçu des fonctions du ClassPad
Port de communication à 3 broches
Voir Chapitre 19 pour plus d’informations.
Écran tactile
Panneau d’icônes
Voir « 1-3 Fonctionnement
de base des applications
internes ».
Pavé directionnel*
1
Port mini-USB à 4 broches
Voir Chapitre 19 pour plus
d’informations.
Stylet
Touche k
Touche f*
*1 Dans ce manuel, le fonctionnement du pavé directionnel est représenté par f, c, d, e.
*2 Il est possible d’affecter certaines fonctions (couper, coller, annuler etc.) ou des opérations de frappes de
touches à des combinaisons de touches qui consistent à appuyer sur la touche f et sur une touche du
clavier tactile. Pour de plus amples détails, voir « 18-2 Configuration des paramètres Système ».
2
Touche K
Touche c
Clavier
Chapitre 1 : Bases 11
Page 12

Mise sous ou hors tension
Lorsque le ClassPad est hors tension, appuyez sur c pour le mettre sous tension.
Pour mettre le ClassPad hors tension, appuyez sur f puis sur c.
Extinction automatique
Le ClassPad présente aussi une fonction d’extinction automatique. C’est-à-dire qu’il se met automatiquement
hors tension s’il n’est pas utilisé pendant un certain temps. Pour le détail, voir « Configurer les propriétés
d’alimentation » à la page 293.
Remarque
Toute information provisoire dans la mémoire vive du ClassPad (graphiques tracés dans la fenêtre du
graphique d’une application, une boîte de dialogue affichée, etc.) est gardée pendant environ 30 secondes
chaque fois que l’alimentation est coupée manuellement ou lors d’une extinction automatique. Cela signifie que
vous pourrez récupérer l’information provisoire dans la mémoire vive si vous rallumez le ClassPad dans les 30
secondes après l’avoir éteint. Après environ 30 secondes, les informations temporaires dans la mémoire vive
sont effacées automatiquement, et lors de la remise en marche, l’écran de démarrage de l’application que vous
utilisiez au moment du dernier arrêt, s’affiche, et les informations précédentes dans la mémoire vive ne sont
plus disponibles.
1-2 Alimentation
Votre ClassPad fonctionne avec quatre piles AAA LR03 (AM4), ou quatre piles NiMH (nickel-hydrure métallique).
L’indicateur de niveau des piles apparaît dans la barre d’état.
piles pleines piles à moitié pleines piles faibles piles vides
Important !
• Veillez à remplacer les piles dès que possible lorsque l’indicateur de niveau des piles (piles faibles).
• Remplacez les piles dès que l’indicateur de niveau des piles indique
communication de données ou certaines fonctions sont impossibles.
• Pour des informations sur la configuration initiale requise après le remplacement des piles, voir «
des piles et préparation du ClassPad » dans le Guide de mise en marche rapide à part.
• Lorsque les piles sont très faibles, votre ClassPad risque de ne pas pouvoir être rallumé avec la touche
c. Si le cas se présente, remplacez immédiatement les piles.
• Le message suivant indique que les piles sont presque mortes. Remplacez-les dès que ce message apparaît.
Si vous continuez d’utiliser le ClassPad, il s’éteindra automatiquement. Vous ne pourrez pas la rallumer tant
que les piles ne seront pas remplacées.
• Remplacez les piles au moins tous les ans, même si vous utilisez peu le ClassPad pendant cette période.
(piles vides). A ce niveau, la
Chargement
Remarque : Les piles fournies avec le ClassPad se déchargent légèrement pendant le transport et
l’entreposage. Elles ne dureront probablement pas aussi longtemps qu’elles le devraient.
Sauvegarde de données
Il est possible de convertir les données du ClassPad au format VCP ou XCP et de stocker les fichiers convertis
sur un ordinateur. Pour plus de détails, voir « 19-2 Transfelt de données entre le ClassPad et un ordinateur
personnel ».
Chapitre 1 : Bases 12
Page 13

1-3 Fonctionnement de base des applications internes
Vous trouverez ici des informations de base et des explications sur les opérations communes à toutes les
applications internes.
Emploi du menu d’applications
Le menu d’applications s’affiche par une tape de m sur le panneau d’icônes. Vous pouvez effectuer les
opérations suivantes avec le menu d’application.
Tapez sur une touche pour
lancer une application. Voir
« Applications internes »
ci-dessous.
En tapant ici, vous pouvez
faire défiler les pages du
menu d’application.
La page du menu
d’application peut
également être modifiée
en balayant l’écran vers la
gauche ou la droite avec le
stylet ou votre doigt.
Tapez ici (ou tapez s sur le panneau d’icônes) pour
afficher le menu suivant.
Fonctions du fichier VCP.
Voir page 300.
Lance l’alignement. du
panneau d’icônes.
Voir page 295.
Affiche les informations
concernant les versions.
Voir page 295.
Applications internes
Le tableau suivant indique les icônes d’applications affichées dans le menu d’applications et ce que l’on peut
faire avec chacune d’elles.
Tapez
sur cette
icône :
Pour lancer cette
application :
Principale
eActivity
Statistiques
Spreadsheet
Graphe & Table
Graphe 3D
Pour effectuer ce type d’opération :
• Calculs généraux, calculs de fonctions compris
• Calculs matriciels
• Système algébrique pour ordinateur
• Création d’un fichier eActivity qui peut être utilisé pour la saisie de
formules, du texte, et d’autres données des applications de ClassPad
• Création d’une liste
• Exécution de calculs statistiques
• Représentation graphique de statistiques
• Saisie de données sur une feuille de calcul
• Manipulation et/ou représentation graphique des données d’une
feuille de calcul
• Exécution de calculs statistiques et/ou représentation graphique de
statistiques
• Représentation graphique d’une fonction
• Enregistrement d’une fonction et création d’une table de solutions par
substitution des différentes valeurs spécifiées comme variables
• Tracer un graphe 3-dimensionnel d’une équation de la forme
z = f (x, y)
ou d’une équation paramétrique
Chapitre 1 : Bases 13
Page 14
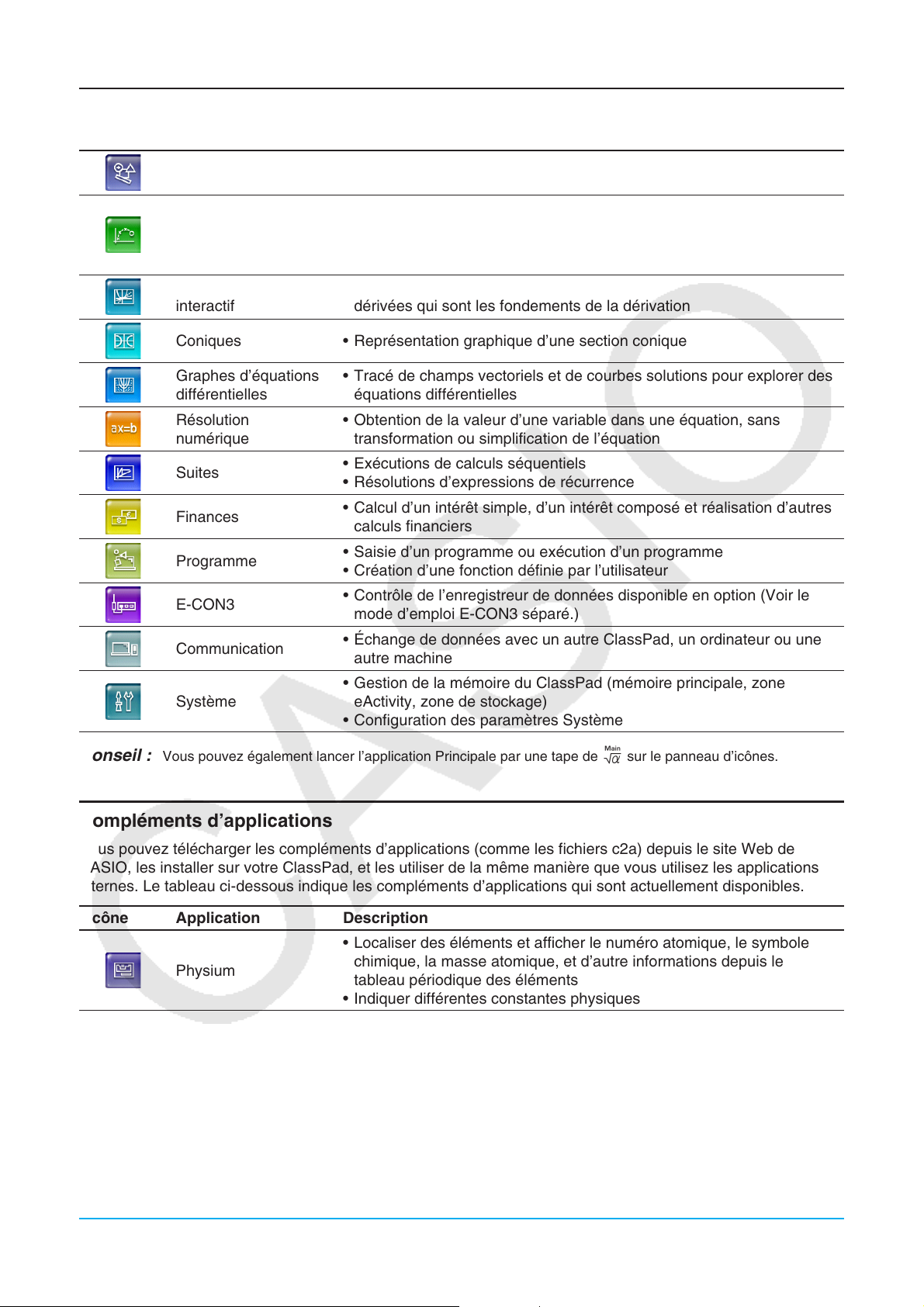
Tapez
sur cette
icône :
Pour lancer cette
application :
Géométrie
Plot Image
Calcul différentiel
interactif
Coniques • Représentation graphique d’une section conique
Pour effectuer ce type d’opération :
• Tracé de figures géométriques
• Création de figures animées
• Marquer des points (représentant des coordonnées) sur une
photographie, une illustration, ou un autre graphique et effectuer
différents types d’analyses basées sur les données marquées
(valeurs des coordonnées)
• Découverte des coefficients différentiels et/ou des formules de
dérivées qui sont les fondements de la dérivation
Graphes d’équations
différentielles
Résolution
numérique
Suites
Finances
Programme
E-CON3
Communication
Système
• Tracé de champs vectoriels et de courbes solutions pour explorer des
équations différentielles
• Obtention de la valeur d’une variable dans une équation, sans
transformation ou simplification de l’équation
• Exécutions de calculs séquentiels
• Résolutions d’expressions de récurrence
• Calcul d’un intérêt simple, d’un intérêt composé et réalisation d’autres
calculs financiers
• Saisie d’un programme ou exécution d’un programme
• Création d’une fonction définie par l’utilisateur
• Contrôle de l’enregistreur de données disponible en option (Voir le
mode d’emploi E-CON3 séparé.)
• Échange de données avec un autre ClassPad, un ordinateur ou une
autre machine
• Gestion de la mémoire du ClassPad (mémoire principale, zone
eActivity, zone de stockage)
• Configuration des paramètres Système
Conseil : Vous pouvez également lancer l’application Principale par une tape de M sur le panneau d’icônes.
Compléments d’applications
Vous pouvez télécharger les compléments d’applications (comme les fichiers c2a) depuis le site Web de
CASIO, les installer sur votre ClassPad, et les utiliser de la même manière que vous utilisez les applications
internes. Le tableau ci-dessous indique les compléments d’applications qui sont actuellement disponibles.
Icône Application Description
• Localiser des éléments et afficher le numéro atomique, le symbole
Physium
chimique, la masse atomique, et d’autre informations depuis le
tableau périodique des éléments
• Indiquer différentes constantes physiques
Remarque
Vous pouvez supprimer tous les compléments d’applications avec l’une des procédures ci-dessous.
• Reset - Storage Memory ou Reset - All (« Supprimer des groupes de données spécifiques (Réinitialisation) »,
page 293)
• Initialize (« Initialiser votre ClassPad », page 293)
Après avoir supprimé les compléments d’applications, vous pouvez utiliser la procédure détaillée dans
« Installer un complément d’application » (page 300) pour les réinstaller.
Chapitre 1 : Bases 14
Page 15

Fenêtre d’application
La fenêtre d’une application interne présente les éléments suivants.
Barre de menus
Barre d’outils
Fenêtre(s) d’application
Fenêtre supérieure
Clavier tactile
Voir page 17.
Barre d’état
Voir page 16.
Fenêtre inférieure
Dans de nombreuses applications, l’écran est partagé entre la fenêtre supérieure et la fenêtre inférieure, qui
contiennent chacune des informations différentes. Lorsque deux fenêtres sont utilisées, la fenêtre sélectionnée
(celle qui est opérationnelle) est appelée « fenêtre active ». Les éléments de la barre de menus, de la barre
d’outils et de la barre d’état s’appliquent à la fenêtre active. La fenêtre active est indiquée par un cadre épais.
Vous pouvez effectuer les opérations suivantes dans une fenêtre d’application.
Pour faire ceci : Effectuez cette opération :
Changer de fenêtre
active
Lorsque deux fenêtres sont affichées, tapez quelque part à l’intérieur de la
fenêtre qui n’est pas entourée d’un cadre épais pour en faire la fenêtre active.
Remarque il n’est pas possible de changer de fenêtre active pendant l’exécution
d’une opération sur cette fenêtre.
Agrandir la fenêtre active
de sorte qu’elle remplisse
Lorsque deux fenêtres sont affichées, tapez sur r. La fenêtre active remplit
tout l’écran. Pour revenir aux deux fenêtres, tapez de nouveau sur r.
tout l’écran
Échanger les fenêtres
supérieure et inférieure
Lorsque deux fenêtres sont affichées, tapez sur S. La fenêtre supérieure
devient la fenêtre inférieure et inversement. L’échange de fenêtres n’a aucun
effet sur leur état. Par exemple, si la fenêtre supérieure est active lorsque vous
tapez sur S elle le reste lorsqu’elle devient la fenêtre inférieure.
Fermer les fenêtres
actives
Lorsque deux fenêtres sont affichées, tapez sur C dans le coin supérieur droit
de la fenêtre. L’autre fenêtre (inactive) remplit ainsi tout l’écran.
Conseil : Si vous tapez sur le bouton r quand les deux fenêtres sont affichées, la fenêtre active remplit tout l’écran,
mais l’autre fenêtre (inactive) ne se ferme pas. Elle reste ouverte, cachée par la fenêtre active. Vous pouvez
donc taper sur S pour voir la fenêtre masquée et la rendre active, et mettre l’autre fenêtre en arrière-plan.
u Modifier l’orientation de l’écran (Uniquement avec le menu d’applications et certaines
applications)
Vous pouvez modifier l’orientation de l’écran vers horizontal lorsqu’un des éléments suivants est affiché : menu
d’applications, application Principale, Graphe & Table, Coniques ou Physium. Tapez sur g pour passer à
l’orientation horizontale (paysage). Pour revenir à l’orientation verticale (portrait), tapez de nouveau surg.
Chapitre 1 : Bases 15
Page 16

Emploi du menu O
Le menu O apparaît dans le coin supérieur gauche de la fenêtre de chaque application, sauf pour l’application
Système. Vous pouvez accéder au menu O en tapant sur m sur le panneau d’icônes, ou bien en tapant sur
le menu O dans la barre de menus.
Les éléments qui apparaissent sur le menu O sont les suivants.
1 En tapant sur [Variable Manager] vous lancez le gestionnaire de variables.
Voir « Emploi du gestionnaire de variables » (page 28) pour le détail.
2 En tapant sur [View Window] vous affichez la boîte de dialogue
permettant de paramétrer la plage d’affichage et d’autres réglages pour
la représentation graphique. Pour le détail, voir les explications sur la
représentation graphique dans les différentes applications (Graphe &
Table, Graphes d’équations différentielles, Statistiques, etc.)
3 En tapant sur un menu, vous affichez la boîte de dialogue permettant
de paramétrer les réglages correspondants. Voir « 1-7 Paramétrage du
format des applications » pour le détail.
4 En tapant sur [Default Setup] vous pouvez rétablir les réglages par
défaut (sauf pour le dossier actuel). Voir « 1-7 Paramétrage du format des applications » pour le détail.
5 En tapant sur [Window] vous pouvez afficher une liste de toutes les fenêtres auxquelles vous pouvez
accéder à partir de l’application actuelle (par exemple, l’application Statistiques). Il suffit de taper sur une
option du menu pour afficher la fenêtre correspondante et la rendre active.
6 [Keyboard] sert à afficher ou masquer le clavier tactile.
1
2
3
4
5
6
7
7 [Close] sert à fermer la fenêtre active actuelle, sauf dans les cas suivants.
• Une seule fenêtre est affichée
• La fenêtre active ne peut pas être fermée par l’application utilisée
Par exemple, vous ne pouvez pas fermer la fenêtre de l’éditeur de graphes à partir de l’application Graphe
& Table.
Informations de la barre d’état
La barre d’état apparaît au bas de la fenêtre de chaque application.
123
Information concernant l’application actuelle
1
Vous pouvez changer le réglage d’un paramètre dans la barre d’outils en tapant dessus. Par exemple
en tapant sur « Cplx » (calculs de nombres complexes) quand l’application Principale est ouverte, vous
sélectionnez le réglage « Real » (calculs de nombres réels). En tapant une nouvelle fois dessus vous
revenez à « Cplx ». Pour plus de détails sur les informations concernant l’application actuelle, voir « 1-7
Paramétrage du format des applications ».
2 Cet indicateur pivote pendant que le processus est en cours.
apparaît pour indiquer qu’une opération est suspendue.
3 Indicateur du niveau des piles (Voir « 1-2 Alimentation ».)
Suspension et arrêt d’une opération
De nombreuses applications internes offrent des fonctions pour suspendre ou arrêter (interrompre) le calcul
d’une expression, la représentation graphique et d’autres opérations.
Chapitre 1 : Bases 16
Page 17

u Pour suspendre une opération
Appuyez sur la touche K pendant le calcul d’une expression, la représentation graphique ou d’autres
opérations pour suspendre l’opération en cours. s’affiche sur le côté droit de la barre d’état pour indiquer
qu’une opération est suspendue. Pour continuer, appuyez une nouvelle fois sur la touche K.
u Arrêt d’une opération
Il faut appuyer sur la touche c pendant le calcul d’une expression, la
représentation graphique d’une fonction ou d’autres opérations pour arrêter
l’opération en cours et afficher une boîte de dialogue « Break » comme celle
indiquée ci-après.
Pour dégager cette boîte, tapez sur la touche [OK].
1-4 Saisie
Les données peuvent être saisies sur le ClassPad soit par le clavier numérique soit par le clavier tactile.
En principe, toute saisie de données exigée par le ClassPad peut être effectuée par le clavier tactile. Le
clavier numérique doit être utilisé pour la saisie de données fréquentes comme les nombres, les opérateurs
arithmétiques, etc.
Emploi du clavier tactile
Le clavier tactile s’affiche au bas de l’écran tactile.
u Pour afficher le clavier tactile
Si le clavier tactile n’est pas à l’écran, appuyez sur la touche
k ou tapez sur le menu O puis sur [Keyboard]. La
clavier tactile s’affiche alors.
• Le clavier tactile dispose de plusieurs jeux de touches
différents comme [Math1], [abc], et [Catalog], que vous
pouvez utiliser pour saisir des fonctions et du texte. Pour
sélectionner un jeu de touches, tapez sur un des onglets sur
le côté gauche du clavier tactile.
• Pour masquer le clavier tactile il suffit d’appuyer de nouveau
sur la touche k ou tapez de nouveau sur le menu O
puis sur [Keyboard].
Clavier tactile
Jeux de touches du clavier tactile
Le clavier tactile dispose de différents jeux de touches qui prennent en charge les divers besoins de saisie de
données. Chaque jeu de touches est indiqué ci-dessous.
Jeux de touches [Math1], [Math2], [Math3], [Trig] (trigonométrique), [Advance]
Ces jeux de touches incluent des touches pour les fonctions de saisie, des opérateurs, et des symboles requis
pour les formules numériques.
Chapitre 1 : Bases 17
Page 18

Math1 Math2 Math3
Trig Advance
Pour plus de détails sur les jeux de touches ci-dessus, voir « Emploi des jeux de touches Math, Trig et
Advance » (page 22).
Jeu de touches [Var] (variable)
Ce jeu de touches inclut uniquement les touches permettant de saisir des
variables à caractère unique. Pour le détail à ce sujet, voir « Emploi de
variables à caractère unique » (page 24).
Jeu de touches [abc]
Utilisez ce jeu de touches pour saisir des caractères alphabétiques. Tapez
sur un des onglets en du haut du clavier (sur toute la droite avec l’orientation
horizontale de l’écran) pour voir les caractères spéciaux, par exemple, tapez
[Math]. Pour le détail à ce sujet, voir « Emploi du clavier alphabétique » (page
25).
Jeu de touches [Catalog]
Ce jeu de touches présente une liste déroulante qui peut être utilisée pour
saisir des fonctions et des commandes prêtes à l’emploi, des variables
système et d’autres fonctions définies par l’utilisateur. Il suffit de taper sur une
commande pour la sélectionner et une nouvelle fois pour l’insérer. Quand un
élément de la liste Form est sélectionné, les commandes disponibles changent.
Pour le détail à ce sujet, voir « Emploi du clavier catalogue » (page 26).
Jeu de touches [Number]
Ce jeu de touches fournit les mêmes touches que celles du clavier. Utilisez
ce jeu de touches lorsque vous voulez uniquement utiliser l’écran tactile pour
la saisie ou à la place du clavier numérique avec l’orientation horizontale de
l’écran (paysage).
Chapitre 1 : Bases 18
Page 19

Saisie de base
Vous trouverez ici un certain nombre d’exemples illustrant la façon de procéder pour saisir des données.
Toutes les procédures décrites requièrent les conditions suivantes.
• L’application Principale doit être ouverte. Voir « Applications internes » (page 13).
• Le clavier tactile doit être affiché. Voir « Emploi du clavier tactile » (page 17).
kSaisie d’une expression
Vous pouvez saisir des expressions tout comme vous les écrivez normalement. Il suffit ensuite d’appuyer sur la
touche E pour exécuter le calcul. Le ClassPad détermine automatiquement l’ordre de priorité des additions,
soustractions, multiplications, divisions et expressions entre parenthèses.
Exemple : Simplifier −2 + 3 − 4 + 10
u Emploi du clavier numérique
cz2+3-4+10E
Si la ligne où vous voulez saisir l’expression de calcul contient déjà une
entrée, assurez-vous d’appuyer sur
u Emploi du clavier tactile
Tapez sur les touches du clavier [Number] pour saisir l’expression du calcul.
c pour l’effacer.
c4-c+d-e+baw
Comme indiqué dans l’exemple ci-dessus, vous pouvez saisir des calculs arithmétiques simples avec le clavier
numérique ou le clavier tactile. Pour saisir des expressions plus complexes, les fonctions, les variables, etc. il
faut utiliser le clavier tactile. Voir le Chapitre 2 pour des informations concernant les expressions de saisie.
Conseil : Dans certains cas, l’expression saisie et l’expression affichée (résultat)
peuvent ne pas être entièrement visibles dans la zone d’affichage. Si le
cas se présente, tapez sur les flèches droite ou gauche qui apparaissent
à l’écran pour faire défiler l’expression et voir la partie non visible.
Vous pouvez également modifier l’orientation de l’écran
vers horizontal (paysage) pour une meilleure lecture
des formules saisies et des résultats de calculs
longs. Voir « Modifier l’orientation de l’écran » (page
15).
kÉdition des termes saisis
u Supprimer un caractère unique
Déplacez le curseur jusqu’à la droite du caractère à supprimer, et appuyez sur K. A chaque pression de
K le caractère à la gauche du curseur est effacé.
Exemple : Remplacer l’expression 369 × × 2 par 369 × 2
1. c369**2
2. dK
Après avoir effectué tous les changements souhaités, appuyez sur E pour calculer le résultat. Pour
ajouter plus de caractères au calcul, revenez à la fin du calcul en appuyant sur e, puis saisissez les termes
nécessaires.
Conseil : Le curseur peut être déplacé sans pression du pavé directionnel, simplement en tapant à l’endroit voulu avec
le stylet. Le curseur se positionne à cet endroit.
Chapitre 1 : Bases 19
Page 20

u Insérer un nouveau terme au milieu d’une expression existante
Utilisez d ou e pour positionner le curseur à l’endroit où vous voulez saisir un nouveau terme et saisissez
le terme nécessaire.
2
Exemple : Remplacer 30
[Math1].)
1. c30x
2. dddds
3. ee)
par sin(30)2 (Pour la saisie, utilisez le clavier numérique et le jeu du clavier tactile
u Remplacer plusieurs termes par de nouveaux
Après avoir fait glisser le stylet sur les termes que vous voulez remplacer, saisissez les nouveaux.
Exemple : Remplacer « 1234567 » par « 10567 »
1. c1234567
2. Faites glisser le stylet sur « 234 » pour le sélectionner.
3. 0
k Emploi du presse-papier pour le copier et le coller
Vous pouvez copier (ou couper) une fonction, une commande ou tout autre terme saisi dans le presse-papier
du ClassPad, puis collez le contenu du presse-papier à un autre endroit. A chaque nouvelle copie ou coupure,
le contenu du presse-papier est remplacé par les nouveaux caractères copiés ou coupés.
u Copier des caractères
1. Faites glisser le stylet sur les caractères que vous voulez copier pour les sélectionner.
2. Sur le clavier tactile, tapez sur p. Ou tapez sur le menu [Edit] puis sur [Copy].
• Les caractères sélectionnés sont copiés dans le presse-papier.
u Couper des caractères
1. Faites glisser le stylet sur les caractères que vous voulez couper pour les sélectionner.
2. Tapez sur le menu [Edit] puis sur [Cut].
• Les caractères sélectionnés sont supprimés et mis dans le presse-papier.
u Coller le contenu du presse-papier
1. Amenez le curseur à la position où vous voulez coller le contenu du presse-papier.
2. Sur le clavier tactile, tapez sur q. Ou tapez sur le menu [Edit] puis sur [Paste].
• Le contenu du presse-papier est collé à la position actuelle du curseur.
Conseil : Le contenu du presse-papier reste dans le presse-papier après avoir été collé. Il peut donc être collé plusieurs
fois de suite.
Copier et coller un message
La « boîte de message » est une case sous la fenêtre graphique (voir Chapitre
3) où une ligne peut être saisie et affichée.
Les deux boutons à la droite de la boîte de message servent à copier le
contenu de la boîte (bouton p), ou à coller le contenu du presse-papier dans
la boîte (bouton q). Le copier et le coller s’effectuent de la même façon que
sur le clavier tactile.
Boîte de message
Chapitre 1 : Bases 20
Page 21

kCopier avec Glisser-Déposer
Vous pouvez également copier une ligne de texte simplement en la sélectionnant et en la faisant glisser dans
un autre emplacement acceptant la saisie de texte.
Exemple 1 : Utiliser l’application Principale pour effectuer le calcul 15 + 6 × 2, modifier en (15 + 6) × 2, puis le
recalculer
1. Dans la zone de travail de l’application Principale, effectuez le calcul ci-
dessous.
c15+6*2E
2. Glissez sur l’expression 15 + 6 × 2 pour la sélectionner, puis faites glisser
l’expression vers le .
• Cela copie 15 + 6 × 2 à l’endroit où vous l’avez déposé.
3. Ajoutez des parenthèses avant et après 15 + 6 puis appuyez sur E.
Conseil : Vous pouvez utiliser le glisser-déposer pour copier à la fois des formules
saisies et des résultats de calculs.
Exemple 2 : Copier une expression que avez saisie avec l’application Principale vers la fenêtre de l’éditeur de
graphes
1. Dans la zone de travail de l’application Principale, saisissez : 2
x^2 + 2x − 1.
c2x{2+2x-1E
2. Tapez sur le bouton fléché vers le bas, à la droite de la barre d’outils. Sur la
palette de boutons qui apparaît, tapez sur !.
• Cela affiche la fenêtre de l’éditeur de graphes dans la moitié inférieure de
l’écran.
3. Sélectionnez l’expression 2
x^2 + 2x − 1 que vous avez saisie avec
l’application Principale, puis faites-la glisser vers le situé à droite du y1:
dans la fenêtre de l’éditeur de graphes.
• Cela copie 2
x^2 + 2x − 1 à l’endroit où vous l’avez déposé.
Conseil
• Une expression que vous copiez à l’aide de l’opération ci-dessus est enregistrée
dans la fenêtre de l’éditeur de graphes de l’application Graphe & Table. Pour plus de
détails sur le fonctionnement de la fenêtre de l’éditeur de graphes, voir Chapitre 3.
• Selon la destination où vous glisser une chaîne de caractères ou une expression,
l’opération de dépose peut la convertir automatiquement en graphique ou en figure. Par exemple, déposer l’expression
de l’exemple 2 dans la fenêtre graphique représentera graphiquement l’expression. Consultez les sections fournies ci-
dessous pour voir des exemples utilisant le glisser-déposer.
- « 2-9 Emploi de l’application Principale en combinaison avec d’autres applications » (Chapitre 2, page 94)
- « 5-4 Représentation graphique d’une expression ou valeur en la déposant dans la fenêtre graphique d’équation
différentielle » (Chapitre 5, page 132)
- « 8-5 Emploi de l’application Géométrie avec d’autres applications » (Chapitre 8, page 182)
- « 13-1 Saisie et Édition du contenu des cellules » (Chapitre 13, page 237), « 13-2 Représentation graphique » (Chapitre
13, page 247)
Différentes opérations du clavier tactile
Dans les paragraphes suivants vous trouverez des explications sur chaque jeu de touches du clavier tactile.
Pour des informations concernant les types de jeux de touches et un aperçu général des jeux de touches, voir
« Jeux de touches du clavier tactile » (page 17). Tous les exemples de cette section requièrent les conditions
suivantes.
• L’application Principale doit être ouverte. Voir « Applications internes » (page 13).
• Le clavier tactile doit être affiché. Voir « Emploi du clavier tactile » (page 17).
Chapitre 1 : Bases 21
Page 22

k Emploi des jeux de touches Math, Trig et Advance
Les jeux de touches [Math1], [Math2], [Math3], [Trig] (trigonométrique), et
[Advance] contiennent des touches pour la saisie d’expressions numériques.
La touche L dans le coin supérieur gauche et toutes les touches de la
rangée inférieure sont communes à tous les jeux de touches. Leurs fonctions
sont décrites ci-dessous.
L Bascule entre la saisie en modèle et la saisie en ligne. Voir « Saisie en
modèle et saisie en ligne » (page 23).
h Effectue la même opération que la touche K du clavier numérique. Supprime le caractère à gauche
de la position actuelle du curseur.
pq Voir « Emploi du presse-papier pour le copier et le coller » (page 20).
D Saisit « ans ». Voir « Emploi de la variable de dernier résultat (ans) » (page 45).
w Effectue la même opération que la touche E du clavier numérique qui exécute des calculs.
Les clés dans le tableau suivant se trouvent sur différents jeux de touches et servent à saisir des fonctions et
des commandes pour effectuer des opérations et des calculs particuliers.
Jeu de touche Touche Description
Math1, Math2,
Math3, Trig
Math1, Math2,
Trig
Math1, Math2
Math1, Math2
Math1, Math3
Math1, Math3
Math1, Math3
Math1, Trig
Math1
N5
p
W
m
sct
QI
4
.
(
)
*R
V"%
« Saisie en modèle et saisie en ligne » (page 23), « Autres
fonctions » (page 50)
Saisit pi (π).
Saisit le symbole de substitution (⇒). « Création d’une nouvelle
variable » (page 33)
« Fonctions logarithmiques et fonctions exponentielles » (page
49)
« Fonctions trigonométriques et trigonométriques inverses »
(page 49)
« Fonctions logarithmiques et fonctions exponentielles » (page
49)
Saisit le symbole de valeur absolue (| |) ou la fonction (abs().
« solve [Action][Equation/Inequality][solve] » (page 83)
Saisit des parenthèses (( )).
Saisit des accolades ({ }). « 2-4 Calculs de listes » (page 58)
r
« Conversion des angles (°,
) » (page 48)
« Fonctions logarithmiques et fonctions exponentielles » (page
49)
Math1
Math1
Math1
Math1
Math2, Math3,
Trig
Math2, Trig
wE
/
a
#
i
e
8
« Autres fonctions » (page 50)
« dms [Action][Transformation][DMS][dms] » (page 65)
« toDMS [Action][Transformation][DMS][toDMS] » (page 65)
« solve [Action][Equation/Inequality][solve] » (page 83)
Saisit l’unité imaginaire (
i).
Saisit le symbole de l’infini (∞).
θ
Saisit la variable
.
Chapitre 1 : Bases 22
Page 23

Jeu de touche Touche Description
Math2, Trig
Math2
Math2
Math3
Math3
Math3
Math3
Math3
Math3
Math3
Math3
Math3
Trig
[
`*7
]_)
678
d
fg
'
+
1
U
[
<>;:=/
~
SCT
Saisit la variables à caractère unique (page 24)
« Emploi du sous-menu Calcul » (page 68)
« 2-5 Calculs de matrices et de vecteurs » (page 58)
« Créer une fonction définie par l’utilisateur avec la commande
Define » (page 211)
Saisit le « f » de f(
« Symbole de dérivée (’) » (page 55)
« dSolve [Action][Equation/Inequality][dSolve] » (page 84)
« Fonction « piecewise » » (page 54)
« Opérateur « with » ( | ) » (page 56)
Saisit des crochets ([ ]). « 2-5 Calculs de matrices et de
vecteurs » (page 58)
« Symboles d’égalité et symboles d’inégalité » (page 55)
« Symbole d’angle (∠) » (page 55)
« Fonctions trigonométriques et trigonométriques inverses »
(page 49)
x), ou le « g » de g(x).
t.
Trig
Advance
Advance
Advance
Advance
Advance
Advance
Advance
Advance
Advance
123
!@#
:!
PN
NM<
hin
r
5%(^
7
6
l
'
« Fonctions hyperboliques et hyperboliques inverses » (page 49)
« Autres Fonctions » (page 50)
« Arrangement (
« Chapitre 6 : Application Suites »
« rSolve » (page 135)
« Emploi du sous-menu Avancé » (page 65)
« Fonction Gamma » (page 57)
« Fonction Delta de Dirac » (page 56)
« Fonction delta
« Fonction échelon de Heaviside » (page 57)
nPr) et Combinaison (nCr) » (page 54)
ième
n
» (page 57)
k Saisie en modèle et saisie en ligne
ClassPad prend en charge deux méthodes de saisie différentes : la saisie en modèle et la saisie en ligne. La
saisie en modèle vous permet de saisir des fractions, des puissances, et d’autres fonctions en utilisant des
formats identiques à ceux des livres. La saisie en ligne utilise un format linéaire pour la saisie des expressions.
2
2'2
2+
( )
'
Saisie en modèle Saisie en ligne
2+ 1
2+ (2 (2) / ( (2) + 1))^2
Chapitre 1 : Bases 23
Page 24

u Passer de la saisie de modèles à la saisie de lignes
∫
Tapez sur la touche L. Chaque tape fait passer la couleur de la touche de blanc (L) à bleu-clair ou viceversa ( ).
Une touche blanche indique un mode de saisie en modèle, alors qu’une touche bleu-clair indique un mode de
saisie en ligne.
Avec le mode de saisie en modèle, vous pouvez effectuer une saisie en modèle à l’aide des touches
comportant la marque
commandes que dans le mode de saisie en ligne.
Exemple 1 : Utiliser le mode de saisie en modèle pour saisi
1. Tapez sur l’onglet [Math1] puis entrer dans le mode de saisie en modèle (touche L blanche).
2. Effectuez l’opération ci-dessous :
2+(N2!2c!2e+1
eem2E
Exemple 2 : Utiliser le mode de saisie en ligne pour saisir la même expression que dans l’exemple 1
(
2+ (2 (2) / ( (2) + 1))^2
ou , comme N et !. Les autres touches saisissent les mêmes fonctions ou
2
2'2
2+
( )
'
)
2+ 1
1. Tapez sur l’onglet [Math1] puis entrer dans le mode de saisie en ligne (touche
2. Effectuez l’opération ci-dessous :
2+(d2!2)N
(!2)+1)ewE
Exemple 3 : Utiliser le mode de saisie en modèle pour saisir
1. Tapez sur l’onglet [Math2] puis entrer dans le mode de saisie en modèle (touche L blanche).
2. Effectuez l’opération ci-dessous :
Oxe1f10exE
Exemple 4 : Utiliser le mode de saisie en modèle pour saisir
1. Tapez sur l’onglet [Math2] puis entrer dans le mode de saisie en modèle (touche L blanche).
2. Effectuez l’opération ci-dessous :
7(1-xm2e)Qxeex
3. Tapez sur la boîte de saisie supérieure droite
Ensuite, tapez sur la boîte de saisie inférieure droite ∫ et appuyez sur 0.
4. Pour exécuter le calcul, appuyez sur E.
puis appuyez sur 1.
()
Y
1
(1 − 2)
∫
0
bleue).
Conseil : Pour des informations sur le contenu et les formats de saisie des fonctions dans l’exemple 3 et l’exemple 4,
voir « 2-7 Emploi du menu Action » (page 62).
k Emploi de variables à caractère unique
Comme le nom le suggère, une variable à caractère unique désigne une variable dont le nom consiste en un
seul caractère, par exemple « a » ou « x ». La saisie des noms de variables consistant en un seul caractère est
soumise à des règles qui diffèrent de la saisie de noms consistant en plusieurs caractères (comme « abc »).
Chapitre 1 : Bases 24
Page 25

u Saisir un nom de variable à caractère unique
Tout caractère saisi avec une des méthodes suivantes est traité comme variable à caractère unique.
• Tape d’une touche du jeu de touches [Var] (variable) (page 18)
• Tape de touches X, Y, ou Z du jeu de la touche [Number]
• Tape de touches [ du jeu de la touche [Math2]
• Pression de la touche x, y, ou Z du clavier numérique
Si vous utilisez ces opérations pour saisir une série de caractères, chacun des caractères sera traité comme
variable à caractère unique. Par exemple, si vous saisissez A, B, C à l’aide du jeu de la touche [Var],
cette série de caractères ne sera pas traitée comme la suite de caractères « abc » mais comme l’expression
mathématique
a × b × c.
Conseil : Les variables à un seul caractère décrites ci-dessus permettent d’effectuer les calculs tels qu’ils apparaissent
dans votre livre.
Exemple 1 : ABCw
Exemple 2 : 2xyE
Conseil : Lorsque vous saisissez une variable à un seul caractère, son nom apparaît en caractère gras et italique. Ceci
permet de savoir qu’il s’agit d’une variable à caractère unique.
u Saisir une suite de caractères
Une suite de caractères (comme « list1 ») peut être utilisée dans les noms de variables, les commandes de
programme, les commentaires, etc. Pour saisir une suite de caractères il faut utiliser le jeu de touches [abc].
Exemple : abcE
Le jeu de touches [abc] peut aussi être utilisé pour saisir les noms de variables à caractère unique. Il suffit alors
de saisir un seul caractère, ou de faire suivre un seul caractère d’un opérateur mathématique.
Exemple : a*b+cE
Conseil : Une variable à caractère unique saisie sur le jeu de touches [abc] est identique à une variable à caractère
unique saisie à l’aide du jeu de touche [Var].
k Emploi du clavier alphabétique
Tapez sur l’onglet [abc] sur la gauche du clavier tactile pour afficher le jeu de
touches [abc] du clavier alphabétique. En plus du jeu de touches [abc], vous
avez le choix entre trois autres jeux de touches désignés par [αβγ] (caractères),
[Math] (symboles mathématiques), et [Symbol] (autres symboles).
Utilisez les onglets au-dessus du clavier alphabétique (sur la droite du clavier
avec l’orientation d’écran horizontale) pour sélectionner un jeu de touches.
Pour revenir au jeu de touche [Math1] depuis le clavier alphabétique, tapez sur
la touches I dans le coin inférieur gauche.
Chapitre 1 : Bases 25
Page 26

k Emploi du clavier catalogue
Le menu « Form » du clavier catalogue sert à sélectionner les cinq catégories décrites-ci dessous.
Func ........ fonctions intégrées (pages 48 et 62)
Cmd ........ commandes et opérateurs intégrés (page 213)
Sys .......... variables système (page 310)
User ........ fonctions définies par l’utilisateur (page 210)
All ............ toutes les commandes, fonctions, etc.
Après avoir sélectionné une catégorie, vous pouvez choisir un élément dans la liste alphabétique qui apparaît
sur le clavier catalogue.
Conseil : Remarque les variables et les programmes définis par l’utilisateur ne peuvent pas être saisis par le clavier
catalogue. Il faut employer le gestionnaire de variables (page 28).
Configuration du clavier catalogue
Tapez sur une lettre pour afficher
les commandes, fonctions ou autres
éléments commençant par cette lettre.
Tapez sur ce bouton pour sélectionner la
catégorie souhaitée ([Func], [Cmd], [Sys],
[User] ou [All]) dans la liste qui apparaît.
Liste alphabétique des commandes,
fonctions et autres éléments disponibles
dans la catégorie sélectionnée avec
« Form ».
Tapez sur ce bouton pour saisir l’élément
actuellement sélectionné dans la liste
alphabétique.
u Utiliser le clavier catalogue
Exemple : Saisir la commande « Plot »
1. Sur le clavier catalogue, tapez sur le bouton fléché de « Form » et sélectionnez [Cmd] dans la liste de
catégories qui apparaît.
2. Tapez sur le bouton + dans le coin supérieur droit jusqu’à ce que le bouton P soit visible.
3. Tapez sur P.
4. Dans la liste alphabétique, tapez sur « Plot », puis tapez sur [INPUT] pour saisir la commande.
• Au lieu de taper sur [INPUT], vous pouvez aussi taper une seconde fois sur la commande pour saisir la
commande.
1-5 Données du ClassPad
Vous trouverez ici des informations sur les divers types des données pouvant être stockées dans la mémoire
du ClassPad, et sur l’emplacement où chaque type de données est stocké. Il est également expliqué comment
utiliser le gestionnaire de variables, qui est un outil qui permet de gérer les données stockées, et également
les opérations sur fichier (sauvegarde de fichier, restitution, suppression, changement de nom, etc.) qui sont
communes à plusieurs applications différentes.
Types de données et emplacements de stockage (Zones de mémoire)
ClassPad utilise une zone de mémoire « mémoire principale » pour stocker les différents types de données.
Exemples :
• L’exécution de « 10⇒
l’application eActivity entraine le stockage de la variable x dans la mémoire principale sous forme de donnée
de type « EXPR » (expression).
x » (qui affecte une valeur de 10 à la variable x) dans l’application Principale ou dans
Chapitre 1 : Bases 26
Page 27

• La création d’une fonction définie par l’utilisateur (page 210) entraine le stockage de la fonction dans la mémoire
principale sous forme de donnée de type « FUNC » (fonction).
• La sauvegarde d’une feuille de calcul en un fichier (en exécutant [File] - [Save] avec l’application
Spreadsheet) enregistre le fichier dans la mémoire principale sous forme de donnée de type « MEM »
(mémoire).
Un fichier eActivity créé avec eActivity est stocké dans une zone de mémoire à part d’eActivity afin de le
dissocier des autres données d’application.
Accès aux données
Il est possible d’accéder aux données de la mémoire principale via n’importe quelle application, en plus de
celle ayant servi à leur création. Elles peuvent également être supprimées, renommés, copiées, déplacées
et consultées autrement à l’aide du gestionnaire de variables (page 28). Seule l’application eActivity permet
d’accéder aux fichiers eActivity.
Types de données de la mémoire principale
Les données stockées dans la mémoire principale ont un attribut de type de données qui est affecté selon
l’application qui a créé les données et le contenu réel des données. Le type de données est indiqué par le
nom du type de données. Ces noms apparaissent dans la liste de variables du gestionnaire de variables et
dans la boîte de dialogue de sélection des données qui apparaît lorsque vous spécifiez une variable dans une
application du ClassPad. Les listes suivantes énumèrent tous les noms des types de données des variables et
donnent la signification de chacun d’eux.
Noms des types
de données
EXPR Données de nombre réel, nombre complexe ou expression
STR Chaîne
LIST Données de liste créées avec l’application Statistiques, l’application Principale, etc.
MAT Données de matrice créées avec l’application Principale, etc.
PRGM* Programme général
EXE* Programme interdit d’édition
TEXT* Données de texte
FUNC* Fonction définie par l’utilisateur
GMEM* Données de la mémoire de graphes sauvegardées avec l’application Graphe & Table
GEO* Données de I’application Géométrie
MEM* Données sauvegardées dans un fichier à l’aide d’une des applications suivantes :
OTHR Autres types de données
Type de données
Pour le détail à ce sujet, voir « Sauvegarde des informations de l’éditeur de graphes
dans la mémoire de graphes » (page 104).
Spreadsheet, Géométrie, Vérifier (page 96), Probabilité (page 97).
Types de variables protégées
Certains types de données sont protégés. Les variables de types protégés ne peuvent pas être remplacées
par d’autres, elles ne risquent donc pas d’être perdues par inadvertance. Les types de variables marqués d’un
astérisque dans la liste précédente sont protégés. Remarque c’est le système qui détermine si un type de
variables doit être protégé ou non. Vous ne pouvez pas changer le statut vous-même.
Conseil : Même si une variable a des données protégées, vous pouvez changer son nom, la supprimer ou la déplacer
si vous voulez. Pour empêcher ces opérations, il faut verrouiller la variable. Voir « Opérations du gestionnaire
de variables » à la page 29.
Chapitre 1 : Bases 27
Page 28

Dossiers de la mémoire Principale
Le ClassPad sauvegarde les variables dans l’un des types de dossiers suivants.
Dossier « main » : Le dossier « main » est un dossier réservé du ClassPad, qui fonctionne comme dossier
actuel par défaut (voir « Dossier actuel » ci-dessous ).
Dossier « library » : C’est également un dossier réservé par le ClassPad. Le dossier « library » sert à
regrouper les données créées par l’utilisateur (variables, programmes, fonctions personnalisées, etc.). Il n’est
pas nécessaire de spécifier un chemin pour accéder aux données sauvegardées dans le dossier « library »,
même si un autre dossier est actuellement spécifié.
Dossier personnel : C’est un dossier que vous devez créer et désigner. Vous pouvez spécifier votre dossier
personnel comme dossier actuel, y transférer des variables, etc. Vous pouvez aussi supprimer et renommer
un dossier personnel, si nécessaire. En tout 87 dossiers personnels peuvent être créés dans la mémoire du
ClassPad.
Conseil : Vous ne pouvez pas mettre un dossier dans un autre.
Dossier actuel
Le dossier actuel est le dossier qui contient les données (sauf les fichiers eActivity) créées par les applications
et à partir duquel vous avez accès à ces données. Le dossier actuel par défaut est le dossier « main ».
Un dossier personnel peut aussi servir de dossier actuel. Pour de plus amples informations à ce sujet, voir
« Opérations du gestionnaire de variables » à la page 29.
Emploi du gestionnaire de variables
Le gestionnaire de variables est un outil qui permet de gérer les variables spécifiées par l’utilisateur, les
programmes, les fonctions personnalisées et d’autres types de données. Bien qu’ici seul le terme de
« variables » soit utilisé, les explications se rapportent aussi aux autres types de données qui peuvent être
traitées par le gestionnaire de variables.
Avec le gestionnaire de variables vous pouvez :
• Créer, supprimer, renommer, verrouiller et déverrouiller des dossier et définir les paramètres du dossier
actuel.
• Supprimer, copier, renommer, déplacer, verrouiller, déverrouiller, rechercher des variables et afficher le
contenu de ces variables.
À propos des types de variables
Les variables avec un nom de lettre comme x et y peuvent être des variables personnelles créées par
l’utilisateur, des variables système ou des variables locales.
• Les variables système sont des variables réservées et prédéfinies et ne peuvent pas être renommées.
Pour le détail sur les noms et d’autres informations sur les variables système, voir « Tableau des variables
système » à la page 310.
• Une variable locale est une variable créée temporairement lorsqu’on définit une fonction, un programme ou
une autre opération dans un but précis. Pour plus d’informations sur les variables locales, voir la commande
« Local » dans « 12-4 Commandes de programmation ».
u Ouverture du gestionnaire de variables
1. Avec n’importe quelle application (sauf
l’application Système) ouverte, tapez sur O
puis sur [Variable Manager].
• La liste des dossiers s’affiche. La liste de
dossiers s’affiche toujours en premier lorsque
vous ouvrez le gestionnaire de variables.
Nom du dossier
Nombre de variables dans
le dossier
Liste de dossiers
Chapitre 1 : Bases 28
Page 29
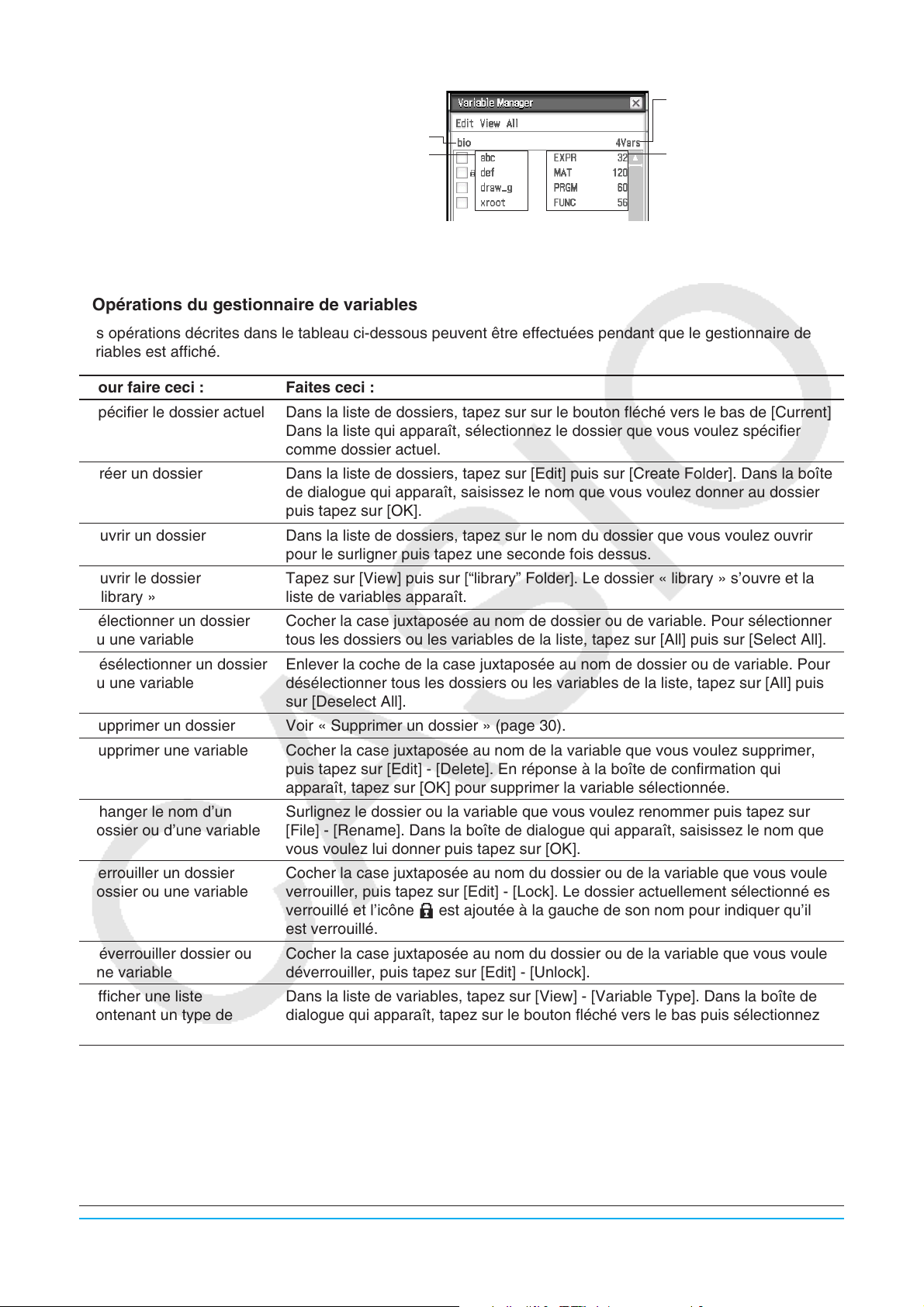
2. Tapez deux fois sur le dossier pour l’ouvrir et
voir son contenu, une liste de variables.
Nom du dossier
Noms des variables
• Pour fermer la liste de variables et revenir à la
Nombre de variables dans
le dossier
Types de données (page 27)
et tailles (octets)
liste de dossiers, tapez sur [Close].
Liste de variables
3. Pour sortir du gestionnaire de variables, tapez sur [Close] dans la liste des dossiers.
u Opérations du gestionnaire de variables
Les opérations décrites dans le tableau ci-dessous peuvent être effectuées pendant que le gestionnaire de
variables est affiché.
Pour faire ceci : Faites ceci :
Spécifier le dossier actuel Dans la liste de dossiers, tapez sur sur le bouton fléché vers le bas de [Current].
Dans la liste qui apparaît, sélectionnez le dossier que vous voulez spécifier
comme dossier actuel.
Créer un dossier Dans la liste de dossiers, tapez sur [Edit] puis sur [Create Folder]. Dans la boîte
de dialogue qui apparaît, saisissez le nom que vous voulez donner au dossier
puis tapez sur [OK].
Ouvrir un dossier Dans la liste de dossiers, tapez sur le nom du dossier que vous voulez ouvrir
pour le surligner puis tapez une seconde fois dessus.
Ouvrir le dossier
« library »
Sélectionner un dossier
ou une variable
Désélectionner un dossier
ou une variable
Tapez sur [View] puis sur [“library” Folder]. Le dossier « library » s’ouvre et la
liste de variables apparaît.
Cocher la case juxtaposée au nom de dossier ou de variable. Pour sélectionner
tous les dossiers ou les variables de la liste, tapez sur [All] puis sur [Select All].
Enlever la coche de la case juxtaposée au nom de dossier ou de variable. Pour
désélectionner tous les dossiers ou les variables de la liste, tapez sur [All] puis
sur [Deselect All].
Supprimer un dossier Voir « Supprimer un dossier » (page 30).
Supprimer une variable Cocher la case juxtaposée au nom de la variable que vous voulez supprimer,
puis tapez sur [Edit] - [Delete]. En réponse à la boîte de confirmation qui
apparaît, tapez sur [OK] pour supprimer la variable sélectionnée.
Changer le nom d’un
dossier ou d’une variable
Surlignez le dossier ou la variable que vous voulez renommer puis tapez sur
[File] - [Rename]. Dans la boîte de dialogue qui apparaît, saisissez le nom que
vous voulez lui donner puis tapez sur [OK].
Verrouiller un dossier
dossier ou une variable
Cocher la case juxtaposée au nom du dossier ou de la variable que vous voulez
verrouiller, puis tapez sur [Edit] - [Lock]. Le dossier actuellement sélectionné est
verrouillé et l’icône b est ajoutée à la gauche de son nom pour indiquer qu’il
est verrouillé.
Déverrouiller dossier ou
une variable
Afficher une liste
contenant un type de
variables précis
Copier ou déplacer une
variable
Cocher la case juxtaposée au nom du dossier ou de la variable que vous voulez
déverrouiller, puis tapez sur [Edit] - [Unlock].
Dans la liste de variables, tapez sur [View] - [Variable Type]. Dans la boîte de
dialogue qui apparaît, tapez sur le bouton fléché vers le bas puis sélectionnez
le type de données dans la liste qui apparait et tapez sur [OK].
Dans la liste de variables, tapez sur [Edit] puis sur [Copy] ou [Move]. Dans
la boîte de dialogue qui apparaît, tapez sur le bouton fléché vers le bas puis
sélectionnez le dossier de destination dans la liste qui apparait et tapez sur
[OK].
Conseil
• Si le même nom de variable existe déjà dans le dossier de destination, la variable est
remplacée dans le dossier de destination par celle que vous copiez ou déplacez.
• Une variable verrouillée ne peut pas être déplacée.
Chapitre 1 : Bases 29
Page 30

Pour faire ceci : Faites ceci :
Afficher le contenu d’une
variable
Saisir le nom d’une
variable ou d’un dossier
dans une application
Rechercher une variable Dans la liste de dossiers, tapez sur [Search]. Dans la boîte de dialogue qui
Dans la liste de variables, tapez sur le nom de la variable dont vous voulez voir
le contenu pour le surligner puis tapez une seconde fois dessus. Le contenu de
la variable figure dans la boîte de dialogue qui apparaît.
Voir « Saisir le nom d’une variable ou d’un dossier dans une application »
(page 31).
apparaît, saisissez le nom de la variable que vous recherchez, puis tapez sur
[OK].
Un point d’exclamation (!) apparaît devant les dossiers contenant un nom de
variables correspondant au nom spécifié.
Remarque : Procédez de la façon décrite ci-dessus pour rechercher un nom
de variable dans le dossier « main » ou un dossier personnel. Remarque vous
ne pouvez pas effectuer la recherche dans le dossier « library ».
Sélectionner un dossier
• Si aucune case n’est cochée dans la liste de dossiers, l’opération effectuée ne concerne que le dossier dont
le nom est actuellement surligné dans la liste. Si la case d’un dossier est cochée, ce dossier est affecté par
l’opération mais pas le dossier surligné dans la liste.
• Lorsque vous cochez la case d’un dossier, toutes les cases des variables à l’intérieur de ce dossier sont
également cochées.
• Lorsque vous changez le nom d’un dossier, seul le dossier dont le nom est surligné dans la liste de dossiers
est renommé. Les dossiers dont les cases sont cochées ne sont pas concernés par ce changement.
Sélectionner une variable
• Si aucune case n’est cochée dans la liste de variables, l’opération effectuée ne concerne que la variable dont
le nom est actuellement surligné dans la liste. Si la case d’une variable est cochée, cette variable est affectée
par l’opération mais pas la variable surlignée dans la liste.
• Lorsque vous changez le nom d’une variable, seul la variable dont le nom est surligné dans la liste de
variables est renommée. Les variables dont les cases sont cochées (variables sélectionnées) ne changent
pas de nom.
Règles de désignation des dossiers et des variables
Lors de la désignation des dossiers et des variables, les règles suivantes s’imposent.
• Les noms des dossiers ou des variables ne peuvent contenir que huit octets.
• Les caractères suivants peuvent être utilisés dans le nom de dossier ou de variable : Caractères majuscules
et minuscules, caractères suffixes, nombres, caractère souligné (_).
• Les noms de dossiers ou des variables sont sensibles aux majuscules/minuscules. Par exemple, chacun des
noms suivants est considéré comme nom de dossier particulier : abc, Abc, aBc, ABC.
• Un mot réservé (noms de variables système, noms de fonctions intégrées, noms de commandes, etc.) ne
peut pas être utilisé comme nom de dossier ou de variable.
• Un nombre, un caractère suffixe ou souligné (_) ne peut pas être utilisé comme premier caractère du nom de
dossier ou de variable.
u Supprimer un dossier
Important !
Avant de supprimer un dossier, assurez-vous que vous n’avez plus besoin des variables qu’il contient. Il est
conseillé, par exemple, de supprimer d’abord les variables dont vous n’avez pas besoin et de mettre les autres
dans un autre dossier, puis de supprimer le dossier vide.
1. Ouvrez le dossier que vous voulez supprimer et vérifiez son contenu.
• Assurez-vous que vous n’avez plus besoin des variables dans le dossier. Si une des variables est
verrouillée, déverrouillez-la.
Chapitre 1 : Bases 30
Page 31

• Après avoir vérifié le contenu du dossier, fermez le dossier et revenez à liste de dossiers.
2. Cochez la case juxtaposée au dossier que vous voulez supprimer.
• Vous pouvez sélectionner et supprimer plusieurs dossiers, si nécessaire.
3. Dans la liste de dossiers, tapez sur [Edit] puis sur [Delete].
4. En réponse à la boîte de confirmation qui apparaît, tapez sur [OK] pour supprimer le dossier.
Conseil : Vous ne pouvez pas supprimer le dossier « library » ni le dossier « main ».
u Saisir le nom d’une variable ou d’un dossier dans une application
1. Dans l’application Principale, l’application Graphe & Table ou une autre application, positionnez le curseur à
l’endroit où vous voulez introduire le nom de la variable.
2. Ouvrez le gestionnaire de variables pour afficher la liste de dossiers.
3. Si vous voulez saisir un nom de variable, tapez deux fois sur le dossier qui inclut la variable dont le nom doit
être saisi. Si vous voulez saisir un nom de dossier, passez à l’étape suivante.
4. Tapez sur le dossier dont le nom doit être saisi de manière à le surligner.
5. Tapez sur [INPUT].
• Le gestionnaire de variables se ferme et le nom du dossier ou de la variable sélectionné à l’étape 4 est
introduit dans l’application à la position du curseur.
Gestion des fichiers d’application
Les applications suivantes peuvent sauvegarder les données en fichiers.
Géométrie (Chapitre 8), eActivity (Chapitre 10), Spreadsheet (Chapitre 13), Fonction Vérifier (page 96),
Probabilité (page 97), Plot Image (Chapitre 15)
Cette section explique les opérations communes pouvant être effectuées sur les fichiers de données créés
avec ces applications.
Conseil : La boîte de dialogue de sauvegarde de fichier eActivity est légèrement différente de la boîte de dialogue de
sauvegarde des autres applications, mais les opérations sont quasiment identiques.
u Enregistrer un fichier
1. Tapez sur [File] puis sur [Save].
2. Dans la boîte de dialogue qui apparaît, tapez sur le nom du dossier où vous voulez sauvegarder le fichier
pour le sélectionner.
3. Dans la boîte d’édition du nom de fichier, désignez un nom de fichier de 8 octets au maximum, puis tapez
sur [Save].
u Ouvrir un fichier existant
1. Tapez sur [File] puis sur [Open].
2. Dans la boîte de dialogue qui s’affiche, appuyez sur le dossier qui contient le fichier que vous voulez ouvrir.
3. Tapez sur le nom du fichier que vous voulez ouvrir pour le sélectionner, puis tapez sur [Open].
u Rechercher un fichier
1. Tapez sur [File] puis sur [Open].
2. Dans la boîte de dialogue qui s’affiche, tapez sur [Search]. La boîte de dialogue de recherche apparaît.
3. Saisissez le nom du fichier que vous recherchez puis tapez sur [Search].
• Les noms de fichiers correspondant au nom saisi sont surlignés. Tapez sur [Open] pour ouvrir un fichier
surligné.
• Pour voir s’il existe d’autres fichiers de ce nom, tapez de nouveau sur [Search] puis sur [Next] dans la boîte
de dialogue de recherche.
Chapitre 1 : Bases 31
Page 32

u Supprimer un dossier ou un fichier
Important !
Lorsque vous supprimez un dossier, tous les fichiers se trouvant à l’intérieur de celui-ci sont également
supprimés. Vérifiez bien le contenu du dossier avant de le supprimer.
1. Tapez sur [File] puis sur [Open].
2. Dans la boîte de dialogue qui s’affiche, cochez la case juxtaposée au dossier ou fichier que vous voulez
supprimer.
• Vous pouvez sélectionner plusieurs dossiers/fichiers si vous voulez.
• Si vous cochez la case juxtaposée au nom du dossier, les cases de tous les fichiers se trouvant à l’intérieur
du dossier sont également cochées.
3. Tapez sur [File] puis sur [Delete].
4. En réponse à la boîte de confirmation qui apparaît, tapez sur [OK] pour supprimer le ou les dossiers ou
fichiers.
Conseil : La sélection d’un dossier supprime le dossier et tout son contenu. Remarque toutefois que le dossier « main »
ne peut pas être supprimé, même s’il est coché.
u Changer le nom d’un dossier ou d’un fichier
1. Tapez sur [File] puis sur [Open].
2. Dans la boîte de dialogue qui apparaît, tapez sur le nom du dossier vous voulez changer pour le
sélectionner.
3. Tapez sur [File] puis sur [Rename]. La boîte de dialogue de changement de nom apparaît.
4. Saisissez le nom que vous voulez lui donner puis tapez sur [OK].
u Déplacer un fichier dans un autre dossier
1. Tapez sur [File] puis sur [Open].
2. Dans la boîte de dialogue qui s’affiche, cochez la case juxtaposée au fichier que vous voulez déplacer.
• Pour déplacer plusieurs fichiers, cochez leurs cases respectives.
3. Tapez sur [File] puis sur [Move].
• La boîte de dialogue de sélection du dossier de destination apparaît.
4. Dans la boîte de dialogue, tapez sur le bouton fléché vers le bas puis sélectionnez le dossier de destination
dans la liste qui apparait.
5. Tapez sur [OK] pour déplacer les fichiers.
u Basculer la vue du menu de fichier entre la Vue en liste et la Vue détaillée (application
eActivity uniquement)
1. Tapez sur [File] puis sur [Open].
2. Dans la boîte de dialogue qui s’affiche, appuyez sur le dossier qui contient les fichiers que vous voulez lister.
3. Pour afficher à la fois le nom et la taille du fichier, tapez sur [View] - [Detail View]. Pour afficher uniquement
les noms des fichiers, tapez sur [View] - [List View].
u Créer un nouveau dossier
1. Tapez sur [File] puis sur [Open].
2. Dans la boîte de dialogue qui s’affiche, tapez sur [File] puis sur [Create Folder], ou tapez sur {.
• La boîte de dialogue de création de dossier apparaît.
3. Entrez un nom de dossier de 8 octets au maximum, puis tapez sur [OK] pour créer un dossier.
Chapitre 1 : Bases 32
Page 33

1-6 Création et emploi de variables
Cette partie explique comment créer une nouvelle variable (variable personnelle) et donne un exemple de
calcul simple illustrant l’emploi d’une variable.
Création d’une nouvelle variable
La façon la plus courante de créer une nouvelle variable est d’affecter une valeur ou une expression au nom de
la variable. Utilisez la touche d’affectation de variable (W) pour affecter des données à une variable.
L’exemple suivant montre comment affecter des données à une variable lorsque « main » est spécifié comme
dossier actuel.
Exemple : Créer une nouvelle variable intitulée « eq1 » et lui affecter l’expression 2
est supposé ne contenir actuellement aucune variable nommée « eq1 » ou « x ».
x + 1 Le dossier « main »
u Opérations sur le ClassPad
1. Lancez l’application Principale.
2. Appuyez sur k pour afficher le clavier tactile puis appuyez sur les touches suivantes.
2x+11W0eqbw
• La variable nommée « eq1 » est créée dans le dossier actuel (ici le dossier
« main ») et l’expression 2
x + 1 lui est affectée.
Conseil
• Si le dossier actuel contient déjà une variable de même nom, le contenu de cette variable est remplacé par les nouvelles
données, à moins que la variable ne soit verrouillée ou protégée. Pour le détail à ce sujet, voir « Opérations du
gestionnaire de variables » (page 29) et « Types de variables protégées » (page 27).
• Pour sauvegarder la variable qui vient d’être créée dans un autre dossier, spécifiez le nom de la variable de la façon
suivante : < nom de dossier >\< nom de variable >.
• Vous pouvez utiliser le gestionnaire de variables pour voir le contenu de la variable qui vient d’être créée. Pour le détail à
ce sujet, voir « Opérations du gestionnaire de variables » (page 29).
• Pour plus d’informations concernant la désignation des variables, voir « Règles de désignation des dossiers et des
variables » (page 30).
Exemple d’emploi de variables
L’exemple suivant emploie la variable créée dans « Création d’une nouvelle variable » ci-dessus.
Exemple : Affecter les valeurs 5 et 10 à
u Opérations sur le ClassPad
1. Affecter 5 à x.
51WxE
2. Contrôlez le contenu de la variable « eq1 ».
0eqbw
• Cela affiche le résultat du calcul 2
3. Affecter 10 à
101WxE
4. Contrôlez le contenu de la variable « eq1 ».
0eqbw
x.
x et vérifier le résultat de eq1 (= 2x + 1)
x + 1 quand x = 5.
Chapitre 1 : Bases 33
Page 34

Variables du dossier « library »
Il est possible d’accéder aux variables du dossier « library » sans spécifier le nom d’un chemin, quel que soit le
dossier actuel.
Exemple : Créer et accéder à deux variables, l’une se trouvant dans le dossier « library » et l’autre se trouvant
dans un autre dossier
u Opérations sur le ClassPad
1. Avec le dossier « main » spécifié comme dossier actuel, effectuez l’opération suivante pour créer un nom de
variable « eq1 » et affectez-lui les données de liste indiquées.
{1, 2, 3} W eq1w
2. En conservant « main » comme dossier actuel, effectuez l’opération suivante pour créer une variable
nommée « eq2 » dans le dossier « library » et affectez-lui les données de liste indiquées.
{4, 5, 6} W library\eq2w
3. Vérifiez le contenu des deux variables.
eq1w
eq2w
(Comme la variable « eq2 » est sauvegardée dans le dossier « library »,
vous n’avez pas besoin d’indiquer le chemin d’accès.)
4. Remplacez la spécification du dossier actuel par « Test ».
• Utilisez le gestionnaire de variables (page 28) pour créer un dossier nommé « Test » et modifiez la
spécification du dossier actuel.
5. Effectuez les opérations suivantes pour voir le contenu des variables « eq1 » et « eq2 ».
eq1E
(Comme cette opération de touches ne permet pas d’accéder au dossier
« main », le nom de variable (« eq1 ») est indiqué sans le contenu.)
main\eq1E
(En spécifiant le chemin du dossier « main » où se trouve « eq1 » vous
pouvez afficher le contenu de la variable.)
eq2E
(Comme la variable « eq2 » est sauvegardée dans le dossier « library »,
vous n’avez pas besoin d’indiquer le chemin d’accès.)
Conseil : Si vous spécifiez le nom d’une variable qui existe dans le dossier actuel et dans le dossier « library » vous
accédez à la variable se trouvant dans le dossier actuel. Pour le détail sur la priorité d’accès aux variables
et la façon d’accéder aux variables enregistrées dans des dossiers particuliers, voir « Règles d’accès aux
variables » ci-dessous.
Règles d’accès aux variables
En principe, il suffit de spécifier le nom de la variable pour y accéder. Les règles énoncées ici concernent
les variables qui ne se trouvent pas dans le dossier actuel ou les variables qui ont un nom identique à celles
d’autres dossiers.
kOrdre de priorité pour la recherche de variables
Lorsqu’un nom de variable est spécifié pour accéder à une variable, la recherche de variable s’effectue dans
l’ordre suivant.
(1) Variables locales (2) Variables du dossier actuel (3) Variables du dossier « library »
Chapitre 1 : Bases 34
Page 35

• Des variables de même nom peuvent exister simultanément comme variable locale, variable du dossier
actuel et variable du dossier « library ». Dans ce cas, le ClassPad recherche les dossiers dans l’ordre indiqué
ci-dessus et s’arrête sur la première variable qu’il trouve. Si vous voulez accéder à une variable se trouvant à
un degré de priorité inférieur, vous devez spécifier le nom du dossier et le nom de la variable comme indiqué
dans le paragraphe suivant « Spécification d’une variable d’un dossier particulier ».
• Si la variable spécifiée ne peut pas être localisée, elle est traitée comme « variable indéfinie ».
• Remarque il faut noter que le dossier « system » n’est pas compris dans la recherche de variables ci-dessus.
Lorsque vous accédez à une variable dans le dossier système, vous devez spécifier le nom de la variable
seulement, sans spécifier le nom du dossier.
Conseil : Seules les variables locales et les variables du dossier actuel sont explorées lors de la sauvegarde de
données de variables ou lorsqu’une commande impliquant une variable (ex. « DelVar ») est exécutée.
Normalement, les variables du dossier « library » ne sont pas explorées. Si vous voulez inclure un dossier
« library » dans la recherche, le dossier « library » faut le spécifier comme variable, de la façon suivante.
kSpécification d’une variable d’un dossier particulier
Vous pouvez sinon accéder à une variable se trouvant dans le dossier « main », le dossier « library » ou un
dossier personnel en spécifiant le nom du dossier et le nom de la variable.
La syntaxe suivante doit être utilisée pour spécifier le nom de la variable :
< nom de dossier >\< nom de variable >
Exemple : Spécifier la variable « abc » se trouvant dans le dossier « main »
main\abc
1-7 Paramétrage du format des applications
Le menu O comprend des réglages de format pour le paramétrage du nombre de chiffres devant apparaître
dans le résultat du calcul affiché et pour le paramétrage de l’unité d’angle, ainsi que des commandes propres
à chaque application. Chacun des réglages et chacune des commandes disponibles sur le menu O sont
indiqués ci-dessous.
Pour faire ceci :
Spécifier un dossier pour les variables et spécifier le format numérique, l’angle
et d’autres réglages pour l’ensemble des applications originales
Paramétrer la fenêtre graphique et les tracés de graphe pour Graphe & Table,
Coniques et d’autres applications utilisant la représentation graphique
Spécifier le format numérique, l’angle et d’autres réglages pour l’application
Géométrie
Paramétrer la transformée de Fourier et FFT Advanced Format
Paramétrer l’application Finances Financial Format
Rétablir tous les réglages par défaut des menus ci-dessus (sauf celui du
dossier actuel spécifié dans la boîte de dialogue du format de base)
u Paramétrer le format des applications
1. Ouvrir une application (sauf l’application Système).
Sélectionnez cette
commande du menu O :
Basic Format
Graph Format
Geometry Format
Default Setup
2. Tapez sur O. Ensuite, tapez sur la commande de menu souhaitée : Basic Format, Graph Format, Geometry
Format, Advanced Format, ou Financial Format.
3. Utilisez la boîte de dialogue pour définir les paramètres souhaités.
• Pour le détail sur les paramètres de chaque boîte de dialogue, voir « Format des applications » ci-dessous.
4. Pour fermer une boîte de dialogue et valider les réglages effectués, tapez sur [Set]. Sinon pour fermer la
boîte de dialogue sans valider les réglages, tapez sur [Cancel] ou sur le bouton C dans le coin supérieur
droit de la boîte de dialogue.
Chapitre 1 : Bases 35
Page 36

Format des applications
Les paramètres pouvant être configurés avec les réglages de format de l’application sont détaillés dans les
paragraphes suivants. Les réglages marqués d’un astérisque (*) dans les tableaux suivants sont les réglages
par défaut du ClassPad.
k Boîte de dialogue du format de base
Utilisez la boîte de dialogue du format de base pour régler les paramètres de base pour les calculs, cellules, et
d’autres paramètres.
Pour spécifier le dossier actuel
Tapez sur 1 puis tapez sur le nom du dossier (main*) que vous voulez.
1
Pour spécifier le format d’affichage des valeurs numériques
Tapez sur 2 puis tapez sur un des paramètres décrits ci-dessous.
2
Normal 1* : Utilise automatiquement le format d’affichage exponentiel
3
lorsque le résultat du calcul
x est : 10
Normal 2 : Utilise automatiquement le format d’affichage exponentiel
lorsque le résultat du calcul
x est : 10
Fix 0 – Fix 9 : Nombre fixe de décimales
Sci 0 – Sci 9 : Nombre fixe de chiffres significatifs
Pour spécifier l’unité d’angle
Tapez sur 3, puis tapez sur « Radian* », « Degree », ou « Grad ».
−2
> |x| ou |x| t 1010.
−9
> |x| ou |x| t 1010.
Pour faire ceci : Faites ceci :
Basculer entre des calculs dans l’ensemble des
nombres complexes (mode complexe) et des calculs
dans l’ensemble des nombres réels (mode réel)
Afficher les résultats sous forme décimale (mode
décimal) ou laisser les résultats sous forme
d’expressions (mode standard)
Activer (mode algèbre) ou désactiver (mode
assistant) la simplification automatique des
expressions
Cocher la case « Complex Format » pour passer
en mode complexe, ou enlever la coche de la case*
pour passer en mode réel*.
Cocher la case « Decimal Calculation » pour passer
en mode décimal, ou enlever la coche de la case*
pour passer en mode standard.
Cocher la case « Assistant » pour passer en mode
assistant, ou enlever la coche de la case* pour
passer en mode algèbre. Voir page 47 pour plus
d’informations.
Spécifier l’ordre décroissant ou l’ordre croissant pour
l’expression du résultat d’un calcul
Cocher la case « Descending Order »* pour afficher
les expressions des résultats de calculs dans l’ordre
décroissant (comme
de la case pour un affichage dans l’ordre croissant
(comme 1 + x + x2).
Spécifier si les variables dans un calcul en mode
complexe doivent être traitées comme nombres réels
ou comme nombres complexes
Cocher la case « Variable is Real » pour traiter
les variables comme nombres réels, ou enlever la
coche de la case* pour traiter les variables comme
nombres complexes.
Conseil : Pour des informations concernant la case « Q
Médiane » (page 146).
1
, Q3 on Data », voir « Méthodes de calcul pour Q1, Q3 et
2
x
+ x + 1), ou enlever la coche
Emploi de la barre d’état pour modifier les format des applications
Avec les applications énumérées dans le tableau ci-dessous, vous pouvez utiliser la barre d’état pour contrôler
et modifier plusieurs réglages de la boîte de dialogue du format de base.
Chapitre 1 : Bases 36
Page 37

Pour cette application : Vous pouvez contrôler et modifier ces réglages :
Principale, eActivity Réglage mode algèbre/mode assistant, réglage mode standard/mode
décimal, réglage mode complexe/mode réel, réglage de l’unité d’angle
Statistiques Réglage mode standard/mode décimal, réglage de l’unité d’angle
Graphe & Table, Coniques,
Graphes d’équations
différentielles, Résolution
numérique, Suites
Réglage mode complexe/mode réel, réglage de l’unité d’angle
u Utiliser la barre d’état pour modifier les réglages de format des applications
Sur la barre d’état, tapez sur le texte du réglage que vous voulez changer.
Application Principale Application Graphe & Table
Chaque tape modifie l’élément tapé comme indiqué ci-dessous.
• « Alg » ↔ « Assist » ... Passe du mode algèbre au mode assistant et vice-versa.
• « Standard » ↔ « Decimal » ... Passe du mode standard au mode décimal et vice-versa.
• « Real » ↔ « Cplx » ... Passe du mode réel au mode complexe et vice-versa.
• « Rad » → « Deg » → « Gra »... Sélectionne le réglage de l’unité d’angle dans l’ordre suivant radian, degré et
grade.
Conseil : Changer un réglage avec la barre d’état a le même effet que changer le réglage correspondant dans la boîte
de dialogue du format de base. Cela signifie que le réglage est modifié pour toutes les applications.
k Boîte de dialogue du format de graphe
Utilisez la boîte de dialogue du format de graphe pour définir les paramètres de la fenêtre graphique et pour
tracer des graphes.
Onglet [Basic]
Pour spécifier l’affichage des axes de la fenêtre graphique
Tapez sur 1 puis tapez sur un des paramètres décrits ci-dessous.
On : afficher l’axe Off : masquer l’axe
1
Number* : afficher l’axe avec une valeur maximale et minimale pour
2
3
4
chaque axe
Pour spécifier l’affichage de la grille de la fenêtre graphique
Tapez sur 2 puis tapez sur un des paramètres décrits ci-dessous.
On : afficher la grille sous forme de points Off : masquer la grille
Line* : afficher la grille sous forme de lignes
Pour sélectionner la spécification de remplissage de l’inégalité
(Inequality Plot)
Tapez sur 3 puis tapez sur un des paramètres décrits ci-dessous.
Union* : remplit les zones où toutes les conditions d’inégalité sont
satisfaites lors de la représentation graphique de plusieurs inégalités
Intersection : remplit les zones où chaque condition d’inégalité est
satisfaite lors de la représentation graphique de plusieurs inégalités
Pour spécifier la couleur des figures et des graphes tracés avec la fonction Dessin (page 115)
Tapez sur 4. Dans la boîte de dialogue qui apparaît, sélectionnez la couleur que vous voulez, puis tapez sur
[OK].
Chapitre 1 : Bases 37
Page 38

Pour faire ceci : Faites ceci :
Activer ou désactiver
l’affichage de noms
des axes de la fenêtre
Cocher la case « Labels »* pour afficher les noms ou enlever la coche de la case
pour masquer les noms.
Conseil : Quel que soit le réglage « Labels », les noms n’apparaissent jamais dans
graphique
Activer ou désactiver
l’affichage des flèches
de la commande
Cocher la case « G-Controller » pour afficher les flèches de la commande
graphique (page 107), ou enlever la coche de la case* pour masquer les flèches de
la commande graphique.
graphique
Spécifier point par
point ou en continu
Cocher la case « Draw Plot » pour spécifier point par point, ou enlever la coche
de la case* pour spécifier en continu la représentation graphique.
pour la représentation
graphique
Activer ou désactiver
l’affichage du nom de
la fonction et de la
Cocher la case « Graph Function »* pour afficher le nom de la fonction et la
fonction sur le graphe, ou enlever la coche de la case pour masquer le nom de la
fonction et la fonction.
fonction
Activer ou désactiver
l’affichage des
Cocher la case « Coordinates »* pour afficher les coordonnées du pointeur de la
fenêtre graphique ou enlever la coche de la case pour masquer les coordonnées.
coordonnées du
pointeur de la fenêtre
graphique
Activer ou désactiver
l’affichage du curseur
Cocher la case « Leading Cursor » pour afficher le curseur d’en-tête, ou enlever
la coche de la case* pour masquer le curseur d’en-tête.
d’en-tête pendant
la représentation
graphique
Spécifier la méthode de
tracé en cas de tracé de
plusieurs graphes
Afficher ou masquer les
valeurs dérivées dans la
fenêtre graphique et la
fenêtre de la table
Cocher la case « Simultaneous Graphs » pour tracer plusieurs graphes
simultanément, ou enlever la coche de la case* pour tracer des graphes l’un
après l’autre.
Cocher la case « Derivative/Slope » pour afficher les valeurs dérivées dans la
fenêtre graphique et la fenêtre de la table, ou enlever la coche de la case* pour
masquer les valeurs dérivées. Pour plus d’informations concernant le contenu
d’affichage, voir « Suivi de courbe et relevé de coordonnées » (page 114) et
« Génération d’une table numérique » (page 110).
la fenêtre graphique de l’application Suites. De même, les noms ne sont
pas affichés pour les types de graphes suivants tracés avec l’application
Statistiques : NPPlot, Histogram, MedBox, NDist Broken.
Chapitre 1 : Bases 38
Page 39

Onglet [Special]
Pour spécifier la largeur de ligne pour l’affichage de l’éditeur de
statistiques et de la table de données
Tapez sur 1, puis sélectionnez un modèle de largeur de cellule : 2 Cells,
1
3 Cells*, ou 4 Cells pour une orientation d’affichage verticale, ou 4 Cells,
5 Cells*, ou 6 Cells une orientation d’affichage horizontale (voir « Modifier
2
l’orientation de l’écran » en page 15).
Pour spécifier une source pour les données d’un tableau
3
Tapez sur 2 puis tapez sur un des paramètres décrits ci-dessous.
Table Input* : Utilise la saisie de données dans une boîte de dialogue
de saisie de table comme source pour la génération d’une table
numérique.
list1 à list6 : Utilise les données de liste dans list1 à list6 comme source
pour la génération d’une table numérique.
<nom de liste> : Utilise les données de liste dans une liste sélectionnée
comme source pour la génération d’une table numérique.
Pour plus d’informations sur la façon de générer une table numérique
à l’aide de chaque réglage, voir « Génération d’une table numérique »
(page 110).
Pour spécifier une source pour les données d’un tableau récapitulatif
Tapez sur 3 puis tapez sur un des paramètres décrits ci-dessous.
View Window* : Utilise les réglages de la fenêtre d’affichage comme source pour la génération d’une table
numérique.
list1 à list6 : Utilise les données de liste dans list1 à list6 comme source pour la génération d’un tableau
récapitulatif.
<nom de liste> : Utilise les données de liste dans une liste sélectionnée comme source pour la génération d’un
tableau récapitulatif.
Pour plus d’informations sur la façon de générer un tableau récapitulatif à l’aide de chaque réglage, voir
« Génération d’un tableau récapitulatif » (page 112).
Pour afficher ou masquer la seconde dérivée pour les tableaux récapitulatifs
Sélectionner la touche On* dans « Summary Table
pour la masquer.
Pour spécifier le réglage auto ou manuel des réglages de la fenêtre d’affichage de l’application
Statistiques
Cocher la case « Stat Window Auto »* pour spécifier un paramétrage automatique, ou enlever la coche de la
case pour un paramétrage manuel.
f (x) » pour afficher la seconde dérivée, ou le bouton Off
Chapitre 1 : Bases 39
Page 40

Onglet [3D Format]
Pour spécifier l’affichage des valeurs des coordonnées
Tapez sur 1, puis sélectionnez « Rectangular* » (afficher des valeurs
des coordonnées rectangulaires), « Polar » (afficher des valeurs
1
des coordonnées polaires), ou « Off » (désactiver l’affichage des
coordonnées).
2
Pour spécifier l’affichage des axes
3
Tapez sur 2, puis sélectionnez « On » (afficher les axes normalement),
« Box » (afficher les axes de coordonnées sous forme de boîte), ou
« Off*» (désactiver l’affichage des axes).
Pour activer ou désactiver l’affichage de noms des axes de la fenêtre
graphique
Tapez sur 3, puis sélectionnez « On » ou « Off*».
k Boîte de dialogue du format Géométrie
Utilisez le boîte de dialogue du format Géométrie pour paramétrer l’application Géométrie.
Conseil : Les informations qui apparaissent dans la zone de prévisualisation au bas de la boîte de dialogue montrent un
aperçu de la fenêtre de l’application Géométrie, compte tenu des réglages effectués dans la partie supérieure
de la boîte de dialogue.
Pour spécifier le format d’affichage des valeurs numériques dans la
fenêtre géométrique
1
Tapez sur 1, puis sélectionner le format que vous voulez. Le réglage
du format de nombre par défaut est Fix2. Pour plus d’informations, voir
2
« Pour spécifier le format d’affichage des valeurs numériques » (page 36).
3
Pour spécifier l’unité de la valeur de la longueur affichée
Tapez sur 2, puis tapez sur un des paramètres décrits ci-dessous.
4
Off* : L’unité de la valeur de longueur n’est pas affichée.
5
mm, cm, m, km, in, ft, yd, mi : Affiche la valeur de longueur dans l’unité
6
Pour spécifier la condition initiale de la fenêtre graphique lors de l’ouverture de l’application Géométrie
Tapez sur 5 puis tapez sur un des paramètres décrits ci-dessous.
On : Afficher les axes Off* : Masquer les axes
Number : Afficher l’axe avec une valeur maximale et minimale pour chaque axe
Pour spécifier l’état initial de la grille lors de l’ouverture de l’application Géométrie
Tapez sur 6 puis tapez sur un des paramètres décrits ci-dessous.
On : Afficher la grille sous forme de points Off* : Masquer la grille
Line : Afficher la grille sous forme de lignes
sélectionnée.
Pour spécifier l’unité d’angle pour la case de mesure
Tapez sur 3, puis tapez sur « Radian », « Degree* », ou « Grad ».
Pour spécifier l’unité d’angle pour la représentation graphique
Tapez sur 4, puis tapez sur « Radian* », « Degree », ou « Grad ».
Chapitre 1 : Bases 40
Page 41

k Boîte de dialogue du format avancé
Utilisez la boîte de dialogue du format avancé pour paramétrer la transformée de Fourier et FFT.
Pour spécifier la formule de la transformée de Fourier
Tapez sur 1 puis tapez sur « Modern Physics », « Pure Math* »,
« Probability », « Classical Physics », ou « Signal Processing ».
1
Pour spécifier la constante d’échelle FFT
Tapez sur 2 puis tapez sur « Pure Math », « Signal Processing* », ou
« Data Analysis ».
Pour spécifier comment sont traitées les variables pour le calcul de
Fourier
Cocher la case « Assume positive real »* pour spécifier que les variables
2
pour le calcul de Fourier sont traitées comme des nombres réels positifs
uniquement. Enlever la coche de la case pour spécifier que les nombres
complexes sont autorisés pour les variables du calcul de Fourier.
k Boîte de dialogue du format Finances
Utilisez le boîte de dialogue du format Finances pour paramétrer l’application Finances.
Onglet [Basic]
Pour spécifier le nombre de jours dans une année
Tapez sur 1, puis tapez sur « 360 days » ou « 365 days* ».
Pour spécifier le début d’une période ou la fin d’une période pour la
1
date de paiement
Tapez sur 2 puis tapez sur « Beginning of period » ou « End of period* ».
2
Pour spécifier le format de date
3
Tapez sur 3 puis tapez sur un des paramètres décrits ci-dessous.
MM/DD/YYYY* : mois/jour/année
DD/MM/YYYY : jour/mois/année
YYYY/MM/DD : année/mois/jour
Pour spécifier le statut des champs de saisie lors du lancement d’un nouveau calcul
Pour faire ceci : Faites ceci :
Lors du changement du type de calcul, copier
automatiquement dans le nouveau calcul le contenu
de tous les champs dans le calcul actuel dont les
noms correspondent aux noms de champs.
Lors du changement du type de calcul, vider tous les
champs.
Cocher la case [Automatically copy common fields to
new calculation]*.
Enlever la coche de la case [Automatically copy
common fields to new calculation].
Chapitre 1 : Bases 41
Page 42

Onglet [Special]
Pour spécifier la gestion des périodes incomplètes
Tapez sur 1 puis tapez sur un des paramètres décrits ci-dessous.
Compound (CI) : Appliquer un intérêt composé à la période incomplète
1
2
3
4
5
Pour spécifier l’utilisation du montant (PRF) ou du pourcentage (r%) pour le calcul du seuil de
rentabilité
Tapez sur 4, puis tapez sur « Amount (PRF)* » ou « Ratio (r%) ».
lors d’un calcul d’intérêt composé
Simple (SI) : Appliquer un intérêt simple à la période incomplète lors d’un
calcul d’intérêt composé
Off* : Ne pas appliquer d’intérêt à la période incomplète lors d’un calcul
d’intérêt composé
Pour spécifier la fréquence de composition
Tapez sur 2, puis tapez sur « Annual* » (une fois par an) ou « Semi-
annual » (deux fois par an).
Pour spécifier l’intervalle des obligations
Tapez sur 3 puis tapez sur un des paramètres décrits ci-dessous.
Term* : Spécifie l’utilisation du nombre de paiements comme durée lors
du calcul des obligations.
Date : Spécifie l’utilisation d’une date comme durée lors du calcul des
obligations.
Pour spécifier le calcul de la quantité des ventes ([QBE]) ou le montant des ventes ([SBE]) pour le
calcul du seuil de rentabilité
Tapez sur 5, puis tapez sur « Quantity* » ou « Sales ». Lorsque « Quantity » est sélectionné, la quantité des
ventes peut être calculée avant le calcul du montant des ventes. Lorsque « Sales » est sélectionné, le montant
des ventes peut être calculé avant le calcul de la quantité des ventes.
Conseil : Lors d’un calcul financier, vous pouvez modifier les réglages avec l’onglet [Format] et la barre d’état de
l’application Finances. Pour le détail à ce sujet, voir « Configuration des réglages de l’application Finances »
(page 194).
Initialisation de tous les réglages de format des applications
La procédure suivante permet de rétablir tous les réglages par défaut de format des applications.
u Opérations sur le ClassPad
1. Tapez sur O puis tapez sur [Default Setup].
2. En réponse au message « Reset Setup Data? » qui apparaît, tapez sur [OK] pour rétablir tous les réglages
par défaut.
• Les réglages sont initialisés sauf le réglage du dossier actuel spécifié dans la boîte de dialogue du format
de base.
1-8 En cas de problème persistant…
Si vous rencontrez un problème pendant que vous effectuez une opération, effectuez les opérations suivantes
avant de supposer que le ClassPad ne fonctionne pas.
1. Initialiser tous les réglages de format des applications.
Effectuer la procédure dans « Initialisation de tous les réglages de format des applications » ci-dessus.
Chapitre 1 : Bases 42
Page 43

2. Effectuer l’opération de Réinitialisation de la RAM (RESTART).
Lorsque le ClassPad se bloque ou ne fonctionne pas comme il devrait, il est nécessaire de réinitialiser la
RAM.
Effectuer l’opération de Réinitialisation de la RAM
Important !
• La réinitialisation de la RAM supprime toutes les données stockées temporairement dans la RAM du
ClassPad. Si vous effectuez une réinitialisation de RAM pendant un calcul, toutes les données du calcul
sauvegardées dans la RAM seront perdues.
• N’effectuez une réinitialisation de RAM que lorsque le ClassPad cesse de fonctionner normalement pour
une raison inconnue.
1. Utilisez le stylet pour appuyer sur le bouton RESTART au dos du
ClassPad.
• Après la réinitialisation, le ClassPad redémarre automatiquement.
Bouton
RESTART
2. Après le redémarrage, configurez le ClassPad. Pour de plus amples informations sur la procédure à
effectuer ici, voir « Chargement des piles et préparation du ClassPad » dans le Guide de mise en marche
rapide à part.
• Le menu d’applications apparaît après la configuration.
3. Réinitialiser le ClassPad.
Avant d’effectuer l’opération de réinitialisation, faites d’abord une copie par écrit de toutes les données
importantes.
Pour des détails, voir « Supprimer des groupes de données spécifiques (Réinitialisation) » (page 293).
Chapitre 1 : Bases 43
Page 44

Chapitre 2 : Application Principale
L’application Principale est une application permettant d’effectuer des calculs numériques et mathématiques
d’ordre général. Elle peut être utilisée pour étudier les mathématiques et résoudre des problèmes
mathématiques. Vous pourrez donc utiliser cette application Principale pour les calculs arithmétiques de base,
les calculs impliquant des listes, des matrices, etc.
A l’ouverture de l’application Principale, un écran vide
contenant une grande zone de travail apparaît. Utilisez
cette zone pour la saisie d’opérations et de commandes. Le
ClassPad utilise aussi cette zone pour afficher les résultats
des calculs.
Expression saisie
Résultat du calcul
Les opérations de base de l’application Principale
consistent essentiellement à saisir l’expression d’un calcul
dans la zone de travail et à appuyer sur E. Le calcul est
alors exécuté et son résultat affiché sur le côté droit de la
zone de travail.
Zone de travail
Boutons et menus spécifiques de l’application Principale
• Supprimer les variables contenant des nombres, des listes et des matrices ...........Edit - Clear All Variables
• Insérer une commande dans la zone de travail (page 62) .....................................................................Action
• Exécuter une commande interactive pour l’expression sélectionnée dans la zone de travail (page 93)
................................................................................................................................................. Interactive
• Commuter l’affichage des résultats de calculs entre le mode standard et le mode décimal ......................u
• Recalculer l’équation sur la ligne où se trouve le curseur ...........................................................................7
• Afficher une expression telle qu’elle a été saisie ........................................................................................0
• Insérer et exécuter la commande Simplify ..................................................................................................S
• Commuter entre bases binaire, octale, décimale ou hexadécimale lors d’un calcul ordinaire (page 61) ...<
• Accéder aux fenêtres de l’application du ClassPad depuis l’application Principale (page 94) ...................$
2-1 Calculs de base
Cette partie du manuel explique comment effectuer des opérations mathématiques de base dans l’application
Principale.
Calculs arithmétiques et calculs entre parenthèses
Vous pouvez effectuer des calculs arithmétiques en saisissant des expressions comme lorsqu’elles sont
écrites. Le ClassPad détermine automatiquement l’ordre de priorité de calcul des additions, soustractions,
multiplications, divisions, fonctions et parenthèses.
0201 Exemples de calculs
Chapitre 2 : Application Principale 44
Page 45

• Tous les exemples de calculs montrés dans 0201 sont effectués sur le clavier numérique ou le jeu de la
touche [Number] du clavier tactile, sauf mention contraire.
• Les exemples de calculs s’effectuent en mode décimal (page 46).
Emploi de la touche e
Utilisez la touche e pour saisir des puissances 10. Vous pouvez aussi saisir des puissances 10 avec la
touche E du jeu de la touche [Number] du clavier tactile.
0202 Exemples de calculs
Omission du signe de multiplication
Le signe de multiplication peut être omis dans chacun des cas suivants.
• Devant une fonction… 2sin (30), 10log (1,2), etc.
• Devant une constante ou une variable… aπ, 2ab, 3ans, etc.
• Devant une ouverture de parenthèses… 3(5 + 6), (a + 1)(b – 1), etc.
Notez qu’il faut utiliser le signe de multiplication lorsque l’expression directement devant l’ouverture de
parenthèses est une variable littérale. Exemple : ab (3 + b) doit être écrit ab × (3 + b). Sinon, l’expression
saisie est considérée comme notation d’une fonction (
f ( x)).
• Devant la touche e ou la touche E (Voir « Emploi de la touche e » ci-dessus.)
• Devant une matrice ou une liste… a {1, 2, 3}, 3 [[1, 2] [3, 4]], etc.
Emploi de la variable de dernier résultat (ans)
Chaque fois que vous exécutez un calcul dans la zone de travail de l’application Principale, le dernier résultat
est automatiquement affecté à la variable nommée « ans » (réponse). Vous pouvez même restituer le contenu
de la mémoire « ans » pour l’utiliser dans un autre calcul en tapant sur la touche D du clavier tactile.
0203 Exemples de calculs
Conseil : Si vous commencez par saisir l’opérateur +, −, ×, ÷ ou ^ au début d’une expression, la variable « ans »
s’insérera automatiquement à la gauche de l’opérateur, même si vous ne tapez pas sur la touche D.
Affectation d’une valeur à une variable
La syntaxe suivante peut être utilisée dans l’application Principale et l’application eActivity pour affecter une
valeur à une variable en plus de la touche d’affectation de variable (W, page 33).
Syntaxe : Variable:= valeur
0204 Affecter 123 à la variable
Important !
« := » ne peut être utilisé que dans l’application Principale et l’application eActivity. Il NE peut PAS être utilisé
dans un programme. Dans l’application Programme, vous devez utiliser W pour mettre une valeur dans une
variable.
x
Chapitre 2 : Application Principale 45
Page 46

Ordre de priorité des calculs
Le ClassPad effectue automatiquement les calculs dans l’ordre suivant.
1 Commandes entre parenthèses (sin(, diff(, etc.)
2 Factorielles (
pourcentages (%)
3 Puissances
4 π, mémoire et multiplications de variables
omettant le signe de multiplication (2π, 5A, etc.),
Commande avec multiplication entre parenthèses
omettant le signe de multiplication (2'3, etc.), ×,
÷
x!), spécifications des degrés (
o, r
),
5 +, –, (–)
6 Opérateurs relationnels (=, , <, >, s, t)
7 and
8 or, xor
9 with ( | )
Conseil
• Les expressions entre parenthèses ont la priorité.
• Dans le cas où une série de calculs comprend dans la même expression plus d’un opérateur 4 à 9 ayant le même
niveau de priorité, les opérations de même niveau sont effectuées de gauche à droite. Une série de calculs de puissance
3 (exemple : 5^2^3) est effectuée de droite à gauche (5^(2^3)).
Exemple :
2 + 3 × (log (sin( 2π2)) + 6,8) = 22,07101691
(En mode algèbre, mode décimal, mode radian)
Modes de calcul
Tous les exemples de calculs suivants sont indiqués dans le mode algèbre seulement.
Mode standard et mode décimal
Le mode standard affiche les résultats des calculs sous forme d’expressions mathématiques lorsque c’est
possible, tandis que le mode décimal convertit les résultats des calculs et les affiche sous forme décimale.
Expression Résultat du mode décimal Résultat du mode standard
2 +
5
4
25
2
2
π
50 ÷ 4 = 12,5 12.5
+ 2 = 3,414213562...
2
π = 3,1415926535...
sin (2,1π) × 5 = 1,5450849718...
• Les résultats du mode décimal dans le tableau ci-dessus montrent ce qui doit apparaître lorsque « Normal 1 »
est sélectionné pour le paramètre [Number Format] dans la boîte de dialogue du format de base.
3.414213562
3.141592654
1.545084972
5 · ( − 1)
u Emploi du bouton u pour commuter entre le mode standard et le mode décimal
Vous pouvez taper sur u pour commuter la valeur affichée entre le mode standard et le mode décimal.
Notez que lorsque vous tapez sur u seul le format de la valeur affichée change. Le réglage du mode
standard/décimal proprement dit ne change pas.
0205 Frappe de u lorsque le ClassPad est configuré pour le mode d’affichage standard (Normal 1)
0206 Frappe de u lorsque le ClassPad est configuré pour le mode d’affichage décimal (Normal 1)
Chapitre 2 : Application Principale 46
Page 47

u Réglages du nombre de décimales, du nombre de chiffres significatifs et de l’affichage
Normal
Les paramètres [Number Format] dans la boîte de dialogue du format de base spécifient le nombre de
décimales, le nombre de chiffres significatifs et le réglage d’affichage normal pour les résultats des calculs
effectués en mode décimal dans l’application Principale. Le tableau suivant montre comment les résultats des
calculs apparaissent pour chaque réglage.
Expression Normal 1 Normal 2 Fix 3 Sci 3
50 ÷ 4 = 12,5 12.5 12.5 12.500 1.25
100 ÷ 6 = 16,6666666... 16.66666667 16.66666667 16.667 1.67
1 ÷ 600 = 0,00166666... 1.666666667
11
÷ 4 = 2.5E + 10 2.5E + 10 2.5E + 10 2.5E + 10 2.50E + 10
10
Le nombre de décimales peut être compris entre 0 et 9 (Fix 0 et Fix 9), et le nombre de chiffres significatifs
entre 0 et 9 (Sci 0 et Sci 9). Pour le détail sur les réglages de [Number Format], voir « Boîte de dialogue du
format de base » à la page 36.
–3 0.00166666666 0.002 1.67E – 3
E
+ 1
E
+ 1
E
Mode complexe et mode réel
Le mode complexe est destiné aux calculs de nombres complexes tandis que le mode réel est limité aux
calculs de nombres réels. L’exécution d’un calcul en mode réel produisant un résultat hors de la plage des
nombres réels entraîne une erreur (Non-Real in Calc).
0207 (Résultats de calculs en mode complexe et en mode réel)
Conseil
• Vous pouvez sélectionner « i » ou « j » comme unité imaginaire. Voir « Spécifier l’unité imaginaire d’un nombre
complexe » à la page 294.
• Si l’expression comprend ⬔(
r,), les résultats de calcul devraient être sous la forme ⬔(r,).
Mode radian, mode degré et mode grade
Vous pouvez spécifier le radian, le degré ou le grade comme unité d’angle pour l’affichage des résultats de
calculs trigonométriques.
u Exemples de résultats de calculs en mode radian, mode degré et mode grade
Expression Mode radian Mode degré Mode grade
sin (π/4)
sin (45) sin (45) sin (45)
sin (50) sin (50) sin (50)
'
sin
π
( )
4
'
sin
Important !
Quelle que soit l’unité d’angle sélectionnée, un calcul contenant un nombre imaginaire avec exposant (par
exemple : e
π
i
) est exécuté en prenant le radian comme unité d’angle (e
π
i
= −1).
π
( )
4
'
Mode assistant et mode algèbre
Le mode algèbre simplifie automatiquement les expressions mathématiques produites par les calculs.
Aucune simplification n’est effectuée en mode assistant. En mode assistant, vous pouvez voir les résultats
intermédiaires, ce qui permet de voir les étapes qui ont conduit à un résultat particulier, comme indiqué dans
0208 (voir l’exemple « expand »).
Chapitre 2 : Application Principale 47
Page 48

0208 (Résultats de calculs en mode assistant et mode algèbre)
Important !
Le mode assistant est disponible dans l’ application Principale et l’application eActivity seulement.
2-2 Emploi de l’historique des calculs
L’historique des calculs dans la zone de travail de l’application Principale peut contenir en tout 30 ensembles
d’expressions/résultats. Vous pouvez retrouver un calcul antérieur, l’éditer et le recalculer, si vous voulez.
• Utilisez la barre de défilement ou les boutons de défilement pour faire défiler la fenêtre de la zone de travail
vers le haut et le bas. Le contenu de l’historique actuel des calculs s’affiche.
• Vous pouvez éditer une expression dans l’historique des calculs et réexécuter le calcul. Il suffit d’appuyer sur
E pour recalculer l’expression où se trouve le curseur ainsi que toutes les expressions postérieures.
0209 Remplacer l’expression « ans × 2 » par « ans × 3 » dans l’exemple ci-dessous, puis la recalculer
Conseil
• Pour recalculer une seule ligne, tapez sur 7. Pour recalculer l’expression à la position du curseur seulement tapez sur
7. Ce qui se trouve avant ou après cette ligne dans l’historique des calculs ne sera pas recalculé.
• Pour recalculer toutes les expressions d’un historique, localisez le curseur sur la toute première ligne et appuyez sur
E.
u Supprimer une partie du contenu de l’historique des calculs
1. Positionnez le curseur sur la ligne de l’expression ou la ligne du résultat des deux lignes que vous voulez
supprimer.
2. Tapez sur [Edit] puis sur [Delete].
Important !
Même si la suppression du résultat des deux lignes a un effet sur les calculs postérieurs, les calculs concernés
ne sont pas automatiquement mis à jour après la suppression. Si vous voulez mettre à jour tout l’historique
des calculs après la suppression d’une expression et de son résultat, positionnez le curseur sur une ligne au-
dessus de celle qui a été supprimée et appuyez sur E.
u Supprimer tout le contenu de l’historique des calculs
Tapez sur [Edit] puis sur [Clear All]. En réponse au message de confirmation qui apparaît, tapez sur [OK].
2-3 Calculs de fonctions
Cette partie du manuel explique comment effectuer des calculs de fonctions dans la zone de travail de
l’application Principale.
• Vous n’avez pas besoin de saisir les fermetures de parenthèses qui précèdent immédiatement une opération
E. Tous les exemples de calcul mentionnés ici omettent les fermetures de parenthèses avant E.
• Les exemples de calculs suivants sont tous effectués dans le mode décimal. Lorsque le mode standard est
utilisé, les résultats sont affichés sous formes de fractions.
Conversion des angles (°, r)
Les deux premiers exemples ci-dessous emploient le « Degree » (indiqué par « Deg » dans la barre d’état)
comme unité d’angle. Le dernier exemple emploie le « Radian » (indiqué par « Rad » dans la barre d’état)
comme unité d’angle. Notez que si une unité d’angle inadéquate est utilisée il ne sera pas possible d’obtenir
des résultats corrects.
Chapitre 2 : Application Principale 48
Page 49

u Changer le réglage d’unité d’angle
1. Sur le menu O tapez sur [Basic Format].
2. Tapez sur le bouton fléché vers le bas de [Angle] et sélectionnez [Radian], [Degree] ou [Grad].
• Vous pouvez aussi changer l’unité d’angle en tapant sur le réglage actuel (Rad, Deg ou Gra) dans la barre
d’état. A chaque frappe, le réglage change.
Problème Opération
Convertir 4,25 radians en degrés.
4.25 Rw
= 243,5070629
47,3° + 82,5rad = 4774,20181°
Convertir 243,5070629° en radians.
= 4,249999999
47.3 + 82.5 Rw
Réglez [Angle] sur le « Radian » et saisissez
243.5070629 *w.
Fonctions trigonométriques et trigonométriques inverses
Problème Opération
π
cos((
) rad) = 0,5
3
2 · sin45° × cos65° = 0,5976724775
Réglez [Angle] sur le « Radian ».
c7/ 3 w ou cN7c 3 w
Réglez [Angle] sur le « Degree ».
2*s 45 )*c 65 w
Peut être omis.
–1
0,5 =30°
sin
S 0.5 w
(Déterminer x pour sinx = 0,5.)
« .5 » peut aussi être utilisé.
Fonctions logarithmiques et fonctions exponentielles
Problème Opération
log1,23 (log
ln90 (log
9 = 2
log
3
4,5
e
= 90,0171313
(–3)4 = (–3) × (–3) × (–3) × (–3) = 81
7
123 (= 123
1,23) = 0,08990511144
10
90) = 4,49980967
e
1
7
) = 1,988647795
" 1.23 w ou V 10 e 1.23 w
I 90 w ou V`e 90 w
V 3 e 9 w ou LV 3 , 9 w
Q 4.5 w
(- 3 ){ 4 w
123 {( 1 / 7 w ou % 7 e 123 w
Fonctions hyperboliques et hyperboliques inverses
Problème Opération
sinh3,6 = 18,28545536
1 3.6 w
cosh
–1
(
) = 0,7953654612
@ 20 / 15 w ou @N 20 c15 w
Chapitre 2 : Application Principale 49
Page 50

Autres fonctions (%, ', x2, x –1, x!, abs, ⬔, signum, int, frac, intg, fRound, sRound)
Problème Opération
Calculer 12% de 1500. (180)
Calculer le pourcentage de 660 par rapport à
880. (75%)
Calculer la valeur supérieure de 15% à
2500. (2875)
Calculer la valeur inférieure de 25% à
3500. (2625)
'2 + '5 = 3,65028154 5 2 e+5 5 w
i) = 1,755317302 + 0,2848487846i
(3 +
2
= (–3) × (–3) = 9
(–3)
2
= –(3 × 3) = –9
–3
1
= 12
1
1
–
4
3
8! (= 1 × 2 × 3 × … × 8) = 40320
Obtenir la valeur absolue du logarithme décimal de
3
?
4
3
⎜log (
)⎟ = 0,1249387366
4
8⬔40° × 5⬔35°
⬔(8,40) × ⬔(5,35) = ⬔(40,75)
Quel est le signe de –3,4567 ? (–1)
(le signe renvoie –1 pour une valeur négative, 1
pour une valeur positive, « Undefined » pour 0, et
$
pour un nombre imaginaire)
²$´
1500 * 12 &w
660 / 880 &w
2500 *( 1 + 15 &
3500 *( 1 - 25 &
Passez au mode complexe (« Cplx » dans la barre
d’état).
5 3 +0w
(- 3 )xw
- 3 xw
( 3 X- 4 X)Xw
ou
N 1 cN 1 c 3 e-N 1 c 4 w
8 !w
4V 10 eN 3 c 4 w
ou L4V 3 / 4 w
Passez au mode degré (« Deg » dans la barre
d’état).
~ 8 , 40 )*~ 5 , 35 )w
[signum] - 3.4567 w
Calculer l’entier de –3,4567. (–3)
Calculer la partie décimale de –3,4567. (–0,4567)
Calculer la partie entière inférieure ou égale à
:- 3.4567 w
[frac] - 3.4567 w
[intg] - 3.4567 w
–3.4567 ? (–4)
Arrondir –3,4567 à deux décimales.
[fRound] - 3.4567 , 2 w
(–3,46)
Arrondir –34567 à quatre chiffres significatifs.
[sRound] - 34567 , 4 w*
(–34570)
* Pour arrondir à 10 chiffres, spécifiez « 0 » comme second argument.
Générateur de nombres aléatoires (rand, randList, randNorm, randBin, RandSeed)
Le générateur de nombres aléatoires du ClassPad peut produire de vrais nombres aléatoires (nombres
aléatoires non séquentiels) et des nombres aléatoires qui suivent un modèle particulier (nombres aléatoires
séquentiels).
Chapitre 2 : Application Principale 50
Page 51

u Commuter entre génération de nombres aléatoires non séquentiels et génération de
nombres aléatoires séquentiels
1. Utilisez la commande « RandSeed » pour configurer les paramètres nécessaires pour la génération de
nombres aléatoires. Voir « Commande RandSeed » à la page 52.
2. Utilisez la fonction « rand », « randList », « randNorm » ou « randBin » pour générer les nombres aléatoires.
u Fonction « rand »
La fonction « rand » génère des nombres aléatoires. Si vous ne spécifiez pas d’argument, « rand » génère des
valeurs décimales à 10 chiffres égales ou supérieures à 0 et inférieures à 1.
En spécifiant deux valeurs entières comme argument vous pouvez générer les nombres aléatoires compris
entre ces deux valeurs.
Problème Opération
Générer des nombres aléatoires entre 0 et 1.
Générer des entiers aléatoires entre 1 et 6.
[rand] w
[rand] 1 , 6 w
u Fonction « randList »
Syntaxe : randList(n [, a, b])
Fonction :
• Lorsque les arguments « a » et « b » sont omis, une liste de
décimales est renvoyée.
• Lorsque les arguments « a » et « b » sont spécifiés, une liste de
entières comprises entre « a » et « b » est renvoyée.
n éléments contenant des valeurs aléatoires
n éléments contenant des valeurs aléatoires
Description :
n » doit être un entier positif.
• «
• Les nombres aléatoires de chaque élément sont générés en accord avec les spécifications de « RandSeed »,
comme avec la fonction « rand ».
Problème Opération
Générer une liste de trois éléments contenant des
valeurs aléatoires décimales.
Générer une liste de cinq éléments contenant des
valeurs aléatoires dans la plage de 1 à 6.
[randList] 3 w
[randList] 5 , 1, 6 w
u Fonction « randNorm »
La fonction « randNorm » génère un nombre aléatoire normal à 10 chiffres à partir de la moyenne spécifiée
et des valeurs de l’écart-type.
Syntaxe : randNorm(
Fonction :
• L’omission de la valeur «
• La spécification de la valeur «
, [, n])
n » (ou la spécification de 1 pour « n ») renvoie le nombre aléatoire généré tel quel.
n » renvoie le nombre spécifié de valeurs aléatoires sous forme de liste.
Chapitre 2 : Application Principale 51
Page 52

Description :
n » doit être un entier positif et « » doit être supérieur à 0.
• «
Problème Opération
Produire de manière aléatoire une taille en utilisant
[randNorm] 8 , 68 w
la répartition normale pour un groupe d’enfants de
moins d’un an, quand la taille moyenne est de 68 cm
et l’écart-type 8.
Produire de manière aléatoire les tailles de cinq
[randNorm] 8 , 68 , 5 w
enfants de l’exemple précédent et les afficher sous
forme de liste.
u Fonction « randBin »
La fonction « randBin » génère des nombres aléatoires binomiaux à partir des valeurs spécifiées comme
nombre d’essais n et probabilité P.
Syntaxe : randBin(
n, P [, m])
Fonction :
• L’omission de la valeur «
• La spécification de la valeur «
m » (ou la spécification de 1 pour « m ») renvoie le nombre aléatoire généré tel quel.
m » renvoie le nombre spécifié de valeurs aléatoires sous forme de liste.
Description :
• «
n » et « m » doivent être des entiers positifs.
Problème Opération
Produire de manière aléatoire le nombre attendu de
[randBin] 5 , 0.5 w
faces selon une distribution binomiale de cinq lancés
de pièces, lorsque la probabilité de tirer face est de
0,5.
Effectuer trois fois les cinq lancés de pièces ci-
[randBin] 5 , 0.5 , 3 w
dessus et afficher le résultat dans une liste.
u Commande « RandSeed »
• Vous pouvez spécifier un entier de 0 à 9 comme argument de cette commande. 0 désigne la génération de
nombres aléatoires non séquentiels. Un entier compris entre 1 et 9 est utilisé comme tête de série pour la
spécification de nombres aléatoires séquentiels. L’argument par défaut de cette commande est 0.
• Les nombres générés par le ClassPad immédiatement après la spécification effectuée suivent toujours le
même modèle aléatoire.
Problème Opération
Générer des nombres aléatoires séquentiels avec 3
[RandSeed] 3 w
comme tête de série.
Générer la première valeur.
Générer la seconde valeur.
Générer la troisième valeur.
[rand] w
[rand] w
[rand] w
Conseil
• Les valeurs aléatoires générées par ces commandes sont des valeurs pseudo-aléatoires.
• Les arguments a et b de « rand(a,b) » et « randList(n,a,b) » doivent être des entiers remplissant les conditions suivantes.
a < b
⎟ a⎟ , ⎟ b⎟ < 1
10 b – a < 1E10
E
Chapitre 2 : Application Principale 52
Page 53

Fonctions des entiers
Ces fonctions prennent les entiers comme arguments seulement et renvoie les entiers.
u Fonction « iGcd »
Syntaxe : iGcd(Exp-1, Exp-2[, Exp-3…Exp-10)]
(Exp-1 à Exp-10 sont tous des entiers.)
iGcd(List-1, List-2[, List-3…List-10)]
(Tous les éléments des listes 1 à 10 sont des entiers.)
Fonction :
• La première syntaxe ci-dessus renvoie le plus grand diviseur commun de deux à dix entiers.
• La seconde syntaxe renvoie, sous forme de liste, le plus grand diviseur commun (GCD) de chacun des
éléments de deux à dix listes. Par exemple, lorsque les arguments sont {
de a et c, et de b et d sera renvoyée.
Description :
• Toutes les listes doivent avoir le même nombre d’éléments.
• Lorsque la syntaxe « iGcd(List-1, List-2[, List-3…List-10)] » est utilisée, une expression (et une seule) (Exp)
peut être incluse comme argument au lieu de la liste.
Problème Opération
Déterminer les plus grands diviseurs communs de
{4, 3}, {12, 6} et {36, 9}.
[iGcd] { 4 , 3 },{ 12 , 6 },{ 36
, 9 })w
a,b}, {c,d}, une liste indiquant le GCD
u Fonction « iLcm »
Syntaxe : iLcm(Exp-1, Exp-2[, Exp-3…Exp-10)]
(Exp-1 à Exp-10 sont tous des entiers.)
iLcm(List-1, List-2[, List-3…List-10)]
(Tous les éléments des listes 1 à 10 sont des entiers.)
Fonction :
• La première syntaxe ci-dessus renvoie le plus petit commun multiple de deux à dix entiers.
• La seconde syntaxe renvoie, sous forme de liste, le plus petit commun multiple (LCM) den chacun des
éléments de deux à dix listes. Par exemple, lorsque les arguments sont {
de a et c, et de b et d sera renvoyée.
Description :
• Toutes les listes doivent avoir le même nombre d’éléments.
• Lorsque la syntaxe « iLcm(List-1, List-2[, List-3…List-10)] » est utilisée, une expression (et une seule) (Exp)
peut être incluse comme argument au lieu de la liste.
Problème Opération
Déterminer les plus petits communs multiples de {4,
3}, {12, 6} et {36, 9}.
[iLcm] { 4 , 3 },{ 12 , 6 },{ 36
, 9 })w
a,b}, {c,d}, une liste indiquant le LCM
u Fonction « iMod »
Syntaxe : iMod(Exp-1/List-1, Exp-2/List-2[)]
Fonction :
• Cette fonction divise un ou plusieurs entiers par un ou plusieurs entiers et renvoie le(s) reste(s).
Description :
• Exp-1 et Exp-2 et tous les éléments des listes 1 et 2 doivent être des entiers.
• Vous pouvez utiliser Exp pour un argument et List pour l’autre argument (Exp, List ou List, Exp) si vous
voulez.
Chapitre 2 : Application Principale 53
Page 54

• Si les deux arguments sont des listes, les deux listes doivent avoir le même nombre d’éléments.
Problème Opération
Diviser 21 par 6 et 7, et déterminer le reste des deux
opérations. (iMod(21, {6, 7})
[iMod] 21 ,{ 6 , 7 })w
Arrangement (nPr) et Combinaison (nCr)
u Nombre total d’arrangements
u Nombre total combinaisons
Problème Opération
Déterminer le nombre d’arrangements et de combinaisons
possibles lors de la sélection de 4 personnes prises dans un
groupe de 10
3
&
²²²²²
²
²²²²²²²
²
10P4
10C4
= 5040
= 210
} 10 , 4 w
{ 10 , 4 w
Jugement de condition (judge, piecewise)
u Fonction « judge »
La fonction « judge » renvoie TRUE lorsqu’une expression est vraie, et FALSE lorsqu’elle est fausse.
Problème Opération
L’expression suivante est-elle vraie ou
fausse ?
1 = 1 TRUE
L’expression suivante est-elle vraie ou
fausse ?
1 < 0 FALSE
[judge] 1 = 1 w
[judge] 1 < 0 w
u Fonction « piecewise »
La fonction « piecewise » renvoie une valeur lorsqu’une expression est vraie et une autre valeur lorsque
l’expression est fausse.
La syntaxe de la fonction « piecewise » est indiquée ci-dessous.
piecewise(<expression de condition>, <renvoie la valeur lorsque vrai>, <renvoie la valeur lorsque faux ou
indéterminé>[ ) ]
ou
piecewise(<expression de la condition>, <renvoie la valeur lorsque vrai>, <renvoie la valeur lorsque faux>,
<renvoie la valeur lorsque indéterminé>[ ) ]
Utilisez le clavier tactile (1) pour saisir la fonction « piecewise » selon la syntaxe suivante.
<renvoie la valeur lorsque vrai>, <expression de la condition>
<renvoie la valeur lorsque faux ou indéterminé>
ou
<renvoie la valeur lorsque la condition 1 est vraie>, <expression de la condition 1>
<renvoie la valeur lorsque la condition 2 est vraie>, <expression de la condition 2>
Problème Opération
Pour l’expression 0 t
lorsque x est égal ou inférieur à 0, et 2 lorsque x
est supérieur à 0 ou indéfini.
Pour l’expression 1 t
lorsque x est égal ou inférieur à 1, et 2 lorsque x
est supérieur à 1.
x (x = variable), renvoyer 1
x (x = variable), renvoyer 1
[piecewise] 0 :X, 1 , 2 w
ou
1 1 c 2 ef 0 :Xw
1 1 c 2 ef 1 :X c 1 <Xw
Chapitre 2 : Application Principale 54
Page 55

Symbole d’angle (∠)
Utilisez ce symbole pour spécifier le format de coordonnées requis par un angle dans un vecteur.
Vous pouvez utiliser ce symbole pour un vecteur seulement.
Problème Opération
Convertir les coordonnées polaires
π/4 en coordonnées rectangulaires. [1, 1]
r = '2 ,
θ
=
Réglez [Angle] sur le « Radian ».
[toRect] [5 2 e,~7/ 4 )]w
Symbole de dérivée (’)
Un seul symbole de dérivée indique la première dérivée d’une équation, dans le format : <nom de variable>’.
Problème Opération
Résoudre l’équation différentielle
{y = 0.5 · x2 + const (1)}
y’ = x.
+Y'=X,X,Yw
Important !
La fonction « dSolve » peut résoudre des équations différentielles du troisième ordre, si bien qu’un maximum
de trois symboles de dérivée (y’’’) peuvent être utilisés. L’exécution d’un calcul « dSolve » contenant plus de
trois symboles de dérivée entraînera une erreur (Invalid Syntax).
Test de primalité (isPrime)
La fonction « isPrime » détermine si le nombre fourni comme argument est premier (renvoie TRUE) ou non
(renvoie FALSE). La syntaxe de la fonction « isPrime » est indiquée ci-dessous.
isPrime(Exp/List[ ) ]
• Exp ou tous les éléments de List doivent être des entiers.
Problème Opération
Déterminer si les nombres 51 et 17 sont des
nombres premiers.
(isPrime({51, 17})
[isPrime] { 51 , 17 })w
Symboles d’égalité et symboles d’inégalité (=, ≠, <, >, s, t)
Vous pouvez utiliser ces symboles pour effectuer un certain nombre de calculs de base.
Problème Opération
Ajouter 3 aux deux côtés de
Soustraire 2 aux deux côtés de
x = 3. x + 3 = 6
(X= 3 )+ 3 w
y s 5. y – 2 s 3 (Y; 5 )- 2 w
Conseil
• Dans les explications de la « Syntaxe » de chaque commande dans « 2-7 Emploi du menu Action », les opérateurs
suivants sont indiqués par « Eq/Ineq » : =, ≠, <, >, s, t. Si les opérateurs « Eq/Ineq » doivent comprendre ou non
l’opérateur « ≠ » une note séparée le spécifie pour chaque commande.
• Une expression qui contient plusieurs opérateurs d’équation ou d’inégalité ne peut pas être saisie comme expression
seulement. Les expressions affichées peuvent avoir plusieurs opérateurs seulement dans le cas d’opérateurs d’inégalité
orientés dans le même sens (exemple : –1 <
x < 1).
Exemple : solve(x2 – 1 < 0, x) w {–1 < x < 1}
Chapitre 2 : Application Principale 55
Page 56

Opérateur « with » ( | )
L’opérateur « with » ( | ) affecte temporairement une valeur à une variable. Vous pouvez utiliser l’opérateur
« with » dans les cas suivants.
• Pour affecter la valeur spécifiée sur le côté droit de | à la variable à la gauche de |
• Pour limiter ou restreindre la plage d’une variable sur la gauche de | conformément aux conditions fournies à
la droite de |
La syntaxe de l’opérateur « with » ( | ) est la suivante.
Exp/Eq/Ineq/List/Mat|Eq/Ineq/List/(opérateur « and »)
Vous pouvez mettre plusieurs conditions dans une liste ou les relier par l’opérateur « and » sur le côté droit.
« » peut être utilisé sur le côté gauche ou le côté droit de |.
Problème Opération
2
x
Évaluer
Pour
+ x + 1 lorsque x = 3. 13
2
x
– 1 = 0, déterminer la valeur de x lorsque
X{ 2 +X+ 1 UX= 3 w
.X{ 2 - 1 = 0 ,X)UX> 0 w
x > 0. {x = 1}
Déterminer la valeur de abs (
x) lorsque x > 0. x
4XeUX> 0 w
Solutions supportées par le ClassPad (TRUE, FALSE, Undefined, No Solution, ∞, const,
constn)
Solution Description Exemple
TRUE Affiché lorsqu’une proposition est vraie.
FALSE Affiché lorsqu’une proposition est fausse.
Undefined Affiché lorsqu’une proposition est indéfinie.
No Solution Affiché lorsqu’il n’y a pas de solution.
∞
const Constante affichée comme const(1) lorsqu’une constante
constn Constante affichée comme constn(1) lorsque la solution
Infini
est incluse dans la solution. S’il y a plusieurs constantes,
elles sont indiquées par const(1), const(2), etc.
comprend une valeur entière qui est une constante.
S’il y a plusieurs constantes, elles sont indiquées par
constn(1), constn(2), etc.
judge (1 = 1) w
judge (1 < 0) w
1/0 w
solve (abs (
lim (1/
dSolve (
{ y = 0.5·x2 + const (1)}
Réglez [Angle] sur le
« Degree ».
solve (sin (
{x = 180·constn (1)}
x) = –1, x) w
2
x
, x, 0) w
y = x, x, y) w
x) = 0, x) w
Fonction Delta de Dirac
« delta » est la fonction delta de Dirac. La fonction delta sert à évaluer des expressions numériques de la façon
suivante.
b
^
b
Les expressions non-numériques passées par la fonction delta ne sont pas évaluées. L’intégrale d’une fonction
delta linéaire est une fonction Heaviside.
Syntaxe : delta(
x)
x : variable ou nombre
0210 (Capture d’écran d’exemples de calcul)
Chapitre 2 : Application Principale 56
Page 57

Fonction delta n
t
La fonction delta n
ième
ième
est la n
ième
différentielle de la fonction delta.
Syntaxe : delta(
x, n)
x : variable ou nombre
n : nombre de différentielles
0211 (Capture d’écran d’exemples de calcul)
Fonction échelon de Heaviside
« heaviside » est la commande de la fonction Heaviside qui sert seulement à évaluer les expressions
numériques suivantes.
H
Les expressions non numériques passées par la fonction Heaviside ne sont pas évaluées, et les expression
numériques contenant des nombres complexes sont renvoyées, sans être définies. La dérivée de la fonction
Heaviside est la fonction Delta.
Syntaxe : heaviside(
!
x)
x : variable ou nombre
0212 (Capture d’écran d’exemples de calcul)
Fonction Gamma
La fonction Gamma est appelée « gamma » par le ClassPad.
+∞
x–1
–t
t
e
Γ(x) =
Pour un entier n le gamma est évalué de la façon suivante.
K
Le gamma est défini pour tous les nombres réels à l’exception du zéro et des entiers négatifs. Il est également
défini pour tous les nombres complexes dont la partie réelle ou la partie imaginaire ne se trouve pas être un
nombre entier.
Le gamma d’une expression symbolique est renvoyé sans être évalué.
Syntaxe : gamma(
∫
0
²
^
d
!
s
x)
x : variable ou nombre
0213 (Captures d’écrans d’un exemple de calcul et d’un graphe)
Chapitre 2 : Application Principale 57
Page 58

2-4 Calculs de listes
Cette partie du manuel explique comment saisir des données et comment effectuer des calculs de base avec
les listes.
Saisie des données de listes dans la zone de travail
0214 Saisir la liste {1, 2, 3} et l’affecter à la variable LIST intitulée « lista » dans la zone de travail de
l’application Principale
Opérations sur les éléments d’une variable LIST
Vous pouvez rappeler la valeur de n’importe quel élément d’une variable LIST. Vous pouvez aussi affecter une
valeur à n’importe quel élément d’une liste.
0215 Rappeler le second élément de la variable de liste intitulée « lista » de l’exemple 0214
0216 Affecter 5 au second élément de « lista »
Emploi d’une liste dans un calcul
Vous pouvez effectuer des opérations arithmétiques entre deux listes, entre une liste et une valeur numérique
ou entre une liste et une expression, une équation ou une inégalité.
Important !
• Lorsque vous effectuez des calculs arithmétiques entre deux listes, les deux listes doivent avoir le même
nombre de cellules. Une erreur se produit si ce n’est pas le cas.
• Une erreur se produit également si une opération entre deux cellules des deux listes produit une erreur.
0217 Effectuer l’opération list3 × {6, 0, 4} lorsque list3 contient {41, 65, 22}
Utilisation d’une liste pour affecter des valeurs différentes à plusieurs variables
Procédez de la façon suivante pour affecter des valeurs différentes à plusieurs variables en utilisant une liste.
Syntaxe : Liste de nombres S liste de variables
0218 Affecter les valeurs 10, 20 et 30 respectivement aux variables
x, y, et z
2-5 Calculs de matrices et de vecteurs
Cette partie du manuel explique comment créer des matrices et effectuer des calculs matriciels élémentaires.
Conseil : Comme un vecteur peut être considéré comme une matrice d’une ligne et n colonnes ou de n lignes et d’une
colonne, vous ne trouverez ici aucune explication spéciale sur les vecteurs. Pour le détail sur les calculs
spécifiques aux vecteurs, voir les explications concernant les éléments du menu [Action] dans « 2-7 Emploi du
menu Action ».
Saisie de données dans une matrice
Vous pouvez saisir les valeurs matricielles sur une seule ligne dans la zone de travail, ou saisir les valeurs
matricielles à l’intérieur d’une matrice.
Chapitre 2 : Application Principale 58
Page 59

Saisir les valeurs matricielles sur une seule ligne
0219 Saisir la matrice
Principale
1 2
3 4
et l’affecter à la variable « mat1 » dans la zone de travail de l’application
Opérations sur les éléments d’une variable matricielle
Vous pouvez rappeler la valeur de n’importe quel élément d’une variable matricielle. Vous pouvez aussi
affecter une valeur à un élément dans une matrice.
0220 Rappeler la valeur des ligne 2 et colonne 1 de la variable matricielle « mat1 » de l’exemple 0219
0221 Affecter « 5 » à l’élément des ligne 1 et colonne 2 de « mat1 »
Saisir les valeurs matricielles à l’intérieur d’une matrice
• Créer une nouvelle matrice de 1 ligne × 2 colonnes .................................................................................. 6
• Créer une nouvelle matrice de 2 lignes × 1 colonne .................................................................................. 7
• Créer une nouvelle matrice de 2 lignes × 2 colonnes ................................................................................ 8
• Ajouter une colonne à la matrice actuellement affichée ............................................................................6
• Ajouter une ligne à la matrice actuellement affichée .................................................................................7
• Ajouter une ligne et une colonne à la matrice actuellement affichée ......................................................... 8
0222 Saisir la matrice
1 2 3
4 5 6
et l’affecter à la variable « mat2 »
Réalisation de calculs matriciels
Cette partie du manuel fournit des exemples de la plupart des calculs matriciels de base.
Addition, soustraction, multiplication et division de matrices
0223 Calculer
0224 Calculer
0225 Multiplier la matrice
1 1
2 1
1 1
2 1
+
×
2 3
2 1
2 3
2 1
1 2
3 4
sur une seule ligne
dans une matrice
par 5
Élévation d’une matrice à une puissance spécifique
Exemple : Élever
0226 Saisie sur une seule ligne
0227 Saisie dans une matrice
1 2
3 4
à la puissance 3
Conseil : Vous ne pouvez élever à une puissance spécifique qu’une matrice carrée. Une erreur se produit si vous
essayez d’élever une matrice non carrée à une puissance spécifique.
Chapitre 2 : Application Principale 59
Page 60

Utilisation d’une matrice pour affecter des valeurs différentes à plusieurs variables
Procédez de la façon suivante pour affecter des valeurs différentes à plusieurs variables en utilisant une
matrice.
Syntaxe : Matrice de nombres ⇒ matrice de variables
(La matrice peut consister en une ligne et plusieurs colonnes, ou plusieurs lignes et une colonne.)
0228 Affecter les valeurs 10, 20 et 30 respectivement aux variables
x, y, et z
2-6 Spécification d’une base numérique
Lorsque vous utilisez l’application Principale, vous pouvez spécifier une base numérique par défaut (binaire,
octale, décimale, hexadécimale). Les conversions entre les bases numériques et les manipulations de bits
avec les opérateurs logiques (not, and, or, xor) sont également possibles.
Notez les restrictions suivantes qui concernent toutes la base numérique (binaire, octale, décimale,
hexadécimale) spécifiée par défaut dans l’application Principale.
• Vous ne pouvez pas utiliser de fonctions scientifiques, ni les commandes des menus [Action] ou [Interactive].
• A part Ans (mémoire de dernier résultat), vous ne pouvez pas utiliser de variables.
• Vous ne pouvez introduire que des entiers. Une erreur (Invalid Syntax) se produit si vous essayez d’introduire
une autre valeur (comme 1,5 ou '2 ).
• Si un calcul produit un résultat autre qu’un entier (nombre avec une partie décimale), le ClassPad tronquera
automatiquement la partie décimale. Par exemple, le calcul de 5 ÷ 2 lorsque décimale est sélectionnée
comme base numérique est 2.
• Un message d’erreur s’affiche si vous essayez d’introduire une valeur incorrecte pour la base numérique
spécifiée. Voici les chiffres qui peuvent être utilisés dans chaque système de notation.
Binaire : 0, 1 Octale : 0 à 7 Décimale : 0 à 9 Hexadécimale : 0 à 9, A, B, C, D, E, F
Limites d’un calcul binaire, octal, décimal et hexadécimal
• La capacité d’affichage et les limites de calcul dans chacune des bases numériques sont les suivantes.
Base numérique Capacité
d’affichage
Binaire 32 chiffres
Octal 11 chiffres
Décimal 10 chiffres
Hexadécimal 8 chiffres
• Les valeurs binaires, octales et hexadécimales négatives sont produites en utilisant le complément de deux
de la valeur d’origine.
Limite de calcul (Positive ; Négative)
x s 01111111111111111111111111111111 ;
0 s
10000000000000000000000000000000 s x s
11111111111111111111111111111111
x s 17777777777 ; 20000000000 s x s 37777777777
0 s
x s 2147483647 ; –2147483648 s x s –1
0 s
x s 7FFFFFFF ; 80000000 s x s FFFFFFFF
0 s
Chapitre 2 : Application Principale 60
Page 61

Sélection d’une base numérique
La base numérique spécifiée dans l’application Principale s’applique à la ligne actuelle (expression, couple de
résultats) et aux lignes suivantes à moins que vous ne changiez de réglage.
u Sélectionner la base pour la ligne où se trouve le curseur
1. Tapez sur le bouton fléché vers le bas juxtaposé au bouton <.
2. Tapez sur le bouton correspondant à la base numérique que vous voulez utiliser :
1 (binaire), 2 octale), 3 (décimale), 4 (hexadécimale).
• La base numérique sélectionnée est indiquée dans la barre d’état.
3. Exécutez le calcul.
Important !
• Une ligne pour laquelle aucune base numérique n’est spécifiée est appelée « ligne de calcul normale ». Pour
revenir à une ligne normale, tapez sur < à l’étape 2 ci-dessus.
• Les résultats de calcul obtenus pour une ligne définie par une base numérique sont suivis des suffixes
suivants, désignant le système numérique.
Système de notation Binaire Octal Décimal Hexadécimal
Suffixes bodh
u Spécifier une base numérique pour la valeur saisie
Vous pouvez ajouter les suffixes suivants pour spécifier la base numérique d’une valeur au moment où
vous l’introduisez : [b] (binaire), [o] (octal), [d] (décimal) et [h] (hexadécimal). Vous pouvez spécifier une
base numérique pour la valeur saisie seulement lorsqu’une base numérique par défaut (hormis normal) est
sélectionnée
Opérations arithmétiques
Vous pouvez utiliser les opérateurs suivants avec les valeurs binaires, octales, décimales et hexadécimales : +,
−, ×, ÷, ^. Vous pouvez aussi utiliser des expressions entre parenthèses.
0229 Calculer 101112 + 11010
0230 Calculer (118 + 78)
0231 Effectuer le calcul 12310 + 10102 pour obtenir un résultat hexadécimal
2
2
Manipulation de bits
Les opérateurs logiques (and, or, xor, not) peuvent être utilisés dans les calculs.
and ...Retourne le résultat d’un produit de bits.
or ......Retourne le résultat d’une somme de bits.
xor ....Retourne le résultat d’une somme logique exclusive de bits.
not ....Retourne le résultat d’un complément (inversion de bits).
0232 Exemples de calculs
Chapitre 2 : Application Principale 61
Page 62

Utilisation de la fonction baseConvert (Transformation du système numérique)
La fonction baseConvert permet de convertir un nombre dans son équivalent d’une base numérique (système
numérique) à une autre.
Important !
• La fonction baseConvert fonctionne seulement pour les entiers positifs.
• La fonction baseConvert ne peut pas être utilisée dans une ligne pour laquelle une base numérique
particulière est spécifiée. Elle peut être utilisée dans une ligne de calcul normale seulement.
Syntaxe : baseConvert (nombre, base actuelle, base souhaitée)
• Le nombre doit être un entier positif consistant en 0 à 9 caractères et/ou A à F.
• La base actuelle et la base souhaitée peuvent être n’importe quel nombre entier de 2 à 16.
0233 Exemples de calculs
2-7 Emploi du menu Action
Le menu [Action] facilite l’emploi des fonctions de transformation et expansion, des fonctions de calcul, des
fonctions statistiques et d’autres opérations mathématiques fréquemment utilisées. Sélectionnez simplement la
fonction souhaitée et saisissez les expressions ou les variables conformément à la syntaxe de la fonction.
Conseil
• Sauf indication explicite différente, toutes les explications présentées ici s’effectuent à partir des modes suivants : Mode
algèbre, mode standard, mode complexe, mode radian et ordre décroissant .
• Vous pouvez utiliser le menu [Interactive] pour sélectionner la plupart des commandes incluses dans le menu [Action].
Pour de plus amples informations sur le menu [Interactive], voir page 93.
Abréviations et ponctuation utilisées dans cette partie du manuel
Les abréviations et la ponctuation utilisées pour les descriptions des syntaxes dans cette partie du manuel ont
la signification suivante.
Exp : Expression (valeur, variable, etc.) List : Liste
Eq : Équation Mat : Matrice
Ineq : Tous les types d’inégalités (a>b, atb, a<b, asb, ab)
Ineqⴝ : Inégalité ab uniquement
[ ] : Les éléments entre crochets peuvent être omis.
{ } : Un des éléments en accolades doit être sélectionné.
Certaines des syntaxes dans les explications suivantes indiquent les paramètres suivants :
Exp/Eq/Ineq/List/Mat
Ces abréviations signifient que vous pouvez utiliser un des paramètres suivants : expression, équation,
inégalité, liste ou matrice.
Chapitre 2 : Application Principale 62
Page 63

Exemples d’écrans
Les écrans suivants sont des exemples de saisie et d’affichage d’expressions sur l’écran du ClassPad. Tous
les exemples mentionnés ici montrent les « expressions complètes ».
Si l’expression saisie n’est pas entièrement visible :
Expression partielle
Si l’expression affichée n’est pas entièrement visible :
Expression partielle
Expression complète
Expression complète
Emploi du sous-menu Transformation
Le sous-menu [Transformation] contient les commandes utilisées pour la transformation d’expressions, par
exemple « expand » et « factor ».
u approx [Action][Transformation][approx]
Fonction : Calcule une approximation numérique d’une expression.
Syntaxe : approx (Exp/Eq/Ineq/List/Mat [ ) ]
Exemple : Obtenir la valeur numérique de '2
u simplify [Action][Transformation][simplify]
Fonction : Simplifie une expression.
Syntaxe : simplify (Exp/Eq/Ineq/List/Mat [ ) ]
Exemple : Simplifier (15'3 + 26)^(1/3)
u expand [Action][Transformation][expand]
Fonction : Développer une expression.
Syntaxe : expand (Exp/Eq/Ineq/List/Mat [ ) ]
expand (Exp,variable [ ) ]
• Si vous spécifiez une variable, Exp est décomposé en fractions partielles
par rapport à la variable.
2
Exemple : Développer (
x + 2)
u factor [Action][Transformation][factor][factor]
Fonction : Factoriser une expression.
Syntaxe : factor (Exp/Eq/Ineq/List/Mat [ ) ]
2
x
Exemple : Factoriser
4x + 4
Chapitre 2 : Application Principale 63
Page 64

u rFactor [Action][Transformation][factor][rFactor]
Fonction : Factorise une expression à sa racine, si possible.
Syntaxe : rFactor (Exp/Eq/Ineq/List/Mat [ ) ]
2
x
Exemple : Factoriser
3
u factorOut [Action][Transformation][factor][factorOut]
Fonction : Factorise une expression par rapport à un facteur donné.
Syntaxe : factorOut (Exp/Eq/Ineq/List/Mat [ ) ]
2
x
Exemple : Factoriser « a » à partir de a
+ bx + c
u combine [Action][Transformation][combine]
Fonction : Réduit au même dénominateur une expression fractionnaire.
Syntaxe : combine (Exp/Eq/Ineq/List/Mat [ ) ]
Exemple : Transformer et réduire (
x + 1)/(x + 2) + x(x + 3)
u collect [Action][Transformation][collect]
Fonction : Réarrange une expression en tenant compte d’une variable particulière.
Syntaxe : collect (Exp/Eq/Ineq/List/Mat[,Exp] [ ) ]
• «
x » est le réglage par défaut lorsque « [,Exp] » est omis.
2
x
Exemple : Réarranger
+ ax + bx par rapport à x
u tExpand [Action][Transformation][tExpand]
Fonction : Emploie les formules de somme et différence pour développer une fonction trigonométrique.
Syntaxe : tExpand(Exp/Eq/Ineq/List/Mat [ ) ]
Exemple : Développer sin (a + b)
u tCollect [Action][Transformation][tCollect]
Fonction : Linéarise une fonction trigonométrique en une expression sous forme de somme.
Syntaxe : tCollect (Exp/Eq/Ineq/List/Mat [ ) ]
Exemple : Linéariser cos(a) × cos(b) en une expression sous forme de somme
u expToTrig [Action][Transformation][expToTrig]
Fonction : Transforme une écriture exponentielle en écriture trigonométrique ou hyperbolique.
Syntaxe : expToTrig (Exp/Eq/Ineq/List/Mat [ ) ]
ix
e
Exemple : Transformer
en écriture trigonométrique (mode radian)
u trigToExp [Action][Transformation][trigToExp]
Fonction : Transforme une écriture trigonométrique ou hyperbolique en écriture exponentielle.
Syntaxe : trigToExp (Exp/Eq/Ineq/List/Mat [ ) ]
Exemple : Transformer coshx en écriture exponentielle
Chapitre 2 : Application Principale 64
Page 65

u toFrac [Action][Transformation][Fraction][toFrac]
Fonction : Transforme une valeur décimale en fraction décimale.
Syntaxe : toFrac (Exp/Eq/Ineq/List/Mat [ ) ]
Exemple : Transformer 5,28 en fraction décimale
u propFrac [Action][Transformation][Fraction][propFrac]
Fonction : Transforme une valeur décimale en écriture fractionnaire anglo-saxonne.
Syntaxe : propFrac (Exp/Eq/Ineq/List/Mat [ ) ]
Exemple : Transformer 1,2 en écriture fractionnaire anglo-saxonne
u dms [Action][Transformation][DMS][dms]
Fonction : Transforme une valeur de format DMS en une valeur équivalente
en degrés seulement.
Syntaxe : dms (Exp/List-1 [,Exp/List-2][,Exp/List-3] [ ) ]
Exemple : Transformer 3° 5’ 6” en valeur équivalente en degrés seulement
• Zéro est le réglage par défaut lorsque [,Exp/List-2] ou [,Exp/List-3][ ) ] est
omis.
Conseil : Vous pouvez saisir 3° 5’ 6” à l’aide de la touche / sur le clavier tactile.
/e 3 e 5 e 6 E
u toDMS [Action][Transformation][DMS][toDMS]
Fonction : Transforme une valeur en degrés seulement en valeur équivalente de format DMS.
Syntaxe : toDMS (Exp/List [ ) ]
Exemple : Transformer 3,085 degrés en valeur équivalente de format DMS
Emploi du sous-menu Avancé
u solve [Action][Advanced][solve]
Pour le détail sur solve, voir page 83.
u dSolve [Action][Advanced][dSolve]
Pour le détail sur dsolve, voir page 84.
u taylor [Action][Advanced][taylor]
Fonction : Trouve un développement limité pour une expression par rapport à une variable spécifique.
Syntaxe : taylor (Exp/List, variable, ordre [,point central] [ ) ]
Exemple : Trouver un développement limité du 5e ordre de sin(
(dans le mode radian)
• Zéro est le réglage par défaut lorsque vous omettez « [,point central] ».
x) en x = 0
u laplace [Action][Advanced][laplace], invLaplace [Action][Advanced][invLaplace]
Fonction : « laplace » est la commande utilisée pour la transformée de
Laplace, et « invLaplace » est la commande utilisée pour la
transformée de Laplace inverse.
Chapitre 2 : Application Principale 65
∞
∫
0
()
–
L[ ()] ()=
Page 66

Syntaxe :
laplace(
f ( t) : expression ;
f ( t), t, s)
t : variable en fonction de laquelle l’expression est
transformée ;
s : paramètre de la transformation
Le ClassPad prend en charge les fonctions suivantes.
x), cos(x), sinh(x), cosh(x), x
sin(
Le ClassPad ne prend pas en charge les fonctions suivantes.
tan(
x), sin
– 1
(x), cos
– 1
(x), tan
n
, 'x, ex, heaviside(x), delta(x), delta(x, n)
– 1
(x), tanh(x), sinh
– 1
(x), cosh
invLaplace(
L(s), s, t)
L(s) : expression ;
s : variable en fonction de laquelle l’expression est
transformée ;
t : paramètre de la transformation
– 1
(x), tanh
– 1
(x), log(x), ln(x), 1/x, abs(x), gamma(x)
Transformée de Laplace d’une équation différentielle
La commande laplace peut être utilisée pour résoudre des équations différentielles ordinaires. Le ClassPad ne
prend pas en charge le Système d’équations différentielles pour laplace.
Syntaxe : laplace(diff eq,
diff eq : équation différentielle à résoudre ; x : variable indépendante dans l’équation différentielle ;
x, y, t)
y : variable dépendante dans l’équation différentielle ; t : paramètre de la transformation
t
Exemple : Résoudre une équation différentielle
l’aide de la transformée de laplace
Lp signifie F(s) = L[ f ( t)] dans le résultat de la transformée d’une équation
différentielle.
x’ + 2x = e
−
lorsque x(0) = 3 à
u fourier [Action][Advanced][fourier], invFourier [Action][Advanced][invFourier]
Fonction : « fourier » est la commande utilisée pour la transformée de Fourier et « invFourier » est la
commande utilisée pour la transformée de Fourier inverse.
Syntaxe : fourier( f ( x), x, w, n) invFourier(F ( w), w, x, n)
x : variable en fonction de laquelle l’expression est transformée ; w : paramètre de la
transformation ; n : 0 à 4, indiquant le paramètre de Fourier à utiliser (optionnel)
Le ClassPad prend en charge les fonctions suivantes.
t), cos(t), log(t), ln(t), abs(t), signum(t), heaviside(t), delta(t), delta(t,n), e
sin(
Le ClassPad ne prend pas en charge les fonctions suivantes.
tan(t), sin
La transformée de Fourier se définit de la façon suivante :
Certains auteurs (en particulier les physiciens) préfèrent écrire la transformée en termes de fréquence
angulaire ω ≡ 2π au lieu de fréquence d’oscillation .
Toutefois, ceci détruit la symétrie et donne la paire de transformées suivante.
– 1
(t), cos
() =
– 1
(t), tan
∞
∫
–∞
– 1
()
(ω) = [()] =
(t), sinh(t), cosh(t), tanh(t), sinh
–2π
∞
∫
–∞
()
–ω
() =
() = –1[(ω)] =
– 1
(t), cosh
∫
–∞
∞
()
– 1
(t), tanh
ti
2π
– 1
(t), gamma(t), 't , e
π
∫
∞
(ω)
–∞
1
2
ω
ω
t
Chapitre 2 : Application Principale 66
Page 67

Pour rétablir la symétrie, la convention suivante est parfois utilisée.
∞
2
1
π
∫
–∞
() = [ ()] =
En général, la paire de transformées de Fourier peut être définie à l’aide de deux constantes arbitraires a et b
comme indiqué ci-dessous.
()
–
() = –1[()] =
2
1
π
∞
∫
–∞
()
1–
∞
∫
–∞
()
ω
() =
n (optionnel) ab
(2
⏐
⏐
π)
1+
∞
(ω)
∫
–∞
–ω
ω
–2π
⏐
(ω) =
Les valeurs de a et b dépendent de la discipline scientifique, qui peut être spécifiée par la valeur de n
(quatrième paramètre optionnel de Fourier et invFourier) comme indiqué ci-dessous.
Malheureusement, un certain nombre de conventions sont couramment utilisées pour a et b. Par exemple,
(0, 1) est utilisé en physiques modernes, (1, –1) est utilisé en mathématique pure et ingénierie système, (1,
1) est utilisé dans la théorie des probabilités pour le calcul de la fonction caractéristique, (–1, 1) est utilisé en
physique classique et (0, –2π) est utilisé dans le traitement de signal.
Définition de la Transformée
Modern Physics (Physique moderne) 0 0 1
Pure Math (Mathématique pure) 1 1 –1
Probability (Probabilité) 2 1 1
Classical Physics (Physique classique) 3 –1 1
Signal Processing (Traitement du signal) 4 0
Conseil : La boîte de dialogue du format avancé peut être utilisée pour paramétrer la transformée de Fourier, par
exemple la définition de la transformée de Fourier, etc. Pour le détail, voir « Boîte de dialogue du format
avancé » à la page 41.
u FFT [Action][Advanced][FFT], IFFT [Action][Advanced][IFFT]
(2
⏐
π)
Fonction : « FFT » est la commande pour la transformée de Fourier rapide, et « IFFT » est la commande
pour la transformée de Fourier rapide inverse. Les valeurs des données 2n sont nécessaires pour
exécuter FFT et IFFT. Sur le ClassPad, FFT et IFFT sont calculés numériquement.
Syntaxe : FFT(liste) ou FFT(liste,
• Les tailles de données doivent être 2
• La valeur pour
utiliser : 0 (Traitement du signal), 1 (Mathématique pure), 2 (Analyse de données).
Les FTT et IFFT sont définis comme suit :
() =
Conseil : La boîte de dialogue du format avancé peut être utilisée pour paramétrer la transformée de Fourier rapide.
Pour le détail voir « Boîte de dialogue du format avancé » à la page 41.
m est optionnelle. Elle peut être comprise entre 0 et 2, et indique le paramètre FFT à
−1
()
∑
=0
m) IFFT(liste) ou IFFT(liste, m)
n
pour n = 1, 2, 3, ...
2π
–——
() =
1
−1
∑
=0
()
2π
——
Chapitre 2 : Application Principale 67
Page 68

Emploi du sous-menu Calcul
∫
Le sous-menu [Calculation] contient les commandes liées au calcul, comme « diff » (dérivation) et « »
(intégration).
u diff [Action][Calculation][diff]
Fonction : Dérive une expression en tenant compte d’une variable donnée.
Syntaxe : diff(Exp/List[,variable] [ ) ]
diff(Exp/List,variable,ordre[,a] [ ) ]
• « a » est le point pour lequel vous voulez déterminer la dérivée.
• « ordre » = 1 lorsque la syntaxe suivante est utilisée : diff(Exp/List[,variable] [ ) ]. «
défaut lorsque vous omettez la « variable ».
6
x
Exemple : Dériver
par rapport à x
u impDiff [Action][Calculation][impDiff]
Fonction : Différencie une équation ou une expression sous forme implicite
en fonction d’une variable précise.
Syntaxe : impDiff(Eq/Exp/List, variable indépendante, variable dépendante)
x » est le réglage par
Exemple : Trouver
y’ par différenciation implicite
Important !
Le symbole de dérivée (’) ne peut pas être utilisé dans l’argument « impDiff( ». Si l’on tente d’utiliser un
symbole de dérivée, l’erreur (Wrong Argument Type) se produira.
u
[Action][Calculation][ ]
Fonction : Intègre une expression par rapport à une variable donnée.
Syntaxe :
(Exp/List[,variable] [ ) ]
(Exp/List, variable, limite inférieure, limite supérieure [,tol ] [ ) ]
• «
x » est le réglage par défaut lorsque vous omettez [,variable].
• «
tol » représente la plage d’erreur tolérée.
• Cette commande renvoie une valeur approximative lorsqu’une plage est spécifiée pour «
• Cette commande renvoie la vraie valeur d’un intervalle défini lorsque «
valeur ne peut pas être obtenue, cette commande effectue un calcul approximatif à l’aide de tol =1E – 5. Si
une valeur approximative peut être obtenue, cette valeur est renvoyée. Un message d’erreur est renvoyé si
une valeur approximative ne peut pas être obtenue ou si le calcul lui-même
n’est pas possible pour une quelconque raison.
Exemple : Intégrer x par rapport à x
tol » n’est pas spécifié. Si une vraie
tol ».
u lim [Action][Calculation][lim]
Fonction : Détermine la limite d’une expression.
Syntaxe : lim (Exp/List, variable, point [,direction] [ ) ]
−
x
e
Exemple : Déterminer la limite de
• Cette fonction renvoie la limite depuis la gauche lorsque « direction » < 0, la limite depuis la droite lorsque
« direction » > 0 et la limite depuis des deux côtés (gauche et droite) lorsque « direction » = 0 ou la direction
est omise.
lorsque x s’approche de ∞
Chapitre 2 : Application Principale 68
Page 69

uΣ [Action][Calculation][Σ]
Fonction : Évalue une expression d’une variable discrète à l’intérieur d’une plage et calcule la somme.
Syntaxe : Σ(Exp/List, variable, valeur inférieure, valeur supérieure [ ) ]
2
x
Exemple : Calculer la somme de
lorsque la valeur de x varie de x = 1 à x
=10
uΠ [Action][Calculation][Π]
Fonction : Évalue une expression d’une variable discrète à l’intérieur d’une plage et calcule un produit.
Syntaxe : Π(Exp/List, variable, valeur inférieure, valeur supérieure [ ) ]
2
x
Exemple : Calculer le produit de
lorsque la valeur de x varie de x = 1 à x =
5
u rangeAppoint [Action][Calculation][rangeAppoint]
Fonction : Trouve une expression ou une valeur satisfaisant une condition dans une plage particulière.
Syntaxe : rangeAppoint (Exp/Eq/List, valeur initiale, valeur finale [ ) ]
• Lorsqu’une équation (Eq) est utilisée comme premier argument, saisissez l’équation en utilisant la syntaxe
Var = Exp. L’évaluation ne sera pas possible si une autre syntaxe est utilisée.
Exemple : Trouver l’expression ou les expressions dans la
liste {
x = π, x = 2π, x = 3π} appartenant à la plage
rapprochée de 0 s x s 5
u mod [Action][Calculation][mod]
Fonction : Renvoie le reste lorsqu’une expression est divisée par une autre expression.
Syntaxe : mod ({Exp/List} -1, {Exp/List} -2 [ ) ]
Exemple : Déterminer le reste lorsque 26 est divisé par 3 (26mod3)
u tanLine [Action][Calculation][line][tanLine]
Fonction : Renvoie le côté droit de l’équation pour la droite tangente (y = ‘expression’) à la courbe au point
spécifié.
Syntaxe : tanLine (Exp/List, variable, valeur de la variable au point de
tangence [ ) ]
3
y = x
Exemple : Déterminer la fonction de la tangente à
en x = 2
u normal [Action][Calculation][line][normal]
Fonction : Renvoie le côté droit de l’équation pour la droite normale (y = ‘expression’) à la courbe au point
spécifié.
Syntaxe : normal (Exp/List, variable, valeur de la variable au point de la
normale [ ) ]
3
y = x
Exemple : Déterminer la fonction de la normale à
en x = 2
u arcLen [Action][Calculation][line][arcLen]
Fonction : Renvoie la longueur de l’arc d’une expression depuis une valeur initiale jusqu’à une valeur finale
par rapport à une variable donnée.
Syntaxe : arcLen (Exp/List, variable, valeur initiale, valeur finale [ ) ]
3
2
y = x
Exemple : Déterminer la longueur d’arc pour
de x = 0 à x = 4
Chapitre 2 : Application Principale 69
Page 70

u fMin [Action][Calculation][fMin/fMax][fMin], fMax [Action][Calculation][fMin/fMax][fMax]
Fonction : Renvoie le point minimal (fMin) / le point maximal (fMax) dans une plage donnée d’une fonction.
Syntaxe : fMin(Exp[,variable] [ ) ]
fMin(Exp, variable, valeur initiale,valeur finale[,
fMax(Exp[,variable] [ ) ]
fMax(Exp, variable, valeur initiale,valeur finale[,
• «
x » est le réglage par défaut lorsque vous omettez « [,variable] ».
• L’infini négatif et l’infini positif sont les réglages par défaut lorsque la syntaxe fMin(Exp[,variable] [ ) ] ou
fMax(Exp[,variable] [ ) ] est utilisée.
• « n » est la précision du calcul, que vous pouvez spécifier en temps qu’entier dans une plage de 1 à 9.
L’utilisation d’une valeur hors de cette plage provoque une erreur.
• Cette commande renvoie à une valeur approximative lorsque la précision du calcul est spécifiée pour «
• Cette commande renvoie une valeur vraie lorsque rien n’est spécifié pour «
pas être obtenue, toutefois, cette commande renvoie une valeur approximative en même temps que n = 4.
• Des points ou sections discontinus fluctuant largement peuvent affecter la précision ou même causer une
erreur.
• La saisie d’un grand nombre pour « n » augmente la précision du calcul, mais aussi le temps nécessaire
pour effectuer le calcul.
• La valeur saisie comme point final de l’intervalle doit être supérieure à la valeur saisie comme point initial.
Sinon, une erreur se produit.
n] [ ) ]
n] [ ) ]
n ».
n ». Si la valeur vraie ne peut
Exemple : Trouver le point minimal de
Exemple : Trouver le point maximal de –x2 + 1 par rapport à x
2
x
– 1 par rapport à x
u gcd [Action][Calculation][gcd/lcm][gcd]
Fonction : Renvoie le plus grand dénominateur commun de deux expressions.
Syntaxe : gcd (Exp/List-1, Exp/List-2 [ ) ]
Exemple : Obtenir le plus grand dénominateur commun de
x + 1 et x
2
– 3x – 4
u lcm [Action][Calculation][gcd/lcm][lcm]
Fonction : Renvoie le plus petit multiple commun de deux expressions.
Syntaxe : lcm (Exp/List-1, Exp/List-2 [ ) ]
2
x
Exemple : Obtenir le plus petit multiple commun de
– 1 et x2 + 2x – 3
u denominator [Action][Calculation][fraction][denominator]
Fonction : Extrait le dénominateur d’une fraction.
Syntaxe : denominator (Exp/List [ ) ]
Exemple : Extraire le dénominateur de la fraction (
y – 2)/(x + 1)
u numerator [Action][Calculation][fraction][numerator]
Fonction : Extrait le numérateur d’une fraction.
Syntaxe : numerator (Exp/List [ ) ]
Exemple : Extraire le numérateur de la fraction (
y – 2)/(x + 1)
Chapitre 2 : Application Principale 70
Page 71

Emploi du sous-menu Complexe
Le sous-menu [Complex] contient les commandes liées aux calculs avec nombres complexes.
u arg [Action][Complex][arg]
Fonction : Renvoie l’argument d’un nombre complexe.
Syntaxe : arg (Exp/Eq/List/Mat [ ) ]
Exemple : Obtenir l’argument du complexe 2 +
i (en mode radian)
u conjg [Action][Complex][conjg]
Fonction : Renvoie le nombre complexe conjugué.
Syntaxe : conjg (Exp/Eq/Ineq/List/Mat [ ) ] (Ineq : Seulement en mode réel)
Exemple : Obtenir le conjugué du complexe 1 +
i
u re [Action][Complex][re]
Fonction : Renvoie la partie réelle d’un nombre complexe.
Syntaxe : re (Exp/Eq/Ineq/List/Mat [ ) ] (Ineq : Seulement en mode réel)
Exemple : Obtenir la partie réelle du nombre complexe 3 – 4
i
u im [Action][Complex][im]
Fonction : Renvoie la partie imaginaire d’un nombre complexe.
Syntaxe : im (Exp/Eq/Ineq/List/Mat [ ) ] (Ineq : Seulement en mode réel)
Exemple : Obtenir la partie imaginaire du nombre complexe 3 – 4
i
u cExpand [Action][Complex][cExpand]
Fonction : Développe une expression complexe en forme rectangulaire (a + bi).
Syntaxe : cExpand (Exp/Eq/List/Mat [ ) ]
• Les variables sont considérées comme des nombres réels.
Exemple : Développer cos
–1
(2) (en mode radian)
u compToPol [Action][Complex][compToPol]
Fonction : Transforme l’écriture algébrique d’un nombre complexe en écriture exponentielle.
Syntaxe : compToPol (Exp/Eq/List/Mat [ ) ]
• Lorsque l’argument est Mat (Matrices), il est possible d’effectuer le calcul en utilisant l’unité d’angle radian
uniquement.
Exemple : Écrire 1 +
Mode radian Mode degré Mode grade
i sous forme exponentielle
Chapitre 2 : Application Principale 71
Page 72

u compToTrig [Action][Complex][compToTrig]
Fonction : Transforme l’écriture algébrique d’un nombre complexe en écriture trigonométrique/hyperbolique.
Syntaxe : compToTrig (Exp/Eq/List/Mat [ ) ]
Exemple : Écrire 1 +
i sous forme trigonométrique (en mode radian)
u compToRect [Action][Complex][compToRect]
Fonction : Transforme l’écriture algébrique d’un nombre complexe en écriture rectangulaire.
Syntaxe : compToRect (⬔(r,) ou r · e^( · i) [ ) ]
Exemple : Transformer l’écriture algébrique
d’un nombre complexe en écriture
rectangulaire
Emploi du sous-menu Création-Liste
Le sous-menu [List][Create] contient des commandes liées à la création de listes.
u seq [Action][List][Create][seq]
Fonction : Génère une liste en accord avec l’expression d’une suite numérique.
Syntaxe : seq (Exp, variable, valeur initiale, valeur finale [,taille du pas] [ ) ]
2
x
Exemple : Générer une liste en accord avec l’expression
lorsque la valeur initiale est 1, la valeur finale 5 et la taille du pas 2
• « 1 » est le réglage par défaut lorsque vous omettez « [,taille du pas] ».
• La taille du pas doit être un facteur de la différence entre la valeur initiale et la valeur finale.
+ 2x
u augment [Action][List][Create][augment]
Fonction : Crée une nouvelle liste en ajoutant une liste à une autre.
Syntaxe : augment (List-1, List-2 [ ) ]
Exemple : Combiner la liste {1, 2} et la liste {3, 4}
u fill [Action][List][Create][fill]
Fonction : Remplace les éléments d’une liste par une valeur ou une expression donnée. Cette commande
peut aussi être utilisée pour créer une nouvelle liste dont les éléments contiennent tous la même
valeur ou expression, ou une nouvelle liste dans laquelle la fréquence de chaque élément de la
première liste est déterminée par l’élément correspondant de la seconde liste.
Syntaxe : fill (Exp/Eq/Ineq, nombres d’éléments [ ) ]
fill (Exp/Eq/Ineq, List [ ) ]
fill (List, List [ ) ]
Exemple : Créer une liste consistant en quatre éléments identiques (2)
u subList [Action][List][Create][subList]
Fonction : Extrait une partie donnée d’une liste pour la mettre dans une nouvelle liste.
Syntaxe : subList (List [,nombre initial] [,nombre final] [ ) ]
Exemple : Extraire les éléments compris entre le deuxième et le quatrième
élément de la liste {1, 2, 3, 4, 5}
• L’élément le plus à gauche est le réglage par défaut lorsque vous omettez le « [,nombre initial] », et
l’élément le plus à droite est le réglage par défaut lorsque vous omettez « [,nombre final] ».
Chapitre 2 : Application Principale 72
Page 73

u shift [Action][List][Create][shift]
Fonction : Renvoie une liste dans laquelle les éléments ont été décalés d’un nombre donné vers la droite ou
la gauche.
Syntaxe : shift (List [,nombre de décalages] [ ) ]
• La spécification d’une valeur négative pour « [,nombre de décalages] » entraîne un décalage vers la droite,
tandis que la spécification d’une valeur positive entraîne un décalage vers la gauche.
• Le décalage d’un (–1) vers la droite est le réglage par défaut lorsque le « [,nombre de décalages] » est
omis.
Exemple : Décaler les éléments de la liste {1, 2, 3, 4, 5, 6} de trois vers la
gauche
u rotate [Action][List][Create][rotate]
Fonction : Renvoie une liste dans laquelle les éléments ont été tournés d’un nombre donné de rotations vers
la droite ou la gauche.
Syntaxe : rotate (List [,nombre de rotations] [ ) ]
• La spécification d’une valeur négative pour « [,nombre de rotations] » fait tourner vers la droite, tandis que la
spécification d’une valeur positive fait tourner vers la gauche.
Exemple : Faire tourner les éléments de la liste {1, 2, 3, 4, 5, 6} de deux
rotations vers la gauche
• Une rotation vers la droite (–1) est le réglage par défaut, lorsque vous omettez le « [,nombre de rotations] ».
u sortA [Action][List][Create][sortA]
Fonction : Trie les éléments de la liste dans l’ordre croissant.
Syntaxe : sortA (List [ ) ]
Exemple : Trier les éléments de la liste {1, 5, 3} dans l’ordre croissant
u sortD [Action][List][Create][sortD]
Fonction : Trie les éléments de la liste dans l’ordre décroissant.
Syntaxe : sortD (List [ ) ]
Exemple : Trier les éléments de la liste {1, 5, 3} dans l’ordre décroissant
u listToMat [Action][List][Create][listToMat]
Fonction : Transforme les listes en matrice.
Syntaxe : listToMat (List-1 [, List-2, ..., List-N] [ ) ]
Exemple : Transformer les listes {3, 5} et {2, 4} en une matrice
u matToList [Action][List][Create][matToList]
• Pour le détail sur matToList, voir page 77.
Emploi des sous-menus Statistiques-Liste et Calcul-Liste
Les sous-menus [List][Statistics] et [List][Calculation] contiennent des commandes liées aux calculs de liste.
u min [Action][List][Statistics][min]
Fonction : Renvoie la valeur minimale d’une expression ou des éléments d’une liste.
Syntaxe : min (Exp/List-1[, Exp/List-2] [ ) ]
Exemple : Déterminer les valeur minimales des éléments de la liste {1, 2, 3}
Chapitre 2 : Application Principale 73
Page 74

u max [Action][List][Statistics][max]
Fonction : Renvoie la valeur maximum d’une expression ou des éléments d’une liste.
Syntaxe : max (Exp/List-1[, Exp/List-2] [ ) ]
Exemple : Déterminer la valeur maximale des éléments de la liste {1, 2, 3}
u mean [Action][List][Statistics][mean]
Fonction : Renvoie la moyenne des éléments d’une liste.
Syntaxe : mean (List-1[, List-2] [ ) ] (List-1 : Données, List-2 : Fréq)
Exemple : Déterminer la moyenne des éléments de la liste {1, 2, 3}
u median [Action][List][Statistics][median]
Fonction : Renvoie la médiane des éléments d’une liste.
Syntaxe : median (List-1[, List-2] [ ) ] (List-1 : Données, List-2 : Fréq)
Exemple : Déterminer la médiane des éléments de la liste {1, 2, 3}
u mode [Action][List][Statistics][mode]
Fonction : Renvoie le mode des éléments d’une liste. S’il y a plusieurs modes, ils sont renvoyés dans une
liste.
Syntaxe : mode (List-1[, List-2] [ ) ] (List-1 : Données, List-2 : Fréq)
Exemple : Déterminer le mode des éléments de la liste {1, 1, 2, 2, 2}
u Q1 [Action][List][Statistics][Q1]
Fonction : Renvoie le premier quartile des éléments d’une liste.
Syntaxe : Q
(List-1[, List-2] [ ) ] (List-1 : Données, List-2 : Fréq)
1
Exemple : Déterminer le premier quartile des éléments de la liste {1, 2, 3, 4, 5}
u Q3 [Action][List][Statistics][Q3]
Fonction : Renvoie le troisième quartile des éléments d’une liste.
Syntaxe : Q3 (List-1[, List-2] [ ) ] (List-1 : Données, List-2 : Fréq)
Exemple : Déterminer le troisième quartile des éléments de la liste {1, 2, 3, 4, 5}
u percentile [Action][List][Statistics][percentile]
Fonction : Trouve le n
Syntaxe : percentile (liste, nombre)
ième
point percentile dans une liste.
u stdDev [Action][List][Statistics][stdDev]
Fonction : Renvoie l’écart-type des éléments d’une liste par rapport à l’échantillon.
Syntaxe : stdDev (List [ ) ]
Exemple : Déterminer l’écart-type de l’échantillon pour les éléments de la liste
{1, 2, 4}
Chapitre 2 : Application Principale 74
Page 75

u variance [Action][List][Statistics][variance]
Fonction : Renvoie la variance des éléments d’une liste par rapport à l’échantillon.
Syntaxe : variance (List [ ) ]
Exemple : Déterminer la variance de l’échantillon pour les éléments de la liste
{1, 2, 4}
u dim [Action][List][Calculation][dim]
Fonction : Renvoie la dimension d’une liste.
Syntaxe : dim (List [ ) ]
Exemple : Déterminer la dimension de la liste {1, 2, 3}
u sum [Action][List][Calculation][sum]
Fonction : Renvoie la somme des éléments d’une liste.
Syntaxe : sum (List-1[, List-2] [ ) ] (List-1 : Données, List-2 : Fréq)
Exemple : Déterminer la somme des éléments de la liste {1, 2, 3}
u prod [Action][List][Calculation][prod]
Fonction : Renvoie le produit des éléments d’une liste.
Syntaxe : prod (List-1[, List-2] [ ) ] (List-1 : Données, List-2 : Fréq)
Exemple : Déterminer le produit des éléments de la liste {1, 2, 3}
u cuml [Action][List][Calculation][cuml]
Fonction : Renvoie les sommes cumulées des éléments d’une liste.
Syntaxe : cuml (List [ ) ]
Exemple : Déterminer les sommes cumulées des éléments de la liste {1, 2, 3}
u Alist [Action][List][Calculation][Alist]
Fonction : Renvoie une liste dont les éléments sont les différences entre deux éléments adjacents d’une autre
liste.
Syntaxe : Alist (List [ ) ]
Exemple : Générer une liste dont les éléments sont les différences entre deux
éléments adjacents de la liste {1, 2, 4}
u percent [Action][List][Calculation][percent]
Fonction : Renvoie le pourcentage de chaque élément d’une liste, dont la
somme est supposée être 100.
Syntaxe : percent (List [ ) ]
Exemple : Déterminer le pourcentage de chaque élément de la liste {1, 2, 3}
u polyEval [Action][List][Calculation][polyEval]
Fonction : Renvoie un polynôme ordonné suivant les puissances décroissantes, de telle sorte que les
coefficients correspondent séquentiellement à chaque élément de la liste saisie.
Syntaxe : polyEval (List [,Exp/List] [ ) ]
x » est le réglage par défaut lorsque « [,Exp/List] » est omis.
• «
Exemple : Créer un polynôme du second degré avec les coefficients {1, 2, 3}
Chapitre 2 : Application Principale 75
Page 76

u sequence [Action][List][Calculation][sequence]
Fonction : Renvoie le polynôme de degré minimal représentant la suite exprimée par la liste saisie. Lorsqu’il
y a deux listes, cette commande renvoie un polynôme qui associe, à chaque valeur de la première
liste, son image correspondante dans la seconde liste.
Syntaxe : sequence (List-1[, List-2] [,variable] [ ) ]
• «
x » est le réglage par défaut lorsque vous omettez « [,variable] ».
Exemple : Déterminer un polynôme pour une suite exprimée par la liste
{3, 5, 7, 9}
u sumSeq [Action][List][Calculation][sumSeq]
Fonction : Trouve le polynôme de degré minimal représentant la suite exprimée par la liste saisie et renvoie la
somme du polynôme. Lorsqu’il y a deux listes, cette commande renvoie un polynôme qui associe,
à chaque valeur de la première liste, son image correspondante dans la seconde liste et renvoie la
somme du polynôme.
Syntaxe : sumSeq (List-1[, List-2] [,variable] [ ) ]
• «
x » est le réglage par défaut lorsque vous omettez « [,variable] ».
Exemple : Déterminer la somme d’un polynôme pour la séquence exprimée par
la liste {3, 5, 7, 9}
Emploi du sous-menu Création-Matrice
Le sous-menu [Matrix][Create] contient des commandes liées à la création de matrices.
u trn [Action][Matrix][Create][trn]
Fonction : Renvoie une matrice transposée.
Syntaxe : trn (Mat [ ) ]
Exemple : Transposer la matrice [[1, 2] [3, 4]]
u augment [Action][Matrix][Create][augment]
Fonction : Renvoie une matrice qui combine deux autres matrices.
Syntaxe : augment (Mat-1, Mat-2 [ ) ]
Exemple : Combiner deux matrices [[1, 2] [3, 4]] et [[5, 6] [7, 8]]
u ident [Action][Matrix][Create][ident]
Fonction : Crée une matrice Identité.
Syntaxe : ident (nombre naturel [ ) ]
Exemple : Créer une matrice Identité 2 × 2
u fill [Action][Matrix][Create][fill]
Fonction : Crée une matrice avec un nombre spécifié de lignes et de colonnes, ou remplace les éléments de
la matrice par une expression donnée.
Syntaxe : fill (Exp, nombre de lignes, nombre de colonnes [ ) ]
fill (Exp, Mat [ ) ]
Exemple : Créer une matrice 2 × 3 dont tous les éléments sont 2
Chapitre 2 : Application Principale 76
Page 77

u subMat [Action][Matrix][Create][subMat]
Fonction : Extrait une section donnée d’une matrice pour la mettre dans une nouvelle matrice.
Syntaxe : subMat (Mat [,ligne initiale] [,colonne initiale] [,ligne finale] [,colonne finale] [ ) ]
• « 1 » est le réglage par défaut lorsque vous omettez « [,ligne initiale] » et « [,colonne initiale] ».
• Le dernier numéro de la ligne est le réglage par défaut lorsque vous
omettez « [,ligne finale] ».
• Le dernier numéro de la colonne est le réglage par défaut lorsque vous
omettez « [,colonne finale] ».
Exemple : Extraire la section de la ligne 2, colonne 2, à la ligne 3, colonne 3
de la matrice [[1, 4, 7] [2, 5, 8] [3, 6, 9]]
u diag [Action][Matrix][Create][diag]
Fonction : Renvoie une matrice à une ligne contenant les éléments de la diagonale principale d’une matrice
carrée.
Syntaxe : diag (Mat[ ) ]
Exemple : Extraire les éléments diagonaux de la matrice [[1, 2] [3, 4]]
u listToMat [Action][Matrix][Create][listToMat]
• Pour le détail sur listToMat, voir page 73.
u matToList [Action][Matrix][Create][matToList]
Fonction : Transforme une colonne donnée d’une matrice en une liste.
Syntaxe : matToList (Mat, numéro de la colonne [ ) ]
Exemple : Transformer la colonne 2 de la matrice [[1, 2] [3, 4]] en une liste
Emploi des sous-menus Calcul-Matrice et Ligne&Colonne-Matrice
Les sous-menus [Matrix][Calculation] et [Matrix][Row&Column] contiennent des commandes liées aux calculs
matriciels.
u dim [Action][Matrix][Calculation][dim]
Fonction : Renvoie les dimensions d’une matrice sous forme de liste à deux éléments {nombre de lignes,
nombre de colonnes}.
Syntaxe : dim (Mat [ ) ]
Exemple : Déterminer les dimensions de la matrice [[1, 2, 3] [4, 5, 6]]
u det [Action][Matrix][Calculation][det]
Fonction : Renvoie le déterminant d’une matrice carrée.
Syntaxe : det (Mat [ ) ]
Exemple : Obtenir le déterminant de la matrice [[1, 2] [4, 5]]
u norm [Action][Matrix][Calculation][norm]
Fonction : Renvoie la norme de Frobenius de la matrice.
Syntaxe : norm (Mat [ ) ]
Exemple : Déterminer la norme de la matrice [[1, 2] [4, 5]]
Chapitre 2 : Application Principale 77
Page 78

u rank [Action][Matrix][Calculation][rank]
Fonction : Trouve le rang d’une matrice.
Cette fonction calcule le rang d’une matrice en appliquant l’élimination de
Gauss sur les lignes d’une matrice. Le rang d’une matrice A est le nombre de
lignes autres que zéro dans la matrice qui en résulte.
Syntaxe : rank (Matrix)
u ref [Action][Matrix][Calculation][ref]
Fonction : Renvoie la forme réduite de Gauss d’une matrice.
Syntaxe : ref (Mat [ ) ]
Exemple : Obtenir la forme réduite de Gauss de la matrice [[1, 2, 3] [4, 5, 6]]
u rref [Action][Matrix][Calculation][rref]
Fonction : Renvoie la forme réduite de Gauss - Jordan d’une matrice.
Syntaxe : rref (Mat [ ) ]
Exemple : Obtenir la forme réduite de Gauss - Jordan de la
matrice [[2, –1, 3, 19] [1, 1, –5, –21] [0, 4, 3, 0]]
u eigVl [Action][Matrix][Calculation][eigVl]
Fonction : Renvoie une liste contenant la ou les valeurs propres de la matrice carrée.
Syntaxe : eigVl (Mat [ ) ]
Exemple : Obtenir la ou les valeurs propres de la matrice [[3, 4] [1, 3]]
u eigVc [Action][Matrix][Calculation][eigVc]
Fonction : Renvoie une matrice dans laquelle chaque colonne représente un vecteur propre d’une matrice
carrée.
• Comme un vecteur propre ne peut en principe pas être déterminé exclusivement, il est standardisé de la
façon suivante lorsque sa norme est 1 :
Lorsque V = [
Syntaxe : eigVc (Mat [ ) ]
Exemple : Obtenir le ou les vecteurs propres de la matrice [[3, 4] [1, 3]]
x1, x2, ..., xn], (⎥ x1⎥
2
+ ⎥ x2⎥ 2 + .... + ⎥ xn⎥ 2 ) = 1.
u LU [Action][Matrix][Calculation][LU]
Fonction : Renvoie la décomposition LU d’une matrice carrée.
Syntaxe : LU (Mat, lVariableMem, uVariableMem [ ) ]
Exemple : Obtenir la décomposition LU de la matrice [[1, 2, 3] [4, 5, 6] [7, 8, 9]]
• La matrice triangulaire inférieure est affectée à la première variable L et
la matrice triangulaire supérieure à la seconde variable U.
Pour afficher la matrice inférieure Pour afficher la matrice supérieure
Lw
Uw
Chapitre 2 : Application Principale 78
Page 79

u QR [Action][Matrix][Calculation][QR]
Fonction : Renvoie la décomposition QR d’une matrice carrée.
Syntaxe : QR (Mat, qVariableMem, rVariableMem [ ) ]
Exemple : Obtenir la décomposition QR de la matrice [[1, 2] [3, 4]]
• La matrice unitaire est affectée à la variable Q et la matrice triangulaire
supérieure à la variable R.
Pour afficher la matrice unitaire Pour afficher la matrice triangulaire supérieure
Qw
Rw
u swap [Action][Matrix][Row&Column][swap]
Fonction : Échange deux lignes d’une matrice.
Syntaxe : swap (Mat, ligne numéro 1, ligne numéro 2 [ ) ]
Exemple : Échanger la ligne 1 et la ligne 2 de la matrice [[1, 2] [3, 4]]
u mRow [Action][Matrix][Row&Column][mRow]
Fonction : Multiplie les éléments d’une ligne donnée d’une matrice par une
expression donnée.
Syntaxe : mRow (Exp, Mat, numéro de ligne [ ) ]
Exemple : Multiplier la ligne 1 de la matrice [[1, 2] [3, 4]] par
x
u mRowAdd [Action][Matrix][Row&Column][mRowAdd]
Fonction : Multiplie les éléments d’une ligne donnée d’une matrice par une expression donnée et ajoute le
résultat à une autre ligne.
Syntaxe : mRowAdd (Exp, Mat, ligne numéro 1, ligne numéro 2 [ ) ]
Exemple : Multiplier la ligne 1 de la matrice [[1, 2] [3, 4]], par x, puis ajouter le
résultat à la ligne 2
u rowAdd [Action][Matrix][Row&Column][rowAdd]
Fonction : Ajoute une ligne donnée d’une matrice à une autre ligne.
Syntaxe : rowAdd (Mat, ligne numéro 1, ligne numéro 2 [ ) ]
Exemple : Ajouter la ligne 1 de la matrice [[1, 2] [3, 4]] à la ligne 2
u rowDim [Action][Matrix][Row&Column][rowDim]
Fonction : Renvoie le nombre de lignes d’une matrice.
Syntaxe : rowDim (Mat [ ) ]
Exemple : Obtenir le nombre de lignes dans la matrice [[1, 2, 3] [4, 5, 6]]
Chapitre 2 : Application Principale 79
Page 80

u rowNorm [Action][Matrix][Row&Column][rowNorm]
Fonction : Calcule la somme des valeurs absolues des éléments de chaque ligne d’une matrice, et renvoie la
valeur maximale des sommes.
Syntaxe : rowNorm (Mat [ ) ]
Exemple : Calculer les sommes des valeurs absolues des éléments de
chaque ligne de la matrice [[1, –2, 3] [4, –5, –6]], et obtenir la valeur
maximale des sommes
u colDim [Action][Matrix][Row&Column][colDim]
Fonction : Renvoie le nombre de colonnes d’une matrice.
Syntaxe : colDim (Mat [ ) ]
Exemple : Obtenir le nombre de colonnes dans la matrice [[1, 2] [3, 4] [5, 6]]
u colNorm [Action][Matrix][Row&Column][colNorm]
Fonction : Calcule la somme des valeurs absolues des éléments de chaque colonne d’une matrice, et renvoie
la valeur maximale des sommes.
Syntaxe : colNorm (Mat [ ) ]
Exemple : Calculer les sommes des valeurs absolues des éléments se
trouvant dans chaque colonne de la matrice [[1, –2, 3][4,
–5, –6][–7, 8, 9]] et obtenir la valeur maximale des sommes
Emploi du sous-menu Vecteur
Le sous-menu [Vector] contient des commandes liées aux calculs de vecteurs.
• Un vecteur est traité comme matrice 1 × N ou N × 1.
• Un vecteur du type 1 × N peut être saisi comme [……] ou [[……]].
Exemple : [1, 2], [[1, 2]]
• Les vecteurs sont considérés sous forme rectangulaire à moins que ∠() soit utilisé pour indiquer une
mesure d’angle.
u augment [Action][Vector][augment]
Fonction : Combine deux vecteurs [Mat-1 Mat-2].
Syntaxe : augment (Mat-1, Mat-2 [ ) ]
Exemple : Combiner les vecteurs [1, 2] et [3, 4]
u fill [Action][Vector][fill]
Fonction : Crée un vecteur contenant un nombre donné d’éléments, ou remplace les éléments d’un vecteur
par une expression donnée.
Syntaxe : fill (Exp, Mat [ ) ]
fill (Exp, 1, nombre de colonnes [ ) ]
Exemple : Remplacer les éléments du vecteur [1, 2] par
x
Exemple : Créer un vecteur 1 × 3 (1 ligne, 3 colonnes) dont tous les éléments
sont « 3 »
Chapitre 2 : Application Principale 80
Page 81

u dim [Action][Vector][dim]
Fonction : Renvoie la dimension d’un vecteur.
Syntaxe : dim (Mat [ ) ]
Exemple : Déterminer la dimension du vecteur [1, 2, 3]
• Le vecteur [1, 2, 3] est traité comme matrice 1 × 3.
u unitV [Action][Vector][unitV]
Fonction : Normalise un vecteur.
Syntaxe : unitV (Mat [ ) ]
• Cette commande peut être utilisée avec une matrice 1 × N ou N × 1
seulement.
Exemple : Normaliser le vecteur [1, 3, 5]
u angle [Action][Vector][angle]
Fonction : Renvoie l’angle formé par deux vecteurs.
Syntaxe : angle (Mat-1, Mat-2 [ ) ]
• Cette commande peut être utilisée avec une matrice 1 × N ou N × 1
seulement.
Exemple : Déterminer l’angle formé par des vecteurs [1, 2] et [3, 4] (en mode
radian)
u norm [Action][Vector][norm]
Fonction : Renvoie la norme d’un vecteur.
Syntaxe : norm (Mat [ ) ]
Exemple : Obtenir la norme du vecteur [1, 2, 3]
u crossP [Action][Vector][crossP]
Fonction : Renvoie le produit vectoriel de deux vecteurs.
Syntaxe : crossP (Mat-1, Mat-2 [ ) ]
• Cette commande peut être utilisée avec une matrice 1 × N ou N × 1 seulement (N = 2, 3).
• Une matrice à deux éléments [a, b] ou [[a], [b]] est automatiquement convertie en matrice à trois éléments
[a, b, 0] ou [[a], [b], [0]].
Exemple : Obtenir le produit vectoriel de deux vecteurs [1, 3, 5] et [2, 4, 6]
u dotP [Action][Vector][dotP]
Fonction : Renvoie le produit scalaire de deux vecteurs.
Syntaxe : dotP (Mat-1, Mat-2 [ ) ]
• Cette commande peut être utilisée avec une matrice 1 × N ou N × 1 seulement.
Exemple : Obtenir le produit scalaire de deux vecteurs [1, 3, 5] et [2, 4, 6]
Chapitre 2 : Application Principale 81
Page 82

u toRect [Action][Vector][toRect]
Fonction : Renvoie les coordonnées rectangulaires [x y] ou [x y z].
Syntaxe : toRect (Mat [,nombre naturel] [ ) ]
• Cette commande peut être utilisée avec une matrice 1 × N ou N × 1 seulement (N = 2, 3).
• Cette commande renvoie «
2, et « z » lorsque le nombre naturel est 3.
• Cette commande renvoie les coordonnées rectangulaires lorsque vous omettez le « nombre naturel ».
Exemple : Transformer les coordonnées polaires ['2 , ∠(π/4)] en
coordonnées rectangulaires (en mode radian)
x » lorsque le « nombre naturel » est 1, « y » lorsque le « nombre naturel » est
u toPol [Action][Vector][toPol]
Fonction : Renvoie les coordonnées polaires [r∠].
Syntaxe : toPol (Mat [,nombre naturel] [ ) ]
• Cette commande peut être utilisée avec une matrice 1 × 2 ou 2 × 1 seulement.
• Cette commande renvoie «
est 2.
• Cette commande renvoie les coordonnées polaires lorsque vous omettez le « nombre naturel ».
Exemple : Transformer les coordonnées rectangulaires [1, 2] en coordonnées
polaires
r » lorsque le « nombre naturel » est 1, et « » lorsque le « nombre naturel »
u toSph [Action][Vector][toSph]
Fonction : Renvoie les coordonnées sphériques [ ρ ∠ ∠φ].
Syntaxe : toSph (Mat [,nombre naturel] [ ) ]
• Cette commande peut être utilisée avec une matrice 1 × 3 ou 3 × 1 seulement.
ρ
• Cette commande renvoie «
2, et « φ » lorsque le nombre naturel est 3.
• Cette commande renvoie les coordonnées sphériques lorsque vous omettez le « nombre naturel ».
Exemple : Transformer les coordonnées rectangulaires [1, 1, 1] en
coordonnées sphériques (en mode radian)
» lorsque le « nombre naturel » est 1, « » lorsque le « nombre naturel » est
u toCyl [Action][Vector][toCyl]
Fonction : Renvoie les coordonnées cylindriques [r∠ z].
Syntaxe : toCyl (Mat [,nombre naturel] [ ) ]
• Cette commande peut être utilisée avec une matrice 1 × 3 ou 3 × 1 seulement.
• Cette commande renvoie «
2, et « z » lorsque le « nombre naturel » est 3.
• Cette commande renvoie les coordonnées cylindriques lorsque vous omettez le « nombre naturel ».
Exemple : Transformer les coordonnées rectangulaires [1, 1, 1] en
coordonnées cylindriques (en mode radian)
r » lorsque le « nombre naturel » est 1, « » lorsque le « nombre naturel » est
Chapitre 2 : Application Principale 82
Page 83

Emploi du sous-menu Équation/Inégalité
Le sous-menu [Equation/Inequality] contient des commandes liées aux équations et aux inégalités.
u solve [Action][Equation/Inequality][solve]
Fonction : Renvoie la solution d’une équation ou d’une inégalité.
Syntaxe 1 : solve(Exp/Eq/Ineq [,variable] [ ) ]
• «
x » est le réglage par défaut lorsque vous omettez « [,variable] ».
Exemple : Résoudre ax + b = 0 pour x
Syntaxe 2 : solve(Exp/Eq/Ineq,variable[, valeur, limite inférieure, limite supérieure] [ ) ]
• La « valeur » est initialement une valeur estimée.
• Cette commande est valide seulement pour les équations et les expressions lorsque la « valeur » et les
éléments suivants sont inclus. Dans ce cas, elle renvoie une valeur approximative.
• Une vraie valeur est renvoyée lorsque la « valeur » et les éléments qui la suivent sont omis. Toutefois,
lorsque la valeur vraie ne peut pas être obtenue, une valeur approximative est renvoyée pour les équations
basées sur la supposition que la valeur est = 0, la limite inférieure est = –
Syntaxe 3 : solve({Exp-1/Eq-1, ..., Exp-N/Eq-N}, {variable-1, ..., variable-N} [ ) ]
• Lorsque « Exp » est le premier argument, on suppose l’équation Exp = 0.
∞, et la limite supérieure est = ∞.
Exemple : Résoudre simultanément les équations linéaires 3
2x – 3y = –8
Vous pouvez aussi saisir les équations simultanées indiquées dans cet exemple avec la touche # du clavier
tactile. La syntaxe devant être saisie est la suivante.
Exp-1/Eq-1
Exp-N/Eq-N
• Les touches utilisées pour saisir cet exemple avec la touche # sont les suivantes.
#dX+eY=fccX-dY=-ieX,Yw
• Pour saisir des équations simultanées à trois inconnues ou plus, appuyez sur la touche # quand le
curseur est dans le champ de saisie Exp-N/Eq-N. À chaque pression du doigt sur la touche #, une ligne
supplémentaire est ajoutée pour la saisie d’une équation.
Syntaxe 4 : Vous pouvez résoudre la relation entre deux points, les droites, les plans, ou les sphères en
variable-1, ..., variable-N
saisissant une équation de vecteur dans la commande solve(. Nous présenterons ici quatre
syntaxes typiques pour résoudre une équation de vecteur avec la commande solve(.
Dans les syntaxes ci-dessous, de Vct-1 à Vct-6 sont des vecteurs-colonnes avec trois (ou deux)
éléments, et
solve(Vct-1 +
• Si le côté droit de l’équation (= Vct-3) est omis dans la syntaxe ci-dessus, tous les éléments du
côté droit sont considérés comme des vecteurs 0.
solve(Vct-1 +
solve(Vct-1 +
solve(Vct-1 +
variable-3, variable-4})
• Les variables (de la variable 1 à la variable 4) peuvent être saisies
dans les éléments de chaque vecteur (Vct-1 à Vct-6) dans les
quatre syntaxes ci-dessus pour résoudre ces variables.
s, t, u et v sont des paramètres.
s * Vct-2 [= Vct-3, {variable-1}])
s * Vct-2 = Vct-3 + t * Vct-4, {variable-1, variable-2})
s * Vct-2 + t * Vct-3 = Vct-4 – u * Vct-5, {variable-1, variable-2, variable-3})
s * Vct-2 + t * Vct-3 = Vct-4 – u * Vct-5 + v * Vct-6, {variable-1, variable-2,
x + 4y = 5,
Chapitre 2 : Application Principale 83
Page 84

0234 Prouver si point P (5, 7, 9) et point Q (5, 7, 8) existent sur la droite l, qui est un vecteur
d’orientation (4, 5, 6) passant par le point A (1, 2, 3)
Remarque
La fonction solve donne comme solution une expression ou une valeur pour l’expression (Exp/Eq) introduite
comme argument. Le message « More solutions may exist » (D’autres solutions peuvent exister) apparaît à
l’écran lorsqu’une valeur est proposée comme solution alors que plusieurs solutions peuvent exister.
La fonction solve peut proposer un maximum de 10 solutions sous forme de valeurs.
Exemple : Résoudre cos (
(Réglage d’unité d’angle : Deg)
x) = 0,5 pour x (valeur initiale : 0)
u dSolve [Action][Equation/Inequality][dSolve]
Fonction : Résout les équations différentielles du premier, second et troisième ordre, ou un système
d’équations différentielles du premier ordre.
Syntaxe : dSolve(Eq, variable indépendante, variable dépendante [, condition initiale 1, condition initiale 2] [,
condition initiale 3, condition initiale 4] [, condition initiale 5, condition initiale 6] [ ) ]
dSolve({Eq-1, Eq-2}, variable indépendante, {variable dépendante 1, variable dépendante 2} [,
condition initiale 1, condition initiale 2, condition initiale 3, condition initiale 4] [ ) ]
• Si vous omettez les conditions initiales, la solution contiendra des constantes arbitraires.
• Saisissez toutes les conditions initiales en utilisant la syntaxe Var = Exp. Toute condition initiale qui emploie
une autre syntaxe est ignorée.
Exemple : Résoudre l’équation différentielle
Exemple : Résoudre le système d’équations différentielles du premier ordre y’ = y + z, z’ = y – z, lorsque « x »
est la variable indépendante, « y » et « z » sont les variables dépendantes et les conditions initiales
sont y = 3 lorsque x = 0, et z = '2 – 3 lorsque x = 0
y’ = x, si y = 1 lorsque x = 0
u rewrite [Action][Equation/Inequality][rewrite]
Fonction : Déplace les éléments du côté droit d’une équation ou d’une inégalité vers le côté gauche.
Syntaxe : rewrite(Eq/Ineq/List [ ) ]
Exemple : Déplacer les éléments du côté droit de
gauche
x + 3 = 5x – x
2
vers le côté
u exchange [Action][Equation/Inequality][exchange]
Fonction : Échange les éléments du côté droit et du côté gauche d’une équation ou d’une inégalité.
Syntaxe : exchange(Eq/Ineq/List [ ) ]
Exemple : Échanger les éléments du côté droit et du côté gauche de
x – 2y
3 > 5
u eliminate [Action][Equation/Inequality][eliminate]
Fonction : Résout une équation par rapport à une variable et remplace la même variable dans une autre
expression par le résultat obtenu.
Syntaxe : eliminate(Eq/Ineq/List-1, variable, Eq-2 [ ) ]
Chapitre 2 : Application Principale 84
Page 85

Exemple : Exprimer
l’expression de x dans 2x + 3y = 5
x en fonction de y dans y = 2x + 3, et substituer
u absExpand [Action][Equation/Inequality][absExpand]
Fonction : Écrit une expression contenant une valeur absolue sans le symbole de valeur absolue.
Syntaxe : absExpand(Eq/Ineq [ ) ]
Exemple : Retirer la valeur absolue de ⎜2
x – 3 ⎜ = 9
u andConnect [Action][Equation/Inequality][andConnect]
Fonction : Combine deux équations ou inégalités en une seule expression.
Syntaxe : andConnect(Eq/Ineq-1, Eq/Ineq-2 [ ) ]
Exemple : Réécrire
x > –1 et x < 3 en une seule inégalité
u getRight [Action][Equation/Inequality][getRight]
Fonction : Extrait les éléments du côté droit d’une équation ou d’une inégalité.
Syntaxe : getRight(Eq/Ineq/List [ ) ]
2
y = 2x
Exemple : Extraire les éléments du côté droit de
+ 3x + 5
u getLeft [Action][Equation/Inequality][getLeft]
Fonction : Extrait les éléments du côté gauche d’une équation ou d’une inégalité.
Syntaxe : getLeft(Eq/Ineq/List [ ) ]
2
x
Exemple : Extraire les éléments du côté gauche de y = 2
+ 3x + 5
u and [Action][Equation/Inequality][Logic][and]
Fonction : Renvoie le résultat du AND logique de deux expressions.
Syntaxe : Exp/Eq/Ineq/List-1 and Exp/Eq/Ineq/List-2
2
x
Exemple : Obtenir le résultat du AND logique de
> 1 and x < 0
u or [Action][Equation/Inequality][Logic][or]
Fonction : Renvoie le résultat du OR logique de deux expressions.
Syntaxe : Exp/Eq/Ineq/List-1 or Exp/Eq/Ineq/List-2
Exemple : Obtenir le résultat du OR logique de
x = 3 or x > 2
u xor [Action][Equation/Inequality][Logic][xor]
Fonction : Renvoie le résultat du OR logique exclusif de deux expressions.
Syntaxe : Exp/Eq/Ineq/List-1 xor Exp/Eq/Ineq/List-2
Exemple : Obtenir le résultat du OR logique exclusif de
x < 2 xor x < 3
u not [Action][Equation/Inequality][Logic][not]
Fonction : Renvoie le NOT logique d’une expression.
Syntaxe : not(Exp/Eq/Ineq/List [ ) ]
Exemple : Obtenir le NOT logique de
x = 1
Chapitre 2 : Application Principale 85
Page 86

Emploi du sous-menu Assistant
Le sous-menu [Assistant] contient quatre commandes liées au mode Assistant.
Notez que les commandes suivantes sont valides dans le mode Assistant seulement. Pour le détail sur le mode
Assistant, voir « Mode assistant et mode algèbre » à la page 47.
u arrange [Action][Assistant][arrange]
Fonction : Ordonne une expression dans l’ordre croissant des coefficients pour chacune des variables.
Syntaxe : arrange (Exp/Eq/Ineq/List/Mat [ ) ]
Exemple : Ordonner 2
x + 3 – 5x + 8y
u replace [Action][Assistant][replace]
Fonction : Remplace la variable d’une expression, équation ou inégalité par la valeur affectée à une variable
en utilisant la commande « store ».
Syntaxe : replace (Exp/Eq/Ineq/List/Mat [ ) ]
Exemple : Remplacer
est affectée à s
s dans l’expression 3x + 2s, lorsque l’expression 2x + 1
u invert [Action][Assistant][invert]
Fonction : Inverse deux variables d’une expression.
Syntaxe : invert (Exp/Eq/Ineq/List [,variable-1, variable-2] [ ) ]
•
x et y sont inversés lorsque les variables ne sont pas spécifiées.
Exemple : Inverser
x et y dans l’expression 2x = y
u Clear_a_z
Fonction : Efface les noms de variables à un seul caractère (a-z et A-Z) dans
le dossier actuel.
Emploi du sous-menu Distribution/Distribution inverse
Le sous-menu [Distribution/Inv.Dist] contient des fonctions de calculs statistiques pour chaque type de
probabilité. Les fonctions dans ce sous-menu permettent d’effectuer les mêmes calculs que les commandes
Distribution disponibles dans l’application Statistiques et dans les applications Principale, eActivity et
Programme.
Pour de plus amples informations sur les expressions numériques utilisées dans les calculs, voir
« Distributions » à la page 155.
Pour de plus amples informations sur la signification des variables utilisées dans les syntaxes des fonctions
présentées dans cette section et sur les variables système contenant les valeurs obtenues lors des calculs, voir
la « Termes de saisie et d’affichage » à la page 159.
Spécification d’arguments dans la fonction Distribution
Vous pouvez spécifier soit des valeurs soit les données d’une liste comme arguments dans la fonction
Distribution. La syntaxe (normPDf(x, , )) de la fonction normPDf (page 87) qui renvoie une densité de
probabilité normale peut être utilisée pour effectuer les calculs indiqués ci-dessous. Le réglage de « Number
Format » est « Fix 2 » pour tous les résultats des calculs.
normPDf(1, 1, 0) = 0,24
normPDf({1, 2}, 1, 0) = {0,24, 0,05}
normPDf(1, {1, 2}, 0) = {0,24, 0,18}
normPDf({1, 2},{1, 2}, 0) = {0,24, 0,12}
normPDf({1, 2},{1, 2},{1, 0}) = {0,40, 0,12}
Chapitre 2 : Application Principale 86
Page 87

Les données de listes se spécifient pour les arguments de la façon suivante et les résultats du calcul se
présentent de la façon suivante.
(a) Spécification des données de listes pour un seul argument
• En principe, vous pouvez spécifier la liste souhaitée, mais chacun des éléments de la liste doit remplir les
conditions exigées par l’argument de la fonction utilisée.
• Le calcul est effectué sur chaque élément de la liste et les résultats se présentent de la façon suivante.
x, {
normPDf(
= {<normPDf(
, 2}, )
1
x,
, ) résultat du calcul>, <normPDf(x, 2, ) résultat du calcul>}
1
(b) Spécification des données de listes pour plusieurs arguments
• Dans ce cas, toutes les listes doivent avoir le même nombre d’éléments. Sinon l’erreur Invalid Dimension
(Dimension incorrecte) se produira.
• Le calcul est effectué sur chaque élément de la liste et les résultats se présentent de la façon suivante.
x
normPDf({
= {<normPDf(
, x2}, {1, 2}, )
1
x
, 1, ) résultats des calculs>, <normPDf(x2, 2, ) résultats des calculs>}
1
Affectation des résultats de calculs avec données de listes aux variables
Lorsque les données d’une liste sont utilisées comme argument dans la fonction Distribution, les résultats du
calcul se présentent sous forme de données de liste, et ces données sont affectées telles quelles à la variable
de dernier résultat « ans ».
Les calculs utilisant la fonction Distribution sont non seulement affectés à la mémoire de dernier résultat
« ans » mais aussi à certaines variables système. Par exemple, la variable de densité de probabilité normale
renvoyée par normPDf est affectée à la variable système prob. Seul le dernier élément des données de la liste
est affecté à une variable système comme résultat d’un calcul.
Dans les explications de la fonction de distribution ci-dessous, les noms des fonctions auxquelles les résultats
de calculs sont affectés sont indiqués dans « Résultats des calculs ».
u normPDf [Action][Distribution/Inv.Dist][Continuous][normPDf]
Fonction : Donne la densité de probabilité normale pour la valeur spécifiée.
x[,
σ
Syntaxe : normPDf(
• Lorsque
σ
et μ sont omis, σ = 1 et μ = 0 sont utilisés.
Résultats des calculs :
, μ)]
prob
Exemple : Déterminer la densité de probabilité normale lorsque x = 37.5,
σ
= 2, μ = 35
u normCDf [Action][Distribution/Inv.Dist][Continuous][normCDf]
Fonction : Donne la probabilité cumulative d’une distribution normale entre une limite inférieure et une limite
supérieure.
σ
Syntaxe : normCDf(valeur inférieure, valeur supérieure[,
• Lorsque
Résultats des calculs :
σ
et μ sont omis, σ = 1 et μ = 0 sont utilisés.
prob, zLow, zUp
Exemple : Déterminer la densité de probabilité normale lorsque la valeur de
la limite inférieure est −
σ
= 2, μ = 35
∞, la valeur de la limite supérieure est 36,
, μ)]
u invNormCDf [Action][Distribution/Inv.Dist][Inverse][invNormCDf]
Fonction : Donne la ou les valeurs limites d’une probabilité de distribution cumulative normale pour les valeurs
spécifiées.
Syntaxe : invNormCDf([tail setting, ]valeur area [,
• Lorsque
σ
et μ sont omis, σ = 1 et μ = 0 sont utilisés.
σ
, μ)]
Chapitre 2 : Application Principale 87
Page 88

• « tail setting » indique l’extrémité spécifiée comme valeur de la probabilité, sachant que Left, Right ou
Center peut être spécifié. Saisissez les valeurs ou les lettres suivantes pour spécifier :
Left : −1, « L », ou « l »
Center : 0, « C », ou « c »
Right : 1, « R », ou « r »
Si vous ignorez ce réglage, « Left » sera utilisé.
• Lorsqu’un argument est omis (résultant en trois arguments), Tail = Left.
μ
• Lorsque deux arguments sont omis (résultant en deux arguments), Tail = Left,
• Lorsque trois arguments sont omis (résultant en un argument), Tail = Left,
• Lorsque « tail setting » est Center, la valeur de la limite inférieure est donnée.
=0.
σ
=1, μ =0.
Résultats des calculs :
Exemple : Déterminer la valeur de la limite supérieure lorsque tail setting =
Left, valeur Area = 0,7, σ = 2, μ = 35
x
InvN, x2InvN
1
u tPDf [Action][Distribution/Inv.Dist][Continuous][tPDf]
Fonction : Donne la densité de probabilité de t de Student pour la valeur spécifiée.
Syntaxe : tPDf(
Résultats des calculs :
Exemple : Déterminer la densité de la probabilité de t de Student lorsque
x, df [ ) ]
prob
x = 2, df = 5
u tCDf [Action][Distribution/Inv.Dist][Continuous][tCDf]
Fonction : Donne la probabilité cumulative d’une distribution t de Student entre une limite inférieure et une
limite supérieure.
Syntaxe : tCDf(valeur inférieure, valeur supérieure,
Résultats des calculs : prob, tLow, tUp
Exemple : Déterminer la probabilité d’une distribution
valeur inférieure = 1,5, la valeur supérieure = ∞, df = 18
df [ ) ]
t de Student lorsque la
u invTCDf [Action][Distribution/Inv.Dist][Inverse][invTCDf]
Fonction : Donne la valeur de la limite inférieure de la probabilité d’une distribution cumulative t de Student
pour les valeurs spécifiées.
Syntaxe : invTCDf(
Résultats des calculs : xInv
Exemple : Déterminer la valeur de la limite inférieure lorsque
0,0754752, df = 18
prob, df [ ) ]
prob =
u chiPDf [Action][Distribution/Inv.Dist][Continuous][chiPDf]
Fonction : Donne la densité de probabilité de χ2 pour les valeurs spécifiées.
Syntaxe : chiPDf(
Résultats des calculs : prob
Exemple : Déterminer la densité de probabilité de χ2 lorsque x = 2, df = 4
x, df [ ) ]
Chapitre 2 : Application Principale 88
Page 89

u chiCDf [Action][Distribution/Inv.Dist][Continuous][chiCDf]
Fonction : Donne la probabilité cumulative d’une distribution χ2 entre une limite inférieure et une limite
supérieure.
Syntaxe : chiCDf(valeur inférieure, valeur supérieure,
Résultats des calculs :
Exemple : Déterminer la probabilité χ2 lorsque la valeur inférieure = 2,7, la
valeur supérieure = ∞, df = 4
prob
df [ ) ]
u invChiCDf [Action][Distribution/Inv.Dist][Inverse][invChiCDf]
Fonction : Donne la valeur de la limite inférieure d’une probabilité de distribution cumulative de χ2 pour des
valeurs spécifiées.
Syntaxe : invChiCDf(
Résultats des calculs :
Exemple : Déterminer la valeur de la limite inférieure lorsque
prob, df [ ) ]
xInv
prob = 0,6092146, df = 4
u fPDf [Action][Distribution/Inv.Dist][Continuous][fPDf]
Fonction : Donne la densité de probabilité F pour une valeur spécifiée.
Syntaxe : fPDf(
Résultats des calculs :
Exemple : Déterminer la densité de probabilité F lorsque x = 1,5, n:df = 24,
x, n:df, d:df [ ) ]
prob
d:df = 19
u fCDf [Action][Distribution/Inv.Dist][Continuous][fCDf]
Fonction : Donne la probabilité cumulative d’une distribution F entre une limite inférieure et une limite
supérieure.
Syntaxe : fCDf(valeur inférieure, valeur supérieure,
Résultats des calculs :
Exemple : Déterminer la probabilité d’une distribution F lorsque la valeur
inférieure = 1,5, la valeur supérieure =
prob
n:df, d:df [ ) ]
∞, n:df = 24, d:df = 19
u invFCDf [Action][Distribution/Inv.Dist][Inverse][invFCDf]
Fonction : Donne la valeur de la limite inférieure d’une probabilité de distribution cumulative F pour les valeurs
spécifiées.
Syntaxe : invFCDf(
Résultats des calculs :
Exemple : Déterminer la valeur de la limite inférieure lorsque
prob, n:df, d:df [ ) ]
xInv
prob = 0,1852,
n:df = 24, d:df = 19
u binomialPDf [Action][Distribution/Inv.Dist][Discrete][binomialPDf]
Fonction : Donne la probabilité de succès obtenu dans une loi binomiale pendant l’essai spécifié.
Syntaxe : binomialPDf(
x, valeur numtrial, pos [ ) ]
Résultats des calculs :
Exemple : Déterminer la probabilité binomiale lorsque x = 5, valeur numtrial = 3,
prob
pos = 0,63
Chapitre 2 : Application Principale 89
Page 90

u binomialCDf [Action][Distribution/Inv.Dist][Discrete][binomialCDf]
Fonction : Donne la probabilité cumulative de succès obtenu dans une distribution binomiale entre la valeur
inférieure et la valeur supérieure spécifiées.
Syntaxe : binomialCDf(valeur inférieure, valeur supérieure, valeur numtrial,
Résultats des calculs :
Exemple : Déterminer la probabilité cumulative binomiale lorsque la valeur
inférieure = 2, la valeur supérieure = 5, la valeur numtrial = 3, pos
= 0,63
prob
pos [ ) ]
u invBinomialCDf [Action][Distribution/Inv.Dist][Inverse][invBinomialCDf]
Fonction : Donne le nombre d’essais minimal dans une distribution de probabilités cumulative binomiale pour
les valeurs spécifiées.
Syntaxe : invBinomialCDf(
Résultats des calculs :
prob, valeur numtrial, pos [ ) ]
xInv, ½xInv
Important !
Lorsque la fonction invBinomialCDf, invPoissonCDf, invGeoCDf, ou
invHypergeoCDf est exécutée, le ClassPad utilise la valeur prob spécifiée
et la valeur correspondant à un, moins le nombre minimal de chiffres
significatifs (valeur ½prob) de la valeur prob pour calculer le nombre d’essais
minimal. Les résultats sont attribués aux variables système xInv (résultat
obtenu avec prob) et ½xInv (résultat obtenu avec ½prob). La fonction ne
donne que la valeur xInv. Toutefois lorsque les valeurs xInv et ½xInv sont
différentes, le message d’avertissement suivant apparaît avec les deux
valeurs.
Les résultats des calculs de la fonction sont des entiers. La précision peut être réduite lorsque le premier
argument a 10 chiffres ou plus. Notez que même une légère différence dans la précision du calcul a une
incidence sur le résultat de ce calcul. Si un message d’avertissement apparaît, vérifiez les valeurs affichées.
Exemple : Déterminer le nombre minimal d’essais lorsque
valeur numtrial = 5, pos = 0,63
prob = 0,609,
u poissonPDf [Action][Distribution/Inv.Dist][Discrete][poissonPDf]
Fonction : Donne la probabilité de succès obtenu dans une distribution de Poisson pendant l’essai spécifié.
Syntaxe : poissonPDf(
Résultats des calculs : prob
Exemple : Déterminer la probabilité de Poisson lorsque x = 10, = 6
x, [ ) ]
u poissonCDf [Action][Distribution/Inv.Dist][Discrete][poissonCDf]
Fonction : Donne la probabilité cumulative de succès obtenu dans une distribution de Poisson entre la valeur
inférieure et la valeur supérieure spécifiées.
Syntaxe : poissonCDf(valeur inférieure, valeur supérieure, [ ) ]
Résultats des calculs :
Exemple : Déterminer la probabilité cumulative selon la loi de Poisson lorsque
la valeur inférieure = 2, la valeur supérieure = 3, = 2,26
prob
Chapitre 2 : Application Principale 90
Page 91

u invPoissonCDf [Action][Distribution/Inv.Dist][Inverse][invPoissonCDf]
Fonction : Donne le nombre d’essais minimal dans une distribution de probabilités cumulative de Poisson
pour les valeurs spécifiées.
Syntaxe : invPoissonCDf(
Résultats des calculs :
prob, [ ) ]
xInv, ½xInv
Important !
Voir « Important ! » sous « invBinomialCDf » à la page 90.
Exemple : Déterminer le nombre d’essais minimal lorsque prob = 0,8074,
= 2,26
u geoPDf [Action][Distribution/Inv.Dist][Discrete][geoPDf]
Fonction : Donne la probabilité de succès obtenu dans une distribution géométrique pendant l’essai spécifié.
Syntaxe : geoPDf(
Résultats des calculs :
Exemple : Déterminer la probabilité géométrique lorsque x = 6, pos = 0,4
x, pos [ ) ]
prob
u geoCDf [Action][Distribution/Inv.Dist][Discrete][geoCDf]
Fonction : Donne la probabilité cumulative de succès obtenu dans une distribution géométrique entre la
valeur inférieure et la valeur supérieure spécifiées.
Syntaxe : geoCDf(valeur inférieure, valeur supérieure,
Résultats des calculs :
prob
pos [ ) ]
Exemple : Déterminer la probabilité géométrique lorsque la valeur inférieure =
2, la valeur supérieure = 3, pos = 0,5
u invGeoCDf [Action][Distribution/Inv.Dist][Inverse][invGeoCDf]
Fonction : Donne le nombre d’essais minimal dans une distribution de probabilités cumulative géométrique
pour les valeurs spécifiées.
Syntaxe : invGeoCDf(
Résultats des calculs :
prob, pos [ ) ]
xInv, ½xInv
Important !
Voir « Important ! » sous « invBinomialCDf » à la page 90.
Exemple : Déterminer le nombre d’essais minimal lorsque prob = 0,875,
pos = 0,5
u hypergeoPDf [Action][Distribution/Inv.Dist][Discrete][hypergeoPDf]
Fonction : Donne la probabilité de succès obtenu dans une distribution hypergéométrique pendant l’essai
spécifié.
Syntaxe : hypergeoPDf(
Résultats des calculs :
Exemple : Déterminer la probabilité hypergéométrique lorsque x = 1, n = 5,
x, n, M, N [ ) ]
prob
M = 10, N = 20
Chapitre 2 : Application Principale 91
Page 92

u hypergeoCDf [Action][Distribution/Inv.Dist][Discrete][hypergeoCDf]
Fonction : Donne la probabilité cumulative de succès obtenu dans une distribution hypergéométrique entre la
valeur inférieure et la valeur supérieure spécifiées.
Syntaxe : hypergeoCDf(valeur inférieure, valeur supérieure,
Résultats des calculs :
Exemple : Déterminer la distribution cumulative hypergéométrique lorsque la
valeur inférieure = 0, la valeur supérieure = 1, n = 5, M = 10, N =
20
prob
n, M, N [ ) ]
u invHypergeoCDf [Action][Distribution/Inv.Dist][Inverse][invHypergeoCDf]
Fonction : Donne le nombre minimal d’essais d’une distribution cumulative hypergéométrique pour les valeurs
spécifiées.
Syntaxe : invHypergeoCDf(
Résultats des calculs :
prob, n, M, N [ ) ]
xInv, ½xInv
Important !
Voir « Important ! » sous « invBinomialCDf » à la page 90.
Exemple : Déterminer le nombre minimal d’essais lorsque prob = 0,3, n = 5,
M = 10, N = 20
Emploi du sous-menu Finances
Le sous-menu [Financial] contient les commandes relatives aux calculs financiers.
Pour des informations sur les fonctions incluses dans ce sous-menu, voir « 11-4 Fonctions de calculs
financiers ».
Emploi du sous-menu Commande
u Define
Fonction 1 : Définit une fonction et l’enregistre avec l’éditeur de graphes.
Syntaxe 1 : Define{
r1() − r100()} = <expression>
Exemple : Définir la fonction
de graphes
Fonction 2 : Crée une fonction définie par l’utilisateur.
Pour le détail à ce sujet, voir « 12-3 Fonctions définies par l’utilisateur ».
u DispStat
Fonction : Affiche les résultats de calculs statistiques antérieurs.
Pour le détail, voir « DispStat » à la page 216 et les exemples 1208 à 1210 dans « Inclusion de fonctions
graphiques et de calculs statistiques dans un programme » à la page 233.
y1(x) − y100(x) ; x1(y) − x100(y) ; yt1(t) − yt100(t) ; xt1(t) − xt100(t) ;
y = sin(x) et l’affecter à la ligne « y3 » de l’éditeur
u Clear_a_z
Fonction : Efface toutes les variables à un seul caractère.
Pour le détail, voir « Clear_a_z » à la page 86.
Chapitre 2 : Application Principale 92
Page 93

u DelVar
Fonction : Supprime la variable spécifiée.
Pour le détail, voir « DelVar » à la page 215.
u Clear All Variables
Fonction : Vide toutes les variables contenant des nombres, des listes ou des matrices.
2-8 Emploi du menu Interactif
Le menu [Interactive] contient la plupart des commandes qui se trouvent dans le menu [Action]. La sélection
d’une commande dans le menu [Action] saisit simplement la commande.
Sur le menu [Interactive] vous tirez le stylet sur l’expression existante dans la zone de travail puis sélectionnez
une commande. L’expression surlignée est incluse dans la commande et une boîte de dialogue s’ouvre si
d’autres arguments sont nécessaires. Si vous sélectionnez un élément du menu [Interactive] sans surligner
d’abord l’expression, la boîte de dialogue dans laquelle les arguments nécessaires doivent être saisis s’ouvre.
Conseil
• Les commandes suivantes du menu [Interactive] fonctionnent de la même manière que les mêmes commandes du menu
[Action]. Pour le détail sur l’emploi de ces commandes, voir « 2-7 Emploi du menu Action ».
[Transformation], [Advanced], [Calculation], [Complex], [List]-[Create], [List]-[Statistics], [List]-[Calculation], [Matrix]-
[Create], [Matrix]-[Calculation], [Matrix]-[Row&Column], [Vector], [Equation/Inequality], [Assistant], [Distribution/Inv.Dist],
[Financial], Define
• Les commandes « DispStat », « Clear_a_z » et « DelVar » du sous-menu [Command] du menu [Action] ne sont pas
incluses dans le menu [Interactive].
Exemple du menu Interactif
Les opérations du menu [Interactive] sont pratiques dans les cas suivants.
• Lorsque vous voulez utiliser une commande pour une expression que vous êtes en train de calculer
• Lorsque vous voulez utiliser une commande qui exige plusieurs arguments
3
x
0235 Factoriser l’expression
0236 Obtenir l’intégrale définie
– 3x2 + 3x – 1
2
x
+ 2x, 1 s x s 2
Emploi de la commande « apply »
La commande « apply » ne se trouve que dans le menu [Interactive]. Vous pouvez utiliser cette commande
pour exécuter une partie précise d’une expression seulement et afficher le résultat.
0237 Calculer le résultat de diff(sin(
l’expression seulement
Remarque : Cet exemple présuppose que le ClassPad est configuré dans les modes suivants :
Algèbre, Complexe, Radian, Ordre Décroissant.
x),x) × cos(x) + sin(x) × diff(cos(x),x), et calculer ensuite une partie de
Chapitre 2 : Application Principale 93
Page 94

2-9 Emploi de l’application Principale en combinaison
avec d’autres applications
Vous pouvez accéder aux fenêtres des autres applications du ClassPad depuis l’application Principale et
effectuer des copier, coller et d’autres opérations entre elles.
Conseil
• Copier des données qui incluent des informations de couleurs d’une autre application et les coller dans l’application
Principale a pour effet d’ignorer les informations de couleurs, et les données collées deviendront noires. Ceci est
également vrai lorsque vous faites un glisser-déposer de données d’une autre application vers l’application Principale.
• Copier des données de l’application Principale et les coller dans une autre application a pour effet d’afficher les données
collées selon les réglages de couleur de l’autre application. Ceci est également vrai lorsque vous faites un glisser-déposer
de données de l’application Principale vers une autre application.
Emploi de la fenêtre d’une autre application
u Ouvrir la fenêtre d’une autre application
1. Tapez sur le bouton fléché vers le bas à la droite de la barre d’outils.
• Une palette d’icônes d’application apparaît.
Éditeur de graphes
Graphe 3D
Graphe
Éditeur de Graphes 3D
Graphique des coniques
Éditeur d’équations différentielles
Résolution numérique
Géométrie
Spreadsheet
Éditeur de statistiques
Éditeur de coniques
Probabilité
Finances
Vérifier
Éditeur de suites
2. Tapez sur le bouton correspondant à la fenêtre que vous voulez afficher.
• La fenêtre correspondant au bouton sur lequel vous avez tapé apparaît dans la fenêtre inférieure.
u Fermer la fenêtre d’une autre application
1. Tapez n’importe où dans la fenêtre que vous voulez fermer.
2. Tapez sur le bouton C dans le coin supérieur droit, ou bien tapez sur O puis sur [Close].
• La zone de travail de l’application Principale s’agrandit et remplit tout l’écran.
Conseil
• Même si vous avez utilisé l’icône r du panneau d’icônes pour agrandir la fenêtre inférieure, la fenêtre de la zone de
travail réapparaît après une frappe sur O puis sur [Close].
• Rien ne se passe si vous tapez sur O puis sur [Close] quand la fenêtre de la zone de travail est active.
u Copier une expression dans la zone de travail et la coller dans la fenêtre de l’éditeur de
graphes
0238 Copier « x2 – 1 » dans la zone de travail et la coller dans la fenêtre de l’éditeur de graphes
• Pour le détail sur la fenêtre de l’éditeur de graphes, voir le Chapitre 3.
Chapitre 2 : Application Principale 94
Page 95

u Représenter graphiquement une fonction en la faisant glisser de la zone de travail vers la
fenêtre graphique
0239 Représenter graphiquement l’expression « x2 – 1 » , qui a déjà été saisie dans la zone de travail
• Comme vous pouvez le voir dans cet exemple, une courbe peut être tracée lorsque vous déposez une
expression de type
f (x) dans la fenêtre graphique.
• Lorsque vous déposez une formule dans la fenêtre graphique 3D au lieu de la fenêtre graphique, la formule
doit être sous la forme
f (x, y) (par exemple x^2+y^2).
Emploi de la fenêtre de l’éditeur de statistiques
Vous pouvez utiliser la fenêtre de l’éditeur de statistiques pour créer de nouvelles variables LIST et éditer les
variables LIST existantes. Vous pouvez aussi utiliser la fenêtre de l’éditeur de statistiques pour spécifier le nom
d’une variable LIST et afficher son contenu.
u Utiliser une variable LIST avec saisie de données à l’aide de l’éditeur de statistiques pour
effectuer un calcul dans la zone de travail
0240 Saisir des données dans « list1 » et « list2 » avec l’éditeur de statistiques puis effectuez le calcul
list1+list2 dans la zone de travail
• Les listes 1 à 6 sont des variables système de type LIST. Pour le détail à ce sujet, voir « Types de données
de la mémoire principale » (page 27).
• Pour le détail sur la saisie et l’édition des données de liste avec l’éditeur de statistiques, voir le Chapitre 7.
u Utiliser l’éditeur de statistiques pour rappeler une variable LIST créée dans la zone de travail
0241 Continuer à la suite de l’exemple 0240 , pour utiliser l’éditeur de statistiques afin de rappeler une
variable « test », créée dans la zone de travail
Utilisation de la fenêtre géométrique
Lorsqu’une fenêtre géométrique est affichée vous pouvez faire glisser des valeurs et des expressions pour les
déposer dedans et tracer la courbe ou la figure de la valeur ou de l’expression. Vous pouvez aussi faire glisser
une figure de la fenêtre géométrique pour la déposer dans la zone de travail pour voir l’expression ou la valeur
correspondante.
u Faire glisser et déposer une expression de la zone de travail dans la fenêtre géométrique
0242 Saisir l’expression x2/52 + y2/22 = 1 dans la zone de travail et la déposer dans la fenêtre géométrique
Conseil : Le tableau suivant montre les types d’expressions qui peuvent être déposées dans la fenêtre géométrique. Si
l’expression n’est pas reconnue, Géométrie l’affiche sous forme de texte.
Si vous déposez ceci dans la fenêtre géométrique : Ceci s’affichera :
Équation linéaire en
Équation d’un cercle en
Équation d’une ellipse en
Équation d’une hyperbole en
Vecteur à 2 dimensions (format 2 lignes × 1 colonne) Un point
Équation
Matrice 2 ×
Matrice
y = f ( x)
n, n t 3
n × 2, n t 3
x et y
x et y
x et y
x et y
Une droite
Un cercle
Une ellipse
Une hyperbole
Une courbe
Un polygone (chaque colonne représentant un sommet du
polygone)
Un polygone ouvert
Chapitre 2 : Application Principale 95
Page 96

u Déposer une expression de la fenêtre géométrique dans la zone de travail
0243 Déposer un point, un cercle, un point et son image de la fenêtre géométrique dans la zone de travail
• Pour le détail sur les opérations possibles sur la fenêtre géométrique, voir le Chapitre 8.
Conseil : Voici ce qui se passe lorsque vous déposez une figure de la fenêtre géométrique dans la zone de travail.
Si vous déposez ceci dans la zone de travail : Ceci s’affichera :
Point Coordonnées sous forme de vecteur (matrice 2 × 1)
Droite Équation de la droite
Vecteur Couple ordonné (tête du vecteur si la queue est à l’origine)
Cercle, Arc, Ellipse, Fonction ou Courbe Équation correspondante
Polygone
Polygone ouvert (créé par une animation)
Deux droites ou segments Système d’équations linéaires
Un point et son image sous une transformation Expression matricielle de la transformation
Matrice 2 ×
Matrice
n × 2
n
2-10 Utilisation de la fonction Vérifier
Vérifier est un outil puissant qui permet de vérifier si les manipulations numériques ou algébriques effectuées
sont correctes. Cette application vous aide à simplifier une expression en vérifiant si l’expression saisie
est équivalente à l’expression originale. Le cas échéant, un logo « souriant » s’affiche pour indiquer que
l’expression est correcte, sinon vous devez corriger votre erreur avant de continuer.
u Lancement de Vérifier
1. Sur la fenêtre de la zone de travail, tapez sur le
bouton fléché vers le bas à la droite de la barre
d’outils.
Expression côté gauche
2. Sur la palette d’icônes qui apparaît, tapez sur W.
Expression côté droit
u Menus et boutons de Vérifier
• Effacer la fenêtre de vérification ..................................................................File - New, Edit - Clear All ou O
• Ouvrir ou sauvegarder un fichier ......................................................................File - Open, File - Save ou {
• Spécifier la plage de calcul d’un nombre complexe pour Vérifier ...............................................................T
• Spécifier la plage de calcul d’un nombre réel pour Vérifier .........................................................................Y
• Spécifier la plage de calcul d’un nombre réel positif pour Vérifier ..............................................................U
• Vérifier l’équation à partir de la première ligne ...........................................................................................!
• Vérifier l’équation à partir de la ligne actuelle ............................................................................................."
0244 Décomposer 50 en produit de facteurs premiers
0245 Continuer à la suite de l’exemple 0244 , pour factoriser
2
x
+ 1 sur le corps des complexes
Chapitre 2 : Application Principale 96
Page 97
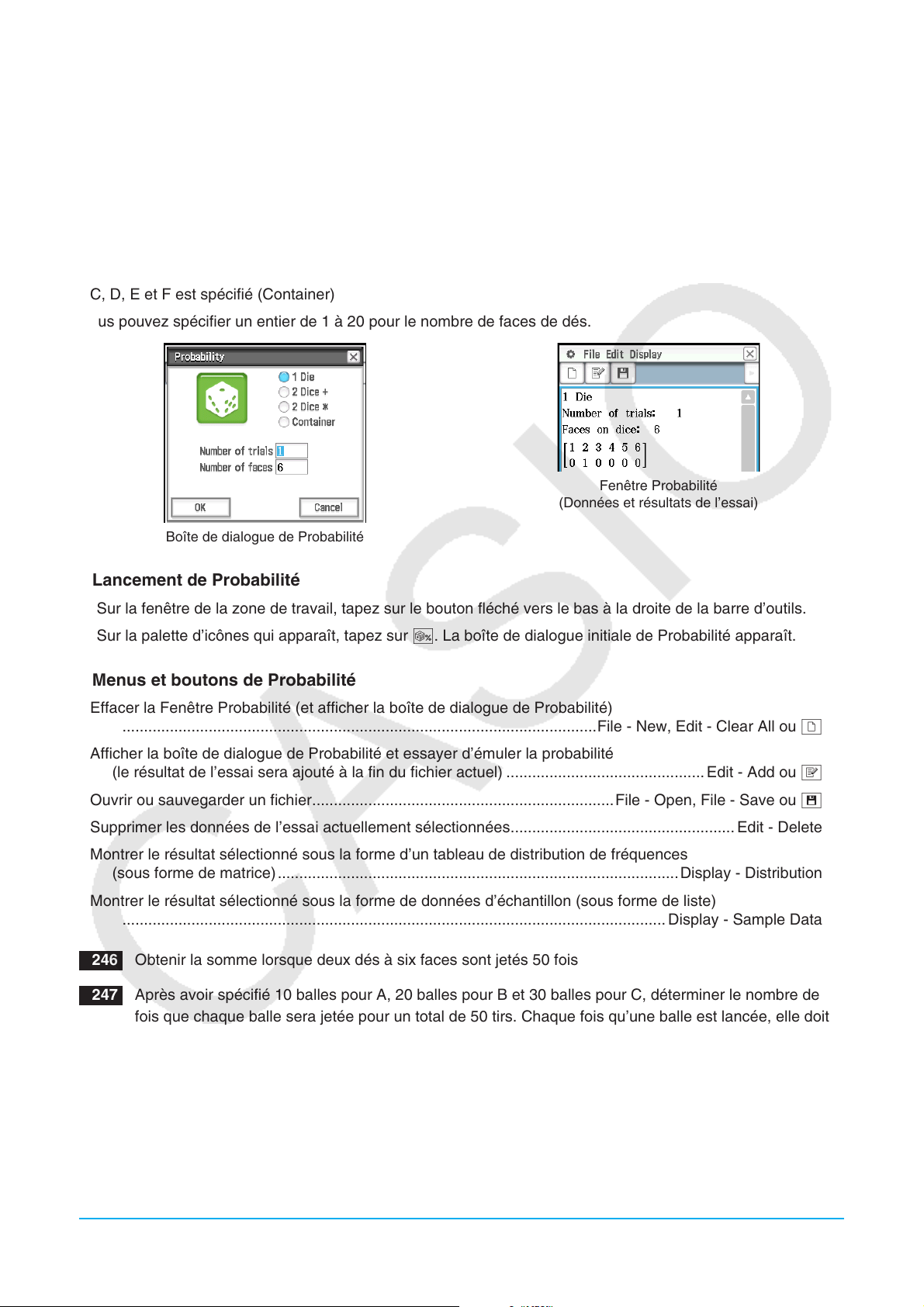
2-11 Emploi de Probabilité
Vous pouvez utiliser Probabilité pour simuler les éléments suivants.
• Les faces visibles d’un dé lorsque un seul dé est jeté un certain nombre de fois (1 Die)
• La somme des données des faces visibles des dés quand une paire de dés est jeté un certain nombre de fois
(2 Dice +)
• Le produit des données des faces visibles des dés quand une paire de dés est jeté un certain nombre de fois
(2 Dice ½)
• Le nombre de fois que chaque balle d’une boîte sera lancée quand un nombre précis de tirs et de balles A, B,
C, D, E et F est spécifié (Container)
Vous pouvez spécifier un entier de 1 à 20 pour le nombre de faces de dés.
Fenêtre Probabilité
(Données et résultats de l’essai)
Boîte de dialogue de Probabilité
u Lancement de Probabilité
1. Sur la fenêtre de la zone de travail, tapez sur le bouton fléché vers le bas à la droite de la barre d’outils.
2. Sur la palette d’icônes qui apparaît, tapez sur P. La boîte de dialogue initiale de Probabilité apparaît.
u Menus et boutons de Probabilité
• Effacer la Fenêtre Probabilité (et afficher la boîte de dialogue de Probabilité)
..............................................................................................................File - New, Edit - Clear All ou O
• Afficher la boîte de dialogue de Probabilité et essayer d’émuler la probabilité
(le résultat de l’essai sera ajouté à la fin du fichier actuel) ..............................................Edit - Add ou P
• Ouvrir ou sauvegarder un fichier ......................................................................File - Open, File - Save ou {
• Supprimer les données de l’essai actuellement sélectionnées .................................................... Edit - Delete
• Montrer le résultat sélectionné sous la forme d’un tableau de distribution de fréquences
(sous forme de matrice) .............................................................................................Display - Distribution
• Montrer le résultat sélectionné sous la forme de données d’échantillon (sous forme de liste)
.............................................................................................................................. Display - Sample Data
0246 Obtenir la somme lorsque deux dés à six faces sont jetés 50 fois
0247 Après avoir spécifié 10 balles pour A, 20 balles pour B et 30 balles pour C, déterminer le nombre de
fois que chaque balle sera jetée pour un total de 50 tirs. Chaque fois qu’une balle est lancée, elle doit
être remise dans la boîte avant le tir suivant.
Chapitre 2 : Application Principale 97
Page 98

Conseil : D’après les réglages par défaut, les résultats de l’essai apparaissent sous la forme d’un tableau de distribution
de fréquences. Lorsque vous sélectionnez des résultats du tableau de distribution et [Sample Data] sur le
menu [Display], ceux-ci apparaissent en données d’échantillon sous la forme d’une liste. Inversement, lorsque
vous sélectionnez les résultats du tableau de distribution et [Distribution] sur le menu [Display], les résultats
apparaissent sous la forme d’un tableau.
Tableau de distribution (forme matricielle)
Données d’échantillon (liste)
2-12 Exécution d’un programme dans l’application
Principale
Vous pouvez exécuter un programme dans l’application Principale ou l’application eActivity.
Syntaxe : Nom de dossier\Nom de programme(paramètre)
• Vous n’avez pas besoin de spécifier le nom de dossier si le programme que vous voulez exécuter se trouve
dans le dossier actuel. Si vous ne changez pas la configuration par défaut du ClassPad, le dossier actuel
pour l’application Programme et l’application Principale est le dossier « main », et il est inutile de changer le
nom.
• A moins de le changer, le dossier actuel de l’application eActivity est le dossier « eAct », et vous devez
toujours spécifier le nom de dossier. Si vous voulez exécuter un programme se trouvant dans le dossier
« main », écrivez « main\Nom de programme(paramètre) ».
Important !
Si la commande de programmation « Pause » est utilisée dans un programme, elle sera ignorée lorsque le
programme sera rappelé de l’application Principale ou eActivity.
Programme application Principale application eActivity
0248 Exécuter le programme intitulé OCTA créé et sauvegardé dans « Création d’un programme » (page 204)
de l’application Principale, et déterminez la surface d’un octaèdre régulier dont le côté mesure 20 cm
Chapitre 2 : Application Principale 98
Page 99

Chapitre 3 : Application Graphe & Table
L’application Graphe & Table permet l’étude graphique d’une fonction, la représentation de courbes en
coordonnées polaires et de courbes paramétrées, ainsi que la représentation de régions du plan définies par
des inégalités. A partir de la courbe, diverses analyses peuvent être effectuées pour déterminer les points
d’intersection de deux courbes, le point d’inflexion, ou bien l’intégrale de la fonction pour des bornes données.
Lorsque vous lancez l’application Graphe & Table, deux fenêtres
apparaissent : 1 la fenêtre de l’éditeur de graphes et 2 la fenêtre
graphique.
• Une feuille de l’éditeur de graphes peut contenir jusqu’à 20 fonctions.
L’éditeur de graphes peut en tout contenir 100 fonctions. Les fonctions
sauvegardées peuvent être représentées graphiquement sur la fenêtre
graphique.
• Les fonctions affichées dans la fenêtre de l’éditeur de graphes peuvent
être utilisées pour générer des tables numériques ou des tableaux
récapitulatifs. Les tables numériques et les tableaux récapitulatifs
apparaissent dans la fenêtre de la table.
1
• Au bas de la fenêtre graphique et de la fenêtre de la table se trouve une
boîte de message dans laquelle apparaissent les expressions et les
valeurs. Cette boîte peut être utilisée pour la saisie ou l’édition.
Boîte de message
Boutons et menus spécifiques de l’application Graphe & Table
Fenêtre de l’éditeur de graphes
• Ouvrir les données sauvegardées dans une variable dans la fenêtre de
l’éditeur de graphes .........................................................................................File - Open Graph Memory
• Sauvegarder toutes les expressions sur la fenêtre de l’éditeur de graphes ..........File - Save Graph Memory
• Sélectionner toute l’expression que vous êtes en train d’éditer .............................................. Edit - Select All
• Supprimer toutes les expressions de la fenêtre de l’éditeur de graphes ..................................Edit - Clear All
• Saisir l’équation d’une courbe de la forme .....................................................................Type -
• Saisir l’équation d’une courbe en coordonnées polaires ...............................................Type -
• Saisir les équations d’une courbe paramétrée ........................................................ Type - ParamType ou g
y=Type ou d
r=Type ou f
2
• Saisir l’équation d’une courbe de la forme
• Saisir une inégalité y en fonction de x
...............................................Type - Inequality - y>Type, y<Type, ytType, ysType ou j, l, ', X
• Saisir une inégalité
...............................................Type - Inequality - x>Type, x<Type, xtType, xsType ou k, ;, Z, C
• Saisir deux fonctions dans une liste et hachurer leur lien ....................................... Type - ShadeType ou y
• Commencer la modification de plusieurs courbes (Dynamic Modify, page 118)
...................................................................................................................... a - Dynamic Graph ou 4
• Afficher la boîte de dialogue de hachure (page 103) ............................................................a - Draw Shade
• Utiliser le modèle d’une fonction intégrée pour représenter graphiquement une fonction ............ a - Built-In
x en fonction de y
x ..................................................................Type - x=Type ou h
Chapitre 3 : Application Graphe & Table 99
Page 100

• Supprimer toutes les expressions sur la feuille active ..............................................a - Sheet - Clear Sheet
• Rétablir le nom de la feuille active par défaut ........................................................a - Sheet - Default Name
• Représenter graphiquement la ou les fonctions sélectionnées ..................................................................$
• Générer un tableau récapitulatif pour la fonction sélectionnée ...................................................................4
• Afficher la boîte de dialogue de la fenêtre d’affichage pour paramétrer la fenêtre graphique ....................6
• Afficher la boîte de saisie de la table pour le paramétrage .........................................................................8
• Générer une table numérique pour la fonction sélectionnée ......................................................................#
Fenêtre graphique
• Supprimer tout le texte de la fenêtre graphique ........................................................................Edit - Clear All
• Effectuer un zoom (page 108) ................................................................................................................Zoom
• Afficher les coordonnées d’un point particulier d’une courbe .....................................Analysis - Trace ou =
• Insérer un point, un graphique ou du texte dans un graphe existant (page 115) ................ Analysis - Sketch
• Effectuer une opération G-Solve (page 116) ..................................................................... Analysis - G-Solve
• Modifier une courbe en changeant la valeur d’un paramètre ................................................Analysis - Modify
• Ouvrir l’image d’une courbe ................................................................................................ a - Open Picture
• Sauvegarder une courbe sous forme d’image .....................................................................a - Save Picture
• Effacer l’image d’une courbe ...............................................................................................a - Clear Picture
• Ajuster la luminosité de l’image d’arrière plan de l’écran de la courbe placée avec la commande
« Open Picture » ................................................................................................................... a - Fade I/O
• Commencer la modification de plusieurs courbes (Dynamic Modify, page 118)
...................................................................................................................... a - Dynamic Graph ou 4
• Afficher la boîte de dialogue de hachure ..............................................................................a - Draw Shade
• Retracer une courbe ................................................................................................................... a - ReDraw
• Rendre active la fenêtre de l’éditeur de graphes ........................................................................................!
• Générer une table numérique pour une courbe existante ..........................................................................#
• Afficher la boîte de saisie de la table pour le paramétrage .........................................................................8
• Générer un tableau récapitulatif pour une courbe existante .......................................................................4
Fenêtre de la table
• Supprimer tout le texte de la fenêtre de la table .......................................................................Edit - Clear All
• Supprimer une ligne d’une table ..............................................................................................T-Fact - Delete
• Insérer une ligne dans la table .................................................................................................. T-Fact - Insert
• Ajouter une ligne après la ligne sélectionnée .............................................................................T-Fact - Add
• Tracer une courbe à tracé continu à partir d’une table .......................................... Graph - G-Connect ou $
• Tracer une courbe point par point à partir d’une table .................................................. Graph - G-Plot ou !
• Sauvegarder le contenu d’une table dans une liste ..............................................................a - Table to List
• Régénérer une table à partir des réglages de la table actuelle ..................................................a - ReTable
• Supprimer la table affichée .................................................................................................. a - Delete Table
• Déplacer le pointeur jusqu’à l’endroit de la courbe correspondant à la valeur sélectionnée dans la table
....................................................................................................................................................a - Link
• Rendre active la fenêtre de l’éditeur de graphes ........................................................................................!
• Afficher la boîte de saisie de la table pour le paramétrage .........................................................................8
Chapitre 3 : Application Graphe & Table 100
 Loading...
Loading...