Casio FX-CP400 operation manual [de]

Download

ClassPad II

fx-CP400

Bedienungsanleitung

Internet-Adresse der CASIO Schulungs-Website

https://edu.casio.com

Laden Sie kostenlose Testsoftware und Support Software herunter

https://edu.casio.com/dl/

Bedienungsanleitungen sind in diversen Sprachen verfügbar unter

https://world.casio.com/manual/calc/

Stellen Sie sicher, dass Sie alle wichtigen Daten in Papierform aufbewahren.

Eine niedrige Batteriespannung oder eine falsche Positionierung der Batterien kann zu einer Beschädigung oder zu einem Verlust der Daten führen. Gespeicherte Daten können ebenfalls durch starke elektrostatische Ladungen oder heftige Stöße beeinträchtigt werden. Es liegt in Ihrer eigenen Verantwortung, Sicherungskopien der Daten anzulegen, um einen Verlust zu verhindern.

Sichern von Daten

ClassPad-Daten können in eine VCP- oder XCP-Datei konvertiert und zu Speicherzwecken an einen Computer übertragen werden. Weitere Informationen finden Sie unter „19-2 Ausführen der Datenkommunikation zwischen dem ClassPad und einem Personal Computer“.

• Bitte bewahren Sie die gesamte Benutzerdokumentation für späteres Nachschlagen auf.

• Die Beispielanzeigen in dieser Bedienungsanleitung dienen lediglich der Veranschaulichung und entsprechen möglicherweise nicht genau den Anzeigen in ClassPad.

• Änderungen des Inhalts dieser Bedienungsanleitung sind ohne Vorankündigung vorbehalten.

• Die Reproduktion dieser Bedienungsanleitung, auch ausschnittsweise, ist ohne die schriftliche Genehmigung des Herstellers nicht gestattet.

• Die CASIO Computer Co., Ltd. übernimmt keine Haftung für bestimmte oder versehentliche Schäden, Kollateralschäden oder Folgeschäden in Zusammenhang mit dem Erwerb und der Verwendung dieser Materialien. Darüber hinaus übernimmt die CASIO Computer Co., Ltd. keinerlei Haftung für jegliche Ansprüche in Bezug auf die Verwendung dieser Materialien durch Dritte.

• Windows® ist eine eingetragene Marke oder Marke der Microsoft Corporation in den Vereinigten Staaten und/oder in anderen Ländern.

• Mac OS, OS X und macOS sind eingetragene Marken oder Marken von Apple Inc. in den Vereinigten Staaten und/oder anderen Ländern.

• In dieser Anleitung genannte Firmen- und Produktnamen sind eventuell eingetragene Marken oder Marken der betreffenden Inhaber.

Beachten Sie, dass Marke ™ und eingetragene Marke ® in dieser Anleitung nicht verwendet werden.

•

Inhalt

Informationen zu dieser Bedienungsanleitung .........................................................................................10

Kapitel 1: Grundlagen ..........................................................................................................11

1-1 Allgemeine Anleitung .............................................................................................................11

ClassPad auf einen Blick..........................................................................................................................11

Ein- und Ausschalten der Stromversorgung .............................................................................................11

1-2 Stromversorgung ....................................................................................................................12

1-3 Grundsätzliche Arbeitsweise in den integrierten Anwendungen .......................................13

Verwenden des Menüs der Anwendungen ..............................................................................................13

Integrierte Anwendungen .........................................................................................................................13

Add-In-Anwendungen...............................................................................................................................14

Anwendungsfenster..................................................................................................................................15

Verwenden des O-Menüs ....................................................................................................................... 16

Interpretieren der Statusleisten-Informationen .........................................................................................16

Pausieren und Beenden einer Operation .................................................................................................17

1-4 Eingabe ....................................................................................................................................17

Verwenden der Software-Tastatur ...........................................................................................................17

Tastensätze der Software-Tastatur ..........................................................................................................18

Grundlagen für die Eingabe .....................................................................................................................19

Verschiedene Operationen auf der Software-Tastatur .............................................................................22

1-5 ClassPad-Daten ......................................................................................................................27

Datentypen und Speicherorte (Speicherbereiche) ...................................................................................27

Hauptspeicher-Datentypen.......................................................................................................................28

Hauptspeicher-Ordner ..............................................................................................................................29

Verwenden des Variablenmanagers ........................................................................................................29

Verwalten von Menü-Dateien ...................................................................................................................33

1-6 Erstellen und Verwenden von Variablen ...............................................................................34

Erstellen einer neuen Variablen ...............................................................................................................34

Beispiel für die Verwendung von Variablen ..............................................................................................35

Variablen des „library“-Ordners ................................................................................................................35

Regeln für den Zugriff auf Variablen ........................................................................................................36

1-7 Konfigurieren der Anwendungsformate ...............................................................................37

Einstellungen der Anwendungsformate ....................................................................................................38

Initialisieren aller Anwendungsformateinstellungen .................................................................................44

1-8 Falls Probleme auftreten… ....................................................................................................44

Kapitel 2: Main-Menü ........................................................................................................... 46

Untermenüs und Schaltflächen des Main-Menüs .....................................................................................46

2-1 Grundrechenarten ..................................................................................................................46

Arithmetische Berechnungen und Klammerrechnung .............................................................................. 46

Verwenden der e-Taste......................................................................................................................47

Weglassen des Multiplikationszeichens ...................................................................................................47

Verwenden der Antwortvariablen (ans) ....................................................................................................47

Wertzuweisung für eine Variable ..............................................................................................................47

Prioritäten der Rechenoperationen während der Berechnung .................................................................48

Berechnungsmodi ....................................................................................................................................48

2-2 Verwenden des zurückliegenden Berechnungsverlaufs ....................................................50

2-3 Berechnungen mit Funktionen ..............................................................................................51

2-4 Listenberechnungen ..............................................................................................................60

Eingeben von Listendaten in den Arbeitsbereich .....................................................................................60

Operationen mit den Elementen einer LIST-Variablen .............................................................................60

Verwenden einer Liste für eine Berechnung ............................................................................................60

Verwenden einer Liste für die Zuordnung verschiedener Werte zu vielfachen Variablen ........................ 61

2-5 Matrizen- und Vektorrechnung ..............................................................................................61

Eingeben von Matrixdaten........................................................................................................................61

Ausführen der Matrizenrechnung .............................................................................................................62

Verwenden einer Matrix für die Zuordnung verschiedener Werte zu vielfachen Variablen ......................62

2-6 Vorgeben eines Zahlensystems ............................................................................................62

Bereiche für binäre, oktale, dezimale und sedezimale Berechnungen ....................................................63

Auswählen eines Zahlensystems .............................................................................................................63

Rechenoperationen ..................................................................................................................................64

Bitweise Verknüpfungen...........................................................................................................................64

Verwenden der baseConvert-Funktion (Zahlbasiswechsel) ..................................................................... 64

2-7 Verwenden des Aktionsmenüs ..............................................................................................64

In diesem Abschnitt verwendete Abkürzungen und Interpunktionen .......................................................65

Screenshot-Beispiele ...............................................................................................................................65

Verwenden des Untermenüs für Transformationen .................................................................................65

Verwenden des Advanced-Untermenüs ...................................................................................................68

Verwenden des Untermenüs für Berechnungen ......................................................................................70

Verwenden des Untermenüs für komplexe Zahlen ..................................................................................73

Verwenden des Untermenüs zur Listenerstellung ....................................................................................75

Verwenden der Untermenüs für Listenstatistik und Listenberechnung .................................................... 76

Verwenden des Untermenüs zur Matrizenerstellung ...............................................................................79

Verwenden der Untermenüs für Matrizenrechnung und Matrizenzeilen und -spalten .............................80

Verwenden des Untermenüs für die Vektorrechnung ..............................................................................83

Verwenden des Untermenüs für Gleichungen und Ungleichungen ........................................................85

Verwenden des Assistenten-Untermenüs ................................................................................................ 89

Verwenden des [Distribution/Inv. Dist.]-Untermenüs ................................................................................89

Verwenden des [Financial]-Untermenüs ..................................................................................................95

Verwenden des [Command]-Untermenüs ................................................................................................ 95

2-8 Verwenden des Interaktiv-Menüs .........................................................................................96

Beispiel für das Interaktiv-Menü ............................................................................................................... 96

Verwenden des „apply“-Befehls ...............................................................................................................97

2-9 Verwenden des Main-Menüs in Kombination mit anderen Anwendungs-Menüs .............97

Verwenden des Fensters eines anderen Anwendungs-Menüs ................................................................ 97

Verwenden des Statistik-Editor-Fensters ................................................................................................. 98

Verwenden des Geometriefensters .......................................................................................................... 98

2-10 Verwenden der Verifizierungs-Funktion .............................................................................99

2-11 Verwenden der Wahrscheinlichkeits-Simulations-Funktion ...........................................100

2-12 Ausführen eines Programms im Main-Menü ....................................................................101

Kapitel 3: Grafik- und Tabellen-Menü .............................................................................. 103

Menüs und Schaltflächen des Grafik- und Tabellen-Menüs ...................................................................103

3-1 Speicherfunktionen ..............................................................................................................105

Verwenden von Grafik-Editor-Blättern ....................................................................................................105

Speichern einer Funktion .......................................................................................................................105

Grafische Darstellung einer gespeicherten Funktion .............................................................................106

Schattieren der von zwei Termen begrenzten Region ...........................................................................107

Überlagern von zwei Ungleichungen in einem Intersection Plot/Union Plot ...........................................108

Speichern der Grafik-Editor-Daten im Grafikspeicher ............................................................................ 108

3-2 Grafikfensteroperationen ..................................................................................................... 109

Konfigurieren der Betrachtungsfenster-Parameter für das Grafikfenster ............................................... 109

Verwenden des Betrachtungsfenster-Speichers .................................................................................... 111

Verschieben des Grafikfensters .............................................................................................................111

Scrollen des Grafikfensters ....................................................................................................................112

Zoomen des Grafikfensters .................................................................................................................... 112

Verwenden von Schnellzoom ................................................................................................................. 113

Verwenden von vorprogrammierten Funktionen für die grafische Darstellung ......................................113

Speichern eines Screenshots einer Grafik ............................................................................................. 114

Anpassen der Helligkeit (Fade I/O) des Grafikfenster-Hintergrundbildes ..............................................114

3-3 Verwenden von Tabelle und Grafik .....................................................................................115

Generieren einer Wertetabelle ...............................................................................................................115

Einblenden von verknüpften Anzeigen für Wertetabellenkoordinaten und Grafikkoordinaten

(Link Trace) ............................................................................................................................................117

Erstellen von Wertetabellenwerten mithilfe einer Grafik .........................................................................117

Erstellen einer Übersichtstabelle ............................................................................................................ 117

3-4 Verwenden von Trace ........................................................................................................... 119

Verwenden von Trace für das Ablesen der Grafikkoordinaten ...............................................................119

3-5 Verwenden des Skizzenmenüs ............................................................................................120

Verwenden der Befehle des Skizzenmenüs ...........................................................................................120

3-6 Analysieren einer für das Zeichnen einer Grafik verwendeten Funktion ........................121

Aktionen unter Verwendung der Befehle des G-Solve-Menüs ............................................................... 121

Verwenden der Befehle des G-Solve-Menüs ......................................................................................... 122

3-7 Modifizieren einer Grafik ......................................................................................................123

Modifizieren einer einzelnen Grafik (Direct Modify) ................................................................................123

Gleichzeitiges Modifizieren von mehreren Grafiken (Dynamic Modify) .................................................. 123

Kapitel 4: Kegelschnitt-Menü ........................................................................................... 126

Menüs und Schaltflächen im Kegelschnitt-Menü ...................................................................................126

4-1 Eingeben einer Kegelschnitt-Gleichung .............................................................................127

4-2 Zeichnen einer Kegelschnittgrafik ......................................................................................127

Zeichnen einer Parabel ..........................................................................................................................127

Zeichnen eines Kreises .......................................................................................................................... 128

Zeichnen einer Ellipse ............................................................................................................................ 128

Zeichnen einer Hyperbel ........................................................................................................................128

Zeichnen eines allgemeinen Kegelschnittes ..........................................................................................128

4-3 Verwenden von G-Solve zur Analyse einer Kegelschnittgrafik ........................................128

Aktionen unter Verwendung der Befehle des G-Solve-Menüs ............................................................... 128

Verwenden der Befehle des G-Solve-Menüs ......................................................................................... 129

4-4 Modifizieren einer Grafik (Dynamic Modify) .......................................................................129

Kapitel 5: Differenzialgleichungsgrafik-Menü ................................................................. 130

Untermenüs und Schaltflächen im Differenzialgleichungseditor-Fenster ............................................... 130

Untermenüs und Schaltflächen im Differenzialgleichungsgrafik-Fenster ............................................... 130

5-1 Grafische Darstellung einer Differenzialgleichung ...........................................................131

Grafische Darstellung einer Differenzialgleichung erster Ordnung ........................................................131

Grafische Darstellung einer Differenzialgleichung zweiter Ordnung ...................................................... 132

Grafische Darstellung einer Differenzialgleichung

Konfigurieren und Modifizieren der Anfangsbedingungen .....................................................................133

Konfigurieren der Parameter für das Differenzialgleichungsgrafik-Betrachtungsfenster ........................134

n-ter Ordnung .......................................................... 133

5-2 Zeichnen der Graphen von Funktionen vom Typ f ( x) und von parametrischen

Funktionen ............................................................................................................................136

5-3 Verwenden der Abtastfunktion zum Ablesen von Grafikkoordinaten ..............................136

5-4 Grafisches Darstellen eines Ausdrucks oder eines Wertes durch Ablegen im

Differenzialgleichungsgrafik-Fenster .................................................................................137

Kapitel 6: Zahlenfolgen-Menü .......................................................................................... 138

Untermenüs und Schaltflächen des Zahlenfolgen-Menüs ......................................................................138

6-1 Rekursive und explizite Darstellung einer Zahlenfolge ....................................................139

Erzeugen einer Zahlentabelle ................................................................................................................139

Bestimmen der expliziten Form einer rekursiv dargestellten Zahlenfolge .............................................. 140

Berechnen der Summe einer Zahlenfolge ..............................................................................................140

6-2 Grafische Darstellung einer Rekursion ..............................................................................141

Kapitel 7: Statistik-Menü ................................................................................................... 142

7-1 Verwendung des Statistik-Editors .......................................................................................142

Grundlegende Listenoperationen ........................................................................................................... 142

Menüs und Schaltflächen für die Listenbearbeitung ..............................................................................144

Verwenden von CSV-Dateien ................................................................................................................144

7-2 Zeichnen einer statistischen Grafik ....................................................................................145

Verfahrensschritte für die Darstellung statistischer Grafiken .................................................................145

Grafische Darstellungen mit einer eindimensionalen Stichprobe ........................................................... 147

Grafische Darstellungen mit einer zweidimensionalen Stichprobe ........................................................148

Überlagern einer Regressionsgrafik in einem Streudiagramm ...............................................................149

Überlagern einer Funktionsgrafik auf einer Statistikgrafik ...................................................................... 150

Menüs und Schaltflächen im Statistik-Grafikfenster ............................................................................... 151

7-3 Ausführung grundlegender statistischer Berechnungen .................................................151

Berechnen statistischer Werte ...............................................................................................................151

Ausführen von Regressionsberechnungen ............................................................................................154

Anzeigen der Ergebnisse der zuletzt ausgeführten statistischen Berechnung (DispStat) .....................155

7-4 Durchführen erweiterter statistischer Berechnungen ......................................................156

Durchführen von Test-, Vertrauensintervall- und Wahrscheinlichkeitsverteilungsberechnungen mit

dem Assistenten ..................................................................................................................................... 156

Tests.......................................................................................................................................................157

Vertrauensintervalle ...............................................................................................................................161

Wahrscheinlichkeitsverteilungen ............................................................................................................162

Ein- und Ausgabebedingungen .............................................................................................................. 166

Kapitel 8: Geometrie-Menü ............................................................................................... 168

Unter-Menüs und Schaltflächen des Geometrie-Menüs ........................................................................168

Konfigurieren der Einstellungen des Geometrie-Betrachtungsfensters .................................................169

Das Geometrieformat-Dialogfeld ............................................................................................................ 169

8-1 Zeichnen von Figuren ..........................................................................................................169

Zeichnen einer Figur ..............................................................................................................................169

Einsetzen von Textketten in die Anzeige ...............................................................................................173

Ansetzen eines Winkelmaßes an eine Figur .......................................................................................... 173

Anzeige der Maße einer Figur ................................................................................................................ 174

Anzeige des Ergebnisses einer Berechnung, die mit Messwerten der Anzeige erstellt wurde .............. 174

Verwendung des „Special Polygon“-Untermenüs ..................................................................................175

Verwendung des „Construct“-Untermenüs ............................................................................................. 175

8-2 Bearbeiten von Figuren ........................................................................................................179

Auswahl und Abwahl von Figuren .......................................................................................................... 179

Verschieben und Kopieren von Figuren ................................................................................................. 180

Verankern einer Anmerkung im Geometriefenster ................................................................................. 180

Festlegen des Zahlenformats eines Messwerts ..................................................................................... 181

Festlegen von Farbe und Linientyp einer angezeigten Figur .................................................................181

Ändern der Anzeigeprioritäten von Figuren ............................................................................................182

8-3 Verwendung des Messfeldes ...............................................................................................183

Anzeigen der Maße einer Figur .............................................................................................................. 183

Festlegen und Beschränken eines Figurenmaßes ................................................................................. 185

Verwenden von Schiebern .....................................................................................................................185

Ändern eines Labels oder Hinzufügen eines Namens zu einem Element .............................................187

8-4 Arbeiten mit Animationen ....................................................................................................187

Verwendung der Animationsbefehle ......................................................................................................187

8-5 Geometrie-Menü in Kombination mit anderen Anwendungs-Menüs ...............................191

Drag & Drop ...........................................................................................................................................191

Kopieren und Einfügen ........................................................................................................................... 191

Kapitel 9: Numerisches-Lösungs-Menü .......................................................................... 192

Menüs und Tasten für die numerische Lösung ......................................................................................192

Eingeben einer Gleichung ...................................................................................................................... 192

Lösen einer Gleichung ...........................................................................................................................192

Kapitel 10: eActivity-Menü ................................................................................................ 194

Unter-Menüs und Schaltflächen des eActivity-Menüs ............................................................................ 194

10-1 Erstellen einer eActivity .....................................................................................................194

Grundlegende Schritte für die Erstellung einer eActivity ........................................................................ 194

Einfügen von Daten in eine eActivity ...................................................................................................... 195

Einfügung eines Anwendungsdatenfeldes .............................................................................................196

Einfügen einer Geometrie-Link-Zeile ......................................................................................................198

10-2 Übertragung von eActivity-Dateien ...................................................................................199

Dateikompatibilität ..................................................................................................................................199

Übertragung von eActivity-Dateien zwischen einem ClassPad und einem Computer ........................... 199

Übertragung von eActivity-Dateien zwischen zwei ClassPads ..............................................................199

Kapitel 11: Finanzmathematik-Menü ................................................................................ 200

11-1 Grundlegende Operationen im Finanzmathematik-Menü ...............................................200

Operationen auf der Seite ......................................................................................................................201

Konfigurieren von Einstellungen im Finanzmathematik-Menü ...............................................................202

11-2 Durchführen von finanzmathematischen Berechnungen ...............................................203

11-3 Berechnungsformeln .......................................................................................................... 204

Einfache Kapitalverzinsung .................................................................................................................... 204

Kapitalverzinsung mit Zinseszins ...........................................................................................................204

Geldflussberechnungen .........................................................................................................................205

Tilgungsberechnungen (Amortisation) ...................................................................................................206

Zinssatz-Umrechnung ............................................................................................................................206

Herstellungskosten, Verkaufspreis, Gewinnspanne ............................................................................... 206

Abschreibung .........................................................................................................................................207

Wertpapieranalyse .................................................................................................................................207

Kostendeckungspunkt ............................................................................................................................208

Gesicherter Gewinn................................................................................................................................208

Finanzstruktur-Risiko ..............................................................................................................................208

Kostenstruktur-Risiko .............................................................................................................................208

Kombiniertes Risiko ................................................................................................................................208

Mengenumrechnung ..............................................................................................................................208

11-4 Finanzmathematische Funktionen ....................................................................................209

11-5 Eingabe- und Ausgabefeldnamen .....................................................................................210

Kapitel 12: Programm-Menü ............................................................................................. 212

Untermenüs und Schaltflächen des Programm-Menüs ..........................................................................212

12-1 Erstellen und Ausführen eines Programms .....................................................................213

Erstellen eines Programms ....................................................................................................................213

Ausführen eines Programms .................................................................................................................. 215

Beenden der Programmausführung ....................................................................................................... 216

Erstellen einer Textdatei.........................................................................................................................216

Verwenden von Textdateien...................................................................................................................217

Umwandeln einer Textdatei in eine Programmdatei ..............................................................................217

Umwandeln einer Programmdatei in eine ausführbare Datei .................................................................217

12-2 Fehlerbeseitigung in einem Programm ............................................................................218

Fehlerbeseitigung nach dem Erscheinen einer Fehlermeldung ............................................................. 218

Fehlerbeseitigung in einem Programm nach unerwarteten Ergebnissen ...............................................218

Bearbeiten eines Programms ................................................................................................................. 218

12-3 Anwenderdefinierte Funktionen ........................................................................................219

Erstellen einer neuen anwenderdefinierten Funktion ............................................................................. 219

Ausführen einer anwenderdefinierten Funktion ......................................................................................220

Bearbeiten einer anwenderdefinierten Funktion .....................................................................................220

12-4 Referenz der Programmbefehle .........................................................................................221

Verwenden dieser Referenz ................................................................................................................... 221

Syntaxkonventionen ...............................................................................................................................221

Befehlsliste .............................................................................................................................................222

12-5 Einbinden von ClassPad-Funktionen in Programme ......................................................243

Einbinden von grafischen Darstellungsfunktionen in einem Programm ................................................. 243

Einbinden von Tabellen- und Grafikfunktionen in einem Programm ...................................................... 243

Einbinden einer Rekursionstabelle und von Rekursionsgrafikfunktionen in einem Programm ..............243

Einbinden von statistischen Grafik- und Berechnungsfunktionen in einem Programm .......................... 243

Einbinden von Finanzberechnungsfunktionen in einem Programm ....................................................... 243

Kapitel 13: Tabellenkalkulation-Menü .............................................................................. 244

Unter-Menüs und Schaltflächen des Tabellenkalkulationsfensters ........................................................ 244

Ändern der Spaltenbreite .......................................................................................................................245

Optionseinstellungen ..............................................................................................................................246

13-1 Eingeben und Bearbeiten von Zelleninhalten ..................................................................247

Auswahl von Zellen ................................................................................................................................247

Eingeben von Daten in eine Zelle ..........................................................................................................247

Eingabe einer Formel ............................................................................................................................. 248

Eingabe einer Zellenreferenz .................................................................................................................248

Typen von Zellendaten (Textdaten und Berechnungsdaten) .................................................................250

Eingeben einer Konstante in eine Zelle des Berechnungsdatentyps ..................................................... 250

Verwenden des Zellenbetrachtungsfensters .......................................................................................... 252

Ändern der Text- und Füllfarbe bestimmter Zellen ................................................................................. 252

Kopieren oder Ausscheiden von Zellen und deren Einfügen an einer anderen Stelle ........................... 253

Neuberechnung der Tabellenkalkulationsausdrücke .............................................................................253

Übertragen von Daten zwischen einer Tabellenkalkulation und CSV-Dateien ......................................254

Importieren und Exportieren von Variablenwerten ................................................................................. 255

13-2 Grafische Darstellungen ....................................................................................................256

Grundlegende Schritte für die grafische Darstellung .............................................................................256

Column Series und Row Series .............................................................................................................257

Grafikfarben und Color Link ...................................................................................................................257

Unter-Menüs und Schaltflächen des Tabellenkalkulations-Grafikfensters ............................................. 258

„Graph“-Menü und Grafikbeispiele ......................................................................................................... 259

Regressionsgrafik-Operationen (Kurvenanpassung) .............................................................................261

Andere Operationen im Grafikfenster .....................................................................................................263

13-3 Statistische Berechnungen ...............................................................................................264

Berechnungen mit Einzelvariablen, Variablenpaaren und Regressionsberechnungen .........................265

Test- und Intervallberechnungen............................................................................................................266

Verteilungsberechnungen ......................................................................................................................268

„DispStat“-Befehl ....................................................................................................................................269

13-4 Zellen- und Listenberechnungen ......................................................................................269

Verwenden der Zellenberechnungsfunktionen ....................................................................................... 269

Verwenden der Listenberechnungsfunktionen ....................................................................................... 269

Kapitel 14: 3D-Grafik-Menü ............................................................................................... 271

Untermenüs und Schaltflächen des 3D-Grafik-Menüs ........................................................................... 271

14-1 Eingeben eines Terms ........................................................................................................272

Verwenden von 3D-Grafik-Editor-Arbeitsblättern ................................................................................... 272

Speichern einer Funktion .......................................................................................................................272

Grafische Darstellung einer gespeicherten Funktion .............................................................................273

14-2 Verwenden des 3D-Grafikfensters ....................................................................................274

Konfigurieren der Parameter für das 3D-Grafik-Betrachtungsfenster ....................................................274

Anzeigen und Ausblenden der Achsen und Label .................................................................................275

Drehen der Grafik ................................................................................................................................... 276

3D-Grafik-Beispiel ..................................................................................................................................276

Verwenden von Trace für das Ablesen der Grafikkoordinaten ...............................................................276

Einfügen von Text in ein 3D-Grafikfenster .............................................................................................277

Berechnen eines

z-Wertes für bestimmte x- und y-Werte bzw. s- und t-Werte ...................................... 277

Kapitel 15: Bildplot-Menü ................................................................................................. 278

Untermenüs und Schaltflächen des Bildplot-Menüs ...............................................................................279

15-1 Verwenden der Plot-Funktion ............................................................................................280

Starten einer Bildplot-Operation ............................................................................................................. 280

Einzeichnen von Punkten in ein c2p-Datei-Bild ......................................................................................280

Einzeichnen von Punkten in ein c2b-Datei-Bild ......................................................................................281

Bearbeiten von Plots auf einem Hintergrundbild .................................................................................... 282

Überlagern einer Grafik auf Hintergrundbild-Plots .................................................................................282

G-Solve ..................................................................................................................................................284

Scrollen des Bildplot-Fensters ................................................................................................................284

15-2 Verwenden der Plotliste .....................................................................................................285

Verwenden des Plotliste-Fensters zum Bearbeiten von Plots ................................................................285

Speichern von Daten in eine Tabellenkalkulation und Importieren von Daten aus einer

Tabellenkalkulation.................................................................................................................................286

Exportieren von Plotdaten in eine Variable und Importieren von Plotdaten aus einer Variable ............. 286

15-3 Anzeigen von Plots auf t-y- oder t-x-Koordinaten ............................................................ 286

15-4 Bildplot-Menü-Dateien ........................................................................................................287

Kapitel 16: Interaktive-Differentialrechnung-Menü ........................................................ 288

Untermenüs und Schaltflächen des DiffCalc-Tabellenfensters .............................................................. 288

16-1 Mehr über Tangenten erfahren mit der [Tangent]-Registerkarte ....................................289

16-2 Ableiten der Ableitung mit der [Deriv]-Registerkarte ......................................................290

16-3 Erstellen einer Wertetabelle sowie grafische Darstellung der ersten und zweiten

Ableitung mithilfe der [D Trace]-Registerkarte ................................................................292

Kapitel 17: Physium-Menü ................................................................................................ 294

Untermenüs und Schaltflächen des Physium-Menüs .............................................................................294

17-1 Periodensystem ..................................................................................................................295

17-2 Grundlegende physikalische Konstanten ........................................................................297

17-3 Vorsichtshinweise...............................................................................................................298

Kapitel 18: System-Menü .................................................................................................. 300

18-1 Verwalten der Speichernutzung ........................................................................................300

Verwenden des „Storage“-Arbeitsblattes ..............................................................................................300

Verwenden des Hauptspeicher („Main Memory“)-Arbeitsblattes und des eActivity-Arbeitsblattes ........301

18-2 Konfigurieren der Systemeinstellungen ...........................................................................302

Untermenüs und Schaltflächen des System-Menüs ..............................................................................302

Konfigurieren der Systemeinstellungen ..................................................................................................303

Kapitel 19: Ausführen der Datenkommunikation ........................................................... 307

19-1 Beschreibung der Datenkommunikation ..........................................................................307

Verwendung des Kommunikations-Menüs des ClassPad ......................................................................307

Das „Select Connection Mode“-Dialogfeld .............................................................................................308

19-2 Ausführen der Datenkommunikation zwischen dem ClassPad und einem Personal

Computer .............................................................................................................................309

Herstellen und Trennen einer Verbindung mit einem Computer im USB-Flash-Modus ......................... 309

Datentransfer zwischen dem ClassPad und einem Personal Computer ................................................310

Installieren einer Add-In-Anwendung .....................................................................................................311

Automatischer Import von VCP-Dateien ................................................................................................311

Regeln für ClassPad-Dateien und Ordner ..............................................................................................312

Arbeiten mit VCP- und XCP-Dateien ......................................................................................................312

19-3 Ausführen der Datenkommunikation zwischen zwei ClassPads ...................................314

Anschluss an ein anderes ClassPad-Gerät ............................................................................................314

Datenübertragung zwischen zwei ClassPads ........................................................................................314

Kommunikationsbereitschaft ..................................................................................................................316

Unterbrechung einer Datenkommunikationsoperation ........................................................................... 316

19-4 Anschluss des ClassPad an den Datenlogger .................................................................316

Anschluss eines ClassPad an den Datenlogger ....................................................................................316

19-5 Anschluss des ClassPad an einen Projektor ...................................................................317

Projizieren von ClassPad-Bildschirminhalten von einem Projektor ........................................................ 317

Vorsichtshinweise beim Anschließen ..................................................................................................... 317

Anhang ............................................................................................................................... 318

Zeichencode-Tabelle....................................................................................................................318

Systemvariablen-Tabelle .............................................................................................................322

Grafiktypen und ausführbare Funktionen .................................................................................326

Tabellen für Fehler- und Warnmeldungen .................................................................................327

Fehlermeldungstabelle .......................................................................................................................... 327

Tabelle der Warnmeldungen .................................................................................................................. 331

Verarbeitung eines Fehlers bei zu geringem Speicherplatz ................................................................... 331

Zurücksetzen und Initialisieren des ClassPad ..........................................................................332

Stellenanzahl und Genauigkeit ...................................................................................................333

Stellenanzahl ..........................................................................................................................................333

Genauigkeit ............................................................................................................................................333

Display-Helligkeit und Lebensdauer der Batterie .....................................................................333

Display-Helligkeit ....................................................................................................................................333

Lebensdauer der Batterie ....................................................................................................................... 333

Spezifikationen ............................................................................................................................334

Prüfungsmodus ................................................................................................................. 336

Kommunikations-Menü - Prüfungsmodus-Menü .................................................................................... 336

Aktivieren des Prüfungsmodus ...............................................................................................................336

ClassPad-Betrieb im Prüfungsmodus ....................................................................................................337

Beenden des Prüfungsmodus ................................................................................................................ 338

Anzeigen der Hilfe für den Prüfungsmodus ............................................................................................339

Informationen zu dieser Bedienungsanleitung

• Die vierstelligen Beispielnummern in fetter Schrift (z. B. 0201 ), die in Kapitel 2 bis 14 vorkommen, weisen

auf Operationsbeispiele hin, die in der separaten Broschüre mit den Beispielen enthalten sind. Sie können die Broschüre mit den Beispielen zusammen mit dieser Bedienungsanleitung verwenden, indem Sie die

entsprechenden Beispielnummern nachschlagen.

• In dieser Bedienungsanleitung werden die Cursortastenoperationen folgendermaßen angegeben: f, c, d, e (1-1 Allgemeine Anleitung).

Kapitel 1: Grundlagen

Dieses Kapitel liefert einen allgemeinen Überblick über den ClassPad und die Anwendungsfunktionen sowie Informationen über Eingabeoperationen und den Umgang mit Daten (Variablen und Ordner), Dateioperationen und das Konfigurieren der Einstellungen von Anwendungsformaten.

1-1 Allgemeine Anleitung

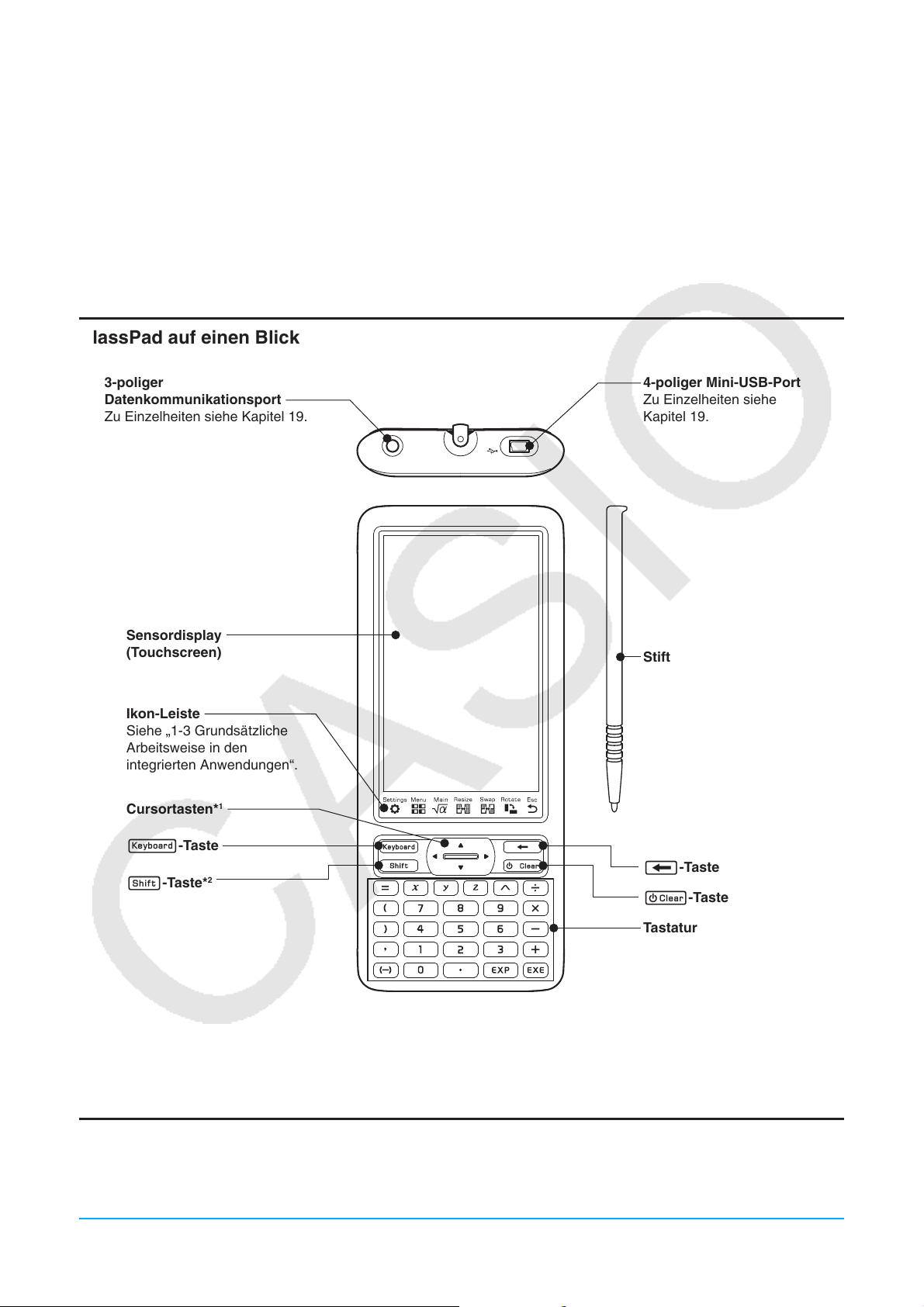
ClassPad auf einen Blick

3-poliger Datenkommunikationsport

Zu Einzelheiten siehe Kapitel 19.

Sensordisplay (Touchscreen)

Ikon-Leiste

Siehe „1-3 Grundsätzliche Arbeitsweise in den integrierten Anwendungen“.

Cursortasten*

4-poliger Mini-USB-Port

Zu Einzelheiten siehe Kapitel 19.

Stift

k-Taste

f-Taste*

*1 In diesem Handbuch wird die Bedienung der Cursortasten als f, c, d, e angegeben. *2 Bestimmte Funktionen (Ausschneiden, Einfügen, Rückgängig usw.) oder Tasteneingabeoperationen können

Tastenkombinationen zugewiesen werden, bei denen die f-Taste und eine Taste auf der Tastatur gedrückt werden. Nähere Informationen hierzu siehe „18-2 Konfigurieren der Systemeinstellungen“.

K-Taste

c-Taste

Tastatur

Ein- und Ausschalten der Stromversorgung

Wenn der ClassPad ausgeschaltet ist, drücken Sie die c-Taste, um das Gerät einzuschalten. Zum Ausschalten des ClassPad drücken Sie f und anschließend c.

Kapitel 1: Grundlagen 11

Ausschaltautomatik

Der ClassPad verfügt auch über eine Ausschaltautomatikfunktion. Diese Funktion schaltet den ClassPad automatisch aus, wenn Sie innerhalb einer festgelegten Zeitspanne keine Operation ausführen. Nähere Einzelheiten hierzu siehe „Konfigurieren der Ein- und Ausschaltfunktionen“ auf Seite 303.

Hinweis

Temporäre Informationen im RAM-Speicher von ClassPad (im Grafikfenster einer Anwendung gezeichnete Grafiken, ein angezeigtes Dialogfeld usw.) werden etwa 30 Sekunden beibehalten, wenn das Gerät manuell oder über die Automatikfunktion ausgeschaltet wird. Das bedeutet, dass Sie die temporären Informationen im RAM wiederherstellen können, wenn Sie den ClassPad innerhalb von 30 Sekunden nach dem Ausschalten wieder einschalten. Nach etwa 30 Sekunden werden die temporären Informationen im RAM automatisch gelöscht. Beim Wiedereinschalten des ClassPad wird dann der Start-Bildschirm der Anwendung angezeigt, die Sie beim letzten Ausschalten verwendet haben. Die zuvor im RAM gespeicherten Informationen sind nicht mehr verfügbar.

1-2 Stromversorgung

Ihr ClassPad wird von vier Mikro-Batterien LR03 (AM4) oder vier Nickel-Metallhydrid-Akkus mit Strom versorgt. Der Batteriepegelindikator wird in der Statusleiste angezeigt.

Voll Mittel Niedrig Verbraucht

Wichtig!

• Tauschen Sie die Batterien möglichst bald aus, wenn der Batteriepegelindikator (Niedrig) angezeigt wird.

• Tauschen Sie die Batterien sofort aus, wenn der Batteriepegelindikator diesem Pegel können Sie keine Datenkommunikation oder andere Funktionen mehr ausführen.

• Weitere Informationen zu den nach einem Batteriewechsel vorzunehmenden Einstellungen finden Sie unter „Aufladen der Batterien und Einstellen des ClassPad“ in der separaten Schnellstartanleitung.

• Wenn die Batteriespannung niedrig ist, wird Ihr ClassPad durch das Drücken der c möglicherweise nicht wieder eingeschaltet. Falls dies eintritt, tauschen Sie die Batterien unverzüglich aus.

• Die folgende Meldung zeigt an, dass die Batterien fast verbraucht sind. Tauschen Sie die Batterien unverzüglich aus, wenn diese Meldung erscheint.

Falls Sie den Betrieb des Rechners fortzusetzen versuchen, schaltet sich dieser automatisch aus. Sie können die Stromversorgung erst dann wieder einschalten, wenn Sie nicht die Batterien ausgetauscht haben.

• Tauschen Sie die Batterien mindestens einmal pro Jahr aus, unabhängig von der Verwendungshäufigkeit des ClassPad während dieses Zeitraumes.

(Verbraucht) angezeigt wird. Bei

-Taste

Hinweis: Die mit dem ClassPad mitgelieferten Batterien werden während des Versands und der Lagerung

etwas entladen. Daher müssen sie vielleicht früher ausgetauscht werden, als es die normale Batterielebensdauer erwarten lässt.

Sichern von Daten

Kapitel 1: Grundlagen 12

1-3 Grundsätzliche Arbeitsweise in den integrierten

Anwendungen

Dieser Abschnitt enthält die grundlegenden Informationen und Bedienungen, die für alle integrierten Anwendungen gleich sind.

Verwenden des Menüs der Anwendungen

Durch Tippen auf m auf der Ikon-Leiste wird das Menü der Anwendungen geöffnet. Sie können die nachfolgend aufgeführten Operationen über das Menü der Anwendungen ausführen.

Tippen Sie auf eine Schaltfläche, um eine Anwendung zu starten. Siehe „Integrierte Anwendungen“ unten.

Durch Tippen auf diesen Bereich wird zwischen den Seiten des Menüs der Anwendungen geblättert. Zwischen den Seiten des Menüs der Anwendungen kann auch durch Wischen auf dem Bildschirm mit dem Stift oder mit dem Finger nach links oder rechts gewechselt werden.

Tippen Sie hier (oder tippen Sie auf s auf der IkonLeiste), um das nächste Menü zu öffnen.

VCP-Dateioperationen. Siehe Seite 312.

Startet das Ausrichtung des Touchscreens. Siehe Seite 305.

Zeigt Versionsinformationen an. Siehe Seite 305.

Integrierte Anwendungen

In der Tabelle unten sind die Ikons der Anwendungen dargestellt, die im Menü der Anwendungen angezeigt werden, mit einer Erläuterung dazu, was Sie in jeder Anwendung tun können.

Tippen Sie auf dieses Ikon:

zum Starten dieser Anwendung:

Main

eActivity

Statistik

Tabellenkalkulation

Grafik und Tabellen

zum Durchführen dieses Typs von Operation:

• Allgemeine Berechnungen einschließlich Funktionsberechnungen

• Matrizenrechnungen

• Computer-Algebra-System

• Erstellen einer eActivity-Datei, die für die Eingabe von Formeln, Text und anderen ClassPad-Anwendungsdaten verwendet werden kann

• Erstellen einer Liste

• Ausführen von statistischen Berechnungen

• Zeichnen einer statistischen Grafik

• Eingeben von Daten in eine Tabellenkalkulation

• Bearbeiten und/oder grafisches Darstellen von Tabellenkalkulationsdaten

• Ausführen von statistischen Berechnungen und/oder Zeichnen einer statistischen Grafik

• Zeichnen einer Grafik

• Abspeichern einer Funktion und Erstellen einer Wertetabelle, indem verschiedene Werte für die Variablen der Funktion eingesetzt werden

Kapitel 1: Grundlagen 13

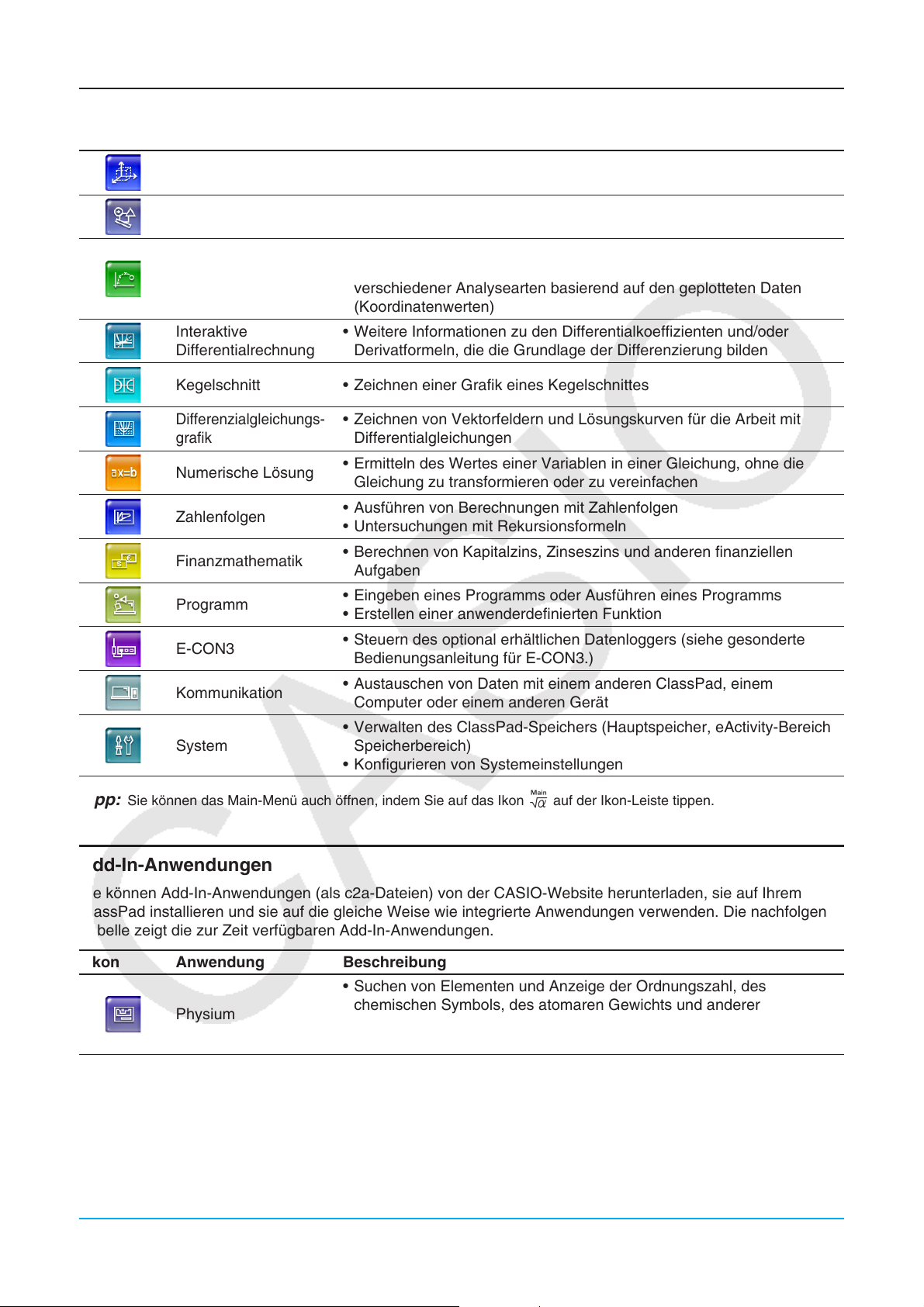
Tippen Sie auf dieses Ikon:

zum Starten dieser Anwendung:

3D-Grafik

Geometrie

Bildplot

Interaktive Differentialrechnung

Kegelschnitt • Zeichnen einer Grafik eines Kegelschnittes

zum Durchführen dieses Typs von Operation:

• Zeichnen einer 3-dimensionalen Grafik einer Gleichung der Form

f (x, y) oder einer Parametergleichung

• Zeichnen von geometrischen Figuren

• Aufbauen von Animationsfiguren

• Plotten von Punkten (die Koordinaten repräsentieren) auf einem Foto, einer Abbildung oder einer anderen Grafik und Ausführen verschiedener Analysearten basierend auf den geplotteten Daten (Koordinatenwerten)

• Weitere Informationen zu den Differentialkoeffizienten und/oder Derivatformeln, die die Grundlage der Differenzierung bilden

z =

Differenzialgleichungs- grafik

Numerische Lösung

Zahlenfolgen

Finanzmathematik

Programm

E-CON3

Kommunikation

System

• Zeichnen von Vektorfeldern und Lösungskurven für die Arbeit mit Differentialgleichungen

• Ermitteln des Wertes einer Variablen in einer Gleichung, ohne die Gleichung zu transformieren oder zu vereinfachen

• Ausführen von Berechnungen mit Zahlenfolgen

• Untersuchungen mit Rekursionsformeln

• Berechnen von Kapitalzins, Zinseszins und anderen finanziellen Aufgaben

• Eingeben eines Programms oder Ausführen eines Programms

• Erstellen einer anwenderdefinierten Funktion

• Steuern des optional erhältlichen Datenloggers (siehe gesonderte Bedienungsanleitung für E-CON3.)

• Austauschen von Daten mit einem anderen ClassPad, einem Computer oder einem anderen Gerät

• Verwalten des ClassPad-Speichers (Hauptspeicher, eActivity-Bereich, Speicherbereich)

• Konfigurieren von Systemeinstellungen

Tipp: Sie können das Main-Menü auch öffnen, indem Sie auf das Ikon M auf der Ikon-Leiste tippen.

Add-In-Anwendungen

Sie können Add-In-Anwendungen (als c2a-Dateien) von der CASIO-Website herunterladen, sie auf Ihrem ClassPad installieren und sie auf die gleiche Weise wie integrierte Anwendungen verwenden. Die nachfolgende Tabelle zeigt die zur Zeit verfügbaren Add-In-Anwendungen.

Ikon Anwendung Beschreibung

• Suchen von Elementen und Anzeige der Ordnungszahl, des

Physium

chemischen Symbols, des atomaren Gewichts und anderer Informationen des Periodensystems der Elemente

• Anzeige verschiedener Naturkonstanten

Hinweis

Sie können alle Add-In-Anwendungen mit einem der folgenden Verfahren löschen.

• Zurücksetzen - Massenspeicher oder Zurücksetzen - Alle („Listenweises Löschen bestimmter Daten (Reset)“, Seite 303)

• Initialisieren („Initialisieren des ClassPad“, Seite 303)

Kapitel 1: Grundlagen 14

Nach dem Löschen von Add-In-Anwendungen können Sie das Verfahren unter „Installieren einer Add-InAnwendung“ (Seite 311) verwenden, um sie neu zu installieren.

Anwendungsfenster

Nachfolgend wird der grundsätzliche Aufbau des Fensters einer integrierten Anwendung dargestellt.

Menüleiste Symbolleiste

Oberes Fenster

Anwendungsfenster

Software-Tastatur

Siehe Seite 17.

Statusleiste

Siehe Seite 16.

Unteres Fenster

In vielen Anwendungen ist das Display in ein oberes Fenster und ein unteres Fenster unterteilt, wobei jedes Fenster unterschiedliche Informationen anzeigt. Wenn zwei Fenster verwendet werden, wird das aktuell ausgewählte Fenster (das Fenster, in dem Sie Operationen ausführen können) als „aktives Fenster“ bezeichnet. Der Inhalt der Menüleiste, Symbolleiste und Statusleiste bezieht sich auf das aktive Fenster. Das aktive Fenster ist an der dicke Umrandung erkennbar.

Sie können die nachfolgend aufgeführten Operationen in einem Anwendungsfenster ausführen.

Um dies zu tun: führen Sie diese Operation aus:

Umschalten des aktiven Fensters

Wenn ein Doppelfenster angezeigt wird, tippen Sie auf eine beliebige Stelle innerhalb des Fensters, das keine dicke Umrandung aufweist, um dieses Fenster zum aktiven Fenster zu machen. Achten Sie darauf, dass Sie das aktive Fenster nicht umschalten können, solange eine Operation im aktuelle Fenster ausgeführt wird.

Ändern der Größe des aktiven Fensters, sodass dieses das Display

Wenn ein Doppelfenster angezeigt wird, tippen Sie auf r. Das aktive Fenster füllt nun das gesamte Display aus. Um zum Doppelfensterdisplay zurückzukehren, tippen Sie erneut auf r.

ausfüllt Vertauschen des oberen

und unteren Fensters

Wenn ein Doppelfenster angezeigt wird, tippen Sie auf S. Dadurch wird das obere Fenster zum unteren Fenster und umgekehrt. Das Vertauschen der Fenster hat keine Auswirkung auf den aktiven Status. Wenn beispielsweise das obere Fenster das aktive Fenster ist, während Sie auf S tippen, dann bleibt dieses Fenster auch das aktive Fenster, nachdem es zum unteren Fenster geworden ist.

Schließen der aktiven Fenster

Wenn ein Doppelfenster angezeigt wird, tippen Sie auf C in der rechten oberen Ecke des Fensters, um das aktive Fenster zu schließen. Das andere (inaktive) Fenster füllt dann die Anzeige.

Tipp: Wenn Sie in einer Doppelfensteranzeige auf das r-Ikon tippen, füllt das gegenwärtig aktive Fenster die Anzeige

aus, aber das andere (inaktive) Fenster wird nicht geschlossen. Es bleibt offen und wird durch das aktive Fenster verdeckt. Das bedeutet, dass Sie durch Tippen auf S das verdeckte Fenster nach vorne bringen können, um es so zum aktiven Fenster zu machen. Das aktuell aktive Fenster rückt dann in den Hintergrund.

Kapitel 1: Grundlagen 15

u Ändern der Display-Ausrichtung (nur Anwendungsmenü und einige Anwendungen)

Sie können das Display während der folgenden Anzeigen horizontal ausrichten: Menü der Anwendungen oder die Menüs Main, Grafik und Tabelle, Kegelschnitt oder Physium. Tippen Sie auf g, um das Display horizontal auszurichten. Um zur vertikalen Display-Ausrichtung zurückzukehren, tippen Sie erneut auf g.

Verwenden des O-Menüs

Das O-Menü erscheint in jeder Anwendung oben links im Fenster, ausgenommen in der Systemanwendung. Sie gelangen zum O-Menü, indem Sie auf der Ikon-Leiste auf m tippen oder auf das O-Menü der Menüleiste tippen.

Nachfolgend sind alle Einträge beschrieben, die im O-Menü erscheinen. 1 Tippen Sie auf [Variable Manager], um den Variablenmanager zu

starten. Näheres hierzu siehe „Verwenden des Variablenmanagers“ (Seite 29).

2 Tippen Sie auf [View Window], um ein Dialogfeld für die Konfigurierung

des Anzeigebereichs und anderer Grafikeinstellungen aufzurufen. Näheres hierzu finden Sie in den Erläuterungen der verschiedenen Anwendungen mit Grafikdarstellungsfunktionen (Grafik und Tabellen, Differenzialgleichungsgrafik, Statistik usw.).

3 Tippen Sie auf eine Menüauswahl, um ein Dialogfeld für die

Konfigurierung der entsprechenden Einstellungseinträge aufzurufen. Näheres hierzu siehe „1-7 Konfigurieren der Anwendungsformate“.

1 2

4 5 6 7

4 Tippen Sie auf [Default Setup], um alle Einstellungen auf die Werksvoreinstellungen zurückzusetzen (außer

der Einstellung des aktuellen Ordners). Näheres hierzu siehe „1-7 Konfigurieren der Anwendungsformate“.

5 Tippen Sie auf [Window], um eine Liste aller Fenster anzuzeigen, auf die von der aktuellen Anwendung aus

zugegriffen werden kann (in diesem Beispiel das Statistik-Menü). Tippen Sie auf eine Menüauswahl, um das entsprechende Fenster anzuzeigen und dieses aktiv zu machen.

6 Tippen Sie auf [Keyboard], um die Anzeige der Software-Tastatur ein- oder auszuschalten. 7 Tippen Sie auf [Close], um das aktuell aktive Fenster zu schließen, ausgenommen in den folgenden Fällen.

• Wenn nur ein Fenster im Display angezeigt wird

• Wenn das gegenwärtig aktive Fenster durch die verwendete Anwendung nicht geschlossen werden kann

Sie können zum Beispiel das Grafik-Editor-Fenster im Grafik- und Tabellen-Menü nicht schließen.

Interpretieren der Statusleisten-Informationen

Die Statusleiste wird am unteren Rand des Fensters jeder Anwendung angezeigt.

123

1 Information über die aktuelle Anwendung

Sie können die Konfigurierung einer in der Statusleiste angezeigten Einstellung durch Antippen ändern. Durch Tippen auf „Cplx“ (zeigt Berechnung komplexer Zahlen an) bei laufendem Main-Menü wird die Einstellung auf „Real“ um (zeigt Berechnung reeller Zahlen an) umgeschaltet. Durch erneutes Antippen wechselt die Einstellung zurück auf „Cplx“. Einzelheiten zu den anwendungsspezifischen Informationen finden Sie unter „1-7 Konfigurieren der Anwendungsformate“.

2 Dieser Indikator dreht sich, während eine Operation ausgeführt wird.

wird hier angezeigt, wenn eine Operation auf Pause geschaltet ist.

3 Batteriepegelindikator (siehe „1-2 Stromversorgung“)

Kapitel 1: Grundlagen 16

Pausieren und Beenden einer Operation

Viele der integrierten Anwendungen bieten Operationen, die eine Pause und Beendigung (Abbruch) der Verarbeitung von Formeln, Grafiken und anderen Operationen gestatten

u Pausieren einer Operation

Durch Drücken der K-Taste, während ein Formelterm, eine Grafik oder eine andere Operation verarbeitet wird, wird auf Pause geschaltet. wird rechts von der Statusleiste angezeigt, wenn für eine Operation Pause eingestellt wurde. Durch erneutes Drücken der K-Taste wird die Operation fortgesetzt.

u Beenden einer Operation

Durch Drücken der c-Taste, während ein Formelterm, eine Grafik oder eine andere Operation verarbeitet wird, wird die Operation beendet und ein „Break“-Dialogfeld wie das nebenstehende angezeigt.

Tippen Sie auf die Schaltfläche [OK] im Dialogfeld, um den Unterbrechungsstatus zu beenden.

1-4 Eingabe

Sie können Daten auf dem ClassPad eingeben, indem Sie dessen Tastatur oder die On-Screen-Software- Tastatur verwenden.

Nahezu alle für Ihren ClassPad erforderlichen Dateneingaben können über die Software-Tastatur ausgeführt werden. Die Tastaturtasten werden für die Eingabe häufig verwendeter Daten wie Zahlen, Arithmetikoperatoren usw. verwendet.

Verwenden der Software-Tastatur

Die Software-Tastatur wird im unteren Teil des Touchscreens angezeigt.

u Anzeigen der Software-Tastatur

Falls die Software-Tastatur nicht auf dem Touchscreen angezeigt wird, drücken Sie die k-Taste oder tippen Sie auf das O-Menü und tippen Sie dann auf [Keyboard]. Die Software- Tastatur wird angezeigt.

• Die Software-Tastatur verfügt über eine Reihe verschiedener Tastensätze, beispielsweise [Math1], [abc] und [Catalog], die Sie für die Eingabe von Funktionen und Text verwenden können. Zur Auswahl eines Tastensatzes tippen Sie auf eine der Registerkarten auf der linken Seite der Software-Tastatur.

• Drücken Sie die k-Taste erneut oder tippen Sie auf das O-Menü und dann erneut auf [Keyboard], um die Software- Tastatur wieder auszublenden.

SoftwareTastatur

Kapitel 1: Grundlagen 17

Tastensätze der Software-Tastatur

Die Software-Tastatur verfügt über eine Reihe verschiedener Tastensätze, die unterschiedliche Anforderungen für die Dateneingabe unterstützen. Die einzelnen verfügbaren Tastensätzen sind nachstehend dargestellt.

Tastensätze [Math1], [Math2], [Math3], [Trig] (Trigonometrie), [Advance]

Diese Tastensätze umfassen Tasten für die Eingabe von Funktionen, Operatoren und Symbolen, die für numerische Formeln benötigt werden.

Math1 Math2 Math3

Trig Advance

Einzelheiten zu den oben dargestellten Tastensätzen sind unter „Verwenden der Math-, Trig- und Advance- Tastensätze“ (Seite 22) zu finden.

Tastensatz [Var] (Variable)

Dieser Tastensatz umfasst nur Tasten für die Eingabe von Variablen mit einem einzigen Zeichen. Nähere Informationen hierzu siehe „Verwenden von Variablen mit einem einzigen Zeichen“ (Seite 25).

Tastensatz [abc]

Verwenden Sie diesen Tastensatz für die Eingabe alphabetischer Zeichen. Tippen Sie auf eine der Registerkarten oben an der Tastatur (rechts, wenn Sie die horizontale Display-Ausrichtung verwenden), um zusätzliche Zeichen anzuzeigen. Tippen Sie beispielsweise auf [Math]. Nähere Informationen hierzu siehe „Verwenden der Alphabet-Tastatur“ (Seite 26).

Tastensatz [Catalog]

Dieser Tastensatz bietet eine scrollbare Liste, die für die Eingabe der integrierten Funktionen, Befehle, Systemvariablen und anwenderdefinierten Funktionen verwendet werden kann. Tippen Sie auf einen Befehl, um diesen auszuwählen, und tippen Sie danach erneut darauf, um diesen einzufügen. Durch Auswählen eines Eintrags aus der „Form“-Liste ändern sich die verfügbaren Befehle. Nähere Informationen hierzu siehe „Verwenden der Catalog-Tastatur“ (Seite 27).

Kapitel 1: Grundlagen 18

Tastensatz [Number]

Dieser Tastensatz liefert dieselben Tasten, die auch die Tastatur bietet. Verwenden Sie diesen Tastensatz, wenn Sie ausschließlich den Touchscreen oder den Touchscreen anstelle der Tastatur zur Eingabe bei Verwendung der horizontalen Display-Ausrichtung verwenden möchten.

Grundlagen für die Eingabe

Dieser Abschnitt umfasst eine Anzahl von Beispielen, die veranschaulichen, wie die grundlegenden Eingabevorgänge auszuführen sind. Alle diese Vorgänge gehen von folgenden Annahmen aus.

• Das Main-Menü wird ausgeführt. Siehe „Integrierte Anwendungen“ (Seite 13).

• Die Software-Tastatur wird angezeigt. Siehe „Verwenden der Software-Tastatur“ (Seite 17).

kEingeben eines Berechnungsterms

Sie können einen Berechnungsterm genau so eingeben, wie er geschrieben ist, und danach einfach die E-Taste drücken, um ihn auszuwerten. Der ClassPad erkennt automatisch die Vorrangregeln für Additionen, Subtraktionen, Multiplikationen, Divisionen und Klammerterme.

Beispiel: Vereinfachen des Terms −2 + 3 − 4 + 10

u Verwenden der Tastaturtasten

cz2+3-4+10E

Wenn die Zeile, in die Sie den Berechnungsterm eingeben möchten, bereits eine Eingabe enthält, achten Sie darauf,

diese zu löschen.

c zu drücken, um

u Verwenden der Software-Tastatur

Tippen Sie auf die Tasten im Tastensatz [Number], um den Berechnungsterm einzugeben.

c4-c+d-e+baw

Wie im Beispiel oben gezeigt können Sie einfache arithmetische Berechnungen eingeben, indem Sie entweder die Tastaturtasten oder die Software-Tastatur verwenden. Die Verwendung der Software-Tastatur ist für die Eingabe von Berechnungstermen, Funktionen, Variablen usw. auf einer höheren Ebene erforderlich. Weitere Informationen zur Eingabe von Termen finden Sie in Kapitel 2.

Tipp: In manchen Fällen passen der Eingabeterm und der Ausgabeterm (Ergebnis)

möglicherweise nicht in den Displaybereich. Wenn dies der Fall ist, tippen Sie auf die Links- oder Rechts-Pfeile, die auf dem Display erscheinen, um die Termanzeige zu scrollen und den nicht in den Displaybereich passenden Teil anzuzeigen.

Sie können auch für das Display auch in die horizontale

Anzeigeausrichtung einstellen, damit lange eingegebene Formeln und Berechnungsergebnisse einfacher abzulesen sind. Siehe „Ändern der Display-Ausrichtung“ (Seite 16).

Kapitel 1: Grundlagen 19

kBearbeiten der Eingabe

u Löschen eines einzelnen Zeichens

Verschieben Sie den Cursor so, dass er unmittelbar rechts von dem zu löschenden Zeichen steht, und drücken Sie dann K. Durch jedes Drücken von K wird ein Zeichen links vom Cursor gelöscht.

Beispiel: Ändern des Terms 369 × × 2 in 369 × 2

1. c369**2

2. dK

Nachdem Sie alle gewünschten Änderungen vorgenommen haben, drücken Sie E, um das Ergebnis zu berechnen. Um weitere Zeichen zu der Berechnung hinzuzufügen, drücken Sie e, um den Cursor an das Ende der Berechnung zu verschieben, und nehmen Sie die gewünschten Eingaben vor.

Tipp: Sie können den Cursor ohne Verwendung der Cursortasten verschieben, indem Sie mit dem Stift auf die

gewünschte Position tippen. Dadurch springt der Cursor an die angetippte Position.

u Einfügen einer neuen Eingabe in der Mitte eines bestehenden Berechnungsterms

Verwenden Sie die d- oder die e-Taste, um den Cursor an die Stelle zu verschieben, an der Sie eine neue Eingabe einfügen möchten, und geben Sie danach die gewünschten Daten ein.

Beispiel: Ändern des Terms 30

Software-Tastensatz.)

in sin(30)2 (zur Eingabe verwenden Sie die Tastatur und den [Math1]-

1. c30x

2. dddds

3. ee)

u Ersetzen einer Eingabezeichenkette durch eine neue Eingabe

Nachdem Sie den Stift über die zu ersetzenden Zeichenkette gezogen haben, führen Sie die neue Eingabe aus.

Beispiel: Ändern von „1234567“ in „10567“

1. c1234567

2. Ziehen Sie den Stift über „234“, um die Zeichenkette zu markieren.

3. 0

k Verwendung der Zwischenablage für das Kopieren und Einfügen

Sie können eine Funktion, einen Befehl oder eine andere Eingabe in die Zwischenablage des ClassPad kopieren (oder ausschneiden) und danach den Inhalt der Zwischenablage an einer anderen Stelle einfügen. Wenn Sie den Kopier- oder Ausschneidevorgang ausführen, wird der Inhalt der Zwischenablage durch die neu kopierten oder ausgeschnittenen Zeichen ersetzt.

u Kopieren von Zeichen

1. Ziehen Sie den Stift über die zu kopierenden Zeichen, um diese zu markieren.

2. Tippen Sie auf der Software-Tastatur auf p, oder tippen Sie auf das [Edit]-Menü und dann auf [Copy].

• Dadurch werden die ausgewählten Zeichen in die Zwischenablage kopiert.

Kapitel 1: Grundlagen 20

u Ausschneiden von Zeichen

1. Ziehen Sie den Stift über die auszuschneidenden Zeichen, um diese zu markieren.

2. Tippen Sie auf das [Edit]-Menü und dann auf [Cut].

• Dadurch werden die ausgewählten Zeichen ausgeschnitten und in die Zwischenablage verschoben.

u Einfügen des Inhalts der Zwischenablage

1. Verschieben Sie den Cursor an die Stelle, an der Sie den Inhalt der Zwischenablage einfügen möchten.

2. Tippen Sie auf der Software-Tastatur auf q. Sie können auch auf das [Edit]-Menü und dann auf [Paste]

tippen.

• Dadurch wird der Inhalt der Zwischenablage an der aktuellen Cursorposition eingefügt.

Tipp: Der Inhalt der Zwischenablage verbleibt in der Zwischenablage, nachdem Sie diesen eingefügt haben. Dies

bedeutet, dass Sie den aktuellen Inhalt so oft wie gewünscht einfügen können.

Kopieren und Einfügen in das Mitteilungsfeld

Das Mitteilungsfeld ist eine Zeile unter dem Grafikfenster und dient als Texteingabe- und Anzeigebereich (siehe Kapitel 3).

Sie können die beiden Schaltflächen rechts vom Mitteilungsfeld verwenden, um den Inhalt des Mitteilungsfeldes zu kopieren (Schaltfläche p) oder den Inhalt der Zwischenablage in das Mitteilungsfeld einzufügen (Schaltfläche q). Kopieren und Einfügen werden auf die gleiche Weise wie die Kopier- und Einfügeoperationen auf der Software-Tastatur ausgeführt.

Mitteilungsfeld

kKopieren mit Drag & Drop

Sie können eine Textzeichenfolge auch kopieren, indem Sie sie einfach auswählen und dann an eine andere Position ziehen, die die Eingabe von Text gestattet.

Beispiel 1: Verwenden des Main-Menüs zum Ausführen der Rechnung 15 + 6 × 2, ändern der Rechnung in

(15 + 6) × 2 und anschließender Neuberechnung

1. Führen Sie im Arbeitsbereich des Main-Menüs die unten stehende

Rechnung aus.

c15+6*2E

2. Ziehen Sie über den Term 15 + 6 × 2, um ihn zu markieren, und ziehen Sie

dann den Term an die Position .

• Dadurch wird 15 + 6 × 2 an die Stelle kopiert, an der Sie den Term abgelegt haben.

3. Fügen Sie Klammen vor und nach 15 + 6 ein, und drücken Sie dann E.

Tipp: Sie können Drag & Drop verwenden, um eingegebene Formeln und

Berechnungsergebnisse zu kopieren.

Kapitel 1: Grundlagen 21

Beispiel 2: Kopieren eines über das Main-Menü eingegebenen Terms in das Grafik-Editor-Fenster

1. Geben Sie im Arbeitsbereich des Main-Menüs Folgendes ein: 2

x^2 + 2x − 1.

c2x{2+2x-1E

2. Tippen Sie auf die Abwärtspfeil-Schaltfläche am rechten Ende der Symbolleiste. Tippen Sie in der Schaltflächenpalette, die angezeigt wird, auf !.

• Das Grafik-Editor-Fenster wird nun in der unteren Hälfte des Bildschirms

angezeigt.

3. Markieren Sie den Term 2

x^2 + 2x − 1, den Sie über das Main-Menü

eingegeben haben, indem Sie darüber ziehen, und ziehen Sie dann den Term an die Position rechts neben y1: im Grafik-Editor-Fenster.

• Dadurch wird 2

x^2 + 2x − 1 an die Stelle kopiert, an der Sie den Term

abgelegt haben.

Tipp

• Ein Term, den Sie in der oben beschriebenen Weise kopiert haben, ist im Grafik-

Editor-Fenster des Grafik- und Tabellen-Menüs registriert. Informationen zum Grafik- Editor-Fenster finden Sie in Kapitel 3.

• Abhängig von der Zielposition, an die Sie eine Zeichenfolge oder einen Term ziehen, kann das Ablegen bewirken, dass

diese bzw. dieser automatisch in eine Grafik oder eine Abbildung umgewandelt wird. Beispielsweise wird durch das Ablegen des Terms in Beispiel 2 im Grafikfenster der Term als Grafik dargestellt. Beispiele für das Verwenden von Drag & Drop finden Sie in den unten stehenden Abschnitten.

- „2-9 Verwenden des Main-Menüs in Kombination mit anderen Anwendungs-Menüs“ (Kapitel 2, Seite 97)

- „5-4 Grafisches Darstellen eines Ausdrucks oder eines Wertes durch Ablegen im Differenzialgleichungsgrafik-Fenster“ (Kapitel 5, Seite 137)

- „8-5 Geometrie-Menü in Kombination mit anderen Anwendungs-Menüs“ (Kapitel 8, Seite 191)

- „13-1 Eingeben und Bearbeiten von Zelleninhalten“ (Kapitel 13, Seite 247), „13-2 Grafische Darstellungen“ (Kapitel 13, Seite 256)

Verschiedene Operationen auf der Software-Tastatur

In diesem Abschnitt wird die Verwendung der einzelnen Tastensätze der Software-Tastatur erklärt. Informationen zu den Tastensatztypen und einen allgemeinen Überblick über Tastensätze finden Sie unter „Tastensätze der Software-Tastatur“ (Seite 18). Bei allen Beispielen in diesem Abschnitt werden folgende Bedingungen angenommen.

• Das Main-Menü wird ausgeführt. Siehe „Integrierte Anwendungen“ (Seite 13).

• Die Software-Tastatur wird angezeigt. Siehe „Verwenden der Software-Tastatur“ (Seite 17).

k Verwenden der Math-, Trig- und Advance-Tastensätze

Die Tastensätze [Math1], [Math2], [Math3], [Trig] (Trigonometrie) und [Advance] enthalten Tasten für die Eingabe numerischer Terme.

Die Taste L oben links und alle Tasten in der unteren Reihe sind allen Tastensätzen gemeinsam. Ihre Funktionen sind nachstehend beschrieben.

L Schaltet zwischen Schablonen- und Zeileneingabe um. Siehe

„Schabloneneingabe und Zeileneingabe“ (Seite 24).

h Führt die gleiche Operation wie die Taste K der Tastatur aus.

Löscht das Zeichen links von der aktuellen Cursorposition. pq Siehe „Verwendung der Zwischenablage für das Kopieren und Einfügen“ (Seite 20). D Gibt „ans“ ein. Siehe „Verwenden der Antwortvariablen (ans)“ (Seite 47). w Führt die gleiche Operation wie die Taste E der Tastatur aus, die Berechnungen ausführt.

Kapitel 1: Grundlagen 22

Die in der folgenden Tabelle aufgeführten Tasten sind in verschiedenen Tastensätzen enthalten. Sie werden verwendet, um Funktionen und Befehle für das Ausführen bestimmter Berechnungen und Operationen einzugeben.

Tastensatz Taste Beschreibung

Math1, Math2, Math3, Trig

Math1, Math2, Trig

Math1, Math2

Math1, Math3

Math1, Trig

Math1

sct

(

)

V"%

„Schabloneneingabe und Zeileneingabe” (Seite 24), „Andere Funktionen“ (Seite 52)

Gibt pi (π) ein. Eingabe des Substitutionssymbols (⇒). „Erstellen einer neuen

Variablen“ (Seite 34) „Logarithmische Funktionen und Exponentialfunktionen“ (Seite

52)

„Trigonometrische Funktionen und Arkusfunktionen“ (Seite 51)

„Logarithmische Funktionen und Exponentialfunktionen“ (Seite

52) Eingabe des absoluten Wertsymbols (| |) oder der Funktion

(abs().

„solve [Action][Equation/Inequality][solve]“ (Seite 85)

Eingabe von Klammern (( )).

Eingabe von Klammern ({

„Winkelumwandlung (°,

}). „2-4 Listenberechnungen“ (Seite 60)

)“ (Seite 51)

„Logarithmische Funktionen und Exponentialfunktionen“ (Seite

52)

Math1

Math2, Math3, Trig

Math2, Trig

Math2

Math3

[

`*7 ]_)

678

„Andere Funktionen“ (Seite 52)

„dms [Action][Transformation][DMS][dms]“ (Seite 67)

„toDMS [Action][Transformation][DMS][toDMS]“ (Seite 68)

„solve [Action][Equation/Inequality][solve]“ (Seite 85)

Eingabe der imaginären Einheit (

i).

Eingabe des Unendlichkeitssymbols (∞).

Eingabe der Variablen

Eingabe der Variablen mit einem einzigen Zeichen (Seite 25)

„Verwenden des Untermenüs für Berechnungen“ (Seite 70)

„2-5 Matrizen- und Vektorrechnung“ (Seite 61)

„Erstellen einer anwenderdefinierten Funktion unter Verwendung des Define-Befehls“ (Seite 220)

Eingabe des „f“ von f(

x) oder des „g“ von g(x).

„Ableitungssymbol (’)“ (Seite 57)

Math3

„dSolve [Action][Equation/Inequality][dSolve]“ (Seite 87)

Kapitel 1: Grundlagen 23

Tastensatz Taste Beschreibung

Math3

Trig

Advance

[

<>;:=/

SCT

123

!@#

NM<

hin

5%(^

„piecewise-Funktion“ (Seite 57)

„with-Operator ( | )“ (Seite 58)

Eingabe von eckigen Klammern ([ ]). „2-5 Matrizen- und Vektorrechnung“ (Seite 61)

„Gleichheits- und Ungleichheitszeichen“ (Seite 58)

„Winkelsymbol (∠)“ (Seite 57)

„Trigonometrische Funktionen und Arkusfunktionen“ (Seite 51)

„Hyperbel- und Areafunktionen“ (Seite 52)

„Andere Funktionen“ (Seite 52)

„Variation/Permutation (

„Kapitel 6: Zahlenfolgen-Menü“

„Über rSolve“ (Seite 140)

„Verwenden des Advanced-Untermenüs“ (Seite 68)

„Gamma-Funktion“ (Seite 60)

nPr) und Kombination (nCr)“ (Seite 56)

Advance

„Dirac-Delta-Distribution“ (Seite 59)

n-te Delta-Distribution“ (Seite 59)

„

„Heaviside-Sprungfunktion“ (Seite 59)

k Schabloneneingabe und Zeileneingabe

Der ClassPad unterstützt zwei verschiedene Eingabemethoden: die Schabloneneingabe und die Zeileneingabe. Die Schabloneneingabe ermöglicht das Eingeben von Brüchen, Potenzen und anderen Funktionen unter Verwendung der Formate eingeben, wie sich auch im Lehrbuch verwendet werden. Bei der Zeileneingabe wird ein lineares Format zur Eingabe von Termen verwendet.

2'2

2 +

( )

Schabloneneingabe Zeileneingabe

2 + 1

2 + (2 (2) / ( (2) + 1))^2

u Umschalten zwischen Schablonen- und Zeileneingabe

Tippen Sie auf die L-Taste. Bei jedem Tippen wechselt die Tastenfarbe zwischen weiß (L) und hellblau ( ). Eine weiße Taste kennzeichnet den Schabloneneingabemodus, eine hellblaue Taste dagegen den Zeileneingabemodus.

Im Schabloneneingabemodus können Sie die Schabloneneingabe unter Verwendung von Tasten vornehmen, bei denen Funktionen oder Befehle wie im Zeilenmodus eingegeben.



oder  auf den Tasten angezeigt wird, z. B. N und !. Mit den anderen Tasten werden dieselben

Kapitel 1: Grundlagen 24

∫

2'2

Beispiel 1: Verwenden des Schabloneneingabemodus zur Eingabe von

1. Tippen Sie auf die Registerkarte [Math1], und aktivieren Sie dann den Schabloneneingabemodus (weiße L-Taste).

2. Führen Sie die folgenden Tastenoperationen aus:

2+(N2!2c!2e+1 eem2E

Beispiel 2: Verwenden des Zeileneingabemodus zur Eingabe desselben Terms wie in Beispiel 1

(

2 + (2 (2) / ( (2) + 1))^2

1. Tippen Sie auf die Registerkarte [Math1], und aktivieren Sie dann den Zeileneingabemodus (hellblaue

-Taste).

2. Führen Sie die folgenden Tastenoperationen aus:

2+(d2!2)N (!2)+1)ewE

Beispiel 3: Verwenden des Schabloneneingabemodus zur Eingabe von

1. Tippen Sie auf die Registerkarte [Math2], und aktivieren Sie dann den Schabloneneingabemodus (weiße L-Taste).

)

2 +

( )

(x)

x=1

2 + 1

2. Führen Sie die folgenden Tastenoperationen aus:

Oxe1f10exE

Beispiel 4: Verwenden des Schabloneneingabemodus zur Eingabe von

1. Tippen Sie auf die Registerkarte [Math2], und aktivieren Sie dann den Schabloneneingabemodus (weiße L-Taste).

2. Führen Sie die folgenden Tastenoperationen aus:

7(1-xm2e)Qxeex

3. Tippen Sie in das Eingabefeld oben rechts von

1. Tippen Sie anschließend auf das Eingabefeld unten rechts von ∫, und drücken Sie dann 0.

4. Zum Durchführen der Berechnung drücken Sie E.

, und drücken Sie dann

(1 − x2)e

∫

Tipp: Informationen zum Inhalt und den Eingabeformaten der Funktionen in den Beispielen 3 und 4 finden Sie im

Abschnitt „2-7 Verwenden des Aktionsmenüs“ (Seite 64).

k Verwenden von Variablen mit einem einzigen Zeichen

Wie die Bezeichnung erkennen lässt, handelt es sich bei einer Variablen mit einem Zeichen um einen Variablennamen, der aus einem einzigen Zeichen besteht, wie zum Beispiel „a“ oder „x“. Die Eingabe von Variablennamen mit einem Zeichen unterliegt anderen Regeln als die Eingabe einer Reihe von mehreren Zeichen (wie „abc“).

u Eingeben eines Variablennamens mit einem einzigen Zeichen

Jedes Zeichen, das Sie unter Verwendung einer der folgenden Techniken eingeben, wird als eine Variable mit einem einzigen Zeichen behandelt.

• Tippen auf eine beliebige Taste des [Var]-Tastensatzes (Variable) (Seite 18).

Kapitel 1: Grundlagen 25

• Tippen auf die Tasten X, Y oder Z des [Number]-Tastensatzes.

• Tippen auf die Taste [ des [Math2]-Tastensatzes.

• Drücken der Tastaturtasten x, y oder Z.

Wenn Sie die oben genannten Tastenoperationen zur Eingabe einer Kette von Zeichen verwenden, wird jedes Zeichen als eine Variable mit einem einzigen Zeichen behandelt. Die Eingabe von A, B, C über den [Var]Tastensatz wird beispielsweise als mathematischer Term „abc“.

a × b × c behandelt und nicht als die Zeichenkette

Tipp: Mit den oben beschriebenen Variablen mit einem einzigen Zeichen können Sie Berechnungen so ausführen, wie sie

typischerweise im Lehrbuch dargestellt werden.

Beispiel 1: ABCw

Beispiel 2: 2xyE

Tipp: Wenn Sie eine Variable mit einem einzigen Zeichen eingeben, wird deren Bezeichnung auf dem Display kursiv

formatiert angezeigt. Auf diese Weise können Sie einfach erkennen, dass es sich bei dem Buchstaben um den Namen einer Variablen mit einem einzigen Zeichen handelt.

u Eingeben einer Kette von mehreren Zeichen

Eine Kette von mehreren Zeichen (beispielsweise „list1“) kann für Variablennamen, Programmbefehle usw. verwendet werden. Verwenden Sie immer den [abc]-Tastensatz, um eine Reihe von mehreren Zeichen einzugeben.

Beispiel: abcE

Sie können den [abc]-Tastensatz auch für die Eingabe von Variablennamen mit einem einzigen Zeichen verwenden. Geben Sie dazu einfach ein einzelnes Zeichen oder ein einzelnes Zeichen gefolgt von einem mathematischen Operator ein.

Beispiel: a*b+cE

Tipp: Eine von Ihnen unter Verwendung des [abc]-Tastensatzes eingegebene Variable mit einem einzigen Zeichen ist

identisch mit einer Variablen mit einem Zeichen, die Sie unter Verwendung des [Var]-Tastensatzes eingeben.

k Verwenden der Alphabet-Tastatur

Tippen Sie auf die Registerkarte [abc] links neben der Software-Tastatur, um die Alphabet-Tastatur, den [abc]-Tastensatz anzuzeigen. Zusätzlich zum [abc]- Tastensatz können Sie auch drei weitere Tastensätze wählen, die Tastensätze [αβγ] (Zeichensymbole), [Math] (mathematische Symbole) und [Symbol] (Sondersymbole).

Verwenden Sie die Registerkarten oberhalb der Alphabet-Tastatur (rechts neben der Tastatur bei Verwendung der horizontalen Bildschirmausrichtung), um einen Tastensatz auszuwählen. Um vom [Math1]-Tastensatz zur AlphabetTastatur zurückzukehren, tippen Sie auf die Taste I links unten.

Kapitel 1: Grundlagen 26

k Verwenden der Catalog-Tastatur

Im „Form“-Menü der Catalog-Tastatur können Sie eine der unten beschriebenen fünf Kategorien auswählen.

Func ........ integrierte Funktionen (Seite 51 und 64)

Cmd ........ integrierte Befehle und Operatoren (Seite 222)

Sys .......... Systemvariablen (Seite 322)

User ........ anwenderdefinierte Funktionen (Seite 219)

All ............ alle Befehle, Funktionen, usw.

Nachdem Sie eine Kategorie ausgewählt haben, können Sie den gewünschten Eintrag aus der alphabetischen Liste auf der Catalog-Tastatur auswählen.

Tipp: Beachten Sie, dass anwenderdefinierte Variablen und anwenderdefinierte Programme nicht über die Catalog-

Tastatur eingegeben werden können. Verwenden Sie dazu den Variablenmanager (Seite 29).

Konfiguration der Catalog-Tastatur

Tippen Sie auf eine Buchstaben- Schaltfläche, um die Befehle, Funktionen oder anderen Einträge anzuzeigen, die mit diesem Buchstaben beginnen.

Dies ist eine alphabetische Liste der Befehle, Funktionen und anderen Einträge, die in der aktuell mit „Form“ gewählten Kategorie zur Verfügung stehen.

Tippen Sie auf die Abwärtspfeil- Schaltfläche, und wählen Sie danach in der angezeigten Liste gewünschte Kategorie ([Func], [Cmd], [Sys], [User] oder [All]) aus.

Tippen Sie auf diese Taste, um den Eintrag einzugeben, der aktuell in der alphabetischen Liste ausgewählt ist.

u Verwenden der Catalog-Tastatur

Beispiel: Eingeben des integrierten Befehls „Plot“

1. Tippen Sie in der Catalog-Tastatur auf die Abwärtspfeil-Schaltfläche für „Form“, und wählen Sie dann [Cmd] in der Liste der angezeigten Kategorien aus.

2. Tippen Sie so lange auf die Schaltfläche + oben rechts, bis die Schaltfläche P sichtbar ist.

3. Tippen Sie auf P.

4. Tippen Sie in der alphabetischen Liste auf „Plot“, und tippen Sie anschließend auf [INPUT], um den Befehl einzugeben.

• Statt auf [INPUT] zu tippen, könnten Sie zur Eingabe des Befehls auch ein zweites Mal auf den Befehl

tippen.

1-5 ClassPad-Daten

Dieser Abschnitt enthält Informationen zu den verschiedenen Typen von Daten, die im ClassPad-Speicher gespeichert werden können, und nennt den Speicherort, an dem die einzelnen Typen von Dateien abgelegt werden. Außerdem wird die Verwendung des Variablenmanagers erläutert, eines Werkzeugs zur Verwaltung gespeicherter Daten und Dateioperationen (Speichern, Aufrufen, Löschen, Umbenennen von Dateien usw.), die einer Reihe verschiedener Anwendungen gemeinsam sind.

Datentypen und Speicherorte (Speicherbereiche)

Der ClassPad verwendet einen „Hauptspeicher“-Bereich, um verschiedene Typen von Daten zu speichern.

Beispiele:

• Das Ausführen von „10⇒

eActivity-Menü bewirkt, dass die Variable x im Hauptspeicher als Daten des Typs „EXPR“ (Term) gespeichert.

x“ (dadurch wird der Variable x der Wert 10 zugewiesen) im Main-Menü oder im

Kapitel 1: Grundlagen 27

• Das Erstellen einer anwenderdefinierten Funktion (Seite 219) bewirkt, dass die Funktion im Hauptspeicher als

Daten des Typs „FUNC“ (Funktion) gespeichert wird.

• Das Speichern von Tabellenkalkulationsdaten in einer Datei (durch Ausführen von [File] - [Save] im

Tabellenkalkulation-Menü) bewirkt, dass die Datei im Hauptspeicher als Daten des Typs „MEM“ (Speicher) gespeichert wird.

Eine mit eActivity erstellte eActivity-Datei wird in einem gesonderten eActivity-Speicherbereich gespeichert, um sie getrennt von anderen Anwendungsdaten aufzubewahren.

Zugreifen auf Daten

Der Zugriff auf Daten im Hauptspeicher ist nicht nur in dem Menü möglich, in der sie ursprünglich erstellt wurden, sondern auch in allen anderen Menüs. Die Daten können auch unter Verwendung des Variablenmanagers gelöscht, umbenannt, kopiert, verschoben oder in anderer Weise genutzt werden (Seite 29). Der Zugriff auf eActivity-Dateien ist nur vom eActivity-Menü aus möglich.

Hauptspeicher-Datentypen

Die im Hauptspeicher gespeicherten Daten haben ein Datentyp-Attribut, das gemäß dem Menü, in dem die Daten erstellt wurden, und gemäß dem tatsächlichen Inhalt der Daten zugewiesen wird. Der Datentyp wird durch einen Datentypnamen angegeben. Die Datentypnamen werden in der Variablenliste des Variablenmanagers sowie im „Select Data“-Dialogfeld angezeigt, das geöffnet wird, wenn Sie eine Variable in einem ClassPad-Menü angeben. In der folgenden Tabelle sind alle Datentypnamen mit einer Erläuterung dazu aufgeführt.

Datentypname Datentyp

EXPR Reelle Zahl, komplexe Zahl oder Formelterm STR Aus Zeichenketten bestehende Daten LIST Listendaten, die unter Verwendung des Statistik-Menüs, des Main-Menüs usw.

erstellt wurden. MAT Matrizendaten, die unter Verwendung des Main-Menüs usw. erstellt wurden. PRGM* Allgemeines Programm EXE* Programm, dessen Bearbeitung nicht zulässig ist TEXT* Textdaten FUNC* Anwenderdefinierte Funktion GMEM* Grafikspeicherdaten, die unter Verwendung des Grafik- und Tabellen-Menüs

gespeichert wurden.

Weitere Informationen hierzu siehe „Speichern der Grafik-Editor-Daten im

Grafikspeicher“ (Seite 108). GEO* Daten des Geometrie-Menüs MEM* Daten, die unter Verwendung eines der folgenden Menüs in eine Datei gespeichert

wurden: Tabellenkalkulation, Geometrie, Überprüfen (Seite 99), Wahrscheinlichkeit

(Seite 100). OTHR Andere als die oben beschriebenen Daten

Geschützte Variablentypen

Einige Datentypen sind geschützt. Eine Variable, deren Datentyp geschützt ist, kann nicht durch eine andere Variablen überschrieben werden, sodass der Variableninhalt vor unbeabsichtigter Änderung geschützt ist. Die Datentypen, deren Namen in der obigen Liste mit einem Sternchen gekennzeichnet sind, sind geschützt. Beachten Sie, dass durch das System festgelegt wird, ob ein Datentyp geschützt ist oder nicht. Sie können den Schutzstatus eines Datentyps nicht selbst ändern.

Tipp: Auch Variablen, deren Datentyp geschützt ist, können Sie umbenennen, löschen oder verschieben. Um diese

Operationen zu deaktivieren, müssen Sie die Variable verriegeln. Siehe „Variablenmanager-Operationen“ auf Seite

30.

Kapitel 1: Grundlagen 28

Hauptspeicher-Ordner

Der ClassPad speichert Daten in einem der folgenden Ordnertypen, die unten beschrieben sind. „main“-Ordner: Der „main“-Ordner ist ein von ClassPad reservierter Ordner, der standardmäßig als aktueller

Ordner fungiert (siehe „Aktueller Ordner“ unten). „library“-Ordner: Der „library“-Ordner ist ebenfalls ein vom ClassPad reservierter Ordner, der für das

Speichern von durch den Anwender erstellten Daten (Variablen, Programme, Anwenderfunktionen usw.) verwendet werden kann. Auf die im „library“-Ordner gespeicherten Daten kann ohne Angabe eines Pfades zugegriffen werden, unabhängig von der aktuellen Ordnereinstellung.

Anwenderordner: Dies ist ein von Ihnen erstellter und benannter Ordner. Sie können einen Anwenderordner zum aktuellen Ordner machen, Variablen in einen Anwenderordner verschieben usw. Sie können einer Anwenderordner auch wie erforderlich löschen und umbenennen. Es können bis zu 87 Anwenderordner gleichzeitig im Hauptspeicher vorhanden sein.

Tipp: Sie können Ordner nicht innerhalb von anderen Ordnern speichern.

Aktueller Ordner

Der aktuelle Ordner ist der Ordner, in dem die in Menüs erstellten Daten (ausgenommen eActivity- Dateien) gespeichert sind und in dem auf diese Daten zugegriffen werden kann. Der anfänglich eingestellte aktuelle Standardordner ist der „main“-Ordner. Sie können auch einen Anwenderordner auswählen, den Sie als aktuellen Ordner erstellt haben. Weitere Informationen zur Vorgehensweise finden Sie unter „Variablenmanager-Operationen“ auf Seite 30.

Verwenden des Variablenmanagers

Der Variablenmanager ist ein Werkzeug für die Verwaltung von Anwendervariablen, Programmen, Anwenderfunktionen und anderer Typen von Daten. Obwohl in diesem Abschnitt nur der Begriff „Variablen“ verwendet wird, beziehen sich die hier aufgeführten Erläuterungen auch auf andere Typen von Daten, die vom Variablenmanager verwaltet werden können.

Mit dem Variablenmanager können Sie folgende Operationen durchführen:

• Erstellen, Löschen, Umbenennen, Verriegeln und Entriegeln von Ordnern und Konfigurieren der aktuellen Ordnereinstellungen.

• Löschen, Kopieren, Umbenennen, Verschieben, Verriegeln, Entriegeln, Suchen von Variablen und Anzeigen des Inhalts der Variablen.

Variablentypen

Eine Variable mit einer Buchstabenbezeichnung wie x und y kann eine anwendererstellte Variable, eine Systemvariable und eine lokale Variable sein.

• Systemvariablen sind vordefinierte, reservierte Variablen, die nicht umbenannt werden können. Informationen zu den Namen und Einzelheiten über die Systemvariablen finden Sie unter „Systemvariablen-Tabelle“ auf Seite 322.

• Eine lokale Variable ist eine Variable, die temporär erstellt wurde, indem eine Funktion, ein Programm oder eine andere Operation für einen bestimmten Zweck definiert wird. Weitere Informationen zu lokalen Variablen finden Sie im Abschnitt zum „Local“-Befehl unter „12-4 Referenz der Programmbefehle“.

Kapitel 1: Grundlagen 29

u Starten des Variablenmanagers

1. Tippen Sie in einem beliebigen Menü (mit

Ausnahme des System-Menüs) auf O, und tippen Sie dann auf [Variable Manager].

• Die Ordnerliste wird geöffnet. Die Ordnerliste wird immer zuerst angezeigt, wenn Sie den Variablenmanager starten.

Ordnername

Anzahl der im Ordner enthaltenen Variablen

Ordnerliste

2. Tippen Sie zweimal auf den Ordnernamen, um den Inhalt des Ordners anzuzeigen, eine

Anzahl der im Ordner enthaltenen Variablen

Variablenliste.

Ordnername

Variablenname

Datentypen (Seite 28) und Größe (Byte)

• Um die Variablenliste zu schließen und zur

Ordnerliste zurückzukehren, tippen Sie auf [Close].

Variablenliste

3. Um den Variablenmanager zu beenden, tippen Sie in der Ordnerliste auf [Close].

u Variablenmanager-Operationen

Die in der nachstehenden Tabelle aufgeführten Operationen können ausgeführt werden, während der Variablenmanager angezeigt wird.

Um dies zu tun: führen Sie dies aus:

Angeben des aktuellen Ordners

Erstellen eines Ordners Tippen Sie in der Ordnerliste auf [Edit] - [Create Folder]. Geben Sie im

Öffnen eines Ordners Tippen Sie in der Ordnerliste auf den Namen des Ordners, den Sie öffnen

Öffnen des „library“- Ordners

Auswählen eines Ordners oder einer Variable

Abwählen eines Ordners oder einer Variable

Löschen eines Ordners Siehe „Löschen eines Ordners“ (Seite 32). Löschen einer Variablen Aktivieren Sie das Kontrollkästchen neben der Variablen, die Sie löschen

Umbenennen eines Ordners oder einer Variablen

Tippen Sie in der Ordnerliste auf die Abwärtspfeil-Schaltfläche [Current]. Wählen Sie in der angezeigten Liste den Ordner aus, den Sie zum aktuellen Ordner bestimmen möchten.

Dialogfeld, das geöffnet wird, den Namen ein, den Sie dem Ordner zuweisen möchten, und tippen Sie dann auf [OK].

möchten, um ihn zu markieren, und tippen Sie dann erneut darauf. Tippen Sie auf [View] und dann auf [“library” Folder]. Der „library“-Ordner wird

geöffnet, und es wird eine Variablenliste mit dem Inhalt des Ordners angezeigt. Aktivieren Sie das Kontrollkästchen neben dem Ordner- oder Variablennamen.

Um alle Ordner oder Variablen in der Liste auszuwählen, tippen Sie auf [All] und dann auf [Select All].

Deaktivieren Sie das Kontrollkästchen neben dem Ordner- oder Variablennamen. Um alle Ordner oder Variablen in der Liste abzuwählen, tippen Sie auf [All] und dann auf [Deselect All].

möchten, und tippen Sie dann auf [Edit] - [Delete]. Als Antwort auf das angezeigte Bestätigungsdialogfeld tippen Sie auf [OK], um die ausgewählte Variable zu löschen.

Markieren Sie den Ordner oder die Variable, den bzw. die Sie umbenennen möchten, und tippen Sie dann auf [File] - [Rename]. Geben Sie im Dialogfeld, das geöffnet wird, den Namen ein, den Sie dem Ordner bzw. der Variablen zuweisen möchten, und tippen Sie dann auf [OK].

Kapitel 1: Grundlagen 30

Um dies zu tun: führen Sie dies aus:

Verriegeln eines Ordners oder einer Variablen

Entriegeln eines Ordners oder einer Variablen

Anzeigen einer Liste eines bestimmten Typs von Variablen

Kopieren oder Verschieben einer Variablen

Aktivieren Sie das Kontrollkästchen neben dem Ordner oder der Variablen, den bzw. die Sie verriegeln möchten, und tippen Sie dann auf [Edit] - [Lock]. Dadurch wird der aktuell ausgewählte Ordner bzw. die Variable verriegelt, und es wird das Ikon b links vom Namen eingefügt, um den verriegelten Zustand anzuzeigen.

Aktivieren Sie das Kontrollkästchen neben dem Ordner oder der Variablen, den bzw. die Sie entriegeln möchten, und tippen Sie dann auf [Edit] - [Unlock].

Tippen Sie in der Variablenliste auf [View] - [Variable Type]. Tippen Sie in dem Dialogfeld, das angezeigt wird, auf die Abwärtspfeil-Schaltfläche, und wählen Sie den Datentyp aus der angezeigten Liste aus. Tippen Sie dann auf [OK].

Tippen Sie in der Variablenliste auf [Edit] und anschließend auf [Copy] oder [Move]. Tippen Sie in dem Dialogfeld, das angezeigt wird, auf die Abwärtspfeil- Schaltfläche, und wählen Sie den Zielordner aus der angezeigten Liste aus. Tippen Sie dann auf [OK].

Tipp

• Wenn im Zielordner bereits eine Variable mit dem gleichen Namen vorhanden ist, wird die Variable im Zielordner durch die kopierte oder verschobene Variable ersetzt.

• Eine verriegelte Variable kann nicht verschoben werden.

Anzeigen des Inhalts einer Variablen

Eingeben eines Ordner- oder Variablennamens in ein Anwendungsfenster

Suchen nach einer Variablen

Tippen Sie in der Variablenliste auf den Namen der Variablen, deren Inhalt Sie anzeigen möchten, sodass diese hervorgehoben ist, und tippen Sie dann erneut darauf. Ein Dialogfeld wird geöffnet, in dem der Inhalt der Variablen angezeigt wird.

Siehe „Eingeben eines Ordner- oder Variablennamens in ein Anwendungsfenster“ (Seite 32).

Tippen Sie in der Ordnerliste auf [Search]. Geben Sie im Dialogfeld, das geöffnet wird, den Variablennamen ein, nach dem Sie suchen, und tippen Sie dann auf [OK]. Ein Ausrufezeichen (!) erscheint vor allen Ordnern, die einen Variablennamen enthalten, der mit dem von Ihnen für die Suche eingegebenen Variablennamen übereinstimmt.

Hinweis: Sie können wie oben beschrieben vorgehen, um den „main“-

Ordner oder einen anwenderdefinierten Ordner nach einem bestimmten Variablennamen zu durchsuchen. Beachten Sie jedoch, dass Sie den „library“- Ordner nicht durchsuchen können.

Auswählen eines Ordners

• Wenn in der Ordnerliste kein Kontrollkästchen aktiviert ist, wird jede Ordneroperation für den Ordner ausgeführt, dessen Name gerade in der Liste hervorgehoben ist. Wenn das Kontrollkästchen für einen Ordner ausgewählt ist, wird die Ordneroperation nur für diesen Ordner ausgeführt. Die Operation hat keine Auswirkung auf den Ordner, dessen Name in der Liste hervorgehoben ist.

• Wenn das Kontrollkästchen für einen Ordner aktiviert wird, werden dadurch auch die Kontrollkästchen für alle Variablen innerhalb dieses Ordners aktiviert.

• Beim Umbenennen eines Ordners wird nur der Ordner umbenannt, dessen Name in der Ordnerliste hervorgehoben ist. Diese Operation hat keine Auswirkungen auf andere Ordner, deren Kontrollkästchen nicht aktiviert sind.

Auswählen einer Variable

• Wenn in der Variablenliste kein Kontrollkästchen aktiviert ist, wird jede Variablenoperation für die Variable ausgeführt, deren Name gerade in der Liste hervorgehoben ist. Wenn das Kontrollkästchen für eine Variable ausgewählt ist, wird die Variablenoperation nur für diese Variable ausgeführt. Die Operation hat keine Auswirkung auf die Variable, deren Name in der Liste hervorgehoben ist.

Kapitel 1: Grundlagen 31

• Beim Umbenennen einer Variable wird nur die Variable umbenannt, deren Name in der Variablenliste hervorgehoben ist. Wenn andere Variablen ausgewählt (markiert) sind, so hat der Vorgang keine Auswirkungen auf diese.

Regeln für Ordner- und Variablennamen

Nachfolgend sind die für Regeln aufgeführt, die für Ordner- und Variablennamen gelten.

• Die Ordner- oder Variablennamen können aus bis zu acht Byte bestehen.

• Folgende Zeichen sind für einen Ordner- oder Variablennamen zulässig: Groß- und Kleinbuchstaben, tiefgestellte Zeichen, Ziffern, Unterstriche (_).

• Bei Ordner- oder Variablennamen wird die Groß- und Kleinschreibung beachtet. Jeder der folgenden Namen wird als unterschiedlicher Ordner-/Variablenname behandelt: abc, Abc, aBc, ABC.

• Ein reserviertes Wort (Systemvariablennamen, vorinstallierte Funktionsnamen, Befehlsnamen usw.) kann nicht als Ordner- oder Variablenname verwendet werden.

• Eine Ziffer, ein tiefgestelltes Zeichen oder ein Unterstrich (_) kann nicht als erstes Zeichen eines Ordner- oder Variablennamens verwendet werden.

u Löschen eines Ordners

Wichtig!

Bevor Sie einen Ordner löschen, vergewissern Sie sich, dass Sie die darin enthaltenen Variablen nicht mehr benötigen. Es ist empfehlenswert, zuerst die nicht mehr benötigten Variablen zu löschen und die noch benötigten Variablen in einen anderen Ordner zu verschieben, bevor Sie den dann leeren Ordner löschen.

1. Öffnen Sie den zu löschenden Ordner, und überprüfen Sie dessen Inhalt.

• Stellen Sie sicher, dass Sie die Variablen im Ordner nicht mehr benötigen. Falls eine der Variablen verriegelt ist, entriegeln Sie diese.

• Nachdem Sie den Inhalt des Ordners überprüft haben, schließen Sie diesen, um zur Ordnerliste zurückzukehren.

2. Aktivieren Sie das Kontrollkästchen neben dem Ordner, den Sie löschen möchten.

• Sie können auch mehrere Ordner auswählen und löschen, wenn Sie dies wünschen.

3. Tippen Sie in der Ordnerliste auf [Edit] und dann auf [Delete].

4. Als Antwort auf das angezeigte Bestätigungsdialogfeld tippen Sie auf [OK], um den Ordner zu löschen.

Tipp: Sie können den „library“-Ordner und den „main“-Ordner nicht löschen.

u Eingeben eines Ordner- oder Variablennamens in ein Anwendungsfenster

1. Verschieben Sie den Cursor im Main-Menü, im Grafik- und Tabellen-Menü oder in einem anderen Anwendungsmenü an die Position, an der Sie den Variablennamen eingeben möchten.

2. Öffnen Sie den Variablenmanager, um die Ordnerliste anzuzeigen.

3. Wenn Sie einen Variablennamen eingeben möchten, tippen Sie zweimal auf den Ordner mit der Variable, deren Namen Sie eingeben möchten. Wenn Sie einen Ordnernamen eingeben, fahren Sie mit dem nächsten Schritt fort.

4. Tippen Sie auf den Ordner oder die Variable, dessen bzw. deren Name Sie eingeben möchten, sodass der Name hervorgehoben wird.

5. Tippen Sie auf [INPUT].

• Dadurch wird der Variablenmanager beendet und der Name des von Ihnen in Schritt 4 gewählten Ordners

bzw. der Variable wird an der aktuellen Cursorposition in das Anwendungsfenster eingefügt.

Kapitel 1: Grundlagen 32

Verwalten von Menü-Dateien

In den unten genannten Menüs können Daten in Dateien gespeichert werden. Geometrie (Kapitel 8), eActivity (Kapitel 10), Tabellenkalkulation (Kapitel 13), Überprüfen (Seite 99),

Wahrscheinlichkeit (Seite 100), Bildplot (Kapitel 15) In diesem Abschnitt werden die allgemeinen Operationen erläutert, die für die in diesem Menüs erstellten

Datendateien ausgeführt werden können.

Tipp: Das Dialogfeld zum Speichern von Dateien in eActivity unterscheidet sich geringfügig vom „Save“-Dialogfeld in

anderen Menüs, aber die Operationen sind im Wesentlichen gleich.

u Speichern einer Datei

1. Tippen Sie auf [File] und dann auf [Save].

2. Geben Sie in dem Dialogfeld, das angezeigt wird, den Namen des Ordners ein, in dem die Datei gespeichert werden soll, sodass er ausgewählt ist.

3. Geben Sie einen bis zu acht Byte umfassenden Dateinamen in das Dateinamen-Bearbeitungsfeld ein, und tippen Sie dann auf [Save].

u Öffnen einer vorhandenen Datei

1. Tippen Sie auf [File] und dann auf [Open].

2. Öffnen Sie in dem Dialogfeld, das angezeigt wird, den Ordner, der die zu öffnende Datei enthält.

3. Tippen Sie auf den Namen der Datei, die Sie öffnen möchten, um sie zu markieren, und tippen Sie dann auf [Open].

u Suchen nach einer Datei

1. Tippen Sie auf [File] und dann auf [Open].

2. Tippen Sie in dem Dialogfeld, das angezeigt wird, auf [Search]. Das „Search“-Dialogfeld wird angezeigt.

3. Geben Sie den Dateinamen ein, nach dem Sie suchen, und tippen Sie dann auf [Search].

• Mit dem eingegebenen Dateinamen übereinstimmende Dateinamen werden auf dem Display markiert.

Tippen Sie auf [Open], um die markierte Datei zu öffnen.

• Um nach dem nächsten Vorkommen des gleichen Dateinamens zu suchen, tippen Sie erneut auf [Search]

und dann auf [Next] im „Search“-Dialogfeld.

u Löschen eines Ordners oder einer Datei

Wichtig!

Durch das Löschen eines Ordners werden auch alle darin befindlichen Dateien gelöscht. Überprüfen Sie daher, ob Sie den Inhalt des Ordners wirklich nicht mehr benötigen, bevor Sie diesen löschen.

1. Tippen Sie auf [File] und dann auf [Open].

2. Aktivieren Sie in dem Dialogfeld, das angezeigt wird, das Kontrollkästchen neben dem Ordner oder der Datei, den bzw. die Sie löschen möchten.

• Sie können auch mehrere Ordner/Dateien zum Löschen auswählen, wenn Sie dies wünschen.

• Durch das Aktivieren eines Kontrollkästchens neben einem Ordnernamen werden automatisch alle

Kontrollkästchen für die Dateien in diesem Ordner aktiviert.

3. Tippen Sie auf [File] und dann auf [Delete].

4. Als Antwort auf das angezeigte Bestätigungsdialogfeld tippen Sie auf [OK], um den Ordner/die Ordner oder die Datei/die Dateien zu löschen.

Tipp: Wenn Sie einen Ordner wie oben beschrieben auswählen, werden der Ordner und sein gesamter Inhalt gelöscht.

Beachten Sie jedoch, dass Sie „main“-Ordner nicht löschen können.

Kapitel 1: Grundlagen 33

u Umbenennen eines Ordners oder einer Datei

1. Tippen Sie auf [File] und dann auf [Open].

2. Geben Sie in dem Dialogfeld, das angezeigt wird, den Namen des Ordners oder der Datei ein, den bzw. die Sie umbenennen möchten, um ihn bzw. sie zu markieren.

3. Tippen Sie auf [File] und dann auf [Rename]. Das „Rename“-Dialogfeld wird angezeigt.

4. Geben Sie den Namen ein, den Sie ihm bzw. ihr zuweisen möchten, und tippen Sie dann auf [OK].

u Verschieben einer Datei in einen anderen Ordner

1. Tippen Sie auf [File] und dann auf [Open].

2. Aktivieren Sie in dem Dialogfeld, das angezeigt wird, das Kontrollkästchen neben der Datei, die Sie verschieben möchten.

• Um mehrere Dateien zu verschieben, aktivieren Sie alle entsprechenden Kontrollkästchen.

3. Tippen Sie auf [File] und dann auf [Move].

• Ein Dialogfeld wird geöffnet, in dem Sie den Zielordner wählen können.

4. Tippen Sie in dem Dialogfeld, das angezeigt wird, auf die Abwärtspfeil-Schaltfläche, und wählen Sie den Zielordner aus der angezeigten Liste aus.

5. Tippen Sie auf [OK], um die Dateien zu verschieben.

u Umschalten des Dateimenüs zwischen List View und Detail View (nur eActivity-Menü)

1. Tippen Sie auf [File] und dann auf [Open].

2. Öffnen Sie in dem Dialogfeld, das angezeigt wird, den Ordner, der die Dateien enthält, die aufgelistet werden sollen.

3. Zur Anzeige von Dateinamen und Dateigröße tippen Sie auf [View] - [Detail View]. Um nur die Dateinamen anzuzeigen, tippen Sie auf [View] - [List View].

u Erstellen eines neuen Ordners

1. Tippen Sie auf [File] und dann auf [Open].

2. Tippen Sie in dem Dialogfeld, das angezeigt wird, auf [File] und dann auf [Create Folder], oder tippen Sie auf {.

• Das „Create Folder“-Dialogfeld wird angezeigt.

3. Geben Sie einen bis zu acht Byte umfassenden Namen für den Ordner ein, und tippen Sie dann auf [OK], um einen Ordner zu erstellen.

1-6 Erstellen und Verwenden von Variablen

Dieser Abschnitt erläutert, wie Sie eine neue Variable (Anwendervariable) erstellen können, und enthält ein einfaches Rechenbeispiel, das die Verwendung einer Variablen illustriert.

Erstellen einer neuen Variablen

Die üblichste Vorgehensweise für das Erstellen einer neuen Variablen ist die Zuordnung eines Wertes oder eines Formelterms zu dem entsprechenden Variablennamen. Verwenden Sie die Variablenzuordnungstaste (W), um Daten einer Variablen zuzuordnen.

Nachfolgend finden Sie ein Beispiel für die Zuordnung zu einer Variablen, während „main“ als der aktuelle Ordner ausgewählt ist.

Kapitel 1: Grundlagen 34

Beispiel: Erstellen einer neuen Variablen mit dem Namen „eq1“ und Zuweisen des Terms 2x + 1 zu dieser.

Im folgenden Beispiel wird von der Annahme ausgegangen, dass momentan im „main“-Ordner keine Variable mit dem Namen „eq1“ oder „x“ abgelegt ist.

u Operationen auf dem ClassPad

1. Starten Sie das Main-Menü.

2. Drücken Sie die k-Taste, um die Software-Tastatur anzuzeigen, und führen Sie anschließend die folgenden Tastenoperationen aus.

2x+11W0eqbw

• Dadurch wird die Variable mit dem Namen „eq1“ im aktuellen Ordner (der

„main“-Ordner in diesem Beispiel) erstellt, und dieser Variable wird der Term 2

x + 1 zugeordnet.

Tipp

• Falls im aktuellen Ordner eine Variable mit dem gewählten Namen bereits vorhanden ist, dann wird der Inhalt der

vorhandenen Variablen durch die neu zugeordneten Daten ersetzt, sofern die vorhandene Variable nicht verriegelt oder geschützt ist. Nähere Informationen hierzu siehe „Variablenmanager-Operationen“ (Seite 30) und „Geschützte Variablentypen“ (Seite 28).

• Um die neu erstellte Variable in einem anderen als dem aktuellen Ordner zu speichern, geben Sie den Variablennamen

wie folgt an: <Ordnername>\<Variablenname>.

• Sie können den Variablenmanager verwenden, um den Inhalt der gerade von Ihnen erstellten Variablen anzuzeigen.

Nähere Informationen hierzu siehe „Variablenmanager-Operationen“ (Seite 30).

• Informationen zu Regeln für Variablennamen siehe „Regeln für Ordner- und Variablennamen“ (Seite 32).

Beispiel für die Verwendung von Variablen

Im folgenden Beispiel wird die Variable verwendet, die wir im Beispiel oben unter „Erstellen einer neuen Variablen“ erstellt haben.

Beispiel: Zuweisen der Werte 5 und 10 zu

x und Überprüfen der Ergebnisse von eq1 (= 2x + 1)

u Operationen auf dem ClassPad

1. Weisen Sie x den Wert 5 zu.

51WxE

2. Überprüfen Sie den Inhalt der Variablen „eq1“.

0eqbw

• Angezeigt wird das Berechnungsergebnis von 2

3. Weisen Sie

101WxE

4. Überprüfen Sie den Inhalt der Variablen „eq1“.

0eqbw

x den Wert 10 zu.

x + 1, wenn x = 5.

Variablen des „library“-Ordners

Auf die Variablen im „library“-Ordner kann ohne Angabe eines Pfades zugegriffen werden, unabhängig von der aktuellen Ordnereinstellung.

Beispiel: Zwei Variablen sind zu erstellen, auf die danach zugegriffen werden soll, wobei eine Variable im

„library“-Ordner und die andere Variable in einem anderen Ordner abgelegt ist.

Kapitel 1: Grundlagen 35

u Operationen auf dem ClassPad

1. Als aktueller Ordner ist „main“ angegeben. Führen Sie die folgende Operation aus, um eine Variable mit dem Namen „eq1“ zu erstellen, der danach die angegebenen Listendaten zugeordnet werden.

{1, 2, 3} W eq1w

2. Als aktueller Ordner ist weiterhin „main“ angegeben. Führen Sie die folgende Operation aus, um eine Variable mit dem Namen „eq2“ im „library“-Ordner zu erstellen, der danach die angegebenen Listendaten zugeordnet werden.

{4, 5, 6} W library\eq2w

3. Überprüfen Sie den Inhalt der beiden Variablen. eq1w

eq2w (Da die Variable „eq2“ im „library“-Ordner gespeichert ist, müssen Sie

keinen Pfad angeben, um auf diese Variable zuzugreifen.)

4. Ändern Sie die Auswahl des aktuellen Ordners in „Test“.

• Verwenden Sie den Variablenmanager (Seite 29), um einen Ordner „Test“ zu erstellen und die Auswahl des

aktuellen Ordners zu ändern.

5. Führen Sie die folgenden Operationen aus, um den Inhalt der Variablen „eq1“ und „eq2“ anzuzeigen. eq1E

(Da bei dieser Tastenoperation nicht auf den „main“-Ordner zugegriffen

wird, wird der Variablenname („eq1“) ohne den Variableninhalt angezeigt.)

main\eq1E (Bei Angabe des Pfads zum „main“-Ordner, in dem sich die Variable „eq1“

befindet, wird der Inhalt der Variablen angezeigt.)

eq2E (Da die Variable „eq2“ im „library“-Ordner abgelegt ist, müssen Sie keinen

Pfad angeben, um auf diese Variable zuzugreifen.)

Tipp: Durch die Angabe eines Variablennamens, der sowohl im aktuellen Ordner als auch im „library“-Ordner vorhanden

ist, wird auf die Variable im aktuellen Ordner zugegriffen. Einzelheiten über die Zugriffsprioritätsfolge der Variablen und den Zugriff auf Variablen in bestimmten Ordnern finden Sie unten unter „Regeln für den Zugriff auf Variablen“.

Regeln für den Zugriff auf Variablen

Normalerweise greifen Sie auf eine Variable zu, indem Sie den Namen der Variablen angeben. Die Regeln in diesem Abschnitt gelten, wenn Sie auf eine Variable zugreifen möchten, die sich nicht im aktuellen Ordner befindet, oder wenn Sie auf eine Variable zugreifen möchten, die den gleichen Namen wie eine oder mehrere Variablen in anderen Ordnern aufweist.

kSuchprioritätsfolge für Variablen

Wenn Sie einen Variablennamen für den Zugriff auf eine Variable angeben, werden die Variablen in der folgenden Reihenfolge gesucht.

(1) Lokale Variablen (2) Variablen des aktuellen Ordners (3) Variablen des „library“-Ordners

• Mehrere Variablen mit dem gleichen Namen können gleichzeitig als eine lokale Variable, als eine Variable

im aktuellen Ordner und als eine Variable im „library“-Ordner vorhanden sein. In diesem Fall durchsucht der ClassPad die Ordner gemäß der oben aufgeführten Reihenfolge und greift auf die zuerst gefundene Variable zu. Wenn Sie auf eine Variable zugreifen möchten, die nach der obigen Prioritätsfolge von niedrigerer Priorität ist, müssen Sie den Ordnernamen zusammen mit dem Variablennamen angeben, wie nachfolgend in „Auswählen einer Variablen in einem bestimmten Ordner“ erklärt.

Kapitel 1: Grundlagen 36

• Wenn eine von Ihnen ausgewählte Variable nicht gefunden werden kann, wird diese wie eine „undefinierte

Variable“ behandelt.

• Beachten Sie, dass der „system“-Ordner nicht in die oben genannte Variablensuche eingeschlossen ist.

Wenn Sie auf eine Variable im Systemordner zugreifen möchten, geben Sie nur den Variablennamen an, ohne den Ordnernamen.

Tipp: Nur lokale Variablen und Variablen des aktuellen Ordners werden im Falle einer Operation, die Variablendaten

speichert, oder eines Befehls, der eine Operation mit einer Variablen ausführt (wie „DelVar“), durchsucht. Normalerweise werden die Variablen im „library“-Ordner nicht durchsucht. Wenn Sie die „library“-Ordner in die Suche einschließen möchten, müssen Sie den „library“-Ordner als die Variablenposition angeben, wie nachfolgend erläutert.

kAuswählen einer Variablen in einem bestimmten Ordner

Sie können auf eine im „main“-Ordner, „library“-Ordner oder in einem bestimmten Anwenderordner enthaltene Variable zugreifen, indem Sie den Ordnernamen gemeinsam mit dem Variablennamen angeben.

Verwenden Sie die folgende Syntax, um einen Ordnernamen anzugeben: <Ordnername>\<Variablenname> Beispiel: Auswählen der Variablen „abc“ im „main“-Ordner

main\abc

1-7 Konfigurieren der Anwendungsformate

Im O-Menü sind Einstellungen für das Format der angezeigten Nachkommastellen oder der signifikanten Ziffern der Berechnungsergebnisse, des Winkelmodus sowie anwendungsbezogene Einstellungen möglich. Nachfolgend sind die im O-Menü enthaltenen Einstellungen und Befehle beschrieben.

Um dies zu tun:

Festlegen des Ordners für Variablen und Konfigurieren des Zahlenformats, des Winkelmodus und anderer Grundeinstellungen für alle integrierten Anwendungen

Konfigurieren der Einstellungen für Grafikfenster und Grafikzeichnung für das Grafik- und Tabellen-Menü, das Kegelschnitt-Menü und andere Menüs mit Grafikdarstellungen

Konfigurieren des Zahlenformats, der Winkeleinstellung und weiterer Einstellungen für das Geometrie-Menü

Konfigurieren der Fouriertransformations- und FFT-Einstellungen Advanced Format Konfigurieren der Einstellungen für das Finanzmathematik-Menü Financial Format Zurücksetzen aller oben genannten Menüeinstellungen auf die Werksvoreinstellungen

(außer der Einstellung des aktuellen Ordners, die im Grundformat-Dialogfeld angegeben ist)

wählen Sie diesen O-Menübefehl:

Basic Format

Graph Format

Geometry Format

Default Setup

u Konfigurieren der Anwendungsformate

1. Öffnen Sie ein Menü (außer dem System-Menü).

2. Tippen Sie auf O. Tippen Sie dann auf den gewünschten Menübefehl: „Basic Format“, „Graph Format“, „Geometry Format“, „Advanced Format“ oder „Financial Format“.

3. Verwenden Sie das Dialogfeld, um die gewünschten Einstellungen vorzunehmen.

• Einzelheiten zu den Einstellungen, die Sie in jedem der Dialogfelder konfigurieren können, finden Sie

unten, unter „Einstellungen der Anwendungsformate“.

4. Um ein Dialogfeld zu schließen und dessen Einstellungen zu bestätigen, tippen Sie auf [Set]. Um ein Dialogfeld zu schließen, ohne dessen Einstellungen anzuwenden, tippen Sie auf [Cancel] oder die Schaltfläche C in der oberen rechten Ecke des Dialogfelds.

Kapitel 1: Grundlagen 37

Einstellungen der Anwendungsformate

Dieser Abschnitt enthält Details über alle Einstellungen, die Sie über die Anwendungsformateinstellungen konfigurieren können. Die nachstehend mit einem Sternchen (*) markierten Einstellungen sind die anfänglichen Vorgabeeinstellungen des ClassPad.

k Grundformat-Dialogfeld

Verwenden Sie das Grundformat-Dialogfeld („Basic Format“), um grundlegende Einstellungen für Berechnungen, Spalten und andere Parameter vorzunehmen.

Angeben des aktuellen Ordners

Tippen Sie auf 1, und tippen Sie dann auf den gewünschten Namen des Ordners (main*).

Angeben des Anzeigeformats für numerische Größen

Tippen Sie auf 2, und tippen Sie dann auf eine der unten beschriebenen Einstellungen.

Normal 1*: Automatische Exponentialanzeige, wenn

Berechnungsergebnis

Normal 2: Automatische Exponentialanzeige, wenn Berechnungsergebnis

−9

x: 10

> |x| oder |x| t 1010 ist. Fix 0 – Fix 9: Feste Anzahl von Dezimalstellen Sci 0 – Sci 9: Feste Anzahl von signifikanten Stellen

Angeben des Winkelmodus

Tippen Sie auf 3, und tippen Sie dann auf „Radian*“, „Degree“ oder „Grad“.

−2

x: 10

> |x| oder |x| t 1010 ist.

Um dies zu tun: führen Sie dies aus:

Umschalten zwischen Berechnungen mit komplexen Zahlen (Komplexmodus) und Berechnungen mit reellen Zahlen (Reeller Modus)

Aktivieren Sie das Kontrollkästchen „Complex Format“, um den Komplexmodus zu starten, oder deaktivieren Sie das Kontrollkästchen*, um den reellen Modus* zu starten.

Anzeigen der Ergebnisse als Dezimalzahl (Dezimalmodus) oder Belassen der Berechnungsergebnisse als exakte Terme (Standardmodus)

Einschalten (Algebramodus) oder Ausschalten (Assistentenmodus) der automatischen Vereinfachung von Termen

Aktivieren Sie das Kontrollkästchen „Decimal Calculation“, um den Dezimalmodus zu starten, oder deaktivieren Sie das Kontrollkästchen*, um den Standardmodus zu starten.

Aktivieren Sie das Kontrollkästchen „Assistant“, um den Assistentenmodus zu starten, oder deaktivieren Sie das Kontrollkästchen*, um den Algebramodus zu starten. Einzelheiten siehe Seite 50.

Festlegen einer absteigenden oder aufsteigenden Reihenfolge für den Term des Berechnungsergebnisses

Aktivieren Sie das Kontrollkästchen „Descending Order“*, um den Term des Berechnungsergebnisses in absteigender Reihenfolge anzuzeigen (z. B. + 1), oder deaktivieren Sie das Kontrollkästchen zur Anzeige in aufsteigender Reihenfolge (z. B. 1 + x +

Festlegen, ob Variablen bei Komplexmodusberechnung als reelle Zahlen oder als komplexe Zahlen zu behandeln sind

Aktivieren Sie das Kontrollkästchen „Variable is Real“, um Variablen als reelle Zahlen zu behandeln, oder deaktivieren Sie das Kontrollkästchen*, um Variablen als komplexe Zahlen zu behandeln.

+ x

Tipp: Informationen zum Kontrollkästchen „Q

152).

, Q3 on Data“ siehe „Berechnungsmethoden für Q1, Q3 und Median“ (Seite

Kapitel 1: Grundlagen 38

Verwenden der Statusleiste zum Ändern der Einstellungen der Anwendungsformate

In den in der Tabelle unten aufgeführten Menüs können Sie über die Statusleiste eine Reihe von Einstellungen des Grundformat-Dialogfelds ändern.

Für dieses Menü: können Sie folgende Einstellungen prüfen und ändern:

Main, eActivity Algebramodus/Assistentenmodus, Standardmodus/Dezimalmodus,

Komplexmodus/Reeller Modus, Winkelmodus Statistik Standardmodus/Dezimalmodus, Winkelmodus Grafik und Tabellen, Kegelschnitt,

Differenzialgleichungsgrafik, Numerische Lösung, Zahlenfolgen

Komplexmodus/Reeller Modus, Winkelmodus

u Verwenden der Statusleiste zum Ändern der Einstellungen der Anwendungsformate

Tippen Sie in der Statusleiste auf den Text der Einstellung, die Sie ändern möchten.

Main-Menü Grafik- und Tabellen-Menü

Durch jedes Tippen ändert sich das angetippte Element wie unten beschrieben.

• „Alg“ ↔ „Assist“ ... Schaltet zwischen dem Algebra- und dem Assistentenmodus um.

• „Standard“ ↔ „Decimal“ ... Schaltet zwischen dem Standard- und dem Dezimalmodus um.

• „Real“ ↔ „Cplx“ ... Schaltet zwischen dem reellen Modus und dem Komplexmodus um.

• „Rad“ → „Deg“ → „Gra“ ... Schaltet die Einstellung für das Winkelmaß zwischen „Radian“, „Degree“ und

„Grad“ um.

Tipp: Das Ändern einer Einstellung über die Statusleiste hat dieselbe Wirkung wie das Ändern der entsprechenden

Einstellung im Grundformat-Dialogfeld. Das bedeutet, dass die Einstellung für alle Anwendungen und Menüs geändert wird.

k Grafikformat-Dialogfeld

Verwenden Sie das „Grafikformat-Dialogfeld“-Dialogfeld, um die Einstellungen für das Grafikfenster und für das Zeichnen von Grafiken vorzunehmen.

[Basic]-Registerkarte

Festlegen der Anzeige der Grafikfensterachsen

Tippen Sie auf 1, und tippen Sie dann auf eine der unten beschriebenen Einstellungen.

On: Achse anzeigen Off: Achse ausblenden Number*: Achsen zusammen mit dem Maximal- und Minimalwert jeder

Achse anzeigen

Festlegen der Anzeige des Grafikfenstergitters

Tippen Sie auf 2, und tippen Sie dann auf eine der unten beschriebenen Einstellungen.

On: Gitter als Punkte anzeigen Off: Gitter ausblenden Line*: Gitter als Linien anzeigen

Auswählen der Festlegung für das Füllen für Ungleichungen (Inequality Plot)

Tippen Sie auf 3, und tippen Sie dann auf eine der unten beschriebenen Einstellungen.

Union*: Bereiche füllen, in denen alle Bedingungen für Ungleichungen

erfüllt sind, wenn mehrere Ungleichungen grafisch dargestellt werden

Intersection: Bereiche füllen, in denen jede Bedingung für Ungleichungen

erfüllt ist, wenn mehrere Ungleichungen grafisch dargestellt werden

Kapitel 1: Grundlagen 39

Festlegen der Farbe von Figuren und Grafiken, die mit der Sketch-Funktion gezeichnet werden (Seite 120)

Tippen Sie auf 4. Wählen Sie im Dialogfeld, das geöffnet wird, die gewünschte Farbe aus, und tippen Sie dann auf [OK].

Um dies zu tun: führen Sie dies aus:

Ein- oder Ausschalten der Anzeige der GrafikfensterachsenLabels

Ein- oder Ausschalten der Anzeige der Grafikcontrollerpfeile

Festlegen von geplotteten Punkten oder durchgehenden

Aktivieren Sie das Kontrollkästchen „Labels“*, um Labels anzuzeigen, oder deaktivieren Sie das Kontrollkästchen, um Labels auszublenden.

Tipp: Unabhängig von der „Labels“-Einstellung werden im Grafikfenster des Zahlenfolgen-

Menüs nie Labels angezeigt. Auch für die folgenden Typen von Grafiken, die im Statistik-Menü erstellt werden, werden keine Labels angezeigt: NPPlot, Histogram, MedBox, NDist Broken.

Aktivieren Sie das Kontrollkästchen „G-Controller“*, damit Grafikcontrollerpfeile eingefügt werden (Seite 112), oder deaktivieren Sie das Kontrollkästchen*, um Grafikcontrollerpfeile auszublenden.

Aktivieren Sie das Kontrollkästchen „Draw Plot“, um geplottete Punkte festzulegen, oder deaktivieren Sie das Kontrollkästchen*, um durchgehende Linien für

Grafikzeichnungen festzulegen. Linien für Grafikzeichnungen

Ein- und Ausschalten der Anzeige von Funktionsname und

Aktivieren Sie das Kontrollkästchen „Graph Function“*, damit Funktionsname

und Funktion in der Grafik angezeigt werden, oder deaktivieren Sie das

Kontrollkästchen, um Funktionsname und Funktion auszublenden. Funktion

Ein- oder Ausschalten der Koordinaten des Grafikfensterzeigers

Ein- und Ausschalten der Anzeige des vorangestellten

Aktivieren Sie das Kontrollkästchen „Coordinates“*, um die Zeigerkoordinaten

im Grafikfenster anzuzeigen, oder deaktivieren Sie das Kontrollkästchen, um die

Koordinaten auszublenden.

Aktivieren Sie das Kontrollkästchen „Leading Cursor“, um den vorangestellten

Cursor anzuzeigen, oder deaktivieren Sie das Kontrollkästchen*, um den

vorangestellten Cursor auszublenden. Cursors während der grafischen Darstellung

Festlegen der Zeichenmethode beim Zeichnen mehrerer

Aktivieren Sie das Kontrollkästchen „Simultaneous Graphs“, um mehrere Grafiken

gleichzeitig zu zeichnen, oder deaktivieren Sie das Kontrollkästchen*, um die

Grafiken nacheinander einzeln zu zeichnen. Grafiken

Anzeigen oder Ausblenden von Ableitungswerten im Grafikfenster und im Tabellenfenster

Aktivieren Sie das Kontrollkästchen „Derivative/Slope“, um Ableitungswerte im

Grafikfenster und im Tabellenfenster anzuzeigen, oder deaktivieren Sie das

Kontrollkästchen*, um Ableitungswerte auszublenden. Einzelheiten zur Anzeige

von Inhalten finden Sie unter „Verwenden von Trace für das Ablesen der

Grafikkoordinaten“ (Seite 119) und „Generieren einer Wertetabelle“ (Seite 115).

Kapitel 1: Grundlagen 40

[Special]-Registerkarte

Festlegen der Zeilenbreite für die Statistik-Editor- und die Datentabellen-Anzeige

Tippen Sie auf 1 und wählen Sie dann ein Muster für die Zellenbreite: 2

Cells, 3 Cells* oder 4 Cells für die vertikale Display-Ausrichtung bzw. 4 Cells, 5 Cells* oder 6 Cells für die horizontale Display-Ausrichtung (siehe

„Ändern der Display-Ausrichtung“ auf Seite 16).

Festlegen einer Quelle für Tabellendaten

Tippen Sie auf 2, und tippen Sie dann auf eine der unten beschriebenen

Einstellungen.

Table Input*: Verwendet die Dateneingabe in einem „Table Input“-

Dialogfeld als Quelle für das Generieren von Zahlentabellen.

list1 bis list6: Verwendet die Listendaten in list1 bis list6 als Quelle für das

Generieren von Zahlentabellen.

<Listenname>: Verwendet die Listendaten in der ausgewählten Liste als

Quelle für das Generieren von Zahlentabellen.

Einzelheiten zum Generieren einer Zahlentabelle unter Verwendung der einzelnen Einstellungen finden Sie unter „Generieren einer Wertetabelle“ (Seite 115).

Festlegen einer Quelle für Übersichtstabellendaten

Tippen Sie auf 3, und tippen Sie dann auf eine der unten beschriebenen Einstellungen. View Window*: Verwendet die Einstellungen des Betrachtungsfensters als Quelle für das Generieren von

Übersichtstabellen. list1 bis list6: Verwendet die Listendaten in list1 bis list6 als Quelle für das Generieren von Übersichtstabellen. <Listenname>: Verwendet die Listendaten in der ausgewählten Liste als Quelle für das Generieren von

Übersichtstabellen. Einzelheiten zum Generieren einer Ergebnistabelle unter Verwendung der einzelnen Einstellungen finden Sie

unter „Erstellen einer Übersichtstabelle“ (Seite 117). Anzeigen oder Ausblenden der zweiten Ableitung in den Übersichtstabellen

Aktivieren Sie die Schaltfläche „On“* unter „Summary Table die Schaltfläche „Off“, um sie auszublenden.

Angeben der automatischen bzw. manuellen Festlegung der Betrachtungsfenster-Einstellungen im Statistik-Menü

Aktivieren Sie das Kontrollkästchen „Stat Window Auto“*, um die automatische Einstellungskonfiguration anzugeben, oder deaktivieren Sie das Kontrollkästchen, um die manuelle Einstellung festzulegen.

[3D Format]-Registerkarte

Festlegen der Anzeige der Koordinatenwerte

Tippen Sie auf 1 und wählen Sie dann „Rectangular*“ (kartesische Koordinatenwerte anzeigen), „Polar“ (Polarkoordinatenwerte anzeigen)

oder „Off“ (Anzeige der Koordinaten ausschalten).

Festlegen der Anzeige der Achsen

Tippen Sie auf 2 und wählen Sie dann „On“ (Achsen normal anzeigen),

„Box“ (umrahmte Koordinatenachsen anzeigen) oder „Off*“ (Anzeige der Achsen ausschalten).

Ein- oder Ausschalten der Anzeige der Achsenbeschriftungen im Grafikfenster

Tippen Sie auf 3 und wählen Sie dann „On“ oder „Off*“.

f (x)“, um die zweite Ableitung anzuzeigen, oder

Kapitel 1: Grundlagen 41

k Geometrieformat-Dialogfeld

Verwenden Sie das Geometrieformat-Dialogfeld, um Einstellungen für das Geometrie-Menü zu konfigurieren.

Tipp: Die als Vorschau im unteren Teil des Dialogfeldes dargestellten Informationen stellen eine Vorschau des

Geometrie-Menüfensters dar, abhängig von den Einstellungen, die in der oberen Hälfte des Dialogfelds vorgenommen sind.

Festlegen des von Zahlenwert-Anzeigeformats im Geometriefenster

Tippen Sie auf 1, und wählen Sie dann das gewünschte Format aus. Die

„Number Format“-Einstellung zu Beginn ist „Fix2“. Weitere Informationen hierzu finden Sie unter „Angeben des Anzeigeformats für numerische

Größen“ (Seite 38).

Festlegen der Einheit des angezeigten Längenwerts

Tippen Sie auf 2, und tippen Sie dann auf eine der unten beschriebenen

Einstellungen.

Off*: Die Einheit für Längenwerte wird nicht angezeigt.

mm, cm, m, km, in, ft, yd, mi: Der Längenwert wird in der ausgewählten

Einheit angezeigt.

Festlegen der Winkeleinheit für das Maßanzeigefeld

Tippen Sie auf 3, und tippen Sie dann auf „Radian“, „Degree*“ oder „Grad“.

Angeben der Winkeleinheit für die grafische Darstellung

Tippen Sie auf 4, und tippen Sie dann auf „Radian*“, „Degree“ oder „Grad“.

Festlegen der Anfangsbedingungen der Grafikfensterachsen bei Öffnen des Geometrie-Menüs

Tippen Sie auf 5, und tippen Sie dann auf eine der unten beschriebenen Einstellungen. On: Achsen anzeigen Off*: Achsen ausblenden Number: Achsen zusammen mit dem Maximal- und Minimalwert jeder Achse anzeigen

Festlegen der Anfangsbedingungen der Grafikfensterachsen bei Öffnen des Geometrie-Menüs

Tippen Sie auf 6, und tippen Sie dann auf eine der unten beschriebenen Einstellungen. On: Gitter als Punkte anzeigen Off*: Gitter ausblenden Line: Gitter als Linien anzeigen

k Zusätzliches-Format-Dialogfeld

Verwenden Sie das Zusätzliches-Format-Dialogfeld, um Einstellungen für Fouriertransformation und FFT vorzunehmen.

Festlegen der Formel für Fouriertransformation

Tippen Sie auf 1, und tippen Sie dann auf „Modern Physics“, „Pure Math*“, „Probability“, „Classical Physics“ oder „Signal Processing“.

Festlegen der FFT-Skalierungskonstante

Tippen Sie auf 2, und tippen Sie dann auf „Pure Math“, „Signal Processing*“ oder „Data Analysis“.

Festlegen der Behandlung von Variablen für Fourier-Berechnungen

Aktivieren Sie das Kontrollkästchen „Assume positive real“*, um anzugeben, dass Variablen für Fourier-Berechnungen nur als positiv

reell behandelt werden sollen. Aktivieren Sie das Kontrollkästchen, um anzugeben, dass komplexe Zahlen für Variablen für FourierBerechnungen zulässig sind.

Kapitel 1: Grundlagen 42

k Finanzmathematisches-Format-Dialogfeld

Verwenden Sie das Finanzmathematisches-Format-Dialogfeld, um Einstellungen für das FinanzmathematikMenü zu konfigurieren.

[Basic]-Registerkarte

Festlegen der Anzahl von Tagen in einem Jahr

Tippen Sie auf 1, und tippen Sie dann auf „360 days“ oder auf „365 days*“.

Festlegen des Beginns oder des Endes der Periode als Zahlungsdatum

Tippen Sie auf 2, und tippen Sie dann auf „Beginning of period“ oder auf

„End of period*“.

Festlegen des Datumsformats

Tippen Sie auf 3, und tippen Sie dann auf eine der unten beschriebenen Einstellungen.

MM/DD/YYYY*: Monat/Tag/Jahr DD/MM/YYYY: Tag/Monat/Jahr YYYY/MM/DD: Jahr/Monat/Tag

Festlegen des Status von Eingabefeldern beim Starten einer neuen Berechnung

Um dies zu tun: führen Sie dies aus:

Beim Wechseln zu einer anderen Berechnungsart automatisch den Inhalt aller Felder der aktuellen Berechnung, deren Namen den Namen der Felder in der neuen Berechnung entsprechen, kopieren

Beim Wechseln zu einer anderen Berechnungsart den Inhalt aller Felder löschen

[Special]-Registerkarte

Festlegen der Behandlung von ungeraden Perioden

Tippen Sie auf 1, und tippen Sie dann auf eine der unten beschriebenen Einstellungen.

Compound (CI): Beim Durchführen einer Zinseszinsberechnung soll

Zinseszins auf die ungerade Periode angewendet werden.

Simple (SI): Beim Durchführen einer Zinseszinsberechnung soll

Kapitalzins auf die ungerade Periode angewendet werden.

Off*: Beim Durchführen einer Zinseszinsberechnung sollen keine Zinsen

auf die ungerade Periode angewendet werden.

Festlegen der Aufzinsungshäufigkeit

Tippen Sie auf 2, und tippen Sie dann auf „Annual*“ (einmal jährlich) oder „Semi-annual“ (zweimal jährlich).

Aktivieren Sie das Kontrollkästchen [Automatically copy common fields to new calculation]*.

Deaktivieren Sie das Kontrollkästchen [Automatically copy common fields to new calculation].

Festlegen des Anleiheintervalls

Tippen Sie auf 3, und tippen Sie dann auf eine der unten beschriebenen Einstellungen.

Term*: Legt die Verwendung einer Reihe von Zahlungen als Dauer für

Pfandbriefberechnungen fest.

Date: Legt die Verwendung eines Datums für Pfandbriefberechnungen

fest.

Kapitel 1: Grundlagen 43

Festlegen der Verwendung des Betrags (PRF) oder des Gewinnverhältnisses (r%) für Rentabilitätsgrenzberechnungen

Tippen Sie auf 4, und tippen Sie dann auf „Amount (PRF)*“ oder „Ratio (r%)“.

Festlegen, ob bei Rentabilitätsgrenzberechnungen zuerst die Umsatzmenge ([QBE]) oder zuerst die Umsatzhöhe ([SBE]) berechnet werden soll

Tippen Sie auf 5, und tippen Sie dann auf „Quantity*“ oder „Sales“. Wenn „Quantity“ ausgewählt ist, kann die Umsatzmenge vor der Berechnung der Umsatzhöhe berechnet werden. Wenn „Sales“ ausgewählt ist, kann die Umsatzhöhe vor der Berechnung der Umsatzmenge berechnet werden.

Tipp: Beim Durchführen einer Finanzberechnung können Sie die Einstellungen über die Statusleiste des

Finanzmathematik-Menüs und die Registerkarte [Format] ändern. Nähere Informationen hierzu siehe „Konfigurieren von Einstellungen im Finanzmathematik-Menü“ (Seite 202).

Initialisieren aller Anwendungsformateinstellungen

Führen Sie die folgende Prozedur durch, wenn Sie alle Anwendungsformateinstellungen auf die Werksvoreinstellung zurücksetzen wollen.

u Operationen auf dem ClassPad

1. Tippen Sie auf O, und tippen Sie dann auf [Default Setup].

2. Als Antwort auf die erscheinende Meldung „Reset Setup Data?“ tippen Sie auf [OK], um alle Einstellungen zu

initialisieren.

• Die Einstellungen werden initialisiert, mit Ausnahme der Einstellung für den aktuellen Ordner, die im Grundformat-Dialogfeld angegeben ist.

1-8 Falls Probleme auftreten…

Falls Probleme bei der Arbeit mit dem Rechner auftreten, ergreifen Sie die folgenden Maßnahmen, bevor Sie einen Defekt in Ihrem ClassPad vermuten.

1. Initialisieren Sie alle Anwendungsformateinstellungen.

Führen Sie die Prozedur unter „Initialisieren aller Anwendungsformateinstellungen“ durch (Seite 44).

2. Führen Sie die RAM-Rückstellung (RESTART) durch.

Führen Sie die RAM-Rückstellung durch, wenn der ClassPad „einfriert“ oder aus einem anderen Grund nicht wie erwartet arbeitet.

Durchführen der RAM-Rückstellungsoperation

Wichtig!

• Die RAM-Rückstellungsoperation löscht alle temporär im RAM des ClassPad abgespeicherten Daten. Durch das Durchführen der RAM-Rückstellungsoperation während einer Berechnung gehen alle durch die Berechnung im RAM abgespeicherten Daten verloren.

• Führen Sie die RAM-Rückstellungsoperation nur aus, wenn Ihr ClassPad aus irgendeinem Grund den normalen Betrieb eingestellt hat.

Kapitel 1: Grundlagen 44

1. Verwenden Sie den Stift, um den RESTART-Knopf auf der

Rückseite des ClassPad zu drücken.

• Im Anschluss an die RAM-Rückstellungsoperation wird der ClassPad wieder automatisch gestartet.

RESTARTKnopf

2. Nachdem der ClassPad wieder gestartet ist, führen Sie die Setup-Operation des ClassPad aus. Weitere Informationen über die Setup-Operation des ClassPad sind unter „Aufladen der Batterien und Einstellen des ClassPad“ in der separaten Schnellstartanleitung zu finden.

• Das Menü der Anwendungen wird geöffnet, nachdem Sie die Setup-Operation beendet haben.

3. Zurücksetzen des ClassPad

Bevor Sie die Rückstelloperation verwenden, fertigen Sie zuerst eine schriftliche Kopie von allen wichtigen Daten an.

Einzelheiten hierzu sind unter „Listenweises Löschen bestimmter Daten (Reset)“ (Seite 303).

Kapitel 1: Grundlagen 45

Kapitel 2: Main-Menü

Das Main-Menü ist ein universelles Anwendungsmenü sowohl für numerische als auch symbolische Berechnungen, das Sie für das Studium der Mathematik und die Lösung von mathematischen Problemen nutzbringend einsetzen können. Sie können das Main-Menü benutzen, um allgemeine Rechenoperationen für die arithmetischen Grundrechenarten, Berechnungen mit Listen (Listenarithmetik), Matrizenrechnungen usw. auszuführen.

Beim Aufrufen des Main-Menüs wird ein großer weißer Arbeitsbereich angezeigt. Verwenden Sie diesen Bereich für die Eingabe der Operationen und Befehle. Der ClassPad verwendet diesen Bereich auch, um die Berechnungsergebnisse auszugeben.

Eingabe des Terms

Berechnungsergebnis

Die grundlegende Operation im Main-Menü besteht darin, einen Berechnungsterm in den Arbeitsbereich einzugeben und E zu drücken. Dadurch wird die Berechnung ausgeführt und das Ergebnis wird auf der rechten Seite des Arbeitsbereichs angezeigt.

Arbeitsbereich

Untermenüs und Schaltflächen des Main-Menüs

• Löschen von Variablen, die Zahlen, Listen und Matrizen enthalten .........................Edit - Clear All Variables

• Einfügen eines Befehls in den Arbeitsbereich (Seite 64) .......................................................................Action

• Ausführen eines interaktiven Befehls für den im Arbeitsbereich

ausgewählten Term (Seite 96) ................................................................................................... Interactive

• Umschalten der Anzeige des Rechenergebnisses zwischen dem

Standardmodus und dem Dezimalmodus ..............................................................................................u

• Neuberechnung der Gleichung nur für die aktuelle Zeile, in der sich der Cursor gerade befindet .............7

• Unveränderte Ausgabe eines eingegebenen Terms ..................................................................................0

• Einfügen und Ausführen des Simplify-Befehls (Vereinfachen) ...................................................................S

• Umschalten zwischen Binär-, Oktal-, Dezimal- oder Sedezimalsystem

während normaler Berechnung (Seite 63) .............................................................................................<

• Zugriff auf die Anwendungs-Fenster des ClassPad vom Main-Menü aus 97) ............................................$

2-1 Grundrechenarten

Dieser Abschnitt erläutert die Ausführung grundlegender mathematischer Operationen im Main-Menü.

Arithmetische Berechnungen und Klammerrechnung

Sie können arithmetische Berechnungen ausführen, indem Sie die Zahlenterme so wie geschrieben eingeben. Der ClassPad erkennt automatisch die Vorrangregeln der Berechnung für Additionen, Subtraktionen, Multiplikationen, Divisionen, Funktionen und Klammerterme.

Kapitel 2: Main-Menü 46

0201 Berechnungsbeispiele

• Alle in 0201 gezeigten Beispielsberechnungen werden unter Verwendung der Tastatur oder des [Number]-

Tastensatzes der Software-Tastatur ausgeführt, sofern nicht anders angegeben.

• Alle Beispielberechnungen werden unter Verwendung des Dezimalmodus ausgeführt (Seite 48).

Verwenden der e-Taste

Verwenden Sie die e-Taste zur Eingabe von Exponenten. Sie können Exponenten auch unter Verwendung der E-Taste im [Number]-Tastensatz der Software-Tastatur eingeben.

0202 Berechnungsbeispiele

Weglassen des Multiplikationszeichens

In den folgenden Fällen können Sie das Multiplikationszeichen weglassen.

• Zahlenfaktor vor einer Funktion… 2sin (30), 10log (1,2) usw.

• Zahlenfaktor im Produkt mit Konstanten oder symbolischen Variablen… aπ, 2ab, 3ans usw.

• Zahlenfaktor oder Klammerterm vor einer geöffneten Klammer… 3(5 + 6), (a + 1)(b – 1) usw.

Beachten Sie, dass Sie das Multiplikationszeichen unbedingt eingeben müssen, wenn der Faktor direkt vor einer geöffneten Klammer eine symbolische Variable ist. Beispiel: ab (3 + b) muss als ab × (3 + b) geschrieben werden. Anderenfalls wird Ihre Eingabe durch den ClassPad als Funktionsnotation ( interpretiert.

f ( x))

• Faktor vor der e-Taste oder der E-Taste (siehe „Verwenden der e-Taste“ oben.)

• Skalarer Faktor vor einer Matrix oder Liste … a {1, 2, 3}, 3 [[1, 2] [3, 4]] usw.

Verwenden der Antwortvariablen (ans)

Jedes Mal, wenn Sie eine Berechnung im Arbeitsbereich des Main-Menüs ausführen, wird das Ergebnis automatisch einer mit „ans“ (answer = Antwort) benannten Variablen zugeordnet. Sie können den aktuellen Wert der „ans“-Variablen durch Tippen auf die D-Taste auf der Software-Tastaturabrufen und diesen in eine andere Berechnung eingeben.

0203 Berechnungsbeispiele

Tipp: Wenn Sie einen Berechnungsterm mit dem Operator +, −, ×, ÷ oder ^ beginnen, wird die „ans“ Variable automatisch

links neben dem Operator eingesetzt, selbst wenn Sie nicht die D-Taste betätigen.

Wertzuweisung für eine Variable

Neben der Verwendung der Variablenzuordnungstaste (W, Seite 34) können Sie auch mit der nachstehenden Syntax im Main-Menü und im eActivity-Menü einer Variablen einen Wert zuordnen.

Syntax: Variable: = Wert

0204 123 die Variable

x zuweisen

Wichtig!

„:=“ kann nur im Main-Menü und im eActivity-Menü verwendet werden Diese Eingabe kann NICHT in einem Programm verwendet werden. Im Programm-Menü müssen Sie W verwenden, um einen Wert in einer Variable abzuspeichern.

Kapitel 2: Main-Menü 47

Prioritäten der Rechenoperationen während der Berechnung

Ihr ClassPad führt die Berechnungen automatisch mit folgenden Vorrangregeln aus.

1 Befehle mit Klammern (sin(, diff(, usw.) 2 Fakultäten (

x!), Gradangaben (

o, r

), Prozente (%)

3 Potenzen 4 π, Speicher- und Variablen-

Multiplikationsoperationen, bei denen das Multiplikationszeichen weggelassen

5 +, –, (–) 6 Relationsoperatoren (=, , <, >, s, t) 7 and 8 or, xor 9 with ( | )

wird (2π, 5A usw.), Befehl mit Klammern- Multiplikationsoperationen, bei denen das Multiplikationszeichen weggelassen wird (2'3 usw.), ×, ÷

Tipp

• Termen in Klammern wird Priorität eingeräumt.

• In Fällen, in denen eine Reihe von Berechnungen im gleichen Term mehr als einen der Operatoren 4 bis 9 beinhaltet,

die das gleiche Prioritätsniveau aufweisen, werden die Operationen gleicher Priorität von links nach rechts ausgeführt. Die Mehrfachpotenzierung 3 (Beispiel: 5^2^3) wird jedoch von rechts nach links (5^(2^3)) ausgeführt.

Beispiel:

2 + 3 × (log (sin( 2π

)) + 6,8) = 22,07101691

(im Algebramodus, Dezimalmodus, Bogenmaßmodus)

Berechnungsmodi

Alle folgenden Berechnungsbeispiele sind nur im Algebramodus (Exaktmodus) dargestellt.

Standardmodus und Dezimalmodus

Der Standardmodus zeigt die Berechnungsergebnisse in mathematisch exakter Form an, sofern dies möglich ist, während der Dezimalmodus die Berechnungsergebnisse in ein Dezimalformat umwandelt (approximative Gleitkomma-Zahlendarstellung).

Berechnungsterm Ergebnis im Dezimalmodus Ergebnis im Standardmodus

50 ÷ 4 = 12,5 12.5

+ 2 = 3,414213562...

π = 3,1415926535...

sin (2,1π) × 5 = 1,5450849718...

3.414213562

3.141592654

1.545084972

(  − 1)

2 +

• Die in der obigen Tabelle aufgeführten Ergebnisse des Dezimalmodus werden im Display angezeigt, wenn

„Normal 1“ für die [Number Format]-Einstellung im Grundformat-Dialogfeld voreingestellt ist.

u Verwenden der u-Schaltfläche zum Umschalten zwischen dem Standardmodus und dem

Dezimalmodus

Sie können auf u tippen, um für die Anzeige eines Zahlenwerts zwischen dem Standard- und dem Dezimalmodusformat umzuschalten.

Beachten Sie, dass durch das Tippen auf u nur die Formatierung eines angezeigten Zahlenwerts umgeschaltet wird. Die aktuelle Standardmodus/Dezimalmodus-Einstellung wird dadurch nicht geändert.

Kapitel 2: Main-Menü 48

0205 Tippen auf u, während der ClassPad für die Anzeige im Standardmodus (Normal 1) konfiguriert ist

0206 Tippen auf u, während der ClassPad für die Anzeige im Dezimalmodus (Normal 1) konfiguriert ist

u Einstellung der Anzahl der Dezimalstellen, der Anzahl der signifikanten Stellen und der

Normalanzeige

Die [Number Format]-Einstellungen im Grundformat-Dialogfeld geben die Anzahl der Dezimalstellen, die Anzahl der signifikanten Stellen und die Normalanzeigeeinstellung für die Darstellung der Berechnungsergebnisse im Dezimalmodus des Main-Menüs vor. Nachfolgend ist dargestellt, wie die Berechnungsergebnisse bei den einzelnen Einstellungen angezeigt werden.

Berechnungsterm Normal 1 Normal 2 Fix 3 Sci 3

50 ÷ 4 = 12,5 12.5 12.5 12.500 1.25 100 ÷ 6 = 16,6666666... 16.66666667 16.66666667 16.667 1.67 1 ÷ 600 = 0,00166666... 1.666666667

÷ 4 = 2,5E + 10 2.5E + 10 2.5E + 10 2.5E + 10 2.50E + 10

Der zulässige Bereich für die Anzahl der Dezimalstellen wird durch Fix 0 bis Fix 9 festgelegt, der Bereich für die Anzahl der signifikanten Stellen wird durch Sci 0 bis Sci 9 festgelegt. Zu Einzelheiten über die [Number Format]-Einstellungen siehe „Grundformat-Dialogfeld“ auf Seite 38.

–3 0.00166666666 0.002 1.67E – 3

+ 1

Komplexer Modus und reeller Modus

Der komplexe Modus dient für Berechnungen mit komplexen Zahlen, während der reelle Modus auf Berechnungen innerhalb des Bereichs der reellen Zahlen beschränkt ist. Wenn im reellen Modus eine Berechnung ausgeführt wird, die zu einem außerhalb des Bereichs der reellen Zahlen liegenden Ergebnis führt, kommt es zu einem Fehler (Non-Real in Calc).

0207 (Berechnungsergebnisse im komplexen Modus und reellen Modus)

Tipp

• Als Imaginäreinheit kann „ i “ oder „ j “ gewählt werden. Siehe „Festlegen der imaginären Einheit einer komplexen Zahl“

auf Seite 304.

• Wenn der Berechnungsterm ⬔(

r,) enthält, müssen die Berechnungsergebnisse die Form ⬔(r,) haben.

Bogenmaßmodus, Altgradmodus und Gon-Modus

Sie können das Bogenmaß, Altgrad oder Gon als das Winkelargument der Ergebnisse von trigonometrischen Berechnungen vorgeben.

u Beispiele für Berechnungsergebnisse im Bogenmaßmodus, Altgradmodus und Gon-Modus

Berechnungsterm Bogenmaßmodus Altgradmodus Gon-Modus

sin (π/4)

sin (45) sin (45) sin (45)

sin (50) sin (50) sin (50)

sin

( )

sin

( )

Wichtig!

Ungeachtet der aktuell gewählten Winkelargument-Einstellung wird eine Berechnung, die eine imaginäre Zahl als Hochzahl (wie z.B. e

) einbezieht, mit Bogenmaß als Winkelargument (e

= −1) ausgeführt.

Kapitel 2: Main-Menü 49

Assistentenmodus und Algebramodus

Der Algebramodus vereinfacht automatisch die von den Berechnungen erzeugten mathematischen Ergebnisse. Im Assistentenmodus wird jedoch keine Vereinfachung ausgeführt. Im Assistentenmodus können Sie auch die Zwischenergebnisse betrachten. Dies ermöglicht es, die Schritte zu sehen, die zu einem bestimmten Ergebnis

führen, so wie in 0208 dargestellt (siehe das „expand“-Beispiel).

0208 (Berechnungsergebnisse im Assistentenmodus und Algebramodus)

Wichtig!

Der Assistentenmodus steht nur im Main-Menü und im eActivity-Menü zur Verfügung.

2-2 Verwenden des zurückliegenden

Berechnungsverlaufs

Der Berechnungsverlauf im Arbeitsbereich des Main-Menüs kann bis zu 30 Paare von Eingabetermen/ Ergebnistermen enthalten. Sie können eine bis zu 30 Schritte zurückliegende Berechnung aufrufen, bearbeiten und danach erneut ausführen, wenn Sie dies wünschen.

• Verwenden Sie die Bildlaufleiste oder die Bildlauf-Schaltflächen, um das Arbeitsbereichsfenster nach oben

oder unten zu scrollen. Dadurch wird der Inhalt des zurückliegenden Berechnungsverlaufs angezeigt.

• Sie können einen Eingabeterm im Berechnungsverlaufsspeicher bearbeiten und danach den sich ergebenden

Term erneut berechnen. Drücken Sie E, um den Term neu zu berechnen, bei dem sich der Cursor aktuell befindet, und um auch alle anderen Terme unterhalb der aktuellen Cursorposition neu zu berechnen.

0209 Der Term „ans × 2“ soll in folgendem Beispiel in „ans × 3“ geändert und anschließend neu berechnet

werden.

Tipp

• Um nur eine einzelne Zeile neu zu berechnen, tippen Sie auf 7. Wenn Sie auf 7 tippen, wird die Berechnung

an der Stelle, an der sich der Cursor gerade befindet, erneut durchgeführt. Dies hat keinen Einfluss auf Inhalte des Berechnungsverlaufs vor oder nach dieser Zeile.

• Um alle Terme im Berechnungsverlauf neu zu berechnen, stellen Sie den Cursor in die oberste Zeile, und drücken Sie

dann E.

u Löschen eines Teils des Inhalts des Berechnungsverlaufs

1. Verschieben Sie den Cursor zu der Eingabezeile oder Ergebniszeile der Zwei-Zeilen-Einheit, die Sie löschen

möchten.

2. Tippen Sie auf [Edit] und anschließend auf [Delete].

Wichtig!

Auch wenn das Ergebnis der gelöschten Zwei-Zeilen-Einheit Auswirkungen auf nachfolgenden Berechnungen hat, werden die davon betroffenen Berechnungen nach dem Löschen nicht automatisch aktualisiert. Wenn Sie den gesamten Berechnungsverlauf aktualisieren möchten, der auf die gelöschte Einheit folgt, verschieben Sie den Cursor an eine Zeile oberhalb der von Ihnen gelöschten Zeile und drücken Sie dann E.

u Löschen des gesamten Inhalts des Berechnungsverlaufs

Tippen Sie auf [Edit] und anschließend auf [Clear All]. Tippen Sie als Antwort auf die erscheinende Bestätigungsmeldung auf [OK].

Kapitel 2: Main-Menü 50

2-3 Berechnungen mit Funktionen

Dieser Abschnitt erläutert, wie Sie Berechnungen mit Funktionen im Arbeitsbereich des Main-Menüs ausführen können.

• Sie müssen keine schließenden Klammern unmittelbar vor der Betätigung der E-Taste eingeben. In

allen Berechnungsbeispielen in diesem Abschnitt wurden die schließenden Klammern vor der E-Taste weggelassen.

• Die nachfolgenden Berechnungsbeispiele sind alle im Dezimalmodus ausgeführt. Bei Verwendung des

Standardmodus werden die Ergebnisse als Brüche angezeigt.

Winkelumwandlung (°, r)

Die ersten zwei Beispiele verwenden „Degree“ (Altgrad) (gekennzeichnet durch „Deg“ in der Statusleiste) als Winkelmoduseinstellung. Das letzte Beispiel verwendet „Radian“ (Bogenmaß) (gekennzeichnet durch „Rad“ in der Statusleiste) als Winkelmoduseinstellung. Beachten Sie, dass die Verwendung der falschen Winkelmoduseinstellung zu falschen Berechnungsergebnissen führt.

u Ändern der Winkelmoduseinstellung

1. Tippen Sie im O-Menü auf [Basic Format].

2. Tippen Sie auf die [Angle]-Abwärtspfeil-Schaltfläche und wählen Sie anschließend [Radian], [Degree] oder

[Grad] aus.

• Sie können die Einstellung des Winkelmodus auch ändern, indem Sie auf die aktuelle Einstellung (Rad, Deg oder Gra) auf der Statusleiste tippen. Das Tippen bewirkt, dass die verfügbaren Einstellungen durchlaufen werden.

Problemstellung Tastenfolge

4,25 rad soll in Altgrad umgerechnet werden. = 243,5070629

47,3° + 82,5 rad = 4774,20181° 243,5070629° entsprechen welchem Wert im

Bogenmaß? = 4,249999999

4.25 Rw

47.3 + 82.5 Rw

[Angle]-Einstellung in „Radian“ (Bogenmaß) ändern und anschließend 243.5070629 *w eingeben.

Trigonometrische Funktionen und Arkusfunktionen

Problemstellung Tastenfolge

cos((

2 · sin45° × cos65° = 0,5976724775

sin (Bestimmen von x für sinx = 0,5.)

) rad) = 0,5

–1

0,5 =30°

[Angle]-Einstellung in „Radian“ (Bogenmaß) ändern. c7/3 w oder cN7c 3 w

[Angle]-Einstellung in „Degree“ (Altgrad) ändern.

2*s 45 )*c 65 w

Kann weggelassen werden.

S 0.5 w

„.5“ kann ebenfalls verwendet werden.

Kapitel 2: Main-Menü 51

Logarithmische Funktionen und Exponentialfunktionen

Problemstellung Tastenfolge

log1,23 (log ln90 (log

9 = 2

log

4,5

= 90,0171313

(–3)

= (–3) × (–3) × (–3) × (–3) = 81

123 (= 123

1,23) = 0,08990511144

90) = 4,49980967

1 7

) = 1,988647795

" 1.23 w oder V 10 e 1.23 w I 90 w oder V`e 90 w

V 3 e 9 w oder LV 3 , 9 w Q 4.5 w

(- 3 ){ 4 w

123 {( 1 / 7 w oder % 7 e 123 w

Hyperbel- und Areafunktionen

Problemstellung Tastenfolge

sinh3,6 = 18,28545536

–1

(

cosh

) = 0,7953654612

1 3.6 w

@ 20 / 15 w oder @N 20 c15 w

Andere Funktionen (%, ', x2, x –1, x!, abs, ⬔, signum, int, frac, intg, fRound, sRound)

Problemstellung Tastenfolge

Wie viel sind 12% von 1500? (180) 660 ist wie viel Prozent von 880? (75%) Welcher Wert ist um 15% größer als

2500? (2875) Welcher Wert ist um 25% kleiner als

3500? (2625) '2 + '5 = 3,65028154 5 2 e+5 5 w

(3 + i) = 1,755317302 + 0,2848487846i In den komplexen Modus wechseln (in der

= (–3) × (–3) = 9

(–3)

= –(3 × 3) = –9

–3

= 12

–

8! (= 1 × 2 × 3 × … × 8) = 40320 Wie groß ist der Absolutwert des Brigg’schen

Logarithmus von

⎜log (

)⎟ = 0,1249387366

8⬔40° × 5⬔35° ⬔(8,40) × ⬔(5,35) = ⬔(40,75)

Welches Vorzeichen weist –3,4567 auf? (–1) (signum ermittelt –1 für einen negativen Wert, 1 für

einen positiven Wert, „Undefined“ für 0 und

²A´

für

eine komplexe Zahl.)

1500 * 12 &w 660 / 880 &w

2500 *( 1 + 15 &

3500 *( 1 - 25 &

Statusleiste als „Cplx“ angezeigt).

5 3 +0w (- 3 )xw

- 3 xw ( 3 X- 4 X)Xw

oder

N 1 cN 1 c 3 e-N 1 c 4 w

8 !w

4V 10 eN 3 c 4 w oder L4V 3 / 4 w

In den Altgradmodus wechseln (in der Statusleiste als „Deg“ angezeigt). ~ 8 , 40 )*~ 5 , 35 )w

[signum] - 3.4567 w

Kapitel 2: Main-Menü 52

Problemstellung Tastenfolge

Welchen ganzzahligen Teil hat –3,4567? (–3) Welchen Dezimalteil hat –3,4567? (–0,4567) Was ist die größte Ganzzahl, die kleiner oder

gleich –3,4567 ist? (–4) Was ergibt –3,4567 gerundet auf zwei

Dezimalstellen? (–3,46) Was ergibt –34567 gerundet auf vier signifikante

Stellen? (–34570)

* Um auf 10 Stellen zu runden, geben Sie „0“ für das zweite Argument ein.

:- 3.4567 w [frac] - 3.4567 w [intg] - 3.4567 w

[fRound] - 3.4567 , 2 w

[sRound] - 34567 , 4 w*

Zufallszahlgenerator (rand, randList, randNorm, randBin, RandSeed)

Der Zufallszahlgenerator des ClassPad kann einzelne Zufallszahlen (also keine Zufallszahlen-Folge) und Zufallszahlen, die einem bestimmten Muster folgen (Zufallszahlen-Folge), erzeugen.

u Umschalten zwischen der Generierung einzelner Zufallszahlen und der Generierung von

Zufallszahlen-Folgen

1. Verwenden Sie den „RandSeed“-Befehl, um die Einstellungen für die Generierung von Zufallszahlen zu konfigurieren. Siehe „RandSeed-Befehl“ auf Seite 55.

2. Verwenden Sie die „rand“-, „randList“-, „randNorm“- oder „randBin“-Funktion, um die Zufallszahlen zu generieren.

u „rand“-Funktion

Die „rand“-Funktion generiert (Pseudo-)Zufallszahlen. Falls Sie kein Argument vorgeben, generiert „rand“ eine 10-stellige positive Dezimalzahl zwischen 0 und kleiner 1. Falls Sie zwei ganze Zahlen als Argument vorgeben, werden zwischen ihnen gleich verteilte ganzzahlige Zufallszahlen generiert.

Problemstellung Tastenfolge

Gleichmäßig verteilte stetige Zufallszahlen zwischen 0 und 1 erzeugen.

Gleichmäßig verteilte stetige Zufallszahlen zwischen 1 und 6 erzeugen.

[rand] w

[rand] 1 , 6 w

u „randList“-Funktion

Syntax: randList(n [, a, b]) Funktion:

• Wenn Sie die Argumente „a“ und „b“ weglassen, wird eine Zufallszahlen-Liste mit

gleich verteilte positive Dezimalzahlen sind.

• Wenn Sie ganzzahlige Argumente „a“ und „b“ vorgeben, wird eine Zufallszahlen-Liste mit

erzeugt, die gleich verteilte ganzzahlige Zufallszahlen im Intervall von „a“ bis „b“ sind.

Beschreibung:

n“ muss eine positive ganze Zahl sein.

• „

• Die (Pseudo-)Zufallszahlen für jedes Listen-Element werden in Abhängigkeit von den „RandSeed“-

Einstellungen der „randList“-Funktion generiert, genau wie bei der „rand“-Funktion.

n Elementen erzeugt, die

n Elementen

Kapitel 2: Main-Menü 53

Problemstellung Tastenfolge

Eine Liste mit drei Elementen generieren, die Dezimalzufallszahlen sind.

Eine Liste mit fünf Elementen generieren, die ganzzahlige Zufallszahlen aus dem Intervall [1, 6] sind.

[randList] 3 w

[randList] 5, 1, 6 w

u „randNorm“-Funktion

Die „randNorm“-Funktion generiert eine 10-stellige normale Zufallszahl, die auf einem vorgegebenen arithmetischen Mittel  und -Werten der Standardabweichung basiert.

Syntax: randNorm( Funktion:

• Weglassen eines Werts für „

Form.

• Vorgeben eines Wertes für „

Beschreibung:

• „

n“ muss eine positive ganze Zahl sein und „ “ muss größer als 0 sein.

Problemstellung Tastenfolge

Einen zufälligen Körperlängen-Wert erzeugen, der entsprechend der Normalverteilung einer Gruppe von Kindern unter einem Jahr mit einer durchschnittlichen Körperlänge von 68 cm und einer Standardabweichung von 8 zu ermitteln ist.

Zufällige Körperlängen von fünf Kindern im obigen Beispiel erzeugen und diese in einer Liste anzeigen.

,  [, n])

n“ (oder Vorgeben von 1 für „n“) ergibt die generierte Zufallszahl in unveränderter

n“ ergibt die vorgegebene Anzahl an Zufallswerten in Listenform.

[randNorm] 8 , 68 w

[randNorm] 8 , 68 , 5 w

u „randBin“-Funktion

Die „randBin“-Funktion generiert binomiale Zufallszahlen auf Basis vorgegebener Werte für die Anzahl der Versuche n und die Wahrscheinlichkeit P.

Syntax: randBin(

n, P [, m])

Funktion:

• Weglassen eines Werts für „

unveränderter Form.

• Vorgeben eines Wertes für „

Beschreibung:

• „

n“ und „m“ müssen positive ganze Zahlen sein.

Problemstellung Tastenfolge

Eine zufällige Zahl für „Kopf“ erzeugen, die entsprechend der Binomialverteilung für fünf Münzwürfe erwartet werden kann, wobei die Wahrscheinlichkeit für „Kopf“ 0,5 beträgt.

Die gleiche Münzwurfsequenz wie oben beschrieben ausführen und die Ergebnisse in einer Liste anzeigen.

m“ (oder Vorgeben von 1 für „m“) ergibt die generierte Zufallszahl in

m“ ergibt die vorgegebene Zahl von Zufallswerten in Listenform.

[randBin] 5 , 0.5 w

[randBin] 5 , 0.5 , 3 w

Kapitel 2: Main-Menü 54

u „RandSeed“-Befehl

• Sie können eine ganze Zahl von 0 bis 9 als Argument dieses Befehls eingeben. 0 bezieht sich auf die

Erzeugung einzelner Zufallszahlen. Eine Ganzzahl von 1 bis 9 verwendet den vorgegebenen Wert als Startpunkt für den jeweiligen Zufallszahlenalgorithmus. Das voreingestellte Vorgabeargument für den „RandSeed“-Befehl ist 0.

• Die durch den ClassPad erzeugten Zufallszahlen unmittelbar nach der Angabe der Zufallszahlenerzeugung

folgen immer dem gleichen Zufallsmuster.

Problemstellung Tastenfolge

Zufallszahlen-Folge unter Verwendung von 3 als

[RandSeed] 3 w

RandSeed-Wert erzeugen. Die erste Zufallszahl der Folge erzeugen.

Die zweite Zufallszahl der Folge erzeugen. Die dritte Zufallszahl der Folge erzeugen.

[rand] w [rand] w [rand] w

Tipp

• Die mit diesen Befehlen erzeugten Zufallszahlen sind Pseudozufallszahlen.

• Die Argumente „a“ und „b“ von „rand(a,b)“ und „randList(n,a,b)“ müssen ganze Zahlen sein und den folgenden

Bedingungen genügen.

a < b

⎟ a⎟ , ⎟ b⎟ < 1

10 b – a < 1E10

Ganzzahlfunktionen

Diese Funktionen verwenden nur Ganzzahlen als Argumente und ergeben Ganzzahlen.

u „iGcd“-Funktion

Syntax: iGcd(Exp-1, Exp-2[, Exp-3…Exp-10)]

(Exp-1 bis Exp-10 sind alles Ganzzahlen.) iGcd(List-1, List-2[, List-3…List-10)] (Alle Elemente von List-1 bis List-10 sind Ganzzahlen.)

Funktion:

• Die erste Syntax oben ergibt den größten gemeinsamen Teiler für zwei bis zehn Ganzzahlen.

• Die zweite Syntax gibt im Listenformat den größten gemeinsamen Teiler (GCD) für jedes Element in zwei bis

zehn Listen aus. Wenn die Argumente beispielsweise {

a,b}, {c,d} sind, erhält man eine Liste mit den GCD für

a und c, und für b und d.

Beschreibung:

• Alle Listen müssen die gleiche Zahl von Elementen enthalten.

• Bei Verwendung der Syntax „iGcd(List-1, List-2[, List-3…List-10)]“ kann ein Ausdruck (Exp) (nur einer)

anstelle einer Liste als Argument einbezogen werden.

Problemstellung Tastenfolge

Die größten gemeinsamen Teiler von {4, 3}, {12, 6} und {36, 9} ermitteln.

[iGcd] { 4 , 3 },{ 12 , 6 },{ 36

, 9 })w

u „iLcm“-Funktion

Syntax: iLcm(Exp-1, Exp-2[, Exp-3…Exp-10)]

(Exp-1 bis Exp-10 sind alles Ganzzahlen.) iLcm(List-1, List-2[, List-3…List-10)] (Alle Elemente von List-1 bis List-10 sind Ganzzahlen.)

Kapitel 2: Main-Menü 55

Funktion:

• Die erste Syntax oben ergibt das kleinste gemeinsame Vielfache für zwei bis zehn Ganzzahlen.

• Die zweite Syntax gibt im Listenformat das kleinste gemeinsame Vielfache (LCM) für jedes Element in zwei

bis zehn Listen aus. Wenn die Argumente beispielsweise {

a,b}, {c,d} sind, erhalten Sie eine Liste mit den LCM

für a und c, und für b und d.

Beschreibung:

• Alle Listen müssen die gleiche Zahl von Elementen enthalten.

• Bei Verwendung der Syntax „iLcm(List-1, List-2[, List-3…List-10)]“ kann ein Ausdruck (Exp) (nur einer)

anstelle einer Liste als Argument einbezogen werden.

Problemstellung Tastenfolge

Die kleinste gemeinsame Vielfachen von {4, 3}, {12, 6} und {36, 9} ermitteln.

[iLcm] { 4 , 3 },{ 12 , 6 },{ 36

, 9 })w

u „iMod“-Funktion

Syntax: iMod(Exp-1/List-1, Exp-2/List-2[)] Funktion:

• Diese Funktion dividiert eine oder mehrere Ganzzahlen durch eine oder mehrere Ganzzahlen und gibt den

Rest bzw. die Reste an.

Beschreibung:

• Exp-1 und Exp-2 sowie alle Elemente von List-1 und List-2 müssen Ganzzahlen sein.

• Sie können Exp für ein Argument und List für das andere Argument (Exp, List oder List, Exp) verwenden.

• Wenn beide Argumente Listen sind, müssen beide Listen die gleiche Zahl von Elementen enthalten.

Problemstellung Tastenfolge

21 durch 6 und 7 dividieren und den Rest von beiden

[iMod] 21 ,{ 6 , 7 })w

Operationen ermitteln. (iMod(21, {6, 7})

Variation/Permutation (nPr) und Kombination (nCr)

u Gesamtanzahl der Variationen/Permutationen

u Gesamtanzahl der Kombinationen

= –––––––

nCr

! (n – r)!

nPr

= –––––

(n – r)!

Problemstellung Tastenfolge

Wie viele Permutationen und Kombinationen sind möglich, wenn aus 10 verschiedenen Personen jeweils 4 ausgewählt werden?

10P4

10C4

= 5040 = 210

} 10 , 4 w { 10 , 4 w

Bedingungsentscheidung (judge, piecewise)

u „judge“-Funktion

Die „judge“-Funktion ermittelt TRUE (wahr), wenn eine Aussage (Gleichung, Ungleichung) wahr ist, und FALSE (falsch), wenn diese falsch ist.

Problemstellung Tastenfolge

Ist die folgende Aussage wahr oder falsch? 1 = 1 TRUE

Ist die folgende Aussage wahr oder falsch? 1 < 0 FALSE

[judge] 1 = 1 w

[judge] 1 < 0 w

Kapitel 2: Main-Menü 56

u „piecewise“-Funktion

Die „piecewise“-Funktion (Kodierung einer Fallunterscheidung) ermittelt unterschiedliche Zahlenwerte (Wahrheitswerte) je nach dem, ob die Aussage wahr, falsch oder nicht entscheidbar ist.

Die Syntax der „piecewise“-Funktion ist nachfolgend dargestellt. piecewise(<Bedingungsaussage>, <ermittelter Wert, wenn Aussage wahr ist>, <ermittelter Wert, wenn

Aussage falsch oder nicht entscheidbar ist> [ ) ] oder piecewise(<Bedingungsaussage>, <ermittelter Wert, wenn Aussage wahr ist>, <ermittelter Wert, wenn Aussage falsch ist >, < ermittelter Wert, wenn Aussage nicht entscheidbar ist> [ ) ]

Verwenden Sie die Software-Tastatur (1) zum Eingeben einer „piecewise“-Funktion mit der unten gezeigten Syntax.

oder

Problemstellung Tastenfolge

Für die Aussage 0 t Wahrheitswert 1, wenn x kleiner oder gleich 0 ist, und 2, wenn x größer als 0 oder nicht definiert ist.

Für die Aussage 1 t Wahrheitswert 1, wenn x kleiner oder gleich 1 ist, und 2, wenn x größer als 1 ist.

x (x = Variable) gilt der

[piecewise] 0 :X, 1 , 2 w oder

1 1 c 2 ef 0 :Xw

1 1 c 2 ef 1 :X c 1 <Xw

Winkelsymbol (∠)

Verwenden Sie dieses Symbol (Winkelsymbol, Versor), um die Koordinatenformatierung zu beschreiben, die für einen Winkel in einem Betrag erforderlich ist. Sie können dieses Symbol nur für Polarkoordinaten verwenden.

Problemstellung Tastenfolge

Die Polarkoordinaten kartesische Koordinaten umwandeln. [1, 1]

r = '2 ,

= π /4 in

[Angle]-Einstellung in „Radian“ (Bogenmaß) ändern. [toRect] [5 2 e,~7/ 4 )]w

Ableitungssymbol (’)

Ein einzelnes Ableitungssymbol zeigt die erste Ableitung eines Terms an, wie nachfolgend dargestellt: <Variablenname>’.

Problemstellung Tastenfolge

Die Differenzialgleichung {y = 0,5 · x2 + const (1)}

y’ = x lösen.

+Y'=X,X,Yw

Wichtig!

Die „dSolve“-Funktion kann Differentialgleichungen bis dritten Grades lösen, weshalb maximal drei Ableitungssymbole (y’’’) verwendbar sind. Bei Ausführung einer „dSolve“-Berechnung mit mehr als drei Ableitungssymbolen erhalten Sie einen „Invalid Syntax“-Fehler.

Primalitätstest (isPrime)

Die „isPrime“-Funktion ermittelt, ob die als Argument gegebene Zahl eine Primzahl (ergibt TRUE) oder keine Primzahl (ergibt FALSE) ist. Für die „isPrime“-Funktion gilt die folgende Syntax.

isPrime(Exp/List[ ) ]

• Exp oder alle Elemente von „List“ müssen Ganzzahlen sein.

Kapitel 2: Main-Menü 57

Problemstellung Tastenfolge

Ermitteln, ob die Zahlen 51 und 17 Primzahlen sind.

[isPrime] { 51 , 17 })w

(isPrime({51, 17})

Gleichheits- und Ungleichheitszeichen (=, ≠, <, >, s, t)

Sie können diese Symbole zur Durchführung verschiedener grundlegender Rechnungen verwenden.

Problemstellung Tastenfolge

Addieren von 3 zu beiden Seiten von x + 3 = 6

x = 3.

(X= 3 )+ 3 w

Subtrahieren von 2 von beiden Seiten von y – 2 s 3

y s 5.

(Y ; 5 )- 2 w

Tipp

• In den „Syntax“-Erläuterungen zu den einzelnen Befehlen unter „2-7 Verwenden des Aktionsmenüs“ sind die folgenden

Operatoren als „Eg/Ineq“ angegeben: =, ≠, <, >, s, t. Ob die „Eq/Ineq“-Operatoren den „≠“-Operator umfassen oder nicht, ist für jeden Befehl in einem separaten Hinweis angegeben.

• Eine Aussage, die mehrere Gleichheits- oder Ungleichheitsoperatoren enthält, kann nicht als einzelner Term eingegeben

werden. Als Ergebnisanzeige kann ein Term mit mehreren Operatoren nur im Falle von Ungleichheitsoperatoren ausgegeben werden, die in die gleiche Richtung weisen (Beispiel: –1 <

x < 1).

Beispiel: solve(x2 – 1 < 0, x) w {–1 < x < 1}

„with“-Operator ( | )

Der „with“-Operator ( I ) ordnet temporär einer Variablen einen Wert zu. Sie können den „with“-Operator in folgenden Fällen verwenden:

• Um den rechts von I beschriebenen Wert der links von | stehenden Variablen zuzuordnen

• Um den Zahlenbereich einer Variablen links von | in Abhängigkeit von den rechts von | stehenden

Bedingungen zu begrenzen oder vorzugeben

Nachfolgend ist die Syntax für den „with“ ( I )-Operator aufgeführt.

Exp/Eq/Ineq/List/Mat|Eq/Ineq/List/(„and“-Operator) Sie können mehrere Bedingungen in eine Liste eintragen oder mit dem „and“-Operator auf der rechten Seite

verbinden. „⫽“ kann auf der linken oder der rechten Seite von | verwendet werden.

Problemstellung Tastenfolge

+ x + 1 berechnen, wenn x = 3 gilt. 13

– 1 = 0 den Wert von x berechnen,

Für

X{ 2 +X+ 1 UX= 3 w .X{ 2 - 1 = 0 ,X)UX> 0 w

wenn x > 0 ist. {x = 1}

– 1 = 0 den Wert von x berechnen, wenn −2

Für < x < 2 ist. { x = −1, x = 1}

Den Wert von abs (

x) berechnen,

.X{ 2 - 1 = 0 ,X)U

- 2 <XpandpX< 2 w 4XeUX> 0 w

wenn x > 0 ist. x

Kapitel 2: Main-Menü 58

Vom ClassPad unterstützte Ergebnisanzeigen (TRUE, FALSE, Undefined, No Solution, ∞, const, constn)

Anzeige Beschreibung Beispiel

TRUE Anzeige, wenn das Ergebnis wahr ist. FALSE Anzeige, wenn das Ergebnis falsch ist. Undefined Anzeige, wenn das Ergebnis nicht definiert ist. No Solution Anzeige, wenn kein Ergebnis vorhanden ist.

∞

const Eine Konstante wird als const(1) angezeigt, wenn ein

constn Eine Konstante wird als constn(1) angezeigt, wenn ein

Unendlich

im Ergebnis enthaltener Wert konstant ist. Im Falle von mehreren Konstanten werden diese mit const(1), const(2) usw. bezeichnet.

im Ergebnis enthaltener Wert ganzzahlig ist. Im Falle von mehreren Konstanten werden diese mit constn(1), constn(2) usw. bezeichnet.

judge (1 = 1) w judge (1 < 0) w 1/0 w solve (abs ( lim (1/ dSolve (

{ y = 0.5·x2 + const (1)}

[Angle]-Einstellung in „Degree“ (Altgrad) ändern. solve (sin ( {x = 180·constn (1)}

x) = –1, x) w

, x, 0) w

y = x, x, y) w

x) = 0, x) w

Dirac-Delta-Distribution

„delta“ bezeichnet die Dirac-Delta-Distribution. Die Delta-Distribution evaluiert numerisch, wie nachstehend dargestellt.

(x) =



{

(x),

= 0

Nicht-numerische Terme, die in die Delta-Distribution übertragen werden, bleiben nicht-evaluiert. Das Integral einer linearen Delta-Distribution ist eine Heaviside-Funktion.

Syntax: delta(

x : Variable oder Zahl

0210 (Berechnungsbeispiel-Screenshot)

n -te Delta-Distribution

Die n-te Delta-Distribution ist das n-te Differential der Delta-Distribution.

Syntax: delta(

0211 (Berechnungsbeispiel-Screenshot)

Heaviside-Sprungfunktion

„heaviside“ ist der Befehl für die Heaviside-Funktion, die nur wie nachstehend gezeigt zu numerischen Termen evaluiert.

H(x) =

x, n) x : Variable oder Zahl n : Anzahl von Differentialen

, x = 0

Jeder an die Heaviside-Funktion weitergeleitete nicht-numerische Term wird nicht evaluiert, und jeder numerische Term, der komplexe Zahlen enthält, wird undefiniert zurückgegeben. Die Ableitung der HeavisideFunktion ist die Delta-Distribution.

Kapitel 2: Main-Menü 59

Syntax: heaviside(x)

x : Variable oder Zahl

0212 (Berechnungsbeispiel-Screenshot)

Gamma-Funktion

Die Gamma-Funktion heißt am ClassPad „gamma“.

+∞

x–1

–t

Γ(x) =

Für eine Ganzzahl n wird Gamma wie nachstehend evaluiert.

∫

(n – 1) !,

(n) =

{

undefined, n

Gamma ist für alle reellen Zahlen mit Ausnahme von Null und negativen Ganzzahlen definiert. Gamma ist auch für alle komplexen Zahlen definiert, wo entweder der reelle oder der imaginäre Teil der komplexen Zahl keine Ganzzahl ist. Gamma eines symbolischen Terms kehrt nicht-evaluiert zurück.

Syntax: gamma(

x : Variable oder Zahl

0213 (Screenshots für Berechnungs- und Grafik-Beispiele)

2-4 Listenberechnungen

Dieser Abschnitt beschreibt, wie Sie Listendaten eingeben und grundlegende Listenberechnungen ausführen.

Eingeben von Listendaten in den Arbeitsbereich

0214 Eingeben der Liste {1, 2, 3} und Zuordnen dieser Liste zu der LIST-Variablen „lista“ im Arbeitsbereich

des Main-Menüs

Operationen mit den Elementen einer LIST-Variablen

Sie können den Wert eines beliebigen Elements einer LIST-Variablen aufrufen. Sie können auch einen Wert einem beliebigen Element in einer Liste zuordnen.

0215 Aufrufen des zweiten Elements der LIST-Variablen „lista“ von Beispiel 0214

0216 Zuordnen von „5“ zum zweiten Element von „lista“

Verwenden einer Liste für eine Berechnung

Sie können arithmetische Operationen zwischen zwei Listen, zwischen einer Liste und einem numerischen Wert, oder zwischen einer Liste und einem Term, einer Gleichung oder Ungleichung ausführen.

Wichtig!

• Wenn Sie eine arithmetische Operation zwischen zwei Listen ausführen, müssen beide Listen die gleiche Anzahl an Elementen aufweisen. Anderenfalls kommt es zu einem Fehler.

• Es kommt auch zu einem Fehler, wenn eine Operation zwischen zwei beliebigen Elementen von zwei Listen zu einem Fehler führt.

Kapitel 2: Main-Menü 60

0217 Ausführen der Operation list3 × {6, 0, 4} aus, wobei list3 die Werte {41, 65, 22} enthält

Verwenden einer Liste für die Zuordnung verschiedener Werte zu vielfachen Variablen

Gehen Sie wie in diesem Abschnitt beschrieben vor, wenn Sie eine Liste verwenden möchten, um vielfachen Variablen mehrere verschiedene Werte zuzuordnen.

Syntax: Liste mit Zahlen S Liste mit Variablen

0218 Zuordnen der Werte 10, 20 und 30 zu den

x, y bzw. z

2-5 Matrizen- und Vektorrechnung

Dieser Abschnitt erläutert, wie Sie Matrizen erstellen und wie Sie die grundlegende Matrizenrechnung ausführen können.

Tipp: Da ein Vektor als eine Matrix mit 1 Zeile und n Spalten (Zeilenvektor) oder als eine Matrix mit n Zeilen und 1 Spalte

(Spaltenvektor) angesehen werden kann, enthält dieser Abschnitt keine speziellen Erläuterungen zu Vektoren. Weitere Informationen über die Vektorrechnung finden Sie in den Erläuterungen zu den betreffenden Optionen des [Action]-Menüs unter „2-7 Verwenden des Aktionsmenüs“.

Eingeben von Matrixdaten

Sie können Matrixwerte in einer einzigen Zeile des Arbeitsbereichs eingeben, oder Sie können Matrixwerte unter Verwendung einer tatsächlichen On-Screen-Matrix eingeben.

Eingeben von Matrixwerten in einer einzigen Zeile

0219 Eingeben der Matrix

des Main-Menüs

1 2 3 4

und Zuordnen dieser Matrix zu der Variablen „mat1“ im Arbeitsbereich

Operationen mit den Elementen einer Matrix-Variablen

Sie können den Wert eines beliebigen Elements einer Matrix-Variablen aufrufen. Sie können auch einem beliebigen Element in einer Matrix einen Wert zuordnen.

0220 Aufrufen des Werts in Zeile 2, Spalte 1 der Matrix-Variablen „mat1“ aus Beispiel 0219

0221 Zuordnen des Wertes 5 zu dem Element in Zeile 1, Spalte 2 von „mat1“

Eingeben der Matrixwerte unter Verwendung einer tatsächlichen On-Screen-Matrix

• Erstellen einer neuen Matrix mit 1 Zeile × 2 Spalten .................................................................................6

• Erstellen einer neuen Matrix mit 2 Zeilen × 1 Spalte .................................................................................7

• Erstellen einer neuen Matrix mit 2 Zeilen × 2 Spalten .............................................................................. 8

• Hinzufügen einer Spalte zur aktuell angezeigten Matrix ............................................................................ 6

• Hinzufügen einer Zeile zur aktuell angezeigten Matrix .............................................................................. 7

• Hinzufügen einer Zeile und einer Spalte zur aktuell angezeigten Matrix ................................................... 8

0222 Eingeben der Matrix

1 2 3 4 5 6

und Zuordnen dieser Matrix zu der Variablen „mat2“

Kapitel 2: Main-Menü 61

Ausführen der Matrizenrechnung

Dieser Abschnitt enthält Beispiele für die Ausführung der elementaren Rechenoperationen der Matrizenrechnung.

Addition, Subtraktion, Multiplikation und Potenzieren von Matrizen

0223 Berechnen von

0224 Berechnen von

0225 Multiplizieren der Matrix

1 1 2 1

2 3

2 1

2 3

2 1

1 2 3 4

in einer einzigen Zeile

unter Verwendung einer tatsächlichen On-Screen-Matrix

mit 5

Potenzieren einer Matrix

Beispiel: Erheben von

0226 Eingeben in einer einzigen Zeile

0227 Eingeben unter Verwendung einer tatsächlichen On-Screen-Matrix

1 2 3 4

zur 3. Potenz

Tipp: Sie können nur quadratische Matrizen potenzieren. Es kommt zu einem Fehler, wenn Sie versuchen, eine nicht

quadratische Matrix zu einer bestimmten Potenz zu erheben.

Verwenden einer Matrix für die Zuordnung verschiedener Werte zu vielfachen Variablen

Gehen Sie wie in diesem Abschnitt beschrieben vor, wenn Sie eine Matrix verwenden möchten, um vielfachen Variablen mehrere verschiedene Werte zuzuordnen.

Syntax: Matrix mit Zahlen ⇒ Matrix mit Variablen

(Die Matrix in einer Zeile mit mehreren Spalten oder aus mehreren Zeilen mit einer Spalte bestehen.)

0228 Zuordnen der Werte 10, 20 und 30 zu den Variablen

x, y bzw. z

2-6 Vorgeben eines Zahlensystems

Bei Verwendung des Main-Menüs können Sie eine standardmäßige Zahlenbasis vorgeben (binär, oktal, dezimal, sedezimal). Außerdem können Sie zwischen Zahlensystemen umwandeln und bitweise Verknüpfungen mittels logischen Operatoren (not, and, or, xor) ausführen lassen.

Beachten Sie die folgenden Einschränkungen, die alle gelten, wenn im Main-Menü eine standardmäßige Zahlenbasis (binär, oktal, dezimal, sedezimal) vorgegeben ist.

• Sie können keine wissenschaftlichen Funktionen oder [Action]- oder [Interactive]-Menübefehle verwenden.

• Mit Ausnahme von „Ans“ (Antwortspeicher-Variable) können keine Variablen verwendet werden.

• Es können nur Ganzzahlen eingegeben werden. Ein Fehler („Invalid Syntax“) tritt auf, wenn Sie einen nichtganzzahligen Wert (wie 1,5 oder '2 ) einzugeben versuchen.

• Falls eine Berechnung ein nicht-ganzzahliges Ergebnis (bei Dezimalteil) erbringt, lässt der ClassPad automatisch die Stellen hinter dem Komma fallen. Beispielsweise ergibt die Berechnung 5 ÷ 2 bei Auswahl des Dezimalsystems das Ergebnis 2.

Kapitel 2: Main-Menü 62

• Eine Fehlermeldung wird angezeigt, falls Sie einen Wert einzugeben versuchen, der für das vorgegebene Zahlensystem ungültig ist. Nachfolgend sind die Ziffern aufgeführt, die im zutreffenden Zahlensystem verwendet werden können.

Binär: 0, 1 Oktal: 0 bis 7 Dezimal: 0 bis 9 Sedezimal: 0 bis 9, A, B, C, D, E, F

Bereiche für binäre, oktale, dezimale und sedezimale Berechnungen

• Nachfolgend sind die Anzeigekapazitäten und Zahlenbereich für jedes Zahlensystem angegeben.

Zahlensystem Anzeigekapazität Berechnungsbereich (positiv; negativ)

Binär 32 Stellen

Oktal 11 Stellen Dezimal 10 Stellen Sedezimal 8 Stellen

• Negative binäre, oktale und sedezimale Werte werden als 2-Komplement des Originalwerts dargestellt.

x s 01111111111111111111111111111111 ;

0 s 10000000000000000000000000000000 s x s 11111111111111111111111111111111

x s 17777777777 ; 20000000000 s x s 37777777777

0 s

x s 2147483647 ; −2147483648 s x s −1

0 s

x s 7FFFFFFF ; 80000000 s x s FFFFFFFF

0 s

Auswählen eines Zahlensystems

Die Festlegung eines standardmäßigen Zahlensystems im Main-Menü wirkt sich für die aktuelle Zeile (Eingabeterm/Ergebnisterm) und alle nachfolgenden Zeilen aus, bis Sie die Einstellung des Standard- Zahlensystems wieder ändern.

u Auswählen des Zahlensystems für die Zeile, in der sich der Cursor gerade befindet

1. Tippen Sie auf die Abwärtspfeil-Schaltfläche neben der <-Schaltfläche.

2. Tippen Sie auf die Schaltfläche, die dem gewünschten Zahlensystem entspricht.

1 (binär), 2 (oktal), 3 (dezimal), 4 (sedezimal).

• Das aktuell ausgewählte Zahlensystem wird in der Statusleiste angezeigt.

3. Führen Sie die Berechnung durch.

Wichtig!

• Eine Zeile, für die kein Zahlensystem vorgegeben ist, wird „normale Berechnungszeile“ genannt. Um eine Zeile wieder zu einer normalen Berechnungszeile zu machen, tippen Sie in Schritt 2 der oben beschriebenen Vorgehensweise auf <.

• Berechnungsergebnisse, die von einer Zeile mit vorgegebenem Zahlensystem erbracht wurden, sind mit einem der nachstehenden Anhangszeichen zur Kennzeichnung des Zahlensystems ausgewiesen.

Zahlensystem Binär Oktal Dezimal Sedezimal Anhangszeichen bodh

u Vorgeben eines Zahlensystems für einen Eingabewert

Sie können die folgenden Anhangszeichen eingeben, um das Zahlensystem eines Werts bei der Eingabe zu bestimmen: [b] (binär), [o] (oktal), [d] (dezimal) und [h] (sedezimal). Das Zahlensystem eines Eingabewerts kann nur festgelegt werden, wenn schon ein Standard-Zahlensystem (neben Normal) ausgewählt wurde.

Kapitel 2: Main-Menü 63

Rechenoperationen

Bei der Eingabe von binären, oktalen, dezimalen und sedezimalen Werten können Sie die folgenden Operatoren verwenden: +, −, ×, ÷, ^. Auch Klammerterme können benutzt werden.

0229 Berechnen von 10111

0230 Berechnen von (118 + 78)

+ 11010

0231 Ausführen der Berechnung 12310 + 10102 so, dass ein sedezimales Ergebnis angezeigt wird

Bitweise Verknüpfungen

Die logischen Operatoren (and, or, xor, not) können für Berechnungen eingesetzt werden.

and ...Erbringt das Ergebnis eines bitweisen Produkts.

or ......Erbringt das Ergebnis einer bitweisen Summe.

xor ....Erbringt das Ergebnis einer bitweisen exklusiven logischen Summe.

not ....Erbringt das Ergebnis eines Komplements (bitweise Inversion).

0232 Berechnungsbeispiele

Verwenden der baseConvert-Funktion (Zahlbasiswechsel)

Mit der baseConvert-Funktion können Sie eine Zahl einer bestimmten Basis (Zahlensystem) in ihr Äquivalent in einer anderen Schreibweise umwandeln.

Wichtig!

• Die baseConvert-Funktion funktioniert nur bei positiven Ganzzahlen.

• Die baseConvert-Funktion kann nicht in einer Zeile benutzt werden, für die ein bestimmtes Zahlensystem vorgegeben ist. Sie kann nur in einer normalen Berechnungszeile verwendet werden.

Syntax: baseConvert (Zahl, Quellbasis, Zielbasis)

• Die Zahl muss eine positive Ganzzahl aus den Ziffern 0 bis 9 und/oder A bis F sein.

• Die Quellbasis und die Zielbasis kann jede ganze Zahl zwischen 2 und 16 sein.

0233 Berechnungsbeispiele

2-7 Verwenden des Aktionsmenüs

Das [Action]-Menü hilft in Ihnen in einfacher Weise, die Transformations- und Expansionsfunktionen, die Differenzial- und Integralfunktionen, die statistischen Funktionen und andere häufig verwendete mathematische Menü-Operationen zu verwenden. Wählen Sie einfach die gewünschte Funktion aus, und geben Sie anschließend die Terme oder Variablen entsprechend der Syntax der Funktion ein.

Tipp

• Wenn nicht speziell anders aufgeführt, werden alle in diesem Abschnitt beschriebenen Vorgänge unter Verwendung der folgenden Modi ausgeführt: Algebramodus, Standardmodus, Komplexer Modus, Bogenmaßmodus, abfallende Reihenfolge.

• Über das [Interactive]-Menü können Sie die meisten Befehle benutzen, die im [Action]-Menü verfügbar sind. Näheres zur Verwendung des [Interactive]-Menüs siehe Seite 96.

Kapitel 2: Main-Menü 64

In diesem Abschnitt verwendete Abkürzungen und Interpunktionen

Nachfolgend sind die Bedeutungen der in den Syntaxbeschreibungen dieses Abschnitts verwendeten Abkürzungen und Interpunktionen erläutert.

Exp: Term (Wert, Variable usw.) List: Liste Eq: Gleichung Mat: Matrix

Ineq: Alle Typen von Ungleichungen (a>b, atb, a<b, asb, ab) Ineqⴝ: Nur Ungleichung ab [ ]: Sie können den (die) Eintrag (Einträge) in den eckigen Klammern weglassen. { }: Wählen Sie einen der Einträge in den geschweiften Klammern.

Manche der Syntaxen in den folgenden Erläuterungen geben Folgendes für die Parameter an:

Exp/Eq/Ineq/List/Mat

Diese Abkürzungen bedeuten, dass Sie jeden der folgenden Einträge als Parameter verwenden können: Term, Gleichung, Ungleichung, Liste oder Matrix.

Screenshot-Beispiele

Die nachfolgenden Screenshots zeigen Beispiele, wie die ein- und ausgegebenen Terme auf dem Display des ClassPad erscheinen. Alle Screenshots in diesem Abschnitt zeigen die Version des „vollständigen Terms“ an.

Wenn der eingegebene Term nicht in die Anzeige passt:

Angezeigter Term

Wenn der ausgegebene Term nicht in die Anzeige passt:

Angezeigter Term

Vollständiger Term

Verwenden des Untermenüs für Transformationen

Das [Transformation]-Untermenü enthält Befehle für die Transformation von Termen, wie zum Beispiel „expand“ und „factor“.

u approx [Action][Transformation][approx]

Funktion: Transformiert einen Term in eine approximative numerische Darstellung. Syntax: approx (Exp/Eq/Ineq/List/Mat [ ) ] Beispiel: Angeben des numerischen Werts von '2

u simplify [Action][Transformation][simplify]

Funktion: Vereinfacht einen Term. Syntax: simplify (Exp/Eq/Ineq/List/Mat [ ) ] Beispiel: Vereinfachen des Terms (15'3 + 26)^(1/3)

Kapitel 2: Main-Menü 65

u expand [Action][Transformation][expand]

Funktion: Expandiert einen Term. Syntax: expand (Exp/Eq/Ineq/List/Mat [ ) ]

expand (Exp,Variable [ ) ]

• Falls Sie eine Variable angeben, wird Exp unter Bezug auf die Variable in

einen Partialbruch zerlegt.

Beispiel: Expandieren des Terms (

x + 2)

u factor [Action][Transformation][factor][factor]

Funktion: Faktorisiert einen Term. Syntax: factor (Exp/Eq/Ineq/List/Mat [ ) ]

Beispiel: Faktorisieren des Terms

 4x + 4

u rFactor [Action][Transformation][factor][rFactor]

Funktion: Faktorisiert einen Term bis hin zu dessen Wurzeln, sofern vorhanden. Syntax: rFactor (Exp/Eq/Ineq/List/Mat [ ) ]

Beispiel: Faktorisieren des Terms

 3

u factorOut [Action][Transformation][factor][factorOut]

Funktion: Ermittelt die Faktoren eines Terms hinsichtlich eines bestimmten Faktors. Syntax: factorOut (Exp/Eq/Ineq/List/Mat, Exp [ ) ]

Beispiel: Ausklammern des Faktors „a“ des Polynoms a

+ bx + c

u combine [Action][Transformation][combine]

Funktion: Transformiert mehrere Brüche in gleichwertige Brüche mit gemeinsamem Nenner (Hauptnenner)

und kürzt diese, wenn möglich. Syntax: combine (Exp/Eq/Ineq/List/Mat [ ) ] Beispiel: Zusammenfassen und Kürzen von (

x + 1)/(x + 2) + x(x + 3)

u collect [Action][Transformation][collect]

Funktion: Ordnet einen Term neu hinsichtlich einer bestimmten Variablen. Syntax: collect (Exp/Eq/Ineq/List/Mat[,Exp] [ ) ]

• „

x“ ist die Standard-Vorgabe, wenn Sie „[,Exp]“ weglassen.

Beispiel: Neuordnen von

+ ax + bx hinsichtlich x

u tExpand [Action][Transformation][tExpand]

Funktion: Verwendet die trigonometrischen Summen- und Differenzformeln (Additionstheoreme), um eine

trigonometrische Funktion zu zerlegen. Syntax: tExpand(Exp/Eq/Ineq/List/Mat [ ) ] Beispiel: Expandieren von sin (a + b)

Kapitel 2: Main-Menü 66

u tCollect [Action][Transformation][tCollect]

Funktion: Verwendet die Produkt- und Summenformeln, um das Produkt einer trigonometrischen Funktion in

einen Term in Summenform zu transformieren. Syntax: tCollect (Exp/Eq/Ineq/List/Mat [ ) ] Beispiel: Transformieren von cos(a) × cos(b) in einen Term in Summenform

u expToTrig [Action][Transformation][expToTrig]

Funktion: Transformiert eine exponentielle Darstellung in eine trigonometrische oder hyperbolische

Darstellung. Syntax: expToTrig (Exp/Eq/Ineq/List/Mat [ ) ]

Beispiel: Transformieren von

(Bogenmaßmodus)

in die trigonometrische Darstellung

u trigToExp [Action][Transformation][trigToExp]

Funktion: Transformiert eine trigonometrische oder hyperbolische Darstellung in die exponentielle

Darstellung. Syntax: trigToExp (Exp/Eq/Ineq/List/Mat [ ) ] Beispiel: Transformieren von cosh

x in die Exponentialdarstellung

u toFrac [Action][Transformation][Fraction][toFrac]

Funktion: Transformiert eine Dezimalzahl in ihre gleichwertige Bruchzahl. Syntax: toFrac (Exp/Eq/Ineq/List/Mat [ ) ] Beispiel: Umformen von 5,28 in den gleichwertigen unechten Bruch

u propFrac [Action][Transformation][Fraction][propFrac]

Funktion: Zerlegt eine Dezimalzahl oder eine gebrochen rationale Funktion in ihren ganzzahligen

(ganzrationalen) Anteil und einen echten Bruch (echt gebrochen rationaler Anteil). Syntax: propFrac (Exp/Eq/Ineq/List/Mat [ ) ] Beispiel: Zerlegen von 1,2 in den ganzzahligen Anteil und den gebrochenen

Rest als echten Bruch

u dms [Action][Transformation][DMS][dms]

Funktion: Transformiert eine Altgrad/Minuten/Sekunden-Darstellung (DMS) in

die gleichwertige Darstellung in Altgrad. Syntax: dms (Exp/List-1 [,Exp/List-2][,Exp/List-3] [ ) ] Beispiel: Transformieren von 3° 5’ 6” in die gleichwertige Altgraddarstellung

• Null ist die Standard-Vorgabe, wenn [,Exp/List-2] oder [,Exp/List-3][ ) ]

weggelassen wird.

Tipp: Sie können 3° 5’ 6” unter Verwendung der /-Taste auf der Software-Tastatur

eingeben.

/e 3 e 5 e 6 E

Kapitel 2: Main-Menü 67

u toDMS [Action][Transformation][DMS][toDMS]

Funktion: Transformiert eine Altgraddarstellung in eine gleichwertige Darstellung im Altgrad/Minuten/

Sekunden-Format. Syntax: toDMS (Exp/List [ ) ] Beispiel: Transformieren von 3,085 Altgrad in die gleichwertige Darstellung im

Altgrad/Minuten/Sekunden-Format

Verwenden des Advanced-Untermenüs

u solve [Action][Advanced][solve]

Informationen über solve finden Sie auf Seite 85.

u dSolve [Action][Advanced][dSolve]

Informationen über dSolve finden Sie auf Seite 87.

u taylor [Action][Advanced][taylor]

Funktion: Findet ein Taylor-Polynom für einen Term bezüglich einer bestimmten Variablen. Syntax: taylor (Exp/List, Variable, Ordnung [,Mittelpunkt] [ ) ] Beispiel: Suchen nach einem Taylor-Polynom fünfter Ordnung für sin(

bezüglich x an der Stelle x = 0 (im Bogenmaßmodus)

• Null ist die Standard-Vorgabe, wenn Sie „[,Mittelpunkt]“ (Entwicklungsstelle)

weglassen.

u laplace [Action][Advanced][laplace], invLaplace [Action][Advanced][invLaplace]

Funktion: Der Befehl für die Laplace-Transformation heißt im ClassPad

„laplace“, und der Befehl für die inverse Laplace-Transformation

heißt im ClassPad „invLaplace“. Syntax:

laplace(

f ( t): Formelterm, Originalfunktion

f ( t), t, s)

t: Variable, bezüglich der der Term transformiert

wird

s: Parameter der Transformation

Der ClassPad unterstützt die Transformation der folgenden Funktionen.

x), cos(x), sinh(x), cosh(x), x

sin( Der ClassPad unterstützt nicht die Transformation der folgenden Funktionen.

tan(

x), sin

– 1

(x), cos

– 1

(x), tan

, 'x, ex, heaviside(x), delta(x), delta(x, n)

– 1

(x), tanh(x), sinh

– 1

(x), cosh

invLaplace(

L(s), s, t)

L(s): Formelterm, Bildfunktion s: Variable, bezüglich der der Term transformiert

wird

t: Parameter der Transformation

– 1

(x), tanh

– 1

(x), log(x), ln(x), 1/x, abs(x), gamma(x)

∞

∫

f(t)e

–st

dtL[ f(t)] (s)=

Laplace-Transformation einer linearen Differenzialgleichung

Der „laplace“-Befehl kann zur Lösung gewöhnlicher Differenzialgleichungen herangezogen werden. Der ClassPad unterstützt mit dem „laplace“ -Befehl jedoch nicht die Lösung eines Systems von Differenzialgleichungen.

Syntax: laplace(diff eq, x, y, t)

diff eq: zu lösende Differenzialgleichung; x: unabhängige Variable in der diff eq (Differenzialgleichung); y: abhängige Variable in der diff eq (Differenzialgleichung); t: Parameter der Transformation (unabhängige Variable der Bildfunktion)

Kapitel 2: Main-Menü 68

Beispiel: Lösen einer Differenzialgleichung

Verwendung der Laplace-Transformation

F(s) = L[ f ( t)] im Ergebnis der Transformation für eine

Lp ist Differenzialgleichung.

x’ + 2x = e

−

, wo x(0) = 3 unter

u fourier [Action][Advanced][fourier], invFourier [Action][Advanced][invFourier]

Funktion: „fourier“ ist der Befehl für die Fourier-Transformation, und „invFourier“ ist der Befehl für die inverse

Fourier-Transformation. Syntax: fourier(

f ( x), x, w, n) invFourier(F ( w), w, x, n)

x: Variable, bezüglich der der Term transformiert wird; w: Parameter der Transformation; n: 0 bis 4,

bezeichnet den zu verwendenden Fourier-Parameter (optional)

Der ClassPad unterstützt die Transformation der folgenden Funktionen. sin(t), cos(t), log(t), ln(t), abs(t), signum(t), heaviside(t), delta(t), delta(t,n), e

Der ClassPad unterstützt nicht die Transformation der folgenden Funktionen. tan(t), sin

Die Fourier-Transformation ist wie folgt definiert:

Manche Autoren (insbesondere Physiker) ziehen es vor, die Transformation mit der Winkelfrequenz ω ≡ 2π anstatt mit der Schwingungsfrequenz  darzustellen.

Dies zerstört allerdings die Symmetrie der Formeln und wird im nachstehenden Transformationspaar beschrieben.

Um die Symmetrie der Transformation wiederherzustellen, wird manchmal die nachstehende Definition verwendet.

– 1

(t), cos

() =

– 1

(t), tan

∞

∫

–∞

– 1

()

(ω) = [()] =

() = [ ()] =

(t), sinh(t), cosh(t), tanh(t), sinh

–2π

∫

–∞



∞

∫

()

∞

()

–∞

–ω



–



() =

() = –1[(ω)] =

() = –1[()] =

– 1

(t), cosh

∫

–∞

∞

()

– 1

(t), tanh

2π

– 1

(t), gamma(t), 't , e



∞

∫

–∞

∞

()

∫

–∞

(ω)



ω



ω

Die Fourier-Transformationspaare werden mit zwei willkürlichen Konstanten a und b definiert, wie unten dargestellt.

1–

∞

∫

–∞

()

ω



() =

⏐

⏐

π)

1+

∞

(ω)

∫

–∞

Kapitel 2: Main-Menü 69

–ω

ω

⏐

(ω) =

Die Werte von a und b sind durch das Wissenschaftsgebiet bestimmt, in dem die Fourier-Transformation zur Anwendung kommen soll. Dazu dient der Wert von n (optionaler vierter Parameter für Fourier und invFourier zur Festlegung der gewünschten Variante der Fourier-Transformation), der wie folgt vorgegeben werden kann.

Es sind eine ganze Reihe von Varianten der schnellen Fouriertransformation in Gebrauch. Mit den Parametern Physik benutzt, (1, –1) wird in der reinen Mathematik benutzt, (1, 1) wird in der Stochastik für die Berechnung der charakteristischen Funktionen benutzt, (–1, 1) wird in der klassischen Physik benutzt, und (0, –2π) wird in der Signalverarbeitung benutzt.

a und b wird diesem Umstand Rechnung getragen. Beispielsweise wird (0, 1) in der modernen

⏐

π)

Transformationsdefinition

Modern Physics (Moderne Physik) 0 0 1 Pure Math (Reine Mathematik) 1 1 –1 Probability (Stochastik) 2 1 1 Classical Physics (Klassische Physik) 3 –1 1 Signal Processing (Signalverarbeitung) 4 0

n (optional) ab

–2π

Tipp: Das Zusätzliches-Format-Dialogfeld kann zur Konfiguration der Einstellungen bezüglich der Fourier-Transformation

verwendet werden, wie z. B. für eine Fourier-Transformationsdefinition. Näheres hierzu finden Sie unter „Zusätzliches-Format-Dialogfeld“ auf Seite 42.

u FFT [Action][Advanced][FFT], IFFT [Action][Advanced][IFFT]

Funktion: „FFT“ ist der Befehl für die schnelle Fourier-Transformation, und „IFFT“ ist der Befehl für die inverse

schnelle Fourier-Transformation. Für die Durchführung von FFT und IFFT sind 2n-Datenwerte

erforderlich. Im ClassPad werden die Befehle FFT und IFFT numerisch ausgeführt. Syntax: FFT(list) oder FFT(list,

• Der Datenumfang muss 2

• Der Wert von Parameter an (Auswahl einer FFT-Variante): 0 (Signalverarbeitung), 1 (Reine Mathematik), 2 (Datenanalyse).

FTT und IFFT sind wie folgt definiert:

() =

m ist optional. Er kann zwischen 0 und 2 liegen und gibt den zu verwendenden FFT-

−1

()

∑

=0

m) IFFT(list) oder IFFT(list, m)

mit n = 1, 2, 3, ... betragen.

2π

–——



() =



−1

∑

=0

()

2π

——



Tipp: Das Zusätzliches-Format-Dialogfeld kann zur Konfiguration der Einstellungen bezüglich der schnellen Fourier-

Transformation verwendet werden. Näheres hierzu finden Sie unter „Zusätzliches-Format-Dialogfeld“ auf Seite 42.

Verwenden des Untermenüs für Berechnungen

Das [Calculation]-Untermenü enthält Berechnungsbefehle wie „diff“ (Differenzial, Ableitung) und „ “ (Integration).

u diff [Action][Calculation][diff]

Funktion: Berechnet die Ableitung eines Terms hinsichtlich einer bestimmten Variablen. Syntax: diff(Exp/List[,Variable] [ ) ]

diff(Exp/List,Variable,Ordnung[,a] [ ) ]

• „a“ ist die Stelle, an der Sie die Ableitung bestimmen möchten.

• „Ordnung“ = 1, wenn Sie die folgende Syntax verwenden: diff(Exp/List[,Variable][ ) ]. Die Vorgabe-Variable ist „

x“, wenn „Variable“ weggelassen wird.

Beispiel: Berechnen der ersten Ableitung von

bezüglich von x

u impDiff [Action][Calculation][impDiff]

Funktion: Berechnet die Ableitung eines Terms in impliziter Form hinsichtlich

einer bestimmten Variablen. Syntax: impDiff(Eq/Exp/List, unabhängige Variable, abhängige Variable) Beispiel: Ermitteln von

y’ mittels impliziter Ableitung

Wichtig!

Das Ableitungssymbol (’) ist im Argument von „impDiff(“ nicht verwendbar. Der Versuch, ein Ableitungssymbol zu verwenden, ergibt einen „Wrong Argument Type“-Fehler.

Kapitel 2: Main-Menü 70

∫

[Action][Calculation][  ]

Funktion: Berechnet das Integral für einen Term bezüglich einer bestimmten Variablen. Syntax:

 (Exp/List[,Variable] [ ) ]  (Exp/List, Variable, untere Grenze, obere Grenze [,tol ] [ ) ]

• „

x“ ist die Standard-Vorgabe, wenn Sie [,Variable] weglassen.

• „

tol“ ist der zulässige Fehler bei einer numerischen Integration.

• Dieser Befehl liefert einen approximativen Integralwert, wenn für „

• Dieser Befehl liefert den numerisch exakten Integralwert über einem definierten Intervall, wenn für

„

tol“ nichts vorgegeben ist. Falls ein exakter Wert nicht erhalten werden kann, führt dieser Befehl eine

Näherungsberechnung mit tol = 1E – 5 durch. Falls ein Näherungswert erhalten werden kann, wird dieser Wert ausgegeben. Eine Fehlermeldung wird ausgegeben, wenn ein Näherungswert nicht erhalten werden kann oder wenn Berechnung selbst aus irgendeinem Grund unmöglich ist.

Beispiel: Unbestimmtes Integrieren von x bezüglich x

tol“ eine Fehlerschranke vorgegeben wird.

u lim [Action][Calculation][lim]

Funktion: Bestimmt den Grenzwert eines Terms. Syntax: lim (Exp/List, Variable, Punkt [,Richtung] [ ) ]

−

Beispiel: Bestimmen des Grenzwerts von

• Diese Funktion liefert den Grenzwert von links, wenn der „Richtungs“-Parameter < 0 ist, den Grenzwert von

rechts, wenn der „Richtungs“-Parameter > 0 ist, und den Grenzwert von beiden Seiten (links und rechts), wenn der „Richtungs“-Parameter = 0 ist oder weggelassen wird.

, wenn x gegen ∞ strebt

uΣ [Action][Calculation][Σ]

Funktion: Interpretiert die Variable in einem Term als diskrete Variable innerhalb eines Lauf-Bereichs und berechnet dann die Summe.

Syntax: Σ(Exp/List, Variable, unterer Wert, oberer Wert [ ) ]

Beispiel: Berechnen der Summe aller

läuft

, wenn der Wert x von x = 1 bis x =10

uΠ [Action][Calculation][Π]

Funktion: Interpretiert die Variable in einem Term als diskrete Variable innerhalb eines Lauf-Bereichs und

berechnet dann das Produkt. Syntax: Π(Exp/List, Variable, unterer Wert, oberer Wert [ ) ]

Beispiel: Berechnen des Produkts von

läuft

, wenn der Wert x von x = 1 bis x = 5

u rangeAppoint [Action][Calculation][rangeAppoint]

Funktion: Sucht nach einem Term oder Wert, die eine vorgegebene Intervall-Bedingung erfüllen. Syntax: rangeAppoint (Exp/Eq/List, Anfangswert, Endwert [ ) ]

• Wenn Sie eine Gleichung (Eq) für das erste Argument verwenden, geben Sie die Gleichung mit der Syntax

Var = Exp ein. Eine Bewertung ist nicht möglich, wenn eine andere Syntax verwendet wird.

Beispiel: Suchen nach dem Gleichungsterm (den

Gleichungstermen) in der Liste { der (die) zu dem abgeschlossenen Intervall 0 s x s 5 gehört (gehören)

x = π, x = 2π, x = 3π},

Kapitel 2: Main-Menü 71

u mod [Action][Calculation][mod]

Funktion: Liefert den Restanteil, wenn ein Term durch einen anderen Term dividiert wird. Syntax: mod ({Exp/List} -1, {Exp/List} -2 [ ) ] Beispiel: Bestimmen des Restanteils, wenn 26 durch 3 dividiert wird (26mod3)

u tanLine [Action][Calculation][line][tanLine]

Funktion: Liefert den Formelterm der Gleichung für die Tangente (y = ‘Formelterm’) an einem bestimmten

Punkt der Kurve. Syntax: tanLine (Exp/List, Variable, Variablenwert am Tangentenpunkt [ ) ]

y = x

Beispiel: Bestimmen der Funktionsgleichung für die Tangente an

wenn x = 2 ist

u normal [Action][Calculation][line][normal]

Funktion: Liefert den Formelterm der Gleichung für die Normale (y ‘Formelterm’) an einem bestimmten Punkt

der Kurve. Syntax: normal (Exp/List, Variable, Variablenwert am Punkt der Normalen [ ) ]

y = x

Beispiel: Bestimmen der Funktionsgleichung der Normalen auf

wenn x = 2 ist

u arcLen [Action][Calculation][line][arcLen]

Funktion: Berechnet mithilfe des Formelterms die Bogenlänge einer Kurve von einem Anfangswert bis zu

einem Endwert bezüglich der vorgegebenen Variablen. Syntax: arcLen (Exp/List, Variable, Anfangswert, Endwert [ ) ]

3 2

y = x

Beispiel: Bestimmen der Bogenlänge für die Kurve

von x = 0 bis x = 4

u fMin [Action][Calculation][fMin/fMax][fMin], fMax [Action][Calculation][fMin/fMax][fMax]

Funktion: Liefert den Minimumpunkt (fMin) / Maximalpunkt (fMax) einer Funktion in einem bestimmten

Intervall. Syntax: fMin(Exp[,Variable] [ ) ]

fMin(Exp, Variable, Anfangswert, Endwert[,

n] [ ) ]

fMax(Exp[,Variable] [ ) ] fMax(Exp, Variable, Anfangswert, Endwert[,

• „

x“ ist die Standard-Vorgabe, wenn Sie [,Variable] weglassen.

n] [ ) ]

• Ein negatives Unendlich und ein positives Unendlich sind die Standard-Vorgaben, wenn die Syntax

fMin(Exp[,Variable] [ ) ] oder fMax(Exp[,Variable] [ ) ] verwendet wird.

• „n“ ist die Berechnungsgenauigkeit, die Sie als Ganzzahl im Bereich von 1 bis 9 vorgeben können. Die

Eingabe eines Wertes außerhalb dieses Bereichs führt zu einer Fehlermeldung.

• Dieser Befehl liefert einen approximativen Wert, wenn die Berechnungsgenauigkeit für „

• Dieser Befehl liefert einen exakten Wert, wenn für „

n“ nichts vorgegeben ist. Falls der exakte Wert nicht

n“ vorgegeben ist.

erhalten werden kann, liefert dieser Befehl jedoch den approximativen Wert mit der Berechnungsgenauigkeit

n = 4.

• Unstetigkeitsstellen oder Abschnitte mit großen Schwankungen der Funktionswerte können die Genauigkeit

beeinträchtigen und sogar zu einem Fehler führen.

• Durch die Eingabe einer größeren Zahl für „

auch die für die Ausführung der Berechnung erforderliche Zeitdauer zunimmt.

• Der für den Endpunkt des Intervalls eingegebene Wert muss größer als der für den Anfangspunkt

eingegebene Wert sein. Andernfalls kommt es zu einer Fehlermeldung.

n“ wird die Genauigkeit der Berechnung erhöht, wobei jedoch

Kapitel 2: Main-Menü 72

Beispiel: Suchen nach dem Minimumpunkt von x2 – 1 bezüglich x

Beispiel: Suchen nach dem Maximalpunkt von –x2 + 1 bezüglich x

u gcd [Action][Calculation][gcd/lcm][gcd]

Funktion: Liefert den größten gemeinsamen Teiler von zwei Termen. Syntax: gcd (Exp/List-1, Exp/List-2 [ ) ] Beispiel: Ermitteln des größten gemeinsamen Teilers von

– 3x – 4

x + 1 und

u lcm [Action][Calculation][gcd/lcm][lcm]

Funktion: Liefert das kleinste gemeinsame Vielfache von zwei Termen. Syntax: lcm (Exp/List-1, Exp/List-2 [ ) ]

Beispiel: Ermitteln des kleinsten gemeinsamen Vielfachen von

+ 2x – 3

– 1 und

u denominator [Action][Calculation][fraction][denominator]

Funktion: Extrahiert den Nenner eines Bruchs oder einer gebrochen rationalen Funktion. Syntax: denominator (Exp/List [ ) ] Beispiel: Extrahieren des Nenners des Bruchs (

y – 2)/(x + 1)

u numerator [Action][Calculation][fraction][numerator]

Funktion: Extrahiert den Zähler eines Bruchs oder einer gebrochen rationalen Funktion. Syntax: numerator (Exp/List [ ) ] Beispiel: Extrahieren des Zählers des Bruchs (

y – 2)/(x + 1)

Verwenden des Untermenüs für komplexe Zahlen

Das [Complex]-Untermenü enthält Befehle, die für Berechnungen mit komplexen Zahlen verwendet werden können.

u arg [Action][Complex][arg]

Funktion: Liefert das Argument einer komplexen Zahl. Syntax: arg (Exp/Eq/List/Mat [ ) ] Beispiel: Berechnen des Arguments der komplexen Zahl 2 +

(im Bogenmaßmodus)

u conjg [Action][Complex][conjg]

Funktion: Liefert die konjugierte komplexe Zahl. Syntax: conjg (Exp/Eq/Ineq/List/Mat [ ) ] (Ineq: nur im reellen Modus) Beispiel: Bestimmen der konjugiert komplexen Zahl zur komplexen Zahl 1 +

Kapitel 2: Main-Menü 73

u re [Action][Complex][re]

Funktion: Liefert den reellen Teil einer komplexen Zahl. Syntax: re (Exp/Eq/Ineq/List/Mat [ ) ] (Ineq: nur im reellen Modus) Beispiel: Bestimmen des reellen Teils der komplexen Zahl 3 – 4

u im [Action][Complex][im]

Funktion: Liefert den imaginären Teil einer komplexen Zahl. Syntax: im (Exp/Eq/Ineq/List/Mat [ ) ] (Ineq: nur im reellen Modus) Beispiel: Bestimmen des imaginären Teils der komplexen Zahl 3 – 4

u cExpand [Action][Complex][cExpand]

Funktion: Expandiert einen komplexen Term in die arithmetische Darstellung (a + bi). Syntax: cExpand (Exp/Eq/List/Mat [ ) ]

• Die Variablen werden als reelle Zahlen angesehen. Beispiel: Angeben von cos

(im Bogenmaßmodus)

–1

(2) in arithmetischer Darstellung

u compToPol [Action][Complex][compToPol]

Funktion: Transformiert eine komplexe Zahl in die Polarform Syntax: compToPol (Exp/Eq/List/Mat [ ) ]

• Wenn das Argument „Mat“ (Matrizen) lautet, kann die Berechnung nur in der Bogenmaßeinheit ausgeführt

werden.

Beispiel: Transformieren von 1 +

Bogenmaßmodus Altgradmodus Gon-Modus

i in die Polarkoordinaten-Darstellung.

u compToTrig [Action][Complex][compToTrig]

Funktion: Transformiert eine komplexe Zahl in ihre trigonometrische/hyperbolische Form. Syntax: compToTrig (Exp/Eq/List/Mat [ ) ] Beispiel: Transformieren von 1 +

(im Bogenmaßmodus)

i in die trigonometrische Darstellung

u compToRect [Action][Complex][compToRect]

Funktion: Transformiert eine komplexe Zahl in ihre kartesische Form. Syntax: compToRect (⬔( Beispiel: Transformieren einer komplexen

Zahl in ihre kartesische Form

r,) oder r · e^( · i)-Form [ ) ]

Kapitel 2: Main-Menü 74

Verwenden des Untermenüs zur Listenerstellung

Das [List][Create]-Untermenü enthält Befehle für das Erstellen von Listen.

u seq [Action][List][Create][seq]

Funktion: Generiert eine Liste in Abhängigkeit von einem numerischen Folgenterm. Syntax: seq (Exp, Variable, Startwert, Endwert [,Schrittweite] [ ) ]

Beispiel: Generieren einer Liste mit Hilfe des Terms

Startwert 1, der Endwert 5 und die Schrittweite 2 betragen

• „1“ ist die Standard-Vorgabe, wenn Sie „[,Schrittweite]“ weglassen.

• Die Schrittweite muss ein Faktor der Differenz zwischen dem Startwert und dem Endwert sein.

u augment [Action][List][Create][augment]

Funktion: Erstellt eine neue Liste, indem eine Liste an eine andere angehängt wird. Syntax: augment (List-1, List-2 [ ) ] Beispiel: Erweitern der Liste {1, 2} durch Anfügen von Liste {3, 4}

u fill [Action][List][Create][fill]

Funktion: Ersetzt die Elemente einer Liste durch einen vorgegebenen Wert oder Term. Dieser Befehl kann

auch verwendet werden, um eine neue Liste zu erstellen, deren Elemente alle den gleichen Wert

oder Term enthalten sollen oder in der die Häufigkeit jedes Elements in der ersten Liste durch das

zugeordnete Element in der zweiten Liste (Häufigkeitsliste) bestimmt wird.

+ 2x , wenn der

Syntax: fill (Exp/Eq/Ineq, Anzahl der Elemente [ ) ]

fill (Exp/Eq/Ineq, List [ ) ] fill (List, List [ ) ]

Beispiel: Erstellen einer Liste, die aus vier identischen Elementen (2) besteht

u subList [Action][List][Create][subList]

Funktion: Extrahiert einen bestimmten Abschnitt einer Liste in eine neue Liste. Syntax: subList (List [,Startindex] [,Endindex] [ ) ] Beispiel: Extrahieren des zweiten bis vierten Elements der Liste {1, 2, 3, 4, 5}

• Das ganz linke Element (Index 1) ist die Standard-Vorgabe, wenn Sie „[,Startindex]“ weglassen, und das

ganz rechte Element ist die Standard-Vorgabe, wenn Sie „[,Endindex]“ weglassen.

u shift [Action][List][Create][shift]

Funktion: Liefert eine Liste, in der die Elemente um eine bestimmte Anzahl von Positionen nach rechts oder

links verschoben wurden. Syntax: shift (List [,Anzahl der Verschiebungen] [ ) ]

• Durch Vorgabe eines negativen Wertes für „[, Anzahl der Verschiebungen]“ erfolgt eine Verschiebung nach

rechts, durch Vorgabe eines positiven Werts eine Verschiebung nach links.

• Eine Verschiebung um eins nach rechts (–1) ist die Vorgabe, wenn Sie „[, Anzahl der Verschiebungen]“

weglassen.

Beispiel: Verschieben der Elemente der Liste {1, 2, 3, 4, 5, 6} um drei

Stellen nach links

Kapitel 2: Main-Menü 75

u rotate [Action][List][Create][rotate]

Funktion: Liefert eine Liste, in der die Elemente um einen bestimmte Anzahl von Positionen nach rechts oder

links rotiert wurden. Syntax: rotate (List [,Anzahl der Positionen der Rotation] [ ) ]

• Durch Vorgabe eines negativen Wertes für „[, Anzahl der Positionen der Rotation]“ erfolgt die zyklische

Verschiebung nach rechts, durch Vorgabe eines positiven Werts eine zyklische Verschiebung nach links.

Beispiel: Zyklisches Verschieben der Elemente der Liste {1, 2, 3, 4, 5, 6} um

zwei Stellen nach links

• Die zyklische Verschiebung um eins nach rechts (–1) ist die Standard-Vorgabe, wenn Sie „[, Anzahl der

Positionen der Rotation]“ weglassen.

u sortA [Action][List][Create][sortA]

Funktion: Sortiert die Elemente der Liste in ansteigender Reihenfolge. Syntax: sortA (List [ ) ] Beispiel: Sortieren der Elemente der Liste {1, 5, 3} in ansteigender

Reihenfolge

u sortD [Action][List][Create][sortD]

Funktion: Sortiert die Elemente der Liste in abfallender Reihenfolge. Syntax: sortD (List [ ) ] Beispiel: Sortieren der Elemente der Liste {1, 5, 3} in abfallender Reihenfolge

u listToMat [Action][List][Create][listToMat]

Funktion: Transformiert Listen in eine Matrix. Syntax: listToMat (List-1 [, List-2, ..., List-N] [ ) ] Beispiel: Übernehmen der Listen {3, 5} und {2, 4} als Spalten in eine Matrix

u matToList [Action][List][Create][matToList]

• Informationen über matToList finden Sie auf Seite 80.

Verwenden der Untermenüs für Listenstatistik und Listenberechnung

Das [List][Statistics]-Untermenü und das [List][Calculation]-Untermenü enthalten Befehle für Berechnungen mit Listen.

u min [Action][List][Statistics][min]

Funktion: Liefert den Minimalwert eines Terms oder der Elemente in einer Liste. Syntax: min (Exp/List-1[, Exp/List-2] [ ) ] Beispiel: Bestimmen der kleinsten Werte der Elemente in der Liste {1, 2, 3}

u max [Action][List][Statistics][max]

Funktion: Liefert den Maximalwert eines Terms oder der Elemente in einer Liste. Syntax: max (Exp/List-1[, Exp/List-2] [ ) ] Beispiel: Bestimmen der größten Werte der Elemente in der Liste {1, 2, 3}

Kapitel 2: Main-Menü 76

u mean [Action][List][Statistics][mean]

Funktion: Liefert der Mittelwert der Elemente in einer Liste. Syntax: mean (List-1[, List-2] [ ) ] (List-1: Daten, List-2: Freq) Beispiel: Bestimmen des Mittelwerts der Elemente in der Liste {1, 2, 3}

u median [Action][List][Statistics][median]

Funktion: Liefert den Medianwert der Elemente in einer Liste. Syntax: median (List-1[, List-2] [ ) ] (List-1: Daten, List-2: Freq) Beispiel: Bestimmen des Medians der Elemente in der Liste {1, 2, 3}

u mode [Action][List][Statistics][mode]

Funktion: Liefert den Modalwert (häufigster Wert) der Elemente in einer Liste. Wenn mehrere Modalwerte

(Elemente mit gleicher maximaler Häufigkeit) vorhanden sind, dann werden diese in einer Liste

ausgegeben. Syntax: mode (List-1[, List-2] [ ) ] (List-1: Daten, List-2: Freq) Beispiel: Bestimmen des Modalwerts der Elemente in der Liste {1, 1, 2, 2, 2}

u Q1 [Action][List][Statistics][Q1]

Funktion: Liefert das erste Quartil der Elemente in einer Liste. Syntax: Q

(List-1[, List-2] [ ) ] (List-1: Daten, List-2: Freq)

Beispiel: Bestimmen des ersten Quartils der Elemente in der Liste {1, 2, 3, 4, 5}

u Q3 [Action][List][Statistics][Q3]

Funktion: Liefert das dritte Quartil der Elemente in einer Liste. Syntax: Q

(List-1[, List-2] [ ) ] (List-1: Daten, List-2: Freq)

Beispiel: Bestimmen des dritten Quartils der Elemente in der Liste {1, 2, 3, 4, 5}

u percentile [Action][List][Statistics][percentile]

Funktion: Findet den n-ten Perzentilpunkt in einer Liste. Syntax: percentile (Liste, Zahl)

u stdDev [Action][List][Statistics][stdDev]

Funktion: Liefert die Stichproben-Standardabweichung der Elemente in einer Liste. Syntax: stdDev (List [ ) ] Beispiel: Bestimmen der Stichproben-Standardabweichung der Elemente in

der Liste {1, 2, 4}

u variance [Action][List][Statistics][variance]

Funktion: Liefert die Stichproben-Streuung der Elemente in einer Liste. Syntax: variance (List [ ) ] Beispiel: Bestimmen der Stichproben-Streuung der Elemente in der Liste

{1, 2, 4}

Kapitel 2: Main-Menü 77

u dim [Action][List][Calculation][dim]

Funktion: Liefert die Dimension (Länge) einer Liste. Syntax: dim (List [ ) ] Beispiel: Bestimmen der Dimension der Liste {1, 2, 3}

u sum [Action][List][Calculation][sum]

Funktion: Liefert die Summe der Elemente in einer Liste. Syntax: sum (List-1[, List-2] [ ) ] (List-1: Daten, List-2: Freq) Beispiel: Bestimmen der Summe der Elemente in der Liste {1, 2, 3}

u prod [Action][List][Calculation][prod]

Funktion: Liefert das Produkt der Elemente in einer Liste. Syntax: prod (List-1[, List-2] [ ) ] (List-1: Daten, List-2: Freq) Beispiel: Bestimmen des Produkts der Elemente in der Liste {1, 2, 3}

u cuml [Action][List][Calculation][cuml]

Funktion: Liefert die kumulativen Summen der Elemente in einer Liste. Syntax: cuml (List [ ) ] Beispiel: Bestimmen der kumulativen Summen der Elemente in der Liste

{1, 2, 3}

u Alist [Action][List][Calculation][Alist]

Funktion: Liefert eine Liste, deren Elemente den Differenzen zwischen zwei benachbarten Elementen einer

anderen Liste entsprechen. Syntax: Alist (List [ ) ] Beispiel: Generieren einer Liste, deren Elemente den Differenzen zwischen

zwei benachbarten Elementen der Liste {1, 2, 4} entsprechen

u percent [Action][List][Calculation][percent]

Funktion: Liefert den Prozentsatz jedes Elements in einer Liste, deren

Summe als 100% angesetzt wird (Häufigkeitsliste). Syntax: percent (List [ ) ] Beispiel: Bestimmen des Prozentsatzes jedes Elements in der Liste {1, 2, 3}

u polyEval [Action][List][Calculation][polyEval]

Funktion: Liefert ein Polynom, das in fallender Reihenfolge der Potenzen aufgebaut ist, sodass die

Koeffizienten in geordneter Reihenfolge jedem Element in der Eingabeliste entsprechen. Syntax: polyEval (List [,Exp/List] [ ) ]

x“ ist die Standard-Vorgabe, wenn Sie „[,Exp/List]“ weglassen.

• „ Beispiel: Erstellen eines Polynoms zweiten Grades mit den Koeffizienten

{1, 2, 3}

Kapitel 2: Main-Menü 78

u sequence [Action][List][Calculation][sequence]

Funktion: Liefert ein Polynom des niedrigsten Grades, das der durch die Eingabeliste ausgedrückten

Zahlenfolge entspricht. Wenn zwei Listen vorhanden sind, dann liefert dieser Befehl ein Polynom,

das jedem Element der ersten Liste das entsprechende Element der zweiten Liste zuordnet. Syntax: sequence (List-1[, List-2] [,Variable] [ ) ]

• „

x“ ist die Standard-Vorgabe, wenn Sie [,Variable] weglassen.

Beispiel: Bestimmen eines Polynoms für eine Zahlenfolge, die durch die Liste

{3, 5, 7, 9} gegeben ist

u sumSeq [Action][List][Calculation][sumSeq]

Funktion: Findet das Polynom niedrigsten Grades, das die durch die Eingabeliste ausgedrückte Zahlenfolge

beschreibt, und liefert die Summe des Polynoms. Wenn zwei Listen vorhanden sind, dann liefert

dieser Befehl ein Polynom, das jedem Element der ersten Liste das entsprechende Element der

zweiten Liste zuordnet, und liefert die Summe des Polynoms. Syntax: sumSeq (List-1[, List-2] [,Variable] [ ) ]

• „

x“ ist die Standard-Vorgabe, wenn Sie [,Variable] weglassen.

Beispiel: Bestimmen der Summe eines Polynoms für eine Folge, die durch die

Liste {3, 5, 7, 9} ausgedrückt wird

Verwenden des Untermenüs zur Matrizenerstellung

Das [Matrix][Create]-Untermenü enthält die Befehle für die Erstellung von Matrizen.

u trn [Action][Matrix][Create][trn]

Funktion: Liefert die transponierte Matrix. Syntax: trn (Mat [ ) ] Beispiel: Transponieren der Matrix [[1, 2] [3, 4]]

u augment [Action][Matrix][Create][augment]

Funktion: Liefert eine neue Matrix, die zwei andere Matrizen

aneinanderfügt. Syntax: augment (Mat-1, Mat-2 [ ) ] Beispiel: Erweitern der Matrix [[1, 2] [3, 4]] durch Anfügen der

Matrix [[5, 6] [7, 8]]

u ident [Action][Matrix][Create][ident]

Funktion: Erstellt eine Einheitsmatrix. Syntax: ident (natürliche Zahl [ ) ] Beispiel: Erstellen einer Einheitsmatrix vom Typ 2 × 2

u fill [Action][Matrix][Create][fill]

Funktion: Erstellt eine Matrix mit einer vorzugebenden Anzahl von Zeilen und Spalten, oder ersetzt die

Elemente einer Matrix durch einen vorzugebenden Term. Syntax: fill (Exp, Anzahl der Zeilen, Anzahl der Spalten [ ) ]

fill (Exp, Mat [ ) ]

Beispiel: Erstellen einer Matrix vom Typ 2 × 3, deren Elemente alle gleich 2

sind

Kapitel 2: Main-Menü 79

u subMat [Action][Matrix][Create][subMat]

Funktion: Extrahiert einen bestimmten Bereich einer Matrix in eine neue Matrix. Syntax: subMat (Mat [,Anfangszeile] [,Anfangsspalte] [,Endzeile] [,Endspalte] [ ) ]

• „1“ ist die Standard-Vorgabe, wenn Sie „[,Anfangszeile]“ und „[,Anfangspalte]“ weglassen.

• Die letzte Zeile (Zeilenindex) ist die Standard-Vorgabe, wenn Sie

„[,Endzeile]“ weglassen.

• Die letzte Spalte (Spaltenindex) ist die Vorgabe, wenn Sie „[,Endspalte]“

weglassen.

Beispiel: Extrahieren als Teilmatrix des Bereichs von Zeile 2, Spalte 2

(oberer linker Anfang des Bereiches) bis zu Zeile 3, Spalte 3 (unteres rechtes Ende des Bereiches) der Matrix [[1, 4, 7] [2, 5, 8] [3, 6, 9]]

u diag [Action][Matrix][Create][diag]

Funktion: Liefert eine einzeilige Matrix (Zeilenvektor), die als Elemente die Hauptdiagonale einer vorgegebenen quadratischen Matrix enthält.

Syntax: diag (Mat[ ) ] Beispiel: Extrahieren der Hauptdiagonal-Elemente der quadratischen Matrix

[[1, 2] [3, 4]] als Zeilenvektor

u listToMat [Action][Matrix][Create][listToMat]

• Informationen über listToMat finden Sie auf Seite 76.

u matToList [Action][Matrix][Create][matToList]

Funktion: Transformiert eine bestimmte Spalte einer Matrix in eine Liste. Syntax: matToList (Mat, Spaltennummer [ ) ] Beispiel: Ausgeben der Spalte 2 der Matrix [[1, 2] [3, 4]] als Liste

Verwenden der Untermenüs für Matrizenrechnung und Matrizenzeilen und -spalten

Das [Matrix][Calculation]-Untermenü und das [Matrix][Row&Column]-Untermenü enthalten Befehle für die Matrizenrechnung.

u dim [Action][Matrix][Calculation][dim]

Funktion: Liefert die Dimension einer Matrix als Liste mit zwei Elementen {Anzahl der Zeilen, Anzahl der

Spalten}. Syntax: dim (Mat [ ) ] Beispiel: Bestimmen der Dimension der Matrix [[1, 2, 3] [4, 5, 6]]

u det [Action][Matrix][Calculation][det]

Funktion: Liefert die Determinante einer quadratischen Matrix. Syntax: det (Mat [ ) ] Beispiel: Berechnen der Determinante der Matrix [[1, 2] [4, 5]]

Kapitel 2: Main-Menü 80

u norm [Action][Matrix][Calculation][norm]

Funktion: Liefert die Frobenius-Norm der Matrix. Syntax: norm (Mat [ ) ] Beispiel: Bestimmen der Frobenius-Norm der Matrix [[1, 2] [4, 5]]

u rank [Action][Matrix][Calculation][rank]

Funktion: Findet den Rang einer Matrix. Die Rangfunktion berechnet den Rang einer Matrix, indem sie eine Gauß-

Elimination der Reihen der gegebenen Matrix durchführt. Der Rang der Matrix A ist die Anzahl von Nicht-Null-Reihen in der resultierenden Matrix.

Syntax: rank (Matrix)

u ref [Action][Matrix][Calculation][ref]

Funktion: Liefert die Zeilenstufenform einer Matrix (Darstellung als obere Dreiecksmatrix). Syntax: ref (Mat [ ) ] Beispiel: Berechnen der Zeilenstufenform der (erweiterten) Matrix

[[1, 2, 3] [4, 5, 6]]

u rref [Action][Matrix][Calculation][rref]

Funktion: Liefert die reduzierte Zeilenstufenform einer Matrix (diagonalisierte Form). Syntax: rref (Mat [ ) ] Beispiel: Berechnen der reduzierten Zeilenstufenform der

(erweiterten) Matrix [[2, –1, 3, 19] [1, 1, –5, –21] [0, 4, 3, 0]]

u eigVl [Action][Matrix][Calculation][eigVl]

Funktion: Liefert eine Liste, die den (die) Eigenwert(e) einer quadratischen Matrix enthält. Syntax: eigVl (Mat [ ) ] Beispiel: Berechnen des bzw. der Eigenwerte der Matrix [[3, 4] [1, 3]]

u eigVc [Action][Matrix][Calculation][eigVc]

Funktion: Liefert eine Matrix, in der die Spalten die normierten Eigenvektoren einer quadratischen Matrix

repräsentieren.

• Da ein Eigenvektor V normalerweise nur bis auf ein skalares Vielfaches eindeutig bestimmt werden kann,

wird er auf die Norm 1 normiert.

Wenn V = [ Syntax: eigVc (Mat [ ) ] Beispiel: Berechnen des bzw. der Eigenvektoren der Matrix [[3, 4] [1, 3]]

x1, x2, ..., xn], (⎥ x1⎥

+ ⎥ x2⎥ 2 + .... + ⎥ xn⎥ 2 ) = 1.

u LU [Action][Matrix][Calculation][LU]

Funktion: Ermittelt die LU-Zerlegung (LR-Zerlegung) einer quadratischen Matrix. Syntax: LU (Mat, lVariableMem, uVariableMem [ ) ] Beispiel: Berechnen der LU-Zerlegung der Matrix [[1, 2, 3] [4, 5, 6] [7, 8, 9]]

• Die untere Dreiecks-Matrix wird, falls nicht anders vorgegeben, der

ersten Variablen L zugeordnet, während die obere Dreiecks-Matrix der

zweiten Variablen U zugeordnet wird.

Kapitel 2: Main-Menü 81

Anzeigen der unteren Matrix Anzeigen der oberen Matrix

u QR [Action][Matrix][Calculation][QR]

Funktion: Liefert die QR-Zerlegung einer quadratischen Matrix. Syntax: QR (Mat, qVariableMem, rVariableMem [ ) ] Beispiel: Berechnen der QR-Zerlegung der Matrix [[1, 2] [3, 4]]

• Die unitäre Matrix wird der Variablen Q zugeordnet, während die obere

Dreiecks-Matrix der Variablen R zugeordnet wird.

Anzeigen der unitären Matrix Anzeigen der oberen Dreiecks-Matrix

u swap [Action][Matrix][Row&Column][swap]

Funktion: Vertauscht zwei Zeilen einer Matrix. Syntax: swap (Mat, Zeilenindex 1, Zeilenindex 2 [ ) ] Beispiel: Vertauschen von Zeile 1 mit Zeile 2 der Matrix [[1, 2] [3, 4]]

u mRow [Action][Matrix][Row&Column][mRow]

Funktion: Multipliziert die Elemente einer bestimmten Zeile in einer Matrix mit

einem bestimmten Term. Syntax: mRow (Exp, Mat, Zeilenindex [ ) ] Beispiel: Multiplizieren der Zeile 1 der Matrix [[1, 2] [3, 4]] mit

u mRowAdd [Action][Matrix][Row&Column][mRowAdd]

Funktion: Multipliziert die Elemente einer bestimmten Zeile in einer Matrix mit einem bestimmten Term und

addiert anschließend das Ergebnis zu einer anderen Zeile. Syntax: mRowAdd (Exp, Mat, Zeilenindex 1, Zeilenindex 2 [ ) ] Beispiel: Multiplizieren der Zeile 1 der Matrix [[1, 2] [3, 4]] mit

anschließend Addieren des Ergebnisses zu Zeile 2

x, und

u rowAdd [Action][Matrix][Row&Column][rowAdd]

Funktion: Addiert eine bestimmte Zeile einer Matrix zu einer anderen Zeile. Syntax: rowAdd (Mat, Zeilenindex 1, Zeilenindex 2 [ ) ] Beispiel: Addieren der Zeile 1 der Matrix [[1, 2] [3, 4]] zu Zeile 2

u rowDim [Action][Matrix][Row&Column][rowDim]

Funktion: Liefert die Anzahl der Zeilen einer Matrix. Syntax: rowDim (Mat [ ) ] Beispiel: Berechnen der Anzahl der Zeilen in der Matrix [[1, 2, 3] [4, 5, 6]]

Kapitel 2: Main-Menü 82

u rowNorm [Action][Matrix][Row&Column][rowNorm]

Funktion: Berechnet die Summe der Beträge der Elemente einer jeden Zeile einer Matrix, und liefert das

Maximum dieser Summen. Syntax: rowNorm (Mat [ ) ] Beispiel: Berechnen der Summe der Beträge der Elemente einer jeden Zeile

einer Matrix [[1, –2, 3] [4, –5, –6]] und Ermitteln des Maximum dieser Summen

u colDim [Action][Matrix][Row&Column][colDim]

Funktion: Liefert die Anzahl der Spalten einer Matrix. Syntax: colDim (Mat [ ) ] Beispiel: Berechnen der Anzahl der Spalten der Matrix [[1, 2] [3, 4] [5, 6]]

u colNorm [Action][Matrix][Row&Column][colNorm]

Funktion: Berechnet die Summe der Beträge der Elemente einer jeden Spalte einer Matrix, und liefert das

Maximum dieser Summen. Syntax: colNorm (Mat [ ) ] Beispiel: Berechnen der Summe der Beträge der Elemente einer jeden

Spalte der Matrix [[1, –2, 3][4, –5, –6][–7, 8, 9]] und Ermitteln des Maximum dieser Summen

Verwenden des Untermenüs für die Vektorrechnung

Das [Vector]-Untermenü enthält die Befehle zur Vektorrechnung.

• Ein Vektor wird wie eine 1 × N Matrix (Zeilenvektor) oder N × 1 Matrix (Spaltenvektor) behandelt.

• Ein Vektor in der Form von 1 × N kann als [......] oder [[......]] eingegeben werden.

Beispiel: [1, 2], [[1, 2]]

• Vektoren werden als kartesische Form interpretiert, wenn nicht das Winkelsymbol ∠() verwendet wird, um

ein Winkelmaß anzugeben.

u augment [Action][Vector][augment]

Funktion: Liefert einen vergrößerten Vektor [Mat-1 Mat-2]. Syntax: augment (Mat-1, Mat-2 [ ) ] Beispiel: Vergrößern des Vektors [1, 2] durch Anfügen von [3, 4]

u fill [Action][Vector][fill]

Funktion: Erstellt einen Vektor, der eine bestimmte Anzahl von Elementen enthält, oder ersetzt die Elemente

eines Vektors durch einen bestimmten Term. Syntax: fill (Exp, Mat [ ) ]

fill (Exp, 1, Anzahl der Spalten [ ) ]

Beispiel: Ersetzen der Elemente des Vektors [1, 2] durch

Beispiel: Erstellen eines Vektors vom Typ 1 × 3 (1 Zeile, 3 Spalten), dessen

Elemente alle „3“ betragen

Kapitel 2: Main-Menü 83

u dim [Action][Vector][dim]

Funktion: Liefert die Dimension eines Vektors. Syntax: dim (Mat [ ) ] Beispiel: Bestimmen der Dimension des Vektors [1, 2, 3]

• Der Vektor [1, 2, 3] wird als eine 1 × 3 Matrix interpretiert.

u unitV [Action][Vector][unitV]

Funktion: Normiert einen Vektor. Syntax: unitV (Mat [ ) ]

• Dieser Befehl kann nur mit einer 1 × N oder N × 1 Matrix verwendet werden. Beispiel: Normieren des Vektors [1, 3, 5]

u angle [Action][Vector][angle]

Funktion: Liefert den von zwei Vektoren gebildeten Winkel. Syntax: angle (Mat-1, Mat-2 [ ) ]

• Dieser Befehl kann nur mit einer 1 × N oder N × 1 Matrix verwendet werden. Beispiel: Bestimmen des Winkels, der von den beiden Vektoren [1, 2] und [3,

4] gebildet wird (im Bogenmaßmodus)

u norm [Action][Vector][norm]

Funktion: Liefert die Euklidische Norm eines Vektors. Syntax: norm (Mat [ ) ] Beispiel: Berechnen der Euklidischen Norm des Vektors [1, 2, 3]

u crossP [Action][Vector][crossP]

Funktion: Liefert das äußere Produkt zweier Vektoren unter Beachtung deren Reihenfolge. Syntax: crossP (Mat-1, Mat-2 [ ) ]

• Dieser Befehl kann nur mit einer 1 × N oder N × 1 Matrix verwendet werden (N = 2, 3).

• Eine aus zwei Elementen bestehende Matrix [a, b] oder [[a], [b]] wird automatisch in eine aus drei

Elementen bestehende Matrix [a, b, 0] oder [[a], [b], [0]] umgewandelt.

Beispiel: Berechnen des Kreuzprodukts der beiden Vektoren [1, 3, 5] und

[2, 4, 6]

u dotP [Action][Vector][dotP]

Funktion: Liefert das innere Produkt zweier Vektoren. Syntax: dotP (Mat-1, Mat-2 [ ) ]

• Dieser Befehl kann nur mit einer 1 × N oder N × 1 Matrix verwendet werden. Beispiel: Berechnen des Skalarprodukts der beiden Vektoren [1, 3, 5] und

[2, 4, 6]

u toRect [Action][Vector][toRect]

Funktion: Liefert eine entsprechende kartesische Darstellung [x y] oder [x y z]. Syntax: toRect (Mat [,natürliche Zahl] [ ) ]

• Dieser Befehl kann nur mit einer 1 × N oder N × 1 Matrix verwendet werden (N = 2, 3).

• Dieser Befehl liefert „

und „z“, wenn die „natürliche Zahl“ gleich 3 ist.

x“, wenn die „natürliche Zahl“ gleich 1 ist, „y“, wenn die „natürliche Zahl“ gleich 2 ist,

Kapitel 2: Main-Menü 84

• Dieser Befehl liefert eine kartesische Darstellung, wenn Sie die „natürliche Zahl“ weglassen. Beispiel: Transformieren der Polarkoordinatendarstellung ['2 , ∠(π/4)] in die

äquivalente arithmetische Darstellung (im Bogenmaßmodus)

u toPol [Action][Vector][toPol]

Funktion: Liefert eine äquivalente Polarkoordinatendarstellung [r∠]. Syntax: toPol (Mat [,natürliche Zahl] [ ) ]

• Dieser Befehl kann nur mit einer 1 × 2 oder 2 × 1 Matrix verwendet werden.

• Dieser Befehl liefert „

ist.

• Dieser Befehl liefert die Polarform, wenn Sie die „natürliche Zahl“ weglassen. Beispiel: Transformieren der kartesischen Darstellung [1, 2] in ihre

äquivalente Polarkoordinatendarstellung

r“, wenn die „natürliche Zahl“ gleich 1 ist, und „“, wenn die „natürliche Zahl“ gleich 2

u toSph [Action][Vector][toSph]

Funktion: Liefert eine äquivalente Kugelkoordinatendarstellung [ ρ ∠ ∠φ]. Syntax: toSph (Mat [,natürliche Zahl] [ ) ]

• Dieser Befehl kann nur mit einer 1 × 3 oder 3 × 1 Matrix verwendet werden.

• Dieser Befehl liefert „

und „φ“, wenn die „natürliche Zahl“ gleich 3 ist.

• Dieser Befehl liefert eine Kugelkoordinatendarstellung, wenn Sie die „natürliche Zahl“ weglassen.

“, wenn die „natürliche Zahl“ gleich 1 ist, „“, wenn die „natürliche Zahl“ gleich 2 ist,

Beispiel: Transformieren des Ortsvektors mit kartesischer Darstellung

[1, 1, 1] in die äquivalente Kugelkoordinatendarstellung (im Bogenmaßmodus)

u toCyl [Action][Vector][toCyl]

Funktion: Liefert eine äquivalente Zylinderkoordinatendarstellung [r∠ z]. Syntax: toCyl (Mat [,natürliche Zahl] [ ) ]

• Dieser Befehl kann nur mit einer 1 × 3 oder 3 × 1 Matrix verwendet werden.

• Dieser Befehl liefert „

und „z“, wenn die „natürliche Zahl“ gleich 3 ist.

• Dieser Befehl liefert eine Zylinderkoordinatendarstellung, wenn Sie die „natürliche Zahl“ weglassen. Beispiel: Transformieren des Ortsvektors mit kartesischer Darstellung

[1, 1, 1] in die äquivalente Zylinderkoordinatendarstellung (im Bogenmaßmodus)

r“, wenn die „natürliche Zahl“ gleich 1 ist, „“, wenn die „natürliche Zahl“ gleich 2 ist,

Verwenden des Untermenüs für Gleichungen und Ungleichungen

Das [Equation/Inequality]-Untermenü enthält die Befehle für Gleichungen und Ungleichungen.

u solve [Action][Equation/Inequality][solve]

Funktion: Liefert die Lösung einer Gleichung oder Ungleichung. Syntax 1: solve(Exp/Eq/Ineq [,Variable] [ ) ]

• „

x“ ist die Standard-Vorgabe, wenn Sie [,Variable] weglassen.

Beispiel: Auflösen von

ax + b = 0 nach x

Kapitel 2: Main-Menü 85

Syntax 2: solve(Exp/Eq/Ineq,Variable[, Wert, untere Intervallgrenze, obere Intervallgrenze] [ ) ]

• „Wert“ ist ein geschätzter Start-Wert für den Lösungsalgorithmus.

• Dieser Befehl gilt nur für Gleichungen und  Terme, wenn „Wert“ und die danach folgenden Einträge

eingeschlossen sind. In diesem Fall liefert dieser Befehl den approximativen Wert (Näherungslösung).

• Ein exakter Wert wird geliefert, wenn Sie „Wert“ und die nachfolgenden Einträge weglassen. Falls jedoch

kein exakter Wert ermittelt werden kann, wird ein approximativer Wert für Gleichungen geliefert, basierend auf der Annahme, dass der Start-Wert = 0, die untere Intervallgrenze = –

∞, und die obere Intervallgrenze =

∞ ist.

Syntax 3: solve({Exp-1/Eq-1, ..., Exp-N/Eq-N}, {Variable-1, ..., Variable-N} [ ) ]

• Wenn „Exp“ das erste Argument ist, wird die Gleichung Exp = 0 angenommen. Beispiel: Auflösen des Gleichungssystems 3

Sie können die in diesem Beispiel gezeigten simultanen Gleichungen auch mit Hilfe der Software-Tastatur- Taste # eingeben. Nachfolgend ist die erforderliche Syntax für die Eingabe aufgeführt.

Exp-1/Eq-1

Exp-N/Eq-N Variable-1, ..., Variable-N

• Nachstehend ist die erforderliche Tastenbedienung zur Eingabe dieses Beispiels unter Verwendung der

#-Taste gezeigt.

#dX+eY=fccX-dY=-ieX,Yw

• Zum Eingeben von simultanen Gleichungen mit drei oder mehr Unbekannten tippen Sie auf die #-Taste,

wenn sich der Cursor im Exp-N/Eq-N-Eingabefeld befindet. Durch jedes Tippen auf # wird eine weitere Zeile als Eingabe in eine Gleichung hinzugefügt.

Syntax 4: Sie können die Beziehung zwischen zwei Punkten, Geraden, Ebenen oder Kugeln berechnen,

indem Sie eine Vektorgleichung in den Befehl solve( eingeben. Hier zeigen wir vier typische

Syntaxen zum Lösen einer Vektorgleichung mit dem Befehl solve(.

In den nachfolgenden Syntaxen sind Vct-1 bis Vct-6 Spaltenvektoren mit drei (oder zwei)

Elementen, und

solve(Vct-1 +

• Wenn die rechte Seite der Gleichung (= Vct-3) in der oben genannten Syntax ausgelassen wurde, wird angenommen, dass alle Elemente auf der rechten Seite 0-Vektoren sind.

solve(Vct-1 + s * Vct-2 = Vct-3 + t * Vct-4, {Variable-1, Variable-2}) solve(Vct-1 + solve(Vct-1 +

Variable-3, Variable-4})

• Variablen (Variable-1 bis Variable-4) können in die Elemente jedes Vektors (Vct-1 bis Vct-6) in den oben genannten vier Syntaxen eingegeben werden, um diese Variablen zu berechnen.

s, t, u und v sind Parameter.

s * Vct-2 [= Vct-3, {Variable-1}])

s * Vct-2 + t * Vct-3 = Vct-4 – u * Vct-5, {Variable-1, Variable-2, Variable-3}) s * Vct-2 + t * Vct-3 = Vct-4 – u * Vct-5 + v * Vct-6, {Variable-1, Variable-2,

x + 4y = 5, 2x – 3y = –8

0234 Überprüfen, ob sich Punkt P (5, 7, 9) und Punkt Q (5, 7, 8) jeweils auf der Gerade

welche ein Ausrichtungsvektor (4, 5, 6) ist, der durch Punkt A (1, 2, 3) verläuft

l befinden,

Hinweis

Als Lösung ermittelt die solve-Funktion einen Ausdruck oder Wert für den als ihr Argument eingegebenen Term (Exp/Eq). Wenn ein Wert als Lösung ermittelt wird, erscheint die Meldung „More solutions may exist“, da mehrere Lösungen vorhanden sein können.

Bei Werten kann die solve-Funktion maximal 10 Lösungen ermitteln.

Kapitel 2: Main-Menü 86

Beispiel: Auflösen von cos (

(Winkelmodus-Einstellung: Deg)

x) = 0,5 nach x (Anfangswert: 0)

u dSolve [Action][Equation/Inequality][dSolve]

Funktion: Löst gewöhnliche Differenzialgleichungen erster, zweiter und dritter Ordnung, oder ein System von

zwei Differenzialgleichungen jeweils erster Ordnung.

Syntax: dSolve(Eq, unabhängige Variable, abhängige Variable [, Anfangsbedingung-1, Anfangsbedingung-2]

[, Anfangsbedingung-3, Anfangsbedingung-4][, Anfangsbedingung-5, Anfangsbedingung-6] [ ) ] dSolve({Eq-1, Eq-2}, unabhängige Variable, {abhängige Variable-1, abhängige Variable-2} [,

Anfangsbedingung-1, Anfangsbedingung-2, Anfangsbedingung-3, Anfangsbedingung-4] [ ) ]

• Wenn Sie die Anfangsbedingungen weglassen, enthält die allgemeine Lösung frei wählbare Konstanten.

• Geben Sie alle Gleichungen mit Anfangsbedingungen unter Verwendung der Syntax Var = Exp ein. Eine Anfangsbedingung, die eine andere Syntax verwendet, wird ignoriert.

Beispiel: Lösen der linearen Differenzialgleichung

Anfangsbedingung x = 0

Beispiel: Lösen des linearen Systems von Differenzialgleichungen erster Ordnung

wobei „x“ die unabhängige Variable ist und „y“ und „z“ die abhängigen Variablen sind, und die Anfangsbedingungen y = 3, wenn x = 0 und z = '2 – 3, wenn x = 0 gegeben sind

y’ = x für y = 1 mit der

y’ = y + z, z’ = y – z,

u rewrite [Action][Equation/Inequality][rewrite]

Funktion: Bringt die Elemente der rechten Seite einer Gleichung oder Ungleichung auf die linke Seite. Syntax: rewrite(Eq/Ineq/List [ ) ] Beispiel: Bewegen der Elemente der rechten Seite von

linke Seite

x + 3 = 5x – x

auf die

u exchange [Action][Equation/Inequality][exchange]

Funktion: Tauscht die Terme der rechten und der linken Seite einer Gleichung oder Ungleichung

gegeneinander aus. Syntax: exchange(Eq/Ineq/List [ ) ] Beispiel: Vertauschen der Seiten der Ungleichung 3 > 5

x – 2y

u eliminate [Action][Equation/Inequality][eliminate]

Funktion: Löst eine Gleichung hinsichtlich einer Variablen auf und ersetzt dann die eliminierte gleiche Variable

in einem anderen Term durch das zuvor erhaltene Ergebnis. Syntax: eliminate(Eq/Ineq/List-1, Variable, Eq-2 [ ) ] Beispiel: Transformieren von

des Zwischenergebnisses in 2x + 3y = 5

y = 2x + 3 in x =, und anschließend Einsetzen

Kapitel 2: Main-Menü 87

u absExpand [Action][Equation/Inequality][absExpand]

Funktion: Löst eine Betragsgleichung/-ungleichung durch Fallunterscheidung auf. Syntax: absExpand(Eq/Ineq [ ) ] Beispiel: Auflösen der Betragsgleichung ⎜2

x – 3 ⎜ = 9

u andConnect [Action][Equation/Inequality][andConnect]

Funktion: Verbindet zwei Gleichungen oder Ungleichungen zu einer fortlaufenden Gleichung/Ungleichung. Syntax: andConnect(Eq/Ineq-1, Eq/Ineq-2 [ ) ] Beispiel: Verbinden von

x > –1 und x < 3 als Ungleichungskette

u getRight [Action][Equation/Inequality][getRight]

Funktion: Extrahiert die Terme der rechten Seite einer Gleichung oder Ungleichung. Syntax: getRight(Eq/Ineq/List [ ) ]

y = 2x

Beispiel: Extrahieren der Terme der rechten Seite von

+ 3x + 5

u getLeft [Action][Equation/Inequality][getLeft]

Funktion: Extrahiert die Terme der linken Seite einer Gleichung oder Ungleichung. Syntax: getLeft(Eq/Ineq/List [ ) ]

Beispiel: Extrahieren der Terme der linken Seite von

y = 2x

+ 3x + 5

u and [Action][Equation/Inequality][Logic][and]

Funktion: Liefert das Ergebnis der logischen AND-Verknüpfung von zwei Termen. Syntax: Exp/Eq/Ineq/List-1 and Exp/Eq/Ineq/List-2 Beispiel: Ermitteln des Ergebnisses der logischen AND-Verknüpfung von

> 1 and x < 0

u or [Action][Equation/Inequality][Logic][or]

Funktion: Liefert das Ergebnis der logischen OR-Verknüpfung von zwei Termen. Syntax: Exp/Eq/Ineq/List-1 or Exp/Eq/Ineq/List-2 Beispiel: Ermitteln des Ergebnisses der logischen OR-Verknüpfung von

x = 3 or x > 2

u xor [Action][Equation/Inequality][Logic][xor]

Funktion: Liefert das Ergebnis der logischen Exklusiv-OR-Verknüpfung von zwei Termen. Syntax: Exp/Eq/Ineq/List-1 xor Exp/Eq/Ineq/List-2 Beispiel: Ermitteln des Ergebnisses der logischen Exklusiv-OR-Verknüpfung

x < 2 xor x < 3

von

u not [Action][Equation/Inequality][Logic][not]

Funktion: Liefert das logische NOT eines Terms. Syntax: not(Exp/Eq/Ineq/List [ ) ] Beispiel: Ermitteln des logischen NOT von

x = 1

Kapitel 2: Main-Menü 88

Verwenden des Assistenten-Untermenüs

Das [Assistant]-Untermenü enthält vier Befehle für den Assistentenmodus. Beachten Sie, dass die folgenden Befehle nur im Assistentenmodus gültig sind. Für weitere Informationen zum

Assistentenmodus siehe „Assistentenmodus und Algebramodus“ auf Seite 50.

u arrange [Action][Assistant][arrange]

Funktion: Sammelt ähnliche Terme und arrangiert diese in fallender Reihenfolge, wobei mit dem Term

begonnen wird, der den kleinsten Koeffizienten enthält. Syntax: arrange (Exp/Eq/Ineq/List/Mat [ ) ] Beispiel: Neuanordnen und Zusammenfassen von 2

Reihenfolge der Variablen

x + 3 – 5x + 8y in der

u replace [Action][Assistant][replace]

Funktion: Ersetzt die Variable in einem Term, einer Gleichung oder einer Ungleichung mit dem Wert, der einer

Variablen unter Verwendung des „store“-Befehls zugeordnet wurde. Syntax: replace (Exp/Eq/Ineq/List/Mat [ ) ] Beispiel: Ersetzen von

zugeordnet

s im Term 3x + 2s, wenn der Term 2x + 1 dem s vorher

u invert [Action][Assistant][invert]

Funktion: Tauscht zwei Variablen in einem Term gegeneinander aus. Syntax: invert (Exp/Eq/Ineq/List [,Variable-1, Variable-2] [ ) ]

•

x und y werden gegeneinander ausgetauscht, wenn Sie die Variablen nicht

anders vorgeben.

Beispiel: Austauschen von

x und y in der Gleichung 2x = y

u Clear_a_z

Funktion: Löscht alle Einzelbuchstaben-Variablennamen (a-z und A-Z) im

gegenwärtigen Ordner.

Verwenden des [Distribution/Inv. Dist.]-Untermenüs

Das [Distribution/Inv.Dist]-Untermenü umfasst Funktionen, die mit verschiedenen Arten der Verteilungswahrscheinlichkeit bei statistischen Berechnungen in Zusammenhang stehen. Die Funktionen in diesem Untermenü führen die gleichen Berechnungen wie die Distribution-Befehle aus, die im Statistik-Menü und im Main-Menü, im eActivity-Menü und im Programm-Menü verfügbar sind. Näheres zu den in Berechnungen verwendeten numerischen Ausdrücken finden Sie unter „Wahrscheinlichkeitsverteilungen“ auf Seite 162. Näheres zu den Bedeutungen der Variablen, die in den Syntaxen der in diesem Abschnitt beschriebenen Funktionen verwendet werden, und zu den Systemvariablen, die die als Rechenergebnis erhaltenen Werte speichern, finden Sie unter „Ein- und Ausgabebedingungen“ auf Seite 166.

Eingeben von Argumenten in der Distribution-Funktion

Sie können für jedes der Argumente in der Distribution-Funktion entweder Werte oder Listendaten eingeben. Die zur Ermittlung der normalen Wahrscheinlichkeitsdichte verwendete Syntax der normPDf-Funktion (Seite

90) (normPDf(x, , )) kann wie unten gezeigt zur Durchführung der Berechnungen verwendet werden. Die „Number Format“-Einstellung für alle Berechnungsergebnisse ist „Fix 2“.

normPDf(1, 1, 0) = 0,24 normPDf({1, 2}, 1, 0) = {0,24, 0,05}

Kapitel 2: Main-Menü 89

normPDf(1, {1, 2}, 0) = {0,24, 0,18} normPDf({1, 2},{1, 2}, 0) = {0,24, 0,12} normPDf({1, 2},{1, 2},{1, 0}) = {0,40, 0,12}

Im Folgenden ist beschrieben, wie Listendaten in Argumente eingegeben und die Berechnungsergebnisse ausgegeben werden.

(a) Eingeben von Listendaten für ein einzelnes Argument

• Im Prinzip kann jede beliebige Liste eingeben werden. Es muss aber jedes Element in der Liste den vom Argument der verwendeten Funktion vorgegebenen Bedingungen entsprechen.

• Die Berechnung erfolgt für jedes Element in der Liste und die Ergebnisse werden wie unten gezeigt ausgegeben.

x, {

normPDf( = {<normPDf(

, 2}, )

x, 

, ) Berechnungsergebnis>, <normPDf(x, 2, ) Berechnungsergebnis>}

(b) Eingeben von Listendaten für multiple Argumente

• In diesem Fall müssen alle Listen die gleiche Zahl an Elementen enthalten. Anderenfalls wird die Fehlermeldung „Invalid Dimension“ angezeigt.

• Die Berechnung erfolgt für jedes Element in der Liste und die Ergebnisse werden wie unten gezeigt ausgegeben.

normPDf({ = {<normPDf(

, x2}, {1, 2}, )

, 1, ) Berechnungsergebnisse>, <normPDf(x2, 2, ) Berechnungsergebnisse>}

Zuordnen von Listendaten-Berechnungsergebnissen zu Variablen

Die Verwendung der Listendaten im Argument der Distribution-Funktion gibt die Berechnungsergebnisse als Listendaten aus, die in unveränderter Form der „ans“-Variablen zugeordnet werden. Zusätzlich zur „ans“-Variablen bewirken Berechnungen, die die Distribution-Funktion verwenden, auch eine Zuordnung der Berechnungsergebnisse zu bestimmten Systemvariablen. Beispielsweise wird die von normPDf ermittelte Variable der Normalwahrscheinlichkeitsdichte der Systemvariablen prob zugeordnet. Als Berechnungsergebnis wird einer Systemvariablen nur das letzte Element der Listendaten zugeordnet.

In den Erklärungen zur Distribution-Funktion finden Sie Näheres dazu, welches Berechnungsergebnis welcher Variablen zugeordnet wird, finden Sie unter „Berechnungsergebnis-Ausgabe“.

u normPDf [Action][Distribution/Inv.Dist][Continuous][normPDf]

Funktion: Ermittelt die Wahrscheinlichkeitsdichte einer Normalverteilung für einen vorgegebenen Wert.

x[,

Syntax: normPDf(

• Bei Auslassung von Berechnungsergebnis-Ausgabe:

, μ)]

und μ werden σ = 1 und μ = 0 verwendet.

prob

Beispiel: Bestimmen der Wahrscheinlichkeitsdichte einer Normalverteilung

bei x = 37.5, σ = 2, μ = 35

u normCDf [Action][Distribution/Inv.Dist][Continuous][normCDf]

Funktion: Ermittelt die kumulative Wahrscheinlichkeit einer Normalverteilung zwischen einem unteren und

einem oberen Grenzwert.

Syntax: normCDf(unterer Wert, oberer Wert[,

• Bei Auslassung von

und μ werden σ = 1 und μ = 0 verwendet.

, μ)]

Berechnungsergebnis-Ausgabe: prob, zLow, zUp Beispiel: Bestimmen der Normal-Wahrscheinlichkeitsdichte bei unterer

Grenzwert = −

∞, oberer Grenzwert = 36,

= 2, μ = 35

Kapitel 2: Main-Menü 90

u invNormCDf [Action][Distribution/Inv.Dist][Inverse][invNormCDf]

Funktion: Ermittelt den (die) Grenzwert(e) einer normalen kumulativen Verteilungswahrscheinlichkeit für

vorgegebene Werte.

Syntax: invNormCDf([tail setting, ]Area-Wert[,

• Bei Auslassung von

• „tail setting“ zeigt die Lage des Anfangspunkts der Wahrscheinlichkeitswerte, wobei Left, Right oder Center vorgegeben werden kann. Geben Sie zum Vorgeben die folgenden Werte oder Buchstaben ein:

Left: −1, „L“ oder „l“ Center: 0, „C“ oder „c“ Right: 1, „R“ oder „r“

Bei Überspringen der Eingabe wird „Left“ verwendet.

• Wenn ein Argument ausgelassen wird (ergibt drei Argumente), Tail = Left.

• Wenn zwei Argumente ausgelassen werden (ergibt zwei Argumente), Tail=Left,

• Wenn drei Argumente ausgelassen werden (ergibt ein Argument), Tail=Left,

• Wenn „tail setting“ auf Center eingestellt ist, wird der untere Grenzwert ausgegeben.

und μ werden σ = 1 und μ = 0 verwendet.

, μ)]

=0.

=1, μ =0.

Berechnungsergebnis-Ausgabe: Beispiel: Bestimmen des oberen Grenzwerts bei Tail setting = Left,

Area-Wert = 0,7, σ = 2, μ = 35

InvN, x2InvN

u tPDf [Action][Distribution/Inv.Dist][Continuous][tPDf]

Funktion: Ermittelt die Wahrscheinlichkeitsdichte einer Student’schen t-Verteilung für einen vorgegebenen

Wert. Syntax: tPDf( Berechnungsergebnis-Ausgabe: Beispiel: Bestimmen der Wahrscheinlichkeitsdichte einer Student’schen

x, df [ ) ]

prob

t-Verteilung bei x = 2, df = 5

u tCDf [Action][Distribution/Inv.Dist][Continuous][tCDf]

Funktion: Ermittelt die kumulative Wahrscheinlichkeit einer Student’schen t-Verteilung zwischen einer oberen

und unteren Grenze. Syntax: tCDf(unterer Wert, oberer Wert, Berechnungsergebnis-Ausgabe: Beispiel: Bestimmen der Wahrscheinlichkeit einer Student’schen t-Verteilung

bei unterer Wert = 1,5, oberer Wert = ∞, df = 18

prob, tLow, tUp

df [ ) ]

u invTCDf [Action][Distribution/Inv.Dist][Inverse][invTCDf]

Funktion: Ermittelt den unteren Grenzwert der kumulativen Wahrscheinlichkeit einer Student’schen

t-Verteilung für vorgegebene Werte.

Syntax: invTCDf( Berechnungsergebnis-Ausgabe: xInv Beispiel: Bestimmen des unteren Grenzwerts bei

prob, df [ ) ]

prob = 0,0754752, df = 18

Kapitel 2: Main-Menü 91

u chiPDf [Action][Distribution/Inv.Dist][Continuous][chiPDf]

Funktion: Ermittelt die Wahrscheinlichkeitsdichte einer χ2-Verteilung für vorgegebene Werte. Syntax: chiPDf( Berechnungsergebnis-Ausgabe: Beispiel: Bestimmen der Wahrscheinlichkeitsdichte einer χ2-Verteilung bei

x, df [ ) ]

prob

x = 2, df = 4

u chiCDf [Action][Distribution/Inv.Dist][Continuous][chiCDf]

Funktion: Ermittelt die kumulative Wahrscheinlichkeit einer χ2-Verteilung zwischen einer unteren und oberen

Grenze. Syntax: chiCDf(unterer Wert, oberer Wert, Berechnungsergebnis-Ausgabe: Beispiel: Bestimmen der Wahrscheinlichkeit einer χ2-Verteilung bei unterer

Wert = 2,7, oberer Wert = ∞, df = 4

prob

df [ ) ]

u invChiCDf [Action][Distribution/Inv.Dist][Inverse][invChiCDf]

Funktion: Ermittelt den unteren Grenzwert der kumulativen Wahrscheinlichkeit einer χ2-Verteilung für

vorgegebene Werte. Syntax: invChiCDf( Berechnungsergebnis-Ausgabe: Beispiel: Bestimmen des unteren Grenzwerts bei prob = 0,6092146, df = 4

prob, df [ ) ]

xInv

u fPDf [Action][Distribution/Inv.Dist][Continuous][fPDf]

Funktion: Ermittelt die Wahrscheinlichkeitsdichte einer F-Verteilung für einen vorgegebenen Wert. Syntax: fPDf( Berechnungsergebnis-Ausgabe: Beispiel: Bestimmen der Wahrscheinlichkeitsdichte einer F-Verteilung bei x =

x, n:df, d:df [ ) ]

prob

1,5, n:df = 24, d:df = 19

u fCDf [Action][Distribution/Inv.Dist][Continuous][fCDf]

Funktion: Ermittelt die kumulative Wahrscheinlichkeit einer F-Verteilung zwischen einer oberen und einer

unteren Grenze. Syntax: fCDf(unterer Wert, oberer Wert, Berechnungsergebnis-Ausgabe: Beispiel: Bestimmen der Wahrscheinlichkeit einer F-Verteilung bei unterer

Wert = 1,5, oberer Wert = ∞, n:df = 24, d:df = 19

prob

n:df, d:df [ ) ]

u invFCDf [Action][Distribution/Inv.Dist][Inverse][invFCDf]

Funktion: Ermittelt den unteren Grenzwert der kumulativen Wahrscheinlichkeit einer F-Verteilung für

vorgegebene Werte. Syntax: invFCDf(

prob, n:df, d:df [ ) ]

Berechnungsergebnis-Ausgabe: Beispiel: Bestimmen des unteren Grenzwertes bei prob = 0,1852, n:df = 24,

xInv

d:df = 19

Kapitel 2: Main-Menü 92

u binomialPDf [Action][Distribution/Inv.Dist][Discrete][binomialPDf]

Funktion: Ermittelt die Wahrscheinlichkeit in einer Binomialverteilung, dass der Erfolg bei einem

vorgegebenen Versuch eintritt. Syntax: binomialPDf( Berechnungsergebnis-Ausgabe: Beispiel: Bestimmen der Binomialwahrscheinlichkeit bei x = 5,

Numtrial-Wert = 3, pos = 0,63

x, Numtrial-Wert, pos [ ) ]

prob

u binomialCDf [Action][Distribution/Inv.Dist][Discrete][binomialCDf]

Funktion: Ermittelt die kumulative Wahrscheinlichkeit in einer Binomialverteilung, dass der Erfolg zwischen

einem vorgegebenen unteren Wert und oberen Wert eintritt. Syntax: binomialCDf(unterer Wert, oberer Wert, Numtrial-Wert, Berechnungsergebnis-Ausgabe: Beispiel: Bestimmen der kumulativen Binomialwahrscheinlichkeit bei unterer

Wert = 2, oberer Wert = 5, Numtrial-Wert = 3, pos = 0,63

prob

pos [ ) ]

u invBinomialCDf [Action][Distribution/Inv.Dist][Inverse][invBinomialCDf]

Funktion: Ermittelt die Mindestzahl von Versuchen einer kumulativen binomialen

Wahrscheinlichkeitsverteilung bei vorgegebenen Werten. Syntax: invBinomialCDf( Berechnungsergebnis-Ausgabe:

prob, Numtrial-Wert, pos [ ) ]

xInv, ½xInv

Wichtig!

Beim Ausführen der invBinomialCDf-, der invPoissonCDf-, der invGeoCDf- oder der invHypergeoCDf-Funktion verwendet der ClassPad zum Berechnen der Werte für die Mindestanzahl von Versuchen den vorgegebenen prob- Wert und den an der kleinsten signifikanten Stelle um eins verminderten

prob-Wert (½prob-Wert). Die Ergebnisse werden den Systemvariablen xInv (Rechenergebnis mit prob) und ½xInv (Rechenergebnis mit ½prob)

zugewiesen. Die Funktion ermittelt stets nur den xInv-Wert. Falls sich jedoch die Werte von xInv und ½xInv unterscheiden, erscheint die unten gezeigte Warnmeldung, die beide Werte zeigt.

Die Rechenergebnisse der Funktion sind Ganzzahlen. Die Genauigkeit kann beeinträchtigt sein, wenn das erste Argument 10 oder mehr Stellen umfasst. Beachten Sie, dass selbst eine geringe Abweichung bei der Berechnung die Rechenergebnisse beeinflusst. Wenn eine Warnmeldung erscheint, überprüfen Sie die angezeigten Werte.

Beispiel: Bestimmen der Mindestzahl von Versuchen bei

Numtrial-Wert = 5, pos = 0,63

prob = 0,609,

u poissonPDf [Action][Distribution/Inv.Dist][Discrete][poissonPDf]

Funktion: Ermittelt die Wahrscheinlichkeit in einer Poisson-Verteilung, dass der Erfolg bei einem

vorgegebenen Versuch eintritt. Syntax: poissonPDf( Berechnungsergebnis-Ausgabe: prob Beispiel: Bestimmen der Poisson-Wahrscheinlichkeit bei x = 10,  = 6

x,  [ ) ]

Kapitel 2: Main-Menü 93

u poissonCDf [Action][Distribution/Inv.Dist][Discrete][poissonCDf]

Funktion: Ermittelt die kumulative Wahrscheinlichkeit in einer Poisson-Verteilung, dass der Erfolg zwischen

einem vorgegebenen unteren Wert und oberen Wert eintritt. Syntax: poissonCDf(unterer Wert, oberer Wert,  [ ) ] Berechnungsergebnis-Ausgabe: Beispiel: Bestimmen kumulativen Poisson-Wahrscheinlichkeit bei unterer

Wert = 2, oberer Wert = 3,  = 2,26

prob

u invPoissonCDf [Action][Distribution/Inv.Dist][Inverse][invPoissonCDf]

Funktion: Ermittelt die Mindestzahl von Versuchen in einer kumulativen Poisson-Wahrscheinlichkeitsverteilung

für vorgegebene Werte. Syntax: invPoissonCDf( Berechnungsergebnis-Ausgabe:

prob,  [ ) ]

xInv, ½xInv

Wichtig!

Siehe „Wichtig!“ unter „invBinomialCDf“ auf Seite 93. Beispiel: Bestimmen der Mindestanzahl von Versuchen bei prob = 0,8074,

 = 2,26

u geoPDf [Action][Distribution/Inv.Dist][Discrete][geoPDf]

Funktion: Ermittelt die Wahrscheinlichkeit in einer geometrischen Verteilung, dass der Erfolg bei einem

bestimmten Versuch eintritt. Syntax: geoPDf( Berechnungsergebnis-Ausgabe:

x, pos [ ) ]

prob

Beispiel: Bestimmen der geometrischen Wahrscheinlichkeit bei x = 6,

pos = 0,4

u geoCDf [Action][Distribution/Inv.Dist][Discrete][geoCDf]

Funktion: Ermittelt die kumulative Wahrscheinlichkeit in einer geometrischen Verteilung, dass der Erfolg

zwischen einem vorgegebenen unteren Wert und oberen Wert eintritt. Syntax: geoCDf(unterer Wert, oberer Wert, Berechnungsergebnis-Ausgabe: Beispiel: Bestimmen der geometrischen Wahrscheinlichkeit bei unterer Wert

= 2, oberer Wert = 3, pos = 0,5

prob

pos [ ) ]

u invGeoCDf [Action][Distribution/Inv.Dist][Inverse][invGeoCDf]

Funktion: Ermittelt die Mindestanzahl von Versuchen einer kumulativen geometrischen

Wahrscheinlichkeitsverteilung für vorgegebene Werte. Syntax: invGeoCDf( Berechnungsergebnis-Ausgabe:

prob, pos [ ) ]

xInv, ½xInv

Wichtig!

Siehe „Wichtig!“ unter „invBinomialCDf“ auf Seite 93. Beispiel: Bestimmen der Mindestanzahl von Versuchen bei

prob = 0,875,

pos = 0,5

Kapitel 2: Main-Menü 94

u hypergeoPDf [Action][Distribution/Inv.Dist][Discrete][hypergeoPDf]

Funktion: Ermittelt die in einer hypergeometrischen Verteilung gegebene Wahrscheinlichkeit, dass der Erfolg

bei einem bestimmten Versuch eintritt. Syntax: hypergeoPDf( Berechnungsergebnis-Ausgabe: Beispiel: Bestimmen der hypergeometrischen Wahrscheinlichkeit für x = 1,

x, n, M, N [ ) ]

prob

n = 5, M = 10, N = 20

u hypergeoCDf [Action][Distribution/Inv.Dist][Discrete][hypergeoCDf]

Funktion: Ermittelt die in einer hypergeometrischen Verteilung gegebene kumulative Wahrscheinlichkeit, dass

der Erfolg zwischen einem vorgegebenen unteren und oberen Wert eintritt. Syntax: hypergeoCDf(unterer Wert, oberer Wert, Berechnungsergebnis-Ausgabe: Beispiel: Bestimmen der kumulativen hypergeometrischen Verteilung bei

einem unteren Wert= 0, oberen Wert = 1, n = 5, M = 10, N = 20

prob

n, M, N [ ) ]

u invHypergeoCDf [Action][Distribution/Inv.Dist][Inverse][invHypergeoCDf]

Funktion: Ermittelt die in einer kumulativen hypergeometrischen Verteilung gegebene Mindestanzahl von

Versuchen für bestimmte Werte. Syntax: invHypergeoCDf( Berechnungsergebnis-Ausgabe:

prob, n, M, N [ ) ]

xInv, ½xInv

Wichtig!

Siehe „Wichtig!“ unter „invBinomialCDf“ auf Seite 93. Beispiel: Bestimmen der Mindestanzahl von Versuchen bei prob = 0.3, n = 5,

M = 10, N = 20

Verwenden des [Financial]-Untermenüs

Das [Financial]-Untermenü enthält Befehle für Finanzberechnungen. Informationen zu den in diesem Untermenü enthaltenen Funktionen sind unter „11-4 Finanzmathematische

Funktionen“ zu finden.

Verwenden des [Command]-Untermenüs

u Define

Funktion 1: Definiert eine Funktion und registriert sie im Grafik-Editor. Syntax 1: Define{

r1() − r100()} = <Term>

Beispiel: Definieren der Funktion

der Zeile „y3“ des Grafik-Editors Funktion 2: Erstellt eine anwenderdefinierte Funktion. Weitere Informationen finden Sie unter „12-3 Anwenderdefinierte Funktionen“.

y1(x) − y100(x) ; x1(y) − x100(y) ; yt1(t) − yt100(t) ; xt1(t) − xt100(t) ;

y = sin(x) und Zuordnen dieser Funktion zu

Kapitel 2: Main-Menü 95

u DispStat

Funktion: Zeigt die vorherigen statistischen Berechnungsergebnisse an. Weitere Informationen finden Sie unter „DispStat“ auf Seite 225 und den Beispielen 1208 bis 1210 unter

„Einbinden von statistischen Grafik- und Berechnungsfunktionen in einem Programm“ auf Seite 243.

u Clear_a_z

Funktion: Löscht alle Einzelbuchstaben-Variablen. Weitere Informationen finden Sie unter „Clear_a_z“ auf Seite 89.

u DelVar

Funktion: Löscht eine bestimmte Variable. Weitere Informationen finden Sie unter „DelVar“ auf Seite 224.

u Clear All Variables

Funktion: Löscht Variablen, die Zahlen, Listen und Matrizen enthalten.

2-8 Verwenden des Interaktiv-Menüs

Mit dem [Interactive]-Menü können Sie die meisten Befehle benutzen, die im [Action]-Menü verfügbar sind. Wenn Sie einen Befehl im [Action]-Menü wählen, wird einfach die Funktion für diesen Befehl eingegeben.

Im [Interactive]-Menü ziehen Sie den Stift über eine vorhandene Eingabe im Arbeitsbereich und wählen dann einen Befehl. Dadurch wird der hervorgehobene Term mit dem Befehl umschlossen und ein Dialogfeld geöffnet, falls mehr Argumente erforderlich sind. Wenn Sie einen [Interactive]-Menüeintrag wählen, ohne zuvor einen Term hervorzuheben, öffnet sich ein Dialogfeld, das Sie zu den erforderlichen Argumenten auffordert.

Tipp

• Die Bedienung der folgenden Befehle des [Interactive]-Menüs ist identisch mit den meisten Befehlen des [Action]-Menüs. Informationen über die Verwendung dieser Befehle finden Sie unter „2-7 Verwenden des Aktionsmenüs“. [Transformation], [Advanced], [Calculation], [Complex], [List]-[Create], [List]-[Statistics], [List]-[Calculation], [Matrix]- [Create], [Matrix]-[Calculation], [Matrix]-[Row&Column], [Vector], [Equation/Inequality], [Assistant], [Distribution/Inv.Dist], [Financial], Define

• Die Befehle „DispStat“, „Clear_a_z“ und „DelVar“ des [Command]-Untermenüs des [Action]-Menüs sind im [Interactive]- Menü nicht enthalten.

Beispiel für das Interaktiv-Menü

Die Operationen im [Interactive]-Menü sind besonders in den folgenden Fällen vorteilhaft.

• Wenn Sie einen Befehl für einem Term verwenden möchten, den Sie gerade bearbeiten.

• Wenn Sie einen Befehl verwenden möchten, der mehrere Argumente erfordert.

0235 Zerlegen des Terms

– 3x2 + 3x – 1 in seine Linear-Faktoren

0236 Berechnen des bestimmten Integrals über

+ 2x für 1 s x s 2

Kapitel 2: Main-Menü 96

Verwenden des „apply“-Befehls

Der „apply“-Befehl ist nur im [Interactive]-Menü enthalten. Sie können diesen Befehl verwenden, um nur einen bestimmten Teil eines Terms zu bearbeiten und dessen Ergebnis anzuzeigen.

0237 Berechnen des Ergebnisses von diff(sin(

Berechnen nur eines Teils des Terms

x),x) × cos(x) + sin(x) × diff(cos(x),x), und anschließend

Hinweis: Dieses Beispiel geht von der Annahme aus, dass der ClassPad für die folgenden

Moduseinstellungen konfiguriert ist: Algebra, Complex, Radian, Descending Order.

2-9 Verwenden des Main-Menüs in Kombination mit

anderen Anwendungs-Menüs

Sie können vom Main-Menü aus auf die Fenster anderer Anwendungen des ClassPad zugreifen und Kopieren, Einfügen, Drag & Drop (Ziehen und Ablegen) und weitere Operationen zwischen diesen Anwendungen ausführen.

Tipp

• Wenn Sie Daten, die Farbinformationen umfassen, in einer anderen Anwendung kopieren und in das Main-Menü einfügen,werden die Farbinformationen nicht berücksichtigt. Die eingefügten Daten werden schwarz. Dies gilt auch, wenn Sie Daten aus einer anderen Anwendung in das Main-Menü ziehen.

• Wenn Sie Daten im Main-Menü kopieren und in eine andere Anwendung einfügen, werden die eingefügten Daten gemäß den Farbeinstellungen dieser anderen Anwendung angezeigt. Dies gilt auch, wenn Sie Daten aus dem Main-Menü in eine andere Anwendung ziehen.

Verwenden des Fensters eines anderen Anwendungs-Menüs

u Öffnen des Fensters eines anderen Anwendungs-Menüs

1. Tippen Sie auf die Pfeilabwärts-Schaltfläche ganz rechts auf der Symbolleiste.

• Eine Palette der Anwendungs-Ikons wird angezeigt.

Grafik-Editor 3D-Grafik

Grafik

3D-Grafik-Editor

Kegelschnitt-Grafik

Differentialgleichungseditor

Numerische Lösung

2. Tippen Sie auf die Schaltfläche, die dem Fenster entspricht, das Sie öffnen möchten.

• Dadurch erscheint das der angetippten Schaltfläche entsprechende Fenster als unteres Fenster.

u Schließen des Fensters eines anderen Anwendungs-Menüs

1. Tippen Sie auf eine beliebige Stelle innerhalb des Fensters, das Sie schließen möchten.

Geometrie Tabellenkalkulation Statistik-Editor Kegelschnitt-Editor Wahrscheinlichkeit Finanzmath Verifizierung Zahlenfolgen-Editor

2. Tippen Sie in der rechten oberen Ecke auf die C-Schaltfläche, oder tippen Sie auf O und dann auf [Close].

• Der Arbeitsbereich des Main-Menüs füllt nun das gesamte Display aus.

Kapitel 2: Main-Menü 97

Tipp

• Auch wenn Sie das r-Ikon der Ikon-Leiste verwenden, um das untere Fenster zu vergrößern, sodass dieses das gesamte Display ausfüllt, wird dieses geschlossen, wenn Sie auf O und anschließend auf [Close] tippen, und Sie kehren zum Fenster des Arbeitsbereichs zurück.

• Es geschieht nichts, wenn Sie auf O und dann auf [Close] tippen, während das Fenster des Arbeitsbereichs aktiv ist.

u Kopieren eines Terms im Arbeitsbereich und Einfügen des Terms in das Grafik-Editor-

Fenster

0238 Kopieren von „x2 – 1“ im Arbeitsbereich und Einfügen des Terms in das Grafik-Editor-Fenster

• Weitere Informationen über das Grafik-Editor-Fenster finden Sie in Kapitel 3.

u Grafisches Darstellen einer Funktion durch Ziehen aus dem Arbeitsbereich in das

Grafikfenster

0239 Grafisches Darstellen des Terms „x2 – 1“, der bereits in den Arbeitsbereich eingegeben wurde

• Wie in diesem Beispiel sichtbar wird, kann eine Grafik gezeichnet werden, indem ein Term in der Form im Grafikfenster abgelegt wird.

• Wenn eine Formel im 3D-Grafikfenster anstatt im Grafikfenster abgelegt wird, muss sie die Form haben (so wie x^2+y^2).

f ( x, y)

Verwenden des Statistik-Editor-Fensters

Sie können das Statistik-Editor-Fenster verwenden, um neue LIST-Variablen zu erstellen und vorhandene LIST-Variablen zu bearbeiten. Sie können das Statistik-Editor-Fenster auch für Eingabe des Namens einer LIST-Variablen und die Anzeige ihres Inhalts verwenden.

u Verwenden einer LIST-Variablen mit Dateneingabe über den Statistik-Editor zur Ausführung

einer Berechnung im Arbeitsbereich

0240 Eingeben von Daten in „list1“ und „list2“ unter Verwendung des Statistik-Editors und anschließend

Ausführen der Berechnung list1+list2 im Arbeitsbereich

• list1 bis list6 sind Systemvariablen des LIST-Typs. Nähere Informationen hierzu siehe „Hauptspeicher- Datentypen“ (Seite 28).

• Informationen über die Eingabe und Bearbeitung von Listendaten unter Verwendung des Statistik-Editors sind in Kapitel 7 zu finden.

f (x)

u Verwenden des Statistik-Editors zum Aufrufen einer LIST-Variablen, die im Arbeitsbereich

erstellt wurde

0241 Unter Fortführung des Beispiels 0240 Verwenden des Statistik-Editors zum Aufrufen einer list-

Variablen „test“, die im Arbeitsbereich erstellt wurde

Verwenden des Geometriefensters

Wenn ein Geometriefenster auf dem Display angezeigt wird, können Sie Werte und Terme in das Geometriefenster ziehen, um die Grafik oder Figur des Wertes oder Terms zu zeichnen. Sie können auch eine Figur vom Geometriefenster in den Arbeitsbereich ziehen, der den entsprechenden Term oder Wert anzeigt.

u Ziehen eines Terms vom Arbeitsbereich in das Geometriefenster

0242 Eingeben des Terms x2/52 + y2/22 = 1 in den Arbeitsbereich und anschließendes Ziehen des Terms in

das Geometriefenster

Kapitel 2: Main-Menü 98

Tipp: Die folgende Tabelle zeigt die Typen der Terme, die Sie im Geometriefenster ablegen können. Wenn der Term nicht

erkannt wird, wird er im Geometriefenster als Text angezeigt.

Ablegen dieses Terms im Geometriefenster: Zeigt Folgendes an:

Lineare Gleichung mit Gleichung eines Kreises mit Gleichung einer Ellipse mit Gleichung einer Hyperbel mit Zweidimensionaler Vektor (im Format von 2 Zeilen × 1

Spalte) Gleichung

2 ×

y = f ( x)

n Matrix, n t 3

x und y

n × 2 Matrix, n t 3

Eine Gerade Ein Kreis Eine Ellipse Eine Hyperbel

Ein Punkt

Eine Kurve Ein geschlossenes Polygon (jede Spalte repräsentiert

einen Eckpunkt des Polygons) Ein offener Polygonzug

u Ziehen einer Figur aus dem Geometriefenster in den Arbeitsbereich

0243 Ziehen eines Punkts, eines Kreises, eines Punkts und seiner Abbildung aus dem Geometriefenster in

den Arbeitsbereich

• Informationen zu Operationen im Geometriefenster finden Sie in Kapitel 8.

Tipp: Nachfolgend ist gezeigt, was geschieht, wenn Sie eine Figur aus dem Geometriefenster in den Arbeitsbereich

ziehen.

Ablegen dieser Figur im Arbeitsbereich: Zeigt Folgendes an:

Punkt Koordinaten als Ortsvektor (2 × 1 Matrix) Gerade Gleichung der Geraden Vektor Koordinaten als freier Vektor (entspricht dem dazu

parallelen Ortsvektor mit gleicher Pfeilrichtung) Kreis, Kreisbogen, Ellipse, Funktion oder Kurve Entsprechende Gleichung Polygon Offener Polygonzug (erstellt durch Animation) Geradenpaar Lineares Gleichungssystem für das Paar Ein Punkt und seine Abbildung unter einer Transformation Matrixterm für die Transformation

2 ×

n Matrix

n × 2 Matrix

2-10 Verwenden der Verifizierungs-Funktion

Die Verifizierungs-Funktion bietet Ihnen ein leistungsstarkes Werkzeug, um prüfen zu können, ob Ihre numerischen oder algebraischen Umformungen richtig sind. „Verify“ unterstützt Sie bei der Vereinfachung von Termen, indem verifiziert wird, ob ein von Ihnen eingegebener Term gleich Ihrem ursprünglichen Term ist. Ist dies der Fall, dann erhalten Sie eine positive Antwort; wenn nicht, müssen Sie Ihren Fehler berichtigen, bevor Sie fortfahren können.

u Starten der Verifizierungs-Funktion

1. Tippen Sie auf die Pfeilabwärts-Schaltfläche ganz rechts auf der Symbolleiste.

2. Auf der erscheinenden Ikon-Leiste tippen Sie auf W.

Term der linken Seite

Term der rechten Seite

Kapitel 2: Main-Menü 99

u Menüs und Schaltflächen der Verifizierungs-Funktion

• Löschen des Verifizierungs-Fensters ....................................................... File - New, Edit - Clear All oder O

• Öffnen oder Speichern einer Datei ...............................................................File - Open, File - Save oder {

• Festlegen des Berechnungsbereichs für komplexe Zahlen für „Verify“ ......................................................T

• Festlegen des Berechnungsbereichs für reelle Zahlen für „Verify“ .............................................................Y

• Festlegen des Berechnungsbereichs für positive reelle Zahlen für „Verify“ ................................................U

• Verifizieren der Gleichung mit Beginn ab der ersten Zeile ..........................................................................!

• Verifizieren der Gleichung mit Beginn ab der aktuellen Zeile ....................................................................."

0244 Vollständiges Zerlegen der Zahl 50 in ihre Faktoren

0245 Unter Fortführung des Beispiels 0244 Faktorisieren des Terms

schreiben)

+ 1 (in der Faktorenform neu

2-11 Verwenden der Wahrscheinlichkeits-Simulations-

Funktion

Mit der Wahrscheinlichkeits-Simulations-Funktion realisieren Sie folgende Experimente:

• Simulation empirischer Häufigkeiten der Würfelseiten (Augenzahlen), die erscheinen, wenn ein idealer Würfel

mit einer vorgegebenen Versuchsanzahl gewürfelt wird (1 Die)

• Simulation empirischer Häufigkeiten auftretender Augensummen, die erscheinen, wenn zwei ideale Würfel mit

einer vorgegebenen Versuchsanzahl geworfen werden (2 Dice +)

• Simulation empirischer Häufigkeiten auftretender Produkte der Augenzahlen, die erscheinen, wenn 2 ideale

Würfel mit vorgegebener Versuchsanzahl gewürfelt werden (2 Dice ½)

• Nachdem Kugeln in den „Farben“ A, B, C, D, E und F mit vorzugebenden Anzahlen in eine Urne gelegt

wurden: Simulation empirischer Häufigkeiten der „Farben“, die auf den zufällig gezogenen Kugeln erscheinen, bei vorgegebener Anzahl von Ziehungen (Container)

Die Anzahl der Würfelseiten können Sie als eine beliebige ganze Zahl von 1 bis 20 vorgeben.

„Simulations“-Fenster

(Versuchsinformationen und Ergebnis)

„Probability“-Dialogfeld

u Starten der Wahrscheinlichkeits-Simulations-Funktion

1. Tippen Sie auf die Pfeilabwärts-Schaltfläche ganz rechts auf der Symbolleiste.

2. Tippen Sie in der nun erscheinenden Ikon-Leiste auf P. Ein anfängliches „Probability“-Dialogfeld wird geöffnet.

u Menüs und Schaltflächen der Wahrscheinlichkeits-Simulations-Funktion

• Löschen des Simulations-Fensters (und Anzeigen des „Probability“-Dialogfelds)

.......................................................................................................... File - New, Edit - Clear All oder O

Kapitel 2: Main-Menü 100

Casio FX-CP400 operation manual [de]

Specifications and Main Features

Frequently Asked Questions

User Manual

Inhalt

Kapitel 1: Grundlagen

1-1 Allgemeine Anleitung

1-2 Stromversorgung

1-4 Eingabe

1-5 ClassPad-Daten

1-6 Erstellen und Verwenden von Variablen

1-7 Konfigurieren der Anwendungsformate

Kapitel 2: Main-Menü

2-1 Grundrechenarten

2-3 Berechnungen mit Funktionen

2-4 Listenberechnungen

2-5 Matrizen- und Vektorrechnung

2-6 Vorgeben eines Zahlensystems

2-7 Verwenden des Aktionsmenüs

2-8 Verwenden des Interaktiv-Menüs

2-10 Verwenden der Verifizierungs-Funktion