How it Works
Casio
Loading...
FX-5800P
Specifications
1 pgs1.48 Mb0
Supplement [es]
18 pgs737.79 Kb0
User Manual
139 pgs5.81 Mb0
User Manual
147 pgs1.23 Mb0
User Manual [it]
147 pgs1.23 Mb0

Casio FX-5800P Supplement [es]

Download
fx-5800P
 Tillägg Supplement Suplemento Ergänzung Supplemento
J E S G I Sw KCh C
http://edu.casio.jp/ http://world.casio.com/edu/
付録
RJA516833-001V01
1-1
m
p
1.67262171×10
–27
kg
3-5
1-2
mn1.67492728×10
–27
kg
3-6
F
96485.3383 C mol
–1
1-3
me9.1093826×10
–31
kg
3-7
e
1.60217653×10
–19
C
1-4
m
1.8835314×10
–28
kg
3-8
N
A
6.0221415×10
23
mol
–1
1-5
a
0
0.5291772108×10
–10
m
4-1
k
1.3806505×10
–23
J K
–1
1-6
h
6.6260693×10
–34
J s
4-2
V
m
22.413996×10
–3
m3 mol
–1
1-7
5.05078343×10
–27
J T
–1
4-3
R
8.314472 J mol
–1
K
–1
1-8
927.400949×10
–26
J T
–1
4-4
C
0
299792458 m s
–1
2-1
H
1.05457168×10
–34
J s
4-5
C
1
3.74177138×10
–16
W m
2
2-2
α 7.297352568×10
–3
4-6
C
2
1.4387752×10
–2
m K
2-3
re2.817940325×10
–15
m
4-7
σ
5.670400×10–8 W m–2 K
–4
2-4
λc2.426310238×10
–12
m
4-8
ε
0
8.854187817×10
–12
F m
–1
2-5
γ
p
2.67522205×108 s
–1
T
–1
5-1
12.566370614×10
–7
N A
–2
2-6
λcp1.3214098555×10
–15
m
5-2
2.06783372×10
–15
Wb
2-7
λcn1.3195909067×10
–15
m
5-3
g
9.80665 m s
–2
2-8
R∞
10973731.568525 m
–1
5-4
G07.748091733×10
–5
S
3-1
u
1.66053886×10
–27
kg
5-5
Z
0
376.730313461 Ω
3-2
1.41060671×10
–26
J T
–1
5-6
t
273.15 K
3-3
–928.476412×10
–26
J T
–1
5-7
G
6.6742×10
–11
m3 kg–1 s
–2
3-4
–0.96623645×10
–26
J T
–1
5-8
atm
101325 Pa
–4.49044799×10
–26
J T
–1
N
µ
B
µ
µ
p
µ
e
µ
n
µ
0
µ
µ
µ
0
φ
#01
– 1 –
#02
a
=
n
Σy
i
–
a.Σx
i
b =
n.Σx
i
2
–
(
Σx
i
)
2
n.Σxiy
i
–
Σx
i
.
Σy
i
r
=
{
n.Σx
i
2
–
(
Σx
i
)
2
}{
n.Σy
i
2
–
(
Σy
i
)
2
}
n.Σxiy
i
–
Σx
i
.
Σy
i
m
y – b
a
=
n = ax + b
#03
Σy
i
= –
a
(
)
–
b
(
)
Σ
x
i
Σx
i
2
b
=
Sxx.Sx2x
2
– (Sxx
2)2
Sxy.Sx2x
2
– Sx
2
y.Sxx
2
a
=
Sxx.Sx2x
2
– (Sxx
2)2
Sx2y.Sxx – Sxy.Sxx
2
(
Σ
x
i
)
2
Sxx = Σx
i
2
–
n
Sxy = Σxiy
i
–
(Σx
i
.
Σy
i
)
Sxx
2
=
Σ
x
i
3
–
(
Σ
x
i
.
Σ
x
i
2
)
Sx2x
2
= Σx
i
4
–
(Σx
i
2)2
Sx2y = Σx
i
2
y
i
–
(Σx
i
2
.
Σy
i
)
m1
=
2a
– b +
b
2
– 4a
(
c
– y
)
m2 =
2a
–
b
–
b
2
– 4a
(
c
– y
)
n = ax2 + bx + c
#04
a =
n
Σy
i
– b
.
Σlnx
i
b =
n
.
Σ
(
lnx
i
)
2
–
(
Σlnx
i
)
2
n
.
Σ
(
lnx
i
)
y
i
– Σlnx
i
.
Σy
i
r =
{n
.
Σ
(
lnx
i
)
2
–
(
Σlnx
i
)
2
}{n
.
Σy
i
2
–
(
Σy
i
)
2
}
n
.
Σ
(
lnx
i
)
y
i
– Σlnx
i
.
Σy
i
m = e
y – a
b
n = a + blnx
– 2 –
a
= exp
(
)
n
Σlnyi – lnb.Σx
i
b = exp
(
)
n.Σx
i
2
–
(
Σx
i
)
2
n.Σx
i
lny
i
– Σx
i
.
Σlny
i
r =
{n
.
Σx
i
2
–
(
Σx
i
)
2
}{n
.
Σ
(
lny
i
)
2
–
(
Σlny
i
)
2
}
n.Σx
i
lny
i
– Σx
i
.
Σlny
i
m =
lnb
lny – lna
n = ab
x
a = exp
(
)
n
Σlnyi – b.Σlnx
i
b =
n.Σ
(
lnx
i
)
2
–
(
Σlnx
i
)
2
n.Σlnx
i
lny
i
– Σlnx
i
.
Σlny
i
r =
{n
.
Σ
(
lnx
i
)
2
–
(
Σlnx
i
)
2
}{n
.
Σ
(
lny
i
)
2
–
(
Σlny
i
)
2
}
n.Σlnx
i
lny
i
– Σlnx
i
.
Σlny
i
m = e
b
ln y – ln a
n = ax
b
#05
#06
#07
a = exp
(
)
n
Σlny
i
– b
.
Σx
i
b =
n.Σx
i
2
–
(
Σx
i
)
2
n.Σx
i
lny
i
– Σx
i
.
Σlny
i
r =
{n
.
Σx
i
2
– (Σx
i
)
2
}{n
.
Σ
(
lny
i
)
2
– (Σlny
i
)
2
}
n.Σx
i
lny
i
– Σx
i
.
Σlny
i
m =
b
lny – lna
n = ae
bx
– 3 –
b =
Sxx
Sxy
r =
Sxx.Syy
Sxy
S
xx = Σ (x
i
–1
)
2
–
Syy = Σy
i
2
–
S
xy = Σ(x
i
–1
)y
i
–
n
(Σx
i
–1
)
2
n
Σx
i
–1
.
Σy
i
n
(
Σy
i
)
2
a =
n
Σy
i
– b
.
Σx
i
–1
#08
m
=
y – a
b
n = a +
x
b
1
2
3
4
5
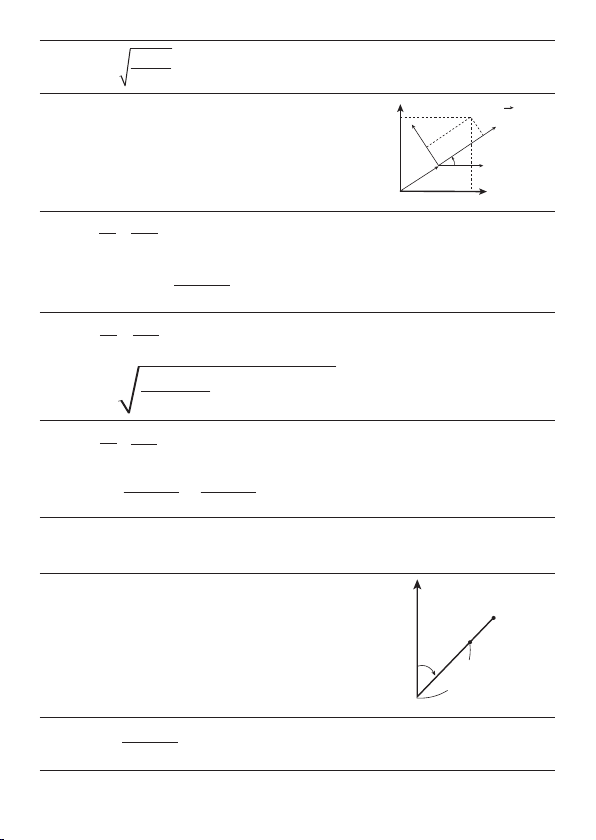
tan
=
θ
m
2 – m1
1 +
m1m2
(m
1m2 G
1)
a
=
t
2 – t1
(t2 >
t1 >
0)
a
b
c
A
B
C
S
=
n{2a + (n – 1)d}
2
#09
θ
y
x
y = m2 x + k
2
y = m
1
x + k
1
cos A =
2
bc
b
2
+ c2 – a
2
cos B =
2
ca
c
2
+ a2 – b
2
cos C =
2
ab
a
2
+ b2 – c
2
2 – 1
υ υ
S
= 0
t + at
2
1 2
(t
> 0)
υ
– 4 –
6
7
8
9
[(xp, yp)→(Xp, Yp)]
Xp = (x
p–x0
)cos + (yp–y0)sin
Yp
= (
y
p–y0
)cos – (xp–x0)sin
α
α
10
11
12
=
(M, T > 0)
3RT
M
[ +
+
Z
=
Const.]
P
γ
2g
P
2
= P
1
+
γ
(
2g
+ Z1 – Z
2
)
(υ, P, , Z > 0)
γ
[ +
+
Z
=
Const.
]
P
γ
2
2g
2g(P
1
– P2)
γ
[ +
+
Z
=
Const.]
P
γ
P
x = nCx
P
x
( 1 – P)
n–x
13
η
=
Q
1
– Q
2
Q
1
( Q
1
G 0)
X
P
= Rcos
+
X
A
α
Y
P
=
Rsin
+
Y
A
α
α
α
y
x
Y
X
(0, 0)
(x0, y0)
α
(x
p
, y
p
)
(X
p
, Y
p
)
(XA, YA)
(Xp, Yp)
(XB, YB)
α
R
υ
2
υ
1
2
– 2
2
υ
υ
υ
+
1
2
+
2g( Z1 – Z2)
υ
( , P, , Z > 0)
γ
υ
2
=
υ
2
2g
υ
γ
( , P, , Z > 0)
γ
υ
Z
2
= + + Z
1
P
1 – P2
1
2
–
2
2
2g
υυ
(
)
0 < P < 1
x = 0, 1, 2······
Pol(X
B
– XA, YB – YA)
– 5 –
14
15
16
17
18
19
20
η
=
T
1
– T
2
T
1
( T
1
G 0)
F = mr
2
ω
(m,
r,
> 0)
ω
F = m
r
S
0
= rR
π
(r,R> 0)
V
=
r2h (r, h > 0)
1 3
π
S
0
= 2 rh
π
(r,
h > 0)
21
V = r2h
π
(r,
h > 0)
24
T
=
1
f
( f > 0)
25
S = r
2
π
(r > 0)
22
T =
2
ω
π
(
G 0)
ω
2
υ
=
T
σ
( T,
> 0 )
σ
υ
23
T
=
2 r
υ
π
( G 0)
υ
(r,
m,
> 0)
υ
26
R =
ρ
R
S
(S,R, > 0)
ρ
[ ]
[ ]
27
ρ
ρ
A
1 1 1
= A
2 2 2
= Const.
υ
υ
ρ
28
A
1 1 1
= A
2 2 2
= Const.
υ
ρ
υ
ρ
(
2
G 0, 2 > 0)
ρ
υ
(A2,
2
> 0)
2
=
υ
A
2 2
ρ
A
1 1 1
ρ
υ
A
2
=
A
1 1 1
ρ
υ
2 2
ρ
υ
– 6 –
X
P
= Rcos
+
X
A
α
Y
P
= Rsin
+
Y
A
α
29
R
1
=
R4R
5
+ R
5R6
+ R
6R4
R
5
R
2
=
R4R
5
+
R5R
6
+
R6R
4
R
6
R
3
=
R4R
5
+ R
5R6
+ R
6R4
R
4
(R4, R5, R6 > 0)
30
R
4
=
,
R
5
R
1R2
R
1
+ R2 + R
3
=
,
R
2R3
R
1
+ R2 + R
3
R
6
=
R
3R1
R
1
+ R2 + R
3
(R1, R2, R3 > 0)
31
[(XA, YA), Rec(R, )→(Xp, Yp)]
α
32
a = b
2
+ c2 – 2bc cos A
(b, c > 0, 0˚ < A < 180˚)
a
2
= b2 + c2 – 2bc cos A →
b
2
= c2 + a2 – 2ca cos B
c
2
= a2 + b2 – 2ab cos C
33
r
2
Qq
F =
4
0
π
ε
1
(r > 0)
34
S = 1
3
+ 2
3
+ ······ + n
3
=
{
}
2
n(n + 1)
2
35
Ai [dB] = 20 log
10
[d B]
(
)
Ι
2
Ι
1
(Ι2 / Ι1 > 0)
36
σ
y = × 10 +
50
x – x
A
( > 0)
σ
(XA, Y
A
)
(Xp, Yp)
α
R
X
– 7 –
υ
W = CV
2
1 2
W =
1 2
C
Q
2
(C > 0)
U
p
=
kx
2
(k, x > 0)
1 2
=
0
t +
υ
S
gt
2
(t > 0)
1 2
37
Pol(X
B
– XA, YB – YA)
38
f = f
0
υ
υ
–
0
– u
(
)
υ
G
υ
0
,
f
0
> 0, > 0
υ
υ
–
0
υ
– u
39
40
41
42
43
W = QV
1 2
44
W = ED
1 2
(E, D > 0)
45
W = E2
1 2
( , E > 0)
ε
ε
46
4
0
r
2
π
ε
Q
E =
( = 9 × 10
9
)
Q
r
2
( r > 0)
47
f =
2
1
π
LC
(L, C > 0)
48
S = ab (a, b > 0)
π
(XA, YA)
(XB, YB)
α
R
X
49
H = U + PV (U, P, V> 0)
– 8 –
P
x
=
(0 < k<N, 0 < n < N)
kCx · N – k C n – x
NCn
sin ic = (1 < n
12
)
1
n
12
55
56
V
e
= BR ( , B, R > 0)
υ
υ
57
P
nRT
V
= (n, T, V > 0)
58
V
nRT
P
= (
n, T, P
> 0)
59
T
PV
nR
= (P, V, n > 0)
60
n
PV RT
= (P, V, T > 0)
61
62
W = LI
2
(L, I > 0)
1 2
S = s(s – a)(s – b)(s – c), s =
a + b + c
)
(
a + b > c
> 0
b + c > a
> 0
c + a > b
> 0
52
S =
(r G 1)
a (rn –1)
r – 1
53
Q = mcT
54
2
50
y
=
e
– x
x > 0
λ
λ
y
= 0
x
< 0
( > 0)
λ
51
(
)
P
x
= ( 1 – P)
x
P
x = 0, 1, 2······
0 < P < 1
– 9 –
63
x
=
n – m
nX
3
– mX1 + Y1 – Y
3
y = m (x – X
1
) + Y
1
)
(
m
=
X
2
– X
1
Y
2
– Y
1
n =
X
4
– X
3
Y
4
– Y
3
64
x =
n – m
nX
3
– mX1 + Y1 – Y
3
y = m (x – X
1
) + Y
1
)
(
m
=
X
2
– X
1
Y
2
– Y
1
n = tan
α
65
P = RI
2
(R > 0)
66
P = (R > 0)
V
2
R
67
68
X
= 2 f L – ( = L – = X
L
– X
C
) ( f, L, C > 0)
π
1
2 f C
π
ω
1
C
ω
69
Z = R
2
+ (2 f L )
2
(= R2 +
2 L2
) (R, f, L > 0)
π
ω
70
Z =
( )
1
R
2
+
( )
2
2 f C –
π
1
2 f L
π
1
(
R, f, C, L > 0)
71
Z =
( )
2
2 f L –
π
1
2 f C
π
R
2
+
( )
=
( )
L –
1
C
R
2
+
ω
ω
(R, f, L, C > 0)
72
F = mH
(m, H > 0)
(X4, Y4)
(X1, Y1)
(X2, Y2)
(X3, Y3)
(x, y)
(X3, Y3)
(X2, Y2)
(X1, Y1)
(x, y)
X
α
U
k
= m
2
1 2
υ
(m, > 0)
υ
– 10 –
F
= iBR
sin
θ
(R> 0, 0˚<   < 90˚)
θ
73
74
T
=
m
2
=
R
2
(m > 0, B > 0, R > 0)
1 2
1 2
m
q
2B2
υ
75
R
1
= Z
0
, R
2
=
1–
Z
0
Z
1
1–
Z
0
Z
1
Z
1
L
min
= 20 log [d B]
( )
–1
Z
1
Z
0
Z
1
Z
0
+
R2
Z0
Z1
R1
(
Z
0 > Z1 > 0)
76
[
]
Z
1
D
1
M
= = =
Z
2
D
2
P
π
M
=
Z
D
(D, Z > 0)
77
[
]
Z
1
D
1
M = = =
Z
2
D
2
P
π
M
=
P
(P > 0)
π
78
[
]
Z
1
D
1
M = = =
Z
2
D
2
P
π
D2
=
(D
1
, Z1, Z2 > 0)
D1Z
2
Z
1
79
[
]
Z
1
D
1
M
= = =
Z
2
D
2
P
π
D =
(P, Z > 0)
PZ
π
80
σ
y = e
–
2
1
π
( > 0)
( x – )
2
2
2
µ
σ
σ
81
YR =
,
Y
X
= 2
f C
–
π
1
2 f L
π
(R, f,C,
L
> 0)
82
S = ab sin
α
( )
a, b > 0
0˚
< < 180˚
α
R
1
– 11 –
Ap [dB] = 10 log
10
[d B] (P
2
/
P
1
> 0)
83
C =
S
d
ε
(S, d > 0)
84
d =
ax1 + by1 + c
a
2
+ b
2
(a, b G 0)
85
R
=
(
x
2
– x
1
)
2
+
(
y
2
– y
1
)
2
86
P
x
=
x !
µ
x
e
–
µ
x
= 0, 1, 2······
0 <
( )
µ
87
Up
= mg h (m, h > 0)
88
ϕ
cos = = (R > 0)
Z
R
( )
P
EI
89
( )
P
2
P
1
90
V
=
Ah
(A, h > 0)
1 3
91
a
2 + b2
= c
2
d
P(x
1
, y1)
ax
1
+ by
1
+ c = 0
b
a
y
1
y
2
y
x
1
R
x
2
– 12 –
V
R
= V · e
–
93
92
S
=
2
(X1 – X
2
) (Y
3
– Y
1
)
+
(X
1
– X
3
) (Y
4
– Y
2
) + (X
1
– X
4
) (Y
1
– Y
3
)
94
Z =
1
2 f C
π
R
2
+
( )
=
1
2C2
R
2
+
ω
(R, f, C > 0)
( )
2
X
Y
(X1, Y1)
(X4, Y4)
(X3, Y3)
(X2, Y2)
CR
t
95
[X
n = XA + n
cos
n, Yn
= Y
A + n
sin n]
α α
θ
α
n
=
0
+ n – 180: X
n = XA + n
cos
n
α
α
Y
n
= Y
A + n
sin
n
α
R
R
R
R
(X1, Y1)
(XA, YA)
X
α
0
α
1
θ
1
R
v
96
n =
sin i sin r
(i, r > 0)
97
nHr
=
r ! (n – 1) !
(n + r – 1) !
0 < r 1 < n
( )
98
n∏r
= n
r
99
R =
v
uR
(v G 0)
100
E = I
2
(I, > 0)
1 2
ω
ω
i
r
I
II
– 13 –
( )
S = rR (r,R> 0)
1 2
101
Z
R
= R, Z
X
= 2 f L –
π
1
2
f C
π
(R, f, L, C,
Z > 0)
102
I
A
C
L
S
R
l
IA
= 2
sin
–1
2R
l
S = – sinI
A
360
π
R2I
A
2
R
2
CL
= × R ×
IA
180
π
103
R
r
104
τ
P
A
= (A, P > 0)
105
τ
= G (G, > 0)
γ
γ
106
θ
θ
F
mg
F = – mg sin (m > 0)
θ
107
F
O
H
mg
x
F
= –
x
R
mg
R> 0
m> 0
108
x = r sin ( r > 0)
θ
109
x = r sin t ( r > 0)
ω
v
– 14 –
110
T
= 2 (
R> 0)
π
R
g
111
R
A
0
sin A
a
=
2R
( )
0˚
< A < 180˚
R > 0
112
[
]
a
= 2
Rsin A
sin A
a
=
2R
[
]
2sin A
a
R =
(0˚<
A
< 180˚, a > 0 )
113
sin A
a
sin B
b
= = =
2
R
sin C
c
V
= r
3
( r > 0)
4 3
115
I = ( r > 0)
P
4 r2
π
116
S = 4 r
2
( r > 0)
π
117
118
T = 2
π
m
k
(m > 0, k > 0)
π
( )
114
C
L
IA
R
T
L
S
L
TL = R tan
IA
2
CL
=
·R·I
A
180
π
SL = R –1
1
cos
IA
2
v
0˚< A, B, C < 180˚
a, b, c, R > 0
( )
– 15 –
S = 1
2
+ 2
2
+ ······ + n
2
= n (n + 1)(2n + 1)
1
6
S = KRcos2 + C cos
α
α
h
=
KRsin2 + C sin
1 2
α
S = (a + b) h (a, b, h > 0)
1 2
119
120
( )
0
< < 90˚
K,R, C > 0
α
121
122
λ
=
R
σ
E
(E, ,R> 0)
σ
123
S
=
bc sin A
1 2
(0˚ < A < 180˚)
124
Y
X
(X1, Y1)
(X2, Y2)
(X3, Y3)
S
=
2
(X
1
– X
2
) (Y
3
– Y
1
)
+
(X
1
– X
3
) (Y
1
– Y
2
)
125
y = a < x < b
b – a
1
y = 0 x < a , x < b
126
F = G
Mm
(M, m, r > 0)
127
[(X
A
, YA) to (XC, YC) → (x, y), R]
R
(XA, YA)
(XB, YB)
(XC, YC)
(x, y)
x =
m +
m
1
mX
A
+ XC – YA + Y
C
m
1
y = Y
A
+ m (x – XA)
R=
(X
C
– x)2 + (YC – y)
2
m =
Y
A
– Y
B
X
A
– X
B
( )
128
α
( )
V
2
V
1
A [d B]= 20 log
10
[d B] (V
2
/
V
1
> 0)
υ
r
2
– 16 –
SA0606-A Printed in China
CASIO COMPUTER CO., LTD.
6-2, Hon-machi 1-chome
Shibuya-ku, Tokyo 151-8543, Japan
Loading...
Buy Points How it Works FAQ Contact Us Questions and Suggestions Privacy Policy Cookie Policy Terms of Use