Casio fx-570MS User Manual

A supplementary reader

for CASIO fx-991MS/ fx-570MS / fx-115MS/fx-100MS

fx-95MS/ fx-82MS / fx-350MS / fx-85MS

SA0204-010002B

Printed in Japan

Worldwide
Education Web

http://world.casio.com/edu_e/

About this book...

This book is a collection of easy-to-understand middle and high school practical problems

that can be solved using a CASIO Scientific Calculator. Problems have been carefully

selected to provide practice in performing calculations that are commonly encountered in

our modern digital information age.

As you will probably discover when you work through the problems in this book, the

scientific calculator is a tool that makes it possible to perform very complex calculations

that would be impossible to perform using manual calculation alone. We hope this lightening

of the calculation load will provide you with more time to spend developing knowledge of

theory and logic, and contribute towards making the study of mathematics more fun.

It is important to remember that this book is not intended to replace the User’s Manual

that comes with your CASIO Scientific Calculator. Make sure you also carefully read the

User’s Manual and familiarize yourself with the features and functions of your calculator

before and while using this book.

When using this book, also remember that it was prepared for a global audience, so

some of the units and contents contained herein may not apply in your particular country or

region.

We at CASIO sincerely hope you enjoy working through the problems in this book, and

that by doing so you are better prepared to meet the challenges of the future digital

information age.

The History of the CASIO Calculator

As the company that developed the world’s first relay-type calculator,

CASIO boasts a proud history of continual innovation and development of

new calculators that expand new horizons and meet the needs of students the

world over. Ever since the 1972 introduction of the fx-1 with simple scientific

function calculator capabilities, CASIO FX Series calculators have been

meeting the needs of teachers, students and other calculator users for some

30 years.

Today, the lineup of CASIO FX Series Scientific Function calculators

covers a wide variety of needs, and are featured in mathematics texts the

world over.

Contents

fx-82MS
fx-85MS fx-95MS

Page fx-350MS

Negative Value Calculations ........................................1 ●●●●

Expression Values and Calculations ............................2 ●●●●

Proportion and Inverse Proportion...............................3 ●●●●

Circles and Sectors ...................................................... 5 ●●●●

Square Roots ................................................................ 7 ●●●●

Pythagorean Theorem ..................................................9 ●●●●

Permutation, Combination ......................................... 10 ●●●●

Trigonometric Function Addition Theorem...............12 ●●●●

Exponential Functions ...............................................13 ●●●●

Logarithmic Functions............................................... 14 ●●●●

Solving Quadratic Equations and Cubic Equations ... 15 ●●●

Solving Simultaneous Equations ...............................18 ●●●

Problems Using CALC and SOLVE..........................22 ●●

Problems Involving Complex Numbers,

with an Emphasis on Polar Form ............................... 25 ●●

fx-100MS fx-570MS
fx-115MS fx-991MS

Statistics Problems ..................................................... 28 ●●●●

Solving Differentials,

with an Emphasis on the Derivative ..........................31 ●●

Solving Integrations,

with an Emphasis on Definite Integrals ..................... 32 ●●

Matrix Problems ........................................................34 ●

Vector Problems .........................................................38 ●

*Please note that some calculator models cannot be used for certain activities.
*Operational procedures may differ depending on the calculator model you use.

Negative Value Calculations

Example

Example

Operation

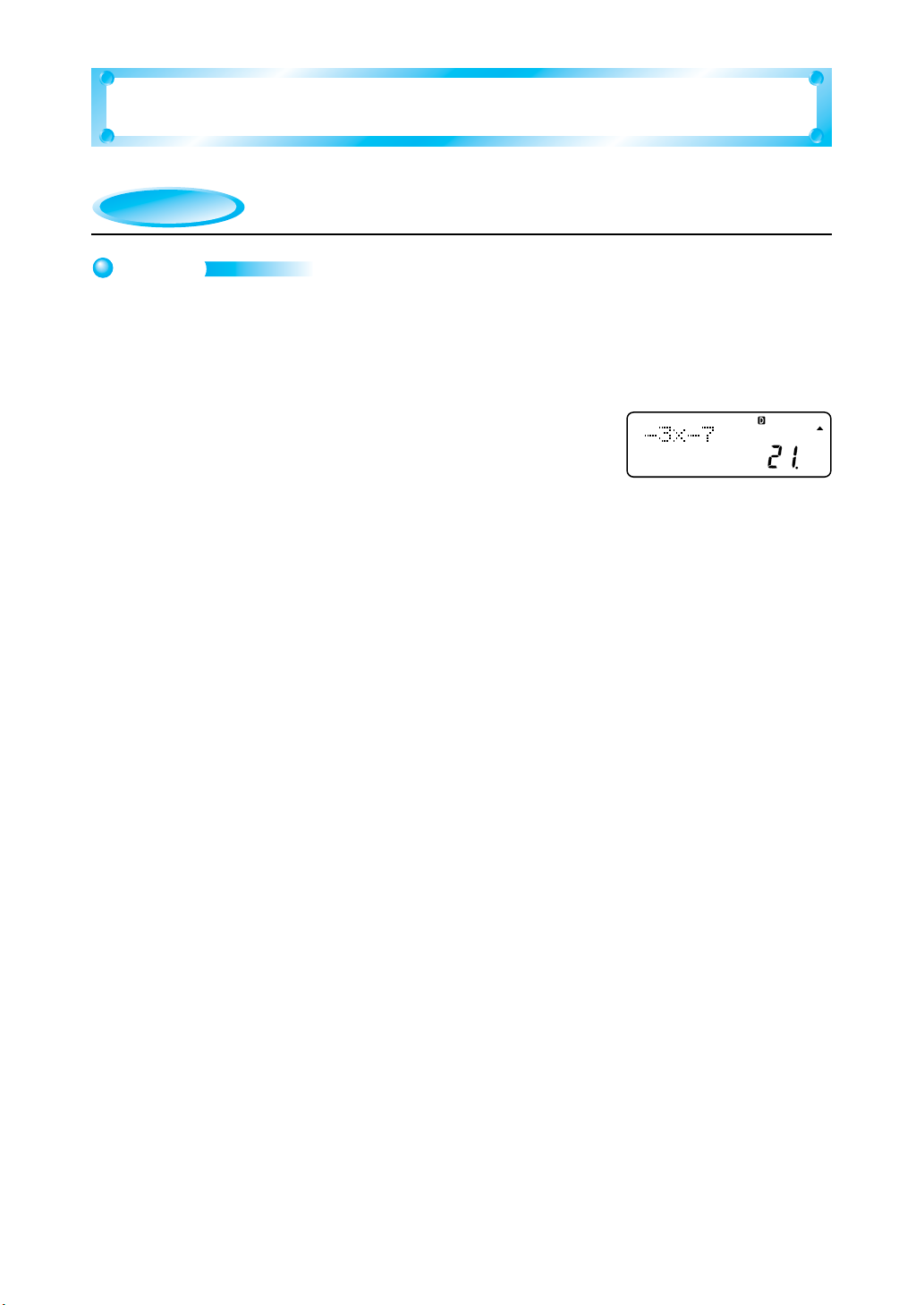
(–3) × (–7) = ?

1. Enter the COMP Mode.

F 1

2. Perform the calculation (–3) × (–7).

D 3 - D 7 =

Result: 21

– 1 –

Expression Values and Calculations

Example

Example

Operation

Determine the value of x2 –

1. Enter the COMP Mode.

F 1

2. Assign 5 to variable X.

5 A J x

3. Assign –3 to variable Y.

D 3 A J y

2

2

4. Determine the value of X

–

Y.

5

p x K , 2 C 5 p y =

Result: 26

1

5

2

y when x = 5 and y = –3.

5

– 2 –

Proportion and Inverse Proportion

y

x

–5

–5

5

5

–10

–10

10

10

Example

Example

For y = 12/x, calculate the values of y for x = 1, 2,
3, 4, 5, 6, to determine how the value of
in proportion to a gradual increase in the value of

x.

Next, calculate the values of
–4, –5, –6, to determine how the value of
changes in proportion to a gradual decrease in
the value of x.

Operation

y for x = –1, –2, –3,

1. Enter the COMP Mode.

F 1

2. Determine the value of y when x = 1.

y changes

y

1 a - 12 =

Result: 12

3. Determine the value of y when x = 2.

2 a - 12 =

Result: 6

4. Likewise, determine the values of y for x = 3, 4, 5, 6.

5. Press the [ key five times to display the value of y = 12 when x = 1.

– 3 –

Proportion and Inverse Proportion

6. Use the ] key to scroll through the values of y for x = 2, 3, 4, 5, 6.

The above reveals that the value of y decreases as the value of x increases.

7. Repeat steps 2 through 6 to calculate the values of y for x = –1 through –6.

○○○

Doing so will reveal that the value of y increases as the value of x decreases.

– 4 –

Circles and Sectors

Example 1

Example 1

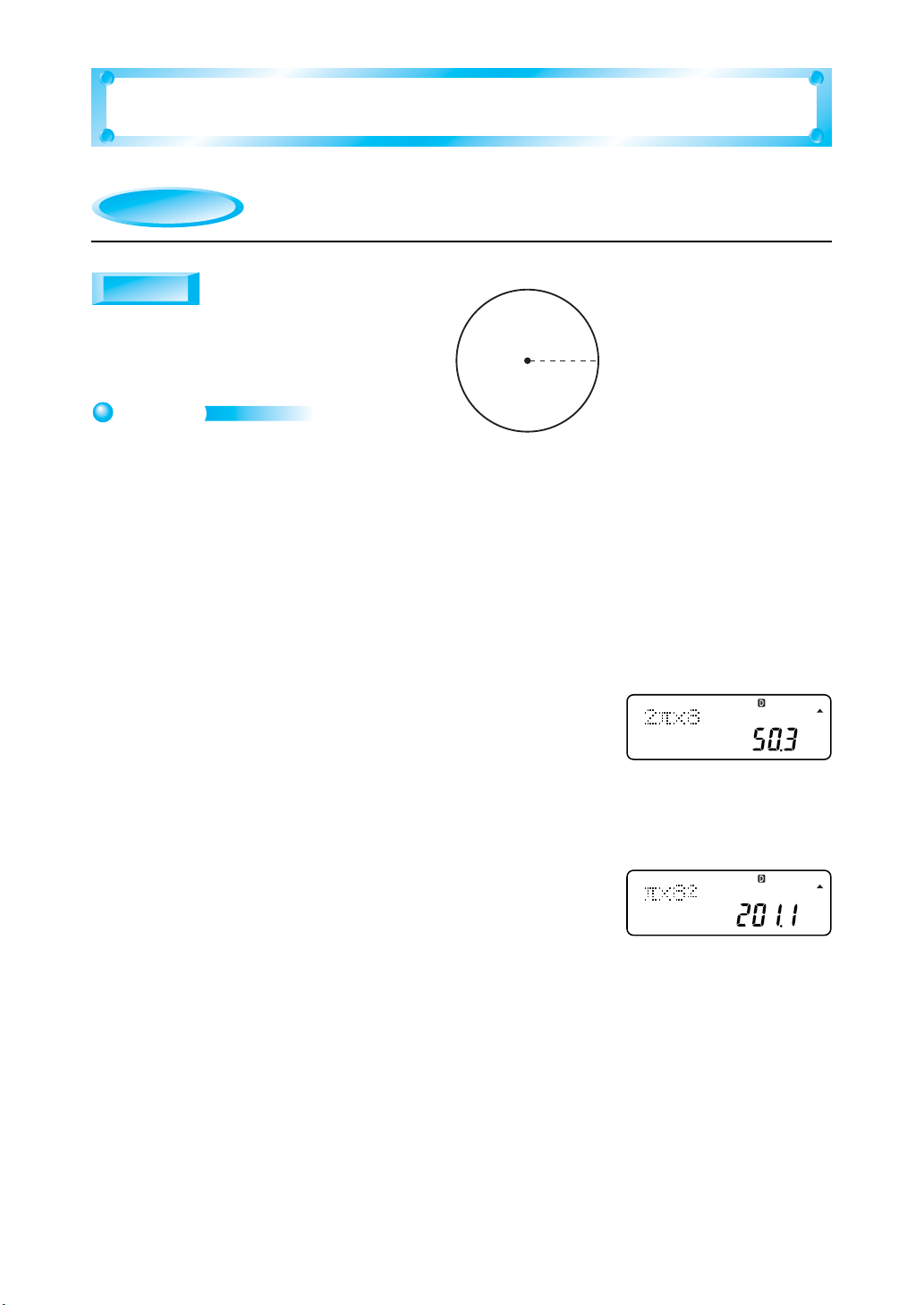
Determine, up to one decimal place, the circumference and
the area of a circle with a radius of 8 cm.

l

Explanation

Explanation

Circumference of a circle: l = 2πr
Area of a circle: S = πr

(Radius = r)

2

r

Operation

1. Enter the COMP Mode.

F 1

2. Press the F key a number of times until 1 (Fix1) is specified as the fixed number of decimal

places.

F

• • •

1(Fix) 1

]

3. Calculate the circumference of the circle.

2 A x - 8 =

FIX

Result: 50.3

The circumference of the circle is approximately 50.3 cm.

4. Calculate the area.

A x - 8 K =

Result: 201.1

The area is approximately 201.1 cm2.

– 5 –

FIX

Circles and Sectors

Example 2

Example 2

Explanation

Explanation

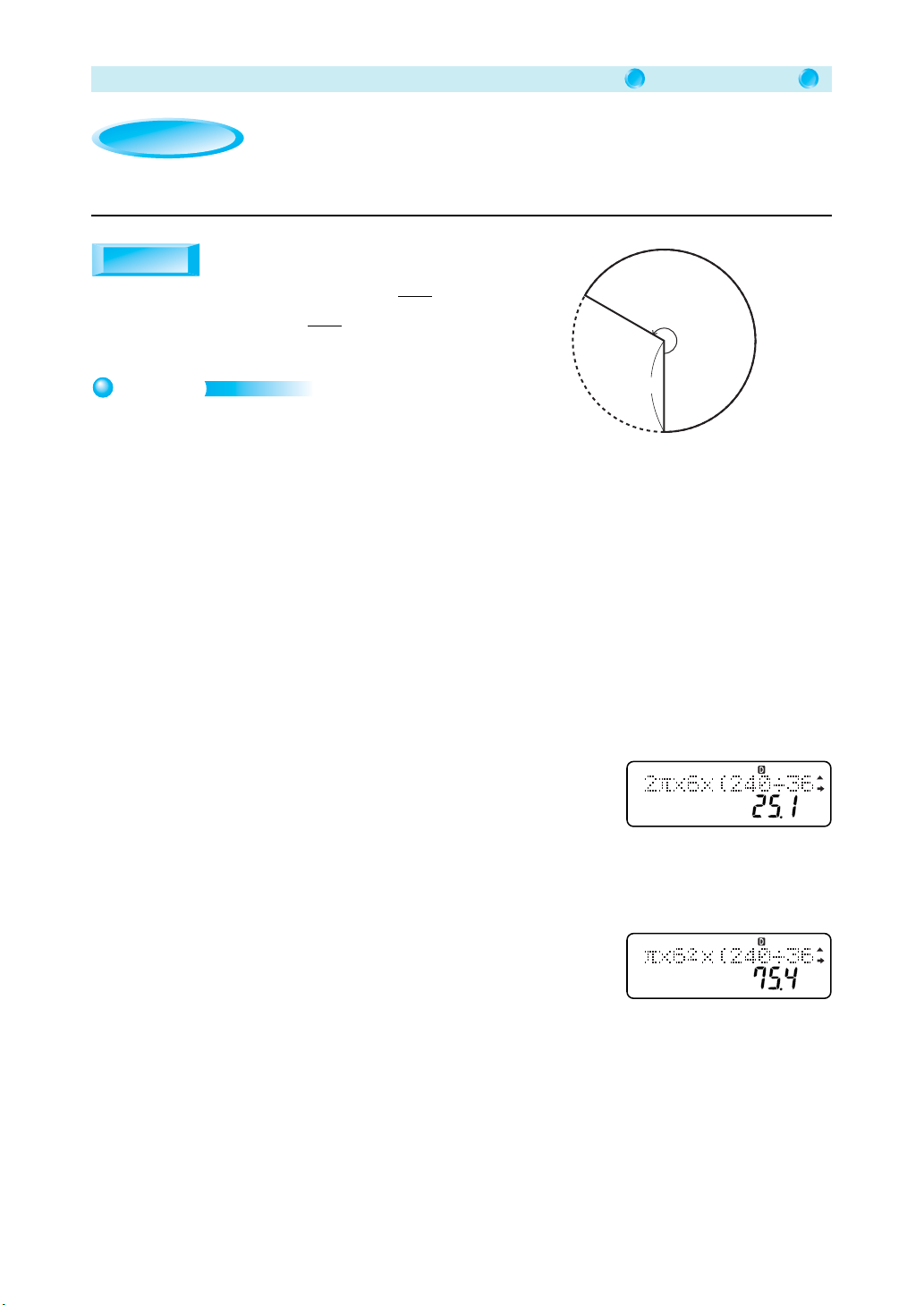
Length of the arc of a sector: l = 2πr ×

Area of a sector: S = πr

(Radius = r, central angle = a°)

Operation

Determine, up to one decimal place, the length of the arc
and area of a sector that has a radius of 6 cm and a
central angle of 240°.

a

a

2

×

360

360

240°

6 cm

1. Enter the COMP Mode.

F 1

2. Press the F key a number of times until degrees (Deg) are specified as the angle unit.

F

• • •

1(Deg)

]

3. Press the F key a number of times until 1 (Fix1) is specified as the fixed number of decimal

places.

F

• • •

1(Fix) 1

]

4. Determine the length of the arc of the sector.

2 A x - 6 - R 240 \ 360 T =

The length of the arc of the sector is approximately 25.1 cm.

5. Calculate the area.

A x - 6 K - R 240 \ 360 T =

The area is approximately 75.4 cm2.

FIX

FIX

– 6 –

Square Roots

Example 1

Example 1

Explanation

Explanation

Operation

Calculate the approximate square root values and then
compare the results.

Arrange the following from smallest to largest.
7, 2.7, 22/3, 18/7

1. Enter the COMP Mode.

F 1

2. Determine the approximate value of 7.

L 7 =

Result: 7  2.645751311]

3. Determine the approximate value of 22/3.

L R 22 \ 3 T =

Result: 22/3  2.708012802

4. Convert 18/7 to its decimal equivalent.

18 \ 7 =

Result: 18/7 = 2.571428571

5. Using the [ key to scroll through and compare the results produced by steps 2 through 4

reveals that the proper ascending order arrangement of the values is: 18/7 < 7 < 2.7 < 22/3.

– 7 –

Square Roots

Example 2

Example 2

Explanation

Explanation

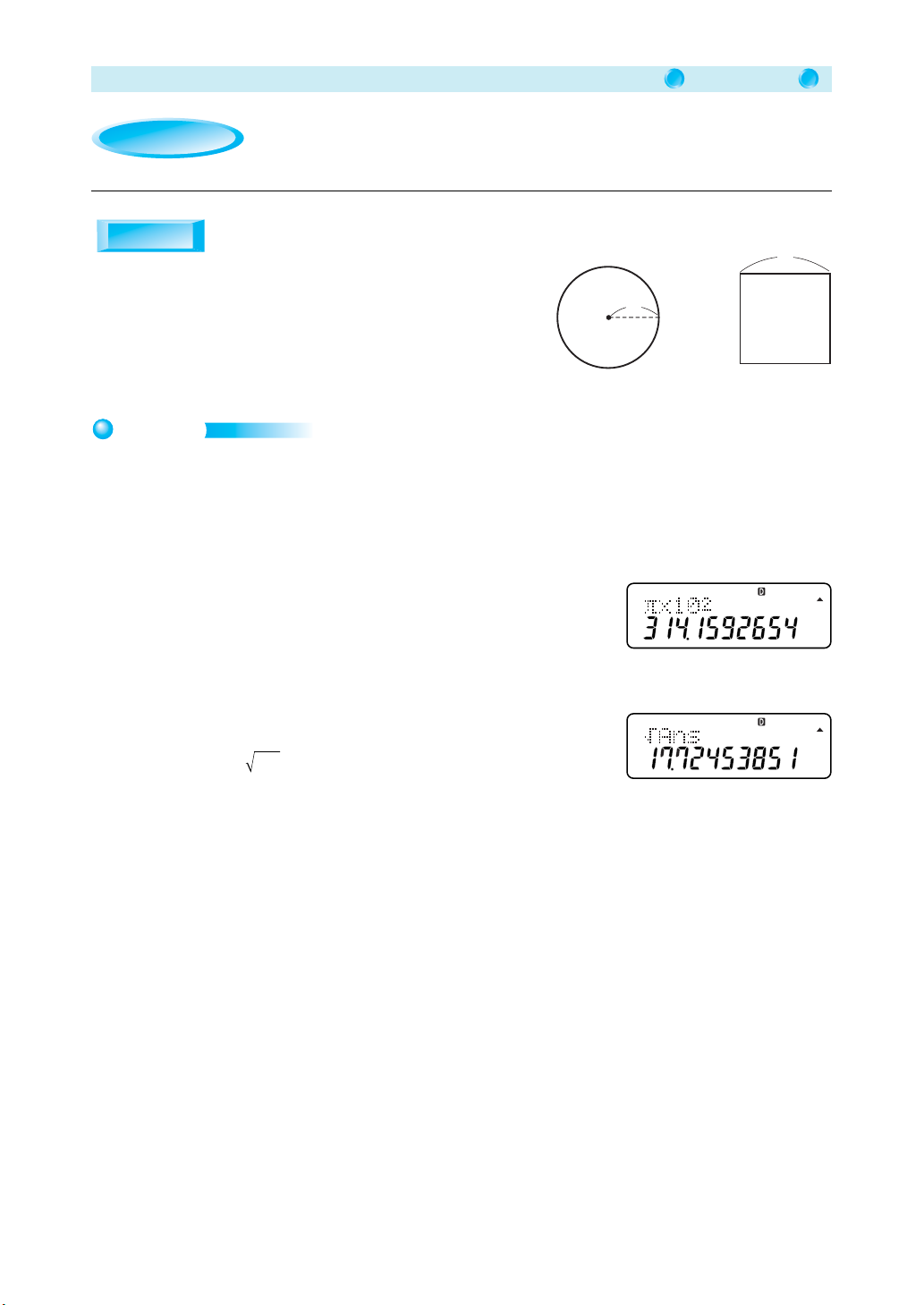
• First, determine the area of the circle.

• If the length of one side of a square is l, the area of the

square is l2. This means that the length of one side of a
square with the same area as the above circle can be
determined by calculating the square root of the area.

Operation

Determine the length of one side of a square whose area is
equal to that of a circle with a radius of 10 cm.

1. Enter the COMP Mode.

F 1

2. First, determine the area of the circle with a 10cm radius.

A x - 10 K =

Result: S = 314.1592654

l

r

SS

=

3. Calculate the square root of the area.

L =

Result: l = S = 17.72453851

The above indicates that the length of one side of a square whose area is equal to that of a circle

with a radius of 10 cm is 17.7 cm.

– 8 –

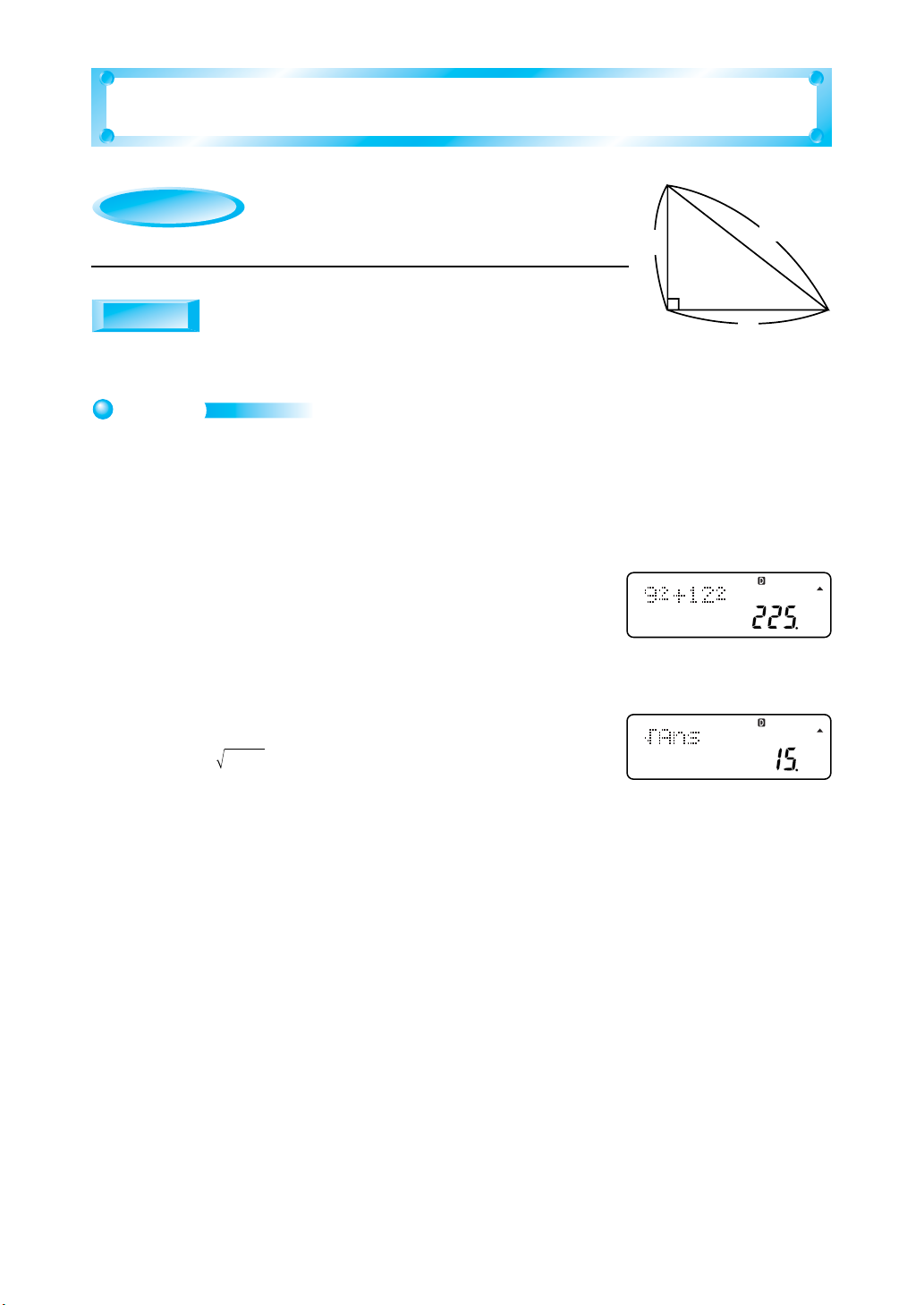
Pythagorean Theorem

Example

Example

Explanation

Explanation

2

a

+ b2 = c

(Two sides = a, b; Hypotenuse = c)

2

Determine the length of the
hypotenuse of a right triangle whose
sides are 9 cm and 12 cm long.

Operation

1. Enter the COMP Mode.

F 1

2. Determine the sum of the squares of the two sides of the right triangle.

9 K + 12 K = ]

3. Calculate the square root.

b

c

a

L =

Result: 225 = 15

The above shows that the length of the hypotenuse is 15 cm.

– 9 –

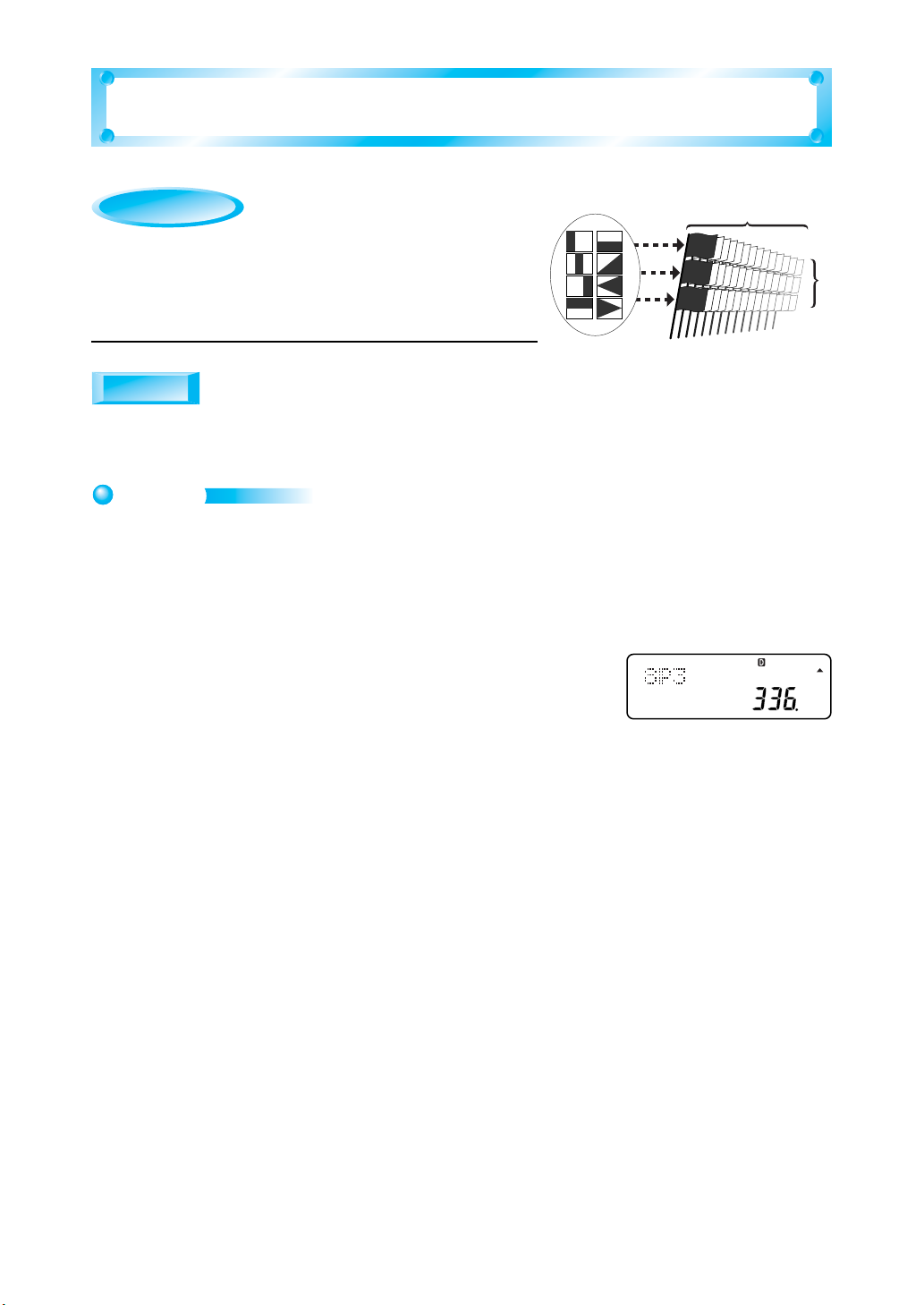
Permutation, Combination

Example 1

Example 1

What would be the maximum number of
different flag signals possible using eight
flags of eight different colors, when each
signal consists of three flags?

Explanation

Explanation

Determine 8P3.

Operation

1. Enter the COMP Mode.

F 1

2. Determine

8 A m 3 =

Result: 8P3 = 336 ]

8P3

.

8

?

3

The above indicates there are 336 different signals possible.

– 10 –

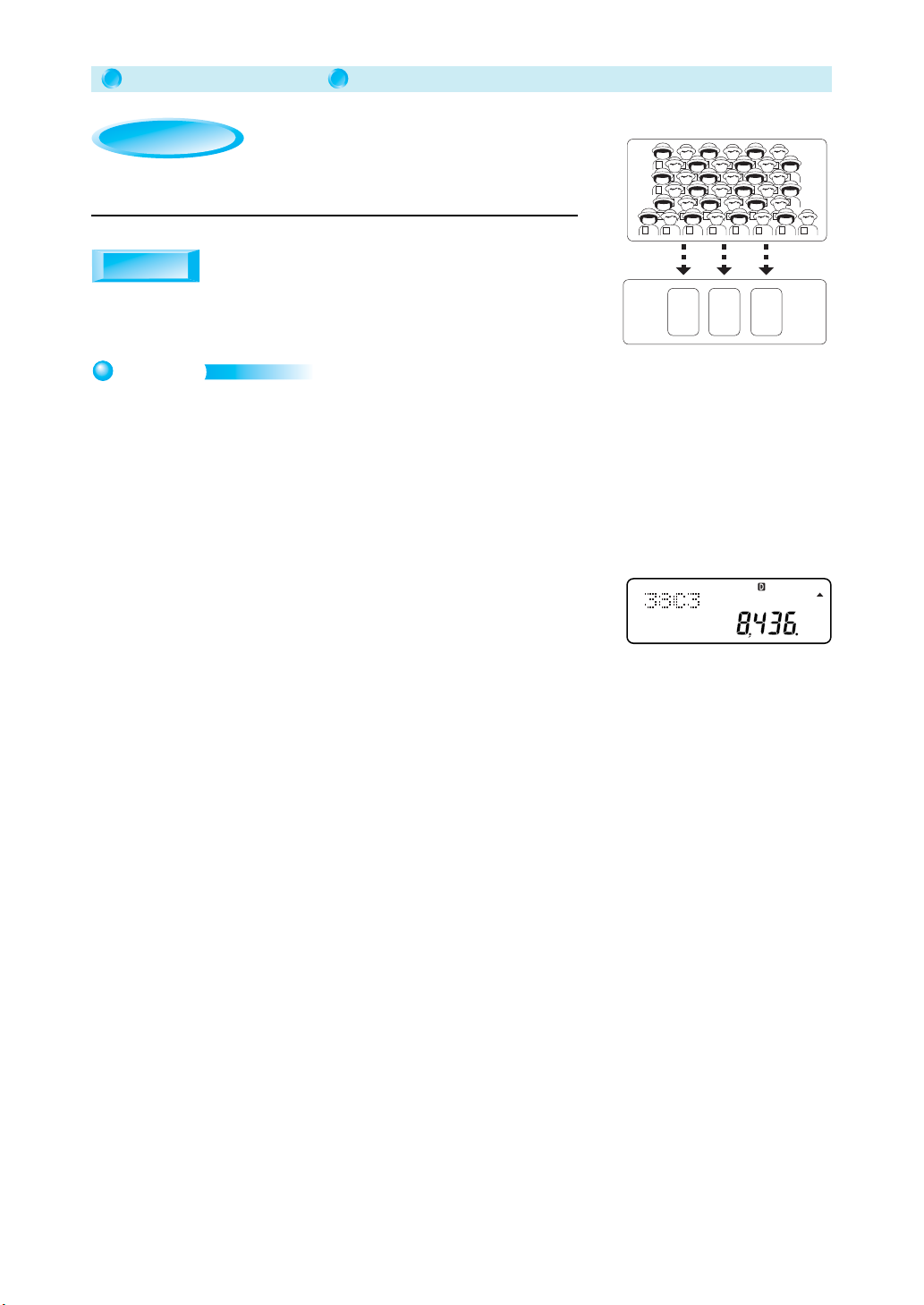
Permutation, Combination

Example 2

Example 2

How many different combinations
are possible when selecting three

38

3

Explanation

Explanation

Determine 38C3.

individuals from a class of 38?

Operation

* The following shows operation using the fx-82MS/85MS/350MS/95MS.

1. Enter the COMP Mode.

F 1

2. Determine

38 n 3 =

Result: 38C3 = 8436 ]

38C3

.

1

3

2

3

7

13

2

3

2

25

26

33

32 38

5

4

6

5

4

3

27

6

5

4

6

5

4

6

29

28

30

35

34

36

1

1

3731

The above shows there are 8436 different combinations possible.

– 11 –

Trigonometric Function Addition Theorem

Example

Example

Explanation

Explanation

sin Function Addition Theorem:
sin(α + β) = sinα cosβ + cosα sin

Operation

Determine the validity of: sin75°
= sin (30° + 45°) = sin30° cos45° + cos30° sin45.

β

1. Enter the COMP Mode.

F 1

2. Press the F key a number of times until degrees (Deg) are specified as the angle unit.

F

• • •

1(Deg)

]

3. Determine value of sin75°.

S 75 =

Result: sin75° = 0.965925826

4. Determine value of sin30° cos45° + cos30° sin45°.

S 30 - W 45 + W 30 - S 45 =

Result: sin30° cos45° + cos30° sin45° = 0.965925826

5. Use the [ key to display the result obtained in step 3 to see if it matches the values obtained in

step 4.

– 12 –

Exponential Function

Example

Example

Explanation

Explanation

• When a ≠ 0: a

• When

a > 0: a

Determine the value of 64

(–p)

= 1/(ap)

(q/p) = p

a

q

Operation

1. Enter the COMP Mode.

F 1

2. Determine the value of 64

64 W R D 2 \ 3 T =

Result: 64

(–2/3)

= 0.0625]

(–2/3)

.

3. Convert to a fraction.

C

(-2/3)

.

The above indicates that 64

(–2/3)

= 0.0625 =

1

––

16

.

– 13 –

Logarithmic Function

Example

Example

Explanation

Explanation

• This calculator has two logarithmic functions: log whose base is e (natural logarithm),

and ln whose base is 10 (common logarithm).

• When the base is something other than that described above, the following formula can

be used to convert the base: When a > 0, b > 0, M > 0 and a b 1, use logaM =
(logbM)/(logba) for the calculation.

Determine the value of log2 .

1

128

≠ ≠

Operation

1. Enter the COMP Mode.

F 1

2. Determine log

1

= (log )/(log 2).

2

128

1

128

R 128 a \ R 2 =

Result: log2 = log /log 2 = –7 ]

1

128

1

128

– 14 –

Solving Quadratic Equations

and Cubic Equations

(fx-95MS/fx-100MS/fx-115MS/fx-570MS/fx-991MS only)

Example 1

Example 1

Operation

*The following shows operation using the fx-100MS/115MS/570MS/

991MS.

1. Select the EQN Mode and then specify the degree of the equation.

In this example we want to solve a quadratic equation,

so you would specify 2.

F F F 1

r

(Degree?) 2

Solve the equation 2x2 – 5x + 2 = 0.

y

2

1

x

21

＿

1
2

2. Input values for a, b, and c in the quadratic equation ax

(a?) 2 =

(b?) D 5 =

(c?) 2 =

3. One of the solutions obtained appears on the display.

4. Display the next solution. ]

The above produces the solutions x = 2 and x = 0.5.

2

+ bx + c = 0.

– 15 –

Example 2

Example 2

Solving Quadratic Equations and Cubic Equations

y

Solve the equation x3 + 2x2 – 2x + 3 = 0 in
the range of complex numbers.

Operation

*The following shows operation using the fx-100MS/115MS/570MS/

991MS.

1. Select the EQN Mode and then specify the degree of the equation.

In this example we want to solve a cubic equation,

so you would specify 3.

F F F 1

r

(Degree?) 3

2. Input values for a, b, c, and d in the cubic equation ax

(a?) 1 =

3

+ bx2 + cx + d = 0.

–3

3

2

1

x

–2 –1

(b?) 2 =

(c?) D 2 =

(d?) 3 =

3. One of the solutions obtained appears on the display.

4. Display the next solution. ]

This causes the symbol R↔I to appear in the upper right corner

of the display.

This indicates that the displayed solution is a complex number,

and the real part is 0.5.

– 16 –

Solving Quadratic Equations and Cubic Equations

5. Display the imaginary part of the solution.

A r

Each press of A r toggles the display between the real part and imaginary part.

6. Display the other solution. ]

A r

This solution is also a complex number, which is the conjugate of the previous solution.

The above example shows us that the solutions for the equation are x = –3, x = 0.5 – 0.866025403i,
and x = 0.5 + 0.866025403i.

– 17 –

Solving Simultaneous Equations

(fx-95MS/fx-100MS/fx-115MS/fx-570MS/fx-991MS only)

Example 1

Example 1

Explanation

Explanation

established and solved as simultaneous equations.

If the number of 50g weights is x and the number of 20g

weights is y, the relation

A group of 13 weights, some weighing 50 grams and some
weighing 20 grams, weigh a combined total of 530 grams.
How many of each type of weight are there?

x + y = 13

{}

x

+ 20y = 530

50

can be

Operation

*The following shows operation using the fx-100MS/115MS/570MS/991MS.

1. Select the EQN Mode and then specify the number of unknowns.

In this example we have two unknowns, x and y, so we would specify 2.

F F F 1

20

g

?

???

????

?????

530

50

g

g

(Unknowns?) 2

2. Input the values for the coefficients of the linear equations with two unknowns

(a1?) 1 =
(b1?) 1 =
(c1?) 13 =
(a2?) 50 =
(b2?) 20 =
(c2?) 530 =

3. One of the solutions obtained appears on the display.

– 18 –

a1x

+

b1y

=

c

1

{}

a2x

+

b2y

=

.

c

2

Solving Simultaneous Equations

4. Display the next solution. ]

The above tells us there are nine 50g weights and four 20g weights.

– 19 –

Solving Simultaneous Equations

x

+

y+z= 170

5

x–3y

=0

x+y–z

=22

{}

Example 2

Example 2

the number of beans given to C is 22 less than the combined total given to
A and B. How many beans each were given to A, B, and C?

Explanation

Explanation

number of beans. This means the total number of beans is x +

y + z = 170. Also, since we know the ratio of beans received

between A (x) and B (y) is 3:5, we can say 5x = 3y, which can
be transformed to 5
beans less than A and B combined, we can say

Combining all of this leaves us with the set of simultaneous equations

we should be able to solve and come up with the answer we need.

Let us say A received x number of beans, B
received y number of beans, and C received z

170 beans are divided among three individuals named A,
B, and C. The ratio of beans given to A and B is 3:5, while

170

x – 3y = 0. Finally, since C (z) received 22

z = x + y – 22.

A B C

, which

Operation

*The following shows operation using the fx-100MS/115MS/570MS/991MS.

1. Select the EQN Mode and then specify the number of unknowns.

In this example we have three unknowns, x, y, and z so we would specify 3.

F F F 1

(Unknowns?) 3

2. Input the values for the coefficients of the linear equations with three unknowns

a1x

+

b1y + c1z

a2x

+

b2y + c2z

{}

a3x

+

b3y + c3z

(a1?) 1 =
(b1?) 1 =
(c1?) 1 =
(d1?) 170 =
(a2?) 5 =
(b2?) D 3 =
(c2?) 0 =
(d2?) 0 =
(a3?) 1 =

=
=
=

d

1

d

2

.

d

3

– 20 –

Solving Simultaneous Equations

(b3?) 1 =
(c3?) D 1 =
(d3?) 22 =

3. Display the solutions.

The above shows us that A received 36 beans, B 60 beans, and C 74 beans.

[ ]

[ ]

– 21 –

Problems Using CALC and SOLVE

21

7

3

y

x

(fx-100MS/fx-115MS/fx-570MS/fx-991MS only)

Example 1

Example 1

Explanation

Explanation

same variable within a single function.

The CALC function comes in handy when substituting
various different values for multiple instances of the

Perform the following steps to sketch the general graph of
the function

2

y = x

+ x + 1.

• Substitute various values for

• Plot the points (

• Connect adjacent points.

Operation

1. Select the COMP Mode.

F 1

2. Input the function and store it.

x, and solve for y.

x, y) on a plane.

p y p u p x K + p x + 1
C

3. Input values for x to display the values obtained for y.

(Input 1.)

1 =

(Input 2.)

C 2 =

< Note >

In this way, use CALC to solve for other values and then draw the graph to see what it looks like.

– 22 –

Problems Using CALC and SOLVE

Example 2

Example 2

An object is dropped from a height of A (m) (free fall). If the speed of the
object when it reaches the ground is B (m/s) and gravitational acceleration is
C = 9.8 (m/s
Determine the speed of the object when it reaches the ground if it is dropped
from a height of 30 meters.
Convert the speed to kilometers per hour.

2

), we can set up the following relation: (1/2) B2 = CA.

Explanation

Explanation

A unit conversion function (fx-570MS/fx-991MS only) lets
you convert from meters per second to kilometers per hour.

gh =2V

g = C = 9.8, h = A = 30, V = B = ?

The SOLVE function lets you solve for the value
of a given relation without changing its form.

1

2

C =

B = ?

9.8 (m/s2)

(m/s)

30m (A)

Operation

1. Select the COMP Mode.

F 1

2. Input the function and store it.

R 1 \ 2 T - p w K p u p e - p q
A I

3. Input values for the variables. Do not input anything for the variable for which you want to solve.

In this example we want to solve for B, so we input values for A and C.

]

9.8 =

30 =

– 23 –

Problems Using CALC and SOLVE

4. Display the variable for which you want to solve, and then run SOLVE.

[ [

A I

(It will take some time before the solution appears.)

5. Now convert the speed to kilometers per hour.

The unit conversion number for converting meters per second to kilometers per hour is 20.

A c 20 =

The above shows us that the approximate speed of the object would be 24.25 meters per second, which

converts to 87.3 kilometers per hour.

– 24 –

Problems Involving Complex Numbers,

with an Emphasis on Polar Form

(fx-100MS/fx-115MS/fx-570MS/fx-991MS only)

Example 1

Example 1

plane, and then determine the point with a ratio of 2 with
the origin as the center.

Rotate 3 – 2i 60 degrees around the origin of the complex

Explanation

Explanation

formed with the positive part of the
express complex number z = a + bi as z = r (cosθ + i sinθ).
This is called polar representation of complex number z.
Using polar representation for z2 in the complex number
multiplication z1 × z2 gives us z2 = r2 (cos
can rotate z1
us a value with a ratio of r

Defining r as the distance of point (a, b) from the

θ

origin on the complex plane and

as the angle

x-axis makes it possible to

θ

+ i sin

θ

2

θ

° around the origin of the complex plane, giving

2

with the origin as the center.

2

). Now we

2

Operation

1. Select the CMPLX Mode.

F 2

2. Specify the angle unit .

F F F F 1(Deg)

imaginary

60°

r

2r

√

3–2i

real

3. Input the polar form of the complex number, with r = 2, and

automatically converted to rectangular form on the display, but you can also display them in polar
form.

θ

= 60. The values you input are

2 A Q 60 =

A r

– 25 –

Problems Involving Complex Numbers, with an Emphasis on Polar Form

4. Multiply by 3 – 2i.

- R L 3 , 2 i T =

A r

The above obtains the complex number 5.196152423 + i.

– 26 –

Problems Involving Complex Numbers, with an Emphasis on Polar Form

Example 2

Example 2

Explanation

Explanation

by determining the absolute value (r) and the argument
(θ) of z1/z2.

You can examine the relationship between
two points on the complex plane (z1 and z2)

Examine the relationship between –5 + 3i and 4 + i, which
are two points on the complex plane.

Operation

1. Select the CMPLX Mode.

F 2

2. Perform the calculation (–5 + 3i ) ÷ (4 + i ).

R D 5 + 3 i T \ R 4 + i T =
A r

3. Convert to polar form and display the result.

–5 + 3

imaginary

i

l

r × l

θ

4 +

i

A Y =

A r

The above indicates that –5 + 3i represents a 135° rotation of 4 + i around the origin, and that it is a

point with a ratio of 1.414213562 (= 2) with the origin as the center.

– 27 –

Statistics Problems

Example 1

Example 1

The following are the measured 100-meter race times for five students.

12.5 11.6 10.8 12.8 11.4 (Unit: Seconds)
Calculate the mean and the sample standard deviation for these results.
Replace the times of the 12-second runners (runner 1 and runner 4) with

11.1 and 11.7 seconds (which are times run by other students), and
calculate the mean and sample standard deviation again.

Explanation

Explanation

When the number of data samples is n, the value of each
data is xi (i = 1...n), and the mean is x :

Sample standard deviation σ

Instead of using these complex formulas, you can obtain the same
results using a simple key operation on the calculator.

Sample standard deviation is a value that expresses
the level of variation among data.

1 =

n-

(Σxi2 – nx

2

)/(n–1)

.

12.5

11.6

10.8

12.8

Operation

*The following shows operation using the fx-82MS/85MS/350MS/95MS.

1. Enter the SD Mode, and clear the statistical memory area.

F 2
A B 1

(Scl) =

2. Input the data.

In the SD Mode, the | key operates as the S key.
Input a value and then press the S key to register it.
To input two sequential values that are identical, input the value and then press S twice..

The display shows how many values have been input (number of samples = n).

11.4

12.5 S 11.6 S 10.8 S 12.8 S 11.4 S

3. Calculate the mean of the data.

t A X 1 =

– 28 –

Statistics Problems

4. Calculate the sample standard deviation of the data.

t A X 3 =

The above shows that the mean is 11.82 seconds, and the sample standard deviation is 0.82.

5. You can view values you have already input by using the ] and [ keys to scroll

them on the display.
You can also edit a displayed value and recalculate, if you want.
For the second part of this problem, first display the first value (12.5 seconds).

t ]

6. Input the new value (11.1) and then press =.

11.1 =

7. Press the ] key a number of times to display the other data item to be edited (12.8 seconds for

runner 4 in this example), and then input the new data (11.7 seconds).

] ] ] ] ] ] 11.7 =

8. Calculate the mean and sample standard deviation of the data.

t A X 1 =

t A X 3 =

The above shows that the mean is 11.32 seconds, and the sample standard deviation is 0.37.

– 29 –

Statistics Problems

58

M

61

M

86

M

61

M

53

M

85

M

72

M

64

M

71

E

68

E

96

E

75

E

84

E

68

E

77

E

80

E

Example 2

Example 2

test results for eight students.

Math 64 72 85 53 61 86 61 58

English 80 77 68 84 75 96 68 71

Use this data to determine the correlation coefficient of the test scores.

The following table shows the mathematics and English

Explanation

Explanation

change in another type of data.
The correlation coefficient r for the two types of data x and y is obtained
using the following expression.

r = =

_

(x_, y

: x, y mean; xσn, yσn: x, y standard deviation)

The correlation coefficient expresses the extent to which
a change in one type of data tends to correspond to a

n

(xi – x)(yi – y)

i = 1

n

(xi – x)

i = 1

2

.

i = 1

n

(yi – y)

n

(xi – x)(yi – y)

i = 1

.

.

xσ

yσ

n

2

n

n

Operation

*The following shows operation using the fx-100MS/115MS/570MS/991MS.

1. Enter the REG Mode and select liner regression (Lin).

First, clear statistical memory.

F F 2 1
A B 1(Scl) = ]]

2. Input the data.

Data items are input in pairs.
Separate each item that makes up a pair with P , and press S to register the pair.

64 P 80 S 72 P 77 S 85 P 68 S 53 P 84 S
61 P 75 S 86 P 96 S 61 P 68 S 58 P 71 S

3. Calculate the correlation coefficient.

A X r r 3(r) =

The correlation coefficient of the above data is about 0.259.

– 30 –

Solving Differentials, with an

Emphasis on the Derivative

(fx-100MS/fx-115MS/fx-570MS/fx-991MS only)

Example 1

Example 1

Explanation

Explanation

Derivative f'(a) at x = a on y = f (x) is the slope of the tangent line at

x = a. Also, the tangent line passes through (a, f (a)), which means

that its equation is y = f'(a) (x – a) + f (a).

Determine the equation for a tangent line at (1, 3) on

2

y = x

– 3x + 5.

Operation

1. Select the COMP Mode.

F 1

2. Determine derivative f'(1) at x = 1 on y = x

2

– 3x + 5.

A J p x K , 3 p x + 5 P 1 T =

3. Determine f'(1) = –1.

f(a)

f(x)

a

tangent line

4. The form of an equation for a tangent line is y = –x + c, which can be transformed to c = y + x.

Since this tangent line passes through (1, 3), substitute these values.

c = y + x

= 3 + 1

5. This produces c = 4.

Based on the above, the equation for the tangent line is y = –x + 4.

– 31 –

Solving Integrations, with an

a

f (x)

axb

Emphasis on Definite Integrals

(fx-100MS/fx-115MS/fx-570MS/fx-991MS only)

Example 1

Example 1

Explanation

Explanation

The area enclosed by y = f(x), the x-axis, and x = a, x = b is generally
determined using the definite integral

Determine the area enclosed by y = x2 + 2, the x-axis, and

x = 1, x = 2.

b

∫

f(x)dx.

a

Operation

1. Select the COMP Mode.

F 1

2. Calculate the value of the definite integral values for y = x

2

+ 2 from x = 1 to x = 2.

d p x K + 2 P 1 P 2 T =

3. This produces a definite integral value of 4.333333333.

The above indicates that the area being calculated is 4.333333333 (= 13/3).

– 32 –

Solving Integrations, with an Emphasis on Definite Integrals

ab

f(x)

Example 2

Example 2

Explanation

Explanation

First, solve y = 4 – x2 and find the x-intercepts. Use this to determine the
integration partition, whose definite integral value is the area.

Determine the area enclosed by y = 4 – x2 and the x-axis.

Operation

1. Select the EQN Mode, and then solve y = 4 – x

2

.

F F F 1 r

(Degree?) 2

(a?) D 1 =
(b?) 0 =
(c?) 4 =

2. The solutions are 2 and –2.

] [

3. Select the COMP Mode and then calculate integration values for y = 4 – x

F 1
d 4 , p x K P D 2 P 2 T =

2

from x = –2 to x = 2.

4. This produces a definite integral value of 10.66666667.

This above tells us that the area being calculated is 10.66666667 (= 32/3).

– 33 –

Matrix Problems

(fx-570MS/fx-991MS only)

Example 1

Example 1

Explanation

Explanation

Operation

Matrix multiplication normally does not follow the commutative law XY = YX.
Consequently, (X + Y) (X – Y) = X2 – XY + YX – Y2 must be used.

Determine X2 – Y2 for two 2 × 2 matrices named X and Y

when X + Y =

3 2

and X – Y =

3 –1

1 –4
7 1

.

1. Select the MAT Mode.

F F F 2

2. Specify the matrix name, and the number of rows and columns, and then input its elements.

For this problem, we need to input X + Y into Matrix A and X – Y into Matrix B.

The following shows input of the elements of Matrix A.

• Specify Matrix A.

A j 1

(Dim)

1

(A)

• Specify 2 for the number of rows (m).

2 =

• Specify 2 for the number of columns (n).

2 =

– 34 –

Matrix Problems

•2 × 2 Matrix A is displayed as

First, input 3 for A

.

11

A11 A12
A21 A22

.

3 =

•Next, input 2 for A12, 3 for A21, and –1 for A22.

2 =

3 =

D 1 =

•The display returns to the initial element (A11) of the matrix after input of values for all elements

is complete.

t

Use the same procedure to input Matrix B elements.

A j 1

1 = D 4 = 7 = 1 = t

(Dim) 2 (B) 2 = 2 =

– 35 –

3. Determine X and Y from X + Y and X – Y.

First, use (X + Y) + (X – Y) = 2X to determine X.

Matrix Problems

A j 3

1

(A)

(Mat)

+

A j 3

1 C 2 - A j 3 (Mat) 4

This produces the result X =

You can use [, ], e, and r to view the other elements of the matrix.

(Mat) 2

(B) =

2 –1

.

5 0

(Ans) =

4. Input result obtained for X into Matrix C.

A j 1

(Dim) 3 (C) 2 = 2 =

2 = D 1 = 5 = 0 = t

5. Now determine Y from (X + Y) – X = Y.

A j 3
A j 3

This produces the result Y =

(Mat) 1
(Mat) 3

(A) ,
(C) =

1 3
–2 –1

.

6. Now perform the calculation Matrix C × Matrix C – Matrix Ans × Matrix Ans (= X

A j 3
A j 3

The above steps show us that X2 – Y2 =

(Mat) 3 (C) K ,
(Mat) 4 (Ans) K =

4 –2
10 0

.

– 36 –

2

– Y2).

Matrix Problems

Example 2

Example 2

Explanation

Explanation

Placing simultaneous equations

makes it possible to express them as AX = B.
This means that if inverse matrix A-1 exists for Matrix A, then X = A-1B.

Operation

Use a matrix to solve the simultaneous equations

2x – 3y = 18

{}

3

x

+ 2y = 1

{}

ax

+ by =

cx

+ dy =

.

k

inside matrices A =

l

1. Select the MAT Mode.

F F F 2

2. Input

2 –3
3 2

A j 1

for Matrix A and

(Dim) 1 (A) 2 = 2 =

2 = D 3 = 3 = 2 = t

18

for Matrix B.

1

a b
c d

, X =

x

, and B =

y

k
l

A j 1

(Dim) 2 (B) 2 = 1 =

18 = 1 = t

3. Determine in inverse for Matrix A.

A j 3

(Mat) 1 (A) a =

4. Multiply the inverse matrix by Matrix B (from the left).

-

A j 3

The above procedure tells us that x = 3 and y = –4.

(Mat) 2 (B) =

– 37 –

Vector Problems

( fx-570MS/fx-991MS only)

tb

→

c

a = (2,1)

→

Express

Example 1

Example 1

Explanation

Explanation

Though this is a vector problem, it can be solved
by solving the following simultaneous equations
for each component.

2s – 3t = 12

{

s

+ 4t = –5

Operation

→

= (–3, 4).

b

= (12, –5) in the form

c

b = (–3,4)

1. Select the EQN Mode and specify 2 as the number of unknowns.

F F F 1

(Unknowns?) 2

2. Input the function and store it.

(a1?) 2 =

=

→

→

+

s

tb

a

when

sa

→

= (2, 1),

a

c = (12, –5) = sa + t b

(b1?) D 3 =
(c1?) 12 =
(a2?) 1 =
(b2?) 4 =
(c2?) D 5 =

3. This shows that the solutions of the simultaneous equations are 3 and 2.

] [

The above tells us that c→=3a→–2b→.

– 38 –

Vector Problems

Example 2

Example 2

Explanation

Explanation

absolute value of its vector, while the angle formed by two
sides is determined using the inner product of their vectors.
For this problem, first lets determine the lengths of the three
sides of triangle ABC.

When determining the properties of a triangle,
the length of a side is determined using the

What type of triangle would be produced by the vertices of
the three points A = (5, 1, 2), B = (1, 0, 1), and C = (2, 4, 2)?

(5, 1, 2)

A

Operation

1. Select the VCT Mode.

x

F F F 3

2. Specify the vector name and dimension, and then input its elements.

The following shows input of the elements of Vector A.

• Specify Vector A.

A z 1

(Dim)

(1, 0, 1)

B

z

(2, 4, 2)

C

y

1

(A)

• Specify three dimensions.

3 =

•3-dimensional Vector A is displayed as (A1 A2 A3). First, input 5 for A1.

5 =

– 39 –

Vector Problems

•Next, input 1 into A2 and 2 into A3.

1 =

2 =

• The display returns to the initial element (A1) after input of values for all elements is complete.

t

Use the same procedure to input elements for Vector B and Vector C.

A z 1

(Dim) 2 (B) 3 =

1 = 0 = 1 = t

A z 1

(Dim) 3 (C) 3 =

2 = 4 = 2 = t

3. Calculate A

B→

= b→– a→.

A z 3 (Vct)

2 (B)

,
A z 3 (Vct) 1

(A) =

– 40 –

Vector Problems

4. Calculate the absolute value of A

The value of AB→ is stored in Ans memory by step 3, so you can use Vct Ans as shown below.

A A A z 3

5. Use the same procedure to obtain absolute values for B

A z 3
A z 3

(Vct) 3 (C) ,
(Vct) 2 (B)

B→

.

(Vct) 4 (Ans) =

C→

and CA→.

=

A A A z 3

(Vct) 4 (Ans) =

A z 3
A z 3

(Vct) 1 (A) ,
(Vct) 3 (C)

=

A A A z 3

The above tells us that the sides of triangle ABC are of equal length, which means it is a regular
triangle.

(Vct) 4 (Ans) =

– 41 –

MEMO

MEMO