Casio ALGEBRA FX 2.0 PLUS, ALGEBRA FX 1.0 PLUS User Manual [de]

Download

ALGEBRA FX 2.0 PLUS

FX 1.0 PLUS

Bedienungsanleitung, Teil 2

http://world.casio.com/edu_e/

CASIO ELECTRONICS CO., LTD. Unit 6, 1000 North Circular Road, London NW2 7JD, U.K.

Wichtig!

Bitte bewahren Sie Ihre Anleitung und alle Informationen griffbereit für spätere Nachschlagzwecke auf.

•••••••••••••••••••

• ••••••••••••••••••

ALGEBRA FX 2.0 PLUS

FX 1.0 PLUS

(Weitere Menüs und Funktionen)

• ••••••••••••••••••

•••••••••••••••••••

• ••••••••••••••••••

•••••••••••••••••••

• ••••••••••••••••••

•••••••••••••••••••

20010901

Inhalt

Kapitel 1 Statistische Schätz-, Test- und Analyseverfahren (STAT)

1-1 Weitere Funktionen im STAT-Menü .................................................. 1-1-1

1-2 Statistische Testverfahren (TEST) .................................................... 1-2-1

1-3 Vertrauensintervalle (INTR).............................................................. 1-3-1

1-4 Wahrscheinlichkeitsverteilungen (DIST)........................................... 1-4-1

Kapitel 2 Finanzmathematik (TVM)

2-1 Vor dem Ausführen finanzmathematischer Berechnungen .............. 2-1-1

2-2 Einfache Kapitalverzinsung .............................................................. 2-2-1

2-3 Kapitalverzinsung mit Zinseszins ..................................................... 2-3-1

2-4 Geldflußberechnungen (Cash-Flow, Investitionsrechnung) ............. 2-4-1

2-5 Tigungsberechnungen (Amortisation) .............................................. 2-5-1

2-6 Zinssatz-Umrechnungen .................................................................. 2-6-1

2-7 Herstellungskosten, Verkaufspreis, Gewinnspanne ......................... 2-7-1

2-8 Berechnung von Zinstagen (Datumsberechnungen)........................ 2-8-1

2-9 Abschreibungsberechnungen (Amortisation) ................................... 2-9-1

2-10 Wertpapieranalyse (Zinsanleihen, Obligationen, ...) ...................... 2-10-1

2-11 TVM-Grafik (weitere grafische Darstellungen) ............................... 2-11-1

Kapitel 3 Differenzialgleichungen (DIFF EQ)

3-1 Zur Lösung von Aufgaben im DIFF EQ - Menü ................................ 3-1-1

3-2 Differenzialgleichungen 1. Ordnung ................................................. 3-2-1

3-3 Lineare Differenzialgleichungen 2. Ordnung .................................... 3-3-1

3-4 Differenzialgleichungen N-ter Ordnung ............................................ 3-4-1

3-5 Systeme von Differenzialgleichungen 1. Ordnung ........................... 3-5-1

Kapitel 4 EA-100 Controller (E-CON)

4-1 Überblick zum E-CON-Menü ............................................................ 4-1-1

4-2 Einrichten des EA-100 (SET UP) ..................................................... 4-2-1

4-3 SET UP - Speicher (Konfigurations-Speicher) ................................. 4-3-1

4-4 SET UP - Programm-File (Konfigurations-Programm) ..................... 4-4-1

4-5 Durchführung einer Datenerfassung ................................................ 4-5-1

Anhang

α-1 Allgemeiner Index ................................................................................α-1

20010901

Kapitel

Statistische Schätz-, Testund Analyseverfahren (STAT)

In der Bedienungsanleitung zum ALGEBRA FX 2.0 PLUS / FX 1.0 PLUS wurden vorrangig die beschreibende Statistik, d.h. die elementare Datenauswertung, statistische Grafiken und verschiedene Regressionsmodelle, behandelt und Wahrscheinlichkeiten mithilfe der Normalverteilung berechnet. In diesem Kapitel werden ergänzend folgende Fragestellungen betrachtet:

•Mittlerer quadratischer Fehler in Regressionsmodellen

•Parametertests zur Überprüfung statistischer Hypothesen

•

Varianz- und Korrelationsanalyse, Tests in Kontingenztafeln

•Vertrauensintervalle für unbekannte Parameter

•Diskrete und stetige Wahrscheinlichkeitsverteilungen

1-1 Weitere Funktionen im STAT-Menü

1-2 Statistische Testverfahren (TEST)

1-3 Vertrauensintervalle (INTR)

1-4 Wahrscheinlichkeitsverteilungen (DIST)

20010901

MSE =

n – 2

i=1

(yi – (axi+ b))

MSE =

n – 3

i=1

(yi – (ax

+ bxi+ c))

MSE =

n – 4

i=1

(yi – (ax

+ bx

+ cx

+d ))

MSE =

n – 5

i=1

(yi – (ax

+ bx

+ cx

+ dx

+ e))

Weitere Funktionen im STAT-Menü

1-1-1

1-1 Weitere Funktionen im STAT-Menü

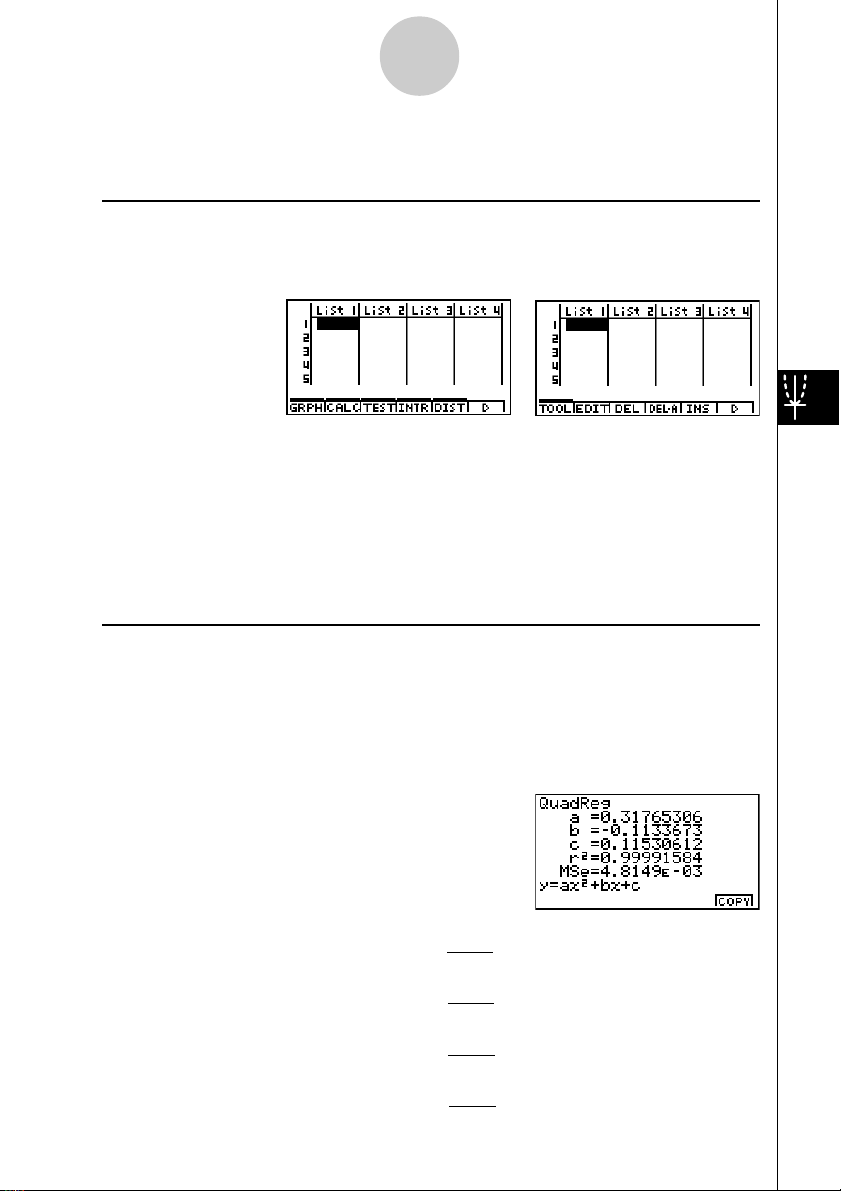
u Funktionstasten im STAT-Eingangsbildschirm

Nachfolgend sind weitere Funktionstasten zum Öffnen entsprechender Untermenüs aufgeführt, die Sie im Eingangsbildschirm (Listeneditor) des STAT-Menüs vorfinden.

Sie können eine der folgenden Funktionstasten drücken, die einem neu hinzugekommenen Untermenü zu weiterführenden statistischen Fragestellungen entspricht.

• 3(TEST) ... Statistische Testverfahren (ab Seite 1-2-1 beschrieben)

• 4(INTR) ... Vertrauensintervalle (ab Seite 1-3-1 beschrieben)

• 5(DIST) ... Wahrscheinlichkeitsverteilungen (ab Seite 1-4-1 beschrieben)

Die Funktionen SORT und JUMP finden Sie im TOOL-Untermenü (6(g)1(TOOL)).

u Berechnung des Bestimmtheitsmaßes (r2) und der Reststreuung (MSE)

Sie können das CALC-Untermenü im STAT-Menü verwenden, um zusätzlich zu den Regressionsanalysen das Bestimmtheitsmaß (r2) in den linearen und quasilinearen Regressionsmodellen (z.B. auch für die quadratische, kubische oder quartische Regression) zu berechnen. Für diese Regressionsmodelle werden auch die Reststreuungen (MSE, mittlere quadratische Fehler) auf Grundlage einer entsprechenden Streuungszerlegung gemäß den folgenden Formeln berechnet.

• Lineare Regression ..............

•Quadratische Regression .....

•Kubische Regression ............

•Quartische Regression .........

20010901

MSE =

n – 2

i=1

(yi – (a + b ln xi ))

MSE =

n – 2

i=1

(ln yi – (ln a + bxi ))

MSE =

n – 2

i=1

(ln yi – (ln a + b ln xi ))

MSE =

n – 2

i=1

(yi – (a sin (bxi + c) + d ))

MSE =

n – 2 1 + ae

-bx

i=1

yi –

Weitere Funktionen im STAT-Menü

1-1-2

• Logarithmische Regression ....

•Exponentielle Regression .......

•Potenz-Regression .................

•Sinus-Regression ...................

• Logistische Regression ...........

u Berechnung eines Schätzwertes für y(x) in Regressionsgrafiken

Wird im STAT-Menü eine Regressionsgrafik erzeugt, können Sie auch die Funktionstaste YCAL nutzen, die für die durchgeführte Regressionsanalyse die Berechnung des (geschätzten)

y-Wertes für einen bestimmten x-Wert mithilfe der ermittelten Regressionsgleichung ermöglicht.

Die Regressionsgrafik beinhaltet die grafische Darstellung der Regressionsfunktion auf Grundlage der zuvor geschätzten Kurvenparameter mithilfe einer zweidimensionalen Stichprobe (die entsprechenden Datenpaare liegen in verbundenen Datenlisten vor).

Nachfolgend wird das allgemeine Vorgehen zur Verwendung der Y-CAL-Funktion beschrieben.

1. Nach dem Zeichnen einer Regressionsgrafik drücken Sie die Tasten 6(g)2(Y-CAL), um die Y-CAL-Funktion aufzurufen. Danach drücken Sie die w-Taste.

Falls sich mehrere Grafiken im Display befinden, verwenden Sie die Cursor-Tasten f und c, um die gewünschte Regressionskurve auszuwählen, danach drücken Sie die w-Taste.

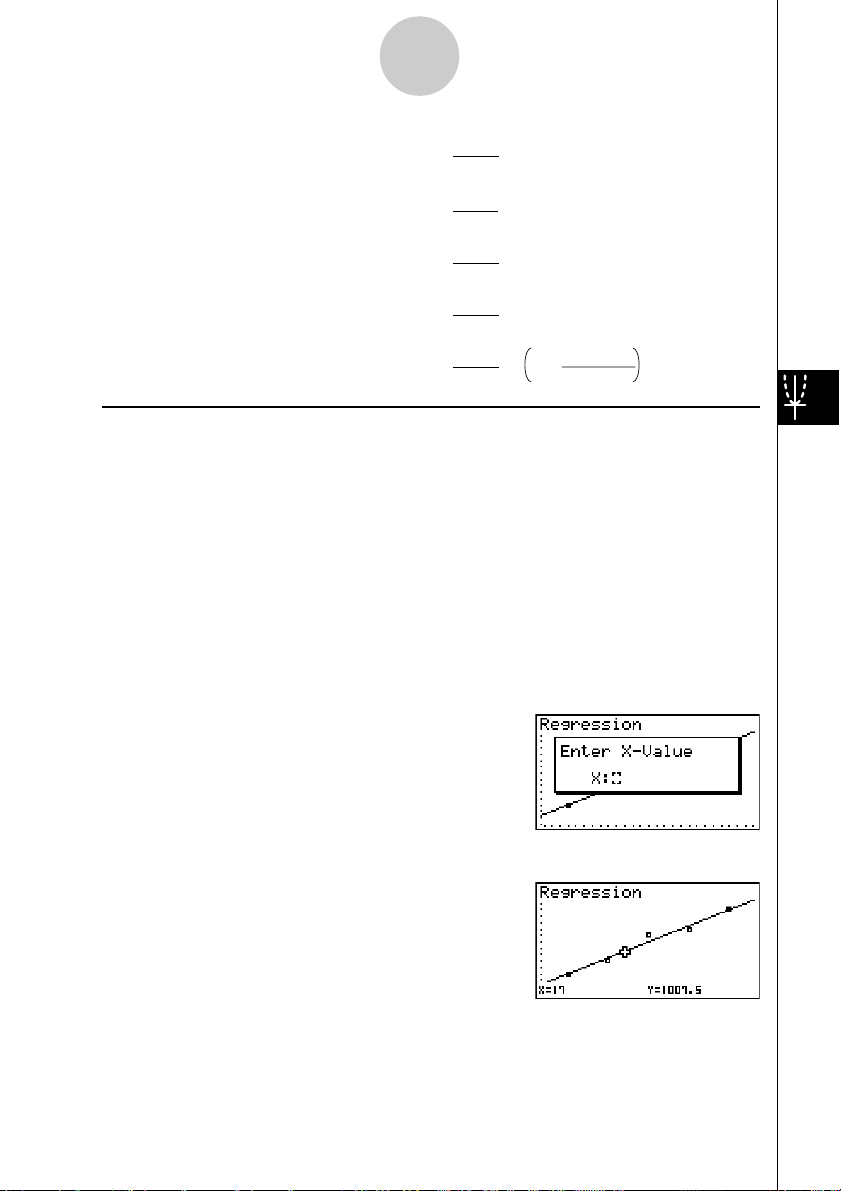
•Es erscheint ein Dialogfenster für die Eingabe des x-Wertes.

2. Geben Sie den gewünschten x-Wert ein und drücken Sie danach die w-Taste.

•Nun erscheinen die Koordinaten für x und y in der Fußzeile des Displays, wobei der Cursor an den entsprechenden Punkt der Regressionsgrafik verschoben wird. Im SET UP - Menü ist dazu vorher Coord: On einzustellen!

3. Drücken Sie erneut die v-Taste oder eine Zifferntaste, um das Dialogfenster für die Eingabe eines weiteren x-Wertes zu öffnen, falls Sie eine weitere Schätzwertberechnung für y ausführen möchten.

20010901

Weitere Funktionen im STAT-Menü

4. Nachdem Sie Ihre Schätzwertberechnungen beendet haben, drücken Sie die i-Taste, um die Koordinatenanzeige und den Cursor vom Display zu löschen.

· Der Cursor erscheint nicht, wenn sich die berechneten Koordinaten nicht innerhalb des Betrachtungsfensters (V-Window) befinden.

· Die Koordinaten erscheinen nicht, wenn [Off] in der Position [Coord] des [SETUP]-Menüs voreingestellt ist.

· Die Y-CAL-Funktion ist auch in einer Kurvendarstellung aktiv, die durch Verwendung der Funktionstaste [DefG] aktiviert wurde.

u Regressionsformel-Kopierfunktion innerhalb der Regressionsrechnungs-

1-1-3

Ergebnisanzeige

Zusätzlich zur normalen Kopierfunktion für Bilder (PICT), die Sie in der Ergebnisanzeige der Regressionsberechnung oder nach dem Zeichnen einer statistischen Grafik (wie z.B. eines Streudiagramms) vorfinden, besitzt das STAT-Menü auch eine COPY-Funktion für Formeln, so dass Sie die im Ergebnis einer Regressionsberechnung erhaltene Regressionsformel auch in den Grafik-Funktionsspeicher kopieren können. Um eine erhaltene Regressionsformel zu kopieren, drücken Sie die Taste 6(COPY).

Testverfahren, Vertrauensintervalle und Wahrscheinlichkeitsverteilungen

Das STAT-Menü enthält Untermenüs für die Durchführung statistischer Tests und die Berechnung von Vertrauensintervallen sowie die Berechnung von Einzelwahrscheinlichkeiten oder Intervallwahrscheinlichkeiten. Sie finden die entsprechenden Erläuterungen dazu in den folgenden Abschnitten: 1-2 Testverfahren, 1-3 Vertrauensintervalle, 1-4 Wahrscheinlichkeitsverteilungen.

u Parametereinstellungen (Vorgabewerte für statistische Aufgabenstellungen)

Nachfolgend sind die beiden Methoden beschrieben, die Sie für die Parametereinstellungen (Vorgabewerte, z.B. Hypothesen für Testverfahren, Konfidenzniveau für Vertrauensintervalle) verwenden können.

• Auswahl einer Variante

Bei dieser Methode drücken Sie im geöffneten Funktionsmenü die Funktionstaste, welche der zu wählenden Fragestellung entspricht (Auswahl unter mehreren Möglichkeiten).

• Direkte Werteingabe von Daten oder Kennzahlen

Bei dieser Methode geben Sie den gewünschten Parameterwert (Vorgabewert) direkt ein. In diesem Fall können Sie nicht über eine Funktionstaste Ihre Eingabe vornehmen.

· Drücken Sie die i-Taste, um zur Listeneingabeanzeige zurückzukehren. Dabei befindet

sich der Cursor an der gleichen Position wie vor dem Beginn der Parametereinstellung.

· Drücken Sie die Tasten ! i(QUIT), um an den Anfang des Listeneditors zurückzukehren.

· Drücken Sie im geöffneten Funktionsmenü in der Position “Execute” einfach die w-Taste ohne

Betätigung der Taste 1(CALC), um die Berechnung auszuführen. Um zur Anzeige der Parametereinstellung zurückzukehren, drücken Sie einfach die i-, A-oder w-Taste.

20010901

Weitere Funktionen im STAT-Menü

1-1-4

u Gemeinsame Funktionen im STAT-Menü

• Das Symbol “■” erscheint während der Ausführung einer Berechnung und während des

Zeichnens einer Grafik in der rechten oberen Ecke der Anzeige. Sie können innerhalb dieser Zeitspanne die A-Taste drücken, um die Berechnungs- oder Zeichnungsoperation abzubrechen (AC Break).

• Sie können die i- oder w-Taste drücken, während ein Berechnungsergebnis oder eine

Grafik im Display angezeigt wird, um in die Anzeige für die Parametereinstellung zurückzukehren. Wenn Sie die Tasten ! i(QUIT) drücken, können Sie an den Anfang des Listeneditors (Listeneingabeanzeige) zurückkehren.

• Sie können die A-Taste drücken, während ein Berechnungsergebnis im Display angezeigt

wird, um in die Anzeige für die Parametereinstellung zurückzukehren.

• Sie können die Tasten u 5(G↔T) nach dem Zeichnen einer Grafik drücken, um zur

Anzeige für die Parametereinstellung (G↔T Funktion) umzuschalten. Falls Sie erneut die Tasten u 5(G↔T) drücken, können Sie zur Grafikanzeige zurückkehren.

• Die G↔T Funktion ist deaktiviert, wenn Sie in der Anzeige für die Parametereinstellung eine

Veränderung vornehmen oder wenn Sie eine u 3(SET UP) oder ! K(V-Window) Operation ausführen.

• Sie können die Speicher- oder Rückruf-Funktion des PICT-Menüs nach dem Zeichnen einer

Grafik ausführen, indem hier ein entsprechendes Untermenü geöffnet wird.

• Die ZOOM-Funktion und die SKETCH-Funktion sind im STAT-Menü deaktiviert.

Die TRACE-Funktion ist deaktiviert, jedoch nicht im Grafikdisplay einer ZweiwegVarianzanalyse (ANOVA). Diese Grafikanzeige kann jedoch nicht gescrollt werden.

• Nach dem Zeichnen einer Grafik, können Sie die Ergebnisspeicherfunktion verwenden, um

die Berechnungsergebnisse in einer bestimmten Liste zu speichern. Grundsätzlich werden alle Positionen (Zahlenwerte) hintereinander abgespeichert, so wie sie angezeigt werden, ausgenommen die erste Zeile mit dem Titel (und ggf. die Alternativhypothese).

• Mit jeder Ausführung der Ergebnisspeicherung (Save Result), werden die in der Liste

vorhandenen Daten durch die neuen Ergebnisse ersetzt.

20010901

Statistische Testverfahren (TEST)

1-2-1

1-2 Statistische Testverfahren (TEST)

Im Untermenü TEST können Sie zwischen 10 verschiedenen Testverfahren auswählen. Das Z-Test-Menü bietet vier oft benutzte Parametertests an, die auf einer(näherungsweise)

N(0,1)-verteilten Testgröße ( Z ) zur Beurteilung der jeweiligen Nullhypothese beruhen. Diese ermöglichen (mit einer vorher festzulegenden Irrtumswahrscheinlichkeit, Signifikanzniveau) die Beurteilung, ob z. B. eine Stichprobe den vermuteten Mittelwert einer Grundgesamtheit genau repräsentiert oder nicht, wobei die Streuung (oder Standardabweichung) der Grundgesamtheit (zum Beispiel die Streuung für ein bestimmtes statistisches Merkmal innerhalb der gesamten Bevölkerung eines Landes) von früheren Tests her bekannt sein muß. Der Z-Test wird z.B. in der Marktforschung oder zur Auswertung von Meinungsumfragen verwendet, die immer wieder durchgeführt werden.

Der 1-Stichproben Z-Test (1-Sample Z-Test) prüft für eine (normalverteilte) Grundgesamtheit eine Mittelwerthypothese, wenn die Grundgesamtheits-Standardabweichung bekannt ist.

Der 2-Stichproben Z-Test (2-Sample Z-Test) prüft eine Gleichheitshypothese für zwei Mittelwerte zweier (normalverteilter) Grundgesamtheiten mittels zweier unabhängiger Stichproben, wenn beide Grundgesamtheits-Standardabweichungen bekannt sind.

Der 1-Prop Z-Test prüft eine Hypothese über einen unbekannten Anteilswert in einer dichotomen Grundgesamtheit auf Grundlage der Trefferquote k/n in n Versuchen.

Der 2-Prop Z-Test prüft eine Gleichheitshypothese für zwei Anteilswerte zweier dichotomer Grundgesamtheiten auf Grundlage der jeweiligen empirischen Trefferquoten in den betrachteten Grundgesamtheiten.

Der t-Test bietet drei oft benutzte Testverfahren und prüft z.B. die entsprechenden Mittelwert- Hypothesen, wenn die Grundgesamtheits-Standardabweichungen unbekannt sind. Die Testgröße ist (näherungsweise) t-verteilt. Die der vermuteten (und im Test vorausgesetzten) Hypothese (

Nullhypothese

Der t-Test wird oftmals zur Untersuchung einer Alternativhypothese verwendet. Eine Ablehnung der Nullhypothese durch das Testverfahren spricht dann für die Alternativhypothese. Die Testentscheidung hängt dabei vom vorzugebenden Signifikanzniveau (Irrtumswahrscheinlichkeit) ab.

Der einfache t-Test (1-Sample t-Test) prüft für eine (normalverteilte) Grundgesamtheit eine Mittelwerthypothese, wenn die Grundgesamtheits-Standardabweichung unbekannt ist.

Der doppelte t-Test (2-Sample t-Test) prüft eine Gleichheitshypothese für zwei Mittelwerte zweier (normalverteilter) Grundgesamtheiten mittels zweier unabhängiger Stichproben, wenn beide Grundgesamtheits-Standardabweichungen unbekannt sind.

Der t-Test zur linearen Regression (LinearReg t-Test) untersucht die Stärke des linearen Zusammenhanges zweier Merkmale X und Y mithilfe verbundener Datenlisten (Datenpaare) und beurteilt gleichzeitig zwei Hypothesen: Nullanstieg im linearen Regressionsmodell bzw. Unkorreliertheit zwischen X und Y (Korrelationsanalyse).

Der

-Test untersucht Hypothesen (Unabhängigkeits- oder Homogenitätshypothesen in Kontingenztafeln) auf Grundlage von zweidimensonalen Häufigkeitstafeln (Matrix der beobachteten Häufigkeiten). Die Testgröße ist (näherungsweise) für zwei kategoriale Variablen (z.B. Ja-Nein-Antworten auswerten) und beurteilt die Unabhängigkeit dieser Variablen. Er könnte z.B. verwendet werden, um anhand der Befragung von Kraftfahrern den Zusammenhang zwischen dem Verursachen von Verkehrsunfällen (Merkmal X) und dem Beherrschen der Verkehrsregeln (Merkmal Y) zu untersuchen.

Der 2-Stichproben F-Test (2-Sample F-Test) prüft eine Hypothese zur Streuungsgleichheit auf Grundlage von Stichproben zweier (normalverteilter) Grundgesamtheiten mithilfe einer F- verteilten Testgröße. Er könnte z.B. verwendet werden, um die krebserregenden Effekte von

) entgegengesetzte Hypothese wird als

-verteilt. Er untersucht z.B. Vierfeldertafeln

20010901

Alternativhypothese

bezeichnet.

Statistische Testverfahren (TEST)

1-2-2

mehreren vermuteten Faktoren zu untersuchen, wie z.B. den Konsum von Tabak, Alkohol, den Vitaminmangel, hohen Kaffeekonsum, Untätigkeit, schlechte Lebensgewohnheiten usw.

Die Varianzanalyse (ANOVA) prüft z.B. die Hypothese zur Mittelwertgleichheit mehrerer (nor- malverteilter) Grundgesamtheiten auf Grundlage entsprechender Stichproben mithilfe einer Streuungszerlegung und einer F-verteilten Prüfgröße. Dieser Test kann z.B. verwendet werden, um zu untersuchen, ob die Kombination verschiedener Werkstoffe oder Herstellungsverfahren eine Auswirkung auf die Qualität und die Lebensdauer eines Endproduktes hat.

Die Einweg-Varianzanalyse (One-Way ANOVA) wird verwendet, wenn nur ein unabhängiger Einflußfaktor A in verschiedenen Abstufungen auf die (abhängige) Variable Y wirkt.

Die Zweiweg-Varianzanalyse (Two-Way ANOVA) wird verwendet, wenn zwei unabhängige Einflußfaktoren A und B in bestimmten Abstufungen auf ein Meßergebnis Y wirken.

Auf den folgenden Seiten werden die oben genannten statistischen Testverfahren und deren Ergebnisdarstellungen genauer erläutert. Weitere Einzelheiten dazu können in speziellen StatistikLehrbüchern nachgelesen werden.

In der Eingangsanzeige des STAT-Menüs drücken Sie die Taste 3(TEST), um das TestUntermenü zu öffnen, das die folgenden Positionen enthält.

• 3(TEST)b(Z) ... Z-Tests (vier Testvarianten, ab Seite 1-2-2)

c(T) ... t-Tests (drei Testvarianten, ab Seite 1-2-10) d(χ2) ... χ2-Tests (ab Seite 1-2-18) e(F) ... 2-Stichproben F-Test (ab Seite 1-2-20) f(ANOVA) ... Varianzanalysen (ab Seite 1-2-22)

k Z-Tests (Tests mit einer N(0,1)-verteilten Testgröße)

u Gemeinsame Funktionen der Z-Tests

Sie können folgende Grafikanalysefunktion nach dem Zeichnen einer Test-Grafik verwenden.

• 1(Z) ... Zeigt den berechneten Wert der (N(0,1)-verteilten) Z-Testgröße an.

Drücken Sie die Taste 1(Z), um die berechnete Z-Testgröße z in der Fußzeile des Displays anzuzeigen, wobei der Cursor an der entsprechenden Position der Grafik angezeigt wird (sofern diese Stelle nicht außerhalb des Betrachtungsfensters liegt). Im Fall eines zweiseitigen Tests werden zwei Punkte -z und z angezeigt. Verwenden Sie die d- und e-Tasten, um den Cursor hin und her zu verschieben. Drücken Sie die i-Taste, um die Anzeige der Z-Testgröße zu löschen.

• 2(P) ... Zeigt den zur berechneten Testgröße gehörenden p-Wert an. Es handelt sich hierbei um die sogenannte kritische Irrtumswahrscheinlichkeit, die der schraffierten Fläche unter der (Gaußschen) Glockenkurve entspricht.

Drücken Sie die Taste 2(P) , um den p-Wert in der Fußzeile des Displays anzuzeigen, ohne dass der Cursor erscheint. Drücken Sie die i-Taste, um die Anzeige des p-Wertes zu löschen.

Folgende Betrachtungsfenstereinstellungen werden für das Zeichnen der Testgrafik (Glockenkurve) verwendet.

Xmin –3,2, Xmax = 3,2, Xscale = 1,

Ymin = –0,1, Ymax = 0,45, Yscale = 0,1

# Durch die Ausführung einer Testfunktion werden

die

z- und p-Werte automatisch in den symboli-

schen Variablen Z bzw. P gespeichert.

20010901

Statistische Testverfahren (TEST)

1-2-3

u1-Stichproben Z-Test (1-Sample Z-Test)

Der 1-Proben Z-Test wird verwendet, um die Mittelwerthypothese Ho: µ=

o zu prüfen, wenn

die Standardabweichung σ der (normalverteilten) Grundgesamtheit bekannt ist.

Testgröße:

Z =

o –

: empirischer Stichprobenmittelwert

o : hypothetischer Mittelwert

: Grundgesamtheits-Standardabweichung

n : Stichprobenumfang

Führen Sie die folgende Tastenbetätigung im STAT-Eingangsmenü (Listeneditor) aus.

3(TEST)

b(Z) b(1-Smpl)

Nachfolgend ist die Bedeutung der einzelnen Positionen im Falle der Datenlistenvorgabe ([Data: List] statt [Data: Variable] eingestellt) beschrieben.

Data ............................ Art der Datenvorgabe (Liste der Stichprobendaten [List] oder

empirische Kennzahlen [Variable])

.................................. Art der Alternativhypothese (“G

kritischen Bereich fest, “< Bereich links fest, “>

0” legt den einseitigen kritischen Bereich

0” legt den zweiseitigen

0” legt den einseitigen kritischen

rechts fest.)

0 ................................ hypothetischer Mittelwert (Nullhypothese Ho:

.................................. bekannte Grundgesamtheits-Standardabweichung (σ > 0)

µ=µ

List .............................. Liste der Stichprobendaten (List 1 bis 20)

Freq ............................. einfache Häufigkeiten [1] oder Häufigkeitsliste (Liste 1 bis 20)

Save Res .................... Listenspeicherplatz zur Speicherung der Berechnungsergeb-

nisse (Keine [None] oder Liste 1 bis 20)

Execute ....................... Führt die Berechnung aus oder zeichnet eine Test-Grafik

(N(0,1)-Glockenkurve)

Nachfolgend ist die Bedeutung der einzelnen Positionen im Falle der Kennzahlenvorgabe [Data: Variable] beschrieben, die sich von der Datenlistenvorgabe [Data: List] unterscheiden.

o .................................. empirischer Stichproben-Mittelwert

n .................................. Stichprobenumfang (positive ganze Zahl)

Nachdem Sie alle Parameter (Vorgabewerte) eingestellt haben, stellen Sie den Cursor auf [Execute] und drücken danach eine der nachfolgend dargestellten Funktionstasten, um die Berechnung auszuführen oder eine Test-Grafik (N(0,1)-Glockenkurve) zu zeichnen.

20010901

Statistische Testverfahren (TEST)

• 1(CALC) ... Führt die Berechnung aus.

• 6(DRAW) ... Zeichnet die Test-Grafik zum Testergebnis.

1-2-4

u u u u u

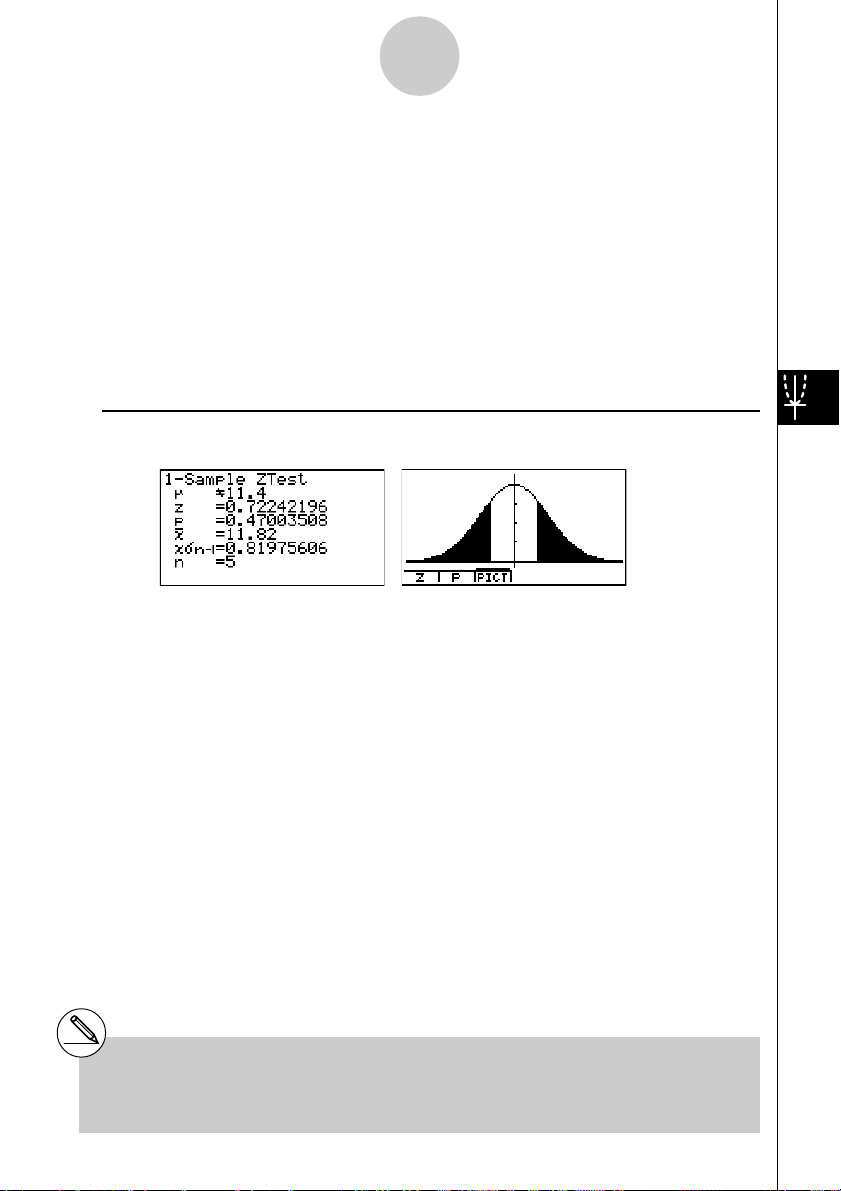
Beispiel Gegeben ist die Stichprobe {12.5, 11.6, 10.8, 12.8, 11.4} = List 1 (aus einer

Berechnungsergebnis-Ausgabebildschirm für 1(CALC) bzw. 6(DRAW)

normalverteilten Grundgesamtheit mit σ =1,30 ) vom Umfang rechnen sind die statistischen Kennzahlen

(unter der Nullhypothese Ho: µ= kritische Irrtumswahrscheinlichkeit p. Kann die Nullhypothese auf Grundlage der vorliegenden Stichprobe abgelehnt werden (Irrtumswahrscheinlichkeit α =

0.05) ?

G11.4

........................

Art der Alternativhypothese (zweiseitiger kritischer Bereich)

o und x

mit

n -1 , sowie die Testgröße

=11.4, HA:

z .................................. berechnete z-Testgröße

p .................................. p-Wert: p

vgl. Bedienungsanleitung zum Taschenrechner S. 6-4-5.

= P

(-|

z | ) + R (| z |

) (kritische Irrtumswahrscheinlichkeit),

o .................................. empirischer Stichproben-Mittelwert

n-1 ............................. empirische Stichproben-Standardabweichung

(Angezeigt nur für Datenlistenvorgabe (Data: List)).

n .................................. Stichprobenumfang

= 5. Zu be-

, ) und die

Entscheidungsregel zum durchgeführten Test:

# [Save Res] speichert die µ-Bedingung in

Zeile 2 (Art der Alternativhypothese) nicht ab.

20010901

p≥

Statistische Testverfahren (TEST)

1-2-5

u 2-Stichproben

Der 2-Stichproben Z-Test wird verwendet, um die Hypothese Ho:

Z-Test (2-Sample Z-Test)

zur Gleichheit zweier

Mittelwerte zu prüfen, wenn die Standardabweichungen der zwei (normalverteilten) Grundgesamtheiten bekannt sind.

Testgröße:

Z =

o1 – o

o1 : empirischer Mittelwert der Stichprobe 1

o2 : empirischer Mittelwert der Stichprobe 2

1 : Standardabweichung der Grundgesamtheit 1

2 : Standardabweichung der Grundgesamtheit 2

n1 : Umfang der Stichprobe 1 n2 : Umfang der Stichprobe 2

Führen Sie die folgende Tastenbetätigung im STAT-Eingangsmenü (Listeneditor) aus.

3(TEST)

b(Z) c(2-Smpl)

Nachfolgend ist die Bedeutung der einzelnen Positionen im Falle der Datenlistenvorgabe ([Data: List] statt [Data: Variable] eingestellt) beschrieben.

Data ...................... Art der Datenvorgabe (Liste der Stichprobendaten [List] oder

1 .......................... Art der Alternativhypothese (“G

1 ........................... bekannte Standardabweichung der Grundgesamtheit 1 (σ1 > 0)

2 ........................... bekannte Standardabweichung der Grundgesamtheit 2 (σ2 > 0)

List(1) .................... Liste der Stichprobendaten 1

List(2) .................... Liste der Stichprobendaten 2

Freq(1) .................. einfache Häufigkeiten [1] oder Häufigkeitsliste 1

Freq(2) .................. einfache Häufigkeiten [1] oder Häufigkeitsliste 2

Save Res............... Listenspeicherplatz zur Speicherung der Berechnungsergeb-

Execute ................. Führt die Berechnung aus oder zeichnet eine Test-Grafik

Nachfolgend ist die Bedeutung der einzelnen Positionen im Falle der Kennzahlenvorgabe [Data: Variable] beschrieben, die sich von der Datenlistenvorgabe [Data: List] unterscheiden.

empirische Kennzahlen [Variable])

2” legt den zweiseitigen

kritischen Bereich fest, “< Bereich links fest, “>

2” legt den einseitigen kritischen

2” legt den einseitigen kritischen Bereich

rechts fest.)

nisse (Keine [None] oder Liste 1 bis 20)

(N(0,1)-Glockenkurve)

20010901

20011201

Statistische Testverfahren (TEST)

1-2-6

o1 ................................. Mittelwert der Stichprobe 1

n1 ................................. Umfang (positive ganze Zahl) der Stichprobe 1

o2 ................................. Mittelwert der Stichprobe 2

n2 ................................. Umfang (positive ganze Zahl) der Stichprobe 2

Nachdem Sie alle Parameter eingestellt haben, stellen Sie den Cursor auf [Execute] und drücken danach eine der folgenden Funktionstasten, um die Berechnung auszuführen oder eine TestGrafik (N(0,1)-Glockenkurve) zu zeichnen.

• 1(CALC) ... Führt die Berechnung aus.

• 6(DRAW) ... Zeichnet die Test-Grafik zum Testergebnis.

u u u u u

Beispiel

Gegeben sind die empirischen Stichprobenmittelwerte

=10.0 (

=3.00 ). Zu be

= 36) (aus normalverteilten Grundgesamtheiten mit

rechnen sind die Testgröße z (unter der Nullhypothese Ho:

, HA:

, ) und die

kritische Irrtumswahrscheinlichkeit p. Kann die

Nullhypothese auf Grundlage der ausgewerteten Stichproben abgelehnt werden (Irrtumswahrscheinlichkeit α = 0.05) ? (Antwort: Ja, wegen p<α , vgl. Entscheidungsregel S. 1-2-4)

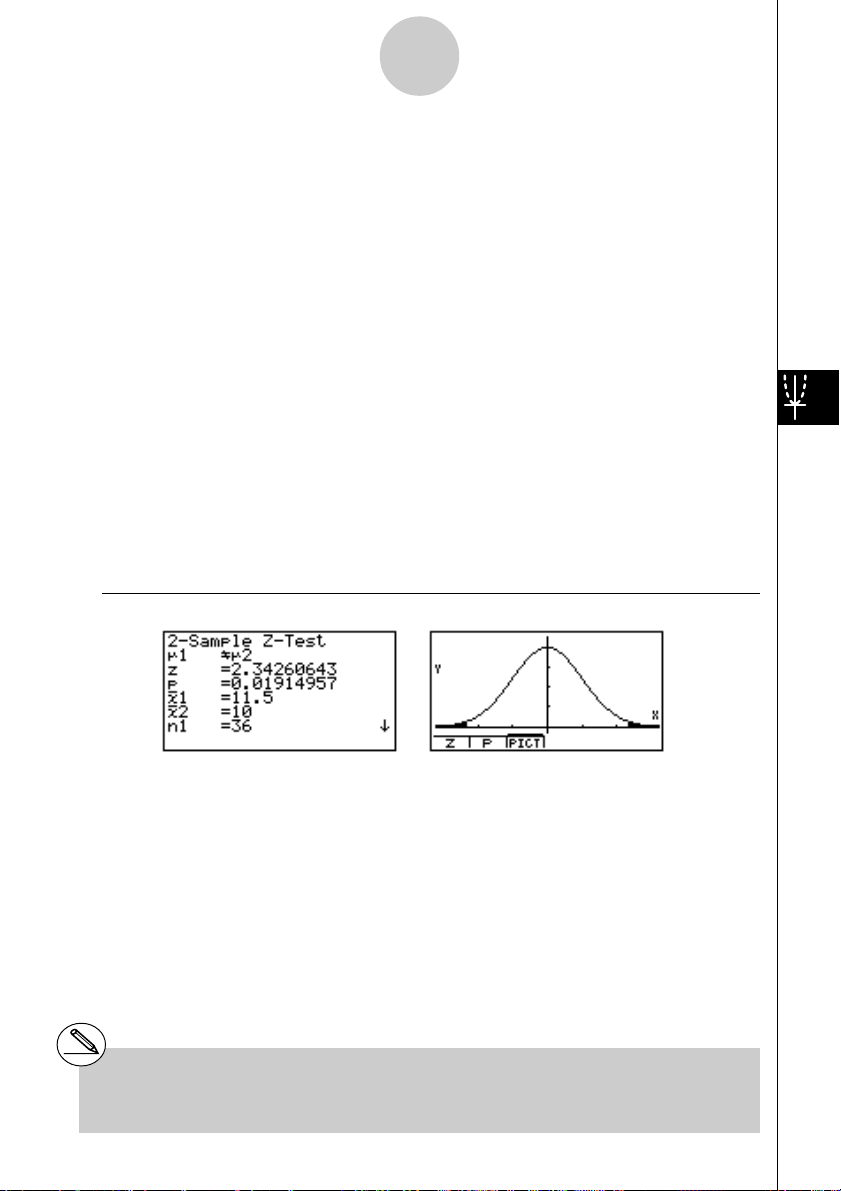
Berechnungsergebnis-Ausgabebildschirm für 1(CALC) bzw. 6(DRAW)

=11.5 (

= 36) und

=2.40 und

2 ........................... Art der Alternativhypothese (zweiseitiger kritischer Bereich)

z .................................. berechnete z-Testgröße

p .................................. p-Wert: p

vgl. Bedienungsanleitung zum Taschenrechner S. 6-4-5.

= P

(-|

z | ) + R (| z |

o1 ................................. empirischer Mittelwert der Stichprobe 1

o2 ................................. empirischer Mittelwert der Stichprobe 2

n-1 ............................ empirische Stichproben-Standardabweichung 1

(Angezeigt nur für Datenlistenvorgabe (Data: List)).

n-1 ............................ empirische Stichproben-Standardabweichung 2

(Angezeigt nur für Datenlistenvorgabe (Data: List)).

.................................

Umfang der Stichprobe 1

n2 ................................. Umfang der Stichprobe 2

# [Save Res] speichert die µ-Bedingung in

Zeile 2 (Art der Alternativhypothese) nicht ab.

20010901

) (kritische Irrtumswahrscheinlichkeit),

Statistische Testverfahren (TEST)

1-2-7

u 1-Prop

Der 1-Prop Z-Test wird für die Prüfung der Hypothese über einen unbekannten Anteilswert (Prop) in einer dichotomen Grundgesamtheit benutzt (Ho: Prop = p0). Für den Test wird eine näherungsweise N(0,1)-verteilte Testgröße Z verwendet:

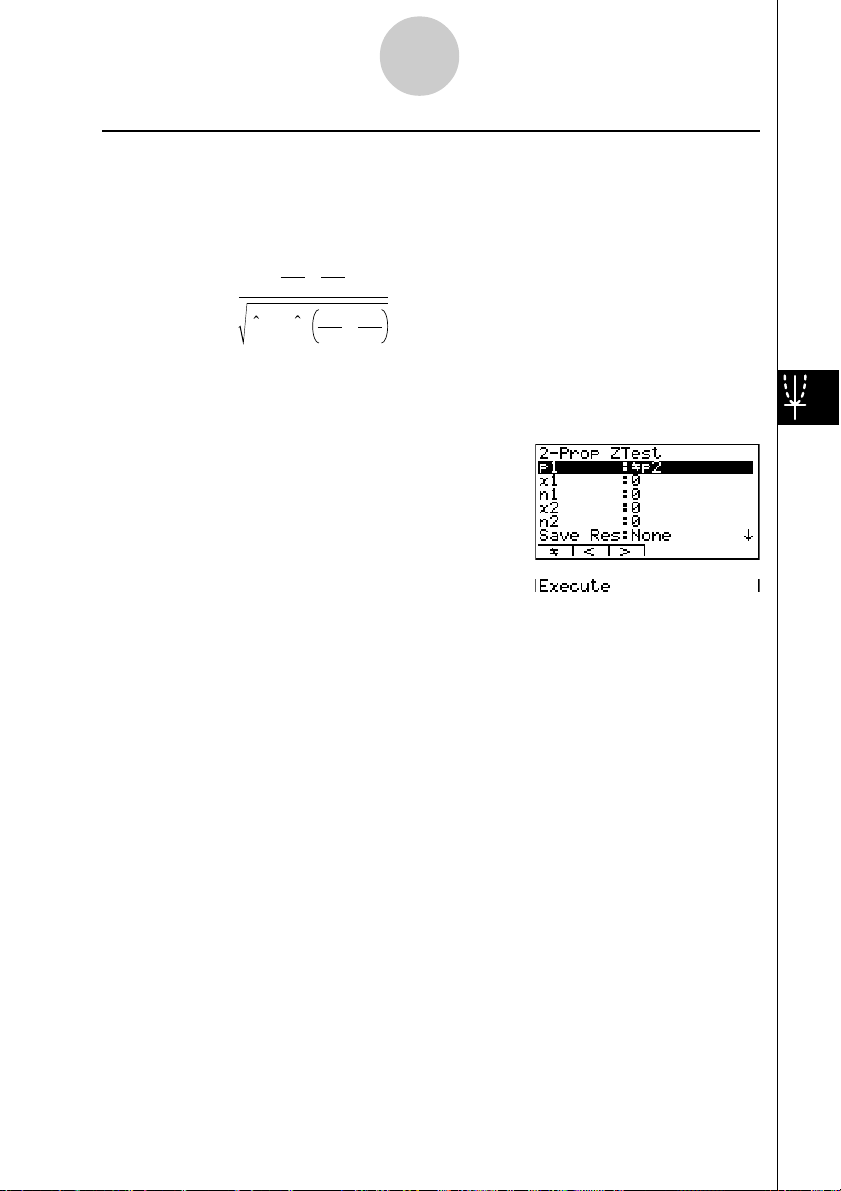
Führen Sie die folgende Tastenbetätigung im STAT-Eingangsmenü (Listeneditor) aus.

Z-Test (Z-Test für einen unbekannten Anteilswert)

– p

Z =

(1– p0)

3(TEST)

b(Z) d(1-Prop)

............................

Prop

.................................

..................................

Save Res

Execute

• 1(CALC) ... Führt die Berechnung aus.

• 6(DRAW) ... Zeichnet die Test-Grafik zum Testergebnis.

....................

.......................

Art der Alternativhypothese (“G p0” legt den zweiseitigen kritischen Bereich fest, “< p0” legt den einseitigen kritischen Bereich links fest, “> p0” legt den einseitigen kritischen Bereich rechts fest.)

hypothetischer Anteilswert (0 < p0 < 1) Anzahl der Treffer in der Stichprobe (x > 0, ganze Zahl) Stichprobenumfang (positive ganze Zahl) Listenspeicherplatz zur Speicherung der Berechnungsergeb-

nisse (Keine [None] oder Liste 1 bis 20) Führt die Berechnung aus oder zeichnet eine Test-Grafik

(N(0,1)-Glockenkurve)

p0 : hypothetischer Anteilswert n : Stichprobenumfang

x : Trefferanzahl

Beispiel: Ausgabebildschirm für 1(CALC) bzw. 6(DRAW), vgl. S.1-2-4

PropG0.5 ...................... Art der Alternativhypothese (zweiseitiger kritischer Bereich)

p ......... p-Wert (kritische Irrtumswahrscheinlichkeit), z ...... berechnete Z-Testgröße,

ˆp = x/n = 2048

# [Save Res] speichert die µ-Bedingung in

Zeile 2 (Art der Alternativhypothese) nicht ab.

4040 ....... Geschätzter Anteilswert, n ...... Stichprobenumfang.

20010901

Statistische Testverfahren (TEST)

1-2-8

u 2-Prop

Der 2-Prop Z-Test wird für die Prüfung der Hypothese der Gleichheit zweier unbekannter Anteilswerte zweier dichotomer Grundgesamtheiten benutzt (Ho: p1 = p2). Für den Test wird eine näherungsweise N(0,1)-verteilte Testgröße Z verwendet:

Führen Sie die folgende Tastenbetätigung

Z-Test (Z-Test zum Vergleich zweier unbekannter Anteilswerte)

x1 : Anzahl der Treffer in der Stichprobe 1 x2 : Anzahl der Treffer in der Stichprobe 2 n1 : Umfang der Stichprobe 1 n2 : Umfang der Stichprobe 2 ˆp :

Geschätzter Anteilswert in der Gesamt

stichprobe

im STAT-Eingangsmenü (Listeneditor) aus.

Z =

3(TEST)

b(Z) e(2-Prop)

p(1 – p )

–

p1 ................................. Art der Alternativhypothese

(“G p2” legt den zweiseitigen kritischen Bereich fest, “< p2” legt den einseitigen kritischen Bereich links fest, “> p2” legt den einseitigen kritischen Bereich rechts fest.)

x1 ................................. Anzahl der Treffer in der Stichprobe 1 (x1 > 0, ganze Zahl)

n1 ................................. Umfang der Stichprobe 1 (positive ganze Zahl)

x2 ................................. Anzahl der Treffer in der Stichprobe 2 (x2 > 0, ganze Zahl)

n2 ................................. Umfang der Stichprobe 2 (positive ganze Zahl)

Save Res .................... Listenspeicherplatz zur Speicherung der Berechnungsergeb-

Execute ....................... Führt die Berechnung aus oder zeichnet eine Test-Grafik

nisse (Keine [None] oder Liste 1 bis 20)

(N(0,1)-Glockenkurve)

1(CALC) ... Führt die Berechnung aus.

• 6(DRAW) ... Zeichnet die Test-Grafik zum Testergebnis.

20010901

Statistische Testverfahren (TEST)

1-2-9

u u u u u

Beispiel In zwei dichotomen Grundgesamtheiten wurden die Trefferanzahlen x1 = 225

und x2 = 230 erzielt (Stichprobenumfang n1 = 300, n2 = 300) sind die statistischen Kennzahlen ˆp 1 , ˆp 2 und ˆp , sowie die Testgröße z (unter der Nullhypothese scheinlichkeit p. Kann die Nullhypothese auf Grundlage der vorliegenden Stichprobe abgelehnt werden (Irrtumswahrscheinlichkeit α = 0.05) ?

Ho: p1 = p2 und HA: p1 > p2

) und die

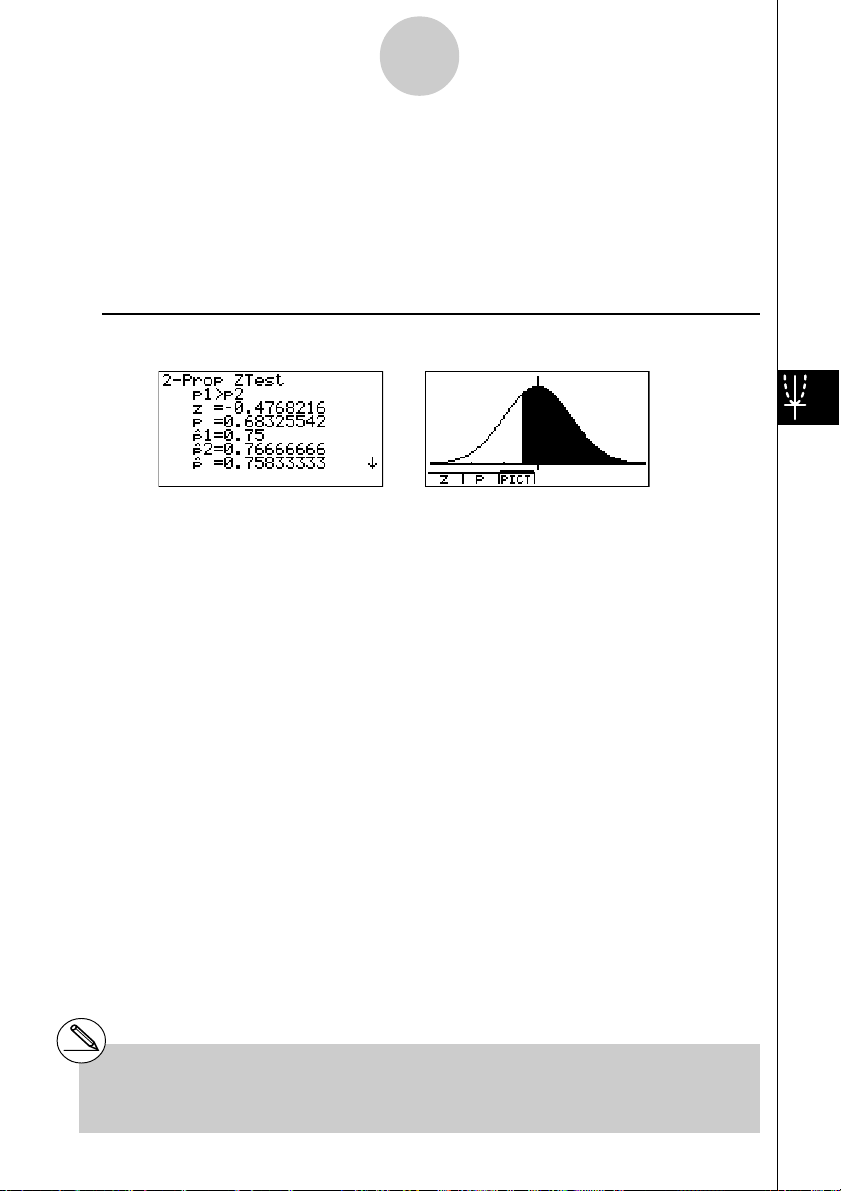
Berechnungsergebnis-Ausgabebildschirm für 1(CALC) bzw. 6(DRAW)

. Zu be

rechnen

kritische Irrtumswahr-

p1>p2 ............................ Art der Alternativhypothese (einseitiger kritischer Bereich,

rechtsseitig)

z .................................. berechnete z-Testgröße ( - 0.4768216 )

p .................................. p-Wert: p

lichkeit, , vgl. Bedienungsanleitung S. 6-4-5)

= R (z ) =

0.68325542 (kritische Irrtumswahrschein-

ˆp 1 ................................. Geschätzter Anteilswert der Grundgesamtheit 1

( 225 / 300 = 0.75 )

ˆp 2 ................................. Geschätzter Anteilswert der Grundgesamtheit 2

( 230 / 300 = 0.76666666... )

ˆp .................................. Geschätzter Anteilswert für die Gesamtstichprobe

( (225+230) / (300+300) = 0.75833333...)

n1 ................................. Umfang der Stichprobe 1 ( 300)

n2 ................................. Umfang der Stichprobe 2 ( 300)

Entscheidungsregel zum durchgeführten Test:

Für eine vorgegebene Irrtumswahrscheinlichkeit α (Signifikanzniveau α , hier α = 0.05 ) wird bei p<α die Nullhypothese abgelehnt (Testgröße im kritischen Bereich) und bei p≥α kein Einwand gegen die Nullhypothese erhoben (Testgröße nicht im kritischen Bereich). In diesem Beispiel gilt d.h. auf Grund des durchgeführten Tests besteht kein Anlaß, die Nullhypothese zu gunsten der Alternativhypothese HA: p1 > p2 abzulehnen.

# [Save Res] speichert die µ-Bedingung in

Zeile 2 (Art der Alternativhypothese) nicht ab.

p≥

, d.h. es besteht kein Einwand gegen die Nullhypthese Ho: p1 = p2 ,

20010901

Statistische Testverfahren (TEST)

1-2-10

t-Tests (Tests mit einer t

u Gemeinsame Funktionen des t-Tests

Sie können folgende Grafikanalysefunktion nach dem Zeichnen einer Test-Grafik verwenden.

• 1(T) ... Zeigt den berechneten Wert der (tm -verteilten) t-Testgröße an.

Drücken Sie die Taste 1(T), um die berechnete t-Testgröße t in der Fußzeile des Displays anzuzeigen, wobei der Cursor an der entsprechenden Position der Grafik angezeigt wird (sofern diese Stelle nicht außerhalb des Betrachtungsfensters liegt).

Im Fall eines zweiseitigen Tests werden zwei Punkte -t und t angezeigt. Verwenden Sie die d- und e-Tasten, um den Cursor hin und her zu verschieben.

Drücken Sie die i-Taste, um die Anzeige der t-Testgröße zu löschen.

Freiheitsgraden entspricht. Die Anzahl der Freiheitsgrade ist vom Stich-

probenumfang und dem verwendeten Testverfahren abhängig.

Drücken Sie die Taste 2(P) , um den p-Wert in der Fußzeile des Displays anzuzeigen, ohne dass der Cursor erscheint.

Drücken Sie die i-Taste, um die Anzeige des p-Wertes zu löschen.

-verteilten Testgröße, m Freiheitsgrade)

Folgende Betrachtungsfenstereinstellungen werden für das Zeichnen der Testgrafik (Dichtefunktion einer t-Verteilung) verwendet.

Xmin = –3,2, Xmax = 3,2, Xscale = 1,

Ymin = –0,1, Ymax = 0,45, Yscale = 0,1

#Durch die Ausführung einer Testfunktion

werden die symbolischen Variablen T bzw. P gespeichert.

20010901

t- und p-Werte automatisch in den

Statistische Testverfahren (TEST)

1-2-11

u Einfacher

t-Test (1-Stichproben t-Test, 1-Sample t-Test)

Der einfache t-Test (1-Stichproben t-Test) wird verwendet, um die Mittelwerthypothese Ho:

µ=µ

o zu prüfen, wenn die Standardabweichung

der (normalverteilten) Grundgesamtheit

unbekannt ist. Für den Test wird eine (näherungsweise) tm-verteilte Testgröße t verwendet:

t =

o –

n–1

o : empirischer Stichprobenmittelwert

0 : hypothetischer Mittelwert

n-1 : Stichproben-Standardabweichung

n : Stichprobenumfang (

m = n

-1)

Führen Sie die folgende Tastenbetätigung im STAT-Eingangsmenü (Listeneditor) aus.

3(TEST)

c(T) b(1-Smpl)

Nachfolgend ist die Bedeutung der einzelnen Positionen im Falle der Datenlistenvorgabe ([Data: List] statt [Data: Variable] eingestellt) beschrieben.

Data ............................ Art der Datenvorgabe (Liste der Stichprobendaten [List] oder

empirische Kennzahlen [Variable])

.................................. Art der Alternativhypothese (“G

kritischen Bereich fest, “< Bereich links fest, “>

0” legt den einseitigen kritischen Bereich

0” legt den zweiseitigen

0” legt den einseitigen kritischen

rechts fest.)

0 ................................ hypothetischer Mittelwert (Nullhypothese Ho:

µ=µ

List .............................. Liste der Stichprobendaten (List 1 bis 20)

Freq ............................. einfache Häufigkeiten [1] oder Häufigkeitsliste (Liste 1 bis 20)

Save Res .................... Listenspeicherplatz zur Speicherung der Berechnungsergeb-

nisse (Keine [None] oder Liste 1 bis 20)

Execute ....................... Führt die Berechnung aus oder zeichnet eine Test-Grafik

(Dichtefunktion einer tm -Verteilung, glockenförmige Kurve)

Nachfolgend ist die Bedeutung der einzelnen Positionen im Falle der Kennzahlenvorgabe [Data: Variable] beschrieben, die sich von der Datenlistenvorgabe [Data: List] unterscheiden.

..................................

n-1

.............................

..................................

empirischer Stichproben-Mittelwert empirische Stichproben-Standardabweichung (x Stichprobenumfang (positive ganze Zahl)

n-1 > 0)

Nachdem Sie alle Parameter eingestellt haben, stellen Sie den Cursor auf [Execute] und drücken danach eine der nachfolgend dargestellten Funktionstasten, um die Berechnung auszuführen oder eine Test-Grafik (Dichtefunktion einer t

-Verteilung, glockenförmige Kurve) zu zeichnen.

20010901

Statistische Testverfahren (TEST)

1-2-12

• 1(CALC) ... Führt die Berechnung aus.

• 6(DRAW) ... Zeichnet die Test-Grafik zum Testergebnis.

u u u u u

Beispiel Gegeben sind die empirischen Kennzahlen

einer normalverteilten Grundgesamtheit mit unbekannten Parametern). Der Stichprobenumfang betrug dabei (unter der Nullhypothese Ho: µ = kritische Irrtumswahrscheinlichkeit p. Kann die Nullhypothese auf Grundlage der ausgewerteten Stichprobe abgelehnt werden (Irrtumswahrscheinlichkeit

= 0.05) ?

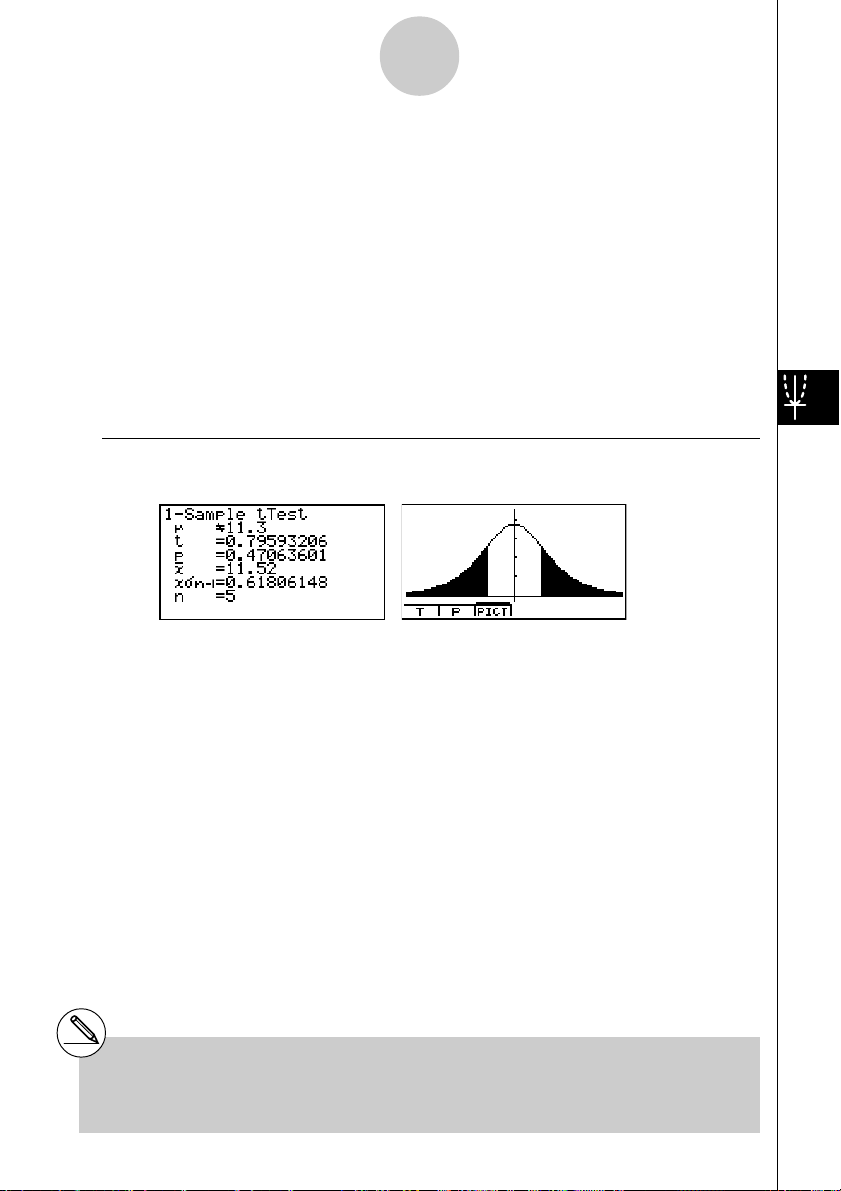
Berechnungsergebnis-Ausgabebildschirm für 1(CALC) bzw. 6(DRAW)

G 11.3 ...................... Art der Alternativhypothese (zweiseitiger kritischer Bereich)

...................................

berechnete t-Testgröße (m = n-1 Freiheitsgrade)

p .................................. p-Wert (kritische Irrtumswahrscheinlichkeit)

o .................................. empirischer Stichproben-Mittelwert

n-1 ............................. empirische Stichproben-Standardabweichung

n .................................. Stichprobenumfang

o = 11.52 und x

= 5. Zu be

mit

n-1 = 0.382

rechnen sind die Testgröße

=11.3, HA:

) und die

1/2

(aus

Entscheidungsregel zum durchgeführten Test:

Für eine vorgegebene Irrtumswahrscheinlichkeit α (Signifikanzniveau α) wird bei p<α die Nullhypothese abgelehnt (Testgröße im kritischen Bereich) und bei p≥α kein Einwand gegen die Nullhypothese erhoben (Testgröße nicht im kritischen Bereich). In diesem Beispiel gilt d.h. es besteht kein Einwand gegen die Nullhypothese. (D.h. der empirische Mittelwert weicht nicht wesentlich (also nicht signifikant, nur unwesentlich) vom hypothetischen Mittelwert ab.)

# [Save Res] speichert die µ-Bedingung in

Zeile 2 (Art der Alternativhypothese) nicht ab.

20010901

p≥

Statistische Testverfahren (TEST)

1-2-13

u Doppelter

Der doppelte t-Test (2-Stichproben t-Test) wird verwendet, um die Hypothese Ho:

t-Test (2-Stichproben t-Test, 2-Sample t-Test)

zur

Gleichheit zweier Mittelwerte zu prüfen, wenn die Standardabweichungen der zwei (normalverteilten) Grundgesamtheiten unbekannt sind. Für den Test wird eine (näherungsweise)

-verteilte Testgröße t verwendet (Anzahl der Freiheitsgrade: m = df ):

Unter der Voreinstellung [Pooled: On] gilt für die Anzahl der Freiheitsgrade:

t =

o1 – o

n–1

o1 :empirischer Mittelwert der

Stichprobe 1

o2 :empirischer Mittelwert der

Stichprobe 2

n-1 :Standardabweichung der

Grundgesamtheit 1

n-1 :Standardabweichung der

Grundgesamtheit 2

= n1 + n2 – 2

n1 : Umfang der Stichprobe 1 n2 : Umfang der Stichprobe 2

n-1 : gemeinsame

Standardabweichung der Gesamtstichprobe (wird nur angezeigt unter der Voreinstellung [Pooled:On].)

df :Freiheitsgrade der

Prüfverteilung

Unter der Voreinstellung [Pooled: Off] gilt für die Anzahl der Freiheitsgrade:

o1 – o

t =

df =

1 n–1

n1–1

2 n–1

(1–C )

n2–1

mit

o1 :empirischer Mittelwert der

Stichprobe 1

o2 :empirischer Mittelwert der

Stichprobe 2

n-1 :Standardabweichung der

Grundgesamtheit 1

n-1 :Standardabweichung der

Grundgesamtheit 2

n1 : Umfang der Stichprobe 1 n2 : Umfang der Stichprobe 2 df :Freiheitsgrade der

Prüfverteilung

Führen Sie die folgende Tastenbetätigung im STAT-Eingangsmenü (Listeneditor) aus.

3(TEST)

c(T)

c(2-Smpl)

20010901

20011201

Statistische Testverfahren (TEST)

1-2-14

Nachfolgend ist die Bedeutung der einzelnen Positionen im Falle der Datenlistenvorgabe ([Data: List] statt [Data: Variable] eingestellt) beschrieben.

Data ............................ Art der Datenvorgabe (Liste der Stichprobendaten [List] oder

empirische Kennzahlen [Variable])

1 ................................. Art der Alternativhypothese (“G µ2” legt den zweiseitigen

kritischen Bereich fest, “< Bereich links fest, “>

2” legt den einseitigen kritischen

Bereich rechts fest.)

List(1) .......................... Liste der Stichprobendaten der 1. Stichprobe

List(2) .......................... Liste der Stichprobendaten der 2. Stichprobe

Freq(1) ........................ einfache Häufigkeiten [1] oder Häufigkeitsliste 1

Freq(2) ........................ einfache Häufigkeiten [1] oder Häufigkeitsliste 2

Pooled ......................... Streuungsgleichheit eingeschaltet ([Pooled: On]) oder

ausgeschaltet ([Pooled: Off])

Save Res .................... Listenspeicherplatz zur Speicherung der Berechnungsergeb-

nisse (Keine [None] oder Liste 1 bis 20)

Execute ....................... Führt die Berechnung aus oder zeichnet eine Test-Grafik

(Dichtefunktion einer t

Verteilung, glockenförmige Kurve)

Nachfolgend ist die Bedeutung der einzelnen Positionen im Falle der Kennzahlenvorgabe [Data: Variable] beschrieben, die sich von der Datenlistenvorgabe [Data: List] unterscheiden.

o1 ................................. empirischer Stichproben-Mittelwert der Stichprobe 1

n-1 ............................ empirische Standardabweichung (x1σn-1 > 0) der Stichprobe 1

n1 ................................. Umfang der Stichprobe 1 (positive ganze Zahl)

o2 ................................. empirischer Stichproben-Mittelwert der Stichprobe 2

n-1 ............................ empirische Standardabweichung (x2σn-1 > 0) der Stichprobe 2

n2 ................................. Umfang der Stichprobe 2 (positive ganze Zahl)

• 1(CALC) ... Führt die Berechnung aus.

• 6(DRAW) ... Zeichnet die Test-Grafik zum Testergebnis.

Verteilung, glockenförmige Kurve) zu zeichnen.

20010901

20011201

Statistische Testverfahren (TEST)

1-2-15

u u u u u

Beispiel Aus zwei (normalverteilten) Grundgesamtheiten, deren (unbekannte) Streu-

ungsparameter als gleich angesehen werden können, wurden die Stichproben 1 und 2 wie folgt entnommen: {105, 108, 86, 103, 103, 107, 124, 124} = List 1, {89, 92, 84, 97, 103, 107, 111, 97} = List 2. dabei jeweils

n-1, x2σn-1 und xpσn-1 sowie die Testgröße

, HA:

= 8. Zu be

, ) und die

rechnen sind die statistischen Kennzahlen o1, o2,

kritische Irrtumswahrscheinlichkeit p. Kann die

Nullhypothese auf Grundlage der ausgewerteten Stichprobe abgelehnt werden (Irrtumswahrscheinlichkeit α = 0.05) ?

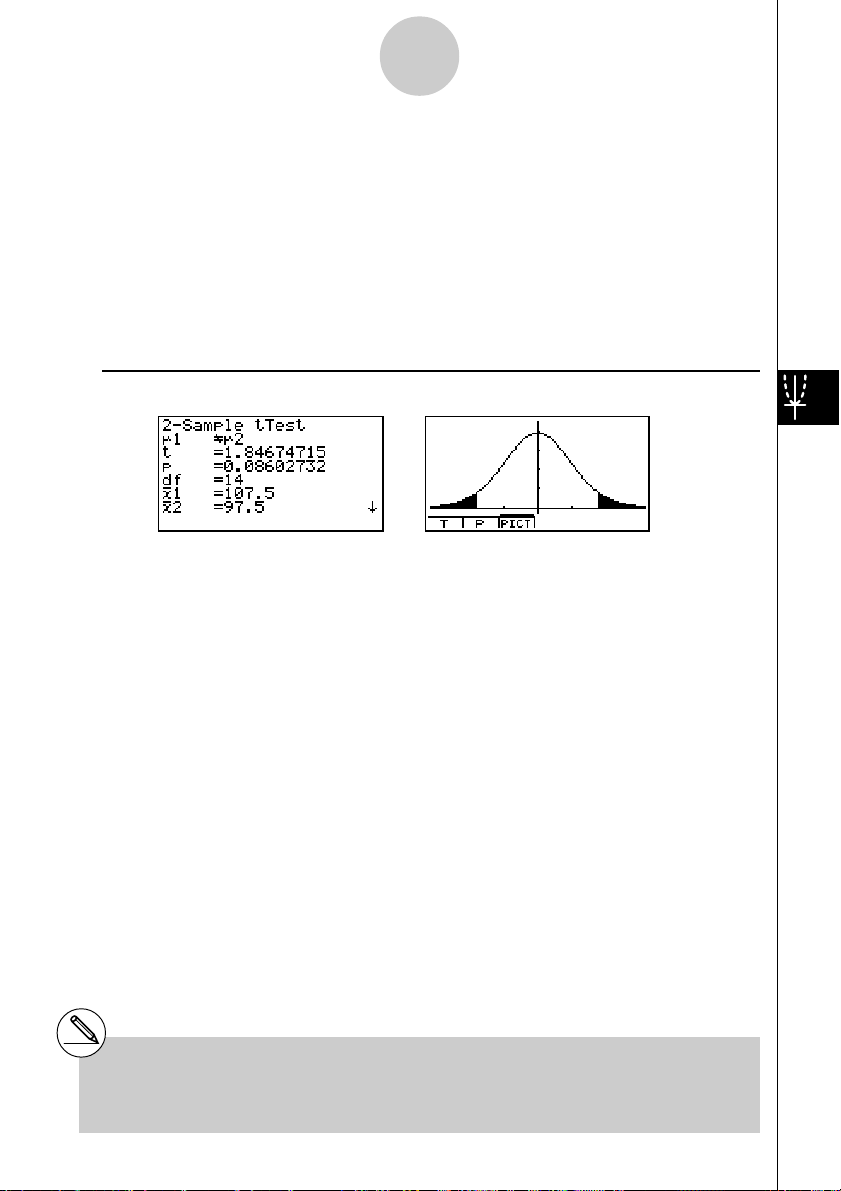
Berechnungsergebnis-Ausgabebildschirm für 1(CALC) bzw. 6(DRAW)

µ1Gµ

2 ........................... Art der Alternativhypothese (zweiseitiger kritischer Bereich)

...................................

berechnete t-Testgröße (df = n1+n2-1 Freiheitsgrade)

p .................................. p-Wert (kritische Irrtumswahrscheinlichkeit)

df ................................. Freiheitsgrade der Prüfverteilung

o1 ................................. empirischer Stichproben-Mittelwert der Stichprobe 1

o2 ................................. empirischer Stichproben-Mittelwert der Stichprobe 2

n-1 ............................ empirische Standardabweichung der Stichprobe 1

n-1 ............................ empirische Standardabweichung der Stichprobe 2

n-1 ............................ gemeinsame Standardabweichung der Gesamtstichprobe (wird

nur angezeigt unter der Voreinstellung [Pooled:On].)

n1 ................................. Umfang der Stichprobe 1

n2 ................................. Umfang der Stichprobe 2

Der Stichprobenumfang betrug

(unter der Nullhypothese Ho:

Entscheidungsregel zum durchgeführten Test:

Für eine vorgegebene Irrtumswahrscheinlichkeit α (Signifikanzniveau α) wird bei p<α die Nullhypothese abgelehnt (Testgröße im kritischen Bereich) und bei p≥α kein Einwand gegen die Nullhypothese erhoben (Testgröße nicht im kritischen Bereich). In diesem Beispiel gilt d.h. es besteht kein Einwand gegen die Nullhypothese. (D.h. die empirischen Mittelwerte unterscheiden sich noch nicht wesentlich (also nicht signifikant, nur unwesentlich). Bei α = würde man jedoch die Nullhypothese wegen vermuteter Unterschiede bereits ablehnen! )

# [Save Res] speichert die

Zeile 2 (Art der Alternativhypothese) nicht ab.

1-Bedingung in

20010901

p≥

0.10

Statistische Testverfahren (TEST)

1-2-16

t-Test zur linearer Regression (LinearReg t-Test) (Korrelationsanalyse)

Der t-Test zur linearer Regression untersucht verbundene Datenlisten des Zufallsvektors (X,

Y) und plottet alle Datenpaare (x

) in einer statistischen Grafik. Danach wird eine

i,yi

Regressioinsgerade (y = a + bx) berechnet und durch die geplottete Punktwolke gelegt. Der Anstieg ␤ (geschätzt durch b) der Regressionsgeraden steht in unmittelbaren Zusammenhang zum (Pearsonschen) Korrelationskoeffizienten ␳ (geschätzt durch r), so dass gleichzeitig die Nulhypothesen "Nullanstieg" bzw. "Unkorreliertheit" untersucht werden können. Für a und b sowie die t

-verteilte Testgröße t gelten die Formeln (Freiheitsgrade: df = n - 2):

a : Achsenabschnitt b : Anstieg der Geraden n : Stichprobenumfang

(n > 3)

r : Korrelationskoeffizient

: Bestimmtheitsmaß

Führen Sie die folgende Tastenbetätigung im STAT-Eingangsmenü (Listeneditor) aus.

3(TEST)

c(T)

d(LinReg)

Nachfolgend ist die Bedeutung der einzelnen Positionen im Falle der Datenlistenvorgabe beschrieben.

& ρ............................ Alternativhypothese für den Anstieg β bzw. den Korrelations-

koeffizienten ρ (“G 0” legt den zweiseitigen kritischen Bereich fest, “< 0” legt den einseitigen kritischen Bereich links fest, “> 0” legt den einseitigen kritischen Bereich rechts fest.)

XList ............................ Liste für die x-Werte der Datenpaare

YList ............................ Liste für die y-Werte der Datenpaare

Freq ............................. einfache Häufigkeiten [1] oder Häufigkeitsliste zu den Daten-

paaren

Save Res..................... Listenspeicherplatz zur Speicherung der Berechnungsergeb-

nisse (Keine [None] oder Liste 1 bis 20)

Execute ....................... Führt die Berechnung aus

Nachdem Sie alle Parameter eingestellt haben, stellen Sie den Cursor auf [Execute] und drücken danach die nachfolgend dargestellte Funktionstaste, um die Berechnung auszuführen.

• 1(CALC) ... Führt die Berechnung aus.

# Sie können für den t-Test zur linearen

Regression keine Test-Grafik zeichnen.

20010901

20011201

Statistische Testverfahren (TEST)

1-2-17

u u u u u

Beispiel Aus zwei (normalverteilten) Grundgesamtheiten X und Y wurden die Stichproben

1 und 2 wie folgt entnommen: { Der Stichprobenumfang betrug dabei jeweils Anstieg b und das Absolutglied a der Regressionsgeraden, der Korrelationskoeffizient r und das Bestimmtheitsmaß r2, sowie die Testgröße z (unter der Nullhypothese Ho: β = tumswahrscheinlichkeit p. Kann die Nullhypothese auf Grundlage der ausgewerteten Stichproben abgelehnt werden (Irrtumswahrscheinlichkeit α = 0.10)? (Antwort: Ja, Ablehnung von statistisch noch nicht gesichert!)

Berechnungsergebnis-Ausgabebildschirm für 1(CALC) und 6(COPY)

G 0 &

G 0 .............. Art der Alternativhypothese (zweiseitiger kritischer Bereich)

t ................................... berechnete t-Testgröße (df = n - 2 Freiheitsgrade)

p .................................. p-Wert (kritische Irrtumswahrscheinlichkeit)

df ................................. Freiheitsgrade (df = n - 2 Freiheitsgrade)

a .................................. Absolutglied der Regressionsgeraden (Schittpunkt mit der y-

Achse)

b .................................. Anstieg der Regressionsgeraden

s .................................. Anpassungsfehler, Wurzel aus der Reststreuung (Restvarianz

mit n - 2 normiert).

r .................................. Korrelationskoeffizient

................................. Bestimmtheitsmaß

0 &

0 , HA:

G 0 &

} = List 1, {

= 5. Zu be

G 0 ,) und die

rechnen sind der

kritische Irr-

Ho wegen p<α . Mit α = 0.05 wäre die Korrelation

} = List 2.

Drücken Sie die Taste 6(COPY), während das Berechnungsergebnis im Display angezeigt wird, um die Regressionsgleichung in den Grafik-Formelspeicher zu kopieren.

Wenn Sie eine Liste für die Position [Resid List] im SET UP-Menü vorgegeben haben, werden die Residuen der linearen Regressionsanalyse automatisch in der vorgegebenen Liste abgespeichert, nachdem die Berechnung abgeschlossen ist.

# [Save Res] speichert die β & ρ -Bedingungen

in Zeile 2 (Alternativhypothese) nicht.

#Wenn die durch [Save Res] benannte Liste die

gleiche Liste ist, wie sie in der Position [Resid List] im SET UP-Menü festgelegt wurde, erfolgt nur eine Speicherung der [Resid List] Daten.

20010901

Statistische Testverfahren (TEST)

1-2-18

-Test (χ2-Homogenitäts- und χ2-Unabhängigkeitstest)

k χ

Der χ2-Test untersucht Homogenitäts- und Unabhängigkeitshypothesen mithilfe von Kontingenztafeln, die im Zusammenhang mit den festgestellten Häufigkeiten

bei k bzw. l Merkmals-

ausprägungen bestehen. Der χ2-Test wird insbesondere für dichotome Variablen (Variable mit zwei möglichen Werten, wie Ja / Nein) verwendet, d.h. k =

= 2 (Vierfeldertafel).

Erwartete Häufigkeiten n : Gesamthäufigkeit (im Fall der Unabhängigkeit (Summe aller bzw. Homogenität):

)

Testgröße, χ2-verteilt mit

(k-1)(l-1) Freiheitsgraden:

χ2 =

ΣΣ

i=1

(xij – Fij)

die folgende Tastenbetätigung im STAT-Eingangsmenü (Listeneditor) aus.

3(TEST)

d(χ2)

Danach bezeichnen Sie die Matrix [Observed], welche die Daten (empirische Häufigkeiten, Kontingenztafel) enthält, und die Matrix [Expected] für die berechneten Häufigkeiten

Nachfolgend ist die Bedeutung der einzelnen Positionen im Eingabefenster aufgeführt.

Observed .................... Name der Matrix (A bis Z), welche die beobachteten Häufig-

keiten (alles positive ganze Zahlen) enthält.

Expected ..................... Name der Matrix (A bis Z), in welcher die erwarteten Häufig-

keiten (unter der Nullhypothese, z.B. Unabhängigkeit) durch den Rechner abspeichert werden.

Save Res..................... Listenspeicherplatz zur Speicherung der Berechnungsergeb-

nisse (Keine [None] oder Liste 1 bis 20)

Execute ....................... Führt die Berechnung aus oder zeichnet eine Test-Grafik

(Dichtefunktion einer χ

Verteilung mit df = (k-1)(l-1) )

Verteilung mit df = (k-1)(l-1) ) zu zeichnen.

• 1(CALC) ... Führt die Berechnung aus.

• 6(DRAW) ... Zeichnet die Test-Grafik zum Testergebnis.

# Die Matrix muss mindestens zwei Zeilen mal

zwei Spalten aufweisen. Es kommt zu einem Fehler, wenn die Matrix nur als Zeilen- oder nur nur als Spaltenmatrix definiert ist.

#Drücken Sie die Taste 2 ('MAT), um die

bezeichneten Matrizen auch im MATRIX-Editor, der für das Betrachten und die Bearbeitung des Inhalts der Matrizen verwendet werden kann, zu definieren.

20010901

Statistische Testverfahren (TEST)

1-2-19

u u u u u

Beispiel Die Komponenten des Zufallsvektors (X,Y) entstammen aus zwei dichotomen

Grundgesamtheiten X und Y . Eine Stichprobenerhebung ergab die folgende Kontingenztafel: Mat A = [ [ ist die Unabhängigkeit der beobachteten Merkmale X und Y. Zu berechnen und unter Mat B abzuspeichern ist die Matrix [ [ hin sind

die Testgröße χ2 (unter der Nullhypothese Ho: P(

P(X=

) P(Y=

die

kritische Irrtumswahrscheinlichkeit p zu bestimmen. Kann die Nullhypothese

) für alle Indexpaare, HA: ... nicht für alle Indexpaare) und

auf Grundlage der vorliegenden Vierfeldertafel abgelehnt werden (Irrtumswahrscheinlichkeit α = 0.10) ? (Antwort: Nein, keine Ablehnung von ausgegangen werden, dass es sich um unabhängige Merkmale handeln könnte.)

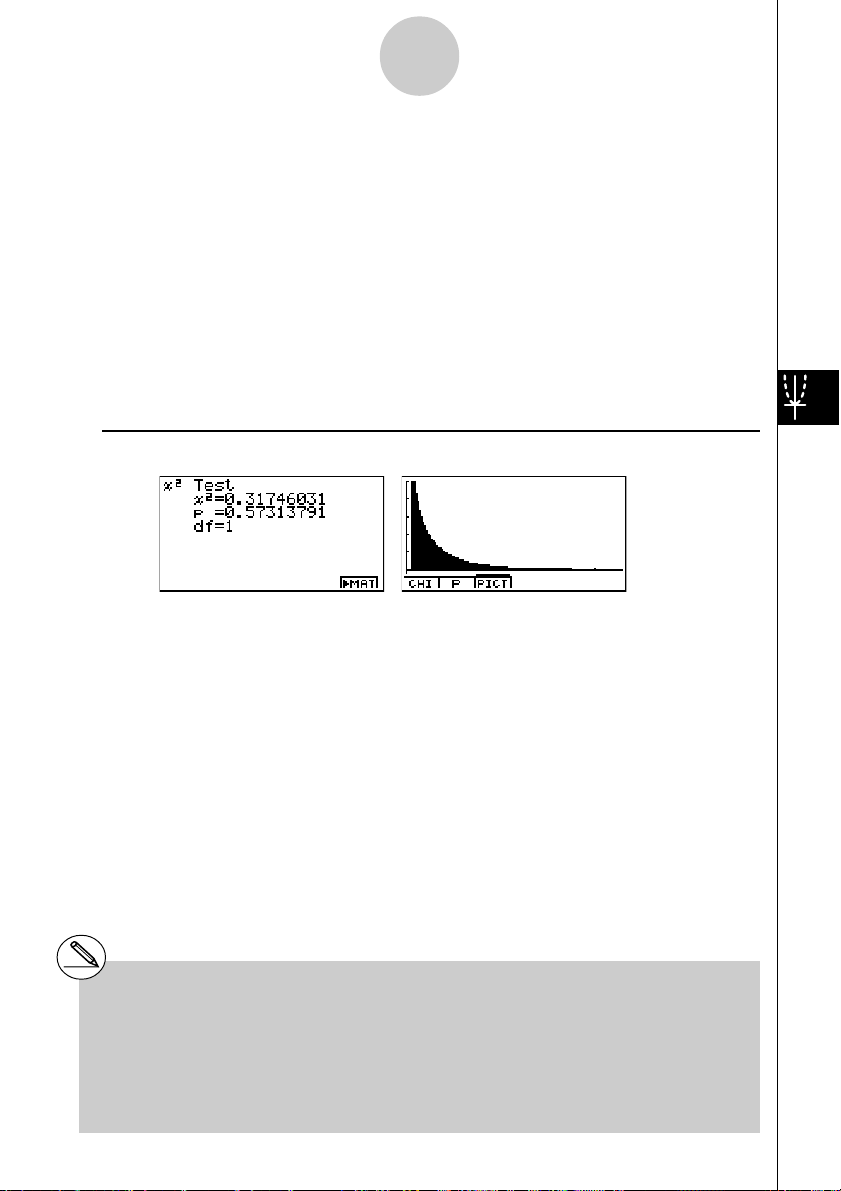
Berechnungsergebnis-Ausgabebildschirm für 1(CALC) bzw. 6(DRAW)

1 2

] [

] ]

, d.h. k = 2, l = 2.

1 2

] [

Zu untersuchen

] ].

(X,Y) =(xi,yj)

Ho wegen p≥α . Es kann also davon

Weiter-

) =

................................. berechnete

-Testgröße (df = 1 Freiheitsgrad)

p .................................. p-Wert (kritische Irrtumswahrscheinlichkeit)

df ................................. Freiheitsgrad

Sie können die folgenden Grafikanalysefunktionen nach dem Zeichnen der Test-Grafik verwenden.

• 1(CHI) ... Zeigt die berechnete

Drücken Sie die Taste 1(CHI), um den wobei der Cursor an der entsprechenden Stelle in der Grafik erscheint (sofern diese Stelle nicht außerhalb des Betrachtungsfensters liegt). Drücken Sie die i-Taste, um die Anzeige des

• 2(P) ... Zeigt den zur berechneten Testgröße gehörenden p-Wert an.

Drücken Sie die Taste 2(P), um den p-Wert in der Fußzeile des Displays anzuzeigen, ohne dass der Cursor erscheint. Drücken Sie die i-Taste, um die Anzeige des p-Wertes zu löschen.

# Drücken Sie die Taste 6('MAT), während ein

Berechnungsergebnis angezeigt wird, um den MATRIX-Editor aufzurufen, den Sie für die Bearbeitung und das Betrachten des Inhalts der Matrizen verwenden können.

# Folgende Betrachtungsfenster-Einstellungen

werden für das Zeichnen der Grafik verwendet:

-Testgröße an.

-Wert in der Fußzeile des Display anzuzeigen,

-Wertes zu löschen.

Xmin = 0, Xmax = 11,5, Xscale = 2,

Ymin = –0,1, Ymax = 0,5, Yscale = 0,1

# Bei der Ausführung des Testverfahrens werden

der

-Wert und der p-Wert automatisch in den

alphabetischen Variablen C bzw. P abgespeichert.

20010901

Statistische Testverfahren (TEST)

1-2-20

k 2-Stichproben F-Test (2-Sample

F-Test) zum Streuungsvergleich

Der 2-Stichproben F-Test prüft die Hypothese zur Gleichheit der Streuungen zweier (normal- verteilter) Grundgesamtheiten mithilfe empirischer Stichprobenstreuungen. Der F-Test beruht auf einer F-verteilten Testgröße mit den Freiheitsgraden n1-1 (Zähler-FG) und n2-1 (NennerFG).

F =

1 n–1

2 n–1

Führen Sie die folgende Tastenbetätigung im STAT-Eingangsmenü (Listeneditor) aus.

3(TEST)

e(F)

Nachfolgend ist die Bedeutung der einzelnen Positionen im Falle der Datenlistenvorgabe ([Data: List] statt [Data: Variable] eingestellt) beschrieben.

Data ............................ Art der Datenvorgabe (Liste der Stichprobendaten [List] oder

empirische Kennzahlen [Variable])

1 ................................. Art der Alternativhypothese (“G σ2” legt den zweiseitigen

kritischen Bereich fest, “< Bereich links fest, “>

2” legt den einseitigen kritischen Bereich

2” legt den einseitigen kritischen

rechts fest.)

List(1) .......................... Liste der Stichprobendaten 1

List(2) .......................... Liste der Stichprobendaten 2

Freq(1) ........................ einfache Häufigkeiten [1] oder Häufigkeitsliste 1

Freq(2) ........................ einfache Häufigkeiten [1] oder Häufigkeitsliste 2

Save Res..................... Listenspeicherplatz zur Speicherung der Berechnungsergeb-

nisse (Keine [None] oder Liste 1 bis 20)

Execute ....................... Führt die Berechnung aus oder zeichnet eine Test-Grafik

(Dichtefunktion einer F

df1,df2

Verteilung)

Nachfolgend ist die Bedeutung der einzelnen Positionen im Falle der Kennzahlenvorgabe [Data: Variable] beschrieben, die sich von der Datenlistenvorgabe [Data: List] unterscheiden.

n-1 ............................ empirische Standardabweichung (x1σn-1

0) der Stichprobe 1

n1 ................................. Umfang der Stichprobe 1 (positive ganze Zahl)

n-1 ............................ empirische Standardabweichung (x2σn-1

0) der Stichprobe 2

n2 ................................. Umfang der Stichprobe 2 (positive ganze Zahl)

20010901

20011201

Statistische Testverfahren (TEST)

1-2-21

• 1(CALC) ... Führt die Berechnung aus.

• 6(DRAW) ... Zeichnet die Test-Grafik zum Testergebnis.

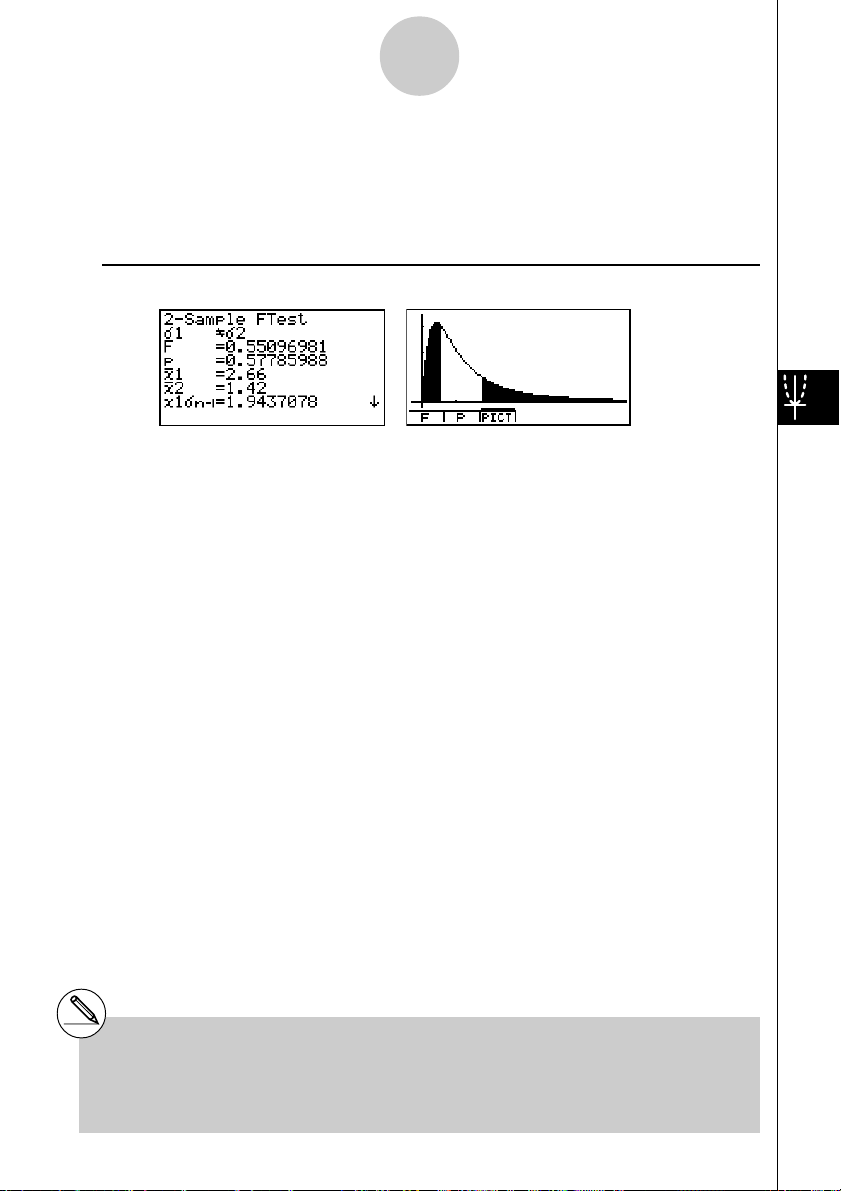
Beispiel: Ausgabebildschirm für 1(CALC) bzw. 6(DRAW)

σ1Gσ

2 .......................... Art der Alternativhypothese (zweiseitiger kritischer Bereich)

F .................................. berechnete F-Testgröße (df 1 = 4, df 2 = 4 Freiheitsgrade)

p .................................. p-Wert (kritische Irrtumswahrscheinlichkeit) ( p≥

=0.10 z.B.)

o1 ................................. empirischer Stichproben-Mittelwert der Stichprobe 1

(Angezeigt nur für Datenlistenvorgabe [Data: List].)

o2 ................................. empirischer Stichproben-Mittelwert der Stichprobe 2

(Angezeigt nur für Datenlistenvorgabe [Data: List].)

n-1 ............................ emp. Standardabweichung der Stichprobe 1 (1.9437078)

n-1 ............................ emp. Standardabweichung der Stichprobe 2 (2.61858741)

n1 ................................. Umfang der Stichprobe 1 (n1 = 5)

n2 ................................. Umfang der Stichprobe 2 (n2 = 5)

Sie können die folgenden Grafikanalysefunktionen nach dem Zeichnen der Test-Grafik verwenden.

• 1(F) ... Zeigt die berechnete F-Testgröße an.

Drücken Sie die Taste 1(F), um den F-Wert in der Fußzeile des Displays anzuzeigen, wobei der Cursor an de entsprechenden Stelle in der Grafik erscheint (sofern diese Stelle nicht außerhalb des Betrachtungsfensters liegt).

Im Falle eines Tests mit zweiseitigem kritischen Bereich werden zwei Punkte angezeigt. Verwenden Sie die d- und e-Taste, um den Cursor zu verschieben.

Drücken Sie die i-Taste, um die Anzeige des F-Wertes zu löschen.

• 2(P) ... Zeigt den zur berechneten Testgröße gehörenden p-Wert an.

Drücken Sie die Taste 2(P), um den p-Wert in der Fußzeile des Displays anzuzeigen, ohne dass der Cursor erscheint. Drücken Sie die i-Taste, um den p-Wert zu löschen.

# [Save Res] speichert die

2 (Alternativhypothese) nicht ab.

# Die Betrachtungsfenstereinstellungen werden

automatisch für das Zeichnen der Grafik optimiert.

1-Bedingung in Zeile

# Bei der Ausführung des Testverfahrens werden

der

F-Wert und der p-Wert automatisch in den

alphabetischen Variablen F bzw. P abgespeichert.

20010901

Statistische Testverfahren (TEST)

1-2-22

k Varianzanalyse (ANOVA)

ANOVA prüft Hypothesen zur Gleichheit von Mittelwerten mehrerer (normalverteilter) Grundgesamtheiten auf Grundlage entsprechender Stichproben mithilfe einer Streuungszerlegung ("Varianzanalyse") und einer oder mehrerer F-verteilter Prüfgrößen. Die Einweg-Varianzanalyse (One-Way ANOVA) wird verwendet, wenn nur ein unabhängiger Einflußfaktor A in verschiedenen Abstufungen Ai auf eine abhängige Variable Yir wirkt. Die Zweiweg-Varianzanalyse (Two-Way ANOVA) wird verwendet, wenn zwei unabhängige Einflußfaktoren A und B in bestimmten Abstufungen Ai und Bj auf eine abhängige Variable

wirken (Indexnotation: i-te Stufe von A, j-te Stufe von B, r=ri-te bzw. r=rij-te Wiederholung).

ijr

Führen Sie die folgende Tastenbetätigung im STAT-Eingangsmenü (Listeneditor) aus.

3(TEST)

f(ANOVA)

Nachfolgend ist die Bedeutung der einzelnen Positionen im Falle der Einweg- bzw. ZweiwegVarianzanalyse beschrieben.

How Many ................... Wählt die Einweg-Varianzanalyse oder Zweiweg-Varianz-

analyse (Anzahl der Einflußfaktoren)

Factor A ....................... Kategorienliste der auf Y wirkenden Faktorstufen A

Dependnt .................... Liste der Stichprobendaten Y

Save Res..................... Listenspeicherplatz zur Speicherung der Berechnungsergeb-

nisse (Keine [None] oder Liste 1 bis 16)*

bzw. Y

ijr

Execute ....................... Führt die Berechnung aus oder zeichnet eine Test-Grafik

(letztes nur für die Zweiweg-Varianzanalyse)

Die folgende Position erscheint nur im Fall der Zweiweg-Varianzanalyse.

Factor B....................... Kategorienliste der auf Y wirkenden Faktorstufen B

Nachdem Sie alle Parameter (Vorgabewerte) eingestellt haben, stellen Sie den Cursor auf [Execute] und drücken Sie danach eine der nachfolgend dargestellten Funktionstasten, um die Berechnung auszuführen oder im Fall einer Zweiweg-Varianzanlyse die Test-Grafik zu zeichnen.

• 1(CALC) ... Führt die Berechnung aus.

• 6(DRAW) ... Zeichnet die Test-Grafik (nur Zweiweg-Varianzanalyse)

Die Berechnungsergebnisse werden in Tabellenform angezeigt, genau wie sie in jedem StatistikLehrbuch zu finden ist.

*1 [Save Res] speichert jede vertikale Spalte der

Tabelle in einer eigenen Liste ab. Die Spalte ganz links wird in der benannten Liste abgespeichert, jede rechts davon angeordnete Spalte wird in der Liste mit der nächstfolgenden

Nummer abgespeichert. Bis zu fünf Listen können für die Speicherung der Spalten verwendet werden. Sie können eine Nummer im Bereich von 1 bis 16 für die erste Liste vorgeben.

20010901

20011201

Statistische Testverfahren (TEST)

1-2-23

Die Einweg-Varianzanalyse benötigt für ihre Auswertung zwei verbundene Datenlisten mit den Datenpaaren ( Datenlisten mit den Datentripeln (

Ai , Yir). Die Zweiweg-Varianzanalyse hingegen benötigt drei verbundene

Ai , Bj , Yijr).

Beispiel: Ausgabebildschirm für eine Einweg- bzw. Zweiweg-Varianzanalyse

Einweg-Varianzanalyse (One-Way ANOVA)

Zeile 1 (A) ................... zum Faktor A: df-Wert, SS-Wert, MS-Wert, F-Wert, p-Wert

Zeile 2 (ERR) .............. zum Fehler: df-Wert, SS-Wert, MS-Wert

Zweiweg-Varianzanalyse (Two-Way ANOVA)

Zeile 1 (A) ................... zum Faktor A: df-Wert, SS-Wert, MS-Wert, F-Wert, p-Wert

Zeile 2 (B) ................... zum Faktor B: df-Wert, SS-Wert, MS-Wert, F-Wert, p-Wert

Zeile 3 (AB) ................. zum Wechselwirkungseffekt (Faktor A × Faktor B):

df-Wert, SS-Wert, MS-Wert, F-Wert, p-Wert

*Die Zeile 3 erscheint nur, wenn für jede Stufen-Kombination

Ai , Bj gleichviele Mehrfach-Beobachtungen vorhanden sind.

Zeile 4 (ERR) .............. zum Fehler: df-Wert, SS-Wert, MS-Wert

F .................................. F-Wert(e) (F = MS / MS

.................................. p-Wert zum jeweiligen F-Wert ( p

................................. Freiheitsgrade

ERR

)

P( F > MS / MS

ERR

) )

SS ................................ Summe der Fehler-Quadrate

MS (= SS / df ) ............

gemittelte Fehler-Quadrat-Summen (gemittelte Streuungsanteile)

Bei der Zweiweg-Varianzanalyse können Sie Grafiken zum Wechselwirkungseffekt zeichnen. Die Anzahl der Graphen ist durch die Anzahl der Stufen des Faktors B bestimmt, die Anzahl der Datenpunkte auf der x-Achse ist durch die Anzahl der Stufen des Faktors A bestimmt. Auf der y-Achse werden die Mittelwerte der Y

zur entsprechenden Kombination(Ai,Bj) abgetragen.

ijr

Sie können die folgende Grafikanalysefunktion nach dem Zeichnen einer Test-Grafik verwenden.

• 1(TRACE) ... Abtastfunktion (Trace) für die berechneten Einzelmittelwerte

Drücken Sie die d- oder e-Taste, um den Cursor auf der Grafik in die entsprechende Richtung zu verschieben. Wenn mehrere Graphen vorhanden sind, können Sie zwischen den Graphen wechseln, indem Sie die f- oder c-Taste drücken. Drücken Sie die i-Taste, um den Zeiger vom Diplay zu löschen.

Die grafische Darstellung steht nur für die Zweiweg-ANOVA zur Verfügung. Die Betrachtungsfenster-Einstellungen werden automatisch ausgeführt, unabhängig von den Vorgaben im SET UP-Menü.

# Bei Verwendung der TRACE-Funktion werden

entsprechend der Cursorposition die Anzahl der Wiederholungen automatisch in der alphabetischen Variablen A bzw. der angezeigte Mittelwert in der Variablen M gespeichert.

20010901

Statistische Testverfahren (TEST)

1-2-24

k ANOVA (Zweiweg)

Darstellung einer Aufgabensituation

Die folgende Tabelle zeigt Messungsergebnisse für ein Merkmal Y (z. B. Festigkeit) eines Metallerzeugnisses, das mittels eines Wärmebehandlungsverfahren unter dem Einfluß zweier Faktoren hergestellt wurde: Zeit (A) und Temperatur (B). Die Messungen wurden zwei Mal unter identischen Bedingungen wiederholt.

B (

Temperatur der Wärmebehandlung

A (Zeit)

A1 113 , 116

Untersuchen Sie mithilfe der Varianzanalyse die folgenden Nullhypothesen, wobei eine Irrtumswahrscheinlichkeit von α = 5% zu verwenden ist.

HA : Die Zeitabstufungen ( HB : Die Temperaturabstufungen ( HAB :

Die Stufenkombinationen (Ai,Bj) sind im Mittel ohne Einfluß auf die Festigkeit

u Lösungsweg

Verwenden Sie die Zweiweg-Varianzanalyse, um die obigen Null-Hypothesen zu prüfen. Geben Sie die obigen Stichprobenwerte (Y-Daten) z.B. wie folgt als verbundene Listen ein.

List 1 = { 1, 1, 1, 1, 2, 2, 2, List 2 = { 1, 1, 2, 2, 1, 1, 2, List 3 = {113, 116, 139, 132, 133, 131, 126, 122 }

Definieren Sie im Eingabemenü zum Testverfahren List 3 (die gemessenen Werte Y ) als abhängig. Ordnen Sie List 1 und List 2 (die Faktorenstufenzuordnung für jeden Werte Y in List 3) dem Faktor A bzw. Faktor B zu. Durch Ausführung der Varianzanalyse werden die folgenden Ergebnisse erhalten.

•Kritische Irrtumswahrscheinlichkeit (Sicherheitsschwelle) p = 0,2458019517 für den Faktor

A (Zeitabstufungen): Der p-Wert (p = 0,2458019517) ist größer als die Irrtumswahrscheinlichkeit (Sicherheitsschwelle α = 0,05), sodass die Null-Hypothese HA nicht verworfen werden kann.

•Kritische Irrtumswahrscheinlichkeit (Sicherheitsschwelle) p = 0,04222398836 für den Faktor

B (Temperaturabstufungen): Der p-Wert (p = 0,04222398836) ist kleiner als die Irrtumswahrscheinlichkeit (Sicherheitsschwelle α = 0,05), sodass die Null-Hypothese HB verworfen werden muss.

•Kritische Irrtumswahrscheinlichkeit (Sicherheitsschwelle) p = 2,78169946E-3 der Interaktion

(Wechselwirkungseffekt) (A × B): Die Sicherheitsschwelle (p = 2,78169946E-3) ist kleiner als die Sicherheitsschwelle (0,05), sodass die Null-Hypothese HAB verworfen werden muss.

Der obige Test zeigt, dass für die Festigkeit des Metallerzeugnisses die Zeitdauer der Wärmebehandlung nicht von Bedeutung ist, wohl aber die Höhe der Temperatur maßgebend und der Wechselwirkungseffekt sehr maßgebend sind.

Ai) sind im Mittel ohne Einfluß auf die Festigkeit Y

(Zweiwegklassifikation, Mehrfachbesetzung)

)B1 B2

139 , 132

133 , 131

Bj) sind im Mittel ohne Einfluß auf die Festigkeit Y

20010901

126 , 122

2} 2}

u Eingabebeispiel

u Ergebnisse

Statistische Testverfahren (TEST)

1-2-25

Hinweis:

Für die Streuungszerlegung (Varianzanalyse) werden folgende mathematische Modelle zur Darstellung von Y mithilfe eines allgemeinen Mittelwertes µ, sowie der individuellen Mittelwertanteile αi bzw. βj bzw. (αβ)ij und des stochastischen Fehlers E benutzt:

Einweg-Varianzanalyse:

SS = SS

+ SS

für Yir = µ + αi + Eir mit E

ERR

僆

N(0,σ

Zweiweg-Varianzanalyse (ohne Wechselwirkungseffet):

SS = SS

+ SSB + SS

für Yir = µ + αi + βj + E

ERR

mit E

ijr

僆

N(0,σ

ijr

Zweiweg-Varianzanalyse (mit Wechselwirkungseffet):

SS = SS

+ SSB + SSAB + SS

ERR

für Y

= µ + αi + βj + (αβ)ij + E

ijr

mit E

ijr

僆

N(0,σ

ijr

Unter den oben genannten Nullhypothesen wurde praktisch stets von Y = µ + E ausgegangen,

d.h. HA : αi = 0 bzw. HB : βj = 0 bzw. HAB : (αβ)

20010901

= 0.

Vertrauensintervalle (INTR)

1-3-1

1-3 Vertrauensintervalle (INTR)

Ein Vertrauensintervall (Konfidenzintervall) ist ein Zahlenbereich (Intervall [Gu, Go]), das den unbekannten Mittelwert einer untersuchten Grundgesamtheit mit hoher Wahrscheinlichkeit einschließen soll. Die Intervallgrenzen Gu, Go werden dabei durch eine Zufallsstichprobe geschätzt unter Berücksichtigung des vorgegebenen Konfidenzniveaus ε.

Bei einem zu breiten Vertrauensintervall ist es nur sehr schwer nachvollziehbar, wo der Mittelwert (wahre Wert) der Grundgesamtheit liegt. Ein zu enges Vertrauensintervall schränkt dagegen den möglichen Mittelwert zu sehr ein und macht es schwierig, zuverlässige Aussagen zu erhalten. Die am häufigsten verwendeten Vertrauenswahrscheinlichkeiten (Konfidenzniveaus, Sicherheitswahrscheinlichkeiten) betragen ε=95% oder ε=99%. Durch das Anheben des Konfidenzniveaus wird das Vertrauensintervall verbreitert, hingegen ein Absenken des Konfidenzniveaus zu einem engeren Vertrauensintervall führt und gleichzeitig aber auch die Gefahr eines ungewollten Ausklammerns des tatsächlichen Mittelwertes in sich birgt. Mit einem Konfidenzniveau von ε=95% z.B. wird der unbekannte Parameter nur mit einer Irrtumswahrscheinlichkeit von α=1-ε= 5% außerhalb des Intervalls [Gu, Go] liegen.

Wenn Sie eine Untersuchung planen, um dann mit den erfaßten Daten ein t-Intervall oder ZIntervall zu bestimmen, müssen Sie auch den Stichprobenumfang, die Breite des Vertrauensintervalls und das Konfidenzniveau bedenken. Das Grenzen Gu, Go des Vertrauensintervalls sind von den Anwendungsbedingungen (Vorgabewerten) abhängig.

Das 1-Stichproben Z-Intervall (1-Sample Z-Interval) beschreibt mithilfe einer Stichprobe das Vertrauensintervall für den unbekannten Mittelwert einer (normalverteilten) Grundgesamtheit, wenn die Standardabweichung der Grundgesamtheit bekannt ist.

Das 2-Stichproben Z-Intervall (2-Sample Z-Interval) beschreibt mithilfe zweier Stichproben das Vertrauensintervall für die Differenz zweier unbekannter Mittelwerte zweier (normalverteilter) Grundgesamtheiten, wenn die Standardabweichungen der zwei Grundgesamtheiten bekannt sind.

Das 1-Prop Z-Intervall beschreibt mithilfe einer Stichprobe das Vertrauensintervall für die Erfolgswahrscheinlichkeit [Prop] in einer dichotomen Grundgesamtheit, wobei die Berechnung der Intervallgrenzen näherungsweise über eine N(0,1)-verteilte Zufallsgröße realisiert wird.

Das 2-Prop Z-Intervall beschreibt mithilfe zweier Stichproben das Vertrauensintervall für die Differenz der Erfolgswahrscheinlichkeit p1 und p2 zweier dichotomer Grundgesamtheiten, wobei die Berechnung der Intervallgrenzen wieder näherungsweise über eine N(0,1)-verteilte Zufallsgröße realisiert wird.

Das 1-Stichproben t-Intervall (1-Sample t-Interval) beschreibt mithilfe einer Stichprobe das Vertrauensintervall für den unbekannten Mittelwert einer (normalverteilten) Grundgesamtheit, wenn die Standardabweichung der Grundgesamtheit unbekannt ist und geschätzt werden muß.

Das 2-Stichproben t-Intervall (2-Sample t-Interval) beschreibt mithilfe zweier Stichproben das Vertrauensintervall für die Differenz zweier unbekannter Mittelwerte zweier (normalverteilter) Grundgesamtheiten, wenn die Standardabweichungen der zwei Grundgesamtheiten unbekannt sind und geschätzt werden müssen.

# Für die Vertrauensintervalle können keine

speziellen Grafiken erstellt werden.

20010901

20011201

Vertrauensintervalle (INTR)

1-3-2

In der Eingangsanzeige (Listeneditor) des STAT-Menüs drücken Sie die Taste 4 (INTR), um das Untermenü für die Vertrauensintervalle anzuzeigen, das die folgenden Positionen enthält.

• 4(INTR)b(Z) ... Z-Intervalle (vier Varianten mithilfe der N(0,1)-Verteilung,

ab S. 1-3-3)

c(T) ... t-Intervalle (zwei Varianten mithilfe der t-Verteilung,

ab S. 1-3-8)

u Allgemeine Hinweise hinsichtlich des Konfidenzniveaus

Durch die Eingabe eines C-Wertes (C-Level, Konfidenzniveau, Sicherheitswahrscheinlichkeit) im Bereich von 0 Konfidenzniveau festgelegt. Durch die Eingabe eines C-Wertes (in %) im Bereich von 1

< C < 1 für die Einstellung des C-Level wird das von Ihnen eingegebene

< C <

100 wird ein C-Wert intern abgespeichert, der dem von Ihnen eingegebenen C-Wert, geteilt durch 100, entspricht.

# Die Eingabe eines Wertes von 100 oder größer

bzw. die Eingabe eines negativen Wertes erzeugt eine Fehlermeldung (Ma ERROR).

20010901

Vertrauensintervalle (INTR)

k Z-Intervalle (mit Quantilen der N(0,1)-Verteilung)

u 1-Stichproben Z-Intervall (1-Sample Z-Interval)

Das 1-Stichproben Z-Intervall beschreibt mithilfe einer Stichprobe das Vertrauensintervall für den unbekannten Mittelwert µ einer (normalverteilten) Grundgesamtheit, wenn die Standardabweichung der Grundgesamtheit bekannt ist.

Die nachfolgenden Formeln beschreiben die Intervallgrenzen Left = Gu , Right = Go .

1-3-3

Es gilt: 1-

ist jedoch das Signifikanzniveau. Der Wert 100 (1–α )

% , d.h. ε = 1-α . Wenn zum Beispiel das Vertrauensniveau 95% beträgt, dann wird durch die Eingabe von 0,95 die Irrtumswahrscheinlichkeit α = 1 – 0,95 = 0,05 erhalten. z das Quantil der Ordnung 1-

Führen Sie die folgende Tastenbedienung im STAT-Eingangsmenü (Listeneditor) aus.

4(INTR)

b(Z)

b(1-Smpl)

Nachfolgend ist die Bedeutung der einzelnen Positionen im Fall der Datenlistenvorgabe ([Data: List] statt [Data: Variable] eingestellt) beschrieben.

Data ............................ Art der Datenvorgabe (Liste der Stichprobendaten [List] oder

C-Level ........................ Konfidenzniveau C (0 < C < 1)

.................................. bekannte Grundgesamtheits-Standardabweichung (σ > 0)

List .............................. Liste der Stichprobendaten

Freq ............................. einfache Häufigkeiten [1] oder Häufigkeitsliste

Save Res..................... Listenspeicherplatz zur Speicherung der Berechnungsergeb-

Execute ....................... Führt die Berechnung der Intervallgrenzen aus

α /

2 einer N(0,1)-Verteilung.

empirische Kennzahlen [Variable])

nisse (Keine [None] oder Liste 1 bis 20)

α /

2 = P( Z

≤ z

vgl. S. 1-4-5 oder

Bedienungsanleitung S. 6-4-5

% entspricht dem Konfidenzniveau 100

α /

) ,

bezeichnet

Nachfolgend ist die Bedeutung der einzelnen Positionen im Fall der Kennzahlenvorgabe [Data: Variable] beschrieben, die sich von der Datenlistenvorgabe [Data: List] unterscheiden.

o .................................. empirischer Mittelwert der Stichprobe

n .................................. Stichprobenumfang (positive ganze Zahl)

20010901

20011201

Vertrauensintervalle (INTR)

1-3-4

Nachdem Sie alle Parameter (Vorgabewerte) eingestellt haben, stellen Sie den Cursor auf [Execute] und drücken Sie danach die folgende Funktionstaste, um die Berechnung auszuführen.

• 1(CALC) ... Führt die Berechnung der Intervallgrenzen aus.

Beispiel:

Ausgabebildschirm (Vorgabewerte: Datenliste,sowie C = 0.95, σ = 15)

Left .............................. Untere Intervallgrenze (Gu) des Konfidenzintervalls für

Right ............................ Obere Intervallgrenze (Go) des Konfidenzintervalls für

o .................................. empirischer Mittelwert der Stichprobe

n-1 ............................. empirische Stichproben-Standardabweichung

(Angezeigt nur für Datenlistenvorgabe [Data: List].)

n .................................. Stichprobenumfang

u 2-Stichproben Z-Intervall (2-Sample Z-Interval)

Das 2-Stichproben Z-Intervall beschreibt mithilfe zweier Stichproben das Vertrauensintervall für die Differenz heiten, wenn die Standardabweichungen der zwei Grundgesamtheiten bekannt sind. α = 1 - ε.

zweier unbekannter Mittelwerte zweier (normalverteilter) Grundgesamt-

Die nachfolgenden Formeln beschreiben die Intervallgrenzen Left = Gu , Right = Go .

o1 :Mittelwert der Stichprobe 1 o2 :Mittelwert der Stichprobe 2

1 :

bekannte Standardabweichung

der Grundgesamtheit 1

2 :

bekannte Standardabweichung

der Grundgesamtheit 2

n1 : Umfang der Stichprobe 1 n2 : Umfang der Stichprobe 2

Für das

/ 2

-Quantil gilt:

/ 2 = P( z

)

, vgl. S. 1-4-5 oder Bedienungsanleitung S. 6-4-5.

/ 2

Führen Sie die folgende Tastenbedienung im STAT-Eingangsmenü (Listeneditor) aus.

4(INTR)

b(Z)

c(2-Smpl)

20010901

Vertrauensintervalle (INTR)

1-3-5

Nachfolgend ist die Bedeutung der einzelnen Positionen im Falle der Datenlistenvorgabe ([Data: List] statt [Data: Variable] eingestellt) beschrieben.

Data ............................ Art der Datenvorgabe (Liste der Stichprobendaten [List] oder

empirische Kennzahlen [Variable])

C-Level ........................ Konfidenzniveau C (0 < C < 1)

1 .................................

2 .................................

bekannte Grundgesamtheits-Standardabweichung 1 ( bekannte Grundgesamtheits-Standardabweichung 2 (

σ σ

> 0)