
ALGEBRA FX 2.0
Bedienungsanleitung
G

CASIO ELECTRONICS CO., LTD.
Unit 6, 1000 North Circular Road,
London NW2 7JD, U.K.
Wichtig!
Bitte bewahren Sie Ihre Anleitung und alle Informationen
griffbereit für spätere Nachschlagzwecke auf.

Vor der erstmaligen Verwendung des Rechners...
Wenn Sie den Rechner erworben haben, enthält dieser noch keine Hauptbatterien. Sie
müssen daher die Batterien wie nachfolgend beschrieben einsetzen, den Rechner zurückstellen und den Kontrast einstellen, bevor Sie den Rechner erstmalig verwenden können.
1. Achten Sie darauf, dass Sie die o-Taste nicht aus Versehen betätigen, schieben Sie
das Gehäuse auf den Rechner und drehen Sie den Rechner um. Entfernen Sie den
rückseitigen Deckel vom Rechner, indem Sie mit Ihrem Finger an der mit
Stelle ziehen.
P
2. Setzen Sie die vier mit dem Rechner mitgelieferten Batterien ein.
•Achten Sie darauf, dass die positiven (+) und negativen (–) Pole der Batterien in die
richtigen Richtungen zeigen.
BACK UP
1 markierten
1
3. Entfernen Sie die Isolierfolie von der mit “BACK UP” markierten Stelle, indem Sie die
Folie in die durch einen Pfeil gekennzeichnete Richtung ziehen.
BACK UP
4. Bringen Sie den rückseitigen Deckel wieder an, wobei Sie darauf achten müssen, dass
die Laschen richtig in die mit 2 markierten Vertiefungen eingreifen. Drehen Sie danach
den Rechner um, so dass dessen Frontseite nach oben zeigt. Der Rechner sollte nun
die Stromversorgung automatisch einschalten und eine Speicherrückstellung ausführen.
2
19990401

5. Drücken Sie die m-Taste.
• Falls das rechts dargestellte Hauptmenü nicht im
Display angezeigt wird, drücken Sie den P-Knopf auf
der Rückseite des Rechners, um eine Speicherrückstellung auszuführen.
P-Knopf
6. Verwenden Sie die Cursortasten (f, c, d, e), um das SYSTEM-Icon zu wählen,
und drücken Sie die w-Taste. Anschließend drücken Sie die 2-Taste(
), um die
Kontrasteinstellungsanzeige zu öffnen.
7. Stellen Sie den Kontrast ein.
•Mit der e-Cursortaste kann der Kontrast des Displays abgedunkelt werden.
•Mit der d-Cursortaste kann der Kontrast des Displays aufgehellt werden.
•Drücken Sie die 1(INIT)-Taste, um den Kontrast auf die Standardvorgabe
zurückzustellen.
8. Um die Kontrasteinstellung des Displays zu verlassen, drücken Sie die m-Taste.
19990401
Schnellstart
Ein- und Ausschalten der Stromversorgung
Auswahl der Menüs
Grundlegende Berechnungen
Wiederholungsfunktion
Bruchrechnung
Exponenten
Grafikfunktionen
Doppelgrafik
Boxzoom
Dynamische Grafik
Tabellenfunktion
19990401

o
OFF
1
Schnellstart
Schnellstart
Willkommen in der Welt der Grafikrechner.
Der Schnellstart ist kein vollständiges Tutorium, führt Sie aber durch die am häufigsten
verwendeten Funktionen, vom Einschalten der Stromversorgung bis hin zu komplexen
Grafikfunktionen. Wenn Sie damit fertig sind, haben Sie die grundlegenden Operationen dieses Rechners kennengelernt und sind in der Lage, mit dem restlichen Teil
dieser Bedienungsanleitung zurechtzukommen, um das gesamte Spektrum der verfügbaren Funktionen zu erlernen.
Jeder Schritt
dass Sie diesem schnell und einfach folgen können. Wenn Sie z.B. die Zahl 57
eingeben müssen, ist dies wie folgt angegeben:
der Beispiele im Schnellstart ist grafisch dargestellt, um zu gewährleisten,
Drücken Sie
Wenn für das Verständnis erforderlich, wurden Beispiele darüber eingefügt, wie das
Display aussehen sollte. Falls Ihr Display nicht diesen Beispielen entspricht, sollten
Sie nochmals ab Beginn starten, indem Sie die
fh
o
-Gesamtlöschtaste drücken.
EIN- UND AUSSCHALTEN DER
STROMVERSORGUNG
Um die Stromversorgung einzuschalten, drücken Sie die o-Taste.
Um die Stromversorgung auszuschalten, drücken Sie die Tasten
Die Stromversorgung des Rechners wird automatisch ausgeschaltet, wenn Sie innerhalb der von Ihnen eingestellten Auslösezeit der Ausschaltautomatik keine Operation
ausführen. Als Auslösezeit können Sie entweder mit sechs Minuten oder mit 60 Minuten vorgeben.
!
.
AUSWAHL DER MENÜS
Dieser Rechner erleichtert die Ausführung einer Vielzahl von Berechnungen, indem
Sie einfach das entsprechende Menü öffnen und nutzen. Bevor Sie aber mit den
eigentlichen Berechnungen und Bedienungsbeispielen beginnen, sollten Sie zuerst
lernen, wie Sie durch die einzelnen Menüs navigieren können.
Wahl des RUN·MAT-Menüs
1. Drücken Sie diem-Taste, um das Hauptmenü
anzuzeigen.
19990401
2
Schnellstart
2. Verwenden Sie die Cursortasten
(
d,e,f,c), um RUN
hervorzuheben, und drücken Sie danach die
•
MAT
w-Taste.
•
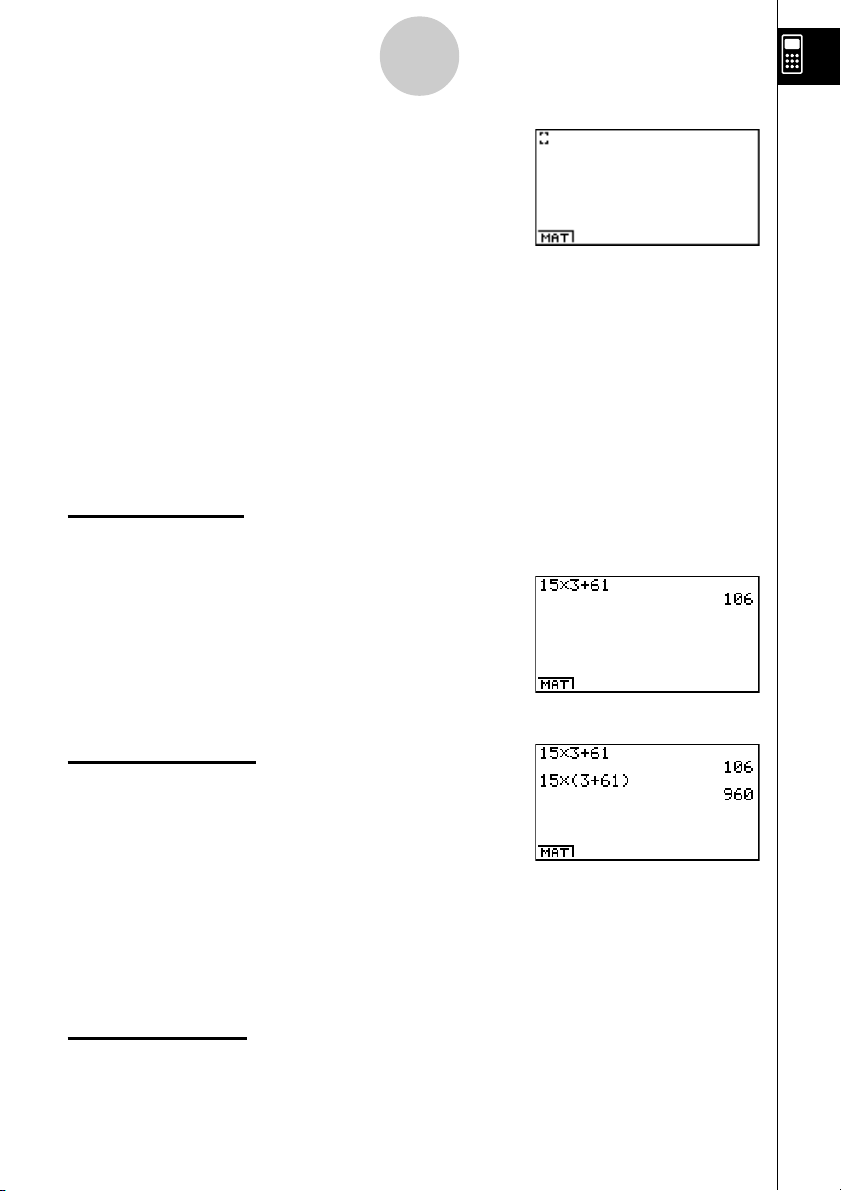
Rechts sehen Sie das Eingangsdisplay des RUN
MAT-Menüs, in dem Sie manuelle Berechnungen und
die Matrizenrechnung ausführen und Programme
ablaufen lassen können.
GRUNDLEGENDE BERECHNUNGEN
Bei manuellen Berechnungen geben Sie den Formelterm von links nach rechts ein, so
wie er auf Papier geschrieben wird. Für Formeln, welche unterschiedliche arithmetische Operationen und Klammern enthalten, benutzt der Rechner automatisch die
korrekte Algebralogik, um das Ergebnis zu ermitteln.
Beispiel:
1. Drücken Sie die
2. Drücken Sie die Tasten
15 × 3 + 61
o-Taste, um ältere Eingaben im Display zu löschen.
bf*d+gbw.
Klammerrechnungen
Beispiel:
1. Drücken Sie die Tasten
15 × (3 + 61)
bf*(d
+gb)w.
Vorhandene höhere mathematische Funktionen
In diesem Rechner sind eine Vielzahl höherer mathematischer Funktionen, einschließlich trigonometrischer, logarithmischer und hyperbolischer Funktionen, bereits fest einprogrammiert.
Beispiel:
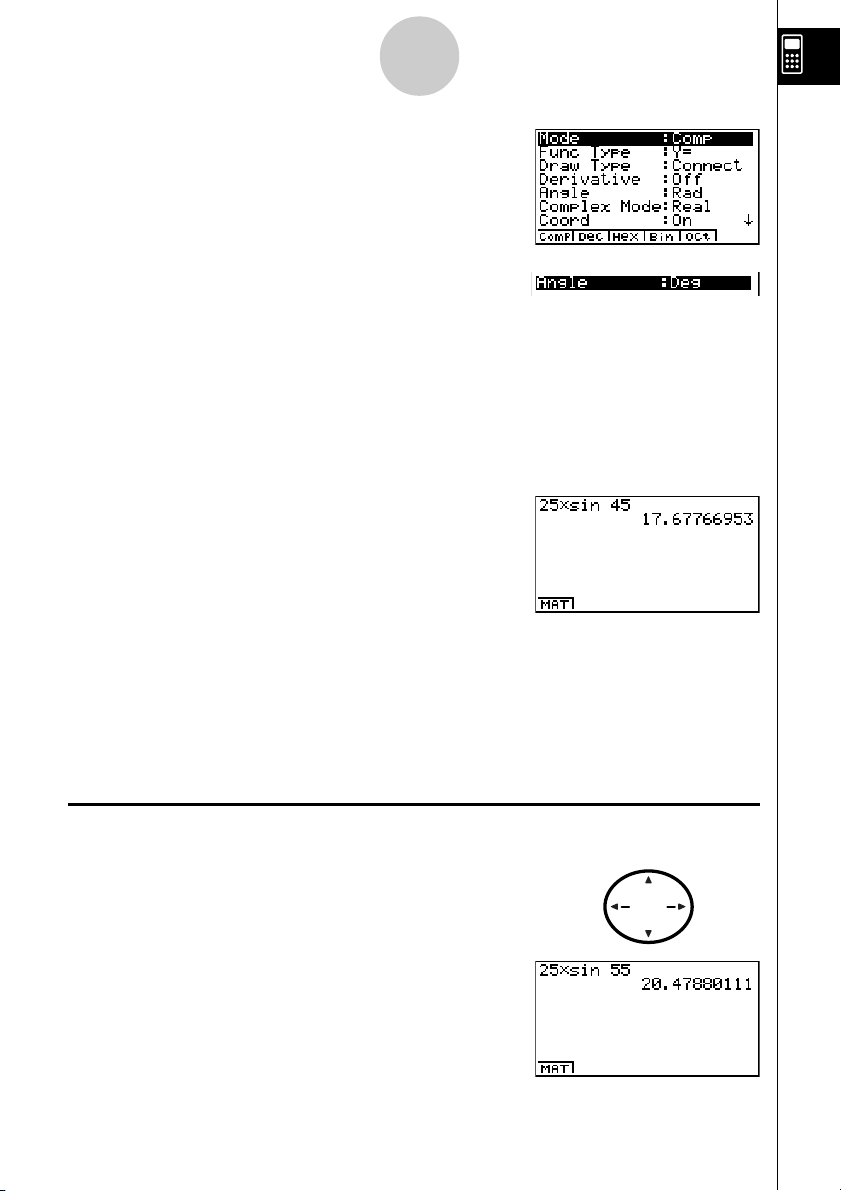
Wichtig!
Stellen Sie unbedingt “Deg” (Altgrad) als Winkelmodus ein, bevor Sie versuchen
dieses Beispiel nachzuvollziehen.
25 × sin 45˚
19990401
SET UP
1. Drücken Sie die Tasten u
Einstellanzeige (SET-UP-Menü) zu öffnen.
3
3
Schnellstart
, um die
2. Drücken Sie die Tasten
cccc
1(Deg), um Altgrad als Winkelmodus vor-
einzustellen.
3. Drücken Sie die
4. Drücken Sie die
5. Drücken Sie die Tasten
i-Taste, um das SET-UP-Menü zu schließen.
o-Taste, um alte Anzeigen im Display zu löschen.
cf*sefw.
WIEDERHOLUNGSFUNKTION
Bei der Wiederholungsfunktion können Sie einfach die d- oder e-Taste
drücken, um die zuletzt ausgeführte Berechnung wieder aufzurufen, so dass Sie Änderungen ausführen oder die Berechnung nochmals unverändert ausführen können.
Beispiel:
1. Drücken Sie die
zurückzuholen und anzuzeigen.
Die Berechnung im letzten Beispiel soll von (25 × sin 45°) auf (25 × sin 55°)
geändert werden.
d-Taste, um die letzte Berechnung
2. Drücken Sie die
Cursor (t) auf die 4 zu verschieben.
3. Drücken Sie die
4. Drücken Sie die f-Taste.
5. Drücken Sie die
erneut auszuführen.
d-Taste zweimal, um den
D-Taste, um die 4 zu löschen.
w-Taste, um die Berechnung
REPLAY
19990401
4
Schnellstart
BRUCHRECHNUNG
Sie können die $-Taste verwenden, um Bruchterme für eine Berechnung einzugeben. Das Symbol “ { ” wird als Trennzeichen verwendet, um die verschiedenen Teile
eines Bruchs (den ganzen Teil, den Zähler und den Nenner einer gemischten Zahl) zu
trennen.
Beispiel:
1. Drücken Sie die o-Taste.
2. Drücken Sie die Tasten
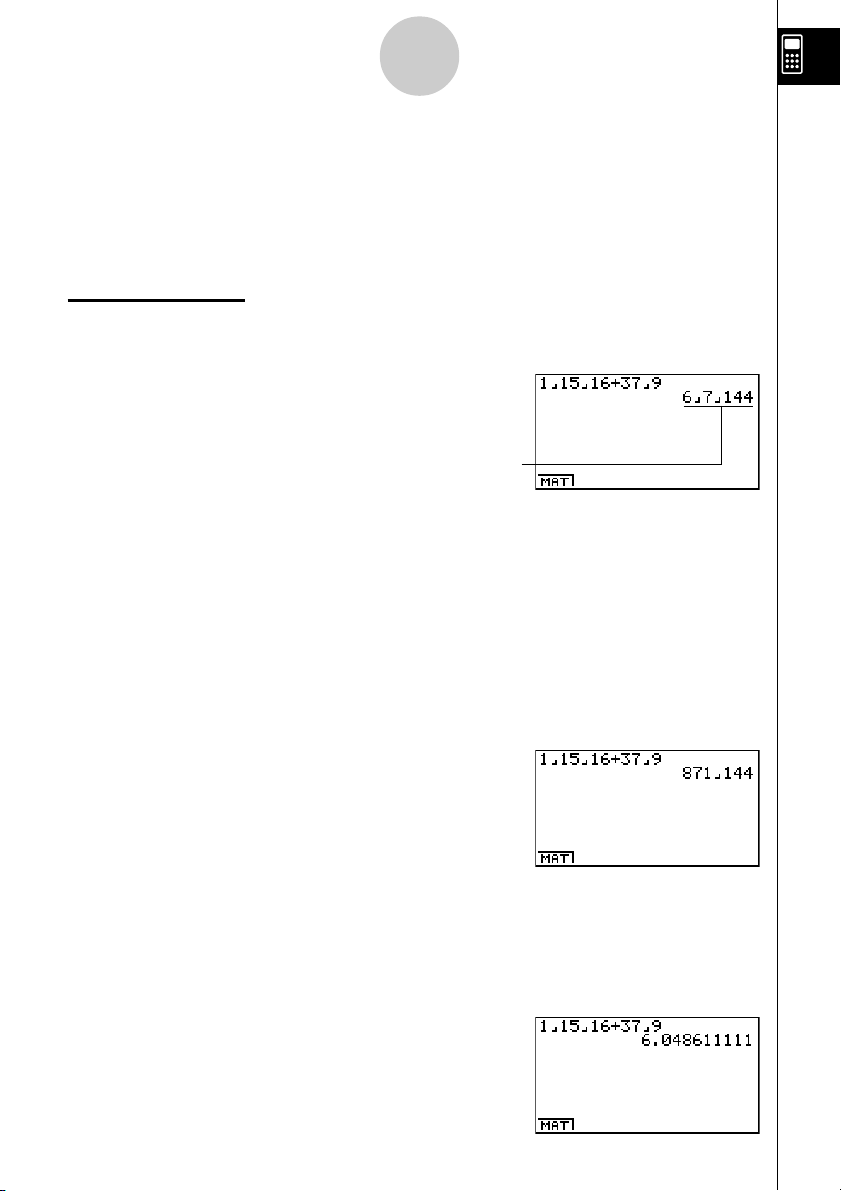
1 15/16 + 37/
9
b$bf$
bg+dh$
jw
.
Zeigt 6 7/
Umwandlung einer gemischten Zahl in einen
unechten Bruch
Während eine gemischte Zahl im Display angezeigt wird, drücken Sie die Tasten
!
Drücken Sie erneut die Tasten
Bruch zurück in eine gemischte Zahl zu verwandeln.
d/c
, um diese in einen unechten Bruch umzuwandeln.
$
!
d/c
, um den unechten
$
144
an.
Umwandlung eines Bruches in seine Dezimalzahlendarstellung (Dezimalbruch)
Während ein Bruch im Display angezeigt wird, drücken Sie die $-Taste, um diesen
in seine Dezimalzahlendarstellung umzuwandeln.
Drücken Sie erneut die
bruch zurück in einen gemeinen Bruch zu verwandeln.
$-Taste, um den Dezimal-
19990401

EXPONENTEN
5
Schnellstart
Beispiel:
1. Drücken Sie die o-Taste.
2. Drücken Sie die Tasten
3. Drücken Sie die
erscheint.
4. Drücken Sie die
5 um den Exponenten einer Potenz handelt.
5. Drücken Sie die
1250 × 2,06
5
bcfa*c.ag.
M-Taste, wodurch das Operationszeichen ^ im Display
f-Taste. Mit ^5 im Display wird angezeigt, dass es sich bei der
w-Taste.
19990401
6
Schnellstart
GRAFIKFUNKTIONEN
Die Grafikfunktionen dieses Rechners ermöglichen die grafische Darstellung von komplexen Grafiken entweder mit kartesischen Koordinaten (horizontale Achse:
Achse:
y) oder Polarkoordinaten (Winkel zur positiven x-Achse:
dinatenursprung:
Alle nachfolgenden Grafikbeispiele werden mit den nach der Zurückstellung wirksamen Einstellungen des Rechners ausgeführt.
r).
θ
; Abstand vom Koor-
x; vertikale
Beispiel
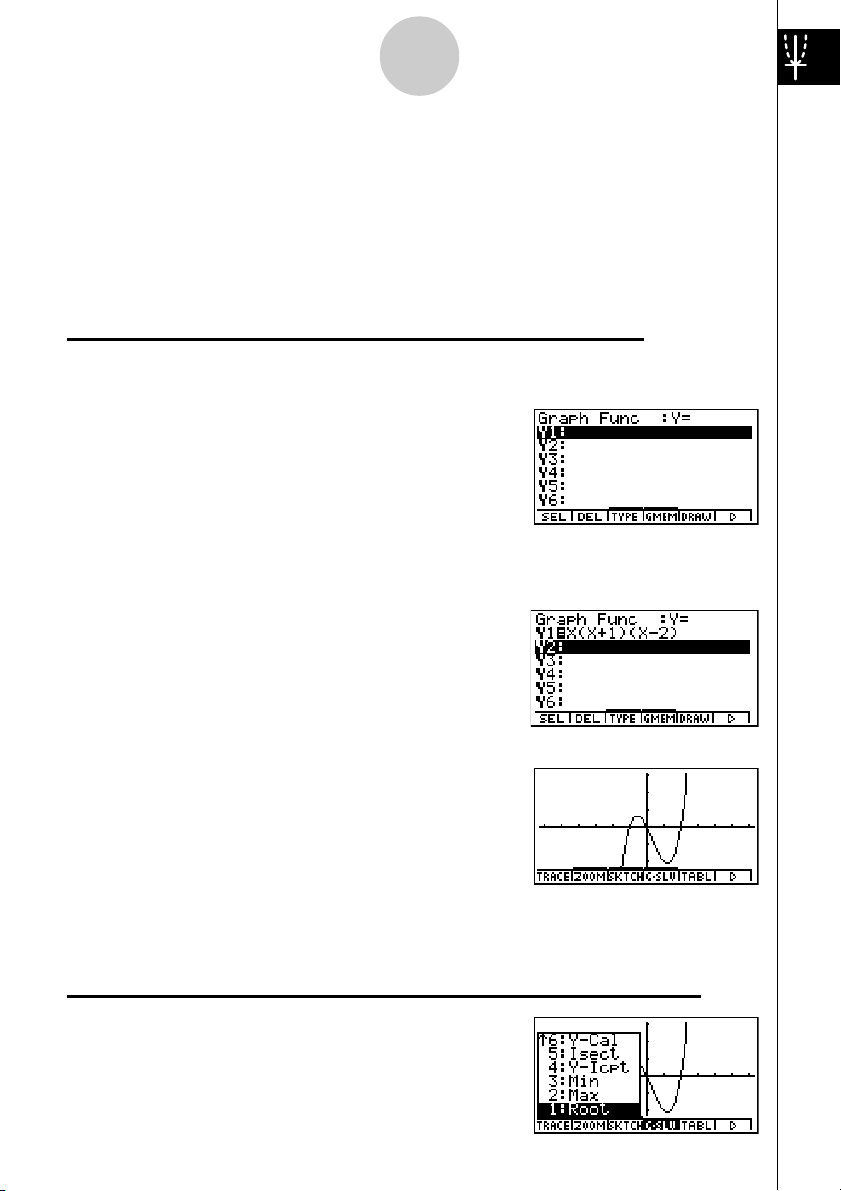
1. Drücken Sie die
2. Verwenden Sie die Cursortasten
3. Geben Sie den Formelterm ein.
1: Zu zeichnen ist der Graph der Funktion Y = X(X + 1)(X – 2)
m-Taste, um in das Hauptmenü zu gelangen.
(
d,e,f,c), um das GRPH
Icon zu markieren. Drücken Sie danach die
w-Taste, um das GRPH
•
TBL-Menü zu öffnen.
•
TBL-
v(v+b)
(v -c)w
4. Drücken Sie die 5 (DRAW)-Taste oder die
w-Taste, um den Graphen zu zeichnen.
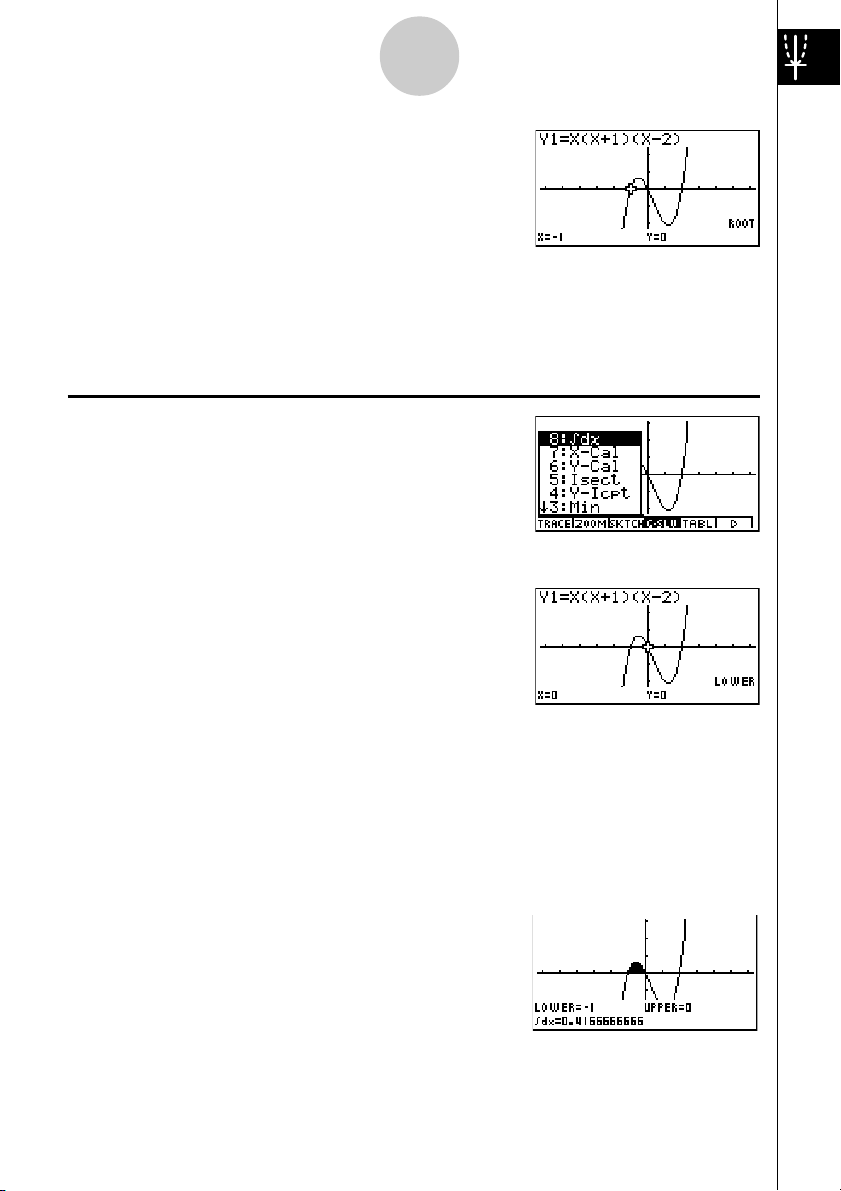
Beispiel
1. Drücken Sie die
tastenmenüs, um das zugehörige Untermenü zu
öffnen.
2: Zu bestimmen sind die Nullstellen der Funktion Y = X(X + 1)(X – 2)
4(G-SLV)-Taste des Funktions-
19990401
7
Schnellstart
2. Drücken Sie die b(Root)-Taste zum Anzeigen
der ersten Nullstelle. Drücken Sie die
zur Ermittlung weiterer Nullstellen.
Beispiel
1. Drücken Sie die Tasten i4(G-SLV)c.
2. Drücken Sie im Untermenü diei(∫dx)-Taste.
3: Zu bestimmen ist der Flächeninhalt zwischen der x-Achse und der Kurve
Y = X(X + 1)(X – 2) im Intervall von X = –1 bis X = 0.
e-Taste
3. Verwenden Sie die d-Taste, um den Cursor auf
den Anfangspunkt X = –1 zu verschieben. Drücken
Sie danach die
den Sie die
Endpunkt X = 0 zu verschieben. Drücken Sie danach die
tionsintervalls abzuschließen und das bestimmte Integral zu berechnen. Die betrachtete Fläche erscheint im Display schattiert, ebenso das Integrationsergebnis 0,4166666666.
Hinweis: Im Ergebnisdisplay unten links wird der Integrand nicht mit angezeigt.
w-Taste. Anschließend verwen-
e-Taste, um den Cursor auf den
w-Taste, um die Eingabe des Integra-
19990401

8
Schnellstart
DOPPELGRAFIK
Mit dieser Funktion können Sie das Display in zwei Fenster unterteilen und zwei
Grafiken gleichzeitig anzeigen.
Beispiel
1. Zur Einstellung der Doppelgrafik drücken Sie
2. Drücken Sie die
: Zeichnen Sie die beiden folgenden Kurven und bestimmen Sie deren Schnitt-
punkt.
Y1 = X(X + 1)(X – 2)
Y2 = X + 1,2
SET UP
u3
um im SET-UP-Menü in der Position Doppelanzeige (Dual Screen) “G+G” vorzugeben.
ccc2(G+G),
i-Taste und geben Sie
danach die beiden Funktionsterme ein.
v(v+b)
(v-c)w
v+b. cw
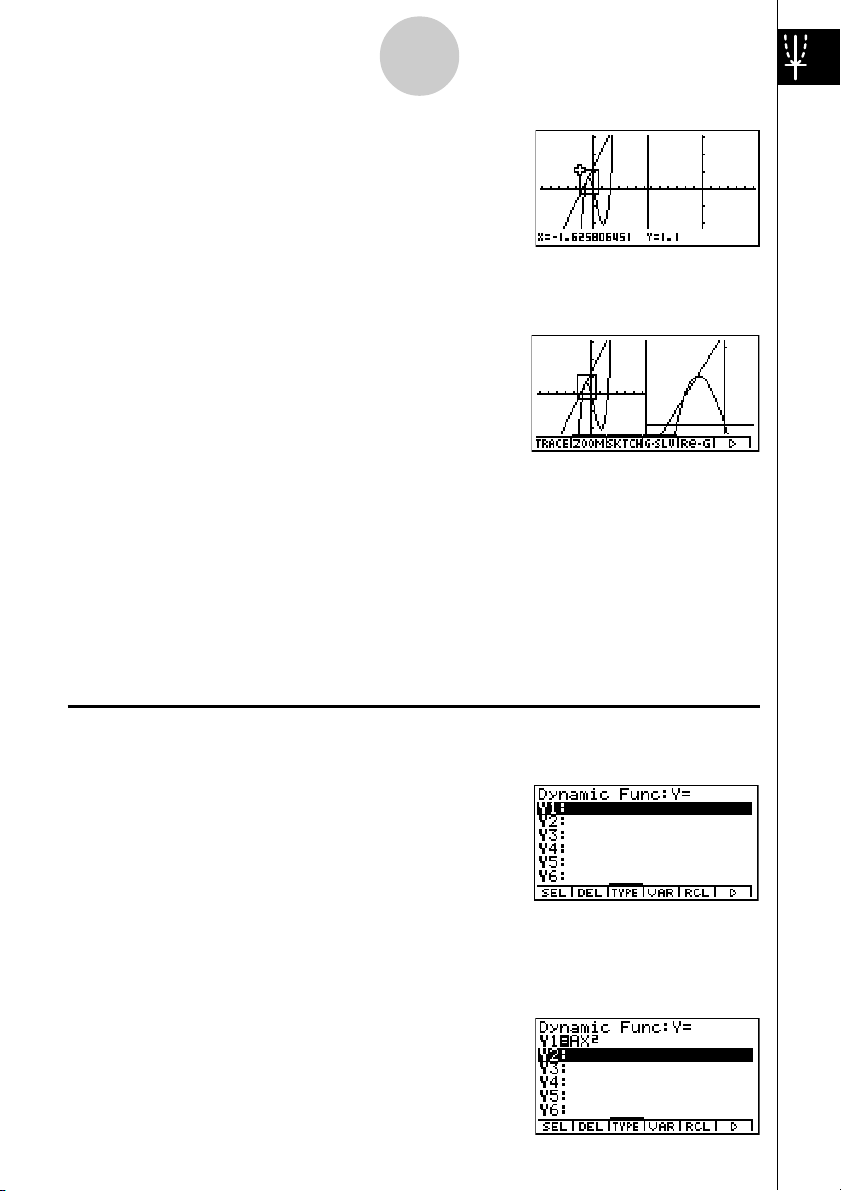
3. Drücken Sie die5(DRAW) -Taste oder die
w-Taste, um die Grafiken zu zeichnen.
BOXZOOM
Verwenden Sie die Boxzoomfunktion, um einen rechteckigen Fensterausschnitt
(Box) einer Grafik für die Vergrößerung festzulegen.
1. Drücken Sie die Tasten
2. Verwenden Sie im linken Hauptfenster die Cursor-
tasten (d,e,f,c), um den Cursor auf
eine Ecke des festzulegenden Rechtecks zu bringen,
und drücken Sie danach die w-Taste.
2(ZOOM) b(Box).
19990401
9
Schnellstart
3. Verwenden Sie die Cursortasten
(d,e,f,c),
verschieben. Wenn Sie dies ausführen, erscheint
im Display ein Rechteck (Box). Verschieben Sie
den Cursor so, dass die Box den Fensterausschnitt
einschließt, den Sie vergrößern möchten.
um
den Cursor erneut zu
4. Drücken Sie die
der vergrößerte Bereich im Nebenfenster (rechte
Seite der Doppelgrafik, inaktive Anzeige).
w-Taste. Dadurch erscheint
DYNAMISCHE GRAFIK
Die dynamische Grafik veranschaulicht als Animation, wie sich die Form einer Grafik
verändert, wenn in der zugehörigen Funktionsgleichung ein enthaltener Parameter
schrittweise verändert wird (Graphen einer Kurvenschar).
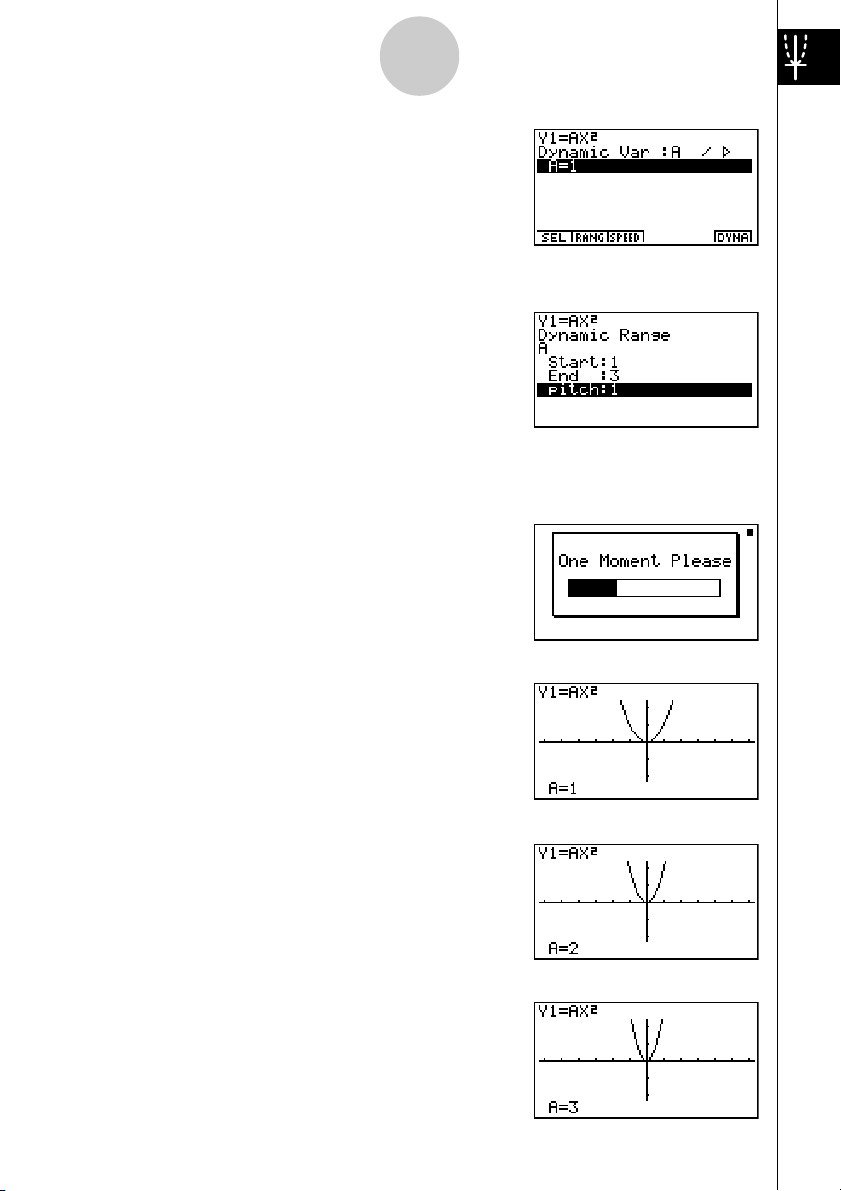
Beispiel:
1. Drücken Sie die m-Taste (Hauptmenü).
2. Verwenden Sie die Cursortasten
d,e,f,c), um das DYNA-Icon zu
(
markieren. Drücken Sie danach die
das DYNA-Menü zu öffnen.
Zu zeichnen sind die Graphen einer Kurvenschar, wenn sich der Scharparameter (Koeffizient A) in der folgenden Funktion in Einerschritten von 1 auf 3
ändert.
Y = AX
2
w-Taste, um
3. Geben Sie den Formelterm ein.
a
A
v
vxw
19990401
10
Schnellstart
4. Drücken Sie die Tasten 4(VAR) bw,
um dem Koeffizienten A den Anfangswert 1
zuzuordnen und A damit als veränderliche Dynamikvariable (Kurvenschar-Parameter) festzulegen.
5. Drücken Sie die Tasten
2(RANG)
bwdwbw, um Anfangs- und
Endwert des Intervalls der Dynamikvariablen A sowie
die Schrittweite für die Veränderung der Werte von A
festzulegen.
6. Drücken Sie die
7. Drücken Sie die
Zeichnen der dynamischen Grafik zu beginnen. Die
Grafiken werden 10 Mal gezeichnet (Animation).
i-Taste.
6(DYNA)-Taste, um mit dem
↓
↓↑
↓↑
19990401

11
Schnellstart
TABELLENFUNKTION
Die Tabellenfunktion ermöglicht das Generieren einer Wertetabelle von Funktionswerten, wenn dem Argument einer Funktion unterschiedliche Werte zugeordnet werden.
Beispiel:
Für die folgende Funktion ist eine Wertetabelle zu erzeugen.
Y = X (X + 1) (X – 2)
1. Drücken Sie die m-Taste (Hauptmenü).
2. Verwenden Sie die Cursortasten
d,e,f,c), um das GRPH
(
Icon auszuwählen. Drücken Sie danach die
w-Taste, um das gewünschte Menü zu öffnen.
3. Geben Sie den obigen Formelterm ein.
•
TBL-
v(v+b)
(v-c)w
4. Drücken Sie die Tasten 6(g)5(TABL),
um die Wertetabelle zu generieren.
Um alle leistungsstarken Eigenschaften dieses Rechners kennenzulernen, lesen Sie
bitte in den entsprechende Kapiteln weiter und probieren Sie alle Rechnerfunktionen
und Rechnerbefehle aus!
19990401

Vorsichtsmaßnahmen bei der
Benutzung des Rechners
•Ihr Rechner besteht aus elektronischen Präzisionsteilen und darf daher niemals zerlegt werden.
•Den Rechner nicht fallen lassen und keinen starken Stößen aussetzen.
•Den Rechner niemals hohen Temperaturen, hoher Luftfeuchtigkeit oder Staub aussetzen. Bei
niedrigen Temperaturen benötigt der Rechner mehr Zeit für die Anzeige der Ergebnisse. Das
Display kann sogar erlöschen. Sobald wieder normale Temperaturen erreicht sind, kehrt das
Display in den Normalzustand zurück.
•Das Display erscheint leer und die Tasten funktionieren nicht, während eine Berechnung ausgeführt wird und der Rechner beschäftigt ist. Daher sollten die Tasten normalerweise nur unter
Beobachtung des Displays verwendet werden, um richtigen Rechnerbetrieb sicherzustellen.
•Die Hauptbatterien sind alle zwei Jahre zu erneuern, auch wenn der Rechner längere Zeit nicht
verwendet wurde. Niemals verbrauchte Batterien im Batteriefach belassen. Sie könnten auslaufen und den Rechner beschädigen.
•Batterien außerhalb der Reichweite von Kindern halten. Falls eine Batterie verschluckt wurde,
ist sofort ärztliche Hilfe in Anspruch zu nehmen!
•Niemals Lösungsmittel wie Verdünner oder Benzin für das Reinigen des Rechners verwenden.
Den Rechner mit einem weichen, trockenen Tuch oder mit einem in neutraler Reinigungslösung
angefeuchteten und gut ausgewrungenen Tuch abwischen.
•Immer vorsichtig vorgehen, wenn Sie Staub vom Display abwischen, um ein Zerkratzen des
Displays zu vermeiden.
•Der Hersteller und die Zulieferanten können nicht verantwortlich gemacht werden für Schäden,
die auf Datenverluste und/oder den Verlust von Formeln aufgrund von Fehlbetrieb, Reparaturen
oder Austausch der Batterien zurückzuführen sind. Der Nutzer des Rechners sollte wichtige
Daten auf Papier festhalten, um solchen Datenverlusten vorzubeugen.
•Die Batterien, die Flüssigkristallanzeige oder andere Teile des Rechners niemals verbrennen.
•Wenn die Meldung “Low Main Batteries!” oder die Meldung “Low Backup Battery!” im Display
erscheinen, sind die Hauptbatterien bzw. die Sicherungsbatterie möglichst bald auszuwechseln.
•Unbedingt die Stromversorgung ausschalten, wenn die Batterien ausgewechselt werden.
•Wird der Rechner einer starken elektrostatischen Ladung ausgesetzt, kann der Speicherinhalt
beschädigt werden oder die Tasten funktionieren nicht mehr. In einem solchen Fall ist die Rückstelloperation durchzuführen, um fehlerhafte Speicherinhalte zu löschen und den normalen
Tastenbetrieb wieder herzustellen.
• Falls der Rechner aus irgend einem Grund blockiert ist und nicht mehr betätigt werden kann,
können Sie mit einem dünnen, spitzen Gegenstand den P-Knopf an der Rückseite des Rechners drücken. Beachten Sie jedoch, dass dadurch alle Daten im Speicher gelöscht werden.
•Starke Erschütterungen oder Stöße während der Programmausführung können das Programm
stoppen oder den Speicherinhalt des Rechners beschädigen.
•Die Verwendung des Rechners in der Nähe eines Fernsehers oder Radios kann zu Interferenzen bei Fernseh- oder Rundfunkempfang führen.
•Bevor Sie einen Fehlbetrieb des Rechners annehmen, ist diese Anleitung aufmerksam durchzulesen und zu überprüfen, ob das Problem nicht auf verbrauchte Batterien, Programmier- oder
Bedienungsfehler zurückzuführen ist.
19990401

Fertigen Sie schriftliche Aufzeichnungen aller wichtigen Daten an!
Niedrige Batteriespannung oder falsches Austauschen der Batterien können dazu führen, dass
die im Speicher dieses Rechners abgelegten Daten verfälscht oder vollständig gelöscht werden.
Die Speicherdaten können auch durch starke elektrostatische Ladungen oder durch starke Stöße
beeinträchtigt werden. Um solchen Datenverlusten vorzubeugen, sollten Sie immer schriftliche
Aufzeichnungen (Kopien) aller wichtigen Daten anfertigen.
CASIO Computer Co., Ltd. ist unter keinen Umständen für spezielle, zusätzliche oder indirekte
Schäden und Schadenersatzansprüche verantwortlich, die sich aus dem Kauf und der Benutzung
dieses Produkts ergeben. Außerdem lehnt CASIO Computer Co., Ltd. jegliche Haftung für
Ansprüche ab, die durch die Verwendung dieses Produkts durch eine dritte Person entstehen.
•Änderungen des Inhalts dieser Bedienungsanleitung ohne Vorankündigung vorbehalten.
•Reproduktion dieser Bedienungsanleitung, auch ausschnittsweise, ist ohne die schriftliche
Genehmigung des Herstellers nicht gestattet.
•Die in Kapitel 10 dieser Bedienungsanleitung beschriebenen Zusatzgeräte sind in bestimm-
ten Ländern nicht erhältlich. Wegen genauer Einzelheiten über die Verfügbarkeit in Ihrem
Land wenden Sie sich bitte an Ihren CASIO-Fachhändler oder an einen Kundendienst.
19990401

• ••••••••••••••••••
•••••••••••••••••••
•••••••••••••••••••
•••••••••••••••••••
•••••••••••••••••••
•••••••••••••••••••
ALGEBRA FX 2.0
•••••••••••••••••••
•••••••••••••••••••
•••••••••••••••••••
•••••••••••••••••••
•••••••••••••••••••
•••••••••••••••••••
•••••••••••••••••••
•••••••••••••••••••
•••••••••••••••••••
•••••••••••••••••••
• ••••••••••••••••••
•••••••••••••••••••
19990401

1
Inhalt
Inhalt
Kapitel 0 Einführung — Bitte dieses Kapitel zuerst durchlesen!
Kapitel 1 Grundlegende Operationen
1-1 Tastenanordnung.............................................................................. 1-1-1
1-2 Display.............................................................................................. 1-2-1
1-3 Eingabe und Editieren von Berechnungsformeln ............................. 1-3-1
1-4 Optionsmenü (OPTN)....................................................................... 1-4-1
1-5 Variablendatenmenü (VARS)............................................................ 1-5-1
1-6 Programmmenü (PRGM) ................................................................. 1-6-1
1-7 Zugeordnetes SET-UP-Menü (Voreinstellungen) ............................. 1-7-1
1-8 Falls Probleme auftreten…............................................................... 1-8-1
Kapitel 2 Manuelle Berechnungen im RUN • MAT - Menü
2-1 Grundrechenarten ............................................................................ 2-1-1
2-2 Spezielle Taschenrechnerfunktionen ................................................ 2-2-1
2-3 Festlegung des Winkelmodus und des Anzeigeformats (SET UP) .. 2-3-1
2-4 Funktionsberechnungen ................................................................... 2-4-1
2-5 Numerische Berechnungen .............................................................. 2-5-1
2-6 Rechnen mit komplexen Zahlen .......................................................2-6-1
2-7 Berechnungen mit Binär-, Oktal-, Dezimal- und
Hexadezimalzahlen .......................................................................... 2-7-1
2-8 Matrizenrechnung............................................................................. 2-8-1
Kapitel 3 Listenoperationen
3-1 Eingabe und Editieren einer Liste .................................................... 3-1-1
3-2 Operationen mit Listendaten ............................................................ 3-2-1
3-3 Arithmetische Operationen mit Listen (Listenarithmetik) .................. 3-3-1
3-4 Umschaltung zwischen Listendateien .............................................. 3-4-1
Kapitel 4 Lösung von Gleichungen im EQUA-Menü
4-1 Eindeutig lösbare lineare Gleichungssysteme ................................. 4-1-1
4-2 Polynomgleichungen höherer Ordnung ............................................ 4-2-1
4-3 Allgemeine Nullstellengleichungen ................................................... 4-3-1
4-4 Was bei Auftreten eines Fehlers zu tun ist ....................................... 4-4-1
19990401

2
Inhalt
Kapitel 5 Grafische Darstellungen
5-1 Grafikbeispiele.................................................................................. 5-1-1
5-2 Voreinstellungen verschiedenster Art für eine optimale
Grafikanzeige ................................................................................... 5-2-1
5-3 Zeichnen einer Grafik ....................................................................... 5-3-1
5-4 Speicherung einer Grafik im Bildspeicher ........................................ 5-4-1
5-5 Zeichnen von zwei Grafiken im gleichen Display ............................. 5-5-1
5-6 Manuelle grafische Darstellung ........................................................ 5-6-1
5-7 Verwendung von Wertetabellen ....................................................... 5-7-1
5-8 Dynamische Grafik (Grafikanimation einer Kurvenschar) ................ 5-8-1
5-9 Grafische Darstellung von Rekursionsformeln (Zahlenfolgen) ......... 5-9-1
5-10 Vervollständigung einer Grafik durch weitere Grafikelemente ....... 5-10-1
5-11 Funktionsanalyse (Kurvendiskussion) ............................................ 5-11-1
Kapitel 6 Statistische Grafiken und Berechnungen
6-1 Vor dem Ausführen statistischer Berechnungen .............................. 6-1-1
6-2 Berechnungen und grafische Darstellungen mit einer
eindimensionalen Stichprobe ........................................................... 6-2-1
6-3 Berechnungen und grafische Darstellungen mit einer
zweidimensionalen Stichprobe .........................................................6-3-1
6-4 Ausführung statistischer Berechnungen und
Ermittlung von Wahrscheinlichkeiten (N(0,1)-Verteilung) ................. 6-4-1
Kapitel 7 Computer-Algebra-System- und Tutorium-Menü
7-1 Nutzung des CAS(Computer-Algebra-System)-Menüs .................... 7-1-1
7-2 Algebra-Menü ................................................................................... 7-2-1
7-3 Tutorium-Menü ................................................................................. 7-3-1
7-4 Hinweise zum Algebra-System......................................................... 7-4-1
Kapitel 8 Programmierung
8-1 Grundlegende Programmierschritte ................................................. 8-1-1
8-2 Programmmenü-Funktionstasten ..................................................... 8-2-1
8-3 Editieren von Programminhalten ...................................................... 8-3-1
8-4 Programmverwaltung ....................................................................... 8-4-1
8-5 Befehlsreferenz ................................................................................ 8-5-1
8-6 Verwendung von Rechnerfunktionen in Programmen ...................... 8-6-1
8-7 Programmmenü-Befehlsliste ............................................................ 8-7-1
8-8 Programmbibliothek ......................................................................... 8-8-1
19990401

3
Inhalt
Kapitel 9 Systemeinstellungsmenü (SYSTEM-Menü)
9-1 Verwendung des Systemeinstellungsmenüs .................................. 9-1-1
9-2 Speicheroperationen (Arbeitsspeicher) .......................................... 9-2-1
9-3 Systemeinstellungen ...................................................................... 9-3-1
9-4 Zurückstellung ................................................................................ 9-4-1
9-5 Sperren des Tutoriums ................................................................... 9-5-1
Kapitel 10 Datenübertragung (LINK-Menü)
10-1 Verbindung von zwei CASIO-Rechnern ....................................... 10-1-1
10-2 Verbindung des Rechners mit einem CASIO-Etikettendrucker .... 10-2-1
10-3 Verbindung des Rechners mit einem Personal Computer ........... 10-3-1
10-4 Ausführung des Datentransfers (LINK-Menü) .............................. 10-4-1
10-5 Hinweise zur Datenübertragung ...................................................10-5-1
10-6 Senden eines aktuellen Bildschirmdisplays (Screen-Shot) .......... 10-6-1
10-7 Add-Ins (Updates und Software-Erweiterungen) ......................... 10-7-1
10-8 MEMORY-Menü (Archivspeicher) ................................................ 10-8-1
Anhang
α
-1 Tabelle der Fehlermeldungen ........................................................α-1-1
α
-2 Für die Eingabe zugelassene Zahlenbereiche ..............................α-2-1
α
-3 Technische Daten..........................................................................α-3-1
α
-4 Allgemeiner Index, Befehlsindex ...................................................α-4-1
α
-5 Tastenindex ....................................................................................α-5-1
α
-6 P-Knopf (falls der Rechner hängen bleibt) ....................................α-6-1
α
-7 Stromversorgung ...........................................................................α-7-1
19990401

Einführung
— Bitte dieses Kapitel
zuerst durchlesen!
Über diese Bedienungsanleitung
u! x( )
Die obige Tastenfolge besagt, dass Sie die !-Taste gefolgt von der x-Taste drücken
sollen. Dadurch wird das -Symbol eingegeben. Auf diese Weise werden alle Tasten dargestellt, die hintereinander gedrückt werden müssen. Die Tastenbezeichnungen sind
aufgeführt, gefolgt von dem tatsächlich eingegebenen Zeichen oder Befehl in Klammern.
0
uFunktionstasten und Menüs
•Viele der in diesem Rechner vorhandenen Operationen können durch Drücken der
Funktionstasten 1 bis 6 ausgeführt werden. Die jeder Funktionstaste zugeordneten
Operationen oder Befehle ändern sich in Abhängigkeit von dem Menü, in dem der
Rechner momentan arbeitet. Dabei werden die aktuell zugeordneten Operationen durch
die Funktionstastenmenüs angezeigt, die im unteren Teil des Displays erscheinen.
•In dieser Bedienungsanleitung ist die aktuell einer Funktionstaste zugeordnete Operation
nach der Tastenbezeichnung in Klammern aufgeführt. So wird zum Beispiel mit 1
(Comp) angezeigt, dass durch das Drücken der 1-Taste die Operation {Comp} gewählt
wird, die auch im Funktionstastenmenü angezeigt ist.
•Wenn ein symbolischer Pfeil (g) im Funktionstastenmenü für die Taste 6 angezeigt
wird, dann bedeutet dies, dass durch das Drücken der 6-Taste das nächste oder
vorhergehende Fenster der Menüoptionen angezeigt wird.
uu
uMenüsymbole
uu
•Die Menüsymbole in dieser Bedienungsanleitung schließen die erforderlichen Tastenbetätigungen ein, um das erläuterte Menü zu öffnen und damit anzuzeigen. Die Tastenbetätigung z.B. für ein Untermenü, das durch Drücken von K gefolgt von {MAT} geöffnet wird,
würde dann wie folgt dargestellt werden: [OPTN]-[MAT].
•Auf die 6(g) -Tastenbetätigungen für das Umschalten auf ein anderes Menüfenster wird
in den Menüsymbol-Tastenbetätigungen nicht extra hingewiesen.
19990401
0-1-1
5-1-1
Grafibeispiele
5-1-2
Grafibeispiele
Einstellung
1. Rufen Sie den GRPH • TBL-Modus aus dem Hauptmenü auf.
Ausführeng
2.Geben Sie die Funktion ein, die Sie grafisch darstellen mhten.
Hier mhten wir das Betrachtungsfenster (V-Window) verwenden, um den Bereich und
die Parameter der Grafik zu spezifizieren. Siehe 5-2-1.
3.eichnen Sie die Grafik.
k Zeichnen einer einfachen Grafik (1)
Beschreibung
Um eine Grafik zu zeichnen, geben Sie einfach die zutreffende Funktion ein.
Procedure
1 m GRPH-TBL
2 dvxw
35(DRAW) (oder w)
Beispiel Die Funktion y = 3x2 ist grafisch darzustellen:
Ergebnisanzeige
19990401 19990401
5-1 Grafikbeispiele
5-1-1
Grafibeispiele
5-1-2
Grafibeispiele
Einstellung
1.Rufen Sie den GRPH • TBL-Modus aus dem Hauptmenü auf.
Ausführeng
2.Geben Sie die Funktion ein, die Sie grafisch darstellen mhten.
Hier mhten wir das Betrachtungsfenster (V-Window) verwenden, um den Bereich und
die Parameter der Grafik zu spezifizieren. Siehe 5-2-1.
3.eichnen Sie die Grafik.
k Zeichnen einer einfachen Grafik (1)
Beschreibung
Um eine Grafik zu zeichnen, geben Sie einfach die zutreffende Funktion ein.
Procedure
1 m GRPH-TBL
2 dvxw
35(DRAW) (oder w)
Beispiel Die Funktion y = 3x2 ist grafisch darzustellen:
Ergebnisanzeige
19990401 19990401
5-1 Grafikbeispiele
Einführung
u Grafiken
In der Regel sind Grafikoperationen und -befehle auf
gegenüberliegenden Seiten dargestellt, wobei sich die
eigentlichen Grafikbeispiele auf der rechten Seite
befinden. Sie können die gleiche Grafik mit Ihrem
Rechner erzeugen, indem Sie die unter "Vorgang"
dargestellten Schritte zum Erhalt der Grafik ausführen.
Informieren Sie sich auf der richtigen Seite (Inhaltsoder Stichwortverzeichnis nutzen) über den Typ der
gewünschten Grafik nach suchen Sie danach die für
diese Grafik angegebene Seite auf. Die Schritte unter
“Vorgang” verwenden immer die dem Rechner
zugrunde liegenden RESET-Einstellungen.
Die Schrittfolgenummern in den Text-Abschnitten “Einstellung” und “Ausführung” auf der jeweils
linken Seite entsprechen den Schrittfolgenummern unter “Vorgang” auf der rechten Seite.
Beispiel:
Linke Seite Rechte Seite
3. Zeichnen Sie die Grafik. 3 5(DRAW)(oder w)
uu
u Befehlsliste
uu
Die Programmmenü-Befehlsliste (Seite 8-7) enthält ein grafisches Flussdiagramm der
verschiedenen Funktionstastenmenüs, die anzeigen, wie Sie in das Menü der erforderlichen Befehle gelangen können.
Beispiel: Die folgende Tastenbetätigung zeigt Xfct an: [VARS]-[FACT]-[Xfct]
Ergänzende Informationen sind im unteren Teil einer Seite in einem mit dem Symbol
Das Symbol * bezeichnet einen Hinweis zu einem Term oder einer Formel, die auf
Das Symbol # bezeichnet einen Hinweis, der allgemeine Informationen zu dem
uu
u Seiteninhalte
uu
Eine dreiteilige Seitennummer befindet sich jeweils
oben in der Mitte auf jeder Seite. Die Seitennummer
“5-1-2” bezeichnet zum Beispiel das Kapitel 5,
Abschnitt 1, Seite 2.
uu
u Ergänzende Informationen
uu
“ (Hinweise)” markierten Rahmen aufgeführt.
der gleichen Seite wie der Hinweis stehen.
Thema enthält, das im gleichen Abschnitt wie der Hinweis dargestellt wird.
19990401

Kapitel
Grundlegende
Operationen
1-1 Tastenanordnung
1-2 Display
1-3 Eingabe und Editieren von Berechnungsformeln
1-4 Optionsmenü (OPTN)
1-5 Variablendatenmenü (VARS)
1-6 Programmmenü (PRGM)
1-7 Zugeordnetes SET-UP-Menü (Voreinstellungen)
1-8 Falls Probleme auftreten …
1
19981001
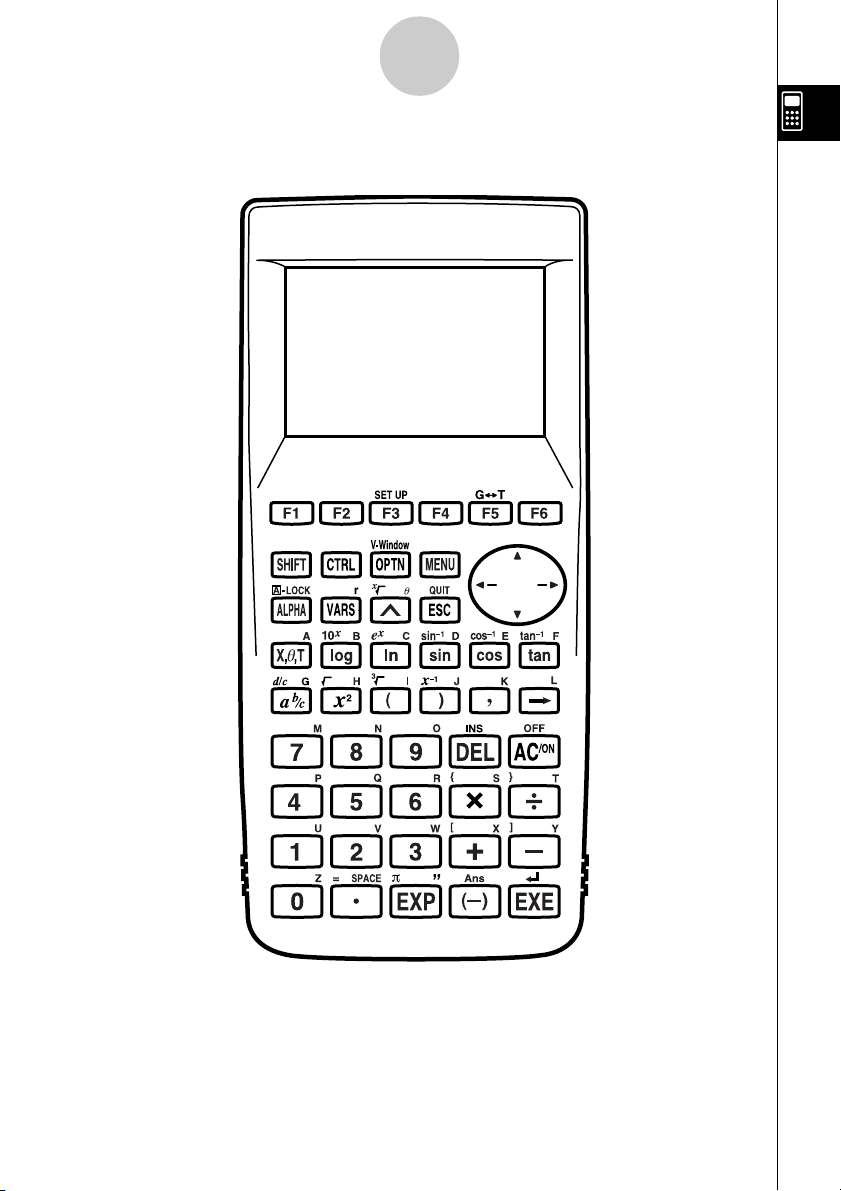
1-1 Tastenanordnung
1-1-1
Tastenanordnung
COPY
PASTE CAT/CAL
PRGM
List
Mat
i
H-COPY
REPLAY
19990401
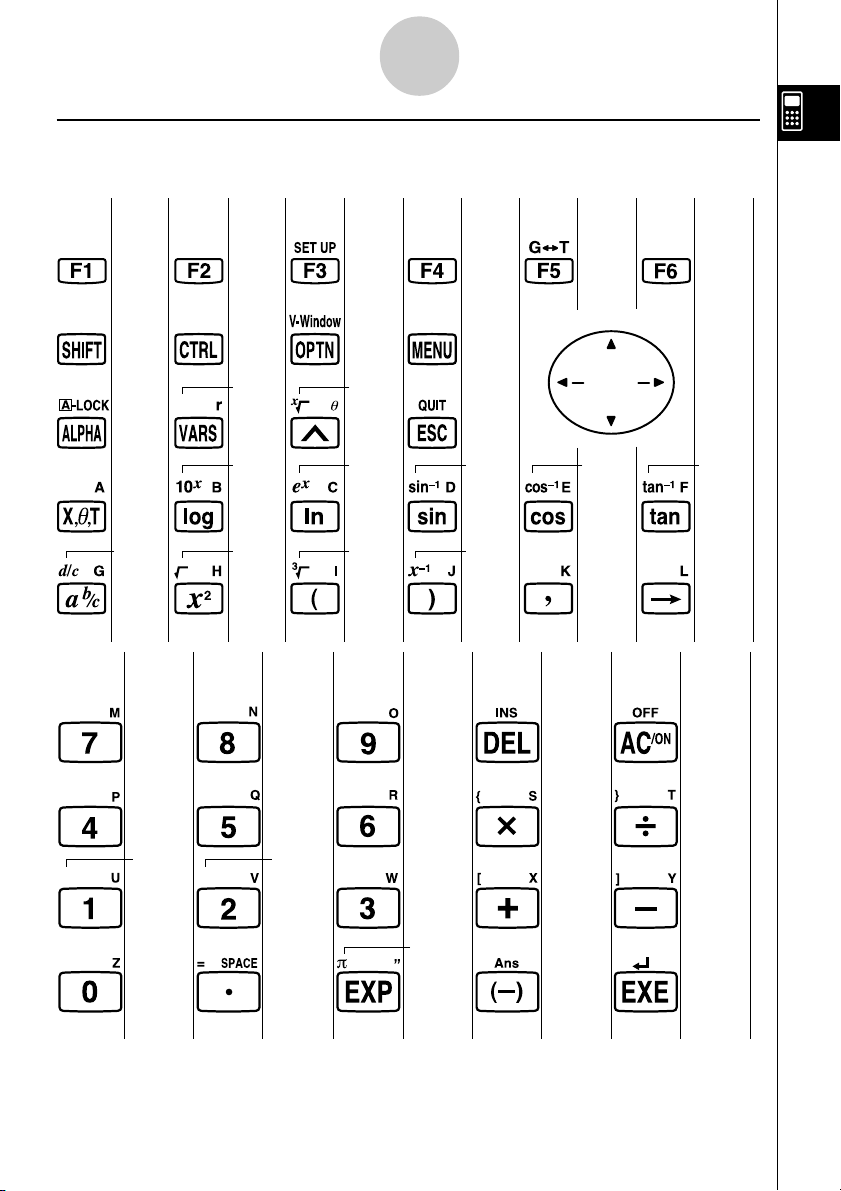
kk
k Tastentabelle
kk
Seite Seite Seite Seite Seite Seite
1-1-2
Tastenanordnung
COPY
1-3-5
1-3-5 1-7-1
PASTE
5-2-1
1-1-3 1-3-4 1-4-1 1-2-1
1-6-1 2-4-4
PRGM
1-1-3 1-5-1 2-4-4
2-4-4 2-4-4
2-4-4 2-4-4
2-4-10
2-4-10
2-4-6 2-4-6
2-4-6
2-4-6
2-1-1
Seite Seite Seite Seite Seite
CAT/CAL
1-3-5 5-3-4 10-6-1
2-4-3 2-4-3
2-4-3 2-4-3
2-1-1
H-COPY
REPLAY
2-4-3
2-4-3
2-2-1
1-3-3
1-3-1
2-1-1
2-1-1
List
i
3-1-2 2-8-11
Mat
2-4-3
19990401
2-1-1
2-2-5
2-1-12-1-1
2-1-1

1-1-3
Tastenanordnung
kk
k Tastenmarkierungen (Mehrfachbelegung einer Taste)
kk
Viele der Tasten des Rechners werden für die Ausführung von mehr als einer Funktion
verwendet. Die auf der Tastatur markierten Funktionen weisen eine Farbcodierung auf, um
Ihnen beim schnellen und einfachen Auffinden der benötigten Funktion zu helfen.
Funktion Tastenbetätigung
1 log l
2 10
x
!l
3 B al
Nachfolgend ist die für die Tastenmarkierungen verwendete Farbcodierung beschrieben.
Farbe Tastenbetätigung
Orange
Rot
# Buchstaben-Feststeller
Wenn Sie normalerweise die a-Taste und
danach eine andere Taste drücken, um ein
alphabetisches Zeichen einzugeben, wird die
Tastatur sofort wieder auf die primären
Funktionen zurückgeschaltet.
Drücken Sie die !-Taste und danach die gewünschte Taste,
um die orange markierte Funktion auszuführen.
Drücken Sie die a-Taste und danach die gewünschte Taste,
um die rot markierte Funktion auszuführen.
19990401
Falls Sie die !-Taste gefolgt von der
a-Taste drücken, wird die Tastatur auf die
Eingabe der alphabetischen Zeichen
solange fest eingestellt, bis Sie die a-
Taste erneut drücken.

1-2-1
Display
1-2 Display
k Wahl eines Icons
Dieser Abschnitt beschreibt, wie Sie ein Icon im Hauptmenü auswählen können, um das
gewünschte Menü aufzurufen.
uu
uWählen eines Icons
uu
1. Drücken Sie die m-Taste, um das Hauptmenü anzuzeigen.
2. Verwenden Sie die Cursortasten (d, e, f, c), um das gewünschte Icon zu
markieren.
Gegenwärtig gewähltes Icon
3. Drücken Sie die w-Taste, um den Eingangsbildschirm des ausgewählten Icons anzuzeigen. Hier wollen wir das STAT-Menü öffnen und erkennen als Eingangsdisplay
den Statistik-Listeneditor.
•Sie können auch ein Menü öffnen, ohne ein Icon im Hauptmenü zu markieren, indem
Sie die Nummer oder den Buchstaben eingeben, die/der in der rechten unteren Ecke
des Icons angegeben ist.
19990401
1-2-2
Display
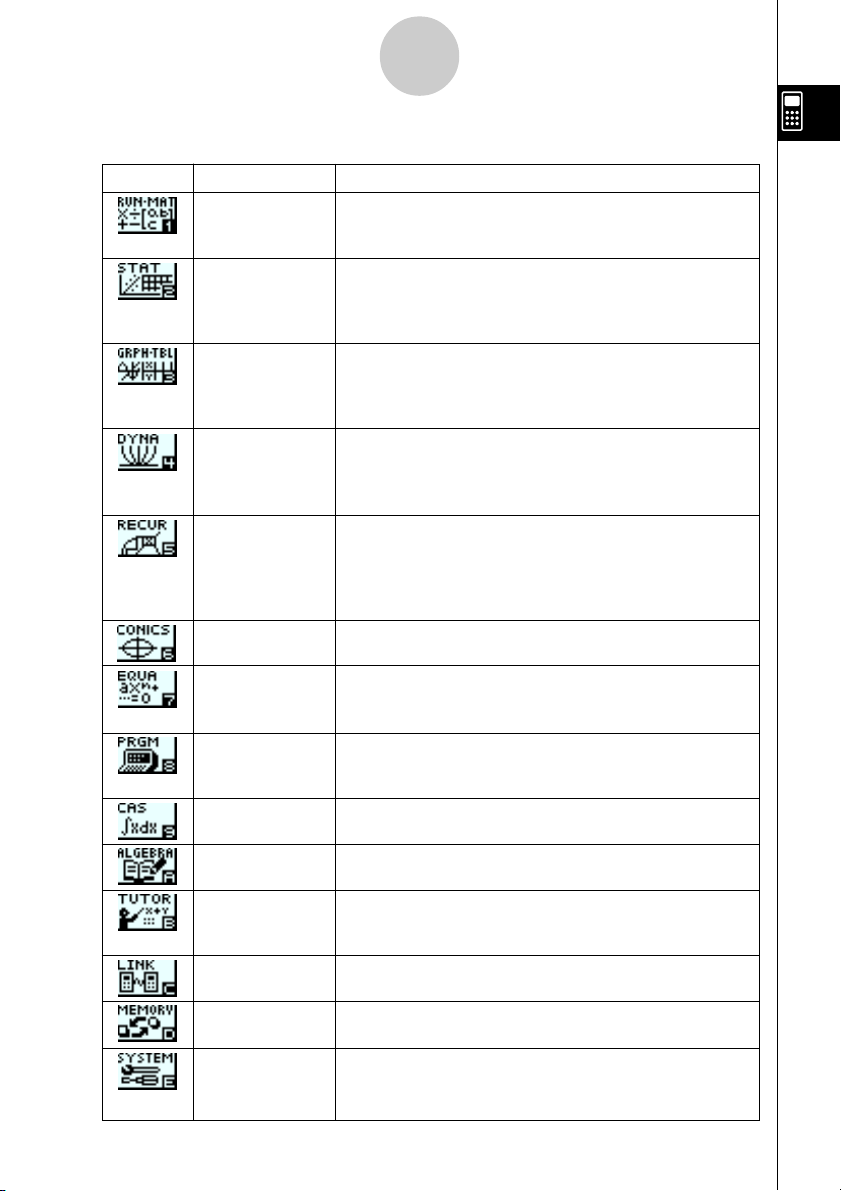
Nachfolgend sind die Bedeutungen der einzelnen Icons (Menüs) erläutert.
Icon
Menübezeichnung
•
RUN
MATrix Verwenden Sie dieses Menü für arithmetische und Funktions-
Bedeutung
(Matrizenrechnung) berechnungen, für Matrizenrechnung sowie für Berechnungen
mit Binär-, Oktal-, Dezimal- und Hexadezimal-Werten.
STATistics Verwenden Sie dieses Menü, um statistische Berechnungen
(Statistik) für eindimensionle Stichproben (z.B. Standardabweichung)
oder zweidimesionale Stichproben (Regression) auszuführen,
Daten zu analysieren und statistische Grafiken zu zeichnen.
GRaPH-TaBLe Verwenden Sie dieses Menü, um Funktionen zu speichern,
(Grafik und Tabelle) eine numerische Wertetabelle verschiedener Funktionswerte
zu erstellen, wenn sich das Argument einer Funktion ändert,
und um Grafiken zu zeichnen.
DYNAmic graph Verwenden Sie dieses Menü, um Funktionen mit einem Para-
(Dynamische Grafik) meter abzuspeichern und mehrere Varianten des Graphen zu
zeichnen, indem die dem Parameter in der Funktion zugeordneten Werte geändert werden (Kurvenschar, Animation).
RECURsion Verwenden Sie dieses Menü, um Rekursionsformeln für
(Rekursion) Zahlenfolgen abzuspeichern, um numerische Tabellen unter-
schiedlicher Werte zu erstellen, wenn sich die dem Folgenindex in einer Folge zugeordneten Werte ändern, und um
Grafiken zu zeichnen (Folgen und Partialsummenfolgen).
CONICS Verwenden Sie dieses Menü für das Zeichen von Grafiken
(Kurven 2. Ordn.) impliziter Funktionen 2. Ordnung (Ellipsen u. a.).
EQUAtion Verwenden Sie dieses Menü, um lineare Gleichungssysteme
(Gleichungslöser) mit 2 bis 30 Unbekannten sowie Polynomgleichungen höherer
Ordnung (bis 30. Grades) und allgem. Gleichungen zu lösen.
PRoGraM Verwenden Sie dieses Menü, um Programme im Programm-
(Programme) bereich zu speichern und um Programme zu editieren und
zu starten.
Computer Algebra
Verwenden Sie dieses Menü für die Ausführung symbolischer
System Rechnungen und algebraischer Umformungen.
ALGEBRA Verwenden Sie dieses Menü für die schrittweise Umformung
(CAS im Detail) und Auflösung numerischer oder symbolischer Formeln.
TUTORial Verwenden Sie dieses Menü, um Aufgabenvarianten und
(CAS-Tutorium) deren Lösungsmodus festzulegen und um Gleichungen
interaktiv zu lösen.
LINK Verwenden Sie dieses Menü, um Speicherinhalte oder
(Übertragung) Sicherungsdaten zu einem anderem Rechner zu übertragen.
MEMORY Verwenden Sie dieses Menü für die Verwaltung der im
(Speicher) Speicher abgelegten Daten.
SYSTEM Verwenden Sie dieses Menü, um alle Speicher neu zu
initialisieren, den Kontrast einzustellen und um andere
Systemeinstellungen auszuführen.
19990401

1-2-3
Display
kk
k Über das Funktionstastenmenü (Untermenüs)
kk
Verwenden Sie die Funktionstasten (1 bis 6), um auf die Menüs und Befehle in der
Menüleiste im unteren Teil der Displayanzeige zuzugreifen. Anhand des Aussehens der
Tastensymbole können Sie entscheiden, ob es sich bei einer der Menüleiste zugeordneten
Funktionstaste um ein Untermenü oder um einen Sofort-Befehl handelt.
• Sofort-Befehl (durch eine dünne Überstreichung markiert, Beispiel: )
Drücken Sie die dem Tastensymbol zugeordnete Funktionstaste, die hier einem Sofort-
Befehl entspricht, um diesen Befehl unmittelbar auszuführen.
• Untermenü (durch eine dicke Überstreichung markiert, Beispiel: )
Drücken Sie die dem Tastensymbol zugeordnete Funktionstaste, die einem Untermenü ent-
spricht, um das Untermenü zu öffnen.
Sie können eine der beiden folgenden Methoden verwen-
den, um einen Befehl aus einem Untermenü auszuwählen.
•Drücken Sie die links von dem Befehl im Untermenü angegebene Taste (Zahl/Buchstabe).
•Verwenden Sie die f- und c-Cursortasten, um den gewünschten Befehl zu markieren.
Drücken Sie danach die w-Taste.
Das Symbol ' rechts von einem Befehl gibt an, dass durch das Ausführen des Befehls ein
weiteres Untermenü geöffnet wird.
Um das Untermenü zu schließen, ohne einen Befehl einzugeben, drücken Sie die i-Taste.
kk
k Über die Displayanzeigen
kk
Dieser Rechner verwendet zwei Arten von Displayanzeigen: eine Textanzeige und eine
Grafikanzeige. Die Textanzeige kann 21 Spalten und acht Zeilen von Zeichen anzeigen,
wobei die unterste Zeile für das Funktionstastenmenü verwendet wird. Die Grafikanzeige
verwendet einen Bereich von 127 (B) × 63 (H) Punkten.
Te xtanzeige Grafikanzeige
Die Inhalte jeder Art von Anzeige werden in unabhängigen Speicherbereichen abgelegt.
Drücken Sie die Tasten u5(G↔T), um zwischen der Grafikanzeige und der Textanzeige
umzuschalten.
# Das Symbol ↑ in der linken oberen Ecke des
Untermenüs zeigt an, dass weitere Befehle in
dem angezeigten Untermenü vorhanden sind.
Ve rwenden Sie die Cursortasten, um den
Menüinhalt nach unten zu rollen und die
darüber angeordneten Befehle anzuzeigen.
19990401

1-2-4
Display
kk
k Normal-Anzeige
kk
Der Rechner zeigt die Zahlenwerte normalerweise mit bis zu 10 Ziffern an. Zahlen, die diese
Grenze überschreiten, werden automatisch im Exponentialformat angezeigt.
u Interpretation des Exponentialformats
1.2E+12 bedeutet, dass das Ergebnis gleichwertig zu 1,2 × 1012 ist. D. h., Sie müssen den
Dezimalpunkt in 1,2 um zwölf Stellen nach rechts verschieben, da der Exponent positiv ist.
Dies ergibt den Wert 1.200.000.000.000.
1.2E–03 bedeutet, dass das Ergebnis gleichwertig zu 1,2 × 10–3 ist. D. h., Sie müssen den
Dezimalpunkt in 1,2 um drei Stellen nach links verschieben, da der Exponent negativ ist.
Dies ergibt den Wert 0,0012.
Sie können innerhalb der Normal-Anzeige zwischen zwei unterschiedlichen Zahlenbereichen
für die automatische Umwandlung in das Exponentialformat wählen.
Norm 1 .................. für |x| < 10–2 (0,01) oder |x| > 10
Norm 2 .................. für |x| < 10–9 (0,000000001) oder |x| > 10
10
(Normal-Anzeige 1)
10
(Normal-Anzeige 2)
Alle in dieser Anleitung aufgeführten Beispiele zeigen die Rechenergebnisse unter der
Voreinstellung (im SET-UP-Menü) auf "Norm 1" an.
Zu Einzelheiten über das Umschalten zwischen Norm 1 und Norm 2 siehe Seite 2-3-2.
19990401

1-2-5
Display
kk
k Spezielle Anzeigeformate
kk
Dieser Rechner verwendet spezielle Anzeigeformate für die Anzeige von gemeinen Brüchen,
Hexadezimalzahlen und Sexagesimalzahlen (Grad/Minuten/Sekunden).
u Brüche (gemischte Zahlen)
................. Bedeutet: 456
u Hexadezimalzahlen
................. Bedeutet: ABCDEF12(16), das ist
gleichwertig mit –1412567278(10)
u Sexagesimalzahlen (Grad/Minuten/Sekunden)
................. Bedeutet: 12° 34’ 56,78”
• Zusätzlich zu den obigen speziellen Anzeigeformaten verwendet der Rechner auch
Indikatoren und Symbole, die dann in den entsprechenden Abschnitten dieser Anleitung
beschrieben sind.
12
––––
23
kk
k Rechnungsausführungsindikator
kk
Immer wenn der Rechner beschäftigt ist, um eine Grafik zu zeichnen oder eine lange,
komplizierte Rechnung bzw. ein Programm auszuführen, blinkt ein schwarzes Kästchen “k”
in der rechten oberen Ecke des Displays. Dieses schwarze Kästchen symbolisiert, dass der
Rechner eine interne Operation ausführt und beschäftigt ist.
19990401

Eingabe und Editieren von Berechnungsformeln
1-3-1
1-3 Eingabe/Editieren von Berechnungsformeln
kk
k Eingabe von Berechnungsformeln
kk
Wenn Sie zur Eingabe einer Berechnungsformel bereit sind, drücken Sie zuerst die ATaste, um bisherige Anzeigen im Display zu löschen. Danach geben Sie ihre Berechnungsformel genau so wie sie auf Papier geschrieben ist von links nach rechts ein und drücken
danach die w-Taste, um das Ergebnis zu erhalten.
○○○○○
Beispiel 1 2 + 3 – 4 + 10 =
Ac+d-e+baw
○○○○○
Beispiel 2 2(5 + 4) ÷ (23 × 5) =
Ac(f+e)/
(cd*f)w
k Editieren von Berechnungsformeln
Verwenden Sie die d- und e-Tasten, um den Cursor an die Stelle zu bringen, die Sie
ändern möchten, und führen Sie danach einen der nachfolgend beschriebenen Vorgänge
aus. Nachdem Sie die Berechnungsformel editiert haben, können Sie diese wiederum durch
Drücken der w-Taste ausführen. Sie können auch die e-Taste verwenden, um an das
Ende der Rechnung zu gelangen oder um weitere Daten einzugeben.
u Ändern einer Position in der Formel (Operand oder Operationszeichen)
○○○○○
Beispiel Ändern Sie cos60 auf sin60
Acga
ddd
D
s
19990401

Eingabe und Editieren von Berechnungsformeln
1-3-2
u Löschen einer Position in der Berechnungsformel
○○○○○
Beispiel Korrigieren Sie 369 × × 2 zu 369 × 2
Adgj**c
ddD
u Einfügen einer Position in der Berechnungsformel
○○○○○
Beispiel Ergänzen Sie 2,362 zu sin2,36
Ac.dgx
ddddd
s
2
u Ändern der zuletzt eingegebenen Position
○○○○○
Beispiel Ändern Sie 396 × 3 auf 396 × 2
Adgj*d
D
c
19990401

Eingabe und Editieren von Berechnungsformeln
1-3-3
kk
k Verwendung des Wiederholungsspeichers
kk
Die zuletzt ausgeführte Berechnungsformel wird immer im Wiederholungsspeicher abgelegt.
Sie können den Inhalt des Wiederholungsspeichers zurückholen, indem Sie die d- oder
e-Taste drücken. Falls Sie die e-Taste drücken, erscheint die Berechnungsformel mit
dem Cursor am Beginn. Drücken Sie dagegen die d-Taste, wird die Berechnungsformel
jetzt mit dem Cursor am Ende der Formel angezeigt. Sie können nun die gewünschten
Änderungen in der Berechnungsformel vornehmen und diese danach nochmals ausführen.
○○○○○
Beispiel 1 Führen Sie die beiden folgenden Berechnungen aus
4,12 × 6,4 = 26,368
4,12 × 7,1 = 29,252
Ae.bc*g.ew
dddd
!D(INS)
h.b
w
Nachdem Sie die A-Taste gedrückt haben, können Sie die f- oder c-Taste betätigen,
um frühere Berechnungsformeln in der Reihenfolge von der neuesten bis zur ältesten
Formel aufzurufen (Multi-Wiederholungsfunktion). Sobald Sie eine ältere Formel aufgerufen
haben, können Sie die e- und d-Tasten verwenden, um den Cursor in der Formel zu
verschieben und die gewünschten Änderungen vorzunehmen, damit eine neue Berechnungsformel entsteht.
○○○○○
Beispiel 2 A bcd+efgw
cde-fghw
A
f (Eine Berechnung zurück)
f (Zwei Berechnungen zurück)
#Durch Drücken der Tasten !D(INS)
ändert sich der Cursor auf ‘‘_’’. Die nächste
Funktion oder der nächste Wert, die/den Sie
eingeben, wird an der Stelle von ‘‘_’’
eingefügt. Um die Einfüge-Operation abzubrechen, drücken Sie erneut die Tasten
!D(INS).
# Eine Berechnungsformel verbleibt solange im
Wiederholungsspeicher, bis Sie eine andere
Berechnung ausführen oder das Menü wechseln.
#Die Inhalte des Wiederholungsspeichers werden
nicht gelöscht, wenn Sie die A-Taste drücken.
Sie können daher eine Berechnung zurück
holen und ausführen, auch nachdem Sie eine
Gesamtlöschoperation vorgenommen haben.
19990401

Eingabe und Editieren von Berechnungsformeln
1-3-4
k Berichtigung der ursprünglichen Berechnungsformel
○○○○○
Beispiel 14 ÷ 0 × 2,3 wurde fehlerhaft anstatt 14 ÷ 10 × 2,3 eingegeben.
Abe/a*c.d
w
Drücken Sie i.
Der Cursor wird automatisch an der Stelle
positioniert, die den Fehler verursacht hat.
Nehmen Sie die erforderlichen Änderungen vor.
db
Führen Sie die Berechnung nochmals aus.
w
kk
k Kopieren und Einfügen
kk
Sie können Befehle, Programme und andere in den Speicher eingegebene Textdaten
vorübergehend in einen als Zwischenablage (“Clipboard”) bezeichneten Speicherbereich
kopieren und danach an einer anderen Stelle im Display einfügen.
u Markieren des Kopierbereichs
1. Verschieben Sie den Cursor (t) an den Beginn oder das Ende des Bereichs des
Textes, den Sie kopieren möchten, und drücken Sie danach die u-Taste. Dadurch
wechselt der Cursor auf “ ”.
2. Verwenden Sie die Cursortasten, um den Cursor zu verschieben und den Bereich des
zu kopierenden (z.B. numerischen) Textes zu markieren.
19990401

Eingabe und Editieren von Berechnungsformeln
1-3-5
3. Drücken Sie die Tasten u1(COPY), um den markierten Text in die Zwischenablage
zu übernehmen. Verlassen Sie danach den KopierbereichAuswahlmodus (COPY-Modus).
Um den markierten Text wieder freizugeben, ohne eine Kopieroperation auszuführen,
drücken Sie die i-Taste.
u Einfügen von (z.B. numerischem) Text
Verschieben Sie den Cursor an die Stelle, an der Sie den Text einfügen möchten, und
drücken Sie danach die Tasten u2(PASTE). Der Inhalt der Zwischenablage wird
dadurch an der Cursorposition eingefügt.
A
u2(PASTE)
kk
k Katalogfunktion
kk
Der Katalog ist eine alphabetische Liste aller in diesem Rechner zur Verfügung stehenden
Befehle. Sie können einen Befehl eingeben, indem Sie den Katalog aufrufen und danach
den gewünschten Befehl auswählen.
u Verwendung des Katalogs für die Eingabe eines Befehls
1. Drücken Sie die Tasten u4(CAT/CAL), um den
Katalog im unteren Teil des Displays anzuzeigen.
2. Drücken Sie die Funktionstaste, die dem ersten Buchstaben des einzugebenden
Befehls entspricht.
3. Wählen Sie den gewünschten Befehl aus dem geöffneten Untermenü aus.
○○○○○
Beispiel 1 Verwendung des Katalogs zur Eingabe des Befehls für das Löschen
der Grafikanzeige (ClrGraph)
Au4(CAT/CAL)3(C~)h(CLR)
b(Graph)
19990401

Eingabe und Editieren von Berechnungsformeln
1-3-6
○○○○○
Beispiel 2 Verwendung des Katalogs für die Eingabe des Programmbefehls
(Prog)
Au4(CAT/CAL)6(g)6(g)
5(P)I(Prog)
Drücken Sie die i-Taste oder die Tasten !i(QUIT), um den Katalog zu schließen.
19990401

1-4-1
Optionsmenü (OPTN)
1-4 Optionsmenü (OPTN)
Das Optionsmenü erlaubt Ihnen den Zugriff auf höhere mathematische Funktionen und
Merkmale, die nicht unmittelbar auf der Tastatur des Rechners angegeben sind. Der Inhalt
des Optionsmenüs unterscheidet sich in Abhängigkeit davon, in welchem Menü Sie sich
gerade befinden, wenn Sie die K-Taste drücken.
Für Einzelheiten über das Optionsmenü (OPTN) siehe “8-7 Programmmenü-Befehlsliste”.
u Optionsmenü im RUN
•
MAT- oder PRGM-Menü
•{LIST} ... {Listenfunktionsmenü}
•{MAT} ... {Matrixoperationsmenü}
•{CPLX} ... {Menü für Berechnungen mit komplexen Zahlen}
•{CALC} ... {Funktionsanalysemenü}
•{NUM} ... {Menü für numerisches Berechnungen}
•{PROB} ... {Menü zur Wahrscheinlichkeitsrechnung}
•{HYP} ... {Hyperbelfunktionsmenü}
•{ANGL} ... {Menü für Winkel-/Koordinatenumwandlung, Sexagesimal-Eingabe/
Umwandlung}
•{STAT} ... {Menü für statistische Berechnungen}
•{FMEM} ... {Funktionsspeichermenü}
•{ZOOM} ... {Zoomfunktionsmenü}
•{SKTCH} ... {Skizzenfunktionsmenü}
•{PICT} ... {Bildspeichermenü}
•{SYBL} ... {Symbolmenü}
•{° ’ ”} … {Grad/Minuten/Sekunden}
•{ ° ’ ”} … {Grad-/Minuten-/Sekunden-Umwandlung}
•{ENG}/{ ENG} … {Technische Notation}
#Das Optionsmenü (OPTN) erscheint nicht,
wenn Binär-, Oktal-, Dezimal- und Hexadezimalberechnungen ausgeführt werden.
19990401

1-4-2
Optionsmenü (OPTN)
Nachfolgend sind die Funktionsmenüs beschrieben, die unter anderen Bedingungen/Menüs
erscheinen.
u Optionsmenü bei Anzeige eine Zahlentabelle im GRPH • TBL- oder RECUR-
Menü
•{LMEM} … {Listenspeichermenü}
•{ ° ’ ”}/{ENG}/{ ENG}
u Optionsmenü im CAS-, ALGEBRA- oder TUTOR-Menü
•{∞} … {Unendlich}
•{Abs} … {Absolutwert}
•{x!} … {Fakultät}
•{sign} … {Signumfunktion}
•{HYP}/{FMEM}
Die Bedeutungen der einzelnen Befehle des Optionsmenüs sind in den Abschnitten
beschrieben, wo das entsprechende Menü behandelt wird.
19990401

Variablendatenmenü (VARS)
1-5-1
1-5 Variablendatenmenü (VARS)
Um abgespeicherte Werte spezieller Vaiablen aufzurufen, drücken Sie die J-Taste, um
das Variablendatenmenü zu öffnen.
{V- WI N }/{FACT}/{STAT}/{GRPH}/{DYNA}/{TABL}/{RECR}/{EQUA*1}
Für Einzelheiten über das Variablendatenmenü (VARS) siehe “8-7 ProgrammmenüBefehlsliste”.
u V-WIN — Aufrufen der Einzelwerte für das Betrachtungsfenster
•{Xmin}/{Xmax}/{Xscale}/{Xdot}
…X-Achse {Minimalwert}/{Maximalwert}/{Skalierung}/{Punktwert*2}
•{Ymin}/{Ymax}/{Yscale}
…Y-Achse {Minimalwert}/{Maximalwert}/{Skalierung}
•{T
θ
min}/{T
θ
max}/{T
θ
ptch}
…T, θ {Minimalwert}/{Maximalwert}/{Schrittweite}
•{R-Xmin}/{R-Xmax}/{R-Xscl}/{R-Xdot}
…X-Achse im Nebenfenster (rechte Grafik) der Doppelgrafik {Minimalwert}/
{Maximalwert}/{Skalierung}/{Punktwert*2}
•{R-Ymin}/{R-Ymax}/{R-Yscl}
…Y-Achse im Nebenfenster (rechte Grafik) der Doppelgrafik {Minimalwert}/
{Maximalwert}/{Skalierung}
•{R-Tmin}/{R-Tmax}/{R-Tpch}
…T-, θ -Einstellung im Nebenfenster (rechte Grafik) der Doppelgrafik
{Minimalwert}/{Maximalwert}/{Schrittweite}
u FACT — Aufrufen des Zoomfaktors
•{Xfact}/{Yfact}
... {Zoom-Faktor der x-Achse}/{Zoom-Faktor der y-Achse}
*1Das EQUA-Untermenü erscheint nur, wenn
Sie aus dem RUN
auf das Variablendatenmenü zugreifen.
# Das Variablendatenmenü erscheint nicht,
wenn J gedrückt wird und das Binär-,
Oktal-, Dezimal- oder Hexadezimalsystem als
das Vorgabe-Zahlensystem eingestellt ist.
•
MAT- oder PRGM-Menü
2
*
Der Punktwert zeigt den Anzeigebereich (XmaxWert – Xmin-Wert) geteilt durch die Punktteilung
(126) des Displays an.
Der Punktwert wird normalerweise automatisch
anhand der Minimal- und Maximalwerte berechnet. Durch eine Änderung des Punktwertes
wird das Maximum automatisch berechnet.
19990401

Variablendatenmenü (VARS)
1-5-2
u STAT — Aufrufen von statistischen Kennzahlen und Parametern
• {n} …{Anzahl der Daten, Stichprobenumfang}
• {X} …{x-Daten einer eindimensionalen oder zweidimensionalen Stichprobe}
oo
•{
o}/{Σx}/{Σx
oo
2
}/{x
σ
n}/{xσn–1}/{minX}/{maxX}
…{Mittelwert}/{Summe der Einzelwerte}/{Summe der Quadrate}/
{Grundgesamtheits-Standardabweichung}/{Stichproben-Standardabweichung}/
{Minimalwert}/{Maximalwert}
• {Y} ... {y-Daten einer zweidimensionalen Stichprobe}
•{
pp
p
}/{Σ
pp
2
y}/{Σ y
}/{Σ
xy}/{ y
σ
n}/{
y
σ
n–1}/{minY}/{maxY}
…{Mittelwert}/{Summe der Einzelwerte}/{Summe der Quadrate}/{Summe
der Produkte der x-Daten und y-Daten}/{Grundgesamtheits-Standardabweichung}/{Stichproben-Standardabweichung}/{Minimalwert}/
{Maximalwert}
•{GRAPH} ... {Grafikdatenmenü}
•{a}/{b}/{c}/{d}/{e}
... {Regressionskoeffizienten linearer oder nichtlinearer Modellgleichungen}
•{r}/{r2}
... {Korrelationskoeffizient}/{Bestimmtheitsmaß}
•{Q1}/{Q3}
... {erstes Quartil}/{drittes Quartil}
•{Med}/{Mod}
... {Median}/{Modalwert} der Eingabedaten
•{H-Strt}/{H-ptch}
... Histogramm {Start-Reduktionslage}/{Klassenbreite}
•{PTS} ... {Datenmenü der Medianpunkte einer Med-Med-Regression}
•{x1}/{y1}/{x2}/{y2}/{x3}/{y3} ... {Koordinaten der Medianpunkte/Summierungspunkte}
19990401

Variablendatenmenü (VARS)
1-5-3
u GRPH — Aufrufen von Grafikfunktionen
•{Yn} /{rn}
... {Funktionsgleichungen oder -ungleichungen in kartesischen Koordinaten }/
{Funktionsgleichungen in Polarkoordinaten}
•{Xtn }/{Ytn}
... Funktionsgleichungen in Parameterdarstellung {Xt}/{Yt}
•{Xn} ... {X=Konstant} vertikale Geraden
(Drücken Sie diese Tasten vor der Eingabe eines Wertes, um den zutreffenden
Speicherbereich auszuwählen.)
u DYNA — Aufrufen der Einstelldaten für eine dynamische Grafik
•{Start}/{End}/{Pitch}
... {Dynamik-Variable/Scharparameter-Startwert}/{Dynamik-Variable/
Scharparameter-Endwert}/{Dynamik-Variable/Scharparameter-Schrittweite}
u TABL — Aufrufen der Tabellen & Grafik-Einstellungswerte- und Tabellen
•{Start}/{End}/{Pitch}
... {Tabellenbereich-Startwert des Arguments}/{Tabellenbereich-Endwert des
Arguments}/{Tabellenbereich-Schrittweite des Arguments}
•{Result*1}
... {Wertetabelle als Matrix}
*1
Die Result-Position erscheint nur dann, wenn
das TABL-Menü im RUN
Menü geöffnet wird.
•
MAT- oder PRGM-
19990401

Variablendatenmenü (VARS)
1-5-4
u RECR — Aufrufen der Rekursionsformeln
*1
, des Tabellenbereichs und der
Wertetabellen
• {FORM}
• {an}/{an+1}/{an+2}/{bn}/{bn+1}/{bn+2}/{cn}/{cn+1}/{cn+2}
... {Datenmenü der Rekursionsformeln}
... {an}/{an+1}/{an+2}/{bn}/{bn+1}/{bn+2}/{cn}/{cn+1}/{cn+2} Formelterme für Zahlenfolgen
• {RANGE} ... {Tabellenbereich-Datenmenü}
• {R-Strt}/{R-End}
... Tabellenbereich {Startwert/Anfangsindex}/{Endwert/Endindex}
• {a0}/{a1}/{a2}/{b0}/{b1}/{b2}/{c0}/{c1}/{c2}
... {a0}/{a1}/{a2} {b0}/{b1}/{b2}/{c0}/{c1}/{c2} Anfangswerte für Zahlenfolgen
• {anStrt}/{bnStrt}/{cnStrt}
... Startwerte {an }/{bn}/{cn} in der WEB-Grafik für eine Konvergenz-/
Divergenzuntersuchung einer Zahlenfolge/Rekursionsformel
• {Result*2} ... {Wertetabelle (der Werte der Folgenglieder) als Matrix
*3
}
u EQUA — Aufrufen der Gleichungskoeffizienten und der Lösungen
•{S-Rslt}/{S-Coef}
... Matrix der {Lösungen}/{Koeffizienten} für ein lineares Gleichungssystem
•{P-Rslt}/{P-Coef}
... Matrix der {Lösungen}/{Koeffizienten} für eine Polynomgleichungen höherer
Ordnung
*4 *
5
*6
*
1
Es kommt zu einer Fehlermeldung, wenn sich
keine Zahlenfolge- oder RekursionsformelWertetabelle im Speicher befindet.
*2
“Result” steht nur im RUN
Menü zur Verfügung.
*
3
Die Tabelleninhalte werden automatisch im
Matrixantwortspeicher (MatAns) gespeichert.
*
4
Die Koeffizienten und Lösungen werden
automatisch im Matrixantwortspeicher
(MatAns) gespeichert.
•
MAT- oder PRGM-
*5
Die folgenden Bedingungen führen zu einer
Fehlermeldung:
—Wenn keine Koeffizienten für die Gleichung
eingegeben wurden.
—Wenn keine Lösungen für die Gleichung
erhalten wurden (z.B. nicht eindeutig
lösbares Gleichungssystem).
*6
Die Koeffizienten- und Lösungsspeicherdaten
für ein lineares Gleichungssystem können nicht
gleichzeitig aufgerufen werden.
19990401

Programmmenü (PRGM)
1-6-1
1-6 Programmmenü (PRGM)
Um das Programmmenü (PRGM) öffnen zu können, müssen Sie zuerst das RUN
•
MAT-
oder PRGM-Menü aus dem Hauptmenü heraus aufrufen. Drücken Sie danach die Tasten
!J(PRGM). Die folgenden Positionen stehen im Programmmenü (PRGM) zur Auswahl
zur Verfügung.
• {Prog} ........ {Programmaufruf}
• {JUMP} ...... {Sprungbefehlsmenü}
• {?} .............. {Eingabeaufforderung}
• {^} ............. {Ausgabebefehl}
• {I/O} ............ {Eingabe/Ausgabe-Steuerungs/Übertragungsbefehlsmenü}
• {IF } ............. {Menü für bedingte Sprungbefehle}
• {FOR} ......... {Schleifen-Steuerungsbefehlsmenü}
• {WHLE}...... {Steuerungsbefehlsmenü für eine bedingte Schleife}
• {CTRL} ....... {Programm-Steuerbefehlsmenü}
• {LOGIC} ..... {Befehlsmenü für Logikoperationen}
• {CLR} ......... {Löschbefehlsmenü}
• {DISP} ........ {Anzeigebefehlsmenü}
• {:} ............... {Mehrfachanweisungs-Verbindungszeichen}
Das folgende Funktionstastenmenü erscheint, wenn Sie die Tasten !J(PRGM) im RUN
•
MAT-Menü oder PRGM-Menü drücken und das Binär-, Oktal-, Dezimal- oder Hexadezimal-
system als das Zahlensystem voreingestellt ist.
• {Prog}/{JUMP}/{?}/{^} /{:}
GG
• {=
G <} ....... {Menü der Bedingungsoperatoren}
GG
Die den Funktionstasten zugeordneten Funktionen sind die gleichen wie im Comp-Modus,
der im SET-UP-Menü voreingestellt werden kann.
Für Einzelheiten zu den Befehlen in den verschiedenen Menüs, die Sie aus dem
Programmmenü aufrufen können, siehe “8. Programmierung”.
19990401

Zugeordnetes SET-UP-Menü (Voreinstellungen)
1-7-1
1-7 Zugeordnetes SET-UP-Menü
(Voreinstellungen)
Jedem Menü, welches aus dem Hauptmenü heraus geöffnet werden kann, ist ein spezielles
SET-UP-Menü zugeordnet, in dem der aktuelle Status der Voreinstellungen eingesehen oder
gewünschte Änderungen vorgenommen werden können. Dies geschieht wie folgt.
u Ändern einer Voreinstellung für ein gewähltes Menü
1. Wählen Sie das gewünschte Icon aus und drücken Sie die w-Taste, um ein Menü
aufzurufen und dessen Eingangsbildschirm anzuzeigen. Hier soll das RUN
geöffnet werden, um dessen zugeordnetes SET-UP-Menü einsehen zu können.
•
MAT-Menü
2. Drücken Sie die Tasten u3(SET UP), um das
SET-UP des RUN
•Die Einstellanzeige (SET UP) ist nur ein mögliches
Beispiel. Der tatsächliche Inhalt der Einstellanzeige
unterscheidet sich in Abhängigkeit von dem Menü,
in dem Sie sich gerade befinden, und ist von
dessen aktuellen Voreinstellungen geprägt.
3. Verwenden Sie die f- und c-Cursortasten, um die Positionen zu markieren, dessen
Vo reinstellung Sie ändern möchten.
4. Drücken Sie die Funktionstaste (1 bis 6), die derjenigen Auswahl-Einstellung
zugeordnet ist, die Sie in das SET UP übernehmen möchten.
5. Nachdem Sie die gewünschten Änderungen ausgeführt haben, drücken Sie die i-
Taste, um in den Eingangsbildschirm des geöffneten Menüs zurückzukehren.
•
MAT-Menüs zu öffnen.
k Funktionstastenmenü im zugeordneten SET-UP-Menü
Dieser Abschnitt beschreibt die Voreinstellungen, die Sie unter Verwendung der
Funktionstasten im zugeordneten SET-UP-Menü ausführen können.
Die Standard-Vorgabeeinstellung ist hier mit einer Wellenlinie unterstrichen.
...
u Mode (Berechnungs/Binär-, Oktal-, Dezimal-, Hexadezimalmodus)
•{Comp} ... {Modus für arithmetische Berechnungen}
•{Dec}/{Hex}/{Bin}/{Oct}
... {Dezimal}/{Hexadezimal}/{Binär}/{Oktal} Modus für spezielle Zahlensysteme.
19990401

Zugeordnetes SET-UP-Menü (Voreinstellungen)
1-7-2
u Func Type (Grafikfunktionstyp)
Drücken Sie eine der folgenden Funktionstasten, um auch die Funktionsweise der v-
Taste umzuschalten.
•{Y=}/{r=}/{Parm}/{X=c}
... Grafiken mit {kartesischen Koordinaten}/{Polarkoordinaten}/{Parameter-
Darstellung}/{X = Konstante}
•{Y>}/{Y<}/{Yt}/{Ys}
... Ungleichungsgrafik {y>f(x)}/{y<f(x)}/{y≥f(x)}/{y≤f(x)}
u Draw Type (Grafikzeichnungsmethode)
•{Con}/{Plot}
... {verbundene Punkte, Liniengrafik}/{nicht verbundene Punkte, Punkteplot}
u Derivative (Anzeige der Ableitung)
•{On}/{Off}
... {Ableitungs-Anzeige eingeschaltet}/{Ableitungs-Anzeige ausgeschaltet}
während Grafik-auf-Tabelle, Tabelle & Grafik oder Trace verwendet werden.
u Angle (Winkelmodus)
•{Deg}/{Rad}/{Gra}
... {Altgrad}/{Bogenmaß}/{Neugrad}
u Complex Mode (Modus für komplexe Zahlen)
•{Real} ... {Berechnungen nur im reellen Zahlenbereich}
•{a + bi}/{r · e^θi}
... {Kartesisches Format, arithmetische Darstellung}/{Polarformat, exponentielle
Darstellung} der Anzeige einer Berechnung mit komplexen Zahlen
u Coord (Koordinaten des Grafikcursors)
•{On}/{Off}
... {Anzeige eingeschaltet}/{Anzeige ausgeschaltet}
u Grid (Grafik-Gitterlinien)
•{On}/{Off}
... {Anzeige eingeschaltet}/{Anzeige ausgeschaltet}
u Axes (Grafikachsen)
•{On}/{Off}
... {Anzeige eingeschaltet}/{Anzeige ausgeschaltet}
u Label (Grafikachsen-Bezeichnungen)
•{On}/{Off}
... {Anzeige eingeschaltet}/{Anzeige ausgeschaltet}
19990401

Zugeordnetes SET-UP-Menü (Voreinstellungen)
1-7-3
u Display (Anzeigeformat der Zahlendarstellung)
•{Fix}/{Sci}/{Norm}/{Eng}
... {Festlegung der Anzahl der Dezimalstellen}/{Festlegung der Mantissenlänge}/
{Normal-Anzeige, in Norm1 oder Norm2 umschaltbar}/{Techniknotation}
u Stat Wind (Einstellung des Betrachtungsfensters der statistischen Grafiken)
•{Auto}/{Man}
... {automatische}/{manuelle} Grafik-Fenstereinstellung
u Reside List (Residuenberechnung)
•{None}/{LIST}
... {keine Berechnung}/{Listenvorgabe für die berechneten Residuen}
u List File (Listendatei-Einstellanzeige)
•{FILE} ... {Einstellung der im Display gewählten Listendatei}
u Va riable (Einstellungen für Tabellengenerierung und Grafikdarstellung)
•{Rang}/{LIST}
... {Tabellenbereichsvorgaben verwenden}/{Listendaten verwenden}
u Graph Func (Anzeige der Funktionsformel in der Grafikdarstellung und bei
Benutzung der Trace-Funktion)
•{On}/{Off}
... {Anzeige eingeschaltet}/{Anzeige ausgeschaltet}
u Dual Screen (Status für Doppelanzeige)
•{T+G}/{G+G}/{G to T}/{Off}
... {Tabelle auf der einen Seite und Grafik auf der anderen Seite der Doppel-
anzeige}/{Grafik auf beiden Seiten der Doppelanzeige}/{Grafik auf der einen
Seite und numerische Wertetabelle auf der anderen Seite der Doppelanzeige}/
{Doppelanzeige ausgeschaltet, d.h. kein unterteilter Bildschirm}
u Simul Graph (Simultaner Grafikmodus)
•{On}/{Off}
... {simultane Grafikdarstellung eingeschaltet (alle Grafiken werden gleichzeitig
gezeichnet)}/{simultane Grafikdarstellung ausgeschaltet (Grafiken werden in der
numerischen Reihenfolge der Speicherbelegung einzeln gezeichnet)}
u Background (Hintergrund der Grafikanzeige)
•{None}/{PICT}
... {keine Hintergrundgrafik}/{Auswahl eines Bildes als Hintergrundgrafik}
19990401

Zugeordnetes SET-UP-Menü (Voreinstellungen)
1-7-4
u Dynamic Type (Animations-Einstellung für dynamische Grafik)
•{Cnt}/{Stop}
... {ohne Stopp (kontinuierlich)}/{automatischer Stopp nach 10 Durchläufen}
u Σ Display (Σ-Wert-Anzeige (Partialsummenfolge) in Zahlenfolge-Tabelle)
•{On}/{Off}
... {Anzeige eingeschaltet}/{Anzeige ausgeschaltet}
u Slope (Anzeige der 1. Ableitung für die aktuelle Cursorposition bei
impliziter Funktionsgrafik - CONICS-Menü)
•{On}/{Off}
... {Anzeige eingeschaltet}/{Anzeige ausgeschaltet}
u Answer Type (Festlegung des Zahlenbereichs für die Ergebnisanzeige)
•{Real}/{Cplx}
... Festlegung auf Darstellung als {reelle Zahl}/{komplexe Zahl}
u H-Copy (Einstellung für das Kopieren des aktuellen Displays)
•{Dirct}/{Mem}
... {direktes Senden zu einem anderen Rechner (PC)}/
{im H-Copy-Speicher abspeichern}
19990401

Falls Probleme auftreten …
1-8-1
1-8 Falls Probleme auftreten …
Falls Probleme bei der Arbeit mit dem Rechner auftreten, ergreifen Sie die folgenden
Maßnahmen, bevor Sie einen Defekt in Ihrem Rechner vermuten.
kk
k Zurückstellung des Rechners auf seine Standard-Voreinstellungen
kk
1. Rufen Sie das SYSTEM-Menü aus dem Hauptmenü heraus auf.
2. Drücken Sie die 5(Reset)-Taste.
3. Drücken Sie die 1(S/U)-Taste und danach die w(Yes)-Taste.
4. Drücken Sie die m-Taste, um in das Hauptmenü zurückzukehren.
Öffnen Sie nun das richtige Menü und führen Sie Ihre Berechnung erneut aus, wobei Sie die
Ergebnisse im Display überwachen.
kk
k Falls der Rechner hängen bleibt
kk
•Sollte der Rechner hängen bleiben und nicht mehr auf Eingaben mit der Tastatur
reagieren, drücken Sie den P-Knopf auf der Rückseite des Rechners, um den Rechner
auf seine Standard-Voreinstellungen zurückzustellen (Siehe Seite α-6-1).
Beachten Sie jedoch, dass dadurch alle Daten aus dem Speicher des Rechners
gelöscht werden.
19990401

Falls Probleme auftreten …
1-8-2
kk
k Meldung für niedrige Batteriespannung
kk
Falls eine der folgenden Meldungen im Display erscheint, schalten Sie den Rechner
unverzüglich aus und wechseln Sie die Batterien, so wie es vorgeschrieben ist.
Falls Sie jedoch den Rechner weiterhin verwenden, ohne die Hauptbatterien auszutauschen,
wird die Stromversorgung schließlich automatisch ausgeschaltet, um die Speicherinhalte zu
schützen. Falls dies eintritt, können Sie die Stromversorgung nicht mehr einschalten, wobei
die Gefahr besteht, dass Speicherinhalte verfälscht oder gar gelöscht werden.
#Sie können keine Datenübertragungen aus-
führen, nachdem eine Meldung für niedrige
Batteriespannung erschienen ist.
# Falls die Hauptbatterien und die Sicherungs-
batterie gleichzeitig verbraucht sind (angezeigt
dadurch, dass beide oben gezeigten Meldungen
gleichzeitig erscheinen), wechseln Sie zuerst die
Sicherungsbatterie und erst danach die
Hauptbatterien aus.
19990401

Kapitel
Manuelle Berechnungen
2
im RUN
2-1 Grundrechenarten
2-2 Spezielle Taschenrechnerfunktionen
2-3 Festlegung des Winkelmodus und des
Anzeigeformats (SET UP)
2-4 Funktionsberechnungen
2-5 Numerische Berechnungen
2-6 Rechnen mit komplexen Zahlen
2-7 Berechnungen mit Binär-, Oktal-, Dezimal- und
Hexadezimalzahlen
2-8 Matrizenrechnung
•
MAT - Menü
19990401

2-1-1
Grundrechenarten
2-1 Grundrechenarten
Rufen Sie aus dem Hauptmenü das RUN•MAT-Menü auf, um das Arbeitsfenster für
manuelle Berechnungen zu öffnen.
kk
k Arithmetische Berechnungen
kk
•Geben Sie die arithmetischen Berechnungsformeln oder Rechenaufgaben wie
geschrieben von links nach rechts ein.
•Verwenden Sie anstatt des Operationszeichens "minus" (--Taste) die --Taste, um
ein Minusvorzeichen vor einem negativen Wert einzugeben.
•Alle Berechnungen werden intern mit einer 15stelligen Mantisse durchgeführt. Das
Ergebnis wird dann auf eine 10stellige Mantisse gerundet, bevor es im Display zur
Anzeige kommt.
•Bei gemischten arithmetischen Operationen werden der Multiplikation und Division
Priorität vor der Addition und Subtraktion eingeräumt (Übliche Vorrangregeln).
Beispiel Tastenfolge
23 + 4,5 – 53 = –25,5 23+4.5-53w
56 × (–12) ÷ (–2,5) = 268,8 56*-12/-2.5w
(2 + 3) × 102 = 500 (2+3)*1E2w*
1
1 + 2 – 3 × 4 ÷ 5 + 6 = 6,6 1+2-3*4/5+6w
100 – (2 + 3) × 4 = 80 100-(2+3)*4w
2 + 3 × (4 + 5) = 29 2+3*(4+5w*
(7 – 2) × (8 + 5) = 65 (7-2)(8+5)w*
6
= 0,3 6 /(4*5)w*
4 × 5
2
3
4
(1 + 2i) + (2 + 3i) = 3 + 5i (b+c!a(i))+(c+
d!a(i))w
(2 + i) × (2 – i) = 5 (c+!a(i))*(c-!a(i)
)w
*1(2+ 3)E2 führt nicht zum korrekten
Ergebnis. Geben Sie diese Aufgabe unbedingt
wie angezeigt ein oder alternativ als
(2+3)*10M2
2
*
Die schließenden Klammern (unmittelbar vor
der Betätigung der w-Taste) können wegge-
lassen werden, wie viele auch erforderlich
wären.
3
Ein Multiplikationssymbol unmittelbar vor einer
*
öffnenden Klammer kann weglassen werden.
4
Dies ist identisch mit 6 / 4 / 5 w.
*
19990401

2-1-2
Grundrechenarten
kk
k Anzahl der Dezimalstellen, Mantissenlänge, Normal-Anzeige
kk
[SET UP]- [Display] -[Fix] / [Sci] / [Norm]
•Auch nachdem Sie die Anzahl der Dezimalstellen oder die Mantissenlänge voreingestellt
haben, werden die internen Rechnungen mit einer 15stelligen Mantisse ausgeführt,
wobei jedoch die berechneten Werte mit einer 10stelligen Mantisse angezeigt werden.
Ve rwenden Sie “Rnd” des numerischen Berechnungsmenüs (NUM) (Seite 2-4-1), um
den angezeigten Wert auf die gewünschte Anzahl der Dezimalstellen und die
gewünschte Mantissenlänge zu runden.
•Die Einstellungen der Anzahl der Dezimalstellen (Fix) und der Mantissenlänge (Sci)
bleiben normalerweise solange wirksam, bis Sie diese ändern oder bis Sie die Einstellungen der Normal-Anzeige (Norm mit Auswahl zwischen Norm1 oder Norm2)
ändern.
○○○○○
Beispiel 100 ÷ 6 = 16,66666666...
Bedingung Tastenfolge Display
100/6w 16.66666667
4 Dezimalstellen u3(SET UP)
cccccccccc
1(Fix)ewiw 16.6667
Mantissenlänge 5 u3(SET UP)
Ersetzt die bisherige u3(SET UP)
cccccccccc
2(Sci)fwiw 1.6667E+01
cccccccccc
1
*
Vo rgabe "Fix" oder "Sci" 3(Norm)iw 16.66666667
*1Die angezeigten Werte werden auf die von
Ihnen vorgegebene Stellenanzahl gerundet.
19990401
1
*

2-1-3
Grundrechenarten
○○○○○
Beispiel 200 ÷ 7 × 14 = 400
Bedingung Tastenfolge Display
200/7*14w 400
3 Dezimalstellen u3(SET UP)
cccccccccc
1(Fix)dwiw 400.000
Berechnung wird mit 200/7w 28.571
maximaler Genauigkeit * Ans ×
fortgesetzt (intern 15 14w 400.000
Stellen, vgl. S. 2-1-2).
• Wenn die gleiche Berechnung mit der vorgegebenen Anzahl von Stellen ausgeführt und
damit mit gerundeten Zwischenergebnissen weitergerechnet wird, erhält man:
200/7w 28.571
Der intern gespeicherte
Wert wird auf die von
Ihnen festgelegten
K5(NUM)e(Rnd)w 28.571
* Ans ×
14w 399.994
Dezimalstellen
gerundet.
kk
k Prioritäten der Rechenoperationen während der Berechnung
kk
Dieser Rechner arbeitet mit der üblichen Algebralogik, um Teilschritte einer Formel mit
folgenden Prioritäten zu berechnen:
1 Koordinatenumrechnung Pol (x, y), Rec (r, θ)
1. und 2. Ableitungen, bestimmte Integrale, Σ-Berechnungen (Partialsummen)
2
d/dx, d
/dx2, ∫dx, Σ, Mat, Solve, FMin, FMax, List→Mat, Seq, Min, Max, Median, Mean,
Augment, Mat → List, P(, Q(, R(, t(, List
2 Funktionen vom Typ A: Bei diesen Funktionen wird zuerst das Argument eingegeben und
danach wird die Funktionstaste gedrückt.
2
x
, x–1, x !, ° ’ ”, ENG-Symbole, Winkelargumente o, r,
3 Potenzen/Wurzeln ^(xy),
4 Gemeine Brüche (gemischte Zahlen) a
x
b
/c
g
5 Abgekürztes Multiplikationsformat (ohne Multplikationszeichen) vor π, vor einer Speicher-
oder Variablenbezeichnung, z.B. 2π, 5A, Xmin, F Start usw.
6 Funktionen vom Typ B: Bei diesen Funktionen wird zuerst die Funktionstaste gedrückt und
danach wird ein Argument eingegeben.
, 3, log, In, ex, 10x, sin, cos, tan, sin–1, cos–1, tan–1, sinh, cosh, tanh, sinh–1, cosh–1,
tanh–1, (–), d, h, b, o, Neg, Not, Det, Trn, Dim, Identity, Sum, Prod, Cuml, Percent, AList,
Abs, Int, Frac, Intg, Arg, Conjg, ReP, ImP
19990401

2-1-4
Grundrechenarten
7 Abgekürztes Multiplikationsformat (ohne Multiplikationszeichen) für Funktionen vom Typ B
2 , A log2 usw.3
8 Variation (Permutation), Kombination nPr, nCr
9 × , ÷
0 +, –
! Relationszeichen >, <, ≥, ≤
@ Ve rgleichsoperator =,
G
# and (Bit-Operation)
$ xnor, xor (Bit-Operationen)
% or (Bit-Operation)
^ And (Logikoperation)
Or (Logikoperation)
○○○○○
Beispiel 2 + 3 × (log sin2π2 + 6,8) = 22,07101691 (Winkelmodus =
1
2
3
4
5
6
Rad (Bogenmaß))
Die Ziffern 1 bis 6 beschreiben hier die Reihenfolge der Rechenschritte.
#Wenn Funktionen mit der gleichen Priorität
hintereinander angewendet werden, erfolgt die
Ausführung von rechts nach links, also von
der inneren zur äußeren Funktion.
x
e
In → ex{In( )}
120 120
Andernfalls erfolgt die Ausführung von links
nach rechts.
#Verkettete Funktionen werden ebenfalls von
rechts nach links ausgeführt.
#Klammerterme haben höchste Priorität.
19990401

2-1-5
Grundrechenarten
k Multiplikationsoperationen ohne Multiplikationszeichen
Sie können das Multiplikationssymbol (×) in allen der folgenden Operationen weglassen.
• Vor der Koordinatenumwandlung und Typ B Funktionen (1 und 6 auf Seite 2-1-3),
ausgenommen bei negativen Vorzeichen
○○○○○
Beispiel 2sin30, 10log1,2, 2 , 2Pol(5, 12) usw.
•Vor Konstanten, Variablen- oder Speicherbezeichnungen
○○○○○
Beispiel 2π, 2AB, 3Ans, 3Y1 usw.
•Vor einer öffnenden Klammer
○○○○○
Beispiel 3(5 + 6), (A + 1)(B – 1) usw.
k Überlauf und Fehler
Bei Überschreiten eines bestimmten Eingabe- oder Berechnungsbereiches bzw. bei unzulässiger Eingabe wird eine Fehlermeldung im Display angezeigt. Während der Fehleranzeige
ist jede weitere Funktion des Rechners unterbrochen. Die folgenden Faktoren verursachen
eine Fehlermeldung im Display.
•Wenn ein Ergebnis (Zwischen- oder Endergebnis) bzw. ein Wert im Speicher die Größe
±9,999999999 × 1099 übersteigt (Ma ERROR).
•Wenn der Versuch unternommen wird, eine Funktionswertberechnung auszuführen, wobei
das Argument den Definitionsbereich übersteigt (Ma ERROR).
•Wenn bei statistischen Berechnungen eine unzulässige Operation ausgeführt wird (Ma
ERROR). Zum Beispiel wenn versucht wird, Kennzahlen zu berechnen, ohne Datenlisten
einzugeben.
•Wenn der falsche Datentyp für das Argument einer Funktionswertberechnung eingegeben
wird (Ma ERROR).
•Wenn die Kapazität des numerischen Wertstapelspeichers oder Befehlsstapelspeichers
überschritten wird (Stack ERROR). Zum Beispiel, Eingabe von 25 aufeinanderfolgenden
Klammern ( gefolgt von 2 + 3 * 4 w.
•Wenn der Versuch unternommen wird, die Berechnung mit einer fehlerhaften Formel auszuführen (Syntax ERROR). Zum Beispiel 5 ** 3 w.
# Während der Programmausführung können
andere Fehler auftreten. Wenn eine
Fehlermeldung erscheint, werden die
meisten Tasten des Rechners gesperrt.
Drücken Sie die i-Taste , um die Fehlermeldung zu löschen und die Fehlerposition
anzuzeigen (siehe Seite 1-3-4).
# Für Informationen über andere Fehler siehe die
“Fehlermeldungstabelle” auf Seite α-1-1.
19990401

2-1-6
Grundrechenarten
•Wenn Sie eine Berechnung versuchen, bei der die Speicherkapazität überschritten wird
(Memory ERROR).
•Wenn Sie einen Befehl verwenden, der ein Argument erfordert, und Sie dabei ein nicht
gültiges Argument eingeben (Argument ERROR).
•Wenn Sie versuchen, eine unzulässige Dimension (unzulässiger Matrixtyp) innerhalb der
Matrizenrechnung zu verwenden (Dimension ERROR).
• Wenn Sie versuchen, eine Berechnung auszuführen, die ein Argument in Form einer
reellen Zahl hat und eine Lösung in Form einer komplexen Zahl ergibt, wobei “Real” in der
Einstellanzeige für “Complex Mode” gewählt ist (Non-Real ERROR).
k Speicherkapazität
Mit jedem Drücken einer Taste werden ein Byte oder zwei Byte verwendet. Einige
Funktionen, die ein Byte benötigen, sind: b, c, d, sin, cos, tan, log, In, und π. Einige
Funktionen, die zwei Byte benötigen, sind: d/dx(, Mat, Xmin, If, For, Return, DrawGraph,
SortA(, PxlOn, Sum und an+1.
#Wenn Sie Zahlenwerte oder Befehle ein-
geben, erscheinen diese linksbündig im
Display. Ergebnisse werden jedoch rechtsbündig angezeigt.
#Der zulässige Bereich sowohl für Eingabe-
als auch für Ausgabewerte beträgt 15 Stellen
für die Mantisse und zwei Stellen für den Exponenten. Die internen Rechnungen werden
ebenfalls unter Verwendung einer 15stelligen
Mantisse und eines zweistelligen Exponenten
ausgeführt.
19990401

Spezielle Taschenrechnerfunktionen
2-2-1
2-2 Spezielle Taschenrechnerfunktionen
kk
k Berechnungen mit Variablen
kk
Beispiel Tastenfolge Display
A erhält den Wert 193,2
193,2 ÷ 23 = 8,4 av(A)/23w 8.4
193,2 ÷ 28 = 6,9 av(A)/28w 6.9
kk
k Speicher
kk
193.2aav(A)w 193.2
uVariablen
Der Rechner verfügt standardmäßig über 28 Variablen. Sie können die Variablen für das
Abspeichern von Werten verwenden, die innerhalb von Berechnungen benötigt werden.
Variablen werden jeweils mit einem Buchstaben bezeichnet, indem die 26 Buchstaben des
Alphabets sowie r und θ verwendet werden. Der Maximalwert, der Variablen zugewiesen
werden kann, weist in Gleitkommadarstellung 15 Stellen für die Mantisse und 2 Stellen für
den Exponenten auf.
u Wertzuweisung für eine Variable
[Wert] a [Variablenbezeichnung] w
○○○○○
Beispiel Wertzuweisung von 123 zur Variablen A
Abcdaav(A)w
○○○○○
Beispiel Abspeicherung der Summe A+456 in der Variablen B
Aav(A)+efgaa
l(B)w
# Die abgespeicherten Werte der Variablen
bleiben erhalten, auch wenn Sie die
Stromversorgung ausschalten.
19990401

Spezielle Taschenrechnerfunktionen
2-2-2
u Anzeige des Wertes einer Variablen
○○○○○
Beispiel Anzeige des abgespeicherten Wertes der Variablen A
Aav(A)w
u Löschen einer Variablen
○○○○○
Beispiel Löschen der Variablen A durch die Wertzuweisung null
Aaaav(A)w
u Wertzuweisung des gleichen Wertes zu mehr als einer Variablen
[Wert]a [erste Variablenbezeichnung*1]K6(g)6(g)4(SYBL)d(~)
[letzte Variablenbezeichnung*1]w
○○○○○
Beispiel Der Wert 10 ist den Variablen A bis F zuzuweisen.
Abaaav(A)
K6(g)6(g)4(SYBL)d(~)
at(F)w
uFunktionsspeicher [OPTN]-[FMEM]
Der Funktionsspeicher (f1~f20) ist nützlich für das temporäre Abspeichern häufig verwendeter
Formelterme. Für eine längere Speicherung wird empfohlen, dass Sie das GRPH
Menü zum Abspeichern für Formelterme und das PRGM-Menü zum Abspeichern für
Programme nutzen.
•{Store}/{Recall}/{fn}/{SEE} ... {Funktionsterm speichern}/{Funktionsterm aufrufen}/
{Funktionsspeicherposition (f1~f20) als Variablenbezeichnung in einem
Te rm}/{Funktionsspeicherliste öffnen}
*1
Sie können hier jedoch “r” oder “θ” nicht als
Va riablenbezeichnung verwenden.
19990401
•
TBL-

Spezielle Taschenrechnerfunktionen
2-2-3
u Abspeichern eines Funktionsterms
○○○○○
Beispiel Abspeichern des Funktionsterms (A+B)(A–B) unter der
Funktionsspeicherposition 1
(av(A)+al(B))
(av(A)-al(B))
K6(g)5(FMEM)
b(Store)bw
u Abruf eines Funktionsterms
○○○○○
Beispiel Abruf des Funktionsterms unter der Funktionsspeicherposition 1
K6(g)5(FMEM)
c(Recall)bw
u Anzeige der Belegung des Funktionsspeichers
K6(g)5(FMEM)
e(SEE)
# Falls die Funktionsspeicherposition, der Sie
einen Funktionsterm zuweisen, bereits einen
Funktionsterm enthält, dann wird der vorhandene Term durch den neuen Term ersetzt.
#Der aufgerufene Funktionsterm erscheint an
der aktuellen Cursorposition im Display.
19990401

Spezielle Taschenrechnerfunktionen
2-2-4
u Löschen eines Funktionsterms
○○○○○
Beispiel Löschen des Funktionsterm unter der Funktionsspeicherposition 1
AK6(g)5(FMEM)
b(Store)bw
•Mit Ausführung der Speicheroperation bei leerem Display wird der Funktionsterm aus der
von Ihnen bezeichneten Funktionsspeicherposition gelöscht.
u Verwendung von abgespeicherten Formeltermen
○○○○○
Beispiel Abzuspeichern sind die Terme x3 + 1, x2 + x im Funktionsspeicher.
Danach soll die folgende Formel grafisch dargestellt werden:
3
y = x
+ x2 + x + 1
Verwenden Sie die folgenden Einstellungen für das Betrachtungsfenster.
Xmin = – 4, Xmax = 4, Xscale = 1
Ymin = –10, Ymax = 10, Yscale = 1
u3(SET UP)c1(Y=)i
AvMd+bK6(g)5(FMEM)b(Store)bw(speichert (x3 + 1))
iAvx+v5(FMEM)b(Store)cw(speichert (x2 + x))
iAK6(g)6(g)2(SKTCH)b(Cls)w
2(SKTCH)e(GRAPH)b(Y=)
K6(g)5(FMEM)d(fn)b+
5(FMEM)d(fn)cw
• Zu vollständigen Einzelheiten über die grafische
Darstellung siehe “5. Grafische Darstellung”.
19990401

Spezielle Taschenrechnerfunktionen
2-2-5
kk
k Antwortspeicherfunktionen der Taschenrechners
kk
Der Taschenrechner besitzt eine Antwortspeicherfunktion sowohl für Zahlenwerte als auch
für Matrizen und Listen. Der Antwortspeicher übernimmt automatisch das letzte Ergebnis,
das Sie durch Drücken der w-Taste erhalten haben (wenn nicht das Drücken der w -Taste
zu einem Fehler geführt hat). Das jeweils letzte Ergebnis wird im Antwortspeicher gespeichert und kann dort abgerufen werden.
Hinweis:
Sowohl für Listen als auch für Matrizen existieren eigene Antwortspeicher "ListAns" bzw.
"MatAns", die genau wie "Ans" durch Kombination der Befehle "List" und "Ans" bzw. "Mat" und
"Ans" abgerufen werden können.
u Verwendung des Inhalts des Antwortspeichers in einer Rechnung
○○○○○
Beispiel 123 + 456 = 579
789 – 579 = 210
Abcd+efgw
hij-!-(Ans)w
kk
k Ausführung von "Ketten-Rechnungen"
kk
Das Ergebnis einer Berechnung kann unmittelbar als erster Operand in der nachfolgenden
Berechnung verwendet werden, indem der Antwortspeicher durch Eingabe eines Operationszeichens automatisch abgerufen wird.
○○○○○
Beispiel 1 ÷ 3 =
1 ÷ 3 × 3 =
Ab/dw
(Fortsetzung)*dw
Eine derartige "Ketten-Rechnung" kann auch mit Typ A Funktionen (x2, x-1, x!, siehe
Seite 2-1-3), +, –, ^(xy), x, ° ’ ” usw. ausgeführt werden.
#Der größte Zahlenwert, der im Antwort-
speicher abgelegt werden kann, weist 15
Stellen für die Mantisse und 2 Stellen für den
Exponenten auf.
# Es können nur numerische Werte und
Rechenergebnisse im Antwortspeicher
gespeichert werden.
# Der Inhalt des Antwortspeichers wird nicht
gelöscht, wenn Sie die A-Taste drücken
oder die Stromversorgung ausschalten.
#Der Inhalt des Antwortspeichers wird durch
eine Operation, die einem anderen Wertspeicher einen Wert zuordnet (wie zum
Beispiel: faav(A)w), nicht
geändert.
19990401

Spezielle Taschenrechnerfunktionen
2-2-6
k Stapelspeicher
Dieser Rechner verwendet für die Speicherung von Werten und Befehlen mit niedriger Priorität Speicherblöcke, die als
numerischen Wertstapelspeicher
und einen
Unterprogramm-Stapelspeicher
dung, wenn Sie eine so komplizierte Rechnung ausführen, dass die Kapazität des verfügbaren numerischen Wertestapelspeichers oder des Befehlsstapelspeichers überschritten
wird, bzw. wenn bei der Ausführung eines Unterprogramms die Kapazität des Unterprogramm-Stapelspeichers überschritten wird.
○○○○○
Beispiel
Stapelspeicher
bezeichnet werden. Der Rechner besitzt einen
mit 10 Ebenen, einen
mit 10 Ebenen. Es kommt zu einer Fehlermel-
Befehlsstapelspeicher
mit 26 Ebenen
#Die Berechnungen werden in Abhängigkeit
von der Prioritätshierarchie ausgeführt. Sobald
eine Berechnung beendet ist, wird sie aus
dem Stapelspeicher gelöscht.
#Die Speicherung einer komplexen Zahl belegt zwei
Ebenen des numerischen Wertestapelspeichers.
#Die Speicherung einer Zwei-Byte-Operation
belegt zwei Ebenen des Befehlsstapelspeichers.
19990401

Spezielle Taschenrechnerfunktionen
2-2-7
k Verwendung von Mehrfachanweisungen
Mehrfachanweisungen werden durch die Verbindung von Einzelanweisungen gebildet, um
sie dann sequentiell abzuarbeiten. Sie können Mehrfachanweisungen in manuellen Berechnungen oder in programmierten Rechenschritten nutzen. Es gibt zwei verschiedene Wege,
wie Sie Einzelanweisungen zu Mehrfachanweisungen verbinden können.
•Doppelpunkt (:)
Anweisungen, die durch Doppelpunkte verbunden sind, werden ohne Unterbrechung von
links nach rechts ausgeführt.
•Ergebnisanzeigebefehl (
^^
^)
^^
Wenn die Programm-Ausführung das Ende einer Anweisung erreicht, dem ein Ergebnisanzeigebefehl folgt, stoppt die Programm-Ausführung. Das bis zu diesem Zeitpunkt erhaltene
Zwischenergebnis erscheint im Display. Sie können mit der Programm-Ausführung fortsetzen,
indem Sie die w-Taste drücken.
○○○○○
Beispiel 6,9 × 123 = 848,7
123 ÷ 3,2 = 38,4375
Abcdaav(A)
!J(PRGM)6(g)6(g)3(:)g.j
*av(A)!J(PRGM)4(^)
av(A)/d.cw
w
#Das Endergebnis einer Mehrfachanweisung
wird immer angezeigt, unabhängig davon, ob
die Berechnung mit einem Ergebnisanzeigebefehl endet.
#Sie können keine Mehrfachanweisung
zusammenstellen, in der eine Einzelanweisung direkt das Ergebnis der vorhergehenden Anweisung verwendet.
Beispiel : 123 × 456: × 5
Ungültig
19990401

Festlegung des Winkelmodus und des Anzeigeformats (SET UP)
2-3-1
2-3 Festlegung des Winkelmodus und des
Anzeigeformats (SET UP)
Vor der erstmaligen Ausführung einer Berechnung sollten Sie die Einstellanzeige (SET-UPMenü) verwenden, um den Winkelmodus und das Anzeigeformat festzulegen.
kk
k Einstellen des Winkelmodus [SET UP]- [Angle]
kk
1. Markieren Sie “Angle” in der Einstellanzeige (SET-UP-Menü).
2. Drücken Sie die Funktionstaste für den festzulegenden Winkelmodus. Drücken Sie
danach die i-Taste.
•{Deg}/{Rad}/{Gra} ... {Altgrad}/{Bogenmaß}/{Neugrad}
•Der Zusammenhang zwischen Altgrad, Bogenmaß und Neugrad lautet
wie folgt:
360° (Altgrad) = 2π (Bogenmaß) = 400 (Neugrad), d.h.
90° (Altgrad) = π/2 (Bogenmaß) = 100 (Neugrad) usw.
kk
k Einstellen des Anzeigeformats für Zahlen [SET UP]- [Display]
kk
1. Markieren Sie “Display” in der Einstellanzeige (SET-UP-Menü).
2. Drücken Sie die Funktionstaste für das einzustellende Anzeigeformat. Drücken Sie
danach die i-Taste.
•{Fix}/{Sci}/{Norm}/{Eng} ... {Festlegung eine festen Anzahl von Dezimalstellen}/
{Festlegung der Mantissenlänge}/{Normal-Anzeige mit Norm1 oder Norm2
einstellbar}/{Technik-Notation}
u Festlegung der Anzahl der Dezimalstellen (Fix)
○○○○○
Beispiel Festlegung auf zwei Dezimalstellen
1(Fix) cw
Drücken Sie die Zahlentaste, die der
Anzahl der Dezimalstellen entspricht,
die Sie festlegen möchten (
#Angezeigte Zahlenwerte werden auf die von
Ihnen festgelegte Anzahl von Dezimalstellen
gerundet.
n
= 0 bis 9).
19990401

Festlegung des Winkelmodus und des Anzeigeformats (SET UP)
2-3-2
u Festlegung der Mantissenlänge (Sci)
○○○○○
Beispiel Einstellung auf die Mantissenlänge 3
2(Sci) dw
Drücken Sie die Zahlentaste, die der Länge
der Mantisse entspricht, die Sie voreinstellen
möchten (
(0 = Mantissenlänge 10.)
n
= 0 bis 9).
u Einstellung auf Normal-Anzeige (Norm 1 oder Norm 2)
Drücken Sie die 3(Norm)-Taste, um zwischen Norm 1 und Norm 2 umzuschalten.
Norm 1: |x| < 10
Norm 2: |x| < 10
–2
(0,01) oder |x| >10
–9
(0,000000001) oder |x| >10
Ab/caaw (Norm 1)
(Die Normal-Anzeige schaltet erst in die Gleitkommazahlendarstellung um, wenn
die voreingestellten Größenordnungen (Norm1 oder Norm2) erreicht werden.)
10
10
(Norm 2)
u Einstellung der Anzeige auf die Technik-Notation (Eng)
Drücken Sie die 4(Eng)-Taste, um zwischen der technischen Schreibweise und der
Standardschreibweise umzuschalten. Der Indikator “/ E” wird im SET-UP-Display angezeigt, wenn die technische Schreibweise wirksam ist. Dabei werden folgende SI-Vorsätze
wirksam (Internationales Einheitensytem), wie zum Beispiel 2.000 (= 2 × 103) → 2k.
E (Exa) × 10
P (Peta) × 10
T (Tera) × 10
G (Giga) × 10
M (Mega) × 10
k (Kilo) × 10
18
15
12
9
6
3
#Die angezeigten Werte werden auf die von Ihnen
vorgegebene Mantissenlänge gerundet.
#Durch die Vorgabe von 0 wird die Mantissen-
länge auf 10 eingestellt.
m (Milli) × 10
µ (Mikro) × 10
n (Nano) × 10
p (Piko) × 10
f (Femto) × 10
#Das SI-Symbol, das die Mantisse auf einem
Wert von 1 bis 1000 eingrenzt, wird automatisch
vom Rechner gewählt, wenn die TechnikNotation voreingesellt ist.
19990401
–3
–6
–9
–12
–15

Funktionsberechnungen
2-4-1
2-4 Funktionsberechnungen
k Funktionsuntermenüs
Dieser Rechner besitzt fünf Funktionsuntermenüs, die Ihnen Zugriff auf höhere mathematische Funktionen ermöglichen, die nicht auf der Tastatur markiert sind.
•Der Inhalt dieser Funktionsuntermenüs unterscheidet sich in Abhängigkeit vom gewählten
Menü, das Sie im Hauptmenü aufgerufen hatten, bevor Sie die K-Taste gedrückt haben.
Die folgenden Beispiele zeigen Funktionsuntermenüs an, die im RUN
erscheinen.
uu
u Numerische Berechnungen (NUM) [OPTN]-[NUM]
uu
•{Abs} ... Um den {Absolutwert / Betrag} einer Zahl zu erhalten, wählen Sie die Abs-
Funktion und geben die Zahl ein.
•{Int}/{Frac} ... Um den {ganzzahligen Teil}/{Bruchteil} einer Zahl zu erhalten, wählen Sie
die Int- oder Frac-Funktion und geben die Zahl ein.
•{Rnd} ... {Rundet} den Wert, der für interne Berechnungen verwendet wird, auf die Man-
tissenlänge 10 (um der Darstellung im Antwortspeicher zu entsprechen) oder auf
die von Ihnen festgelegte Anzahl von Dezimalstellen (Fix) oder die von Ihnen festgelegte Mantissenlänge (Sci).
•{Intg} ... Um für eine vorgegebene Zahl die {größte ganze Zahl} zu erhalten, die nicht
größer als die Zahl selbst ist, wählen Sie die Intg-Funktion und geben die Zahl ein.
•{E-SYM} ... {Technik-Notation, SI-Symbole} SI-Verkleinerungs-/Vergrößerungsvorsätze
•{m}/{µ}/{n}/{p}/{f} ... {Milli (10–3)}/{Mikro (10–6)}/{Nano (10–9)}/{Piko (10
{Femto (10
•{k}/{M}/{G}/{T}/{P}/{E} ... {Kilo (103)}/{Mega (106)}/{Giga (109)}/{Tera (1012)}/
{Peta (1015)}/{Exa (1018)}
–15
)}
•
MAT-Menü
–12
)}/
uu
u Wahrscheinlichkeitsrechnung (PROB) [OPTN]-[PROB]
uu
•{x!} ... Nach der Eingabe eines Wertes zu drücken, um die {Fakultät} dieses Wertes zu
erhalten. Anzahl der {Permutationen} (ohne Wiederholung).
•{nPr}/{nCr} ... Anzahl der {Variationen}/{Kombinationen} (ohne Wiederholung).
•{Ran#}... {Generieren einer stetig gleichverteilten Pseudo-Zufallszahl (zwischen 0 und 1)}
•{P(}/{Q(}/{R(} ... Wahrscheinlichkeiten {P(t)}/{Q(t)}/{R(t)} der N(0,1)-Verteilung (Standard-
normalverteilung) über den Intervallen (-∞ ,t] , [0, |t|] bzw. [t, ∞).
•{t(} ... Wert des standardisierten Arguments {t(x)} der N(0,1)-Verteilungsfunktion zum
nichtstandardisierten Argument x.
19990401

Funktionsberechnungen
2-4-2
uu
u Hyperbolische und Areafunktionen (HYP) [OPTN]-[HYP]
uu
•{sinh}/{cosh}/{tanh} ... Hyperbolische {Sinus-}/{Cosinus-}/{Tangens-}Funktion
•{sinh–1}/{cosh–1}/{tanh–1} ... Area-Hyperbel-{Sinus-}/{Cosinus-}/{Tangens-}Funktion
uu
u Winkelsymbole, Koordinatenumrechnung, Sexagesimal-Operationen
uu
(ANGL)
•{°}/{r}/{g} ... Bezeichnet {Altgrad}/{Bogenmaß}/{Neugrad} für einen Eingabewert.
•{° ’ ”} ... Bezeichnet {Grad (Stunden), Minuten und Sekunden}, wenn ein Sexagesimalwert
eingegeben wird.
•{'DMS} ... {Wandelt einen Dezimalwert in einen Sexagesimalwert um.}
•{Pol(}/{Rec(} ... Umwandlung von {kartesischen in Polarkoordinaten}/
{Polar- in kartesische Koordinaten}
uu
u Sofortumformungen
uu
•{ ° ’ ” } ... {Wandelt einen erhaltenen Dezimalwert in einen Sexagesimalwert (Grad/
Minuten/Sekunden) um.}
•{ENG}/{ ENG} ... Verschiebt das Komma im berechneten Wert um drei Stellen nach
{rechts}/{links} und {vermindert}/{erhöht} den Exponenten um drei. Wenn Sie die
technische Schreibweise verwenden, wird das SI-Symbol ebenfalls entsprechend
geändert.
•Die Operationen des { ° ’ ” }-, {ENG}- und { ENG}-Menüs stehen nur dann zur
Ve rfügung, wenn ein Berechnungsergebnis im Display angezeigt wird.
[OPTN]-[ANGL]
kk
k Winkelmodus
kk
Um den Winkelmodus eines Eingabewertes zu ändern, drücken Sie zuerst die Tasten
K3(ANGL). Im erscheinenden Untermenü wählen Sie “°”(Altgrad), “r”(Bogenmaß)
oder “g”(Neugrad).
•Wählen Sie in der Einstellanzeige (SET UP) unbedingt “Comp” für “Mode”.
Beispiel Tastenfolge
Umwandlung von 4,25 rad u3(SET UP)cccc1(Deg)i
in Altgrad: 243,5070629 4.25K6(g)3(ANGL)c(r)w
47,3° + 82,5rad = 4774,20181°
# Sobald Sie einen Winkelmodus eingestellt
haben, bleibt dieser wirksam, bis Sie einen
anderen Winkelmodus voreinstellen.
47.3+82.5K6(g)3(ANGL)c(r)w
Der Winkelmodus bleibt auch erhalten, wenn Sie
die Stromversorgung ausschalten.
19990401

Funktionsberechnungen
2-4-3
kk
k Trigonometrische und Arkusfunktionen
kk
•Stellen Sie unbedingt den Winkelmodus korrekt ein, bevor Sie Berechnungen mit
trigonometrischen oder Arkusfunktionen ausführen.
Hinweis:
90° (Altgrad) =––– rad (Bogenmaß) = 100 Gon (Neugrad)
π
2
•Wählen Sie in der Einstellanzeige (SET UP) unbedingt “Comp” für “Mode”.
Beispiel Tastenfolge
sin 63° = 0,8910065242 u3(SET UP)cccc1(Deg)i
s63w
π
cos (–– rad) = 0,5 u3(SET UP)cccc2(Rad)i
3
c(!E(π)/d)w
tan (– 35Gon) = – 0,6128007881
u3(SET UP)cccc3(Gon)i
t-35w
2 • sin 45° × cos 65° = 0,5976724775
u3(SET UP)cccc1(Deg)i
2*s45*c65w*
1
cosec 30° =
1
= 2 1/s30w
sin30°
arcsin0,5 = 30° !s(sin–1)0.5*2w
(x = arcsin 0,5 , dann sinx = 0,5)
Hinweis:
Die Notation der Arkusfunktion lautet y=arcsin x oder y=arccos x oder y=arctan x , die verkürzte
Taschenrechnernotation ist y=sin
Kehrwertbildung verwechselt werden.
z.B. (sin x)
(arcsin x)
*1* kann weggelassen werden. *2Die Eingabe von vorangestellten Nullen ist nicht
–1
= 1 / sin x = sin
–1
= 1 / arcsin x = (sin
–1
x oder y=cos–1x oder y=tan–1x und darf nicht mit der
–1
x in Schriftform und andererseits
–1x)–1
sin x in verkürzter Taschenrechnernotation!
G
erforderlich.
19990401

Funktionsberechnungen
2-4-4
k Logarithmische und Exponentialfunktionen (Potenzen)
•Wählen Sie in der Einstellanzeige (SET UP) unbedingt “Comp” für “Mode”.
Beispiel Tastenfolge
log 1,23 (log101,23) = 8,990511144 × 10
(Zehnerlogarithmus)
In 90 (loge90) = 4,49980967 I90w
(Natürlicher Logarithmus)
1,23
10
= 16,98243652
(Berechnung der Zehnerpotenz mit dem
Exponenten 1,23. Damit ist 1,23 der
Zehnerlogarithmus von 16,98243652.)
4,5
e
= 90,0171313 !I(ex)4.5w
(Berechnung der e-Potenz mit dem Expo nenten 4,5. Damit ist 4,5 der natürliche
Logarithmus von 90,0171313.)
(–3)4 = (–3) × (– 3) × (–3) × (–3) = 81 (-3)M4w
(Potenz einer negativen Zahl)
–34 = –(3 × 3 × 3 × 3) = –81 -3M4w
(Negative Potenz einer Zahl)
1
7
123
_
(= 123
7) = 1,988647795 7!M(x )123w oder
(Wurzeln und Potenzen)
2 + 3 × 3 – 4 = 10 2+3*3!M( x ) 64-4w*
64
(Wurzeln und Potenzen)
–2
l1.23w
!l(10x)1.23w
123M(1/7)w
2+3*!(( 3 ) 64-4w oder
2+3*64M(1/3)-4w
1
oder
*1^ (xy) und x haben Vorrang vor
Multiplikationen und Divisionen.
19990401

Funktionsberechnungen
2-4-5
k Hyperbolische und Areafunktionen
•Wählen Sie in der Einstellanzeige (SET UP) unbedingt “Comp” für “Mode”.
Beispiel Tastenfolge
sinh 3,6 = 18,28545536 K6(g)2(HYP)b(sinh)3.6w
cosh 1,5 – sinh 1,5 K6(g)2(HYP)c(cosh)1.5-
= 0,2231301601 2(HYP)b(sinh)1.5w
–1,5
= e
(Anzeige: –1,5) I!-(Ans)w
(Beispiel für cosh
20
arcosh
x ± sinh x = e
= 0,7953654612
15
Bestimmung des Wertes für x,
wenn tanh(4x) = 0,88 beträgt:
artanh 0,88
x =
4
= 0,3439419141
Hinweis:
Die Notation der Areafunktion lautet y=arsinh x oder y=arcosh x oder y=artanh x , die verkürzte
Taschenrechnernotation ist y=sinh
Kehrwertbildung verwechselt werden.
z.B. (sinh x)
(arsinh x)
–1
= 1 / sinh x = sinh
–1
= 1 / arsinh x = (sinh
±x
)
K6(g)2(HYP)f(cosh–1)(20/15)w
K6(g)2(HYP)g(tanh–1)0.88/4w
–1
x oder y=cosh–1x oder y=tanh–1x und darf nicht mit der
–1
x in Schriftform und andererseits
–1x)–1
sinh x in verkürzter Taschenrechnernotation!
G
19990401

Funktionsberechnungen
2-4-6
k Andere Funktionen
•Wählen Sie in der Einstellanzeige (SET UP) unbedingt “Comp” für “Mode”.
Beispiel Tastenfolge
+ =
25
3,65028154 !x( )2+!x( )5w
(3 + i)
1,755317302
=
+0,2848487846i
!x( )(d+!a(i))w
(–3)2 = (–3) × (–3) = 9 (-3)xw
–32 = –(3 × 3) = –9 -3xw
1
–––––– = 12
11
–– – ––
34
(3!)(x
–1
)-4!)(x–1))!)(x–1)w
8! (= 1 × 2 × 3 × .... × 8) 8K6(g)1(PROB)b(x!)w
= 40320
3
Wie groß ist der Absolutwert des
Zehnerlogarithmus von
3
log | = 0,1249387366
|
4
= 42
3
?
4
3
!(
(
)
(36*42*49
)w36 × 42 × 49
K5(NUM)b(Abs)l(3/4)w
Was ist der ganzzahlige Teil K5(NUM)c(Int)-3.5w
von – 3,5? – 3
Was ist der Dezimalteil von K5(NUM)d(Frac)-3.5w
– 3,5? – 0,5
Was ist die größte ganze Zahl, K5(NUM)f(Intg)-3.5w
die – 3,5 nicht übersteigt? – 4
19990401

Funktionsberechnungen
2-4-7
k Generieren einer stetig gleichverteilten Pseudo-Zufallszahl (Ran#)
Diese Funktion generiert einzelne Pseudo-Zufallszahlen mit 10 Dezimalstellen oder eine
Zufallszahl aus einer Zufallszahlenfolge. Die Zufallszahlen sind größer als Null und kleiner
als 1.
•Eine einzelne Zufallszahl wird generiert, wenn Sie kein Argument vorgeben.
Beispiel Tastenfolge
Ran # (Generiert eine Zufallszahl.) K6(g)1(PROB)e(Ran#)w
(Mit jedem Drücken der w-Taste wird eine w
neue Zufallszahl generiert.) w
•Falls Sie ein Argument von 1 bis 9 vorgeben, wird eine Zufallszahl aus der gewählten
Zufallszahlenfolge 1 bis 9 generiert.
•Falls Sie das Argument 0 vorgeben, wird der Zufallszahlenalgorithmus neu initialisiert.*
Beispiel Tastenfolge
Ran# 1 (Generiert die erste Zufallszahl aus der 1(PROB)e(Ran#)bw
Zufallszahlen-Folge 1.)
(Generiert die zweite Zufallszahl aus der w
Zufallszahlen-Folge 1.)
Ran# 0 (Initialisiert den Algorithmus.) 1(PROB)e(Ran#)aw
Ran# 1 (Generiert erneut die erste Zufallszahl der 1(PROB)e(Ran#)bw
Zufallszahlen-Folge 1.) usw.
1
*1Durch Übergang zu einer anderen ZZ-Folge
oder durch das Generieren einer vollständig
anderen Zufallszahl (ohne ein Argument) wird
der Zufallszahlen-Algorithmus initialisiert.
19990401

k Koordinatenumwandlung
uu
u Kartesische Koordinaten
uu
Funktionsberechnungen
2-4-8
uu
u Polarkoordinaten
uu
•In Polarkoordinaten wird der Winkel θ innerhalb des Hauptwinkelbereichs von –180°<
< 180° berechnet und angezeigt (im Bogenmaß oder Neugrad entsprechend).
•Wählen Sie in der Einstellanzeige (SET UP) unbedingt “Comp” für “Mode”.
Beispiel Tastenfolge
Berechnen Sie r und θ° für x = 14 und y = 20,7 u3(SET UP)cccc1(Deg)i
1 24,989 → 24,98979792 (r)
2 55,928 → 55,92839019 (θ)
K6(g)3(ANGL)g(Pol()
14,20.7)w
Berechnen Sie x und y für r = 25 und θ = 56° u3(SET UP)cccc1(Deg)i
1 13,979 → 13,97982259 (x)
2 20,725 → 20,72593931 (y)
K6(g)3(ANGL)h(Rec()
25,56)w
θ
19990401

Funktionsberechnungen
2-4-9
k Variation (Permutation) und Kombination
uu
u Variation (Permutation)
uu
ohne Wiederholung ohne Wiederholung
n! n!
nPr = ––––– nCr = –––––––
(n – r)! r! (n – r)!
•Wählen Sie in der Einstellanzeige (SET UP) unbedingt “Comp” für “Mode”.
○○○○○
Beispiel Berechnung der möglichen Anzahl der Variationen, wenn 4 unter-
schiedliche Elemente aus 10 möglichen ausgewählt werden.
Formel Tastenfolge
10P4 = 5040 10K6(g)1(PROB)c(nPr)4w
○○○○○
Beispiel Berechnung der möglichen Anzahl der Kombinationen, wenn 4 unter-
schiedliche Elemente aus 10 möglichen ausgewählt werden.
Formel Tastenfolge
uu
u Kombination
uu
10C4 = 210 10K6(g)1(PROB)d(nCr)4w
Hinweis: Die eigentliche Permutation ist n! , d.h. n!=nPr mit r=n.
nCr ist der Binomialkoeffizient "n über r".
19990401

Funktionsberechnungen
2-4-10
kk
k Gemeine Brüche (gemischte Zahlen)
kk
•Unechte Brüche werden mit der Ganzzahl, gefolgt von Zähler und Nenner dargestellt.
•Wählen Sie in der Einstellanzeige (SET UP) unbedingt “Comp” für “Mode”.
Beispiel Tastenfolge
2113
(Anzeige: 3{13{20) 2$5+3$1$4w
–– + 3 –– = 3 –––
5420
= 3,65 $(Umwandlung in einen Dezimalbruch)
$(Umwandlung in einen gemeinen Bruch)
11
––––– + –––––
2578 4572
= 6,066202547 × 10
–4
1$2578+1$4572w
(Anzeige: 6,066202547E–04*1)
(Anzeigeformat Norm 1)
1
–– × 0,5 = 0,25*
2
1,5 + 2,3i = 1–– + 2––i
1
= ––
4
13
210
2
1$2*.5w
$
1.5+2.3!a(i)w
3
Anzeige:
$$*
1{1{2
+2{3{10i
15
–––––– = 1––
11 7
–– + ––
34
(Anzeige: 1{5{7)
1$(1$3+1$4)w*
4
Hinweis: Gemischte Zahlen dürfen nicht mit einer Multiplikation (ohne Multiplikationszeichen)
verwechselt werden.
*1Wenn die Gesamtanzahl der Zeichen für die
ganze Zahl, Zähler, Nenner und Begrenzungszeichen 10 übersteigt, dann wird der
eingegebene Bruch automatisch im
Dezimalzahlenformat angezeigt.
2
*
Berechnungen, die sowohl gemeine Brüche
als auch Dezimalzahlen enthalten, werden im
Dezimalzahlenformat ausgeführt.
3
Wenn Sie die $-Taste einmal drücken, um das
*
Dezimalzahlenformat einer komplexen Zahl in
einen Bruch umzuwandeln, werden auf verschiedenen Zeilen zuerst der Realteil und dann
der Imaginärteil angezeigt.
4
*
Sie können auch Bruchterme innerhalb des
Zählers oder Nenners eines Bruches verwenden, indem Sie den Zähler oder Nenner in
Klammern setzen.
19990401

Funktionsberechnungen
2-4-11
k Berechnungen in technischer Notation (SI-Symbole)
Unter Verwendung des Untermenüs für die technische Schreibweise können Sie die SISymbole (Internationales Einheitensystem) eingeben.
•Wählen Sie in der Einstellanzeige (SET UP) unbedingt “Comp” für “Mode”.
Beispiel Tastenfolge
u3(SET UP)cccccccccc
4(Eng)i
999k (Kilo) + 25k (Kilo) 999K5(NUM)g(E-SYM)g(k)+255(NUM)
= 1,024M (Mega) g(E-SYM)g(k)w
9 ÷ 10 = 0,9 = 900m (Milli) 9/10w
= 0,9 K6(g)6(g)6(g)3( ENG)*
= 0,0009k (Kilo) 3( ENG)*
= 0,9 2(ENG)*
= 900m 2(ENG)*
1
1
2
2
*1Wandelt den angezeigten Wert in die nächst
höhere SI-Einheit um, indem der Dezimalpunkt um drei Stellen nach links verschoben
wird.
*2Wandelt den angezeigten Wert in die nächst
niedrigere SI-Einheit um, indem der Dezimalpunkt um drei Stellen nach rechts verschoben
wird.
19990401

Numerische Berechnungen
2-5-1
2-5 Numerische Berechnungen
Nachfolgend sind die Befehle beschrieben, die in den Untermenüs zur Verfügung stehen, die
Sie für die Berechnung von 1. und 2. Ableitungen, von bestimmten Integralen, von Partialsummen für Zahlenreihen (Σ-Berechnungen), für die Maximal-/Minimalwert- und Nullstellenberechnungen verwenden können.
Wenn das Optionsmenü im Display angezeigt wird, drücken Sie die 4(CALC)-Taste, um
das Funktionsanalysemenü anzuzeigen. Die Befehle dieses Menüs werden verwendet,
wenn bestimmte Fragestellungen untersucht werden sollen.
•{d/dx}/{d2/dx2}/{∫dx}/{Σ}/{FMin}/{FMax}/{Solve} ... numerische Berechnung der {1. Ab-
leitung}/{2. Ableitung}/{bestimmtes Integral}/{Partialsumme, Σ(Sigma)-Berechnung}/
{Minimalwert}/{Maximalwert}/{Nullstelle}
Nullstellenberechnung
Nachfolgend ist die Syntax für die Verwendung des Solve-Befehls in einem Programm
aufgeführt.
Solve( f(x), n, a, b)(a: untere Grenze für x, b: obere Grenze für x, n: Startwert zur
Nullstellensuche von f(x))
•Es gibt zwei unterschiedliche Methoden zur Eingabe der Nullstellengleichung:
direkte Eingabe eines Formelterms oder Eingabe mittels Koeffiziententabelle.
Bei der direkten Eingabe eines Formelterms (die hier beschriebene Methode), nutzen
Sie den Funktionsterm zur Berechnung der Funktionswerte. Diese Art der Eingabe ist
identisch mit der Eingabe, die Sie mit dem Solve-Befehl im PRGM-Menü verwenden
können.
Die Eingabe mittels Koeffiziententabelle wird im EQUA-Menü verwendet. Diese Eingabemethode wird in den meisten Fällen praktiziert und empfohlen.
Es kommt zu einer Fehlermeldung (Iteration ERROR), wenn das Iterationsverfahren
zur Nullstellenbestimmung nicht konvergiert und keine Nullstelle gefunden wird.
19990401

Numerische Berechnungen
2-5-2
k Ableitungsberechnungen (1. Ableitung) [OPTN]-[CALC]-[d
Um eine 1. Ableitung numerisch zu berechnen, öffnen Sie zuerst das Funktionsanalysemenü
und geben danach die in der nachfolgenden Reihenfolge gezeigten Größen ein.
K4(CALC)b(d/dx) f(x),a,tol)
d
d/dx ( f (x), a) ⇒ ––– f (a) mit x = a .
dx
Die Berechnung der Ableitung wird wie üblich über den Differenzenquotienten definiert:
f '(a) = lim ––––––––––––– (Grenzwert des Differenzenquotienten)
In dieser Definition wird ein
f (a + Ax) – f (a)
AxAx→0
unendlich kleiner
ersetzt. Das Ergebnis liegt in der Nähe von f ' (a) (sofern keine Unstetigkeit vorliegt) und wird
wie folgt berechnet:
f (a + Ax) – f (a)
f '(a) –––––––––––––
Ax
Um die bestmögliche Genauigkeit zu erhalten, verwendet dieser Rechner die Zentraldifferenz f (a + Ax / 2) – f (a – Ax / 2), um eine numerische Ableitung zu ermitteln.
Verwendung der Ableitungsberechnung in einer Grafikfunktion
• Wenn der Ableitungsbefehl in einer Grafikfunktion verwendet wird, kann durch Weg-
lassen des Toleranzwertes (tol) die Ableitungsberechnung in der Grafikdarstellung vereinfacht werden. In einem solchen Falle wird auf die Genauigkeit verzichtet, um ein
schnelleres Zeichnen zu ermöglichen. Wird der Toleranzwert vorgegeben, erfolgt das
Zeichnen der Grafik mit der gleichen Genauigkeit, wie Sie es bei normalen Ableitungsberechnungen gewöhnt sind.
• Sie können auch die Eingabe der Ableitungsstellen weglassen, indem Sie die folgende
Syntax für die Grafik der 1. Ableitung nutzen: z.B. Y2 = d/dx(Y1). In diesem Fall wird der
Wert der X-Variablen als variable Ableitungsstelle verwendet.
(a: Stelle, an der Sie die Ableitung bestimmen
möchten,
Wert durch einen
tol: To leranz)
ausreichend kleinen
Wer t Ax
/dx]
19990401

Numerische Berechnungen
2-5-3
○○○○○
Beispiel Zu bestimmen ist die 1. Abeitung für die Funktion y = x3 + 4x2 + x – 6 an
der Stelle x = 3 mit einer Genauigkeit von “tol” = 1E – 5 .
Geben Sie die Funktion f(x) ein.
AK4(CALC)b(d/dx)vMd+evx+v-g,
Geben Sie die Stelle x = a ein, an der Sie die 1. Ableitung bestimmen möchten.
d,
Geben Sie die Genauigkeitsschranke ein.
bE-f)
w
#In der Funktion f(x) kann nur X als die
Va riable des Funktionsterms verwendet
werden. Andere Variablen (A bis Z, r,
werden wie Konstanten behandelt und der
aktuell diesen Variablen zugeordnete Wert
wird während der Berechnung verwendet.
# Die Eingabe des Toleranzwertes (tol) und der
schließenden Klammern kann weggelassen
werden. Falls Sie den Toleranzwert (tol)
weglassen, verwendet der Rechner
automatisch den Wert 1
E-10 für tol.
θ
)
# Vorgegeben werden kann ein Toleranzwert
(tol) von 1
Fehlermeldung (Iteration ERROR), wenn kein
Ergebnis gefunden werden kann, das die vorgegebene Genauigkeit (Toleranz) besitzt.
#Unstetigkeitsstellen oder Intervalle mit sehr
steilen Anstiegen können die Genauigkeit beeinträchtigen oder sogar einen Berechnungsfehler verursachen.
19990401
E-14 oder größer. Es kommt zu einer

Numerische Berechnungen
2-5-4
u Rechenregeln mit Ableitungen (1. Ableitung) und deren Anwendung
•Ableitungen können miteinander addiert, subtrahiert, multipliziert und dividiert werden.
dd
Mit der Symbolik für x = a können Sie daher
––– f (a) = f '(a), ––– g (a) = g'(a)
dx dx
die Terme berechnen.
f '(a) + g'(a), f '(a) × g'(a) usw.
•Die Ableitungsbefehle und damit die berechneten Ableitungen können sofort in Additionen, Subtraktionen, Multiplikationen, Divisionen und in Funktionen verwendet werden.
2 × f '(a), log( f '(a)) usw.
• Funktionsterme können in jedem der Argumente ( f (x), a, tol) des Differenzialoperators
verwendet werden.
d
––– (sinx + cosx, sin0.5, 1E - 8) usw.
dx
#Achten Sie darauf, dass ein Ableitungsbefehl
für die 1. oder 2. Ableitung, ein Integrations-,
Σ-, Maximalwert-/Minimalwert- oder Nullstellenberechnungsbefehl (Solve-Befehl) nicht
innerhalb eines Ableitungsbefehls selbst verwendet werden kann.
#Das Drücken der A-Taste während der Be-
rechnung einer Ableitung (wenn der Cursor nicht
im Display angezeigt wird) unterbricht die Berechnung.
#Verwenden Sie immer das Bogenmaß (Rad-
Modus) als Winkelmodus für die Ableitungsberechnung bei trigonometrischen Funktionen.
19990401

Numerische Berechnungen
2-5-5
kk
k Berechnung zweiter Ableitungen [OPTN]-[CALC]-[d
kk
Nachdem das Funktionsanalysemenü geöffnet wurde, können Sie 2. Ableitungen unter
Verwendung des folgenden Eingabe-Formates numerisch berechnen.
K4(CALC)c(d2/dx2) f(x),a,tol)
(a: Ableitungsstelle, tol: Toleranz)
2
d
––– (f (x), a) ⇒ ––– f (a) mit x = a .
2
dx
2
d
2
dx
Die Berechnung zweiter Ableitungen erfolgt näherungsweise unter Verwendung der folgenden Differenzenformel der zweiten Ordnung, die auf der Newtonschen Polynom-Interpolation
beruht.
2 f(a + 3h) – 27 f(a + 2h) + 270 f (a + h) – 490 f(a)+270 f (a – h) – 27 f(a – 2h) +2 f(a – 3h)
= –––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––
f''(a)
180h
2
In dieser Formel werden “ausreichend kleine Zuwächse von h” verwendet, um einen
Näherungswert zu erhalten, der sich an f ”(a) annähert.
○○○○○
Beispiel Zu bestimmen ist die zweite Ableitung der Funktion y = x3 + 4x2 + x – 6
an der Stelle x = 3.
Hier soll eine Genauigkeit von tol = 1E – 5 verwendet werden.
Geben Sie die Funktion f(x) ein.
AK4(CALC)c(d2/dx2) vMd+
evx+v-g,
2
/dx2]
Geben Sie 3 als die Stelle a ein, an der die 2. Ableitung berechnet werden soll.
d,
Geben Sie die Genauigkeitsschranke (Toleranzwert) ein.
bE-f)
w
#In der Funktion f(x) kann nur X als die Variable
des Funktionsterms verwendet werden.
Andere Variablen (A bis Z, r,
Konstanten behandelt und der aktuell diesen
Va riablen zugeordnete Wert wird während der
Berechnung verwendet.
θ
) werden wie
#Die Eingabe des Toleranzwertes (tol) und der
schließenden Klammer kann weggelassen
werden.
#Unstetigkeitsstellen oder Intervalle mit sehr
steilen Anstiegen können die Genauigkeit beeinträchtigen oder sogar einen Berechnungsfehler
verursachen.
19990401

Numerische Berechnungen
2-5-6
u Rechenregeln mit Ableitungen (zweite Ableitung) und deren Anwendung
•Arithmetische Operationen können unter Verwendung von berechneten zweiten
Ableitungen ausgeführt werden.
2
d
Mit der Symbolik für x = a können Sie daher
––– f (a) = f ''(a), ––– g (a) = g''(a)
2
dx
die Terme f ''(a) + g''(a), f ''(a) × g''(a) usw. berechnen.
•Das Ergebnis der Berechnung zweiter Ableitungen kann in einer nachfolgenden
arithmetischen oder in einer Funktionsberechnung verwendet werden.
2 × f ''(a), log( f ''(a) ) usw.
• Funktionen können innerhalb der Argumente ( f(x), a, tol) des Differenzialoperators
verwendet werden.
2
d
––– (sin x + cos x, sin 0.5, 1E - 8) usw.
2
dx
2
d
2
dx
#Achten Sie darauf, dass ein Ableitungsbefehl
für die 1. oder 2. Ableitung, ein Integrations-,
Σ-, Maximalwert-/Minimalwert- oder Nullstellenberechnungbefehl (Solve-Befehl) nicht
innerhalb eines Ableitungsbefehls für die 2.
Ableitung selbst verwendet werden kann.
# Vorgegeben werden kann ein Toleranzwert
(tol) von 1
einer Fehlermeldung (Iteration ERROR),
wenn kein Ergebnis gefunden werden kann,
das die vorgegebene Genauigkeit besitzt.
E-14 oder größer. Es kommt zu
#Sie können die Berechnung einer 2. Ableitung
durch Drücken der A-Taste unterbrechen.
#Verwenden Sie immer das Bogenmaß (Rad-
Modus) als Winkelmodus, wenn Sie 2. Ableitungen für trigonometrische Funktinen berechnen.
# Zur die Verwendung einer 2. Ableitung in einer
grafischen Darstellung (Grafikfunktion) siehe
Seite 2-5-2.
19990401

Numerische Berechnungen
kk
k Integralrechnung (bestimmte Integrale) [OPTN]-[CALC]-[
kk
Um ein bestimmtes Integral zu berechnen, öffnen Sie zuerst das Funktionsanalysemenü und
geben danach die in der nachfolgenden Reihenfolge gezeigten Größen ein.
K4(CALC)d (∫dx) f(x) , a , b , tol )
2-5-7
(a: Anfangspunkt, b: Endpunkt, tol: Tol e ranz)
∫
dx]
( f(x), a, b, tol) ⇒
∫
Wie in der obigen Abbildung zu erkennen ist, werden die bestimmten Integrale ermittelt, indem die vorzeichenbehafteten Flächenanteile zwischen dem Graphen y = f (x) und der x-
Achse über dem Intervall von a bis b aufsummiert werden. Gilt f (x) > 0 für a < x < b, dann
liegt die in der Abbildung dargestellte Situation vor. Damit wird der Flächeninhalt des in der
Abbildung dargestellten Gebietes als bestimmtes Intergral berechnet.
∫
a
b
f(x)dx
Berechnet wird die Fläche
b
f(x)dx.
∫
a
# Falls f (x) < 0 für a < x < b gilt, ergibt das
bestimmte Integral zur Flächenberechnung
zunächst einen negativen Wert, d.h.
Flächeninhalt = Integralwert × (– 1).
# Vgl. auch S. 7-1-12: Integral-Befehl (CAS-
Menü: unbestimmtes Integral)
19990401

Numerische Berechnungen
2-5-8
○○○○○
Beispiel Zu berechnen ist das bestimmte Integral von x = 1 bis x = 5 für die
nachfolgend angegebene Funktion. Die Toleranz ist “tol” = 1 E – 4.
5
(2x2 + 3x + 4) dx
∫
1
Geben Sie den Integranden, d.h. die Funktion f (x), ein.
AK4(CALC)d(∫dx)cvx+dv+e,
Geben Sie die Integrationsgrenzen, d.h.den Anfangspunkt und den Endpunkt, ein.
b,f,
Geben Sie die Genauigkeitsschranke, d.h.den Toleranzwert, ein.
bE-e)
w
uu
u Rechenregeln mit bestimmten Integralen und deren Anwendung
uu
•Integrale können hier mit anderen Rechenoperationen (Additionen, Subtraktionen,
Multiplikationen und Divisionen) kombiniert und damit mehrfach benutzt werden.
b
f(x) dx +
∫
a
d
g(x) dx usw.
∫
c
•Ergebnisse der numerischen Integration können in Additionen, Subtraktionen,
Multiplikationen, Divisionen und in anderen Funktionen verwendet werden.
b
2 ×
f(x) dx oder log (
∫
a
b
f(x) dx) usw.
∫
a
• Funktionsterme können in allen Argumenten ( f(x), a, b, tol) eines Integral-Befehls
verwendet werden.
cos 0,5
(sin x + cos x) dx = ∫(sin x + cos x, sin 0,5, cos 0,5, 1E - 4)
∫
sin 0,5
#In der Funktion f(x) kann nur X als die
Va riable des Funktionsterms verwendet
werden. Andere Variablen (A bis Z,
werden wie Konstanten behandelt, und der
aktuell diesen Variablen zugeordnete Wert
wird während der Berechnung verwendet.
#Die Eingabe von “tol” und der schließenden
Klammern kann weggelassen werden. Falls
Sie “tol,” weglassen, verwendet der Rechner
automatische den tol-Vorgabewert von 1
r,
θ
)
E-5.
# Für Integrationen kann eine lange Zeitspanne bis
zur Beendigung benötigt werden.
#Achten Sie darauf, dass ein Ableitungsbefehl für
die 1. oder 2. Ableitung, ein Integrations-, Σ-,
Maximalwert-/Minimalwert- oder Nullstellenberechnungbefehl (Solve-Befehl) nicht
innerhalb eines Integrations-Befehls verwendet
werden kann.
19990401

Positiver
Anteil (S
2-5-9
)
1
Negativer Anteil (S2)
Numerische Berechnungen
Achten Sie bei einer Flächeninhaltsberechnung auf folgende Punkte, um richtige Integrationsergebnisse zu erhalten.
(1) Wenn Funktionen mit wechselndem Vorzeichen integriert werden, führen Sie die Berech-
nung für einzelne Intervalle mit vorzeichenkonstanten Funktionswerten aus oder integrieren zunächst über alle positiven Flächenanteile und dann über alle negativen Flächenanteile. Anschließend werden die Teilergebnisse zusammengefaßt: z.B. S = S1 - S2 .
b
f(x)dx =
∫
a
Positiver Anteil
(2) Wenn viele Oszillationen innerhalb des Integrationsbereiches zu großen Abweichungen
im Integrationsergebnis führen können, berechnen Sie die Flächenanteile stückweise (die
Abschnitte mit großen Oszillationen in kleinere Abschnitte zerlegen). Fassen Sie abschließend die Teilergebnisse zusammen.
b
f(x)dx =
∫
a
(3) Das Integrationsergebnis Null bedeutet nicht zwangsläufig, dass der Integrand identisch
Null gewesen ist.
#Durch Drücken der A-Taste während der
Berechnung eines Integrals (während der
Cursor nicht im Display angezeigt wird) können Sie die Rechnung unterbrechen.
#Verwenden Sie immer das Bogenmaß (Rad-
Modus) als Winkelmodus, wenn Sie trigonometrische Funktionen integrieren.
∫
c
f(x)dx + (–
∫
a
x1
f(x)dx +
a
x2
∫
x1
# Es kommt zu einer Fehlermeldung (Iteration
ERROR), wenn kein Integrationsergebnis
gefunden werden kann, das die geforderte
Genauigkeit (Toleranzwert) aufweist.
b
f(x)dx)
∫
c
(S1)
Negativer Anteil
f(x)dx +.....+
b
∫
x4
f(x)dx
(S2)
19990401

Numerische Berechnungen
2-5-10
kk
k Σ-Berechnungen (Partialsummen einer Zahlenfolge) [OPTN]-[CALC]-[Σ ]
kk
Um Σ-Berechnungen auszuführen, öffnen Sie zuerst das Funktionsanalysemenü und geben
danach die in der nachfolgenden Reihenfolge gezeigten Größen ein:
K4(CALC)e(Σ) ak , k , α , β , n )
○○○○○
(ak , k, α, β, n) = Σ ak = aα + a
Σ
β
k = α
+n
α
+ . . . + a
(Anfangsindex
β
α
, Endindex β, Schrittweite n)
Beispiel Folgende Partialsumme ist zu berechnen:
6
(k2 – 3k + 5)
Σ
k = 2
Hinweis: Ve rwenden Sie als Schrittweite n = 1 (Standardschrittweite).
AK4(CALC)e(Σ)a,(K)x
-da,(K)+f,
a,(K),c,g,b)w
#Sie können nur eine Variable (k) in der Funktion
ak = f (k) für die Eingabefolge (ak) verwenden.
#Geben Sie nur ganze Zahlen für den Anfangs-
index (
α
) und den Endindex (β) der Folge (ak)
ein.
#Sie können die Eingabe von
schließenden Klammer weglassen.
Wenn Sie
automatisch
19990401
n weglassen, wird in der Summation
n = 1 verwendet.
n und der

Numerische Berechnungen
2-5-11
u Rechenregeln mit Partialsummen und deren Anwendungen
•Arithmetische Operationen unter Verwendung der Σ-Berechnungsbefehle
nn
Σ-Berechnung:
Sn = Σ ak, Tn = Σ bk
k = 1 k = 1
Mögliche Operationen: Sn + Tn, Sn – Tn usw.
•Arithmetische und Funktionsoperationen, die die Ergebnisse der Σ-Berechnung
verwenden:
2 × Sn oder log (Sn) usw.
• Funktionsoperationen in den Argumenten (ak, k) der Σ-Berechnungsterme:
Σ (sink, k, 1, 5) usw.
#Achten Sie darauf, dass ein Ableitungsbefehl
für die 1. oder 2. Ableitung, ein Integrations-,
Σ-, Maximalwert-/Minimalwert- oder Nullstellenberechnungbefehl (Solve-Befehl) nicht
innerhalb eines Σ-Berechnungsbefehls
verwendet werden kann.
#Achten Sie darauf, dass der im Endindex
verwendete Wert größer als der im Anfangsindex
α
verwendete Wert ist. Anderenfalls
kommt es zu einer Fehlermeldung.
#Um eine laufende Σ-Berechnung (wenn der
Cursor nicht im Display angezeigt wird) zu
unterbrechen, drücken Sie die A-Taste.
19990401
β

Numerische Berechnungen
2-5-12
kk
k Maximal/Minimalwertrechnungen [OPTN]-[CALC]-[FMin]/[FMax]
kk
Nach den Öffnen des Funktionsanalysenmenüs können Sie Maximalwert- / Minimalwertberechnungen unter Verwendung der nachfolgenden Formate eingeben und so die Punkte
für das Maximum oder Minimum einer Funktion innerhalb des Intervalls a < x < b berechnen.
(a: Anfangspunkt des Intervalls, b: Endpunkt des Intervalls, n: Genauigkeit (n = 1 bis 9))
uu
uMinimalwert
uu
K4(CALC)f(FMin) f(x) , a , b , n )
uu
uMaximalwert
uu
K4(CALC)g(FMax) f(x), a , b , n )
○○○○○
Beispiel 1 Für die Funktion y = x
2
– 4x + 9 ist der Minimalwert innerhalb des
durch den Anfangspunkt a = 0 und den Endpunkt b = 3 festgelegten
Intervalls zu bestimmen (Genauigkeitsparameter n = 6).
Geben Sie die Funktion f(x) ein.
AK4(CALC)f(FMin) vx-ev+j,
Geben Sie die Grenzen des Such-Intervalls ein: a = 0, b = 3.
a,d,
Geben Sie den Genauigkeitsparameter n = 6 ein.
g)
w
Hinweis:
Das Ergebnis wird als ListAns-Display angezeigt und im [List]-[Ans]-Speicher einge tragen, siehe Seite 2-2-5 "Antwortspeicherfunktion". Das erste Listenelement ist das
Argument (Minimumstelle), das zweite der Funktionswert (Minimalwert).
19990401

Numerische Berechnungen
2-5-13
○○○○○
Beispiel 2 Für die Funktion y = –x
2
+ 2x + 2 ist der Maximalwert innerhalb des
durch den Anfangspunkt a = 0 und den Endpunkt b = 3 festgelegten
Intervalls zu bestimmen (Genauigkeitsparameter n = 6).
Geben Sie die Funktion f(x) ein.
AK4(CALC)g(FMax) -vx+cv+c,
Geben Sie die Grenzen des Such-Intervalls ein: a = 0, b = 3.
a,d,
Geben Sie den Genauigkeitsparameter n = 6 ein.
g)
w
Hinweis:
Das Ergebnis wird als ListAns-Display angezeigt und im [List]-[Ans]-Speicher einge tragen, siehe Seite 2-2-5 "Antwortspeicherfunktion". Das erste Listenelement ist das
Argument (Maximumstelle), das zweite der Funktionswert (Maximalwert).
#In der Funktion f(x) kann nur X als die
Va riable des Funktionsterms verwendet
werden. Andere Variablen (A bis Z,
werden wie Konstanten behandelt und der
aktuell diesen Variablen zugeordnete Wert
wird während der Berechnung verwendet.
#Sie können die Eingabe von
schließenden Klammer weglassen.
#Unstetigkeitsstellen oder Intervalle mit sehr
steilen Anstiegen können die Genauigkeit
beeinträchtigen und sogar einen Berechnungsfehler verursachen.
#Achten Sie darauf, dass ein Ableitungsbefehl
für die 1. oder 2. Ableitung, ein Integrations-,
Σ-, Maximalwert-/Minimalwert- oder Nullstellenberechnungbefehl (Solve-Befehl) nicht
innerhalb eines Maximalwert-/MinimalwertBefehls verwendet werden kann.
r,
n und der
θ
)
#Durch Eingabe eines größeren Wertes für
die Genauigkeit der Berechnung erhöht, wobei
jedoch die für die Ausführung der Berechnung
erforderliche Zeitspanne zunimmt.
#Der für den Endpunkt des Intervalls (
eingegeben Wert muss größer sein als der für
den Anfangspunkt (
Anderenfalls kommt es zu einer Fehlermeldung.
#Sie können die Ausführung einer Maximal/wert-
Minimalwertrechnung durch Drücken der A-
Taste unterbrechen.
#Sie können eine ganze Zahl im Bereich von 1
bis 9 als Wert für
Wertes außerhalb dieses Bereichs führt zu einer
Fehlermeldung.
19990401
a) eingegebene Wert.
n eingeben. Die Eingabe eines
b)
n wird

Rechnen mit komplexen Zahlen
2-6-1
2-6 Rechnen mit komplexen Zahlen
Mit komplexen Zahlen können Sie Additionen, Subtraktionen, Multiplikationen, Divisionen,
Klammerrechnungen, Funktionswerteberechnungen und Speicherrechnungen ausführen,
genau wie in den auf den Seiten 2-1-1 und 2-4-6 beschriebenen manuellen Berechnungen.
Sie können den Darstellungsmodus für komplexe Zahlen festlegen, indem Sie in der Einstellanzeige (SET UP) die Position für “Complex Mode” eine der folgenden Einstellungen auswählen.
• {Real} ... Berechnungen nur im reellen Zahlenbereich*
1
• {a+bi} ... Berechnungen mit komplexen Zahlen und Anzeige der Ergebnisse in
arithmetischer Darstellung (kartesische Koordinaten)
• {re^
θ
i} ... Berechnungen mit komplexen Zahlen und Anzeige der Ergebnisse in
exponentieller Darstellung (Polarkoordinaten)*
2
Drücken Sie die Tasten K3(CPLX), um das Untermenü für das Rechnen mit komplexen
Zahlen anzuzeigen, welches die folgenden Positionen enthält.
• {Abs}/{Arg} ... Berechnung des {Absolutwertes (Betrages)}/{Arguments (Winkels)}
• {Conjg} ... {Berechnung der konjugiert komplexen Zahl}
• {ReP}/{ImP} ... Berechnung des {Realteils}/{Imaginärteils} einer komplexen Zahl
• {'re^
θ
i}/{'a+bi} ... Umwandlung des Ergebnisses in {Polarkoordinaten}/{kartesische
Koordinaten}
*1Falls in einer Eingabegröße ein Imaginärteil
als Argument vorhanden ist, wird die Berechnung in komplexen Zahlen ausgeführt, wobei
das Ergebnis in kartesischen Koordinaten
angezeigt wird.
Beispiel: (Komplexer Hauptwert von ln 2i )
ln 2i = 0,6931471806 + 1,570796327i
Jedoch:
ln 2i + ln (- 2 ) = (Non-Real ERROR)
2
*
Die Form des angezeigten Hauptwinkelbereiches für
θ
der Einstellanzeige (SET UP) unter “Angle”
eingestellt wurde:
hängt vom Winkelmodus ab, der in
• Deg ... –180 <
• Rad ... – π <
• Gon ... –200 <
θ
θ
< π
θ
< 180
< 200
# Die im Real-Modus bzw. im a+bi / re^θi -Modus
erhaltenen Ergebnisse sind beim allgemeinen
Potenzieren mit (x
und y = m/n rational ist, wobei n eine ungerade
Zahl darstellt:
Beispiel:
x
3
(- 8) = – 2 (reelle Zahl) oder
Im ersten Fall handelt es sich um die
(komplexe) Nebenwurzel (mit Imaginärteil 0):
x
3
Im zweiten Fall handelt es sich um die
(komplexe) Hauptwurzel:
# Vgl. auch S. 7-1-10: cExpand-Befehl (CAS-
Menü)
(- 8) = – 2 (reelle Zahl)
x
3
(- 8) = 1 + 1,732050808i(a+bi / re^ θi)
y
) unterschiedlich, wenn x < 0
= 1 + 1,732050808i (a+bi
/ re^θi)
19990401

Rechnen mit komplexen Zahlen
2-6-2
kk
k Absolutwert und Argument [OPTN]-[CPLX]-[Abs]/[Arg]
kk
Der Rechner interpretiert jede komplexe Zahl in der Form Z = a + bi als Punkt oder Koordinatenpaar (a, b) in der der Gauß'schen Zahlenebene und berechnet den Absolutwert Z und
das Argument (arg Z) mit Hilfe des Koordinatenpaares (a, b).
○○○○○
Beispiel Zu berechnen sind der Absolutwert (r) und das Argument (θ) für die
komplexe Zahl 3 + 4i, wobei der Winkelmodus auf Altgrad eingestellt
werden soll.
Imaginäre Achse
reelle Achse
AK3(CPLX)b(Abs)
(d+e!a(i))w
(Berechnung des Absolutwertes (Betrages))
AK3(CPLX)c(Arg)
(d+e!a(i))w
(Berechnung des Arguments (Winkels))
#Das Ergebnis der Argumentberechnung
unterscheidet sich in Abhängigkeit vom
aktuell eingestellten Winkelmodus (Altgrad,
Bogenmaß, Neugrad).
19990401

Rechnen mit komplexen Zahlen
2-6-3
kk
k Konjugiert komplexe Zahlen [OPTN]-[CPLX]-[Conjg]
kk
Eine komplexe Zahl der Gestalt a + bi wird in die konjugiert komplexe Zahl der Gestalt
a – bi umgeformt.
○○○○○
Beispiel Zu berechnen ist die konjugiert komplexe Zahl zur komplexen Zahl
2 + 4i.
AK3(CPLX)d(Conjg)
(c+e!a(i))w
kk
k Berechnung des Real- und des Imaginärteils
kk
Verwenden Sie den folgenden Vorgang, um den Realteil a oder den Imaginärteil b einer
komplexen Zahl der Gestalt a + bi zu berechnen.
○○○○○
Beispiel Zu berechnen sind der Real- und der Imaginärteil der komplexen Zahl
2 + 5i
AK3(CPLX)e(ReP)
(c+f!a(i))w
(Berechnung des Realteils)
[OPTN]-[CPLX]-[ReP]/[lmP]
AK3(CPLX)f(ImP)
(c+f!a(i))w
(Berechnung des Imaginärteils)
Hinweis: Beachten Sie, dass der Realteil und Imaginärteil stets reelle Zahlen sind.
#Der Ein/Ausgabebereich für komplexe Zahlen
umfaßt für jede Koordinate 10 Stellen für die
Mantisse
#Wenn eine komplexe Zahl mehr als 21 Stellen
# Falls der Realteil oder der Imaginärteil einer
und zwei Stellen für den Exponenten.
einnimmt, werden der Realteil und der Imaginärteil in unterschiedlichen Zeilen des Displays angezeigt.
komplexen Zahl gleich Null sind, wird dieser
Te il bei arithmetischer Darstellung nicht angezeigt.
# 18 Byte des Speichers werden verwendet, wenn
Sie eine komplexe Zahl einer Variablen
zuordnen.
#Die folgenden Funktionen können auf
komplexen Zahlen angewendet werden:
, x2, x–1, ^(x
cos, tan, sin
sinh
Int, Frac, Rnd, Intg, Fix, Sci, ENG, ENG, ° ’ ”,
° ’ ”, a b/c, d/c
19990401
y
3
),
, x, In, log, 10x, ex, sin,
–1
, cos–1, tan–1, sinh, cosh, tanh,
–1
, cosh–1, tanh
–1

Rechnen mit komplexen Zahlen
2-6-4
kk
k Umrechnung zwischen exponentieller und arithmetischer Darstellung
kk
[OPTN]-[CPLX]-[
''
're^
''
Verwenden Sie den folgenden Vorgang, um eine in arithmetischer Darstellung angezeigte
komplexe Zahl in die exponentielle Darstellung umzurechnen bzw. umgekehrt.
○○○○○
Beispiel Die arithmetische Darstellung der komplexen Zahl 1 + 3
i ist in die
exponentielle Darstellung umzuformen.
Ab+(!x( )d)! a(i)
K3(CPLX)g('re^θi)w
θ
i]
19990401

Berechnungen mit Binär-, Oktal-, Dezimal- und Hexadezimalzahlen
2-7-1
2-7 Berechnungen mit Binär-, Oktal-, Dezimal-
und Hexadezimalzahlen
Sie können das RUN • MAT-Menü mit der Binär-, Oktal-, Dezimal- oder Hexadezimaleinstellung (SET UP) verwenden, um Berechnungen mit Binär-, Oktal-, Dezimal- oder Hexadezimalzahlen auszuführen. Sie können auch Umrechnungen zwischen den Zahlensystemen und logische Operationen ausführen.
•Sie können die höheren mathematischen Funktionen nicht für Berechnungen mit Binär-,
Oktal-, Dezimal- oder Hexadezimalzahlen verwenden.
•Sie können nur ganze Zahlen in Berechnungen mit Binär-, Oktal-, Dezimal- oder Hexadezimalzahlen verwenden, d.h. Dezimalbrüche oder gemeine Brüche sind nicht zulässig.
Falls Sie einen Wert mit einem Dezimalstellenanteil eingeben, schneidet der Rechner
den Dezimalstellenanteil automatisch ab und geht zu einer ganzen Zahl über.
•Falls Sie den Versuch unternehmen, einen nicht zugelassenen Wert für das verwendete
Zahlensystem einzugeben (binär, oktal, dezimal oder hexadezimal), zeigt der Rechner
eine Fehlermeldung an. Nachfolgend sind die zwei bis maximal 16 Ziffern aufgeführt, die
im zutreffenden Zahlensystem verwendet werden können.
Binär: 0, 1
Oktal: 0, 1, 2, 3, 4, 5, 6, 7
Dezimal: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Hexadezimal: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, u, v, w, x, y, z
•Negative Binär-, Oktal- sowie Hexadezimalwerte werden durch das Komplement des
ursprünglichen Wertes zu "Null" erzeugt, so dass X + Neg X = "Null" = (1)0...0 gilt. Die
führende Ziffer (1) wird wegen Überschreitung der Anzeigekapazität nicht dargestellt.
•Nachfolgend sind die Anzeigekapazitäten für jedes Zahlensystem angegeben.
Zahlensystem Anzeigekapazität
Binär 16 Stellen
Oktal 11 Stellen
Dezimal 10 Stellen
Hexadezimal 8 Stellen
#Die für Hexadezimalzahlen verwendeten
alphabetischen Zeichen erscheinen in
anderer Darstellung, um sie von den
normalen Textzeichen unterscheiden zu
können.
Normaler Text: A, B, C, D, E, F
Hexadezimalziffern: u, v, w, x, y, z
19990401

Berechnungen mit Binär-, Oktal-, Dezimal- und Hexadezimalzahlen
2-7-2
•Nachfolgend sind die Zahlenbereiche der einzelnen Zahlensysteme aufgeführt, innerhalb
derer Berechnungen durchgeführt werden können.
Binärzahlen (Dualzahlen, Anzeige mit 16 Stellen))
Positiv: 0000000000000000 < x < 0111111111111111 (Vorzeichenbit=0)
Negativ: 1000000000000000 < x < 1111111111111111 (Vorzeichenbit=1)
Oktalzahlen (Anzeige mit 11 Stellen)
Positiv: 00000000000 < x < 17777777777
Negativ: 20000000000 < x < 37777777777
Dezimalzahlen
Positiv: 0 < x < 2147483647
Negativ: –2147483648 < x < –1
Hexadezimalzahlen (Anzeige mit 8 Stellen)
Positiv: 00000000 < x < 7FFFFFFF
Negativ: 80000000 < x < FFFFFFFF
uu
u Ausführen einer Binär-, Oktal-, Dezimal- oder Hexadezimalzahlenrechnung
uu
[SET UP]- [Mode] -[Dec]/[Hex]/[Bin]/[Oct]
1. Wählen Sie das RUN • MAT-Menü im Hauptmenü aus.
2. Drücken Sie die Tasten u3(SET UP) und wählen Sie danach Ihr Vorgabe-Zahlensystem durch Drücken der Taste 2(Dec), 3(Hex), 4(Bin) oder 5(Oct) aus.
3. Drücken Sie die i-Taste, um in das Display für die Berechnungseingabe zu wechseln. Hierbei erscheint das Funktionsmenü mit den folgenden Positionen.
•{d~o}/{LOGIC}/{DISP}/{SYBL} ... {Zahlensystem-Identifikationsmenü}/{Logikoperations-
Menü}/{Dezimal-/Hexadezimal-/Binär-/Oktal-Umrechnungsmenü}/{Symbolmenü}
19990401

Berechnungen mit Binär-, Oktal-, Dezimal- und Hexadezimalzahlen
kk
k Auswahl eines Zahlensystems
kk
Sie können das Dezimal-, Hexadezimal-, Binär- oder Oktalzahlensystem als das VorgabeZahlensystem einstellen, indem Sie die Einstellanzeige (SET UP) verwenden. Nachdem Sie
die dem gewünschten System entsprechende Funktionstaste gedrückt haben, drücken Sie
die w-Taste, um die Einstellanzeige zu schließen.
uu
u Auswahl eines Zahlensystems für einen Eingabewert direkt im Display
uu
Sie können für jeden Eingabewert jeweils ein individuelles Zahlensystem nutzen. Drücken
Sie die 1(d~o)-Taste, um ein Untermenü der Zahlensystemsymbole anzuzeigen. Drücken
Sie danach die Funktionstaste gemäß dem Symbol, das Sie wählen möchten, und geben Sie
dann unmittelbar danach den Wert ein.
•{d}/{h}/{b}/{o} ... {dezimal}/{hexadezimal}/{binär}/{oktal}
uu
u Eingabe von Zahlenwerten bei unterschiedlichen Zahlensystemen
uu
○○○○○
Beispiel Einzugeben sind 12310 oder 10102, wenn das voreingestellte Zahlen-
system das Hexadezimalzahlensystem ist.
2-7-3
u3(SET UP)3(Hex)i
A1(d~o)b(d)bcdw
1(d~o)d(b)babaw
kk
k Arithmetische Operationen
kk
○○○○○
Beispiel 1 Zu berechnen ist 101112 + 110102
u3(SET UP)4(Bin)i
Ababbb+
bbabaw
19990401

Berechnungen mit Binär-, Oktal-, Dezimal- und Hexadezimalzahlen
2-7-4
○○○○○
Beispiel 2 Einzugeben und auszuführen ist 1238 × ABC16, wenn das Vorgabe-
Zahlensystem das Dezimal- oder Hexadezimalzahlensystem ist.
u3(SET UP)2(Dec)i
A1(d~o)e(o)bcd*
1(d~o)c(h)ABCw
3(DISP)c(Hex)w
kk
k Negative Werte und Logikoperationen
kk
Drücken Sie die 2(LOGIC)-Taste, um ein Untermenü der Negation und Logikoperationen
zu öffnen.
•{Neg} ... {Negation eines Zahlenwertes, Übergang zum negativen Wert}
•{Not}/{and}/{or}/{xor}/{xnor} ... {NOT}/{AND}/{OR}/{XOR}/{XNOR} (Logikoperationen)
u Negative Werte
○○○○○
Beispiel Der negative Wert von 1100102 ist zu bestimmen.
u3(SET UP)4(Bin)i
A2(LOGIC)b(Neg)
bbaabaw
u Logikoperationen
○○○○○
Beispiel 1 Einzugeben und auszuführen ist “12016 and AD16”
u3(SET UP)3(Hex)i
Abca2(LOGIC)
d(and)ADw
19990401
 Loading...
Loading...