Casio ALGEBRA FX 1.0 PLUS, ALGEBRA FX 2.0 PLUS, ALGEBRA PLUS FX 2.0 User Manual

ALGEBRA FX 2.0 PLUS

FX 1.0 PLUS

User’s Guide

(

Additional Functions

)

http://world.casio.com/edu_e/

CASIO ELECTRONICS CO., LTD. Unit 6, 1000 North Circular Road, London NW2 7JD, U.K.

Important!

Please keep your manual and all information handy for future reference.

•••••••••••••••••••

• ••••••••••••••••••

•••••••••••••••••••

ALGEBRA FX 2.0 PLUS

FX 1.0 PLUS

(Additional Functions)

•••••••••••••••••••

• ••••••••••••••••••

•••••••••••••••••••

• ••••••••••••••••••

20010101

Contents

Chapter 1 Advanced Statistics Application

1-1 Advanced Statistics (STAT) .............................................................. 1-1-1

1-2 Tests (TEST) .................................................................................... 1-2-1

1-3 Confidence Interval (INTR)............................................................... 1-3-1

1-4 Distribution (DIST) ............................................................................ 1-4-1

Chapter 2 Financial Calculation (TVM)

2-1 Before Performing Financial Calculations ........................................ 2-1-1

2-2 Simple Interest ................................................................................. 2-2-1

2-3 Compound Interest ........................................................................... 2-3-1

2-4 Cash Flow (Investment Appraisal) .................................................... 2-4-1

2-5 Amortization ..................................................................................... 2-5-1

2-6 Interest Rate Conversion.................................................................. 2-6-1

2-7 Cost, Selling Price, Margin ............................................................... 2-7-1

2-8 Day/Date Calculations ...................................................................... 2-8-1

2-9 Depreciation ..................................................................................... 2-9-1

2-10 Bonds ............................................................................................. 2-10-1

2-11 TVM Graph ..................................................................................... 2-11-1

Chapter 3 Differential Equations

3-1 Using the DIFF EQ Mode ................................................................. 3-1-1

3-2 Differential Equations of the First Order ........................................... 3-2-1

3-3 Linear Differential Equations of the Second Order ........................... 3-3-1

3-4 Differential Equations of the Nth Order ............................................ 3-4-1

3-5 System of First Order Differential Equations .................................... 3-5-1

Chapter 4 E-CON

4-1 E-CON Overview .............................................................................. 4-1-1

4-2 EA-100 Setup ................................................................................... 4-2-1

4-3 Setup Memory .................................................................................. 4-3-1

4-4 Program Converter ........................................................................... 4-4-1

4-5 Starting a Sampling Operation ......................................................... 4-5-1

Index

20010101

Chapter

Advanced Statistics Application

1-1 Advanced Statistics (STAT)

1-2 Tests (TEST)

1-3 Confidence Interval (INTR)

1-4 Distribution (DIST)

20010101

1-1-1

Advanced Statistics (STAT)

1-1 Advanced Statistics (STAT)

uFunction Menu

The following shows the function menus for the STAT Mode list input screen.

Pressing a function key that corresponds to the added item displays a menu that lets you select one of the functions listed below.

• 3(TEST) ... Test (page1-2-1)

• 4(INTR) ... Confidence interval (page1-3-1)

• 5(DIST) ... Distribution (page1-4-1)

SORT and JUMP functions are located in the TOOL menu (6(g)1(TOOL)).

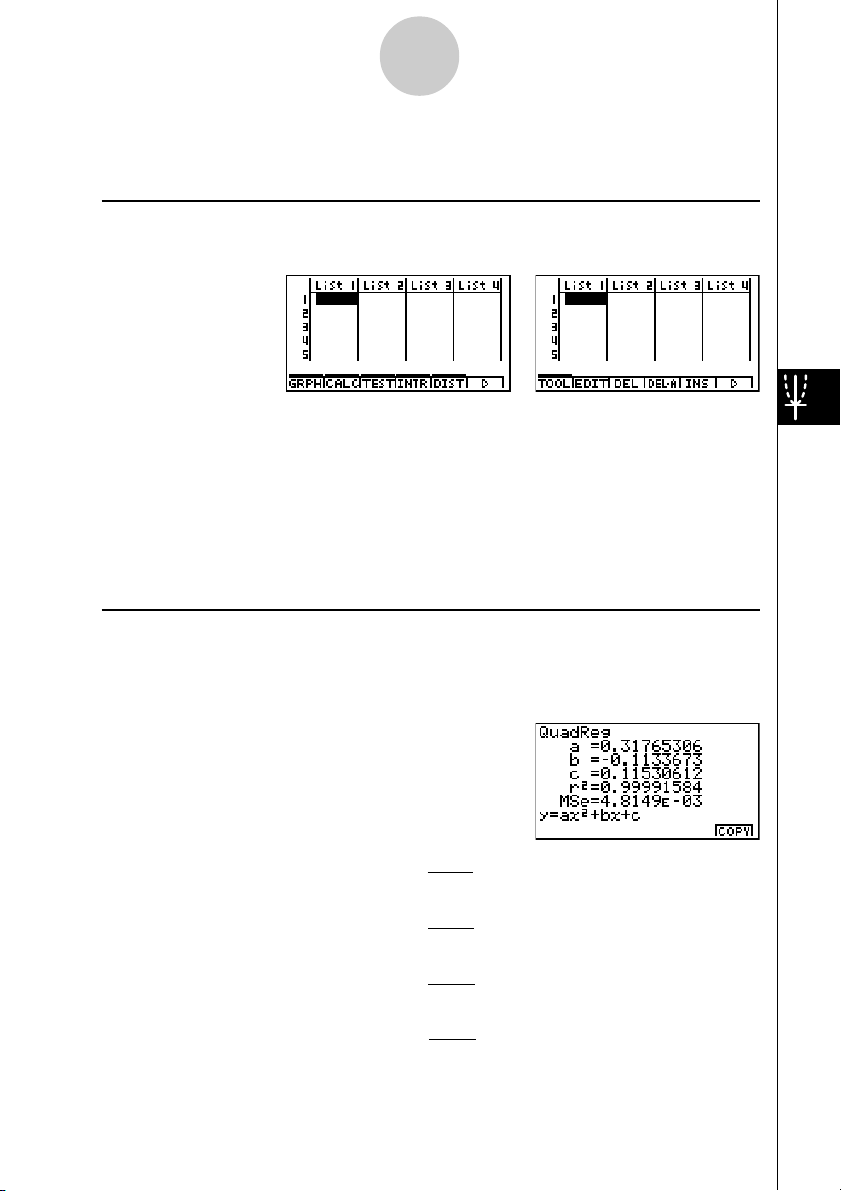
uCalculation of the Coefficient of Determination (r2) and MSE

You can use the STAT Mode to calculate the coefficient of determination (r2) for quadratic regression, cubic regression, and quartic regression. The following types of MSE calculations are also available for each type of regression.

•Linear Regression ...

•Quadratic Regression ...

•Cubic Regression ...

•Quartic Regression ...

20010101

n – 2

n – 3

n – 4

n – 5

(yi – (axi+ b))

i=1

(yi – (ax

i=1

(yi – (ax

i=1

(yi – (ax

i=1

MSE =

+ bxi+ c))

+ bx

+ cx

+d ))

+ dx

+ e))

1-1-2

Advanced Statistics (STAT)

• Logar ithmic Regression ...

•Exponential Repression ...

•Power Regression ...

•Sin Regression ...

• Logistic Regression ...

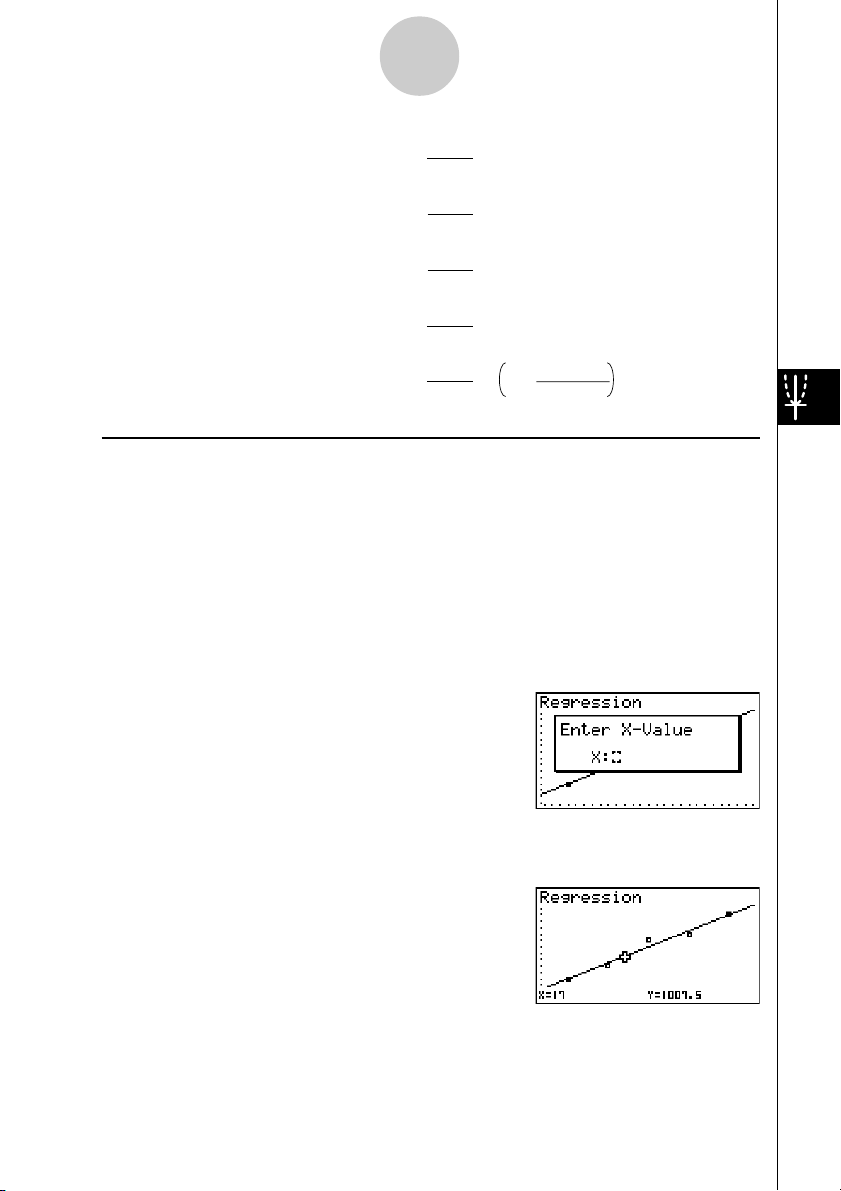
uEstimated Value Calculation for Regression Graphs

The STAT Mode also includes a Y-CAL function that uses regression to calculate the estimated y-value for a particular x-value after graphing a paired-variable statistical regression.

The following is the general procedure for using the Y-CAL function.

1. After drawing a regression graph, press 6(g)2(Y-CAL) to enter the graph selection mode, and then press w.

If there are multiple graphs on the display, use f and c to select the graph you want, and then press w.

• This causes an x-value input dialog box to appear.

MSE =

(yi – (a + b ln xi ))

n – 2

i=1

(ln yi – (ln a + bxi ))

n – 2

i=1

(ln yi – (ln a + b ln xi ))

n – 2

i=1

(yi – (a sin (bxi + c) + d ))

n – 2

i=1

n – 2 1 + ae

i=1

yi –

-bx

2. Input the value you want for x and then press w.

• This causes the coordinates for x and y to appear at the bottom of the display, and moves the pointer to the corresponding point on the graph.

3. Pressing v or a number key at this time causes the x-value input dialog box to reappear so you can perform another estimated value calculation if you want.

20010101

20011101

1-1-3

Advanced Statistics (STAT)

4. After you are finished, press i to clear the coordinate values and the pointer from the display.

· The pointer does not appear if the calculated coordinates are not within the display range.

·The coordinates do not appear if [Off] is specified for the [Coord] item of the [SETUP] screen.

· The Y-CAL function can also be used with a graph drawn by using DefG feature.

u Regression Formula Copy Function from a Regression Calculation Result

Screen

In addition to the normal regression formula copy function that lets you copy the regression calculation result screen after drawing a statistical graph (such as Scatter Plot), the STAT Mode also has a function that lets you copy the regression formula obtained as the result of a regression calculation. To copy a resulting regression for mula, press 6(COPY).

k Tests, Confidence Interval, and Distribution Calculations

The STAT Mode includes functions for performing tests, and confidence interval and distribution calculations. You can find explanations of each of these functions in the following sections: 1-2 Tests, 1-3 Confidence Interval, and 1-4 Distr ibution.

uParameter Settings

The following describes the two methods you can use to make parameter settings for test, confidence interval, and distribution calculations.

• Selection

With this method, you press the function key that corresponds to the setting you want to select from the function menu.

• Value Input

With this method, you directly input the parameter value you want to input. In this case, nothing appears in the function menu.

·Pressing i returns to the list input screen, with the cursor in the same position it was at

before you started the parameter setting procedure.

· Pressing ! i(QUIT) returns to the top of list input screen.

· Pressing w without pressing 1(CALC) under “Execute” item advances to calculation

execution. To return to the parameter setting screen, press i, A, or w.

20010101

1-1-4

Advanced Statistics (STAT)

uCommon Functions

• The symbol “■” appears in the upper right corner of the screen while execution of a

calculation is being performed and while a graph is being drawn. Pressing A during this time terminates the ongoing calculation or draw operation (AC Break).

• Pressing i or w while a calculation result or graph is on the display returns to the

parameter setting screen. Pressing ! i(QUIT) returns to the top of list input screen.

· Pressing A while a calculation result is on the display returns to the parameter setting screen.

• Pressing u 5(G↔T) after drawing a graph switches to the parameter setting screen

(G↔T function). Pressing u 5(G↔T) again returns to the graph screen.

· The G↔T function is disabled whenever you change a setting on the parameter setting screen, or

when you perfor m a u 3(SET UP) or ! K(V-Window) operation.

• You can perform the PICT menu's screen save or recall functions after drawing a graph.

· The ZOOM function and SKETCH function are disabled.

The TRACE function is disabled, except for the graph display of two-way ANOVA.

The graph screen cannot be scrolled.

• After drawing a graph, you can use a Save Result feature to save calculation results to a

specific list. Basically, all items are saved as they are displayed, except for the first line title.

·Each time you execute Save Result, any existing data in the list is replaced by the new results.

20010101

20011101

1-2-1

Tests (TEST)

1-2 Tests (TEST)

The Z Test provides a variety of different standardization-based tests. They make it possible to test whether or not a sample accurately represents the population when the standard deviation of a population (such as the entire population of a country) is known from previous tests. Z testing is used for market research and public opinion research, that need to be performed repeatedly.

1-Sample Z Test tests for the unknown population mean when the population standard deviation is known.

2-Sample Z Test tests the equality of the means of two populations based on independent samples when both population standard deviations are known.

1-Prop Z Test tests for an unknown proportion of successes.

2-Prop Z Test tests to compare the proportion of successes from two populations.

The t Test tests the hypothesis when the population standard deviation is unknown. The hypothesis that is the opposite of the hypothesis being proven is called the while the hypothesis being proved is called the

alternative hypothesis

applied to test the null hypothesis. Then a determination is made whether the null hypothesis or alternative hypothesis will be adopted.

1-Sample t Test tests the hypothesis for a single unknown population mean when the population standard deviation is unknown.

2-Sample t Test compares the population means when the population standard deviations are unknown.

LinearReg t Test calculates the strength of the linear association of paired data.

null hypothesis

. The t-test is normally

Test tests hypothesis concerning the proportion of samples included in each of a number of independent groups. Mainly, it generates cross-tabulation of two categorical variables (such as yes, no) and evaluates the independence of these variables. It could be used, for example, to evaluate the relationship between whether or not a driver has ever been involved in a traffic accident and that person’s knowledge of traffic regulations.

2-Sample F Test tests the hypothesis for the ratio of sample variances. It could be used, for example, to test the carcinogenic effects of multiple suspected factors such as tobacco use, alcohol, vitamin deficiency, high coffee intake, inactivity, poor living habits, etc.

ANOVA tests the hypothesis that the population means of the samples are equal when there are multiple samples. It could be used, for example, to test whether or not different combinations of materials have an effect on the quality and life of a final product.

One-Way ANOVA is used when there is one independent variable and one dependent variable.

Two-Way ANOVA is used when there are two independent variables and one dependent variable.

20010101

20011101

1-2-2

Tests (TEST)

The following pages explain various statistical calculation methods based on the principles described above. Details concerning statistical principles and terminology can be found in any standard statistics textbook.

On the initial STAT Mode screen, press 3(TEST) to display the test menu, which contains the following items.

• 3(TEST)b(Z) ... Z Tests (p. 1-2-2)

c(T) ... t Tests (p. 1-2-10)

d(χ2) ... χ2 Test (p. 1-2-18) e(F) ... 2-Sample F Test (p. 1-2-20)

f(ANOVA) ... ANOVA (p. 1-2-22)

k Z Tests

uZ Test Common Functions

You can use the following graph analysis functions after drawing a graph.

• 1(Z) ... Displays z score.

Pressing 1 (Z) displays the z score at the bottom of the display, and displays the pointer at the corresponding location in the graph (unless the location is off the graph screen). Tw o points are displayed in the case of a two-tail test. Use d and e to move the pointer. Press i to clear the z score.

• 2(P) ... Displays p-value.

Pressing 2 (P) displays the p-value at the bottom of the display without displaying the pointer. Press i to clear the p-value.

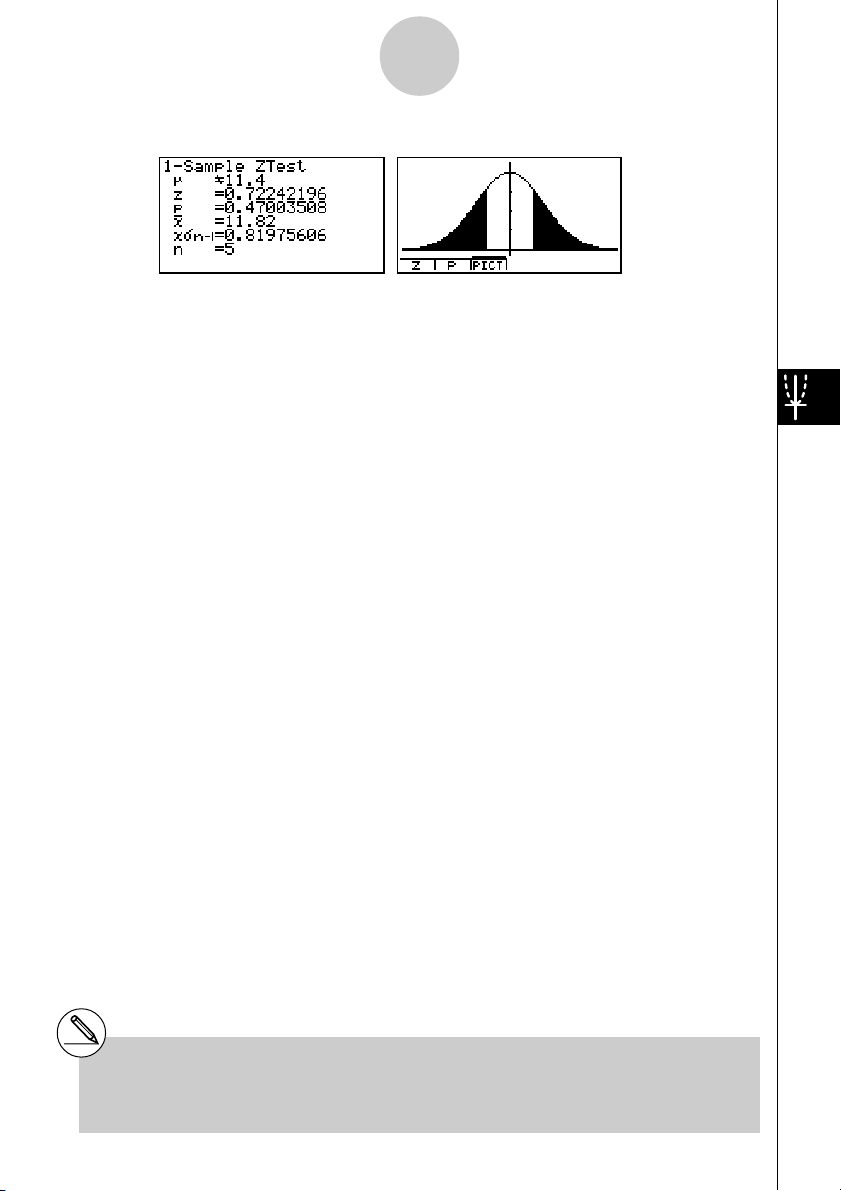
u1-Sample Z Test

This test is used when the population standard deviation is known to test the hypothesis. The 1-Sample Z Test is applied to the normal distribution.

Z =

o –

o : mean of sample

o : assumed population mean

: population standard deviation

n : s ize of sample

# The following V-Window settings are used for

drawing the graph.

Xmin = –3.2, Xmax = 3.2, Xscale = 1, Ymin = –0.1, Ymax = 0.45, Yscale = 0.1

#Executing an analysis function automatically

stores the z and p values in alpha variables Z and P, respectively.

20010101

20011101

1-2-3

Tests (TEST)

Perform the following key operations from the statistical data list.

3(TEST)

b(Z)

b(1-Smpl)

The following shows the meaning of each item in the case of list data specification.

Data ............................ data type

.................................. population mean value test conditions (“G

two-tail test, “<

0” specifies lower one-tail test, “> µ0”

0” specifies

specifies upper one-tail test.)

0 ................................. assumed population mean

.................................. population standard deviation (σ > 0)

List .............................. list whose contents you want to use as data (List 1 to 20)

Freq ............................. frequency (1 or List 1 to 20)

Save Res..................... list for storage of calculation results (None or List 1 to 20)

Execute ....................... executes a calculation or draws a graph

The following shows the meaning of parameter data specification items that are different from list data specification.

o .................................. mean of sample

n .................................. size of sample (positive integer)

After setting all the parameters, align the cursor with [Execute] and then press one of the function keys shown below to perform the calculation or draw the graph.

• 1(CALC) ... Performs the calculation.

• 6(DRAW) ... Draws the graph.

20010101

20011101

Tests (TEST)

Calculation Result Output Example

G11.4

........................

direction of test

z .................................. z score

p .................................. p-value

o .................................. mean of sample

n-1 ............................. sample standard deviation

(Displayed only for Data: List setting.)

n .................................. size of sample

1-2-4

# [Save Res] does not save the µ condition in

line 2.

20010101

1-2-5

Tests (TEST)

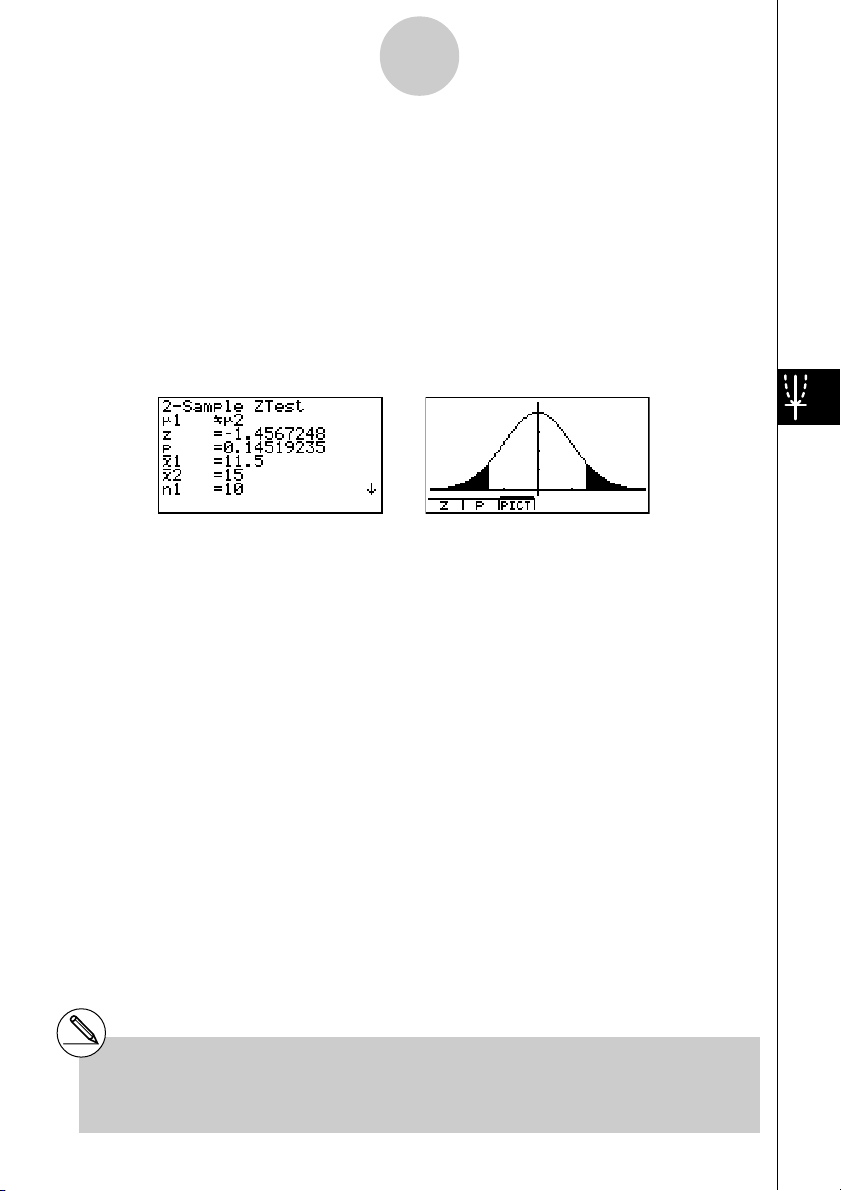
u2-Sample Z Test

This test is used when the standard deviations for two populations are known to test the hypothesis. The 2-Sample Z T est is applied to the normal distribution.

Z =

o1 – o

o1 : mean of sample 1 o2 : mean of sample 2

1 : population standard deviation of sample 1

2 : population standard deviation of sample 2

n1 : siz e of sample 1 n2 : siz e of sample 2

Perform the following key operations from the statistical data list.

3(TEST)

b(Z)

c(2-Smpl)

The following shows the meaning of each item in the case of list data specification.

Data ............................ data type

1 ................................. population mean value test conditions (“G µ2” specifies two-

tail test, “< smaller than sample 2, “>

2” specifies one-tail test where sample 1 is

2” specifies one-tail test where

sample 1 is greater than sample 2.)

1 ................................. population standard deviation of sample 1 (σ1 > 0)

2 ................................. population standard deviation of sample 2 (σ2 > 0)

List(1) .......................... list whose contents you want to use as sample 1 data

(List 1 to 20)

List(2) .......................... list whose contents you want to use as sample 2 data

(List 1 to 20)

Freq(1) ........................ frequency of sample 1 (1 or List 1 to 20)

Freq(2) ........................ frequency of sample 2 (1 or List 1 to 20)

Save Res..................... list for storage of calculation results (None or List 1 to 20)

Execute ....................... executes a calculation or draws a graph

The following shows the meaning of parameter data specification items that are different from list data specification.

20010101

20011101

1-2-6

Tests (TEST)

o1 ................................. mean of sample 1

n1 ................................. size (positive integer) of sample 1

o2 ................................. mean of sample 2

n2 ................................. size (positive integer) of sample 2

After setting all the parameters, align the cursor with [Execute] and then press one of the function keys shown below to perform the calculation or draw the graph.

• 1(CALC) ... Performs the calculation.

• 6(DRAW) ... Draws the graph.

Calculation Result Output Example

2 ........................... direction of test

z ................................... z score

p .................................. p-value

o1 ................................. mean of sample 1

o2 ................................. mean of sample 2

n-1 ............................ standard deviation of sample 1

(Displayed only for Data: List setting.)

n-1 ............................ standard deviation of sample 2

(Displayed only for Data: List setting.)

n1 ................................. size of sample 1

n2 ................................. size of sample 2

# [Save Res] does not save the

line 2.

1 condition in

20010101

1-2-7

Tests (TEST)

u1-Prop Z Test

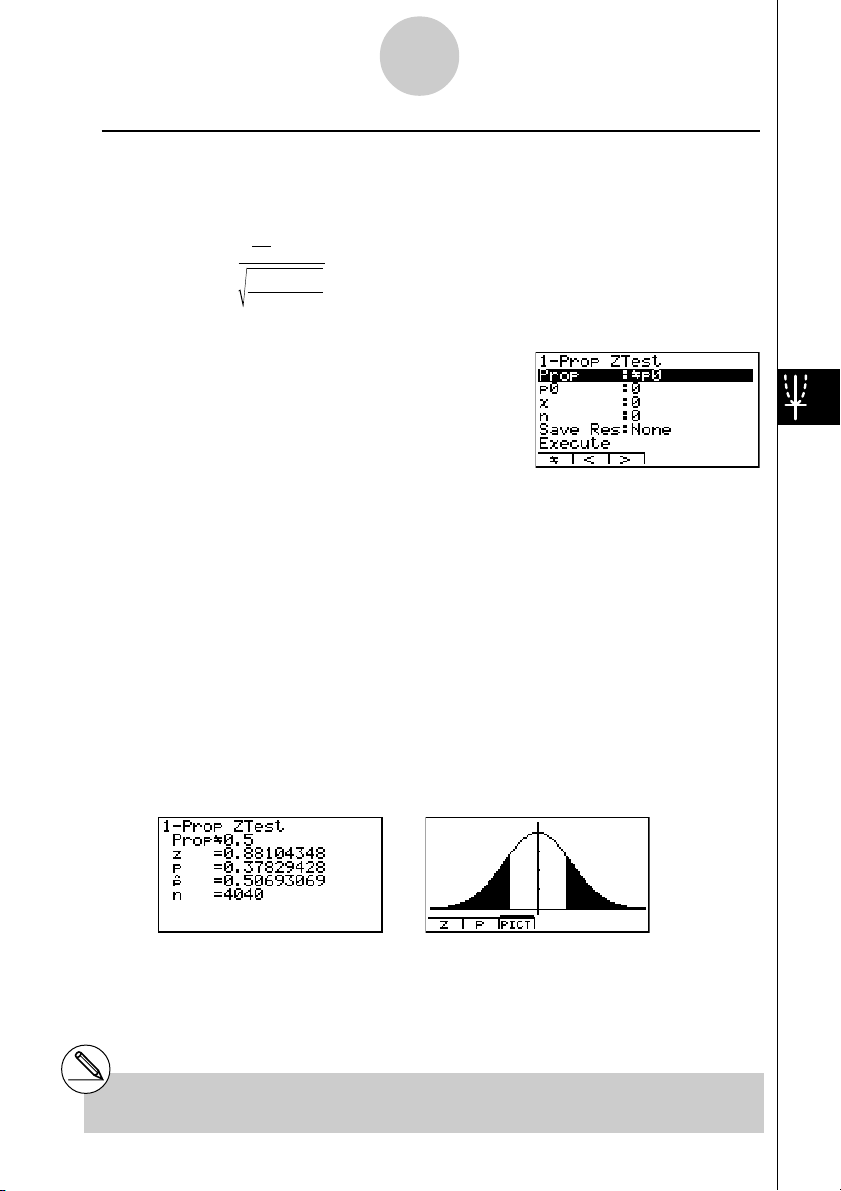
This test is used to test for an unknown proportion of successes. The 1-Prop Z Test is applied to the normal distribution.

p0 : expected sample proportion n : s ize of sample

Z =

x n

(1– p0)

– p

Perform the following key operations from the statistical data list.

3(TEST)

b(Z)

d(1-Prop)

Prop ............................ sample proportion test conditions (“G p0” specifies two-tail

test, “< p0” specifies lower one-tail test, “> p0” specifies upper one-tail test.)

p0 ................................. expected sample proportion (0 < p0 < 1)

x .................................. sample value (x > 0 integer)

n .................................. size of sample (positive integer)

Save Res..................... list for storage of calculation results (None or List 1 to 20)

Execute ....................... executes a calculation or draws a graph

After setting all the parameters, align the cursor with [Execute] and then press one of the function keys shown below to perform the calculation or draw the graph.

• 1(CALC) ... Performs the calculation.

• 6(DRAW) ... Draws the graph.

Calculation Result Output Example

PropG0.5 .................... direction of test

z ................................... z score

p .................................. p-value

ˆp .................................. estimated sample proportion

n .................................. size of sample

# [Save Res] does not save the Prop condition

in line 2.

20010101

20011101

1-2-8

Tests (TEST)

u2-Prop Z Test

This test is used to compare the proportion of successes. The 2-Prop Z Test is applied to the normal distribution.

–

p(1 – p )

Z =

Perform the following key operation from the statistical data list.

3(TEST)

b(Z) e(2-Prop)

x1 : data value of sample 1 x2 : data value of sample 2 n1 : siz e of sample 1 n2 : siz e of sample 2 ˆp : estimated sample proportion

p1 ................................. sample proportion test conditions (“G p2” specifies two-tail

test, “< p2” specifies one-tail test where sample 1 is smaller than sample 2, “> p2” specifies one-tail test where sample 1 is greater than sample 2.)

x1 ................................. data value (x1 > 0 integer) of sample 1

n1 ................................. size (positive integer) of sample 1

x2 ................................. data value (x2 > 0 integer) of sample 2

n2 ................................. size (positive integer) of sample 2

Save Res..................... list for storage of calculation results (None or List 1 to 20)

Execute ....................... executes a calculation or draws a graph

After setting all the parameters, align the cursor with [Execute] and then press one of the function keys shown below to perform the calculation or draw the graph.

• 1(CALC) ... Performs the calculation.

• 6(DRAW) ... Draws the graph.

Calculation Result Output Example

20010101

20011101

1-2-9

Tests (TEST)

p1>p2 ............................ direction of test

z .................................. z score

p .................................. p-value

ˆp 1 ................................. estimated proportion of sample 1

ˆp 2 ................................. estimated proportion of sample 2

ˆp .................................. estimated sample proportion

n1 ................................. size of sample 1

n2 ................................. size of sample 2

# [Save Res] does not save the p1 condition in

line 2.

20010101

1-2-10

Tests (TEST)

k t Tests

u t Test Common Functions

You can use the following graph analysis functions after drawing a graph.

• 1(T) ... Displays t score.

Pressing 1 (T) displays the t score at the bottom of the display, and displays the pointer at the corresponding location in the graph (unless the location is off the graph screen).

Tw o points are displayed in the case of a two-tail test. Use d and e to move the pointer.

Press i to clear the t score.

• 2(P) ... Displays p-value.

Pressing 2 (P) displays the p-value at the bottom of the display without displaying the pointer.

Press i to clear the p-value.

# The following V-Window settings are used for

drawing the graph.

Xmin = –3.2, Xmax = 3.2, Xscale = 1, Ymin = –0.1, Ymax = 0.45, Yscale = 0.1

#Executing an analysis function automatically

stores the t and p values in alpha variables T and P, respectively.

20010101

1-2-11

Tests (TEST)

u1-Sample t Test

This test uses the hypothesis test for a single unknown population mean when the population standard deviation is unknown. The 1-Sample t T est is applied to t-distribution.

t =

o –

n–1

o : mean of sample

0 : assumed population mean

n-1 : sample standard deviation

n : siz e of sample

Perform the following key operations from the statistical data list.

3(TEST)

c(T)

b(1-Smpl)

The following shows the meaning of each item in the case of list data specification.

Data ............................ data type

.................................. population mean value test conditions (“G

tail test, “<

0” specifies lower one-tail test, “> µ0” specifies

upper one-tail test.)

0 ................................. assumed population mean

List .............................. list whose contents you want to use as data (List 1 to 20)

Freq ............................. frequency (1 or List 1 to 20)

Save Res..................... list for storage of calculation results (None or List 1 to 20)

Execute ....................... executes a calculation or draws a graph

0” specifies two-

The following shows the meaning of parameter data specification items that are different from list data specification.

o .................................. mean of sample

n-1 ............................. sample standard deviation (xσn-1 > 0)

n .................................. size of sample (positive integer)

After setting all the parameters, align the cursor with [Execute] and then press one of the function keys shown below to perform the calculation or draw the graph.

• 1(CALC) ... Performs the calculation.

• 6(DRAW) ... Draws the graph.

20010101

20011101

Calculation Result Output Example

G 11.3 ...................... direction of test

...................................

t score

p .................................. p-value

o .................................. mean of sample

n-1 ............................. sample standard deviation

n .................................. size of sample

1-2-12

Tests (TEST)

# [Save Res] does not save the µ condition in

line 2.

20010101

+ 46 hidden pages