ANALOG DEVICES LTC 1966 CMS8 Datasheet

Download

Page 1

Precision Micropower

∆∑ RMS-to-DC Converter

FeaTures DescripTion

Simple to Use, Requires One Capacitor

True RMS DC Conversion Using DS Technology

High Accuracy:

0.1% Gain Accuracy from 50Hz to 1kHz

0.25% Total Error from 50Hz to 1kHz

High Linearity:

0.02% Linearity Allows Simple System Calibration

Low Supply Current:

155µA Typ, 170µA Max

Ultralow Shutdown Current:

0.1µ A

Constant Bandwidth:

Independent of Input Voltage

800kHz –3dB, 6kHz ±1%

Flexible Supplies:

2.7V to 5.5V Single Supply Up to ±5.5V Dual Supply

Flexible Inputs:

Differential or Single-Ended

Rail-to-Rail Common Mode Voltage Range Up to 1V

Flexible Output:

Differential Voltage

PEAK

Rail-to-Rail Output Separate Output Reference Pin Allows Level Shifting

Wide Temperature Range:

–55°C to 125°C

Small Size:

Space Saving 8-Pin MSOP Package

The LTC®1966 is a true RMS-to-DC converter that utilizes an innovative patented DS computational technique. The internal delta sigma circuitry of the LTC1966 makes it simpler to use, more accurate, lower power and dramatically more flexible than conventional log antilog RMS-to-DC converters.

The LTC1966 accepts single-ended or differential input signals (for EMI/RFI rejection) and supports crest factors up to 4. Common mode input range is rail-to-rail. Differential input range is 1V

PEAK

Unlike previously available RMS-to-DC converters, the superior linearity of the LTC1966 allows hassle free system calibration at any input voltage.

The LTC1966 also has a rail-to-rail output with a separate output reference pin providing flexible level shifting. The LTC1966 operates on a single power supply from 2.7V to

5.5V or dual supplies up to ±5.5V. A low power shutdown mode reduces supply current to 0.5µA.

The LTC1966 is insensitive to PC board soldering and stresses, as well as operating temperature. The LTC1966 is packaged in the space saving MSOP package which is ideal for portable applications.

applicaTions

True RMS Digital Multimeters and Panel Meters

True RMS AC + DC Measurements

L, LT, LTC, LTM, Linear Technology and the Linear logo are registered trademarks and No Latency DS is a trademark of Linear Technology Corporation. All other trademarks are the property of their respective owners. Protected by U.S. Patents including 6359576, 6362677, 6516291 and 6651036.

LTC1966

, and offers unprecedented linearity.

Typical applicaTion

Single Supply RMS-to-DC Converter

2.7V TO 5.5V

OUTPUT

DIFFERENTIAL

INPUT

0.1µF

OPT. AC

COUPLING

IN1

LTC1966

OUT RTN

IN2

EN GND

AVE

1µF

1966 TA01

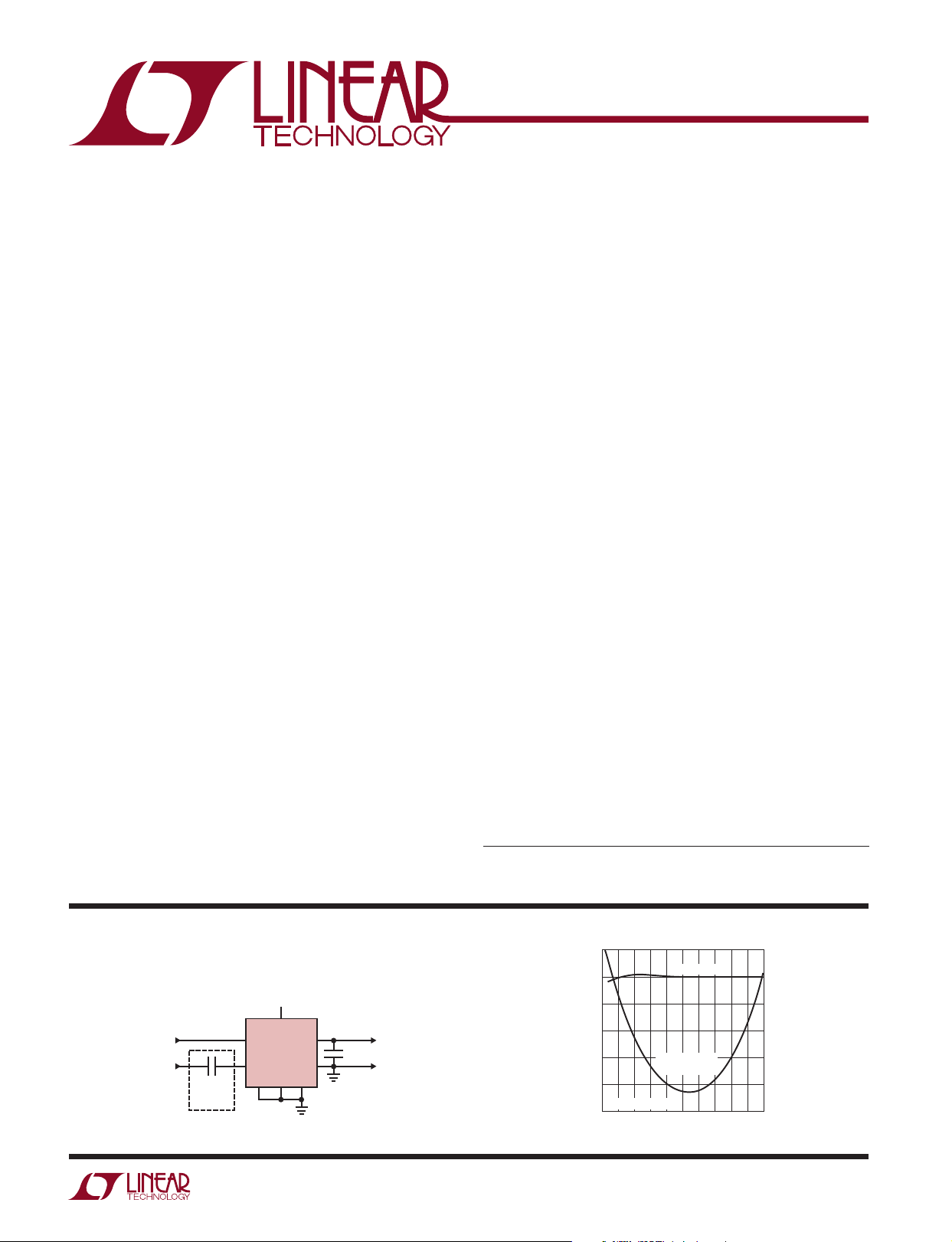
Quantum Leap in Linearity Performance

)

0.2

RMS

mV AC

–0.2

mV DC – V

–0.4

OUT

–

OUT

–0.6

–0.8

60Hz SINEWAVES

–1.0

LINEARITY ERROR (V

100 200 300 400

LTC1966, ∆∑

CONVENTIONAL

LOG/ANTILOG

VIN (mV AC

RMS

1966 TA01b

500500 150 250 350 450

1966fb

)

Page 2

LTC1966

(Note 1)

Supply Voltage

to GND ............................................. – 0.3V to 7V

to VSS ............................................ –0.3V to 12V

to GND ............................................. –7V to 0.3V

Input Currents (Note 2) ...................................... ± 10mA

Output Current (Note 3) ..................................... ± 10mA

ENABLE Voltage ....................... V

OUT RTN Voltage ............................... V

Operating Temperature Range (Note 4)

LTC1966C/LTC1966I ............................ –40°C to 85°C

LTC1966H .......................................... –40°C to 125°C

LTC1966MP ....................................... –55°C to 125°C

Specified Temperature Range (Note 5)

LTC1966C/LTC1966I ............................ –40°C to 85°C

LTC1966H .......................................... –40°C to 125°C

LTC1966MP ....................................... –55°C to 125°C

Maximum Junction Temperature ......................... 150°C

Storage Temperature Range ................. –65°C to 150°C

Lead Temperature (Soldering, 10 sec) .................. 300°C

– 0.3V to VSS + 12V

– 0.3V to V

pin conFiguraTionabsoluTe MaxiMuM raTings

TOP VIEW

GND

IN1

IN2

MS8 PACKAGE

8-LEAD PLASTIC MSOP

= 150°C, θJA = 220°C/W

JMAX

ENABLE

OUT RTN

OUT

orDer inForMaTion

LEAD FREE FINISH TAPE AND REEL PART MARKING* PACKAGE DESCRIPTION TEMPERATURE RANGE

LTC1966CMS8#PBF LTC1966CMS8#TRPBF LTT G 8-Lead Plastic MSOP 0°C to 70°C LTC1966IMS8#PBF LTC1966IMS8#TRPBF LTT H 8-Lead Plastic MSOP –40°C to 85°C LTC1966HMS8#PBF LTC1966HMS8#TRPBF LTT G 8-Lead Plastic MSOP –40°C to 125°C LTC1966MPMS8#PBF LTC1966MPMS8#TRPBF LTT G 8-Lead Plastic MSOP –55°C to 125°C Consult LTC Marketing for parts specified with wider operating temperature ranges. *The temperature grade is identified by a label on the shipping container.

For more information on lead free part marking, go to: http://www.linear.com/leadfree/ For more information on tape and reel specifications, go to: http://www.linear.com/tapeandreel/

elecTrical characTerisTics

The l denotes the specifications which apply over the full operating temperature range, otherwise specifications are at TA = 25°C. VDD = 5V, VSS = –5V, V V

= 0.5V unless otherwise noted.

ENABLE

SYMBOL PARAMETER CONDITIONS MIN TYP MAX UNITS

Conversion Accuracy

LIN

ERR

OOS

Conversion Gain Error 50Hz to 1kHz Input (Notes 6, 7)

Output Offset Voltage (Notes 6, 7)

Linearity Error 50mV to 350mV (Notes 7, 8)

ERR

LTC1966C, LTC1966I LTC1966H, LTC1966MP

OUTRTN

= 0V, C

l l

= 10µF, VIN = 200mV

AVE

±0.1 ±0.3

0.1

0.02 0.15 %

±0.4 ±0.7

0.2

0.4

0.6

RMS

mV mV mV

% % %

1966fb

Page 3

LTC1966

elecTrical characTerisTics

The l denotes the specifications which apply over the full operating temperature range, otherwise specifications are at TA = 25°C. VDD = 5V, VSS = –5V, V V

= 0.5V unless otherwise noted.

ENABLE

SYMBOL PARAMETER CONDITIONS MIN TYP MAX UNITS

PSRR Power Supply Rejection (Note 9)

IOS

Input Offset Voltage (Notes 6, 7, 10)

Accuracy vs Crest Factor (CF)

CF = 4 60Hz Fundamental, 200mV CF = 5 60Hz Fundamental, 200mV

Input Characteristics

Input Voltage Range (Note 14) Input Impedance Average, Differential (Note 12)

CMRRI Input Common Mode Rejection (Note 13) V V

IMAX

IMIN

Maximum Input Swing Accuracy = 1% (Note 14) Minimum RMS Input

PSRRI Power Supply Rejection V

Output Characteristics

OVR Output Voltage Range Z

OUT

Output Impedance V

CMRRO Output Common Mode Rejection (Note 13) V

OMAX

Maximum Differential Output Swing Accuracy = 2%, DC Input (Note 14)

PSRRO Power Supply Rejection V

Frequency Response

10P

–3dB

1% Additional Error (Note 15) C 10% Additional Error (Note 15) C ±3dB Frequency (Note 15) 800 kHz

Power Supplies

Positive Supply Voltage Negative Supply Voltage (Note 16) Positive Supply Current IN1 = 20mV, IN2 = 0V

Negative Supply Current IN1 = 20mV, IN2 = 0V

Shutdown Characteristics

DDS

SSS

Supply Currents V Supply Currents V

ENABLE Pin Current High V

LTC1966C, LTC1966I LTC1966H, LTC1966MP

(Note 11)

RMS

(Note 11)

RMS

Average, Common Mode (Note 12)

Supply (Note 9)

= 0.5V (Note 12)

ENABLE

= 4.5V

ENABLE

Supply (Note 9)

= 10µF 6 kHz

AVE

= 10µF 20 kHz

AVE

IN1 = 200mV, IN2 = 0V

= 4.5V

ENABLE

= 4.5V

ENABLE

LTC1966H, LTC1966MP

= 4.5V

ENABLE

OUTRTN

= 0V, C

l l

= 10µF, VIN = 200mV

AVE

RMS

0.02 0.15

0.20

0.3

0.02 0.8

1.0

–1 2 mV

–20 30 mV

100

MΩ MΩ

7 200 µV/V

1 1.05 V

5 mV

250 120

75 85

600 300

µV/V µV/V

95 kΩ

30 16 200 µV/V

1.0

1.05 V

0.9 250 501000

500

µV/V µV/V

2.7 5.5 V

–5.5 0 V

155

170 µA

158

12 20 µA

0.5 10 µA

–1

–0.1 µA

–2

–0.3 –0.05 µA

%V %V %V

mV mV

kΩ

µA

1966fb

Page 4

LTC1966

elecTrical characTerisTics

The l denotes the specifications which apply over the full operating temperature range, otherwise specifications are at TA = 25°C. VDD = 5V, VSS = –5V, V V

= 0.5V unless otherwise noted.

ENABLE

SYMBOL PARAMETER CONDITIONS MIN TYP MAX UNITS

HYS

ENABLE Pin Current Low V

ENABLE Threshold Voltage VDD = 5V, VSS = –5V

ENABLE Threshold Hysteresis 0.1 V

= 0.5V

ENABLE

LTC1966H, LTC1966MP

= 5V, VSS = GND

= 2.7V, VSS = GND

OUTRTN

= 0V, C

l l

= 10µF, VIN = 200mV

AVE

–2

–1 –0.1 µA

–10

2.4

2.1

1.3

RMS

µA

V V V

Note 1: Stresses beyond those listed under Absolute Maximum Ratings may cause permanent damage to the device. Exposure to any Absolute Maximum Rating condition for extended periods may affect device reliability and lifetime.

Note 2: The inputs (IN1, IN2) are protected by shunt diodes to V V

. If the inputs are driven beyond the rails, the current should be limited

and

to less than 10mA. Note 3: The LTC1966 output (V

) is high impedance and can be

OUT

overdriven, either sinking or sourcing current, to the limits stated. Note 4: The LTC1966C/LTC1966I are guaranteed functional over

the operating temperature range of –40°C to 85°C. The LTC1966H/ LTC1966MP are guaranteed functional over the operating temperature range of –55°C to 125°C.

Note 5: The LTC1966C is guaranteed to meet specified performance from 0°C to 70°C. The LTC1966C is designed, characterized and expected to meet specified performance from –40°C to 85°C but is not tested nor QA sampled at these temperatures. The LTC1966I is guaranteed to meet specified performance from –40°C to 85°C. The LTC1966H is guaranteed to meet specified performance from –40°C to 125°C. The LTC1966MP is guaranteed to meet specified performance from –55°C to 125°C.

Note 6: High speed automatic testing cannot be performed with C

= 10µF. The LTC1966 is 100% tested with C

AVE

= 22nF. Correlation

AVE

tests have shown that the performance limits above can be guaranteed with the additional testing being performed to guarantee proper operation of all the internal circuitry.

Note 7: High speed automatic testing cannot be performed with 60Hz inputs. The LTC1966 is 100% tested with DC and 10kHz input signals. Measurements with DC inputs from 50mV to 350mV are used to calculate the four parameters: G

ERR

, V

OOS

, V

and linearity error. Correlation tests

IOS

have shown that the performance limits above can be guaranteed with the additional testing being performed to guarantee proper operation of all internal circuitry.

Note 8: The LTC1966 is inherently very linear. Unlike older log/antilog circuits, its behavior is the same with DC and AC inputs, and DC inputs are used for high speed testing.

Note 9: The power supply rejections of the LTC1966 are measured with DC inputs from 50mV to 350mV. The change in accuracy from V V

= 5.5V with VSS = 0V is divided by 2.8V. The change in accuracy from

= 0V to VSS = –5.5V with VDD = 5.5V is divided by 5.5V.

= 2.7V to

Note 10: Previous generation RMS-to-DC converters required nonlinear input stages as well as a nonlinear core. Some parts specify a DC reversal error, combining the effects of input nonlinearity and input offset voltage. The LTC1966 behavior is simpler to characterize and the input offset voltage is the only significant source of DC reversal error.

Note 11: High speed automatic testing cannot be performed with 60Hz inputs. The LTC1966 is 100% tested with DC stimulus. Correlation tests have shown that the performance limits above can be guaranteed with the additional testing being performed to verify proper operation of all internal circuitry.

Note 12: The LTC1966 is a switched capacitor device and the input/ output impedance is an average impedance over many clock cycles. The input impedance will not necessarily lead to an attenuation of the input signal measured. Refer to the Applications Information section titled Input Impedance for more information.

Note 13: The common mode rejection ratios of the LTC1966 are measured with DC inputs from 50mV to 350mV. The input CMRR is defined as the change in V input levels of V output CMRR is defined as the change in V V

and OUT RTN = VDD – 350mV divided by VDD – VSS – 350mV.

measured between input levels of VSS to VSS + 350mV and

IOS

– 350mV to VDD divided by VDD – VSS – 350mV. The

measured with OUT RTN =

OOS

Note 14: Each input of the LTC1966 can withstand any voltage within the supply range. These inputs are protected with ESD diodes, so going beyond the supply voltages can damage the part if the absolute maximum current ratings are exceeded. Likewise for the output pins. The LTC1966 input and output voltage swings are limited by internal clipping. The maximum differential input of the LTC1966 (referred to as maximum input swing) is 1V. This applies to either input polarity, so it can be thought of as ±1V. Because the differential input voltage gets processed by the LTC1966 with gain, it is subject to internal clipping. Exceeding the 1V maximum can, depending on the input crest factor, impact the accuracy of the output voltage, but does not damage the part. Fortunately, the LTC1966’s ∆∑ topology is relatively tolerant of momentary internal clipping. The input clipping is tested with a crest factor of 2, while the output clipping is tested with a DC input.

Note 15: The LTC1966 exploits oversampling and noise shaping to reduce the quantization noise of internal 1-bit analog-to-digital conversions. At higher input frequencies, increasingly large portions of this noise are aliased down to DC. Because the noise is shifted in frequency, it becomes a low frequency rumble and is only filtered at the expense of increasingly long settling times. The LTC1966 is inherently wideband, but the output accuracy is degraded by this aliased noise. These specifications apply with C

= 10µF and constitute a 3-sigma variation of the output rumble.

AVE

Note 16: The LTC1966 can operate down to 2.7V single supply but cannot operate at ±2.7V. This additional constraint on V

mathematically as –3 • (V

– 2.7V) ≤ VSS ≤ Ground.

can be expressed

1966fb

Page 5

Typical perForMance characTerisTics

GAIN ERROR (%)

LTC1966

Gain and Offsets vs Input Common Mode

0.5 VDD = 5V

0.4

= –5V

0.3

0.2

0.1

–0.1

GAIN ERROR (%)

–0.2

–0.3

–0.4

–0.5

–5

GAIN ERROR

OOS

IOS

–4 –2

–3

–1

INPUT COMMON MODE (V)

Gain and Offsets vs Output Common Mode

0.5 VDD = 5V

0.4

= –5V

0.3

0.2

GAIN ERROR

0.1

–0.1

GAIN ERROR (%)

–0.2

–0.3

–0.4

–0.5

–4 –2

–5

–3

OUTPUT COMMON MODE (V)

–1

0 54

IOS

0 54

1966 G03

OOS

1966 G06

0.5

0.4

0.3

0.2

0.1

–0.1

–0.2

–0.3

–0.4

–0.5

0.5

0.4

0.3

0.2

0.1

–0.1

–0.2

–0.3

–0.4

–0.5

0.5

0.4

0.3

OFFSET VOLTAGE (mV)

0.2

0.1

–0.1

–0.2

–0.3

–0.4

–0.5

0.5

0.4

0.3

OFFSET VOLTAGE (mV)

0.2

0.1

–0.1

GAIN ERROR (%)

–0.2

–0.3

–0.4

–0.5

Gain and Offsets vs Input Common Mode

VDD = 5V

= GND

0.5 1.5

1.0

INPUT COMMON MODE (V)

2.0

IOS

OOS

GAIN ERROR

3.5

2.5 5.04.5

3.0

Gain and Offsets vs Output Common Mode

VDD = 5V

= GND

IOS

OOS

GAIN ERROR

0.5 1.5

1.0

OUTPUT COMMON MODE (V)

2.0

3.5

2.5 5.04.5

3.0

4.0

1966 G02

1966 G05

0.5

0.4

0.3

0.2

0.1

–0.1

–0.2

–0.3

–0.4

–0.5

0.5

0.4

0.3

0.2

0.1

–0.1

–0.2

–0.3

–0.4

–0.5

0.5

0.4

0.3

OFFSET VOLTAGE (mV)

0.2

0.1

–0.1

GAIN ERROR (%)

–0.2

–0.3

–0.4

–0.5

0.5

0.4

0.3

OFFSET VOLTAGE (mV)

0.2

0.1

–0.1

GAIN ERROR (%)

–0.2

–0.3

–0.4

–0.5

Gain and Offsets vs Input Common Mode

VDD = 2.7V

= GND

0.3 0.9

0.6 INPUT COMMON MODE (V)

IOS

GAIN ERROR

OOS

1.5 2.7

1.8

1.2

Gain and Offsets vs Output Common Mode

VDD = 2.7V

= GND

GAIN ERROR

OOS

0.3 0.9

0.6

OUTPUT COMMON MODE (V)

IOS

1.5 2.7

1.8

1.2

2.1

2.4

1966 G01

2.4

1966 G04

1.0

0.8

0.6 OFFSET VOLTAGE (mV)

0.4

0.2

–0.2

–0.4

–0.6

–0.8

–1.0

1.0

0.8

0.6 OFFSET VOLTAGE (mV)

0.4

0.2

–0.2

–0.4

–0.6

–0.8

–1.0

Gain and Offsets vs Temperature

0.5 VDD = 5V

0.4

= –5V

0.3

0.2

GAIN ERROR

0.1

–0.1

GAIN ERROR (%)

–0.2

–0.3

–0.4

–0.5

–40 –20

–60

IOS

40 602080

0 TEMPERATURE (°C)

OOS

100 120

1966 G09

0.5

0.4

0.3 OFFSET VOLTAGE (mV)

0.2

0.1

–0.1

–0.2

–0.3

–0.4

–0.5

140

Gain and Offsets vs Temperature

0.5 VDD = 5V

0.4

= GND

0.3

0.2

0.1

GAIN ERROR

–0.1

GAIN ERROR (%)

–0.2

–0.3

–0.4

–0.5

–60

–40

–20 0

TEMPERATURE (°C)

402060

80 100 120

Gain and Offsets vs Temperature

1966 G07

1.0

0.8

0.6 OFFSET VOLTAGE (mV)

0.4

0.2

–0.2

–0.4

–0.6

–0.8

–1.0

140

1966fb

0.5

0.4

IOS

0.3

0.2

OOS

0.1

–0.1

–0.2

–0.3

–0.4

–0.5

140

1966 G08

0.5 VDD = 2.7V

0.4

= GND

0.3

OFFSET VOLTAGE (mV)

0.2

0.1

–0.1

GAIN ERROR (%)

–0.2

–0.3

–0.4

–0.5

–60

–40

–20

IOS

GAIN ERROR

OOS

402060

TEMPERATURE (°C)

80 100 120

Page 6

LTC1966

Typical perForMance characTerisTics

Gain and Offsets vs VSS Supply

0.5 VDD = 5V

0.4

0.3

0.2

GAIN ERROR

0.1

–0.1

GAIN ERROR (%)

–0.2

–0.3

–0.4

–0.5

–6

NOMINAL

–5

SPECIFIED

CONDITIONS

–4

VSS (V)

OOS

–2–3–1

Performance vs Large Crest Factors

230

220

210

200

190

180

170

OUTPUT VOLTAGE (mV DC)

160

150

FUNDAMENTAL

FREQUENCY

200mV

RMS

= 4.7µF

AVE

= 5V

5%/DIV

2 3 5

20Hz

100Hz

SCR WAVEFORMS

CREST FACTOR

60Hz

6 7 8

1966 G11

250Hz

1966 G12

IOS

0.5

0.4

0.3

0.2

0.1

–0.1

–0.2

–0.3

–0.4

–0.5

0.5 VSS = GND

0.4

0.3

OFFSET VOLTAGE (mV)

0.2

0.1

–0.1

GAIN ERROR (%)

–0.2

–0.3

–0.4

–0.5

2.5

3.0

AC Linearity

0.20 60Hz SINEWAVES

= 1µF

AVE

0.15

)

RMS

0.10

0.05

(mV AC

–0.05

(mV DC) – V

–0.10

OUT

–0.15

–0.20

= GND

IN2

100 200 300 50035050 150 250 450

GAIN ERROR

3.5

(mV AC

IN1

IOS

OOS

4.0

VDD (V)

RMS

4.5

Performance vs Crest FactorGain and Offsets vs VDD Supply

5.0

1966 G10

5.5

0.8

0.6

0.4

0.2

–0.2

–0.4

–0.6

–0.8

–1.0

201.0 200mV

AVE

200.8

OFFSET VOLTAGE (mV)

O.1%/DIV

200.6

200.4

200.2

OUTPUT VOLTAGE (mV DC)

200.0

199.8

1.0

SCR WAVEFORMS

RMS

= 10µF

= 5V

1.5 2.5

2.0 3.0 CREST FACTOR

20Hz 60Hz

100Hz

3.5

4.0

4.5

5.0

1966 G15

Output Accuracy vs Signal Amplitude

1% ERROR

)

RMS

(mV

–5

–1% ERROR

–10

(mV DC) – V

OUT

–15

–20

400

)

1966 G13

AC INPUT

= 3V

0.5 1 1.5 2 V

IN1

AC INPUTS = 60Hz SINEWAVES V

= GND

IN2

AC INPUT

= 5V

DC INPUT

VDD = 5V

)

RMS

2.5

1966 G24

| (mV)

INDC

– |V

OUTDC

0.10

0.08

0.06

0.04

0.02

–0.02

–0.04

–0.06

–0.08

–0.10

DC Linearity

= 1µF

AVE

= GND

IN2

–300

–500

–100

(mV)

IN1

EFFECT OF OFFSETS MAY BE POSITIVE OR NEGATIVE

100

300

1966 G14

500

Quiescent Supply Currents vs Supply Voltage

200

175

150

125

100

SUPPLY CURRENT (µA)

–25

2 6

1 5

VDD SUPPLY VOLTAGE (V)

VSS = GND

1966 G16

Shutdown Currents vs ENABLE Voltage

250

VDD = 5V

200

150

100

SUPPLY CURRENT (µA)

–50

–100

1 2

ENABLE PIN VOLTAGE (V)

3 5

4 6

1966 G18

ENABLE PIN CURRENT (nA)

500

250

–250

–500

1966fb

Page 7

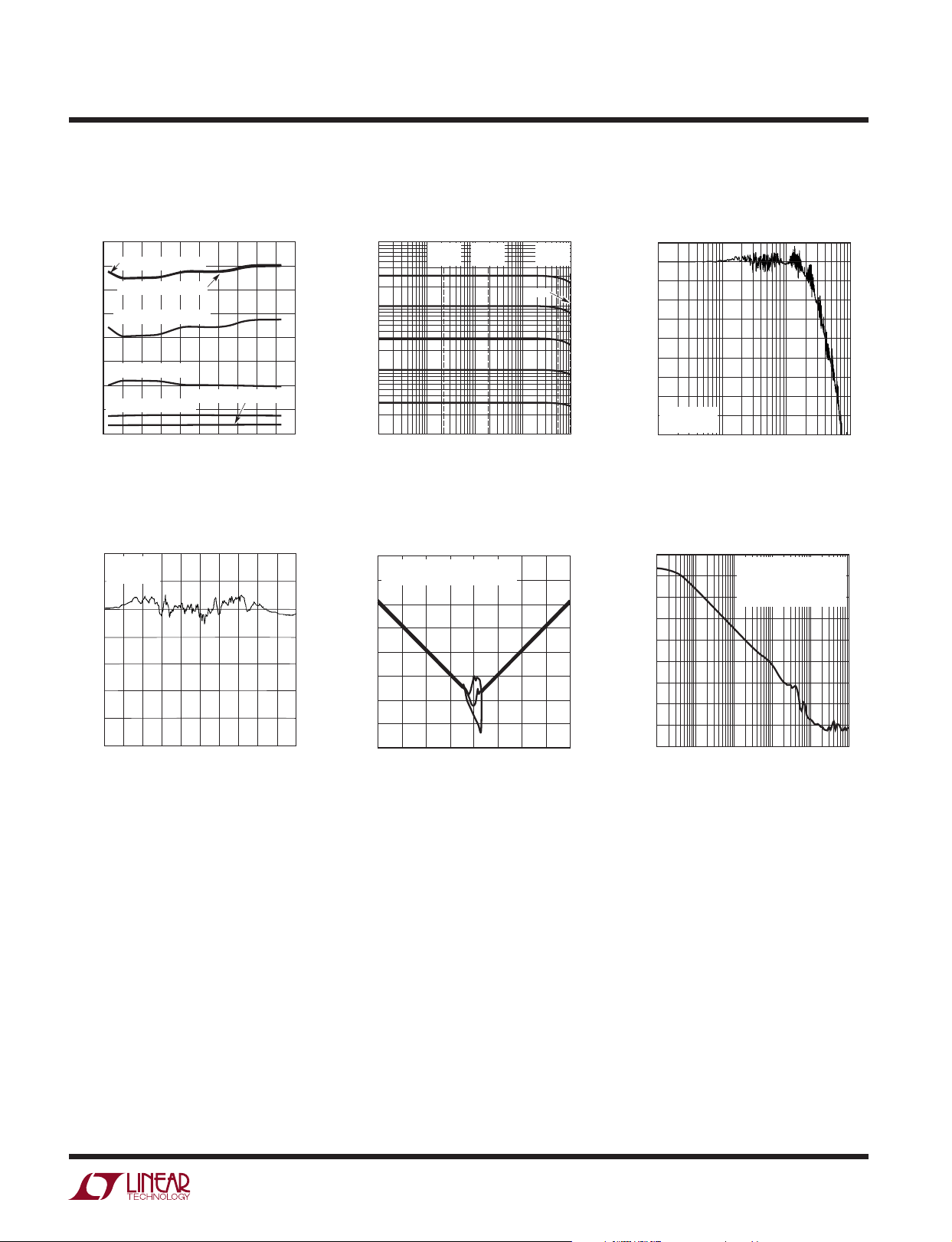
Typical perForMance characTerisTics

Quiescent Supply Currents vs Temperature

170

VDD = 5V, VSS = –5V

160

VDD = 5V, VSS = GND

150

140

VDD = 2.7V, VSS = GND

(µA)

130

120

VDD = 5V, VSS = –5V

110

VDD = 5V, VSS = GND

100

–40 –20 6040

–60

0 20 TEMPERATURE (°C)

Bandwidth to 100kHz

202

0.5%/DIV = 47µF

AVE

201

200

199

198

197

OUTPUT DC VOLTAGE (mV)

196

195

INPUT FREQUENCY (kHz)

VDD = 2.7V, VSS = GND

80 100 120 140

1966 G17

60 80

1966 G21

100

(µA)

Input Signal Bandwidth

1000

100

OUTPUT DC VOLTAGE (mV)

1 100 1K

0.1%

ERROR1%ERROR

INPUT SIGNAL FREQUENCY (Hz)

10K 100K 1M

DC Transfer Function Near Zero

= GND

IN2

THREE REPRESENTITIVE UNITS

(mV DC)

OUT

–5

–10

–20

–15

–10

–5

IN1

(mV DC)

–3dB

10%

ERROR

1966 G19

1966 G22

LTC1966

Input Signal Bandwidth

202

200

198

196

194 192

190

188

OUTPUT DC VOLTAGE (mV)

186

1%/DIV

184

= 2.2µF

AVE

182

Common Mode Rejection Ratio vs Frequency

110

100

COMMON MODE REJECTION RATIO (dB)

10 1k 10k 1M

10 100 1000

INPUT FREQUENCY (kHz)

VDD = 5V

= –5V

±5V INPUT CONVERSION

TO DC OUTPUT

100

FREQUENCY (Hz)

1966 G20

100k

1966 G23

1966fb

Page 8

LTC1966

––

()

pin FuncTions

GND (Pin 1): Ground. A power return pin. IN1 (Pin 2): Differential Input. DC coupled (polarity is

irrelevant). IN2 (Pin 3): Differential Input. DC coupled (polarity is

irrelevant).

(Pin 4): Negative Voltage Supply. GND to – 5.5V.

(Pin 5): Output Voltage. This is high impedance.

OUT

The RMS averaging is accomplished with a single shunt capacitor from this node to OUT RTN. The transfer function is given by:

V OUT RTN Average IN IN

()

OUT







 



OUT RTN (Pin 6): Output Return. The output voltage is created relative to this pin. The V are not balanced and this pin should be tied to a low impedance, both AC and DC. Although it is typically tied to GND, it can be tied to any arbitrary voltage, V

RTN < (V

OUT RTN = GND.

(Pin 7): Positive Voltage Supply. 2.7V to 5.5V.

ENABLE (Pin 8): An Active Low Enable Input. LTC1966 is debiased if open circuited or driven to V operation, pull to GND, a logic low or even V

– Max Output). Best results are obtained when

and OUT RTN pins

OUT

. For normal

< OUT

1966fb

Page 9

applicaTions inForMaTion

LTC1966

START

READ

RMS-TO-DC

CONVERSION

CONTACT LTC BY PHONE OR

AT www.linear.com AND

GET SOME NOW

YOU ALREADY TRY OUT

READ THE TROUBLESHOOTING

GUIDE. IF NECESSARY, CALL

LTC FOR APPLICATIONS SUPPORT

NOT

SURE

DID

THE LTC1966?

YES NO

DO YOU

NEED TRUE RMS-TO-DC

CONVERSION?

YES

DO YOU

HAVE ANY LTC1966s

YET?

YES

DID

YOUR CIRCUIT

WORK?

DO YOU WANT TO

KNOW HOW TO USE THE

LTC1966 FIRST?

FIND SOMEONE WHO DOES

AND GIVE THEM THIS

DATA SHEET

YES

READ THE DESIGN COOKBOOK

CONTACT LTC

AND PLACE YOUR ORDER

YES

WELL ENOUGH THAT YOU

YES

NOW DOES YOUR

RMS CIRCUIT WORK

ARE READY TO BUY

THE LTC1966?

READ THE TROUBLESHOOTING

GUIDE AGAIN OR CALL LTC

FOR APPLICATIONS SUPPORT

1966 TA02

1966fb

Page 10

LTC1966

applicaTions inForMaTion

RMS-TO-DC CONVERSION

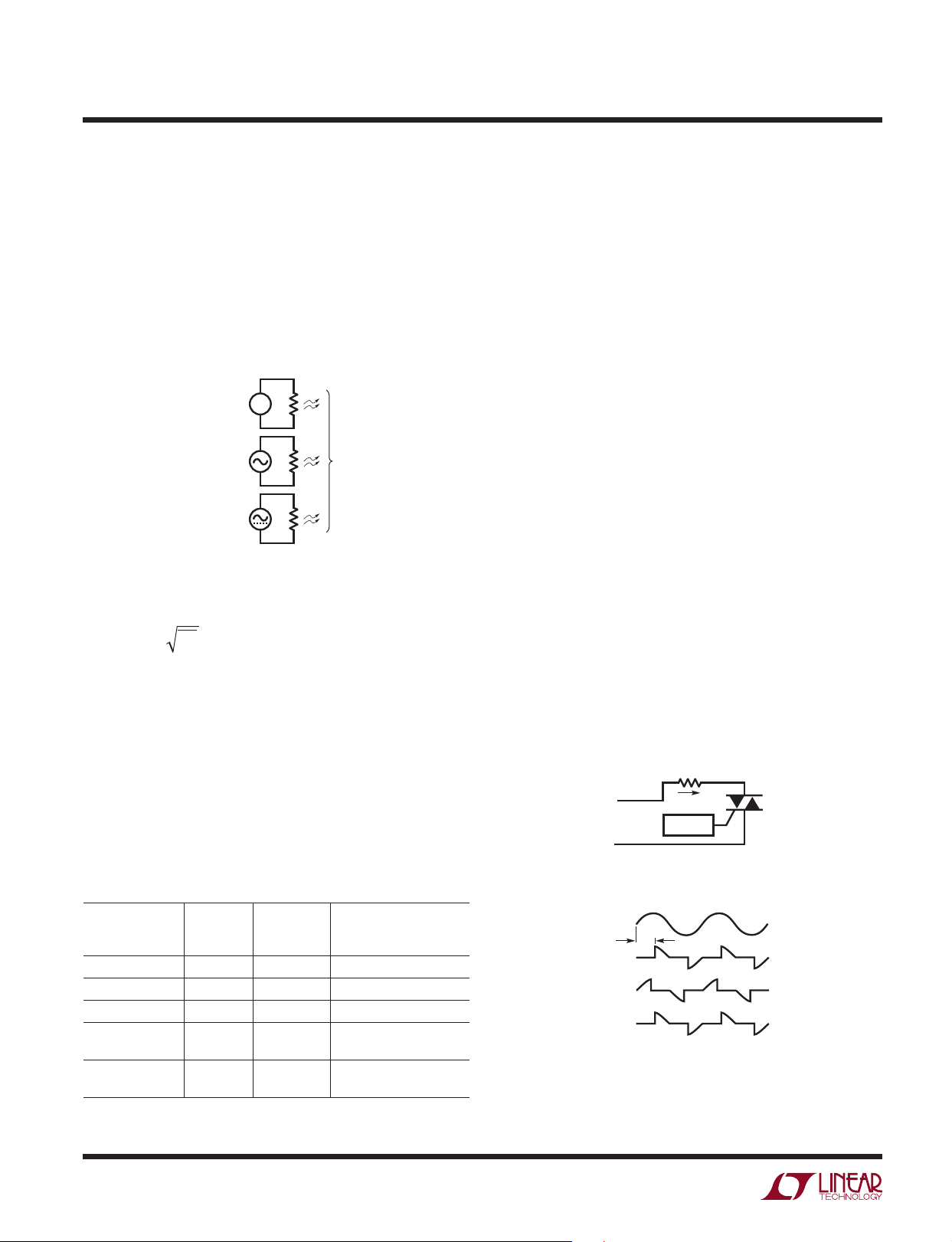
Definition of RMS

RMS amplitude is the consistent, fair and standard way to measure and compare dynamic signals of all shapes and sizes. Simply stated, the RMS amplitude is the heating potential of a dynamic waveform. A 1V

AC waveform

RMS

will generate the same heat in a resistive load as will 1V DC.

R1V DC

–

1V AC

RMS

R1V (AC + DC) RMS

SAME HEAT

1966 F01

Figure 1

Mathematically, RMS is the root of the mean of the square:

RMS

Alternatives to RMS

Other ways to quantify dynamic waveforms include peak detection and average rectification. In both cases, an average (DC) value results, but the value is only accurate at the one chosen waveform type for which it is calibrated, typically sine waves. The errors with average rectification are shown in Table 1. Peak detection is worse in all cases and is rarely used.

Table 1. Errors with Average Rectification vs True RMS

AVERAGE

RECTIFIED

WAVEFORM V

Square Wave 1.000 1.000 11% Sine Wave 1.000 0.900 *Calibrate for 0% Error Triangle Wave 1.000 0.866 –3.8% SCR at 1/2 Power,

Θ = 90° SCR at 1/4 Power,

Θ = 114°

RMS

1.000 0.637 –29.3%

1.000 0.536 –40.4%

(V) ERROR*

The last two entries of Table 1 are chopped sine waves as is commonly created with thyristors such as SCRs and Triacs. Figure 2a shows a typical circuit and Figure 2b shows the resulting load voltage, switch voltage and load currents. The power delivered to the load depends on the firing angle, as well as any parasitic losses such as switch ON voltage drop. Real circuit waveforms will also typically have significant ringing at the switching transition, dependent on exact circuit parasitics. For the purposes of this data sheet, SCR waveforms refers to the ideal chopped sine wave, though the LTC1966 will do faithful RMS-to-DC conversion with real SCR waveforms as well.

The case shown is for Θ = 90°, which corresponds to 50% of available power being delivered to the load. As noted in Table 1, when Θ = 114°, only 25% of the available power is being delivered to the load and the power drops quickly as Θ approaches 180°.

With an average rectification scheme and the typical calibration to compensate for errors with sine waves, the RMS level of an input sine wave is properly reported; it is only with a nonsinusoidal waveform that errors occur. Because of this calibration, and the output reading in

, the term true RMS got coined to denote the use of

RMS

an actual RMS-to-DC converter as opposed to a calibrated average rectifier.

LOAD

–

MAINS

LOAD

LINE

THY

LINE

–

LOAD

CONTROL

Figure 2a

Figure 2b

–

1966 F02a

1966 F02b

THY

1966fb

Page 11

applicaTions inForMaTion

()

LTC1966

How an RMS-to-DC Converter Works

Monolithic RMS-to-DC converters use an implicit computation to calculate the RMS value of an input signal. The fundamental building block is an analog multiply/ divide used as shown in Figure 3. Analysis of this topology is easy and starts by identifying the inputs and the output of the lowpass filter. The input to the LPF is the calculation from the multiplier/divider; (V

)2/V

OUT

. The lowpass filter will take the average of this to create the output, mathematically:



OUT

()

  

Because V is DC,

 

 

VVor

()

VVRMS V



()

 

OUT

 

()



OUT

OUT IN

OUT IN IN



 

OUT



OUT

 

OUT

()



()



OUT

 

and

How the LTC1966 RMS-to-DC Converter Works

The LTC1966 uses a completely new topology for RMSto-DC conversion, in which a ∆S modulator acts as the divider, and a simple polarity switch is used as the multiplier as shown in Figure 4.

OUT

∆–∑

REF

±1

LPF

Figure 4. Topology of LTC1966

OUT

The ∆S modulator has a single-bit output whose average duty cycle (D) will be proportional to the ratio of the input signal divided by the output. The ∆S is a 2nd order modulator with excellent linearity. The single bit output is used to selectively buffer or invert the input signal. Again, this is a circuit with excellent linearity, because it operates at only two points: ±1 gain; the average effective multiplication over time will be on the straight line between these two points. The combination of these two elements again creates a lowpass filter input signal proportional to (VIN)2/V

OUT

which, as shown above, results in RMS-to-DC conversion.

()

OUT

Figure 3. RMS-to-DC Converter with Implicit Computation

× ÷

LPF

1966 F03

OUT

Unlike the prior generation RMS-to-DC converters, the LTC1966 computation does NOT use log/antilog circuits, which have all the same problems, and more, of log/antilog multipliers/dividers, i.e., linearity is poor, the bandwidth changes with the signal amplitude and the gain drifts with temperature.

The lowpass filter performs the averaging of the RMS function and must be a lower corner frequency than the lowest frequency of interest. For line frequency measurements, this filter is simply too large to implement on-chip, but the LTC1966 needs only one capacitor on the output to implement the lowpass filter. The user can select this capacitor depending on frequency range and settling time requirements, as will be covered in the Design Cookbook section to follow.

This topology is inherently more stable and linear than log/antilog implementations primarily because all of the signal processing occurs in circuits with high gain op amps operating closed loop.

1966fb

Page 12

LTC1966

applicaTions inForMaTion

More detail of the LTC1966 inner workings is shown in the Simplified Schematic towards the end of this data sheet. Note that the internal scalings are such that the ∆S output duty cycle is limited to 0% or 100% only when VIN

exceeds ± 4 • V

OUT

Linearity of an RMS-to-DC Converter

Linearity may seem like an odd property for a device that implements a function that includes two very nonlinear processes: squaring and square rooting.

However, an RMS-to-DC converter has a transfer function, RMS volts in to DC volts out, that should ideally have a 1:1 transfer function. To the extent that the input to output transfer function does not lie on a straight line, the part is nonlinear.

A more complete look at linearity uses the simple model shown in Figure 5. Here an ideal RMS core is corrupted by both input circuitry and output circuitry that have imperfect transfer functions. As noted, input offset is introduced in the input circuitry, while output offset is introduced in the output circuitry.

Any nonlinearity that occurs in the output circuity will corrupt the RMS in to DC out transfer function. A nonlinearity in the input circuitry will typically corrupt that transfer function far less, simply because with an AC input, the RMS-to-DC conversion will average the nonlinearity from a whole range of input values together.

But the input nonlinearity will still cause problems in an RMS-to-DC converter because it will corrupt the accuracy as the input signal shape changes. Although an RMS-to-DC converter will convert any input waveform to a DC output, the accuracy is not necessarily as good for all waveforms as it is with sine waves. A common way to describe dynamic signal wave shapes is crest factor. The crest factor is the ratio of the peak value relative to the RMS value of a waveform. A signal with a crest factor of 4, for instance, has a peak that is four times its RMS value. Because this peak has energy (proportional to voltage squared) that is 16 times (4

) the energy of the RMS value, the peak is

necessarily present for at most 6.25% (1/16) of the time. The LTC1966 performs very well with crest factors of 4

or less and will respond with reduced accuracy to signals with higher crest factors. The high performance with crest factors less than 4 is directly attributable to the high linearity throughout the LTC1966.

The LTC1966 does not require an input rectifier, as is common with traditional log/antilog RMS-to-DC converters. Thus, the LTC1966 has none of the nonlinearities that are introduced by rectification.

The excellent linearity of the LTC1966 allows calibration to be highly effective at reducing system errors. See System Calibration section following the Design Cookbook.

INPUT CIRCUITRY

INPUT OUTPUT

• V

IOS

• INPUT NONLINEARITY

Figure 5. Linearity Model of an RMS-to-DC Converter

IDEAL

RMS-TO-DC

CONVERTER

OUTPUT CIRCUITRY

• V

OOS

• OUTPUT NONLINEARITY

1966 F05

1966fb

Page 13

applicaTions inForMaTion

LTC1966

DESIGN COOKBOOK

The LTC1966 RMS-to-DC converter makes it easy to implement a rather quirky function. For many applications all that will be needed is a single capacitor for averaging, appropriate selection of the I/O connections and power supply bypassing. Of course, the LTC1966 also requires power. A wide variety of power supply configurations are shown in the Typical Applications section towards the end of this data sheet.

Capacitor Value Selection

The RMS or root-mean-squared value of a signal, the root of the mean of the square, cannot be computed without

some averaging to obtain the mean function. The LTC1966 true RMS-to-DC converter utilizes a single capacitor on the output to do the low frequency averaging required for RMS-to-DC conversion. To give an accurate measure of a dynamic waveform, the averaging must take place over a sufficiently long interval to average, rather than track, the lowest frequency signals of interest. For a single averaging capacitor, the accuracy at low frequencies is depicted in Figure 6.

However, if the output is examined on an oscilloscope with a very low frequency input, the incomplete averaging will be seen, and this ripple will be larger than the error depicted in Figure 6. Such an output is depicted in Figure7. The ripple is at twice the frequency of the input because of the computation of the square of the input. The typical values shown, 5% peak ripple with 0.05% DC error, occur with C

= 1µF and f

AVE

INPUT

= 10Hz.

If the application calls for the output of the LTC1966 to feed a sampling or Nyquist A/D converter (or other circuitry that will not average out this double frequency ripple) a larger averaging capacitor can be used. This trade-off is depicted in Figure 8. The peak ripple error can also be reduced by additional lowpass filtering after the LTC1966, but the simplest solution is to use a larger averaging capacitor.

This frequency dependent error is in addition to the static errors that affect all readings and are therefore easy to trim or calibrate out. The Error Analyses section to follow discusses the effect of static error terms.

ACTUAL OUTPUT WITH RIPPLE f = 2 × f

INPUT

PEAK

RIPPLE

(5%)

IDEAL

OUTPUT

ERROR

(0.05%)

Figure 6 depicts the so-called DC error that results at a given combination of input frequency and filter capacitor

values

. It is appropriate for most applications, in which the output is fed to a circuit with an inherently band limited frequency response, such as a dual slope/integrating A/D converter, a ∆S A/D converter or even a mechanical analog meter.

–0.2

C = 4.7µF

–0.4

–0.6

–0.8

–1.0

–1.2

DC ERROR (%)

–1.4

–1.6

–1.8

–2.0

C = 10µF

C = 2.2µF

C = 1.0µF

C = 0.47µF

INPUT FREQUENCY (Hz)

Figure 6. DC Error vs Input Frequency

OUTPUT

PEAK

ERROR =

DC ERROR +

PEAK RIPPLE

(5.05%)

TIME

AVERAGE

OF ACTUAL

OUTPUT

1966 F07

Figure 7. Output Ripple Exceeds DC Error

C = 0.22µF

10 20 50 60 100

C = 0.1µF

1966 F06

1966fb

Page 14

LTC1966

applicaTions inForMaTion

–0.2

–0.4

C = 100µF

–0.6

–0.8

–1.0

–1.2

PEAK ERROR (%)

–1.4

–1.6

–1.8

–2.0

C = 47µF

C = 22µF C = 10µF

Figure 8. Peak Error vs Input Frequency with One Cap Averaging

C = 4.7µF

10 20 50 60 100

INPUT FREQUENCY (Hz)

C = 2.2µF C = 1µF

1966 F08

A 1µF capacitor is a good choice for many applications. The peak error at 50Hz/60Hz will be <1% and the DC error will be <0.1% with frequencies of 10Hz or more.

Note that both Figure 6 and Figure 8 assume AC-coupled waveforms with a crest factor less than 2, such as sine waves or triangle waves. For higher crest factors and/or AC + DC waveforms, a larger C

will generally be required.

AVE

See Crest Factor and AC + DC Waveforms.

Capacitor Type Selection

The LTC1966 can operate with many types of capacitors. The various types offer a wide array of sizes, tolerances, parasitics, package styles and costs.

Ceramic chip capacitors offer low cost and small size, but are not recommended for critical applications. The value stability over voltage and temperature is poor with many types of ceramic dielectrics. This will not cause an RMS-to-DC accuracy problem except at low frequencies, where it can aggravate the effects discussed in the previous section. If a ceramic capacitor is used, it may be necessary to use a much higher nominal value in order to assure the low frequency accuracy desired.

Another parasitic of ceramic capacitors is leakage, which is again dependent on voltage and particularly temperature.

If the leakage is a constant current leak, the I • R drop of

the leak multiplied by the output impedance of the LTC1966 will create a constant offset of the output voltage. If the leak is Ohmic, the resistor divider formed with the LTC1966 output impedance will cause a gain error. For < 0.1% gain accuracy degradation, the parallel impedance of the

capacitor leakage will need to be > 1000 times the LTC1966 output impedance. Accuracy at this level can be hard to achieve with a ceramic capacitor, particularly with a large value of capacitance and at high temperature.

For critical applications, a film capacitor, such as metalized polyester, will be a much better choice. Although more expensive, and larger for a given value, the value stability and low leakage make metal film capacitors a trouble free choice.

With any type of capacitor, the self resonance of the capacitor can be an issue with the switched capacitor LTC1966. If the self resonant frequency of the averaging capacitor is 1MHz or less, a second smaller capacitor should be added in parallel to reduce the impedance seen by the LTC1966 output stage at high frequencies. A capacitor 100 times smaller than the averaging capacitor will typically be small enough to be a low cost ceramic with a high quality dielectric such as X7R or NPO/COG.

Input Connections

The LTC1966 input is differential and DC coupled. The LTC1966 responds to the RMS value of the differential voltage between Pin 2 and Pin 3, including the DC portion of that difference. However, there is no DC-coupled path from the inputs to ground. Therefore, at least one of the two inputs must be connected with a DC return path to ground.

Both inputs must be connected to something. If either input is left floating, a zero volt output will result.

1966fb

Page 15

applicaTions inForMaTion

LTC1966

For single-ended DC-coupled applications, simply connect one of the two inputs (they are interchangeable) to the signal, and the other to ground. This will work well for dual supply configurations, but for single supply configurations it will only work well for unipolar input signals. The LTC1966 input voltage range is from railto-rail, and when the input is driven above V

(ground for single supply operation) the gain and

or below

offset errors will increase substantially after just a few hundred millivolts of overdrive. Fortunately, most single supply circuits measuring a DC-coupled RMS value will include some reference voltage other than ground, and the second LTC1966 input can be connected to that point.

For single-ended AC-coupled applications, Figure 9 shows three alternate topologies. The first one, shown in Figure 9a uses a coupling capacitor to one input while the other is grounded. This will remove the DC voltage difference from the input to the LTC1966, and it will therefore not be part of the resulting output voltage. Again, this connection will work well with dual supply configurations, but in single supply configurations it will be necessary to raise the voltage on the grounded input to assure that the signal at the active input stays within the range of V

to VDD. If there

is already a suitable voltage reference available, connect the second input to that point. If not, a midsupply voltage can be created with two resistors as shown in Figure 9b.

Finally, if the input voltage is known to be between V and V

, it can be AC-coupled by using the configuration

shown in Figure 9c. Whereas the DC return path was provided through Pin 3 in Figures 9a and 9b, in this case, the return path is provided on Pin 2, through the input signal voltages. The switched capacitor action between the two input pins of the LTC1966 will cause the voltage

on the coupling capacitor connected to the second input to follow the DC average of the input voltage.

For differential input applications, connect the two inputs to the differential signal. If AC coupling is desired, one of the two inputs can be connected through a series capacitor.

In all of these connections, to choose the input coupling capacitor, C

, calculate the low frequency coupling time

constant desired, and divide by the LTC1966 differential input impedance. Because the LTC1966 input impedance is about 100 times its output impedance, this capacitor is typically much smaller than the output averaging capacitor. Its requirements are also much less stringent, and a ceramic chip capacitor will usually suffice.

Output Connections

The LTC1966 output is differentially, but not symmetrically, generated. That is to say, the RMS value that the LTC1966 computes will be generated on the output (Pin 5) relative to the output return (Pin 6), but these two pins are not interchangeable. For most applications, Pin 6 will be tied to ground (Pin 1), and this will result in the best accuracy. However, Pin 6 can be tied to any voltage between V (Pin 4) and V swing desired. This last restriction keeps V within the range of V

(Pin 7) less the maximum output voltage

itself (Pin 5)

OUT

to VDD. If a reference level other

than ground is used, it should be a low impedance, both AC and DC, for proper operation of the LTC1966.

Use of a voltage in the range of V

– 1V to VDD – 1.3V can

lead to errors due to the switch dynamics as the NMOS transistor is cut off. For this reason, it is recommended that OUT RTN = 0V if V

is ≤3V.

LTC1966

IN1

IN2

(9a)

Figure 9. Single-Ended AC-Coupled Input Connection Alternatives

100k

R2 100k

IN1

IN2

(9b)

LTC1966

IN1

(9c)

IN2

1966 F09

OR GND

1966fb

–

Page 16

LTC1966

applicaTions inForMaTion

In any configuration, the averaging capacitor should be connected between Pins 5 and 6. The LTC1966 RMS DC output will be a positive voltage created at V with respect to OUT RTN (Pin 6).

Power Supply Bypassing

The LTC1966 is a switched capacitor device, and large transient power supply currents will be drawn as the switching occurs. For reliable operation, standard power supply bypassing must be included. For single supply operation, a 0.01µF capacitor from V

(Pin 7) to GND

(Pin1) located close to the device will suffice. For dual supplies, add a second 0.01µF capacitor from V to GND (Pin 1), located close to the device. If there is a good quality ground plane available, the capacitors can go directly to that instead. Power supply bypass capacitors can, of course, be inexpensive ceramic types.

The sampling clock of the LTC1966 operates at approximately 200kHz, and most operations repeat at a rate of 100kHz. If this internal clock becomes synchronized to a multiple or submultiple of the input frequency, significant conversion error could occur. This is particularly important when frequencies exceeding 10kHz can be injected into the LTC1966 via supply or ground bounce. To minimize this possibility, capacitive bypassing is recommended on both supplies with capacitors placed immediately adjacent to the LTC1966. For best results, the bypass capacitors should be separately routed from Pin 7 to Pin 1, and from Pin 4 to Pin 1.

OUT

(Pin 5)

(Pin 4)

–1

–2

(V)

–3

–4

–5

–6

2.5

Figure 10. VSS Limits vs V

3.5 4 4.5

LTC1966

OPERATES IN THIS RANGE

5 5.5

VDD (V)

1966 F10

Up and Running!

If you have followed along this far, you should have the LTC1966 up and running by now! Don’t forget to enable the device by grounding Pin 8, or driving it with a logic low.

Keep in mind that the LTC1966 output impedance is fairly high, and that even the standard 10MΩ input impedance of a digital multimeter (DMM) or a 10× scope probe will load down the output enough to degrade its typical gain error of 0.1%. In the end application circuit, either a buffer or another component with an extremely high input impedance (such as a dual slope integrating ADC) should be used. For laboratory evaluation, it may suffice to use a bench top DMM with the ability to disconnect the 10MΩ shunt.

If you are still having trouble, it may be helpful to skip ahead a few pages and review the Troubleshooting Guide.

The LTC1966 needs at least 2.7V for its power supply, more for dual supply configurations. The range of allowable negative supply voltages (V voltages (V

constraint is:

–3 • (V

) is shown in Figure 10. Mathematically, the

– 2.7V) ≤ VSS ≤ GND

) vs positive supply

The LTC1966 has internal ESD absorption devices, which are referenced to the V

and V

in-circuit ESD immunity, the V

supplies. For effective

and VSS pins must be

connected to a low external impedance. This can be accomplished with low impedance power planes or simply with the recommended 0.01µF decoupling to ground on each supply.

What About Response Time?

With a large value averaging capacitor, the LTC1966 can easily perform RMS-to-DC conversion on low frequency signals. It compares quite favorably in this regard to prior generation products because nothing about the ∆S circuitry is temperature sensitive. So the RMS result doesn’t get distorted by signal driven thermal fluctuations like a log/antilog circuit output does.

However, using large value capacitors results in a slow response time. Figure 11 shows the rising and falling step responses with a 1µF averaging capacitor. Although they both appear at first glance to be standard exponential

1966fb

Page 17

applicaTions inForMaTion

120

= 1µF

AVE

100

120

100

LTC1966

= 1µF

AVE

LTC1966 OUTPUT (mV)

0.1 0.2 0.3 0.4 TIME (SEC)

Figure 11a. LTC1966 Rising Edge with C

SETTLING ACCURACY (%)

0.1

0.01

LTC1966 OUTPUT (mV)

0.5

1966 F11a

= 1µF Figure 11b. LTC1966 Falling Edge with C

AVE

1 100.1 100

SETTLING TIME (SEC)

0.2 0.4 0.6 0.8

Figure 12. LTC1966 Settling Time with One Cap Averaging

TIME (SEC)

1966 F11b

AVE

= 1µF

C = 100µFC = 47µFC = 22µFC = 10µFC = 4.7µFC = 2.2µFC = 0.47µFC = 0.22µFC = 0.1µF C = 1µF

1966 F12

decay type settling, they are not. This is due to the nonlinear nature of an RMS-to-DC calculation. Also note the change in the time scale between the two; the rising edge is more than twice as fast to settle to a given accuracy. Again this is a necessary consequence of RMS-to-DC calculation.

Although shown with a step change between 0mV and 100mV, the same response shapes will occur with the LTC1966 for ANY step size. This is in marked contrast to prior generation log/antilog RMS-to-DC converters, whose averaging time constants are dependent on the signal level, resulting in excruciatingly long waits for the output to go to zero.

The shape of the rising and falling edges will be dependent on the total percent change in the step, but for less than the 100% changes shown in Figure 11, the responses will be less distorted and more like a standard exponential

decay. For example, when the input amplitude is changed from 100mV to 110mV (+10%) and back (–10%), the step responses are essentially the same as a standard exponential rise and decay between those two levels. In such cases, the time constant of the decay will be in between that of the rising edge and falling edge cases of Figure 11. Therefore, the worst case is the falling edge response as it goes to zero, and it can be used as a design guide.

Figure12 shows the settling accuracy vs settling time for a variety of averaging capacitor values. If the capacitor value previously selected (based on error requirements) gives an acceptable settling time, your design is done.

To convince oneself of this necessity, consider a pulse train of 50% duty cycle between 0mV and 100mV. At very low frequencies, the LTC1966 will essentially track the input. But as the input frequency is increased, the average result will converge to the RMS value of the input. If the rise and fall characteristics were symmetrical, the output would converge to 50mV. In fact though, the RMS value of a 100mV DC-coupled 50% duty cycle pulse train is 70.71mV, which the asymmetrical rise and fall characteristics will converge to as the input frequency is increased.

1966fb

Page 18

LTC1966

applicaTions inForMaTion

But with 100µF, the settling time to even 10% is a full 38 seconds, which is a long time to wait. What can be done about such a design? If the reason for choosing 100µF is to keep the DC error with a 75mHz input less than 0.1%, the answer is: not much. The settling time to 1% of 76 seconds is just 5.7 cycles of this extremely low frequency. Averaging very low frequency signals takes a long time.

However, if the reason for choosing 100µF is to keep the peak error with a 10Hz input less than 0.05%, there is another way to achieve that result with a much improved settling time.

Reducing Ripple with a Post Filter

The output ripple is always much larger than the DC error, so filtering out the ripple can reduce the peak error substantially, without the large settling time penalty of simply increasing the averaging capacitor.

Figure 13 shows a basic 2nd order post filter, for a net 3rd order filtering of the LTC1966 RMS calculation. It uses the 85kΩ output impedance of the LTC1966 as the first resistor of a 3rd order Sallen-Key active RC filter. This topology features a buffered output, which can be desirable depending on the application. However, there are disadvantages to this topology, the first of which is that the op amp input voltage and current errors directly degrade the effective LTC1966 V

. The table inset in Figure 13 shows these

OOS

errors for four of Linear Technology’s op amps.

LTC1966 C

OP AMP

LTC1966 V

OOS

IOS

• R

B/OS

TOTAL OFFSET

VALUE

38.3k

AVE

1µF

LT1494

±375µV

±73µV

±648µV

294k

1µA

169k

1µF

LT1880

±150µV ±329µV ±679µV SHORT

1.2mA

–

0.1µF

LT1077

±200µV

±60µV ±329µV ±589µV

294k 48µA

LT1880

LT 2050

±27µV ±230µV SHORT

750µA

±3µV

1966 F13

A second disadvantage is that the op amp output has to operate over the same range as the LTC1966 output, including ground, which in single supply applications is the negative supply. Although the LTC1966 output will function fine just millivolts from the rail, most op amp output stages (and even some input stages) will not. There are at least two ways to address this. First of all, the op amp can be operated split supply if a negative supply is available. Just the op amp would need to do so; the LTC1966 can remain single supply. A second way to address this issue is to create a signal reference voltage a half volt or so above ground. This is most attractive when the circuitry that follows has a differential input, so that the tolerance of the signal reference is not a concern. To do this, tie all three ground symbols shown in Figure 13 to the signal reference, as well as to the differential return for the circuitry that follows.

Figure 14 shows an alternative 2nd order post filter, for a net 3rd order filtering of the LTC1966 RMS calculation. It also uses the 85kΩ output impedance of the LTC1966 as the first resistor of a 3rd order active RC filter, but this topology filters without buffering so that the op amp DC error characteristics do not affect the output. Although the output impedance of the LTC1966 is increased from 85kΩ to 285kΩ, this is not an issue with an extremely high input impedance load, such as a dual slope integrating ADC like the ICL7106. And it allows a generic op amp to be used, such as the SOT-23 one shown. Furthermore, it easily works on a single supply rail by tying the noninverting input of the op amp to a low noise reference as optionally shown. This reference will not change the DC voltage at the circuit output, although it does become the AC ground for the filter, thus the (relatively) low noise requirement.

LTC1966 C

200k

AVE

1µF

OTHER

REF VOLTAGE,

SEE TEXT

0.22µF

–

LT1782

681k

0.22µF

1066 F14

Figure 13. Buffered Post Filter

Figure 14. DC Accurate Post Filter

1966fb

Page 19

applicaTions inForMaTion

LTC1966

Step Responses with a Post Filter

oth of the post filters, shown in Figures 13 and 14,

B are optimized for additional filtering with clean step responses. The 85kΩ output impedance of the LTC1966 working into a 1µF capacitor forms a 1st order LPF with a –3dB frequency of ~1.8Hz. The two filters have 1µF at the LTC1966 output for easy comparison with a 1µF only case, and both have the same relative (Bessel-like) shape. However, because of the topological differences of pole placements between the various components within the two filters, the net effective bandwidth for Figure 13 is

slightly higher (≈1.2 • 1.8 ≈ 2.1Hz) than with 1µF alone,

while the bandwidth for Figure 14 is somewhat lower

(≈0.7 • 1.8 ≈ 1.3Hz) than with 1µF alone. To adjust the

bandwidth of either of them, simply scale all the capacitors by a common multiple, and leave the resistors unchanged.

The step responses of the LTC1966 with 1µF only and with the two post filters are shown in Figure 15. This is the rising edge RMS output response to a 10Hz input starting at t = 0. Although the falling edge response is the worst case for settling, the rising edge illustrates the ripple that these post filters are designed to address, so the rising edge makes for a better intuitive comparison.

an issue with input frequency bursts at 50Hz or less, and even with the overshoot, the settling to a given level of accuracy improves due to the initial speedup.

As predicted by Figure 6, the DC error with 1µF is well under 1mV and is not noticeable at this scale. However, as predicted by Figure 8, the peak error with the ripple from a 10Hz input is much larger, in this case about 5mV. As can be clearly seen, the post filters reduce this ripple. Even the wider bandwidth of Figure 13’s filter is seen to cut the ripple down substantially (to <1mV) while the settling to 1% happens faster. With the narrower bandwidth of Figure 14’s filter, the step response is somewhat slower, but the double frequency output ripple is just 180µV.

Figure 16 shows the step response of the same three cases with a burst of 60Hz rather than 10Hz. With 60Hz, the initial portion of the step response is free of the boost seen in Figure 15 and the two post filter responses have less than 1% overshoot. The 1µF only case still has noticeable 120Hz ripple, but both filters have removed all detectable ripple on this scale. This is to be expected; the first order filter will reduce the ripple about 6:1 for a 6:1 change in frequency, while the third order filters will reduce the

ripple about 6

:1 or 216:1 for a 6:1 change in frequency.

The initial rise of the LTC1966 will have enhanced slew rates with DC and very low frequency inputs due to saturation effects in the ∆S modulator. This is seen in Figure 15 in two ways. First, the 1µF only output is seen to rise very quickly in the first 40ms. The second way this effect shows up is that the post filter outputs have a modest overshoot, on the order of 3mV to 4mV, or 3% to 4%. This is only

1966 F15

200mV/

DIV

20mV/ DIV

INPUT

BURST

1µF ONLY FIGURE 13 FIGURE 14

STEP

RESPONSE

100ms/DIV

Figure 15. Step Responses with 10Hz Burst

Again, the two filter topologies have the same relative shape, so the step response and ripple filtering trade-offs of the two are the same, with the same performance of each possible with the other by scaling it accordingly. Figures 17 and 18 show the peak error vs. frequency for a selection of capacitors for the two different filter topologies. To keep the clean step response, scale all three capacitors

1966 F16

200mV/

DIV

20mV/ DIV

1966fb

INPUT

BURST

1µF ONLY FIGURE 13 FIGURE 14

STEP

RESPONSE

100ms/DIV

Figure 16. Step Responses with 60Hz Burst

Page 20

LTC1966

applicaTions inForMaTion

–0.2

–0.4

–0.6

–0.8

–1.0

–1.2

PEAK ERROR (%)

–1.4

–1.6

–1.8

–2.0

–0.2

–0.4

–0.6

–0.8

–1.0

–1.2

PEAK ERROR (%)

–1.4

–1.6

–1.8

–2.0

C = 10µF

C = 4.7µF C = 2.2µF C = 1.0µF C = 0.47µF C = 0.22µF

Figure 17. Peak Error vs Input Frequency with Buffered Post Filter

C = 10µF

C = 4.7µF

C = 2.2µF C = 1.0µF C = 0.47µF C = 0.22µF C = 0.1µF

Figure 18. Peak Error vs Input Frequency with DC Accurate Post Filter

C = 0.1µF

10 100

INPUT FREQUENCY (Hz)

1966 F17

10 100

INPUT FREQUENCY (Hz)

1966 F18

within the filter. Scaling the buffered topology of Figure 13 is simple because the capacitors are in a 10:1:10 ratio. Scaling the DC accurate topology of Figure 14 can be done with standard value capacitors; one decade of scaling is shown in Table 2.

Table 2. One Decade of Capacitor Scaling for Figure 14 with EIA Standard Values

AVE

1µF 0.22µF

1.5µF 0.33µF

2.2µF 0.47µF

3.3µF 0.68µF

4.7µF 1µF

6.8µF 1.5µF

C1 = C2 =

Figures 19 and 20 show the settling time versus settling accuracy for the buffered and DC accurate post filters, respectively. The different curves represent different scalings of the filters, as indicated by the C

value. These are

AVE

comparable to the curves in Figure 12 (single capacitor case), with somewhat less settling time for the buffered post filter, and somewhat more settling time for the DC accurate post filter. These differences are due to the change in overall bandwidth as mentioned earlier.

The other difference is the settling behavior of the filters below the 1% level. Unlike the case of a 1st order filter, any 3rd order filter can have overshoot and ringing. The filter designs presented here have minimal overshoot and ringing, but are somewhat sensitive to component mismatches. Even the ±12% tolerance of the LTC1966 output impedance can be enough to cause some ringing. The dashed lines indicate what can happen when ±5% capacitors and ±1% resistors are used.

1966fb

Page 21

applicaTions inForMaTion

()

SETTLING ACCURACY (%)

LTC1966

C = 100µFC = 47µFC = 22µFC = 10µFC = 4.7µFC = 2.2µFC = 1.0µFC = 0.47µFC = 0.22µFC = 0.1µF

0.1

0.01

SETTLING ACCURACY (%)

0.1

0.01

Figure 19. Settling Time with Buffered Post Filter

Figure 20. Settling Time with DC Accurate Post Filter

SETTLING TIME (SEC)

Although the settling times for the post filtered configurations shown on Figures 19 and 20 are not that much different from those with a single capacitor, the point of using a post filter is that the settling times are far better for a given level peak error. The filters dramatically reduce the low frequency averaging ripple with far less impact on settling time.

Crest Factor and AC + DC Waveforms

In the preceding discussion, the waveform was assumed to be AC-coupled, with a modest crest factor. Both assumptions ease the requirements for the averaging capacitor. With an AC-coupled sine wave, the calculation engine squares the input, so the averaging filter that follows is required to filter twice the input frequency, making its job easier. But with a sinewave that includes DC offset, the square of the input has frequency content

10.1 10 100

1066 F14

C = 100µFC = 47µFC = 22µFC = 10µFC = 4.7µFC = 2.2µFC = 1.0µFC = 0.47µFC = 0.22µFC = 0.1µF

10.1 10 100

1066 F20

at the input frequency and the filter must average out that lower frequency. So with AC + DC waveforms, the required value for C

should be based on half of the

AVE

lowest input frequency, using the same design curves presented in Figures 6, 8, 17 and 18.

Crest factor, which is the peak to RMS ratio of a dynamic signal, also effects the required C

value. With a higher

AVE

crest factor, more of the energy in the signal is concentrated into a smaller portion of the waveform, and the averaging has to ride out the long lull in signal activity. For busy waveforms, such as a sum of sine waves, ECG traces or SCR chopped sine waves, the required value for

should be based on the lowest fundamental input

AVE

frequency divided as such:

INPUT MIN

•–

1966fb

DESIGN

Page 22

LTC1966

()

applicaTions inForMaTion

using the same design curves presented in Figures 6, 8, 17 and 18. For the worst-case of square top pulse trains, that are always either zero volts or the peak voltage, base the selection on the lowest fundamental input frequency divided by twice as much:

INPUT MIN

•–

DESIGN

The effects of crest factor and DC offsets are cumulative. So for example, a 10% duty cycle pulse train from 0V to 1V

(CF = √10 = 3.16) repeating at 16.67ms (60Hz)

PEAK

input is effectively only 30Hz due to the DC asymmetry and is effectively only:

DESIGN

6316 2

•.–

378

for the purposes of Figures 6, 8, 17 and 18. Obviously, the effect of crest factor is somewhat simplified

above given the factor of 2 difference based on a subjective description of the waveform type. The results will vary somewhat based on actual crest factor and waveform dynamics and the type of filtering used. The above method is conservative for some cases and about right for others.

The LTC1966 works well with signals whose crest factor is 4 or less. At higher crest factors, the internal ∆∑ modulator will saturate, and results will vary depending on the exact frequency, shape and (to a lesser extent) amplitude of the input waveform. The output voltage could be higher or lower than the actual RMS of the input signal.

The ∆∑ modulator may also saturate when signals with crest factors less than 4 are used with insufficient averaging. This will only occur when the output droops to less than 1/4 of the input voltage peak. For instance, a DC-coupled pulse train with a crest factor of 4 has a duty cycle of

6.25% and a 1V

input is 250mV

PEAK

50Hz, repeating every 20ms, and C

. If this input is

RMS

= 1µF, the output

AVE

will droop during the inactive 93.75% of the waveform. This droop is calculated as:

INACTIVE TIME

1–



−

 

2 • Z• C

OUT AVE



MIN

RMS

 





 

  

For the LTC1966, whose output impedance (Z

) is 85kΩ,

OUT

this droop works out to –5.22%, so the output would be reduced to 237mV at the end of the inactive portion of the input. When the input signal again climbs to 1V

PEAK

, the

peak/output ratio is 4.22. With C

= 10µF, the droop is only –0.548% to 248.6mV

AVE

and the peak/output ratio is just 4.022, which the LTC1966 has enough margin to handle without error.

For crest factors less than 3.5, the selection of C

AVE

as previously described should be sufficient to avoid this droop and modulator saturation effect. But with crest factors above 3.5, the droop should also be checked for each design.

Error Analyses

Once the RMS-to-DC conversion circuit is working, it is time to take a step back and do an analysis of the accuracy of that conversion. The LTC1966 specifications include

, V

three basic static error terms, V

OOS

and GAIN. The

IOS

output offset is an error that simply adds to (or subtracts from) the voltage at the output. The conversion gain of the LTC1966 is nominally 1.000 V

DCOUT/VRMSIN

and the gain error reflects the extent to which this conversion gain is not perfectly unity. Both of these affect the results in a fairly obvious way.

Input offset on the other hand, despite its conceptual simplicity, effects the output in a nonobvious way. As its name implies, it is a constant error voltage that adds directly with the input. And it is the sum of the input and

that is RMS converted.

IOS

This means that the effect of V nonlinear RMS conversion. With 0.2mV (typ) V a 200mV

AC input, the RMS calculation will add the

RMS

is warped by the

IOS

, and

DC and AC terms in an RMS fashion and the effect is negligible:

= √(200mV AC)2 + (0.2mV DC)2

OUT

= 200.0001mV = 200mV + 1/2ppm

1966fb

Page 23

applicaTions inForMaTion

LTC1966

But with 10× less AC input, the error caused by V

IOS

100× larger:

= √(20mV AC)2 + (0.2mV DC)2

OUT

= 20.001mV = 20mV + 50ppm

This phenomena, although small, is one source of the LTC1966’s residual nonlinearity.

On the other hand, if the input is DC-coupled, the input offset voltage adds directly. With +200mV and a +0.2mV

, a 200.2mV output will result, an error of 0.1% or

IOS

1000ppm. With DC inputs, the error caused by V

IOS

can be positive or negative depending if the two have the same or opposing polarity.

The total conversion error with a sine wave input using the typical values of the LTC1966 static errors is computed as follows:

= (√(500mV AC)2 + (0.2mV DC)2) • 1.001 + 0.1mV

OUT

= 500.600mV = 500mV + 0.120%

= (√(50mV AC)2 + (0.2mV DC)2) • 1.001 + 0.1mV

OUT

= 50.150mV = 50mV + 0.301%

= (√(5mV AC)2 + (0.2mV DC)2) • 1.001 + 0.1mV

OUT

= 5.109mV = 5mV + 2.18%

As can be seen, the gain term dominates with large inputs, while the offset terms become significant with smaller inputs. In fact, 5mV is the minimum RMS level needed to keep the LTC1966 calculation core functioning normally, so this represents the worst-case of usable input levels.

Using the worst-case values of the LTC1966 static errors, the total conversion error is:

= (√(500mV AC)2 + (0.8mV DC)2) • 1.003 + 0.2mV

OUT

= 501.70mV = 500mV + 0.340%

= (√(50mV AC)2 + (0.8mV DC)2) • 1.003 + 0.2mV

OUT

= 50.356mV = 50mV + 0.713%

= (√(5mV AC)2 + (0.8mV DC)2) • 1.003 + 0.2mV

OUT

= 5.279mV = 5mV + 5.57%

These static error terms are in addition to dynamic error terms that depend on the input signal. See the Design Cookbook for a discussion of the DC conversion error with low frequency AC inputs. The LTC1966 bandwidth limitations cause additional errors with high frequency inputs. Another dynamic error is due to crest factor. The LTC1966 performance versus crest factor is shown in the Typical Performance Characteristics.

Monotonicity and Linearity

The LTC1966, like all implicit RMS-to-DC convertors (Figure 3), has a division with the output in the denominator. This works fine most of the time, but when the output is zero or near zero this becomes problematic. The LTC1966 has multiple switched capacitor amplifier stages, and depending on the different offsets and their polarity, the DC transfer curve near zero input can take a few different forms, as shown in the Typical Performance Characteristics graph titled DC Transfer Function Near Zero.

Some units (about 1 of every 16) will even be well behaved with a transfer function that is the upper half of a unit rectangular hyperbola with a focal point on the y-axis of

a few millivolts.

For AC inputs, these units will have a

monotonic transfer function all the way down to zero input. The LTC1966 is trimmed for offsets as small as practical,

and the resulting behavior is the best statistical linearity provided the zero region troubles are avoided.

It is possible, and even easy, to force the zero region to be well behaved at the price of additional (though predictable) V

and some linearity error. For large enough input

OOS

signals, this linearity error may be negligible.

In general, every LTC1966 will have a DC transfer function that is essentially a unit rectangular hyperbola (the gain is not always exactly unity, but the gain error is small) with an X- and Y- offset equal to V sigma section gets confused. While some units will be the north half of a north south pair, other units will have two upper halfs of the conjugate, east west, hyperbolas. The circuit of Figure 23 will assure a continuous transfer function.

IOS

and V

, respectively, until the inputs are small enough that the delta

OOS

1966fb

Page 24

LTC1966

applicaTions inForMaTion

To do this, inject current into the output. As shown in Figure 21, the charge pump output impedance is 170kΩ, with the computational feedback cutting the closed loop output impedance to the 85kΩ specification. By injecting 30nA of current into this 170Ω, with zero input, a 5mV offset

LTC1966

IN1

IN2

RMS TO DC

CONVERSION

CHARGE PUMP

170kΩ

OUTPUT

1966 F21

INJECT

AVE

Figure 21. Behavioral Block Diagram of LTC1966

is created at the output feedback point, which is sufficient to overcome the 5mV minimum signal level. With large enough input signals, the computational feedback cuts the output impedance to 85kΩ so the transfer function asymptotes will have an output offset of 2.5mV, as shown in Figure 22. This is the additional, predictable, V

OOS

that is added, and should be subtracted from the RMS results, either digitally, or by an analog means.

(mV DC)

5mV MIN

OUT

Figure 22b. AC Transfer Function with I

IDEAL

VIN (mV AC)

ASYMPTOTES

SHIFTED +2.5mV

10 15

1966 F22b

INJECT

= 30nA

Figure 23 shows an analog implementation of this with the offset and gain errors corrected; only the slight, but necessary, degradation in nonlinearity remains. The circuit works by creating approximately 300mV of bias at the junction of the 10MΩ resistors when the LTC1966’s input/output are zero. The 10MΩ resistor to the LTC1966 output therefore feeds in 30nA. The loading of this resistor causes a slight reduction in gain which is corrected, as is the nominal 2.5mV offset, by the LT1494 op amp.

(mV DC)

OUT

–20

–15

IDEAL

–10

5mV MIN

0 5–510

VIN (mV DC)

Figure 22a. DC Transfer Function with I

ASYMPTOTES

SHIFTED +2.5mV

1966 F22a

INJECT

= 30nA

IN1

IN2

–5V

LTC1966

OUTRTN

OUT

ENGND

10MΩ

85kΩ

10MΩ

1µF

750k

10MΩ

84.5k

100pF

LT1494

–

–5V

Figure 23. Monotonic AC Response with Offset and Gain Corrected

1966 F23

OUT

1966fb

Page 25

applicaTions inForMaTion

LTC1966

The two 10MΩ resistors not connected to the supply can be any value as long as they match and the feed voltage is changed for 30nA injection. The op amp gain is only

1.00845, so the output is dominated by the LTC1966 RMS results, which keeps errors low. With the values shown, the resistors can be ±2% and only introduce ±170ppm of gain error. The 84.5k resistor is the closest match in the 1% EIA values but if the 2% EIA value of 82k were used instead, the gain would only be reduced by 248ppm.

This low error sensitivity is important because the LTC1966 output impedance is 85kΩ ±11.8%, which can create a gain error of ±0.1%; enough to degrade the overall gain accuracy somewhat. This gain variation term is increased with lower value feed resistors, and decreased with higher value feed resistors.

A bigger error caused by the variation of the LTC1966 output impedance is imperfect cancelation of the output offset introduced by the injected current. The offset correction provided by the LT1494 will be based on a consistent

84.5kΩ times the injected current, while the LTC1966 output impedance will vary enough that the output offset will have a ±300µV range about the nominal 2.5mV. If this level of output offset is not acceptable, either system calibration or a potentiometer in the LT1494 feedback may be needed.

If the two 10MΩ feed resistors to the LT1494 have significant mismatch, cancellation of the 2.5mV offset would be further impacted, so it is probably worth paying an extra penny or so for 1% resistors or even the better temperature stability of thin film devices. The 300mV feed voltage is not particularly critical because it is nominally cancelled, but the offset errors due to these resistance mismatches is scaled by that voltage.

Note that the input bias current of the op amp used in Figure 23 is also nominally cancelled, but it will add or subtract to the total current injected into the LTC1966 output. With the 1nA I While it is possible to eliminate the feed resistors by using an op amp with a PNP input stage whose I

of the LT1494 this is negligible.

BIAS

is 30nA

BIAS

or more, I this circuit needs a minimum of 30nA, therefore such an approach may not always work.

Because the circuit of Figure 23 subtracts the offset created by the injected current, the LT1494 output with zero LTC1966 input will rest at +2.5mV, nominal before offsets, rather then the 5mV seen in Figure 22.

Output Errors Versus Frequency

As mentioned in the Design Cookbook, the LTC1966 performs very well with low frequency and very low frequency inputs, provided a large enough averaging capacitor is used.

However, the LTC1966 will have additional dynamic errors as the input frequency is increased. The LTC1966 is designed for high accuracy RMS-to-DC conversion of signals into the audible range. The input sampling amplifiers have a –3dB frequency of 800kHz or so. However, the switched capacitor circuitry samples the inputs at a modest 100kHz nominal. The response versus frequency is depicted in the Typical Performance Characteristics titled Input Signal Bandwidth. Although there is a pattern to the response versus frequency that repeats every sample frequency, the errors are not overwhelming. This is because LTC1966 RMS calculation is inherently wideband, operating properly with minimal oversampling, or even undersampling, using several proprietary techniques to exploit the fact that the RMS value of an aliased signal is the same as the RMS value of the original signal. However, a fundamental feature of the ∆S modulator is that sample estimation noise is shaped such that minimal noise occurs with input frequencies much less than the sampling frequency, but such noise peaks when input frequency reaches half the sampling frequency. Fortunately the LTC1966 output averaging filter greatly reduces this error, but the RMS-to-DC topology frequency shifts the noise to low (baseband) frequencies. So with input frequencies above 5kHz to 10kHz, the output will slowly wander around ±a few percent.

is usually only specified for maximum and

BIAS

1966fb

Page 26

LTC1966

V V

R R

M k

IN SOURCE

SOURCE

Ω + Ω

8 100

1 25– . %

applicaTions inForMaTion

Input Impedance

The LTC1966 true RMS-to-DC converter utilizes a 2.5pF capacitor to sample the input at a nominal 100kHz sample frequency. This accounts for the 8MΩ input impedance. See Figure 24 for the equivalent analog input circuit. Note however, that the 8MΩ input impedance does not directly affect the input sampling accuracy. For instance, if a 100k source resistance is used to drive the LTC1966, the sampling action of the input stage will drag down the voltage seen at the input pins with small spikes at every sample clock edge as the sample capacitor is connected to be charged.

The time constant of this combination is small, 2.5pF •

100kΩ = 250ns, and during the 2.5µs period devoted to sampling, ten time constants elapse. This allows each sample to settle to within 46ppm and it is these samples that are used to compute the RMS value.

IN1

IN2

IN1

IN2

RSW (TYP)

IIN

()

2.5pF

RSW (TYP)

(TYP)

2.5pF (TYP)

1966 F24

IIN

()

= Ω

AVG

−

IN IN

−

Figure 24. LTC1966 Equivalent Analog Input Circuit

This is a much higher accuracy than the LTC1966 conversion limits, and far better than the accuracy computed via the simplistic resistive divider model:

This resistive divider calculation does give the correct model of what voltage is seen at the input terminals by a parallel load averaged over a several clock cycles, which is what a large shunt capacitor will do—average the current spikes over several clock cycles.

When high source impedances are used, care must be taken to minimize shunt capacitance at the LTC1966 input so as not to increase the settling time. Shunt capacitance of just

2.5pF will double the input settling time constant and the error in the above example grows from 46ppm to 0.67% (6700ppm). A 13pF scope probe will increase the error to almost 20%. As a consequence, it is important to not try to filter the input with large input capacitances unless driven by a low impedance. Keep time constant <<2.5µs.

When the LTC1966 is driven by op amp outputs, whose low DC impedance can be compromised by sharp capacitive load switching, a small series resistor may be added. A 10k resistor will easily settle with the 2.5pF input sampling capacitor to within 1ppm.

These are important points to consider both during design and debug. During lab debug, and even production testing, a high value series resistor to any test point is advisable.

Output Impedance

The LTC1966 output impedance during operation is similarly due to a switched capacitor action. In this case, 59pF of on-chip capacitance operating at 100kHz translates into 170kΩ. The closed loop RMS-to-DC calculation cuts that in half to the nominal 85kΩ specified.

In order to create a DC result, a large averaging capacitor is required. Capacitive loading and time constants are not an issue on the output.

1966fb

Page 27

applicaTions inForMaTion

LTC1966

However, resistive loading is an issue and the 10MΩ impedance of a DMM or 10× scope probe will drag the output down by –0.85% typ.

During shutdown, the switching action is halted and a fixed 30k resistor shunts V

to OUT RTN so that C

OUT

AVE

is discharged.

Guard Ringing the Output

The LTC1966’s combination of precision and high output impedance can present challenges that make the use of a guard ring around the output a good idea for many applications.

As mentioned above, a 10M resistive loading to ground will drag down the gain far more than the specificed gain tolerance. On a printed circuit board, contaminants from solder flux residue to finger grime can create parasitic resistances, which may be very high impedance, but can have deleterious effects on the realized accuracy. As an example, if the output (Pin 5) is routed near V

(Pin 4)

in a ±5V application, a parasitic resistance of 1G (1,000M) is enough to introduce a –425µV output offset error, more than the specified limit of the LTC1966 itself.

Use of a guard ring, wherein the LTC1966 output node is completely surrounded by a low impedance voltage, can reduce leakage related errors substantially. The ground ring can be tied to OUTRTN (Pin 6) and should encircle the output (Pin 5), the averaging capacitor terminal, and the destination terminal at the ADC, filter op amp, or whatever else may be next.

Figure 24a shows a sample PCB layout for the circuit of Figure 13, wherein the guard ring trace encloses R1, R2, and the terminals of C1, C2, and the op amp input connected to the high impedance LTC1966 Output. For the circuit of figure 14, the guard ring should enclose R1 and the terminals of C1 and C2, as well as the terminal at the ultimate destination.

Figure 24b shows a sample PCB layout for the circuit of Figure 23. The summing node of the LT1494 has the same high impedance and high accuracy as the LTC1966 output, so here the guard ring encircles both of them. Any leakage between them is benign because the LT1494 forces them to the same nominal voltage.

0.1µF

LTC1966

MS8

1µFC

AVE

Figure 24a. PCB Layout of Figure 13 with Guard Ring

0.1µF

1966 F24a

LT1880

SO8

LTC1966

MS8

1966 F24b

1µFC

AVE

Figure 24b. PCB Layout of Figure 23 with Guard Ring

LT1494

SO8

1966fb

Page 28

LTC1966

applicaTions inForMaTion

Interfacing with an ADC

The LTC1966 output impedance and the RMS averaging ripple need to be considered when using an analog-todigital converter (ADC) to digitize the LTC1966 RMS result.

The simplest configuration is to connect the LTC1966 directly to the input of a type 7106/7136 ADC as shown in Figure 25a. These devices are designed specifically for DVM/DPM use and include display drivers for a 3 1/2 digit LCD segmented display. Using a dual slope conversion, the input is sampled over a long integration window, which results in rejection of line frequency ripple when integration time is an integer number of line cycles. Finally, these parts have an input impedance in the GΩ range, with specified input leakage of 10pA to 20pA. Such a leakage, combined with the LTC1966 output impedance, results in just 1µV to 2µV of additional output offset voltage.

LTC1966

OUT RTN

Figure 25a. Interfacing to DVM/DPM ADC

LTC1966

OUTPUT

OUT RTN

Figure 25b. Interfacing to LTC2420

OUTPUT

LTC2420

REF

AVE

GND

AVE

SDO

SCK

1966 F25b

7106 TYPE

IN HI

IN LO

SERIAL DATA

DIGITALLY CORRECT LOADING ERRORS

1966 F25a

Another type of ADC that has inherent rejection of RMS averaging ripple is an oversampling ∆∑. With most, but not all, of these devices, it is possible to connect the LTC1966 output directly to the converter input. Issues to look out

for are the input impedance, and any input sampling currents. The input sampling currents drawn by ∆∑ ADCs often have large spikes of current with short durations that can confuse some op amps, but with the large C

AVE

needed by the LTC1966 these are not an issue. The average current is important, as it can create LTC1966

errors; if it is constant it will create an offset, while average currents that change with the voltage level create gain errors. Some converters run continuously, others only sample upon demand, and this will change the results in ways that need to be understood. The LTC1966 output impedance has a loose tolerance relative to the usual resistors and the same can be true for the input impedance of ∆∑ ADC, resulting in gain errors from part-to-part. The system calibration techniques described in the following section should be used in applications that demand tight tolerances.

One example of driving an oversampling ∆∑ ADC is shown in Figure 25b. In this circuit, the LTC2420 is used with a 1V V

. Since the LTC1966 output voltage range is about

REF

1V, and the LTC2420 has a ±12.5% extended input range, this configuration matches the two ranges with room to spare. The LTC2420 has an input impedance of 16.6MΩ, resulting in a gain error of –0.4% to –0.6%. In fact, the LTC2420 DC input current is not zero at 0V, but rather at one half its reference, so both an output offset and a gain error will result. These errors will vary from part to part, but with a specific LTC1966 and LTC2420 combination, the errors will be fixed, varying less than ±0.05% over temperature. So a system that has digital calibration can be quite accurate despite the nominal gain and offset error. With 20 bits of resolution, this part is more accurate than the LTC1966, but the extra resolution is helpful because it reduces nonlinearity at the LSB transitions as a digital gain correction is made. Furthermore, its small size and ease of use make it attractive.

1966fb

Page 29

applicaTions inForMaTion

LTC1966

As is shown in Figure 25b, where the LTC2420 is set to continuously convert by grounding the CS pin. The gain error will be less if CS is driven at a slower rate, however, the rate should either be consistent or at a rate low enough that the LTC1966 and its output capacitor have fully settled by the beginning of each conversion, so that the loading errors are consistent.

Note that in this circuit, the input current of the LTC2420 is being used to assure monotonicity. The LTC2420 Z

16.6MΩ is effectively connected to half the reference voltage, so when the LTC1966 has zero signal, 500mV/16.6MΩ = 30nA is provided.

Alternatively, a 5V V

can be used, but in this case the

REF

LTC1966 output span will only use 20% of the LTC2420’s input voltage range. Furthermore, if the OUTRTN remains grounded, the injected current with zero signal will be 150nA, resulting in 5× the offset error and nonlinearity shown in Figure 22.

In both of the circuits of Figure 25, a guard ring only has to encircle three terminals, the LTC1966 output, the top of the averaging capacitor, and the ADC input. Figure 26 shows the top copper patterns for example PCB layouts of each.

The low power consumption of the LTC1966 makes it well suited for battery powered applications, and its slow output (DC) makes it an ideal candidate for a micropower ADC.

LTC1966

MS8

1µfC

AVE

Figure 26b. PCB Layout of Figure 25b with Guard Ring

LTC2420

SO8

1966 F26b

Figure 10 in Application Note 75, for instance, details a 10-bit ADC with a 35ms conversion time that uses just 29µA of supply current. Such an ADC may also be of use within a 4mA to 20mA loop.

Other types of ADCs sample the input signal once and perform a conversion on that one sample. With these ADCs (Nyquist ADCs), a post filter will be needed in most cases to reduce the peak error with low input frequencies. The DC accurate filter of Figure 14 is attractive from an error standpoint, but it increases the impedance at the ADC input. In most cases, the buffered post filter of Figure13 will be more appropriate for use with Nyquist analog-todigital converters.

SYSTEM CALIBRATION

LTC1966

MS8

ICL7106

MQFP

1µfC

AVE

Figure 26a. PCB Layout of Figure 25a with Guard Ring

1966 F26a

The LTC1966 static accuracy can be improved with end system calibration. Traditionally, calibration has been done at the factory, or at a service depot only, typically using manually adjusted potentiometers. Increasingly, systems are being designed for electronic calibration where the accuracy corrections are implemented in digital code wherever possible, and with calibration DACs where necessary. Additionally, many systems are now designed for self calibration, in which the calibration occurs inside the machine, automatically without user intervention.

1966fb

Page 30

LTC1966

applicaTions inForMaTion

Whatever calibration scheme is used, the linearity of the LTC1966 will improve the calibrated accuracy over that achievable with older log/antilog RMS-to-DC converters. Additionally, calibration using DC reference voltages are essentially as accurate with the LTC1966 as those using AC reference voltages. Older log/antilog RMS-to-DC converters required nonlinear input stages (rectifiers) whose linearity would typically render DC based calibration unworkable.

The following are four suggested calibration methods. Implementations of the suggested adjustments are dependent on the system design, but in many cases, gain and output offset can be corrected in the digital domain, and will include the effect of all gains and offsets from the LTC1966 output through the ADC. Input offset voltage, on the other hand, will have to be corrected with adjustment to the actual analog input to the LTC1966.

The methods below assume the unaltered linearity of the LTC1966, i.e. without the monotonicity fix of Figure 21. If this is present, the V taken out before using either method for which V not calibrated. Also, the nonlinearity it introduces will increase the 20mV readings discussed below by 0.78% but increase the 200mV readings only 78ppm. There are a variety of ways to deal with these errors, including possibly ignoring them, but the specifics will depend on system requirements. Designers are cautioned to avoid the temptation to digitally take out the hyperbolic transfer function introduced because if the offsets are not exactly the nominals assumed, the system will end up right back where it began with a potential discontinuity with zero input, either from a divide by zero or from a square root of a negative number in the calculations to undo the hyperobic transfer function. An adaptive algorithm would most likely be necessary to safely take out more than half of the introduced nonlinearity.

If a 5V reference is used in the connection of Figure 25b, the V

and nonlinearity created would be even larger,

OOS

shift it introduces should be

OOS

and will no doubt be more tempting to correct for. Designers are likewise cautioned against correcting for all of the nonlinearity.

AC-Only, 1 Point

The dominant error at full-scale will be caused by the gain error, and by applying a full-scale sine wave input, this error can be measured and corrected for. Unlike older log/antilog RMS-to-DC converters, the correction should be made for zero error at full scale to minimize errors through

The best frequency for the calibration signal is roughly ten times the –0.1% DC error frequency. For 1µF, –0.1% DC error occurs at 8Hz, so 80Hz is a good calibration frequency, although anywhere from 60Hz to 100Hz should suffice.

The trade-off here is that on the one hand, the DC error is input frequency dependent, so a calibration signal frequency high enough to make the DC error negligible should be used. On the other hand, as low a frequency as can be used is best to avoid attenuation of the calibrated AC signal, either from parasitic RC loading or insufficient op amp gain. For instance, with a 1kHz calibration signal, a 1MHz op amp will typically only have 60dB of open loop gain, so it could attenuate the calibration signal a full 0.1%.

AC-Only, 2 Point

The next most significant error for AC-coupled applications will be the effect of output offset voltage, noticeable at the bottom end of the input scale. This too can be calibrated out if two measurements are made, one with a full-scale sine wave input and a second with a sine wave input (of the same frequency) at 10% of full-scale. The trade-off in selecting this second level is that it should be small enough that the gain error effect becomes small compared to the gain error effect at full-scale, while on the other hand, not using so small an input that the input offset voltage becomes an issue.

out the dynamic range.

1966fb

Page 31

applicaTions inForMaTion

LTC1966

The calculations of the error terms for a 200mV full-scale case are:

Gain =

Output Offset =

DC, 2 Point

DC based calibration is preferable in many cases because a DC voltage of known, good accuracy is easier to generate than such an AC calibration voltage. The only down side is that the LTC1966 input offset voltage plays a role. It is therefore suggested that a DC based calibration scheme check at least two points: ±full-scale. Applying the –fullscale input can be done by physically inverting the voltage or by applying the same +full-scale input to the opposite LTC1966 input.

For an otherwise AC-coupled application, only the gain term may be worth correcting for, but for DC-coupled applications, the input offset voltage can also be calculated and corrected for.

Reading at 200mV – Reading at 20mV

180mV

Reading at 20mV

Gain

–20mV

Note: Calculation of and correction for input offset voltage are the only way in which the two LTC1966 inputs (IN1, IN2) are distinguishable from each other. The calculation above assumes the standard definition of offset; that a positive offset is the case of a positive voltage error inside the device that must be corrected by applying a like negative voltage outside. The offset is referred to whichever pin is driven positive for the +full-scale reading.

DC, 3 Point

One more point is needed with a DC calibration scheme to determine output offset voltage: +10% of full scale.

The calculation of the input offset is the same as for the 2-point calibration above, while the gain and output offset are calculated for a 200mV full-scale case as:

Gain =

Output Offset = Reading at 200mV +Reading at – 200mV – 400mV •Gain

Reading at 200mV –Reading at 20mV

180mV

The calculations of the error terms for a 200mV full-scale case are:

Gain =

Input Offset =

Reading at 200mV + Reading at – 200mV

400mV

Reading at – 200mV –Reading at 200mV

2•Gain

1966fb

Page 32

LTC1966

applicaTions inForMaTion

TROUBLESHOOTING GUIDE

Top Ten LTC1966 Application Mistakes

1. Circuit won’t work–Dead On Arrival–no power drawn.

– Probably forgot to enable the LTC1966 by pulling Pin8 low.

Solution: Tie Pin 8 to Pin 1.

2. Circuit won’t work, but draws power. Zero or

very little output, single-ended input application. – Probably didn’t connect both input pins.

Solution: Tie both inputs to something. See Input

Connections in the Design Cookbook.

CONNECT PIN 3

IN1

LTC1966

IN2

1966 TS02

3. Screwy results, particularly with respect to linearity

or high crest factors; differential input application. – Probably AC-coupled both input pins.

Solution: Make at least one input DC-coupled. See

Input Connections in the Design Cookbook.

4. Gain is low by a few percent, along with other screwy results.

– Probably tried to use output in a floating, differential

manner.

Solution: Tie Pin 6 to a low impedance. See Output

Connections in the Design Cookbook.

GROUND PIN 6

LTC1966

OUT

OUT RTN

TYPE 7136

ADC

1966 TS04

5. Offsets perceived to be out of specification because 0V in ≠ 0V out. – The offsets are not specified at 0V in. No RMS-to-DC converter works well at 0 due to a divide-by-zero calculation.

Solution: Measure V

readings > ±5mV

IOS/VOOS

by extrapolating

6. Linearity perceived to be out of specification particularly with small input signals.

– This could again be due to using 0V in as one of the

measurement points.

Solution: Check Linearity from 5mV

to 500mV

RMS

DC CONNECT ONE INPUT

–

The input offset voltage can cause small AC

DC CONNECT ONE INPUT

linearity errors at low input amplitudes as well. See Error Analyses section.

IN1

LTC1966

IN2

IN1

LTC1966

IN2

1966 TS03

Possible Solution: Include a trim for input offset.

1966fb

Page 33

applicaTions inForMaTion

LTC1966

7. Output is noisy with >10kHz inputs. – This is a fundamental characteristic of this topol-

ogy. The LTC1966 is designed to work very well with inputs of 1kHz or less. It works okay as high as 1MHz, but it is limited by aliased ∆S noise.

Solution: Bandwidth limit the input or digitally filter the resulting output.

8. Large errors occur at crest factors approaching, but less than 4.

– Insufficient averaging.

Solution: Increase C

. See Crest Factor and AC + DC

AVE

Waveforms section for discussion of output droop.

9. Screwy results, errors > spec limits, typically 1% to 5%.

– High impedance (85kΩ) and high accuracy (0.1%)

require clean boards! Flux residue, finger grime, etc. all wreak havoc at this level.

Solution: Wash the board.

Helpful Hint: Sensitivity to leakages can be reduced significantly through the use of guard traces.

KEEP BOARD CLEAN

10. Gain is low by ≅ 1% or more, no other problems. – Probably due to circuit loading. With a DMM or

a 10× scope probe, Z

= 10MΩ. The LTC1966

output is 85kΩ, resulting in –0.85% gain error. Output impedance is higher with the DC accurate post filter.

Solution: Remove the shunt loading or buffer the

output.

– Loading can also be caused by cheap averaging

capacitors.

Solution: Use a high quality metal film capacitor

for C

AVE

LOADING DRAGS DOWN GAIN

LTC1966

OUT

OUT RTN

85k

10M

200mV

–0.85%

RMS

DCV

DMM

1966 TS10

LTC1966

1966fb

Page 34

LTC1966

Typical applicaTions

±5V Supplies, Differential, DC-Coupled

RMS-to-DC Converter

DC + AC

INPUTS

(1V

PEAK

DIFFERENTIAL)

LTC1966

IN1 DC OUTPUT

IN2

–5V

OUT

OUT RTN

GND ENV

1966 TA03

C 1µF

AVE

2.7V Single Supply, Single Ended, AC-Coupled RMS-to-DC Converter with Shutdown

2.7V/3V CMOS

OFF

AC INPUT

(1V

PEAK

0.1µF

)

2.7V

LTC1966

IN1 DC OUTPUT

IN2 V

OUT

OUT RTN

GND

1966 TA04

C 1µF

AVE

5V Single Supply, Differential, AC-Coupled

RMS-to-DC Converter

AC INPUTS

(1V

DIFFERENTIAL)

PEAK

0.1µF

LTC1966

IN1 DC OUTPUT

OUT

IN2

OUT RTN

GND ENV

1966 TA05

±2.5V Supplies, Single Ended, DC-Coupled

RMS-to-DC Converter with Shutdown

GND

OUT

0.1µF X7R

C 1µF

1966 TA06

2.5V

OFF

–2V

DC + AC

INPUT

(1V

PEAK

)

LTC1966

IN1 DC OUTPUT

IN2

OUT RTN

–2.5V –2.5V

C 1µF

AVE

–2.5V

Battery Powered Single-Ended AC-Coupled

RMS-to-DC Converter

AC INPUT

)

(1V

PEAK

IN1

IN2

LTC1966

OUT RTN

GND

1966 TA07

GND

LT1175CS8-5

SHDN

OUT

SENSE

0.1µF

0.1µF X7R

OUT

ENV

C 1µF

AVE

DC OUTPUT

1966fb

Page 35

siMpliFieD scheMaTic

GND

LTC1966

C12

Y1 Y2

IN1

IN2

2nd ORDER ∆∑ MODULATOR

C5C3

TO BIAS CONTROL

–

OUTPUT

1966 SS

AVE

A2A1

–

C10

C11

SHUTDOWN

CLOSED DURING

OUT RTN

30k BLEED RESISTOR FOR C

AVE

1966fb

Page 36

LTC1966

package DescripTion

MS8 Package

8-Lead Plastic MSOP

(Reference LTC DWG # 05-08-1660 Rev F)

0.889 ± 0.127 (.035 ± .005)

5.23

(.206)

MIN

0.42 ± 0.038

(.0165 ± .0015)

TYP

RECOMMENDED SOLDER PAD LAYOUT

NOTE:

1. DIMENSIONS IN MILLIMETER/(INCH)

2. DRAWING NOT TO SCALE

3. DIMENSION DOES NOT INCLUDE MOLD FLASH, PROTRUSIONS OR GATE BURRS. MOLD FLASH, PROTRUSIONS OR GATE BURRS SHALL NOT EXCEED 0.152mm (.006") PER SIDE

4. DIMENSION DOES NOT INCLUDE INTERLEAD FLASH OR PROTRUSIONS. INTERLEAD FLASH OR PROTRUSIONS SHALL NOT EXCEED 0.152mm (.006") PER SIDE

5. LEAD COPLANARITY (BOTTOM OF LEADS AFTER FORMING) SHALL BE 0.102mm (.004") MAX

3.20 – 3.45

(.126 – .136)

0.65

(.0256)

BSC

GAUGE PLANE

0.18

(.007)

0.254

(.010)

DETAIL “A”

0° – 6° TYP

DETAIL “A”

0.53 ± 0.152 (.021 ± .006)

SEATING

PLANE

3.00 ± 0.102

(.118 ± .004)

(NOTE 3)

4.90 ± 0.152

(.193 ± .006)

0.22 – 0.38

(.009 – .015)

TYP

1.10

(.043)

MAX

1 2

0.65

(.0256)

BSC

0.52

(.0205)

REF

3.00 ± 0.102

(.118 ± .004)

(NOTE 4)

0.86

(.034)

REF

0.1016 ± 0.0508 (.004 ± .002)

MSOP (MS8) 0307 REV F

1966fb

Page 37

LTC1966

revision hisTory

REV DATE DESCRIPTION PAGE NUMBER

B 5/11 Revised entire data sheet to add H- and MP- grades 1 to 38

(Revision history begins at Rev B)

Information furnished by Linear Technology Corporation is believed to be accurate and reliable. However, no responsibility is assumed for its use. Linear Technology Corporation makes no representation that the interconnection of its circuits as described herein will not infringe on existing patent rights.

1966fb

Page 38

LTC1966

Typical applicaTion

RMS Noise Measurement

70A Current Measurement

AC CURRENT

71.2A MAX

50Hz TO 400Hz

T1: CR MAGNETICS CR8348-2500-N www.crmagnetics.com

10Ω

IN1

IN2

–5V

LTC1966

OUT RTN

GND ENV

VOLTAGE

NOISE IN

100Ω

OUT

–

100Ω

1.5µF

C 1µF

1/2

LTC6203

–5V

100k

V 4mVDC/A

AVE

OUT

1966 TA09

RMS

10k

0.1µF

LTC1966

IN1

OUT RTN

IN2

GND ENV

–5V

AC CURRENT

71.2A MAX

50Hz TO 400Hz

OUT

1mV

1µV

RMS

C 1µF

OUT

1966 TA10

BW 1kHz TO 100kHz INPUT SENSITIVITY = 1µV

Single Supply RMS Current Measurement

10Ω

0.1µF

NOISE

AVE

RMS

100k

TYP

LTC1966

IN1

IN2

OUT

OUT RTN

GND ENV

AVE

1µF

1966 TA08

T1: CR MAGNETICS CR8348-2500-N www.crmagnetics.com

OUT

= 4mVDC/A

RMS

relaTeD parTs

PART NUMBER DESCRIPTION COMMENTS

1077 Micropower, Single Supply Precision Op Amp 48µA ISY, 60µV V

LT LT1175-5 Negative, –5V Fixed, Micropower LDO Regulator 45µA IQ, Available in SO-8 or SOT-223 LT1494 1.5µA Max, Precision Rail-to-Rail I/O Op Amp 375µV V

OS(MAX)

LT1782 General Purpose SOT-23 Rail-to-Rail Op Amp 40µA ISY, 800µV V LT1880 SOT-23 Rail-to-Rail Output Precision Op Amp 1.2mA ISY, 150µV V LTC1967 Precision, Extended Bandwidth RMS to DC Converter 330µA ISY, ∆∑ RMS Conversion to 4MHz LTC1968 Precision, Wide Bandwidth RMS to DC Converter 2.3mA I LTC2050 Zero Drift Op Amp in SOT-23 750µA I

, ∆∑ RMS Conversion to 15MHz

, 3µV V

LT2178/LT2178A 17µA Max, Single Supply Precision Dual Op Amp 14µA ISY, 120µV V LTC2402 LTC2420 LTC2422

2-Channel, 24-bit, Micropower, No Latency ∆S 20-bit, Micropower, No Latency ∆S ADC in SO-8 2-Channel, 20-bit, Micropower, No Latency ∆S ADC

™

ADC

200µA I 200µA I

, 4ppm INL, 10ppm TUE

, 8ppm INL, 16ppm TUE

Dual Channel Version of LTC2420

Linear Technology Corporation

1630 McCarthy Blvd., Milpitas, CA 95035-7417

(408) 432-1900 ● FAX: (408) 434-0507

●

www.linear.com

OS(MAX)

, 100pA I

OS(MAX)

, 450pA I

, 75pA I

OS(MAX)

, 2nA I

OS(MAX)

, 900pA I

, 350pA I

OS(MAX)

B(MAX)

OS(MAX)

 LINEAR TECHNOLOGY CORPORATION 2001

1966fb

LT 0511 REV B • PRINTED IN USA