Page 1
Engineer-to-Engineer Note EE-228
a
Technical notes on using Analog Devices DSPs, processors and development tools
Contact our technical support at dsp.support@analog.com and at dsptools.support@analog.com
Or vi sit our o n-li ne r esou rces htt p:/ /www.analog.com/ee-notes and http://www.analog.com/processors
Switching Regulator Design Considerations for ADSP-BF533 Blackfin®
Processors
Contributed by Bob Libert, Brian Erisman, and Joe Beauchemin Rev 1 – February 2, 2005
Introduction
The Blackfin® embedded processor’s on-chip
voltage regulator is a switching buck regulator
that requires external components to function
properly. This application note describes how
buck converters work and provides guidelines for
choosing the external components for the control
circuit to work with ADSP-BF531 / ADSPBF532 / ADSP-BF533 Blackfin processors.
Since the design of the internal voltage regulator
is similar to other Blackfin processors, this note
applies to the ADSP-BF534 / ADSP-BF536 /
ADSP-BF537 and the ADSP-BF561 processors
as well.
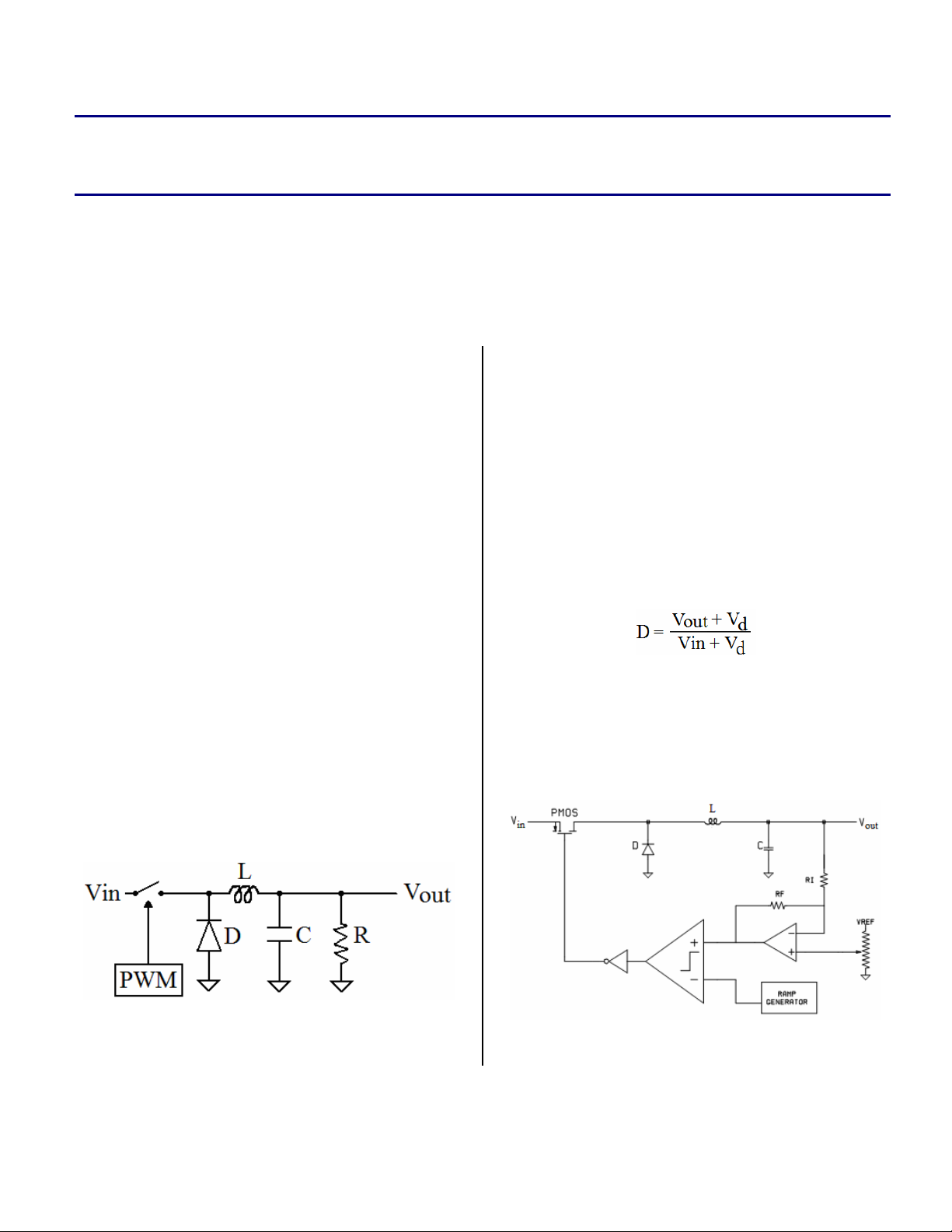
A buck converter consists of a switch, an
inductor, a diode, a capacitor, and a pulse-width
modulator (PWM), as shown in Figure 1.
The PWM controller is internal to Blackfin
processors, and the rest of the components are
external.
A control loop senses the regulator voltage and
sets the duty ratio (D) of the PWM to generate
the programmed voltage, where D is
approximately:
As can be seen in this equation, the forward
Internal Voltage Regulator
The internal voltage regulator on Blackfin
processors is a buck converter that reduces the
input voltage, which can range from 2.25 V to
voltage of the diode (Vd) contributes to both
terms. Variations in the diode’s forward voltage
and input and output voltages cause D to range
from approximately 30% to 63%.
3.6 V, to the voltage applied to the core, which is
programmable from 0.8 V to 1.2 V.
Figure 1. Basic Buck Converter
Figure 2. Internal Voltage Regulator Circuit
Copyright 2005, Analog Devices, Inc. All rights reserved. Analog Devices assumes no responsibility for customer product design or the use or application of
customers’ products or for any infringements of patents or rights of others which may result from Analog Devices assistance. All trademarks and logos are property
of their respective holders. Information furnished by Analog Devices applications and development tools engineers is believed to be accurate and reliable, however
no responsibility is assumed by Analog Devices regarding technical accuracy and topicality of the content provided in Analog Devices’ Engineer-to-Engineer Notes.
Page 2
a
The internal voltage regulator circuit (Figure 2)
consists of a voltage reference, an error
amplifier, a ramp generator, a comparator, and a
driver.
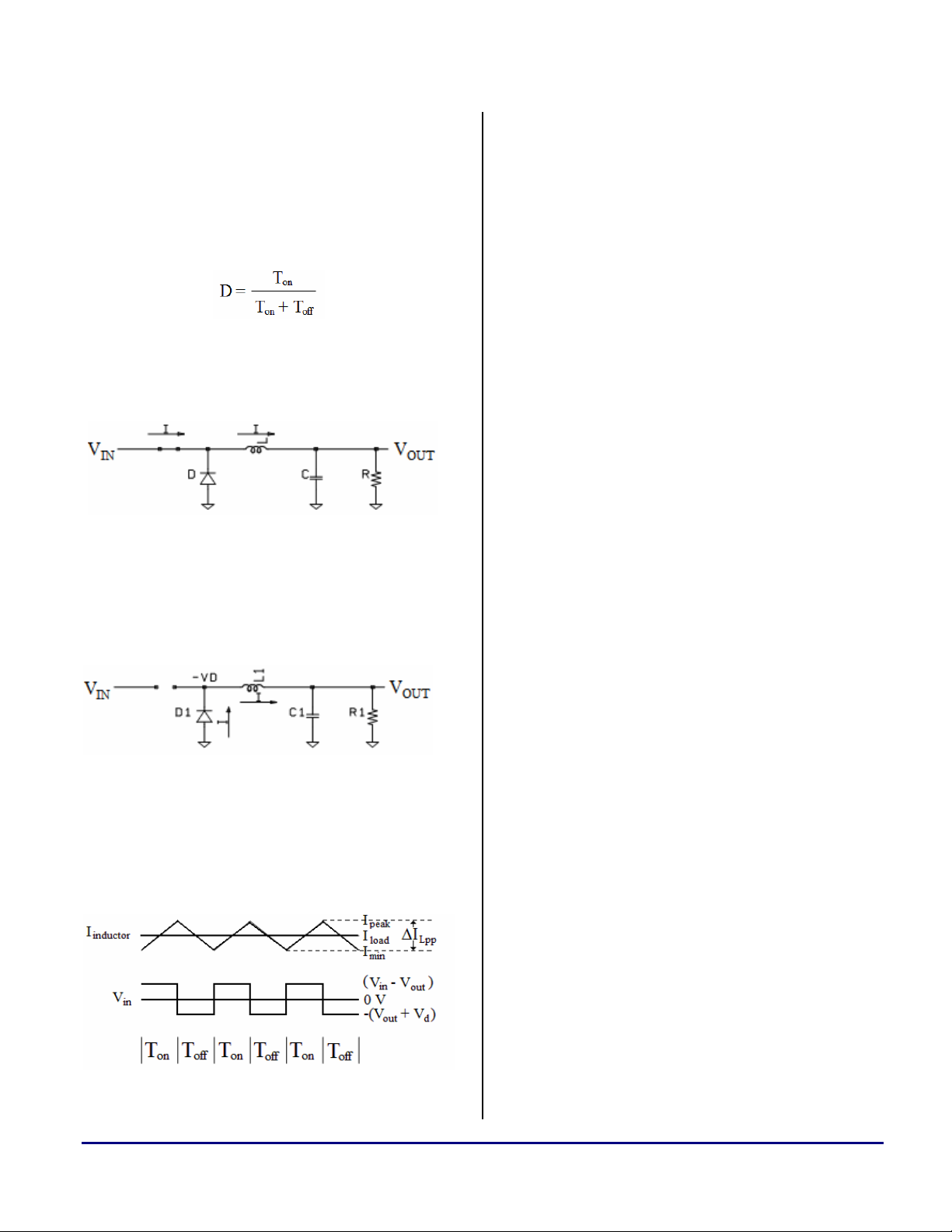
There are two states for the switch, closed (Ton)
and open (T
), where D is defined as:
off
During T
, the switch connects the supply
on
voltage (Vin) to the inductor (L), causing the
current in the inductor to ramp up.
Figure 3. Switch Behavior During Ton
During T
, the switch is off and the diode turns
off
on, which results in a negative voltage across the
inductor. This, in turn, causes the current to
decrease.
Another parameter introduced in Figure 5 is the
inductor ripple current (∆I
). This is the peak-
Lpp
to-peak measurement of current values that can
be expected to flow through the inductor.
The real circuit will also contain a number of
parasitic elements associated with the external
components. The PMOS FET has two parasitic
elements which reduce its efficiency. The first is
R
, the resistance between the drain and the
DS(on)
source. The power lost between the drain and the
source (P
) is the power dissipated within the
RDS
channel of the FET itself, which is present only
during the T
period, and is simply:
on
P
RDS
= I
load
2
* R
DS(on)
* D
The second parameter affecting the FET's
efficiency is its gate charge (QG). The loss due to
QG (PQG) occurs during both switching periods,
when the gate driver charges and discharges the
gate (Vgs). The value of PQG depends on the
switching frequency (fSW) and the turn on (Tr)
and turn off (Tf) times of the gate, and is defined
as:
PQG = f
* ((Vin/2)*(I
SW
*(Tr+Tf)) + (QG*Vgs))
load
The inductor has a DC resistance (RL). The loss
due to RL (PRL) is defined as:
Figure 4. Switch Behavior During T
The average current is load current (I
waveforms for the inductor current (I
off
). The
load
) and
inductor
the voltage at the input to the inductor (Vin)
should resemble Figure 5.
= I
P
RL
The largest contributor to overall loss is within
the diode. The diode limits its efficiency (PD)
because it has a forward voltage (V
during the T
time and is dependent on I
off
load
2
* RL
) that is on
d
. The
load
efficiency degradation caused by the diode is
implicit in the equation:
P
= I
D
* Vd * (1 – D)
load
The output filter capacitor has a parasitic
inductance (L
) and resistance (R
ESL
). Parasitic
ESR
inductance has no first-order effect on efficiency,
Figure 5. Inductor Wave Forms
Switching Regulator Design Considerations for ADSP-BF533 Blackfin® Processors (EE-228) Page 2 of 8
but degrades the filter performance by increasing
the output ripple and raising the burden on other
load bypass capacitors. Parasitic resistance
Page 3
degrades efficiency and directly translates
inductor ripple current into what is usually the
dominant component of output ripple voltage.
The power loss due to R
P
= (∆I
ESR
Lpp
ESR
2
* R
is given by:
) / 12
ESR
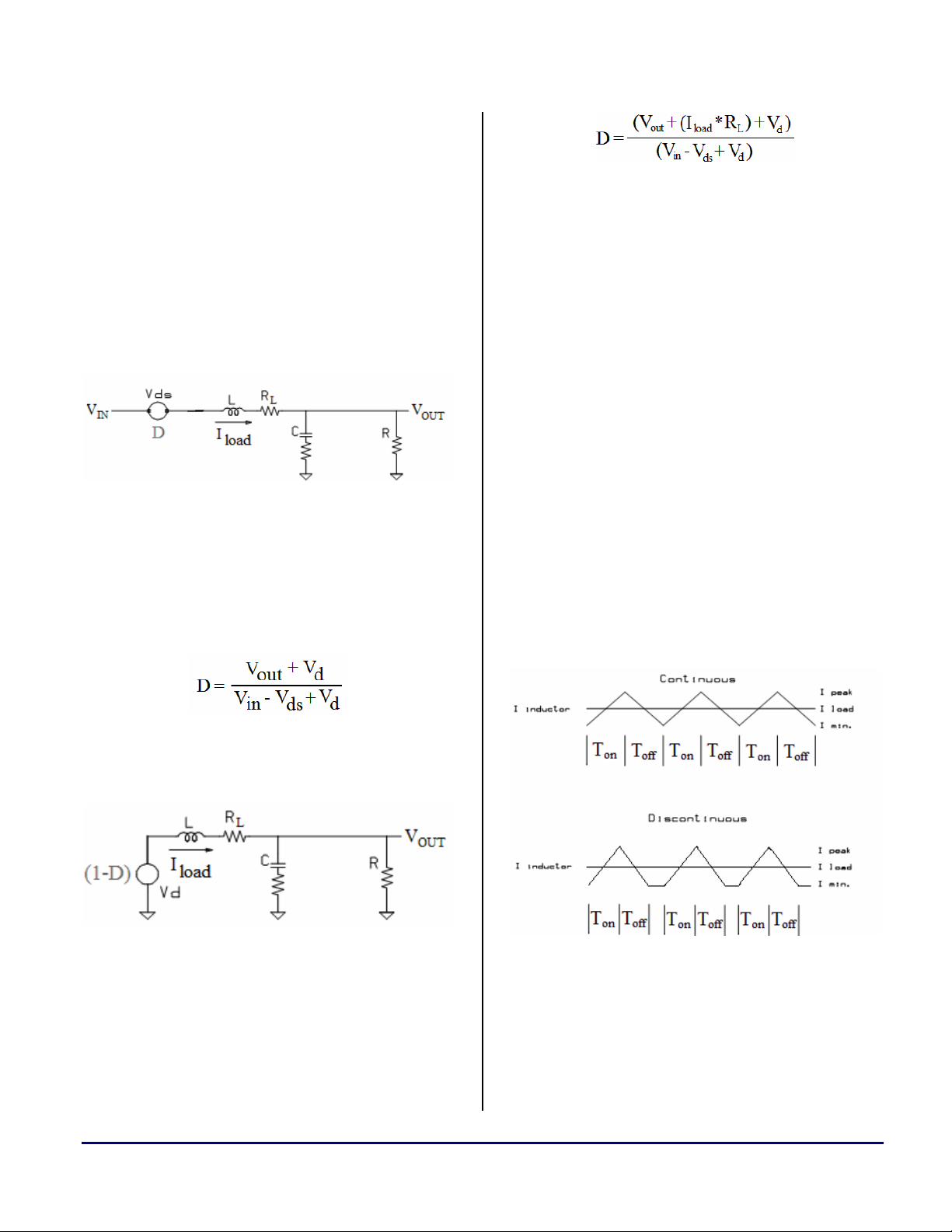
Analyzing the loss models for the two switchstates yields two simple observations. Figure 6
shows the equivalent circuit diagram with the
switch on, which eliminates the diode.
Figure 6. On-State Loss Model
Figure 6 shows that the switch’s on-state loss is
in series with the input source Vin, therefore, an
equivalent voltage loss term, Vds, can be
subtracted from the input voltage in the D
equation:
a
Buck converters usually work in what is called
the continuous mode. In the continuous mode of
operation, the current through the inductor rises
during the T
and the switching frequency (f
state and falls during the T
on
) spans the two
SW
states:
fSW = 1 / (Ton + T
off
)
The voltage regulator runs in continuous mode
during normal Blackfin processor operation (i.e.,
in Full On mode and Active mode).
The other mode of operation, discontinuous
mode, is the mode in which there is a period of
time after T
when there is no current flowing in
off
the inductor. This occurs when the Blackfin
processor is in a low-power state with a low
voltage on the core supply. Usually, this is a
mode to be avoided because it changes the loop
characteristics. Figure 8 shows the impact on
inductor current for the two modes of operation:
state,
off
Similarly, Figure 7 depicts the equivalent circuit
diagram with the switch open:
Figure 7. Off-State Loss Model
Here, the observation can be made that the
output inductance loss is in series with the
output, so an equivalent voltage loss term can be
added to the output, and is simply the inductor’s
equivalent resistance (R
current (I
Switching Regulator Design Considerations for ADSP-BF533 Blackfin® Processors (EE-228) Page 3 of 8
). Thus, the D equation becomes:
load
) multiplied by the load
L
Figure 8. Continuous IL vs Discontinuous IL
In the discontinuous plot above, the space
between T
and the subsequent Ton is referred to
off
as “dead time”.
Page 4

a
External Component Selection
The four external components of the regulator
and the bypass capacitor on the input supply
voltage need to be chosen to fit the operation of
the Blackfin processor’s internal switching
regulator. Tradeoffs can be made with respect to
cost or efficiency. Each component has parasitic
elements. Reducing these parasitics usually
improves efficiency, but may add cost.
Power Transistor (FET)
The gate drive inside the Blackfin processor’s
internal regulator was designed to provide a
maximum drive current of 200 mA. A small
internal current-limiting resistor, parasitics from
bond wires, and package leads limit the actual
charge time and reduce the efficiency. The FET
to be chosen should have a gate charge (QG) of
less than 20 nC.
The other critical parameter of the FET is its
R
since the supply voltage (Vgs) can vary from
2.25 V to 3.6 V, be sure to examine the R
vs. Vgs curve in the FET data sheet. Check the
R
. In general, lower is better; however,
DS(on)
component for the minimum Vgs.
DS(on)
DS(on)
Inductor
Given a pre-selected switching frequency and
fixed PWM control, the inductor controls the
amount of current ripple, the response of the
control loop, and whether the regulator runs in
continuous mode or discontinuous mode. The
minimum value for the inductor (L
) can be
min
calculated from the following equation:
Recall that the ∆I
term is the peak-to-peak
Lpp
magnitude of the ripple current in the inductor,
which, under steady-state conditions, is the
current that flows into the output capacitor.
Under steady-state conditions, the duty ratio (D)
is adjusted by the feedback loop in such a way
that the magnitude of ramp-up and ramp-down
currents in the inductor will be equal (Figure 8).
However, note that a minimum load current is
necessary to keep the regulator in continuous
mode. This current is known as the critical
current, and is represented as I
depicts how I
relates to ∆I
critical
Lpp
critical
:
. Figure 9
The breakdown voltage (BVDSS) should not be a
problem, since most FETs have breakdowns
greater than 12 V. Since the maximum Vin is
3.63 V, the expected diode voltage should result
in a total voltage of around 4 V. Being ultraconservative, the specified BVDSS should exceed
roughly twice this value. The power dissipation
on the switch should be specified to be greater
than 0.5 W.
In summary, the FET should meet these
minimum requirements:
R
@Vgs = 2.5V or less < 0.2Ω
DS(on)
Figure 9. Inductor Current
For minimal inductance values, ∆I
to be twice I
critical
.
is assumed
Lpp
Because of the wide range of operating
conditions, the choice of inductor involves some
compromise. The calculated values for all load
Gate charge < 20nC
Power dissipation > 0.5W
BVD
> 10V
SS
conditions range from 0.9 µH to 68 µH. One
value will not allow continuous operation or fast
response to transients. A 10 µH inductor was
chosen to cover most of the operating range at
the 1 MHz default clock frequency.
Switching Regulator Design Considerations for ADSP-BF533 Blackfin® Processors (EE-228) Page 4 of 8
Page 5

a
Choosing the inductor value alone is not
sufficient, as there are other parameters that
should also be considered when selecting the
inductor for the regulator circuit.
Minimize the DC resistance in the inductor (RL)
to about 0.1-0.25 Ω (typical). The inductor’s
resistance (R
) and load impedance (R) also
L
affect the DC gain.
The RMS current rating (I
) must be able to
rms
handle the maximum current expected from the
Blackfin processor. Refer to the application note
Estimating Power for ADSP-BF533 Blackfin
Processors (EE-229)
[1]
for details regarding how
to compute this value.
The saturation current (I
the I
I
sat
plus ½ ∆I
rms
Lpp
maximum specifications state that the
) must be greater than
sat
plus a safety margin. Some
maximum is when the inductance is reduced by
10%.
Finally, the inductor should be specified for
1 MHz to support all three programmable
switching frequencies.
Capacitors
Two capacitors must be specified, each with its
own requirements.
The first capacitor is the power supply bypass
capacitor. Because of the switching transients
that may adversely affect the power supply, a
low ESR (R
), >68 µF electrolytic capacitor
ESR
and a 0.01 µF (or 0.1 µF) ceramic capacitor must
be connected as close as possible to the source of
the switching FET.
The filter capacitor should have R
of 20 to 40 mΩ, because the R
in the range
ESR
adds zero to
ESR
the loop response, which cancels one of the LC
poles. This restriction is true by virtue of voltage
mode control use:
The R
One equation for the minimum value (C
also contributes to the ripple:
ESR
∆V
out
= ∆I
Lpp
* R
ESR
) of
min
the filter capacitor is:
However, since the value of the capacitor also
affects the loop response, a minimal value may
cause excess ripple and/or oscillations. To meet
the loop response criteria and provide good
transient response, the inductor value should be
near its minimum and the capacitor/inductor pole
should be set to about 10 kHz. The zero from the
R
and capacitor should be about three to five
ESR
times the pole frequency.
Diode
A Schottky diode is recommended to reduce the
loss associated with the forward diode voltage
(Vd), although any switching diode can be used
with a reduction in efficiency. The diode should
also be able to handle the maximum load current.
Design Example
The following is a sample design that can be
used as a reference. The sample has the
following parameters:
V
= 3.3V
in
= 1.2V (default)
V
out
fSW = 1MHz (default)
I
= 300mA
load
∆I
= 30% of I
Lpp
<10mV (ripple voltage)
∆V
out
(ripple current)
load
RL = 0.046Ω
R
Switching Regulator Design Considerations for ADSP-BF533 Blackfin® Processors (EE-228) Page 5 of 8
Q
= 0.18Ω
DS(on)
= 8.5nC
G
Page 6

a
Tr = Tf = 35ns
Vd = 375mV
R
= ~60mΩ
ESR
Some of the above specifications are taken from
data sheets of specifically chosen components.
For this design example, the following
components are being used:
Inductor – Miller PM3316 15µH [2]
FET – Fairchild FDS9431A [3]
Diode – Zetex ZHCS1000 [4]
Capacitor – Tantalum 100µF
From this particular design example’s sample
characteristics and the specifications given by the
chosen components, the theories discussed in this
note can be applied to obtain values for
minimum inductance (L
capacitance (C
frequency (F
frequency (F
). From there, the pole
min
), the capacitor and R
pole
), and efficiency (η) can be
zero
) and minimum
min
zero
ESR
calculated as well.
Note that this D value falls within the expected
range of 30% to 63%.
The second unknown in the L
equation is the
min
ripple current:
∆I
= 30% * I
Lpp
∆I
= 0.3 * 300mA = 90mA
Lpp
This value can be substituted into the L
load
min
equation along with D:
L
> 10.27µΗ
min
A 15 µH inductor satisfies the above L
min
requirement. If a 15 µH inductor is chosen, the
ripple current then becomes:
In addition to the parameters detailed above, the
duty ratio and ripple current must first be
obtained before using the given equations for the
inductor and capacitor.
Before solving for D, Vds must first be obtained:
Vds = I
= 300mA * 0.18Ω
V
ds
V
= 54mV
ds
load
* R
DS(on)
This Vds value is then substituted into the D
equation:
D = 0.44
∆I
= 62mA
Lpp
Now the minimum capacitance can be computed.
Knowing that the 10 mV specification is a
maximum voltage ripple number, the C
equation can be used:
C
= 6.2µF
min
The transient response depends on the output
impedance of the filter (Z), which is:
min
Switching Regulator Design Considerations for ADSP-BF533 Blackfin® Processors (EE-228) Page 6 of 8
Page 7

a
P
= 300mA2 * 0.18Ω * 0.44
RDS
Z = 1.56Ω
To reduce the output impedance and improve the
transient response, the cap is increased to
100 µF. Z then becomes 0.39 Ω.
Next, the pole (F
) can be calculated:
pole
F
= 4109 Hz = ~5kHz
pole
And the zero (F
) becomes:
zero
P
= 7.1mW
RDS
Computing PQG:
P
= fSW * ((I
QG
P
= 1MHz*((300mA*(35ns+35ns))+(8.5nC*3.3V))
QG
P
= 49mW
QG
* (Tr + Tf)) + (QG *Vgs))
load
Computing PRL:
P
= I
RL
= 300mA2 * 0.046Ω
P
RL
P
= 4.1mW
RL
load
2
* RL
Computing PD:
PD = I
* Vd * T
load
off
PD = 300mA*375mV*(1-0.44)
PD = 63mW
Computing P
ESR
:
F
= 26.5kHz
zero
These F
pole
and F
values are within the desired
zero
limit for stability.
To address efficiency, the total power loss in the
circuit must be accounted for and subtracted
from the total power output (P
= V
P
out
P
= 1.2V * 300mA
out
P
= 360mW
out
out
* I
) at the load:
out
load
The losses in the circuit, as described previously,
are P
Computing P
, PQG, PRL, PD, and P
RDS
:
RDS
P
= I
RDS
load
2
* R
ESR
.
DS(on)
* D
P
= (∆I
ESR
P
= (62mΑ2 * 60mΩ) / 12
ESR
P
= 0.02mW
ESR
Lpp
2 * R
ESR
) / 12
The final loss comes from the power required to
drive the PWM switcher itself (PL
), which is
PWM
0.5 mW. Taking all these losses into
consideration, the total power loss (PL
TOT
) can
be described by the following:
PL
= P
TOT
PL
= (7.1 + 49 + 4.1 + 63 + 0.02 + 0.5)mW
TOT
PL
= 124mW
TOT
+ PQG + PRL + PD + P
RDS
ESR
+ PL
PWM
After calculating the total power loss, the
efficiency (η) of the circuit can be calculated:
η = P
out
/ (P
out
+ PL
TOT
)
η = 360mW / (360mW + 124mW)
η = 74.4%
Switching Regulator Design Considerations for ADSP-BF533 Blackfin® Processors (EE-228) Page 7 of 8
Page 8

a
The efficiency will be lower at low load currents
because the 49 mW switching loss is independent
of load.
Board Layout Considerations
The board layout must minimize the connection
between the VROUT[1:0] pins and the gate pin of
the FET. The trace resistance and inductance
must be low enough to handle 1 MHz switching
speeds and 200 mA of switching current. The
traces to and from the FET's source and the
V
should, if possible, be Kelvined to their power
supply to avoid transient effects on other devices
supply pin on the Blackfin processor
DDEXT
connected to the same supply. The connection
paths to the FET's drain, the diode, inductor, and
capacitors should be as short as possible and able
to handle the load current.
The same is true for the ground connections,
since they will carry the same load currents as
the supply during the T
through the diode) and the gate switching current
during Ton.
Lastly, locate the electrolytic capacitors at the
FET source and the output side of the inductor.
Add ceramic 0.1 or 0.01 µF capacitors in parallel
to reduce the high frequency impedance.
time (the load current
off
References
[1] Estimating Power for ADSP-BF533 Blackfin® Processors (EE-229). Rev 1, February 2004. Analog Devices, Inc.
[2] PM3316-100M Inductor Data Sheet. J.W. Miller Magnetics.
[3] FDS9431A P-Channel 2.5V Specified MOSFET Data Sheet. September 1999. Fairchild Semiconductor.
[4] ZHCS1000 Schottky Rectifier Diode Data Sheet. Zetex Semiconductors.
Document History
Revision Description
Rev 1 – February 2, 2005
by Bob Libert, Brian Erisman,
and Joe Beauchemin
Initial Release
Switching Regulator Design Considerations for ADSP-BF533 Blackfin® Processors (EE-228) Page 8 of 8
 Loading...
Loading...