Page 1

New Technologies for Wide Impedance
Range Measurements to 1.8 GHz
Product Note 4291-1
HP 4291B RF Impedance/
Material Analyzer
Introduction
With the current trends in the
communications and data
processing industries requiring
higher performance, smaller
physical size, lower cost, and
higher reliability, accurate and
efficient electronic component
characterization is an increasingly
important part of product design.
Many of these advanced products
are operating at frequency in the
RF range.
Older low-frequency or indirect
methods of component evaluation
are often not able to provide the
high quality impedance parameter
information required for
HP 4291B RF Impedance/Material Analyzer with SMD fixtures
understanding component
performance under actual
operating conditions in the RF
range. This product note
describes new impedance
measurement techniques and
innovations contained in the
HP 4291B RF Impedance/
Material Analyzer that allow
accurate and efficient direct
impedance measurement and
analysis from 1 MHz to 1.8 GHz.
Five general topics will be
discussed:
Limitations of traditional
methods of impedance analysis.
Extending the frequency range
and impedance magnitude
range, while maintaining high
accuracy.
1
Making high accuracy Quality
Factor (Q) and Dissipation Factor
(D) measurements at RF.
Increasing test flexibility by
extending the device-under-test
(DUT) location 1.8 meters from
the instrument while maintaining
accuracy.
Eliminating fixture errors
critical issues for accurate RF
measurements.
Limitations of traditional
impedance measurement
solutions
Most conventional measuring
instruments such as traditional
LCR meters and impedance
analyzers are limited to lower
frequency analysis where the
4-terminal pair method can
provide very high accuracy. For
higher frequencies a vector
network analysis approach is
often used by first measuring the
reflection coefficient, then
calculating impedance values.
This indirect method may be
useful for impedance values near
50 Ω, but can be inaccurate for
impedance values significantly
higher or lower than 50 Ω. In
addition, calibration and removal
of test fixturing errors can be a
tedious procedure and in some
cases, not possible. The issue of
fixturing at RF can be a major
Page 2
source of error and expense. In
general, impedance measurements
in the RF range in the past have
been very difficult and often
yield widely varying results with
questionable accuracy. For
today's RF component or circuit
designer, a new solution is
needed to provide the accuracy
and test efficiency required for
complete RF impedance
characterization of circuit
elements.
Hewlett-Packard now offers a
new analyzer dedicated to the
direct measurement of
impedance and material
parameters from 1 MHz to 1.8 GHz
that overcomes many of the
limitations of previous approaches.
The HP 4291B provides highly
accurate RF impedance
measurements and offers a
family of surface mount device
(SMD) test fixtures. With a color
display and powerful firmware,
up to 15 impedance parameters
as well as equivalent circuit
models and more are easily
measured and displayed. The
following topics describe this
new analyzer's capabilities and
measurement technology.
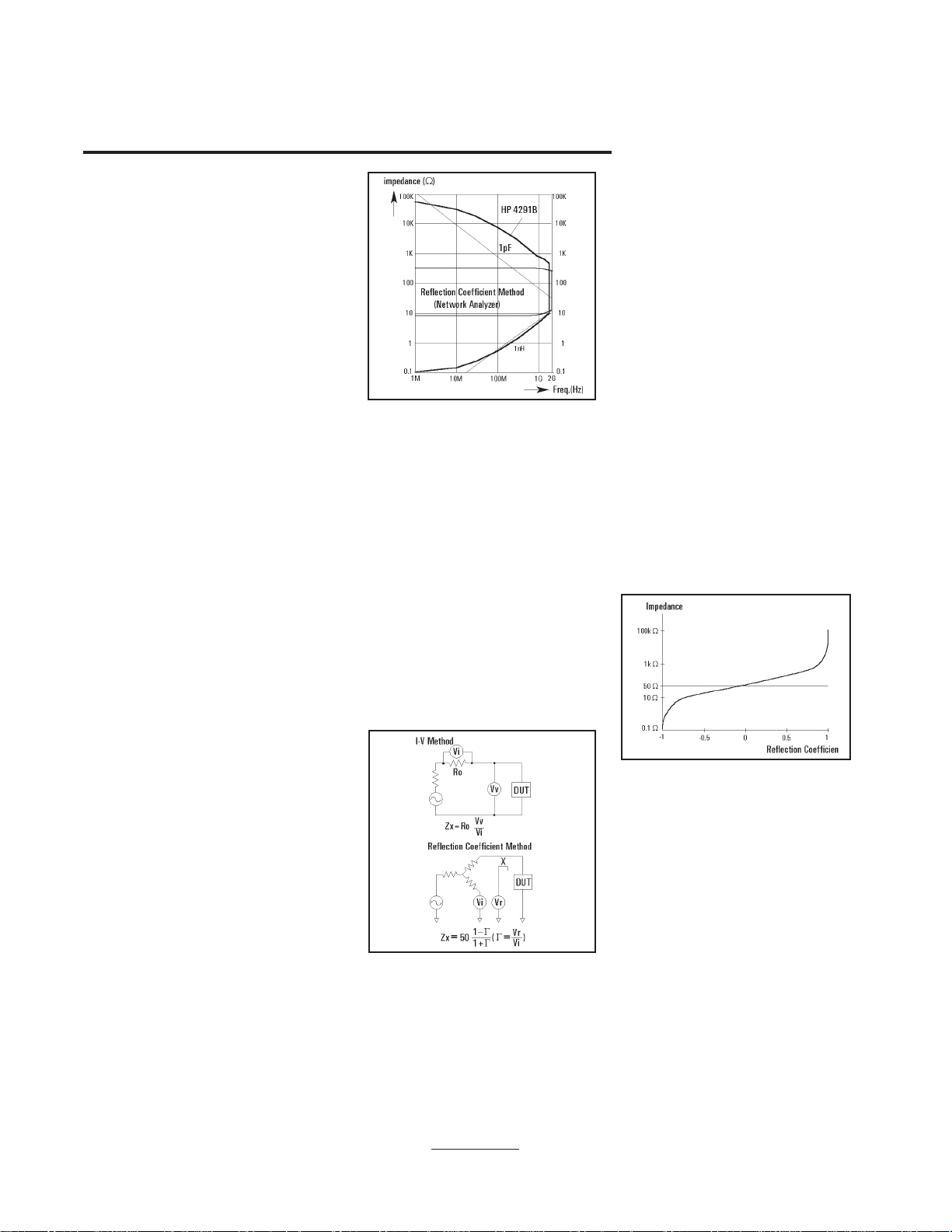
Figure 1. Ranges of impedance
measurement (Accuracy of
measurement: 10%)
The HP 4291B achieves its
accuracy over these wide
impedance ranges using tow new
techniques:
Direct impedance using
the RF I-V method
The analyzer uses a new method
to measurement impedance; the
RF I-V method. Figure 2 shows
the basic principles of the RF I-V
method and reflection coefficient
method (conventional method
using a vector network analyzer).
and reflection coefficient
methods, the impedance is given
by ratios of the readings of the
two voltmeters. Therefore one
would expect that the accuracy
of both methods would be similar.
However, the reflection
coefficient method magnifies the
measurement error when
converting reflection coefficient
to impedance. As impedance
goes away from 50 Ω, Figure 3
shows that a small changes in
reflection coefficient value
produces a large change in
impedance. In other words, a
small error in the reflection
coefficient leads to a large error
in impedance. (For example, for
an impedance of 2 kΩ, a 1 % error
of reflection coefficient results
in a 24 % error in impedance.)
Figure 3. Relationship between
impedance and reflection coefficient
Expanding the range of
impedance magnitudes
As shown in Figure 1, the
HP 4291B provides an
exceptionally wide range of
impedance measurements. It is
the ideal instrument for measuring
very small capacitance (1 pF)
and inductance (1 nH) values in
the RF range.
Figure 2. I-V method and reflection
coefficient impedance method
As can be seen from the equations
in Figure 2, the RF I-V method
measures impedance directly,
while the reflection coefficient
method measures reflection
coefficient and concerts it to
impedance. In both the RF I-V
2
The RF I-V method measures
impedance directly from a ratio
of voltage and current, without
converting the measured data.
Therefore, the RF I-V technique
maintains consistent accuracy
even if the impedance is
significantly larger or smaller
than 50 Ω. Thus for measuring
non-50 Ω components, the
HP 4291B using the RF I-V
technique is recommended.
Page 3

High/Low impedance circuit
The HP 4291B employs highimpedance and low-impedance
circuits, as shown in Figure 4, to
expand the range of impedance
measurements. When measuring
a high-impedance device,
accurate measurement of the
DUT current is most critical. The
high-impedance circuit solves
this problem by connecting the
current detection circuit directly
in series with the DUT, ensuring
accurate DUT current
measurement and not measuring
current flowing in the voltage
sensing circuit.
On the other hand, when
measuring a low-impedance
device, the voltage across the
DUT is most critical. In this case,
the low-impedance circuit
connects the voltage detection
circuit directly to the DUT,
ensuring accurate voltage
measurement and not measuring
the voltage drop from the current
sensing impedance. By using the
right measuring circuit for the
impedance being measured, it is
possible to extend the range of
impedance magnitudes measured
for a given accuracy.
Figure 4. High-impedance and lowimpedance measuring circuits
High Accuracy Q and D
measurements
As shown in Figure 5,
the HP 4291B is capable of
evaluating a sample with Q = 100
within ±15 % accuracy at 1 GHz.
This capability is targeted for
evaluating the loss of low-loss
components at RF. The accuracy
of Q and D measurements depend
on the accuracy of phase
measurement. See Figure 6.
The HP 4291B improves the
accuracy of phase measurements
by requiring an additional phase
calibration step. (Conventional
one-port calibration uses open,
short, and 50 Ω load standards.)
This type of one-port calibration
does not provide satisfactory
accuracy for phase measurements
because of the phase uncertainty
of the 50 Ω standard. By using a
low-loss air capacitor as a phase
standard, the HP 4291B lowers
the phase uncertainty to 1 mrad or
less (corresponding to D = 0.001),
ensuring improved accuracy for
Q and D measurements.
Error-free 1.8m cable
extension
The cable connecting the main
body of the HP 4291B to the test
station has been extended to
1.8 meters without adding
additional errors. See Figure 7.
The long cable allows easy
access to remote DUT locations.
This temperature chamber,
scanner/handler, or custom test
setup, for example.
These two measuring circuits are
implemented as two different test
heads in the HP 4291B, so users
can select and switch the circuits
easily to optimize the measurement
range and accuracy to best
match the DUT impedance.
Figure 5. Q measurement accuracy
Figure 6. Q and D measurement and
phase measurement
3
Figure 7. Extended test cable
Normally, extending the cable
increases measurement error
due to increased noise,
temperature differentials, cable
resistance, etc. However, as
illustrated in Figure 8, the
HP 4291B measures the current
and voltage signals using the
same circuit and alternates the
measurement with fast timedivision multiplexing.
Page 4

Since the measurements are
made at an alternating interval of
several milliseconds, the same
cable-induced errors occur in
both the current and voltage
measurement data. These errors
are then canceled out when the
impedance is obtain from the
ratio of voltage to current.
Furthermore, by measuring
current and voltage with the same
circuit, errors in the measuring
instrument caused by temperature
changes are offset in the same
manner, resulting in significant
temperature characteristic
improvement.
Figure 8. Time-division multiplexing
of cuurent/voltage measurement
Test fixtures have a large impact
on measurement accuracy,
especially at higher test
frequencies. An important factor
in getting accurate measurements
is eliminating errors introduced
by the DUT fixturing. Calibration
insures high accuracy at the plane
of calibration (measurement point
where the standards are applied),
but in actual practice, the test
fixture can add additional error
terms beyond the calibration
plane. This is why fixture error
compensation is so important.
Electrical properties of the test
fixture (which occur after the
calibration point), consist of a
phase rotation due to the
physical length of the electrodes
and other unwanted stray
parasitics between electrodes.
Both of these can cause significant
measurement errors in the RF
band. Conventional measuring
instruments often have no
convenient method to eliminate
them effectively. The HP 4291B
uses electrical length
compensation to remove the
errors caused by phase rotation
and OPEN/SHORT compensation
(at the DUT location in the fixture)
for removing fixture parasitic
impedance.
Conclusion
The HP 4291B RF impedance
and material analyzer provides
highly accurate impedance and
material measurements by
incorporating new technologies
and offering an integrated
package including a family of
SMD and material fixtures. The
analyzer overcomes many
limitations of conventional
impedance analysis and, for the
first time, provides an efficient
and accurate measurement
solution for passive component
analysis over the RF range.
For detailed technical information
of the HP 4291B RF impedance
and material analyzer, refer the
HP 4291B Technical Information
in page 5.
For more information, request
following literatures from your
local HP representative:
HP4291B 1.8 GHz impedance/Material
Analyzer Product Overview P/N 59661501E
HP 4291B Technical Specifications P/N
5966-1543E
Highly Accurate Evaluation of Chip
Capacitors using the HP 4291B
Application Note 1300-1 P/N 59661850E
Evaluating Chip Inductors using the HP
4291B Application Note 1300-2 P/N
5966-1848E
Permittivity Measurements of PC Board
and Substrate Materials using the HP
4291B and HP 16453A
Application Note 1300-3 P/N 59661847E
Permeability Measurements using the
HP 4291B and HP 16454A Application
Note 1300-4 P/N 5966-1844E
Electronic Characterization of IC
Package Application Note 1300-5 P/N
5966-1849E
Impedance Characterization of
Magneto-Resistive Disk Heads Using
the HP 4291B Impedance/Material
Analyzer Application Note 1300-6 P/N
5966-1096E
On-Chip Semiconductor Device
Impedance Mesurements Using the HP
4291B Application Note 1300-7
P/N 5966-1845E
Evaluating Temperature Characteristics
using a Temperature Chamber and the
HP 4291B Product Note
4291-2 P/N 5966-1927E
Impedance Measurements Using the HP
4291B and the Cascade Microtech
Prober Product Note 4291-3 P/N
5966-1928E
Dielectric Comnstant Evaluation of
Rough Surfaced Materials Product Note
4291-5 P/N 5966-1926E
4
Page 5
Appendix.
New Technologies used in the High Frequency
Impedance Analyzer
HP 4291B RF Impedance/Material Analyzer
Technical information
Abstract
A new one-port impedance analyzer has been
developed for analysis of high frequency devices
and materials up to 1.8 GHz.
Traditionally, impedances near 50 Ω have been
measured accurately by the null method using a
directional bridge. However, this new analyzer
uses a voltmeter/ammeter method and offers
precise measurement capability over a wide
impedance range. Furthermore, a special
calibration method using a low-loss capacitor
realizes an accurate high-Q device measurement.
This paper describes the advantages of these
techniques. Impedance traceability of the
instrument will also be discussed.
Finally, many types of test fixtures are introduced,
because they are a key element in any test system.
1. Introduction
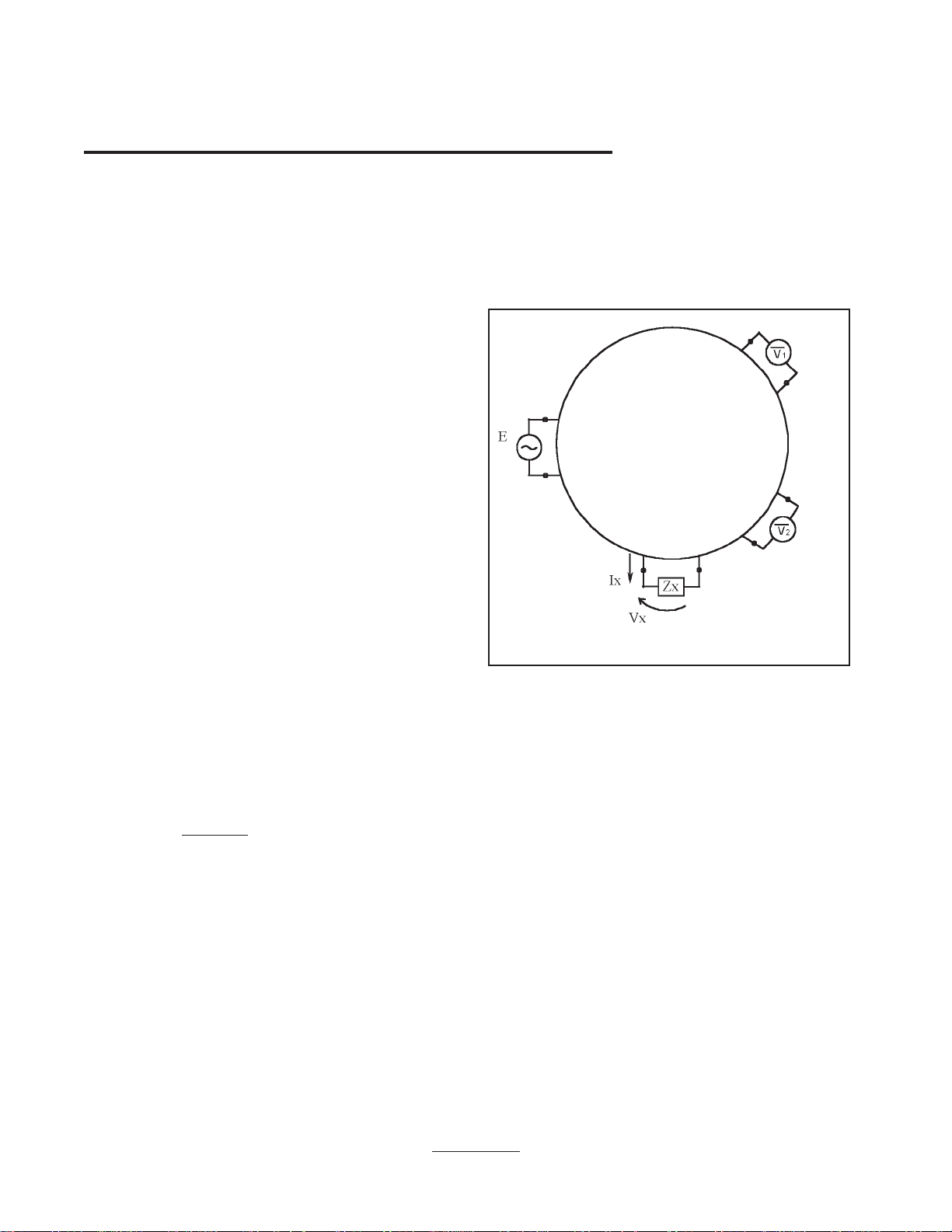
A general impedance measurement schematic
using two vector voltmeters is shown in Fig. 1. In
this case, the true impedance (Zx) of a device under
test (DUT) is determined by measuring the voltages
of any two different sets of points in a linear circuit.
Zx = K1 × (1)
where
K1, K2, K3 : complex constant
In the process of deriving the equation above,
linearity is assumed but reciprocity is not assumed.
Therefore, the existence of active devices in the
circuitry is not prohibited.
There are at most three unknown parameters
related to the circuit in the equation (1). Once we
know these parameters, we can calculate any
impedance of the DUT from the measured voltage
K2+Vr
1+K3×Vr
Vr : voltage ratio
E: signal source V1: vector voltmeter1
V2: vector voltmeter2 Zx: DUT
Figure 1. General schematic for impedance measurement
using two vector voltmeters
ratio (Vr). The procedure that estimates these
circuit parameters is called "calibration" and one
method is "Open-Short-Load (OSL) calibration."
Calculation of Zx from the measured voltage ratio
(Vr) according to equation (1) is called
"correction."
2. Transducer
We call a linear circuit such as the one in Fig. 1
(one that relates a signal source, two vector
voltmeters and a DUT) a "transducer."
Transducers are the key element in impedance
measurement. For example, two types of
transducers, the "directional bridge" and the
transducer in a "voltmeter/ammeter (V-I) method,"
are compared in terms of sensitivity to the gain
variance.
2-1. Directional bridge type
Directional bridges (see Fig. 2-1) are used in many
network analyzers.
5
Page 6

In this case, the bilinear transformation is
1+
Zx = −R
Γ
× (2)
0
1−
Γ
where
(Z
−
R0)
Γ
Vr = = (− ) ×
R
x
= : reflection coefficient
(Z
+
R0)
x
V
2
V
1
= 50Ω : characteristic impedance
0
1
Γ
8
Parameters corresponding to those in equation (1)
are
K1 = - Ro, K2 = 1, K3 = - 1
E: signal source V1: vector voltmeter1
V2: vector voltmeter2 Zx: DUT
R@ Ro = 50 Ω
Ro: characteristic impedance
Figure 2-1. Directional bridge circuit
2-2. V-I method
Fig. 2-2 shows the simplest transducer in the V-I
method. The bilinear transformation in this case is
Zx = R
× Vr (3)
0
where
R
= 50Ω : resistor that converts DUT current
0
to a voltage
V
Vr =
2
V
1
Parameters corresponding to those in equation (1)
are
E: signal source V1: vector voltmeter1
V2: vector voltmeter2 Zx: DUT
R: resistor converting DUT current to a voltage
R@ Ro = 50 Ω
Figure 2-2. V-I method
2-3. Sensitivity to gain variance
In this section we discuss the relationship between
the impedance measurement error and the gain
variance of the vector voltmeters.
2-3-1. Directional bridge type
We assume that the vector voltmeters in Fig. 2-1
are not ideal but have some gain variance. In this
situation, the measured voltages (V1 and V2) and
the calculated impedance (Zx) are:
V
= E ×
1
V2 =
Zx = −R
α
1
( − )
8
×
0
1
× E × Γ ×
1+
Γ
1−
Γ
α
2
where
α
: gain of the vector voltmeter1
1
α
: gain of the vector voltmeter2
2
Γ
=
−
8 × Vr ×
V
2
Vr = : voltage ratio
V
1
α
2
α
= : ratio of voltmeter gains
2
α
α
: measured reflection coefficient
r
1
K1 = R, K2 = 0, K3 = 0
6
Page 7

We define the calculated impedance sensitivity (S)
to the voltmeters' gain variance as follows:
δZ
x
Z
S = (4)
x
δ
α
r
α
r
This sensitivity can be considered as the inverse of
the "magnification on gain variance." The smaller S
is, the smaller the error of the calculated
impedance is. In this case, equation (4) is given as
follows:
δ
Z
δΓ
S = × ×
x
δΓ
1
= ( ) ×
2
δα
Z
r
2
− R
x
Zx × R
α
r
Z
x
2
o
o
1
(− ) × ( ) for |Z
2
R
o
Z
x
| << Ro
x
= 0 for |Zx| = Ro
1
( ) × ( ) for |Z
2
Z
x
R
o
| >> Ro
x
This implies
1) This type of transducer has little sensitivity to
the voltmeter gain variance when the DUT
impedance is near Ro (50 Ω).
2) The gain variance of the voltmeters behaves as
the offset impedance with a magnitude of
(1/2)*Ro*| ∆α r/α r | when the DUT impedance is
far smaller than Ro.
3) The gain variance of the voltmeters behaves as
the offset admittance with a magnitude of
(1/2)*Go*| ∆α r/ α r| when the DUT impedance is
far larger than Ro.
where
∆αr: change in gain ratio α
r
Go : 1 / Ro
Fig. 2-3 shows this characteristic.
Figure 2-3. Sensitivity to the voltmeter gain variance
2-3-2. V-I method
We also assume that there is some gain variance in
the vector voltmeters in Fig. 2-2. The relationship
among measured voltages (V1 and V2) and the
calculated impedance (Zx) are:
R
V1 = E ×
V2 = E ×
Zx = Ro × Vr
o
Zx + R
Z
x
Zx + R
× α
r
× α
1
o
× α
2
o
where
α
: gain of the vector voltmeter1
1
α
: gain of the vector voltmeter2
2
V
Vr = : voltage ratio
α
2
V
1
α
1
= : ratio of voltmeter gains
r
α
2
In this case, the sensitivity is given by the following:
The error ratio (∆Zx/Zx) is always constant and
equal to unity. For example, if the voltmeter gain
7
Page 8

ratio ar changes 1%, an impedance error of 1% is
caused for any DUT.
δZ
x
Z
x
S = = 1
δ
α
r
α
r
3.Schematic of new RF impedance
analyzer
From the discussion in section 2, we find that the
voltmeter gain variance is neither suppressed nor
magnified for all DUT impedances in a "V-I method
type transducer." This characteristic is desirable
for wide impedance measuring capability.
Therefore we adopted this type of transducer for
our new one-port RF impedance meter.
3-1. Basic transducer circuit
Fig. 3-1 shows the basic circuit of the transducer in
New RF Impedance Meter which is modified from
Fig. 2-2. The high impedance configuration realizes
perfect OPEN and imperfect SHORT conditions. On
the other hand the low impedance configuration
realizes imperfect OPEN and perfect SHORT
conditions.
Moreover, this circuit has the following
characteristic:
3-2. Actual transducer circuit
Actual transducer circuits are shown in Fig. 3-2 (a)
and Fig. 3-2 (b).
We took the following things into account when
designing the actual transducer circuits:
(a) for high impedance measurement
* the output impedance at the DUT port is always Ro in
either switch position
E: signal source V1: vector voltmeter1
V2: vector voltmeter2 Zx: DUT
R@ Ro: characteristic impedance
switch: ON for high impedance measurement
switch: OFF for low impedance measurement
Figure 3-1. Basic transducer circuit in New RF
impedance Analyzer
(b) for low impedance measurement
E: signal source V1: vector voltmeter1
V2: vector voltmeter2 Zx: DUT
R@Ro
Ro: characteristic impedance
Figure 3-2. The actual transducer circuit
1) Because a wideband switch with small nonlinearity and with small transients over a
wide signal range is not easily realized, we
divided the circuit in Fig. 3-1 into two separate
circuits.
2) Because the minimum frequency of the new
meter is 1 MHz, the floating voltmeter (V1),
8
Page 9

which corresponds to the current meter, is easily
realized by using a balun.
3) In order to prevent the error caused by by-pass
current we adopted a circuit in which the exciting
impedance of the balun is parallel connected not
to the current meter (V1) but to the signal source
(E).
3-3. Simplified block diagram of new impedance
analyzer
The followings are other key features of the
instrument:
1) time division multiplex
Two voltmeters are obtained by time division
multiplexing one voltmeter. The multiplexing
eriod is 2msec. This ensures that the slow drift
of the voltmeter gain does not affect the
impedance measurement. The signal path
after the multiplexer can be extended. This
instrument uses a 1.8m cable between the
transducer and the instrument main frame.
This allows wide flexibility in constructing a
test system using automatic device handlers.
Good temperature characteristics are also
derived even with an extended cable by the
single path configuration.
Figure 3-5. (a) Typical errors for impedance magnitude
with the transducer for high impedance
Figure 3-5. (b) Typical errors for impedance magnitude
with the transducer for low impedance
4. A special calibration for high Q measurement
Normally the accuracy requirement for the
impedance phase is greater than that of the
impedance magnitude. Our New Impedance Meter
has a special, but easy-to-use, calibration for high
Q (quality factor) device measurements. We
discuss this calibration technique in this section.
(2) impedance ranging
At frequencies below 200 MHz there exists an
"expand range." In the expand range there is a
gain difference between the voltage channel
and the current channel in the earlier stage of
the multiplexer. This impedance ranging offers
stable measurements for DUTs with
impedances that differ greatly from 50 Ω.
Fig.3-3 (a), Fig. 3-3 (b) shows the typical
measurement errors for impedanceof the
instrument. The errors mainly consist of the
uncertainties for standards (STDs) used in the
calibration, non-repeatabilities in connections,
temperature coefficients, noise and errors in the
interpolations. The impedance phase errors can be
reduced by using a special calibration (see Section
4).
4.1 Outline of the special calibration
Even if the stability of the instrument is good
enough, accurate Q measurements are not
performed without correct markings on the phase
scale of the instrument. For instance, if we want to
measure the Q factor with 10% uncertainty for a
DUT whose Q value is almost 100, the uncertainty
for phase scaling must be smaller than 1E-3. The
phase accuracy of the instrument is determined
almost entirely by the uncertainty of the 50Ω LOAD
STD used in the OSL calibration. One method to
improve phase measurement accuracy is to use a
phase calibrated LOAD STD. However, it is not
ensured that phase uncertainty for a calibrated
50Ω LOAD is smaller than 1E-3 at high frequencies
(such as 1 GHz).
In addition to the normal OPEN-SHORT-LOAD
STDs, using a low-loss air-capacitor as the second
LOAD (LOAD2), whose dissipation factor (D) is
kept below 1E-3 at around 1 GHz, offers the
following feature:
9
Page 10

* the uncertainty for the measured phase is
decreased from the phase uncertainty of the 50Ω
LOAD (LOAD1) to the uncertainty of
D of the low-loss capacitor (LOAD2) for almost
all DUT impedances.
4.2 Details of the modified OSL calibration
using an additional load
We want to have the calibration method which
reduces the error in phase measurement in spite of
the existence of phase error for the 50Ω LOAD.
Consider the case that we have the 50Ω LOAD STD
whose impedance phase is not known but
impedance magnitude is known. In this situation
how about adding another LOAD (LOAD2) whose
impedance magnitude is not known but impedance
phase is known? We use a low-loss capacitor as the
second LOAD. The number of unknown circuit
parameters are still three at most. However, two
more unknowns related to STDs are added. Let us
define the problem. There are eight real unknown
parameters:
1) circuit parameter K1 (two real parameters)
2) circuit parameter K2 (two real parameters)
3) circuit parameter K3 (two real parameters)
Zlmi : measured impedance for LOAD STD
(i = 1 : LOAD1, i = 2 : LOAD2)
Zlsi : true impedance for LOAD STD
(i = 1 : LOAD1, i = 2 : LOAD2)
Zls
= Zabs_ls1*EXP(j*θls1)
1
Zls
= Zabs_ls2*EXP(j*θls2)
2
θls1 = θ2 - θ1 + θls2
Zabs_ls2 = A1/A2*Zabs_ls1
Zabs_ls1 : impedance magnitude for LOAD1
(50Ω) : known
θls2 : impedance phase for LOAD2
(low-loss capacitor) : known
θ1 = arg((1 - Zlm
θ2 = arg((1 - Zlm
*Yom)/(Zlm1 - Zsm))
1
*Yom)/(Zlm2 - Zsm))
2
A1 = |(1 - Zlm1 *Yom)/(Zlm1 - Zsm)|
A2 = |(1 - Zlm2 *Yom)/(Zlm2 - Zsm)|
For the actual cases these circuit parameters are
expressed by far more complicated equations.
Therefore
we adopted a simpler procedure consisting of two
steps:
4) impedance phase qls1 of the 50Ω LOAD
(one real parameter)
5) impedance magnitude Zabs_ls2 of the low-loss
capacitor LOAD2 (one real parameter)
We solved this problem analytically. For the
simplest case where both the OPEN and the SHORT
STD are ideal, the three circuit parameters are
found as follows :
K1 = A × Zls × R
−
Z
K2 =
K3 = −Ysm x R
sm
R
o
o
o
(5)
where
Ro : characteristic impedance
A = (1 - Zlmi *Yom)/(Zlmi - Zsm)
Yom : measured admittance for OPEN STD
Zsm : measured impedance for SHORT STD
1) step 1
*Regard the impedance of the 50Ω LOAD as
Zls1 = 50+j*0 (that is, the phase of LOAD1 is
zero).
*Find the circuit parameters K1, K2, and K3 by
normal OSL calibration using the LOAD value
(Zls1).
*Execute correction for LOAD2 and get the
corrected impedance (Zcorr2).
*Calculate the phase difference (∆θ) between the
phase of Zcorr2 and the true phase of LOAD2
2) step 2
*Modify the impedance of LOAD1 to Zls1'
whose phase is -∆θ and whose impedance
magnitude is still 50 Ω
*Calculate the circuit parameters again by
normal OSL calibration using modified
LOAD impedance Zls1'.
10
Page 11

Although this is an approximate method, actually
just performing the two steps is accurate enough
for our purpose. We call this method the "modified
OSL calibration."
4.3 Phase measurement error using modified
OSL calibration
We considered the following error factors during
phase measurement in the modified OSL
calibration:
1) uncertainty for impedance magnitude of
LOAD1
For example, the relationship between the phase
measurement error and the uncertainty for the
impedance phase of LOAD2 (∆θls2) is shown in
Fig. 4-1. Fig. 4-2 shows the relationship between
the phase measurement error and the uncertainty
for admittance magnitude of OPEN (∆Yopen).
From the above discussion the phase measurement
error when using the modified OSL calibration is
mainly determined by
* uncertainty for the impedance phase of LOAD2
* uncertainty for the admittance magnitude of
OPEN
2) impedance phase of LOAD1
3) impedance magnitude of LOAD2
4) uncertainty for impedance phase of LOAD2
5) uncertainty for admittance magnitude of OPEN
Notice that factor 2 and factor 3 do not cause any
error if we use the analytical solution. By
computer simulations the phase error is shown to
behave as follows:
1) Sensitivity of phase measurement error due to
the uncertainty of impedance magnitude for
LOAD1 is small.
2) Sensitivity of phase measurement error due to
the impedance phase of LOAD1 is small.
3) Sensitivity of phase measurement error due to
the impedance magnitude of LOAD2 is small.
4) Uncertainty for the impedance phase of LOAD2
directly affects the phase measurement error.
5) Sensitivity of the phase measurement error due
to the uncertainty for admittance magnitude of
OPEN (| ∆Yopen|) is reduced to
|Ro*∆Yopen|*(Copen/Cls2) in the case of
reactive DUT. In the case of resistive DUTs, the
sensitivity is the same as in the normal OSL
calibration.
where
Ro : characteristic impedance = 50 Ω
Copen : capacitance of OPEN STD
Cls2 : capacitance of LOAD2 (low-loss
capacitor)
Now we evaluate these two items. The D factor for
the capacitor (3pF) used in the calibration can be
small because its dimensions are small and the
space between the inner and outer conductors is
filled almost completely with air. The D value is
verified as 500E-6 at 1GHz from the residual
resistance measurement at the series resonant
frequency. The D factor is in proportion to Freq
due to the skin effect. By using zero as the D value
for the capacitor during calibration a phase
measurement error of 500E-6 is realized at 1 GHz.
On the other hand, the uncertainty for the OPEN
capacitance is +/-5fF at most.
This leads to a phase measurement error less than
+/-100E-6 at 1 GHz. In all, a phase measurement
uncertainty of 500E-6 is realized by using the
modified OSL calibration.
5. Impedance tracability
For an impedance performance check using the
top-down method [1] we set up a kit traceable to the
National Standards. This kit is calibrated annually
at our standard laboratory. Two major items in the
kit are the 50Ω LOAD and 10 cm long, 50Ω
beadless air line. The 50Ω LOAD is desirable
because its frequency characteristic for
impedance is very flat. The structure of the air line
is very simple. Therefore, it is easy to predict its
frequency characteristic and it is convenient to
realize various impedances by changing
frequencies with the OPEN or SHORT terminated.
The traceability path for the kit is shown in Fig. 5.
The impedance characteristic of OPEN ended and
SHORT ended air lines can be calculated
theoretically from their dimensions and resistivity.
11
1.5
Page 12

[2] However, it is not easy to design the syst offring
calibrated dimensions with the individual kit.
Freq. = 1GHz
|Zopen| : impedance of OPEN STD @ 2 kΩ
Dqls2: uncertainty for impedance phase of LOAD2 (low-loss
capacitor) = 500E-6
Figure 4-1. Relationship between the phase measurement
error and the uncertainty for the impedance phase of
LOAD2
Therefore, the periodical calibration of dimensions
is performed only to the reference air line of the
standard laboratory. Calibration for the individual
air line is executed by the network analyzer
calibrated from the reference air line. The 50Ω
LOAD calibration is done mainly by the quarter
wave impedance method and DCR measurement.
The OPEN termination is calibrated by a
capacitance bridge at low frequencies and by the
network analyzer at high frequencies. The SHORT
termination is treated as an ideal one.
Uncertainties for it consists of the skin effect and
non-repeatabilities.
Freq. = 1GHz
Ro: characteristic impedance = 50 Ω
|Zopen| : impedance of OPEN STD @ 2kΩ
Dq1 = |Ro*DYopen|*Copen/Cls2
|DYopen| : uncertainty for admittance magintude of OPEN = 30mS
Copen = 82 fF, Cls2 = 3pF
Figure 4-2. Relationship between the phase measurement
error
6. Test fixtures
In the actual measurement test fixtures
corresponding to different shaped DUTs are
needed. As the frequency range goes up higher,
people need fixtures that are able to handle smaller
devices. We have developed four types of
fixtures:
* a fixture for surface mount devices (SMDs) with
bottom electrodes
* a fixture for SMDs with side electrodes
* a fixture for very small SMDs
* a fixture for lead components
To reduce the error at the fixture terminal it is
necessary to minimize the length from the
reference APC-7 plane to the fixture terminal and
to minimize the connection non-repeatability.
The new fixtures improved repeatability by almost
five times compared with our old ones.The typical
non-repeatability of the SMD fixtures is
12
Page 13

* +/-50 pH, +/- 30 mΩ for SHORT measurement
* +/- 5 fF, +/- 2 µS for OPEN measurement
Furthermore, we installed "fixture compensations"
in the firmware which corresponds to the
corrections at the reference plane. This reduces the
errors generated in the circuit between the
reference plane and the fixture terminal. The best
choice for the compensation is the OSL. However, it
is not easy to prepare a LOAD having excellent
frequency characteristics. As the more realistic
way we prepare the following compensation
functions:
* fixture port extension
* OPEN-SHORT correction at the fixture plane
Fig. 6 shows the typical additional error when using
the above corrections at the same time. These
values are almost three times better than the errors
for our former type of fixtures.
Figure 6. Typical additional errors after fixture
compensations
7. Conclusion
Selection of "transducers" is important for accurate
impedance measurement . A new type of
transducers, which are based on the voltmeter/
ammeter method and have wide impedance
measuring capability, are proposed. By adopting
these transducers the New RF Impedance Analyzer
has been developed. We also proposed a new
phase calibration technique modified from the OSL
calibration. It utilizes a low-loss capacitor as the
second LOAD. This calibration enables accurate Q
measurements.
References
[1] Hewlett Packard, "Traceability and the HP8510
Network Analyzer," Nov. 1 1985
[2] Robert E. Nelson, Marlene R. Coryell,
"Electrical Parameters of Precision, Coaxial,
Air-Dielectric Transmission Lines," NBS
Monograph96, June 30 1966
13
Page 14

For more information about HewlettPackard test & measurement products,
applications, services, and for a current
sales office listing, visit our web site,
http://www.hp.com/go/tmdir. You can
also contact one of the following
centers and ask for a test and measurement sales representative.
United States:
Hewlett-Packard Company
Test and Measurement Call Center
P.O. Box 4026
Englewood, CO 80155-4026
1 800 452 4844
Canada:
Hewlett-Packard Canada Ltd.
5150 Spectrum Way
Mississauga, Ontario
L4W 5G1
(905) 206 4725
Europe:
Hewlett-Packard
European Marketing Centre
P.O. Box 999
1180 AZ Amstelveen
The Netherlands
(31 20) 547 9900
Japan:
Hewlett-Packard Japan Ltd.
Measurement Assistance Center
9-1, Takakura-Cho, Hachioji-Shi,
Tokyo 192, Japan
Tel: (81) 426 56 7832
Fax:(81) 426 56 7840
APC-7 ® is a U.S. registered trademark
of the Bunker Ramo Corporation.
14
Latin America:
Hewlett-Packard
Latin American Region Headquarters
5200 Blue Lagoon Drive
9th Floor
Miami, Florida 33126
U.S.A.
Tel: (305) 267-4245
(305) 267-4220
Fax:(305) 267-4288
Australia/New Zealand:
Hewlett-Packard Australia Ltd.
31-41 Joseph Street
Blackburn, Victoria 3130
Australia
Tel: 1 800 629 485 (Australia)
0800 738 378 (New Zealand)
Fax:(61 3) 9210 5489
Asia Pacific:
Hewlett-Packard Asia Pacific Ltd.
17-21/F Shell Tower, Times Square,
1 Matheson Street, Causeway Bay,
Hong Kong
Tel: (852) 2599 7777
Fax:(852) 2506 9285
Copyright © 1998
Hewlett-Packard Company
Printed in U.S.A. 10/98
5966-2046E
 Loading...
Loading...