Texas Instruments CC-40 A Collection Of Information

A

Collection

of

Information

c

an

The

TI

CC-

-40

Computer

fey

Palmer

0.

Hanson,

Jr.

June

1985

This

collection

is

a

compilation

of

articles

on

the

CC-4-0

which

appeared

in

the

1983

and

1984

issues

of

TI

PPG

Notes.

This material is not copyrighted and may be reproduced for

personal

use.

In/hen

material

is

used

elsewhere

we ask as a

matter of courtesy that

TI

PPC

Notes

be

mentioned.

The

use

of the material in this compilation is entirely at the risk of the

user.

No responsibility as

to

the accuracy and the

consequences

due

to

the

lack

of

it

will

be

borne

by

either

the

club

or

the

editor.

Volume

8,

Number

3 *

May/June

1983

The BIG NEWS is the Texas Instruments Compact

Computer,

40 (CC-40).

Maurice Swinnen and I had received engineering models some time ago for

evaluation. As a result this issue of TI PPC Notes contains

our

pre

liminary impressions together with some sample programs. There seems

to be

an

emphasis

on

scientific applications as

evidenced

by

thirteen

(sometimes

fourteen)

digit

arithmetic,

trigonometric

functions

such as

arcsin and arccos, use of trigonometric arguments in radians, degrees,

or grads,

and

the like. A

calculator

mode

is

provided

which

has

an

unexpected quirk for a TI machine (see page

5)-

Example speed checks

show that

the

CC-40

is much

faster

than

the

TI-59-

The keyboard is

small—too

small to touch type, but large enough to not feel cramped.

The

CC-40

is not a pocket computer—but then neither are most other

so-called "pocket" computers, unless one is talking about.the pockets

in

the

winter

overcoatsofRussian

infantrymen.

The

announcementsTaf

the peripherals describe a^complete.capability including Wafertape drives for recording, RS-232 interfaces for printing, and even a video

interface which will circumvent one of the

major

limitations

of

the

baseline

CC-40,

namely the

single

line,

display.

It is downright

difficult to debug programs without a printer and only a single line

display. While the CC-40 is now available from retailers the periph

erals

are

not, at least

not

in

the Tampa

Bay

area.

V8N3

P23

THE

CC-40^-

Maurice

Swinnen

writes:

The

CC-40

is a good computer

...

the

keyboard is smaller than the one on the typewriter. It

has a lot of one-keystroke entries for programming such as PRINT,

FOR,

NEXT,

etc.

The Basic is enhanced by a lot of subprograms which you

can reach by

CALL

XXXXX.

All information on memory mapping is given

such that it is easy to do assembly language programming. It has

both

CALL

PEEK

and

CALL

POKE

commands,

plus

a

CALL

DEBUG. I

wrote

several

programs—JIVE TURKEY and

others.

Because I sorely missed

a printer I concocted

an

RS-232 interface and

now

I

can

use.any

printer on

it.

(Editor's

Note:

Late news releases from TI indicate

that

peripherals

for

the

CC-40

should

be

available.

As I

write

this

the CC-40 is available

in

retail stores in this area,

but

the peripherals

are not.)

lfoe

speed on

the

CC-40*

is much

faster

than on the 59$ of

course.

Count

ing from 1

to

100

was

fast

this

time,

too

fast to clock

directly.

So

I put it in a loop and let it

count

to

100 one hundred

times.

That

took 34 seconds, which makes the time for counting to 100 equal to

0.34 seconds. Not bad? Then I tried to compute factorials. The

highest

factorialIcould

generate

directly

before

overflow

was

84.

It took exactly

1-.37

seconds, again measured in a loop-of 100 for

accuracy.

Editor's

Note:

Maurice's JIVE TURKEY program appears on the following

page.

I

have

also

had

an

engineering

model

of

the

CC-40

for

about

a month, and performed other speed comparisons. The keyboard is what

TI

calls

a.3/4

keyboard,

meaning

it

is

3/4

the

distance

between

the

keys relative

to

a full size

keyboard.

That means it is essentially

impossible

to

touch

type*

The

HP-75

has

approximately a

0.8

keyboard.

Touch typing is trying at best. The Radio Shack Model 100 has a full

size keyboard.

/

TI

PPC NOTES

V8N3P24

JIVE

TURKEY

an the CC-40. Maurice E.T.

Suinnen

100 DISPLAY AT(6)"* JIVE TURKEY GAME *":PAUSE 2 110 SCORE=Q:FIB=0:RANDOMIZE:SECRET=INTRND(100)

120 DISPLAY ERASE ALL"PROBABILITY OF

TRUTH?

0-100? ;

130

ACCEPT AT(29)BEEP VALIDATE(DIGIT);PROB

140 ROLL=INTRND(100):SC0RE=SC0RE+1:DISPLAY"YOUR

GUES?

0-100";

150

ACCEPT

AT(20)BEEP

VALIDATE(DIGIT);GUESS:IF

GUESS=SECRET THEN 190

160 IF PROB>ROLL THEN FLAG=1 ELSE FLAG =0:IF FLAG=0 THEN FIB=FIB+1 170 IF

GUESSOECRET

THEN IF FLAG=1 THEN 240 ELSE 230

180 IF GUESS>SECRET THEN IF FLAG=1 THEN 230 ELSE 240

190

PRINT»CONGRATULATIONS!

YOU

DID

IT!":PAUSE

3

200

DISPLAY

AT

(3)"SC0RE=";SC0RE,"#OFFIBS=";FIB:PAUSE

210

DISPLAY"SAME

GAME

AGAIN?

Y/N";:ACCEPT AT(22)BEEP VALIDATE("YNyn"),ANSWERS

220 IF

ANSUER$="Y"

OR

ANSWER$="y"

THEN

110

ELSE

250

230

PRINT"GUESS

TOO

HIGH":PAUSE

1:G0T0

140

240

PRINT"GUESS

TOO LOW"".PAUSE

1:G0T0

140

250

DISPLAY AT(5)ERASE ALL"BYE,

HAVE

A NICE DAY!":PAUSE 3:END

PALINDROMIC

NUMBERS

IN BASIC -

Palmer

Hanson.

Page

6

of

this

issue

reports

the

results

of

some

exten

sive

tests

of

the

TI-59

generating

palindromic

numbers

using

digit

reverser

techniques.

Albert

Smith

found

23

numbers

between

1

and

1900

which

would

not

reach

a

palindromic

number

within

the

range

of

the

TI-59.

I

wrote

the

following

BASIC

program

for

the

CC-40

to

investigate

those

numbers

further.

10

INPUT

"fl$

«";fl*

15

N « 9

.

20

L •

LEN<

fl$

>

25

6$

s

""

30

FOR

I = L TO 1

STEP

-1

35

B$

* B-$ &

SEG*<fl$,ia>

40

50

IF

fl$

•

B$

THEN

290

100

C*

•

""••R10

* 0

'

105

FOR I = L TO 1

STEP

-1

110

fl •

VflL<SEG*<fi**Iil>>

+

VflL<SEG*<B*,

I,l>>

+

fU0

115

IF

fl > 9

THEN

C * fl -

10

ELSE

C • fl

120

C$

»

STR$<C>

8<

C$

125

IF

1=1

> 9

THEN

1=110

* 1

ELSE

fll0

- 0

135

140

IF

fllO

- 1

THEN

C*

-

"1"

fc

C*

145

N.«

N + 1

150

PRINT

N

155

fl*

*

C$

160

GOTO

20

200

PRINT

fl*;N

210

PAUSE

10

220

GOTO

10

999

END

TI PPC NOTES

V8N3P25

PALINDROMIC NUMBERS IN BASIC (cont)

The program

uses

digit by

digit

string manipulation such that its

operation is independent of the word length of an individual computer.

Variations of the program were also

run

on a Radio Shack Color Computer,

a Radio

Shack

TRS-80

Model

100

Portable

Computer,

and

an

Apple.

The

relative execution times to change 89 into 8813200023188 in 24 steps

were

i

TI-59

in normal mode 4 min 51 sec

TI-59

in EE mode 4 min 37 sec

TI-58C in normal mode 6 min 7 sec

CC-40 27

seconds

Color Computer 18 seconds

Apple 10 seconds

Model

100

18

seconds

With the insertion of a CLEAR 1024 command at line number 5 the string

limitation

which

limited

the

number

of

iterations

to

about

140

was

removed

with

the

Model

100

and

raised

to

about

580

iterations.

Tests

showed

that not one of the 23

numbers

listed on page 6 would reach

a palindromic number where the final number

prior

to

string

overflow

was 255 digits long! I also noticed that there was a pattern in the

numbers

1495

through

1857

on page 6 which suggested that

the

numbers

1945

and

1947

would

also

fail

to

yield

a

palindromic

number,

and

verified

that

with

the

Model

100.

FINDING PI IN BASIC - Palmer

Hanson.

The CC-40 implementation of BASIC

provides

a PI

function

and

permits

the

arguments

for the trigonometric functions to be entered in

-degrees,

radians, or

grads—one indication of the

emphasis

on scientific useage for the

CC-40.

For those BASIC mechanizations which do not provide a PI function and

which are limited to radian

arguments

for the trigonometric functions

the programmer

often

wants the value of PI

for

use

in

conversions

from

degrees to radians. An old programmer's trick which recovers the value

of PI to the accuracy of the individual machine is to

use

the

function

PI

=

4*ATN(l).

I

had

used

that

technique

satisfactorily

on

many

com

puters

until

I

encountered

the Radio

Shack

Model

100.

When

using

the

conversion

factor

derived

from

ATN(l)A5

(equivalent

to

4*ATN(l)/l80)

I found that

the

cosine

of 60

degrees

was returned as .5000000001147 f

Which is

simply

not

consistent

with a fourteen digit

machine.

After

some

experimentation

I

found

that the

use

of

a

conversion

factor

de

rived

from

ATN(3E13)/90

would

result

in

the

cosine

of

60

degrees

being

returned as

.49999999999998

—respectable accuracy in anyone's

book.

Similar improvements in the accuracy of the trigonometric functions on

the Model 100 were found for other functions and other arguments. I

have tentatively concluded that the ATN

function

on

the -Model 100 is weak.

With this information in hand I decided to

examine*

the capability of

other calculators and computers to evaluate pi. I found a wide range

of capability ranging from the nine digit capability of the Apple

II,

the

Radio

Shack

Color

Computer

and

the

Atari

400,

through

the

ten

digit

capability pf the HP product line of programmable calculators to the

fourteen digit capability of the Model 100t The table on the following

page

summarizes

my

experience.

TI

PPC

NOTES

V8N3P26

DERIVING

PI

IN

BASIC

(cont)

From

4*ATN(1)

From

2*ATN(N)

AMS-55

Reference

.3.1^15

92553

58979

3.1415

92653

58979

Commodore

VIC-20

3.1415

9266

3.1415

9266

Color

Computer

3.1415

9266

3.1415

9266

Apple

II

3.1^15

9266

3.1415

9266

Atari

400

3.1415

9267

3.1415

9264

HP-11

3.1415

92654

3.1415

92654

TI-57

3.1415

92653

2

3.1415

92653

6

TI-55H

&

TI-57LCD

3.1415

92653

5

3.1415

92653

4

TI-58/58C/59

3.1415

92653

588

3.1415

92653

590

TI-99/4A

3.1415

92653

59

3.1415

92653

59

CC-40

3.1415

92653

59

3.1415

92653

59

Model

100

3.1415

92653

1932

3.141.5

92653

5898

In

the table the N in 2*ATN(N) is a number sufficiently large

such

tnat

no

further

changes

in

ATN(N)

will

occur

with

larger

N.

For

the

Model

100 that value is about

3E13.

For the CC-40 that value is about

2E12.

For

the

TI

programmable

calculators

and

the

CC-40

the

values

listed

are

those internal to the machine

not

those displayed.

The

predominance

of

TI

machines,

including

the

CC-40,

at

the

high

accuracy

end

of

the

table

is

as

expected.

The

CC-40

also

provides

the

arcsin

ahd'arccos

functions

which

are

not

available

on

the

other

"home"

computers—one more

instance

of attention to scientific applications.

TI

PPC

NOTES

V9N4P7

FOURTEEN

DIGITS

OF

PI

FROM

THE

99/4

AND

CC-40

-

Myer

Boland

"Finding-Piin

BASIC"

in

V8N3P26

reported

that

both

the

TI-99/4A

and

the

CC-40

returned

the

twelve

digits

3«l4l5

92653

59

in

response

to

the BASIC instruction P = 4*ATN(l) . Myer Boland reports that one

can

recover

fourteen

digits

with

the

equation

P =

4000*ATN(1)

on

the

TI-99/4A,

andIverify

the

same

result,

with

the

CC-40j

Pi

x

1000

exact

4000*ATN(1>

3141.5 92653 58979 3

3141.5 92653 5898

Unfortunately,

at

least

on

the

CC-40,

if one

tries

to.

convert

to

the

value

of

pi,

not

lOOOxpi,

by

dividing

the

result

by

1000,

the

end

result

reverts

to

the

twelve

digit

value

3.1415

92653

59

.

This

is

one more illustration of the kind of results

which

occur

with

BASIC,

but

which,

we would not expect with the typical calculator.

TI PPC NOTES V8N3P5

A CC-40 QUIRK - Palmer Hanson. The

second

chapter

of

the TI Compact

Computer User's Guide describes

how

to use the CC-40

as a calculator. The discussion of chain calculations on page 2-8

cautions "•..A loss of accuracy occasionally results when you chain

calculations. See Appendix F for accuracy information. ...H The

discussion of accuracy in Appendix F begins with a discussion of

the

5/4

rounding

technique

which

will

remind

the

TI-58/59

user

of

a similar discussion on page C-l of Personal Programming. As with

the TI-58/59 the

CC-40

uses a minimum of 13 digits to perform

calculations and rounds the results to 10 digits for the normal

display

format.

Actually,

some

calculations

are

carried

to

14

digits as in the example on page F-l:

2/3=

.66666666666667

and

1/3

=

.33333333333333

2/3-1/3

-

1/3

=

.00000000000001

which

is

dispalyed

as

l.E-14

Note that both fractions yield fourteen digit values. Furthermore,

the

fraction

2/3

yields

a 7 in

the

fourteenth

of

least

significant

place.

The

TI

calculators

have

typically

yielded

a 6 in

the

least

significant place of the display register in response to the

sequence 2 DIV 3 = . The fact that the TI calculators truncated

to

the

display

register

was

sometimes

useful.

An

example

appeared

in

my

article

"There's

Gold

in

Those

Guard

Digits"

in

the

May/June

1982

issue

of

PPX

Exchange»

where

I

described

the

use

of

the

truncation feature to implement an effective integer function when

a thirteen digit integer was divided by a small integer such that

the quotient still had a thirteen digit number to the left of the

decimal point*

Now

if

we'alter

the

sequence

above

slightly

in

order

to

view

the

intermediate

result,

say

to the

sequence

2/3

ENTER

-1/3-1/3

ENTER

then the result in the display will be 3.334E-11 . Insertion of

= before each ENTER will not change the result. Investigation

will

reveal

that

the

different

result

occurs

because

the

ENTER

command

causes

the

calculator

mode

to

truncate

to

the

display

value.

TI-58/59

users

will

recognize

this

effect

as

being

similar

to

the

use of an EE-INV-EE sequence to truncate to the display value. If

one

performs

the

sequence

2

DIV

3 =

EE

INV

EE

- 1

DIV

3-1

DIV

3 =

with a

TI-58

or

TI-59

the

result will be 3.34E-11 where the

difference

from

the CC-40

result

above is due to the

use

of

fourteen

dibits

by

the

CC-40

and

thirteen

digits

by

the

TI-58/59.

This

effect

of

the

interruption of a chain calculation

to

display an intermediate

result

is

an

important

difference

between

the

use of

the

CC-40

in

the calculator

ftiode

and the use of TI calculators. The equivalent

sequence in a BASIC mode does not yield the truncation effect. The

sequence y s 2/3

PRINT

Y

.x = Y -

1/3

-

1/3

PRINT

X

yields l.E-14 in the

display.

We will discuss other aspects of

accuracy of the CC-40 in future

issues.

TI

PPC

NOTES

V8N4P10

CC-40

GRAPHICS

-

Maurice

Swinnen.

These

whimsical little programs

illustrate the use of the CHAR command

(page

5-15

of the

CC-40

User's

Guide

to generate user defined characters.

The characters are then called in sequence to provide

an

illusion

of motion. The first program moves a character across the screen

while performing the old "jumping

jack"

exercise. The second

program

uses

seven

characters

(all

that

are

allowed)

to

generate

a "soccer" figure which moves the

"ball

back

and

forth across the

screen.

JUMPIHi

^JFIOK

100

CALL

CHAR'C0,"0E0E150E04048A11',

>'CALL

CHARX

1,"0E0E840E15840404'

118

FOR

1=1

TO

31'FOR

J=9

TO

1=DISPLAY

AT,CHR*<J>=PAUSE

.3

120

I

130

FOR

K=31

TO

1

STEP

-l'FOR

L=9

TO

1 =

DISPLAY

AT<

fO,

CHR$<

L >

140

K

150

GOTO

110

SOCCER

100

CALL

CHAR<

Q>"

0E0E158E04040A11"

>«CALL

CHAR<

1, "

881A1A1B0S820509

" >

110

CALL

CHARX

2,"0001050305191919">'CALL

CHAR<3,"000185031D191981">

128

CALL

CHAR<4,,,150E84048A110E0E"

>'CALL

CHARTS,"8018141314131313">

138

CALL

CHAR<S,"008B081B8C8S1412">

148

FOR

fl*10

TO

21=FOR

B-0

TO

S'DISPLAY

AT<A>,CHR*'PAUSE

.1

150

A'PAUSE

.5

160

FOR

A=21

TO

10

STEP

-l'FOR

B'6

TO

0

STEP

-1

170

DISPLAY

flT<R),CHR*<e>-PflUSE

.1

138

A'PAUSE

.5'GOTO

140

TI

PPC

NOTES

V9N1P19

What

is

the

memory

protection

-for

the

CC—40?

Can

I

safely

bridge

a

battery

removal

by

having

the

AC

adapter

connected?

You

will

recall

that

we

were

cautioned

that

having

the

Adapter/Charger

connected

to

a

TI—58C

or

TI=59

with

the

battery

pack

removed

could

damage

the

calculator.

The

CC—40

manual

provides

no

information.

I

did

not

want

to

do

a

test

with

my

CC-40

since

I

run

the

risk

of

destroying

all

my

accumulated

programs.

Maurice

Sw'innen

says

that

he

has

changed

batteries

without

losing

his

programs.

He

thinks

it

took

about

a

minute

to

make

the

change.

As

soon

as

I

have

some

sort

o-f

recording

device

for

the

CC-40

I will

run

the

appropriate

tests.

In

the

meantime

I

have

asked

TI

for

clarification.

TI

PPC

NOTES

V8N4P11

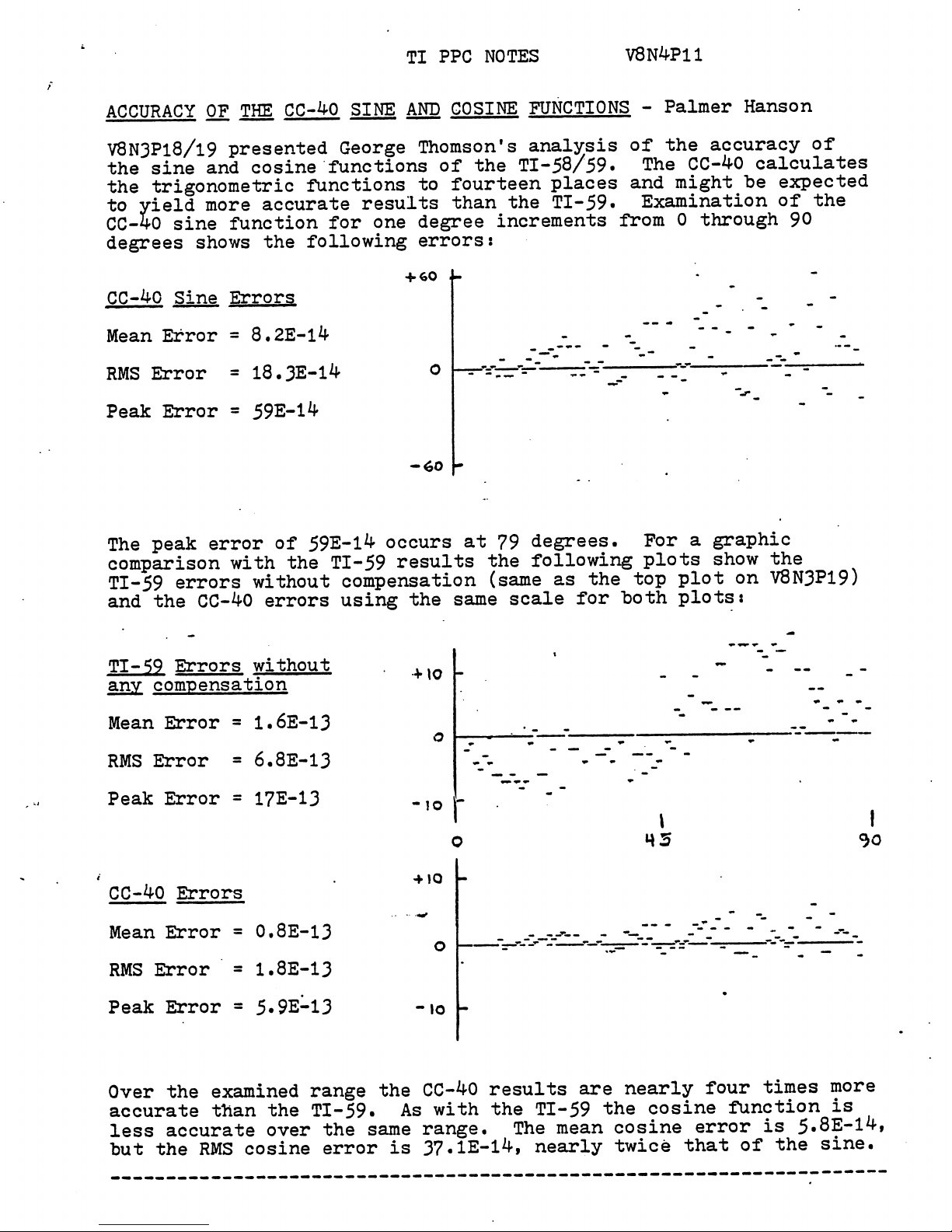
ACCURACY OF THE CC-40 SINE AND COSINE FUNCTIONS - Palmer Hanson

V8N3P18/19

presented

George

Thomson's

analysis

of

the

accuracy

of

the

sine

and

cosine

functions

of

the

TI-58/59.

The

CC-40

calculates

the

trigonometric

functionstofourteen

places

and

might

"be

expected

to

yield

more

accurate

results

than

the

TI-59.

Examinationofthe

CC-40

sine

function

for one

degree

increments

from 0 through 90

degrees

shows

the

following

errors:

CC-40

Sine

Errors

Mean

Error

=

8.2E-14

RMS Error = 18.3E-14 Peak Error = 59E-14

+

60

-60

The

peak

error

of

59E-14

occurs

at

79

degrees.

For

a

graphic

comparison

with

the

TI-59

results

the

following

plots

show

the

•TI-59

errors

without

compensation

(same

as

the

top

plot

on

V8N3P19)

and

the

CC-40

errors

using

the

same

scale

for

"both

plots*

TI-59

Errors

without

any

compensation

Mean Error = 1.6E-13

RMS

Error = 6.8E-13

Peak

Error

=

17E-13

CC-40

Errors

Mean

Error

= 0.8E-13

RMS

Error

= 1.8E-13

Peak

Error

=

5.9E-13

+ »o -

-10

o

4»0

-

-10

I

MS

I

30

Over

the

examined

range

the

CC-40

results

are

nearly

four

times

more

accurate

than

the

TI-59.

As

with

the

TI-59

the

cosine

function

is

less

accurate

over

the

same

range.

The

mean

cosine

error

is

5.8E-14,

but the RMS

cosine

error

is

37.1E-14,

nearly twice that of the

sine.

TI

PPC

NOTES

V8N4P12

PROMPTING

ON

THE

CC-40

- In

V7N7/8P24

Maurice

Swinnen

described

a

multi-language

capability

built

into

the

TI-88

such

that

prompting

could

be

in

English,

German

or

French,

The

CC-40

provides

an

extended

multi-language

prompting

capability

through

the

use

of

the

CALL

SETLANG(n)

command.

The

assigned

language codes are:

0 English

1

German

2

French

3

Italian

4

Dutch

5 Swedish

6 Spanish

For

n = 1

the

system

messages

and

error

messages

are

in

German.

For

example,

the

responsetothe

incorrect

entry

sequence

ATN(

ENTER

is

"ungleiche

Klammern".

For

any

other

value

of n

the

system

messages

and

error

messages

are

in

English.

In

response

to

the

incorrect

sequence

ATN(

ENTER

the

English

response

is

"Unmatched

parenthesis".

This

output

of

error

messages

in

text

is

one

of

the

attractive

features of the

CC-40.

The user need not memorize error codes or

translation

tables

to avoid frequent reference to

th'e

manual. The

manual does provide extended discussion of each error

message.*

TM

For

programs

fromaSolid

State

Software

module

the

prompts

and

messages

from

the

module

may

be

in

any

of

the

languages

if

supported

by

the

particular

module.

My

Mathematics

module

supports

English,

German and French. For the Prime Factors program the various messages

ares

English"

PRIME

FACTORS

Use

Printer?

Enter # To Be

Factored:

Exit Program?

German

PRIMZAHLEN

Drucker

benutzen?

- >

Zahl:

French

FACTEURS

PREMIERS

Utilisation

d'une

Imprimante?

- >

Nb

a

Decomposer:

Programm

verlassen?

Fin du

Programme?

The

responsestothe

questions

asking

for

yes/no

answers

areYor

N

in

English,Jor

N in

German,

and

0

or

N in

French.

I

have

not

found

any

information

in

the

manual

for

the

Mathematics

module

which

would

tell

me

which

languages

are

supported.

Language

codes3through

6

result in English

messages

for that

module.

PRIME FACTORS WITH THE CC-40 MATHEMATICS MODULE - The speed of the

prime

factors

program

in

the

CC-40

Mathematics

module

is

disappointing,

about

ten

to

.forty

percent

faster

than

the

fastest

program

for

the

TI-59t

but

substantially

slower

than

some

programs

for

the

HP-41.

Representative

speeds for some of the standard problems are:

Program/machine

CC-40

Fast

Mode

Modulo

210

Leeds

FM

(V8N2P26)

Acosta

FM

58C

M/JJ

Module

- 59

111111111111

1035698<?9

987654321

9999999967

11

sec

32

sec

4l

sec

1 hr 55

min

I

45 sec

58 sec

2

hr

8

min

17

sec

46

sec

61

sec

2 hr 31

min

27

sec

6l

sec

79

sec

3 hr 6 min

43 sec

163 sec

215

sec

TI

PPC NOTES V8N4-P13

PRIME FACTORS ON THE CC-40

(cont)

For

large

primes

such

as

9999999967

the

execution

speed

of

the

CC-40

Mathematics

module

program

is

about

0.069VN

.

Page

19 of

the

July

1981

issue

of

the

PPC

Calculator

Journal

reported

a

speed

of

0.035VN

for

the

HP-MC;

hut

the

HP-^IC

cannot

maintain

that

speed

for

input

integers

of

more

than

ten

digits.

The

CC-4-0

Mathematics

module

program

has

other

deficiencies:

*

The

program

stops

as

each

factor

is

found.

A

better

technique

is to

store

the

factors

as they are

found

and

continue

the

search

until

all

factors

are

found.

This

minimizes

operator

attention.

A

simple

additional

routine

provides

for

recall

of

the

factors.

The

technique

was

illustrated

in

Laurance

Leeds'

Speedy

Factor Finder

in

V8N2P26.

*

Multiplicityoffactors

is

not

indicated.

Indicationofthe

multiplicity

usingatechnique

such

as

that

devised

by

George.

-

Vogel

in

his

prime

factor

programinthe

article

"It

Pays

to

Analyze

Your

Problem"inthe

January/February

1981

issue

of

PPX

Exchange

would

be

preferred.

As

George

said

in

that

article

"Piecemeal

presentationofresults

is

slow

and

inconvenient

(try

factoring

7.2^7.757.312).

Yet

it

is

not

difficulttomake

the

program

count

the

number

of

times

each

prime

factor

occurs,

and

output

the

count."

George

usedadecimal

point

notation

where

the

number

after

the

decimal

point

indicated

the

mult

iplicity.

For

the

number

mentioned

the

output

would

be

2.28

and

3.03

meaning

22°x3J

.

*

Although

the

CC-^K)

program

can

factor

input

integersofup

to

twelve

digits,itdoes

not

provideanability

to

recall

the

input

integer

correctly

for

more

than

ten

digits.

For

example,

factor

the

number

111,111,1111111.

You

will

obtain

the

correct

solution

on

the

first

pass,

and

an

"N"

in

response

to

the

prompt

"Exit

Program?"

will

bring

the

input

value

back

to

the

display

but

in

exponential

notation

1.1111111E+11.If

you

run

with

that

-

value

you

will

get

the

factors

for

111,111,100,000

J

We

will

have

to

wait

until

someone

finds

out

how

to

download

the

programsinthe

modules

beforewecan

know

if

there

will

be

ways

to

use

segmentsofthe

module

programs,

say

in

the

manner

in

which

we

can

enter

the

library

modules

of

the

TI-59

with

the

sequence

Pgm-XX-SBR-nnn .

4

CC-40

PERIPHERALS-Peripherals

for

the

CC-40

includeaPrinter/Plotter

a

Wafertape™

Digital

Tape

Drive,

and

ar..

RS-232

interface.

Currently,

none

of

these

are

available

in

the

Tampa

Bay

area.

The

devices

are

listed

in

the

Sears

Fall/Winter

1983

catalog

(page

869),inthe

Educalc

Mail

Store

catalog

issue

16

(page

3*0»

and

in

the

Elek-Tek

catalog

Volume

VI

(page

17).

Inquiries

indicate

the

peripherals

will

be

available

in

early

fall.

Although

the

Manufacturer's

Suggested

Retail

Price

for

the

CC-40

is

$24-9.95,

catalog

prices

range

from

$199-99

(Sears)

through

$189.95

(Educalc)to$189.00

(Elek-Tek).Ihave

seen

the

CC-40

at

local

discount'houses

for

as

low

as

$179.95.

The

CC-40

packsalot

of

"bang

for

the

buck"

at

those

prices.

TI

PPC

NOTES

V8N5P14

MATRIX

OPERATIONS

WITH

THE

CC-40

MATHEMATICS

MODULE

-

In

V8N4P12/13

I

re

ported

that

the

execution

speed

of

the

prime

factors

program

in

the

CC-40

Mathematics

module

was

disappointing,

and

that

the

module

had

other

deficiencies

as

well. I

am

happy

to

report

that

the

matrix

manipulation

programs

seem

to

be

more

carefully

constructed.

The

capabilities

are

similar

to

those

of

the

ML-02

and

ML-03

programs

in

the

Master

Library

module

of

the

TI-59.

In

fact,

the

discussion

of

the

use

of

the

lower

upper

(LU)

decomposition

method

is

identical

for

the

CC-40

Mathematics

module

and

the

TI-S9

ML-02

programs.

Execution

speed

is

substantially

improved.

The

CC-40

finds

the

determi

nant

for

the

third

order

matrix

problem

on

page

12

of

the

manual

for

the

TI

-59 Master Library module in about two seconds,

while

the

TI-59 requires

sixteen

seconds

to

complete

the

same

problem.

The

CC-40

finds

the

determinant

of a

fifth

order

matrix

in

about

six

seconds,

while

the

TI-59

requires about

fifty-three

seconds

for

the

same

problem

using

ML-02.

A

deficiency

of

the

CC-40

program is that

the

result

is

brought

to

the

display with a BASIC Print command and

the

user

cannot

perform

any

chain

calculations on the result without reentering

the

value. The reentering

process

necessarily

drops

any

digits

which

were

not

displayed.

The

TI-59

solution

is

displayed

in a

manner

such

that

chain

calculations

on

the

displayed

result is possible.

The

loss in

accuracy

for

the

chain

calcu

lations with

the

CC-40 caused by

the

reentry

can

be

duplicated

with

the

TI-

59 by performing EE-INV-EE to truncate to

the

displayed

value

before

proceeding

with

user

entered

chain

calculations.

If

the

variable

names

of

the

solution

were

available

the

user could recall

the

solutions

as a part

of

his

keyboard

BASIC

chain

calculations

and

retain

the

full accuracy; but

the

documentation

with

the

CC-40

provides

no

information

as

to

the

variable

names.

To

remedy

this

situation

I

have

written

a

short

demonstration

program

for

solution

of a

system

of

linear

equations

(AX = B)

which

provides

identification

of

variable

names

for

at

least

some

elements

of

the

solution:

100

DIM

A(S,9),C(S,S),B(S)

110

R =

PI

120

INPUT

"Enter

Order

of

Matrix

-

";N

150

CALL

MI("A",A<,),1,N,N,0>

200

CALL

AK("B",BO

,

1,N,0)

250

PRINT

"Solving"

300

CALL

MATS(A(,),C<,),BO,1,1,5,1,N,1,R>

350

IF

RO0

THEN

400

360

PRINT

"MATRIX

IS

SINGULAR":PAUSE

400

FOR

I = 1

TO

N

410

X*

-

"X"

&

STR*(I>

& "

=*

"

420

PRINT

X$JA<1,1):PAUSE

430

999

STOP

Line

100 -

The

dimension statement

sets

up

the

array

names

to

be

used

in

the

various

subroutine

calls.

For

reasons

that

are

not

very

clear

to

me

the

array

for

the

entry

matrix

A(m,n)

must

have

one

more

column

than

the

order

of

the

problem

if

the

MATS

subroutine

call

at

line

300

is

to

operate

properly.

Line

110

-

The

dummy

variable

R

will

be

used

to

indicate

whether

or

not

the

input

matrix

is

singular.

See

the

discussion

of

the

TEST

variable

on

page

94

of

the

Mathematics

Module

manual.

TI

PPC

NOTES

V8N5P15

Matrix

Operations

with

the

CC-40

Mathematics

Module

- (cont)

Line 120 - Provides operator control of the order of the problem to be

solved.

Line 150 - This subroutine call provides for input

and

edit of

the

elements

of

the

matrix A into a

two

dimensional array.

See

page

95

of

the

manual.

The single line subroutine

call

provides a thorough set of prompts for

entry and

editing,

including indication of the row and column on each

element

to

be

entered.

Line 200 - This subroutine call provides for input and edit of the elements

of

the

vector

B

into

a

one

dimensional

array.

See

pages

85-86

of

the

manual.

Again,

the subroutine

call

also provides a thorough set of

prompts..

Line 250 - This only provides a clear indication that the computer has

changed from the edit mode to the solve mode.

Line 300 - This subroutine call provides

the

solution for

the

set of linear

equations.

See

page

94

of

the

manual.

The subroutine ends

with

the

elements

of

the

solution

in

the

subscript

1

column

of

the

A array,

and

with

the inverse of the A matrix in array

C.

If

the input A matrix was singular

then

R

is

changed

to

zero.

Line

350

-

Tests

the

value

of R

to

determine

if

the

input

matrix

A

was

singular.

Line 360 - Displays an appropriate message if the input matrix was

singular.

~

Lines 400 to 430 - Display the elements of the solution with appropriate

annotation.

To illustrate use of the program use the problem on page 12 of the manual

for

the

TI-59

Master

library

module:

1.

Press RUN and ENTER. See

the

prompt "Enter Order of Matrix -

".

2.

Press 3 and press ENTER. See the prompt "Enter A(l,l):"

3.

Press 4 and press ENTER to insert the A(1,1) element. The computer

accepts

the

input

and

returns

with

the

prompt

"Enter

A(l,2):".

Continue to

enter the

re?maining

elements of the

matrix.

Note that the CC-40 accepts

the matrix elements by row in contrast with the TI-59 which accepted the

elements by

column.

But

note that there is nothing to remember since the

MI

subroutine

call

supplies the necessary

prompts.

When the last element A

(3,3)

has

been

entered

the

computer

responds

with

the

prompt

"Edit?".

If

you

choose

to

edit

by

responding

with

a Y the

computer

response

is the

prompt

"Edit

All

Input?".

If

you

respond

with

a N the

computer

response

is

"Enter

Row

To

Be

Edited:".

You

enter

the

row

number

and

the

computer

response is

another

prompt

"Enter

Column

to Be

Edited:".

You

enter

the

column

number

and

the

computer

response is

"Enter

A(i,j):

Aij"

where i

and

j are the row

and

column

you

selected,

and

Aij

is the value

which

was

entered for that element earlier. If you

decide

to

edit

that

element

you

replace the

displayed

value

with

the

desired

one and press

ENTER.

If

you

decide not to change the element you simply press ENTER. In either case

the computer responds with the prompt "Edit Other Elements?".

TI

PPC

NOTES

V8N5P16

flatrix

Operations

with

the

CC-40

Mathematics

Module

- (cont)

4.

When

you

have

completed

any

editing

of

the

A

matrix

the

final N

response

to

the

edit

prompts

will

cause

the

computer

to

move

forward

to

the

entry

of

the

vector

elements.

The

prompt

message

will

be

"Enter

B(D".

You

proceed

to

enter

the

elements

of

the

vector

in a

manner

similar

to

that

used

for

the

matrix.

Again,

you

will

be

given

an

opportunity

to

edit.

The

important

point

is

that

all

the

prompts

for

the

entry

of

both

matrix

elements

and

vector

elements

are

provided

by

the

module

in

response

to

the

subroutine

calls

MI

and

AK.

5.

When

you

have

completed

the

editing

process

by

responding

with

an

N at

the

appropriate

point

the

program

immediately

proceeds

to

solution

of

the

problem,

with

the

indication

"Solving"

in

the

display.

When

the

solution

is

complete

the

computer

response

is

the

display

"XI = 4" if

you

entered

the

problem

from

page

12 of

the

Master

Library

correctly.

Press

ENTER

as

many

times

as

needed

to

see

the

remainder

of

the

solution.

6.

After

the

display

of

the

solution

has

been

completed

you

may

use

keyboard

BASIC

(or

you

may

add

commands

to

the

program)

to

read

out

other

parameters,

or

the

same

parameters

in

other

formats.

The

elements

of

the

input

matrix

have

been

destroyed.

The

elements

of

the

inverse

of

the

input

matrix

appear

in

array

C

properly

located;

that

is,

the

i,j

element

of

the

inverse

can

be

recalled

with

the

command

PRINT

C(i,j).

For

our

example,

the

sequence

PRINT

C(2,2)

will

yield

a

ten

digit

display

of

.0416666667.

The

user

can

view

additional

digits

with

the

command

PRINT

USING

".##############"JC(2,2)

to

yield

a

fourteen

digit

display

of

.04166666666667

; or, in a

technique

similar

to

that

used

to

observe

the

guard

digits

of

the

TI-59,

the

user

can

use

the

command

PRINT

(C(2,2)-.04166)*100000

to

yield

a

display

of

.666666667

•

7. " If

the

user

changes

the

sixth

element

in

the

argument

for

the

MATS

subroutine

call

from

a 5

to

a 4,

then

the

program

will

only

proceed

through

.the

calculation

of

the

inverse

of

the

input

matrix.

The

elements

of

the

inverse will appear in

array

C,

again with

the

appropriate

subscripts.

The

elements

of

the

inverse

will

also

appear

in

array

A,

but

with

the

first

and

second

columns

interchanged.

This

is

exactly

the

same

orientation

in which

the inverse appears in a TIr59, where

there

is

also

an indication of

the

interchanged columns through observation of

the

pivoting index; that is,

for

the

particular third order example used

here

TI-59

memory

registers

R17,

R18 and R19

will

contain the numbers

2,

1,

and 3 respectively. I have

been

unable

to find a way to recall

the

pivoting index

from

the

CC-40

solution. Hopefully, this helps to explain the note in the discussion of

"Inversion" on page 52 of the manual for

the

Mathematics

module

which

states "..The inverse of A may be stored with its columns, permuted and must

be reentered for subsequent calculations."

That

statement

is

true

if one

uses

the

CALL

"MAT"

method

to

obtain

the

inversion.

If

one

uses

the

CALL

MATS

method

illustrated

here

then

the

columns

in

array

A

may

(or

may

not)

be permuted depending on the particular input matrix, but

the

inverse which

appears in array C will not have permuted columns and can be used directly

for

further

calculations.

A least squares polynomial curve fitting program using

the

techniques

described

here

appears

on

the

following

page.

TI

PPC

NOTES

V8N5P17

LEAST SQUARES POLYNOMIAL CURVE FIT WITH THE CC-40 MATHEMATICS MODULE

This

program

uses

the

same

techniques

described

on

the

with

the addition of a

call

of subroutine AU (see pages 87-38 of the

manual)

to

provide

entry

of

the

data

pairs

into

two

one-dimensional

arrays.

Again,

the

subroutine

call

provides

valuable

prompts.

I

believe

that the

prompts

with

this

program

are

sufficient

such

that

no

detailed

program

description

is

required.

There

is

one

idiosyncrasy

of

the

prompts

for

editing

the

entry

of

the

data

pairs

which

is

described

on page 18

of

this

issue.

100 DIM A<8,9),B(S),C(8,8),H(8),X<50),Y(50)

110

INPUT

"Number

of

Data

Pairs?

";K

120

CALL

AU("X","Y",X(),Y(),1,K,0)

130 INPUT "Degree of

Polynomial?

"JN

140

PRINT

"Solving"

150

n=n+i:r=i:p*="":Q*=""

160

FOR

1=1

TO

N:F0R

J=l

TO

N

170

A(I,J)=0:NEXT

J

180

b(D=o:next

I

190

FOR

L=l

TO

K

200

H(1>=1

210

FOR

1=2

TO

N

220

H<I)=H(I-1)*X(L):NEXT

I

230

FOR

1=1

TO

N:F0R

J=l

TO

N

240 A(I,J)=A(I,J)+H<I)*H<J):NEXT J

250

B=B<I)+H(I)*Y<L):NEXT

I

260

270 CALL MATS(A(,),C(,),BO,l,l,5,l,N,l,R)

280

IF

ROO

THEN

300

290

PR-INT

"Matrix is

singular":PAUSE:GOTO

470

300

FOR

1=1

TO

N

310

X*="A"8<STR*(I-1)8<"

• "

320

PRINT

xs;a<i,1):pause:next

I

330 INPUT "Display Residuals (Y/N)? "JP*

340

S1=0

350

FOR

I

=1

TO

K

360

Y1=A(N,1>

370

FOR

J=(N-1)

TO

1

STEP

-1

380

Yt=A<J,l)+X(I)*Yl:NEXT

J

390

D1=Y(I)-Y1

400 IF P*="y" OR P*="Y" THEN 410 ELSE 430

410

A*="d"&STR*(I)&"

= "

'

420

PRINT

A*5Dl:PAUSE

430

S1=S1+D1*D1:NEXT

I

440

PRINT

"Standard

Error

=

";SQR<S1/(K-N)):PAUSE

450

INPUT "Try a

Different

Degree

460 IF 3*="y" OR Q*="Y" THEN 130

470

STOP

LANGUAGES ON THE CC-40 - VSN4P12 discussed

the

various

languages

which

are

available

with

the

CC-40

by

using

the

CALL SETLANG

command.

The Mathematics and Statistics modules support

English,

German,

and

French.

Tne

Finance

module

supports

only

English

and

German.

TI

PPC

NOTES

V8N5P18

A PROMPTING ANOMALY IN THE MATHEMATICS MODULE FOR THE CC-40

There

is

an

apparent

error

in

that

portion

of

the

Mathematics

module

for

the

CC-40

which

provides

for

editing

of

the

entry

of

two

one-dimensional

arrays.

An

example

occurs

when

running

the

Cubic

Splines

program.

Go

to

page

31

of

the

manual

and

follow

the

example

through

step

13.

At

that

point

the

display

will

read

"Edit?".

Do

not

proceed

to

step

14.

Rather

respond

with

a Y

for

yes

and

press

ENTER.

The

display

will

prompt

with

the

message

"Edit

All

Input?".

This

time

respond

with

an

N

for

no

and

press

ENTER.

The

display

will

prompt

with

the

message

"Enter

Element

to Be

Edited:".

Press 3 and ENTER and see "Enter X

(3)

:

1"

in the display. The

1 was

loaded

into

that location by step

10.

Press ENTER again assuming

that

you

did

not

want

to

edit

the

value

inX(3).The

display

changes

to

"Enter X(3): .3413".

You

would

have

expected

the

display

to

read

"Enter

Y(3):'

.8413". Although the indication of which element is

available to be edited is incorrect, the value displayed is that which was

stored in

Y(3)

at step

11.

There is no harm done by the improper

indication,

but

it

will

surprise

an

unwary

operator.

The

same

effect

can

be

seen

when

using

the AU

routine

on

page

87 in the

manual.

Users

of

the

Least

Squares

Polynomial

Curve

Fit

on

page

17

of

this

issue

can

expect

to

encounter

this

anomaly.

TI PPC

NOTES

V9N3P17

MEMORY

PROTECTIONONTHE

CC-40-V9N1P19

discussed

memory

protection

. on the CC-40 during replacement of

the

batteries.

Maurice

Swinnen

had

reported

successful

changes

without

losing

memory

when

the

time

to

replace

was

less

thanaminute.

In

late

MayIpurchasedanAC

Adapter

for

my

CC-40

from

Educalc#

(Stock

No.

AC-9201,

$14.95

plus

shipping

and

handling).

Just

in

time!

.In

mid

June

the

battery

low

indicator

appearedonmy

CC-40.

I

connected

the

AC

adapter,

replaced

the

batteriesata

leisurely

pace,

and

found

no

loss

of

memory.

Further

experiments

showed

that

the

CC-40

will

work

satisfactorily

with

either

the

batteriesorthe

AC

adapter,

whichever

is

available.

If

the

batteries

are

installed,

and

you

connect

the

AC

adapter

cable,

but

do

not

plug

into

AC

power,

the

CC-40

still

runs

from

battery

power.

That

featureisnot

available

with

some

other

portables.

The

Radio

Shack

Model

100

mechanization

disconnects

the

batteries

when

the

AC

.power

adapterisconnected.

The

instructions

are

very

explicit--first,

you

connect

the

adaptertoan

AC

outlet,

then

you

connect

the

adapter

cabletothe

computer.

If

the

adapter

cable

is

connectedtothe

computer

withoutaconnectiontoAC

power

the

computer

will

not

operate.

Memory

is

held

up

by

the

NiCad

memory

retention

battery.

This

would

seem

to

permitaconditioninwhich

inadvertently

leaving

the

adapter

connected

to

the

computer

arid

not

connectedtoAC

power

could

eventually

cause

a

loss

of

memory

as

the

NiCad

battery

runs

down.

I

have

written

to

Radio

Shack

for

information.Ihave

also

writtentoTI

for

approval

•

of

the

use

of

the

AC

Adapter

during

battery

replacement.

TI

PPC

NOTES

V8N6P18

ACCURACY

OF

THE

SOLUTIONS

FOR

SYSTEMS

OF

LINEAR

EQUATIONS

Several

different programs for solution of systems of linear equations with

the

TI-59

have

been

discussed

in

this

issue.

How

does

the

user

decide

which

program

to

use?

The discussion in previous pages of this issue has

addressed

considerations

such

as

user

friendliness,

system

size,

and

the

like.

Another important issue is accuracy of the solution, and we will see

that the Ohlsson program and its derivatives atrre less accurate. How do we

raeasure

accuracy? George Thomson provided some thoughts on that subject.

R&Y^e

are some

practical

tips for testers of matrix inversion

programs.

The

workhorse

test

matrices

are

the

,,HilbertsM5

the

first

row

is

1,

1/2, 1/3,

...f

the

second

row is

1/2,

1/3,

1/4,

...,

the third row is

1/3,

1/4,

1/5,

...,

and so

on.

Their inverses have horrendously huge integers and are

available. See for example,

I.

R.

Savage and

E.

Lukacs, National Bureau of

Standards

flMS

No.

39,

pp.

187-108

(1954)

for

the

inverses up

to

10 x

IB.

The seventh

row,

seventh column of the 18 x 18 inverse is 348 06739 96800 .

Others are almost as

large.

The Msub-Hilberts" with

the

first row

1/2,

1/3,

1/4,

...,

the second row

1/3,

1/4,

1/5,

...,

and so on are even harder to

invert

correctly. I suggest as a guinea pig

the

7x7

subHHilbert, with

ones

on

the

right

hand

side:

1/2

1/3

1/4

1/3

1/4

1/5

1/4

1/5

1/6

1/5

1/6

1/7

l/e

1/7

1/6

1/7

1/8

1/9

1/3

1/9

1/H

1/5 1/6 1/7

1/8

1/6

1/7

1/8

1/9

1/8

1/9

1/19

1/8

1/9

1/10

1/11

1/9

1/10

1/11

1/12

1/10

1/11

1/12

1/13

1/10

1/11

1/12

1/13

1/14

1

The exact

solution

of

the

simultaneous

equations

is

56, -1512, 12600,

-46230, 83160, -72072, and 24024. All

the

elements

of

the

inverse

are

.integers,

the

largest

is

6915

58560.

The

most

practical

measure of the

accuracy

of a solution is to calculate the relative

error,

i.e.,

(answer

-

true result)/(true result) for each element

and

take

the

largest value.

This

measure

is related

to

the

number

of

meaningful

significant

digits

in

the

results.

Readers

who

are familiar with

52

Notes will recall that V2N12P5 described

the use of the

Hilbert

matrices

(Oij

=

l/(i+j-l)

as a test of the ability

of a matrix inversion routine

to

handle

ill-conditioned

matrices.

All

the ML-02 deriviatives yield identical results. Therefore, description

of the results

from

any one of the

ML-02

programs defines the accuracy of

all

of

them.

Similarly,

the Ohlsson

program

and the derivatives by Prins

and

Ristanovic

yield

identical

results,

and

a

single

description

of

results

will

suffice

for all three.

For

the

7x7

sub-Hilbert

test

suggested

by

George

Thomson

the

various

algorithms

yield

the

following

resultsx

TI

PPC

NOTES

V8N6P19

Ohlsson/

TI-59

Anderson

Nick

and

CC-40

Ristanovic/

ML-02

Row

Ristanovic

Mathematics

Pr

ins

Reduct

ion

PPX

V4N5P8

"Gauss'*

Module

Programbiten

V7N6P13

V8N5P14

55.9233

56.0082

56.0081

56.0076

56.000032

-1510.2276

-1512.1896

-1512.

1865

-1512.1732

-1512.000787

12587.0911

12601.3863

12601.3511

12601.2536

12600.0059

-46157.9673

-46204.5344

-46204.3822

-46204.0623

-46200.

0192

83091.9632

83167.3718

83167.

0718

83166.

5503

83160.0311

-72018.4333

-72077.8274

-72077.5542

-72077.

1412

-72072.0246

24007.

6425

24025.7860

24025.

6926

24025.

5659

24024.

0074

1.37E-3

1.46E-4

1.45E-4

1.35E-4

.

5.71E-7

The

ML-02

solution,

the

Anderson

row

reduction

solution,

and

the

Nick/

Ristanovic

solution

yield

nearly

identical

results

from

an

accuracy

standpoint.

The

Ohlsson

program

and

its

derivatives

yield

a solution

that

is an order of

magnitude

less

accurate.

The CC-40 yields a

much

more

accurate solution than any of the TI-59 programs.

This

is somewhat

surprising since

the

manual for the CC-40 Mathematics Module indicates that

the

method

of

solution

is

the

same

as

for

ML-02,

and

the

CC-40

carries

only

one additional

digit.

To attain that

level

of accuracy with the CC—4©

it

is

necessary

to

calculate

the

matrix

elements

in the

program.

If one tries

to enter the values from the keyboard then the quirk described in V8N3P5

takes

over,-and

only

ten

digits

are

used.

The

error

in

the

resulting

solution

is

6.94E-3.

One

can

obtain

similar

errors

with

ML-02

by

pressing

EE-INV-EE

after

calculating

each

reciprocal,

and

before

entering

the

element for use by

the

program.

fls

an

additional

comparison of the capability of the CC-40 I entered an old

"•workhorse"

simultaneous equation solution into the CC-40 and several other

home/personal

computers.

Gene

Friel

also

providedasolution

using

the

Math-Pac Application Module

with

the HP-41C which uses a Gauss elimination

method.

The results, again using George Thomson's

7x7

test were:

HP-41

Color

Comp

Apple

11+

CC-40

Model

100

56.6667

55.5926

56.1869

56.000198

55.999816

-1527.3832

-1502.

465

-1516.2347

-1512.00461

-1511.99596

12712.2414

12529.8262

12630.3122

12600.0337

12599.

9716

-46566.

4960

-45969.5924

-46297.3343

-46200.1101

-46199.

9102

83755.0102

S27S4.5266

83315.8117

83160.

1785

83159.8577

•72541.8140

-71774.

7464

-72193.5851

-72072.1406

-72071.8899

24167.

8491

23932.811

24060.

8602

24024.0429

24023.

9669

1.19E-2

7.27E-3

3.34E-3

3.53E-6

3.28E-06

The superiority of the CC-40 and Radio Shack Model

100,

both 14 decimal

digit

computers,

is

obvious.

But

this

solution

on

the

CC-40

is

an

order

of

magnitude less accurate than that from the program in the Mathematics

module.

TI

PPC

NOTES

V8N6P20

Accuracyofthe

Solutions

for

SystemsofLinear

Equations-(cont)

For

reference

the

common

program

used

to

evaluate

the

four

computers

is:

100

DIM

A<10,10),B(10)

110

INPUT

"Enter

order";N

120

N =

N-l

130

K=0

135

FOR

I = 0

TO

N

140

FOR

J = 0

TO

N

145

A(I,J)=l/<J+K+2)

150

155

B(I)=1

160

K=K+1

.

165

200

FOR

K = 0

TO

N

210

P -

A<K,K)

250

FOR

J - K

TO

N

260 A<K,J) - A(K,J)/P

270

280

B(K)

-

B(K)/P

290

FOR

I - 0

TO

N

300

IF

I • K

THEN

360

310

F =

A(I,K)

320

FOR

J - K

TO

N

330

A<I,J)

«

A(I,J)

-

F*A<K,J>

340

350

BCD

•

B<I)

-

F*B(K)

360

370

490

FOR

I • 0

TO

N

500 PRINT "X"+STR*+" - "; B(I)

510

600

END

Lines

130

through

165

provide

automatic

entry

of

the

appropriate

sub-

Hilbert

problemasdefinedbyGeorge

Thomsononpage

18.

If

you

wish

to

use

the

program

for

other

solutions

simply

replace

those

steps

with

appropriate

stepstoaccept

the

appropriate

matrix

elements.

MORE

SUBPROGRAMS

FOR

THE

CC-40

STATISTICS

CARTRIDGE-Experiments

show

that

the

CC-40

Statistics

cartridge has a

subprogram

for

input

and

editofa

two-dimensional

array

whichisvery

similartothat

in

ihe

Mathematics

cartridge.

Even

the

call

MI

is

the

same.

™*

^"P*s.ar*

the

sameasthose

describedonVSN5P15

except

thatatthe

end

of

an

edit

of

all

input

the

Statistics

cartridge

implementation

leaves

the

subprogram,

while

the

Mathematics

cartridge

implementation

returns

for

additional

editing.

There

^

obviously

other

unlisted

subprogramsinthe

Statistics

cartridge.

Jcall

for

an

AK

subprogram

for

input

and

entry

ofaone-dimensional

array

as

tn

the

Mathematics

cartridge

yields

the

error

«f^e

"Program

not

found".Acall

for

an

AU

subprogram

for

input

and

editof*^

«-"

dimensional

arraysaswith

the

^the^atics

cartrxdge

yieWs

the

error

message

"Illegal

Syntax",

which

suggests

thereisa

subprogrammthe

Statistics

cartridge

with

the AU

name.

TI

PPC

NOTES

V8N6P21

SORTING

ON

THE

CC-40

-

The

Statistics

cartridge

for

the

CC-40

has

a

shell

sort

subprogram.

The

program

requires

that

the

elements

to

be

sorted

have

already

been

assembled

into

a

one

dimensional

array.

The

following

program

provides

entry

of

data

into

an

array,

sorting,

and

display

of

the

sorted

elements:

100

DIM

XC100)

110

INPUT

"Number

of

Elements?

";K

120

FOR

I - 1

TO

K

130

INPUT

"Enter

XfiSTRSd)*"):

";X(I>

140

PRINT

"Press

<ENTER>

to

Sort":PAUSE

150

PRINT

"Sorting"

160

CALL

SORT(X(),K)

170

FOR

I * 1

TO

K

180

PRINT

"SX("&STR*&")

-

"{Xd)

190

PAUSE:

200

END

This

program

is

much

faster

than

the

sorting

program

in

the

Math/Utilities

module

for

the

TI-59

(MU—06)•

The

CC—40

sorts

60

random

numbers

in

31

seconds.

The

TI-59

takes

4

minutes

55

seconds.

TI PPC NOTES V8N5P18

FACTORIALS

WITH

THE

CC-40

MATHEMATICS

MODULE

Factorials

can

be

calculated

with

the

Mathematics

module

o-f

the

CC-40

by

recognizing

that

N! *

Gamma(N+l).

With

this

technique

the

CC-40

with

the

Mathematics

module

installed

will,

return

Ln(Gamma(70))

=

226.19054S3

in

about

one

second

and

pressing

ENTER

will

immediately

yield

Gamma(70)

=

1.711225E+98

"which is equal to 69!. By

comparison

the

ML-16

program

on

the

TI-59

takes

about

16

seconds

to

obtain

the

equivalent

answer;

but,

the

MU-

11

program

in

the

Math/Utilities

module

-for

the

TI-59

will

find

69!

in

about

four

seconds

with

the

Gamma

function

method.

The

CC-40

can

obtain

factorials

up

to

85! =

3.31424E+126

with

this

method.

TI

PPC

NOTES

V9N5P11

CC-40

STATUS

- In

late

November

I

called

Educalc

for

information

on

peripherals and supplies for the CC-40. I was told

that TI was discontinuing the

CC-40.

A call to the TI Consumer

Hotline,

800-842-2737t confirmed that the CC-40 development had been stopped.

There will be repair support for CC-40 hardware both in and out of

warranty, but no

new

products will be released* We

will

continue to

provide coverage of the CC-40 and peripherals in TI PPC

Notes.

Some

peripherals

continue to be for sale at the TI exchange centers*

Other

sources for

supplies

are

available.

I have used the Radio Shack ink

cartridges

.successfullyinthe

Printer/Plotter.

••<

XI

to

rf

XI

rf

o-

<

Ol

"O

Ol

PO

3

Ol

rf

ri-

o-

to

3

XJ

•-*•

3

3Z

vO

-»

Ol

OO

CD

-^

ON

2»

VJ1

Ol

O.

rr

•*-

O.

V>4

ro

o-

a

3

k-4

rf

CD

rr

3"

rf

PO

1

5*.

o o

Ol

CD

3"

C

O

»—•

CD

o.

n

-»

-o

*-••

H-•

3"

zr

v<

Ol

o

1

Ol

O •

Ol

CD

•

»-••

•

r~*

•

c

O

zr

•

CD

•

Ol

•

CD

3*

Ol

3-

O

CD |

O

c a

to

1—-

CD

rt-

»-»•

-»

3

o

CD

*

X)

CO

CD

•+

r±

to

o 3

-1

rf

r-•

H-«

x>

3

CD

to

3

O

to

tt>

rr

CD

3

< I

«£

CO

CD

rt-

rf

Ol

I--

to

w>

c

O

!-••

rf

tO

C

CD

r*»

CO

>-•

O

x>

Ol

-1

o.

3*

rr

>»

CD

o-

•"*• 1

3»

rf

CD

3

O

—»

3P

*-<

•—-

rf

-»

—4

CD

3

—|

to

H-»

-»

£

Ol

r-•

CO

o

Ol

•-••

CO

-x*

£

-o

-1

*-»•

-*»

CD

PO

CO

1

J*

Ol

O)

•—•

CD

CD |

Z

o •

PO

rr

m

to

CD

«*

Ol

o

3*

«*

or

Ol

CO

»—•

»•<

-♦>

*•<

Ol

O

1—•

»—•

f~»

O^l

OO

CD

zr

Ol

CD 3

-1

CP

CD

O O

x>

o

—i

3

-»

Ol

CO

£

__«

£ 1

tr>

CD

z:

C

to

3

-♦»

CD

H"

CD

1

o

Ol

3

-i

Ol

ri

o

Ol

3

CD

-I

o>

Ol

CD

r*»

O

o.

Ol

rf

zr

r--

rf

Ol

O.

rf

H»«

O

3"

m

»—»

O

—4

—«

O

rf

»-<

3

to

oo

c

O

rf

O

al

-h

-1

Ol

CD

f*»

Ol

o.

Ol

rr

.a

to

X>

rr

CD

Ol

¥-*•

CD O

CD

rf

-»

Ol

rf

-4%

•-•♦

or

i

(3

»-••

4—4

rf

-o

m

"»

»-H

c

Ol

C

»-••

o

H-«

o

»-••

oo

«-i-

O-

o

3"

-h

3

*—•

cr

CD

r*»

*-*•

O

c

O

to

1

Ol

. <

Ol

O.

H»»

rf

3-

Ol

*•<

i

3

-♦»

Ol

-1

PO

CD

1

H-»

rf

k->*

to

o

O.

Ol

•o

O.

to

o

c

-♦»

£

oi4

rf

«•

CD

to

1

Ol

<

o

CD

-»

r-•

z

CD

3

•—»

^

-t»

3

M»

Ol

m

CD

3

o

XI

vO

O.

CD

rf

c

O

3"

*—•

-1

CD

m

c

"%

CD

rf

-»

3*

3"

o.

--^

•—•

!-••

CD

3

rr

3

CD

«^<

•^

-♦>

o O

PC"

Ol

rf

3

•-••

3:

i

r—

*-<

(O

lO

PC-

C

vO

3

3"

-♦»

-1

Ol

t—•

O

to

m

CD

»-••

rf

t-t-

3*

»-••

o.

CD

£

-o

O

to

•

zr

O

rf

3 O

X)

»-*•

Ol

o.

O

CD

c

«»

rf

3-

Ol

oi

|

rn

V>4 O

C

-1

CD

»-••

•

to

CD

c=

to

rf

< CD

iO

l

to

»—*

r-t-

3*

3"

»-••

rf

x>

rf

-I

Ol

o

3

f-»

CD

»^

CD O

-♦»

c

!—•

CD

c

Ol

O

-»

r*>

CD

c

CI

rs>

c

f-•

Ol

*^<

->

-|r-

c

3

*—•*

CD

3*

CD

O.

-»

3

to

^<

o

H»-

CD

Ol

rf

-♦»

to

•n

CD

O

-1

pc-

O

3

»--•

rr

O

»—*

H-•

a

rf

Ol

O

X

rf

1

O

o>

3

•

CD

»>

—♦»

rf

to

1—*

^

CD

Ol

rt-

O

CD

Ol

CD

-1

rf

o

O

rr

Ol

o

£

rf

o.

-n

»-»•

Ol

CD o CD

O

to

*-<

3

Ol

2

rf

3"

»-••

PO

•

XI

-»

-♦»

to

o

-<

CD

-♦»

3

zr

o.

O.

t-t-

X>

3

3 o

Ol

O"

rr

CD

H-»

•—»

-^*>

1

H-«

o o

Ol

rf

1

3

c

O.

Ol

-»

co

o

1—4

*n

to

*-<

•—s

CD

3

O"

O

3

-1

to

CD

c

»-••

zr

3

*n

O

3

Ol

r»*

H-»

O

x>

3

c

t—*

XI

Ol

O.

O

»—»

Ol

»•<

o

rf

Ol

CD

<->

»—4

<o

«-♦•

CD

3=

O

rt-

-»

O

CD

•o

c O

O

~*

to

H-»

*-••

to

CD

Ol

H»«

O.

o-

o

Ol

CD

o

cr

Ol

CD

Ol

-»

o

O

•

1

o

Ol

vO

CD

to

"»

3"

O

-♦»

•«*

-♦»

Ol

o

XI

CD

c

3"

3

-1

»-••

3

»—•

3

CD CD

rf

CO

O

c

Ol

-<

Ol

!-••

3

»—•

XI

o

to

»-••

!-••

f—

»—•

Ol

O 3

rr

O

Ol

♦—•

CD

-»

o

m

1—

to

c

-»

CD .

*-••

o

»—•

<

o

•*

•a

o

1—•

3 CD

>—•

k—•

^

-»

>—•

•

Ol

rf

Ol

Q~

3

CD

3

»-<

•—•

-»

rf

r**

•^

~»

CD

rf

3

o.

c

•

*<

-o

CD CD

rt

3 O

3

rf

CD

Ol

>-••

"O

o

»-••

M-

CD

f-•

Q-

!--•

r*»

o

3*

O

-1

3

O

o.

Ol

a

to

CD

3"

Ol

•-••

—4

^^

m

O

f-f

o

3

O

3"

3

-o

-»

CD

3

•n

£

CD

3

rf

O

rf

S~>.

3

H*»

Ol

-•»

3

Ol

O

o

c

CD

r*'

to

_4

•

XI

CD

rf

3

rf

•

2S

c

=r

4—•

O

»-••

O

rf

CD CD

rf

I-"*

to

O.

c

O

3*

Ol

rf

»-••

C

-♦»

3

O

3C

O.

v<

c->

x>

3

H-•

—«

I-*-

Ol

3

rf

3

H-»

-•

3

3"

♦-••

Ol

3*

CI

co

o>

CD

rr

x>

3

3*

O.

»-»•

3

!-••

to

Ol

to

f"

-»

Ol

rf

o.

Ol

<

«•

CD

Ol

I—•

x>

o

O

r-•

»--•

O.

-1

CD

r*»

Ol

3

CD

Ol

"^1

O

-1

CO

1—4

-o

-1

•

4—•

CD

»—»

f-

3

rf

O

Ol

CD

o-

-i

O

^C

f—

CD

fir

3

CD

<

o

1—•

CD CD

c

3~

rf

3

Ol

rf

3

Ol

OO

rr

H«-

Ol

^<"

3

£

•y

h3

""*

2E

••o

4-**

oi

»-••

rf

to

o 3

rf

-1

O

Ol

zr

3

O.

zr

CD

1

Ol

!-••

-♦»

o

-1

O.

»—*

CD

•

Ol

3

<

1—•

»-••

c

rf

o O

O

3

o

•-»•

i-n

CD |

to

o

O

"O

3

M*

^

1

c

3

2

CD

-♦»

CD

Ol

3

Ol

c

Ol

o-

-1

»—•

Ol

• O

»—•

3"

»—•

*•<

•—•

Ol

3

XI

O.

3

r*i

M

tO

PC"

-<

CO

CD

O

-»

CD

3

rf

O

rf

£

t-k-

to

3

O

O.

3

o

*-••

O.

r*r

o.

f-»

Ol

3

rf

»^

Ol

-4%

m

3

rr

CD

»-••

O CD

3

O

c

C

3

PO

CO CD

-^^.

CD

XI

3

O

CO

3"

-t»

3"

-i

Ol

-1

CD

-1

3

zr

rf

r*»

CD

Ol

3

O

I-—

o

•

CO

o o

»-••

Ol

f-«

3

Ol

o.

Ol

O

O.

Ol

1—•

CD

»—4

'»d

•d

o

^<

as

CD

O

*•<

-o

o

CD

.»

c

CD

*-••

rf

€-*-

PC-

CD

f-»

3

O

»-••

•

f-4

O

rf

O.

CD

o

zr

•"••

—»

Ol

/*-N

•

XI

-♦»

CD

o

Ol

CD

c

*—*

CD

3

1

2S

rf

•*

3

«*

to

o

c

CD

o>

3"

PO

rf-

3"

zr

CD

1—•

3 O

rf

Q-

3

CD

3 CD

X

XI

3

ar

-n

•—•

o •

Ol

rf

1—•

r»»

•

CT>

zr

«*

Ol

c

rf

to

O

»-••

-H

CD

rf

CO CD

to

fr—•

-1

3"

C

X>

O

Ol

3

Ol

-♦>

^~s

CD

•

i—-

»-••

CD

*—•

rf

r-t

3

CD

rr

—♦»

co

!-••

-1

CD

to

3"

3

o

H-»

O

3 CD

-1

Ol

rf

^<

CD

»—•

»-••

C">

Ol

O

r*-

O

•

-♦»

«<

£

-1

CD

3

1

»—»

rr

o

^

^<

O

3

CD

—•»

cr

-»

•

CD

3"

-1

rf

O.

3

to

CD

€-*•

•

3"

CD

3

Ol

-1

-*»

»-••

-1

O

*<-N

CD

f

-♦»

O.

-♦»

o

•-4

£

CD

O.

-1

I o

3

-<

*-•

3

O

•—•

Ol

N—•

rf

3

Ol

zr

CD

Ol

—i

•

-I

Ol

o

Ol

CD 3

c->

Ol

•n

3

o

#*—s

£

Ol

CD

£

•-••

3

c

•—4

Ol

1

o.

o

1

«"f

o.

-»

CD

3

k-»*

O

3

£

3

Ol

•o

3

Ol

CD

<=

<

r-i

rf

^<

3

rir

3

r*»

<

o

3

^<

O.

-»

—4

>-••

CD

M-

CD

Ol

»—-

3

rf

| c

3

pc-

=r

to

Ol

»—4

3

O

Ol

to

-1

CD

"»

3

m

Ol

1

3"

CD

zr

to

C

CD

3

O-

O

3

-1

rf

Ol

O.

3

<

3-

zr

CD

O

O.

3*

1 1—•

CD CO

oi

CD

rf

£

3

CD

G

?r

-1

c

-o

O

CD

-4.

m

»-••

\J\

1—1

CD

H-»»

rf

CD

to

3

Ol

-1

x»

3"

£

Ol

3*

H-*

cr

tO

CD

O

• CD

CD

I CD

»-<

-•

to

X

3"

CD

O.

•

•—»

CD

b—*

-1

to

3

(.0

O

1

f-•

vD

Ol

CD

I-*-

Ol

CD

Ol

f-«

OO

Ol

•••• 3

1—•

Ol

1

»—i

c

1

C

to

Ol

-1

rf

O.

to

Ol

o

-:

%xt

to

<

->

3

Ol

«*

3*

O

-1

rt-

<

»—*

-h

!--•

CD

c

3 3

rr

Ol

-1

o

XI

-»

rr

Ol

C~> 1

-•»

^-v

i-»-

!-»•

3

rf

*-*-

zr

SS

o

-1

to

Ol

3

CD

rf

O

or

Ol

-•

3

£

CD

1

C

O

rf

rr

O.

CO

zr

-♦»

CD

-I

7*-

-1

O

zr

Ol

CO

Ol

CD

CI

I o

O 3

to

•o

!-••

3"

*-••

c

K

3

-•»

-1

3

3 < 3

C

o.

!—•

CT

<

CD O

O

O 3

rr

1—•

3 CD

rr

^C

CD o

Ol

CD

O

Ol

cr

r*»

-4*

1

"1

-»

3

4—•

to

3

CD

to

rf

-»

»-••

t-t-

Ol

CD

3

c

CD

C

CD

O.

o

Ol

•^

CD

rf

-1

r-»

Ol

/-\lQ

3

o.

Ol

rf

3

c

^~

1—•

to

CD

»-••

•-••

to

rf

o

3

»-••

-1

—1

-»

Ol

H--

•

rf

•-••

f-«

3

Ol

1

O

•

-»

f-»

CD

»-••

3

1—•

O

-I

CD

H-•

4—•

o

1

rf

o> ©

«,

3

rf

<->

"O

-♦»

rf

3"

3

Ol

rf

CD

Ol

rf-

O

<

*•*•

3

3 3

/-N

~n

£

3 O

3

Ol

O

3

Ol

rr

Q.

m

*-<

3

1

zr

=> c

2»

XI

3"

C"5

-«

O

CD

Ol

CD

-o

€-ir

Ol

1—•

—»

CD

rf

CD

to

3

CD

to

••<

o

CD

»—1

o

O

3"

<

O

Ol

CD

3

rf

zr

Ol

r-*

CD

4—4

1 CD

*•< CD

«/f

i—•

CD

1

o

-•

PC-

o

zr

PO

CO

CD

•—'

-♦»

—1

3"

CD

to

-1

3

»-••

-»

<

3

CD

Ol

CD

3

Ol

O

f—

^<

CD

-•»

Ol

-1

»—•

«-<

-*-to

»-••

CD

—«

f-•

Ol

J*

to

-1

»-<

o

3-

CD

3

*—*

CD

Ol

rr

Ol

-h

Ol

rf

CD

!-••

"1

-♦»

O.

O

• •

Ol

«•

O CD

Ol

3"

1

rf

o

rf

f—

O-

o

-%

rf

to

HH

Ol

c*-

2

to

c

-1

CD

«^<

H»«

-1

!-••

1—«

£

CD

O

3

o-

zr

-»

-O

Ol

-♦»

XI

*-»•

rf

CD

•

Ol

1

3"

rf

O

©

3

xi

f—

*•

a>

3"

1

-1

•

c

o-

rf

—1

Ol

o

Ol

o

-#

o

•-<

c

CD

Ol

>-••

O

1

rr

c~>

Ol

-t

»—•

<

1 CD

ar

-i

CD

-1

to

3

CD O

Ol

v-n

c

O"

XJ

zr

1—4

rt-

O

Ol

CD

rf

£

3

•

3

rf

H-»

1

CD

3

O

Ol

a

3

r*»

CD

P"?

CD

xi

3

»—•

vO

Ol

to

-1

-»

Ol

zr

3

f--

<

• O

•

N—^

-1

rr

O

3"

O

zr

Ol

rr

x-

M»

3

£

I

O.

O

C

2»

1

CI

-•

c

m

__A

to

»—•

o

Ol

(O

3

«•

3 CD

3»

O

o

3

CD

>—•

f-«

CD

-l

o

Ol

zr

rr

£

r*»

"1

»—•

CD

x>

XI

Ol

-P-

Ol

3

»—•

Ol

1

CI

-o

-<

ro

Ol

3

Q>

-4»

o

O-

to

c

to

Ol

*<

-»

pc-

/—N

-h

rr

CD

Ol

1

to

Ol

l_l.

3

f-•

Ol

o

1—1

*—•

XI

rf

CD

1 1

PC*

XI

*r>

o

»-••

»"<

CD

rf

»-••

CD

to

o-

r±

—1

3"

o.

—«

3"

Ol

H-4

!-••

*-*•

to

o

x>

3"

-»

3

rr

CD

c

3"

CD

1

4r-

CD CD

•

3

,•

1

CD

3

c

c±

c

<

rf

Ol

»-••

Ol

CD

HH

X>

Ol

•—•

3 3

1

O

—-4

O

rr

Ol

CD

Ol

CO

to

X

1—•

Ol

3"

m

Ol

O

3

1 o

»><

-1

to

PC-

O

CD

rf

!-••

£

3 3

3

1

-1

Q.

to

3*

rf

<*

f-»

r*»

Ol

-♦»

-*»

o

3

Ol

3

1—•

C

| •

^

t—4

CD

3"

O

-»

Ol

O o

CD

to

—

o

OO

O

Ol

3

r*»

3"

1

O <

Ol

-»

Ol

o

O

-1

£

Ol

O.

<

tO

»-»•

to

Ol

vO

-•»

o

3

-♦l

3

CD CD

to

•

to

3

oo

to

Ol

rf

vc

Ol

to

CD

x>

v-n

-l

CD

CD <

-1

-♦»

O

1

»—•

CD

»-••

-♦»

3"

O

2i

o

o>

«-f

o

f-»-

•—•

rf

o

1

to

X

•—»

—»

CD

rf

t-t

-»

vO

Ol

-♦l

-O

Ol

3

O

XI

r»

rf

3

¥•*•

-»

to

c

o

»—•

-1

XI

Ol

H-«

3~

€•*• <

c

Ol

rf

^<

Ol

"%

CD

O O

•

IM

Ol

*->»

C

!-*•

,rr

rf

Ol

O.

zr

cr

CD CD

r-t

-h

CD

0>

o.

-"»

•—•

CD

C

3

»-••

CD

o-

3

-1

—4

~ CD 3

3

*-••

3

x>

-H

XI

ri-

o-

v«>

•»<

3

c7

CD

»—•

-•»

zr

Ol

"oi

CD

»-••

CD

O.

Ol

«-♦•

«*

!-»•

♦-••

o

to

CD

-♦l

CD

3

H»»

-»

x>

-o

CD

zr

CD

rf

o.

o

X>

H-«

1—1

-1

zr

Ol

O.

3

Ol

-l

CD

Ol

CD

-1

-♦»

-1

ZT

rf

to

sz

c

-o

•CD

to

3

to

-1

H-•

•

CD

rf

£

Or

c

rf

3

•«

o

•n

ar

Ol

-1

O

O"

o

O

•*

-1

3

»-••

rf

CD

^

O

Ol

to

-o

CD

O

M-

C

«*

Ol

o CD »•<

3"

CD

•-••

zr

Ol

!-••

to

CD

M«

ar

XI

Ol

^

f-•

3

rr

-h

C

3

O

CD

«-•-

*-*

»—•

oi

o.

3

to

o

rf

to

•

3

rf

Ol

O

1

CD

»—-

o

Ol

•

CD

r*»

f-•

m

o.

to

•—•

*-»•

-t»

Ol

♦—*

to

o-

O

-♦»

3"

-♦»

T»

O

CO

Ol

v»->

rf

t-t-

Ol

3

Ol

%•

!-••

c

Ol

o

rr

3

C

3"

CD

m

o

-1

Ol

3 3

O

*<

»—•

cr

CD

c

^<

O

CD o

Ol

-h

c

-»

*<

£

3"

rf

•—•

3

rf

Ol

o

-♦»

zr

CD

XI

r*»

1

r*'

!-••

CD

Ol

3

Ol

CD

-»

to

o

•^<

•

to

rf

3

r-t-

-1

3

rf

CD

Ol

o.

o O

ri-

rf

*-<

f-«

3

O

CD

to

O

3

Ol

<

O.

rf

c

CD CD

o-

zr

C~>

Ol

rf

to

»-••

-1

zr

3T

rf

<

XI

'

-»

o.

rf

zr

-»

o

tO

r*»

»—•

«-•-

—*

»•<

rf

to

2

O.

to

H»»

CD

C~>

^-<

• •

3"

rf

CO

Ol

o.

rf

!-••

o

3*

Ol

3*

CD

c

-♦»

o

O

1

o,

Ol

CD

f—

Ol

CD V>J

o

ZT

x>

O

>•

,*

3

1

o

f—

3-

3"

3

O

£

Ol

C

Ol

3

O

»-••

rf

Ol

-»

3

XI

Ol

c

rf

£

rf

r-*

-1

O

c

CD

*<

-t

to

•-••

TO

-F-

c

Ol

CD

Ol

XI

£

O

-1

to

Ol

o.

-♦»

Ol

rf.

Ol

!-••

CD

Ol

O)

H-•

zr

-♦»

rr

»—-

-i

o CD

rf

c

-1

3

Ol

O

•

no

*<

-1

t—•

—i

rf

3

f

zr

•-<

rf

O.

X)

!-*•

Ol

2

CD

H»«

r*»

CD

4—•

to

c

to

3 CD

to

•

PO

€-t

CD

>-••

3*

»•»••

rf

Ol

X>

M«

CD

C

3

Ol

O

Ol

CD

H-»

CD

XI

CD

—i

3

to

O

!-»•

Ol

rf

CD

O.

to

€-t-

»-»•

3

CD

t—*

CD

-♦>

O CD o

•—•

CD

ro

3

£

H-*

rf

•n

<-*- 3

CD

¥-»

O

X3

o_

to

•

—4

3*

Ol

O

3

rir

3

to

O

rf

Ol

rr

Ol

3

Ol

3

O

3

o

Ol

-1

3"

-h

O.

3"

O

3"

Q,

to

rf

3

C

Ol

CD

3"

CD

3

3"

Ol

cr

o

CD

to

Ol

3

zr

-»

zr

f-•

CD

*^>

Ol

o-

O

rf

rr

3 O

CD

o CD

Ol

<

CD CO

1

o

tO

1

CD

1 1

H-*

CD

*^

O.

1

*^<

*<.

—h

3

to

•*

Ol

CD

^-<

CD

1

• • CD

^<

o

zr

O-

CD 3

-1

M

-1

rf

CD

TI

PPC

NOTES V9N1P11

100

OISPLAY

AT(2)"EE module in

place?

Y/N":A$=KEY$

110

IF

A$="N"

OR

A$="n'»

THEN

360

120

OISPLAY

AT(2)"Rectangular

to

Polar?

Y/N":A$=KEY$

130

IF

A$="N"

OR

A$=nn"

THEN

320

140

OISPLAY

AT(2)nX-coordinate?";

150

ACCEPT

AT(18)VALI0ATE(NUMERIC)BEEP,X

160 DISPLAY

AT(2)"Y-coordinate?";

170

ACCEPT

AT(18)VALIDATE(NUMERIC)BEEP,Y

180

CALL

RP(X,Y,M,A)

190

DISPLAY

AT(2)"Magnitude='»;M:PAUSE

200

DISPLAY

AT(2)"Angle=";A;"degrees":PAUSE

210

GOTO

120

220

OISPLAY

AT(2)«Polar to

Rectangular?

Y/N":A$=KEY$

230

IF A$="N"

OR

A$='»n«

THEN

350

240

DISPLAY

AT(2)"Magnitud-e?";

' '250

ACCEPT

AT(18)VALI0ATE(NUMERIC)BEEP,M

260

DISPLAY

AT(2)"Angle

in

degrees?";

"270

ACCEPT

AT(20)VALIDATE(NUMERIC)BEEP,A

280

CALL

PR(M,A,X,Y)

290 DISPLAY

AT(2)"X-coordinate=";X:PAUSE

300 DISPLAY

AT(2)nY-coordinate=";Y:PAUSE

310

GOTO

220

320

DISPLAY

AT(5)"Exit

program? Y/N'»:A$=KEY$

330

IF

A$="N"

OR

A$="n"

THEN

220

ELSE

END

340

DISPLAY

AT(5)"Exit

program? Y/N":A$=KEY$

350

IF A$="N'»

OR

k$=«n"

THEN

120

ELSE

END

360 DISPLAY

AT(4)"Insert

EE

module,

please!":PAUSE

4

370

END •

EDITOR'S

NOTE - My

sentiments

about

the

lack

o-f

peripherals

are

the

same

as

Maurice's.

I

am

using

the

Mathematics

module

and

have

a

set

of

interacting

programs

which

perform

polynomial

regressions,

compute

residuals,

solve

sets

of

linear

equations

by

various

methods,

and

the

like.

One

inadvertent

NEW

would

be

a

disaster.

The

CC-40

is

beginning

to

get

some

favorable

press.

In

the

article

"Choosing

a

Notebook

Computer"

in

the

January

1984

issue

of

Creative

Computing

author

Oavid

Ahl

discusses

price

versus

performance:

"...

But

perhaps

most

interesting

are

the

five

machines

'that

fall

below

the

curve,

and

thus

represent

relative

bargains.

At

the

low

end

is

the

TI

CC-40.

For

professionals,

students,

and

engineers,

this

is

an

unbeatable

machine

at

only

$250,

frequently

discounted

to

well

under

$200.

..."

TI

PPC

NOTES

V9N3P23

SIMULTANEOUS EQUATIONS WITH THE CC-40 MATHEMATICS MODULE -

P.

Hanson

V8N5P14-16

discussed

the

matrix

operations

programs

in

the

CC-40

mathematics

module.

V8N6P19

reported excellent results using those

techniques

to

solve

the

7x7

sub-Hilbert,

but

presented

the

results

only

to

enough

digits

to

establish

the

relative

error.

James

Walters

proposed

another

method

of

error

evaluation,

that

is,

multiplying

the

solution

vector

by

the

original

matrix

56.00003229

and

comparing

the

result

with

the

input

unity

vector.

-1512.000787

To

use

that

method

it

was

important

to

use

all

of

the

12600.00591

digitsofthe

solution.

No

difficulties

were

found

-46200.0192

in

doing

that

with

any

of

the

TI-59

solutions,

or

83160.0311

for

any

of

the"

solutionsonpersonal

computers

using"-72072.0246

the

programonV8N6P20;

but

the

Mathematics

module

24024.007436

solution from the CC-40 would only yield the 9 to

11

digits

shown

at

the

right.

Afteralot

of

agonizing

over

items

such

as

whether

my

application

of

"PRINT

USING"

was

proper,

and

the

like,

I

finally

found

that

the

truncated

result

from

the

CC-40

Mathematics

module is a direct result of the method of solution.

I

had

assumed

that

the

method

of

solution

from

the

CC-40

Mathematios

module

and

from

the

TI-59

Master

Library

(ML-02)

was

the

same.

The

discussions

under

"Method

Used"

on

page

13 of

the

Master

Library

manual

and

on

pages

53-54

of

the

CC-40

Mathematics

module

manual

are

identical.

Experiments

show

that

the

methods

for

solution

of

linear

equations

must

be

quite

different.

The

ML-02

solution

on

the

TI-59

does

not

seem

to

make

direct

use

of

the

inverse

of

the

matrix.

The

CC-40

solution

seems

to obtain the

inverse,

and simply multiply the inverse by the vector

to

get

the

solution.

Where

the

vector

is

the

unity

vector

as

in

our

7x7

sub-Hilbert

test

problem,

the

solution

may

be

obtained

by

simply

adding

up

the

rows

of

the

inverse

«,„„•..«,.

matrix.

-For

the

7x7

problem,

the

C(7,l)

=

168,168.045

045

95

seventh

(or

bottom

row)

of

the

C(7,2)

=

-4,036,033.121

075

inverse

matrix

is

listed

at

the

C(7,3)

=

-30,270,248.620

461

right.

Now,

if

you

sum

the

terms

C(7,4)

=

-100,900,829.259

5

in

the

row

from

the

top,

as

would

C(7t5)

=

166,486,368.937.

2

be

reasonable

foraloop

in

the

C(7,6)

=

-133,189,095.560

0

computer,

then

you

will

obtain

C(7,7)

=

41,225,196.345

304

exactly the solution for the #

seventh

element

in

the

table

at

the

top

of

the

page.

Similar

results

can

be

obtained

for

the

other

elements

of

the

solution

by

reading

out

the

elements

of

the

inverse

matrix.

You

must

remember

to

always

truncate

each

intermediate

sum

to

the

fourteen

digit

limit

of

the

computer.

The

truncated

output

arises

because

the

last

summation

is

between

two

'numbers

of

about

4l million but of

opposite

sign,

yielding an

answer

of

about

24

thousand.

The

same

sort

of

result

can

be

obtained

with

the

ML-02

programsbynot

solving

simultaneous

equations

with

ML-02

Program

E,

but

rather

obtaining

the

inverse

matrix

with

ML-02

Program

B',

and

summing

the

rows.

The

printout

on

the

left

below

is

the

ML-02

solution

using

the

standard

method.

The

printout

at

the

right

was

obtained

using

the

inverse

matrix

method.

Agair,

the

truncation

effect

is evident. Until TI choses

...

_.,_,__.

to

release

the

program

details

56.0081897448

5b.UOSlbVb

of

the

CC-40

Solid State

Mod-

-1512.

189567-129

'^l2-

^^J3

ules

we

can

only

continue

to

12601.

38627848

12601.

38624

try

to

understand

through

ex-

-46204.

53435755

-46204.5337

perimentation.

83167.37180486 83167.3708

-72077.82742612

-72077.8273

24025.7860121

24025.78576

TI

PPC

NOTES

V9N5P6

NUMERIC

REPRESENTATION

IN

THE

TI-99/4

AND

CC-40

-

Laurance

Leeds

In V9N4P7 Myer Boland reported that he could recover fourteen digits of

pi

on

the

TI-99/4

with

the

equation

P *

4000«ATN(1>.

If

one

tries

to

convert

the answer from 1000«pi to pi by dividing by 1000, then the end result

reverts to a twelve digit value. The same results were reported for the

CC-40.

These

results

follow

directly

from

the

radix

100

arithmetic

mechanization (see page F-2 of the CC-40 Manual or page 111-13 of the

TI-99/4

manual.

Both

machines

use

seven

radix

100

bytes

for

the

mantissa.

This

is

just

another way of saying that the arithmetic is performed using seven

blocks,

each of two decimal digits, with the value of

each

block ranging from zero

through

99.

The exponent is selected so that the decimal point of the

mantissa immediately follows the most significant digit. In short, the

arithmetic

is in

base

100.

The

mechanization

explains

why

40

» ATN<1)

gives

14

digits

of

pi

400

* ATN(l)

gives

12

digits

of

pi

4000

• ATN(l)

gives

14

digits

of

pi

40000

»

ATN(1>

gives

12

digits

of

pi

and also why

(4000«ATN(1>)

/1000

gives

a 12 digit

result.

We

will

see that

the twelve

digit

results

are thirteen

digit

results

which

include a

trailing

(non-displayed)

zero.

In

the

same

manner

the

thirteen

digit

TI-59

yields

an

apparent

twelve

digit

value,

but

actually

a

correctly

rounded

13

digit

value

for

pi.

Consider

two representative calculations:

400

« ATN(l)

4000

»

ATN(1>

ATN(1> = 78.53 98 16 33 97 45 x 100 ='78.53 98 16 33 97 45 x 100

400

=

4.00

00

00 00

00 00 x

100

+1

4000

=

40.00

00 00 00 00 00 x

100+

*

3

12

31

20

2

12

21

20

3

92

39

20

0

64

6

40

1

32

13

20

3

88

38

80

1

80

18

00

3

14.15

92

65

35

89

80

x

100°

31

41.59

26

53

58

98

00

x

100°

Rounding to seven radix 100 digits yields:

3

14.15

92

65 35

90

31

41.59

26

53 58

98

and scaling the mantissa and exponent yields:

3.14

15

92

65

35

90

x

100

3

A similar exercise for dividing 4000«ATN(1> by 1000 is left to

the

reader.

3.14

15

92

65

35

90

x

100^

31.41

59

26

53 58

98

x

100

*

TI

PPC

NOTES

V9N5P7

Numeric

Representation

in

the

TI-99/4

and

CC-40

-

(cont)

Although

both

the

CC-40

and

the

TI-99/4

allow

entry

of

a

fourteen

digit

base

ten

number,

the

storage

of

the

number

depends

upon

the

location

of

the

decimal

point.

For

example.

The

entry

1234567.8912345

translates

to

1.23

45

67

89

12

34

50

x

100

which rounds to 1.23 45 67 89 12 35 x 1003

The

rounding

of

the

seventh

radix

100

digit

(the

13th

and

14th

base

10

digits)

in

accordance

with

the

value

of

the

eighth

radix

100

digit

occurs

immediately

after

the

calculation.

This

precludes

the

use

of

the

seventh

block

for

programs

which

require

all

of

the

base

10

digits

to

be

exact,

as

in

multi-precision

work.

A

safe

rule

is

to

program

as

though

the

machine

is

an

exact

twelve

digit

calculator,

never

permitting

any

overflow

into

the

seventh

block

if

this

information

can

affect

the

result.

Since

the

rounding

also

occurs

in

division,

modulo

division

may

not

give

the

desired

result.

For

example,

we

ask

for

the

residue

when

N =

12345678901563

is

divided

by

547.

Since

N

is

a

fourteen

digit

number

we

use

modulo

division,

say

with

the

algorithm

N

mod

M = N - M «

INT(N/M)

Both

the

CC-40

and

the

TI-99/4A

return

-2

as

the

answer.

The

correct

answer

is

545.

The

base

100

arithmetic

is

not

the

culprit;

the

rounding

is.

While

-it

is

true

that

in

this

example

N

is

congruent

to

-2

mod

547,

this

result

could

surely

mess

up

program

calculations.

Editor*s

Note: My

Radio

Shack

Model

100

which

also

does

14

digit

arithmetic

gets

the

correct

answer

using

the

algorithm

above.

Texas Instruments CC-40 A Collection Of Information

Specifications and Main Features

Frequently Asked Questions

User Manual