Texas Instruments BA II PLUS User guide



BA II PLUS™

Calculator

Important

Texas Instruments makes no warranty, either expressed or implied, including but not limited to any implied warranties of merchantability and fitness for a particular purpose, regarding any programs or book materials and makes such materials available solely on an “as-is” basis.

In no event shall Texas Instruments be liable to anyone for special, collateral, incidental, or consequential damages in connection with or arising out of the purchase or use of these materials, and the sole and exclusive liability of Texas Instruments, regardless of the form of action, shall not exceed the purchase price of this calculator. Moreover, Texas Instruments shall not be liable for any claim of any kind whatsoever against the use of these materials by any other party.

US FCC Information Concerning Radio Frequency Interference

This equipment has been tested and found to comply with the limits for a Class B digital device, pursuant to Part 15 of the FCC rules. These limits are designed to provide reasonable protection against harmful interference in a residential installation. This equipment generates, uses, and can radiate radio frequency energy and, if not installed and used in accordance with the instructions, may cause harmful interference with radio communications. However, there is no guarantee that interference will not occur in a particular installation.

If this equipment does cause harmful interference to radio or television reception, which can be determined by turning the equipment off and on, you can try to correct the interference by one or more of the following measures:

•

Reorient or relocate the receiving antenna.

•

Increase the separation between the equipment and receiver.

•

Connect the equipment into an outlet on a circuit different from that to which the receiver is connected.

•

Consult the dealer or an experienced radio/television technician for help.

Caution:

approved by Texas Instruments may void your authority to operate the equipment.

Any changes or modifications to this equipment not expressly

1: Overview of Calculator Operations 1

Turning the Calculator On and Off

Resetting the Calculator

Keys and 2nd Functions

The Display

..................................................

Display Indicators

.......................................

............................................

Setting Calculator Formats

Clearing the Calculator

Correcting Entry Errors

Math Operations

........................................

.......................................

..............................................

Appendix: Reference Information 115

Formulas

Error Conditions

Accuracy Information

IRR Calculations

AOSé (Algebraic Operating System) Calculations

Battery Information

In Case of Difficulty

Texas Instruments (TI) Support and Service Information

Texas Instruments (TI) Warranty Information

.............................................

.......................................

...................................

.......................................

.............

.....................................

.......

................

116

125

128

129

131

132

133

134

135

Index 137

Overview of Calculator Operations

This chapter contains information on:

•

Basic calculator operation

•

Clearing and correcting

•

Math operations

•

Memory

•

Last Answer

•

Worksheets

1: Overview of Calculator Operations 1

Turning the Calculator On and Off

Turning the Calculator On

Press

to turn the calculator on.

•

If you turned the calculator off by pressing calculator returns to operation in the standard-calculator mode. A value of zero is displayed and the values in all of the worksheets are the same as you left them, as are the formats for numbers, angle units, dates, separators, and calculation method.

•

If the APD™ feature turned the calculator off, the calculator, including the display and any error condition, returns exactly as you left it.

, the

Turning the Calculator Off

When you press

•

The displayed value is cleared.

•

Any unfinished standard-calculator operation is canceled.

•

Any worksheet calculation in progress is canceled.

•

Any error condition is cleared.

•

The Constant Memory™ feature retains all worksheet values and settings, including the contents of the 10 memories and all format settings.

to turn the calculator off:

Automatic Power Down™ (APD™) Feature

To prolong the life of the battery, the Automatic Power Down (APD) feature turns the calculator off automatically if you do not press any key for approximately 10 minutes.

2 BA II PLUS™ Calculator

Resetting the Calculator

Resetting the calculator restores all default settings and clears all data. Because you can clear only selected portions of data, you should reserve the reset function for appropriate situations. You might choose to reset when you first purchase the calculator or when you start a new project.

Effects of Resetting

•

Clears the display and any unfinished calculation.

•

Clears all 10 memories.

•

Clears all worksheet data and restores the default settings. (For information on specific worksheets, refer to the specific worksheet chapters.)

•

Returns the calculator to the standard-calculator mode.

Alternatives to Resetting

Before resetting the calculator, consider the other methods for clearing described in this chapter. For example, if you need to clear only one worksheet, you can do so without resetting.

Procedure: Resetting the Calculator

If necessary, first press P to clear any error condition.

쐃

Press &

RST ?

쐇

To reset the calculator, press

}

and the

indicator are displayed.

ENTER

RST

and

0.00

are

displayed.

To cancel the reset operation instead, press

Note:

displayed.

& U

0.00

The calculator is in standard-calculator mode.

1: Overview of Calculator Operations 3

Keys and 2nd Functions

The primary function of each key is printed on the key. For example, press

Some keys provide a secondary function. which is printed in yellow above the key. When you press &, the character, abbreviation, or word printed above a key becomes active for the next keystroke. For example, press & U to leave a worksheet and return to standard-calculator mode.

The Display

The display shows entries and results with up to 10 digits. The indicators along the top of the display provide information about the status of the calculator and tell you what keys are available at different times.

ABC

represents the spaces where the three-letter abbreviations

for the variable labels are displayed.

to turn the calculator on or off.

4 BA II PLUS™ Calculator

Display Indicators

Indicator Meaning

2nd

INV

HYP

COMPUTE

ENTER

SET

# $

DEL

INS

BGN

RAD





The calculator will access the second function of the next key pressed.

The calculator will access the inverse function of the next key or key sequence pressed.

The calculator will access the hyperbolic function of the next key or key sequence pressed.

You can compute a value for the displayed variable by pressing

You can enter a value for the displayed variable by keying in a value and pressing

The displayed variable is a setting that you can change by pressing & V.

You can press " to view previous variables in the current worksheet or # to view subsequent variables.

You can press & W to delete a cash flow or a statistical data point.

You can press & X to insert a cash flow or a statistical data point.

You have selected beginning-of-period payments for TVM calculations. If the in the TVM worksheet, end-of-period payments are selected.

The calculator is in the radian mode. All angle values are displayed and must be entered as radians. If the not displayed, all angle values are displayed and must be entered as degrees.

The displayed value has been entered in a worksheet. After a computation, the  indicators are cleared.

The displayed value has been computed in a worksheet. If you make a change to the worksheet that invalidates a previously computed value, the  indicator is removed from that value.

The displayed value is “assigned” to the variable represented by the label in the display. If the = indicator is not displayed, the displayed value is not assigned to the displayed variable.

The displayed value is negative.

indicator is not displayed when you are

BGN

RAD

indicator is

1: Overview of Calculator Operations 5

Setting Calculator Formats

You can set formats for five aspects of the calculator.

Format Options Default

Number of decimal places

Angle units degrees (

Dates

Number separatorsUS format 1,000.00 or

Calculation method

The sections that follow give details about each format and instructions for changing the format.

Number of Decimal Places

The calculator internally stores numeric values to an accuracy of 13 digits. You can specify the number of decimal places to be displayed. The default is two decimal places, rounding if necessary.

The decimal format setting affects only the display; it does not round the internal value, except for amortization and depreciation results. To round the internal value, use the round function.

Examples in this guidebook assume a setting of two decimal

Note:

places. Other settings may show different results.

0 – 9 (floating-decimal format = 9)

format mm-dd-yyyy or

(European) format dd-mm-yyyy

(European) format 1.000,00

Chn

(chain) or

Operating System) calculations

DEG

) or radians (

AOS

Eur

™

(Algebraic

places

RAD)DEG

(degrees)

Chn

format

(chain)

6 BA II PLUS™ Calculator

Procedure: Changing the Number of Decimal Places

쐃

Press &

is displayed with the current

DEC=

decimal-place setting.

쐇

Enter the number of decimal places to be displayed (0 through 9) and press

. To specify a floating-decimal

format, enter 9.

쐋

Choose one of the following to continue:

To continue setting formats, press #.

To return to the standard-calculator mode, press &

To access a worksheet, press the appropriate worksheet key or key sequence.

Angle Unit Format

You can enter and display angle values in either degrees or radians. You can specify which method you require.

The default setting for angle units is degrees. There is no display indicator for this setting. However, if you specify radians, the

indicator is displayed in the upper right-hand

RAD

corner of the display.

Procedure: Changing the Angle Unit Format

쐃

If necessary, press &

| #

The most recently selected angle-units format is displayed, either

쐇

Press & V repeatedly to set either

쐋

Choose one of the following to continue:

To continue setting formats, press # or ".

To return to the standard-calculator mode, press &

To access a worksheet, press the appropriate worksheet

DEG

RAD

DEG

RAD

key or key sequence.

1: Overview of Calculator Operations 7

Date Format

Both the Bond and Date worksheets use dates. You can select either the US or the European display format. The default setting for dates is the US format.

US format (US): Month Day Year

12 - 31 - 1990

European format (

EUR

): Day Month Year

31 - 12 - 1990

Procedure: Changing the Date Format

쐃

If necessary, press &

| # #

The most recently selected date format is displayed, either

쐇

Press & V repeatedly to select either

쐋

Choose one of the following to continue:

To continue setting formats, press # or ".

To return to the standard-calculator mode, press &

To access a worksheet, press the appropriate worksheet

EUR

key or key sequence.

8 BA II PLUS™ Calculator

Separator Format

You can select either the US or the European format for the display of separators in numbers. The default setting for separators is the US format.

US and UK format (US):

European format (

EUR

1,000.00

1.000,00

Procedure: Changing the Separator Format

쐃

If necessary, press &

| # # #

The most recently selected separator format is displayed, either

쐇

Press & V repeatedly to select either

쐋

Choose one of the following to continue:

EUR

To continue setting formats, press # or ". To return to the standard-calculator mode, press & To access a worksheet, press the appropriate worksheet

key or key sequence.

1: Overview of Calculator Operations 9

Calculation Method

You can select either the chain calculation method or the

AOS

(algebraic operating system) calculation method. The default setting for calculation method is chain (

When the calculation method is set to

Chn

(chain), the

Chn

calculator solves problems in the order that you enter them. This calculation method is used in most financial calculators.

For example, in

when you enter 3 H 2 < 4 N, the answer is

Chn

20 (3 + 2 = 5, 5 * 4 = 20).

When the calculation method is set to

(the algebraic

AOS

operating system), the calculator solves problems according to the standard rules of algebraic hierarchy. In AOS, multiplication and division operations are completed before addition and subtraction operations.

This calculation method is used in most scientific calculators.

For example, in

when you enter 3 H 2 < 4 N, the answer

AOS

is 11 (2 Q 4 = 8; 3 + 9 = 11). The multiplication operation is completed before the addition operation.

Procedure: Changing the Calculation Method

쐃

If necessary, press &

| # # # #

The most recently selected calculation method is displayed, either

(Chain) or

Chn

(Algebraic Operating System).

AOS

쐇

Press & V repeatedly to select either

쐋

Choose one of the following to continue:

To continue setting formats, press # or ".

To return to the standard-calculator mode, press &

To access a worksheet, press the appropriate worksheet

Chn

AOS

key or key sequence.

10 BA II PLUS™ Calculator

Clearing the Calculator

To clear . . . Keystrokes

. . . one character at a time from the display (including decimal points).

. . . an incorrect entry, an error condition, or an error message from the display.

. . . out of a worksheet and return to standard-calculator mode.

. . . all pending operations in the standard-calculator mode and display zero.

. . . in a worksheet, a value you have keyed into the display but not yet entered as a variable value. The previous value returns.

. . . any calculation you have started but have not yet completed.

. . . the TVM worksheet and return the values in the worksheet to a known starting point.

. . . any worksheet (not TVM) and return the values in the worksheet to a known starting point. Also returns you to the first variable in the worksheet.

. . . all 10 memories.

. . . one of the 10 memories without affecting the others.

& U

P P

& U & ^

& z

& { & z

Q D

key for the number of the memory (0–9)

and the

* When you are in a worksheet, press P repeatedly to return to standard-calculator

mode.

1: Overview of Calculator Operations 11

Correcting Entry Errors

If you enter an incorrect number but have not yet pressed an operation key (such as H or 4), you can correct the number without clearing the calculation.

•

Remove the last digit or decimal point from a number you have keyed in by pressing the backspace key * and then enter the correct digit.

•

Erase the entire number by pressing P once, then key in the correct number and continue with your calculation.

Pressing

Note:

pressed an operation key clears any calculation in progress.

Example: Correcting an Entry Error

Compute 3 Q 1234.56, but accidentally enter .86 instead of .56. Use * to correct the mistake, and then continue with your calculation.

Procedure Keystrokes Display

Clear the calculator.

Begin the expression.

Enter the second number incorrectly.

Erase the 86.

Complete the number correctly.

Compute the result.

to correct a numeric entry immediately after you have

& U

1234.86 1,234.86

* *

56 1,234.56

0.00

3.00

1,234.

3,703.68

12 BA II PLUS™ Calculator

Math Operations

When the calculation method is set to chain (

), mathematical

Chn

expressions, such as 3 + 2 Q 4, are evaluated in the order that you enter them. The N key completes an operation and displays the result.

Operation Example Keystrokes Display

Addition 6 + 4

Subtraction 6 N 4

Multiplication 6 Q 4

Division 6 P 4

Universal power 3

1.25

Parentheses 7 Q (3 + 5)

Percent 4% of $453

Percent ratio 14 is what percent of

25?

Percent add-on $498 + 7% sales tax

Percent discount $69.99 N 10% discount

Square 6.3

Combinations n = 52, r = 5

Permutations n = 8, r = 3

H 4

B 4

< 4

6 4

1.25

< 4 2

6 25 2

H 7

;

< 9 3 H 5 :

453 14

498

69.99

B 10

6.3 52

& s 5

& m 3

10.00

2.00

24.00

1.50

3.95

56.00

18.12

56.00

34.86

532.86

7.00

62.99

39.69

2,598,960.00

336.00

1: Overview of Calculator Operations 13

Math Operations (cont.)

Some operations are performed immediately and do not require that you press N.

Operation Example Keystrokes Display

Square root

15.5

Reciprocal 1/3.2

Factorial 5!

Natural logarithm ln 203.45

Natural antilogarithm e

.69315

Round Round 2 P 3 to the set

decimal format

Random number* Generate random

number

Store “seed” value

Sine** sin(11.54°)

Cosine** cos(120°)

Tangent** tan(76°)

Arcsine** sin

Arccosine** cos

Arctangent** tan

(.2)

(-.5)

(4)

Hyperbolic sine sinh(.5)

Hyperbolic cosine cosh(.5)

Hyperbolic tangent tanh(.5)

Hyperbolic arcsine sinh

Hyperbolic arccosine cosh

Hyperbolic arctangent tanh

(5)

(.5)

15.5

3.2

203.45

.69315

6 3 N &

& a

D & a

11.54 120 76

S 8

& c

& c 8

3.94

0.31

120.00

5.32

2.00

0.67

0.86

0.20

0.50

4.01

11.54

120.00

75.96

0.52

1.13

0.46

2.31

2.29

0.55

* The random number generated when you press & a may not be the one shown

here.

** Angles are interpreted according to the current setting for angle units (degrees or

radians). These examples show angles in degrees.

14 BA II PLUS™ Calculator

More on Selected Math Operations

Universal Power

;

lets you raise a positive number to any power (2 example). However, you can raise a negative number only to an integer power or the reciprocal of an odd number. In either case, the power can be either positive or negative.

Parentheses

Parentheses let you control the order in which a numeric expression is evaluated. The portion of an expression enclosed in parentheses is evaluated separately. Up to 15 levels of parentheses are available, with up to 8 pending operations.

If an expression would end in a series of closed parentheses you can omit pressing :. Press N to close all of the parentheses automatically, evaluate the expression, and display the end result. To see intermediate results, press : repeatedly.

Factorial

To compute the factorial of a displayed number, press & g. The number must be a positive integer 69.

or 2

(1/3)

, for

Random Numbers

To generate a random real number between zero and one (0<x<1) from a uniform distribution, press &

To repeat a sequence of random numbers, you must first store a “seed” value in the random number generator. To store a seed value, key in an integer greater than zero and press D

. This lets you recreate experiments by generating the

same series of random numbers.

Combinations

& s

computes the number of combinations of n items taken

r at a time.

nCr

1: Overview of Calculator Operations 15

nr r

−×

()

Permutations

& m

computes the number of permutations of n items taken

r at a time.

−

()

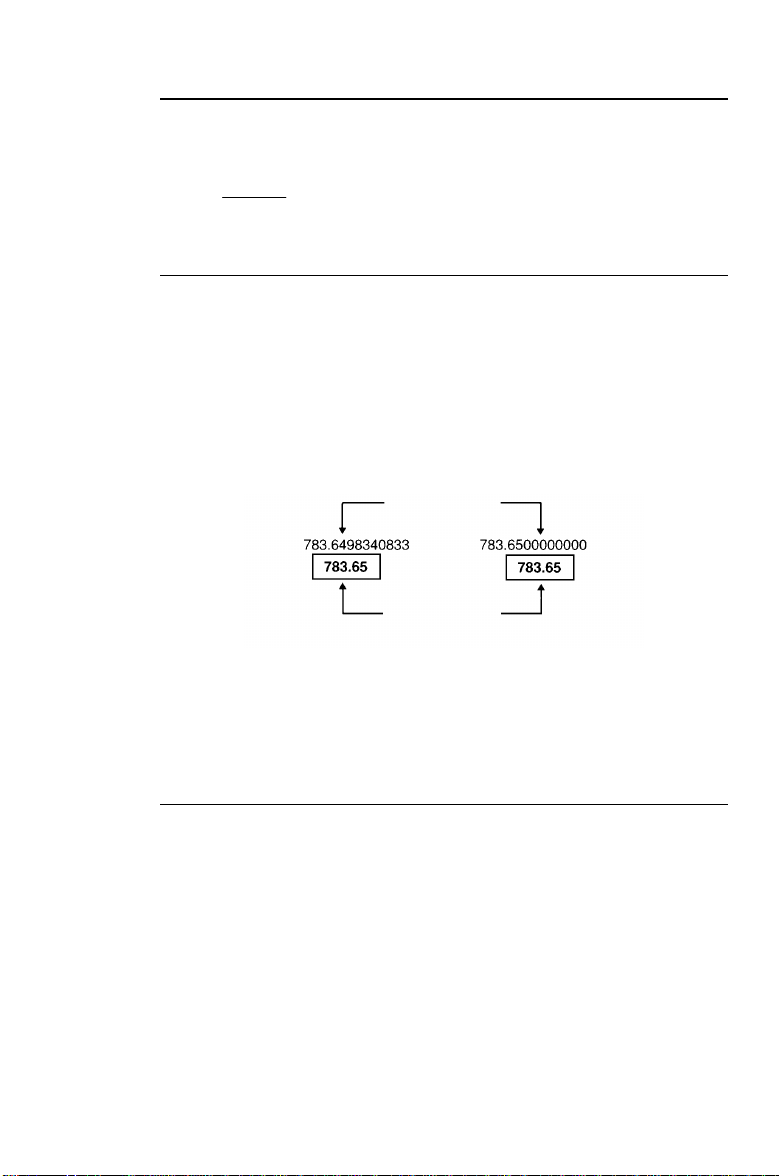
Rounding

The round function is useful when you need to perform a calculation using the displayed form of a number rather than the unrounded value that the calculator stores internally. The decimal format setting does not round the calculator’s internally stored value, only the displayed value.

& o

lets you change the internal value to match its

displayed form.

Internal value

Displayed value

Before rounding

After rounding

For example, in the Bond worksheet, you might want to round a computed selling price to the nearest penny (two decimal places) before continuing with your calculation.

Scientific Notation

If you compute a value that is larger or smaller than the calculator can display in standard decimal format, the value is displayed in scientific notation. A value in scientific notation is displayed as a base value (sometimes called a mantissa), followed by a blank space, followed by an exponent.

You cannot directly enter a number in scientific notation, but when the AOS calculation method is selected, you can use the

;

key to enter a number in scientific notation.

For example, for 3 Q 10

16 BA II PLUS™ Calculator

, key in 3 <

;

Memory Operations

Your calculator always has 10 memories available.

•

The memories can hold any numeric value within the range of the calculator.

•

The memories are numbered access each memory using a single keystroke.

Clearing Memory

There are two ways to clear memory.

•

Storing a zero in an individual memory clears the memory (shown in “Memory Examples” below).

through M9. This lets you

•

To clear all of the memories simultaneously, press &

& z

to clear the Memory worksheet.

{

Storing to Memory

To store a displayed value to a memory (0 through 9), press and a digit key 0 through 9.

•

Any previous value in that memory is replaced by the new value.

•

When you turn the calculator off, the Constant Memory feature retains all stored values.

Recalling from Memory

To recall a number stored in a memory to the display, press and a digit key 0 through 9. The number is displayed, but also remains in memory.

Memory Examples

Function Keystrokes

Store a zero in memory 4 (clear memory 4).

Store 14.95 in memory 3.

Recall a value from memory 7.

14.95

1: Overview of Calculator Operations 17

Memory Arithmetic

Memory arithmetic allows you to perform a calculation on a stored value and then store the result with a single operation.

•

Memory arithmetic does not change the displayed value, only the value in the affected memory.

•

Memory arithmetic does not complete any calculation in progress.

The table below shows the memory arithmetic functions available with the calculator. In each case, the result is stored in the specified memory.

These examples assume that a value is already in the display.

Function Keystrokes

Add the value in the display to the value in

D H

D B

D <

D 6

D ;

memory 9.

Subtract the value in the display from the value in memory 3.

Multiply the value in memory 0 by the value in the display.

Divide the value in memory 5 by the value in the display.

Raise the value in memory 4 to the power of the displayed value.

18 BA II PLUS™ Calculator

Calculations Using Constants

& `

stores a number and an operation for use in repetitive

calculations.

After you store the constant, you can use it in subsequent calculations by entering a new value and pressing N. The constant is cleared when you press any key other than a numeric entry key or N.

Example: Multiply 3, 7, and 45 by 8.

Procedure Keystrokes Display

Clear calculator.

Begin first calculation.

Store Q 8 in the constant register.

Compute 7 Q 8.

Compute 45 Q 8.

Keystrokes for Constant Calculations

The following table shows how to set the constant for addition, subtraction, multiplication, division, universal power, and percent. The constant value is denoted by c.

Keystrokes Function

H & ` c

B & ` c

< & ` c

6 & ` c

; & ` c

H & ` c 2 NAdds c% of each subsequent entry to that entry.

B & ` c 2 NSubtracts c% of each subsequent entry from that

Adds c to each subsequent entry.

Subtracts c from each subsequent entry.

Multiplies each subsequent entry by c.

Divides each subsequent entry by c.

Raises each subsequent entry to the power of c.

entry.

& U

3 3

< & `

0.00

24.00

56.00

360.00

Repeat constant calculations with n N.

1: Overview of Calculator Operations 19

Last Answer Feature

To display the last answer, press & x. If your current equation calls for the last answer repeatedly, you can retrieve the value of

You can use the last answer feature to copy a value:

•

From one place to another within the same worksheet.

•

From one worksheet to another.

•

From a worksheet to the standard-calculator mode.

•

From the standard-calculator mode to a worksheet.

is updated when:

ANS

more than once.

ANS

•

You enter a value by pressing

•

You compute a value by pressing %.

•

You press N to complete a calculation.

•

The calculator automatically computes a value.

Example: Last Answer

Procedure Keystrokes Display

Clear the calculator.

Enter a calculation and complete it with the equal key.

Begin a new calculation.

Recall the last answer.

Complete the calculation.

& U

H 1

;

& x

0.00

4.00

2.00

4.00

16.00

20 BA II PLUS™ Calculator

Using Worksheets: Tools for Financial Solutions

What Is a Worksheet?

Each worksheet is designed as a framework for a set of variables. The formulas that define the relationships between the variables, though not visible, are built into each worksheet.

•

Each worksheet is designed to solve specific types of problems such as time-value-of money, cash-flow, bond, or depreciation problems.

•

You access the Time-Value-of-Money (TVM) worksheet variables with the five TVM keys on the third row of the keyboard (,, -, ., /, 0).

•

All other worksheets are prompted. For example, the

key sequence lets you access the variables in the

prompted worksheet to amortization calculations.

•

You select settings for some variables, assign known values to other variables, and compute values for the unknown variables.

•

Variable labels are displayed one at a time, along with any value previously assigned to the variable.

•

By changing the values of the variables, you can quickly perform “what if” calculations.

•

Generally, each worksheet is independent of the others; operations you perform in one worksheet do not affect variables in other worksheets.

•

All current worksheet data is retained when you stop using a worksheet, even if you turn off the calculator.

1: Overview of Calculator Operations 21

Types of Worksheets

The calculator has two modes.

•

In the standard-calculator mode, you can perform standard math operations and compute TVM values (

•

In the prompted worksheet modes, you are guided through specialized tasks such as amortization calculations and cash-flow analyses.

Worksheet Variables

TVM Variables

You access the five time-value-of-money variables with the five TVM keys on the third row of the keyboard. You can access other parts of the TVM worksheet and other TVM functions by pressing the & key.

Z[\ ]^ ,-. /0

You can enter values using the five basic TVM keys at any time, even when you are in another worksheet. However, to compute TVM values or clear the TVM worksheet, you must be in the standard-calculator mode. To return to the standard-calculator mode, press &

N, I/V, PV, PMT

22 BA II PLUS™ Calculator

Prompted-worksheet Variables

To access the column of variables within a prompted worksheet (or portion of a prompted worksheet), press the appropriate worksheet key or key sequence.

For example, to access the amortization variables

PRN,

and

(first payment in a range, last payment in a range,

INT

remaining balance, principal, and interest), press &

P1, P2, BAL

This is the prompted worksheet for amortization calculations.

Press # and " to move to the next or previous variable in a prompted worksheet. Different variable labels and values are displayed. Indicators in the display prompt you to select settings, enter values, or compute results.

To return to standard-calculator mode, press &

There are five types of worksheet variables:

•

Enter-only

•

Compute-only

•

Automatic-compute

•

Enter-or-compute

•

Settings

Enter-Only Variables

You cannot compute a value for enter-only variables. Values may be limited to a specified range. An enter-only variable can be:

•

Entered directly from the keyboard.

•

The result of a math calculation.

•

Recalled from memory.

•

Obtained from another worksheet using the last answer feature.

When you access an enter-only variable, the variable label and the

indicator are displayed. The

ENTER

indicator also reminds you that once you have keyed a value into the display, you must press

to assign that value to the variable. An = sign is displayed between the label and the value when the value has been assigned to the variable.

1: Overview of Calculator Operations 23

Compute-Only Variables

For compute-only variables, you compute values by displaying the appropriate label and pressing %; you cannot enter a value for this type of variable.

When you access a compute-only variable, the variable label and the

COMPUTE

indicator are displayed. This indicator reminds you to press % to compute a value for the displayed variable. An = sign is displayed between the label and the value when the value has been assigned to the variable.

Automatic-Compute Variables

For automatic-compute variables, you do not have to press %; a value is automatically computed and displayed when you access the variable by pressing # or ". After a value is automatically computed, an = sign is displayed between the label and the value.

Enter-or-Compute Variables in the TVM Worksheet

The five variables in the TVM worksheet (N,

) are enter-or-compute variables. It is not necessary to be in

I/Y, PV, PMT

, and

the standard-calculator mode when you enter values for these variables. However, you must be in the standard-calculator mode to compute values for these variables.

•

To enter a TVM value, key a value into the display and press the appropriate variable key.

•

To compute a TVM value, press % and the appropriate variable key.

24 BA II PLUS™ Calculator

Enter-or-Compute Variables in Prompted Worksheets

Some prompted worksheets contain variables that you can either enter or compute. When you access an enter-or-compute variable, the variable label is displayed along with both the

and

ENTER

•

The

COMPUTE

indicator reminds you that if you key in a value

ENTER

for the variable, you must press

indicators.

to assign the value to

the variable.

•

The

COMPUTE

indicator reminds you that if you want to

compute a value for the variable, you must press %.

After you press

or %, an = sign is displayed between

the label and the value.

Selecting Worksheet Settings

Most prompted worksheets have variables with two or more options (settings). When you access a setting, the variable label and the

indicator are displayed. The label that is displayed

SET

indicates the current setting.

Press & V repeatedly to cycle through the options to the one you want.

Indicators

When you enter a value for a variable, the calculator displays . When you compute a value for a variable, the calculator displays . If you make a change to a worksheet that invalidates previously entered or computed values, the  and  indicators are removed.

1: Overview of Calculator Operations 25

Clearing Worksheets and Setting Defaults

Label

& }

N I/Y PV PMT FV P/Y C/Y END /

BGN P1 P2 BAL PRN INT

Note: & } US number separators, CHN calculations).

12 12

END END

& ^& [

also sets the calculator formats (2 decimal places, DEG, US dates,

& z

& ]

& z

& \

& z

26 BA II PLUS™ Calculator

Time-Value-of-Money and

Amortization Worksheets

The Time-Value-of-Money and Amortization worksheets are useful in applications where the cash flows are equal, evenly spaced, and either all inflows or all outflows. They help you solve problems involving annuities, loans, mortgages, leases, and savings. You can also generate an amortization schedule.

Press # and " to move through each set of variables.

Z[\]^

,-./0

2: TVM and Amortization Worksheets 27

TVM and Amortization Worksheet Labels

Keys Label Meaning

& [ #

& ] & V

& \ # # # #

N I/Y PV PMT FV P/Y C/Y

END BGN P1 P2 BAL PRN INT

Notes about the TVM and Amortization Worksheets

Number of periods Enter/compute

Interest rate per year Enter/compute

Present value Enter/compute

Payment Enter/compute

Future value Enter/compute

Number of payments per year Enter-only

Number of compounding periods per year

End-of-period payments Setting

Beginning-of-period payments Setting

Starting payment Enter-only

Ending payment Enter-only

Balance Auto-compute

Principal paid Auto-compute

Interest paid Auto-compute

Type of Variable

Enter-only

& } !

♦

C/Y=12; END

& ^

♦

affect

P/Y, C/Y

& [ & z

♦

& ] & z

♦

& \ & z

♦

INT=0

When solving a problem using only four of the five TVM

♦

sets

(not

BGN

sets

N, I/Y, PV, PMT

, or the

N=0, I/Y=0, PV=0, PMT=0, FV=0; P/Y=12

);

P1=1, P2=1; BAL=0, PRN=0, INT=0

, and FV to zero; does not

BGN/END

sets

setting.

and

P/Y=12

(not

END

P1=1, P2=1, BAL=0, PRN=0

BGN

C/Y=12

, and

variables, make sure the unused variable is zero.

28 BA II PLUS™ Calculator

Notes about TVM and Amortization Worksheets (cont.)

♦

Enter values for

PV, PMT

, and FV as negative if they are outflows (cash paid out) or as positive if they are inflows (cash received). To enter a negative value, press S after entering the number.

♦

Enter automatically converts values for

♦

When you enter a value for automatically entered for

♦

The

as the nominal interest rate. The TVM worksheet

I/Y

to a “per period” rate based on the

I/Y

P/Y

END/BGN

and

setting lets you specify whether the transaction

C/Y

, the same value is

P/Y

. (You can change

C/Y

is an ordinary annuity or an annuity due.

In ordinary annuities, the payments occur at the end of each payment period. Most loans are in this category. For ordinary annuities, select

In annuities due, payments occur at the beginning of each

END

payment period. Most leases are in this category. For annuities due, select

♦

Pressing % when

or P2 is displayed updates P1 and P2 to

BGN

represent the next range of payments.

♦

A computed value for

after a specified number of

BAL

payments may be slightly different than a computed value for

after the same number of payments.

When solving for the

value rounded to the number of decimal places

PMT

BAL, PRN

, and

, the calculator uses

INT

specified by the decimal format.

When solving for value for

2: TVM and Amortization Worksheets 29

PMT

, the calculator uses the unrounded

Entering, Recalling, and Computing TVM Values

You enter a TVM value by keying in a value and pressing the appropriate TVM key (,, -, ., /, or 0). The value is stored in the TVM variable (

N, I/Y, PV, PMT

, or FV).

You recall a TVM value to the display by pressing J and the TVM key.

When you enter or recall a value for any of the five TVM variables (

N, I/Y, PV, PMT

, or FV), you can be in either standard calculator mode or a worksheet mode. The display responds differently according to the mode you are in.

•

In standard calculator mode (accessed by pressing

), the variable label, the = sign, and the value you

entered or recalled are displayed.

•

In worksheet mode, only the value you entered or recalled is displayed. Any label previously in the display remains.

To compute a TVM value, press % and the appropriate TVM key. When you compute a TVM value, you must be in standard calculator mode. Press &

to return to standard

calculator mode.

Entering a Value for N Using [xP/Y]

You can use &

to enter a value for N. Pressing &

automatically multiplies a displayed number by the value stored in the

variable (number of payments per year).

P/Y

By entering the number of years (for example, 30) and pressing

& Z

, you can compute the number of payments required to pay off an annuity. Press , to enter that value as the number of payments in a TVM calculation.

30 BA II PLUS™ Calculator

Compound Interest

Many lending institutions add the interest you earn to the principal. The interest you earn from the previous compounding period becomes part of the principal for the next compounding period. Compound interest enables you to earn a greater amount of interest on your initial investment.

In order to earn compound interest, the interest must remain with the principal. For example, if you invest $100 at an annual interest rate of 10% compounded annually, you earn $10 interest after one year. At the end of the second year, the interest is calculated on $110 ($100 principal plus $10 accumulated interest), so you earn $11 in the second year. As additional interest accumulates, your interest earnings increase each year.

2: TVM and Amortization Worksheets 31

Time-Line Diagrams

A time-line diagram can help you visualize cash flows by showing the amounts paid or received (cash outflows or cash inflows) at various points in time.

•

Cash flows received are shown with arrows pointing up, as with the loan amount at the left.

•

Cash flows invested have arrows pointing down, as with the 35 regular payments and the balloon payment at the right.

Loan amount 23,000 Enter inflows as positive.

Time

- 400- 400 Pmt 2 Pmt 3 Pmt 34 Pmt 35

400- 400

15,000

Balloon

Pmt

Entering Inflows and Outflows

The calculator follows the established convention of treating inflows of cash (cash received) as positive and outflows of cash (cash paid out) as negative.

•

You must enter inflows as positive values and outflows as negative values.

•

The calculator displays computed inflows as positive values and computed outflows as negative values.

32 BA II PLUS™ Calculator

Procedure: Using the TVM Worksheet

The worksheet stores the values and settings you enter until you clear the worksheet or change the values or settings. Therefore, you may not need to do all the steps in the procedure every time you work a TVM problem.

쐃

Press & (

N=0, I/Y=0, PV=0, PMT=0, FV=0; P/Y=12, C/Y=12; END; P1=1

P2=1; BAL=0, PRN=0, INT=0

쐇

P/Y

key in the number of payments per year, and press

쐋

Press #.

} !

to reset all variables to their defaults

(payments per year) should not be 12, press & [,

(compounding periods per year) and its

C/Y=

current value are displayed. When you enter a value for the same value is automatically entered for

C/Y

. If the

compounding periods per year is different than the

END

is the

payments per year, key in the value and press

쐏

If you want beginning-of-period payments ( default setting), press & ] & V.

If beginning-of-period payments are selected, the

BGN

indicator is displayed; no indicator is displayed for end-ofperiod payments.

쐄

Press &

쐂

Enter values for the four known variables. Key in each value

to return to standard calculator mode.

and press the appropriate key (,, -, ., /, or 0). The value of the unknown variable is 0.

쐆

Press % and the key for the unknown variable to compute its value.

P/Y

2: TVM and Amortization Worksheets 33

Procedure: Generating an Amortization Schedule

The worksheet for amortization calculations uses the values you entered and computed in the TVM worksheet to compute amortization data. The procedures on these pages give you two ways to generate an amortization schedule.

쐃

Press & (

N=0, I/Y=0, PV=0, PMT=0, FV=0; P/Y=12, C/Y=12; END; P1=1

P2=1; BAL=0, PRN=0, INT=0

쐇

Press &

P1=

쐋

Specify the range of payments.

To enter a value for key in a value and press

To enter a value for press #, enter a value, and press

쐏

Press # repeatedly to display the automatically computed

} !

to reset all variables to their defaults

and its current value are displayed.

(the first payment in the range),

(the last payment in the range),

values:

쐄

Press &

— the remaining balance after payment

BAL

— the principal

PRN

— the interest paid over the specified range

INT

or, if

is displayed, press # to display

INT

again.

쐂

Repeat steps 2 and 3 for each range of payments to generate an amortization schedule.

34 BA II PLUS™ Calculator

Procedure: Automatically Generating a Schedule

After you enter the initial values for P1 and P2, as described above, you can automatically compute an amortization schedule.

쐃

Press &

P1=

쐇

Press %. This automatically updates both

or, if

INT

and its current value.

is displayed, press # to display

and P2 to

represent the next range of payments.

The calculator computes the next range of payments using the same number of periods as in the previous range of payments. For example, if the previous range was 1 through 12 (12 payments), pressing % updates the range to 13 through 24 (12 payments).

쐋

Press # to display

If you pressed % when for

is automatically displayed. (You can still enter a

new value for

If you did not press % when press % when

and P2 for the next range of payments.

쐏

Press # as needed to display the automatically computed values for

쐄

Repeat steps 1 through 4 until the schedule is complete.

BAL, PRN

was displayed, a new value

, if necessary.)

was displayed, you can

is displayed to enter values for both

, and

for the next range of payments.

INT

2: TVM and Amortization Worksheets 35

Basic Loan Calculations—Interest

Example: Interest Rate

You have a 30-year mortgage for $75,000 and make payments each month of $576.69. What is the interest rate of your mortgage?

Procedure Keystrokes Display

Set all variables to defaults.

Enter number of payments using payment multiplier.

Enter loan amount.

Enter payment amount.

Compute interest rate.

The interest rate is 8.5% per year.

& } !

& Z

75000

576.69

% -

RST 0.00

N= 360.00 PV= 75,000.00 PMT= -576.69 I/Y= 8.50





36 BA II PLUS™ Calculator

Basic Loan Calculations—Payments

Example: Monthly Payment

You are considering a 30-year mortgage at 8.5% for $75,000.

How much would the monthly payment be?

Procedure Keystrokes Display

Set all variables to defaults.

Enter number of payments using payment multiplier.

Enter interest rate.

Enter loan amount.

Compute payment.

The monthly payment would be $576.69.

Example: Quarterly Payment

(continued from previous example)

Your mortgage company also offers an option for a quarterly mortgage with quarterly compounding.

How much would your quarterly payment be? (You do not need to enter the loan amount or the interest rate. The compounding periods is automatically reset to equal the payments periods.)

& } !

& Z

8.5

75000

% /

RST 0.00

N= 360.00 I/Y= 8.50 PV= 75,000.00 PMT= -576.69





Procedure Keystrokes Display

Set payments per year to 4.

Return to calculator mode.

Enter number of payments using payment multiplier.

Compute payment.

& [

& U

% /

& Z

P/Y= 4.00

0.00

N= 120.00 PMT= -1,732.71

The quarterly payment would be $1,732.71.

2: TVM and Amortization Worksheets 37





Future Value of Savings

Example: Future Value of Savings

You have opened a savings account with $5,000. The bank pays 5%, compounded at the end of each year. What is the future value of the account after 20 years?

Procedure Keystrokes Display

Set all variables to defaults.

Set payments per year to 1.

Return to calculator mode.

Enter number of payments.

Enter interest rate.

Enter beginning balance.

Compute future value.

The future value is $13,266.49.

& } !

& [

& U

5 5000

% 0

RST 0.00 P/Y= 1.00

0.00 N= 20.00 I/Y= 5.00 PV= -5,000.00 FV= 13,266.49





38 BA II PLUS™ Calculator

Present Value of Savings

Example: Future Value of Savings

You are opening a savings account that you want to be worth $10,000 in 20 years. The bank pays 5%, compounded at the end of each year. How much do you need to deposit now?

Procedure Keystrokes Display

Set all variables to defaults.

Set payments per year to 1.

Return to calculator mode.

Enter number of payments.

Enter interest rate.

Enter final balance.

Compute future value.

The present value is $3,768.89. This is the amount you need to deposit.

& } !

& [

& U

5 10000

% .

RST 0.00 P/Y= 1.00

0.00 N= 20.00 I/Y= 5.00 FV= 10,000.00 PV= -3,768.89





2: TVM and Amortization Worksheets 39

Present Value in Present-Value Annuities

Example: Present Value of Cost Savings

The Furros Company purchased a machine that provides annual savings of $20,000 per year for the next 10 years. Using an annual discount rate of 10%, compute the present value of the savings using an ordinary annuity and an annuity due.

•

For a present value ordinary annuity:

PV = ?

$20,000 $20,000 $20,000

. . .

0 1 9 N = 10

I/Y = 10

•

For a present value annuity due for a leasing agreement:

PV = ?

$20,000 $20,000 $20,000

. . .

0 1 9 N = 10

I/Y = 10

40 BA II PLUS™ Calculator

Example: Present Value of Cost Savings (cont.)

Procedure Keystrokes Display

Set all variables to defaults.

Set payments per year to 1.

Return to calculator mode.

Enter number of payments.

& } !

& [

& U

RST 0.00 P/Y= 1.00

0.00

N= 10.00

Enter interest rate per payment period.

Enter payment.

10 20000

I/Y= 10.00 PMT= -20,000.00

Compute PV for an ordinary annuity.

Set beginning-of-period payments.

Return to calculator mode.

Compute PV for annuity due.

% .

& ] & V

& U

% .

PV= 122,891.34

BGN

0.00

PV= 135,180.48

The present value is $122,891.34 with an ordinary annuity and $135,180.48 with an annuity due.



…

2: TVM and Amortization Worksheets 41

Perpetual Annuities

A perpetual annuity consists of equal payments that continue indefinitely. An example of a perpetual annuity is a preferred stock that yields a constant dollar dividend.

These time-line diagrams represent a perpetual annuity as an ordinary annuity and as an annuity due.

•

For a perpetual ordinary annuity:

PMT PMT

01 2

•

For a perpetual annuity due:

PMT PMT PMT

01 2

Because the term (1 + I/Y / 100) equations approaches zero as N becomes larger, you can use the following equations to solve for the present value of a perpetual annuity.

. . . to infinity

in the present value annuity

•

For a perpetual ordinary annuity:

(

I/Y

PMT

/ 100)

(

I/Y

PMT

/ 100)

PV =

•

For a perpetual annuity due:

PV = PMT +

42 BA II PLUS™ Calculator

Example: Present Value of Perpetual Annuities

The Land of OZ has issued perpetual bonds for replacing bricks in their highway system. The bonds pay $110 per $1000 bond. You plan to purchase the bonds if you can earn 15% annually. What price should you pay for the bonds?

Procedure Keystrokes Display

Clear.

Calculate PV for a perpetual ordinary annuity.

Calculate PV for a perpetual annuity due.

& U P P

110

6 15 2

110

0.00

733.33

843.33

You should pay $733.33 for a perpetual ordinary annuity and $843.33 for a perpetual annuity due.

2: TVM and Amortization Worksheets 43

Variable Cash Flows

In annuities, all payments are equal. In variable cash flows, however, the payments are unequal. You can solve for the present value of variable cash flows by treating the cash flows as a series of compound interest payments.

The present value of variable cash flows is the value of cash flows occurring at the end of each payment period discounted back to the beginning of the first cash flow period (time zero).

PV = ?

01 N

Example: Present Value of Annual Savings

The ABC Company is purchasing a machine that will save the following end-of-year amounts.

Year 1234

Amount $5000 $7000 $8000 $10000

Assuming a discount rate of 10%, does the present value of the cash flows exceed the original cost of $23,000?

. . .

j-1

PV = ?

$5,000 $7,000 $8,000 $10,000

0 1 2 3 N=4

44 BA II PLUS™ Calculator

Example: Present Value of Annual Savings

Procedure Keystrokes Display

Set all variables to defaults.

Set payments per year to 1.

Return to calculator mode.

Enter interest rate per cash flow period.

Enter 1st cash flow.

Enter period number of 1st cash flow.

Compute present value of 1st cash flow.

Store in M1.

Enter 2nd cash flow.

Enter period number.

Compute present value of 2nd cash flow.

Sum to memory.

Enter 3rd cash flow.

Enter period number.

Compute present value of 3rd cash flow.

Sum to memory.

Enter 4th cash flow.

Enter period number.

Compute present value of 4th cash flow.

Sum to memory.

Recall total present value.

Subtract original cost.

& } !

& [

RST 0.00 P/Y= 1.00

& U

5000

% .

7000

% .

D H

8000

% .

D H

10000

% .

D H

1 23,171.23

23000

I/Y= 10.00 FV= -5,000.00

N= 1.00

PV= 4,545.45

FV= -7,000.00 N= 2.00

PV= 5,785.12

FV= -8,000.00 N= 3.00

PV= 6,010.52

FV= -10,000.00 N= 4.00

PV= 6,830.13

0.00

171.23



…



…



…



…

The present value of the cash flows is $23,171.23, which exceeds the machine’s cost by $171.23. This is a profitable investment for the company.

2: TVM and Amortization Worksheets 45

Lease-or-Buy Decision

Your business is considering getting a new computer server. If you lease, you would pay $36,000 per year for five years at the first of each year. You could buy it for $125,000. The server is expected to save the company $46,000 per year. It will have no resale value at the end of the five years. The company can borrow at 15% annual interest. You require a 20% annual return on projects and investments of this kind. Ignoring tax effects, should you acquire it, and if so, should you lease or purchase it?

Example: Present Value of Cost Savings

Procedure Keystrokes Display

Set all variables to defaults.

Set payments per year to 1.

Return to calculator mode.

Enter number of periods.

Enter required annual return rate.

Enter annual savings.

Compute present value of savings.

& } !

& [

& U

20 46000

% .

RST 0.00 P/Y= 1.00

0.00

N= 5.00

I/Y= 20.00 PMT= -46,000.00

PV= 137,568.16



…

The present value of the annual savings exceeds the purchase price (i.e., the investment will exceed your annual required return rate). Acquiring the server is a good financial move. Should you lease or buy it?

46 BA II PLUS™ Calculator

Example: Present Value of Lease Payments

Procedure Keystrokes Display

Set all variables to defaults.

Set payments per year to 1.

Set beginning-of-period payments.

Return to calculator mode.

Enter number of periods.

& } !

& [

& ] & V

& U

RST 0.00 P/Y= 1.00

BGN

0.00

N= 5.00

Enter periodic interest rate at which your firm can borrow.

Enter annual lease payment.

15 36000

I/Y= 15.00 PMT= -36,000.00

Compute present value of lease payments.

% .

PV= 138,779.22

The present value of the lease payments is greater than the purchase price of $125,000, so it would be best to buy the server outright.





2: TVM and Amortization Worksheets 47

Present Value of Lease with Residual Value

The Peach Bright Company wants to purchase a machine that it is currently leasing from your company. You offer to sell it for the present value of the lease discounted at an annual interest rate of 22% compounded monthly. The machine has a residual value of $6500, and 46 monthly payments of $1200 remain on the lease. If the payments are due at the beginning of each month, how much should you charge for the machine?

The total value of the machine is the present value of the residual value plus the present value of the lease payments.

Procedure Keystrokes Display

Set all variables to defaults.

Set payments per year to 1.

Set beginning-of-period payments.

Return to calculator mode.

Enter number of payments.

Calculate and enter periodic interest rate.

Enter residual value of asset.

Compute present value of residual.

Enter amount of lease payment.

Compute present value of lease payments.

& } !

& [

& ] & V

& U

6 12 N

6500

% .

1200

% .

RST 0.00 P/Y= 1.00

BGN

N= 46.00

I/Y= 1.83 FV= -6,500.00

PV= 2,818.22

PMT= -1,200.00

PV= 40,573.18



0.00









Peach Bright should pay your company $40,573.18 for the machine.

48 BA II PLUS™ Calculator

Monthly Payments

You are planning to purchase a new small desk and chair set that is sale priced at $525. You can finance your purchase at 20% APR, compounded monthly, for two years. How much is the monthly payment?

PV = $525 FV = $0

PMT = ? PMT = ? PMT = ?

0 1 23 N = 24

Example: Monthly Payments

Procedure Keystrokes Display

Set all variables to defaults.

Enter number of payments using payment multiplier.

Enter interest rate.

Enter loan amount.

Compute payment.

. . .

I/Y = 20 ÷ 12

& } !

& Z

20 525

% /

RST 0.00

N= 24.00 I/Y= 20.00 PV= -525.00 PMT= 26.72





Your monthly payment is $26.72.

2: TVM and Amortization Worksheets 49

Yield to Maturity on Bond Purchased on Interest Date

A 9% $1,000 semiannual commercial bond has 13 remaining coupon payments. You can purchase the bond for $852.50 (ignoring commissions). At this price, what is your yield to maturity and the annual effective rate?

Example: Yield to Maturity

Procedure Keystrokes Display

Set all variables to defaults.

Set payments per year to 2.

Return to calculator mode.

Enter number of remaining coupon payments.

Enter bond price.

Calculate the coupon payment.9 2 6 2 <

Enter bond redemption value.

Compute annual yield.

Store in memory.

& } !

& [

& U

852.5

N /

1000

% -

Example: Effective Annual Interest

1000

RST 0.00 P/Y= 2.00

N= 13.00 PV= -852.50

PMT= 45.00 FV= 1,000.00 I/Y= 12.37



0.00





(continued from previous example)

Use the Interest Conversion worksheet (Chapter 7) to calculate the effective annual interest rate.

Procedure Keystrokes Display

Select and clear Interest Conversion worksheet.

Recall rate from memory.

Enter compounding periods.

Compute annual effective rate."

& v & z

# #

NOM= 0.00 NOM= 12.37

C/Y= 2.00 EFF= 12.75

The annual yield to maturity is 12.37% with semiannual compounding. The equivalent annual effective rate is 12.75%.

50 BA II PLUS™ Calculator





Saving for the Future by Making Monthly Deposits

Accounts with payments made at the beginning of the period are referred to as “annuity due” accounts. Interest on annuity due accounts starts accumulating earlier and produces slightly higher yields.

An individual has decided to invest $200 at the beginning of each month in a retirement plan. What will the account balance be at the end of 20 years if the fund earns an annual interest of

7.5 % compounded monthly, assuming beginning-of-period payments?

Future value(FV) = ?

Interest = 7.5%

Number of payments (N) = 240

. . .

Payment amount (PMT) = $200

Example: Regular Deposits (Annuity Due)

Procedure Keystrokes Display

Set all variables to defaults.

Set beginning-of-period payments.

Return to calculator mode.

Enter number of payments using payment multiplier.

Enter interest rate.

Enter amount of payment.

Compute future value.

& } !

& ] & V

& U

& Z

7.5 200

% 0

RST 0.00

BGN

N= 240.00 I/Y= 7.50 PMT= -200.00 FV= 111,438.31

0.00





Depositing $200 at the beginning of each month for 20 years results in a future amount of $111,438.31.

2: TVM and Amortization Worksheets 51

Amount to Borrow and Down Payment

You want to buy a car that sells for $5,100. The finance company charges 13.51% APR, compounded monthly, on a 48-month loan. If you can afford a monthly payment of $125, how much can you borrow? How much do you need for the down payment?

Example: Loan Amount and Down Payment

Calculate the loan amount. Then subtract it from the cost of the car to find the down payment.

PV = ? FV = $0

$125 $125 $125

. . .

0 1 47 N=48

I/Y = 13.51 ÷ 12

Procedure Keystrokes Display

Set all variables to defaults.

Enter number of payments using payment multiplier.

Enter monthly interest rate.

Enter payment.

Compute loan amount.

Calculate down payment.

& } !

& Z

13.51 125

% .

5100

RST 0.00

N= 48.00 I/Y= 13.51 PMT= -125.00 PV= 4,615.73

-484.27





To buy the car, you can borrow $4,615.73 and make a down payment of $484.27.

52 BA II PLUS™ Calculator

Regular Deposits for a Specified Future Amount

You plan to open a savings account and deposit the same amount of money at the beginning of each month. In 10 years, you want to have $25,000 in the account. How much should you deposit if the annual interest rate is 7% with quarterly compounding?

(compounding periods per year) is automatically set to

C/Y

equal

Example: Monthly Deposits Compounded Quarterly

Procedure Keystrokes Display

Set all variables to defaults.

Set compounding periods to 4.

Set beginning-of-period payments.

Return to calculator mode.

Enter number of deposits using payment multiplier.

Enter interest rate.

Enter future value.

Compute deposit amount.

(payments per year), so you need to set

P/Y

& } !

& [ #

& ] & V

& U

& Z

7 25000

% /

C/Y

RST 0.00 P/Y=

C/Y=

BGN

N= 120.00 I/Y= 7.00 FV= 25,000.00 PMT= -143.92

12.00

4.00

0.00





You need to make monthly deposits of $143.92.

2: TVM and Amortization Worksheets 53

Time Value of Money/Amortization Schedule

This two-part example shows you how to use the TVM and Amortization worksheets to compute the monthly payment on a 30-year loan and then generate an amortization schedule for the first three years of the loan.

Example: Mortgage Payment

Using the TVM worksheet, determine the monthly payment on a 30-year mortgage with a loan amount of $120,000 and an annual percentage rate of 9.125%.

Procedure Keystrokes Display

Set all variables to defaults.

Enter number of payments using payment multiplier.

Enter interest rate.

Enter loan amount.

Compute payment.

& } !

& Z

9.125 120000

% /

Notice that the interest rate displays as 9.13, even though you entered 9.125. The calculator uses 9.125 for calculation. To see the stored value of digits, press &

! & U J

I/Y

RST 0.00

N= 360.00 I/Y= 9.13 PV= 120,000.00 PMT= -976.36

to make the

I/Y

displayed with three

I/Y





The computed monthly payment is $976.36. Because

PMT

money paid out, it is displayed as a negative number.

54 BA II PLUS™ Calculator

Example: Loan Amortization

(continued from previous example)

Use the Amortization worksheet to generate an amortization schedule for the first three years of the loan. Assume that the first payment is in April; therefore, the first year has 9 payment periods. There are 12 payment periods per year thereafter.

Procedure Keystrokes Display

Select the Amortization worksheet.

Set ending period to 9.

Display first year amortization data.

Change beginning period to 10.

Change ending period to 21.

Display second year amortization data.

Move to P1 and press % to enter next range of payments.

Display P2.

Display third year amortization data.

& \

# # #

# %

# # #

P1= 1.00

P2= 9.00 BAL=

PRN= INT=

P1= 10.00

P2= 21.00 BAL=

PRN= INT=

P1= 22.00 P2= 33.00 BAL=

PRN= INT=

119,407.46

-592.54

-8,194.70

118,551.85

-855.61

-10,860.71

117,614.86

-936.99

-10,779.33













Note that the principal and interest are displayed as negative because they are outflows.

2: TVM and Amortization Worksheets 55

Interest and Loan Balance after Specified Payment

To evaluate the financial advisability of financing all or some of the sale price of a property, a seller must know the amount of interest that will be received and the remaining balance at the end of the term (balloon payment).

A seller is asked to finance $82,000 at 10% annual interest, amortized over a 30-year term but with a balloon payment due after five years.

The seller wants to know:

•

The amount of the monthly payment.

•

The amount of interest he will receive.

•

The amount of the balloon payment.

Example: Compute Monthly Payment

Procedure Keystrokes Display

Set all variables to defaults.

Enter number of payments using payment multiplier.

Enter interest rate.

Enter loan amount.

Compute payment.

& } !

& Z

82000

% /

RST 0.00

N= 360.00 I/Y= 10.00 PV= 82,000.00 PMT= -719.61





Example: Compute Amortization Schedule

(continued from previous example)

Procedure Keystrokes Display

Select Amortization worksheet.

Enter end period after five years.

View computed balance due after five years.

View computed interest paid after five years.

& \

& Z

# #

P1= 1.00

P2= 60.00

BAL= 79,190.83

INT= -40,367.43

If the seller financed the sale, he would receive:

•

$719.61 each month for five years.

•

$40,367.43 in interest over the five-year term.

•

$79,190.83 as the balloon payment.

56 BA II PLUS™ Calculator





Canadian Mortgages

Canadian mortgages typically require the borrower to make monthly payments, although interest is compounded semiannually. Additionally, mortgages are usually refinanced at the end of a fixed period of time, such as five years.

A home buyer borrows $60,000 for 20 years at an annual interest rate of 13 % compounded semiannually. How much are the monthly payments and the amount necessary to pay off the mortgage after five years?

Example: Payment

Procedure Keystrokes Display

Set all variables to defaults.

Leave payments per year at 12.

Set compounding periods per year to 2.

Return to calculator mode.

Enter number of payments using payment multiplier.

Enter interest rate per year.

Enter present value.

Compute payment.

& } !

& [

& U

& Z

13 60000

% /

RST 0.00 P/Y= 12.00

C/Y= 2.00

0.00

N= 240.00 I/Y= 13.00 PV= 60,000.00 PMT= -688.52





Example: Amortization Schedule

(continued from previous example)

Procedure Keystrokes Display

Select Amortization worksheet.

Enter number of payments as

using payment multiplier.

View balance after five years.

& \

& Z

P1= 1.00

P2= 60.00 BAL= 55,389.85

The monthly payment is $688.52, and $55,389.85 is required to pay off the mortgage after five years.

2: TVM and Amortization Worksheets 57





58 BA II PLUS™ Calculator

Cash Flow Worksheet

Three keys are used for performing cash-flow calculations.

(

)

Press # and " to move through each set of variables.

lets you enter cash flow data.

lets you compute net present value.

lets you compute internal rate of return.

3: Cash Flow Worksheet 59

Cash Flow Worksheet Labels

Key Label Meaning Variable Type

' # #

( #

)

CFo

* Amount of

* Frequency of

NPV IRR

Initial cash flow Enter-only

Discount rate Enter-only

Net present value Compute-only

Internal rate of return Compute-only

cash flow Enter-only

*nn represents the number of the cash flow (

corresponding frequency (

F01–F24

C01–C24

) or the number of the

Notes about the Cash Flow Worksheet

♦

' & z

♦

& } !

To enter cash-flow values and frequencies, press '. You can

♦

enter the initial cash flow (

sets all variable values to zero.

) plus up to 24 cash flows,

CFo

each of which can be a unique value. Enter inflows (cash received) as positive and outflows (cash paid out) as negative. Use S to enter a negative value.

♦

The

INS

and

indicators in the display let you know that

DEL

you can use & X and & W to insert or delete cash flows.

60 BA II PLUS™ Calculator

Interpreting the Results of IRR Calculations

When you compute a value for

(internal rate of return), the

IRR

calculator displays either a solution or an error message.

When a solution is displayed, there are two possibilities.

•

The displayed solution is the only solution.

•

There may be additional solutions. This occurs when there are two or more sign changes in the cash flow sequence.

When an error message is displayed, there are two possibilities.

•

No solution for

IRR

exists (

). This occurs when there

Error 5

are no sign changes in the cash flow sequence.

•

The calculator is unable to determine a value for a maximum number of iterations (

Error 7

For a detailed description of sign changes as they relate to

IRR

within

IRR

refer to “IRR Calculations” in the Appendix.

3: Cash Flow Worksheet 61

Uneven and Grouped Cash Flows

Uneven Cash Flows

The Cash Flow worksheet lets you analyze the value of money over equal time periods. It allows you to enter uneven values, each of which can be either an inflow (cash received) or an outflow (cash paid out).

Similar to an annuity’s present value (PV) in the TVM worksheet, a typical cash-flow problem usually has an initial cash flow (labeled

Grouped Cash Flows

In some cash-flow problems, every cash flow may be a unique value. In other cash-flow problems, there may be consecutive cash flows of equal value.

). This is always a known, entered value.

CFo

You must enter unequal cash flows separately, but you can save time and space by using the

variable to enter groups of

consecutive cash flows of equal value.

62 BA II PLUS™ Calculator

Entering Cash Flows

You can enter the initial cash flow and up to 24 additional cash flows, each of which can be a unique value. Enter inflows as positive and outflows as negative. If you have consecutive cash flows of equal value, you can enter the cash-flow value and then a frequency of up to 9,999 for the number of times the value occurs.

Procedure: Entering Cash Flows

쐃

Press ' to select the cash flow entry portion of the Cash Flow worksheet.

and its current value are displayed.

CFo=

쐇

If necessary, press &

쐋

Key in a value for

쐏

Press # to display

(initial cash flow) and press

CFo

C01

to clear the worksheet.

Key in a value for the first cash flow or group of cash flows and press

. Enter an inflow (cash received) as a positive number; enter an outflow (cash paid out) as a negative number.

쐄

Press # to display

F01

If there are multiple, consecutive, equal occurrences of the cash flow you entered, key in the number of occurrences (frequency) and press

쐂

Press # to display the next available cash flow.

Key in the value of the cash flow(s) and press

쐆

Press #.

. The default value is

If there are multiple, consecutive, equal occurrences of the cash flow you entered, key in a value for the frequency and

press

쐊

Repeat steps 6 and 7 until all cash flows and frequencies are

entered.

When you have entered all the cash-flow data, you can press

or " to review the entries.

3: Cash Flow Worksheet 63

Deleting Cash Flows

When you delete a cash flow, the calculator decreases the numbers of subsequent cash flows .

Before deleting After deleting

8,000 cash flow 8,000 cash flow

Procedure: Deleting a Cash Flow

The

indicator lets you know when you can delete a cash

DEL

flow.

쐃

Press # or " until the cash flow you want to delete is displayed.

쐇

Press & W.

The cash flow you specified (and its frequency) is deleted. The calculator decreases the numbers of subsequent cash flows so that there is no gap.

64 BA II PLUS™ Calculator

Inserting Cash Flows

When you insert a cash flow, the calculator increases the numbers of the current and subsequent cash flows.

When inserting cash flows, remember that the most cash flows you can enter is 24.

Procedure: Inserting a Cash Flow

The

indicator lets you know when you can insert a cash

INS

flow.

쐃

Press # or " until the display shows the current cash flow where you want to insert the new cash flow.

For example, if you want to insert a new second cash flow, display

쐇

Press & X.

쐋

Key in the value of the new cash flow and press

C02

The new cash flow is entered “before” the current cash flow. The calculator increases the numbers of the current and subsequent cash flows. For example,

쐏

If necessary, press #, enter a value for the frequency, and

press

becomes

C02

C03

3: Cash Flow Worksheet 65

Computing NPV and IRR

(internal rate of return) is the interest rate at which the net

IRR

present value of the cash flows is equal to zero. present value) is the sum of the present values for the cash inflows (cash received) and outflows (cash paid out).

NPV

(net

A positive value for

indicates a profitable investment.

NPV

Procedure: Computing Net Present Value

쐃

Press (.

and its current value are displayed.

쐇

Key in a value for

쐋

Press # to display the

쐏

Press % to compute the net present value of the series of

(discount rate) and press

variable label.

NPV

cash flows.

The calculator computes and displays the value.

Procedure: Computing Internal Rate of Return

쐃

Press ).

and its current value are displayed.

IRR=

쐇

Press % to compute the internal rate of return. The calculator computes and displays the value.

66 BA II PLUS™ Calculator

Uneven Cash Flows

A company plans to pay $7,000 for a new machine. The company would like a 20% annual return on its investment. Over the next six years, the company expects to receive the annual cash flows shown below.

Year Cash Flow Number Cash Flow Estimate

1 1 3,000

2–5 2 5,000 each year

6 3 4,000

The following time line shows that these cash flows are a combination of equal and unequal values. Because the initial cash flow (

On the next few pages, you will enter cash flow data, edit the data when a change is necessary, and compute the net present value and internal rate of return.

) is an outflow, it is a negative value.

CFo

Example: Entering Cash Flow Data

Procedure Keystrokes Display

Set all variables to defaults.

Select Cash Flow worksheet.

Enter initial cash flow.

Enter cash flow for first year.#

Enter cash flows for years two through five.

Enter cash flow for sixth year.

& } !

3000

5000 4

4000

7000

# #

3: Cash Flow Worksheet 67

RST 0.00 CFo= 0.00

CFo=-7,000.00 C01=

F01= C02=

F02= C03=

F03=

3,000.00

1.00

5,000.00

4.00

4,000.00

1.00



Example: Editing Cash Flow Data

(continued from previous example)

After entering the data, you learn that the cash flow projections you were given were incorrect. The $4,000 cash-flow value should occur in the second year instead of the sixth. Otherwise, the entries are correct.

Year Incorrect Cash Flow Correct Cash Flow

1 3,000 3,000

2 5,000 4,000

3 5,000 5,000

4 5,000 5,000

5 5,000 5,000

6 4,000 5,000

Edit the existing data in the Cash Flow worksheet by deleting the $4,000 value for year 6 and inserting it for year 2.

Procedure Keystrokes Display

Move to third cash flow.

Delete third cash flow.

Move to second cash flow.

Insert new second cash flow.

Move to next cash flow to verify data.

& W

" "

& X #

# #

4000

C03= 4,000.00 C03= 0.00 C02= 5,000.00

C02= F02=

C03= F03=

4,000.00

1.00

5,000.00

4.00



68 BA II PLUS™ Calculator

Example: Computing Net Present Value

(continued from previous example)

Compute the net present value ( period (

Procedure Keystrokes Display

Access

Enter interest rate per period.

Compute net present value.

[

) of 20%.

NPV

) using an interest rate per

NPV

(

# %

[

= 0.00

[

= 20.00

NPV= 7,266.44

Example: Computing Internal Rate of Return

(continued from previous example)

Compute the internal rate of return (

Procedure Keystrokes Display

IRR

Access

Compute internal rate of return.

)

IRR

IRR= 0.00 IRR= 52.71

The internal rate of return is 52.71%.





3: Cash Flow Worksheet 69

Value of a Lease with Uneven Payments

A lease with an uneven payment schedule usually accommodates seasonal or other anticipated fluctuations in the lessee’s cash position.

Suppose a 36-month lease has the following payment schedule, with beginning-of-period payments.

Number of Months Payment Amount

4$0

8 $5000

3$0

9 $6000

2$0

10 $7000

If the required earnings rate is 10% annually with monthly compounding:

•

What is the present value of these lease payments?

•

What even payment amount at the beginning of each month would result in the same present value?

Because the cash flows are uneven, use the Cash Flow worksheet to determine the net present value ( lease.

NPV

) of the

70 BA II PLUS™ Calculator

Example: Compute Net Present Value of Cash Flows

The cash flows for the first four months are stated as a group of four $0 cash flows. Because the lease specifies beginning-ofperiod payments, you must treat the first cash flow in this group as the initial investment ( three cash flows on the cash flow screens (

The BGN/END setting in the TVM worksheet does not affect the

Note:

Cash Flow worksheet.

Net present value (NPV) = ?

Interest (I) = 10%

C01 C02 C03 C04 C05 C06

$0 $5000 $0 $6000 $0 $7000

F01 = 3 F02 = 8 F03 = 3 F04 = 9 F05 = 2 F06 = 10

Initial investment (CFo) = $0

Procedure Keystrokes Display

Set all variables to defaults.

Select Cash Flow worksheet.

Enter first group of cash flows.

Enter second group of cash flows.

Enter third group of cash flows.

Enter fourth group of cash flows.

Enter fifth group of cash flows.

Enter sixth group of cash flows.

Select NPV.

Enter monthly earnings rate.10 6 12

Compute NPV.

Store in memory 0.

& } !

# #

(

# %

) and enter the remaining

CFo

and

C01

RST 0.00 CFo= 0.00 C01=

5000 8

3 6000

2 7000

0 NPV -138,088.44

F01= C02=

F02= C03=

F03= C04=

F04= C05=

F05= C06=

F06=

[

= 0.00

[

=0.83

NPV= -138,088.44

F01

5000.00

6000.00

7000.00

0.00

3.00

8.00

0.00

3.00

9.00

0.00

2.00

10.00





3: Cash Flow Worksheet 71

Example: Compute Equivalent Monthly Payments

(continued from previous example)

Use the net present value ( as the present value (

) from the Cash Flow worksheet

NPV

) in the TVM worksheet to compute the equivalent even monthly payment that is equivalent to the uneven cash flows.

Present value (PV) = NPV from Cash Flow worksheet

Interest (I/Y) = 10%

Number of payments (N) = 36

. . .

Payment amount (PMT) = ?

Procedure Keystrokes Display

Set beginning-of-period payments.

Return to calculator mode.

NPV

Enter

as PV and make it

positive.

Enter interest per year.

Enter number of payments.

Compute payment.

& ] & V

& U

% /

BGN

0.00

PV= 138,088.44 I/Y= 10.00 N= 36.00 PMT= -4,418.90

At the required earnings rate of 10%, the present value of the lease payments is $138,088.44. An even monthly payment of $4,418.90 would result in the same present value.





72 BA II PLUS™ Calculator

Bond Worksheet

To access the Bond worksheet, press &

Press # and " to move through each set of variables.

4: Bond Worksheet 73

Bond Worksheet Labels

Label Meaning Variable Type

SDT CPN RDT RV ACT* 360* 2/Y* 1/Y* YLD PRI AI

* Press & V repeatedly to view the options for day-count method or

Settlement date Enter-only

Annual coupon rate in percent Enter-only

Redemption date Enter-only

Redemption value (percentage of par value) Enter-only

Actual/actual day-count method Setting

30/360 day-count method Setting

Two coupons per year Setting

One coupon per year Setting

Yield to redemption Enter/compute

Dollar price Enter/compute

Accrued interest Auto-compute

coupons per year.

Notes about the Bond Worksheet

♦

& l & z

(

SDT, RDT

, day-count method, and coupon frequency are not

sets

RV=100, CPN=0, YLD=0

, and

PRI=0

affected.)

2/Y

sets

RV=100, CPN=0, YLD=0

♦

& } !

and

to 12-31-1990; day-count method to

RDT

frequency to

If you have not entered the necessary values, an error occurs

♦

, and

ACT

PRI=0; SDT

; coupon

when you press # or " to move through the worksheet.

You can enter dates in US format (MM.DDYY) or European

♦

format (DD.MMYY). Dates are displayed with hyphens, either MM-DD-YYYY (US format) or DD-MM-YYYY (European format).

You can enter dates from January 1, 1950, through December

♦

31, 2049.

When you enter a value for

♦

, remember that it is the

CPN

annual coupon rate as a percent—not the dollar amount of the coupon payment.

74 BA II PLUS™ Calculator

Notes about the Bond Worksheet (cont.)

♦

Enter a date for

(redemption date) in the date format

RDT

you selected (U.S. or European). The calculator assumes that the redemption date (

For “to maturity” calculations, enter the maturity date for

RDT

For “to call” calculations, enter the call date for

♦

Redemption value (

) coincides with a coupon date.

RDT

) is a percentage of the bond’s par

RDT

value.

For “to maturity” analysis, enter 100 for

For “to call” analysis, enter the call price for

♦

When either

ACT

is displayed, you can set the day-

360

count method by pressing & V repeatedly to select either

(actual/actual) or

ACT

♦

When either

1/Y or 2/Y

repeatedly to set coupon frequency as payments per year) or

♦

To compute a value for

♦

To compute a value for

♦

A value for

is computed automatically in terms of dollars

(30/360).

360

is displayed, you can press &

(two coupon

2/Y

(one coupon payment per year).

1/Y

, enter a value for

YLD

, enter a value for

PRI

YLD

per $100 of par value.

4: Bond Worksheet 75

Terminology

The following terminology applies to the Bond worksheet.

Call Date

before the bond’s maturity date is a callable bond. The call date for such a bond is printed in the bond contract.

Coupon Payment

of the bond as interest.

Coupon Rate

Dollar Price

dollars per $100 of par value.

Par Value (or face value)

Premium Bond

the par value sells at a premium.

Discount Bond

sells at a discount.

Redemption Date

retires the bond. This date may be the date of maturity or, for a callable bond, a call date.

Redemption Value

bond when it is retired. If the bond is redeemed at the maturity date, the redemption value is the par value printed on the bond. If the bond is redeemed at a call date, the redemption value is the bond’s par value plus any call premium. The calculator treats the redemption value in terms of dollars per $100 of par value.

— A bond that can be retired by the issuing agency

— The periodic payment made to the owner

— The annual interest rate printed on the bond.

— Price of the security expressed in terms of

— The value printed on the bond.

— A bond that sells for an amount greater than

— A bond selling for less than the par value

— The date on which the issuing agency

— The amount paid to the owner of the

Settlement Date

for funds.

Yield to Maturity

from payments of principal and interest, with interest compounded semiannually at the stated yield rate. The yield to maturity takes into account the amount of premium or discount, if any, and the time value of the investment.

76 BA II PLUS™ Calculator

— The date on which a bond is exchanged

— The rate of return to the investor earned

Entering Bond Data and Computing Results

Before computing values for price or yield and accrued interest, enter the four known values (settlement date, coupon rate, redemption date, and redemption value). If necessary, change the day-count method and coupon frequency settings. The worksheet stores values and settings until you clear the worksheet or change the values and settings.

Procedure: Entering Bond Data

First enter the known values:

쐃

Press &

SDT

쐇

Press &

쐋

Key in a value for

쐏

Press # repeatedly and enter values for

RDT

you did for

is displayed, along with the previous date.

to clear the worksheet.

(settlement date) and press

SDT

CPN

(coupon rate),

(redemption date), and RV (redemption value) just as

SDT

Procedure: Selecting Bond Settings

After entering the known values, select the settings:

쐃

Press # until

ACT

is displayed to select the day-count

360

method.

To select the actual/actual day-count method, press

& V

To select the 30/360 day-count method, press & repeatedly until

쐇

Press # until

repeatedly until

is displayed.

360

2/Y

is displayed to select coupon

1/Y

is displayed.

ACT

frequency.

To select two coupons per year, press & V repeatedly until

To select one coupon per year, press & V repeatedly until

is displayed.

2/Y

is displayed.

1/Y

4: Bond Worksheet 77

Procedure: Computing Bond Price (PRI)

쐃

Press # until

쐇

Key in a value for

쐋

Press # to display

A value for

is displayed.

YLD

and press

YLD

, and then press %.

PRI

is computed and displayed.

PRI

Procedure: Computing Bond Yield (YLD)

쐃

Press # until

쐇

Key in a value for

쐋

Press # to display

A value for

is displayed.

PRI

and press

PRI

, and then press %.

YLD

is computed and displayed.

YLD

Computing Accrued Interest (AI)

A value for AI (accrued interest) is computed and displayed automatically when you access the variable.

is computed in

terms of dollars per $100 of par value.

Press # repeatedly until

and its value are displayed.

78 BA II PLUS™ Calculator

Bond Price and Accrued Interest Example

You want to purchase a semiannual corporate bond that matures on 12/31/97 to settle on 6/12/96. The bond is based on the 30/360 day-count method with a coupon rate of 7%. It will be redeemed at 100% of its par value. For an 8% yield to maturity, compute the bond’s price and the accrued interest.

Example: Entering Bond Data

Procedure Keystrokes Display

Set all variables to defaults.

Select Bond worksheet.

Enter settlement date.

Enter coupon rate.

Enter redemption date.

Leave redemption value as is.

& } !

& l

6.1296

12.3197

Example: Computing Bond Price and Accrued Interest

(continued from previous example)

Select 30/360 day-count method.

Leave two coupon payments per year.

Enter yield.

Compute price

View accrued interest.

# & V

# %

RST 0.00 SDT = 12-31-1990 SDT = 6-12-1996 CPN = 7.00

RDT = 12-31-1997 RV = 100.00

360

2/Y YLD = 8.00 PRI = 98.56 AI = 3.15





For an 8% yield to maturity, the price of the bond is $98.56 per 100 and the accrued interest is $3.15 per 100.

4: Bond Worksheet 79

80 BA II PLUS™ Calculator

Depreciation Worksheet

To access the Depreciation worksheet, press & p. Then choose a depreciation method, enter the known values, and compute the unknown values.

To choose a depreciation method, press & V repeatedly until the desired method is displayed.

Press # and " to move through each set of variables.

5: Depreciation Worksheet 81

Depreciation Worksheet Labels

Label Meaning Variable Type

* Straight line method Setting

* Sum-of-the-years’-digits method Setting

SYD

* Declining-balance method Setting/Enter

DB DBX*DB

* French straight-line method Setting/Enter

SLF

* French declining balance method Setting/Enter

DBF LIF M01 DT1 CST SAL YR DEP RBV RDV

* Press & V repeatedly to view all of the options for depreciation method.

Notes about the Depreciation Worksheet

method with crossover to

Life of the asset in years Enter-only

Starting month Enter-only

Starting date (

Cost of the asset Enter-only

Salvage value of the asset Enter-only

Year to compute Enter-only

Depreciation for the year Auto-compute

Remaining book value at the end of the year Auto-compute

Remaining depreciable value Auto-compute

) Enter-only

SLF

Setting/Enter

♦

& p & z

sets

LIF=1, M01=1, YR=1; CST=0, SAL=0

The depreciation method is not affected.

♦

& } !

sets the depreciation method to

declining-balance percent (for

M01=1, YR=1; CST=0, SAL=0

(straight-line, French method) and

♦

SLF

and

DBX

only) to

(declining-

DBF

;

200; LIF=1

balance, French method) are European depreciation methods. They are only available if you have selected the European format for entering dates or entering separators in numbers.

♦

DEP, RBV

(initial date) is available only for

DT1

, and

are computed a year at a time. Results are

RDV

SLF

rounded to the number of decimal places specified by the display format.

82 BA II PLUS™ Calculator

Notes about the Depreciation Worksheet (cont.)

♦

Values for

DEP, RBV

, and

are computed and displayed

RDV

automatically when you press # to display each variable.

♦

If you choose

as the depreciation method, enter a

DBX

value for declining-balance percent when you display the or

label. The value you enter must be a positive number.

DBX

(The default value is 200.)

♦

The value you enter for

SYD, DB, DBX

♦

The value you enter for

is selected, a positive real number.

SLF

, or

must be:

LIF

is selected, a positive integer.

DBF

has two parts. The integer

M01

portion represents the month that the asset is placed into service. The decimal portion represents the fraction of the initial month in which the asset begins to depreciate. For example, entering 1.5 specifies that the asset begins to depreciate in the middle of the first month. Entering 4.25 specifies that the asset begins to depreciate a quarter of the way through the fourth month.

♦

When computing depreciation, the value you enter for must be a positive integer.

♦

From

, you can press # to return to YR. To represent the

RDV

next depreciation year, press % to increment the value for

by one.

♦

Repeatedly returning to value for

, and computing values for

, pressing % to increment the

DEP, RBV

, and

RDV

computes a depreciation schedule. The schedule is complete when

5: Depreciation Worksheet 83

equals zero.

RDV

Entering Data and Computing Results

Because the worksheet stores previous values and settings until you change them or clear the worksheet, you may not need to do all the steps every time you work a depreciation problem.

Procedure: Selecting a Depreciation Method

쐃

Press & p to select the Depreciation worksheet.

The label for the current depreciation method is displayed.

쐇

Press &

쐋

Press & V repeatedly until the depreciation method you want is displayed (

쐏

If you select

to clear the worksheet.

SL, SLF, SYD, DB, DBX

, key in a value for the declining-

DBX

, or

DBF

balance percent. The default value is 200.

Procedure: Entering Depreciation Data

쐃

Press # to display

쐇

Key in a value for

쐋

Repeat for

To use

SLF

M01, DT1

DBF

, do not forget to set either the European date

format or the European format for separators (&

LIF

and press

LIF

(if

SLF

CST, SAL

, and YR.

Computing Results

After entering the data, press # repeatedly to automatically compute and display values for

DEP, RBV

, and

RDV

The  symbol in the display lets you know that each value has been computed.

Procedure: Generating a Depreciation Schedule

To generate a depreciation schedule and compute values for other years:

쐃

Press # to display the

variable, and then press % to

increment the value by one.

쐇

Press # repeatedly to automatically compute and display new values for

84 BA II PLUS™ Calculator

DEP, RBV

, and

RDV

Declining Balance with Straight-Line Crossover Example

In mid-May, a company begins to depreciate a machine with a seven-year life and no salvage value. The machine cost is $100,000. Use the declining-balance with straight-line crossover method to compute the depreciation expense, remaining book value, and remaining depreciable value for the first two years. The declining-balance percent is 200.

Example: Declining-Balance Data

Procedure Keystrokes Display

Set all variables to defaults.

Select Depreciation worksheet.

Select declining-balance crossover method.

Enter life in years.

Enter starting month.

Enter cost.

Leave salvage value at 0.

Leave year at 1.

Display depreciation amount, remaining book value, and remaining depreciable value.

View second year.

Display second year depreciation data.

& } !

& p

& V & V & V

5.5

# # #

# %

# # #

100000

RST 0.00

DBX = 200.00 LIF = 7.00 M01 = 5.50 CST = 100,000.00 SAL = 0.00 YR = 1.00 DEP =

RBV = RDV =

YR = YR =

DEP = RBV = RDV =

17,857.14 82,142.86 82,142.86

1.00

2.00

23,469.39 58,673.47 58,673.47









For the first year, the depreciation amount is $17,857.14, the remaining book value is $82,142.86, and the remaining depreciable value is $82,142.86.

For the second year, the depreciation amount is $23,469.39, the remaining book value is $58,673.47, and the remaining depreciable value is $58,673.47.

5: Depreciation Worksheet 85

Straight-Line Depreciation Example

In mid-March, a company begins depreciation of a commercial building with a 31½ year life and no salvage value. The building cost $1,000,000. Use the straight-line depreciation method to compute the depreciation expense, remaining book value, and remaining depreciable value for the first two years.

Example: Entering Straight-Line Depreciation Data

Procedure Keystrokes Display

Set all variables to defaults.

Select Depreciation worksheet.

Enter life in years.

Enter starting month.

Enter cost.

Leave salvage value as is.

Leave year as is.

Display depreciation amount, remaining book value, and remaining depreciable value.

View second year.

Display second year depreciation data.

& } !

& p

# !

# # #

# %

# # #

31.5

3.5 1000000

RST 0.00

SL LIF = 31.50 M01 = 3.50 CST = 1,000,000.00

SAL = 0.00 YR = 1.00 DEP =

RBV = RDV =

YR = YR =

DEP = RBV = RDV =

25,132.28 974,867.72 974,867.72

1.00

2.00

31,746.03 943,121.69 943,121.69









For the first year, the depreciation amount is $25,132.28, the remaining book value is $974,867.72, and the remaining depreciable value is $974,867.72.

For the second year, the depreciation amount is $31,746.03, the remaining book value is $943,121.69, and the remaining depreciable value is $943,121.69.

86 BA II PLUS™ Calculator

Statistics Worksheet

Two keys are used for performing statistics calculations.

& j

& k

Press # and " to move through each set of variables.

lets you enter statistical data.

lets you choose a statistics calculation method and compute results.

6: Statistics Worksheet 87

Statistics Worksheet Labels

Keys Label Meaning Variable Type

& j #

& k & V

(as needed)

Y LIN

Ln EXP PWR 1-V

Current X value

Current Y value

Standard linear regression Logarithmic regression Exponential regression Power regression One-variable statistics

Number of observations Mean (average) of X values Sample standard deviation of X Population standard deviation of X Mean (average) of Y values Sample standard deviation of Y Population standard deviation of Y Linear regression y-intercept Linear regression slope Correlation coefficient Predicted X value Predicted Y value Sum of X values Sum of X squared values Sum of Y values Sum of Y squared values

Sum of XY products

Enter-only Enter-only

Setting Setting Setting Setting Setting

Auto-compute Auto-compute Auto-compute Auto-compute Auto-compute Auto-compute Auto-compute Auto-compute Auto-compute Auto-compute Enter/compute Enter/compute Auto-compute Auto-compute Auto-compute Auto-compute Auto-compute

*nn indicates the number of the current X or Y value. ** Not displayed for one-variable statistics.

88 BA II PLUS™ Calculator

Notes about the Statistics Worksheet

& j & z

sets all

and Y values and all values in

the Stat portion of the worksheet to zero, but does not affect the statistics calculation method.

& k & z

and all values to zero.

LIN

& } !

, and all other values to zero.

X, Y

You can enter up to 50 (

sets the statistics calculation method to

x,y

) data points.

LIN

If you have not entered any data points, an error will occur when you press # or " to move through the portion of the worksheet that displays results.

When you are entering data for one-variable statistics,

represents the value and

specifies the number of

occurrences (frequency). When you enter a value for value for

To analyze one-variable statistics, select

, Sx,

defaults to 1.

. Only values for n,

, and

are computed and displayed for one-

1-V

, the

variable statistics.

When analyzing two-variable statistics, you have four regression methods to choose from:

and

•

— Standard linear regression analysis

LIN

•

— Logarithmic regression analysis

•

Except for

— Exponential regression analysis

EXP

— Power regression analysis

PWR

and Y', the values for the statistics variables are

automatically computed and displayed when you access them.

You can use the You can enter a value for

to compute X'.

6: Statistics Worksheet 89

and Y' variables for regression predictions.

to compute Y', or enter a value for

Regression Models

For two-variable data, the Statistics worksheet has four regression models for curve fitting and forecasting.

value is interpreted as the independent variable and the

The

value as the dependent variable.

Model Formula Restrictions

LIN

Linear (

Logarithmic (Ln) Y = a + b ln(X) All X values > zero

Exponential (

Power (

The statistical results are computed using transformed values:

•

The linear model uses X and Y.

•

The logarithmic model uses ln(X) and Y.

•

The exponential model uses X and ln(Y).

•

The power model uses ln(X) and ln(Y).

) Y = a + b X

EXP

PWR

) Y = a X

) Y = a b

All Y values > zero

All X and Y values > zero

The calculator determines the values for

and b that create the

line or curve that best fits the data.

Correlation Coefficient

The calculator also determines r (the correlation coefficient) which measures the goodness of fit of the equation with the data.

In general, the closer

is to 1 or -1, the better the fit; the closer

is to zero, the worse the fit.

90 BA II PLUS™ Calculator

Entering Statistical Data

& j

lets you enter and display up to 50 data points. The Statistics worksheet stores the values you enter until you clear the worksheet or change the values. Therefore, you may not need to do all the steps each time you perform a Statistics calculation.

Procedure: Entering Data Points

쐃

Press & j to select the data-entry portion of the Statistics worksheet.

is displayed, along with any previous value.

X01

쐇

Press &

쐋

Key in a value for

If you are entering one-variable data,

to clear the worksheet.

and press

X01

is the first data

X01

point.

If you are entering two-variable data,

is the first

X01

value.

쐏

Press # to display the and press

If you are entering one-variable data, you can enter the

number of times the

variable. Key in a value for

Y01

value occurs (frequency). The

Y01

default value is 1.

If you are entering two-variable data, enter the first

value.

쐄

Press # to display the next

variable.

쐂

Repeat steps 3 through 5 until all of the data points are entered.

Displaying Data Points

As with other worksheets, you can move up and down through the data-entry portion of the Statistics worksheet by pressing

or ".

6: Statistics Worksheet 91

Editing Statistical Data

Pressing & j also lets you insert or delete data points. You may not need to do all the steps each time you perform a Statistics calculation.

Procedure: Deleting a Data Point

When the

indicator is displayed, you can delete a data

DEL

point.

쐃

Press # or " until the data point you want to delete is displayed.

쐇

Press & W.

The data point you specified (both

and Y) is deleted. The

calculator decreases the numbers of subsequent data points so that there is no gap.

Procedure: Inserting a Data Point

When the

쐃

Press # or " until the display shows the current

indicator is displayed, you can insert a data point.

INS

variable

of the data point where you want to insert the new data.

For example, if you want to insert a new second data point, display

쐇

Press & X.

쐋

Key in the new

The new

X02

value and press

value is entered “above” the current data point.

The calculator increases the numbers of the current and subsequent data points. For example,

X02

becomes

X03

쐏

If necessary, press #, and then key in a value for the variable and press

92 BA II PLUS™ Calculator

Computing Statistical Results

Procedure: Selecting a Statistics Calculation Method

쐃

Press & k to select the statistical calculation portion of the Statistics worksheet.

The most recently selected statistics calculation method is displayed (

쐇

Press & V repeatedly until the statistics calculation method you want is displayed.

LIN, Ln, EXP, PWR

, or

1-V

If you are analyzing one-variable data, select

쐋

Press # to begin computing results.

1-V

Computing Results

To compute results based on the current data set, press

repeatedly after you have selected the statistics calculation method.

The results of the statistical calculations (except for

and Y')

are computed and displayed automatically when you access them.

For one-variable statistics, only values for

are computed and displayed.

, Sx,

, and

Procedure: Computing Y'

쐃

If necessary, press & k.

쐇

Press " or # until

쐋

Key in a value for

쐏

Press # to display the

쐄

Press % to compute a predicted

is displayed.

and press

variable.

value.

6: Statistics Worksheet 93

Procedure: Computing X'

쐃

If necessary, press & k.

쐇

Press " or # until

is displayed.

쐋

Key in a value for

쐏

Press " to display the

쐄

Press % to compute an

and press

variable.

value.

94 BA II PLUS™ Calculator

Texas Instruments BA II PLUS User guide

Specifications and Main Features

Frequently Asked Questions

User Manual

Important

US FCC Information Concerning Radio Frequency Interference

Appendix: Reference Information 115

Index 137

Turning the Calculator On and Off

Turning the Calculator On

Turning the Calculator Off

Automatic Power Down™ (APD™) Feature

Resetting the Calculator

Effects of Resetting

Alternatives to Resetting

Procedure: Resetting the Calculator

Keys and 2nd Functions

The Display

Display Indicators

Setting Calculator Formats

Number of decimal places

Procedure: Changing the Number of Decimal Places

Angle Unit Format

Procedure: Changing the Angle Unit Format

Date Format

Procedure: Changing the Date Format

Separator Format

Procedure: Changing the Separator Format

Calculation Method

Procedure: Changing the Calculation Method

Clearing the Calculator

Correcting Entry Errors

Example: Correcting an Entry Error

Math Operations

Math Operations (cont.)

More on Selected Math Operations

Universal Power

Parentheses

Factorial

Random Numbers

Combinations

Permutations

Rounding

Scientific Notation

Memory Operations

Clearing Memory

Storing to Memory

Recalling from Memory

Memory Examples

Memory Arithmetic

Calculations Using Constants

Keystrokes for Constant Calculations

Last Answer Feature

Example: Last Answer

Using Worksheets: Tools for Financial Solutions

What Is a Worksheet?

Types of Worksheets

Worksheet Variables

TVM Variables

Prompted-worksheet Variables

Enter-Only Variables

Compute-Only Variables

Automatic-Compute Variables

Enter-or-Compute Variables in the TVM Worksheet

Enter-or-Compute Variables in Prompted Worksheets

Selecting Worksheet Settings

Indicators

Clearing Worksheets and Setting Defaults

TVM and Amortization Worksheet Labels

Notes about the TVM and Amortization Worksheets

Notes about TVM and Amortization Worksheets (cont.)

Entering, Recalling, and Computing TVM Values

Entering a Value for N Using [xP/Y]

Compound Interest

Time-Line Diagrams

Entering Inflows and Outflows

Procedure: Using the TVM Worksheet

Procedure: Generating an Amortization Schedule

Procedure: Automatically Generating a Schedule

Basic Loan Calculations—Interest