ST AN2450 Application note

AN2450

Application note

LLC resonant half-bridge converter design guideline

Introduction

The growing popularity of the LLC resonant converter in its half-bridge implementation (see

Figure 1) is due to its high efficiency, low level of EMI emissions, and its ability to achieve

high power density. Such features perfectly fit the power supply demand of many modern
applications such as LCD and PDP TV or 80+ initiative compliant ATX silver box. One of the
major difficulties that engineers are facing with this topology is the lack of information
concerning the way the converter operates and, therefore, the way to design it in order to
optimize its features.

The purpose of this application note is to provide a detailed quantitative analysis of the
steady-state operation of the topology that can be easily translated into a design procedure.

Exact analysis of LLC resonant converters (see [1.] ) leads to a complex model that cannot
be easily used to derive a handy design procedure. R. Steigerwald (see [2]) has described a
simplified method, applicable to any resonant topology, based on the assumption that input­to-output power transfer is essentially due to the fundamental Fourier series components of
currents and voltages.

This is what is commonly known as the "first harmonic approximation" (FHA) technique,
which enables the analysis of resonant converters by means of classical complex ac-circuit
analysis. This is the approach that has been used in this paper.

The same methodology has been used by Duerbaum (see [3] ) who has highlighted the
peculiarities of this topology stemming from its multi-resonant nature. Although it provides
an analysis useful to set up a design procedure, the quantitative aspect is not fully complete
since some practical design constraints, especially those related to soft-switching, are not
addressed. In (see [4] ) a design procedure that optimizes transformer's size is given but,
again, many other significant aspects of the design are not considered.

The application note starts with a brief summary of the first harmonic approximation
approach, giving its limitations and highlighting the aspects it cannot predict. Then, the LLC
resonant converter is characterized as a two-port element, considering the input
impedance, and the forward transfer characteristic. The analysis of the input impedance is
useful to determine a necessary condition for Power MOSFETs' ZVS to occur and allows
the designer to predict how conversion efficiency behaves when the load changes from the
maximum to the minimum value. The forward transfer characteristic (see Figure 3) is of
great importance to determine the input-to-output voltage conversion ratio and provides
considerable insight into the converter's operation over the entire range of input voltage and
output load. In particular, it provides a simple graphical means to find the condition for the
converter to regulate the output voltage down to zero load, which is one of the main benefits
of the topology as compared to the traditional series resonant converter.

October 2007 Rev 5 1/32

www.st.com

Contents AN2450

Contents

1 FHA circuit model . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4

2 Voltage gain and input impedance . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8

3 ZVS constraints . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14

4 Operation under overload and short-circuit condition . . . . . . . . . . . . 17

5 Magnetic integration . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18

6 Design procedure . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21

7 Design example . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23

8 Electrical test results . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26

8.1 Efficiency measurements . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26

8.2 Resonant stage operating waveforms . . . . . . . . . . . . . . . . . . . . . . . . . . . 27

9 Reference . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31

10 Revision history . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31

2/32

AN2450 List of figures

List of figures

Figure 1. LLC resonant half-bridge converter . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4

Figure 2. FHA resonant circuit two port model. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7

Figure 3. Conversion ratio of LLC resonant half-bridge . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9

Figure 4. Shrinking effect of l value increase . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11

Figure 5. Normalized input impedance magnitude . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12

Figure 6. Capacitive and inductive regions in M - fn plane . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13

Figure 7. Circuit behavior at ZVS transition . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15

Figure 8. Voltage gain characteristics of the LLC resonant tank . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17

Figure 9. Transformer's physical model . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19

Figure 10. Transformer's APR (all-primary-referred) model. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 19

Figure 11. Transformer construction: E-cores and slotted bobbin . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20

Figure 12. LLC resonant half-bridge converter electrical schematic . . . . . . . . . . . . . . . . . . . . . . . . . . 25

Figure 13. Circuit efficiency versus output power at various input voltages. . . . . . . . . . . . . . . . . . . . . 27

Figure 14. Resonant circuit primary side waveforms at nominal dc input voltage and full load . . . . . . 28

Figure 15. Resonant circuit primary side waveforms at nominal dc input voltage and light load . . . . . 28

Figure 16. Resonant circuit primary side waveforms at nominal dc input voltage and no-load . . . . . . 29

Figure 17. Resonant circuit primary side waveforms at nominal dc input voltage and light load . . . . . 29

Figure 18. +200 V output diode voltage and current waveforms . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30

Figure 19. +75 V output diode voltage and current waveforms . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30

3/32

FHA circuit model AN2450

m

d

d

1 FHA circuit model

The FHA approach is based on the assumption that the power transfer from the source to
the load through the resonant tank is almost completely associated to the fundamental
harmonic of the Fourier expansion of the currents and voltages involved. This is consistent
with the selective nature of resonant tank circuits.

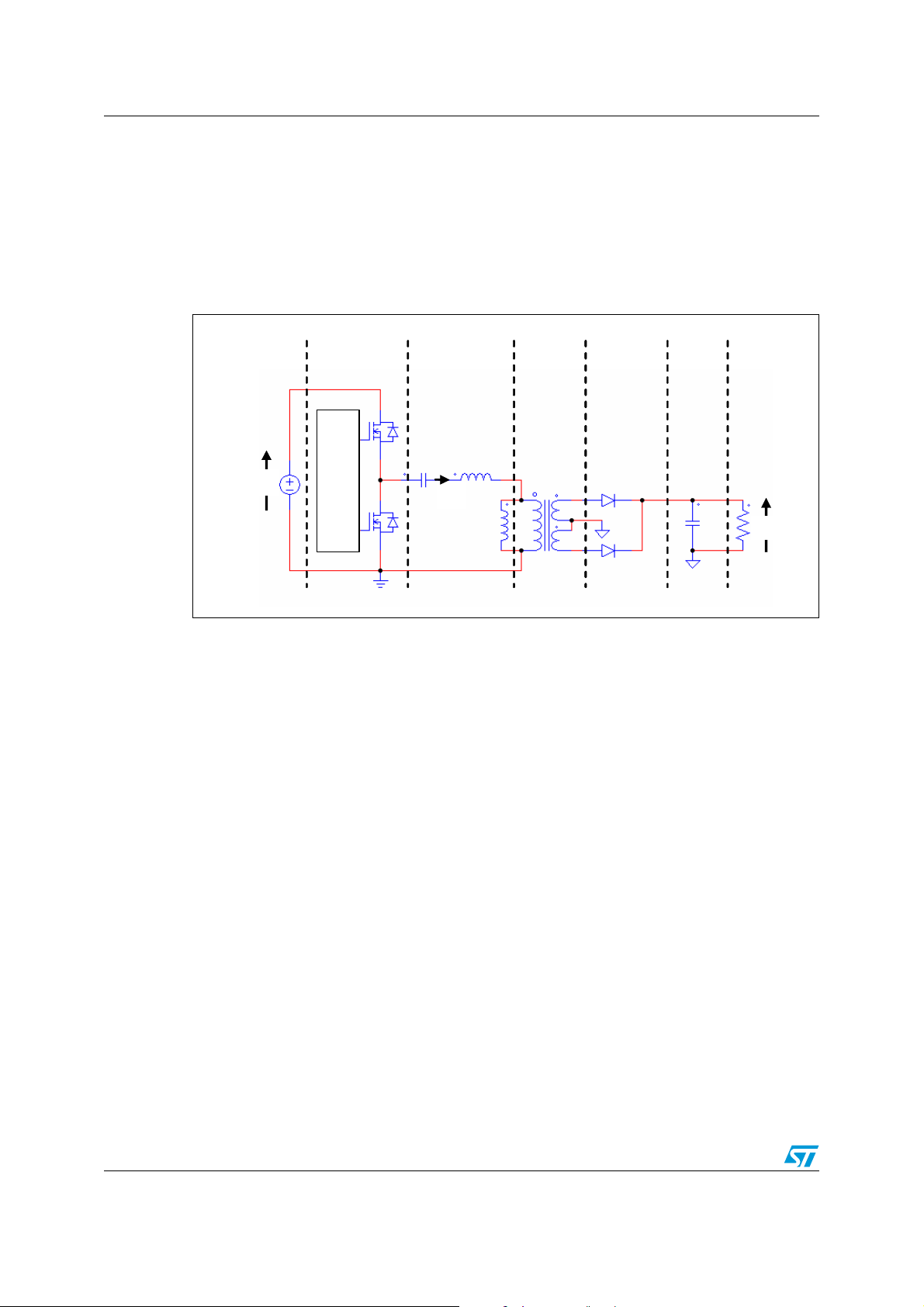
Figure 1. LLC resonant half-bridge converter

Input source

V

dc

Controlle

Switch Network

Q

Half-bridge

Driver

Q

Resonant

tank

1

C

L

r

r

I

rt

Ideal

transformer

n:1

Uncontrolle

rectifier

D

1

L

2

D

2

Low-pass

filter

C

out

Load

R

out

V

out

The harmonics of the switching frequency are then neglected and the tank waveforms are
assumed to be purely sinusoidal at the fundamental frequency: this approach gives quite
accurate results for operating points at and above the resonance frequency of the resonant
tank (in the continuous conduction mode), while it is less accurate, but still valid, at
frequencies below the resonance (in the discontinuous conduction mode).

It is worth pointing out also that many details of circuit operation on a cycle-to-cycle time
base will be lost. In particular, FHA provides only a necessary condition for MOSFETs' zero­voltage switching (ZVS) and does not address secondary rectifiers' natural ability to work
always in zero-current switching (ZCS). A sufficient condition for Power MOSFETs' ZVS will
be determined in Section 3: ZVS constraints still in the frame of FHA approach.

Let us consider the simple case of ideal components, both active and passive.

The two Power MOSFETs of the half-bridge in Figure 1 are driven on and off symmetrically
with 50% duty cycle and no overlapping. Therefore the input voltage to the resonant tank
v

(t) is a square waveform of amplitude Vdc, with an average value of Vdc/2. In this case the

sq

capacitor C
voltage across C

The input voltage waveform v

acts as both resonant and dc blocking capacitor. As a result, the alternate

r

is superimposed to a dc level equal to Vdc/2.

r

(t) of the resonant tank in Figure 1 can be expressed in

sq

Fourier series:

Equation 1

V

vsqt()

4/32

---------

2

dc

2

-- -

V

dc

π

n 135.,,=

∑

1

-- -

n2πfswt()sin+=

n

..

AN2450 FHA circuit model

whose fundamental component v

(t) (in phase with the original square waveform) is:

i.FHA

Equation 2

2

t()

-- -

V

π

dc

2πfswt()sin=

of the input voltage fundamental

i.FHA

v

iFHA

.

where fsw is the switching frequency. The rms value V
component is:

Equation 3

2

v

iFHA

.

As a consequence of the above mentioned assumptions, the resonant tank current i
be also sinusoidal, with a certain rms value I

-------

=

V

dc

π

and a phase shift Φ with respect to the

rt

(t) will

rt

fundamental component of the input voltage:

Equation 4

irtt() 2I

2πfswt Φ–()sin 2I

rt

Φcos 2πfswt()2Irt–sin•Φ2πfswt()cos•sin==

rt

This current lags or leads the voltage, depending on whether inductive reactance or
capacitive reactance dominates in the behavior of the resonant tank in the frequency region
of interest. Irrespective of that, i

(t) can be obtained as the sum of two contributes, the first

rt

in phase with the voltage, the second with 90° phase-shift with respect to it.

The dc input current I

from the dc source can also be found as the average value, along a

i.dc

complete switching period, of the sinusoidal tank current flowing during the high side
MOSFET conduction time, when the dc input voltage is applied to the resonant tank:

Equation 5

T

sw

---------

2

1

---------

where T

is the time period at switching frequency.

sw

The real power P

I

=

idc

.

, drawn from the dc input source (equal to the output power P

in

irtt() td

∫

T

sw

0

ideal case) can now be calculated as both the product of the input dc voltage V
average input current I

and the product of the rms values of the voltage and current's first

i.dc

-------

2

I

Φcos=

rt

π

in this

out

times the

dc

harmonic, times cosΦ :

Equation 6

P

inVdc

I

idc

.

V

.

iFHAIrt

Φcos==

the two expressions are obviously equivalent.

The expression of the apparent power P

and the reactive power Pr are respectively:

app

Equation 7

P

=

appViFHAIrt

.

PrV

iFHAIrt

.

Φsin=

Let us consider now the output rectifiers and filter part. In the real circuit, the rectifiers are
driven by a quasi-sinusoidal current and the voltage reverses when this current becomes
zero; therefore the voltage at the input of the rectifier block is an alternate square wave in
phase with the rectifier current of amplitude V

out

.

5/32

FHA circuit model AN2450

4

The expressions of the square wave output voltage v

o.sq

(t) is:

Equation 8

4

t()

-- -

V

=

π

V

.

osq

which has a fundamental component v

out

n135.,,=

o.FHA

∑

(t):

1

-- -

n

..

n2πf

sw

t Ψ–()sin

Equation 9

t()

-- -

V

π

out

2(πfswt Ψ)–sin=

V

oFHT

.

whose rms amplitude is:

Equation 10

22

V

oFHA

.

---------- -

V

=

out

π

where Ψ is the phase shift with respect to the input voltage. The fundamental component of
the rectifier current

(t) will be:

irect

Equation 11

i

t() 2I

rect

where I

is its rms value.

rect

Also in this case we can relate the average output current to the load I
ac current I

flowing into the filtering output capacitor:

c.ac

rect

2(πfswt Ψ)–sin=

and also derive the

out

Equation 12

T

sw

---------

I

out

2

---------

T

sw

2

i

rect

∫

0

t() td

22

---------- -

π

I

rect

P

V

out

out

out

-----------==

R

out

---------- -==

V

Equation 13

2

2

I

–=

out

.

out

where P

Since v

is the output power associated to the output load resistance R

out

o.FHA

(t) and i

(t) are in phase, the rectifier block presents an effective resistive load

rect

to the resonant tank circuit, R

I

cac

, equal to the ratio of the instantaneous voltage and

o.ac

I

.

rect

current:

Equation 14

8

-----

π

V

------------- -

2

P

2

out

out

8

-----

====

R

out

2

π

t()

t()

V

oFHA

.

---------------- -

I

rect

v

.

oFHA

.

oac

---------------------- -

i

rect

R

Thus, in the end, we have transformed the non linear circuit of Figure 1 into the linear circuit
of Figure 2, where the ac resonant tank is excited by an effective sinusoidal input source
and drives an effective resistive load. This transformation allows the use of complex ac­analysis methods to study the circuit and, furthermore, to pass from ac to dc parameters
(voltages and currents), since the relationships between them are well-defined and fixed
(see equations Equation 3, Equation 5, Equation 6, Equation 10 and Equation 12 above).

6/32

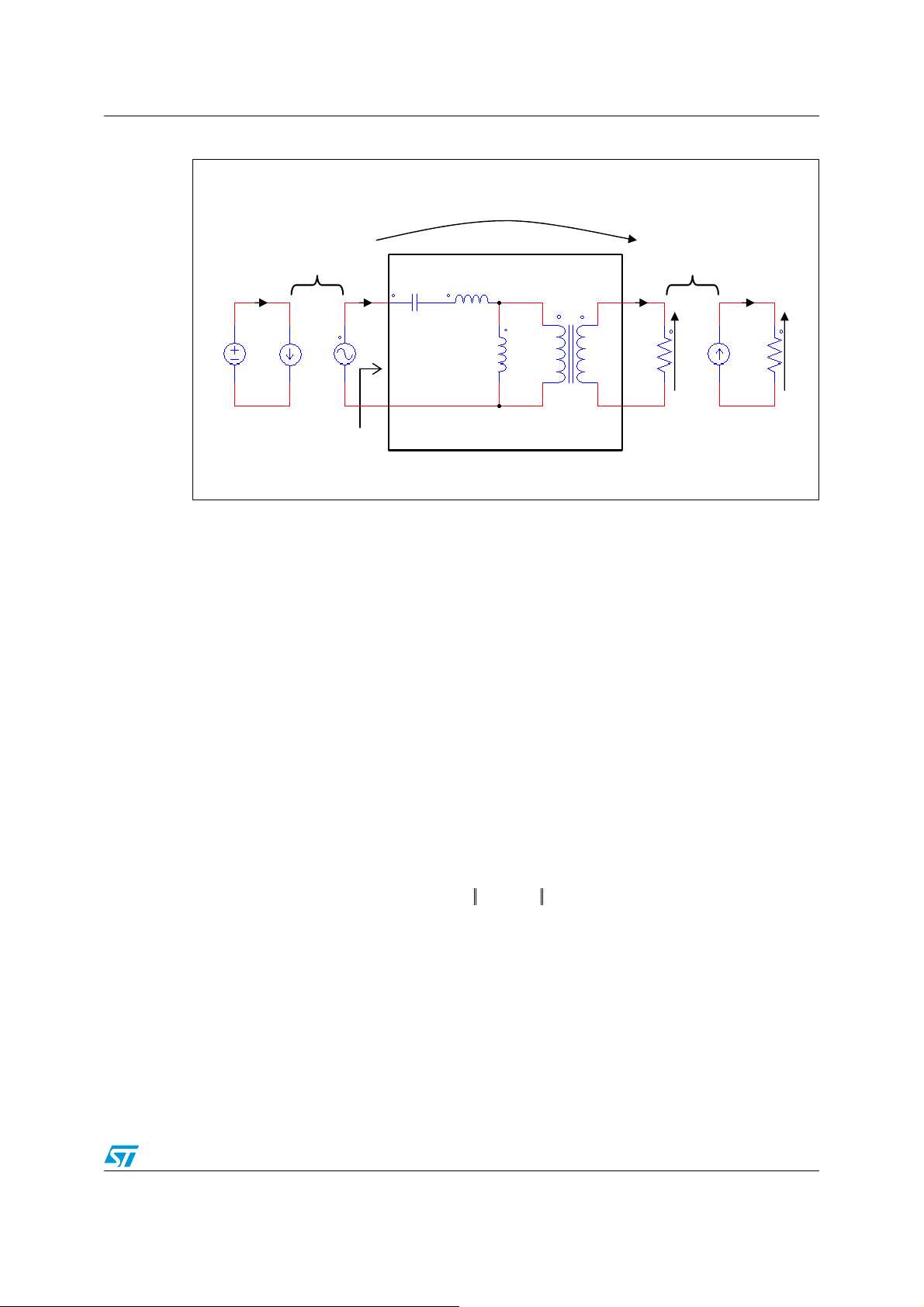
AN2450 FHA circuit model

k

2

Figure 2. FHA resonant circuit two port model

H(jȦ)

V

dc

dc input

I

i.dc

controlled

switch

networ

V

i.

FHA

n :1

I

rt

Cr L

L

r

m

I

rect

R

o.ac

rectifier &

low-pass

filter

V

o.

FHA

dc output

I

out

R

out

V

out

(jȦ)

Z

in

ac resonant tank

The ac resonant tank in the two-port model of Figure 2 can be defined by its forward transfer
function H(s) and input impedance Z

in

(s):

Equation 15

Hs()

V

s()

.

oFHA

------------------------ -

V

s()

iFHA

.

n

1

-- -

--------------------------------------

==

n

||

R

.

oac

Z

sL

m

s()

in

Equation 16

Zins()

iFHA

-----------------------

s()

I

rt

1

--------- sLrn2R

++==

sC

r

oac

||

sL

.

m

V

s()

.

For the discussion that follows it is convenient to define the effective resistive load reflected
to the primary side of the transformer R

ac

:

Equation 17

R

n2R

=

ac

and the so-called "normalized voltage conversion ratio" or "voltage gain" M(f

oac

.

):

sw

Equation 18

V

.

oFHA

Mfsw()nHj2πfsw()n

==

---------------- -

V

.

iFHA

It can be demonstrated (by applying the relationships Equation 3, Equation 10 and Equation

18 to the circuit in Figure 2) that the input-to-output dc-dc voltage conversion ratio is equal

to:

Equation 19

V

---------- -

V

out

dc

1

------ -

2n

Mfsw()=

In other words, the voltage conversion ratio is equal to one half the module of resonant
tank's forward transfer function evaluated at the switching frequency.

7/32

Voltage gain and input impedance AN2450

2 Voltage gain and input impedance

Starting from Equation 18 we can obtain the expression of the voltage gain:

Equation 20

Mfnλ Q,,()

with the following parameter definitions:

---------------------------------------------------------------------------- -=

⎛⎞

1 λ

⎜⎟
⎝⎠

1

2

λ

------ -–+

2

f

n

⎛⎞

Q2f

+

⎝⎠

2

1

----–

n

f

n

resonance frequency:

f

r

characteristic impedance:

Z

o

---------

quality factor:

inductance ratio:

normalized frequency:

Q

R

ac

L

r

λ

------ -=

L

m

f

n

1

----------------------=

2π L

Z

o

Z

o

------------------ -

n2R

oac

.

f

sw

-------=

f

r

rCr

L

r

----- - 2πfrL
C

r

2

Z

π

0

-----

------

===

2

8

n

r

P

out

------------- -

2

V

out

1

---------------- -===

2πfrC

r

Under no-load conditions, (i.e. Q = 0) the voltage gain assumes the following form:

Equation 21

1

MOLfnλ,()

-----------------------------=

1 λ

λ

------ -–+

2

f

n

Figure 3 shows a family of plots of the voltage gain versus normalized frequency. For

different values of Q, with λ = 0.2, it is clearly visible that the LLC resonant converter
presents a load-independent operating point at the resonance frequency f

(fn = 1), with

r

unity gain, where all the curves are tangent (and the tangent line has a slope -2λ).
Fortunately, this load-independent point occurs in the inductive region of the voltage gain
characteristic, where the resonant tank current lags the input voltage square waveform
(which is a necessary condition for ZVS behavior).

The regulation of the converter output voltage is achieved by changing the switching
frequency of the square waveform at the input of the resonant tank: since the working region
is in the inductive part of the voltage gain characteristic, the frequency control circuit that
keeps the output voltage regulated acts by increasing the frequency in response to a
decrease of the output power demand or to an increase of the input dc voltage. Considering
this, the output voltage can be regulated against wide loads variations with a relatively
narrow switching frequency change, if the converter is operated close to the load­independent point. Looking at the curves in Figure 3, it is obvious that the wider the input dc

8/32

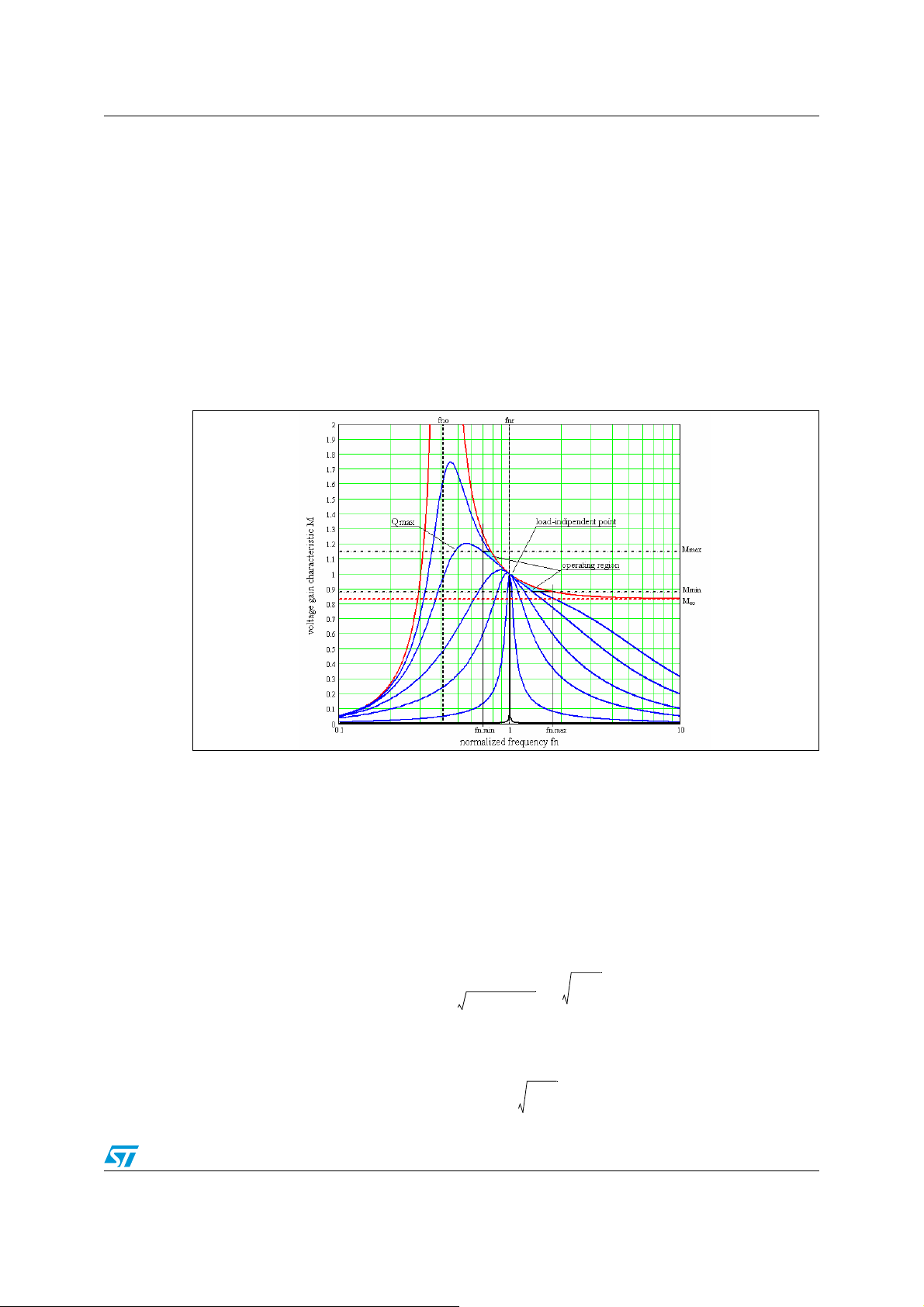
AN2450 Voltage gain and input impedance

voltage range is, the wider the operating frequency range will be, in which case it is difficult
to optimize the circuit. This is one of the main drawbacks common to all resonant topologies.

This is not the case, however, when there is a PFC pre-regulator in front of the LLC
converter, even with a universal input mains voltage (85 V
the input voltage of the resonant converter is a regulated high voltage bus of ~400 V

- 264 Vac). In this case, in fact,

ac

dc

nominal, with narrow variations in normal operation, while the minimum and maximum
operating voltages will depend, respectively, on the PFC pre-regulator hold-up capability
during mains dips and on the threshold level of its over voltage protection circuit (about 10­15% over the nominal value). Therefore, the resonant converter can be optimized to operate
at the load-independent point when the input voltage is at nominal value, leaving to the step­up capability of the resonant tank (i.e. operation below resonance) the handling of the
minimum input voltage during mains dips.

Figure 3. Conversion ratio of LLC resonant half-bridge

The red curve in Figure 3 represents the no-load voltage gain curve M
frequency going to infinity, it tends to an asymptotic value M

:

∞

; for normalized

OL

Equation 22

M∞MOLfn∞λ,→()

Moreover, a second resonance frequency f

can be found, which refers to the no-load

o

------------ -==

1 λ+

1

condition or when the secondary side diodes are not conducting (i.e. the condition where
the total primary inductance L

+ Lm resonates with the capacitor Cr); fois defined as:

r

Equation 23

-----------------------------------------

f

o

2π L

1

+()C

rLm

r

λ

------------ -==

f

r

1 λ+

or in normalized form:

Equation 24

f

o

----

f

no

f

λ

------------ -==

1 λ+

r

9/32

Voltage gain and input impedance AN2450

At this frequency the no-load gain curve MOL tends to infinity.

By imposing that the minimum required gain M
the asymptotic value M

, it is possible to ensure that the converter can work down to no-load

∞

(at max. input dc voltage) is greater than

min

at a finite operating frequency (which will be the maximum operating frequency of the
converter):

Equation 25

The maximum required gain M

V

out

M

min

(at min. input dc voltage) at max. output load (max. P

max

------------------ -

2n

V

.

dcmax

>=

1

------------ -

1 λ+

that is at max. Q, will define the min. operating frequency of the converter:

Equation 26

V

out

M

max

Given the input voltage range (V

● always below resonance frequency (step-up operations)

● always above resonance frequency (step-down operations)

● across the resonance frequency (shown in Figure 3).

dc.min

- V

----------------- -

2n

=

V

.

dcmin

), three types of operations are possible:

dc.max

Looking at Figure 4, we can see that an increase of the inductance ratio value λ has the
effect of shrinking the gain curves in the M - f
(which means the no-load resonance frequency f
reduces the asymptotic level M

of the no-load gain characteristic. At the same time the

∞

plane toward the resonance frequency fnr

n

increases) and contemporaneously

no

peak gain of each curve increases.

out

),

10/32

AN2450 Voltage gain and input impedance

Figure 4. Shrinking effect of λ value increase

Starting from Equation 16 we can obtain the expression of the normalized input impedance

of the resonant tank:

Z

n

Equation 27

Z

infn

Znfnλ Q,,()

---------------------------------- -

λ Q,,()

Z

o

jf

n

-------------------- -

λ jfnQ+

1f

–

n

----------------+==

jf

n

2

whose magnitude is plotted in Figure 5, at different Q values, with λ = 0.2.

The red and blue curves in the above mentioned figure represent the no-load and short
circuit cases respectively, and are characterized by asymptotes at the two normalized
resonance frequencies f
normalized frequency f

and fnr (= 1). All the curves at different values of Q intercept at

no

:

n.cross

Equation 28

f

ncross

.

At frequencies higher than the crossing frequency f
such that at increasing output current Iout (that is at increasing P
(coherently to the load resistance); the opposite happens at frequencies lower than f

----------------=

12λ+

2λ

n.cross

, the input impedance behaves

and Q) it decreases

out

n.cross

where the input impedance increases, while the output load resistance decreases.

,

11/32

Voltage gain and input impedance AN2450

2

2

Figure 5. Normalized input impedance magnitude

The ac analysis can also help to estimate converter's efficiency η

φ and predict how this

changes with the load. Considering the generic model similar to the one in Figure 2, where
the resonant tank includes also the dissipative elements (i.e. series resistors for magnetic
components winding losses and capacitor's ESR, and parallel resistors for magnetic losses
of inductors and transformer), we can compute the transfer function H
impedance Z
Z

in.LOSS

, we get:

in.LOSS

(jω). By calculating input and output power in terms of H

(jω) and the input

LOSS

LOSS

and

Equation 29

2

jω()

jω()[]

.

inLOSS

) and the input and output power are

where Y

η

is the admittance (reciprocal of Z

in.LOSS

P

out

---------- -

P

H

LOSS

--------------------------------------------------------- -==

R

.

oac

Re Y

in.LOSS

in

expressed as:

Equation 30

PinV

.

iFHAIrt

Φcos V

==

iFHA

.

2

Re

1

-------------------------------

Z

inLOSS

jω()

.

.

Equation 31

.

oac

V

.

iFHA

------------------

R

oac

.

H

LOSS

jω()===

V

.

oFHA

P

out

V

.

oFHAIrect

------------------- -

R

The region on the left-hand side of the diagram in Figure 5, i.e. for a normalized frequency
lower than f
voltage; at normalized frequency higher than the resonance frequency f

, is the capacitive region, where the tank current leads the half-bridge square

no

(= 1), on the right-

nr

hand side region, the input impedance is inductive, and the resonant tank current lags the
input voltage. In the region between the two resonance frequencies the impedance can be
either capacitive or inductive, depending on the value of the impedance phase angle.

By imposing that the imaginary part of Z
has zero phase angle, as Z

12/32

is real and does not affect the phase), we can find the

o

, λ, Q) is zero (which means imposing that Zin

n(fn

AN2450 Voltage gain and input impedance

boundary condition between capacitive and inductive mode operation of the LLC resonant
converter.

The analytical results are the following:

Equation 32

fnZλ Q,()

Q2λ 1 λ+()– Q2λ 1 λ+()–[]

---------------------------------------------------------------------------------------------------------------- -=

2Q

2

2

++

4Q2λ

2

Equation 33

2

λ

λ

⎛⎞

----

–=

⎝⎠

2

f

n

n

where f

QZfnλ,()

represents the normalized frequency where, for a fixed couple (λ- Q), the input

nZ

---------------­–

1f

resonant tank impedance is real (and only real power is absorbed from the source); while
Q

is the maximum value of the quality factor, below which, at a fixed normalized frequency

Z

and inductance ratio (f

- λ) the tank impedance is inductive; hence, the maximum voltage

n

gain available in that condition is also found:

Equation 34

M

λ Q,()MfnZλ Q ),λQ,,(()=

MAX

By plotting the locus of operating points [M

(λ, Q), fnZ(λ,Q)], whose equation on M - fn

MAX

plane is the following:

Equation 35

f

MZfnλ,()

-------------------------------------- -=

2

f

n

n

1 λ+()λ–

we can draw the borderline between capacitive and inductive mode in the region between
the two resonance frequencies, shown in Figure 6 It is also evident that the peak value of
the gain characteristics for a given quality factor Q value, already lies in the capacitive
region.

Figure 6. Capacitive and inductive regions in M - f

plane

n

13/32

ZVS constraints AN2450

Moreover, by equating the second term of (Equation 35) to the maximum required gain
M

(at minimum input voltage), and solving for fn, we get the minimum operating

max

frequency f

which allows the required maximum voltage gain at the boundary between

n.min

capacitive and inductive mode:

Equation 36

f

nmin

.

---------------------------------------------- -=

1

1

1

-----------------

M

max

⎞
⎟

2

⎠

⎛

1

-- -

1

–

+

⎜

λ

⎝

Furthermore, by substituting the minimum frequency (Equation 36) into the Equation 33, we
get the maximum quality factor Q

which allows the required maximum voltage gain at the

max

boundary between capacitive and inductive mode:

Equation 37

2

max

--------------

M

max

Q

λ

M

1

max

---

--------------------------+=

λ

2

M

max

1–

Finally, by equating the second term of the no-load transfer function (Equation 21) to the
minimum required voltage gain M
normalized frequency f

n.max

:

, it is possible to find the expression of the maximum

min

Equation 38

3 ZVS constraints

The assumption that the working region lies inside the inductive region of operation is only a
necessary condition for the ZVS of the half bridge MOSFETs, but not sufficient; this is
because the parasitic capacitance of the half bridge midpoint, neglected in the FHA
analysis, needs energy to be charged and depleted during transitions. In order to
understand ZVS behavior, refer to the half bridge circuit in Figure 7, where the capacitors
C

and C

oss

MOSFETs and the total stray capacitance present across the resonant tank impedance, so
that the total capacitance C

Equation 39

which, during transitions, swings by ∆V = V
such that a dead time T
the beginning of the ON-time of the other one, so that both are not conducting during T

are, respectively, the effective drain-source capacitance of the Power

stray

is inserted between the end of the ON-time of either MOSFET and

D

f

nmax

.

at node N is:

zvs

C

zvs

1

----------------------------------------- -=

1

-- -

+

1

λ

2C

OSSCstray

. To allow ZVS, the MOSFET driving circuit is

dc

1

⎛⎞

------------ -–

1

⎝⎠

M

min

+=

.

D

14/32

AN2450 ZVS constraints

Figure 7. Circuit behavior at ZVS transition

Vg1

Vg2

Irt

T

D

Vsq

Vdc

I

zvs

Due to the phase lag of the input current with respect to the input voltage, at the end of the
first half cycle the inductor current I
deplete C

so that its voltage swings from ∆V to zero (it will be vice versa during the

ZVS

is still flowing into the circuit and, therefore it can

rt

second half cycle).

In order to guarantee ZVS, the tank current at the end of the first half cycle (considering the
dead time negligible as compared to the switching period, so that the current change is
negligible as well) must exceed the minimum value necessary to deplete C
dead time interval T

, which means:

D

within the

ZVS

Equation 40

T

sw

⎛⎞

I

zvsirt

---------

===

⎝⎠

2

V∆

-------

C

zvs

T

D

2C

OSSCstray

+()

V

---------

T

dc

D

This current equals, of course, the peak value of the reactive current flowing through the
resonant tank (it is 90° out-of-phase); the one that determines the reactive power level into
the circuit:

Equation 41

I

zvs

2IrtΦsin=

15/32

ZVS constraints AN2450

Moreover, as the rms component of the tank current associated to the active power is:

Equation 42

P

I

actIrt

in

Φcos

---------------==

V

iFHA

.

we can derive also the rms value of the resonant tank current and the phase lag Φ between
input voltage and current (that is the input impedance phase angle at that operating point):

Equation 43

I

rt

2

I

Φ)2( I

rt

2

Φ)2(sin+cos

rt

P

in

⎛⎞

---------------

⎝⎠

V

.

iFHA

I

zvs

----------- -+==

2

2

2

Equation 44

P

in

⎛⎞

Φ a

-------------------- -

cos=

⎝⎠

V

iFHAIrt

.

Thus we can write the following analytic expression:

Equation 45

Im Z

---------------------------------------------- -

Φ()tan

Re Z

λ Q,,()[]

nfn

λ Q,,()[]

nfn

≥=

C

----------- -

πT

zvs

D

V

dc

----------- -

P

in

2

which is the sufficient condition for ZVS of the half-bridge Power MOSFETs, to be applied to
the whole operating range. The solution of Equation 45 for the quality factor Q

zvs

that
ensures ZVS behavior at full load and minimum input voltage is not convenient. Therefore,
we can calculate the Q

value (at max. output power and min. input voltage), where the

max

input impedance has zero phase, and take some margin (5% - 10%) by choosing:

Equation 46

zvs1

90=

.

max

%

%

Q

•

95÷Q

and check that the condition (Equation 45) is satisfied at the end of the process, once the
resonant tank has been completely defined. The process will be iterated if necessary.

Of course the sufficient condition for ZVS needs to be satisfied also at no-load and
maximum input voltage; in this operating condition it is still possible to find an additional
constraint on the maximum quality factor at full load to guarantee ZVS. In fact the input
impedance at no-load Z

has the following expression:

in.OL

Equation 47

1

Z

() jZofn1

inOLfn

.

⎛⎞
⎝⎠

1

-- -+

----–=

λ

f

n

Taking into account that:

Equation 48

ZoRacQ=

and writing the sufficient condition for ZVS in this operating condition, that is:

Equation 49

V

.

iFHAmax

-------------------------------------- -

Z

()

inOLfnmax

.

I

zvs Vdcmax()

------------------------------- -

≥

2

16/32

AN2450 Operation under overload and short-circuit condition

we get the constraint on the quality factor for the ZVS at no-load and maximum input
voltage:

Equation 50

Q

2

-------------------------------------------- -

-- -

≤

.

zvs2

π

λ 1+()f

λf

nmax

.

nmax

.

2

T

--------------------- -

RacC

λ–

D

zvs

Therefore, in order to guarantee ZVS over the whole operating range of the resonant
converter, we have to choose a maximum quality factor value lower than the smaller of
Q

zvs.1

and Q

zvs.2

.

4 Operation under overload and short-circuit condition

An important aspect to analyze is the converter's behavior during output over-load and/or
short-circuit.

Referring to the voltage gain characteristics in Figure 8, let us suppose that the resonant
tank has been designed to operate in the inductive region for a maximum output power
P
(corresponding to the horizontal line M = M

When the output power is increased from zero to the maximum value, the gain characteristic
relative to each power level changes progressively from the red curve (Q = 0) to the black
one (Q
moves along the horizontal line M = M
is given by the abscissa of the crossover between the horizontal line M = M
gain characteristic relevant to the associated value of Q.

(corresponding to the curve Q = Q

out.max

). The control loop keeps the value of M equal to Mx, then the quiescent point

max

) at a given output-to-input voltage ratio

max

) greater than 1,

x

and the operating frequency at each load condition

x

and the voltage

x

Figure 8. Voltage gain characteristics of the LLC resonant tank

17/32

Magnetic integration AN2450

If the load is increased over the maximum specified (associated to the curve Q = Q

max

)
eventually the converter's operating point will invariably enter the capacitive region, where
hard switching of power MOSFETs may cause device failures, if no corrective action is
taken.

In fact, for values of Q sufficiently greater than Q

the intersection with the M = Mx line will

max

take place on the left-hand side of the borderline curve and, then, in the capacitive region;
moreover, if Q exceeds the value corresponding to the characteristic curve tangent to M =
M

there will no longer be a possible operating point with M=Mx. This means that the

x

converter will no longer be able to keep the output voltage regulated and the output voltage
will fall despite the reduction of the operating frequency (feedback reversal).

Limiting the minimum operating frequency (e.g. at the frequency value corresponding to the
intersection of M=M

with Q=Q

x

) is not enough to prevent the converter from entering the

max

capacitive region of operation. In fact, as the minimum frequency is reached, from that point
onwards a further load increase will make the operating point move along the vertical line
f=f

and eventually cross the borderline.

min

Limiting the minimum operating frequency is effective in preventing capacitive mode
operation only if the minimum (normalized) frequency value is greater than 1. This suggests
that, in response to an overload / short circuit condition at the output, the converter
operating frequency must be pushed above the resonance frequency (it is better if well
above it) in order to decrease power throughput.

It is worth noticing that, if the converter is specified to deliver a peak output power (where
output voltage regulation is to be maintained) greater than the maximum continuous output
power for a limited time, the resonant tank must be designed for peak output power to make
sure that it will not run in capacitive mode. Of course, its thermal design will consider only
the maximum continuous power.

In any case, whatever the converter specified, short circuit conditions or, in general,
overload conditions exceeding the maximum specified for the tank circuit, need to be
handled with additional means, such as a current limitation circuit.

5 Magnetic integration

The LLC resonant half-bridge is well suited for magnetic integration, i.e. to combine the
inductors as well as the transformer into a single magnetic device. This can be easily
recognized looking at the transformer's physical model in Figure 9, where the topological
analogy with the inductive part of the LLC tank circuit is apparent. However, the real
transformer has leakage inductance on the secondary side as well, which is completely
absent in the model considered so far. To include the effect of secondary leakage in the FHA
analysis, we need a particular transformer model and a simplifying assumption.

It is well known that there are an infinite number of electrically equivalent models of a given
transformer, depending on the choice of the turn ratio of the ideal transformer included in the
model. With an appropriate choice of this "equivalent" turn ratio n (obviously different from
the "physical" turn ratio n
on the primary side.

= N1/N2) all the elements related to leakage flux can be located

t

18/32

AN2450 Magnetic integration

This is the APR (All-Primary-Referred) model shown in Figure 10, which fits the circuit
considered in the FHA analysis. It is possible to show that the APR model is obtained with
the following choice of n:

Equation 51

L

nk

with k transformer's coupling coefficient, L

1

inductance of each secondary winding. Note that L

1

----- -=

L

2

inductance of the primary winding and L2

still has physical meaning: it is the

r

primary inductance measured with the secondary windings shorted. Note also that the
primary inductance L

Figure 9 and Figure 10, hence, L

must be unchanged. It is only differently split in the 2 models of

1

will be the difference between L1 and Lr.

m

In the end, the analysis done so far is directly applicable to real-world transformers provided
they are represented by their equivalent APR model. Vice versa, a design flow based on the
FHA analysis will provide the parameters of the APR model; hence, an additional step is
needed to determine those of the physical model. In particular this applies to the turn
number n
L

L1+Lµ=L1

, since Lr and Lm still have a connection with the physical world (Lr+Lm =

t

).

Figure 9. Transformer's physical model

Ideal Transformer

Prim. leakage

Prim. leakage

inductance

inductance

Magnetizing

Magnetizing

inductance

inductance

L

L

L1

L1

Ideal Transformer

n

n

Lµ

Lµ

: 1 : 1

: 1 : 1

t

t

L

L

L2a

L2a

L

L

L2b

L2b

Figure 10. Transformer's APR (all-primary-referred) model

Ideal Transformer

L

L

r

r

L

L

m

m

Ideal Transformer

n : 1 : 1

n : 1 : 1

Sec. leakage

Sec. leakage

inductance

inductance

Sec. leakage

Sec. leakage

inductance

inductance

The problem is mathematically undetermined: there are 5 unknowns (L
L

) in the physical model and only three parameters in the APR model. The simplifying

L2b

, Lµ, nt, and L

L1

L2a

assumption that overcomes this issue is that of magnetic circuit symmetry: flux linkage is

19/32

,

Magnetic integration AN2450

assumed to be exactly the same for both primary and secondary windings. This provides the
two missing conditions:

Equation 52

L

L

L2aLL2b

With this assumption it is now possible to find the relationship between n and n

L1

-------- -==

2

n

t

:

t

Equation 53

L

+

ntn

mLr

------------------ n1 λ+==

L

m

Figure 11. Transformer construction: E-cores and slotted bobbin

Slotted
bobbin

Separator

Air gap symmetrically
placed between the
windings

Top view

Winding

Ferrite
E half-cores

Winding

It is not difficult to find real-world structures where the condition of magnetic symmetry is
quite close to reality. Consider for example the ferrite E-core plus slotted bobbin assembly,
using side-by-side winding arrangement, shown in Figure 11.

20/32

AN2450 Design procedure

f

6 Design procedure

Based on the analysis presented so far, a step-by-step design procedure of an LLC
resonant converter is now proposed, which fulfills the following design specification and
requires the additional information listed below:

● Design specification:

– Input voltage range: V

– Nominal input voltage: V

– Regulated output voltage: V

– Maximum output power: P

– Resonant frequency: f

– Maximum operating frequency: f

●

Additional info:

– Parasitic capacitance at node N: C

– Dead time of driving circuit: T

●

General criteria for the design:

– The converter will be designed to work at resonance at nominal input voltage.

– The converter must be able to regulate down to zero load at maximum input

voltage.

– The converter will always work in ZVS in the whole operating range.

● 10 step procedure:

– Step 1 - to fulfill the first criterion, impose that the required gain at nominal input

voltage equals unity and calculate the transformer turn ratio:

dc.min

dc.nom

r

out

- V

out

dc.max

max

zvs

D

Equation 54

V

out

M

nom

2n

-------------------

V

.

dcnom

1==

⇒

V

1

.

dcnom

-- -

-------------------

n

=

2

V

out

– Step 2 - calculate the max. and min. required gain at the extreme values of the

input voltage range:

Equation 55

V

out

M

max

----------------- -

2n

=

V

dcmin

.

Equation 56

V

out

=

2n

------------------ -

V

.

dcmax

M

min

– Step 3 - calculate the maximum normalized operating frequency (according to the

definition):

Equation 57

f

nmax

.

max

---------- -=

f

r

21/32

Design procedure AN2450

2

– Step 4 - calculate the effective load resistance reflected at transformer primary

side, from Equation 14 and Equation 17:

Equation 58

V

8

2

out

-----

R

ac

------------- -

n

=

2

P

out

π

– Step 5 - impose that the converter operates at maximum frequency at zero load

and maximum input voltage, calculating the inductance ratio from Equation 38:

Equation 59

λ

1M

----------------------

=

–

M

min

min

f

.

nmax

--------------------------

2

f

nmax

.

1–

2

– Step 6 - calculate the max Q value to work in the ZVS operating region at

minimum input voltage and full load condition, from Equation 37 and Equation 46:

Equation 60

2

Q

zvs1

•

λ

--------------

M

max

%

Q

95=

.

max

%

95=•

M

1

-- -

λ

max

--------------------------+

2

M

max

1–

– Step 7 - calculate the max Q value to work in the ZVS operating region at no-load

condition and maximum input voltage, applying Equation 50:

Equation 61

Q

zvs2

2

-- -

-------------------------------------------- -

=

.

π

λ 1+()f

λf

nmax

.

nmax

.

2

T

----------------------

RacC

λ–

D

zvs

– Step 8 - choose the max quality factor for ZVS in the whole operating range, such

that:

Equation 62

Q

min Q

{, }≤

zvs

..

zvs1Qzvs2

– Step 9 - calculate the minimum operating frequency at full load and minimum input

voltage, according to the following approximate formula:

Equation 63

f

minfr

– Step 10 - calculate the characteristic impedance of the resonant tank and all

component values (from definition):

Equation 64

1

---------------- -=

ZoQ

=

zvsRac

22/32

C

r

2πfrZ

----------------------------------------------------------------- -=

1

-- -

1

+

λ

o

1

⎛⎞
⎜⎟
⎜⎟

1

⎜⎟
⎜⎟
⎝⎠

L

1

---------------------------------------–

1

M

max

Z

o

----------=

r

2πf

Q

zvs

⎛⎞

-------------

+

⎝⎠

Q

max

L

r

4

L

r

---- -=

m

λ

AN2450 Design example

7 Design example

Here below, a design example follows for a 400 W resonant converter intended to be
operated with a front-end PFC with a typical regulated bus voltage of about 400 V.

The STMicroelectronics resonant controller L6599 is particularly suitable for this application.
In fact it incorporates the necessary functions to properly drive the two half-bridge
MOSFETs by a 50 percent fixed duty cycle with a fixed dead-time T
and low side MOSFET driving signals), changing the frequency according to the feedback
signal in order to regulate the output voltages against load and input voltage variations. The
main features of the L6599 are a non linear soft-start, a new current protection mode
allowing to program the hiccup mode timing, a dedicated pin for sequencing or brown-out
(pin LINE) and a stand-by pin (pin STBY) allowing for the burst mode operation at light load.

The converter specification data are the following:

– Nominal input DC voltage: 390 V

– Input DC voltage range: from 320 to 420 V

– Output voltages: 200 V@ 1.6 A continuous current - 75 V@ 1.0 A continuous

current

– Resonance frequency: 120 kHz

– Max operating frequency: 150 kHz

– Delay time (L6599 data-sheet): 270 ns

– Foreseen half-bridge total stray capacitance (at node N): 350 pF

, (between high side

D

The calculations have been done assuming that all power is delivered to the 200 V output
voltage. Afterward, once the turn ratio has been defined, the transformer is designed to
deliver the two output voltages, using the correct number of turns and the proper wire
section.

The results of the 10 step procedure are summarized in Ta bl e 1 :

Table 1. Desing results

Step Parameter

1 n = 0.975

M

= 1.22

2

3f

4R

5 λ = 0.21

6Q

7Q

8Q

9f

Z

10

o

L

max

=0.93

M

min

= 1.25

n.max

= 77.05 Ω

ac

= 0.41

zvs.1

= 1.01

zvs.2

= 0.41

zvs

= 80.6 kHz

min

= 31.95 Ω Cr = 41.51 nF

= 42 µH Lm = 197 µH

r

23/32

Design example AN2450

The chosen standard value of the resonant capacitor is 4 7nF. The transformer has been
designed using a two slot coil-former and integrating both the series inductance L
shunt inductance L

, in order to obtain a magnetic component with the following

m

and the

r

parameters:

● primary inductance (with secondary windings open)

L

pSO()LrLm

240 µH=+=

L

● primary inductance with secondary windings shorted

pSS()Lr

ntn1λ+• 1.08==

● transformer turn ratio

40 µH==

The number of primary turns has been found experimentally, by measuring the "specific
leakage inductance" (i.e. the leakage inductance per square turns) of a few suitable ferrite
cores, using a two slot winding configuration. The procedure consists of winding a few layers
of turns on both slots of the coil-former (same copper area for primary and secondary) and
then measuring the inductance of one winding with the other one short circuited. Dividing
this measured value by the squared number of turns gives the specific leakage inductance
of the core - coil-former construction. The chosen ferrite core is a ER-49-27-17 type,
material grade PC44, and the necessary number of primary turns to obtain the required
leakage inductance is 19. Therefore, the total number of secondary turns for 200 V output is
18 (from the required turn ratio n

).

t

The secondary side of the transformer consists of two center-tap windings, one for each
output, and the two output voltages (+75 V and +200 V) are obtained by series connecting
the two secondary windings on the DC side (refer to the electrical schematic in Figure 12 for
better understanding of circuit configuration). The bottom winding (for +75 V output) has 7
turns, while the top winding consists of 11 (18-7) turns.

24/32

AN2450 Design example

C21

470nF

C11

100nF

C10

10uF/50V

R10

47

R15

10k

C18

10nF

+200V

PWM-Latch

R14

1k5

C12

4nF7

R11

10

R21

1k5

LINE

Vaux

+75V

1234567

8

J1

CON8

R27

6k2

R28

2k7

R20

75k

R22

1k0

R26

1k0

R19

3k3

U3

TL431

C22

47nF

D9

C-12V

C19

10uF/50V

L2

22uH

C16

220uF/100V

C17

220uF/100V

R3

2k7

C14

47uF/100V

D6

STTH1002C

U2A

SFH617A-2

U2B

SFH617A-2

C20

47nF

C1

470nF

Q1

BC327

R1

560k

R18

56k

R17

56k

C2

100nF

R16

56k

R24

470R

C3

470nF

T1

T-RES-ER49-400W

C5

270pF

R9

2M2

R8

16k

Q2

STP14NK50Z

C7

47nF/630V

Q3

STP14NK50Z

D2

BYT08P-400D4BYT08P-400

Vdc

C6

22uF/250VC9100uF/250V

C8

100uF/250V

L1

10uH

R12

150

C13

220pF/630V

D8

LL4148

D7

LL4148

C15

1uF0

R13

100R

D5

STTH1002C

R23

75k

R7

47

R2

0R

R5

47

D1

LL4148

D3

LL4148

R6

0R

CSS

DELAYCFRFMIN

STBY

ISEN

LINE GND

LVG

VCC

NC

OUT

HVG

VBOOT

DIS PFC-STOP

U1

L6599

R4

0R

C4 100nF

R25

220R

JP

Figure 12. LLC resonant half-bridge converter electrical schematic

25/32

Electrical test results AN2450

8 Electrical test results

8.1 Efficiency measurements

Ta bl e 2 , Ta bl e 3 and Ta bl e 4 below show the output voltage and current measurements at

the various dc input voltage (nominal 390 Vdc, min 360 Vdc and max 420 Vdc) and several
load conditions. For all measurements, both at full load and at light load operation, the input
power has been measured by a digital power meter (Yokogawa WT-210). Particular attention
has to be paid when measuring input power at full load in order to avoid measurement errors
due to the voltage drop on cables and connections (connecting the WT-210 voltmeter
termination to the board input connector). For the same reason, the measurements of the
output voltages have been taken directly at the output connector, by using the remote sense
option of the active load (Chroma 63108 and 63103) connected to the outputs.

Table 2. Efficiency measurements @ V

+200 V @load(A) +75 (V) @load (A) Pout (W) Pin (W) Efficiency %

198.76 1.603 76.74 1.010 396.12 408.80 96.90%

198.75 1.300 76.80 0.811 320.66 330.81 96.93%

198.76 1.001 76.87 0.613 246.08 253.90 96.92%

198.79 0.751 76.95 0.414 181.15 187.54 96.59%

198.84 0.500 77.03 0.200 114.83 120.24 95.50%

198.87 0.151 77.06 0.107 38.27 42.70 89.64%

Table 3. Efficiency measurements @ Vin = 360 V

+200 V @load(A) +75 (V) @load (A) Pout (W) Pin (W) Efficiency %

198.68 1.603 76.68 1.010 395.93 409.47 96.69%

198.64 1.301 76.74 0.811 320.67 331.26 96.80%

198.62 1.000 76.81 0.613 245.70 254.17 96.67%

198.60 0.751 76.88 0.414 180.98 187.23 96.66%

198.57 0.500 76.94 0.198 114.52 120.43 95.09%

198.57 0.151 76.94 0.107 38.22 43.20 88.46%

= 390 V

in

dc

dc

Table 4. Efficiency measurements @ Vin = 420V

+200 V @load(A) +75 (V) @load (A) Pout (W) Pin (W) Efficiency %

198.35 1.601 76.57 1.008 394.74 407.45 96.88%

198.20 1.301 76.55 0.808 319.71 329.70 96.97%

197.87 1.001 76.47 0.609 244.64 252.55 96.87%

196.85 0.750 76.20 0.410 178.88 185.13 96.62%

26/32

dc

AN2450 Electrical test results

p

)

Table 4. Efficiency measurements @ Vin = 420Vdc (continued)

+200 V @load(A) +75 (V) @load (A) Pout (W) Pin (W) Efficiency %

198.01 0.504 76.74 0.198 114.99 119.78 96.00%

198.67 0.151 76.98 0.107 38.24 41.92 91.21%

The measurements have been done after 30 minutes of warm-up at maximum load. The
circuit efficiency has been calculated at each load condition and input dc voltage and is
plotted in Figure 13, showing very high values at maximum load level, higher than 96.5%.
Also at light load, at an output power of about 10% of the maximum level, the converter
efficiency is very good, reaching a value better than 88% in the whole DC input voltage
range.

Figure 13. Circuit efficiency versus output power at various input voltages

98.00%

97.00%

96.00%

95.00%

94.00%

93.00%

Efficiency (%)

92.00%

91.00%

90.00%

89.00%

88.00%

0.00 50.00 100.00 150. 00 200.00 250.00 300.00 350. 00 400.00 450.00

Out

ut power (W

@ 390 Vdc

@ 360 Vdc

@ 420 Vdc

8.2 Resonant stage operating waveforms

Figure 14 shows some waveforms during steady state operation of the resonant circuit at

nominal dc input voltage and full load. The Ch1 waveform is the half-bridge square voltage
on pin 14 of L6599, driving the resonant circuit. The trace Ch2 represents the transformer
primary current flowing into the resonant tank. As shown, it is almost sinusoidal, because
the operating frequency (about 123 kHz) is close to the resonance of the leakage
inductance of the transformer and the resonant capacitor (C6). In this condition the circuit
has a good margin for ZVS operation, providing good efficiency, while the almost sinusoidal
current waveform just allows for an extremely low EMI generation.

27/32

Electrical test results AN2450

Figure 14. Resonant circuit primary side waveforms at nominal dc input voltage and

full load

Ch1: half-bridge square voltage
Ch2: resonant tank current
Ch3: +200 V output voltage

Figure 15 and Figure 16 show the same waveforms as Figure 14 with both outputs lightly

loaded (50 mA each) and not loaded, respectively. These graphs demonstrate the ability of
the converter to operate down to zero load, with the output voltages still within regulation
limits (as can be seen looking at Ch3 waveform, representing the +200 V output voltage).
The resonant tank current, in this load condition, assumes, obviously, an almost triangular
shape and represents the magnetizing current flowing into the transformer primary side.

Figure 15. Resonant circuit primary side waveforms at nominal dc input voltage and

light load

Ch1: half-bridge square voltage
Ch2: resonant tank current
Ch3: +200 V output voltage

28/32

AN2450 Electrical test results

Figure 16. Resonant circuit primary side waveforms at nominal dc input voltage and

no-load

Ch1: half-bridge square voltage
Ch2: resonant tank current
Ch3: +200 V output voltage

In Figure 17, the Ch1 waveform shows a detail of the half-bridge square voltage (directly
taken across pin14 and pin10 of L6599 controller) to highlight the softness of voltage edge,
without abrupt negative voltage spikes that would be generated in presence of large stray
inductance of wiring. The layout is very critical in this respect and needs to be optimized in
order to minimize this effect, which could damage the controller itself.

In Figure 18 and Figure 19, waveforms relevant to the secondary side are represented. The
rectifiers reverse voltage is measured by CH1 (for both +200 V and +75 V outputs) and the
peak-to-peak value is indicated on the right of the graph. Waveform CH2 shows the current
flowing into one of the two output diodes for each output voltage (respectively D6 and D8).
Also this current shape is almost a sine wave, whose average value is one half the output
current.

Figure 17. Resonant circuit primary side waveforms at nominal dc input voltage and

light load

Ch1: half-bridge square voltage
(between pin14 and 10 of L6599)

Ch2: resonant tank current

Ch3: low side MOSFET gate
drive signal

29/32

Electrical test results AN2450

Figure 18. +200 V output diode voltage and current waveforms

+200 V output waveforms:
Ch1: +200 V diode reverse voltage
Ch2: diode D6 current

Figure 19. +75 V output diode voltage and current waveforms

+75 V output waveforms:
Ch1: resonant tank current
Ch2: diode D8 current

30/32

AN2450 Reference

9 Reference

1. Steady-state Analysis of the LLC Resonant Converter, Applied Power Electronics

Conference and Exposition, 2001. APEC 2001. Pages: 728 - 735

2. A Comparison of Half Bridge Resonant Converter Topologies, IEEE Trans. on Power

Electronics, 1988. Pages: 174 - 182.

3. First harmonic approximation including design constraints, Telecommunications Energy

Conference, 1998. INTELEC. Pages: 321 - 328

4. Design Optimization for an LCL-Type Series Resonant Converter,

http://www.powerpulse.net/features/techpaper.php?paperID=76

5. L6599 high voltage resonant controller data-sheet, STMicroelectronics

10 Revision history

Table 5. Document revision history

Date Revision Changes

11-Jan-2007 1 First issue

06-Mar-2007 2 Minor text change

26-Mar-2007 3 Equation 53 modified

24-Jul-2007 4 Quality factor (Q) modified

25-Oct-2007 5 Modified: Equation 14 and Equation 33

31/32

AN2450

Please Read Carefully:

Information in this document is provided solely in connection with ST products. STMicroelectronics NV and its subsidiaries (“ST”) reserve the
right to make changes, corrections, modifications or improvements, to this document, and the products and services described herein at any
time, without notice.

All ST products are sold pursuant to ST’s terms and conditions of sale.

Purchasers are solely responsible for the choice, selection and use of the ST products and services described herein, and ST assumes no
liability whatsoever relating to the choice, selection or use of the ST products and services described herein.

No license, express or implied, by estoppel or otherwise, to any intellectual property rights is granted under this document. If any part of this
document refers to any third party products or services it shall not be deemed a license grant by ST for the use of such third party products
or services, or any intellectual property contained therein or considered as a warranty covering the use in any manner whatsoever of such
third party products or services or any intellectual property contained therein.

UNLESS OTHERWISE SET FORTH IN ST’S TERMS AND CONDITIONS OF SALE ST DISCLAIMS ANY EXPRESS OR IMPLIED
WARRANTY WITH RESPECT TO THE USE AND/OR SALE OF ST PRODUCTS INCLUDING WITHOUT LIMITATION IMPLIED
WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE (AND THEIR EQUIVALENTS UNDER THE LAWS
OF ANY JURISDICTION), OR INFRINGEMENT OF ANY PATENT, COPYRIGHT OR OTHER INTELLECTUAL PROPERTY RIGHT.

UNLESS EXPRESSLY APPROVED IN WRITING BY AN AUTHORIZED ST REPRESENTATIVE, ST PRODUCTS ARE NOT
RECOMMENDED, AUTHORIZED OR WARRANTED FOR USE IN MILITARY, AIR CRAFT, SPACE, LIFE SAVING, OR LIFE SUSTAINING
APPLICATIONS, NOR IN PRODUCTS OR SYSTEMS WHERE FAILURE OR MALFUNCTION MAY RESULT IN PERSONAL INJURY,
DEATH, OR SEVERE PROPERTY OR ENVIRONMENTAL DAMAGE. ST PRODUCTS WHICH ARE NOT SPECIFIED AS "AUTOMOTIVE
GRADE" MAY ONLY BE USED IN AUTOMOTIVE APPLICATIONS AT USER’S OWN RISK.

Resale of ST products with provisions different from the statements and/or technical features set forth in this document shall immediately void
any warranty granted by ST for the ST product or service described herein and shall not create or extend in any manner whatsoever, any
liability of ST.

ST and the ST logo are trademarks or registered trademarks of ST in various countries.

Information in this document supersedes and replaces all information previously supplied.

The ST logo is a registered trademark of STMicroelectronics. All other names are the property of their respective owners.

© 2007 STMicroelectronics - All rights reserved

STMicroelectronics group of companies

Australia - Belgium - Brazil - Canada - China - Czech Republic - Finland - France - Germany - Hong Kong - India - Israel - Italy - Japan -

Malaysia - Malta - Morocco - Singapore - Spain - Sweden - Switzerland - United Kingdom - United States of America

www.st.com

32/32