Sharp EL-9900C,EL-9900 User Manual

Sharp EL-9900

Graphing Calculator

Basic Keyboard Activities

General Mathematics

Algebra

Programming

Advanced Keyboard Activities

Algebra

Calculus

Statistics

Trigonometry

Programming

Sharp EL-9900

Graphing Calculator

Basic Keypad

EL-9900

SUB

SPLIT

TBLSET

DRAW

FORMAT

CALC

OPTION

LIST

CLIP

OFF

A-LOCK

STAT

PLOT

SLIDE SHOW

2ndF

ALPHA

Y

=

GRAPH

TABLE

WINDOW

ZOOM

TRACE

ON

+

–

.

–

+

MATH

Simp

a

STAT

A

GH I J K

a

b

c

LMN

789

QRST

4

VW

1

0

PRGM

BCDEF

b

a

c

a

b

c

b

a

SET UP

INS

DEL BS

A.

xxx

RCL VARS

,

{}

(

5

2

SPACE ENTRY ANS

6

3



x

X

+

(–)

%

.

int

STO

O

CATALOG

Y

xp

QUIT

CL

–1

x

2

x

P

)

U

.

–

Z

–

ENTER

1

Basic Keyboard/GENERAL MATHEMATICS USING THE SHARP EL-9900

Press to access the calculation screen.

1. Add 9 to 27 twice.

STEP 1: Enter 27 by pressing 2 7 . STEP 2: Add by pressing the + key. STEP 3: Enter 9 by pressing 9 . STEP 4: Find the first sum by pressing the ENTER key. STEP 5: Add 9 again by pressing + 9 ENTER .

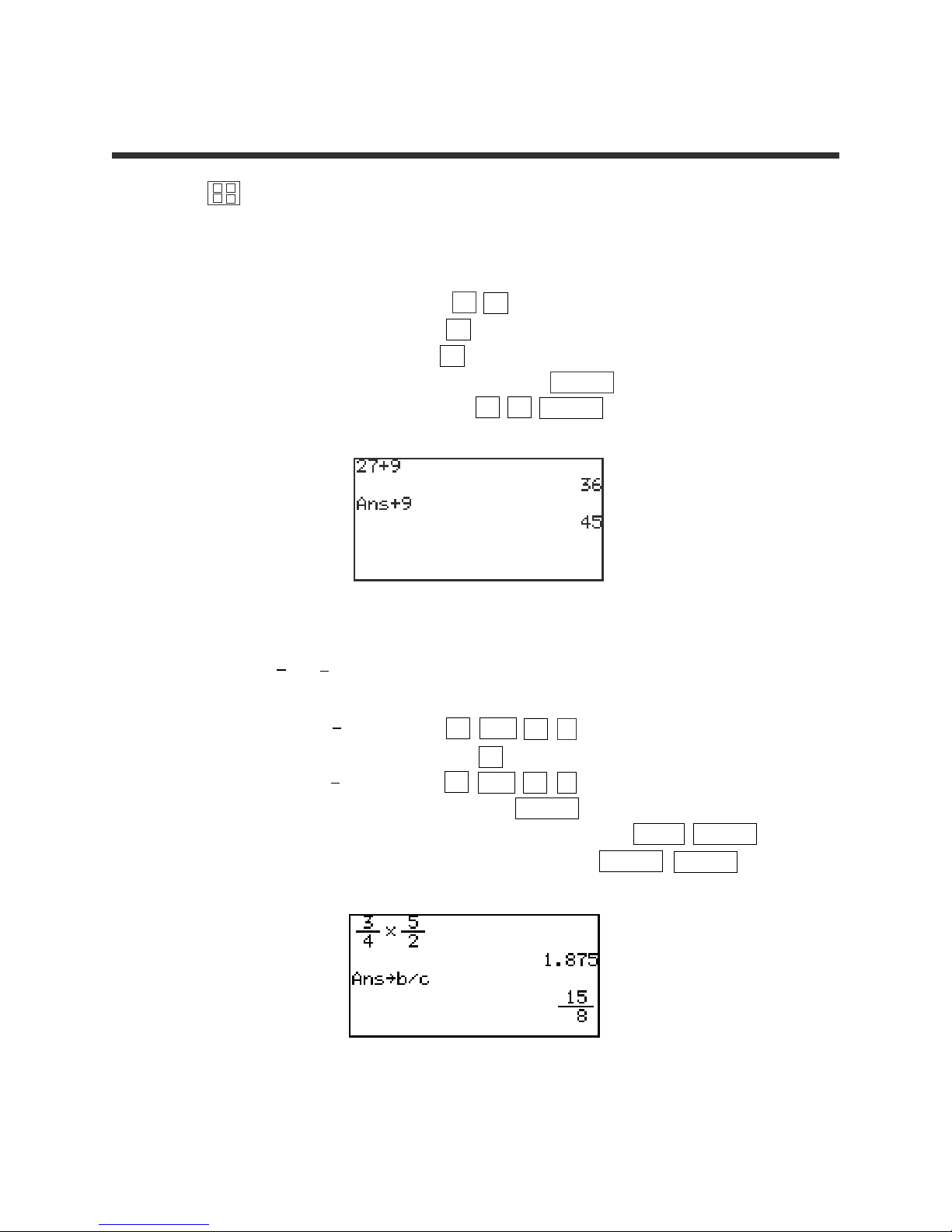
2. Multiply to . Then, convert to a decimal.

STEP 1: Enter by pressing 3 a/b 4 . STEP 2: Multiply by pressing the × key. STEP 3: Enter by pressing 5 a/b 2 . STEP 4: Find the product by pressing ENTER . STEP 5: Convert to an improper fraction by pressing ➞b/c ENTER . STEP 6: Convert to a mixed number by pressing ➞ab/c ENTER .

BASIC ARITHMETIC

×

+

–

÷

▼

3 4

5 2

3 4

5 2

▼

2

Basic Keyboard/GENERAL MATHEMATICS USING THE SHARP EL-9900

Press to access the calculation screen.

A trapezoid is a four-sided figure where two of the sides are parallel and the other two sides are not parallel.

The area of a trapezoid is defined to be Area = ( )•(b

1

+ b2) where h

is the height or distance between the parallel sides b

1

and b2.

1. Calculate ( ) × (3 + 4).

STEP 1: Enter ( ) by pressing

(

5 a/b 2

)

.

STEP 2: Multiply by pressing the × key. STEP 3: Enter (3 + 4) by pressing

(

3 + 4 ).

STEP 4: Calculate by pressing the ENTER key.

The answer is 17.5

2. Edit the previous calculation to find ( )•(7 + 4).

STEP 1: Edit the previous calculation by pressing 2ndF ENTRY

to move the blinking cursor to highlight the 3. STEP 2: Delete the 3 by pressing DEL to backspace delete. STEP 3: Insert the 7 by pressing 7 . STEP 4: Calculate by pressing the ENTER key.

The answer is 27.5.

PARENTHESES AND EDITING

×

+

–

÷

h

2

5 2

▼

h

b

1

b

2

▼

3

Basic Keyboard/GENERAL MATHEMATICS USING THE SHARP EL-9900

Press to access the calculation screen.

Mixtures contain two or more components. Percents are often used to express the amount of a component in a mixture.

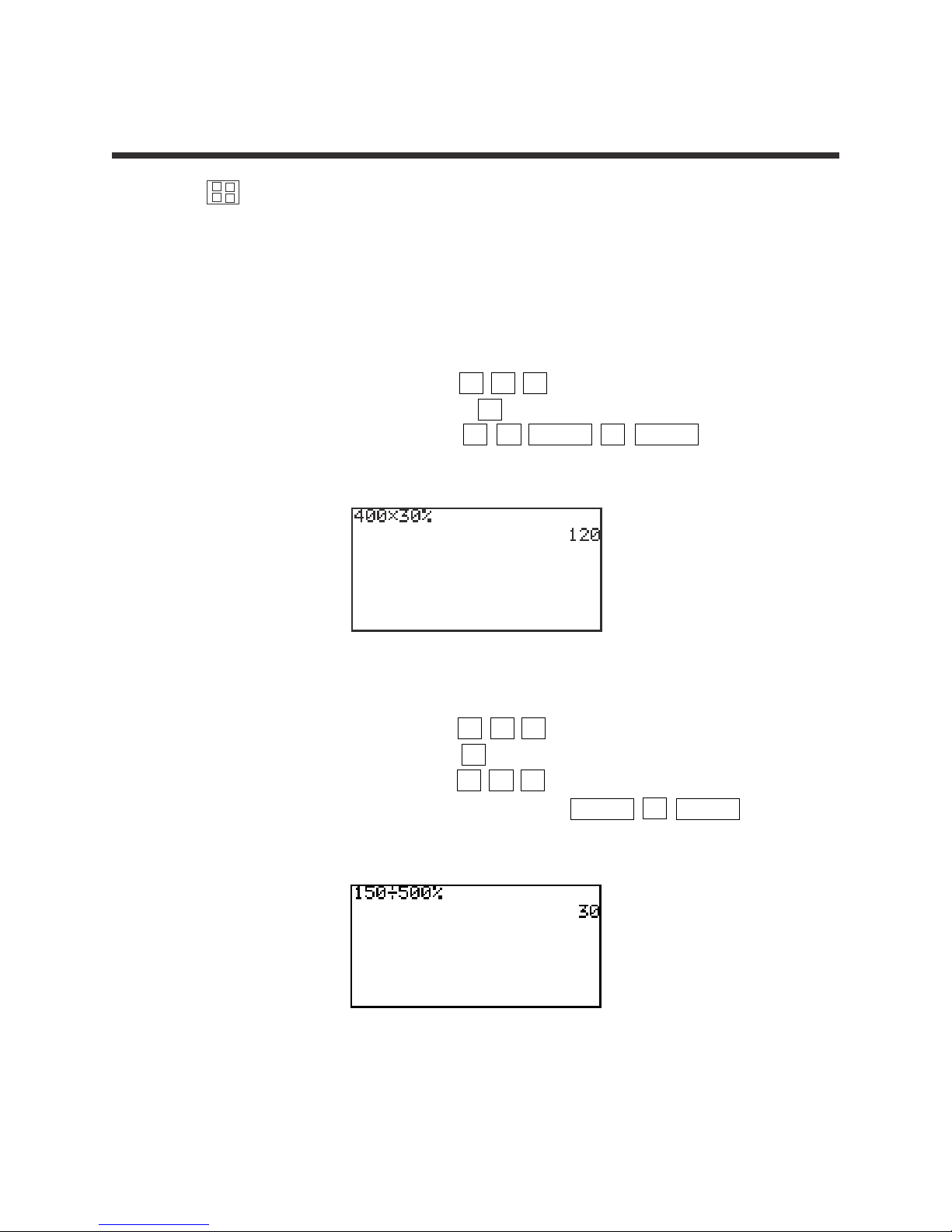
1. Find 30% of 400.

STEP 1: Enter 400 by pressing 4 0 0 . STEP 2: Multiply by pressing the × key. STEP 3: Enter 30% by pressing 3 0 2ndF % ENTER .

The answer is 120.

2. Find what percent of 500 is 150.

STEP 1: Enter 150 by pressing 1 5 0 . STEP 2: Divide by pressing the ÷ key. STEP 3: Enter 500 by pressing 5 0 0 . STEP 4: Calculate by percentage by pressing 2ndF % ENTER .

The answer is 30%.

PERCENTS

×

+

–

÷

4

Basic Keyboard/GENERAL MATHEMATICS USING THE SHARP EL-9900

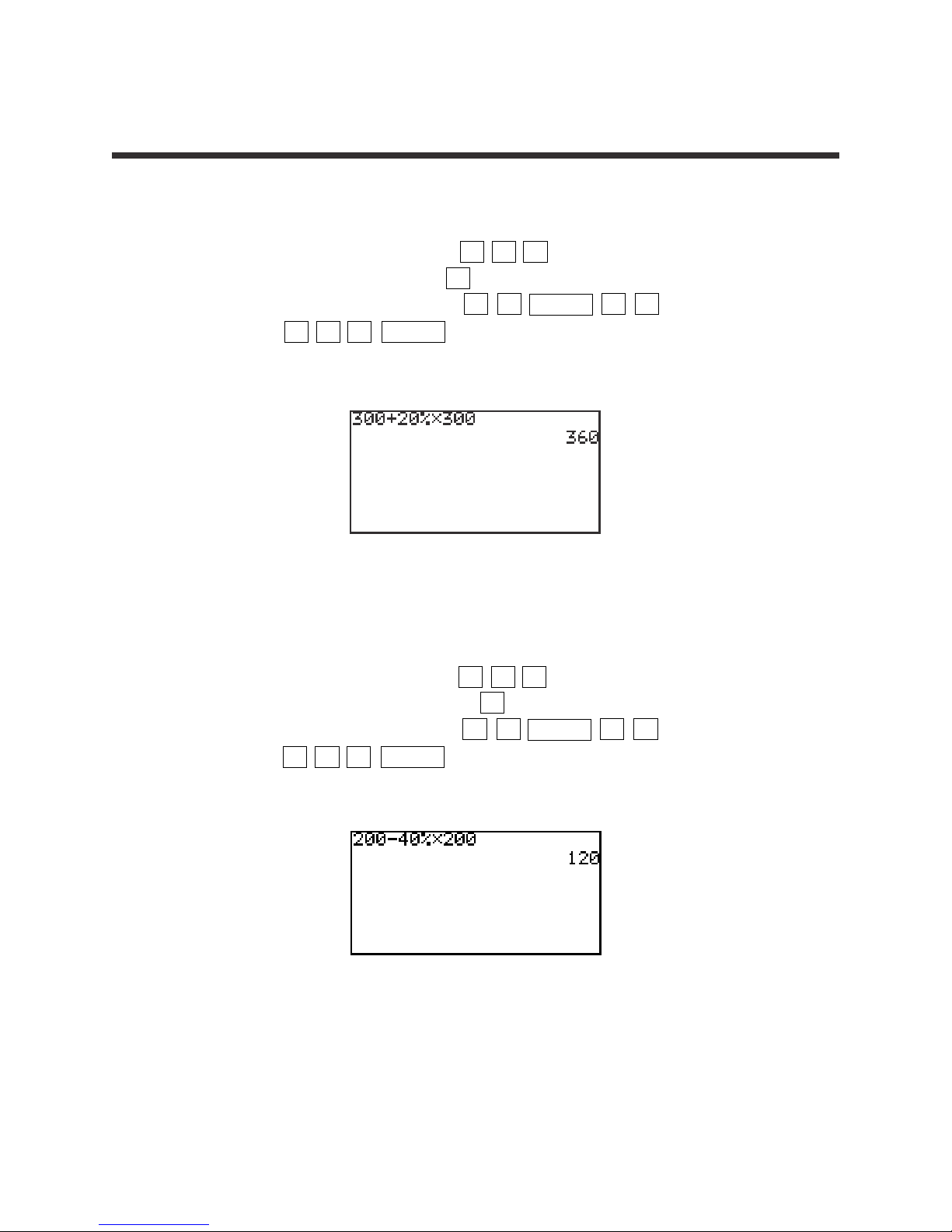
3. Add 20% to 300.

STEP 1: Enter 300 by pressing 3 0 0 . STEP 2: Add by pressing the + key. STEP 3: Enter 20% by pressing 2 0 2ndF % ×

3 0 0 ENTER .

The answer is 360.

4. Subtract 40% from 200.

STEP 1: Enter 200 by pressing 2 0 0 . STEP 2: Subtract by pressing the – key. STEP 3: Enter 40% by pressing 4 0 2ndF % ×

2 0 0 ENTER .

The answer is 120.

PERCENTS (continued)

5

Basic Keyboard/GENERAL MATHEMATICS USING THE SHARP EL-9900

Press to access the calculation screen.

1. Calculate 2 • 3 and store the value in A. Recall the A to

see the product stored in A.

STEP 1: Multiply 2 and 3 by pressing 2 × 3 ENTER .

The product is 6. STEP 2: Store 6 into A by pressing STO ALPHA A ENTER . STEP 3: Clear the screen by pressing CL . STEP 4: Recall A by pressing ALPHA A ENTER .

2. Calculate 3 • 5 and store the value in M. Calculate 4 • 5

and add this product to M. Then, recall the M to see the sum of the products.

STEP 1: Multiply 3 and 5 by pressing 3 × 5 ENTER .

The product is 15. STEP 2: Store 15 into M by pressing STO ALPHA M ENTER . STEP 3: Multiply 4 and 5 by pressing 4 × 5 ENTER .

The product is 20. STEP 4: Add 20 to M by pressing + ALPHA M .

The sum of the products is 35.

3. Recall the previous answer.

STEP 1: With the display screen cleared, recall the previous answer

by pressing 2ndF ANS ENTER .

MEMORY USAGE

×

+

–

÷

6

Basic Keyboard/GENERAL MATHEMATICS USING THE SHARP EL-9900

Press to access the calculation screen.

1. Calculate 152.

STEP 1: Enter 15 by pressing 1 5 . STEP 2: Square by pressing the x

2

key.

STEP 3: Calculate by pressing the ENTER key.

The answer is 225.

2. Calculate 34.

STEP 1: Enter 3 by pressing 3 . STEP 2: Exponentiate by pressing the a

b

key. STEP 3: Enter 4 by pressing 4 . STEP 4: Calculate by pressing the ENTER key.

The answer is 81.

3. Calculate √196.

STEP 1: Enter the square root by pressing 2ndF √ . STEP 2: Enter 196 by pressing 1 9 6 . STEP 3: Calculate by pressing the ENTER key.

The answer is 14.

POWERS AND ROOTS

×

+

–

÷

7

Basic Keyboard/GENERAL MATHEMATICS USING THE SHARP EL-9900

Press to access the calculation screen.

1. Find log 3.

STEP 1: Enter log by pressing MATH A 4 . STEP 2: Enter 3 by pressing the 3 key. STEP 3: Calculate by pressing the ENTER key.

The answer is 0.4771.

2. Find 10

(3÷4)

.

STEP 1: Enter 10 by pressing MATH A 5 . STEP 2: Enter (3 ÷ 4) by pressing 3 ÷ 4 . STEP 3: Calculate by pressing the ENTER key.

The answer is 5.6234.

LOGARITHMS AND EXPONENTIALS

×

+

–

÷

8

Basic Keyboard/GENERAL MATHEMATICS USING THE SHARP EL-9900

The definitions of the trigonometric functions with regard to the right triangle can be used to find distances between points. The sine function is defined to be opposite side/hypotenuse, the cosine function is adjacent side/hypotenuse, and the tangent function is opposite side/adjacent side.

Put the calclator in degree mode by pressing 2ndF SETUP B 1 .

1. Find sin 30°.

STEP 1: Press to access the calculation screen. STEP 2: Enter sin 30 by pressing MATH Α 1 3 0 . STEP 3: Calculate by pressing the ENTER key.

The answer is 0.5.

2. Find 3cos 20°.

STEP 1: Enter 3 cos 20 by pressing 3 MATH Α 2 2 0 . STEP 2: Calculate by pressing the ENTER key.

The answer is 2.819

3. Find tan 50°.

STEP 1: Enter tan 50 by pressing MATH Α 3 5 0 . STEP 2: Calculate by pressing the ENTER key.

The answer is 1.19.

Remember that cotangent = 1/tangent, secant = 1/cosine, and cosecant = 1/sine.

TRIGONOMETRIC FUNCTIONS

×

+

–

÷

hypotenuse opposite side

adjacent side

θ

9

Basic Keyboard/GENERAL MATHEMATICS USING THE SHARP EL-9900

Put the calclator in radian mode by pressing 2ndF SETUP B 2 .

1. Find sin 2.1.

STEP 1: Press to access the calculation screen. STEP 2: Enter sin 2.1 by pressing MATH Α 1 2

.

1.

STEP 3: Calculate by pressing the ENTER key.

The answer is .8632

2. Find cos (-1.7).

STEP 1: Enter 3 cos (-1.7) by pressing 3 MATH Α 2

(−)

1

.

7.

STEP 2: Calculate by pressing the ENTER key.

The answer is -.3865

3. Find tan 0.

STEP 1: Enter tan 0 by pressing MATH Α 3 0 . STEP 2: Calculate by pressing the ENTER key.

The answer is zero.

TRIGONOMETRIC FUNCTIONS (continued)

×

+

–

÷

10

Basic Keyboard/GENERAL MATHEMATICS USING THE SHARP EL-9900

Angles can be expressed in degrees and radians. Degrees can be expressed in either decimal degrees or degrees-minutes-seconds. The sum of the angles of a triangle is 180° or π radians.

Press to access the calculation screen.

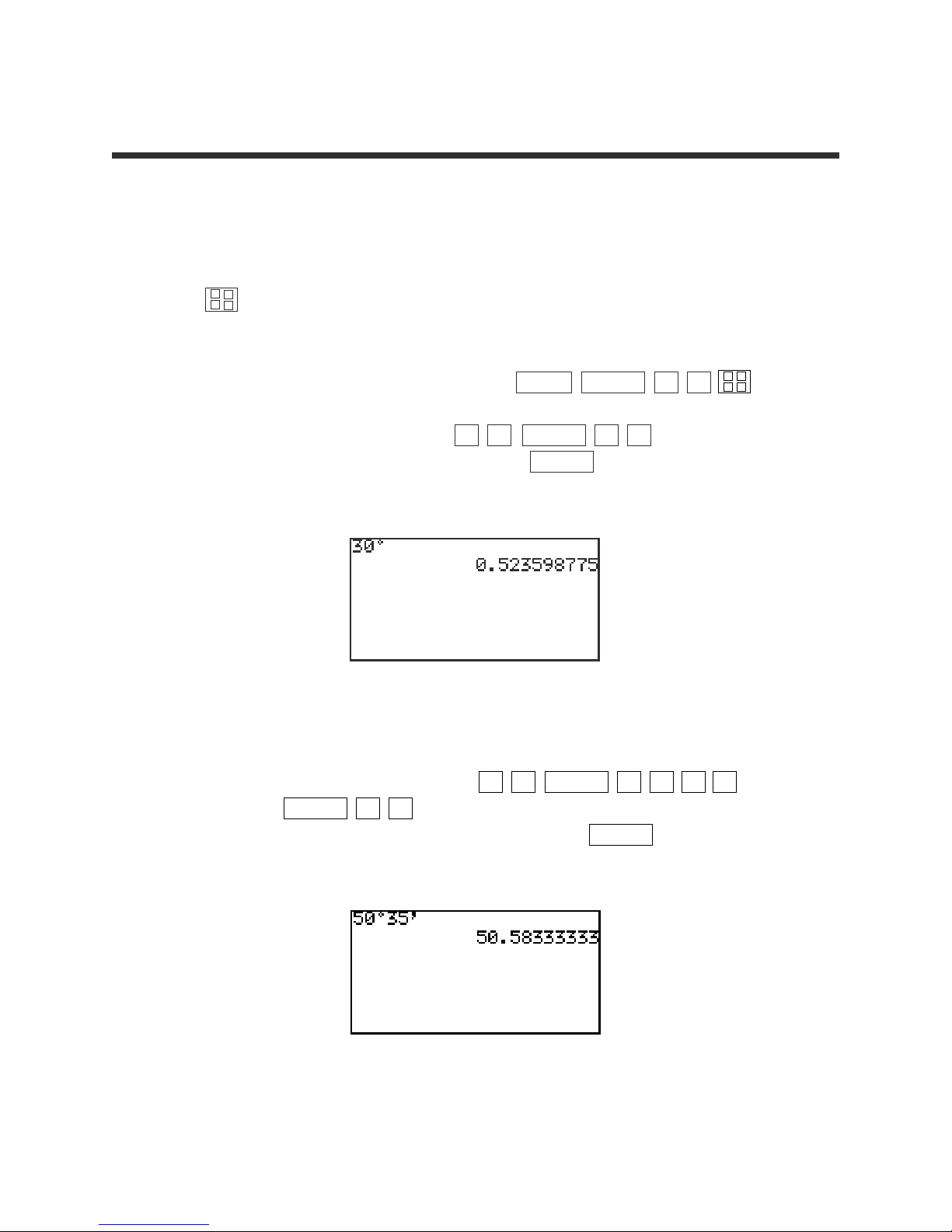
1. Convert 30° to radians.

Put the calclator in radian mode by pressing 2ndF SETUP B 2 .

STEP 1: Enter 30° by pressing 3 0 MATH Ε 1 . STEP 2: Convert to radians by pressing ENTER .

The answer is 0.5236.

2. Convert 50°35’ to decimal degrees.

STEP 1: Enter 50°35’ by pressing 5 0 MATH E 1 3 5

MATH Ε 2 .

STEP 2: Calculate decimal degrees by pressing ENTER .

The answer is 50.5833.

ANGLE CONVERSIONS

×

+

–

÷

×

+

–

÷

11

Basic Keyboard/GENERAL MATHEMATICS USING THE SHARP EL-9900

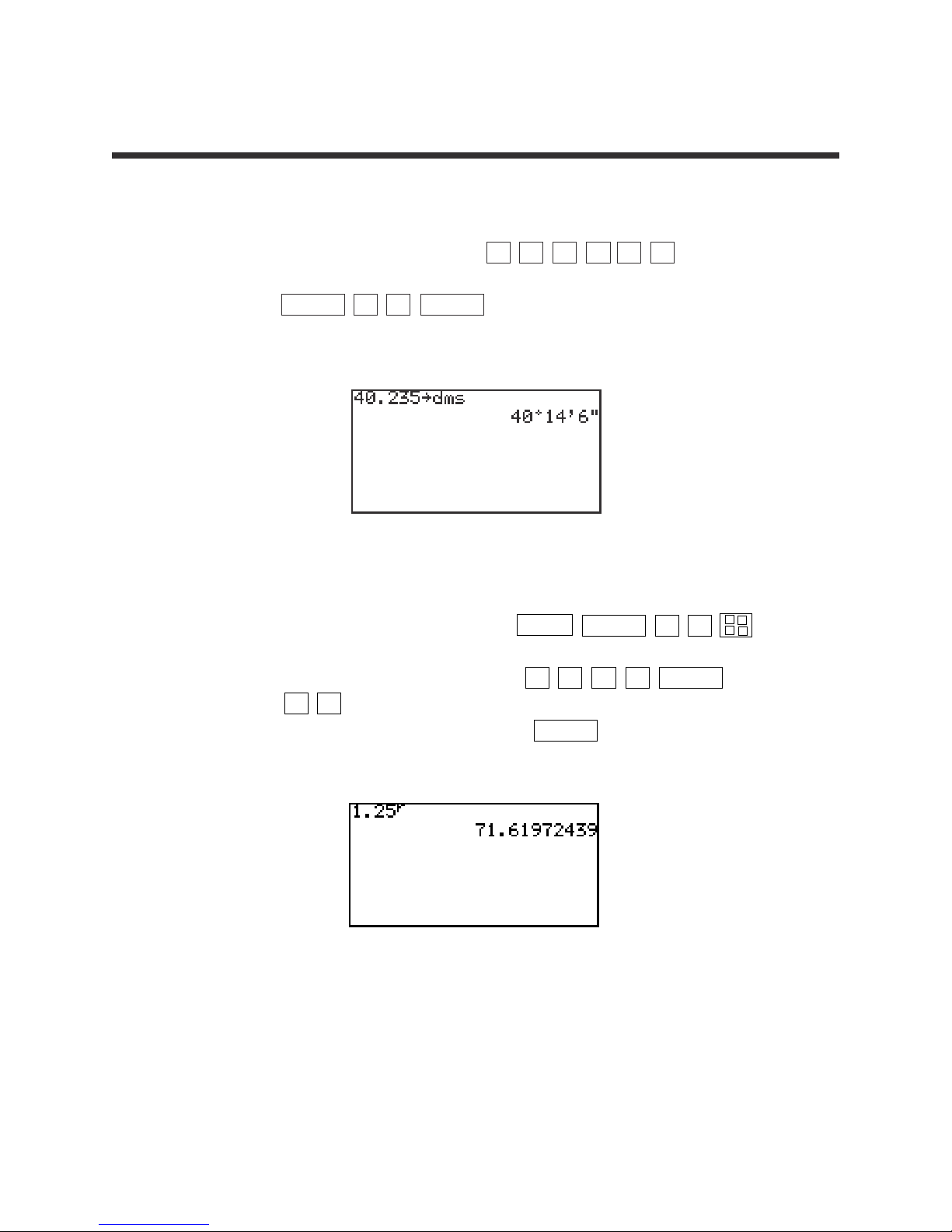
3. Convert 40.235° to degrees-minutes-seconds.

STEP 1: Enter 40.235° by pressing 4 0

.

23 5 .

STEP 2: Calculate degrees-minutes-seconds by pressing

MATH D 2 ENTER .

The answer is 40°14’06”.

4. Convert 1.25 radians to degrees.

Put the calclator in degree mode by pressing 2ndF SETUP B 1 .

STEP 1: Enter 1.25 radians by pressing 1

.

2 5 MATH

E4 .

STEP 2: Convert to degrees by pressing ENTER .

The answer is 71.6°.

ANGLE CONVERSIONS (continued)

×

+

–

÷

12

Basic Keyboard/GENERAL MATHEMATICS USING THE SHARP EL-9900

Press to access the calculation screen.

1. Find five factorial or 5!.

STEP 1: Enter 5! by pressing 5 MATH C 7 . STEP 2: Calculate by pressing ENTER .

The answer is 120.

2. Find the number of combinations of 2 from a group of 5.

STEP 1: Enter the large number 5 by pressing 5 . STEP 2: Enter the combination symbol by pressing MATH C 6 . STEP 3: Enter the small number 2 and calculate by pressing

2 ENTER .

The answer is 10.

Permutations are found in the same manner.

3. Randomly select a person from an ordered group of 10.

STEP 1: Access the random integer command by pressing

MATH C 2 . STEP 2: Enter the lower bound of 1 by pressing 1 ,. STEP 3: Enter the upper bound of 10 by pressing 1 0 ). STEP 4: Calculate the random person by pressing ENTER .

Answers will vary.

PROBABILITY

×

+

–

÷

13

Basic Keyboard/GENERAL MATHEMATICS USING THE SHARP EL-9900

1. Calculate statistics for a one-variable data set.

STEP 1: Turn the calculator on and press STAT to enter the statistics menu.

Press A (EDIT) ENTER to view the statistics data entry screen. If there is a data set present within the lists on your calculator, use the arrow keys to move to the list, if necessary, and press ▲ to highlight the list label. Press DEL ENTER to delete the old data. Repeat for other lists of data.

STEP 2: Move the highlighter to the cell directly below the L1 in the table.

Enter the following data set: 25 32 28 33 31 27 40 38 29 30

STEP 3: Check the data you have entered and correct any errors you may find.

Press 2ndF QUIT to exit the data entry screen. To calculate the numerical descriptions of the data set, press STAT C (CALC) and 1 (1_Stats). Press ENTER and the statistical results will appear.

2. The statistics displayed are:

1. the average or mean value of the data set, ;

2. the standard deviation assuming the data set is a sample from a population, sx;

3. the standard deviation assuming the data set represents the entire population, σx;

4. the sum of the data values, ∑x;

5. the sum of the squared data values, ∑x

2

;

Press ▼ five times to see more of the statistics.

6. the number of values in the data set, n;

7. the minimum value in the data set, xmin;

8. the first quartile (25th percentile), Q1;

9. the median (50th percentile), Med;

10. the third quartile (75th percentile), Q3; and Press ▼ one more time to see the final statistic.

11. the maximum value in the data set, xmax.

ONE-VARIABLE STATISTICS

x

14

Basic Keyboard/GENERAL MATHEMATICS USING THE SHARP EL-9900

Steps for creating a data set's histogram

STEP 1: Turn the calculator on, press STAT A (EDIT) ENTER to view the

statistics data entry screen. Delete old data sets.

STEP 2: Move the highlighter to the cell directly below the L1 in the table and enter

the following data set: 15 28 17 36 38 19 13 25 27 41

STEP 3: Check the data you have entered by pressing ▲ to move back through

the data.

STEP 4: To graph a histogram that represents the data set, you must first press

STAT PLOT A (PLOT1) and press ENTER . A PLOT1 setup screen will appear. Turn the plot on by pressing ENTER . Select one-variable data by pressing ▼ ENTER . Set the list to L1 by pressing ▼

2ndF L1 ENTER . A blank Freq: prompt indicates the data is non-weighted

and the frequencies are one. Choose the histogram graph by pressing ▼

STAT PLOT A (HIST) and 1 (Hist).

STEP 5: Set the calculator to rectangular graphing by pressing 2ndF SET UP

E (COORD) 1 (Rect) and press 2ndF QUIT .

STEP 6: Set the viewing window by pressing WINDOW . Set the horizontal axis to

10 < x < 50 with Xscl = 10 by pressing 1 0 ENTER 5 0 ENTER 1

0 ENTER . Set the vertical axis to 0 < y < 5 with Yscl = 1 by pressing 0 ENTER 5 ENTER 1 ENTER .

View the histogram by pressing GRAPH .

HISTOGRAM FOR A ONE-VARIABLE DATA SET

15

Basic Keyboard/GENERAL MATHEMATICS USING THE SHARP EL-9900

Steps for creating a data set's box-and-whisker chart

STEP 1: Press STAT to enter the statistics menu. Delete old data and enter the

following data set in L1: 1112222344

STEP 2: To construct a box-and-whisker chart, first press STAT PLOT A

ENTER . Press ENTER to turn PLOT1 on. Press ▼ ENTER to choose one-variable data. Press ▼ 2ndF L1 ENTER to enter L1 as the data list. Leave the Freq prompt blank. Set the graph to a box-and-whisker chart by pressing ▼ STAT PLOT E (BOX) 1 Box.

STEP 3: In the example, the data is discrete with a smallest value of 1 and a largest

value of 4. Set the viewing window to 0 < x < 5 with Xscl = 1. Next, set the vertical axis to 0 < y < 1 with Yscl = 1.

STEP 4: To view the box-and-whisker chart for the data, press GRAPH .

STEP 5: Press TRACE followed by and to view the five values making up the

box-and whisker chart.

STEP 6: Turn PLOT1 off by pressing STAT PLOT ENTER ENTER

2ndF QUIT .

BOX-AND-WHISKER CHART FOR A ONE-VARIABLE DATA SET

▼

16

Basic Keyboard/GENERAL MATHEMATICS USING THE SHARP EL-9900

Steps for creating a pie chart from count data

STEP 1: Press STAT to enter the statistics menu. Delete old data and enter the

following data set in L1 using weights in L2: 24 18 40 10

STEP 2: To construct a pie chart, first press STAT PLOT ENTER . Press ENTER

to turn PLOT1 on. Press ▼ ENTER to choose one-variable data. Press ▼

2ndF L1 ENTER to enter L1 as the data list. Leave the Freq prompt blank. Set the graph to a pie chart by pressing ▼ STAT PLOT F (PIE) 1 (PIE) .

STEP 3: To view the pie chart for the data, press GRAPH .

STEP 4: Press TRACE followed by and to highlight and mark the pieces

of the pie chart.

STEP 5: Turn PLOT1 off by pressing STAT PLOT ENTER ENTER

2ndF QUIT .

PIE CHART FOR A ONE-VARIABLE DATA SET

▼

17

Basic Keyboard/GENERAL MATHEMATICS USING THE SHARP EL-9900

Steps for calculating statistics for a two-variable data set

STEP 1: Turn the calculator on and press STAT to enter the statistics menu. Press

A (EDIT) ENTER to access the data entry screen. Delete old data

by highlighting L1 and pressing DEL ENTER . Repeat for other lists.

STEP 2: Enter the following data set:

X

Y 25 32 28 33 31 27 40 38 29 30

STEP 3: Check the data you have entered and correct any errors you may find.

To calculate the numerical descriptions of the two variables, press 2ndF

QUIT STAT C (CALC) 2 2_Stats. Press ENTER and the statistical

results will appear.

STEP 4: Press ▼ to view the remaining statistics.

The statistics displayed are:

1. the average or mean value of the variable, or ;

2. the standard deviation assuming the data points are a sample from a population, sx or sy;

3. the standard deviation assuming the data points represents the entire population, σx or σy;

4. the sum of the values, ∑x or ∑y;

5. the sum of the squared values, ∑x

2

or ∑y2;

6. the number of data points, n;

7. the minimum variable value, xmin or ymin;

8. the maximum variable value, xmax or ymax; and

9. the sum of the x and y products, ∑xy.

STATISTICS FOR A TWO-VARIABLE DATA SET

x

y

18

Basic Keyboard/GENERAL MATHEMATICS USING THE SHARP EL-9900

Steps for drawing a scatter diagram for a two-variable data set

STEP 1: Consider the following table listing the revenue for a large corporation:

Y

ear Revenue (in millions of dollars)

1 48.63 2 48.86 3 48.91 4 49.69 5 51.10 6 52.00 7 52.03

STEP 2: Access the statistics data entry screen and delete old data.

STEP 3: Enter the data using L1 for the year and L2 for the revenue (in millions

of dollars). Check the data and correct any errors you may find.

STEP 4: Press STAT PLOT A (PLOT1) ENTER to access the PLOT1 set up

screen. To turn PLOT 1 on, press ENTER . Press ▼ ENTER to set the data to two-variable. Set L1 for the x variable by pressing

▼ 2ndF LIST A 1 ENTER . Press 2ndF LIST 2 ENTER to set L2

for the y variable. To set the graph to scatter diagram, press STAT PLOT

G (S.D.) and 3 (Scattr ).

STEP 5: Construct an autoscaled scatter diagram of this data set by pressing ZOOM

A (ZOOM) 9 (Stat).

Press TRACE and press repeatedly to verify that Xmin= 1, Xmax= 7, Ymin= 48.63, and Ymax= 52.03.

SCATTER DIAGRAM FOR A TWO-VARIABLE DATA SET

▼

19

Basic Keyboard/GENERAL MATHEMATICS USING THE SHARP EL-9900

Steps for calculating the best-fitting line

STEP 1: Turn the calculator on and press STAT to enter the statistics menu.

Access the data entry screen by pressing A (EDIT) ENTER . Delete old data and enter the following data set:

X

Y 25 32 28 33 31 27 40 38 29 30 Check the data you have entered and correct any errors you may find.

STEP 2: To find the best-fitting line (regression line) for the data, press STAT

D (REG) 0 2 (Rg_ax+b) and press ENTER .

STEP 3: To overlay the regression line and the scatter diagram for the data, you must

first set up the scatter diagram by pressing STAT PLOT A (PLOT1)

ENTER ENTER ▼ ENTER ▼ 2ndF LIST A 1 ENTER 2ndF

LIST 2 ENTER STAT PLOT G (S.D.) and 3 (Scattr ).

STEP 4: Display the scatter diagram for the data by pressing WINDOW and setting

Xmin = 20, Xmax = 45, Xscl = 5, Ymin = 25, Ymax = 40, and Yscl = 5. Press

GRAPH to view the scatter diagram.

STEP 5: To view the overlay of the regression line and the scatter diagram, press

Y= CL 2ndF VARS H (STAT) ENTER B (REGEQN) 1 (RegEqn)

GRAPH .

LINEAR REGRESSIONS

×

+

–

÷

▼

1

Basic Keyboard/ALGEBRA USING THE SHARP EL-9900

1. Turn the calculator on and press Y= .

2. Press CL to remove an old Y1 expression.

3. Enter the linear equation ( y = 3x + 1 ) for Y1 by pressing 3 x

+ 1 .

4. Enter the viewing window range by pressing ZOOM A (ZOOM) 5 (Default). This establishes the default viewing ranges for graphing

equations. These ranges are -10 < x < 10 and -10 < y < 10. The scale for the x and y axes are 1.

5. To graph another equation, press Y= CL to access and clear the Y1=

prompt.

6. Enter the next equation, and press GRAPH to view the graph.

7. If the line does not appear in the default viewing window, press ZOOM 4 (OUT) to enlarge the viewing window.

GRAPHING LINEAR EQUATIONS

2

Basic Keyboard/ALGEBRA USING THE SHARP EL-9900

1. Graph the equation y = 1x by pressing Y= CL to remove an old Y1

expression, and press x to enter the equation.

2. Press ZOOM A (ZOOM) 5 (Default) to view the graph.

3. Changing the slope to 2 will result in the equation y = 2x.

Enter this equation for Y2 by pressing Y= ▼ 2 x .

4. To view both the graphs on the same coordinate axes, press GRAPH .

The graph y = 2x has a greater slope than y = x.

5. Changing the slope to will result in the equation y = x. Enter this

equation for Y2 by pressing Y= ▼ CL 1 a/b 2 x .

6. To view both the graphs on the same coordinate axes, press GRAPH .

The graph y = x has less slope than y = x.

7. Changing the slope to -1 will result in the equation y =-x.

Enter this equation for Y2 by pressing Y= ▼ CL

(-)

x .

8. To view both the graphs on the same coordinate axes, press GRAPH .

The graph y =-x has the opposite slope of y = x.

CHARACTERISTICS OF SLOPE

1 2

▼

1 2

3

Basic Keyboard/ALGEBRA USING THE SHARP EL-9900

1. Graph the equation y = x by pressing Y= CL to remove an old Y1

expression, and press x to enter the equation.

2. Press ENTER CL to clear Y2 or additional prompts.

3. Use the default viewing range, and press ZOOM A (ZOOM) 5 (Default) to view the graph.

4. Adding 2 will result in the equation y = x + 2. Enter this equation for Y2 by

pressing Y= ▼ x

+

2 .

5. To view both the graphs on the same coordinate axes, press GRAPH .

The graph y = x + 2 has shifted up from the graph of y = x . The y - intercept is now y = 2.

6. Subtracting 2 will result in the equation y = x – 2. Enter this equation for Y2

by pressing Y= ▼ CL x – 2 .

7. To view both the graphs on the same coordinate axes, press GRAPH .

The graph y = x – 2 has shifted down from the graph of y = x . The y - intercept is now y =-2.

CHARATERISTICS OF THE y-INTERCEPT

4

Basic Keyboard/ALGEBRA USING THE SHARP EL-9900

1. Enter the equations Y1 = 3X + 1 and Y2 = 3X + 2 by pressing Y= CL 3

x

+ 1 ENTER CL 3 x + 2 .

2. Press ZOOM A (ZOOM) 5 (Default) to view the graphs.

3. These lines are called parallel since they have an equal slope but different

y-intercepts. These lines will not intersect.

4. Enter the equations Y1 = 3X - 1 and Y2 = -1/3 X + 1 by pressing Y= CL 3 x – 1 ENTER CL

(-)

1 a/b 3 x

+ 1 .

5. Press ZOOM A 7 to view the graphs.

6. These line are called perpendicular since they have slopes that are negative

reciprocals of each other (m

1

= -1/m2). Notice, these intersecting lines form

four equal angles.

7. Graph two lines with unequal slopes (not negative reciprocals). What do

you see? Are the lines parallel, perpendicular or neither?

PARALLEL AND PERPENDICULAR LINES

▼

5

Basic Keyboard/ALGEBRA USING THE SHARP EL-9900

Graphing and translations of quadratic equations

1. Turn the calculator on and press Y= . Press CL to remove an old Y1

expression. Press ENTER CL to remove an old Y2 expression.

2. To enter the quadratic equation ( y = x

2

) for Y1, press x x2.

Enter the viewing window range by pressing ZOOM A (Zoom) 7 (Dec).

3. When 2 is added to x2, the resulting equation is y = x2+ 2. Enter this

function for Y2 by pressing Y=

▼ x x

2

+ 2 . Press GRAPH .

What does the addition of 2 do?

4. When -2 is added to x2, the resulting equation is y = x2– 2. To change Y2

for this expression, press Y=

▼ CL x x

2

– 2 ENTER GRAPH .

What does the addition of -2 do?

QUADRATIC EQUATIONS

6

Basic Keyboard/ALGEBRA USING THE SHARP EL-9900

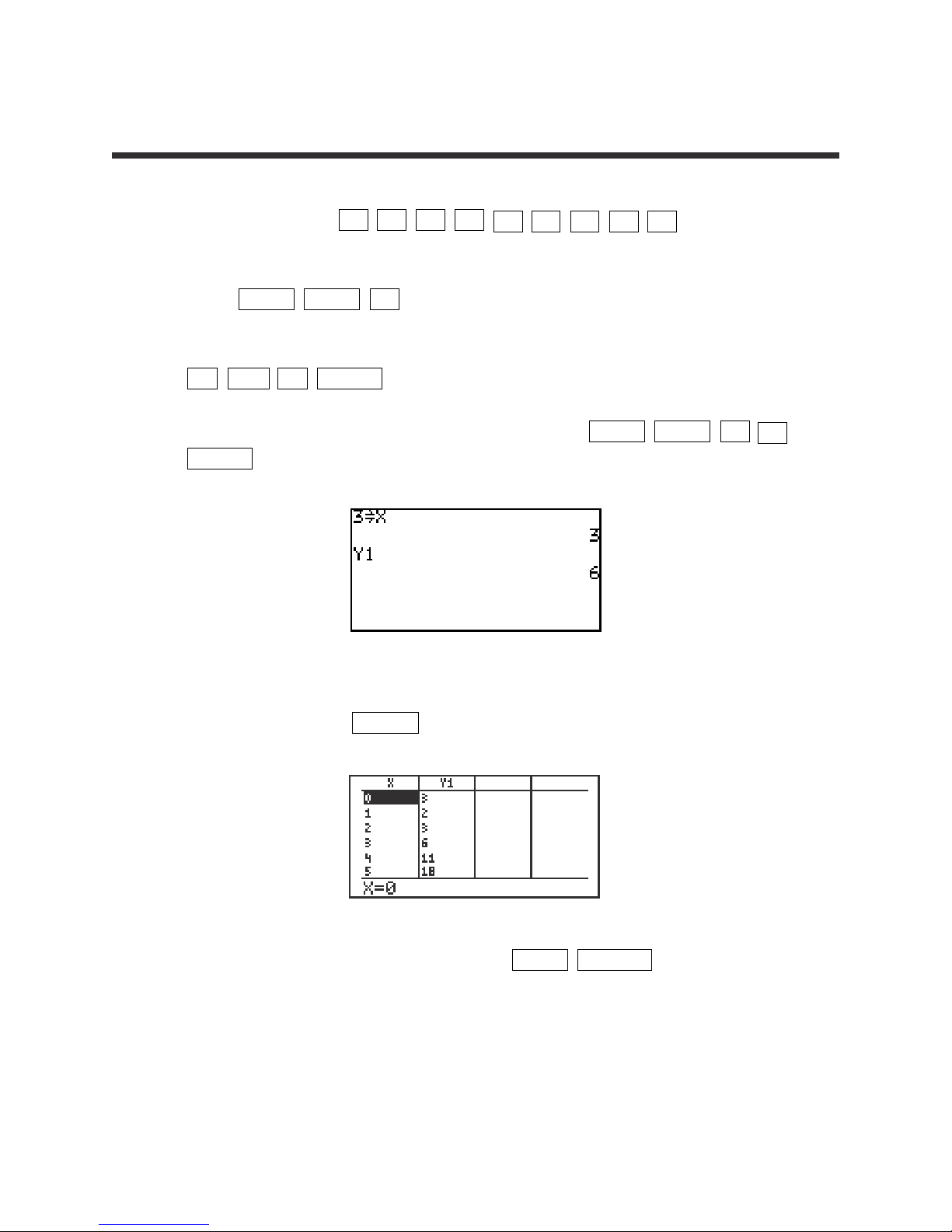
1. For example, to evaluate f(x)=x

2

-

2x + 3 for x=3, you will enter the function

for Y1 by pressing Y= CL x x

2

– 2 x + 3 . Be sure

to clear any other expressions.

2. Press 2ndF QUIT CL to return to and clear the calculation screen.

3. To evaluate the function at x = 3, first store 3 into the X variable by pressing 3 STO x ENTER .

4. Evaluate the function stored in Y1 at 3 by pressing 2ndF VARS A 1

ENTER .

5. Another way to evaluate a function for several values is using the Sharp’s

table feature. Press TABLE to view a table of values.

6. You can customize the table by pressing 2ndF TBLSET . You can set

the table’s minimum x value (TBLStrt) to another value than zero, and you can change the table’s increment value (TBLStep) from 1 to another value.

EVALUATING A FUNCTION

7

Basic Keyboard/ALGEBRA USING THE SHARP EL-9900

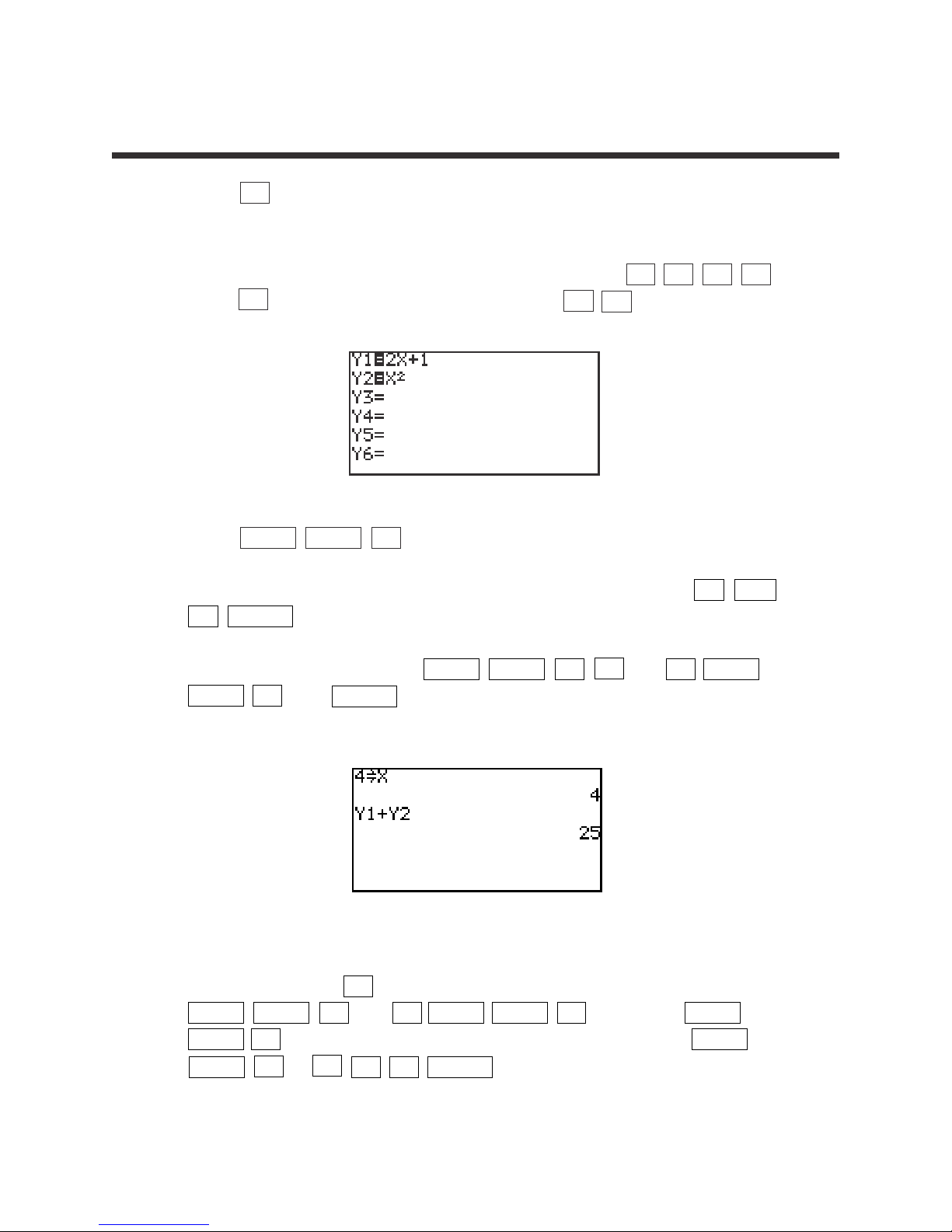
1. Press Y= and clear old expressions.

2. Enter the functions for Y1 and Y2. For example, enter f(x)=2x + 1 for Y1 and

g(x)=x

2

for Y2 by moving the cursor to Y1 and pressing 2 x + 1 ,

press ▼ to move the cursor to Y2, and press x x

2

.

3. Press 2ndF QUIT CL to return to and clear the calculation screen.

4. To evaluate (f+g)(4), first store 4 into the X variable by pressing 4 STO x ENTER .

5. Evaluate (f+g)(4) by pressing 2ndF VARS A 1 (Y1) + 2ndF

VARS 2 (Y2) ENTER . This can be repeated for (f-g)(x), (fg)(x), and

(f/g)(x).

6. Another way to conduct an operation on functions and evaluate it for a value

is to use Y3. Press Y= and enter the operation (f-g)(x) into Y3 by pressing

2ndF VARS 1 (Y1) – 2ndF VARS 2 (Y2). Press 2ndF

QUIT CL to return to and clear the calculation screen. Press 2ndF

VARS 3 Y3

(

4

)

ENTER .

OPERATIONS ON FUNCTIONS

8

Basic Keyboard/ALGEBRA USING THE SHARP EL-9900

1. Press Y= and clear old expressions.

2. Enter the two functions to be composed for Y1 and Y2. For example, enter

y=x

2

–1 for Y1 by pressing x x

2

– 1 ENTER and y=x+1 for Y2 by

pressing x

+

1 ENTER .

3. Enter the composition of Y2 into Y1 for Y3 by pressing 2ndF VARS A 1 (Y1)

(

2ndF VARS 2 (Y2)

)

ENTER .

4. Keep Y1 and Y2 graphs from appearing by deselecting Y1 and Y2. Do this by

pressing ENTER ENTER .

5. Press ZOOM A 7 (Dec) to view the composition of Y2 into Y1 in the

decimal window.

6. Change the Y3 composition to Y1 in Y2 by pressing Y= CL 2ndF VARS 2 (Y2)

(

2ndF VARS 1 (Y1) ).

7. Press ZOOM A 7 (Decimal) to view the composition of Y1 into Y2 in

the decimal window.

COMPOSITION OF FUNCTIONS

▼▼▼

▼

▼ ▼

9

Basic Keyboard/ALGEBRA USING THE SHARP EL-9900

1. Press 2ndF QUIT CL to return to and clear the calculation screen.

2. To evaluate the formula for the area of a trapezoid (Area=(h/2)(a+b), where

‘h’ is the height between the two bases (‘a’ and ‘b’) for different values, you must first type in the formula. For example, to enter the area formula for a trapezoid, press

(

ALPHA H ÷ 2

)(

ALPHA A +

ALPHA B

)

ENTER .

3. Now, store the values for ‘h,’ ‘a,’ and ‘b’ into the calculator. Use h=1, a=2,

and b=3. Store these by pressing 1 STO ALPHA H ENTER 2

STO ALPHA A ENTER 3 STO ALPHA B ENTER .

4. Clear the screen by pressing CL . Recall the formula by pressing 2ndF ENTRY four times. Press ENTER to evaluate the formula for the stored

values.

5. Change the height to 4 by pressing 4 STO ALPHA H ENTER .

Recall the formula by pressing 2ndF ENTRY two times and press

ENTER to re-evaluate the formula for the new value.

FORMULAS

10

Basic Keyboard/ALGEBRA USING THE SHARP EL-9900

1. Press Y= and clear old expressions. Press ZOOM A 7 to view a

clear viewing window.

2. To graph the circle in the form (x–h)

2

+ (y–k)2= r2, you will use the circle

drawing feature. For example, in the circle (x–3)

2

+ (y–2)2= 12, h=3, k=2 and r=1. Press 2ndF DRAW A 9 (Circle). Move the cursor right to an ‘h’ of x=3 by pressing repeatedly until x=3. Move the cursor up to a ‘k’ of y=2 by pressing repeatedly until y=2. Press ENTER to set the center point.

3. Move the cursor the length of the radius in one direction away from the center. In the example use the arrow key. Move the cursor 1 unit away from the center and press ENTER . The circle will be drawn with the cursor appearing at the point in the circle to which you moved.

4. If the circle will not completely appear in the viewing window, zoom out on the decimal window to a larger window, because any other windows may distort the circle. Draw the circle again in the larger window.

GRAPHING CIRCLES

▼

11

Basic Keyboard/ALGEBRA USING THE SHARP EL-9900

1. Turn the calculator on and press Y= . Y prompts will appear on the viewing window. Press CL to remove old Y expressions. Setup the calculator with rectangular coordinates and the equation editor mode by pressing 2ndF

SET UP E (COORD) 1 (Rect) G (EDITOR) and 1 (Equation). Press CL

to exit the menu and return to the Y prompts.

2. To enter the polynomial y = –3x

2

+ x + 1, press

(–)

3 x x

2

+

x

+

1 .

3. Press ZOOM A (Zoom) 7 (Dec) to establish the decimal viewing window and view the graph. Press TRACE to engage the trace feature. Press to move the cursor near the left-hand root.

4. Press ZOOM A (ZOOM) 3 (In) to zoom in on the left- hand root. Press TRACE and move the tracer to approximate the root.

5. Press ZOOM G (RCL) 2 (PreWin) to return to the decimal viewing window. Press TRACE and move the tracer to find the right-hand root.

6. Press ZOOM A (ZOOM) 3 (In) to zoom in. Press TRACE and move the tracer to approximate the root.

ZOOMING TO FIND ROOTS

▼

12

Basic Keyboard/ALGEBRA USING THE SHARP EL-9900

1. Press Y= CL to return to and clear the Y1 prompt.

2. To enter the polynomial y = –5x

2

–3x + 1, press

(–)

5 xx2– 3

x + 1 .

3. View the graph in the decimal viewing window by pressing ZOOM

A (ZOOM) 7 (Dec).

4. Press TRACE and move cursor to the left of the left-hand root. Press 2ndF

CALC to view the calculate menu.

5. Press 5 (X_Incpt) to find the left-hand root.

6. Press 2ndF CALC 5 (X_Incpt) to find the next root.

JUMPING TO FIND ROOTS

13

Basic Keyboard/ALGEBRA USING THE SHARP EL-9900

1. To solve 3(4 – 2x) ≥ 5 – x, rewrite it as 3(4 – 2x) – 5 + x ≥ 0 and determine the values of x where the function y = 3(4 – 2x) – 5 + x is on or above the x-axis.

2. To do this, press Y= CL and enter 3(4 – 2x) – 5 + X in the Y1 location.

3. Set the viewing window of the graph by pressing ZOOM A (ZOOM)

5 (Default). You should be able to clearly view the x-intercept.

4. Locate the x-intercept at the point (1.4, 0) by pressing 2ndF CALC and

5 (X_Incpt).

5. Since the graph is above the x-axis, to the left of the x-intercept, the solution to the inequality 3(4 – 2x) – 5 + x ≥ 0 is all values of x such that x ≤ 1.4.

INEQUALITIES

14

Basic Keyboard/ALGEBRA USING THE SHARP EL-9900

1. To solve the inequality 3(4 – 2x) ≥ 5 – x, press Y= CL , enter 3(4 – 2X) for Y1 and 5 – X for Y2.

2. Set the viewing window by pressing ZOOM A (ZOOM) 5 (Default).

3. Next, shade the set of points that make the inequality true by pressing 2ndF

DRAW G (SHADE) 1 (Set) to access the “Set Shade” screen. Since the

inequality you are solving is Y1 ≥ Y2 the solution is where the graph of Y1 is “on the top” and Y2 is "on the bottom." Do this by pressing 2ndF VARS A

ENTER 2 2ndF VARS ENTER 1 . Press GRAPH to view the

shaded region.

4. Press 2ndF CALC 2 (Intsct) to find where the graphs intersect.

5. Since the shaded region is to the left of x = 1.4, the solution to the inequality 3(4 – 2x) ≥ 5 – x is all values of x such that x ≤ 1.4.

6. Turn off the shading by pressing 2ndF DRAW G (SHADE) 2 (INITIAL).

INEQUALITIES

▼

15

Basic Keyboard/ALGEBRA USING THE SHARP EL-9900

1. The inequality -1 ≤ 2x – 5 ≤ 7 is commonly referred to as a “double” inequality.

2. Clear any previously entered functions by pressing Y= CL .

3. Enter Y1 = -1, Y2 = 2X – 5, and Y3 = 7.

4. Press ZOOM A (ZOOM) 5 (Default) to view the line y = 2x – 5 between the lines y = -1 and y = 7.

5. Press 2ndF CALC 2 (Intsct) to find the point of intersection of the lines y = 2x – 5 and y =-1 at (2, -1). Press ▲ to move the tracer to the y = 7 line. Press 2ndF CALC 2 (Intsct) to find y = 2x – 5 and y = 7 at (6, 7).

6. The solution to the “double” inequality -1 ≤ 2x – 5 ≤ 7 consists of all values of x in between, and including, 2 and 6 (i.e., x ≥ 2 and x ≤ 6). The solution is 2 ≤ x ≤ 6.

DOUBLE INEQUALITIES

16

Basic Keyboard/ALGEBRA USING THE SHARP EL-9900

Graphing a system of equations and using the calculate feature to find the solutions

1. Turn the calculator on and press Y= .

2. Press CL to clear an old Y1 expression. Press ENTER CL to clear additional Y prompts.

3. To enter the system of equations: y = x

2

– 1

y = 2x

press xx

2

– 1 ENTER 2 x . View the graphs by pressing ZOOM

A (Zoom) 5 (Default).

4. Press 2ndF CALC to access the calculate feature. Press 2 (Intsct). The left-hand intersection will appear on the screen.

5. Press 2ndF CALC to access the calculate feature again. Press 2

(Intsct). The right-hand intersection will appear on the screen.

SOLVING A SYSTEM OF EQUATIONS

1

Basic Keyboard/PROGRAMMING USING THE SHARP EL-9900

1. The Basic keyboard can only execute a program. Use the Advanced Keyboard to enter and check the program.

2. Turn the calculator on and press PRGM to enter the programming menu. The menu consists of commands to execute, edit, and create new programs.

3. Press C (NEW) and ENTER to open a new program. The calculator is now locked in ALPHA mode and is prepared to accept a name for the new program. Enter the program name.

4. You can now enter the program. All program commands are obtained in the program menu. You cannot type program commands using the ALPHA key. To reach this menu, press PRGM . All the program commands begin with an uppercase letter.

5. Press CL to exit the program commands. When entering a new program, you must press ENTER at the end of each line.

6. If you make a mistake entering a program, use the calculator's editing feature to correct the error. First, you can press the arrow keys to move around the program. Second, you can use the DEL key which deletes a highlighted item, the BS key which backspace deletes an item, and the

2ndF INS keys which allow you to insert new items. Third, the calculator operates in typeover mode which allows you to simply type over a mistake. You must press ENTER after correcting a mistake for the correction to be saved for future use.

CREATING A NEW PROGRAM

2

Basic Keyboard/PROGRAMMING USING THE SHARP EL-9900

1. After entering the program with the Advanced Keyboard, press 2ndF QUIT to save the program and exit the editing mode.

2. Execute a program by pressing PRGM A (EXEC) and select the program

using the arrow keys and press ENTER .

3. If you receive an error statement, press to go to the line within the

program in which the error occurs. Compare your line with the correct one above to find the error. Correct the error using the editing features of the calculator and press ENTER to save the correction. Press 2ndF QUIT and try to execute the program again.

4. Once the program is working, you can execute the program from the Basic

Keyboard.

EXECUTING A PROGRAM

▼

3

Basic Keyboard/PROGRAMMING USING THE SHARP EL-9900

1. Program the calculator to find the prime factorization of a whole number

greater than 2. This method decomposes a number into the prime factors 2, 3, 5, etc.

2. Create a new program with the name DECOMP. Enter the following program

and remember to press ENTER at the end of each line. If you make a mistake, use the calculator’s editing features to correct the error.

3. Enter the following program using the Advanced Keyboard:

Input N PRGM A 3 ALPHA N ENTER 2⇒D 2 STO ALPHA D ENTER

Label A PRGM B 0 1 ALPHA A ENTER

If (N

÷D) = int PRGM B 0 3

(

ALPHA N ÷

(N÷D) Goto B ALPHA D

)

ALPHA = MATH B 0 5

(

ALPHA N ÷ ALPHA D

)

PRGM B 0 2 ALPHA B ENTER

D+1⇒D ALPHA D

+

1 STO ALPHA D

ENTER

If D ≤√N Goto A PRGM B 0 3 ALPHA D MATH

F 6 2ndF √ ALPHA N PRGM

B 0 2 ALPHA A ENTER

Goto C PRGM B 0 2 ALPHA C ENTER

Label B PRGM B 0 1 ALPHA B ENTER

N

÷D⇒N ALPHA N ÷ ALPHA D STO ALPHA

N ENTER

Print D PRGM A 1 ALPHA D ENTER

Goto A PRGM B 0 2 ALPHA A ENTER

Label C PRGM B 0 1 ALPHA C ENTER

Print N PRGM A 1 ALPHA N ENTER

End PRGM A 6 ENTER

Press 2ndF QUIT to exit the editor.

PRIME FACTORIZATION

4

Basic Keyboard/PROGRAMMING USING THE SHARP EL-9900

4. Execute the DECOMP program from the Basic Keyboard by pressing

PRGM and selecting DECOMP. Enter the number for which you want to find the prime factorization. Try 56. Press 5 6 ENTER to find the prime factorization of 56. You should then see the following prime factorization.

You can repeat this program for other numbers by pressing ENTER to execute the program over and over again. Press CL to clear the screen.

PRIME FACTORIZATION (continued)

5

Basic Keyboard/PROGRAMMING USING THE SHARP EL-9900

1. Program the calculator to find the common factors and the greatest common factor of any pair of whole numbers.

2. Create a new program with the name FACTORS. Enter the following program and remember to press ENTER at the end of each line. If you make a mistake, use the calculator’s editing features to correct the error.

3. Enter the following program using the Advanced Keyboard:

Input A PRGM A 3 ALPHA A ENTER

Input B PRGM A 3 ALPHA B ENTER 2⇒D 2 STO ALPHA D ENTER

Label A PRGM B 0 1 ALPHA A ENTER If fpart (A÷D)π0 PRGM B 0 3 MATH B 4

(

Goto B ALPHA A ÷ ALPHA D

)

MATH F

2 0 PRGM B 0 2 ALPHA B

ENTER

If fpart (B÷D)π0 PRGM B 0 3 MATH B 4

(

Goto B ALPHA B ÷ ALPHA D

)

MATH F

2 0 PRGM B 0 2 ALPHA B

ENTER

Print D PRGM A 1 ALPHA D ENTER

Label B PRGM B 0 1 ALPHA B ENTER D+1⇒D ALPHA D + 1 STO ALPHA D

ENTER

If D≤min(A,B) PRGM B 0 3 ALPHA D MATH

Goto A F 6 MATH B 6 ALPHA A ,

ALPHA B

)

PRGM B 0 2

ALPHA A ENTER

End PRGM A 6 ENTER

COMMON FACTORS

6

Basic Keyboard/PROGRAMMING USING THE SHARP EL-9900

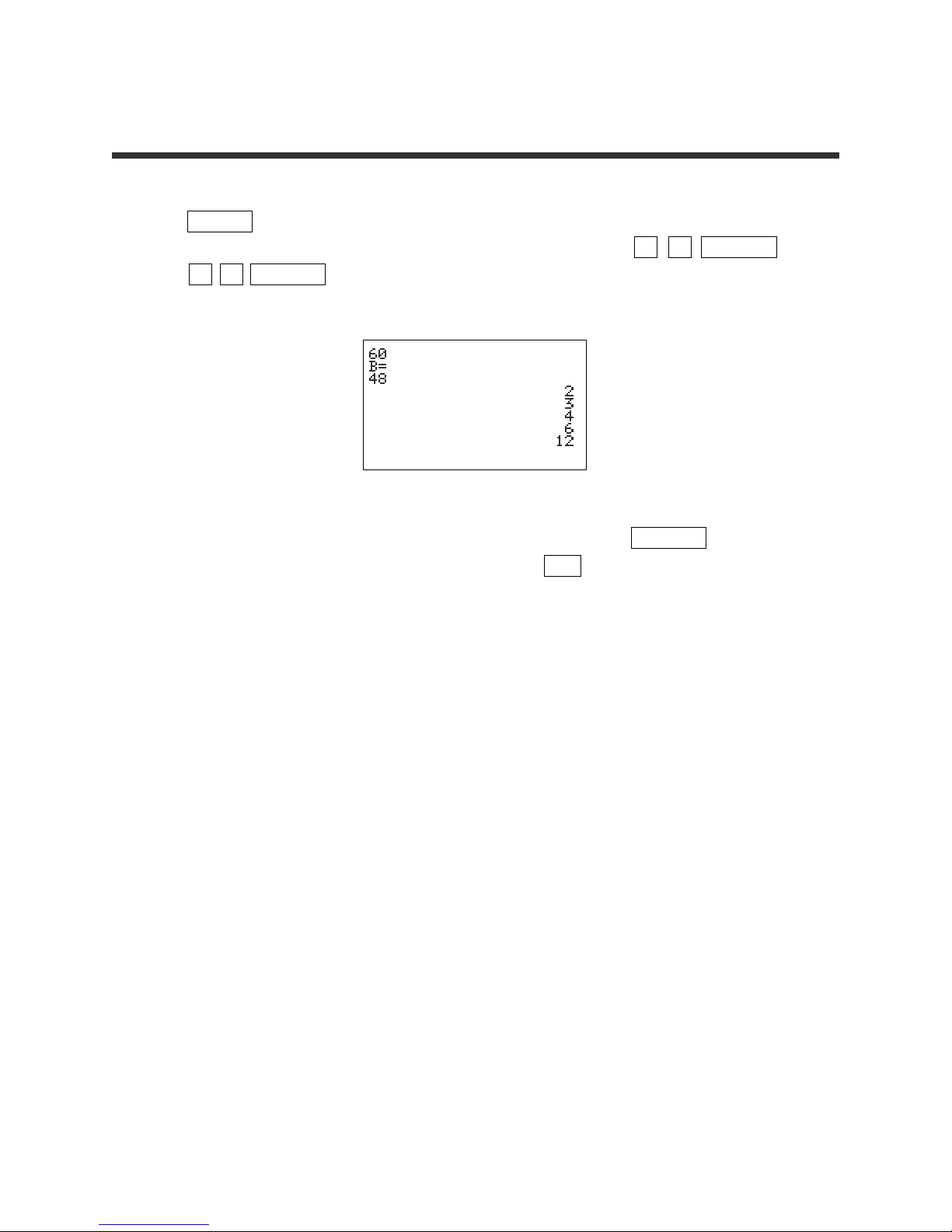
4. Execute the FACTORS program from the Basic Keyboard by pressing

PRGM and selecting FACTORS. Enter the numbers for which you

want to find the common factors. Try 60 and 48. Press 6 0 ENTER

4 8 ENTER to find the common factors of 60 and 48. You should

then see the following common factors.

You can repeat this program for other numbers by pressing ENTER to execute the program over and over again. Press CL to clear the screen.

COMMON FACTORS (continued)

7

Basic Keyboard/PROGRAMMING USING THE SHARP EL-9900

1. Program the calculator to perform synthetic division of a polynomial by a linear divisor.

2. Create a new program with the name SYNTHETI. Enter the following program and remember to press ENTER at the end of each line. If you make a mistake, use the calculator’s editing features to correct the error.

3. Enter the following program using the Advanced Keyboard:

Input D PRGM A 3 ALPHA D ENTER 0⇒P 0 STO ALPHA P ENTER {D+1,1}⇒ 2ndF

{

ALPHA D + 1 , 1 2ndF

dim(mat A) } STO 2ndF MATRIX C 0 1 2ndF

MATRIX A 1

)

ENTER

Print “COEFFIC PRGM A 1 PRGM 2

IENTS P(X) 2ndF A-LOCK C O E F F I

C I E N T S SPACE P ALPHA

( X/θ/T/n ) ENTER

Label A PRGM B 0 1 ALPHA A ENTER P+1⇒P ALPHA P + 1 STO ALPHA P

ENTER

Input C PRGM A 3 ALPHA C ENTER C⇒mat A(P,1) ALPHA C STO 2ndF MATRIX A 1

(

ALPHA P , 1

)

ENTER

If P<D+1 PRGM B 0 3 ALPHA P MATH

Goto A F 5 ALPHA D + 1 PRGM

B 0 2 ALPHA A ENTER

Label B PRGM B 0 1 ALPHA B ENTER

Input R PRGM A 3 ALPHA R ENTER

Label C PRGM B 0 1 ALPHA C ENTER 1⇒P 1 STO ALPHA P ENTER 0⇒S 0 STO ALPHA S ENTER

SYNTHETIC DIVISION

8

Basic Keyboard/PROGRAMMING USING THE SHARP EL-9900

Print “COEFFIC PRGM A 1 PRGM 2

IENTS Q(X) 2ndF A-LOCK C O E F F I C

I E N T S SPACE Q ALPHA

(

X/θ/T/n

)

ENTER

Label D PRGM B 0 1 ALPHA D ENTER mat A(P,1)⇒F 2ndF MATRIX A 1

(

ALPHA P , 1

)

STO ALPHA F ENTER

F+S⇒Q ALPHA F + ALPHA S STO ALPHA

Q ENTER

Print Q PRGM A 1 ALPHA Q ENTER

Wait PRGM A 4 ENTER R×Q⇒S ALPHA R × ALPHA Q STO ALPHA

S ENTER

P+1⇒P ALPHA P + 1 STO ALPHA P

ENTER

If P<D+1 PRGM B 0 3 ALPHA P MATH

Goto D F 5 ALPHA D + 1 PRGM B 0

2 ALPHA D ENTER

mat A(P,1)⇒F 2ndF MATRIX A 1

(

ALPHA P , 1

)

STO ALPHA F ENTER

F+S⇒Q ALPHA F + ALPHA S STO ALPHA

Q ENTER

Print PRGM A 1 PRGM 2 2ndF

“REMAINDER A-LOCK R E M A I N D E R

ALPHA ENTER

Print Q PRGM A 1 ALPHA Q ENTER

End PRGM A 6 ENTER

Press 2ndF QUIT to exit the editor.

SYNTHETIC DIVISION (continued)

9

Basic Keyboard/PROGRAMMING USING THE SHARP EL-9900

4. Execute the SYNTHETI program from the Basic Keyboard by pressing

PRGM and selecting SYNTHETI. Use synthetic division to divide

P(x) = 2x

3

+ 3x2+ 4x + 5 by x – 1. Enter the degree for P(x) by pressing 3 ENTER . Next enter the coefficients and constant for P(x) by pressing 2 ENTER 3 ENTER 4 ENTER 5 ENTER . Enter the r

value of 1 by pressing 1 ENTER . The first coefficient of Q(x) will appear. Press ENTER to see additional coefficients. The remainder will be shown to end the program. You should then see the following coefficients, constant and remainder (Q(x) = 2x

2

+ 5x + 9, remainder = 14).

You can repeat this program for other numbers by pressing ENTER to execute the program over and over again. Press CL to clear the screen.

SYNTHETIC DIVISION (continued)

10

Basic Keyboard/PROGRAMMING USING THE SHARP EL-9900

1. Program the calculator to graph a random walk. A random walk can go in any direction for a random distance. This program stops when the graph tries to go outside the calculator display.

2. Create a new program with the name WALK. Enter the following program and remember to press ENTER at the end of each line. If you make a mistake, use the calculator’s editing features to correct the error.

3. Enter the following program using the Advanced Keyboard:

ClrDraw 2ndF DRAW A 1 ENTER 0⇒D 0 STO ALPHA D ENTER .5⇒X . 5 STO X/θ/T/n ENTER .5⇒Y . 5 STO ALPHA Y ENTER

Label A PRGM B 0 1 ALPHA A ENTER .2(random–.5)⇒H . 2

(

MATH C 1 – . 5 )STO

ALPHA H ENTER

.2(random–.5)⇒K . 2

(

MATH C 1 – . 5

)

STO

ALPHA K ENTER

Line(X,Y,X+H, 2ndF DRAW A 2 X/θ/T/n , ALPHA Y+K) Y , X/θ/T/n + ALPHA H , ALPHA

Y + ALPHA K

)

ENTER

X+H⇒XX/θ/T/n + ALPHA H STO X/θ/T/n ENTER Y+K⇒Y ALPHA Y + ALPHA K STO ALPHA

Y ENTER

If X<0 Goto B PRGM B 0 3 X/θ/T/n MATH F

5 0 PRGM B 0 2 ALPHA B ENTER

If X>1 Goto B PRGM B 0 3 X/θ/T/n MATH F 3 1

PRGM B 0 2 ALPHA B ENTER

If Y<0 Goto B PRGM B 0 3 ALPHA Y MATH F 5 0

PRGM B 0 2 ALPHA B ENTER

RANDOM WALKS

11

Basic Keyboard/PROGRAMMING USING THE SHARP EL-9900

If Y>1 Goto B PRGM B 0 3 ALPHA Y MATH F 3

1 PRGM B 0 2 ALPHA B ENTER

D+√(H

2+K2

)⇒D ALPHA D + 2ndF √

(

ALPHA H

x

2

+ ALPHA K x

2

)

STO ALPHA

D ENTER

Goto A PRGM B 0 2 ALPHA A ENTER

Label B PRGM B 0 1 ALPHA B ENTER

Print D PRGM A 1 ALPHA D ENTER

End PRGM A 6 ENTER

4. First, press Y= and CL to clear the Y1 prompt. Press CL to clear additional prompts if necessary. Set the viewing window for the graphing by pressing WINDOW 0 ENTER 1 ENTER 1 ENTER 0

ENTER 1 ENTER 1 ENTER . Execute the WALK program by pressing PRGM and selecting WALK. The program will show you the random walk and then display the distance traveled in the walk. If your walk is short, then press ENTER to execute the program again. When you have a long walk, press GRAPH to view the graph. A long walk is greater than 10.

RANDOM WALKS (continued)

▼

12

Basic Keyboard/PROGRAMMING USING THE SHARP EL-9900

1. Program the calculator to roll a set of dice.

2. Create a new program with the name ROLLING. Enter the following program and remember to press ENTER at the end of each line. If you make a mistake, use the calculator’s editing features to correct the error.

3. Enter the following program using the Advanced Keyboard:

Print “NUMBER PRGM A 1 PRGM A 2 2ndF

OF DICE A-LOCK N U M B E R

SPACE O F SPACE D I C E ENTER

Input N PRGM A 3 ALPHA N ENTER 0⇒K 0 STO ALPHA K ENTER

Label A PRGM B 0 1 ALPHA A ENTER

Print int ( PRGM A 1 MATH B 5

(

random × 6)+1 MATH C 1 × 6

)

+ 1 ENTER

K+1⇒K ALPHA K + 1 STO ALPHA K

ENTER

If K<N PRGM B 0 3 ALPHA K MATH

Goto A F 5 ALPHA N PRGM B 0 2

ALPHA A ENTER

End PRGM A 6 ENTER

ROLLING DICE

13

Basic Keyboard/PROGRAMMING USING THE SHARP EL-9900

4. Execute the ROLLING program by pressing PRGM and selecting ROLLING. Enter the number of dice, up to eight, that you wish the calculator to roll for you. Roll five dice by pressing 5 ENTER . The program will show the five values for the dice on the screen. You should see a screen similar to the following (the values for the dice should be different).

ROLLING DICE (continued)

14

Basic Keyboard/PROGRAMMING USING THE SHARP EL-9900

1. Program the calculator to find Pythagorean triples. Pythagorean triples are three numbers x, y, and z that satisfy x

2

+ y2= z2.

2. Create a new program with the name PYTHAG. Enter the following program and remember to press ENTER at the end of each line. If you make a mistake, use the calculator’s editing features to correct the error.

3. Enter the following program using the Advanced Keyboard:

Input N PRGM A 3 ALPHA N ENTER 2⇒J 2 STO ALPHA J ENTER 1⇒K 1 STO ALPHA K ENTER

Label A PRGM B 0 1 ALPHA A ENTER If √(J

2+K2

)≠ipart PRGM B 0 3 2ndF √

(

ALPHA J

(√(J

2+K2

)) Goto B x2+ ALPHA K x

2

)

MATH F 2

MATH B 3

(

2ndF √

(

ALPHA

J x

2

+ ALPHA K x

2

))

PRGM B

0 2 ALPHA B ENTER

Print J PRGM A 1 ALPHA J ENTER

Print K PRGM A 1 ALPHA K ENTER Print √(J

2+K2

) PRGM A 1 2ndF √

(

ALPHA

J x

2

+ ALPHA K x

2

)

ENTER

Print “ PRGM A 1 PRGM A 2 ENTER

Wait PRGM A 4 ENTER

Label B PRGM B 0 1 ALPHA B ENTER K+1⇒K ALPHA K + 1 STO ALPHA K ENTER If K≤(J–1) PRGM B 0 3 ALPHA K MATH

Goto A F 6 ( ALPHA J – 1

)

PRGM B 0

2 ALPHA A ENTER

J+1⇒J ALPHA J + 1 STO ALPHA J ENTER 1⇒K 1 STO ALPHA K ENTER If J≤N PRGM B 0 3 ALPHA J MATH

PYTHAGOREAN TRIPLES

15

Basic Keyboard/PROGRAMMING USING THE SHARP EL-9900

Goto A F 6 ALPHA N PRGM B 0 2

ALPHA A ENTER

End PRGM A 6 ENTER

4. Execute the PYTHAG program by pressing PRGM and selecting PYTHAG. Enter the upper bound for the Pythagorean triples. Set the upper bound to 15 by pressing 1 5 ENTER . The program will show the first Pythagorean triple. Press ENTER to view additional triples. You should see screens similar to the following ones.

PYTHAGOREAN TRIPLES (continued)

Sharp EL-9900

Graphing Calculator

Advanced Keypad

EL-9900

SUB

SPLIT

TBLSET

DRAW

FORMAT

CALC

OPTION

LIST

CLIP

OFF

A-LOCK

STAT PLOT

SLIDE SHOW

2ndF

ALPHA

Y

=

GRAPH

TABLE

WINDOW

ZOOM

TRACE

ON

sin cos

+

–

.

–

+

TOOL

MATRIX

MATH

sin

a

uvw

STAT

–1

A

cos

GH I J K

b

c

L

789

QRST

L4 L5 L6

4

VW

L1 L2 L3

1

0

<

0

SOLVER

PRGM

–1

BCDEF

tan

a

b

MN

–1

tan

a

INS

DEL BSInCL

x

10

log

b

,

{}

SET UP

RCL VARS

(

X

=

x

FINANCE

+

ENTRY

5

2

i

SPACE

6

3



(–)

x

e

STO

O

CATALOG

Y Z

EXE

. .

xp

ENTER

QUIT

–1

x

2

x

X/0/T/n

P

)

U

.

–

ANS

1

Advanced Keyboard/ALGEBRA USING THE SHARP EL-9900

Graphing and translations of quadratic equations

1. Turn the calculator on and press Y= . Press CL to remove an old Y1 expression. Press ENTER CL to remove an old Y2 expression.

2. To enter the quadratic equation ( y = x

2

) for Y1, press X/θ/T/n x2.

Enter the viewing window range by pressing ZOOM A (Zoom) 7 (Dec).

3. When 2 is added to x2, the resulting equation is y = x2+ 2. Enter this function for Y2 by pressing Y=

▼ X/θ/T/n x

2

+ 2 . Press GRAPH .

What does the addition of 2 do?

4. When -2 is added to x2, the resulting equation is y = x2– 2. To change Y2 for this expression, press Y=

▼ CL X/θ/T/n x

2

– 2 .

ENTER GRAPH . What does the addition of -2 do?

5. Summarize the effect of k within the standard equation y = a(x – h)

2

+ k.

QUADRATIC EQUATIONS

2

Advanced Keyboard/ALGEBRA USING THE SHARP EL-9900

Steps for solving an equation using the equation method

1. Turn the calculator on and press 2ndF SOLVER to access the solver feature. A blank screen should appear. If the screen is not blank, then press

CL to clear the screen.

2. Select the Equation method for solving by pressing 2ndF SOLVER ,

A (METHOD) 1 (Equation).

3. Enter the formula P = L 1 – ( 1 + I÷12)

–

N

-

1

I÷12

Press ALPHA P ALPHA = ALPHA L

(

a/b 1 –

(

1

+ ALPHA I ÷ 1 2

)

a

b

(-)

ALPHA N

ALPHA I ÷ 1 2

)

a

b

(-)

1 .

This equation is referred to as the amortization formula, with a loan (L) with a fixed rate of interest (I).

4. Press ENTER to view the variable list. To find the monthly payment on a $15,000 car loan made at 9% interest over four years (48 months), enter the values by pressing ▼ 1 5 0 0 0 ENTER • 0 9

ENTER 4 8 ENTER . Press and notice the payment ( P) is now highlighted by the cursor, press 2ndF EXE to solve for the payment.

5. Pressing CL will return you to the variable screen. You can now change or solve for any of the values. Save this formula by pressing 2ndF

SOLVER C (SAVE) ENTER and entering the formula name. Give the

formula the name AMORT by pressing A M O R T ENTER .

FORMULAS OR LITERAL EQUATIONS

▼

[

]

3

Advanced Keyboard/ALGEBRA USING THE SHARP EL-9900

Steps for solving an equation using the graphic method

1. Turn the calculator on and press 2ndF SOLVER to access the solver feature. Press CL to clear the formula entry screen. Select the Graphic method for solving by pressing 2ndF SOLVER A (METHOD) 3 (Graphic).

2. Enter the formula V = π r

2

h by pressing ALPHA V ALPHA = 2ndF

π ALPHA R a

b

2 ALPHA H .

3. This equation is the formula for calculating the volume of a cylinder ( V) in terms of the cylinder's height ( H) and radius ( R). Press ENTER to view the variable list.

4. To find the radius of a cylinder with a volume of 30 cubic inches, and a height of 10 inches, enter the values by pressing 3 0 ENTER ▼ 1

0 ENTER . Press ▲ and notice the radius ( R) is now highlighted by

the cursor.

5. Press 2ndF EXE to solve for the radius. The graphic solver will prompt you for a variable range to solve within. Set the variable range to 0 and 2 by pressing 0 ENTER 2 ENTER .

6. Press 2ndF EXE to solve.

7. Pressing CL will return you to the variable screen. You can now change or solve for any of the values. Save this formula by pressing 2ndF SOLVER ,

C (SAVE) pressing ENTER , and entering the formula name. Give

the formula the name VCYL by pressing V C Y L ENTER .

FORMULAS OR LITERAL EQUATIONS

▼

4

Advanced Keyboard/ALGEBRA USING THE SHARP EL-9900

Solving an equation using Newton's method

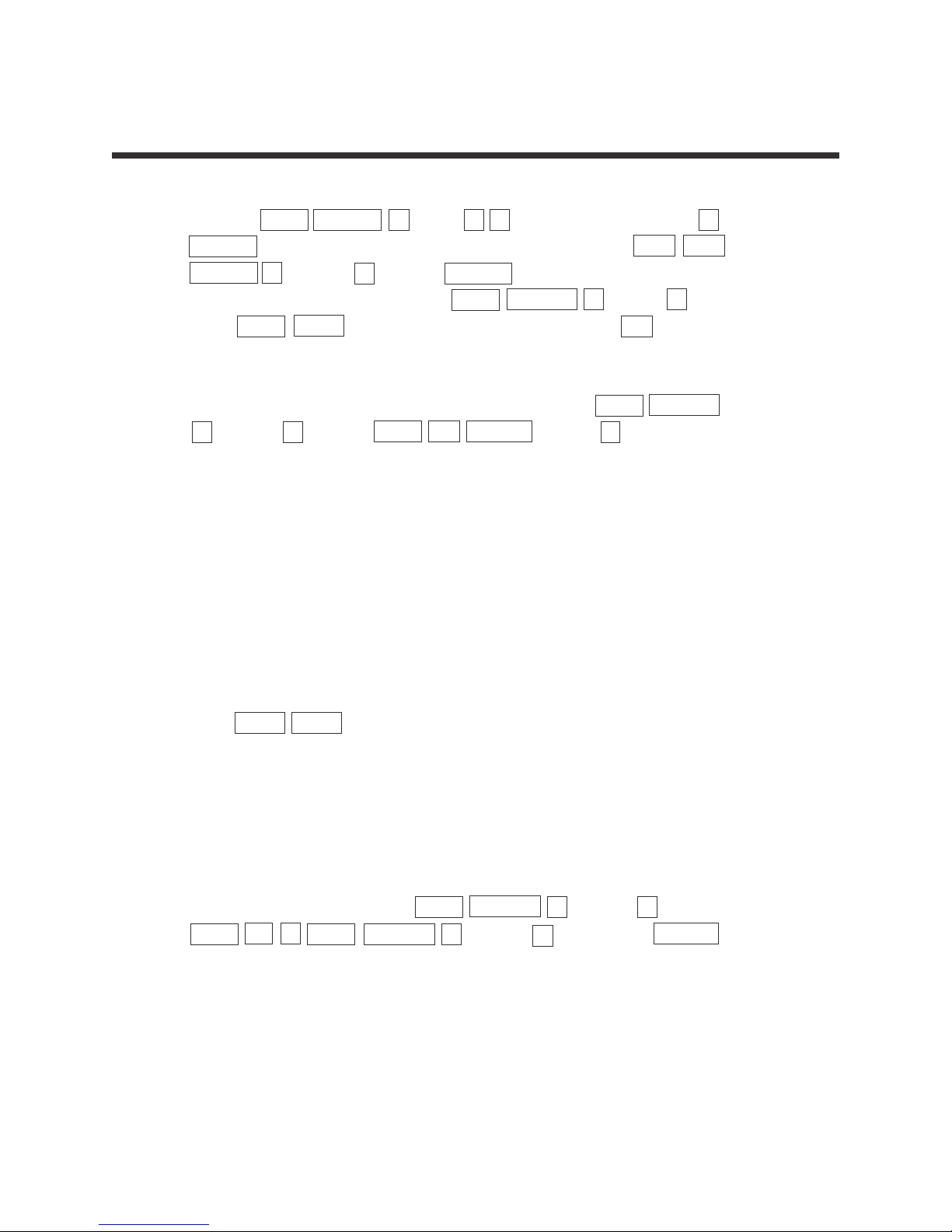
1. Press 2ndF SOLVER to enter the solver feature. Press CL to clear the formula entry screen.

2. Select the Newton's method for solving by pressing 2ndF SOLVER ,

A (METHOD) 2 (Newton). Enter the formula A = H(B + C) by pressing

ALPHA A ALPHA = 1 a/b 2 ALPHA H

(

ALPHA B +

ALPHA C ).

3. Press ENTER to view the variable list. To find the height of a trapezoid with an area of 25 in

2

, and bases of length 5 and 7 inches, enter the values by pressing 2 5 ENTER ▼ 5 ENTER 7 ENTER ▲▲. Notice the height (H) is now highlighted by the cursor.

4. Press 2ndF EXE to continue. Newton's method will prompt you for a guess or starting point. Enter a starting point of 1 by pressing 1 ENTER .

5. Press 2ndF EXE to solve. A height of 4.1667 will appear on the screen.

6. Pressing CL will return you to the variable screen. You can now change or solve for any of the values. Save this formula by pressing 2ndF SOLVER ,

C (SAVE) ENTER and entering the formula name. Give the formula the

name "ATRAP," by pressing A T R A P ENTER .

FORMULAS OR LITERAL EQUATIONS

1 2

▼

5

Advanced Keyboard/ALGEBRA USING THE SHARP EL-9900

Graphing a polynomial and zooming to find the roots

1. Turn the calculator on and press Y= . Y prompts will appear on the viewing window. Press CL to remove old Y expressions. Setup the calculator with rectangular coordinates and the equation editor mode by pressing 2ndF

SET UP E (COORD) 1 (Rect) G (EDITOR) and 1 (Equation). Press CL

to exit the menu and return to the Y prompts.

2. To enter the polynomial y = x

3

– 3x2+ x + 1, press X/θ/T/n ab3

– 3 X/θ/T/n x

2

+

X/θ/T/n

+

1 .

3. Press ZOOM A (Zoom) 7 (Dec) to establish the decimal viewing window and view the graph. Press TRACE to engage the trace feature. Press to move the cursor near the left-hand root.

4. Set the zoom factors to 5 by pressing ZOOM B (FACTOR) press

ENTER 5 ENTER 5 ENTER . Press ZOOM A (ZOOM) 3 (In) to zoom in on the left- hand root. Press TRACE and move the tracer to approximate the root.

5. Press ZOOM H (RCL) 2 (PreWin) to return to the decimal viewing window. Press TRACE and move the tracer to find the middle root.

6. Press repeatedly to move the tracer near the right-hand root. Press

ZOOM A (ZOOM) 3 (In) to zoom in. Press TRACE and move the tracer

to approximate the root.

GRAPHING POLYNOMIALS AND FINDING THE ROOTS

▼

6

Advanced Keyboard/ALGEBRA USING THE SHARP EL-9900

Graphing a polynomial and jumping to find the roots

1. Press Y= CL to return to and clear the Y1 prompt.

2. To enter the polynomial y = x

4

+ x3–5x2–3x + 1, press X/θ/T/n ab4

+ X/θ/T/n a

b

3

–

5 X/θ/T/nx2– 3 X/θ/T/n + 1 .

3. View the graph in the decimal viewing window by pressing ZOOM

A (ZOOM) 7 (Dec).

4. Press TRACE and move cursor to the left of the left-hand root. Press 2ndF

CALC to view the calculate menu.

5. Press 5 (X_Incpt) to find the left-hand root.

6. Press 2ndF CALC 5 (X_Incpt) to find the next root.

7. Press 2ndF CALC 5 (X_Incpt) to find the next root.

8. Press 2ndF CALC 5 (X_Incpt) to find the next root.

GRAPHING POLYNOMIALS AND FINDING THE ROOTS

▼

7

Advanced Keyboard/ALGEBRA USING THE SHARP EL-9900

Graphing a system of equations and using the calculate feature to find the solutions

1. Turn the calculator on and press Y= .

2. Press CL to clear an old Y1 expression. Press ENTER CL to clear additional Y prompts.

3. To enter the system of equations: y = x

2

– 1

y = 2x

press X/θ/T/nx

2

– 1 ENTER 2 X/θ/T/n . View the graphs

by pressing ZOOM A (Zoom) 5 (Default).

4. Press 2ndF CALC to access the calculate feature. Press 2 (Intsct). The left-hand intersection will appear on the screen.

5. Press 2ndF CALC to access the calculate feature again. Press 2

(Intsct). The right-hand intersection will appear on the screen.

SOLVING A SYSTEM OF EQUATIONS

8

Advanced Keyboard/ALGEBRA USING THE SHARP EL-9900

Solving a system of linear equations using the tool feature

1. Press 2ndF TOOL to access the tool menu.

2. Press B (SYSTEM) 2 (2) to view the entry screen for solving a linear-system of equations. Systems up to six variables and six equations can be solved.

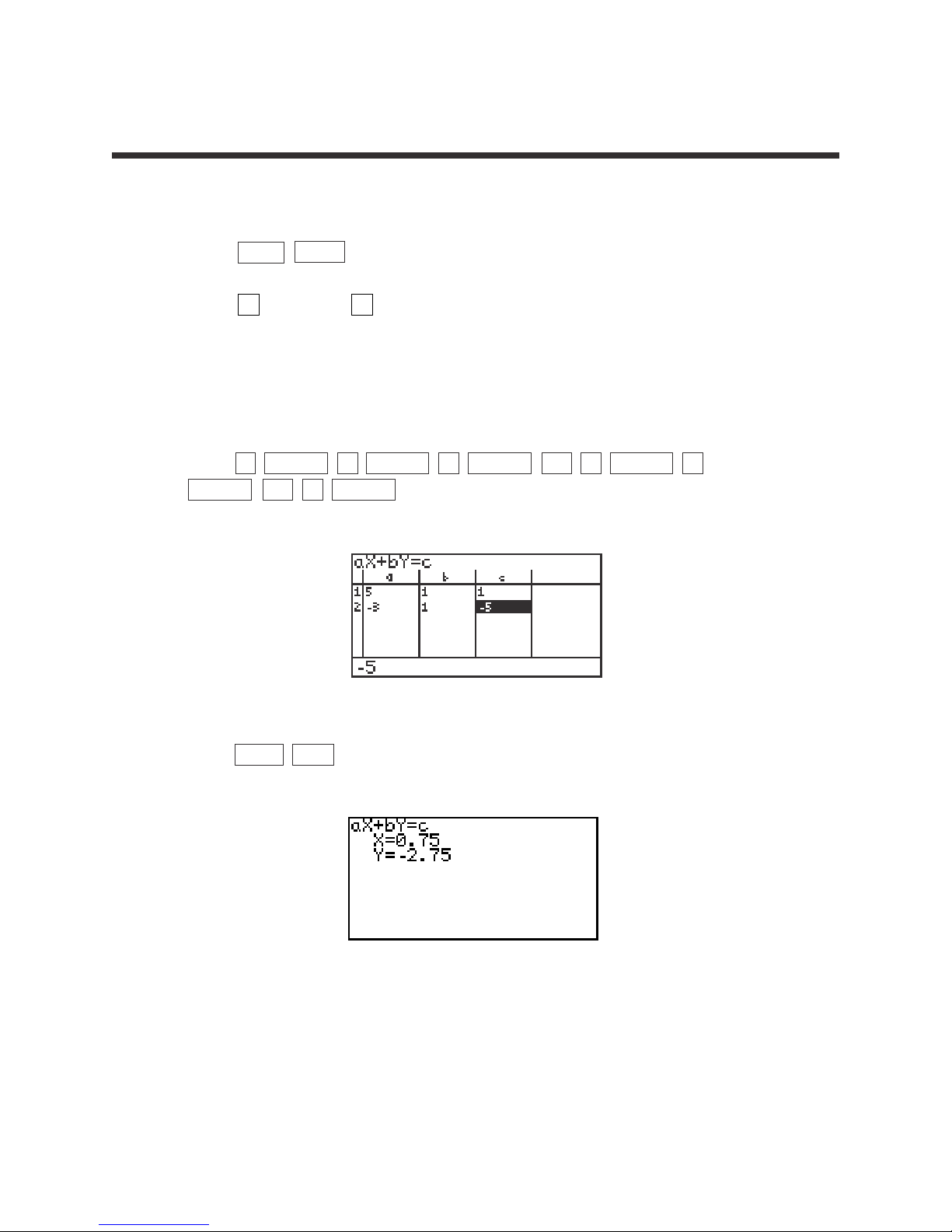
3. To enter the system of equations: 5x + y = 1

-

3x + y =-5

Press 5 ENTER 1 ENTER 1 ENTER

(–)

3 ENTER 1

ENTER

(–)

5 ENTER .

4. Press 2ndF EXE to solve the system.

SOLVING A SYSTEM OF EQUATIONS

9

Advanced Keyboard/ALGEBRA USING THE SHARP EL-9900

1. Press 2ndF MATRIX to access the matrix menu.

2. Press B (EDIT) 1 (mat A) to select matrix A.

3. Now, enter the size or dimension of the matrix. We will enter the 3

× 3 matrix. 1 2 1

2 1 -1

1 1 -2 Press 3 ENTER 3 ENTER to set the dimension of the matrix at three rows by three columns.

4. The calculator will now prompt you for the matrix. Enter the elements of the matrix by pressing 1 ENTER 2 ENTER 1 ENTER 2 ENTER

1 ENTER

(–)

1 ENTER 1 ENTER 1 ENTER

(–)

2 ENTER .

5. Press 2nd QUIT to exit the display of matrix A.

6. Repeat the process to enter a 3

× 3 matrix B = 1 2 3

4 5 6 7 8 9 .

7. Matrix multiplication can be performed if the number of columns of the first matrix is equal to the number of rows of the second matrix. In the matrix multiplication A

× B, the elements in the first row of A are multiplied to the

corresponding elements in the first column of B. The sum of these multiplications is placed in the 1,1(first row, first column) position of the resulting matrix. This process is repeated until each row of A has been multiplied to each column of B. Press 2nd QUIT to leave matirx entry mode.

8. To multiply the matrices A and B together, press 2ndF MATRIX A (NAME)

1 (mat A)

× 2ndF MATRIX 2 (mat B) and ENTER .

MATRIC SOLUTIONS TO SYSTEMS OF LINEAR EQUATIONS

[

]

[

]

10

Advanced Keyboard/ALGEBRA USING THE SHARP EL-9900

1. The calculator will directly establish an identity matrix of a given size by pressing 2ndF MATRIX C (OPE) 0 5 (identity) and pressing 3

ENTER . To save the identity matrix in matrix C, press STO 2ndF

MATRIX A (NAME) 3 (mat C) ENTER . Confirm that the identity matrix is stored in matrix C by pressing 2ndF MATRIX B (EDIT) 3 (mat C). Press 2ndF QUIT to exit the matrix editor and press CL to clear the screen.

2. Find the inverse of the square matrix A by pressing 2ndF MATRIX A (NAME) 1 (mat A) 2ndF x

-

1

ENTER . Press to see more of

the matrix.

3. To solve the system of equations x + 2y + z = 8

2x + y – z = 1

x + y – 2z =-3 using matrices, use the matrix A entered previously as the coefficient matrix, and enter the constants on the right side of the equal sign into matrix B, where B = 8

1

-

3 . Press 2ndF QUIT to exit the display of the B matrix. The solution matrix X is found by multiplying mat A

-1

B • mat B.

4. This multiplication is derived from the equation AX= B, A

-1

• A • X = A-1• B (multiply both sides by A-1)

I • X = A

-1

•B (A-1• A = I, identity matrix)

X = A

-1

• B (I • X = X )

Multiply A

-1

• B by pressing 2ndF MATRIX A (NAME) 1 (mat A)

2ndF x

-

1

× 2ndF MATRIX A (NAME) 2 (mat B) and ENTER .

The solution matrix will appear.

MATRIC SOLUTIONS TO SYSTEMS OF LINEAR EQUATIONS

▼

[

]

11

Advanced Keyboard/ALGEBRA USING THE SHARP EL-9900

1. To solve 3(4 – 2x) ≥ 5 – x, rewrite it as 3(4 – 2x) – 5 + x ≥ 0 and determine the values of x where the function y = 3(4 – 2x) – 5 + x is on or above the x-axis.

2. To do this, press Y= CL and enter 3(4 – 2x) – 5 + X in the Y1 location.

3. Set the viewing window of the graph by pressing ZOOM A (ZOOM)

5 (Default). You should be able to clearly view the x-intercept.

4. Locate the x-intercept at the point (1.4, 0) by pressing 2ndF CALC and

5 (X_Incpt).

5. Since the graph is above the x-axis, to the left of the x-intercept, the solution to the inequality 3(4 – 2x) – 5 + x ≥ 0 is all values of x such that x ≤ 1.4.

INEQUALITIES

12

Advanced Keyboard/ALGEBRA USING THE SHARP EL-9900

1. To solve the inequality 3(4 – 2x) ≥ 5 – x, press Y= CL , enter 3(4 – 2X) for Y1 and 5 – X for Y2.

2. Set the viewing window by pressing ZOOM A (ZOOM) 5 (Default).

3. Next, shade the set of points that make the inequality true by pressing 2ndF

DRAW G (SHADE) 1 (Set) to access the “Set Shade” screen. Since the

inequality you are solving is Y1 ≥ Y2 the solution is where the graph of Y1 is “on the top” and Y2 is "on the bottom." Do this by pressing 2ndF VARS A

ENTER 2 2ndF VARS ENTER 1 . Press GRAPH to view the

shaded region.

4. Press 2ndF CALC 2 (Intsct) to find where the graphs intersect.

5. Since the shaded region is to the left of x = 1.4, the solution to the inequality 3(4 – 2x) ≥ 5 – x is all values of x such that x ≤ 1.4.

6. Turn off the shading by pressing 2ndF DRAW G (SHADE) 2 (INITIAL).

INEQUALITIES

▼

13

Advanced Keyboard/ALGEBRA USING THE SHARP EL-9900

1. The inequality -1 ≤ 2x – 5 ≤ 7 is commonly referred to as a “double” inequality.

2. Clear any previously entered functions by pressing Y= CL .

3. Enter Y1 = -1, Y2 = 2X – 5, and Y3 = 7.

4. Press ZOOM A (ZOOM) 5 (Default) to view the line y = 2x – 5 between the lines y = -1 and y = 7.

5. Press 2ndF CALC 2 (Intsct) to find the point of intersection of the lines y = 2x – 5 and y =-1 at (2, -1). Press ▲ to move the tracer to the y = 7 line. Press 2ndF CALC 2 (Intsct) to find y = 2x – 5 and y = 7 at (6, 7).

6. The solution to the “double” inequality -1 ≤ 2x – 5 ≤ 7 consists of all values of x in between, and including, 2 and 6 (i.e., x ≥ 2 and x ≤ 6). The solution is 2 ≤ x ≤ 6.

DOUBLE INEQUALITIES

14

Advanced Keyboard/ALGEBRA USING THE SHARP EL-9900

1. The solution region of a system of inequalities consists of all points (a, b) such that when x = a and y = b, all inequalities in the system are true.

2. For example, to graph the solution region for the system

2x + y ≥ 1

x

2

+ y ≤ 1,

first rewrite each inequality in the system so that the left-hand-side is y:

y ≥ 1 – 2x y ≤ 1 – x

2

3. Press Y= CL and enter 1 – 2X in Y1 and 1 – X2in Y2.

4. Next, shade the points that have a y-value less than Y2 and greater than Y1. Do this by pressing 2ndF DRAW G (SHADE) 1 (Set) 2ndF VARS A

ENTER 1 2ndF VARS ENTER 2 .

5. Graph the system by pressing ZOOM A (ZOOM) 7 (Dec).

6. Turn off the shading by pressing 2ndF DRAW G (SHADE) 2 (INITIAL).

SYSTEMS OF INEQUALITIES

▼

15

Advanced Keyboard/ALGEBRA USING THE SHARP EL-9900

1. Evaluate |-2(5 – 1)| by pressing to access the home or computation screen. Enter the absolute value symbol by pressing MATH B (NUM)

1 (abs). You should see | | on the screen. Enter -2(5-1) inside the

absolute value symbols and evaluate by pressing

(–)

2

(

5 – 1

)

ENTER .

2. Graph y = |x| by pressing Y= CL to clear the Y1 prompt. Press ENTER

CL to clear the remaining prompts if necessary. Enter |x| in Y1 by pressing MATH B (NUM) 1 (abs) and pressing X/θ/T/n . Press ZOOM A

(ZOOM) 5 (Default) to draw the graph.

ABSOLUTE VALUE

×

+

–

÷

16

Advanced Keyboard/ALGEBRA USING THE SHARP EL-9900

1. Solve |5 – 4x| = 6 by first pressing Y= CL to clear the Y1 prompt.

2. Enter |5 – 4x| in Y1 with the keystrokes MATH B (NUM) 1 (abs)

5 – 4 X/θ/T/n .

3. Next, press ENTER CL 6 to enter 6 in Y2.

4. Press ZOOM A (ZOOM) 5 (Default) to view the two points of intersection of the absolute value and the horizontal line y = 6.

5. Press 2ndF CALC 2 (Intsct) to find one point of intersection of the two graphs. Press 2ndF CALC 2 (Intsct) again to find the other point of intersection.

6. The solution to the equation |5 – 4x| = 6 consists of the two values-0.25 and 2.75.

ABSOLUTE VALUE EQUATIONS

17

Advanced Keyboard/ALGEBRA USING THE SHARP EL-9900

1. To solve < 8 , rewrite the inequality so that the right-hand side of the inequality is zero: – 8 < 0.

2. Press Y= and clear all the Y prompts.

3. Enter the left-hand side of the inequality – 8 in Y1 by pressing

MATH B (NUM) 1 (abs) a/b 2 0 – 6 X/θ/T/n 5

–

8 .

4. Graph the expression by pressing ZOOM A (Zoom) 5 (Default). The x-intercepts of the graph are clearly visible.

5. Press 2ndF CALC 5 (X_Incpt) to find the first x-intercept. Press 2ndF

CALC 5 (X_Incpt) to find the second x-intercept.

6. Since the graph is below the x-axis for x in between the two x-intercepts, the solution is -3.33 < x < 10.

ABSOLUTE VALUE INEQUALITIES

20 – 6x

5

20 – 6x

5

20 – 6x

5

▼

18

Advanced Keyboard/ALGEBRA USING THE SHARP EL-9900

1. To solve the inequality |3.5x + 4| ≥ 10, press Y= CL to clear the Y1 prompt. Press ENTER CL to clear additional prompts.

2. Enter the function |3.5x + 4| in Y1 by pressing MATH B (NUM)

1 (abs) 3 • 5 X/θ/T/n + 4 ENTER . Enter 10 in Y2 by pressing 1 0 .

3. Access the Set Shade screen by pressing 2ndF DRAW G (SHADE) 1 (SET). Since Y2 is the function "on the bottom," press 2ndF VARS A

ENTER 2 (Y2) and since Y1 is the function "on the top," press 2ndF

VARS ENTER 1 (Y1).

4. Set the viewing window by pressing ZOOM A (Zoom) 5 (Default). Press

ZOOM 4 (out) to see the intersection.

5. Press 2ndF CALC 2 (Intsct) to locate a point of intersection. Repeat to find the other. The intersections are (-4, 10) and (1.714, 10). The solution of the inequality |3.5x + 4| > 10 is all values of x such that x ≤-4 or x ≥ 1.714.

6. Turn off the shading by pressing 2ndF DRAW G (SHADE) 2 (INITIAL).

ABSOLUTE VALUE INEQUALITIES

▼

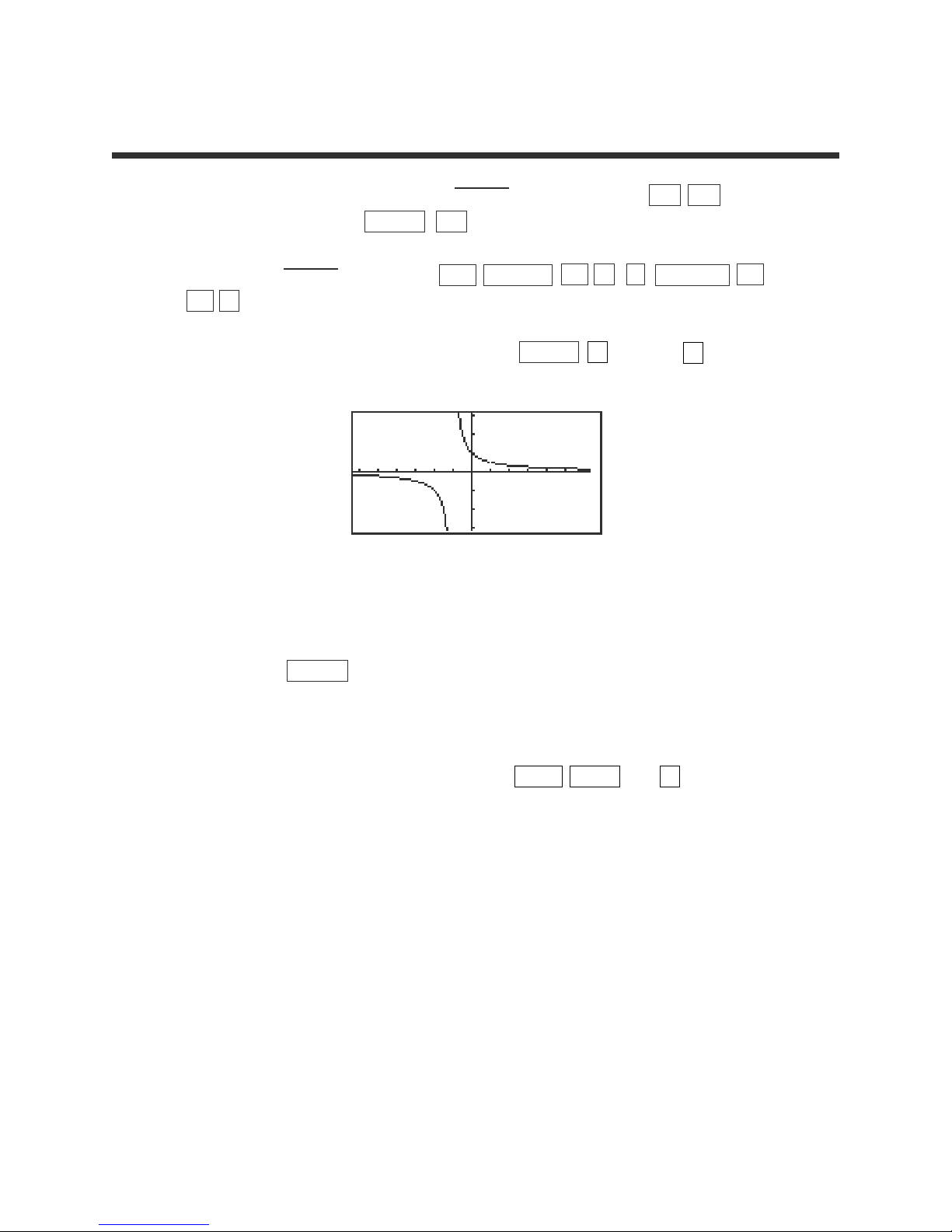
19

Advanced Keyboard/ALGEBRA USING THE SHARP EL-9900

1. Graph the rational function f(x) = by first pressing Y= CL to clear the Y1 prompt. Press ENTER CL to clear additional Y prompts.

2. Enter Y1 = by pressing a/b X/θ/T/n – 1 X/θ/T/nx

2

– 1 .

3. Graph in the decimal window by pressing ZOOM A (ZOOM) 7 (Dec).

4. The function consists of two branches separated by the vertical asymptote (the line x =-1). Look closely at the graph and observe the “hole” in it at x = 1. Press TRACE and investigate the "hole." Note that the hole will be seen only when the window is a "friendly" or decimal window.

5. Notice that there are no x-intercepts for the graph. The y-intercept can easily be found at x = 0, y = 1 by pressing 2ndF CALC and 6 (Y_Incpt).

6. Observe that the line y = 0 is very likely a horizontal asymptote of f(x).

RATIONAL FUNCTIONS

(x – 1)

(x

2

– 1)

(x – 1)

(x

2

– 1)

▼

20

Advanced Keyboard/ALGEBRA USING THE SHARP EL-9900

1. Solve the inequality ≤ 2 using the intersection method with shading, by first pressing Y= CL to clear the Y1 prompt.

2. Enter the left-hand side of the inequality in Y1 by pressing MATH B (NUM)

1 (abs) pressing a/b X/θ/T/n 1 – X/θ/T/nx

2

ENTER . Enter 2

in Y2 by pressing 2 ENTER .

3. Press 2ndF DRAW G (SHADE) 1 (SET) 2ndF VARS A ENTER 1 (Y1)

2ndF VARS ENTER 2 (Y2).

4. View the graph by pressing ZOOM A (ZOOM) 7 (Dec).

5. Press 2ndF CALC 2 (Intsct) repeatedly, to locate the x-values of the points of intersection, x =-1.281,-0.781, 0.781, and 1.281. The solution is all values of x such that x ≤-1.281 or -0.781 ≤ x ≤ 0.781 or x ≥ 1.281.

6. Turn off the shading by pressing 2ndF DRAW G (SHADE) 2 (INITIAL).

RATIONAL INEQUALITIES

x

(1 – x

2

)

▼

21

Advanced Keyboard/ALGEBRA USING THE SHARP EL-9900

Steps for graphing a parabola in rectangular mode

1. Graph the parabola x = y2– 2 by first rewriting as y = ± (x + 2).

2. Press Y= CL to clear the Y1 prompt. Press ENTER CL to clear additional prompts. Enter (x + 2) in Y1 with the keystrokes 2ndF

X/θ/T/n + 2 .

3. Press ENTER and enter -Y1 = -(x + 2) in Y2 with the key strokes

(–)

2ndF

VARS A (EQVARS) ENTER 1 (Y1).

4. View the graph by pressing ZOOM A (ZOOM) 7 (Dec).

Steps for graphing a parabola in parametric mode

1. Change to parametric mode by pressing 2ndF SET UP E (COORD)

2 (Param). Press 2ndF QUIT to exit the set-up screen.

2. Press Y= CL to clear the X1T prompt. To rewrite x = y

2

– 2 in parametric

form, simply let y = T and substitute in x = y

2

– 2 to obtain x = T2– 2. Enter

X1T = T

2

– 2 in the calculator by pressing X/θ/T/nx2– 2 ENTER .

Enter Y1T = T by pressing X/θ/T/n .

3. View the graph by pressing ZOOM A (ZOOM) 7 (Dec).

4. Notice that only a half of the parabola is drawn. To see the rest of the parabola, press WINDOW and adjust the Tmin. Set Tmin to -6 by pressing

(–)

6 ENTER . Press GRAPH to view the complete parabola.

5. Change the calculator back to rectangular mode by pressing 2ndF SET UP

E (COORD) 1 (Rect).

CONIC SECTIONS

√

22

Advanced Keyboard/ALGEBRA USING THE SHARP EL-9900

Steps for graphing a circle in rectangular mode

1. To graph the circle x2+ y2= 4, solve for y in terms of x . The result is y =±4 – x

2

.

2. Press Y= CL to clear the Y1 prompt. Enter Y1 = (4 – X

2

) by pressing

2ndF 4 – X/θ/T/nx

2

ENTER and then enter Y2 = -(4 – X2) by

pressing CL

(–)

2ndF VARS A (EQVARS) ENTER A (XY) 1 (Y1).

View the graph by pressing ZOOM A (ZOOM) 7 (Dec).

Steps for graphing a circle not in standard form

1. First solve the equation for y by completing the square on the y-term and solving for y. For example, draw the graph of the circle x

2

– 2x + y2+ 4y = 2

by rewriting as y = ± (6 – x

2

+ 2x) – 2.

2. Enter Y1 = (6 – x

2

+ 2x), Y2 = Y1 – 2 and Y3 = -Y1 – 2. “Turn off” Y1 so that it will not graph by pressing ▲ to move the blinking cursor to the Y1 expression. Press to position the blinking cursor over the = sign, and press ENTER so that “=” is no longer darkened.

3. To view the graph, press ZOOM 7 (Dec).

4. Adjust the screen to see the bottom part of the circle by pressing ZOOM A (ZOOM) 4 (OUT).

CONIC SECTIONS (continued)

√

▼

1

Advanced Keyboard/CALCULUS USING THE SHARP EL-9900

1. Set the calculator to floating point decimal display by pressing 2ndF SET UP C (FSE) and 1 (Float Pt). Set the calculator to rectangular

coordinates E (COORD) and 1 (Rect). Press 2ndF QUIT to exit the set up menu.

2. Consider the function f(x) = . Press Y= CL to access and clear the

Y1 prompt. Press ENTER CL to clear the remaining prompts.

3. Construct a graph of f(x) in the Decimal viewing window by first entering

Y1= with the keystrokes a/b 2 X/θ/T/n + 2 X/θ/T/n

x

2

– 1 , and then press ZOOM A (ZOOM) 7 (Dec) to see

the graph.

4. Notice that even though is not defined at x =-1 (as evidenced by the

hole in the graph at that point), the functional values appear to be getting closer and closer to -1. A careful observation of the graph leads to the following estimates:

lim f(x) = 0, x → -∞

lim f(x) = -1,

x →-1

lim f(x) does not exist, x → 1

and lim f(x) = 0.

x →∞

5. It also appears that the line y = 0 is a horizontal asymptote and the line x = 1

is a vertical asymptote for this function.

EVALUATING LIMITS

(2x + 2) (x

2

– 1)

(2x + 2) (x

2

– 1)

(2x + 2) (x

2

– 1)

▼

2

Advanced Keyboard/CALCULUS USING THE SHARP EL-9900

6. Tables of functional values sometimes provide more detailed information

than a graph when investigating limits. The TABLE feature will assist you in constructing a numerical table of values. Press TABLE to access the TABLE feature.

7. Notice the table provides the x-values and their corresponding y-values

according to Y1. You can change the table settings by pressing 2ndF

TBLSET . You can change the table start value and the table step value.

Verify the following values using the the TABLE feature.

x gets smaller and smaller→

x-10

-

50

-

100

-

250

-

500

-

1000

-

10,000

y-.18182-.03922-.01980 .00797

-

.00399

-

.00200

-

.00020

y = f(x) appears to get closer and closer to 0

This provides evidence that lim f(x) = 0.

x →∞

x approaches -1 from the left x approaches -1 from the right

x-1.05

-

1.01

-

1.001

-

1.0001

-

.9999

-

.999

-

.99

-

.90

y-.9756-.99502

-

.9995

-

.9999

-

1.0001-1.0005-1.0051-1.0526

y = f(x) gets closer and closer to -1 from above y = f(x) gets closer and closer to -1 from below

This provides evidence that lim f(x) = -1.

x →-1

EVALUATING LIMITS (continued)

3

Advanced Keyboard/CALCULUS USING THE SHARP EL-9900

1. The calculator has a built-in function denoted by d/dx that uses numerical

methods to estimate the derivative of a function at a given value. The entry form of the derivative function is d/dx (f(x), a).

2. Estimate f’(2) for f(x) = x

2

using the derivative function. Press MATH

A (CALC) 05(d/dx() X/θ/T/nx

2

,

2 )to input: d/dx (X

2

, 2).

Press ENTER to compute.

3. The calculator also has a derivative trace.

Activate the derivative trace by pressing 2ndF FORMAT C (Y') and

1 (ON). Press 2ndF QUIT to exit the FORMAT menu.

4. Press Y= CL and enter the function for Y1 by pressing X/θ/T/nx

2

.

5. Draw the graph by pressing ZOOM A (Zoom) 7 (Dec).

6. Press TRACE to activate the trace and press to the values for the derivative.

7. Be sure to turn off the derivative trace.

DERIVATIVES

×

+

–

÷

▼

4

Advanced Keyboard/CALCULUS USING THE SHARP EL-9900

Enter and execute a program for finding a tangent line to a curve at a given point.

1. Turn the calculator on and press PRGM to enter the programming menu.

2. Press C (NEW) and ENTER to open a new program.

3. Name the new program TANGENT by pressing T A N G E N T

ENTER .

4. Press ENTER at the end of each line. If you make a mistake, use the calculator's editing features to correct the error. Enter the following program:

PROGRAM KEYSTROKES Input X PRGM A 3 X/θ/T/n ENTER

(Y1,X)⇒M MATH A 0 5 2ndF VARS A ENTER A 1

,

X/θ/T/n )

STO ALPHA M ENTER

Y1(X)⇒Y 2ndF VARS A ENTER 1 ( X/θ/T/n ) STO ALPHA

Y ENTER

-

M

xX+Y⇒B (–) ALPHA M × X/θ/T/n + ALPHA Y STO ALPHA

B ENTER ClrT PRGM C 1 ENTER Print PRGM A 1 PRGM 2 2ndF A-LOCK T A N G "TANGENT E N T SPACE L I N E = ALPHA ENTER LINE= PRGM 1 PRGM 2 ALPHA Y ALPHA = ALPHA Print M X/θ/T/n + ALPHA B ENTER "Y=MX+B

TANGENT LINES

d

dx

5

Advanced Keyboard/CALCULUS USING THE SHARP EL-9900

Continue to enter the TANGENT program.

Print "M= PRGM 1 PRGM 2 ALPHA M ALPHA = ENTER Print M PRGM 1 ALPHA M ENTER Print "B= PRGM 1 PRGM 2 ALPHA B ALPHA = ENTER Print B PRGM 1 ALPHA B ENTER End PRGM 6 ENTER

5. Press 2ndF QUIT to save the program and exit the editing mode.

6. Enter f(x) =x

3

– x2+1 for Y1 by pressing Y= CL X/θ/T/n ab3

–

X/θ/T/nx

2

+ 1 ENTER .

7. Execute the TANGENT program by pressing PRGM A (EXEC) and selecting TANGENT.

8. Enter an X of 1 by pressing 1 ENTER . You should then see the equation for the tangent line to the curve at x = 1.

9. You can repeat this process for other x values. Press ENTER to execute the program over and over again.

10. If you receive an error statement, press or to go to the line within the program in which the error occurs. Compare your line with the correct one above to find the error. Correct the error using the editing features of the calculator and save the corrections by pressing ENTER . Press 2ndF QUIT and try executing the program again.

TANGENT LINES (continued)

▼

6

Advanced Keyboard/CALCULUS USING THE SHARP EL-9900

Draw the tangent line to a function at a given point.

1. To draw the tangent line on a displayed graph, you must first enter the graph for Y1. Enter the function f(x) = x

3

– x2+ 1 for Y1 by pressing Y=

CL X/θ/T/n a

b

3 – X/θ/T/nx2+ 1 ENTER .

2. Graph the function by pressing ZOOM A (ZOOM) 7 (Dec).

3. Draw the tangent line at x = 1 by pressing 2ndF DRAW A (DRAW)

5 (T_line

(), move the tracer right to x =1 by pressing repeatedly,

and then press ENTER .

TANGENT LINES

▼

7

Advanced Keyboard/CALCULUS USING THE SHARP EL-9900

1. Set the graphing calculator to rectangular graphing by pressing 2ndF

SET UP E (COORD) 1 (Rect). Press 2ndF QUIT to exit the SET UP

menu.

2. Consider f(x) = 2x

3

– 7x2– 70x + 75. Press Y= CL to access and clear Y1.

Press ENTER CL to clear additional Y prompts. Enter f(x) for Y1 by pressing 2 X/θ/T/n a

b

3 – 7 X/θ/T/nx2– 7 0 X/θ/T/n

+ 7 5 .

3. Graph the function by pressing WINDOW

(–)

1 0 ENTER 1 0 ENTER

1 ENTER ZOOM A (Zoom) 1 (Auto).

4. To determine the point at which the relative maximum occurs, press

2ndF CALC 4 (Maximum). The maximum occurs at x =-2.44.

5. Find the point at which the relative minimum occurs by pressing 2ndF

CALC 3 (Minimum). The minimum occurs at x = 4.776.

6. Combining this information with a view of the graph, we see that f(x) is increasing for x = -∞ to-2.4427 and from 4.776 to ∞ while f(x) is decreasing for x between-2.4427 and 4.776.

RELATIVE EXTREMA

▼

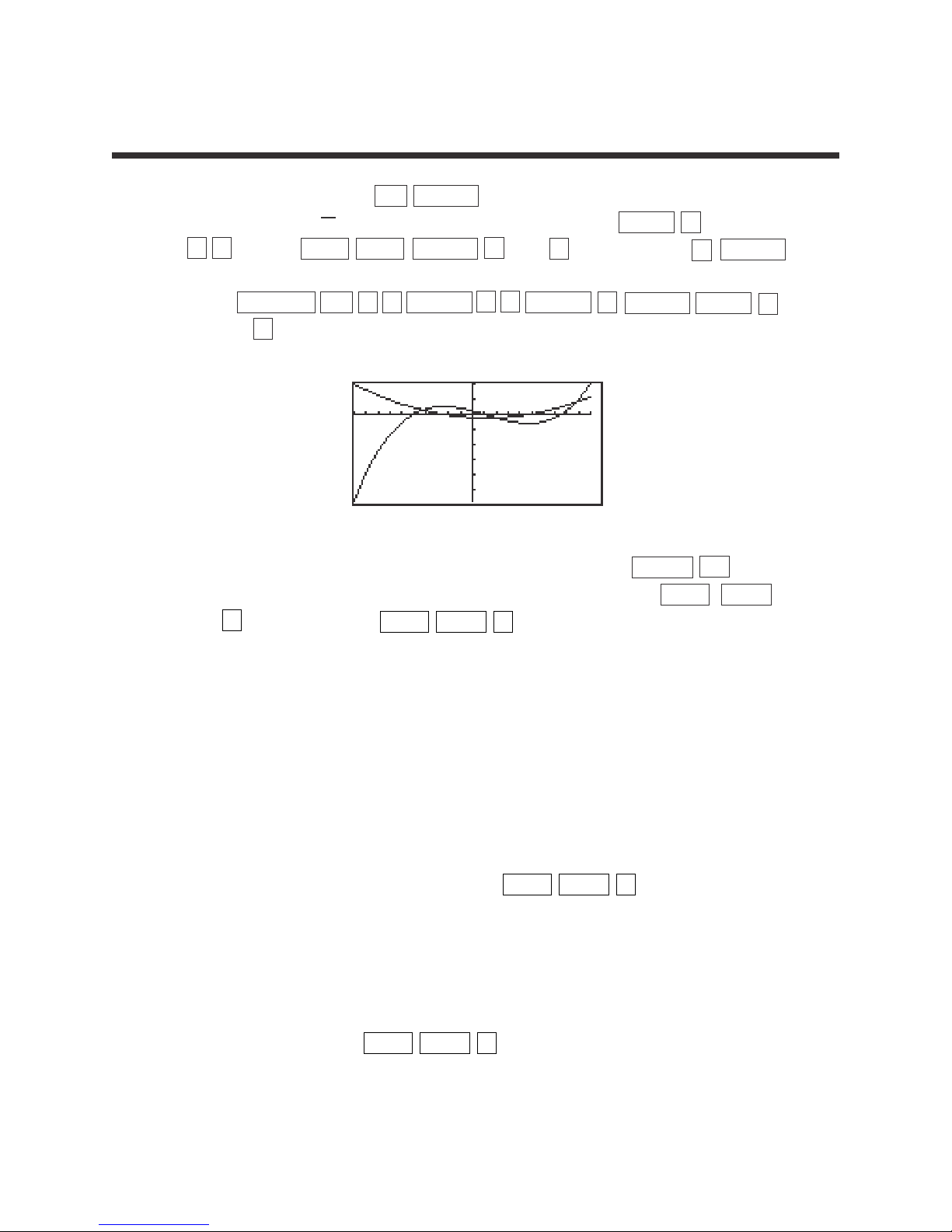
8

Advanced Keyboard/CALCULUS USING THE SHARP EL-9900

1. Graph f ’(x) by pressing Y= ENTER entering f(x)= 2x3– 7x2– 70x + 75 for Y1, and entering (Y1) for Y2. Enter Y2 by pressing MATH A (CALC)

0 5 (d/dx

() 2ndF VARS ENTER A (XY) 1 (Y1) and press ) ENTER .

2. Press WINDOW

(–)

1 0 ENTER 1 0 ENTER 1 ENTER ZOOM A

(Zoom) 1 (Auto) to obtain the graphs of f(x) and f ’(x).

3. We now want to find the two x-intercepts of f’(x). Press TRACE ▼ to place the tracer on the graph of the derivative. Then, press 2ndF CALC and 5 (X_Incpt). Press 2ndF CALC 5 (X_Incpt) again to obtain the other x-intercept.

4. Comparing these values to the x-coordinates of the points at which the maxima and minima of f(x) occur, we see they are the same.

5. Where is f’(x) positive? Notice this is where the graph of f(x) is increasing. Where is f’(x) negative? Notice this is where f(x) is decreasing.

6. Next, find the minimum point of f ’(x) by first making sure the trace cursor is on the graph of the derivative, pressing 2ndF CALC 3 (Minimum).

7. Look at f(x) and observe that this appears to be the point at which the function “bends a different way.”

8. Find the point of inflection directly by moving the cursor to the original function and pressing 2ndF CALC 7 (Inflec).

GRAPHS OF DERIVATIVES

d dx

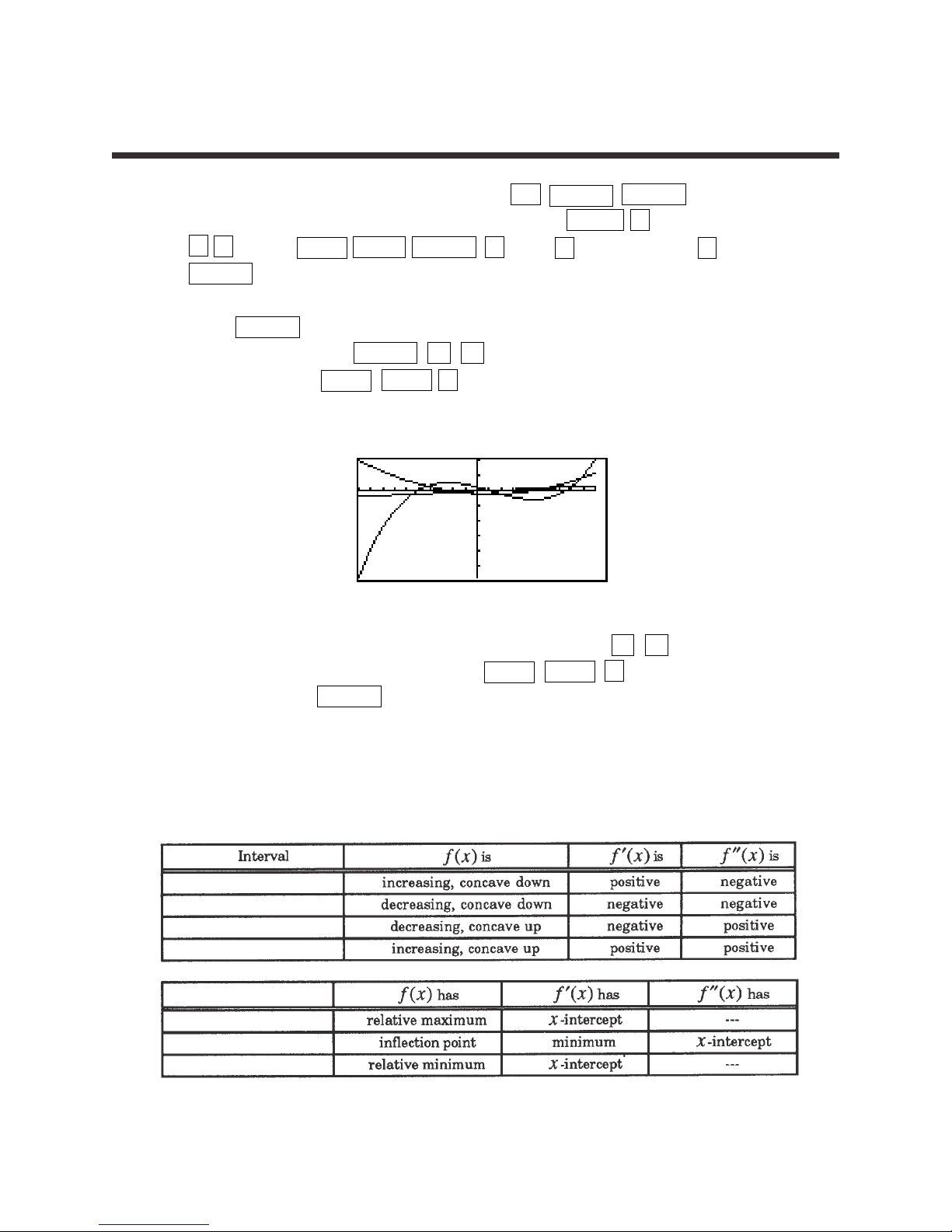
9

Advanced Keyboard/CALCULUS USING THE SHARP EL-9900

9. Graph the second derivative by pressing Y= ENTER ENTER , and input d/dx (Y2) in the Y3 location with the keystrokes MATH A (CALC)

0 5 (d/dx

() 2ndF VARS ENTER A (XY) 2 (Y2) and press )

ENTER .

10. Press GRAPH to obtain the graphs of f(x), f ’(x), and f’’(x). Where is f’’(x). zero? After pressing TRACE ▼▼to place the tracer on the second derivative, press 2ndF CALC 5 (X_Incpt) to find that f’’(x) = 0 at X= 1.167.

11. Find the y-value of this point of inflection by pressing ▲▲to move the cursor to the original function. Press 2ndF CALC 1 (Value) and enter

1.167 and press ENTER .

12. The connections we have discovered between the graphs of f(x), f ’(x), and f’’(x) are summarized in the tables below.

GRAPHS OF DERIVATIVES (continued)

x <-2.4427

-

2.4427 < x < 1.1656

1.1656 < x < 4.776

x > 4.776

x – value

x =-2.4427

x = 1.16567

x = 4.776

10

Advanced Keyboard/CALCULUS USING THE SHARP EL-9900

1. Set the calculator to rectangular graphing by pressing 2ndF SETUP E (Coord) 1 (Rect). Press 2ndF QUIT to exit the setup menu.

2. A new product was introduced through a television advertisement appearing during the Super Bowl. Suppose that the proportion of people that purchased the product x days after the advertisement appeared is given by f(x) = . When did maximum sales occur and what proportion of people purchased the product at that time?

3. Press Y= CL to clear the Y1 prompt. Press ENTER CL to clear additional prompts. Enter f(x) in the Y1 location with the keystrokes a/b

5

•

3 X/θ/T/n X/θ/T/nx2+ 1 5 .

4. Let’s examine the graph for the first 25 days after the advertisement appeared. Press WINDOW , enter Xmin = 0, Xmax = 25, Xscl = 5, Ymin = 0, Ymax = 1, Yscl = 1.

5. Press GRAPH to view the graph.

6. When did maximum sales occur and what proportion of people purchased the product at that time? Press 2ndF CALC and

4 (Maximum) to find a maximum sales at x = 3.87 days with a 68%

proportion.

OPTIMIZATION

(5.3x)

(x2+ 15)

▼

11

Advanced Keyboard/CALCULUS USING THE SHARP EL-9900

1. Find an estimate of 2xdx.

2. Integrate a function by pressing MATH A (CALC) 0 6

( ∫ ).

3. Enter 0 for the lower limit. Press ▲ , input 1 for the upper limit, and press

. Next, press 2 X/θ/T/n to input the integrand. Enter the “dx” by

pressing MATH 0 7 (dx). Press ENTER to compute.

4. Shade the region by first pressing Y= CL to access and clear the Y1 prompt. Clear additional prompts by pressing ENTER CL .

5. Enter f(x) in Y1 with the keystrokes 2 X/θ/T/n . Press WINDOW and enter Xmin = 0 and Xmax = 1. Draw the graph by pressing ZOOM

A (ZOOM) 1 (Auto).

6. Shade the region by pressing 2ndF DRAW G (SHADE) and 1 (Set) to access the shading screen.

7. Since Y1= 2X is the function “on the top,” press 2ndF VARS ENTER

A (XY) 1 . Leave the lower bound location empty. Press GRAPH

to view the shaded region.

8. Turn off the shading by pressing 2ndF DRAW G (SHADE) 2 (INITIAL).

SHADING AND CALCULATING AREAS REPRESENTED BY AN INTEGRAL

×

+

–

÷

▼

∫

0

1

▼

12

Advanced Keyboard/CALCULUS USING THE SHARP EL-9900

1. Calculate and draw a graph of the area of the region between f(x) = 5x – x

2

+ 12 and g(x) = ex+ 5.

2. Return to and clear the Y prompts by pressing Y= CL . Clear additional prompts if necessary.

3. Input f(x) in Y1 with the keystrokes 5 X/θ/T/n – X/θ/T/nx

2

+ 1

2 ENTER . Input g(x) in Y2 with the keystrokes 2ndF e

x

X/θ/T/n

+ 5 .

4. Enter the viewing window -5 < x < 5 and-5 < y < 20. Your viewing window should clearly show the region between f(x) and g(x) and, if applicable, display the intersections of the functions. Press GRAPH to view the graphs.

5. Shade the region between the two curves by pressing 2ndF DRAW

G (SHADE) 1 (SET). Since Y2 is the function "on the bottom," press

2ndF VARS ENTER A (EQVARS) ENTER 2 (Y2) and since Y1 is the function “on the top," press 2ndF VARS ENTER 1 (Y1). Press GRAPH to view the shaded region.

6. Next, find the limits of integration. Press 2ndF CALC 2 (Intsct). Do this twice to obtain the x-coordinates of the two points of intersection. The points of intersection are x =-1.09 and x = 2.58.

7. Find the approximate area by pressing CL MATH A (CALC) 06 ( ∫) enter-1.09, press ▲ , enter 2.58, press , enter the function “on the top,” 5x – x

2

+ 12, press – ( , enter the function “on the bottom,”

e

x

+ 5, press )MATH 0 7 (dx). Press ENTER to obtain the approximate

area of 20.34.

AREA BETWEEN CURVES

▼

×

+

–

÷

13

Advanced Keyboard/CALCULUS USING THE SHARP EL-9900

Enter and execute a program for finding the rectangular approximation for an area,

1. Press 2ndF PRGM to enter programming mode. Press C (NEW) to enter a new program, followed by ENTER . Name the new program RECTAPP by pressing R E C T A P P followed by ENTER .

2. You can now enter in the RECTAPP program. Remember to press ENTER at the end of each line. If you make a mistake, use the calculator's editing features to make corrections. Enter the following program:

PROGRAM KEYSTROKES Input N PRGM A 3 ALPHA N ENTER

Input A PRGM 3 ALPHA A ENTER

Y1(A)⇒L 2ndF VARS A ENTER A 1 (ALPHA A )STO

ALPHA L ENTER

Input B PRGM 3 ALPHA B ENTER

Y1(B)⇒R 2ndF VARS ENTER 1 (ALPHA B )STO ALPHA

R ENTER

(B–A)÷N⇒W

(

ALPHA B – ALPHA A )÷ ALPHA N STO

ALPHA W ENTER

A+W÷2⇒X ALPHA A + ALPHA W ÷ 2 STO X/θ/T/n

ENTER

Y1(X)⇒M 2ndF VARS ENTER 1 (X/θ/T/n

)

STO ALPHA

M ENTER

A+W⇒X ALPHA A + ALPHA W STO X/θ/T/n ENTER

Label LOOP PRGM B 0 1 2ndF A-LOCK L O O P

ALPHA ENTER

Y1(X)+L⇒L 2ndF VARS ENTER 1 (X/θ/T/n

)

+ ALPHA L STO

ALPHA L ENTER

PROGRAM FOR RECTANGULAR APPROXIMATION OF AREA

14

Advanced Keyboard/CALCULUS USING THE SHARP EL-9900

Y1(X)+R⇒R 2ndF VARS ENTER 1

(

X/θ/T/n

)

+ ALPHA R STO

ALPHA R ENTER

X+W÷2⇒XX/θ/T/n + ALPHA W ÷ 2 STO X/θ/T/n ENTER

Y1(X)+M⇒M 2ndF VARS ENTER 1

(

X/θ/T/n

)

+ ALPHA M STO

ALPHA M ENTER

X+W÷2⇒XX/θ/T/n + ALPHA W ÷ 2 STO X/θ/T/n ENTER

If X<BGoto PRGM B 0 3 X/θ/T/n MATH F 5 ALPHA

LOOP B PRGM B 0 2 2ndF A-LOCK L O O P

ALPHA ENTER

ClrT PRGM C 1 ENTER

Print "LEFT= PRGM A 1 PRGM 2 2ndF A-LOCK L E F T =

ALPHA ENTER

Print W×L PRGM 1 ALPHA W × ALPHA L ENTER

Print "MID= PRGM 1 PRGM 2 2ndF A-LOCK M I D

= ALPHA ENTER

Print W×M PRGM 1 ALPHA W × ALPHA M ENTER

Print "RIGHT= PRGM 1 PRGM 2 2ndF A-LOCK R I G H T

= ALPHA ENTER

Print W× R PRGM 1 ALPHA W × ALPHA R ENTER

End PRGM 6 ENTER

Press 2ndF QUIT to save the program and exit the editing mode.

PROGRAM FOR RECTANGULAR APPROXIMATION OF AREA (continued)

15

Advanced Keyboard/CALCULUS USING THE SHARP EL-9900

Executing a program

3. Enter the function f(x) = cos x, by pressing Y= CL cos X/θ/T/n . Press ENTER CL to clear additional prompts.

4. Execute the RECTAPP program, press PRGM A , highlight the 'RECTAPP' program, and press ENTER . Enter 'N' of 5 by pressing 5

ENTER , followed by 'A' of 0 and 'B' of 1. You will see a display of left, midpoint and right rectangular approximations for the area under the cosine function between 0 and 1 with 5 intervals in the partition.

5. You can repeat this process for a different number of partitions, different limits, or another function. Press ENTER to execute the program over and over again. Press CL to exit the program.

6. If you receive an error statement, press or to go to the line within the program in which the error occurs. Compare your line with the correct one above to find the error. Correct the error using the editing features of the calculator and save the program by pressing 2ndF QUIT . Try executing the program again.

PROGRAM FOR RECTANGULAR APPROXIMATION OF AREA (continued)

▼

16

Advanced Keyboard/CALCULUS USING THE SHARP EL-9900

A program for finding the trapezoidal approximation for an area.

Input N PRGM A 3 ALPHA N ENTER

Input A PRGM 3 ALPHA A ENTER

Y1(A)⇒L 2ndF VARS A ENTER A 1 (ALPHA A )STO

ALPHA L ENTER

Input B PRGM 3 ALPHA B ENTER

Y1(B)⇒R 2ndF VARS ENTER 1 (ALPHA B )STO ALPHA R

ENTER

0⇒Z 0 STO ALPHA Z ENTER

(B–A)÷N⇒W

(

ALPHA B – ALPHA A )÷ ALPHA N STO

ALPHA W ENTER

A+W⇒X ALPHA A + ALPHA W STO X/θ/T/n ENTER

Label LOOP PRGM B 0 1 2ndF A-LOCK L O O P

ALPHA ENTER

2Y1(X)+Z⇒Z 2 2ndF VARS ENTER 1 (X/θ/T/n

)

+ ALPHA Z STO

ALPHA Z ENTER

X+W⇒XX/θ/T/n + ALPHA W STO X/θ/T/n ENTER

If X<BGoto PRGM B 0 3 X/θ/T/n MATH F 5 ALPHA B

LOOP PRGM 0 2 2ndF A-LOCK L O O P ENTER

ClrT PRGM C 1 ENTER

Print "TRAP= PRGM A 1 PRGM 2 2ndF A-LOCK T R A P =

PRGM 2 ENTER

Print (W÷2) PRGM 1 (ALPHA W ÷ 2

)(

ALPHA

(L+Z+R) L + ALPHA Z + ALPHA R )ENTER

End PRGM 6 ENTER

Execute like the rectangular program to find an approximate area of .83866.

TRAPEZOIDAL APPROXIMATION OF AREA

17

Advanced Keyboard/CALCULUS USING THE SHARP EL-9900

Steps for graphing the hyperbolic sine function.

1. Turn the calculator on and press Y= CL to access and clear the Y1 prompt. Press ENTER CL to remove additional expressions.

2. To enter the hyperbolic sine function ( y = sinh x ) for Y1, press MATH ,

A (CALC) 15(sinh) and press X/θ/T/n .

3. Enter the viewing window by pressing ZOOM F (HYP) 1 (sinh x).

Steps for graphing the hyperbolic cosine function.

4. Press Y= CL to remove the hyperbolic sine function.

5. To enter the hyperbolic cosine function ( y = cosh x ) for Y1, press MATH

1 6 (cosh x) press X/θ/T/n .

6. Press GRAPH to view the graph.

HYPERBOLIC FUNCTIONS

18

Advanced Keyboard/CALCULUS USING THE SHARP EL-9900

1. Turn the calculator on and set the calculator to sequence mode by pressing

2ndF SET UP E (COORD) 4 (Seq).

2. Press 2ndF QUIT Y= to access the sequence prompts. Clear any sequences by presing CL .

3. Enter the sequence generator a

n

= n2– n for u(n) by pressing X/θ/T/n

x

2

– X/θ/T/n ENTER . Enter n1= 1 for u(nMin) by pressing

1 ENTER .

4. View a table of sequence values by pressing TABLE .

5. Graph the sequence by first setting the format to time and drawing to dot mode. Do this by pressing 2ndF FORMAT G (TYPE) 2 (Time). Press 2ndF QUIT to exit the FORMAT menu. Change to dot mode by pressing 2ndF DRAW D (LINE) ENTER ENTER . Enter the viewing window by pressing WINDOW 1 ENTER 1 0 ENTER 1 ENTER

1 ENTER

(–)

1 ENTER 1 1 ENTER 1 ENTER

(–)

1 0

ENTER 1 0 0 ENTER 1 0 ENTER . View the sequence by

pressing GRAPH .

6. Turn off sequence mode and dot mode.

SEQUENCES

▼

19

Advanced Keyboard/CALCULUS USING THE SHARP EL-9900

1. Change to sequence mode, time format, and dot mode.

2. Enter the recursive sequence generator a

n

= a

n – 1

+ 2n for u(n) by pressing

Y= CL 2ndF u

(

X/θ/T/n – 1

)

+ 2 X/θ/T/n ENTER .

Enter a

1

= 1 by pressing 1 ENTER .

3. View a table of sequence values by pressing TABLE .

4. Graph the sequence in the window as -1< x < 11, -10 < y < 100 by pressing

GRAPH .

5. Turn off sequence mode and dot mode.

RECURSIVE SEQUENCES

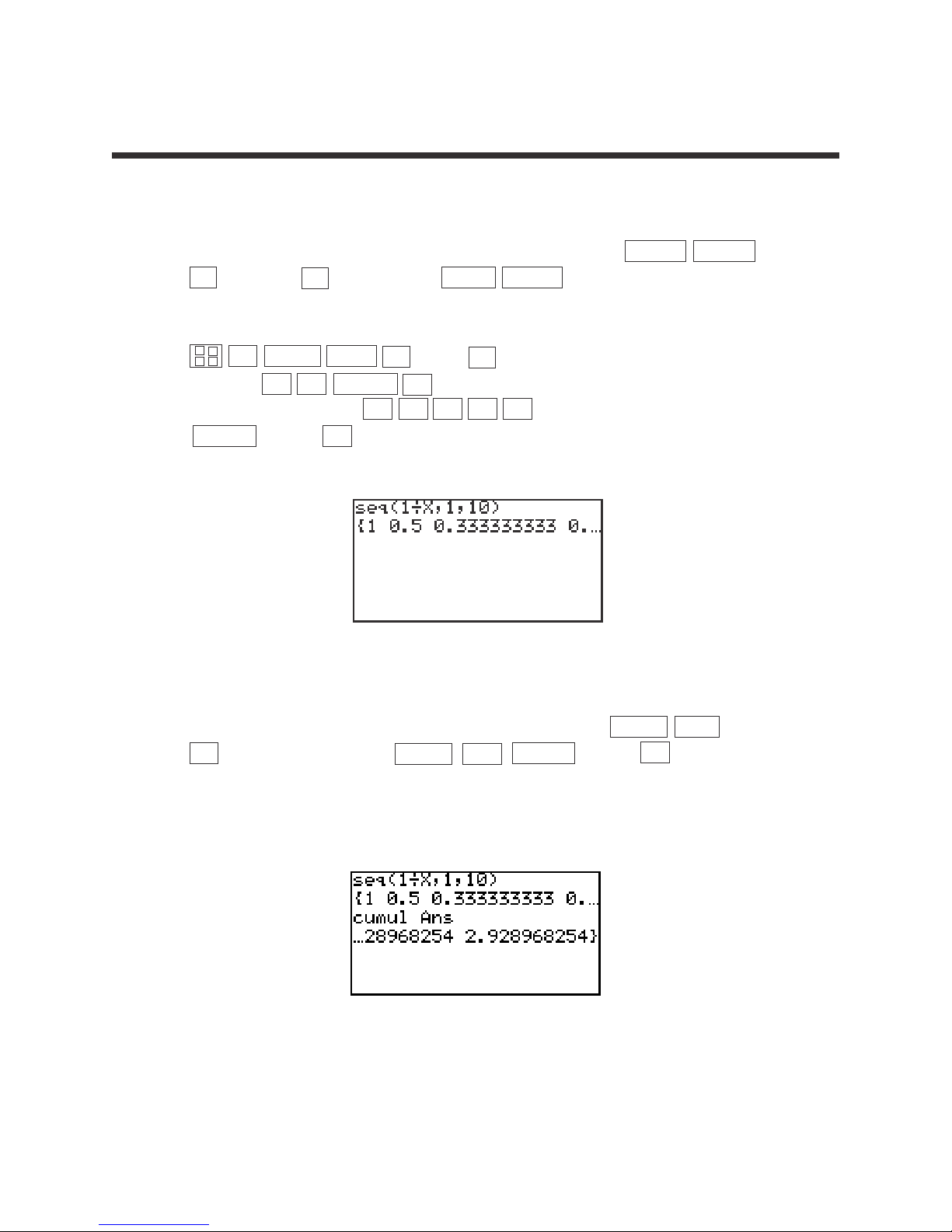
20

Advanced Keyboard/CALCULUS USING THE SHARP EL-9900

Find the partial sum of a series, ∑ 1/X, for the first 10 terms.

1. Make sure the SET UP to rectangular mode by pressing 2ndF SET UP ,

E (COORD) 1 (Rect). Press 2ndF QUIT to exit the SET UP menu.

2. First find the sequence of the first 10 terms of series ∑ 1/X by first pressing

CL 2ndF LIST A (OPE) 5 (seq

( ). Enter the generator 1/X by

pressing 1

÷ X/θ/T/n

,

. Enter the lower and upper bounds for the

sequence by pressing 1

,

1 0

)

. Find the sequence by pressing

ENTER . Press to see more of the sequence.

3. Find the partial sum of the first 10 terms by pressing 2ndF LIST

6 (cumul) and pressing 2ndF ANS ENTER . Press to move right in the sequence of partial sums until the last term is seen. The partial sum of the first 10 terms is 2.9289.

PARTIAL SUM OF A SERIES

▼

×

+

–

÷

21

Advanced Keyboard/CALCULUS USING THE SHARP EL-9900

Steps for graphing a polar function:

1. Turn the calculator on and press 2ndF SET UP E (COORD) 3 (Polar) to change to polar mode. While in the SET UP menu, the

calculator should be setup in radian mode. To complete this setup, press

B (DRG) 2 (Rad). Press 2ndF QUIT to exit the SET UP menu.

2. Make sure calculator is in connected mode by pressing 2ndF DRAW D

(LINE) ENTER . The first option should be reflected for R1. Set the calculator to display polar coordinates when tracing, by pressing 2ndF

FORMAT F (CURSOR) and 2 (PolarCoord). Also, set the calculator to display the expression during tracing by pressing B (EXPRESS) 1 (ON). Press 2ndF QUIT to exit the FORMAT menu.

3. Press Y= to access the R1 prompt. Press CL to remove an old R1 expression. Press ENTER CL to clear additional R prompts.

4. Enter the polar function r = 2(1 – cos θ) for R1, by pressing 2 (1 –

cos X/θ/T/n

)

. Notice, when in polar mode the X/θ/T/n key

provides a θ for equation entry.

5. Now, graph the polar function in the Decimal viewing window by pressing

ZOOM A (ZOOM) 7 (Dec).

6. This particular shape of curve is called a cardoid. Trace the curve by pressing TRACE . Notice the expression is displayed at the top of the screen.

GRAPHING POLAR EQUATIONS

22

Advanced Keyboard/CALCULUS USING THE SHARP EL-9900

Steps for graphing a parametric function:

1. Turn the calculator on and press 2ndF SET UP E (COORD)

2 (Param) to change to parametric mode. Press 2ndF QUIT

to exit the SET UP menu.

2. Make sure calculator is set to display rectangular coordinates when tracing by pressing 2ndF FORMAT F (CURSOR) 1 (RectCoord)

. Press 2ndF

QUIT to exit the FORMAT menu.

3. To enter the parametric function X1T = 2(cos T)

3

, Y1T = 2(sin T)3, press

Y= CL 2

(

cos X/θ/T/n

)

a

b

3 ENTER CL 2

(

sin

X/θ/T/n

)

a

b

3 ENTER . Notice, when in parametric mode the

X/θ/T/n key provides a T for equation entry.

4. Now, graph the parametric function in the Decimal viewing window by pressing ZOOM A (ZOOM) 7 (Dec).

5. Press TRACE and notice the expression and T values now appear on the range screen.

GRAPHING PARAMETRIC EQUATIONS

1

Advanced Keyboard/STATISTICS USING THE SHARP EL-9900

Steps for creating a non-weighted one-variable data set

1. Turn the calculator on and press STAT to enter the statistics menu.

2. Touch A (EDIT) ENTER , to view the statistics data entry screen. If there is a data set present within the lists on your calculator, use the arrow keys to move to the list, if necessary, and press ▲ to highlight the list label.

3. Press DEL ENTER to delete the old data. Repeat for other lists of data.

4. Move the highlighter to the cell directly below the L1 in the table. Enter the following data set:

58768935

by pressing 5 ENTER 8 ENTER 7 ENTER 6 ENTER 8 ENTER

9 ENTER 3 ENTER 5 ENTER .

5. To check the data you have entered, press ▲ to move back through the data values.

6. To sort your data set in an ascending manner, press STAT B (OPE) 1 (sortA) 2ndF L1 ) ENTER . Press STAT A (EDIT)

ENTER . Notice this first cell now contains the smallest value 3.

7. To save this data set, press 2ndF LIST C (L_DATA) 1 (StoLD) 1 ENTER . You can store up to ten sets of six lists.

8. To retrieve a data set matrix into a statistical data set, press 2ndF

LIST C (L_DATA) 2 (RclLD) 1 ENTER .

CREATION OF A ONE-VARIABLE DATA SET

×

+

–

÷

×

+

–

÷

×

+

–

÷

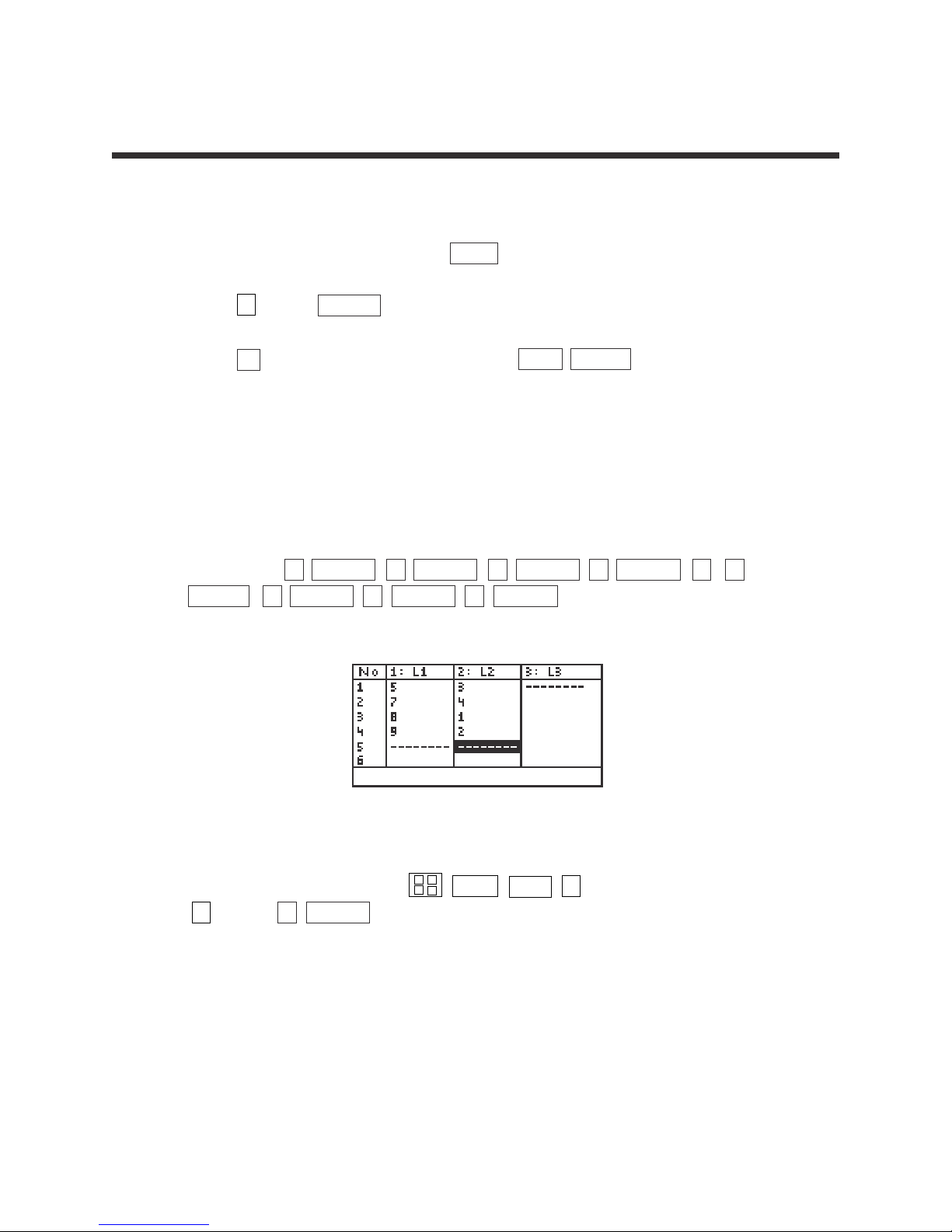
2

Advanced Keyboard/STATISTICS USING THE SHARP EL-9900

Steps for creating a weighted one-variable data set

1. Turn the calculator on and press STAT to enter the statistics menu.

2. Press A (EDIT) ENTER , to view the statistics data entry screen. Remove old data by using the arrow keys to move to the list of data, and press ▲ to highlight the list label. Press DEL ENTER to delete the old data. Repeat for other lists of data.

3. Move the highlighter to the cell directly below the L1 in the table. Enter the following data set into L1 with the frequencies entered into L2. If a value appears three times within a data set, its weight or frequency is 3. Enter the following data set using the weights: 5557777899 by pressing 5 ENTER 7 ENTER 8 ENTER 9 ENTER 3

ENTER 4 ENTER 1 ENTER 2 ENTER .

4. To save this data set, press 2ndF LIST C (L_DATA)

1 (StoLD) 2 ENTER .

CREATION OF A ONE-VARIABLE DATA SET

▼

×

+

–

÷

3

Advanced Keyboard/STATISTICS USING THE SHARP EL-9900

Steps for calculating numerical descriptions of a one-variable non-weighted data set

1. Turn the calculator on and press STAT to enter the statistics menu. Press A (EDIT) ENTER to view the statistics data entry screen. If there is a data set present within the lists on your calculator, use the arrow keys to move to the list, if necessary, and press ▲ to highlight the list label. Press DEL ENTER to delete the old data. Repeat for other lists of data.

2. Move the highlighter to the cell directly below the L1 in the table. Enter the following data set: 25 32 28 33 31 27 40 38 29 30

3. Check the data you have entered and correct any errors you may find. Press 2ndF QUIT to exit the data entry screen. To calculate the numerical descriptions of the data set, press STAT C (CALC) and 1 (1_Stats). Press ENTER and the statistical results will appear.

4. The statistics displayed are:

1. the average or mean value of the data set, ;

2. the standard deviation assuming the data set is a sample from a population, sx;

3. the standard deviation assuming the data set represents the entire population, σx;

4. the sum of the data values, ∑x;

5. the sum of the squared data values, ∑x

2

;

Press ▼ five times to see more of the statistics.

6. the number of values in the data set, n;

7. the minimum value in the data set, xmin;

8. the first quartile (25th percentile), Q1;

9. the median (50th percentile), Med;

10. the third quartile (75th percentile), Q3; and Press ▼ one more time to see the final statistic.

11. the maximum value in the data set, xmax.

NUMERICAL DESCRIPTION OF A ONE-VARIABLE DATA SET

x

Sharp EL-9900C,EL-9900 User Manual

Specifications and Main Features

Frequently Asked Questions

User Manual