Sharp EL-9650 Owner Manual
EL-9650
GRAPHING CALCULATOR
MODEL
EL-9650
GRAPHING CALCULATOR
OPERATION MANUAL
SHARP CORPORATION
00BUP (TINSE0397THZZ)
PRINTED IN CHINA / IMPRIMÉ EN CHINE
gewijzigd door 93/68/EEG.
Dette udstyr overholder kravene i direktiv nr. 89/336/EEC med
tillæg nr. 93/68/EEC.
Quest’apparecchio è conforme ai requisiti della direttiva 89/
336/EEC come emendata dalla direttiva 93/68/EEC.
89/336/,
93/68/.
Este equipamento obedece às exigências da directiva 89/336/
CEE na sua versão corrigida pela directiva 93/68/CEE.
Este aparato satisface las exigencias de la Directiva 89/336/
CEE, modificada por medio de la 93/68/CEE.
Denna utrustning uppfyller kraven enligt riktlinjen 89/336/EEC
så som kompletteras av 93/68/EEC.
Dette produktet oppfyller betingelsene i direktivet 89/336/EEC i
endringen 93/68/EEC.
Tämä laite täyttää direktiivin 89/336/EEC vaatimukset, jota on
muutettu direktiivillä 93/68/EEC.
This equipment complies with the requirements of Directive 89/
336/EEC as amended by 93/68/EEC.
Dieses Gerät entspricht den Anforderungen der EG-Richtlinie
89/336/EWG mit Änderung 93/68/EWG.
Ce matériel répond aux exigences contenues dans la directive
89/336/CEE modifiée par la directive 93/68/CEE.
Dit apparaat voldoet aan de eisen van de richtlijn 89/336/EEG,
• The information provided in this manual is subject to change without notice.
• SHARP assumes no responsibility, directly or indirectly, for financial losses or claims
for data lost or otherwise rendered unusable whether as a result of improper use,
repairs,defects, battery replacement, use after the specified battery life has expired,
or any other cause.
from third persons resulting from the use of this product and any of its functions, the
loss of or alteration of stored data, etc.
• SHARP strongly recommends that separate permanent written records be kept of all
important data. Data may be lost or altered in virtually any electronic memory
product under certain circumstances. Therefore, SHARP assumes no responsibility
• The material in this manual is supplied without representation or warranty of any
kind. SHARP assumes no responsibility and shall have no liability of any kind,
consequential or otherwise, from the use of this material.
manual on hand for reference.
Congratulations on purchasing the EL-9650 Graphing Scientific Calculator. Please read
this operation manual carefully to familiarize yourself with all the features of the
calculator and to ensure years of reliable operation. Also, please keep this operation
INTRODUCTION
NOTICE
i
5. When Using for the First Time ................................................................................... 5
(1) Inserting batteries ................................................................................................5
(2) Resetting the calculator .......................................................................................6
(3) Jumping .............................................................................................................33
(2) Moving the cursor vertically ...............................................................................33
(1) Moving the cursor horizontally ........................................................................... 33
13. Moving the Cursor ...................................................................................................33
12. Display Format of the Cursor Pointer ......................................................................32
(2) One-line edit mode ............................................................................................ 31
(1) Equation edit mode ............................................................................................25
11. Edit Modes ..............................................................................................................25
(2) SET UP menu ....................................................................................................20
(1) Checking SET UP contents................................................................................ 20
10. SET UP Menu ......................................................................................................... 20
9. Precedence of Calculations ..................................................................................... 19
8. Operating Modes .....................................................................................................18
7. Using Menus ...........................................................................................................15
(2) Entering alphabet letters ....................................................................................14
(1) Using secondary functions (2ndF) ..................................................................... 14
6. Using Secondary Functions (2ndF) and Alphabet Letters (ALPHA)........................14
5. Using Functions ....................................................................................................... 13
4. Correcting Errors .....................................................................................................12
6. Inserting and Removing the Touch-pen .....................................................................7
7. Caring for Your Calculator .........................................................................................8
CHAPTER 1 GENERAL INFORMATION ........................................................................9
1. Entering Numeric Values ........................................................................................... 9
2. Common Math Operations ......................................................................................10
3. Changing Entered Characters and Expressions ..................................................... 11
(3) Adjusting the contrast...........................................................................................6
(4) Turning the power off ...........................................................................................7
GETTING STARTED .......................................................................................................1
1. Names of Parts .......................................................................................................... 1
2. Function of Each Part ................................................................................................2
3. Explanation of Keys ................................................................................................... 3
4. Using the Protective Cover ........................................................................................ 4
CONTENTS
ii
(2) Using the reset switch ........................................................................................34
14. Resetting the Calculator ..........................................................................................34
(1) Reset .................................................................................................................. 34
CHAPTER 2 UNIQUE FUNCTIONS .............................................................................37
(2) Using the touch-pen on the normal function calculation screen ........................40
(1) Using the touch-pen on the menu screen ..........................................................37
1. Pen-touch Operations .............................................................................................37
(3) Select RESET from the menu ............................................................................35
2. Solver Function .......................................................................................................45
(2) CHANGE function ..............................................................................................48
4. SHIFT/CHANGE Functions .....................................................................................47
(1) SHIFT function ...................................................................................................47
CHAPTER 3 MANUAL CALCULATIONS ......................................................................49
1. Arithmetic Calculations ............................................................................................49
(2) Decimals shown as binary, octal, and hexadecimal numbers............................63
3. Binary, Octal, and Hexadecimal Calculations..........................................................63
(1) Binary, octal, decimal and hexadecimal numbers .............................................. 63
4. Test Functions .........................................................................................................67
5. Boolean Operations ................................................................................................. 67
(2) Usable functions (menus) for complex numbers ................................................ 70
(1) Usable function keys (main unit keys) in the complex number mode ................69
6. Calculations Using Complex Numbers ....................................................................69
(1) Table of true values for boolean operations .......................................................67
(4) Binary, octal, and hexadecimal calculations (arithmetic calculations)................65
(3) Binary, octal, decimal and hexadecimal conversion .......................................... 64
7. Convenient and Useful Functions ...........................................................................72
(1) Last entry function.............................................................................................. 72
(2) Continuing calculations using last answer ......................................................... 73
(3) Memory calculations ..........................................................................................74
(4) TOOL menu........................................................................................................76
iii
(2) Functions selected from menus (MATH menu)..................................................53
2. Function Calculations ..............................................................................................51
(1) Input examples of functions accessible directly from keys ................................52
(2) Advancing the demonstration screen by one page ............................................46
(1) Viewing the installed demonstration screen....................................................... 46
3. SLIDE SHOW Function ...........................................................................................46
(4) Using the touch-pen on other screens ...............................................................44
(3) Using the touch-pen on the graph screen ..........................................................42
CHAPTER 4 GRAPHING FUNCTIONS ........................................................................79
1. Function Graphing Procedures ...............................................................................79
2. Graph Modes ........................................................................................................... 79
(2) Checking the format (See page 97 for details.) .................................................80
3. Rectangular Coordinate Graphing ........................................................................... 80
(1) Setting the rectangular coordinate graph mode .................................................80
4. Parametric Graphing ...............................................................................................92
5. Polar Coordinate Graphs ......................................................................................... 93
6. Sequence Graphing ................................................................................................95
7. FORMAT Setting ..................................................................................................... 97
8. Entering Functions ..................................................................................................98
9. Zoom Functions ..................................................................................................... 100
10. Selecting a Line Type for a Graph .........................................................................103
11. Setting a Window ..................................................................................................104
12. Draw Operations ...................................................................................................106
13. CALC Functions ....................................................................................................117
14. Tables ....................................................................................................................121
(2) Rapid window ................................................................................................... 127
(1) Rapid GRAPH ..................................................................................................124
15. Useful Functions ................................................................................................... 124
(1) Table Setting .................................................................................................... 123
(1) Draw menu configuration .................................................................................106
(12) Split screen ......................................................................................................91
(11) Displaying tables (See page 121 for details.) ...................................................90
(10) Shading ............................................................................................................88
(9) CALC functions (See page 117 for details.)....................................................... 87
(8) Displaying numerical derivative Y’ of graphs ..................................................... 87
(7) Trace function for moving the cursor pointer on the graph ................................84
(6) Displaying equations ..........................................................................................83
(5) Zooming in on graphs ........................................................................................82
(4) Displaying graphs ..............................................................................................82
(3) Entering a function (See page 98 for details.) .................................................... 81
CHAPTER 5 MATRIX FUNCTIONS............................................................................ 135
1. Inputting a Matrix ...................................................................................................135
2. Matrix Calculations ................................................................................................138
(3) Rapid zoom ......................................................................................................128
(4) Split screen ...................................................................................................... 130
(5) Substitution graph ............................................................................................131
iv
(2) MATH ...............................................................................................................143
3. Calculations Using Special Matrix Functions ........................................................139
(1) OPE .................................................................................................................139
CHAPTER 6 LIST FUNCTIONS ................................................................................145
1. List Calculations Using List Number ...................................................................... 146
2. Drawing a Function Graph Using a List ................................................................. 148
(1) Inputting and editing the data using the list table.............................................155
4. Editing and Easy Input of List Data ....................................................................... 155
(3) L_Data .............................................................................................................154
CHAPTER 7 STATISTICS/ REGRESSION CALCULATIONS ..................................157
(2) Statistics ........................................................................................................... 158
1. Statistics ................................................................................................................157
(1) Calculating statistics ........................................................................................157
2. Regression ............................................................................................................ 172
3. Statistic Testing ...................................................................................................... 178
4. Distribution Function .............................................................................................. 190
CHAPTER 8 FINANCIAL FUNCTIONS ...................................................................... 197
(2) Cash flow diagrams .........................................................................................199
(1) Differences between simple interest and compound interest ..........................197
1. Before Starting Financial Calculations ..................................................................197
(10) Data list operation function (B OPE) ..............................................................170
(9) Trace function of statistical graphs...................................................................169
(8) Specifying statistical graph and graph functions .............................................. 168
(7) Explanation of graph types ..............................................................................166
(6) Graphing statistical data ..................................................................................163
(5) Editing statistical data ...................................................................................... 162
(4) Calculating statistics (CALC menu) .................................................................160
(3) Entering statistical data .................................................................................... 159
2. The Financial Function ..........................................................................................200
(1) Setting of payment due (at the beginning/end of a period) ..............................200
(2) SOLVER function .............................................................................................200
(3) Calculation using the CALC mode ...................................................................204
(4) VARS menu...................................................................................................... 210
v
(2) MATH ...............................................................................................................152
(1) OPE .................................................................................................................148
3. Special List Function Groups Built into the Menu .................................................. 148
(3) Calculation using [ ] .......................................................................................... 144
CHAPTER 9 SOLVER FUNCTION ............................................................................. 211
1. Inputting an Equation and Finding Its Solution ...................................................... 211
(2) Graph method ..................................................................................................215
2. Selecting the Solution Analysis Method ................................................................ 213
(1) Newton’s method ............................................................................................. 214
3. Registering an Equation ........................................................................................217
4. Calling Up the Solver Equation .............................................................................218
5. Renaming the Solver Equation .............................................................................. 219
CHAPTER 10 SLIDE SHOW FUNCTIONS ................................................................ 221
1. Built-in Slide Show ................................................................................................221
2. Creating an Original Slide Show ...........................................................................223
3. Viewing the Original Slide Show ...........................................................................226
(2) Deleting the registered screen (DEL) ............................................................... 227
4. Editing the Original Slide Show .............................................................................226
(1) Changing the order of the screens (MOVE)..................................................... 226
CHAPTER 11 SHIFT/CHANGE FUNCTIONS ............................................................229
1. SHIFT Function ....................................................................................................... 229
2. CHANGE Function .................................................................................................. 236
CHAPTER 12 PROGRAMMING FUNCTION ............................................................. 239
1. Creating a New Program .......................................................................................239
2. Programming .........................................................................................................240
3. Program Input and Edit .........................................................................................240
4. Variables................................................................................................................241
(2) B BRNCH menu ...............................................................................................245
(1) A PRGM menu .................................................................................................243
5. Programming Commands .....................................................................................243
(3) Renaming the registered title (RENAME) ........................................................ 228
6. Other Functions Often Used in Programs ............................................................. 251
(3) C SCRN menu ................................................................................................. 247
(4) D I/O menu ...................................................................................................... 247
(5) E COORD menu ............................................................................................. 248
(6) F FORM memu ...............................................................................................249
(7) G S_PLOT menu.............................................................................................250
(8) H COPY menu ................................................................................................ 251
(1) Inequalities .......................................................................................................251
(2) Graphing functions ........................................................................................... 252
vi
vii
6. Explanation of EL-9650 menus ............................................................................. 282
5. Calculation Range .................................................................................................276
(3) Distribution function .........................................................................................274
(2) Error conditions during financial claculations ...................................................274
(1) Financial ........................................................................................................... 272
4. Calculation Equation Error Conditions Used by This Unit .....................................272
3. Error Codes and Error Messages .......................................................................... 270
2. Specifications ........................................................................................................ 267
(3) Replacing the memory backup battery ............................................................266
(2) Replacing the operating batteries .................................................................... 265
(1) Battery precautions ..........................................................................................265
1. Replacing the Batteries ......................................................................................... 265
APPENDIX ..................................................................................................................265
(1) When trouble occurs ........................................................................................264
5. Reset Function ......................................................................................................263
(2) Data communication between the EL-9650 and a Personal computer............ 263
(1) To link with another EL-9650 (Communication between EL-9650s) ................261
4. Link Function .........................................................................................................261
3. Deleting Files ......................................................................................................... 260
2. Checking Memory Usage ......................................................................................259
1. Adjusting Screen Contrast ..................................................................................... 259
CHAPTER 13 OPTION FUNCTIONS .........................................................................259
(2) Random substitution of numbers ..................................................................... 256
(1) Conversion of temperatures from Celsius to Fahrenheit .................................254
8. Sample Program ...................................................................................................254
7. Error Messages .....................................................................................................254
viii
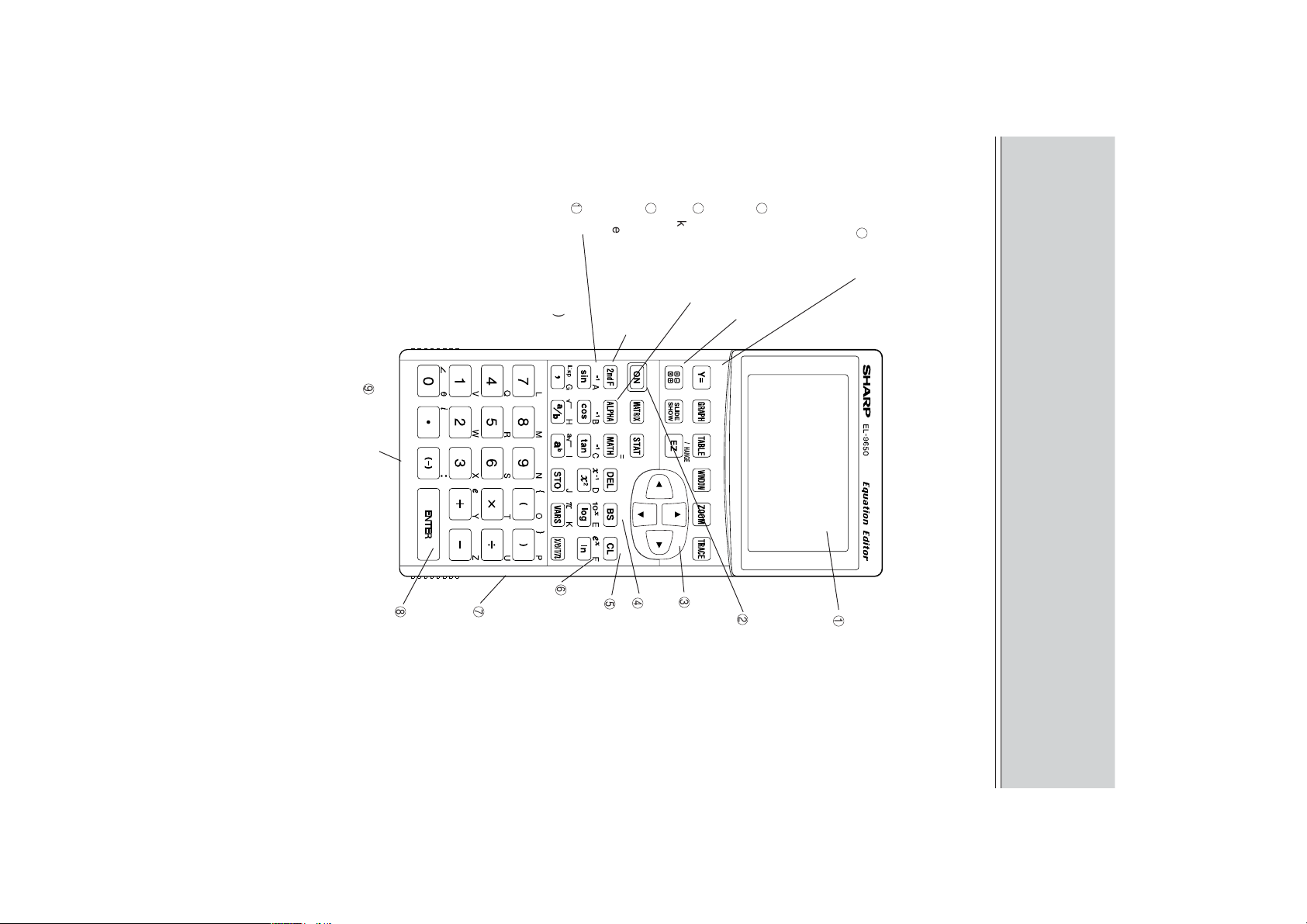
F
COMMUNICATION PORT
LIST
FI
NC
PT
UI
ST
Secondary function
(printed in yellow)
specification (2nd F)
key
G
Secondary function
H
Alphabet specification
key
calculation screen
selection key
I
Normal function
1. Names of Parts
J
Graphing keys
GETTING STARTED
u v w
L4 L5 L6
sin
OFF
ST
SOLVER
AT PLOT
9
Peripheral connection terminal
COMMUNICATION PORT
L
2
SPACE
ENTRY
L3L1
1
LIST
ANS
8
Calculation execute key
FI
EXE
NANC
E
7
Reset switch (on the
back of unit)
cos
A LOCK
PRGM DRAW
CLIP
TOOL
tan
RCL
OPT
ION
INS
SET UP
QUI
T
SHIFT CHANGE
6
Alphabet key (printed in blue)
5
Clear/Quit key
3
4
Cursor movement keys
Set up key
SPLIT
TBLSET
SUB
FORMAT
CALC
2
Power supply ON/OFF
key
GENERAL INFORMATION
1
Display screen
4
6
7
8
9
F
G
H
I
required since all memory contents will be deleted when pressing the reset switch.
executing calculations.
screen which performs numerical calculations or calculations using functions.
Alphabet specification key: Used when specifying an operation printed in blue
Normal function calculation screen selection key: Used when selecting the
in mustard-yellow above a key (upper left).
above a key (upper right).
cables or a PC link cable (not a power supply).
Secondary function: Used with
Secondary function specification key: Used when specifying an operation printed
Calculation execution key: Used when specifying calculation commands and
Peripheral connection terminal: Terminal used when connecting separately sold
Alphabet key: Used with
Reset switch: Used when replacing batteries or when errors occur. Caution is
Å
5
(this may vary according to setting or display screen). These keys are also used
when selecting menus.
format of this graphing scientific calculator.
programs, etc., or when returning to the previous screen. This key is also used when
clearing errors.
Set up key: Mode setting key that determines the calculation method and display
Clear/Quit key: Used when clearing numerical values, calculation commands,
bers. The cursor is indicated using “_” when there is no number or character. The
cursor is indicated using a flashing “
2. Function of Each Part
1
2
3
n
Cursor movement keys: Specifies location to input/correct characters and num-
Display screen
Power supply ON/OFF key: Press
to turn off the power supply.
GETTING STARTED
Ï
2
to input secondary functions.
to enter letters.
” when overlapping a number or character
˚
to turn on the power supply. Press
Ï
<Example>
Operation of
3. Explanation of Keys
• Most keys have more than two functions.
• To use a function printed on a key, simply press the button.
• To specify a function (secondary function) printed in yellow above a key or on the
• To specify a function a character printed in blue on the upper right side of a key,
• : This function is used for studying graphs and to aid understanding.
•
upper left, press
press the
However, there are exceptions to this rule, as in the Menu selection screen, etc.,
where
•
•
J
Graph related keys:
Various settings for graphing can be made using the group of keys indicated in the
box.
•
Å
sÅ
sin
-1
A
▼
▼
▼
Ïz
s
: Specify sin
A : Specify character A
does not have to be pressed first.
Å
key first.
Ï
first.
: Draws a graph using the formula inputted in .
: The user can move graph curves and change formats directly with a touch
(For details, see CHAPTER 4 “15. Useful Functions” on page 124.)
of a pen (For details, see page 229).
: Introduces the user to a mode where expansion and reduction of the
graphing screen, input of main functions and graphing settings can be
performed with ease.
: Used to open the formula input screen for drawing graphs.
(For details, see page 221.)
: Specify sin
3
-1
GETTING STARTED
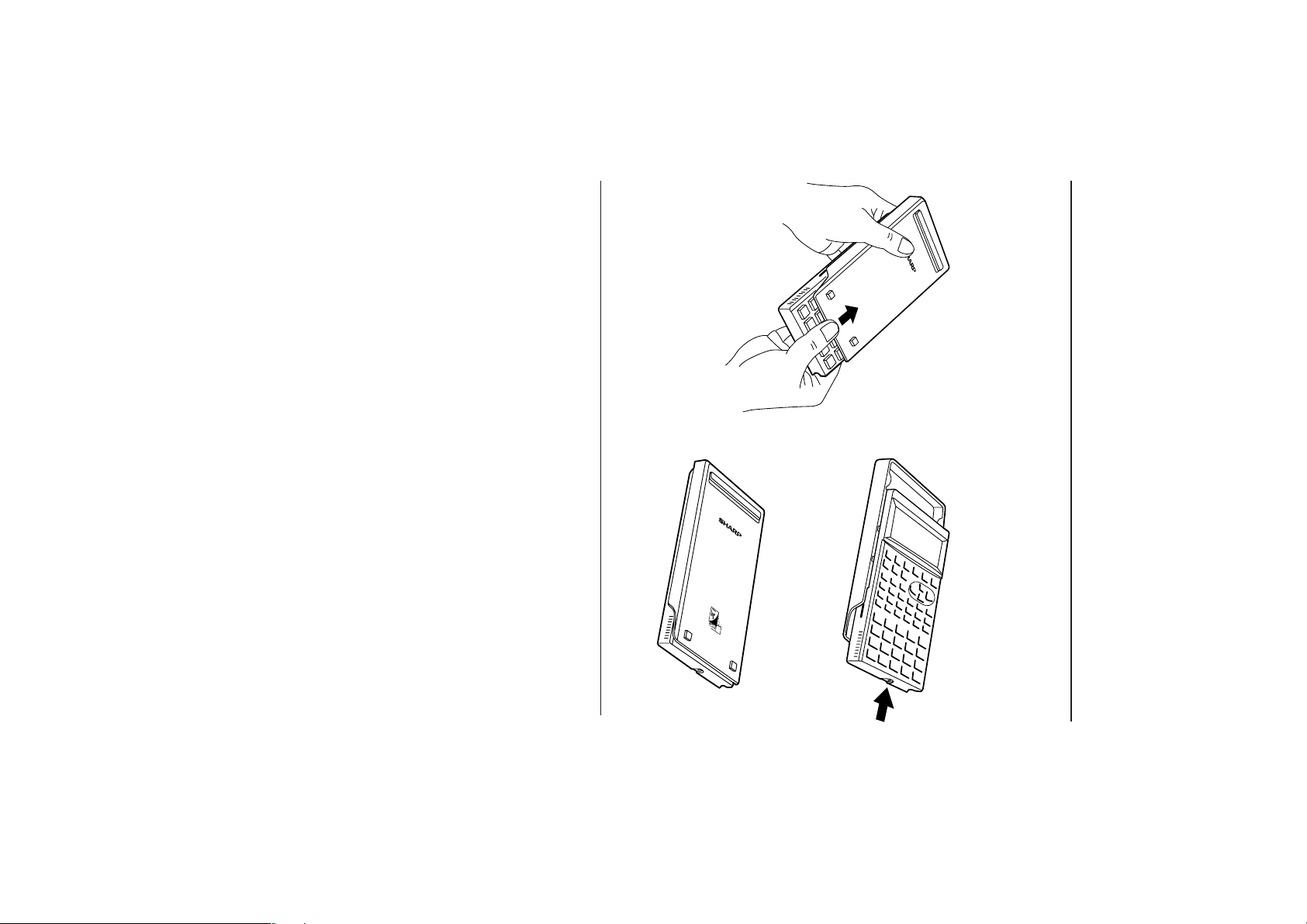
CAUTION
Be careful not to drop the touch-pen when removing the unit from its protective cover.
To open the cover:
4. Using the Protective Cover
GETTING STARTED
4
When not in use:
When in use:
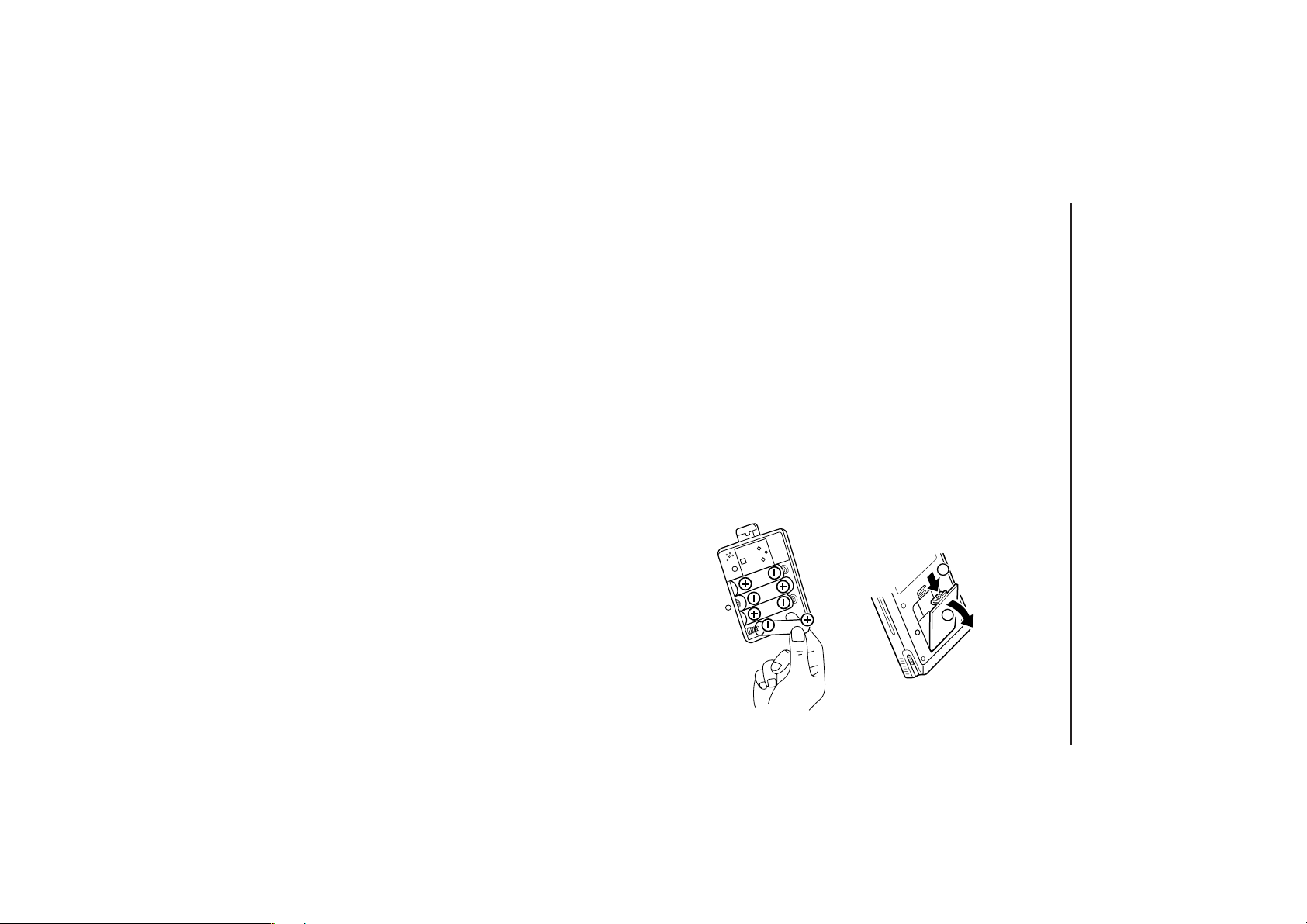
(1) Inserting batteries
3. Close the battery cover.
The unit is automatically reset when closing the
battery cover. The display “WAIT” will appear
while the unit initializes settings.
Since the cover also functions as a reset switch,
power will not turn on unless the cover is
attached.
5
Make sure that the tab that was pulled when
opening the cover is inserted completely and a
snapping sound is heard.
Do not remove the label since it
contains backup battery for
memory protection.
the correct direction.
2. Insert batteries as shown in the
Be careful to insert the batteries in
diagram to the right.
down on the tab then lift up.
1. Open the battery cover located on
To remove the battery cover, pull
the back of the unit.
1
5. When Using for the First Time
2
GETTING STARTED
Operation:
3. Press
Ϝ
to return to the previous screen.
6
2. The contrast can be adjusted using
+
-
: Increases the contrast
: Decreases the contrast
+-
.
1. Press
The Optional functions menu will appear (see the
diagram on the right).
Ïq
.
(3) Adjusting the contrast
Display contrast may vary with the ambient temperature and remaining battery
power. Adjust accordingly for the best view.
procedure indicated above.
* The message shown to the right may appear when not
performing the above procedure. To prevent loss of
data, etc., reset the calculator by following the
• Move to the standard function calculation screen by
pressing any key.
• Press the
shown to the right, indicating that all data within the
internal memory of the calculator has been cleared).
¬
key (the display will change to that
• A “WAIT” display will appear momentarily when
unit to clear all data within the calculator’s memory.
pressing the RESET switch. When the display
disappears, the screen shown to the right will appear.
GETTING STARTED
(2) Resetting the calculator
1. Press the RESET switch located on the back of the
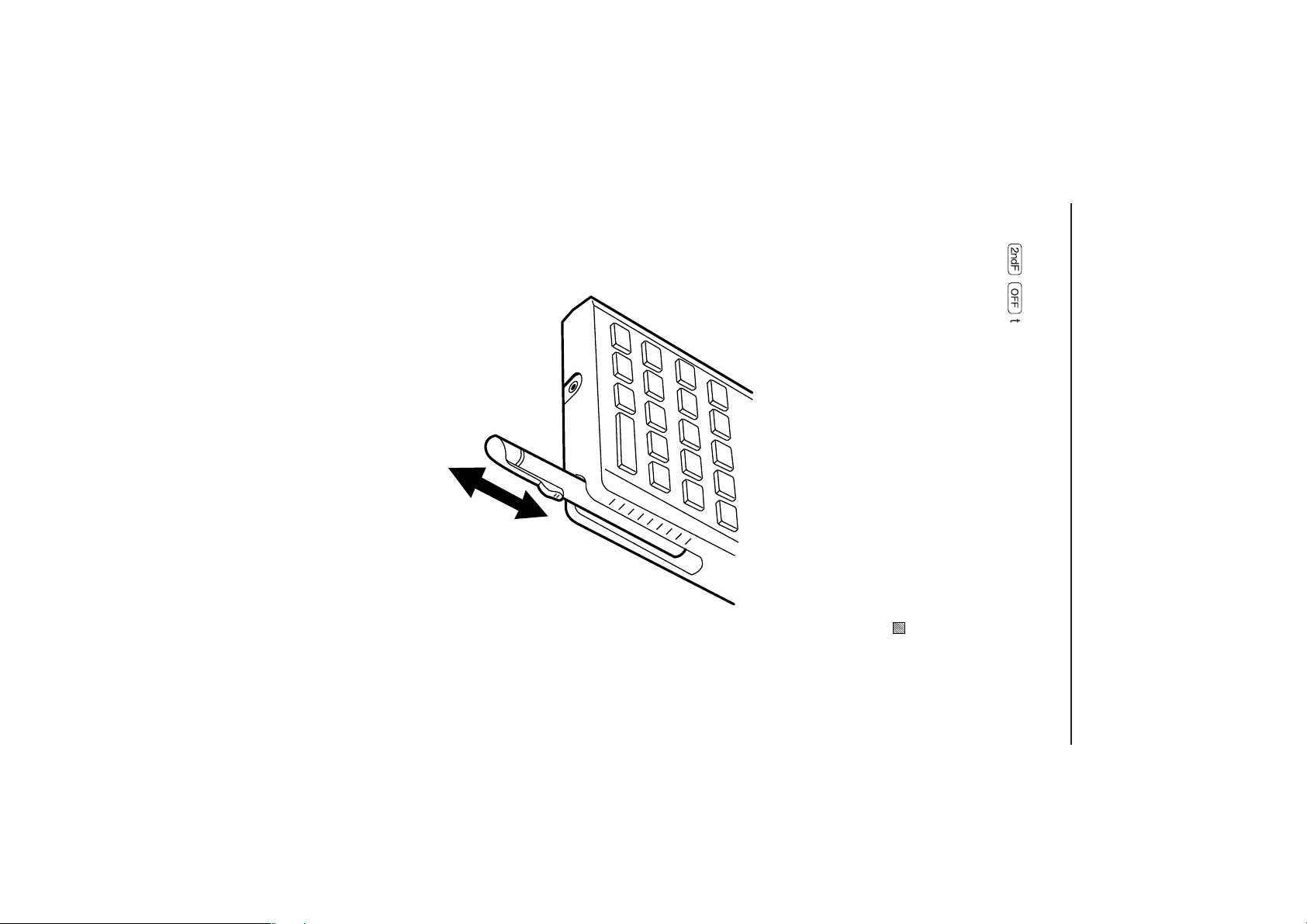
6. Inserting and Removing the Touch-pen
It is possible to store the touch-pen on the side of the main unit when not in use.
7
This function will not operate while executing calculations (flashing “
right side of the screen).
Ï˙
to turn the power off.
GETTING STARTED
” on the upper
(4) Turning the power off
Press
Regarding the automatic power-off function:
The power supply is automatically turned off when there is no operation for a period of
approximately 10 minutes to save battery consumption (the time varies by a few
minutes according to use).
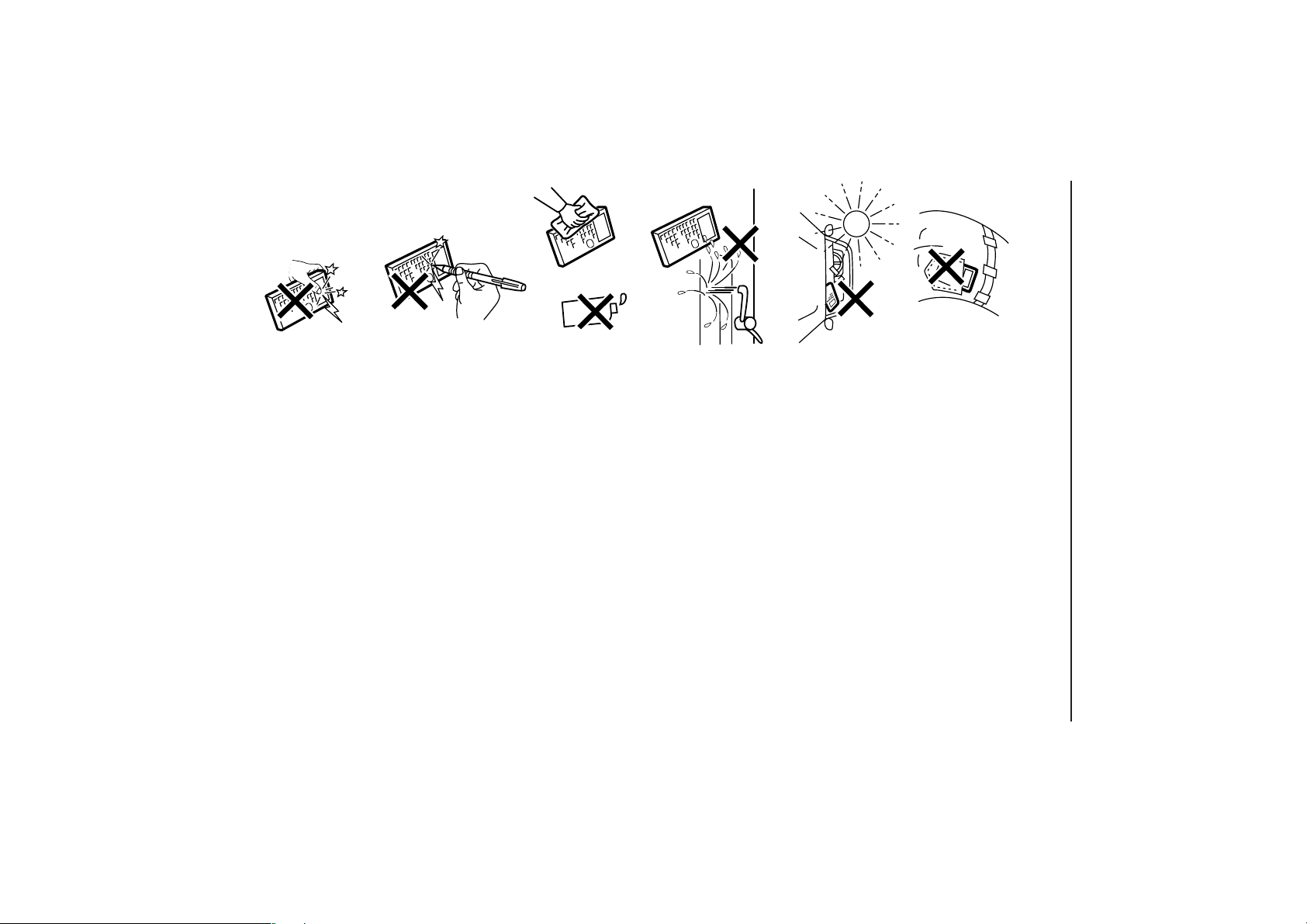
7. Caring for Your Calculator
Keep the calculator away from extreme heat such as
on a car dashboard or near a heater, and avoid
exposing it to excessively humid or dusty environ-
Do not use a sharp pointed object or exert too much
Avoid excessive physical stress.
8
force when pressing keys.
Clean with a soft, dry cloth using no solvents.
perspiration, etc. will also cause malfunction.
Since this product is not waterproof, do not use it or
store it where fluids, for example water, can splash
onto it. Raindrops, water spray, juice, coffee, steam,
ments.
Do not carry the calculator around in your back
pocket, as it may break when you sit down. The
display is made of glass and is particularly vulnerable.
GETTING STARTED
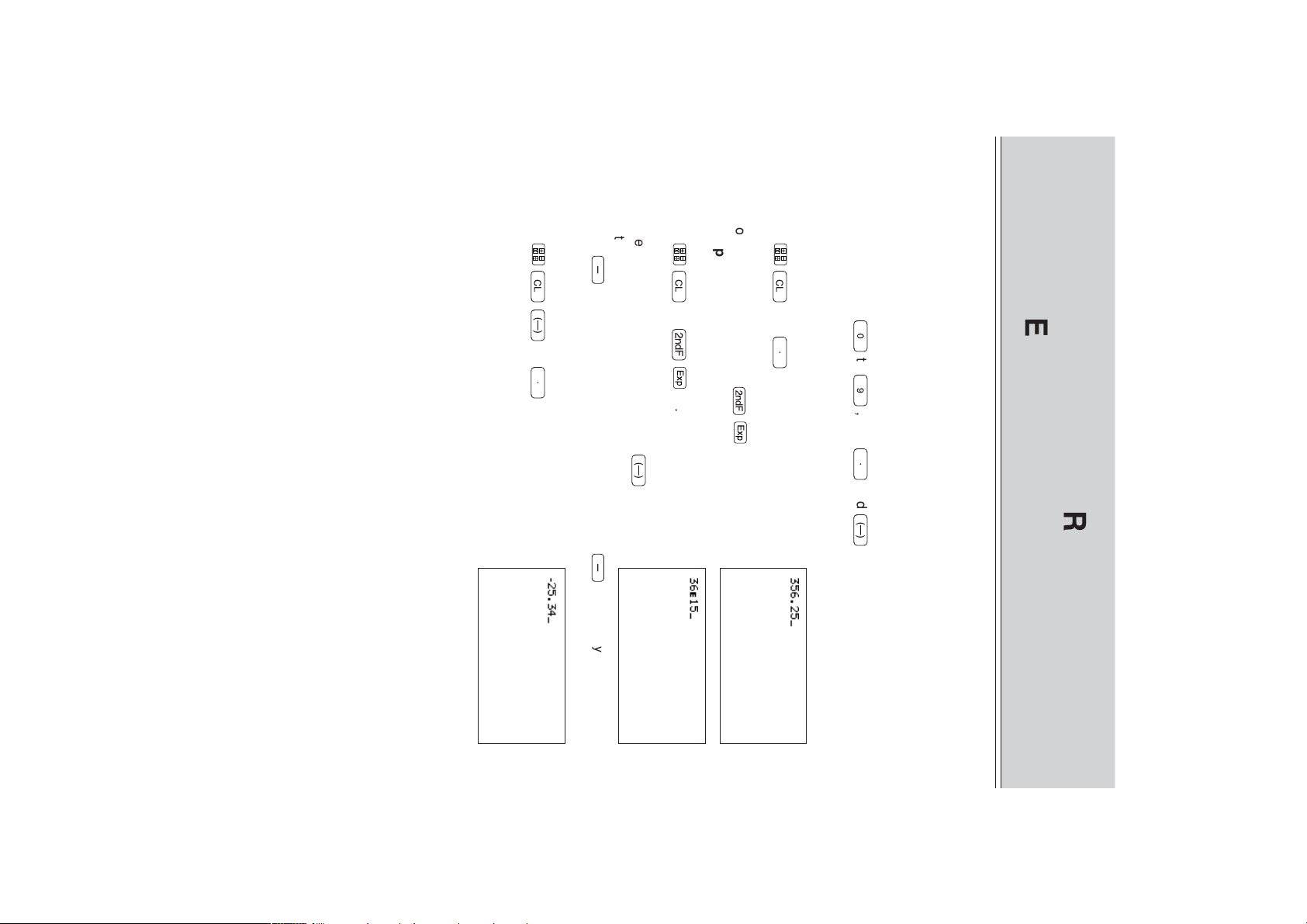
<Example>
To enter “-25.34”
Press
* Using
entering the number.
• To enter a negative (-) number, press
To enter “36×10
Press
<Example>
• To enter an exponent, use
Press
values.
<Example>
To enter “356.25”
procedures described here show how to perform calculations with common math
1. Entering Numeric Values
The number keys (
functions. This chapter also explains the main set-up functions (mode settings).
This chapter describes the basic key operations (input rules) of the calculator. The
¬—
-
to enter a negative number generates an error.
25
.
34.
9
-
is used only for subtraction.
—
before
¬
36
”
Ï
15.
15
Ï
.
¬
356
.
25.
GENERAL INFORMATION
0
to
9
CHAPTER 1
), and
.
and
—
are used to enter numeric
GETTING STARTED
10
2. Common Math Operations
The calculator can be used in the same way as a standard calculator for calculations
using common math operations.
<Example>
To obtain the answer of “(100+256)×2÷85–9”
Press
/
Press
calculation appears on the right side of the display below the expression. The display
does not include an equal (=) sign.
85
®
-
¬(
to execute the calculation. The result of the
9.
100
+
256
)j
2
CHAPTER 1
85
dj®
-
9 , enter <<<< <
<Example>
To change “÷” in the expression
to, “×”.
After entering
•
¬
previous calculation.
: clears an entire expression that has been entered and the result of the
* When the INSERT mode is selected, the mode stays active until
again. In the equation edit mode (see CHAPTER 1 “11.Edit Modes” on page 25), the
INSERT mode automatically becomes active.
•
Ï◊
one space to the left and deletes the character or expression entered in that
location.
the left side of the cursor. (When the one line edit mode is selected.)
* When the INSERT mode is selected, the cursor changes to the “ ” symbol.
•
•
d
Ú
the cursor is located is deleted.
sions
: deletes an entry. When this key is pressed, the character or expression where
: moves the cursor backward. Each time
To change a character or expression before executing the calculation, follow the
procedure below.
Move the cursor to the location for correction. The new content will be inserted to the
left of the cursor when entered (during Equation edit mode).
Move the cursor to the character or expression to be changed, and enter a new
character or expression. (When the one line edit mode is selected)
3. Changing Entered Characters and Expres-
11
(
to make the change.
100
+
256
“(
100
)j
+
256)×2÷85–9”
2
/
: after pressing these keys, a character or expression can be inserted to
Ú
is pressed, the cursor moves
GENERAL INFORMATION
Ï◊
are pressed
12
Example B: This display indicates that a memory error
has occurred. To correct it, follow the procedure below.
Example C: When any error except one described above occurs, follow the procedure
below.
• Use < or > to move the cursor to the error location, and correct error. (The
• The display will vary depending on the error message.
* For the details of error codes and messages, see APPENDIX “3.Error Codes and Error
Messages” on page 270.
expression on the screen can be changed.)
• Use <, >, or
entered expression will be deleted.)
¬
to clear the error. (The
• Use
to the primary screen. The entered expression will
be deleted.)
¬
to clear the error. (The display will return
below), and stops operating.
The method of correcting an error varies depending on the error code.
Example A: This display indicates that a syntax error
has occurred. To correct it, follow the procedure below.
• Use < or > to move the cursor to the error
location, and correct error. (The expression on the
screen can be changed.)
4. Correcting Errors
When an error is generated, the calculator displays an error message (examples shown
CHAPTER 1
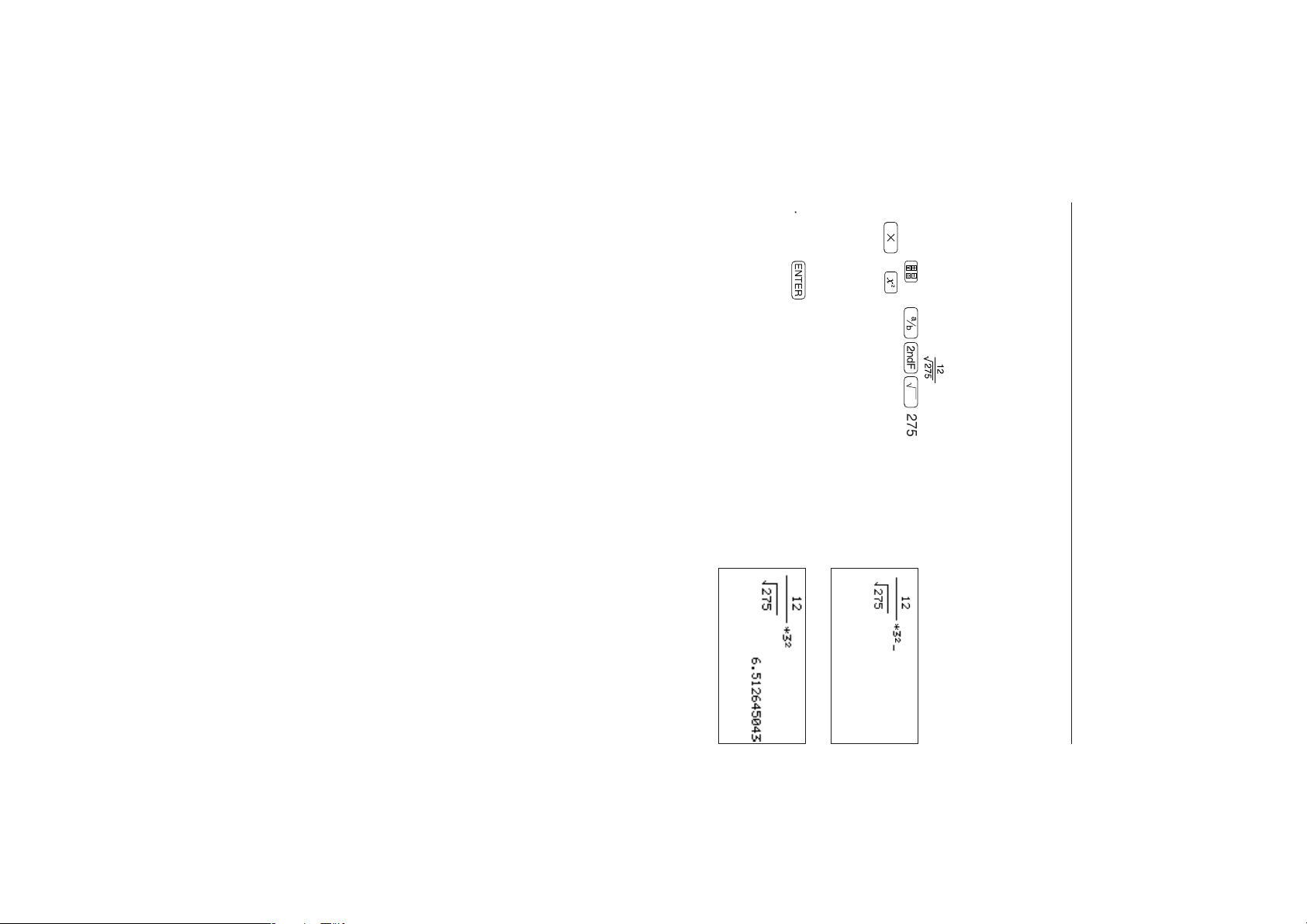
2. Press
1. Press 12
j
5. Using Functions
The following shows an example of a calculation using
functions that are directly accessible from the keys
(functions indicated on keys and secondary functions).
<Example>
To obtain the answer of “ × 3
13
®
.
3 .
;Ï
2
”
275 >>
GENERAL INFORMATION
14
ÅY1
executing.
To input a graph equation named “Y1”, press
will display “Y1” on the screen, but an error will be returned when
A®A1
names (L1 to L6) etc., should not be typed out. Instead, the appropriate key must be
pressed or menu item selected.
<Example>
• To change from the ALPHA LOCK mode to the normal mode, press
For successful usage, function names, graph equation names (Y1 to Y9 and Y0), list
cursor changes from “
A” to “_”.)
Å
• Press
Å
mode. In this mode, alphabet letters can be entered
continuously from the keyboard.
A1 2 3
Ï
Ï
to set to the ALPHA LOCK
BCD
θ
.
(2) Entering alphabet letters
<Example>
To enter “A123BCDθ”
Secondary function of “sin” key
Press
<Example>
To obtain the answer “sin
Ïz
↑
.5
-1
®
0.5” (Angle mode: Radian)
(1) Using secondary functions (2ndF)
The secondary functions include function entries, menu screen display, and mode
settings.
• The functions and characters printed to the left and right sides above the keys
• When
• When
become active for the next keystroke when
pressed, the characters printed in blue become active.
setting has been changed. (See CHAPTER 1 “12.Display Format of the Cursor
Pointer” on page 32 for details.)
6. Using Secondary Functions (2ndF) and
CHAPTER 1
Alphabet Letters (ALPHA)
Ï
Ï
or
is pressed, the functions printed in yellow become active. When
Å
is pressed, the shape of the cursor changes to indicate that the
Ï
or
Å
is pressed.
. Pressing
(The
Å
is
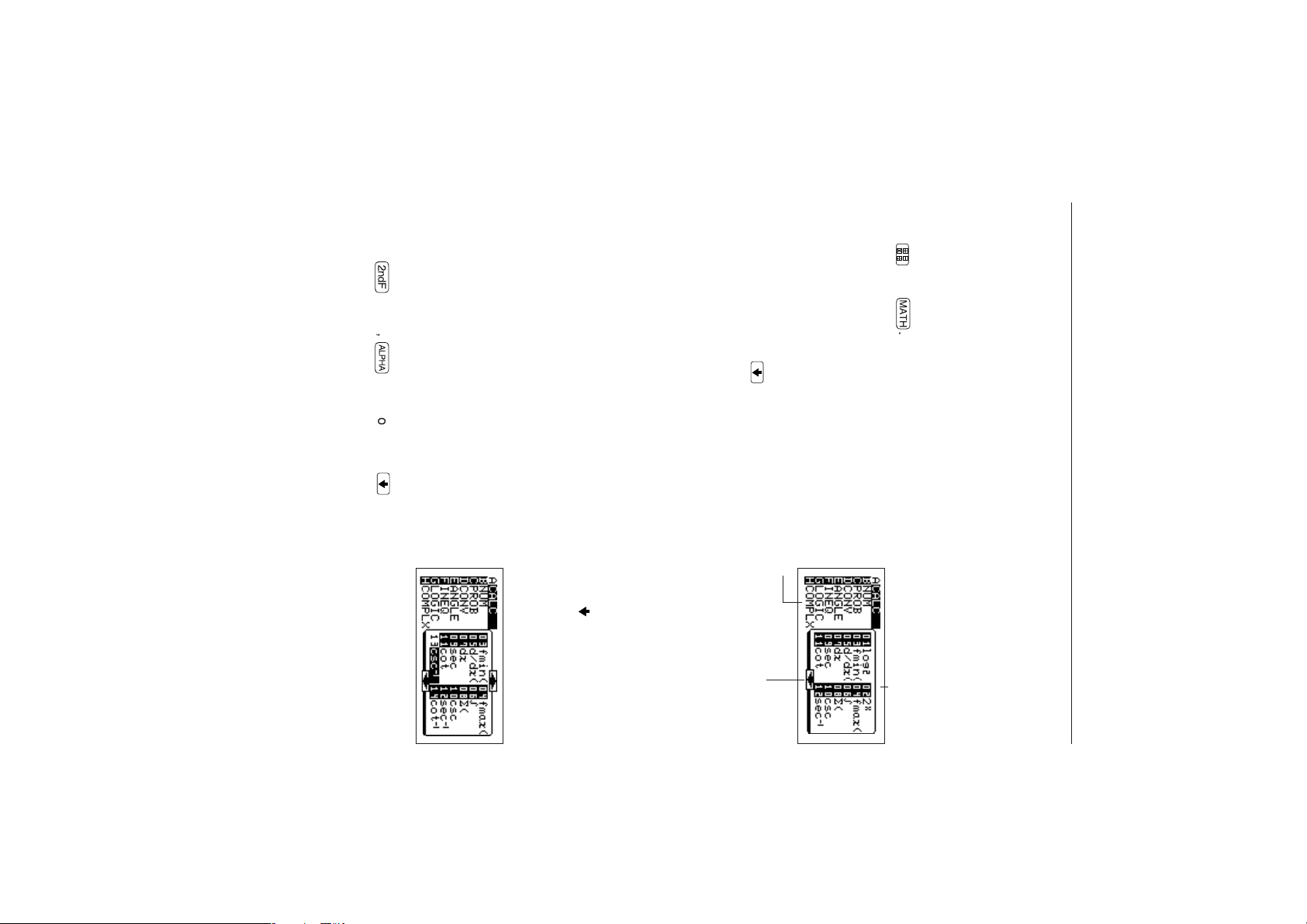
to the sub-menu, and scroll down the sub-menu.
In the example above, press > to move the cursor
to the sub-menu side, and press ≥≥≥
≥≥≥ (6 times). The display should look
like the one shown on the right (items 01 and 02
disappear from the display, and items 13 and 14
appear at the bottom).
Press
advance the sub-menu screen.
• To see how many items are in the sub-menu, move the cursor from the main menu
that there are more items that are not currently shown on the screen.)
however, the number indications are highlighted. This indicates that no function is
currently selected. The sub-menu shows items 01 to 12. The “
• On this display, the highlighted function or mode name (not the alphabet letter or
(In the above example, [A CALC] is currently selected. In the [A CALC] sub-menu,
number) is currently selected.
• The display changes to the screen shown above.
• The main menu lists items A to H (the number of items varies in each menu). Each
item on the main menu has a sub-menu.
<Example>
Press
grouped by function type and item type. Calculations and mode settings can be
executed by selecting appropriate functions.
7. Using Menus
This calculator is equipped with function menus that allow many functions other than
those printed on the keys and main unit to be used. These additional functions are
15
Ï
≥,
Å
≥ or touch
on the screen with the touch-pen to
” symbol indicates
and
≥
.
: This symbol appears when there are more items after No. 12.
Main menu items
GENERAL INFORMATION
Sub-menu items
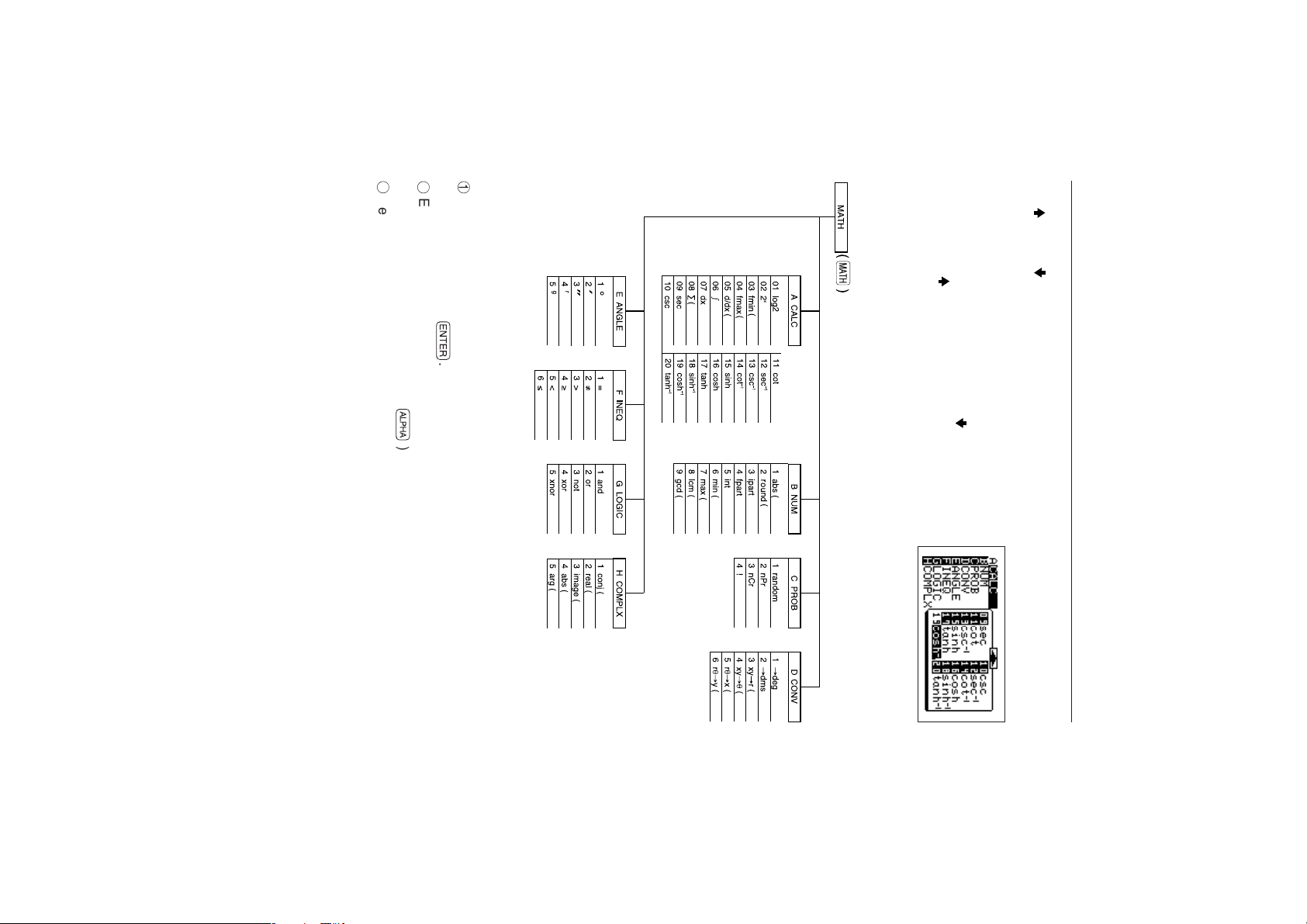
There are three ways to select a menu.
1
2
3
Use <, >, ≥, and ≤, to move the cursor and highlight the selected
function, and press
Enter the letter (A, B, etc.) or number of the selected menu to directly access the
menu. (There is no need to press
Select a menu item by pressing the item on the screen twice with the tip of the
touch-pen provided.
®
.
Å
• Press ≥≥≥ (3 times). The display should
displays the “ ” symbol, there are no more sub-menu
When the screen no longer shows the “ ” symbol but
items below (end of the page). (There are 20 sub-menu
items in the [A CALC] menu.)
The following diagram shows the main menu and sub-
menu structure described above.
currently shown on the display.
look like the one shown on the right.
•“
CHAPTER 1
” and “ ” symbols indicate that there are more items before and after those
16
.)
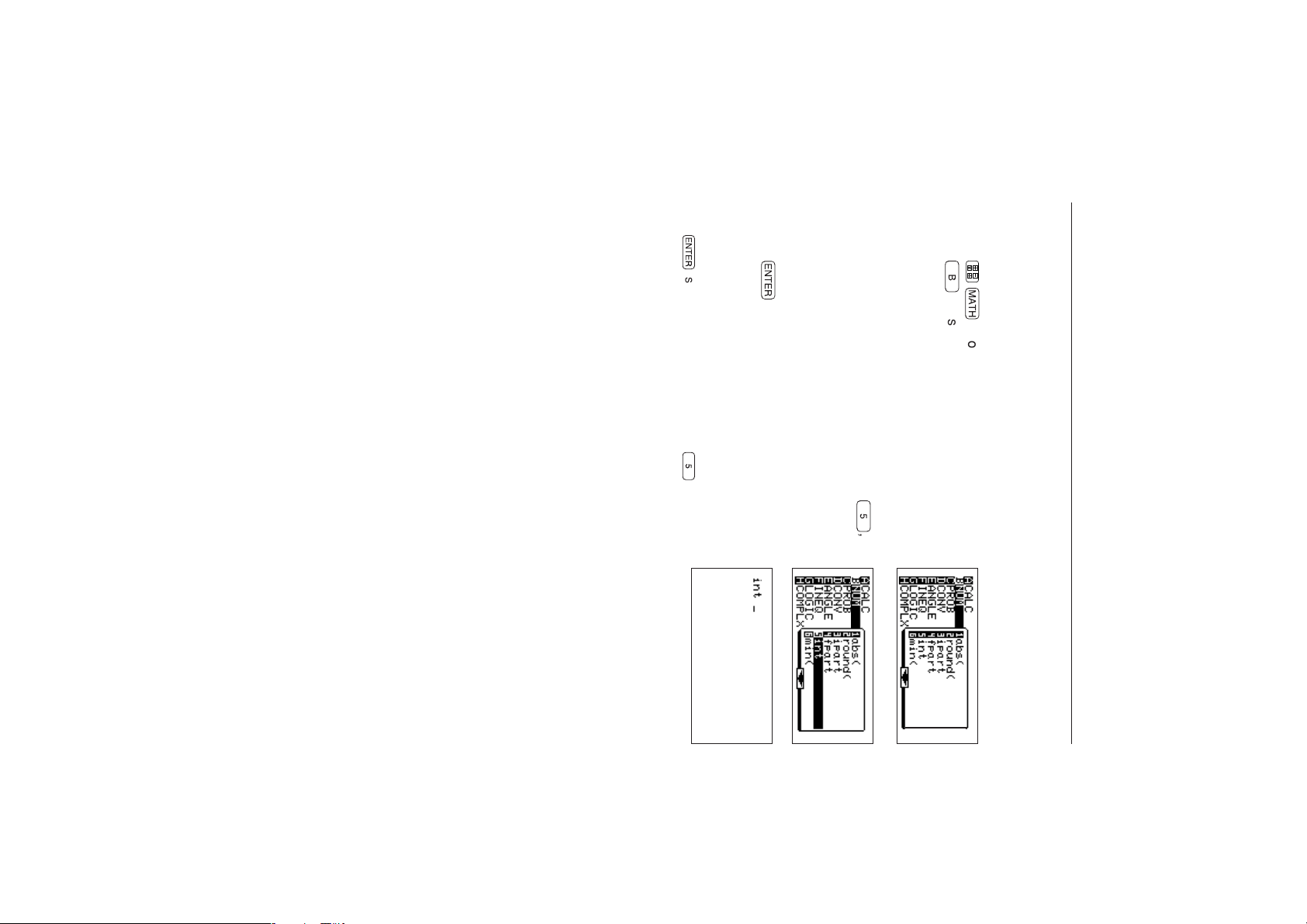
4. Press
* In this calculator, functions are grouped and stored in menus. This allows the many functions
3.
to be used easily.
®
is not necessary when pressing
again.
displayed before the menu screen appeared.
®
The “int” indication appears on the screen that was
*
, or select [5 int] with the touch-pen
3. Press > ≥≥≥≥ (or press
or select [5 int] with the touch-pen).
1. Press
2. Press
touch-pen).
<Example>
To use the “int” function to obtain a whole number (The “int” function is in the [B NUM]
sub-menu of the MATH menu.)
B
≥
(or select [B NUM] using ≥ or the
to open the MATH menu.
17
5
of procedure
5
,
GENERAL INFORMATION
18
• The style of
• If display or calculation results are not what is expected, check to see whether there
are errors in the setting by following the chart to the left.
settings.
, in addition to is influenced by .
To view the flow chart:
• SLIDE SHOW is unrelated to the SET UP menu.
• The normal function calculation mode
is influenced heavily by the SET UP
8. Operating Modes
• The EL-9650 has many modes and commands that are related to the display
• Expected results cannot be obtained when errors are made in the default settings.
• Modes that influence various calculations and processes have been organized into a
* In reality, each command and mode are related in a complex manner.
For example, (equation input) and are related. However a vertical line is not drawn on
This is to show the horizontal relationship (modes that have the most influence) in the most
the flow chart.
simple way.
flow chart.
method of equations, graphs, lists, calculation results and key input
CHAPTER 1
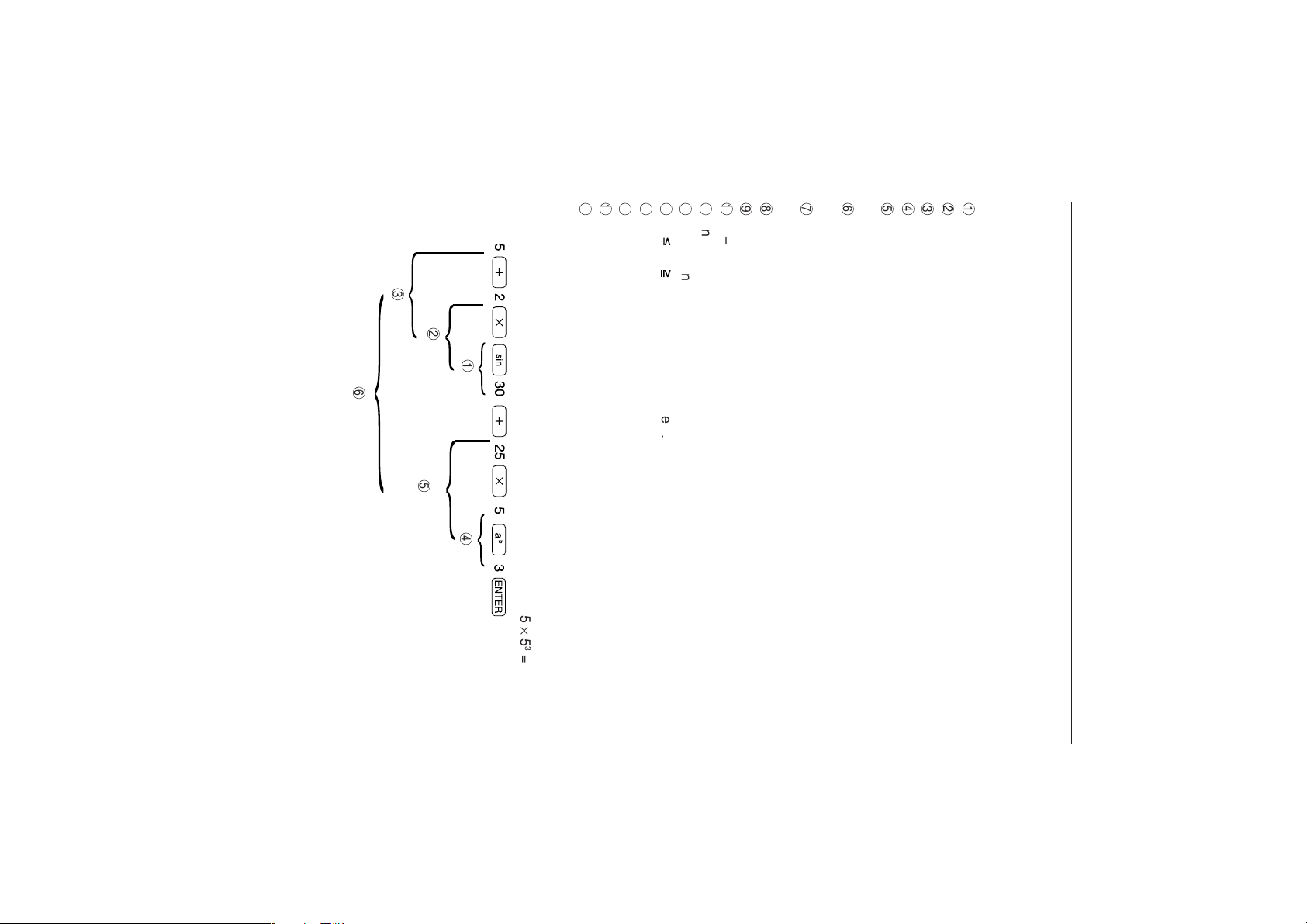
6
3
2
1
<Example>
The key operation and calculation precedence of 5 + 2 × sin 30 + 25 × 5
M
{, [, STO, etc.
J
I
)K (L }, ]
<,
, >, , ≠, =, → deg, → dms, etc.
G
H
and
or, xor, xnor
F
+, –
9
Permutation/combined functions (nPr, nCr)
function that follows a numerical value (3 cos 20, etc.).
×, ÷
6
Multiplication with omitted “×” commands immediately before a single calculation
Single calculation functions that are irnmediately after a numerical value (sin, cos,
tan, sin
-1
,cos
-1
, tan
-1
, log, 10
x
,In, e
x
, ◊,abs, int, ipart, fpart, (–), not, neg etc.).
7
8
4
5
Single calculation functions immediately before a numerical value (X
Exponential functions (a
Multiplications with omitted “×” commands immediately before variables such as π or
stored memory and 2π, 2A, etc.
b
,
a
◊ etc.)
Complex angles (∠)
Fraction calculations (a/b)
• This unit is equipped with a function that detects calculation precedence.
• The calculation precedence is as follows:
1
2
3
9. Precedence of Calculations
19
5
4
GENERAL INFORMATION
2
3
=
, X
–1
, !, °,
r
,
g
).
20
[3 Grad]: Set to gradient
The above display will appear when
menu is used for displaying the current settings, the menus that can be set are B
through G, with sub-menus for each. The functions of these are explained below.
[B DRG]: Used to set the angle unit (default setting: Rad)
[1 Deg]: Set to degree
[2 Rad]: Set to radian
}
The relationships are:
Ï
are pressed. Since item A of the main
(2) SET UP menu
* “A” is highlighted and current settings are displayed when
Contents displayed on the right side of the screen when
selecting [A] are the current settings.
entering the SET UP mode. In this case, it is not necessary to
press
A
.
(1) Checking SET UP contents
Press
Ï
.
• Be sure to set the SET UP mode according to desired calculations and graph
plotting since there may be differences in the results depending on the set conditions
of SET UP.
10. SET UP Menu
• SET UP is a function that sets input and display methods.
• Please select each method according to use.
CHAPTER 1
Loading...